形模型，模型参数的确定需依赖同步相量测量单元（Phasor Measurement Unit, PMU）的实时量测。上述研究表明了变压器对GIC有明显的电感效应，但尚未基于此形成动态GIC计算模型与方法。摘要 考虑高空核电磁脉冲晚期成分（HEMP E3）的动态特性，研究了变压器电感对HEMP E3在电网内所产生地磁感应电流（GIC）的阻碍作用，以及E3 GIC引起的直流偏磁下变压器无功损耗特性。通过场路耦合仿真计算了直流偏磁下特高压变压器的等效电感及无功损耗特性，并提出实现快速计算的简化解析方法。基于上述特性建立考虑电感效应的变压器回路动态GIC计算模型，并应用于E3 GIC及其造成的变压器无功损耗的计算。结果表明：变压器的等效电感（包括励磁电感和漏电感）阻碍GIC的快速增长，其数值随直流偏磁程度的增大而迅速下降，该电感效应使GIC滞后于E3的变化且峰值变平缓，忽略此特征则会高估GIC对设备的损害，误判事件的严重性；变压器的无功损耗在GIC较大时表现出明显的饱和特性，不考虑此特征会高估电力系统响应的灾害性风险，影响核爆期间应对措施的科学性。由于简化解析法不涉及暂态仿真，可以在保证一定精度的基础上快速预测E3作用下电网GIC与变压器无功损耗。
关键词：地磁感应电流 变压器 高空核电磁脉冲晚期成分 动态特性 无功损耗
高空核电磁脉冲（High-altitude Electromagnetic Pulse, HEMP）的晚期成分（HEMP E3）是由核爆炸晚期的空气离子和碎片在地磁场中运动所产生的电磁脉冲[1]，表现出磁流体动力学特性，具有低频、低幅值、持续时间长[2-3]的特点。HEMP E3引起地磁场剧烈变化并产生地面感应电场，进而在电网中产生地磁感应电流（Geomagnetically Induced Currents, GIC），其原理与直流输电系统单极运行方式或太阳活动引发的地磁暴在电网中产生的GIC[4-6]相似。低频的E3 GIC通过接地中性点流入变压器，引起变压器直流偏磁现象[7-8]，导致谐波增多、无功损耗增大、振动与噪声增大、温升加剧[9-12]等问题。核爆影响区域内所有接地变压器同时发生直流偏磁，产生的群发性无功损耗可能造成电网无功波动、电压下降，甚至引发电压崩溃[13-14]。现有研究主要针对HEMP早期（E1）或中期（E2）作用下电力系统及其关键设备的耦合与损害效应[15-18]，而对E3引起的系统失稳风险研究较少。故准确计算E3作用下的电网GIC及其造成的变压器无功效应对于认识、评估E3引起的系统风险以及研究应对措施、增强电网抵御HEMP打击的能力都具有重要的意义。
针对HEMP E3作用下电网GIC计算，国内外已有了一些研究。文献[19]建立电网等效模型计算了某750 kV电网E3感应电流。文献[20]利用节点导纳法计算了北美特定地区电网E3 GIC分布情况。文献[21]基于E3感生电场的等效电压源列写回路阻抗方程，提出了牵引供电系统的E3 GIC算法。目前，已有研究主要采用地磁暴期间GIC的计算方法，将E3 GIC视为准直流，忽略电网元件的电感效应，基于系统直流参数将问题转化为求解直流电路模型[22-23]。然而E3电场的脉冲波形相比地磁暴感生电场变化更快，这种动态特性使电网元件的电感效应更显著，导致原有的基于直流参数的计算方法可能存在精度不足的问题。
变压器因其铁心的高磁导率而对E3 GIC有显著的电感效应。文献[24]利用EMTP进行了变压器直流偏磁暂态仿真，论证了变压器电感明显延长了变压器进入饱和的时间，其电感效应阻碍GIC的快速增长。然而铁心的非线性使该效应无法简单地等效为线性电感元件。文献[25]通过解析法推导了GIC下的变压器等效电感。文献[26]基于功率守恒推导了变压器在GIC作用下的等效励磁电抗。文献[27]建立了反映变压器直流偏磁期间励磁支路阻抗变化的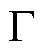形模型，模型参数的确定需依赖同步相量测量单元（Phasor Measurement Unit, PMU）的实时量测。上述研究表明了变压器对GIC有明显的电感效应，但尚未基于此形成动态GIC计算模型与方法。
E3 GIC导致变压器直流偏磁下无功损耗的增加是造成系统失稳风险的重要因素。文献[28]将E3下变压器无功损耗纳入电力系统暂态稳定性分析。文献[29]在其仿真算例中考虑了E3下变压器无功效应对电网电压的影响。以上研究一定程度上揭示了变压器在E3作用下的次生无功扰动（GIC-Q）特性，但主要采用K值法，即认为无功损耗与GIC满足比例系数为K的线性关系[30]，而相关研究[31-32]都指出K值法在大GIC和考虑GIC动态特性下的局限性，这种局限性在地磁暴事件中也许不显著，但由于E3 GIC峰值更高、变化更快，可能影响E3事件中对变压器无功损耗的预测精度。文献[7]基于电磁暂态仿真总结了E3下变压器无功损耗的变化规律，结果显示Q与GIC的比例系数随E3电场的增大而明显减小。能否准确预测E3下变压器的实时无功损耗直接影响系统电压稳定性分析，对评估事件风险[33]具有重要意义。
本文计及HEMP E3的动态特性研究了变压器电感对GIC增长的作用，通过场路耦合仿真计算了直流偏磁下特高压变压器的等效电感与无功损耗特性，并提出了实现快速计算的简化解析法。建立了考虑电感效应的变压器回路E3 GIC动态计算模型，为预测HEMP E3作用下电网GIC与变压器无功损耗提供了较为准确且有效的方法。
标准IEC 61000-2-9[34]给出HEMP E3电场的标准双指数函数波形如图1所示，适用于电导率为10-4 S/m的均匀大地。
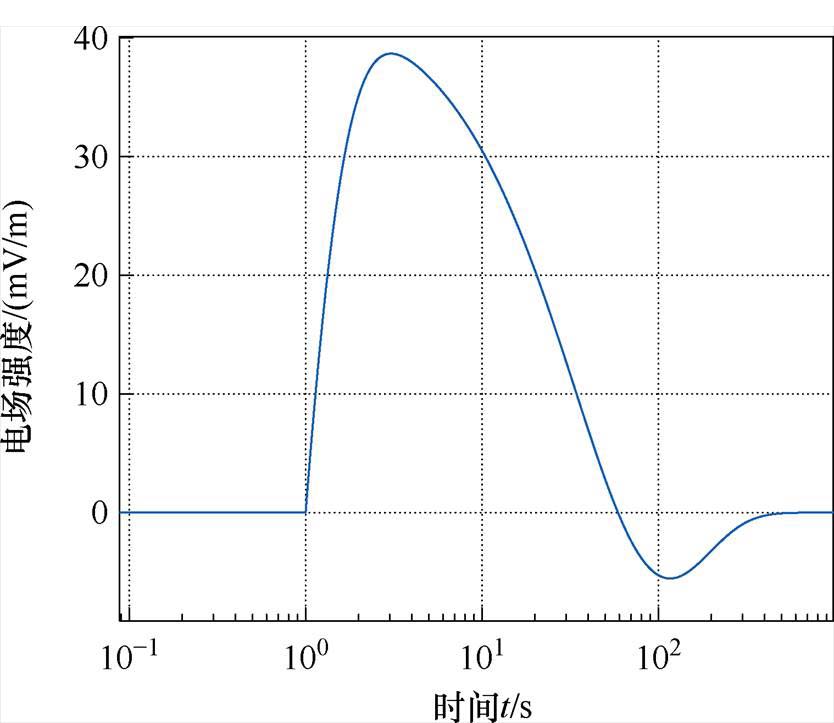
图1 HEMP E3标准波形
Fig.1 Standard HEMP E3 waveform
类似地，磁暴感生电场作用机制，HEMP E3感生地面电场在电网接地点间产生电位差，其作用可等效为串联在接地点间输电线路上的电压源，数值为地电场沿线路的积分[22]，即
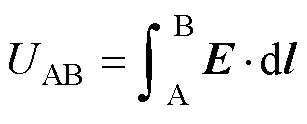（1）
式中，UAB为接地点A、B之间的E3等效电压源；dl为接地点间输电线路的长度微分；E为E3感生地电场强度。
在电位差作用下，GIC经接地变压器的中性点流入电网，流过输电线路，最后通过其他接地中性点流回大地构成通路，电网内单个变压器的GIC回路如图2a所示，假设电网每相参数相同，则三相GIC相同，且流过中性点接地电阻的GIC是流过单相线路的3倍。原有方法[35-36]（以下简称为N方法）将GIC视为准直流，基于电网元件的直流参数建立了如图2b所示的单相变压器回路的GIC等效计算模型，其中Udc为E3感生电场等效电压源，RL、RN、RT分别为线路直流电阻、接地点接地电阻、变压器一次绕组电阻。该准直流计算模型忽略了元件对GIC的电感效应，如果应用于变化缓慢的地磁暴感生电场，可能具有较高的精度[37]，然而，如图1所示，E3电场上升时间仅为0.9 s，在短暂的几秒内迅速达到38.7 mV/m的高峰值，这种快速变化的动态特性使元件电感效应更显著，可能影响计算精度。因此，建立图2c所示的动态GIC计算模型，其中Lmef为变压器等效电感（包括励磁电感与漏电感），变压器内GIC大小影响铁心的饱和程度，进而影响等效电感大小，因此Lmef为非线性元件。
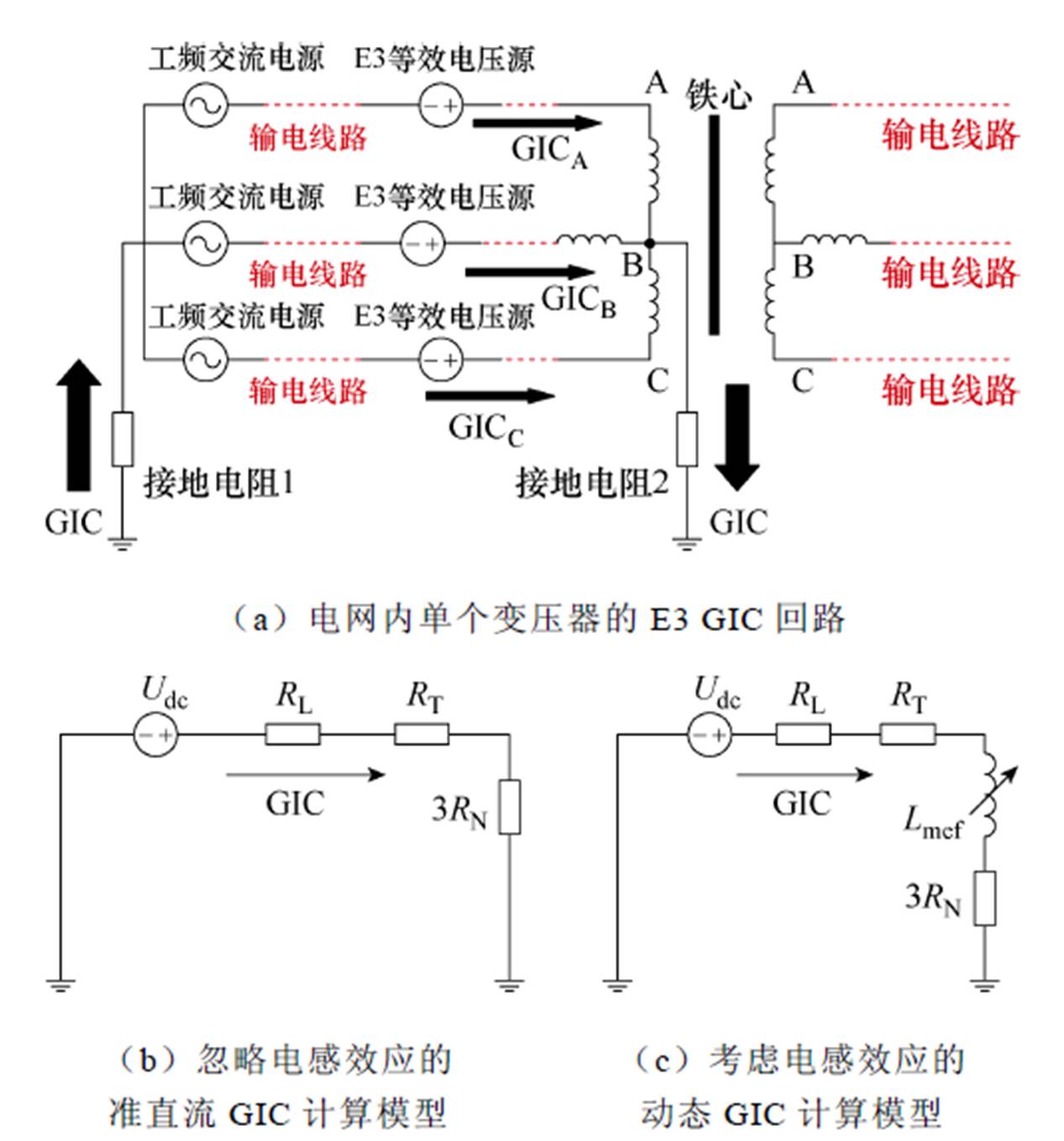
图2 单相变压器GIC计算等效电路模型
Fig.2 Single-phase transformer circuit model for GIC calculation
为研究等效电感Lmef，分析变压器的直流偏磁工作状态：E3感生电场在电网中诱导的GIC流入变压器后，产生的直流磁通叠加在正常工况的交流磁通上，深入非线性磁化曲线的饱和区，导致铁心半波饱和与励磁电流畸变。变压器铁心直流偏磁工作状态示意图如图3所示。由于E3 GIC的频率成分相比工频依然属于低频成分，可以假设每个工频周期内GIC不变，即为直流量Idc。励磁电感在周期内随磁通瞬时值动态变化，等效电感Lmef的数值与这种动态变化有关。
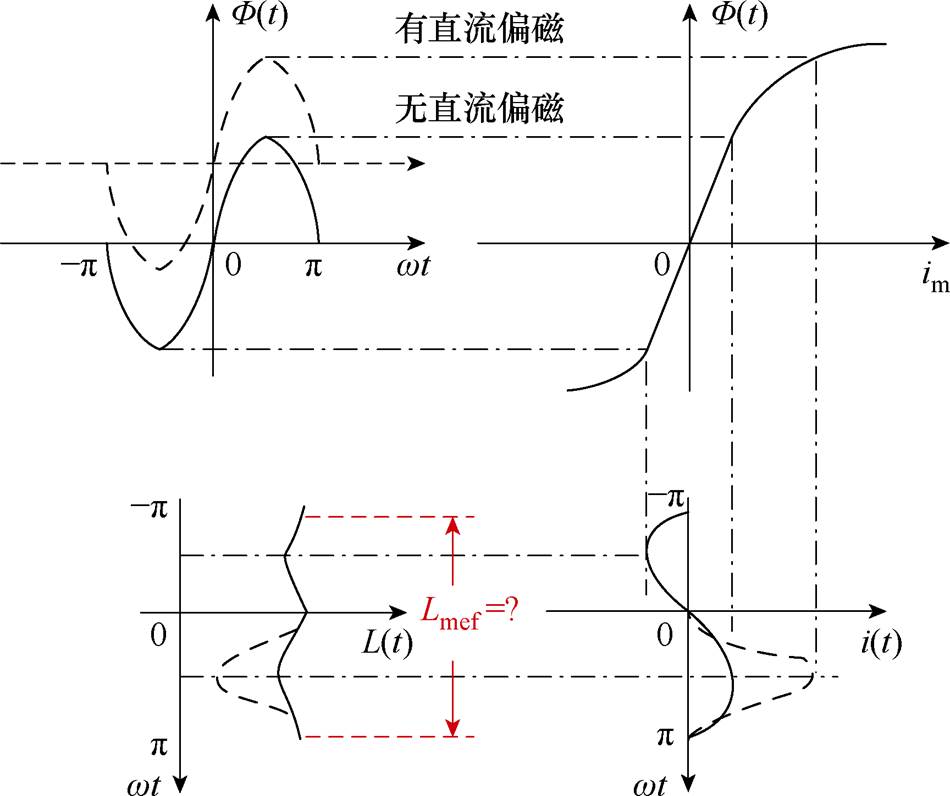
图3 变压器铁心直流偏磁工作状态示意图
Fig.3 Schematic of transformer direct current (DC) bias
为确定等效电感与瞬时电感动态变化之间的关系，建立图4a所示的直流偏磁下单个变压器瞬态电路，um为变压器一次侧额定交流电压源，i(t)为回路电流（包括交流分量与直流分量），R为回路总直流电阻，即R=RL+RT+3RN。LT为变压器的瞬时电感，包括励磁电感与漏电感。认为一个工频周期内电气量的直流成分不变。
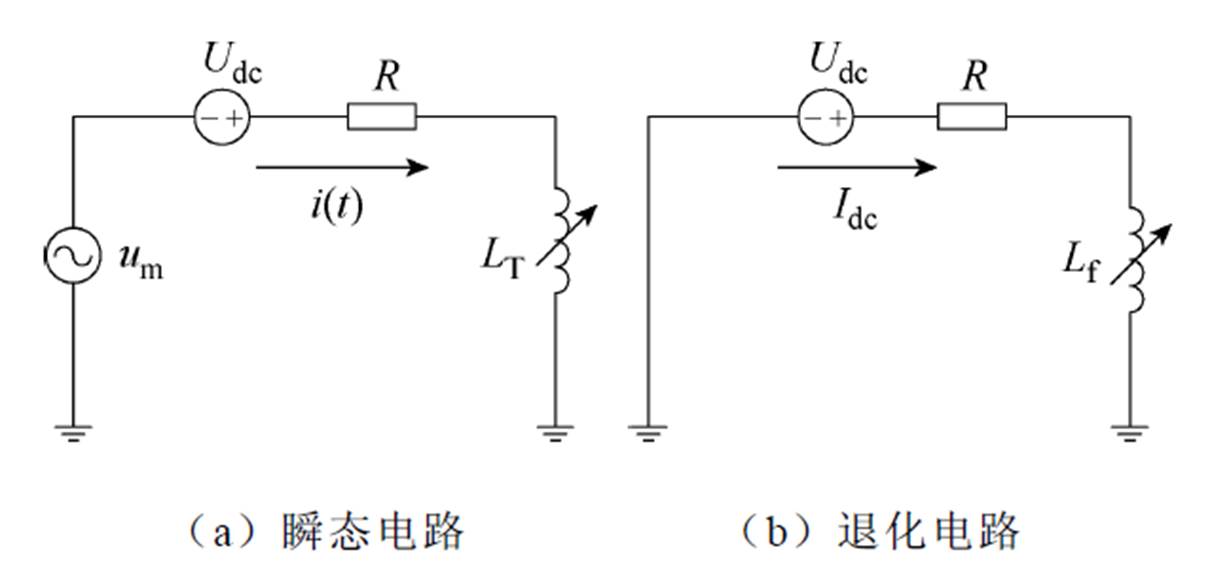
图4 单个变压器直流偏磁回路
Fig.4 Single transformer DC bias circuit
由瞬态电路列出的微分方程为
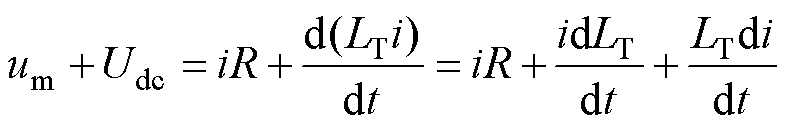（2）
定义电流的平均变化率[38]为
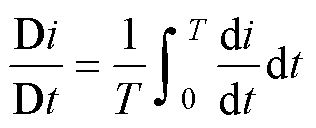（3）
式中，T为工频周期。将式（2）代入式（3），由于交流分量一个周期的积分为0，可得
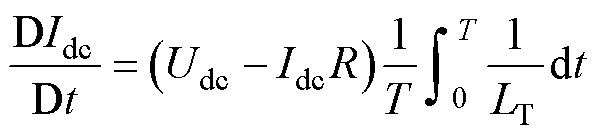（4）
式中，Idc为电流的直流分量，即该周期内GIC。式（3）和式（4）的推导过程详见文献[39]。假设令
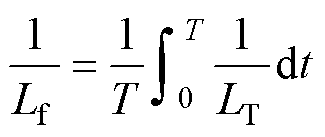（5）
则式（4）变为式（6），形式上为一阶RL电路的微分方程，基于此，电路退化为图4b。
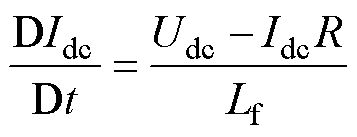（6）
对比图2c与图4b可知，Lf即为变压器等效电感Lmef，表示为
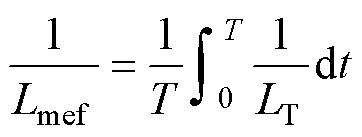（7）
Lmef受变压器直流偏磁程度影响，是随周期内直流量Idc变化的非线性元件。
为定量研究Lmef-Idc特性，进行大量不同Idc下的变压器直流偏磁仿真，同时计算变压器无功损耗以研究Q-Idc特性。特高压（Ultra High Voltage, UHV）电网由于输电线路长且采用单位长度电阻更小的分裂导线，易产生更大的E3 GIC；其中的特高压变压器直流电阻小，更易受到E3 GIC的侵害，进而引起无功损耗增大导致电网无功功率波动。因此，以单相特高压自耦变压器为研究对象，仿真计算其等效电感与无功损耗，并提出简化解析方法以实现快速计算。特高压变压器相关参数见附表2。
通过变压器直流偏磁场路耦合仿真计算特高压变压器的等效电感与无功损耗特性。
图5a和图5b分别为变压器空载电路模型和1/8磁场模型。其中，电路模型中的Udc为直流电压源，Rk为缩短过渡过程的串联电阻，r1、r2为高、中压绕组的电阻，us、u1、u2分别为工频交流电压源、变压器一次电压和二次电压，由于低压绕组空载且与高、中压绕组没有电的联系，因此电路模型忽略低压绕组。Lm1、Lm2、M12分别为高、中压绕组自感和高中压绕组的互感，变压器总电感LT=Lm1+Lm2+ 2M12。电路模型微分方程的求解由自编程实现。基于有限元商业软件Ansys建立磁场模型，用棱边有限元方法计算非线性磁场，方法准确性已得到验证[40]。计算忽略了铁心磁滞与涡流损耗，其中的铁心磁滞可能导致励磁电感的动态变化波形不对称，但影响很小[41]。铁心硅钢片型号为27ZH095，磁化曲线如图5c所示。仿真中，将电路模型计算的电流代入磁场模型作为激励，基于能量扰动原理[42]计算该时刻的瞬时电感值，并回代入电路模型求解下一时刻电流。仿真的具体过程与其准确性的实验验证详见文献[9, 43]。
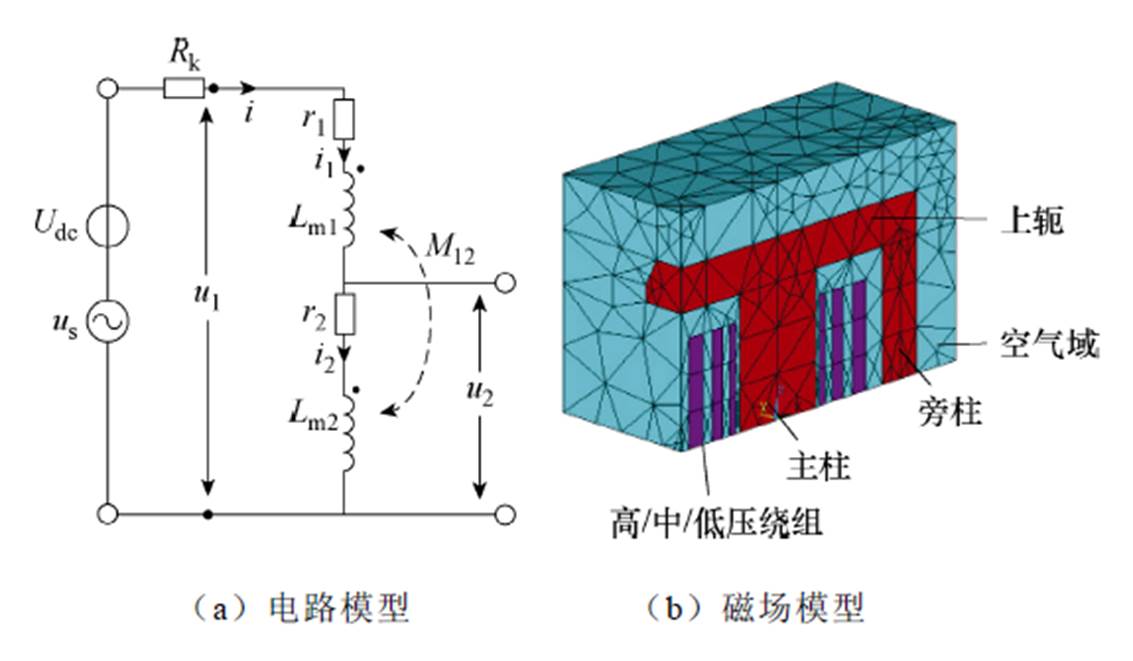
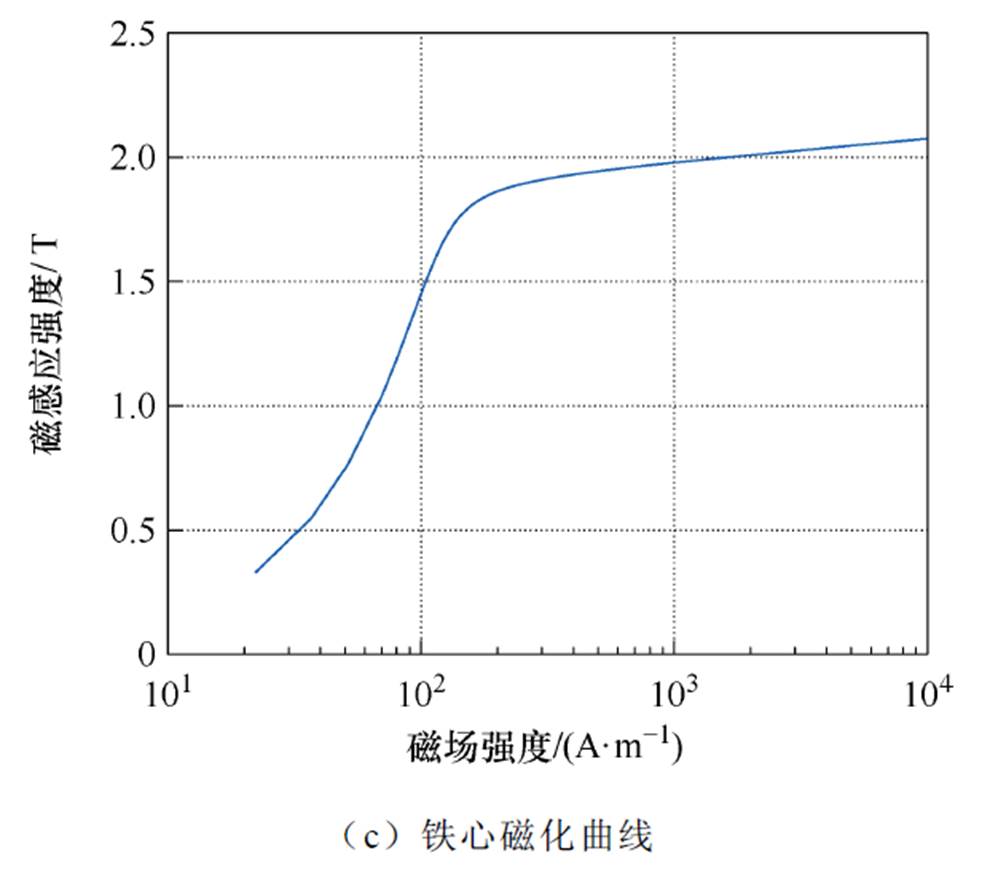
图5 变压器直流偏磁场路耦合仿真法示意图
Fig.5 The field-circuit coupled simulation for transformer DC bias
图6展示了直流量分别为5、10、50 A时仿真计算的励磁电流与对应的瞬时电感。0.015 s时刻瞬时电感下降，是由于励磁电流达到负峰值，使铁心进入初步饱和。
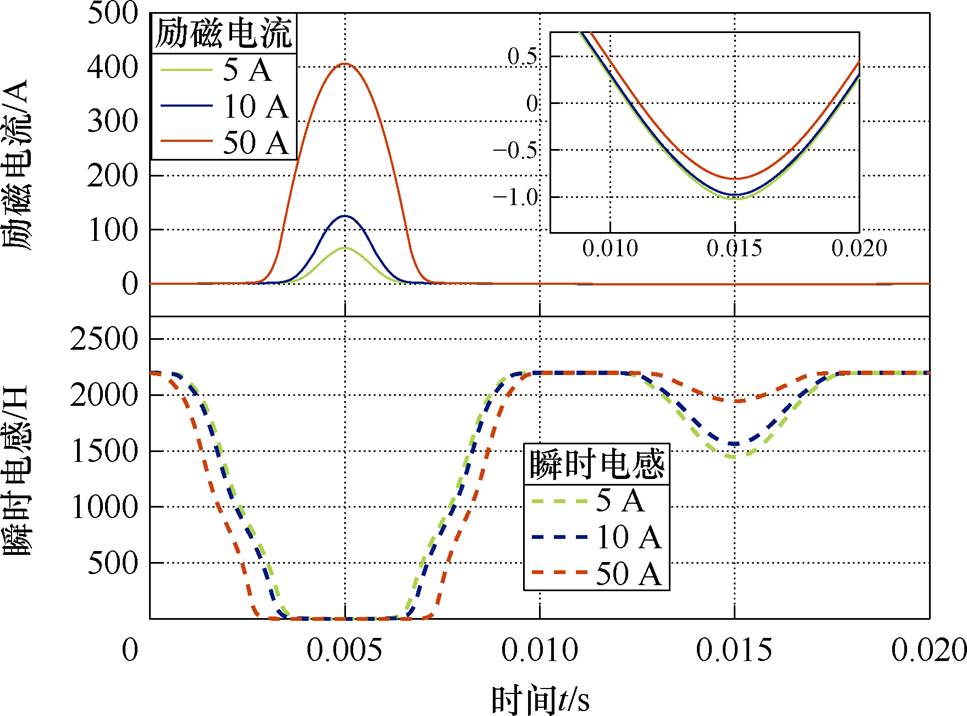
图6 直流量为5、10、50 A时的励磁电流与对应的瞬时电感
Fig.6 The magnetization current and corresponding instantaneous magnetization inductance at DC of A, 10 A, and 50 A
为计算定直流量下的等效电感，式（7）变为
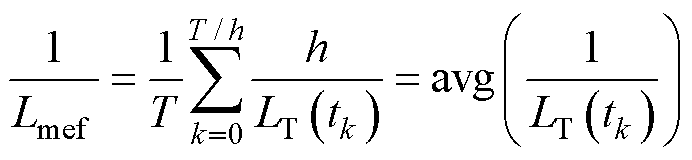（8）
式中，h为仿真步长，此处设置为(0.02/2 000) s；LT(tk)为一个工频周期内第k个时间步长的电感瞬时值。求得直流量为5、10、50 A时的Lmef分别为18.81、11.52、5.878 H。
进行大量不同直流电流量下的仿真分析，由式（8）计算相应Lmef，得到Lmef-Idc特性曲线如图7a所示。
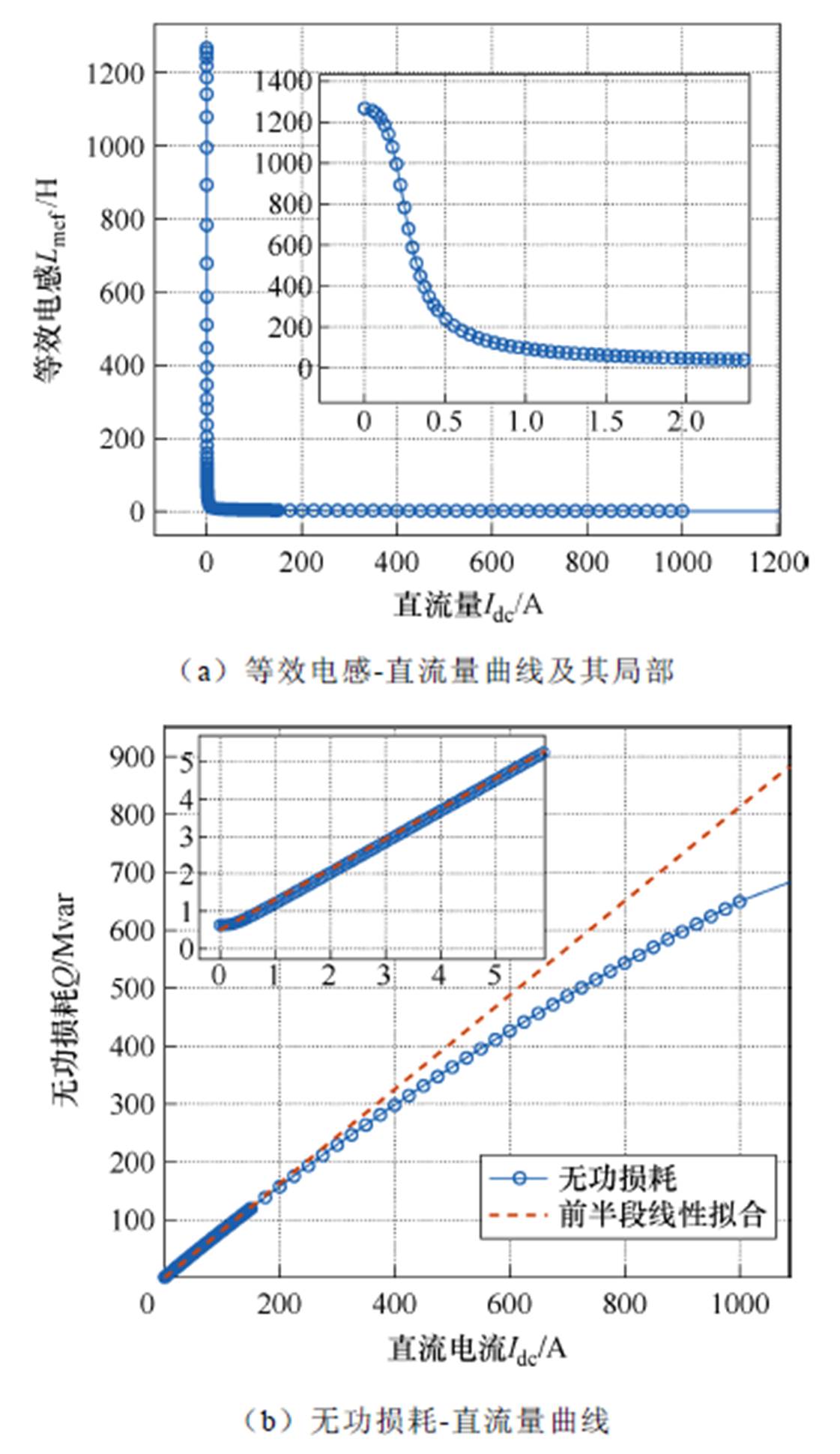
图7 仿真计算的等效电感及无功损耗与直流量曲线
Fig.7 Equivalent inductance vs. DC curve and reactive power loss vs. DC curve of simulation
假设变压器一次电压在GIC导致的直流偏磁时波形保持不变，同时忽略铁心磁滞、涡流损耗及数值很小的绕组电阻分压，励磁电流与一次电压的相位差为90°，因此，单相特高压变压器直流偏磁下的无功损耗计算式为
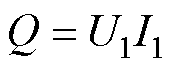（9）
式中，U1为额定基频电压有效值；I1为对波形进行傅里叶分解得到的基频电流有效值。图7b为Q-Idc特性曲线。
图7a所示的等效电感Lmef在直流量Idc很小时有一个短暂平台期维持在很大数值，这是由于此时的峰值磁通尚未使铁心深度饱和，平台期的临界直流量约为0.2 A左右。Idc增大至超过临界直流量后，瞬时电感动态波形出现数值很小的深度饱和低谷阶段，导致Lmef急剧下降，较小的直流增量便造成Lmef的大幅下降：在1 A处，已减小为无直流偏磁时的8%。Lmef足够小后，其衰减速度随Idc继续增大而减缓，直至铁心在工频周期内完全饱和。
图7b所示无功损耗Q在平台期也因电流畸变不显著而增长缓慢。Idc超过临界直流量后，Q大致以一定比例随Idc增大，可以用K值法即图中线性虚线近似表示。然而，随着Idc继续增大，Q增长趋缓与Idc的比例系数明显减小，如800 A时K值法预测的无功损耗已高于仿真值的20%。直流量越大，无功损耗的饱和特性越显著，直至铁心在工频周期内完全饱和时，无功损耗达到极限。HEMP E3在电网内产生的GIC峰值可达几百上千安培[7, 19]，因此K值法可能会高估E3 GIC波峰处的变压器无功损耗。
上述计算依赖大量的场路耦合有限元仿真，效率有限。因此，提出简化解析法，采用两段式简化磁化曲线，通过解析实现变压器Lmef-Idc与Q-Idc特性的快速计算。图8为简化后变压器铁心直流偏磁工作状态[25, 38]的示意图。
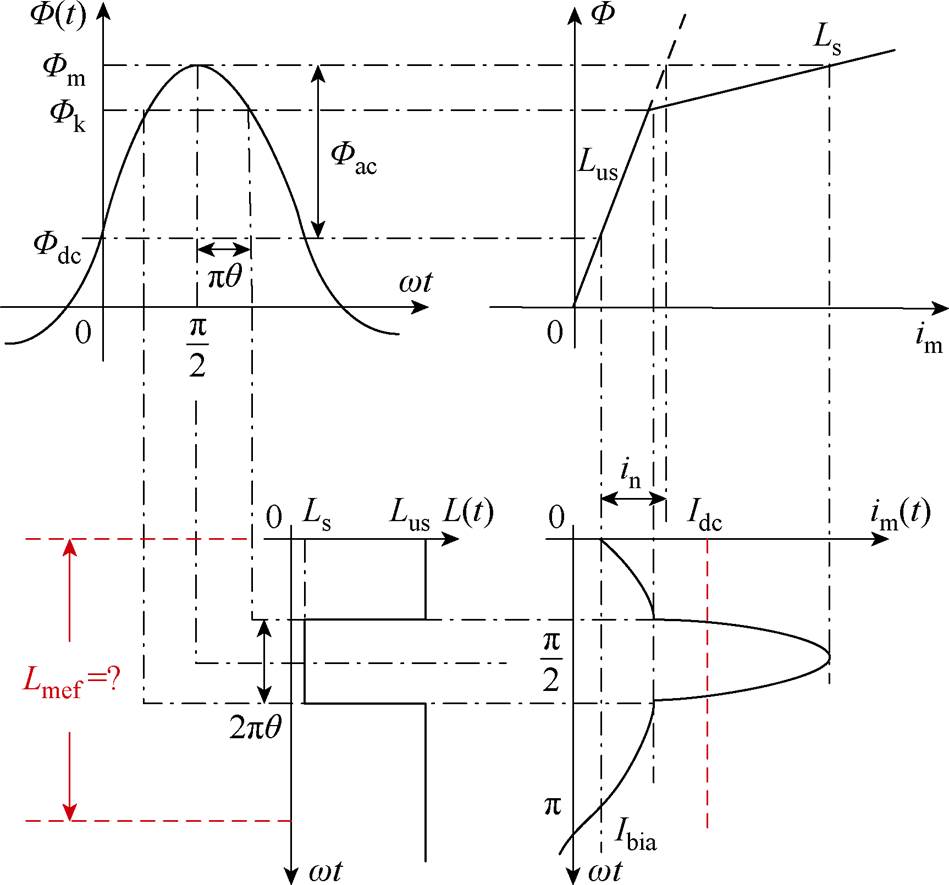
图8 使用两段式磁化曲线的变压器铁心直流偏磁示意图
Fig.8 The DC bias working state of the transformer core with two-segment magnetization curve
基于此分析磁通与励磁电流的各类成分。铁心磁通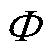
叠加了额定工况下峰值为
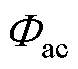的正弦交流磁通与直流量Idc产生的直流磁通
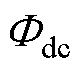，即
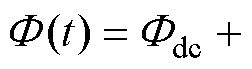
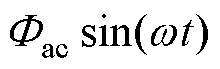，其中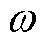
为工频角频率。忽略漏电感，仅分析励磁电感的变化：其数值随着瞬时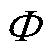磁通与膝点磁通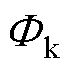
的数值关系在不饱和电感Lus与饱和电感Ls之间切换[32]。
直流磁通较小时，叠加后的磁通峰值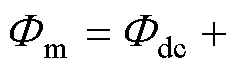
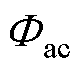未超过膝点磁通，铁心不饱和，因此类似2.1节的平台期，存在一个临界直流磁通即临界直流量Icr，在此之前变压器电感恒为Lus，该临界直流Icr为
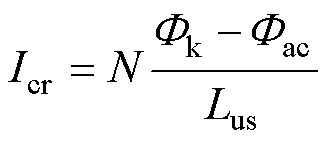（10）
式中，N为变压器一次绕组匝数，即串联绕组与公共绕组匝数之和。
直流量Idc超过Icr后，铁心部分饱和，设一个工频周期内饱和时间占空比为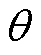
，则饱和角为
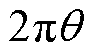，磁通关系满足
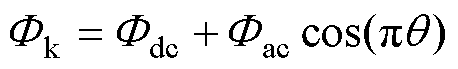。则式（7）变为
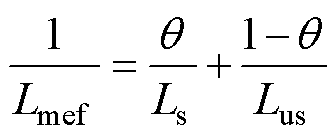（11）
即简化解析法下的变压器等效电感解析式。
由图8可知，铁心饱和时变压器励磁电流为
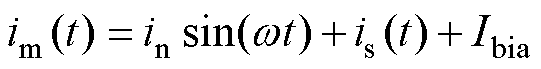（12）
式中，in为额定励磁电流峰值，即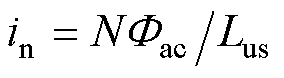
；
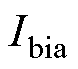为直流磁通引起的偏置直流电流分量；
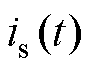为饱和区磁通贡献的励磁电流部分，表示为
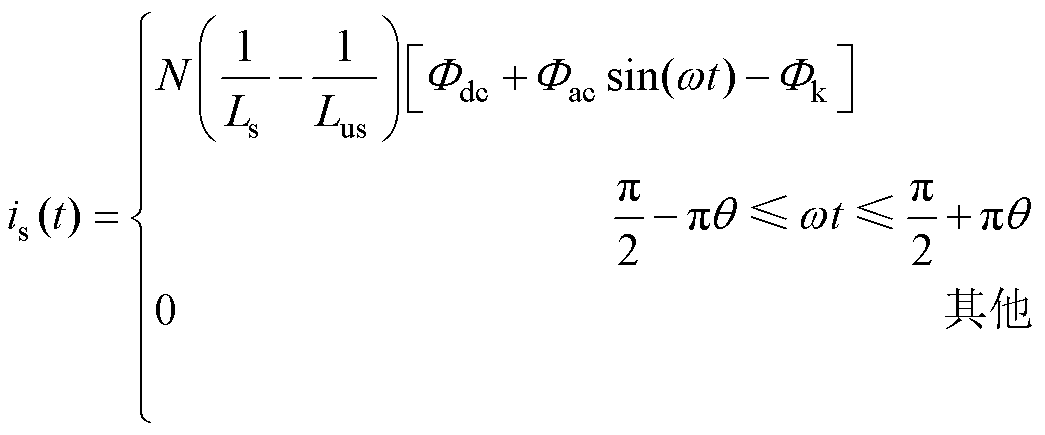（13）
式中，不饱和电感Lus远大于饱和电感Ls，可认为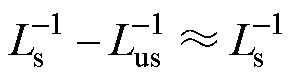
，由式（12）、式（13）得到直流量为
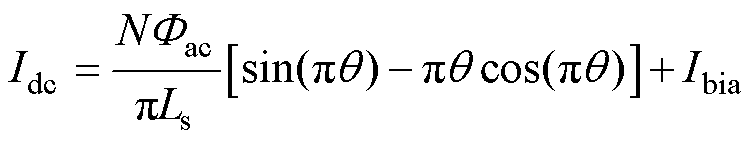（14）
忽略铁心磁滞与涡流损耗，认为变压器一次电压为峰值Um的额定工频交流电压，则电压电流基波分量有效值为
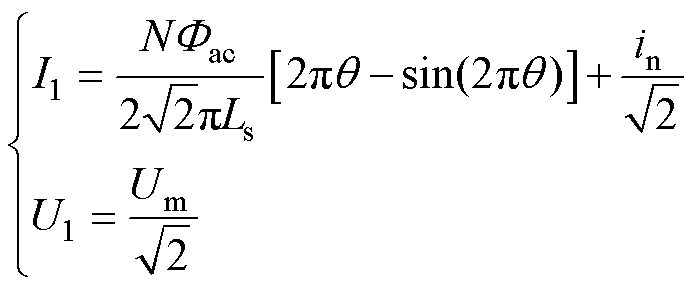（15）
代入式（9）得到无功损耗与占空比的关系为
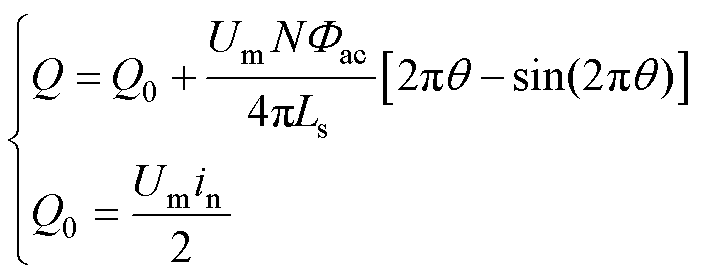（16）
式中，Q0为变压器不饱和时的无功损耗。
式（11）、式（14）、式（16）分别为Lmef、Idc和Q的解析式，联立计算得Lmef-Idc与Q-Idc特性曲线并与上文的仿真计算结果对比如图9所示。分别将场路耦合仿真与简化解析法简称为A方法与B方法。
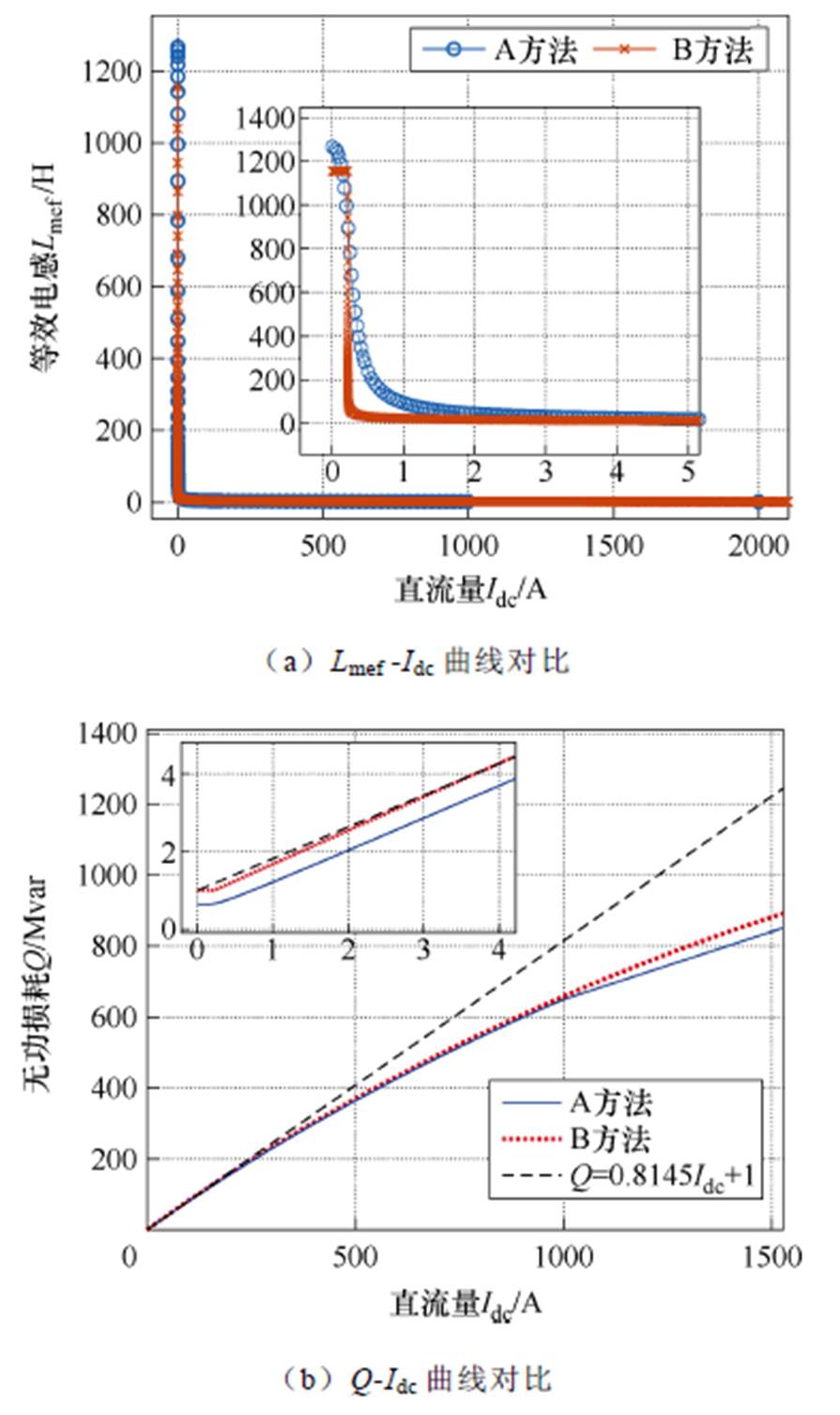
图9 等效电感与无功损耗曲线对比
Fig.9 Comparison of equivalent inductance and reactive power loss
由式（10）计算的临界直流量为0.219 A，与仿真观察到的平台期数值接近。图9a中B方法的Lmef在Idc较小时相比A方法数值衰减更快，这主要是由于简化的磁化曲线忽略了膝点附近的过渡过程；GIC超过4 A左右后，两方法的Lmef均已下降至很小且数值相近。图9b所示两方法计算的无功损耗结果误差很小，均在Idc值较大时表现出明显饱和特性。图中线性虚线基于GIC-K的工程算法[25,44]得出，作为与本文方法计算结果的对比。
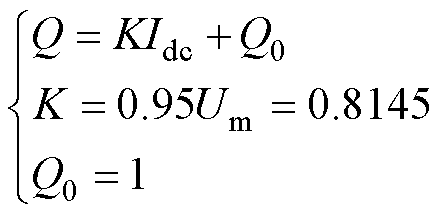（17）
简化解析法不涉及长时间暂态仿真，通过解析实现变压器等效电感与无功损耗特性的快速计算，误差较小且主要集中在直流量较低的条件下。该方法的技术路线如图10所示。磁化曲线的简化方法见附录。
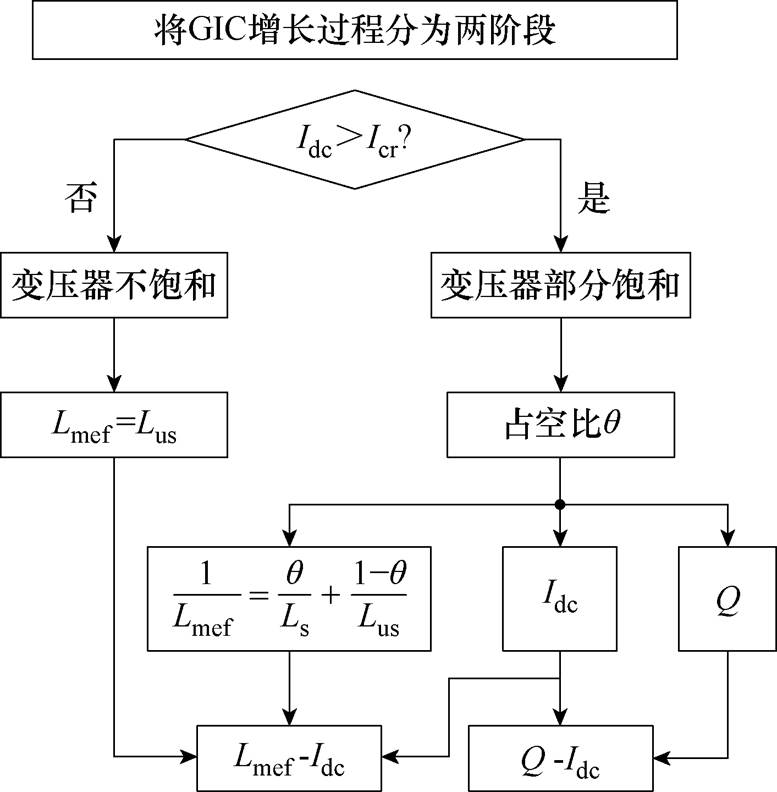
图10 简化解析法技术路线
Fig.10 Technical roadmap of simplified analytical method
将变压器等效电感与无功损耗特性应用于图2c的动态GIC计算模型，快速计算GIC与其造成的变压器无功损耗：由初始GIC（设置为0 A）插值Lmef-Idc曲线得到初始Lmef，以一个工频周期为迭代步长求解电路微分方程，计算动态GIC，并插值Q-Idc曲线得到每个时刻的无功损耗。
设回路直流电阻之和为5 W，Udc为在t=1 s时跃变的幅值分别为50 V和2 500 V的阶跃电压，以模拟小GIC和大GIC情形。分别基于A方法和B方法的Lmef-Idc计算得到图11所示的回路GIC和变压器无功损耗波形，并添加N方法计算的GIC及K值法计算的无功损耗。基于算例参数进行仿真，将上述方法与仿真值对比。
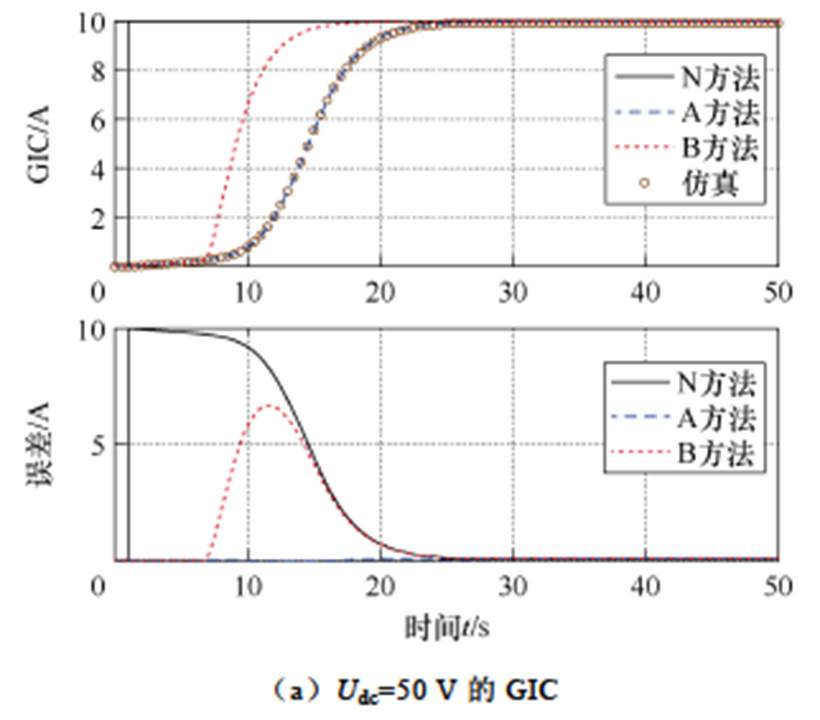
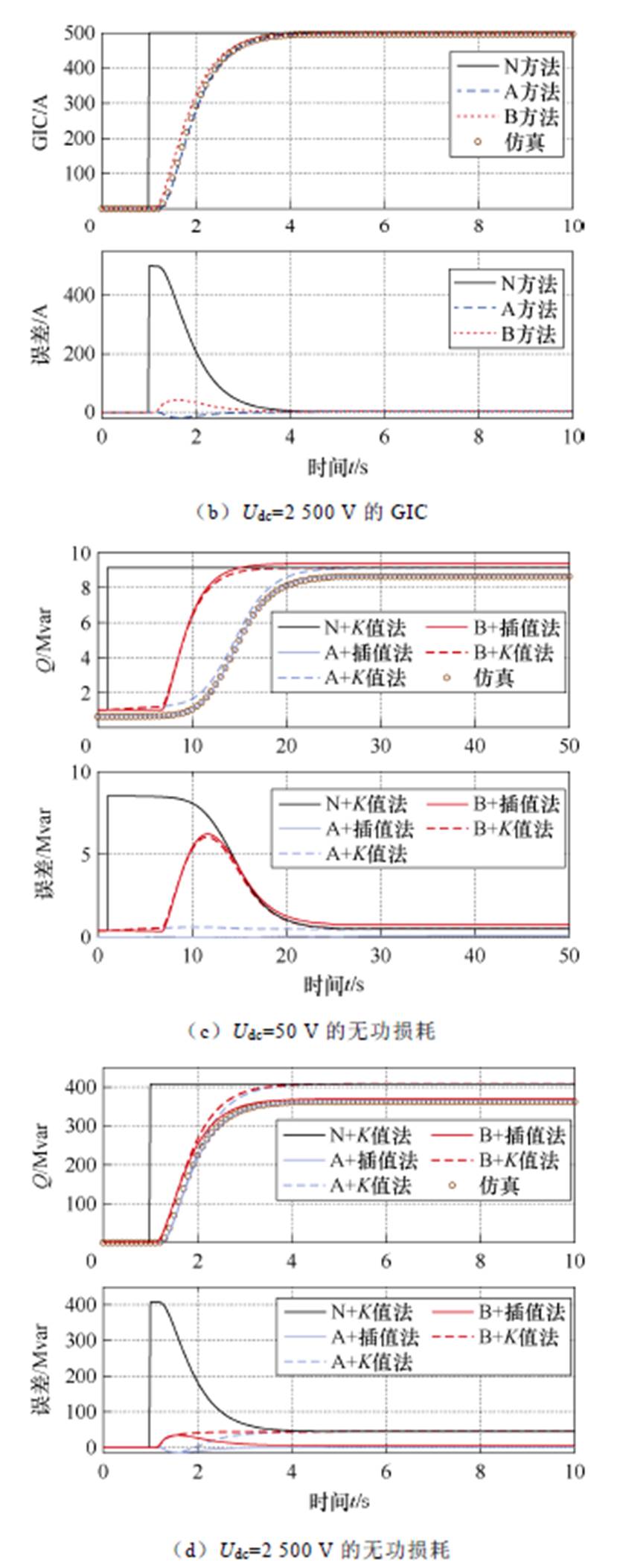
图11 回路内GIC与无功损耗波形，及各方法与仿真值之间的误差（R=5 W）
Fig.11 GIC growth waveforms and reactive power loss growth waveforms within the circuit, along with the errors between each method and the simulation results (R=5 W)
由图11可知，N方法计算GIC没有考虑电感效应，误差较大；基于A方法Lmef-Idc计算GIC并插值Q-Idc曲线计算无功损耗的结果与仿真值之间误差很小。
小幅值（50 V）感应电场下计算与仿真结果如下：
1）如图11a所示，不饱和大电感阻碍GIC的快速增长与变压器的饱和，表现出显著的电感效应。GIC超过临界直流量后，Lmef快速下降导致GIC增长变快，但由于等效电压较小，GIC达到稳态数值Udc/R依然需要一定时间。此时B方法结果存在一定误差，原因如图9a所示，B方法的Lmef在小直流量阶段下降更陡峭，使变压器更快达到稳定饱和。
2）图11c的无功损耗也相应存在数十秒的明显滞后。由于GIC较小，Q与GIC近似呈线性关系，因此插值Q-Idc曲线与K值法计算的无功功率损耗差别不大。
大幅值（2 500 V）感应电场下计算与仿真结果 如下：
1）如图11b所示，GIC仅数秒就快速上升到稳态值，此时B方法的计算结果与仿真值接近，因为大等效电压使变压器快速进入B方法误差很小的大GIC饱和后期。
2）如图11d所示，无功损耗的时延不显著，但在大GIC下出现饱和特性，K值法误差明显。
结果表明，变压器的电感效应在小感应电场下显著阻碍GIC与Q快速增长；大感应电场下电感阻碍作用不明显，但无功的饱和特性显著。HEMP E3波形在短暂几秒内快速上升到很高的峰值，因此上述特性是影响计算精度的重要因素。评估E3引发的系统风险时，重点关注其中的高峰值阶段，而简化解析法在高感生电场下具有较好的精度，因此适用于E3作用下GIC与变压器无功损耗的快速准确 计算。
图2c为考虑电感效应的E3 GIC动态计算模型，变压器选用上文的特高压变压器。由于三华特高压1 000 kV电网中的蒙西-晋北段所在的M1板块大地浅层（＜90 km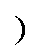
电导率接近HEMP E3标准波形的适用范围，因此采用该段的线路参数与接地点参数见表1，作为计算参数[45]。
假设该段大地是电导率为10-4 S/m的均匀大地，HEMP E3感生地电场方向与蒙西-晋北输电线夹角为0，采用E3标准波形，由式（1）计算E3等效电压源。以50 km输电线路为基准，计算E3 GIC与造成的变压器无功损耗如图12所示，N方法与K值法计算结果作为对照组。
表1 蒙西-晋北段GIC模型计算参数
Tab.1 Calculation parameters of GIC model for the Mengxi-Jinbei section
参 数数 值 变电站接地电阻/W0.1 线路单位长度直流电阻/(W/m)0.009 5 线路回数2 电压等级/kV1 000
图12 HEMP E3下回路内GIC与无功损耗波形
Fig.12 Waveforms of GIC and reactive power loss in he circuit under HEMP E3
如图12a所示，动态E3 GIC的增长受变压器等效电感阻碍作用的影响，导致其峰值变平缓。在GIC过零点处，变压器回到不饱和状态，显著阻碍了GIC的极性变换与反向增长，造成数秒的平台期。N方法预测的E3 GIC在3.06 s时达到峰值2 174.7 A，而A、B两方法分别在7.9 s和7.64 s达到峰值1 857.7 A和1 874.8 A，相比N方法的波峰时间分别延后约4.8 s和4.6 s，N方法峰值误差达到17%。对E3 GIC上升速度与峰值的估计偏差将导致对核爆事件中关键电力设备如变压器等故障失效概率大小的误判，进而误判事件严重性，导致过于保守的应对决策，造成不必要的财产损失。
图12b所示的无功损耗波形除了时间滞后，还在波峰处表现出明显饱和特性，N方法计算GIC进而用K值法计算的无功损耗峰值高估了接近800 Mvar，误差达到81%，即使基于动态GIC采用K值法，依然有536 Mvar的明显高估与54.8%的误差。无功损耗直接影响电网电压稳定性分析[28-29]，对无功损耗的高估导致对电力系统响应灾害性风险的保守评估，这大大影响调度决策的科学性，可能造成不必要的减负荷与退运行，因此在HEMP E3的波峰阶段应该对K值修正。
简化解析法不依赖仿真，且总体计算误差很小，可以实现特高压电网E3 GIC与其造成的变压器无功效应的快速计算，这是保证快速准确分析电网电压稳定性并及时科学应对灾害的重要前提。
通过场路耦合仿真定量分析了特高压变压器的Lmef-Idc和Q-Idc特性，并提出了实现快速计算的简化解析法。基于上述特性，应用动态GIC计算模型计算了变压器回路的动态E3 GIC及其造成的变压器无功损耗。得出结论如下：
1）变压器等效电感Lmef阻碍GIC的快速增长，从而使E3 GIC滞后于E3感生电场的变化且峰值变平缓，并间接导致变压器动态无功的滞后。Lmef数值随直流偏磁程度的增大而急剧减小，因此对小GIC阻碍作用更显著，使E3 GIC在流向改变时出现平台期。
2）变压器无功损耗Q-Idc特性在直流量Idc较小时近似呈线性关系，但在Idc较大时出现明显饱和特性，且Idc越大，饱和特性越显著。这大大影响了E3 GIC（尤其是峰值阶段）下变压器无功损耗的计算精度，导致K值法的高估，误差可达数百Mvar。为保证电压稳定性分析精度，应对K值法修正。
3）提出的简化解析法不涉及仿真，因此不要求变压器的具体几何参数，且保证了一定计算精度。基于该方法与变压器回路动态GIC计算模型，可实现HEMP E3作用下GIC及其造成的变压器无功损耗的快速准确计算。
本文假设大地电导率均匀，因此有一定局限性，但结论依然可以为评估并预防E3引起的设备损坏和系统风险奠定基础。
附 录
1. 标准IEC 61000-2-9[34]HEMP E3的双指数函数波形表达式为
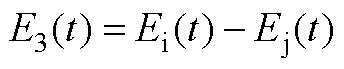（A1）
其中
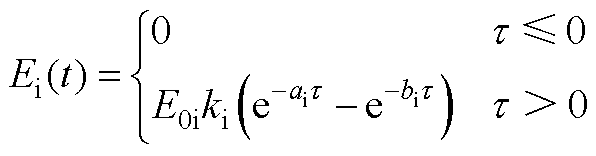
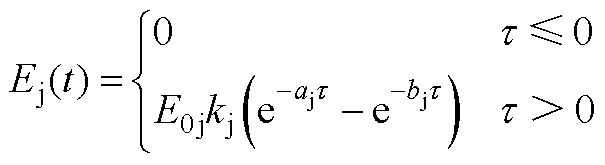
附表1为适用于电导率为10-4 S/m的均匀大地的HEMP E3标准波形参数。
附表1 HEMP E3标准波形参数
App.Tab.1 Parameters of standard HEMP E3 waveform
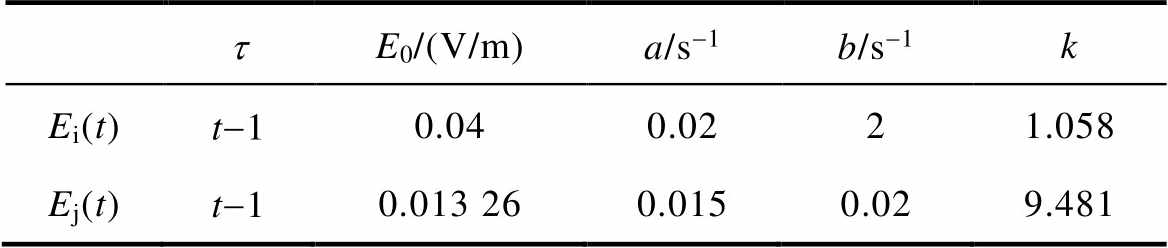
tE0/(V/m)a/s-1b/s-1k Ei(t)t-10.040.0221.058 Ej(t)t-10.013 260.0150.029.481
2. 本文研究的特高压变压器参数见附表2。
附表2 特高压自耦变压器参数
App.Tab.2 Parameters of UHV transformer
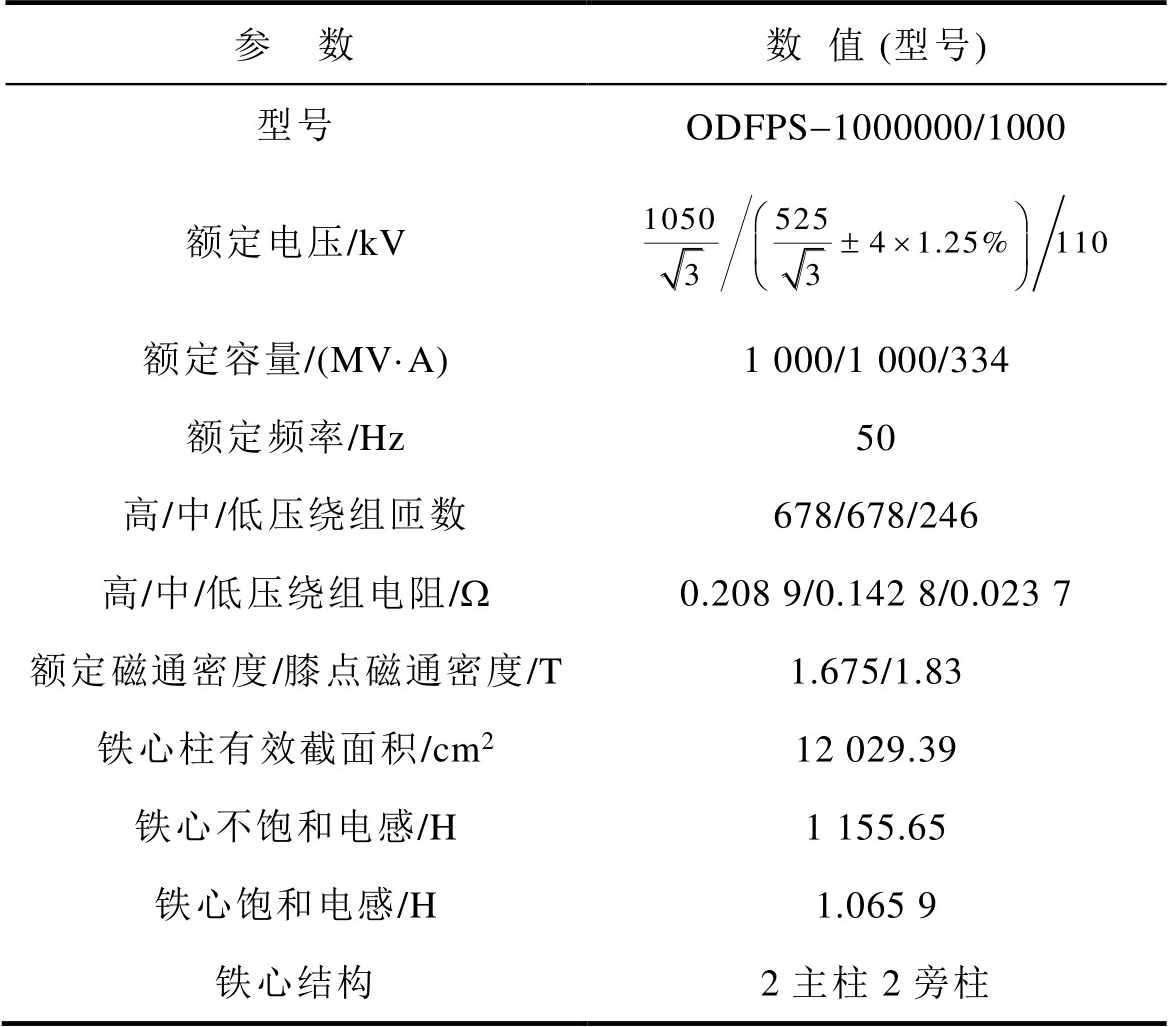
参 数数值 (型号) 型号ODFPS-1000000/1000 额定电压/kV 额定容量/(MV·A)1 000/1 000/334 额定频率/Hz50 高/中/低压绕组匝数678/678/246 高/中/低压绕组电阻/W0.208 9/0.142 8/0.023 7 额定磁通密度/膝点磁通密度/T1.675/1.83 铁心柱有效截面积/cm212 029.39 铁心不饱和电感/H1 155.65 铁心饱和电感/H1.065 9 铁心结构2主柱2旁柱
3. 简化的磁化曲线可由三个参数确定：膝点磁通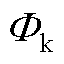
、不饱和电感Lus及饱和电感Ls。
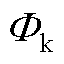：基于未简化的非线性磁化曲线，不饱和段与饱和段近似为两段直线，延长后交点纵坐标为膝点磁通密度
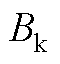[31]，由式（A2）计算
。
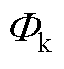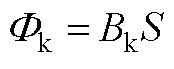（A2）
式中，S为铁心主柱有效截面积。
Lus：2.2节的无直流偏磁下额定励磁电流峰值in满足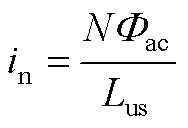
，因此由式（A3）计算Lus。
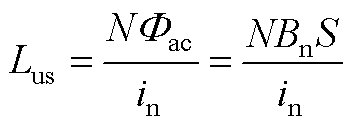（A3）
式中，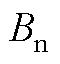
为变压器额定磁通密度；in近似视作一次侧施加额定电压时的空载电流峰值，通过空载实验确定。
Ls计算式为
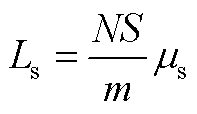（A4）
式中，m为与铁心尺寸有关的结构系数；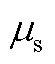
为铁心饱和微分磁导率，是未简化的B-H曲线在深度饱和段的近似直线斜率。式（A4）在参考文献[32]中由安培环路定理和磁通连续性定理推导得出。
参考文献
[1] 刘彤宇, 李丽, 王亚楠, 等. 高空电磁脉冲晚期环境下电力系统效应研究进展[J]. 强激光与粒子束, 2024, 36(5): 134-150.
Liu Tongyu, Li Li, Wang Yanan, et al. Research progress on power system effects in late-time high- altitude electromagnetic pulses environment[J]. High Power Laser and Particle Beams, 2024, 36(5): 134- 150.
[2] Klein K W, Barnes P R, Zaininger H W. Electro- magnetic pulse and the electric power network[J]. IEEE Transactions on Power Apparatus and Systems, 1985, PAS-104(6): 1571-1577.
[3] Radasky W A. Rezaei-Zare A. Behavior of single- phase transformers under geomagnetically induced current conditions[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 916-925.
[4] 党存禄, 马雄文. 基于复杂网络理论的变电站直流偏磁治理研究[J]. 高压电器, 2024, 60(4): 193-198.
Dang Cunlu, Ma Xiongwen. Research on DC bias control of substation based on complex network theory[J]. High Voltage Apparatus, 2024, 60(4): 193-198.
[5] 刘春明. 中低纬电网地磁感应电流及其评估方法研究[D]. 北京: 华北电力大学, 2009.
Liu Chunming. Mid-low latitude power grid geomag- netic induced currents and its assessing method[D]. Beijing: North China Electric Power University, 2009.
[6] 辛文凯, 王泽忠, 刘春明, 等. 基于磁流体力学模型与模型预测控制的地磁暴期间超高压、特高压电网电压波动平抑优化调度[J]. 电工技术学报, 2024, 39(13): 4003-4014.
Xin Wenkai, Wang Zezhong, Liu Chunming, et al. Optimal dispatch for smooth voltage fluctuation of EHV and UHV power grid during geomagnetic storms based on magnetohydrodynamics model and model predictive control method[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4003-4014.
[7] 杨一帆, 刘民周, 谢彦召, 等. 高空电磁脉冲晚期成分作用下500 kV变压器无功损耗仿真研究[J]. 电工技术学报, 2024, 39(1): 267-277.
Yang Yifan, Liu Minzhou, Xie Yanzhao, et al. Simulation research on reactive power loss characteri- stic of 500 kV transformer under late-time high- altitude electromagnetic pulses[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 267-277.
[8] 陈宇浩, 谢彦召, 刘民周, 等. 高空电磁脉冲作用下电力系统主要效应模式分析[J]. 强激光与粒子束, 2019, 31(7): 49-54.
Chen Yuhao, Xie Yanzhao, Liu Minzhou, et al. Analysis of high-altitude electromagnetic effect models on power system[J]. High Power Laser and Particle Beams, 2019, 31(7): 49-54.
[9] 李冰, 王泽忠, 刘恪, 等. 特高压变压器直流偏磁对绕组电流的影响[J]. 电工技术学报, 2020, 35(7): 1422-1431.
Li Bing, Wang Zezhong, Liu Ke, et al. Research on winding current of UHV transformer under DC- bias[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1422-1431.
[10] Zhang Xiaoyue, Liu Xinghua, Guo Fanghong, et al. Calculation of DC bias reactive power loss of converter transformer via finite element analysis[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 751-759.
[11] 潘超, 安景革, 刘闯, 等. 变压器偏磁效应噪声特性的多场耦合分析与抑制[J]. 电工技术学报, 2023, 38(18): 5077-5088.
Pan Chao, An Jingge, Liu Chuang, et al. Multi-field coupling analysis and suppression for biased magnetic noise in transformer[J]. Transactions of China Elec- trotechnical Society, 2023, 38(18): 5077-5088.
[12] 邢军强, 王菲, 韩刚, 等. 大地直流偏磁影响下电力变压器损耗及温升计算研究[J]. 电气技术, 2020, 21(1): 20-24, 30.
Xing Junqiang, Wang Fei, Han Gang, et al. Research on loss and temperature rise calculation method of power transformer under the influence of geomag- netically induced current[J]. Electrical Engineering, 2020, 21(1): 20-24, 30.
[13] Gilbert J, Kappenman J, Radasky W, et al. The late-time (E3) high-altitude electromagnetic pulse (HEMP) and its impacton the U.S. power grid[R]. Goleta: Oak Ridge National Laboratory, 2010.
[14] Pierre B J, Krofcheck D J, Hoffman M J, et al. Modeling framework for bulk electric grid impacts from HEMP E1 and E3 effects (tasks 3.1 final report): SAND2021-0865[R]. Sandia National Lab. (SNL- NM), Albuquerque, NM (United States), 2021.
[15] 公延飞, 郝建红, 蒋璐行, 等. 有损大地上传输线HEMP响应的研究[J]. 电工技术学报, 2018, 33(21): 4901-4908.
Gong Yanfei, Hao Jianhong, Jiang Luhang, et al. The research for the transient response of overhead trans- mission line on lossy ground excited by HEMP[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4901-4908.
[16] 秦锋, 王旭桐, 陈伟, 等. 强电磁脉冲下线路绝缘子闪络特性试验研究[J]. 电工技术学报, 2023, 38(13): 3640-3650.
Qin Feng, Wang Xutong, Chen Wei, et al. Experi- mental study on flashover characteristics of line insulator under strong electromagnetic pulse[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3640-3650.
[17] 谢海燕. 系统级HEMP耦合分析方法研究进展[J]. 现代应用物理, 2023, 14(2): 14-20.
Xie Haiyan. Research progress of system level HEMP coupling analysis methods[J]. Modern Applied Physics, 2023, 14(2): 14-20.
[18] 秦锋, 王旭桐, 陈伟, 等. 高空电磁脉冲作用下配电变压器瞬态响应与失效机理[J]. 中国电机工程学报, 2023, 43(17): 6924-6933.
Qin Feng, Wang Xutong, Chen Wei, et al. Transient response and failure mechanism of distribution trans- former under high-altitude electromagnetic pulse[J]. Proceedings of the CSEE, 2023, 43(17): 6924-6933.
[19] 赵志斌, 柯俊吉, 马丽斌. 高空核电磁脉冲晚期效应对电网稳定性影响的研究[J]. 电气技术, 2015, 16(9): 16-19.
Zhao Zhibin, Ke Junji, Ma Libin. Research on impact of late-time HEMP to stability of power grids[J]. Electrical Engineering, 2015, 16(9): 16-19.
[20] Lee R H, Shetye K S, Birchfield A B, et al. Using detailed ground modeling to evaluate electric grid impacts of late-time high-altitude electromagnetic pulses (E3 HEMP)[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1549-1557.
[21] 高志伟, 周于翔, 朱思熠. 晚期HEMP作用下铁路牵引供电系统GIC算法研究[J]. 强激光与粒子束, 2021, 33(9): 093001.
Gao Zhiwei, Zhou Yuxiang, Zhu Siyi. Study on GIC algorithm of railway traction power supply system under action of late time HEMP[J]. High Power Laser and Particle Beams, 2021, 33(9): 093001.
[22] Horton R, Boteler D, Overbye T J, et al. A test case for the calculation of geomagnetically induced currents[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2368-2373.
[23] 郑宽, 刘连光, David H. Boteler, 等. 多电压等级电网的GIC-Benchmark建模方法[J]. 中国电机工程学报, 2013, 33(16): 179-186, 3.
Zheng Kuan, Liu Lianguang, Boteler D H, et al. Modelling geomagnetically induced currents in multiple voltage levels of a power system illustrated using the GIC-benchmark case[J]. Proceedings of the CSEE, 2013, 33(16): 179-186, 3.
[24] Bolduc L, Gaudreau A, Dutil A. Saturation time of transformers under DC excitation[J]. Electric Power Systems Research, 2000, 56(2): 95-102.
[25] 王泽忠, 黄天超. 变压器地磁感应电流-无功功率动态关系分析[J]. 电工技术学报, 2021, 36(9): 1948- 1955.
Wang Zezhong, Huang Tianchao. Analysis of geomagnetically induction current-reactive power dynamic relationship of transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1948-1955.
[26] Vakhnina V V, Kuvshinov A A, Chernenko A N. Modulation of the power transformer magnetizing inductance by variations of geomagnetically induced currents during geomagnetic disturbances[C]//2021 International Ural Conference on Electrical Power Engineering (UralCon), Magnitogorsk, Russian Federation, 2021: 49-54.
[27] Xin Wenkai, Liu Chunming, Rezaei-Zare A, et al. Real-time monitoring method of power grid voltage stability during geomagnetic storms[J]. IEEE Transa- ctions on Power Delivery, 2024, 39(1): 192-201.
[28] Hutchins T R, Overbye T J. Power system dynamic performance during the late-time (E3) high-altitude electromagnetic pulse[C]//2016 Power Systems Com- putation Conference (PSCC), Genoa, Italy, 2016: 1-6.
[29] Overbye T J, Snodgrass J, Birchfield A, et al. Towards developing implementable high altitude electromagnetic pulse E3 mitigation strategies for large-scale electric grids[C]//2022 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2022: 1-6.
[30] 辛文凯, 王泽忠, 刘春明, 等. 地磁暴影响下特高压交流电网电压稳定性量化评估方法[J]. 电工技术学报, 2023, 38(21): 5771-5780.
Xin Wenkai, Wang Zezhong, Liu Chunming, et al. Quantitative evaluation method of voltage stability of UHV AC power network under geomagnetic storm[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5771-5780.
[31] Rezaei-Zare A. Behavior of single-phase transformers under geomagnetically induced current conditions[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 916-925.
[32] 王泽忠, 黄天超. 特高压变压器地磁感应电流和无功功率关系的定量分析[J]. 电工技术学报, 2020, 35(22): 4709-4716.
Wang Zezhong, Huang Tianchao. Quantitative analysis of geomagnectically induced current-Q relation of UHV transformer[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4709- 4716.
[33] 胡博, 谢开贵, 邵常政, 等. 双碳目标下新型电力系统风险评述: 特征、指标及评估方法[J]. 电力系统自动化, 2023, 47(5): 1-15.
Hu Bo, Xie Kaigui, Shao Changzheng, et al. Commentary on risk of new power system under goals of carbon emission peak and carbon neutrality: characteristics, indices and assessment methods[J]. Automation of Electric Power Systems, 2023, 47(5): 1-15.
[34] International Electrotechnical Commission. Electro- magnetic compatibility (EMC)-part 2-9: environment- description of HEMP environment-radiated dis- turbance: IEC 61000-2-9[S]. International Electro- technical Commission, 1996.
[35] Pirjola R. Review on the calculation of surface electric and magnetic fields and of geomagnetically induced currents in ground-based technological systems[J]. Surveys in Geophysics, 2002, 23(1): 71-90.
[36] Hutchins T. Modeling, simulation, and mitigation of the impacts of the late time (E3) high-altitude electromagnetic pulse on power systems[D]. Champaign, IL, USA: University of Illinois at Urbana-Champaign, 2016.
[37] Liu Chunming, Li Yunlong, Pirjola R. Observations and modeling of GIC in the Chinese large-scale high-voltage power networks[J]. Journal of Space Weather and Space Climate, 2014, 4: A03.
[38] Boteler D H, Bradley E. On the interaction of power transformers and geomagnetically induced currents[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2188-2195.
[39] Boteler D H. Characteristics of time-varying inductance[J]. IEEE Transactions on Magnetics, 1994, 30(2): 172-176.
[40] 王泽忠, 潘超, 周盛, 等. 基于棱边有限元的变压器场路耦合瞬态模型[J]. 电工技术学报, 2012, 27(9): 146-152.
Wang Zezhong, Pan Chao, Zhou Sheng, et al. Transient magnetic-circuit coupled model of trans- former based on edge finite element method[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 146-152.
[41] Chen Zhiwei, Li Hongmei, Liu Liuwen, et al. DC bias treatment of hybrid type transformer based on magnetic flux modulation mechanism[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1700204.
[42] Pan Chao, Wang Zezhong, Li Hailong, et al. Stability analysis based on transient magnetic-circuit coupled method for DC-biased transformer[C]//2012 Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 2012: 1-4.
[43] 谭瑞娟. 单相特高压自耦变压器直流偏磁电磁特性研究[D]. 北京: 华北电力大学, 2017.
Tan Ruijuan. Research on electromagnetic characteri- stics of single-phase UHV autotransformer under DC bias[D]. Beijing: North China Electric Power University, 2017.
[44] 刘连光, 朱溪, 王泽忠, 等. 基于K值法的单相四柱式特高压主体变的GIC-Q损耗计算[J]. 高电压技术, 2017, 43(7): 2340-2348.
Liu Lianguang, Zhu Xi, Wang Zezhong, et al. Calculation for reactive power loss of single-phase four limbs UHV main transformer due to geomag- netically induced currents with parameter K[J]. High Voltage Engineering, 2017, 43(7): 2340-2348.
[45] 郑宽. 大电网地磁感应电流影响因素及建模方法研究[D]. 北京: 华北电力大学, 2014.
Zheng Kuan. Research on influence factors and modeling methods of geomagnetically induced currents in large power grid[D]. Beijing: North China Electric Power University, 2014.
Abstract The late-time high-altitude electromagnetic pulses (HEMP E3) induce potential differences between grounding points in the power grid, subsequently generating geomagnetic induced current (GIC). E3 GIC causes direct current (DC) bias in power grid transformers, leading to increased harmonics, reactive power loss, vibration, and temperature rise, adversely impacting operational performance. Notably, the widespread increase in reactive power losses of all transformers in the affected area can cause grid-wide voltage fluctuations or even collapse. Therefore, accurate calculation of E3 GIC and its associated transformer reactive power loss is crucial for assessing system risks under E3 and developing effective countermeasures. Existing studies primarily calculate GIC based on the DC parameters of power grids and use the K-parameter method to estimate transformer reactive power loss, assuming a linear relationship with GIC. However, these methods neglect the inductive effects of transformers on GIC or the saturation of reactive power loss under high GIC. Therefore, the paper investigates the hindrance of transformer inductance on GIC and the characteristics of reactive power losses under DC bias induced by E3 GIC.
Based on the transient circuit of a single-phase transformer under DC bias, the equivalent inductance of the transformer (including magnetizing and leakage inductance) is derived. It is a nonlinear component influenced by the level of DC bias. Subsequently, a dynamic E3 GIC calculation model for a single power grid transformer circuit is established, considering the transformer inductance effect.
The equivalent inductance and reactive power loss characteristics of a single-phase ultra-high-voltage (UHV) transformer are calculated under DC bias through field-circuit coupled finite element simulations. A simplified analytical method for rapid calculation is proposed with a two-segment simplified magnetization curve. It is shown that the equivalent inductance decreases rapidly as the DC current increases. Under low DC, the reactive power loss exhibits an approximately linear relationship with DC current levels. However, the growth slows under high DC, and the saturation characteristics become more pronounced as the DC current increases. These are applied to calculate dynamic GIC and transformer reactive power loss under step voltage as the induced electric field. The results indicate that GIC and reactive power loss are delayed by tens of seconds under a low-induced electric field, and the saturation of reactive power loss becomes more pronounced under a high-induced electric field, suggesting greater overestimation by the K-parameter method. The simplified analytical method yields minor errors, especially under a high-induced electric field.
The E3 GIC and the associated transformer reactive power loss are calculated using the dynamic GIC calculation model with a 50 km transmission line as a reference. The results suggest that: (1) The transformer equivalent inductance hinders the rapid growth of GIC, both directly and indirectly delaying dynamic E3 GIC and reactive power loss relative to E3-induced electric field, with more flattened peaks. The waveforms exhibit zero-crossing plateaus. Ignoring the inductive effect can cause misjudgment of equipment damage and event severity. (2) The reactive power loss exhibits saturation characteristics at the E3 peak, which implies substantial errors in the K-parameter engineering algorithm, over predicting by several hundred Mvar. It affects the catastrophic risk prediction in power system response and the scientific accuracy of optimization scheduling decisions. The proposed simplified analytical method can rapidly predict E3 GIC and reactive power loss in the transformer circuit under HEMP E3 while maintaining reasonable accuracy.
keywords：Geomagnetically induction current (GIC), transformer, late-time high-altitude electromagnetic pulses, dynamic characteristics, reactive power loss
中图分类号：TM41
DOI: 10.19595/j.cnki.1000-6753.tces.241453
国家自然科学基金资助项目（52177081）。
收稿日期 2024-08-14
改稿日期2024-10-28
王古玥 男，2000年生，博士研究生，研究方向为电力系统电磁兼容。E-mail: w120181010715@163.com
刘春明 男，1972年生，教授，博士生导师，研究方向为电网安全运行与灾变控制。E-mail: liuchunming@ncepu.edu.cn（通信作者）
（编辑 郭丽军）