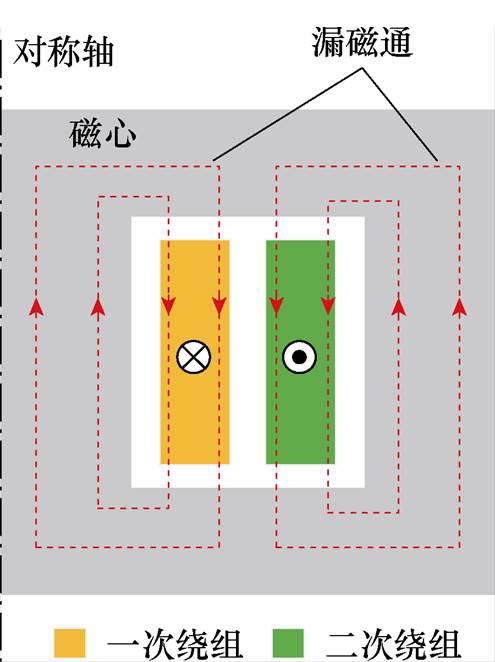
图1 磁通泄漏路径
Fig.1 Path of leakage flux
摘要 高频变压器漏感是影响电力电子变压器运行可靠性和功率传输特性的一个至关重要的参数。利兹线绕组复杂的绞合结构使得变压器漏感精确计算面临挑战。由于高频变压器优化设计过程中对漏感计算速度和准确性要求较高,传统有限元法需要对利兹线绕组进行精细化建模,对计算机硬件成本要求高,计算耗时长,因此目前常采用解析计算法。基于一维磁场假设的解析计算法虽然能快速计算变压器漏感,但忽略了绕组端部效应和内、外磁心窗口磁场强度分布差异的影响,导致计算误差较大。为此该文建立一种基于镜像原理的双二维利兹线绕组高频变压器漏感解析计算模型,在考虑内、外磁心窗口磁场强度分布差异的同时,兼顾绕组的端部效应和频变特性。最后,绕制了三台不同型号的样机,并进行实验验证与对比分析。实验结果表明,所建立的模型能够实现圆形和矩形利兹线绕组高频变压器漏感的精确、高效计算。
关键词:高频变压器 利兹线 漏感 双二维模型 镜像法 频变特性
随着智能电网、能源互联网等未来电网技术的快速发展,电力电子变压器逐渐成为研究热点[1]。高频变压器是电力电子变压器DC-DC环节关键的组成部分[2],在电气隔离和电压等级变化中发挥着重要作用。高频工况下,漏感作为高频变压器的重要寄生参数,其作用不能忽略[3]。例如,谐振拓扑结构中通常将高频变压器漏感作为谐振网络的一部分[4],进而减小无源元件的体积,提高功率密度[5-6]。然而利兹线绕组复杂的绞合结构使得漏感精确计算非常困难,因此,在电力电子变压器DC-DC环节的优化设计中,准确、快速地预测变压器漏感至关重要。
高频变压器漏感的计算方法主要分为数值法和解析法两类[7]。有限元法是一种典型的数值法,通过有限元仿真软件对高频变压器进行涡流场有限元数值分析[7]。文献[8]基于有限元分析方法,研究了绕组交叉换位以及绕组层数在宽频区间内对漏感和绕组损耗的影响规律。文献[9]提出了一种绕组分段概念的漏感计算方法,通过有限元法计算漏感值。文献[10]提出了双二维有限元模型计算利兹线绕组高频变压器漏感。对于有限元法,随着变压器工作频率的不断升高,导体的涡流效应影响显著,变压器漏感随着频率升高造成的衰减不可忽略。为了保证计算的精度,需要对宽频段内若干频点进行扫频计算来考虑漏感的频变特性,导致计算量的大大增加,计算过程复杂,耗时长。在高频变压器的设计阶段,首先需要通过优化程序来确定设计参数,需要相关参数的模型,如高频变压器漏感计算模型、绕组损耗计算模型等,在优化过程中,这些模型将被执行数千次,对模型的计算效率提出了较高的要求。
与数值法相比,解析法具有形式简单、计算速度快等优势,广泛应用于高频变压器优化设计[11]。然而,由于解析法在磁场计算时均进行了一定程度的简化,不可避免地产生误差。
现有的解析计算法主要是基于P. L. Dowell提出的一维磁场假设下的漏感和绕组损耗计算模型[12],虽然考虑了高频下绕组的涡流效应,但仅在理想的铜箔绕组排布下计算精度较高。文献[13-14]基于Dowell模型,对磁心窗口各区域进一步细分,通过引入孔隙率因子和洛氏系数提高了模型计算的精度。但通过洛氏系数进行绕组高度等效时未能充分考虑端部效应的影响[15]。在高频条件下计算精度显著下降。文献[16]以矩形利兹线绕组为研究对象,将每层矩形利兹线等效为多层细股线绕组的组合,提出适用于矩形利兹线的漏感参数计算模型。由于该模型基于面积等效法推导得到,在高频条件下同样存在较大的计算误差。针对面积等效法的不足,张珂等[17]提出采用极坐标系来表征利兹线绕组的磁场分布,并将利兹线等效为圆导线,通过引入两个归一化因子,考虑绕组的频变特性,实现了对利兹线绕组高频变压器漏感参数的计算。但仅沿磁心窗口区域纵向分布的外部磁场假设,导致绕组端部效应的表征不准确。文献[18-19]利用镜像法提取磁心窗口的二维磁场分布,这种方法不受端部效应的影响,利用Matlab编程语言实现计算,并且易于后处理和集成在变压器优化设计中,但是并未考虑高频下涡流效应带来的影响。文献[20]中,通过引入两个归一化因子来考虑高频下圆导线变压器的涡流效应,但仅实现了圆导线变压器漏感的精确预测。以上文献都是通过高频变压器内部磁心窗口计算漏感的单二维模型,忽略了变压器内、外磁心窗口磁场强度的差异。
为了实现利兹线绕组高频变压器漏感的准确、快速计算,本文建立了一种计及利兹线绕组高频变压器内、外磁心窗口磁场分布差异,并且考虑高频下利兹线绕组变压器涡流效应和端部效应的漏感解析计算模型。该模型适用于利兹线绕组高频变压器,计算成本低、计算速度快,并且通过Matlab编程语言实现,易于集成到高频变压器优化设计程序中。
在变压器中,一次绕组交流励磁产生的所有磁通并不能与二次绕组完全相连,部分磁通会从磁心泄漏并通过空气、绕组层和绝缘层返回,造成一次、二次绕组之间的不完全耦合,泄漏的磁通就是变压器漏感产生的原因[14],磁通泄漏路径如图1所示。

图1 磁通泄漏路径
Fig.1 Path of leakage flux
面积等效模型是基于能量法对漏感进行计算的单二维模型,该模型通过内部磁心窗口单位长度的漏磁能量计算变压器的漏磁能量。漏感和漏磁能量的关系为
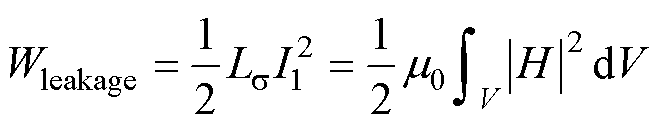 (1)
(1)
式中,Wleakage为变压器漏磁能量;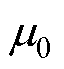 为空气磁导率;I1为一次绕组电流有效值;
为空气磁导率;I1为一次绕组电流有效值;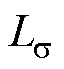 为归算至一次绕组的漏感;H为磁场强度;V为积分体积。
为归算至一次绕组的漏感;H为磁场强度;V为积分体积。
当高频变压器使用利兹线绕组时,由于其多股独立绝缘细导线绞合的结构,使得每根股线都能穿过导线横截面每个位置,此时可认为电流均匀分布在所有股线上。复杂的几何结构导致传统Dowell模型难以精确计算高频变压器的漏感,因此需要对Dowell模型进行修正[16]。将图2a所示直径为DL的圆形N股利兹线等效成图2b所示的DL×DL方形区域排列[21],并进一步等效为图2c中面积相同的方形股线,等效宽度为
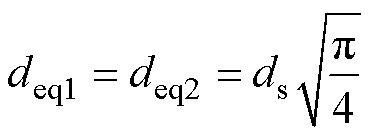 (2)
(2)
式中,ds为利兹线股线直径。
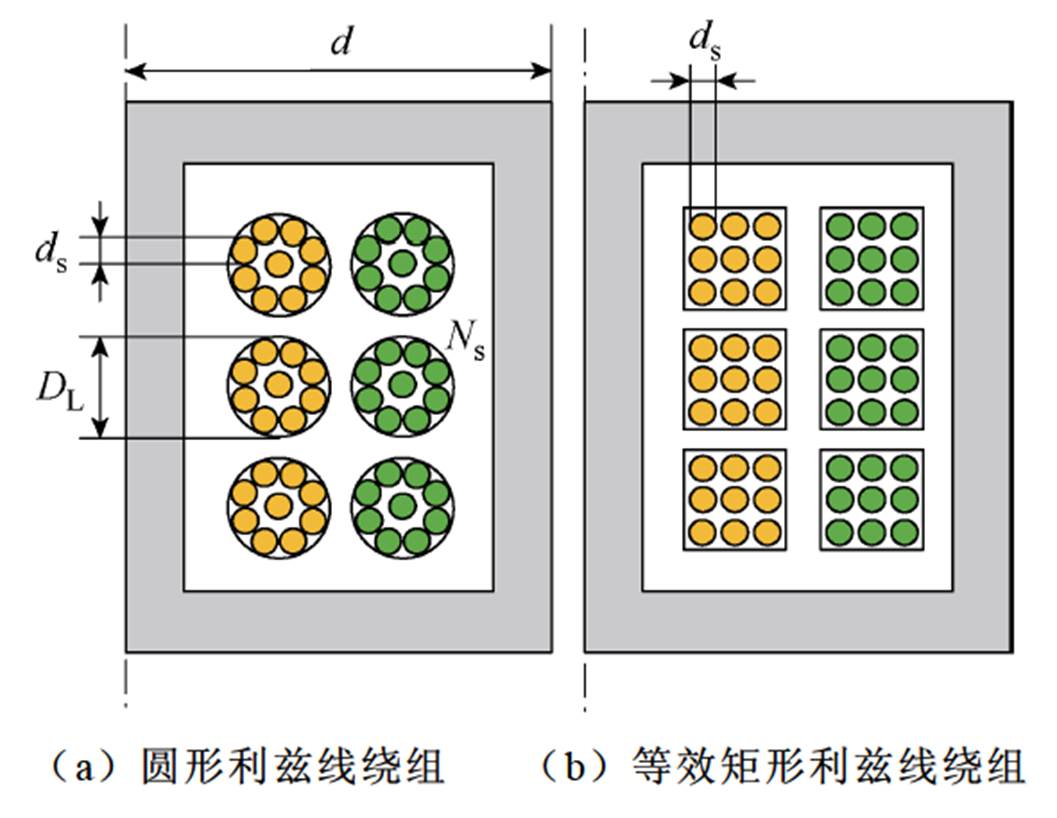
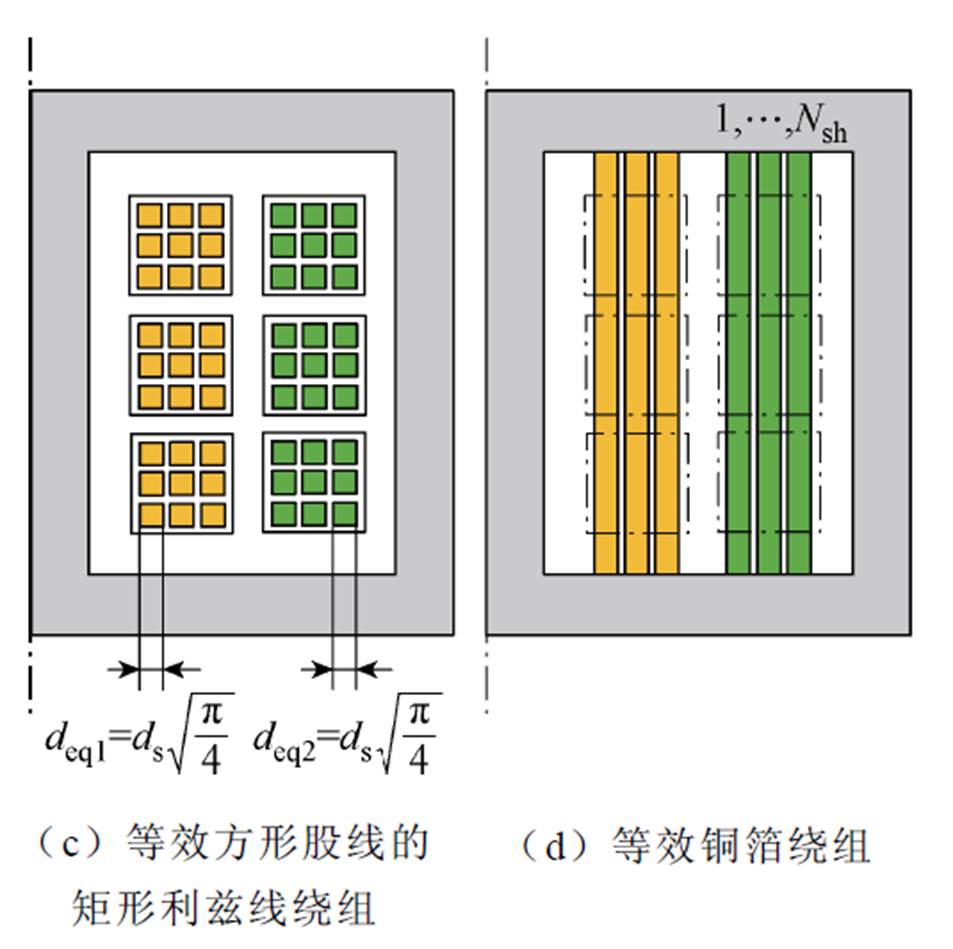
图2 圆形利兹线绕组面积等效
Fig.2 Circular Litz wire winding area equivalent
将方形股线等效成宽度相同的铜箔绕组,由于等效后绕组的横截面积发生改变,为使绕组整体电导率相同,需要引入等效孔隙率因子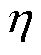 ,以保证等效前后绕组具有相同的导电能力,如式(3)所示。为了减小端部效应的影响,通过洛氏系数对绕组的高度进行修正,如式(4)所示。
,以保证等效前后绕组具有相同的导电能力,如式(3)所示。为了减小端部效应的影响,通过洛氏系数对绕组的高度进行修正,如式(4)所示。
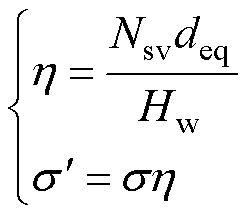 (3)
(3)
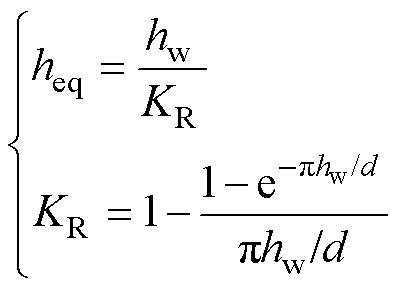 (4)
(4)
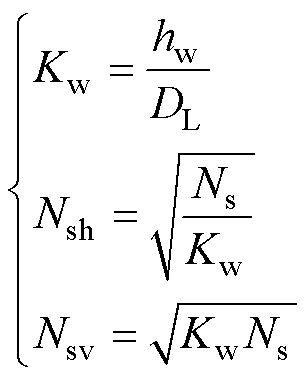 (5)
(5)
式中,Hw为磁心窗口的高度; 为电导率;
为电导率;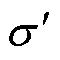 为等效电导率;KR为洛氏系数,hw为绕组高度;heq为绕组等效高度;Ns为总股线数;Kw为绕组高度和利兹线直径的比值因子,引入Kw是为了确定等效后水平和垂直方向的利兹线股数;Nsv和Nsh分别为等效后垂直方向的总股数和水平方向的总股数。
为等效电导率;KR为洛氏系数,hw为绕组高度;heq为绕组等效高度;Ns为总股线数;Kw为绕组高度和利兹线直径的比值因子,引入Kw是为了确定等效后水平和垂直方向的利兹线股数;Nsv和Nsh分别为等效后垂直方向的总股数和水平方向的总股数。
将磁心窗口漏磁能量分解为以下三部分,并通过安培环路定律计算一次、二次绕组导体漏磁能量,一次、二次绕组层间绝缘区域漏磁能量,一次、二次绕组主绝缘区域漏磁能量。
一次、二次绕组导体漏磁能量Wp和Ws分别为
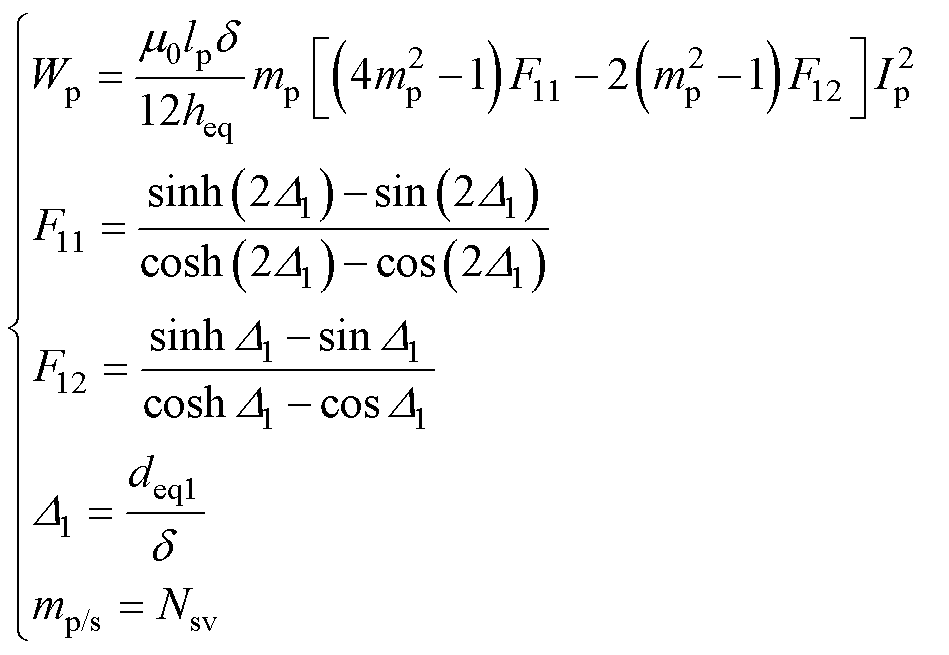 (6)
(6)
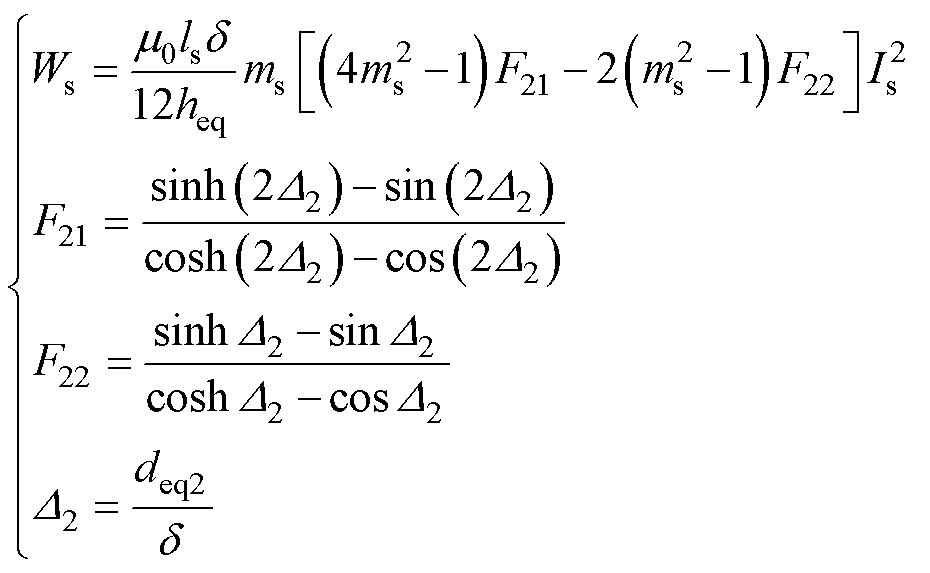 (7)
(7)
式中,lp和ls为一次绕组和二次绕组平均磁路长度;Ip和Is为一次绕组和二次绕组电流有效值;mp和ms为一次绕组和二次绕组的层数;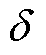 为趋肤深度;
为趋肤深度;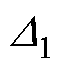 、
、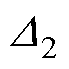 为Dowell模型中提出来的归一化厚度[12];F11、F12为Dowell模型中推导出来与频率相关的因子,表征漏磁能量与频率的关系。
为Dowell模型中提出来的归一化厚度[12];F11、F12为Dowell模型中推导出来与频率相关的因子,表征漏磁能量与频率的关系。
一次、二次绕组层间绝缘区域漏磁能量Wp_ins、Ws_ins分别为
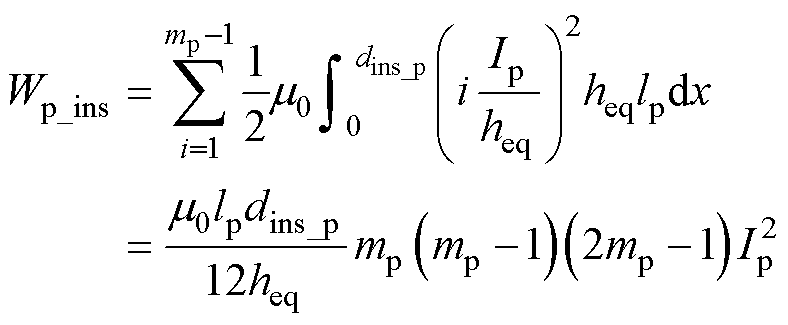 (8)
(8)
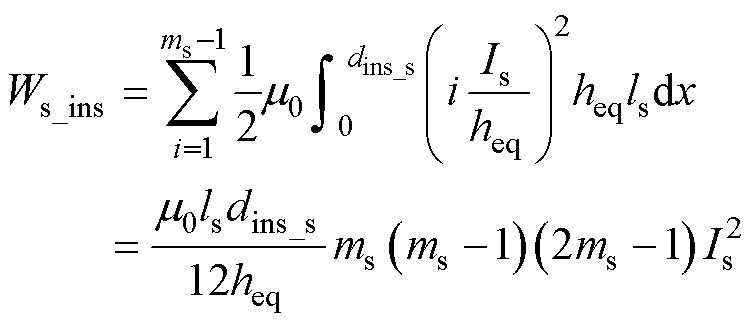 (9)
(9)
式中,dins_p、dins_s分别为一次、二次绕组层间绝缘距离。
一次、二次绕组主绝缘区域漏磁能量为
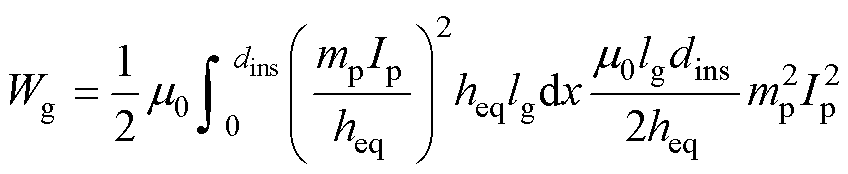 (10)
(10)
式中,dins为一次、二次绕组间主绝缘距离;lg为主绝缘区域平均磁路长度。
折算到一次绕组的高频变压器漏感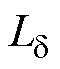 为
为
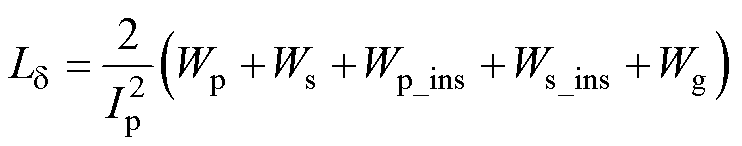 (11)
(11)
传统的面积等效法难以精确计算高频变压器漏感,并且厚度修正因子也缺乏可靠的物理解释。
变压器内部磁心窗口(IW)四边都是高磁导率磁心,而外部磁心窗口(OW)仅一面是高磁导率磁心。因此,内、外磁心窗口的磁场强度存在差异,如图3所示。这种内、外磁心窗口磁场强度的差异会在只考虑内部磁心窗口漏磁能量的单二维计算模型中引入误差。
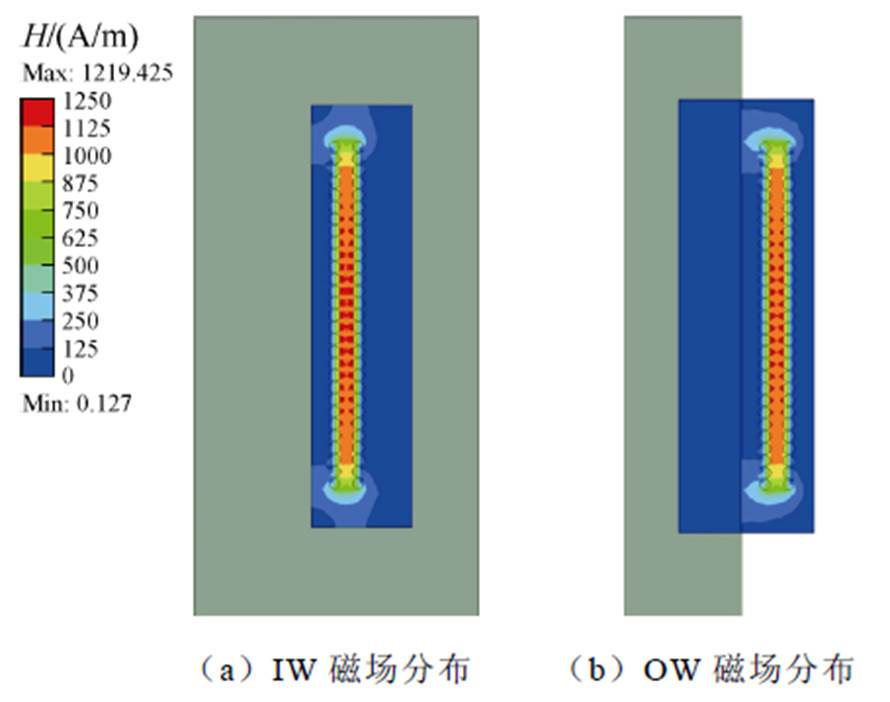
图3 内、外磁心窗口磁场分布
Fig.3 Magnetic field distribution inside and outside core window
为了考虑内、外磁心窗口磁场强度的差异,本文提出了双二维漏感计算模型,将变压器漏磁能量通过两个平面(IW平面和OW平面)进行计算;同时采用镜像法对二维磁场进行分析并提取内、外磁心窗口静磁场下的漏磁能量。利用镜像原理可以得到内、外磁心窗口的二维磁场分布,考虑绕组端部效应的同时避免了泊松方程的复杂求解。在低频时漏磁能量可以近似为直流漏磁能量,然而随着频率升高,绝缘区域无电流通过,漏磁能量衰减很小,可认为其保持恒定;导体区域漏磁能量衰减明显,为了考虑导体区域漏磁能量的频变特性,引入两个与频率相关的因子考虑导体内的趋肤效应和邻近效应。
因此,本文针对利兹线绕组高频变压器建立了一个双二维镜像法漏感计算模型,通过内/外两个磁心窗口平面进行漏磁能量提取,在采用镜像原理的基础上,考虑了高频涡流效应的影响,双二维镜像法计算模型如图4所示。
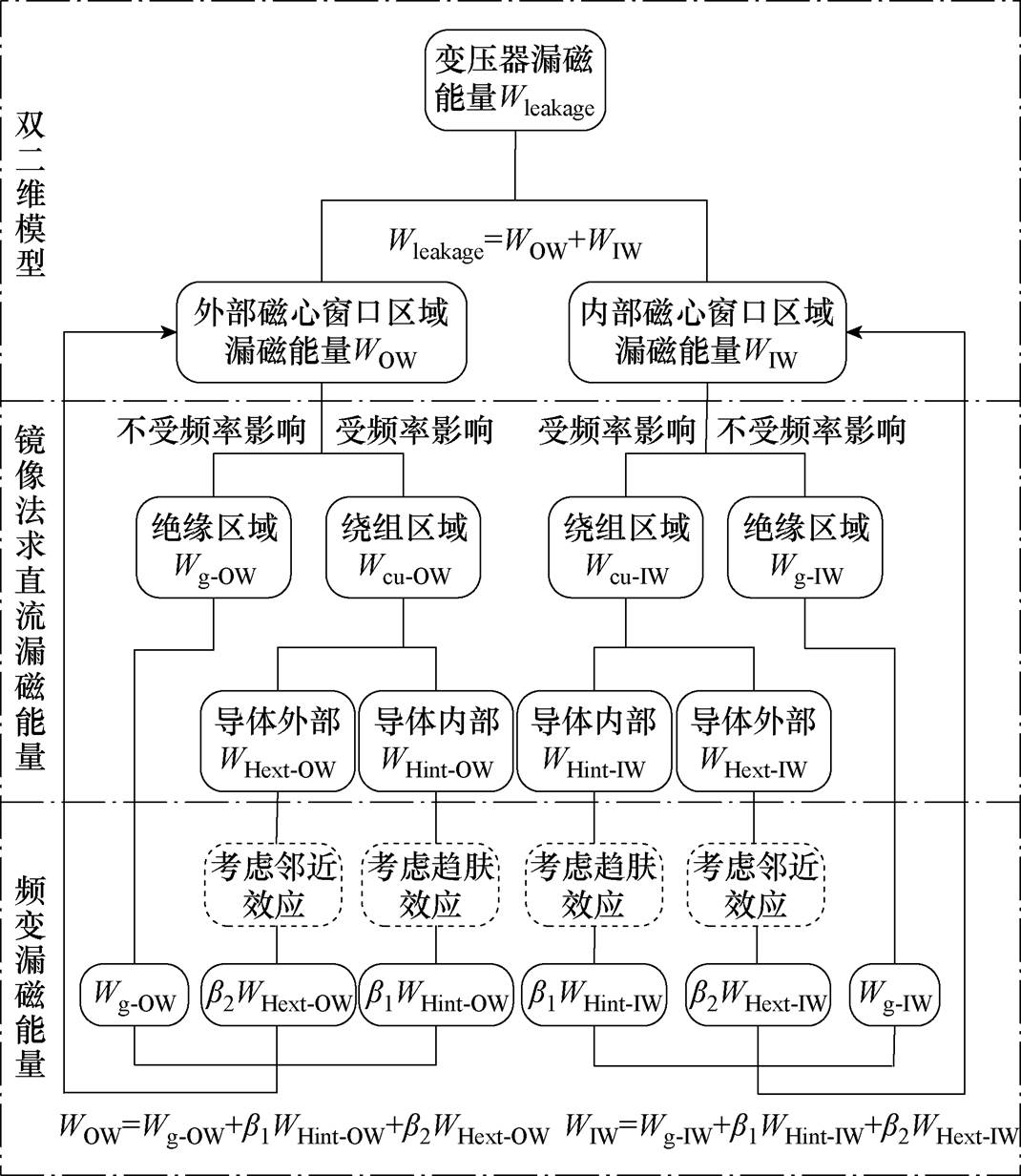
图4 双二维镜像法计算模型
Fig.4 Double-2-D image method calculation model
2.1.1 双二维模型建模过程
双二维模型是基于变压器的两个横截面计算漏磁能量[22],如图5所示,该模型考虑了内部磁心窗口截面和外部磁心窗口截面磁场强度的差异,能够更加精确地模拟高频变压器三维结构特性。
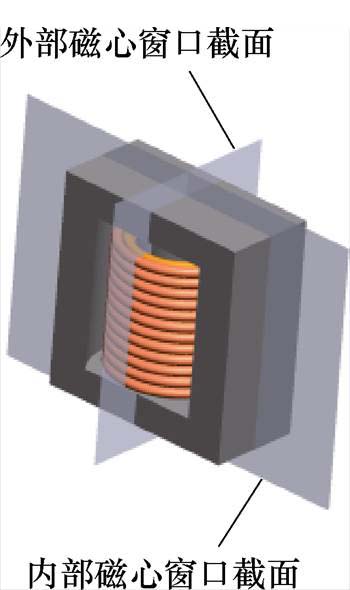
图5 内、外磁心窗口截面
Fig.5 Cross section of inside and outside core window
双二维模型建模步骤:
1)基于镜像法建立内部磁心窗口平面(IW)和外部磁心窗口平面(OW)模型并提取磁场分布数据,使用计及双二维模型计算内、外磁心窗口平面单位长度漏磁能量。
2)引入内、外磁心窗口平面能量加权半径dIW、dOW计算内、外磁心窗口平面平均匝长,从而得到高频变压器漏磁能量Wleakage。
2.1.2 内、外磁心窗口平面的平均匝长
根据磁能分布可计算得到磁心窗口平面的平均匝长。对于壳式变压器,在弯曲的绕组中,需要考虑磁场的曲率。因此,引入能量加权半径来计算内、外磁心窗口平面的平均匝长。
内、外磁心窗口平面的能量加权半径为
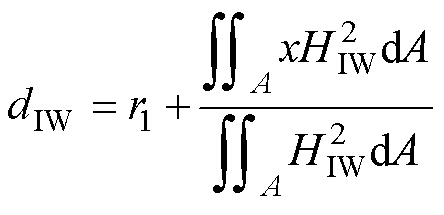 (12)
(12)
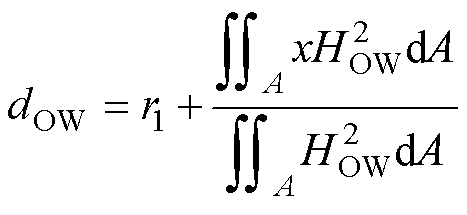 (13)
(13)
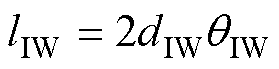 (14)
(14)
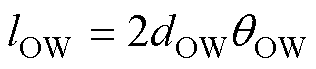 (15)
(15)
式中,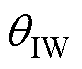 、
、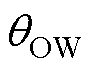 分别为内、外磁心窗口平面对应的角度;r1为圆形磁心中柱半径;HIW、HOW分别为内、外磁心窗口平面的磁场强度;lIW、lOW分别为内、外磁心窗口平面的平均匝长。壳式变压器俯视图如图6所示。
分别为内、外磁心窗口平面对应的角度;r1为圆形磁心中柱半径;HIW、HOW分别为内、外磁心窗口平面的磁场强度;lIW、lOW分别为内、外磁心窗口平面的平均匝长。壳式变压器俯视图如图6所示。
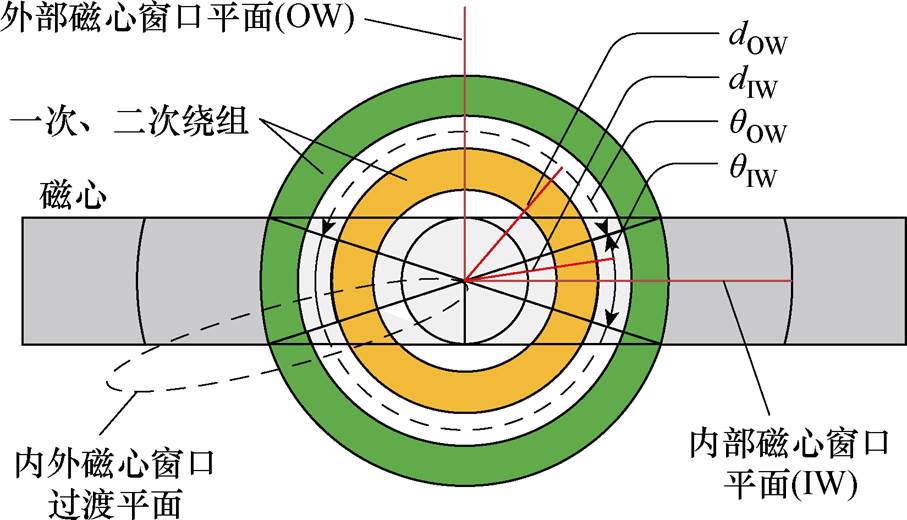
图6 壳式变压器俯视图
Fig.6 Top view of shell type transformer
在二维磁场分析中,经常使用镜像法提取平面内磁场强度。根据镜像原理,磁心对任意放置在它附近的载流导体起反射作用。如果通过实际导体的电流是I,那么通过镜像导体的电流Iimage为
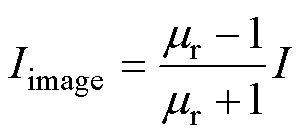 (16)
(16)
式中,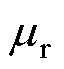 为磁心的相对磁导率。在中高频变压器中,采用的都是
为磁心的相对磁导率。在中高频变压器中,采用的都是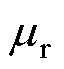 ≥1 000的高磁导率磁心,因此使用镜像法时Iimage
≥1 000的高磁导率磁心,因此使用镜像法时Iimage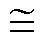 I[23]。
I[23]。
2.2.1 镜像法提取内部磁心窗口磁场强度
变压器内部磁心窗口平面以四边磁心为边界,为该平面内的导体提供了两对反射介质,理论上在x和y方向上产生无限数量的镜像导体[18],如图7a所示。内部磁心窗口中任意一点的磁场强度都是由原始导体和相应镜像导体共同产生得到的,内部磁心窗口内任意一点P(x, y)处,单个导体(xi, yj)及镜像导体在P处激发的磁场强度由毕奥-萨伐尔定律和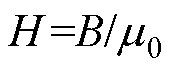 计算得到,即
计算得到,即
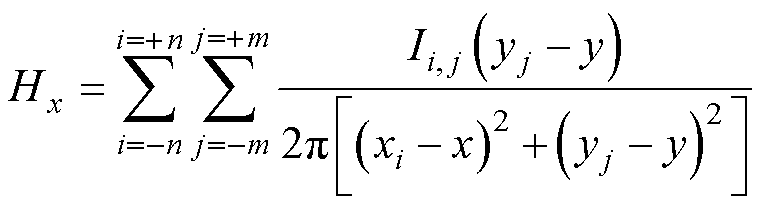 (17)
(17)
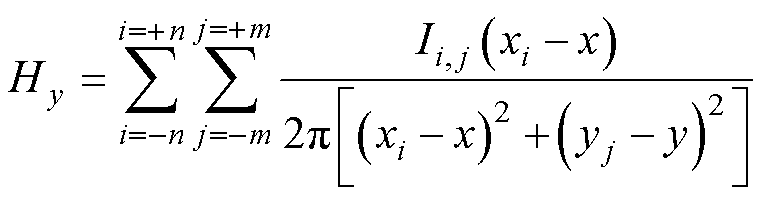 (18)
(18)
式中,m→∞,n→∞,(i, j)为镜像磁心窗口的位置,当i=j=0时表示原始磁心窗口。在P(x, y)处所有导体共同激发的磁场强度为
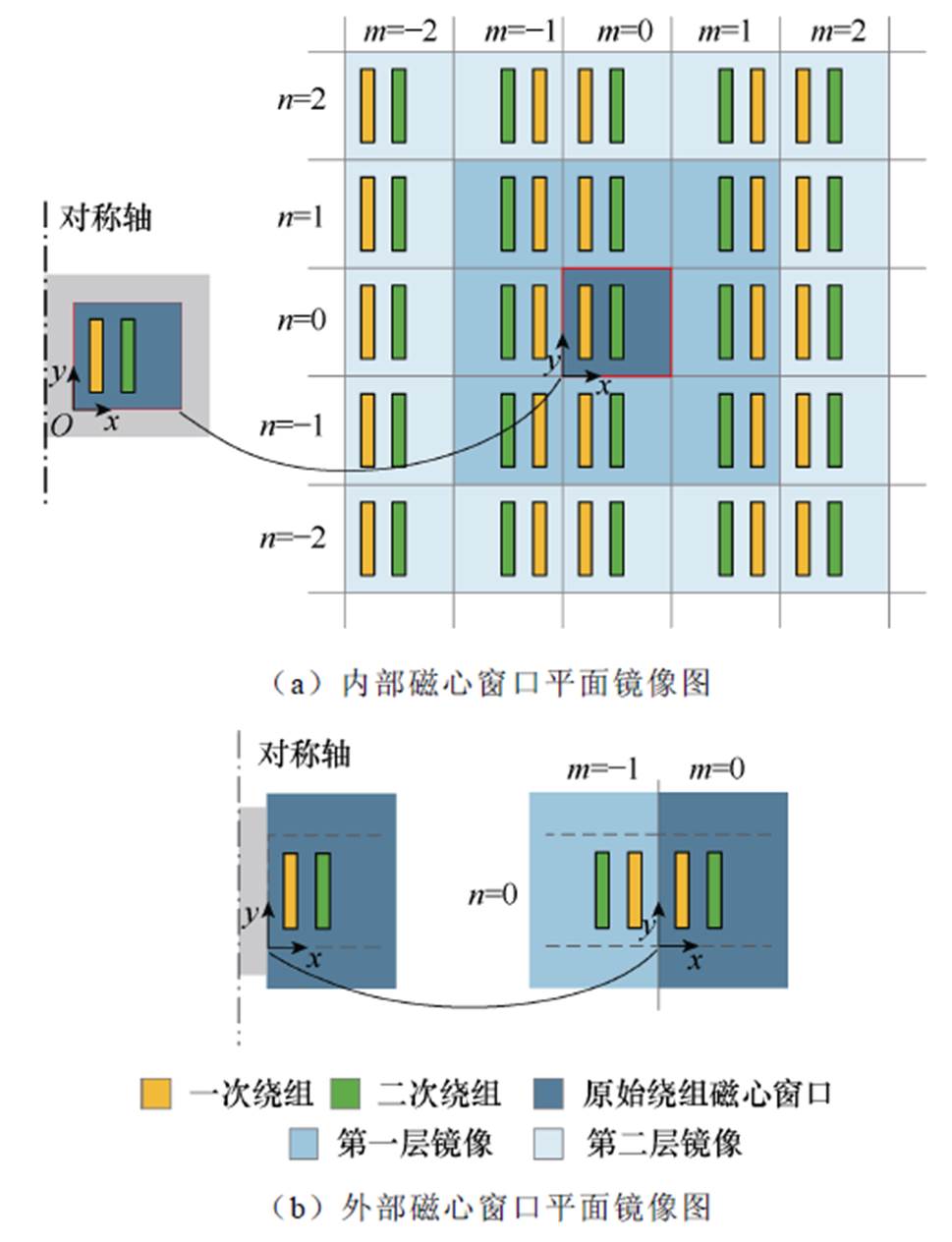
图7 内、外磁心窗口内实际导体和镜像导体
Fig.7 Original and mirrored conductorsinside and outside core window
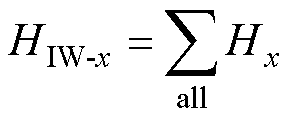 (19)
(19)
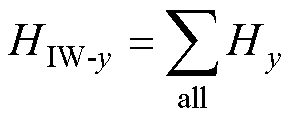 (20)
(20)
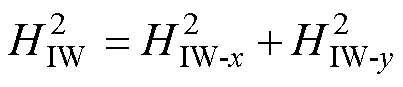 (21)
(21)
内部磁心窗口区域漏磁能量为
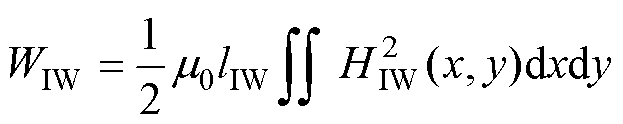 (22)
(22)
2.2.2 镜像法提取外部磁心窗口磁场强度
变压器外部磁心窗口平面仅一侧是高磁导率磁心,该平面的导体仅产生一个镜像导体,如图7b所示。外部磁心窗口平面内任意一点Q(x, y)处,单个导体(xi, yj)及镜像导体在Q处激发的磁场强度为
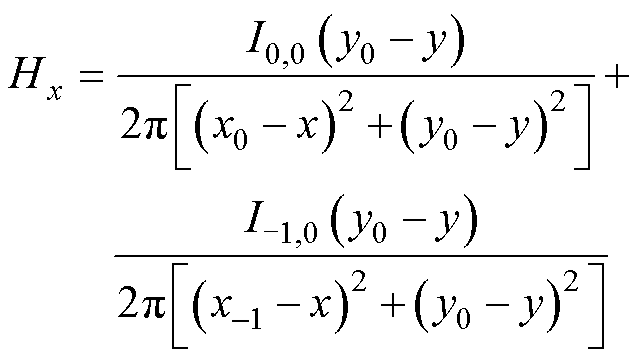 (23)
(23)
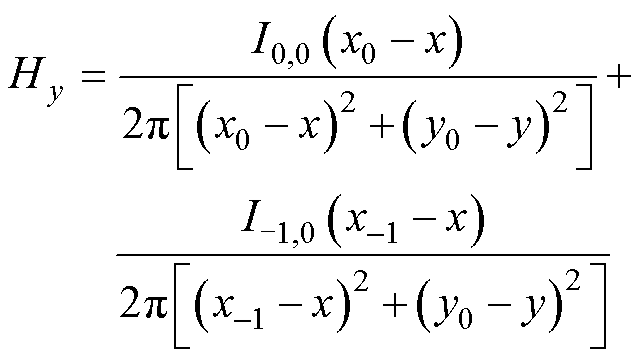 (24)
(24)
在Q(x, y)处所有导体共同激发的磁场强度为
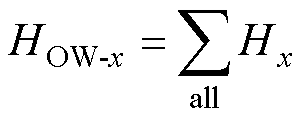 (25)
(25)
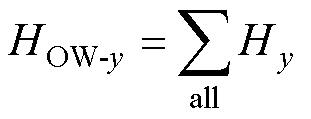 (26)
(26)
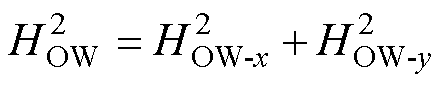 (27)
(27)
外部磁心窗口区域漏磁能量为
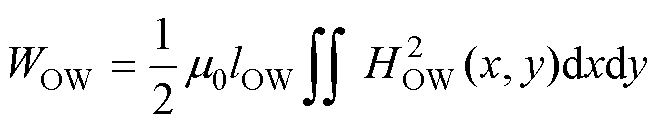 (28)
(28)
变压器处于低频工作状态时,漏磁能量可以近似为直流漏磁能量,变压器的漏磁能量为
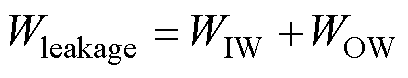 (29)
(29)
式中,WIW和WOW通过式(22)和式(28)得到。由于绝缘区域没有电流通过,绝缘区域内的漏磁能量几乎不随频率变化,可以认为保持恒定;随着变压器工作频率的升高,受趋肤效应和邻近效应的影响,导体内部的漏磁能量衰减明显。因此,在利兹线绕组高频变压器漏感计算中需要将绝缘区域和导体区域的漏磁能量单独处理。在利兹线绕组变压器中,直接计算不规则的绝缘区域漏磁能量十分困难,因此,通过镜像法分别计算磁心窗口区域和导体区域的漏磁能量,两者之差即为不规则的绝缘区域漏磁能量,如图8a和图8b所示。
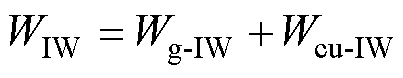 (30)
(30)
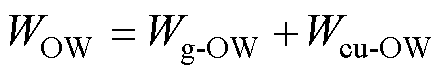 (31)
(31)
式中,Wg-IW、Wg-OW分别为内、外磁心窗口绝缘区域漏磁能量;Wcu-IW、Wcu-OW分别为内、外磁心窗口导体区域漏磁能量。
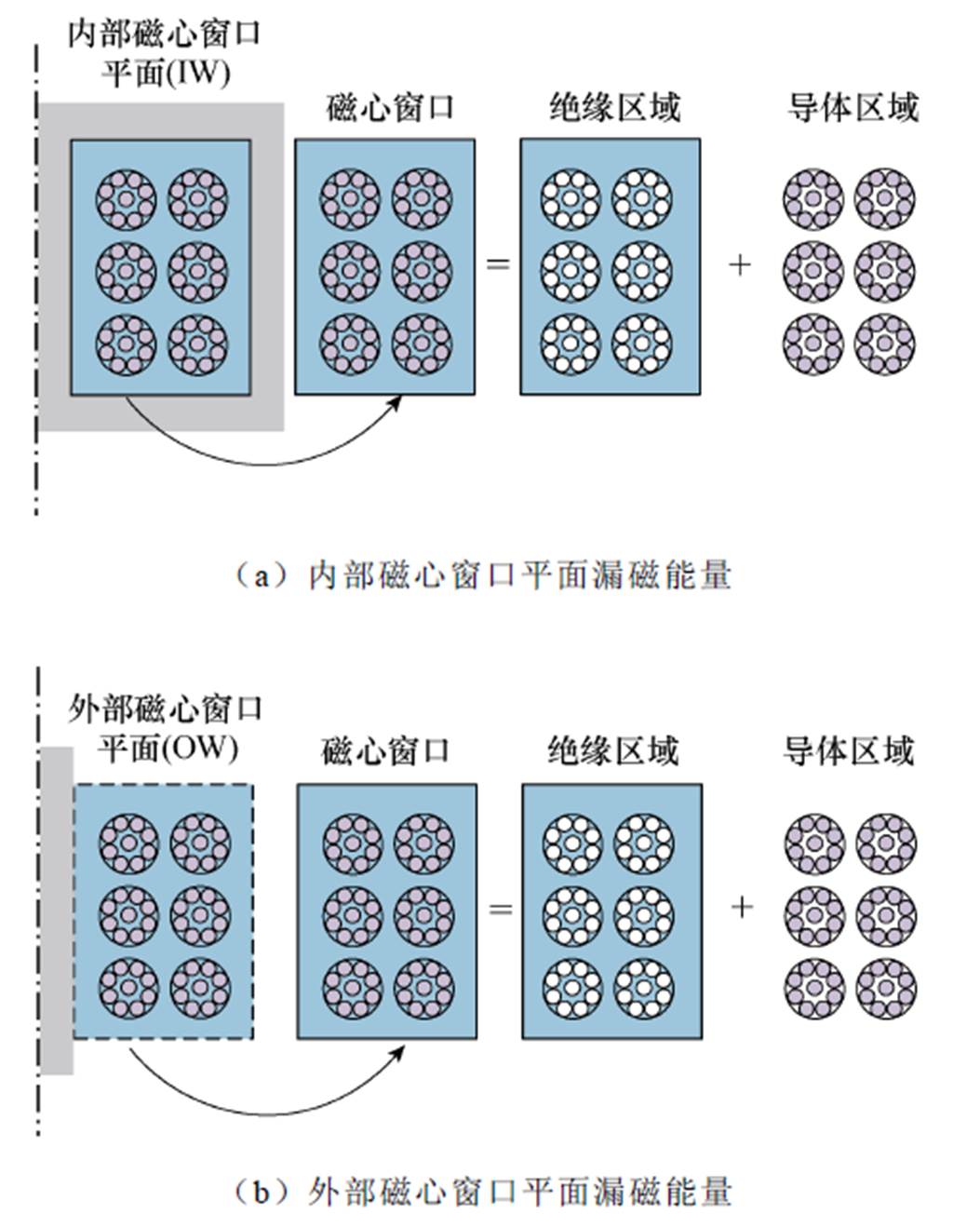
图8 内、外磁心窗口漏磁能量
Fig.8 The core window leakage energy inside and outside core window
利兹线结构和磁场分布如图9所示,导体内股线的磁场由自身磁场Hint和外部股线产生磁场Hext组成。导体内漏磁能量为
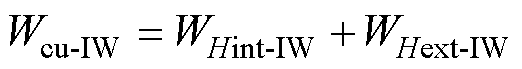 (32)
(32)
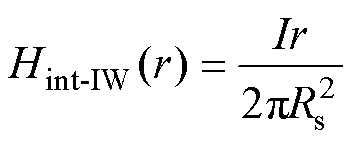 (33)
(33)
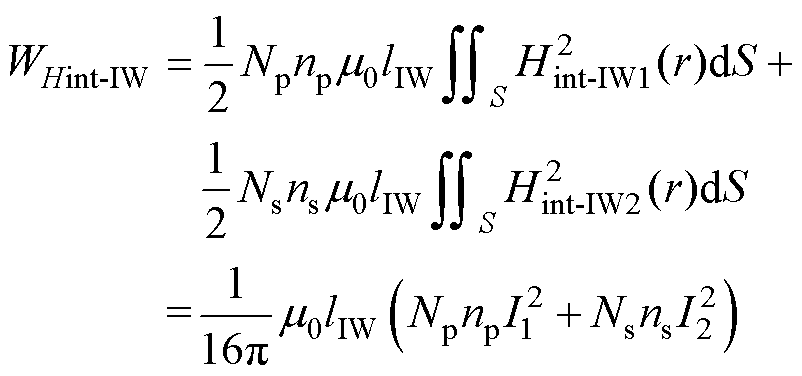 (34)
(34)
式中,Rs为股线半径;Hint-IW为股线内磁场强度;由安培环路定理求得;WHint-IW为股线内磁场Hint-IW产生的漏磁能量;Np和Ns分别为一次绕组、二次绕组利兹线股数;np和ns分别为一次绕组、二次绕组利兹线匝数;I1和I2分别为一次绕组、二次绕组股线的电流幅值。由于利兹线多股独立绝缘细导线绞合的结构,使得每根股线都能穿过利兹线横截面每个位置,可以认为一束利兹线内所有股线通过的电流大小相等。
WHext-IW是外部股线磁场Hext-IW产生的漏磁能量,有
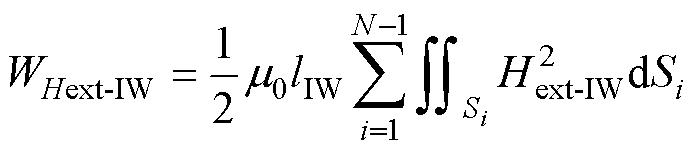 (35)
(35)
式中,N为变压器利兹线的总股数;Si为股线i区域。内、外磁心窗口绝缘区域漏磁能量为
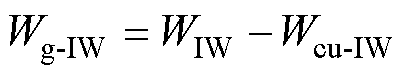 (36)
(36)
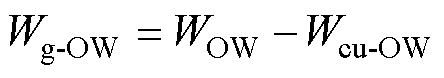 (37)
(37)
利兹线变压器直流漏磁能量为
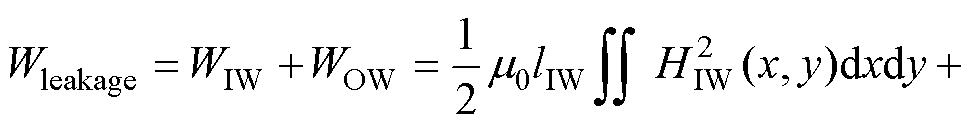
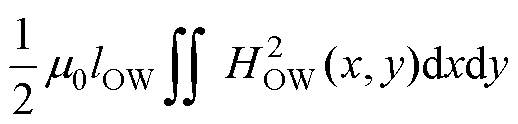 (38)
(38)
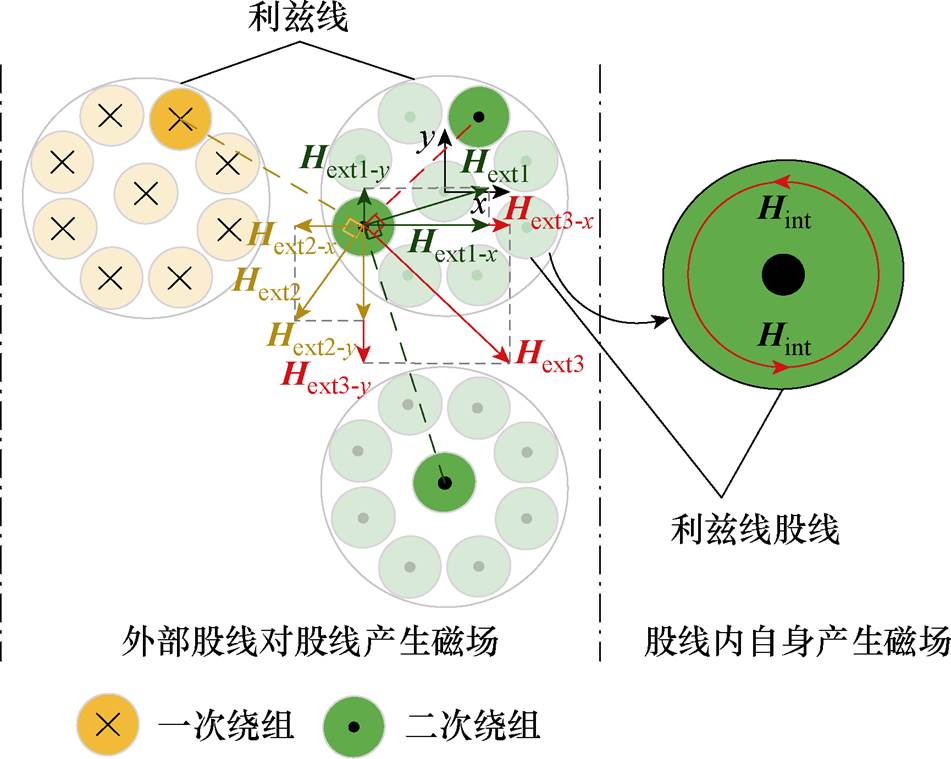
图9 利兹线内Hint和Hext磁场分布
Fig.9 Distribution of magnetic fields Hint and Hext inside the Litz wire
随着频率升高,股线中涡流效应显著,利兹线股线中储存的漏磁能量明显衰减,因此需要对导体区域直流漏磁能量进行修正。由于股线中的趋肤效应和邻近效应是正交的[24],可以将二者单独处理。
2.4.1 趋肤效应和邻近效应
当半径为Rs的圆导线中通过幅值为I、频率为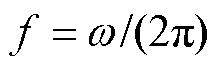 的正弦电流时,导线内部的磁场强度可以由麦克斯韦方程求解,即
的正弦电流时,导线内部的磁场强度可以由麦克斯韦方程求解,即
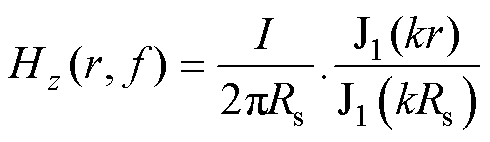 (39)
(39)
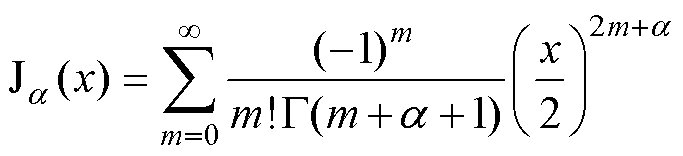 (40)
(40)
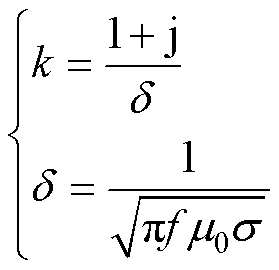 (41)
(41)
式中,Hz(×)为圆导线产生的z轴方向磁场强度(圆导线与z轴方向平行);f为通入电流的频率;r为圆导线内任意一点到圆心的距离;J1(x)为一阶贝塞尔函数;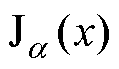 为
为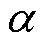 阶贝塞尔函数;k为复传播系数;
阶贝塞尔函数;k为复传播系数;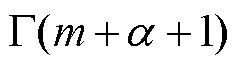 为伽玛函数,也叫第二类欧拉积分,
为伽玛函数,也叫第二类欧拉积分,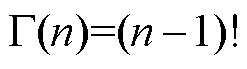 。
。
当圆导线位于幅值为H、频率为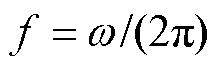 的时变磁场中,导线内部磁场强度为
的时变磁场中,导线内部磁场强度为
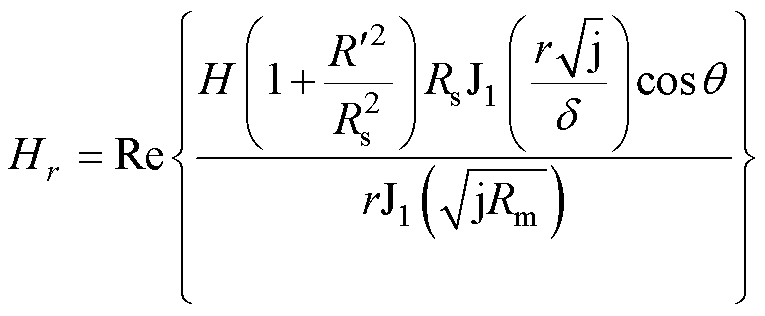 (42)
(42)
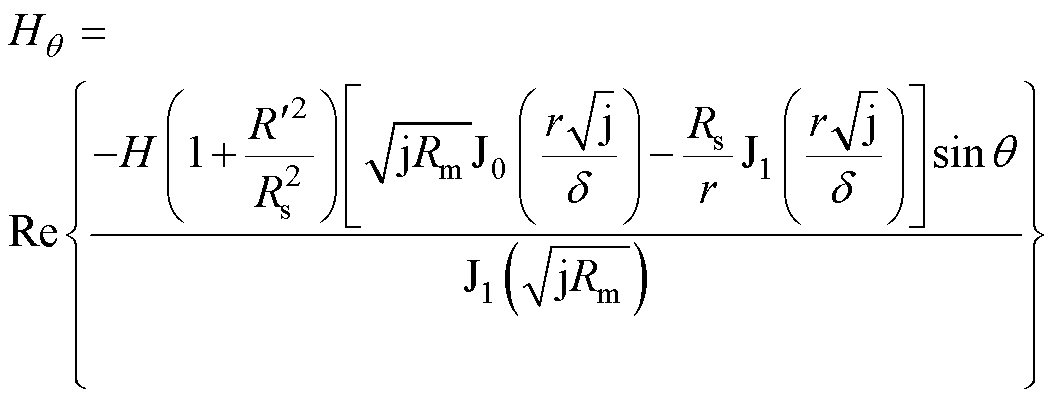 (43)
(43)
式中,Hr(×)为圆导线产生的r方向磁场强度;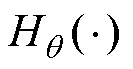 为圆导线产生的轴向磁场强度;Rm为磁雷诺数,Rm和
为圆导线产生的轴向磁场强度;Rm为磁雷诺数,Rm和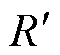 的计算式为
的计算式为
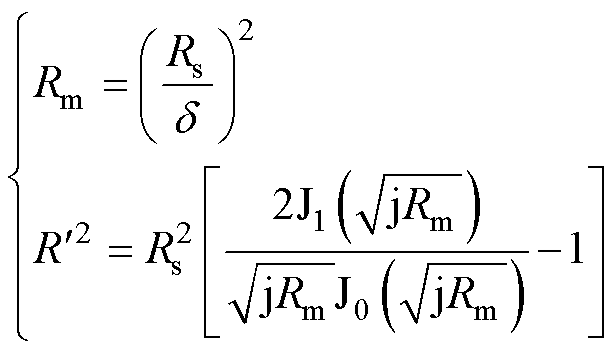 (44)
(44)
通过归一化处理,可得到两个与频率相关的股线归一化因子,趋肤因子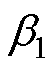 和邻近因子
和邻近因子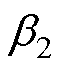 分别为
分别为
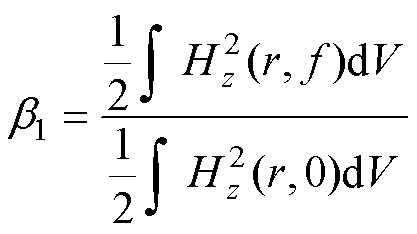 (45)
(45)
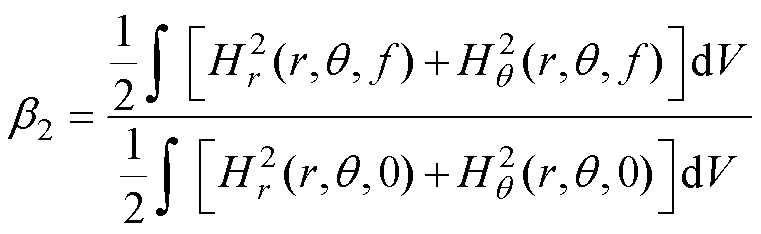 (46)
(46)
2.4.2 频变漏磁能量
为考虑涡流效应造成的导体区域漏磁能量衰减,引入趋肤因子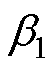 和邻近因子
和邻近因子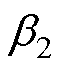 对导体区域直流漏磁能量修正,即可得到利兹线绕组高频变压器导体区域的频变漏磁能量计算公式为
对导体区域直流漏磁能量修正,即可得到利兹线绕组高频变压器导体区域的频变漏磁能量计算公式为
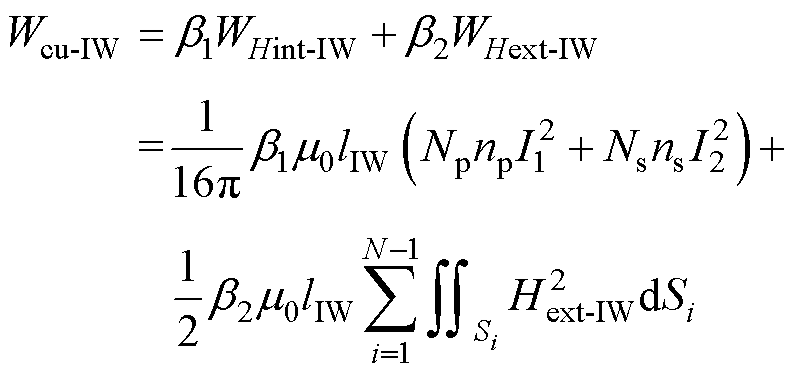 (47)
(47)
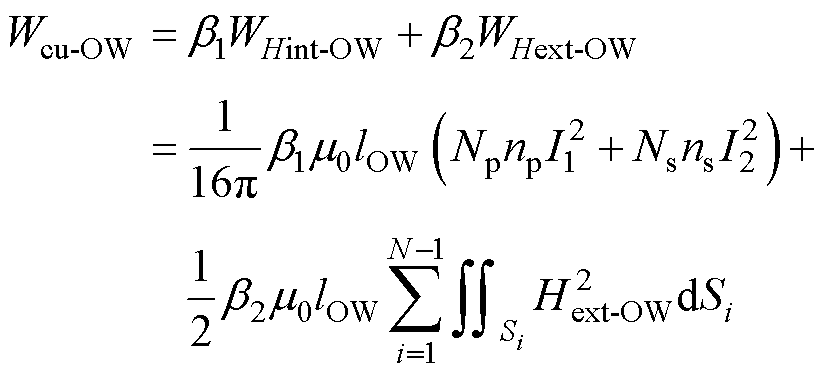 (48)
(48)
将式(47)和式(48)代入式(30)和式(31)中,再将式(30)和式(31)代入式(29)中,得到利兹线绕组高频变压器漏感表达式为
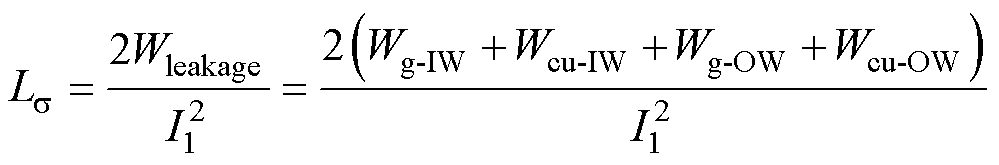 (49)
(49)
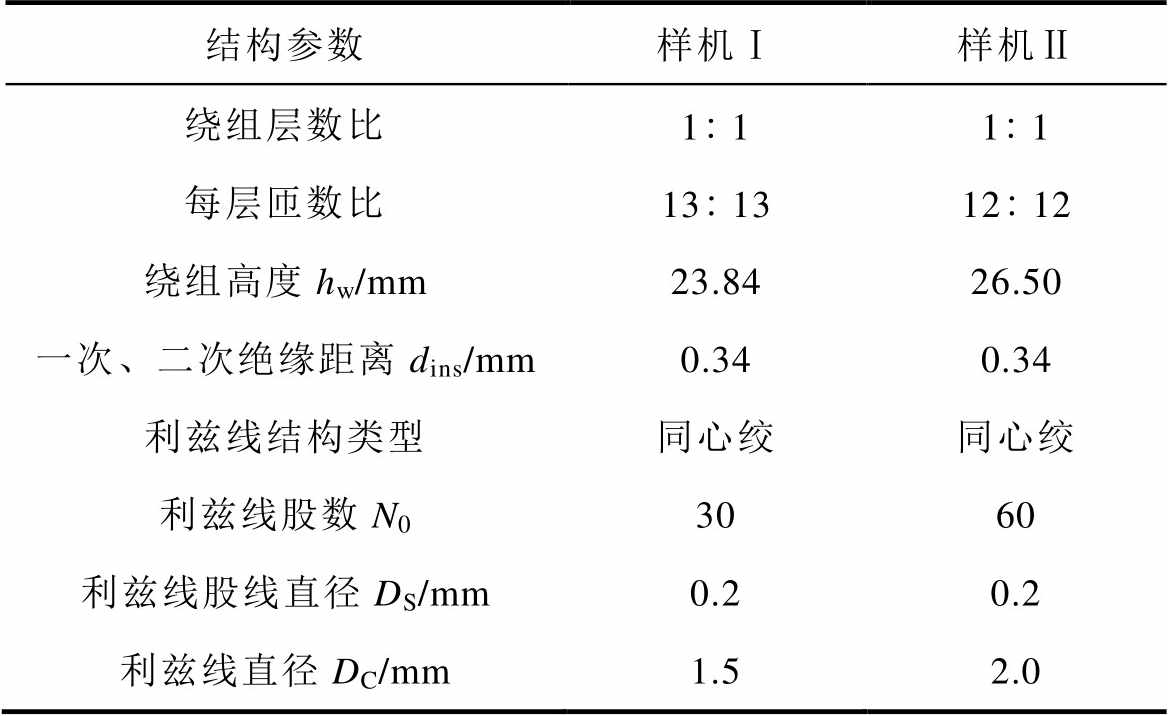
圆形利兹线是高频变压器中比较常见的利兹线绕组结构,本文利用不同型号的圆形利兹线绕制了两台变压器样机来验证所提漏感解析计算模型的准确性。图10所示为绕制的圆形利兹线绕组高频变压器样机,两台样机利兹线绕组的股数不同,具体参数见表1,磁心材料选用型号为EC4220铁氧体。

图10 圆形利兹线绕组高频变压器样机
Fig.10 Prototype of high-frequency transformer with circular Litz-wire winding
表1 样机Ⅰ和样机Ⅱ的参数
Tab.1 Parameters of Prototype Ⅰ and Prototype Ⅱ
结构参数样机Ⅰ样机Ⅱ 绕组层数比1111 每层匝数比13131212 绕组高度hw/mm23.8426.50 一次、二次绝缘距离dins/mm0.340.34 利兹线结构类型同心绞同心绞 利兹线股数N03060 利兹线股线直径DS/mm0.20.2 利兹线直径DC/mm1.52.0
高频变压器一般具有对称结构,因此本文在进行有限元建模过程中,采用降维处理方法,通过二维有限元模型模拟变压器的磁场强度分布,在保证计算精度的前提下,降低建模难度和计算量[25]。
应用二维有限元仿真Ansys Electronic Suite 2019 R1中的Maxwell 软件对样机进行二维有限元仿真,二维有限元仿真的磁场强度分布如图11所示;使用KEYSIGHT E4990A阻抗分析仪测量样机漏感,图12为高频变压器样机漏感测量平台,测量频率设置为100 kHz~2 MHz的宽频范围,在实验测量过程中,保持高频变压器样机二次绕组短路,一次绕组与测量探头KEYSIGHT 16047E相连,根据变压器的T型等效电路,实验测量数据为不同频率下高频变压器样机一次绕组漏感和二次绕组漏感归算到一次绕组的漏感之和[26]。为了进一步说明本文采用双二维模型的必要性,对比了单二维的面积等效模型,实验结果对比如图13所示。
由图13可知,以实验测量值为基准值,本文模型与基准值在宽频100 kHz~2 MHz范围内,变压器样机Ⅰ的平均相对误差为1.54%,变压器Ⅱ的平均相对误差为2.50%,两种不同型号圆形利兹线绕组样机计算误差均在5.00%以内。
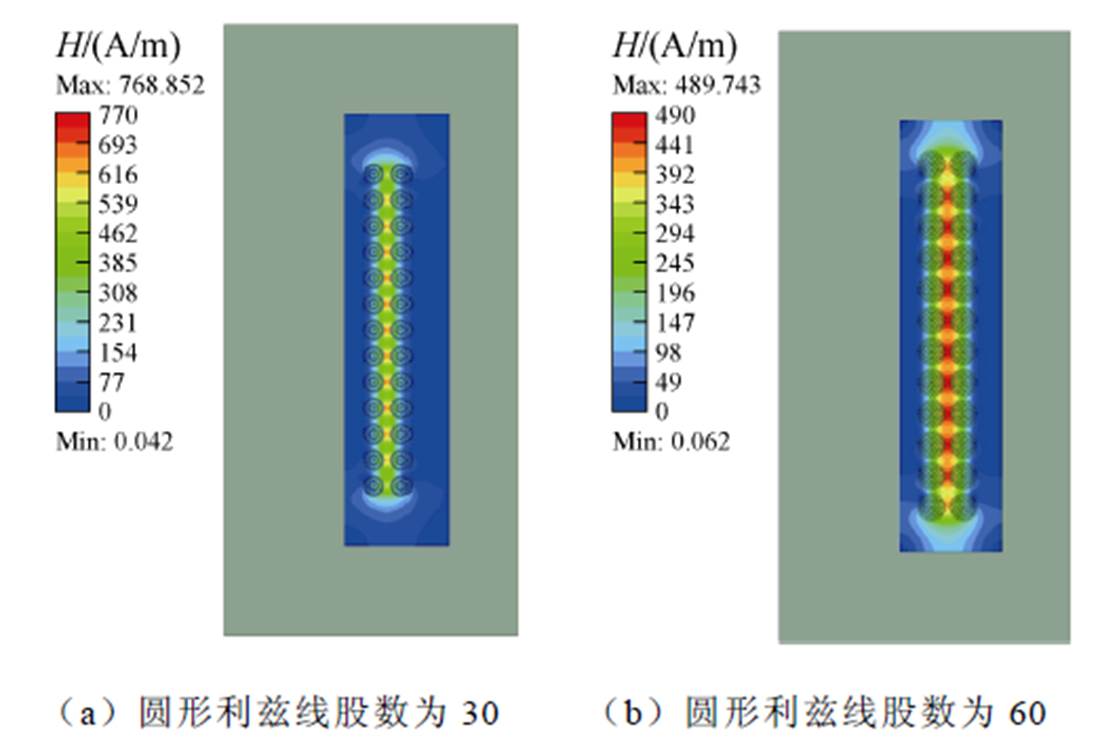
图11 样机Ⅰ和样机Ⅱ的二维有限元仿真
Fig.11 2-D finite element simulation of Prototype Ⅰ and Prototype Ⅱ

图12 高频变压器样机漏感测试平台
Fig.12 High-frequency transformer prototype leakage inductance measurement platform
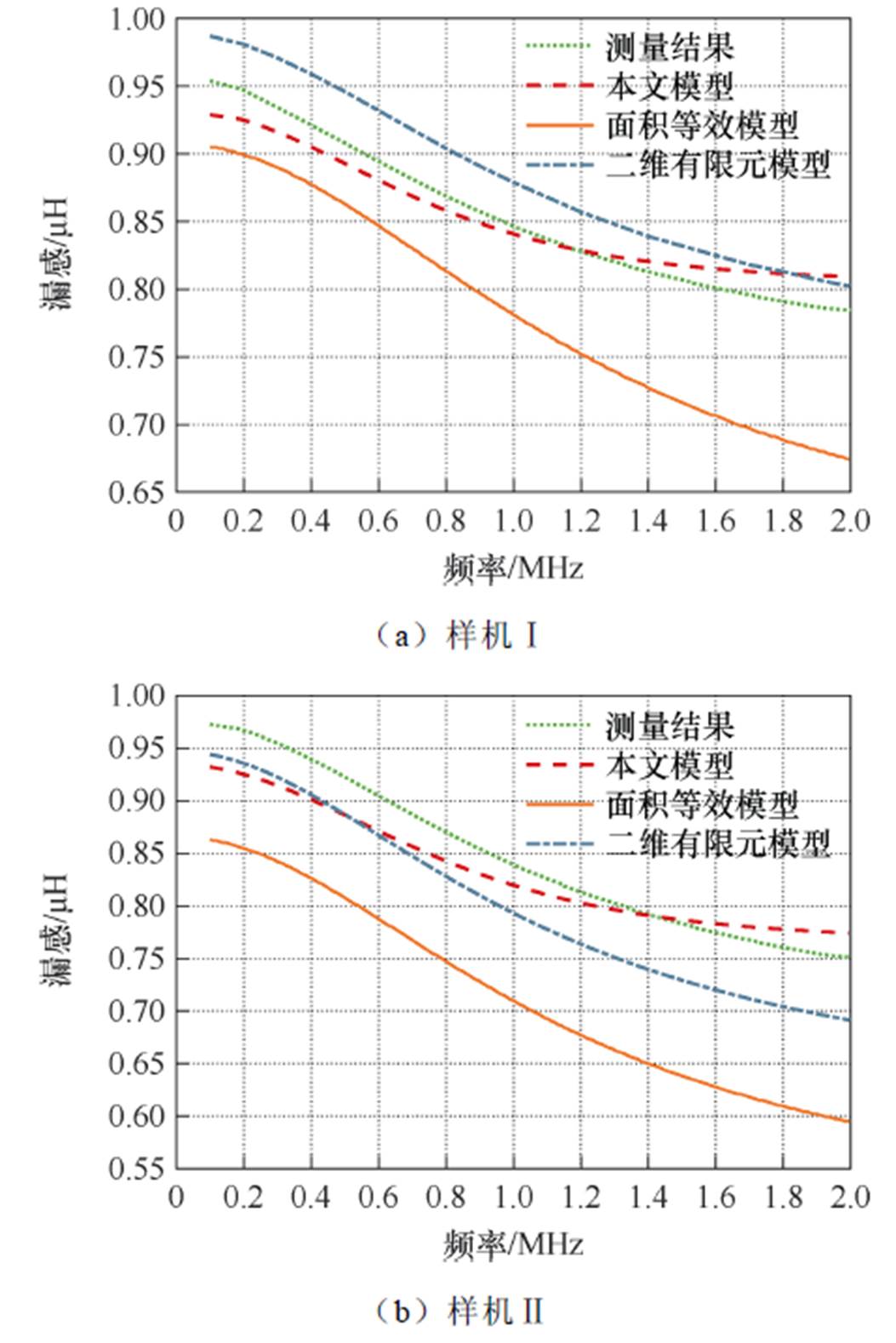
图13 样机实验数据对比
Fig.13 Comparison of prototype experimental data
矩形利兹线又被称为定型利兹线,是由多根绝缘导线绞合并通过机械压制定型成矩形截面导线。本文绕制了一台矩形利兹线绕组高频变压器样机来验证所提漏感计算模型的准确性。如图14所示为绕制矩形利兹线绕组高频变压器样机,具体参数见表2,磁心材料选用的型号为EC4220铁氧体。

图14 矩形利兹线绕组高频变压器样机
Fig.14 Prototype of high-frequency transformer with rectangular Litz-wire winding
表2 样机Ⅲ的参数
Tab.2 Parameters of Prototype Ⅲ
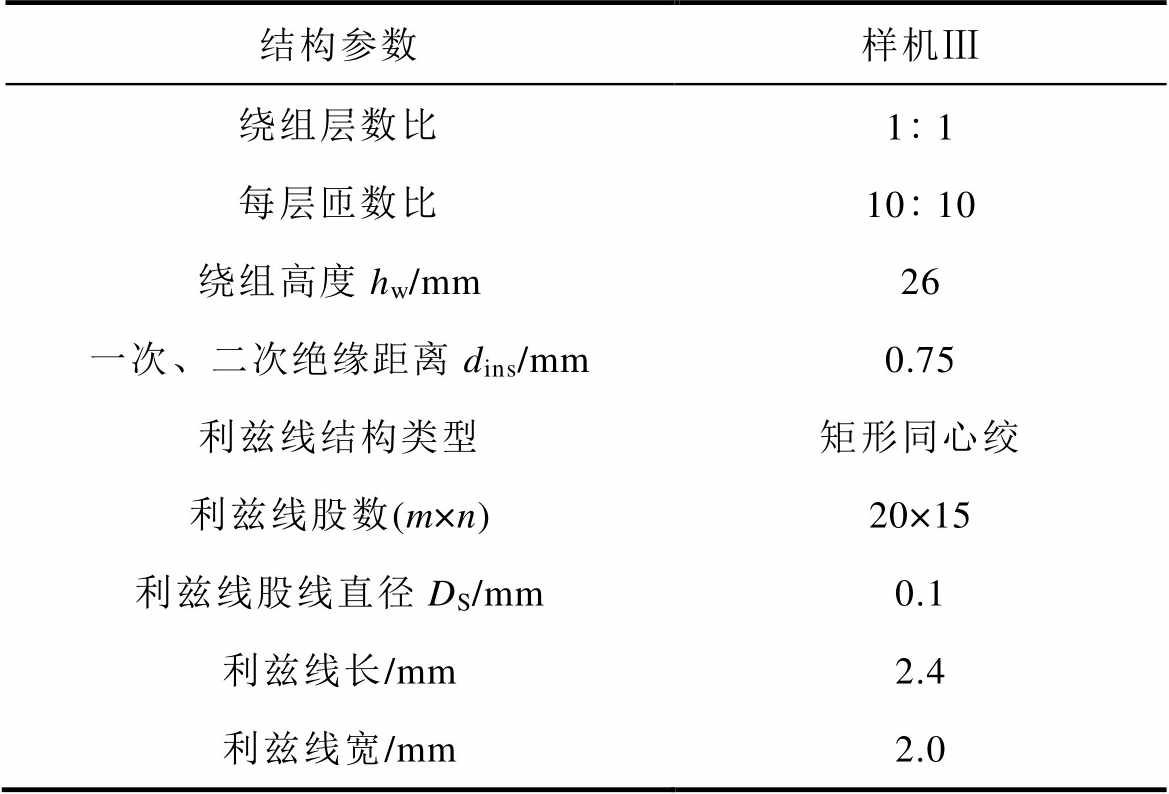
结构参数样机Ⅲ 绕组层数比11 每层匝数比1010 绕组高度hw/mm26 一次、二次绝缘距离dins/mm0.75 利兹线结构类型矩形同心绞 利兹线股数(m×n)20×15 利兹线股线直径DS/mm0.1 利兹线长/mm2.4 利兹线宽/mm2.0
矩形利兹线绕组样机二维有限元仿真的磁场强度分布如图15所示。实验结果对比如图16所示,在宽频100 kHz~2 MHz范围内矩形利兹线绕组样机的平均相对误差为5.10%。
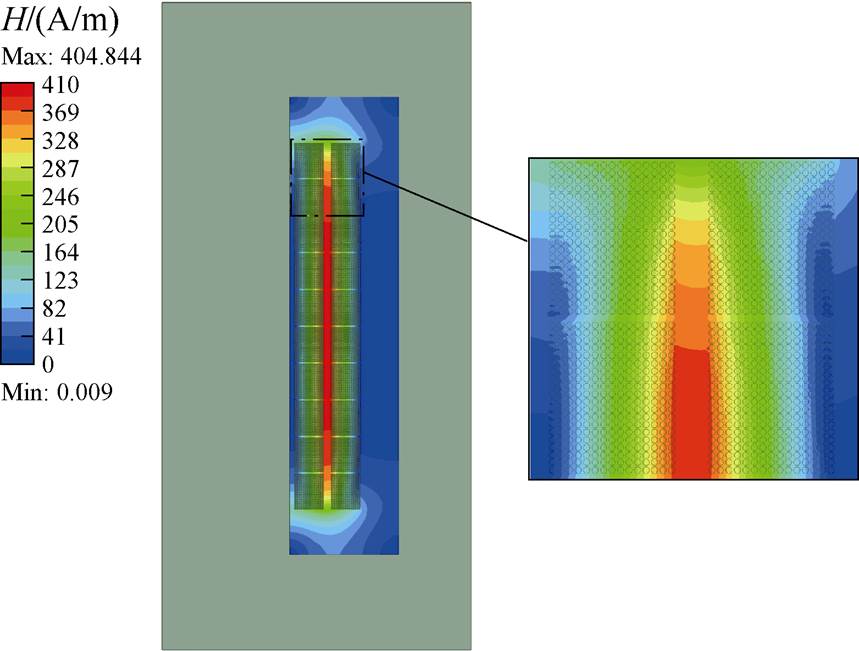
图15 样机Ⅲ的二维有限元仿真
Fig.15 2-D finite element simulation of Prototype Ⅲ
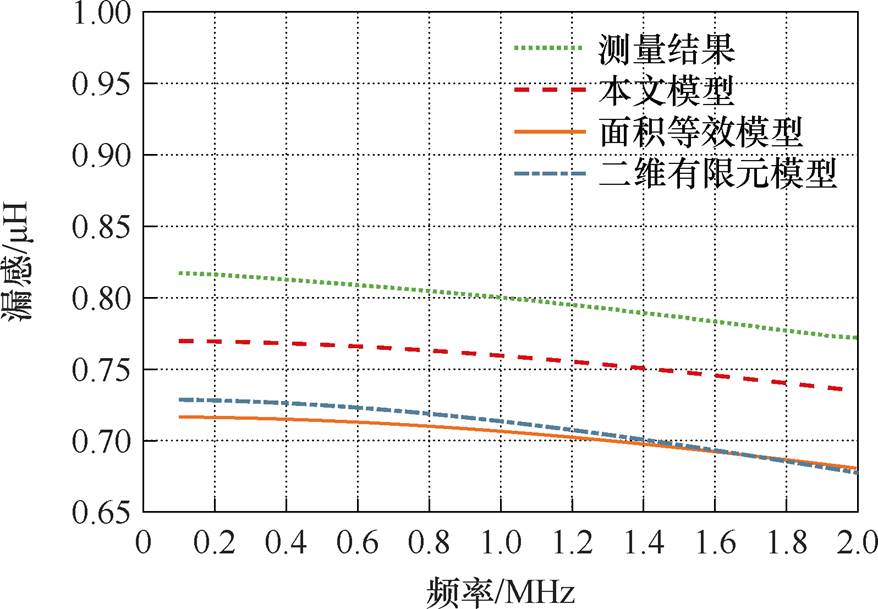
图16 样机实验数据对比
Fig.16 Comparison of prototype experimental data
本文中所有的数值计算和仿真均在CPU为AMD EPYC 7763及128GB RAM的计算机上进行。本文所建模型与二维有限元模型的计算耗时对比见表3,由实验结果可知,本文所建模型能有效降低计算时间。
表3 本文模型与二维有限元模型计算时间对比
Tab.3 Comparison of calculation time between the model in this paper and the 2-D finite element model (单位: s)

样机二维有限元模型本文模型 Ⅰ300131 Ⅱ960144 Ⅲ10 800417
与实验测量结果对比,本文所建立模型的计算结果在高频条件下下降趋势减缓,这是因为忽略了高频下绝缘区域漏磁能量的衰减。本文模型与实验测量结果的平均相对误差不超过6.00%,能够实现在宽频范围内圆形和矩形利兹线绕组样机漏感的精确、快速计算。
1)本文分析了变压器内、外磁心窗口磁场强度分布的差异,对高频变压器内、外磁心窗口两个平面分别进行建模,建立了双二维计算模型,提高了变压器漏磁能量的计算精度。
2)采用镜像法进行内、外磁心窗口静磁场下的漏磁能量提取以考虑绕组的端部效应,引入两个归一化因子考虑高频下导线的趋肤效应和邻近效应,实现了宽频范围内利兹线绕组高频变压器漏感的精确预测。
3)搭建了三台不同型号变压器样机,将本文模型的计算结果与测量结果对比,样机的平均相对误差分别为1.54%、2.50%、5.10%,由数据对比可知,本文模型能够实现利兹线绕组高频变压器漏感的精确计算。同时如表3所示,将本文模型与二维有限元模型的计算时间进行对比,由实验结果可知,本文模型能够避免二维有限元的复杂建模和仿真过程,节省了计算成本。
参考文献
[1] 程鹤, 徐恺, 李朋圣, 等. 三相CLLC谐振变换器磁集成平面变压器设计与优化[J]. 电工技术学报, 2024, 39(12): 3774-3786.
Cheng He, Xu Kai, Li Pengsheng, et al. Design and optimization of three-phase CLLC resonant converter with magnetic integrated planar transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3774-3786.
[2] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wang Tao, Wen Jifeng, et al. Three- dimensional temperature calculation and optimization design method for high power high-frequency transformer[J]. Transactions of China Electrotech- nical Society, 2023,38(18): 4994-5005, 5016.
[3] 赵志刚, 白若南, 陈天缘, 等. 基于智能优化算法的高频变压器电磁结构优化设计[J]. 电工技术学报, 2024, 39(18): 5610-5625.
Zhao Zhigang, Bai Ruonan, Chen Tianyuan, et al. Optimization design of electromagnetic structure of high frequency transformer based on intelligent optimization algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5610-5625.
[4] 宋猛, 秦苏新, 朱子锐, 等. 基于噪声源钳位的输入并联输出串联全桥变换器共模噪声抑制方法[J]. 电工技术学报, 2025, 40(14): 4558-4566.
Song Meng, Qin Suxin, Zhu Zirui, et al. Common mode noise reduction for input-parallel output-series full-bridge converter based on noise source clamping[J]. Transactions of China Electrotechnical Society, 2025, 40(14): 4558-4566.
[5] 陈润田, 李楚杉, 姚文熙, 等. 基于等效励磁电感的SiC串联器件型中压双有源桥变换器的软开关技术[J]. 电工技术学报, 2024, 39(12): 3732-3745.
Chen Runtian, Li Chushan, Yao Wenxi, et al. Soft- switching technique for medium voltage dual active bridge converter with series-connected SiC devices based on equivalent magnetizing inductance[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3732-3745.
[6] Guo Xuan, Li Chi, Zheng Zedong, et al. General analytical model and optimization for leakage inductances of medium-frequency transformers[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(4): 3511-3524.
[7] 李朋, 郝治国, 张保会, 等. 基于有限元法的变压器漏感计算在绕组变形中的应用[J]. 电力自动化设备, 2007, 27(7): 49-53.
Li Peng, Hao Zhiguo, Zhang Baohui, et al. Leakage inductance calculation based on finite element method for power transformer and its application to winding deformation analysis[J]. Electric Power Automation Equipment, 2007, 27(7): 49-53.
[8] 陈彬, 李琳, 刘海军, 等. 基于有限元法的高频变压器漏电感和绕组损耗计算与分析[J]. 电工电能新技术, 2018, 37(1): 8-14.
Chen Bin, Li Lin, Liu Haijun, et al. Calculation and analysis of leakage inductance and winding loss of high-frequency transformer based on finite element method[J]. Advanced Technology of Electrical Engineering and Energy, 2018, 37(1): 8-14.
[9] 刘星亮, 邱祁, 王若宇, 等. 基于有限元仿真的高频高压变压器分段绕组漏感设计方法[J]. 高电压技术, 2020, 46(2): 610-617.
Liu Xingliang, Qiu Qi, Wang Ruoyu, et al. Design method for leakage inductance of high-frequency high-voltage transformer with winding segmented based on finite element simulation[J]. High Voltage Engineering, 2020, 46(2): 610-617.
[10] Chen Tianyuan, Zhao Zhigang, Shen Zhan, et al. A homogenized FEM data-driven model for calculating leakage inductance of high-frequency transformer with Litz-wire winding[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2024, 12(2): 2067-2081.
[11] 江进波, 姚延东, 赵青, 等. 基于有限元的高频变压器分布参数计算与分析[J]. 高压电器, 2024, 60(12): 66-74.
Jiang Jinbo, Yao Yandong, Zhao Qing, et al. Calcu- lation and analysis of distributed parameters of high- frequency transformer based on finite-solid-element method[J]. High Voltage Apparatus, 2024, 60(12): 66-74.
[12] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387.
[13] Bahmani M A, Thiringer T. Accurate evaluation of leakage inductance in high-frequency transformers using an improved frequency-dependent expression[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5738-5745.
[14] Ouyang Ziwei, Zhang Jun, Hurley W G. Calculation of leakage inductance for high-frequency trans- formers[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5769-5775.
[15] Wan Zhenyu, Li Yongjian, Wang Haoming, et al. An improved calculation method of leakage inductance for high-frequency transformer based on precise analysis of magnetic field[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2024, 12(1): 707-717.
[16] Mogorovic M, Dujic D. Medium frequency trans- former leakage inductance modeling and experimental verification[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 419-424.
[17] Zhang Ke, Chen Wu, Cao Xiaopeng, et al. Accurate calculation and sensitivity analysis of leakage inductance of high-frequency transformer with Litz wire winding[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3951-3962.
[18] Fouineau A, Raulet M A, Lefebvre B, et al. Semi-analytical methods for calculation of leakage inductance and frequency-dependent resistance of windings in transformers[J]. IEEE Transactions on Magnetics, 2018, 54(10): 8400510.
[19] Sharma A, Kimball J W. Evaluation of transformer leakage inductance using magnetic image method[J]. IEEE Transactions on Magnetics, 2021, 57(11): 8401912.
[20] 赵志刚, 郑宇萱, 陈天缘, 等. 基于镜像法的高频圆导线变压器漏感计算模型[J]. 中国电机工程学报, 2024, 44(16): 6697-6707.
Zhao Zhigang, Zheng Yuxuan, Chen Tianyuan, et al. Leakage inductance calculation model of high- frequency round conductor transformer based on image method[J]. Proceedings of the CSEE, 2024, 44(16): 6697-6707.
[21] Gu W J, Liu R. A study of volume and weight vs. frequency for high-frequency transformers[C]// Proceedings of IEEE Power Electronics Specialist Conference-PESC'93, Seattle, WA, USA, 1993: 1123- 1129.
[22] Schlesinger R, Biela J. Leakage inductance modelling of transformers: accurate and fast models to scale the leakage inductance per unit length[C]//2020 22nd European Conference on Power Electronics and Applications (EPE'20 ECCE Europe), Lyon, France, 2020: P.1-P.11.
[23] Hammond P. Electric and magnetic images[J]. Proceedings of the IEE Part C: Monographs, 1960, 107(12): 306.
[24] Ferreira J A, van Wyk J D. A new method for the more accurate determination of conductor losses in power electronic converter magnetic components[C]// Third International Conference on Power Electronics and Variable-Speed Drives, London, UK, 2002: 184- 187.
[25] 赵志刚, 刘朝阳, 贾慧杰, 等. 圆形利兹线绕组高频损耗三维快速计算模型[J]. 中国电机工程学报, 2024, 44(19): 7901-7911.
Zhao Zhigang, Liu Zhaoyang, Jia Huijieet al. Fast three-dimensional calculation mode for high frequ- ency loss of circular Litz-wire windings[J]. Pro- ceedings of the CSEE, 2024, 44(19): 7901-7911
[26] 杨思莹, 王松, 陈志豪, 等. 基于优化算法的变压器绕组等效电路建模[J]. 电气技术, 2023, 24(8): 29-36, 49.
Yang Siying, Wang Song, Chen Zhihao, et al. Equivalent circuit modeling of transformer winding based on optimization algorithms[J]. Electrical Engineering, 2023,24(8): 29-36, 49.
Abstract High-frequency transformer leakage inductance is an important parameter that affects the operational reliability and power transfer characteristics of power electronic transformers. The complex stranded structure of the Litz-wire winding makes it challenging to calculate transformer leakage inductance accurately. The difference in magnetic field strength between the transformer's inner and outer core windows introduces errors in the single 2-D calculation model, which only considers the magnetic field strength of the inner core window. Additionally, the complex structure of the Litz-wire makes it difficult to extract the magnetic field strength accurately. Therefore, this paper establishes a leakage inductance analytical calculation model that considers the difference in magnetic field distribution between the inner and outer core windows of a high-frequency transformer with a Litz wire winding, as well as the eddy current effect and edge effect of the transformer with a Litz wire winding at high frequencies.
Firstly, this paper proposes a double-2D leakage inductance calculation model, which calculates the transformer leakage energy through two planes. Then, the mirror method is employed to analyze the two-dimensional magnetic field and extract the leakage energy of the inner and outer core windows. The two-dimensional magnetic field distribution of the core window can be obtained using the mirror principle, avoiding the complex solution of the Poisson equation while considering the edge effect. Secondly, to assess the frequency-variable characteristics of the leakage magnetic energy in the conductor region, two frequency- dependent factors are introduced to evaluate the skin and proximity effects. Finally, three prototypes of different models are verified.
The following conclusions are drawn. (1) This paper analyzes the difference in the distribution of magnetic field strength between the inner and outer core windows, thereby improving the accuracy of transformer leakage energy calculations by separately extracting the magnetic field strengths of the inner and outer core windows. (2) The mirror method extracts the leakage energy of the static magnetic field from the inner and outer core windows to account for the edge effect of the windings. The introduction of two normalization factors accounts for the conductor skin effect and proximity effect at high frequencies, enabling the accurate prediction of high-frequency transformer leakage inductance in Litz-wire windings across a wide frequency range. (3) Compared with the measurement results, the average relative error of the prototypes is no more than 6%. Compared with the 2-D finite element (FEM), the proposed model saves the calculation time by avoiding the complex modeling and simulation process.
keywords:High-frequency transformer, Litz wire, leakage inductance, double-2-D models, image method, frequency-variable characteristic
中图分类号:TM433
DOI: 10.19595/j.cnki.1000-6753.tces.241280
国家自然科学基金(52077053, 52377008)和中央引导地方科技发展基金(226Z1601G)资助项目。
收稿日期 2024-07-17
改稿日期2024-08-20
赵志刚 男,1981年生,教授,博士生导师,研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用。E-mail: zhaozhigang@hebut.edu.cn
王 凯 男,1998年生,硕士研究生,研究方向为高频变压器优化设计与工程电磁场数值仿真及应用。E-mail: 202221401108@stu.hebut.edu.cn(通信作者)
(编辑 郭丽军)