表1 锂离子电池循环老化工况条件
Tab.1 Cyclic aging conditions for lithium-ion batteries
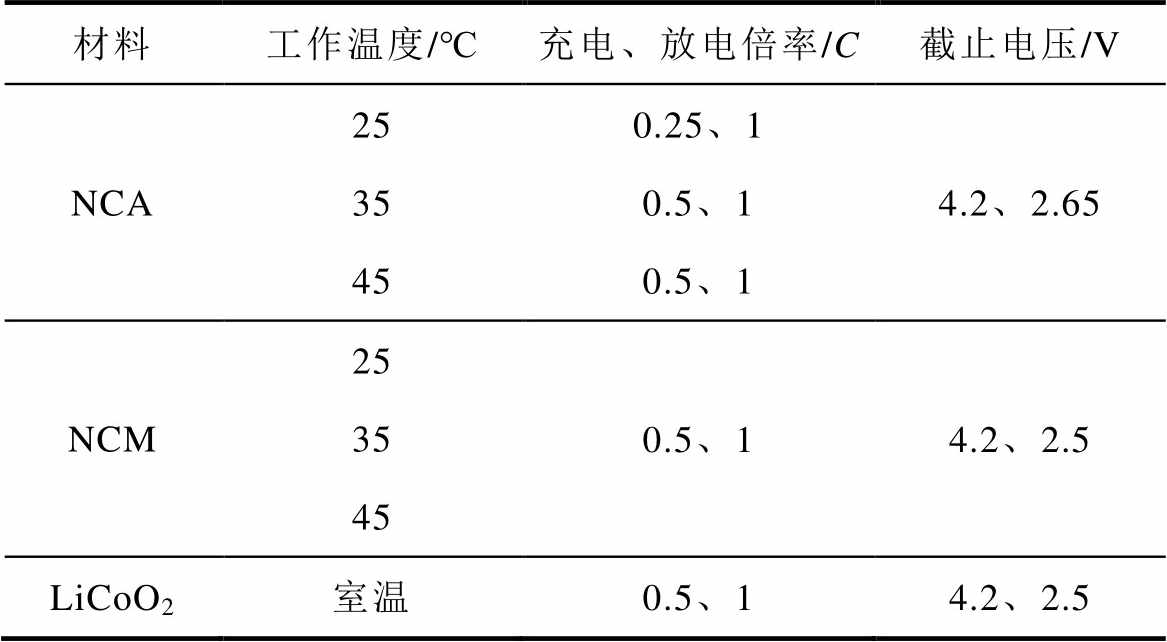
材料工作温度/℃充电、放电倍率/C截止电压/V NCA250.25、1 350.5、14.2、2.65 450.5、1 NCM25 350.5、14.2、2.5 45 LiCoO2室温0.5、14.2、2.5
摘要 容量是衡量电池性能的关键指标,当前容量估计存在特征实用性差、模型准确度与泛化性不足的问题。鉴于此,该文提出一种结合极化衰减特征与通道关注混合神经网络的锂离子电池容量在线估计方法。首先,利用恒压电流和弛豫电压衰减的去极化特性,提取不受充电起点影响的多维实用特征,同时引入相关系数法和主成分分析法对特征进行预处理以用于容量在线估计;其次,通过融合深度置信网络(DBN)、长短期记忆网络(LSTM)和挤压-激励(SE)机制,构建具有自适应通道关注能力的混合神经网络以提高容量估计精度;最后,利用多种工况、多种材料的电池数据,对所提的方法进行了验证。结果表明,容量估计的平均绝对百分比误差、方均根百分比误差分别在1.2%、1.5%以内,验证了该方法的准确性与有效性。
关键词:锂离子电池 容量在线估计 极化衰减特征 混合神经网络 通道注意力
锂离子电池因其高能量密度、长循环寿命、无污染等优点,被广泛应用于便携式电子设备、新能源电动汽车、大规模储能电站等关键领域[1-2]。然而,电池在长期存储或频繁充放电过程中,内部结构会发生改变,如可循环锂损失、集电极腐蚀等,进而导致电池性能逐渐退化[3]。而容量作为衡量电池性能的关键参数,不仅能够反映电池的健康状态(State of Health, SOH)与剩余使用寿命(Remaining Useful Life, RUL),还是评判电池组内单体不一致的重要依据[4]。因此,准确预测电池容量对电池的整体监控与安全管理具有重要意义。
目前,电池容量估算方法主要分为两类:基于模型的方法和基于数据驱动的方法[5-6]。基于模型的方法是通过构建数学关系表达式来反映锂离子电池的容量衰退过程,主要包括等效电路模型和电化学模型。S. Amir等[7]提出一种动态等效电路模型,并用非线性最小二乘曲线拟合逼近模型参数,以在线获得电池容量。Li Chaofan等[8]提出一种改进的分数阶等效电路模型,并利用参数来估计电池健康状态。基于等效电路模型的方法虽然应用广泛,但其精度受电池工况影响较大。随着对电池内部机理研究的深入,基于电化学模型的状态估计逐渐成熟。例如,熊瑞等[9]利用有限元分析方法简化了电化学模型,并结合遗传算法进行电池模型参数辨识,建立了电池容量与模型中5个参数之间的关系;A. Allam等[10]提出一种基于电化学模型的自适应互联观测器来估算电池模型参数与容量。基于电化学模型的方法估计精度较高,但参数较多、计算成本较高,实际应用困难。基于模型的方法能够较好地解释电池内部复杂的电化学动力过程,然而电池模型的构建是具有挑战性的,需要对电池的电化学特性有一个全面、深入的了解。另外,模型参数的精确辨识较为困难,通常依赖滤波算法的收敛性与收敛速度,并且辨识结果与环境温度、电池材料等有较大关系。
基于数据驱动的方法不需要考虑电池内部复杂的电化学反应过程,而是直接利用历史数据对电池容量进行估计,具有较高的可迁移性与泛化性[11]。数据驱动方法包括高斯过程回归(Gaussian Process Regression, GPR)、支持向量机(Support Vector Machine, SVM)、神经网络(Neural Network, NN)等方法[12]。其中神经网络算法能够利用表层数据形成更抽象的高层次特征来表示数据分布规律,具有卓越的处理复杂非线性问题的能力,因此在电池状态预测与故障诊断领域得到广泛应用[13]。例如,K. Park等[14]提出了一种多对一结构的长短期记忆(Long Short Term Memory, LSTM)神经网络估计电池容量;Xu Jiangtao等[15]构建了一种图增强型LSTM网络用于锂离子电池的容量估计。除了LSTM等时间序列模型,深度置信网络(Deep Belief Networks, DBN)等特征提取模型也因高效的数据处理和优异的特征优选能力,逐渐应用于状态估计领域[16]。例如,Liu Datong等[17]利用DBN与卡尔曼滤波(Kalman Filtering, KF)实现了动态工况下锂离子电池荷电状态(State of Charge, SOC)的估计;Cao Mengda等[18]提出了一种基于DBN网络的容量估计框架,并使用NASA的PCoE数据集验证了方法的有效性;Wang Yujie等[19]构建了DBN与粒子群优化(Particle Swarm Optimization, PSO)算法的融合模型,并使用电池不完全放电数据,实现了电池SOH的估计。
基于数据驱动的方法,估计结果的准确性取决于输入特征的质量和模型的预测能力[20]。因此,除了确定合适的建模算法外,对于能够表征电池容量退化趋势特征的选择也相当重要[21]。Zhang Yingda等[22]提取了等压降放电时间和放电期间达到最高温度的时间作为特征;Tang Ruoli等[23]根据恒流放电数据,从统计角度、时间角度和曲线角度提取了20个指标作特征。然而,电池在实际使用中,放电数据受负载影响而表现出动态变化,因此基于电池放电数据进行特征提取很难在实际中应用。相比于放电过程,电池充电过程更加稳定。Lin Chuanping等[24]选择特定电压区间的恒流充电时间作为特征;Guo Peiyao等[25]通过从电压、电流和温度曲线中提取了八种特征进行电池容量估计,但值得注意的是,这些特征均是基于完整充电情况下获取的。另外,除了直接利用充电阶段的电压、电流、温度等原始数据外,增量容量(Incremental Capacity, IC)、差分温度(Differential Temperature, DT)等微分变换曲线也能够实现对电池老化程度的诊断,进而实现电池容量估计[26]。例如,Jiang Bo等[27]从IC曲线提取两个峰值、一个峰谷作为特征用于老化诊断,Wang Zhenpo等[28]从差热伏安(Differential Thermal Voltammetry, DTV)曲线中提取峰值位置、峰值、谷值作为特征用于容量估计。但是基于微分曲线提取的特征在大倍率恒流充电、多级恒流快充及随机初始电量充电情况下面临峰值畸变和消失的问题,另外微分曲线的获取需要研究复杂滤波方法,以平滑原始曲线。综上所述,目前特征提取主要存在以下问题:①特征易受到随机充电起点的影响,在线应用困难;②特征只适用于固定工况或材料的电池,泛化性较差;③针对单一过程提取的多维特征拥有较多冗余信息,模型训练困难。
鉴于此,本文提出了一种结合极化衰减特征和混合神经网络的锂离子电池容量在线估计方法。考虑到电池极化效应与电池老化状态的密切相关性,首先分析了去极化过程(恒压充电与弛豫放松)中电流电压随容量衰减的变化规律,并在此阶段提取了不受充电起点影响的多维原始特征。同时引入相关系数法和主成分分析(Principal Components Analysis, PCA)法对特征进行分析与融合降维,并将预处理后的降维特征用于容量在线估计。其次通过融合深度置信网络、长短期记忆神经网络、挤压-激励(Squeeze and Excitation, SE)机制,构建了具有自适应通道关注能力的改进深度置信网络-长短期记忆神经网络(IDBN-LSTM)混合神经网络以提高容量估计精度。最后使用本文方法对多种工况、多种材料的电池数据进行了全面对比验证。实验结果表明,即使在数据质量较差、样本较少的情况下,本文提出的方法依然具有较高的估计精度和较好的稳定性。
本文首先介绍了本文使用数据集,并阐述了极化衰减特征的提取方法与预处理过程;然后介绍了相关基础模型,并构建具有自适应通道关注能力的混合神经网络;最后从多个角度设计了实验,并根据实验结果分析了方法的有效性。
本文使用两个数据集的电池数据对所提出的方法进行有效性验证,其中数据集1来自同济大学清洁能源汽车工程中心[29],数据集2来自实验室自建老化数据集,两种数据集共包含三种材料、八种工况的电池数据。
数据集1包括18块商用18650锂离子电池, 正极材料为LiNi0.86Co0.11Al0.03O2(NCA)或LiNi0.83Co0.11Mn0.07O2(NCM),电池的标称容量均为3.5 A·h。数据集2包括2块18650锂离子电池,正极材料为钴酸锂(LiCoO2),电池的标称容量为2.6 A·h。所有电池的循环过程均遵循恒流-恒压(Constant Current-Constant Voltage, CC-CV)充电模式,充电完成后静置30 min,随后进行CC放电,再静置30 min。恒压充电截止电流为0.05C,其他循环老化条件见表1。NCA类、NCM类、LiCoO2类电池容量衰减曲线如图1a、图1b、图1c所示。其中,图例中的“NCA-25-025_1#4”表示该电池的正极材料为NCA,工作温度为25℃,充电倍率为0.25C,放电倍率为1C,序号为4。对于LiCoO2类电池,循环老化实验是在室温条件下进行,图例中未做特别标注。
表1 锂离子电池循环老化工况条件
Tab.1 Cyclic aging conditions for lithium-ion batteries

材料工作温度/℃充电、放电倍率/C截止电压/V NCA250.25、1 350.5、14.2、2.65 450.5、1 NCM25 350.5、14.2、2.5 45 LiCoO2室温0.5、14.2、2.5
特征提取过程的选择需要适应电池充放电的工作状态,以使锂离子电池的容量估计无需依赖特定的工作条件。放电状态受负载变化影响,特征提取困难。充电条件受电池管理系统(Battery Manage- ment System, BMS)控制,较为稳定,另外大部分用户,尤其是大型充电站、储能电站等企业,倾向于在电网负荷低谷时进行充电,以实现经济效益。而负荷低谷通常在夜间并持续较长时间,这使得电池可以采用稳定的充电方式(如标准充放电协议)将电量充满,并有充足的时间进行静置。但充电起始点的不确定性给恒流充电下特定范围电压的获取带来偶然性,输入特征可能无法满足实际应用。因此本文选择在恒压充电过程以及电压弛豫过程进行特征提取,以满足BMS对容量估计的实时在线性要求。
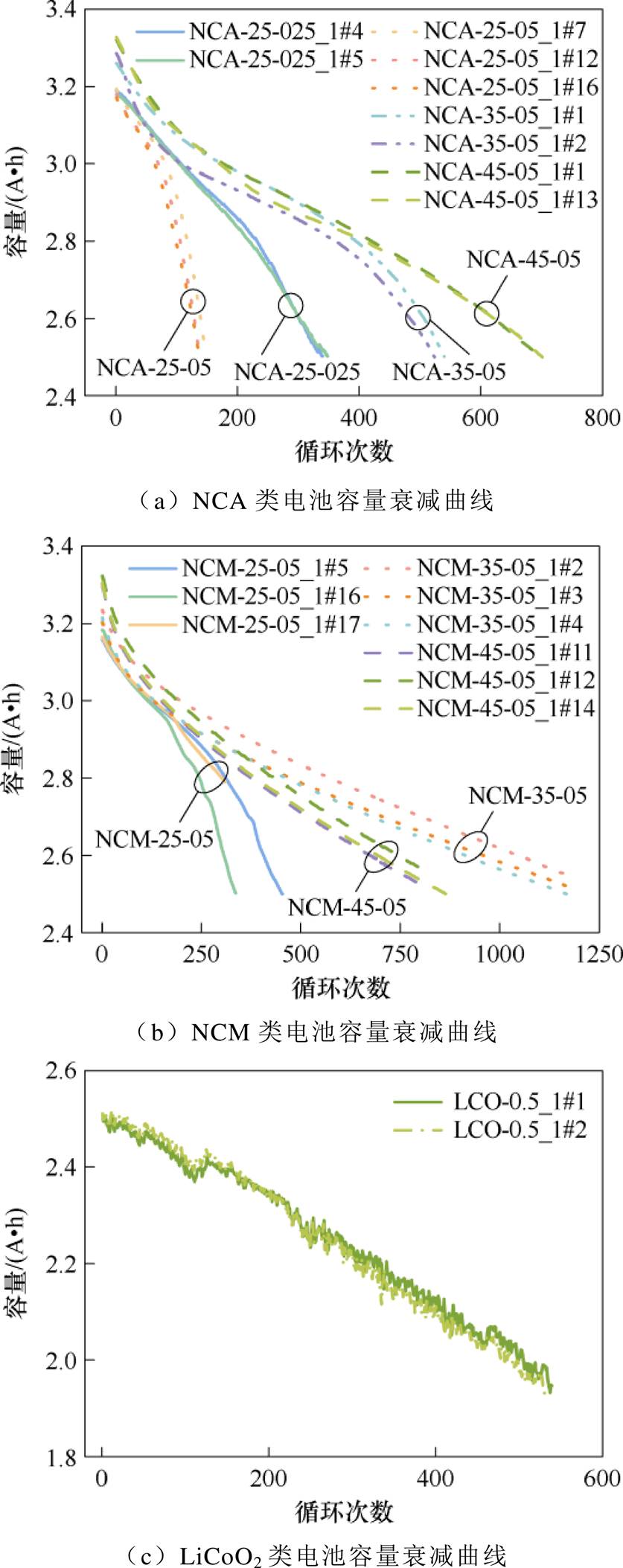
图1 数据集容量衰减曲线
Fig.1 Dataset capacity degradation curves
电池在充电过程中会导致电极电势偏离平衡电位,这种现象称为电池的极化效应。根据极化产生的原因,可以将其分为欧姆极化、活化极化和浓差极化,相应的内阻分别为欧姆极化内阻、活化极化内阻和浓差极化内阻,具体如图2锂离子电池双极化等效电路模型中的Ro、Ra、Rc所示。在锂离子电池容量衰减过程中会出现固体电解质界面(Solid Electrolyte Interphase, SEI)膜增长、电解液分解、电极结构破坏等副反应,从而导致电池内阻增加,即极化内阻增加,因此电池极化程度的强弱与电池老化程度之间具有密切关系。而在恒压充电过程中,充电电流逐渐减小,导致极化电压降低,极化程度减弱。对于电压弛豫环节,电池处于开路状态,故电池内部只有活化极化与浓差极化反应发生,而由于极化电容的存在,将导致弛豫电压以指数形式衰减,直至达到平衡电位。综上所述,恒压与弛豫过程与电池去极化反应有直接关系,理论上完全可以表征电池容量。下面将详细介绍特征的提取方法与处理过程。
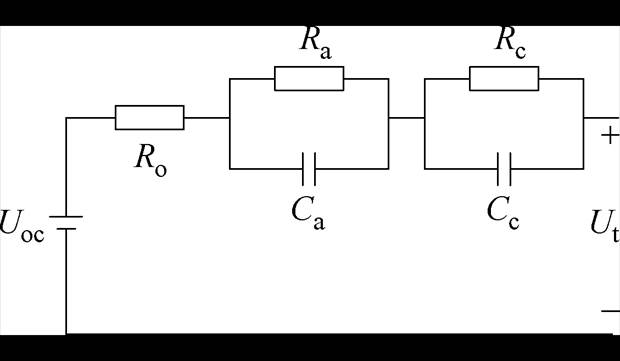
图2 锂离子电池双极化等效电路模型
Fig.2 Bipolarized equivalent circuit model for lithium-ion batteries
1.2.1 恒压过程特征提取
CV充电是电池达到满电的必要阶段,且只要电压低于上限即可进行充电。图3a显示了电池不同循环下CV充电过程中电流的变化情况。可以看出,随着电池容量的衰减,恒压充电的整体时间呈现增加趋势,且电流曲线斜率在充电后期呈现明显减少的趋势。为了更加清晰地观察充电后期电流情况,绘制了CV充电结束前1 000 s的电流曲线,如图3b所示。可以看到,在恒压充电后期,随着循环次数的增加,电流最大值呈现减少趋势,且电流曲线逐渐趋近平滑。
根据上述恒压充电后期存在的特性,选取充电结束时刻前最后10 min的电流初始值、平均值以及充电容量为前三个特征,分别记为It、Im、Qt。由于充电结束时间无法提前确定,同时为了减少BMS的数据负担,另外选取恒压充电电流从0.15C到充电结束所持续的时间和充电容量为第四和第五个特征,分别记为T和Qi。因此,整个恒压阶段特征的数据采集只需在充电电流到0.15C时开始进行即可。本文使用的恒压充电电流数据的采样间隔为10 s。
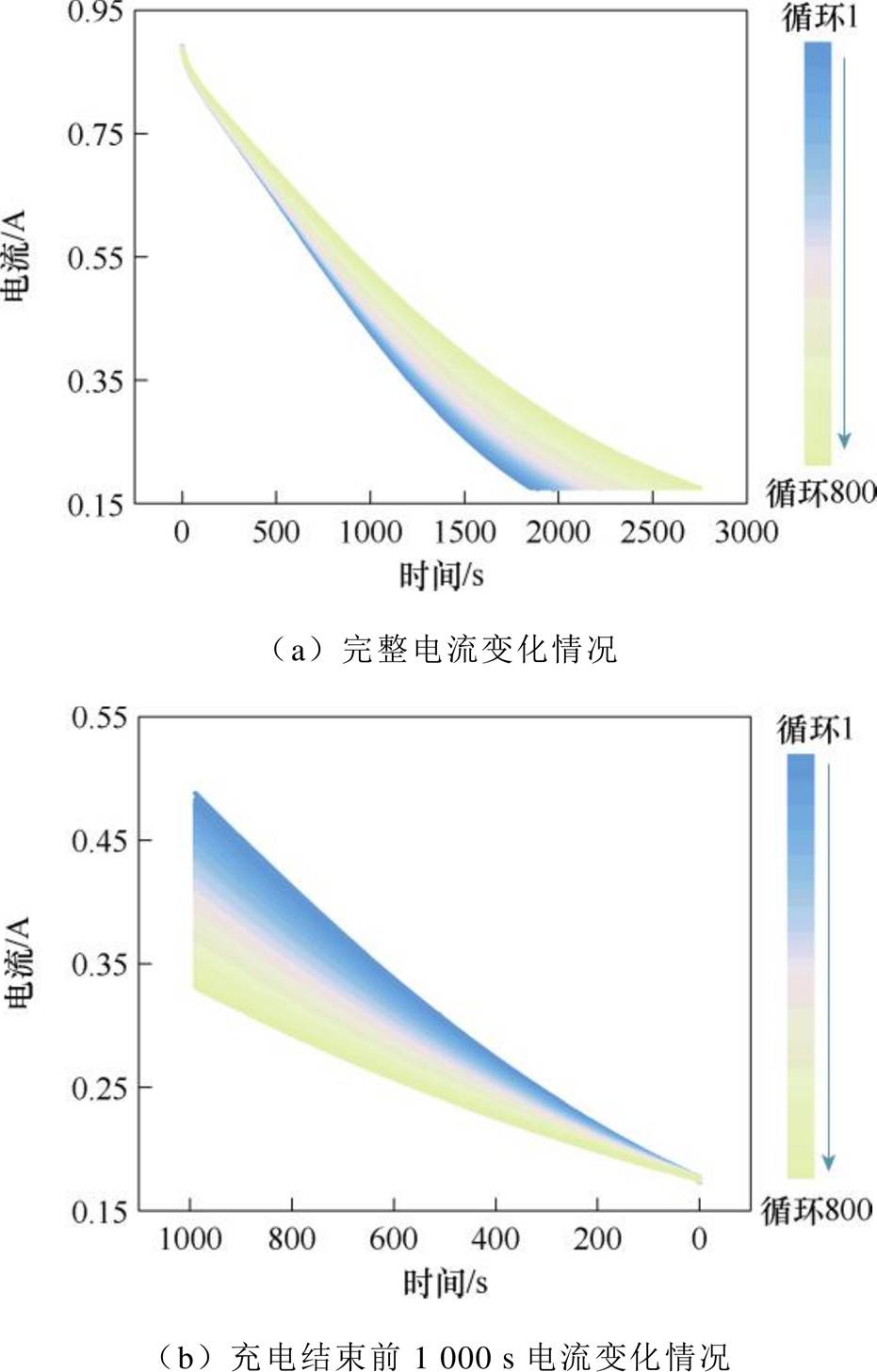
图3 不同循环下恒压充电期间电流变化情况
Fig.3 Variation of current during constant voltage charging under different cycles
1.2.2 弛豫过程特征提取
图4显示了电池不同循环下弛豫电压的变化情况。从图4中可以看出,电池弛豫电压曲线呈现明显下降的趋势,且随着时间的增加,电压的差值逐渐增大。为了更清晰地描述电压曲线,使用指数函数对曲线进行拟合,公式为
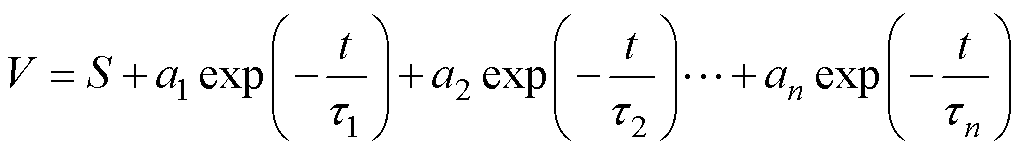 (1)
(1)
式中,V为拟合电压;S为截距;a1~an为指数衰减环节幅值;t1~tn为时间常数。
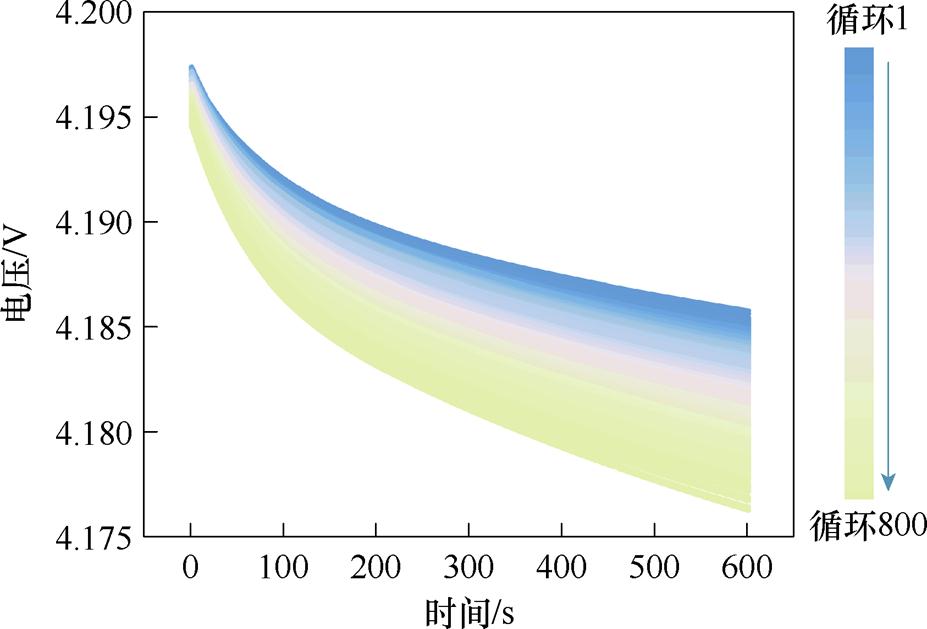
图4 不同循环下弛豫电压变化情况
Fig.4 Changes in relaxation voltage under different cycles
决定系数(Coefficient of Determination)R2和方均根误差(Root Mean Square Error, RMSE)两个指标被用来评估曲线拟合效果。
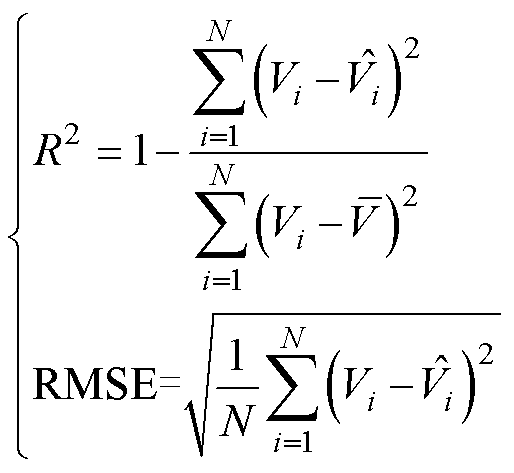 (2)
(2)
式中,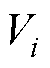 为第i个真实电压;
为第i个真实电压;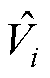 为第i个拟合电压;
为第i个拟合电压;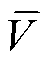 为真实电压的平均值;N为采样点数量。
为真实电压的平均值;N为采样点数量。
为了确定指数环节的最佳阶数,绘制了R2和RMSE随指数环节阶数变化的曲线,如图5所示。当指数环节阶数为1时,拟合精度最低;当指数环节阶数为2时,R2>0.99,RMSE<0.001;随着指数环节阶数的增加,拟合精度的提升并不显著,但计算量将直线上升。因此指数环节选择2为最佳。
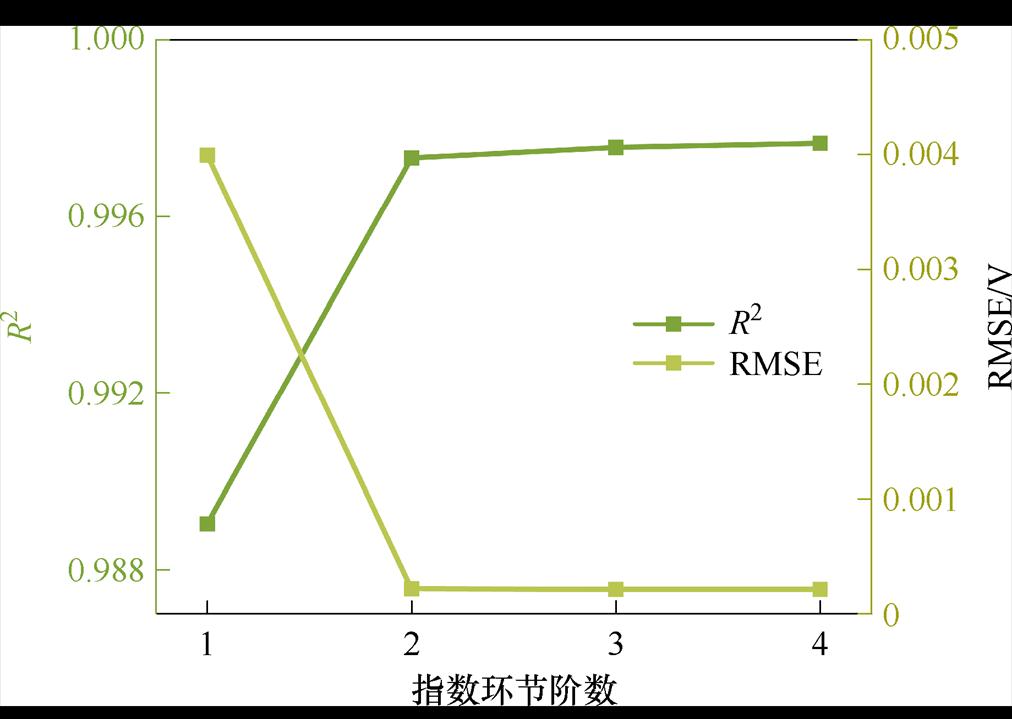
图5 R2和RMSE随阶数的变化情况
Fig.5 Variation of R2 and RMSE with order
图6为所有电池数据单元的拟合误差分布情况。其中R2主要集中在0.999 7附近,且最小值大于0.997,RMSE主要集中在0.000 12 V附近,且最大值小于0.000 4 V,表明二阶指数函数能够很好地拟合弛豫电压曲线。因此将拟合系数S、a1、a2、t1、t2记为第6~10个特征。通过对弛豫电压数据进行函数拟合,实现了高维电压序列向低维系数向量的转换,降低了模型的计算复杂度,同时也能起到数据降噪的作用。本文使用的弛豫电压数据的采样间隔为120 s。
虽然前面对特征与容量的相关性进行了直观描述,但缺乏定量分析。因此采用Pearson和Spearman相关性分析方法,对特征与容量之间的关系进行定量分析。Pearson和Spearman的计算公式为
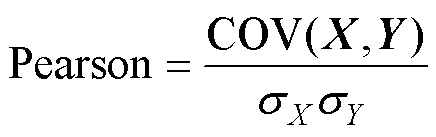 (3)
(3)
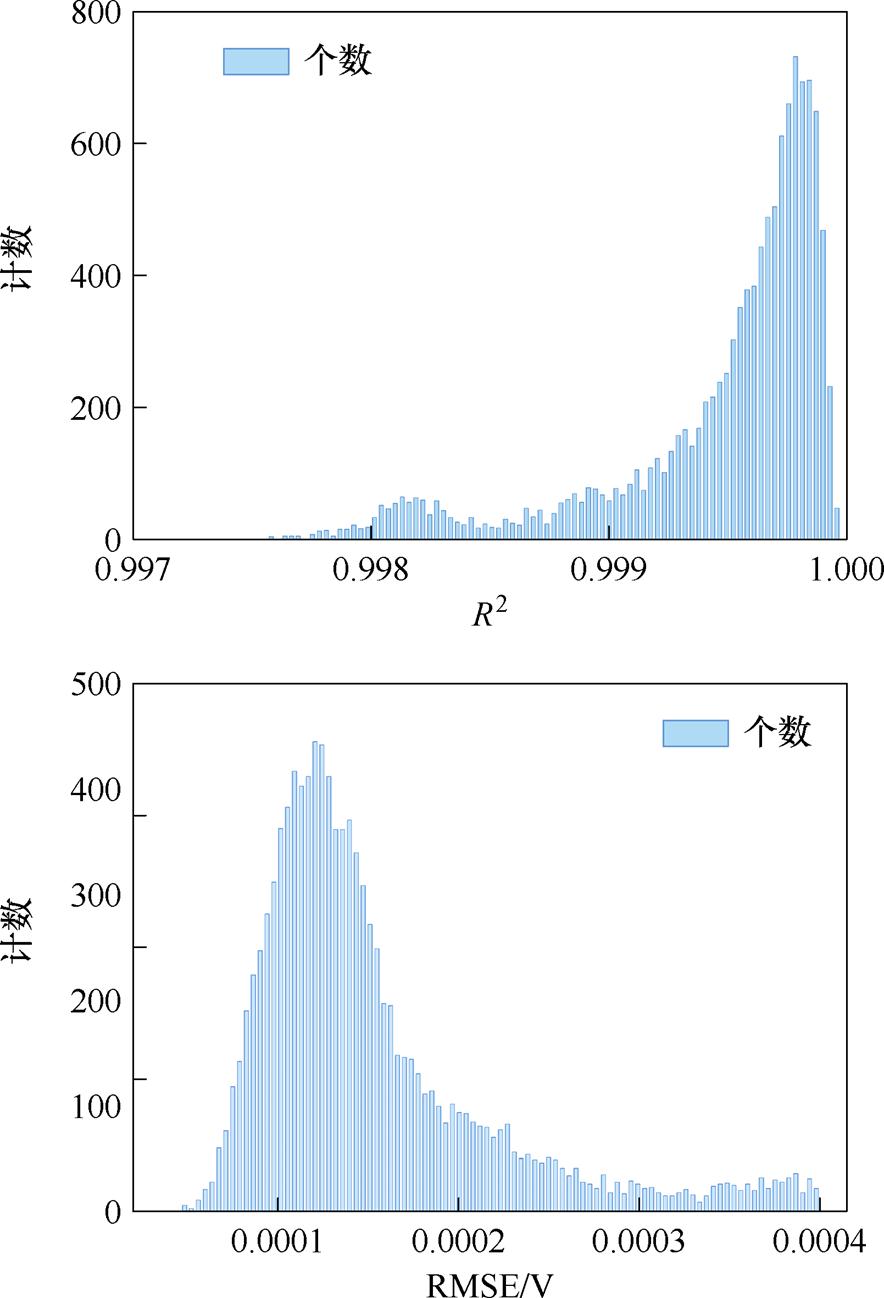
图6 拟合曲线R2和RMSE误差分布
Fig.6 Fitting curve R2 and RMSE error distribution
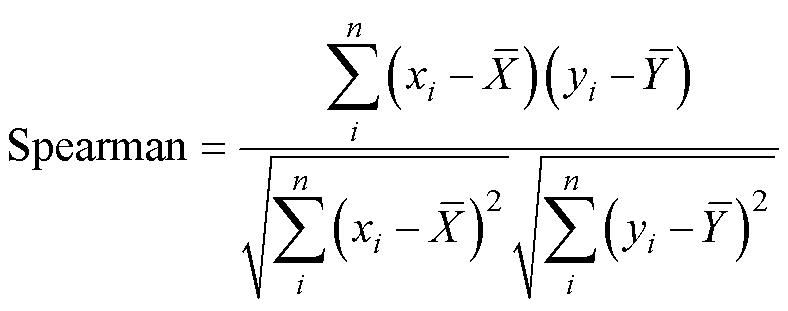 (4)
(4)
式中,X、Y分别为特征向量和目标向量;COV(X,Y)为X和Y协方差;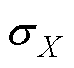 、
、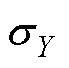 分别为X和Y的标准差,
分别为X和Y的标准差, 和
和 分别为X和Y平均值;xi和yi分别为X和Y中的元素。
分别为X和Y平均值;xi和yi分别为X和Y中的元素。
提取的特征与电池容量的Pearson和Spearman相关系数结果分别见表2和表3。从表2和表3中可以看出,在恒压环节提取的五个特征两种相关系数绝对值均大于0.9。而在弛豫过程中提取的五个特征中,电池的t2特征相关系数的绝对值几乎都小于0.6,故舍弃该特征。a1和a2的相关性会随着电池种类和工况的不同表现出较大差异,例如NCM-35- 05_1电池a1的相关性较低,a2的相关性较高,而对于NCA-25-05_1电池,情况正好相反。但可以发现,a1和a2特征均与电池容量呈负相关,因此采用线性组合将两个特征进行融合,从表2和表3中可以看出,融合后的特征相关系数绝对值均大于0.82,相较于融合之前具有较大提升。根据相关性分析结果,初步筛选确定恒压环节It、Im、Qt、T、Qi和弛豫电压拟合系数a1+a2、S、t1八个特征。
表2 特征与容量间的Pearson相关系数结果
Tab.2 Pearson correlation coefficient results between characteristics and capacity
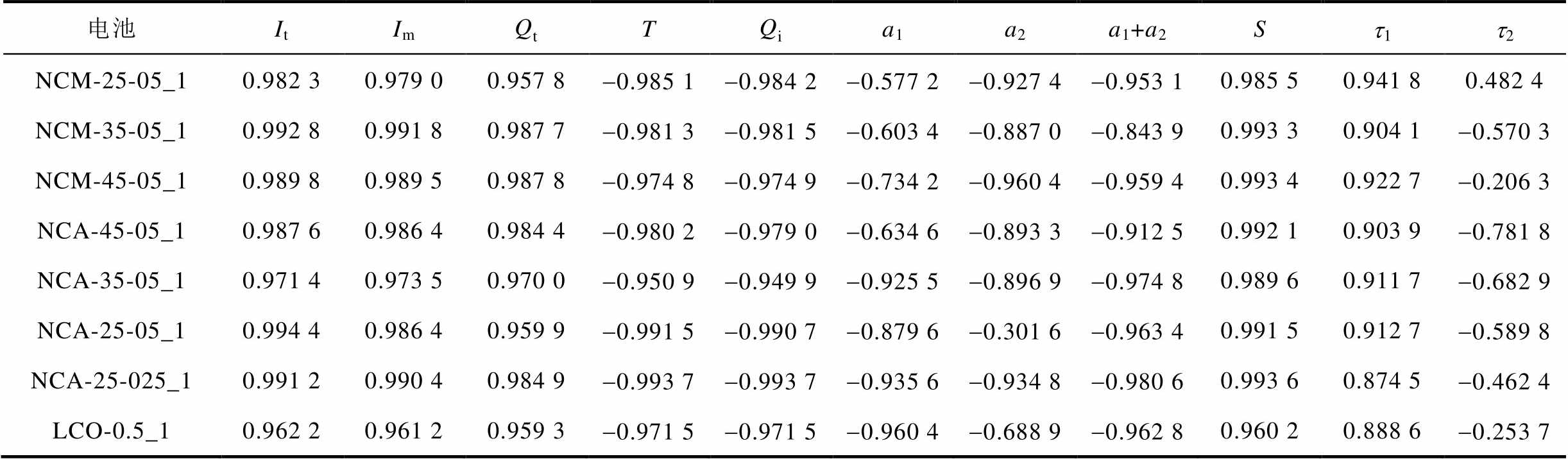
电池ItImQtTQia1a2a1+a2St1t2 NCM-25-05_10.982 30.979 00.957 8-0.985 1-0.984 2-0.577 2-0.927 4-0.953 10.985 50.941 80.482 4 NCM-35-05_10.992 80.991 80.987 7-0.981 3-0.981 5-0.603 4-0.887 0-0.843 90.993 30.904 1-0.570 3 NCM-45-05_10.989 80.989 50.987 8-0.974 8-0.974 9-0.734 2-0.960 4-0.959 40.993 40.922 7-0.206 3 NCA-45-05_10.987 60.986 40.984 4-0.980 2-0.979 0-0.634 6-0.893 3-0.912 50.992 10.903 9-0.781 8 NCA-35-05_10.971 40.973 50.970 0-0.950 9-0.949 9-0.925 5-0.896 9-0.974 80.989 60.911 7-0.682 9 NCA-25-05_10.994 40.986 40.959 9-0.991 5-0.990 7-0.879 6-0.301 6-0.963 40.991 50.912 7-0.589 8 NCA-25-025_10.991 20.990 40.984 9-0.993 7-0.993 7-0.935 6-0.934 8-0.980 60.993 60.874 5-0.462 4 LCO-0.5_10.962 20.961 20.959 3-0.971 5-0.971 5-0.960 4-0.688 9-0.962 80.960 20.888 6-0.253 7
表3 特征与容量间的Spearman相关系数结果
Tab.3 Spearman correlation coefficient results between characteristics and capacity
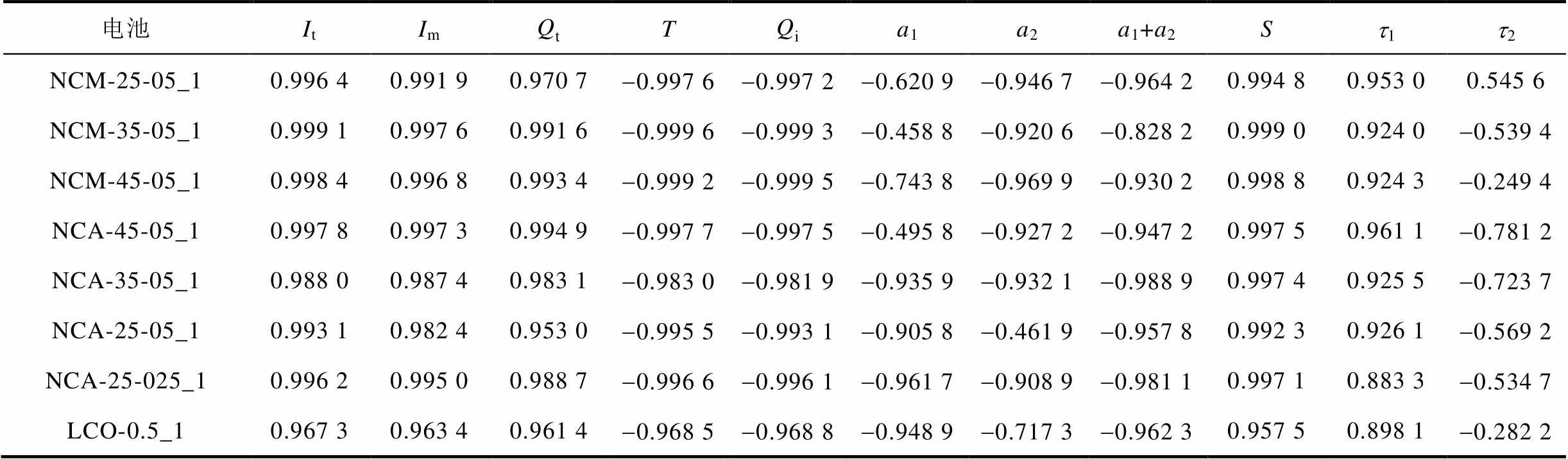
电池ItImQtTQia1a2a1+a2St1t2 NCM-25-05_10.996 40.991 90.970 7-0.997 6-0.997 2-0.620 9-0.946 7-0.964 20.994 80.953 00.545 6 NCM-35-05_10.999 10.997 60.991 6-0.999 6-0.999 3-0.458 8-0.920 6-0.828 20.999 00.924 0-0.539 4 NCM-45-05_10.998 40.996 80.993 4-0.999 2-0.999 5-0.743 8-0.969 9-0.930 20.998 80.924 3-0.249 4 NCA-45-05_10.997 80.997 30.994 9-0.997 7-0.997 5-0.495 8-0.927 2-0.947 20.997 50.961 1-0.781 2 NCA-35-05_10.988 00.987 40.983 1-0.983 0-0.981 9-0.935 9-0.932 1-0.988 90.997 40.925 5-0.723 7 NCA-25-05_10.993 10.982 40.953 0-0.995 5-0.993 1-0.905 8-0.461 9-0.957 80.992 30.926 1-0.569 2 NCA-25-025_10.996 20.995 00.988 7-0.996 6-0.996 1-0.961 7-0.908 9-0.981 10.997 10.883 3-0.534 7 LCO-0.5_10.967 30.963 40.961 4-0.968 5-0.968 8-0.948 9-0.717 3-0.962 30.957 50.898 1-0.282 2
为了更直观地观察特征随容量的变化趋势,以NCM-35-05_1#2电池为例,绘制了归一化处理后的八个特征与容量之间的变化趋势曲线,如图7所示。
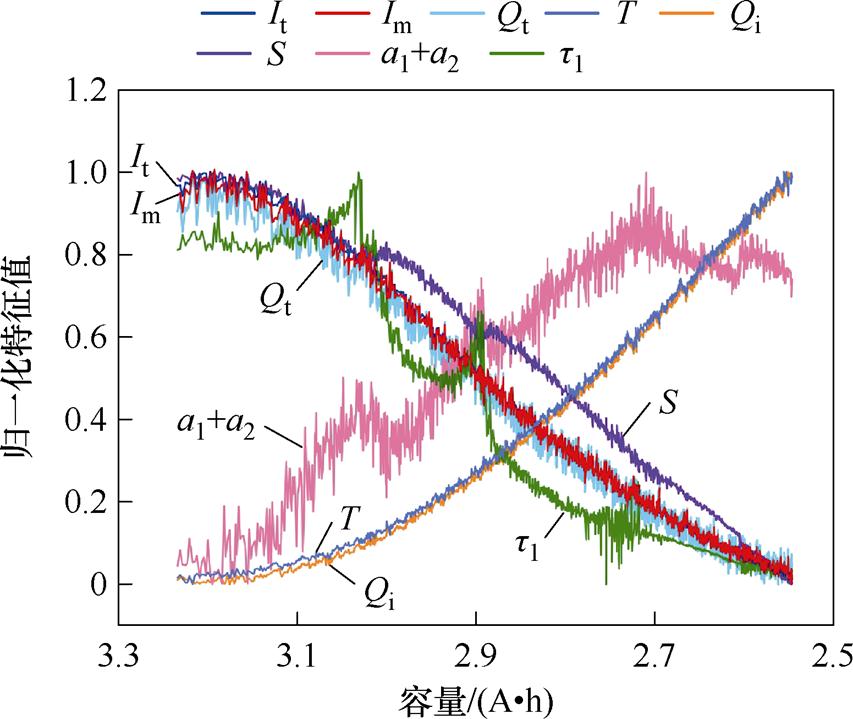
图7 归一化特征随容量的变化趋势
Fig.7 Trend of normalized features with capacity
从图7可以看出,除了t1特征有波动外,其余七个特征与容量均呈现近似线性的关系,说明提取的特征与容量之间确实存在良好的映射关系。但对比曲线间的位置关系发现,归一化后的部分特征存在一定的曲线重叠,说明特征之间可能存在冗余信息,而这些冗余信息可能导致模型训练不稳定,因此本文使用PCA方法对特征进行进一步的分析与处理。PCA的主要步骤如下:
(1)对八个特征组成的矩阵A进行归一化处理,得到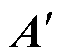 ,矩阵中各元素计算公式为
,矩阵中各元素计算公式为
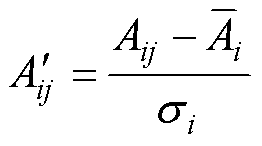 (5)
(5)
式中,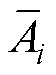 和
和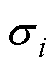 分别为第i列的平均值和方差。
分别为第i列的平均值和方差。
(2)计算特征矩阵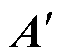 的协方差矩阵D,公式为
的协方差矩阵D,公式为
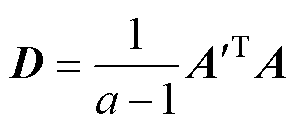 (6)
(6)
式中,a为样本数量。
(3)计算特征值和特征向量,公式为
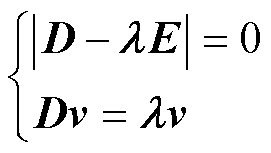 (7)
(7)
式中,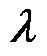 为特征值;E为单位矩阵。将特征值按照降序排列,即
为特征值;E为单位矩阵。将特征值按照降序排列,即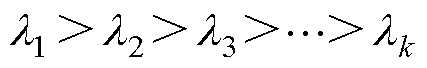 ,并求出对应的特征向量为
,并求出对应的特征向量为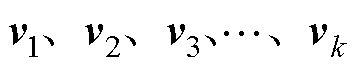 ,此向量组成的矩阵Vk即为经过主成分分析得到的间接特征矩阵。
,此向量组成的矩阵Vk即为经过主成分分析得到的间接特征矩阵。
(4)计算每个主成分的方差贡献率Ci和特征变换后的新数据特征Anew,公式为
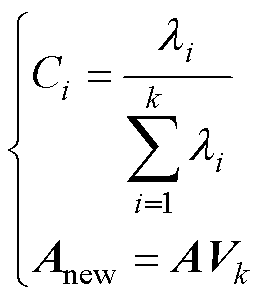 (8)
(8)
式中,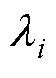 为第i个特征值。
为第i个特征值。
表4给出了电池各主成分的方差贡献率。从中可以看出,对于不同类型的电池,各个主成分的方差贡献率差异较大,但前四个主成分的累计贡献率均达到99%以上,说明这四个主成分能够代表数据的整体变化情况,因此本文选择PC1、PC2、PC3、PC4计算得到的新数据作为特征降维特征。通过PCA处理,将具有极化衰减特性的原始特征进行了融合降维,降低了输入数据维度与模型训练的难度。
表4 各类电池PCA分析结果
Tab.4 PCA analysis results for various types of batteries
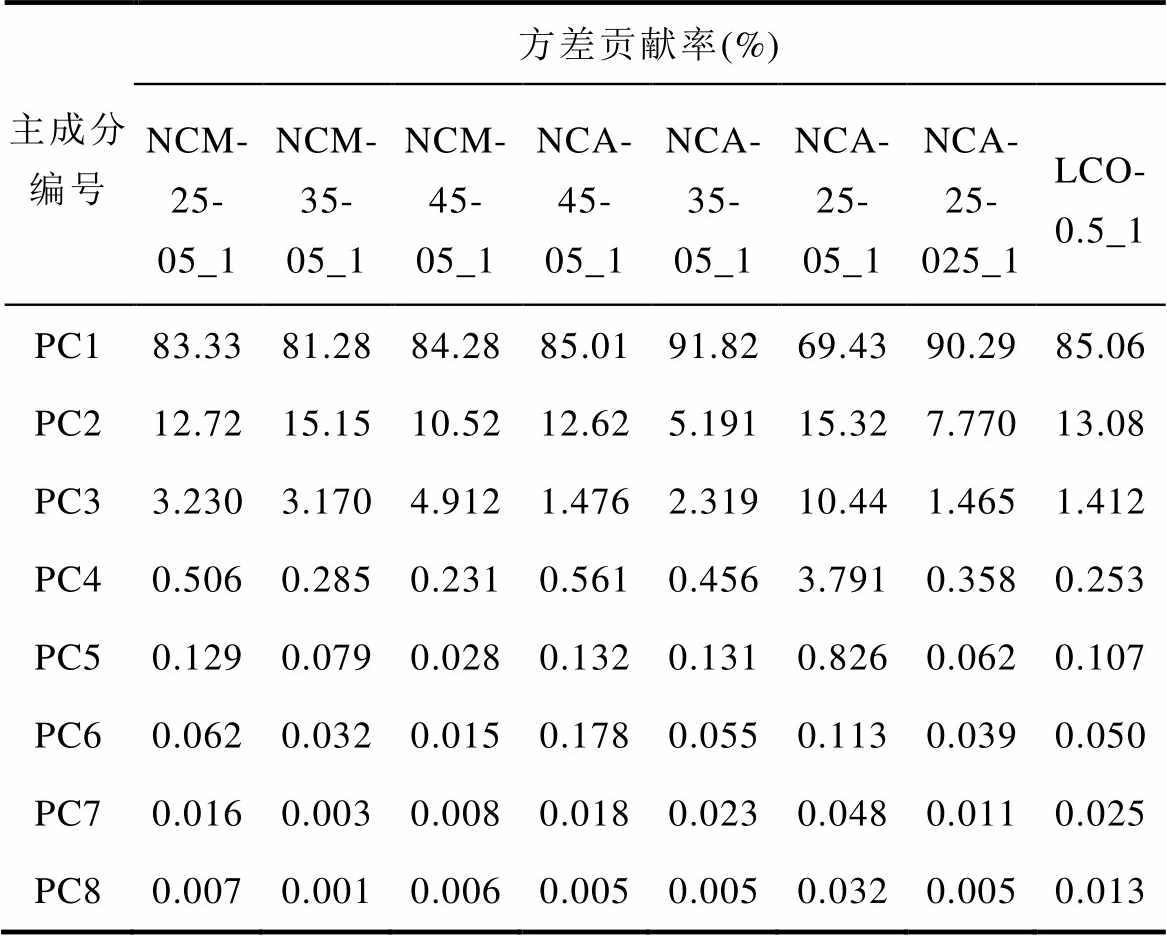
主成分编号方差贡献率(%) NCM-25-05_1NCM-35-05_1NCM-45-05_1NCA-45-05_1NCA-35-05_1NCA-25-05_1NCA-25-025_1LCO-0.5_1 PC183.3381.2884.2885.0191.8269.4390.2985.06 PC212.7215.1510.5212.625.19115.327.77013.08 PC33.2303.1704.9121.4762.31910.441.4651.412 PC40.5060.2850.2310.5610.4563.7910.3580.253 PC50.1290.0790.0280.1320.1310.8260.0620.107 PC60.0620.0320.0150.1780.0550.1130.0390.050 PC70.0160.0030.0080.0180.0230.0480.0110.025 PC80.0070.0010.0060.0050.0050.0320.0050.013
DBN是一种概率生成的深度网络模型,由受限玻耳兹曼机(Restrict Boltzmann Machine, RBM)堆叠而成。RBM是基于能量的概率图模型,可见向量v与隐藏向量h的联合能量函数E和联合概率分布P可表示为
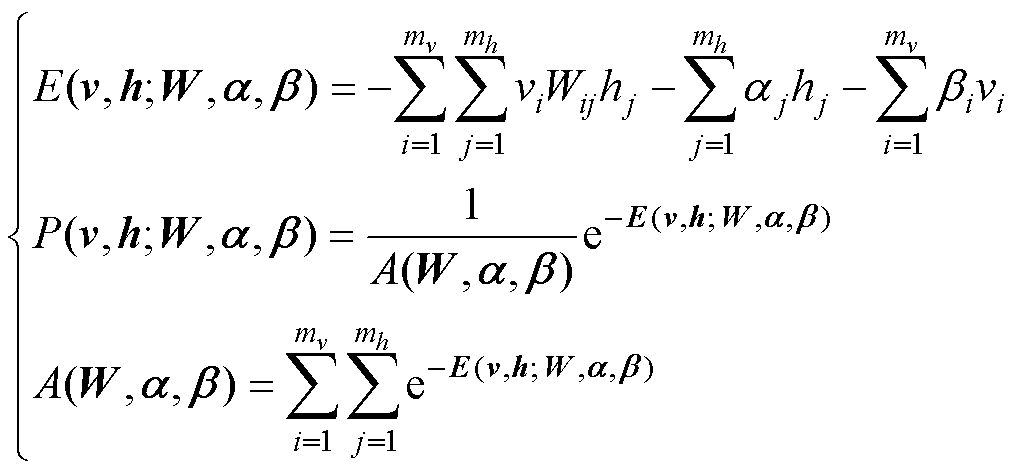 (9)
(9)
式中,mv、mh分别为可见神经元与隐藏神经元个数;Wij为从第i个可见神经元到第j个隐藏神经元之间的权值;aj、bi分别为第j个隐藏神经元和第i个可见神经元的偏置;A(W, a, b)为分配函数。
RBM的每个神经元输出为二值状态,即0或1,分别代表神经元的未激活状态和激活状态。当给出可见层(隐藏层)神经元状态时,隐藏层(可见层)神经元将独立于RBM,因此隐藏层(可见层)激活概率函数可表示为
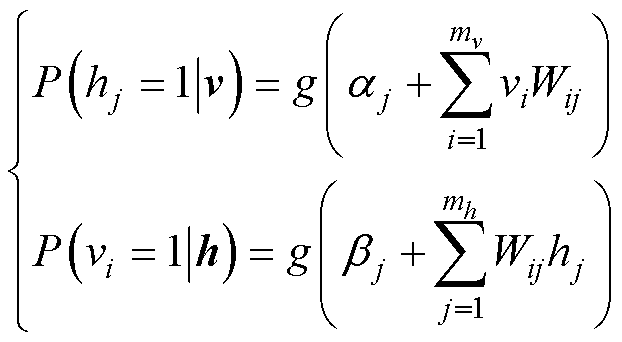 (10)
(10)
式中,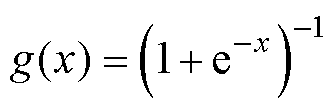 表示激活函数Sigmoid。
表示激活函数Sigmoid。
DBN的训练包括无监督学习和有监督微调两个过程。无监督学习过程不会提供训练数据的标签,参数更新是基于对比散度(Contrastive Divergence, CD)算法推导的,可描述为
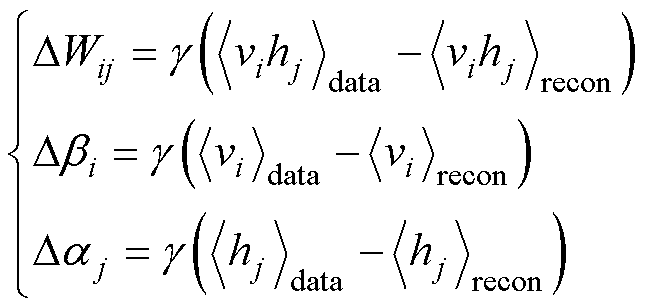 (11)
(11)
式中,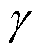 为RBM训练学习率;
为RBM训练学习率;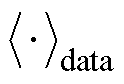 为数据分布的期望值;
为数据分布的期望值;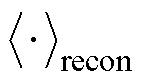 为模型重构后的期望值。
为模型重构后的期望值。
在无监督训练结束后,将采用带标签的数据进行监督式微调,该过程利用反向传播(Back Pro- pagation, BP)算法更新模型参数。
LSTM是循环神经网络(Recurrent Neural Net- work, RNN)的改进版,具有强稳定性和高精度的特点。LSTM通过引入三个门控机制(输入门、遗忘门、输出门)有效解决了传统RNN在训练过程中可能出现的梯度消失和梯度爆炸的问题,其基本原理公式为
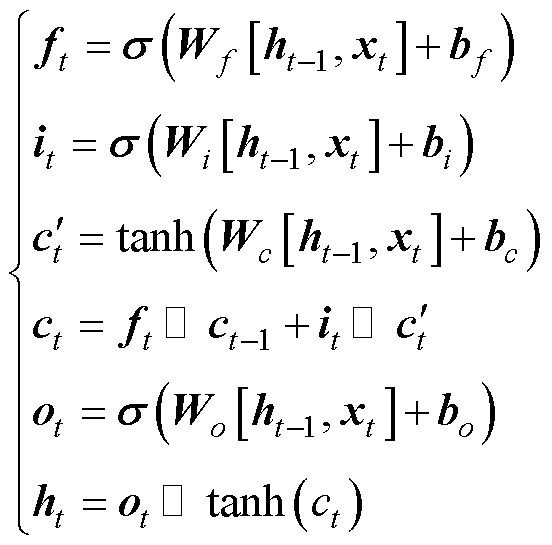 (12)
(12)
式中,it、ft和ot分别为输入门、遗忘门和输出门的激活向量;xt和ht分别为当前时刻的输入和隐藏状态;W和b分别为网络中需要学习的权重矩阵和偏置向量;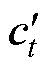 和
和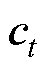 分别为单元的中间状态和输出状态;
分别为单元的中间状态和输出状态;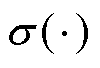 为Sigmoid激活函数;tanh为双曲正切函数。
为Sigmoid激活函数;tanh为双曲正切函数。
挤压-激励注意力是基于注意力原理设计的,其能通过自动计算每个通道的权重来评估各个通道在执行固定任务时的重要程度,从而聚焦关键信息并降低次要信息的影响,达到提高模型精度的目的。SE通道注意力由挤压、激励和缩放三部分组成,基本结构如图8所示。
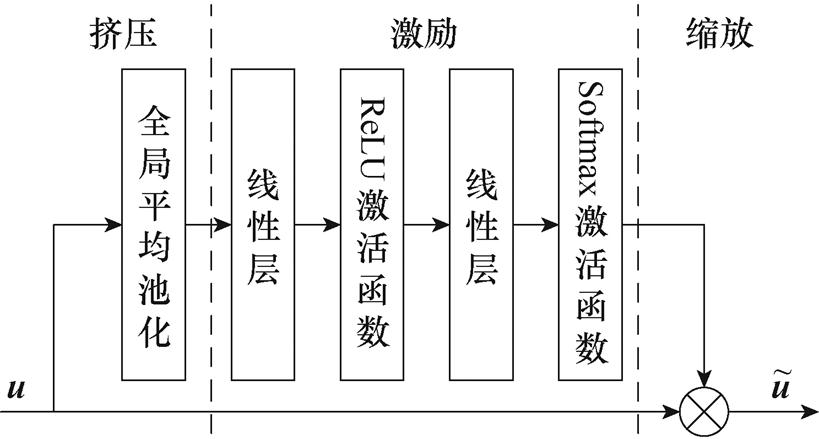
图8 SE注意力模块结构
Fig.8 Structure diagram of the SE attention module
挤压块:使用全局平均池化层将通道全局信息压缩到通道描述符中,表达式为
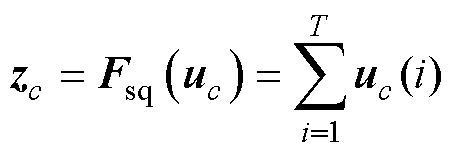 (13)
(13)
式中,c为第c个通道;T为总通道数量(隐藏层神经元的数量);z为通道描述符;u为特征图;u(i)为通道中第i个位置的特征值。
激励块:使用Sigmoid激活函数计算各个通道的权重,表达式为
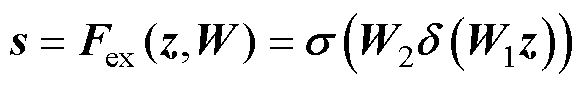 (14)
(14)
式中,W1、W2为线性层;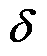 为ReLU激活函数。
为ReLU激活函数。
缩放块:将学习到的通道注意力权重s应用到原通道,表达式为
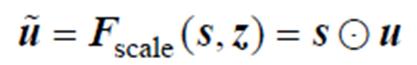 (15)
(15)
式中,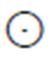 表示Hadamard运算。
表示Hadamard运算。
经典DBN网络一般采用简单的线性层来完成预测任务,而锂离子电池容量非线性衰减是复杂电化学反应导致的,简单的线性层对于容量与输入特征映射关系的学习可能无法达到较好的效果,因此本文使用学习能力更强、稳定性更好且适合处理时间序列问题的LSTM网络来构建DBN-LSTM模型,以提高模型整体学习能力。另外将SE自适应通道注意力模块融入DBN网络的RBM层中,使得模型能够动态调整每个隐藏层中各个神经元的权重,以确保重要信息在各层之间的有效传递,从而增强DBN网络的高阶信息挖掘能力。通过上述的模型改进策略,将最终构建的混合神经网络命名为IDBN-LSTM。
基于极化衰减特征与IDBN-LSTM混合神经网络构建了锂离子电池容量在线估计框架,如图9所示。具体实现流程如下:
(1)特征提取。根据电池极化反应强度与电池容量的关系,利用恒压充电电流与弛豫放松电压的去极化特性数据,提取不受充电起始点影响的多维实用特征。
(2)数据处理。首先,对特征进行标准化处理;然后使用相关性分析与PCA技术进行分析与特征融合,确定四个主成分作为间接特征;最后将处理后的电池数据划分为训练集和测试集,分别用于模型的离线训练与在线评估。
(3)模型构建与训练。利用SE自适应通道注意力模块优化RBM的隐藏层,同时使用LSTM网络改善DBN模型的输出效果,构建具有通道关注能力的IDBN-LSTM网络。然后使用训练集特征与容量数据训练模型,得到具有最优权重和偏置项的容量估计模型。
(4)预测与结果评估。利用预测集数据和训练好的估计模型实现容量的在线估计,然后根据估计容量与真实容量计算评价指标,实现对模型性能的全面评估。
表5为IDBN-LSTM模型的详细参数。为了更好地量化本文提出的锂离子电池容量估计方法,引入相对误差(Relative Error, RE)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、方均根百分比误差(Root Mean Square Percentage Error, RMSPE)和决定系数R2验证其准确性与有效性,四个指标计算公式为
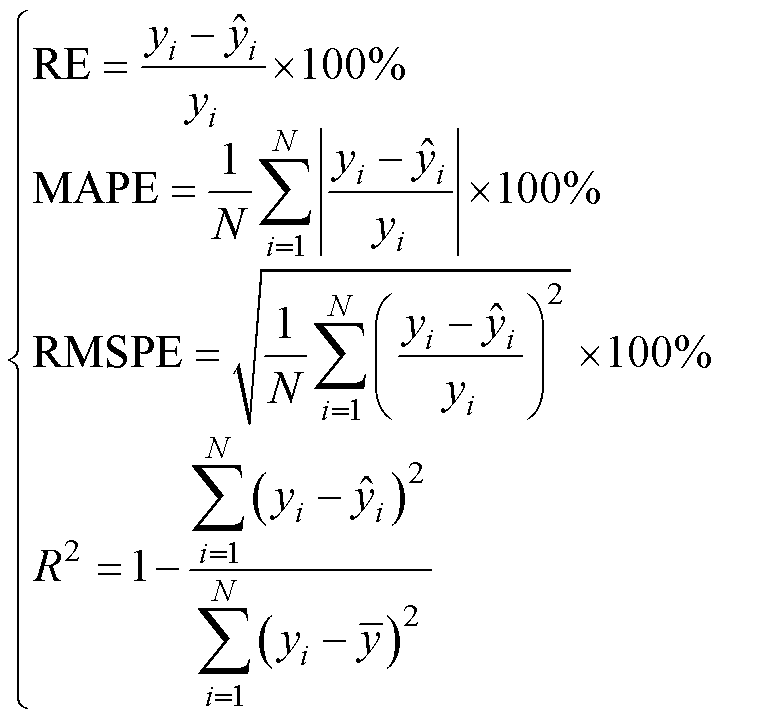 (16)
(16)
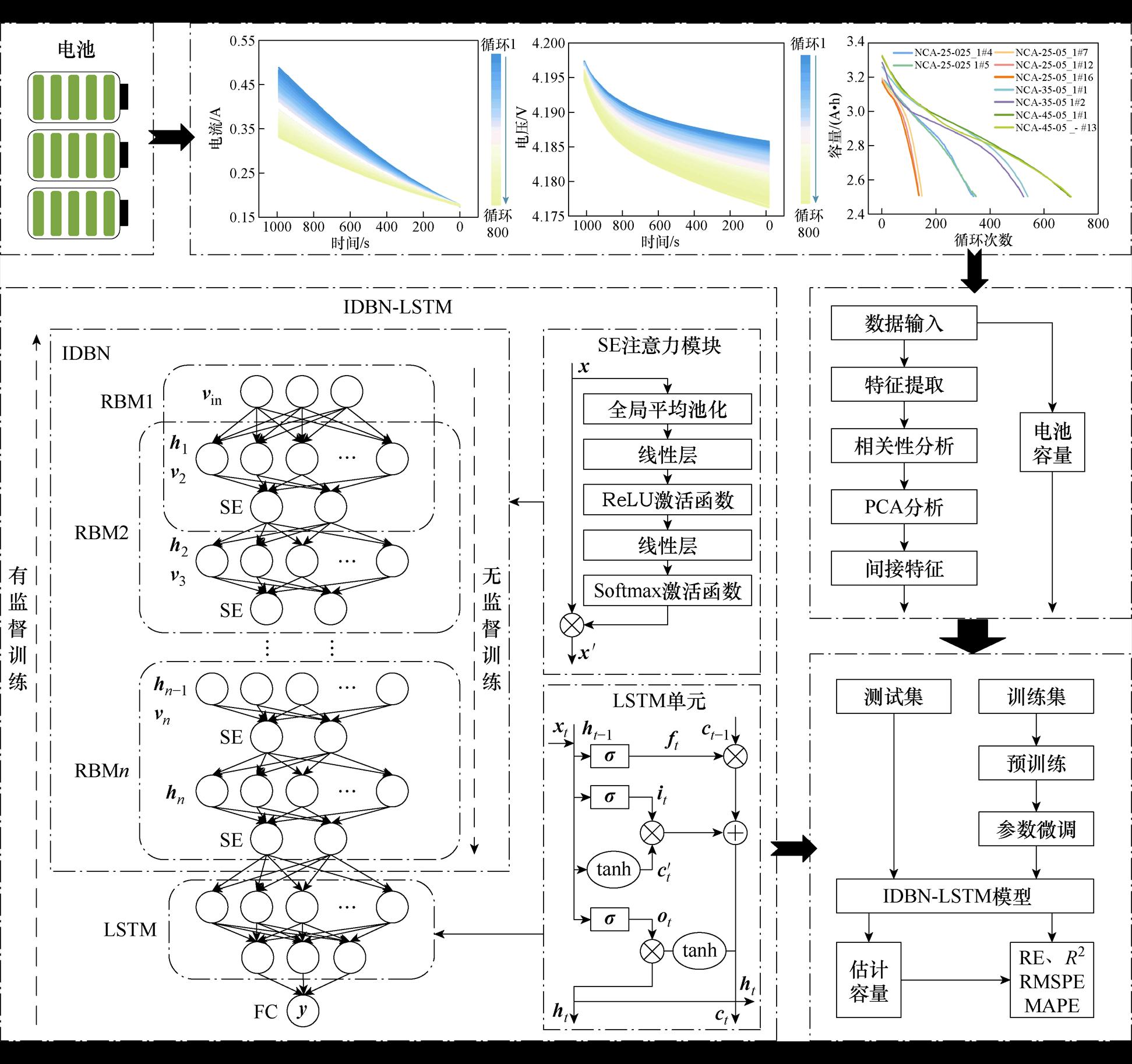
图9 锂离子电池容量估计框架
Fig.9 Lithium-ion battery capacity estimation framework
式中,N为样本个数;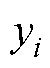 为实际值;
为实际值;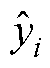 为预测值;
为预测值;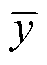 为样本均值。
为样本均值。
表5 IDBN-LSTM模型参数设置
Tab.5 IDBN-LSTM model parameter settings
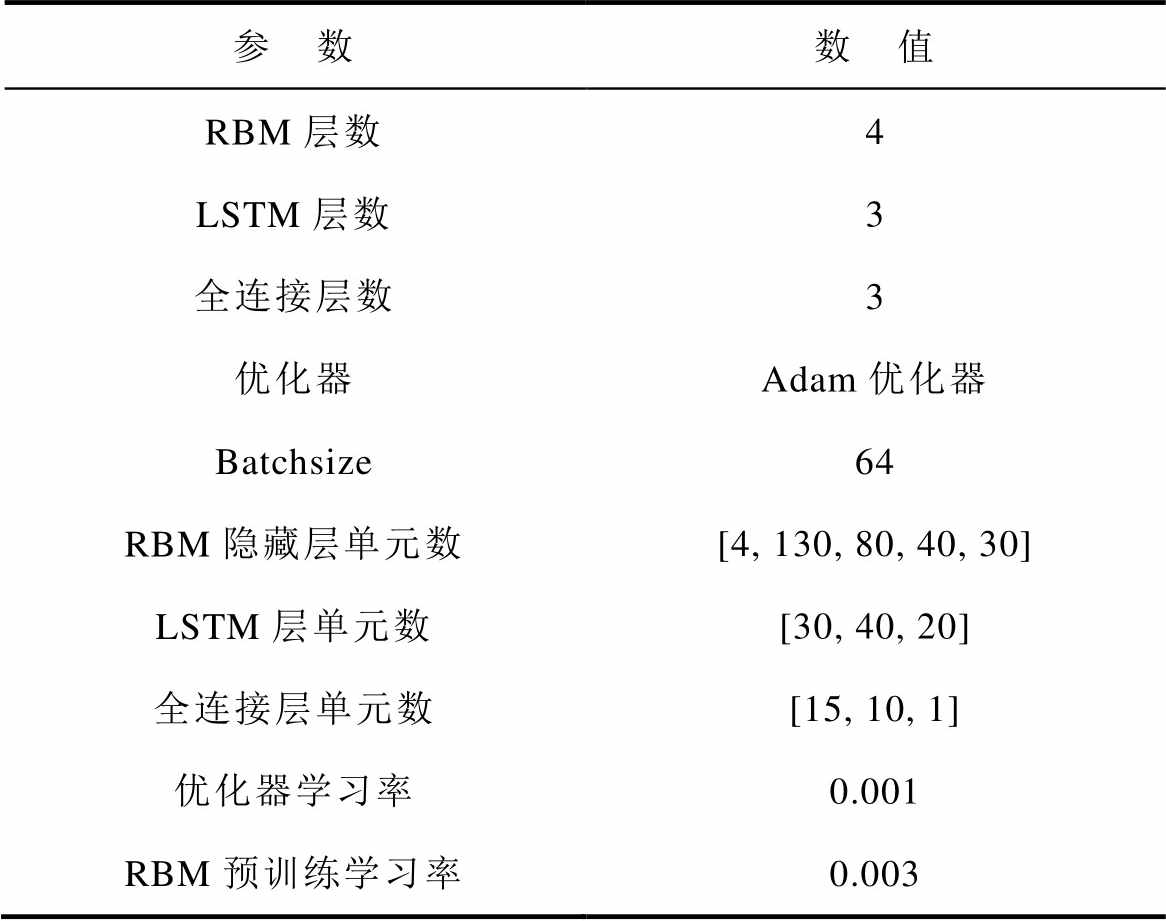
参 数数 值 RBM层数4 LSTM层数3 全连接层数3 优化器Adam优化器 Batchsize64 RBM隐藏层单元数[4, 130, 80, 40, 30] LSTM层单元数[30, 40, 20] 全连接层单元数[15, 10, 1] 优化器学习率0.001 RBM预训练学习率0.003
为了验证本文提出方法的有效性,设计了对比实验。对比实验详细内容如图10所示。
针对不同的电池数据结构,设计了多电池交叉验证(实验A)、小样本性能测试(实验B)、单电池性能测试(实验C)和模型泛化性验证(实验D)四组实验。实验A采用三个电池数据,其中两个电池数据作训练集,余下的一个电池数据作预测集,并通过交叉验证的方式评估模型在电池数据充足下的综合表现。实验B采用电池循环次数较少的两个电池数据,分别作训练集和预测集,验证模型在小样本条件下的精度。实验C采用一个电池数据,其中前60%作训练集,后40%作预测集,验证模型在同一电池不同老化阶段的表现。实验D使用不同充电条件下的多个电池作为训练集和测试集,验证模型对电池充电条件的敏感程度及其泛化能力。
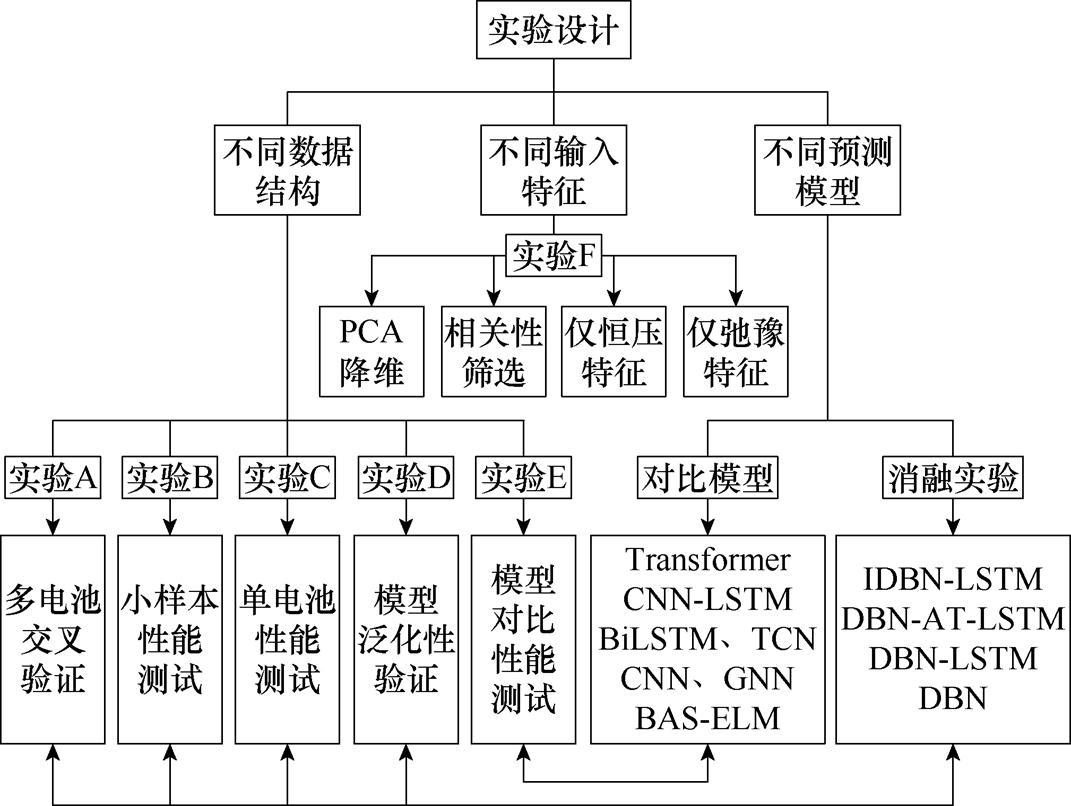
图10 对比实验详细内容
Fig.10 Details of the comparison experiment
为了验证本文提出的IDBN-LSTM(M1)模型架构的有效性,选取DBN-AT-LSTM(M2)、DBN- LSTM(M3)以及DBN(M4)模型进行消融实验分析。其中M2是仅在DBN的最后一层隐藏层添加SE注意力模块。同时,选取Transformer[30]、时序卷积网络(Temporal Convolutional Network, TCN)[31]、图神经网络(Graph Neural Networks, GNN)[32]、CNN-LSTM网络[33]等前沿算法,以及双向长短期神经网络(Bidirectional Long Short-Term Memory, BiLSTM)[34]、卷积神经网络(Convolutional Neural Network, CNN)[35]、天牛须搜索算法(Beetle Antennae Search algorithm, BAS)优化极限学习机(Extreme Learning Machine, ELM)[36]、多层感知机(Multi-Layer Perceptron, MLP)等基础算法进行不同模型的对比验证(实验E)。
为了验证本文特征提取与处理方法的有效性,选择仅恒压电流特征、仅弛豫电压特征、经相关性筛选特征与经PCA降维特征进行对比验证(实验F)。各实验的训练预测集划分情况见表6。
实验A的估计结果如图11所示,对应的相对误差如图12所示。从图11可以看出,在训练数据充足的条件下,M1模型表现稳定,在电池老化的全生命周期中,M1的估计结果相较于其他模型明显更接近电池真实容量衰减曲线,且交叉验证组之间的预测结果没有显著偏差。此外,在电池老化中期,所有模型都展现出不错的估计效果,这也证明所选特征能够较好地反映电池容量。
表6 数据集划分情况
Tab.6 Division of the data sets
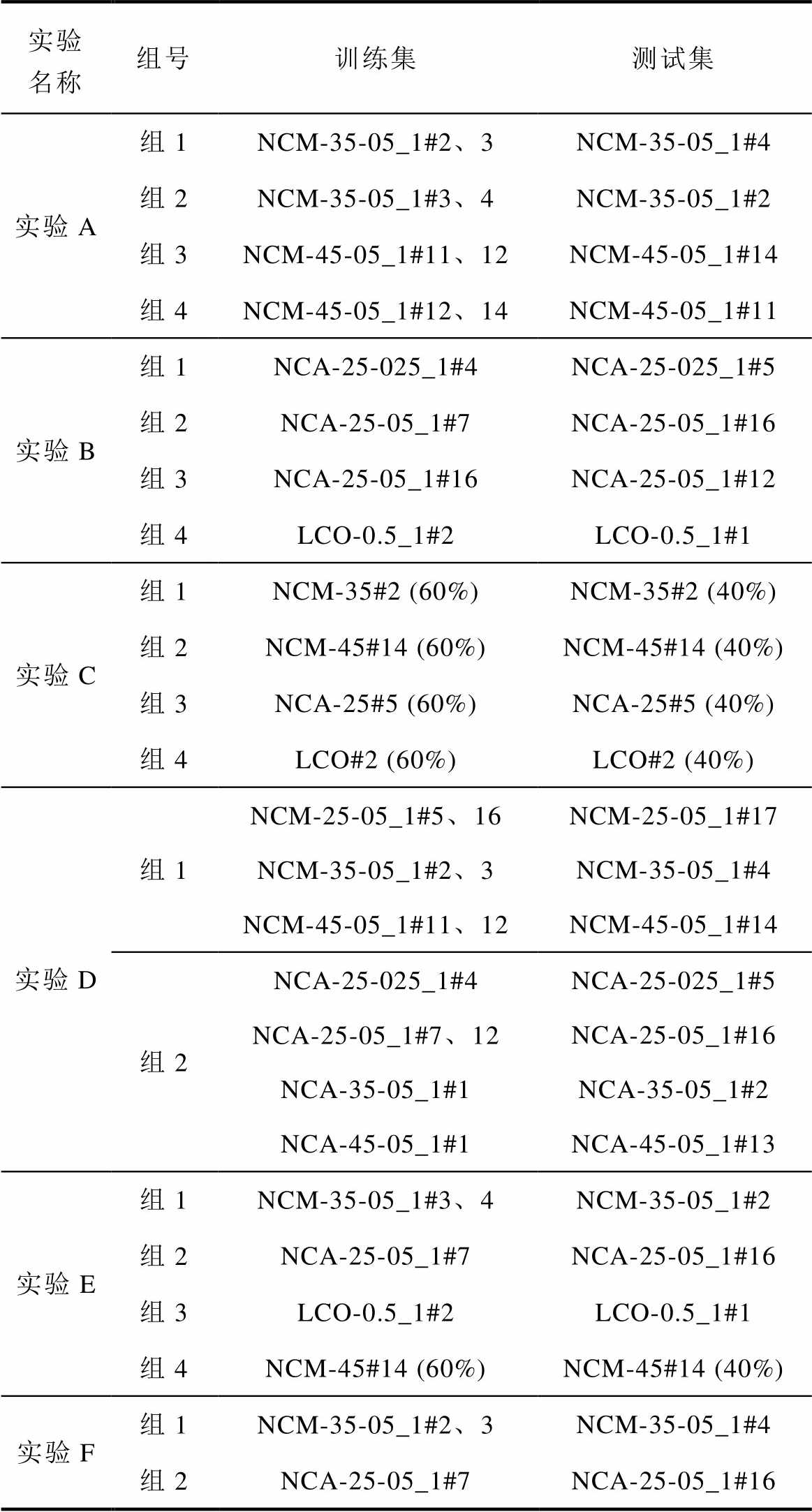
实验名称组号训练集测试集 实验A组1NCM-35-05_1#2、3NCM-35-05_1#4 组2NCM-35-05_1#3、4NCM-35-05_1#2 组3NCM-45-05_1#11、12NCM-45-05_1#14 组4NCM-45-05_1#12、14NCM-45-05_1#11 实验B组1NCA-25-025_1#4NCA-25-025_1#5 组2NCA-25-05_1#7NCA-25-05_1#16 组3NCA-25-05_1#16NCA-25-05_1#12 组4LCO-0.5_1#2LCO-0.5_1#1 实验C组1NCM-35#2 (60%)NCM-35#2 (40%) 组2NCM-45#14 (60%)NCM-45#14 (40%) 组3NCA-25#5 (60%)NCA-25#5 (40%) 组4LCO#2 (60%)LCO#2 (40%) 实验D组1NCM-25-05_1#5、16NCM-35-05_1#2、3NCM-45-05_1#11、12NCM-25-05_1#17NCM-35-05_1#4NCM-45-05_1#14 组2NCA-25-025_1#4NCA-25-05_1#7、12NCA-35-05_1#1NCA-45-05_1#1NCA-25-025_1#5NCA-25-05_1#16NCA-35-05_1#2NCA-45-05_1#13 实验E组1NCM-35-05_1#3、4NCM-35-05_1#2 组2NCA-25-05_1#7NCA-25-05_1#16 组3LCO-0.5_1#2LCO-0.5_1#1 组4NCM-45#14 (60%)NCM-45#14 (40%) 实验F组1NCM-35-05_1#2、3NCM-35-05_1#4 组2NCA-25-05_1#7NCA-25-05_1#16
从图12可以看出,M1模型的相对误差波动最小,相对误差绝对值维持在1%以内,展示了较高的稳定性与准确性。M2模型在中后期表现不错,相对误差水平接近M1模型,但在电池老化前期,估计误差普遍较大,准确性较差。M3只在组1和组3中显示较低的误差水平,泛化性较差;而M4模型无论在前期还是后期,相对误差均显著高于M1模型,且误差波动明显,未能实现电池容量的有效估计。
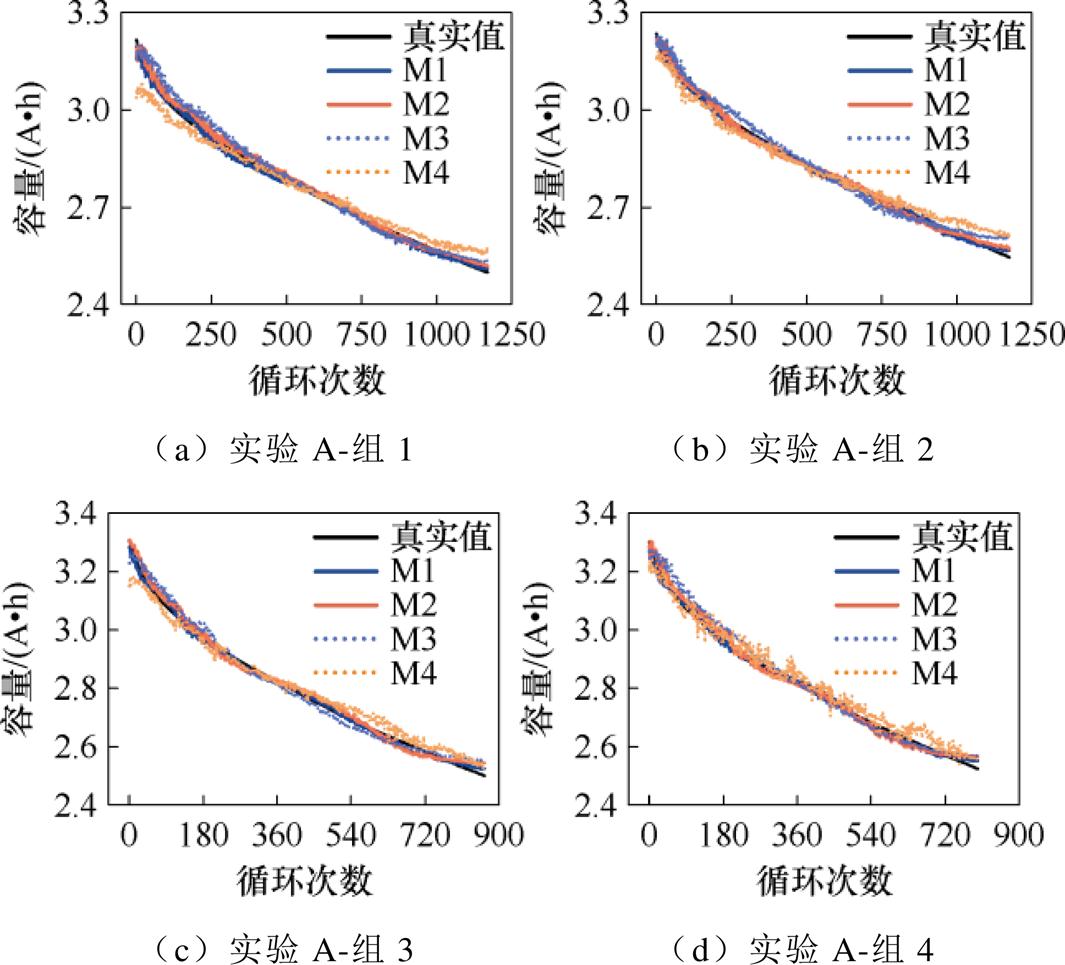
图11 实验A各模型估计结果
Fig.11 Experiment A estimation results for each model
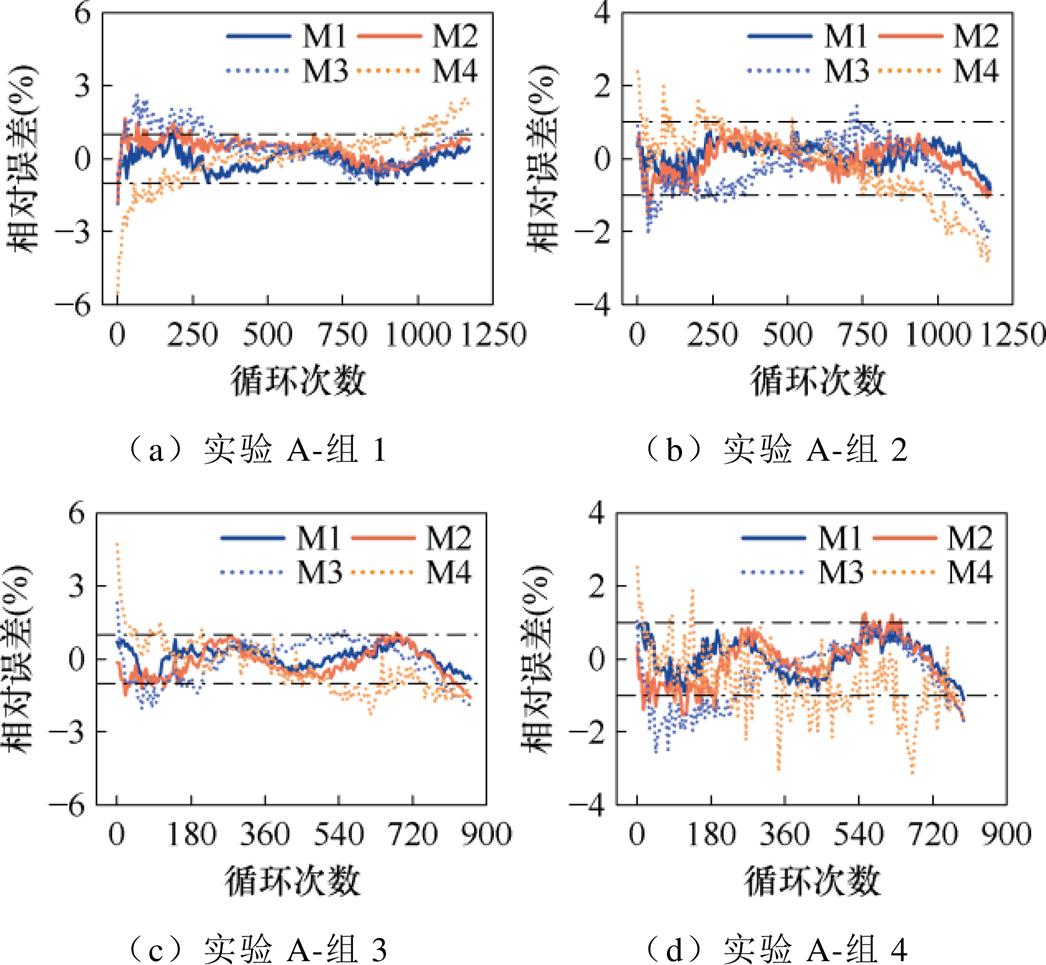
图12 实验A各模型相对误差
Fig.12 Experiment A estimated errors for each model
为了更直观地观察误差分布,绘制了实验A的相对误差箱型图,如图13所示,图中箱体表示误差分布10%~90%分位数,箱体越小,说明数据波动性越小,箱线表示误差的最大、最小值。以实验A-组1为例,各模型相对误差主要分布如下:M1的相对误差主要集中在[-0.57%, 0.49%]区间内,此区间最短且中心接近于零线,表明模型具有最高的精度和稳定性;M2的相对误差主要集中在[-0.26%, 0.86%]区间,虽然区间长度与M1相差不多,但中心偏离零线约0.3%,平均相对误差较大;M3的相对误差主要集中在[-0.48%, 1.59%]区间,区间较长,中心偏离零线约0.5%,模型效果不佳;而M4的相对误差主要集中在[-1.42%, 1.37%]区间,区间最长,说明相对误差波动最大,模型精度与稳定性最差。
实验A各模型的评价指标见表7。数据表明,在样本充足的情况下,M1模型的表现明显优于其他模型,其MAPE低于0.443%,RMSPE低于0.61%,R²高于0.99。以组1为例,M4在电池容量衰减的早期和晚期表现较差,其评价指标最高。M3通过引入LSTM网络,增强了模型对输入数据的学习能力,使得整体性能比M4提升10%以上。M2在DBN网络后添加通道注意力,帮助LSTM网络更好地关注关键信息,其MAPE为0.528%,RMSPE为0.605%,表现良好。M1通过对RBM层的改进,防止关键信息在RBM层间传递过程中丢失,从而显著提升了性能,MAPE和RMSPE降至0.352%、0.420%。与M2模型相比,M1模型的MAPE和RMSPE降低了约30%,与M3、M4相比,降低了约55%和60%。结果证明,在充足样本量的条件下,本文提出的方法能够实现电池工作寿命内容量的精确估计。
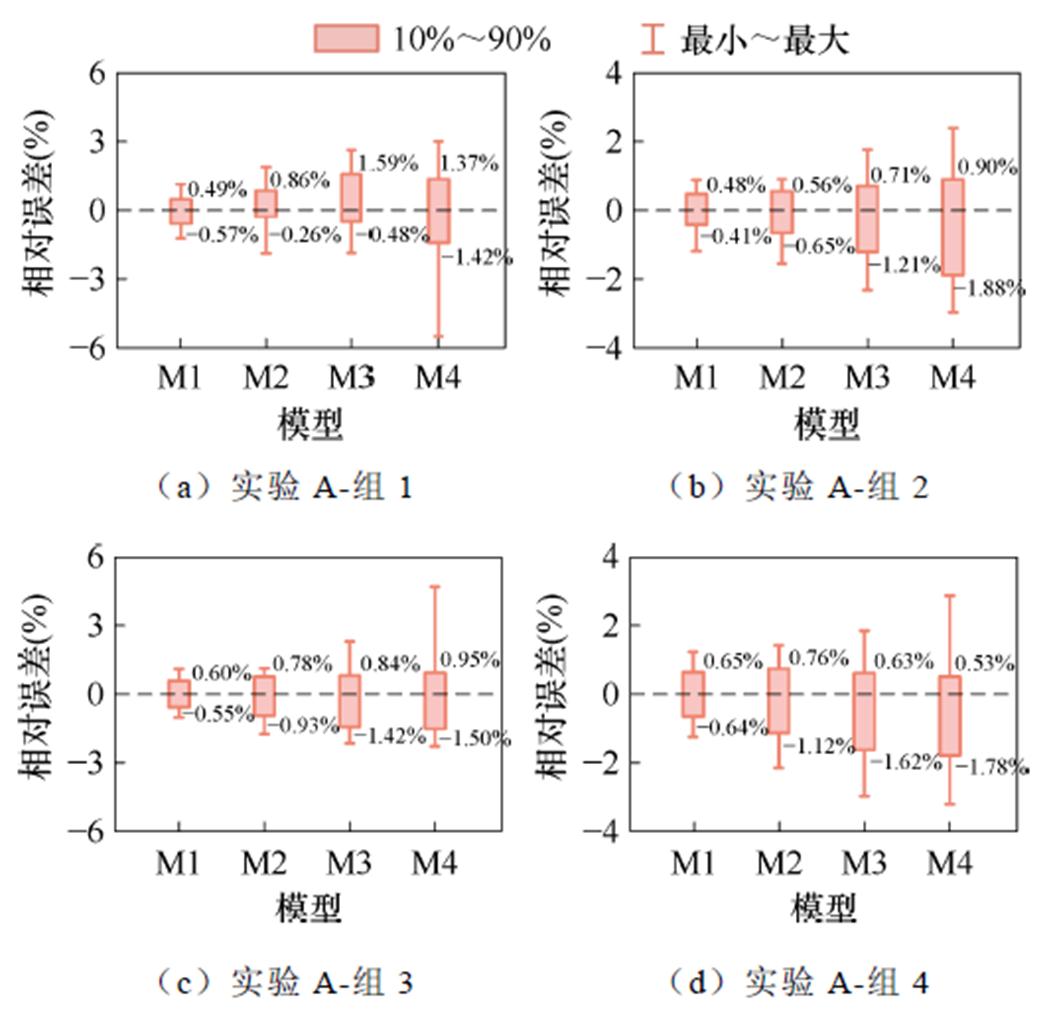
图13 实验A误差分布箱型图
Fig.13 Experiment A error distribution box plot
表7 实验A各模型评价指标
Tab.7 Evaluation metrics for each model in experiment A
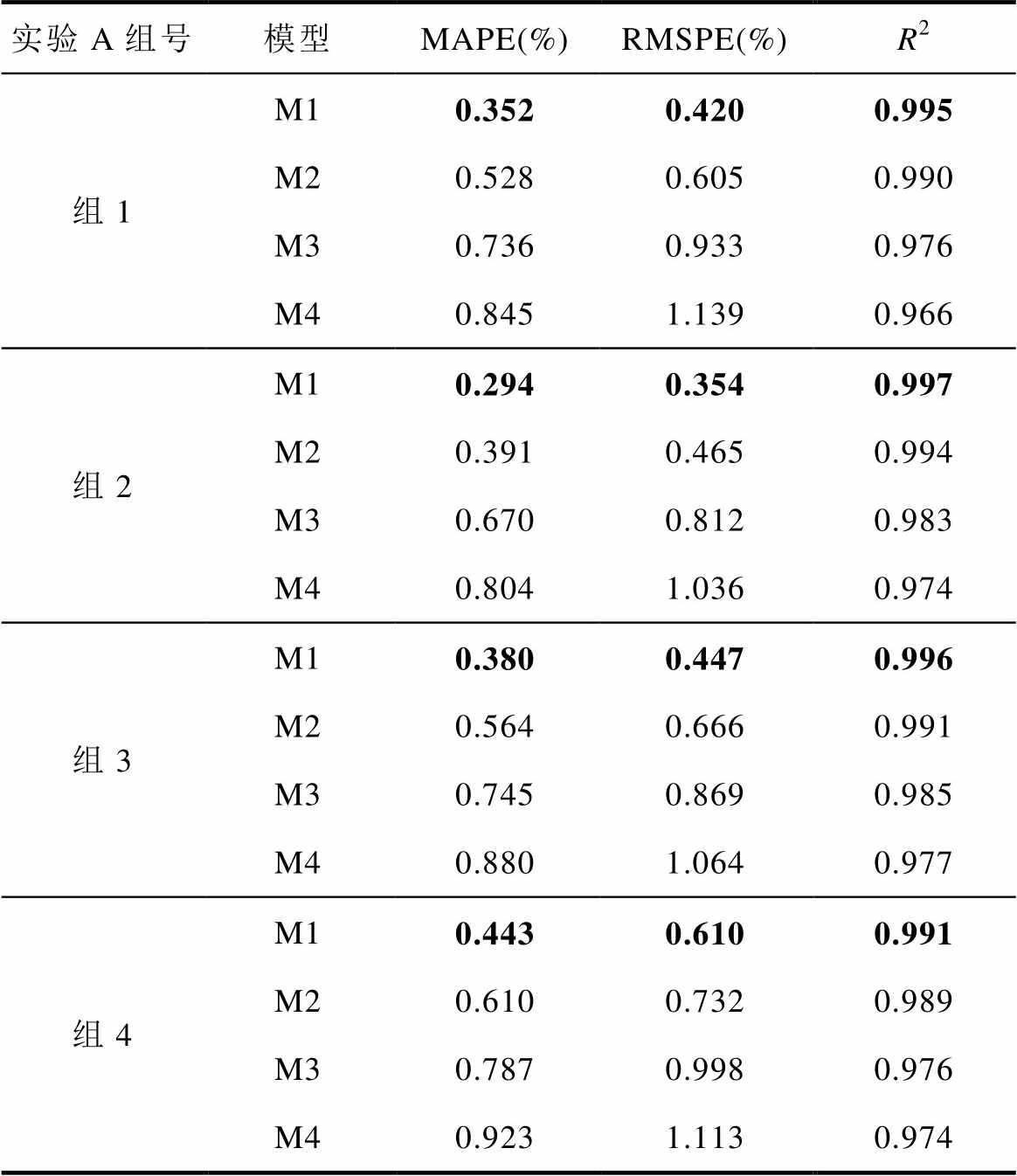
实验A组号模型MAPE(%)RMSPE(%)R2 组1M10.3520.4200.995 M20.5280.6050.990 M30.7360.9330.976 M40.8451.1390.966 组2M10.2940.3540.997 M20.3910.4650.994 M30.6700.8120.983 M40.8041.0360.974 组3M10.3800.4470.996 M20.5640.6660.991 M30.7450.8690.985 M40.8801.0640.977 组4M10.4430.6100.991 M20.6100.7320.989 M30.7870.9980.976 M40.9231.1130.974
实验B的估计结果如图14所示,对应的相对误差如图15所示。从图14可以看出,M1的估计结果能较好地拟合真实的电池容量衰减曲线,且能够在电池拐点后准确地预测容量的变化情况。另外,尽管组4电池的容量波动较大,导致M1的估计效果相比其他组实验表现稍逊,但与组4其他模型相比,其容量波动仍是最小的,说明M1模型仍具有良好的稳定性。从图15可以看出,在前三组实验中,M1模型的相对误差绝对值几乎控制在1%以内。而在波动性较大的组4中,M1模型的相对误差绝对值也能基本保持在2%以内。因此,即使在使用单电池且小样本数据训练的情况下,M1模型的表现依然出色。
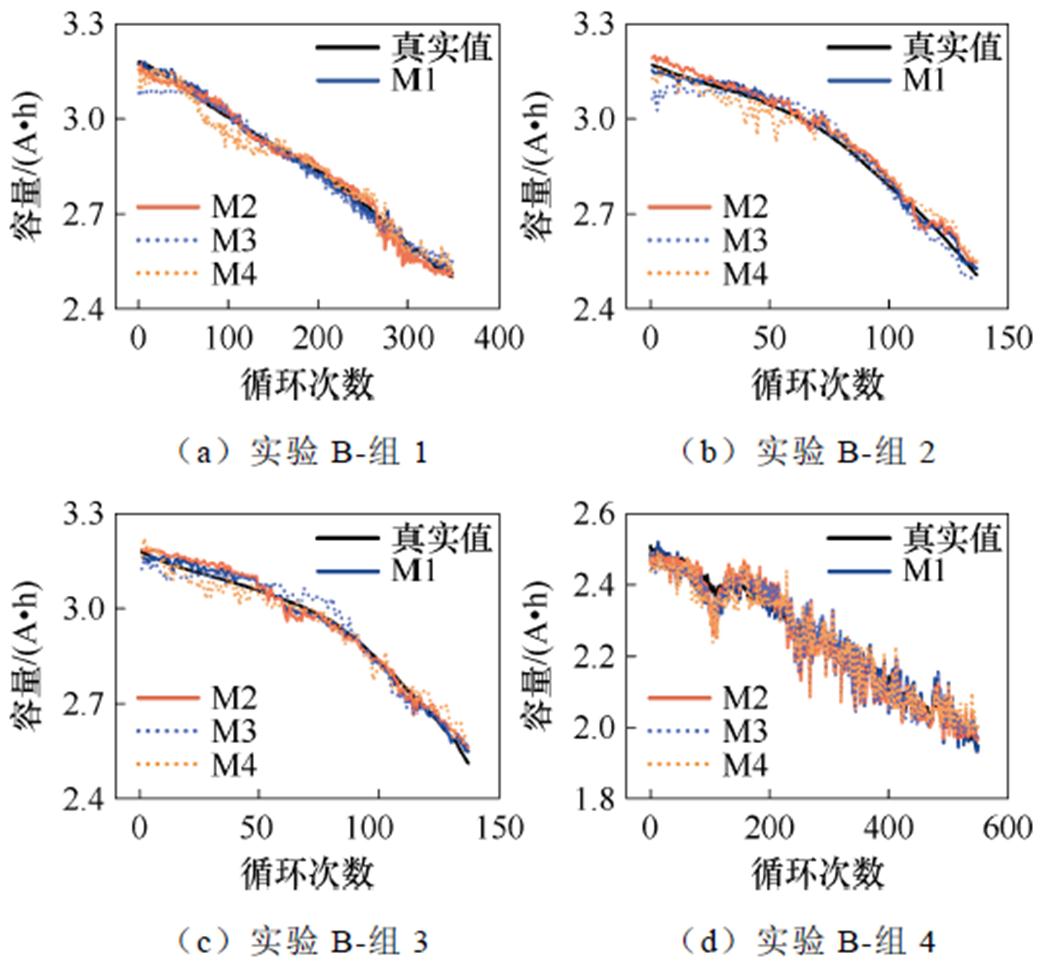
图14 实验B各模型估计结果
Fig.14 Experiment B estimation results for each model
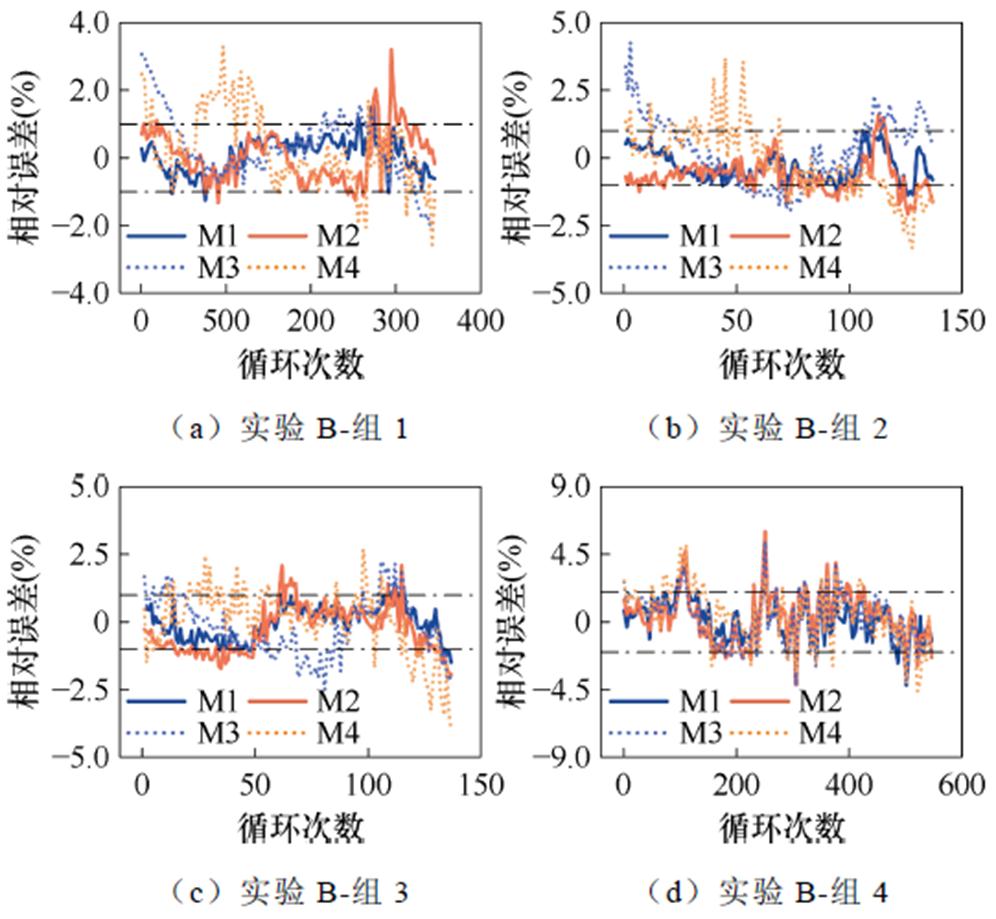
图15 实验B各模型相对误差
Fig.15 Experiment B estimated errors for each model
图16为实验B的相对误差主要分布情况。以组1为例,M4模型的相对误差主要分布在[-0.95%, 1.87%]区间,最大和最小误差绝对值均超过3%。M3模型通过结合LSTM网络,误差分布主要在[-0.88%, 1.58%]区间,区间长度较M4缩小约10%。M2模型的误差分布主要在[-0.81%,1.02%]区间,而M1模型在[-0.69%, 0.72%]区间,主要区间长度较M2缩小约20%,说明通过在RBM隐藏层引入注意力机制显著提升了模型的稳定性与准确性。
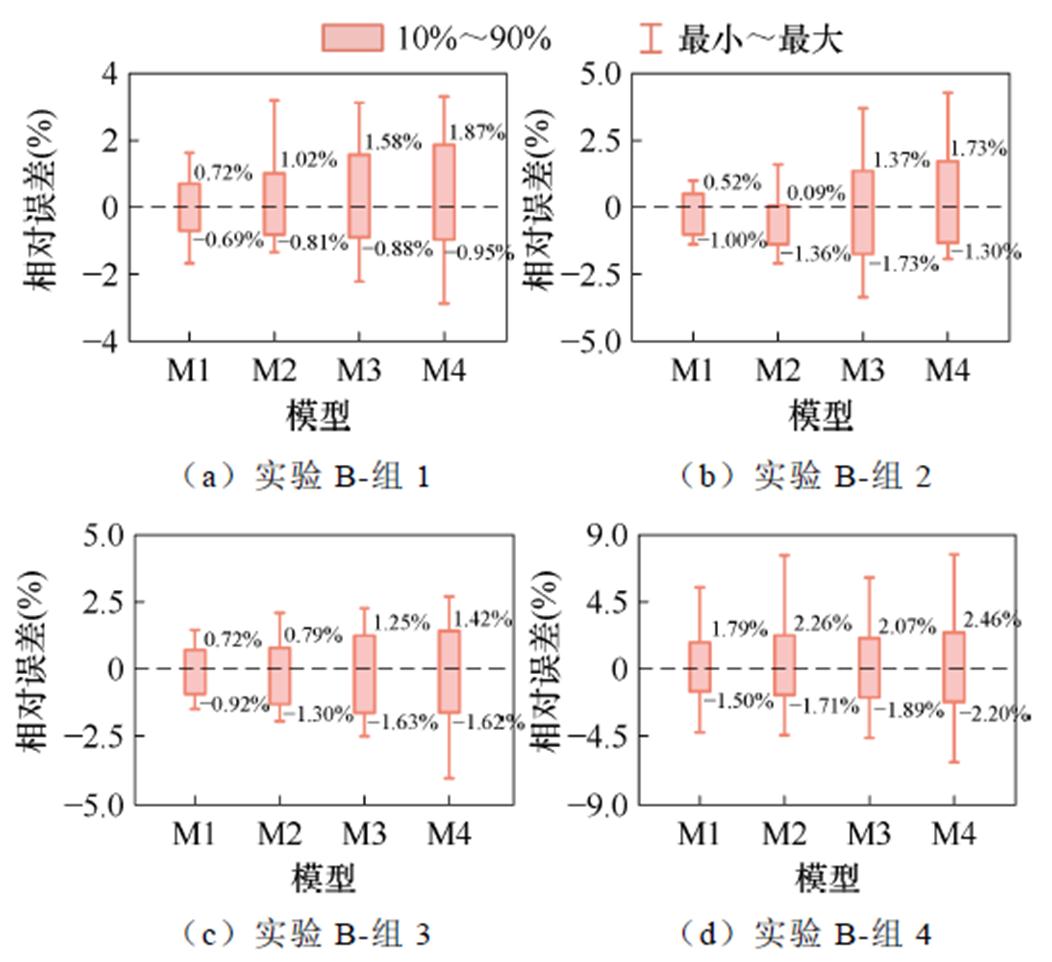
图16 实验B误差分布箱型图
Fig.16 Experiment B error distribution box plot
实验B各模型的评价指标见表8。从中可以看出,对于前三组实验,数据样本量较少,且电池容量衰减过程存在拐点,但M1模型的MAPE仍控制在0.57%以内,RMSPE控制在0.66%以内。而对于组4来说,电池老化过程中出现大量的容量再生点,数据分布更接近电池的实际工作情况,但M1模型的MAPE和RMSPE分别为1.084%和1.382%,估计准确度仍能满足工程需要。
对比表7和表8的数据可以看出,实验B中的MAPE和RMSPE的数值略有增加。原因在于,当使用两个电池数据作为训练集时,电池单体间的差异性被相对削弱,训练出的模型具有更强的泛化能力;而仅使用一个电池数据训练模型时,电池单体间的不一致性会变得较为明显,因此导致模型在新数据上的效果略有下降,但平均误差仍在1.1%以内。
表8 实验B各模型评价指标
Tab.8 Evaluation index of each model in experiment B
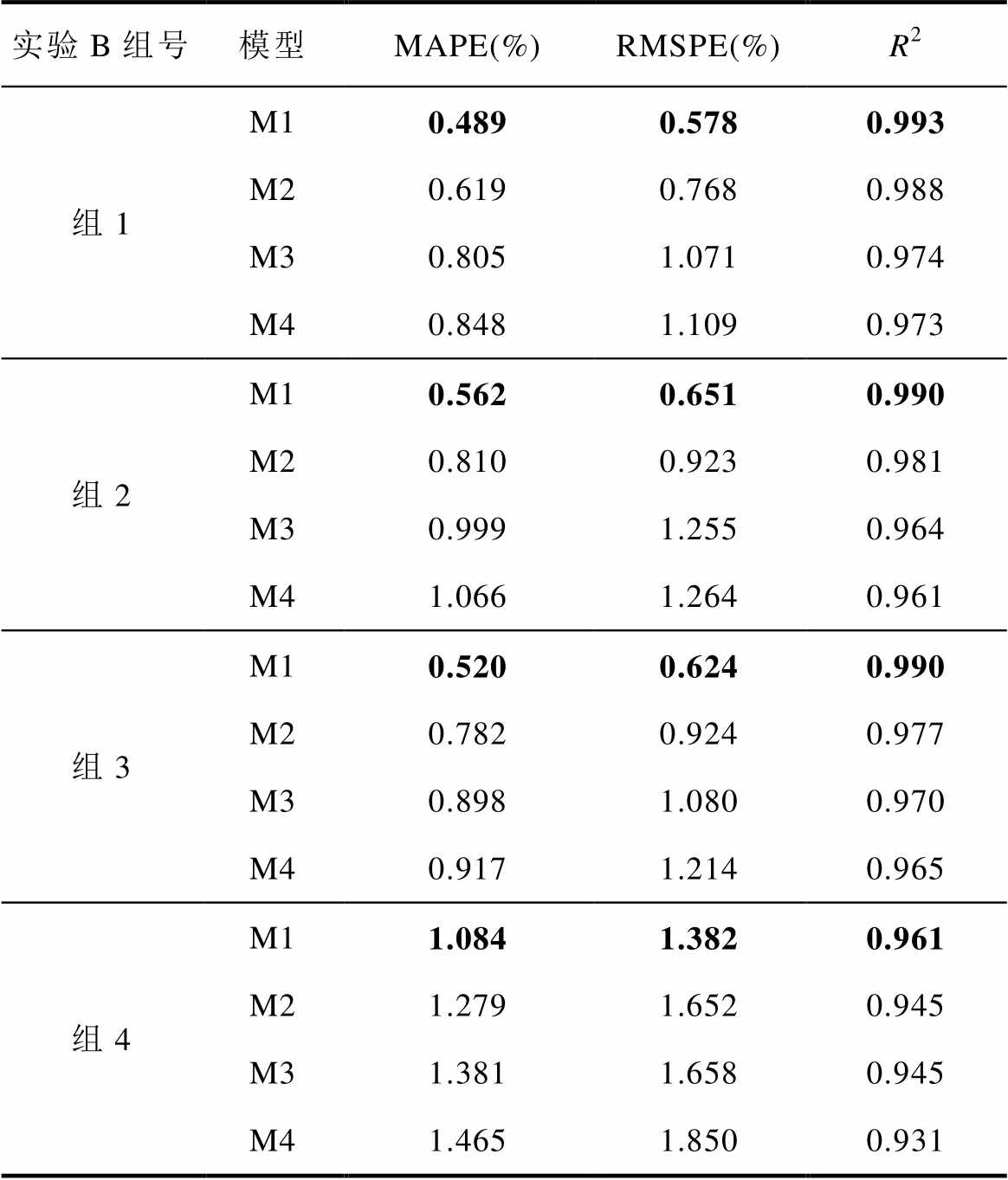
实验B组号模型MAPE(%)RMSPE(%)R2 组1M10.4890.5780.993 M20.6190.7680.988 M30.8051.0710.974 M40.8481.1090.973 组2M10.5620.6510.990 M20.8100.9230.981 M30.9991.2550.964 M41.0661.2640.961 组3M10.5200.6240.990 M20.7820.9240.977 M30.8981.0800.970 M40.9171.2140.965 组4M11.0841.3820.961 M21.2791.6520.945 M31.3811.6580.945 M41.4651.8500.931
实验C的估计结果如图17所示,对应的相对误差如图18所示,各模型的评价指标见表9。从图17和图18分析可知,当使用同一电池的老化数据作为训练和预测集时,四个模型的估计误差在后期均逐渐增加。这主要是因为训练数据集中在电池较新状态时期,此阶段电池的老化模式相对固定;而在老化的后期,由于电池内部副反应的增多,老化模式变得更加复杂,使得仅依赖前期数据训练的模型难以适应后期复杂的电池老化状态,因此导致预测精度下降。然而对于M1模型,其预测结果出现较大偏差的时间点相比其他模型更为延后。从表9中可以直观地看到,M1模型在所有模型中误差指标最小,预测效果最佳。在公开数据集中,M1的MAPE在0.67%以内,RMSPE在0.93%以内;在实验室数据集中,M1模型MAPE和RMSPE分别为1.198%和1.487%。
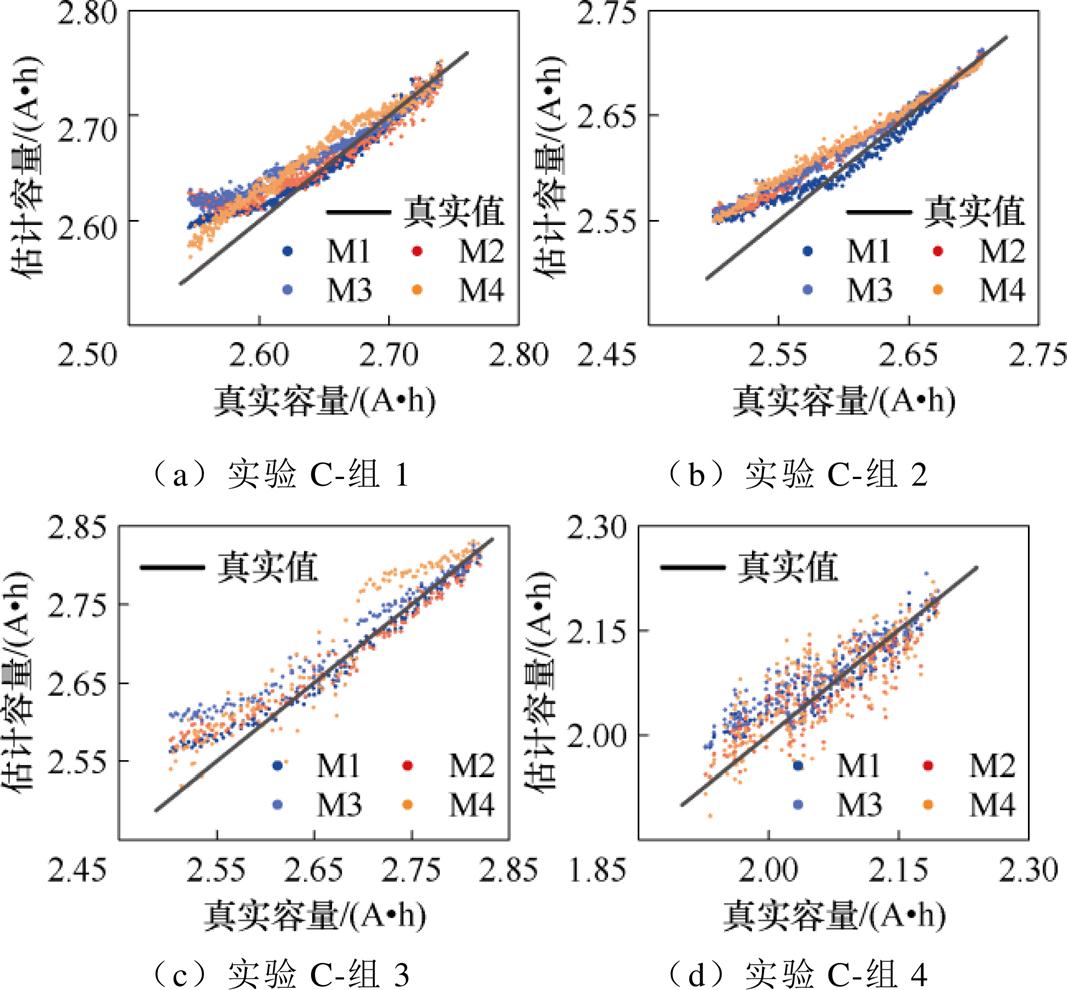
图17 实验C各模型估计结果
Fig.17 Experiment C estimation results for each model
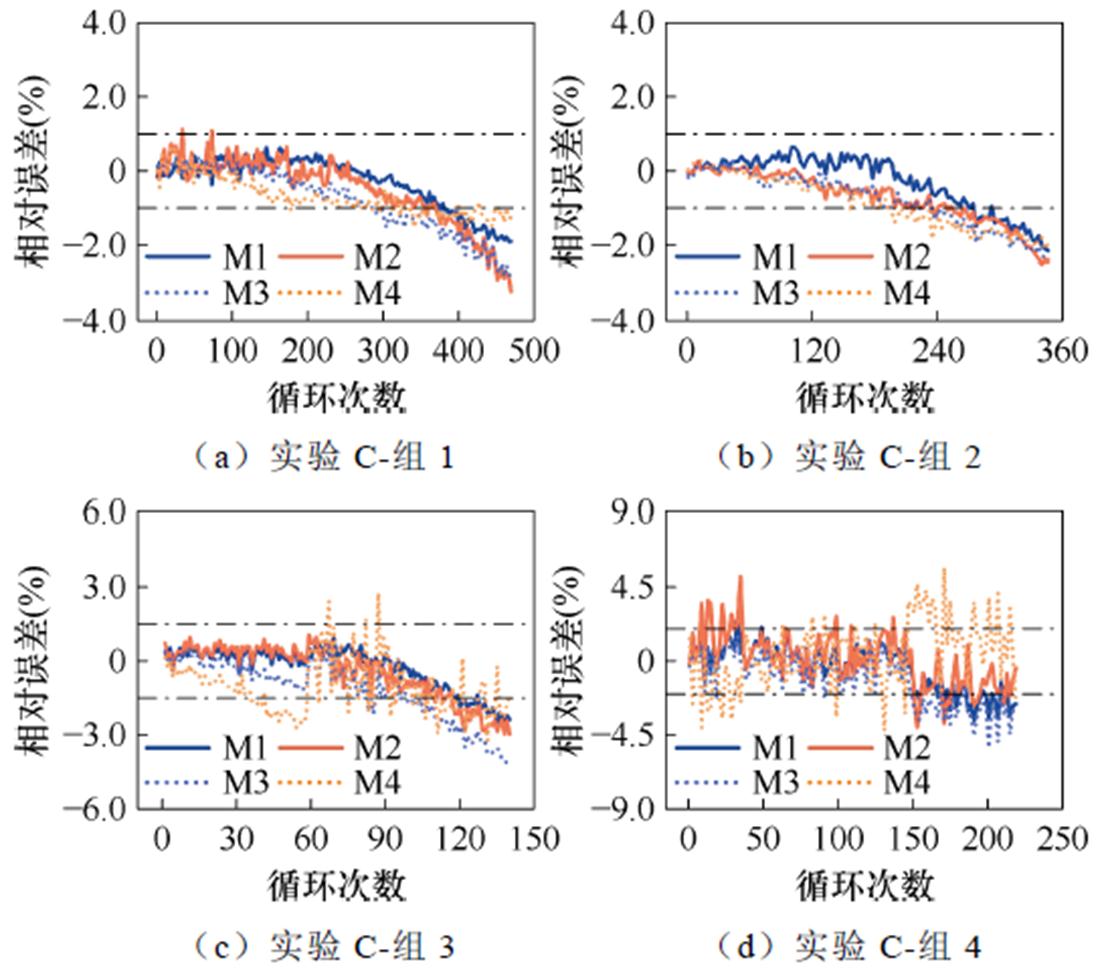
图18 实验C各模型相对误差
Fig.18 Experiment C estimated errors for each model
表9 实验C各模型评价指标
Tab.9 Evaluation index of each model in experiment C
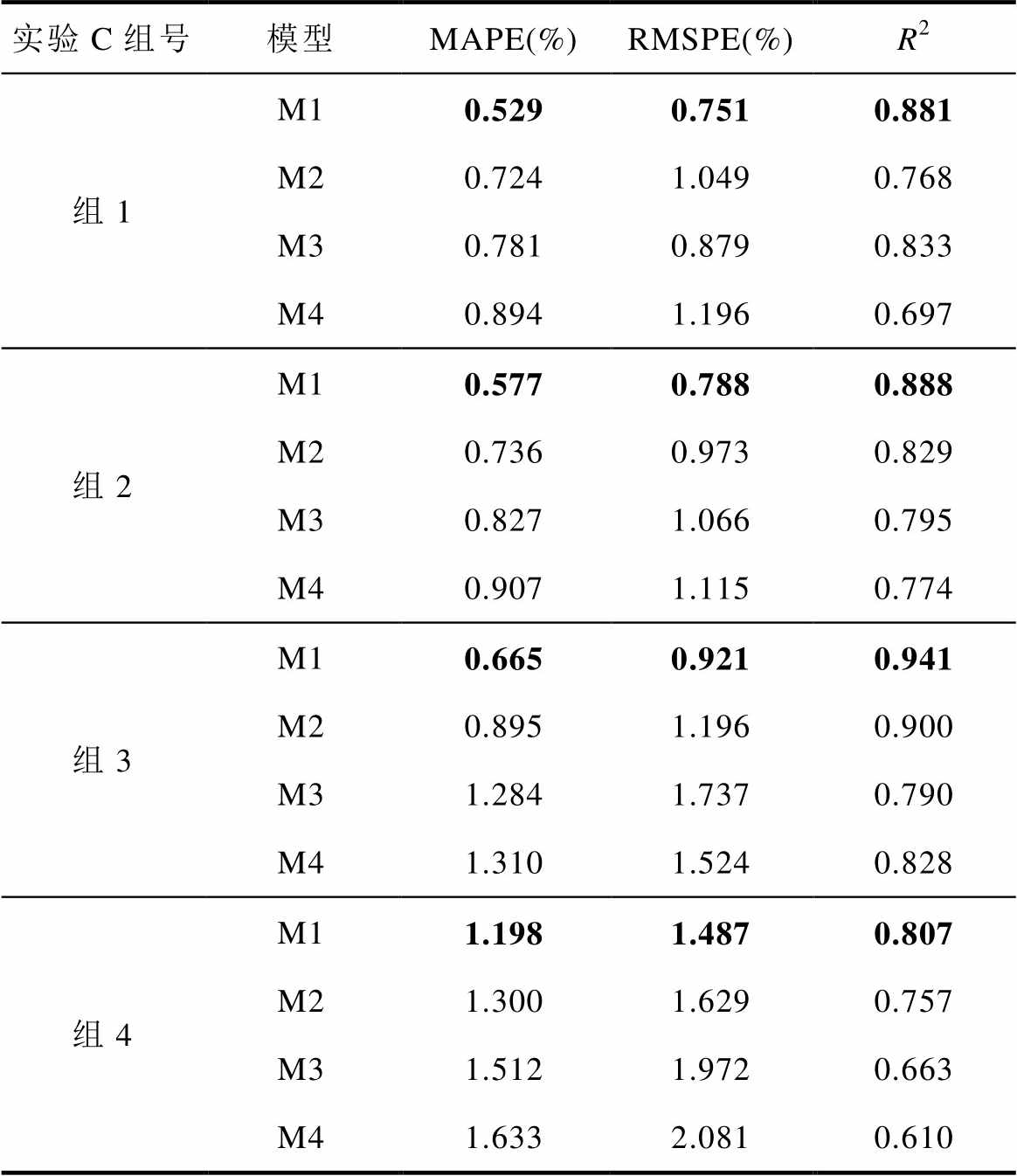
实验C组号模型MAPE(%)RMSPE(%)R2 组1M10.5290.7510.881 M20.7241.0490.768 M30.7810.8790.833 M40.8941.1960.697 组2M10.5770.7880.888 M20.7360.9730.829 M30.8271.0660.795 M40.9071.1150.774 组3M10.6650.9210.941 M20.8951.1960.900 M31.2841.7370.790 M41.3101.5240.828 组4M11.1981.4870.807 M21.3001.6290.757 M31.5121.9720.663 M41.6332.0810.610
实验D的组1估计结果与误差如图19所示,各个模型的评价指标见表10。组2估计结果如图20所示,相对误差分布如图21所示,各个模型的评价指标见表11。
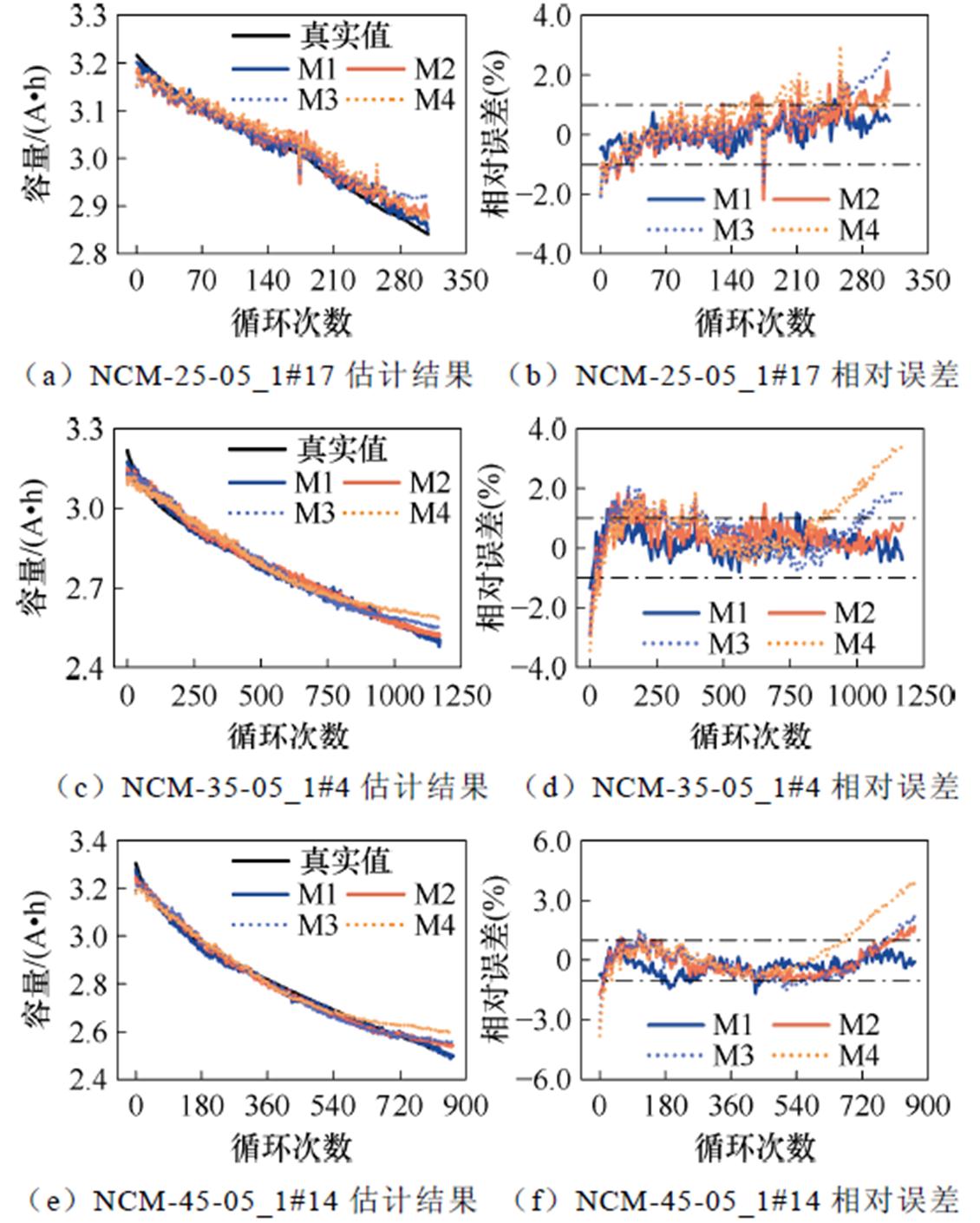
图19 实验D组1不同电池的估计结果与误差
Fig.19 Experiment D group 1 estimation results and errors for different batteries
表10 实验D组1的各模型的评价指标
Tab.10 Evaluation index of each model for experiment D group 1
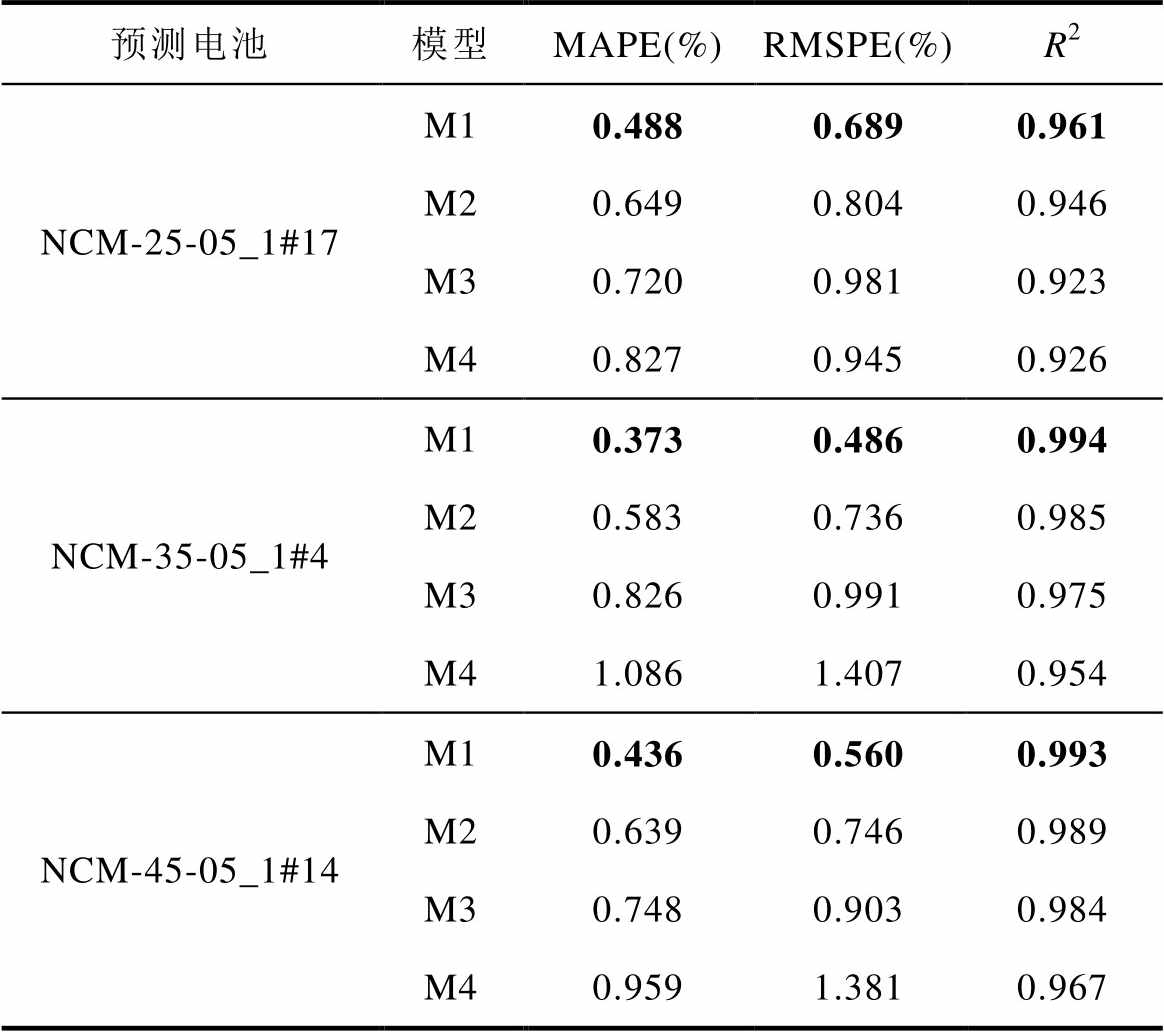
预测电池模型MAPE(%)RMSPE(%)R2 NCM-25-05_1#17M10.4880.6890.961 M20.6490.8040.946 M30.7200.9810.923 M40.8270.9450.926 NCM-35-05_1#4M10.3730.4860.994 M20.5830.7360.985 M30.8260.9910.975 M41.0861.4070.954 NCM-45-05_1#14M10.4360.5600.993 M20.6390.7460.989 M30.7480.9030.984 M40.9591.3810.967
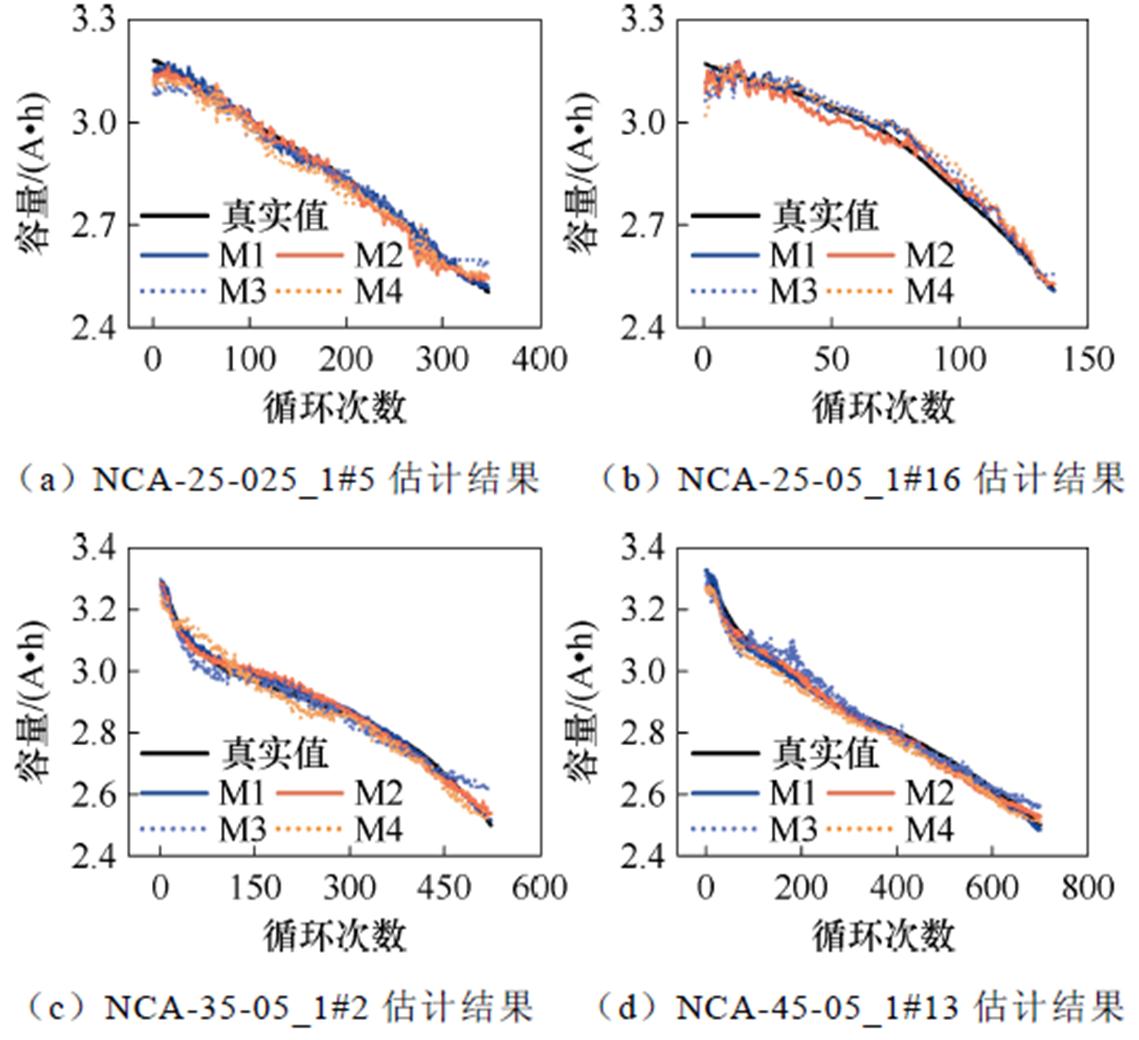
图20 实验D组2不同电池的估计结果
Fig.20 Experiment D group 2 estimation results for different batteries
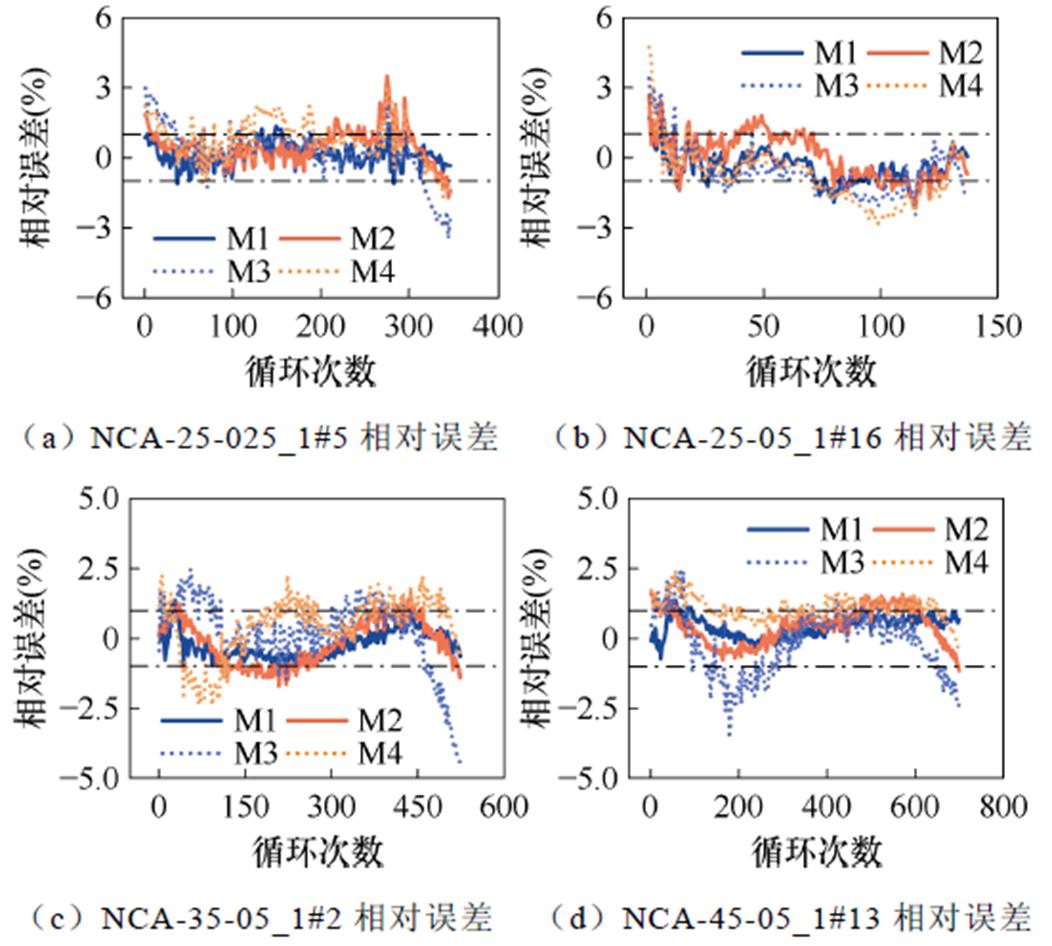
图21 实验D组2不同电池的相对误差
Fig.21 Experiment D group 2 estimation errors for different batteries
从图19~图21的结果可以看出,M1模型在估计效果上表现最佳,其相对误差基本保持在±1%以内,表明模型具有较好的估计性能。此外,相较于其他模型,M1模型的输出结果在电池老化的前期和后期都较为稳定。从表10与表11的评价指标中可以看出,M1模型在各项指标上均表现最优,MAPE与RMSPE分别控制在0.7%和0.9%以内,说明模型能够同时准确估计不同充电条件下的电池容量,具有良好的泛化能力。对于实际使用中的电池而言,由于充电器的参数已固定,充电倍率通常保持不变,但电池所处环境温度会受到天气、季节等外部因素的影响,表现为非周期性的波动。在实验D的两组实验中,充分考虑了电池工作温度的影响,且模型表现良好。因此,本文提出的模型及特征提取方法具有良好的在线应用能力。
表11 实验D组2的各模型的评价指标
Tab.11 Evaluation index of each model for experiment D group 2
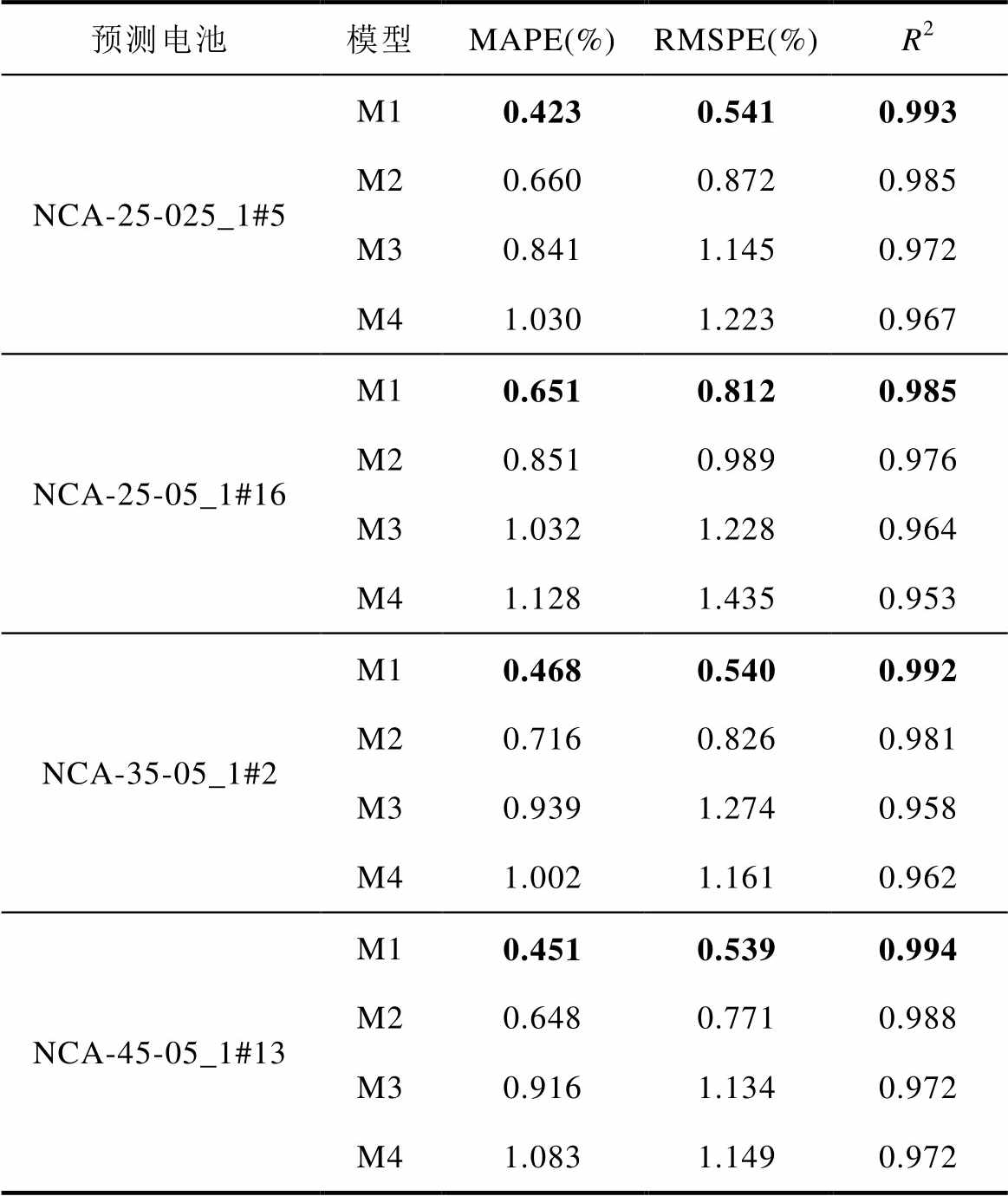
预测电池模型MAPE(%)RMSPE(%)R2 NCA-25-025_1#5M10.4230.5410.993 M20.6600.8720.985 M30.8411.1450.972 M41.0301.2230.967 NCA-25-05_1#16M10.6510.8120.985 M20.8510.9890.976 M31.0321.2280.964 M41.1281.4350.953 NCA-35-05_1#2M10.4680.5400.992 M20.7160.8260.981 M30.9391.2740.958 M41.0021.1610.962 NCA-45-05_1#13M10.4510.5390.994 M20.6480.7710.988 M30.9161.1340.972 M41.0831.1490.972
综合上述四组实验中的M3和M4估计结果可知,在DBN的BP层前添加LSTM网络能够提升模型的性能约5%以上,这是因为RBM层学习到的重要信息是相对固定的,并且信息在层间传递时可能出现重要信息丢失的问题。而对比模型M1、M2与M3的估计结果可知,在每个RBM隐藏层中融合自适应学习通道重要性的SE模块后,极大地增强了模型对输入特征中关键信息的挖掘能力,从而使模型性能提升20%以上。
实验E部分模型估计结果如图22所示,评价指标见表12。从组1~组3的结果可知,IDBN-LSTM的估计效果明显优于其他对比模型。虽然在组4中,IDBN-LSTM的评价指标并非最低(Transformer为最低),但从图22d可以看到,IDBN-LSTM模型的预测曲线在相邻容量预测点间波动较小,表现出比Transformer更好的稳定性。对于实际工作中的电池,其最大容量在短期内通常不会出现剧烈波动,这进一步说明本文提出的模型更符合在线应用的要求。
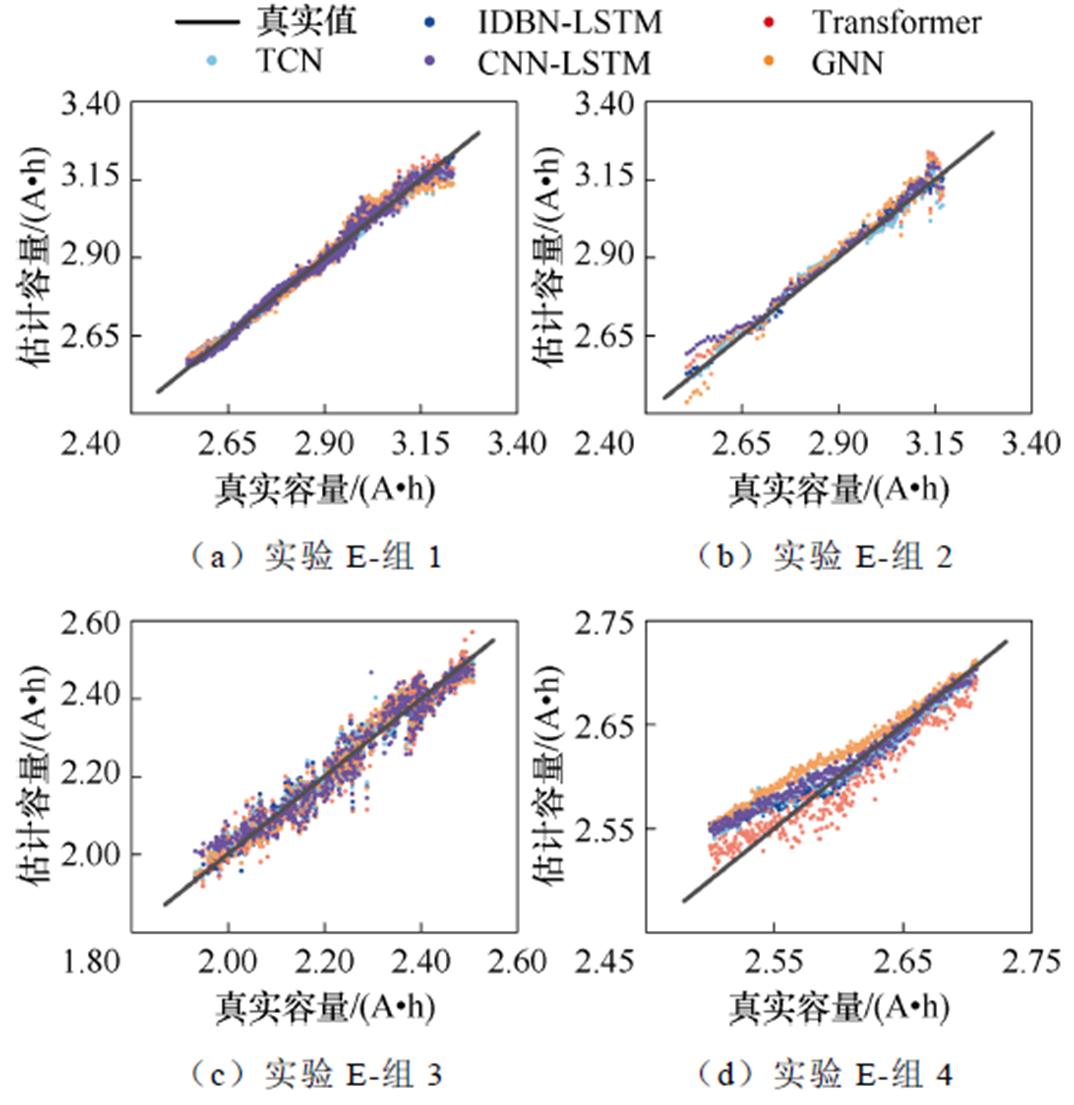
图22 实验E模型估计结果
Fig.22 Experiment E estimation results for each model
表12 实验E各模型评价指标
Tab.12 Evaluation index of each model in experiment E
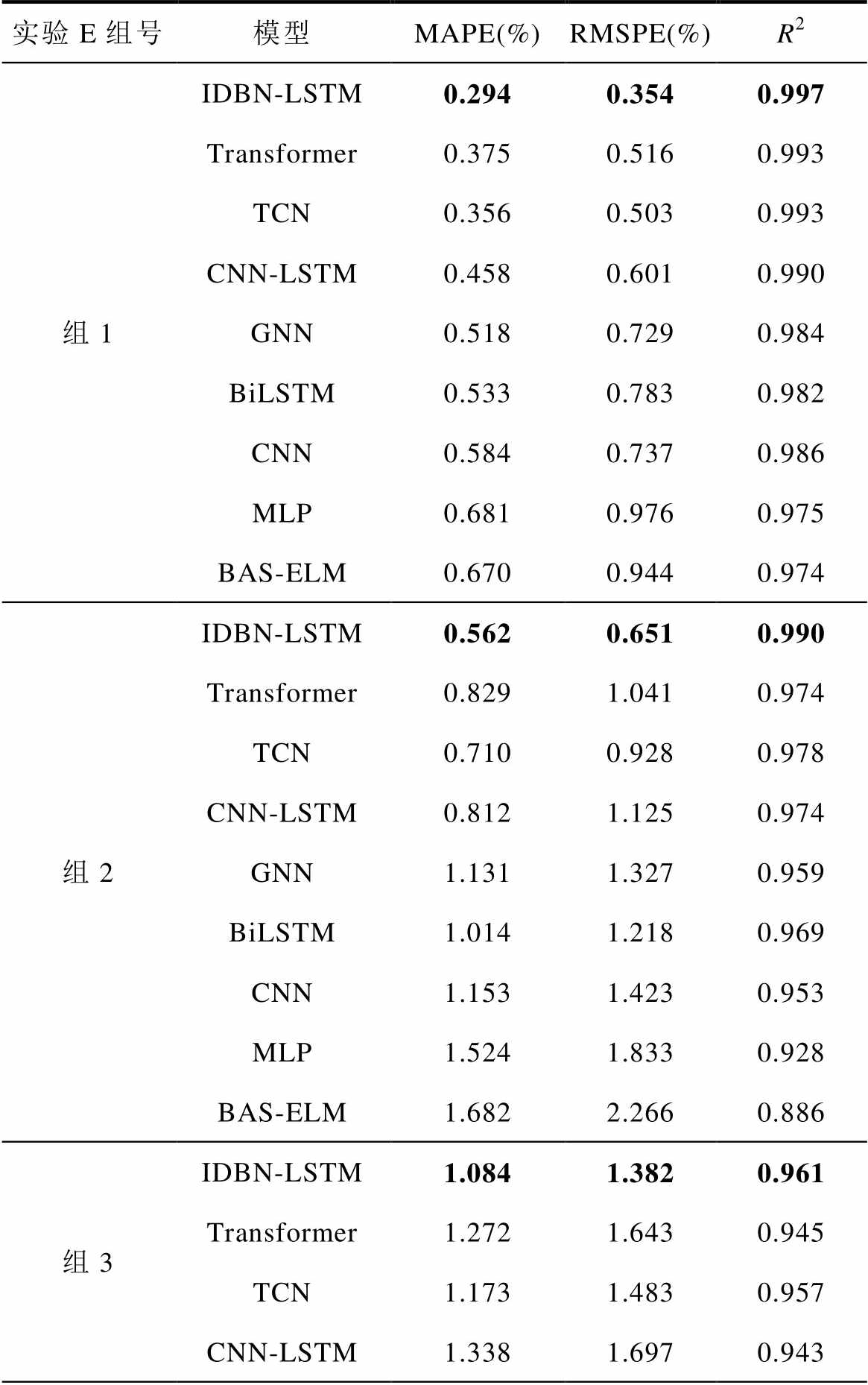
实验E组号模型MAPE(%)RMSPE(%)R2 组1IDBN-LSTM0.2940.3540.997 Transformer0.3750.5160.993 TCN0.3560.5030.993 CNN-LSTM0.4580.6010.990 GNN0.5180.7290.984 BiLSTM0.5330.7830.982 CNN0.5840.7370.986 MLP0.6810.9760.975 BAS-ELM0.6700.9440.974 组2IDBN-LSTM0.5620.6510.990 Transformer0.8291.0410.974 TCN0.7100.9280.978 CNN-LSTM0.8121.1250.974 GNN1.1311.3270.959 BiLSTM1.0141.2180.969 CNN1.1531.4230.953 MLP1.5241.8330.928 BAS-ELM1.6822.2660.886 组3IDBN-LSTM1.0841.3820.961 Transformer1.2721.6430.945 TCN1.1731.4830.957 CNN-LSTM1.3381.6970.943
(续)
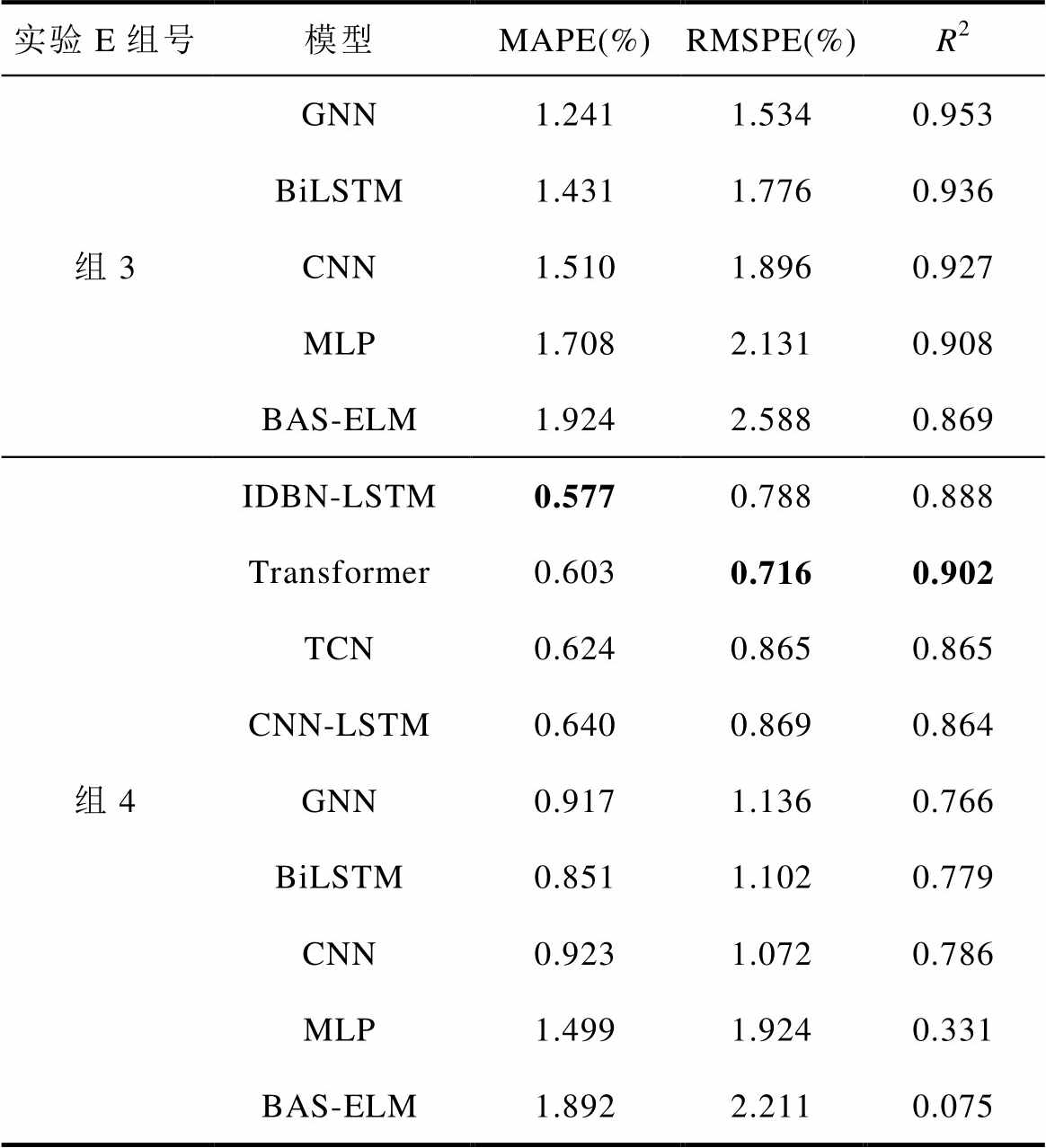
实验E组号模型MAPE(%)RMSPE(%)R2 组3GNN1.2411.5340.953 BiLSTM1.4311.7760.936 CNN1.5101.8960.927 MLP1.7082.1310.908 BAS-ELM1.9242.5880.869 组4IDBN-LSTM0.5770.7880.888 Transformer0.6030.7160.902 TCN0.6240.8650.865 CNN-LSTM0.6400.8690.864 GNN0.9171.1360.766 BiLSTM0.8511.1020.779 CNN0.9231.0720.786 MLP1.4991.9240.331 BAS-ELM1.8922.2110.075
不同输入特征下容量估计结果与误差如图23所示,评价指标见表13。通过双去极化过程的特征提取实现了恒压电流特征与弛豫电压特征的优势互补,通过相关性分析的初步筛选与主成分分析的融合降维之后,实现了对输入数据的全面精炼与特征间的关联解耦,从而使模型更容易捕捉特征与容量间的映射关系。从表13中可以看出,本文提出的特征处理方法能够使估计精度提高约35%,验证了本文在特征工程上所做工作的有效性。
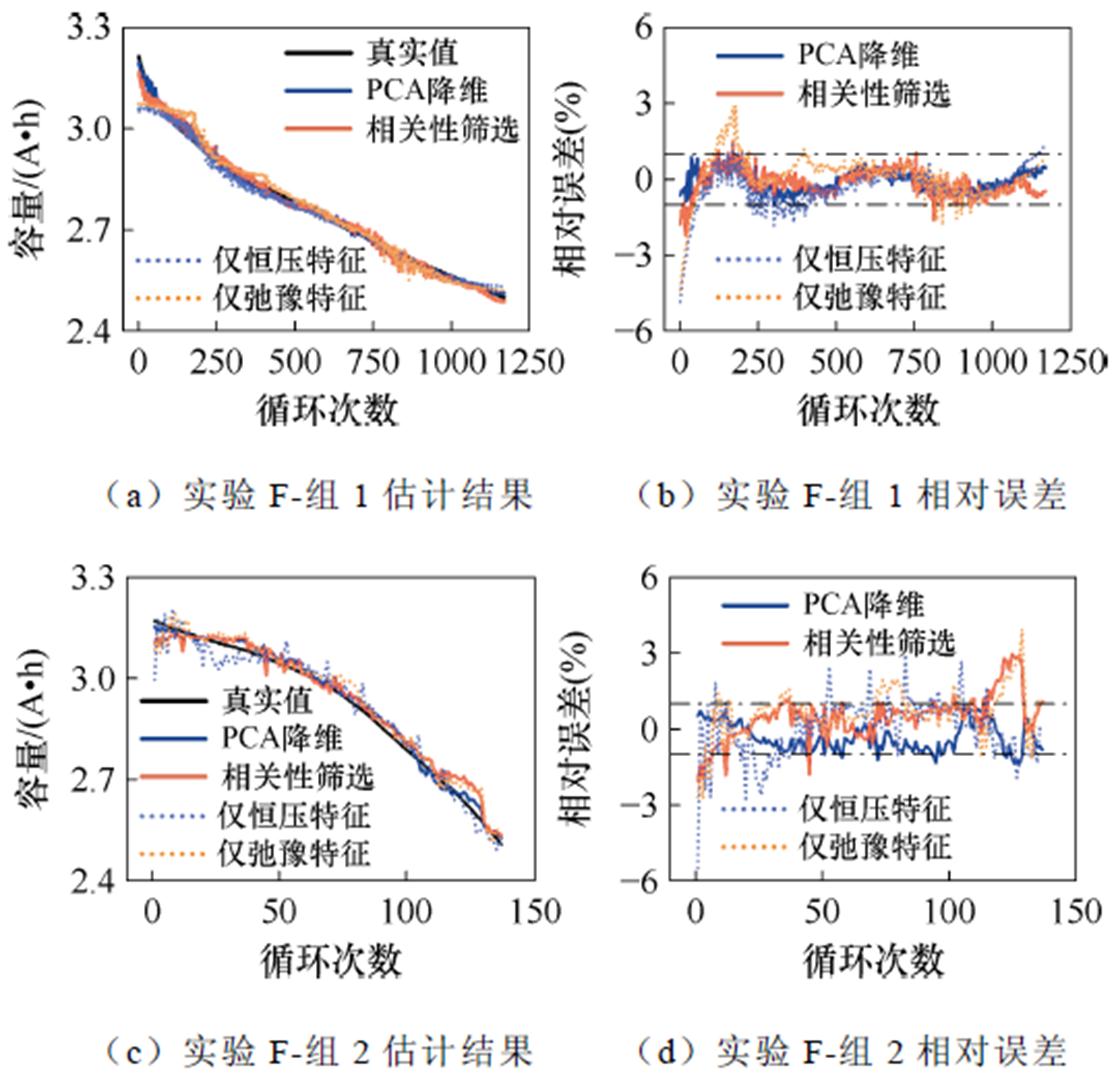
图23 实验F估计结果与误差
fig.23 Experiment F estimation results and errors
表13 不同输入特征下模型的评价指标
Tab.13 Evaluation metrics for models with different input characteristics
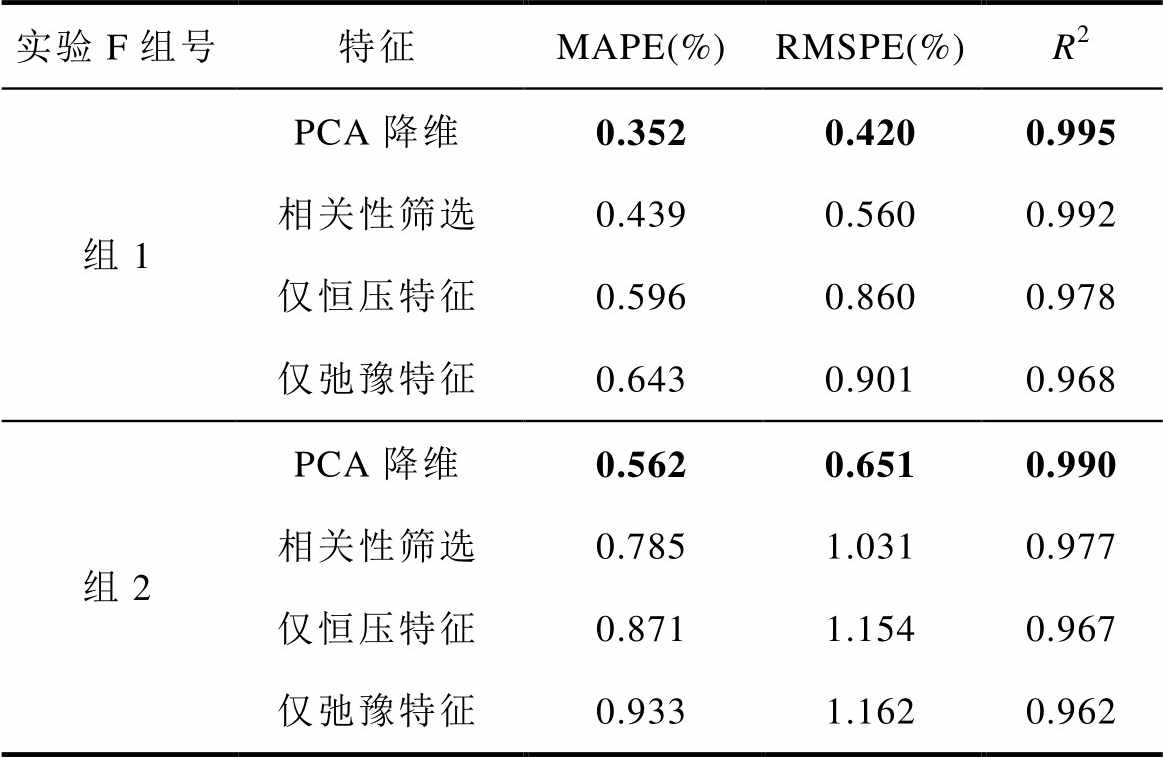
实验F组号特征MAPE(%)RMSPE(%)R2 组1PCA降维0.3520.4200.995 相关性筛选0.4390.5600.992 仅恒压特征0.5960.8600.978 仅弛豫特征0.6430.9010.968 组2PCA降维0.5620.6510.990 相关性筛选0.7851.0310.977 仅恒压特征0.8711.1540.967 仅弛豫特征0.9331.1620.962
本文针对锂离子电池容量估计中特征实用性差与模型泛化性低等问题,提出了一种结合极化衰减特征与通道关注混合神经网络的锂离子电池容量在线估计方法。在此基础上,利用多种工况、多种材料的电池数据与不同输入特征、不同预测模型进行了比较和测试,具体结论如下:
1)利用恒压电流与弛豫电压衰减的去极化特性,提取了不受充电起点影响的多维实用特征,并对其进行相关性分析与PCA处理。结果表明,极化衰减特征提取容易且满足在线应用要求,同时在经过特征预处理后,相关系数均高于0.8,且相比于仅单一过程特征,估计精度提高约35%。
2)构建了集成DBN、LSTM和SE机制的混合神经网络。结果表明,LSTM因其强大的时间序列处理能力能够提升DBN的预测性能,SE自适应通道注意力机制能够增强DBN的高阶信息挖掘能力。相比之下,SE的通道关注能力对模型性能的贡献更大,且效果稳定,但LSTM网络同样不可或缺,两者协同作用,使模型性能提升25%以上。
3)从多个角度出发,全面进行了实验验证。实验结果表明,本文提出方法的各种评价指标均呈现最优,且在数据较少、质量较差的情况下,MAPE、RMSPE分别保持在1.2%、1.5%以内,证明了本文提出方法的准确性与有效性。
参考文献
[1] Zhang Lei, Hu Xiaosong, Wang Zhenpo, et al. Hybrid electrochemical energy storage systems: an overview for smart grid and electrified vehicle applications[J]. Renewable and Sustainable Energy Reviews, 2021, 139: 110581.
[2] 衣思彤, 刘雅浓, 马耀浥, 等. 基于贝叶斯优化-卷积神经网络-双向长短期记忆神经网络的锂电池健康状态评估[J]. 电气技术, 2024, 25(5): 1-10, 21.
Yi Sitong, Liu Yanong, Ma Yaoyi, et al. State of health assessment of lithium battery based on Bayesian optimization-convolution neural network- bi-directional long short term memory neural network[J]. Electrical Engineering, 2024, 25(5): 1-10, 21.
[3] 李英顺, 阚宏达, 郭占男, 等. 基于数据预处理和VMD-LSTM-GPR的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(10): 3244-3258.
Li Yingshun, Kan Hongda, Guo Zhannan, et al. Prediction of remaining useful life of lithium-ion battery based on data preprocessing and VMD- LSTM-GPR[J]. Transactions of China Electrotech- nical Society, 2024, 39(10): 3244-3258.
[4] 戴俊彦, 夏明超, 陈奇芳. 基于双重注意力机制的电池SOH估计和RUL预测编解码模型[J]. 电力系统自动化, 2023, 47(6): 168-177.
Dai Junyan, Xia Mingchao, Chen Qifang. Encoding and decoding model of state of health estimation and remaining useful life prediction for batteries based on dual-stage attention mechanism[J]. Automation of Electric Power Systems, 2023, 47(6): 168-177.
[5] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[6] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[7] Amir S, Gulzar M, Tarar M O, et al. Dynamic equivalent circuit model to estimate state-of-health of lithium-ion batteries[J]. IEEE Access, 2022, 10: 18279-18288.
[8] Li Chaofan, Yang Lin, Li Qiang, et al. SOH estimation method for lithium-ion batteries based on an improved equivalent circuit model via elec- trochemical impedance spectroscopy[J]. Journal of Energy Storage, 2024, 86: 111167.
[9] Xiong Rui, Li Linlin, Li Zhirun, et al. An electro- chemical model based degradation state identification method of Lithium-ion battery for all-climate electric vehicles application[J]. Applied Energy, 2018, 219: 264-275.
[10] Allam A, Onori S. Online capacity estimation for lithium-ion battery cells via an electrochemical model-based adaptive interconnected observer[J]. IEEE Transactions on Control Systems Technology, 2021, 29(4): 1636-1651.
[11] 王宁, 陈志强, 刘明义, 等. 基于模糊综合评价的锂离子电池健康状态评估[J]. 发电技术, 2022, 43(5): 784-791.
Wang Ning, Chen Zhiqiang, Liu Mingyi, et al. Health status assessment of lithium-ion battery based on fuzzy comprehensive evaluation[J]. Power Generation Technology, 2022, 43(5): 784-791.
[12] 张若可, 郭永芳, 余湘媛, 等. 基于数据驱动的锂离子电池RUL预测综述[J]. 电源学报, 2023, 21(5): 182-190.
Zhang Ruoke, Guo Yongfang, Yu Xiangyuan, et al. Review of data-driven RUL prediction for lithium-ion batteries[J]. Journal of Power Supply, 2023, 21(5): 182-190.
[13] 周才杰, 汪玉洁, 李凯铨, 等. 基于灰色关联度分析-长短期记忆神经网络的锂离子电池健康状态估计[J]. 电工技术学报, 2022, 37(23): 6065-6073.
Zhou Caijie, Wang Yujie, Li Kaiquan, et al. State of health estimation for lithium-ion battery based on gray correlation analysis and long short-term memory neural network[J]. Transactions of China Electro- technical Society, 2022, 37(23): 6065-6073.
[14] Park K, Choi Y, Choi W J, et al. LSTM-based battery remaining useful life prediction with multi-channel charging profiles[J]. IEEE Access, 2020, 8: 20786- 20798.
[15] Xu Jiangtao, Qu Jie, Xu Haitao. Capacity estimation of lithium-ion batteries with automatic feature extraction and graph-enhanced LSTM[J]. Journal of Energy Storage, 2024, 85: 111131.
[16] Sesidhar D V S R, Badachi C, Green R C II. A review on data-driven SOC estimation with Li-Ion batteries: Implementation methods & future aspirations[J]. Journal of Energy Storage, 2023, 72: 108420.
[17] Liu Datong, Li Lü, Song Yuchen, et al. Hybrid state of charge estimation for lithium-ion battery under dynamic operating conditions[J]. International Journal of Electrical Power & Energy Systems, 2019, 110: 48-61.
[18] Cao Mengda, Zhang Tao, Wang Jia, et al. A deep belief network approach to remaining capacity estimation for lithium-ion batteries based on charging process features[J]. Journal of Energy Storage, 2022, 48: 103825.
[19] Wang Yujie, Li Kaiquan, Peng Pei, et al. Health diagnosis for lithium-ion battery by combining partial incremental capacity and deep belief network during insufficient discharge profile[J]. IEEE Transactions on Industrial Electronics, 2023, 70(11): 11242-11250.
[20] 史永胜, 任嘉睿, 李锦, 等. 基于DeepAR与特征选择的锂离子电池在线状态估计[J]. 电源学报, 2023, 21(2): 163-171.
Shi Yongsheng, Ren Jiarui, Li Jin, et al. Online state estimation of lithium-ion batteries based on DeepAR and feature selection[J]. Journal of Power Supply, 2023, 21(2): 163-171.
[21] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342.
Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium-ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
[22] Zhang Yingda, Ma Hongyan, Wang Shuai, et al. Indirect prediction of remaining useful life for lithium-ion batteries based on improved multiple kernel extreme learning machine[J]. Journal of Energy Storage, 2023, 64: 107181.
[23] Tang Ruoli, Zhang Peng, Ning Siwen, et al. Prediction of battery SOH and RUL based on cooperative characteristics in voltage-temperature- time dimensions[J]. Journal of the Electrochemical Society, 2023, 170(6): 060535.
[24] Lin Chuanping, Xu Jun, Shi Mingjie, et al. Constant current charging time based fast state-of-health estimation for lithium-ion batteries[J]. Energy, 2022, 247: 123556.
[25] Guo Peiyao, Cheng Ze, Yang Lei. A data-driven remaining capacity estimation approach for lithium- ion batteries based on charging health feature extraction[J]. Journal of Power Sources, 2019, 412: 442-450.
[26] Li Xiaoyu, Wang Zhenpo, Zhang Lei, et al. State- of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis[J]. Journal of Power Sources, 2019, 410: 106-114.
[27] Jiang Bo, Dai Haifeng, Wei Xuezhe. Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging con- dition[J]. Applied Energy, 2020, 269: 115074.
[28] Wang Zhenpo, Yuan Changgui, Li Xiaoyu. Lithium battery state-of-health estimation via differential thermal voltammetry with Gaussian process regression[J]. IEEE Transactions on Transportation Electrification, 2021, 7(1): 16-25.
[29] Zhu Jiangong, Wang Yixiu, Huang Yuan, et al. Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation[J]. Nature Communications, 2022, 13(1): 2261.
[30] Wang Wentao, Yang Kaiyi, Zhang Lisheng, et al. An end-cloud collaboration approach for online state- of-health estimation of lithium-ion batteries based on multi-feature and transformer[J]. Journal of Power Sources, 2024, 608: 234669.
[31] Zhang Hao, Gao Jingyi, Kang Le, et al. State of health estimation of lithium-ion batteries based on modified flower pollination algorithm-temporal convolutional network[J]. Energy, 2023, 283: 128742.
[32] Zhou K Q, Qin Yan, Yuen C. Graph neural network- based lithium-ion battery state of health estimation using partial discharging curve[J]. Journal of Energy Storage, 2024, 100: 113502.
[33] Jiao Zhipeng, Ma Jian, Zhao Xuan, et al. A methodo- logy for state of health estimation of battery using short-time working condition aging data[J]. Journal of Energy Storage, 2024, 82: 110480.
[34] Li Kaiquan, Wang Yujie, Chen Zonghai. A com- parative study of battery state-of-health estimation based on empirical mode decomposition and neural network[J]. Journal of Energy Storage, 2022, 54: 105333.
[35] Zhang Shaowen, Zhu Haiping, Wu Jun, et al. Voltage relaxation-based state-of-health estimation of lithium- ion batteries using convolutional neural networks and transfer learning[J]. Journal of Energy Storage, 2023, 73: 108579.
[36] Hou Xiaokang, Guo Xiaodong, Yuan Yupeng, et al. The state of health prediction of Li-ion batteries based on an improved extreme learning machine[J]. Journal of Energy Storage, 2023, 70: 108044.
Online Estimation of Lithium-Ion Battery Capacity Based on Polarization Decay Feature and Hybrid Neural Network with Channel Attention
Abstract The capacity of a lithium-ion battery is a key indicator of the state of health (SOH) and remaining useful life (RUL) of the battery, as well as the state of charge (SOC) and equalization management within the battery pack. Therefore, accurate estimation of battery capacity is crucial for the battery management system (BMS). However, in practice, the battery capacity often cannot be measured directly, and needs to be estimated indirectly by combining relevant methods and accessible parameters. Therefore, this paper extracts multidimensional features reflecting the polarization strength of the battery based on a data-driven approach, and constructs a hybrid neural network with adaptive channel focusing capability, so as to realize online accurate estimation of lithium-ion battery capacity.
First, considering that the microscopic manifestation of battery capacity decay is the increase of battery polarization internal resistance, and the constant voltage charging and voltage relaxation processes are directly related to the battery depolarization reaction, the depolarization characteristics of constant voltage current and relaxation voltage decay are utilized to extract the multidimensional practical features that are not affected by the charging starting point. Data preprocessing of the original multidimensional features is performed by correlation coefficient method and principal component analysis (PCA) to complete the screening and dimensionality reduction and fusion of the features, and finally four indirect features are identified as model inputs. Next, the squeeze-excitation (SE) module is integrated into each hidden layer of the deep belief network (DBN) to construct an enhanced DBN network with channel attention capability, and the higher-order feature information extracted from the DBN is used to perform time-series prediction using a long- and short-term memory (LSTM) network to capture the mapping relationship between the battery capacity and the input features. Finally, six sets of simulation experiments are designed for different data structures, prediction models and input features to verify the effectiveness and accuracy of the method proposed in this paper in all aspects.
The simulation results show that the method proposed in this paper can effectively improve the accuracy of capacity estimation. Under different training and prediction data structures, the mean absolute percentage error (MAPE) and root mean square percentage error (RMSPE) of capacity estimation are controlled within 1.2% and 1.5%, respectively, and the model has the ability to simultaneously estimate the battery capacity under different charging conditions with good generalization. For different prediction models, the fusion of DBN network, SE mechanism and LSTM network effectively improves the accuracy of capacity estimation, especially the SE module contributes more significantly to the stability and accuracy of the model, but the LSTM network is equally indispensable, and the synergistic effect of both of them improves the performance of the model by more than 25%. Meanwhile, compared with other advanced algorithms, the model proposed in this paper demonstrates better stability while ensuring higher estimation accuracy, which verifies the effectiveness of the model improvement strategy in this paper. Compared with the original input features, the capacity estimation accuracy is improved by about 30% by combining the complementary features of constant pressure and relaxation dual depolarization processes and data preprocessing methods, which validates the effectiveness of the work done on feature engineering in this paper.
Keywords:Lithium-ion battery, capacity estimation online, polarization decay feature, hybrid neural network, channel attention
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.241344
国家自然科学基金项目(52307238)、省部共建电工装备可靠性与智能化国家重点实验室优秀青年创新基金项目(EERI_OY2023007)、河北省省级科技计划(225676163GH)、河北省燕赵青年科学家项目(E2024202109)和天津市重点项目(22JCZDJC00620)资助。
收稿日期 2024-07-28
改稿日期 2024-09-28
徐志成 男,1995年生,副教授,硕士生导师,研究方向为锂离子电池高精建模与状态感知、储能系统多源监测与安全管理等。
E-mail: xzc@hebut.edu.cn
张 献 男,1983年生,教授,博士生导师,研究方向为无线电能传输技术、工程电磁场与磁技术、储能系统安全管理等。
E-mail: zhangxian@hebut.edu.cn(通信作者)
(编辑 郭丽军)