
图1 100 A×h磷酸铁锂电池
Fig.1 100 A×h lithium iron phosphate battery
摘要 为提高储能用锂离子电池组在不同环境温度及电池老化状态下的荷电状态(SOC)估算精度,提出一种考虑温度及老化的储能用锂离子电池组SOC估算算法。利用带外源性输入的非线性自回归模型(NARX)神经网络来代替传统二阶RC等效电路模型中的RC回路,根据不同温度、不同老化状态下的实验数据对模型进行训练,进而建立考虑温度和老化影响的电池模型。为解决电池组SOC估算问题,电池组模型选择均值差异模型,通过自适应无迹卡尔曼滤波(AUKF)算法分别计算均值及差异模型SOC,并通过模糊控制计算SOC融合权值,实现电池组SOC融合及估算。最后搭建硬件在环仿真平台,在不同工况下将所提算法与扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)算法进行对比,结果表明所提算法估算精确度更高、鲁棒性更好。
关键词:电池组荷电状态(SOC)估算带外源性输入的非线性自回归模型(NARX)神经网络 均值差异模型 自适应无迹卡尔曼(AUKF) 模糊控制
储能电池因其容量大、低碳、环保等优点在储能系统中发挥着越来越重要的作用[1]。但在实际应用中,储能电池时常面临着过充、过放、电池寿命短等问题,因此储能电池荷电状态(State of Charge,SOC)的精准估算显得异常重要,也因此成为电池管理系统(Battery Manegement System, BMS)研究重点之一[2]。
目前,国内外储能电池SOC估算方法大致可分为三类:传统实验法、数据驱动法、模型法[3]。传统实验法主要包括安时积分法、开路电压法[4]。安时积分法[5]只需要对电流进行时间积分便可实现SOC估计,但估算精确度很大程度上依赖SOC初始值,且会产生累计误差。开路电压法[6]只需要确定电池开路电压(Open Circuit Voltage,OCV)与SOC的关系即可确定电池SOC。虽然开路电压法操作简单,但其不能够在线测量,测量时必须静置足够长时间,若静置时间不足,就无法得到准确的SOC值,因此不适用于运行状态的SOC估算。基于数据驱动的方法包括神经网络法、深度学习法、支持向量机等。此类方法不要求了解电池内部反应机理,但必须使用大量的数据处理来做训练样本,运算量大,对计算机处理器能力有一定要求[7]。模型法有电化学模型、等效电路模型[8]等。电化学模型虽然可以较为真实地反映电池内部变化机理,物理特征明确,估算精度高,但模型复杂,某些参数需要进行标定才能确定,计算量大[9]。等效电路模型[10]通过电压、电阻、电容等电路元器件构成,需要辨识的参数少,计算方便,具有良好的实时性,经常结合卡尔曼滤波法一起使用,具有很强的鲁棒性。
由于电池运行工况为非线性工况,传统卡尔曼滤波适用于线性系统,因此不能直接用于储能电池SOC估算[11]。许多研究人员对此进行了改进,如S. Afshar等[12]使用扩展卡尔曼滤波(Extended Kalman Filter, EKF)将非线性系统通过泰勒级数展开转变为线性系统,但忽略了二阶及以上的高阶项,因此在有高阶次系统时,算法精度低,且因需要计算雅可比矩阵,计算较为复杂;钱伟、王浩宇等[13]使用改进滑模观测器(Improved Sliding Mode Observer, ISMO)-自适应扩展卡尔曼滤波(Adaptive Extended Kalman Filter, AEKF)算法进行电池SOC估算,虽然在一定程度上提高了SOC估算精度,但AEKF算法计算复杂度较大,在某些条件下收敛速度慢,影响估算实时性。Chen Kui等[14]使用鲸鱼算法(Whale Optimization Algorithm, WOA)与多核相关向量机(Multi-Kernel Relevance Vector Machine, MK-RVM)算法进行SOC估算,结合了全局优化和局部建模的优势,算法适应性较强,但算法计算复杂度较高,参数调优较为困难。
上述研究方法,只适用于常温下的电池SOC估计,未考虑到环境温度、电池老化对电池SOC估计造成的影响,且未考虑电池成组后SOC变化情况,因此实际意义不大[15-16]。针对以上问题,靳立强 等[17]提出一种电池-温度模型,并改进了EKF算法,在高低温时SOC估算精度均有提升,且能够抑制电流漂移噪声干扰,但算法并未考虑电池老化对SOC估算的影响,算法适用性无法保证。针对电池老化问题,郑涛等[18]提出一种容积卡尔曼滤波(Cubature Kalman Filter, CKF)算法,能够更新电池容量,实现在线SOC估计,但未考虑环境温度变化情况。刘光军等[19]提出基于分段聚合和卡尔曼滤波的锂电池组SOC估算方法,实现了电池组SOC估算,但研究过程中,设定变化条件太过单一,估算结果存在一定误差。申江卫等[20]基于迁移模型对宽温度范围电池组SOC估计展开研究,实现了宽温度环境下的电池组SOC估算,然而并未考虑电池老化对电池组SOC估算的影响,且未考虑极限温度下算法的适用性。
针对储能用锂离子电池组SOC估算问题,本文采用带外源非线性自回归(Nonlinear Auto-Regressive with Exogenous Inputs, NARX)神经网络来代替传统二阶RC等效电路模型中的RC回路,根据不同温度、不同老化状态下的实验数据对模型进行训练,建立考虑温度和老化影响的电池模型。并在此基础上提出均值差异模型来解决电池组SOC估算问题,使用自适应无迹卡尔曼滤波(Adaptive Unscented Kalman Filter, AUKF)算法分别对均值及差异模型进行SOC估计,利用模糊控制确定SOC融合权值,实现电池组电池SOC融合及估算。最后搭建硬件在环仿真平台,在-20℃、0℃、50℃等多种工况下将所提算法与EKF、UKF算法进行对比,结果表明所提算法估算准确度更高、鲁棒性更好。
储能系统锂离子电池在工作时,SOC估算精度会受很多因素影响,例如环境温度、充放电倍率、电池老化状态、运行时间、电池内阻等。因此为了能够建立准确的电池模型,必须要通过相关实验来分析这些因素对电池产生的影响。
本文选择使用合作企业生产的100 A·h磷酸铁锂电池进行实验,进而保证实验的准确性及可靠性,所用电池如图1所示,该电池的主要性能参数见 表1。图2为所搭建的充放电测试平台,由计算机数据处理平台、动力电池测试系统、充放电测试支架、100 A×h磷酸铁锂电池组成。

图1 100 A×h磷酸铁锂电池
Fig.1 100 A×h lithium iron phosphate battery
表1 电池的主要性能参数
Tab.1 The main performance parameters of the battery

参 数数 值 标称电压/V3.2 标称容量/(A·h)100 电池循环次数≥1 200 电池额定容量/(A·h)100 充电截止电压/V3.65 放电截止电压/V2.5 最大充放电电流1C

图2 充放电测试平台
Fig.2 Charge and discharge test platform
1.1.1 不同温度、老化状态下OCV与SOC关系
为确定不同温度、不同老化工况下OCV与SOC之间关系,使用可编程式恒温恒湿试验机结合充放电测试平台进行测试,由于储能系统工作温度范围多为-20℃~50℃,因此在此范围内,每隔10℃进行一次测试,首先进行混合功率脉冲特性(Hybrid Pulse Power Characteristic, HPPC)测试,记录不同温度下电池OCV与SOC关系曲线。上述温度范围为八种环境温度,选择8块一致性好的电池,分别对应其中一个工作温度,进行电池老化测试,以0.5C电流恒流恒压充电以0.5C恒流放电,使电池逐渐老化,电池健康状态(State of Health, SOH)每降5%,记录一次该老化状态下的SOC与OCV关系曲线。以此类推,当电池SOH=80%时,认为电池达到退役状态,结束实验。图3为SOH=100%时,不同温度下电池OCV与SOC关系曲线。图4为环境温度为20℃时,不同老化状态下OCV与SOC的变化情况。
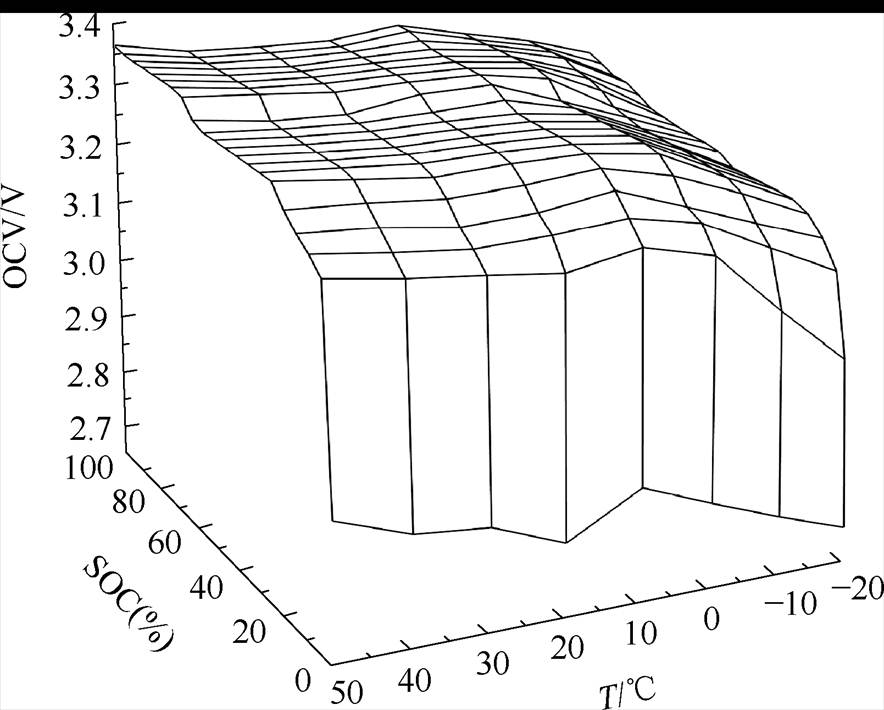
图3 SOH=100%时,不同温度SOC-OCV关系曲线
Fig.3 SOH=100%, SOC-OCV relationship curves at different temperatures
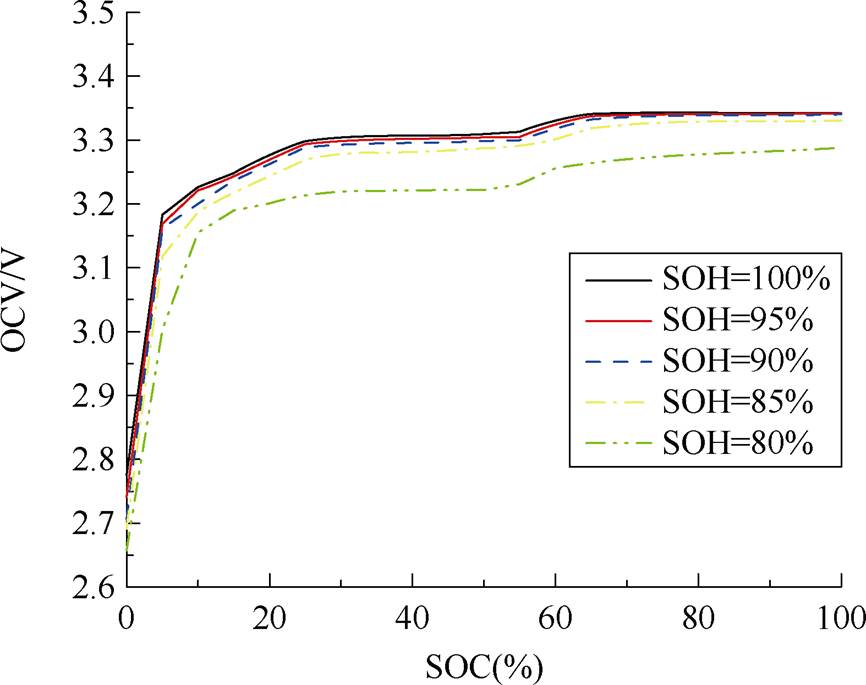
图4 20℃时,不同老化状态SOC-OCV关系曲线
Fig.4 SOC-OCV relationship curves of different aging states at 20℃
1.1.2 不同温度、老化状态下内阻与SOC关系
电池内阻分为欧姆内阻与极化内阻,内阻的大小决定了电池内离子在电极间转换的难易程度,是影响电池性能的一个主要因素。本小节研究欧姆内阻在不同环境温度、老化状态情况下与SOC的关系,进行回弹电压特性测试,并通过实验分析其实验数据。根据欧姆定律,可计算出电池SOC每增加5%时,对应的欧姆内阻R0值。图5为SOH=100%时,不同温度下R0与SOC之间的关系,图6为环境温度为20℃时,不同老化状态下R0与SOC之间的关系。
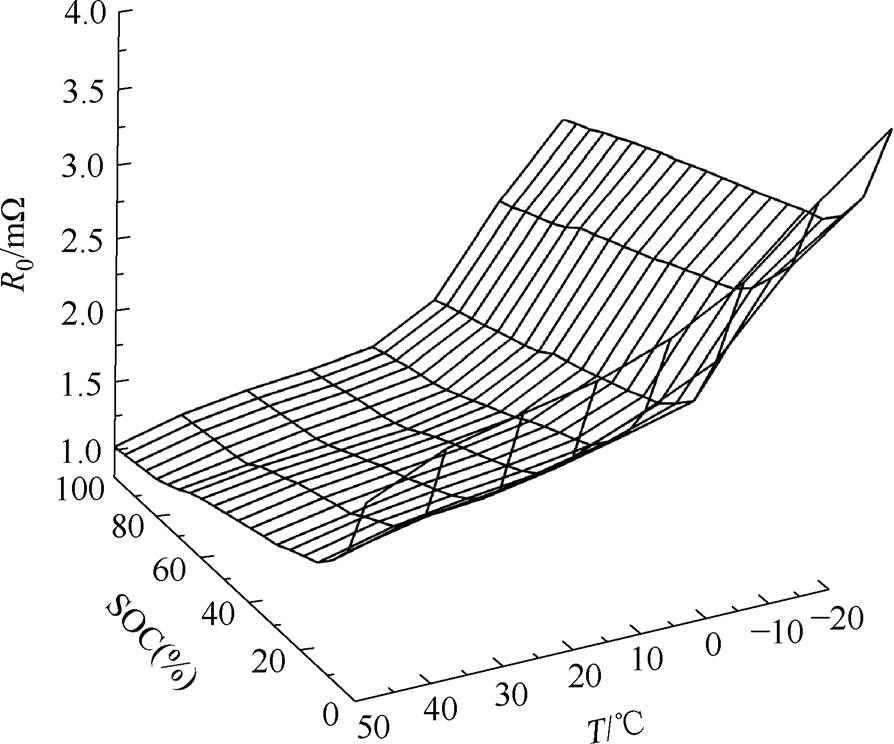
图5 SOH=100%时,不同温度下R0与SOC关系曲线
Fig.5 SOH=100%, the relationship between R0 and SOC at different temperatures
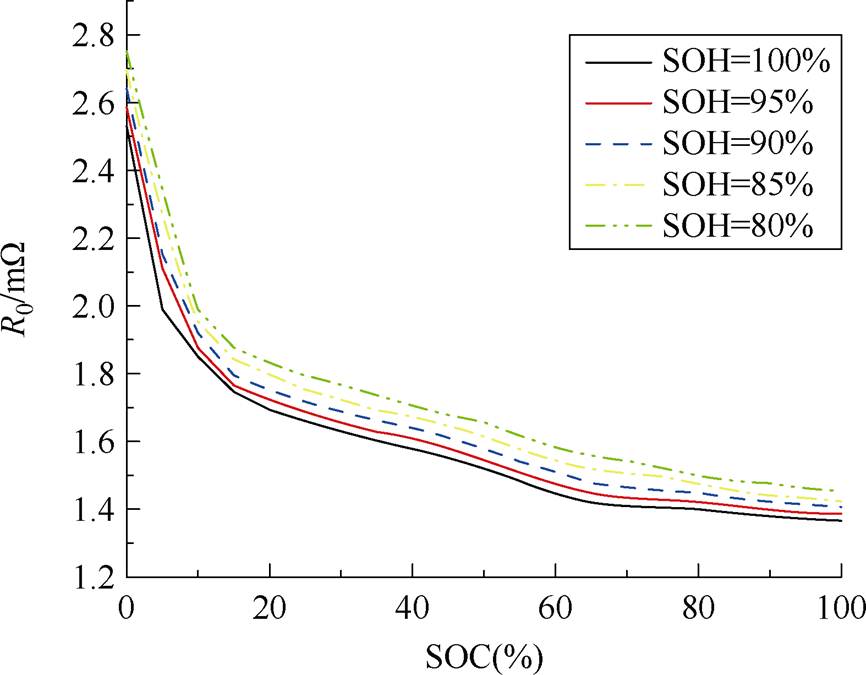
图6 20℃时,不同老化状态下R0与SOC关系曲线
Fig.6 R0 and SOC relationship curves under different aging states at 20℃
1.1.3 不同温度下、老化状态下极化电压与SOC关系
通过回弹电压特性测试实验可知,当充放电初始时,电池端电压会发生突变;当充放电结束时,电池端电压先缓慢变化,最后趋于平衡。以上变化均是电池极化效应造成的,图7为极化效应外特性示意图。
由图7可知,电池端电压缓慢变化阶段则是受电化学极化与浓度差极化影响,后文将这两种极化统称为极化现象,对极化现象的研究主要是对极化电压进行分析[21],图8为在同一SOC值时,不同温度下极化电压曲线。图9为在20℃时不同老化状态下极化电压曲线。
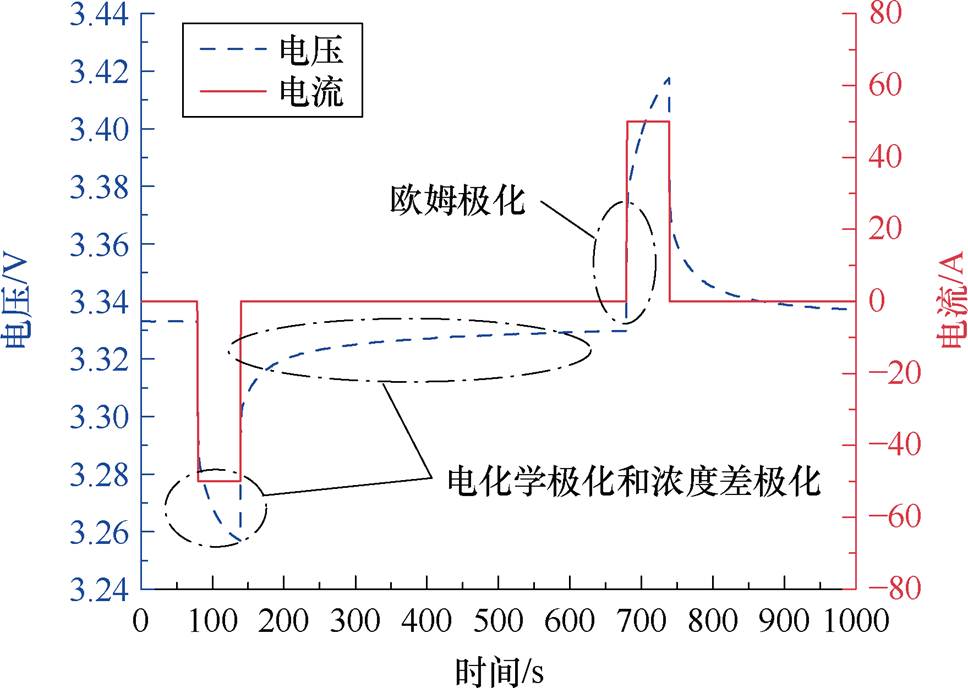
图7 极化效应外特性示意图
Fig.7 Schematic diagram of external characteristics of polarization effect
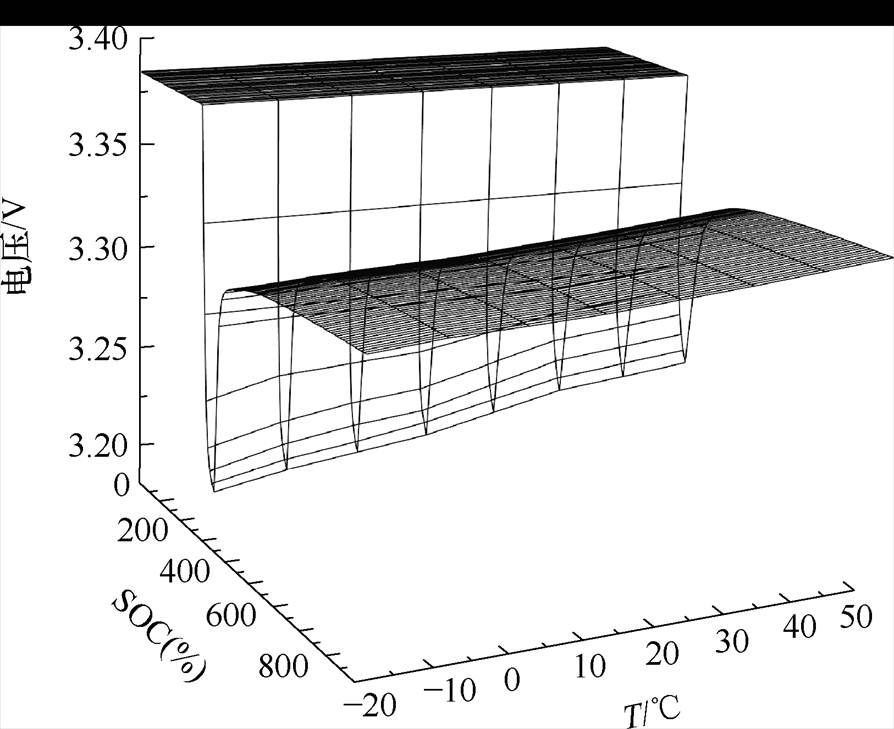
图8 极化电压与温度关系
Fig.8 Relationship between polarization voltage and temperature
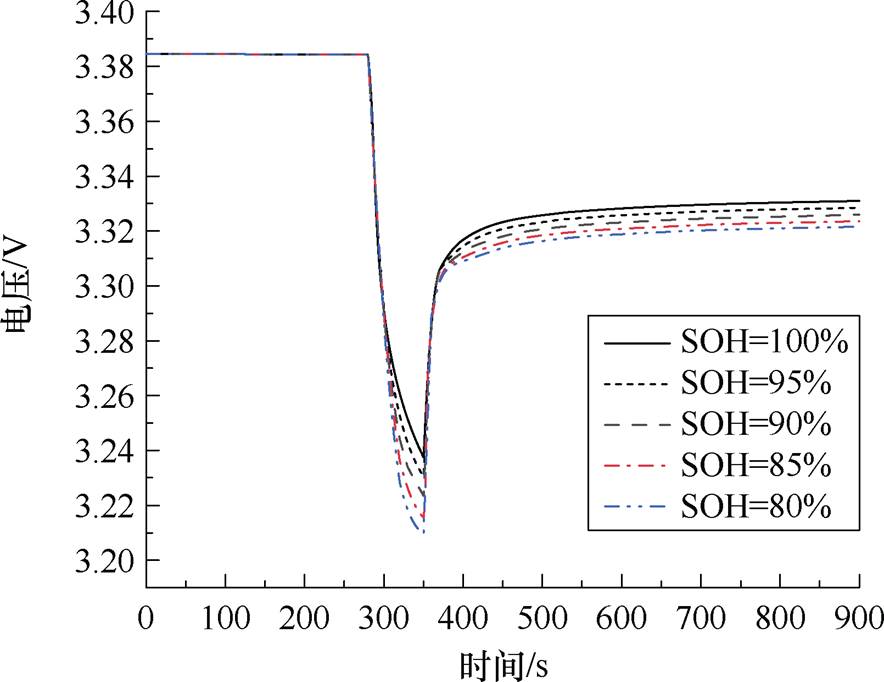
图9 20℃时,极化电压与电池老化状态关系
Fig.9 Relationship between polarization voltage and battery aging state at 20℃
目前最为常用的电池模型是等效电路模型。等效电路模型由电压源、电容、电阻等电子元件搭 建[22],主要包括电阻模型、Thevenin模型、PNGV模型、二阶以及多阶RC等效电路模型、通用非线性(General Non-Linear, GNL)模型等。
上述模型均是在电阻模型的基础上添加电阻、电容元器件构成。现常用的模型主要为Thevenin模型及二阶RC等效电路模型。由于电池存在两种极化,而Thevenin模型只有一个RC回路,因此不能很好地表征电池特性[23]。而二阶RC等效电路模型则是在Thevenin模型的基础上又加上一个RC电路,能更好地表征电池的极化现象和电压回流效应[24]。一定程度上,等效电路模型中RC环节越多,估算精度也就越高,但随着RC环节的增多,算法计算量也就随之增大,耗时也就越长[25]。考虑到电池模型的复杂程度以及精确度,并考虑到环境温度及电池老化对电池参数的影响,本文选择使用二阶RC等效电路模型[26],如图10所示。
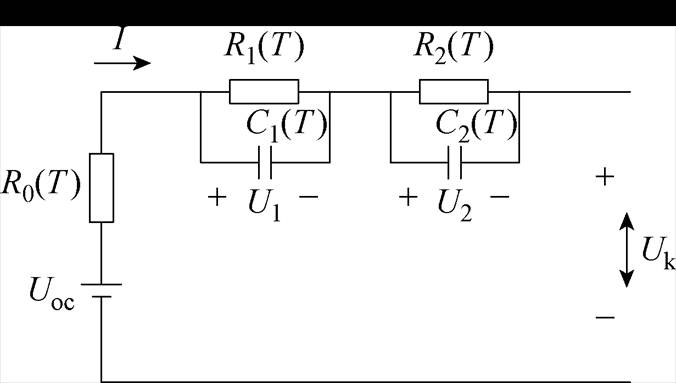
图10 二阶RC等效电路模型
Fig.10 Second order RC equivalent circuit model
根据等效电路模型可得
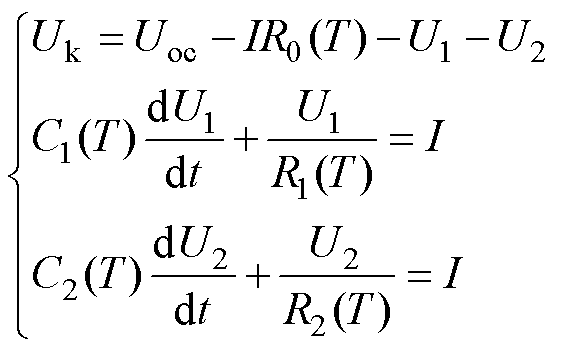 (1)
(1)
式中,I为电流;Uk为端电压;R0(T)为欧姆内阻,T为温度;Uoc为开路电压;R1(T)为电化学极化内阻;R2(T)为浓差极化内阻;C1(T)为电化学极化电容;C2(T)为浓差极化电容;U1为R1(T)C1(T)回路的电压;U2为R2(T)C2(T)回路的电压。
电池在充放电过程中电压为时变的序列,传统等效电路模型中的RC回路主要用来模拟电池中极化电压的变化,它的本质正是对电池电压在时域上的变化趋势进行建模。传统等效电路模型采用带有外部输入的线性自回归模型(Auto-Regressive Exogenous Model, ARX)描述电池极化电压动态特性,而ARX对电池极化特性的非线性描述准确度有限,由于电池在使用过程中运行工况复杂多变,数据量较大,因此通过机器学习的方式对大量数据进行训练并对电池进行建模是一种具有较高应用价值和可行性的新思路。
具有外部输入的非线性自回归(NARX)神经网络在传统BP神经网络的基础上引入输入延时单元与输出反馈,因此它不仅是一种拥有反馈单元的动态神经网络,也是一种递归型神经网络。由于输出可以反馈到输入,以此来作为此信号的历史信息,加以复用,因此便有了记忆功能和较强的学习能力。与时间序列的预测相比,普通前馈神经网络表现更佳,电池在充放电过程中电压电流就是时变的时间序列,因此NARX神经网络非常适用于电池系统[27]。它的函数表达式为
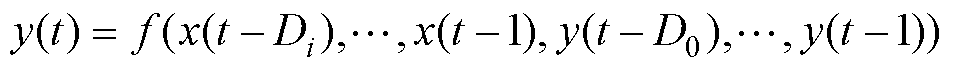 (2)
(2)
式中,Di为输入时延最大阶数;x((t-Di),…, x(t-1))为相对于t时刻的历史输入;D0为输出时延最大阶数;y((t-D0),…, y(t-1))为相对于t时刻的历史输出;f为拟合得到的非线性函数。图11为NARX神经网络(Neutral Network, NARXNN)结构,第一层为输入层,带有延时环节;第二层为隐含层,隐含层的数量由所研究对象的复杂度决定,可自行调整;第三层则为输出层。
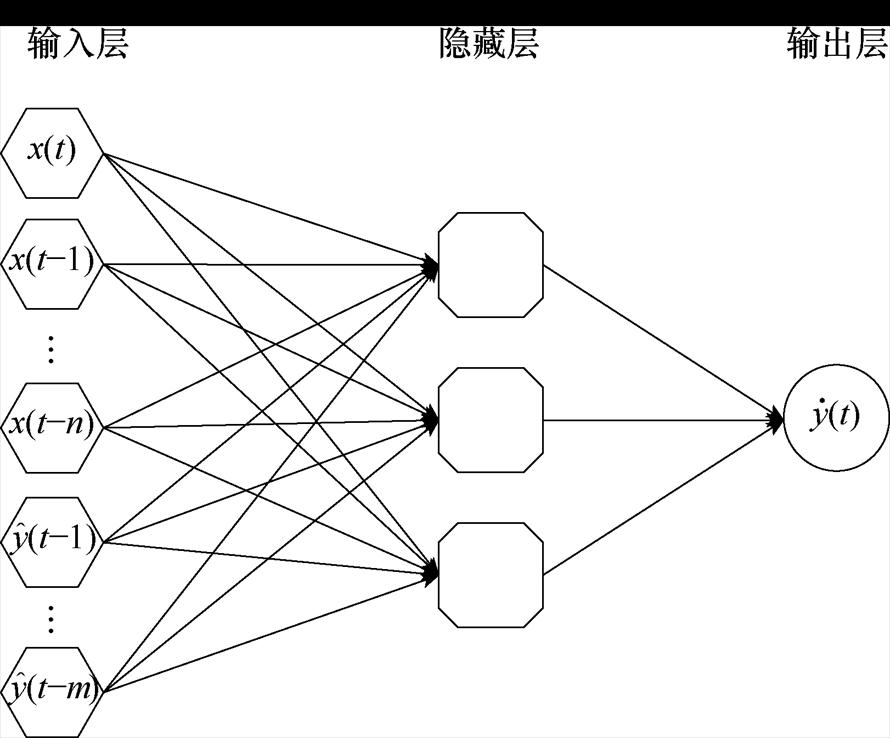
图11 NARXNN结构
Fig.11 NARXNN structure diagram
NARXNN的隐含层函数为双曲正切函数,表示为
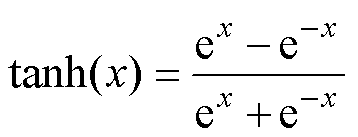 (3)
(3)
输出层为线性函数,即
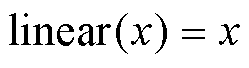 (4)
(4)
当隐含层的节点数量较多时,网络精度更优。但训练时长也会随之增加,也有可能带来过拟合现象。为解决此问题,选择Levenberg-Marquardt(L-M)算法优化神经网络,L-M算法不需要计算Hessian矩阵,同时可以控制步长,对初始值依赖性小,即使初始值距离最优值很远,也可以迅速找到局部最优值[28]。各层系数权重更新公式为
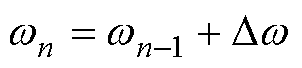 (5)
(5)
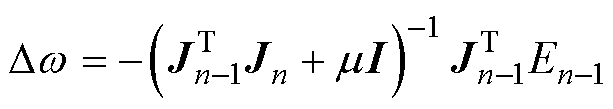 (6)
(6)
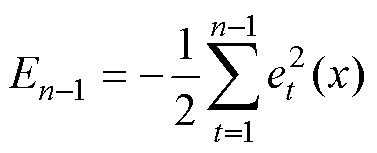 (7)
(7)
式中,En-1为n-1时刻的误差函数;Jn-1为En-1的雅可比矩阵;I为单位矩阵;et(x)为训练误差;wn、wn-1分别为第n次和第n-1次进行网络迭代时各层系数权重值;m 为比例系数。
由电池特性测试可知,电池极化效应受电流作用时间、大小以及相位影响,为尽可能地模拟实际工况,所选择脉冲电流序列包含以下两种工况:一种为规律脉冲电流,即充电/放电—静置—充电/放电—静置工况,使NARX神经网络学习基本运行模式下电池极化电压变化情况;第二种为混合运行工况,即电流变化较快,存在持续放电之后瞬间进入充电模式,或者充电放电工况多次瞬间转变。考虑到储能电池运行工况较为复杂,规律性的电流激励可能很少,因此单一工况不能完全代表电池组实际运行工况。为了使NARX神经网络能够更好地模拟电池极化电压,增强SOC估算准确性,必须进行第二种工况的训练。
将合作企业数据库中的大量现有工况数据作为数据集,合并多个数据集,组成了200个训练样本,上述两种工况在每个样本中随机均匀分布,每个样本时长为25 000 s,通过在Matlab中编写脚本,设置训练完成条件为最大迭代次数为1 000,神经网络延迟分别设置为1、5、10、20以及隐藏层节点数设置为10、20、50,梯度设置为1.0×10-7,考虑到神经网络计算复杂度,将网络层数设置为1层,进行神经网络训练,具体训练流程如图12所示。
为防止模型出现过拟合现象,提升网络的泛化能力,将满足精度的训练数据进行分类处理,分别作为训练集、测试集、验证集,三个数据集之间互不干涉,三个数据集占原始数据比例分别为80%、10%、10%。经过多次参数调整,并进行电池SOC估算,最终确定NARX神经网络隐藏层取一层,隐藏层节点数为10,延迟阶数取1时,此时估算精度较高,且计算相对简便。图13为训练过程中网络性能随迭代次数的变化曲线,当训练迭代次数达到74次后,达到最佳性能,停止训练。此时方均误差为1.082 5´10-6。
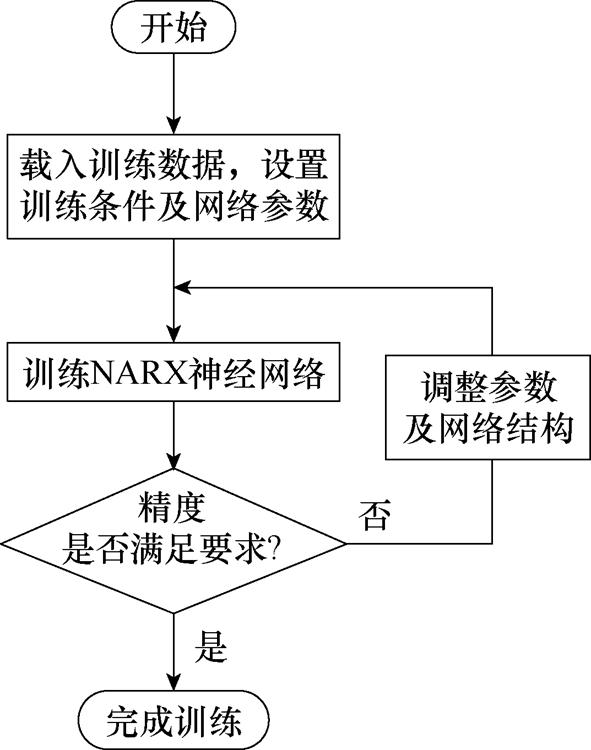
图12 NARX神经网络训练过程
Fig.12 NARX neural network training process
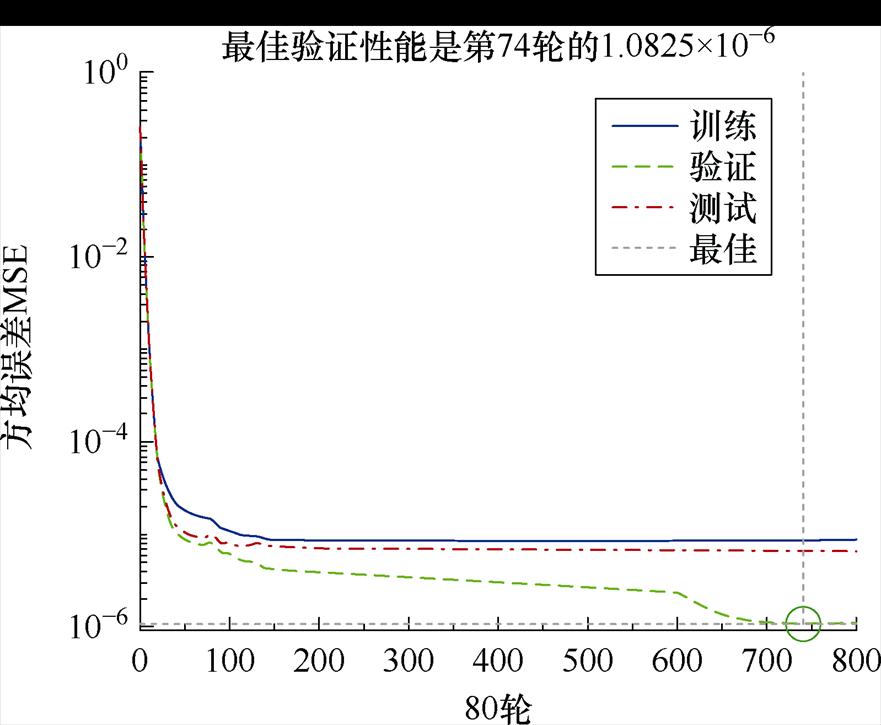
图13 网络性能随迭代次数变化曲线
Fig.13 Network performance curves with the number of iterations
图14为神经网络训练误差直方图,从图中看出,此时训练误差集中在-0.000 53上,说明此时网络具有较高的训练精度。图15为三个数据集的回归分析图,横坐标为归一化后的SOC值,纵坐标为归一化后网络预测的SOC值,三个数据的预测值与实际值相关系数均接近1,说明预测值接近实际值,训练效果理想。
将上文训练好的NARX神经网络与传统二阶RC等效电路模型进行结合,实现对不同工况下电池极化电压的预测,提高电池模型精度,进而提高电池SOC估算精度,优化后的等效电路模型如图16所示。
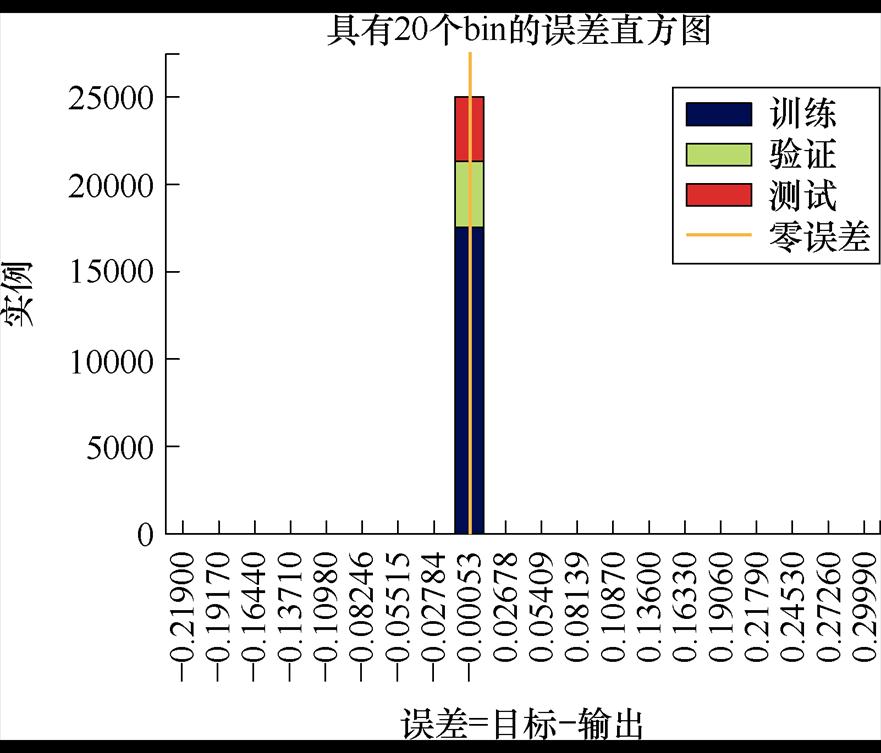
图14 神经网络训练误差直方图
Fig.14 Neural network training error histogram
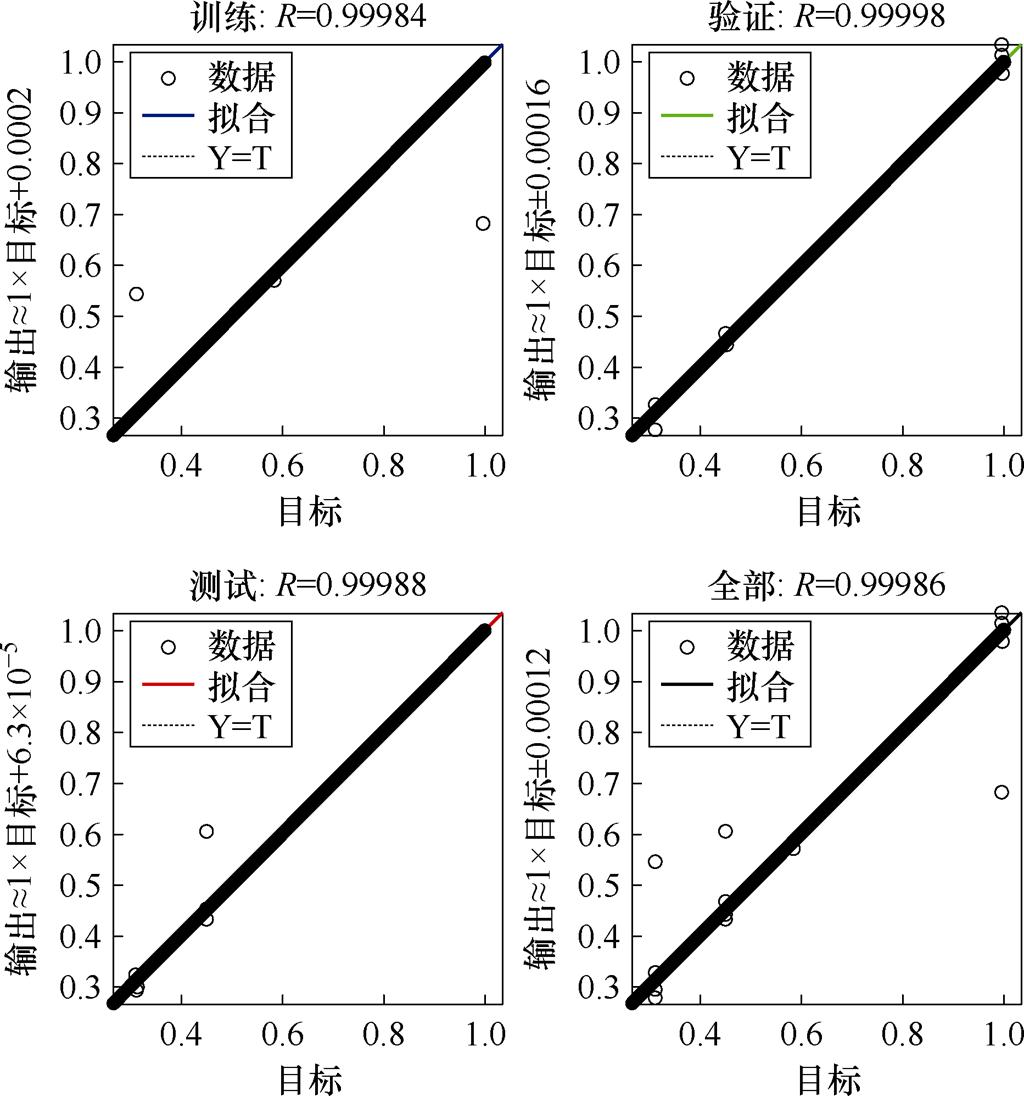
图15 神经网络在三个数据集上的回归结果
Fig.15 Regression results of neural network on three data sets
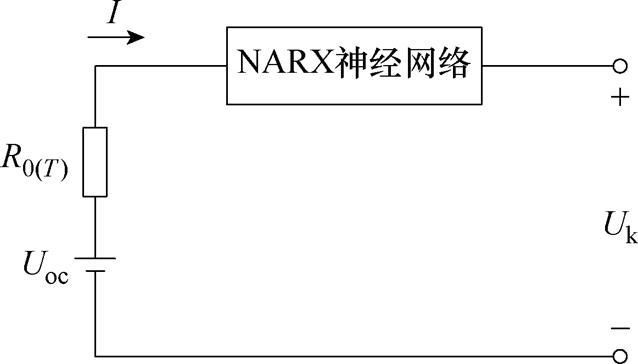
图16 NARX神经网络优化等效电路模型
Fig.16 NARX neural network optimization equivalent circuit model
通过将上文在不同工况下所测的数据代入神经网络进行训练,然后将运行电压、电流及上一时刻极化电压历史数据代入神经网络中即可得到该时刻极化电压预测值。通过前一时刻SOC值,可得到此时电池欧姆内阻,将此数据代入电池模型,最终通过估算算法得到电池的SOC值。图17为使用NARX神经网络优化的等效电路模型估计电池SOC流程。
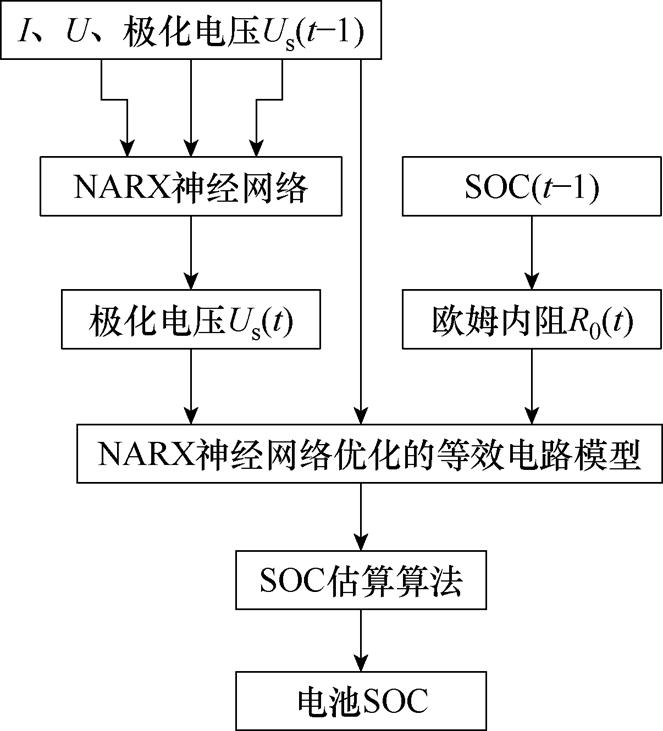
图17 估算SOC流程
Fig.17 Estimating SOC flow chart
为验证NARX神经网络优化效果,从企业数据库中随机选择一种工况,对其进行SOC估算,相比传统二阶RC等效电路模型两种算法,得到SOC估算结果与误差如图18所示。
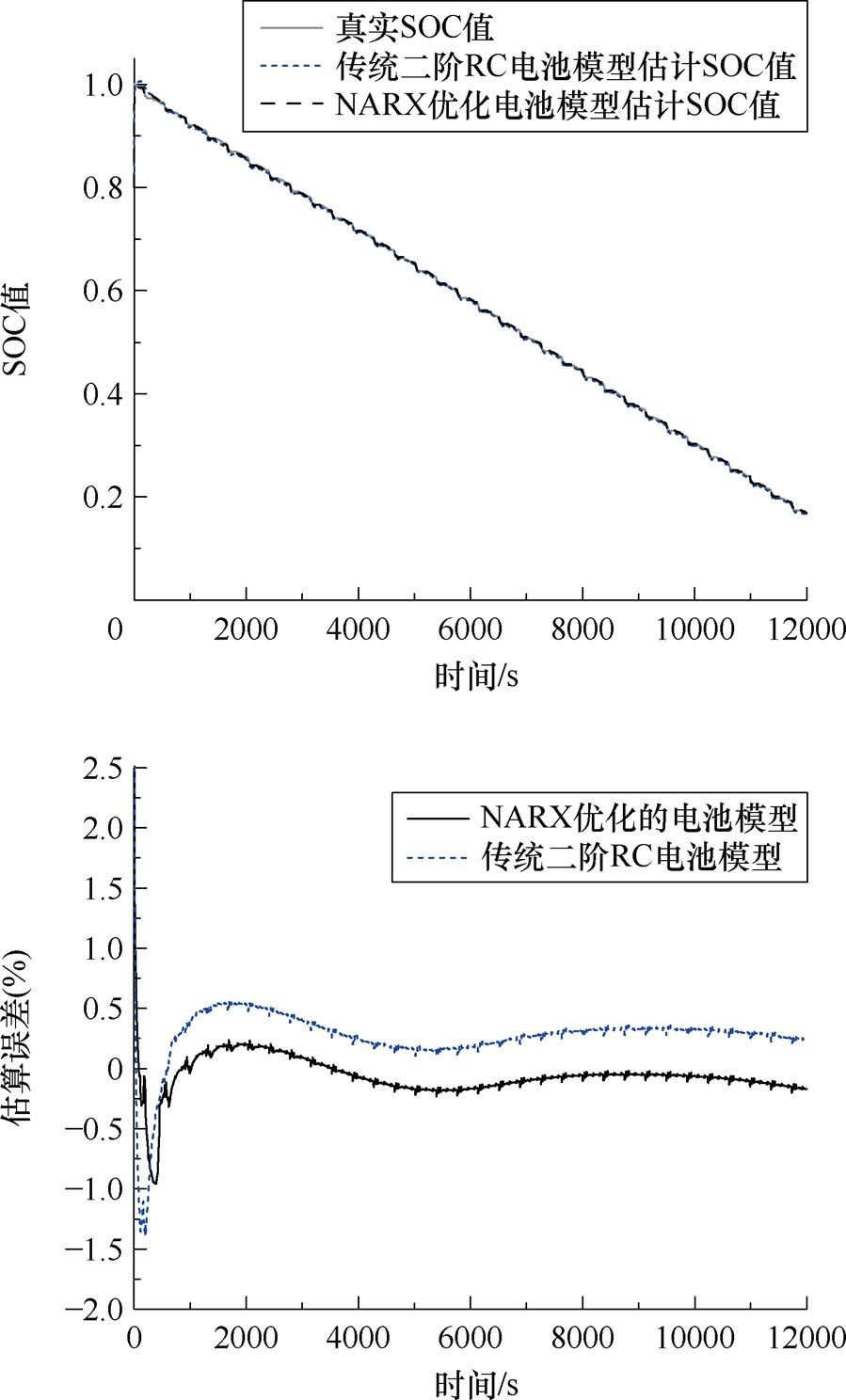
图18 两种算法估算结果与误差
Fig.18 Two algorithms estimate results and errors
从图18误差图中可以看出,NARX神经网络优化的电池模型收敛速度略慢于传统二阶RC等效电路模型,而优化后的电池模型估计误差远小于传统电池模型,因此,改进后的电池模型表现更优,更适合作为后续电池组SOC估算基础模型。
目前,基于等效电路模型的电池组建模主要分为大单体模型、电压最大最小模型以及均值差异模型[29]三大类。大单体模型将整个电池组视为一个整体,虽然建模简单,计算复杂度低,但本质上仍为单体,无法考虑电池组中各单体之间的差异,除此之外,对于串联电池数目多的模型来说,大单体模型计算量非常大。电压最大最小模型考虑的是电池组中第一个过充电电池与第一个过放电电池,由于这两个电池限制了整组电池的可用容量,因此电池组SOC值实际为这两个电池的SOC值,又因为电池SOC与OCV具有线性关系,因此,只需确定最高最低电压,即可估算电池组SOC值。虽然简单易行,但误差非常大。均值差异模型包含一个均值模型及多个差异模型,均值模型用来表示电池组的平均状态,输出用SOCm表示。差异模型用来表示各单体之间与均值的差距,输出用SOCi表示。差异模型由于考虑的因素不同,模型选择也不同,考虑因素越多,模型复杂度越高。目前,差异模型主要考虑的因素包括SOC差异、容量差异、自放电率差异及内阻差异,如图19所示。

图19 四种差异模型分类
Fig.19 Four kinds of differential model classification
综上所述,根据电池特性测试并考虑到模型的复杂度以及模型准确度,选择使用均值差异模型搭建电池组模型,其中差异模型选择考虑SOC差异及内阻差异。
由于锂离子电池为高度非线性系统,且受外部环境、噪声影响较为严重,因此传统的卡尔曼滤波算进行SOC估算[30]效果不是很好。为解决此问题,已有很多改进的卡尔曼滤波算法,其中UKF算法虽然适用于非线性系统,但忽略了系统噪声变化特性,进而影响了估计的精度[31]。因此为提高估算精度与稳定性,降低噪声协方差影响,本文选择自适应无迹卡尔曼滤波(AUKF)分别对均值模型及差异模型SOC进行估算。AUKF估算SOC具体公式如下。
1)均值模型状态向量为
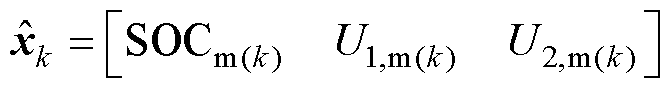 (8)
(8)
式中,SOCm(k)、U1,m(k)、U2,m(k)为模型参数在k时刻的估计值。
(1)初始化状态变量均值及协方差
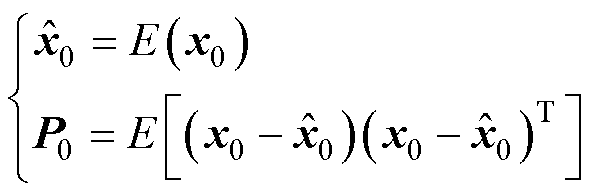 (9)
(9)
式中,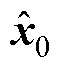 为初始变量均值;
为初始变量均值;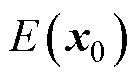 为期望;x0为初始状态变量;P0为初始状态协方差。
为期望;x0为初始状态变量;P0为初始状态协方差。
(2)Sigma点计算

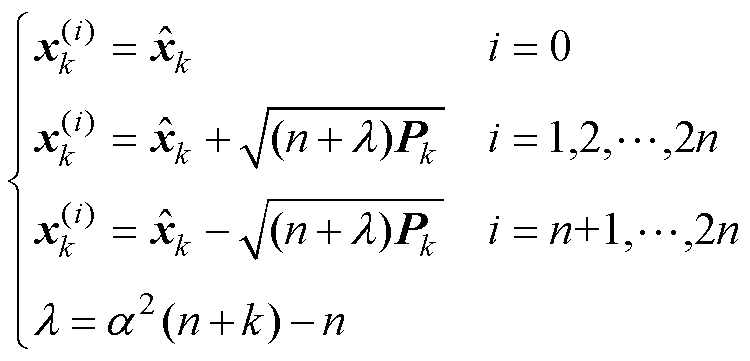 (10)
(10)
式中,上标i表示Sigma点的索引号,用于区分不同的采样点生成方式,i=0对应中心点,i=1, 2,…, n对应沿协方差矩阵正方向的Sigma点;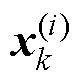 为2n+1个Sigma点;
为2n+1个Sigma点;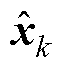 为上一时刻状态变量最优值;
为上一时刻状态变量最优值;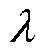 为缩放比例参数;
为缩放比例参数;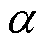 为比例因子,满足10-4≤
为比例因子,满足10-4≤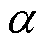 ≤1;n为状态变量维度,本文取n=3;
≤1;n为状态变量维度,本文取n=3;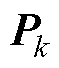 为误差协方差矩阵;
为误差协方差矩阵;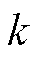 用来控制点集的扩散。
用来控制点集的扩散。
(3)计算Sigma加权系数
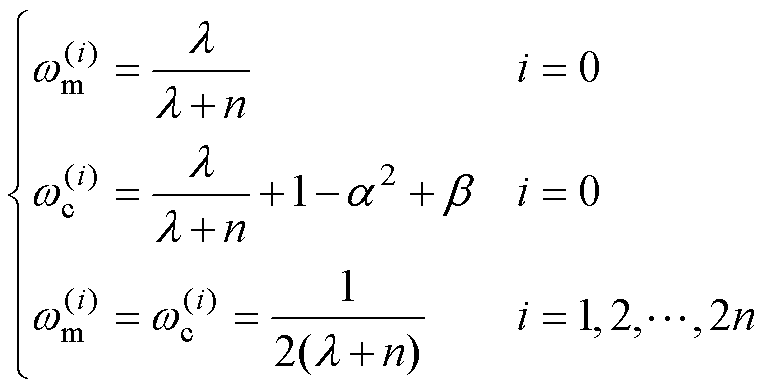 (11)
(11)
式中,wc为协方差权重;wm为均值权重;b 为高斯分布,本文取b =2。
(4)时间更新
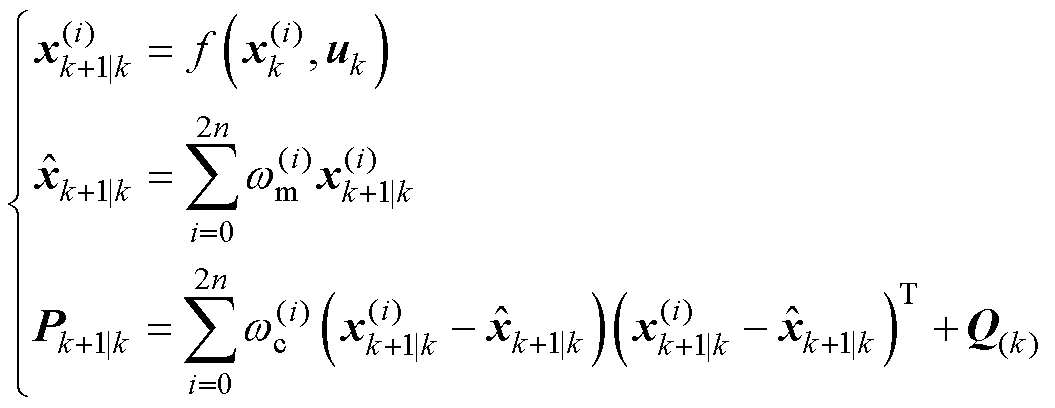 (12)
(12)
其中
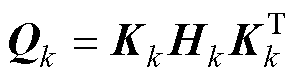
式中,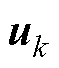 为控制输入;
为控制输入;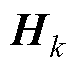 为新息实时估计协方差函数,
为新息实时估计协方差函数,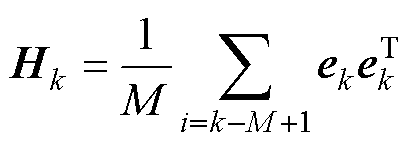 ;
;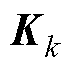 为卡尔曼增益;M为累计新息数量,本文取M=3;
为卡尔曼增益;M为累计新息数量,本文取M=3;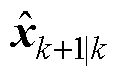 为状态变量预测值;
为状态变量预测值;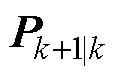 为协方差预测值。
为协方差预测值。
(5)计算下一时刻新Sigma点
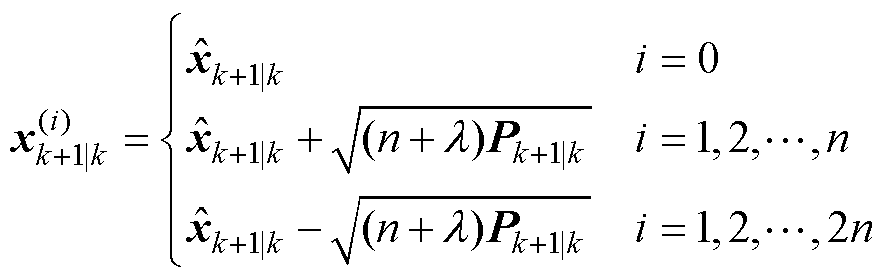 (13)
(13)
式中,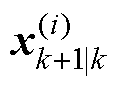 为2n+1个新的Sigma点。
为2n+1个新的Sigma点。
(6)观测变量更新
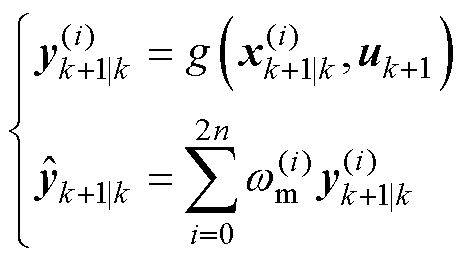 (14)
(14)
式中,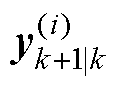 为预测观测值;
为预测观测值;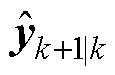 为预测观测值均值。
为预测观测值均值。
(7)卡尔曼增益与误差协方差更新
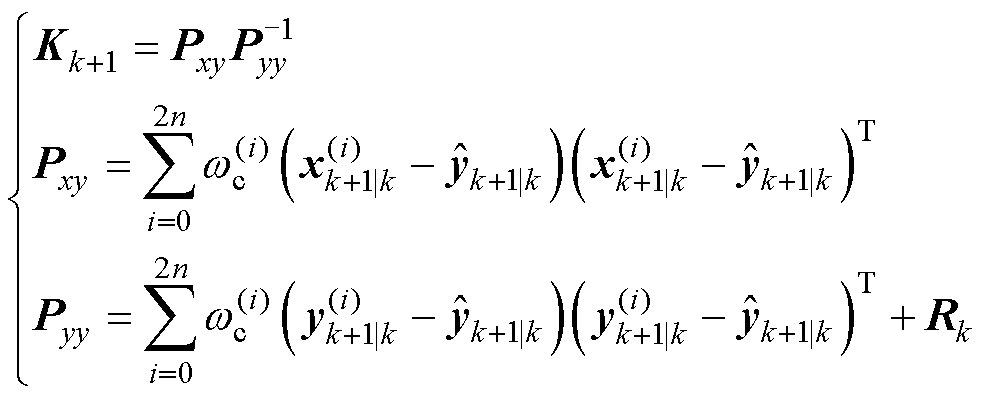 (15)
(15)
式中,Pxy为预测观测协方差;Pyy为预测观测方差;Kk+1为卡尔曼增益;xk+1为最优状态估计;Pk+1为协方差矩阵;Rk为测量噪声协方差。
(8)更新状态变量与协方差矩阵
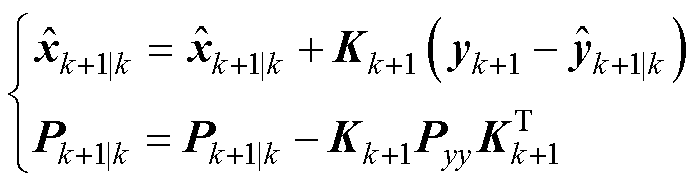 (16)
(16)
(9)更新观测噪声与状态噪声协方差
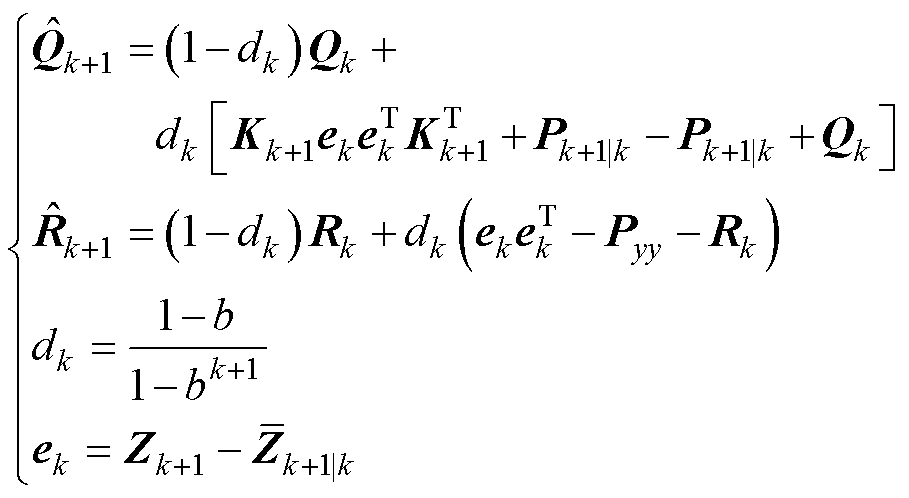 (17)
(17)
式中,ek为残差;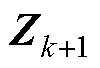 为观测量;
为观测量;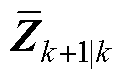 为预测均值;dk为自适应因子;b为遗忘因子,一般0.95≤b≤1,本文取b=0.975。
为预测均值;dk为自适应因子;b为遗忘因子,一般0.95≤b≤1,本文取b=0.975。
通过式(17)改进UKF算法估算SOC值时,能够确保状态噪声协方差与测量噪声协方差实现实时更新,保证噪声的非负定性。但状态噪声以及观测噪声协方差为互不相关高斯白噪声,且会影响到状态变量协方差,当状态变量协方差为非对称的正定矩阵时,不能够实现楚列斯基(Cholesky)分解,进而使得算法无法进行。因此需要对状态噪声以及观测噪声协方差进行修正,修正公式为
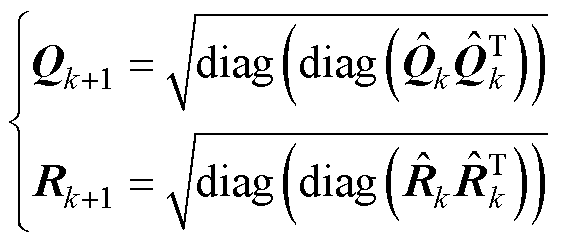 (18)
(18)
2)差异模型状态表达式为
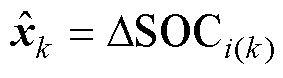 (19)
(19)
初始化状态变量均值及协方差为
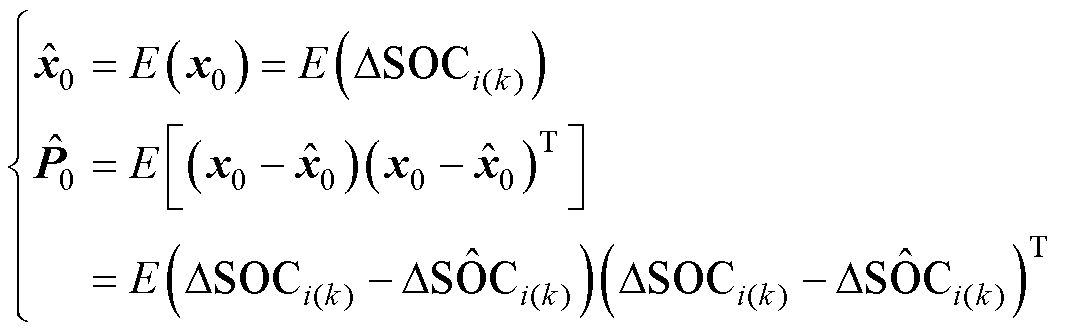 (20)
(20)
其他步骤均与均值模型一样,而差异模型仅一个DSOC状态量,因此相较于均值模型计算复杂度会降低。
因为电池电压一致性分布规律遵循正态分布[32],又因为电池SOC与电压线性相关,因此SOC分布规律也近似遵循正态分布。正态分布概率分布函数为
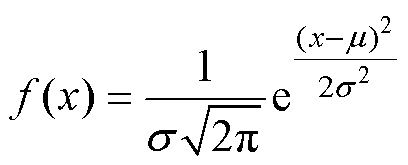 (21)
(21)
由式(21)可知,正态分布概率分布函数由m 与s 两个参数决定,其表征电池SOC分布状态。实现电池组SOC融合需要确定每个单体电池SOC概率密度分布情况,因此得到的函数的值同时也是SOC融合权重值wi。
首先通过上文AUKF算法确定电池均值模型SOCm值,将SOCm值以及电流I作为输入,输入差异模型,获得各单体电池终端电压,以此来确定差异模型SOCi值。获得的SOCm与SOCi的值通过式(22)可得到均值模型标准差SOCs。由于电池SOC受环境温度及老化的影响,不同阶段SOC融合权重不同,为实现准确、实时、可靠的电池组SOC估算,因此选择使用模糊控制实现融合权重确定,通过计算正态分布参数,根据模糊规则进行融合权重重新分配。
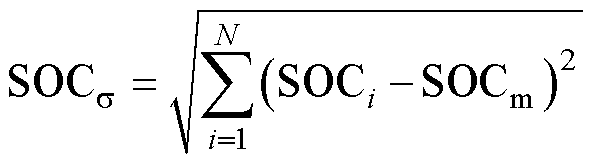 (22)
(22)
式中,N为电池单体总数。
模糊控制是在美国Zadeh(扎德)教授提出的模糊集合理论基础上发展而来,模糊控制系统构成如图20所示,所提出的“隶属度函数”正是模糊控制的基础也是关键。隶属度函数用来表示系统获得的输入值与隶属度函数确定的模糊值之间的映射关系,不同隶属度函数形状也不同。
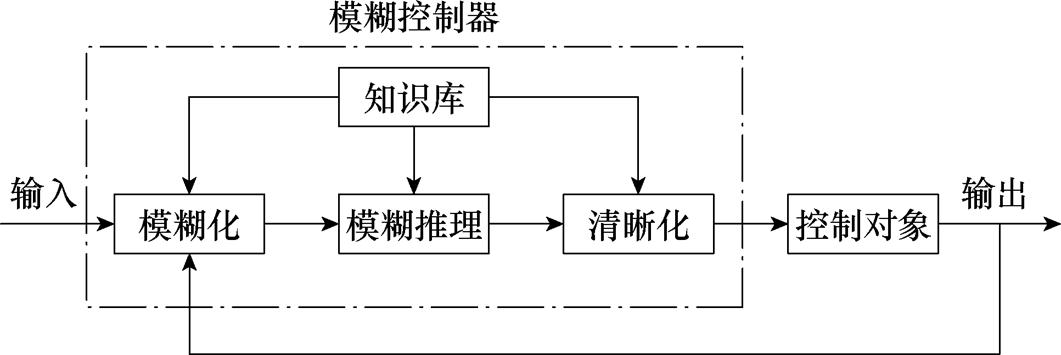
图20 模糊控制系统构成
Fig.20 The constitution of fuzzy control system
要确定电池组融合权重,首先要确定m 与s2的值。SOCm决定m 的值,SOCm与SOCs共同决定s 的值。
SOCm的隶属度函数由高斯函数表征,将SOCm划分为7个域,SOCm与m 隶属度函数如图21所示。将SOCs划分为3个域,SOCs与s 隶属度函数如图22所示。m 的输出结果如图23所示,s 随SOCm与SOCs的变化趋势如图24所示。
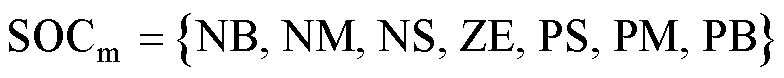 (23)
(23)
由3.2节已得到均值模型及差异模型的SOC,并通过上述方法,可得到电池组SOC分布规律的m 及s,因此可通过计算得到融合权值wi。将所有单体SOC融合权值wi进行融合,便可实现电池组SOC融合。电池组SOC融合公式为
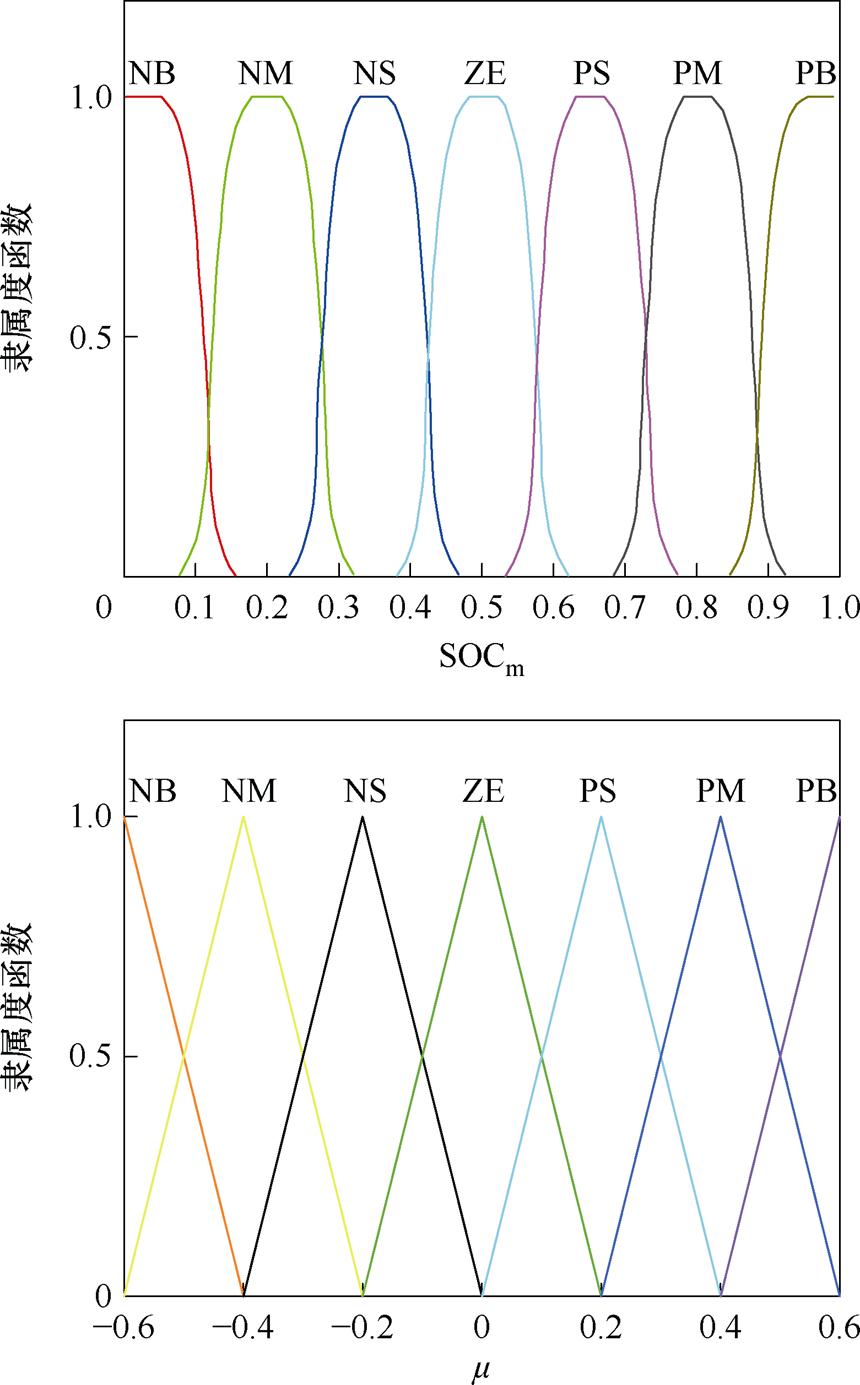
图21 SOCm与m 隶属度函数
Fig.21 Membership function of SOCm and m
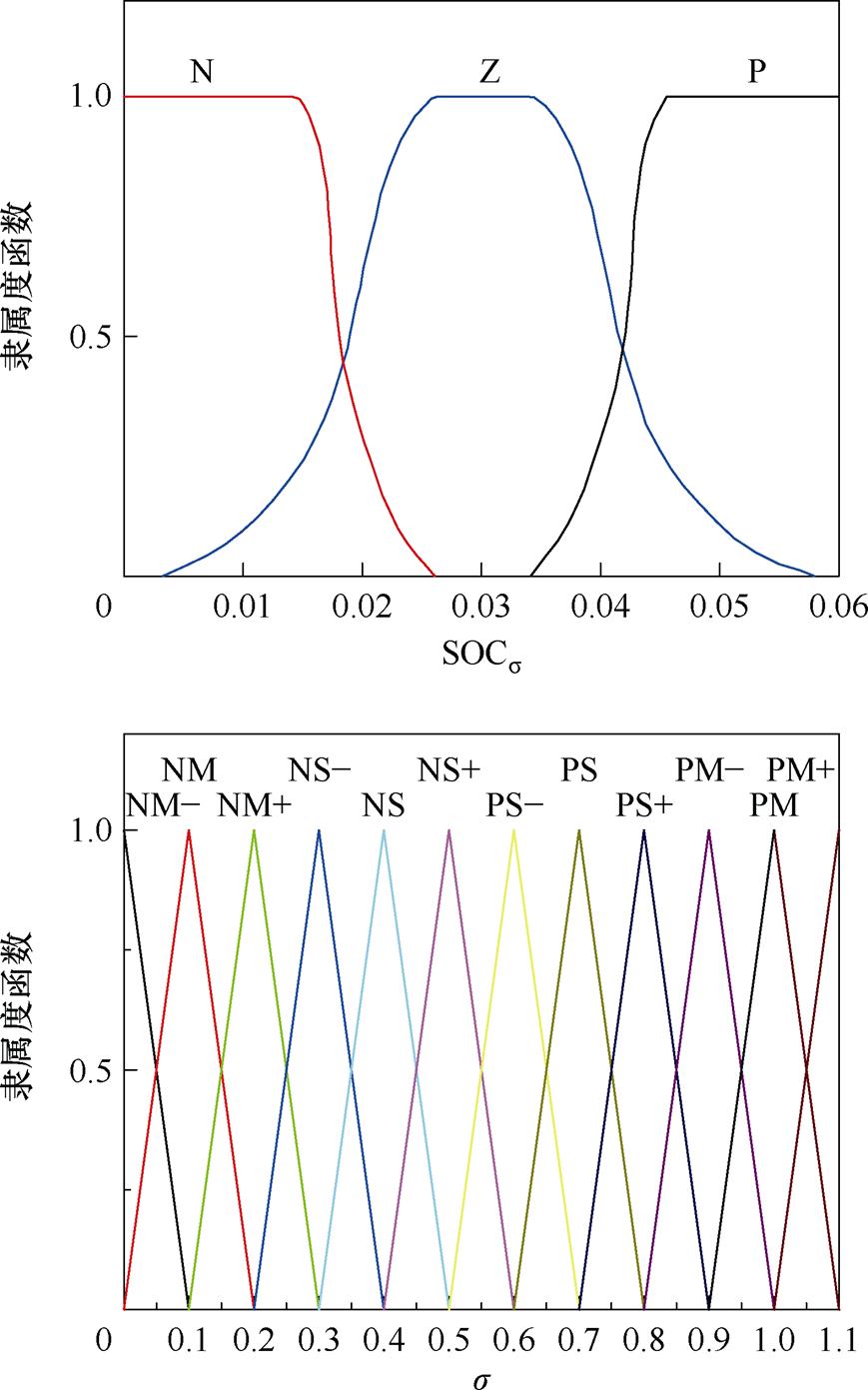
图22 SOCs与s 隶属度函数
Fig.22 Membership function of SOCs and s
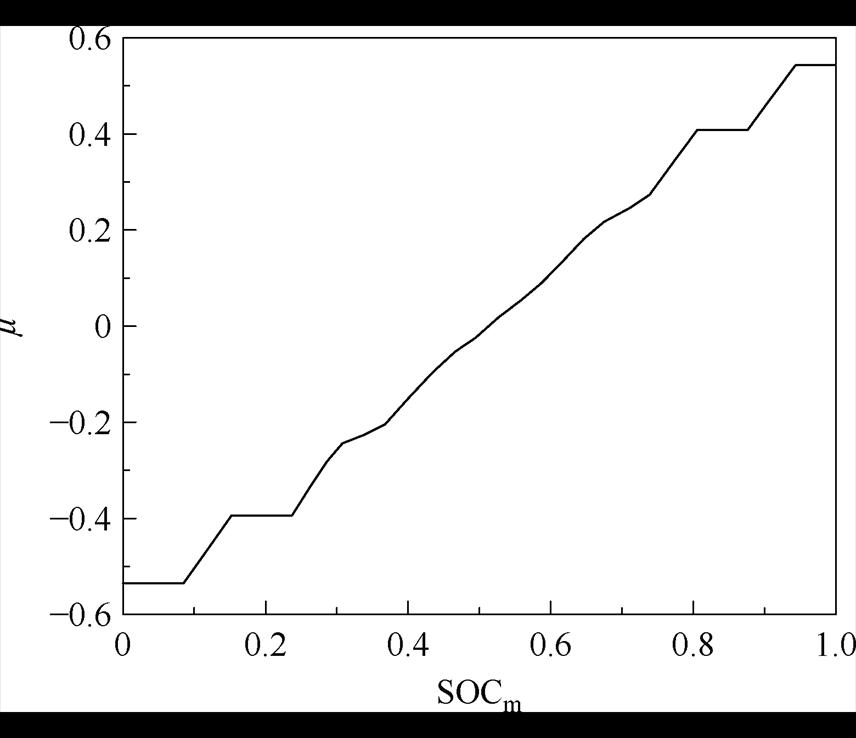
图23 m 的输出结果
Fig.23 The output of m
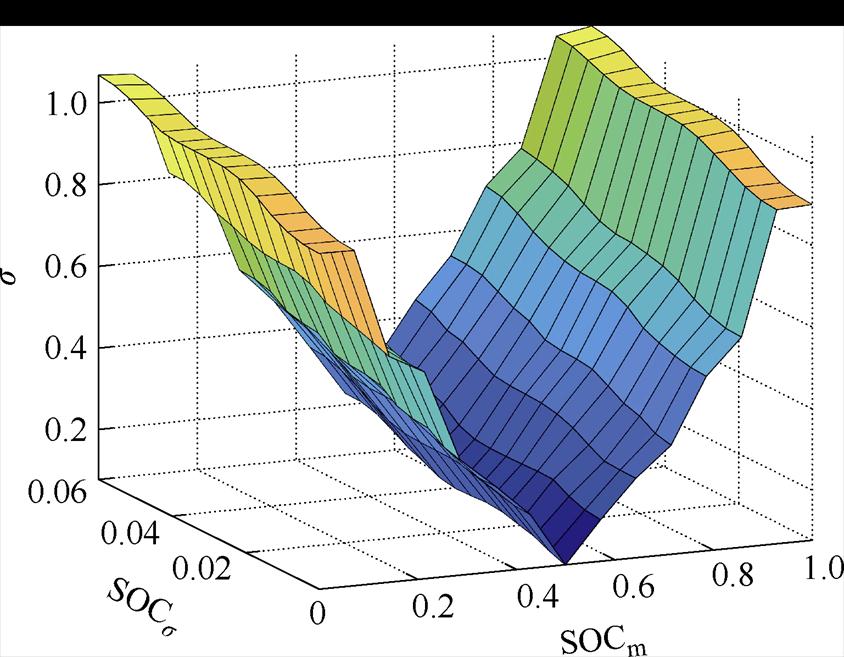
图24 s 随SOCm与SOCs变化趋势
Fig.24 strends to change with SOCm and SOCs
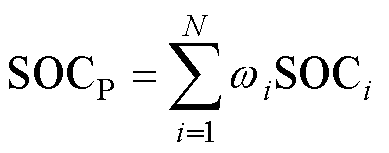 (24)
(24)
式中,SOCP为电池组SOC;N为电池单体数;SOCi为第i个单体电池SOC。
为验证本文所提算法的准确性及鲁棒性,搭建硬件在环仿真平台,将锂离子电池组放入恒温恒湿实验环境中,并通过充放电设备对电池组进行充放电,将所搭建的SOC估算法输入Speed Goat实时机中,电流、电压数据作为输入,并通过上位机观察输出结果,验证所提算法的准确性及鲁棒性,硬件在环(Hardware in the Loop, HiL)平台如图25所示。
首先,通过从合作企业现有数据中选择一种电池运行工况对算法准确性进行验证,环境温度为25℃,电池为全新电池。将电流作为输入,输出为电池组SOC估计结果与估计误差,结果如图26 所示。

图25 硬件在环仿真平台
Fig.25 HiL simulation platform
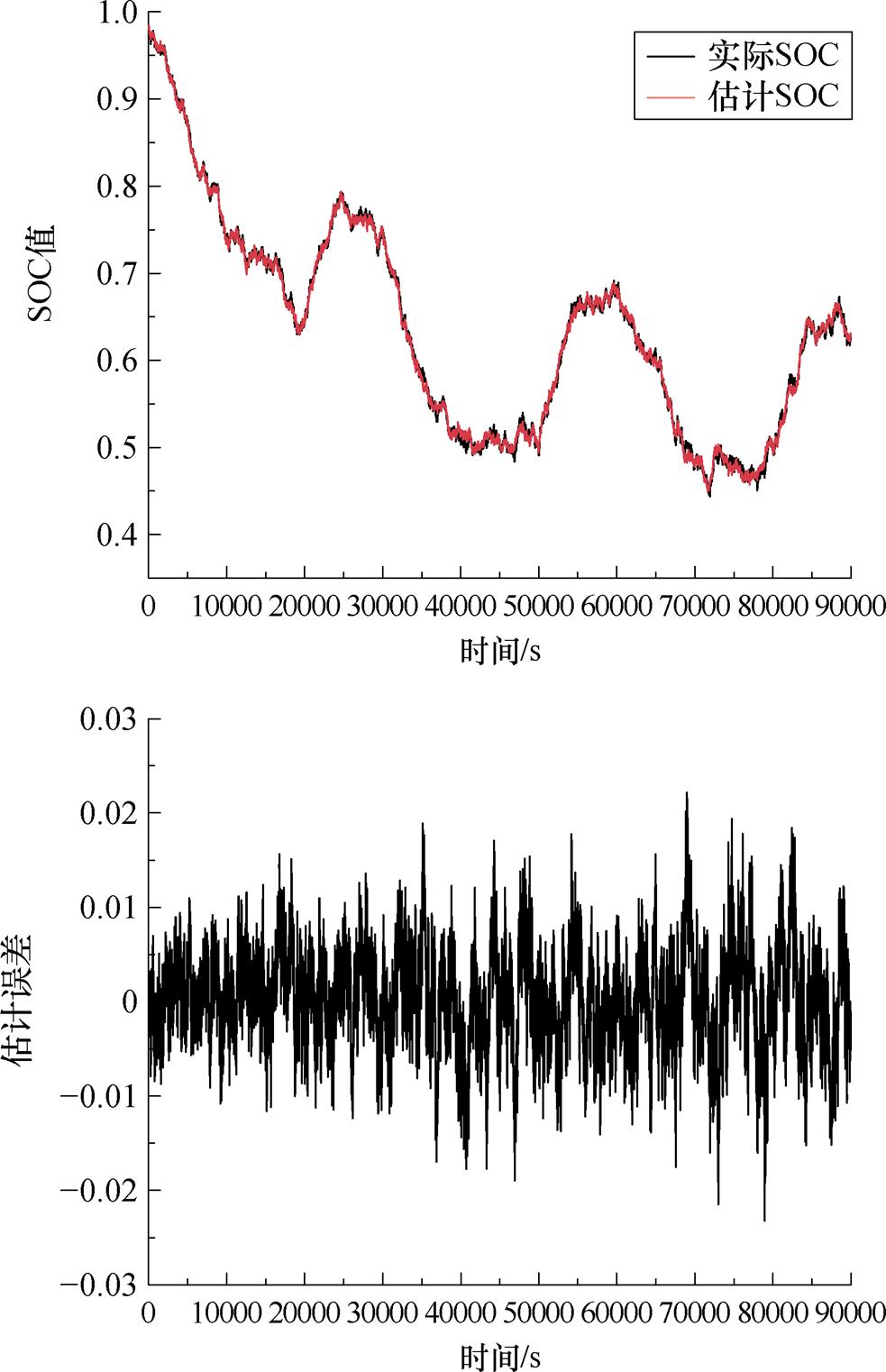
图26 SOC估计结果与误差
Fig.26 SOC estimated results and errors
由硬件在环实验结果可知,全新锂离子电池在常温环境下,使用本文所提算法可保证电池组SOC估算误差在2.5%以内。高低温极端环境是目前影响电池性能的重要因素,因此选择在-20℃、0℃、50℃以及电池可用容量为90%、80%条件下进行实验,并通过与传统EKF、UKF估算算法进行对比,验证本文所提算法准确性及鲁棒性,实验结果如图27~图31所示。三种算法估计误差平均值对比见表2。
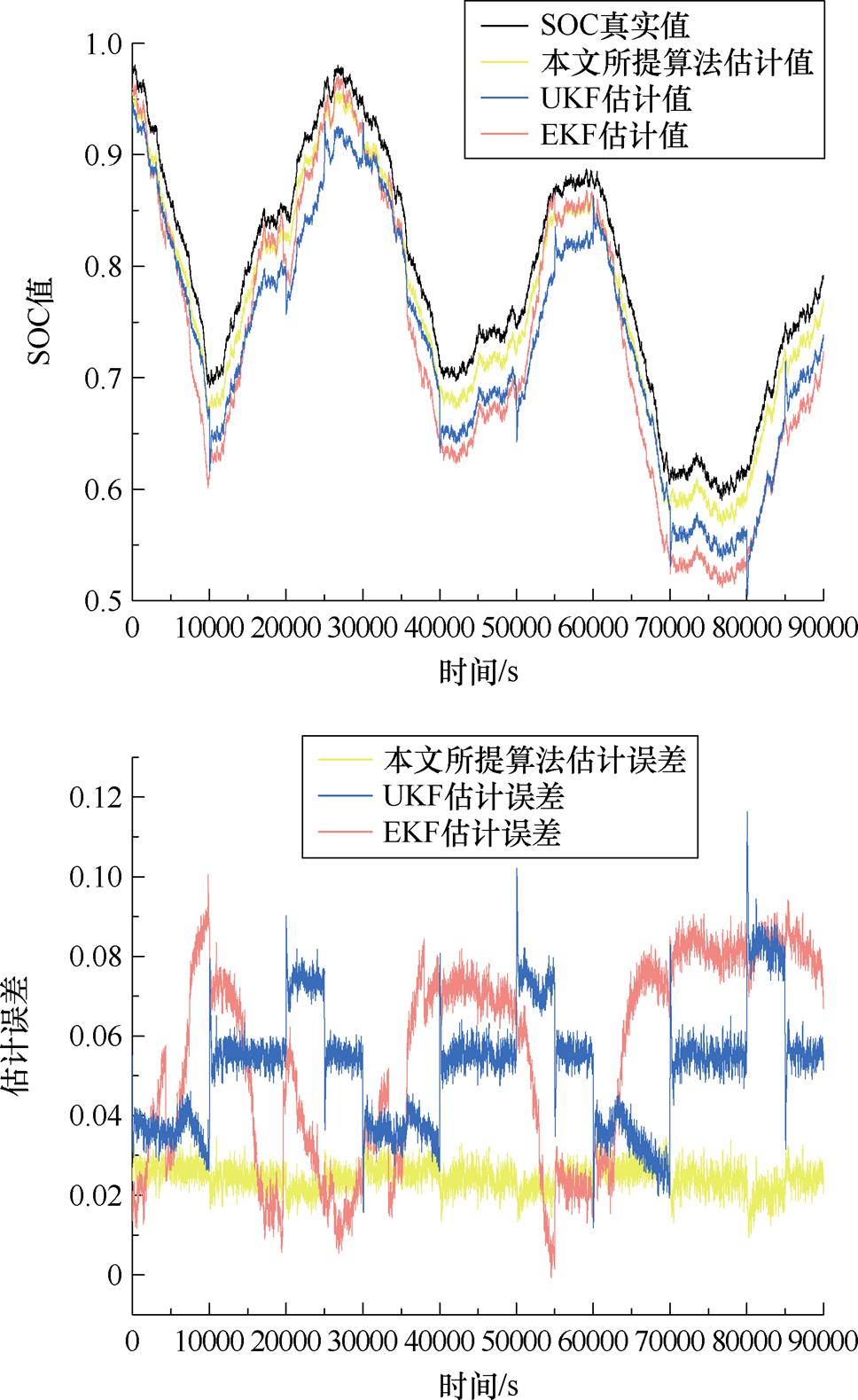
图27 在-20℃下,SOC估计结果与误差
Fig.27 At -20℃, SOC estimates results and errors
1)NARX神经网络优化后的二阶RC等效电路模型,相比传统二阶RC等效电路模型应对环境温度、电池老化变化更加灵活,能够实现多种工况下电池极化电压的精准预测,提高电池模型精度。
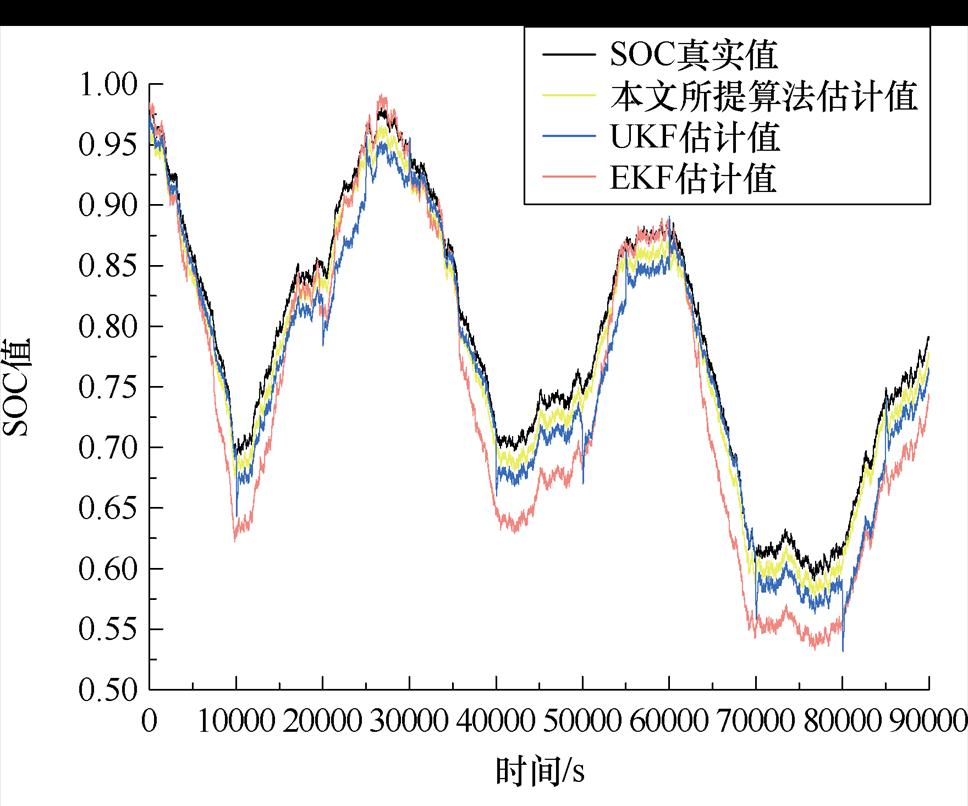
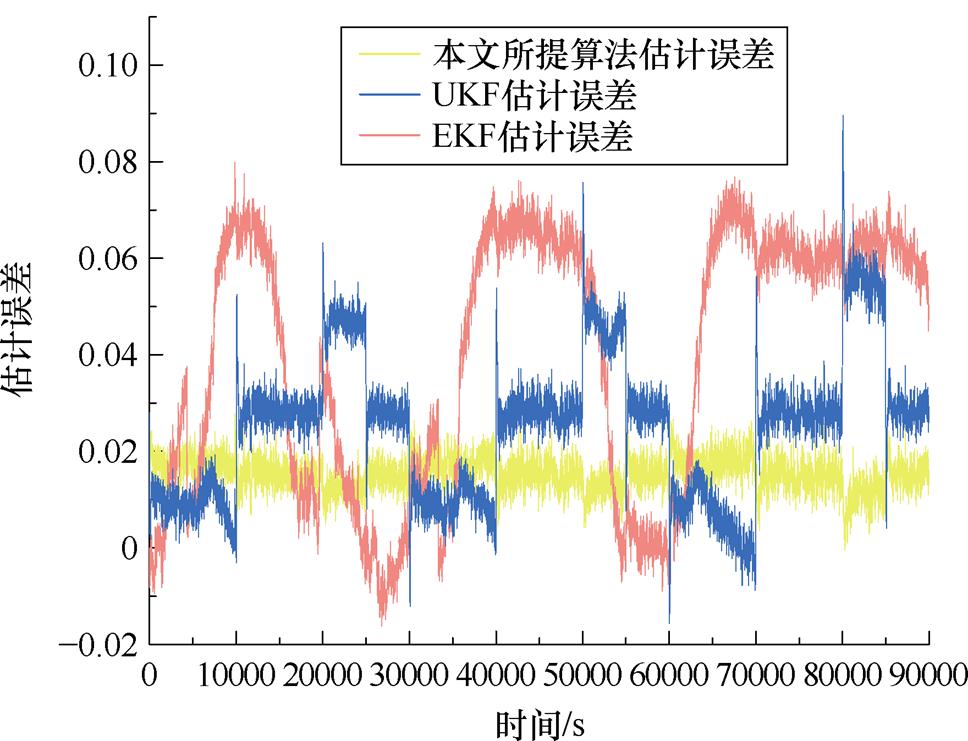
图28 在0℃下,SOC估计结果与误差
Fig.28 At 0℃, SOC estimated results and errors
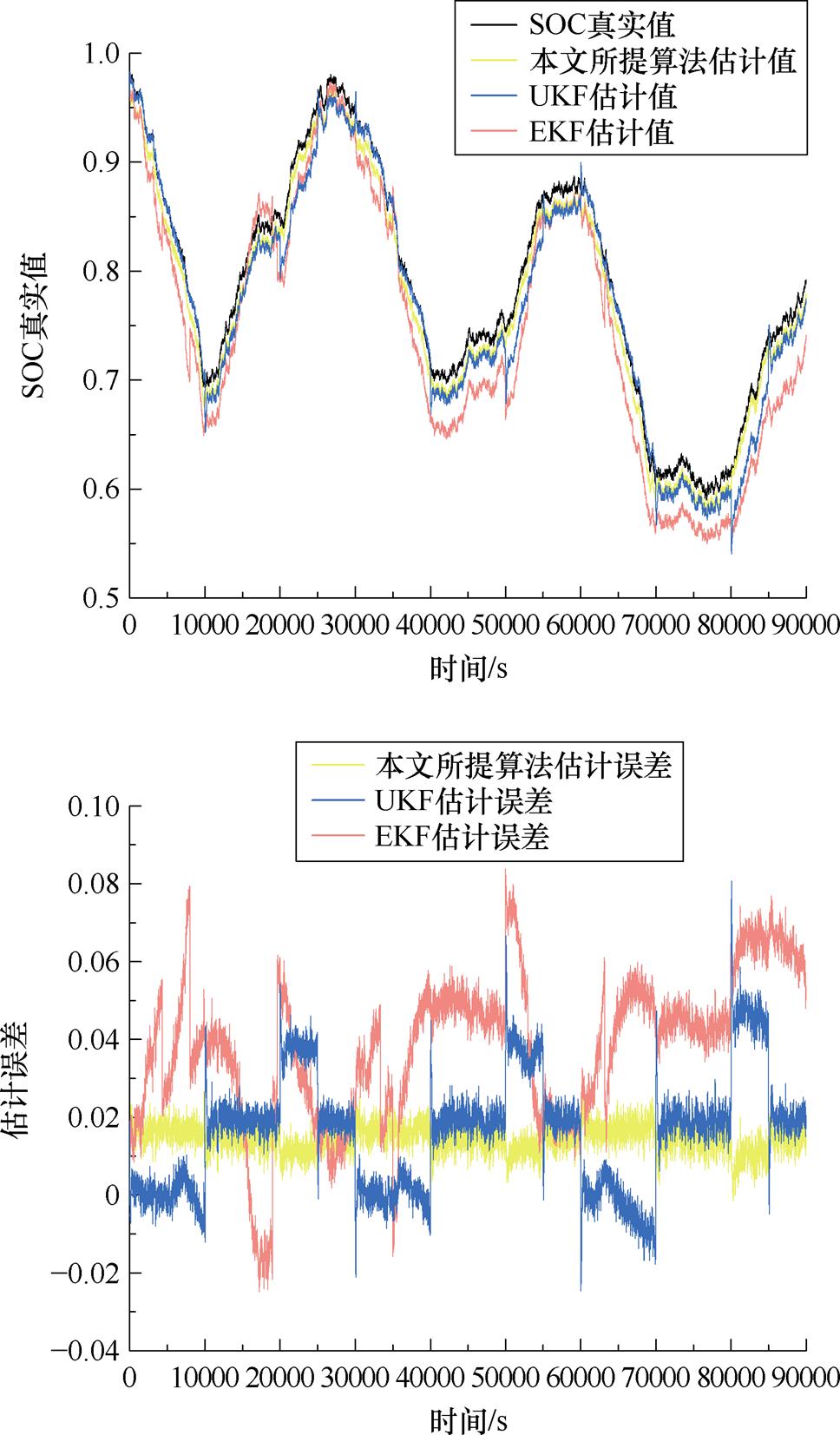
图29 在50℃下,SOC估计结果与误差
Fig.29 At 50℃, SOC estimated results and errors
2)均值差异模型能够更好地表征电池组中各电池状态,使用AUKF算法分别对均值及差异模型进行估算,并使用模糊控制确定电池SOC融合权重,实现了电池组SOC估算。
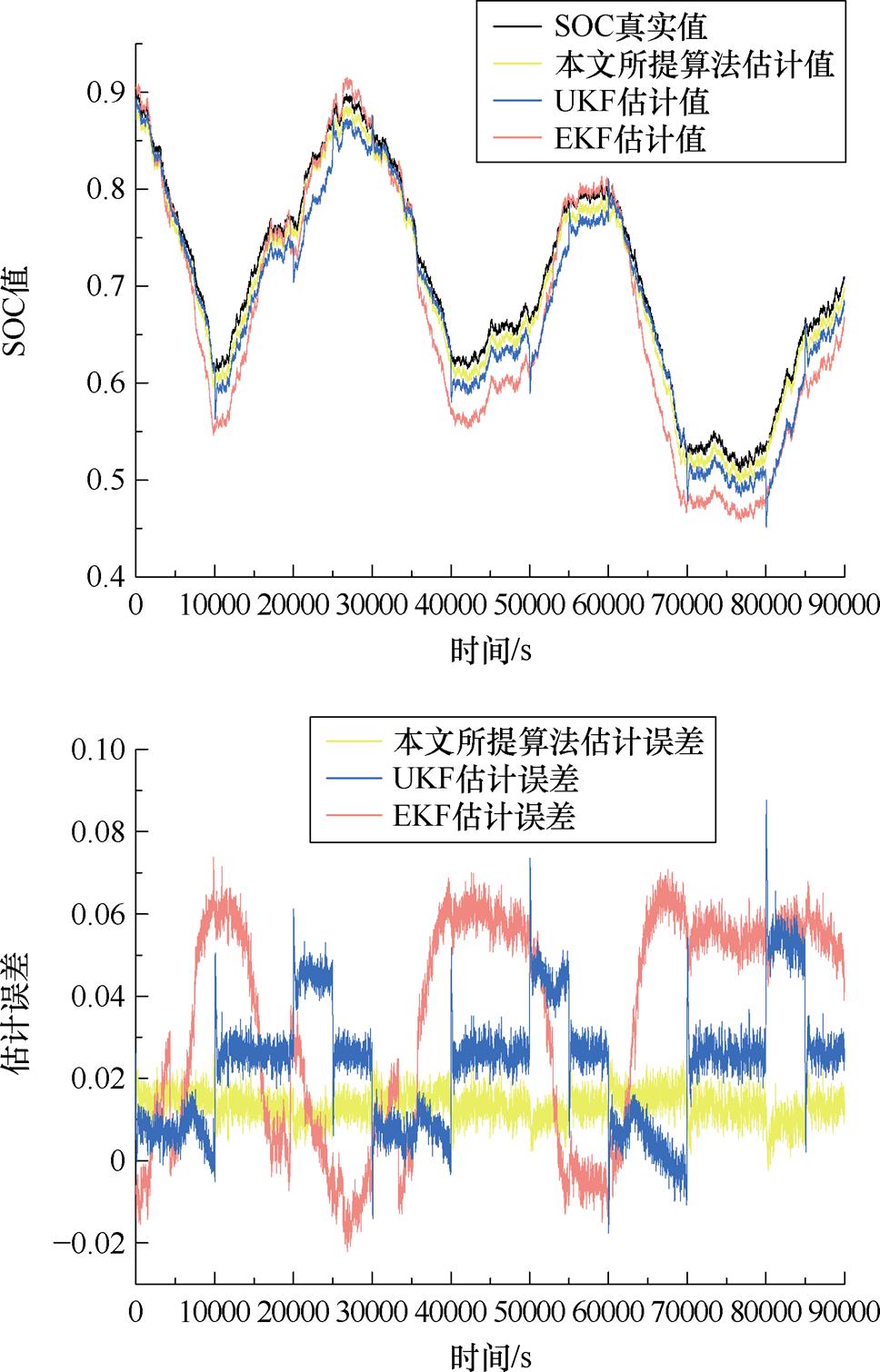
图30 25℃,可用容量90%时,SOC估计结果与误差
Fig.30 When the available capacity is 90% at 25℃, SOC estimation results and errors
3)通过多种不同温度、不同老化条件的运行工况,将本文所提算法与EKF及UKF算法进行对比,实验结果表明,本文所提算法估算误差在2.5%以内,且估算误差平均值均在3%以内,估算误差及误差平均值均优于EKF、UKF算法,验证了本文所提算法的准确性及鲁棒性。
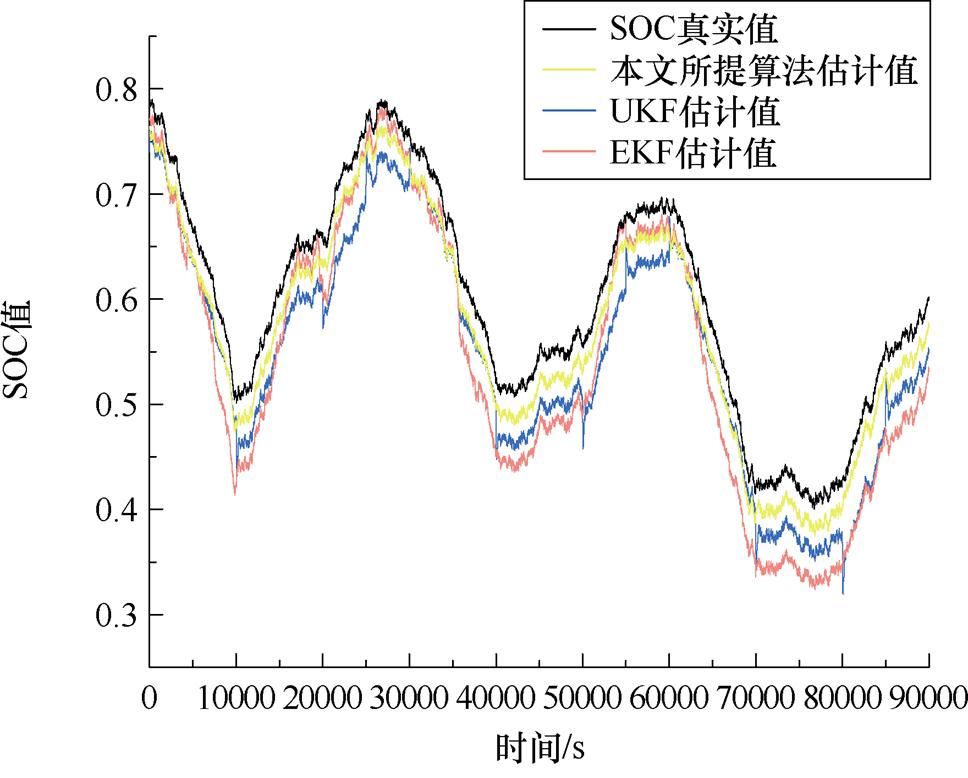
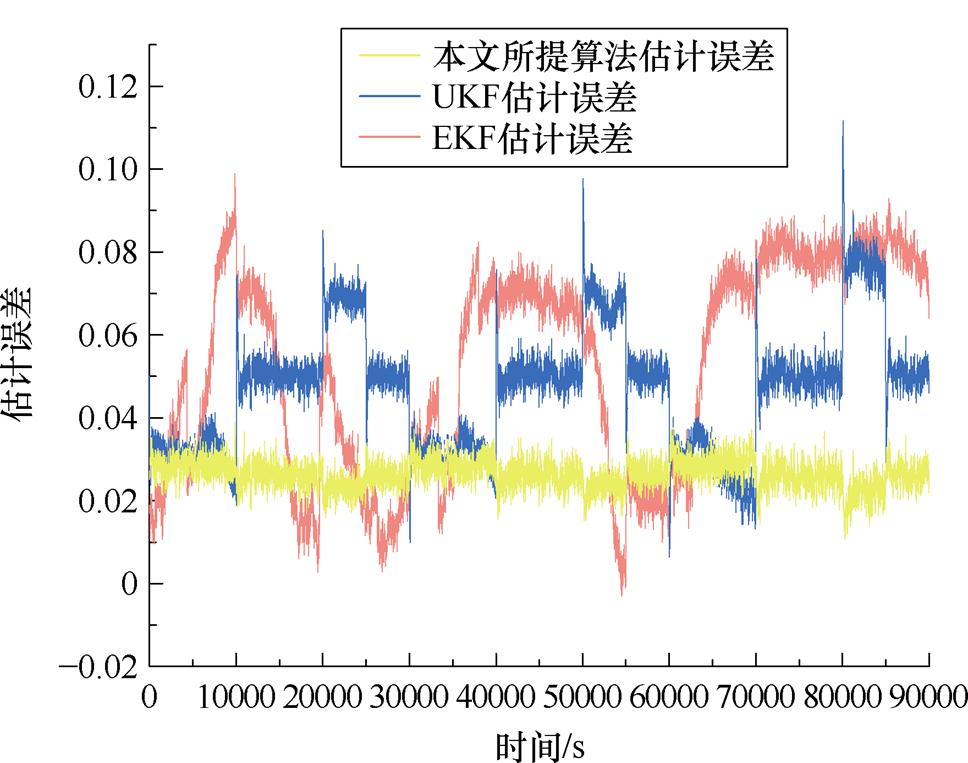
图31 25℃,可用容量80%时,SOC估计结果与误差
Fig.31 When the available capacity is 80% at 25℃, SOC estimation results and errors
表2 三种算法估计误差平均值对比
Tab.2 Comparison of the average estimation error of the three algorithms(%)
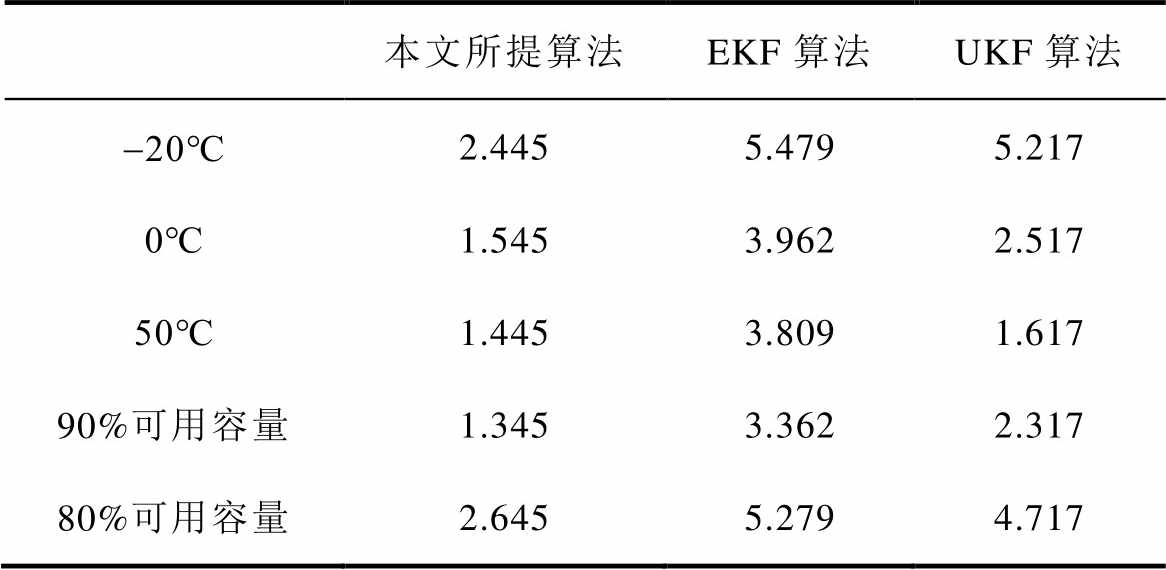
本文所提算法EKF算法UKF算法 -20℃2.4455.4795.217 0℃1.5453.9622.517 50℃1.4453.8091.617 90%可用容量1.3453.3622.317 80%可用容量2.6455.2794.717
参考文献
[1] 王新栋, 董政, 王书华, 等. 基于改进开路电压模型和自适应平方根无迹卡尔曼滤波的锂离子电池宽温度多工况SOC估计[J]. 电工技术学报, 2024, 39(24): 7950-7964.
Wang XinDong, Dong Zheng, Wang Shuhua, et al. Wide temperature multi-condition SOC estimation for Li-ion batteries based on improved open circuit voltage model and adaptive square root untrace Kalman filter[J]. Transactions of China Electro- technical Society, 2024, 39(24): 7950-7964.
[2] 宗梦然. 电网储能用电池管理系统设计与实现[D].郑州: 郑州大学, 2020.
Zong Mengran. The design and implementation of battery management system for grid energy storage[D]. Zhengzhou: Zhengzhou University, 2020.
[3] Zhou W, Zheng Y, Pan Z, et al. Review on the battery model and SOC estimation method[J]. Processes, 2021, 9(9): 1685.
[4] Shi Meihua, Yuan Jingchao, Dong Li, et al. Com- bining physicochemical model with the equivalent circuit model for performance prediction and optimization of lead-acid batteries[J]. Electrochimica Acta, 2020, 353: 136567.
[5] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint SOC and SOH estimation method based on the fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[6] Yang Jufeng, Huang Wenxin, Xia Bing, et al. The improved open-circuit voltage characterization test using active polarization voltage reduction method[J]. Applied Energy, 2019, 237: 682-694.
[7] Boujoudar Y, Elmoussaoui H, Lamhamdi T. Lithium- ion batteries modeling and state of charge estimation using artificial neural network[J]. International Journal of Electrical and Computer Engineering, 2019, 9(5): 3415.
[8] 华菁, 阮观强, 胡星, 等. 基于TVFFRLS-ACKF的锂离子电池SOC估算[J].电子测量技术, 2022, 45(24): 22-28.
Hua Jing, Ruan Guanqiang, Hu Xing, et al. SOC Estimation of lithium-ion battery based on TVFFLS- ACKF[J]. Electronic Measurement Technology, 2022, 45(24): 22-28.
[9] 周韦润. 动力电池参数辨识和荷电状态估计研究[D]. 镇江: 江苏科技大学, 2019.
Zhou Weirun. Power battery parameter identification and state of charge estimation[D]. Zhenjiang: Jiangsu University of Science and Technology, 2019.
[10] Manh-Kien Tran, Anosh Mevawala, Satyam Panchal, et al. Effect of integrating the hysteresis component to the equivalent circuit model of lithium-ion battery for dynamic and non-dynamic applications[J]. Journal of Energy Storage, 2020, 32: 101785.
[11] Luo Yong, Qi Pengwei, Kan Yingzhe, et al. State of charge estimation method based on the extended Kalman filter algorithm with consideration of time varying battery parameters[J]. International Journal of Energy Research, 2020, 44(13): 10538-10550.
[12] Afshar S, Morris K, Khajepour A. State-of-charge estimation using an EKF-based adaptive observer[J]. IEEE Transactions on Control Systems Technology, 2018, 27(5): 1907-1923.
[13] 钱伟, 王浩宇, 郭向伟, 等. 联合改进滑模观测器的自适应卡尔曼滤波荷电状态估计[J]. 电工技术学报, 2025, 40(6): 1984-1994.
Qian Wei, Wang Haoyu, Guo Xiangwei, et al. Adaptive Kalman filter state of charge estimation for a combined improved sliding mode observer[J]. Transactions of China Electrotechnical Society, 2025, 40(6): 1984-1994.
[14] Chen Kui, Zhou Shuyuan, Liu Kai, et al. State of charge estimation for lithium-ion battery based on whale optimization algorithm and multi-kernel relevance vector machine[J]. The Journal of Chemical Physics, 2023, 158(10): 104110.
[15] 张君鸣. 基于神经网络方法的锂离子电池状态估计研究[D]. 济南: 山东大学, 2021.
Zhang Junming. Research on state estimation of li-ion battery based on neural network[D]. Jinan: Shandong University, 2021.
[16] 余杰, 廖思阳, 徐箭, 等. 考虑环境温度的磷酸铁锂电池SOC实时修正及频率控制方法[J]. 电工技术学报, 2023, 38(17): 4564-4573.
Yu Jie, Liao Siyang, Xu Jian, et al. Real-time SOC correction and frequency control method for lithium iron phosphate batteries considering ambient tempera- ture[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4564-4573.
[17] 靳立强, 孙志祥, 刘志茹, 等. 不同温度下锂电池剩余电量估算的仿真研究[J]. 汽车工程, 2019, 41(5): 590-598, 606.
Jin Liqiang, Sun Zhixiang, Liu Zhiru, et al. Simulation research on estimation of residual charge of lithium battery at different temperatures[J]. Automotive Engineering, 2019, 41(5): 590-598, 606.
[18] 郑涛, 张里, 侯杨成, 等. 基于自适应CKF的老化锂电池SOC估计[J]. 储能科学与技术, 2020, 9(4): 1193-1199.
Zheng Tao, Zhang Li, Hou Yangcheng, et al. SOC Estimation of aging lithium batteries based on adaptive CKF[J]. Energy Storage Science and Technology, 2020, 9(4): 1193-1199.
[19] 刘光军, 吴思齐. 基于分段聚合和卡尔曼滤波的锂电池组SOC估算[J]. 江苏大学学报(自然科学版), 2024, 45(3): 281-285.
Liu Guangjun, Wu Siqi. SOC estimation of lithium battery pack based on segmented polymerization and Kalman filter[J]. Journal of Jiangsu University (Natural Science Edition), 2024, 45(3): 281-285.
[20] 申江卫, 刘伟强, 高承志, 等. 宽温度环境下基于迁移模型的锂电池组SOC估计[J]. 中国公路学报, 2024, 37(5): 383-396.
Shen Jiangwei, Liu Weiqiang, Gao Chengzhi, et al. State of charge estimation of lithium battery packs in wide temperature environments based on migration model[J]. China Journal of Highway and Transport, 2024, 37(5): 383-396.
[21] 张宇翔. 基于NARX神经网络的锂离子电池建模及SOC估计的研究[D]. 上海: 上海交通大学, 2019.
Zhang Yuxiang. Lithium-ion battery modelling and SOC estimation based on NARX neural networks[D]. Shanghai: Shanghai Jiao Tong University, 2019.
[22] 赵英杰, 张闯, 刘素贞, 等. 基于电极等效电路模型的锂离子电池无析锂快充策略优化研究[J]. 电工技术学报, 2024, 39(18): 5868-5882.
Zhao Yingjie, Zhang Chuang, Liu Suzhen, et al. Optimization of fast charging strategy for lithium-ion batteries without dissolving lithium based on elec- trode equivalent circuit model[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5868- 5882.
[23] 陈玉伟, 顾钟凡, 李承澳, 等. 基于BP-AUKF算法和FFRLS的蓄电池SOC估计[J]. 电力设备管理, 2021(9): 211-213.
Chen Yuwei, Gu Zhongfan, Li Cheng’ao, et al. Battery SOC estimation based on BP-AUKF algo- rithm and FFRLS[J]. Electric Power Equipment Management, 2021(9): 211-213.
[24] 刘雨洋. 基于H∞ 滤波的锂电池SOC与SOP联合估计研究[D]. 绵阳: 西南科技大学, 2023.
Liu Yuyang. Joint estimation of lithium battery SOC and SOP based on H∞ filtering[D]. Mianyang: Southwest University of Science and Technology, 2023.
[25] 王文亮, 何锋, 蒋雪生, 等. 基于双扩展卡尔曼滤波锂电池荷电状态估算研究[J]. 电子测量技术, 2020, 43(19): 49-52.
Wang Wenliang, He Feng, Jiang Xuesheng, et al. Research on charge state estimation of lithium battery based on double extended Kalman filter[J]. Electronic Measurement Technology, 2020, 43(19): 49-52.
[26] Barcellona S, Piegari L. Lithium ion battery models and parameter identification techniques[J]. Energies, 2017, 10(12): 2007.
[27] 徐鹏, 王潺, 万世斌, 等. 基于NARXNN变工况下锂离子电池SOC间接估计[J]. 电源技术, 2022, 46(10): 1161-1166.
Xu Peng, Wang Chan, Wan Shibin, et al. Li-ion battery SOC indirect estimation under varying working profile based on NARX neural network[J]. Chinese Journal of Power Sources, 2022, 46(10): 1161-1166.
[28] 秦潇涵. 基于循环神经网络的锂电池SOC估计[D].杭州: 杭州电子科技大学, 2020.
Qin Xiaohan. SOC estimation for lithium ion batteries based on recurrent neural network[D]. Hangzhou: Hangzhou Dianzi University, 2020.
[29] 候亚虹. 动力电池组不一致性建模及SOC融合估计研究[D]. 西安: 长安大学, 2021.
Hou Yahong. Inconsistency modeling of power battery pack and SOC fusion estimation[D]. Xi’an: Changan University, 2021.
[30] 何志刚, 李尧太, 盘朝奉, 等. 基于AIUKF的锂离子电池SOC估算[J]. 电源技术, 2020, 44(4): 518-521.
He Zhigang, Li Yaotai, Pan Chaofeng, et al. Lithium- ion battery SOC Estimation based on AIUKF[J]. Chinese Journal of Power Sources, 2020, 44(4): 518-521.
[31] Lin Xinyou, Tang Yunliang, Ren Jing, et al. State of charge estimation with the adaptive unscented Kalman filter based on an accurate equivalent circuit model[J]. Journal of Energy Storage, 2021, 41: 102840.
[32] 高文帅. 基于T-S模糊神经网络的Hammerstein模型预测控制[D]. 抚顺: 辽宁石油化工大学, 2020.
Gao Wenshuai. Predictive control of Hammerstein model based on T-S fuzzy neural network[D]. Fushun: Liaoning Shihua University, 2020.
SOC Estimation Algorithm of Lithium-Ion Battery Pack for Energy Storage Considering Temperature and Aging
Abstract The traditional state of charge (SOC) estimation algorithm does not consider the ambient temperature and aging state of the battery changes when using the lithium-ion battery pack for energy storage. In practical applications, the adaptability is poor, and the estimation accuracy is low. In recent years, several SOC estimation algorithms for battery packs have been proposed, taking into account temperature or battery aging. However, most remain incomplete and exhibit high computational complexity. This paper proposes a SOC estimation algorithm for lithium-ion battery packs used in energy storage, which considers temperature and aging, to enhance the accuracy and robustness of SOC estimation in battery packs under various ambient temperatures and aging states.
First, the 100 A·h lithium iron phosphate battery produced by Zhongke De Fang (Hebei) New Energy Co., Ltd. is used as the research object, and its characteristics are tested under various temperatures and aging conditions. Depending on the characteristics of the selected battery, the second-order RC equivalent circuit model is chosen as the basic battery model. A nonlinear autoregressive neural network with external input (NARX) is chosen to replace the RC circuit in the second-order RC equivalent circuit model, and the NARX neural network structure is determined by training the model through actual working conditions data. Then, a battery model considering ambient temperature and battery aging is established. The working condition data is randomly selected from the enterprise database. SOC estimation is performed to verify the computation and accuracy of the optimized NARX neural network battery model. The experimental results show that although the convergence rate of the NARX neural network optimized battery model is slightly slower than that of the traditional second-order RC equivalent circuit model, the estimated error of the optimized battery model is much smaller than that of the conventional battery model. Therefore, the improved battery model performs better and is more suitable for SOC estimation of subsequent battery packs. Considering SOC and internal resistance differences, a battery pack mean difference model is proposed. An adaptive unscented Kalman filtering (AUKF) algorithm is selected to estimate the mean model and difference model, and the SOC of the difference model is modified to obtain the SOC of the single battery pack. A fuzzy control strategy determines the battery pack's SOC fusion weight.
Finally, a hardware-in-the-loop simulation platform is built to verify the SOC estimation algorithm for battery packs. The proposed algorithm is compared with the traditional extended Kalman filter (EKF) and unscented Kalman filter (UKF) algorithms at ambient temperatures of -20℃, 0℃, and 50℃, and for aging states of the battery of 90% and 80%. Experimental results demonstrate that the proposed algorithm ensures an average estimation error of less than 3% under various temperatures and aging operating conditions. Under any working conditions, the average estimation error of the proposed algorithm is lower than that of traditional EKF and UKF algorithms.
Keywords:Battery pack SOC estimation, NARX neural network, mean difference model, AUKF algorithm, fuzzy control
中图分类号:TM912.9
DOI: 10.19595/j.cnki.1000-6753.tces.241201
河北省引进留学人员项目(CL201704)和河北省高等学校科学技术研究项目(ZD2019023)资助。
收稿日期 2024-07-06
改稿日期 2024-08-13
姬 鹏 男,1977年生,博士,教授,博士生导师,研究方向为新能源车辆动力学与控制、电动汽车智能化。
E-mail: Pj180@126.com
吕泽旭 男,2000年生,硕士研究生,研究方向为电池SOC估算。
E-mail: 862318211@qq.com(通信作者)
(编辑 郭丽军)