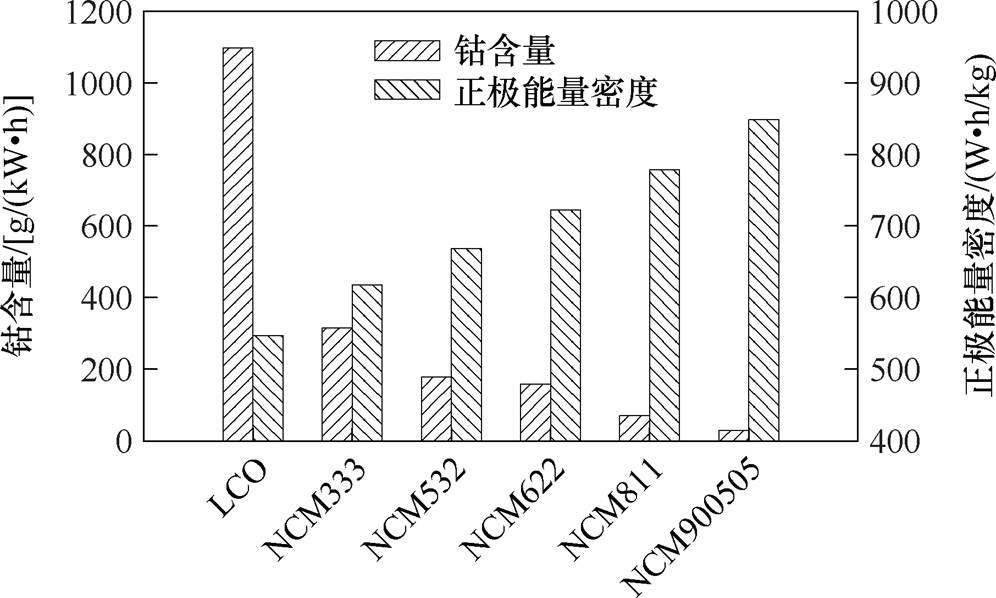
图1 不同含钴量正极材料的能量密度[2]
Fig.1 Energy density of cathode materials with different cobalt content[2]
摘要 无钴正极材料可以打破钴元素阻碍锂离子电池发展的壁垒，对新能源汽车可持续发展具有重要意义。电化学模型是分析无钴电池内外部特性参数的桥梁，是研究电池状态估计和老化诊断的理论基础。宽温域下无钴电池建模存在精度低、参数获取困难的问题，为提高宽温域无钴电池电化学模型的仿真能力，该文提出基于多维度灵敏度分析的高敏感度模型参数确定方法。研究表明，电池正负极固相扩散系数、反应速率常数、材料颗粒半径等参数对温度和倍率的依赖性显著；为解决低温大部分模型参数灵敏度急剧增加而导致参数辨识失效的问题，采用Arrhenius方程描述高灵敏度电化学参数随温度的变化规律，建立宽温度域电化学模型参数修正方法，-5～50℃范围内模型方均根误差20 mV以内。利用改进的电化学模型，揭示了无钴电池的电化学参数与电性能的关联关系，结果表明扩散类参数与电池的容量和能量指标紧密关联，为无钴电池老化状态诊断和智能管理提供重要的理论支撑。
关键词：无钴锂离子电池 P2D模型 灵敏度分析 宽温度区域
锂离子电池因其高比能、轻量化和环保等特点，已成为电动汽车的理想动力源之一。锂离子电池的能量密度主要由正极材料决定，其占据了电池总成本的40%～50%。正极的成本主要取决于原材料的成本，如锂、镍、钴等元素，其中广泛应用的钴元素存在着价格波动大和供应链脆弱等问题[1]。根据InfoMine报道，截至2024年5月，钴的成交价为12.47$/lb（1 lb=0.453 592 37 kg），远超镍、锰等元素的价格，因此降低锂离子电池中钴元素的含量已成行业发展的当务之急。为避免钴元素对锂离子电池发展的限制，研究人员提出了磷酸铁锂体系以及具有高比能特点的镍钴锰层状氧化物正极体系（Nickel-Cobalt- Manganese, NCM）等，从NCM333发展到NCM811再到无钴镍锰体系，逐步减少钴元素的占比，也提高了正极材料的能量密度，不同含钴量正极材料的能量密度如图1所示。
图1 不同含钴量正极材料的能量密度[2]
Fig.1 Energy density of cathode materials with different cobalt content[2]
无论是NCM还是无钴镍锰材料均是层状氧化物，由氧原子层分隔的锂离子层和过渡金属离子层组成。根据XRD图谱显示，无钴正极材料的（003）反射的峰值强度与（104）反射的峰值强度之比（I(003)/I(104)）低于NCM材料，增大钴元素和镍元素的含量可以明显降低正极材料中阳离子Ni2+/Li+的混合程度[3]。文献[4]提出存在于过渡金属层中的钴元素，通过减小层间和层内的磁阻来削弱阳离子混排效应。文献[5-6]采用其他元素替代钴元素的作用，但仍然存在初始库仑效率低和倍率性能差的问题，经分析主要是因为H1相的动力性能差所引起。然而，文献[7]研究了通过参杂其他元素抑制LiNiO2多重相变，发现与Al、Mn和Mg不同，较低含量的钴（尤其是低于5%占比）不能有效抑制相变，对于高镍材料无法提供安全性支撑。因此，在过渡金属层中钴元素并非必不可少，也有研究表明一定程度的阳离子混排可以缩减高荷电状态下的层间距离，有利于电池循环过程中的结构稳定[8]。为实现电池的最佳性能可以采取掺杂阳离子、取代特殊元素、材料表面包覆等优化策略[9]。
目前，对于无钴动力电池的性能及温度依赖性研究较少，为探究宽温度区域无钴电池电性能及内部主导因素，需要在准确搭建电化学模型的基础上提取电化学参数与电性能指标，发展能够揭示演变规律和互联效应的特征作为快速无损检测指标。J. Newman等提出了一种结合微观颗粒行为和宏观动力学行为的准二维（Pseudo-Two-Dimensional, P2D）模型，用于描述锂离子电池内部的锂离子扩散、迁移和界面反应等物理和化学过程，同等效电路模型相比，可以更准确地仿真电池的性能和行为[10]。因此，P2D模型的大多参数都具有物理含义，这为深入了解电池性能提供了机会。然而P2D模型具有数十个待辨识的参数且部分存在强耦合，同时受温度影响较大，给宽温度区间高精度机理建模带来困难。为了厘清电池在不同环境温度和运行工况时电化学参数的影响程度，需要分析参数的灵敏度，从而提升参数的可靠性以保证模型的仿真精度。文献[11]在常温下基于不同倍率和放电深度，采用局部灵敏度方法分析26个参数的敏感性，确定参数的可识别性，但未考虑温度变化对电化学参数的影响。文献[12]采用初等效应检验方法在多种工况下对电池P2D模型参数的全局灵敏度进行评估，提出新的无损参数辨识方法。研究表明，电化学参数的灵敏度往往受电池荷电状态和倍率的约束，因此需要从多维度出发，综合考虑温度、倍率和荷电状态这三者对建模参数的影响。随后，需要准确获取可识别性高的参数，一般多采用直接测量，或者粒子群优化算法等方式确定[13]。文献[14]按照参数的时变特征分组，使用恒流脉冲识别8个快速动态参数，再利用准静态测试数据识别8个慢速动态参数。参数辨识往往面临一种实验能否有效区别多个具体参数值的问题，因此需要选择更为细致的分离方式。对于研究电化学参数的温度效应，文献[15]实现了一维电化学模型和三维热模型的耦合计算，采用Arrhenius方程修正温度对部分动力学参数的影响，文献[16]则引入更多随温度和电解液浓度变化的电化学参数及其经验公式，或是直接用常数值表示。
宽温域下无钴镍锰体系电池建模存在精度低的问题，特别是在低温时常规的P2D控制方程不能满足仿真精度的要求，同时电池的电化学参数和外特性之间的关联关系尚不清晰。为探究以上问题，本文首先通过分析无钴电池的电性能，得出易受温度和倍率影响的动力学障碍区域和电性能指标的电热依赖性。然后阐述了多维度电化学参数对模型输出的影响，提取出高灵敏度的参数，辨识并发现在低温下各电化学参数的灵敏度均大幅增加，通过辨识实验确定参数值的难度增大；提出利用温度修正方程改进低温时电化学参数的获取方法，建立宽温度域的电化学模型并验证其精度。最后，利用模型作为媒介，分析了无钴电池电化学参数与电性能间的关联关系，将扩散类的电化学参数与电池的容量和能量等电性能类指标相关联，作为后续研究无钴电池健康状态的一个重要指标。
本文选择了一款软包电池进行实验测试，其参数信息见表1。测试过程中为了将电池环境温度恒定在要求数值，将电池放入生化培养箱，整体的实验装置由生化培养箱（SPX-250BIII）、电池充放电测试系统（NEBULA 100A）及其上位机组成，如图2所示。
表1 无钴电池参数信息
Tab.1 Cobalt-free battery parameters
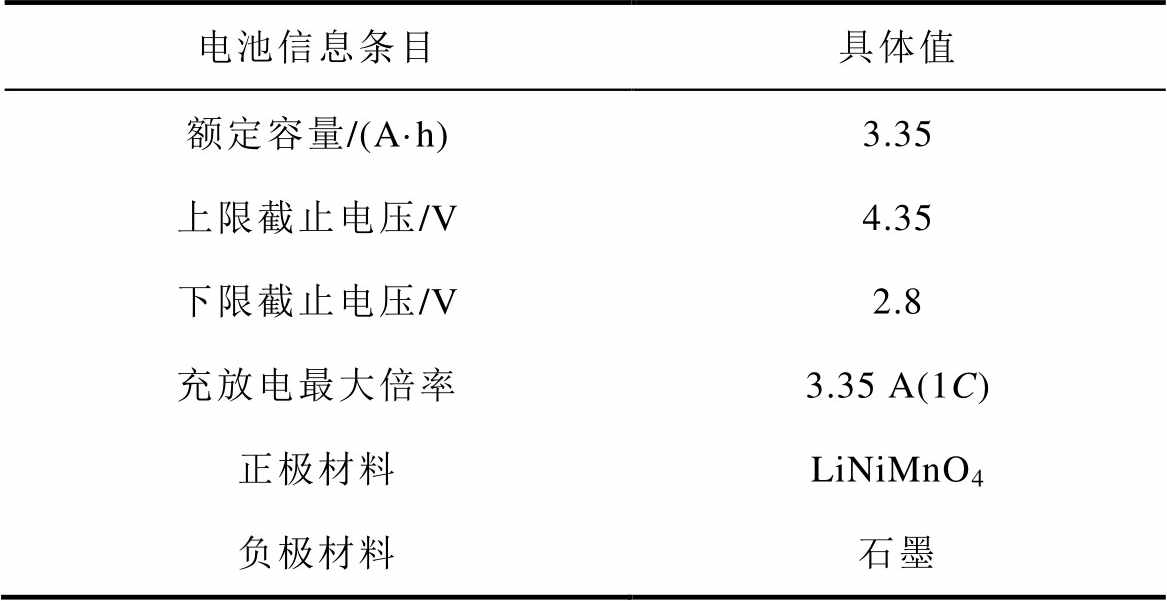
电池信息条目具体值 额定容量/(A·h)3.35 上限截止电压/V4.35 下限截止电压/V2.8 充放电最大倍率3.35 A(1C) 正极材料LiNiMnO4 负极材料石墨
将电池样本分别置于不同温度（-5℃、5℃、25℃、45℃）的生化培养箱中，采用恒流恒压充电和恒流放电的制式循环3次，分别设置倍率为0.2C、0.5C、0.8C、1C，作为无钴电池的电性能测试方案。无钴电池在不同温度下的开路电压容量增量曲线（以下简称IC曲线）如图3所示，使用与文献[17]相同的方法标记峰特征。其中，填充颜色的标号表示负极相变（如
），未填充颜色的标号表示正极相变（如①），★表示正极相变和负极相变的共同作用。
图2 电池测试平台
Fig.2 Battery test platform
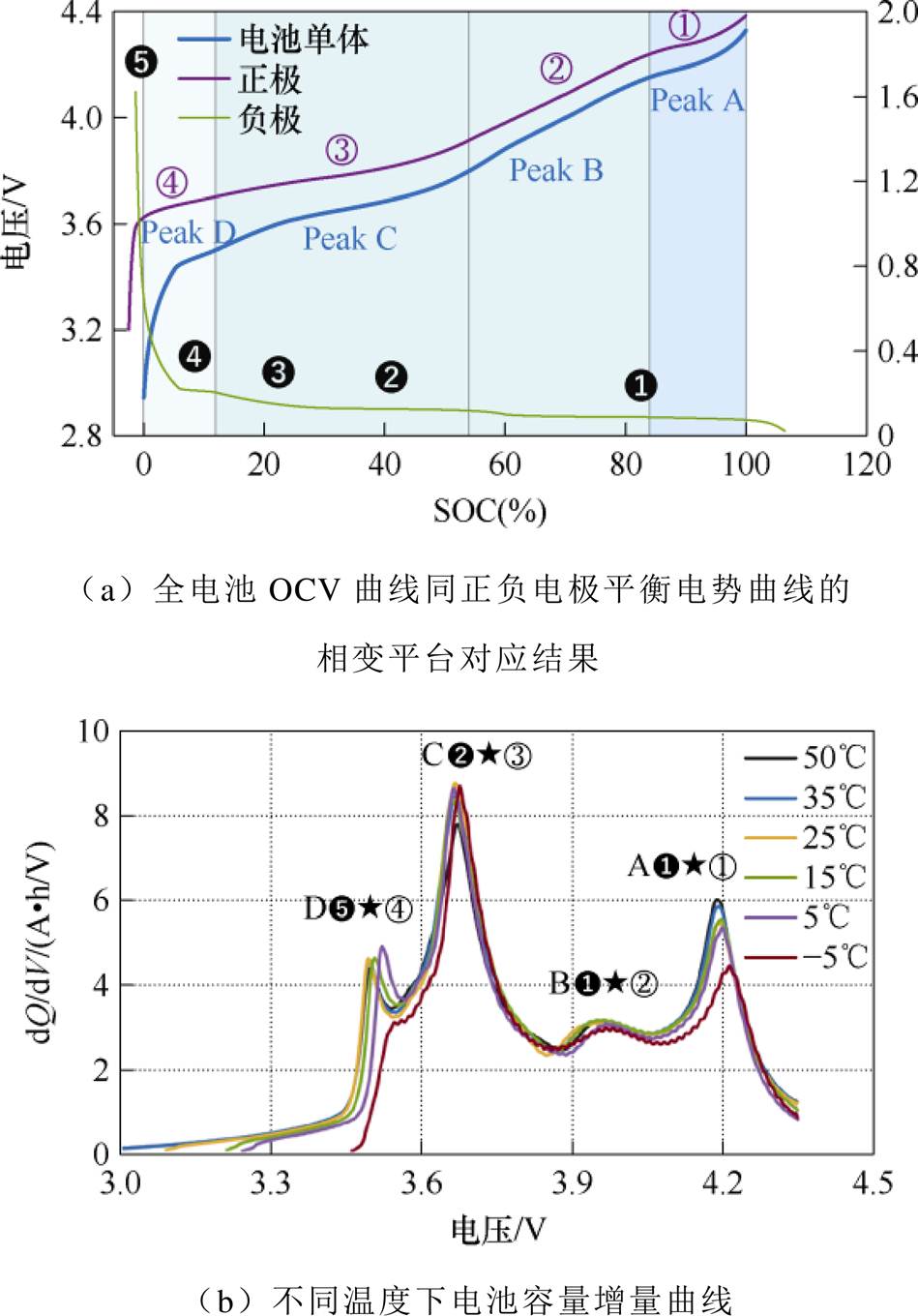
图3 全电池OCV曲线同正负电极平衡电势曲线的相变平台对应结果和不同温度下电池容量增量曲线
Fig.3 The OCV curve of cell corresponds to the phase transition platform of the balance potential curve of electrode and battery IC curve at different temperatures
在充放电过程中无钴材料经历了从六方晶系（H1）到单斜晶系（M），再到六方晶系（H2），最后到六方晶系（H3）的一系列相变过程[18-19]。随着电池环境温度的降低，可以发现峰A的峰值高度显著降低，特别是在-5℃，这个现象主要是因为电池的荷电状态（State of Charge, SOC）较高时，正极材料处于严重脱锂状态，即从六方晶系H2到H3的相变中，该相变会引起晶格C轴的收缩并产生机械应力，进而材料内部容易产生裂纹，造成电解液渗入发生副反应[19]；且负极因温度较低，锂离子的扩散和迁移效应变缓。由于充电初期正极出现了显著的电压极化现象，峰D在低温时也趋于消失，右移至3.55 V左右，变温静置的过程中电池的起始电压逐渐增大，开始充电后未及时积累电量就已经进入峰C区域。综上所述，峰A和峰D区域共同组成了无钴电池动力学受限的电压区域。需要通过研究物理含义更为全面的电化学模型来阐述温度对无钴电池内部性能的影响[20]。
对实验数据处理后提取了五种关于无钴电池电性能的参数指标，分别是容量、能量、库仑效率、能量效率和电池直流内阻。容量表示在某种条件下电池可储存的电量，结合其自身的体积可以预测大规模电池组的占用空间；通过对电池电压和容量的充放电曲线进行积分即可得到能量指标表征电池的动力性能[21]。库仑效率用以评估每次循环后电荷的可逆性，其中，与容量相关的库仑损失主要来源于电解液和电极活性物质的损失，而与容量不相关的库仑损失则是电池的自放电及析锂等副反应引起的。直流内阻表示电池接通电流后发生化学反应所产生的阻力大小，可以直接影响电池的发热和系统的响应速度。这五种电性能指标可直接通过充放电测试系统的数据计算得到，从电池外特性的角度反映电池性能与外部施加应力的关系。
无钴电池电性能参数随温度和倍率变化的三维图如图4所示。电池的容量和能量随着温度的升高而显著增大，但随着倍率增大却趋于下降。由于无钴材料中镍元素的含量较高，可以弥补钴元素缺失对倍率性能的影响，与NCM电池相比，其倍率性能的差异主要取决于镍元素的占比。因此电池的库仑效率受温度和倍率的影响较小，基本稳定在99.5%左右。而电池的能量效率则同时受到两者的共同影响，而且相对而言，倍率应力影响更为突出。当温度升高时，电池的内阻显著降低后趋于平稳，原因是电解液作为电池内部的电介质，往往随着温度的升高电导率增大，因而随着温度的升高电池的内阻表现为减小。经过定性分析后，选择25℃下0.5C恒流工况的电性能参数指标作为基准值，与其他15种情况下的指标作偏差比较，显示电性能参数指标对环境温度应力和倍率应力的依赖性，不同温度、不同倍率下无钴电池的电性能参数依赖性分析见表2（“+”符号的数量表征了电性能参数对倍率和温度因素的依赖程度，采用1～4个“+”进行评估，“+”越多依赖性越强），容量和能量的相关量依赖倍率，因为两者的计算方式与电池的电流和电压有关，在大倍率时电池的极化加重，造成可用容量和能量的显著减少。而内阻和效率的相关量对温度的依赖性更大，内阻的变化反映了低温条件下电池的内部损耗增加，更易诱发副反应；而效率则因其计算方式为放电数据除以充电数据的百分数从而抵消了倍率因素的影响。根据这五种外特性指标的变化规律选择适当的外界应力施加于无钴电池，使得电池能够发挥出更加优良的动力性能。
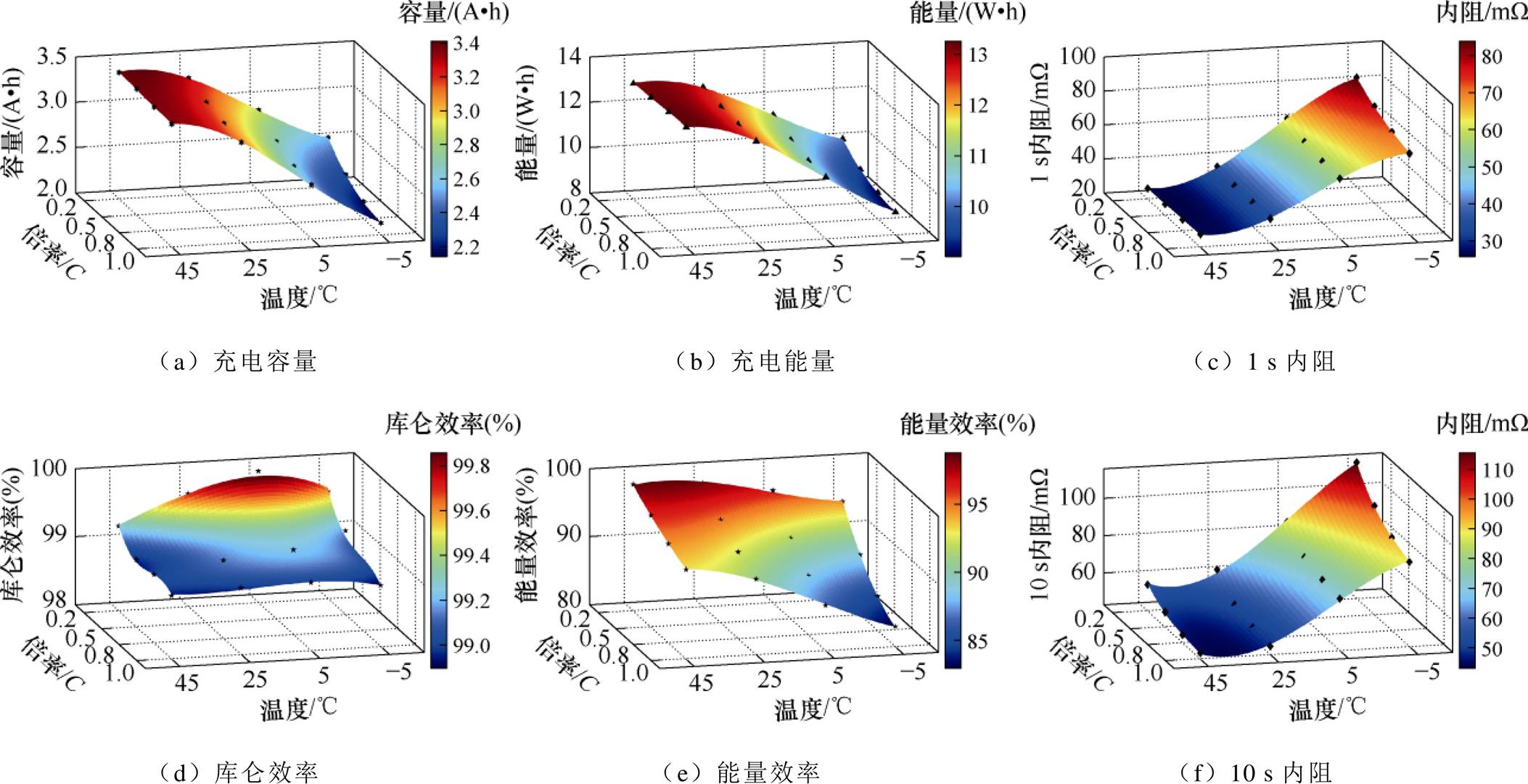
图4 无钴电池电性能参数随温度和倍率变化的三维图
Fig.4 Three-dimensional diagram of electric performance parameters of cobalt-free battery with temperature and rate
表2 不同温度不同倍率无钴电池电性能参数依赖性分析
Tab.2 Dependence analysis of electric performance parameters of cobalt-free batteries at different temperatures and rates
参 数倍率依赖性温度依赖性 容量Q/(A·h)+++++ 能量E/(W·h)+++++ 库仑效率CE(%)+++++ 能量效率EE(%)+++++ 1 s直流内阻R/W+++++ 10 s直流内阻R/W+++++
在P2D建模方法中，锂离子电池通常被视为一个由正极、负极和隔膜共同组成的整体。锂离子电池电化学模型示意图及电化学参数说明（充电过程）如图5所示。其充电过程中，锂离子从正极固体颗粒的内部扩散到颗粒表面，然后在颗粒表面发生氧化性动力学反应，生成的锂离子通过电解质中的扩散和传导穿越隔膜向负极移动。锂离子进入负极之后，在负极颗粒表面发生还原性动力学反应，从而逐渐扩散到石墨颗粒内部，直到充电结束。两个电极的化学反应方程如式（1）和式（2）所示，电池充电和放电为可逆反应。
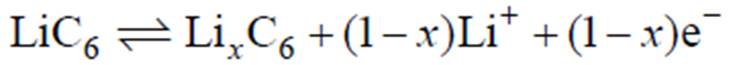（1）
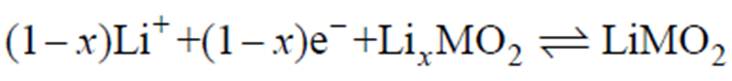（2）
P2D模型通常采用大小相同并且均匀分布的球形颗粒等效固体电极材料，锂离子在正极和负极材料中的扩散过程是P2D模型中的重点[22]。其扩散过程描述了固相材料中锂离子浓度随时间和位置变化的分布情况，遵循Fick第二定律，其中扩散系数Ds决定了锂离子在电极材料中的传输速率。因为电极活性材料整体具有电阻性能，通常使用微分形式的欧姆定律来表示电荷守恒定律。除了考虑电极材料中的反应原理，还需要考虑电解液中的离子传输和扩散过程，这些传输过程通常基于Nernst-Planck方程来描述。在电解液中，锂离子不仅会受到浓度差引起的扩散效应影响，另一方面还会受到外部施加电场造成的迁移效应影响。当电池接通电流之后，厚度方向上的锂离子浓度将由原本的静态初值逐渐分布不均匀。同时考虑扩散浓度变化和电解液自身的欧姆特性，综合得到液相电荷守恒方程。以上分别阐述了活性颗粒材料和电解液这两种不同物质形态所对应的反应控制方程，如何将这两者实现物理层面的沟通，则需要通过基于Butler-Volmer方程的电极动力学方程来描述锂离子孔壁流量与电荷传递过电势之间的关系。最后，引入负极表面存在固体电解质界面（Solid Electrolyte Interphase, SEI）膜阻抗造成的欧姆过电势，计算电池整体的电势守恒方程，得到电池的输出端电压，具体控制方程见附表1。
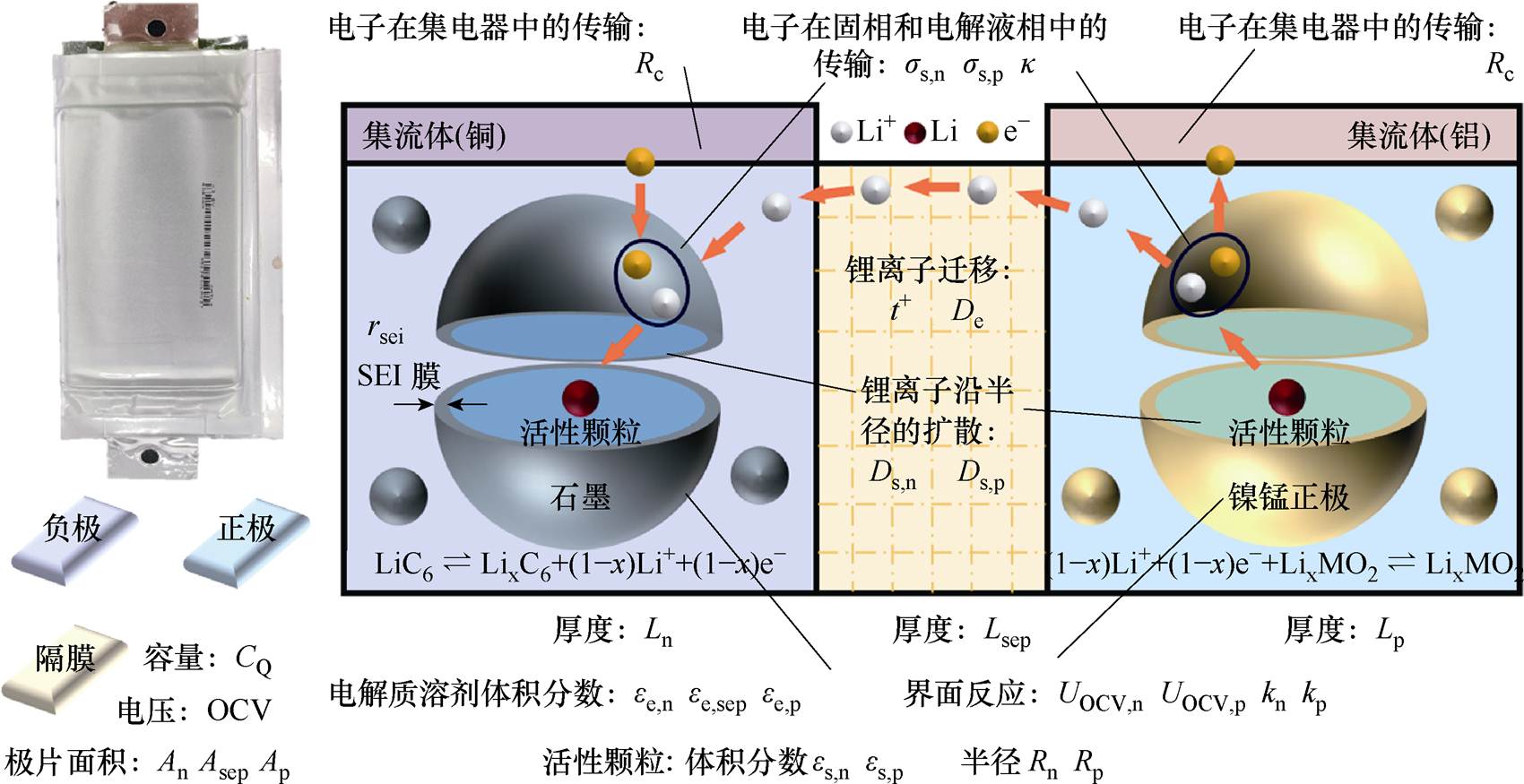
图5 锂离子电池电化学模型示意图及电化学参数说明（充电过程）
Fig.5 Schematic diagram of electrochemical model of lithium-ion battery and description of electrochemical parameters (charging)
P2D模型中的参数众多且易受电池所处状态的影响，因此在辨识合理的电化学参数之前，需要经过灵敏度分析，筛选出值得仔细辨识的待确定参数，既可以加速模型搭建，也为后续参数分析奠定基础。根据搭建无钴电池电化学模型的需求选取了18个重点参数值，分为结构参数、热力学参数和动力学参数三大类。其中，一共10个结构参数，共同表示电池的几何结构，包含电极颗粒半径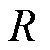
、极片厚度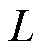
、极片表面积
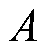、活性物质体积分数
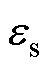和电解液体积分数
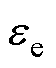等。通过粒子群优化算法对真实全电池曲线与拟合后曲线的方均根误差进行最小化寻优，获取正负极活性材料的最大锂离子浓度
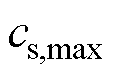和初始嵌锂状态
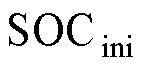等热力学参数，用以描述电池内部各种形式能量的转换过程[23]。该方法辨识出的热力学参数可直接导入电化学模型中使用，所以不再分析热力学参数的灵敏度结果。动力学参数获取一方面依据Butler-Volmer动力学，提取反应速率常数
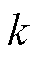和SEI膜阻抗
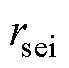表示电荷转移能力；另一方面，考虑各类材料传输粒子的能力，如正负电极和电解液中的扩散系数（
&
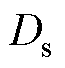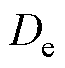）、锂离子转移数
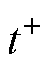、电导率（
&
）、
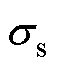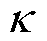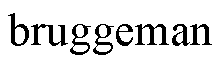系数等。
一次一项（One-at-a-Time, OAT）灵敏度分析是一种常用于数学建模和统计分析的方法，其本质是计算函数对输入变量的偏导数，即一个线性变换过程。由于Comsol Multiphysics®工具的有限元方法在每个单元内采用线性插值函数，将非线性方程在局部范围内线性化，从而降低了求解难度。与此同时，还可以通过限制参数扰动范围的方式，保证模型的输出在参数空间中的特定区间附近与输入参数的扰动间的关系呈线性。文中待分析的电化学模型参数范围均来自文献中常用的参考取值，参数值的变化不会对模型的输出结果产生显著的非线性影响，更适用于多维度分析，有助于在建模初期了解模型中各个参数对输出结果的影响，进而优化和调整参数取值。算法实施流程如图6所示。
首先，已将需要分析的参数放入附表2中，并且确定了这些参数的变化范围。在各自的范围内取10个均分值，随后设置不同的温度、倍率和SOC区间进行充电仿真，实现定量化描述。bupper和blower分别是选定参数范围的上、下限，有些动力学参数的数量级非常小且存在跨数量级现象，可以采用对数尺度表示。
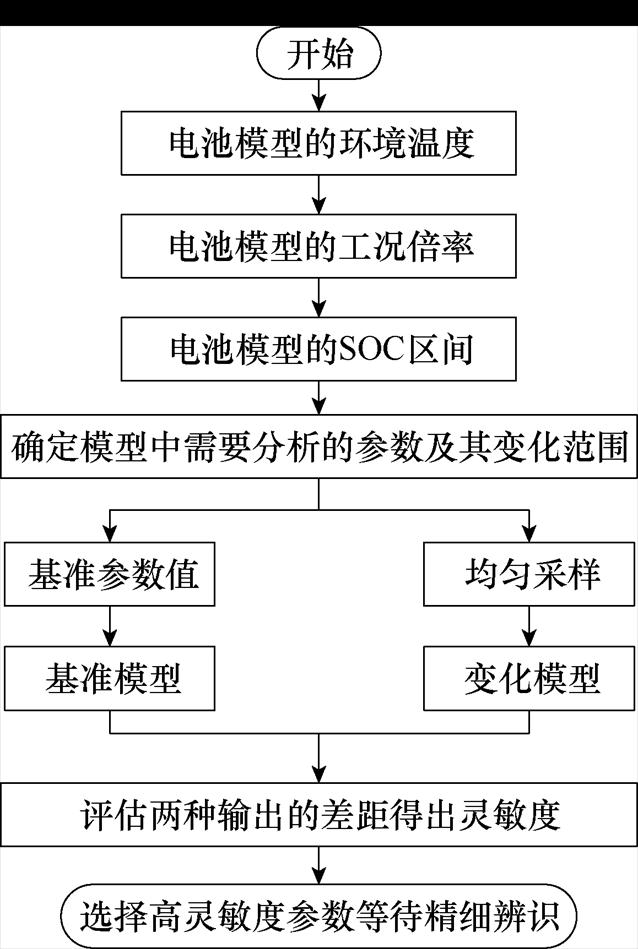
图6 电化学参数灵敏度分析流程
Fig.6 Flow chart of sensitivity analysis of electrochemical parameters
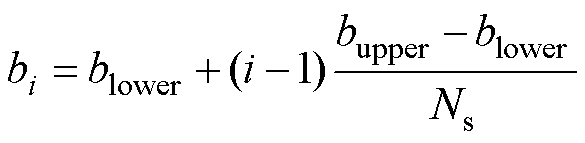（3）
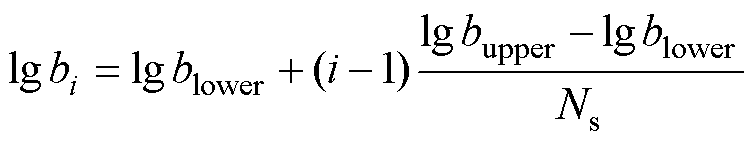（4）
式中，bi为逐一输入的参数。
随后，设定平均值作为输入参数的基准值，形成一个基准模型用于每次研究的比较计算。按照一次改变一个参数的原则，逐一变化每个选定的参数，同时保持其他参数不变。每个参数的灵敏度分析考虑了不同温度（-5℃、25℃、50℃）、充电倍率（0.2C、0.5C、0.8C、1C）和SOC区间（0%～10%、10%～40%、40%～60%、60%～80%、80%～100%），共同组成了一个包含60种工况的仿真矩阵。通过输入参数
求取以上各种工况的输出并与基准模型对比，求得方均根误差后对整体结果进行均一化处理。
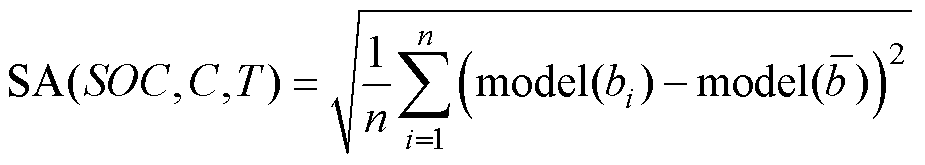（5）
式中，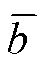
为输入参数的平均值。
运行过程中无钴电池的动力性能往往受温度、倍率和电池荷电状态三者的综合影响，为了提升模型在不同工况下的普适和准确程度，相比于单因素条件的局限性，采用多维度因素分析参数的灵敏度是更加贴合需求的。首先，对18个参数生成灵敏度矩阵。25℃不同倍率和不同SOC区间电化学参数的归一化灵敏度矩阵如图7所示。其中每个矩阵包含20个灵敏度元素（4个倍率，5个SOC区间），每个点表示在一定的SOC区间和倍率下的归一化灵敏度指标，圆点的面积越大，表示在该情况下参数的灵敏度越高。通过25℃的灵敏度分析结果可知，Rn、Rp、kn、kp、Ds,n、Ds,p、De等7个参数的灵敏度变化显著，与50℃和-5℃的灵敏度结果基本一致。其中，正、负电极的反应速率常数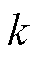随倍率和SOC区间的变化尤为显著，属于需要重点关注和辨识的参数；通过参数灵敏度分析结果来看，在10个结构参数中，正负极材料的颗粒半径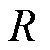是影响模型精度的高灵敏度参数，因此对于无钴电池而言，需要采用扫描电子显微镜（Scanning Electron Microscope, SEM）等手段测量较为准确的颗粒半径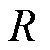；液相扩散系数De对倍率的增加更为敏感，而固相扩散系数Ds则是随不同SOC区间的差异较为显著。其余一部分参数的灵敏度指标较低甚至接近0，可以在一定范围内忽略这些值对电池性能的影响，直接使用经验值代入模型。因此，筛选出高灵敏度的参数值可以提高参数辨识的可靠性，且在高倍率工况下有助于识别各类电化学参数，提升调参效率。
通过解耦电池的温度、倍率和SOC这三者对电化学参数的影响，在只考虑其中一类因素的前提下分析模型受不同电化学参数的影响程度，即将包含60种灵敏度元素的归一化矩阵按照单一影响因素进行求和，解耦后不同维度下电化学参数的灵敏度结果如图8所示。对于5个不同的SOC区间，上文所提出的7个参数仍有较高灵敏度，随着充电的进行，电池的SOC增加，各参数的灵敏度整体上升，特别是前60% SOC为0～60%的区域内变化显著，这意味着在建立模型时需要确保电池的起始SOC的准确度。在4个不同倍率状态下，随着倍率增大，7个高灵敏度参数的灵敏度值变化较明显，其辨识结果对端电压的影响较大，而其他参数的灵敏度值基本无变化。最后，需要特别关注温度的影响，电池处于低温状态时，所有电化学参数的灵敏度均大幅增加，其中颗粒半径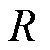的灵敏度最高，与文献[24]的结论一致，原本灵敏度接近于0的固液相体积分数
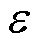等参数的灵敏度值与其他参数趋于一致，表明每个参数对模型输出的影响是同时增大的，因此常规的电化学辨识实验基本失效。
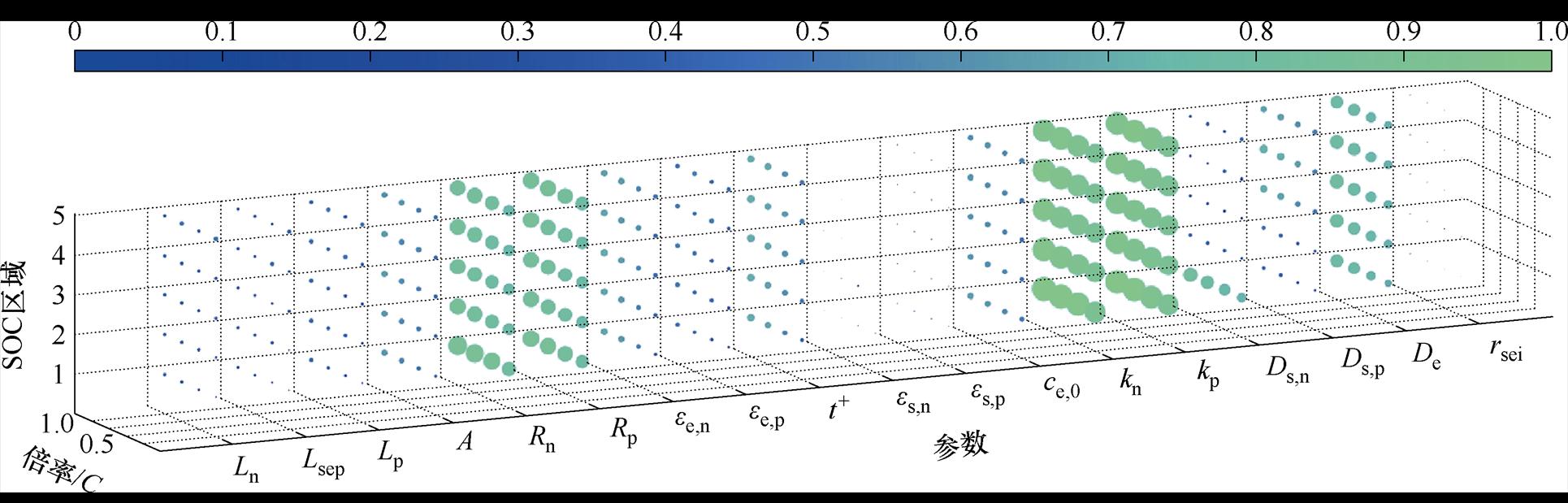
图7 25℃不同倍率和不同SOC区间电化学参数的归一化灵敏度矩阵
Fig.7 Normalized sensitivity matrix of electrochemical parameters at different rates and SOC ranges at 25℃
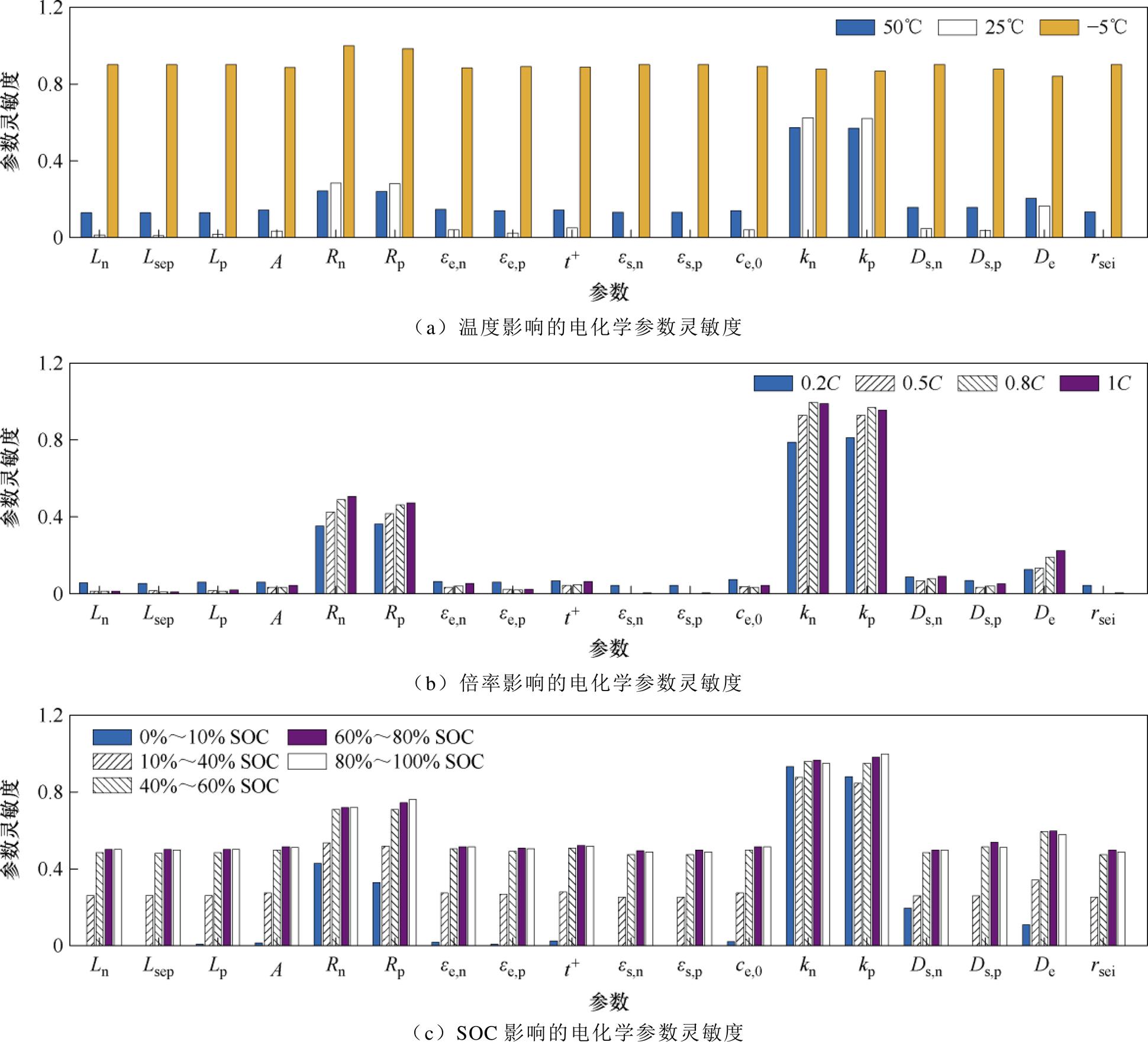
图8 解耦后不同维度下电化学参数的灵敏度结果
Fig.8 Sensitivity results of electrochemical parameters under different dimensions after decoupling
通过分离不同时间尺度特性的参数，设计相应的短时间尺度和长时间尺度参数辨识实验[25]。如图9所示以短时间脉冲实验为例，当温度为15℃时，辨识反应速率常数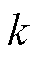后的脉冲电压拟合结果良好；而当温度下降至5℃后，脉冲拟合曲线的精度出现较大误差，基于参数辨识实验和温度拟合式两种方法得到的恒流工况曲线差距较大，而温度拟合式法更接近实测数据曲线。此情况随温度下降愈发突出，印证了低温时由于各参数的灵敏度大幅上升造成经实验实现参数辨识的难度加剧。所以需要获取高于5℃的模型参数辨识值并对每个参数作温度相关的拟合方程，进而探索参数的温度演变规律获得低温下的可靠参数值，如图10所示。
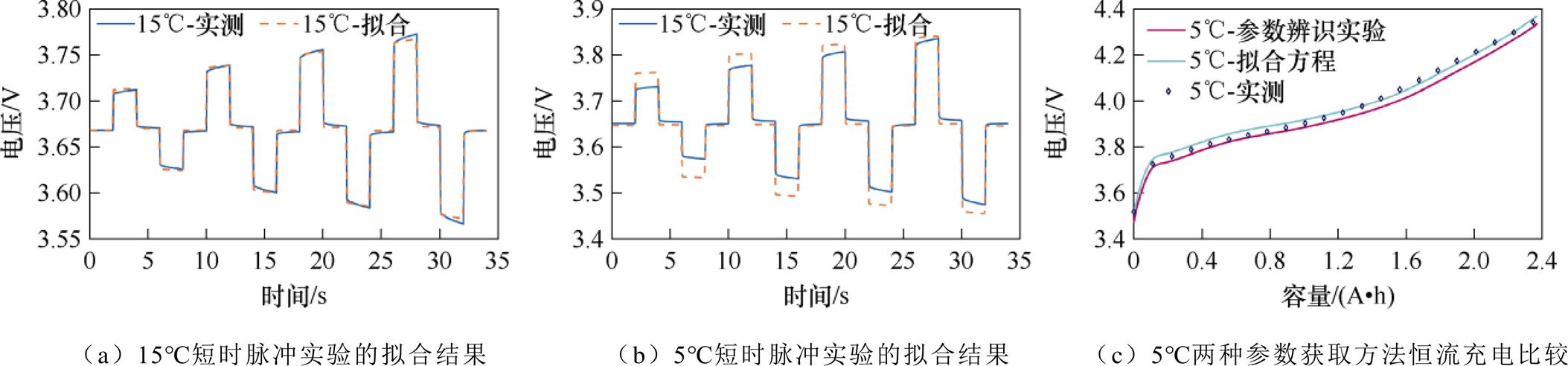
图9 不同温度短时脉冲实验的拟合结果和5℃参数辨识实验法和温度拟合式法恒流充电比较
Fig.9 Fitting results of short-term pulse experiments at different temperatures and comparison of constant current charging with parameter identification experimental method and temperature fitting method at 5℃
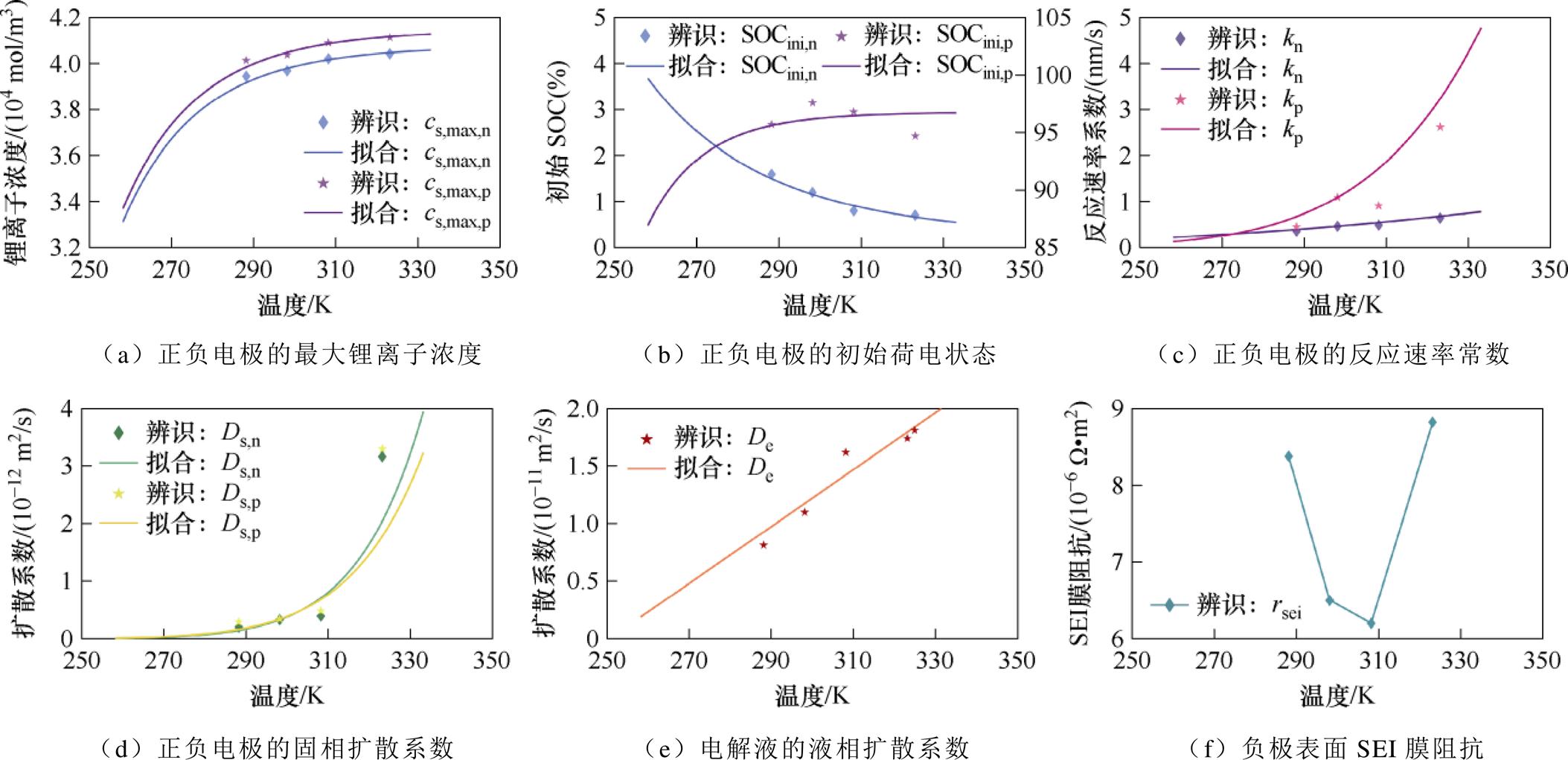
图10 电化学参数随温度的变化规律
Fig.10 The variation of electrochemical parameters with temperature
在宽温域下测试无钴电池的开路电压，采用正负电极活性材料的平衡电势曲线拟合全电池开路电压曲线的方法获取不同温度下的热力学参数，发现其受温度的影响显著。其中，提取了正、负极活性材料的最大锂离子浓度cs,max,p、cs,max,n和初始嵌锂状态SOCini,p、SOCini,n这四个参数，可以发现cs,max,n和cs,max,p随温度上升的变化规律基本相同，而SOCini,n和SOCini,p随温度上升的变化规律相反，正极初始嵌锂状态SOCini,p逐渐增大而负极初始嵌锂状态SOCini,n逐渐减小，因为未在高温区域测试正负极半电池的平衡电势曲线，造成SOCini,p参数值在高温区域波动严重。进而采用温度变量相关的幂函数修正了正、负极材料的最大锂离子浓度和初始嵌锂程度。
对于动力学参数，提取了正、负电极的反应速率常数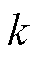、固相扩散系数Ds和电解质的液相扩散系数De、以及负极表面的SEI膜阻抗rsei。其中，在适合的温度范围内反应速率常数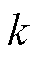和固相扩散系数Ds通常采用Arrhenius方程修正参数的温度效应[26]，可以通过计算得到以上4个参数的活化能，从而获得温度拟合方程。液相扩散系数De呈现出线性排布规律，而SEI膜阻抗rsei随温度变化没有明确的规律。动力学参数普遍展示出随温度上升而逐渐增大的趋势，表明无论是电解质还是活性材料中的分子无规则热运动都变得剧烈，促使反应物中的活化分子数增加并且分子间的有效碰撞次数增加，加快了反应速率，同时存在浓度差的区域加速了扩散。9个参数的温度拟合式见表3。无钴电池层状氧化物正极中缺少钴元素，不仅增加了电极中阻碍扩散的阳离子混排效应，而且降低了正极固相扩散系数对低温的耐受性，导致电池在低温下的倍率性能较差[3, 27]。
表3 电化学参数的温度拟合式
Tab.3 Temperature fitting formula of electrochemical parameters
参数拟合式R2 cs,max,n0.988 2 cs,max,p0.988 2 SOCini,n0.988 3 SOCini,p0.702 5 kn0.956 6 kp0.857 5 Ds,n0.857 1 Ds,p0.827 5 De0.946 5
该模型使用基于有限元法的建模仿真工具Comsol Multiphysics®进行求解。附表2中汇总了25℃电化学模型所使用到的参数值，采用多种倍率恒流充电工况验证模型的准确性，具体为0.2C、0.5C、0.8C、1C。每个倍率下实验值和仿真值的方均根误差均在11 mV以下，绝对误差主要集中在充电初期。通过电性能测试结果发现，电池以恒流1C充电时电池表面的最大温升不会超过3℃，因此不再考虑某一具体环境温度下电池运行造成的温升现象对电池性能的影响。
宽温域共包含-5℃、5℃、15℃、25℃、35℃、50℃共6个温度点。图11中先行绘制了15℃、25℃、35℃、50℃这4个温度点的模型仿真结果，表明该条件下电化学模型的拟合结果良好，进而证明通过参数辨识实验获取高灵敏度电化学参数的方法是可行的。当环境温度在15℃及其以上的常温区域和高温区域时，1C恒流充电的端电压拟合结果较为良好，方均根误差稳定在9 mV左右，而绝对平均误差稳定在7 mV。但根据图8a结果表明，基于参数辨识实验的方法在低温条件下失效，电化学模型中众多参数的灵敏度均大幅上升，导致无法区分出高灵敏度参数进行着重辨识，每一个参数的取值变化都会引发模型输出的偏移。因此需要建立高灵敏度参数随温度变化的函数来计算主要影响模型精度的参数在低温时的取值。由于电池未经过老化循环实验，所以不考虑电池结构参数的变化，只提取一部分可辨识的热力学参数和灵敏度较高的动力学参数结果，见表3。最终，通过图12a和图12b可得该方法有效改善了低温电化学模型精度低的问题。
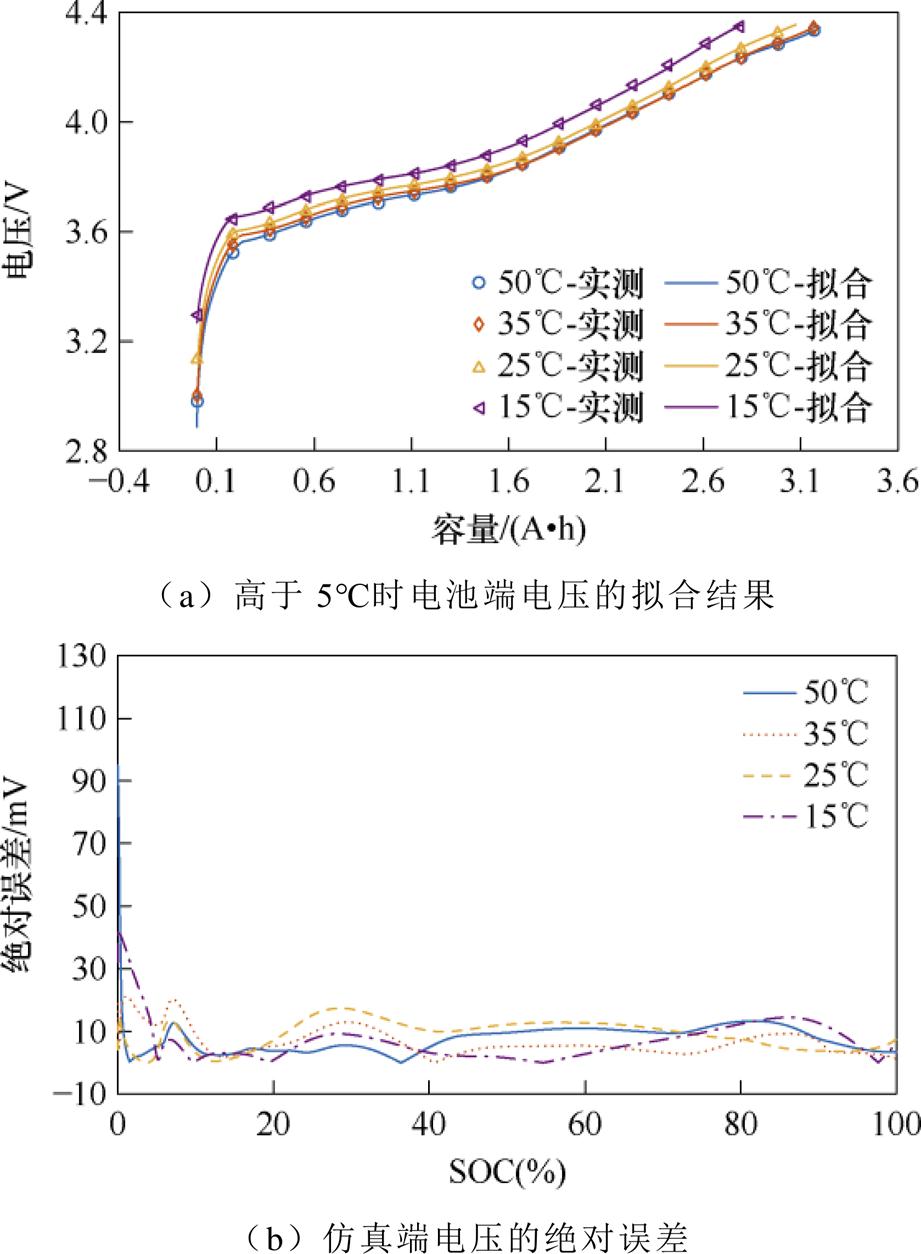
图11 高于5℃时电池端电压的拟合结果及其绝对误差
Fig.11 The fitting result and absolute error of battery terminal voltage above 5℃
为了确保所提取参数温度拟合方程的高可信度，需要验证低温下电池端电压的拟合精度，如图12b所示。不同温度电池端电压的拟合误差见表4。从表4看出，低温区域的端电压拟合误差较大，这是因为随着温度的降低，电池的动力学性能削弱，电化学参数对模型输出的影响愈发突出，无法通过参数辨识实验获取可信的参数值，相比于原始参数辨识方法（改进前）采用温度经验方程修正的方法（改进后）可将误差控制在可接受的20 mV范围内。
为探究不同充电倍率时电化学参数对无钴电池电性能相关的参数影响程度，图13绘制了常温25℃条件下，选择5个高灵敏度的动力学参数（视作自变量）对四类高灵敏性的电性能参数（视作因变量）的影响。每个自变量的变化范围取为已确定参数值的上下40%区间，采样次数为10次，一个自变量选定三个点绘制结果（分别为下界值、中间值、上界值）。因变量包含了充电工况的容量、能量以及外界施加电流后1 s和10 s的直流内阻值。
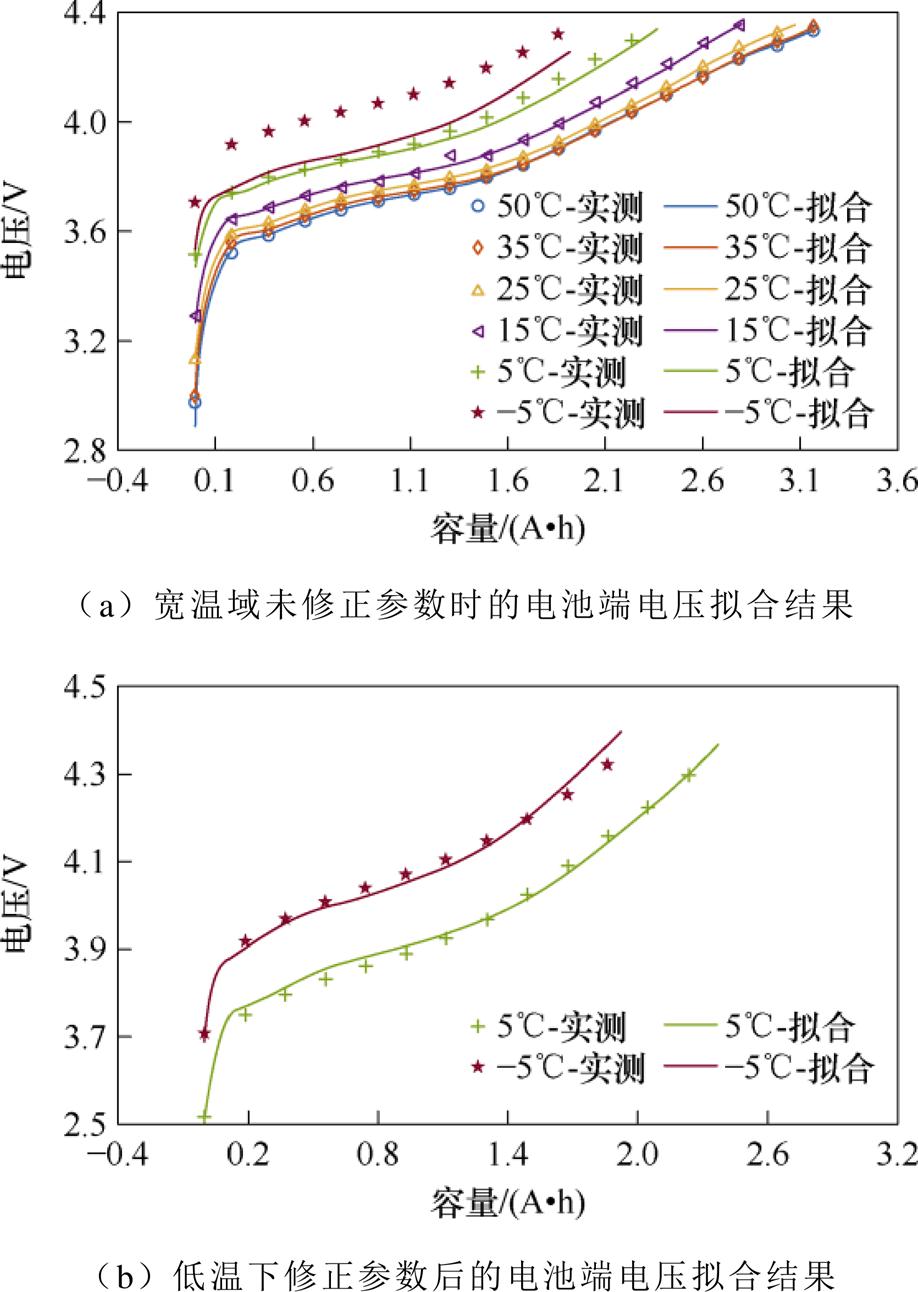
图12 宽温域未修正参数时和低温下修正参数后的电池端电压拟合结果
Fig.12 Fitting results of battery terminal voltage with uncorrected parameters at a wide temperature range and corrected parameters at a low temperature range
表4 不同温度电池端电压的拟合误差
Tab.4 The fitting error of battery terminal voltage at different temperatures
通过对比发现，尽管同一种自变量在不同充电倍率会引起电池电性能参数的改变，但具体到自变量自身的变化所带来的影响，不同的自变量参数则有不同的效果，不同倍率时电性能指标对动力学参数的依赖性见表5（“☆”符号的数量表征了不同倍率下电性能指标对电化学模型动力学参数的依赖性，表示电池电化学模型与外特性的联系程度，采用1～4个“☆”进行评估，“☆”越多依赖性越强）。反应速率常数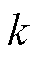的变化对电池可充入的容量和能量影响甚微。在较大倍率时，固相扩散系数Ds和液相扩散系数De的这类传输性质的自变量产生的效果较明显，代表了电池中的离子从高浓度区向低浓度区移动的速率，从而影响电荷的传输速率，最终造成容量指标发生波动。对于电池内阻而言，自变量的变化确实会造成内阻因变量的波动，但除负极扩散系数之外的波动范围普遍较小，说明负极扩散系数较大时离子在电极颗粒内部移动的阻力较弱，起始1 s时的直流内阻值自然会偏小，而10 s直流内阻因为接通电流的时间略长，极化效应开始积累，所以数值变化微弱。综上所述，可以将扩散类的参数与电池的容量和能量等电性能指标相关联，作为后续研究无钴电池健康状态分析的一个重要指标。而电荷反应类的参数则主要考虑其与电池温度及自身活化能的关系，视为电化学反应方程式的动力系数，直接使用温度拟合函数表达。
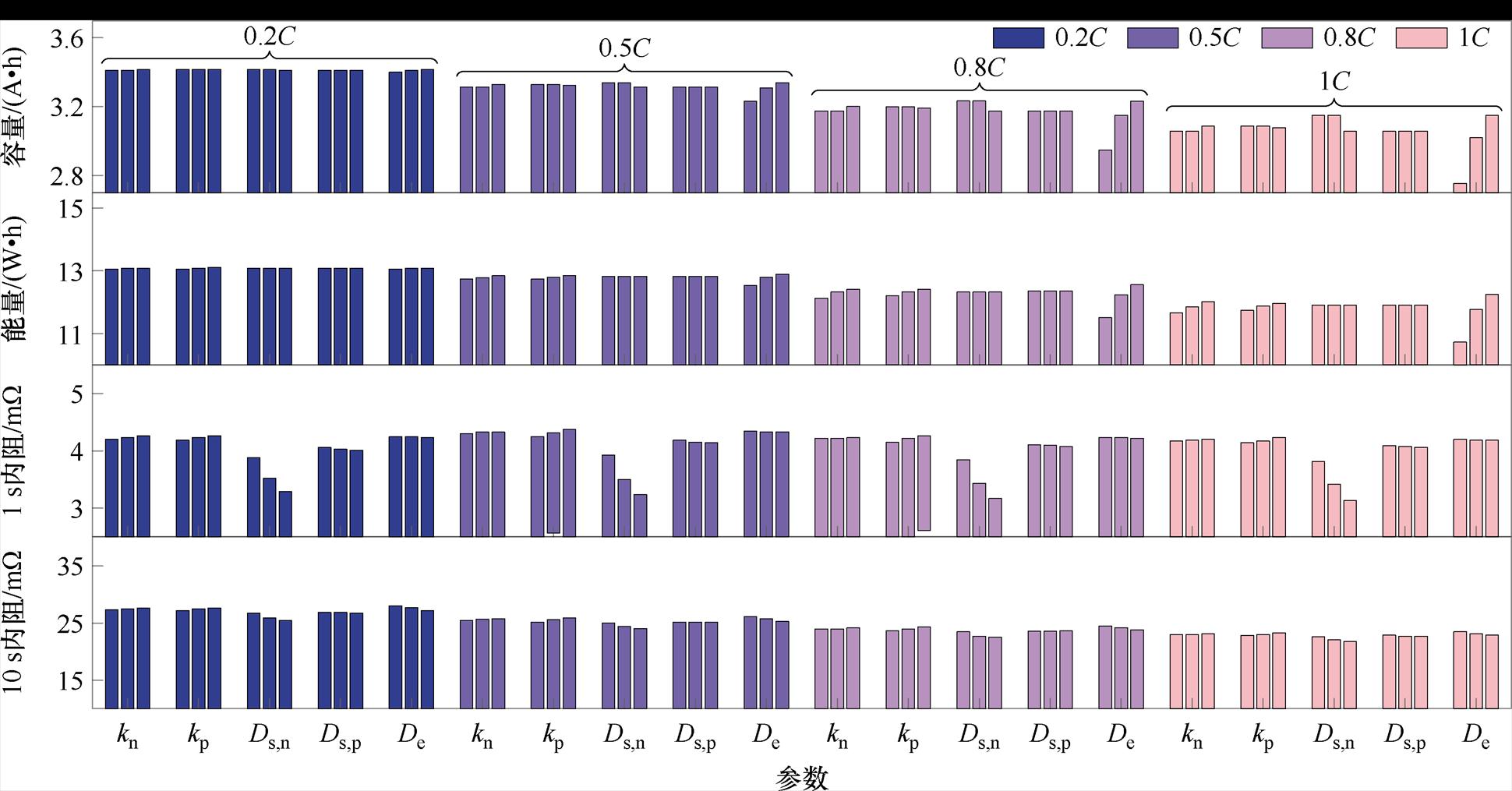
图13 25℃不同倍率动力学参数对电性能参数的影响
Fig.13 Diagram of the influence of dynamic parameters at different rates of 25℃ on electrical performance parameters
表5 不同倍率电性能指标对动力学参数的依赖性
Tab.5 Analysis of the dependence of electric properties of different magnification on dynamic parameters
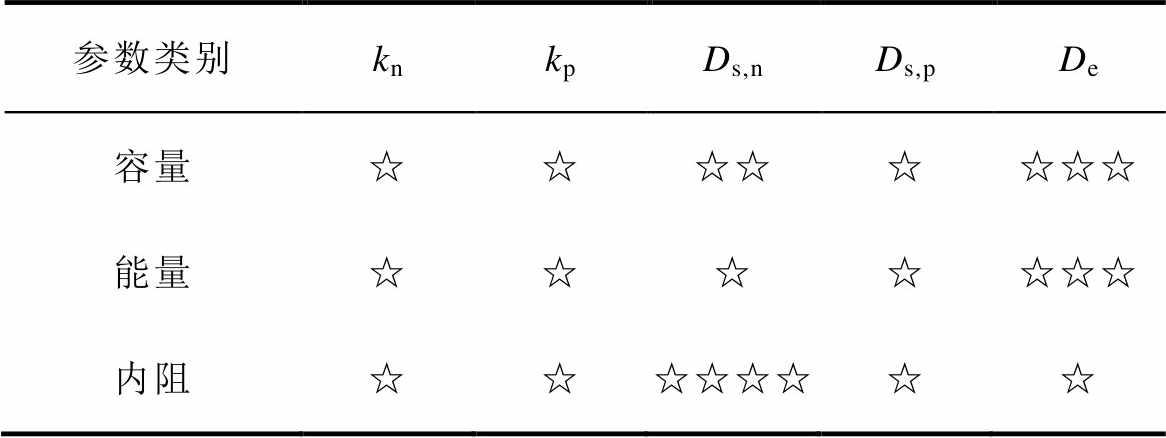
参数类别knkpDs,nDs,pDe 容量☆☆☆☆☆☆☆☆ 能量☆☆☆☆☆☆☆ 内阻☆☆☆☆☆☆☆☆
无钴正极材料作为目前最新兴的层状氧化物，与助力实现锂离子电池摆脱钴元素的限制，同时起到提高电池能量密度的目的。通过对无钴电池样本进行实验分析，探究其在电热耦合作用下的电性能变化特性。由于缺乏钴元素，仅靠掺杂锰元素抑制氧化镍材料的多重相变问题，从实验结果可知，电池在高温下的倍率性能与NCM三元电池相当，但是在低温条件下性能不及NCM三元电池，究其原因是低温削弱了离子扩散系数的耐受度，开路电压IC曲线的峰A和峰D构成了动力学障碍的电压区域。随后选定五种关于无钴电池电性能的参数指标，在电热耦合的情况下分析得到容量和能量指标对倍率更敏感，而内阻和效率对温度更敏感，相比于NCM电池，无钴正极中镍元素的占比较大，因此库仑效率的表现稳定。
基于P2D模型原理，采用OAT灵敏度分析方法研究多维度电化学参数的灵敏度，结果表明电池的正负极固相扩散系数、反应速率常数、材料颗粒半径和液相扩散系数等对倍率和SOC的依赖性显著；而在低温下众多电化学参数的灵敏度急剧增加导致参数辨识失效。根据高于5℃的4个较精确模型结果提取出高灵敏度的电化学参数，引入Arrhenius方程等温度相关的拟合方程式求解电池各部分的活化能及变化规律。进而获得低温下的可信电化学参数值，有效地提高了宽温域下无钴电池建模的精度并解决了参数获取困难的问题，-5℃～50℃范围内方均根误差在20 mV以内。最后，利用改进后的模型构建起电化学模型内部参数与电性能外部参数的沟通桥梁，结果表明扩散类参数与电池的容量和能量相关联，而电荷传输类参数则主要考虑其与电化学反应温度间的关系，为后续研究无钴电池老化状态诊断和智能管理提供理论支撑。
附 录
附表1 锂离子电池P2D模型的控制方程
App.Tab.1 The governing equation of P2D model of lithium ion battery
控制方程边界及初始条件 [1]固相锂离子分布 [2]液相锂离子分布
（续）
控制方程边界及初始条件 [3]固相电势分布 [4]液相电势 [5]电极动力学 [6]端电压
附表2 无钴电池电化学参数灵敏度分析的取值范围及常温（25℃）电化学参数的辨识结果汇总表
App.Tab.2 The value range of sensitivity analysis of electrochemical parameters of cobalt-free cells and the identification results of electrochemical parameters at 25℃
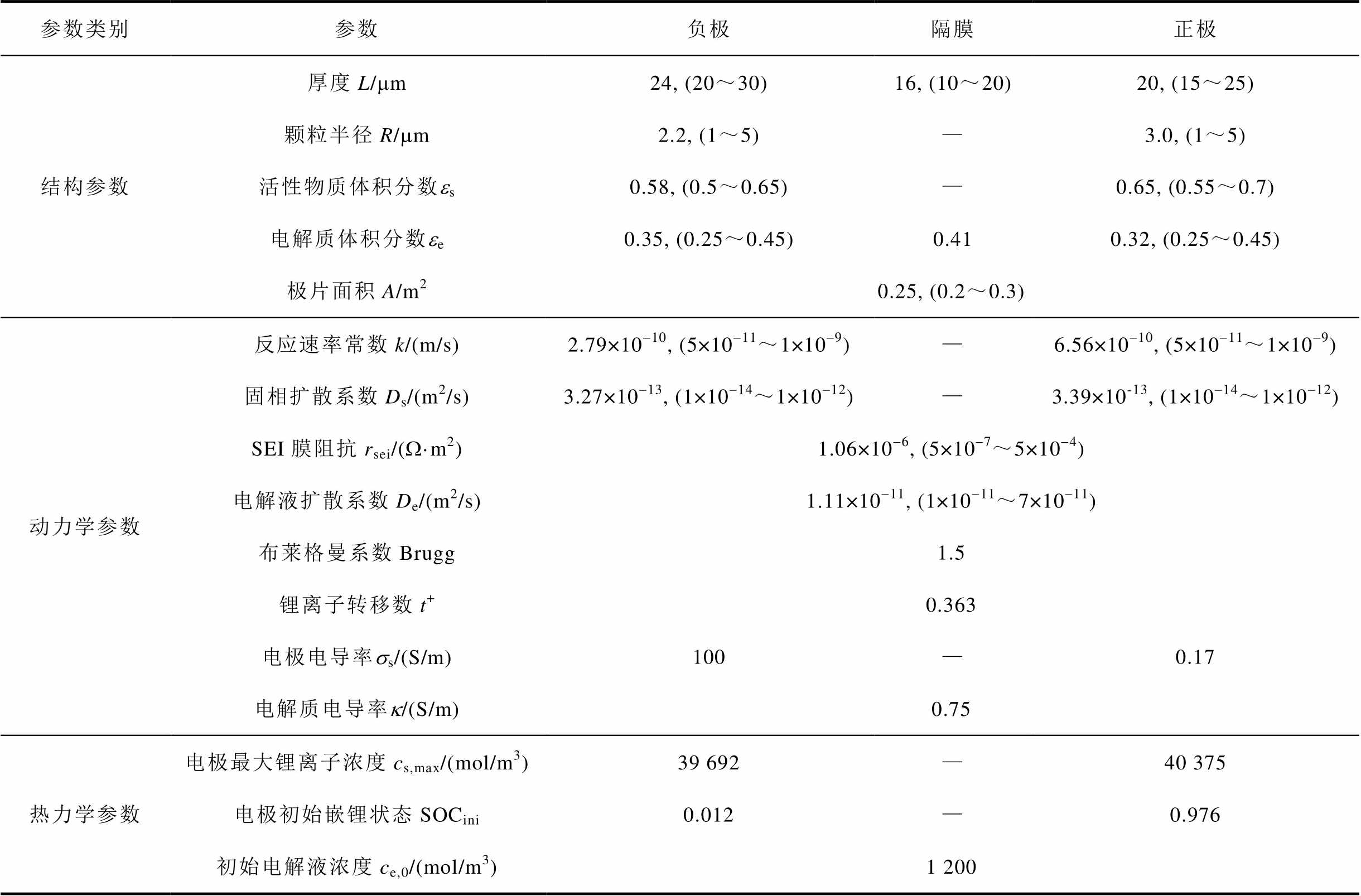
参数类别参数负极隔膜正极 结构参数厚度L/mm24, (20～30)16, (10～20)20, (15～25) 颗粒半径R/mm2.2, (1～5)—3.0, (1～5) 活性物质体积分数es0.58, (0.5～0.65)—0.65, (0.55～0.7) 电解质体积分数ee0.35, (0.25～0.45)0.410.32, (0.25～0.45) 极片面积A/m20.25, (0.2～0.3) 动力学参数反应速率常数k/(m/s)2.79×10-10, (5×10-11～1×10-9)—6.56×10-10, (5×10-11～1×10-9) 固相扩散系数Ds/(m2/s)3.27×10-13, (1×10-14～1×10-12)—3.39×10-13, (1×10-14～1×10-12) SEI膜阻抗rsei/(W·m2)1.06×10-6, (5×10-7～5×10-4) 电解液扩散系数De/(m2/s)1.11×10-11, (1×10-11～7×10-11) 布莱格曼系数Brugg1.5 锂离子转移数t+0.363 电极电导率ss/(S/m)100—0.17 电解质电导率k/(S/m)0.75 热力学参数电极最大锂离子浓度cs,max/(mol/m3)39 692—40 375 电极初始嵌锂状态SOCini0.012—0.976 初始电解液浓度ce,0/(mol/m3)1 200
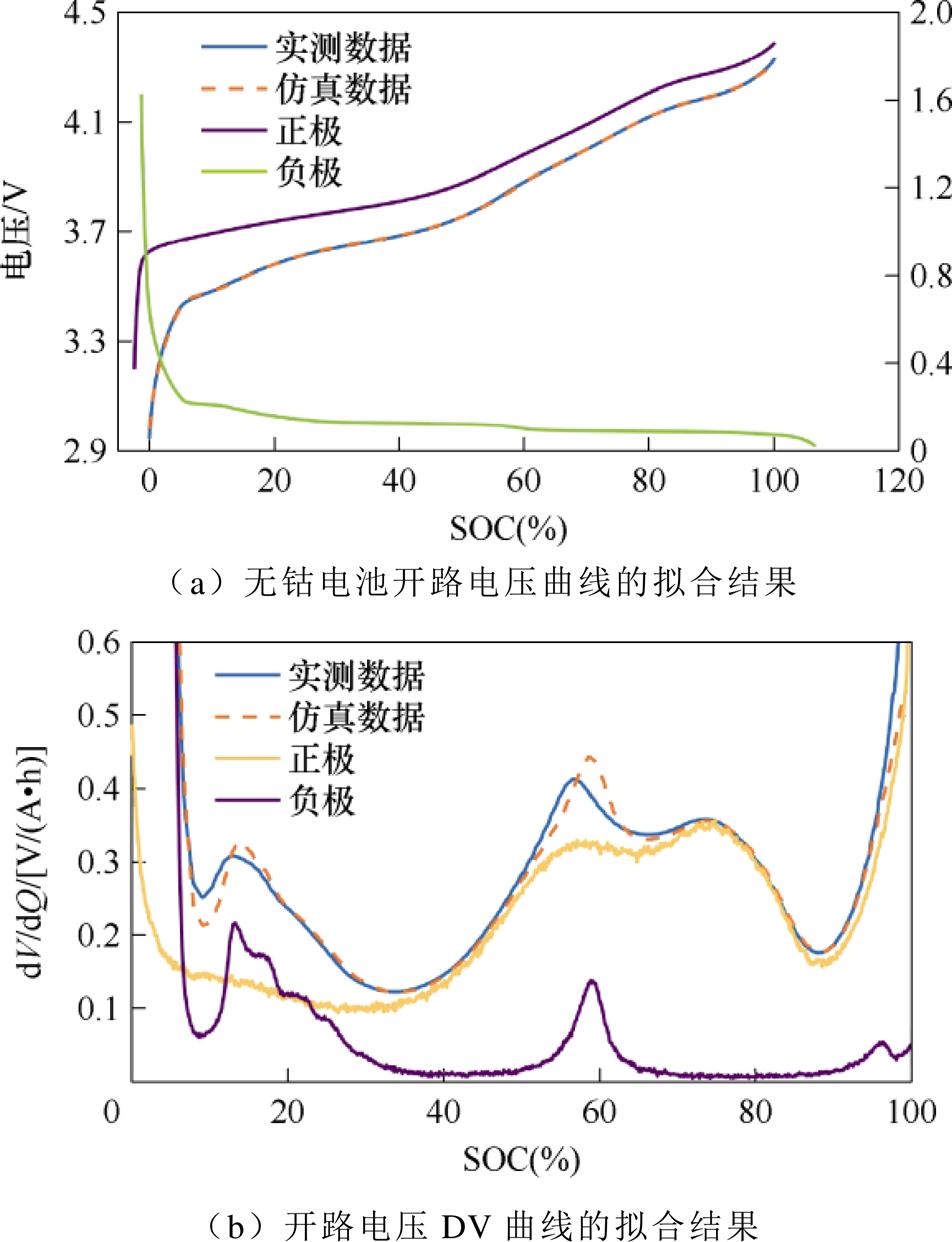
附图1 25℃无钴电池的开路电压曲线和DV曲线的拟合结果
App.Fig.1 Fitting results of open circuit voltage curve and DV curve of 25℃ cobalt-free battery
参考文献
[1] Lee S, Manthiram A. Can cobalt be eliminated from lithium-ion batteries?[J]. ACS Energy Letters, 2022, 7(9): 3058-3063.
[2] Li Wangda, Erickson E M, Manthiram A. High-nickel layered oxide cathodes for lithium-based automotive batteries[J]. Nature Energy, 2020, 5: 26-34.
[3] Ryu H H, Kang G C, Ismoyojati R, et al. Intrinsic weaknesses of co-free Ni-Mn layered cathodes for electric vehicles[J]. Materials Today, 2022, 56: 8-15.
[4] Zheng Jiaxin, Teng Gaofeng, Xin Chao, et al. Role of superexchange interaction on tuning of Ni/Li disordering in layered Li(NixMnyCoz)O2[J]. The Journal of Physical Chemistry Letters, 2017, 8(22): 5537-5542.
[5] Aishova A, Park G T, Yoon C S, et al. Cobalt-free high-capacity Ni-rich layered Li[Ni0.9Mn0.1]O2 cathode[J]. Advanced Energy Materials, 2020, 10(4): 1903179.
[6] Kim Y, Seong W M, Manthiram A. Cobalt-free, high- nickel layered oxide cathodes for lithium-ion batteries: Progress, challenges, and perspectives[J]. Energy Storage Materials, 2021, 34: 250-259.
[7] Li Hongyang, Cormier M, Zhang Ning, et al. Is cobalt needed in Ni-rich positive electrode materials for lithium ion batteries?[J]. Journal of the Electro- chemical Society, 2019, 166(4): A429-A439.
[8] Urban A, Lee J, Ceder G. The configurational space of rocksalt-type oxides for high-capacity lithium battery electrodes[J]. Advanced Energy Materials, 2014, 4(13): 1400478.
[9] Noerochim L, Suwarno S, Idris N H, et al. Recent development of nickel-rich and cobalt-free cathode materials for lithium-ion batteries[J]. Batteries, 2021, 7(4): 84.
[10] Doyle M, Fuller T F, Newman J. Modeling of galvanostatic charge and discharge of the lithium/ polymer/insertion cell[J]. Journal of the Electro- chemical Society, 1993, 140(6): 1526-1533.
[11] Li Weihan, Cao Decheng, Jöst D, et al. Parameter sensitivity analysis of electrochemical model-based battery management systems for lithium-ion batteries[J]. Applied Energy, 2020, 269: 115104.
[12] Xu Le, Lin Xianke, Xie Yi, et al. Enabling high- fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification[J]. Energy Storage Materials, 2022, 45: 952-968.
[13] 贠祥, 张鑫, 王超, 等. 基于联合参数辨识的粒子群优化扩展粒子滤波的锂电池荷电状态估计[J]. 电工技术学报, 2024, 39(2): 595-606.
Yun Xiang, Zhang Xin, Wang Chao, et al. State of charge estimation of Li-ion battery using particle swarm optimization extended Kalman particle filter based on joint parameter identification[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(2): 595-606.
[14] Gu Yuxuan, Wang Jianxiao, Chen Yuanbo, et al. Electrochemical parameter identification for lithium- ion battery sources in self-sustained transportation energy systems[EB/OL]. 2022: 2206.10099. https:// arxiv.org/abs/2206.10099v2.
[15] Yu Shuyang, Xu Chao, Mao Ya, et al. Heat generation mechanism and parameter sensitivity analysis of NCA-graphite battery based on electrochemical- thermal coupling model[J]. Journal of the Electro- chemical Society, 2023, 170(6): 060514.
[16] Wang Dafang, Huang Huanqi, Tang Zhihao, et al. A lithium-ion battery electrochemical-thermal model for a wide temperature range applications[J]. Electro- chimica Acta, 2020, 362: 137118.
[17] Fly A, Chen R. Rate dependency of incremental capacity analysis (dQ/dV) as a diagnostic tool for lithium-ion batteries[J]. Journal of Energy Storage, 2020, 29: 101329.
[18] Li Hang, Wang Li, Song Youzhi, et al. Understanding the insight mechanism of chemical-mechanical degradation of layered co-free Ni-rich cathode materials: a review (small 32/2023)[J]. Small, 2023, 19(32): 2302208.
[19] 王亚松. 镍锰二元富镍正极材料的合成与机理研究[D]. 哈尔滨: 哈尔滨工业大学, 2022.
Wang Yasong. Synthesis and mechanism research of Ni-Mn binary Ni-rich cathode materials[D]. Harbin: Harbin Institute of Technology, 2022.
[20] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703- 1725.
[21] Yao Yanxin, Lei Jiafeng, Shi Yang, et al. Assessment methods and performance metrics for redox flow batteries[J]. Nature Energy, 2021, 6: 582-588.
[22] 李长龙. 车用锂离子电池机理建模与并联模组不一致性研究[D]. 济南: 山东大学, 2022.
Li Changlong. Physics-based modeling of Li-ion batteries and inconsistency analysis of parallel modules[D]. Jinan: Shandong University, 2022.
[23] Oca L, Miguel E, Agirrezabala E, et al. Physico- chemical parameter measurement and model response evaluation for a pseudo-two-dimensional model of a commercial lithium-ion battery[J]. Electrochimica Acta, 2021, 382: 138287.
[24] Gholami J, Barzoki M F. Electrochemical modeling and parameter sensitivity of lithium-ion battery at low temperature[J]. Journal of Energy Storage, 2021, 43: 103189.
[25] 高洋. 三元材料锂离子电池老化诊断、评估与建模方法[D]. 北京: 北京交通大学, 2019.
Gao Yang. Aging diagnosis, evaluation and modeling of lithium ion batteries with Li(NiMnCo)O2 cathode[D]. Beijing: Beijing Jiaotong University, 2019.
[26] Wang Dafang, Huang Huanqi, Tang Zhihao, et al. A lithium-ion battery electrochemical-thermal model for a wide temperature range applications[J]. Electro- chimica Acta, 2020, 362: 137118.
[27] 吴立峰, 刘昊, 林仲钦, 等. 低温环境下锂离子电池荷电状态与超声透射飞行时间的关系研究[J]. 电工技术学报, 2022, 37(21): 5617-5626.
Wu Lifeng, Liu Hao, Lin Zhongqin, et al. Relationship between state of charge of lithium-ion battery and ultrasonic transmission flight time at low temperature[J]. Transactions of China Electrotech- nical Society, 2022, 37(21): 5617-5626.
Abstract There is a growing interest in cobalt-free nickel-manganese layered oxides as a new cathode material. Eliminating cobalt reduces costs and improves energy density, making it ideal for the increasing demands of electronic devices and electric vehicles.
Due to the lack of cobalt, doping with manganese can partially suppress the multiple-phase transitions of nickel oxide materials. Experimental results show that the battery's rate performance at room temperature and above is comparable to that of nickel-cobalt-manganese (NCM) batteries. However, under low-temperature conditions, its performance is inferior to that of NCM ternary batteries. The peaks A and D in the battery's incremental capacity curve of open-circuit voltage constitute a voltage region of kinetic barriers. The underlying reason is that low temperature weakens the tolerance of the lithium-ion diffusion coefficient. Subsequent analysis under coupled electro thermal conditions indicates that capacity and energy metrics are more sensitive to charge rate (C-rate), whereas internal resistance and efficiency exhibit greater temperature sensitivity. A comprehensive electrochemical model is warranted to better understand cobalt-free batteries' temperature-dependent behavior.
The insufficient simulation accuracy of the parameters of the traditional P2D model is particularly evident when modeling cobalt-free nickel-manganese system batteries at low temperatures. The simulation accuracy is very low using the parameters obtained through electrochemical parameter identification at low temperatures. Furthermore, the correlation between the electrochemical parameters of the battery and its external performance remains unclear. Therefore, the sensitivity of battery C-rate and state of charge (SOC) is studied for multi-dimensional electrochemical parameters using the one-at-a-time (OAT) sensitivity analysis method. Results show that parameters, such as solid-phase diffusion coefficients in both cathode and anode electrodes, reaction rate constants, particle radius, and liquid-phase diffusion coefficient, have a significant impact on battery performance and are closely correlated with C-rate and SOC.
The significantly enhanced sensitivity of electrochemical parameters at low temperatures makes parameter identification more challenging. This paper extracts high-sensitivity electrochemical parameters by analyzing the results of multiple models at temperatures above 5℃. It employs temperature-dependent fitting equations, such as the Arrhenius equation, to calculate reliable electrochemical parameters, improving cobalt-free battery modeling accuracy over a wide temperature range. The root mean square error (RMSE) is within 20 mV over the temperature range of -5℃ to 50℃. A robust correlation is established between internal electrochemical parameters and external electrical performance. The study demonstrates that diffusion-related parameters strongly correlate with battery capacity and energy, while charge transfer-related parameters are susceptible to the temperature of electrochemical reactions. This paper provides a solid foundation for future investigations into the state of health diagnosis of cobalt-free batteries and the development of advanced battery management systems.
Keywords：Cobalt-free lithium-ion battery, P2D model, sensitivity analysis, wide temperature region
中图分类号：TM912
DOI: 10.19595/j.cnki.1000-6753.tces.241141
国家重点研发计划资助项目（2022YFB2502304）。
收稿日期 2024-06-29
改稿日期 2024-07-17
张彩萍 女，1982年生，博士，教授，博士研究生导师，研究方向为电动汽车动力电池和储能电池在电力系统中的应用。
E-mail: zhangcaiping@bjtu.edu.cn（通信作者）
乔 波 女，1999年生，硕士研究生，研究方向为锂离子电池建模及性能分析。
E-mail: 22121493@bjtu.edu.cn
（编辑 郭丽军）