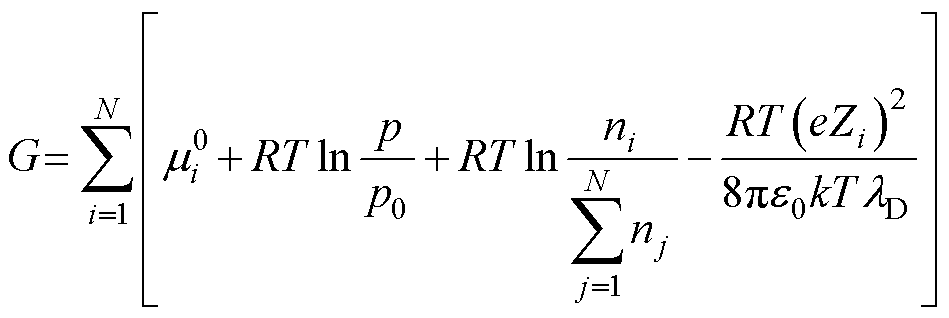（1）
摘要 开关电弧通常会在弧后电流零区的关键开断时刻表现出极强的非平衡现象，从而显著影响断路器的灭弧效果，然而针对工程背景下SF6及其环保替代气体的非平衡电弧物理特性则鲜有研究。该文基于双温配分函数与质量作用定律建立电弧等离子体组分求解模型，根据非平衡热力学关系及相互作用理论计算物性参数，研究了弧后非平衡态SF6与C4F7N等离子体的微观粒子组分及宏观物理特征，并探讨了非平衡与气压条件等对其热动属性与输运系数的影响机制。结果表明：非平衡状态会显著改变等离子体内解离与电离反应的主导顺序，进而影响其物理性质；相较于SF6，复杂的C4F7N气体受双温条件的影响更为显著，其非平衡效应在环保气体灭弧特性评估中不可忽略；双温等离子体输运系数的变化主要归因于粒子组分与碰撞温度的综合作用。研究结果可为开关电弧的非平衡数值模拟与参数评估提供基础数据。
关键词：开关电弧 非平衡等离子体 SF6 C4F7N 热动属性 输运系数
高压气体断路器作为维系电力系统安全稳定运行的关键设备，是应对电力系统短路故障危害的重要保障[1]。随着新型电力系统建设的不断推进，系统容量持续攀升，其对高压开关设备的开断能力及可靠性也提出了更高要求。大电流开断的电弧现象是一个多物理场强耦合的复杂过程，其弧后介质恢复与能量输入的复杂竞争是决定断路器开断成功与否的关键[2]。研究开断过程气体电弧的弧后动态特征与演化行为，对支撑新一代开关装备研制具有重要意义。
国内外学者针对开关电弧等离子体开展了大量数值模拟与弧后评估工作。Q. Zhang等[3]基于计算流体动力学（Computational Fluid Dynamics, CFD）研究了电流零区SF6电弧在平衡态假设下的衰减行为与弧后击穿过程，ABB[4]、西门子[5]、伊顿[6]公司也将电弧的磁流体动力学（Magnetohydrodynamic, MHD）仿真广泛应用于SF6高压断路器的研发设计领域。近年来，由于SF6气体极强的温室效应[7]，研究人员针对电气设备中SF6的环境友好型替代气体开展了大量的研究[8-9]，其中，C4F7N被认为是最具潜力的新型环保绝缘气体，以其混合气体作为灭弧介质是当前极具可行性的方案之一[10]。Bian Chenxi等[11]基于MHD仿真研究了C4F7N气体的燃弧特性；张博雅等[12]通过数值模拟及热动属性评估等方法研究了C4F7N在40.5 kV高压环保断路器中的应用；ABB[13]与GE[14]公司也同样针对C4F7N系列开关设备开展了大量仿真评估研究。
然而，上述研究大都基于局域热力学平衡（Local Thermodynamic Equilibrium, LTE）假设，难以精确描述弧后气体绝缘介质瞬态转化的复杂过程。事实上，在电流零区的弧后关键开断时刻，气体介质温度在强对流冷却作用下快速下降，等离子体粒子间碰撞频率骤减。由于电子与重粒子质量差距较大且能量交换不足，往往呈现电子温度高于重粒子温度的非热力学平衡现象[15]。研究表明，电流过零时刻电弧等离子体的非平衡度q 可达9以上（非平衡度为电子温度Te与重粒子温度Th之比，即q=Te/Th），远远偏离局域热力学平衡假设[16]。同时，非平衡电弧中高温电子的活跃状态会极大程度地改变等离子体的物理特性，进而显著影响高压断路器的零区数值模拟与弧后击穿特性评估结果[17]。S. Eda等[18]基于双温模型对Ar电弧进行仿真研究，发现非平衡电弧模型中温度的计算结果与平衡态假设下存在较大差距；S. A. Al-Mamun 等[19]研究了双温条件下CO2-H2等离子体的演化特性，并表示其非热平衡的影响十分重要；石岩等[20]从电子密度角度出发分析了SF6开关电弧的双温现象，结果表明将等离子体简单地考虑为LTE状态可能会引起数值评估的较大误差。由此可见，非热平衡现象对于电弧衰减行为及弧后击穿的评估是不可忽略的，而目前针对非平衡电弧的研究大都集中于Ar[21]、He[22]等简单惰性气体，限制其进一步发展的核心问题在于缺乏复杂气体电弧非平衡建模所必需的非平衡物性参数[23]。
等离子体的热动属性与输运系数等物性参数是电弧数值模拟与参数评估的基础[24]，目前针对开关电弧的实验手段尚无法直接测量等离子体的物性参数，通常基于统计物理的方法进行科学计算获得[25]。M. I. Boulos等[26]整理了Ar、N2、O2等单元素气体的最新基础物性参数，并表明热动与输运特性是任何等离子体建模的必要先决条件；Y. Cressault[27]研究了CO2等常用灭弧介质的物性参数；李静[28]及Ding Can等[29]分别计算了热平衡条件下SF6电弧等离子体的热力学与输运特征；Li Xingwen等[30]研究了C5F10O环保混合气体与SF6物性参数的区别；Zhang Boya等[31]从rcp（密度×比定压热容）等参数角度研究了C4F7N等环保气体的灭弧性能；Wu Yi等[32]完整计算了C4F7N替代气体在热平衡条件下的热动属性与输运系数，为环保型C4F7N开关设备的MHD模拟提供了基础参数。在非热平衡等离子体方面，已有学者系统地计算了双温SF6的物理特征参 数[33-35]，支撑SF6电弧非平衡衰减行为研究；Zhong Linlin等[36-37]研究了双温C4F7N的组分及固体沉积效应，为环保气体等离子体非平衡计算提供了重要参考。目前关于C4F7N灭弧介质的热平衡物理特性已有较为全面的计算研究，而其非平衡物性参数则未见报道。针对高压开关设备持续向大容量发展的前景，需进一步考虑高充气压力下的维里修正与Debye-Hückel修正作用，并基于C4F7N等离子体的双温热化学及相互作用过程，研究弧后非平衡态SF6与C4F7N的物性参数。
综上所述，本文基于双温粒子相互作用模型建立了气体电弧的非平衡物性参数求解方法，计算了SF6与C4F7N弧后双温等离子体的粒子组分、热力学参数与输运系数，并研究了气压与非平衡度等因素对等离子体理化特性的影响规律。研究结果可为气体电弧的非平衡数值模拟与参数评估提供基础数据，进而支撑新一代高压气体开关装备研制。
获得电弧等离子体的粒子组分是计算其热动属性与输运系数的前提。传统平衡条件下的等离子体组分通常基于系统吉布斯自由能最小化原理得到，综合考虑维里修正与Debye-Hückel修正，系统的吉布斯自由能可表示[38]为
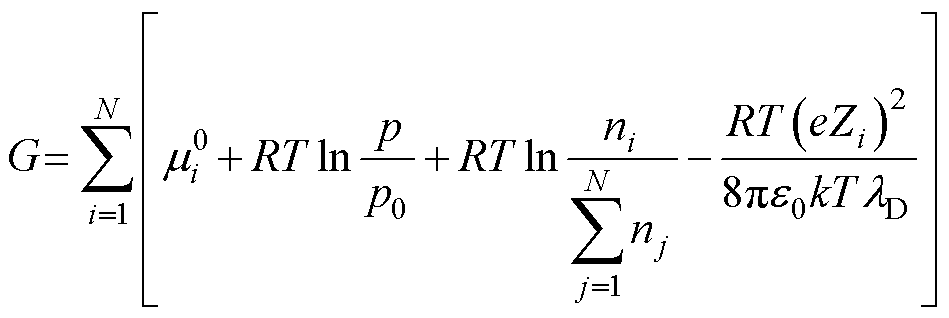（1）
式中，N为系统中粒子种类的数量；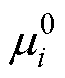
为粒子i的标准态化学势，可基于美国国家标准与技术研究院（National Institute of Standards and Technology, NIST）数据库公开的最小二乘法拟合粒子热化学函数计算获得；R为理想气体常数；T、p分别为气体温度与压强；p0为参考压强；ni为粒子i的数密度；e为元电荷；Zi为粒子i所带电荷；e0为真空介电常数；k为玻耳兹曼常数；lD为德拜长度，主要考虑了电子屏蔽的作用，表达式为
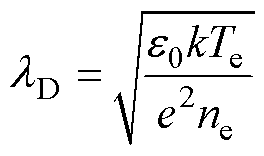（2）
式中，ne为电子密度。
在弧后非LTE等离子体中，由于电子与重粒子实际质量差距较大，电子从电场获取的能量难以及时通过碰撞传递给重粒子，因此通常采用双温度模型描述等离子体系统状态。非平衡条件下，系统吉布斯自由能最小化原理不再完全适用，通常采用双温质量作用定律求解。对此，A. V. Potapov与M. C. M. Van de Sanden分别提出了不同的双温质量作用定律形式[39]。可以证明，Potapov方法与吉布斯自由能最小化原理在数学层面等价，而Van de Sanden方法则基于熵最大原理推导得出，目前已有研究人员从理论层面论证了两者的等价性[36]。多数学者认为Potapov方法的电子-重粒子能量交换假设在多温度电弧中并不适用，基于此，本文利用双温质量作用定律的Van de Sanden形式，计算了非平衡条件下SF6与C4F7N等离子体的粒子组分，并将其非平衡度q=1的情况与吉布斯自由能最小化的求解结果进行了对比验证。Van de Sanden方法可表示为
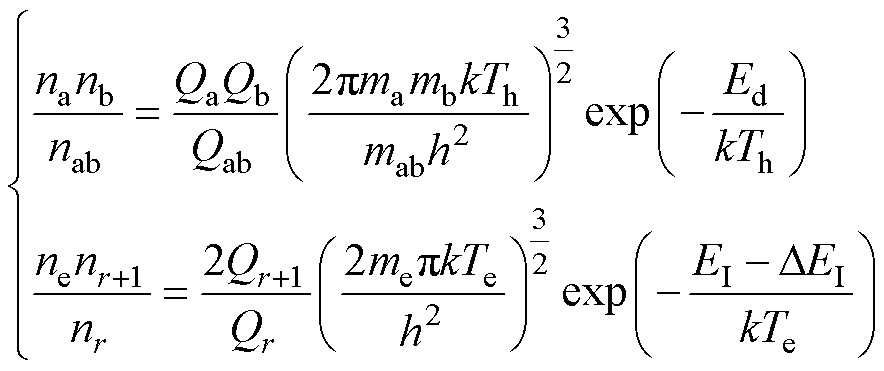（3）
式中，Qi为粒子i的双温配分函数，是联系粒子微观量子状态与宏观物理特性的桥梁；mi为粒子i的绝对质量；下角标“ab”表示解离前的分子，“a”“b”表示ab的解离产物，“e”表示电子，“r”为粒子的电离阶数；h为普朗克常数；Ed、EI分别为化学反应对应的解离能与电离能；DEI为带电粒子间相互作用引起的电离能降落，与德拜长度有关。
由此可见，求解非平衡电弧等离子体粒子组分的关键是获得其双温配分函数。粒子的配分函数Qt由平动配分函数Qtr与内配分函数Qint构成，其中Qtr的贡献已经包含在质量作用定律方程中，而Qint则主要考虑电子激发Qel、粒子振动Qvib、粒子转动Qrot及原子核Qnucl的贡献，即
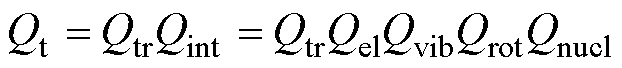（4）
在双温等离子体模型中，电子平动配分函数与电子配分函数主要与电子碰撞有关，故其计算所用温度指标为电子温度Te，其他以重粒子平动、振动、转动等为主要贡献的配分函数则基于重粒子温度Th进行计算。其中各类双温配分函数可表示为
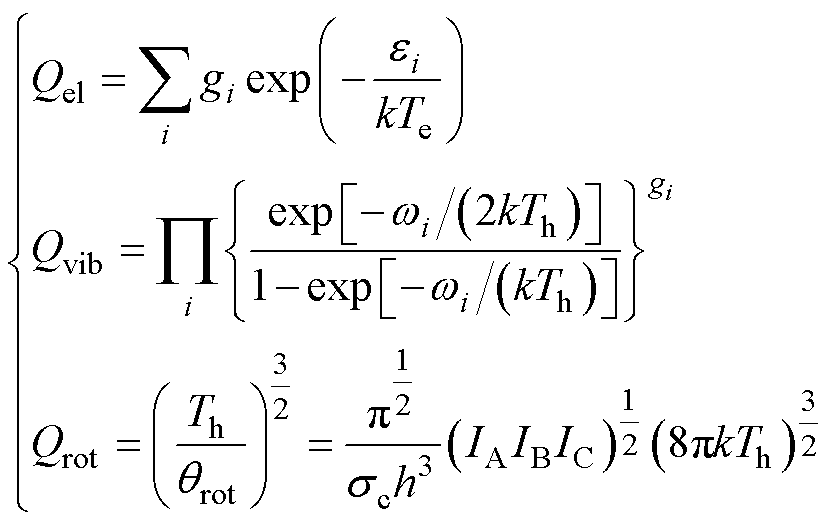（5）
式中，gi为粒子i的能级统计权重；ei为粒子i的电子能级能量；wi为粒子i的基本振动频率；qrot为转动常数；sc为粒子的对称常数；IA、IB、IC为粒子转动的三个惯性矩。
目前等离子体热动属性计算工作中采用的粒子基本热化学函数大都来自美国航空航天局（National Aeronautics and Space Administration, NASA）发布的平衡态最小二乘拟合结果[40]，而未考虑基于配分函数的理论推导求解方法，与真实物理状态可能存在一定的拟合偏差，且无法满足非平衡计算需求。本文综合考虑电子激发、粒子振动与粒子转动的贡献，基于完整双温配分函数计算了SF6与C4F7N等离子体的非平衡热动属性，并将相关粒子的热化学函数求解结果与NIST实验测量数据点进行对比验证，其中双温粒子的热力学属性可表示为
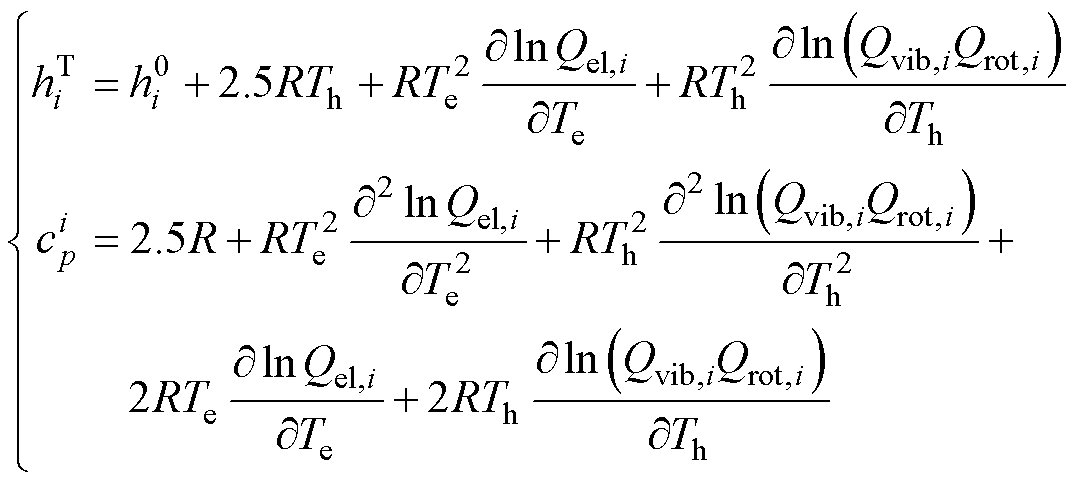（6）
式中，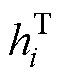
为双温粒子i的比焓；
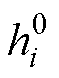为粒子i的标准生成焓；
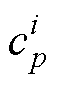为双温粒子i的比定压热容，其表示为比焓对温度的偏导数。
非平衡电弧的宏观热动属性计算主要建立在等离子体组分与双温粒子热化学函数的基础上，其中不同学者对比定压热容等参数的计算方式尚存在争议。V. Colombo等[41]将双温等离子体的宏观比焓hT对电子温度Te求偏导，定义了电子温度主导下的非平衡比定压热容；Wu Yi等[32]分别考虑了电子与重粒子能量对等离子体比热容的作用，定义了以气体温度为主导的非平衡比定压热容。本文根据大多数学者的推荐，将双温电弧等离子体的宏观热动属性表示为
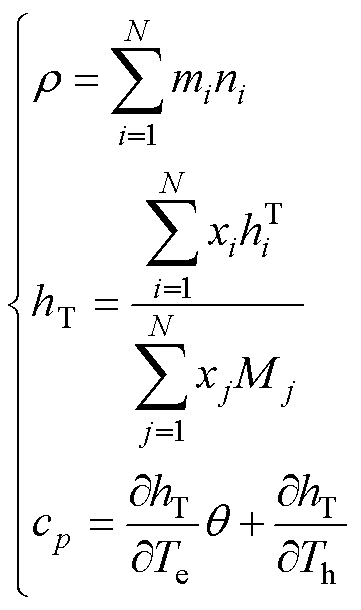（7）
式中，r 为双温电弧的宏观质量密度；xi为粒子i的摩尔分数；Mi为粒子i的摩尔质量；cp为电弧等离子体的宏观比定压热容。
电弧等离子体宏观输运特性的计算通常基于Chapman-Enskog方法，假定粒子运动速度满足一阶微扰的麦克斯韦分布函数，将Boltzmann方程的解表示为Sonine多项式的高阶展开。获得等离子体宏观输运系数的关键在于如何精确描述微观粒子间相互作用的碰撞过程，对此，R. S. Devoto[42]与V. Rat等[43]分别提出了忽略电子与重粒子相互作用的简化解耦方法以及完全考虑两者相互作用的计算方法。研究表明，R. S. Devoto提出的简化解耦处理方法相对于完整考虑电子与重粒子耦合作用的复杂方法而言，其误差可忽略不计[44]，完全满足电弧等离子体的数值模拟要求。在双温非平衡等离子体的相互作用研究方面，通常基于约化碰撞温度描述各类粒子间的碰撞过程，不同学者分别考虑了约化温度的不同表达形式[33, 45]。本文从平衡态下的Chapman- Enskog计算方法出发，计算了约化温度控制下的等离子体粒子相互作用积分，研究了Sonine多项式的高阶展开形式在双温条件下的应用方法，并给出了基于约化碰撞温度的输运系数的实用计算公式。其中约化温度与关键碰撞参数可表示为
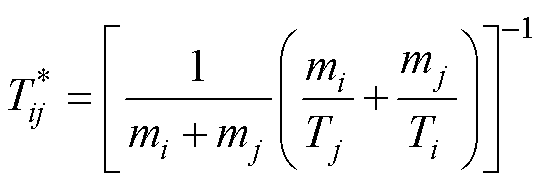（8）
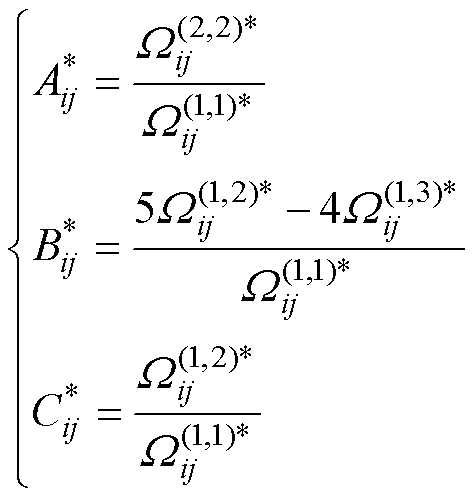（9）
式中，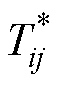
为双温等离子体中粒子i与粒子j相互作用的约化碰撞温度；Ti为粒子i的温度；
、
、
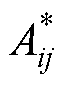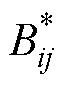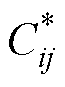为约化温度控制下粒子碰撞的相互作用系数，是求解非平衡输运特性的关键参数；
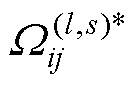为双温粒子间相互作用的约化碰撞积分，与Sonine多项式的展开级数有关，其中上角标 (l,s) 表征碰撞积分的类型。
根据R. S. Devoto的电子解耦理论，综合考虑电子的浓度扩散与热扩散，同时对Sonine多项式进行三阶展开近似，将双温等离子体电导率s 描述为
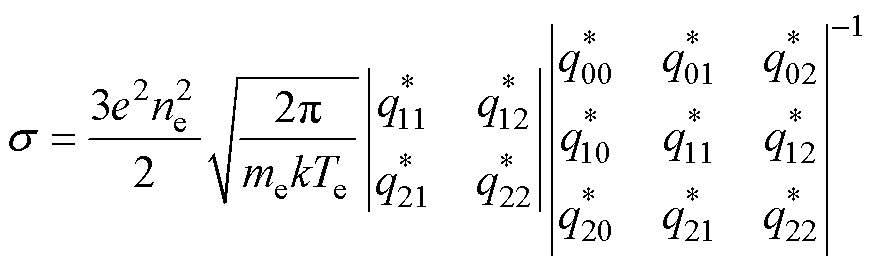（10）
式中，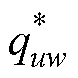
为约化温度下的电子输运碰撞参数，可用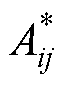、、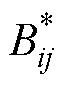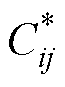表示[42]。
黏度用于描述等离子体粒子发生相对运动时的内摩擦性质，是表征流体对抗形变与流动能力的重要输运参数，与碰撞时的粒子质量存在较强的相关性。本文基于Sonine多项式的一阶展开近似，将双温电弧的黏度描述为
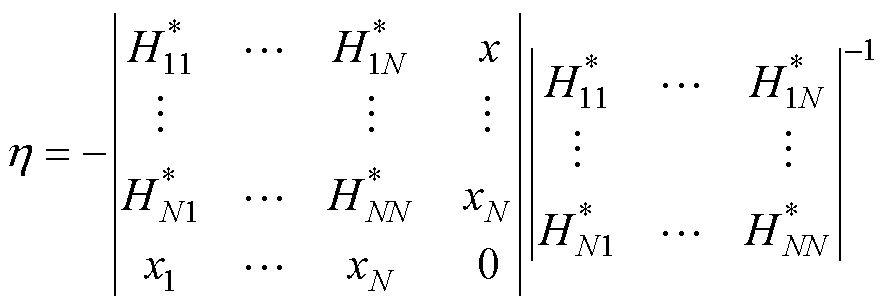（11）
式中，h 为非平衡等离子体黏度；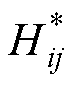
为约化温度控制的双温黏度矩阵求解系数，可用粒子摩尔质量以及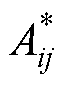、、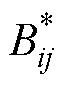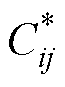表示。针对上述高阶黏度矩阵的行列式运算，本文基于克莱姆法则以及行列式展开的方法，将其转换为关于系数矩阵
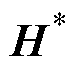的线性方程组求解问题，用于计算非平衡等离子体的黏度。
双温等离子体热导率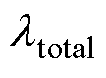
由电子平动热导率
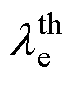、重粒子平动热导率
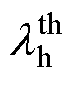、内部热导率lint与反应热导率lreac四部分贡献组成，其中电子平动热导率和重粒子平动热导率分别基于Sonine多项式的三阶与二阶展开近似表示，其计算方法与电导率和黏度相似[42]。内部热导率与反应热导率则主要与粒子的双温比热容以及化学反应焓变有关，表示为
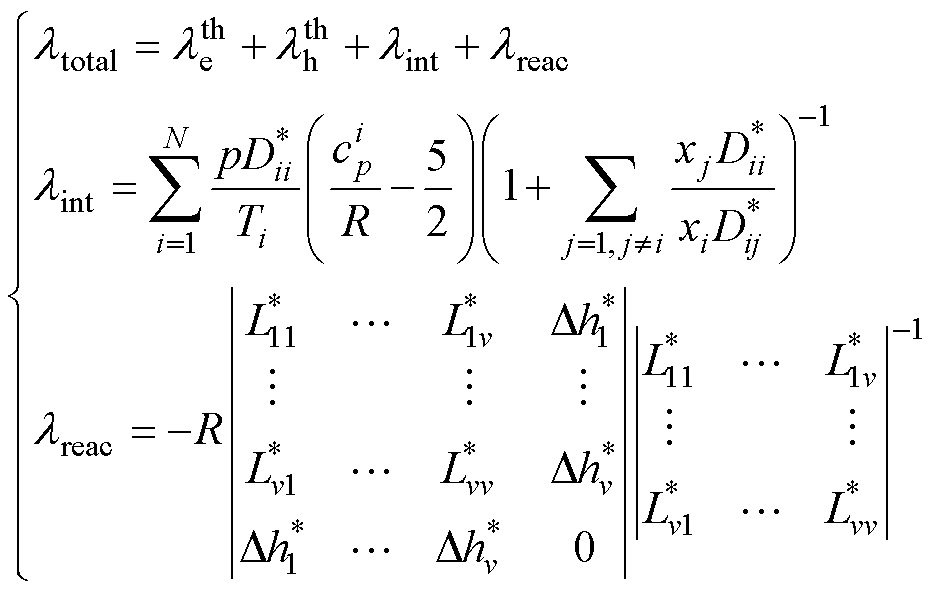（12）
式中，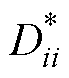
为约化温度控制下粒子i的自扩散系数；
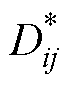为约化温度控制下粒子i与粒子j间的二元扩散系数；
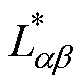为双温反应热导率求解矩阵的约化系数，a,b=1, 2,…,v；v为系统中存在的化学反应总数；
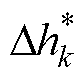为双温状态下化学反应k产生的焓变与RT的比值，反映系统的化学反应进程以及能量变化情况。
综上所述，非平衡态电弧等离子体热动属性与输运特性求解模型与计算流程如图1所示。
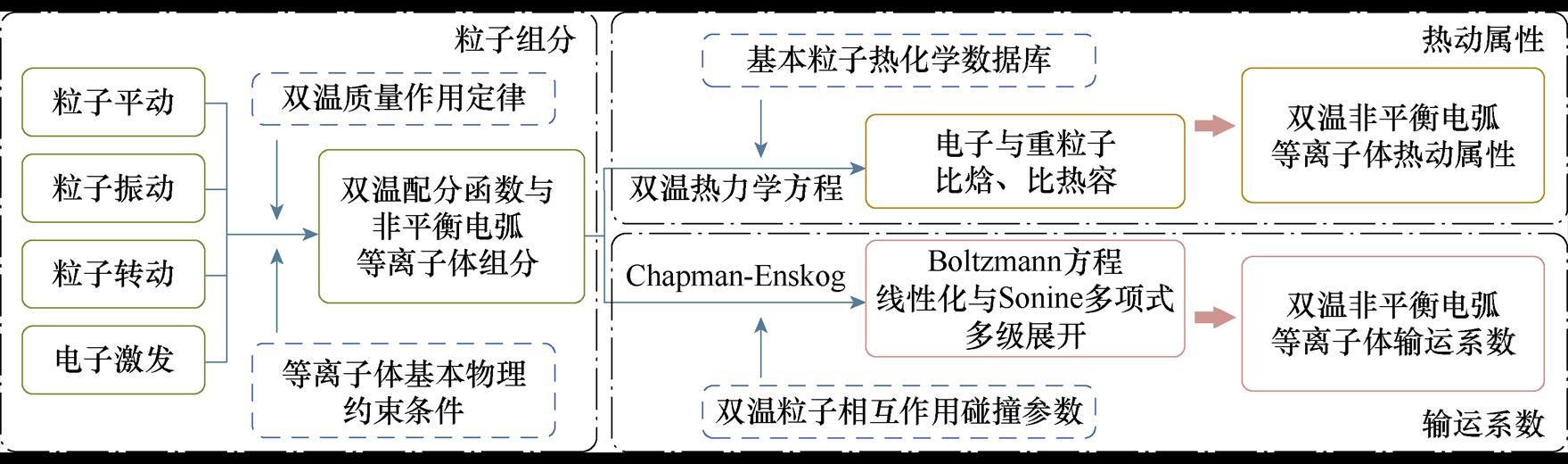
图1 非平衡电弧等离子体热动属性与输运特性计算流程
Fig.1 Flow chart for calculation of thermodynamic and transport properties of non-equilibrium arc plasma
现有的SF6及环保型高压断路器充气压力通常处于0.6～0.8 MPa[12-14, 46]，基于上述非平衡电弧等离子体物理特性计算方法，本文首先求解了0.8 MPa SF6电弧等离子体在不同非平衡条件下的微观粒子组分构成，并与平衡状态的吉布斯自由能最小化算法求解结果进行了对比，计算中考虑的主要粒子见表1。
表1 非平衡SF6等离子体中计算考虑的主要粒子
Tab.1 The main particles considered in the calculation of non-equilibrium SF6 plasma
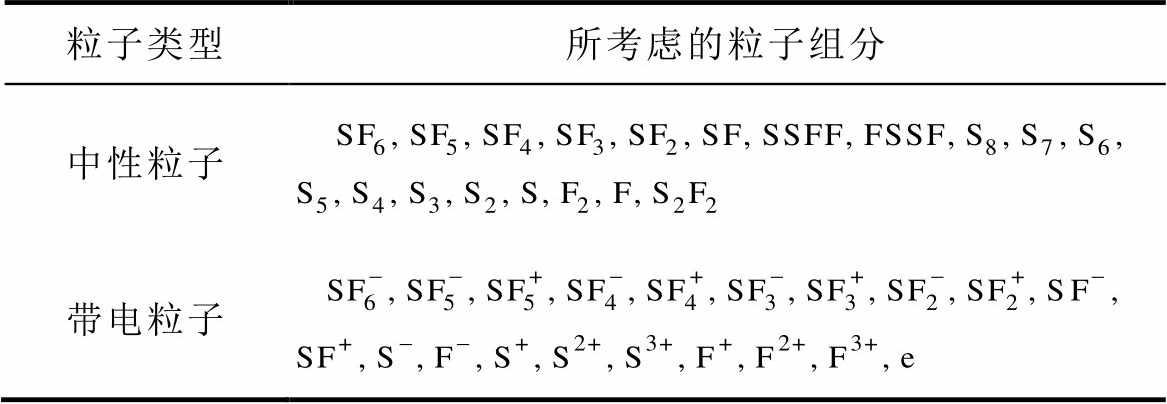
粒子类型所考虑的粒子组分 中性粒子 带电粒子
图2为化学平衡假设下不同非平衡度的双温SF6电弧等离子体在0.8 MPa时的微观粒子组分，其中非平衡度q=1的粒子组分与吉布斯自由能最小化的平衡态计算结果吻合较好，在一定程度上验证了该非平衡计算方法的正确性。由双温等离子体组分随电子温度演化情况可知，q=4的非平衡条件会极大地抑制解离反应的进行。这是由于分子的解离过程主要与重粒子温度有关，电子配分函数对解离反应的贡献较小，如SF6分子发生解离的电子温度由约1 500 K变化至约6 000 K，对应的重粒子温度大致相等。而在电子温度为20 000 K以上的高温区域，多原子粒子已充分解离，非平衡现象对粒子组分的影响几乎可以忽略。通常情况下，由于S原子的一阶电离能（10.36 eV）小于F原子（17.42 eV），平衡态SF6中S电离的过程（约6 000 K）优先于F（约10 000 K）发生；而在较强的非平衡条件下，由于SF6的逐级分解尚未完全进行，体系内S原子含量较少，等离子体中F原子的电离将优先于S原子在8 700 K的电子温度附近占主导地位，这会在一定程度上对电弧的热动与输运特性产生影响。此外，在0.8 MPa的开断工况下，即使计算中已考虑了三体间相互作用的第三维里系数修正项，其对低温区粒子组分的影响依然较小，这与A. B. Murphy等的研究结果一致[47]；而高温区Debye-Hückel修正对于双温SF6组分计算的影响则相对显著，这主要是由带电粒子相互作用引发的能量变化所导致的。
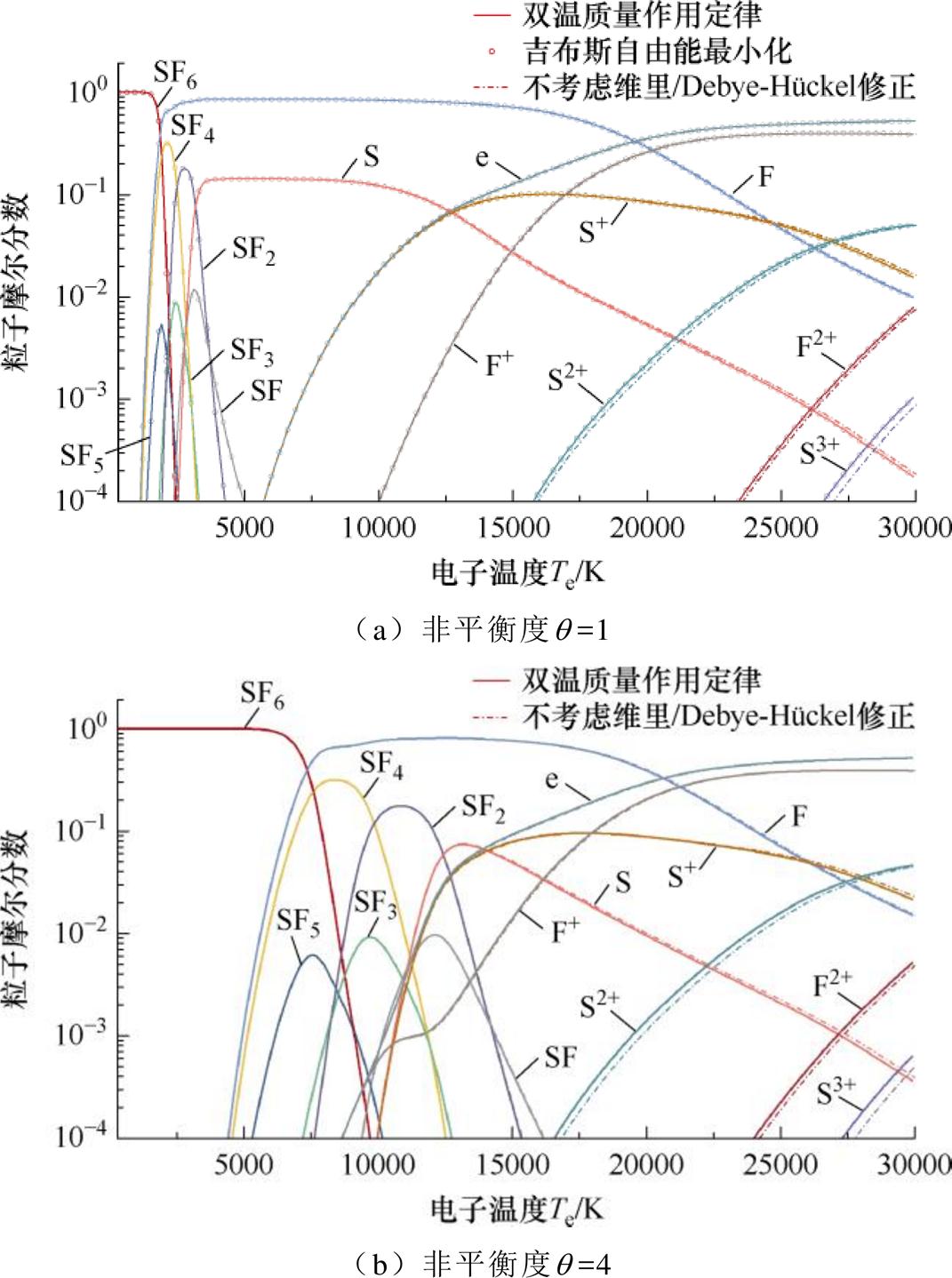
图2 不同非平衡度下0.8 MPa SF6电弧等离子体粒子组分
Fig.2 Particle composition of 0.8 MPa SF6 arc plasma at different non-equilibrium degrees
NIST数据库将微观粒子的热化学性质表示为温度的最小二乘拟合函数[40]，以此获得任意温度下粒子的物理特性。由于其依托的实验参数范围相对有限（通常为298～6 000 K），此类函数逼近结果可能在高温区间内使拟合精度降低，且无法完全满足双温条件的粒子参数需求。基于此，本文利用双温内配分函数求解了300～30 000 K温度范围内粒子的热化学性质，并应用于非平衡电弧的宏观热动属性计算。图3展示了q=1条件下SF6相关粒子的热化学函数计算结果，同时与NIST数据库的公开实验数据进行了对比，结果可验证上述粒子热化学函数求解方法的准确性。
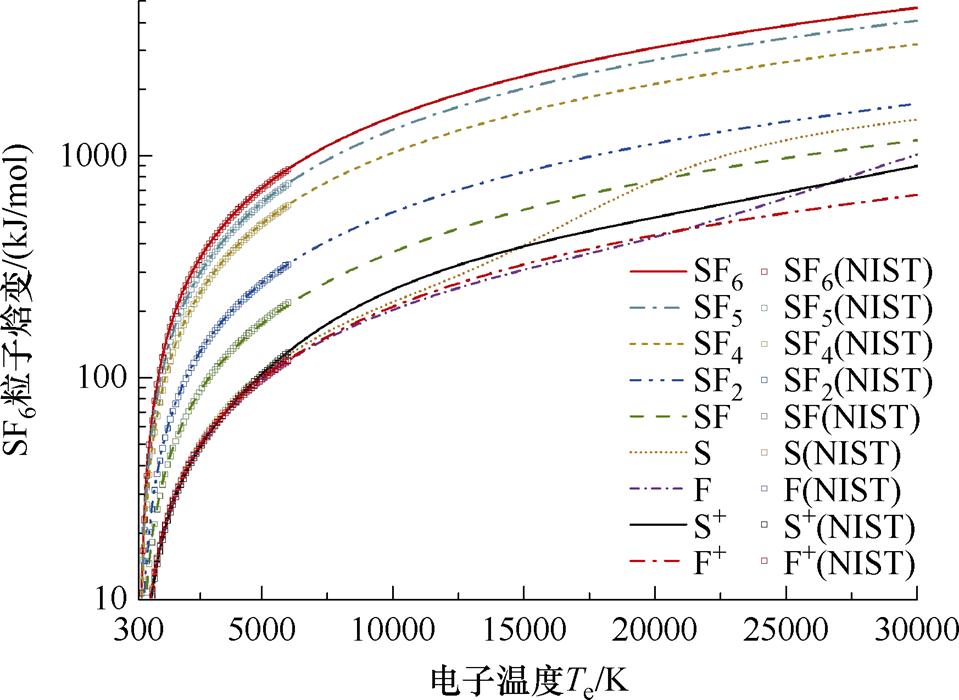
图3 SF6相关粒子热化学函数计算结果与NIST对比
Fig.3 Comparison of the calculated thermochemical functions of SF6 particles with NIST results
图4展示了0.8 MPa、非平衡度q=1～20状态下SF6双温电弧等离子体的质量密度、比焓及比定压热容等热动属性，并将计算结果与西安交通大学公开电弧物性参数基础数据库[48]中的平衡态参数以及Wang Weizong等[33]在q=3状态下的比热容参数进行了对比。由图4可见，三者整体结果较为一致，其中比定压热容在重粒子温度4 000 K附近存在的部分差异主要与考虑的粒子组分及选用的基础数据不同有关。根据前文的研究结果，非平衡现象会极大地阻碍气体分子的解离过程，提高等离子体中大质量重粒子所占比例；同时根据Dalton分压定律的双温形式，更低的重粒子温度致使其拥有更大的粒子数密度，故随着非平衡度的增大，SF6等离子体质量密度也显著提升。此外，在相同的电子温度下，非平衡电弧中重粒子的温度与内能均处于较低水平，系统内高能粒子含量较少，比焓也相应地随着非平衡度的增大而降低。等离子体的比定压热容主要取决于其内部的化学反应进程，如平衡态SF6在5 000 K以下的比热容峰值对应其逐级解离，而在7 000 K以上的波动则主要由S与F原子的电离决定。随着非平衡度的提高，化学反应的迟滞会显著减缓比定压热容的演化进程，同时根据2.1节微观粒子组分的计算结果，较强的非平衡状态可能会在一定程度上改变系统中物理化学过程的主导顺序与反应结果，导致其在非平衡条件下的比定压热容演化趋势与数值大小发生一定变化。
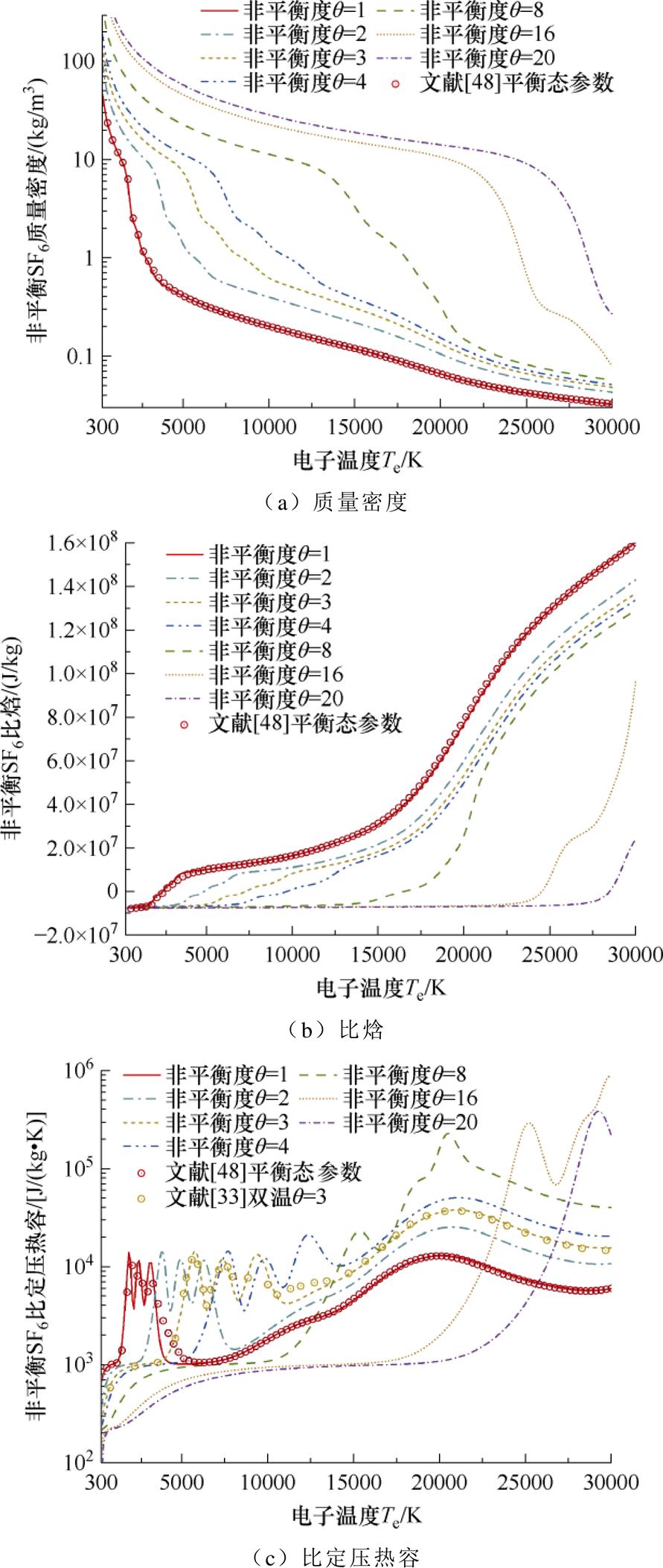
图4 0.8 MPa下双温SF6电弧等离子体热动属性
Fig.4 Thermodynamic properties of 2-T SF6 arc plasma under 0.8 MPa
气体输运系数主要与粒子间碰撞的相互作用强度以及化学反应过程有关，故非平衡条件下等离子体的输运特性取决于粒子组分、相互作用温度、热力学函数以及系统反应焓变等多种物理化学过程的综合影响。本文基于Devoto电子-重粒子解耦方法，建立了双温粒子相互作用积分模型，求解非平衡SF6电弧等离子体输运系数，并将其与GDPLAD数据库和Wang Weizong等[33]的公开结果进行对比，如图5所示。
根据非平衡粒子组分的求解结果，q=1与q=4状态下的SF6等离子体分别在电子温度6 000 K及9 000 K附近发生显著电离，对应其电导率明显增大的拐点。在较低的电子温度区间内，由于非平衡现象对粒子解离与电离反应的抑制作用，其电导率随非平衡度的增加而显著降低；而当电子温度处于较高的区间时，等离子体相对完全电离，此时重粒子温度越低，其热运动对电子定向迁移的阻碍越小，非平衡电弧的宏观电导率则越大。
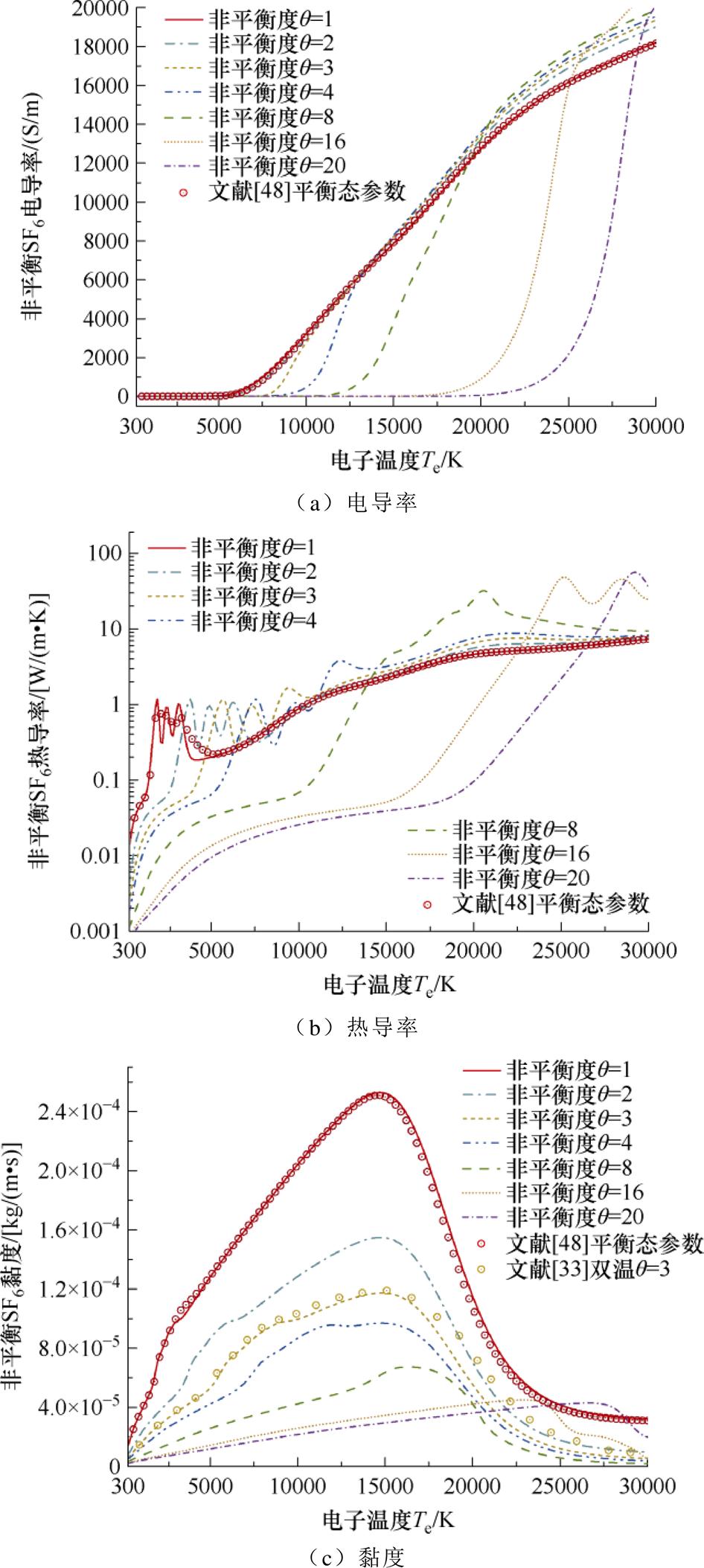
图5 0.8 MPa下双温SF6电弧等离子体输运系数
Fig.5 Transport coefficients of 2-T SF6 arc plasma under 0.8 MPa
图6展示了0.8 MPa、q=4条件下各类物理过程对非平衡SF6电弧等离子体热导率的贡献，其中内部热导率lint在重粒子温度Th＜1 000 K的区间内占主导，电子平动热导率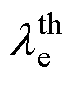对电子温度Te＞9 000 K的显著电离区间贡献较大，而总热导率的波峰则主要取决于化学反应的影响。故在图5b所示的非平衡SF6热导率中，随着非平衡度的增大，内部热导率在更宽的温度范围内占主导地位，而电子平动热导率的主导则发生在更高的电子温度下。此外，由于非平衡等离子体中重粒子温度较低，重粒子平动热导率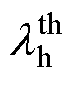的贡献相对较小，这与平衡态等离子体中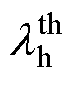贡献较大但lint贡献较小的研究结果存在一定差异。而非平衡度q 对于反应热导率lreac的影响则与比定压热容类似。
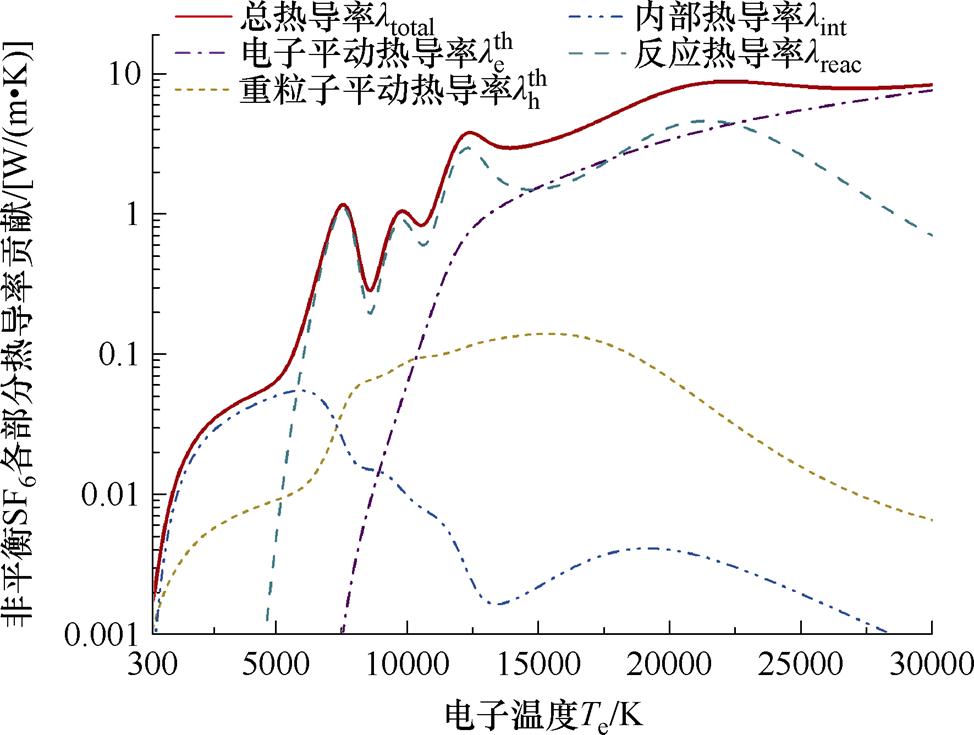
图6 各类物理过程对非平衡SF6热导率的贡献（q=4）
Fig.6 Contribution of various physical processes to the thermal conductivity of non-equilibrium SF6 (q=4)
气体的黏度主要由质量较大的重粒子间的相互作用决定。在较低的温度区间内，重粒子间碰撞的相互作用随着温度的升高而持续增大，黏度也随之攀升，而在电子温度Te＞15 000 K以上的显著电离区域，同极性正离子间的排斥作用使得等离子体黏度大幅降低。非平衡状态等离子体中重粒子温度较低，其宏观黏度也随之显著下降；同时，由于粒子电离受阻，其黏度演化曲线峰值也随之向更高的电子温度区域移动。本文双温SF6黏度与Wang Weizong等[33]的报道在低温区间内较为一致，而在15 000 K以上存在部分差异，其主要归因于德拜长度的定义不同。Wang Weizong等在计算过程中考虑了离子屏蔽的作用，本文则主要根据R. S. Devoto等[49]的推荐，认为仅考虑电子屏蔽效应可能与实验结果更加吻合。
由于C4F7N分子结构与反应路径的复杂性，其通常在电弧的高温与放电环境下表现出不可逆的分解过程[31]，致使弧后C4F7N等离子体的粒子组分与热动属性相较于原气体发生较大改变。本文综合考虑过往学者对电弧作用下C4F7N化学反应与分解产物的研究结果[50-52]，基于计算化学方法建立了对应物种的粒子模型，并求解了化学平衡假设下的弧后双温C4F7N等离子体微观粒子组分如图7所示。双温质量作用定律与吉布斯自由能最小化算法在q=1条件下的计算结果仍表现出较强的一致性。计算中考虑的粒子组分与分解产物在表2中列出，其中忽略了部分过渡态以及同分异构体的影响。
由于C4F7N大分子复杂分解过程涉及的化学反应能量消耗高于SF6分子的逐级分解，平衡条件下C4F7N相关多原子粒子的充分解离温度（约11 000 K以上）显著高于SF6（约5 000 K）。此外，与SF6电弧等离子体相比，C4F7N分解产物与相关粒子质量较大且构型复杂，同时涉及解离反应众多、相互作用过程相互耦合，故非平衡状态对C4F7N等离子体的粒子组分与物理特性影响更为显著。在非平衡度q=4时，鉴于各类粒子数密度控制下化学反应间的强耦合性，CF、N2等多种物质组分含量演化规律发生了明显的改变，如C2N等多原子分子彻底分解的电子温度延缓至22 000 K以上，远高于同条件下SF6的非平衡解离温度（约16 000 K）。高温状态的原子电离过程同样因非平衡解离规律的变化而受到较大的影响：等离子体中电离反应的主要贡献次序由C→N→F改变为F→C→N，原子的电离从电负性与电离能为主导（C、N、F的一阶电离能分别为11.26、14.53、17.42 eV）转化为粒子数密度为主导；且非平衡C4F7N等离子体中低质量中性粒子的含量显著减小，与SF6相比，大分子间及带电粒子间的碰撞主导作用更为显著，这将对其输运过程产生更大影响。
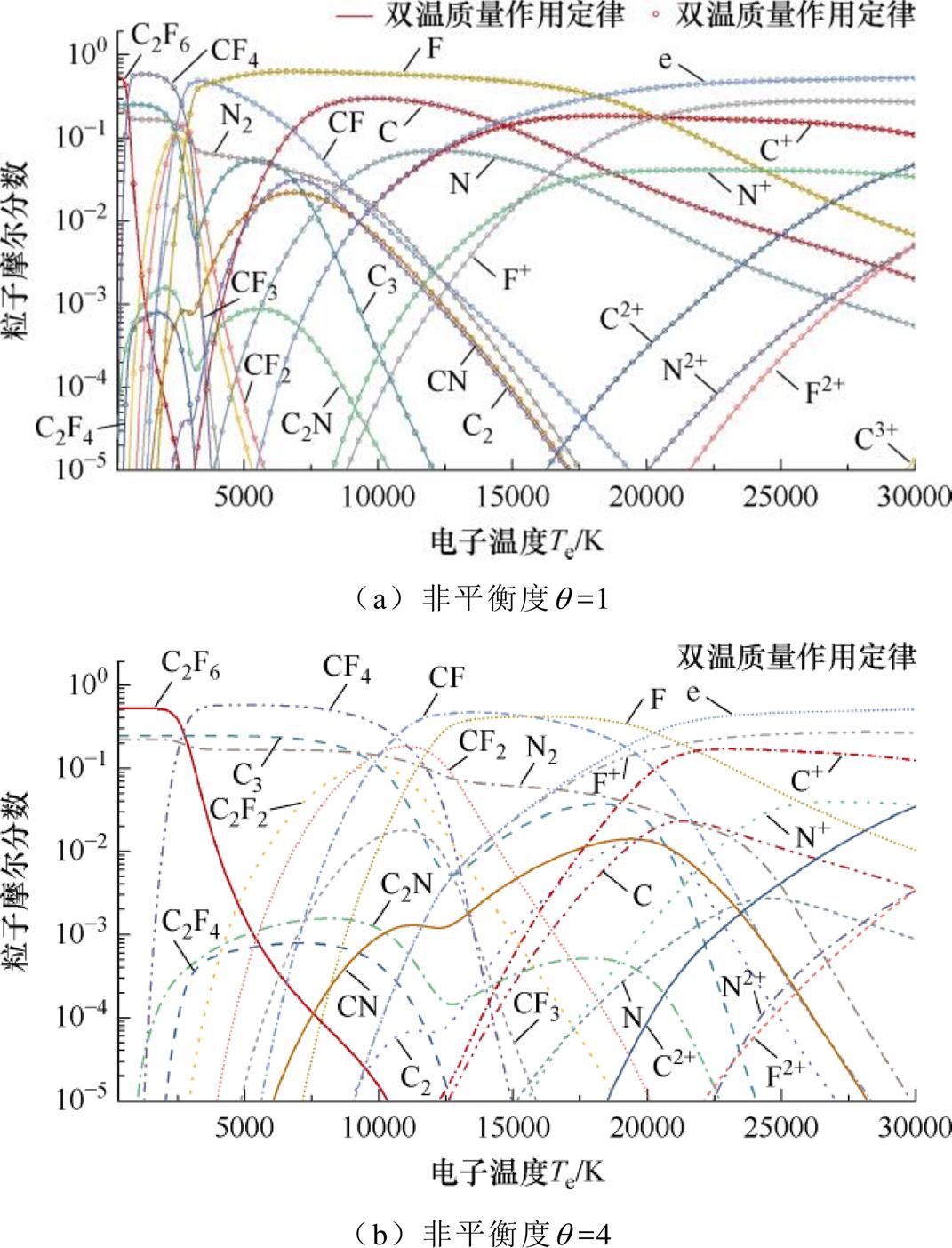
图7 不同非平衡度下0.8 MPa C4F7N电弧等离子体粒子组分
Fig.7 Particle composition of 0.8 MPa C4F7N arc plasma at different non-equilibrium degrees
表2 非平衡C4F7N等离子体中计算考虑的主要粒子
Tab.2 The main particles considered in the calculation of non-equilibrium C4F7N plasma
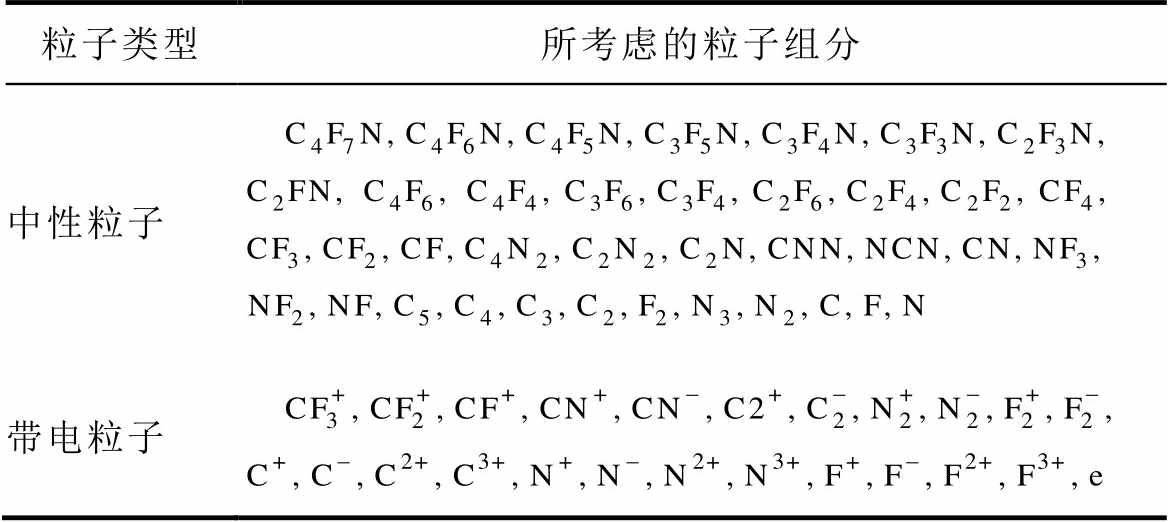
粒子类型所考虑的粒子组分 中性粒子 带电粒子
此外，Zhong Linlin等[36]基于质量作用定律的Potapov形式计算了双温C4F7N等离子体在q=3条件下的粒子组分，其中部分典型C4F7N弧后分解产物与本文Van de Sanden方法的对比如图8所示。Zhong Linlin等研究了碳固体沉积对于非平衡粒子组分的影响，本文则主要考虑到目前开关电弧MHD建模方法的限制，未将石墨固体列入计算的物种范围。故与本文计算结果相比，Zhong Linlin等报道结果中与C元素相关的CF3、CF2、CF等粒子含量均相对较少，而F原子则出现更早且含量更高，这是由石墨沉积消耗了等离子体中的C原子而导致的。同时，由于Potapov方法允许双温系统中的电子-重粒子能量交换，故Zhong Linlin等结果中的电离反应更易发生，且C+、e等带电粒子的生成发生在更低的温度，这与其先前的研究结论一致[53]。综上所述，双温组分求解方法以及可能存在的碳沉积过程会在一定程度上影响C4F7N等离子体的粒子构成，进而改变其比热容、电导率及黏度等热动与输运特征，考虑固体沉积的C4F7N气体电弧建模方法及物性参数仍有待进一步探索。
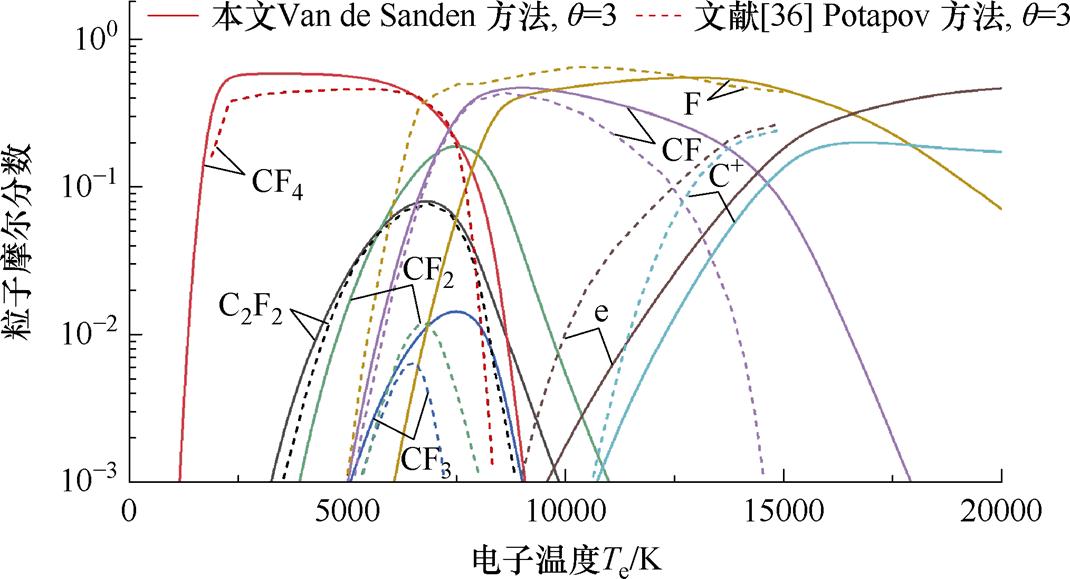
图8 0.1 MPa、q=3双温C4F7N等离子体典型粒子组分
Fig.8 Typical particle composition of two-temperature C4F7N plasma at 0.1 MPa, q=3
图9展示了0.8 MPa双温C4F7N电弧等离子体在q=1～20范围内的热力学参数，并将q=1状态的计算结果与Wu Yi等[32]已发表的C4F7N平衡态物性参数进行了比较。其中两者的比定压热容在低温区间内存在部分差异，主要是由于考虑的C4F7N分解产物以及选用的基础数据不完全相同，故系统内发生的化学反应以及生成的粒子不同。Wu Yi等较好地考虑和模拟了C4F7N气体分子解离过程的物理特性；而本文则主要基于过往对复杂环保气体分解行为的试验结果，尽可能地还原了高能流密度电弧分解下的弧后C4F7N等离子体微观粒子及物性参数。
与前文粒子组分的研究结果相匹配，非平衡现象对C4F7N等离子体热动属性的影响远比SF6更为显著。LTE状态下C4F7N质量密度与比焓的演化趋势与SF6大致趋同，而在q=16～20条件下，C4F7N非平衡等离子体于高温区的质量密度可达SF6的10倍以上，且比焓数值极小。这是由于其内部粒子组分仍以尚未分解的大分子为主，解离反应与电离反应暂未大规模发生。此外，非平衡状态C4F7N比定压热容演化进程的延缓现象同样相较于SF6而言更为显著，且曲线形态的变化更加明显，与LTE下的数值差别更大，这主要是由于多类复杂的解离与电离反应在较低的重粒子温度下堆积，并在较高的电子温度下一同进行导致的。鉴于非平衡条件下C4F7N等离子体热动属性的明显区别，rcp与rhT等参数作为衡量环保气体电弧开断能力的重要参考之一[31]，其受非平衡条件的影响不可被忽略。图10展示了0.8 MPa下非平衡SF6与C4F7N电弧等离子体的rcp计算结果，其中5 000 K以下的rcp峰值表明气体介质有着较好的湍流热耗散能力与灭弧性能，而10 000 K以上的峰值则代表电弧的高温弧芯区域易发生径向膨胀从而难以调控[54]。由结果可知，即使在非热平衡状态下，SF6气体的能量耗散仍保持在较高水平，有着相对出色的灭弧性能；而非平衡C4F7N等离子体在5 000 K以下的湍流耗散能力则相较于LTE假设下更弱，灭弧性能相对较差。根据Wang Weizong等[16]的研究结果，高压断路器电流零区关键湍流区域内的电弧等离子体约处于q=2～4的非平衡态。选用非平衡条件下的rcp参数作为环保气体弧后湍流耗散与灭弧性能的评估标准，在一定程度上更具有科学性。
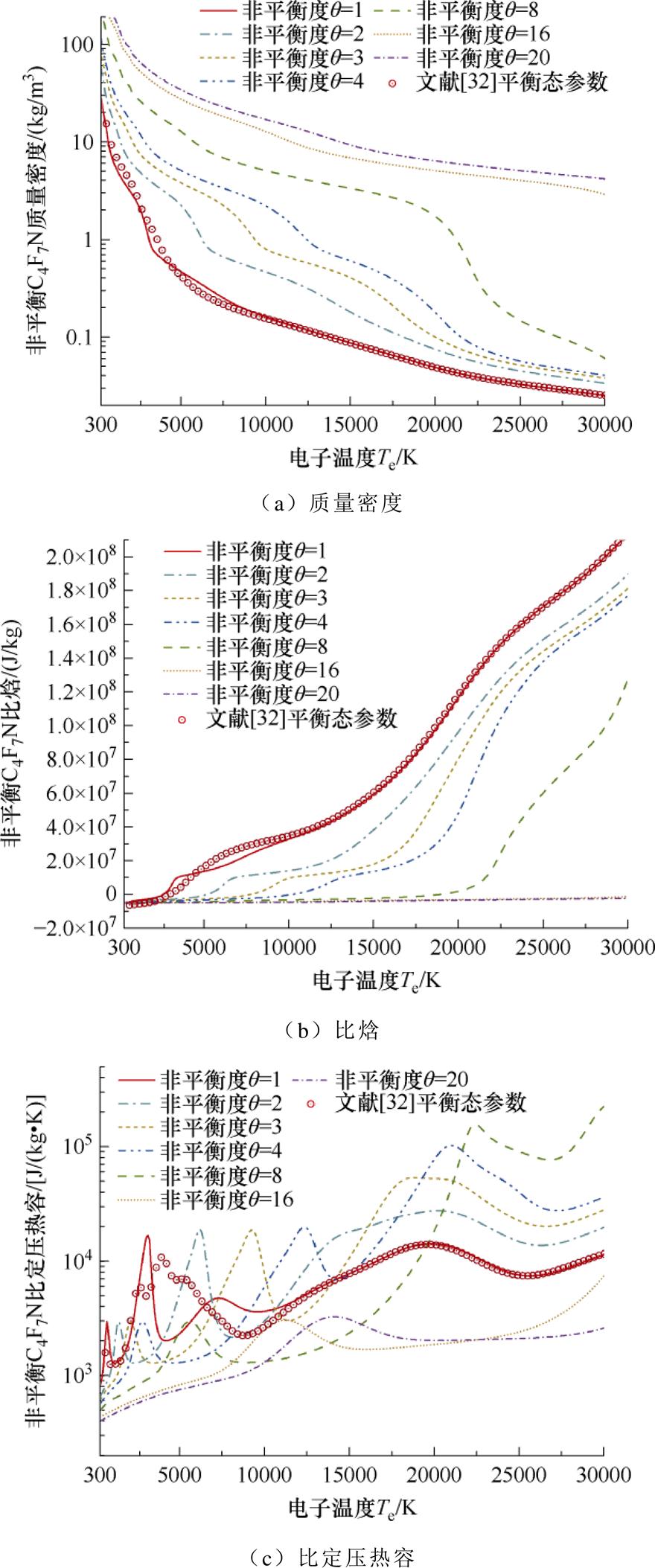
图9 0.8 MPa下双温C4F7N电弧等离子体热动属性
Fig.9 Thermodynamic properties of 2-T C4F7N arc plasma under 0.8 MPa
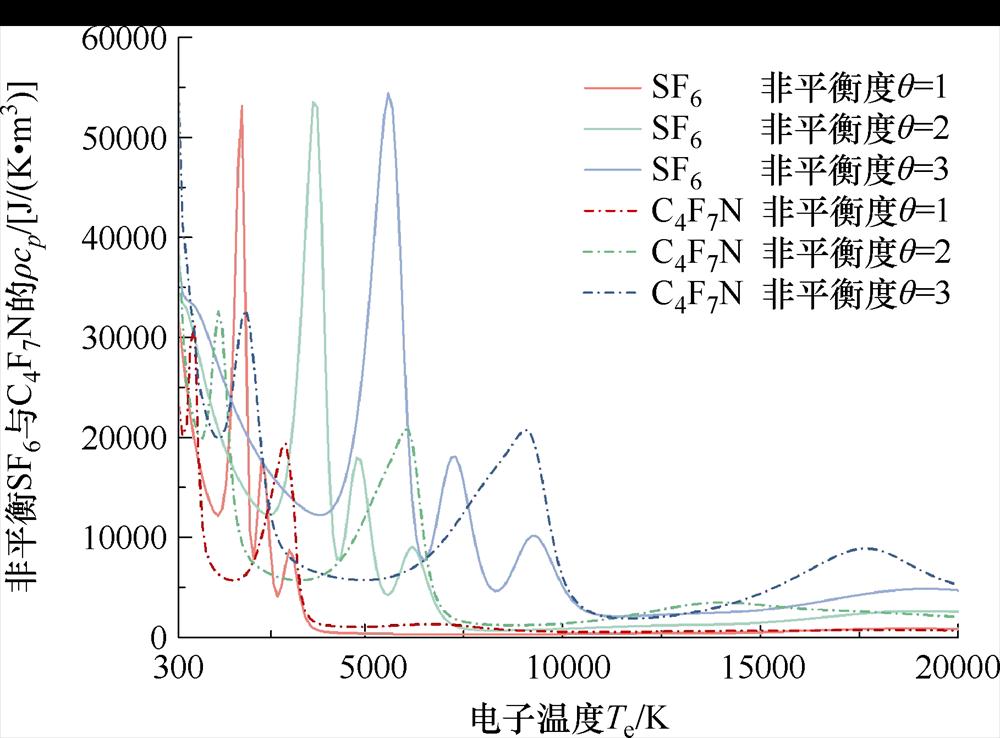
图10 0.8 MPa下非平衡SF6与C4F7N等离子体的rcp
Fig.10 rcp of non-equilibrium SF6 and C4F7N plasmas under 0.8 MPa
弧后非平衡C4F7N等离子体在0.8 MPa条件下的输运系数计算结果及其与Wu Yi等[32]的LTE公开数据对比情况如图11所示。平衡态C4F7N与SF6等离子体电导率的演化规律较为相似；而在非平衡条件下，较低的重粒子温度在极大程度上阻碍了C4F7N气体的复杂解离与电离过程，使其电子数密度与电导率发生较大改变。在q≤4的非平衡等离子体中，SF6解离过程对电离反应的影响较小，故电导率的变化并不明显，而对C4F7N来说该现象则十分显著，其中q=2状态对C4F7N电导率的影响约相当于q=5下的SF6。热导率计算结果与Wu Yi等研究结果存在的小部分差异主要由反应热导率的贡献引起，其产生原因与比定压热容相同。由于化学反应及电子平动等多方面的作用，非平衡现象对C4F7N等离子体热导率的影响同样显著大于SF6，其中强非平衡C4F7N气体中内部热导率与重粒子平动热导率的贡献开始占主导地位。此外，由于电离反应与正离子生成过程受到更大的影响，与SF6相比，C4F7N等离子体的黏度峰值也随非平衡度的增大而产生更显著的后移，这意味着在非平衡电弧磁流体模型中，C4F7N的对流过程对应着更大的黏度。
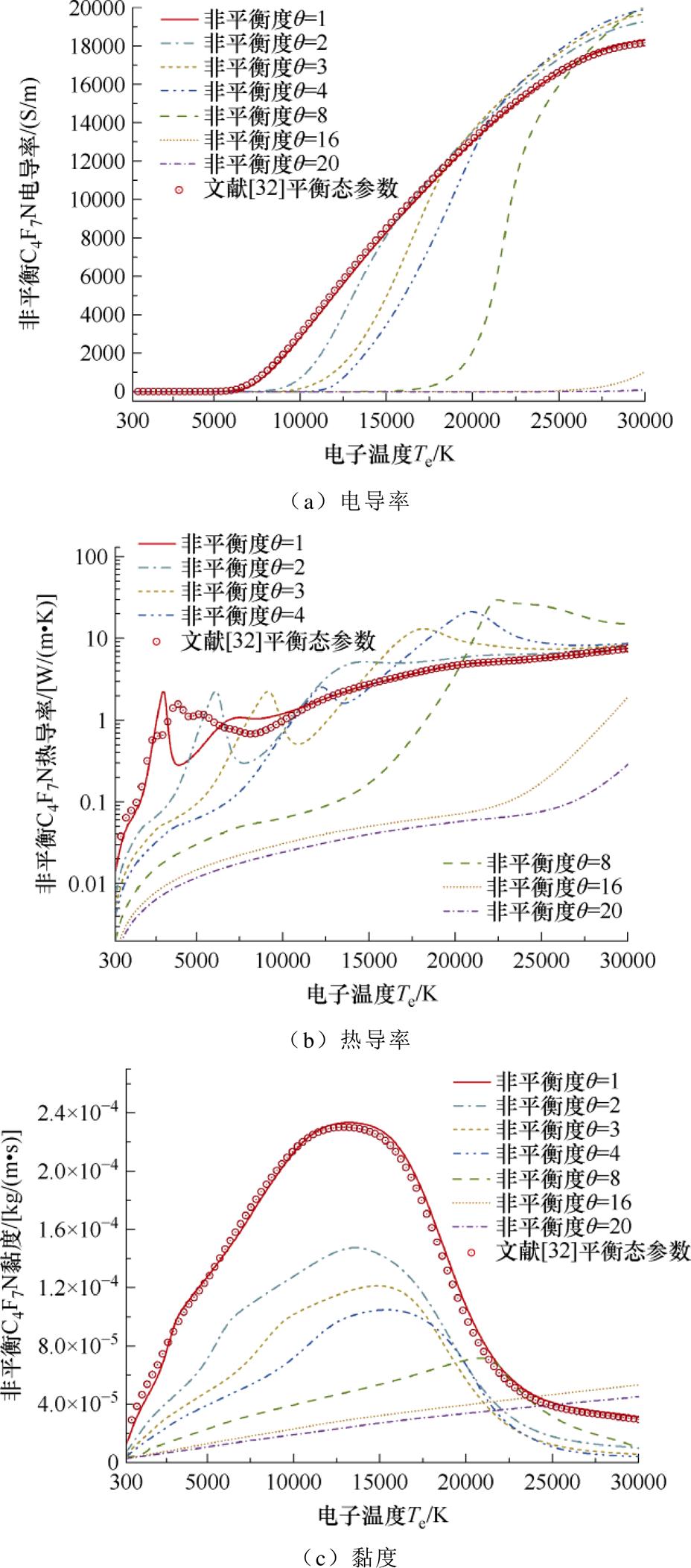
图11 0.8 MPa 下双温C4F7N电弧等离子体输运系数
Fig.11 Transport coefficients of 2-T C4F7N arc plasma under 0.8 MPa
气压对等离子体物性参数的影响一直以来都是电弧等离子体物理特性研究的一个重要话题。根据勒夏特列原理，气压的增大会阻碍等离子体中解离与电离反应的进行，这一特征与非平衡现象的作用类似。图12展示了不同气压以及非平衡状态下的C4F7N部分典型热动属性与输运系数。虽然更高气压下等离子体的比定压热容演化进程因化学反应受到抑制而呈现一定程度的延缓，但对整体比热容数值大小的影响较小；而非平衡条件下其数值大小则会发生较大的改变。此外，由于气压增大改变了等离子体中的粒子数密度，致使高温区间内等离子体的电子密度及电导率显著提升，而非平衡等离子体的电导率差异则主要表现在较低的温度范围内。需要注意的是，气压对粒子间碰撞相互作用的影响较小，故其对黏度的影响主要是由于粒子电离进程的差异，而非平衡等离子体中双温粒子温度的差异将直接影响其碰撞相互作用的强弱，进而改变宏观黏度等输运特性。
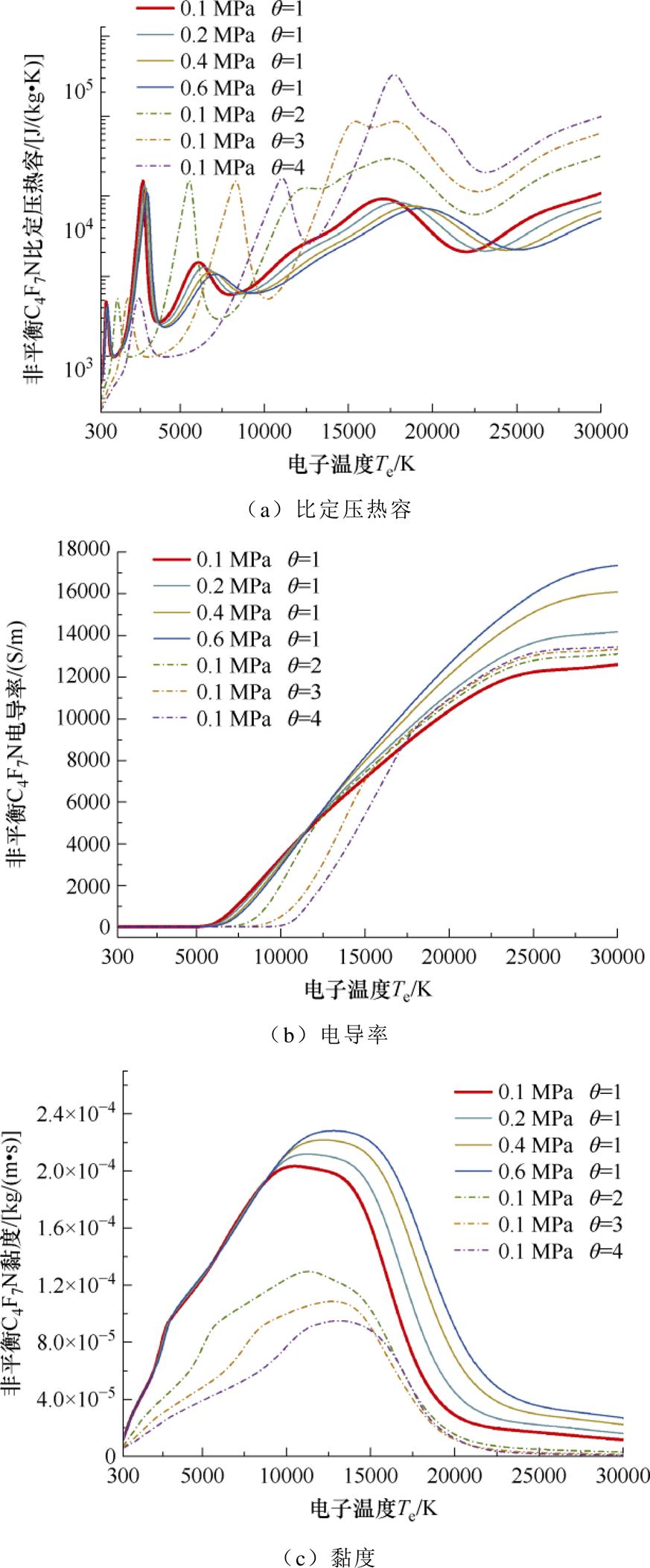
图12 气压与非平衡度对C4F7N电弧等离子体物性参数的影响
Fig.12 Effect of pressure and non-equilibrium degree on thermal physical parameters of C4F7N arc plasma
本文基于双温配分函数与相互作用模型建立了弧后非平衡态等离子体的物性参数计算方法，并针对电力开关设备实际运行工况求解了高气压、强非平衡条件下SF6与C4F7N等离子体的粒子组分、热动属性及输运系数，得出以下结论：
1）该双温方法在q=1状态下与LTE状态的吉布斯自由能最小化算法及其他公开数据的结果基本一致，部分差异归因于所选择的粒子组分种类及计算方法不同。非平衡现象会在极大程度上改变电弧等离子体中的粒子解离规律与电离主导次序，同时由于分子结构及反应路径的复杂性，C4F7N气体组分受非平衡条件的影响相较于SF6更加显著。
2）非平衡现象对气体电弧热动属性的影响极大，这主要是由双温等离子体中分子解离过程的延迟以及不同粒子温度对气体状态方程的贡献不同导致的。非平衡C4F7N与SF6的热动特征与LTE假设下差别较大，而rcp与rhT等热力学参数作为衡量环保气体开断特性的关键参考，其弧后关键开断时刻的非平衡状态不可忽略。以非平衡条件下的rcp参数作为灭弧介质的零区湍流耗散评估指标在一定程度上更具科学性。
3）电弧等离子体输运特性受非平衡度的影响规律主要取决于微观粒子组分及碰撞相互作用的综合作用。一方面非平衡现象抑制了解离与电离过程的进行；另一方面由于重粒子热运动对电子定向迁移的阻碍减小，反而提升了电子平动对输运系数的贡献，故非平衡电导率呈现低温区减小而高温区增大的特征。气体的非平衡黏度则因重粒子的相互作用温度降低而显著减小。
4）增大气压同样会阻碍等离子体化学反应的进行，物性参数随气压的变化主要归因于反应进程及粒子数密度的差异；而非平衡状态除会对粒子组分产生影响之外，亦会改变粒子能量与碰撞作用强度，进而影响电子与重粒子的宏观物理特征。此外，考虑到高充气压力下C4F7N与CO2/O2气体混合使用的实际应用背景，仍有必要进一步研究其混合物等离子体的非平衡物理特征。
参考文献
[1] 李辰辉, 褚继峰, 龙潇, 等. 基于弧触头接触振动特征分析的高压SF6断路器电寿命在线监测方法[J]. 电工技术学报, 2024, 39(15): 4883-4895.
Li Chenhui, Chu Jifeng, Long Xiao, et al. Online monitoring method of electrical life of high voltage SF6 circuit breaker based on analysis of arcing contact vibration characteristics[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4883-4895.
[2] 崔建, 孙帅, 张国钢, 等. 基于双温度磁流体电弧仿真改进Mayr电弧模型的特快速暂态过电压仿真方法[J]. 电工技术学报, 2024, 39(16): 5149-5161.
Cui Jian, Sun Shuai, Zhang Guogang, et al. The very fast transient overvoltage simulation method based on two-temperature MHD arc simulation to improve Mayr arc model[J]. Transactions of China Elec- trotechnical Society, 2024, 39(16): 5149-5161.
[3] Zhang Q, Liu J, Yan J D, et al. The modelling of an SF6 arc in a supersonic nozzle: II. current zero behaviour of the nozzle arc[J]. Journal of Physics D: Applied Physics, 2016, 49(33): 335501.
[4] Dhotre M T, Ye Xiangyang, Linares F, et al. Multiobjective optimization and CFD simulation for a high-voltage circuit breaker[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2105-2112.
[5] Petchanka A, Reichert F, Gonzalez J J, et al. Modelling of the deformation of PTFE-nozzles in a high voltage circuit breaker due to multiple inter- ruptions[J]. Journal of Physics D: Applied Physics, 2016, 49(13): 135201.
[6] Rümpler C, Zacharias A, Chechare R B, et al. Coupling of magneto-hydrodynamics and structural models to predict wall deformation due to arcing[J]. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2023, 8: 343-353.
[7] Li Xingwen, Zhao Hu, Murphy A B. SF6-alternative gases for application in gas-insulated switchgear[J]. Journal of Physics D Applied Physics, 2018, 51(15): 153001.
[8] Guo Ze, Liu Shungui, Pu Yunjie, et al. Study of the arc interruption performance of CO2 gas in high-voltage circuit breaker[J]. IEEE Transactions on Plasma Science, 2019, 47(5): 2742-2751.
[9] 崔兆轩, 林莘, 钟建英, 等. C4F7N/CO2混合气体特高压母线通流温升特性研究[J]. 电工技术学报, 2023, 38(9): 2491-2499.
Cui Zhaoxuan, Lin Xin, Zhong Jianying, et al. Study on the temperature rise characteristics of C4F7N/CO2 mixed gas ultra high voltage bus[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2491- 2499.
[10] Zhang Boya, Zhou Ran, Wang Kai, et al. Arc interruption performance of C4F7N-CO2 mixture in a 126 kV disconnector[J]. IEEE Transactions on Power Delivery, 2022, 38(2): 1197-1207.
[11] Bian Chenxi, He Baina, Lin Xin, et al. Research on interruption performance of environmentally friendly C4F7N mixed-gas-insulated switchgear[J]. Energies, 2022, 15(18): 6500.
[12] 张博雅, 周然, 郝迈, 等. C4F7N混合气体在40.5kV断路器中的应用研究(一): 燃弧特性仿真与灭弧性能评估[J]. 中国电机工程学报, 2022, 42(23): 8750- 8762.
Zhang Boya, Zhou Ran, Hao Mai, et al. Research on application of C4F7N gas mixture in 40.5kV circuit breaker (part Ⅰ): simulation and evaluation of arc extinguishing performance[J]. Proceedings of the CSEE, 2022, 42(23): 8750-8762.
[13] Korbel J, Ostrowski J, Stoller P, et al. Convective performance of C5-flouroketone-based (C5-FK) and C4-flouronitrile-based (C4-FN) gas mixtures and SF6[J]. Journal of Thermal Science and Engineering Applications, 2023, 15(1): 011002.
[14] Hermosillo V F, Schirmer M, Irwin T, et al. Development of an SF6-free AC HV dead-tank circuit breaker rated 145 kV, 63 kA[C]//2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 2023: 1-5.
[15] 荣命哲, 吴翊, 杨飞, 等. 开关电弧电流零区非平衡态等离子体仿真研究现状[J]. 电工技术学报, 2017, 32(2): 1-12, 23.
Rong Mingzhe, Wu Yi, Yang Fei, et al. Review on the simulation method of non-equilibrium arc plasma during current zero period in the circuit breaker[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 1-12, 23.
[16] Wang Weizong, Yan J D, Rong Mingzhe, et al. Theoretical investigation of the decay of an SF6 gas-blast arc using a two-temperature hydrodynamic model[J]. Journal of Physics D: Applied Physics, 2013, 46(6): 065203.
[17] Tanaka Y, Iijima T. Hybrid thermofluid modeling with LTE and non-LTE assumption for decaying molecular gas arcs[C]//2022 6th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Seoul, Republic of Korea, 2022: 93-98.
[18] Eda S, Ogino Y, Asai S, et al. Non-equilibrium modeling of arc plasmas in the gas-metal arc-welding process[J]. Journal of Physics D: Applied Physics, 2021, 54(32): 325204.
[19] Al-Mamun S A, Tanaka Y, Uesugi Y. Two- temperature two-dimensional non chemical equilibrium modeling of Ar-CO2-H2 induction thermal plasmas at atmospheric pressure[J]. Plasma Chemistry and Plasma Processing, 2010, 30(1): 141-172.
[20] 石岩, 崔博源, 陈允, 等. 开关电弧非平衡态电导率的研究[J]. 高压电器, 2020, 56(2): 27-33.
Shi Yan, Cui Boyuan, Chen Yun, et al. Study on non-equilibrium state conductivity of switching arc[J]. High Voltage Apparatus, 2020, 56(2): 27-33.
[21] Zhang Xiaoning, Li Heping, Murphy A B, et al. Comparison of the transport properties of two- temperature argon plasmas calculated using different methods[J]. Plasma Sources Science and Technology, 2015, 24(3): 035011.
[22] Guo Xiaoxue, Murphy A B, Li Xingwen. Thermo- dynamic properties and transport coefficients of two-temperature helium thermal plasmas[J]. Journal of Physics D: Applied Physics, 2017, 50(12): 125202.
[23] 仲林林, 王逸凡, 顾琦. C4F7N气体电弧的辐射输运特性研究[J]. 电工技术学报, 2023, 38(19): 5316- 5329.
Zhong Linlin, Wang Yifan, Gu Qi. Study on radiation transport characteristics of C4F7N gaseous arc[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5316-5329.
[24] Zhong Linlin, Wang Jiayu, Xu Jie, et al. Effects of buffer gases on plasma properties and arc decaying characteristics of C4F7N-N2 and C4F7N-CO2 arc plasmas[J]. Plasma Chemistry and Plasma Processing, 2019, 39(6): 1379-1396.
[25] Nikjou V, Kebriaee A, Momeni M, et al. A model for determining thermodynamic and transport properties of electric arc plasmas at elevated pressures and temperatures and its validations[J]. The European Physical Journal D, 2023, 77(6): 119.
[26] Boulos M I, Cressault Y, Fauchais P L, et al. Thermodynamic and transport properties of gases over the temperature range 300-30, 000 K[M]// Boulos M I, Fauchais P L, Pfender E. Handbook of Thermal Plasmas. Cham: Springer International Publishing, 2023: 1807-1921.
[27] Cressault Y. Basic knowledge on radiative and transport properties to begin in thermal plasmas modelling[J]. AIP Advances, 2015, 5(5): 057112.
[28] 李静, 荐雯, 曹云东, 等. SF6替代气体C4F7N/CO2喷口灭弧性能分析[J]. 高压电器, 2024, 60(9): 92-98.
Li Jing, Jian Wen, Cao Yundong, et al. Arc interruption performance analysis of nozzle filled with C4F7N/CO2 gas mixture instead of SF6 gas[J]. High Voltage Apparatus, 2024, 60(9): 92-98.
[29] Ding Can, Ding Qingchang, Wang Zhenyi, et al. Comparison of algorithms for predicting plasma physical parameters of SF6-Cu mixtures at local thermodynamic equilibrium state via machine learning[J]. AIP Advances, 2021, 11(11): 115102.
[30] Li Xingwen, Guo Xiaoxue, Murphy A B, et al. Calculation of thermodynamic properties and transport coefficients of C5F10O-CO2 thermal plasmas[J]. Journal of Applied Physics, 2017, 122(14): 143302.
[31] Zhang Boya, Xiong Jiayu, Chen Li, et al. Funda- mental physicochemical properties of SF6-alternative gases: a review of recent progress[J]. Journal of Physics D: Applied Physics, 2020, 53(17): 173001.
[32] Wu Yi, Wang Chunlin, Sun Hao, et al. Properties of C4F7N-CO2 thermal plasmas: thermodynamic properties, transport coefficients and emission coefficients[J]. Journal of Physics D: Applied Physics, 2018, 51(15): 155206.
[33] Wang Weizong, Rong Mingzhe, Wu Yi, et al. Thermodynamic and transport properties of two- temperature SF6 plasmas[J]. Physics of Plasmas, 2012, 19(8): 083506.
[34] Wu Yi, Chen Zhexin, yang Fei, et al. Two- temperature thermodynamic and transport properties of SF6-Cu plasmas[J]. Journal of Physics D: Applied Physics, 2015, 48(41): 415205.
[35] Wang Xiaohua, Gao Qingqing, Fu Yuwei, et al. Dominant particles and reactions in a two-temperature chemical kinetic model of a decaying SF6 arc[J]. Journal of Physics D Applied Physics, 2016, 49(10): 105502.
[36] Zhong Linlin, Gu Qi, Wu Bingyu. Graphite production in two-temperature non-LTE plasmas of C4F7N and C5F10O mixed with CO2, N2, and O2 as eco-friendly SF6 replacements: a numerical study[J]. Plasma Processes and Polymers, 2021, 18(8): 2100036.
[37] Zhong Linlin, Baheti B, Wu Qi. Particle condensation in two-temperature (2T) arc plasmas of various SF6 replacements[J]. Plasma Chemistry and Plasma Processing, 2024, 44(5): 1867-1882.
[38] Guo Xiaoxue, Li Xingwen, Murphy A B, et al. Calculation of thermodynamic properties and transport coefficients of CO2-O2-Cu mixtures[J]. Journal of Physics D: Applied Physics, 2017, 50(34): 345203.
[39] Gleizes A, Chervy B, Gonzalez J J. Calculation of a two-temperature plasma composition: bases and application to SF6[J]. Journal of Physics D: Applied Physics, 1999, 32(16): 2060-2067.
[40] McBride B J, Gordon S. Computer program for calculating and fitting thermodynamic functions[R]. Cleveland: NASA, 1992.
[41] Colombo V, Ghedini E, Sanibondi P. Thermodynamic and transport properties in non-equilibrium argon, oxygen and nitrogen thermal plasmas[J]. Progress in Nuclear Energy, 2008, 50(8): 921-933.
[42] Devoto R S. Simplified expressions for the transport properties of ionized monatomic gases[J]. Physics of Fluids, 1967, 10(10): 2105-2112.
[43] Rat V, André P, Aubreton J, et al. Transport properties in a two-temperature plasma: theory and application[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2001, 64(2): 026409.
[44] Colombo V, Ghedini E, Sanibondi P. Two- temperature thermodynamic and transport properties of argon-hydrogen and nitrogen-hydrogen plasmas[J]. Journal of Physics D: Applied Physics, 2009, 42(5): 055213.
[45] Zhang Xiaoning, Li Heping, Murphy A B, et al. A numerical model of non-equilibrium thermal plasmas. I. transport properties[J]. Physics of Plasmas, 2013, 20(3): 033508.
[46] CIGRE WG A3.41. Current interruption in SF6-free switchgear[R]. Paris: CIGRE, 2022.
[47] Murphy A B, Tam E. Thermodynamic properties and transport coefficients of arc lamp plasmas: argon, krypton and xenon[J]. Journal of Physics D: Applied Physics, 2014, 47(29): 295202.
[48] 西安交通大学. 特种电气技术研究中心电弧物性参数数据库[DB/OL]. (2024-08-12)[2024-08-22]. https:// aet.xjtu.edu.cn/sjxzzx1/dhwxcs/zlmd.htm.
[49] Devoto R S. Transport coefficients of ionized argon[J]. Physics of Fluids, 1973, 16(5): 616-623.
[50] 李祎, 张晓星, 傅明利, 等. 环保绝缘气体C4F7N研究及应用进展Ⅰ: 绝缘及电、热分解特性[J]. 电工技术学报, 2021, 36(17): 3535-3552.
Li Yi, Zhang Xiaoxing, Fu Mingli, et al. Research and application progress of eco-friendly gas insulating medium C4F7N, part Ⅰ: insulation and electrical, thermal decomposition properties[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3535- 3552.
[51] Chen Li, Zhang Boya, Li Xingwen, et al. Decomposition pathway of C4F7N gas considering the participation of ions[J]. Journal of Applied Physics, 2020, 128(14): 143303.
[52] Chen Li, Zhang Boya, Yang Tao, et al. Thermal decomposition characteristics and kinetic analysis of C4F7N/CO2 gas mixture[J]. Journal of Physics D: Applied Physics, 2020, 53(5): 055502.
[53] Zhong Linlin, Murphy A B, Wang Xiaohua, et al. Calculation of two-temperature plasma composition: I. mass action law methods and extremum searching methods[J]. Journal of Physics D: Applied Physics, 2020, 53(6): 065202.
[54] 柯学, 王安阳, 刘伟, 等. CF3SO2F及其混合气体电弧等离子体粒子组分与物性参数计算[J]. 电工技术学报, 2024, 39(19): 6145-6161.
Ke Xue, Wang Anyang, Liu Wei, et al. Calculation of particle composition and physical property parameters of arc plasma particles of CF3SO2F and its gas mixtures[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6145-6161.
Thermodynamic Properties and Transport Coefficients of Post-Arc Nonequilibrium SF6 and C4F7N Plasmas
Abstract Switching arcs typically exhibit a strong non-equilibrium state at the critical moment of current interruption in the post-arc current zero region, which subsequently affects the current interruption performance of high-voltage switchgear. However, current research on switching arcs predominantly relies on the assumption of local thermodynamic equilibrium (LTE), making it challenging to accurately describe the post-arc decay process. To address this issue, this study investigates the non-equilibrium thermodynamic properties and transport coefficients of SF6 and C4F7N in the post-arc state. It compares the physical characteristics of the arc decay process of C4F7N under high-pressure conditions with those of SF6, providing fundamental parameters for the non-equilibrium arc modeling of both gases.
Firstly, the two-temperature partition functions were calculated, and a model for solving the composition of non-equilibrium plasma was established based on the two-temperature mass action law. Secondly, various thermodynamic properties of the non-equilibrium plasma were computed based on the 2-T composition and partition functions. Finally, using the computed data, a system for solving the transport coefficients of non-equilibrium plasma was established based on the 2-T Chapman-Enskog theory. Through these computations, this work investigated the effects of non-equilibrium conditions on the composition and thermophysical parameters, and compared the differences in the impact of pressure and non-equilibrium conditions.
The computational data for post-arc non-equilibrium SF6 and C4F7N plasmas indicate that, due to the first ionization energy of sulfur atoms (10.36 eV) being lower than that of fluorine atoms (17.42 eV), sulfur in the SF6 plasma will undergo significant ionization preferentially over fluorine at 6 000 K under the LTE assumption. However, in a plasma with a non-equilibrium degree (q=Te/Th) of 4, fluorine atom ionization will dominate over sulfur near an electron temperature of 8 700 K; a similar phenomenon occurs in C4F7N. Additionally, the significant dissociation temperature of polyatomic particles in the non-equilibrium C4F7N plasma increases from 11 000 K to over 22 000 K, which is significantly higher than the 16 000 K observed in SF6 under the same conditions. Under conditions of q=16～20, the mass density of non-equilibrium C4F7N can exceed that of SF6 by more than tenfold, indicating that the thermodynamic properties are significantly influenced by the non- equilibrium state. The impact of q=2 on the electrical conductivity of C4F7N plasma is approximately equivalent to that of q=5 on SF6, suggesting that the transport coefficients are primarily determined by the plasma composition and the intensity of interactions between particles. Therefore, complex large molecules are more sensitive to the influence of non-equilibrium conditions.
The analysis of the computational data leads to the following conclusions: (1) The established non-equilibrium computational model yields results under LTE conditions that are generally consistent with other published data. Due to the complexity of C4F7N molecules, the effects of non-equilibrium phenomena are more pronounced in C4F7N compared to SF6. (2) The thermodynamic properties of non-equilibrium plasmas differ significantly from those under the LTE assumption, using the rcp parameter under non-equilibrium conditions provides a more accurate assessment of the arc-extinguishing performance of gases. (3) Non-equilibrium conditions simultaneously alter the plasma's particle composition and collision intensity, resulting in complex nonlinear variations in transport properties as the degree of non-equilibrium changes. (4) Both increased pressure and higher degrees of non-equilibrium suppress chemical reactions; however, the difference lies in their impact on particle number density and particle energy.
Keywords：Switching arc, non-equilibrium plasma, SF6, C4F7N, thermodynamic properties, transport coefficients
中图分类号：TM561
DOI: 10.19595/j.cnki.1000-6753.tces.241486
国家电网有限公司科技项目资助（5500-202320105A- 1-1-ZN）。
收稿日期 2024-08-23
改稿日期 2024-10-10
汪冠宇 男，2000年生，博士研究生，研究方向为SF6环保替代气体开关电弧。
E-mail: wangguanyu@stu.xjtu.edu.cn
张博雅 男，1990年生，教授，博士生导师，研究方向为高电压与大电流、气体放电与等离子体。
E-mail: zhangby@xjtu.edu.cn（通信作者）
（编辑 李 冰）