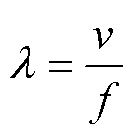 (1)
(1)
摘要 瞬时性电弧击穿是电力电缆永久性故障的重要前兆,依靠电弧信号在线监测此类故障的难度较大,考虑到瞬时性电弧会在电缆绝缘中产生击穿炭化通道,可利用行波反射法对该通道缺陷进行诊断。该文首先建立电力电缆的频域等效电路模型,基于频域反射法(FDR),利用Z变换向电缆特征频谱中调制双曲正割脉冲信号,对FDR进行优化改进,在保证高定位精度及灵敏度的同时,实现缺陷类型的判别;其次在仿真电力电缆上设置不同类型及数量的缺陷,以验证所提算法的有效性;最后设计并搭建瞬时性电弧击穿试验平台,制备瞬时性电弧击穿通道,利用改进算法对缺陷电缆的首端反射系数谱进行处理。诊断结果表明,击穿通道的位置相对误差小于0.5%,其类型为感性缺陷。
关键词:电力电缆 瞬时性电弧击穿 缺陷诊断 反射系数 Z变换
电力电缆作为电力系统中传输电能的一次设备,保障其安全可靠运行至关重要。然而,电缆在长期运行中受电、热、机械、化学及环境等因素的影响,绝缘状态会逐渐下降,出现缺陷,随着缺陷劣化加剧最终形成电缆永久性故障[1-4]。研究表明,电缆线路在产生永久性故障前,会捕捉到电压、电流间歇性扰动,随即又恢复正常,这些异常信号扰动的本质是瞬时性电弧[5-6]。在电应力作用下,此类电弧会在电缆绝缘本体累积炭化物质,形成未贯穿线芯及金属屏蔽的击穿通道[7-8]。瞬时性电弧击穿又被称为潜伏性故障[9-10],作为永久性故障的重要前兆,其对电缆健康状态的预警具有重要意义。
目前识别潜伏性故障的主要策略为监测瞬时性电弧信号,然而该信号具有很强的随机性及瞬时性,无法被传统继电保护设备有效识别,且对在线行波采集装置的灵敏度及时间校准能力有较高要求,难以被有效捕捉。因此,可考虑在离线检测中,针对瞬时性电弧[10-11]引发后留存的击穿通道进行缺陷诊断。
以时域反射法(Time Domain Reflectometry, TDR)为代表的行波反射法在电缆离线定位中的研究及应用较为成熟[12-15]。TDR通过行波在电缆异常处的反射信息进行故障定位,但其受信号高频分量较少的影响,仅对开路、短路等硬故障有较好的定位效果。考虑到电缆在瞬时性电弧击穿后依然具有一定的绝缘强度,TDR可能并不适用。
近年来出现的频域反射法(Frequency Domain Reflectometry, FDR)弥补了TDR对高阻故障等软故障定位能力不佳的缺点,其利用时频域转换算法对宽频阻抗谱(Broadband Impedance Spectrum, BIS)、反射系数谱(Reflection Coefficient Spectrum, RCS)等电缆反射频谱信息进行处理,实现缺陷定位[16-18]。在时频域处理算法中,目前较为主流的算法有线性谐振分析法(Line Resonance Analysis, LIRA)、快速傅里叶变换法(Fast Fourier Transform, FFT)及积分变换法(Integral Transform, IT)等。但这些算法也存在诸多限制,其中LIRA的诊断曲线中易出现误判信息,且算法尚未公开[19];FFT类算法的定位灵敏度及精度相较LIRA得到了有效提升,但受频谱泄漏及栅栏效应的影响,无法从诊断曲线中判断缺陷或故障的所属类型,其依然易产生干扰误判峰[20-21]。IT算法基于拉普拉斯变换,大幅降低了干扰峰的影响,但该算法的识别灵敏度有所降低,且需提前获取健康电缆的传输系数,否则没有闭式解,在工程应用上有较大困难[22]。
针对上述问题,相关研究进一步做出了优化改进。本课题组在之前的研究中通过施加chebyshev窗[23-24],文献[25-26]也通过施加Kaiser、Blackman窗等窗函数,抑制频谱泄漏的影响,突出主瓣波形,进一步提高了FDR定位的精度及灵敏度,但依然无法判断缺陷所属类型。文献[27]通过设计反射系数对比函数,有效地判别出电缆开路、短路等故障类型,但缺乏对阻抗变化微弱的绝缘缺陷等软故障判别效果的研究。文献[28]利用虚拟入射波形的FFT变换,实现了电缆故障类型的判别,但该方法需对RCS做插值预处理,降低了计算效率。文献[29]利用线性调频Z变换对RCS进行算法处理,在有效地避免冗余频谱信息产生干扰峰的同时,也无需进行FFT中时域与频域数据不一致带来的插值处理操作,但该算法依然无法根据诊断曲线给出缺陷类型判据。
判断瞬时性电弧击穿通道的缺陷所属类型,需准确表征行波在时间域的极性变化。双曲正割脉冲(Hyperbolic Secant Pulse, HSP)作为一种单极性波,具备能量集中、衰减迅速且过渡平滑的特点,对行波的极性信息有着良好的表征特性,在信号处理、通信、光纤等领域有着广泛的应用[30-32]。本文基于前人研究基础,利用该脉冲的频域信息对Z变换算法进行优化改进,处理电缆首端反射系数谱,在保证高定位精度及灵敏度的同时,实现缺陷类型的判别。然后设计试验制备瞬时性电弧击穿通道,利用改进算法对RCS进行处理,在精准定位瞬时电弧击穿通道的同时,给出其缺陷类型判据。
电力电缆中,电磁波波长l 与其频率f的关系为
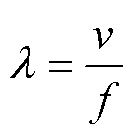 (1)
(1)
式中,v为行波波速度,约为光速的一半。
由于FDR研究的频域范围可达几十MHz甚至上百MHz[33-34],由式(1)可知,此时电缆结构尺寸不满足远小于信号波长的条件,故不可忽略波过程的影响,应利用分布参数模型对电力电缆进行建模研究,该模型下电缆的等效电路如图1所示。
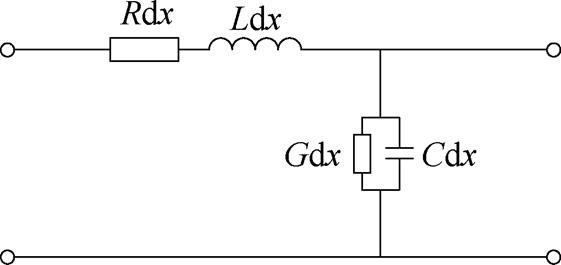
图1 分布参数模型下电缆等效电路
Fig.1 Equivalent circuit of cable distributed parameters
图1中,R、L、C、G分别为单位长度下电缆的电阻、电感、电容及电导,dx为电缆长度。电缆的分布参数为频变参数,其中R主要由电缆内外导体的电导率决定,L主要由电缆内外导体的自感与互感决定。此外,高频信号下,导体的趋肤效应与临近效应加剧,R、L及轴向阻抗Z分别近似表示为
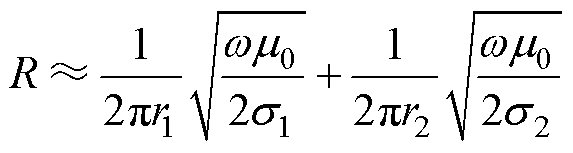 (2)
(2)
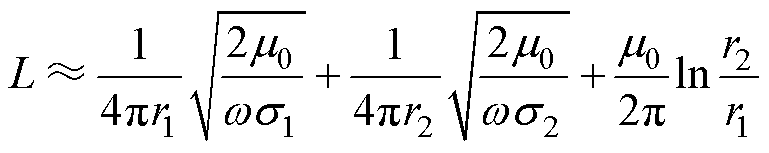 (3)
(3)
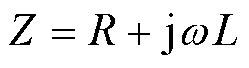 (4)
(4)
式中,r1与s1分别为线芯的外半径及电导率;r2与s2分别为金属屏蔽的半径及电导率;m0为真空磁导率;w 为角频率。
电缆的分布电容C与分布电导G由绝缘介质决定,主要受材料介电参数的影响。径向导纳Y计算式为
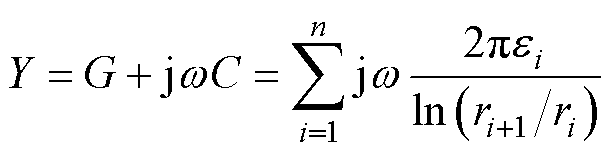 (5)
(5)
式中,ei、ri+1、ri分别为电缆绝缘第i层电介质的复介电常数、外半径及内半径。
表征电缆中的行波传输特性的波阻抗Z0及传输系数g 可分别表示为
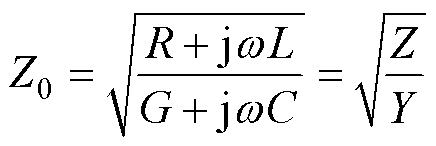 (6)
(6)
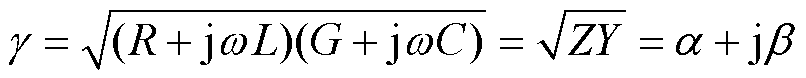 (7)
(7)
式中,a 为表征行波幅值衰减特性的衰减系数;b 为表征行波相位变化特性的相位系数。
当一根全长为l的电缆末端开路时,距电缆首端x处的输入阻抗及反射系数可分别表示为
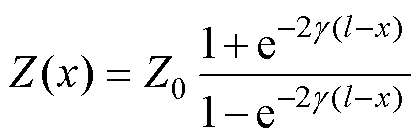 (8)
(8)
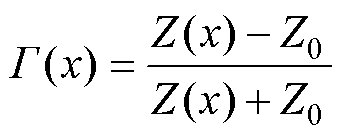 (9)
(9)
由式(7)~式(9)可知,在宽频带下,g 为随频率变化的频变参数,故Z(0)与G(0)均为行波在电缆中的频域反射信息。当x=0时,Z(0)即为BIS,G(0)即为RCS。
FDR定位的空间分辨率Dl[35]为
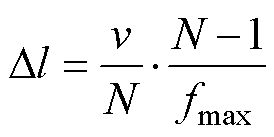 (10)
(10)
式中,N为BIS/RCS的采样点数;fmax为BIS/RCS的频域上限。
假设在距离电缆首端l1处存在一瞬时性电弧击穿通道,由于击穿通道尺寸极其微小,相当于在电缆电路中引入一个集总参数Zf;考虑到FDR的空间分辨率为Dl,则需将Zf嵌入长为Dl的电缆段lf中进行行波规律分析。此时电缆等效电路模型如图2所示,Zf所在电缆段lf产生阻抗不匹配,行波在入射lf及出射lf时均会产生折反射,引入新的反射分量Gf,表示为
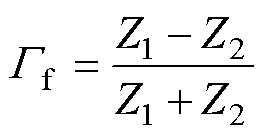 (11)
(11)
式中,Z1为行波入射处的特征阻抗;Z2为行波出射处的特征阻抗。以RCS为例,此时利用相关变量可将G(0)表示为
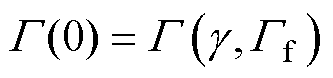 (12)
(12)
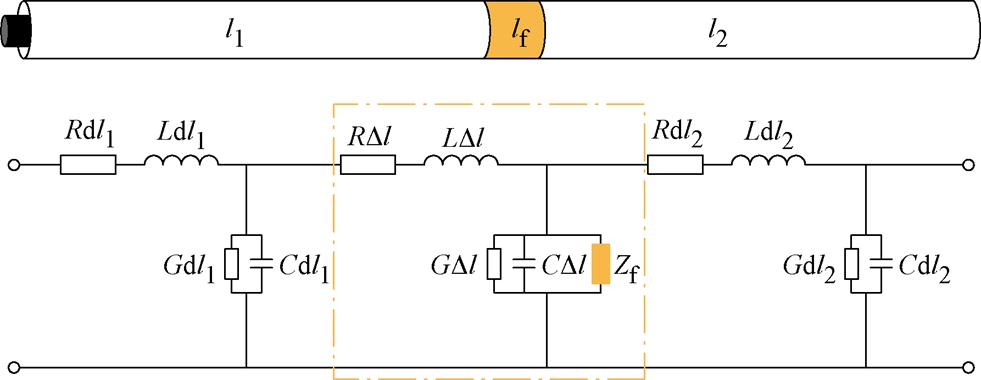
图2 含缺陷电缆的等效电路模型
Fig.2 Equivalent circuit model of a cable with defect
因此,对故障电缆的RCS/BIS进行空间域转换,将异常反射信息转换为空间域对应位置的畸变信息,可实现故障的定位。
Z变换是一种时间-复频域离散信号转换算法,其定义式为
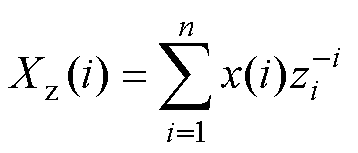 (13)
(13)
式中,i为计数变量;n为采样点数;x(i)为离散采样信号;Xz(i)为采样数据进行Z变换后的输出信号;zi为采样复变量,定义为
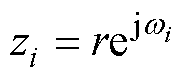 (14)
(14)
式中,r为复变量模;wi为采样幅角。
为简化Z变换处理过程,将r设为1,考虑离散信号在电缆首端入射后又反射至首端的时间间隔为ti,定义wi为
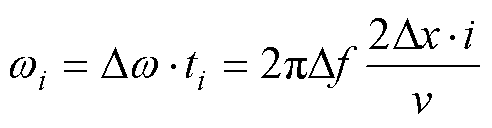 (15)
(15)
式中,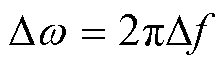 ;Df为采样频率间隔;Dx为定位曲线的空间域间隔,其取值需大于空间分辨率Dl。
;Df为采样频率间隔;Dx为定位曲线的空间域间隔,其取值需大于空间分辨率Dl。
相较BIS,RCS可直接反映波反射的特征信息,故选取G(0)作为x(i)进行Z变换处理。由于G(0)已经是频域数据,需对其进行共轭处理,结合式(13)~式(15),定位算法表达式为
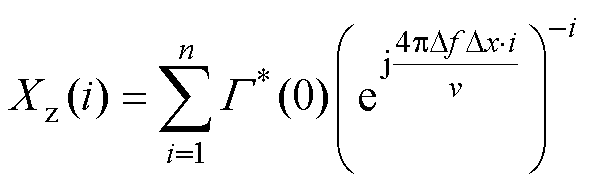 (16)
(16)
由于受测试仪器的带宽限制,G(0)无法覆盖全频带,致使频域反射信息在进行频域-空间域转换时受频谱泄漏及栅栏效应的影响,在空间域反射波形的主峰两侧出现大量的旁瓣。
由式(6)、式(11)可知,不同类型的故障或缺陷会造成电缆异常处特征阻抗增大或减小,进而在反射系数的空间域波形中表现出不同的极性信息。然而旁瓣的存在会湮没主瓣的波形信息,大大影响反射系数极性的重现,阻碍故障类型的正确判别,无法给出瞬时性电弧击穿通道的故障判据。
为解决上述问题,考虑向现有的电缆首端反射信息中引入调制双曲正割脉冲信号S(t),其时域表达式为
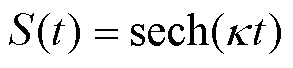 (17)
(17)
式中,sech( · )为双曲正割函数;k 为脉宽控制因子,k 越大,时域脉宽越窄,S(t)对应的频域脉宽越大。
S(t)的频域表达式为
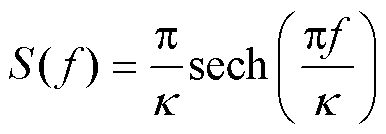 (18)
(18)
调制脉冲后的故障诊断算法表达式为
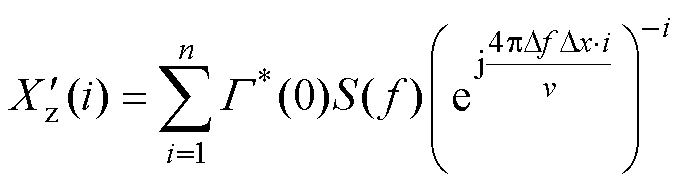 (19)
(19)
以100 MHz左右带宽的调制脉冲为例,其时域及频域波形如图3所示。由该信号的时频域表达式及图3可知,该脉冲无论是在时域还是在频域皆为双曲正割型函数,有着良好的自稳定性。且时域波形为能量集中的单极性峰,频域波形中心频率集中在低频段,可在起到窗函数滤除旁瓣信息作用的同时,有效地还原反射系数的极性信息。
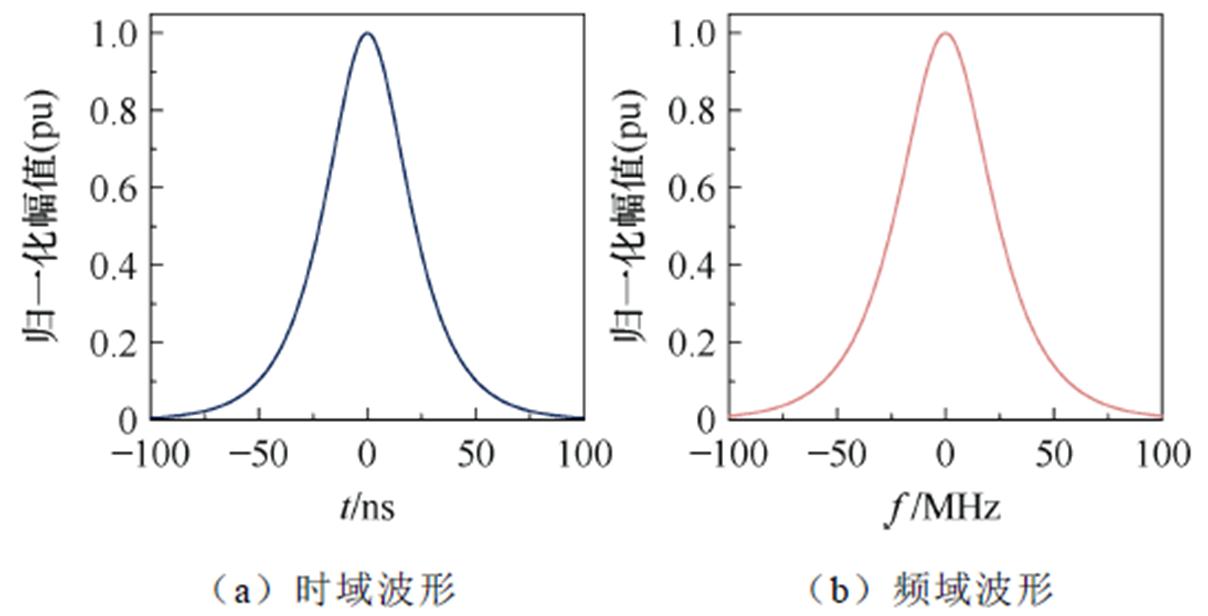
图3 双曲正割脉冲的时域及频域波形
Fig.3 Time-domain and frequency-domain waveform of hyperbolic secant pulse
为使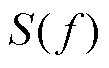 与G(0)的频域范围尽可能重叠,对k 进行约束,需满足
与G(0)的频域范围尽可能重叠,对k 进行约束,需满足
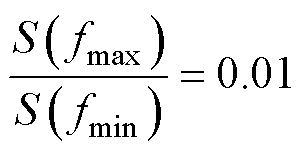 (20)
(20)
式中,fmax与fmin分别为G(0)的频带上限与下限。
为更加直观地显示改进算法效果,仿真计算Z变换算法改进前后不同长度的10 kV电力电缆反射波形的空间域变化。设置反射波形频带为9 kHz~ 18 MHz,绘制Z变换算法改进前后的反射波形如图4所示。
由图4a可知,受时频域转换中的栅栏效应及频谱泄漏影响,Z变换直接处理后的反射波形呈现极性振荡,无法还原反射系数的极性信息,造成电缆故障或缺陷类型的误判;由图4b改进Z变换算法处理得到的反射波形所示,随着传播距离的变化,反射波形均为单极性波,反射系数极性还原度明显提高,为后续电缆瞬时击穿缺陷类型的判别提供了有效的算法支持。
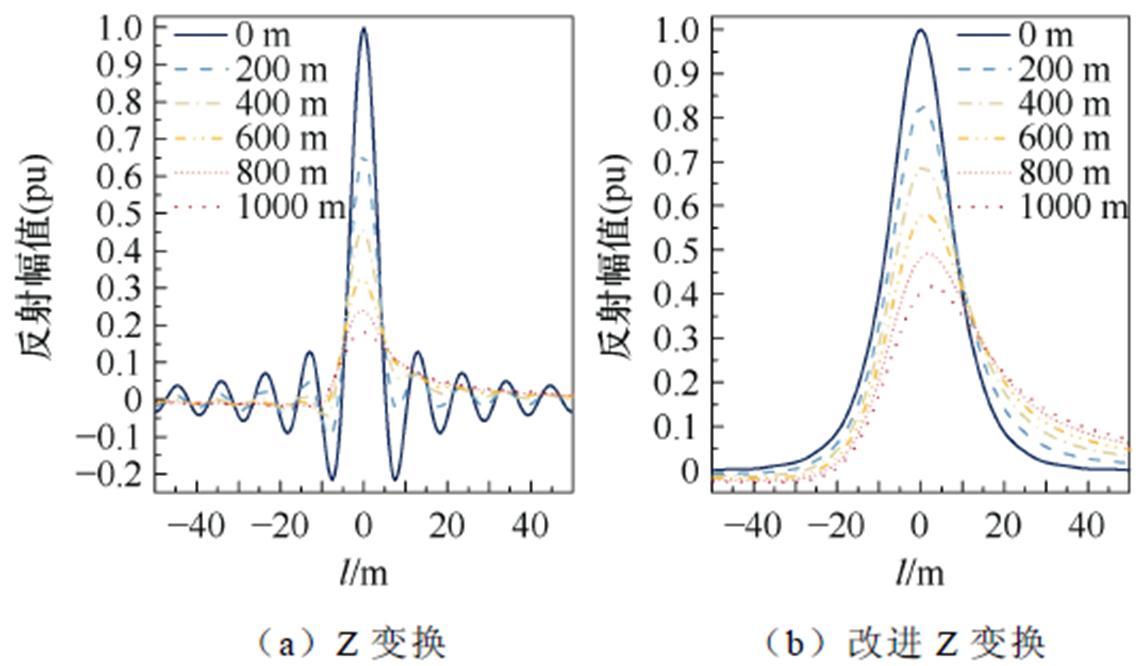
图4 Z变换算法改进前后的反射波形
Fig.4 Reflection waveform before and after the improvement of the Z-transform algorithm
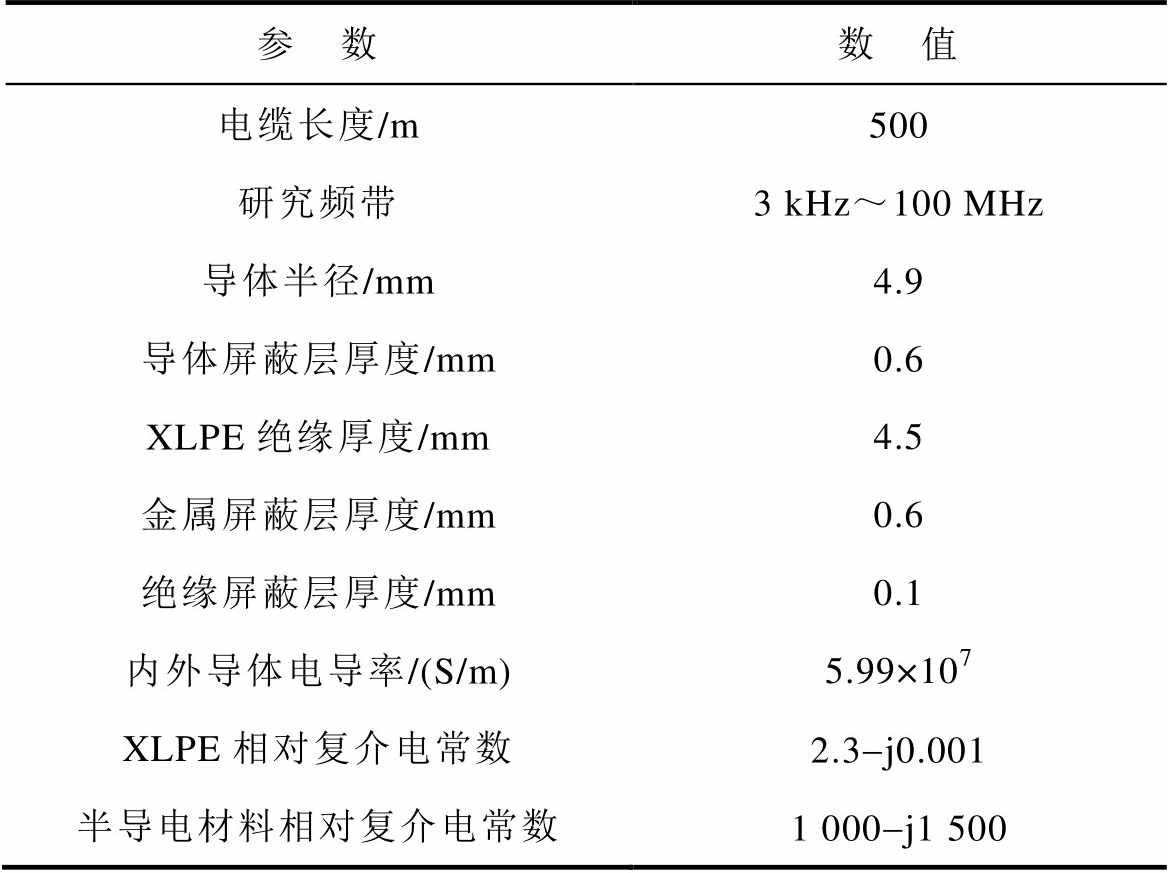
为验证提出的改进Z变换算法可应用于电缆瞬时性电弧通道的精准定位,并给出其缺陷所属类型的有效判据,本节以10 kV电力电缆为仿真对象,模拟设置不同类型缺陷并进行诊断研究。仿真电缆参数及缺陷设置分别见表1和表2。
表1 仿真电缆参数设置
Tab.1 Parameter settings for cable simulation
参 数数 值 电缆长度/m500 研究频带3 kHz~100 MHz 导体半径/mm4.9 导体屏蔽层厚度/mm0.6 XLPE绝缘厚度/mm4.5 金属屏蔽层厚度/mm0.6 绝缘屏蔽层厚度/mm0.1 内外导体电导率/(S/m)5.99×107 XLPE相对复介电常数2.3-j0.001 半导电材料相对复介电常数1 000-j1 500
表2 仿真电缆缺陷设置
Tab.2 Defect settings for cable simulation
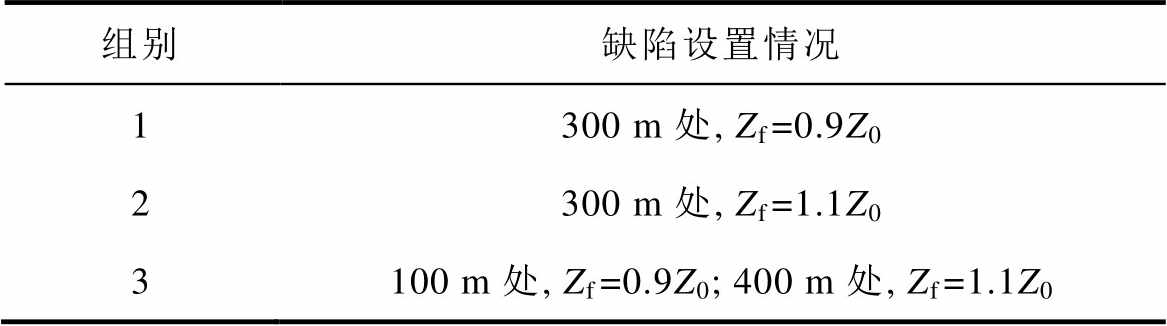
组别缺陷设置情况 1300 m处, Zf=0.9Z0 2300 m处, Zf=1.1Z0 3100 m处, Zf=0.9Z0; 400 m处, Zf=1.1Z0
由表2可知,第1组缺陷设置中300 m处特征阻抗减小,对应一个容性缺陷;第2组缺陷设置中300 m处特征阻抗增大,对应一个感性缺陷;第3组缺陷设置中设置了两处特征阻抗变换类型不同的缺陷。三组电缆的仿真诊断结果如图5所示。观察分析可知,受旁瓣信息影响,传统FDR诊断曲线虽确定了缺陷位置,但曲线底噪严重,且对于不同类型的缺陷,其识别结果均为一正极性峰,无法判别缺陷类型。
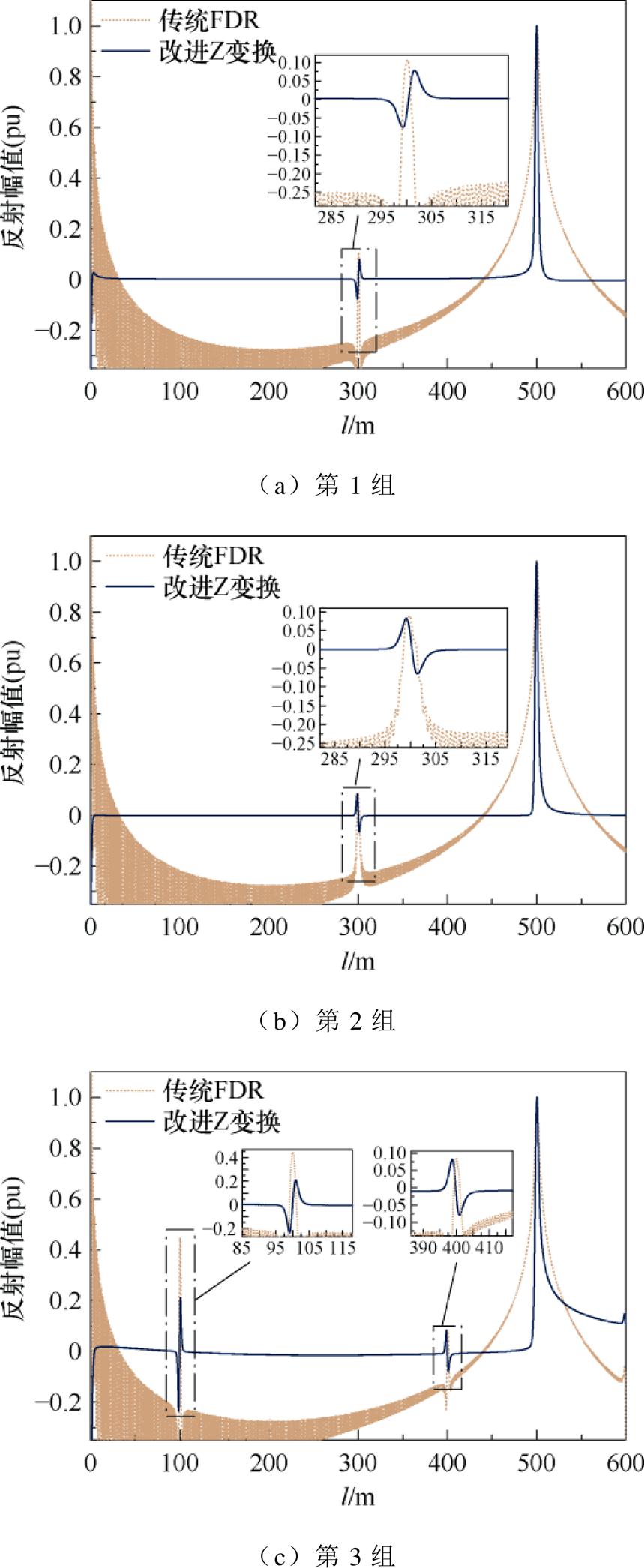
图5 仿真电缆的缺陷诊断曲线
Fig.5 Simulated cable’s defect diagnostic curves
对比之下,改进Z变换定位曲线滤除了旁瓣等杂波对主瓣信息的干扰,抑制了波形展宽,定位分辨率大幅提升;并且反映了反射系数的极性信息,其中容性缺陷的波形极性为先负后正,感性缺陷的波形极性为先正后负。对于第3组中的多缺陷场景,改进Z变换定位曲线同样能在精确定位的同时给出其类型判据。这为在工程应用中筛选、识别瞬时性电弧击穿通道这一绝缘缺陷提供了方法基础。
为提取反射系数在空间域的变化规律,给出瞬时性电弧击穿通道的识别判据,选用一根10 m长的YJV-15/8.7 3×70全新电力电缆作为试验对象,并搭建试验平台,在此电缆上制备潜伏性故障。
在制备瞬时性电弧击穿通道前,利用矢量网络分析仪(Vector Network Analyzer, VNA)对电缆进行RCS的采集,以作为参照数据留存。VNA型号为Keysight E5071C(仪器带宽为300 kHz~20 GHz),采集RCS时的平台设置如图6所示。VNA利用一根同轴射频线与电缆的A相线芯及金属屏蔽相连接,扫频范围设为300 kHz~270 MHz;使用计算机对扫频所得数据进行后续缺陷识别算法处理。
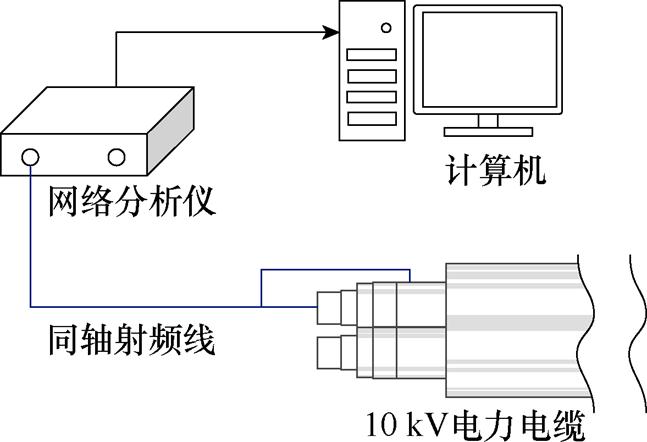
图6 电缆的RCS采集平台
Fig.6 RCS testing platform of cable
为加快瞬时击穿的试验进程,需在电缆本体上制造一处微弱的绝缘薄弱点,其示意图如图7所示。首先,在距离电缆首端4.1 m处剥除约10 cm长的外护套与填充层,使各相金属屏蔽裸露。其次,在A相金属屏蔽绕包带的间隙处,利用直径为0.6 mm的钻头,在绝缘屏蔽上径向打入约4 mm深的缺陷,随后恢复金属屏蔽的绕包,并将薄弱段埋设入湿润土壤中,以模拟敷设环境。最后对电缆进行RCS的采集,分析发现,由于此处制备的缺陷薄弱点极其微弱,无论是RCS扫频曲线还是改进Z变换处理后的缺陷识别曲线,相较健康电缆数据均未识别出异常,故可排除绝缘薄弱点对后续击穿通道定位及识别效果的影响。
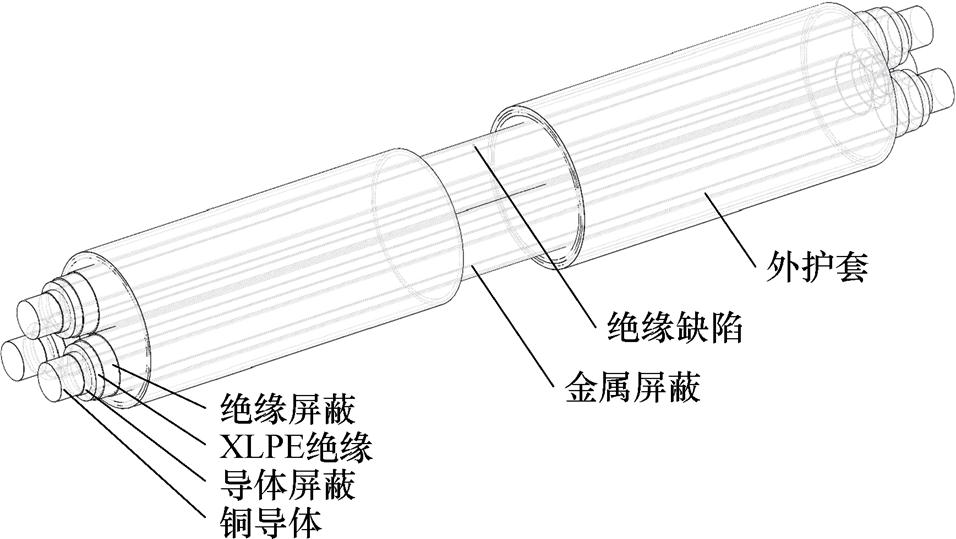
图7 绝缘薄弱点示意图
Fig.7 Schematic of insulation weak points
考虑现实线路中瞬时性电弧需在线路投运时引发,故利用试验变压器对电缆持续加压。瞬时性电弧击穿通道制备平台如图8所示。试验电路的接线从变压器引出,经过限流电阻与保护电阻后,接至电缆A相首端线芯处,B相及C相首端作开路处理,并与A相首端保持0.5 m左右的安全距离。随后在A相金属屏蔽上引出接地线并接地。线芯电压信号通过分压器与电压探头采集,接地电流则通过电流探头采集,计算机通过采集卡对两信号进行实时采集,以证明制备所得击穿通道是由瞬时性电弧引 起的。
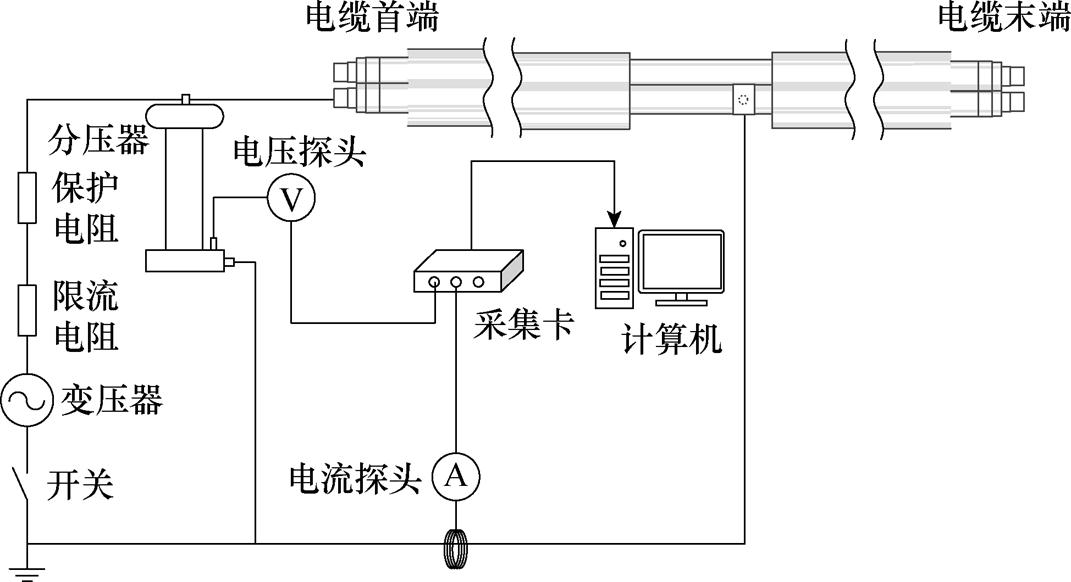
图8 瞬时性电弧击穿通道制备平台
Fig.8 The preparation platform of transient arc breakdown channel
在持续施加额定电压约50 min后,伴随着电弧放电的声音,采集卡捕捉到了瞬时性电弧信号,该信号持续约1/4周期,电压电流波形如图9所示。观察发现,电压信号在某一正半周期峰值附近骤降,然后立即上升,电流信号则突然升高形成脉冲;随后电压在负半周期峰值处再次出现下降的趋势,整个过程持续时间为ms级,且击穿后信号恢复正常,对外表现为绝缘恢复,这与瞬时性电弧信号特征一致[9-11]。另外,试验过程中也关注了电缆击穿前后的局部放电及绝缘电阻水平变化。在瞬时击穿前的稳压过程中,采集卡捕捉到了局部放电信号,但次数极少,放电强度较低,在A相瞬时性击穿后,其局部放电频率及强度均有显著提升。利用绝缘电阻测试仪(Megger MIT515,测试电压为5 kV)对电缆进行绝缘水平测试发现,瞬时性击穿后,A相绝缘电阻由击穿前的69 GW 降至42 GW,绝缘水平下降,但仍符合运行要求。
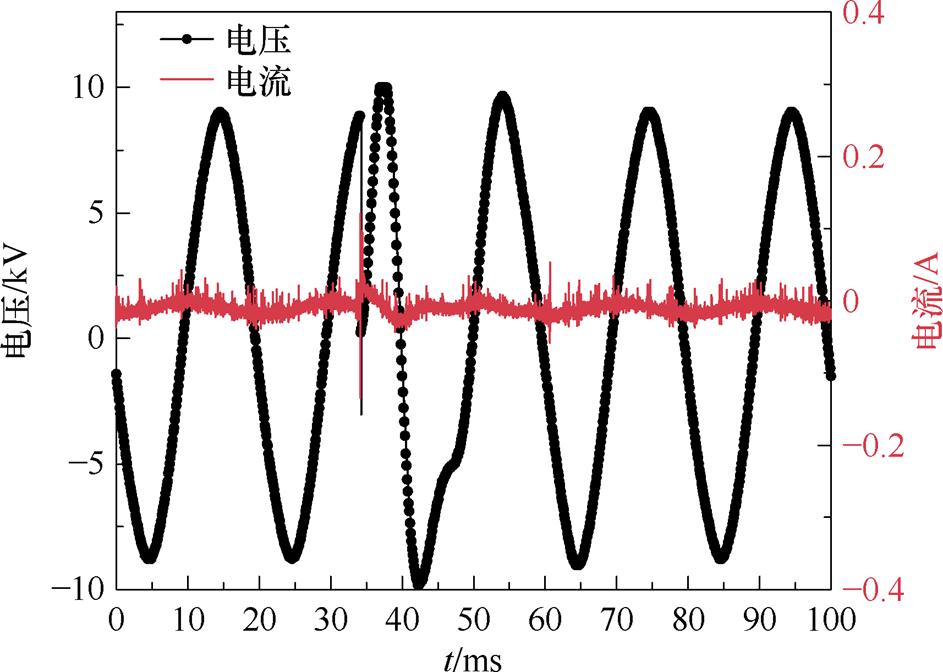
图9 瞬时性电弧的电压电流波形
Fig.9 Voltage and current waveforms of transient arcs
关闭电源,再次采集电缆的RCS,随后剥除4.1 m处A相金属屏蔽,得到绝缘状况如图10a所示。观察发现,此处形成一处炭化通道,通道直径约为1.5 mm,绝缘屏蔽上有明显的灼烧痕迹,其表面及金属屏蔽上附着大量的炭黑。沿炭化通道径向进行解剖如图10b所示,可知此通道尚未贯穿线芯和导体屏蔽,且在电子显微镜下观察发现,通道内壁也存在明显的灼烧痕迹,且附着炭化颗粒。从电弧信号的波形及通道状态来看,本试验制备出了瞬时性电弧击穿通道。

图10 瞬时性电弧击穿引发的炭化通道
Fig.10 Carbonized channel induced by transient arc breakdown
瞬时性电弧击穿前后的电缆首端反射系数谱对比如图11所示。观察发现,RCS的幅值谱及相位谱均呈现较强的周期性,且在相位谱过零点附近,幅值谱变化迅速。瞬时性电弧击穿后,RCS的幅值及相位均产生极其微弱的偏移,但无法根据这些频谱信息实现击穿通道的定位,更无法判别其类型。
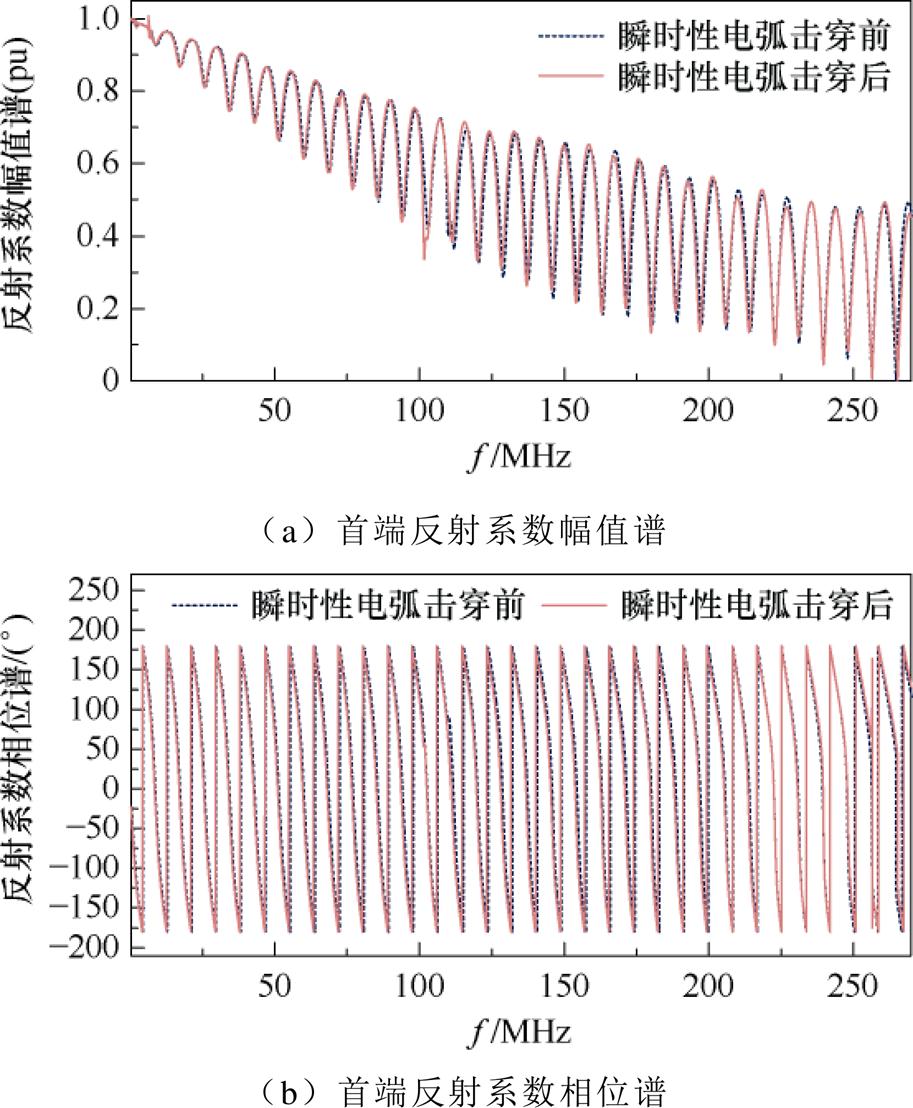
图11 瞬时性电弧击穿前后电缆RCS对比
Fig.11 Comparison of cable’s RCS before and after transient arc breakdown
对图11中的RCS进行改进Z变换算法处理,诊断曲线如图12所示。观察发现,瞬时性电弧击穿后,在距离电缆首端4.15 m处出现一畸变反射波,定位相对误差小于0.5%,反射波形极性先正后负,对应缺陷类型为特征阻抗增大的感性缺陷。从电缆等效电路角度分析,由于击穿通道的形成,XLPE绝缘介质缺失,导致电缆线芯与屏蔽间的容性效应减弱,进而使得击穿通道所在电缆段特征阻抗减小,故行波在入射缺陷段时极性为正,出射缺陷段时极性为负。
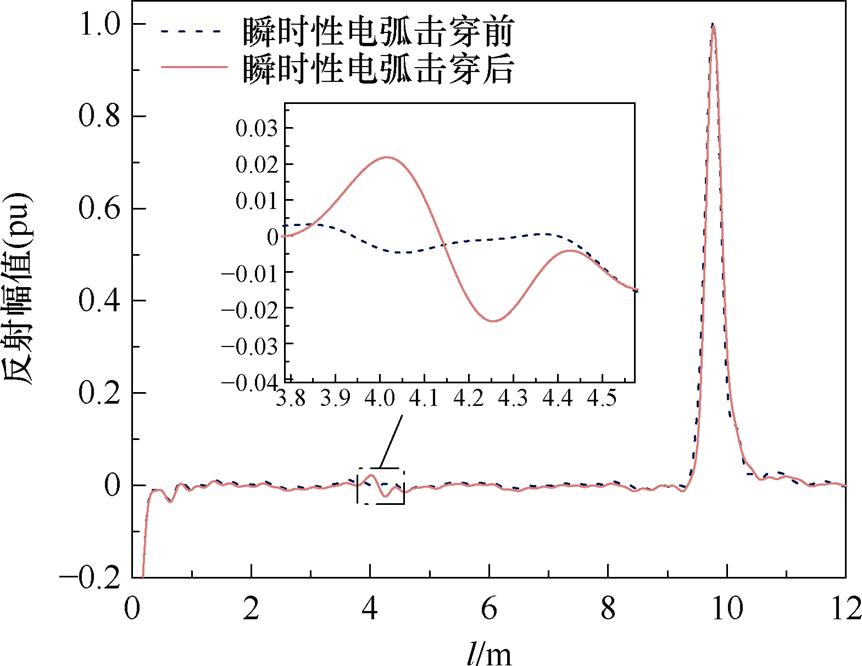
图12 瞬时击穿前后10 kV电缆的改进Z变换诊断曲线
Fig.12 Improved Z-transform diagnostic curve of a 10 kV cable before and after instantaneous breakdown
为进一步确定改进Z变换算法的有效性,并与感性缺陷诊断特征曲线进行对比,将一根同轴电缆(电缆型号SYV-50-3,长48.2 m)的10 m及34 m处挤压变形,此类损伤会导致电缆局部特征阻抗减小,属于容性缺陷。设置VNA扫频范围为3 kHz~50 MHz,诊断结果如图13所示。可发现相较于受挤压前,挤压后的电缆缺陷诊断曲线的10 m及34 m处均出现了极性先负后正的畸变波形,符合容性缺陷的时域特征反射波形。
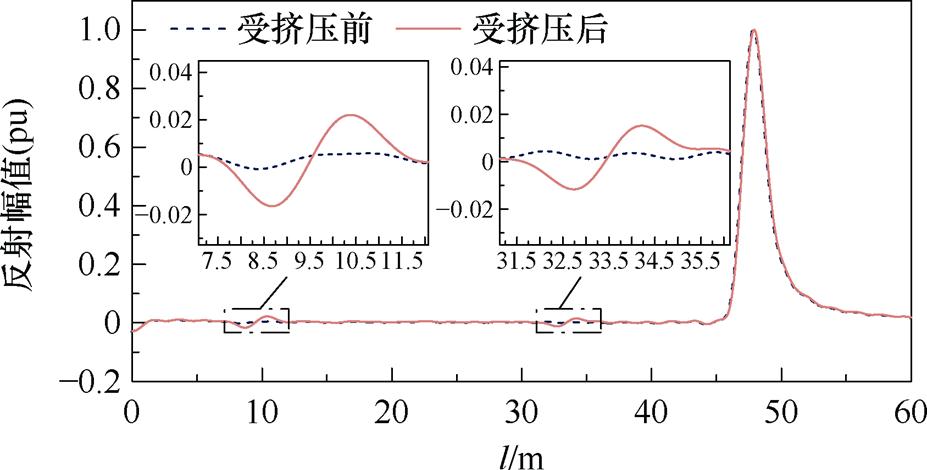
图13 容性缺陷下同轴电缆的改进Z变换诊断曲线
Fig.13 Improved Z-transform diagnostic curve of a coaxial cable under capacitive defects
同时,给出某商用TDR定位仪及传统FDR定位方法的诊断结果分别如图14和图15所示,与图12中瞬时击穿前后10 kV电缆的改进Z变换诊断结果进行对比。图14中,TDR定位仪的脉宽设置为50 ns,波速度设置为172 m/ms,由于TDR信号源高频分量较少,空间分辨率不足,无法确定缺陷位置。由图15可知,传统FDR曲线在4.47 m处出现畸变峰,缺陷定位误差约为6%,且受旁瓣干扰,定位分辨率降低,主瓣的极性信息被湮没,无法给出击穿通道的缺陷类型判据。
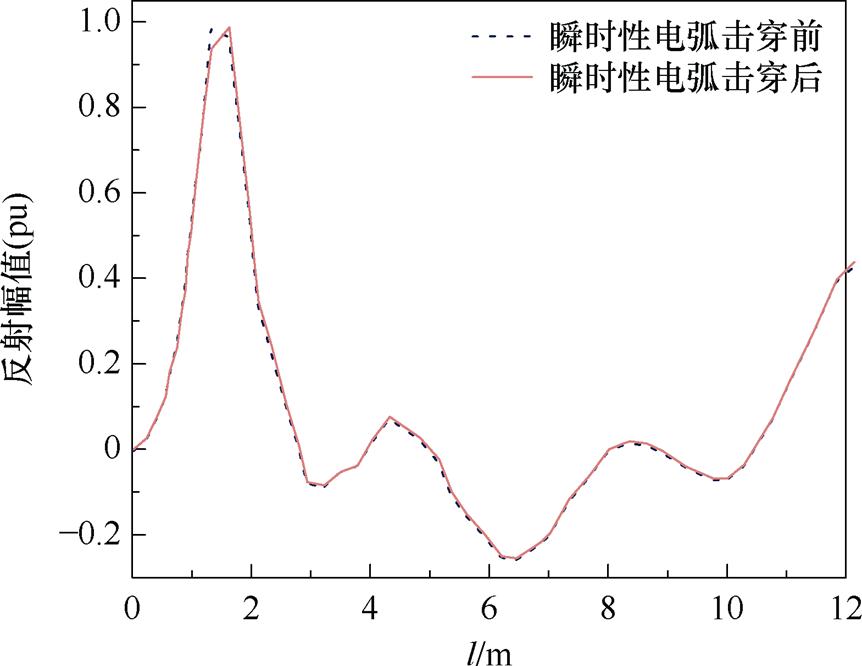
图14 TDR诊断曲线
Fig.14 Diagnostic curve of TDR
本文基于电缆首端反射系数,利用改进Z变换时频域转换算法,实现了瞬时性电弧击穿通道的缺陷诊断,具体结论如下:
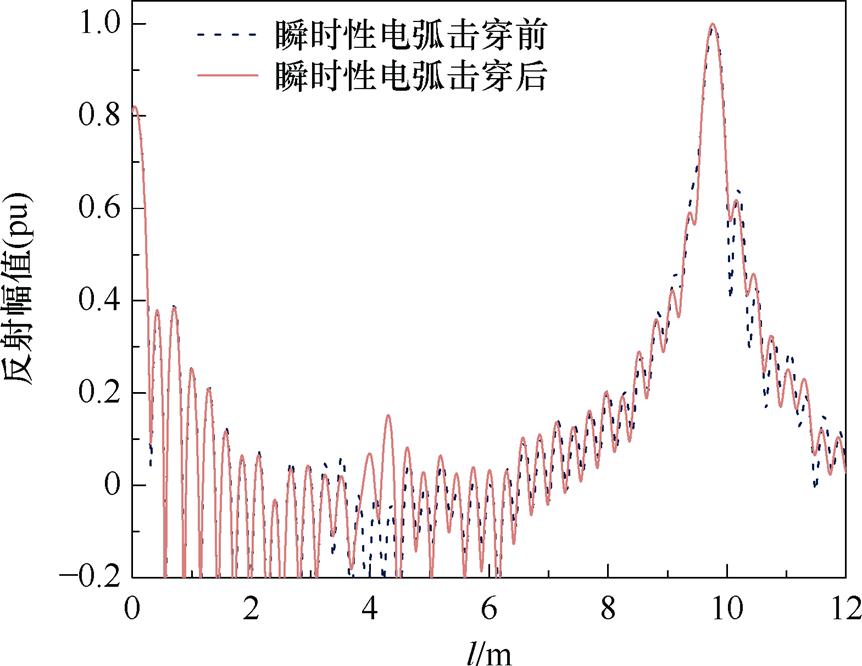
图15 传统FDR诊断曲线
Fig.15 Diagnostic curve of Traditional FDR method
1)针对电缆频谱信息的时频域转换算法,以Z变换为基础,向RCS中调制双曲正割脉冲信号,使得算法在实现精准定位缺陷的同时,可根据反射系数空间域的极性变化信息给出缺陷类型判据,并在仿真中设置不同类型的缺陷,对改进算法的有效性予以验证。
2)设计并搭建瞬时性电弧击穿试验平台,在10 kV电力电缆上制备出瞬时性电弧引发的击穿通道。随后利用改进Z变换算法、传统FDR算法对扫频数据进行处理,并将TDR定位仪所得结果作为效果参照。对比之下,本文所提出的改进Z变换算法可在保证瞬时性电弧击穿通道定位精度小于0.5%的同时,给出其缺陷类型判据,推断其属于感性缺陷。这为在后续电缆输配电线路的运维检修中,诊断该类潜伏性故障提供了有效的算法及合理的判据。
参考文献
[1] 赵书静, 詹博博, 龚梁涛, 等. 基于调频连续波相位敏感特性的电缆局部缺陷检测方法[J]. 电工技术学报, 2023, 38(11): 3009-3021.
Zhao Shujing, Zhan Bobo, Gong Liangtao, et al. Research on cable local defect detection method based on phase-sensitive characteristics of frequency modulated continuous wave[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3009-3021.
[2] 王昊月, 王晓威, 孙茂伦, 等. XLPE电缆绝缘热老化的高压频域介电谱诊断方法[J]. 电工技术学报, 2022, 37(17): 4497-4507.
Wang Haoyue, Wang Xiaowei, Sun Maolun, et al. High voltage frequency domain dielectric spectroscopy diagnosis method for thermal aging of XPLE cables[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4497-4507.
[3] 罗潘, 任志刚, 徐阳, 等. 退役高压交联聚乙烯电缆绝缘老化状态分析[J]. 电工技术学报, 2013, 28(10): 41-46.
Luo Pan, Ren Zhigang, Xu Yang, et al. Aging condition analysis of high voltage XLPE cables out of service[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 41-46.
[4] 吴春芳, 陈云, 黄韬, 等. 电力电缆状态感知与检测技术研究综述[J]. 高压电器, 2024, 60(10): 86- 103.
Wu Chunfang, Chen Yun, Huang Tao, et al. Overview of condition sensing and detection technology for power cables[J]. High Voltage Apparatus, 2024, 60(10): 86-103.
[5] 任广振, 王云鹤, 曹俊平, 等. 电力电缆初期绝缘故障检测方法综述[J]. 重庆大学学报, 2023, 46(11): 1-12.
Ren Guangzhen, Wang Yunhe, Cao Junping, et al. Review of incipient insulation fault detection methods for power cables[J]. Journal of Chongqing University, 2023, 46(11): 1-12.
[6] 李露露, 李永培, 周新月, 等. 10kV交联聚乙烯电缆内部多形态间歇性电弧故障建模[J]. 电工技术学报, 2022, 37(23): 6104-6115.
Li Lulu, Li Yongpei, Zhou Xinyue, et al. Modeling of internal multiform intermittent arc fault for 10kV XLPE cable[J]. Transactions of China Electro- technical Society, 2022, 37(23): 6104-6115.
[7] Rowland S, Wang Miao. Fault development in wet, low voltage, oil-impregnated paper insulated cables[J]. IEEE Transactions on Dielectrics and Electrical Insu- lation, 2008, 15(2): 484-491.
[8] 瞿科, 张文海, 肖先勇, 等. 基于波形衰减因子的电缆接头绝缘早期故障状态监测[J]. 高电压技术, 2022, 48(1): 318-327.
Qu Ke, Zhang Wenhai, Xiao Xianyong, et al. Condition monitoring for incipient faults of cable joint insulation based on waveform attenuation factor[J]. High Voltage Engineering, 2022, 48(1): 318-327.
[9] Izadi M, Mohsenian-Rad H. Synchronous waveform measurements to locate transient events and incipient faults in power distribution networks[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 4295-4307.
[10] Kojovic L A, Williams C W. Sub-cycle detection of incipient cable splice faults to prevent cable damage[C]//2000 Power Engineering Society Summer Meeting, Seattle, WA, USA, 2000: 1175-1180.
[11] 区伟潮, 葛阳, 朱延廷, 等. 基于双端原理的中压电缆潜伏性故障定位方法[J]. 山东大学学报 (工学版), 2022, 52(5): 84-91.
Ou Weichao, Ge Yang, Zhu Yanting, et al. Method for locating latent faults of medium voltage cables based on double-ended principle[J]. Journal of Shandong University (Engineering Science), 2022, 52(5): 84- 91.
[12] CIGRE TF D1.02.05. Practical aspects of the dete- ction and location of PD in power cables[R]. Paris: CIGRE, 2006.
[13] 叶源, 胡晓. 计及双界面的电缆绝缘水树缺陷时域反射解析模型[J]. 电工技术学报, 2024, 39(1): 55-64.
Ye Yuan, Hu Xiao. A dual interface analytical model for time-domain reflectometry of water tree defects in power cables[J]. Transactions of China Electro- technical Society, 2024, 39(1): 55-64.
[14] 操雅婷, 周凯, 孟鹏飞, 等. 基于正交匹配-伪魏格纳分布的电缆缺陷定位[J]. 电工技术学报, 2023, 38(16): 4489-4498.
Cao Yating, Zhou Kai, Meng Pengfei, et al. Cable defect location based on orthogonal matching pursuit and pseudo Wigner-ville distribution[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4489-4498.
[15] 梁栋, 徐丙垠, 谢伟, 等. 基于小波脉冲相关的电缆故障时域反射测距方法[J]. 中国电机工程学报, 2020, 40(24): 8050-8057, 8241.
Liang Dong, Xu Bingyin, Xie Wei, et al. A time- domain-reflectometry cable fault location method using wavelet pulses and cross-correlation[J]. Pro- ceedings of the CSEE, 2020, 40(24): 8050-8057, 8241.
[16] Toman G J, Fantoni P F. Cable aging assessment and condition monitoring using line resonance analysis (LIRA)[C]//16th International Conference on Nuclear Engineering, Orlando, Florida, USA, 2009: 177-186.
[17] Hirai N, Yamada T, Ohki Y. Comparison of broad- band impedance spectroscopy and time domain reflectometry for locating cable degradation[C]//2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 2012: 229-232.
[18] 唐作鑫, 周凯, 徐叶飞, 等. 考虑衰减补偿的频域反射单元平均恒虚警率电缆缺陷识别方法[J]. 电工技术学报, 2024, 39(16): 5194-5205.
Tang Zuoxin, Zhou Kai, Xu Yefei, et al. Frequency domain reflectometry cell average constant false alarm rate cable defect identification method considering attenuation compensation[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(16): 5194-5205.
[19] Fantoni P F. Condition monitoring of electrical cables using line resonance analysis (LIRA)[C]//17th Inter- national Conference on Nuclear Engineering, Brussels, Belgium, 2010: 171-178.
[20] 任广振, 曹俊平, 邹星宇, 等. 基于宽频阻抗谱的电力电缆缓冲层缺陷定位研究[J]. 高压电器, 2025, 61(2): 111-119.
Ren Guangzhen, Cao Junping, Zou Xingyu, et al. Research on power cable buffer layer defect localization based on broadband impedance spectro- scopy[J]. High Voltage Apparatus, 2025, 61(2): 111- 119.
[21] Ohki Y, Yamada T, Hirai N. Precise location of the excessive temperature points in polymer insulated cables[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(6): 2099-2106.
[22] Zhou Zhiqiang, Zhang Dandan, He Junjia, et al. Local degradation diagnosis for cable insulation based on broadband impedance spectroscopy[J]. IEEE Transac- tions on Dielectrics and Electrical Insulation, 2015, 22(4): 2097-2107.
[23] Hu Yuxiao, Chen Lu, Liu Ying, et al. Principle and verification of an improved algorithm for cable fault location based on complex reflection coefficient spectrum[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 30(1): 308-316.
[24] Jin Yan, Hu Yuxiao, Shi Chaoqun, et al. An improved algorithm of cable fault diagnosis considering signal attenuation compensation[C]//2024 IEEE 5th Inter- national Conference on Dielectrics (ICD), Toulouse, France, 2024: 1-4.
[25] 李蓉, 周凯, 万航, 等. 基于输入阻抗谱的电力电缆本体局部缺陷类型识别及定位[J]. 电工技术学报, 2021, 36(8): 1743-1751.
Li Rong, Zhou Kai, Wan Hang, et al. Identification and location of local defects in power cable body based on input impedance spectroscopy[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(8): 1743-1751.
[26] 李蓉, 周凯, 万航, 等. 基于频域反射法的10 kV配电电缆中间接头受潮定位[J]. 电网技术, 2021, 45(2): 825-832.
Li Rong, Zhou Kai, Wan Hang, et al. Moisture location of 10 kV cable joints in medium voltage distribution grid based on frequency domain reflection[J]. Power System Technology, 2021, 45(2): 825-832.
[27] 刘鹏程, 田立斌, 高磊, 等. 基于反射系数谱相关系数的电缆故障检测方法[J]. 绝缘材料, 2023, 56(5): 95-102.
Liu Pengcheng, Tian Libin, Gao Lei, et al. Detection method of cable fault based on correlation coefficient of reflection coefficient spectrum[J]. Insulating Materials, 2023, 56(5): 95-102.
[28] 饶显杰, 周凯, 谢敏, 等. 基于频域反射法的特征时域波形恢复技术[J]. 高电压技术, 2021, 47(4): 1420-1427.
Rao Xianjie, Zhou Kai, Xie Min, et al. Recovery technique of characteristic time domain waveform based on frequency domain reflection method[J]. High Voltage Engineering, 2021, 47(4): 1420-1427.
[29] 王尉军, 陈旻, 殷慧, 等. 基于反射系数谱Z变换的电缆缺陷定位方法[J]. 绝缘材料, 2024, 57(1): 109-115.
Wang Weijun, Chen Min, Yin Hui, et al. Cable defect location method based on Z transformation of reflection coefficient spectrum[J]. Insulating Materials, 2024, 57(1): 109-115.
[30] 贾楠, 李唐军, 孙剑, 等. 高非线性光纤正常色散区利用皮秒脉冲产生超连续谱的相干特性[J]. 物理学报, 2014, 63(8): 178-186.
Jia Nan, Li Tangjun, Sun Jian, et al. Coherence properties of supercontinuum generated by a picosecond pulse in normal dispersion region of highly nonlinear fiber[J]. Acta Physica Sinica, 2014, 63(8): 178-186.
[31] Li Qian, Jian Ziyun, Lu Wei, et al. Combination and compression of multiple optical pulses in nonlinear fibers with the exponentially decreasing dispersion[J]. IEEE Journal of Quantum Electronics, 2018, 54(2): 1-10.
[32] 杨振峰, 杨振军, 张书敏. 超短双曲正割脉冲的两种脉冲宽度比较[J]. 光子学报, 2008, 37(9): 1722- 1725.
Yang Zhenfeng, Yang Zhenjun, Zhang Shumin. Comparison of two kinds of pulse width of ultrashort hyperbolic secant pulses[J]. Acta Photonica Sinica, 2008, 37(9): 1722-1725.
[33] 饶显杰, 徐忠林, 刘翔宇, 等. 基于反射系数与核函数构建的新型电缆缺陷诊断方法[J]. 电工技术学报, 2024, 39(7): 2184-2192, 2213.
Rao Xianjie, Xu Zhonglin, Liu Xiangyu, et al. A new cable defect diagnosis method based on reflection coefficient and kernel function construction[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2184-2192, 2213.
[34] 金琰, 胡钰骁, 石超群, 等. 基于反射系数的电缆故障定位及评估优化算法[J]. 高电压技术, 2025, 51(5): 2436-2446.
Jin Yan, Hu Yuxiao, Shi Chaoqun, et al. Cable fault location and assessment optimization algorithm based on reflection coefficient[J]. High Voltage Engin- eering, 2025, 51(5): 2436-2446.
[35] 陈璐, 李光茂, 杨森, 等. 频域响应法在电力电缆缺陷定位中的研究综述[J]. 南方电网技术, 2023, 17(10): 53-64.
Chen Lu, Li Guangmao, Yang Sen, et al. Review of research on frequency domain response method and its application in defect location of power cables[J]. Southern Power System Technology, 2023, 17(10): 53-64.
Abstract Transient arc breakdown is recognized as an important precursor to permanent faults in power cables. Currently, diagnostic methods for such faults primarily depend on the online monitoring of arc signals. Due to the randomness and rapid changes associated with transient arcs, along with interference from noise signals, the challenges in locating and identifying these faults of this method are significant. Given that transient arcs may create carbonized breakdown channels in cable insulation, causing reflections of traveling waves, the feasibility of employing offline wave reflection methods for diagnostics has been explored. The frequency domain reflection (FDR) method, noted for its high sensitivity to slight impedance changes, is utilized in this study to diagnose channel defects induced by transient arc breakdown and to establish identification criteria. However, traditional FDR diagnostic curves are plagued with many interfering waveforms, making it challenging to determine the type of defect. To address these issues, an improved Z-transform algorithm is proposed in this paper, and transient arc breakdown channel defects are prepared, ensuring high location accuracy and sensitivity while facilitating the discrimination of defect types.
First, an equivalent electrical circuit model of the power cable under distributed parameters is constructed, from which the reflection coefficient spectrum (RCS) at the cable’s head end is derived. The application of the Z-transform algorithm to process the RCS and the settings of various parameters are then thoroughly analyzed. Despite these measures, the diagnostic results still contain numerous sidebands and interfering waveforms, and the polarity information of the reflection coefficients cannot be discerned. Considering the wide applications of the hyperbolic secant pulse, a rapidly attenuating and smoothly transitioning unipolar wave in fields such as signal processing, communications, and fiber optics, this pulse is employed to modulate the RCS and to refine the Z-transform. Moreover, various types of defects are set up on a 500-meter-long simulated cable for diagnostic validation. The improved algorithm is shown to maintain high location accuracy and sensitivity, providing correct criteria for defect types based on the polarity information of the reflection coefficients.
Subsequently, an experimental platform for transient arc breakdown is designed and assembled using experimental transformers, voltage divider, voltage probes and current probes among other devices. The defects produced experimentally are confirmed as transient arc breakdown channels through the analysis of online waveforms and defect cross-sections. And then the improved algorithm and traditional FDR method are applied to process the reflection coefficient spectrum at the first end of the defective cable, and time-domain reflectometry (TDR) is used for comparison in diagnosing the defective cable. The diagnostic results from the improved Z-transform algorithm indicate that the position error of the breakdown channel is less than 0.5%, identifying it as an inductive defect. In contrast, TDR results are unable to ascertain the defect's location, and although the traditional FDR method achieves defect localization, it does so with a location error of approximately 6%, accompanied by numerous interfering waveforms, failing to provide criteria for defect type.
In conclusion, the improved Z-transform algorithm proposed in this paper ensures a location accuracy of less than 0.5% for transient arc breakdown channels and provides criteria for their classification, deducing them to be inductive defects. This offers a potent algorithm and valid criteria for diagnosing such incipient faults in the maintenance of cable transmission and distribution lines.
Keywords:Power cable, transient electric arc breakdown, defect diagnosis, reflection coefficient, Z- transform
中图分类号:TM247
DOI: 10.19595/j.cnki.1000-6753.tces.241599
国家电网有限公司总部科技项目资助(5500-202318538A-3-2-ZN)。
收稿日期 2024-09-10
改稿日期 2024-11-03
何光华 女,1978年生,研究员级高级工程师,研究方向为电力电缆施工、运维与检修。
E-mail: 13585086631@163.com(通信作者)
金 琰 男,2000年生,硕士研究生,研究方向为电力电缆故障诊断与状态评估。
E-mail: jy123456@stu.xjtu.edu.cn
(编辑 李 冰)