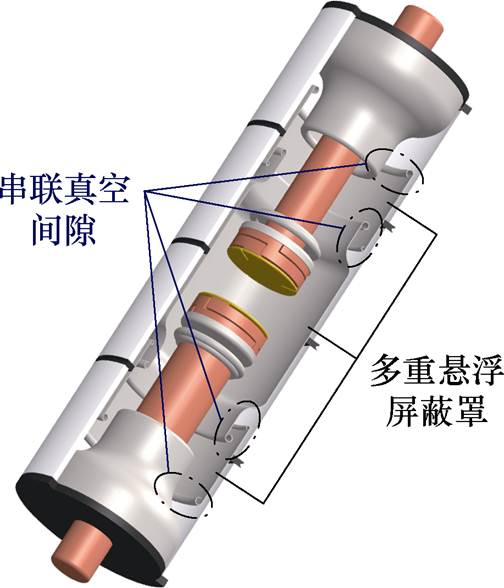
图1 典型126 kV真空灭弧室结构
Fig.1 Structure of typical 126 kV vacuum interrupter
摘要 串联真空间隙击穿电压的极性效应是影响高电压真空设备绝缘性能的重要因素。该文以球-板电极真空间隙为对象，通过试验研究了雷电冲击电压极性对于串联双间隙击穿特性的影响，结合电场仿真分析了串联双间隙极性效应的产生机理，进而提出了一种基于阴极最大电场强度的串联双间隙正、负极性击穿电压评估方法。研究结果表明，串联双球-板真空间隙的正极性击穿电压高于负极性，并且随着间隙距离的增加，正、负极性击穿电压的差值逐渐增大，极性效应越发显著。此外，正、负极性冲击电压下双间隙的阴极最大电场强度与击穿电压之间遵循近乎相同的负指数关系，阐明了阴极电场强度的差异是造成串联间隙击穿电压具有极性效应的主要原因。经试验验证，阴极最大电场强度与击穿电压间的拟合关系可用于评估不同极性雷电冲击电压下串联双真空间隙的耐压能力，评估误差在10%以内。研究结果可为高电压真空绝缘结构的设计提供理论依据。
关键词：真空击穿 串联双间隙 极性效应 雷电冲击电压 阴极电场强度
目前，SF6气体断路器以其优异的灭弧和绝缘性能在110 kV及以上的高电压等级电力系统中占据主导地位，然而SF6是一种强温室效应气体，其地球暖化系数是CO2的23 900倍[1]。基于《京都议定书》的签订以及我国“双碳”目标的提出，限制并替代SF6气体的使用、发展环保型高压开关设备已成为电气领域的研究热点[2-5]。
真空断路器具有环境友好、大容量开断能力强及免维护等优势，因此发展高电压等级真空断路器是取代SF6断路器的重要手段[6-9]。真空灭弧室是真空断路器中耐受高电压、开断大电流的核心部件，电压等级的提升对真空灭弧室的绝缘性能提出了更高的要求[10]。一方面，可在灭弧室内设置多重悬浮屏蔽罩结构，以起到均匀电场分布、阻挡金属蒸气喷溅的作用[1, 11]，典型126 kV真空灭弧室结构如 图1所示；另一方面，可通过将多个灭弧室串联构成多断口结构，以减缓长真空间隙击穿电压的饱和效应[12-13]。以上两种结构均可等效为串联真空间隙。
电力开关设备需要同时具备耐受正、负极性雷电冲击电压（Lightning Impulse Voltage, LIV）的能力[10]，而真空绝缘结构的击穿电压往往存在极性效应[14-16]。一方面，由于真空开关设备中电场分布非均匀，可能导致正、负极性电压下的场致发射强度不同，进而造成耐压能力产生差异[17-18]；另一方面，真空击穿起始于阴极表面的绝缘缺陷，而两侧电极上缺陷结构和数量的差异也可能导致击穿电压具有极性效应[19]。此外，串联真空间隙的击穿电压受其中各个间隙耐压能力的影响，并且不同极性电压下多间隙的击穿过程可能存在差异，因此增加串联间隙数量会加剧极性效应[20-23]。由此可见，串联真空间隙的击穿极性效应是影响高压真空灭弧室绝缘性能的重要因素。然而，目前尚无串联真空间隙击穿极性效应的定量研究，对于串联间隙极性效应的产生机理仍不清楚，同时也缺乏串联间隙正、负极性击穿电压的评估方法，导致高压真空灭弧室的绝缘结构设计十分困难，制约了真空断路器电压等级的提升。
图1 典型126 kV真空灭弧室结构
Fig.1 Structure of typical 126 kV vacuum interrupter
针对上述问题，本文旨在定量研究LIV极性对于串联双真空间隙耐压能力的影响规律。首先，通过试验获得正、负极性LIV作用下串联双真空间隙的击穿特性；其次，结合电场仿真分析不同极性电压下双间隙阴极电场强度对于击穿电压的影响关系；最后，在此基础上，阐明串联双真空间隙击穿极性效应的产生机理，进而提出一种串联双间隙正、负极性击穿电压的评估方法，并利用试验结果验证该方法的可行性。研究结果有助于加深对串联真空间隙击穿机理的认识，可为高压真空灭弧室的绝缘结构设计提供理论依据，促进输电等级真空开关设备的发展。
串联双真空间隙雷电冲击击穿试验电路示意图如图2所示。本文将球-板电极安装在陶瓷真空管内构成试验用真空间隙。双真空间隙垂直串联于绝缘支架上，中间采用铜导线连接（长约0.5 m），根据与接地点的相对位置分别命名为高压侧间隙和低压侧间隙。为获得串联真空间隙实际分压情况下的击穿特性[20-26]，本文未对双间隙设置屏蔽环。
试验中，将雷电冲击发生器输出的标准LIV（1.2/50 ms）施加到高压侧间隙，低压侧间隙接地。双间隙的击穿电压和击穿电流分别由分压器和Pearson线圈测得。采用升降法逐次施加LIV，即当施加峰值为U的冲击电压时，若试品未发生击穿，下一次施加电压增加DU，直至试品被击穿，再将施加电压降低DU，该过程持续约400次。为了准确地获得击穿电压，设置DU为2 kV。串联间隙是否被击穿通过测量得到的电压电流波形判断，典型击穿试验波形如图3所示。击穿试验前，各真空间隙在1.0 mm间距下分别进行LIV老炼，直至间隙击穿电压达到饱和。
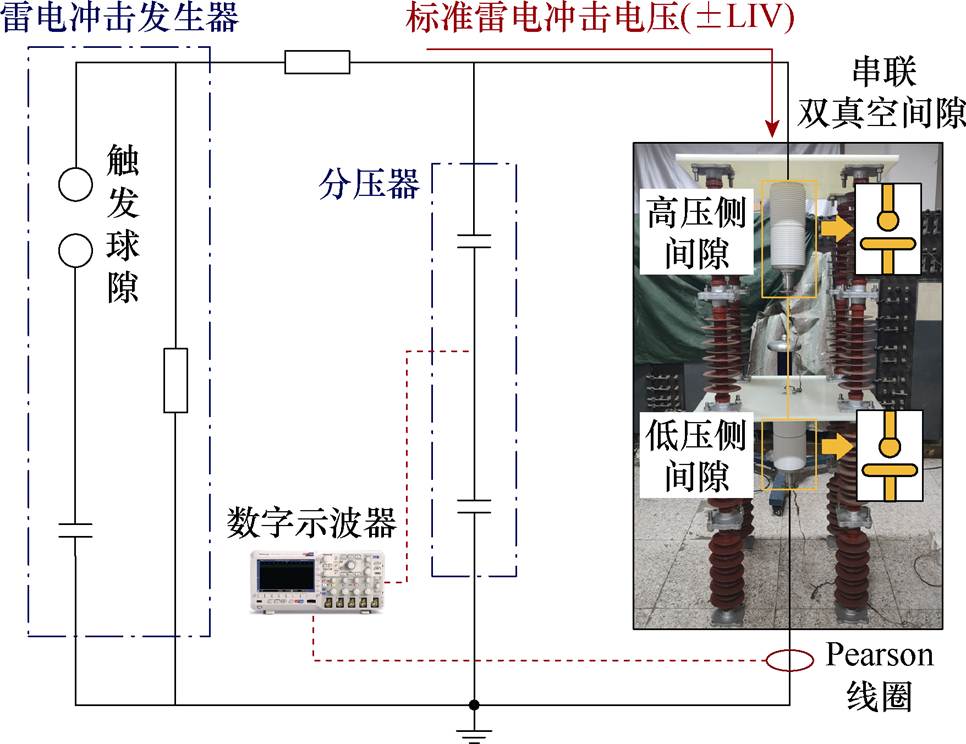
图2 试验电路示意图
Fig.2 Schematic of experimental circuit
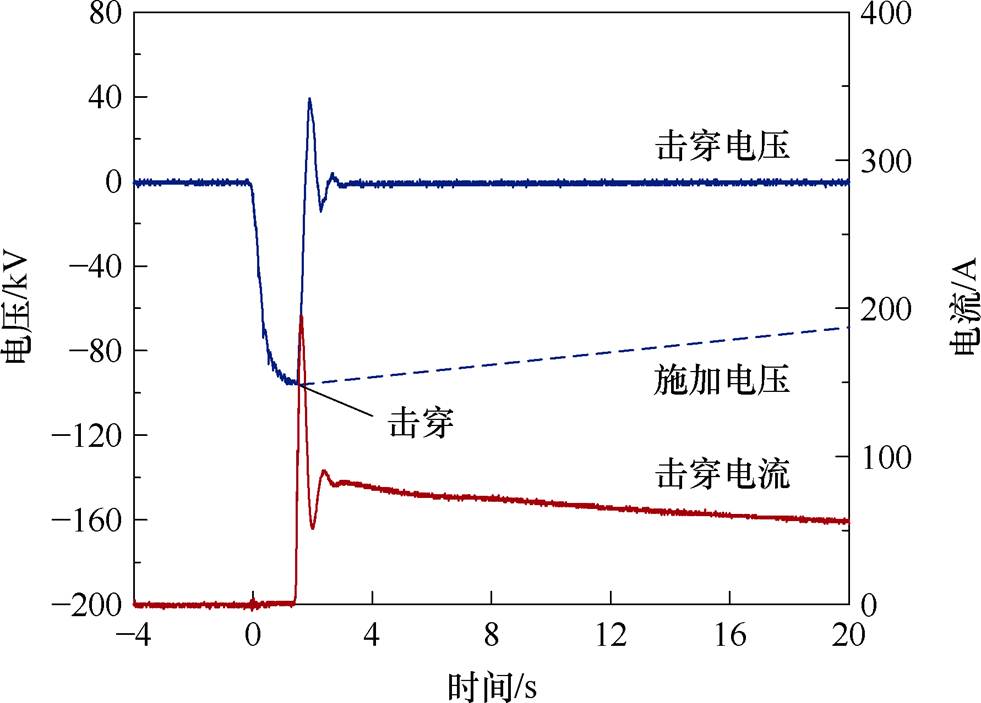
图3 典型击穿试验波形
Fig.3 Typical waveforms of breakdown test
串联双真空间隙电极结构示意图如图4所示。考虑到球-板电极系统为典型的稍不均匀电场结构（均匀度在0.5～1.0范围内），其研究结果应能较好地反映灭弧室内部间隙的击穿特性；并且，球-板电极真空间隙击穿电压的分散性较低，因此本文采用该结构来研究串联间隙的击穿极性效应[25, 27]。双间隙采用完全相同的电极结构，球电极的直径为18 mm，板电极的直径为50 mm，电极材料为无氧铜，电极表面粗糙度为1.6 mm。串联双真空间隙的间距设置见表1。表中，dh和dl分别表示高压侧间隙和低压侧间隙的距离。两间隙距离均分布在0.5～2.0 mm范围内，包含五种情况：第1、3、5组为dl固定1.0 mm不变，dh从0.5 mm增加至2.0 mm；第2、3、4组为dh固定1.0 mm不变，dl从0.5 mm增加至2.0 mm。在每种间距条件下分别开展正、负极性雷电冲击击穿试验，进而研究不同极性电压下两间隙距离对串联结构击穿特性的影响。
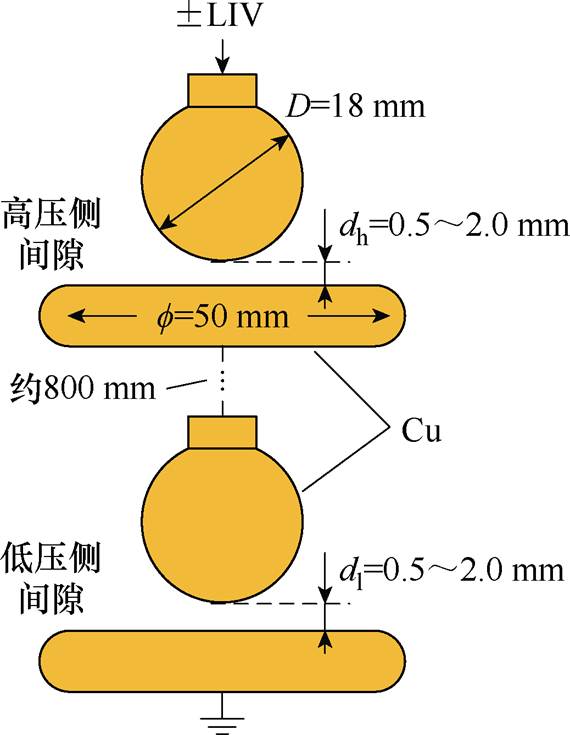
图4 串联双真空间隙电极结构示意图
Fig.4 Schematic of electrode configuration for double vacuum gaps in series
表1 串联双真空间隙距离设置
Tab.1 Distance setup of double vacuum gaps in series
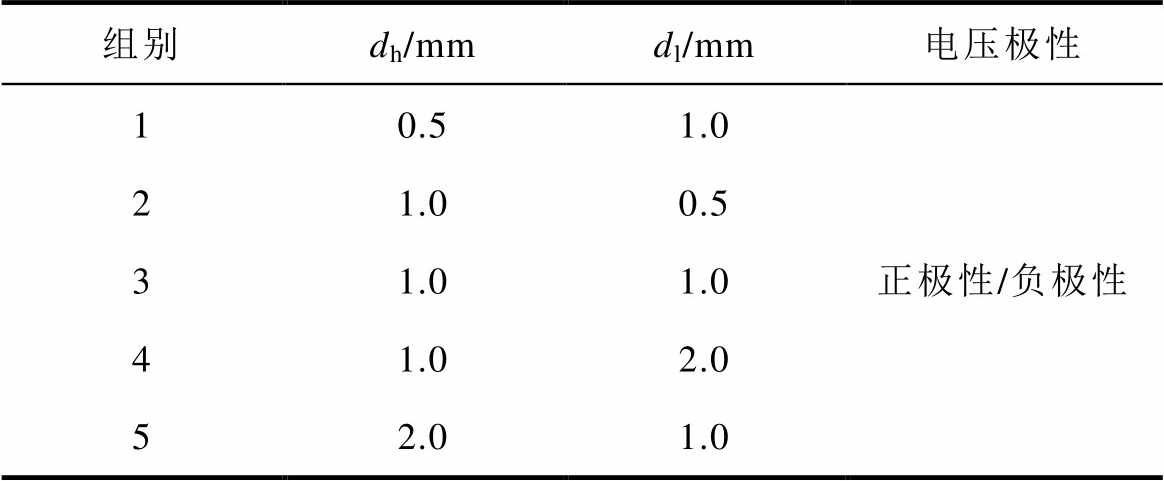
组别dh/mmdl/mm电压极性 10.51.0正极性/负极性 21.00.5 31.01.0 41.02.0 52.01.0
本节通过试验确定正极性LIV下串联双真空间隙的击穿特性，结合前期已发表的负极性雷电冲击击穿特性[25]，基于Weibull函数统计分析击穿电压的概率分布，进而获得不同极性电压下间隙距离对串联双间隙50%击穿电压U50的影响规律。试验中，其中一个间隙从0.5 mm增加至2.0 mm，另一间隙固定为1.0 mm不变。
正、负极性LIV下串联双真空间隙击穿电压的升降法测试结果如图5所示。图中，空心符号表示正极性击穿电压Ub+；实心符号表示负极性击穿电压Ub-。图5a～图5e分别为表1中五种间距条件下的测试结果。可以看出，在接近400组击穿试验中，各间距条件下串联双间隙的击穿电压均在稳定的范围内波动，说明试验前的老炼过程已使两间隙击穿电压达到饱和状态。对于总间距为1.5 mm的第1组和第2组间隙，Ub+的分布区间分别为56～92 kV和58～100 kV，均略微高于Ub−的分布区间46～88 kV和54～100 kV，相差在10 kV以内；当总间距增加至3.0 mm时（第4组和第5组），Ub+的分布区间分别增加至99～165 kV和111～174 kV，此时已经显著大于Ub−的分布区间78～147 kV和93～156 kV，差值接近20 kV。上述结果表明，对于具有球-板电极结构的串联双真空间隙，正极性击穿电压的分布区间高于负极性击穿电压，并且随着总间隙距离的增加，正、负极性击穿电压的差值逐渐增大。
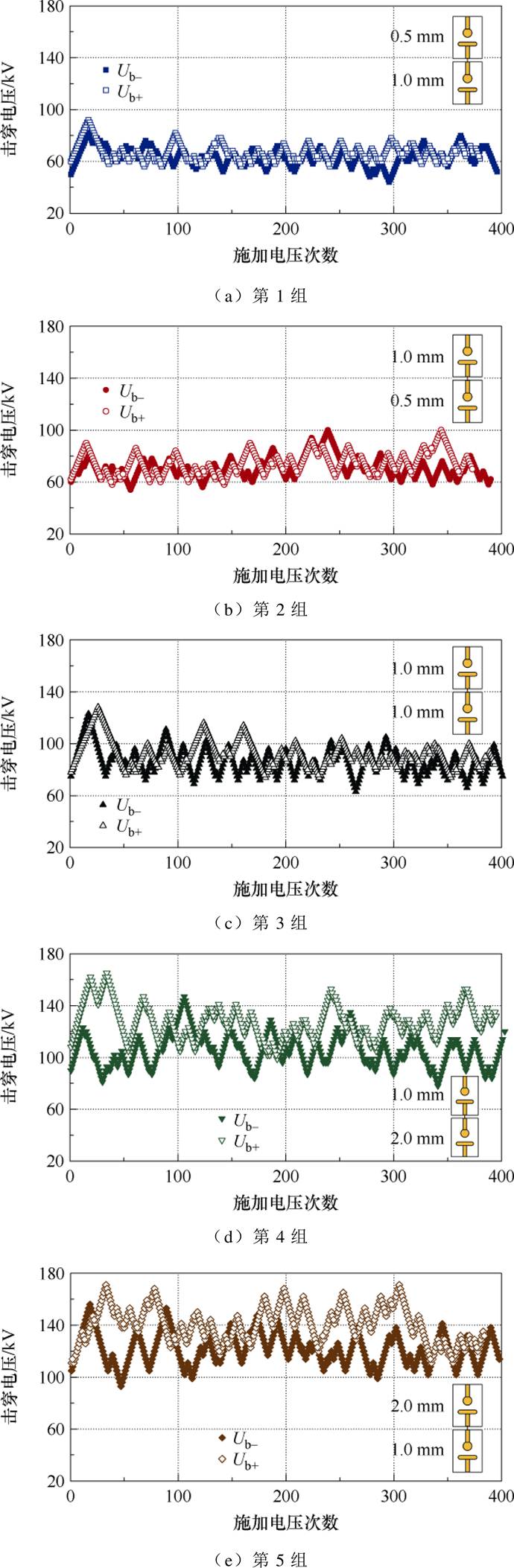
图5 击穿电压升降法测试结果
Fig.5 Experimental results of breakdown voltage by up-down method
通过统计图5中的测试结果可以确定串联双真空间隙击穿电压的累积概率分布，如图6所示。本文采用式（1）描述的三参数Weibull函数对击穿概率进行分析，拟合得到的击穿概率Weibull分布参数见表2。从表2中看出，任一间隙距离、电压极性条件下的拟合度R2均大于0.99，这说明串联双真空间隙的击穿概率能较好地服从Weibull分布。为便于与现有研究进行对比分析[10, 28]，本文采用50%击穿电压U50来表征串联双真空间隙的绝缘强度。根据所得Weibull拟合函数，可计算得到相应条件下双间隙的U50，同样见表2。
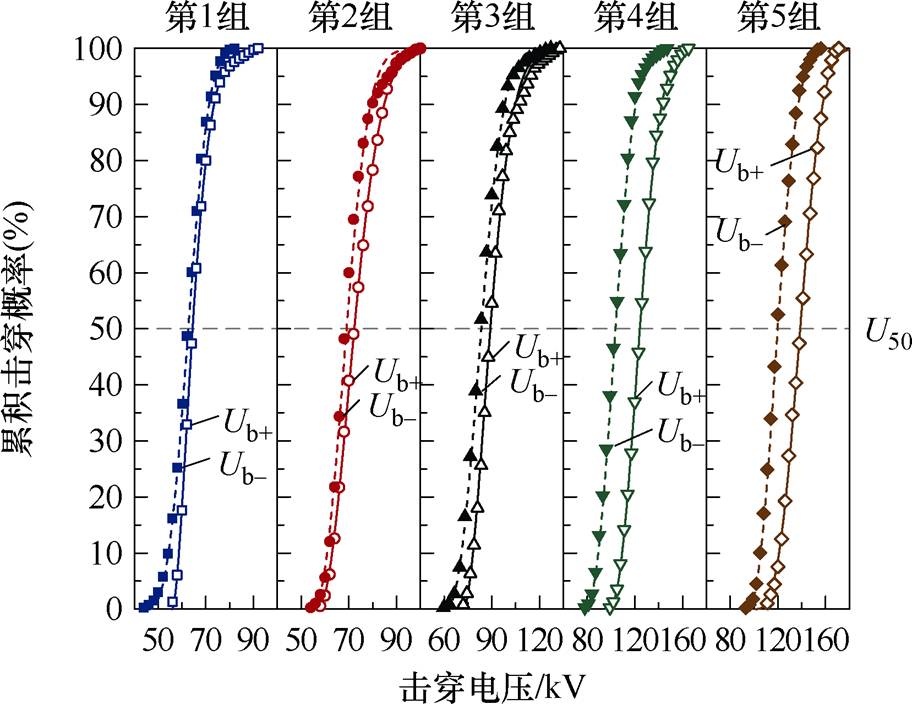
图6 击穿电压的累积概率分布
Fig.6 Cumulative probability distribution of breakdown voltage
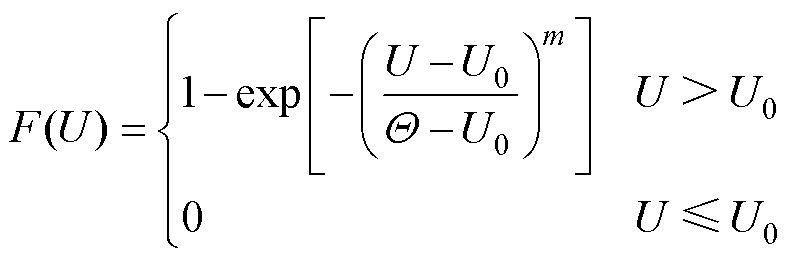（1）
表2 击穿概率Weibull分布参数
Tab.2 Parameter values of breakdown probability Weibull distribution
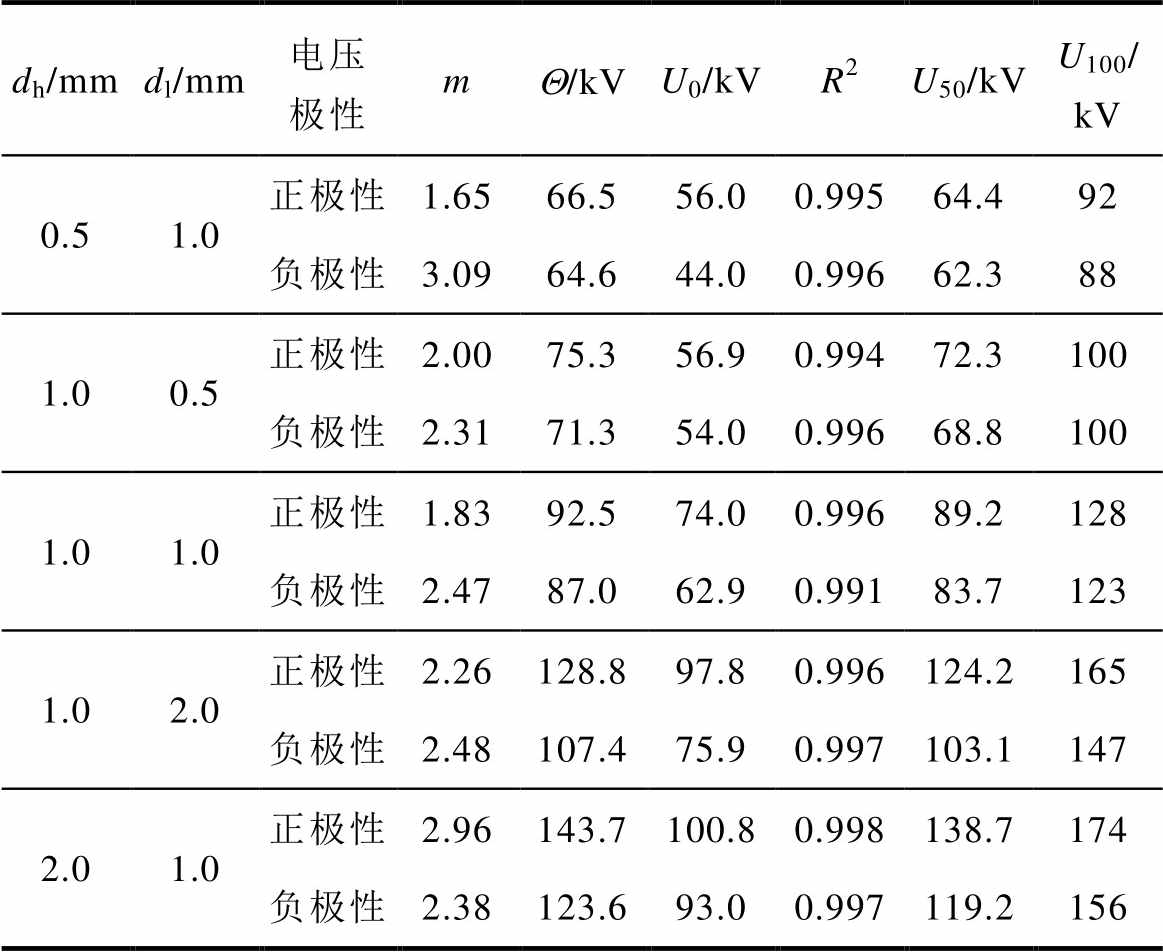
dh/mmdl/mm电压极性mQ/kVU0/kVR2U50/kVU100/kV 0.51.0正极性1.6566.556.00.99564.492 负极性3.0964.644.00.99662.388 1.00.5正极性2.0075.356.90.99472.3100 负极性2.3171.354.00.99668.8100 1.01.0正极性1.8392.574.00.99689.2128 负极性2.4787.062.90.99183.7123 1.02.0正极性2.26128.897.80.996124.2165 负极性2.48107.475.90.997103.1147 2.01.0正极性2.96143.7100.80.998138.7174 负极性2.38123.693.00.997119.2156
式中，F(U)为击穿电压的累积概率；U0为位置参数，即击穿概率为0%的临界击穿电压值；m为形状因子；Q 为尺度参数。
根据表2中的计算结果，可以确定正、负极性LIV下串联双真空间隙U50与间隙距离之间的关系，如图7所示。图7中，圆圈表示正极性LIV下的U50，方块表示负极性LIV下的U50，误差棒表示图5中击穿电压的波动范围。
图7a为dl固定为1.0 mm，dh从0.5 mm增加至2.0 mm的结果。可以看出，当总间距为1.5 mm时，正、负极性LIV下的U50分别为64.4 kV和62.3 kV，二者仅相差2.1 kV；随着总间距增加至3.0 mm，正、负极性LIV下的U50分别增加至138.7 kV和119.2 kV，增加了115.4%和91.3%，并且二者的差值达到19.5 kV。图7b为dh固定为1.0 mm，dl从0.5 mm增加至2.0 mm的结果，随着总间距从1.5 mm增加至3.0 mm，正极性LIV下的U50从72.3 kV增加至124.2 kV，增加了71.8%，而负极性LIV下的U50从68.8 kV增加至103.1 kV，增加了49.9%，二者间的差值从3.5 kV显著增加至21.1 kV。此外，通过表2可以看出，双间隙100%击穿电压U100与U50的变化趋势相近，随着总间距的增加，正、负极性LIV下U100的差值逐渐增大，总间距为3.0 mm时差值接近20 kV。
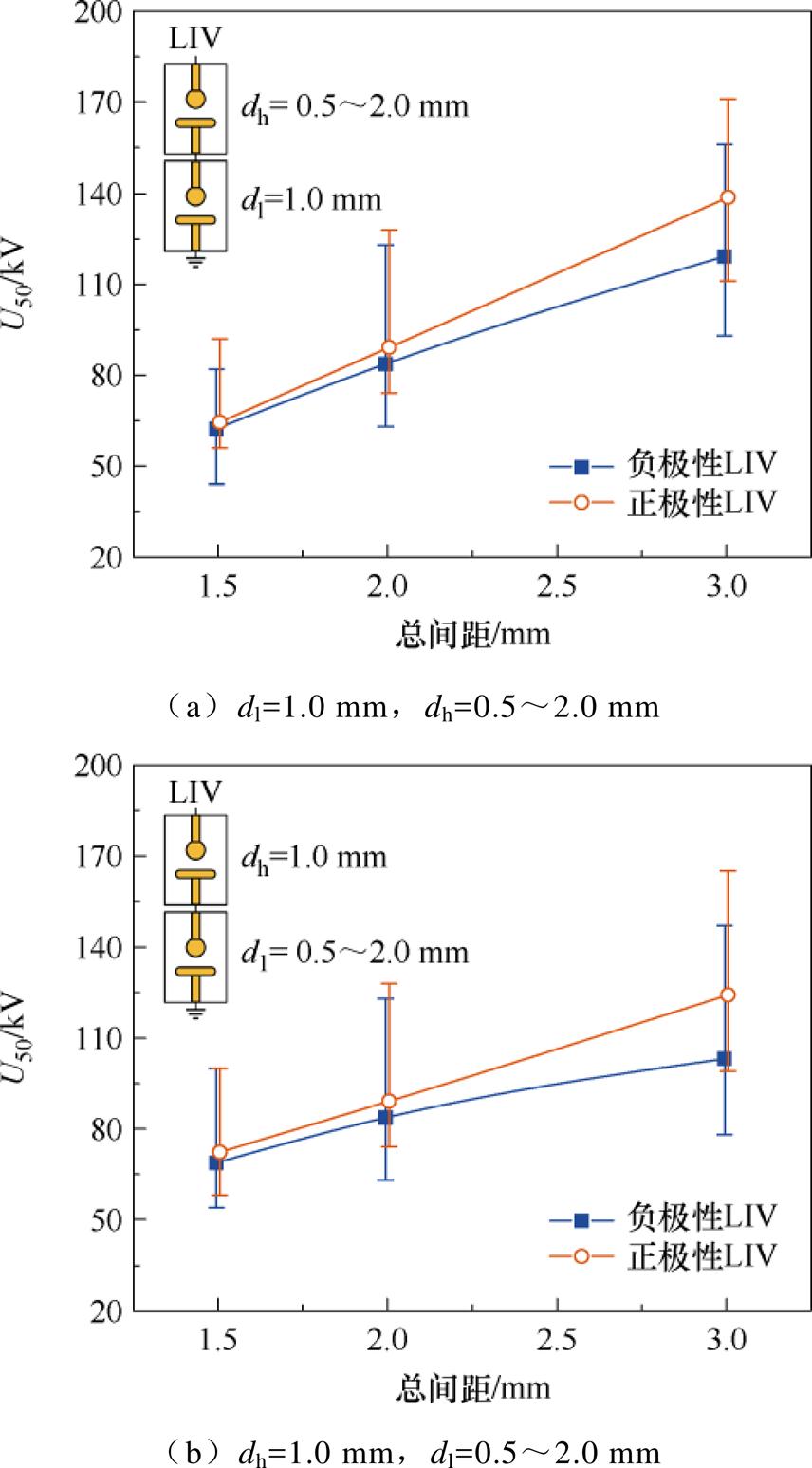
图7 串联双真空间隙U50与间隙距离之间的关系
Fig.7 Relationship between U50 and gap distances of double vacuum gaps in series
以上结果表明，当总间距处于1.5～3.0 mm范围内时，串联双真空间隙在正极性LIV下的绝缘强度高于负极性LIV下的情况，说明串联双真空间隙存在击穿极性效应。并且，当总间距为1.5 mm时，正、负极性LIV下U50的差值在4 kV以内，此时极性效应较弱，而随着双间隙中任一间距的增大，极性效应越发显著，总间距为3.0 mm时该差值将接近20 kV。此外，无论施加何种极性LIV，两间隙对串联结构绝缘强度的影响程度不同，高压侧间隙对串联结构绝缘强度的影响相较于低压侧间隙均更为显著。
本节通过有限元法（Finite Element Method, FEM）计算串联双真空间隙在正、负极性单位直流电压下的电场分布，获得双间隙的电压分布比与阴极表面最大电场强度，并结合击穿特性试验结果进一步分析不同极性电压下双间隙阴极最大电场强度对击穿电压的影响规律。
串联双真空间隙电场仿真模型示意图如图8所示，该模型是根据图2中双间隙的实际布置方式精确构建的。高压侧间隙中球电极的电位设置为±1 kV，中间悬浮导体部分设置为悬浮电位，低压侧间隙的板电极以及大地电位设置为0 V，边界条件为无限远处电位为0 V。
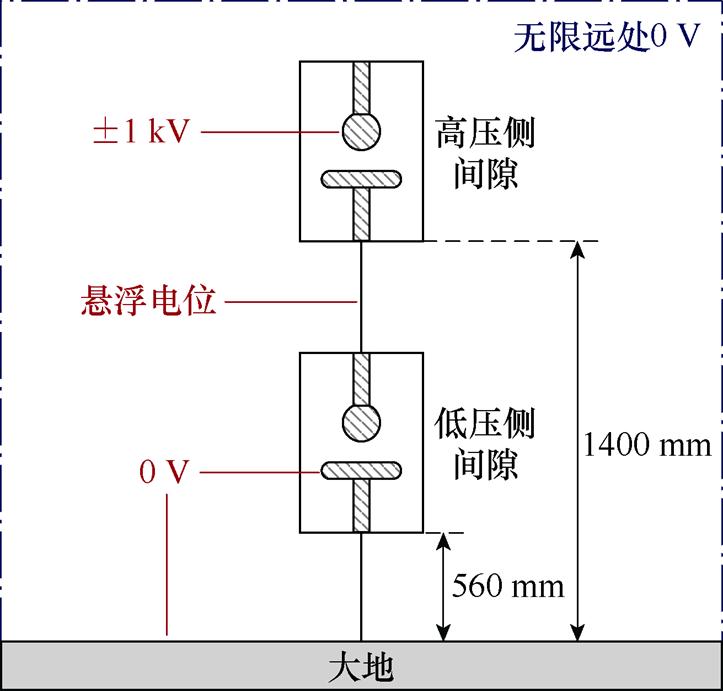
图8 串联双真空间隙电场仿真模型示意图
Fig.8 Schematic of electric field simulation model for double vacuum gaps in series
图9为正、负极性电压下串联双真空间隙的典型电场分布（dh=dl=1.0 mm）。从图9可以看出，当施加不同极性电压时，双间隙的电场分布近似，高压侧间隙的电场强度显著高于低压侧间隙，并且两间隙的最大电场强度均位于球电极端部。不同之处在于，当施加负极性电压时，两间隙中的球电极为阴极，板电极为阳极；而在正极性电压下则相反，板电极为阴极，球电极为阳极。
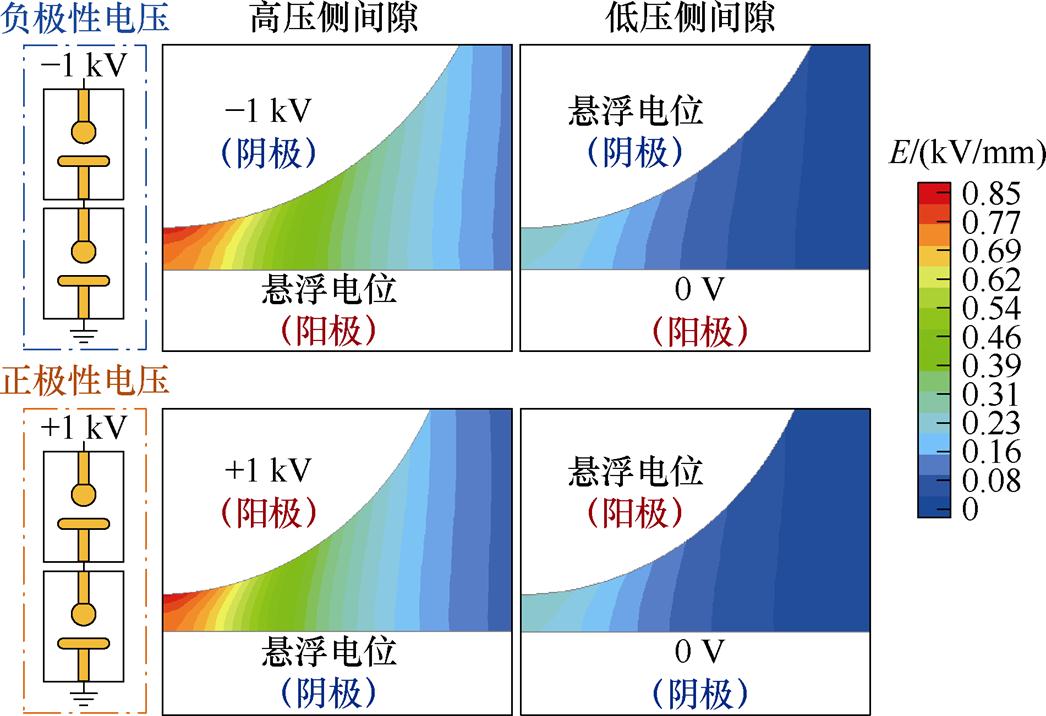
图9 串联双真空间隙典型电场分布（dh=dl=1.0 mm）
Fig.9 Typical electric field distributions of double vacuum gaps in series (dh=dl=1.0 mm)
计算得到的正、负极性电压下双真空间隙的电压分布见表3。表中，Uh%和Ul%分别为高压侧间隙和低压侧间隙所承受电压占总电压的百分比。结果表明，不同极性电压下两间隙的电压分布几乎相同，仅相差不到1%，高压侧间隙和低压侧间隙分别承担约75%和25%的总电压。根据前人的研究[1, 26, 29]，该结果能较好地反映实际串联间隙的分压情况。由于串联双真空间隙的电压分布主要取决于等效电路，当双间隙的布置方式和接地位置确定后，其等效电路的拓扑及参数将保持不变。并且，悬浮导体对地杂散电容的存在导致低压侧间隙的等效电容增大，使其承担的电压相较于高压侧间隙更低[30-31]。总之，当接地位置不变时，施加电压极性对串联双间隙电压分布的影响可忽略不计。
表3 正、负极性电压下双真空间隙的电压分布
Tab.3 Voltage distributions of double vacuum gaps under positive and negative voltages
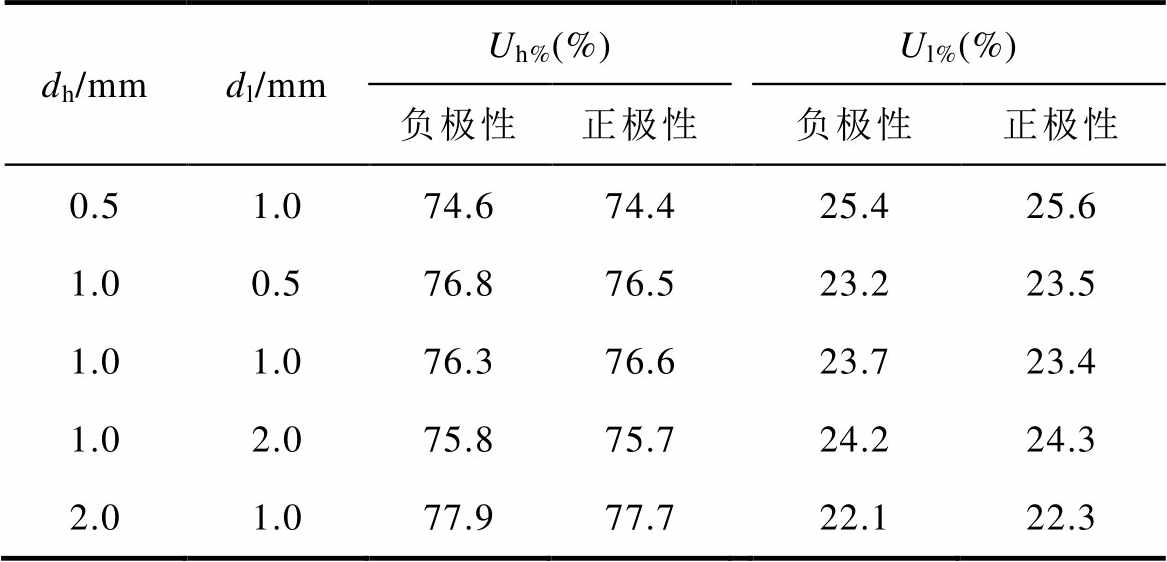
dh/mmdl/mmUh%(%)Ul%(%) 负极性正极性负极性正极性 0.51.074.674.425.425.6 1.00.576.876.523.223.5 1.01.076.376.623.723.4 1.02.075.875.724.224.3 2.01.077.977.722.122.3
由于阴极的场致电子发射被认为是真空击穿发展的关键[32]，本文将着重分析串联双真空间隙的阴极最大电场强度。计算得到的正、负极性电压下双间隙的阴极最大电场强度见表4。表中，Ecmax(h)和Ecmax(l)分别为高压侧间隙和低压侧间隙的阴极最大电场强度值。由图9中的电场分布可知，负极性电压下的阴极最大电场强度为球电极表面的电场强度峰值，而正极性电压下则为板电极表面的电场强度峰值。由于施加电压为±1 kV，计算结果为双间隙在单位电压下的电场强度，该值仅取决于真空间隙的几何结构。
表4 正、负电压下双真空间隙的阴极最大电场强度
Tab.4 Maximum field strengths at cathode of double vacuum gaps under positive and negative voltages
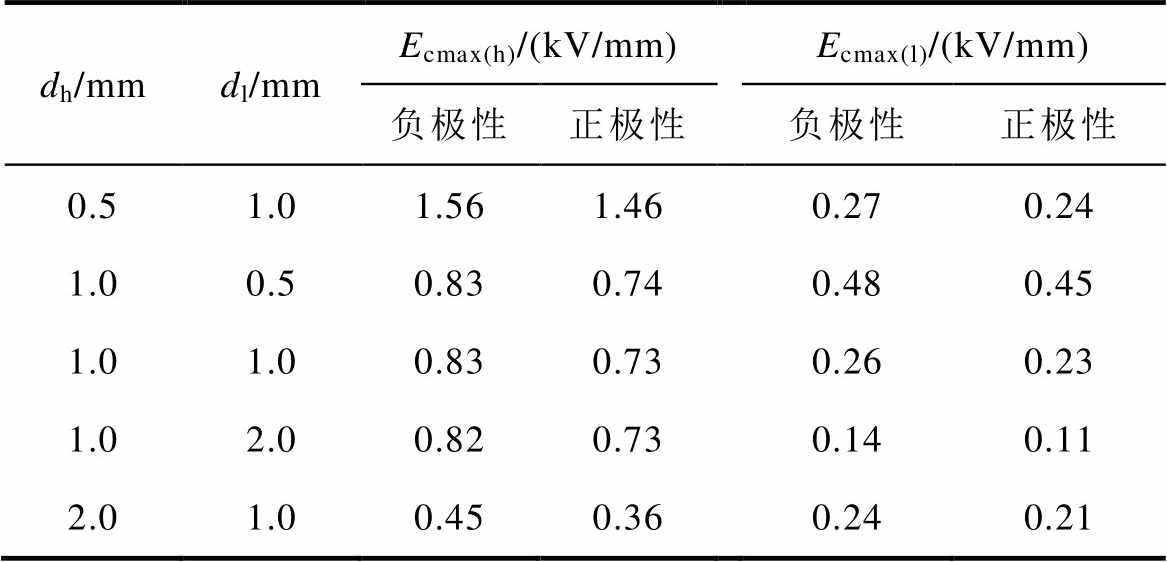
dh/mmdl/mmEcmax(h)/(kV/mm)Ecmax(l)/(kV/mm) 负极性正极性负极性正极性 0.51.01.561.460.270.24 1.00.50.830.740.480.45 1.01.00.830.730.260.23 1.02.00.820.730.140.11 2.01.00.450.360.240.21
由表4可知，当dh固定为1.0 mm，dl从0.5 mm增加至2.0 mm时，正、负极性电压下Ecmax(l)显著降低70%以上，而Ecmax(h)几乎恒定为0.73 kV/mm与0.83 kV/mm；相似地，当dl固定为1.0 mm，dh从0.5 mm增加至2.0 mm时，正、负极性电压下Ecmax(h)的下降幅度同样超过70%，而Ecmax(l)略有降低。上述结果表明，两间隙的阴极最大电场强度主要取决于自身的间距，而另一间隙对其的影响较小。并且，由于球-板间隙电场分布的不对称性，正极性电压下的Ecmax(h)和Ecmax(l)分别要比负极性电压下平均低0.1 kV/mm和0.03 kV/mm。
结合试验确定的雷电冲击击穿电压（见表2）与计算得到的阴极最大电场强度（见表4），可以确定正、负极性LIV作用下串联双真空间隙的阴极最大电场强度与U50之间的关系，如图10所示。考虑到两间隙的阴极最大电场强度主要取决于自身的间距，Ecmax(h)和Ecmax(l)对U50的影响应相互独立，下面将依次进行分析。Ecmax(h)与U50之间的关系如图10a所示。可以看出，当Ecmax(h)从0.3 kV/mm增加至1.6 kV/mm时，正、负极性LIV下双间隙U50均呈指数趋势下降，并且二者的拟合曲线高度吻合。
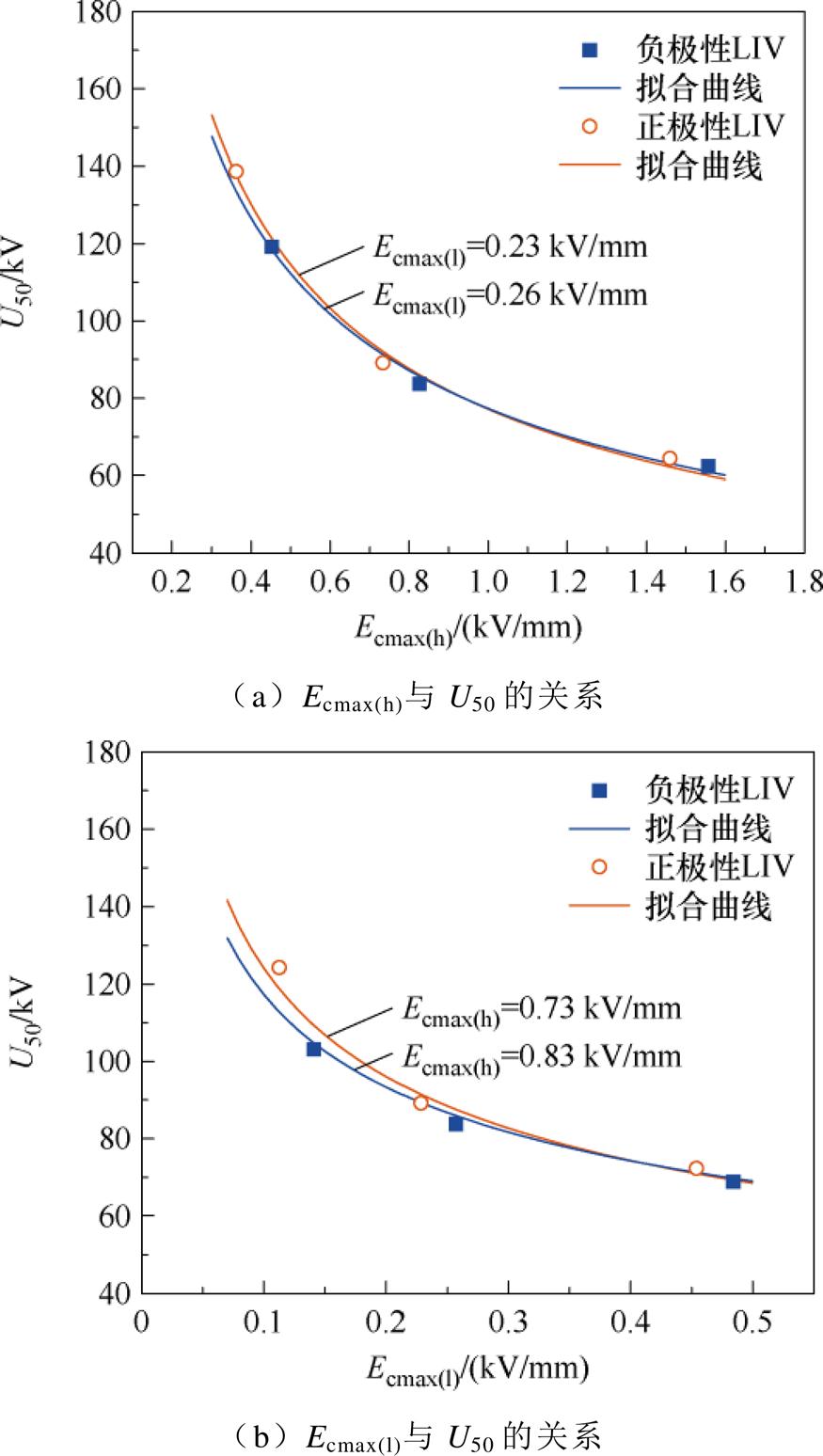
图10 串联双真空间隙阴极最大电场强度与U50之间的关系
Fig.10 Relationship between maximum field strengths at cathode and U50 of double vacuum gaps in series
Ecmax(l)与U50之间的关系如图10b所示，当Ecmax(l)处于0.1～0.5 kV/mm范围内时，随着Ecmax(l)的增加，不同极性电压下U50同样呈指数趋势下降。不过，正极性LIV下的拟合曲线整体略高于负极性，考虑到此时正极性电压下的Ecmax(h)要比负极性电压下低0.1 kV/mm，而Ecmax(h)的降低将使U50增加。假设Ecmax(h)保持恒定，正、负极性LIV下Ecmax(l)与U50的拟合曲线也近乎一致。
以上结果表明，无论施加何种极性的LIV，随着两间隙阴极最大电场强度的增加，串联间隙的击穿电压均呈指数趋势下降。并且可以合理地假设：在正、负极性LIV下，双真空间隙的阴极最大电场强度与50%击穿电压之间遵循相同的定量关系。
普遍认为，真空击穿起始于阴极表面的微观缺陷，如微凸起等[33]，由于缺陷不规则的几何形状使得阴极局部电场强度倍增，高电压下将引起场致电子发射，这会对真空击穿的发展起着十分重要的作用[10, 34]，而场致发射强度取决于阴极最大电场强度。当阴极最大电场强度超过一定值后，场致发射产生的热量将使电极表面温度升至沸点从而释放金属蒸气，金属蒸气在高能电子束的撞击下将发生强电离并引发间隙击穿[32]。本文暂不考虑间隙电极材料不对称的情况，假设在相同电极材料条件下，真空间隙阴极电场强度的击穿临界值Ec保持恒定[35]。对于非均匀电场分布，Ec的表达式[10]为
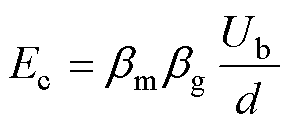（2）
式中，Ub为击穿电压；d为间隙距离；bm和bg分别为微观、宏观场致增强系数。
式（3）为本文计算的单位电压（±1 kV）下理想球-板间隙的阴极宏观最大电场强度，该值仅与间隙的几何结构有关，并未考虑电极表面的微观形貌。
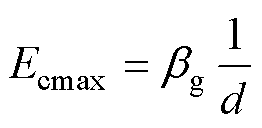（3）
联立式（2）和式（3）可得到Ub的表达式，即
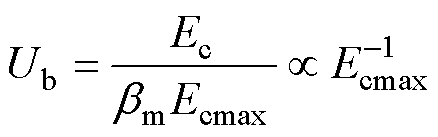（4）
结果表明，真空击穿电压与Ecmax和bm呈负指数关系，其中bm取决于电极表面的微观形貌。一般认为，若两侧电极经过相同的加工和打磨过程，其表面的微观形貌近乎一致，由此假设bm也保持恒定[10]。此外，鉴于球、板电极的强电场区域面积相近且很小，施加不同极性电压时二者发生电子发射的概率差异不大，面积效应较弱[19, 25, 36]。因此，真空间隙的击穿电压主要由阴极宏观最大电场强度决定。
由于串联多真空间隙的完全贯穿是由各间隙共同击穿所引发[37-38]，而式（4）表明各间隙的击穿电压主要取决于阴极最大电场强度，并呈负指数关系。因此，串联双间隙的击穿电压将由两间隙阴极最大电场强度共同决定，这解释了图10中在正、负极性LIV作用下击穿电压和阴极最大电场强度遵循相同负指数关系的原因。
根据4.1节的分析，串联双真空间隙的击穿电压主要取决于两间隙的阴极最大电场强度。另外，由表3可知，电压极性对双间隙分压特性的影响可忽略不计，高压侧间隙承担约75%的总电压UT。以此为基础，图11比较了正、负极性LIV下串联双真空间隙的击穿发展情况（dh=dl）。从图11中可看出，尽管电压极性对两间隙电场分布的影响较小，但其决定了阴极的位置，正极性电压下阴极位于板电极，而负极性电压下则位于球电极，由于球-板间隙不对称的电场分布，正极性LIV下Ecmax(h)和Ecmax(l)均低于负极性LIV下的情况，具体见表4。
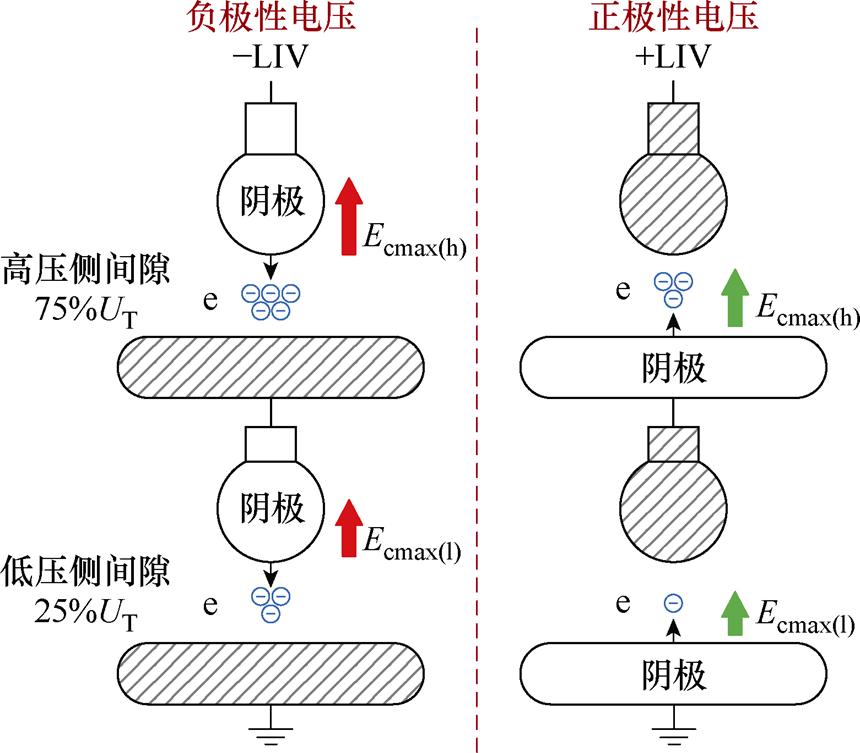
图11 串联双真空间隙击穿发展情况示意图
Fig.11 Schematic of breakdown development situations for double vacuum gaps in series
当施加峰值相同的LIV时，由于负极性电压下的阴极电场强度较高，两间隙的场致发射强度相较于正极性情况更剧烈，这意味着负极性LIV下双间隙发生非同步击穿（高压侧间隙先击穿）的概率更高[25, 37]，可能在较低的电压下就能实现串联间隙的完全贯穿，因此串联双球-板间隙在正极性LIV下的绝缘强度高于负极性，如图5和图7所示。综上所述，阴极电场强度的差异是造成串联双真空间隙击穿电压具有极性效应的主要原因。
由于阴极电场强度取决于电极结构，若两间隙的电极结构差异较大（例如球-板电极串联板-球电极），电压极性改变后可能会出现Ecmax(h)＜Ecmax(l)的情况。此时，低压侧间隙的耐压能力显著降低，两间隙的击穿次序将发生转变，先由低压侧间隙击穿，随后双间隙完全贯穿[25, 37]。由此可见，相较于单一真空间隙，阴极电场强度对串联间隙极性效应的作用机制更加复杂。不同极性LIV下，阴极电场强度的变化不仅会影响串联结构中各间隙的耐压能力，还将影响多间隙的击穿发展过程，二者共同导致了击穿电压的差异。
此外，由于阴极电场强度与击穿电压之间遵循负指数的关系（见式（4）），短间隙条件下阴极电场强度较高，电场强度变化对于击穿电压的影响不显著；而对于长间隙，阴极电场强度较低，不同极性电压下电场强度微小的变化都可能导致双间隙击穿电压产生较大的差异，如图10所示。因此，串联双真空间隙在短间距条件下正、负极性击穿电压的差异较小，而随着双间隙中任一间距的增大，极性效应越发显著，总间距为3.0 mm时该差值接近20 kV，如图7所示。参考现有研究[18-19]，对于具有非对称电极的单一真空间隙，不同极性LIV下耐压能力的差异较为明显，间距为3.0 mm时正、负击穿电压的差值约为15～20 kV。考虑到串联间隙的击穿电压受其中各间隙耐压能力的影响，极性效应理应比单一间隙更显著，因此双间隙的正、负击穿电压差接近20 kV是合理的。
在前期的研究中已通过拟合得到了负极性LIV作用下串联双真空间隙U50与阴极最大电场强度之间的定量关系[25]，表示为
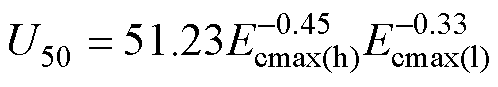（5）
经验证，该式可用于评估不同电极结构、间隙距离条件下串联双间隙的负极性击穿电压。根据本文研究结果可知，阴极最大电场强度是影响串联双真空间隙绝缘强度的关键因素，不同极性LIV下U50与阴极最大电场强度之间遵循近乎相同的负指数关系，如图10所示，因此式（5）理论上也能够评估正极性LIV下串联双间隙的耐压能力。
接下来利用本文击穿特性试验结果，验证式（5）评估正极性LIV下串联双真空间隙U50的可行性，如图12所示。图中，“n”表示dl=1.0 mm，dh=0.5～2.0 mm条件下的试验值，见图7a；“r”表示dh=1.0 mm，dl=0.5～2.0 mm条件下的试验值，见图7b；虚线为式（5）的评估值。可以看出，在两种间距变化条件下，双间隙U50的评估值与试验值都能较好地吻合，最大评估误差为7.6%。考虑到真空间隙U100为U50的1.3～1.4倍[10, 21]，可进一步对U100进行评估，以确定串联双间隙的最高耐受电压。
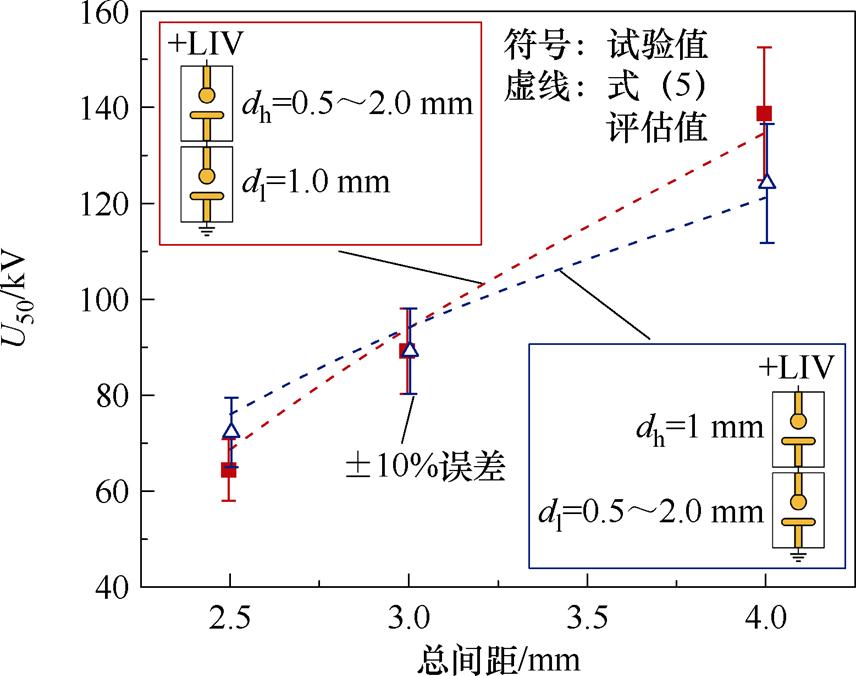
图12 正极性LIV下串联双真空间隙U50评估结果
Fig.12 Estimation results of U50 for double vacuum gaps in series under positive LIV
上述结果表明，可以利用阴极最大电场强度对不同极性LIV下串联双真空间隙的耐压能力进行定量评估，方法总结如下：首先，根据串联双真空间隙的实际布置方式精确构建电场仿真模型；其次，确定施加不同极性电压时两间隙中阴极的位置，并计算单位电压下（±1 kV）的阴极最大电场强度；最后，利用阴极最大电场强度与U50之间的拟合关系（式（5））评估正、负极性LIV下串联双间隙的击穿电压。
本文通过试验研究了正、负极性雷电冲击电压作用下串联双真空间隙的击穿特性，结合电场仿真分析了不同极性电压下双间隙阴极电场强度对击穿电压的影响关系，在此基础上阐明了串联双间隙击穿极性效应的产生机理，进而提出了一种串联双间隙正、负极性击穿电压的评估方法，并利用试验结果验证了该方法的可行性。所得结论如下：
1）串联双真空间隙的雷电冲击击穿电压存在极性效应。对于球-板间隙结构，正极性LIV下的U50高于负极性，当总间距为1.5 mm时极性效应较弱，正、负极性LIV下U50的差值在4 kV以内，而随着双间隙中任一间距的增大，极性效应越发显著，总间距为3.0 mm时该差值将接近20 kV。
2）阴极电场强度是影响串联双真空间隙耐压能力的关键因素，正、负极性LIV下双间隙的阴极最大电场强度与击穿电压之间遵循近乎相同的负指数关系。由于间隙电场分布的不对称性，阴极电场强度的差异是造成串联双真空间隙击穿电压具有极性效应的主要原因。
3）提出了基于阴极最大电场强度的串联双真空间隙正、负极性雷电冲击击穿电压评估方法。通过电场仿真确定双间隙在不同极性单位电压下的阴极最大电场强度，进而利用阴极最大电场强度与U50之间的拟合关系实现击穿电压的定量评估，经试验验证评估误差在10%以内。
本文基于典型的球-板电极结构研究了串联双真空间隙击穿极性效应的产生机理，同时所提方法在评估正、负极性击穿电压方面效果较好。但实际真空灭弧室内悬浮电极多、击穿随机性大，如何准确地评估灭弧室复杂绝缘结构的击穿电压及极性效应有待进一步研究。
参考文献
[1] 王建华, 张国钢, 闫静, 等. 高压开关电器发展前沿技术[M]. 北京: 机械工业出版社, 2020.
[2] Reilly J, Prinn R, Harnisch J, et al. Multi-gas assessment of the Kyoto protocol[J]. Nature, 1999, 401(6753): 549-555.
[3] 黄小龙, 赵双伟, 王勇, 等. 环保型高压电力开关设备研究进展综述[J]. 工程科学与技术, 2023, 55(3): 14-29.
Huang Xiaolong, Zhao Shuangwei, Wang Yong, et al. A review of research progress on environment- friendly high-voltage power switchgear[J]. Advanced Engineering Sciences, 2023, 55(3): 14-29.
[4] 柯学, 王安阳, 刘伟, 等. CF3SO2F及其混合气体电弧等离子体粒子组分与物性参数计算[J]. 电工技术学报, 2024, 39(19): 6145-6161.
Ke Xue, Wang Anyang, Liu Wei, et al. Calculation of particle composition and physical property parameters of arc plasma particles of CF3SO2F and its gas mixtures[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6145-6161.
[5] 崔兆轩, 林莘, 钟建英, 等. C4F7N/CO2混合气体特高压母线通流温升特性研究[J]. 电工技术学报, 2023, 38(9): 2491-2499.
Cui Zhaoxuan, Lin Xin, Zhong Jianying, et al. Study on the temperature rise characteristics of C4F7N/CO2 mixed gas ultra high voltage bus[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2491- 2499.
[6] 张在秦, 刘志远, 王闯, 等. 大电流真空电弧中阳极熔化过程的实验与仿真研究[J]. 电工技术学报, 2024, 39(7): 2143-2152, 2160.
Zhang Zaiqin, Liu Zhiyuan, Wang Chuang, et al. Experimental and numerical study on anode melting in high current vacuum arcs[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2143-2152, 2160.
[7] 程显, 白青林, 葛国伟, 等. 真空与气体一体化串联机械开关及其直流快速转移应用[J]. 电工技术学报, 2024, 39(5): 1464-1473.
Cheng Xian, Bai Qinglin, Ge Guowei, et al. High speed switch with series-connected vacuum and gas interrupters and its DC fast transfer application[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1464-1473.
[8] 刘洋, 管臣, 姚晓飞, 等. 72.5kV快速真空断路器技术研究及开发[J]. 高压电器, 2024, 60(8): 11-19.
Liu Yang, Guan Chen, Yao Xiaofei, et al. Research and development on 72.5 kV fast vacuum circuit breaker technology[J]. High Voltage Apparatus, 2024, 60(8): 11-19.
[9] 吴文海, 吴晟玮, 沈丰慧, 等. 252 kV环保型GIS双断口真空断路器并联电容的电场分析计算[J]. 高压电器, 2024, 60(9): 114-125.
Wu Wenhai, Wu Shengwei, Shen Fenghui, et al. Electric field analysis and calculation of parallel capacitors for 252 kV environment-friendly GIS double-break vacuum circuit breaker[J]. High Voltage Apparatus, 2024, 60(9): 114-125.
[10] Slade P G. The Vacuum Interrupter: Theory, Design, and Application[M]. 2nd ed. Boca Raton: CRC Press, 2020.
[11] 李烁, 修士新, 贾申利, 等. 金属罐体对真空灭弧室内部电场分布的影响[J]. 高电压技术, 2024, 50(2): 570-578.
Li Shuo, Xiu Shixin, Jia Shenli, et al. Influence of metal tank on the internal electric field distribution of vacuum interrupter[J]. High Voltage Engineering, 2024, 50(2): 570-578.
[12] 钟建英, 孙广雷, 杨葆鑫, 等. 高电压等级真空断路器研究现状及展望[J]. 高电压技术, 2024, 50(2): 451-466.
Zhong Jianying, Sun Guanglei, Yang Baoxin, et al. Research status and prospect of high voltage vacuum circuit breaker[J]. High Voltage Engineering, 2024, 50(2): 451-466.
[13] 葛国伟, 王文博, 程显, 等. 基于两间隙异步联动的一体化高压真空灭弧室电场设计[J]. 电工技术学报, 2024, 39(17): 5555-5564.
Ge Guowei, Wang Wenbo, Cheng Xian, et al. Electric field design of integrated high-voltage vacuum interrupter based on two-gap asynchronous linkage[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5555-5564.
[14] Arora R, Mosch W. High voltage and electrical insulation engineering[M]. Hoboken NJ: Wiley-IEEE, 2011.
[15] Li Shimin, Yamano Y, Geng Yingsan, et al. Gas desorption induced discharge in vacuum and its polarity effect[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(3): 799-805.
[16] Li Shimin, Yamano Y, Geng Yingsan, et al. Polarity effect of impulse conditioning characteristics under a uniform electric field in vacuum[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2021, 28(3): 838-844.
[17] Yu Yongxiang, Wang Jianhua, Yang He, et al. Asymmetrical AC field emission current charac- teristics of vacuum interrupters subjected to inrush current[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(1): 49-57.
[18] Shioiri T, Ohshima I, Honda M, et al. Impulse voltage field emission characteristics and breakdown dependency upon field strength in vacuum gaps[J]. IEEE Transactions on Power Apparatus and Systems, 1982, PAS-101(10): 4178-4184.
[19] Toya H, Hayashi T, Shinozaki Y, et al. Statistical property of breakdown between electrode and shield in high-voltage vacuum interrupter[J]. IEEE Transa- ctions on Plasma Science, 1985, 13(5): 311-314.
[20] 廖敏夫, 段雄英, 邹积岩. 单断口和三断口串联真空灭弧室绝缘击穿统计特性[J]. 中国电机工程学报, 2007, 27(12): 97-102.
Liao Minfu, Duan Xiongying, Zou Jiyan. Dielectric strength and statistical property of single and triple breaks vacuum interrupters in series[J]. Proceedings of the CSEE, 2007, 27(12): 97-102.
[21] Ma Hui, Shen Jingyu, Ding Jian’gang, et al. Prediction method of the breakdown probability for multiple vacuum gaps in series considering dielectric recovery under a lightning impulse voltage[J]. IEEE Transac-tions on Dielectrics and Electrical Insulation, 2022, 29(2): 753-761.
[22] Shen Jingyu, Ma Hui, Li Junyi, et al. Breakdown characteristics of double vacuum gaps in series under lightning impulse voltage: optimal gap distance distribution[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 30(2): 869-876.
[23] Shen Jingyu, Ma Hui, Ding Jian’gang, et al. Breakdown characteristics of triple vacuum gaps in series under lightning impulse voltage: Effect of floating potential gap[J]. Vacuum, 2022, 205: 111453.
[24] 阮江军, 舒胜文, 黄道春, 等. 串联真空灭弧室工频预击穿电流的自均压作用[J]. 高电压技术, 2010, 36(6): 1353-1358.
Ruan Jiangjun, Shu Shengwen, Huang Daochun, et al. Self-voltage sharing effects of power frequency prebreakdown current flowing through vacuum inter- rupters in series[J]. High Voltage Engineering, 2010, 36(6): 1353-1358.
[25] Shen Jingyu, Ma Hui, Ma Xiangteng, et al. Double short vacuum gaps in series under lightning impulse voltage: Estimation of breakdown voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(4): 1297-1304.
[26] 吴高波, 阮江军, 黄道春, 等. 126kV模块化三断口真空断路器静、动态均压设计[J]. 中国电机工程学报, 2013, 33(19): 215-223.
Wu Gaobo, Ruan Jiangjun, Huang Daochun, et al. Static and dynamic voltage sharing design of 126 kV modular triple-break vacuum circuit breaker[J]. Proceedings of the CSEE, 2013, 33(19): 215-223.
[27] 马慧, 刘志远, 耿英三, 等. 高电压等级真空灭弧室绝缘设计研究[J]. 真空电子技术, 2019(5): 7-13.
Ma Hui, Liu Zhiyuan, Geng Yingsan, et al. Investigation on insulation design of high voltage vacuum interrupters[J]. Vacuum Electronics, 2019(5): 7-13.
[28] 王建华, 耿英三, 刘志远. 输电等级单断口真空断路器理论及其技术[M]. 北京: 机械工业出版社, 2017.
[29] Kulkarni S, Hemachander M, Kumar S A, et al. Concept of series connected vacuum interrupters[C]// 2012 25th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV), Tomsk, Russia, 2012: 517-520.
[30] 程显, 杜帅, 葛国伟, 等. 环保型罐式多断口真空断路器均压配置研究[J]. 电工技术学报, 2021, 36(15): 3154-3162.
Cheng Xian, Du Shuai, Ge Guowei, et al. Study on voltage-sharing configuration of environment-friendly tank type multi-break vacuum circuit breakers[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3154-3162.
[31] 黄道春, 王华清, 全万霖, 等. 考虑混合式直流断路器整机结构的多断口串联机械开关均压设计[J]. 中国电机工程学报, 2022, 42(6): 2407-2415.
Huang Daochun, Wang Huaqing, Quan Wanlin, et al. Voltage sharing design of series multi-break mechanical switch considering the whole structure of hybrid DC circuit breaker[J]. Proceedings of the CSEE, 2022, 42(6): 2407-2415.
[32] Mesyats G A, Proskurovsky D I. Pulsed electrical discharge in vacuum[M]. Berlin: Springer Berlin Heidelberg, 1989.
[33] Zhang Yingyao, Deng Fanping, Ma Yuan, et al. Dynamic temperature characteristics of cathode microprotrusion under electron emission based on smoothed particle hydrodynamics[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2023, 30(5): 1941-1949.
[34] Zhou Zhipeng, Kyritsakis A, Wang Zhenxing, et al. Direct observation of vacuum arc evolution with nanosecond resolution[J]. Scientific Reports, 2019, 9(1): 7814.
[35] 李世民, 江希茜, 李镇廷, 等. 脉冲电压老炼过程中真空击穿机制演化机理[J]. 高电压技术, 2023, 49(11): 4790-4797.
Li Shimin, Jiang Xixi, Li Zhenting, et al. Evolution law of vacuum breakdown mechanisms in impulse voltage conditioning process[J]. High Voltage Engineering, 2023, 49(11): 4790-4797.
[36] Zhao Liang, Su Jiangcang, Li Rui, et al. Development of centimeter-class vacuum breakdown characteristics under microsecond pulses[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(2): 649-654.
[37] Ding Jiangang, Liu Xue, Yao Xiaofei, et al. Lightening impulse breakdown of vacuum gaps in series: part I: partial breakdown[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2022, 29(4): 1365-1372.
[38] Kong Fei, Nakano Y, Kojima H, et al. Discharge characteristics for various discharge patterns under negative lightning impulse voltage in vacuum[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(2): 813-818.
Abstract Vacuum gaps in series are widely used in high-voltage vacuum equipment to improve the insulation performance.It is well-known that one vacuum gap has different dielectric strengths under positive and negative voltages, termed as polarity effect, and this difference might be enlarged as the number of series-gap increases. Therefore, the polarity effect of vacuum gaps in series is an important factor influencing the insulation performance of vacuum equipment. However, there is no quantitative research on the polarity effect of multiple vacuum gaps and also a lack of related evaluation methods. This makes it difficult to design the insulation structure in high-voltage vacuum equipment. To address these issues, this article quantitatively investigated the influence of lightning impulse voltage (LIV) polarity on the breakdown characteristics of double vacuum gaps in series. The mechanism of polarity effect was revealed and an evaluation method for positive and negative breakdown voltages was proposed. The results can help to further understand the breakdown mechanism of vacuums gaps in series and provide theoretical basis for the design of high-voltage insulation structure in vacuum.
Firstly, based on sphere-plane electrodes, the breakdown characteristics of double vacuum gaps in series were experimentally determined under positive and negative LIVs. The up-down method was adopted in voltage application. The cumulative probability of breakdown voltage was analyzed by the 3-parameters Weibull distribution and the 50% breakdown voltage U50 was obtained to represent the dielectric strength of double gaps. Secondly, the electric fields of double vacuum gaps were calculated by the finite element method. The voltage distribution and field strengths at cathode of double gaps were obtained. Combining with the experimental results, the influence of maximum field strength at cathode on U50 under positive and negative LIVs was determined. Then, according to the breakdown theory in vacuum, the mechanism of polarity effect was illustrated by analyzing the relationship between the field strengths at cathode and breakdown voltage of double vacuum gaps. Finally, a method for evaluating the breakdown voltages of double gaps under both positive and negative LIVs was proposed based on the maximum field strength at cathode and validated by the experimental results.
The conclusions were drawn as following: (1) The lightning impulse breakdown voltage of double vacuum gap in series showed a polarity effect. For the double sphere-plane gaps, the positive breakdown voltage was higher than the negative one. As the gap distance increased, their difference gradually became larger and the polarity effect was more significant. (2) The electric field strength at cathode was the key factor affecting the dielectric strength of double vacuum gaps. Under positive and negative LIVs, the maximum field strength at cathode and breakdown voltage followed a similar negative-exponential relationship. Due to the asymmetric electric field distribution, the difference in field strength at cathode should be the main reason for the polarity effect. (3) Validated by experiments, the fitted relationship between maximum field strength at cathode and U50(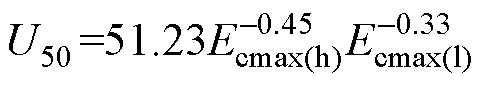
) can be used to evaluate the breakdown voltages of double gaps under LIVs with both polarities. The estimation error was within 10%.
Keywords：Vacuum breakdown, double gaps in series, polarity effect, lightning impulse voltage (LIV), electric field strength at cathode
中图分类号：TM561.2
DOI: 10.19595/j.cnki.1000-6753.tces.241608
国家重点研发计划（2022YFB2403700）和国家自然科学基金（52207149, 52277136）资助项目。
收稿日期 2024-09-10
改稿日期 2024-10-14
沈靖宇 男，1995年生，讲师，硕士生导师，研究方向为高压真空断路器、真空放电与绝缘、开关电器仿真技术。
E-mail: shenjy@fzu.edu.cn（通信作者）
许志红 女，1963年生，教授，博士生导师，研究方向为电器及其智能化技术。
E-mail: 641936593@qq.com
（编辑 李 冰）