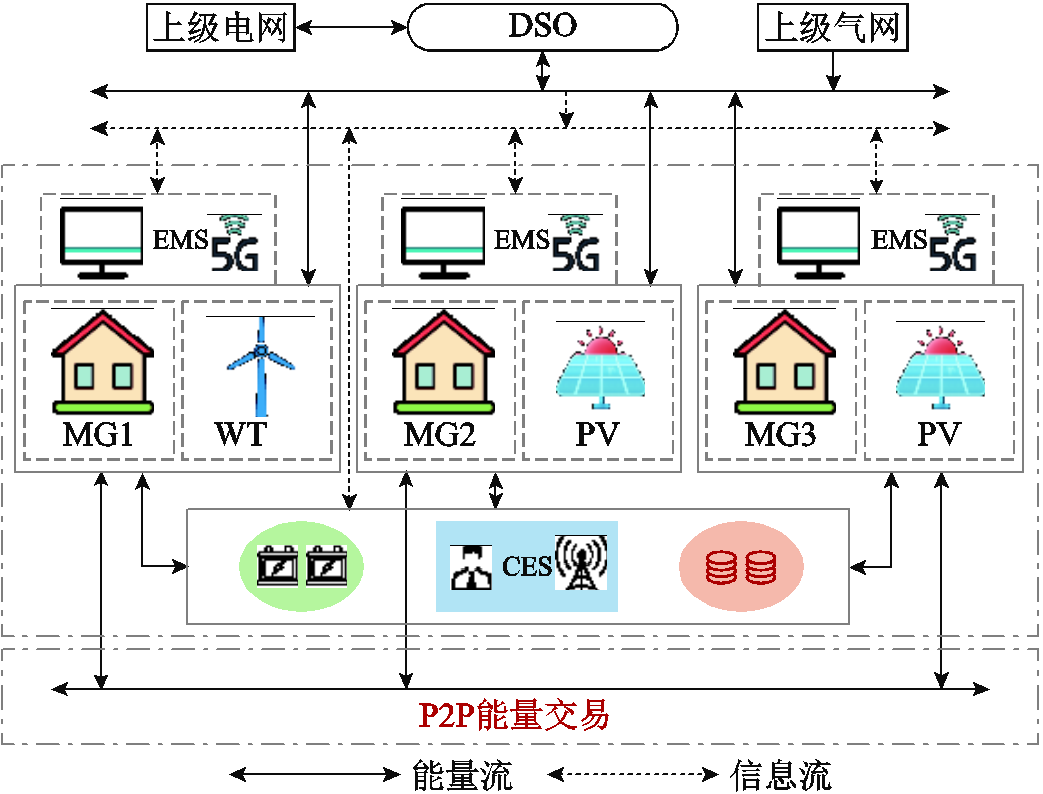
图1 系统运行框架图
Fig.1 System framework diagram
摘要 新能源的强烈不确定性给多微电网协同运行带来了可靠性和安全性的巨大挑战,为此提出一种基于改进条件生成对抗网络(CGAN)的多微电网配电系统分布鲁棒协同优化调度模型。首先,为更准确地描述新能源的不确定性,该模型以改进CGAN和K-means++聚类算法削减得到的场景集作为分布鲁棒优化集合的初始新能源场景,其中改进CGAN模型使用Wasserstein距离作为判别器损失函数,以新能源日前预测值作为生成对抗网络的条件变量;其次,构建一种考虑动态潮流约束和云储能租赁的配电网-多微电网协同运行模型,上层利用Stackelberg博弈描述配电网与多微电网间的关系,下层建立基于多能点对点交易贡献率的利益分配方法;然后,为保护各主体隐私并提高求解效率,提出一种耦合可并行计算列与约束生成的二分法求解能量交易问题,并用改进交替乘子算法求解利益分配问题;最后算例结果表明,所提方法能更准确、更有效地描述新能源的不确定性,能兼顾系统的鲁棒性、经济性和安全性,并保证每个参与主体的利益。
关键词:改进条件生成对抗网络 云储能 分布鲁棒优化 配电网-多微电网协同运行
微电网(Microgrid,MG)[1]作为一种灵活高效的能源管理系统,能有效地应对能源危机,并助力“双碳”目标的实现。然而,单个微电网的工作能力有限,且抗干扰能力在运行环境变化时表现不佳[2]。随着微电网技术的不断发展,多个微电网通过互联构成多微电网系统(Multi-Microgrid, MMG)。MMG不仅可以接入配电系统,还支持微电网之间的点对点(Peer-to-Peer, P2P)能量交互。这种系统能够实现微电网之间的智能协调和灵活的能源交易,有效地解决更大范围内新能源的消纳和利用问题,降低社会成本[3]。然而,随着可再生能源渗透率的不断增长,其固有的不确定因素给MMG的稳定协同运行带来了巨大的挑战。
目前,随机优化[4]和鲁棒优化[5]是处理MMG不确定性的两种主要方法。随机优化需要大量数据和准确的概率分布来提高优化精度,但实际应用中,不确定性的真实分布往往难以精确获知,且大规模的离散场景计算耗时过长,限制了其更广泛的应用。相较之下,鲁棒优化无需概率信息,通过不确定性集描述参数的波动范围,但过于强调最坏情况而导致其是过于保守的解决方案[6]。近年来,新兴的分布鲁棒优化(Distributionally Robust Optimization, DRO)结合了这两种方法的优点,展现了更好的性能。该方法无需预设概率分布的类型和参数,而是通过数据驱动的方式构造概率分布模糊集,并针对最差的概率分布进行决策。基于概率距离或矩信息构造模糊集是DRO中的两种常见手段。文献[7]基于Wasserstein距离构建随机变量的概率分布模糊集,建立了虚拟电厂的分布鲁棒优化模型。文献[8]基于Wasserstein距离建立风光发电的概率分布模糊集,用于解决可在生能源参与的储能系统容量配置问题。文献[9]利用矩信息建立鲁棒优化不确定集,解决了配电系统日前日内优化的风电不确定性问题。然而,这些研究大多通过偏转线性决策规则和对偶定理构造凸优化模型,且0-1变量的增加也会增加模型的转换和求解的难度,相应的NP-hard问题也很复杂。另外一种基于数据驱动的DRO方法,通过并行求解有效地避免了推导对偶形式以及引入0-1变量造成的求解效率低的问题[10]。该方法利用历史数据样本生成并计算典型场景的初始概率分布,通过以1-范数和∞-范数作为综合范数约束其概率分布模糊集,然后制定不确定因素在最恶劣概率分布下的最优决策[10-11]。
目前,针对风光等可再生能源常用的场景生成方法主要基于统计学习和深度学习。传统的统计学模型如马尔可夫链法[12]、时间序列法[13]、场景树生成法[14],依据可再生能源出力的历史数据确定相应的参数,未能充分考虑新能源发电序列的时空相关性及其他未知信息。相比于统计学习,深度学习方法可以通过无监督学习和自主学习,更准确地反映随机变量的时空特征,展现出更强的泛化能力和数据表达能力。在最新的研究中,学者们应用生成对抗网络来生成符合概率分布的可再生能源功率曲线,以及在不同条件下的可再生能源功率曲线[15]。同时,一种基于条件生成对抗网络的可再生能源日前场景生成方法也被提出,通过对条件生成对抗网络(Conditional Generative Adversarial Networks, CGAN)模型进行博弈训练,使其学会学习预测曲线与实际曲线之间的映射关系,相较于传统的马尔可夫链场景生成方法,能够更精确地描述风电不确定性[16]。此外,针对电力系统运行规划中不同条件下的场景,还提出了一种基于Wasserstein距离的CGAN模型,用于风电功率极端场景的生成,相较于传统的基于Wasserstein距离的GAN生成的场景集质量更佳。
另外,MMG中各微电网隶属于不同的利益主体,有自身利益的考虑。文献[17]建立了分布式光伏产销者社区的合作运营模式,并采用Shapley值法分配合作收益。但Shapley方法只考虑通过边际贡献进行利益分配,无法保证全局利益最大化。文献[18-19]提出了一种非对称纳什议价模型,综合考虑了合作参与者之间的利益、策略和信息等问题,在处理参与者之间的非独立性和交互性方面更合理。上述文献研究了多微电网的P2P能源交易优化问题,但现有的合作联盟通常是配电网运营商(Distribution System Operator, DSO)或上网电价的被动接受者,无法根据各自的能源需求进行有效的互动。文献[20]基于Stackelberg博弈建立了DSO引导下的多产消者日前调度模型。文献[21]建立了考虑分区定价的多微电网P2P能源交易模型,并基于Stackelberg博弈确定了唯一均衡解。这些研究表明,通过DSO设定价格信号来指导下层联盟的优化运行,可以提高可再生能源的利用率并降低对电网的依赖。然而,上述研究并未考虑除电能以外的交易和运行过程中的线路潮流问题。
基于以上研究,本文提出了一种基于改进条件生成对抗网络的多微电网配电系统分布鲁棒协同优化运行策略。与现有研究相比,本研究的主要创新点和贡献如下:
1)提出一种基于改进CGAN的场景生成方法,用于生成DRO集合的初始新能源场景。该CGAN模型使用Wasserstein距离作为判别器损失函数,以优化训练过程中梯度消失和模式崩溃的问题。同时,以新能源功率日前预测值作为改进CGAN的条件变量,使改进CGAN能够学习满足条件的噪声分布与真实数据训练集之间的映射关系,从而更准确地描述新能源出力的随机特性。
2)构建一种考虑动态潮流约束和云储能租赁的DSO-MMG协同运行模型,上层利用Stackelberg博弈描述DSO与MMG的关系,下层建立基于P2P多能交易贡献率的非对称纳什议价模型,确保各参与主体的利益。
3)为提高模型求解效率并有效保护各主体隐私,提出一种耦合可并行计算列与约束生成(Column and Constraint Generation, C&CG)的二分算法求解能源交易问题,并用改进ADMM算法求解利益分配问题。
图1为本文提出的系统运行模型框架。MG与DSO直接相连,可以根据DSO指定价格进行购能,也可以在微电网间进行P2P交易。微电网运营商会根据自身供给需求,通过议价方式进行能量交换,减小对上级电网的依赖,降低自身的运行成本。同时,微电网运营商通过租赁云储能(Cloud Energy Storage, CES)来降低在微电网内部建设储能系统的高额投资成本,促进可在生能源的消纳。此外,各微电网配备了能量管理系统,采用先进的5G通信技术,以实现实时能源交互和价格传输,保证在高效率的同时兼顾MG隐私保护要求[18]。

图1 系统运行框架图
Fig.1 System framework diagram
本文的混合博弈模型如图2所示。上层为Stackelberg博弈[21],DSO作为博弈主体,根据MMG的能源需求制定交易价格,以最大化其利益。下层为MMG间的合作博弈,通过协调微电网间的能源交易量和价格来最大化自身利益。同时,引入分布鲁棒优化来处理博弈过程中的不确定因素,从而更好地消纳新能源出力并降低调度成本。
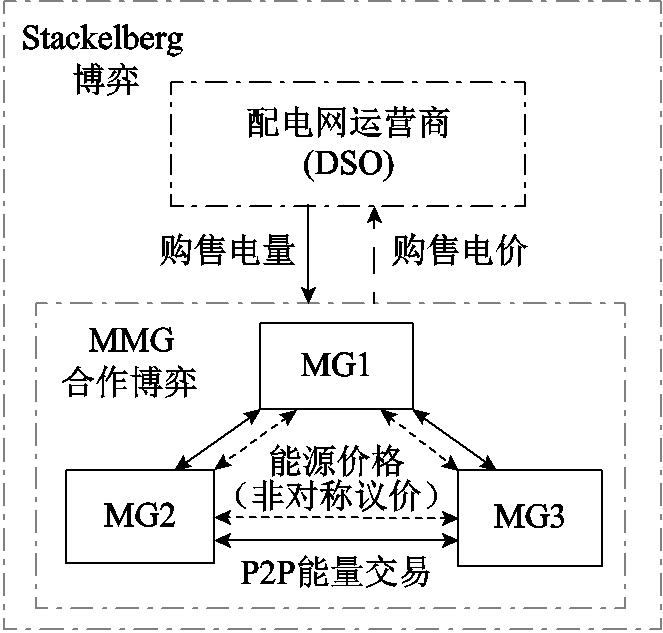
图2 混合博弈模型
Fig.2 Mixed game model
该模型可分为以下步骤:
1)根据纳什议价理论[18],将微电网的合作博弈问题分解为联盟收益最大化(P1)和能源支付问题(P2)。
2)在Stackelberg博弈中,DSO的目标是最大化自身收益,MMG的目标是最大化联盟收益(P1)。该过程中考虑到新能源发电的不确定性问题,采用分布鲁棒进行各微电网的内部优化。
3)根据非对称纳什议价理论和各微电网的P2P能量贡献,计算能源支付问题(P2)。
GAN[22]是一种基于博弈论的无监督生成式模型。它通过生成器网络(Generator Network, GN)和判别器网络(Discriminator Network, DN)之间相互对抗博弈逐渐生成与真实样本相似的数据样本。而CGAN将监督学习与半监督学习结合,允许在生成样本的过程中将附加信息作为生成器的输入,指导样本的生成过程,其基本架构如图3所示。其中,判别器损失函数采用Wasserstein距离,以解决训练过程中可能出现的梯度消失和模式崩溃问题。同时,将风光功率日前预测值作为条件信息c输入CGAN中,使得模型能够学习条件噪声分布与实际数据之间的映射关系。整个模型的设计旨在更准确地描述风光的随机性和不确定性,为风光场景生成提供了一种有效的方法。使用Wasserstein距离来代替CGAN中的JS散度,其目标函数表示为
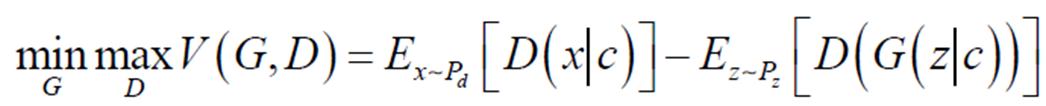 (1)
(1)
式中,G(·)为发生器函数;D(·)为鉴别器函数;V(·)为生成器与鉴别器样本的距离;E(·)为期望函数;x为生成样本;z为随机噪声;c为条件信息;Pd和Pz分别为真实样本和噪声的概率分布。
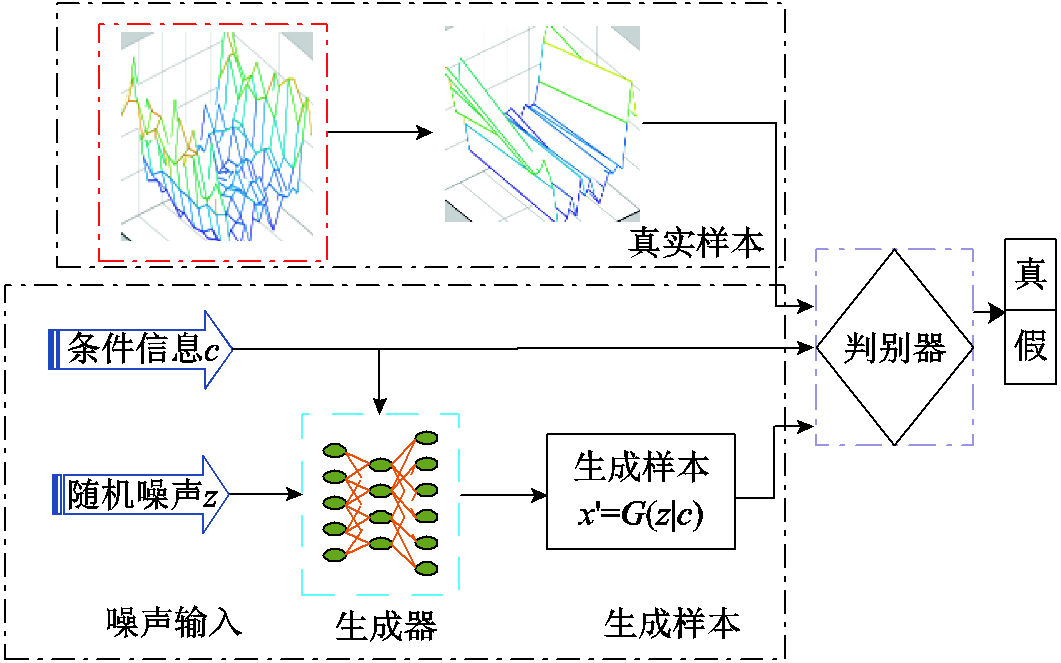
图3 条件生成对抗网络的结构
Fig.3 Structure of CGAN
通过对CGAN鉴别器的梯度范数进行惩罚,解决了CGAN不能在1-Lopschitz约束下约束鉴别器的问题。带梯度惩罚项的CGAN整体训练的目标函数表示为[16]
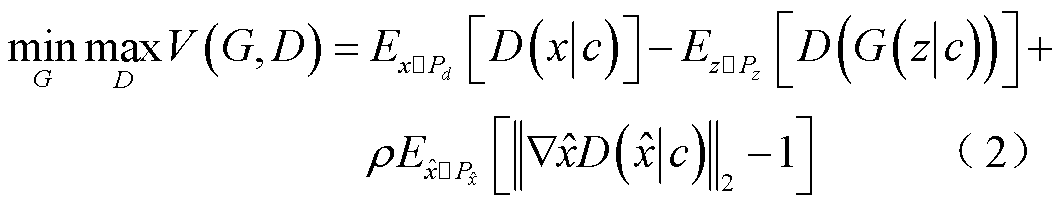
式中,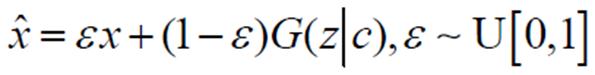 ;
;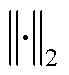 表示2-范数;ρ为梯度惩罚系数;
表示2-范数;ρ为梯度惩罚系数;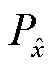 为服从
为服从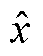 的概率分布。
的概率分布。
相对于K-means算法,K-means++聚类算法[23]在选取初始聚类中心方面进行优化,在电力系统场景聚类过程更加简单高效。本文采用K-means++算法对改进CGAN生成的大量场景进行聚类。通过Davies Bouldin指数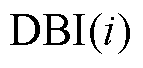 和廓形系数
和廓形系数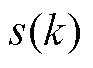 两个典型内部效度指标进行定量分析,分别表示为
两个典型内部效度指标进行定量分析,分别表示为
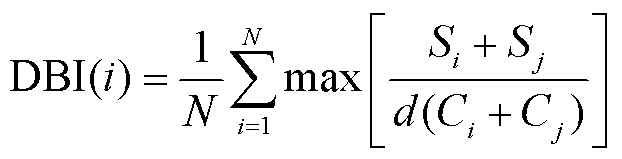 (3)
(3)
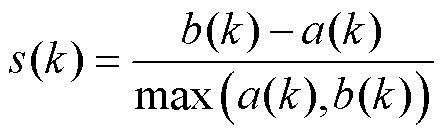 (4)
(4)
式中,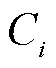 为第i个簇的中心;
为第i个簇的中心;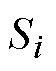 为簇i中所有样本到
为簇i中所有样本到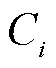 的平均距离;
的平均距离;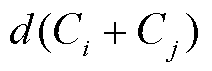 为簇中心
为簇中心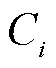 与
与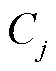 之间的距离;
之间的距离;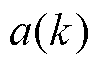 为第k个样本与集群内所有样本之间的平均距离;
为第k个样本与集群内所有样本之间的平均距离;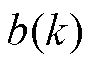 为第k个样本与集群外其他样本之间的平均距离;N为簇的数量。
为第k个样本与集群外其他样本之间的平均距离;N为簇的数量。
3.1.1 DSO成本模型
DSO在Stackelberg博弈中扮演着领导者的角色,以自身的利益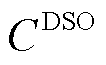 最大化为目标函数,包括与上级电网交易成本
最大化为目标函数,包括与上级电网交易成本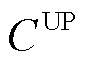 、与下级微电网交易成本
、与下级微电网交易成本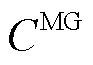 以及网损成本
以及网损成本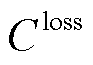 ,即
,即
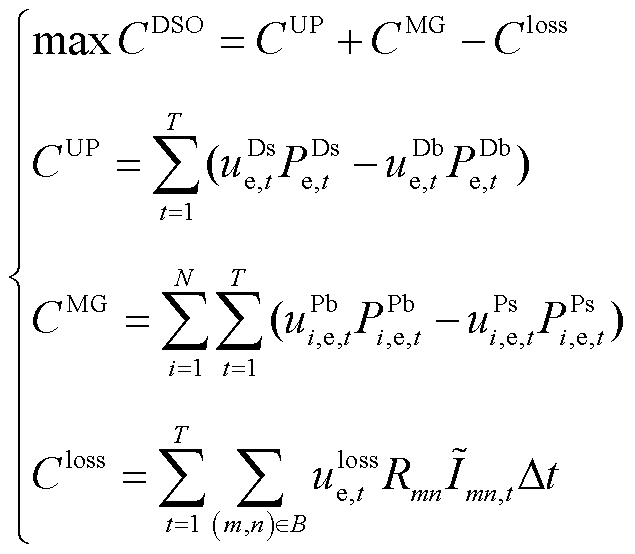 (5)
(5)
式中,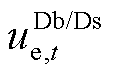 、
、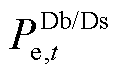 分别为DSO向上级电网的购售电价和购售电量;
分别为DSO向上级电网的购售电价和购售电量;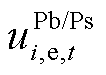 、
、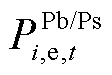 分别为MG向DSO的购售电价和购售电量;
分别为MG向DSO的购售电价和购售电量;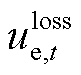 为电能损耗价格;
为电能损耗价格;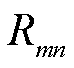 为mn支路电阻;
为mn支路电阻;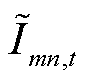 为mn支路电流二次方;
为mn支路电流二次方;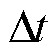 为时间间隔;B为网络中所有节点集合。
为时间间隔;B为网络中所有节点集合。
3.1.2 约束条件
1)电价约束
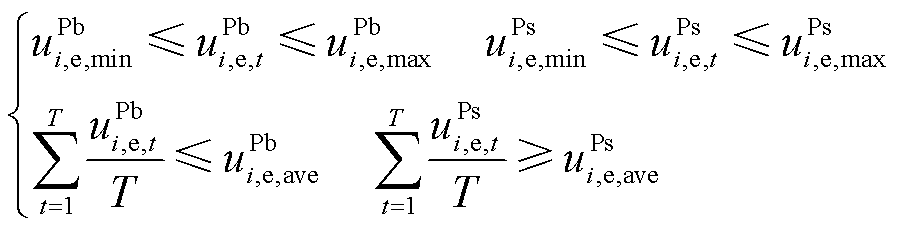 (6)
(6)
式中,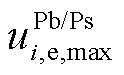 、
、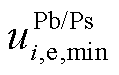 分别为DSO制定MG联盟购售电价的上、下限;
分别为DSO制定MG联盟购售电价的上、下限;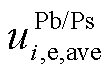 为购售电价的平均值;
为购售电价的平均值;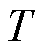 为一个时间周期。
为一个时间周期。
2)潮流约束
为更准确地反映系统的动态运行,确保构建模型更符合实际运行情况,本文采用基于二阶锥松弛的动态最优潮流模型[24],即
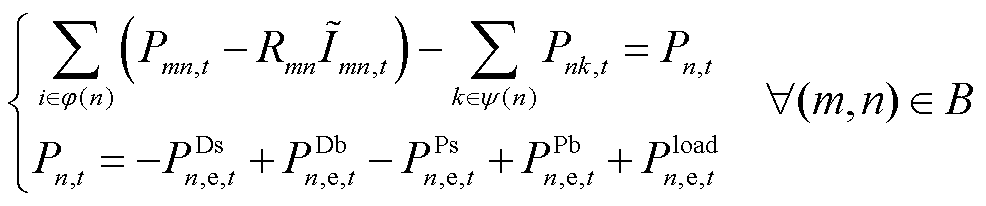 (7)
(7)
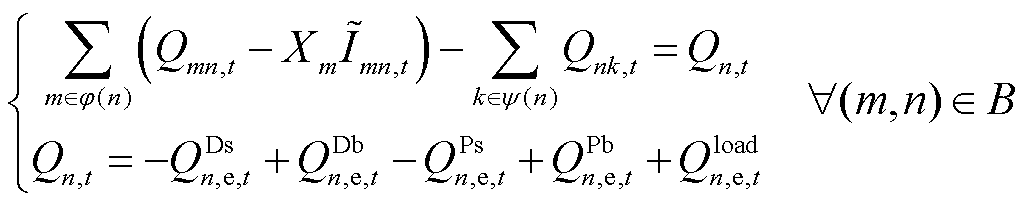 (8)
(8)
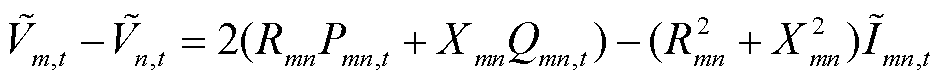 (9)
(9)
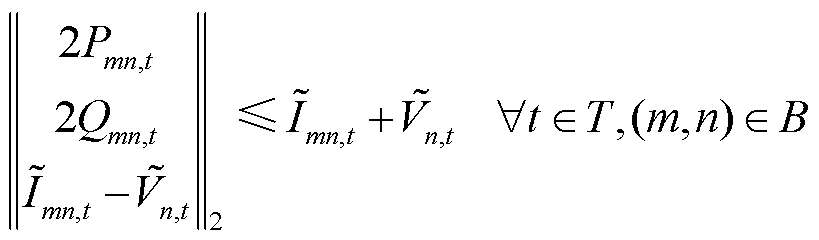 (10)
(10)
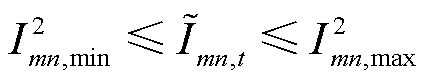 (11)
(11)
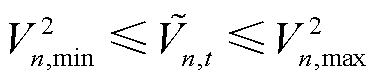 (12)
(12)
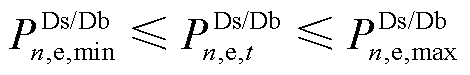 (13)
(13)
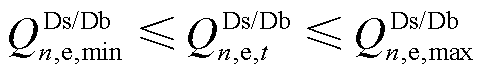 (14)
(14)
式中,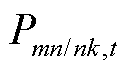 、
、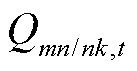 为mn/nk支路的有功功率和无功功率;
为mn/nk支路的有功功率和无功功率;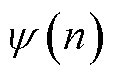 为以n为首端节点的支路末端节点集合;
为以n为首端节点的支路末端节点集合;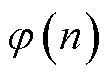 为以n为末端节点的支路首端节点集合;
为以n为末端节点的支路首端节点集合;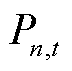 、
、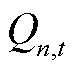 分别为n节点的有功功率和无功功率;
分别为n节点的有功功率和无功功率;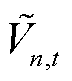 为n节点电压二次方;
为n节点电压二次方;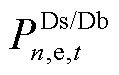 、
、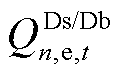 分别为n节点向上级电网购售电有功功率和无功功率;
分别为n节点向上级电网购售电有功功率和无功功率;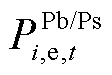 、
、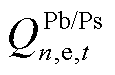 分别为n节点向DSO购售电量有功功率和无功功率;
分别为n节点向DSO购售电量有功功率和无功功率;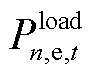 、
、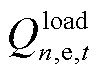 分别为n节点的负荷有功功率和无功功率;
分别为n节点的负荷有功功率和无功功率;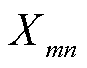 为mn支路电抗;
为mn支路电抗;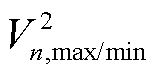 、
、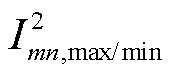 分别为n节点电压二次方上/下限和mn支路电流二次方上/下限;
分别为n节点电压二次方上/下限和mn支路电流二次方上/下限;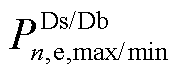 、
、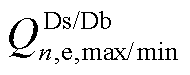 分别为向上级电网购售电有功功率上/下限和无功功率上/下限。
分别为向上级电网购售电有功功率上/下限和无功功率上/下限。
3.2.1 云储能设备
为降低储能的投资成本和使用成本,云储能[25]模式成为微电网运营商的一种选择。CES服务商根据单位容量为CES服务提供定价。各微电网运营商根据自身的储能需求,向CES服务商购买相应容量电、热的云储能设备使用权。云储能服务商和微电网之间通过通信系统交换信息和费用,通过电网和热网进行能源交互。MG通过云储能i的实时储电容量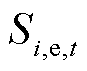 和实时储热容量
和实时储热容量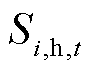 用矩阵形式表示为
用矩阵形式表示为
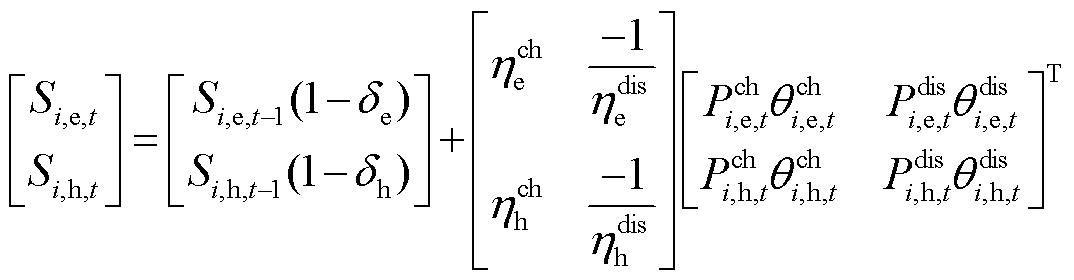 (15)
(15)
式中,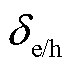 为云储电/热的自损耗系数;
为云储电/热的自损耗系数;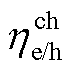 为充电/热的效率;
为充电/热的效率;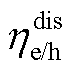 为放电/热的效率;
为放电/热的效率;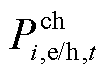 为实时充电/热功率;
为实时充电/热功率;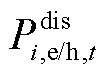 为实时放电/热功率;
为实时放电/热功率;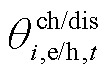 为充放电/热的状态变量。
为充放电/热的状态变量。
MG的云储能实时容量约束表示为
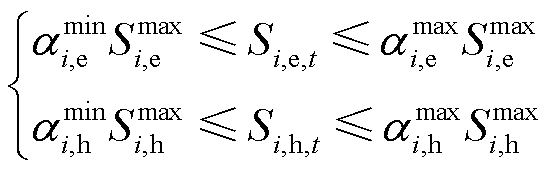 (16)
(16)
式中,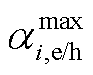 、
、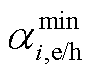 分别为CES荷电/热状态上下限占比系数。
分别为CES荷电/热状态上下限占比系数。
MG租用的云储电容量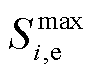 和云储热容量
和云储热容量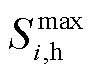 约束为
约束为
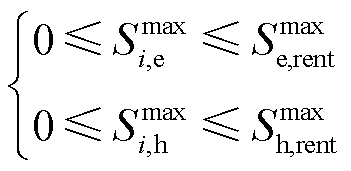 (17)
(17)
式中,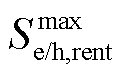 为MG可租用的最大云储电/储热容量。
为MG可租用的最大云储电/储热容量。
为保证下一个周期储能系统的正常运行,应保持储能初始状态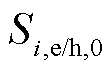 与调度周期结束时储能状态
与调度周期结束时储能状态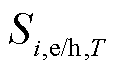 的连续性,有
的连续性,有
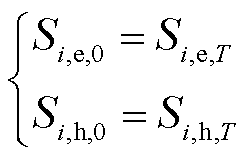 (18)
(18)
为防止CES同时充能、放能,设置约束为
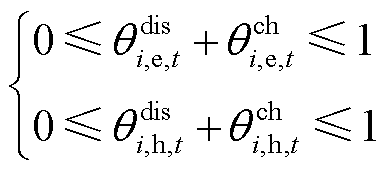 (19)
(19)
MG租用的CES充放电功率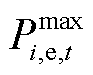 和充放热功率
和充放热功率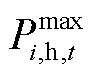 约束为
约束为
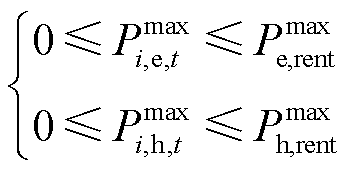 (20)
(20)
式中,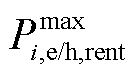 为MG租用的CES最大充放电/热功率。
为MG租用的CES最大充放电/热功率。
MG的实时充放能功率约束表示为
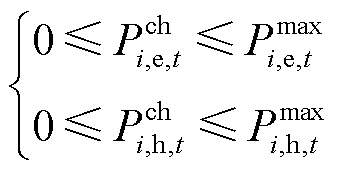 (21)
(21)
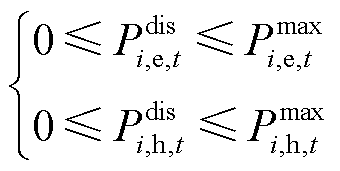 (22)
(22)
3.2.2 微电网内部设备
微电网内部模型如图4所示,微电网根据自身的地理位置等条件选择适合的分布式发电能源。为实现多能利用,加入燃气轮机、热泵、吸收式制冷机、电制冷机等[18]能源耦合设备。同时引入碳捕集和电转气[19]设备来降低CO2的排放,并考虑柔性负荷[18],进一步提高新能源的消纳水平和用户参与的积极性。
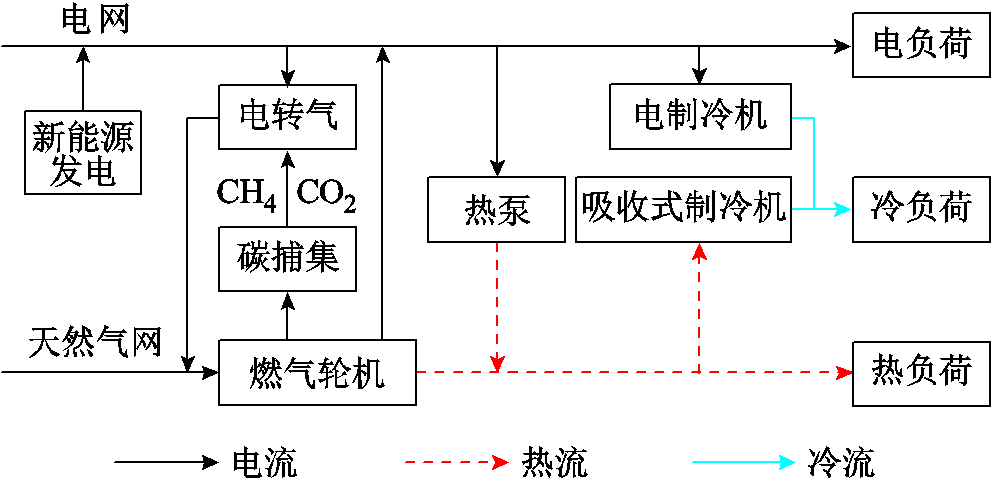
图4 微电网的内部模型
Fig.4 Internal system model of a microgrid
3.2.3 成本模型
微电网与DSO的交互成本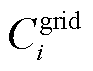 表示为
表示为
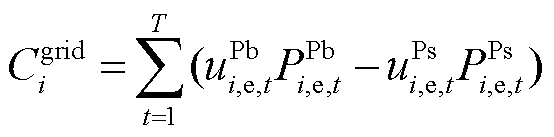 (23)
(23)
微电网的购气成本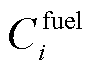 表示为
表示为
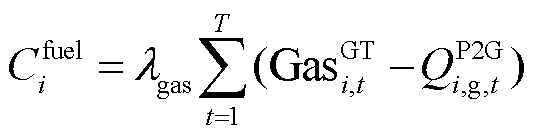 (24)
(24)
式中,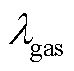 为购气价格;
为购气价格;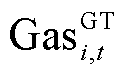 为燃气轮机(GT)耗气量;
为燃气轮机(GT)耗气量;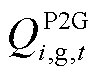 为P2G产气量。
为P2G产气量。
需求响应成本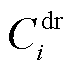 表示为
表示为
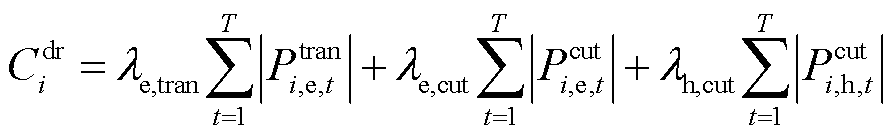 (25)
(25)
式中, 、
、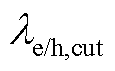 分别为可转移电负荷和可削减电热负荷的补偿价格;
分别为可转移电负荷和可削减电热负荷的补偿价格;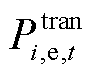 为可转移电负荷;
为可转移电负荷;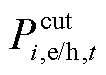 为可削减电/热负荷。
为可削减电/热负荷。
MG内的设备运维成本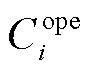 表示为
表示为
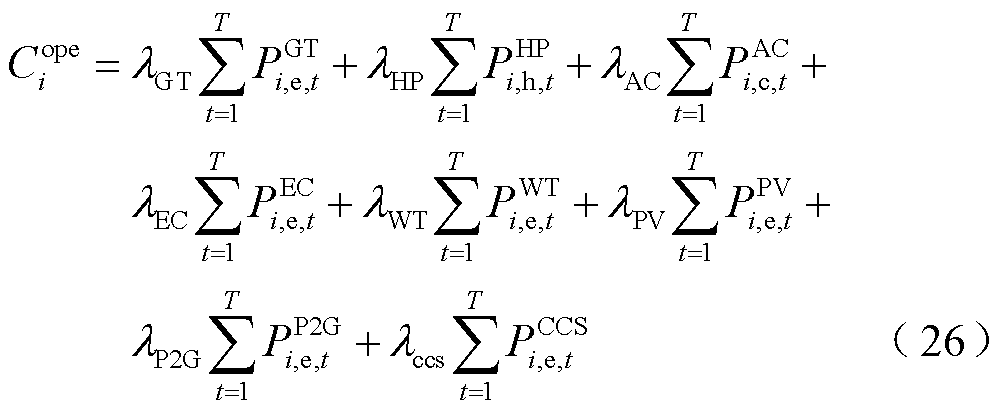
式中,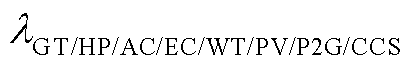 、
、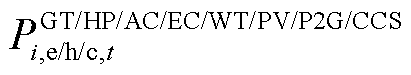 分别对应GT、热泵(HP)、吸收式制冷机(AC)、电制冷机(EC)、风力机组(WT)、光伏机组(PV)、电转气设备(P2G)、碳捕集设备(CCS)的运维价格系数和产能量。
分别对应GT、热泵(HP)、吸收式制冷机(AC)、电制冷机(EC)、风力机组(WT)、光伏机组(PV)、电转气设备(P2G)、碳捕集设备(CCS)的运维价格系数和产能量。
碳交易成本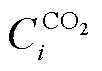 表示为
表示为
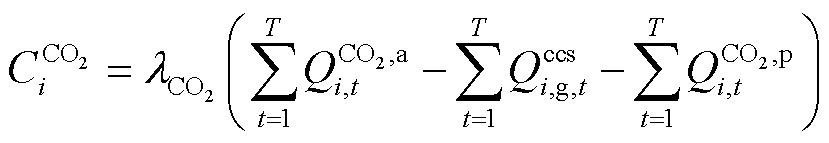 (27)
(27)
式中,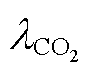 为碳排放价格系数;
为碳排放价格系数;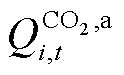 为设备产生CO2量;
为设备产生CO2量;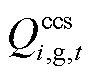 为CCS耗碳量;
为CCS耗碳量;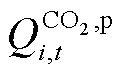 为微电网的CO2配额。
为微电网的CO2配额。
MG每日租借的云储能成本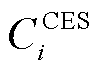 为
为
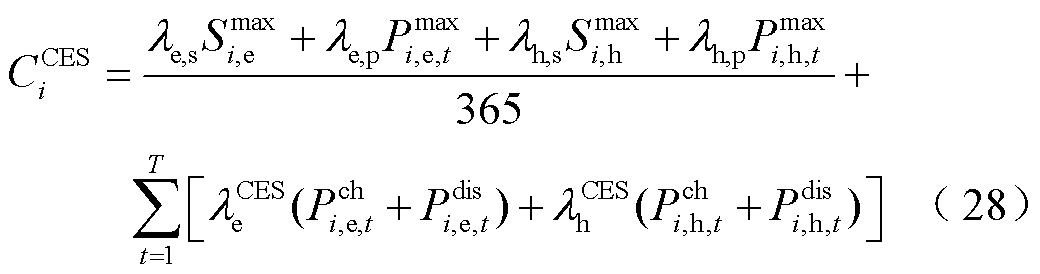
式中,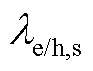 、
、 分别为云储电热的租赁价格系数和运维价格系数;
分别为云储电热的租赁价格系数和运维价格系数; 为CES的充放电热价格系数。
为CES的充放电热价格系数。
微电网的总成本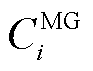 表示为
表示为
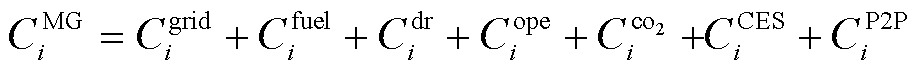 (29)
(29)
式中,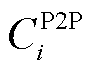 为微电网间的交易支付成本。
为微电网间的交易支付成本。
3.2.4 能量平衡约束
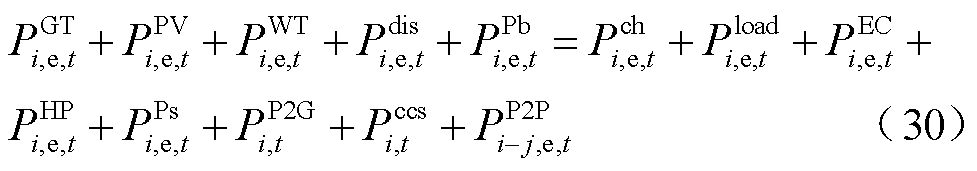
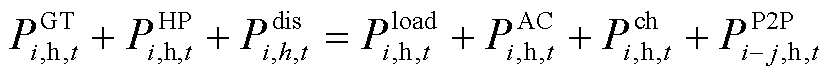 (31)
(31)
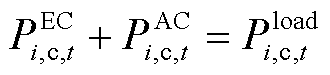 (32)
(32)
式中,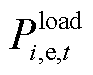 、
、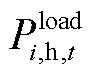 、
、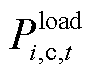 分别为微电网的电负荷、热负荷和冷负荷。
分别为微电网的电负荷、热负荷和冷负荷。
根据微电网的能量贡献进行收益分配,所提非对称纳什议价模型为
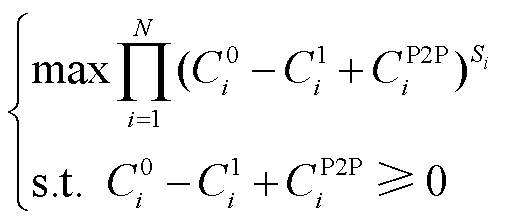 (33)
(33)
式中,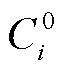 为谈判破裂点,即微电网i合作前的最优成本;
为谈判破裂点,即微电网i合作前的最优成本;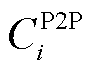 为微电网间的交易支付成本;
为微电网间的交易支付成本;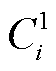 为微电网i不考虑支付的合作成本;
为微电网i不考虑支付的合作成本;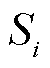 为各微电网议价能力,求解过程见附录。文献[18-20]已证明纳什议价模型可以等价为求解合作效益最大化子问题和能源支付子问题。
为各微电网议价能力,求解过程见附录。文献[18-20]已证明纳什议价模型可以等价为求解合作效益最大化子问题和能源支付子问题。
子问题1:合作效益最大化(P1)
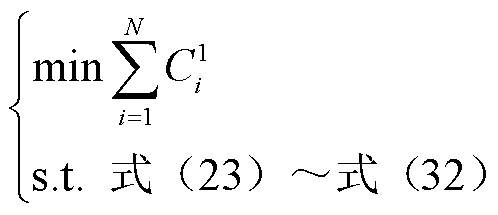 (34)
(34)
子问题2:能源支付子问题(P2)
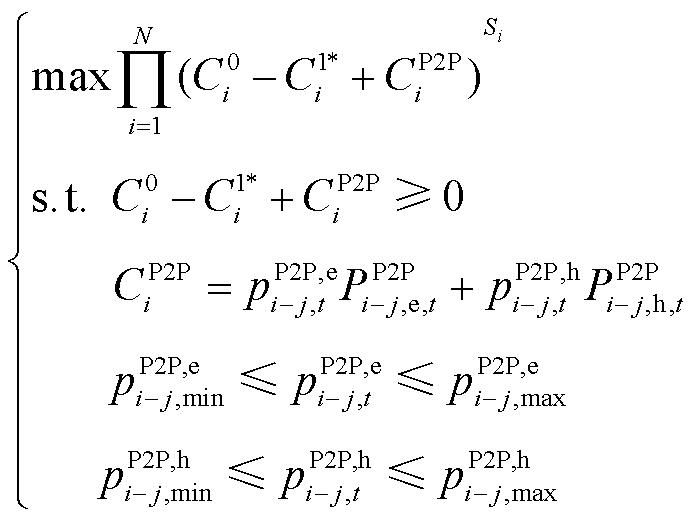 (35)
(35)
式中,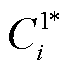 为子问题1求得的最优解;
为子问题1求得的最优解;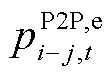 为交互电价;
为交互电价;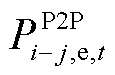 为交互电量;
为交互电量;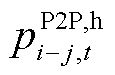 为交互热价;
为交互热价;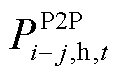 为交互热量;
为交互热量;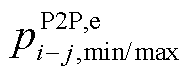 、
、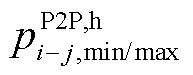 分别为交互电价和交互热价上、下限约束。
分别为交互电价和交互热价上、下限约束。
本文采用两阶段分布鲁棒模型,第一阶段min问题先于不确定性发生前决策与外界的能量交易计划,包含微电网向DSO的购售电量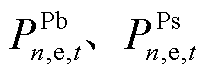 以及微电网间的P2P能源交易量
以及微电网间的P2P能源交易量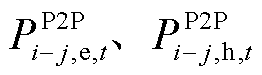 ,用
,用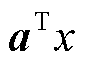 表示,称为预调度阶段;第二阶段max-min问题是在给定第一阶段决策后在不确定集内寻找考虑最恶劣新源出力场景概率下的调度计划,将其反馈给第一阶段重新调整适应该场景的决策,包括微电网自身的设备出力以及云储能的充放能情况,用
表示,称为预调度阶段;第二阶段max-min问题是在给定第一阶段决策后在不确定集内寻找考虑最恶劣新源出力场景概率下的调度计划,将其反馈给第一阶段重新调整适应该场景的决策,包括微电网自身的设备出力以及云储能的充放能情况,用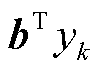 表示,称为再调度阶段。第一阶段与第二阶段通过不断交替优化直到第一阶段决策满足不确定集内所有场景的要求,即
表示,称为再调度阶段。第一阶段与第二阶段通过不断交替优化直到第一阶段决策满足不确定集内所有场景的要求,即
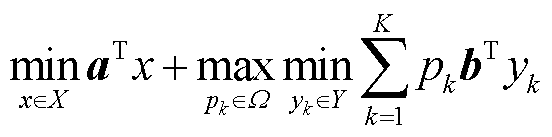 (36)
(36)
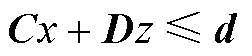 (37)
(37)
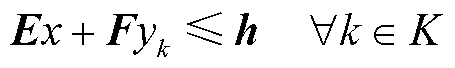 (38)
(38)
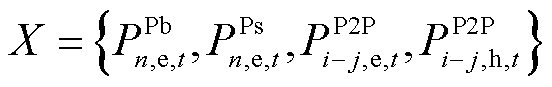 (39)
(39)
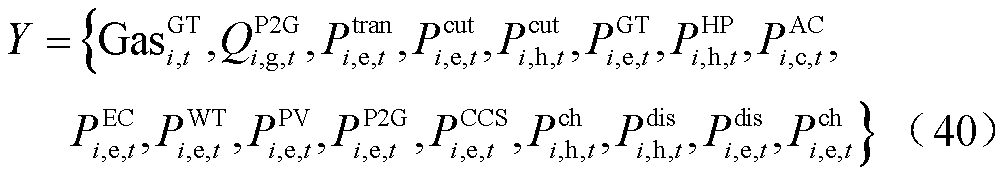
式中,X和Y分别为第一阶段和第二阶段决策变量的集合;C、D、E、F、d、h为常数系数矩阵;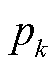 为聚类后情景k出现的概率;
为聚类后情景k出现的概率;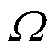 为综合范数的置信区间;K为典型离散场景总数。
为综合范数的置信区间;K为典型离散场景总数。
通过场景聚类得到的场景概率分布存在一定的误差。为使概率分布更接近真实数据,本节给出的不确定性置信集以初始概率分布为中心,通过综合范数对情景概率分布进行约束,得到每个离散情景的最差概率分布。由1-范数和∞-范数组成的综合范数概率置信区间表示为
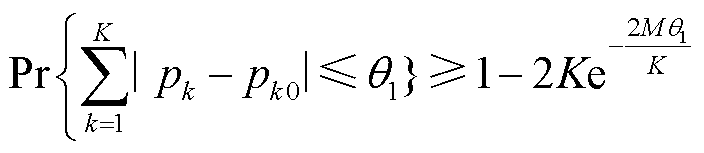 (41)
(41)
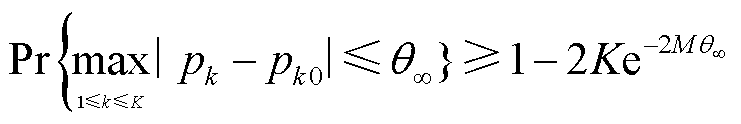 (42)
(42)
式中,Pr{·}为概率算子;M为生成的样本个数;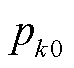 为情景k的初始概率值;
为情景k的初始概率值;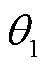 和
和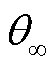 分别为1-范数和∞-范数对应约束下的概率允许偏差极限。
分别为1-范数和∞-范数对应约束下的概率允许偏差极限。
为方便表示,令式(41)和式(42)的等式右边部分分别等于α1和α∞,α1和α∞表示概率分布需要满足的不确定性置信度。式(41)和式(42)可以变换为
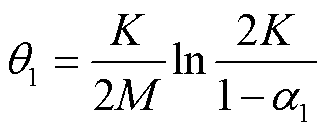 (43)
(43)
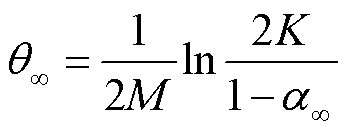 (44)
(44)
概率分布所满足的置信集表示为
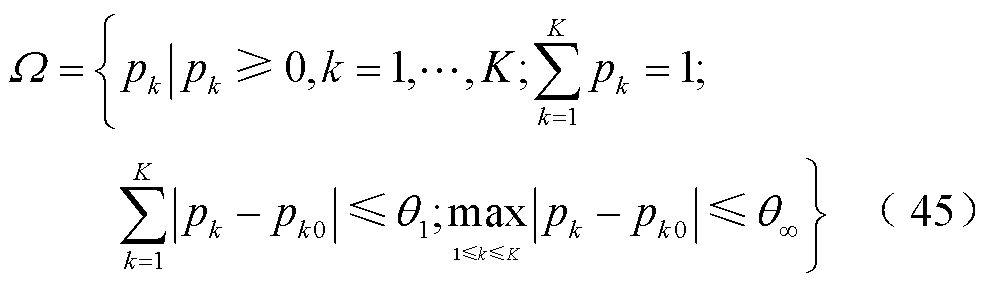
本文采用二分法分布式优化算法[20]来加快DSO对微电网购、售电电价波动的收敛速度。如果两个连续迭代的解相同则使用二分法收缩边界,并迅速收敛到最终迭代结果,求解过程如图5所示。
1)当 ,添加约束条件式(46)。
,添加约束条件式(46)。
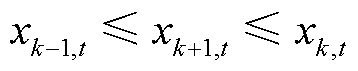 (46)
(46)
2)当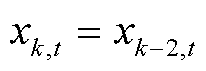 ,添加约束条件式(47)。
,添加约束条件式(47)。
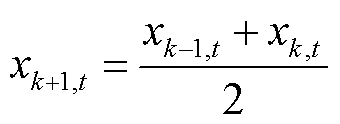 (47)
(47)
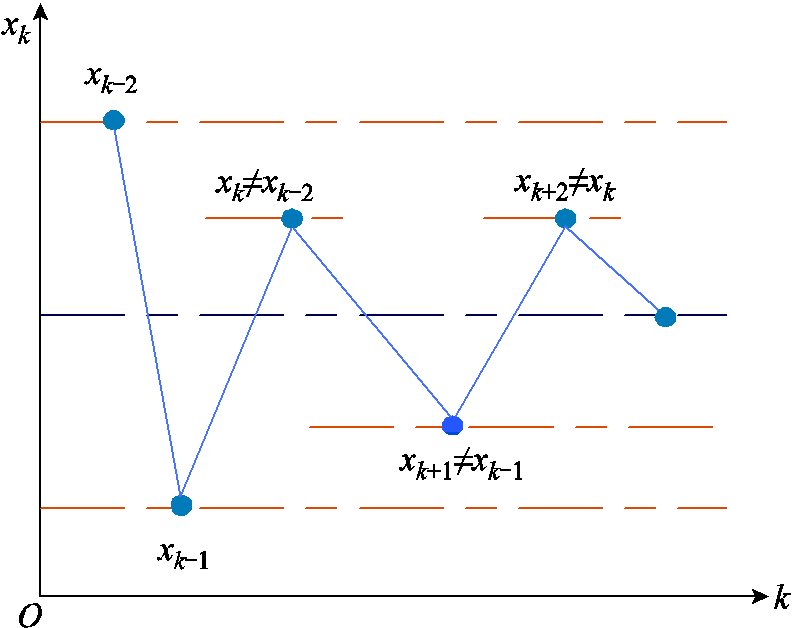
图5 二分法求解流程
Fig.5 Bisection-based method solution process
式中,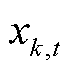 为第k次迭代的电能价格,并设此时为区间上界。
为第k次迭代的电能价格,并设此时为区间上界。
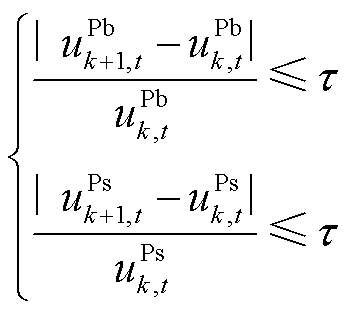 (48)
(48)
在迭代过程中,判断是否满足式(48)的收敛系数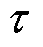 。如果满足收敛,则跳出迭代循环,并输出最优解。
。如果满足收敛,则跳出迭代循环,并输出最优解。
在DSO与微电网联盟的Stackelberg博弈中,采用分布鲁棒优化处理不确定性问题。分布鲁棒优化问题时由于各个场景问题相互独立,可以采用并行求解的方法进行处理。首先分别求解k个min问题,然后再求解max问题,从而避免推导对偶形式以及引入0-1变量造成的求解效率低的问题。在得到最恶劣的场景概率后,再通过C&CG算法进行主、子问题迭代求解。
1)主问题
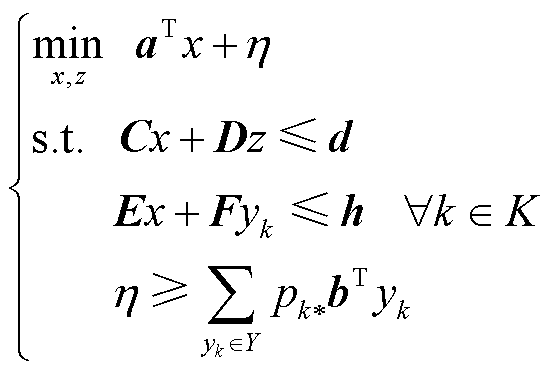 (49)
(49)
式中,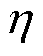 为引入的辅助变量;
为引入的辅助变量;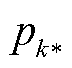 为子问题求得的最恶劣概率分布的优化结果。
为子问题求得的最恶劣概率分布的优化结果。
2)子问题
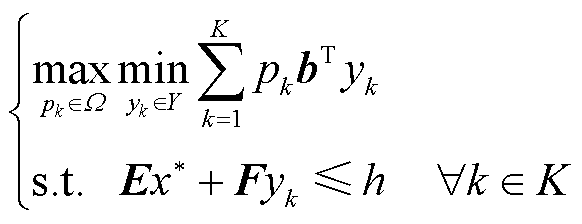 (50)
(50)
式中,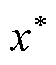 为主问题求得的优化结果,在子问题中为已知量。由于不同场景下内层决策变量相互独立,故子问题的内层可以分解为k个独立的线性规划问题,并利用并行计算方法同时求解。因此子问题式(50)可等效为
为主问题求得的优化结果,在子问题中为已知量。由于不同场景下内层决策变量相互独立,故子问题的内层可以分解为k个独立的线性规划问题,并利用并行计算方法同时求解。因此子问题式(50)可等效为
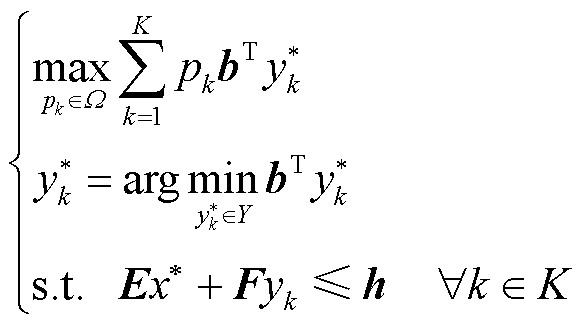 (51)
(51)
式中,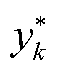 为k场景对应线性规划问题的最优解。
为k场景对应线性规划问题的最优解。
在求解得到微电网间的最优电热交易功率后,根据附录中式(A1)~式(A9)计算各微电网的议价能力,并采用改进ADMM算法求解微电网间的能源交易价格。
5.3.1 改进ADMM算法
考虑到ADMM算法收敛速度主要受到拉格朗日乘子和步长的影响,常规ADMM算法在迭代过程中仅考虑拉格朗日乘子的更新而步长保持不变,从而导致在算法后期可能出现收敛效率降低的问题。因此,本文通过在每次迭代过程中,根据原始残差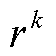 和对偶残差
和对偶残差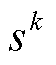 的相对变化动态调整步长
的相对变化动态调整步长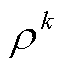 ,从而提升算法的求解效率,即
,从而提升算法的求解效率,即
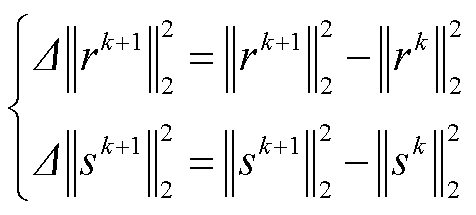 (52)
(52)
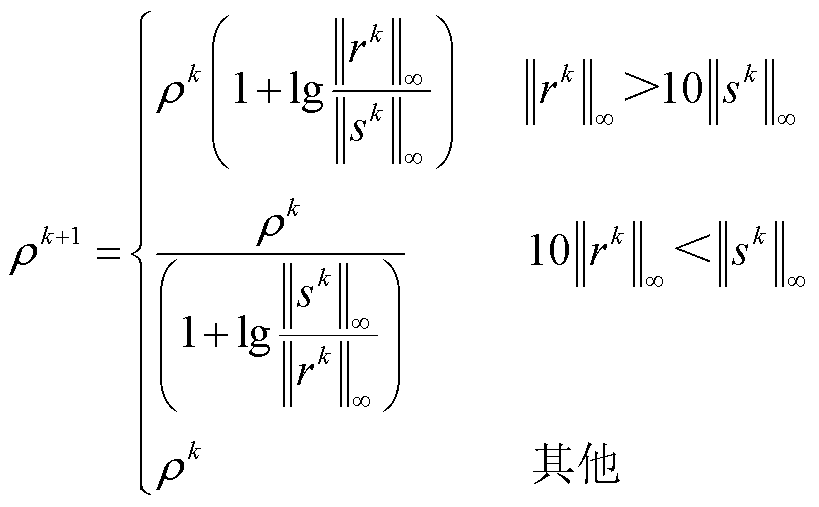 (53)
(53)
式中,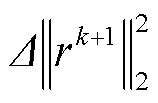 、
、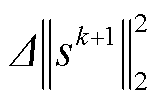 分别为第k次迭代原始残差和对偶残差的值变化。若原始残差和对偶残差的值变化均大于设定值
分别为第k次迭代原始残差和对偶残差的值变化。若原始残差和对偶残差的值变化均大于设定值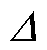 ,则说明收敛性能良好,保持原步长进行下一次迭代。否则,按式(53)对步长进行更新,如果原始残差远大于对偶残差,则步长将增大,从而导致违反原始可行性的严重惩罚;如果对偶残差远大于原始残差,则由于对偶可行性收敛,步长减小。在这种情况下,原始可行度和对偶可行度的收敛可以交替平衡。
,则说明收敛性能良好,保持原步长进行下一次迭代。否则,按式(53)对步长进行更新,如果原始残差远大于对偶残差,则步长将增大,从而导致违反原始可行性的严重惩罚;如果对偶残差远大于原始残差,则由于对偶可行性收敛,步长减小。在这种情况下,原始可行度和对偶可行度的收敛可以交替平衡。
5.3.2 改进ADMM算法求解过程
为确保两个微电网间的交易价格相等,对其P2P交易价格进行解耦,有
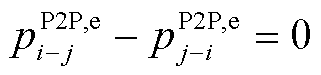 (54)
(54)
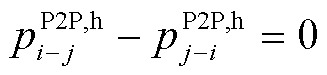 (55)
(55)
改进ADMM算法过程:
1)根据式(A1)~式(A9)计算各微电网议价能力。
2)建立式(35)的增广拉格朗日函数,有
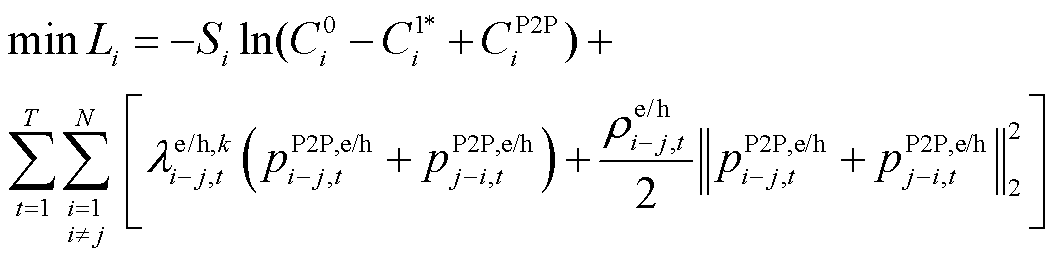
3)各微电网按照以下步骤更新。
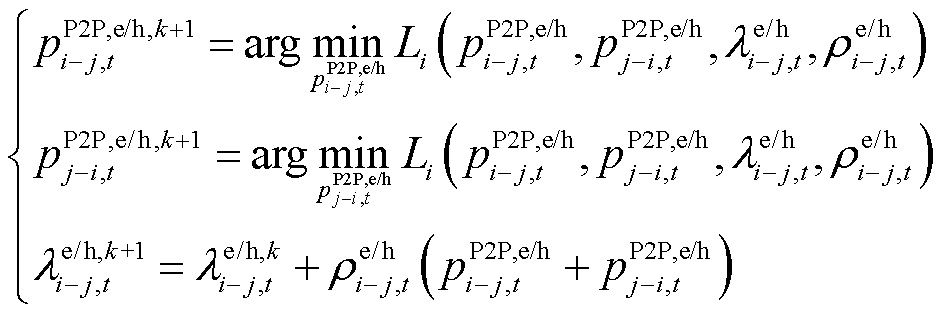
4)判断每个微电网是否均满足收敛条件,若满足则停止迭代,输出多园区系统调度结果;否则,更新拉格朗日乘子和步长,返回步骤2)继续迭代。
图6为本研究构建的分层调度求解框架。上层是考虑分布鲁棒优化的Stackelberg博弈,采用二分法和列与生成算法求解。下层为合作博弈的利益分配问题,采用改进ADMM算法求解。
具体流程为:
1)初始化二分法参数,生成初始DSO电价 、
、 。
。
2)在二分法的每次迭代中,各微电网根据DSO电价基于C&CG算法并行计算各自内部优化问题,保证微电网联盟收益最大化(P1)。基于C&CG算法的求解流程如下:
(1)初始化不确定变量。设定下界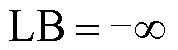 ,上界
,上界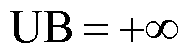 ,迭代次数
,迭代次数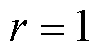 ,收敛误差
,收敛误差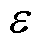 。
。
(2)求解主问题式(49)。将主问题的目标函数值作为新的下界。
(3)求解子问题式(51)。将求得的主问题最优解代入子问题中,求解得到子问题的目标函数值,更新上界。
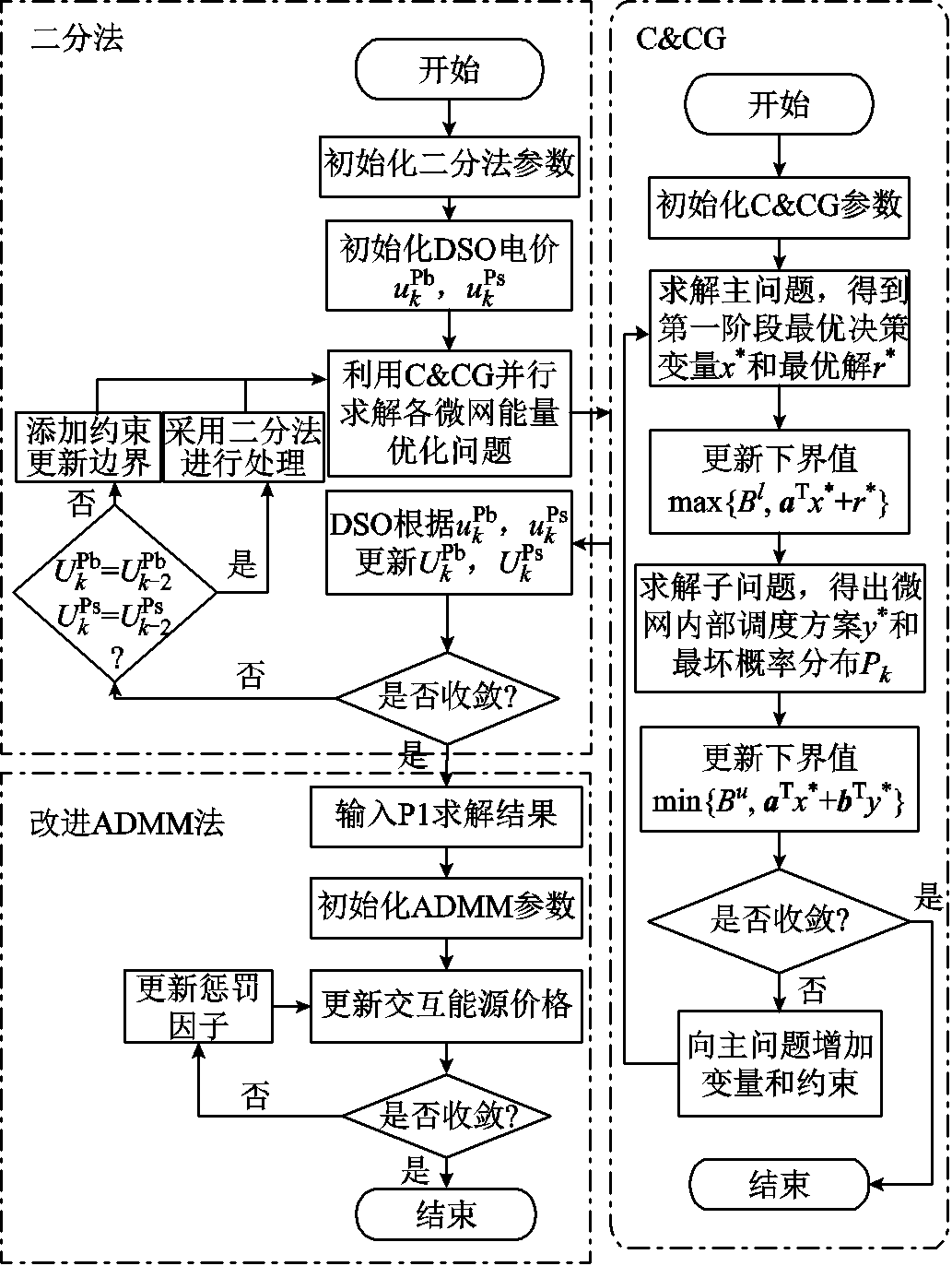
图6 分层调度求解框架
Fig.6 Hierarchical scheduling solution framework
(4)满足收敛条件,则停止迭代,返回微电网i的最优解;否则,在主问题中增加关于场景约束继续迭代。
3)DSO根据各微电网的购售电能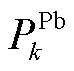 、
、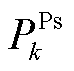 更新电价
更新电价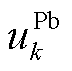 ,
,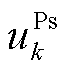 ,保证自身利益最大化。
,保证自身利益最大化。
4) 判断是否满足二分法收敛条件,若不满足,使用二分法添加约束,并返回步骤2)继续迭代;若满足收敛条件,将微电网间的能量交易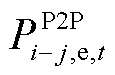 、
、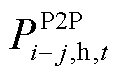 发送至下层,并采用改进ADMM算法求解微电网间的能源交易价格问题(P2)。
发送至下层,并采用改进ADMM算法求解微电网间的能源交易价格问题(P2)。
本文采用IEEE 33节点算例进行实例分析,3个微电网分别放在6、9、28节点,并使用Matlab R2020b结合工具包Matpower,调用商业求解器Gurobi 9.1对优化程序进行求解。以华北某地区2年的PV和WT的日前功率预测数据及实际功率数据作为样本集,数据间隔为1 h。其中,样本集的80%用于模型训练,20%用于测试。IEEE 33节点运行状态见附录第2小节,微电网参数与能源价格见附表1~附表3。
6.1.1 基于Wasserstein距离的CGAN的性能评估
在本节中,使用以下两个评价指标来评估本文所提CGAN场景生成方法的性能。
1)Wasserstein距离[26]。模型训练的目标是使损失尽可能小,即最小化真实分布和生成分布之间的Wasserstein距离。随着Wasserstein距离不断减小,最终判别器将无法准确区分输入样本的来源,可再生能源输出场景将充分反映历史数据的真实分布。
2)最大平均差异(Maximum Mean Discrepancy, MMD)[27]是希尔伯特空间中两个分布之间差异的度量,它可用于测量生成的数据集和真实数据集之间的距离。MMD度量越小,两个分布越接近,意味着训练性能越好。
以微电网1为例,评价指标在训练过程中的变化如图7所示。可以发现,本文的CGAN方法生成的场景与风电真实值之间的误差很小,能很好地反映新能源的真实场景。
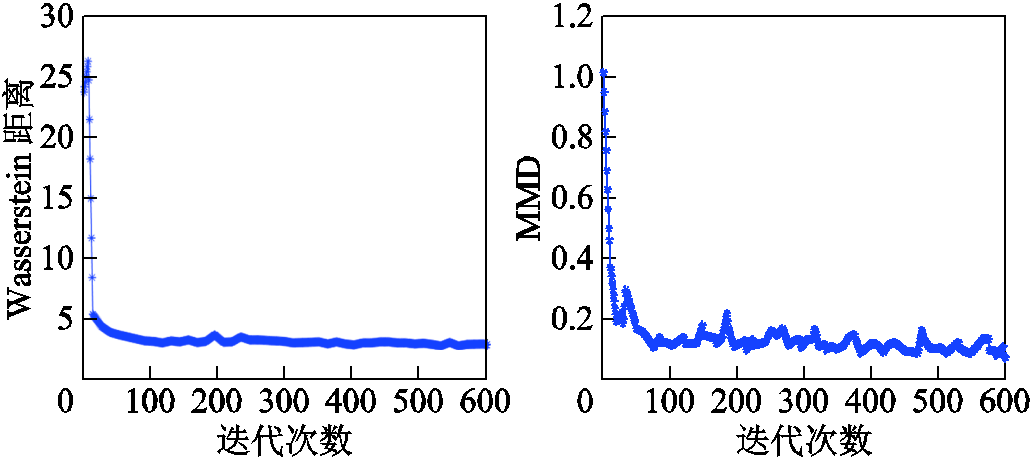
图7 训练期间评估指标的变化
Fig.7 Changes of the evaluation metrics during training
6.1.2 基于Wasserstein距离的CGAN性能对比
为进一步验证本文所提场景生成方法的有效性,将本文提出的考虑Wasserstein距离的CGAN与基于拉丁超立方法(Latin Hypercube Sampling, LHS)[28]以及常规CGAN的场景生成方法[15]进行对比,以风机发电场景生成为例,具体分析如下。
不同风电场景生成方法性能对比见表1。可以看出,LHS方法除期望与真实场景相近外,峰度指标具有明显的误差,且LHS场景与常规CGAN场景的MMD值均大于本文所提CGAN场景,这表明本文提出的的CGAN方法能够更准确地学习真实样本的出力特征。此外,本文的场景生成时间低于常规CGAN,这是由于本文考虑Wasserstein距离的CGAN方法消除了模式崩溃和梯度消失问题,从而进一步提升了算法的求解效率。
表1 不同场景生成方法对比
Tab.1 Comparison of different scenario generation methods

场景期望值/MW, 误差(%)峰度,误差(%)MMD运行时间/s 真实1.50, 03.73, 0—— LHS1.53, 23.81, 2.140.26431.7 常规CGAN1.54, 2.73.7, 0.80.17407.51 本文CGAN1.53, 23.68, 1.30.11326.89
图8显示了通过改进CGAN场景生成和 K-means++聚类获得的典型可再生输出场景及其概率。由图8可以看出,本文的改进CGAN方法生成的1 000个场景集几乎可以覆盖真实功率曲线的范围,且功率区间宽度较小。各微电网聚类后的Davies Bouldin指数分别为为1.22、1.31、1.42,廓形系数分别为0.46、0.4、0.35。结果表明聚类性能良好,且聚类得到典型场景可以完全包含真实功率曲线,这表明所提场景生成与削减方法能够很好地刻画新能源出力的不确定性区间。
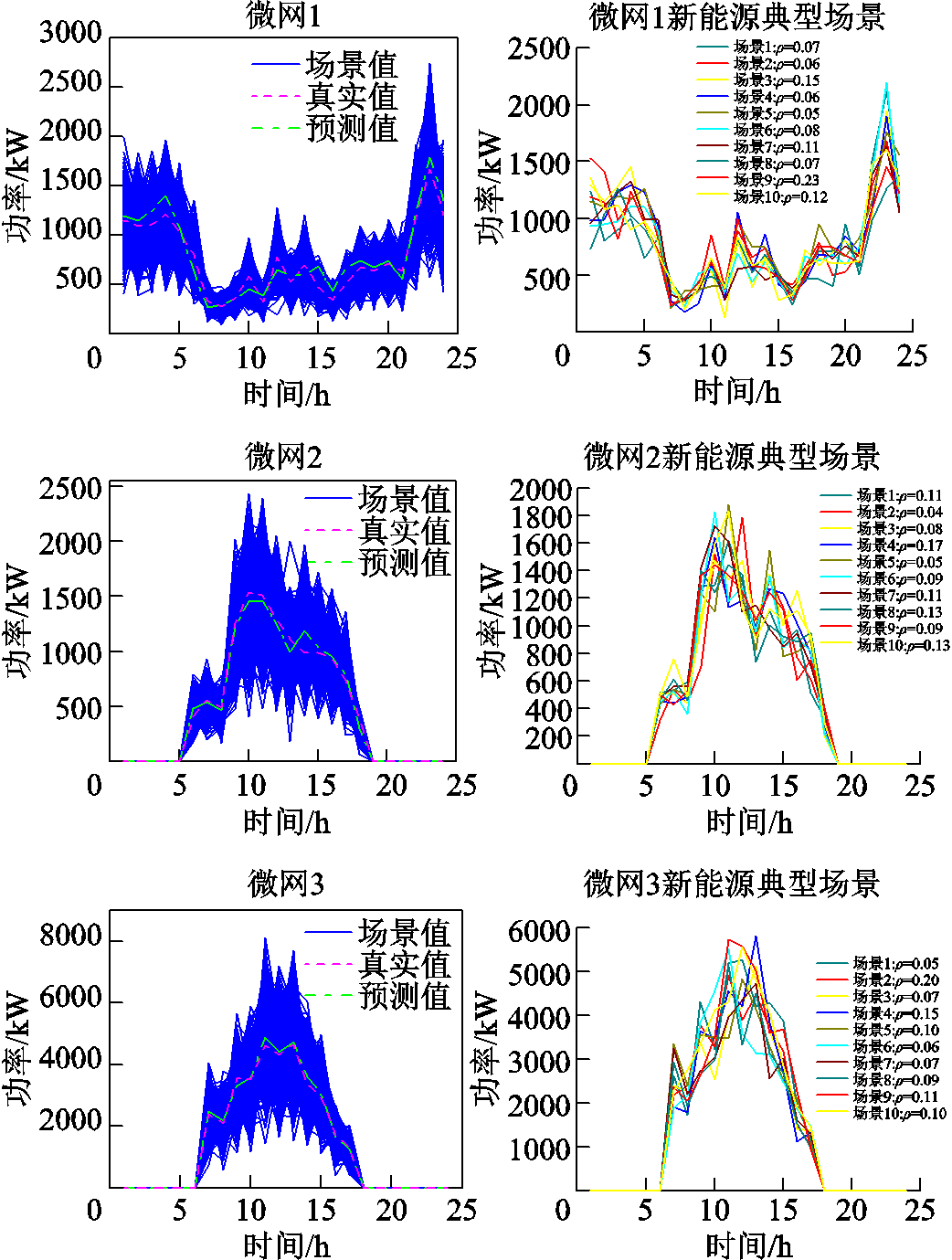
图8 各微电网的场景生成与聚类结果
Fig.8 Scenario generation and clustering results for MG
为进一步验证配电网最优潮流优化对系统经济稳定运行的影响,本节设定两种对比方案进行分析。方案1为本文的动态潮流约束,方案2为不考虑配电网潮流约束。对两种方案的网损,电压偏移和配电网的网损成本[24]进行分析。
上述两种方案下配电网运行指标对比分析见表2。可以看出,方案1相较于方案2,网损降低49.94%、电压偏移指标降低57.45%,配电网网损成本降低639.63元,表明本文所提模型有利于提高系统运行的稳定性和经济性。
表2 运行指标对比分析
Tab.2 Comparative analysis of operation indicators

方案网损/(kW·h)电压偏移(%)配电网网损成本/元 11 347.64±2673.82 22 691.94±4.71 313.45
6.4.1 Stackelberg博弈结果
上层优化迭代结果如图9所示。由图9可以看出,Stackelberg博弈的均衡解在第19次迭代后收敛,表明了二分法在解决该问题上的有效性。此外,经计算得出内嵌C&CG算法的平均迭代次数为2.1次,可以做到快速收敛,体现了本文所提算法的良好性能,能够满足提前调度的需求。
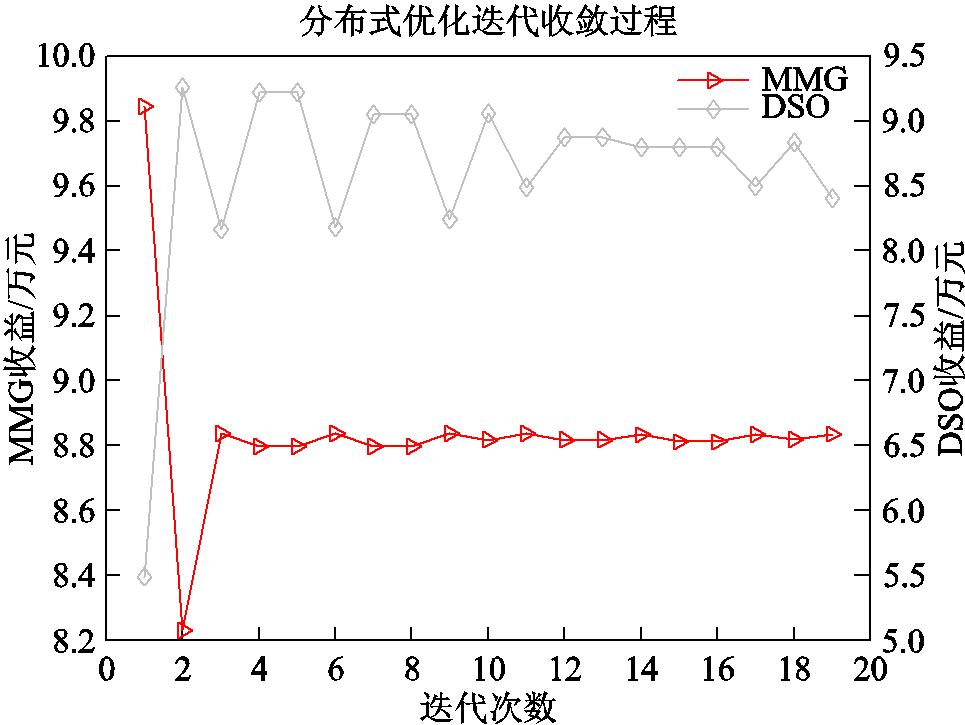
图9 上层优化迭代结果
Fig.9 Iterative results of upper optimization
上层调度中DSO对MMG的购售电价如图10所示,可以得出DSO向MMG购售电价与DSO向主电网购售电价的趋势是大致相同的。而根据购售电价信息,07:00—22:00时段DSO向主网购电价偏高,DSO向MMG售电价也偏高,因此MMG更倾向于进行内部微电网之间的能量交易,减少向DSO购电的需求。
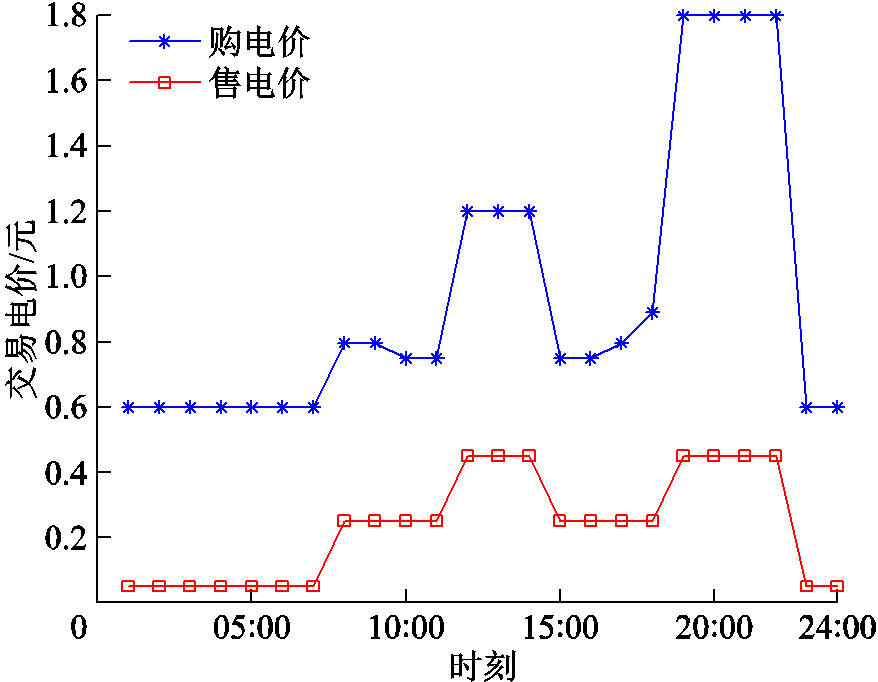
图10 DSO制定电价
Fig.10 Electricity price of DSO
6.4.2 合作博弈结果
在DSO电价的指导下,下层微电网合作运营的电能和热能交易情况如图11所示。在01:00—07:00期间,由于风电能源发电量较高,因此MG1承担了主要的电力交易量。在08:00—15:00期间,MG2光伏发电量大,用电量少,产生的过剩电量向其他微电网出售。在热能交易过程中,MG1需要的热能较多,MG3会产生过剩热能并向其他两个微电网出售。同时,可以看出微电网间的能量交互功率和为0,满足电能热能间的交互约束。
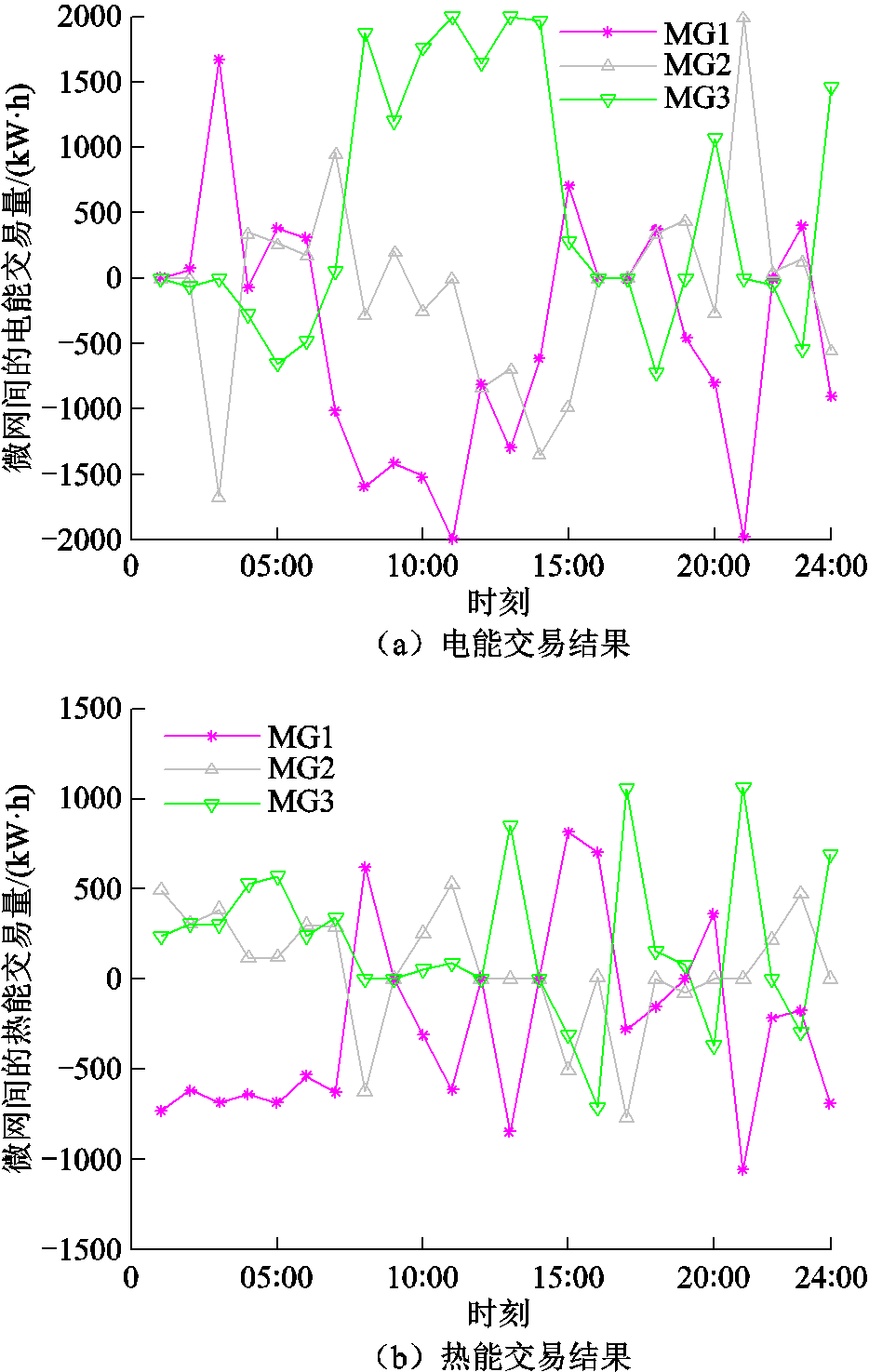
图11 微电网间的能量交易
Fig.11 Energy interaction results between microgrids
微电网间的能量交易价格与交易量相对应,如图12所示,各微电网参与P2P交易贡献的能量越多,微电网的议价能力也随之增强,从而获得更高的能量交易价格。此外,微电网间的交互电价低于DSO制定的购电价格,各微电网能够更有效地进行能量交互,促进多主体之间的合作,同时也保障了各个参与者自身利益。
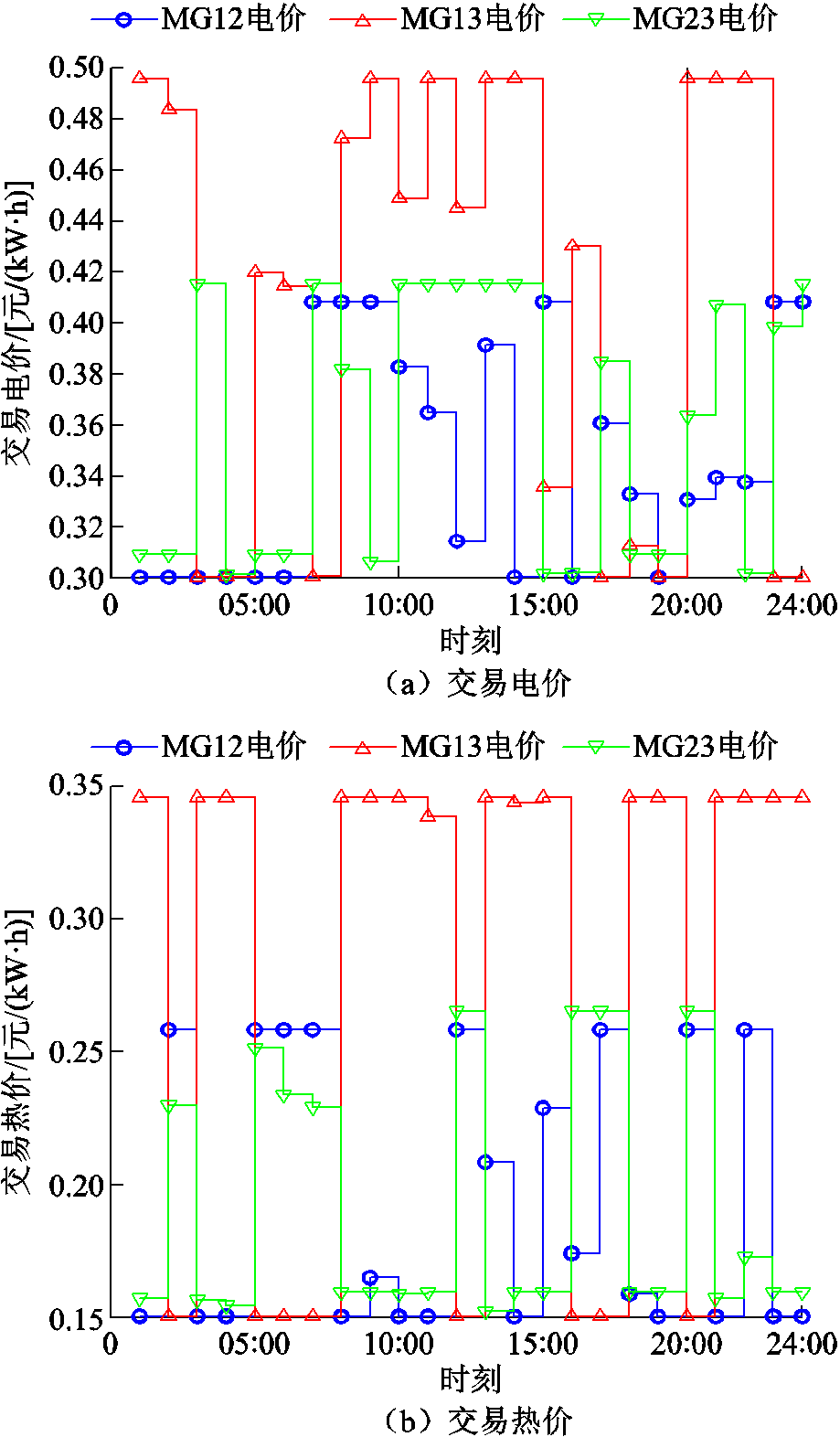
图12 微电网间的能量交易价格
Fig.12 Energy trading prices between microgrids
6.4.3 微电网内部优化结果
图13为微电网1内部能量优化结果。微电网1风力充沛,00:00—06:00和13:00—16:00处于本地用电低谷时段,多余的风力发电量通过EC、P2G-CCS以及HP进行消纳,多余的电力出售给外电网和其他微电网。07:00—12:00和16:00—23:00时段处于用电高峰期,消纳全部的风电出力后,微电网1还通过增强GT机组出力,向其他微电网购电,云储能系统放电、向上级电网购电以及需求响应等措施来满足负荷的需求,降低了园区的总用能成本。在热功率的优化方面,在00:00—07:00时,微电网1通过HP出力、GT出力、云储能充热需求响应以及P2P热能交易等手段维持热力平衡。在19:00—22:00时,GT机组热出力过多,通过AC机组耗热和云储能放热消纳多余的热量,缓解EC的压力。冷功率的分析同理。总体来看,微电网1通过P2P交易,有效地降低了向DSO的购电成本,并提高微电网系统的收益。
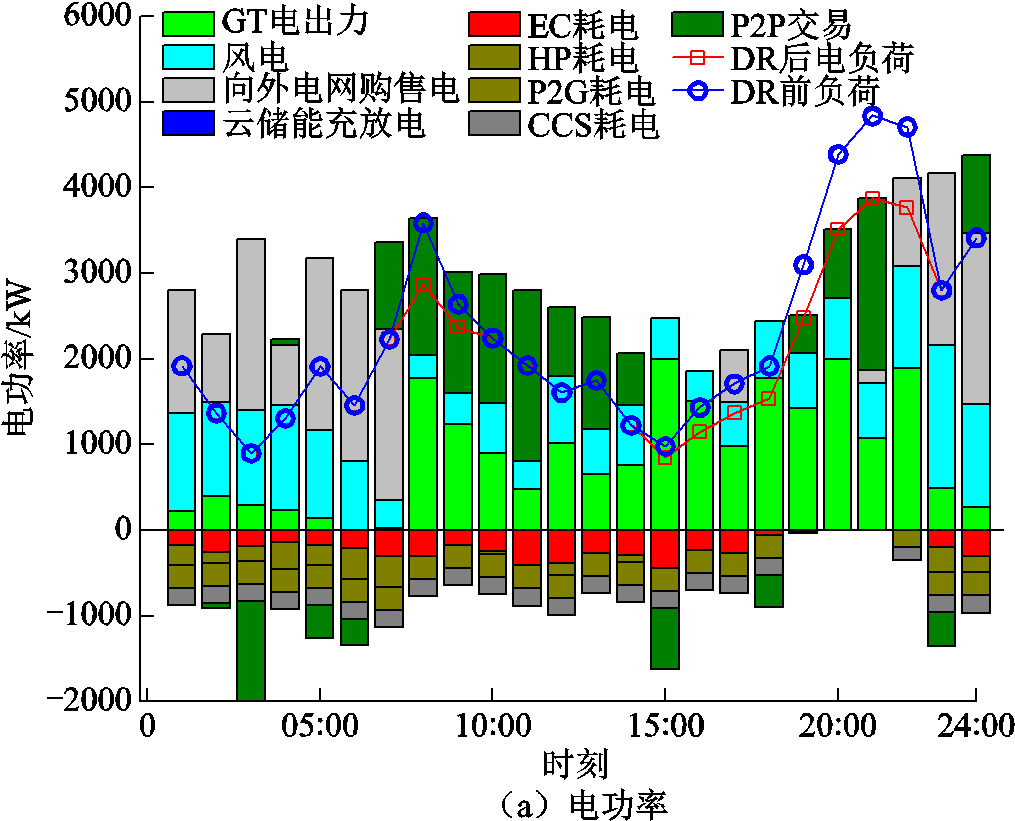
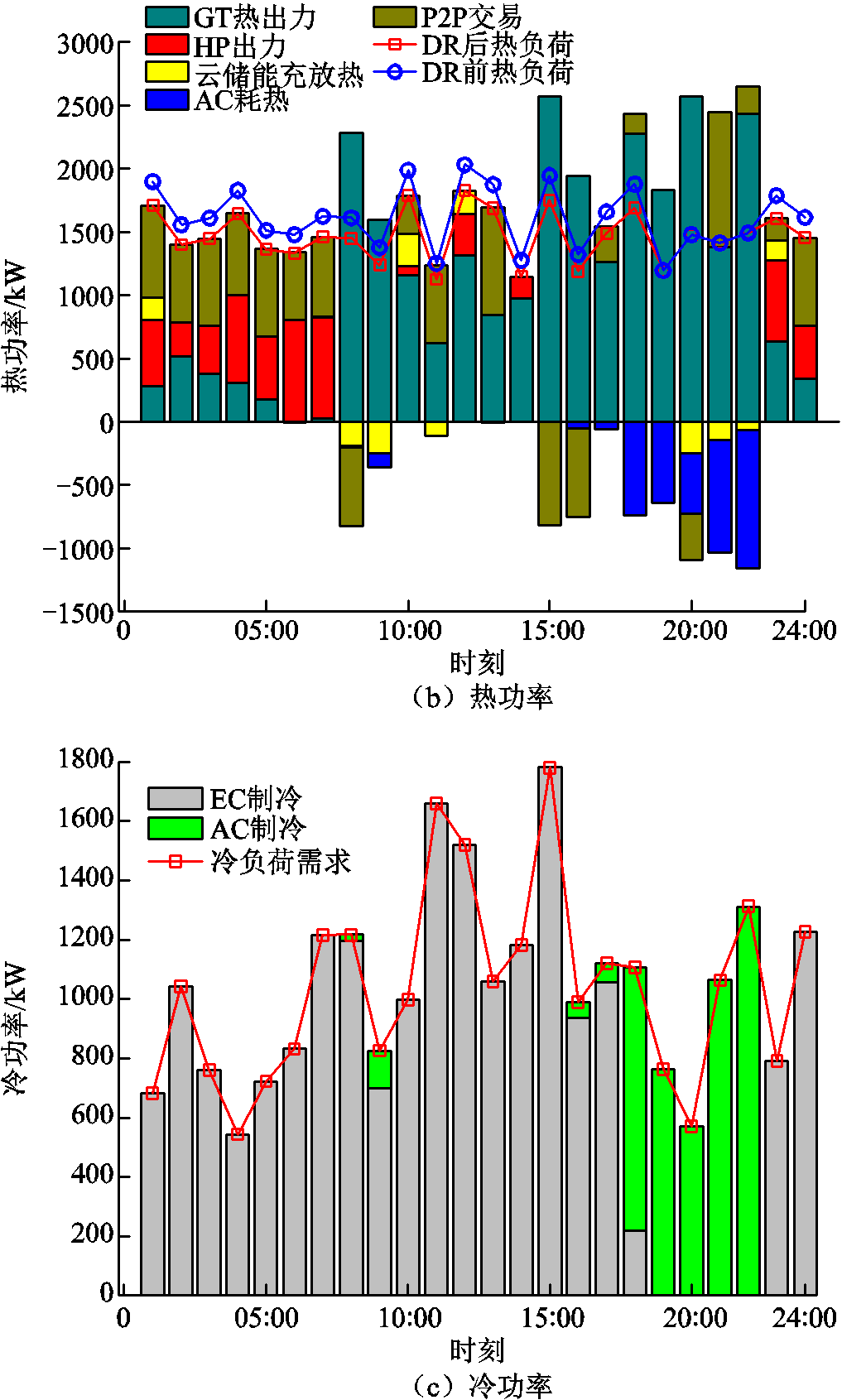
图13 微电网1的功率平衡
Fig.13 Power balance of MG1
为验证本文所提方法的有效性,设置了以下四种不同模式进行对比分析,不同模式下的优化结果见表3。
模式1:仅考虑上层配电网与下层微电网联盟之间的Stackelberg博弈,不考虑联盟内各微电网之间的P2P能量交易,微电网内不考虑储能系统。
模式2:在模式1的基础上,考虑联盟内各微电网之间的P2P能量交易,并采用一般的纳什议价理论解决各主体间的利润分配问题。
模式3:在模式2的基础上,增加了各微电网租赁云储能的情况。
模式4:在模式3的基础上,采用非对称纳什议价理论解决各主体间的利润分配问题,即本文研究模型。
与模式1相比,模式2的三个微电网的最终成本以及联盟总成本均呈现下降趋势,分别降低了1.69%、3.90%、11.67%和4.66%,这表明微电网之间的P2P能量交易能够显著降低各微电网的运行成本。与模式2相比,模式3中的微电网联盟减少了向上层配电网的购电功率19 354.64 kW,同时降低了微电网联盟总成本4 356.64元。这是由于模式3中云储能设备的加入降低了下层微电网联盟对上层配电网的依赖,且在电价低或发电量大的时段存储多余的电能,并在高峰时段释放,从而有效地减少了微电网的购电成本。相较于模式3,模式4在利益分配方面考虑了微电网间的非对称纳什议价方式,根据能量贡献的大小进行利益分配。其中微电网3能量贡献较大,获得更高的能量交易收益,进一步降低了其运营成本,这表明本文的非对称议价方式可以更公平合理地分配微电网的合作收益。
表3 不同模式下的优化结果
Tab.3 Optimization results under different scenarios
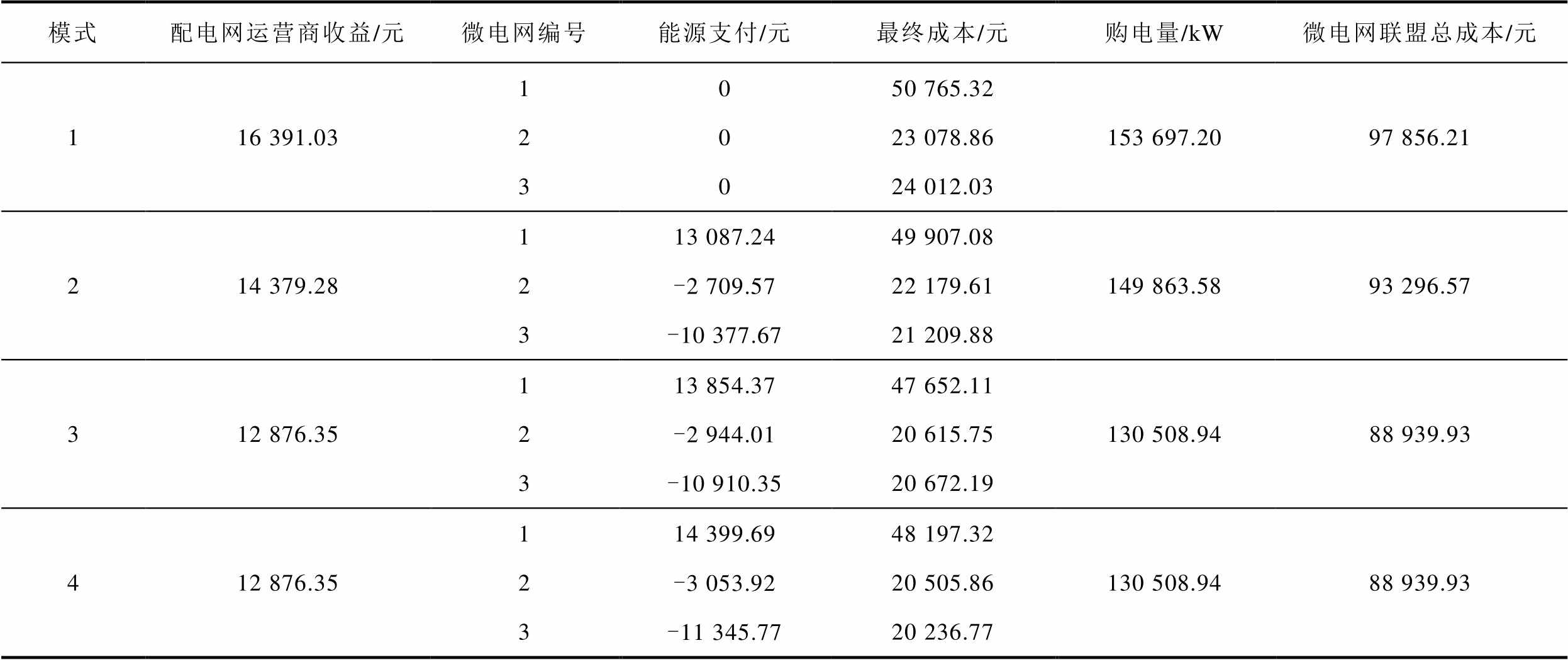
模式配电网运营商收益/元微电网编号能源支付/元最终成本/元购电量/kW微电网联盟总成本/元 116 391.031050 765.32153 697.20 97 856.21 2023 078.86 3024 012.03 214 379.28113 087.2449 907.08149 863.58 93 296.57 2-2 709.5722 179.61 3-10 377.6721 209.88 312 876.35113 854.3747 652.11130 508.94 88 939.93 2-2 944.0120 615.75 3-10 910.3520 672.19 412 876.35114 399.6948 197.32130 508.94 88 939.93 2-3 053.9220 505.86 3-11 345.7720 236.77
6.6.1 优化方法对比
不同的两阶段优化方法的经济性对比见表4。由表4可以看出,两阶段随机优化的总调度成本最低,这是由于随机优化对于典型场景是基于概率分布进行的,忽略了场景的波动性,在实际运行中需要增加额外成本去应对。传统两阶段鲁棒优化成本最高,这是因为仅考虑最恶劣典型场景,故采用该方法的系统决策者保守性最强。混合两阶段鲁棒的再调度成本和总调度成本位于两阶段随机优化和传统两阶段鲁棒优化之间,能够克服传统两阶段鲁棒优化过于保守的问题。
表4 不同优化方法经济性对比
Tab.4 Economic comparison of different optimization methods

优化方法成本/元 预调度再调度总调度 两阶段随机优化40 012.71441 077.61781 091.332 传统两阶段鲁棒优化37 132.36255 641.89992 774.261 两阶段分布鲁棒优化40 485.87648 454.05288 939.928
6.6.2 不同置信水平的分析
为了分析置信水平对MMG运营成本的影响,设置M=1 000。不同置信水平下合作联盟运营成本对比见表5。随着置信水平α1和α∞的增加,合作联盟的成本增加。原因是置信区间变大,新能源发电最恶劣场景出现的概率增加,各微电网需要调控成本来应对风光的不确定性,从而导致合作联盟总的成本增加。
表5 不同置信水平运营成本对比
Tab.5 Cost comparison of results at different confidence levels

联盟总成本/元 0.588 810.7988 890.0688 903.79 0.888 876.9488 897.5288 953.27 0.9988 915.4188 939.9389 010.14
为了进一步分析综合范数置信区间的优越性,表6选取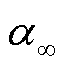 为0.8,
为0.8,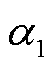 分别为0.2、0.5、0.99的综合范数与仅考虑∞-范数约束的优化结果进行比较。可以看出,当历史数据数量不变时,综合范数置信区间下的优化结果比只考虑∞-范数置信区间下的优化结果更经济。这是因为综合范数置信区间更小,可以更准确地表征风光发电的不确定性,从而降低了运营成本。表7为综合范数与仅考虑1-范数的优化结果比较。同样地,综合范数约束条件下的联盟总成本值较仅考虑1-范数约束条件下的更低,保守度更低。
分别为0.2、0.5、0.99的综合范数与仅考虑∞-范数约束的优化结果进行比较。可以看出,当历史数据数量不变时,综合范数置信区间下的优化结果比只考虑∞-范数置信区间下的优化结果更经济。这是因为综合范数置信区间更小,可以更准确地表征风光发电的不确定性,从而降低了运营成本。表7为综合范数与仅考虑1-范数的优化结果比较。同样地,综合范数约束条件下的联盟总成本值较仅考虑1-范数约束条件下的更低,保守度更低。
表6 综合范数与∞-范数成本对比
Tab.6 Comparison of comprehensive norm and ∞-norm costs

联盟总成本/元 综合范数∞-范数 0.288 876.9489 037.12 0.588 897.5289 037.12 0.9988 953.2789 037.12
表7 综合范数与1-范数成本对比
Tab.7 Comparison of comprehensive norm and 1-normcost

联盟总成本/元 综合范数1-范数 0.588 890.0689 019.72 0.888 897.5289 019.72 0.9988 939.9389 019.72
为验证本文改进ADMM算法的有效性,在本小节主要比较了集中式算法、传统ADMM算法和本文的改进ADMM算法性能。算法性能对比见表8。
表8 算法性能对比
Tab.8 Comparison of the algorithm efficiency

算法计算时间/s迭代次数能源支付/元(微电网1) 集中式103—14 350.14 传统ADMM2313314 431.72 改进ADMM1241714 399.69
由表8可以看出,改进ADMM算法的计算时间和迭代次数明显小于传统ADMM算法,表明本文的方法有助于提高算法的收敛性能。改进ADMM算法与集中式算法在计算时间和运行结果上差别不大,表明改进ADMM的分布式求解可以接近全局最优解。而改进ADMM算法只需要参与者之间有限的信息交换,具有保护参与者隐私的优点。
本文以考虑新能源出力不确定场景下的多微电网接入配电网能量交易为研究对象,提出了一种基于混合博弈的DSO与MMG的两阶段分布鲁棒优化模型。上层利用Stackelberg博弈描述DSO与MMG的关系,下层建立基于P2P多能交易贡献率的非对称纳什议价模型,主要结论如下:
1)提出了一种改进CGAN的场景生成方法,用于生成DRO集合的初始新能源场景,能够更准确地描述新能源的不确定性。此外,本文提出的两阶段DRO模型在保证鲁棒性的基础上能够避免传统两阶段鲁棒优化过于保守的问题,通过选择合适的综合范数的概率不确定度预算,可以很好地平衡微电网系统的经济性和保守性。
2)MMG通过租赁云储能系统、实施需求侧响应策略和进行微电网间电能与热能交易,降低了微电网联盟的运行成本。在与DSO进行互动的同时,又降低了对配电网的依赖,以更大程度地实现自身的能源独立,并促进新能源的消纳。
3)本文构建的混合博弈模型确定了DSO的购售价格和微电网间的能源交易价格,从而确保DSO和MMG的协同运行,并按照微电网的多能交易能量贡献大小合理分配合作收益,有效地激发了微电网主体参与能量交易的积极性。
4)提出了一种耦合C&CG的二分法求解上层能源交易问题,并用改进ADMM算法求解利益分配问题,各主体间仅交换有限的信息,有效地保护了各主体隐私,并提高了模型的求解效率。
在后续的研究中,为提升模型的准确性,将进一步考虑各微电网的热能交易过程中产生的热损耗问题以及损耗成本的分配问题。
附 录
1. 微电网间的议价能力
议价能力是决定收益分配的重要因素,因此通过非线性能量映射法[18]量化各主体的议价能力。本文将各微电网的电能贡献和热能贡献进行量化,具体为
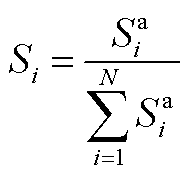 (A1)
(A1)
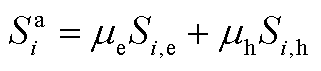 (A2)
(A2)
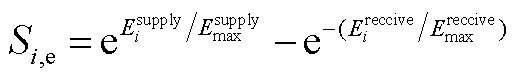 (A3)
(A3)
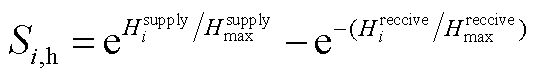 (A4)
(A4)
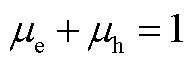 (A5)
(A5)
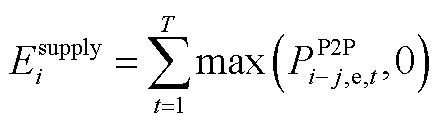 (A6)
(A6)
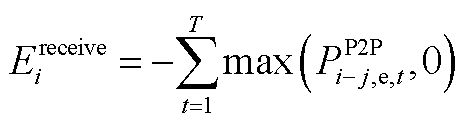 (A7)
(A7)
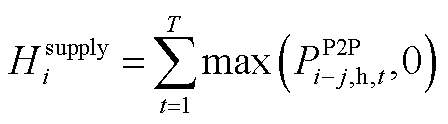 (A8)
(A8)
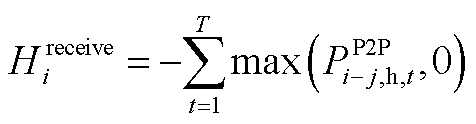 (A9)
(A9)
式中,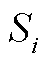 为各微电网议价能力
为各微电网议价能力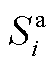 的归一化量化值;
的归一化量化值;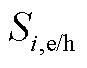 分别为各微电网电能/热能议价能力的量化值;
分别为各微电网电能/热能议价能力的量化值;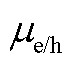 为电能热能对议价的贡献占比;
为电能热能对议价的贡献占比;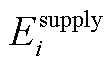 、
、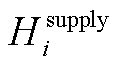 分别为微电网参与合作时总体提供的电能和热能;
分别为微电网参与合作时总体提供的电能和热能;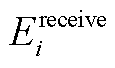 、
、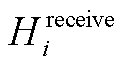 分别为微电网参与合作时总体接受的电能和热能。
分别为微电网参与合作时总体接受的电能和热能。
2. IEEE 33节点运行状态
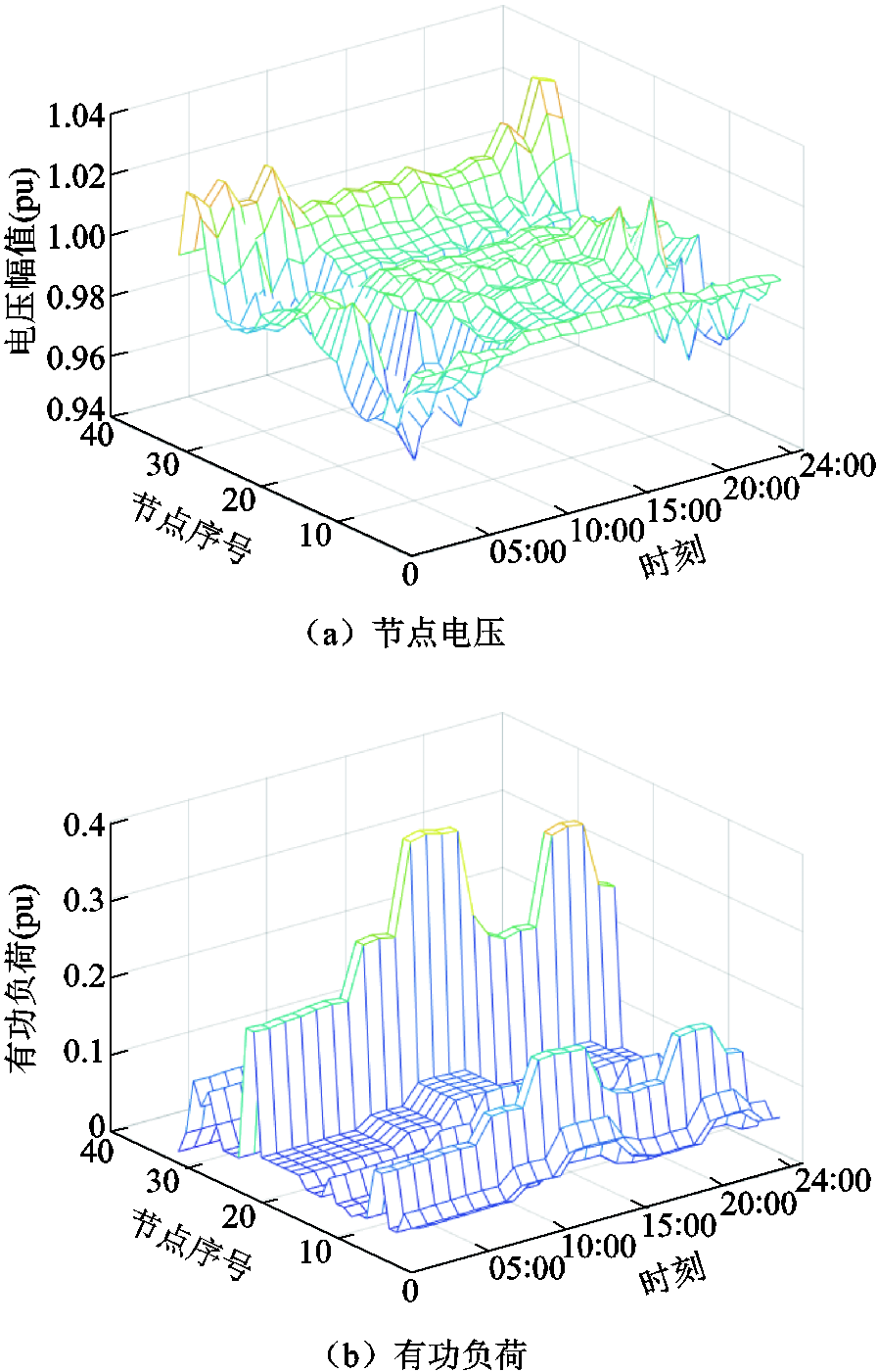
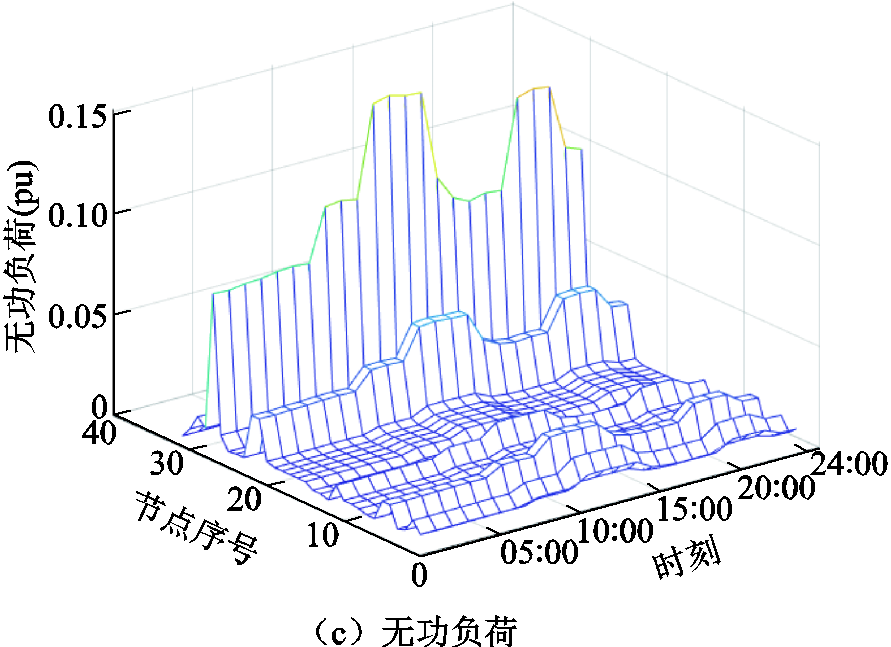
附图1 IEEE 33节点运行状态
App.Fig.1 Node running status of IEEE 33
3.系统参数
附表1 微电网运行参数
App.Tab.1 Microgrid operation parameters
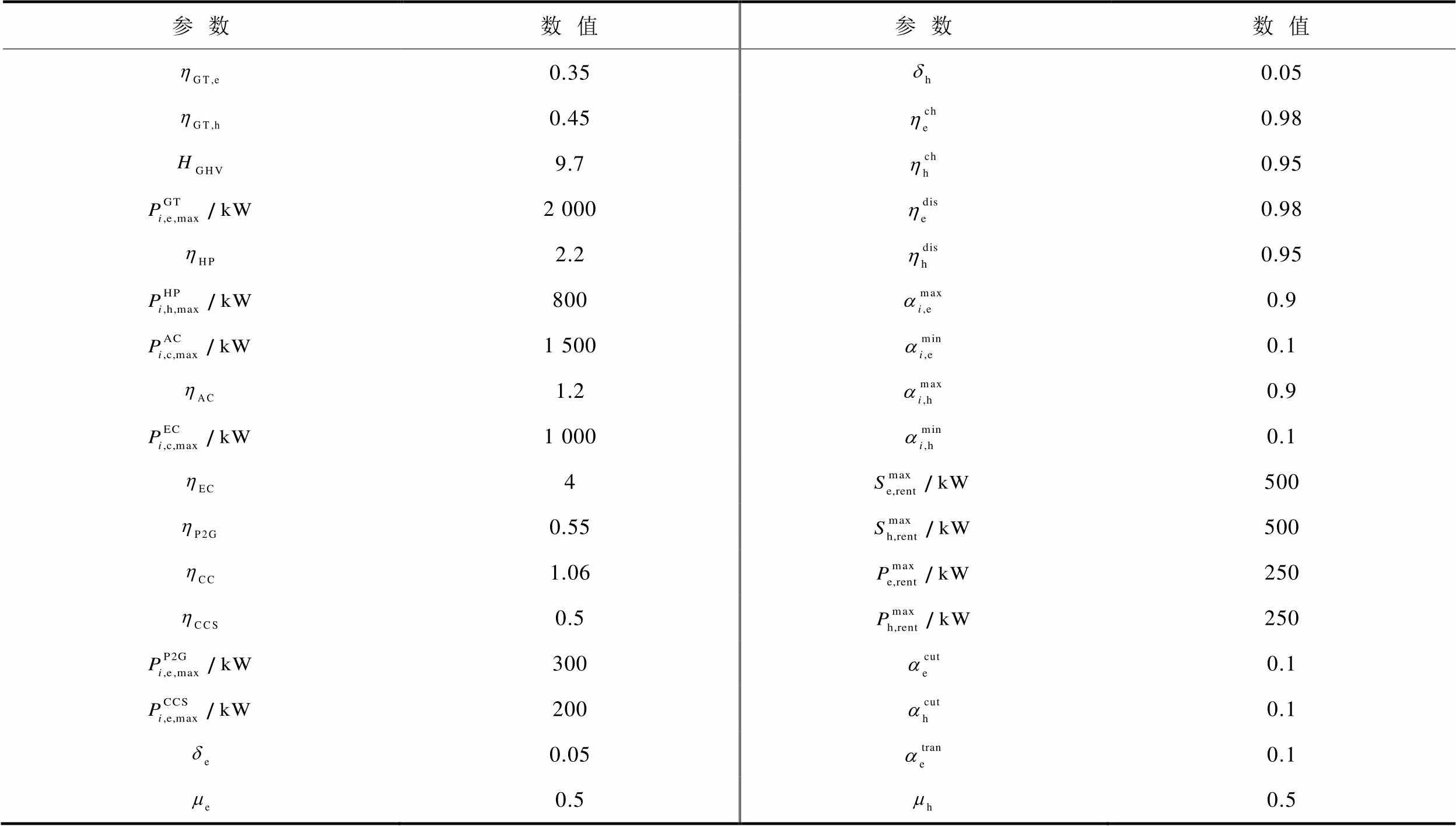
参数数值参数数值 0.350.05 0.450.98 9.70.95 2 0000.98 2.20.95 8000.9 1 5000.1 1.20.9 1 0000.1 4500 0.55500 1.06250 0.5250 3000.1 2000.1 0.050.1 0.50.5
附表2 能源价格
App.Tab.2 Energy prices
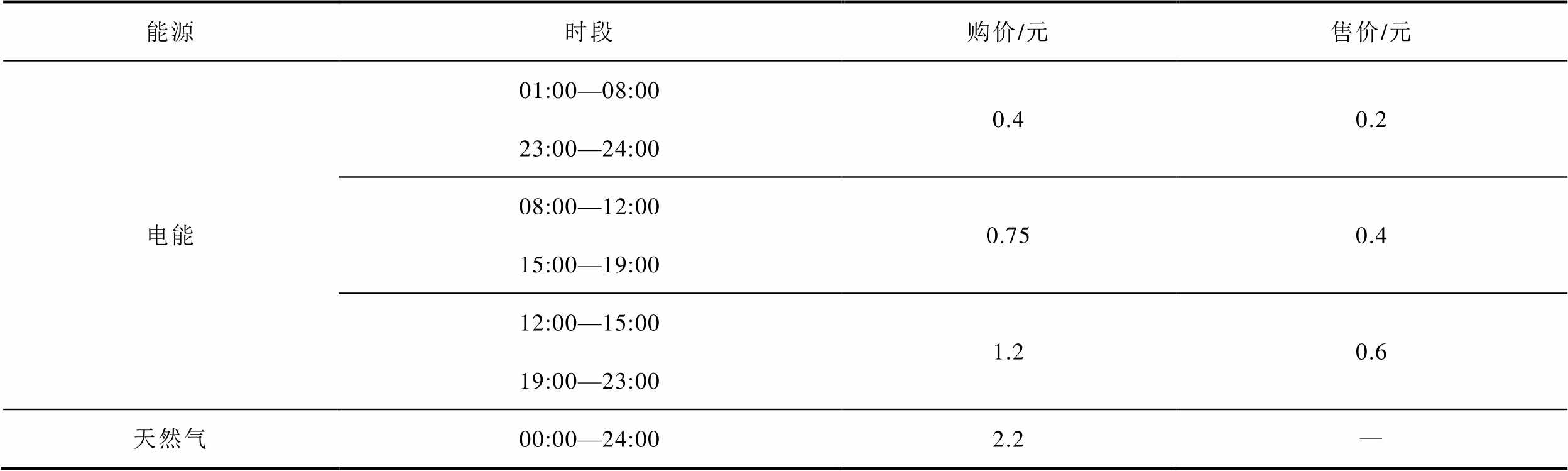
能源时段购价/元售价/元 电能01:00—08:000.40.2 23:00—24:00 08:00—12:000.750.4 15:00—19:00 12:00—15:001.20.6 19:00—23:00 天然气00:00—24:002.2—
附表3 微电网运维成本参数
App.Tab.3 Microgrid O&M cost parameters

参数数值 ,0.03,0.25 0.15 0.03/0.02/0.025/0.01 0.11/0.08/0.015/0.025 0.4 ,110/37 ,30/10 ,0.01/0.005
参考文献
[1] 梁紫雯, 牟龙华, 何楚璇. 微能源网互联系统的频率调节和消纳能力研究[J]. 电工技术学报, 2022, 37(增刊1): 74-82.
Liang Ziwen, Mu Longhua, He Chuxuan. Research on frequency modulation and accommodation capability of interconnected system of micro-energy network[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 74-82.
[2] Chang Weiguang, Yang Qiang. Low carbon oriented collaborative energy management framework for multi-microgrid aggregated virtual power plant considering electricity trading[J]. Applied Energy, 2023, 351: 121906.
[3] 朱振山, 刘秉庚, 郭磊. 考虑动态氢价机制的综合能源多微电网系统分布式优化调度[J]. 电网技术, 2023, 47(12): 5036-5054.
Zhu Zhenshan, Liu Binggeng, Guo Lei. Distributed optimal dispatch of integrated energy multi-microgrid system considering dynamic hydrogen price mechanism[J]. Power System Technology, 2023, 47(12): 5036-5054.
[4] 王学杰, 赵会茹, 曹艺琼, 等. 基于随机-Nash-Harsanyi讨价还价博弈的光伏-氢储能多主体分散协同调度[J]. 电工技术学报, 2024, 39(9): 2652-2666.
Wang Xuejie, Zhao Huiru, Cao Yiqiong, et al. Photovoltaic-hydrogen energy storage multi-agent decentralized cooperative scheduling based on stochastic-Nash-Harsanyi bargaining game[J]. Tran-sactions of China Electrotechnical Society, 2024, 39(9): 2652-2666.
[5] Shams M H, Shahabi M, MansourLakouraj M, et al. Adjustable robust optimization approach for two-stage operation of energy hub-based microgrids[J]. Energy, 2021, 222: 119894.
[6] 郑诗程, 许浩, 郎佳红, 等. 计及光伏不确定性的多区域综合能源系统多场景分布鲁棒优化调度[J]. 太阳能学报, 2024, 45(3): 460-469.
Zheng Shicheng, Xu Hao, Lang Jiahong, et al. Multi-scenario distributed robust optimal scheduling of multi-area integrated energy systems considering photovoltaic uncertainty[J]. Acta Energiae Solaris Sinica, 2024, 45(3): 460-469.
[7] 刘鑫, 李扬, 史云鹏, 等. 计及用户参与不确定性的虚拟电厂分布鲁棒优化模型[J]. 电力自动化设备, 2022, 42(7): 84-93.
Liu Xin, Li Yang, Shi Yunpeng, et al. Distributionally robust optimization model of virtual power plant considering user participation uncertainty[J]. Electric Power Automation Equipment, 2022, 42(7): 84-93.
[8] 朱玲, 李威, 王骞, 等. 基于校正条件生成对抗网络的风电场群绿氢储能系统容量配置[J]. 电工技术学报, 2024, 39(3): 714-730.
Zhu Ling, Li Wei, Wang Qian, et al. Wind farm-green hydrogen energy storage system capacity sizing method based on corrected-conditional generative adversarial network[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 714-730.
[9] 李勇, 凌锋, 乔学博, 等. 基于网侧资源协调的自储能柔性互联配电系统日前-日内优化[J]. 电工技术学报, 2024, 39(3): 758-773, 923.
Li Yong, Ling Feng, Qiao Xuebo, et al. Day-ahead and intra-day optimization of flexible interconnected distribution system with self-energy storage based on the grid-side resource coordination[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 758-773, 923.
[10] 滕孟杰, 陈晨, 赵宇鸿, 等. 不确定风电接入下计及煤电机组深调和储能的电力系统分布鲁棒优化日前调度方法[J]. 电网技术, 2024, 48(8): 3122-3132.
Teng Mengjie, Chen Chen, Zhao Yuhong, et al. Distribution robust optimal day-ahead dispatch method for power systems with uncertain wind power access considering deep peak regulation of coal-fired units and energy storage[J]. Power System Technology, 2024, 48(8): 3122-3132.
[11] 胡俊杰, 童宇轩, 刘雪涛, 等. 计及精细化氢能利用的综合能源系统多时间尺度鲁棒优化策略[J]. 电工技术学报, 2024, 39(5): 1419-1435.
Hu Junjie, Tong Yuxuan, Liu Xuetao, et al. Multi-time-scale robust optimization strategy for integrated energy system considering the refinement of hydrogen energy use[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1419-1435.
[12] 刘洁, 林舜江, 梁炜焜, 等. 基于高阶马尔可夫链和高斯混合模型的光伏出力短期概率预测[J]. 电网技术, 2023, 47(1): 266-275.
Liu Jie, Lin Shunjiang, Liang Weikun, et al. Short-term probabilistic forecast for power output of photovoltaic station based on high order Markov chain and Gaussian mixture model[J]. Power System Technology, 2023, 47(1): 266-275.
[13] Serrano Ardila V M, Maciel J N, Ledesma J J G, et al. Fuzzy time series methods applied to (in)direct short-term photovoltaic power forecasting[J]. Energies, 2022, 15(3): 845.
[14] Li Li, Wang Jing, Zhong Xiaoyi, et al. Combined multi-objective optimization and agent-based modeling for a 100% renewable island energy system considering power-to-gas technology and extreme weather conditions[J]. Applied Energy, 2022, 308: 118376.
[15] 黄棋悦, 严楠, 钟旭佳. 基于生成对抗网络的风电爬坡功率预测[J]. 太阳能学报, 2023, 44(1): 226-231.
Huang Qiyue, Yan Nan, Zhong Xujia. Wind power ramping events prediction based on generative adversarial network[J]. Acta Energiae Solaris Sinica, 2023, 44(1): 226-231.
[16] 张帅, 刘文霞, 万海洋, 等. 基于改进条件生成对抗网络的可控场景生成方法[J]. 电力自动化设备, 2024, 44(6): 9-17.
Zhang Shuai, Liu Wenxia, Wan Haiyang, et al. Controllable scenario generation method based on improved conditional generative adversarial network [J]. Electric Power Automation Equipment, 2024, 44(6): 9-17.
[17] 王再闯, 陈来军, 李笑竹, 等. 基于合作博弈的产销者社区分布式光伏与共享储能容量优化[J]. 电工技术学报, 2022, 37(23): 5922-5932.
Wang Zaichuang, Chen Laijun, Li Xiaozhu, et al. Capacity optimization of distributed PV and shared energy storage of prosumer community based on cooperative game[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5922-5932.
[18] Chen Yujia, Pei Wei, Ma Tengfei, et al. Asymmetric Nash bargaining model for peer-to-peer energy transactions combined with shared energy storage[J]. Energy, 2023, 278: 127980.
[19]Cui Shichang, Wang Yanwu, Liu Xiaokang, et al. Economic storage sharing framework: asymmetric bargaining-based energy cooperation[J]. IEEE Transactions on Industrial Informatics, 2021, 17(11): 7489-7500.
[20] Liu Hong, Li Jifeng, Ge Shaoyun, et al. Distributed day-ahead peer-to-peer trading for multi-microgrid systems in active distribution networks[J]. IEEE Access, 2020, 8: 66961-66976.
[21] Liu Xubin, Chen Xinyu, Jin Tianyu, et al. Network-Constrained Peer-to-Peer energy trading for multiple microgrids considering zoning pricing[J]. International Journal of Electrical Power & Energy Systems, 2023, 147: 108837.
[22] 叶畅, 曹侃, 丁凯, 等. 基于广义储能的多能源系统不确定优化调度策略[J]. 电工技术学报, 2021, 36(17): 3753-3764.
Ye Chang, Cao Kan, Ding Kai, et al. Uncertain optimal dispatch strategy based on generalized energy storage for multi-energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3753-3764.
[23] 赵书强, 要金铭, 李志伟. 基于改进K-means聚类和SBR算法的风电场景缩减方法研究[J]. 电网技术, 2021, 45(10): 3947-3954.
Zhao Shuqiang, Yao Jinming, Li Zhiwei. Wind power scenario reduction based on improved K-means clustering and SBR algorithm[J]. Power System Technology, 2021, 45(10): 3947-3954.
[24] 黄小庆, 李隆意, 徐鹏鑫, 等. 多主体博弈共赢的电动汽车充电桩共享方法[J]. 电工技术学报, 2023, 38(11): 2945-2961.
Huang Xiaoqing, Li Longyi, Xu Pengxin, et al. Electric vehicle charging pile sharing method based on multi-subject game and win-win[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2945-2961.
[25] 麻秀范, 孟祥玉, 朱秋萍, 等. 计及通信负载的5G基站储能调控策略[J]. 电工技术学报, 2022, 37(11): 2878-2887.
Ma Xiufan, Meng Xiangyu, Zhu Qiuping, et al. Control strategy of 5G base station energy storage considering communication load[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2878-2887.
[26] Zhang Yufan, Ai Qian, Xiao Fei, et al. Typical wind power scenario generation for multiple wind farms using conditional improved Wasserstein generative adversarial network[J]. International Journal of Electrical Power & Energy Systems, 2020, 114: 105388.
[27] Li Yang, Li Jiazheng, Wang Yi. Privacy-preserving spatiotemporal scenario generation of renewable energies: a federated deep generative learning approach[J]. IEEE Transactions on Industrial Informatics, 2022, 18(4): 2310-2320.
[28] 付文杰, 王喻玺, 申洪涛, 等. 基于拉丁超立方抽样和场景消减的居民用户基线负荷估计方法[J]. 电网技术, 2022, 46(6): 2298-2307.
Fu Wenjie, Wang Yuxi, Shen Hongtao, et al. Residential customer baseline load estimation based on Latin hypercube sampling and scenario subtraction [J]. Power System Technology, 2022, 46(6): 2298-2307.
Abstract The strong uncertainty of renewable energy poses significant challenges to the reliability and safety of multi-microgrid (MMG). As the integration of renewable sources continues to grow globally, their inherent variability could lead to fluctuations in energy supply that complicate grid management. To address this, a distributed robust cooperative optimization scheduling model for MMG distribution systems based on an improved conditional generative adversarial network (CGAN) is proposed.
Firstly, to accurately describe the uncertainty of renewable energy, the model uses scenario sets generated by the improved CGAN and reduced by the K-means++ clustering algorithm as the initial renewable energy scenarios for the distributionally robust optimization set. The improved CGAN model uses the Wasserstein distance as the discriminator loss function, effectively addressing issues of gradient vanishing and mode collapse during the optimization training process. By using day-ahead forecasts of renewable energy output as conditional variables, the improved CGAN learns the mapping between the conditional noise distribution and actual data, enhancing its ability to capture the stochastic characteristics of renewable energy production. Secondly, a DSO-MMG model considering dynamic power flow constraints and cloud storage leasing is constructed. The upper layer uses a Stackelberg game to describe the relationship between the DSO and MMG, while the lower layer establishes a benefit distribution method based on the contribution rate of multi-energy peer-to-peer (P2P) transactions. Dynamic power flow constraints reasonably limit the electric power flow during energy transactions, preventing overloads or voltage anomalies, thereby enhancing system stability and economic efficiency. The application of cloud energy storage reduces investment and management costs for microgrid storage, enabling them to store excess energy during surplus periods and release it during shortages, which decreases reliance on traditional grids and reduces operational costs. To address the benefit allocation issue, an asymmetric Nash bargaining model based on multi-energy P2P transaction contribution rates is proposed, ensuring fair distribution among participants and encouraging collaboration among microgrids. Then, a bisection method that couples parallel computing C&CG is proposed to solve the energy trading problem, allowing parallel operation of multiple computing units to accelerate the solving process. the improved ADMM is used to solve the benefit distribution problem. safeguarding participant privacy and improving algorithmic efficiency.
The results show that the improved CGAN method proposed in this paper can describe the uncertainty of renewable energy more accurately and effectively, and the two-stage DRO model can avoid the overly conservative nature of traditional two-stage robust optimization while ensuring robustness, effectively balancing the economic efficiency and conservativeness of the microgrid system. In addition, the constructed hybrid game model effectively reduces the operation cost of multi-microgrids and stimulates the active participation of various stakeholders in energy trading. The solution algorithm of the model significantly improves the solution efficiency and protects the privacy of each subject.
Keywords:Improved conditional generative adversarial network, cloud storage, distributionally robust optimization, distribution-multi-microgrid coordinated operation
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.241227
国家自然科学基金资助项目(51607068)。
收稿日期 2024-07-11
改稿日期 2024-09-28
李 虹 女,1979年生,硕士生导师,研究方向为新能源电力系统分析与控制。
E-mail:lxy.lh@163.com
韩雨萌 男,2000年生,硕士研究生,研究方向为微电网系统能源优化调度。
E-mail:hym2877598344@163.com(通信作者)
(编辑 赫 蕾)