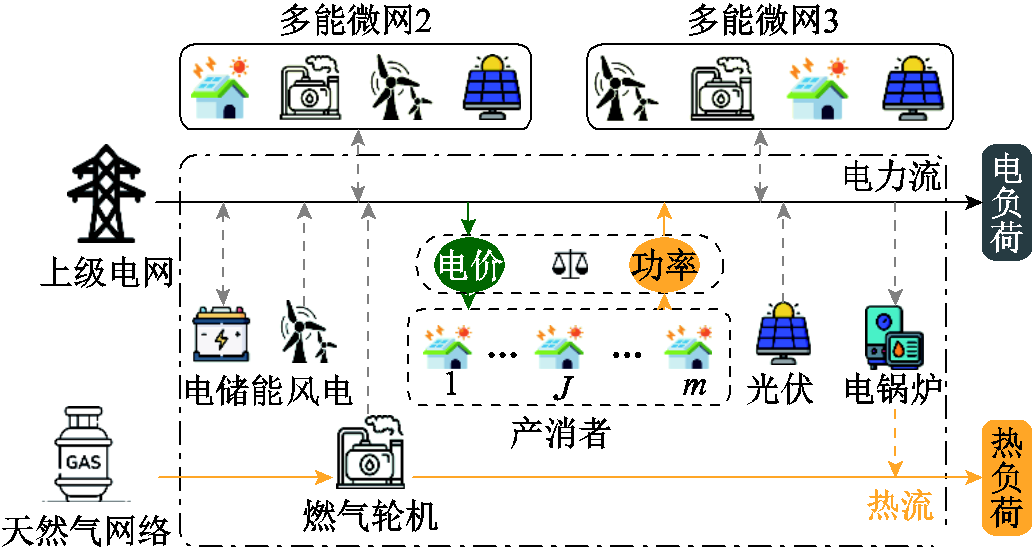
图1 多能微网框架模型
Fig.1 Framework for the model of MEMG
摘要 多能微网在运行过程中会受到电价以及新能源出力等多重不确定因素的影响。针对该问题,该文提出一种基于Wasserstein两阶段分布鲁棒优化的多主体多能微网合作博弈优化模型。首先,考虑多能微网和其内部产消者的互动关系,提出了“上层为多能微网,下层为产消者”的双层优化模型;其次,采用基于Wasserstein距离的模糊集分别构建了电价、多能微网新能源出力以及内部产消者光伏出力的不确定性模型;然后,在多主体多能微网之间,构建了考虑合作博弈和隐私保护的能源交互模型,并采用交替方向乘子法(ADMM)结合列与约束生成法(C&CG)对模型进行分布式求解;最后,基于包含三主体多能微网的系统进行算例分析,验证了该文所提模型和算法的有效性。
关键词:双层优化 两阶段分布鲁棒优化 多能微网 合作博弈 分布式算法
构建新型电力系统对于服务新能源规模开发,保障替代传统能源的安全性,助推电力系统绿色转型,达成“双碳”目标具有重要意义。多能微网(Multi-Energy Microgrid, MEMG)集成多种分布式能源(如风电、光伏)、冷热电联产机组以及储能等设备,可以实现多类型能源的生产、互补与高效利用,对新型电力系统的发展至关重要[1]。
单一的多能微网规模较小,容易受到运行环境的影响[2],而其内部可再生能源容量越来越高,导致运行稳定性会进一步下降。另一方面,随着社会的发展,电力需求不断增加,由于多能微网生产的电能不足,导致其无法参与电力市场交易[3],这进一步限制了其发展。上述问题可以通过“网间互联互通”的方式解决。和单一的多能微网相比,该方式能有效提升多主体多能微网的稳定性、可靠性和灵活性[4],同时减小远距离输电损耗[5]。与此同时,这种运行模式给点对点(Peer-to-Peer, P2P)能源交易提供了平台[6],它允许相邻的多能微网进行能源交易,从而获得额外的收益[7];此外,P2P能源交易还能进一步提升多能微网的运行灵活性与新能源消纳能力[8]。目前,基于多主体P2P能源交易是电力市场的热门研究领域。文献[2]提出多主体微网的P2P能源交互策略,并采用交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)保护各主体隐私性。文献[9]提出一种考虑交通运输的合作博弈优化策略,其中多主体多能微网之间进行电能和氢能交易。以上研究将多能微网作为一个独立主体,忽略了对内部产消者的分析与建模,造成了一定的误差因素。
同时,上述文献忽略了电价、新能源出力等不确定性因素的影响,这可能导致决策过于乐观。为了应对这些不确定性,通常引入随机优化(Stochastic Optimization, SO)[10]或鲁棒优化(Robust Optimization, RO)[11]进行处理。其中,随机优化依赖精确的概率分布函数,但在实际操作中分布可能难以获得;而鲁棒优化则假设不确定参数在一个不确定集中波动,并针对不确定集的最恶劣情况进行优化,但可能导致解过于保守。分布鲁棒优化(Distributionally RO, DRO)是一种新兴的优化方法[12],其保守性通常介于随机优化和鲁棒优化之间。分布鲁棒的形式主要包括均值方差模型[7,13],Wasserstein球[14]、散度模型[15]及综合范数[16]。由于均值方差模型只包含了部分矩信息,不能较好地刻画真实分布;而采用散度模型会引入指数项,给计算求解带来困难。相比之下,基于Wasserstein距离的分布鲁棒优化可以更有效地利用历史数据,从而降低决策保守性[17]。因此,分布鲁棒的研究热点开始偏向Wasserstein球(以下简称W球),主要应用领域包括两阶段备用容量优化[18]、两阶段机组组合[19]、“配电网-充电站”分布协同优化[20-21],以及单一多能微网[1,22]、能源枢纽[17]和虚拟电厂[23]的优化调度,但在多主体能源交易领域,尚未有研究结合Wasserstein两阶段分布鲁棒模型进行处理。
基于上述问题,本文提出了一种基于Wasserstein两阶段分布鲁棒的多主体多能微网合作博弈能源交易模型,主要工作如下:
1)建立多能微网的典型架构,并构建了描述多能微网和内部产消者互动关系的双层优化模型。
2)结合Wasserstein模糊集分别构建了多能微网的两阶段分布鲁棒模型以及内部产消者的分布鲁棒机会约束(Distributionally Robust Chance Constraint, DRCC)模型,充分考虑了多重不确定性对系统的影响。
3)基于ADMM和列与约束生成法(Column and Constraint Generation algorithm, C&CG)将所提模型转为分布式优化问题,并在多主体多能微网系统中进行算例仿真,验证所提方法的可行性和有效性。
本文构建的多能微网框架模型如图1所示,主要包含了新能源设备(风电、光伏)、电储能、电锅炉、燃气轮机,以及产消者。每个多能微网包含电、热两类负荷,其中热负荷主要由燃气轮机和电锅炉进行供应。

图1 多能微网框架模型
Fig.1 Framework for the model of MEMG
根据博弈类型不同,整个模型可以分为以下两部分[24]:
1)多能微网和内部产消者构成了双层优化模型。其中多能微网作为上层主体,负责给产消者制定合理的电价以引导其用电行为;而产消者接受多能微网制定的电价之后,在满足需求的前提下以最小化自身的成本为目标,决策出向多能微网的购电功率。该模型本质上是多能微网和产消者的主从博弈。
2)任一多能微网既能根据上级电网制定的电价调整购售电功率,也能和相邻的多能微网进行能源交互。该模型为基于纳什谈判的多主体多能微网合作博弈。
多能微网在运行中会受到电价、新能源出力等多重不确定量的影响,由于二者均具有较强的波动性,其实际数值通常与预测值不完全一致,直接代入对应的预测曲线进行计算不能反映真实的系统运行成本,所以需要将预测值的波动考虑在内[25-27]。为此,本节采用Wasserstein距离分别构造两者的不确定集。
以新能源出力为例,其基于Wasserstein距离的模糊集形式为
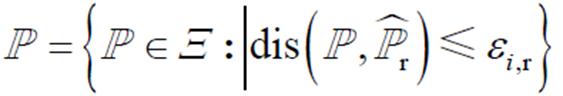 (1)
(1)式中,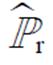 为t时刻新能源出力的经验分布;
为t时刻新能源出力的经验分布;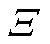 为对应的支撑集(即概率分布的集合);模糊集
为对应的支撑集(即概率分布的集合);模糊集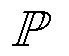 表示以经验分布为圆心、与经验分布的距离小于或等于
表示以经验分布为圆心、与经验分布的距离小于或等于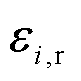 的分布集合。两个分布之间的距离表达式为
的分布集合。两个分布之间的距离表达式为
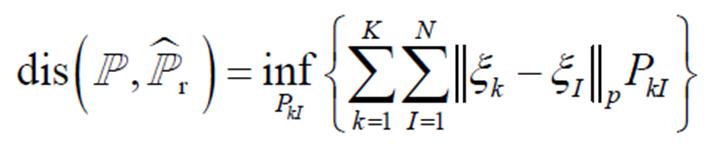 (2)
(2)
式中,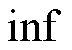 表示下确界;
表示下确界;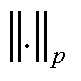 代表p范数,在研究中通常取1(即1-范数);K和
代表p范数,在研究中通常取1(即1-范数);K和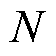 分别为分布
分别为分布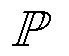 和
和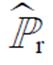 所包含的总样本数;
所包含的总样本数;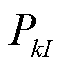 为联合分布(
为联合分布(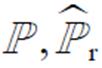 )取样本(
)取样本(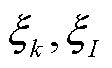 )的概率。当样本趋向无穷时(或分布为连续型随机变量),式(2)可转换为积分的形式[14],即
)的概率。当样本趋向无穷时(或分布为连续型随机变量),式(2)可转换为积分的形式[14],即
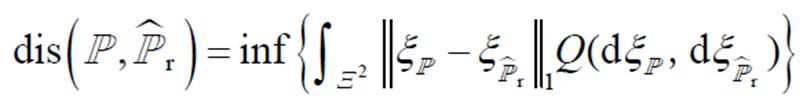 (3)
(3)式中,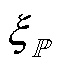 和
和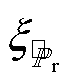 分别为服从
分别为服从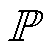 和
和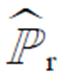 的随机变量;
的随机变量;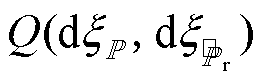 为对应的联合分布。
为对应的联合分布。
多能微网和上级电网的购售电价模糊集与新能源出力类似,本节不再赘述。
多能微网i以最小化运行成本为目标,其基于Wasserstein两阶段分布鲁棒优化的模型为
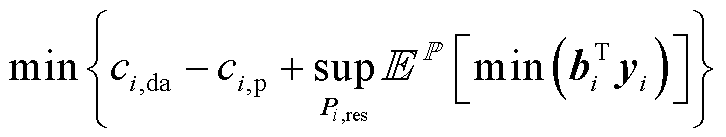 (4)
(4)式中,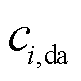 和
和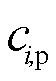 分别为日前运行成本与合作博弈利益,两者均在新能源出力的不确定性之前决策;Pi,res为多能微网i新能源出力的模糊集,
分别为日前运行成本与合作博弈利益,两者均在新能源出力的不确定性之前决策;Pi,res为多能微网i新能源出力的模糊集,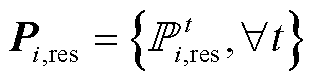 ;
;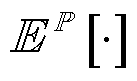 表示对随机变量进行期望运算;
表示对随机变量进行期望运算;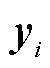 为日内第二阶段的决策变量;
为日内第二阶段的决策变量;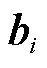 为第二阶段成本函数对应的相关系数矩阵;sup表示上确界。
为第二阶段成本函数对应的相关系数矩阵;sup表示上确界。
1)日前成本函数
由前文可知,多能微网i的日前成本包括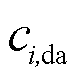 和
和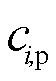 两部分,对应的表达式为
两部分,对应的表达式为
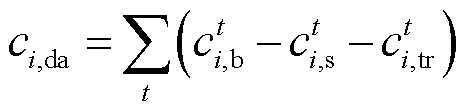 (5)
(5)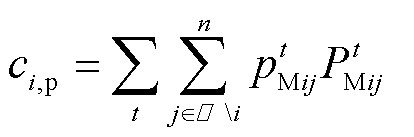 (6)
(6)
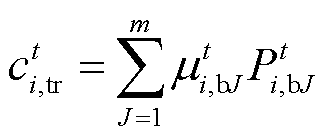 (7)
(7)
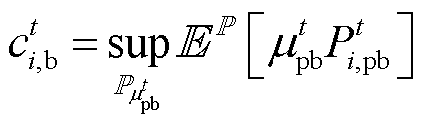 (8)
(8)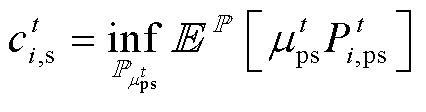 (9)
(9)
式中,n和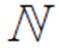 分别为多能微网的总数与集合;i和j为其对应索引;m为多能微网i内部产消者总数;J为对应的产消者索引;
分别为多能微网的总数与集合;i和j为其对应索引;m为多能微网i内部产消者总数;J为对应的产消者索引;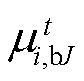 为多能微网i制定给第J个产消者的售电电价;
为多能微网i制定给第J个产消者的售电电价;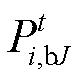 为该产消者的购电功率;
为该产消者的购电功率;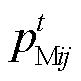 为多能微网i和j的交互电价;
为多能微网i和j的交互电价;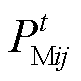 为两者的交互功率;
为两者的交互功率;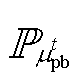 、
、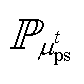 分别为t时刻购、售电电价的模糊集;
分别为t时刻购、售电电价的模糊集;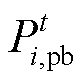 和
和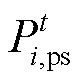 分别为多能微网i与上级电网的购、售电功率。式(8)、式(9)分别为多能微网i在t时刻购售电价分布最恶劣的情况下与上级电网的购电成本和售电利润期望值。
分别为多能微网i与上级电网的购、售电功率。式(8)、式(9)分别为多能微网i在t时刻购售电价分布最恶劣的情况下与上级电网的购电成本和售电利润期望值。
2)日内成本函数
多能微网i的日内调度主要包括内部储能恶化成本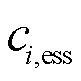 、天然气购买成本
、天然气购买成本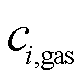 以及电锅炉的运行成本
以及电锅炉的运行成本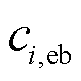 。
。
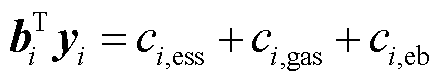 (10)
(10)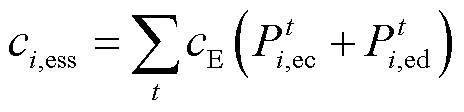 (11)
(11)
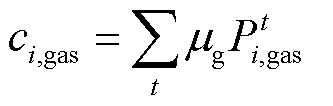 (12)
(12)
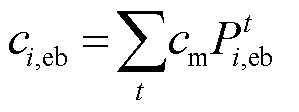 (13)
(13)式中,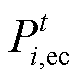 和
和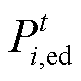 分别为储能的充、放电功率;
分别为储能的充、放电功率;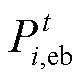 为燃气轮机的输入功率;
为燃气轮机的输入功率;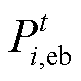 为电锅炉的用电功率;
为电锅炉的用电功率;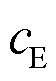 为储能的单位恶化成本;
为储能的单位恶化成本;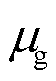 为单位天然气购买成本;
为单位天然气购买成本;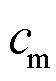 为电锅炉单位运维成本。
为电锅炉单位运维成本。
1)储能约束
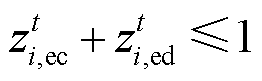 (14)
(14)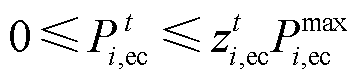 (15)
(15)
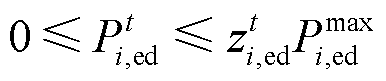 (16)
(16)
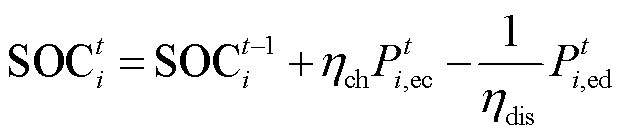 (17)
(17)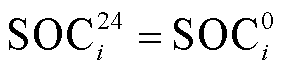 (18)
(18)
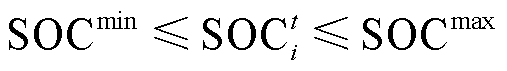 (19)
(19)
式中,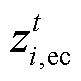 和
和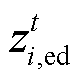 分别为充、放电0-1变量;
分别为充、放电0-1变量;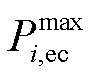 和
和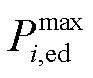 分别为最大充、放电功率;
分别为最大充、放电功率;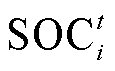 为储能的荷电状态;
为储能的荷电状态;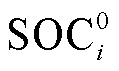 为储能的初始容量;
为储能的初始容量;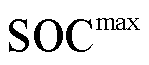 和
和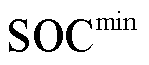 分别为荷电状态(State of Charge, SOC)上、下限;
分别为荷电状态(State of Charge, SOC)上、下限;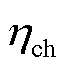 和
和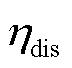 分别为充、放电效率。
分别为充、放电效率。
2)燃气轮机约束
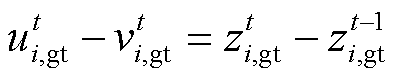 (20)
(20)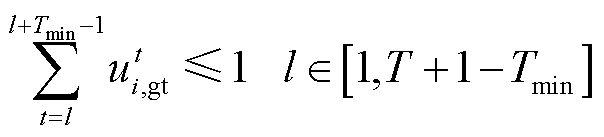 (21)
(21)
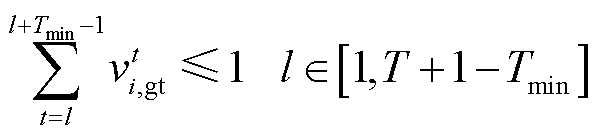 (22)
(22)
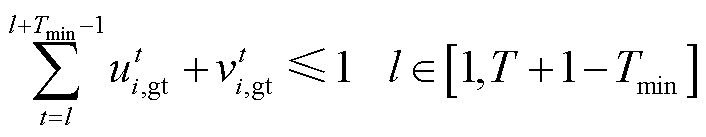 (23)
(23)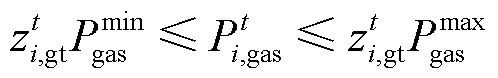 (24)
(24)
式中,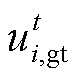 、
、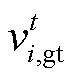 和
和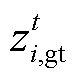 为0-1变量,分别为燃气轮机的启、停和运行状态;
为0-1变量,分别为燃气轮机的启、停和运行状态;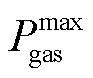 和
和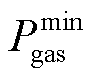 分别为燃气轮机输入功率上、下限;
分别为燃气轮机输入功率上、下限;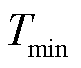 为燃气轮机最短运行时长;
为燃气轮机最短运行时长;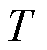 为总时段数。
为总时段数。
3)电锅炉约束
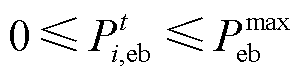 (25)
(25)式中,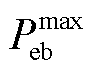 为电锅炉的最大用电功率。
为电锅炉的最大用电功率。
4)购售电约束
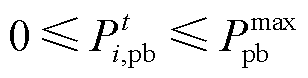 (26)
(26)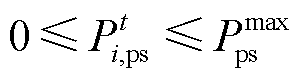 (27)
(27)
式中,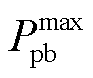 和
和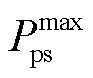 分别为购、售电功率上限。
分别为购、售电功率上限。
5)耦合约束
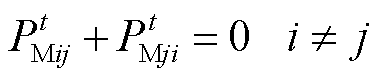 (28)
(28)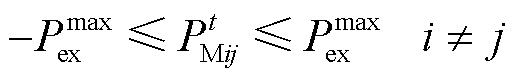 (29)
(29)
式中,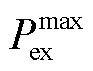 为相邻多能微网之间功率交互上限。
为相邻多能微网之间功率交互上限。
6)功率平衡约束
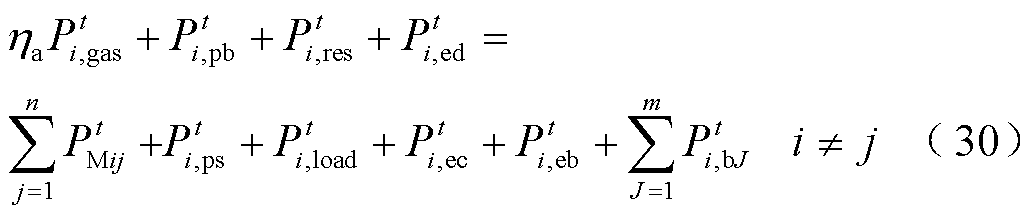
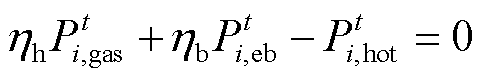 (31)
(31)
式中,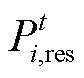 、
、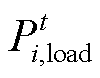 和
和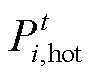 分别为可再生能源出力、电负荷、热负荷的大小;
分别为可再生能源出力、电负荷、热负荷的大小;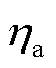 、
、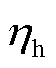 和
和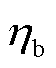 分别为燃气轮机的产电效率、产热效率及电锅炉的产热效率。
分别为燃气轮机的产电效率、产热效率及电锅炉的产热效率。
7)售电电价约束
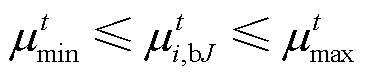 (32)
(32)式中,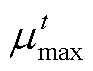 和
和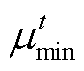 分别为多能微网i制定给内部产消者的电价上、下限。
分别为多能微网i制定给内部产消者的电价上、下限。
多能微网i内部任一产消者J的目标函数为
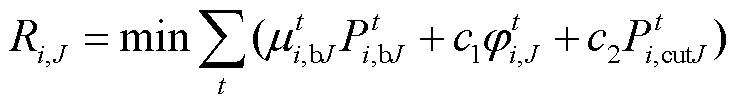 (33)
(33)式中,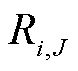 为多能微网i内部第J个产消者的总成本,包括向多能微网i的购电成本、自身参与需求响应的平移负荷成本以及中断负荷成本;
为多能微网i内部第J个产消者的总成本,包括向多能微网i的购电成本、自身参与需求响应的平移负荷成本以及中断负荷成本;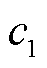 和
和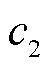 分别为单位平移成本和单位切负荷成本;
分别为单位平移成本和单位切负荷成本;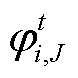 为对应的辅助变量;
为对应的辅助变量;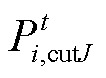 为产消者J的可中断负荷。
为产消者J的可中断负荷。
1)需求响应约束
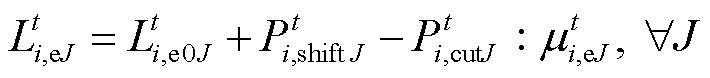 (34)
(34)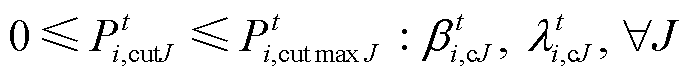 (35)
(35)
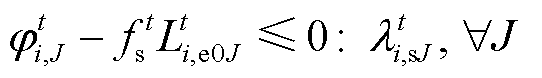 (36)
(36)
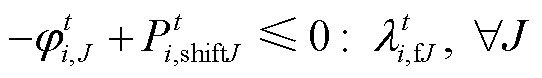 (37)
(37)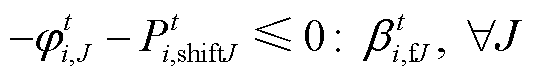 (38)
(38)
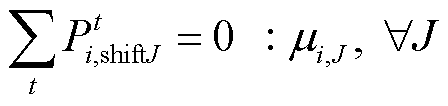 (39)
(39)
式中,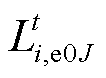 、
、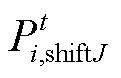 分别为产消者J的原始负荷、可平移负荷;
分别为产消者J的原始负荷、可平移负荷;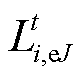 为产消者J经过需求响应后的实际负荷;
为产消者J经过需求响应后的实际负荷;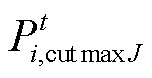 为产消者J内部可中断负荷的上限;
为产消者J内部可中断负荷的上限;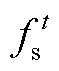 为产消者J最大可平移负荷占原始负荷的比例;
为产消者J最大可平移负荷占原始负荷的比例;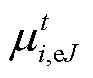 、
、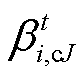 、
、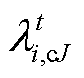 、
、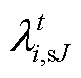 、
、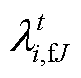 、
、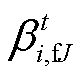 和
和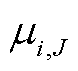 为约束对应的拉格朗日乘子。
为约束对应的拉格朗日乘子。
2)购电功率约束
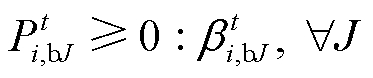 (40)
(40)式中,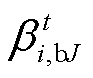 为对应的拉格朗日乘子。
为对应的拉格朗日乘子。
3)功率平衡约束
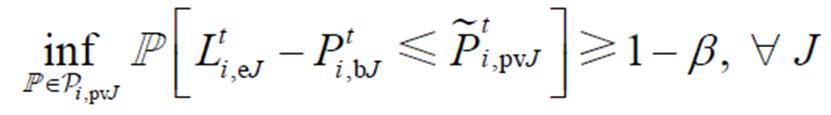 (41)
(41)式中,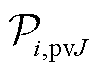 为
为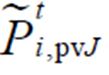 的支撑集,其定义和式(3)类似;
的支撑集,其定义和式(3)类似;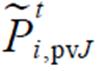 为光伏随机变量。式(41)表示产消者内部基于DRCC的功率平衡约束,主要用于描述下层产消者J内部光伏出力不确定性。其含义为光伏随机变量
为光伏随机变量。式(41)表示产消者内部基于DRCC的功率平衡约束,主要用于描述下层产消者J内部光伏出力不确定性。其含义为光伏随机变量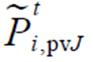 在最恶劣的分布下,仍然能以至少
在最恶劣的分布下,仍然能以至少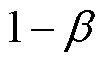 的概率满足产消者内部的供电需求,对应的参数
的概率满足产消者内部的供电需求,对应的参数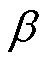 为DRCC的违反概率。
为DRCC的违反概率。
为简化求解,本节将对模型进行重构。
第1节所提的多能微网模型中,式(4)和式(8)、式(9)均构成了双层优化。根据文献[28],可将其转换为式(42)~式(44)的形式,具体的推导见附录1。
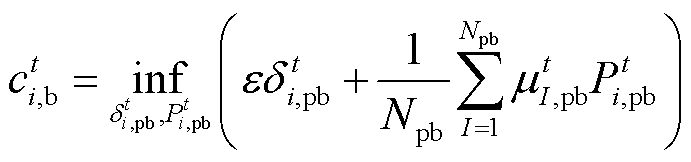 (42)
(42)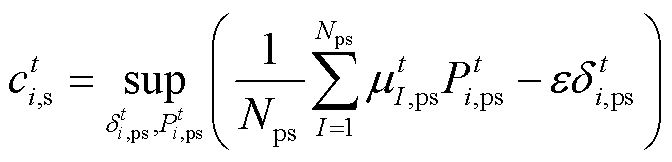 (43)
(43)
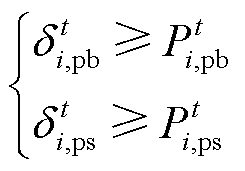 (44)
(44)
式中,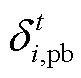 和
和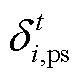 为拉格朗日乘子;
为拉格朗日乘子;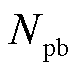 和
和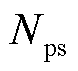 分别为购、售电价对应的总样本数;
分别为购、售电价对应的总样本数;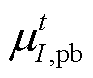 和
和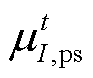 分别为购、售电价的第I个样本;
分别为购、售电价的第I个样本;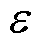 为电价的W球半径。
为电价的W球半径。
求解式(41)的方法主要包括条件风险价值(Conditional Value at Risk, CVaR)[29]、混合整数规划(Mixed Integer Linear Programming, MILP)[30]。以及边界支撑[31]。由于CVAR转换结果较为保守,而MILP容易生成不合理的结果[21],因此本文采用边界支撑法将其转换为
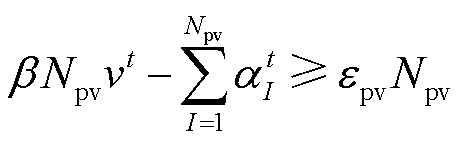 (45)
(45)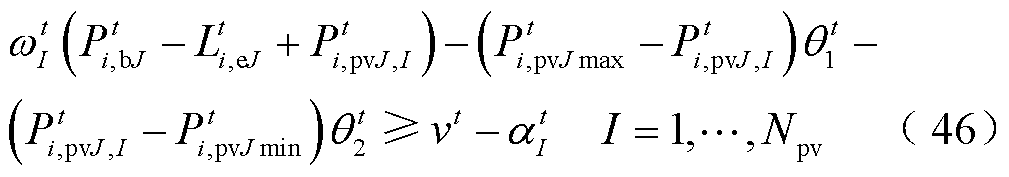
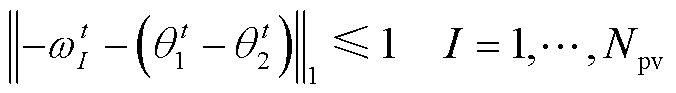 (47)
(47)
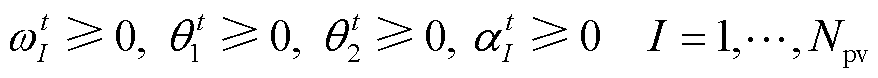 (48)
(48)式中,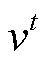 、
、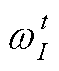 、
、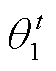 、
、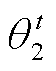 和
和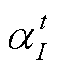 为辅助变量;
为辅助变量;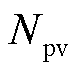 为多能微网i第J个产消者的光伏样本数;
为多能微网i第J个产消者的光伏样本数;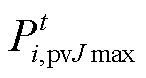 和
和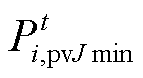 分别为该产消者的光伏出力上、下限;
分别为该产消者的光伏出力上、下限;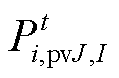 为产消者的第I个历史数据;
为产消者的第I个历史数据;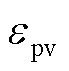 为随机变量
为随机变量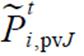 对应的W球半径。
对应的W球半径。
通过式(45)~式(48)可知,样本数和约束数量成正比。为了降低样本数过多导致的求解困难,可将式(41)重构为
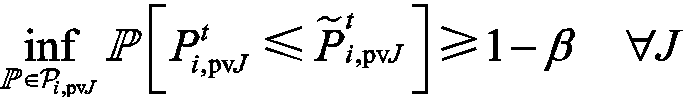 (49)
(49)式中,变量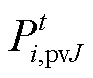 嵌套在式(50)的右侧。
嵌套在式(50)的右侧。
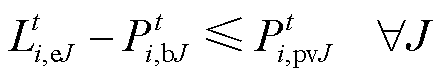 (50)
(50)
在符合概率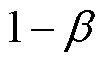 的前提下,越大的
的前提下,越大的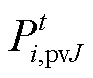 越符合实际工程需求。因此,式(41)可作为以下优化问题的约束:
越符合实际工程需求。因此,式(41)可作为以下优化问题的约束:
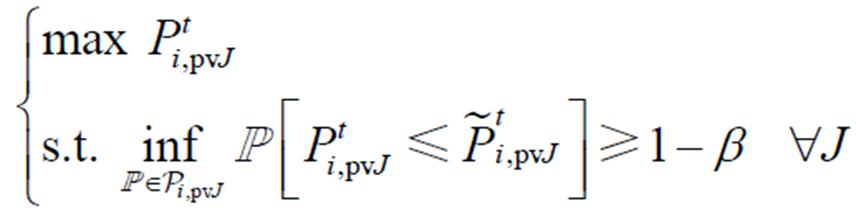 (51)
(51)为了求解式(51),重新采用边界支撑法进行等效,最终得到
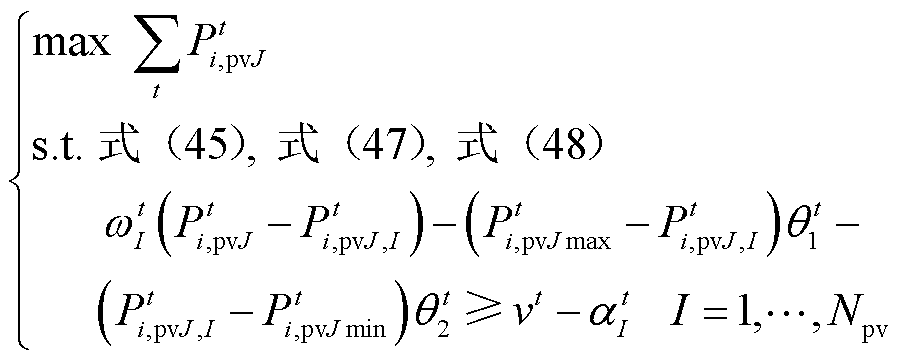 (52)
(52)
式(52)是一个独立的优化模型,可以采用商业求解器Gurobi进行求解,所得最优解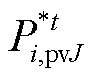 可作为定值代入产消者的功率平衡约束,有
可作为定值代入产消者的功率平衡约束,有
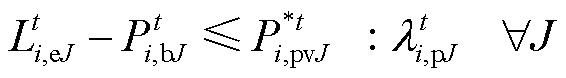 (53)
(53)式中,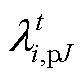 为对应的拉格朗日乘子。
为对应的拉格朗日乘子。
由式(33)~式(40)、式(53)可知,产消者模型为线性规划问题,可进一步通过库恩-塔克条件(Karush-Kuhn-Tucker, KKT)、大M法将“多能微网-产消者”双层模型转换为带有均衡约束的数学规划[32],从而确保双方在交易过程中实现纳什均衡。转换过程对应的约束见附录2。式(7)可通过强对偶定理转换为式(54),具体过程见附录3。
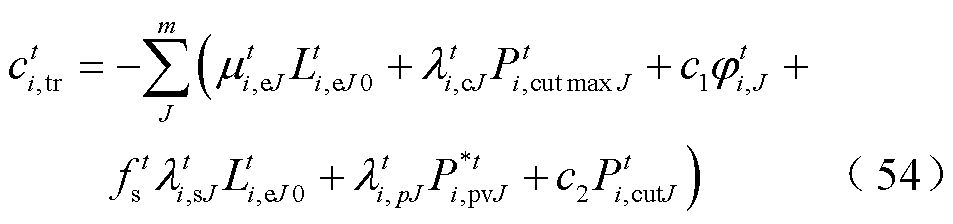
求解Wasserstein两阶段分布鲁棒的方法包括凸均值法[33]、仿射变换[1,22,34]、强对偶变换[23],以及多面体近似法[35]等。由于仿射变换要求不确定主体和决策呈线性关系,但在实际中这种线性关系无法保证[36];而强对偶变换和多面体近似法效率较低,因此本文采用凸均值法对模型进行转换。
2.4.1 不确定集等效转换
基于凸均值法,多能微网i的新能源出力不确定集可以转换为
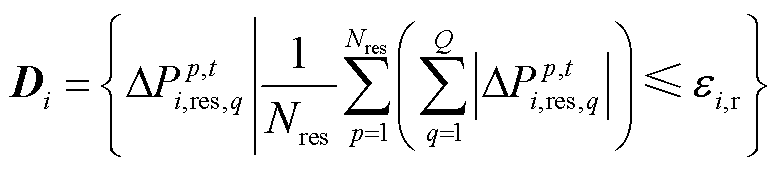 (55)
(55)式中,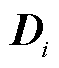 为模型转换后所对应的不确定集;
为模型转换后所对应的不确定集;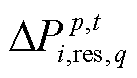 为t时刻多能微网i第q类新能源所对应第p个样本
为t时刻多能微网i第q类新能源所对应第p个样本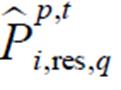 的波动值;
的波动值;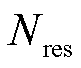 为t时刻多能微网i内部每个新能源出力的总样本数;Q为安装的新能源总数。
为t时刻多能微网i内部每个新能源出力的总样本数;Q为安装的新能源总数。
相应地,式(30)调整为
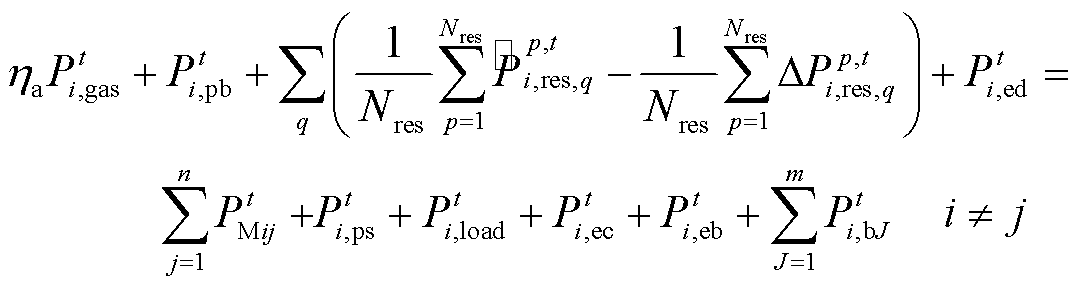 (56)
(56)2.4.2 目标函数等效变换
基于式(42)~式(44)、式(54)~式(56),可将式(4)进一步等效为
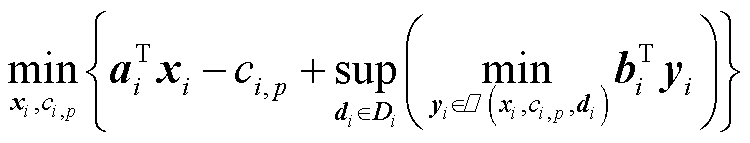 (57)
(57)式中,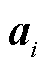 为日前运行成本
为日前运行成本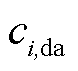 的相关系数矩阵;
的相关系数矩阵;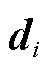 为不确定变量;
为不确定变量;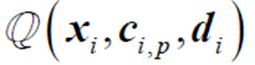 为日内第二阶段变量的可行域。经过上述变换,基于Wasserstein两阶段分布鲁棒模型被转换为对应的两阶段鲁棒模型。
为日内第二阶段变量的可行域。经过上述变换,基于Wasserstein两阶段分布鲁棒模型被转换为对应的两阶段鲁棒模型。
对于多主体多能微网,它们在满足自身用电需求的前提下可以通过合作的方式最大化联盟的收益。根据纳什谈判理论[37],多主体多能微网联盟的目标函数为
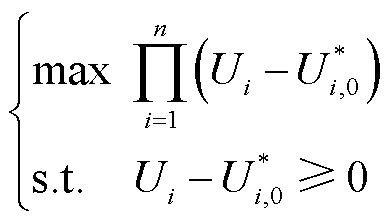 (58)
(58)式中,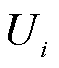 为多能微网i参与合作的最大利润(即运行成本的相反数);
为多能微网i参与合作的最大利润(即运行成本的相反数);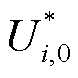 为谈判破裂点。式(58)是高度非凸的模型,需要将其拆分为电能子问题SP1和电价子问题SP2后进行求解[38]。
为谈判破裂点。式(58)是高度非凸的模型,需要将其拆分为电能子问题SP1和电价子问题SP2后进行求解[38]。
2.5.1 子问题SP1模型
基于均值不等式,多主体多能微网的电能子问题SP1可以建模为
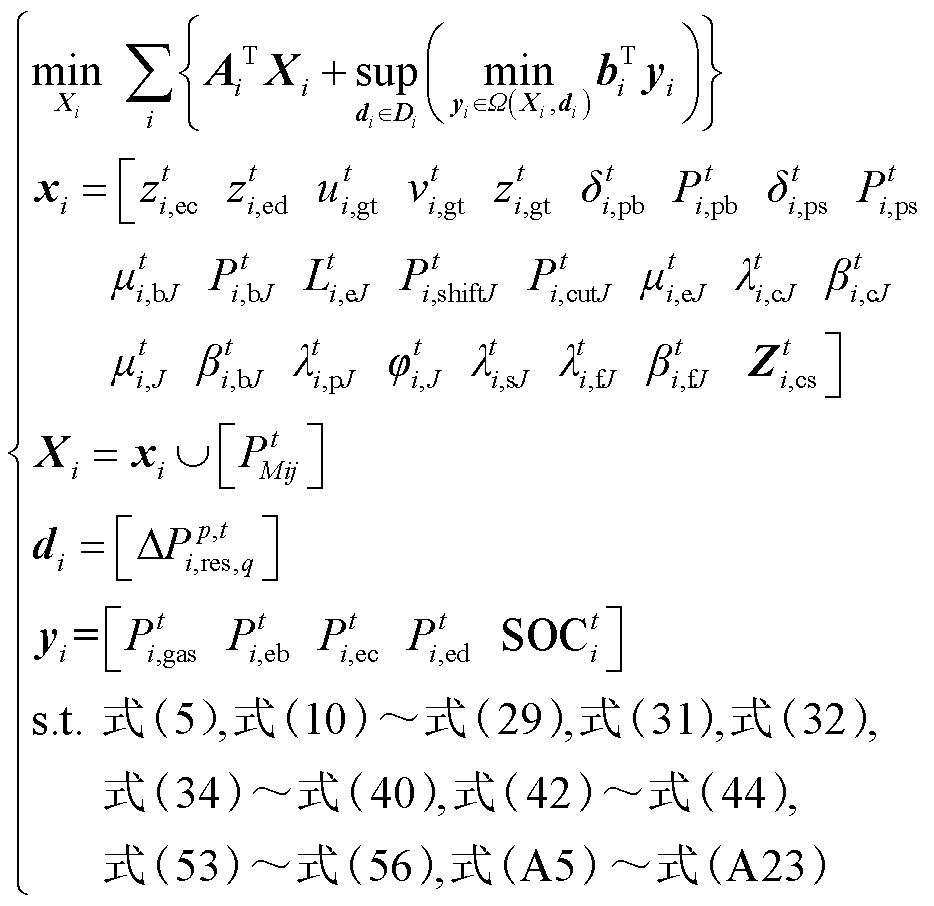 (59)
(59)式中,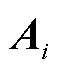 为子问题SP1第一阶段对应的相关系数矩阵;Ω为yi的可行域;
为子问题SP1第一阶段对应的相关系数矩阵;Ω为yi的可行域;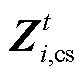 为大M法引入的整数变量集合,其包含的变量见附录2。
为大M法引入的整数变量集合,其包含的变量见附录2。
2.5.2 子问题SP2模型
在SP1求解结束后,相邻多能微网之间的交互量已经确定,但是由于交互电价未知,因此合作利益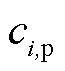 无法计算。为此,需要构造电价子问题SP2进行求解,其对应的表达式为
无法计算。为此,需要构造电价子问题SP2进行求解,其对应的表达式为
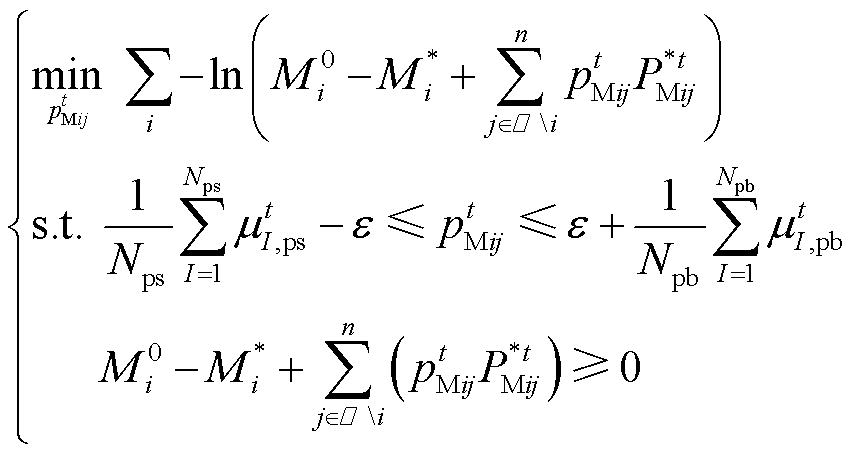 (60)
(60)式中,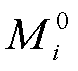 为多能微网i不参与P2P合作的最优运行成本(即
为多能微网i不参与P2P合作的最优运行成本(即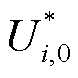 的相反数);
的相反数);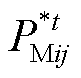 和
和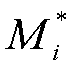 分别为SP1模型所对应的多能微网i的最优解和最优值。
分别为SP1模型所对应的多能微网i的最优解和最优值。
在求解子问题SP1和SP2时,需要保护各主体多能微网的隐私性。由于ADMM算法能有效地保护各主体隐私,且在迭代中仅要求各主体进行有限的信息交互,不会影响能源市场机制[9,38]。因此本文采用该法对两个子问题进行分布式求解。
基于式(28)和式(59),SP1的增广拉格朗日函数为
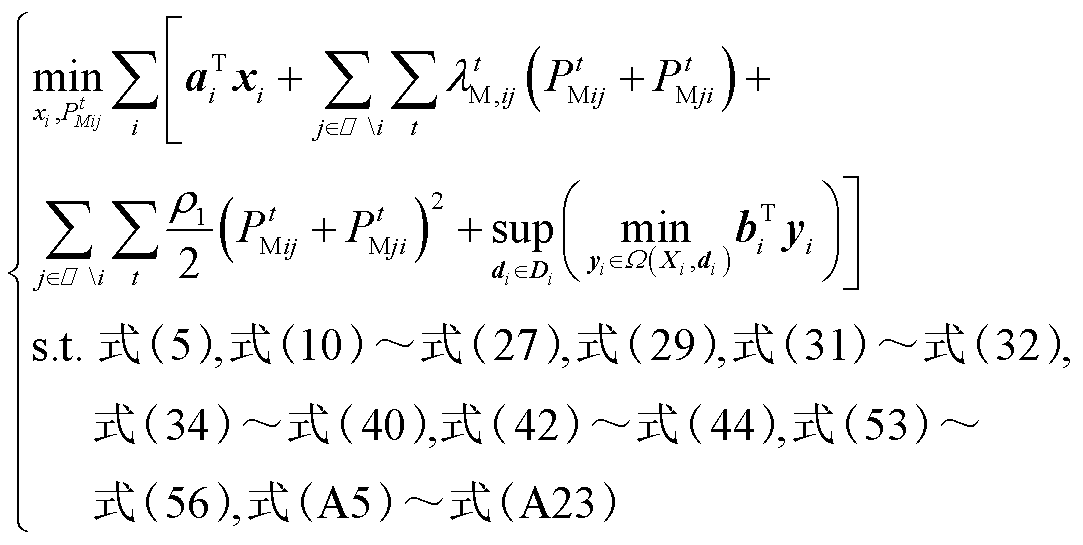 (61)
(61)式中,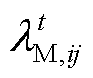 为多能微网i和j耦合约束的拉格朗日乘子;
为多能微网i和j耦合约束的拉格朗日乘子;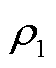 为对应的罚参数。基于ADMM算法,式(61)可拆分为每个多能微网对应的子模型。以多能微网i为例,其子模型为
为对应的罚参数。基于ADMM算法,式(61)可拆分为每个多能微网对应的子模型。以多能微网i为例,其子模型为
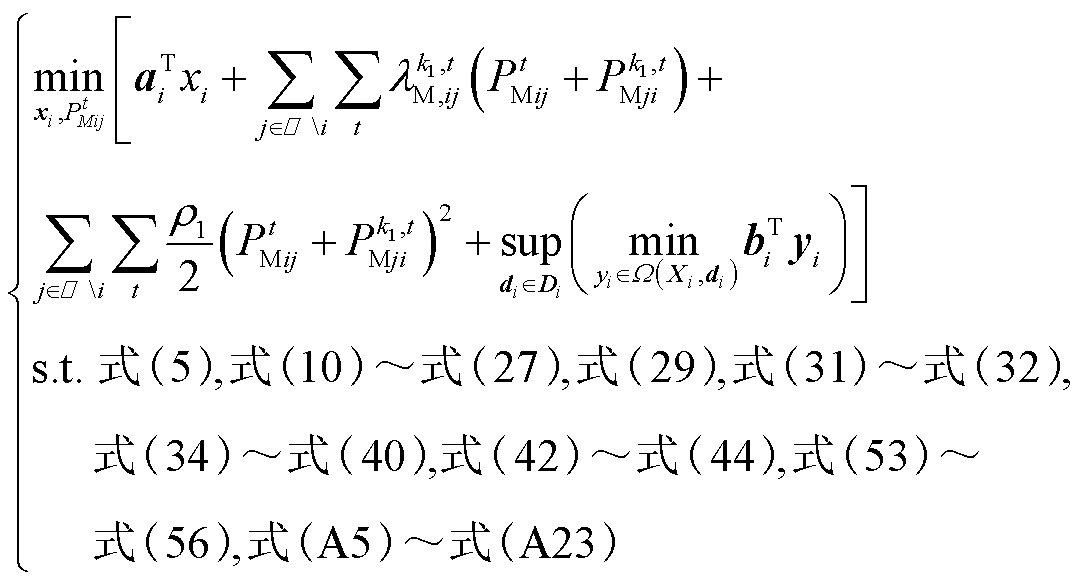 (62)
(62)
式中,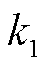 为ADMM的迭代次数;
为ADMM的迭代次数;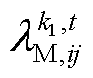 为第
为第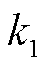 次迭代对应的耦合约束乘子;
次迭代对应的耦合约束乘子;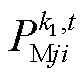 为第
为第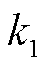 次迭代其余多能微网传递的交互功率。
次迭代其余多能微网传递的交互功率。
为求解式(62),采用C&CG算法[11]将其拆分为主问题(Master Problem, MP)和子问题(Subproblem, SP)进行迭代,其中MP为
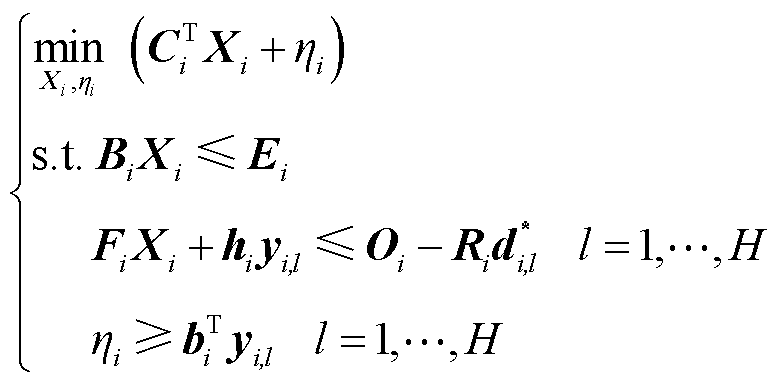 (63)
(63)式中,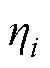 为辅助变量;
为辅助变量;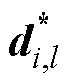 为历次迭代中求解SP得到的不确定解;
为历次迭代中求解SP得到的不确定解;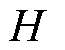 为C&CG的迭代次数;
为C&CG的迭代次数;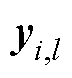 为MP构造的第l组日内决策变量;
为MP构造的第l组日内决策变量;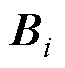 、
、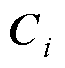 、
、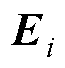 、
、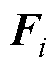 、
、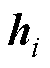 、
、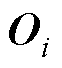 、
、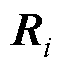 为MP的相关系数矩阵。
为MP的相关系数矩阵。
SP表达式为
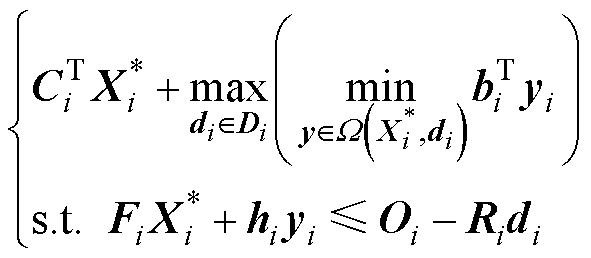 (64)
(64)式中,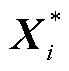 为MP的最优解。
为MP的最优解。
将式(63)的最优值记为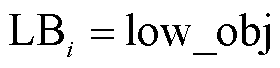 ;同时记式(64)的最优值为
;同时记式(64)的最优值为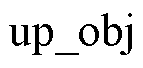 ,并令
,并令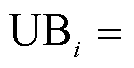
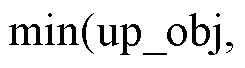
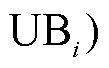 ,则子模型的C&CG收敛条件为
,则子模型的C&CG收敛条件为
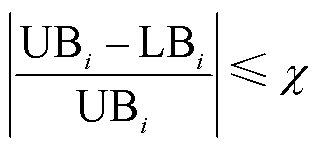 (65)
(65)式中,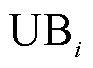 和
和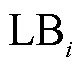 分别为多能微网i子模型的上、下界;
分别为多能微网i子模型的上、下界;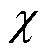 为C&CG算法的收敛阈值。当C&CG算法收敛后,将求得的交互功率送至对应的多能微网子模型继续迭代,直至满足ADMM算法的收敛条件,即
为C&CG算法的收敛阈值。当C&CG算法收敛后,将求得的交互功率送至对应的多能微网子模型继续迭代,直至满足ADMM算法的收敛条件,即
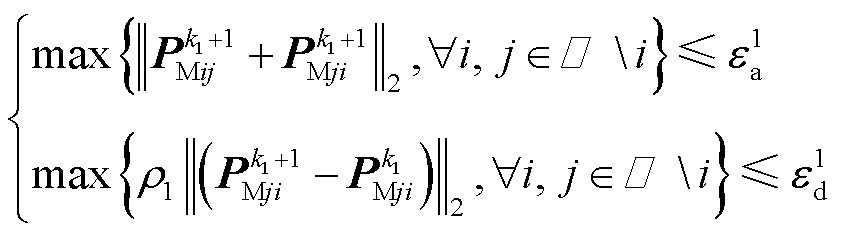 (66)
(66)
式中,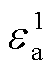 和
和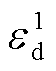 分别为子问题SP1原始残差和对偶残差的收敛阈值。
分别为子问题SP1原始残差和对偶残差的收敛阈值。
为了对SP2进行分布式求解,需要构造相邻多能微网的电价耦合约束为
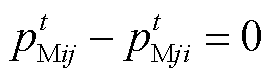 (67)
(67)基于式(60)和式(67),SP2的增广拉格朗日函数为
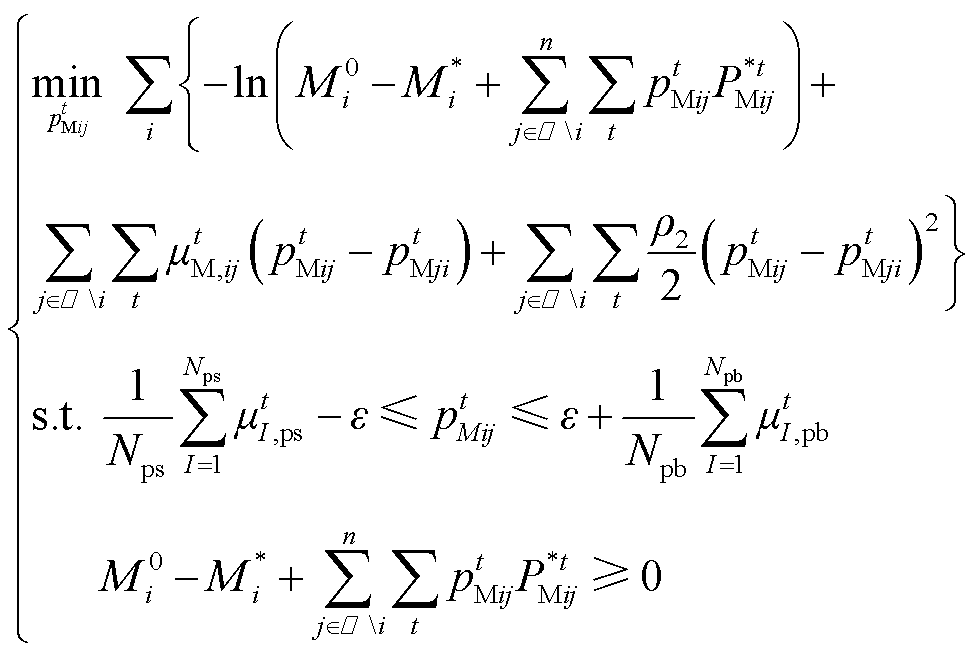 (68)
(68)
式中,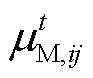 为多能微网i和j电价耦合约束的拉格朗日乘子;
为多能微网i和j电价耦合约束的拉格朗日乘子;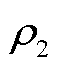 为对应的罚参数。类似地,可基于ADMM算法,将式(68)拆分为每个多能微网对应的电价子模型,以多能微网i为例,其子模型为
为对应的罚参数。类似地,可基于ADMM算法,将式(68)拆分为每个多能微网对应的电价子模型,以多能微网i为例,其子模型为
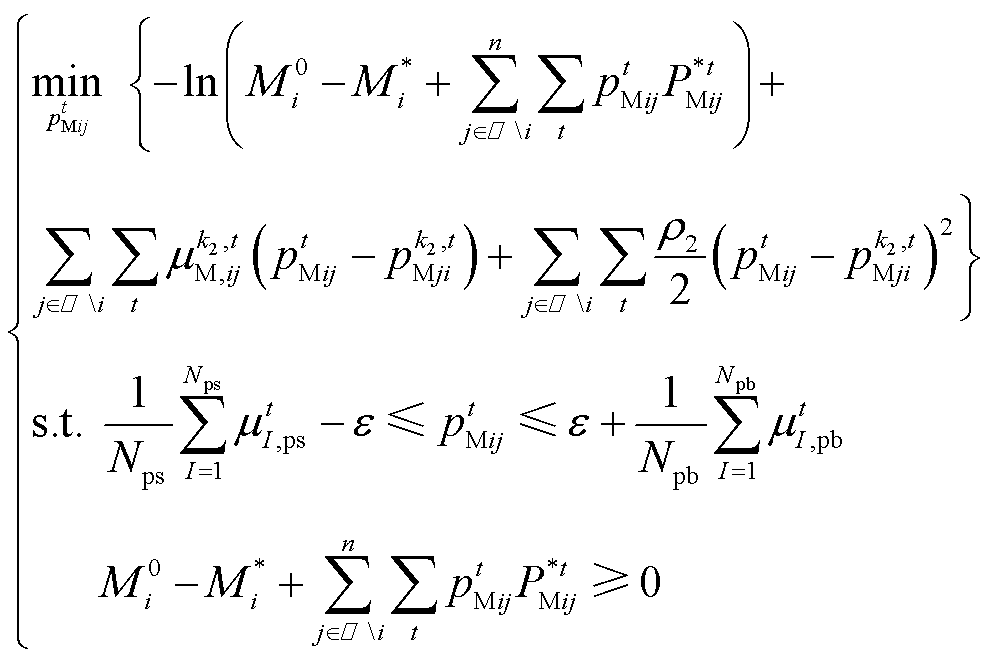 (69)
(69)式中,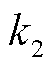 为ADMM的迭代次数;
为ADMM的迭代次数;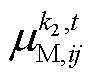 为第
为第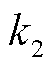 次迭代对应的耦合约束乘子;
次迭代对应的耦合约束乘子;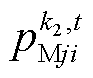 为第
为第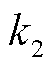 次迭代其余多能微网传递的交互电价。将求得的交互电价送至对应的多能微网继续迭代,直至满足收敛条件式(70)。
次迭代其余多能微网传递的交互电价。将求得的交互电价送至对应的多能微网继续迭代,直至满足收敛条件式(70)。
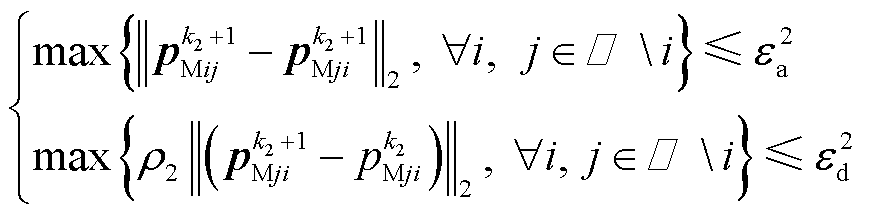 (70)
(70)
式中,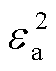 和
和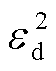 分别为子问题SP2原始残差和对偶残差的收敛阈值。算法的整体迭代流程如图2所示,对应的伪代码见附录4。
分别为子问题SP2原始残差和对偶残差的收敛阈值。算法的整体迭代流程如图2所示,对应的伪代码见附录4。
本文以三个多能微网为基础进行仿真测试,所使用的软件为Python3.6.5和Gurobi9.1.2。多能微网内部元件以及相关算法的参数见附表1。其中每个多能微网配置的燃气轮机、储能的数量均为1,且相同元件的容量相等;每个多能微网内部的产消者数量统一设置为3,且均配备了总容量为100 kW的屋顶光伏。多能微网1的新能源设备为风电,多能微网2的新能源设备为光伏,多能微网3的新能源设备为风电和光伏,具体的架构如附图1所示。各多能微网内部可再生能源出力、电负荷以及热负荷的预测曲线如附图2~附图4所示,本文假设每个多能微网新能源出力的预测误差服从均值为0、方差为0.1的正态分布[12]。多能微网和上级电网的平均购售电价如附图5所示,多能微网制定给产消者的售电电价范围如附图6所示。所有数据的采样频率为1 h,对应的总时段T=24 h。
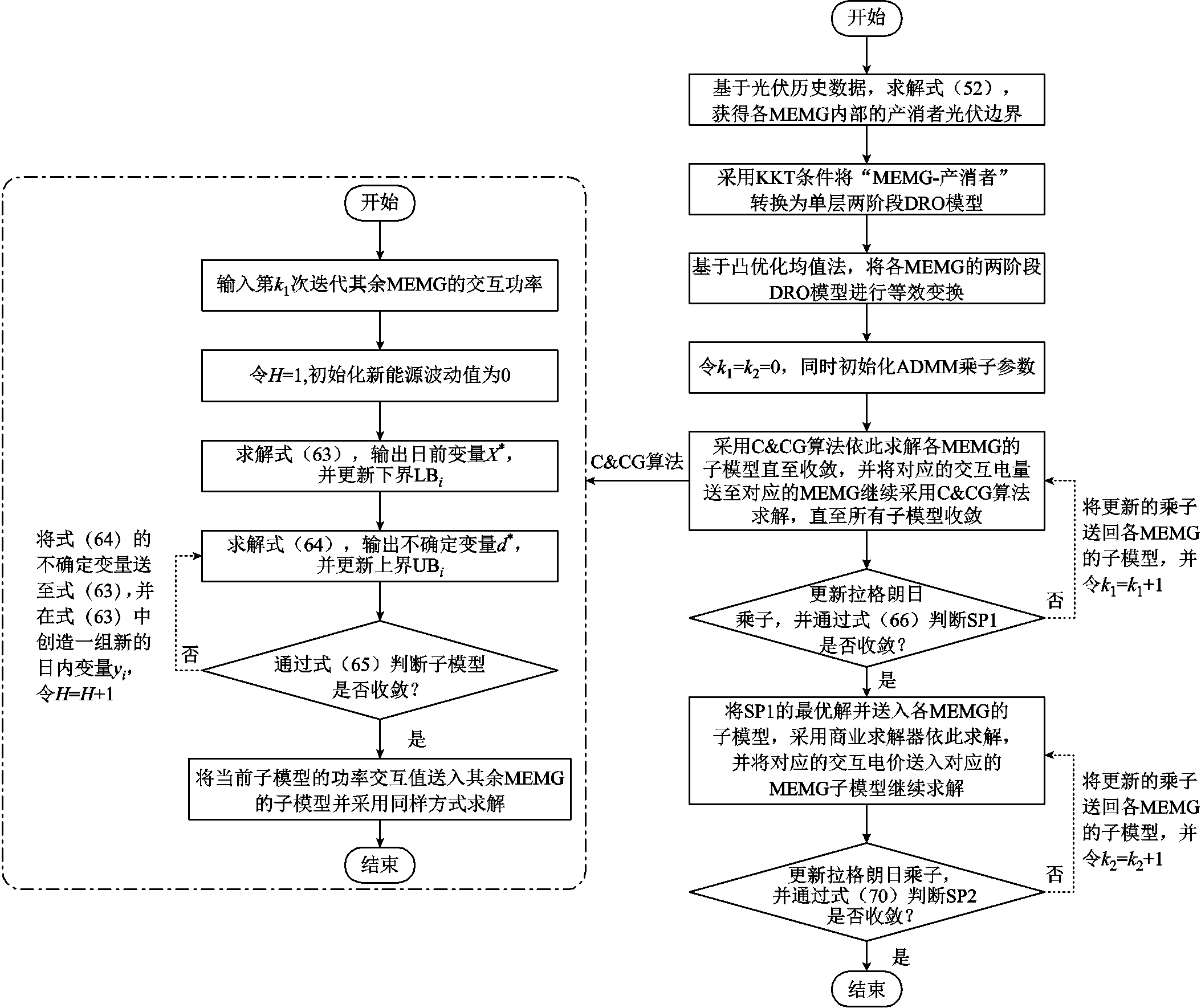
图2 算法求解流程
Fig.2 Algorithm iteration flow chart
本文对应的算法收敛情况如图3所示,其中SP1子问题的迭代次数为38次,而SP2的迭代次数为67次,对应的计算时间分别为189.59 s和25.93 s。该计算成本对于多能微网的日前调度规划是完全充足的。
4.2.1 电能优化分析
各多能微网的电能交互结果如图4所示,通过分析可以证明它们在不同时段的出力互补性。具体来说,在1:00—5:00,多能微网2新能源出力为0,因此其向多能微网1和3进行购电;而多能微网1在该时段负荷较重,因此选择向多能微网3购买少量电能,同时也提供电能给多能微网2获得利润;在7:00—16:00,多能微网2新能源出力充裕,可以为其余多能微网提供电能。在17:00—21:00,多能微网1为充裕型微网,可以为其余多能微网提供电能。类似地,在22:00—24:00,多能微网3表现为充裕型微网。
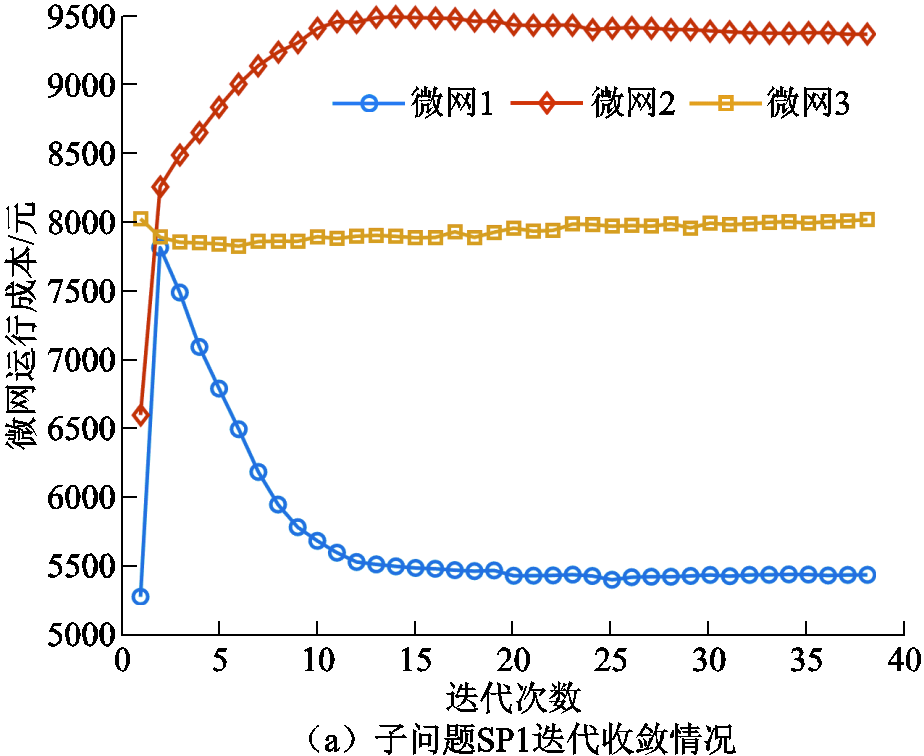
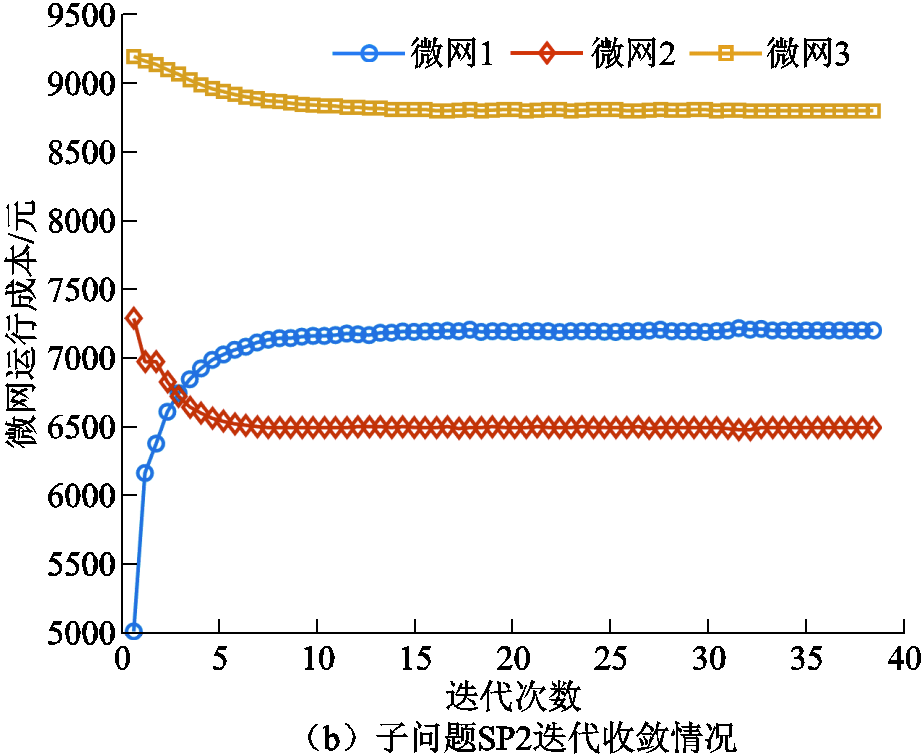
图3 算法收敛清况
Fig.3 Convergence of the algorithm
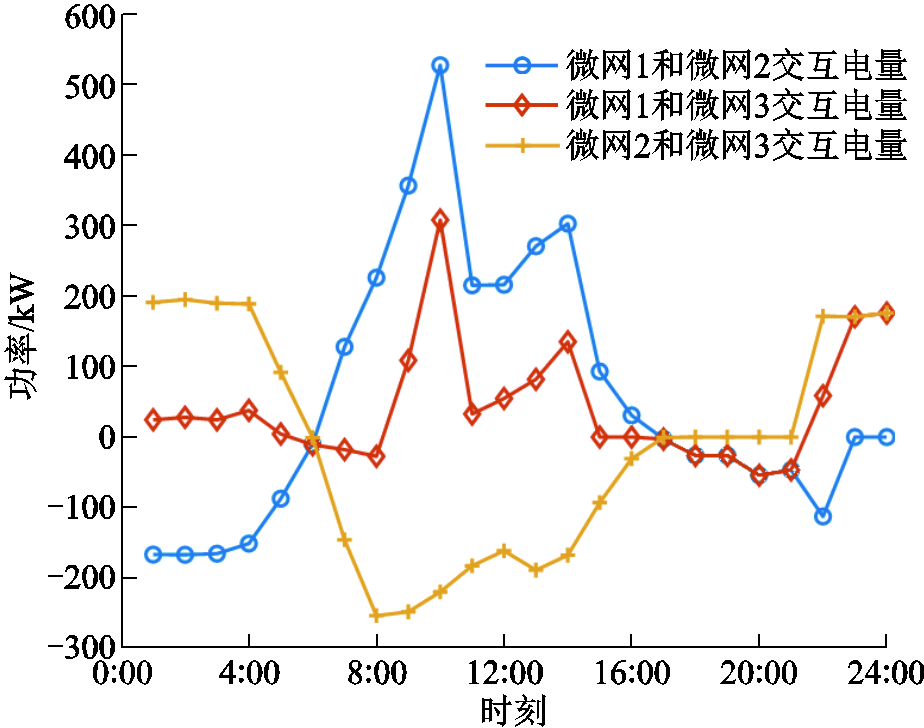
图4 多主体多能微网交互功率
Fig.4 Electric energy trading between each MEMG
多能微网之间的交互电价如图5所示,其结果介于其和上级电网的等效购售电价之间,从而为P2P交易提供了合理的平台。以多能微网2为例,在7:00—16:00,相比向上级电网售电,多能微网2可以以更高的价格将电能卖给多能微网1和3;而在其余时段,其通过更低的价格向多能微网1和3买电,从而提升了运行效益。
图6以多能微网2为例,给出了其电功率平衡情况;而其余多能微网的电功率平衡情况如附图7、附图8所示。
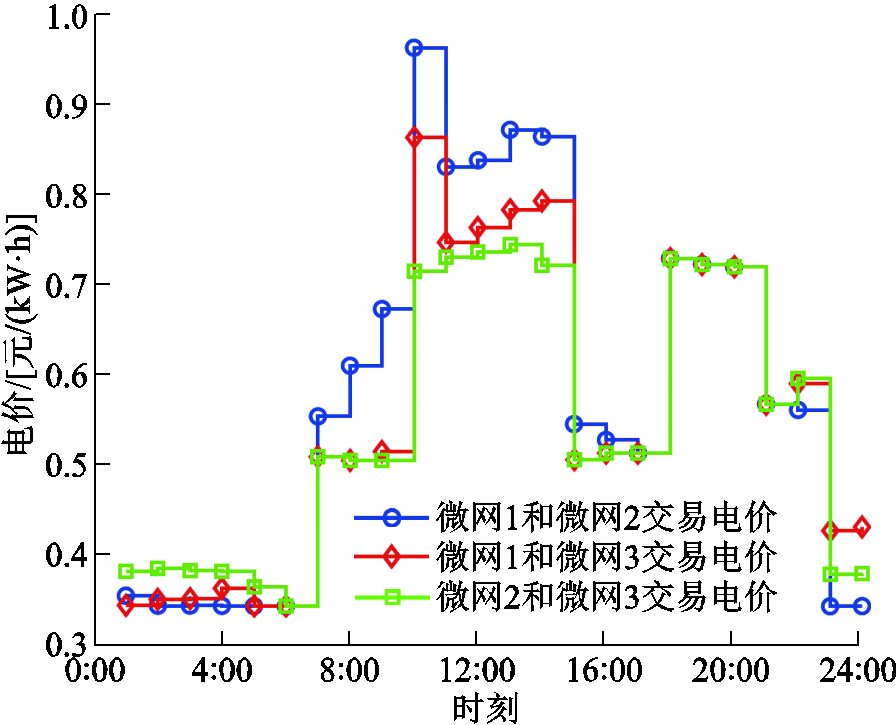
图5 多主体多能微网交互电价
Fig.5 Electric trading price between each MEMG
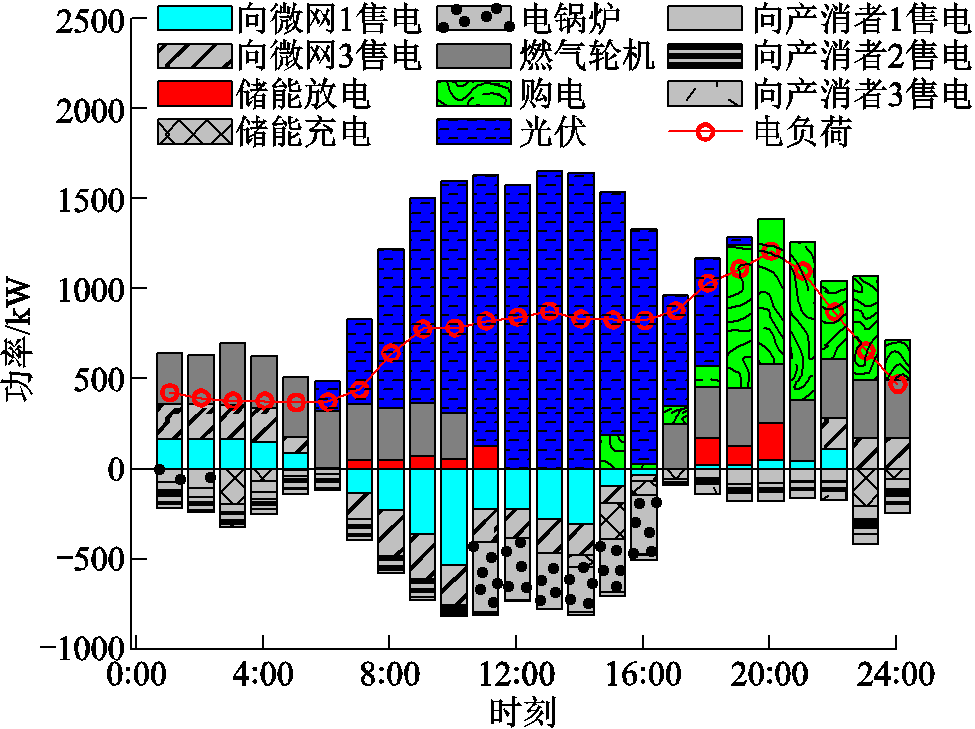
图6 基于合作博弈的多能微网2电功率平衡条件
Fig.6 Electric energy balance conditions of MEMG 2 based on cooperation game
4.2.2 热能优化分析
由于燃气轮机具备“热电联产”的效应,因此热功率平衡条件和燃气轮机的运行情况直接相关。以多能微网1为例,其热功率平衡条件如图7所示。
对于多能微网1而言,在11:00—22:00时段内其电负荷和热负荷均处于较高水平,为了满足高负荷下的功率平衡,该时段多能微网1的燃气轮机开始投入运行。根据附表1可知,本文设置的燃气轮机最低产热功率为360 kW,而在其余时段多能微网1的热负荷低于该值,因此仅通过电锅炉进行热负荷供应。类似地,其余多能微网的热功率平衡条件如附图9、附图10所示。
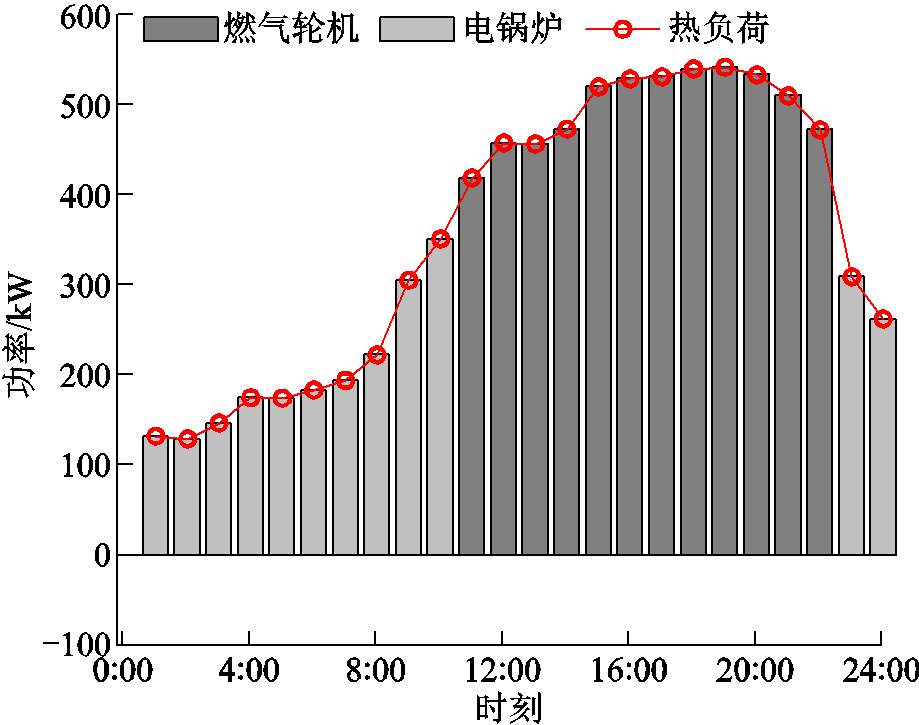
图7 多能微网1热功率平衡条件
Fig.7 Heat energy balance conditions of MEMG 1
4.2.3 产消者优化分析
图8以多能微网3内部的1号产消者为例,给出其基于50天历史数据得到的优化边界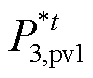 。
。
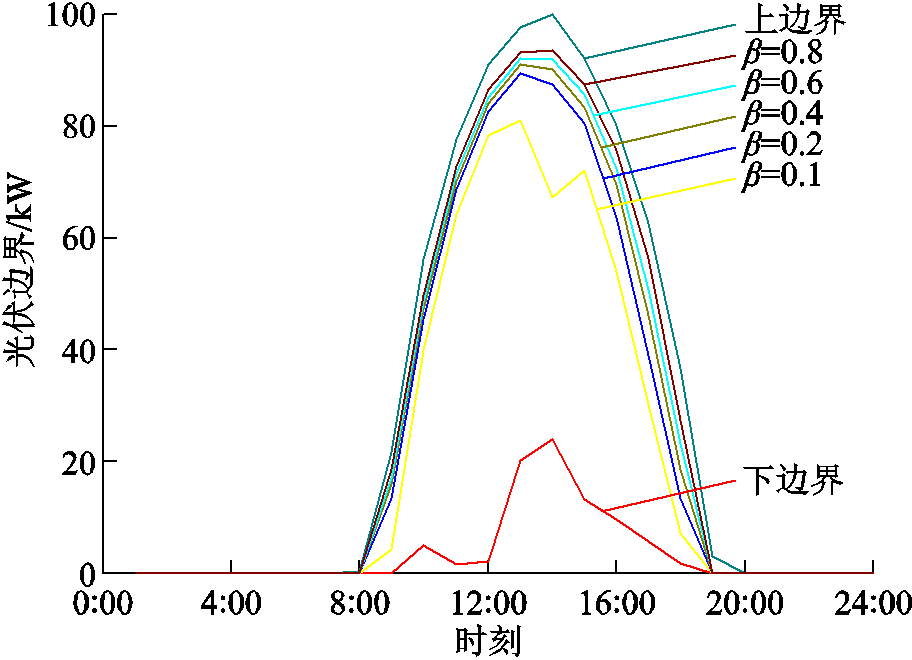
图8 基于DRCC的产消者不确定性分析
Fig.8 Uncertainty analysis of prosumer based on DRCC
图8表明,光伏的边界出力随着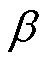 的增大而增大,符合概率论里上分位点的理论。当
的增大而增大,符合概率论里上分位点的理论。当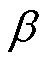 取值过小,光伏的出力下界也会小于绝大多数场景,导致式(52)的优化结果较为保守。该产消者的内部电功率平衡条件如图9所示。
取值过小,光伏的出力下界也会小于绝大多数场景,导致式(52)的优化结果较为保守。该产消者的内部电功率平衡条件如图9所示。
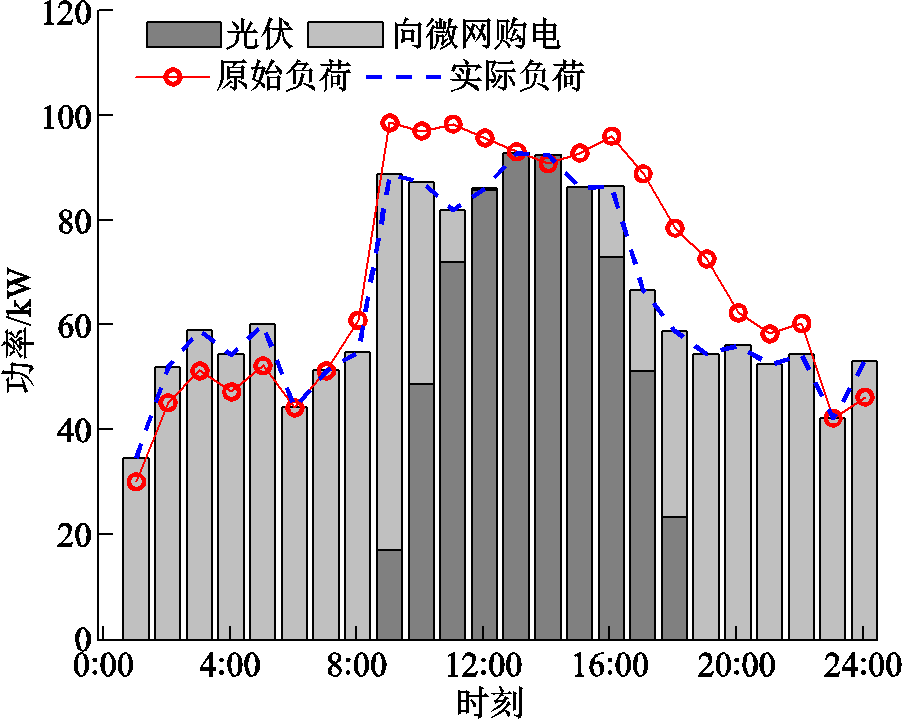
图9 多能微网3内部产消者1的电功率平衡条件
Fig.9 Electric energy balance conditions of prosumer 1 in MEMG 3
从图9中可知,在一些特定的时段(如1:00—8:00,19:00—24:00),光伏边界为0。这是因为该时段所对应的光伏历史出力全为0(或只有极少数据不为0),此时采用式(52)计算对应的光伏边界会极大地增加计算成本,同时得到不合理的求解结果(如负值)。因此,产消者在该时段内通过需求响应调整负荷,并向多能微网购电以满足自身需求;而在9:00—17:00时段,产消者将优先通过光伏进行供电,缺额部分则通过向多能微网购电获得。多能微网3和内部产消者的交互电价如图10所示,而各产消者的运行成本见表1。
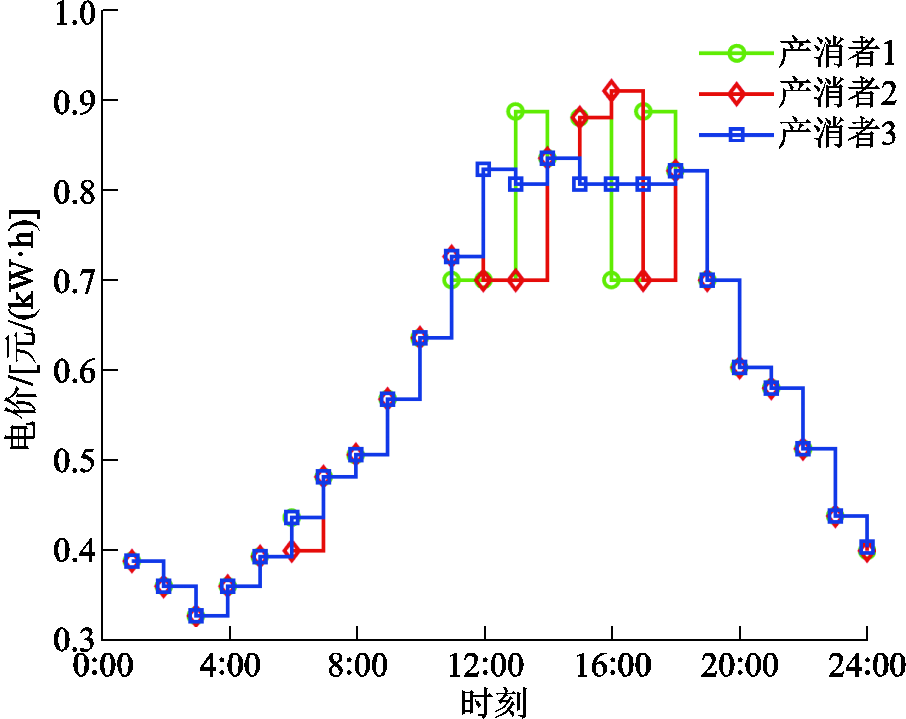
图10 多能微网3与内部产消者的交互电价
Fig.10 Electric trading price between MEMG 3 and each prosumer
表1 多能微网3内部产消者运行成本
Tab 1 Opreating cost of each prosumer in MEMG 3

产消者编号运行成本/元 1523.35 2550.71 3402.04
4.3.1 不同W球半径下的成本比较
根据第2节、第3节可知,不确定主体的W球半径会对优化结果产生影响。本文以多能微网的新能源出力为例,设置三组W球半径进行对比,分析其对系统成本的影响[39]。其中第1组的W球半径为0,即模糊集仅含经验分布;第2组中多能微网1和2的新能源出力W球半径取30,多能微网3取60;第3组中多能微网1和2的W球半径取50,多能微网3取100。三组半径对应的系统总成本如图11所示。
从图11中可知,系统运行成本随着W球半径的增大而增大。一方面,当W球半径较小时,模糊集包含的分布较少,因此系统应对最劣分布的成本也较低;另一方面,因为随着半径的增大,模糊集内的分布增多,新能源出力不确定性进一步增强,从而导致系统应对最劣分布的成本增加。
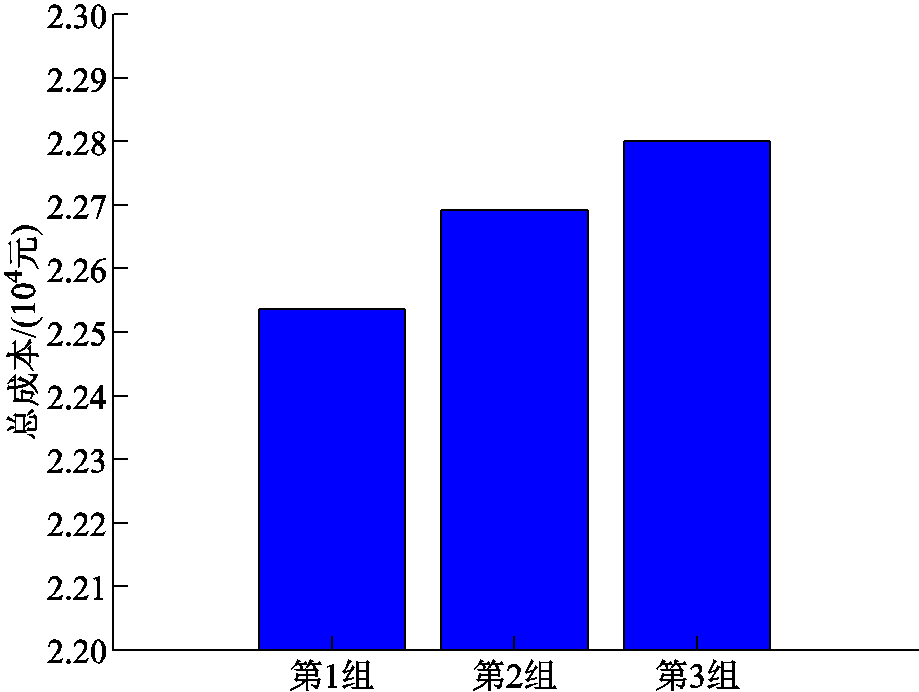
图11 不同新能源出力W球半径对应的系统成本
Fig.11 Total cost under different radius of Wasserstein ball
4.3.2 不同鲁棒模型下的成本比较
为了验证本文模型和传统鲁棒模型的区别及有效性,本文设置如下场景进行比对。场景1:所有多能微网采用Wasserstein两阶段分布鲁棒,且不参与合作;场景2:多能微网采用Wasserstein两阶段分布鲁棒,同时相互之间进行P2P合作博弈;场景3:多能微网采用传统的两阶段鲁棒,且不参与合作;场景4:多能微网采用两阶段鲁棒,同时相互之间进行P2P合作博弈。场景3和4对应的新能源出力不确定集取自文献[40]。四种场景对应的多能微网运行成本见表2。
表2 不同场景多能微网运行成本
Tab.2 Opreating cost of each MEMG under different scenario

场景运行成本/元总成本/元 MEMG 1MEMG 2MEMG 3 18 071.857 930.658 389.6824 392.18 27 538.797 400.597 860.8622 800.24 38 095.387 947.728 702.2424 745.34 47 509.617 362.548 117.9122 990.06
对比场景1和场景2可知,每个多能微网均可以通过合作博弈降低成本约530元。若不考虑合作博弈,三个多能微网均存在向上级电网售电的行为;而参与合作博弈后,所有多能微网不再向上级电网进行售电,且向上级电网的购电频率也有显著减小。该结果一方面证明与直接和上级电网交互相比,合作博弈为多能微网提供了更经济的调度方案;另一方面也说明通过合作博弈可以促进多能微网的新能源消纳水平,避免其过多售电对上级电网带来的冲击。类似地,对比场景3和场景4,每个多能微网均可以通过合作博弈降低成本约585元,可知无论采用何种鲁棒模型,合作博弈都能有效降低运行成本。对比场景1和场景3可知,基于Wasserstein的两阶段分布鲁棒能够有效地缓解两阶段鲁棒的保守问题;同样地,对比场景2和场景4可知,总成本由22 800.24元上升到22 990.06元,但由于两阶段鲁棒的不确定集范围更大,在合作博弈中可能会促进电能交互并增加P2P收益,基于场景2的多主体多能微网总交互功率为7 921.82 kW,而场景4则为8 059.41 kW,扩大了多能微网之间的交互量。
本文考虑了多重不确定主体对多能微网优化运行的影响,提出了基于Wasserstein两阶段分布鲁棒的多能微网合作博弈模型,主要结论如下:
1)考虑了多能微网的典型架构,构建了“多能微网-产消者”的双层优化模型,能够有效地体现两者的互动影响。
2)充分考虑了多能微网新能源出力、电价以及内部产消者光伏出力等多重不确定性主体对系统优化的影响,构建了基于Wasserstein两阶段分布鲁棒模型,在改善传统鲁棒决策保守的同时提升了系统应对不确定性的能力。
3)在问题求解方面,采用凸均值法对两阶段分布鲁棒模型进行等效变换,降低了模型求解难度;并通过ADMM嵌套C&CG算法,实现对两阶段分布鲁棒与合作博弈模型的有效求解。
本文所提模型的主要研究对象为相邻的多能微网,因此下一步将对不同电力市场机制下(如跨区域、跨国等情况)的多能微网合作模式进行深入研究。此外,后续将进一步分析市场动态变化以及极端天气导致的可再生能源高波动性对多能微网运行的影响。
附 录
1. 购电成本与售电利润转换
多能微网在t时刻向上级电网的购电成本可等效为[14,28]
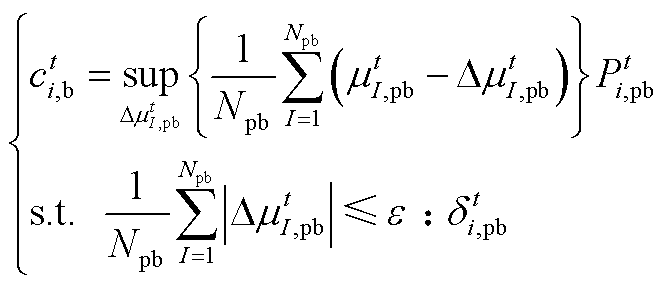 (A1)
(A1)其对应的拉格朗日函数为
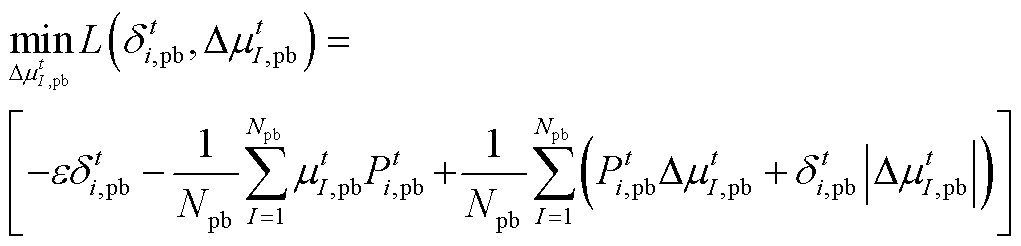 (A2)
(A2)
式(A2)的最小值为
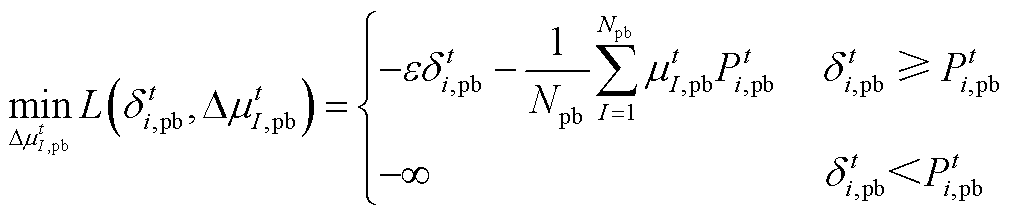 (A3)
(A3)因此,式(A1)的对偶问题为
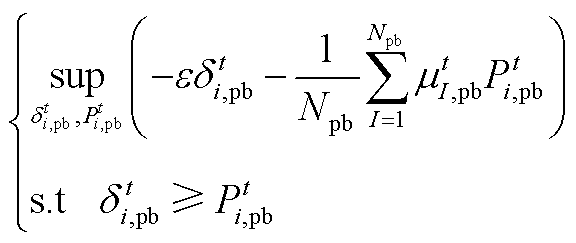 (A4)
(A4)
根据对偶问题和原问题的关系,并结合式(A4),文中式(8)最终可转换为式(42)的形式。类似地,多能微网在t时刻和上级电网的售电利润可由式(9)转换为式(43),具体推导过程不再赘述。
2. 产消者约束
下层产消者J的一阶平稳条件为
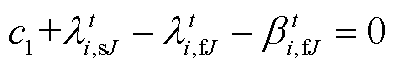 (A5)
(A5)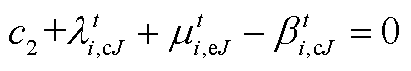 (A6)
(A6)
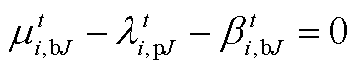 (A7)
(A7)
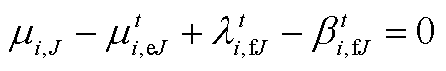 (A8)
(A8)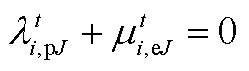 (A9)
(A9)
产消者J对应的对偶可行域以及互补松弛大M约束为
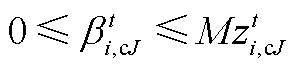 (A10)
(A10)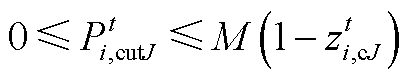 (A11)
(A11)
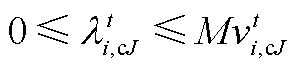 (A12)
(A12)
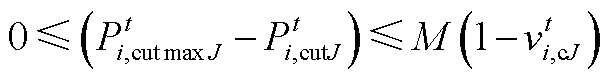 (A13)
(A13)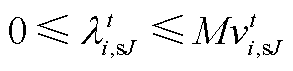 (A14)
(A14)
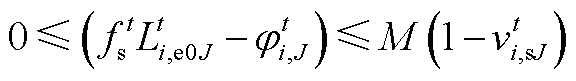 (A15)
(A15)
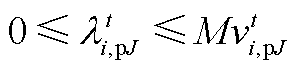 (A16)
(A16)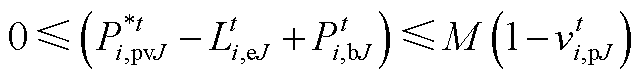 (A17)
(A17)
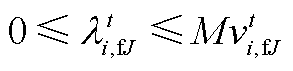 (A18)
(A18)
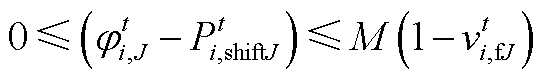 (A19)
(A19)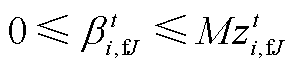 (A20)
(A20)
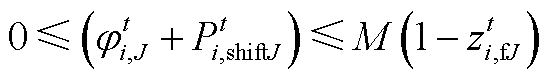 (A21)
(A21)
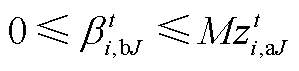 (A22)
(A22)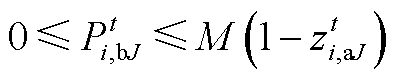 (A23)
(A23)
式中,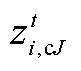 、
、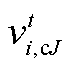 、
、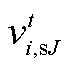 、
、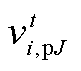 、
、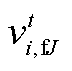 、
、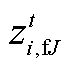 和
和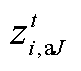 均为0-1变量,本文记它们的集合为
均为0-1变量,本文记它们的集合为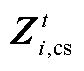 。
。
3. “多能微网-产消者”交互利润转换
对于一个线性规划问题,其紧凑形式为
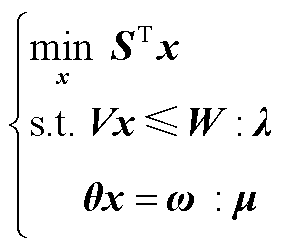 (A24)
(A24)对应的对偶问题为
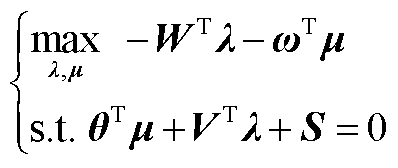 (A25)
(A25)
根据强对偶定理,式(A24)和式(A25)的最优值相等。因此,产消者的目标函数可以转换为
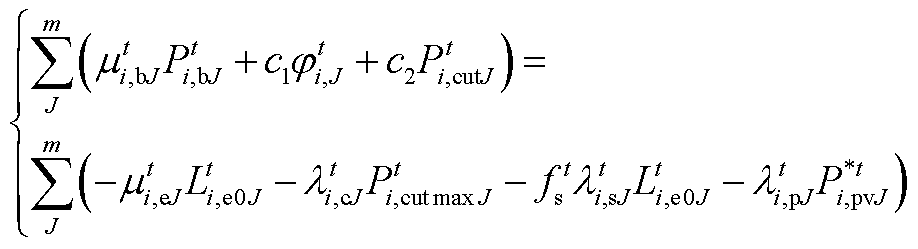 (A26)
(A26)对式(A26)进行移项,即得式(54)。
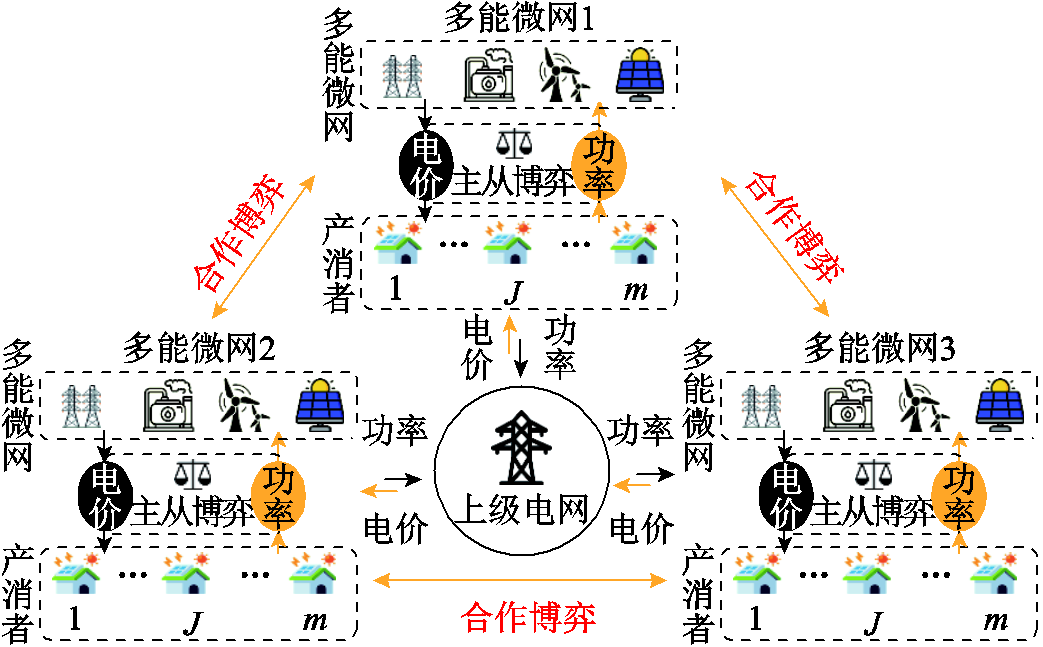
附图1 结构示意图
App.Fig.1 Framework of model
4. 算法伪代码

基于ADMM嵌套C&CG算法的迭代求解 设置SP1的收敛精度和与最大迭代次数,并初始化迭代次数 for do for each MEMG i∈do 设置C&CG算法收敛精度,初始化迭代次数H=1,并令 while abs((UBi-LBi)/UBi)>: 求解MP式(63) 输出至SP, 并令最优值为 求解SP式(64) 输出至MP, 记最优值为,并令 H=H+1 end while 将交互功率输入对应的MEMG end for 更新拉格朗日乘子 until 式(66)成立 end for 设置SP2的收敛精度和与最大迭代次数,并初始化迭代次数 for do for each MEMG i∈do 求解式(69) 将交互电价送至对应的MEMG end for 更新拉格朗日乘子 until 式(70)成立 end for
5. 系统参数
附表1 主要参数
App.Tab.1 Main parameters

参数数值 购/售电功率上限/kW2 000/2 000 储能充/放电功率上限/kW200/200 储能充放电成本系数/[元/(kW·h)]0.05 储能充/放电效率0.95/0.95 储能电量上/下限/(kW·h)540/60 储能电量初始值/(kW·h)300 燃气轮机输入上/下限/kW1 600/800
(续)

参数数值 燃气轮机最短/最长运行时间/h2/24 燃气轮机产电/产热效率(%)30/45 单位天然气购买成本系数/[元/(kW·h)]0.35 电锅炉功率上限/kW1 000 电锅炉产热效率(%)90 电锅炉单位运行成本系数/[元/(kW·h)]0.1 产消者单位平移负荷成本系数/[元/(kW·h)]0.15 产消者单位中断负荷成本系数/[元/(kW·h)]0.5 最大切负荷比例/最大平移负荷比例(%)10/15 电价/产消者的W球半径0.01 MEMG 1/2/3新能源出力W球半径50/50/100 SP1罚参数0.01 SP2罚参数15 大M变量10 000 C&CG/SP1收敛精度0.005 SP2收敛精度10-8 DRCC违反概率(%)60
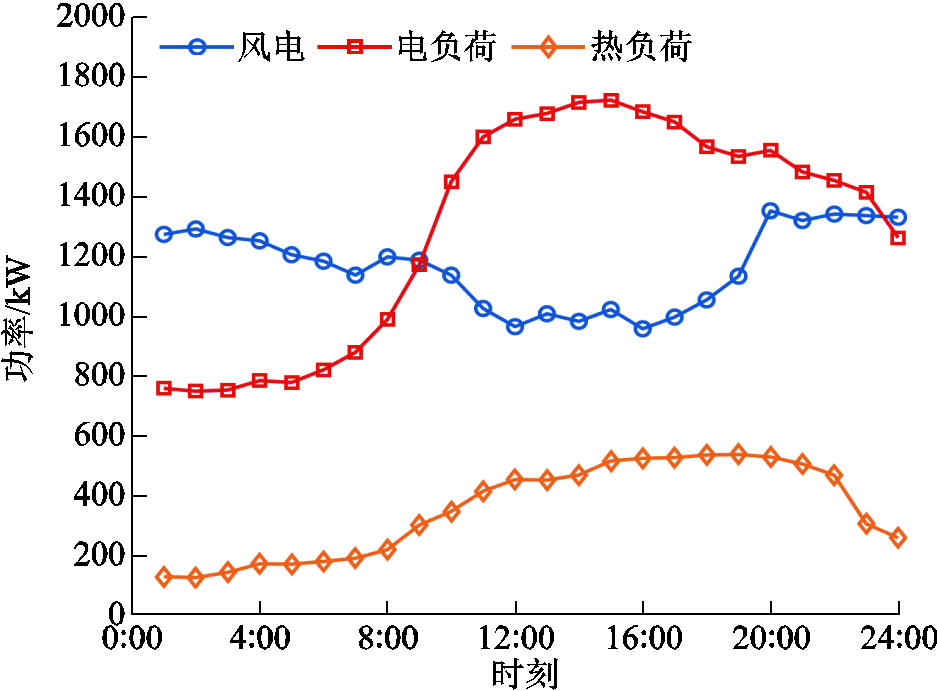
附图2 多能微网1的基础数据
App.Fig.2 Basic data of MEMG 1
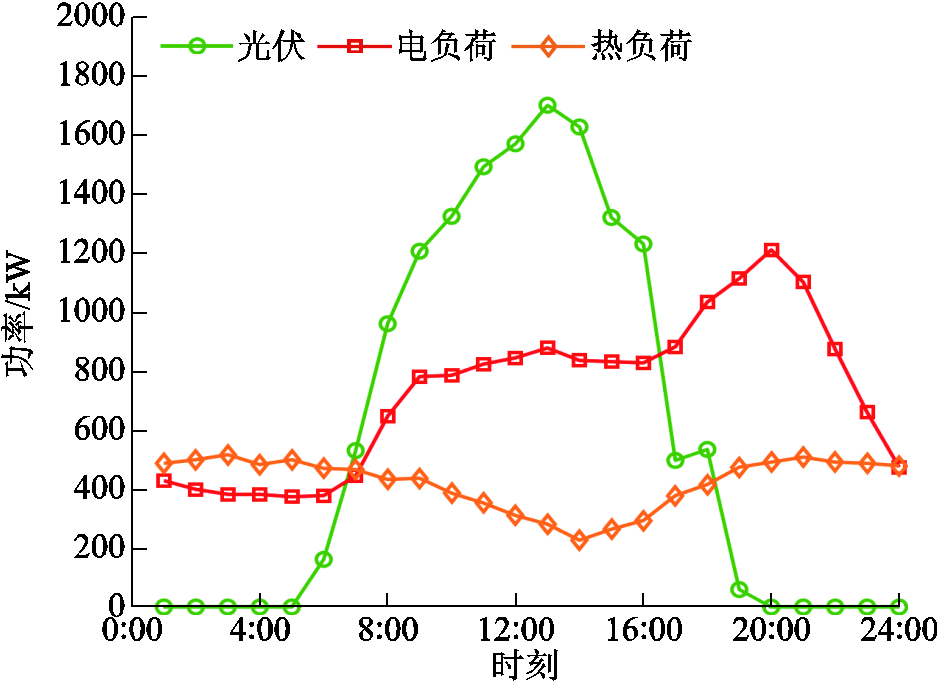
附图3 多能微网2的基础数据
App.Fig. 3 Basic data of MEMG 2
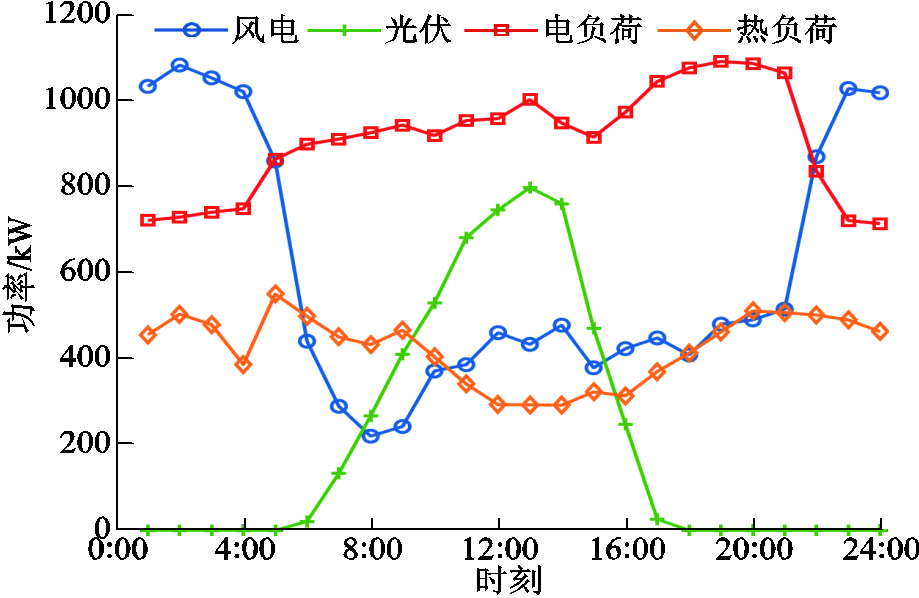
附图4 多能微网3的基础数据
App.Fig.4 Basic data of MEMG 3
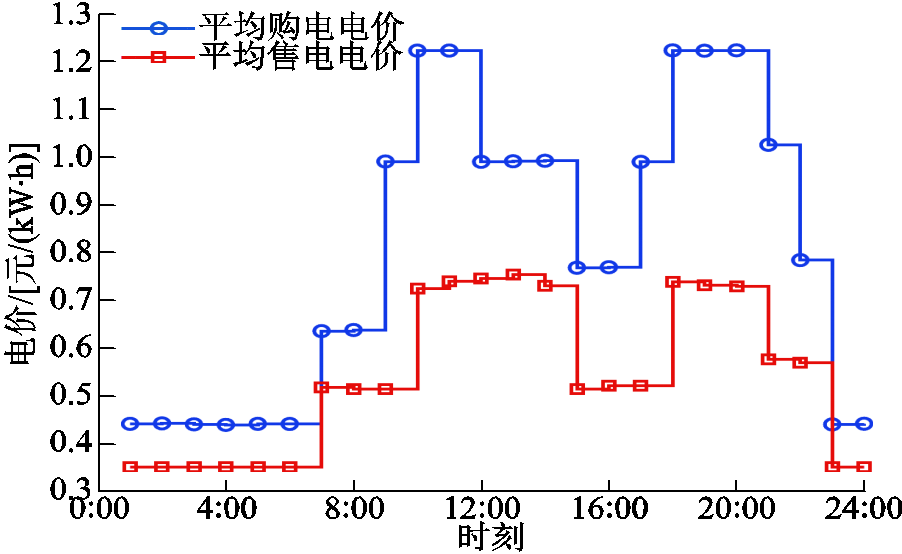
附图5 平均电价曲线
App.Fig.5 Curves of average electricity price
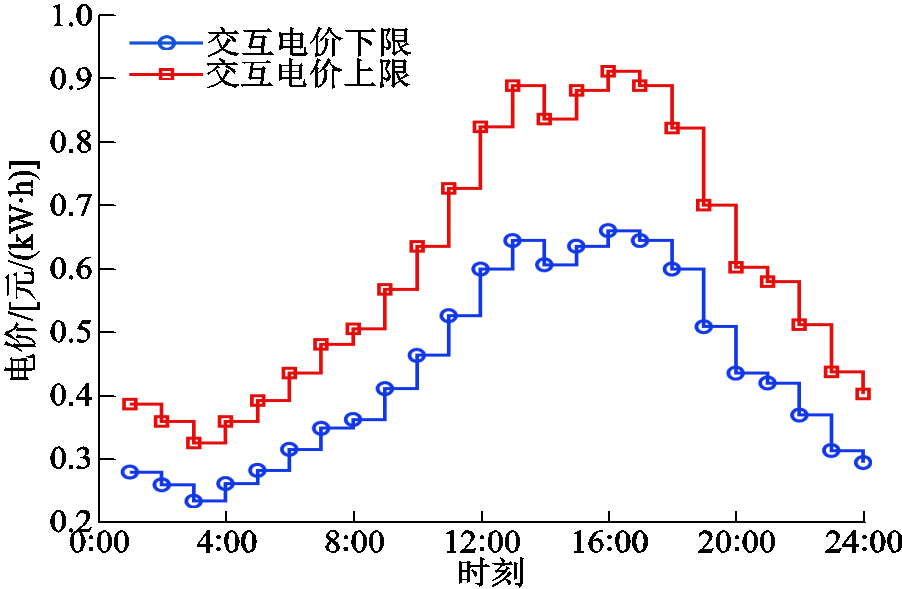
附图6 “多能微网-产消者”电价交互范围
App.Fig. 6 The range of interaction electricity price between MEMG and prosumer
6. 优化调度结果
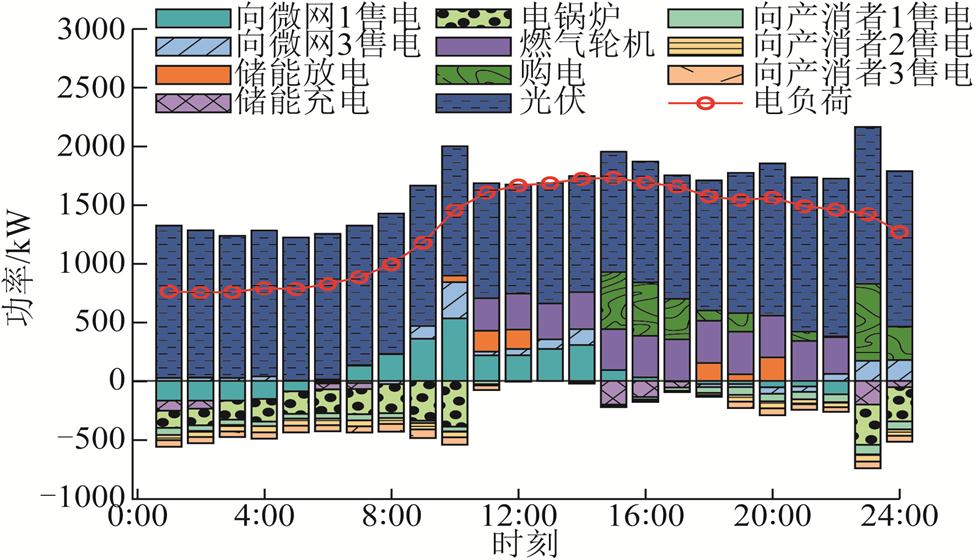
附图7 基于合作博弈的多能微网1电功率平衡条件
App.Fig.7 Electric energy balance conditions of MEMG 1 based on cooperation game
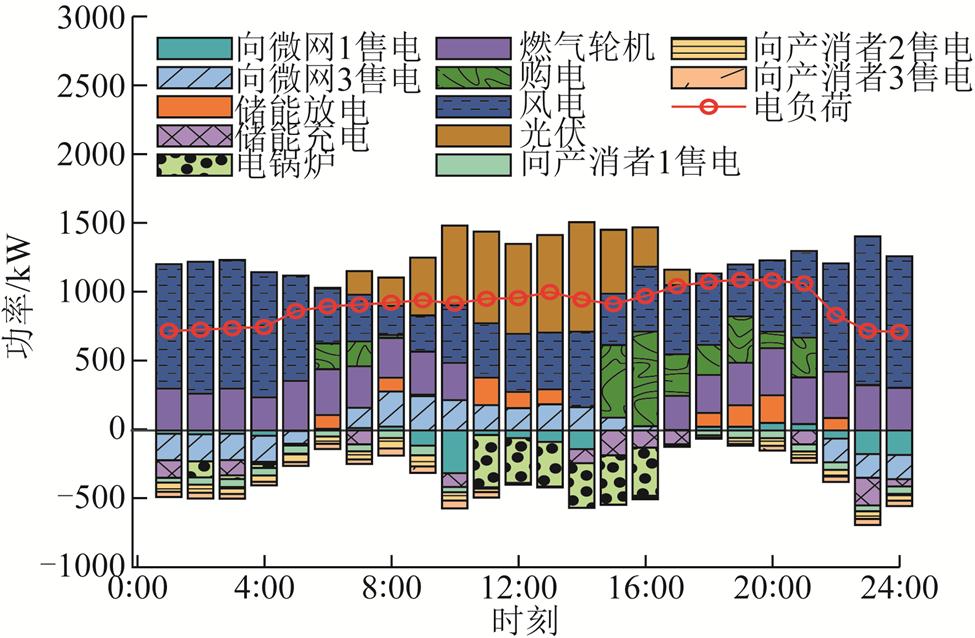
附图8 基于合作博弈的多能微网3电功率平衡条件
App.Fig.8 Electric energy balance conditions of MEMG 3 based on cooperation game
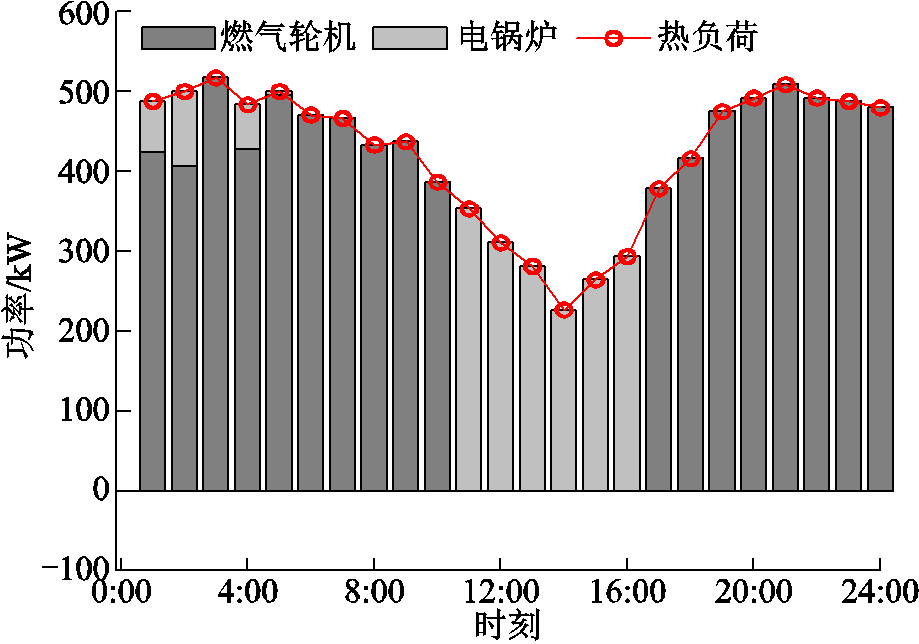
附图9 多能微网2热功率平衡条件
App.Fig.9 Heat energy balance conditions of MEMG 2
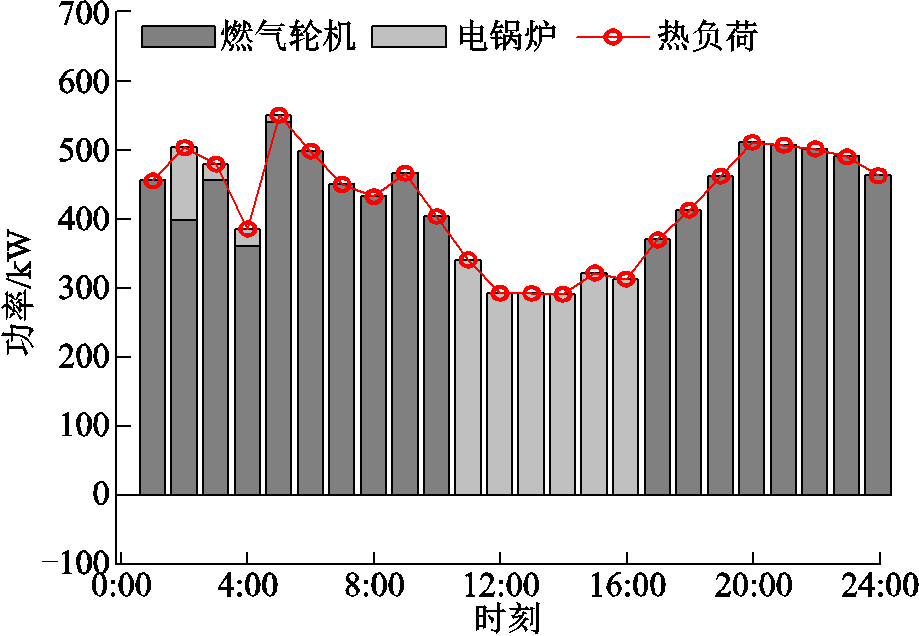
附图10 多能微网3热功率平衡条件
App.Fig.10 Heat energy balance conditions of MEMG 3
参考文献
[1] 李鸿, 朱继忠, 董瀚江. 考虑协变量因素的多能微电网两阶段分布鲁棒优化调度[J]. 中国电机工程学报, 2025, 45(3): 822-834.
Li Hong, Zhu Jizhong, Dong Hanjiang. Two-stage distributionally robust optimization scheduling for multi-energy microgrid considering covariate factors [J]. Proceedings of the CSEE, 2025, 45(3): 822-834.
[2] Chen Weidong, Wang Junnan, Yu Guanyi, et al. Research on day-ahead transactions between multi-microgrid based on cooperative game model[J]. Applied Energy, 2022, 316: 119106.
[3] Zhang Chenghua, Wu Jianzhong, Zhou Yue, et al. Peer-to-peer energy trading in a microgrid[J]. Applied Energy, 2018, 220: 1-12.
[4] Islam M, Yang Fuwen, Amin M. Control and optimisation of networked microgrids: a review[J]. IET Renewable Power Generation, 2021, 15(6): 1133-1148.
[5] Wu Zhi, Xu Zheng, Gu Wei, et al. Decentralized game-based robustly planning scheme for distribution network and microgrids considering bilateral energy trading[J]. IEEE Transactions on Sustainable Energy, 2022, 13(2): 803-817.
[6] Mohseni S, Pishvaee M S. Energy trading and scheduling in networked microgrids using fuzzy bargaining game theory and distributionally robust optimization[J]. Applied Energy, 2023, 350: 121748.
[7] Nasiri N, Zeynali S, Najafi Ravadanegh S, et al. Moment-based distributionally robust peer-to-peer transactive energy trading framework between networked microgrids, smart parking lots and electricity distribution network[J]. IEEE Transactions on Smart Grid, 2024, 15(2): 1965-1977.
[8] Wang Zhuo, Hou Hui, Zhao Bo, et al. Risk-averse stochastic capacity planning and P2P trading collaborative optimization for multi-energy microgrids considering carbon emission limitations: an asymmetric Nash bargaining approach[J]. Applied Energy, 2024, 357: 122505.
[9] Pu Yuchen, Li Qi, Luo Shuyu, et al. Peer-to-peer electricity-hydrogen trading among integrated energy systems considering hydrogen delivery and transportation [J]. IEEE Transactions on Power Systems, 2024, 39(2): 3895-3911.
[10] 王学杰, 赵会茹, 曹艺琼, 等. 基于随机-Nash-Harsanyi讨价还价博弈的光伏-氢储能多主体分散协同调度[J]. 电工技术学报, 2024, 39(9): 2652-2666.
Wang Xuejie, Zhao Huiru, Cao Yiqiong, et al. Photovoltaic-hydrogen energy storage multi-agent decentralized cooperative scheduling based on stochastic-Nash-Harsanyi bargaining game[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2652-2666.
[11] Zeng Bo, Zhao Long. Solving two-stage robust optimization problems using a column-and-constraint generation method[J]. Operations Research Letters, 2013, 41(5): 457-461.
[12] Wang Lingling, Jiang Chuanwen, Gong Kai, et al. Data-driven distributionally robust economic dispatch for distribution network with multiple microgrids[J]. IET Generation, Transmission & Distribution, 2020, 14(24): 5712-5719.
[13] Lu Shuai, Gu Wei, Xu Yijun, et al. Unlock the thermal flexibility in integrated energy systems: a robust nodal pricing approach for thermal loads[J]. IEEE Transactions on Smart Grid, 2023, 14(4): 2734-2746.
[14] Mohajerin Esfahani P, Kuhn D. Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations[J]. Mathematical Programming, 2018, 171(1): 115-166.
[15] Zhong Junjie, Li Yong, Wu Yan, et al. Optimal operation of energy hub: an integrated model combined distributionally robust optimization method with Stackelberg game[J]. IEEE Transactions on Sustainable Energy, 2023, 14(3): 1835-1848.
[16] Li Yang, Han Meng, Shahidehpour M, et al. Data-driven distributionally robust scheduling of community integrated energy systems with uncertain renewable generations considering integrated demand response[J]. Applied Energy, 2023, 335: 120749.
[17] Zhong Junjie, Zhao Yirui, Li Yong, et al. Synergistic operation framework for the energy hub merging stochastic distributionally robust chance-constrained optimization and Stackelberg game[J]. IEEE Transactions on Smart Grid, 2025, 16(2): 1037-1050.
[18] Lin Zhenjia, Wu Qiuwei, Chen Haoyong, et al. Scenarios-oriented distributionally robust optimizationfor energy and reserve scheduling[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2943-2946.
[19] Zheng Xiaodong, Chen Haoyong. Data-driven distributionally robust unit commitment with Wasserstein metric: tractable formulation and efficient solution method[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4940-4943.
[20] Nguyen H T, Choi D H. Decentralized distributionally robust coordination between distribution system and charging station operators in unbalanced distribution systems[J]. IEEE Transactions on Smart Grid, 2023, 14(3): 2164-2177.
[21] Nguyen H T, Choi D H. Distributionally robust model predictive control for smart electric vehicle charging station with V2G/V2V capability[J]. IEEE Transactions on Smart Grid, 2023, 14(6): 4621-4633.
[22] 侯慧, 甘铭, 吴细秀, 等. 考虑移动氢能存储的港口多能微网两阶段分布鲁棒优化调度[J]. 中国电机工程学报, 2024, 44(8): 3078-3093.
Hou Hui, Gan Ming, Wu Xixiu, et al. Two-stage distributionally robust optimal scheduling for port multi-energy microgrid considering mobile hydrogen energy storage[J]. Proceedings of the CSEE, 2024, 44(8): 3078-3093.
[23] 俞鸿飞, 王韵楚, 吕瑞扬, 等. 考虑灵活爬坡产品的虚拟电厂两阶段分布鲁棒优化运营策略[J]. 电力系统自动化, 2024, 48(14): 16-27.
Yu Hongfei, Wang Yunchu, Lü Ruiyang, et al. Two-stage distributionally robust optimization operation strategy of virtual power plants considering flexible ramping products[J]. Automation of Electric Power Systems, 2024, 48(14): 16-27.
[24] 张玉敏, 李竞锐, 吉兴全, 等. 考虑电-碳市场决策协同的园区综合能源系统双层博弈调度[J]. 电力系统自动化, 2025, 49(12): 45-59.
Zhang Yumin, Li Jingrui, Ji Xingquan, et.al. Bi-level game dispatch of park integrated energy system considering decision-making synergy of electricity-carbon markets[J]. Automation of Electric Power Systems, 2025, 49(12): 45-59.
[25] 陈春宇, 黄宸恺, 王剑晓, 等. 考虑风电不确定性的调频辅助服务市场多时间尺度出清调度策略[J]. 电工技术学报, 2024, 39(21): 6804-6818.
Chen Chunyu, Huang Chenkai, Wang Jianxiao, et al. Multi-time-scale frequency regulation market clearing and dispatch strategy considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6804-6818.
[26] 宋梦, 林固静, 高赐威, 等. 考虑多重不确定性的广义共享储能优化配置方法[J]. 电工技术学报, 2025, 40(5): 1521-1539.
Song Meng, Lin Gujing, Gao Ciwei, et al. A generalized shared energy storage optimization configuration method considering multiple uncertainties [J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1521-1539.
[27] 江岳文, 陈梅森. 基于鲁棒后悔度的日前市场购电联合优化[J]. 电工技术学报, 2019, 34(9): 1971-1983.
Jiang Yuewen, Chen Meisen. Joint optimization of electricity purchase in the day-ahead market based on robust regret[J]. Transactions of China Electro-technical Society, 2019, 34(9): 1971-1983.
[28] 葛少云, 杜咏梅, 郭玥, 等. 基于分布鲁棒优化的车-站-网日前能量管理与交易[J]. 电力系统自动化, 2024, 48(5): 11-20.
Ge Shaoyun, Du Yongmei, Guo Yue, et al. Day-ahead energy management and trading of electric vehicles, charging stations and distribution networks based on distributionally robust optimization[J]. Automation of Electric Power Systems, 2024, 48(5): 11-20.
[29] 文艺林, 胡泽春, 宁剑, 等. 基于分布鲁棒机会约束的充电运营商参与调峰市场投标策略[J]. 电力系统自动化, 2022, 46(7): 23-32.
Wen Yilin, Hu Zechun, Ning Jian, et al. Bidding strategy of charging operator participating in peak regulation market based on distributionally robust chance constraint[J]. Automation of Electric Power Systems, 2022, 46(7): 23-32.
[30] Xie Weijun. On distributionally robust chance constrained programs with Wasserstein distance[J]. Mathematical Programming, 2021, 186(1): 115-155.
[31] Arrigo A, Ordoudis C, Kazempour J, et al. Wassersteindistributionally robust chance-constrained optimization for energy and reserve dispatch: an exact and physically-bounded formulation[J]. European Journal of Operational Research, 2022, 296(1): 304-322.
[32] 黄大为, 郭念康, 于娜, 等. 面向系统灵活性提升的大用户激励型需求响应优化策略[J]. 电工技术学报, 2024, 39(21): 6778-3792.
Huang Dawei, Guo Niankang, Yu Na, et al. Optimization strategy for enhancing system flexibility through incentive demand response of large-scale users[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6778-3792.
[33] Li Junkai, Xu Zhengyang, Liu Hong, et al. A Wasserstein distributionally robust planning model for renewable sources and energy storage systems under multiple uncertainties[J]. IEEE Transactions on Sustainable Energy, 2023, 14(3): 1346-1356.
[34] Wang Yuwei, Yang Yuanjuan, Fei Haoran, et al. Wasserstein and multivariate linear affine based distributionally robust optimization for CCHP-P2G scheduling considering multiple uncertainties[J]. Applied Energy, 2022, 306: 118034.
[35] 张锞, 王旭, 杨宏坤, 等. 数据中心集群灵活边界下电力系统分布鲁棒优化调度方法[J]. 电力系统自动化, 2024, 48(7): 235-247.
Zhang Ke, Wang Xu, Yang Hongkun, et al. Distributionally robust optimal scheduling method for power system under flexibility boundaries of data center clusters[J]. Automation of Electric Power Systems, 2024, 48(7): 235-247.
[36] Qiu Haifeng, Sun Qirun, Lu Xi, et al. Optimality-feasibility-aware multistage unit commitment considering nonanticipative realization of uncertainty[J]. Applied Energy, 2022, 327: 120062.
[37] Nash J F. The bargaining problem[J]. Econometrica, 1950, 18(2): 155.
[38] 董雷, 李扬, 陈盛, 等. 考虑多重不确定性与电碳耦合交易的多微网合作博弈优化调度[J]. 电工技术学报, 2024, 39(9): 2635-2651.
Dong Lei, Li Yang, Chen Sheng, et al. Multi-microgrid cooperative game optimization scheduling considering multiple uncertainties and coupled electricity-carbon transactions[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2635-2651.
[39] 郭方洪, 冯秀荣, 杨淏, 等. 基于数据模型双驱动的新能源微电网分布鲁棒优化调度[J]. 电力系统自动化, 2024, 48(20): 36-47.
Guo Fanghong, Feng Xiurong, Yang Hao, et.al. Data-model-dual-driven based distributionally robust optimization scheduling of renewable energy microgrid[J]. Automation of Electric Power Systems, 2024, 48(20): 36-47
[40] Wang Lingling, Zhu Zean, Jiang Chuanwen, et al. Bi-level robust optimization for distribution system with multiple microgrids considering uncertainty distribution locational marginal price[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1104-1117.
Multi-Agent Multi-Energy Microgrid Cooperative Game Scheduling Based on Wasserstein Two Stage Robust Optimization
Abstract As the core of the energy system, multi-energy microgrid (MEMG) integrates distribution generation unit (such as wind turbine, photovoltaic), combing cooling, heat and power units, and energy storage to provide diverse energy supplies to customers for enhanced energy efficiency. However, the uncertainties in electricity prices and renewable generation are inevitably during the operation performance of MEMG. To tackle these uncertainties while enhancing economic benefits, this paper proposes a cooperative energy trading model for MEMGs based on Wasserstein two-stage distributionally robust optimization.
First, to describe the interaction between MEMG and prosumer, a bilevel programming is established where the MEMG plays a leader and multiple prosumers are regarded as followers. Based on the electricity purchase power obtained from each prosumer, the MEMG optimizes the transactive price and send to followers. In each follower model, prosumer minimizes its operation cost under the given electric price which from MEMG. Meanwhile, the ambiguous set based on Wasserstein distance are utilized to capture the uncertainty of electricity price, renewable energy and photovoltaic in prosumer, respectively. The model of MEMG is formulated as a Wasserstein two stage distributionally optimization problem (WDRO) considering uncertain price and renewable energy, while the uncertainty of prosumers can be addressed by introducing the distributionally robust chance constraint (DRCC). Then various methods are employed to transform the WDRO and DRCC into finite linear terms, such as convex theory and physical support method, respectively. On this basis, the bilevel programming for “MEMG-prosumer” can be replaced by single-level model via KKT conditions, strong duality theory and big-M method. Additionally, an energy interaction model considering cooperative game and privacy protection has been developed among MEMGs, and the alternating direction multiplier method (ADMM) combined with column and constraint generation algorithm (C&CG) are used to solve the problem.
Simulation results included three MEMGs verify the effectiveness of operation strategy proposed in this paper. The results indicate that: (1) The proposed bilevel programming can simultaneously provide optimal energy scheduling and price strategic for MEMG and prosumer. (2) The Wasserstein ambiguous set can effectively capture the price, renewable output and prosumer uncertainty, making it more comprehensive and less conservative compared to traditional robust optimization. (3) The effectiveness of the proposed energy trading model as well as the efficiency of the ADMM and C&CG algorithms are demonstrated by corresponding simulation results.
Keywords:Bilevel programming,two stage distributionally robust optimization, multi-energy microgrid, cooperation game theory, distributed algorithm
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.241525
国家重点研发计划资助项目(2021YFB2401300)
收稿日期 2024-08-30
改稿日期 2024-09-23
王 波 男,1978年生,教授,博士生导师,研究方向为电力深度视觉、边缘计算等。
E-mail:whwdwb@whu.edu.cn
王 蔚 男,1995年生,博士研究生,研究方向为电力系统不确定性分析。
E-mail:d77mvp@whu.edu.cn(通信作者)
(编辑 赫 蕾)