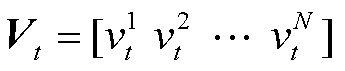与
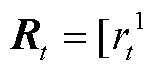
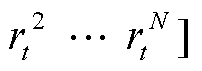。输入矩阵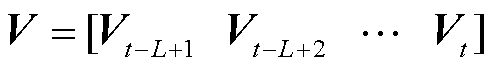
和R=[Rt-L+1 Rt-L+2 … Rt]分别表示所有风机在过去L时刻内的风速与风向数据，其中L为输入预测模型的历史特征序列长度。多风机短期风速概率预测问题描述如图1所示。摘要 在风机呈不规则排布的风电场中，对多风机各自风速的概率预测，有利于量化风速的不确定性与波动性，进而为风电场精细化控制提供更为丰富的信息。对此，该文提出了一种基于贝叶斯图卷积神经网络（BGCNN）的多风机风速超短期概率预测模型。为提取风机排布的空间特征信息，该模型首先以风机历史数据为依据构建了风电场的初始图结构；其次，针对固定图结构难以考虑建模误差的问题，采用BGCNN将风电场图模型参数化，并通过训练其参数改变图信息，从而提取风机间空间特征，同时，在BGCNN的图卷积神经网络模块后接入长短时记忆网络，实现时间特征提取，由此，综合空间和时间相关性特征信息，得到考虑时-空二维相关性的多风机风速预测结果；最后，利用蒙特卡洛法抽样多组模型输出值，进一步得到对应概率预测结果。在呈不规则分布的多台风机上的仿真结果验证了所提概率预测方法的有效性。
关键词：概率预测 风速预测 图卷积神经网络 空间相关性 超短期预测
随着全球能源结构的转变，新能源发电在电力系统的占比逐步提高[1]。其中，风力发电是缓解环境污染和实现“双碳”目标的重要手段[2-3]。2023年，我国累计风电装机容量约4.4亿kW，同比增长20.7%[4]。随着风电的大规模集群并网，其输出功率的随机性和不确定性等特点，将给电网安全稳定运行带来隐患[5]。风电功率主要由风速决定，因此对风速的准确预测有助于优化电网的调度控制，保证电力系统的安全稳定运行[6]。
国内外学者对风速预测已经取得了一定的研究成果。纵览已有的预测方法，根据其预测结果形式的不同，可划分为点预测和概率性预测方法[7]。由于风速本身的随机波动性，传统点预测方法只能得到单点预测值，不能定量描述风速不确定性，因此风速概率预测成为当前风速预测研究的热点[8]。根据是否假定风速概率预测区间服从某一分布形式，概率预测又可进一步分为参数法与非参数法[9]。参数法用假定的概率分布模型对风速不确定性进行拟合，如t分布[10]、Weibull分布[11]、正态分布[12]等，其优点是参数求取简单，但由于实时风速的概率分布特性不同，简单的分布拟合难以满足实际情况的需求，误差较大[13-14]。非参数法并不提前假设实时风速符合的概率分布模型，常见的方法包括分位数回归法[15]、经验分布拟合[16]、核密度估计（Kernel Density Estimation, KDE）法[17]等。由于规避了分布假设不合理的问题，非参数法在刻画风速不确定性方面更为灵活。近年来，伴随着深度学习的热潮，深度神经网络也被广泛应用于风速概率预测[18]。文献[19]为了避免分位数模型伴随的交叉问题，提出了一种基于多尺度特征的非交叉分位数风速概率预测模型。文献[20]首先将风速序列进行集合经验模式分解，再分别对各分量建立高斯回归模型，最后叠加预测结果实现了风速概率预测。
我国近年来重点建设“沙戈荒”大规模新能源基地，相应风电场呈现出占地面积广、风机分布不规则等特点，由此造成各风机本地风速差异显著[21]。因此，若能实现风电场内多风机风速的概率预测，则不仅有助于更加准确地感知大型风电场运行态势、为其精细化控制提供更加丰富全面的信息，同时也可助力电力系统的概率稳定性分析，优化电力系统控制策略。
将卷积神经网络（Convolutional Neural Network, CNN）和长短时记忆网络（Long Short Term Memory network, LSTM）融合形成组合预测模型，并对模型进行贝叶斯化，可以得到多风机风速概率预测结果[22]。但CNN利用卷积核提取空间信息，且具有平移不变性，不适用于大型风电场内风机呈不规则分布的情景。相较于传统的CNN，使用图卷积神经网络（Graph Convolutional Neural Network, GCNN）提取风机空间特征，更符合风机呈非欧式空间分布的实际情况[23-24]。然而，这种方法所定义的图结构是固定的，忽略了建模假设与数据噪声所导致的误差。并且模型只能得到单点预测值，难以描述风速预测结果的不确定性。
针对以上问题，本文提出一种基于贝叶斯图卷积神经网络（Bayesian Graph Convolutional Neural Network, BGCNN）的多风机风速概率预测模型。BGCNN在图结构中引入不确定性，不仅能调整图结构，准确地描述风机间空间相关关系，同时也可提高模型的泛化能力[25]。本文模型首先以各风机历史数据为依据构建风电场初始图结构。随后将风电场图模型输入BGCNN，实现图信息的改变，从而提取多风机空间相关性。与此同时，将LSTM接入BGCNN中的GCNN模块后，使其对蕴含风机间空间信息的特征矩阵进行时间特征提取，由此得到考虑时-空二维相关性的多风机风速预测结果。在模型训练过程中，利用蒙特卡洛法抽样多组模型输出值，最终实现多风机风速概率预测。
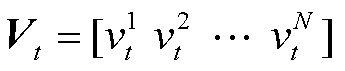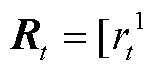
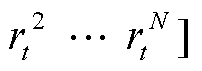大型风电场内的多风机风速超短期概率预测，基于各风机的历史风速与风向数据，采用BGCNN与LSTM集成预测模型，捕捉各风机风速之间的时-空二维相关性，由此得到预测结果。假设某风电场建有N个不规则排布的风机，则风机在t时刻的本地风速与风向值分别为与。输入矩阵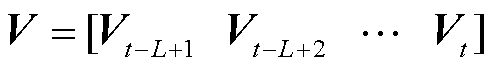和R=[Rt-L+1 Rt-L+2 … Rt]分别表示所有风机在过去L时刻内的风速与风向数据，其中L为输入预测模型的历史特征序列长度。多风机短期风速概率预测问题描述如图1所示。
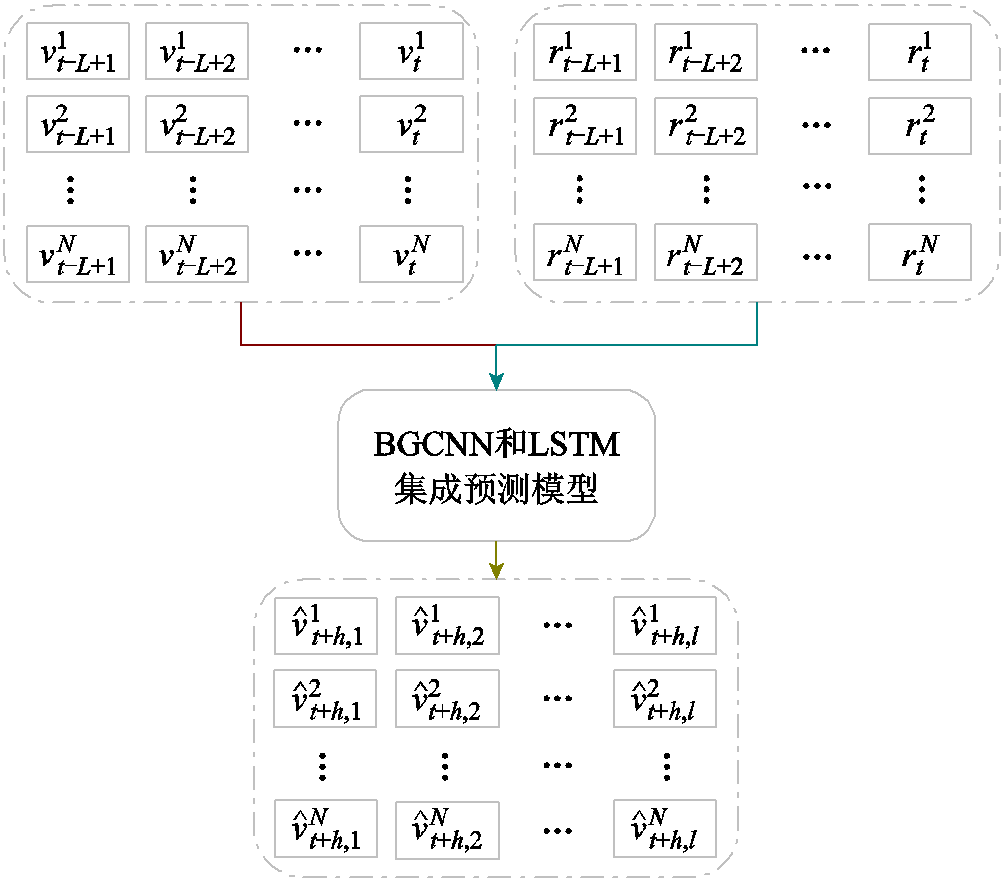
图1 多风机短期风速概率预测问题描述
Fig.1 Problem description of short-term wind speed probabilistic forecasting for multiple turbines
图1中，集成概率预测模型建立了从历史风速矩阵V、历史风向矩阵R到t+h时刻风速矩阵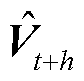
的映射f，该映射可表示为
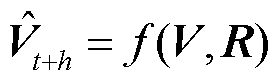，其中h代表预测时域。本文以预测分布的分位数表示概率预测结果，在分位数td下各风机预测风速的分位数为
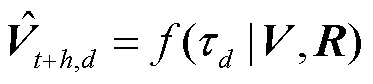，为获得更全面的概率分布信息，共取l个分位点，且0＜t1＜…＜td＜…＜tl＜1。
GCNN将卷积运算从欧式数据拓展至图数据，可以对图数据进行节点分类、图分类、边预测等。GCNN的本质是将当前节点及其相邻节点的特征聚合在一起，并生成当前节点的新特征。基于此，每个节点的预测结果都会受到相邻节点的影响，从而进一步挖掘数据的潜在特征联系。
图结构由集合g=(I, E)定义。其中，I代表N个节点的集合，E代表边的集合。每个节点有D维特征，节点的特征构成一个N×D维的特征矩阵X，节点间的边关系构成一个N×N维的邻接矩阵A。
从结构上看，GCNN是一个神经网络层，层与层之间的传播方式可以表示为
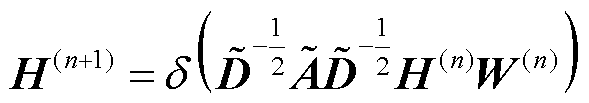（1）
式中，n为神经网络层数；H为每一层的输入特征，特征矩阵X为第一层的输入；W为每一层需要训练的权值矩阵；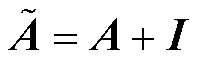
，I为单位矩阵；
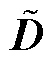为
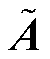的度矩阵；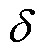
为非线性激活函数。
2019年，BGCNN被首次提出并应用于半监督节点分类问题中[25]。与GCNN保持不变的图结构不同，BGCNN中的图片拓扑由不断更新的参数生成。GCNN是BGCNN的重要组成部分，通过GCNN实现确定性预测后，BGCNN的其余模块可以根据预测结果生成新的图结构，并以新图结构的预测效果为依据更新GCNN模型权重。对定义随机图参数、模型权重和节点输出特征的联合后验进行推理，可以计算出节点最终输出。计算公式为
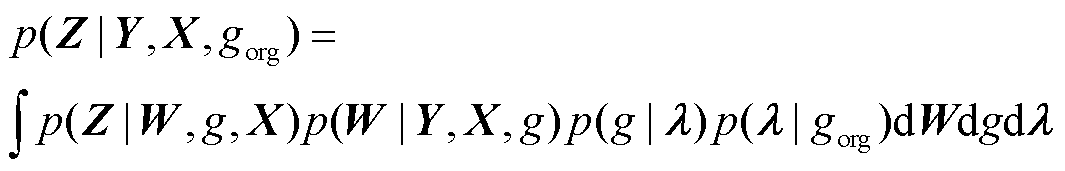（2）
式中，p为似然估计；gorg为最初搭建的图结构；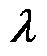
为定义随机图的参数；g为由参数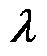生成的新图结构；W为新图g对应的GCNN权值矩阵；Y为输入特征对应的输出值；Z为BGCNN最终层的输出特征。
由于式（2）中的积分难以直接计算，一般采用蒙特卡洛近似表达为
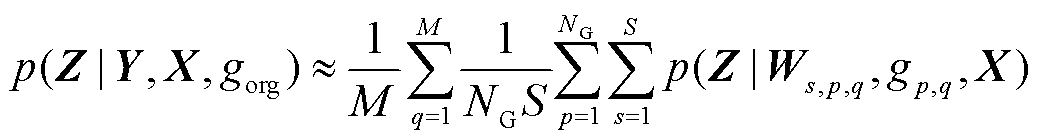（3）
式中，M为由后验p(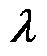|gorg)所生成参数
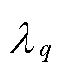的数量；NG为从后验概率p(g|
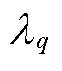)中抽取图片gp,q的数量；S为从基于图片gp,q的BGCNN模型中抽取权值矩阵的数量；Ws,p,q为基于图gp,q对应BGCNN模型的权值矩阵；gp,q为由gorg演变而来的新图结构。
文献[26]提出了一种分类混合隶属随机块模型（assortative Mixed Membership Stochastic Block Model, a-MMSBM），被应用于BGCNN的新图生成。该方法能搭建具有复杂结构的图，但要求定义图结构的参数分为两类，因此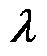可以表示为
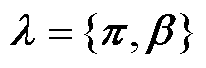（4）
为防止抽样图片gp,q和gorg结构差距过大，用最大似然估计法代替参数π和β的积分，有
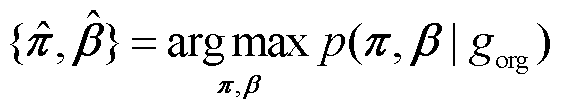（5）
根据蒙特卡洛抽样、式（2）及式（5），节点最终输出也可以表达为
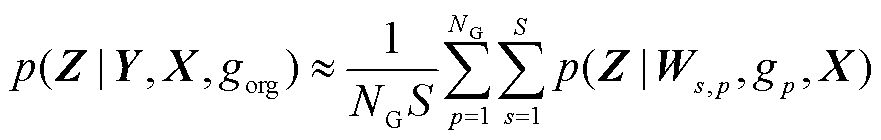（6）
式中，gp为从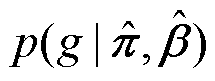
中抽样得到的图；Ws,p为从后验
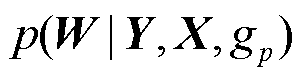中抽样得到的权重矩阵。
在a-MMSBM模型中，对于点集I中的任意点a，它隶属于每个社区的概率构成了K维概率矩阵πa=[πa1…πaK]。将同属一个社区的节点建立连接的可能性设为βk。由式（5）可知，参数π和β联合后验最大值的求取至关重要，其表达式为
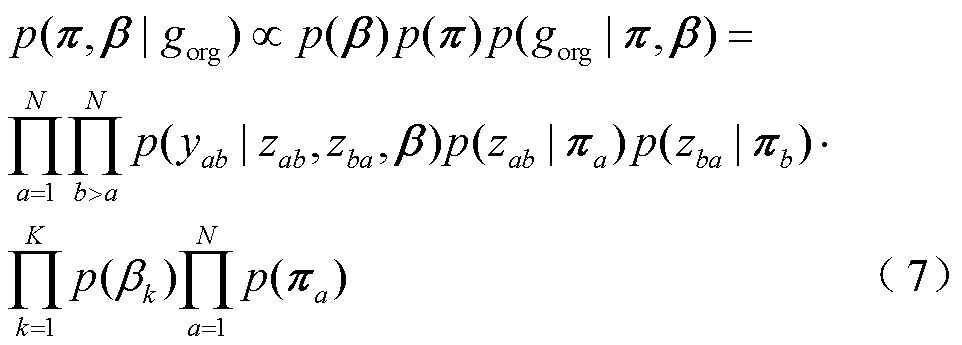
在式（7）中，βk、πakÎ(0,1)，且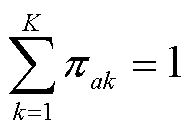
。由于梯度更新的迭代算法不能满足这两条约束条件，因此引入参数q和f对参数π和β重新参数化，从而计算参数π和β的联合后验最大值。
参数q和f与参数π和β之间的关系为
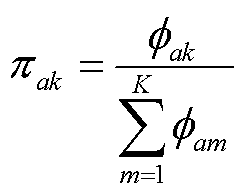（8）
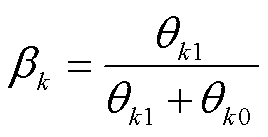（9）
式中，fak≥0，fak从Gamma分布取值作为先验，即fak～Gamma(a,r)；qki≥0，qki从Gamma分布取值作为先验，即qki～Gamma(h,r)。
使用预条件梯度上升法最大化式（7）在参数q和f上的联合后验，推导得参数q和f的更新规则为
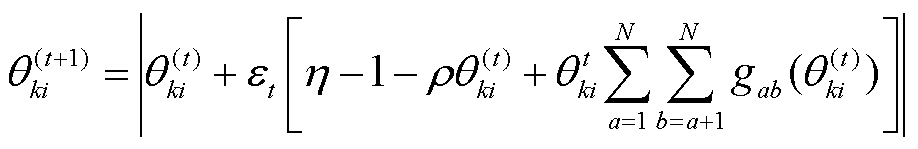（10）
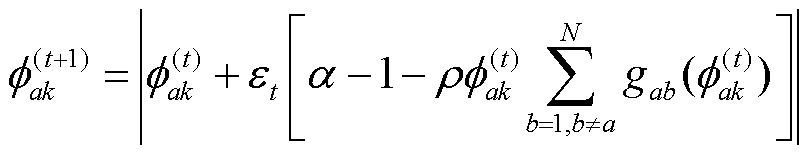（11）
式（10）与式（11）中参数的详细表达式可以参考文献[25]。
BGCNN给出的图结构参数化原理适用于风速预测中风机呈不规则分布的情景，它能不断地改变图结构信息，充分捕捉各风机间空间相关性，提高预测准确性。
风电场内各风机间的本地风速数据具有显著的空间相关性，因而可以利用这种相关性构造图结构。在包含N个不规则排布风机的风电场中，风电场图结构由集合g=(I, E)定义，其中I为N个节点的集合，每个节点代表一个风机，E为边的集合。各风机本地风速的相关性构成了N×N维的邻接矩阵A，矩阵内元素A(i, j)反映了风机i与风机j的边关系。
任一风机i有过去H时间长度的历史风速向量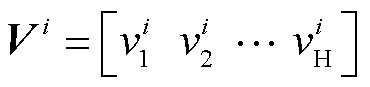
。对风机间历史风速数据Pearson相关性进行分析，得到相关系数为
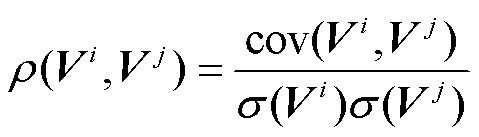（12）
式中，i、j分别为风机i与风机j；Vi、Vj分别为两风机对应的历史风速向量；cov(·)为两个向量的协方差；σ(·)为向量的标准差。
相关系数r值越大则说明两风机间本地风速的相关性越显著。设置参数ε＞0，若风机i、j的相关系数r＞ε，节点i、j建立连接；若不满足该条件，则两节点无关[24,27]。因此，反映边关系的邻接矩阵A定义为
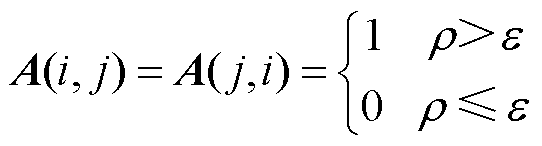（13）
由2.2节中对BGCNN的原理介绍可知，随机图结构由a-MMSBM的后验生成。然而，若参数π和β初始值随机设定，则会导致模型生成的新图难以贴合实际风电场中风机之间的空间关系，影响预测结果。因此，以GCNN-LSTM模型所输出的风速预测结果为依据初始化参数π和β，可以降低参数π和β的取值随机性，提高预测有效性。
参数π表示节点隶属度，π=[π1π2 … πN]T为图中所有节点的隶属度矩阵，其中任意一个节点a的隶属度矩阵为πa=[πa1πa2…πaK]，K为节点可以隶属的社区数量。在分类问题中，含N个节点的GCNN模型的输出特征矩阵为ZN×B，其中B为标签数，同时也可以看作社区数量，因此输出矩阵Z可以直接作为π的初始值。与分类问题不同，在本文所研究的风速回归预测问题中，模型输出值并没有类别的概念。GCNN与LSTM组合模型的输出特征矩阵为ZN´T，表示N个风机在未来T个时刻的风速预测值。为了实现参数π初始化，即满足其划分社区类别的要求，需要对各风机的本地风速预测结果进行分类。
聚类算法能够实现数据集的分类。它将一个数据集中的样本划分为若干子集。每个子集称为一个簇，簇中的数据具有相似特征。K-means是聚类算法的一种，其中簇的数量需要提前定义。K-means可以基于点与点之间距离的相似度来计算最佳类别归属，原理简单，容易实现，因此得到广泛应用。
使用K-means聚类法对各风机节点进行分类，其目标函数为
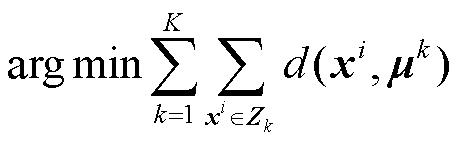（14）
式中，xi为第i个风机的输出特征，同时也是节点i的坐标；mk为簇k的质心；Zk为隶属于簇k的多风机特征矩阵合集；d(xi,mk)为节点i与其簇心k的距离，计算公式为
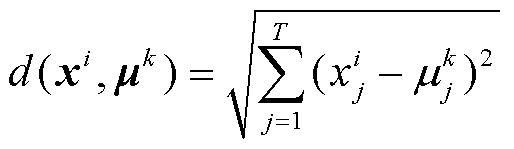（15）
式中，T为节点i的特征数量；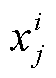
和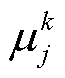
分别为组成节点i与簇心k的特征。
在确定各簇簇心后，再求取各节点隶属于每个社区的概率，计算公式为
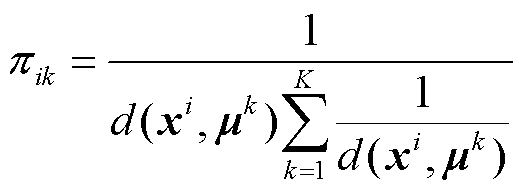（16）
式中，πik为节点i隶属于社区k的概率，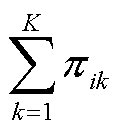
=1。
根据上述计算过程，可以实现参数π的初始化。参数β的初始化基于参数π实现，与BGCNN处理分类问题的初始化方法一致[25]。
基于BGCNN的概率预测模型，通过学习风电场中呈不规则分布的各风机风速与风向时空相关性来实现多风机本地风速概率预测。与2.2节中BGCNN的运行原理一致，本文模型也通过计算随机图参数、模型权重和节点输出特征的联合后验实现预测。本文模型的改进点在于在GCNN模型后接入了LSTM模块，使得输出特征矩阵可以同时包含时-空二维相关性。预测框架可以分为图结构生成和概率预测两个部分，分别如图2和图3所示。
图2展示的图结构生成部分与式（2）中p(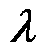
|gorg)以及p(g|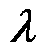)部分对应。在图2中，GCNN与LSTM组合模型可以获得多风机的风速点预测结果。在GCNN-LSTM模型后插入a-MMSBM模块，该模块可以根据GCNN-LSTM模型的输出特征矩阵生成定义风电场图结构的参数λ，不同参数λ可以定义各类风电场图结构g。
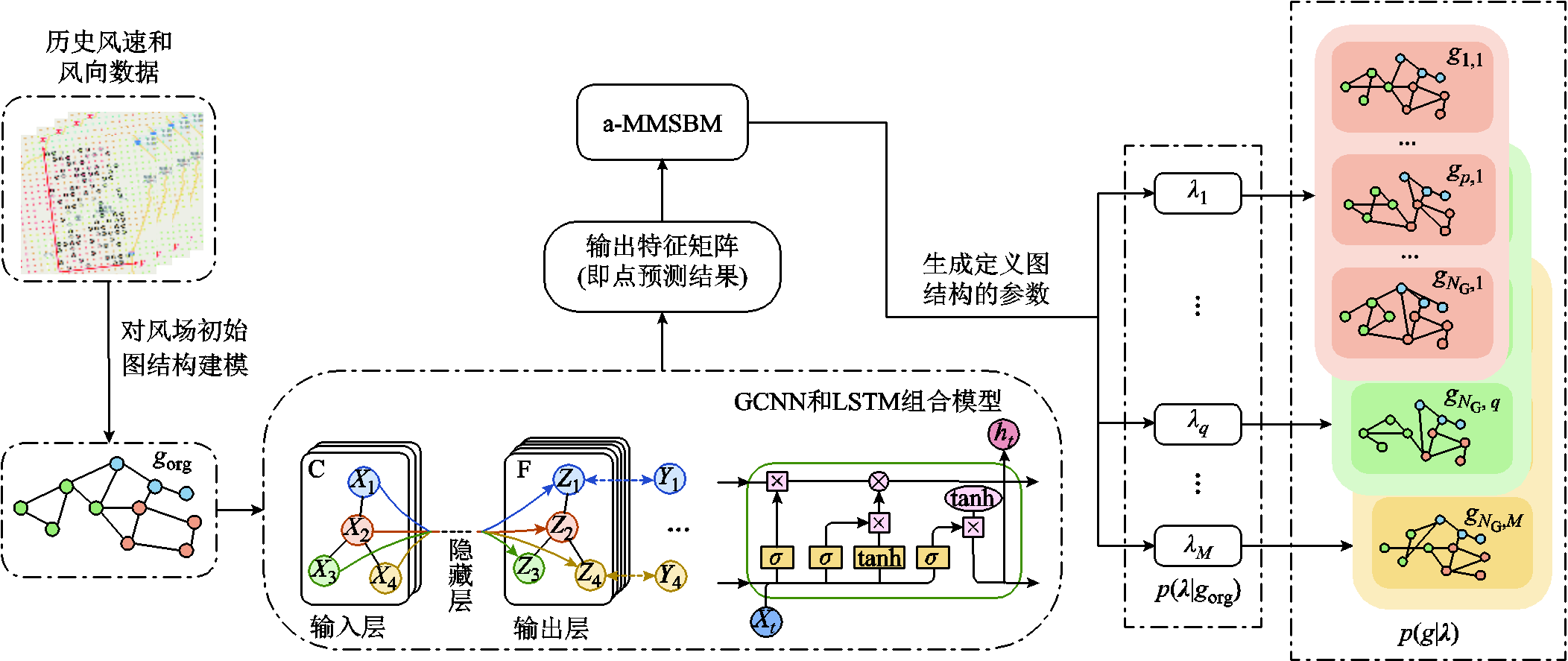
图2 风电场图结构生成框架
Fig.2 Framework for the generation of wind farm graph structures
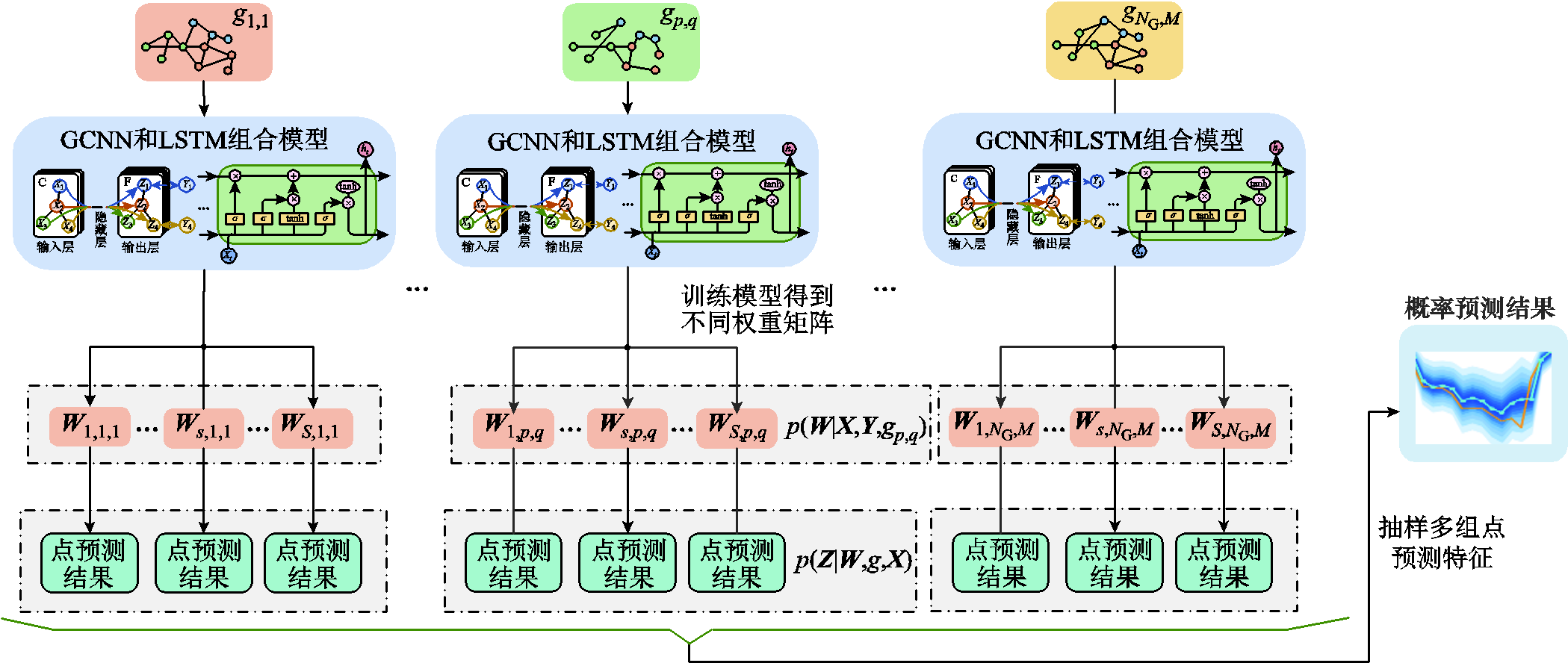
图3 以各类风电场图结构为输入样本的组合模型训练与预测框架
Fig.3 Framework for training and forecasting of the combined model using various types of wind farm graph structures as input samples
图3展示的概率预测部分与式（2）中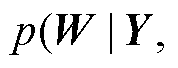
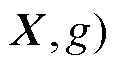和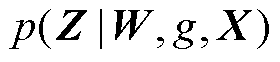
部分相对应。在图3中，各类图结构g均可以作为GCNN-LSTM模型的输入。随后，通过训练得到GCNN-LSTM模型对应不同图结构的最优权重W。每个图结构及其对应权重均能求取一组风速点预测结果，再根据蒙特卡罗法抽样多组风速预测结果，最终可以获得概率预测结果。
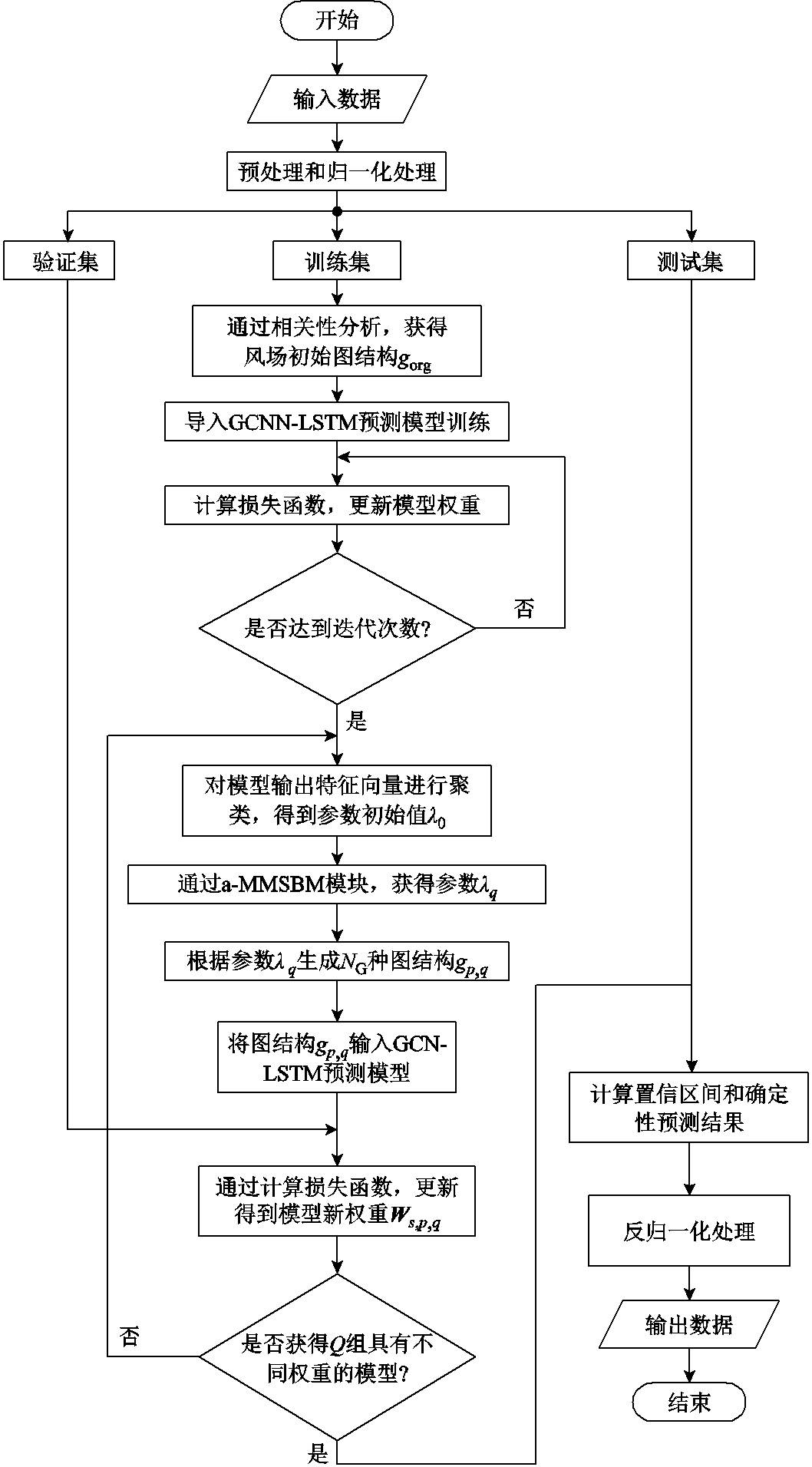
本文所提模型的训练和预测流程如附图1所示，具体步骤如下：
1）输入风电场内各个风机历史风速与风向数据，并对数据进行预处理和归一化处理。随后，将数据集划分为训练集、验证集和测试集。
2）对训练集中各风机历史数据进行Pearson相关性分析，获得集合gorg=(I, E)表征风电场初始图结构。
3）将gorg对应的邻接矩阵A、训练集数据导入GCNN-LSTM模型训练。
4）计算损失函数，采用Adam优化算法，更新模型网络权重和偏置。同时基于验证集观察优化效果。
5）判断是否达到最大迭代次数，是则进行步骤6），否则返回步骤4）。
6）将gorg对应的邻接矩阵A以及测试集数据导入此时的GCNN-LSTM模型，并对模型输出特征向量进行K-means聚类，得到定义风电场图结构的参数初始值λ0。
7）将λ0输入a-MMSBM模块，根据式（7）求取后验，生成参数λq。
8）利用参数λq生成NG种新的图结构。
9）将从NG种图结构中抽样得到的图结构gp,q输入此时的GCNN-LSTM模型，并计算损失函数，通过Adam算法优化权重矩阵，此时的新权重矩阵为Ws,p,q。同时保存此时的模型输出矩阵。
10）判断是否保存了Q组预测结果，是则进行步骤11），否则返回步骤6）。
11）根据保存的Q组模型输出矩阵，计算各风机风速点预测结果，以及各置信度条件下的置信区间，并对预测结果进行反归一化处理。
本文模型在训练与优化后，就可以被部署到实际的风电场中。实际应用中，风速与风向数据通过加密的数据文件传输至预测服务器，进行超短期预测后，再以加密文件形式传输至安全服务器，并最终向外提供数据服务。在系统部署过程中，应确保系统硬件的可靠性和网络通信的稳定性。同时，为确保预测系统的持续运行和效益最大化，还需要定制有效的维护策略，如定期的设备检查和维修。
本文采用的数据集来自美国国家可再生能源实验室，包含2007—2013年美国超过12万个站点的100 m轮毂风速和风向数据等，站点间距为 2 km×2 km，呈网格排布。由于绝大部分风机并不是以理想的规则形式分布，因此从数据集中随机抽取100台风机，被选中的风机位于美国怀俄明州楚格沃特附近，其分布如图4所示。图4中，将编号为76和33的风机分别用绿色圆圈和蓝色方块标出。
图4 不规则分布的100台风机
Fig.4 100 wind turbines irregularly distributed
本文仿真选用了从2012年1月1日到2012年6月22日的100台风机风速和风向数据，时间分辨率为5 min，共计50 000条。其中，训练集、验证集和测试集的数据量比例为8:1:1。
风机风向数据在0°～360°范围内，但359°与1°附近的风向数据虽然数值差距极大，物理意义却相近，直接使用该类数据会增大预测误差。因此对风向数据进行三角函数化预处理，此时风速、sin风向及cos风向构成了每台风机的三维特征向量，并且将预处理后的三维数据作为预测模型的输入数据。
为验证基于BGCNN的多风机风速概率预测模型的预测性能，将它与基于贝叶斯神经网络的BCNN-LSTM和基于分位数回归的Q-CNN-LSTM模型进行对比。同时，为验证BGCNN提取空间相关性对单个风机概率预测精度的提高，再将其与贝叶斯LSTM（Bayesian LSTM, BLSTM）以及LSTM分位数回归模型（Quantile Regression LSTM, Q-LSTM）模型进行对比。预测模型均在python3.9环境下搭建，实验硬件配置为2.10 GHz Intel®Core(TM)/i7-12700CPU/16 GB内存。本文模型的参数设置见表1。
表1 本文模型的参数设置
Tab.1 Parameter settings of the model
参数数值 训练轮数1 350 学习率0.001 GCNN层数2 K-means聚类簇的数量6 LSTM隐藏层数1
本文模型与对比模型将从点预测与概率预测两方面进行对比。本节以单风机为例介绍评价指标，由于各类评价指标结果均非负，因此，对于多风机风速概率预测模型，以各风机评价指标的均值衡量其对风电场内风机的整体预测效果。
5.2.1 点预测评价指标
仿真采用平均绝对误差（Mean Absolute Error, MAE）和方均根误差（Root Mean Square Error, RMSE）作为点预测的评价指标。MAE与RMSE值越小，表示预测效果越好。对于单个风机的本地风速预测效果，两个预测误差指标的表达式为
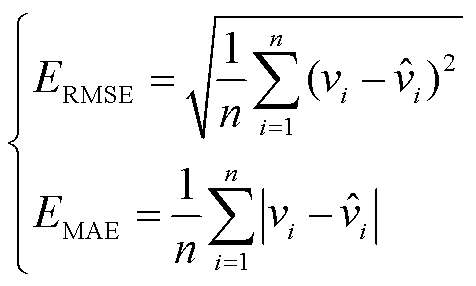（17）
式中，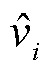
为第i个样本的风机本地风速预测值；vi为第i个样本的风机本地风速实际值。
5.2.2 概率预测评价指标
本次仿真的概率预测结果采用可靠度（reliability）、锐度（sharpness）和Pinball评分三类指标进行综合评价。
1）可靠度指标
采用预测区间覆盖率（Prediction Interval Coverage Probability, PICP）衡量预测区间可靠性。覆盖率越接近置信度a，表明预测可靠性越高。对任一风机概率预测效果，PICP的计算公式为
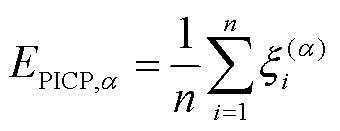（18）
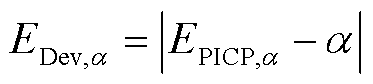（19）
式中，EDev,a为偏差指数，用来评价概率预测结果的无偏性；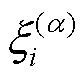
为第i个样本的示性函数，其定义为
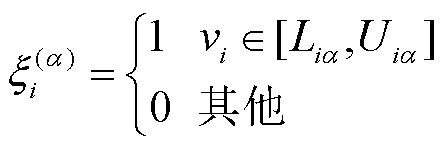（20）
式中，Uia和Lia分别为第i个样本在置信度a下预测风速的上界与下界。
2）锐度指标
锐度通过预测区间的标准方均根宽度来衡量，反映了概率预测分布的离散程度。锐度越小，代表预测分布更集中，预测效果越好。定义置信度a下的锐度计算公式为
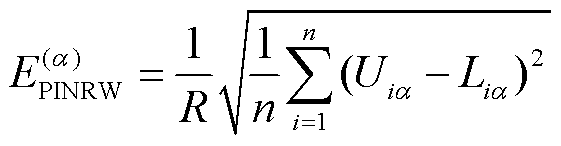（21）
式中，R为样本中风速最大值与最小值之差。
3）Pinball评分指标
Pinball分数能综合反映预测结果的可靠度和锐度。它的数值越小，说明概率预测效果越好。Pinball分数计算公式为
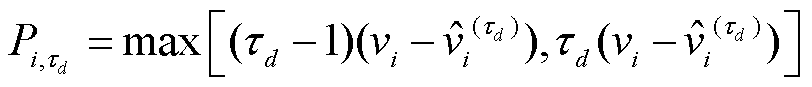（22）
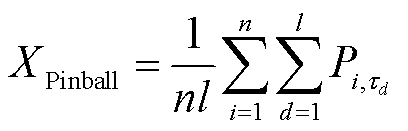（23）
式中，Xpinball为概率预测结果的平均Pinball分数值；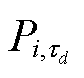
为第i个样本在td分位点下的Pinball分数值。
本文模型采用滚动预测的方法，对风机未来4 h 10 min的风速进行超短期预测。以测试集中2012年6月18日为例，图5a给出了76号风机的风速概率预测结果。图5中，较低置信度的预测区间可以较好地嵌入较高置信度的预测区间中，且不同置信度下预测区间的上下限均与实际风速曲线具有相似的趋势，这表明基于BGCNN构建的本文模型能很好地捕捉风速变化的动态特征。其他风机的风速概率预测结果如附图2所示。
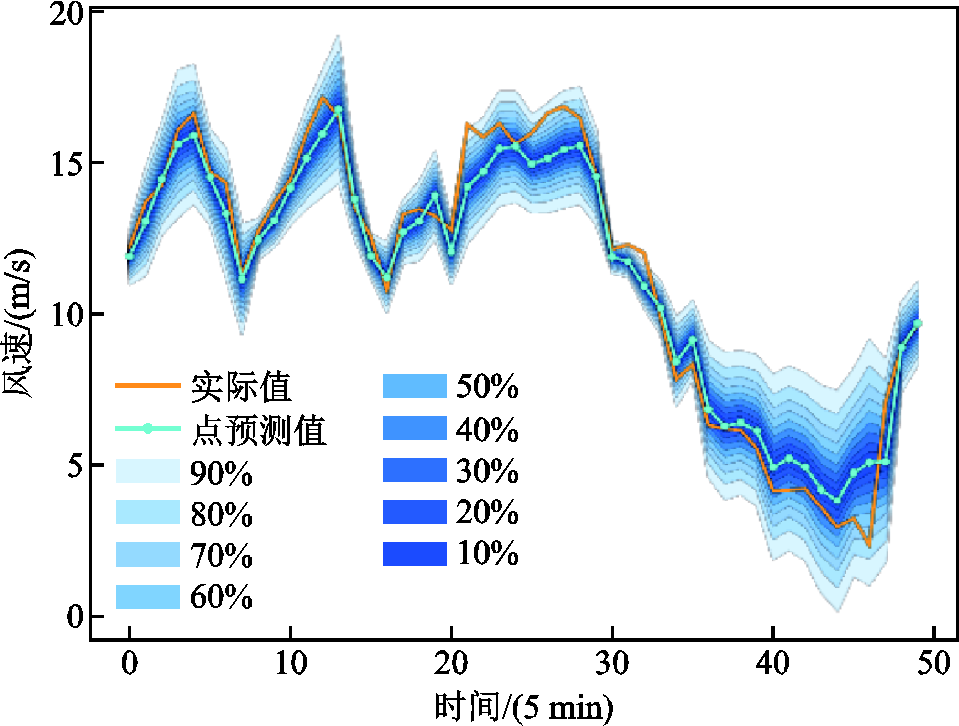
图5 76号风机在夏季的风速概率预测结果
Fig.5 Probabilistic forecasting output of ID 76 wind turbin in summer
多风机依照风速数据进行聚类后的结果如图6所示，可以看出100台风机被划分为六类不同的簇。聚类结果是风电场图结构的构建依据。风电场图结构展现了风机间的关联性，在仿真运行过程中，它会随训练轮数的增加而改变。图7呈现了不同训练轮数下的风场图结构信息。图7中，不同的图结构体现出多风机间不同的空间相关信息，风速概率预测结果的不确定性就来自BGCNN引入的图结构不确定性。从图7中可以看出，随着训练轮数增加，验证集的损失函数逐级递减，表明呈现各风机边关系的图结构越来越准确，权重矩阵不断优化，使确定性预测结果精度提高。
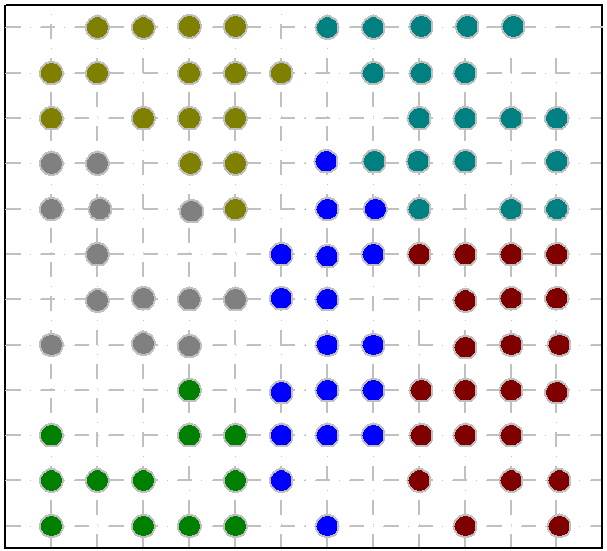
图6 风机聚类结果示意图
Fig.6 Schematic of turbine clustering results
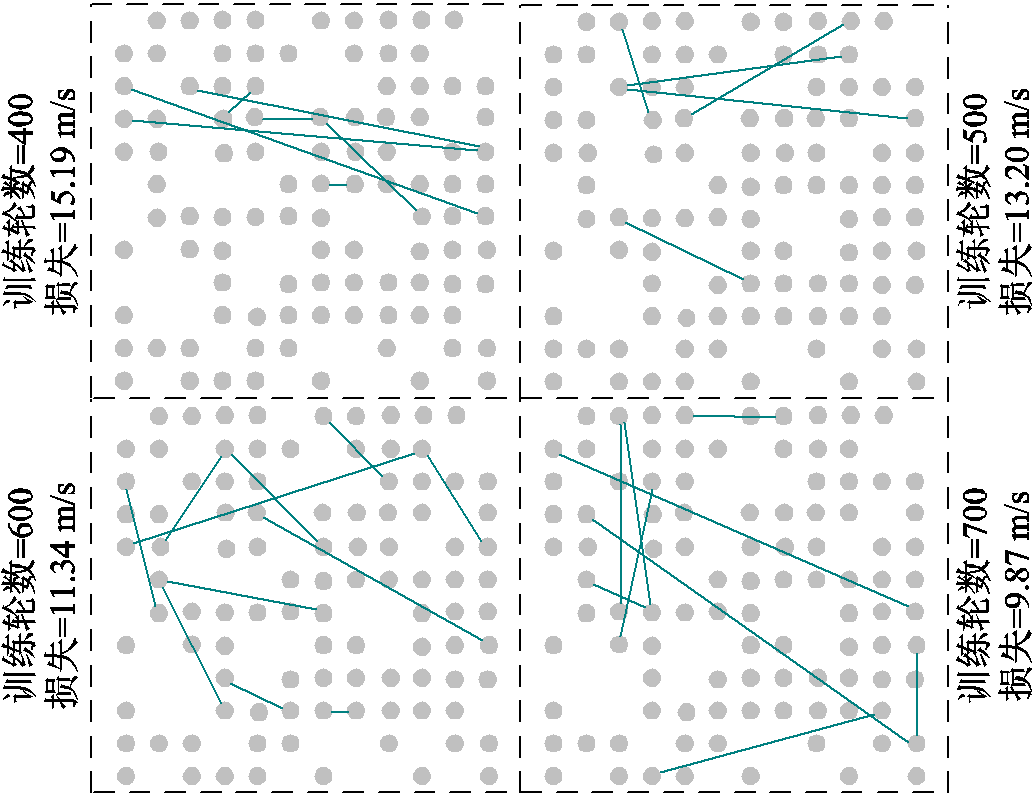
图7 不同训练轮数下的风电场图结构
Fig.7 Wind farm graph structure under different epoch
5.3.1 风速点预测结果对比分析
对于同时输出多风机预测结果的模型，本文模型以及BCNN-LSTM模型的点预测结果通过计算抽样结果的均值获得，Q-CNN-LSTM模型则通过中位数预测得到。多风机点预测误差如图8a所示，本文模型与BCNN-LSTM和Q-CNN-LSTM模型相比，MAE误差别分下降了0.399 m/s与0.067 m/s，RMSE误差分别下降了0.419 m/s与0.066 m/s，表明本文模型的点预测精度更高。
对于单风机风速预测模型，BLSTM模型的点预测结果由计算抽样结果的均值获取，Q-LSTM模型则通过中位数预测得到。随机选取33号风机，关于该风机的点预测误差如图8b所示，图9为使用本文模型在连续采样时刻的33号风机本地风速点预测结果。由图8b可知，本文模型的MAE与RMSE误差是三个模型中的最小值，分别为1.044 m/s与1.498 m/s。表明合理利用风电场中风机间的空间相关性，可以有效提高风机风速的预测精度。
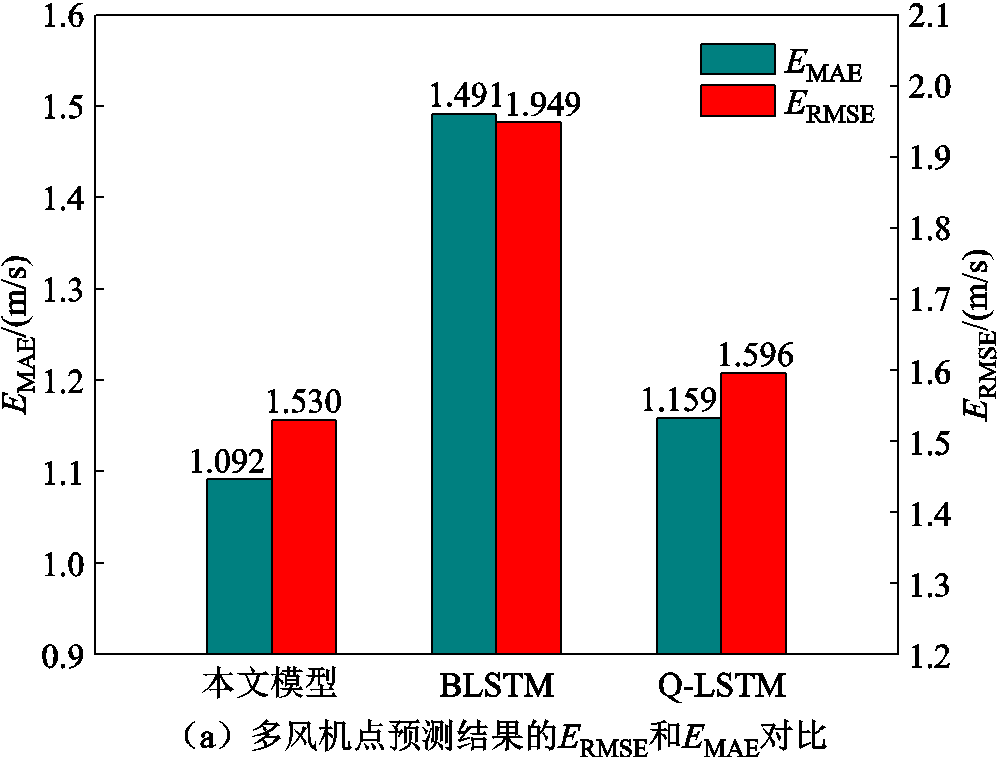
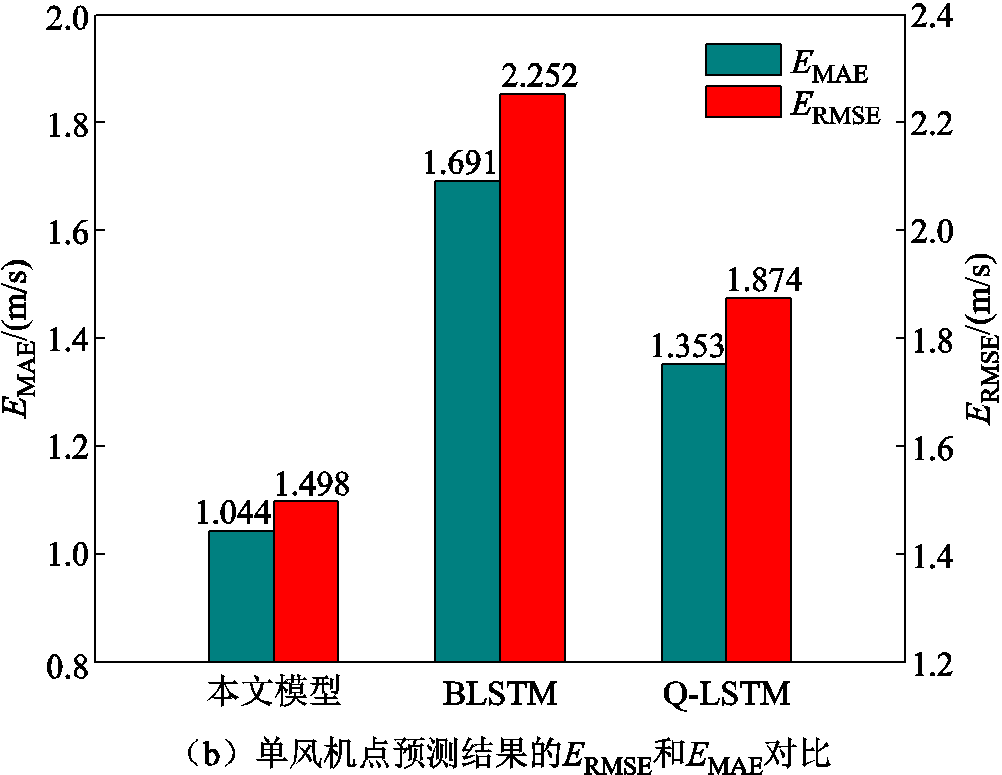
图8 点预测评价标准直方图
Fig.8 Histogram of point forecast evaluation indicators
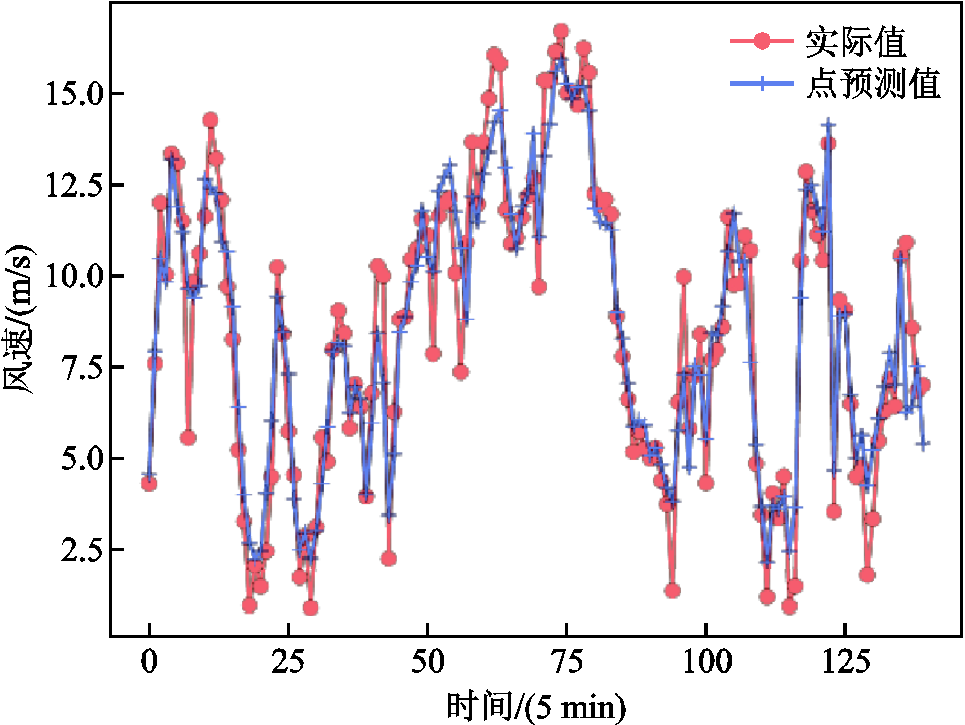
图9 33号风机的风速点预测结果
Fig.9 Point forecasting output of ID 33 wind turbine
5.3.2 风速概率预测结果对比分析
多风机概率预测模型预测结果的可靠性和锐度对比见表2和表3。表2列出了不同置信度下预测模型的EPICP和EDev对比，其中EAD为各置信度下偏差指数EDev的均值；表3列出了不同置信度下模型的EPINRW以及XPinball对比。图10a给出了各模型预测结果的EPICP曲线，越接近理想曲线表明预测效果越好；图10b给出了各模型预测结果的EPINRW曲线，越接近横轴表明预测区间锐度指标越好。
在预测区间可靠性方面，结合表2和图10a可以看出，尽管在10%与30%～50%置信度下BCNN-LSTM模型的预测区间覆盖率EPICP最接近理想值，但其对应置信度下的EPINRW锐度指标高于本文模型，说明该模型预测区间过宽，预测分布不集中。虽然在70%置信度下Q-CNN-LSTM模型的EPICP值最理想，但图10a中该模型曲线与理想曲线差距较大，预测效果并不好。在其余置信度下，本文模型生成的预测区间覆盖率EPICP都更接近理想值，同时EAD（3.10%）也远低于对比模型，可见本文所提模型能够生成具备有效覆盖率的预测区间。
表2 不同多风机风速预测模型的EPICP和EDev对比
Tab.2 Comparison of EPICP and EDevfor different multi-wind turbine speed forecasting models（%）
模型EPICPEDev均值EAD 置信度10%置信度20%置信度30%置信度40%置信度50%置信度60%置信度70%置信度80%置信度90% 本文模型11.4621.9033.6744.7555.1565.0173.3681.4088.753.10 BCNN-LSTM9.0417.3827.0436.2945.3054.5463.2372.2781.934.78 Q-CNN-LSTM13.9317.0724.8530.9443.6453.7667.7176.3681.225.38
表3 不同多风机风速预测模型的EPINRW和XPinball对比
Tab.3 Comparison of EPINRWand XPinballfor different multi-wind turbine speed forecasting models
模型EPINRWEPINRW均值EAPXPinball/(m/s) 置信度10%置信度20%置信度30%置信度40%置信度50%置信度60%置信度70%置信度80%置信度90% 本文模型0.0210.0390.0610.0830.1070.1330.1640.2030.2600.1190.669 BCNN-LSTM0.0260.0500.0770.1050.1350.1690.2060.2570.3280.1500.672 Q-CNN-LSTM0.0270.0460.0570.0850.0930.1340.1660.2090.2710.1210.674
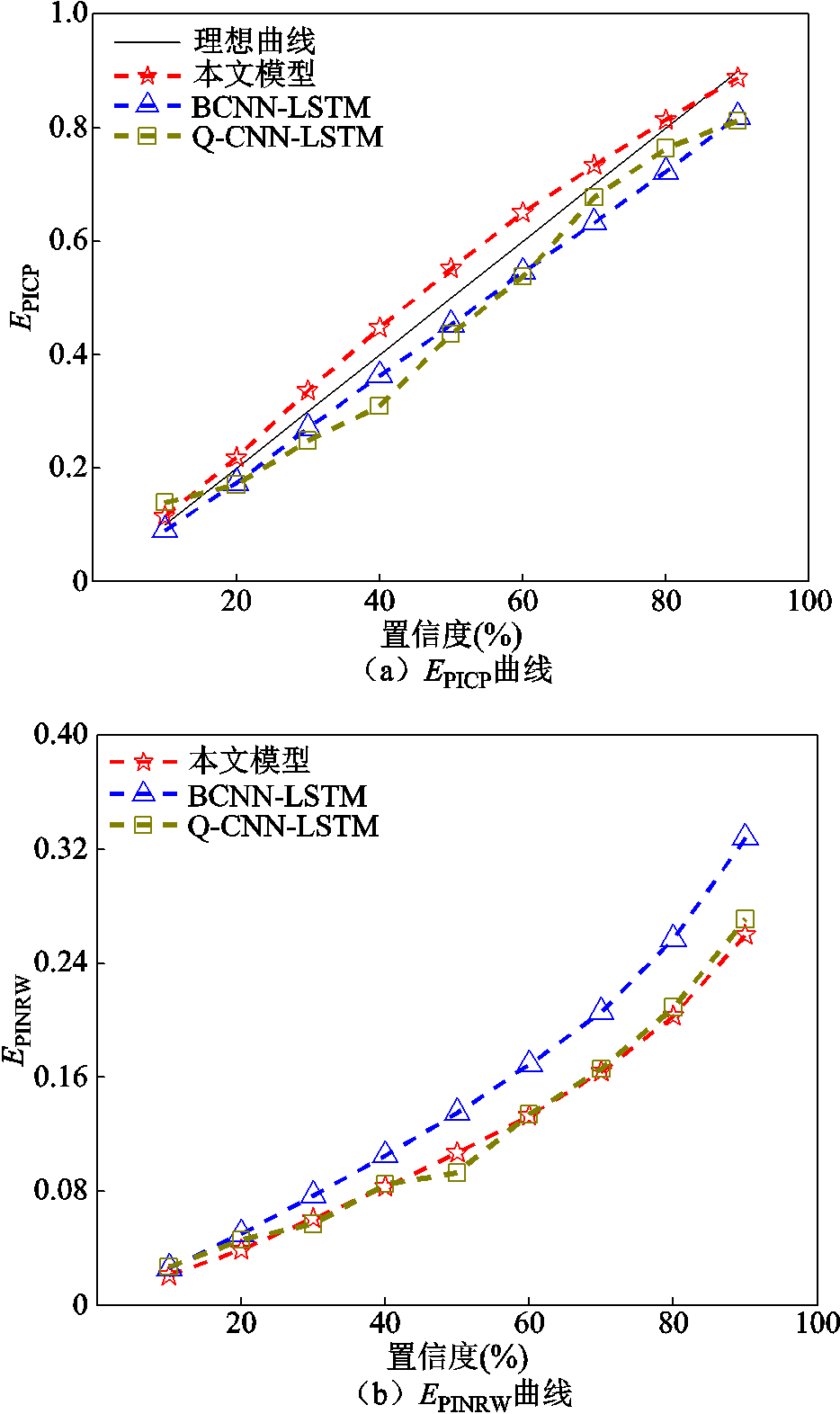
图10 不同模型的可靠性和锐度评价指标折线图
Fig.10 Reliability and sharpness evaluation indicators polylines for different models
在预测区间锐度方面，由表3和图10b可以看出，本文模型生成EPINRW均值低于对比模型，并且在多数置信度下，本文模型的EPINRW曲线更接近横轴。表明本文模型预测结果生成的预测区间更加集中，预测效果更好。
在预测区间Pinball分数方面，根据表3可以看出本文模型的XPinball值最低。与BCNN-LSTM和Q-CNN-LSTM模型相比，XPinball值分别下降了0.003 m/s与0.005 m/s。因此本文模型的概率预测质量最高。
为了验证本文模型对风电场中任意单个风机概率预测效果的提高，表4列出了单风机风速预测模型与本文模型对于33号风机的EDev均值EAD、EPINRW均值EAP以及XPinball的结果对比，不同置信度下各模型的EPICP以及EPINRW结果见附表1和附表2。
表4 不同单风机风速预测模型评价指标对比
Tab.4 Comparison of evaluation indexes for different single turbine speed forecasting models
模型EAD(%)EAPXPinball/(m/s) 本文模型1.680.1230.431 BLSTM3.700.1820.576 Q-LSTM2.800.1250.478
由表4可知，对于33号风机的概率预测结果，在可靠性方面，本文模型的偏差指数均值EAD（1.68%）远低于对比模型，表现出更接近置信度的预测区间覆盖率；在锐度方面，本文模型EPINRW均值低于对比模型，表明预测区间更加紧致；在Pinball分数方面，本文模型得分最低，展现了较好的概率预测性能。
对于风电场中呈不规则排布的多风机风速概率预测问题，本文提出了一种基于BGCNN和LSTM的时空集成概率预测方法。该方法能够充分利用风机间风速与风向数据的时空相关性，提高预测性能。仿真算例结果表明：
1）本文使用聚类方法对GCNN-LSTM模型输出特征进行分类，并将风机节点的聚类结果类比为分类问题的标签值。这使得BGCNN能够运用在回归问题中，并能很好地提取风机数据间的空间特征。
2）相较于BCNN-LSTM与Q-CNN-LSTM模型，本文模型在点预测和概率预测方面均能获得更高的预测精度，由预测结果计算得到的预测区间偏差小且分布集中，明显优于对比模型。
3）对于风电场中的单个风机，本文模型预测精度高于只针对单风机的概率预测模型，这反映了合理有效地提取空间特征有利于减小预测误差。
附 录
附图1 基于BGCNN的多风机风速预测概率流程
App.Fig.1 Flow chart for wind speed probabilistic forecasting for multiple wind turbines based on BGCNN
附图2 不同风机的风速概率预测结果
App.Fig.2 Probabilistic forecasting outputs for different turbines
附表1 不同单风机风速预测模型的EPICP和EDev对比
App.Tab.1 Comparison of EPICP and EDev for different single turbine speed forecasting models （%）
模型EPICPEDev均值EAD 置信度10%置信度20%置信度30%置信度40%置信度50%置信度60%置信度70%置信度80%置信度90% 本文模型13.2520.8832.1339.3649.0059.4471.0881.1285.541.68 BLSTM8.0316.0626.9142.1755.0267.8775.1079.9285.943.70 Q-LSTM10.8416.4733.7337.7545.7854.2272.2977.9189.562.80
附表2 不同单风机风速预测模型的EPINRW对比
App.Tab.2 Comparison of EPINRW for different single turbine speed forecasting models
模型EPINRWEPINRW均值EAP 置信度10%置信度20%置信度30%置信度40%置信度50%置信度60%置信度70%置信度80%置信度90% 本文模型0.0210.0410.0630.0860.1100.1380.1690.2100.2690.123 BLSTM0.0310.0600.0930.1270.1630.2040.2500.3110.3980.182 Q-LSTM0.0230.0330.0710.0850.1020.1430.1780.2110.2770.125
参考文献
[1] 金梦, 朱鑫要, 周前. 新能源对电网调峰特性影响定量评估及应用[J]. 高压电器, 2023, 59(4): 70-76.
Jin Meng, Zhu Xinyao, Zhou Qian. Quantitative assessment of influence of renewable energy on peak regulation characteristics of power grid and its application[J]. High Voltage Apparatus, 2023, 59(4): 70-76.
[2] 刘雨佳, 樊艳芳, 白雪岩, 等. 基于特征交叉机制和误差补偿的风力发电功率短期预测[J]. 电工技术学报, 2023, 38(12): 3277-3288.
Liu Yujia, Fan Yanfang, Bai Xueyan, et al. Short-term wind power prediction based on feature crossover mechanism and error compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3277-3288.
[3] 李阳, 沈小军, 张扬帆, 等. 基于速度-关联约束的风电机组风速感知异常数据识别方法[J]. 电工技术学报, 2023, 38(7): 1793-1807.
Li Yang, Shen Xiaojun, Zhang Yangfan, et al. Cleaning method of wind speed outliers for wind turbines based on velocity and correlation constraints [J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1793-1807.
[4] 国家能源局.国家能源局发布2023年全国电力工业统计数据[EB/OL]. [2024-01-26]. https://www.nea. go v.cn/2024-01/26/c_1310762246.htm.
[5] 顾雪平, 魏佳俊, 白岩松, 等.基于分层模型预测控制的含风电电力系统恢复在线决策方法[J]. 电工技术学报, 2025, 40(5): 1471-1486.
Gu Xueping, Wei Jiajun, Bai Yansong, et al. Online decision-making method for wind power integrated power system restoration based on hierarchical model predictive control[J]. Transactions of China Electro-technical Society, 2025, 40(5): 1471-1486.
[6] 陈臣鹏, 赵鑫, 毕贵红, 等. 基于多模式分解和麻雀优化残差网络的短期风速预测模型[J]. 电网技术, 2022, 46(8): 2975-2985.
Chen Chenpeng, Zhao Xin, Bi Guihong, et al. SSA-res-GRU short-term wind speed prediction model based on multi-model decomposition[J]. Power System Technology, 2022, 46(8): 2975-2985.
[7] 徐询, 谢丽蓉, 梁武星, 等. 考虑风电预测误差时序性及风电可信度的双层优化模型[J]. 电工技术学报, 2023, 38(6): 1620-1632, 1661.
Xu Xun, Xie Lirong, Liang Wuxing, et al. Bi-level optimization model considering time series characteristic of wind power forecast error and wind power reliability[J]. Transactions of China Electro-technical Society, 2023, 38(6): 1620-1632, 1661.
[8] 黎静华, 骆怡辰, 杨舒惠, 等. 可再生能源电力不确定性预测方法综述[J]. 高电压技术, 2021, 47(4): 1144-1157.
Li Jinghua, Luo Yichen, Yang Shuhui, et al. Review of uncertainty forecasting methods for renewable energy power[J]. High Voltage Engineering, 2021, 47(4): 1144-1157.
[9] 韩丽, 乔妍, 景惠甜. 基于误差分类的风电功率区间评估[J]. 电力系统自动化, 2021, 45(1): 97-104.
Han Li, Qiao Yan, Jing Huitian. Interval estimation of wind power based on error classification[J]. Automation of Electric Power Systems, 2021, 45(1): 97-104.
[10] 杨茂, 杜刚. 基于t Location-Scale分布的风电功率概率预测研究[J]. 中国电力, 2017, 50(1): 140-145.
Yang Mao, Du Gang. Wind power probability prediction based on t location-scale distrabution[J]. Electric Power, 2017, 50(1): 140-145.
[11] 岳国华, 杜志叶, 蔡泓威, 等. 基于风速概率分布与风切变指数的直流输电线路离子流场数值模拟方法[J]. 电工技术学报, 2024, 39(9): 2907-2915.
Yue Guohua, Du Zhiye, Cai Hongwei, et al. Numerical simulation method of ion flow field in DC transmission line based on wind speed probability distribution and wind shear exponent[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2907-2915.
[12] Chen Niya, Qian Zheng, Nabney I T, et al. Wind power forecasts using Gaussian processes and numerical weather prediction[J]. IEEE Transactions on Power Systems, 2014, 29(2): 656-665.
[13] 余建明, 庞传军. 考虑数据和模型不确定性的短期风电功率概率预测[J]. 电网技术, 2022, 46(5): 1926-1933.
Yu Jianming, Pang Chuanjun. Short-term wind power probabilistic prediction considering data and model uncertainties[J]. Power System Technology, 2022, 46(5): 1926-1933.
[14] 刘洪波, 刘珅诚, 盖雪扬, 等. 高比例新能源接入的主动配电网规划综述[J]. 发电技术, 2024, 45(1): 151-161.
Liu Hongbo, Liu Shencheng, Gai Xueyang, et al. Overview of active distribution network planning with high proportion of new energy access[J]. Power Generation Technology, 2024, 45(1): 151-161.
[15] 李丹, 张远航, 杨保华, 等. 基于约束并行LSTM分位数回归的短期电力负荷概率预测方法[J]. 电网技术, 2021, 45(4): 1356-1364.
Li Dan, Zhang Yuanhang, Yang Baohua, et al. Short time power load probabilistic forecasting based on constrained parallel-LSTM neural network quantile regression mode[J]. Power System Technology, 2021, 45(4): 1356-1364.
[16] Pinson P, Kariniotakis G. Conditional prediction intervals of wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1845-1856.
[17] 宋宇, 李涵. 基于核密度估计和Copula函数的风、光出力场景生成[J]. 电气技术, 2022, 23(1): 56-63.
Song Yu, Li Han. Typical scene generation of wind and photovoltaic power output based on kernel density estimation and Copula function[J]. Electrical Engineering, 2022, 23(1): 56-63.
[18] 臧海祥, 赵勇凯, 张越, 等. 基于低风速功率修正和损失函数改进的超短期风电功率预测[J]. 电力系统自动化, 2024, 48(7): 248-257.
Zang Haixiang, Zhao Yongkai, Zhang Yue, et al. Ultra-short-term wind power prediction based on power correction under low wind speed and improved loss function[J]. Automation of Electric Power Systems, 2024, 48(7): 248-257.
[19] 宋萌萌. 基于深度学习技术的风速预测方法研究[D]. 长沙: 中南大学, 2023.
Song Mengmeng. Research on wind speed forecasting method based on deep learning techniques[D]. Changsha: Central South University, 2023.
[20] 甘迪, 柯德平, 孙元章, 等. 基于集合经验模式分解和遗传-高斯过程回归的短期风速概率预测[J]. 电工技术学报, 2015, 30(11): 138-147.
Gan Di, Ke Deping, Sun Yuanzhang, et al. Short-term wind speed probabilistic forecasting based on EEMD and coupling GA-GPR[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 138-147.
[21] 王晨, 寇鹏. 基于卷积神经网络和简单循环单元集成模型的风电场内多风机风速预测[J]. 电工技术学报, 2020, 35(13): 2723-2735.
Wang Chen, Kou Peng. Wind speed forecasts of multiple wind turbines in a wind farm based on integration model built by convolutional neural network and simple recurrent unit[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2723-2735.
[22] Zou Mingzhe, Holjevac N, Đaković J, et al. Bayesian CNN-BiLSTM and vine-GMCM based probabilistic forecasting of hour-ahead wind farm power outputs[J]. IEEE Transactions on Sustainable Energy, 2022, 13(2): 1169-1187.
[23] Zhao Yanfang, Pu Haitao, Dai Yingjian, et al. Short-term wind power prediction method based on GCN-LSTM[C]//2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 2023: 1329-1333.
[24] Khodayar M, Wang Jianhui. Spatio-temporal graph deep neural network for short-term wind speed forecasting[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 670-681.
[25] Zhang Yingxue, Pal S, Coates M, et al. Bayesian graph convolutional neural networks for semi-supervised classification[C]//Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, Hawaii, USA 2019: 5829-5836.
[26] Li Wenzhe, Ahn S, Welling M. Scalable MCMC for mixed membership stochastic blockmodels[C]// Artificial Intelligence and Statistics, Proceedings of Machine Learning Research, Cadiz, Spain, 2016: 723-731.
[27] Yu Yunjun, Hu Guoping. Short-term solar irradiance prediction based on spatiotemporal graph convolutional recurrent neural network[J]. Journal of Renewable and Sustainable Energy, 2022, 14(5): 053702.
Speed Probabilistic Forecasting of Multiple Wind Turbines in Wind Farm Based on Bayesian Graph Convolutional Neural Network
Abstract Wind speed is characterized by randomness and volatility, which makes the point forecast results cannot quantify the uncertainty of wind speed. Therefore, probabilistic wind speed forecasting is a hot topic in current wind speed forecasting research. In wind farms with large turbine intervals and irregular rows, the local wind speed of each turbine has significant differences. However, the traditional wind speed probabilistic forecasting models tend to treat the wind speeds in an area as the same value, which is not conducive to the detailed control of wind farms. To solve the above problems, this paper proposes a probabilistic wind speed forecasting model for multiple wind turbines based on Bayesian graph convolutional neural network (BGCNN).
Firstly, the original graph model of wind field was constructed based on the historical data of wind speed and wind direction of each turbine. After that, the wind field graph model was inputted into BGCNN, which can parameterize the graph model to change the graph information and extract the multi-turbine spatial correlation. In this process, the long and short-term memory network (LSTM) was plugged into the back of GCNN module in the BGCNN model, so that the feature matrix containing spatial information among turbines was inputted into the LSTM for temporal feature extraction, and the wind speed forecast results of multiple turbines considering the time-space two-dimensional correlation were obtained. Finally, the Monte Carlo method was used to sample multiple sets of model output values to achieve probabilistic wind speed forecasting for multiple turbines.
Simulation results on the wind farm data show that, multiple turbines in a wind farm present different graph structures under different epochs, indicating that the proposed model can fully consider various spatial relationships among different turbines. For point forecasting results, which are obtained by calculating the mean of the sampling results, the mean absolute error of the proposed model is 1.092 m/s for all 100 wind turbines, and the root mean squared error among them is 1.530 m/s. There are both smaller than the comparison model, BCNN-LSTM and Q-CNN-LSTM. For probabilistic forecasting, the reliability and sharpness of the proposed model are not all the best at different confidence level, such as in the case of 30%, 50% confidence level, etc. Nevertheless, the average forecast interval coverage bias index and average sharpness of the forecast results are 3.10% and 0.119, respectively, which are lower than the two comparison models. For turbine number 33, compared with the single turbine forecasting model, the probabilistic forecasting results of the proposed model are the best, with the smallest forecast interval coverage bias index, sharpness and Pinball score, which are 1.68%, 0.123～0.431 m/s, respectively.
The following conclusions can be drawn from the simulation analysis: (1) In this paper, the clustering method is used to classify the output features of the GCNN-LSTM model, which enables the BGCNN to be used in regression problems and to extract the spatial features among wind turbine data well. (2) Compared to the comparison models, the model in this paper achieves higher forecast accuracy in both point forecasting and probabilistic forecasting, and the forecast intervals calculated from the forecast results have small deviations and concentrated distribution. (3) For a single wind turbine in a wind farm, the forecast accuracy of this paper's model is higher than that of the probabilistic forecasting model only for a single wind turbine, which reflects that the reasonable and effective extraction of spatial features is conducive to the reduction of forecast errors.
Keywords：Probabilistic forecasting, wind speed forecast, graph convolutional neural network, spatial correlation, ultra-short-term forecasting
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.241651
国家自然科学基金资助项目（52077165）。
收稿日期 2024-09-23
改稿日期 2025-01-02
郭美仑 女，2001年生，硕士研究生，研究方向为风电概率预测、电力系统不确定性分析。
E-mail：gml0317@stu.xjtu.edu.cn
寇 鹏 男，1983年生，教授，博士生导师，研究方向为电力系统预测与控制，可再生能源并网等。
E-mail：koupeng@mail.xjtu.edu.cn（通信作者）
（编辑 赫 蕾）