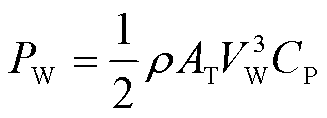 (1)
(1)
摘要 面向新型电力系统大规模清洁能源并网带来的强随机扰动导致控制性能及电网频率稳定性变差的问题,该文从自动发电控制的角度提出泰勒双延迟深度确定性策略梯度算法来获取多区域协同最优解,进而提高大规模清洁能源并网后电力系统的控制性能及频率稳定性。所提算法采用泰勒级数展开更新价值网络,改善了强化学习中存在的动作价值高估,有助于提升算法的控制精度;同时引入可减少训练样本损失的经验回放策略替代训练样本的随机采样,以提升算法寻优正确率,进而减少随机扰动对控制性能的影响。通过搭建改进的IEEE标准两区域负荷频率控制模型和风光水火储一体化三区域互联负荷频率控制模型并进行仿真,验证了所提算法的有效性。相较于其他强化学习算法,该文所提算法具有更优的控制性能和更稳定的频率响应。
关键词:自动发电控制 强化学习 多区域协同 泰勒双延迟
随着新型电力系统的不断推进,以风电、光伏发电为代表的清洁能源开发规模持续扩大[1]。具有较强随机性和间歇性的清洁能源大规模并网会给电网带来强随机扰动,影响电力系统控制性能及频率稳定性。目前工程应用的自动发电控制(Automatic Generation Control, AGC)方法以优先确保自身区域控制性能最优的集中式模式[2-5]为主,由于通信延迟和地理位置等因素,集中式AGC难以充分调动各区域间的协同控制。
面向分布式模式的新型电力系统将整个系统划分为相互关联的子系统,为保证多区域电网间的协同,分布式AGC应运而生。学者们对分布式AGC进行探索[6-12],以期在获取多区域协同的同时,解决不断接入的清洁能源带来的强随机扰动导致电网控制性及频率稳定性越来越差的问题。此过程中基于多智能体的强化学习逐渐被学者们认可,不仅是因为多智能体强化学习可以进行多区域协同,而且基于马尔科夫决策过程的强化学习对于解决随机问题具有优势。
强化学习中最经典的算法为Q学习及其衍生算法,学者们针对AGC的研究多以Q学习框架为主流研究方法。如文献[13]提出多步回溯Q(λ)学习算法,解决了火电机组大时滞环节带来的延时回报。文献[14]提出基于平均报酬最优准则的R(λ)算法,解决了复杂扰动环境下Q学习收敛性差的问题。文献[15]提出一致性迁移Q学习,解决了机组规模较大导致的维数灾难问题。然而,Q框架体系算法存在对Q值估计不准确的问题[16],导致获取到的动作值与真实状态之间有较大的偏差,影响电力系统控制性能及频率稳定性。
文献[17]提出双Q学习算法,将Q值计算拆分为最优动作选择和Q值估计两个步骤,有效地缓解了Q学习算法估值不准确的问题。针对可再生能源消纳的协同控制,文献[18]在双Q学习的基础上引入加权思想,解决了传统Q学习的动作估值偏差问题,并且在大规模电网中验证了其有效性。针对大型风电并网,文献[19]提出乐观双Q算法,可减缓动作值高估并且避免算法陷入局部最优解,有效地提升了控制性能。文献[20]提出重复更新Q学习算法,从理论上解决Q值估值不准确问题,并且引入拉格朗日松弛原理提升算法学习效率,从而提升电力系统频率响应的稳定性。
然而,上述方法虽然解决了Q值估值不准确问题,但Q学习及其衍生算法均为离散算法,需要针对不同的控制系统设计不同的动作空间,而大规模清洁能源并网导致电力系统运行状态变得更加复杂,离散算法已无法提供足够高的控制精度,导致电力系统频率误差较大。文献[21]提出基于演员-评论家框架的深度确定性策略梯度(Deep Deterministic Gradient, DDPG)算法,能够通过建立策略网络和价值网络实现连续控制。DDPG通过策略网络获取动作,价值网络对动作进行打分指导策略网络做出改进。然而DDPG为获得最优的策略,价值网络会对动作价值进行最大化处理,这会导致算法对真实动作价值的高估[22],进而导致较大的频率偏差。其次,DDPG需要建立一个样本池,算法在训练时不断地从样本池中采样,而当采集到由随机扰动或噪声所产生的样本进行训练时,会影响算法的准确性和稳定性。
因此,面向分布式新型电力系统,本文从分布式AGC视角,提出泰勒双延迟深度确定性策略梯度减少损失(Taylor twin Delayed Deep Deterministic policy gradient Reducible Loss, TaTD3-ReLo)算法。所提算法是基于泰勒时间差分(Taylor Temporal Difference, TaTD)算法[23],采用泰勒级数展开更新价值网络,解决了DDPG中存在的动作价值高估问题,以获得更准确的动作响应,从而降低电力系统频率误差。同时,通过减少训练样本损失(Reducible Loss, ReLo)策略[24]对采集到的实时数据进行优先排序,向由随机扰动和噪声等能够导致低学习能力的样本分配较低优先级,向具有高学习能力的样本赋予更多优先级,以提升控制系统的稳定性,进而解决规模化清洁能源并网带来的强随机扰动导致电网控制性能及频率偏差越来越差的问题。最后,通过搭建两区域负荷频率控制(Load Frequency Control, LFC)模型和三区域风光水火储一体化模型进行仿真,验证所提算法的有效性。
由于风力和光伏具有不确定性和随机性,直接导致了风力发电和光伏发电的间歇性和波动性,使得并网后的电力系统调峰能力不足,而抽水蓄能和风电、光伏发电有着明显的互补效应,可以显著降低风力发电、光伏发电大规模并网对电网的影响,提高风电和光伏的消纳水平[25]。
因此,本文对风力发电和光伏发电通过抽水蓄能进行消纳,搭建风光水火储一体化系统模型。通过抽水蓄能进行发电,确保在并网时电力系统的稳定性,同时也最大化了风电和光伏发电的利用效率。
本文搭建的风电机组中[26],由Matlab/Simulink中的白噪声模块产生随机量,采用风速乘以随机量模拟风速波动。风机输出功率为
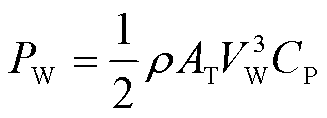 (1)
(1)
式中,ρ为空气密度(kg/m3);AT为旋翼截掠面积(m2);VW为额定风速(m/s);CP为风能利用系数。建立风电机组模型如图1所示。
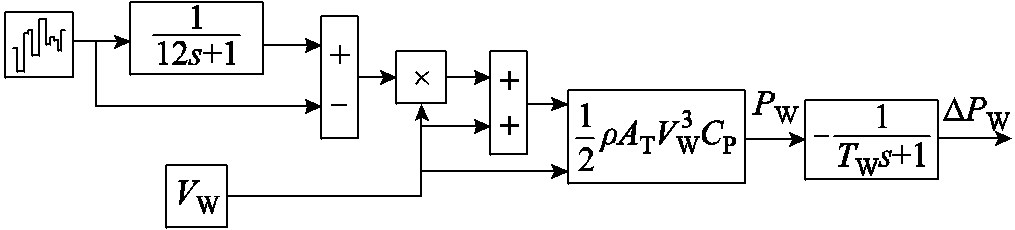
图1 风电机组模型
Fig.1 Wind turbine models
由于光伏发电系统[26]的输出功率受天气的影响是不规律的,因此,考虑均匀日照和非均匀日照的偏差,利用Matlab中的白噪声模块建立光伏发电机组模型如图2所示。图2中,PS为光伏功率偏差,TP为光伏机组时间常数,DPPV为光伏功率偏差。通过式(2)模拟实际光伏功率变化的功率偏差。
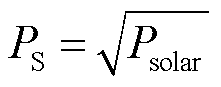 (2)
(2)
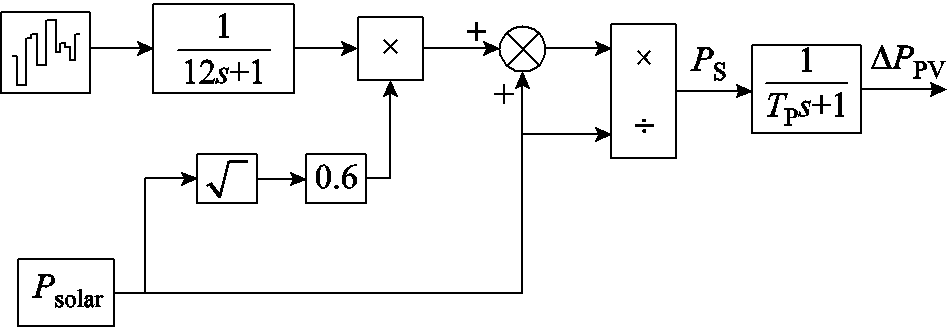
图2 光伏发电机组模型
Fig.2 Photovoltaic turbine models
抽水蓄能一般分为发电和抽水两种运行工况[27]。发电工况中包含调速器和水轮机两部分;抽水工况中,水泵机组与发电机组等效为相同的异步电动机。抽水蓄能运行框图如图3所示。图3中,TW为启动时间常数,Tg为调速器时间常数,T2为补偿器参数,T1为复位参数,T0为调速系数,Kg为电机增益,Tr为再启动时间常数,Tt为惯性系数,∆f为系统频率偏差,PG为发电功率,PP为抽水功率。
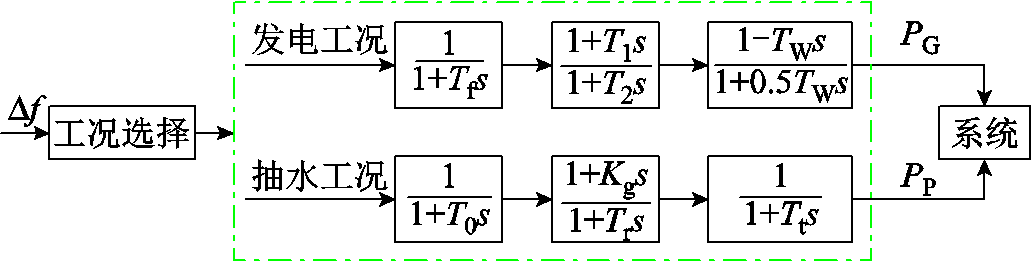
图3 抽水蓄能运行框图
Fig.3 Pumped storage operation block diagram
传统火电机组可简化为调速器和汽轮机,水电机组可简化为调速器和水轮机[28]。通过传递函数构建火电机组和水电机组的数学模型为
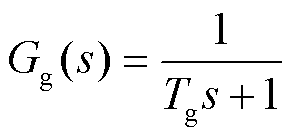 (3)
(3)
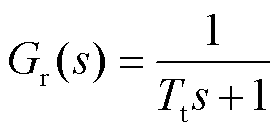 (4)
(4)
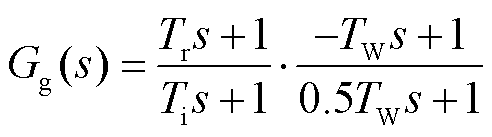 (5)
(5)
式中,Gg为汽轮机调速器传递函数;Gr为水轮机调速器传递函数;Ti为水轮机调节阀时间常数。
TaTD3-ReLo是以DDPG算法为基础的深度强化学习算法,通过寻求最优控制策略以获得准确的动作响应,从而提升电力系统频率的稳定性。
TaTD3算法用于改善价值网络高估动作价值的问题。通过泰勒级数展开更新价值网络,使价值网络可以给出更为准确的动作价值,从而更好地指导策略网络做出改进,以获得最优控制策略。TaTD3算法中策略网络更新规则为
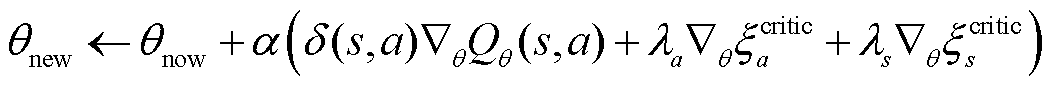 (6)
(6)
式中,θnew为策略网络更新后的参数;θnow为策略网络当前参数;Qθ(s, a)为状态s执行动作a时所获得的动作价值;δ(s, a)为时间差分(Temporal Difference, TD)误差,表示当前时刻动作价值与下一时刻动作价值之间的差值;α为学习率;λa为动作协方差;λs为状态协方差;ξacritic、ξscritic分别为Qθ(s, a)和δ(s, a)的余弦距离,计算公式为
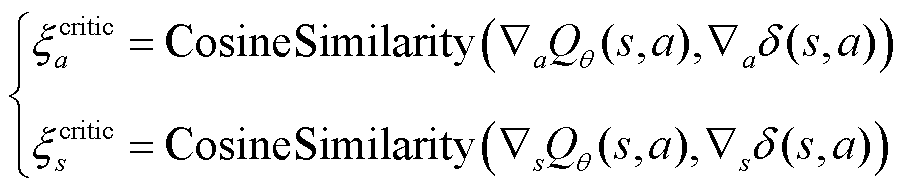 (7)
(7)
式中,CosineSimilarity为余弦相似度;ÑaQθ(s, a)为动作价值对当前动作a进行微分;Ñaδ(s, a)为TD误差对当前动作a进行微分;ÑsQθ(s,a)为Q值对当前状态s进行微分;Ñsδ(s, a)为TD误差对当前状态s进行微分。由于TaTD3在更新价值网络时需要对状态s和动作a进行微分,因此需要引入一个环境转换的微分模型和奖励模型计算Ñaδ(s, a)和Ñsδ(s, a)。TaTD3在更新价值网络时需要不断地从经验池中随机抽取样本进行训练,但这种随机采样会导致一些学习性高的样本被较少地选取或者被完全忽略,从而影响算法的学习效率和性能。
ReLo原理按照可学习性对经验池中的样本进行分类,优先选取可学习性较高的样本进行训练,而不是从经验池中随机采样,以提升算法稳定性和学习效率。ReLo原理通过训练网络(具有参数θ)和目标网络(具有参数θ-)的损失之差确定样本的可学习性,其数学表达式为
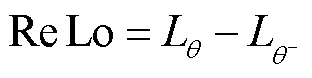 (8)
(8)
式中,Lθ为网络参数为θ的损失函数;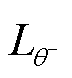 为网络参数为θ-的损失函数。损失函数数学表达式为
为网络参数为θ-的损失函数。损失函数数学表达式为
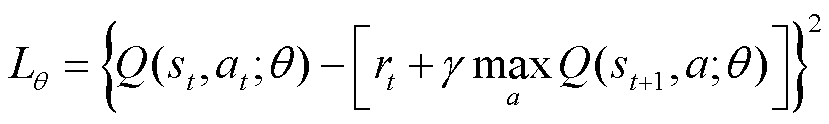 (9)
(9)
式中,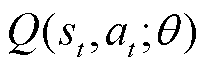 为t时刻价值函数;
为t时刻价值函数;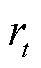 为t时刻奖励函数,st为t时刻状态值;at为t时刻动作值;γ为折扣因子。
为t时刻奖励函数,st为t时刻状态值;at为t时刻动作值;γ为折扣因子。
确定样本的可学习性后,对于经验池中的每一个样本都分配采样概率P(k),在训练智能体时基于概率对经验池进行采样。采样概率计算公式为
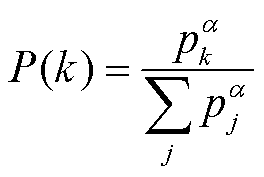 (10)
(10)
式中,α∈[0,1];pk为样本k的可学习性,计算公式为
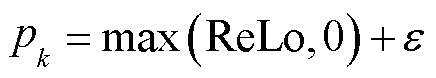 (11)
(11)
式中,ε为一个非常小的常数,保证最低采样概率非零。
为了克服诸如DDPG等连续控制算法中存在的动作价值高估问题,以及算法在随机采样过程中随机扰动对算法学习效率及稳定的影响,提出TaTD3-ReLo。所提算法通过截断双Q学习策略、目标网络和策略网络延迟更新、目标策略网络中加入噪声三种方法,进而能够保证算法的稳定性和训练效率。
1)截断双Q学习策略
为更好地解决动作价值的高估问题,TaTD3-ReLo算法使用两个价值网络和一个策略网络,每个网络都对应一个目标网络。通过目标价值网络对策略网络得出的动作进行评价,得到两个动作价值,采用动作价值中的最小值计算TD目标,从而抑制对动作价值的高估问题。采用截断双Q学习策略后的TD目标计算公式为
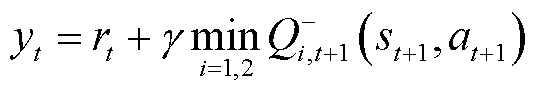 (12)
(12)
式中,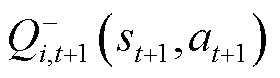 为第i目标价值网络在t +1时刻的目标价值网络参数;i为价值网络。
为第i目标价值网络在t +1时刻的目标价值网络参数;i为价值网络。
2)目标网络和策略网络延迟更新
TaTD3-ReLo在更新价值网络d次后更新目标网络和策略网络,确保在更新策略网络时将价值网络产生的误差降到最低,从而提高策略网络的更新质量。当电力系统存在随机扰动时,价值网络本身不可靠,无助于改进策略网络,因此通过延迟更新目标网络可减少价值网络的评价误差。目标价值网络更新公式为
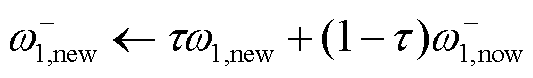 (13)
(13)
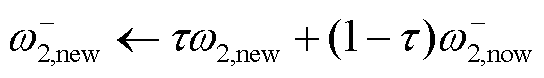 (14)
(14)
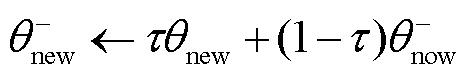 (15)
(15)
式中,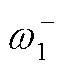 、
、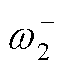 为两个目标策略网络的参数;τ∈(0,1)。
为两个目标策略网络的参数;τ∈(0,1)。
3)目标策略网络中加入噪声
为增加探索样本的随机性和多样性,TaTD3-ReLo在目标策略网络μ计算动作时加入随机噪声,改进后的动作值为
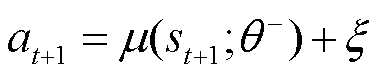 (16)
(16)
式中,ξ为噪声,其值从截断正态分布中抽取。截断正态分布记作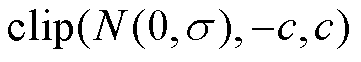 ,表示均值为0、标准差为σ的正态分布,使用截断,保证噪声大小不会超过[-c, c]的范围。
,表示均值为0、标准差为σ的正态分布,使用截断,保证噪声大小不会超过[-c, c]的范围。
TaTD3-ReLo算法框架如图4所示。
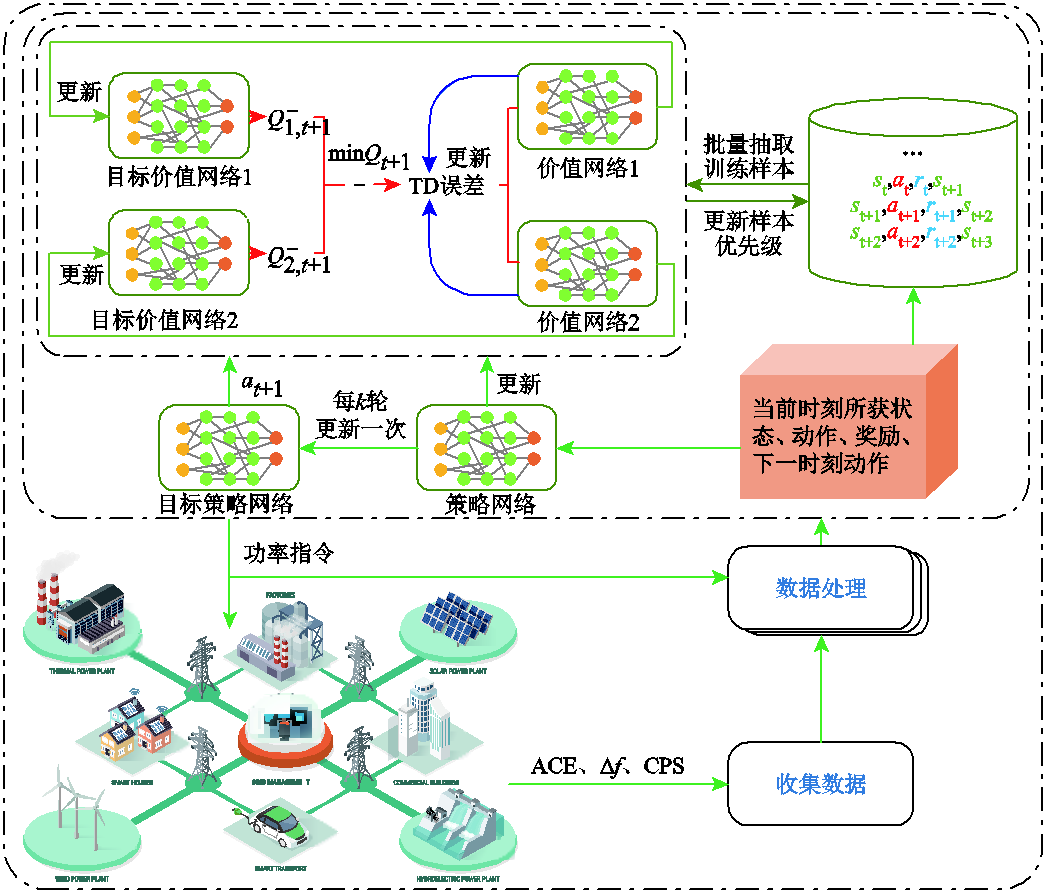
图4 TaTD3-ReLo算法框架
Fig.4 TaTD3-ReLo algorithmic framework
为评估基于TaTD3-ReLo算法AGC控制器的性能,引入北美电力可靠性委员会提出的控制性能标准(Control Performance Standards, CPS)[29]。AGC控制器性能应该尽量保持CPS指标和频率偏差∆f在合格范围内,其具体指标如下:
1)CPS1≥200%,且CPS2为任意值,CPS指标合格。
2)100%≤CPS1<200%,且CPS2≥90%,CPS指标合格。
3)CPS1<100%,CPS指标不合格。
4)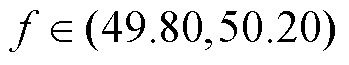 Hz,频率指标合格。
Hz,频率指标合格。
对于AGC系统而言,智能体为AGC控制器,环境为电力系统,状态为区域控制误差(Area Control Error, ACE)。智能体通过动作与环境进行交互,在交互过程中,环境给出一个即时奖励(奖励函数如2.1节所示),用于衡量智能体执行当前动作的好坏,并且根据奖励对下一回合的动作进行修正。
ACE是区域控制指标和实时动作好坏的直接反映。为了使ACE输出平稳并且CPS指标长期稳定,本文对ACE和CPS指标进行归一化处理,并对ACE(i)(ACE的瞬时值)和CPS进行加权作为奖励函数。目标奖励函数为
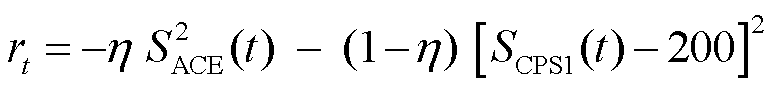 (17)
(17)
式中,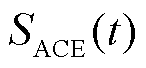 为t时刻ACE的值;
为t时刻ACE的值; 为t时刻CPS1的值;η为权重系数。通过实验验证,η=0.5时AGC系统可获得更优的控制性能。其中,ACE和CPS计算公式为
为t时刻CPS1的值;η为权重系数。通过实验验证,η=0.5时AGC系统可获得更优的控制性能。其中,ACE和CPS计算公式为
 (18)
(18)
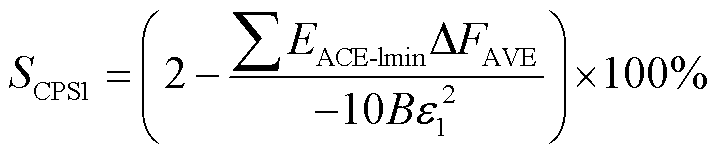 (19)
(19)
式中,Δf为频率偏差;ΔPtie为联络线功率;B为频率响应系数;EACE-1min为1 min内ACE的平均值;ΔFAVE为1 min内的频率偏差平均值;e1为全年 1 min内频率平均偏差的方均根。
1)学习率α∈(0,1),决定算法收敛速度。较大的α可加快学习速度,较小的α可获得更优的控制策略。
2)折扣因子γ∈[0,1],表示智能体对未来奖励的重视程度。γ越大,表示智能体越重视未来奖励;γ越小,表示智能体越重视当前奖励。
3)经验池容量E,太小的容量会导致样本利用率低,太大会增加存储和计算成本。
所有参数设置见表1。
表1 参数设置
Tab.1 Parameters setting

参数数值 策略网络学习率α110-4 价值网络学习率α210-4 折扣因子γ0.95 目标动作噪声方差ξ0.03 策略网络更新间隔d5 经验池容量E1 000
抽水蓄能是目前技术最成熟、经济性最优、最具大规模开发条件的电力系统绿色低碳灵活调节电源[30]。通过减少火电机组起停频率,抽水蓄能不仅能提高发电效率,而且增强了电力系统的供电能力[25]。此外,水电机组相较于火电机组具有响应速度快、调节能力强等优点[28],在电力系统中具有调峰调频的作用。因此本文在标准两区域LFC模型基础上,搭建含有火电机组、水电机组和抽水蓄能的改进两区域LFC模型,如图5所示。图5中,TP与KP为频率响应系数,∆PLA为区域A负荷功率,T12为联络线时间常数。
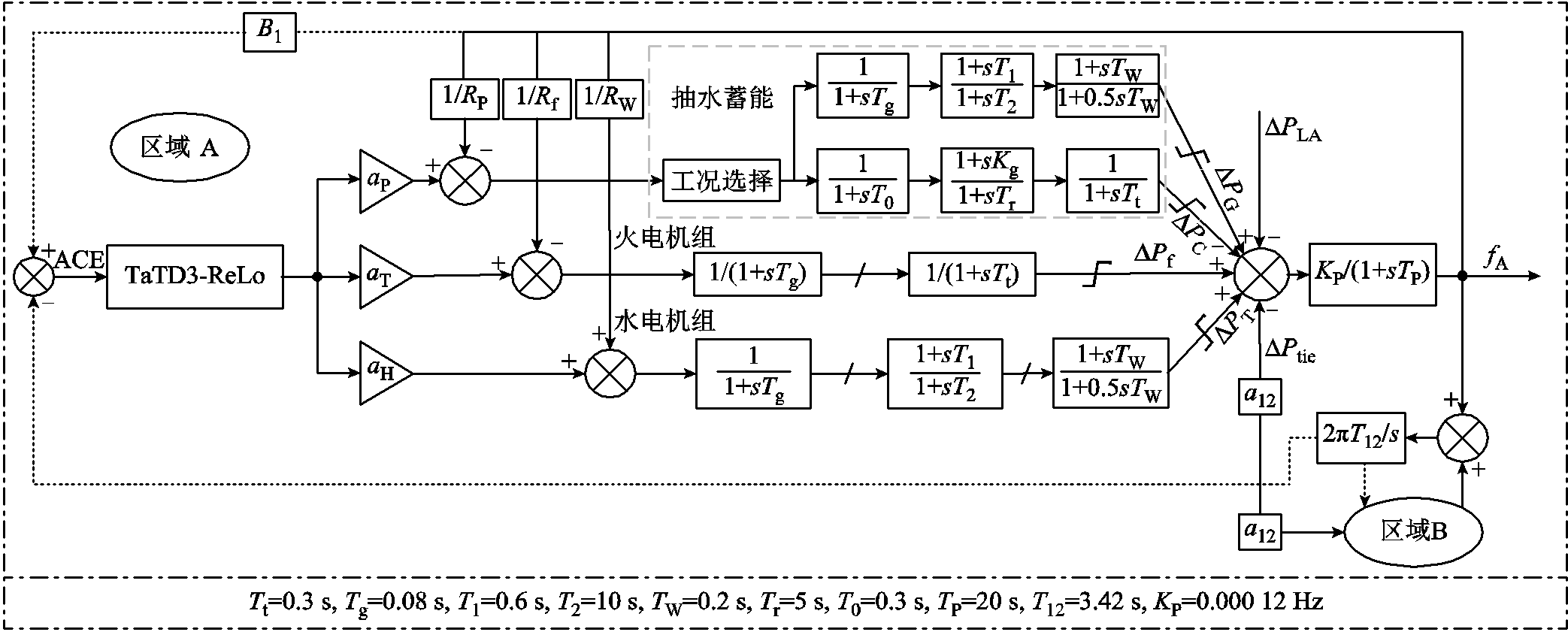
图5 改进的IEEE标准两区域LFC模型
Fig.5 Improved IEEE standard two-area LFC model
4.1.1 预学习
在正式投入运行前,强化学习算法需要充足的预学习以获得最优控制策略,预学习完成后便可直接投入AGC系统运行,无需再次进行训练,以满足大型AGC的实时性要求。本文对两区域模型引入周期为5 000 s、幅值为1 000 MW的正弦负荷进行回合训练,并与DQN[31]、DDPG[21]、TD3[22]、TaTD3[23]四种算法进行对比,通过奖励值曲线是否趋于稳定来判断算法的收敛性,取训练结束后各算法运行数据进行对比,评估所提算法的控制性能。五种算法预学习及预学习完成后的控制性能如图6所示(以区域A为例)。
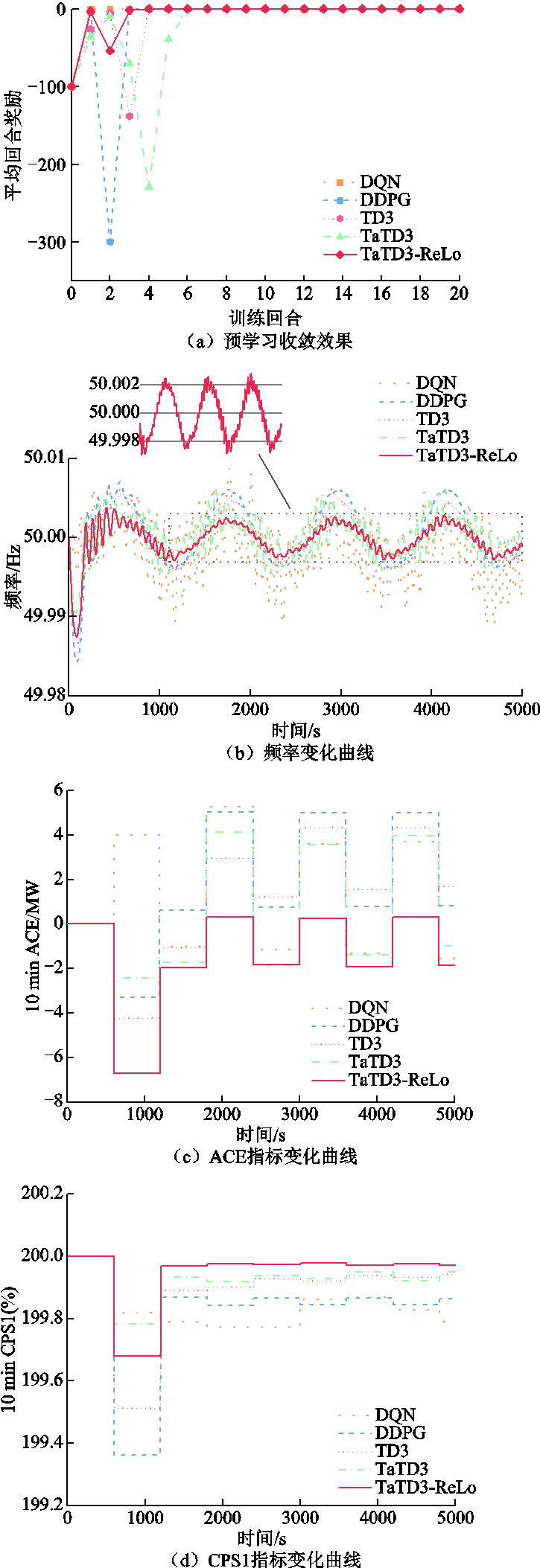
图6 预学习性能指标
Fig.6 Pre-learning performance indicators
由图6a可知,TaTD3-ReLo在三回合后奖励值趋于平稳,相较于其他算法收敛速度有明显优势。图6b~图6d为训练结束后各算法的性能指标,通过CPS1平均值、ACE平均值和频率对控制性能进行评估。由图6b可知,TaTD3-ReLo频率偏差最大值为0.01 Hz,远小于频率偏差阈值±0.2 Hz;在 1 000 s之后,频率上下波动误差为±0.002 Hz,相较于其他算法更为稳定;由图6c可知,TaTD3-ReLo可将ACE平均值维持在±2 MW之内,远优于其他算法;由图6d可知,TaTD3-ReLo的CPS1平均值相较于其他算法更为稳定,其最大误差为0.31%,最小误差为0.02%。另外,由图6b可以看出,相对于DQN算法,DDPG算法具有更准确的控制精度,可以获得更稳定的频率响应。
4.1.2 阶跃扰动
考虑到系统实际运行过程中负荷突增的情况,引入阶跃负荷扰动进行模拟,检验算法的控制性能。在两区域模型中选取幅值相同的阶跃扰动,采用相同的奖励函数对DQN、TD3、DDPG、TaTD3和TaTD3-ReLo算法进行仿真实验,各算法控制性能指标如图7所示(以区域A为例)。
由图7a可知,TaTD3-ReLo算法在负荷突增的情况下,ACE的绝对值更小,并且在负荷稳定后,ACE值更趋近0;相较于其他算法,ACE可减少29.5%~87.4%。由图7b可知,TaTD3-ReLo算法的CPS1值更趋于200%,可以更好地满足CPS标准;相较于其他算法,CPS1可提高4.41%~37.53%。由图7c可知,DDPG算法由于存在动作价值高估问题,导致频率上下波动较大,而TaTD3算法采用泰勒级数展开克服了DDPG算法存在的动作价值高估问题,大幅提高了频率响应的稳定性,频率稳定性可提高26.6%~74.9%。综上所述,TaTD3-ReLo算法在面对负荷突增的情况时控制性能最优,TaTD3次之。
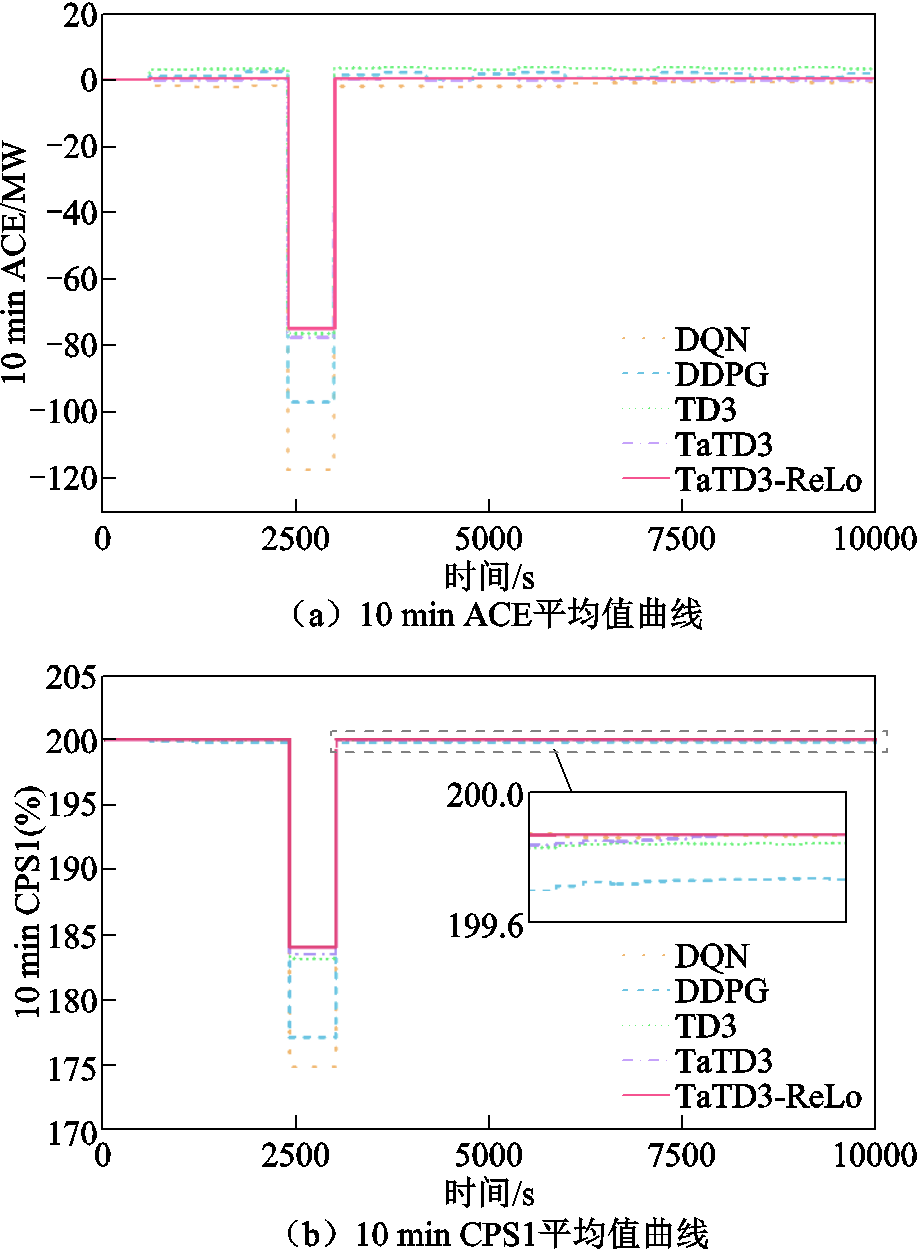
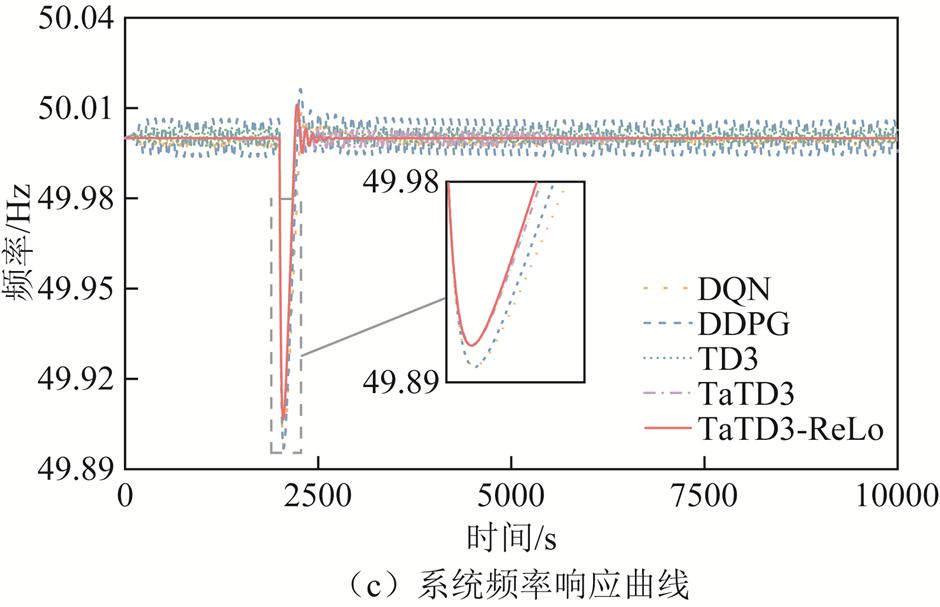
图7 阶跃扰动性能指标
Fig.7 Step disturbance performance index
4.1.3 随机方波扰动
对于负荷不断突增或突减的情景,引入随机方波进行模拟,以30 000 s为周期进行实时仿真。各算法运行功率输出效果如图8所示(以区域A为例)。
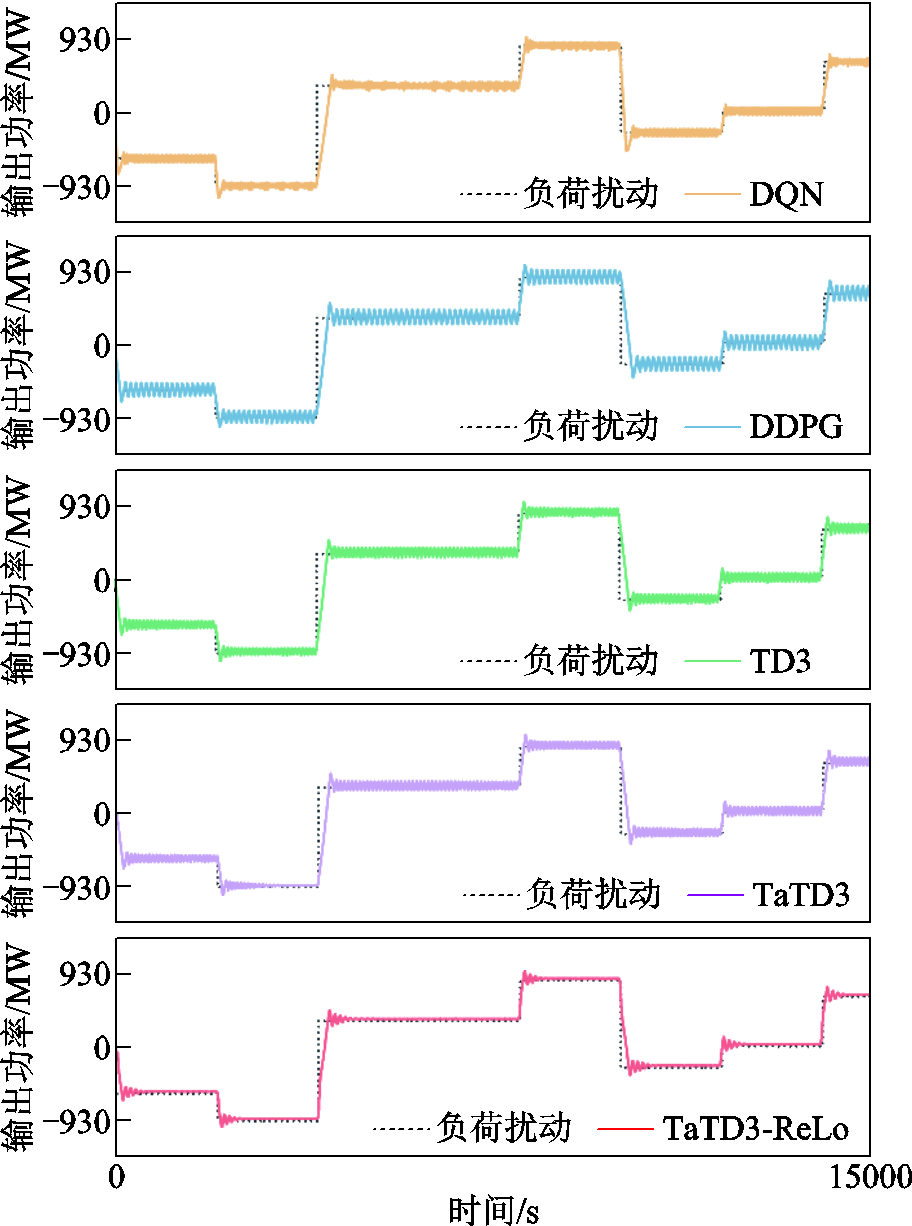
图8 随机方波扰动机组出力曲线
Fig.8 Random square wave disturbed unit output curves
由图8可知,TaTD3-ReLo算法在面对随机方波扰动时稳定性最好,并且在面对负荷突增或突减时有较小的超调量。图9为上述五种算法的各项性能指标,其中,| ∆f |为整个仿真周期频率误差的绝对值;|ACE|为整个仿真周期ACE绝对值的平均值。相对于其他算法,TaTD3-ReLo算法的|ACE|可减少25%~44%;|∆f |降低了42%~85%,并且CPS1值也更高。
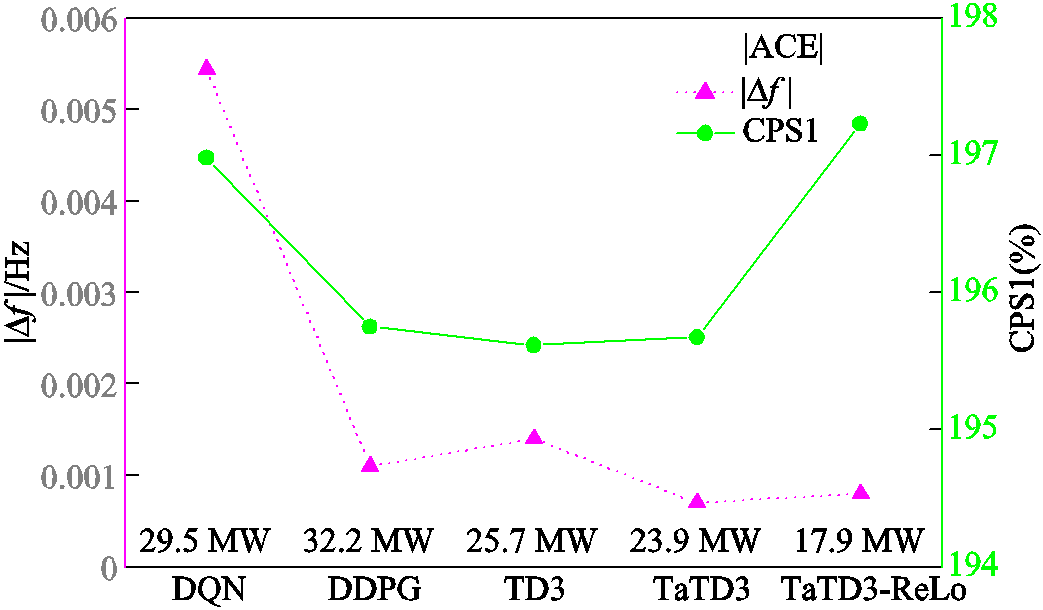
图9 随机方波扰动下各算法的控制性能
Fig.9 Control performance of each algorithm under random square wave disturbance
上述仿真结果表明,TaTD3-ReLo算法在面对负荷突增或者负荷持续突增突减的情况下仍具有最优的控制性能。
风光水火储一体化三区域互联电网模型包括:传统的火电机组、水电机组、风力机组、光伏机组和抽水蓄能机组,如图10所示。各机组模型参数见表2,其中,传统机组和风光发电采用西南电网数据[20]。
表2 机组模型参数
Tab.2 Parameters for unit model

机组参数 火电机组Tg=0.08 s, Tt=0.3 s 水电机组Tgh=0.08 s, TW1=0.6 s, TW2=10 s, TWh=0.2 s 风电机组TW=1.5 s 光伏机组TP=1.85 s 抽水蓄能机组Tf=0.06 s, T1=0.6 s, T2=10 s, TW=0.2 s, TP=0.3 s, Kg=0.2(pu), Tr=5 s, Tt=0.8 s
4.2.1 白噪声扰动
引入随机白噪声扰动模拟电网时刻都在变化的负荷扰动。以 30 000 s为考核周期进行仿真,验证TaTD3-ReLo算法控制性能。以重庆地区为例,其负荷跟踪曲线如图11所示,频率响应曲线如图12所示。
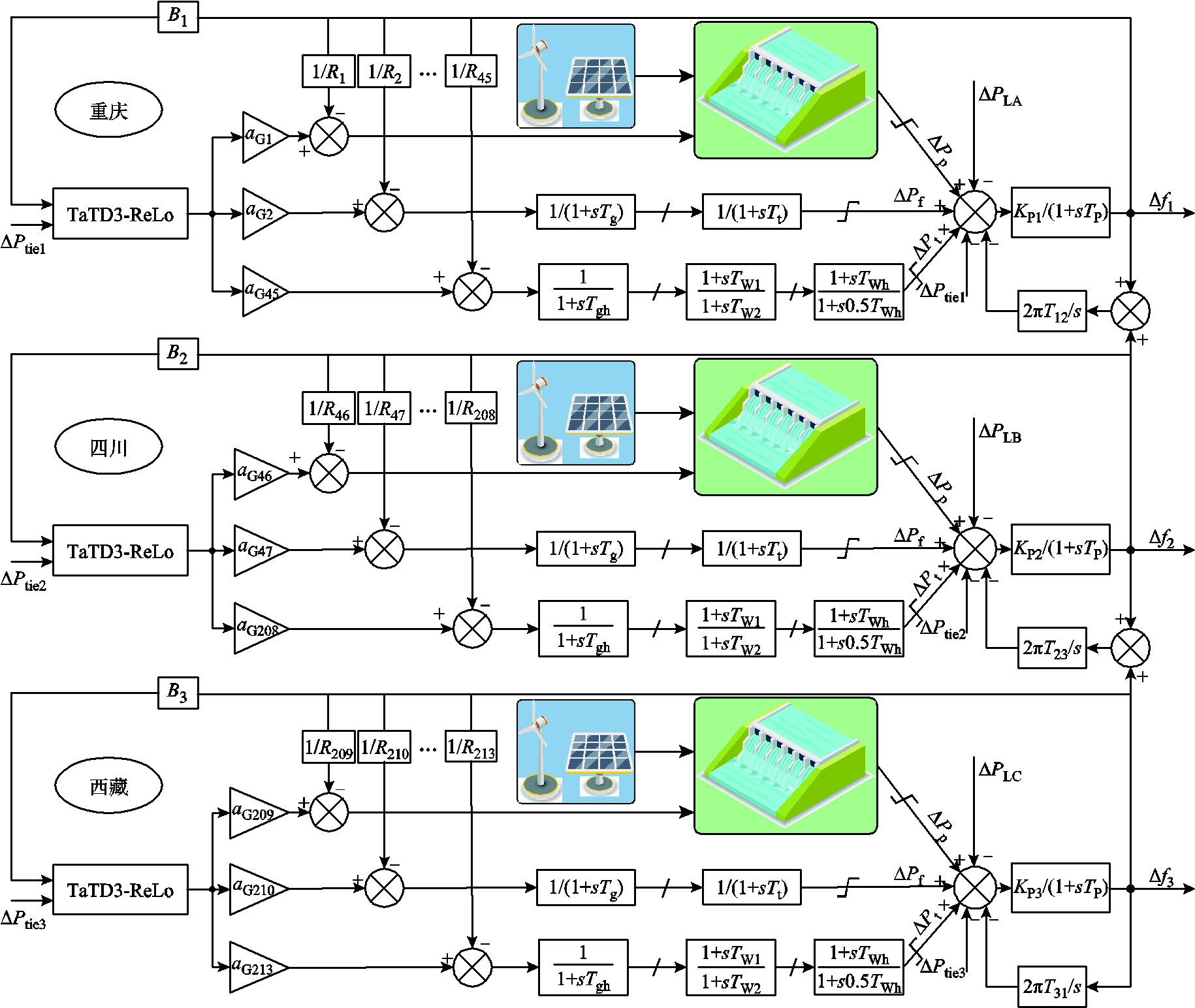
图10 风光水火储一体化三区域模型
Fig.10 Integrated wind-solar-hydro-thermal-storage three-area model
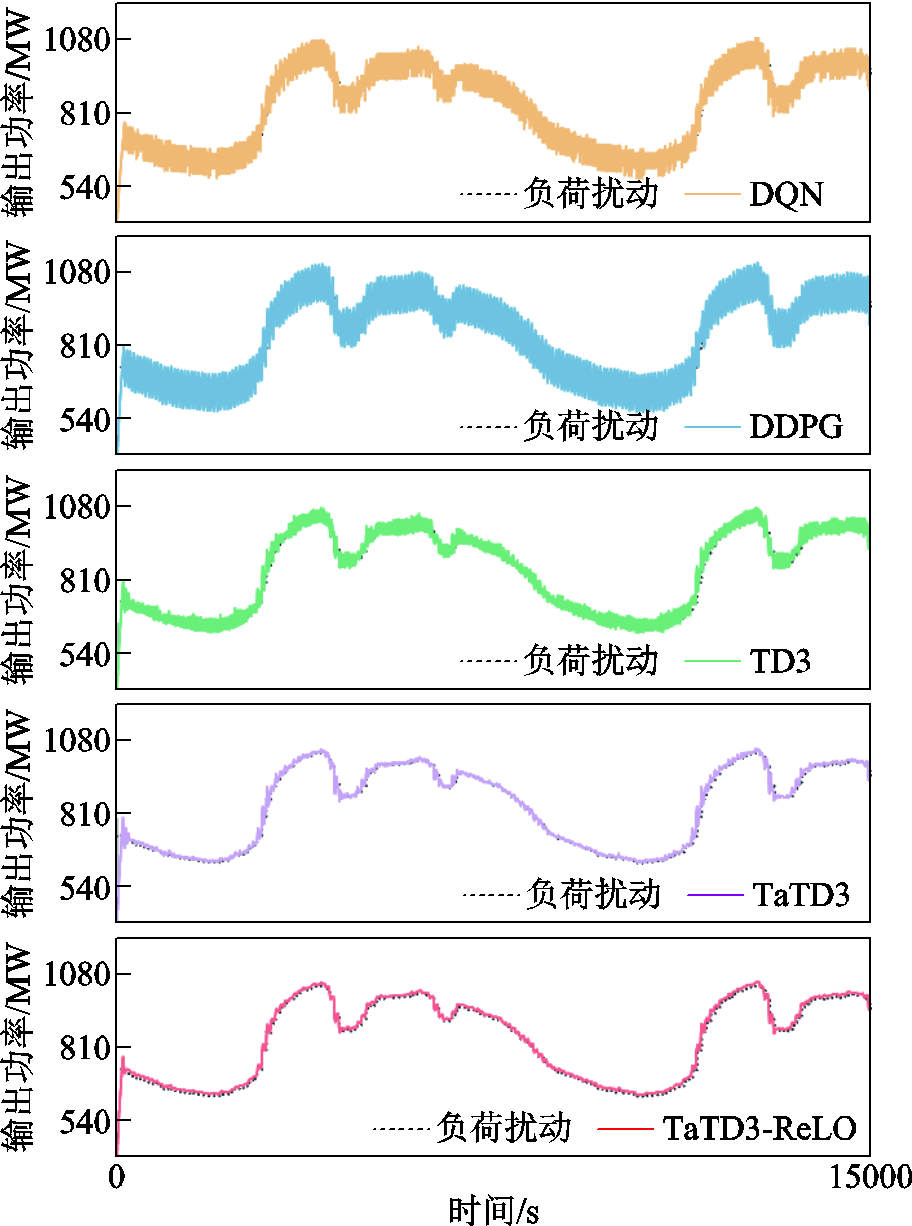
图11 白噪声扰动机组出力曲线
Fig.11 White noise disturbed unit output curves
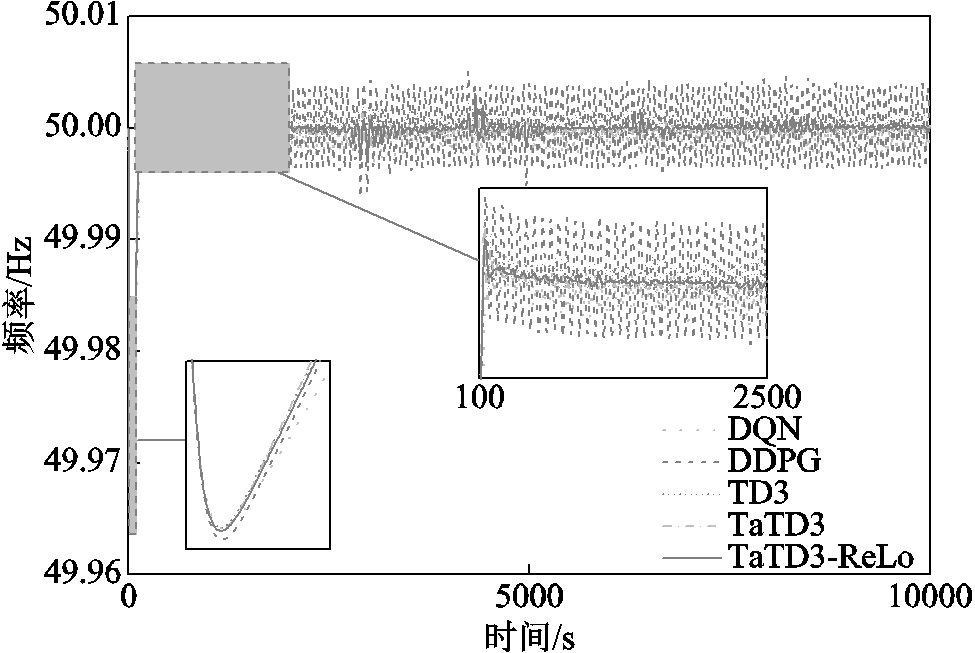
图12 白噪声扰动系统频率响应曲线
Fig.12 Frequency response curves of white noise disturbed system
结合图11、图12可以看出,TaTD3-ReLo算法具有更平滑的曲线,可以更好地跟踪电网负荷扰动,并且具有更稳定的频率响应。白噪声扰动下算法控制性能如图13所示。综合图13的三区域控制性能指标,在多区域随机电网环境下,TaTD3-ReLo算法有较强的适应力和更优的控制性能。在满足CPS1标准的情况下,具有更低的区域控制误差和频率偏差。以重庆地区为例,相较于其他算法,|ACE|减少56%~86%,| ∆f |降低20%~86%。
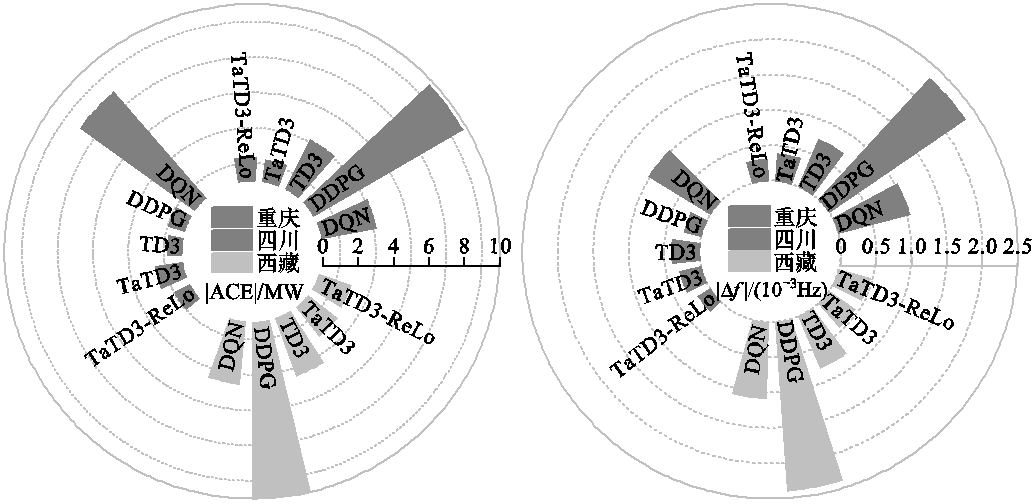
图13 白噪声扰动下算法控制性能
Fig.13 Algorithm control performance under white noise
4.2.2 随机负荷扰动
考虑到实际分布式能源接入的强随机性,引入无规则随机负荷信号模拟真实电网环境,进行24 h实时仿真,验证TaTD3-ReLo算法在实际工程中的应用效果。图14为光伏、风力发电的功率输出曲线,图15为TaTD3-ReLo算法跟踪负荷扰动的输出曲线,图16为各算法频率响应曲线(各项数据取重庆地区为例)。可以看出TaTD3-ReLo算法不仅可以更准确地跟踪负荷扰动而且频率响应也更稳定。
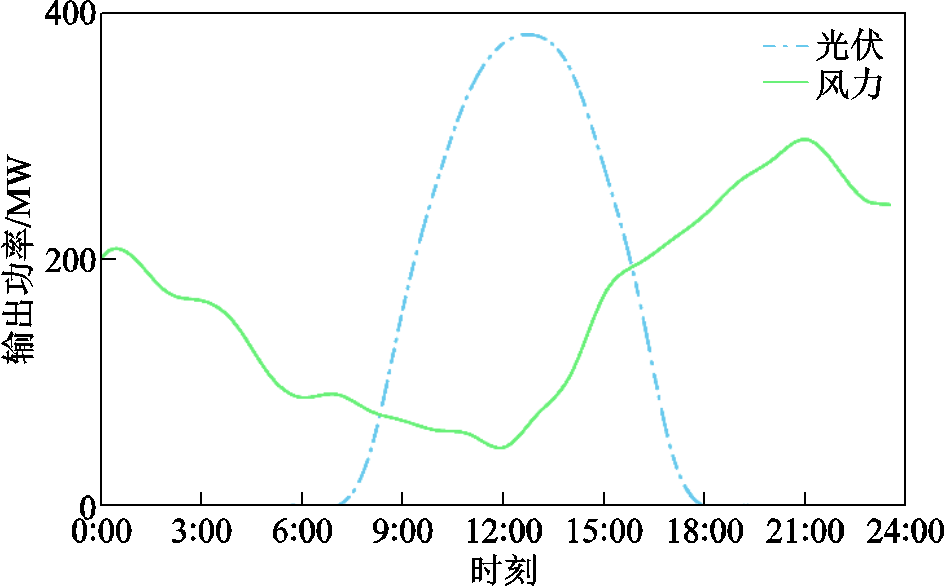
图14 风电、光伏功率输出曲线
Fig.14 Wind and photovoltaic power output curves
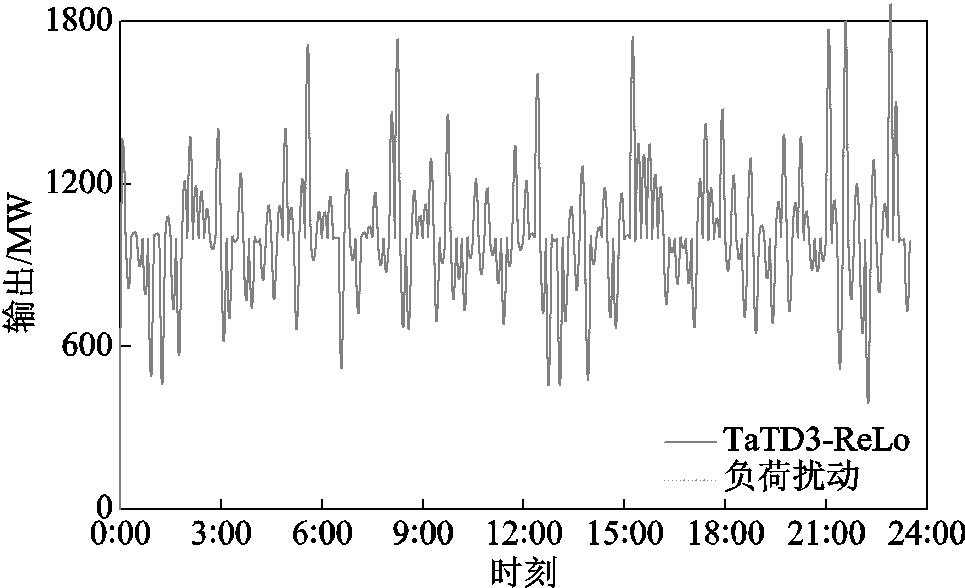
图15 TaTD3-ReLo控制器机组功率输出曲线
Fig.15 TaTD3-ReLo algorithm power output curves
各算法在不同区域的控制性能指标见表3。以重庆地区为例,分析数据可以得到,相较于其他算法,TaTD3-ReLo算法|ACE|可减少43.57%~81.84%;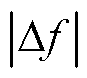 可降低29.33%~76.96%;CPS1可提升18.60%~70.33%。根据仿真结果分析,在不同的运行工况下,TaTD3-ReLo算法均可满足AGC控制性能指标,并且在面对强随机扰动时,TaTD3-ReLo算法具有更稳定的频率响应,同时具有更优的控制性能。
可降低29.33%~76.96%;CPS1可提升18.60%~70.33%。根据仿真结果分析,在不同的运行工况下,TaTD3-ReLo算法均可满足AGC控制性能指标,并且在面对强随机扰动时,TaTD3-ReLo算法具有更稳定的频率响应,同时具有更优的控制性能。
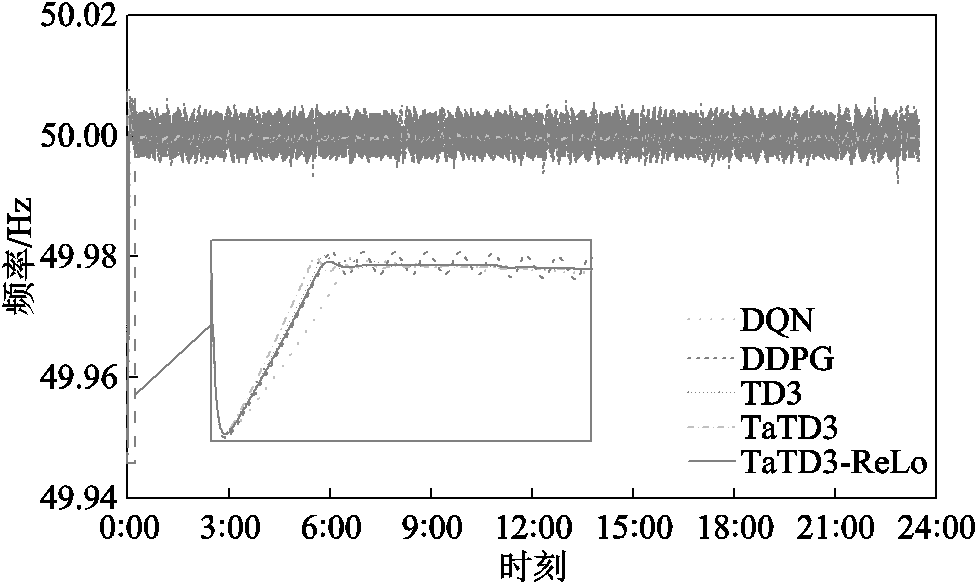
图16 随机负荷各算法频率响应
Fig.16 Frequency response of algorithm for random load
表3 随机负荷控制性能指标
Tab.3 Random load control performance indicators
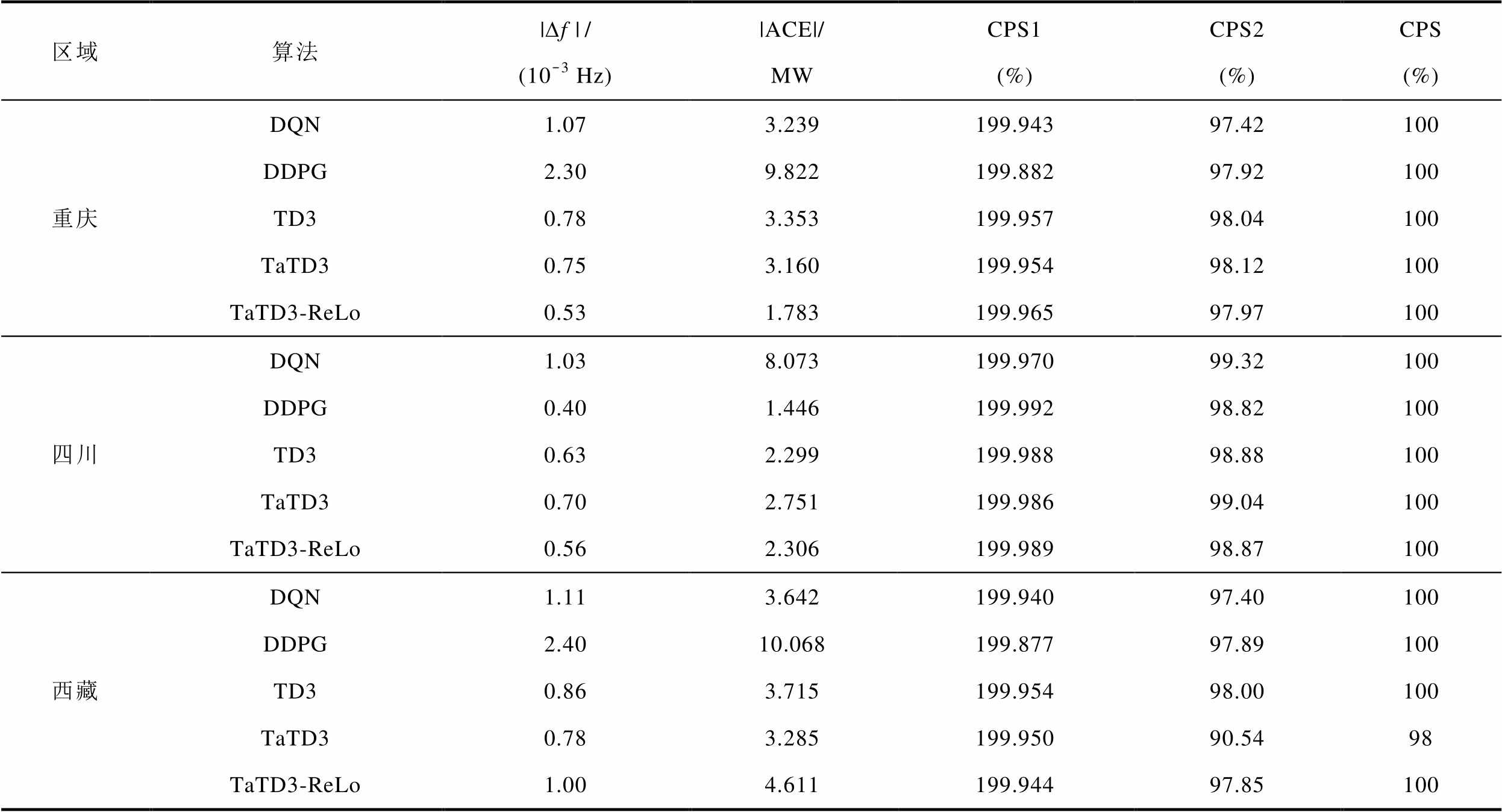
区域算法|∆f |/(10-3 Hz)|ACE|/MWCPS1(%)CPS2(%)CPS(%) 重庆DQN1.073.239199.94397.42100 DDPG2.309.822199.88297.92100 TD30.783.353199.95798.04100 TaTD30.753.160199.95498.12100 TaTD3-ReLo0.531.783199.96597.97100 四川DQN1.038.073199.97099.32100 DDPG0.401.446199.99298.82100 TD30.632.299199.98898.88100 TaTD30.702.751199.98699.04100 TaTD3-ReLo0.562.306199.98998.87100 西藏DQN1.113.642199.94097.40100 DDPG2.4010.068199.87797.89100 TD30.863.715199.95498.00100 TaTD30.783.285199.95090.5498 TaTD3-ReLo1.004.611199.94497.85100
为解决大规模清洁能源并网后电力系统控制性能及频率稳定性变差的问题,本文提出TaTD3-ReLo算法。
TaTD3-ReLo算法使用泰勒级数展开更新策略网络以获得更准确的动作价值,进而获取最优的控制策略,解决了连续算法中存在的动作价值高估问题。同时,ReLo策略根据训练样本的可学习性进行排序,以减少噪声或随机扰动对系统产生的影响,从而提升算法的收敛能力和稳定性。
仿真结果表明,所提算法具有更优的控制性能,且可以有效地实现新型电力系统模式下分布式多区域互联电网协同,进而解决大规模清洁能源并网后电力系统控制性能及频率稳定性变差的问题。
所提算法应用泰勒级数展开获取更准确的动作价值估计,但这会引入额外的超参数,需要大量实验以获得最优性能。因此,通过元学习自动学习最优参数是下一步研究的重点。
参考文献
[1] 李军徽, 潘雅慧, 穆钢, 等. 高比例风电系统中储能集群辅助火电机组调峰分层优化控制策略[J]. 电工技术学报, 2025, 40(7): 2127-2145.
Li Junhui, Pan Yahui, Mu Gang, et al. Hierarchical optimal control strategy for storage cluster-assisted thermal unit peaking in high-ratio wind power system [J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2127-2145.
[2] Debbarma S, Saikia L C, Sinha N. Automatic generation control using two degree of freedom fractional order PID controller[J]. International Journal of Electrical Power & Energy Systems, 2014, 58: 120-129.
[3] Sahu R K, Panda S, Yegireddy N K. A novel hybrid DEPS optimized fuzzy PI/PID controller for load frequency control of multi-area interconnected power systems[J]. Journal of Process Control, 2014, 24(10): 1596-1608.
[4] Sahu B K, Pati S, Mohanty P K, et al. Teaching–learning based optimization algorithm based fuzzy-PID controller for automatic generation control of multi-area power system[J]. Applied Soft Computing, 2015, 27: 240-249.
[5] Liu Fang, Li Yong, Cao Yijia, et al. A two-layer active disturbance rejection controller design for load frequency control of interconnected power system[J]. IEEE Transactions on Power Systems, 2016, 31(4): 3320-3321.
[6] 王磊, 胡国, 吴海, 等. 基于分层深度强化学习的分布式能源系统多能协同优化方法[J]. 电力系统自动化, 2024, 48(1): 67-76.
Wang Lei, Hu Guo, Wu Hai, et al. Multi-energy collaborative optimization method for distributed energy systems based on hierarchical deep reinforcement learning[J]. Automation of Electric Power Systems, 2024, 48(1): 67-76.
[7] Yin Linfei, Zhang Chenwei, Wang Yaoxiong, et al. Emotional deep learning programming controller for automatic voltage control of power systems[J]. IEEE Access, 2021, 9: 31880-31891.
[8] Zhang Xiao shun, Yu Tao, Pan Zhen ning, et al. Lifelong learning for complementary generation control of interconnected power grids with high-penetration renewables and EVs[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4097-4110.
[9] 罗清局, 朱继忠. 基于多参数规划改进ADMM的线性电-气综合能源系统分布式优化调度[J]. 电工技术学报, 2024, 39(9): 2797-2809.
Luo Qingju, Zhu Jizhong. Distributed optimal dispatch of linear integrated electricity and gas system based on multi-parameter programming modified ADMM[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2797-2809.
[10] Li Jiawen, Yu Tao, Zhu Hanxin, et al. Multi-agent deep reinforcement learning for sectional AGC dispatch[J]. IEEE Access, 2020, 8: 158067-158081.
[11] 张薇, 王浚宇, 杨茂, 等. 基于分布式双层强化学习的区域综合能源系统多时间尺度优化调度[J/OL]. 电工技术学报, 2024: 1-16. https://doi.org/ 10.19595/j.cnki.1000-6753.tces.240907.
Zhang Wei, Wang Junyu, Yang Mao, el al. The multi-time-scale optimal scheduling for regional integrated energy system based on the distributed bi-layer reinforcement learning[J]. Transactions of China Electrotechnical Society, 2024: 1-16. https://doi.org/ 10.19595/j.cnki.1000-6753.tces.240907.
[12] Li Jiawen, Yu Tao. Virtual generation alliance automatic generation control based on deep reinfo-rcement learning[J]. IEEE Access, 2020, 8: 182204-182217.
[13] Yu Tao, Zhou Bin, Chan K W, et al. Stochastic optimal relaxed automatic generation control in non-Markov environment based on multi-step Q(λ) learning[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1272-1282.
[14] Yu T, Zhou B, Chan K W, et al. R(λ) imitation learning for automatic generation control of interconnected power grids[J]. Automatica, 2012, 48(9): 2130-2136.
[15] Zhang Xiaoshun, Li Qing, Yu Tao, et al. Consensus transfer Q(λ)-learning for decentralized generation command dispatch based on virtual generation tribe[J]. IEEE Transactions on Smart Grid, 2018, 9(3): 2152-2165.
[16] Thrun S, Schwartz A. Issues in using function approximation for reinforcement learning[C]//Procee-dings of the 1993 connectionist models summer school, Hillsdale, NJ, USA, 1993: 255-263.
[17] Hasselt H. Double Q-learning[C]//Proceedings of the 24th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2010, 2: 2613-2621.
[18] 李彦营, 席磊, 郭宜果, 等. 基于权重双Q-时延更新学习算法的自动发电控制[J]. 中国电机工程学报, 2022, 42(15): 5459-5471.
Li Yanying, Xi Lei, Guo Yiguo, et al. Automatic generation control based on the weighted double Q-delayed update learning algorithm[J]. Proceedings of the CSEE, 2022, 42(15): 5459-5471.
[19] Xi Lei, Li Haokai, Zhu Jizhong, et al. A novel automatic generation control method based on the large-scale electric vehicles and wind power integration into the grid[J]. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(5): 5824-5834.
[20] 席磊, 刘治洪, 李彦营. 基于拉格朗日松弛强化学习算法的自动发电控制[J]. 中国电机工程学报, 2023, 43(4): 1359-1369.
Xi Lei, Liu Zhihong, Li Yanying. Automatic generation control based on Lagrangian relaxation reinforcement learning algorithm[J]. Proceedings of the CSEE, 2023, 43(4): 1359-1369.
[21] Lillicrap T, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning[J]. arXiv preprint arXiv:150902971, 2015.
[22] Vaswani S, Kazemi A, Babanezhad R, et al. Addressing function approximation error in actor-critic methods: supplementary material A. proof of convergence of clipped double Q-learning[C]// Proce-edings of the International Conference on Machine Learning, PMIL, 2018: 1587-1596.
[23] Garibbo M, Robeyns M, Aitchison L. Taylor TD-learning[C]//Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 2023: 1061-1081.
[24] Sujit S, Nath S, Braga P, et al. Prioritizing samples in reinforcement learning with reducible loss[J]. Advances in Neural Information Processing Systems, 2023, 36: 23237-23258.
[25] 甘伟, 艾小猛, 方家琨, 等. 风-火-水-储-气联合优化调度策略[J]. 电工技术学报, 2017, 32(增刊1): 11-20.
Gan Wei, Ai Xiaomeng, Fang Jiakun, et al. Coordinated optimal operation of the wind, coal, hydro, gas units with energy storage[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 11-20.
[26] Magdy G, Shabib G, Elbaset A A, et al. Renewable power systems dynamic security using a new coordination of frequency control strategy based on virtual synchronous generator and digital frequency protection[J]. International Journal of Electrical Power & Energy Systems, 2019, 109: 351-368.
[27] 赵熙临, 周红玉, 付波, 等. 一种用于微网调频的风电与抽水蓄能综合控制方法[J]. 河南理工大学学报(自然科学版), 2023, 42(4): 121-129.
Zhao Xilin, Zhou Hongyu, Fu Bo, et al. A comprehensive control method for wind power and pumped storage in the frequency regulation of microgrid[J]. Journal of Henan Polytechnic University (Natural Science), 2023, 42(4): 121-129.
[28] 李嘉文, 余涛, 张孝顺, 等. 基于改进深度确定性梯度算法的AGC发电功率指令分配方法[J]. 中国电机工程学报, 2021, 41(21): 7198-7212.
Li Jiawen, Yu Tao, Zhang Xiaoshun, et al. AGC power generation command allocation method based on improved deep deterministic policy gradient algorithm[J]. Proceedings of the CSEE, 2021, 41(21): 7198-7212.
[29] Jaleeli N, VanSlyck L S. NERC’s new control performance standards[J]. IEEE Transactions on Power Systems, 1999, 14(3): 1092-1099.
[30] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[31] Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[J]. ArXiv e-Prints, 2013. arXiv: 1312.5602.
Abstract The proportion of clean energy in modern power systems is steadily increasing. The large-scale integration of clean energy, which is highly random and intermittent, introduces significant stochastic disturbances that severely impact the control performance and frequency stability of power systems. This paper explores the challenges of declining control performance and frequency stability caused by large-scale clean energy integration from the perspective of automatic generation control (AGC). Currently, AGC methods in engineering applications mainly follow a centralized model. Since centralized control prioritizes optimizing performance within its own region, it is difficult to achieve coordinated control across different areas. In addition, factors such as communication delays and geographical location further limit the coordination and consistency of centralized control methods.
The new power systems based on a distributed model divide the system into interconnected subsystems. Load frequency control (LFC) is used to regulate the output of each generator, ensuring coordinated operation across multiple areas of the grid. In this process, reinforcement learning algorithms based on Markov decision processes have advantages in solving random problems and enabling multi-area coordinated control. As a result, they are gradually being introduced into AGC to achieve optimal control performance and frequency stability in multi-area grids. However, reinforcement learning algorithms often suffer from the problem of overestimating action values, which can lead to larger frequency deviations in power systems.
To address this issue in distributed power systems, we propose the Taylor twin delayed deep deterministic policy gradient algorithm to obtain the optimal multi-area coordinated solution. This approach aims to improve control performance and frequency stability in power systems with large-scale clean energy integration. The proposed algorithm uses a Taylor series expansion to update the value network, which mitigates the issue of action value overestimation commonly found in reinforcement learning. This improvement enhances the control accuracy of the algorithm, thereby improving the frequency stability of the power system. Additionally, an experience replay strategy is introduced to replace random sampling of training data. This strategy assigns lower priority to samples affected by random disturbances and noise, which tend to reduce learning capability, while giving higher priority to samples with greater learning potential. This approach increases the accuracy of optimization, thus reducing the impact of random disturbances on control performance.
To validate the effectiveness of the proposed algorithm, we developed an improved IEEE standard two-area LFC model and a wind-solar-hydro-thermal-storage integrated three-area interconnected LFC model. Simulations were conducted by introducing step disturbances, random square wave disturbances, and other load variations. The control performance of the TaTD3-ReLo, TaTD3, TD3, DDPG, and DQN algorithms was analyzed under different operating conditions. The series of simulation results demonstrated that the TaTD3-ReLo algorithm exhibits strong robustness and high learning capability. Compared to other reinforcement learning algorithms, the proposed algorithm shows superior control performance and more stable frequency responses. It also enables effective coordination among distributed multi-area interconnected grids in the new power system model, addressing the decline in control performance and frequency stability caused by the large-scale integration of clean energy.
Keywords:Automatic generation control, reinforcement learning, multi-area collaboration, Taylor twin delayed
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.241673
国家自然科学基金资助项目(52277108, 52477104)。
收稿日期 2024-09-25
改稿日期 2024-10-23
席 磊 男,1982年生,博士生导师,研究方向为电力系统运行与控制、自动发电控制、信息物理系统网络攻击与防御、智能控制方法。
E-mail:xilei2014@163.com(通信作者)
王文涛 男,1999年生,硕士研究生,研究方向为自动发电控制。
E-mail:antony322@163.com
(编辑 赫 蕾)