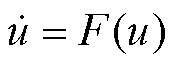 ,假设初值为u(0),其在t0时刻和t时刻的解分别为u(t0)、u(t),且满足
,假设初值为u(0),其在t0时刻和t时刻的解分别为u(t0)、u(t),且满足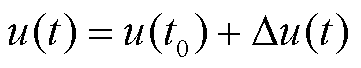 ,则有
,则有摘要 新能源电力系统中电力电子设备控制切换特性增加了暂态电压稳定状态准确评估的难度,现有暂态电压稳定指标和稳定判据在噪声干扰和控制切换影响下易发生电压稳定状态误判。为此,该文提出一种基于切换补偿李雅普诺夫指数(SCMLE)的新能源电力系统暂态电压稳定评估方法。首先,依据最大李雅普诺夫指数(MLE)稳定判别机理,将电压稳定问题转换为积分终值矩阵的特征值变化问题,进而分别构建系统受扰前后的电压轨线变分方程,充分计及控制环节动态特性对电压稳定性的影响;然后,采用电压轨线变分方程积分终值矩阵特征值计算SCMLE,克服现有MLE指标需设置符号观测窗口的缺陷;其次,构建了表征系统非光滑扭曲程度的切换补偿矩阵用于修正积分结果,弥补指标在系统非光滑点处的计算误差,实现暂态电压稳定状态的快速、准确评估;最后,通过光伏场站接入单机无穷大系统和某实际电网系统的仿真分析,验证了所提方法的准确性和有效性。
关键词:新能源电力系统 暂态电压稳定评估 控制切换 李雅普诺夫指数
随着“双碳”战略的稳步推进,我国电力系统逐渐转变为含高比例新能源和高比例电力电子设备的“双高”电力系统[1-2]。系统中新能源并网变流器的多时间尺度响应特性及受扰情况下的控制投切行为,使系统暂态电压演变特性迥异于传统交流电力系统[3-6]。因此,亟须构建适用于新能源电力系统的暂态电压稳定评估方法,为调度人员制定有效的暂态电压稳定控制策略提供参考依据,保障新能源电力系统安全稳定运行。
目前,模型驱动的暂态电压稳定分析及评估方法主要包括时域仿真法[7]、能量函数法[8-9]、单调系统分析法[10-11]及最大李雅普诺夫指数(Maximum Lyapunov Exponent, MLE)指标[12-14]等。时域仿真法具有较高的计算精度,但需建立全系统的详细数学模型,耗时长。能量函数法有效地避免了时域仿真法计算量大的不足,可以确定系统暂态电压稳定的临界切除时间或运行边界,但能量函数构建困难,当系统拓扑变化或控制切换时需重新构建能量函数,普适性不强。为此,有学者尝试根据单调系统理论,采用增益函数雅可比矩阵谱半径作为系统稳定判据,分析了系统参数对暂态电压稳定性的影响,但尚未应用于暂态电压稳定状态快速评估。而MLE作为非线性动力系统稳定性分析的重要分支之一,可以描述系统相空间中两相邻轨线的收敛或发散程度,避免了复杂的能量函数构建过程且计算速度快,已被应用于电力系统的暂态电压稳定评估。
现有MLE根据计算方法的不同主要分为基于时间延时嵌入的MLE(Time-delayed embedding Maximum Lyapunov Exponent, TMLE)[15]、基于离散映射模型的MLE[16]以及基于QR分解的MLE(Maximum Lyapunov Exponent based on QR decomposition, QRMLE)[17]。其中,文献[18]采用相位校正法重新构建初始时间窗口,提出基于相位校正李雅普诺夫指数的暂态电压稳定评估方法,有效抑制了电压相位变化对电压稳定判别准确度的影响。文献[19]构建了基于系统响应信息的网络无功能量函数,通过无功能量演化轨迹计算MLE指标,实现了系统暂态电压稳定状态判别。然而,嵌入参数选取不当易导致TMLE符号特征振荡,延长了电压稳定判别时间,且TMLE难以计及控制投切期间系统的运行状态差异性,降低了其电压稳定评估的准确度。对此,文献[20]基于变流器多种运行模式下的离散映射模型,通过雅可比矩阵特征值计算MLE,分析系统不同运行模式下的稳定边界。文献[21-22]通过构建变流器频闪映射模型,采用基于雅可比矩阵特征值的MLE分析系统稳定参数域。然而,离散映射模型通常以固定开关周期作为窗口函数进行建模,难以计及新能源变流器的多时间尺度控制特性,使得离散映射模型构建困难。并且,新能源变流器的低电压穿越(Low Voltage Ride Through, LVRT)控制投切将导致系统非光滑特性加剧,QRMLE在系统非光滑点处难以包含全部动态信息,进一步降低了暂态电压稳定评估的准确度。
针对以上问题,本文提出一种基于切换补偿李雅普诺夫指数(Switching Compensation Maximum Lyapunov Exponent, SCMLE)的新能源电力系统暂态电压稳定评估方法。首先,根据非线性动力系统MLE稳定判别原理,分别构建正常运行工况和电压跌落运行工况下的电压轨线变分方程,有效计及控制系统动态特性对电压稳定性的影响;其次,构建了衡量LVRT控制切换下系统非光滑扭曲程度的切换补偿矩阵,弥补了QRMLE在系统控制切换时刻的计算误差;最后,给出了SCMLE指标的完整计算流程及暂态电压稳定判据,并通过光伏场站接入单机无穷大系统和某实际电网系统验证了所提方法的准确性和有效性。
基于TMLE的电压评估指标已被用于系统暂态电压稳定状态判别。然而,大量新能源场站的并网使得电压响应特性发生改变,并呈现非光滑特征,严重影响TMLE的判别准确度。对此,本节首先揭示MLE符号特征与新能源并网节点电压轨迹演变特性之间的关系;然后分析控制切换对TMLE判别准确度的影响,为SCMLE指标构建提供理论支撑。
对于电压微分模型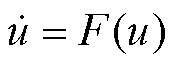 ,假设初值为u(0),其在t0时刻和t时刻的解分别为u(t0)、u(t),且满足
,假设初值为u(0),其在t0时刻和t时刻的解分别为u(t0)、u(t),且满足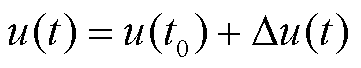 ,则有
,则有
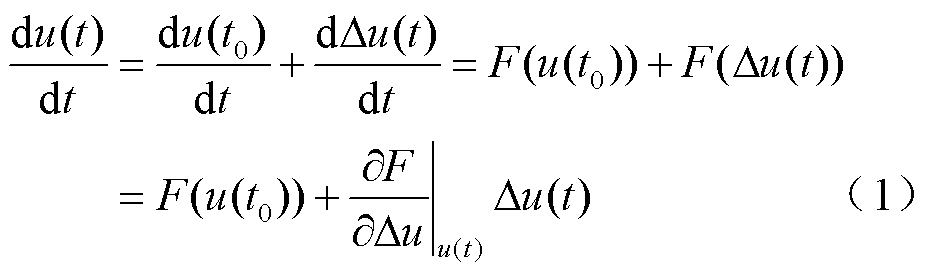
即
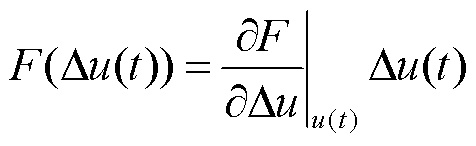 (2)
(2)
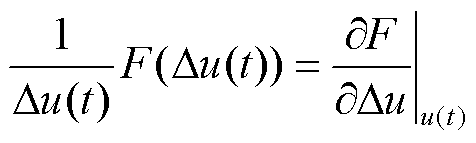 (3)
(3)
式中,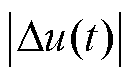 可看作是t时刻两相邻电压轨迹之间的距离。电压轨迹演变情况如图1所示。
可看作是t时刻两相邻电压轨迹之间的距离。电压轨迹演变情况如图1所示。
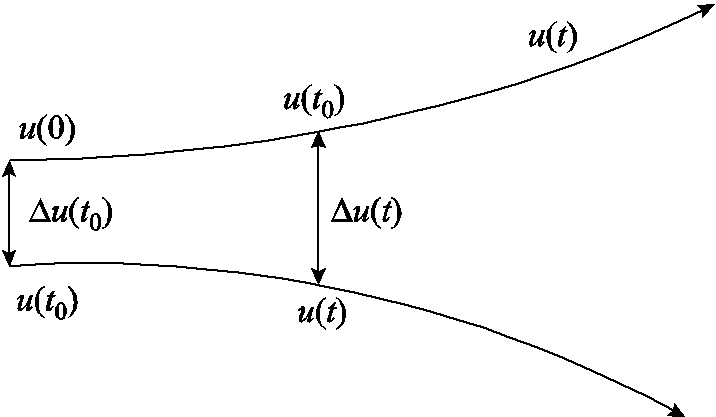
图1 电压轨迹演变情况
Fig.1 Evolution of voltage trajectories
为度量电压轨迹经演变后收敛或发散的平均速率,需计算经演变后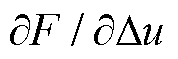 的平均值,有
的平均值,有
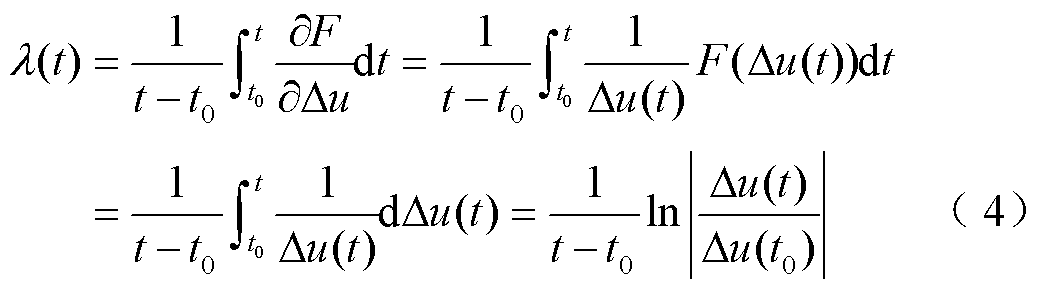
式中,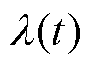 为系统的李雅普诺夫指数(Lyapunov Exponent, LE)。
为系统的李雅普诺夫指数(Lyapunov Exponent, LE)。
根据式(4)及LE稳定判别标准[23-24],若电压轨迹发散,则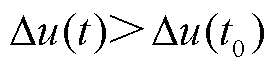 ,此时
,此时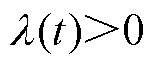 ,暂态电压失稳;若电压轨迹收敛,则
,暂态电压失稳;若电压轨迹收敛,则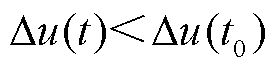 ,此时
,此时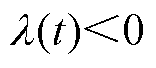 ,暂态电压稳定。因此,LE可用于判别暂态电压响应轨迹的收敛或发散行为。
,暂态电压稳定。因此,LE可用于判别暂态电压响应轨迹的收敛或发散行为。
进一步地,将上述一维系统拓展到二维。根据LE定义,若在某一运行点(u1, u2)处系统雅可比矩阵特征值为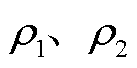 ,则其实部就是该点的LE。
,则其实部就是该点的LE。
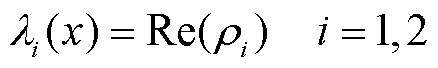 (5)
(5)
式中,将最大的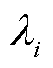 称为系统的MLE,其代表系统暂态电压的稳定或失稳程度。
称为系统的MLE,其代表系统暂态电压的稳定或失稳程度。
在实际应用中,为在线计算各节点电压时间序列数据的MLE,可在式(4)的基础上进行简化,并采用延时嵌入技术获取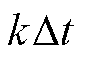 时刻电压轨迹的MLE指标,即TMLE。
时刻电压轨迹的MLE指标,即TMLE。
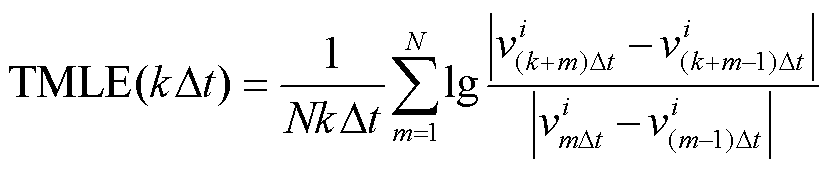 (6)
(6)
式中,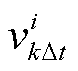 为节点i在
为节点i在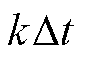 时刻的电压幅值;m=1, 2, …, N,N为嵌入时间窗口长度。
时刻的电压幅值;m=1, 2, …, N,N为嵌入时间窗口长度。
可见,TMLE基于LE计算式简化得到,具有计算速度快的特点。但对于含有控制切换的新能源电力系统,其存在电压稳定性误判的问题,下面将做进一步分析。
上述TMLE指标已被用于传统电力系统暂态电压稳定状态判别。然而,由式(6)可知,TMLE仅能判别嵌入步长下的电压轨迹发散或收敛行为,未严格遵循LE计算原理。当电压轨迹出现由于电力电子设备快动态作用引入的噪声干扰或控制反复投切造成的等幅振荡时,易引起TMLE符号特征长时间临界振荡,影响暂态电压稳定判别。
图2为考虑LVRT控制前后的新能源并网节点暂态电压演变曲线,图3为TMLE演变曲线。由图3可知,当TMLE用于电力电子设备控制环节反复投切场景时,由于控制切换易造成电压演变曲线等幅振荡,为准确获得电压轨迹的收敛或发散趋势,仅基于节点量测数据的TMLE曲线符号特征会在零附近振荡,难以准确识别电力系统暂态电压稳定运行状态。
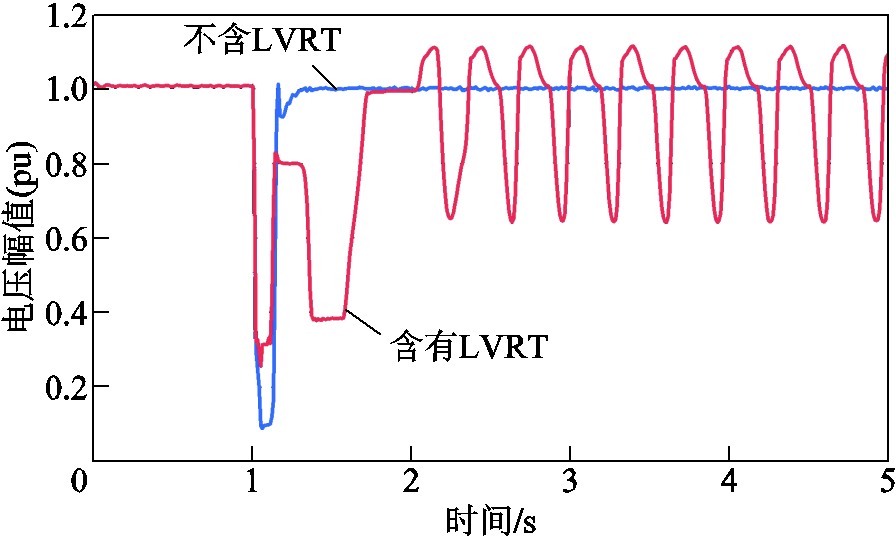
图2 新能源并网节点电压演变曲线
Fig.2 Voltage evolution curves of renewable energy grid-connected node
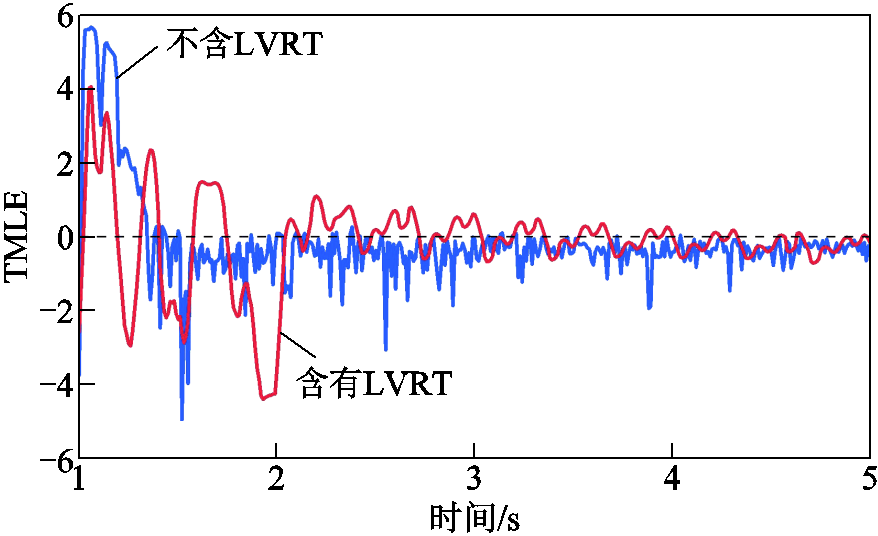
图3 TMLE演变曲线
Fig.3 Evolution curves of TMLE
根据MLE计算原理,其本质为求解系统某一运行点处的雅可比矩阵特征值。为此,本文分别构建正常运行和电压跌落期间的电压轨线变分方程,并借助积分终值矩阵特征值判别电压稳定状态,避免采用电压轨迹局部演变特征进行电压稳定状态判别产生的局限性。此外,为弥补控制切换时刻系统非光滑特性引起的计算误差,本文通过构建切换补偿矩阵修正积分结果,进一步提高MLE的电压判别速度和准确度。
暂态期间的LVRT控制投切使得系统电压轨迹在受扰前后呈现迥异的动态响应特性,影响暂态电压稳定判别。因此,本节分别构建新能源并网节点受扰前后电压轨线变分方程,以准确表征各控制模式下的暂态电压响应特性,为SCMLE计算提供模型基础。
计及LVRT控制的跟网型光伏场站电路拓扑及控制框图如图4所示。其中ug为无穷大电源电压,u1为公共耦合点(Point of Common Coupling, PCC)电压,i1为流过滤波电感的电流,i2为场站注入电网的电流。
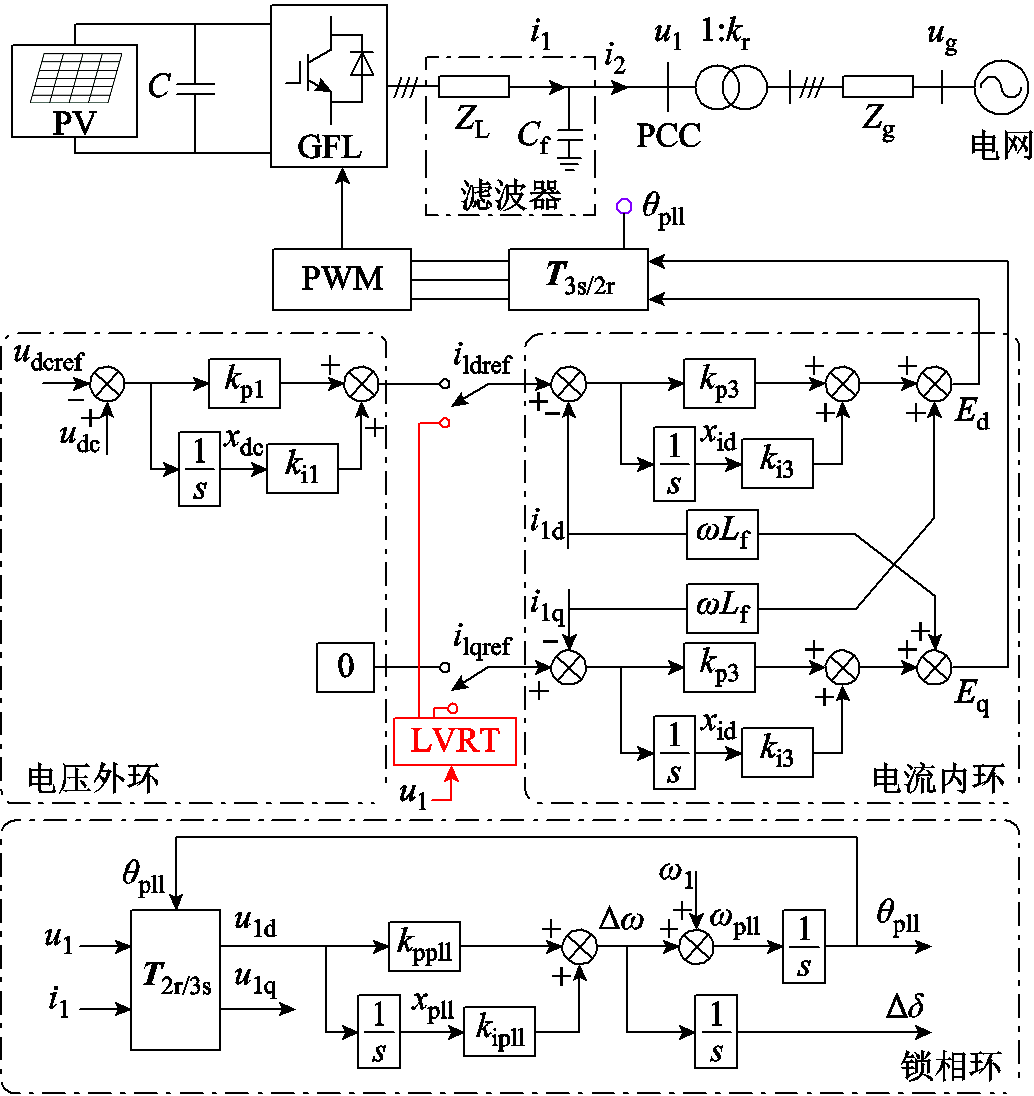
图4 跟网型光伏场站电路拓扑及控制框图
Fig.4 Single diagram and control strategy of photovoltaic power plant with grid-following control strategy
正常运行期间,跟网型变流器通过电压外环跟踪直流母线电压,生成有功电流指令值、无功电流指令值为零,并由电流内环生成参考电动势Ed、Eq。根据图4可得Ed、Eq表达式为
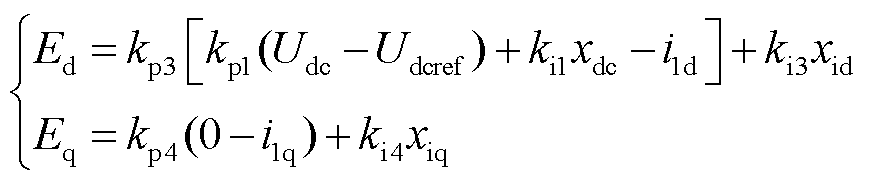 (7)
(7)
式中,kp1、kp3、kp4、ki1、ki3、ki4为控制器参数;Udc、Udcref分别为直流母线电压和直流电压参考值;i1d、i1q分别为光伏场站注入PCC电流的d、q轴分量;xdc、xid、xiq为控制系统内部信号。
忽略滤波器动态过程,建立网络接口方程为
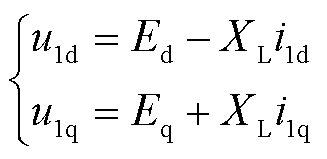 (8)
(8)
式中,u1d、u1q分别为PCC电压d、q轴分量;XL为变流器出口滤波器电抗。
将式(7)代入式(8),可得光伏场站输出电流dq轴分量为
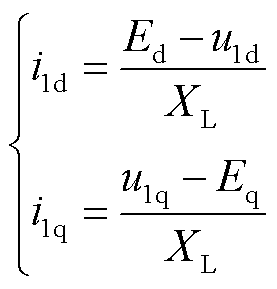 (9)
(9)
此外,PCC电压微分方程为
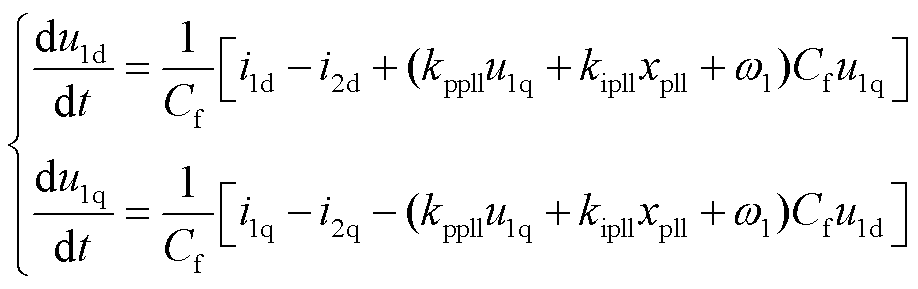 (10)
(10)
式中,kppll、kipll为锁相环控制参数;Cf为滤波电容;i2d、i2q分别为电网注入PCC电流i2的d、q轴分量;w1为电网同步角频率;xpll为锁相环积分器输出。
然后将式(9)中i1d、i1q分别代入式(10)即可得到正常运行工况下PCC电压微分方程(具体表达式见附录中式(A1))。
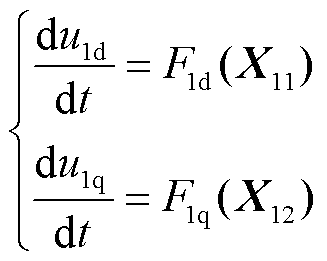 (11)
(11)
其中
X11=[u1d u1q i2d]T X12=[u1d u1q i2q]T
进一步地,将式(11)中的F1d(X11)、F1q(X12)分别对u1d、u1q求偏导数,得到雅可比矩阵J1中各元素,进而得到正常运行工况下的电压轨线变分方程为
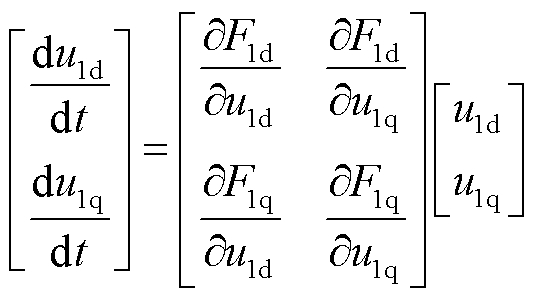 (12)
(12)
用矩阵形式将其表示为
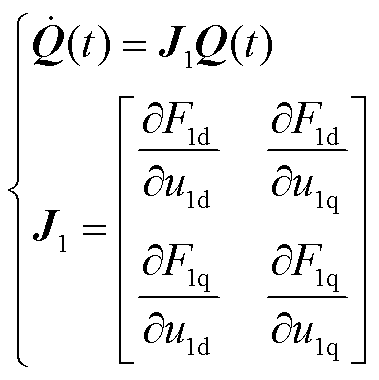 (13)
(13)
式中,Q(t)=[u1d u1q]T;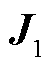 为正常运行工况下的雅可比矩阵,具体元素表达式见式(A2)。
为正常运行工况下的雅可比矩阵,具体元素表达式见式(A2)。
在电压跌落期间,光伏场站将切换到LVRT控制模式,此时电压外环退出运行,有功及无功电流指令由式(14)确定。根据新能源场站并网标准,在此将切换阈值设置为0.9倍PCC电压基准值[25]。
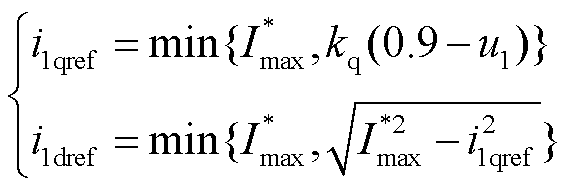 (14)
(14)
式中,kq为无功电流控制增益;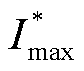 为变流器所能承受的最大电流标幺值;i1dref和i1qref分别为LVRT控制期间有功、无功电流指令值。
为变流器所能承受的最大电流标幺值;i1dref和i1qref分别为LVRT控制期间有功、无功电流指令值。
此时,参考电动势Eds、Eqs将改写为
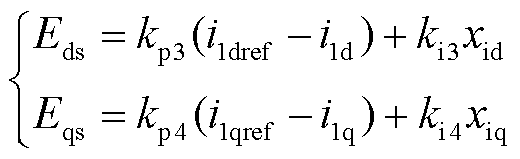 (15)
(15)
同理,将式(15)代入式(9)即可得到输出电流i1ds、i1qs,然后将其代入式(10)得到电压跌落期间PCC电压微分方程(具体表达式见式(A3)、式(A5))。
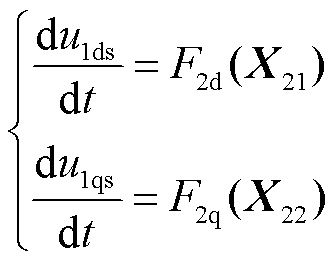 (16)
(16)
式中,X21=[u1ds u1qs i2d]T;X22=[u1ds u1qs i2q]T;u1ds、u1qs分别为电压跌落期间PCC电压d、q轴分量。
进一步地,将其转换为电压轨线变分方程,有
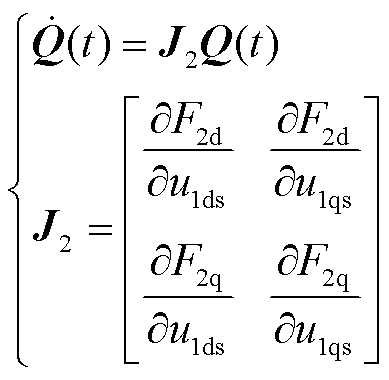 (17)
(17)
式中,J2为电压跌落工况下的雅可比矩阵,具体表达式见式(A4)、式(A6)。
综上所述,式(13)和式(17)共同构成光伏场站正常运行工况和电压跌落工况的电压轨线变分方程,本文将在不同运行工况下采用对应的变分方程计算SCMLE指标值。
根据第2节建立的电压轨线变分方程,同时考虑控制切换时刻系统非光滑特性带来的MLE计算误差问题,本节将从SCMLE指标计算、暂态电压稳定判据构建及评估框架三个方面,提出考虑控制切换的新能源电力系统暂态电压稳定评估方法。
本文在QRMLE的基础上,通过切换补偿矩阵修正系统控制切换时刻的QRMLE计算误差,提出一种考虑控制切换的暂态电压稳定评估指标,具体计算步骤如下。
1)针对LVRT控制投切的切换补偿矩阵构建。控制投切前后系统相邻轨线x1(t):a→b和x2(t):c→d的变化情况如图5所示。图5中,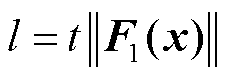 为轨线x1(t)在时间t内从a到b的长度,
为轨线x1(t)在时间t内从a到b的长度,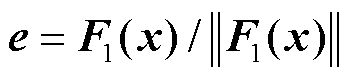 为切换前轨线x1(t)单位切矢量,r为切换后轨线x2(t)单位切矢量,即切换面单位法矢量。若切换面方程s(x)可微,则有
为切换前轨线x1(t)单位切矢量,r为切换后轨线x2(t)单位切矢量,即切换面单位法矢量。若切换面方程s(x)可微,则有
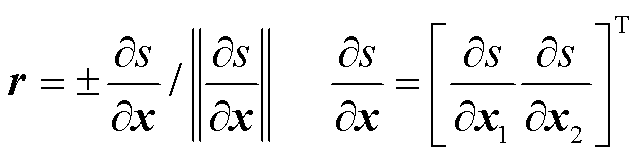 (18)
(18)
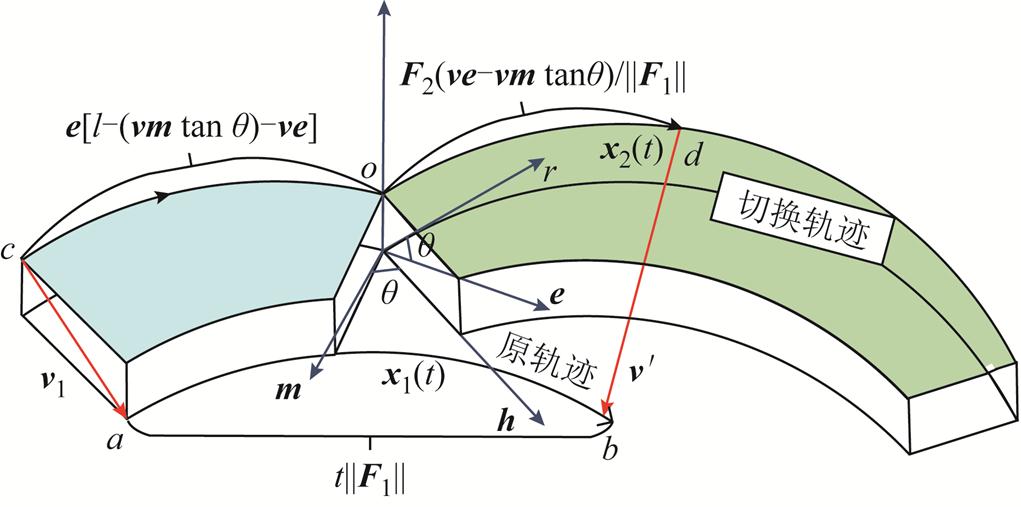
图5 切换补偿算法模型
Fig.5 The model of switching compensation algorithm
由图5可知,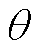 为矢量r和e之间的夹角,
为矢量r和e之间的夹角,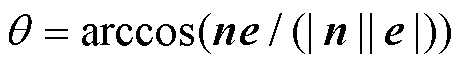 ,m为垂直于e的单位矢量,则可推导得
,m为垂直于e的单位矢量,则可推导得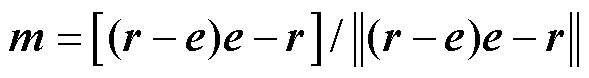 。
。
为量化轨线x1到x2之间的非光滑扭曲程度,需推导矢量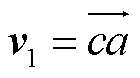 和
和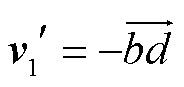 间的函数关系。由图5中几何关系可得
间的函数关系。由图5中几何关系可得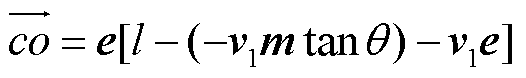 ,系统轨线从点c到o的演变时间为
,系统轨线从点c到o的演变时间为
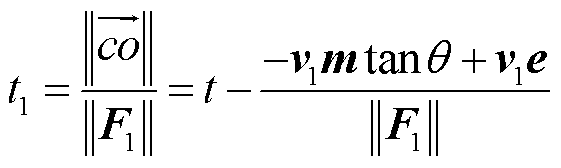 (19)
(19)
式中,F1为系统切换前电压解矢量。
进而可以得到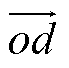 轨线的长度为
轨线的长度为
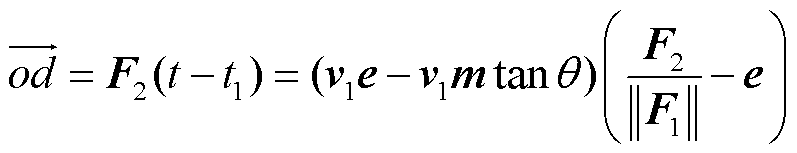 (20)
(20)
式中,t1为系统轨迹从点c演变到点o所经历时间;F2为系统切换后电压解矢量。
如图5所示,由于轨线环绕a、b、d、o、c一周的矢量和为零,即
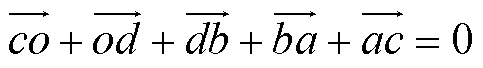 (21)
(21)
将计算得到的各矢量值代入式(21)即可建立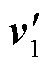 和
和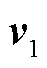 之间的关系,具体为
之间的关系,具体为
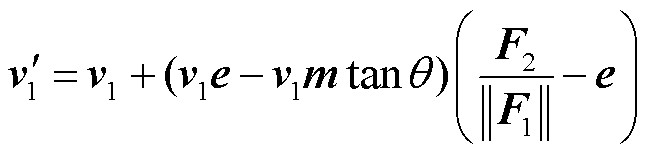 (22)
(22)
因此,控制投切时刻两相邻轨线的非光滑扭曲程度即切换补偿矩阵可以表示为
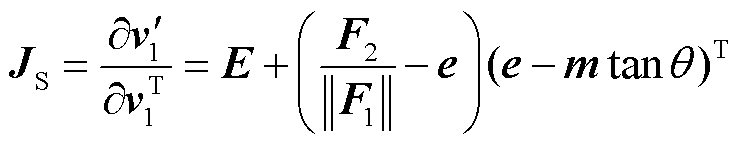 (23)
(23)
式中,E为单位矩阵。
对于LVRT控制投切行为,定义LVRT控制投出期间的系统为子系统1,投入期间的系统为子系统2,则切换面方程可写为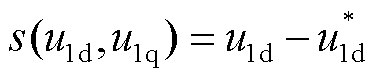 ,其中
,其中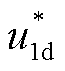 为控制切换时PCC电压d轴分量。从子系统1正向穿越切换面到达子系统2时,垂直于切换面的单位矢量为n=[1 0]T,从子系统2反向穿过切换面到达子系统1时,n=[-1 0]T。
为控制切换时PCC电压d轴分量。从子系统1正向穿越切换面到达子系统2时,垂直于切换面的单位矢量为n=[1 0]T,从子系统2反向穿过切换面到达子系统1时,n=[-1 0]T。
2)正常运行工况下SCMLE指标求解。首先在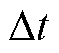 时段内求解式(13),然后对积分终值矩阵
时段内求解式(13),然后对积分终值矩阵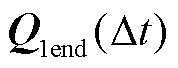 进行QR分解,得到矩阵Q和矩阵R。
进行QR分解,得到矩阵Q和矩阵R。
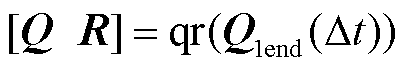 (24)
(24)
式中,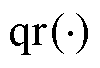 为QR分解函数。
为QR分解函数。
进一步将矩阵R的n个对角线元素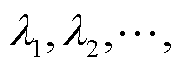
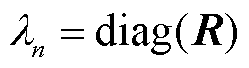 代入式(25),根据式(26)得到第
代入式(25),根据式(26)得到第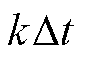 时刻的SCMLE。并将分解得到的矩阵Q作为下一时刻的Q(0)计算新的积分终值矩阵。
时刻的SCMLE。并将分解得到的矩阵Q作为下一时刻的Q(0)计算新的积分终值矩阵。
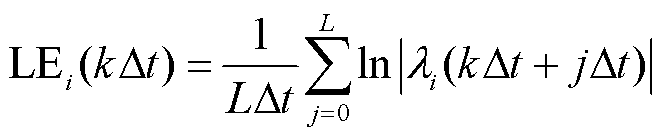 (25)
(25)
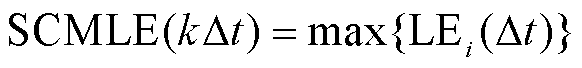 (26)
(26)
式中,L为计算时间窗口长度。
3)电压跌落工况下计及切换补偿的SCMLE指标求解。PCC电压跌落至0.9UB以下时,LVRT控制投入,此时利用式(23)计算由子系统1到子系统2的切换补偿矩阵JS12。然后使用JS12修正当前时刻积分终止矩阵,进行QR分解。
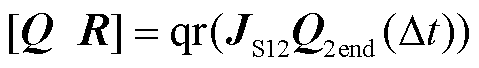 (27)
(27)
进一步将矩阵R的对角线元素代入式(25)并根据式(26)得到电压跌落时刻的SCMLE,此时跳转到子系统2利用式(17)求解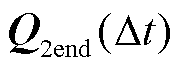 及电压跌落期间的SCMLE。
及电压跌落期间的SCMLE。
4)电压恢复状态下的SCMLE指标求解。在故障清除时刻,若电压恢复至0.9UB以上,则LVRT控制投出,利用式(23)计算由子系统2到子系统1的切换补偿矩阵JS21,并修正积分结果。
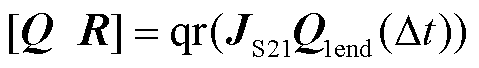 (28)
(28)
同理将矩阵R的对角线元素代入式(25),并根据式(26)得到故障清除时刻的SCMLE,返回子系统1。重复上述步骤1)~步骤3),即可获取多种运行模式交替切换下系统的SCMLE曲线。
通过对PCC电压进行连续监测,计算得到SCMLE曲线,根据MLE稳定判据并结合SCMLE曲线演变特征,给出以下暂态电压稳定判据。
判据一:从故障清除时刻开始,监测SCMLE曲线符号特征及回摆顶点,若连续两次SCMLE回摆顶点数值均小于零,则判别暂态电压稳定。
判据二:从故障清除时刻开始,监测SCMLE曲线符号特征及回摆顶点,若SCMLE幅值连续0.4 s大于零,则判别暂态电压将失去稳定。
此外,将判据一(二)中判别系统暂态电压稳定(失稳)时刻所对应的SCMLE数值作为该场景下系统的稳定性指标值。
进一步结合暂态电压稳定判据示意图6对所提判据进行说明。若电压轨迹趋于稳定,则SCMLE曲线呈衰减趋势,识别其连续两次回摆顶点均小于零则判别暂态电压将趋于稳定;反之,若电压轨迹发散,SCMLE数值逐渐增加并持续大于零,则判别暂态电压失稳。相较于传统TMLE,所提方法无需预先设置观测延时窗口躲过MLE符号特征振荡,通用性更强。
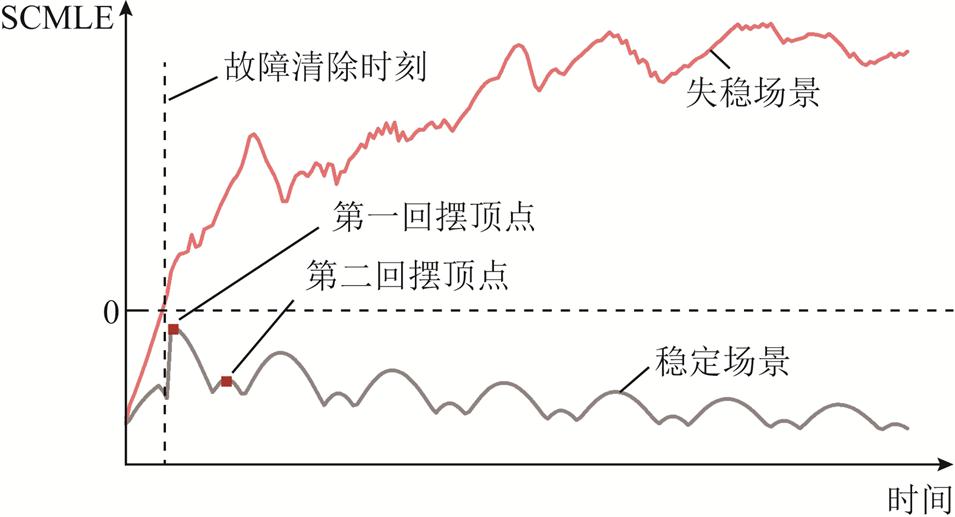
图6 暂态电压稳定判据示意图
Fig.6 Schematic diagram of transient voltage stability criteria
基于SCMLE的暂态电压稳定评估框架如图7所示,具体计算步骤如下。
1)在正常运行工况下,PCC电压高于0.9UB,使用子系统1的积分终值矩阵计算SCMLE。
2)当PCC电压发生跌落时,在其低于0.9UB的第1个时刻计算切换补偿矩阵JS12及当前时刻考虑切换补偿的SCMLE。
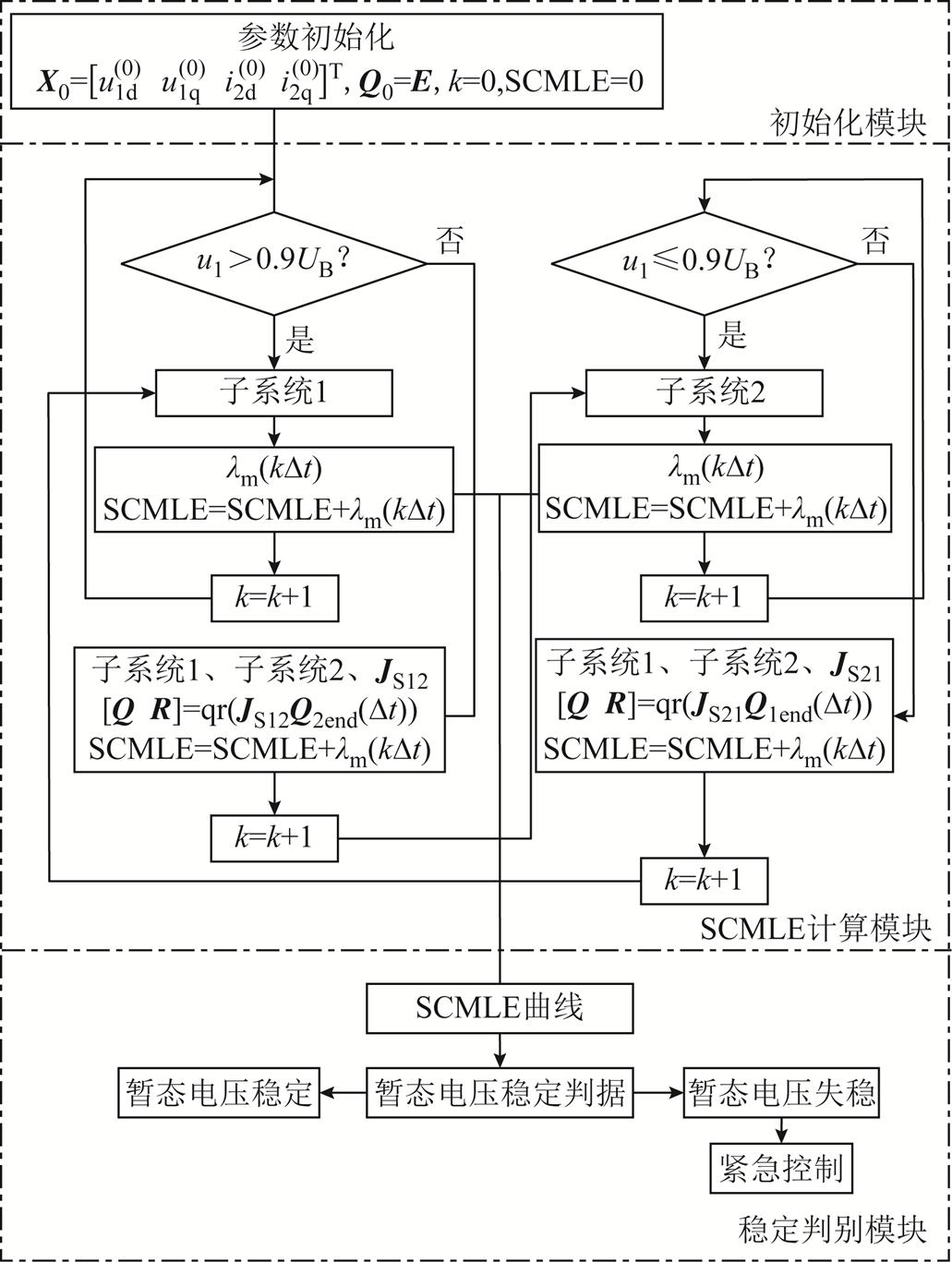
图7 基于SCMLE的暂态电压稳定评估框架
Fig.7 Transient voltage stability assessment framework based on SCMLE
3)在LVRT控制投入期间,采用子系统2的积分终值矩阵计算SCMLE。
4)当PCC电压恢复后,在其大于0.9UB的第1个时刻计算切换补偿矩阵JS21及当前时刻考虑切换补偿的SCMLE。
5)重复步骤2)~步骤4),直至达到电压稳定判别标准,计算结束。
本节通过对光伏场站接入单机无穷大系统和某实际电网系统进行仿真分析,验证所提暂态电压稳定评估方法的准确性和有效性。
借助Matlab/Simulink搭建如图4所示系统进行暂态电压稳定与失稳场景的仿真分析,设置仿真时长5 s,仿真步长0.01 ms。
4.1.1 暂态电压稳定评估有效性验证
为直观体现电压轨迹演化特性,将其转换到ΔVmag-Vmagcr-t空间,分析故障后电压轨迹是否存在稳定平衡点,其中ΔVmag及Vmagcr计算公式[26]为
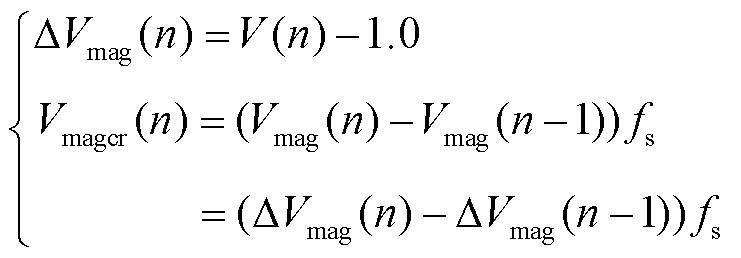 (29)
(29)
式中,V(n)为第n个采样时刻的电压幅值;fs为电压测量数据采样频率;ΔVmag(n)为第n个采样时刻的电压幅值变化量;Vmagcr(n)为第n个采样时刻的电压幅值变化率。
然后,在不同场景下将SCMLE与QRMLE[17]、TMLE[15]、相位校正李雅普诺夫指数(Phase Correction Maximum Lyapunov Exponent, PCMLE)[18]的计算结果进行对比分析,验证考虑切换补偿对提升暂态电压稳定判别速度和准确度的有效性。
1)场景1:暂态电压稳定场景
当电网侧发生三相短路故障,故障开始时刻为1 s、故障持续时间0.1 s时,系统电压稳定。电压稳定场景的电压幅值曲线及电压相轨迹如图8所示,MLE曲线如图9所示。由图8可知,故障切除后并网节点电压趋于稳定,且电压轨迹经过演变后稳定在故障后的平衡点。同时,图9分别给出不同MLE的计算结果,可以看出SCMLE曲线在故障后呈衰减振荡,且在t=1.38 s时满足连续两次回摆顶点小于零,根据3.2节判据一即可在1.38 s时判别暂态电压稳定。然而,由于QRMLE在控制切换时刻未包含系统全部动态信息,导致所需电压稳定判别时间更长;而PCMLE需在故障清除后延时两倍嵌入时长(0.6 s)实现暂态电压稳定判别,判别时间较SCMLE滞后0.36 s;此外,由于TMLE曲线在零轴附近长时间振荡,难以准确判别暂态电压稳定状态。可见,SCMLE相较于QRMLE、PCMLE分别缩短了24.18%和20.69%的电压稳定判别时间。
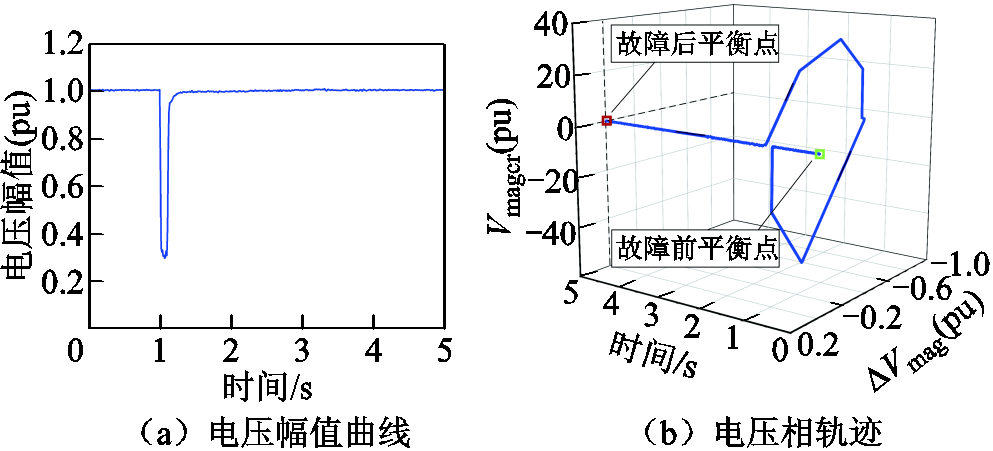
图8 电压稳定场景下的并网点电压演变轨迹
Fig.8 Voltage evolution trajectory at grid-connected node under voltage stability scenario
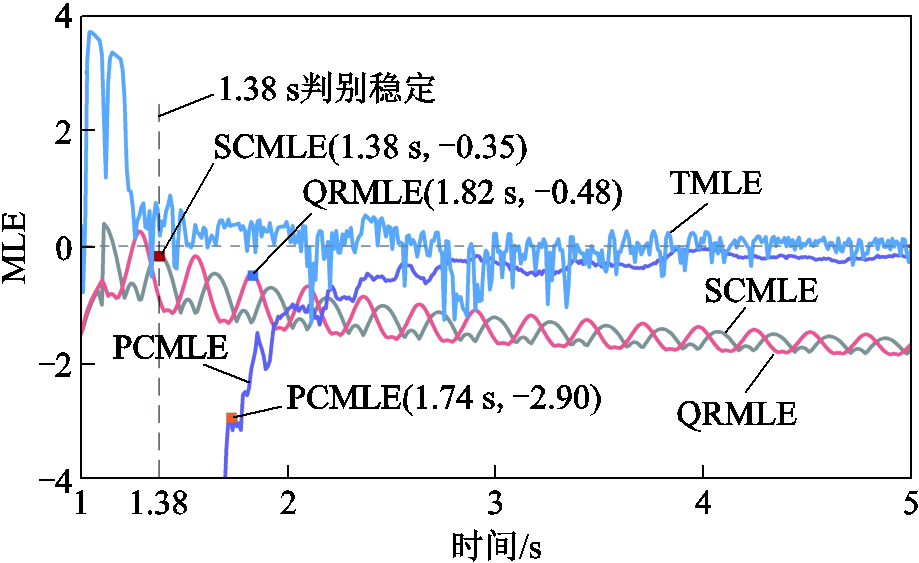
图9 电压稳定场景的MLE曲线
Fig.9 MLE curves for voltage stability scenario
2)场景2:暂态电压失稳场景
进一步将故障持续时间延长到0.15 s,并网节点暂态电压失稳。电压失稳场景下的电压幅值曲线及电压相轨迹如图10所示,MLE曲线如图11所示。由图10可知,故障切除后电压轨迹混沌,无法收敛到稳定平衡点。由于暂态电压持续失稳,从图11可以看出SCMLE数值逐渐增加并越过零点,且此后符号特征不发生改变。根据第3.2节中判据二,即可在t=1.6 s时迅速判断电压将失去稳定。
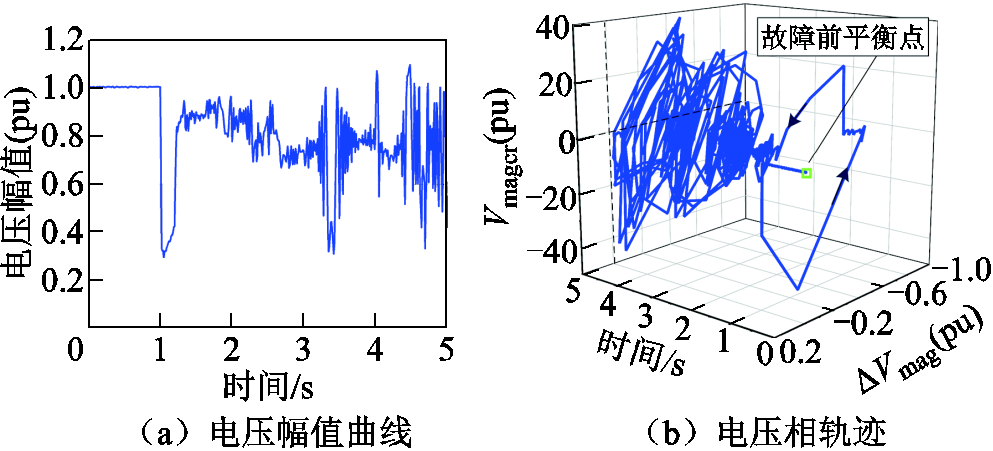
图10 电压失稳场景下的并网点电压演变轨迹
Fig.10 Voltage evolution trajectory at grid-connected node under voltage instability scenario
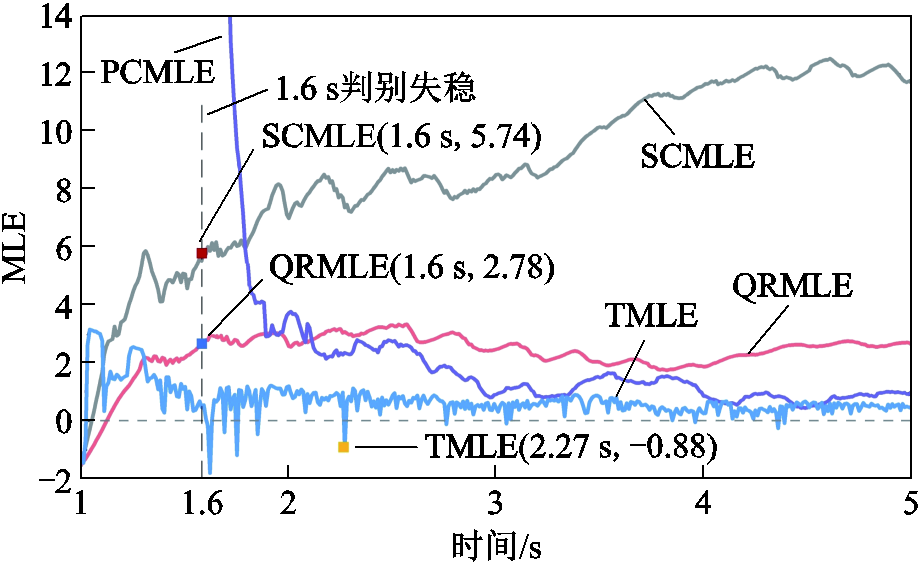
图11 电压失稳场景的MLE曲线
Fig.11 MLE curves for voltage instability scenario
在电压失稳场景下,SCMLE、QRMLE、PCMLE均能准确判别暂态电压失稳,但PCMLE所需时间更长,QRMLE响应速度较慢;而TMLE直至t=2.27 s后仍有为负的符号特征,将干扰暂态电压稳定判别。
3)场景3:有/无新能源LVRT控制投切场景
为验证切换补偿对MLE计算结果及暂态电压稳定判别准确性的影响。首先,在无LVRT控制投切场景下将SCMLE与传统MLE的电压稳定判别结果进行对比分析,如图12所示。由于系统不存在控制策略切换,SCMLE与QRMLE计算结果相同,SCMLE和传统MLE均能正确判别暂态电压稳定/失稳状态。
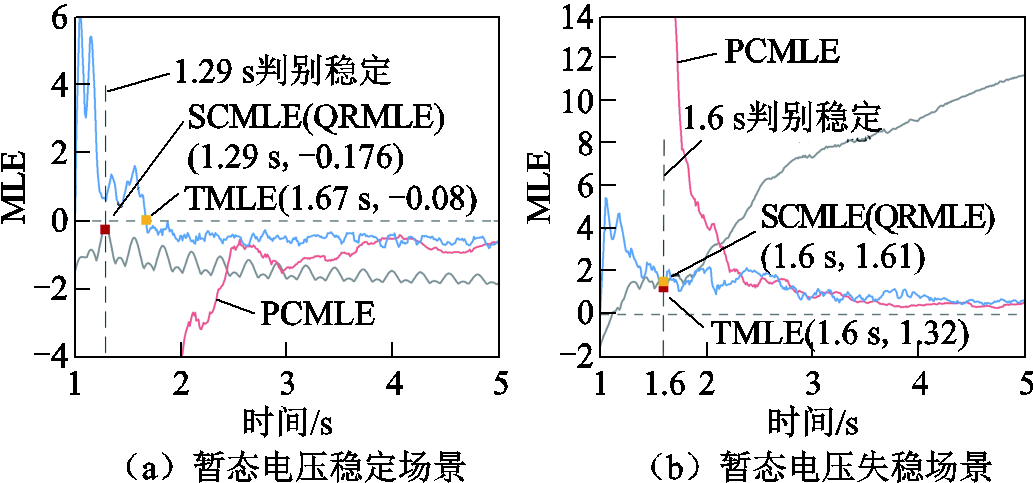
图12 无LVRT控制投切时的MLE曲线
Fig.12 MLE curves without LVRT control switching
然后,在LVRT控制反复投切场景下,分别将SCMLE与传统MLE的计算结果进行对比分析,验证所提切换补偿矩阵的有效性,电压幅值曲线及MLE曲线如图13所示。由图13b可知,SCMLE在系统非光滑点处不断对积分终值矩阵进行修正,能够更准确地反映电压轨迹的实际演化特性,SCMLE曲线在t=1.2 s时越过零轴,且符号特征始终保持正确的演变趋势,根据3.2节判据二,可在t=1.6 s时判别为暂态电压失稳。然而,QRMLE在控制切换时刻难以包含系统全部动态信息,存在计算误差,由于误差累积导致其逐渐向零轴靠近,易造成电压稳定状态误判;此外,由于PCMLE和TMLE采用延时嵌入方法求解,难以考虑控制切换对暂态电压稳定判别结果的影响,在该场景下易误判为暂态电压稳定。
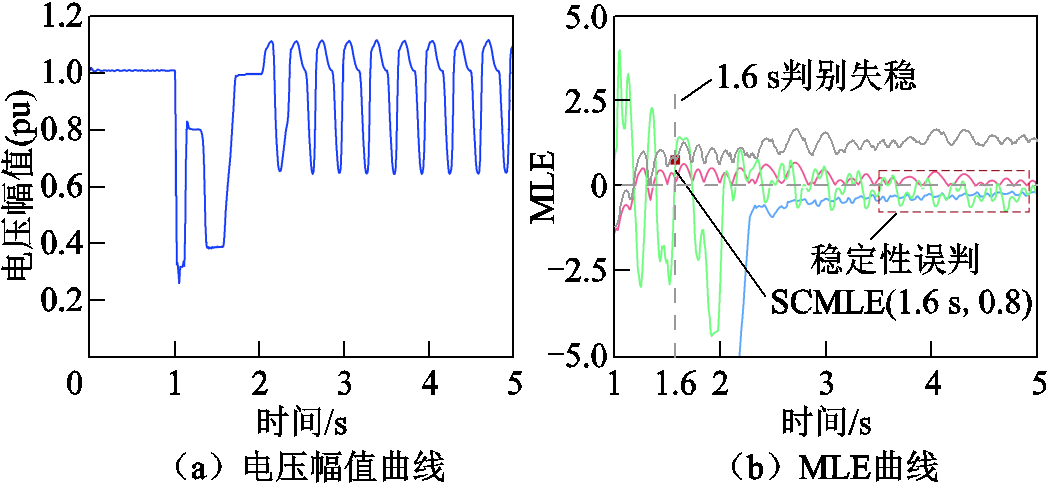
图13 LVRT反复投切下的电压幅值曲线及MLE曲线
Fig.13 Voltage amplitude and MLE curve under repeated LVRT activation
4.1.2 鲁棒性分析
为验证所提方法的抗噪性能,分别在电压稳定和失稳量测数据中加入随机噪声来模拟同步向量测量装置(Phasor Measurement Unit, PMU)噪声,并分别计算TMLE、QRMLE及SCMLE,电压稳定/失稳场景下的判别结果如图14所示。
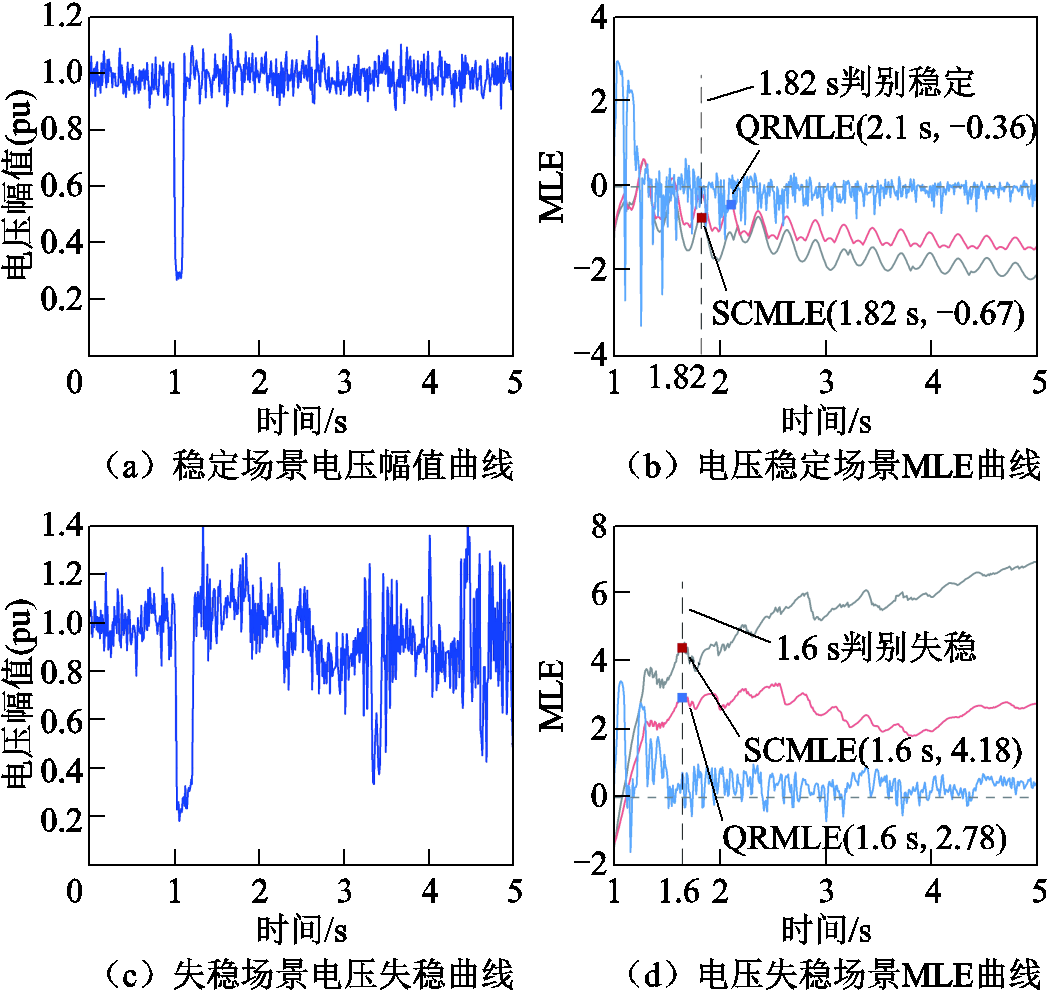
图14 测量噪声对MLE的影响
Fig.14 Influence of measurement noise on MLE
由图14b可知,在量测噪声干扰下,SCMLE曲线仅出现一次回摆顶点大于零,根据3.2节判据一,在t=1.82 s准确判别为暂态电压稳定。而QRMLE出现连续两次回摆顶点过零,需进一步监测符号特征,在t=2.1 s时才能判别为暂态电压稳定;其次,由于测量噪声的干扰,TMLE符号特征在零附近振荡,难以准确判别暂态电压稳定性。此外,由图14d可知,在电压失稳场景下SCMLE迅速发散,根据3.2节判据二在t=1.6 s时准确判别为暂态电压失稳。可以看出,所提SCMLE在电压稳定和失稳场景下均具有较好的抗噪声性能。
4.1.3 控制参数对系统暂态电压稳定性影响
在新能源并网系统中,变流器控制系统动态响应特性将影响受扰后系统暂态电压稳定状态。为此,在相同故障场景下(网侧故障,故障持续时间0.1 s),通过改变电流内环控制参数,利用SCMLE分析控制参数对PCC暂态电压稳定性的影响。
将比例增益系数kp3,4设置在0.2~0.6范围内、积分增益系数ki3,4设置在5~15范围内。不同控制参数组合下暂态电压稳定状态及判别结果见表1。根据表1可知,由于SCMLE计及系统控制切换特性,在电压稳定和失稳场景下均能准确判别。
表1 不同控制参数下SCMLE暂态电压稳定判别结果
Tab.1 Transient voltage stability assessment results of SCMLE under different control parameters

参数组合kp3,4ki3,4仿真结果判别结果 10.215稳定稳定 20.415稳定稳定 30.615失稳失稳 40.315稳定稳定 50.310稳定稳定 60.35失稳失稳
进一步对系统暂态电压稳定性进行全局分析,控制参数对暂态电压稳定性的影响如图15所示。由图15可知,当kp3,4超过0.5后,由于引入的高频分量增加,易造成系统暂态电压失稳且SCMLE指标迅速越过零平面;当ki3,4减小到5以下时,由于系统等效阻尼减小,受扰后暂态电压失去稳定,SCMLE指标越过零平面。
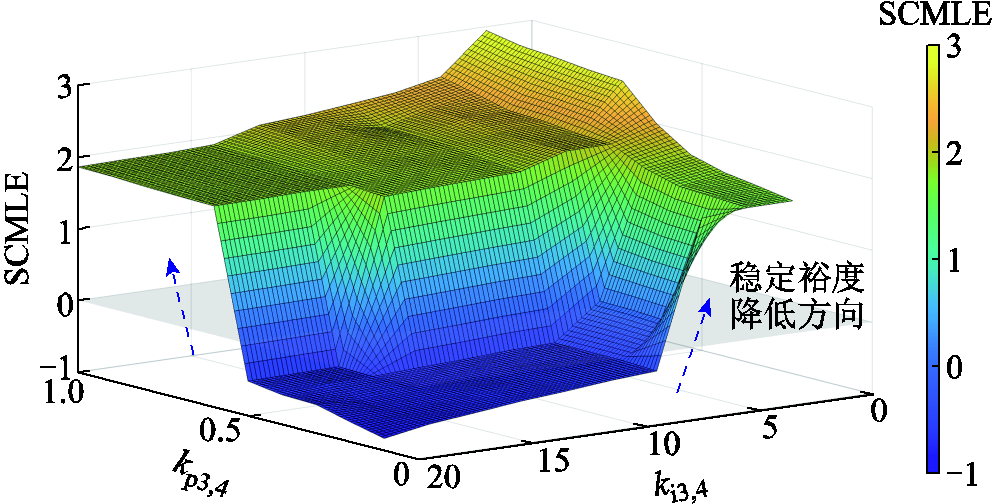
图15 控制参数对暂态电压稳定性的影响
Fig.15 Influence of control parameters on transient voltage stability
此外,图16给出了可维持暂态电压稳定的稳定参数域,其中,在参数组合3和参数组合6下系统暂态电压失稳,SCMLE指标大于零。针对本文系统,易维持系统暂态电压稳定的控制参数范围为kp3,4:0.1~0.4,ki3,4:10~20。
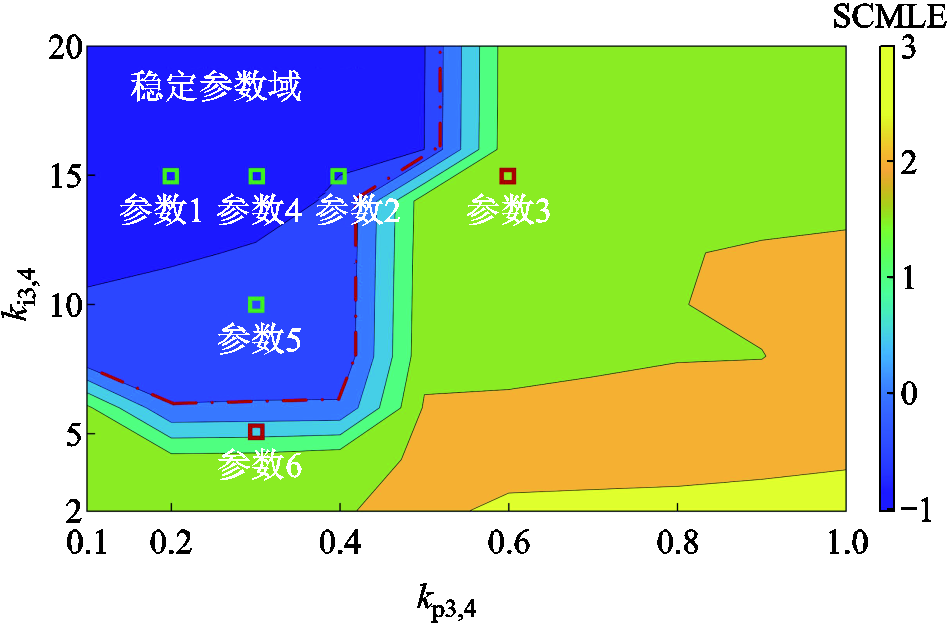
图16 电压稳定参数域
Fig.16 Voltage stability region of control parameters
本节在某高比例新能源电网中验证所提方法有效性。该区域电网共102个节点,其中新能源场站节点52个,总新能源外送功率6 850 MW,部分网架结构如图17所示。采用电力系统分析综合程序(Power System Analysis Software Package, PSASP)进行仿真,仿真时长10 s,仿真步长10 ms。
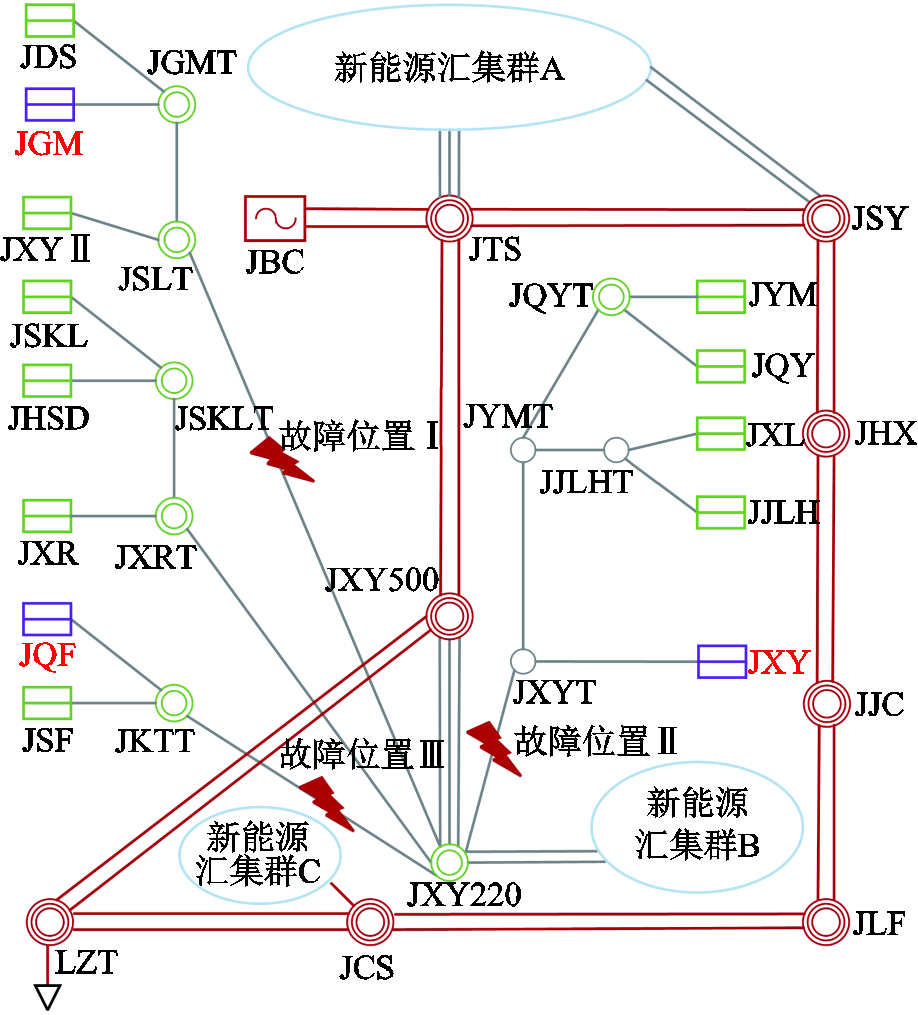
图17 某实际电网网架结构
Fig.17 The structure of an actual power grid
通过在线路JXY220-JSLT、JXY220-JXYT、JXY220-JKTT上分别设置三相短路故障(故障持续时间为0.1 s),得到场景Ⅰ、场景Ⅱ和场景Ⅲ,在各场景下对JGM、JXY、JQF三个新能源场站节点的电压稳定状态进行判别。图18、图19、图20分别给出了各节点电压幅值曲线和受扰相对严重节点的MLE曲线。
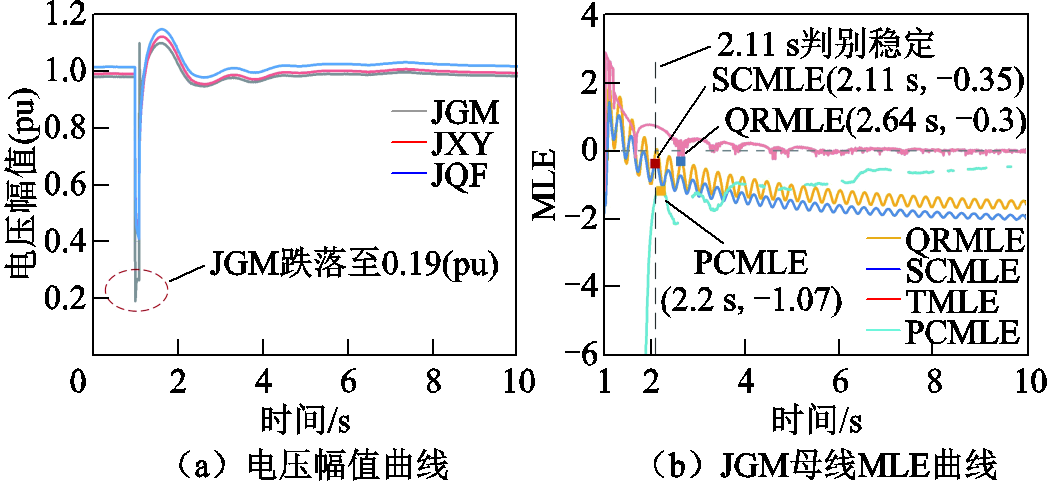
图18 故障场景Ⅰ下的电压曲线及MLE曲线
Fig.18 Voltage curve and MLE curves for fault scenario I
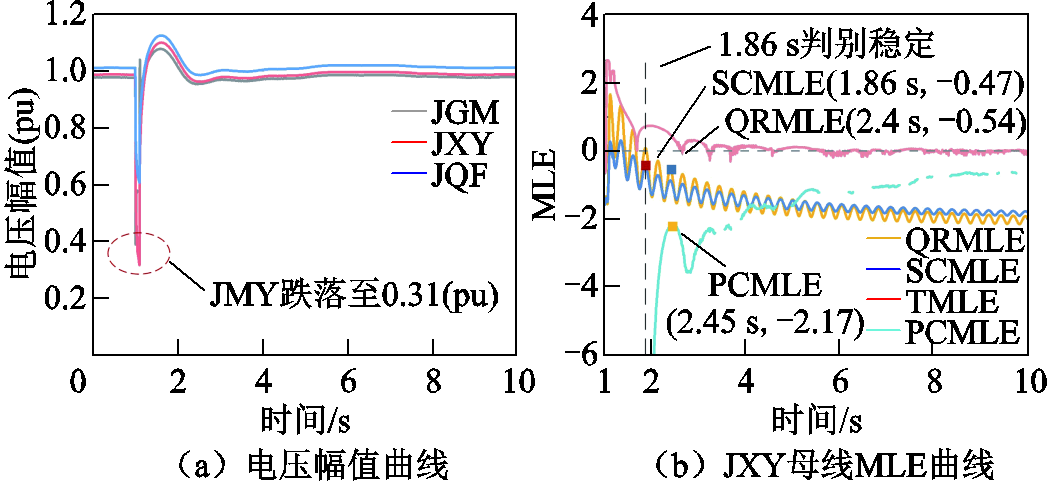
图19 故障场景Ⅱ下的电压曲线及MLE曲线
Fig.19 Voltage curves and MLE curve for fault scenario Ⅱ
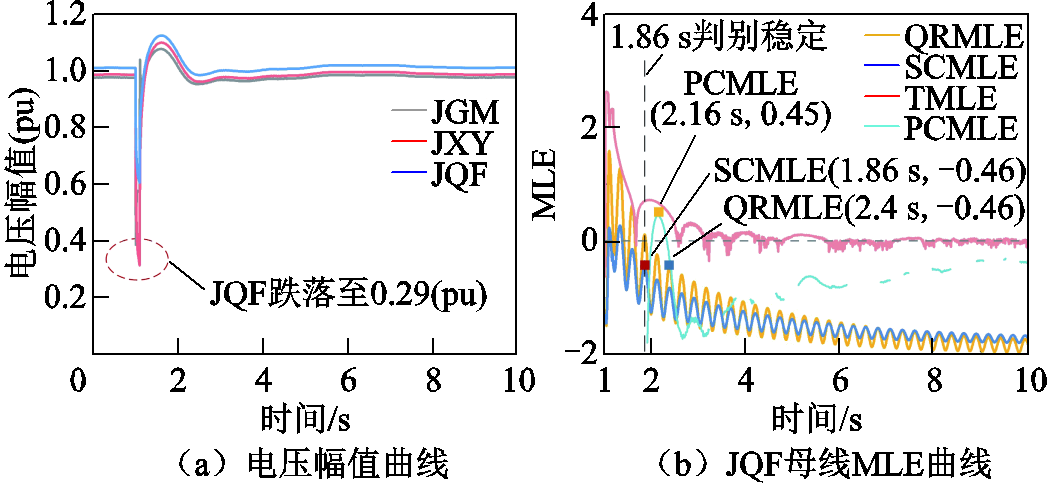
图20 故障场景Ⅲ下的电压曲线及MLE曲线
Fig.20 Voltage curves and MLE curves for fault scenario Ⅲ
同时,所提SCMLE与QRMLE、PCMLE、TMLE的暂态电压稳定判别结果见表2。由表2可知,在三种故障场景下所提SCMLE对各新能源场站节点的电压稳定状态均做出快速、准确的判别。而QRMLE在控制切换时刻未对积分结果进行补偿,电压稳定判别时间明显大于SCMLE;此外,由于受电压轨迹轻微波动及测量噪声影响,TMLE符号特征在零附近长时间振荡,难以做出有效判别。上述结果表明,在实际电网中,所提SCMLE的电压稳定判别准确度高于QRMLE和TMLE、所需判别时间小于PCMLE,有效地提升了控制切换下暂态电压稳定状态判别的计算效率。
表2 SCMLE与QRMLE、PCMLE、TMLE判别结果
Tab.2 Assessment results of SCMLE with QRMLE, PCMLE and TMLE
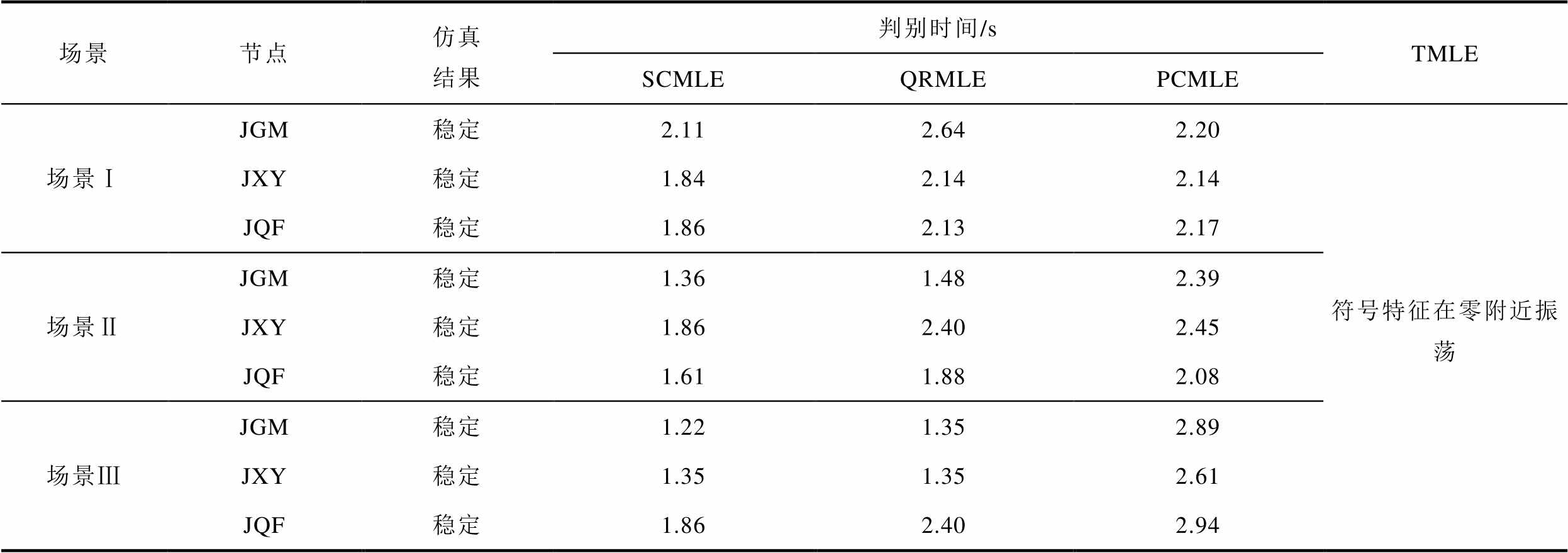
场景节点仿真结果判别时间/sTMLE SCMLEQRMLEPCMLE 场景ⅠJGM稳定2.112.642.20符号特征在零附近振荡 JXY稳定1.842.142.14 JQF稳定1.862.132.17 场景ⅡJGM稳定1.361.482.39 JXY稳定1.862.402.45 JQF稳定1.611.882.08 场景ⅢJGM稳定1.221.352.89 JXY稳定1.351.352.61 JQF稳定1.862.402.94
本文提出一种基于SCMLE的新能源电力系统暂态电压稳定评估方法,在光伏场站接入单机无穷大系统和某实际电网系统中进行仿真分析和验证,相关结论如下:
1)所提方法基于非线性动力系统混沌理论,将电压稳定问题转换为积分终值矩阵的特征值变化问题,具有较严格的理论依据。
2)所提SCMLE分别缩短了QRMLE、PCMLE指标24.18%、20.69%的电压稳定判别时间,且有效地避免了TMLE符号特征振荡问题,在实际电网系统中仍具备良好评估性能。
3)所提SCMLE可分析控制参数对系统暂态电压稳定性的影响,确定当前运行状态距电压稳定边界的距离,为稳控措施制定提供信息参考。
本文通过场站侧微分方程分析新能源控制切换下的系统暂态电压稳定问题,推导过程中对电网拓扑结构进行了一定简化。下一步研究将考虑电网拓扑变化、电网节点电压空间分布以及新能源场站分布对系统暂态电压稳定性的影响,为后续分析源-网交互作用下的新能源电力系统暂态电压稳定问题提供理论基础。
附 录
正常运行工况及电压跌落工况下的PCC电压微分方程及Jacobi矩阵元素具体如下。
1)正常运行工况。PCC电压微分方程为
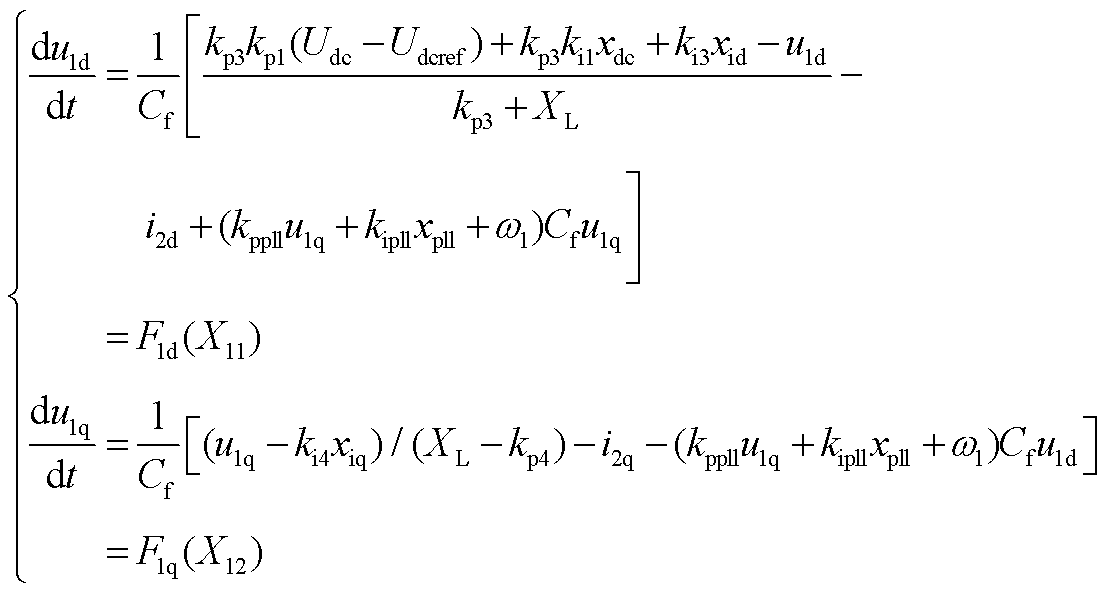 (A1)
(A1)
式中,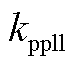 、
、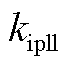 为锁相环控制参数。
为锁相环控制参数。
然后将F1d(X11)、F1q(X12)对u1d、u1q求偏导数,得到系统正常运行工况下的Jacobin矩阵J1,各元素具体为
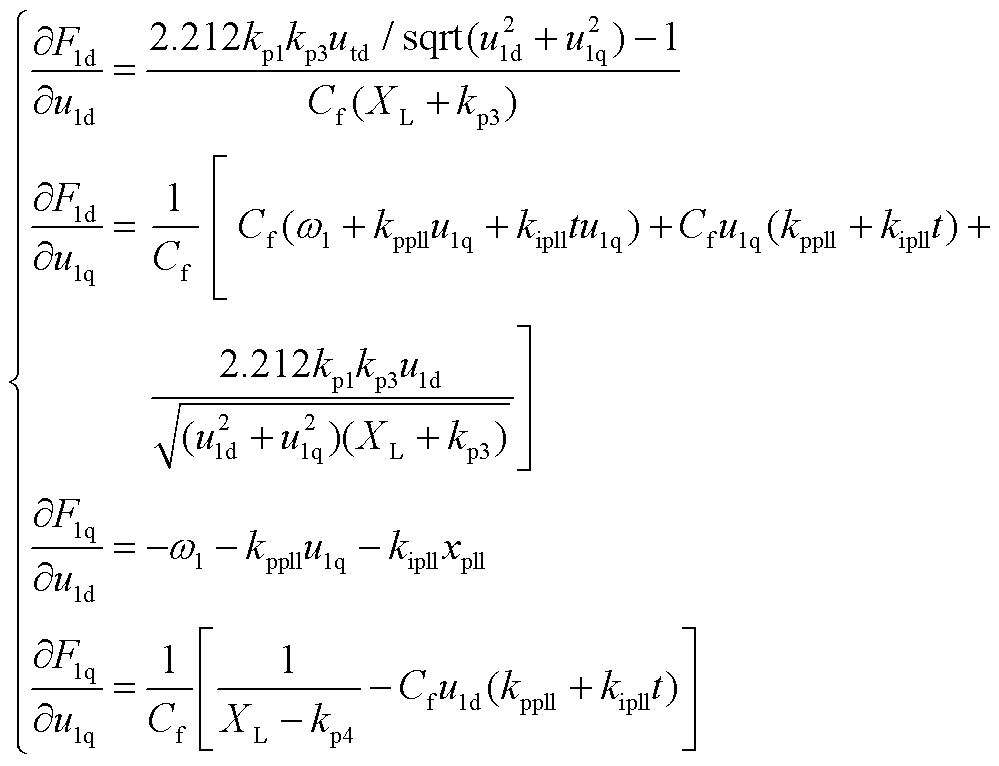 (A2)
(A2)
式中,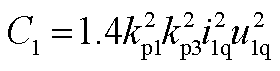 ,
,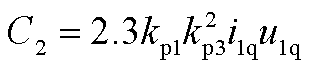 ,
,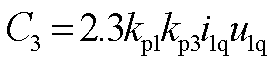 ,
,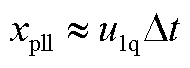 ,
,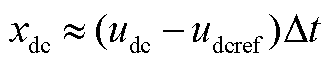 ,
,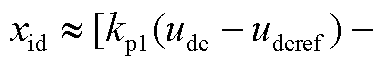
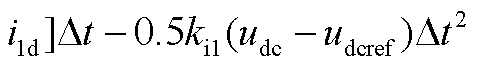 。
。
2)电压跌落工况。PCC电压跌落至0.9UB以下时,系统切换至LVRT控制模式。若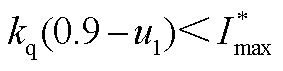 ,则此时
,则此时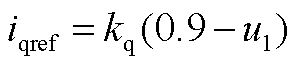 、
、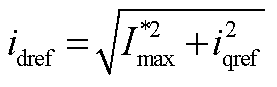 ,新能源场站电压微分方程为
,新能源场站电压微分方程为
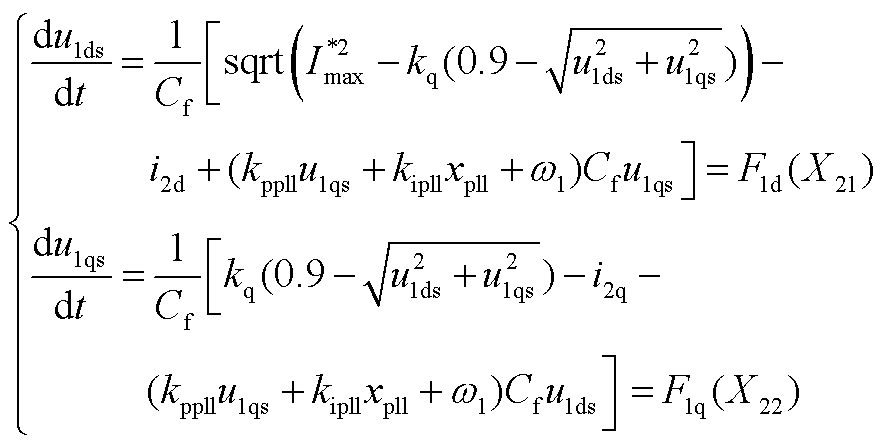 (A3)
(A3)
式中,kq为无功电流控制增益。
然后将F1d(X21)、F1q(X22)对u1ds、u1qs求偏导数,得到LVRT控制模式下的Jacobin矩阵J2。J2中各元素为
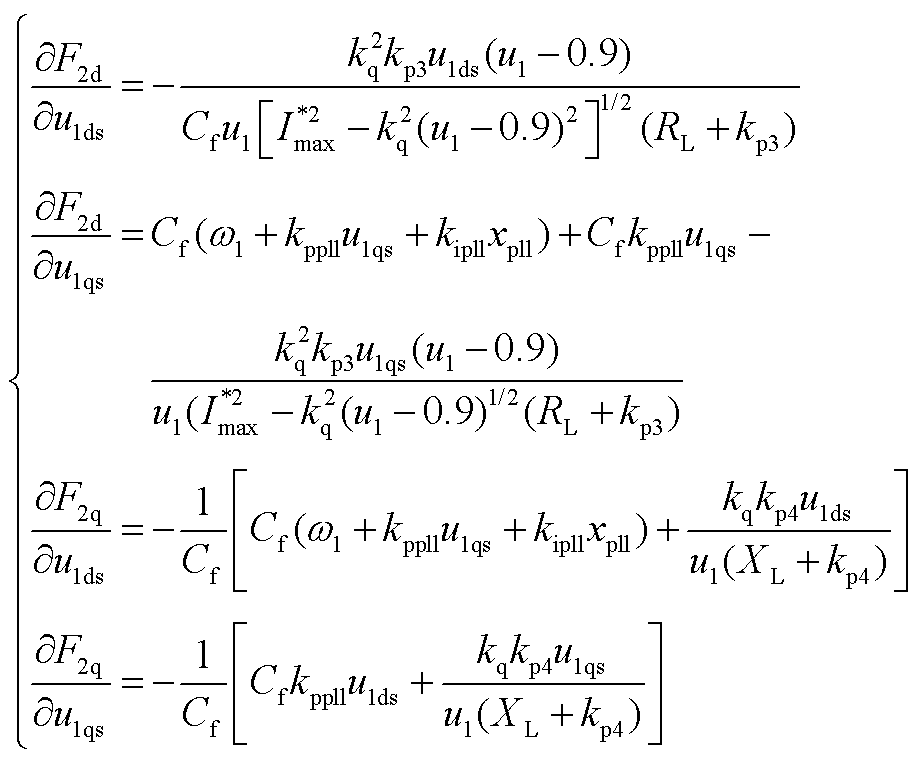 (A4)
(A4)
式中,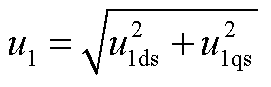 。
。
若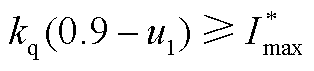 ,则此时
,则此时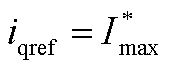 ,
,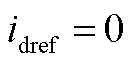 ,新能源场站电压微分方程为
,新能源场站电压微分方程为
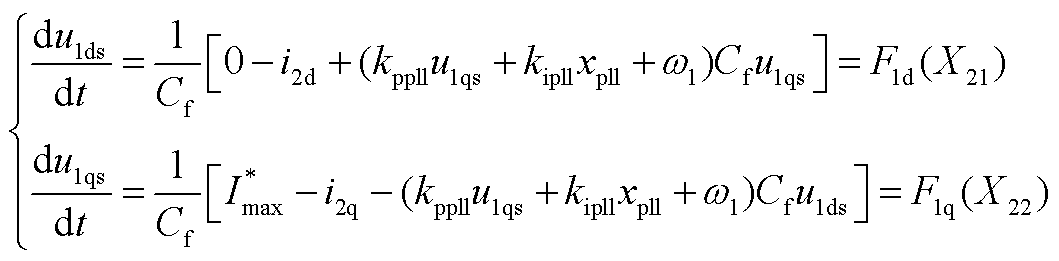 (A5)
(A5)
此时J2中各元素为
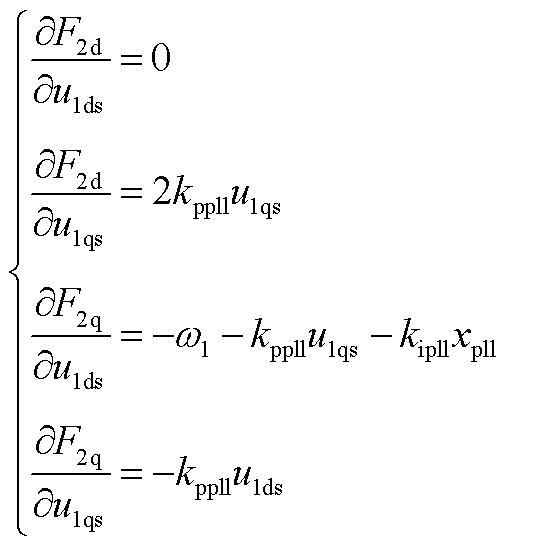 (A6)
(A6)
参考文献
[1] 赵郅毅, 许寅, 吴翔宇, 等. 含异构微源的混合型孤岛微电网暂态有功响应分析与控制策略[J]. 电工技术学报, 2024, 39(19): 6072-6084.
Zhao Zhiyi, Xu Yin, Wu Xiangyu, et al. Transient active power response analysis and control strategy of hybrid island microgrid containing heterogeneous microsources[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6072-6084.
[2] 陈国平, 董昱, 梁志峰. 能源转型中的中国特色新能源高质量发展分析与思考[J]. 中国电机工程学报, 2020, 40(17): 5493-5506.
Chen Guoping, Dong Yu, Liang Zhifeng. Analysis and reflection on high-quality development of new energy with Chinese characteristics in energy transition[J]. Proceedings of the CSEE, 2020, 40(17): 5493-5506.
[3] 杨铭, 曹武, 赵剑锋, 等. 受控电压/电流源型变流器混合多机暂态电压支撑策略[J]. 电工技术学报, 2023, 38(19): 5207-5223, 5240.
Yang Ming, Cao Wu, Zhao Jianfeng, et al. Transient voltage support strategy for hybrid multi-converter of controlled voltage/current source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5207-5223, 5240.
[4] 徐式蕴, 王一鸣, 孙华东, 等. 国外新能源脱网事故对中国电网安全稳定运行的启示[J]. 电力系统自动化, 2024, 48(13): 1-8.
Xu Shiyun, Wang Yiming, Sun Huadong, et al. Insights from renewable energy outage accidents abroad for secure and stable operation of power grids in China[J]. Automation of Electric Power Systems, 2024, 48(13): 1-8.
[5] 杨金洲, 李业成, 熊鸿韬, 等. 新能源接入的受端电网暂态电压失稳高风险故障快速筛选[J]. 电工技术学报, 2024, 39(21): 6746-6758.
Yang Jinzhou, Li Yecheng, Xiong Hongtao, et al. A fast screening method for the high-risk faults with transient voltage instability in receiving-end power grids interconnected with new energy[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6746-6758.
[6] 刘昊, 方天治, 张惠丽, 等. 弱电网下应对复杂稳定性问题的并网逆变器改进电压前馈通路研究[J]. 电工技术学报, 2024, 39(16): 4955-4967.
Liu Hao, Fang Tianzhi, Zhang Huili, et al. Research on an improved voltage feedforward path of grid-connected inverter coping with complex stability issues in weak grid[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 4955-4967.
[7] 仲悟之, 汤涌. 电力系统微分代数方程模型的暂态电压稳定性分析[J]. 中国电机工程学报, 2010, 30(25): 10-16.
Zhong Wuzhi, Tang Yong. Transient voltage stability analysis of differential-algebra equation in power system[J]. Proceedings of the CSEE, 2010, 30(25): 10-16.
[8] 杜兆斌, 黄昌树, 陈智颖, 等. 基于主导不稳定平衡点法的暂态电压稳定性研究[J]. 电测与仪表, 2022, 59(12): 64-70.
Du Zhaobin, Huang Changshu, Chen Zhiying, et al. Research on transient voltage stability analysis based on controlling UEP method[J]. Electrical Measurement & Instrumentation, 2022, 59(12): 64-70.
[9] Zhang Xu, Hao Zhiguo, Li Jiapeng, et al. Transient DC-link voltage oscillation stability assessment of VSC-HVDC systems using Lyapunov direct method [J]. International Journal of Electrical Power & Energy Systems, 2024, 157: 109873.
[10] 王波, 朱晓杰, 李振垚, 等. 基于单调系统理论的光伏并网系统暂态电压稳定性分析[J]. 电力系统自动化, 2023, 47(3): 19-29.
Wang Bo, Zhu Xiaojie, Li Zhenyao, et al. Analysis on transient voltage stability of power system with photovoltaic based on monotone system theory[J]. Automation of Electric Power Systems, 2023, 47(3): 19-29.
[11] 陈民权, 张谦, 甘德强, 等. 基于混合单调系统理论的电压动态响应分析[J]. 电力系统自动化, 2021, 45(18): 85-93.
Chen Minquan, Zhang Qian, Gan Deqiang, et al. Analysis of dynamic voltage response based on mixed monotone system theory[J]. Automation of Electric Power Systems, 2021, 45(18): 85-93.
[12] Dasgupta S, Paramasivam M, Vaidya U, et al. Real-time monitoring of short-term voltage stability using PMU data[J]. IEEE Transactions on Power Systems, 2013, 28(4): 3702-3711.
[13] Yoon K, Choi D, Lee S H, et al. Optimal placement algorithm of multiple DGs based on model-free Lyapunov exponent estimation[J]. IEEE Access, 2020, 8: 135416-135425.
[14] Eckmann J P, Ruelle D. Ergodic theory of chaos and strange attractors[J]. Reviews of Modern Physics, 1985, 57(3): 617-656.
[15] Rosenstein M T, Collins J J, De Luca C J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D: Nonlinear Phenomena, 1993, 65(1/2): 117-134.
[16] Aniszewska D, Rybaczuk M. Lyapunov type stability and Lyapunov exponent forexemplary multiplicative dynamical systems[J]. Nonlinear Dynamics, 2008, 54(4): 345-354.
[17] Ramasubramanian K, Sriram M S. A comparative study of computation of Lyapunov spectra with different algorithms[J]. Physica D: Nonlinear Phenomena, 2000, 139(1/2): 72-86.
[18] 王长江, 姜涛, 陈厚合, 等. 基于相位校正李雅普诺夫指数的电力系统暂态电压稳定评估[J]. 电工技术学报, 2021, 36(15): 3221-3236.
Wang Changjiang, Jiang Tao, Chen Houhe, et al. Transient voltage stability assessment of power systems based on phase correction maximum Lyapunov exponent[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3221-3236.
[19] 刘铖, 周元通, 曹志冲, 等. 基于网络无功能量最大李雅普诺夫指数的暂态电压稳定评估[J/OL]. 高电压技术, 1-16[2025-04-02].https://doi.org/10.13336/ j.1003-6520.hve.20241322.
Liu Cheng, Zhou Yuantong, Cao Zhichong, et al. Transient voltage stability assessment based on maximum Lyapunov exponent of network energy reactive term[J/OL]. High Voltage Engineering, 1-16 [2025-04-02]. https://doi.org/10.13336/j.1003-6520. hve.20241322.
[20] Xie Fan, Yang Ru, Zhang Bo. Bifurcation and border collision analysis of voltage-mode-controlled flyback converter based on total ampere-turns[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2011, 58(9): 2269-2280.
[21] Jia Zirui, Liu Ling, Liu Chongxin. Dynamic analysis and fractional-order terminal sliding mode control of a fractional-order buck converter operating in discontinuous conduction mode[J]. International Journal of Bifurcation and Chaos, 2022, 32(4): 2250045.
[22] Yu Yongjin, Zhang Chao. Bifurcation analysis of cascaded H-bridge converter controlled by proportional resonant[J]. International Journal of Electrical Power & Energy Systems, 2021, 125: 106476.
[23] Skokos C, Gottwald G A, Laskar J. Chaos Detection and Predictability[M]. Berlin, Heidelberg: Springer, 2016.
[24] Yan Jie, Liu C C, Vaidya U. PMU-based monitoring of rotor angle dynamics[J]. IEEE Transactions on Power Systems, 2011, 26(4): 2125-2133.
[25] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 风电场接入电力系统技术规定: GB/T 19963—2011[S]. 北京: 中国标准出版社, 2012.
[26] Gurusinghe D R, Rajapakse A D. Post-disturbance transient stability status prediction using synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3656-3664.
Transient Voltage Stability Assessment Approach for Renewable Energy Power System Considering Switching Compensation
Abstract The large-scale integration of renewable energy and power electronic devices into the power system has led to transient voltage evolution characteristics that significantly differ from conventional AC power systems. As a result, existing transient voltage stability indices and criteria are prone to misjudging voltage stability states under the influence of noise interference and control switching. To address these problems, this paper proposed a transient voltage stability assessment approach for renewable energy power system based on switching compensation Lyapunov exponent (SCMLE). The approach improves the accuracy of transient voltage stability assessment by the impact of control switching. It provides dispatchers with reliable transient voltage stability information for formulating voltage stability control strategies, which enhances the reliability and stability of renewable energy power system.
Firstly, based on the transient voltage stability discriminant mechanism of the maximum Lyapunov exponent (MLE), the voltage stability issue is transformed into an eigenvalue variation problem of the integral final value matrix and ensures a rigorous theoretical foundation of assessment results. Subsequently, the variational equation of the PCC voltage trajectory was formulated for both the normal operation mode and low voltage ride-through (LVRT) operation mode. The influence of system control characteristics and operating modes on transient voltage response features was fully considered. The SCMLE was then computed using the eigenvalues of the final value matrix derived from the variational equations. This approach overcame the limitation of the time-delayed embedding maximum Lyapunov exponent (TMLE), which required a predefined observation window. Thirdly, to reduce the impact of LVRT control switching on transient voltage stability assessment, a switching compensation matrix was constructed to represent the non-smooth distortion degree of the system. This matrix was used to correct the calculation error of the integral final value matrix at non-smooth points, improving both the speed and accuracy of the transient voltage stability assessment. Finally, the validity and effectiveness of the proposed approach were verified through simulation results from a single-machine infinite bus system with a photovoltaic power plant and a real power system. The simulation results show that the SCMLE was less sensitive to the observation time window and exhibited strong robustness under noise interference.
The following conclusions can be drawn: (1) The proposed approach, based on the stability discrimination mechanism of MLE, transforms the voltage stability problem into an eigenvalue variation problem of the integral terminal matrix, ensuring a rigorous theoretical foundation of assessment results. (2) The SCMLE reduces transient voltage stability assessment time by 24.18% and 20.69% compared to the maximum Lyapunov exponent based on QR decomposition (QRMLE) and the phase correction maximum Lyapunov exponent (PCMLE), respectively. Additionally, it effectively avoids the symbolic feature oscillations near the zero-axis and maintains robust assessment performance in real power grids. (3) The SCMLE analyzed the impact of control parameters on the transient voltage stability of the system and provides the stability region for control parameters. The proportional gain coefficient required to maintain transient voltage stability ranged from 0.1 to 0.4, while the integral gain coefficient ranged from 10 to 20. It offers valuable insights for control parameters design and the formulation of transient voltage stability control strategies.
Keywords:Renewable energy power system, transient voltage stability assessment, control switching, Lyapunov exponent
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241606
华北电力科学研究院有限责任公司资助项目(KJZ2023086)。
收稿日期 2024-09-10
改稿日期 2025-04-04
王长江 男,1989年生,实验师,博士,硕士生导师,研究方向为电力系统安全性与稳定性、新能源消纳、人工智能技术。
E-mail:cjwangneepu@163.com
刘先超 男,1995年生,博士研究生,研究方向为电力系统安全性与稳定性。
E-mail:liuxianchao2017@aliyun.com(通信作者)
(编辑 赫 蕾)