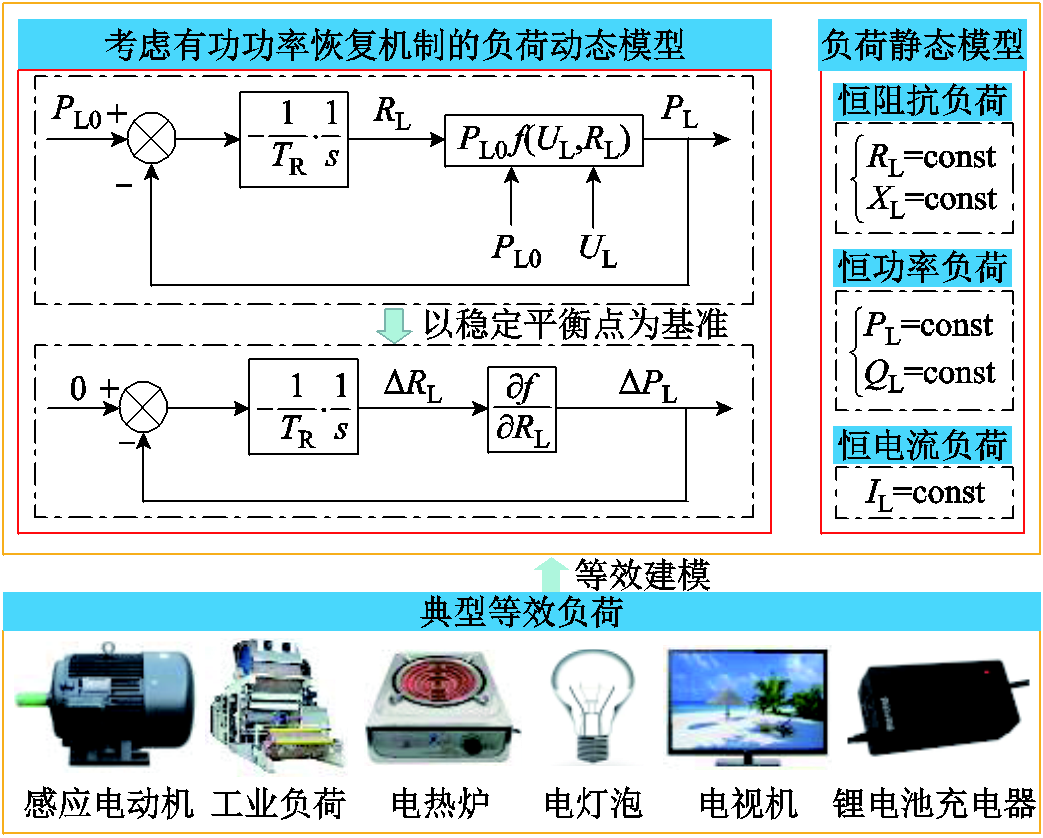
图1 电力系统典型负荷建模
Fig.1 Modeling of typical loads in power system
摘要 利用易量测电气量和正反馈规律判别暂态电压失稳，符合新型电力系统对响应式紧急控制技术的需求。然而传统的正反馈判据基于电力系统的理想戴维南等效电路提出，实际应用中可能存在测量电气量难以获取，或者判据在电压迅速下降时短时失效的问题。该文力图从暂态电压的本质失稳机理出发，提升判据性能。首先，基于负荷功率恢复机制和模型，以表征失稳机理的负荷阻抗状态变量刻画电压失稳区域；然后，依据功率因数与负荷阻抗在暂态电压失稳过程中的一致性变化规律，借助功率因数等效表达状态变量以利于量测，构建功率因数映射正反馈不稳定域的暂态电压失稳判据；最后，与功率电流传统判据对比，分析该文所提判据的适用性，并在中国电力科学研究院发布的暂态电压崩溃标准算例及万节点测试系统中进行了验证。
关键词：功率因数 暂态电压失稳 正反馈 不稳定域
电力系统暂态电压稳定的识别长期以来倍受关注[1-3]。随着系统规模日益扩大、运行方式日趋复杂，传统“离线计算、在线匹配”的预案式电压失稳判别和控制技术逐渐显现出一定的局限性，基于响应特征识别失稳势在必行[4-5]。
电压问题存在多种场景，尤其涉及新能源[6]和直流输电[7-8]时更为复杂。暂态电压失稳通用判别方法主要包括时域仿真[9]、能量函数[10-11]等，然而此类方法普遍依赖经验，且能量函数的构造较为困难。业界普遍认为，机电时间尺度下最为常见的暂态电压失稳仍是由负荷特性主导[12]。在过去几十年，科研人员针对负荷侧高占比的感应电动机开展了大量研究。文献[13]提出感应电动机幅相运动模型，文献[14]基于分岔理论发现高比例感应电动机易引发电压失稳。基于感应电动机动态特性，有研究发现电磁转矩小于机械转矩时，转差率不断增大，感应电动机吸收无功功率大增，可导致系统无功不足而引发暂态电压失稳[15]。这些研究工作旨在解释负荷主导的暂态电压的失稳机理。另一方面，亦有学者致力于此类暂态电压失稳的判据构建，文献[16]结合感应电动机转差率极限和机端电压构造失稳判据，但是转差率极限又受工作状态和节点电压影响，确定难度较大。另有部分学者基于戴维南等效电路，比较节点负荷阻抗和戴维南等值阻抗以判断暂态电压失稳[17]，但是系统戴维南等效阻抗随运行方式变化。文献[18]改进戴维南等值参数辨识算法，借助阻抗比指标实现判别。然而上述判据中电动机转差率和戴维南等值阻抗等特征电气量或多或少面临不易量测的问题[19]，难以适应系统多变运行方式对基于响应识别失稳的需求。
作为最直接的响应特征，电压幅值可以反映电力系统电压暂态规律。利用受扰后电压运行轨迹和跌落面积，并设定阈值判断暂态电压失稳[20-21]是基于响应的基本判据形式。但是若节点电压恢复较慢，可能导致误判。亦有学者利用关键节点电压幅值变化率计算李雅普诺夫指数，并通过此特征量的时间序列实施电压轨迹趋势跟踪[22]。类似地，借助机端电压幅值偏差序列，也可实现基于最大李雅普诺夫指数与电压幅值偏差率的暂态电压失稳判别[23]。文献[24]对电压跌落程度赋权并提出相应的多二元表判据。然而上述判据属于数据驱动的判稳方法，仅依靠节点电压数据，未结合具体失稳机理，判稳准确性与时效性受阈值影响较大，且不利于甄别失稳的原因。
为了揭示负荷动态特性导致暂态电压失稳的本质并提高判稳准确度，相关研究团队在主导稳定形态识别[25]的基础上提出暂态电压失稳主要与负荷的功率获取机制相关[26]。在此基础上，文献[27]发现负荷侧暂态电压失稳伴随线路电流持续增大但有功功率反而减小的恶性循环过程，开辟了依托反馈关系并利用易量测信息实现电压稳定判别的研究路线，并提出了传统的线路功率电流判据。然而此判据使用戴维南等效电路的线路功率和电流，实际应用时通常较难在输电网中找到完全对应的具体线路。另外，传统的线路功率电流判据未考虑电压下降较快时，可能造成的电流短时变化趋势与整体趋势不相符的问题，从而导致判据短时失效。
本文仍基于正反馈关系和易量测信息的响应特征，开展暂态电压失稳的判别研究，试图从本质失稳机理出发提升判据性能。首先，基于负荷功率恢复机制模型，以描述暂态电压失稳机理的负荷阻抗状态变量刻画电压失稳区域；然后，借助功率因数等效表达负荷阻抗变化，提出利用功率因数映射负荷动态正反馈不稳定域的暂态电压失稳判据；最后，分析本文所提判据的适用性，尤其针对传统判据可能发生错判的场景，并以中国电力科学研究院发布的暂态电压崩溃（China Electric Power Research Institute’s Voltage Collapse, CEPRI-VC）标准算例[28]以及万节点测试系统验证本文判据的有效性。
电力负荷可建模为动态或静态模型[29]。其中，负荷动态特性通常不失一般性地建模为受扰后的功率恢复机制[12,26]，电力系统典型负荷建模如图1所示。图1中，RL、XL分别为负荷等效电阻、电抗，TR为电阻变化时间常数，PL0、PL与QL分别为负荷有功功率预设目标、吸收的有功功率和无功功率，UL为负荷节点电压，IL为负荷电流，1/s代表积分环节。受扰后，动态负荷吸收的有功功率若偏离预设目标，其将按照物理规律或控制逻辑调整电阻，以减少功率偏差。
以负荷等效电阻为状态变量描述的功率恢复机制动态模型[26]为
图1 电力系统典型负荷建模
Fig.1 Modeling of typical loads in power system
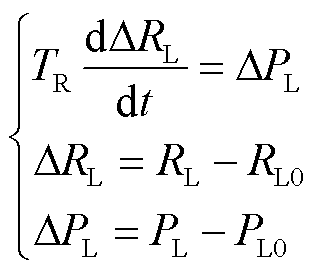（1）
式中，RL0为负荷等效电阻初始值。
基于戴维南定理，将电源经输电网络向负荷供电的场景等效为图2a所示电路。而将负荷消耗有功功率PL与其等效电阻RL的关系如图2b所示电路。可确定B右侧曲线为负荷状态运动的正反馈区域，该区域中若存在非零功率偏差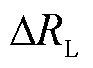
，功率恢复机制控制的RL变化将进一步增加功率偏差。同理，O与B之间曲线段为负反馈区域。
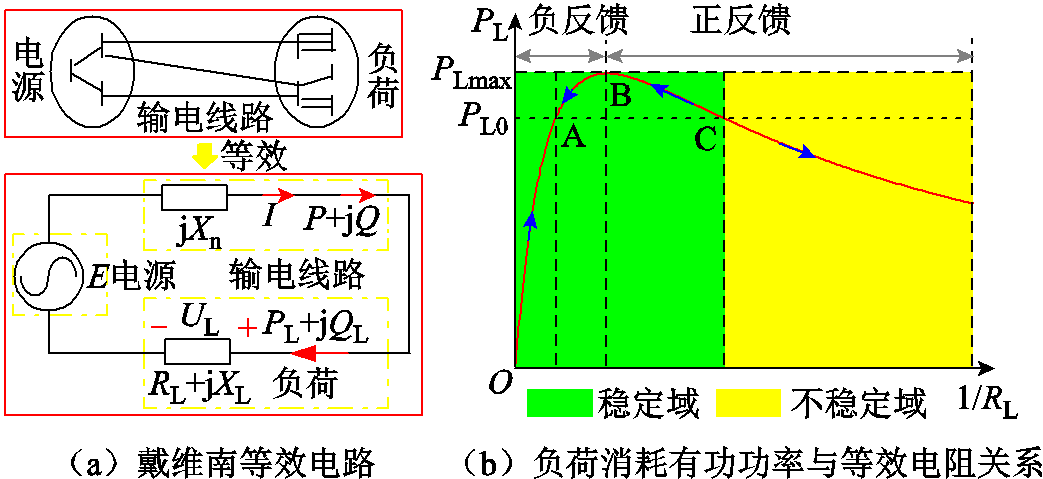
图2 负荷消耗有功功率与其等效电阻的关系示意图
Fig.2 The relationship between active power of load and its equivalent resistance
然而并不是所有的正反馈区域均为不稳定域。若负荷状态位于B与C之间，虽然此时处于正反馈区域，但是负荷状态经运动会越过B，并最终稳定于平衡点A，因此B与C之间为稳定域，仅C右侧为不稳定域。扰动若使负荷状态进入正反馈不稳定域，其等效电阻持续减小，功率因数持续变差，从而增加了无功功率消耗。电网无功支撑能力不变的情况将导致负荷节点电压崩溃。电压稳定是局部问题，若能判断某节点的负荷状态进入正反馈不稳定域，可判定该节点将发生暂态电压失稳。
根据1.1节功率恢复模型的机理分析，负荷状态位于不稳定域而引发暂态电压失稳时，伴随有负荷等效电阻减小而消耗功率下降的正反馈过程。因此，可以构建暂态电压失稳的机理判据为
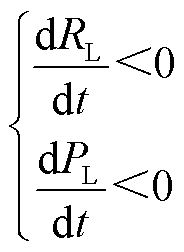（2）
然而，负荷等效电阻通常不便于量测，因此考虑使用响应电气量实现式（2）的可量测化。功率恢复过程中负荷的功率因数为
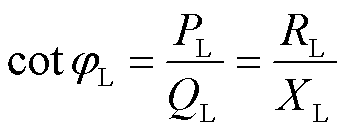（3）
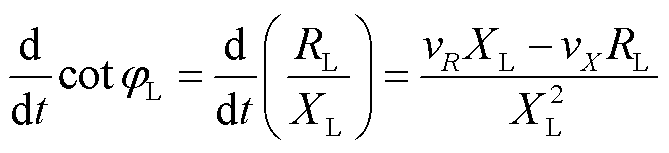（4）
式中，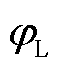
为负荷功率因数角；
、
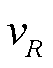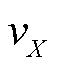分别为等效电阻和电抗的变化率。
为阐述可使用功率因数角的余切值等效表达暂态电压失稳的机理判据（2），做如下分类讨论。当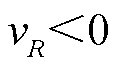
，
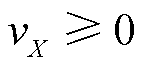时，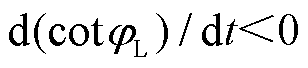
，负荷功率因数角的余切值与等效电阻的变化方向一致；当，
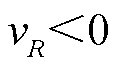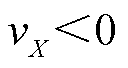时，在满足式（5）的前提下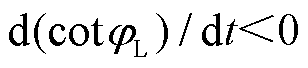，，功率因数角的余切值与等效电阻的变化方向一致。同理，可证明当负荷等效电阻增大，即
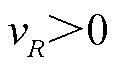时，满足相似规律。
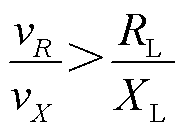（5）
负荷功率恢复机制通常仅调节其等效电阻，不改变或较少改变等效电抗，通常式（5）均成立。负荷功率因数角的余切值与等效电阻变化规律一致，为式（2）的可量测化创造了条件。可等效推出功率因数映射负荷正反馈不稳定域的暂态电压失稳判据，如式（6）所示，负荷有功功率、无功功率均可在母线节点测得。
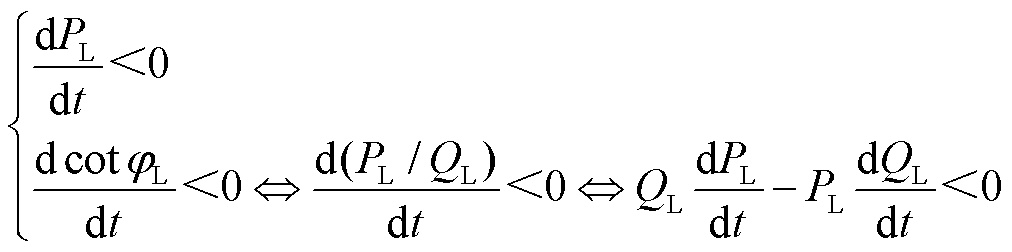（6）
考虑到导数计算中除法运算造成的数值传递误差，可将式（6）中的导数运算改进为差分形式。另外，工程实践中通常将电压安全与暂态电压失稳同时判别，可附加电压安全门槛Ux与判据持续时间阈值T [27]。
在以往研究中，已有同样基于正反馈规律的暂态电压失稳判据。其中较为常见的是如式（7）所示的功率电流判据[27]，使用线路电气量实现判稳。
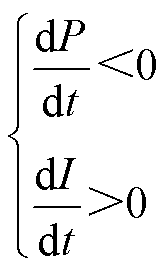（7）
式中，P为线路有功功率；I为线路电流。
然而传统判据的构建前提与实际电网情况通常存在差异。例如，功率电流判据由图2a戴维南等效系统推导得出，其将整个输电网等效为理想的单一线路，基于戴维南等效的线路功率和电流构成失稳判据。现实中仅少数电网结构能找到与图2a等效对应的电气量。例如，存在明显联络线且功率电流单向流动的链式电网，联络线电流和功率可分别等效对应图中线路电流和功率，从而基于式（7）对联络线某一侧的区域电网得到较为满意的暂态电压判稳结果。但是戴维南等效电气量大多数情况无法在实际电网中找到等效对应。例如，在高度互联的网状电网结构中就较难找到与图2a理想线路电流完全等效的具体线路电流。因此，实际情况可能会影响基于线路电气量测量的传统功率电流判据实施。本文利用母线功率以及功率因数映射状态变量而构成失稳判据，可避免此实施困难。
另外，多负荷节点的区域电网中各母线电压存在差异。考虑负荷状态受扰进入不稳定域而发生暂态电压失稳，失稳过程中部分节点电压可能下降较快。若负荷等效电阻某时段内下降相对较慢，则会导致短时间内线路电流不升反降，与电流整体变化趋势不一致，传统功率电流判据式（7）无法在短时间内判出暂态电压失稳。本文构建的失稳判据式（2）和式（6）基于暂态电压失稳的本质机理直接提出，因此不存在此问题。随电压下降，功率曲线如图3所示，由实线过渡至虚线，同时负荷状态由S变化至T。可以看出，此时负荷仍位于不稳定域，将继续失稳，负荷状态按照R→S→T运行。此过程中负荷功率PL在减小，负荷等效电阻RL也呈现减小的一致趋势，负荷节点电压下降并不影响本文判据。
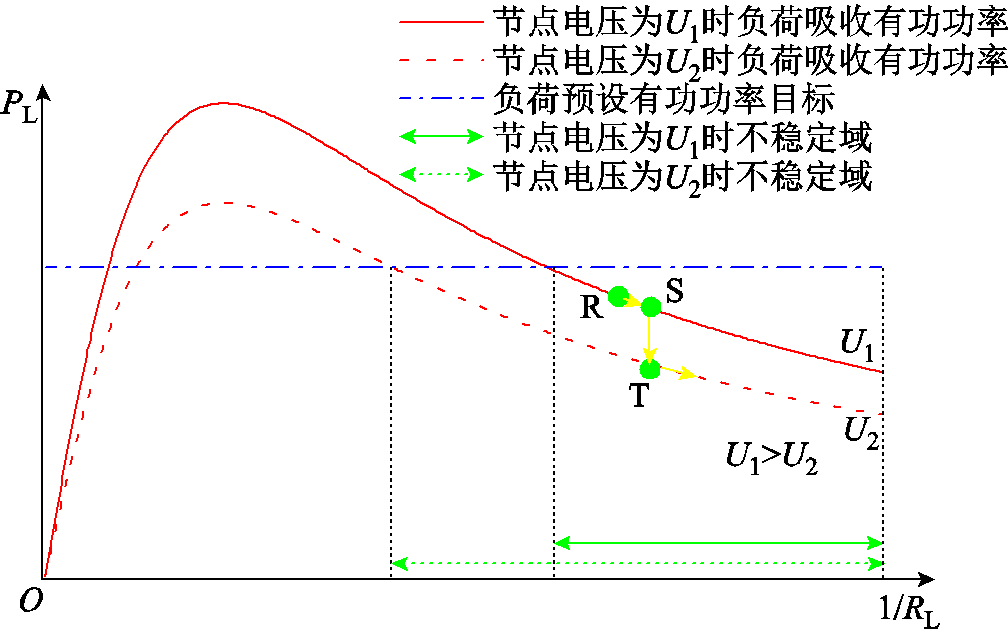
图3 负荷节点电压下降时不稳定域变化
Fig.3 The change of instability region in case that the bus voltage drops
诚然，本文判据也有局限性，在新型电力系统的适用性值得探讨。本文判据面向负荷侧主导的暂态电压失稳识别，由负荷功率恢复机制及其动力学模型推理构建，电气量测量于负荷母线。因此，讨论本文判据的适用性仅需从负荷母线观察，关注负荷功率恢复机制以及式（1）模型在新型电力系统是否仍成立。在直流馈入和集中式新能源场景下，负荷构成并未改变，故本文判据依然适用。在分布式新能源高比例渗透至负荷侧时，由于低电压穿越过程中新能源发出无功，并非呈现式（1）描述的功率恢复动态特性，本文判据存在失效风险。但若考虑新能源保护在其低电压穿越失败时切除新能源，本文判据仅时效性有所降低。
为了验证本文所提出的暂态电压失稳判据，本节在CEPRI-VC标准算例[28]及万节点测试系统进行仿真分析。
PSD-BPA仿真软件搭建的CEPRI-VC标准算例见附图1。标准算例共包含100个母线节点，以500 kV电网为主网架，负荷模型由65%的感应电动机动态负荷和35%的静态负荷构成。受扰后由PSD-BPA仿真暂态样本，在500 kV负荷节点应用本文暂态电压失稳判据。
若节点bus1至节点bus2的交流线路于1 s发生三相接地短路故障，短路故障发生后0.1 s故障线路被切除，500 kV节点的电压暂态如图4a所示。故障切除后，节点电压均在10 s内恢复至额定值附近，根据电力系统安全稳定导则[30-31]，该样本为暂态电压稳定样本。以bus4节点为例，节点电压、有功功率以及功率因数角余切值如图4b所示。应用本文暂态电压失稳判据，该节点被判定为未发生电压失稳。相似地验证其他500 kV负荷节点（因篇幅所限，未能逐节点列出相关电气量），判据做出同样判断。所以本文判据将此样本识别为暂态电压稳定样本，与真实情况相符，判据输出结果正确。
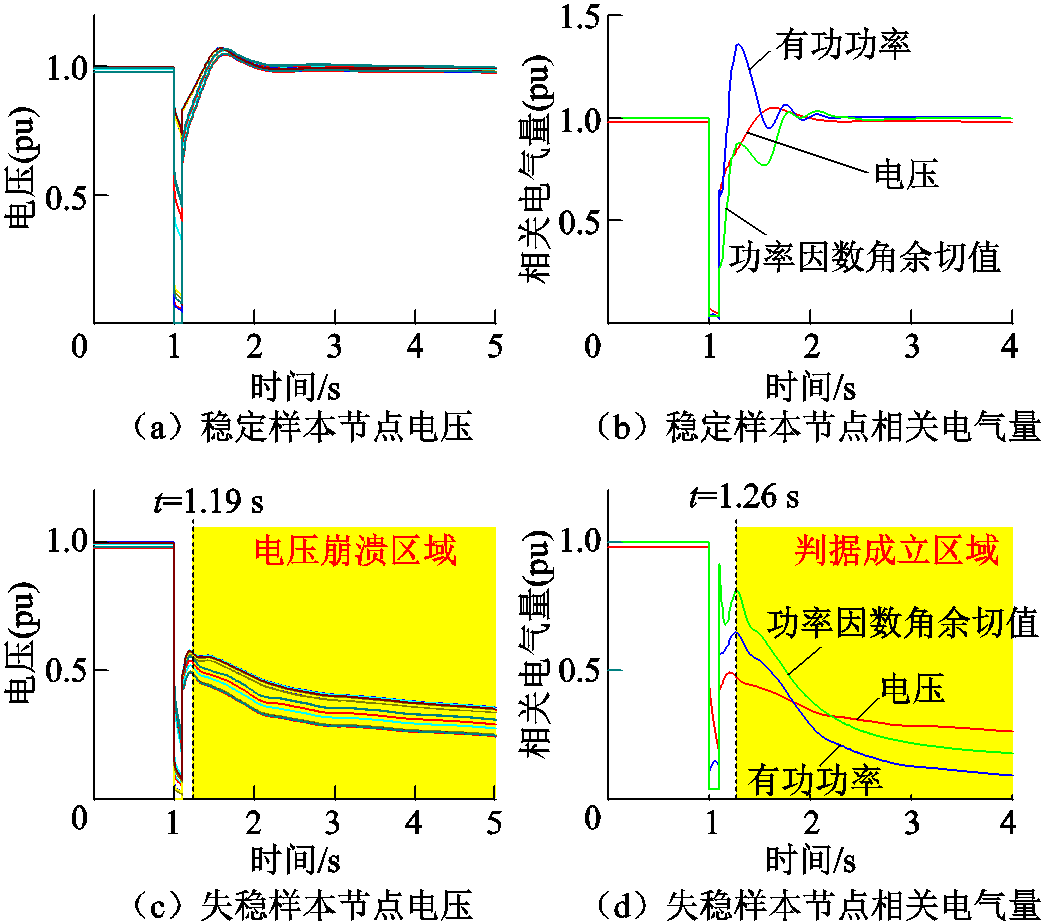
图4 CEPRI-VC标准算例仿真结果
Fig.4 Simulation in CEPRI-VC benchmark system
若节点bus12至节点bus13的交流线路、节点bus1至节点bus2的交流线路以及节点bus2至节点bus3的交流线路于1 s同时发生三相接地故障，0.1 s后切除故障线路，500 kV节点电压波形如图4c所示。由于部分节点电压低于0.75(pu)的持续时间超过1 s，该样本为暂态电压失稳样本[30-31]。以bus4节点为例，节点电压、有功功率以及功率因数角的余切值示于图4d。从1.26 s开始本文判据持续成立，图中亦标注了判据成立的时间范围。根据判据将该节点判别为电压失稳，亦与真实情况相符，判据输出结果正确。
通过设置多种类型故障，生成400个案例样本，利用稳定样本误判率（False Alarm Rate, FAR）与失稳样本漏判率（Missing Alarm Rate, MAR）两个性能评价指标[32]对本文判据的准确性进行统计，本文判据与常用的功率电流判据性能对比见表1。结果表明传统功率电流判据与本文判据均能较为准确地判断暂态电压失稳，而本文判据在失稳样本漏判率MAR方面略优于传统的功率电流判据。
表1 CEPRI-VC标准算例本文判据与功率电流判据性能对比
Tab.1 Performance comparison between the proposed criterion and the popular power vs. current criterion in CEPRI-VC benchmark system
判据误差率(%)漏判率(%) 功率电流判据8.500.94 本文所提判据8.500
保持电压安全门槛Ux=0.75(pu)不变，改变判据成立持续时间阈值T，本文判据与功率电流判据的误漏判率随T变化趋势如图5所示。结果表明，增加判据成立需持续的时间阈值能够降低上述两个判据的误判率FAR。但是，随着T值变大，功率电流判据的漏判率MAR明显上升，而本文判据并没有发生明显变化。本文判据鲁棒性更好，在判别暂态电压失稳场景时准确性更高。本文判据与功率电流判据的判别时效随T变化如图6所示。由图6可知增加T会延长判据做出判断所需时间，从而降低判据时效性。
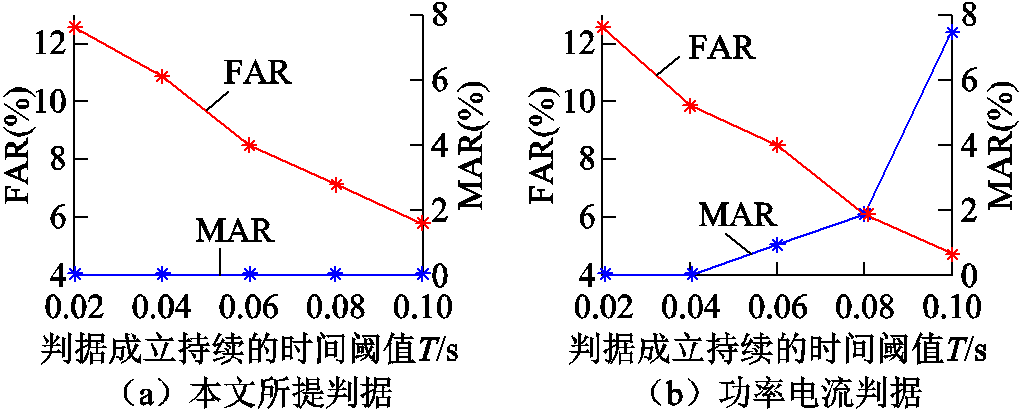
图5 CEPRI-VC标准算例T变化时判据准确性对比
Fig.5 Comparison of criterion accuracy in case of various T in CEPRI-VC benchmark system
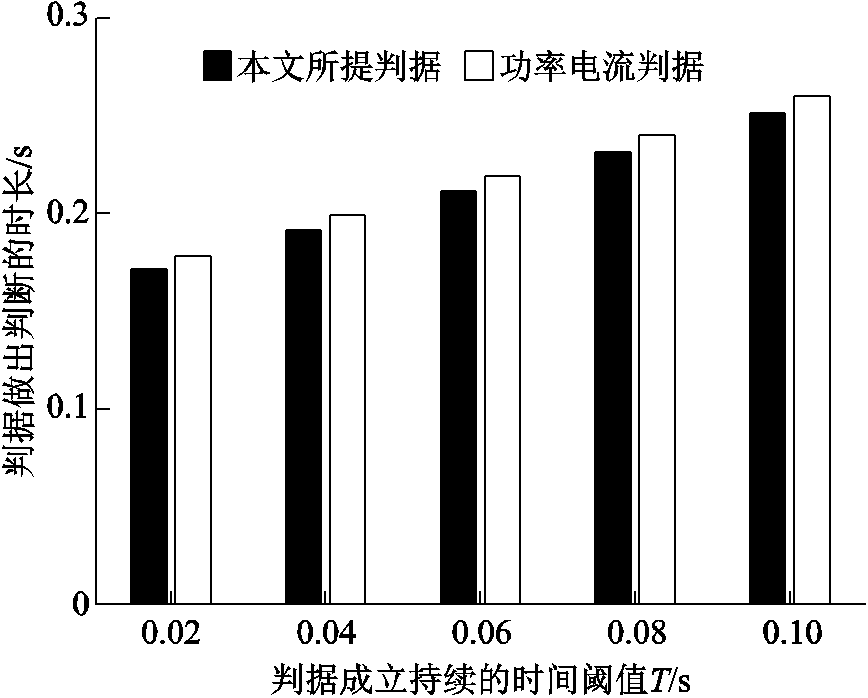
图6 CEPRI-VC标准算例T变化时判据时效性对比
Fig.6 Comparison of criterion rapidity in case of various Tin CEPRI-VC benchmark system
保持判据成立持续时间阈值T=0.06 s，改变电压安全门槛Ux，可做类似验证，如图7和图8所示。降低Ux能够降低上述两个判据的误判率FAR。但是，随着Ux取值变小，功率电流判据漏判率MAR明显上升，而本文判据并没有发生明显变化。可认为本文判据准确性更高。在时效性方面，降低Ux并未明显降低判据时效性。
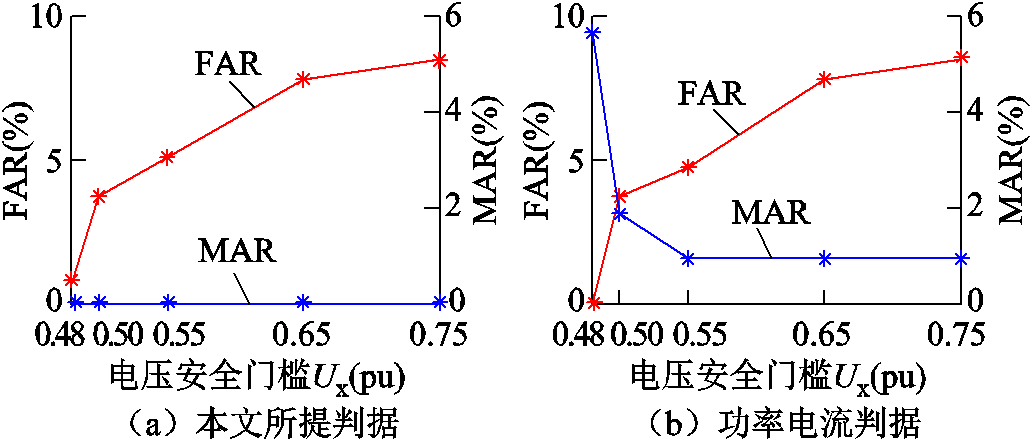
图7 CEPRI-VC标准算例Ux变化时判据准确性对比
Fig.7 Comparison of criterion accuracy in case of various Ux in CEPRI-VC benchmark system
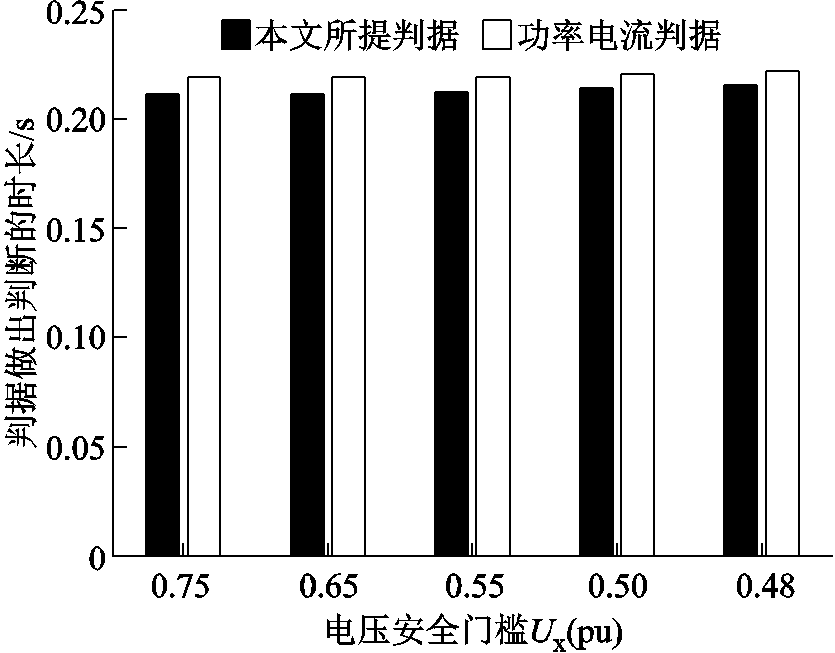
图8 CEPRI-VC标准算例Ux变化时判据时效性对比
Fig.8 Comparison of criterion rapidity in case of various Ux in CEPRI-VC benchmark system
以节点bus16至节点bus17的交流线路、节点bus1至节点bus2的交流线路以及节点bus2至节点bus3的交流线路于1 s同时发生三相接地故障为例，解释判据准确性呈现上述规律的原因。短路故障发生0.1 s后切除故障线路，通过电压暂态波形判断该样本为暂态电压失稳样本。bus4节点电压、有功功率与功率因数角余切值的变化关系如图9a所示，有功功率与电流的变化关系如图9b所示。发现功率电流判据与本文判据最终均能正确识别系统发生了暂态电压失稳。但是，在1.31 s和1.49 s后的一段时间内，电流不升反降，功率电流判据在该段时间内不成立。虽然在1.24～1.3 s功率电流判据已经成立，但是由于受判据成立持续时间阈值限制，功率电流判据直至1.49 s才最终判断该样本为失稳样本。而从1.24 s开始本文判据持续成立，即可在1.32 s做出正确判断。
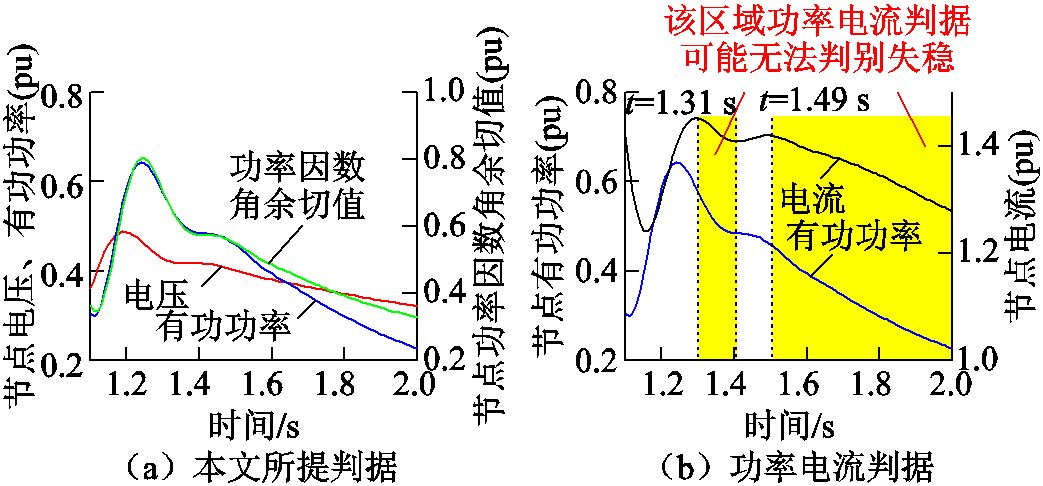
图9 CEPRI-VC标准算例失稳样本判别过程对比
Fig.9 Comparison of detailed procedure for an instability example in CEPRI-VC benchmark system
本节在某万节点测试系统验证本文判据。该测试系统如附图2所示，测试系统共包含10 575个母线节点，送受端系统均以500 kV为主网架，送端系统负荷模型由70%的感应电动机动态负荷和30%的静态负荷构成，受端系统负荷模型由60%的感应电动机动态负荷和40%的静态负荷构成，系统扰动后暂态过程由PSD-BPA仿真。
若节点1RB01151至节点1RB01451双回交流线路于1 s发生三相接地故障，故障发生0.1 s后线路切除，500 kV主网架节点电压波形如图10a所示。故障切除后，系统内所有节点电压均在10 s内恢复，该样本为暂态电压稳定样本。以3RB27821节点为例，节点电压、有功功率以及功率因数角余切值如图10b所示。应用本文所提出的暂态电压失稳判据，该节点被判定为未发生电压失稳。相似地验证其他500 kV负荷节点，判据也做出同样判断。所以本文判据将此样本识别为暂态电压稳定样本，与真实情况相符，判据输出结果正确。
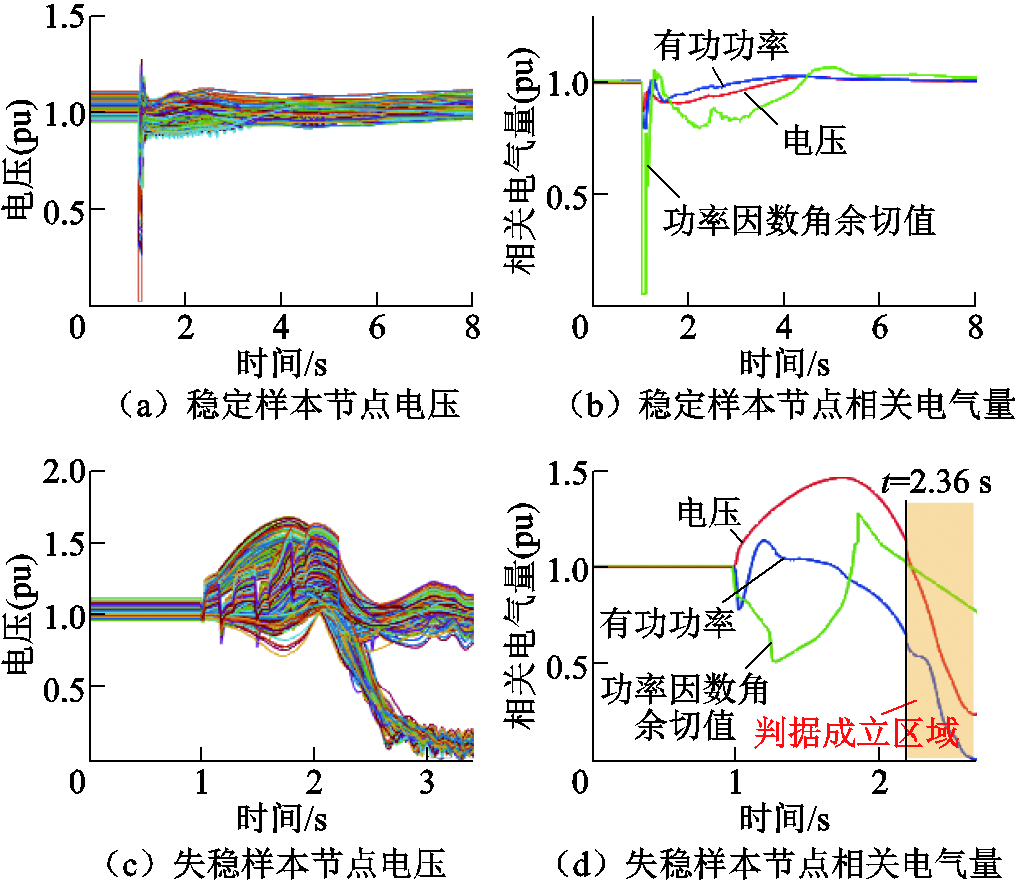
图10 万节点测试系统仿真结果
Fig.10 Simulation results in testing system with 10 575 buses
若直流1、2、3、5同时发生闭锁故障，500 kV主网架节点电压波形如图10c所示。由于部分节点电压低于0.75(pu)的持续时间超过1 s，该样本为暂态电压失稳样本。以3RB27821节点为例，节点电压、有功功率以及功率因数角余切值波形如图10d所示。应用本文暂态电压失稳判据，从2.36 s开始判据持续成立，判定为暂态电压失稳，判据输出结果正确。
通过设置多种故障获得2 000个样本，利用稳定样本误判率FAR与失稳样本漏判率MAR两个性能评价指标验证本文判据，本文判据与常用的功率电流判据性能对比见表2。结果表明，功率电流判据与本文判据均能够较为准确地判断暂态电压失稳。
表2 万节点测试系统本文所提判据与功率电流判据性能对比
Tab.2 Performance comparison between the roposedcriterion and the popular power vs. current criterion in testing system with 10 575 buses
判据误判率(%)漏判率(%) 功率电流判据1.814 本文所提判据2.380
保持电压安全门槛Ux而改变判据成立持续时间阈值T，本文判据与功率电流判据误判率和漏判率统计结果如图11所示。可得到与CEPRI-VC标准算例相同的结论，增加T能够降低上述两个判据的误判率FAR，但是随着T取值增大，功率电流判据与本文判据漏判率MAR均会上升。本文判据漏判率MAR始终低于功率电流判据，说明本文判据的鲁棒性更好，在暂态电压失稳场景时准确性更高。
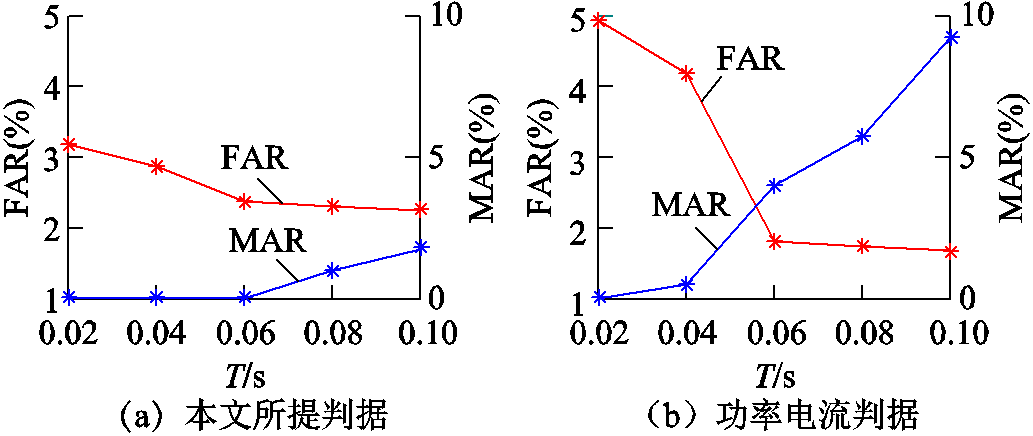
图11 万节点测试系统T变化时判据准确性对比
Fig.11 Comparison of criterion accuracy in case of various T in testing system with 10 575 buses
判据成立持续时间阈值T取不同值时，本文判据与功率电流判据做出判断的时长如图12所示。结果表明，增加T会延长判据做出判断的时长，从而降低判据时效性。
保持判据成立持续时间阈值T而改变电压安全门槛Ux，做类似验证，Ux变化时判据准确性和时效性对比分别如图13和图14所示。降低Ux能够降低上述两个判据的误判率FAR。随着Ux取值变小，功率电流判据与本文判据的漏判率MAR均会上升，但是本文判据漏判率MAR始终低于功率电流判据。可以认为，本文判据在判别暂态电压失稳场景时准确性更高。在时效性方面，降低Ux明显地降低了判别速度。
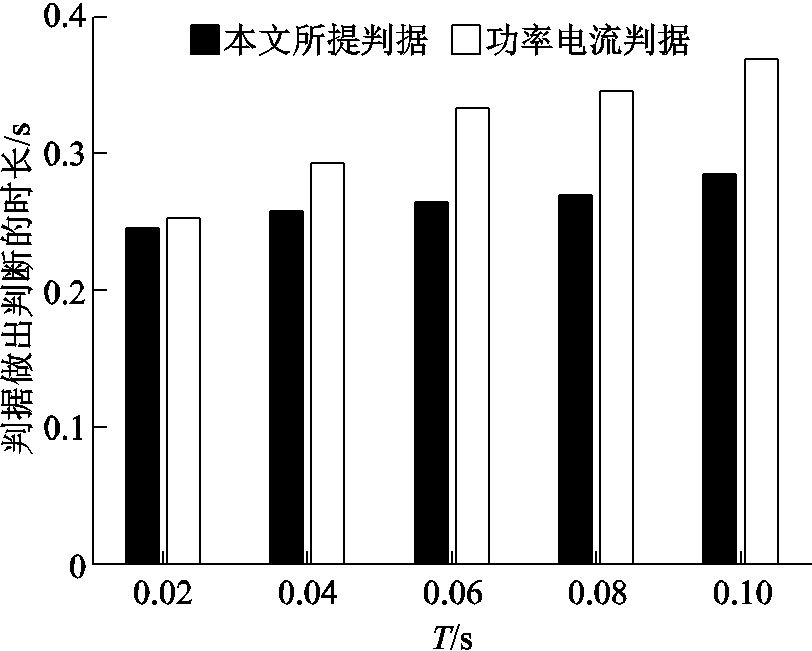
图12 万节点测试系统T变化时判据时效性对比
Fig.12 Comparison of criterion rapidity in case of various T in testing system with 10 575 buses
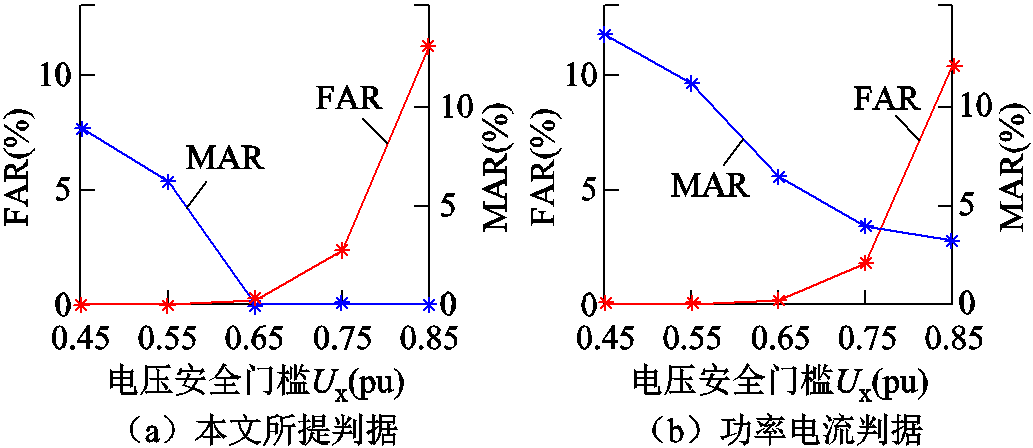
图13 万节点测试系统Ux变化时判据准确性对比
Fig.13 Comparison of criterion accuracy in case of various Ux in testing system with 10 575 buses
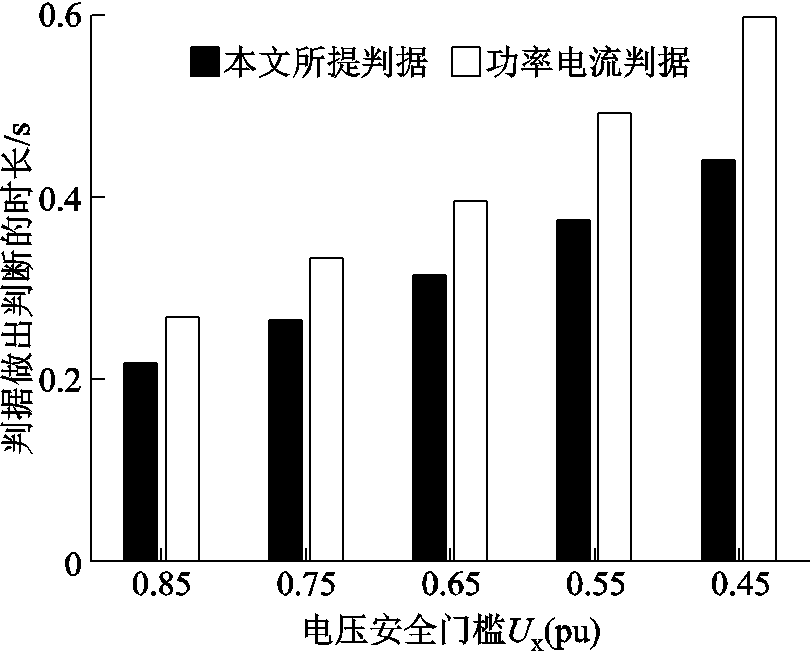
图14 万节点测试系统Ux变化时判据时效性对比
Fig.14 Comparison of criterion rapidity in case of various Ux in testing system with 10 575 buses
以直流1、3、6同时闭锁场景为例，解释判据准确性呈现上述规律的原因。通过电压暂态波形可判断该样本为暂态电压失稳样本。1RB01721节点的电压、有功功率与功率因数余切角变化关系如图15a所示，有功功率与电流的变化关系如图15b所示。发现功率电流判据与本文判据最终均能判别系统发生暂态电压失稳。但是，在1.93 s和2.05 s后的一段时间，电流不升反降，功率电流判据在该段时间内不会成立，功率电流判据直至2.15 s才做出最终判断。由于节点电压在2.03 s下降至电压安全门槛0.75(pu)以下，且在此之前有功功率与功率因数角余切值持续下降时间已超过0.06 s，本文判据在第2.03 s即可做出判断。
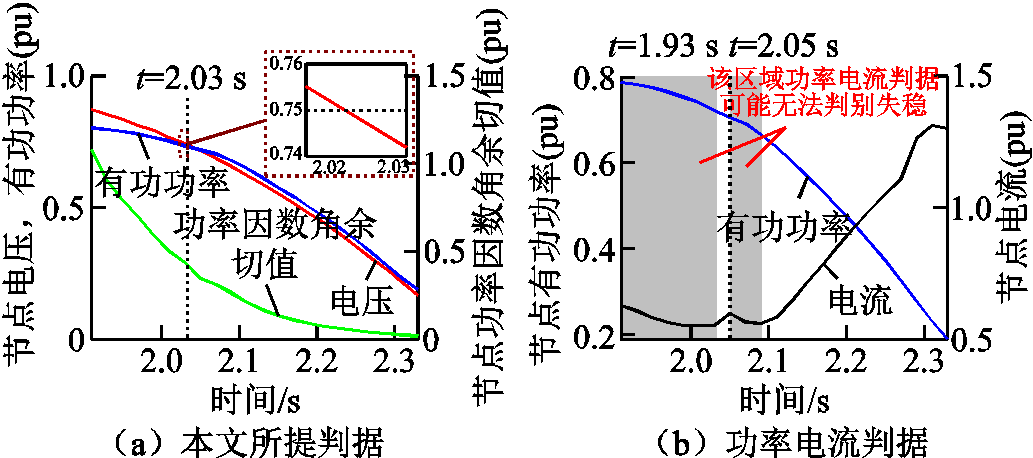
图15 万节点测试系统失稳样本判别过程对比
Fig.15 Comparison of detailed procedure for an instability example in testing system with 10 575 buses
基于响应特征识别暂态电压失稳，本文提出一种利用功率因数映射负荷正反馈不稳定域的暂态电压失稳判据，并在中国电力科学研究院发布的暂态电压崩溃标准算例以及万节点测试系统验证了该判据的有效性，主要结论如下：
1）相较于正反馈规律的其他传统判据（例如线路功率电流判据），本文所提判据以负荷功率恢复特性的等效电阻作为状态变量，描述暂态电压不稳定域，更能体现暂态电压失稳的机理本质。
2）功率因数与电压暂态失稳的等效电阻状态变量存在一致性变化规律，以功率因数映射正反馈不稳定域而构建的失稳判据，具有易量测的优点。
3）相较于正反馈规律的其他传统判据，本文所提判据摆脱了电压变化条件对判据准确性的约束，在负荷节点电压下降较快时鲁棒性更好。
虽然本文判据基于负荷侧暂态电压失稳的本质机理提出，但是在电压稳定性识别的工程实践中，通常综合考虑电压安全因素，本文判据附加的电压安全门槛以及判据持续时间阈值可考虑借助人工智能方法确定，值得进一步研究。另外，分布式新能源占比对本文判据适用性的影响，亦值得深入探讨。
附 录
1. CEPRI-VC标准算例
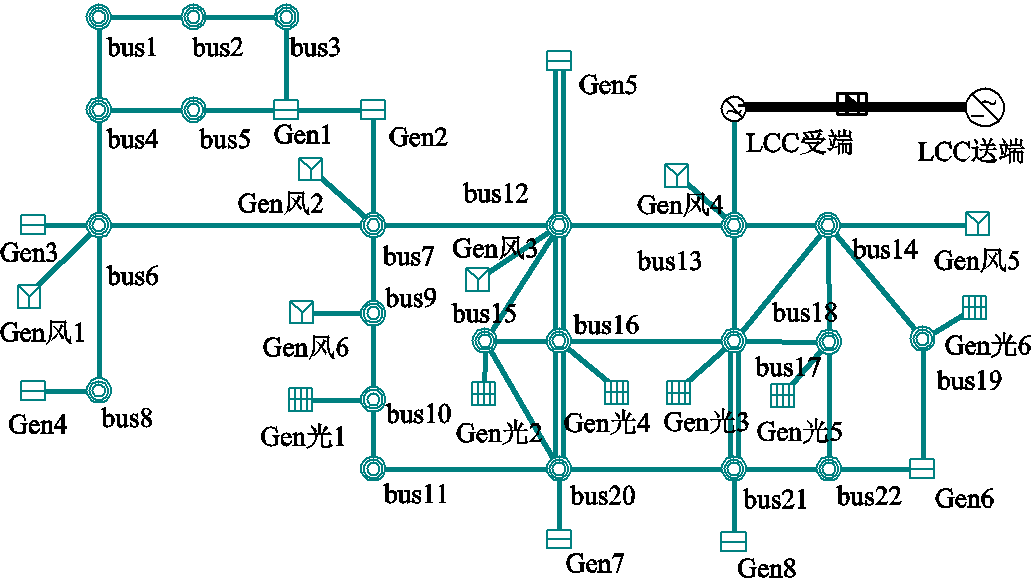
附图1 CEPRI-VC标准算例接线图
App.Fig.1 Diagram of CEPRI-VC benchmark system
附表1 CEPRI-VC标准算例感应电动机参数
App.Tab.1 Parameters of induction motor in CEPRI-VC benchmark system
参数数值 惯性时间常数/s2.037 2 定子电阻(pu)0.033 1 定子电抗(pu)0.109 5 励磁电抗(pu)2.965 转子电阻(pu)0.019 2 转子电抗(pu)0.11
2. 万节点测试系统
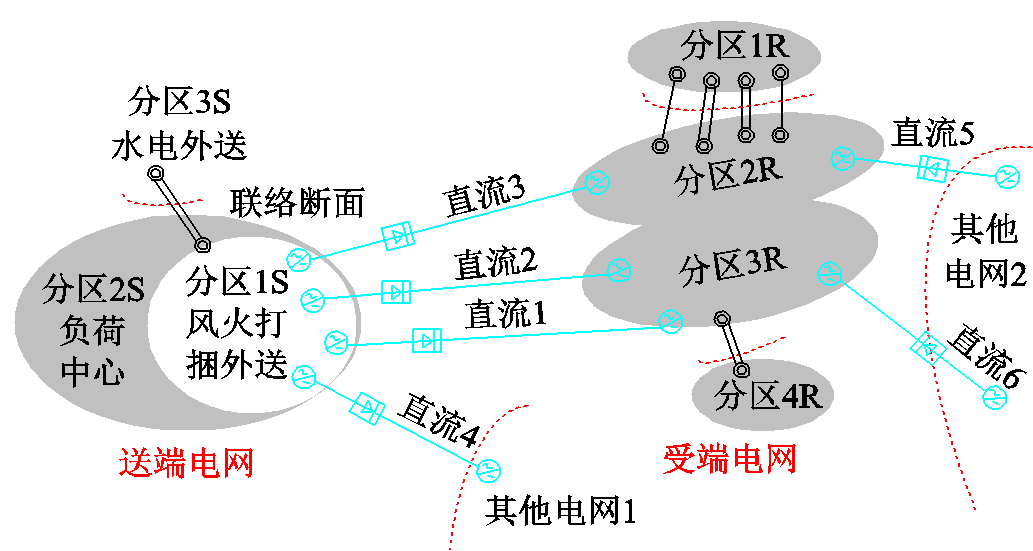
附图2 万节点测试系统示意图
App.Fig.2 Diagram of testing system with 10 575 buses
附表2 万节点测试系统感应电动机参数
App.Tab.2 Parameters of induction motor in testing system with 10 575 buses
参数数值 电动机惯性时间常数/s2 定子电阻(pu)0.02 定子电抗(pu)0.18 励磁电抗(pu)3.499 转子电阻(pu)0.02 转子电抗(pu)0.12
参考文献
[1] 刘文华, 宋强, 滕乐天, 等. 暂态电压稳定与新型动态无功补偿装置[J]. 电工技术学报, 2007, 22(7): 18-23.
Liu Wenhua, Song Qiang, Teng Letian, et al. Transient voltage stability and static synchronous compensator [J]. Transactions of China Electrotechnical Society, 2007, 22(7): 18-23.
[2] 杨金洲, 李业成, 熊鸿韬, 等. 基于阻抗的新能源接入的受端电网暂态电压失稳高风险故障快速筛选方法[J]. 电工技术学报, 2024, 39(21): 6746-6758.
Yang Jinzhou, Li Yecheng, Xiong Hongtao, et al. A fast screening method for the high-risk faults with transient voltage instability in receiving-end power grids interconnected with new energy based on impedance [J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6746-6758.
[3] 冉慧娟, 王治钟, 高本锋, 等. 适用于高压直流输电受端系统的两阶段暂态电压评估方法[J]. 电网技术, 2023, 47(10): 4272-4284.
Ran Huijuan, Wang Zhizhong, Gao Benfeng, et al. Two-stage transient voltage evaluation suitable for HVDC receiving systems[J]. Power System Technology, 2023, 47(10): 4272-4284.
[4] 杨浩, 伍柏臻, 刘铖, 等. 基于暂态关键特征逻辑推理的复杂电网响应驱动暂态稳定性判别[J]. 电工技术学报, 2024, 39(13): 3943-3955.
Yang Hao, Wu Baizhen, Liu Cheng, et al. Response-driven transient stability assessment for complex power grids based on logical reasoning with transient key feature[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3943-3955.
[5] 郑超, 孙华东, 曲仝. 基于广域支路响应的电压失稳主动解列控制[J]. 中国电机工程学报, 2021, 41(22): 7563-7574.
Zheng Chao, Sun Huadong, Qu Tong. Active splitting control of voltage instability based on wide area branches' response[J]. Proceedings of the CSEE, 2021, 41(22): 7563-7574.
[6] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[7] 刘乔, 王俊生. 背靠背直流输电故障闭锁后过电压分析和优化[J]. 电气技术, 2024, 25(3): 79-84.
Liu Qiao, Wang Junsheng. Analysis and optimization of overvoltage after fault blocking in back-to-back DC transmission[J]. Electrical Engineering, 2024, 25(3): 79-84.
[8] 王奕鑫, 唐宇, 叶琳, 等. 多馈入直流系统电压稳定中静态负荷影响的定量分析和评估方法[J]. 电工技术学报, 2024, 39(23): 7379-7393.
Wang Yixin, Tang Yu, Ye Lin, et al. Quantitative analysis and evaluation method for the impact of static loads on voltage stability in multi-infeed direct current systems[J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7379-7393.
[9] 韩圣泽. 暂态电压稳定评估方法综述[J]. 电工技术, 2023(4): 166-170.
Han Shengze. Survey of transient voltage stability evaluation methods[J]. Electric Engineering, 2023(4): 166-170.
[10] 詹富均. 基于能量函数法的电力系统暂态电压稳定域研究[D]. 广州: 华南理工大学, 2017.
Zhan Fujun. Research on transient voltage stability region of power system based on energy function method[J]. Guangzhou: South China University of Technology, 2017.
[11] 刘晔, 沈沉. 交直流混联系统的能量函数构造方法综述与探究[J]. 中国电机工程学报, 2022, 42(8): 2842-2853.
Liu Ye, Shen Chen. Review and research on construction methods of energy function for hybrid AC-DC power system[J]. Proceedings of the CSEE, 2022, 42(8): 2842-2853.
[12] 孙元章, 王志芳. 负荷恢复模型对电压无功稳定性的影响[J]. 电力系统自动化, 1997, (1): 33-36.
Sun Yuanzhang, Wang Zhifang. Dynamic load restoration modeling and its impact on voltage stability[J]. Automation of Electric Power Systems, 1997, (1): 33-36.
[13] 王青子, 袁小明. 异步电动机幅相运动方程模型及动态过程机理分析[J]. 中国电机工程学报, 2021, 41(1): 363-373, 425.
Wang Qingzi, Yuan Xiaoming. Amplitude-phase motion equation model of induction motor and analysis of dynamic process mechanism[J]. Proceedings of the CSEE, 2021, 41(1): 363-373, 425.
[14] 李文俏, 王振树, 李中强. 基于分岔理论的负荷模型对交直流混联系统电压稳定性的影响[J]. 电力自动化设备, 2020, 40(11): 144-149.
Li Wenqiao, Wang Zhenshu, Li Zhongqiang. Influence of bifurcation theory based load model on voltage stability of AC/DC hybrid system[J]. Electric Power Automation Equipment, 2020, 40(11): 144-149.
[15] Balanathan R, Pahalawaththa N C, Annakkage U D. Modelling induction motor loads for voltage stability analysis[J]. International Journal of Electrical Power & Energy Systems, 2002, 24(6): 469-480.
[16] 张文朝, 张博, 潘捷, 等. 基于感应电动机网荷互馈特性的暂态电压失稳机理探析[J]. 电力系统自动化, 2017, 41(7): 8-14.
Zhang Wenchao, Zhang Bo, Pan Jie, et al. Mechanism analysis for transient voltage instability based on crossfeed characteristics between power network and load of induction motor[J]. Automation of Electric Power Systems, 2017, 41(7): 8-14.
[17] 罗华伟, 吴政球, 戴庆华, 等.电网戴维南等值参数的快速计算[J]. 中国电机工程学报, 2009, 29(1): 35-39.
Luo Huawei, Wu Zhengqiu, Dai Qinghua, et al. Fast computation of thevenin equivalent parameters[J]. Proceedings of the CSEE, 2009, 29(1): 35-39.
[18] 吕钦刚. 基于戴维南等值参数解析辨识的中长期电压稳定在线监视[D]. 哈尔滨: 哈尔滨工业大学, 2019.
Lü Qingang. On-line monitoring of mid-long term voltage stability based on the analytical identification method of Thevenin equivalent parameters[D]. Harbin: Harbin Institute of Technology, 2019.
[19] 郑超, 孙华东, 陈怡君. 基于广域支路响应特征的失稳预判与紧急控制[J]. 中国电机工程学报, 2021, 41(17): 5866-5877.
Zheng Chao, Sun Huadong, Chen Yijun. Instability prejudge and emergency control based on the response characteristic of wide-area branches[J]. Proceedings of the CSEE, 2021, 41(17): 5866-5877.
[20] 邓晖, 赵晋泉, 吴小辰, 等. 基于受扰电压轨迹的电力系统暂态失稳判别: (一)机理与方法[J]. 电力系统自动化, 2013, 37(16): 27-32, 46.
Deng Hui, Zhao Jinquan, Wu Xiaochen, et al. Transient instability detection of power system based on perturbed voltage trajectories part one theory and method[J]. Automation of Electric Power Systems, 2013, 37(16): 27-32, 46.
[21] 邓晖, 赵晋泉, 吴小辰, 等. 基于受扰电压轨迹的电力系统暂态失稳判别(二)算例分析[J]. 电力系统自动化, 2013, 37(17): 58-63.
Deng Hui, Zhao Jinquan, Wu Xiaochen, et al. Transient instability detection of power system based on perturbed voltage trajectories part two case analysis[J]. Automation of Electric Power Systems, 2013, 37(17): 58-63.
[22] 王长江, 姜涛, 陈厚合, 等. 基于相位校正李雅普诺夫指数的电力系统暂态电压稳定评估[J]. 电工技术学报, 2021, 36(15): 3221-3236.
Wang Changjiang, Jiang Tao, Chen Houhe, et al. Transient voltage stability assessment of power systems based on phase correction maximum Lyapunov exponent[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3221-3236.
[23] 张晓英, 高金, 王琨, 等. 基于电压时间序列的电力系统暂态电压稳定分析[J]. 智慧电力, 2021, 49(3): 51-58.
Zhang Xiaoying, Gao Jin, Wang Kun, et al. Transient voltage stability analysis of power system based on voltage time series[J]. Smart Power, 2021, 49(3): 51-58.
[24] 薛安成, 周健, 刘瑞煌, 等. 采用多二元表判据的实用暂态电压稳定裕度指标研究[J]. 中国电机工程学报, 2018, 38(14): 4117-4125, 4317.
Xue Ancheng, Zhou Jian, Liu Ruihuang, et al. A new practical transient voltage stability margin index based on multiple-two-element notation criterion[J]. Proceedings of the CSEE, 2018, 38(14): 4117-4125, 4317.
[25] 郑超, 孙华东, 赵兵. 基于关键支路sBTTC指数幅相相关性的主导稳定形态判别与多级主动控制[J]. 中国电机工程学报, 2022, 42(7): 2474-2486.
Zheng Chao, Sun Huadong, Zhao Bing. Dominant stability mode discrimination and multilevel stability control based on amplitude-phase correlation of critical branch’s sBTTC index[J]. Proceedings of the CSEE, 2022, 42(7): 2474-2486.
[26] 汤涌, 仲悟之, 孙华东, 等. 电力系统电压稳定机理研究[J]. 电网技术, 2010, 34(4): 24-29.
Tang Yong, Zhong Wuzhi, Sun Huadong, et al. Study on mechanism of power system voltage stability[J]. Power System Technology, 2010, 34(4): 24-29.
[27] 汤涌, 易俊, 孙华东, 等. 基于功率电流变化关系的电压失稳判别方法[J]. 中国电机工程学报, 2010, 30(28): 7-11.
Tang Yong, Yi Jun, Sun Huadong, et al. Voltage instability criterion based on variation relationship of power and current[J]. Proceedings of the CSEE, 2010, 30(28): 7-11.
[28] 赵兵, 徐式蕴, 兰天楷, 等. 新型电力系统标准算例(3)：电压稳定CSEE-VS[J]. 中国电机工程学报, 2024, 44(21): 8353-8364.
Zhao Bing, Xu Shiyun, Lan Tiankai, et al. Benchmark for AC-DC hybrid system with high penetration of renewables (3): voltage stability benchmark CSEE-VS[J]. Proceedings of the CSEE, 2024, 44(21): 8353-8364.
[29] 沈一鸣. 基于电网稳态及暂态量测数据的负荷模型参数辨识方法研究[D]. 杭州: 浙江大学, 2022.
Shen Yiming. Research on load model parameters identification method based on power system steady-state and transient measurement data[D]. Hangzhou: Zhejiang University, 2022.
[30] 国家市场监督管理总局, 国家标准化管理委员会. 电力系统安全稳定导则: GB 38755—2019[S]. 北京: 中国标准出版社, 2019.
[31] 国家市场监督管理总局, 国家标准化管理委员会. 电力系统安全稳定计算规范: GB/T 40581—2021[S]. 北京: 中国标准出版社, 2021.
[32] 甄永赞, 阮程. 基于代价敏感支持向量机和多变量决策树的分级自适应暂态电压稳定评估[J]. 电网技术, 2024, 48(2): 778-791.
Zhen Yongzan, Ruan Cheng. Hierarchical self-adaptation transient voltage stability assessment based on cost-sensitive SVM and multivariate decision tree [J]. Power System Technology, 2024, 48(2): 778-791.
Transient Voltage Instability Identification Based on Positive-Feedback Unstable Region Mapped by Power Factor during Load Dynamics
Abstract New-type modern power systems require the emergency control responding to system transients more than event-records. Hence the identification of voltage instability using the measurable electrical quantities and the positive-feedback mechanism is more adapted to such requirement. However, the conventional and typical criteria of such a kind are derived from Thevenin equivalent circuit. They are possibly difficult to capture the exactly-same measurement consistent to ideal Thevenin equivalence, when they are applied on practical power grids. If the system voltage drops rapidly, these criteria are also prone to invalidity for some intermittent short-periods, causing time-delay of judgement.
This paper aimed to promote the performance of the response-driven identification on the transient voltage instability by deriving the criteria from the deduction on essential dynamics. The mechanism of such instability due to load dynamics was found out to be associated with the intrinsic feature of power-recovery in loads. Then the unstable region in mathematics could be formulated by the state variables of loads’ equivalent resistance in the differential equations modeling such a power-recovery feature. The positive-feedback characteristics in the unstable region were depicted on the basis of these state variables. The consistency in the changing trend between power factor and these state variables during voltage transients was discussed. The criteria mapping the positive-feedback unstable region with power factor and equivalent power quantities were proposed. The adaptability of the proposed criteria was explored, emphasizing the analysis on why the conventional positive-feedback criteria tend to be invalid in the scenario of rapid voltage-drop.
The proposed criteria were validated by the benchmark system, namely China Electric Power Research Institute’s Voltage Collapse (CEPRI-VC) system, as well as the ten-thousand-node testing system with 10575 buses in specific. The results confirmed the effectiveness of the proposed positive-feedback criteria mapping the unstable region by power factor. The proposed criteria resulted in the missing alarm rate (MAR) of 0% in both systems. They also resulted in the false alarm rate (FAR) of 8.50% in CEPRI-VC system and 2.38% in the ten-thousand-node testing system, respectively. The performance of the proposed criteria could be promoted furtherly by increasing the parameter of criteria-holding duration threshold and/or decreasing the parameter of voltage-safety threshold. Fig.9 and Fig.15 demonstrated the variation of relevant electrical quantities during transients in case of voltage instability. They indicated the judgement process of the proposed criteria, which were always satisfied even if voltage dropped rapidly. The figures also showed the intermittent failures in the conventional criteria, explaining why they retarded the discrimination speed.
This paper reached the following conclusions. The unstable region depicted by the dynamics of equivalent resistance in load model of power recovery can reflect the essential mechanism of transient voltage instability. There exists the consistent variation between power factor and the equivalent load resistance in unstable region of voltage transient instability. Mapping the unstable region with the positive-feedback variation of power factor can facilitate the construction of measurable criteria. The proposed criteria get rid of the constraint of voltage variation speed on the judgement accuracy, demonstrating robustness in case that the voltage drops rapidly.
Keywords：Power factor, transient voltage instability, positive feedback, unstable region
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241494
国家重点研发计划资助项目（2021YFB2400800）。
收稿日期 2024-08-26
改稿日期 2024-11-19
王晓辉 男，1979年生，博士，副教授，研究方向为电力电子化电力系统分析与控制。
E-mail：wangxiaohui@sdu.edu.cn
党崇阳 男，1999年生，硕士研究生，研究方向为响应驱动的受端电网暂态电压稳定判别。
E-mail：dcy04272021@163.com（通信作者）
（编辑 赫 蕾）