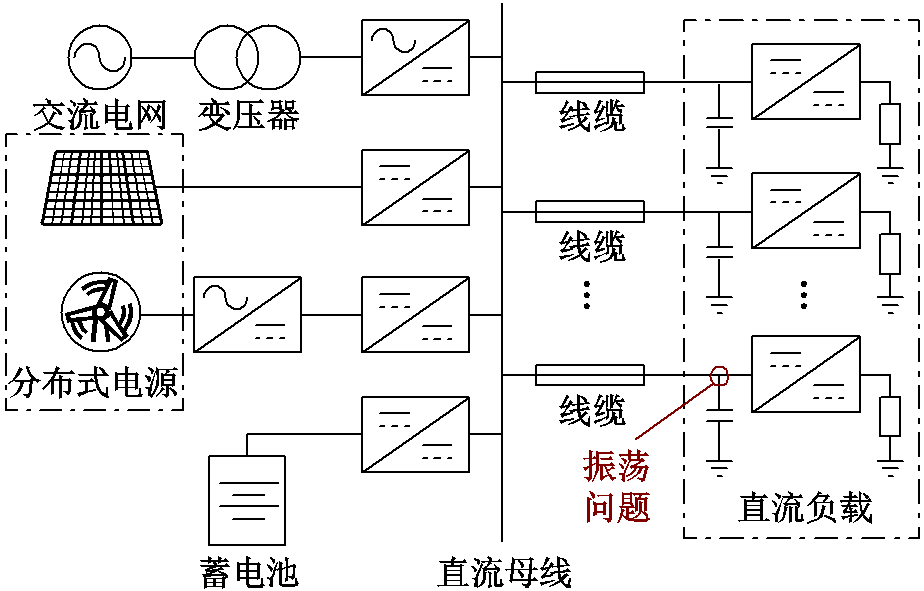
图1 直流配电系统结构示意图
Fig.1 Structure of DC distribution power system
摘要 直流配电系统中电力电子设备分布集中,总体呈现弱阻尼特性,易引发一系列小信号稳定性问题。随着人工智能集群计算等供电需求的大幅增长,供电密度相应提升,使得阻抗不匹配点逐渐向高频段移动,尤其是数字控制延时所导致的高频振荡问题逐渐凸显。针对此问题,该文提出一种基于相位补偿器的直流配电系统高频振荡抑制策略,首先考虑了系统中的数字控制延时,构建级联直流系统的修正阻抗小信号模型,提升高频段建模结果的准确性;然后,基于修正模型,对配电系统进行了高频振荡机理的分析;最后,考虑高频振荡的主要影响因素,提出了相位补偿策略,通过修改系统的控制回路重塑负载变换器的闭环输入阻抗,对直流配电系统中的高频振荡进行有效抑制,提升系统的供电稳定性。在240 V直流配电系统中对该方法进行了测试,实验结果验证了系统稳定性分析结果的正确性以及相位补偿策略的良好性能。
关键词:相位补偿 直流配电系统 高频振荡 小信号稳定性 数字控制
随着可再生能源分布式发电和以电动汽车为主的直流负荷的快速发展,直流配电系统由于具有高效、易维护、灵活可控等特点而被广泛关注,大量应用于数据中心、楼宇供电、空间站及舰船等领域[1-4]。典型直流配电系统的结构示意图如图1所示。为保证稳定的直流母线电压,蓄电池通常被安置在靠近直流母线的位置,而远端的直流负载则通过长线缆连接到直流母线上。可见,直流配电系统中包含众多电力电子设备,使得系统惯性及阻尼降低,从而引起变换器端口的振荡现象,具体表现为直流负载输入端电压电流大幅度波动、交流侧功率因数降低等问题,同时带来不可避免的异常高频噪声[5-8]。

图1 直流配电系统结构示意图
Fig.1 Structure of DC distribution power system
级联结构是直流配电系统中最基本的连接形式[9],因此可将直流配电系统简化为级联系统进行稳定性问题分析。对于级联系统的小信号稳定性问题多聚焦于负载变换器作为恒功率负载时的负阻抗特性所导致的低频振荡问题,相关学者已通过采用在级联端口加入无源器件的无源方法[10]或修改系统控制回路重塑系统阻抗的有源方法[11-14]等,有效地解决了低频振荡问题。然而,随着人工智能(Artificial Intelligence, AI)集群计算等供电需求的大幅增长,系统供电密度要求相应提高。为满足功率密度要求,直流配电网中负载变换器趋向于降低输入电容值,这就会使阻抗不匹配点移至高频段。而由于数字控制系统的高可靠性及灵活性,系统中的电力电子设备多采用数字控制,由此带来的延时就会导致高频振荡问题的产生。因此为不影响下一代高密度高效电源的改进,直流配电系统中的高频振荡问题亟须解决。
目前对于数字控制导致的延时问题已有较为广泛的研究,主要有两种解决方案。一种是直接减少数字控制延时,文献[15]采用过采样的方式,通过提高采样率减小计算延时,但会引入开关噪声,造成信号混叠,对系统控制造成不良影响。当数字控制环路延时难以直接减小时,就需要采用第二种方法,通过控制策略对延时进行补偿。文献[16]使用状态预估延时补偿法,重塑并网逆变器输出阻抗,从而提高系统稳定性,但该方法的效果依赖于模型预测的准确性。文献[17]采用陷波器改进延时补偿策略,但对谐振频率的准确性较为敏感。文献[18-21]分别采用不同形式的相位补偿器补偿数字控制延时带来的相位滞后,该方法不受预测信息影响,相比于状态观测器和陷波器更具有普适性,但会由于相位补偿器在Nyquist频率附近的增益过大而导致高频噪声放大。文献[22]在电网电压前馈中加入带通滤波器,并在比例谐振控制器上并联谐波补偿器,以提高并网系统鲁棒性,并抑制电网电压谐波。文献[23]采用类似方法,针对控制延时对风电场侧换流站阻抗的影响进行深入分析,在电压前馈通路中加入低通滤波器,并在电压控制项中引入虚拟阻抗,以消除延时对高频阻抗的影响。可见,现有控制策略的研究大多基于交流场景,如风电场、并网逆变器等,而对于直流场景下高频振荡的抑制策略鲜有研究。
鉴于此,本文提出了一种适用于直流配电系统的相位补偿策略。首先,考虑实际系统中的数字控制环路中各环节的影响,构建了负载变换器的修正小信号模型,并通过Matlab/Simulink仿真平台进行频率扫描,与理论建模结果进行对比,验证了模型的准确性;其次,基于修正模型,进一步分析了直流配电系统中的稳定性问题以及高频振荡问题的主要影响因素;然后,在控制回路中添加相位超前补偿器,并对补偿器参数进行详细设计,理论分析了所添加策略对系统稳定性能的提升以及动态性能的影响;最后,搭建了一个3 kW、240~400 V的级联系统对所提出的相位补偿策略的稳定性能及动态性能进行了实验验证,证明了理论分析的正确性及所提方法的有效性。
在数据中心、空间站及船舶供电系统等领域,为保证直流配电系统的高可靠性,直流母线电压由交流电网经不间断电源(Uninterrupted Power Supply, UPS)和蓄电池等不同类型的电源提供,故该情况下将直流母线简化为一稳定电压源,得到简单的直流配电系统。为便于稳定性分析,母线引出的多条线缆间进行进一步解耦,将直流配电系统简化为线缆和变换器构成的级联直流系统,线缆-Boost变换器级联系统结构如图2所示。将直流母线电压视为稳压源Vdc,长距离线缆等效为电感Lw和电阻Rw,Cin为负载变换器的输入电容,并将其划入源侧。负载变换器为一电流模式控制的Boost变换器。利用阻抗判据[24]分析系统稳定性时,需要分别对源侧输出阻抗Zs_out及负载侧输入阻抗Zl_in进行建模。
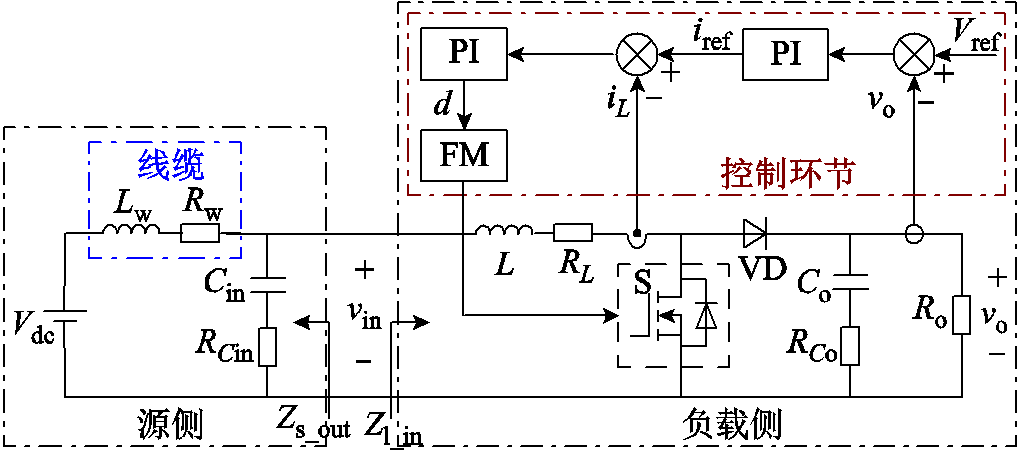
图2 线缆-Boost变换器级联系统结构
Fig.2 Structure of the cascaded system with cable and Boost converter
Boost变换器的闭环控制框图如图3所示。其中,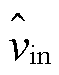 、
、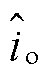 、
、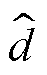 、
、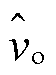 、
、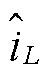 、
、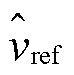 、
、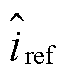 分别为输入电压、输出电流、占空比、输出电压与电感电流及其参考值的小信号扰动变量,Gvg(s)、Zout(s)、Gvd(s)、Yin(s)、Gio(s)、Gid(s)为通过状态空间平均法建立的Boost开环小信号传递函数,表达式见表1,Gv(s)、Gi(s)分别为系统电压环和电流环补偿器的传递函数,均采用PI控制。红色框图部分为数字控制等效环节,忽略数字控制延时时,控制延时Gd(s)、电流采样延时Gsh_i(s)以及电压采样延时Gsh_v(s)视为1。
分别为输入电压、输出电流、占空比、输出电压与电感电流及其参考值的小信号扰动变量,Gvg(s)、Zout(s)、Gvd(s)、Yin(s)、Gio(s)、Gid(s)为通过状态空间平均法建立的Boost开环小信号传递函数,表达式见表1,Gv(s)、Gi(s)分别为系统电压环和电流环补偿器的传递函数,均采用PI控制。红色框图部分为数字控制等效环节,忽略数字控制延时时,控制延时Gd(s)、电流采样延时Gsh_i(s)以及电压采样延时Gsh_v(s)视为1。
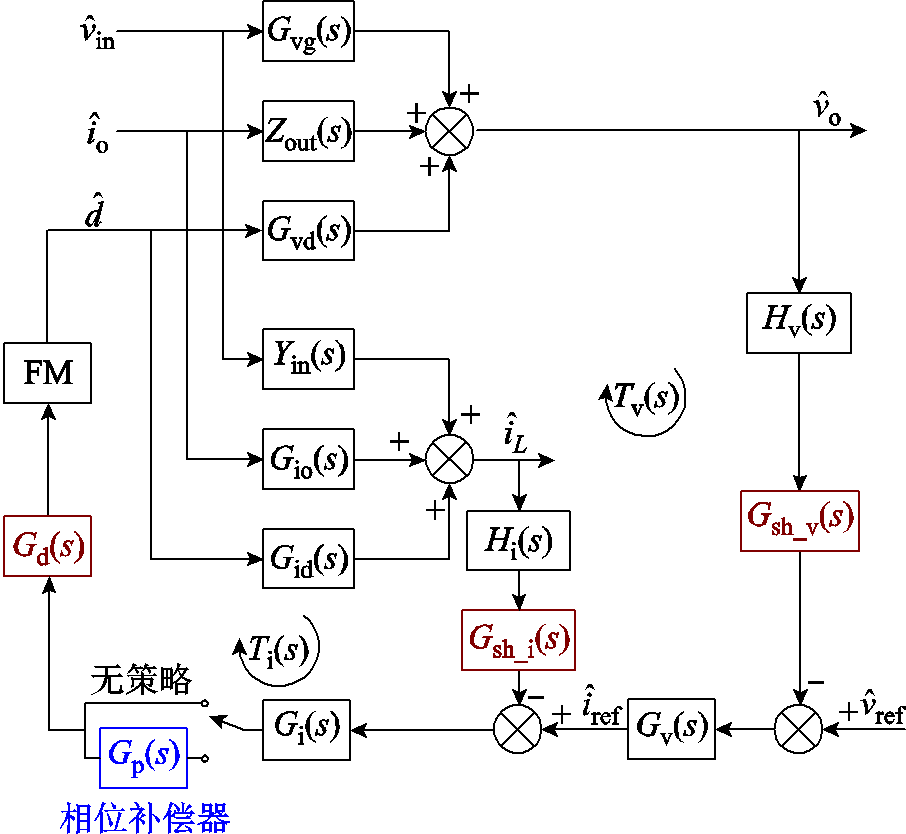
图3 Boost变换器闭环控制框图
Fig.3 Closed loop small-signal control block diagram of Boost converter
表1 Boost开环小信号传递函数
Tab.1 Open loop small-signal transfer functions of Boost converter

物理意义表达式 音频灵敏度 输出阻抗 控制到输出电压传递函数 输入导纳 反向电流比 控制到电感电流传递函数
表1中,Vin、Ro和D分别为Boost变换,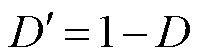 ,
,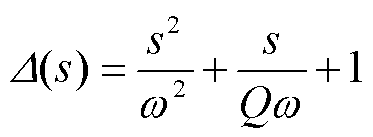 ,
,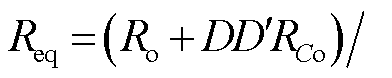
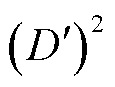 ,
,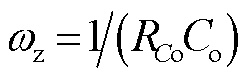 ,
,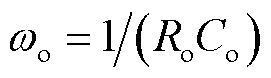 ,
,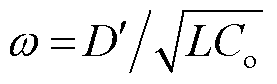 ,
,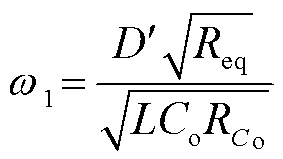 ,
,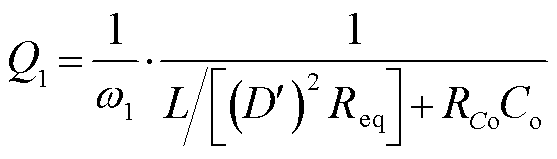 ,
,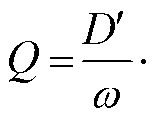
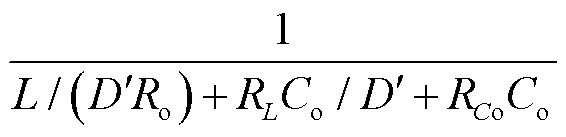 ,L、Co和
,L、Co和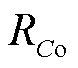 分别为Boost变换器的电感、输出电容及其等效串联电阻值。
分别为Boost变换器的电感、输出电容及其等效串联电阻值。
根据图3所示的控制框图,由梅森增益公式可求解得到忽略数字控制延时的情况下,Boost闭环输入阻抗Zl_inc为
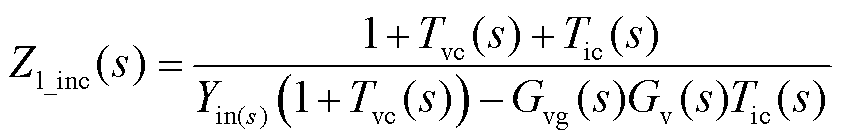 (1)
(1)
式中,Tvc(s)、Tic(s)分别为忽略数字控制延时的情况下电压环、电流环环路增益,表示为
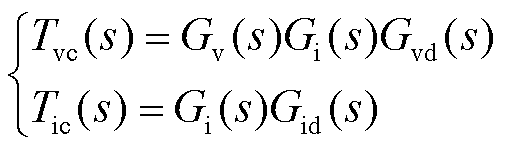 (2)
(2)
该阻抗模型能够保证在低频段的准确性,常用于低频振荡问题的分析[10, 12-14]。然而,实际中的数字控制所导致的延时会对系统高频段特性产生影响[25-26],此时一般阻抗模型的准确性不足以支撑高频振荡问题的分析。因此在建模过程中需要考虑数字控制环节对系统的影响,得到准确的小信号模型,为后续的稳定性分析奠定基础。
数字控制环路中主要包括采样保持、数字补偿器和数字脉宽调制(Pulse Width Modulation, PWM)等环节。
对于采样保持环节,采样开关的影响根据采样原理可等效为采样周期的倒数,同时保持效果可利用零阶保持器进行等效,因此得到采样保持在连续域中的传递函数Gsh(s)为
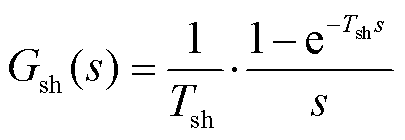 (3)
(3)
式中,Tsh为采样周期。
对于数字补偿器,由于连续时间补偿器和双线性变换后补偿器频率特性曲线基本一致,仅在接近奈奎斯特采样频率处开始产生区别,因此数字补偿器可直接使用其s域小信号模型。
对于数字PWM,其导致的环路中的控制延时主要包括数字信号微处理器带来的计算延时和数字调制器的采样特性带来的调制延时,调制延时的时间取决于数字PWM的调制形式,具体见表2,其中,Ts为开关管的开关周期。因此,控制延时构成的传递函数可表示为
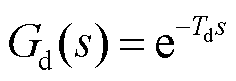 (4)
(4)
式中,Td为环路中的控制延时,由调制延时Tm和计算延时Tc构成。
表2 不同数字PWM调制形式下的调制延时
Tab.2 Modulation delay time under different digital PWM modulation forms

调制方式调制延时Tm 前沿调制DTs 后沿调制(1-D)Ts 对称调制Ts/2
采样保持环节传递函数形式较为复杂,且延时项e-τs的存在不利于传递函数的求解,其不包含零极点信息,利用根轨迹等方式进行分析时不能完全体现其对系统的影响,因此常需要对其进行简化及近似。下面对采样保持环节进行近似。
1)近似方法一:将采样保持环节近似为
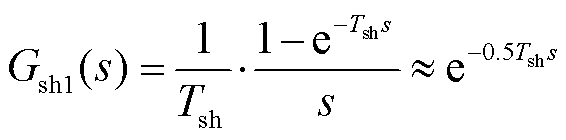 (5)
(5)
便于与控制延时合并。
2)近似方法二:直接对采样保持环节中的延时项进行泰勒展开,得到
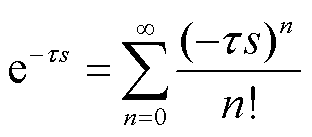 (6)
(6)
式中,n为Padé近似的阶数,阶数越高则精度越高,同时表达式也越复杂,这里保留3次项对延时项进行近似,得到
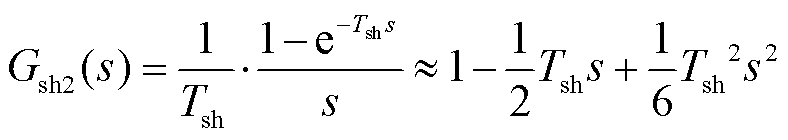 (7)
(7)
3)近似方法三:通过对采样保持环节中延时项的倒数进行泰勒展开得到其近似形式为
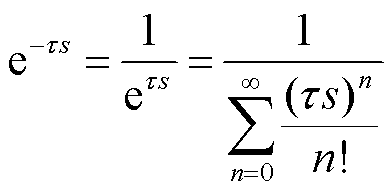 (8)
(8)
通常将其近似为一阶惯性环节1/(τs+1),则采样保持环节可被近似为
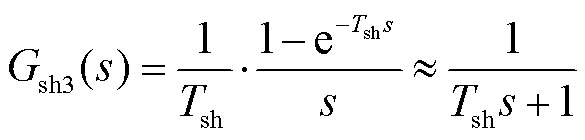 (9)
(9)
该方法只在延时时间较小时具有较高精度,在大延时系统中往往具有较大误差。
4)近似方法四:将采样保持环节中的延时项利用有理式进行近似,最经典的方法为Padé近似,通常较泰勒近似更为准确,其表达式为
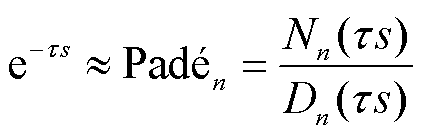 (10)
(10)
其中
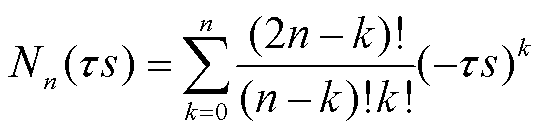 (11)
(11)
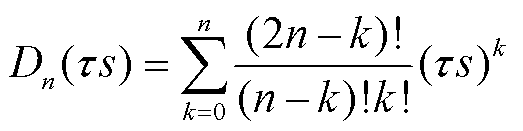 (12)
(12)
阶数越高则精度越高,同时表达式也越复杂,这里选用三阶Padé近似式对延时项进行近似,得到
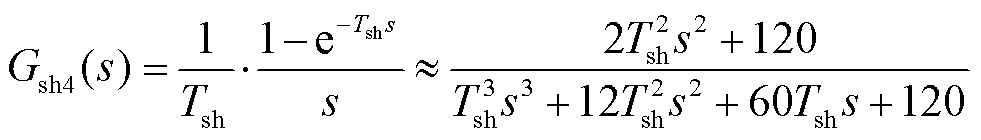 (13)
(13)
其中,近似方法一的近似结果中仍包含延时项,不利于传递函数的求解,故不采用近似方法一。近似方法二、三均基于泰勒级数展开对延时项进行近似,而近似方法四基于Padé逼近进行近似。一般情况下,要使得泰勒级数展开的估计误差小于Padé近似,需令泰勒级数展开的阶数为Padé近似阶数的2倍以上,这必然导致表达式阶数升高,不利于简化计算。故同样阶数下,Padé近似要比泰勒级数展开具有更高的准确性。因此,对于采样保持环节采用式(13)所示近似式,同时对于控制延时采用三阶Padé近似式进行近似,得到
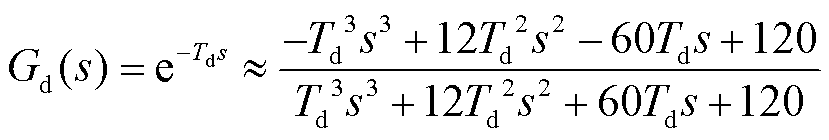 (14)
(14)
进一步,为展示频域下四种近似方法的近似效果,利用Mathcad对四种近似方法进行对比,设置采样周期Tsh=100 μs,得到伯德图如图4所示。近似方法一对相频特性近似效果较好,但幅频特性曲线在2 kHz处开始与原曲线产生差别。近似方法二对相频特性曲线拟合较好,但幅频特性曲线在2 kHz处开始抬升,误差较大。近似方法三对幅频特性曲线近似效果较好,但相频特性曲线在400 Hz处就开始产生较大误差。而近似方法四对原曲线的相频特性曲线及幅频特性曲线的近似在10 kHz之前都能够保持较高的准确性。
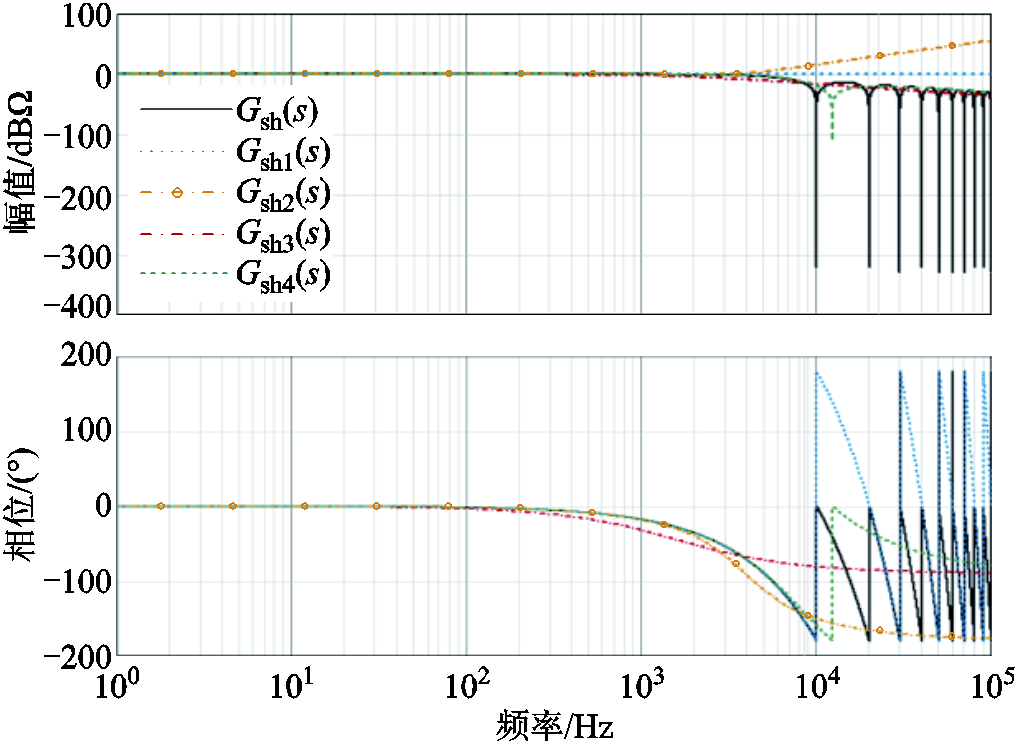
图4 不同近似方法下采样保持环节伯德图
Fig.4 Bode diagrams of the sampling holders with different approximation methods
因此考虑数字控制时,Boost闭环输入阻抗为
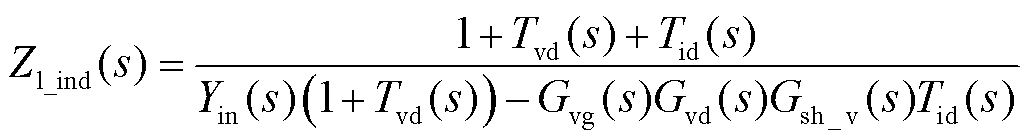 (15)
(15)
式中,Tvd(s)、Tid(s)分别为考虑数字控制时的电压环、电流环环路增益,表示为
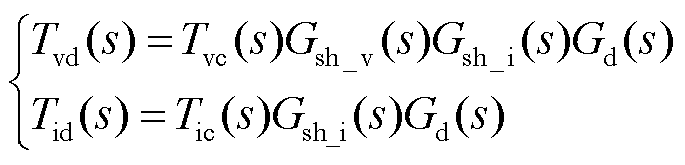 (16)
(16)
为验证所建立小信号阻抗模型的准确性,绘制Boost变换器修正前后的闭环输入阻抗理论建模及仿真扫频伯德图,并进行对比分析。
典型级联直流系统参数见表3。绘制系统闭环输入阻抗伯德图,并在Matlab/simulink中搭建离散的仿真模型进行扫频,扫频结果Zl_ins(s)与考虑数字控制前后的理论建模结果Zl_inc(s)、Zl_ind(s)对比如图5所示。对比修正前阻抗模型与扫频结果,修正前阻抗模型只在较低频段能够保证一定准确性,高频段特性与扫频结果会产生较大偏差,当阻抗不匹配发生于高频段时将会对系统稳定性的分析产生误导,凸显考虑数字控制延时对系统建立精确模型的必要性。对比修正后阻抗模型与仿真扫频结果,所建立的修正小信号模型无论在低频段还是高频段都能够保证高准确性,为后续的稳定性分析奠定坚实基础。对比修正前后的建模结果可得,数字延时抬升了负载变换器闭环输入阻抗在高频段的相位,使得系统高频段稳定性降低,易发生振荡。
表3 典型级联直流系统参数
Tab.3 Parameters of the cascaded DC system
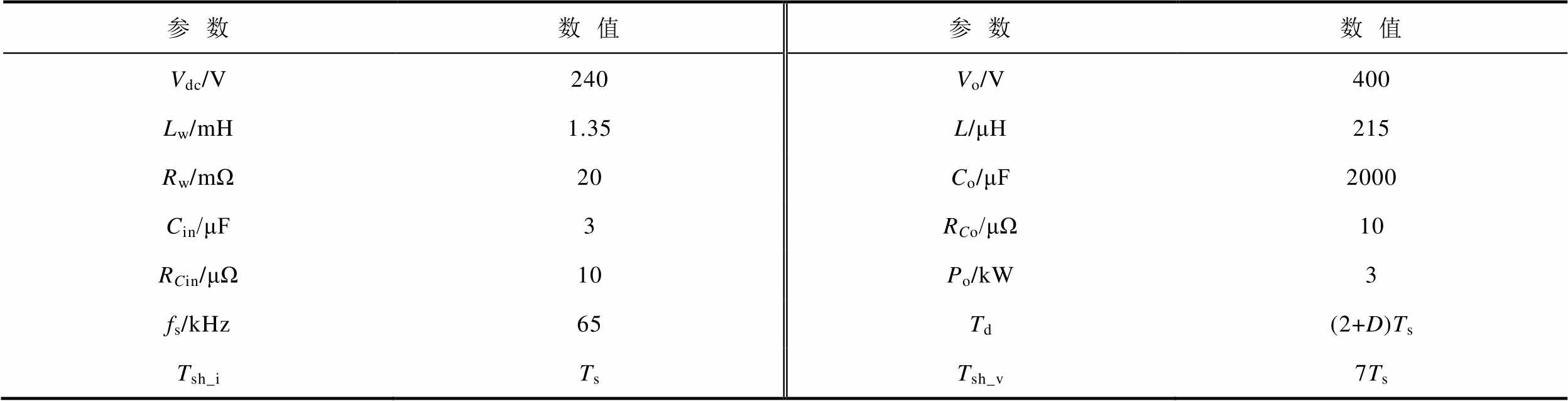
参数数值参数数值 Vdc/V240Vo/V400 Lw/mH1.35L/μH215 Rw/mΩ20Co/μF2000 Cin/μF3RCo/μΩ10 RCin/μΩ10Po/kW3 fs/kHz65Td(2+D)Ts Tsh_iTsTsh_v7Ts
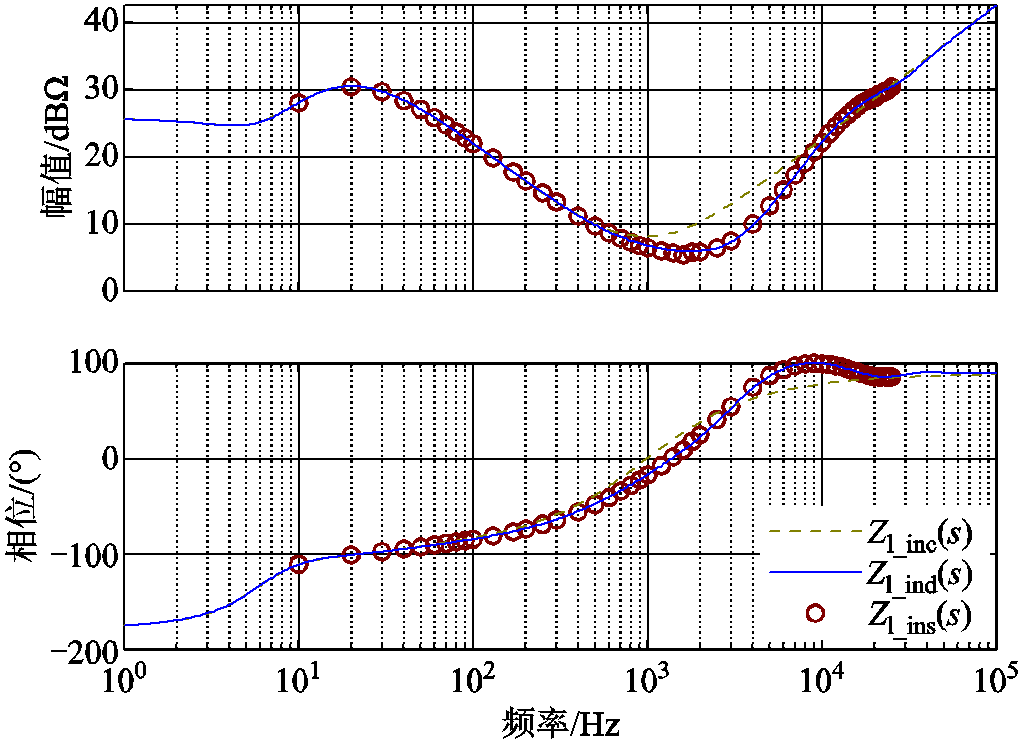
图5 Boost变换器闭环输入阻抗理论建模与扫频结果伯德图
Fig.5 Bode diagrams of theoretical modeling and sweep frequency result of closed loop input impedance of Boost converter
基于修正的负载变换器小信号模型对级联直流系统的稳定性进行分析,还需要对源侧输出阻抗进行建模。
图2中源侧输出阻抗可表示为
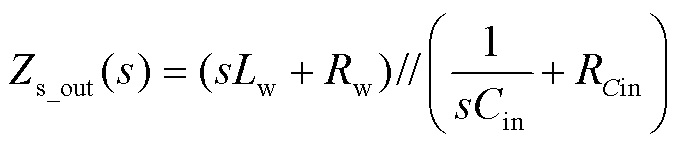 (17)
(17)
分别绘制不同输入电容情况下,级联直流系统的端口阻抗特性伯德图如图6所示。当输入电容较大时,负载变换器闭环输入阻抗Zl_in (s)和源侧输出阻抗Zs_out1 (s)在LC谐振频率fr1附近fi11和fi12处出现两个交点。当系统带宽较高时,交点发生的频点fi11处系统将呈现负阻抗特性,使得对应的相位差大于180°,系统发生低频振荡,并且实际振荡频率
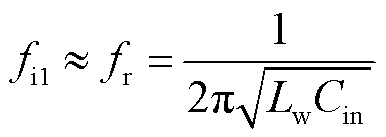 (18)
(18)
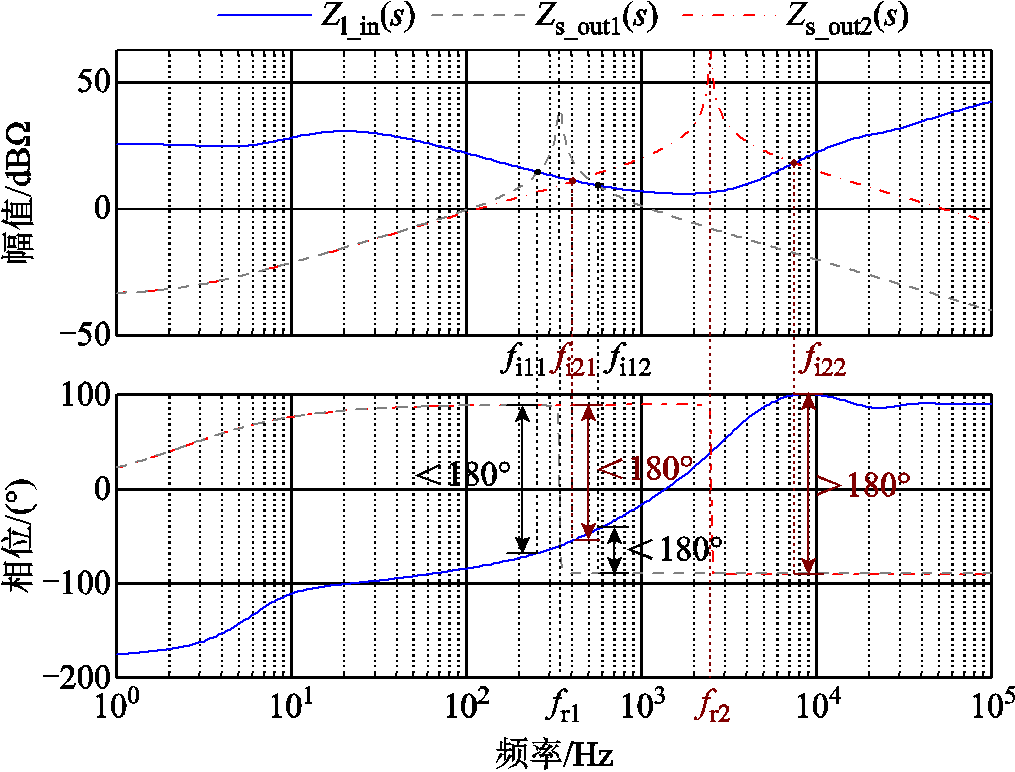
图6 级联系统端口阻抗特性伯德图
Fig.6 Bode diagrams of impedance characteristics of cascaded system
当输入电容较小时,Zl_in (s)和源侧输出阻抗Zs_out2 (s)在远离LC谐振频率fr2的fi21和fi22处出现两个交点。将fr2左侧的交点fi21称为低频交点,其右侧的交点fi22称为高频交点。根据级联系统阻抗判据,当低频交点对应的相位差大于180°时将会出现交点频率的低频振荡,而当高频交点对应的相位差大于180°时将会出现交点频率的高频振荡。
因此对于高压等级直流母线的直流配电网,其振荡问题可分为低频振荡和高频振荡两类。对于低频振荡问题,目前已有较为广泛的研究[10-14, 27],然而对于直流配电网中环路延时所导致的高频振荡问题研究较少,故本文主要对高频振荡的影响因素进行进一步分析。
根据图6对比可知,输入电容小是产生高频振荡的根本原因。当输入电容较大时,阻抗交叉主要发生在低频段,从根本上避免了高频振荡的发生。然而,当输入电容较小时,高频交点出现,此时当数字控制环路导致的延时较大时就会使得系统发生高频振荡。下面通过绘制级联系统奈奎斯特曲线分别对数字控制中三个主要环节(计算延时Tc、电流环采样周期Tsh_i及电压环采样周期Tsh_v)对系统稳定性的影响进行分析。
当计算延时Tc分别等于开关周期Ts和2Ts时,Tsh_v固定,改变Tsh_i观察系统稳定性,绘制级联系统奈奎斯特曲线如图7a、图7b所示,将系统幅值裕度h绘制柱状图如图8a所示。可以看到,当Tc=2Ts时,系统不稳定,随着Tsh_i的减小,系统稳定裕度增大,但仍为负值,系统始终存在高频振荡;当Tc=Ts时,系统稳定,但Tsh_i持续增大时会使得系统失稳。因此,Tc是影响高频振荡的主导因素,Tsh_i对系统稳定性次之,Tc、Tsh_i越大,系统稳定性越差。
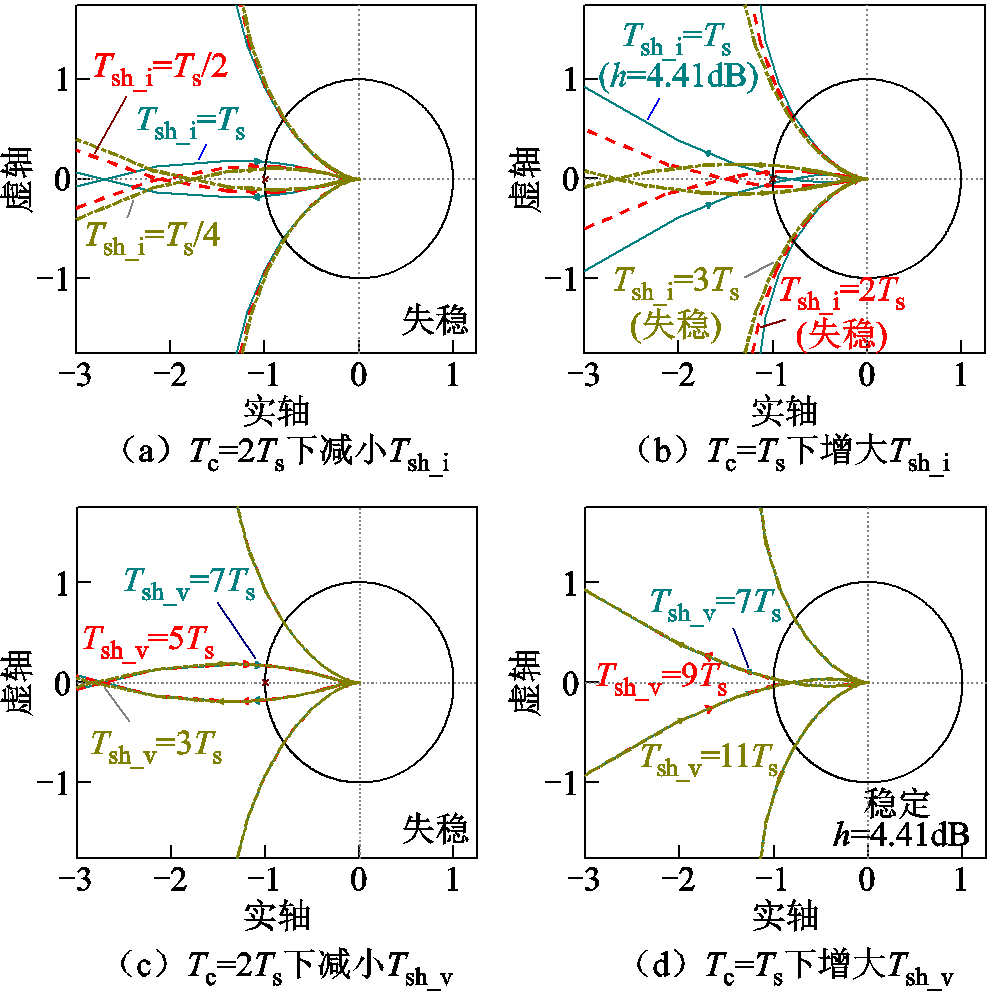
图7 各数字控制环节延时变化时系统奈奎斯特曲线
Fig.7 Nyquist diagrams of the system with the time delay of each digital control link changing
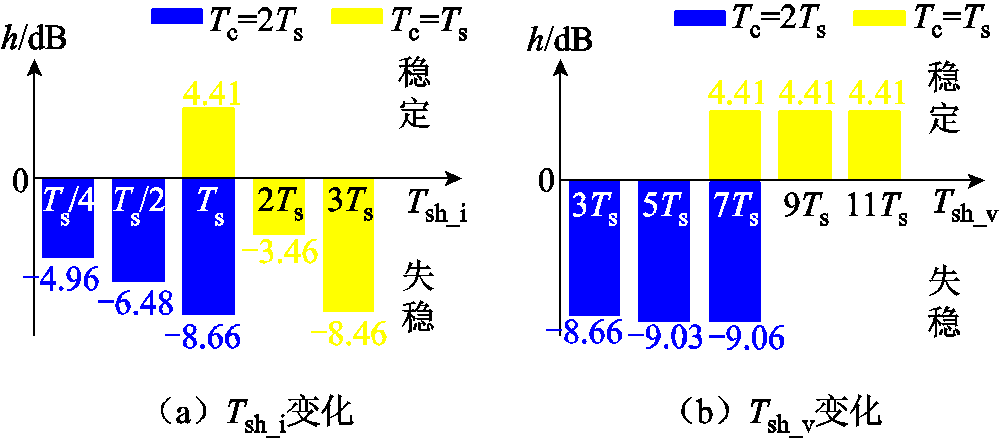
图8 各数字控制环节延时变化时系统稳定裕度柱状图
Fig.8 Histograms of system stability margin with the time delay of each digital control link changing
与分析Tsh_i的影响类似,令Tc分别等于开关周期Ts和2Ts时,Tsh_i固定,改变Tsh_v观察系统稳定性,绘制级联系统奈奎斯特曲线如图7c、图7d所示,将系统幅值裕度绘制柱状图如图8b所示。可以看到,Tsh_v对系统稳定性的影响很小,当Tc=2Ts时减小Tsh_v,系统持续失稳;当Tc=Ts时增大Tsh_v,系统仍保持稳定。
综上所述,输入电容小和数字控制延时大均为高频振荡的必要条件。其中,输入电容值决定潜在的振荡类型是由负载变换器负阻抗特性导致的低频振荡还是由数字控制延时导致的高频振荡;数字控制延时进一步对高频振荡是否发生产生影响,其中,计算延时对系统高频稳定性影响最大,其次是电流环延时,电压环延时的影响可忽略不计。
为解决数字控制带来的延时问题,根据前述高频振荡影响因素的分析,最直接的方式是增大输入电容。然而随着AI集群计算等供电需求的大幅增长,系统供电趋于高密度高效发展,较大的输入电容值与这一趋势相违背。因此本文通过补偿器对控制延时进行补偿。控制延时中对高频振荡产生影响的因素主要为计算延时和电流采样导致的电流环延时,故本文直接针对这两种因素进行补偿,提出一种相位超前补偿策略,在电流内环加入相位超前补偿器,从而补偿系统在高频段的相位,进一步抑制高频振荡的发生。
添加的相位超前补偿器能够在所设置的频率附近提供0°~45°的相位补偿功能,且对系统低频段的相幅特性影响较小。在连续域中该环节的传递函数表达式为
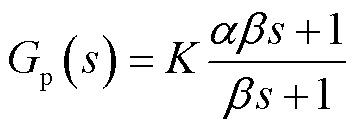 (19)
(19)
式中,α、β、K为该环节的补偿参数。参数α用来确定相位最大补偿量φ,如式(20)所示;参数β用来确定相位补偿中心频率fc,如式(21)所示;比例系数K用来调节该环节对系统幅值响应的影响,一般情况下取值范围为0~1。
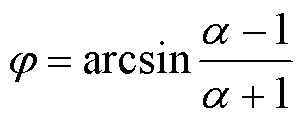 (20)
(20)
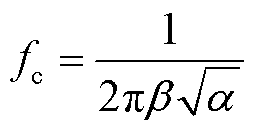 (21)
(21)
根据图3给出的加入相位超前补偿环节后的系统控制框图,由梅森增益公式得到引入相位补偿环节后的变换器输入导纳为
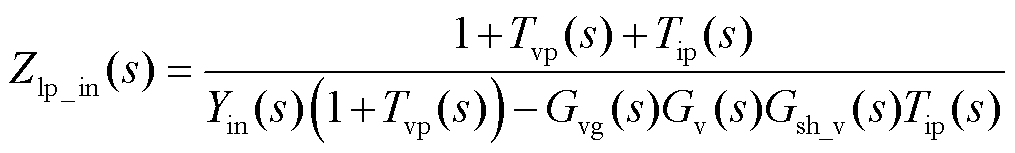 (22)
(22)
式中,Tvp(s)、Tip(s)分别为添加相位补偿环节后的电压环及电流环环路增益,表示为
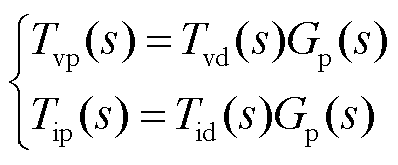 (23)
(23)
为指导相位补偿环节参数设计,进一步分析所提策略中各参数对系统稳定性的影响,固定比例系数K=0.4,改变相位最大补偿量φ及相位补偿中心频率fc绘制奈奎斯特曲线,进行理论分析,得到各参数情况下系统增益裕度曲面如图9所示。可以看到,随着φ增大,系统增益裕度单调递增,同时,随着fc增大,系统稳定性总体上呈现先增大后减小的趋势。当fc=10 kHz时,随着φ增大系统稳定性提升的速度最快,因此,最终选取fc=10 kHz,φ=45°作为最佳补偿参数。
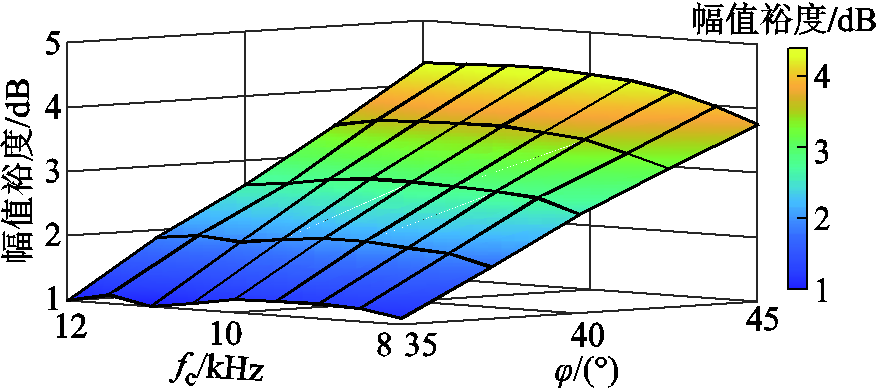
图9 不同补偿器参数下系统幅值裕度曲面
Fig.9 Surface diagram of system amplitude margin with different compensator parameters
当fc=10 kHz,φ=45°时改变K,绘制不同K下系统奈奎斯特曲线如图10所示。可见,随着K减小,系统稳定裕度增大,系统稳定性增强。然而当K<1时必然会使得电流环带宽降低,影响系统动态性能,因此在设计过程中需要对稳定性能与动态性能折中考虑,同时留有一定的稳定裕度,故选取K=0.4。
由3.2节分析,针对级联系统设计相位超前补偿策略φ=45°,fc=10 kHz,K=0.4。
为分析系统稳态性能,绘制系统添加相位补偿策略前后的端口阻抗特性伯德图如图11a所示,添加相位补偿策略后,系统4~11 kHz处的相位被压低,使得高频交点处的相位差小于180°,系统稳定。
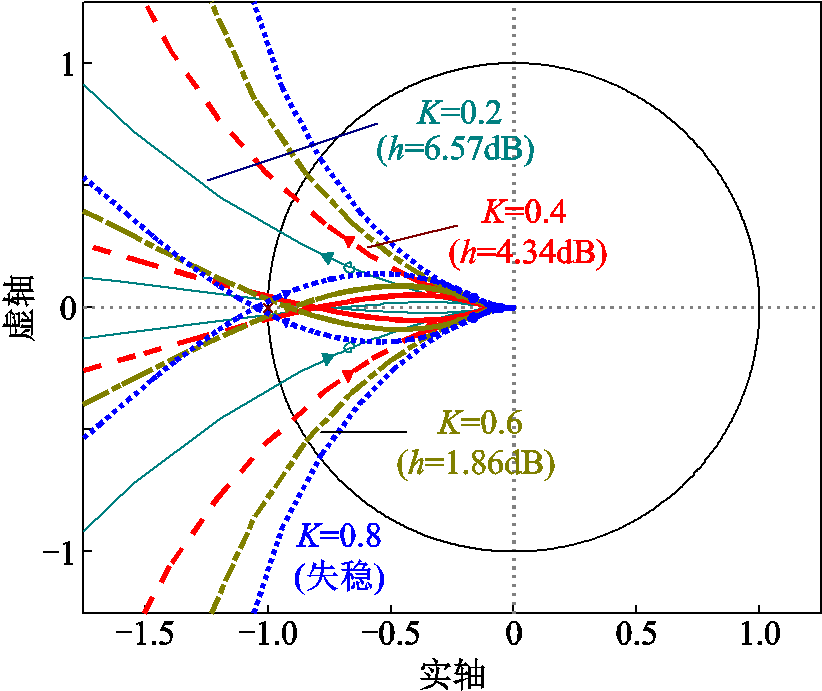
图10 不同K下系统奈奎斯特曲线
Fig.10 Nyquist diagrams of the system with different K
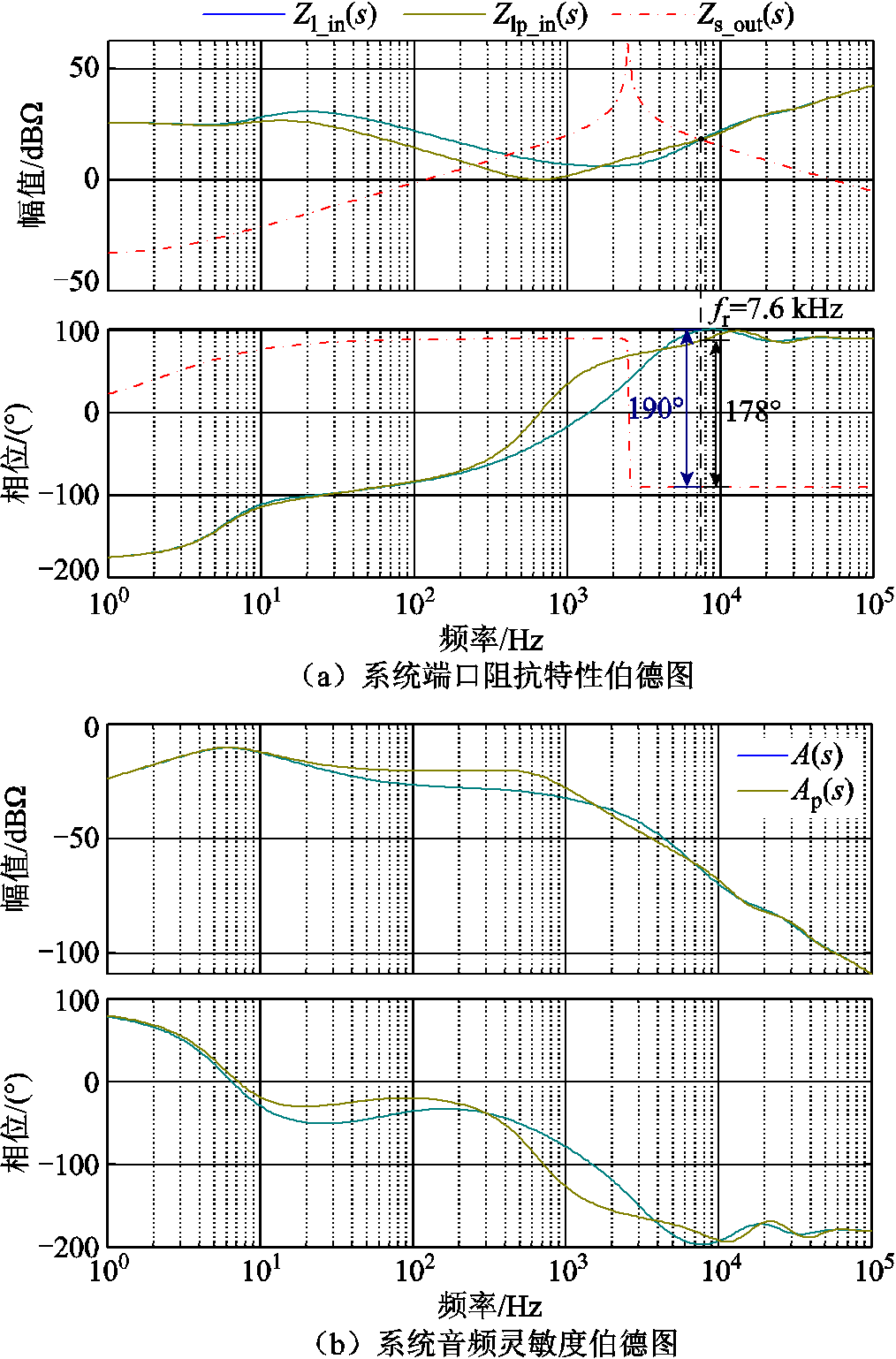
图11 添加相位补偿环节前后系统稳态及动态特性伯德图
Fig.11 Bode diagrams of steady-state and dynamic characteristics of the system before and after adding phase compensator
同时,在变换器控制系统中加入相位补偿策略后需对其动态性能进行分析。由于相位补偿策略改变了变换器的控制环路,会对变换器的闭环控制产生影响,从而影响系统动态性能,该现象在以往的文献中多有提及。对于变换器动态性能的评估可以由音频灵敏度特性来体现。音频灵敏度为输入电压到输出电压的传递函数,表示变换器受到输入电压扰动时输出电压的响应。因此,音频灵敏度越低,输出电压跟随给定值而不受输入电压波动干扰的特性越好。故根据图3所示的小信号控制框图计算得到系统加入补偿策略之前的音频灵敏度传递函数为
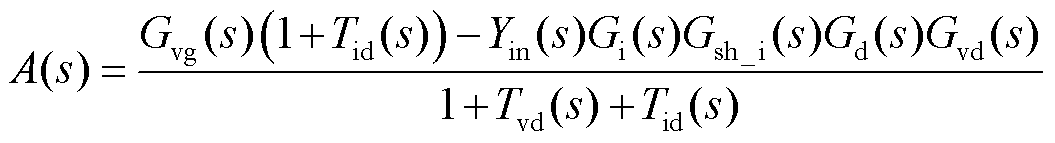 (24)
(24)
同样,根据图8所示的小信号控制框图计算得到系统加入补偿策略后的音频灵敏度传递函数为
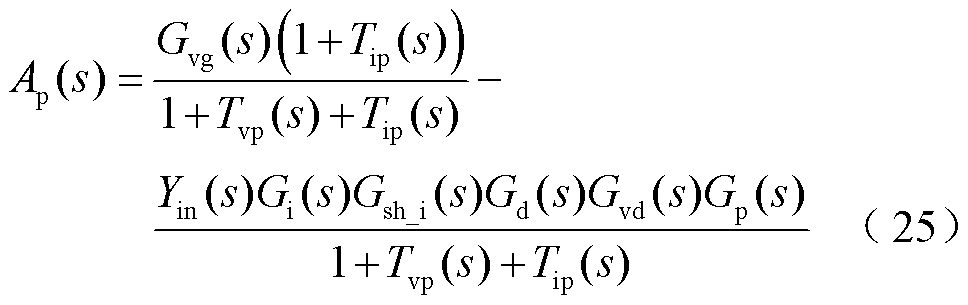
进一步绘制系统添加相位补偿策略前后的音频灵敏度曲线如图11b所示。添加相位补偿策略后系统音频灵敏度曲线最大值不变,证明所添加策略对系统的动态电压跌坑影响较小。
综上所述,添加相位补偿策略后,系统高频段相位得到补偿,使得高频交点处的相位差小于180°,系统稳定。同时对于系统动态性能,添加相位补偿策略后,系统输入电压突然跌落时,输出电压跌坑将不会恶化。
为验证相位补偿策略对系统高频振荡抑制的有效性,搭建了一个240~400 V、3 kW的级联直流系统,连接示意图如图12所示,系统参数见表3。
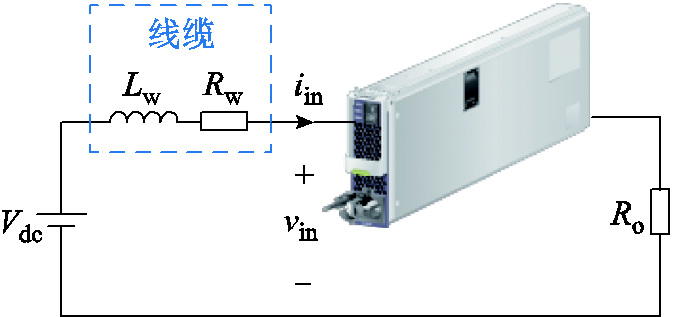
图12 级联系统连接示意图
Fig.12 Connection diagram of the cascaded system
为了验证稳定性能,在系统满载的情况下分别进行无策略和添加相位补偿策略的测试,得到端口输入电压电流波形如图13所示。无策略时系统发生振荡,振荡频率为7.69 kHz,振荡峰峰值最高达到263 V,与理论分析结果相符;t=85 ms时添加相位补偿策略,经过5 ms系统恢复稳定,端口输入电压纹波峰峰值为2.8 V,级联直流系统的高频振荡问题得到了有效抑制。
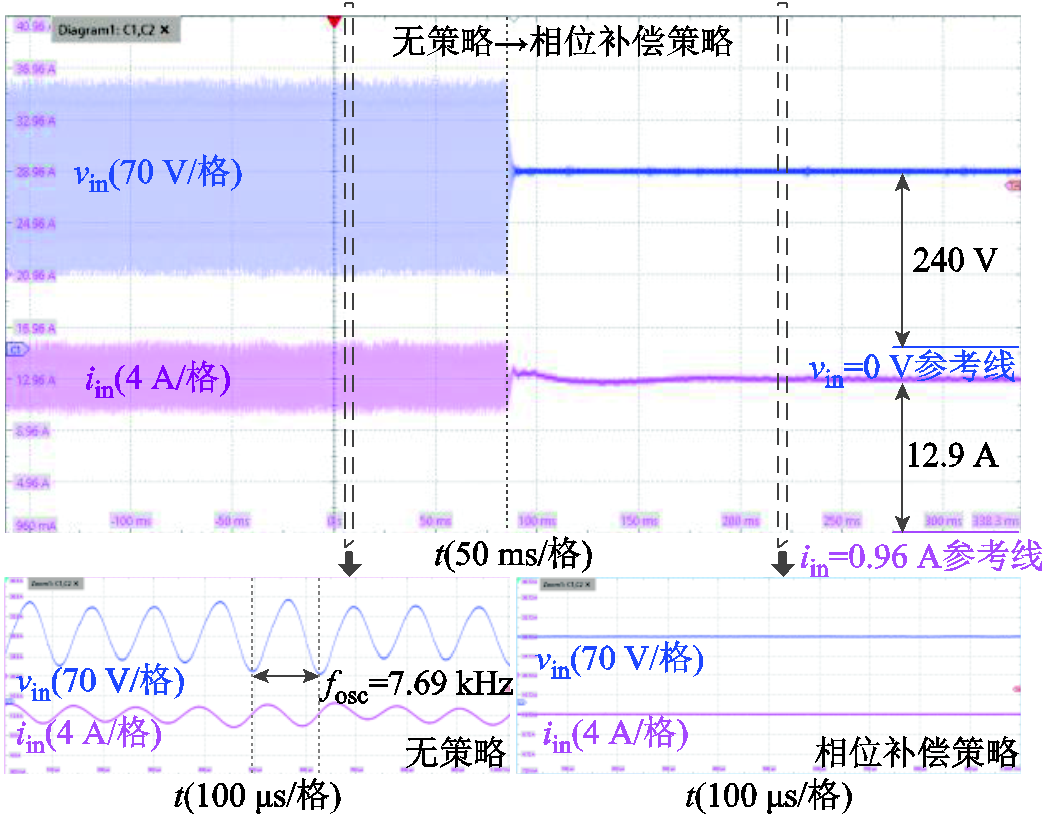
图13 级联系统端口电压电流波形
Fig.13 Waveforms of the port voltage and current of the cascaded system
为了验证动态性能,将输入电压Vdc从240 V跌落至210 V,对单电源分别进行无策略和添加相位补偿策略的测试,得到输出电压波形如图14所示。t=0 s引入输入电压跌落时,无策略情况下输出电压跌坑Δvo为12.03 V,加入相位补偿策略后Δvo为12.37 V。故加入相位补偿策略基本不会影响输出电压跌落Δvo的大小,即相位补偿策略不会对系统本身的动态性能产生负面影响。
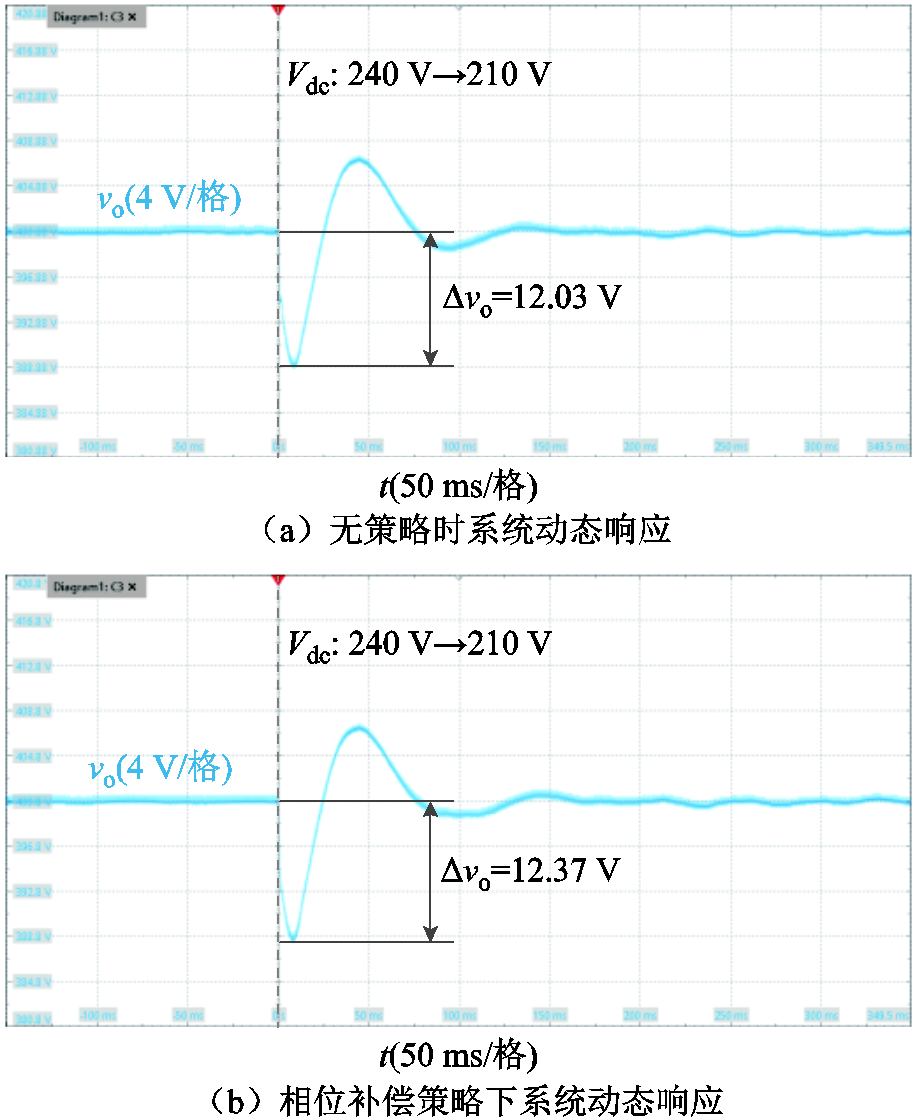
图14 输入电压跌落时输出电压波形
Fig.14 Waveforms of the output voltage when the input voltage drops
为了验证相位补偿策略的鲁棒性,在系统负载功率、输入电压、开关频率及线缆长度分别发生变化时进行测试,得到不同系统参数下相位补偿策略的补偿效果,绘制端口输入电压纹波Δvin柱状图如图15所示。可以看出,所提出的相位补偿策略在负载功率变化、输入电压在220~380 V、开关频率在60~70 kHz、线缆等效电感在1.35/4~1.35×4 mH的情况下均能够抑制系统级联端口高频振荡的发生,保证级联直流系统的稳定性,具有良好的鲁棒性。
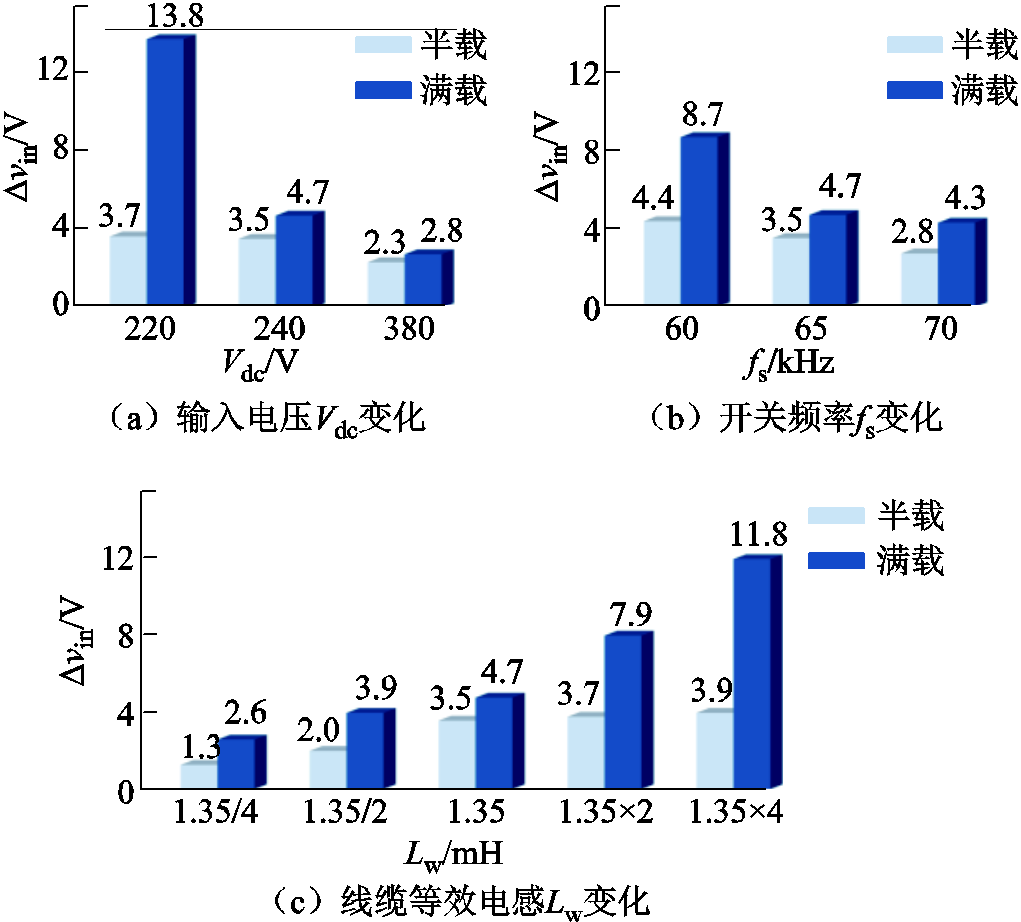
图15 不同系统参数下相位补偿策略的补偿效果
Fig.15 The compensation effect of phase compensation strategy under different system parameters
本文通过建立考虑数字控制延时的级联直流系统阻抗小信号模型,对直流配电系统的高频振荡机理进行了深入研究,完善了直流配电系统的振荡场景,并对振荡影响因素进行了详细分析。在此基础上,针对高频振荡问题提出相位补偿策略,通过修改系统的控制回路补偿系统在高频段的相位,提升系统的稳定性,从而解决直流配电系统中的高频振荡问题。最后在240 V直流配电系统中对该方法进行了实验验证,主要研究结论如下:
1)所提出的负载变换器闭环输入阻抗小信号模型考虑了实际系统中的数字控制环节,保证了系统在高频段的建模准确性,为系统稳定性分析奠定了理论基础。
2)依据阻抗判据进行直流配电系统稳定性分析,提出小信号振荡问题的低频振荡和高频振荡分类法,发现低频振荡发生的决定性因素为控制器带宽,而高频振荡发生的决定性因素为负载变换器输入电容与数字控制延时的大小。
3)数字控制延时主要包括控制延时与电压电流采样延时,其中计算延时是影响系统稳定性的主导因素,电流环采样延时次之,电压环采样延时的影响可忽略不计。
4)所提出的相位补偿策略能够提高直流配电系统的小信号稳定性,解决了级联直流系统的高频振荡问题,同时保证了优异的系统动态性能。
参考文献
[1] 张泽华, 宋桂英, 张晓璐, 等. 考虑恒功率负载的直流微电网稳定性与鲁棒性控制策略[J]. 电工技术学报, 2023, 38(16): 4391-4405.
Zhang Zehua, Song Guiying, Zhang Xiaolu, et al. Stability and robustness control strategy of DC microgrid considering constant power load[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4391-4405.
[2] 刘笑, 杨建, 李力, 等. 基于机器学习的带被动阻尼直流微电网系统的稳定性检测[J]. 电工技术学报, 2024, 39(8): 2281-2293, 2324.
Liu Xiao, Yang Jian, Li Li, et al. Stability detection of DC microgrid systems with passive damping based on machine learning[J]. Transactions of China Electro-technical Society, 2024, 39(8): 2281-2293, 2324.
[3] 李霞林, 郭力, 王成山, 等. 直流微电网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(1): 2-17.
Li Xialin, Guo Li, Wang Chengshan, et al. Key technologies of DC microgrids: an overview[J]. Proceedings of the CSEE, 2016, 36(1): 2-17.
[4] 王晴, 刘增, 韩鹏程, 等. 基于变流器输出阻抗的直流微电网下垂并联系统振荡机理与稳定边界分析[J]. 电工技术学报, 2023, 38(8): 2148-2161.
Wang Qing, Liu Zeng, Han Pengcheng, et al. Analysis of oscillation mechanism and stability boundary of droop-controlled parallel converters based on output impedances of individual converters in DC microgrids [J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2148-2161.
[5] 吴翔宇, 张晓红, 尚子轩, 等. 基于频域阻抗网络建模分析的交直流微电网振荡问题研究[J]. 电工技术学报, 2024, 39(8): 2294-2310.
Wu Xiangyu, Zhang Xiaohong, Shang Zixuan, et al. Research on the oscillation problem of AC-DC microgrids based on frequency domain impedance network modeling and analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2294-2310.
[6] 李周, 王宇涵, 顾伟, 等. 直流电网及其运行控制策略发展趋势[J]. 电力系统自动化, 2024, 48(24): 1-21.
Li Zhou, Wang Yuhan, Gu Wei, et al. Development trend of DC power grid and its operation and control strategy[J]. Automation of Electric Power Systems, 2024, 48(24): 1-21.
[7] 郑凯元, 杜文娟, 王海风. 聚合恒功率负荷对直流微电网稳定性影响的阻抗法分析[J]. 电网技术, 2021, 45(1): 134-148.
Zheng Kaiyuan, Du Wenjuan, Wang Haifeng. DC microgrid stability affected by aggregated constant power loads based on impedance method[J]. Power System Technology, 2021, 45(1): 134-148.
[8] 庄莹, 裴玮, 刘子奇, 等. 提升低压直流配电稳定性的时滞模型预测附加控制[J]. 电工技术学报, 2023, 38(12): 3248-3263.
Zhuang Ying, Pei Wei, Liu Ziqi, et al. Time-delay model predictive additional control strategy to improve the stability of low-voltage DC distribution system[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3248-3263.
[9] 杜韦静, 张军明, 钱照明. Buck变流器级联系统直流母线电压补偿控制策略[J]. 电工技术学报, 2015, 30(1): 135-142.
Du Weijing, Zhang Junming, Qian Zhaoming. Compensation methodology for DC bus voltage of cascaded system formed by Buck converters[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 135-142.
[10] Cespedes M, Xing Lei, Sun Jian. Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1832-1836.
[11] 王成山, 李微, 王议锋, 等. 直流微电网母线电压波动分类及抑制方法综述[J]. 中国电机工程学报, 2017, 37(1): 84-98.
Wang Chengshan, Li Wei, Wang Yifeng, et al. DC bus voltage fluctuation classification and restraint methods review for DC microgrid[J]. Proceedings of the CSEE, 2017, 37(1): 84-98.
[12] Zhang Xin, Ruan Xinbo, Zhong Qingchang. Improving the stability of cascaded DC/DC converter systems via shaping the input impedance of the load converter with a parallel or series virtual impedance [J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7499-7512.
[13] He Bangbang, Chen Wu, Li Xin, et al. A power adaptive impedance reshaping strategy for cascaded DC system with buck-type constant power load[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 8909-8920.
[14] Wu Mingfei, Lu D D C, Tse C K. Direct and optimal linear active methods for stabilization of LC input filters and DC/DC converters under voltage mode control[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2015, 5(3): 402-412.
[15] Zeng Chengbi, Wang Hanwen, Li Sudan, et al. Grid-voltage-feedback active damping with lead compensation for LCL-type inverter connected to weak grid[J]. IEEE Access, 2021, 9: 106813-106823.
[16] 谢文浩, 刘一琦, 王建赜, 等. 提高LCL型并网逆变器阻抗重塑控制鲁棒性的延时补偿方法[J]. 电工技术学报, 2017, 32(增刊1): 178-185.
Xie Wenhao, Liu Yiqi, Wang Jianze, et al. A delay compensation method of the grid-connected inverter with LCL filter to improve robustness of the impedance shaping control[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 178-185.
[17] Yao Wenli, Yang Yongheng, Zhang Xiaobin, et al. Design and analysis of robust active damping for LCL filters using digital Notch filters[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2360-2375.
[18] 金国彬, 苑忠奇, 李国庆, 等. 基于无源性的并网逆变器扩展阻尼区域方法研究[J]. 电力系统保护与控制, 2022, 50(19): 25-35.
Jin Guobin, Yuan Zhongqi, Li Guoqing, et al. A method of extending the damping region of a grid-connected inverter based on passivity[J]. Power System Protection and Control, 2022, 50(19): 25-35.
[19] 王林, 孙鹏菊, 薛统宇, 等. 一种提高LCL型并网逆变器电流控制性能的延时补偿方法[J]. 中国电机工程学报, 2020, 40(19): 6320-6330.
Wang Lin, Sun Pengju, Xue Tongyu, et al. A delay compensation method to improve the current control performance of the LCL-type grid-connected inverter[J]. Proceedings of the CSEE, 2020, 40(19): 6320-6330.
[20] 姜鑫, 易皓, 卓放, 等. 基于直流电压同步的构网型变流器低频振荡分析与阻尼控制[J]. 电力系统自动化, 2024, 48(16): 30-39.
Jiang Xin, Yi Hao, Zhuo Fang, et al. Low-frequency oscillation analysis and damping control for grid-forming converters based on DC voltage synchro-nization[J]. Automation of Electric Power Systems, 2024, 48(16): 30-39.
[21] 刘海春, 过仕安, 钱强, 等. 基于基准频率自适应谐波准谐振控制器的宽变频逆变电源控制研究[J]. 电工技术学报, 2024, 39(20): 6462-6474.
Liu Haichun, Guo Shian, Qian Qiang, et al. Research on control of wideband variable-frequency inverters based on harmonics quasi resonant controller with frequency reference adapting[J]. Transactions of China Electrotechnical Society, 2024, 39(20): 6462-6474.
[22] 杨龙月, 郭锐, 张乐, 等. 非理想电网下逆变器并网电流质量改善策略[J]. 电力系统保护与控制, 2020, 48(15): 10-18.
Yang Longyue, Guo Rui, Zhang Le, et al. Improvement strategy for grid-connected current quality of an inverter under non-ideal grid conditions[J]. Power System Protection and Control, 2020, 48(15): 10-18.
[23] 熊小玲, 罗博晨, 刘京波, 等. 计及SVG的双馈风电场高频阻抗建模及振荡分析[J]. 电网技术, 2023, 47(7): 2905-2917.
Xiong Xiaoling, Luo Bochen, Liu Jingbo, et al. High frequency impedance modeling and oscillation analysis of DFIG-based station considering SVG[J]. Power System Technology, 2023, 47(7): 2905-2917.
[24] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[25] Agorreta J L, Borrega M, López J, et al. Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 770-785.
[26] 曹子恒, 肖先勇, 马俊鹏, 等. 提高LCL型并网逆变器鲁棒性的改进型电容电流反馈有源阻尼策略[J]. 高电压技术, 2020, 46(11): 3781-3790.
Cao Ziheng, Xiao Xianyong, Ma Junpeng, et al. Novel capacitor current feedback active damping strategy for enhancing robustness of LCL-type grid-connected inverters[J]. High Voltage Engineering, 2020, 46(11): 3781-3790.
[27] Su Xinyang, Wang Minghao, Zhao Bi’an, et al. An adaptive compensated virtual impedance method for oscillation suppression in DC distribution power systems[J/OL]. IEEE Transactions on Industrial Electronics, 2024, DOI:10.1109/TIE.2024.3476912.
Phase Compensation-Based High-Frequency Oscillation Suppression of DC Power Distribution Systems
Abstract With the access of a large number of distributed power supplies and various types of DC loads, the distribution of power electronic equipment in the DC distribution system becomes more concentrated, leading to the inertia and damping of the system being reduced, which makes it easy that small-signal stability problems occur, divided into low-frequency oscillation and high-frequency oscillation. Among them, the problem of low-frequency oscillation caused by the negative impedance characteristic of constant power load has been concerned and solved widely. However, with the substantial growth of power supply demand of AI cluster computing and so on, the system power supply density requirements are increased correspondingly, so the input capacitance of the converter is reduced constantly, making the impedance mismatch point move to the high-frequency band gradually. Because the digital control is flexible and reliable, it is often used for the control of converters, which makes the high-frequency oscillation problem become more and more prominent. Therefore, in order to promote the improvement of the next generation of high-density and high-efficiency power supply, the high-frequency oscillation problem in the DC distribution system needs to be solved.
To solve this issue, the mechanism of high-frequency oscillation in DC distribution system was analyzed. Firstly, considering the influence of each link in the digital control loop of the actual system, the modified small- signal model of the load converter impedance was constructed, making the accuracy range of the model be extended to the kHz level. Secondly, based on the modified model, the stability problem of DC distribution system was further analyzed, and the classification of low-frequency oscillation and high-frequency oscillation of small-signal oscillation problem was proposed, and the main factors of high-frequency oscillation problem were analyzed. The digital control delay includes control delay and voltage and current sampling delay, in which the calculation delay is the main factor affecting the stability of the system, the current loop sampling delay is the second, and the voltage loop sampling delay can be negligible.
A phase compensation-based high-frequency oscillation suppression method was proposed for DC power distribution system. Firstly, the phase compensator was added to the control loop to compensate the dominant factor of high-frequency oscillation in DC distribution system. Secondly, the compensator parameters were designed to compensate the phase of the system in the high-frequency band and improve the stability of the system, so as to solve the high-frequency oscillation problem in the DC distribution system. Finally, the influence of the added strategy on the stability and dynamic performance of the system was analyzed theoretically.
The experimental results based on 3 kW, 240~400 V experimental platform validated the correctness of the stability analysis results and the performance of the phase compensation strategy. The results show that the proposed small-signal model of modified impedance converter can reflect the digital control link in the actual system, and ensure the accuracy of the system modeling in high-frequency band. At the same time, the proposed phase compensation strategy can improve the small-signal stability of DC distribution system, solve the problem of high-frequency oscillation of cascaded DC system, and ensure the excellent dynamic performance of the system. In addition, when the load power, input voltage, switching frequency or equivalent inductance of the cable changes, the proposed control strategy can ensure good stability and robustness of the system.
Keywords:Phase compensation, DC distribution power system, high-frequency oscillation, small-signal stability, digital control
中图分类号:TM721.1; TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241488
收稿日期 2024-08-23
改稿日期 2024-11-19
王彤鹭 女,2000年生,硕士研究生,研究方向为直流配电系统的阻抗建模、控制及稳定性分析。
E-mail:tlwang@stu.xjtu.edu.cn
王 跃 男,1972年生,教授,博士生导师,研究方向为新能源变流器控制与稳定性分析、柔性直流输电等。
E-mail:davidwangyue@mail.xjtu.edu.cn(通信作者)
(编辑 赫 蕾)