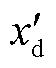为调相机暂态电抗，XT为升压变压器电抗，令XSC为两者之和，USC为调相机暂态电抗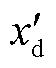后的暂态电动势，δSC为调相机功角；Iv和φi分别为新能源输出电流和功率因数角；Up和δp分别为公共耦合点（Point of Common Coupling, PCC）电压的幅值和相位；Ug和δg分别为无穷大电网电压的幅值和相位，本文以无穷大电网电压为基准（δg=0）；Xg为系统并网点与无穷大电网之间的等值电抗；PSC、Pv和Pg分别为调相机输出有功功率、新能源输出有功功率和注入电网的有功功率。摘要 在大型新能源基地中配置同步调相机是提高新能源承载能力的一种有效的技术方案，然而该方案中调相机存在暂态功角失稳风险。现有文献针对特定工况下的调相机暂态失稳问题开展了分析，但并未综合考虑系统参数对调相机功角特性的影响，导致不同失稳形态下的暂态失稳机理缺乏系统的理解。为此，该文拟从能量视角分析系统功率传递关系并建立等效同步机模型，借鉴传统同步机暂态稳定的分析方法，归纳并分析调相机不同失稳形态背后的暂态失稳机理。首先，解析了调相机功角特性并给出了等效同步机建模方法，基于等效同步机模型和传统同步机的能量函数给出了系统的能量函数；其次，分析了暂态期间系统能量转换过程并揭示了调相机暂态失稳机理，研究表明，调相机暂态期间存在首摆失稳和二摆失稳两种形态，前者与传统同步机失稳形态类似，后者经历首摆减速而二摆加速失稳的过程且存在与前者不同的失稳边界；然后，通过分析系统参数对调相机失稳形态和系统稳定裕度的影响，为系统稳定提升控制设计提供了理论基础；最后，通过电磁暂态仿真验证了所提失稳机理以及影响因素分析的正确性。
关键词：新能源基地 同步调相机 等效同步机 暂态功角稳定性 Lyapunov能量函数
在“双碳”目标指引下，我国正加快推进新型电力系统建设[1]。建设大规模新能源基地是推进新型电力系统建设取得实效的行动之一[2]。新能源基地因短路容量和转动惯量不足而存在电压和频率失稳风险，因此具有电压和惯量支撑能力的同步调相机被广泛配置在新能源基地附近[3-9]。然而当系统发生短路故障时，作为和同步发电机类似的同步旋转设备，同步调相机同样会因功率不平衡而暂态功角失稳。
由于同步调相机和同步发电机与电网的同步机制均由转子运动方程决定，因此在分析新能源基地中同步调相机的暂态稳定性时，可以参考新能源接入对同步发电机暂态稳定性影响的相关研究[10-19]。文献[11]采用阻抗模型等效描述双馈风机的外特性，分析了双馈风机接入对同步机暂态稳定性的影响，得到风机接入导致同步机首摆功角变化范围减小的结论。文献[12-13]基于双馈风机等效阻抗模型，分析了风机接入方式和接入容量对同步机暂态稳定性的影响。文献[14-16]将双馈风机建模为功率注入模型并推导了其对同步机功角特性的影响，随后揭示了系统暂态稳定机理并分析了影响系统暂态稳定性的关键因素。文献[17]基于等面积定则分析了风机采用低电压穿越控制策略时的无功比例系数和有功电流对同步机暂态稳定性的影响规律，同时给出了能够提升系统暂态稳定性的改进故障穿越控制策略。文献[18-19]基于等效接地导纳将风电场对系统功角特性的影响等效为对同步机之间电气距离的影响，随后分析了风电接入容量对系统暂态稳定性的影响。
此外，由于构网型设备模拟了同步机与电网的同步方式[20]，因此有关跟网/构网混联系统暂态同步稳定性的研究同样具有参考价值。文献[21-22]通过建立描述跟网和构网型设备同步过程的动态方程，分析了两者动态交互对系统暂态稳定性的影响，得到了跟网型设备输出无功电流增大有助于提升构网型设备稳定性的结论。进一步地，文献[23]基于矢量图法和相平面法分析了跟网和构网型设备控制参数对系统暂态稳定性的影响，给出了控制器参数设计原则。文献[24]通过解析含构网型静止无功发生器的新能源送出系统的功角特性，结合等面积定则揭示了其暂态失稳机理。然而相比于同步机和构网型设备，调相机由于没有原动机提供机械功率，且不具备包含功率参考值的外环控制环节，因而其有功调控能力较弱，导致其运行特性与同步机和构网型设备存在显著差异。因此，在新能源基地附近配置调相机后需重新审视调相机的暂态功角稳定性。
已有文献分析了新能源基地附近调相机的暂态功角稳定性。文献[25-26]研究表明，金属性故障下新能源的有功功率无法全部注入电网，调相机因承担此盈余有功功率而面临转子加速失稳的风险。文献[27-28]针对单相接地短路故障场景，揭示了在新能源低电压穿越深度较高的情况下，调相机存在首摆减速而后摆加速的功角失稳形态，随后分析了影响调相机暂态稳定的关键因素。文献[29]基于相量法定性分析了过渡电阻和新能源低电压穿越控制策略对调相机暂态摇摆过程的影响。然而，现有研究尚局限于故障参数或新能源控制策略等因素主导系统暂态特性的特定工况，未选取有效视角深入归纳不同失稳形态背后的暂态失稳机理，未能综合考虑不同失稳形态下系统参数对调相机暂态稳定性的影响，无法为调相机稳定提升控制设计提供普适的理论依据。
针对上述问题，本文的主要工作为：①分析联合系统和传统同步机系统的异同之处，揭示联合系统中调相机与传统同步机存在不同暂态失稳形态的本质原因；②基于等效同步机视角，从转子承担的不平衡功率出发归纳并揭示调相机不同暂态失稳形态背后的失稳机理；③量化调相机不同暂态失稳形态的边界条件和稳定裕度，分析系统参数对调相机失稳形态和稳定裕度的影响。
考虑如图1所示的新能源和调相机联合送出系统（后文简称联合系统）的拓扑。图1中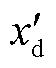，为调相机暂态电抗，XT为升压变压器电抗，令XSC为两者之和，USC为调相机暂态电抗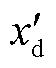后的暂态电动势，δSC为调相机功角；Iv和φi分别为新能源输出电流和功率因数角；Up和δp分别为公共耦合点（Point of Common Coupling, PCC）电压的幅值和相位；Ug和δg分别为无穷大电网电压的幅值和相位，本文以无穷大电网电压为基准（δg=0）；Xg为系统并网点与无穷大电网之间的等值电抗；PSC、Pv和Pg分别为调相机输出有功功率、新能源输出有功功率和注入电网的有功功率。
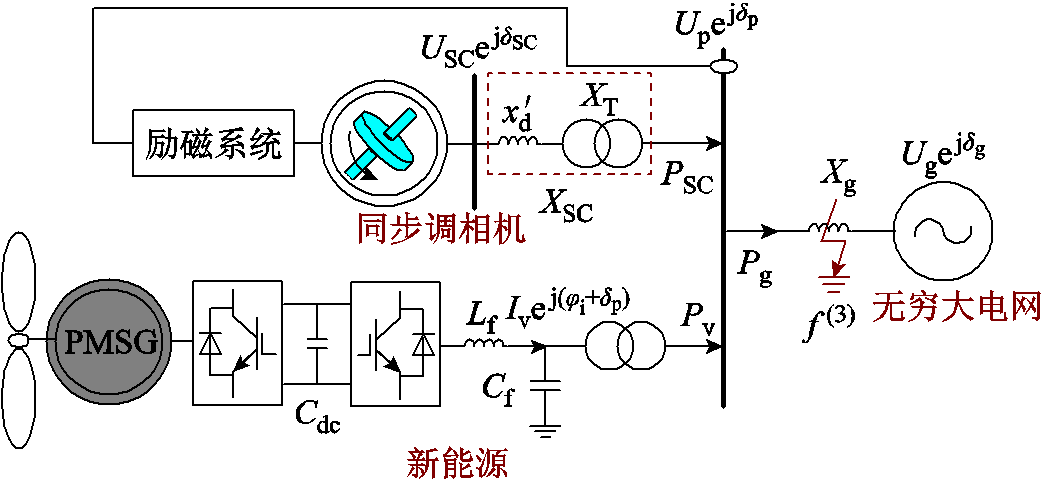
图1 新能源和调相机联合送出系统模型
Fig.1 Associationsystem model of renewable energy base co-located with condenser
为了突出说明联合系统中调相机暂态功角失稳机理，在转子运动时间尺度下采用如下假设以简化分析：①考虑到阻尼绕组时间常数远小于转子摆动周期，调相机采用同步机三绕组模型[30]；②新能源稳态期间采用单位功率因数控制，忽略新能源电流内环和锁相环的动态过程且不考虑锁相环失稳的场景[31-34]；③忽略线路电阻以及频率变化对系统参数的影响[25,35]。
基于图1所示的系统模型，推导系统短路故障下调相机的功角特性方程。首先对三相短路的故障电路进行戴维南等效处理，模型如图2所示。图2中，df为故障与并网点之间的距离，Rf和Xf分别为过渡电阻和接地电抗。
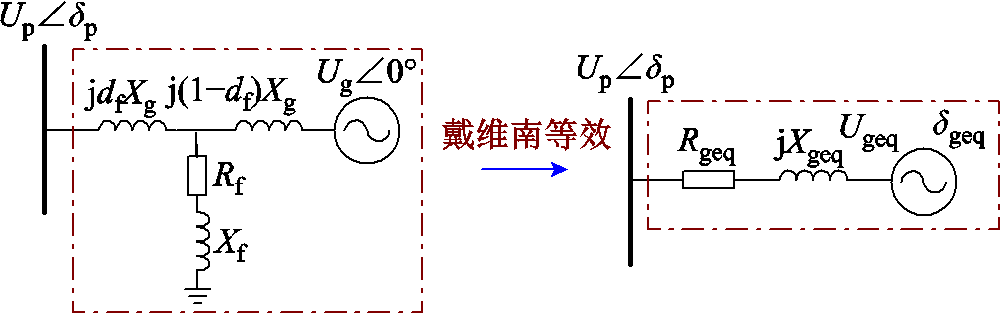
图2 三相短路故障戴维南等效模型
Fig.2 Thévenin equivalent model of three-phase short-circuit fault
由图2可知，并网点与无穷大电网之间的等效线路阻抗为
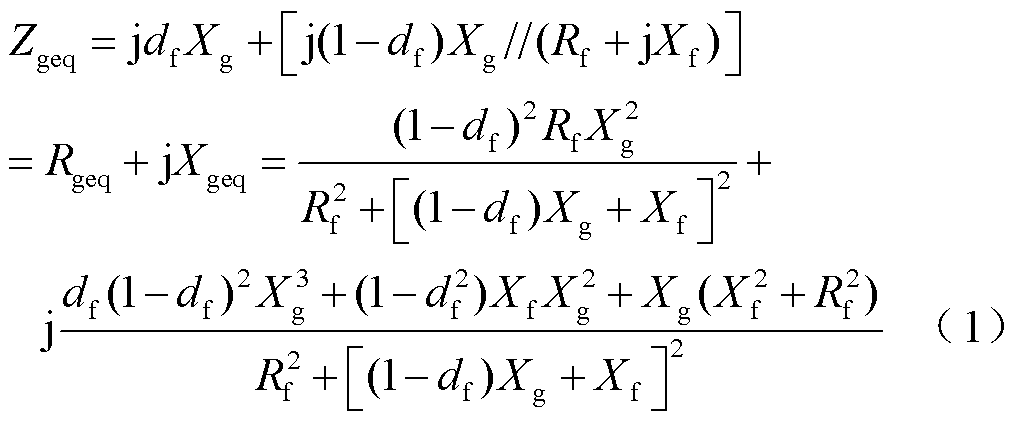
式中，Rgeq和Xgeq分别为等效线路电阻和电抗。
无穷大电网等效电动势为
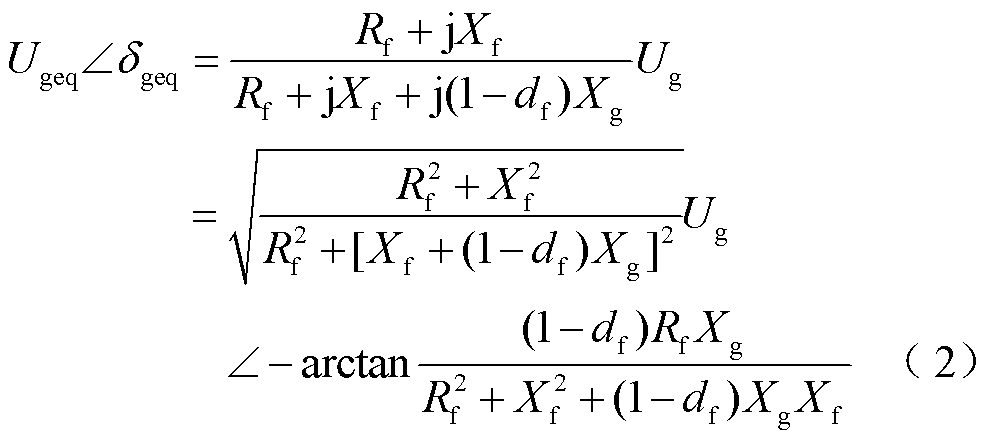
故障期间，新能源需依据并网导则切换至低电压穿越控制策略，此时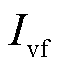
的有功电流和无功电流[36]为
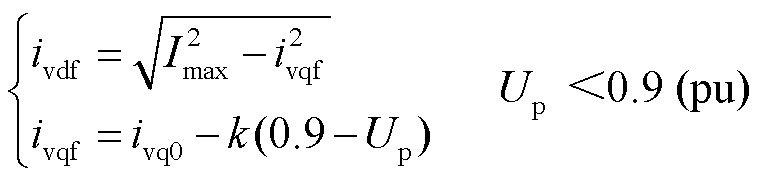（3）
式中，Imax为新能源换流器电流容量；ivq0为新能源故障前控制模式下的q轴电流指令值；k为动态无功电流比例系数。
文献[37]表明低电压穿越期间新能源可等效建模为电流源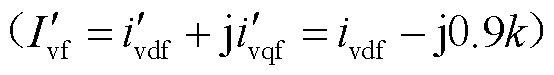
并联虚拟电抗（j/k）的形式，为了分析低电压穿越控制参数对调相机功角特性的影响，前述戴维南等效过程中考虑j/k后可得
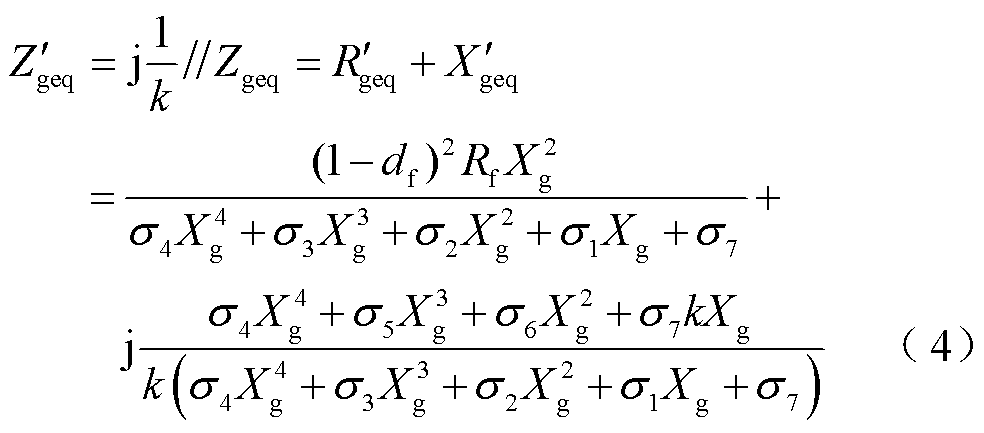
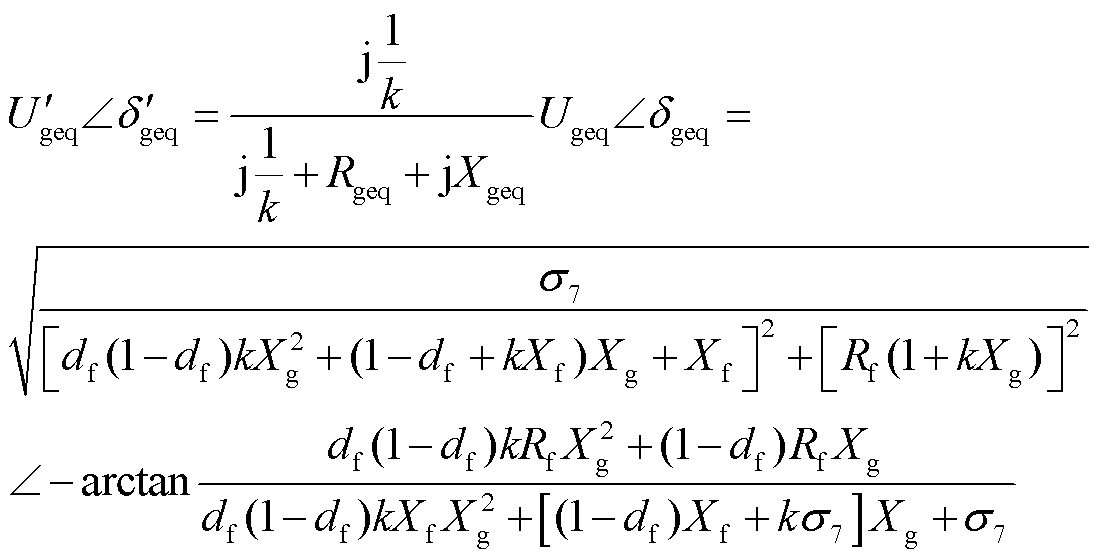（5）
式（4）和式（5）中有关σ的参数详见附录第1节。
结合图1和图2，依据叠加定理可得故障期间PCC电压表达式为
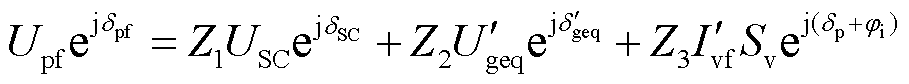（6）
其中
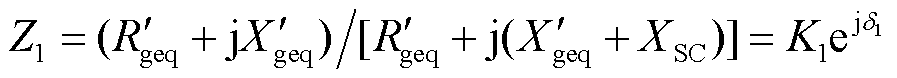
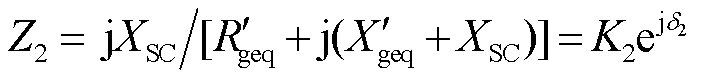
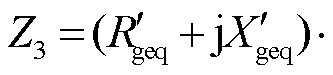
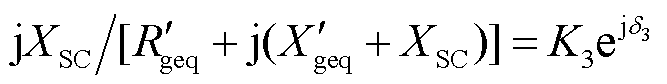
根据式（6）可以解出PCC电压幅值为
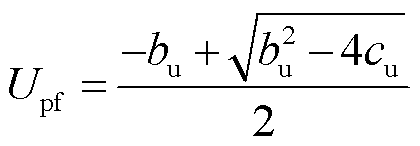（7）
其中
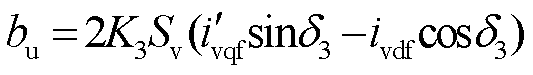
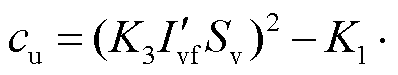
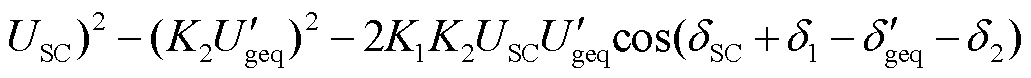
同理由式（6）可得PCC电压相位为
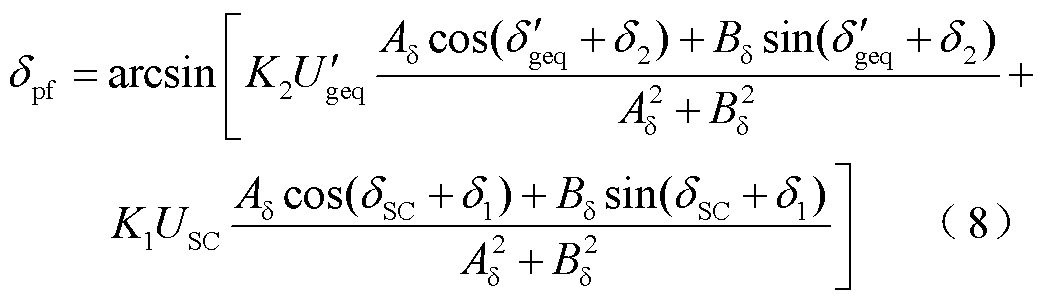
式中，Aδ=K3Sv(i′vqfcosδ3+ivdfsinδ3)；Bδ=Upf−K3Sv(ivdf·cosδ3−i′vqfsinδ3)；Sv为以系统额定容量为基准归算后的新能源容量；Upf和δpf的推导过程详见附录第1节。
从并网点向无穷大电网看去，注入电网的有功功率为
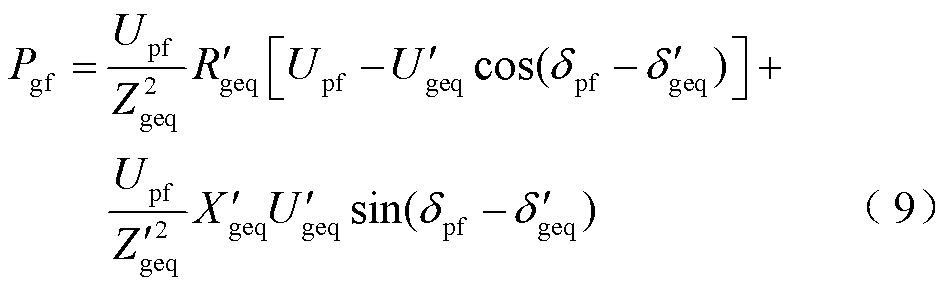
由系统有功功率平衡关系可得调相机输出有功功率为
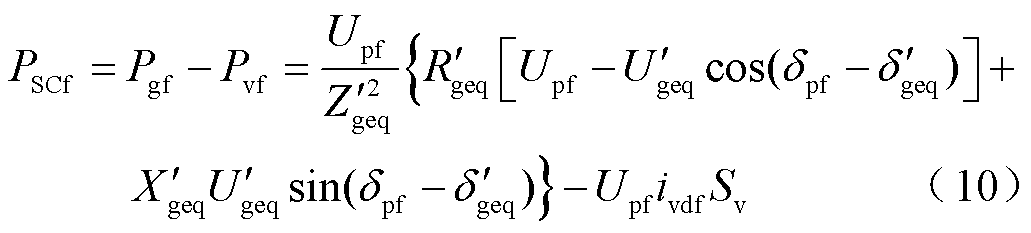
将式（7）和式（8）代入式（10）中可得联合系统发生短路故障时调相机的功角特性方程。系统稳态运行时，将df=1、Rf=∞和k=0代入式（4）、式（5）、式（7）、式（8）和式（10）中可得调相机稳态功角特性PSC(δSC)。本文中带有下标“f”的符号表示故障期间的参量，未带下标“f”的符号表示稳态参量；式（4）和式（5）中带上标“′”的符号表示对处于低电压穿越控制的新能源进行等效建模后推导得到的参量。
值得一提的是，若系统发生不对称短路故障，依据正序等效定则可知系统短路点与接地点间存在附加电抗XΔ，此时采用前述故障等效方法可得正序增广网络中并网点和电网间的等值联络电抗。随后参考前述推导方法同理可得调相机功角特性。
考虑到调相机的动态特性与同步机一样均由转子运动过程主导，且传统同步机功角稳定的机理明确，稳定分析理论体系成熟，因此本文拟建立等效同步机模型分析联合系统中调相机暂态失稳问题。
由系统有功功率平衡关系可知：PSCf=Pgf −Pvf。注入电网的有功功率Pgf由电网有功功率需求决定，其受线路参数和故障类型等因素影响。新能源有功功率Pvf受自身控制策略、通流容量和并网点电压影响。考虑到暂态期间电网有功功率需求因故障扰动而发生改变，此时新能源在低电压穿越控制和换流器电流限幅的作用下，其有功功率无法满足电网有功功率需求。调相机无调速系统，其有功功率调节能力弱，暂态期间承担新能源和电网间的不平衡功率Pgf−Pvf而吸收/发出有功功率PSCf。因此，从并网点向设备侧看，调相机转子的动能将依据新能源发出功率大小而相应改变，以满足电网有功功率需求，即调相机转子为系统能量转换的“媒介”。
联合系统的等效同步机建模如图3所示。将新能源和调相机分别视为等效同步机的原动机和发电机后[25-26]可得
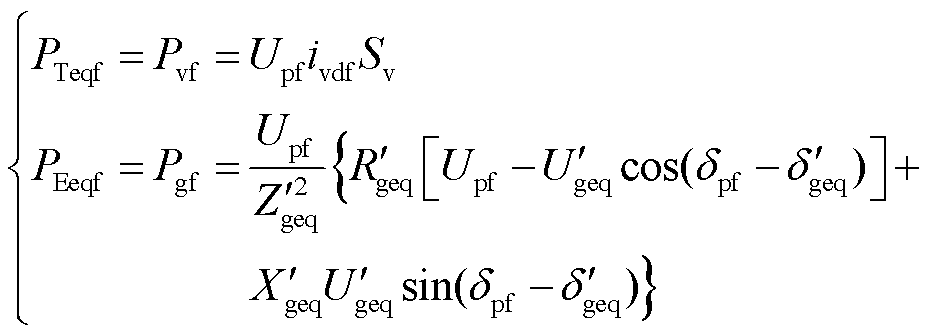（11）
式中，PTeqf和PEeqf分别为等效同步机的机械功率和电磁功率。
值得一提的是，传统同步机具有暂态期间机械功率恒定为1(pu)的特性[30]，故障期间其因机械功率大于电磁功率而呈现转子正向摆动的形态。由式（11）可知，当系统发生短路故障时，并网点电压Upf跌落且新能源通常因进入低电压穿越控制策略而发出小于稳态值（ivd=1.0(pu)）的有功电流，此时新能源输出有功功率Pvf相较于稳态值（Pv=1.0(pu)）大幅下降。因此，不同于传统同步机，联合系统中调相机存在因PTeqf＜PEeqf而功角反向摆动的情况。
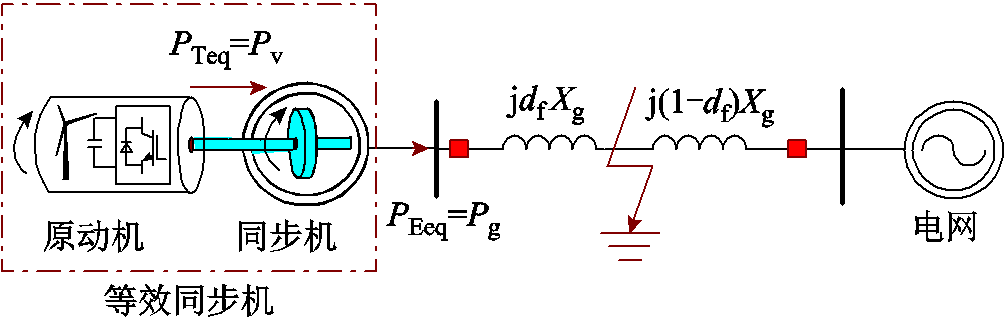
图3 联合系统等效同步机模型
Fig.3 Equivalent synchronous generator model of the association system
由式（11）可知，不同的控制策略和网络参数将改变新能源输出有功功率和电网有功功率需求，导致调相机转子承担性质不同的不平衡功率。故障期间，若电网有功功率需求大幅下降且小于此时新能源发出的有功功率，典型场景如系统发生金属性短路故障[25-26]，此时新能源有功功率因无法注入外电网而注入附近的调相机，导致等效同步机转子上PTeqf＞PEeqf，转子在驱动功率作用下开始加速；若新能源输出功率无法满足网侧有功功率需求，典型场景如系统发生高阻接地故障[29]，此时调相机因自身有功功率调节能力弱而发出有功功率，导致等效同步机转子上PTeqf＜PEeqf，转子在制动功率作用下开始减速。由此可见，在不同的系统参数下，调相机暂态期间存在两种摇摆形态。本节基于等效同步机模型，参考传统同步机的能量函数给出系统的相对动能和势能表达式，从系统能量转换角度揭示两种摇摆形态下调相机暂态功角失稳机理。
结合式（10）可得调相机转子运动方程为
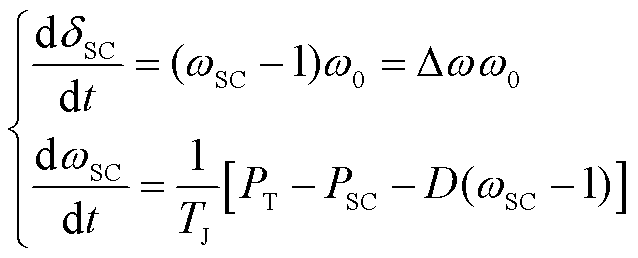（12）
式中，ωSC为调相机转子角频率；ω0为系统额定角频率；∆ω为与δ′处于同一时刻的转速偏差；TJ为调相机惯性时间常数；PT为调相机的机械功率，近似为零；D为调相机阻尼系数。
由传统同步机的能量函数可知，运行轨迹上任意一点的转子相对动能Ek和系统势能Ep分别[30]为
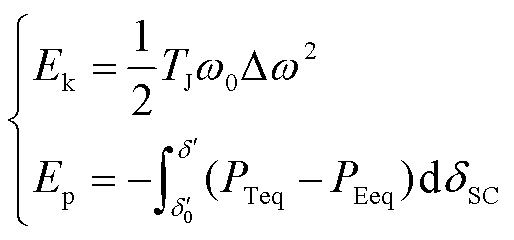（13）
式中，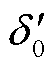
为系统运行轨迹的稳定平衡点；δ′为任一时刻调相机功角。考虑到本文关注功角摇摆过程中系统能量变化情况，取同一运行轨迹上任意两点的相对动能和势能增量进行后续分析。
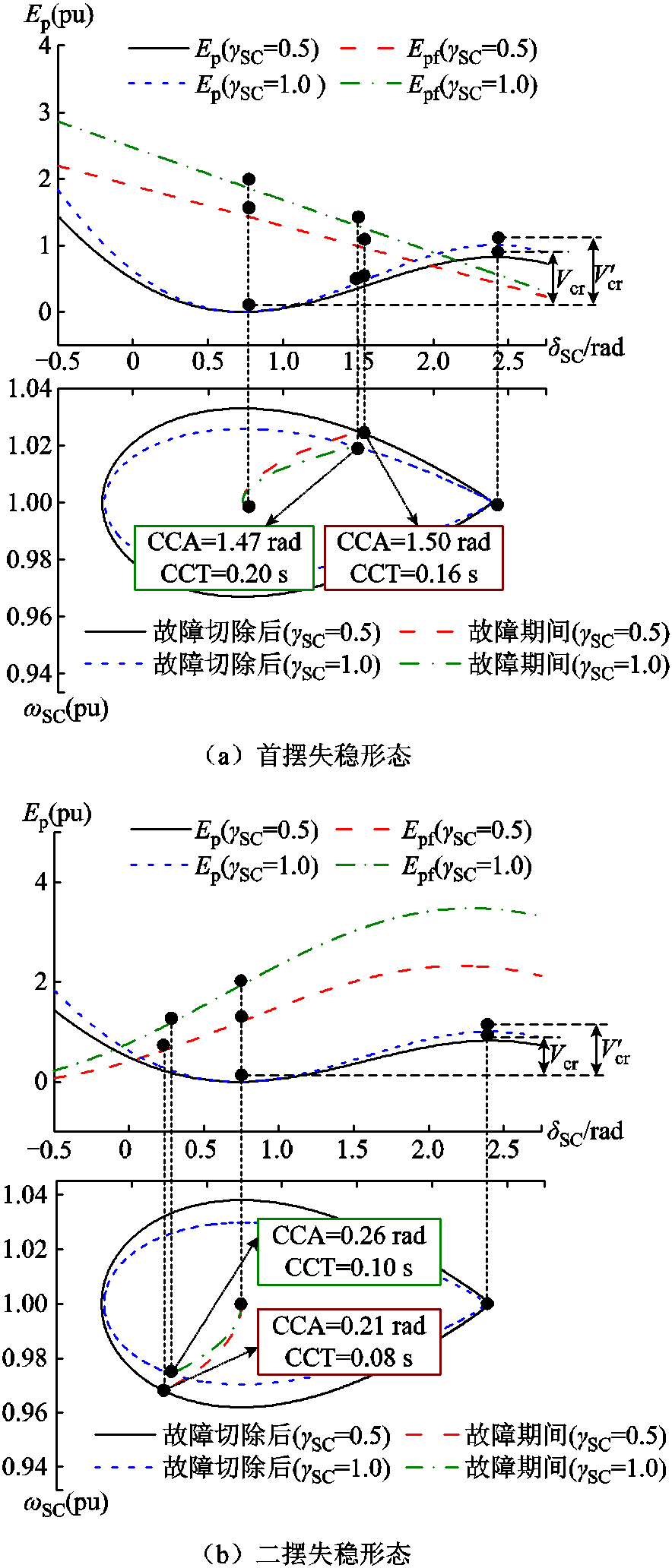
基于式（11）～式（13）可得导致故障期间PTeqf＞PEeqf和PTeqf＜PEeqf的两种工况下等效同步机功角特性曲线和系统势能曲线分别如图4a和图4b所示。图4中，tcl为故障切除时间，δcl为故障切除时调相机功角，δre为调相机反向摆动阶段转速恢复为同步转速时对应的功角，δmax为系统不稳定平衡点处对应的功角。稳态工况下，系统运行点位于稳定平衡点a处，对应的功角为δ0。此时PTeq=PEeq，新能源有功功率全部注入至外电网中且满足网侧有功功率需求。
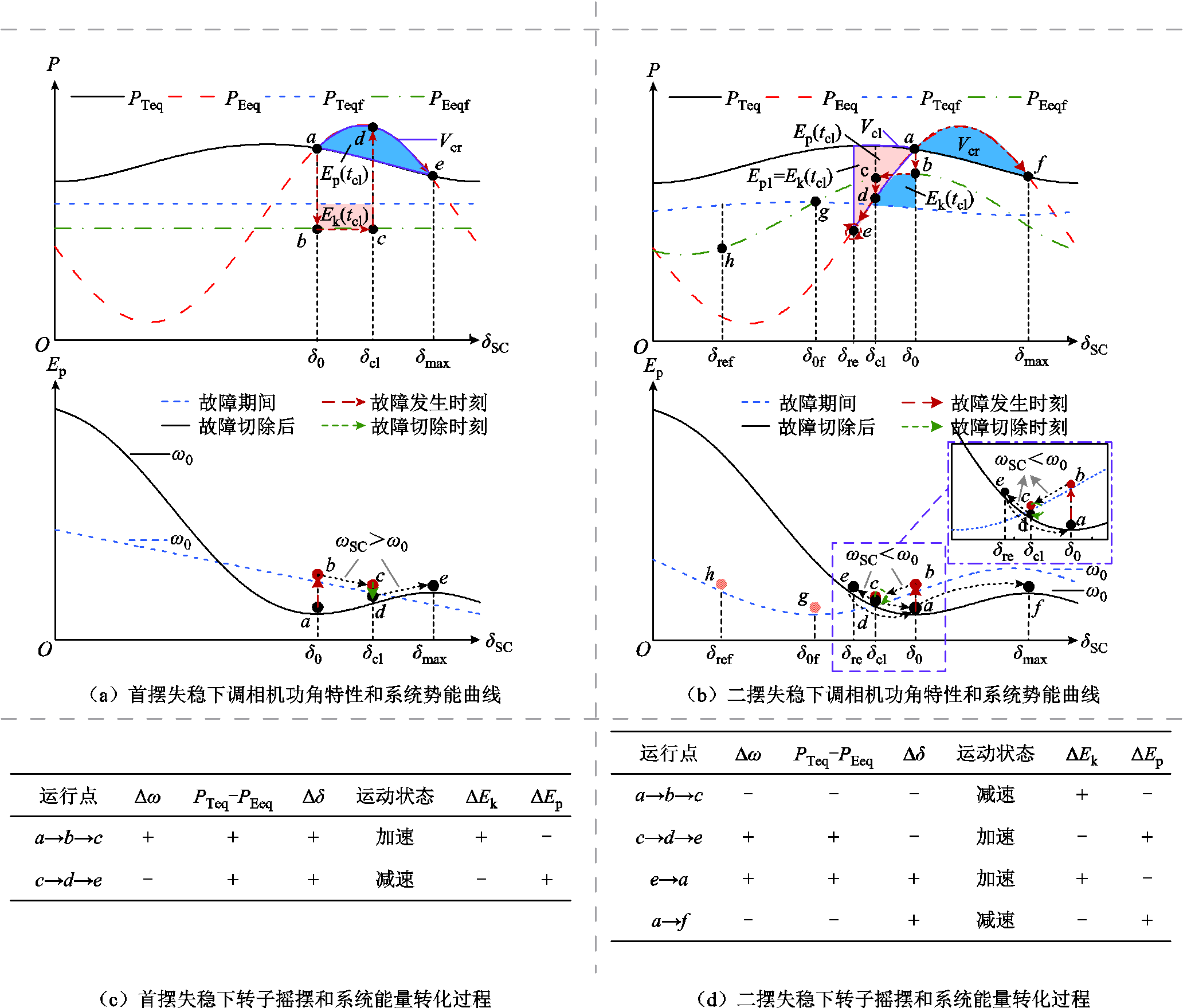
图4 不同失稳形态下调相机的暂态失稳机理
Fig.4 Transient instability mechanism of the condenser with different instability forms
对于导致故障期间PTeqf＞PEeqf的工况，转子摇摆和能量转换过程如图4c所示。此工况下调相机暂态失稳形态与传统同步机首摆加速失稳类似[25-26]，后文简称此失稳形态为首摆失稳。
对于导致故障期间PTeqf＜PEeqf的工况，转子摇摆和能量转换过程如图4d所示。可以看出，故障期间转子减速并积累相对动能Ek(tcl)。故障切除后转子加速，功角在惯性的作用下继续减小直至转速恢复同步速（d→e阶段），此阶段Ek(tcl)转换为系统势能Ep1。随后调相机进入功角增大的正向摇摆阶段，在e→a阶段转子加速，此时系统势能Ep1+Ep(tcl)转换为相对动能。a→f阶段转子减速，若Ep1+Ep(tcl)大于f点处系统势能（临界能量Vcr），则系统暂态失稳。此工况下调相机经历首摆功角反向摆动而二摆转子正向加速失稳的暂态过程，后文简称此失稳形态为二摆失稳。
值得一提的是，二摆失稳工况下，故障期间等效同步机PTeqf和PEeqf曲线存在交点g，且此点处dPEeqf/dδSC＞0，表明其为稳定平衡点。若故障切除时间较长，调相机在故障期间完成首摆功角减小过程（b→h阶段）并进入二摆转子加速且功角增大的阶段（h→c阶段），期间经历“相对动能→系统势能→相对动能”的能量转换过程。在故障切除后因转子转速大于同步速而功角继续增大，进入前述d→f阶段，若故障切除时刻的系统能量Vcl＞Vcr则暂态失稳。
忽略阻尼影响，对式（12）进行首次积分可得系统的能量函数为
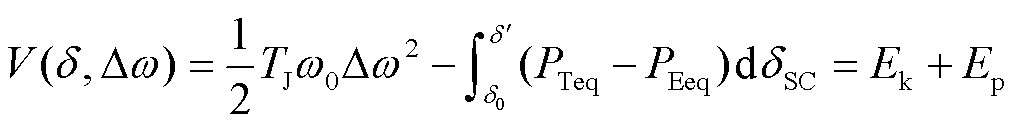（14）
由前述分析可知，当Ek(tcl)+Ep(tcl)≤Vcr时系统暂态稳定。Ek(tcl)+Ep(tcl)=Vcr时对应的故障切除时间和调相机功角分别为极限切除时间（Critical Clearance Time, CCT）和极限切除角（Critical Clearance Angle, CCA）。结合式（14）可知系统临界能量为
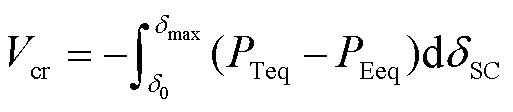（15）
式中，δmax为不稳定平衡点处对应的功角。
结合前述系统能量转换过程可知，两种失稳形态下故障切除时刻的转子相对动能和系统势能均可通过式（16）计算。
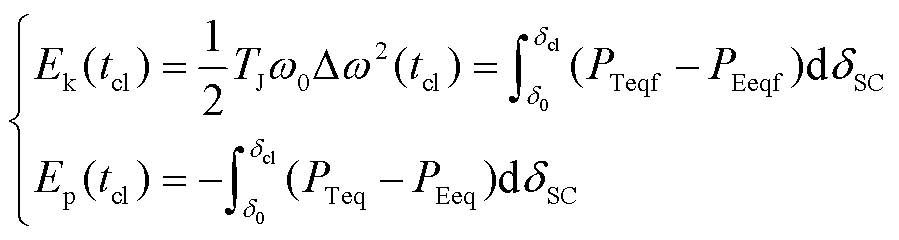（16）
因此，两种失稳形态下以能量形式表示的系统暂态稳定裕度为
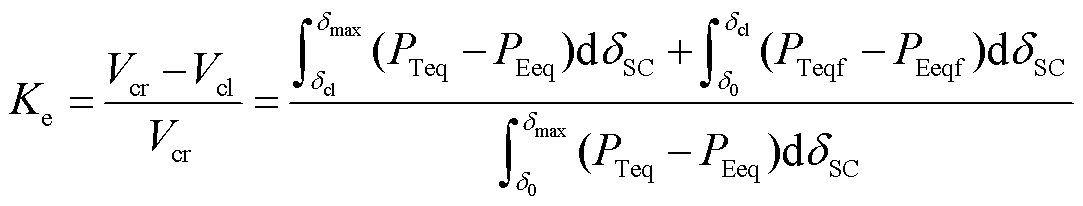（17）
为了便于实际应用并揭示两种失稳形态下系统暂态稳定边界的差异性，有必要分析以CCT表示的系统暂态稳定裕度。首摆失稳形态下，由图4a可知，系统仅在c点处切除故障时满足Ek(tcl)+ Ep(tcl)=Vcr，表明系统存在唯一的CCA。由于故障期间运动至c点的路径唯一，系统存在唯一的CCT。因此，以CCT表示的系统暂态稳定裕度为
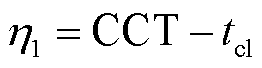（18）
二摆失稳形态下，由图4b可知，系统仅在c点处切除故障时满足Ek(tcl)+Ep(tcl)=Vcr，表明系统的CCA唯一。由于故障期间运行点到达c点存在b→c和b→h→c两个路径，故系统存在两个CCT。令运行点沿b→c路径运动的时间为CCT1，沿b→h→c路径运动的时间为CCT2，结合势能曲线可知，系统在CCT1＜tcl＜CCT2的条件下因Ek(tcl)+Ep(tcl)＞Vcr而失稳。因此，此形态下系统的暂态稳定裕度为
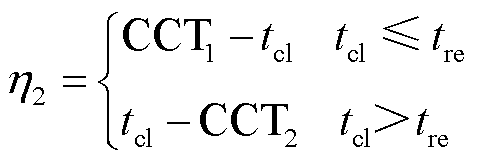（19）
式中，tre为运行点沿b→h路径运动的时间。为简化分析，仅关注故障期间运行点沿b→h→b路径运动的过程，后续摇摆过程忽略不计。
由此可知，在实际工程中若发现调相机进入二摆失稳形态，在故障期间的首摆功角减小阶段迅速切除故障，或在故障期间的功角增大阶段适当延长故障切除时间均有助于保障调相机暂态稳定。
在调相机不同的失稳形态下，系统暂态稳定裕度不同。为了计算系统暂态稳定裕度以指导保护控制设计，有必要解析调相机暂态失稳形态发生变化的边界，从而预先分析实际场景下系统发生短路故障时调相机的暂态摇摆过程。因此，本节通过解析故障瞬间转子上不平衡功率为零时对应的系统参数，从而得到调相机失稳形态由首摆失稳变化至二摆失稳的必要条件。
考虑到故障期间新能源通常采用低电压穿越控制策略，此时不同的过渡电阻将导致调相机进入不同的失稳形态[25-26,29]。因此本文以过渡电阻为例，解析导致调相机失稳形态发生变化的过渡电阻范围。
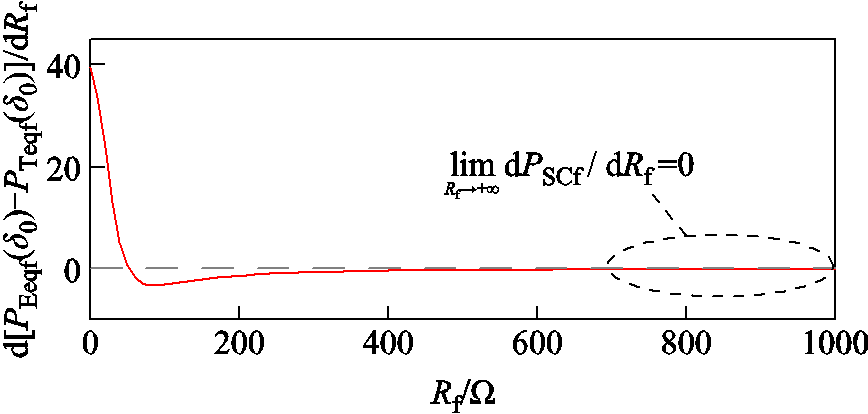
增大过渡电阻后，故障瞬间调相机有功功率与过渡电阻的灵敏度曲线如附图1所示。考虑到当过渡电阻为无穷大时短路支路开路，此时系统为稳态运行状态，等效同步机转子不平衡功率为零，即Rf→∞时PTeqf(δ0)−PEeqf(δ0)=0。由附图1可知，随着Rf的增大，d[PEeqf(δ0)−PTeqf(δ0)]/dRf先正后负，且Rf→∞时d[PEeqf(δ0)−PTeqf(δ0)]/dRf=0，表明较大的Rf将导致PEeqf(δ0)＞PTeqf(δ0)。
结合式（10）和式（11）可知稳态工况下等效同步机机械功率和电磁功率分别为
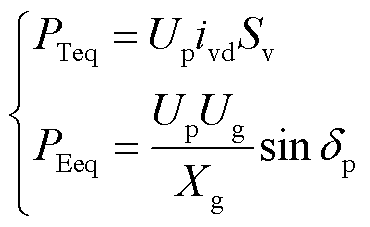（20）
由于稳态时调相机不发出有功功率，因此其功角近似等于并网点相位，同时令PTeq=PEeq可得调相机稳态运行时的功角为
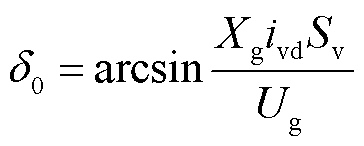（21）
故障期间等效同步机的机械功率和电磁功率分别为
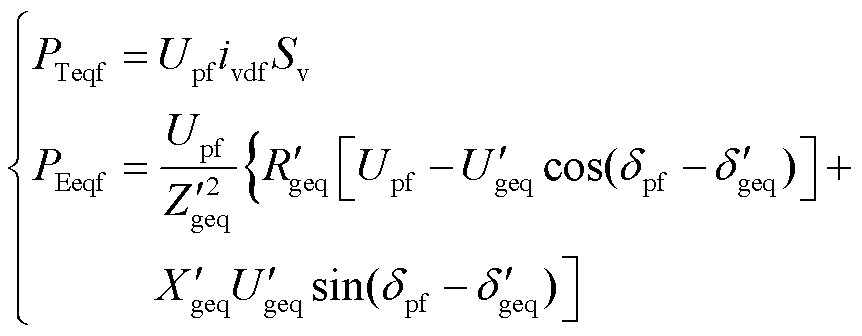（22）
为了计算导致调相机由首摆失稳变化至二摆失稳形态的临界过渡电阻，令PTeqf(δ0)=PEeqf(δ0)可得
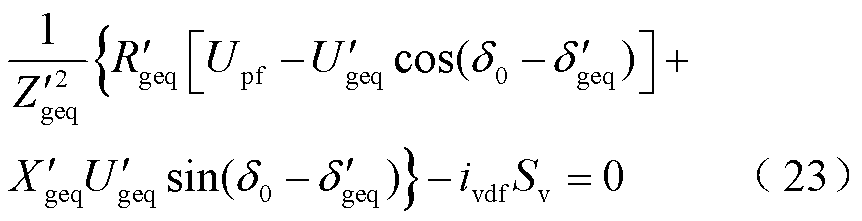
在线路电抗Xg∈[0.125, 0.5]，故障距离df∈[0.1, 0.9]的范围内对式（23）进行数值分析可得
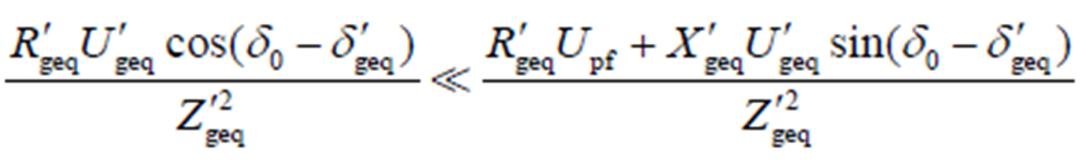（24）
因此忽略式（23）中的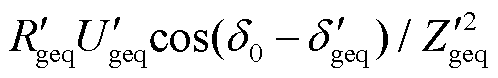
项后可得
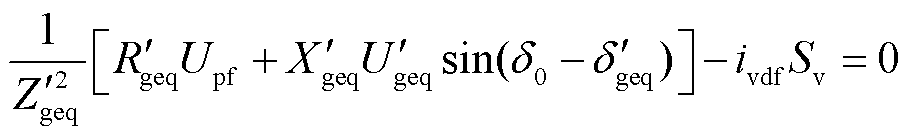（25）
将戴维南等效参数代入式（25）中并整理可得
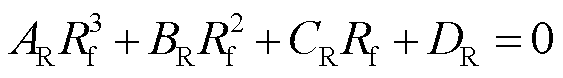（26）
求解式（26）并忽略不符合实际的解可得前述临界过渡电阻为
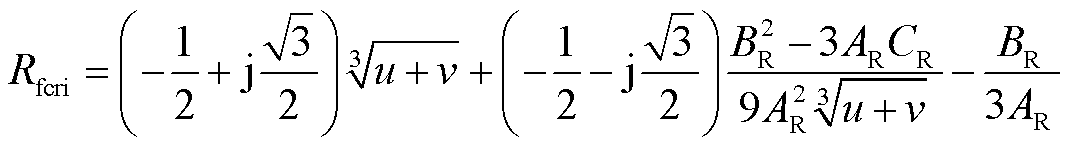（27）
式（26）和式（27）中系数表达式详见附录第2节。
结合前述分析可得不同线路电抗和故障距离下，导致调相机暂态期间进入二摆失稳形态的过渡电阻范围，如附图2所示。参考此分析方法，同理可得导致调相机失稳形态变化的其他系统参数范围。
前述分析表明调相机暂态期间存在两种失稳形态。本节从等效同步机转子上承担的不平衡功率出发，探究系统参数对调相机失稳形态以及系统暂态稳定裕度的影响。
由式（10）和式（14）可知，提高ivdf不会改变系统临界能量Vcr，但会使新能源暂态有功功率Pvf=UpfivdfSv增大，从而导致等效同步机中原动机提供的机械功率PTeqf增大。由此可知，增大ivdf将导致调相机由二摆失稳形态向首摆失稳形态变化。
对于系统暂态稳定裕度，在首摆失稳形态下，故障期间PTeqf＞PEeqf，PTeqf增大导致转子承担的不平衡功率增大，从而此阶段积累相对动能Ek(tcl)的能力增强，Vcl=Vcr的条件下允许转子故障期间摆开的角度减小，因此系统的CCA和CCT减小。在二摆失稳形态下，故障期间PTeqf＜PEeqf，PTeqf增大使得转子上不平衡功率减小，从而此阶段积累相对动能Ek(tcl)的能力下降，导致CCA和CCT均增大。
动态无功电流比例系数k增大时，新能源暂态期间输出更多的无功功率从而导致Upf增大，同时整理式（10）可得
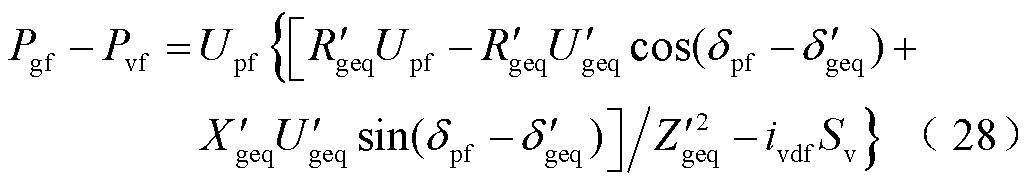
由式（28）可以看出，Upf增大，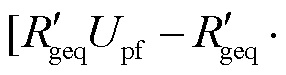
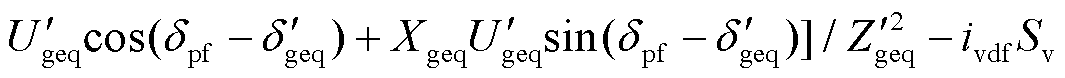相应增大，表明尽管新能源有功出力Pvf小幅上升，但不及电网有功功率需求Pgf的增大程度，此时等效同步机转子上ΔPEeqf＞ΔPTeqf。由此可见，增大k将导致调相机由首摆失稳形态向二摆失稳形态变化。
对于系统暂态稳定裕度，由于增大k导致ΔPEeqf＞ΔPTeqf，因此在首摆失稳形态下故障期间积累Ek(tcl)的能力减弱，同时考虑到增大k不会改变Vcr，因此CCA和CCT均增大。而在二摆失稳形态下，故障期间积累Ek(tcl)的能力增强，因此CCA和CCT均减小。
上述结果表明，为了提升调相机暂态稳定性，若暂态期间调相机进入首摆失稳形态，则新能源故障期间应减发有功功率并增发无功功率；而当调相机进入二摆失稳形态时，新能源应增发有功功率并减发无功功率。
定义调相机容量占比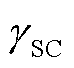
为调相机容量SSC与新能源容量SVSC之比，则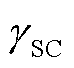与调相机支路电抗XSC和调相机惯量TJ间关系为
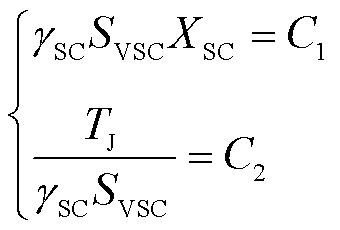（29）
式中，C1和C2为常数。
由式（29）可知，SVSC固定时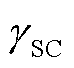，增大使得XSC减小，进而导致调相机支路功率送出极限增大，此时调相机发出的有功功率和无功功率增大。有功功率增大意味着等效同步机PEeq增大，同时由式（21）可知δ0和δmax不变，因此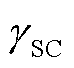增大能够提升Vcr。无功功率增大使得并网点电压升高，从而产生类似于增大新能源无功功率对系统稳定性的影响。由附图3可知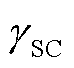，增大将导致两种失稳形态下积累Ek(tcl)的能力均增强，表明首摆失稳形态下ΔPTeqf＞ΔPEeqf，二摆形态下ΔPEeqf＞ΔPTeqf，因此增大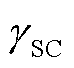对调相机失稳形态的变化存在非线性影响。
对于系统暂态稳定裕度，由附图3可知，综合考虑Ek(tcl)和Vcr增大的影响后，两种形态下CCA均减小。考虑到TJ随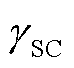增大而增大，有助于减缓转子摇摆动态从而增大了CCT。
系统强度与线路电抗Xg成反比关系，系统强度减弱意味着Xg增大，此时线路功率送出极限下降，导致等效同步机PEeqf和PEeq减小。同时由式（21）可知Xg增大导致δ0增大和δmax减小，结合式（14）可知Vcr减小。由PEeqf随Xg的增大而减小可知，Xg增大导致调相机失稳形态由二摆失稳向首摆失稳变化。
在首摆失稳形态下，PEeqf减小使得故障期间转子承担不平衡功率增大从而积累Ek(tcl)的能力增强，因此CCA和CCT均减小。在二摆失稳形态下，PEeqf减小使得故障期间转子承担不平衡功率减小从而积累Ek(tcl)的能力下降，但结合附图4可知|ΔVcr|＞|ΔEk(tcl)|，因此CCA和CCT下降。
为了验证前述调相机暂态失稳机理和各因素影响规律的正确性，本节基于PSCAD/EMTDC搭建了如图1所示的联合系统模型，系统参数见表1。
表1 联合送出系统参数
Tab.1 Main parameters of the associate system
参数数值 交流系统基准容量Sb/(MV·A)150 无穷大电网电压Ug/kV230 线路电抗Xg(pu)0.33 线路电阻Rg(pu)0.033 调相机暂态电抗x′d(pu)0.14 升压变电抗XT(pu)0.1 惯性时间常数TJ/s3.0
为了验证调相机暂态期间存在两种失稳形态，设置线路中点发生持续0.2 s的三相短路接地故障，过渡电阻Rf分别为0.001 Ω和20 Ω，得到各设备有功功率、调相机功角和转速的时域仿真波形如图5所示。可以看出，Rf=0.001 Ω时，暂态期间调相机进入首摆失稳形态。此时调相机故障期间因Pvf＞Pgf而吸收有功功率，其转子加速且功角增大。故障切除后转子减速，功角因惯量作用继续增大直至越过系统不稳定平衡点而失稳。Rf=20 Ω时，暂态期间调相机进入二摆失稳形态，此时调相机故障期间因Pvf＜Pgf而发出有功功率，其转子减速且功角随之减小。故障切除后，新能源向调相机注入有功功率使其转子加速，功角先减小后增大。上述仿真结果与理论分析所得两种暂态失稳过程一致。
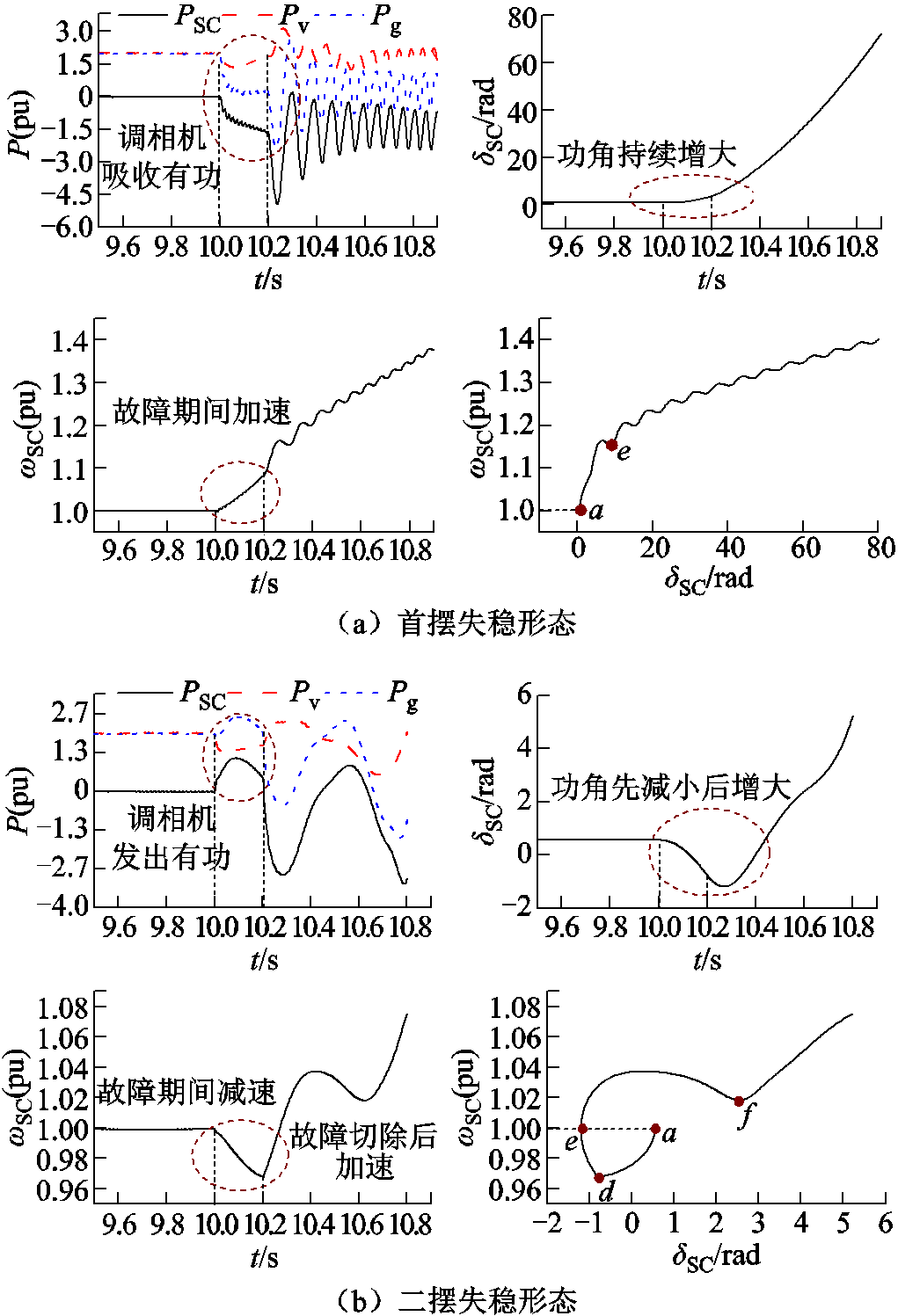
图5 不同失稳形态下系统时域仿真波形
Fig.5 Time-domain simulation waveforms of the system under different instability forms
4.2.1 首摆失稳形态下影响因素验证
本节设置短路故障发生于线路中点，过渡电阻Rf=0.001 Ω，故障切除时间为0.2 s，验证各因素对首摆失稳形态下调相机暂态稳定影响规律的正确性。
固定其他参数而增大新能源暂态有功电流ivdf后得到的系统时域仿真波形如图6a所示。可以看出，在ivdf =0.1(pu)时调相机功角稳定，而随着ivdf增大，故障期间转子承担更多的不平衡功率（由调相机有功功率大小体现），且故障切除时刻转速偏差增大，表明故障期间转子产生了更多的相对动能，系统暂态稳定性下降。图6b为增大动态无功电流比例系数k后的仿真波形，可以看出k=2.5时系统暂态稳定，而减小k后系统失稳。上述结果表明，故障期间新能源减发有功功率和增发无功功率有助于提升系统暂态稳定性。
图6c为不同线路电抗Xg下的仿真波形。可以看出，Xg较小时调相机功角稳定，增大Xg至0.33(pu) 时系统失稳，表明Xg增大导致系统暂态稳定性下降。
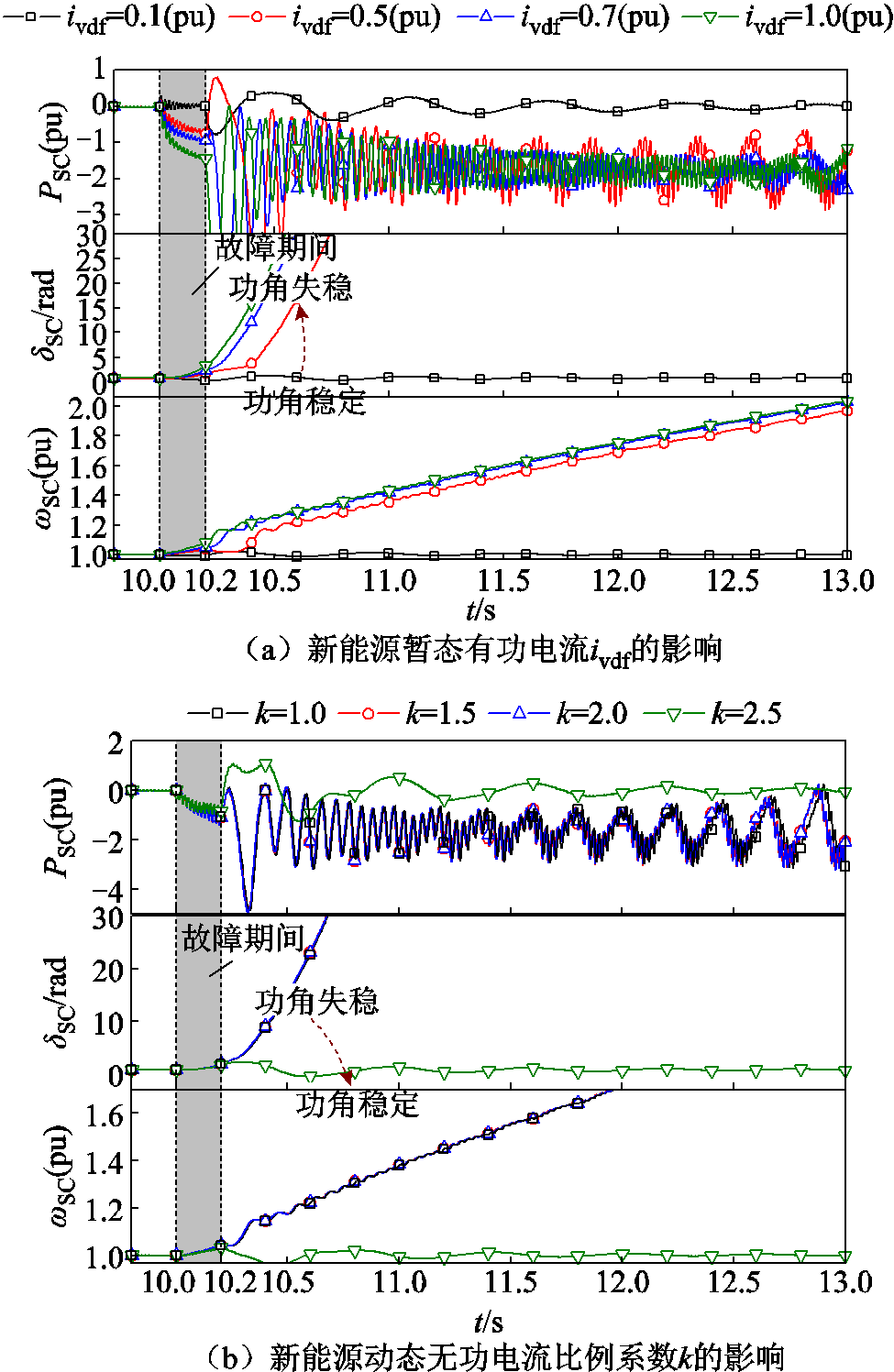
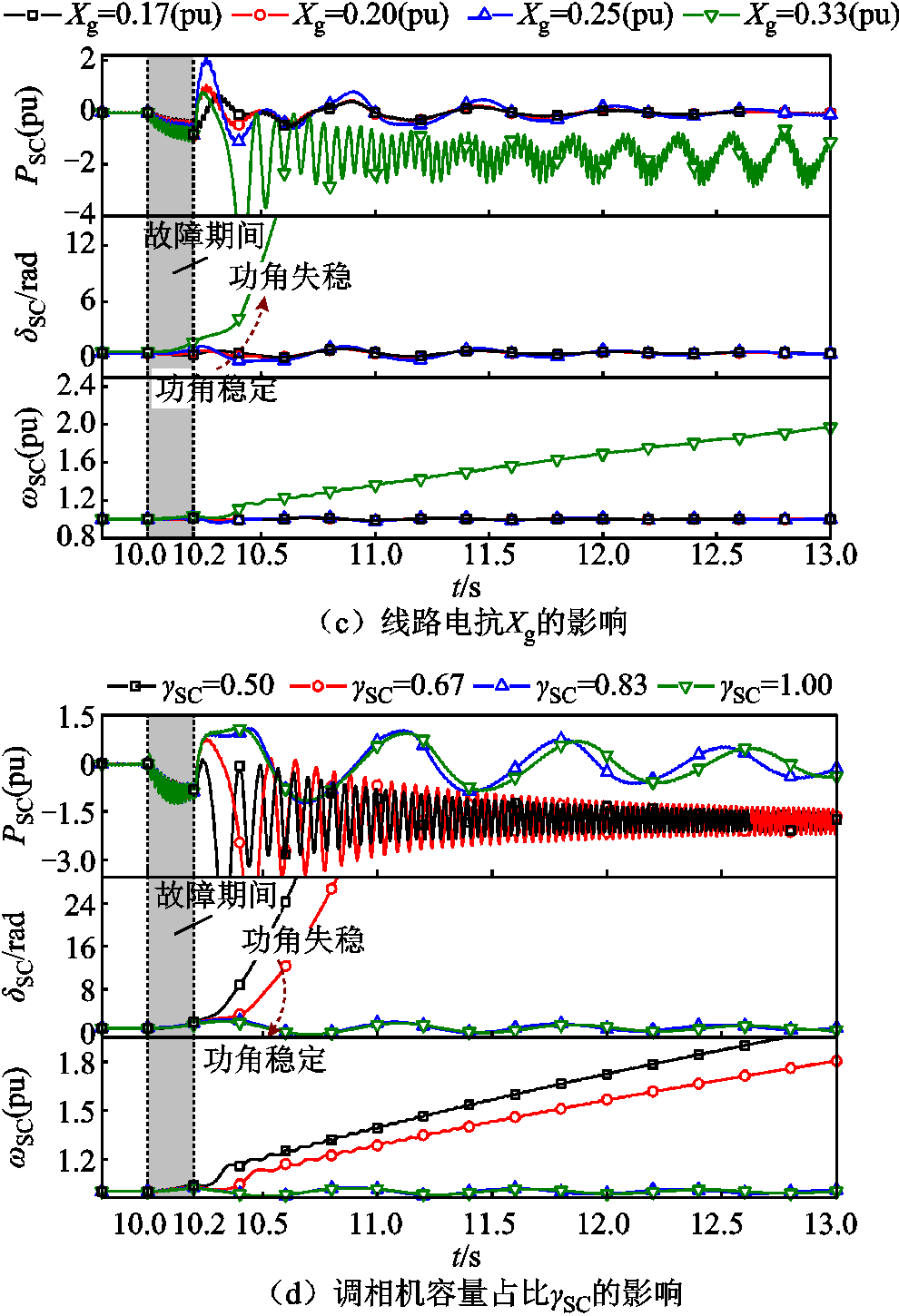
图6 首摆失稳形态下暂态稳定影响因素验证
Fig.6 Influence of different factors on the transient stability under first-swing instability form
增大调相机容量占比后得到的仿真波形如图6d所示。可以看出，调相机容量占比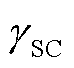为0.50和0.67时系统失稳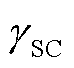，增大后系统能够保持稳定。因此，增大调相机容量占比有利于提升系统暂态稳定性。
4.2.2 二摆失稳形态下影响因素验证
本节设置短路故障发生于线路中点，过渡电阻Rf=20 Ω，故障切除时间为0.1 s，验证各因素对二摆失稳形态下调相机暂态稳定影响规律的正确性。
不同新能源暂态有功电流下系统时域波形如图7a所示。可以看出，故障期间随着新能源输出有功电流ivdf增大，等效同步机转子上不平衡功率减少。同时故障切除时转子转速偏差减小，表明故障期间产生的相对动能下降。当ivdf =1.0(pu)时，调相机功角稳定。图7b为不同动态无功电流比例系数下系统时域波形。可以看出，动态无功电流比例系数k增大会使等效同步机转子承担更多不平衡功率，从而导致转子转速偏差增大并产生更多相对动能。当k=1.0时，调相机功角稳定。上述结果表明，故障期间新能源增发有功功率和降低无功功率有助于提升调相机的暂态稳定性。
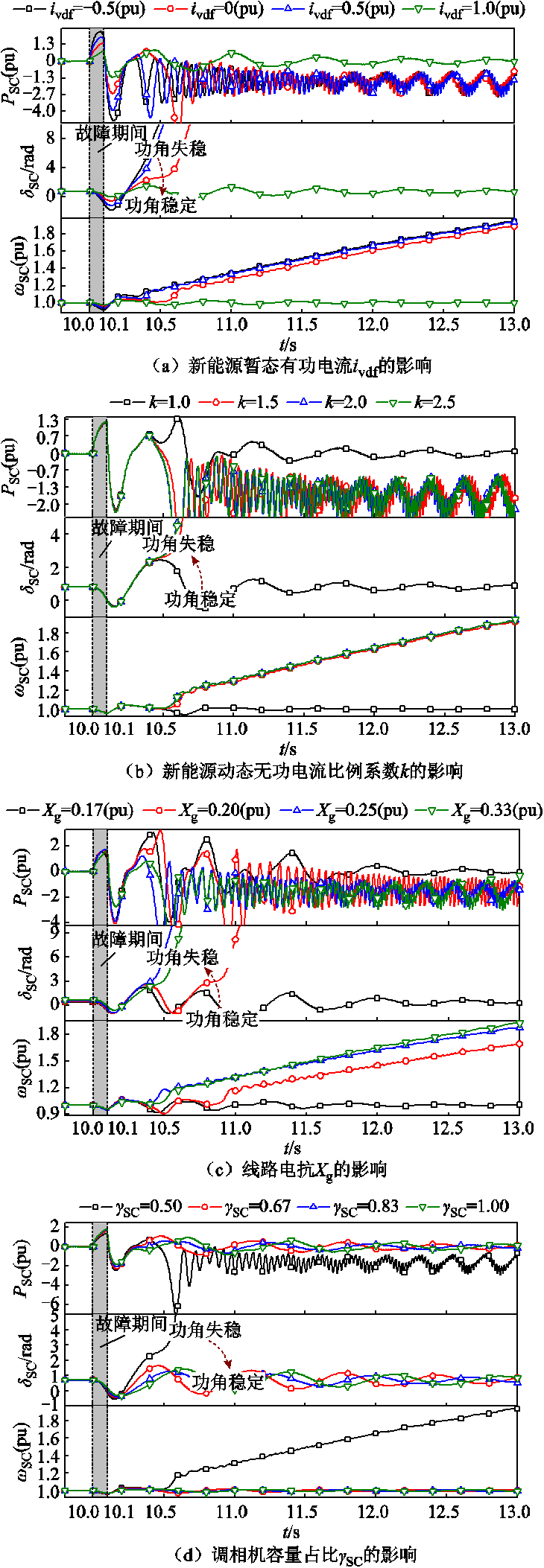
图7 二摆失稳形态下暂态稳定影响因素验证
Fig.7 Influence of different factors on the transient stability under second-swing instability form
不同线路电抗Xg下系统时域波形如图7c所示。可以看出，Xg=0.17(pu)时调相机功角稳定，Xg增大后系统暂态稳定性下降。此外，Xg增大使得调相机稳态功角增大，与前述理论分析一致。
增大调相机容量占比可得系统时域波形如图7d所示。可以看出，调相机容量占比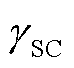=0.5时系统失稳，随着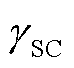增大，故障期间等效同步机转子上不平衡功率增大，但转速偏差因惯量的同步增大而减小。因此，增大调相机容量占比有利于提升系统暂态稳定性。
针对大型新能源基地附近调相机的暂态功角失稳问题，本文基于等效同步机模型，从转子承担的不平衡功率出发，归纳并揭示了调相机暂态失稳机理，随后探究了系统参数对调相机功角稳定性的影响规律，得到的主要结论如下：
1）不同运行工况下，调相机存在首摆加速失稳和首摆减速而二摆加速失稳两种形态。前者与传统同步机暂态稳定类似。后者在首摆阶段经历类似于“压缩弹簧”的势能积累过程，为二摆阶段提供初始能量，若此能量大于系统临界能量则功角失稳。
2）两种失稳形态下调相机暂态稳定边界不同。首摆失稳形态下系统存在唯一的CCT，当故障切除时间大于CCT时系统失稳；二摆失稳形态下系统存在两个CCT，当故障切除时间处于两个CCT之间时系统失稳。因此为指导系统保护控制设计，需分析调相机的暂态摇摆形态并计算对应的失稳边界。
3）由于降低故障期间调相机承担的不平衡功率有助于提升系统暂态稳定性，因此首摆失稳形态下新能源应减发有功功率并增发无功功率；二摆失稳形态下新能源应增发有功功率并减发无功功率。此外，增大调相机容量占比或提高系统强度有利于保障调相机暂态稳定。
本文所得结论适用于锁相环能够与系统保持同步的场景，分析锁相环失稳后对系统暂态稳定性的影响是未来的研究工作。
附 录
1. 调相机功角特性推导
式（4）和式（5）中的系数表达式为
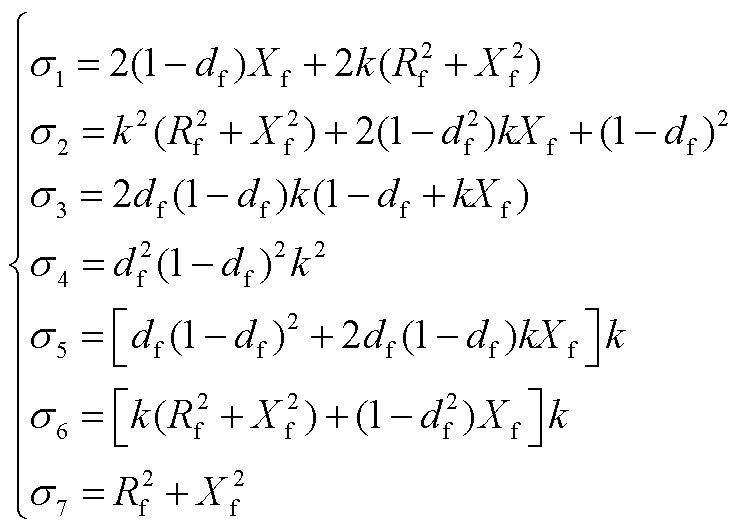（A1）
推导PCC电压幅值Upf和相位δpf的详细过程如下。
由式（6）可得有关PCC电压的方程为
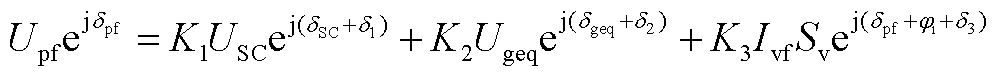（A2）
式（A2）展开可得
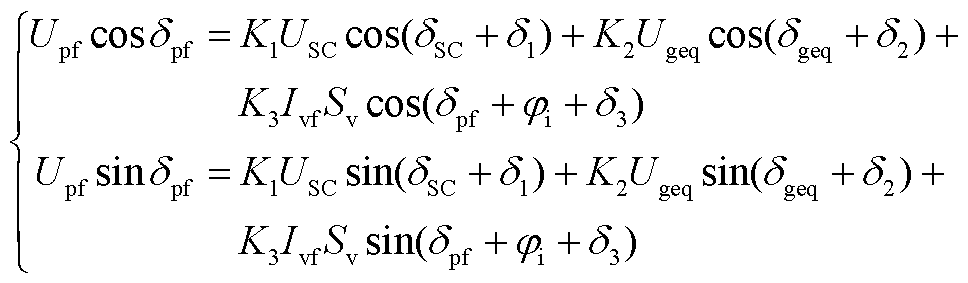（A3）
根据式（A3）所示方程组，整理后可得有关δSC−δpf的方程组为
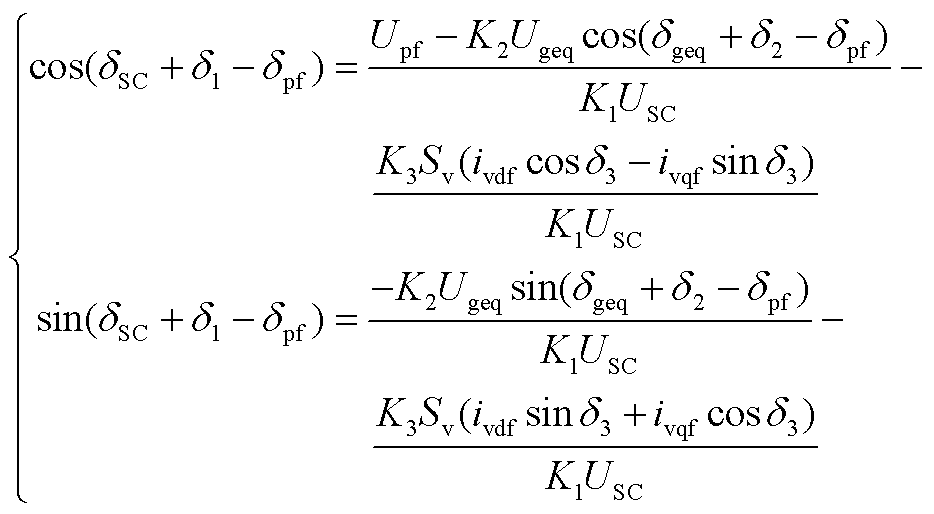（A4）
通过对式（A3）进行整理变换，然后将式（A4）代入式（A3）中可得关于Upf的二次方程为
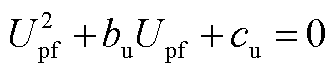（A5）
其中
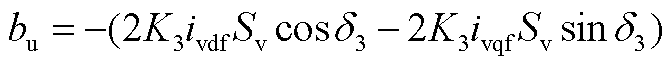（A6）
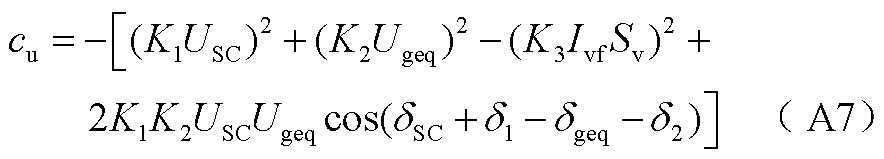
求解此一元二次方程并舍去不符合系统电压实际情况的项，可得PCC电压幅值详细表达式为
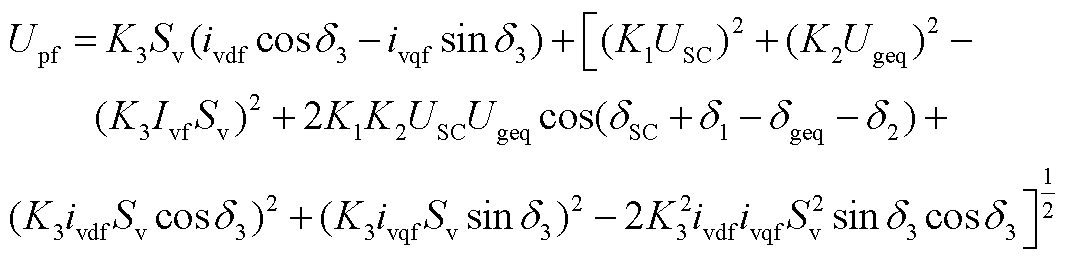（A8）
根据式（A3）可以得到有关PCC电压相位δpf的方程组，即
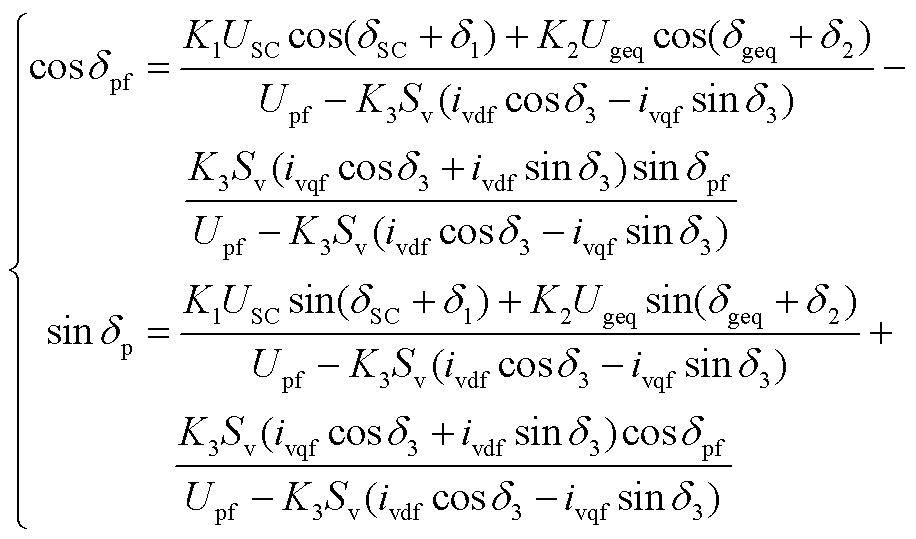（A9）
将式（A9）中两个方程联立求解可得PCC电压相位详细表达式为
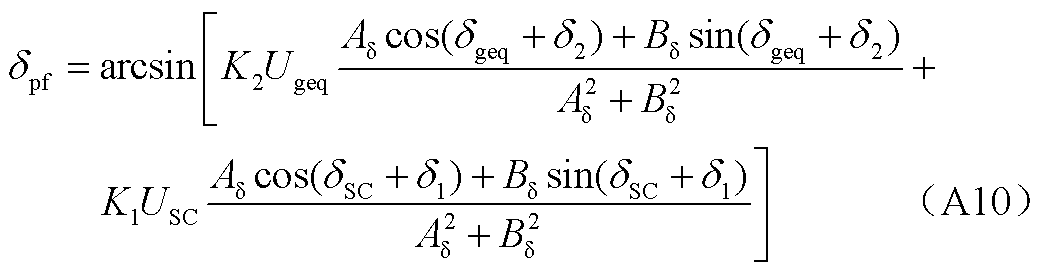
其中
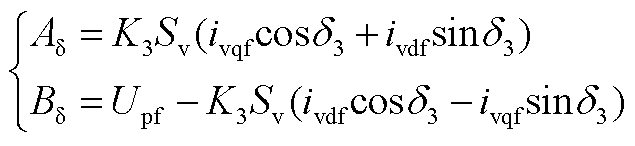（A11）
至此，得到了联合系统PCC电压幅值Upf和相位δpf的解析表达式。
2. 过渡电阻对调相机暂态失稳形态的影响
附图1 故障瞬间调相机有功功率与Rf的灵敏度曲线
App.Fig.1 The sensitivity curve of the condenser active power at the moment of fault occurrence and Rf
式（26）和式（27）中的系数表达式为
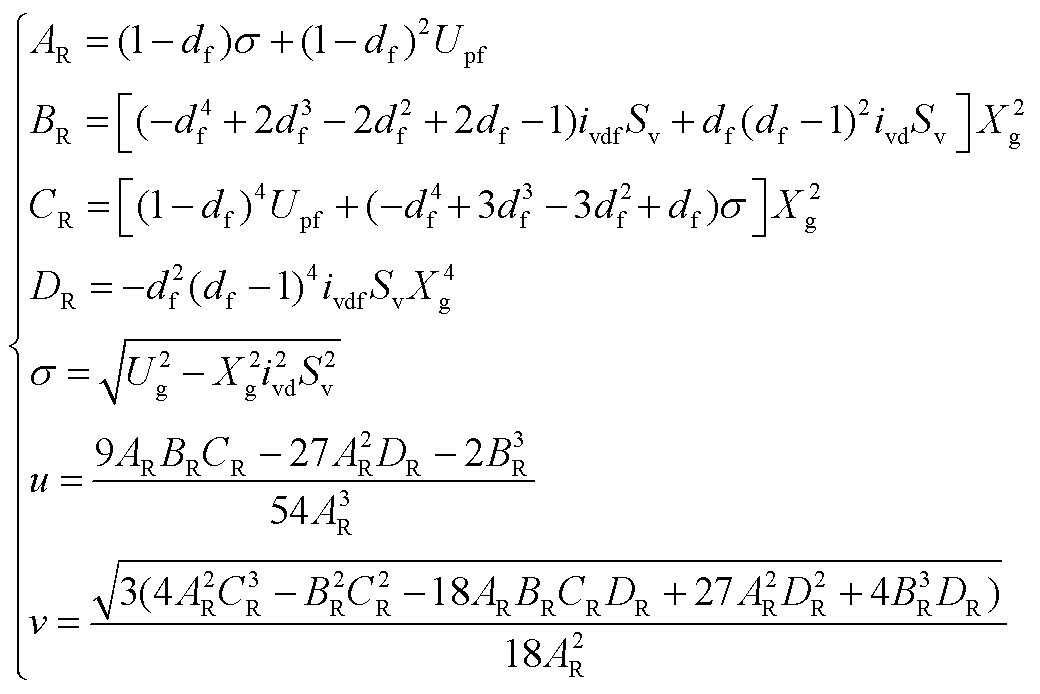（A12）
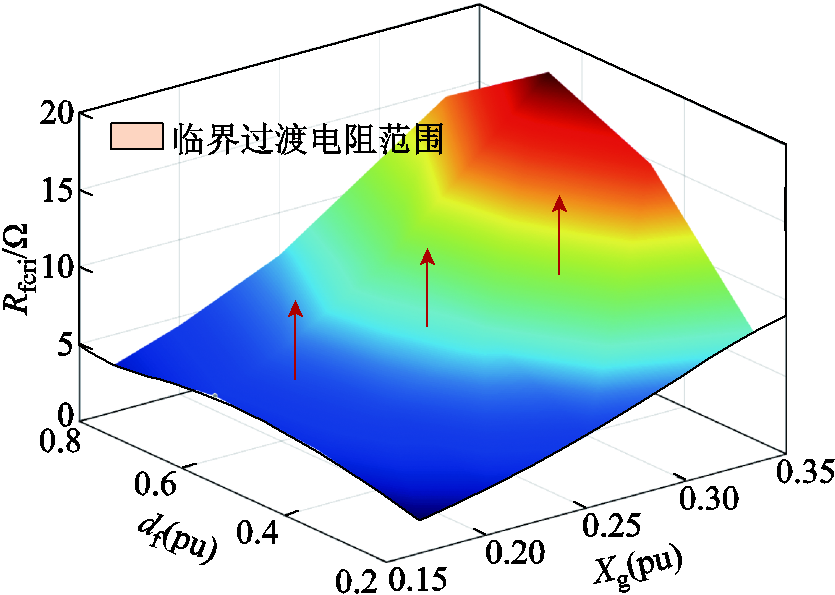
附图2 临界过渡电阻范围
App.Fig.2 The range of critical transition resistance
3. 系统参数对暂态稳定性的影响
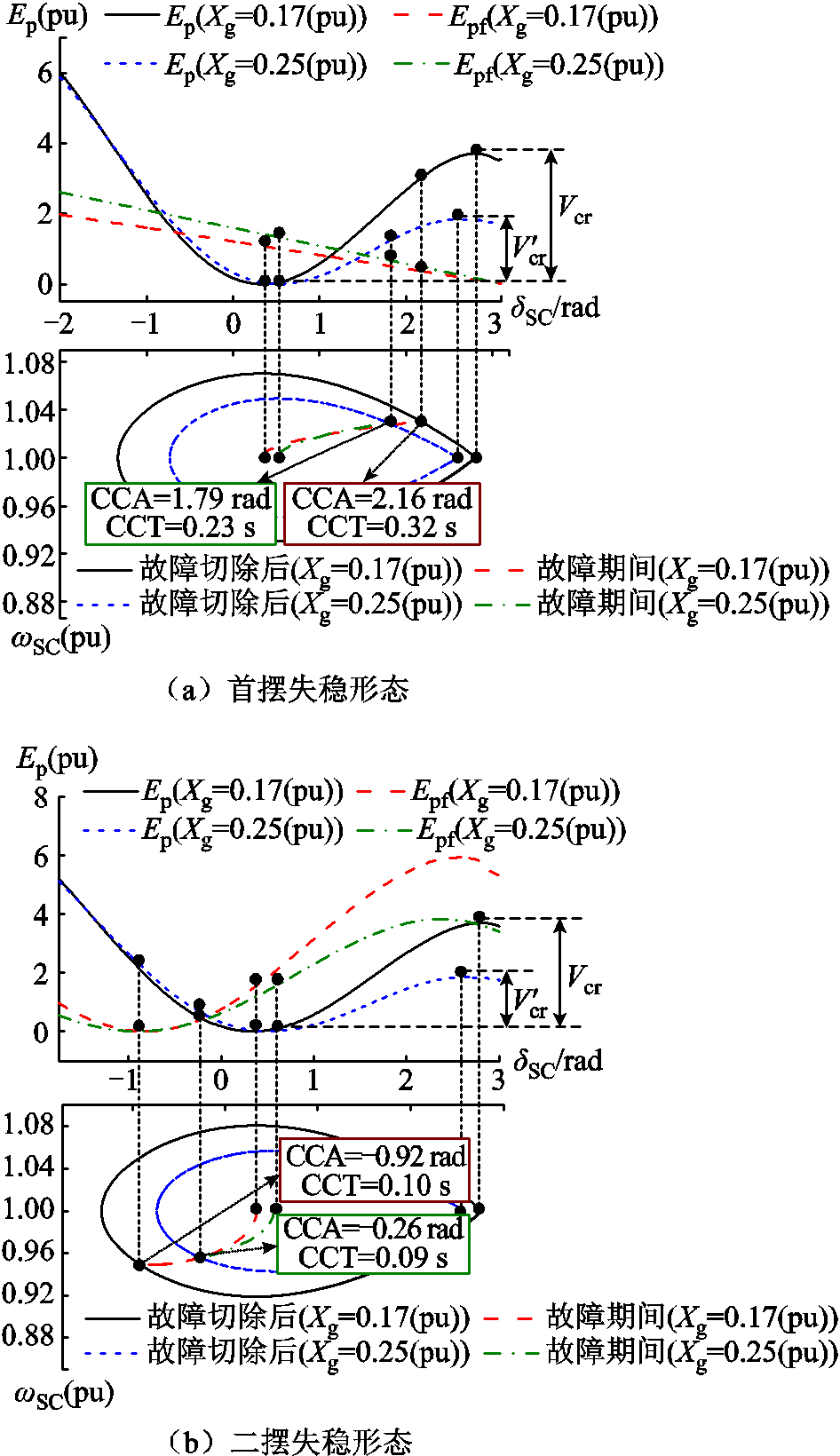
附图3 Xg对系统暂态稳定性的影响
App.Fig.3 Infulence of Xg on transient stability of the system
附图4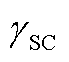 
对系统暂态稳定性的影响
App.Fig.4 Infulence of 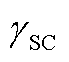on transient stability of the system
参考文献
[1] 舒印彪, 陈国平, 贺静波, 等. 构建以新能源为主体的新型电力系统框架研究[J]. 中国工程科学, 2021, 23(6): 61-69.
Shu Yinbiao, Chen Guoping, He Jingbo, et al. Building a new electric power system based on new energy sources[J]. Strategic Study of CAE, 2021, 23(6): 61-69.
[2] 国家发展改革委, 国家能源局, 国家数据局. 《加快构建新型电力系统行动方案(2024—2027年)》答记者问[J]. 电力设备管理, 2024(15): 7-8.
[3] 胡光, 高晖胜, 辛焕海, 等. 考虑电压动态的电力系统频率强度量化方法[J]. 电力系统自动化, 2024, 48(8): 67-78.
Hu Guang, Gao Huisheng, Xin Huanhai, et al. Quantification method for power system frequency strength considering voltage dynamics[J]. Automation of Electric Power Systems, 2024, 48(8): 67-78.
[4] 杨金洲, 李业成, 熊鸿韬, 等. 新能源接入的受端电网暂态电压失稳高风险故障快速筛选[J]. 电工技术学报, 2024, 39(21): 6746-6758.
Yang Jinzhou, Li Yecheng, Xiong Hongtao, et al. A fast screening method for the high-risk faults with transient voltage instability in receiving-end power grids interconnected with new energy[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6746-6758.
[5] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[6] 江一航, 赵书强, 王慧, 等. 计及风电、调相机支撑特性的频率安全约束分布鲁棒机组组合调度方法[J]. 电工技术学报, 2025, 40(1): 80-95.
Jiang Yihang, Zhao Shuqiang, Wang Hui, et al. Distributionally robust frequency constrained unit commitment with frequency support of wind power and synchronous condenser[J]. Transactions of China Electrotechnical Society, 2025, 40(1): 80-95.
[7] 郭强, 李志强. 同步调相机发展综述[J]. 中国电机工程学报, 2023, 43(15): 6050-6064.
Guo Qiang, Li Zhiqiang. Summarization of synchronous condenser development[J]. Proceedings of the CSEE, 2023, 43(15): 6050-6064.
[8] 王雅婷, 张一驰, 周勤勇, 等. 新一代大容量调相机在电网中的应用研究[J]. 电网技术, 2017, 41(1): 22-28.
Wang Yating, Zhang Yichi, Zhou Qinyong, et al. Study on application of new generation large capacity synchronous condenser in power grid[J]. Power System Technology, 2017, 41(1): 22-28.
[9] 金一丁, 于钊, 李明节, 等. 新一代调相机与电力电子无功补偿装置在特高压交直流电网中应用的比较[J]. 电网技术, 2018, 42(7): 2095-2102.
Jin Yiding, Yu Zhao, Li Mingjie, et al. Comparison of new generation synchronous condenser and power electronic reactive-power compensation devices in application in UHV DC/AC grid[J]. Power System Technology, 2018, 42(7): 2095-2102.
[10] 林旻威, 温步瀛. 大规模风电接入对电力系统暂态稳定性影响研究综述[J]. 电气技术, 2017, 18(4): 1-8, 38.
Lin Minwei, Wen Buying. The overview of influence of large scale wind generation on transient stability of power system[J]. Electrical Engineering, 2017, 18(4): 1-8, 38.
[11] 于强, 孙华东, 汤涌, 等. 双馈风电机组接入对电力系统功角稳定性的影响[J]. 电网技术, 2013, 37(12): 3399-3405.
Yu Qiang, Sun Huadong, Tang Yong, et al. Impact on angle stability of power system with doubly fed induction generators connected to grid[J]. Power System Technology, 2013, 37(12): 3399-3405.
[12] 王清, 薛安成, 郑元杰, 等. 双馈型风电集中接入对暂态功角稳定的影响分析[J]. 电网技术, 2016, 40(3): 875-881.
Wang Qing, Xue Ancheng, Zheng Yuanjie, et al. Impact of DFIG-based wind power integration on the transient stability of power systems[J]. Power System Technology, 2016, 40(3): 875-881.
[13] 牟澎涛, 赵冬梅, 王嘉成. 大规模风电接入对系统功角稳定影响的机理分析[J]. 中国电机工程学报, 2017, 37(5): 1325-1334.
Mu Pengtao, Zhao Dongmei, Wang Jiacheng. Influence mechanism analysis of large-scale wind power integration on power system angle stability[J]. Proceedings of the CSEE, 2017, 37(5): 1325-1334.
[14] 汤蕾, 沈沉, 张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(一): 理论基础[J]. 中国电机工程学报, 2015, 35(15): 3832-3842.
Tang Lei, Shen Chen, Zhang Xuemin. Impact of large-scale wind power centralized integration on transient angle stability of power systems: part Ⅰ: theoretical foundation[J]. Proceedings of the CSEE, 2015, 35(15): 3832-3842.
[15] 汤蕾, 沈沉, 张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(二): 影响因素分析[J]. 中国电机工程学报, 2015, 35(16): 4043-4051.
Tang Lei, Shen Chen, Zhang Xuemin. Impact of large-scale wind power centralized integration on transient angle stability of power systems: part Ⅱ: factors affecting transient angle stability[J]. Proceedings of the CSEE, 2015, 35(16): 4043-4051.
[16] 于珍, 沈沉, 张雪敏. 双馈风机故障穿越后功率恢复速率对系统暂态稳定的影响分析[J]. 中国电机工程学报, 2018, 38(13): 3781-3791, 4019.
Yu Zhen, Shen Chen, Zhang Xuemin. Analysis on the impact of post-fault power recovery speed of doubly-fed induction generators on power system transient stability[J]. Proceedings of the CSEE, 2018, 38(13): 3781-3791, 4019.
[17] 张锋, 陈武晖, 康佳乐, 等. 双馈风电场故障穿越控制策略对风火打捆系统暂态稳定性影响及提升控制策略研究[J]. 电工技术学报, 2025, 40(3): 717-729.
Zhang Feng, Chen Wuhui, Kang Jiale, et al. Research on the effect of fault ride-through control strategy of doubly-fed wind farms on transient stability of wind-fire bundling system and enhancement control strategy [J]. Transactions of China Electrotechnical Society, 2025, 40(3): 717-729.
[18] 姜惠兰, 吴玉璋, 周照清, 等. 含双馈风力发电场的多机系统暂态功角稳定性分析方法[J]. 中国电机工程学报, 2018, 38(4): 999-1005, 1276.
Jiang Huilan, Wu Yuzhang, Zhou Zhaoqing, et al. A method to analyze the transient angle stability of multi-machine system with DFIG-based wind farm[J]. Proceedings of the CSEE, 2018, 38(4): 999-1005, 1276.
[19] 姜惠兰, 周照清, 蔡继朝. 风电接入比例对电力系统暂态功角稳定性影响的分析方法[J]. 电力自动化设备, 2020, 40(7): 53-67.
Jiang Huilan, Zhou Zhaoqing, Cai Jizhao. Analysis method of influence of wind power access proportion on transient power angle stability of power system[J]. Electric Power Automation Equipment, 2020, 40(7): 53-67.
[20] 王伟, 周少泽, 黄萌, 等. 构网型技术：演进历程、功能定位及应用展望[J]. 电力系统自动化, 2025, 49(1): 1-13.
Wang Wei, Zhou Shaoze, Huang Meng, et al. Grid-forming technologies: evolution history, functional positioning, and application perspectives[J]. Automation of Electric Power Systems, 2025, 49(1): 1-13.
[21] Li Mingfei, Quan Xiangjun, Wu Zaijun, et al. Modeling and transient stability analysis of mixed-GFM-GFL-based power system[C]//2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 2021.
[22] 耿华, 何长军, 刘浴霜, 等. 新能源电力系统的暂态同步稳定研究综述[J]. 高电压技术, 2022, 48(9): 3367-3383.
Geng Hua, He Changjun, Liu Yushuang, et al. Overview on transient synchronization stability of renewable-rich power systems[J]. High Voltage Engineering, 2022, 48(9): 3367-3383.
[23] 黄森, 姚骏, 钟勤敏, 等. 含跟网和构网型新能源发电单元的混联电力系统暂态同步稳定分析[J]. 中国电机工程学报, 2024, 44(21): 8378-8392.
Huang Sen, Yao Jun, Zhong Qinmin, et al. Transient synchronization stability analysis of hybrid power system with grid-following and grid-forming renewable energy generation units[J]. Proceedings of the CSEE, 2024, 44(21): 8378-8392.
[24] 邱硕, 庄可好, 汤波, 等. 基于直流电容自同步的构网型SVG暂态同步稳定分析与提升策略[J/OL]. 电网技术, 2024: 1-15. https://doi.org/10.13335/j. 1000-3673.pst.2024.1040.
Qiu Shuo, Zhuang Kehao, Tang Bo, et al. Transient synchronous stability analysis and enhancement strategy for DC capacitor self-synchronisation- based constructed grid type SVGs[J/OL]. Power System Technology, 2024: 1-15. https://doi.org/10.13335/j. 1000-3673.pst.2024.1040.
[25] 沈广进, 辛焕海, 刘昕宇, 等. 大型新能源基地中调相机同步失稳机理与影响因素分析[J]. 电力系统自动化, 2022, 46(20): 100-108.
Shen Guangjin, Xin Huanhai, Liu Xinyu, et al. Analysis on synchronization instability mechanism and influence factors for condenser in large-scale renewable energy base[J]. Automation of Electric Power Systems, 2022, 46(20): 100-108.
[26] Liu Xinyu, Xin Huanhai, Zheng Di, et al. Transient stability of synchronous condenser co-located with renewable power plants[J]. IEEE Transactions on Power Systems, 2024, 39(1): 2030-2041.
[27] 杨松浩, 李秉芳, 赵天骐, 等. 新能源场站分布式同步调相机暂态功角失稳形态及机理[J]. 电力系统自动化, 2023, 47(3): 12-18.
Yang Songhao, Li Bingfang, Zhao Tianqi, et al. Transient angle instability mode and mechanism of distributed synchronous condensers in renewable energy station[J]. Automation of Electric Power Systems, 2023, 47(3): 12-18.
[28] 赵天骐, 李秉芳, 杨松浩, 等. 新能源场站分布式同步调相机暂态功角稳定性影响因素分析[J]. 电力系统自动化, 2023, 47(16): 114-122.
Zhao Tianqi, Li Bingfang, Yang Songhao, et al. Analysis of influence factors for transient rotor-angle stability of distributed synchronous condensers in renewable energy stations[J]. Automation of Electric Power Systems, 2023, 47(16): 114-122.
[29] 王彤, 王潇桐, 韩梓畅, 等. 分布式调相机暂态特性分析与暂态功角稳定性机理研究[J]. 电工技术学报, 2025, 40(1): 36-51.
Wang Tong Wang Xiaotong Han Zichang, et al. Research on transient characteristic analysis and transient stability mechanism of distributed condenser [J]. Transactions of China Electrotechnical Society, 2025, 40(1): 36-51.
[30] Leonard L. 电力系统稳定与控制[M]. 李相俊, 李生虎, 金恩淑, 译. 3rd ed. 北京: 机械工业出版社. 2018.
[31] 辛焕海, 李子恒, 董炜, 等. 三相变流器并网系统的广义阻抗及稳定判据[J]. 中国电机工程学报, 2017, 37(5): 1277-1293.
Xin Huanhai, Li Ziheng, Dong Wei, et al. Generalized-impedance and stability criterion for grid-connected converters[J]. Proceedings of the CSEE, 2017, 37(5): 1277-1293.
[32] He Xiuqiang, Geng Hua. Transient stability of power systems integrated with inverter-based generation[J]. IEEE Transactions on Power Systems, 2021, 36(1): 553-556.
[33] Zhao Mingquan, Yuan Xiaoming, Hu Jiabing, et al. Voltage dynamics of current control time-scale in a VSC-connected weak grid[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2925-2937.
[34] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[35] 张庆海, 彭楚武, 陈燕东, 等. 一种微电网多逆变器并联运行控制策略[J]. 中国电机工程学报, 2012, 32(25): 126-132, 18.
Zhang Qinghai, Peng Chuwu, Chen Yandong, et al. A control strategy for parallel operation of multi-inverters in microgrid[J]. Proceedings of the CSEE, 2012, 32(25): 126-132, 18.
[36] 国家市场监督管理总局, 国家标准化管理委员会. 风电场接入电力系统技术规定第1部分：陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[37] Xin Huanhai, Liu Xinyu, Zheng Di, et al. Risk assessment of post-fault temporary overvoltage using generalized short-circuit ratio[J]. IEEE Transactions on Power Systems, 2024, 39(1): 1837-1849.
Transient Power Angle Instability Mechanism and Stability Margin Analysis of Synchronous Condenser Co-Located with Renewable Energy Base Based on Equivalent Synchronous Generator
Abstract Configuring synchronous condensers (SCs) in large renewable energy base is an effective technical solution to improve the carrying capacity of renewable energy. However, there is a risk of transient power angle instability of the SC in this scheme. Existing literatures have analyzed the transient instability of the SC under specific operating conditions, but they have not comprehensively considered the influence of system parameters on the power angle characteristics of the SC, resulting in a lack of systematic understanding of the transient instability mechanism of the SC under different instability forms. In order to solve the above problems, this paper intends to summarize and analyze the transient instability mechanism behind the different instability forms of the SC based on the equivalent synchronous generator model, quantify the change boundary of the instability forms of the SC and the transient stability margin of the system under the different instability forms by drawing on the analysis methods of transient stability of the traditional synchronous generator.
Firstly, the power angle characteristics of the SC are analyzed based on the equivalent model of the associated system of a renewable energy base co-located with a SC and the Thévenin equivalent method. Subsequently, the active power transfer relationship between the equipment and the grid is analyzed, and the equivalent synchronous generator modeling method is provided. Secondly, the energy function of the associated system is developed based on the equivalent synchronous generator model and the energy function of the traditional synchronous generator. The energy conversion process of the system during the transient period is analyzed, and at the same time, the transient instability forms and mechanisms of the SC are summarized and revealed. Thirdly, based on the unbalanced power borne by the rotor during the fault period, the boundary conditions leading to changes in the instability forms of the SC are quantified. The transient stability margin of the system under different instability forms are derived based on the energy function and the critical clearance time (CCT), and the influence of the system parameters on the instability forms and transient stability margin of the SC is analyzed. Finally, the correctness of the proposed instability mechanisms and the analysis of the influencing factors are verified through electromagnetic transient simulations.
The following conclusions can be drawn: (1) Under different operating conditions, there are two types of instability forms of the SC: first-swing accelerated instability and first-swing decelerated and second-swing accelerated instability. The former is similar to the transient instability process of the traditional synchronous generator. The latter accumulates potential energy in the first swing stage and converts the potential energy into kinetic energy in the second swing stage. (2) The transient stability boundaries of the SC under the two types of instability forms are different. In the first-swing instability form, there is one CCT, and the system is unstable when the fault clearance time is larger than the CCT. In the second-swing instability form, there are two CCTs, and the system is unstable when the fault clearance time is in the middle of the two CCTs. (3) Since reducing the unbalanced power borne by the SC during the fault helps improve the transient stability of the system, renewable energy should adjust its power output by reducing active power and increasing reactive power under the first-swing instability form, while increasing active power and reducing reactive power under the second-swing instability form. In addition, increasing the capacity proportion of the SC or improving system strength will help improve the transient stability of the SC.
Keywords：Renewable energy base, synchronous condenser, equivalent synchronous generator, transient power angle stability, Lyapunov energy function
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241690
国家电网有限公司科技资助项目（SGNW0000FGJS2400312）。
收稿日期 2024-09-27
改稿日期 2024-12-03
单永鹏 男，2001年生，硕士研究生，研究方向为高比例新能源电力系统稳定分析与控制。
E-mail：shanyp@zju.edu.cn
辛焕海 男，1981年生，教授，博士生导师，研究方向为交直流混联电力系统和高比例新能源电力系统稳定性分析和控制。
E-mail：xinhh@zju.edu.cn（通信作者）
（编辑 赫 蕾）