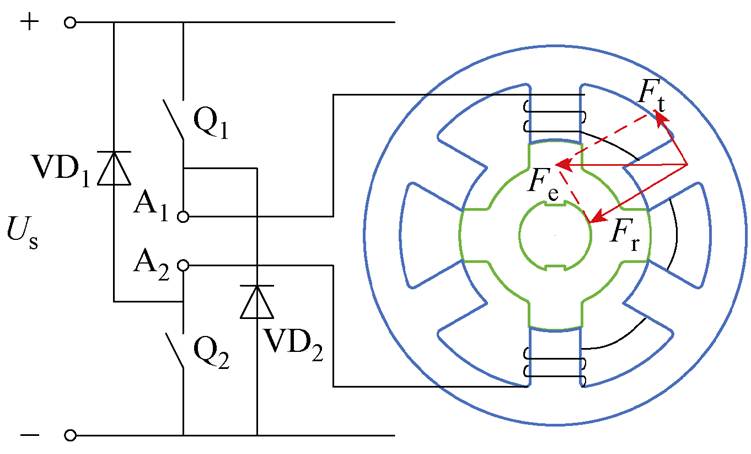
图1 SRM工作原理
Fig.1 SRM working principle
摘要 开关磁阻电机（SRM）的双凸极结构和工作原理引发了电机的转矩脉动与径向力脉动问题，进而导致电机振动。而传统的振动抑制策略对两者的综合抑制能力较弱，极大地限制了SRM在高精度需求等领域的应用。为实现对两者的同时抑制，该文提出一种基于磁链波形规划的径向力与转矩分配函数（TSF），并改进电压矢量表，为径向力的降低预留充足的时间，进而抑制径向力脉动；在此基础上，构建磁阻预测值与实际值间的差值模型，利用磁阻与电流的关系提出一种基于磁阻预测的电流误差补偿方法提高模型预测控制（MPC）的精度，进一步提升对转矩脉动和径向力脉动的抑制效果。经不同工况下的实验得出，与传统电流斩波控制（CCC）、脉冲宽度调制（PWM）、模型预测转矩控制（MPTC）法相比，采用新的控制策略可同时使转矩脉动和径向力脉动至少分别降低10.10%和23.47%，电机的振动加速度频谱也验证了具有误差补偿的振动抑制策略的有效性。
关键词：开关磁阻电机 模型预测控制 振动 误差补偿
开关磁阻电机（Switched Reluctance Machine, SRM）不需要永磁体，具有成本低廉、控制灵活、调速范围宽、起动转矩大、运行效率高等优点，被广泛应用于工业传动等领域，在未来的电机驱动系统中有很大的应用潜力[1-2]。但由于其双凸极结构与断续工作的特点，运行期间SRM会产生较大的振动[3-4]，这些缺点限制了SRM在某些高精度伺服需求或对振动敏感领域中的应用。
引发SRM振动的主要因素为电机的转矩脉动与径向力脉动[2]。目前SRM振动抑制的研究大体分为电机本体优化设计与控制抑制方法。从电机本体结构优化角度，可以通过改变电机参数来改变径向力或电机自身固有频率以避免共振。文献[5-6]对定转子进行斜极设计或优化转子极数减弱SRM的振动。文献[7-8]则改变相绕组联结方式抑制电机运行期间的振动。在控制径向力以抑制电机振动的方法中，两步换相法和三步换相法有较好的抑制效果[9]。文献[10]通过改变电流二次谐波幅值和相位来减少定子齿径向力总和的变化，并利用小型SRM验证了所提方法的有效性。而直接瞬时力控制可以保持总的径向力不变以消除零阶振动模型的激励，但不利于减小转矩脉动[11-12]。而抑制转矩脉动的方法有转矩分配函数（Torque Sharing Functions, TSF）[13]、直接转矩控制[14]、直接瞬时转矩控制等。文献[15]提出一种区间分段型TSF的控制方法，利用前后相的去磁、励磁能力和转矩跟踪能力，使SRM输出的总电磁转矩维持恒定值。而文献[16]提出了一种新的直接转矩控制方法，该方法去除了磁通的滞环控制，建立了新的电压矢量选取规则，输出转矩可以精确地跟踪参考值，从而减少转矩脉动。文献[17]提出了一种基于改进滑模控制策略的直接瞬时转矩控制方法，在传统滑模面和滑模趋近律的基础上引入状态变量，降低了不同工况下电机的转矩波动和电机动态过程调整时间，该方法在稳态和变速变载工况下具有良好的性能。文献[18-19]采用模型预测控制（Model Predictive Control, MPC）对转矩与径向力脉动进行抑制，以代价函数实现多目标控制，但未能有效地实现转矩与径向力的闭环控制。
综合国内外学者的研究成果可以看出，针对SRM的转矩脉动、径向力脉动及振动等问题逐渐形成了可靠的解决方法，但仍存在以下问题：①从控制策略方面，大多数研究针对转矩脉动或径向力脉动进行控制，并且采取的控制方法在减小转矩脉动的同时往往会增大径向力峰值，反之亦然。②作为常用的振动抑制策略，MPC法对参考模型的精度有较高的要求，精度较低的模型在多步预测中自身误差逐步累积，严重影响了算法的控制效果。
针对以上问题，本文基于MPC策略提出了一种基于磁阻预测的电流误差补偿方法，在磁链规划转矩与径向力分配函数（Force Sharing Function, FSF）的基础上进一步降低了转矩与径向力脉动，以实现对振动的抑制。
SRM定转子凸极间变化的电磁力可被正交分解为径向与切向，图1为定转子间电磁力及工作 原理。
图1 SRM工作原理
Fig.1 SRM working principle
图1中，Us为母线电压，VD1、VD2为二极管，A1、A2连接A相绕组的两端，Q1、Q2为开关管。电磁力Fe切向分量Ft的切向力波动通过轴承等连接件影响控制系统的振动；电磁力Fe径向分量Fr的径向力波动引发的定子振动传播到其他部件，影响电机整体的振动。此外，为提升电机的转矩密度，在设计阶段便将SRM气隙设定得较低，使得定转子间的径向力更大。SRM的双凸极结构和工作原理决定了径向力脉动与切向力脉动是SRM振动的主要原因，总结分析如下：
1）SRM的转矩脉动问题。由图1可知，当给SRM单相线圈绕组励磁时，相绕组产生的磁吸力使转子朝着磁路磁阻最小的方向旋转。切向磁吸力Ft产生了使SRM能够运行所需要的电磁力矩T。转矩T与电流i、转子位置角qph的非线性关系T(i, qph)如图2所示。由于转矩与电流、转子位置角有关且呈非线性关系，使得转矩难以控制且脉动较大，转矩脉动通过连接器、基座等部件引发驱动系统的振动，使定子凸极部分产生振动形变。当电机与负载的同心度存在一定偏差时，这种振动将会尤为明显。转矩脉动的增加将不可避免地加大电机本体振动。
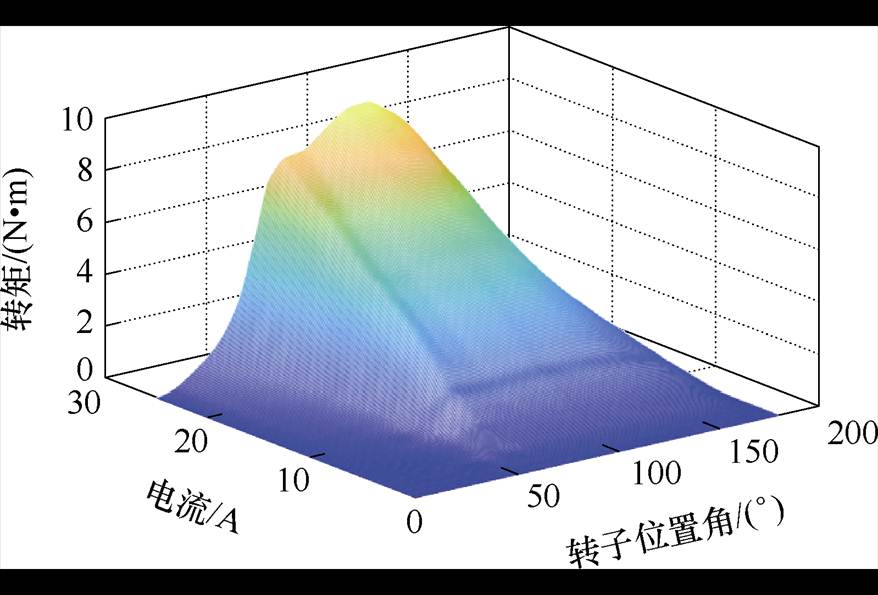
图2 T(i,qph)非线性关系
Fig.2 Non-linear relationship of T(i,qph)
2）定子所承受的周期性变化的径向力。SRM中大部分的电磁噪声由定转子之间的径向力引起。定转子间气隙对线性磁路有
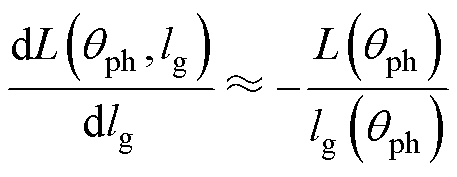（1）
所以，径向磁吸力Fr的线性模型表达式为
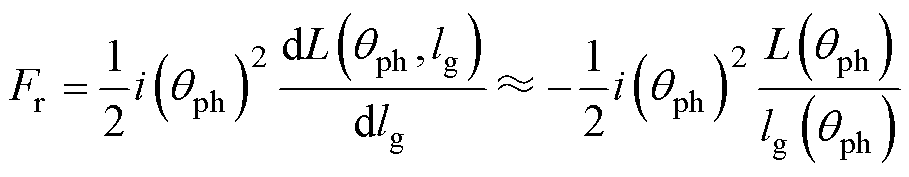（2）
式中，lg为定子和转子之间的气隙长度；L为相绕组的自感；负号表示径向力令定转子间气隙缩短。从式（2）可以看出，径向力随转子位置和电流的变化而波动，如图3所示。当定子齿与转子齿主轴线重合时径向力较大；而当定子齿与转子槽主轴线重合时则较小。定子受脉动径向力影响做压缩和扩张运动，产生振动。当其谐波频率与定子或基座等部件的固有频率一致时，引发共振。定子振动通过电机内部接触点传播到转子、绕组等部件，引起整个电机振动。
为实现振动抑制，基于以上对其产生原因的分析，转矩脉动和径向力脉动是最常见的控制目标。因此，对SRM振动抑制问题的研究可以归结为对其径向力脉动和转矩脉动抑制的研究。
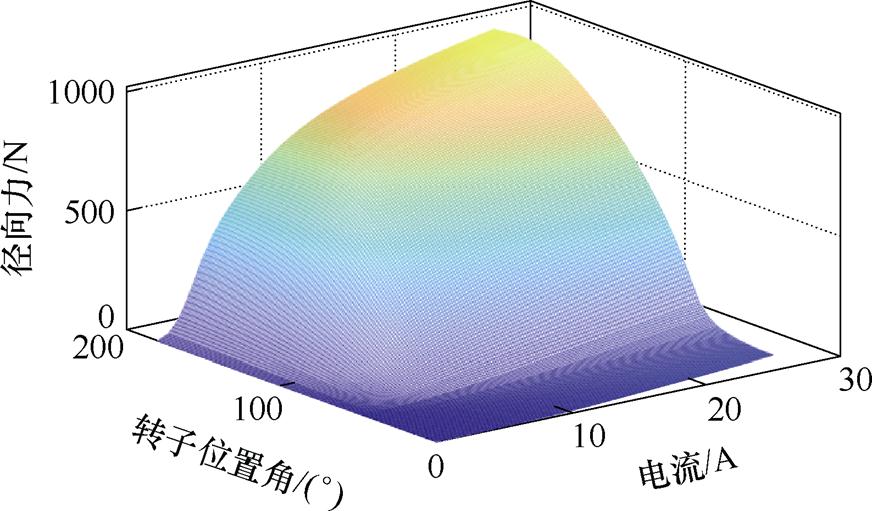
图3 Fr(i,qph)非线性关系
Fig.3 Non-linear relationship of Fr(i,qph)
TSF作为一种参考转矩规划曲线，将总转矩分解为前后相的目标转矩，通过直接转矩控制或间接转矩控制的方法，使前后相分别追踪目标转矩以保证总转矩恒定[20-21]，使合成瞬时转矩脉动最小化。本文利用TSF抑制SRM由于自身非线性导致的较大的转矩脉动。转矩与径向力均是由电机内多物理场作用下的电磁力产生的。转矩因切向电磁力产生，径向力则因径向电磁力产生，故可将TSF原理应用于电磁径向力上，构建FSF，以使电机运行期间的总电磁径向力保持不变，减少总径向力脉动。
根据电机磁链曲线设计TSF，并按此原理构建FSF。如式（3）所示，通过调整开通角qon来规划励磁区的磁链yup曲线；如式（4）所示，换相重叠角qov根据电机定转子参数计算。
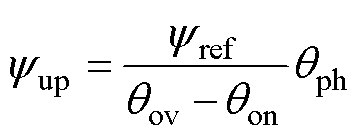（3）
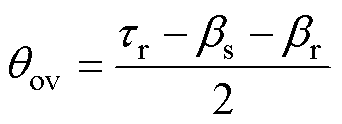（4）
式中，yref为qov处的磁链，可根据参考转矩Tref和qov通过转矩查找表y(T,qph) 获得；tr为SRM的转子极距；bs为定子极弧；br为转子极弧。通过转矩、磁链和位置二维查找表得到励磁相转矩Tup关于位置qph的函数为
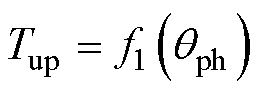（5）
退磁相转矩函数Tdown为
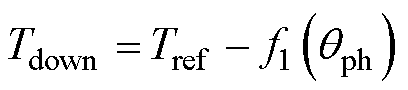（6）
则TSF表示为
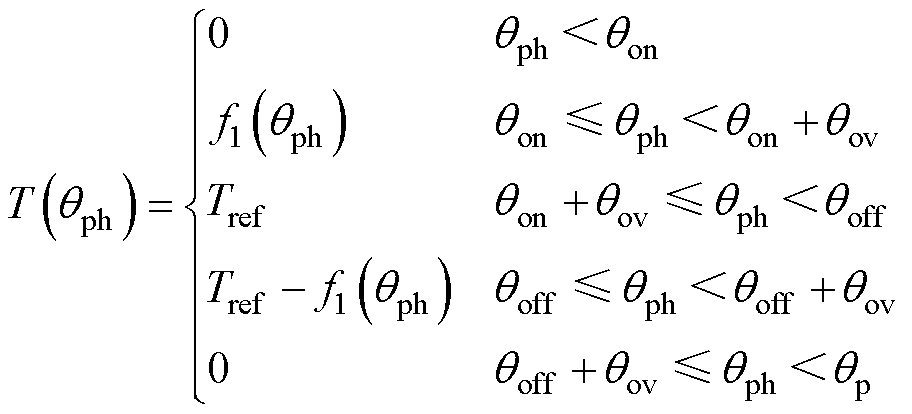（7）
式中，关断角qoff可通过转子周期角qp计算得到，即
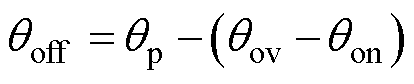（8）
与TSF原理相同，Fref为给定的径向力振幅，在换相阶段，根据计算得到的SRM换相导通区内相磁链轨迹函数，通过磁链、径向力和位置二维查找表得到励磁相径向力关于位置的函数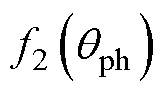
，则FSF可表示为
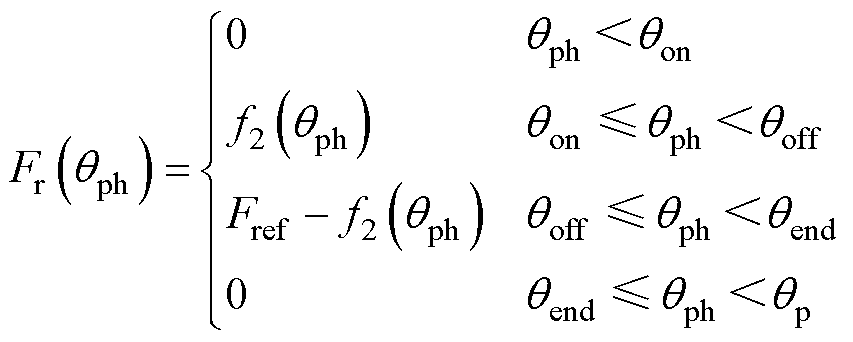（9）
式中，qend为径向力降至零的角度。为使径向力曲线对称，令qend=2qoff−qon。
调整开通角qon、关断角qoff会影响电机磁链曲线，进而影响电机转矩与径向力，构建的TSF和FSF将会影响转矩和径向力脉动。
建立转矩、径向力与开通角之间的函数关系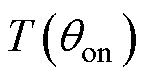
和
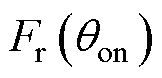，以便优化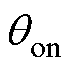
。通过计算得到转矩脉动Trip和径向力脉动Fr-rip，后经归一化构造多目标优化函数
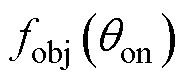，并最小化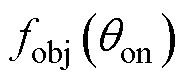确定最优开通角。
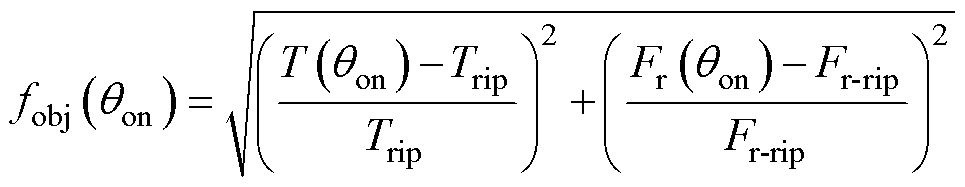（10）
式中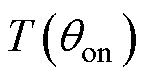，为开通角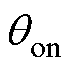与转矩T之间的函数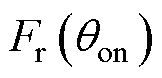；为开通角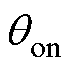与径向力Fr之间的函数。
转矩脉动定义为
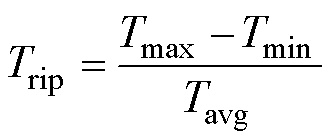（11）
式中，Tmax为总转矩的最大值；Tmin为总转矩的最小值；Tavg为总转矩的平均值。
径向力脉动同转矩脉动的构造一致，可根据式（12）计算。
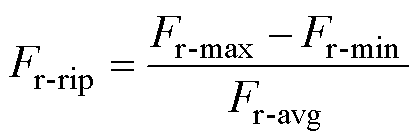（12）
式中，Fr-max为总径向力的最大值；Fr-min为总径向力的最小值；Fr-avg为总径向力的平均值。
通过二次规划寻找合适的qon以使构造的多目标函数fobj值最小，进而确定最优控制角。基于电机磁链曲线在线获取最优规划函数。
SRM运行过程中各相可能出现开通、续流、关断三种状态，即功率变换器的通断状态分别为{1, 0, -1}。因此预测控制中下一时刻电机开关状态共有27种。为降低预测给处理器造成的运算负担，对三相12/8极SRM运行阶段的单个电周期进行划分，以简化不同时刻的开关状态，具体如图4所示。
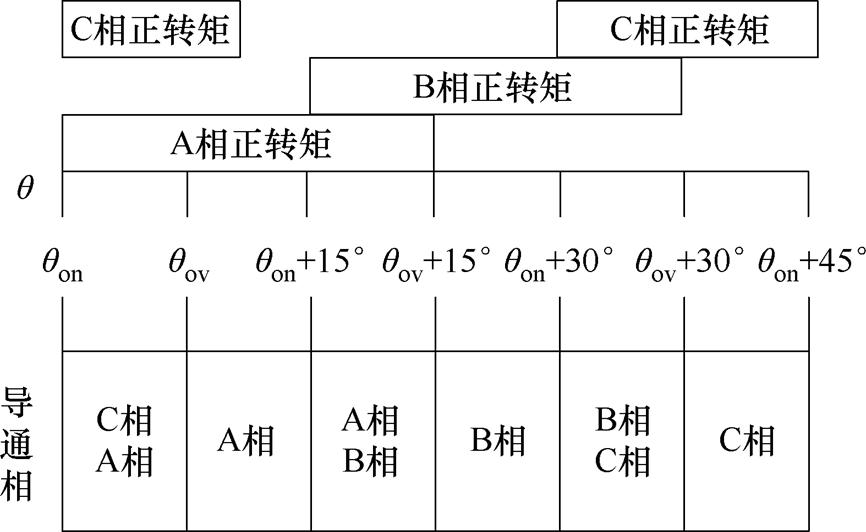
图4 三相12/8极SRM单个电周期区域划分示意图
Fig.4 Three-phase 12/8-pole SRM single electrical cycle area division schematic diagram
当转子位置处于单相区时，只有当前导通相的开关状态需要被预测，其余相开关状态均为-1，故单相导通区仅需要预测开通、续流、关断三种开关状态；当转子位置处于换相区时，则需预测正在换相的两相开关状态。而另外一相产生负转矩，开关状态为-1。励磁相与退磁相均有开通、续流、关断三种开关状态。若将qon设定为0°、qov设定为7.5°，则根据三相12/8极SRM开关状态的不同构建电压矢量表，见表1。
表1 MPC简化后的电压矢量表
Tab.1 MPC simplified voltage vector table
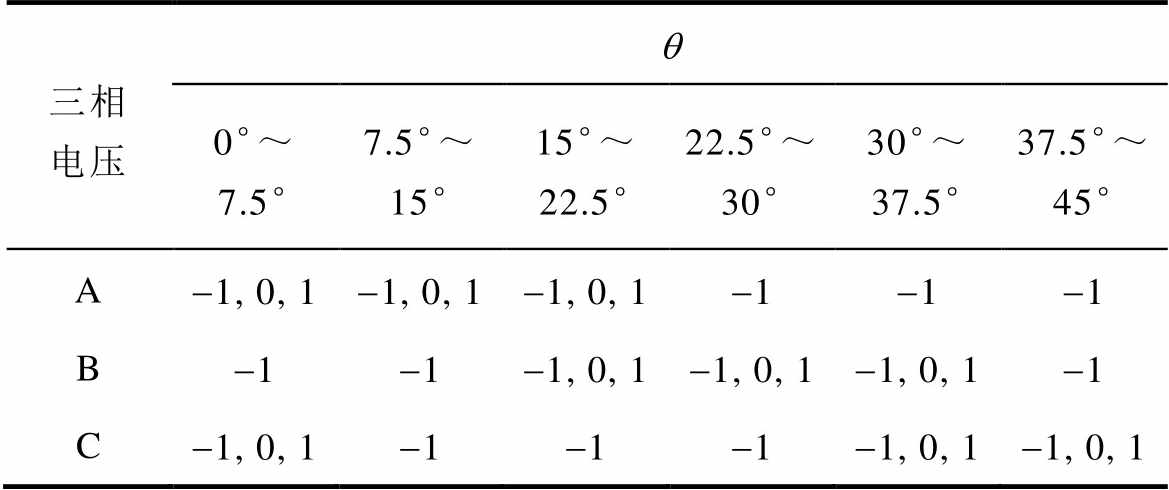
三相电压q 0°～ 7.5°7.5°～ 15°15°～22.5°22.5°～30°30°～37.5°37.5°～45° A-1, 0, 1-1, 0, 1-1, 0, 1-1-1-1 B-1-1-1, 0, 1-1, 0, 1-1, 0, 1-1 C-1, 0, 1-1-1-1-1, 0, 1-1, 0, 1
从SRM转矩特性的角度，以上方法可以达到简化的目的。但从电磁径向力的角度，这种方法反而会加剧电机运行过程中的振动。鉴于相转矩在 0°～180°电角度导通期间从0增长至最大值后衰减至0，而相径向力在导通阶段不断上升，于对齐位置处达到最大值。故直接沿用传统模型预测转矩控制（Model Predictive Torque Control, MPTC）的开关状态会因在对齐位置关断导通相使得该相径向力迅速衰减至0，进而使总径向力发生突变。
为实现对转矩和径向力脉动的综合抑制，对三相12/8极SRM单个电周期的区域重新进行划分，优化电压矢量表。在换相区，依旧只对励磁相与退磁相的开关状态进行预测，其余相保持关断状态-1；不同的是，为避免上一导通相转子位置经过对齐位置后出现该相径向力迅速减小的不利情况，在单相导通区依旧预测退磁相的开关状态，保证退磁相径向力可缓慢减小，为径向力的降低预留充足的时间，进而抑制径向力脉动。该方法的原理即在励磁相转子位置进入电感下降区后延迟该相进入负压关断的时间，保证相径向力有足够的时间归零。具体措施为在退磁相的qoff和qend之间添加零压续流“0”状态和正压励磁“1”状态。表2为考虑径向力衰减变化的各相电压矢量预测情况。
表2 考虑径向力衰减变化的电压矢量表
Tab.2 Table of voltage vectors considering changes in radial force attenuation
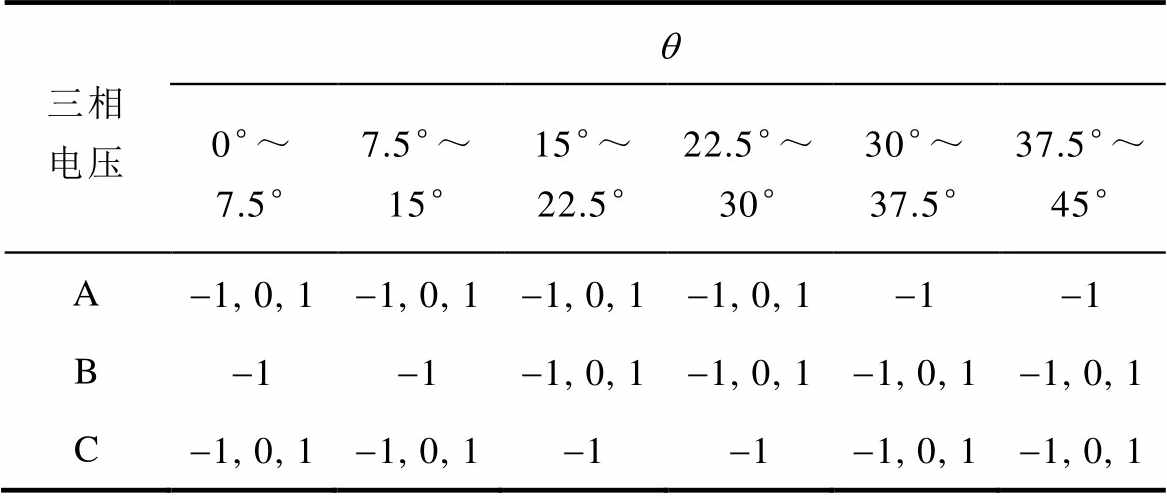
三相电压q 0°～ 7.5°7.5°～ 15°15°～22.5°22.5°～30°30°～37.5°37.5°～45° A-1, 0, 1-1, 0, 1-1, 0, 1-1, 0, 1-1-1 B-1-1-1, 0, 1-1, 0, 1-1, 0, 1-1, 0, 1 C-1, 0, 1-1, 0, 1-1-1-1, 0, 1-1, 0, 1
以上部分实现了TSF、FSF的设计，电压矢量表的改进以及对SRM转矩、径向力特性模型的构建，本节将基于MPC思想对SRM转矩脉动与径向力脉动进行联合抑制。
首先，对电机电压方程和速度表达式进行离散化处理：由电流与转速位置传感器测量获得当前k时刻的相电流iph(k)和转子位置qph(k)，基于电机电磁特性计算电机各相磁链yph(k)，并根据离散化的电压平衡方程预测下一时刻的各相磁链yph-p(k+1)，即
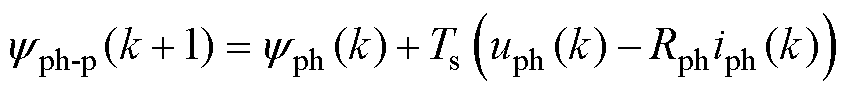（13）
式中，uph(k)为k时刻的相电压；Rph为相电阻；Ts为采样步长。
假设电机转速w 在预测范围内恒定，下一时刻转子位置qph-p(k+1)可表示为
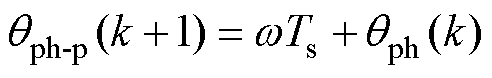（14）
式中，w 为k时刻的电机转速。
然后，根据下一时刻的相磁链yph-p(k+1)与转子位置qph-p(k+1)采用反插值法预测各相电流iph-p(k+1)，即
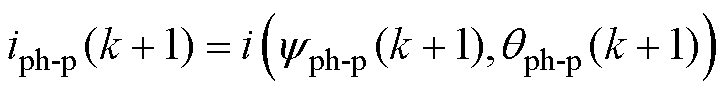（15）
鉴于处理器流水线的运算机理，处理器从获取采样信息至发送控制指令共需要两个指令周期，故采取预测一个控制步长的传统MPC方式具有一定的延迟性，控制算法的稳定性也有所降低。为提升模型预测转矩与径向力控制（Model Predictive Torque and Force Control, MPTFC）策略的实时性，本文提出的控制方法进行两个控制步长的预测，并在预测一个控制步长的电机状态后，进行如下假设：①第一次预测值与实际值一致；②处理器计算频率较高，w 在预测算法中恒定不变。
据式（13）可知，k+1步相磁链yph-p(k+1)采用实际的k时刻相电压uph(k)进行预测，而k+2步相磁链yph-p(k+2)则利用模型预测的电压矢量y与母线电压Udc相乘进行预测，作为k+2步电压平衡方程的相电压，具体计算方式如下。
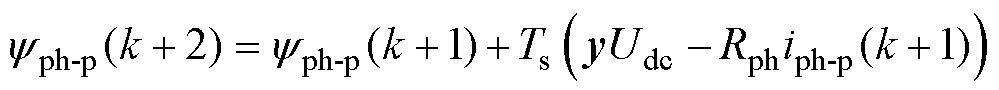（16）
同样以反插值法预测k+2时刻的相电流iph-p(k+2)为
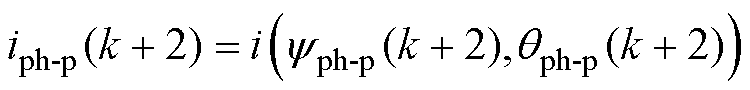（17）
基于构建的SRM转矩与径向力模型以查找表（Look-Up Table, LUT）插值的方式预测k+2时刻的各相转矩Tph(k+2)与电磁径向力Fr-ph(k+2)分别为
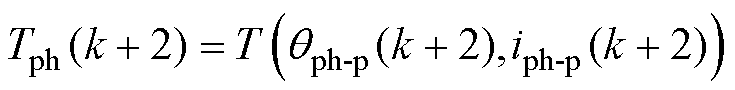（18）
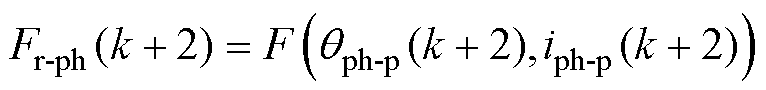（19）
为实现转矩与径向力的预测值对基于TSF和FSF构建的各相转矩与径向力参考值的实时跟踪，构建如式（20）的代价函数J，通过寻找使代价函数最小的开关状态实现转矩脉动和径向力脉动的联合抑制。
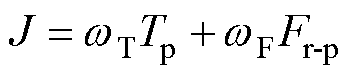（20）
式中，wT、wF分别为转矩脉动、径向力脉动权重；Tp、Fr-p分别为转矩部分、径向力部分代价函数。
Tp与Fr-p定义为i(j)相预测值Tj、Fj(Tj, Fj)与分配函数构造的参考值Tref、Fref之间的完全平方差，即
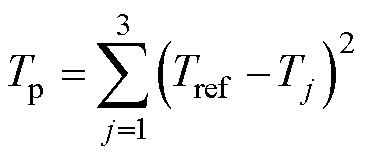（21）
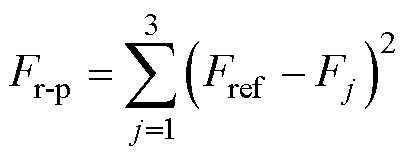（22）
MPC法由于具有概念直观、多目标优化以及易于理解等优势已成为处理具有复杂约束条件的非线性动态系统的有效策略[22-24]。但其控制性能依赖电机特性模型的准确性，实际控制系统难以获得控制对象的理想模型进而导致模型失配，预测不准确；且电机运行阶段，即使在固定工况下，参数的测量误差在实际电机中也不可避免，导致电机参数与实际参数存在偏差，造成预测误差。而不同的工作条件也会导致电机参数出现一定的差异；若将此类电磁特性模型用于MPC，预测步长越多累计的模型误差越大，算法的控制效果越差[25]。为进一步提升第2节提出的MPTFC的性能，减少电机运行期间电机参数变化对控制算法效果的影响，本节提出一种基于误差补偿的MPTFC（Model Predictive Torque and Force Control based on Current Error Compensation, CEC-MPTFC）法，进一步减小电机的转矩脉动与径向力脉动。
以电机相电流和转子位置为变量可构建SRM磁链特性、转矩特性以及径向力特性模型。其中，转子位置在某一稳态转速下可通过离散方程极为准确地预测未来时刻的参数值，而为简化计算，相电流的预测必然要通过精确度较差的数据表。故相电流可作为综合影响SRM转矩特性与径向力特性的关键电磁参数，以提升自身预测精度进而提升MPTFC的精确度，最终实现SRM振动抑制算法的优化。
本文提出的基于磁阻补偿的SRM电流预测方法通过电磁特性对电流进行初步预测，进而得到预测磁阻，后基于电压平衡方程，利用采集的相电流和相电压对预测磁阻进行补偿使其更接近实际磁阻，根据补偿后的磁阻计算反电动势预测下一控制周期的相电流，进而提高电流预测的精度。
首先，根据2.3节式（13）～式（15）计算获取k+1时刻预测电流iph-p(k+1)。对电压平衡方程进行离散化处理，可获得k+1时刻的电流预测结果为
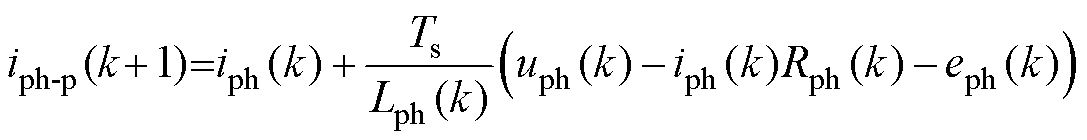（23）
式中，iph-p(k+1)为该相k+1时刻的预测电流值；eph(k)为该相k时刻的反电动势。从式（23）可知，影响电流预测精度的参数有k时刻相电流iph(k)、相电感Lph(k)、相电压uph(k)以及相电阻Rph(k)。作为极易受到扰动且变化较大的电机参数，iph(k)、Lph(k)对实际电流的计算结果影响极大；uph(k)作为MPC中设置的不同开关状态直接影响的参数，需要作为变量直接参与到电机参数的预测过程中，影响着代价函数对多种开关状态的选择；而Rph(k)因其温度变化特性，在实际运行中参数值变化较小，且在电流预测中与相电流的乘积数值较低，对预测结果的扰动较小。故为降低实际相电流预测环节的复杂度，忽略对相电流扰动较小的Rph(k)，将磁阻Rm(k)代入SRM电压平衡方程，基于离散化思想可计算得到相邻两时刻的相电流差值为
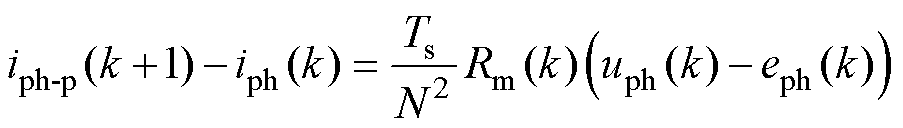（24）
式中，N为相绕组匝数。
类比相邻两时刻实际电流差值的计算方法，将基于LUT获得的相电感Lph及基于Lph计算得到的相磁阻Rph-m(k)、相电流iph (k)等电磁参数定义为预测量Lph-p、Rph-m-p(k)、iph-p(k)，获得相邻两时刻预测电流的差值为
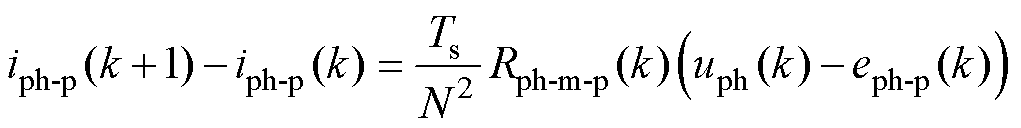（25）
式中，Rph-m-p(k)为该相k时刻的预测磁阻；eph-p(k)为该相k时刻的预测反电动势。而预测磁阻Rph-m-p(k)可基于预测电感Lph-p(k)与N计算，即
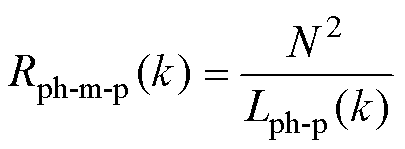（26）
Lph-p(k)可基于数据表L(i,q)采用LUT计算，即
（27）
对预测电流与实际电流求取差值，假设预测反电动势和实际电动势相差不大，可计算出k时刻的实际磁阻Rm(k)为
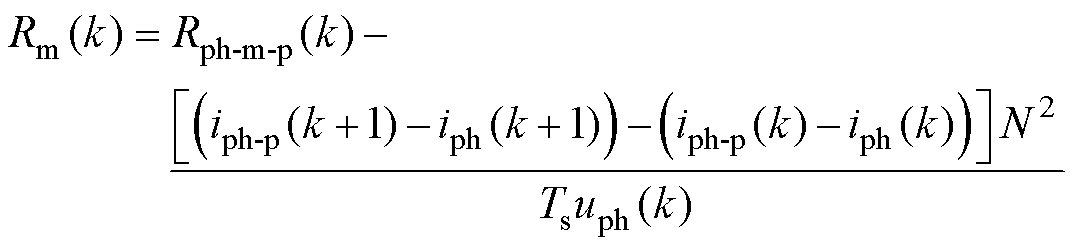（28）
得到k时刻的实际磁阻Rm(k)后，由式（25）减去式（24），可计算出k时刻的实际反电动势eph(k)、预测反电动势eph-p(k)分别为
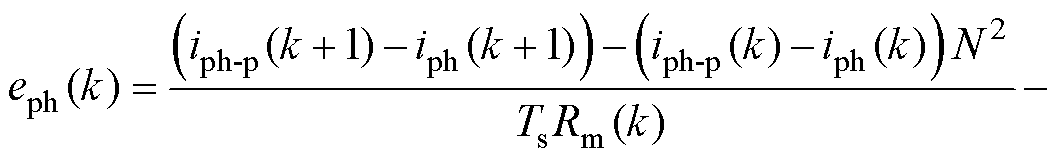
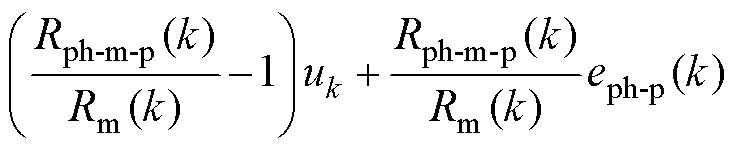（29）
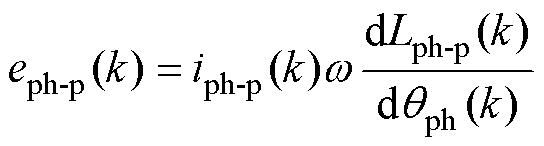（30）
经该简化通过式（31）预测k+1时刻的相电流。
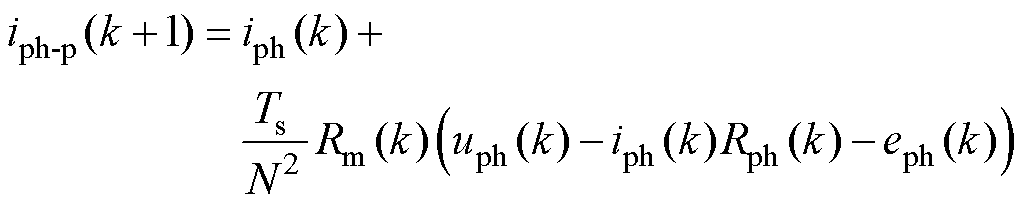（31）
为降低算法复杂度，提出的电流误差补偿方法仅对导通相的磁阻与电流进行预测补偿，即仅预测磁阻下降沿部分，得到的相电流预测值更接近实际电流，相电流补偿前后的波形对比如图5所示。
可以看到，基于磁链预测补偿后的相电流与实际电流之间差值远小于未经补偿的预测电流与实际电流差值，说明该方法可降低MPC对离线SRM静态特性数据表精确度的依赖性，提升了采用LUT的MPC效果。
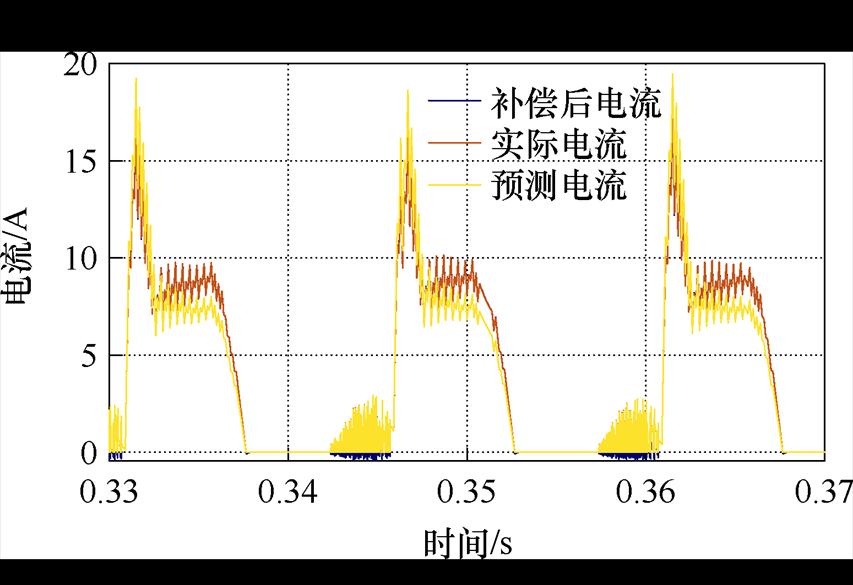
图5 相电流补偿对比
Fig.5 Comparison of phase current compensation
将电流误差补偿方法与MPTFC相结合，以更好地实现SRM转矩脉动和径向力脉动的抑制，所构建的SRM振动抑制框架如图6所示。
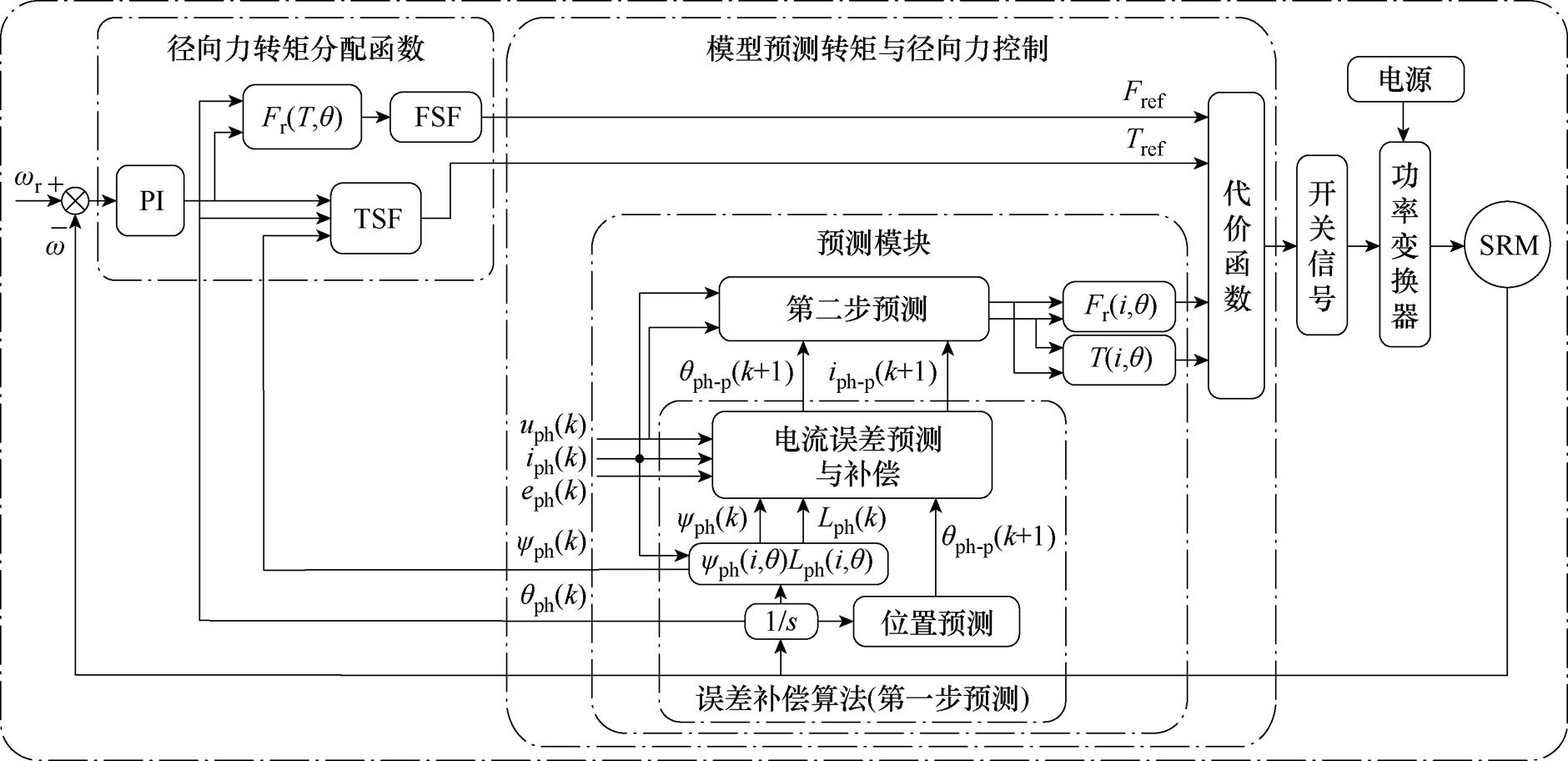
图6 CEC-MPTFC法原理示意图
Fig.6 Schematic diagram of the principle of the CEC-MPTFC
通过实验测量或有限元分析获取SRM磁链、转矩与径向力特性模型；基于磁阻预测对电流误差进行预测并补偿，提升预测过程参考模型的精度；构建TSF和FSF，规划各相转矩与径向力波形曲线，通过判断是否处于换相区，计算各相转矩与径向力以同时实现对两者的抑制；在MPC的代价函数中设置转矩与径向力的权重，以平衡量级实现平稳抑制。
在两步预测模块中搭建两步电流误差补偿模块，该部分可依照如图7所示的原理示意图构建。具体基于误差补偿的SRM两步预测MPTFC流程如图8所示。具体步骤如下：
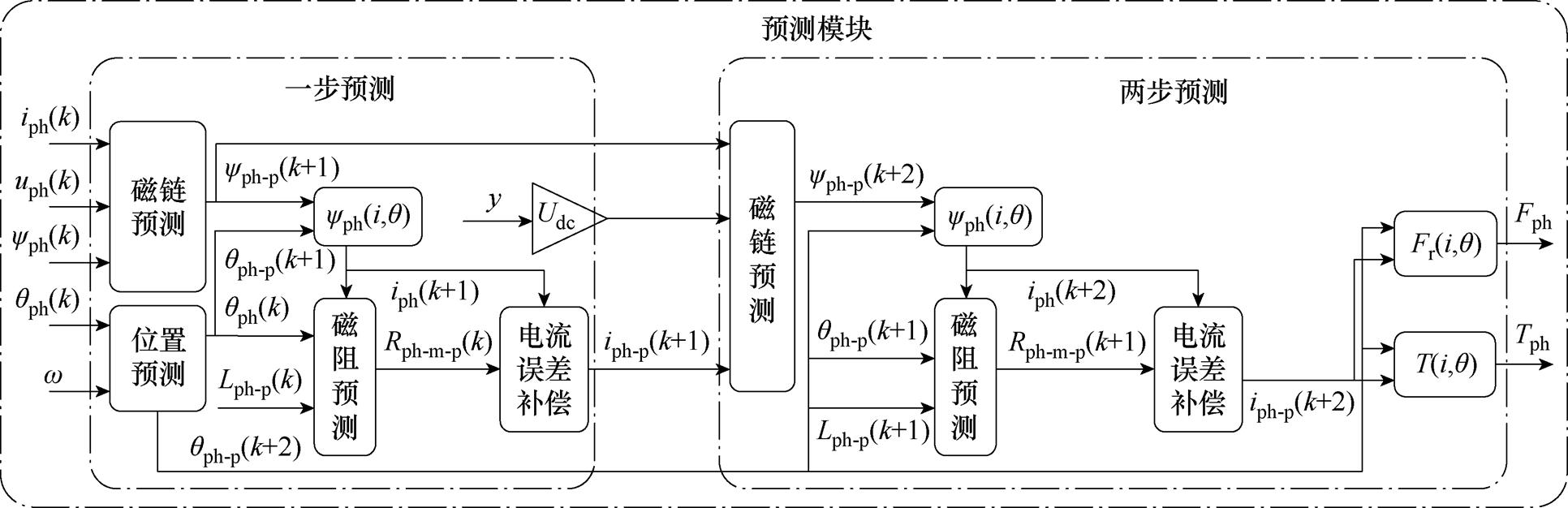
图7 基于误差补偿的预测模块原理示意图
Fig.7 Schematic diagram of the prediction module based on error compensation
（1）根据式（10）寻找最优开通角规划最优磁链曲线并确定TSF、FSF。
（2）根据式（15）利用磁链、位置预测值反插值进行第一步电流预测。
（3）根据式（31）利用补偿后的磁阻计算反电动势预测下一控制周期的相电流，进行第一次磁阻预测补偿电流误差。
（4）通过改进的电压矢量表2及式（16）进行第二步电流预测。
（5）根据式（31）进行第二次磁阻预测补偿电流误差，类同第一次误差补偿。
（6）根据式（18）、式（19）插值获取预测转矩和径向力，计算其与参考值之间的差值代入式（20）代价函数寻找最优开关状态并应用于功率变换器。
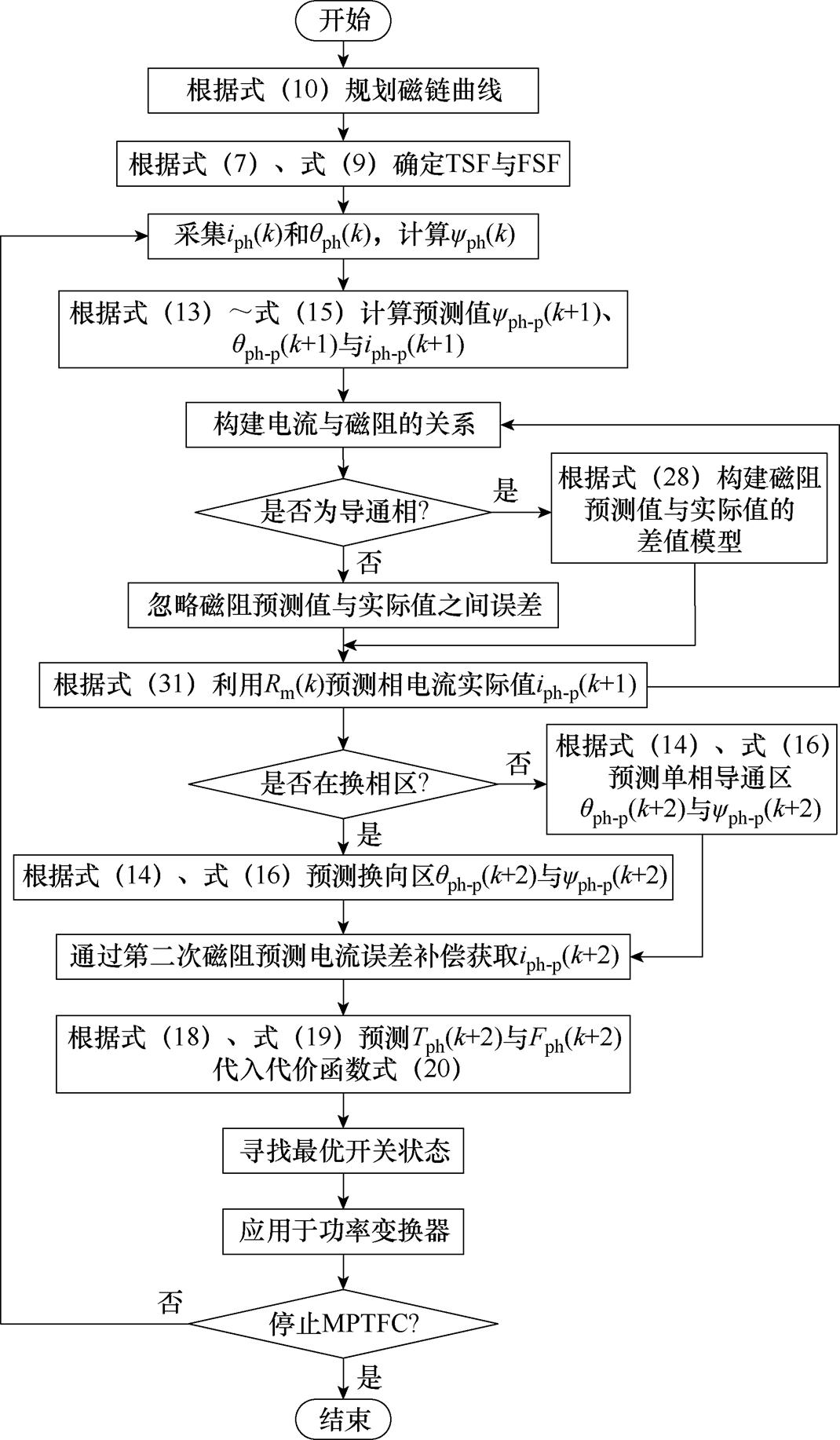
图8 CEC-MPTFC流程
Fig.8 CEC-MPTFC flow chart
本节基于三相12/8极SRM半物理实验平台，完成CEC-MPTFC的振动抑制实验验证。实验平台具体电气部分如图9a所示，机械部分如图9b所示。实验所使用的三相12/8极SRM样机参数见表3。
SRM控制方式包括脉宽调制控制（Pulse Width Modulation, PWM）方式、电流斩波控制（Current Chopper Control, CCC）方式和角度位置控制（Angular Position Control, APC）方式，其中PWM用于低、高速运行，其调速系统动态响应快、抗干扰能力强，但低速时转矩脉动大；CCC是一种对电流峰值进行限制的恒转矩控制方法，适用于低速或起动运行工况，相比于APC方式控制效果更精确、转矩变化更平稳；APC保持绕组电压不变，通过调整qon与qoff，改变相绕组的导通关断时间，适用于在控制电机额定转速以上运行。本文采用500 r/min、1 000 r/min带载1 N×m、2 N×m的四种稳定工况进行实验验证。为从抑制转矩脉动方面突出本文提出的CEC-MPTFC法抑制振动效果的优越性，分别在相同工况下与CCC、MPTC与MPTFC进行实验对比。
图9 SRM驱动系统实验平台
Fig.9 Experimental platform of SRM drive system
表3 SRM关键参数
Tab.3 Someparameters of SRM
参 数数 值 额定功率/W600 额定转速/(r/min)2 000 额定电流/A25 定子相数12 转子相数8 每极匝数119
在CCC模型中，设置qon=0°，qoff=18°；MPTC法转矩部分权重系数wT=1，电流部分权重系数wi=0.04；MPTFC中转矩部分权重系数wT=1，径向力部分权重系数wF=0.000 05。以相电流、转矩波形、径向力波形为关键指标，评判四种方法控制效果优劣。其中，低转速500 r/min搭载1 N×m负载下四种方法的实验结果如图10所示。
可以看到，CCC对转矩脉动与径向力脉动的抑制效果均不够理想；MPTC作为专注对转矩脉动抑制的控制方法，其对转矩脉动的抑制效果较好，但径向力没有得到控制；而提出的MPTFC基于构建的TSF、FSF以及考虑径向力变化特性的电压矢量表，使得退磁相在经过转子对齐位置后继续导通，令径向力衰减速度变缓并产生较小的负转矩，使转矩脉动与径向力脉动得到同时抑制。在引入电流误差补偿策略后，相电流波形变得更为平滑，使单相导通区总转矩更为平稳，总转矩波形的抖动也明显降低，相电流的精确度得到了提升，退磁相在经过转子对齐位置后继续导通，令径向力衰减速度变缓，并产生较小的负转矩，使电机转矩脉动与径向力脉动均有小幅度下降。
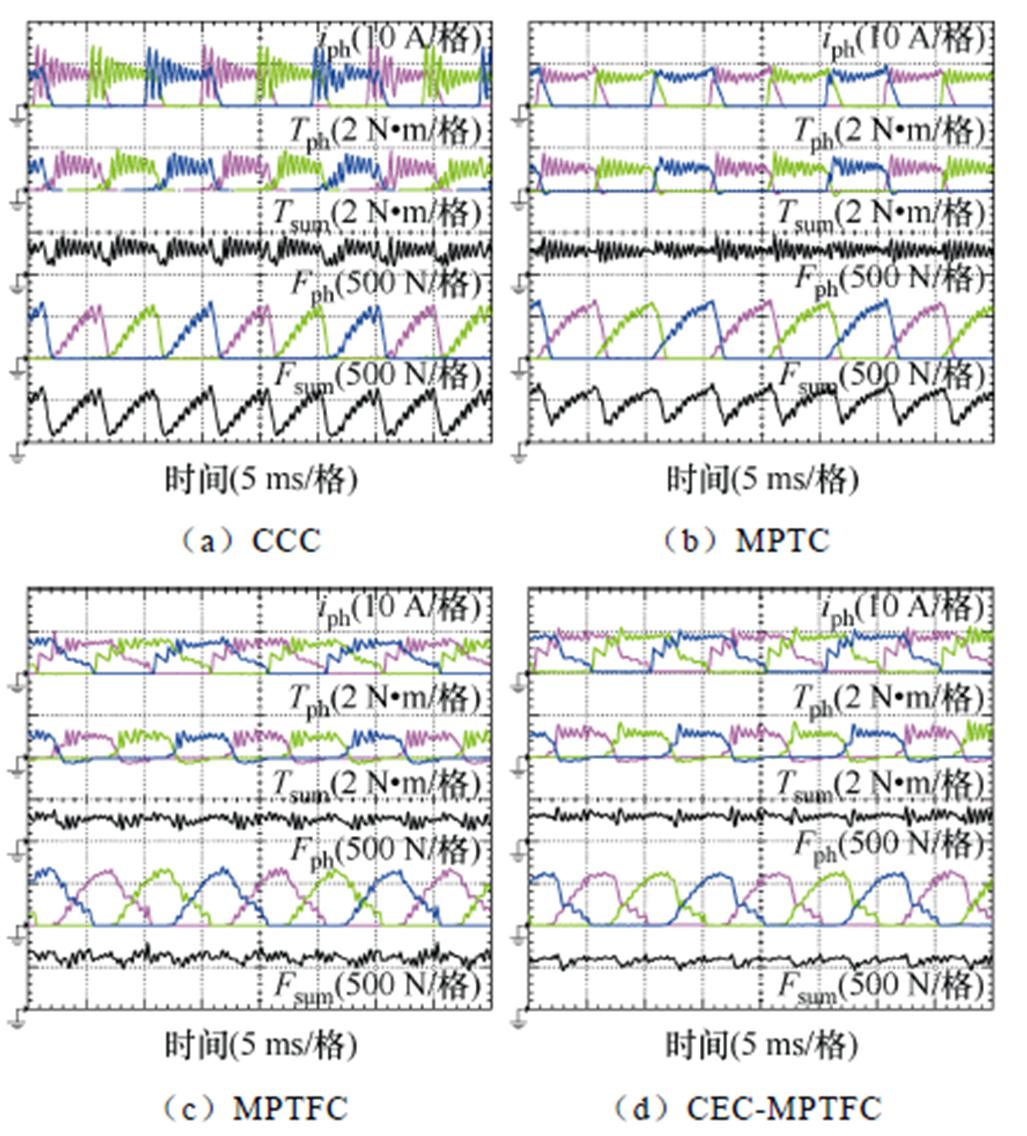
图10 500 r/min、1 N·m工况下四种方法实验结果
Fig.10 Experimental results of four methods at 500 r/min, 1 N·m operating condition
500 r/min不同负载下四种方法振动加速度频谱如图11所示，从各控制方法在500 r/min转速下电机机壳的振动加速度频谱可以看出，MPTFC对电机振动的抑制效果优于CCC与MPTC。MPTC只对电机的转矩脉动进行控制，但该方法在一定程度上也减弱了电机的振动，该现象恰好验证了第1节中的结论，即转矩脉动与径向力脉动影响着SRM的振动。同时，也可以看出CEC-MPTFC法对电机振动的抑制效果优于另三种方法。
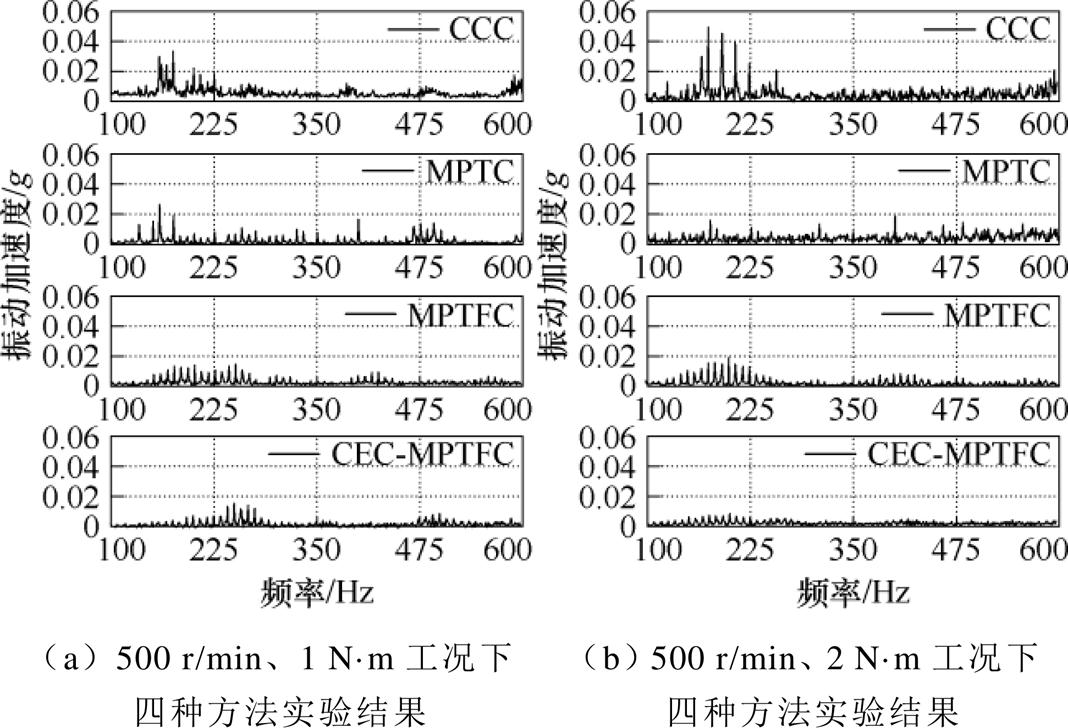
图11 500 r/min不同负载下四种方法振动加速度频谱
Fig.11 Vibration acceleration spectra of four methods under different loads at 500 r/min
1 000 r/min、1 N·m工况下四种方法实验结果如图12所示，随着转速上升，MPTFC下退磁相产生的负转矩逐步增大，使总转矩在换相阶段的平稳度下降。在1 000 r/min转速下MPTFC对转矩脉动的抑制效果降低，从略优于MPTC变至与MPTC近似。高转速下，MPTC退磁相关断较慢，产生了较大的负转矩，但也因此使得径向力衰减速度降低，在一定程度上抑制了径向力脉动，因此在1 000 r/min下MPTC的径向力脉动变小。
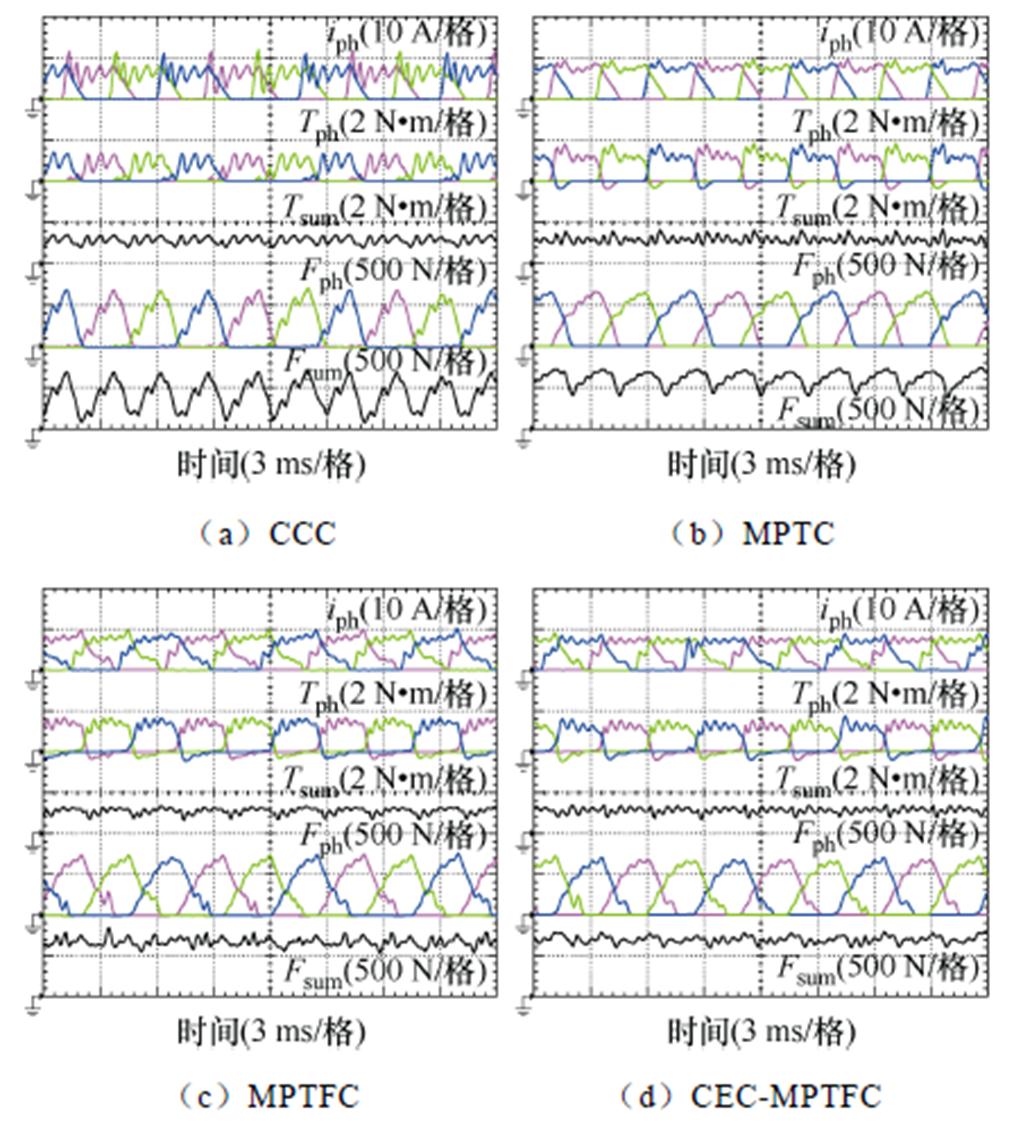
图12 1 000 r/min、1 N·m工况下四种方法实验结果
Fig.12 Experimental results of four methods at 1 000 r/min, 1 N·m operating condition
1 000 r/min不同负载下四种方法振动加速度频谱如图13所示。可以看出，在MPTFC对转矩脉动的抑制效果变弱的情况下，由于其相比于MPTC对径向力脉动的抑制效果更好，依旧有效地实现了转矩脉动与径向力脉动的同时抑制，因此其对电机振动的抑制效果仍优于CCC与MPTC。而基于误差补偿的振动抑制策略的振动加速度明显小于其他三种方法。在1 500 r/min负载1 N·m工况下与PWM控制法的对比如图14所示，振动加速度频谱如图15所示。
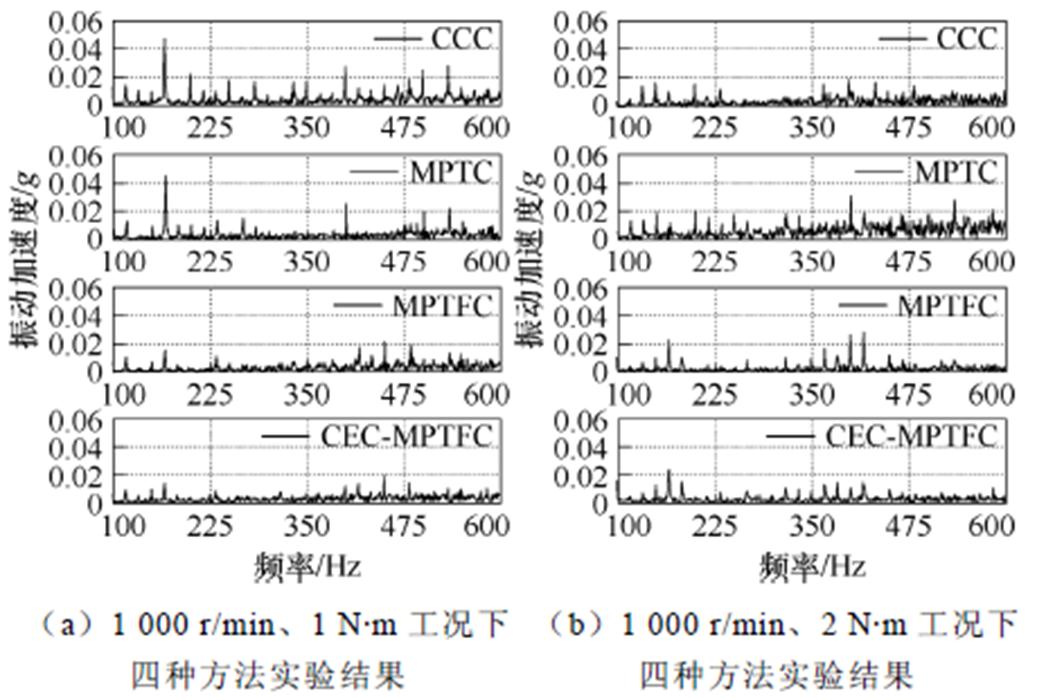
图13 1 000 r/min不同负载下四种方法振动加速度频谱
Fig.13 Vibration acceleration spectra of four methods under different loads at 1 000 r/min
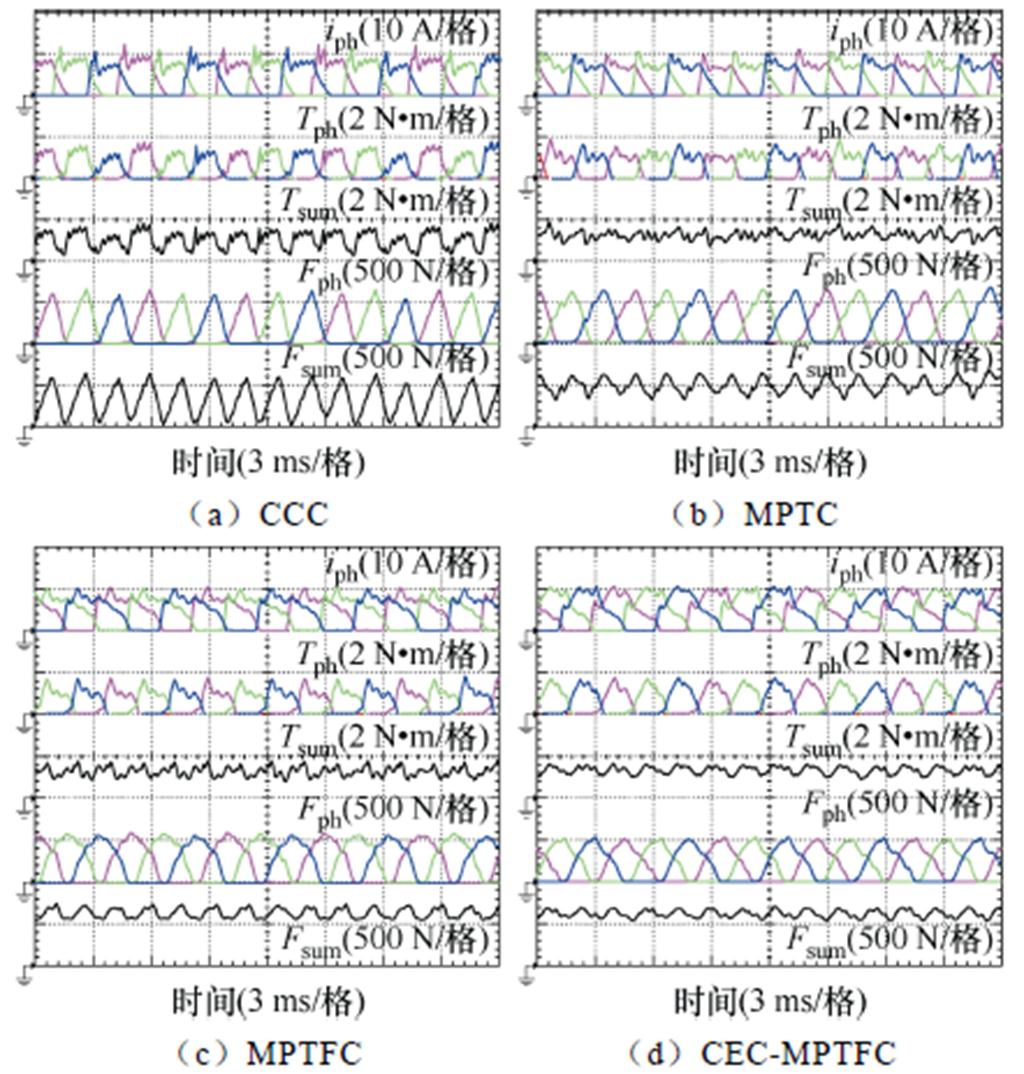
图14 1 500 r/min、1 N·m工况下四种方法实验结果
Fig.14 Experimental results of four methods at 1 500 r/min, 1 N·m operating condition
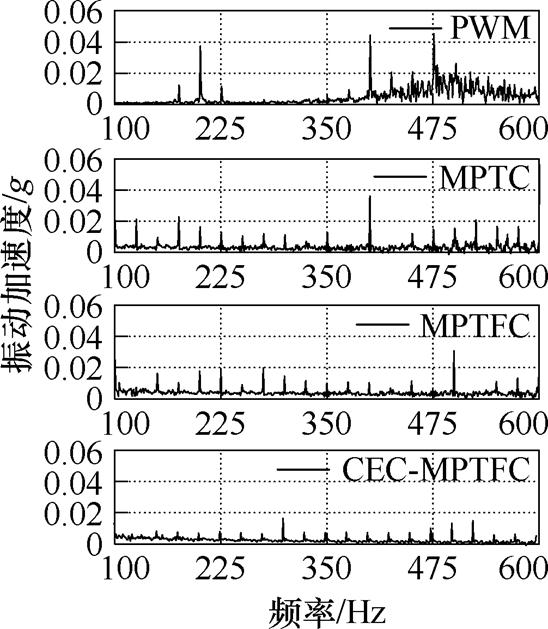
图15 1 500 r/min、1 N·m工况下四种方法振动加速度频谱
Fig.15 Vibration acceleration spectra of four methods at 1 500 r/min, 1 N·m operating condition
可以看出，在高速时与宽调速范围的PWM控制方法相比，本文提出的CEC-MPTFC法同样具有振动抑制的优越性。为更清晰地比较CEC-MPTFC法与其他三种方法的控制效果，构建以上不同方法的性能对比，见表4。以转矩脉动Trip、径向力脉动Fr-rip两个重要指标作为评判依据。从表4可以看出，MPTFC法相比于CCC、PWM和MPTC法，基本实现了对转矩脉动与径向力脉动的抑制，同时也提高了径向力平均值。本文提出的CEC-MPTFC法相比于MPTFC法对转矩脉动与径向力脉动的抑制效果进一步提升，同时由于模型预测中相电流预测值的精确度上升，使得相电流幅值减小，各相径向力幅值随之减小，从一定程度上减小了径向力平均值。与MPTFC的实验对比结果从侧面验证了3.1节提出的基于磁阻预测的电流误差补偿策略对MPC性能的提升。
表4 五种工况下四种方法的控制性能对比
Tab.4 Comparison of control performance of four methods under five operating conditions
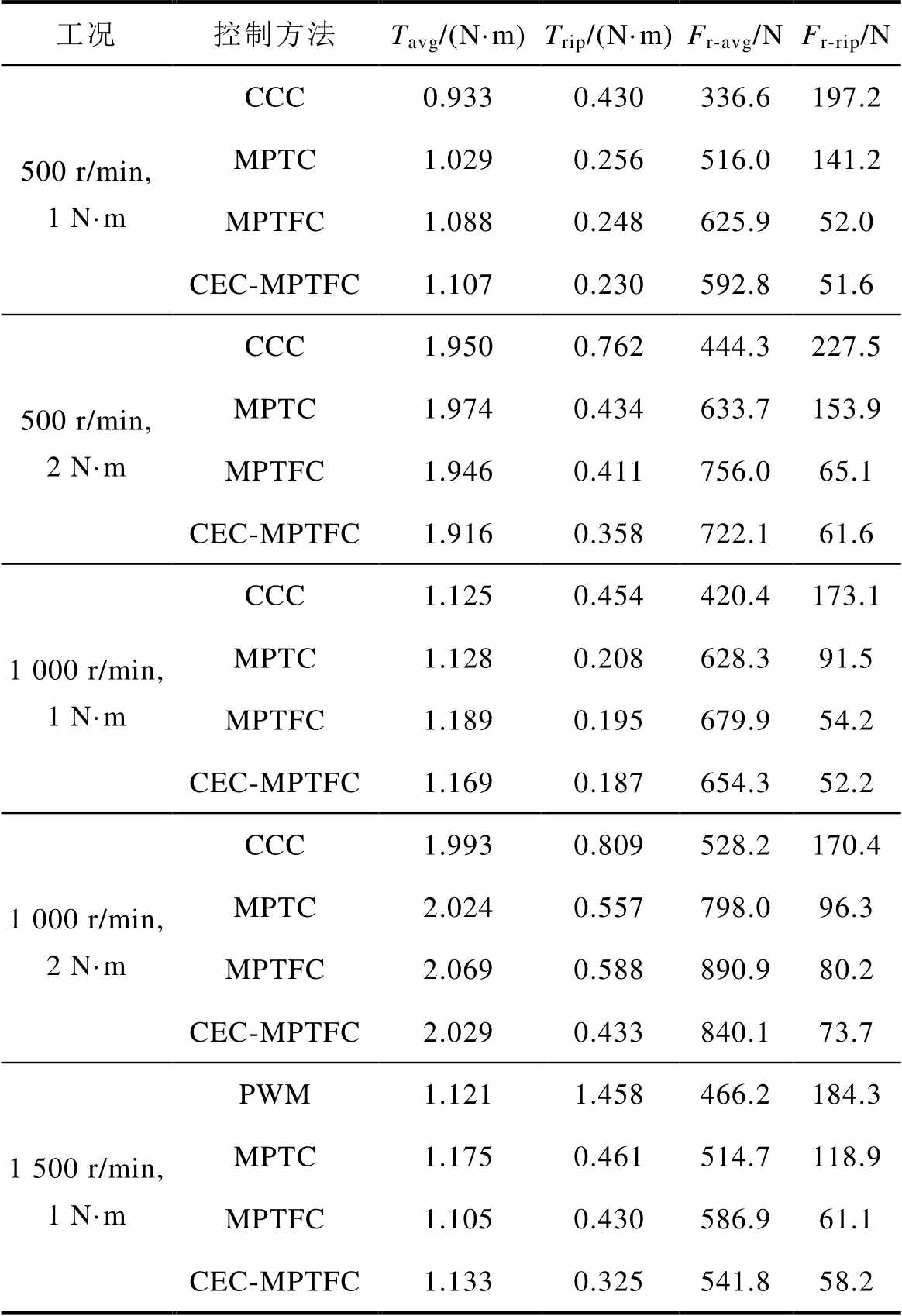
工况控制方法Tavg/(N·m)Trip/(N·m)Fr-avg/NFr-rip/N 500 r/min,1 N·mCCC0.9330.430336.6197.2 MPTC1.0290.256516.0141.2 MPTFC1.0880.248625.952.0 CEC-MPTFC1.1070.230592.851.6 500 r/min, 2 N·mCCC1.9500.762444.3227.5 MPTC1.9740.434633.7153.9 MPTFC1.9460.411756.065.1 CEC-MPTFC1.9160.358722.161.6 1 000 r/min, 1 N·mCCC1.1250.454420.4173.1 MPTC1.1280.208628.391.5 MPTFC1.1890.195679.954.2 CEC-MPTFC1.1690.187654.352.2 1 000 r/min, 2 N·mCCC1.9930.809528.2170.4 MPTC2.0240.557798.096.3 MPTFC2.0690.588890.980.2 CEC-MPTFC2.0290.433840.173.7 1 500 r/min, 1 N·mPWM1.1211.458466.2184.3 MPTC1.1750.461514.7118.9 MPTFC1.1050.430586.961.1 CEC-MPTFC1.1330.325541.858.2
本文针对SRM 的振动问题，从转矩脉动和径向力脉动的基本原理出发，提出了基于误差补偿的SRM振动抑制策略，结合实验结果对比验证了该技术对振动的抑制效果，并得出以下主要结论：
1）通过规划磁链波形构造径向力与转矩分配函数，实现转矩与径向力同时控制；重新规划电压矢量表，减小因退磁相关断造成的径向力脉动。
2）针对MPC受到参数模型精度影响的问题，提出了一种基于磁阻预测的电流误差补偿方法。将电流误差补偿方法与模型预测转矩与径向力控制结合，进一步提升对转矩脉动与径向力脉动的抑制 效果。
参考文献
[1] 方成辉, 陈昊, Galina Demidova, 等. 开关磁阻电机无电流传感器控制方法[J]. 电工技术学报, 2023, 38(2): 365-374.
Fang Chenghui, Chen Hao, Demidova G, et al. Current sensorless control method of switched reluctance motors[J]. Transactions of China Elec- trotechnical Society, 2023, 38(2): 365-374.
[2] 杨帆, 陈昊, 李晓东, 等. 一种优化开关磁阻电机换相区控制策略的高效率转矩分配函数[J]. 电工技术学报, 2024, 39(6): 1671-1683.
Yang Fan, Chen Hao, Li Xiaodong, et al. An efficient torque sharing function for optimizing the com- mutation zone control strategy of switched reluctance motors[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1671-1683.
[3] 吴长龙, 徐衍亮, 付东山, 等. 电动工具用高速两相开关磁阻电机研究[J]. 微电机, 2015, 48(11): 5-8, 25.
Wu Changlong, Xu Yanliang, Fu Dongshan, et al. Research of high-speed two-phase switched relu- ctance motor in electric tool[J]. Micromotors, 2015, 48(11): 5-8, 25.
[4] 李宗霖, 陈昊, 戚湧, 等. 基于自抗扰滑模控制的开关磁阻电机转矩分配控制策略[J]. 电工技术学报, 2024, 39(18): 5639-5656.
Li Zonglin, Chen Hao, Qi Yong, et al. Torque sharing function control strategy for switched reluctance motor based on active disturbance rejection sliding mode control[J]. Transactions of China Electro- technical Society, 2024, 39(18): 5639-5656.
[5] Gundogmus O, Das S, Yasa Y, et al. Acoustic noise mitigation in high pole count switched reluctance machines utilizing skewing method on stator and rotor poles[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 5581-5593.
[6] 闫文举, 陈昊, 马小平, 等. 不同转子极数下磁场解耦型双定子开关磁阻电机的研究[J]. 电工技术学报, 2021, 36(14): 2945-2956.
Yan Wenju, Chen Hao, Ma Xiaoping, et al. Development and investigation on magnetic field decoupling double stator switched reluctance machine with different rotor pole numbers[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2945- 2956.
[7] Song Shoujun, Xia Zekun, Zhang Zhihui, et al. Control performance analysis and improvement of a modular power converter for three-phase SRM with Y-connected windings and neutral line[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6020-6030.
[8] Hua Wei, Hua Hao, Dai Ningyi, et al. Comparative study of switched reluctance machines with half-and full-teeth-wound windings[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1414-1424.
[9] 薛秀慧, 陈强, 庞瀚文, 等. 开关磁阻电机的精确延时两步换相控制[J]. 电力电子技术, 2019, 53(10): 75-78.
Xue Xiuhui, Chen Qiang, Pang Hanwen, et al. Two-stage commutation method with precise time delay for switched reluctance motor control[J]. Power Electronics, 2019, 53(10): 75-78.
[10] Kurihara N, Chiba A, Yamada K, et al. A relationship of radial force sum and current waveforms in switched reluctance motor for noise reduction[C]// 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 5560-5566.
[11] 任浩天, 甘醇, 曲荣海, 等. 基于电流转矩协同控制的开关磁阻电机新型直接瞬时转矩控制策略[J]. 中国电机工程学报, 2024, 44(19): 7794-7806.
Ren Haotian, Gan Chun, Qu Ronghai, et al. Current-torque coordinated control based direct instantaneous torque control strategy for switched reluctance motor[J]. Proceedings of the CSEE, 2024, 44(19): 7794-7806.
[12] Hofmann A, De Doncker R W. Hysteresis-based DIFC in SRM: eliminating switching harmonics while improving inverter efficiency[C]//7th IET Inter- national Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 2014: 1-6.
[13] 贲彤, 聂恒, 陈龙, 等. 一种正弦补偿型转矩分配函数的SRM转矩脉动抑制策略[J]. 电机与控制学报, 2022, 26(8): 100-111.
Ben Tong, Nie Heng, Chen Long, et al. SRM torque ripple suppression strategy based on sinusoidal compensation torque sharing function[J]. Electric Machines and Control, 2022, 26(8): 100-111.
[14] Ye Jin, Bilgin B, Emadi A. An extended-speed low-ripple torque control of switched reluctance motor drives[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(3): 1457-1470.
[15] 胡艳芳, 康智勇, 孙德博, 等. 基于区间分段转矩分配函数的开关磁阻电机转矩脉动抑制[J]. 电机与控制学报, 2023, 27(10): 54-62.
Hu Yanfang, Kang Zhiyong, Sun Debo, et al. Torque ripple suppression of switched reluctance motor based on interval segmentation torque sharing function[J]. Electric Machines and Control, 2023, 27(10): 54-62.
[16] Yan Ning, Cao Xin, Deng Zhiquan. Direct torque control for switched reluctance motor to obtain high torque–ampere ratio[J]. IEEE Transactions on Indu- strial Electronics, 2019, 66(7): 5144-5152.
[17] 韩国强, 陆哲, 吴孟霖, 等. 基于改进滑模控制策略的开关磁阻电机直接瞬时转矩控制方法[J]. 电工技术学报, 2022, 37(22): 5740-5755.
Han Guoqiang, Lu Zhe, Wu Menglin, et al. Direct instantaneous torque control method for switched reluctance motor based on an improved sliding mode control strategy[J]. Transactions of China Elec- trotechnical Society, 2022, 37(22): 5740-5755.
[18] Ge Lefei, Fan Zizhen, Du Nan, et al. Model predictive torque and force control for switched reluctance machines based on online optimal sharing function[J]. IEEE Transactions on Power Electronics, 2023, 38(10): 12359-12364.
[19] Ge Lefei, Yuan Ruilin, Cheng Qiyuan, et al. Model predictive torque and force control of an switched reluctance machine[C]//2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 2021: 280-284.
[20] 屈资喻, 黄朝志, 陈军, 等. 减小开关磁阻电机转矩脉动的九区间DITC控制策略[J]. 河南理工大学学报(自然科学版), 2022, 41(4): 117-125.
Qu Ziyu, Huang Chaozhi, Chen Jun, et al. Direct instantaneous torque control strategy at 9 regions for reducing torque ripple of switched reluctance motor[J]. Journal of Henan Polytechnic University (Natural Science), 2022, 41(4): 117-125.
[21] 费晨, 颜建虎, 汪盼, 等. 基于改进的转矩分配函数法的开关磁阻电机转矩脉动抑制[J]. 电工技术学报, 2018, 33(增刊2): 394-400.
Fei Chen, Yan Jianhu, Wang Pan, et al. Torque ripple suppression of switched reluctance motor based on modified torque sharing function[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 394-400.
[22] 刘忠永, 范涛, 何国林, 等. 高性能永磁同步电机显式模型预测控制算法研究[J]. 电工技术学报, 2023, 38(22): 6039-6058.
Liu Zhongyong, Fan Tao, He Guolin, et al. Research on high-performance explicit model predictive control algorithm for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6039-6058.
[23] 梅杨, 吕宁, 魏铮. 间接矩阵变换器-双异步电机调速系统的模型预测控制权重因数整定[J]. 电工技术学报, 2024, 39(23): 7554-7565.
Mei Yang, Lü Ning, Wei Zheng. Model predictive control weight factor tuning method for indirect matrix converter-double induction motors speed control system[J]. Transactions of China Elec- trotechnical Society, 2024, 39(23): 7554-7565.
[24] 向超群, 杜京润, Zhang Xinan, 等. 电容电压平衡的四电平有源中性点钳位逆变器的改进模型预测电流控制[J]. 电工技术学报, 2024, 39(18): 5826- 5838.
Xiang Chaoqun, Du Jingrun, Zhang Xinan, et al. An improved model predictive control of four-level active neutral point clamped inverter with balanced capacitor voltage[J]. Transactions of China Elec- trotechnical Society, 2024, 39(18): 5826-5838.
[25] 周汉斌, 杨建, 黄连生, 等. 基于有限状态机的三电平逆变器双矢量模型预测控制策略[J]. 电力系统自动化, 2023, 47(11): 155-164.
Zhou Hanbin, Yang Jian, Huang Liansheng, et al. Double-vector model predictive control strategy of three-level inverter based on finite state machine[J]. Automation of Electric Power Systems, 2023, 47(11): 155-164.
Abstract With its simple and robust structure and wide speed regulation range, switched reluctance machine (SRM) has a wide range of application scenarios in the fields of multi-all-electric airplanes, electric vehicles, and new energy power generation. However, due to its double-convex pole structure and pulse-powered operation mode, SRM has the shortcomings of large torque ripple and strong vibration during operation, which seriously affects its practical application in the industrial field.
In view of the above problems, this paper firstly explores the generation mechanism of vibration noise of SRM, and identifies torque ripple and radial force ripple as the two major causes of motor vibration noise. Based on the idea of model predictive control (MPC), a multi-objective control method of SRM torque ripple and radial force ripple based on the MPC method is proposed along with the control logic of torque predictive control. Based on the magnetic chain waveform planning, the radial force and torque share function (TSF) is constructed, and the torque and radial force waveforms of each phase are planned to realize the simultaneous control of the torque and radial force; considering the changing characteristics of the radial force, the voltage vector table of single-phase conduction area under the MPC is optimized, so that the radial force ripple caused by demagnetization correlation breaks can be reduced; the predicted torque and radial force are taken as the parameters to the cost function, so that the on-line optimization of the switching status of the minimum torque ripple and radial force ripple can be performed.
In MPC, the accuracy of the motor electromagnetic characteristic model seriously affects the stability of the control algorithm, in order to improve the stability of the model predictive torque and radial force control (MPTFC) algorithm, and reduce the vibration of the motor, propose a current error compensation method based on the prediction of reluctance. Combined with the operating characteristics of the SRM variable reluctance, from the nonlinear inductance characteristics, according to the parameters of each phase current and voltage, to obtain the relationship between the predicted reluctance and the actual reluctance; combined with the motor state equations, the inverse deduction to obtain a more accurate value of current prediction, to improve the control performance of the MPC algorithm.
Finally, a semi-physical experimental verification platform based on a 600 W three-phase 12/8-pole SRM is constructed to experimentally validate the proposed error compensation-based vibration suppression control strategy. Comparisons are made with current chopper control (CCC), PWM control, MPC, model predictive torque control (MPTC), and MPTFC methods at 500 r/min, 1 000 r/min, and 1 500 r/min with a load of 1 N·m and 2 N·m. The experimental results show that, compared with the traditional CCC, PWM and MPTC, the MPTFC strategy has significant suppression effects on torque ripple and radial force ripple, and the vibration acceleration spectrum shows that this method effectively reduces the vibration of the whole machine; the model predictive torque and force control based on current error compensation (CEC-MPTFC) further strengthens the suppression effect, and reduces the torque ripple and radial force ripple by 10.10% and 23.47%, which provides a reference to improve the reliability of the SRM.
Keywords：Switched reluctance machine, model predictive control, vibration, error compensation
中图分类号：TM301.4+2; V233.7+1
DOI: 10.19595/j.cnki.1000-6753.tces.241292
国家自然科学基金（52107055）和航空科学基金（20220040051002）资助项目。
收稿日期 2024-07-19
改稿日期 2024-11-17
葛乐飞 男，1992年生，博士，副教授，博士生导师，研究方向为起动/发电一体化电机系统。
E-mail: lge@nwpu.edu.cn（通信作者）
宋佳赫 女，2001年生，硕士研究生，研究方向为开关磁阻电机振动抑制及故障诊断。
E-mail: sjhhhhh@mail.nwpu.edu.cn
（编辑 郭丽军）