图1 MMT-MLPMLSM电机结构示意图
Fig.1 Schematic diagram of the structure of MMT-MLPMLSM
摘要 针对动磁式磁悬浮永磁直线同步电机，该文提出并设计了一种H2/H∞混合鲁棒控制策略，有效地提升了电机悬浮子系统的鲁棒性和动态性。首先，分析动磁式磁悬浮永磁直线同步电机的运行机理，建立了电机系统数学模型，并指出传统H∞鲁棒控制策略存在无法考虑系统内部干扰的问题。在此基础上，提出并设计H2/H∞混合鲁棒控制器，进一步分析了控制器加权矩阵参数对系统动态性和鲁棒性的影响，给出参数的选取原则。最后，搭建了磁悬浮永磁直线同步电机悬浮系统的实验平台，对所提出的H2/H∞混合鲁棒控制策略进行了仿真和实验验证，其结果证明了该文研究内容的正确性和有效性。
关键词：动磁式磁悬浮直线电机 磁悬浮系统数学模型 加权矩阵 H2/H∞混合鲁棒控制
悬浮永磁直线同步电机从根本上消除了传统永磁直线同步电机中存在于运动平台和静止导轨之间的摩擦力[1-3]，可以实现非接触的精密直线定位运动，具有无摩擦、高精度、高速高加速度、高响应、高可靠性等优点。相比于气悬浮，磁悬浮具有刚度大、承载力高的优点，可以适应超洁净和真空制造环境，无需精密加工的气浮支撑表面，从而降低制造成本[4-6]，是新一代光刻机等高端装备中精密直线定位运动的最佳选择之一[7-9]。
磁悬浮永磁直线同步电机从动子和定子的结构上可以简单分为动圈式和动磁式两类。动圈式悬浮永磁直线同步电机（Moving Coil Type Magnetic Levitation Permanent Magnet Linear Synchronous Motor, MCT-MLPMLSM）的电磁模型虽然简单，但由于动子上放置了励磁线圈，电缆会给电机带来额外的扰动，还会限制电机的行程和动子的运动自由度[10-12]。相反，动磁式悬浮永磁直线同步电机（Moving Magnet Type Magnetic Levitation Permanent Magnet Linear Synchronous Motor, MMT-MLPMLSM）的动子上放置了永磁体，无需线缆和散热装置，能够真正实现动子与导轨的无接触运动，但是其电磁特性较为复杂，且磁悬浮系统本质上是耦合的、不稳定的[13-15]。因此，建立磁悬浮系统的精确数学模型，实现系统的解耦并设计有效的控制策略通常是一项复杂的工作[16-18]。在过去的几年里，许多学者对MMT- MLPMLSM的结构和控制策略进行了大量研究。
文献[19]将管状线性执行器与磁悬浮轴承相结合，提出了一种磁悬浮管状永磁直线同步电机，利用同一套绕组来产生电磁推力和磁悬浮力。文献[20]提出了一种由线性磁滞电机驱动的新型磁悬浮直线移动工作台。利用移动工作台左右两侧定子绕组的磁链与次级的磁滞效应相互作用产生电磁推力，利用两侧定子绕组的磁链差产生横向磁阻力，从而控制工作台的悬浮力。文献[21]针对长初级永磁直线同步电机，提出了一种双边绕组协调的主动悬浮控制方法，然而该方法需要给双边绕组通入对称的电流进行PI控制，但是由于加工装配误差，双边绕组无法做到完全一致，因此法向力与推力之间仍然存在耦合。
以上文献的MMT-MLPMLSM在实现悬浮和推进功能时共用一套绕组，悬浮力控制与推力控制间存在耦合，增大了系统控制难度，阻碍了系统定位和跟踪性能的提升。
文献[22]采用两套绕组来分别控制悬浮系统和推进系统，两套绕组分布于初级的不同位置。通过理论分析，建立了两个系统耦合量的精确模型，并设计了H∞鲁棒控制器。文献[23]则将两套绕组叠加嵌套在同一初级铁心齿上进行正交解耦控制，一套专门用于产生电磁推力，另一套则专门用于产生磁悬浮力，通过这种方式实现悬浮力与推进力的解耦，但由于两套绕组磁路相同，当铁心饱和时，两者磁路不能线性叠加，悬浮力与推力控制仍然会存在一定程度的耦合。文献[24]针对该电机提出了一种H∞鲁棒控制方法，提升了系统的抗干扰能力，但只考虑了系统外部的扰动，并未对系统内部扰动进行抑制。针对这一问题，文献[25-26]将鲁棒控制与滑模控制相结合，利用滑模控制能抑制内部参数扰动的特点，来同时提升磁悬浮系统对内、外扰动的鲁棒性，但滑模控制存在抖振的问题。
针对以上挑战，本文采用一种双绕组结构的MMT-MLPMLSM，简化了悬浮系统与推进系统的数学模型，降低了控制器的设计难度。针对这一款电机的悬浮子系统，本文提出并设计了一种H2/H∞混合鲁棒控制器，同时考虑了系统的内外扰动，有效提升了系统的动态性和鲁棒性。
本文首先详细介绍了电机的结构、运行原理和系统控制框图，建立了磁悬浮系统数学模型。其次，给出了H2/H∞鲁棒控制器的设计过程，研究了加权矩阵参数对系统动态性和鲁棒性的影响。然后，推导了系统的传递函数，通过伯德图和零极点分布图分析了系统的稳定性，并对所提出的H2/H∞混合鲁棒控制策略与传统H∞鲁棒控制策略进行了对比仿真，证明了该方法的可行性。最后，搭建了磁悬浮系统的实验平台，对所提出的方法进行了实验验证，证明了该方法的有效性。
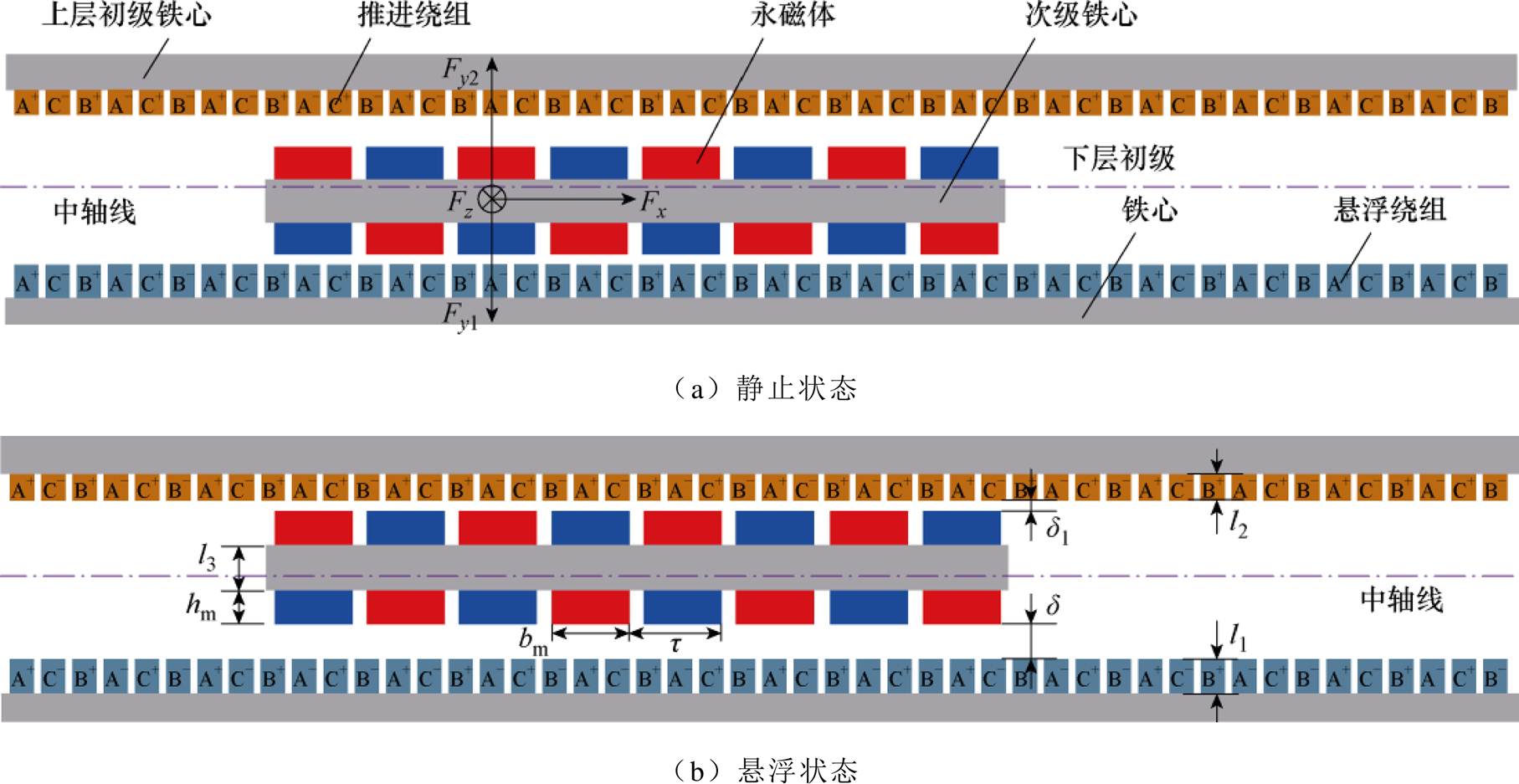
本文研究的MMT-MLPMLSM结构示意图如 图1所示。该电机为非对称双边结构，初级为定子，次级为动子。初级分为上层和下层，分别装有推进绕组和悬浮绕组。上层初级和下层初级均为无槽结构，避免了齿槽效应的影响。推进绕组和悬浮绕组的厚度和匝数不同，但相序的连接顺序相同。次级双边的磁极采用表面安装结构，且所有永磁体的尺寸一样，电机主要结构参数见表1。
图1 MMT-MLPMLSM电机结构示意图
Fig.1 Schematic diagram of the structure of MMT-MLPMLSM
MMT-MLPMLSM可以实现对动子四个自由度的控制。推进绕组和悬浮绕组分别控制x轴和y轴的平移自由度。由于永磁体、上铁心、下铁心和动子铁心宽度相同，MMT-MLPMLSM还可以实现动子y轴旋转自由度和z轴平移自由度的被动控制。
推进绕组和悬浮绕组均采用三相正弦交流电励磁，推进绕组采用id=0控制策略实现推力的稳定输出，悬浮绕组采用iq=0控制策略调节悬浮力的大小。
表1 电机主要结构参数
Tab.1 Main structural parameters of the motor
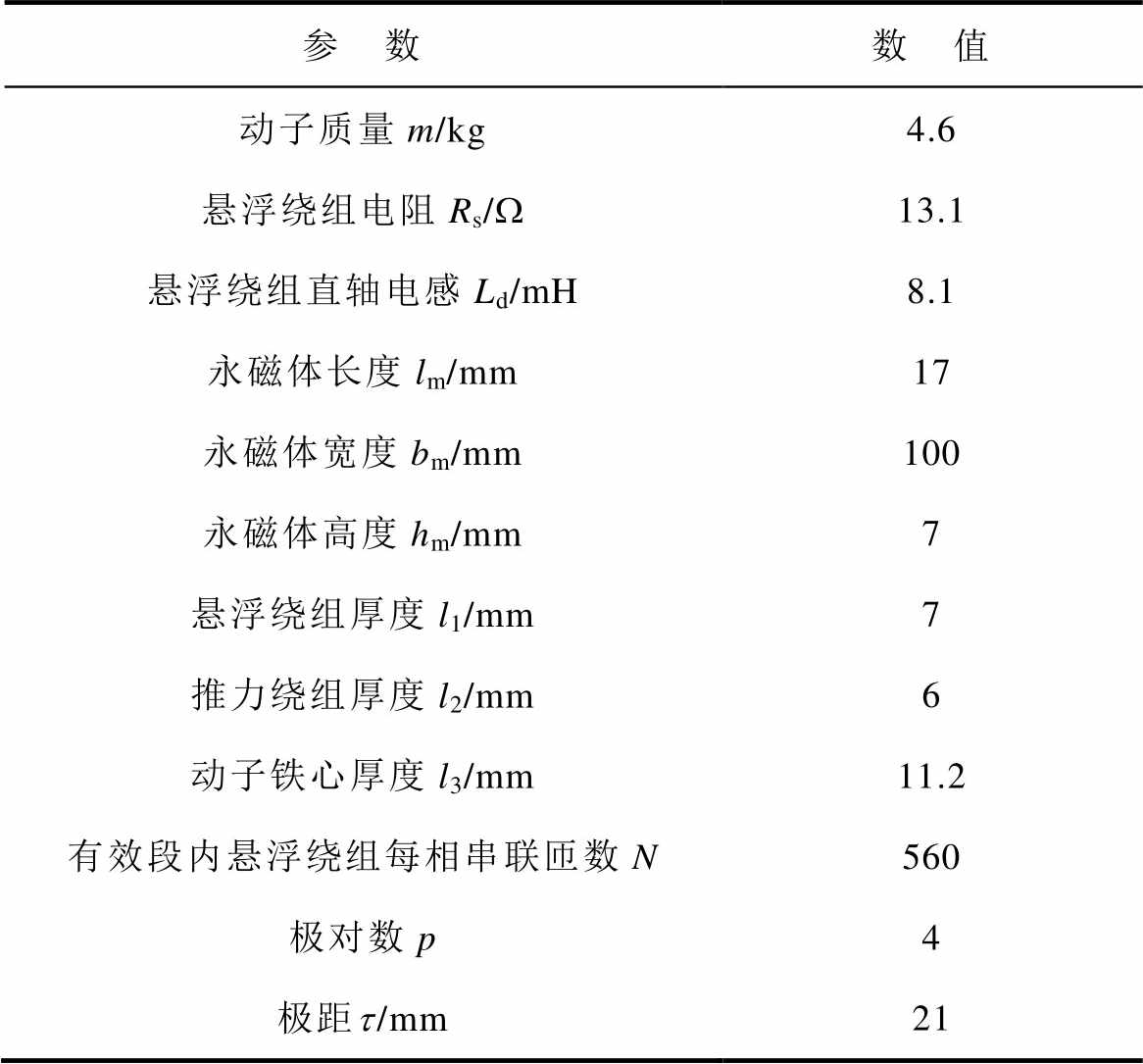
参 数数 值 动子质量m/kg4.6 悬浮绕组电阻Rs/W13.1 悬浮绕组直轴电感Ld/mH8.1 永磁体长度lm/mm17 永磁体宽度bm/mm100 永磁体高度hm/mm7 悬浮绕组厚度l1/mm7 推力绕组厚度l2/mm6 动子铁心厚度l3/mm11.2 有效段内悬浮绕组每相串联匝数N560 极对数p4 极距t/mm21
电机采用两侧气隙宽度不均匀的设计方案。在静止状态时，电机次级停靠在下层初级侧，如图1a所示，此时上层气隙宽度大于下层气隙宽度。当电机起动时，通过给悬浮绕组通入电流来调整下层磁场，从而调节双边初级与次级间的空载法向力。当电机稳定运行时，双边初级与次级间空载法向力之差等于重力，上层气隙宽度小于下层气隙宽度，如图1b所示。
此种电机结构有以下优势：
（1）通过双边、双绕组的结构，简化了系统数学模型，降低了系统控制难度。
（2）利用双边初级与次级间空载法向力之差作为悬浮力，在电机稳定运行时，悬浮绕组电流只需要抑制法向力的波动，降低了悬浮系统的功率损耗。
（3）采用动磁式设计，次级无需馈电电缆和冷却装置，消除线缆力扰动的同时进一步简化了装置结构。
（4）双边气隙不等宽的设计，增强了悬浮力与推力、负载重力间的适配性，解决了传统单边式结构中存在的“法向力远大于重力和推力”的问题。
为了使系统解耦，分别对推进系统和悬浮系统采用id=0和iq=0的控制策略，得到磁悬浮系统的电压方程为
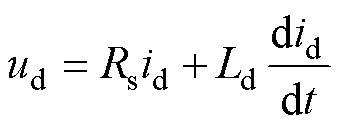（1）
式中，ud为悬浮绕组直轴电压分量；Rs为悬浮绕组电阻；id为悬浮绕组直轴电流分量；Ld为悬浮绕组直轴电感。
磁悬浮系统的磁路回路示意图如图2所示。在一对极的情况下，采用等效法进行磁悬浮力的推导。图2表明磁悬浮力是由Fy1、Fy2两部分组成，其中Fy1为下层初级对次级的吸引力，方向向下，Fy2为上层初级对次级的吸引力，方向向上。将次级在一对极下受到的磁悬浮合力记为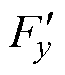
，规定其方向向上，则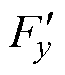=Fy2-Fy1。
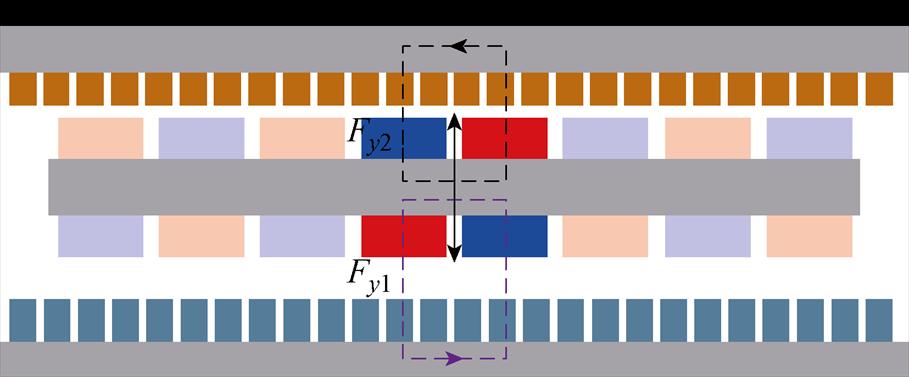
图2 磁悬浮系统的磁路回路示意图
Fig.2 Schematic diagram of the magnetic circuit loop of a maglev system
由场能理论及虚位移原理得到Fy1表达式为
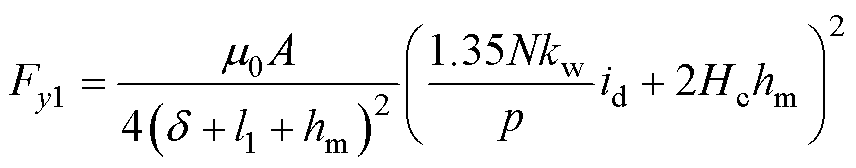（2）
式中，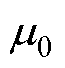
为真空磁导率；
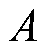为一对极下磁路有效面积；
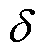为下层气隙高度；
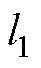为悬浮绕组厚度；
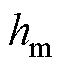为永磁体高度；
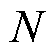为有效段内悬浮绕组每相串联匝数；
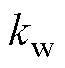为悬浮绕组的绕组因数；
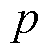为极对数；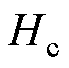
为永磁体矫顽力的数值。
由场能理论及虚位移原理得到Fy2表达式为
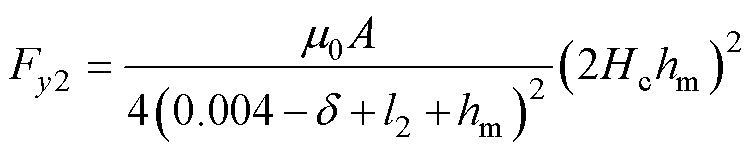（3）
式中，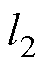
为推进绕组厚度。
本文采用的电机是4对极的，因此次级受到的总磁悬浮力Fy=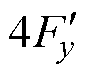
，其表达式为
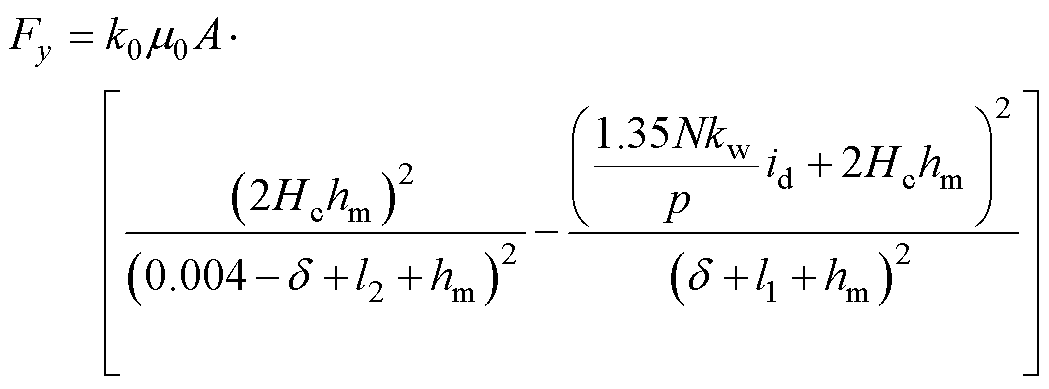（4）
式中，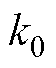
为校正系数。
记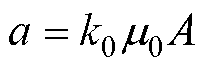
，
，
，
，
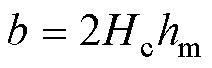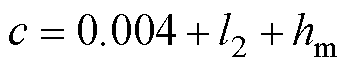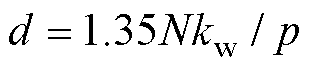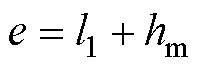，则悬浮力方程可写为
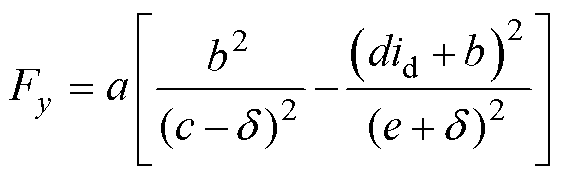（5）
由式（5）可知，悬浮系统具有很强的非线性特点，磁悬浮系统作为定位执行器需要在平衡位置稳定悬浮，因此为了便于控制器的设计，可以对磁悬浮系统的模型进行线性化处理[21-24]。在平衡点（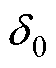
, 
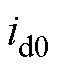）附近对磁悬浮系统进行泰勒展开，有
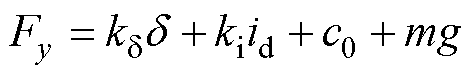（6）
其中
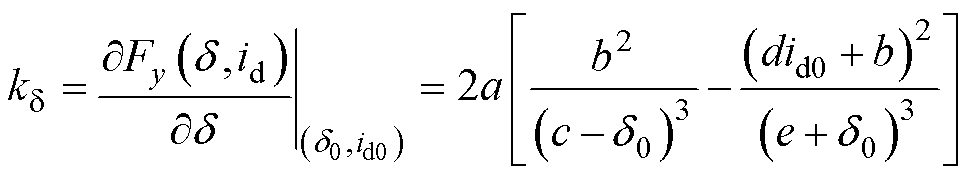
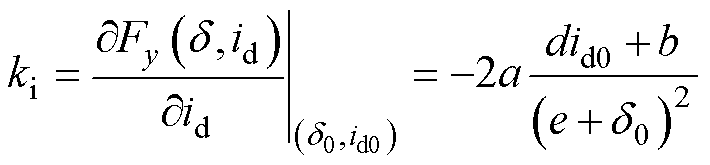
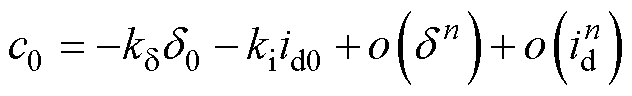（7）
式中，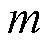
为动子质量；
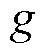为重力加速度；
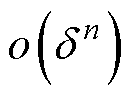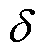为的二次及以上的高次项；
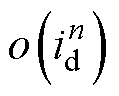为
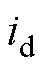的二次及以上的高次项；c0可以看成是泰勒展开式中高次项在向平衡点靠近时所产生的内部扰动。
悬浮方向上的运动方程为
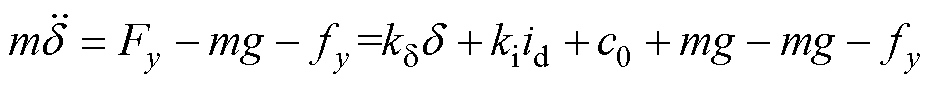
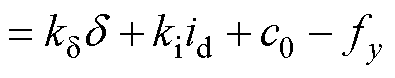（8）
式中，fy为悬浮方向上受到的外部扰动。
悬浮系统的空间状态方程为
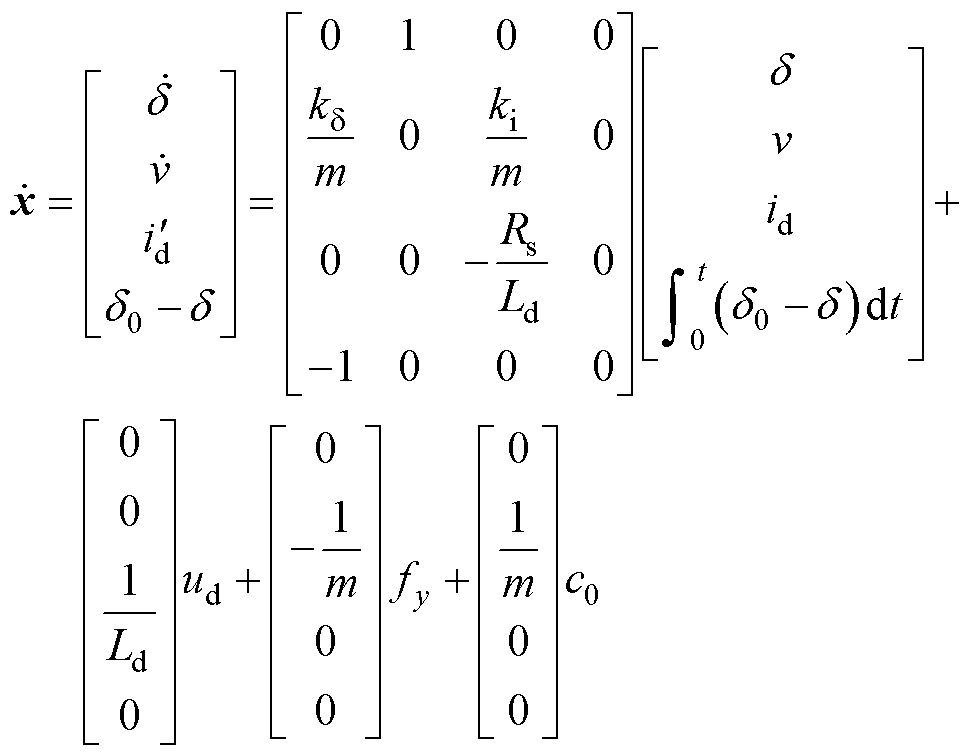
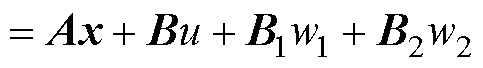（9）
式中，v为电机悬浮方向上的速度；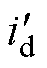
为悬浮绕组直轴电流的导数；u=ud，w1=fy，w2=c0；A、B、B1、B2为四个矩阵。
针对图1所示的MMT-MLPMLSM，其整个系统的控制框图如图3所示。图中，iq1、id1分别为推进绕组的交、直轴电流；iq2、id2分别为悬浮绕组的交、直轴电流；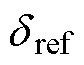
、xref分别为悬浮方向和推进方向的位置给定。
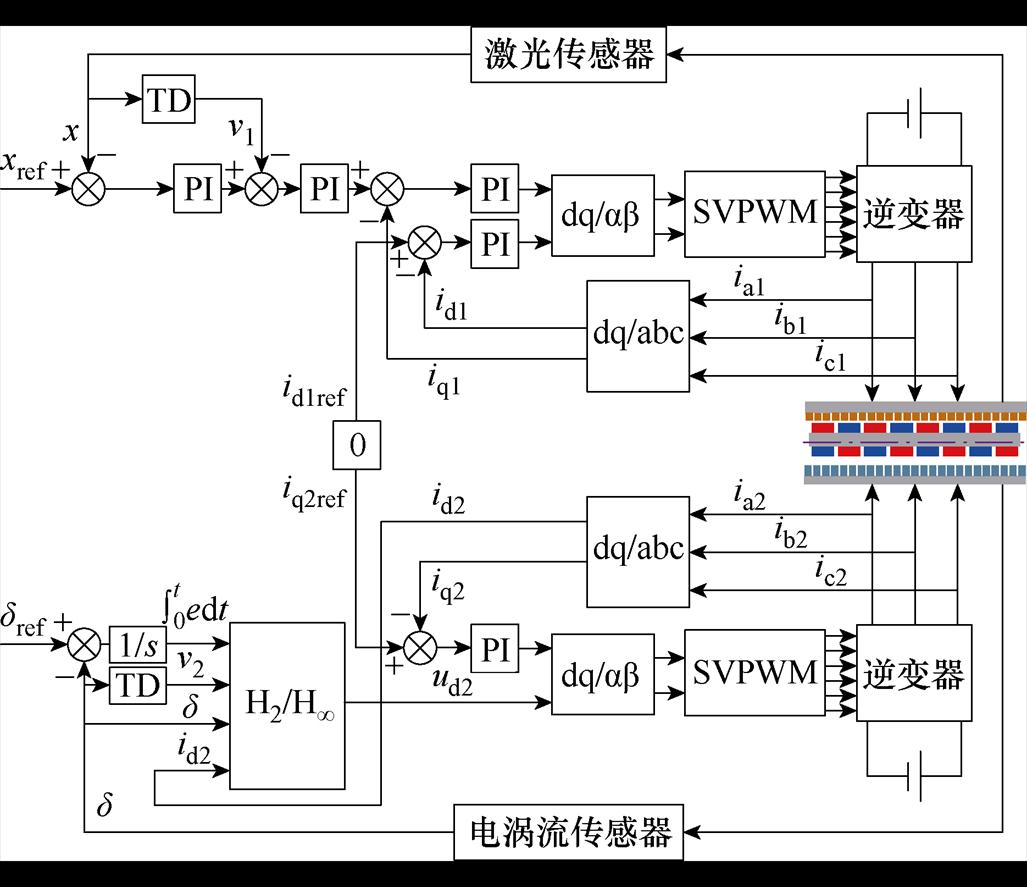
图3 系统控制框图
Fig.3 System control block diagram
id1=0, iq1控制MMT-MLPMLSM的电磁推力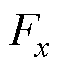
, iq2=0, id2和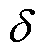共同控制MMT-MLPMLSM的磁悬浮力Fy，实现了两个系统的解耦控制。在此基础上，采用如图3所示的系统控制方案。电涡流传感器检测电机动子y方向的悬浮高度，并通过跟踪微分器（Tracking Differentiator, TD）计算出速度，将检测到的气隙高度、
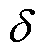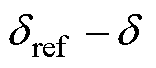的积分、速度v2、d轴电流id2输入H2/H∞混合鲁棒控制器中，控制器输出d轴电压ud2。激光传感器检测电机动子x方向的推进位移，并通过跟踪微分器TD计算出速度，将检测到的位移x与参考位移xref进行比较，并将误差输入PI控制器中，然后依次进行速度环、电流环的控制。
因此，可以将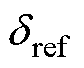
设置为平衡点，通过H2/H∞混合鲁棒控制器后得到ud2，进而调节磁悬浮力Fy，使电机次级达到平衡位置。随后设置推进方向的位移xref，通过三环调节电磁推力Fx，使电机次级达到给定位置，实现悬浮系统与推进系统的独立控制。
针对图1所示双绕组结构MMT-MLPMLSM的悬浮子系统，本文设计了H2/H∞混合鲁棒控制器，其控制框图如图4所示。
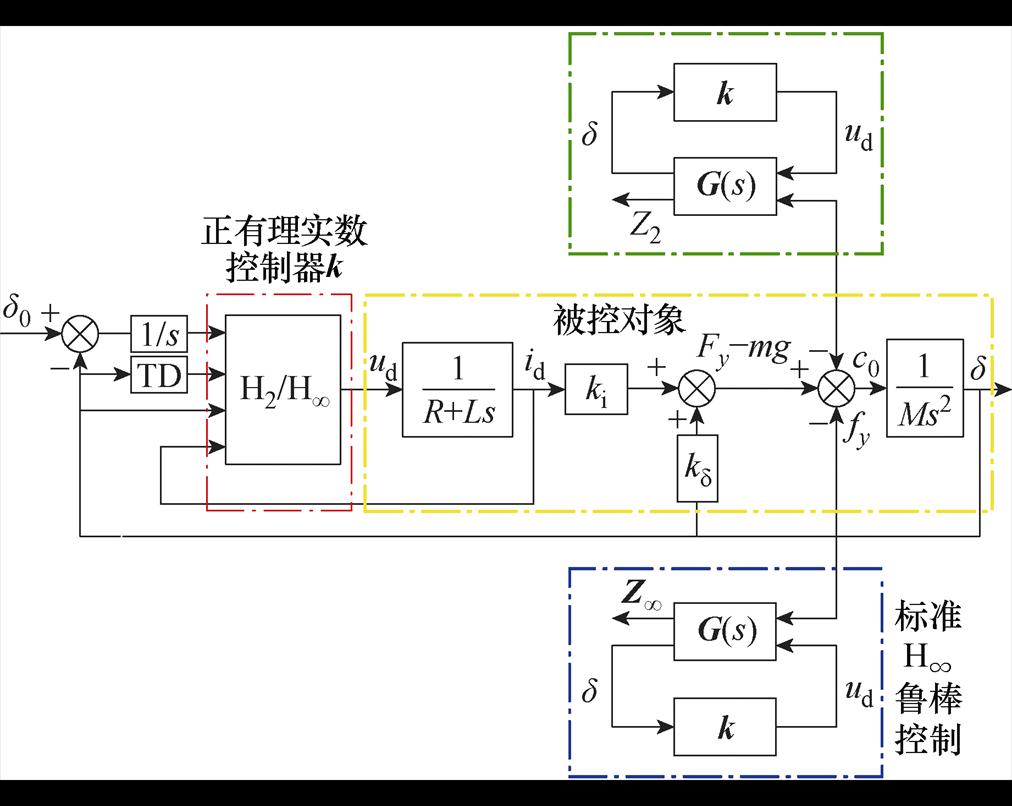
图4 H2/H∞混合鲁棒控制的框图
Fig.4 Block diagram of H2/H∞ robust control
标准H∞鲁棒控制的框图如图4所示。其中，fy为有界的外部输入信号（一般指干扰信号），ud为控制系统的输入信号，Z∞为被控输出量（也可认为是为了设计要求所界定的评价信号），G(s)为被控对象，k为控制器。
H∞鲁棒控制的目的就是对于图4所示的被控对象G(s)（即黄色部分），求解一个正有理实数控制器k（即红色部分），使得闭环系统稳定的同时，外部扰动fy到被控输出量Z∞闭环传递函数的H∞范数Tzw(s)∞最小，让扰动对输出的影响极小。
通过式（4）可知，系统中除了外部扰动外，在对悬浮力进行线性化处理时，其泰勒展开式中的高次项部分也是一种扰动，这属于系统内部的扰动。本文引入H2范数来对这部分扰动进行抑制，使得内部扰动c0到被控输出量Z2闭环传递函数的H2范数最小，即让c0到Z2的能量衰减过程加快，以此来提升系统的快速性和鲁棒性，如图4绿色部分（右上角）所示。
被控对象的状态空间方程可表示为
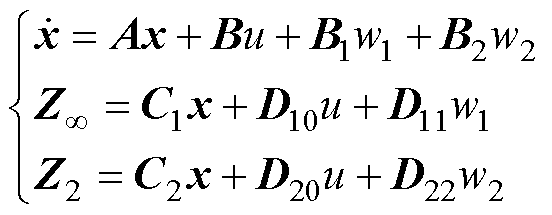（10）
式中，C1、D10、D11、C2、D20、D22为加权矩阵，为方便求解控制器，通常情况下D11、D22取为0。
对一个给定的标量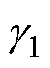
＞0，若存在对称正定矩阵X以及W满足式（11），则说明系统的H2/H∞混合控制器是存在的，同时K=W/X即为控制器的控制律。
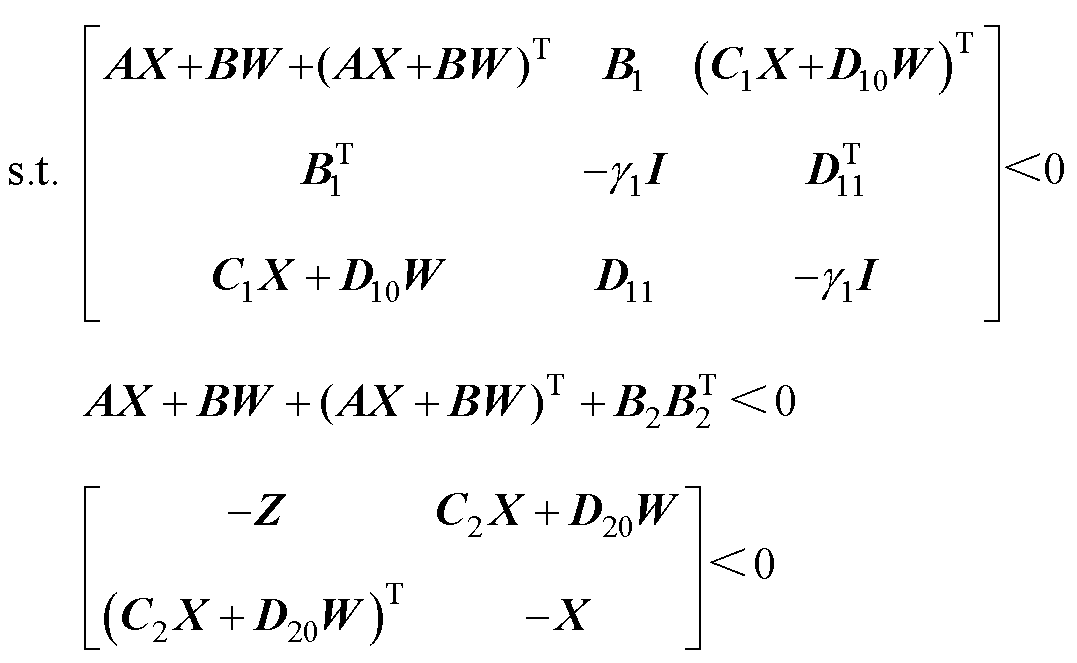
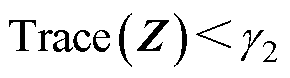（11）
式中，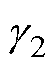
为正实数；I为单位矩阵；Z为正定矩阵。
为了验证所设计的H2/H∞混合鲁棒控制器的正确性和有效性，保持H∞鲁棒控制加权矩阵C1和D10不变的情况下，选取H2/H∞的加权矩阵C2和D20。
加权矩阵C2对角线元素的值以及D20非零元素值的选择对系统的性能影响显著，但是加权矩阵随着被控对象和设计指标的不同，产生的差异也不 同[22, 24]，因此并无特定的规律可以遵循。本文探究了加权矩阵参数对被控磁悬浮系统动态性和鲁棒性的影响规律。
C2、D20的形式为
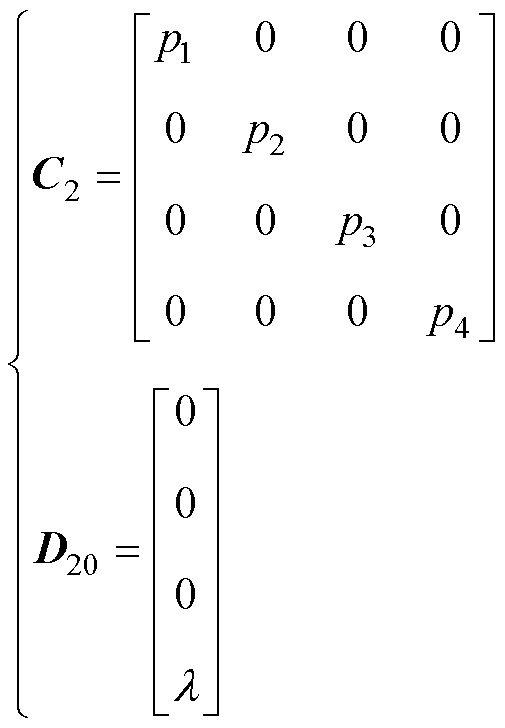（12）
式中，p1、p2、p3、p4、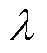
为正实数。
控制器k的形式为
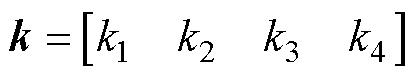（13）
式中，k1、k2、k3、k4为正实数。
2.3.1 k1～k4对系统的影响
先通过不断试取参数，求解出一个使系统稳定的控制器，然后在保证系统依旧稳定的前提下改变k1～k4的数值，对系统造成的影响如图5所示。
研究结果表明：
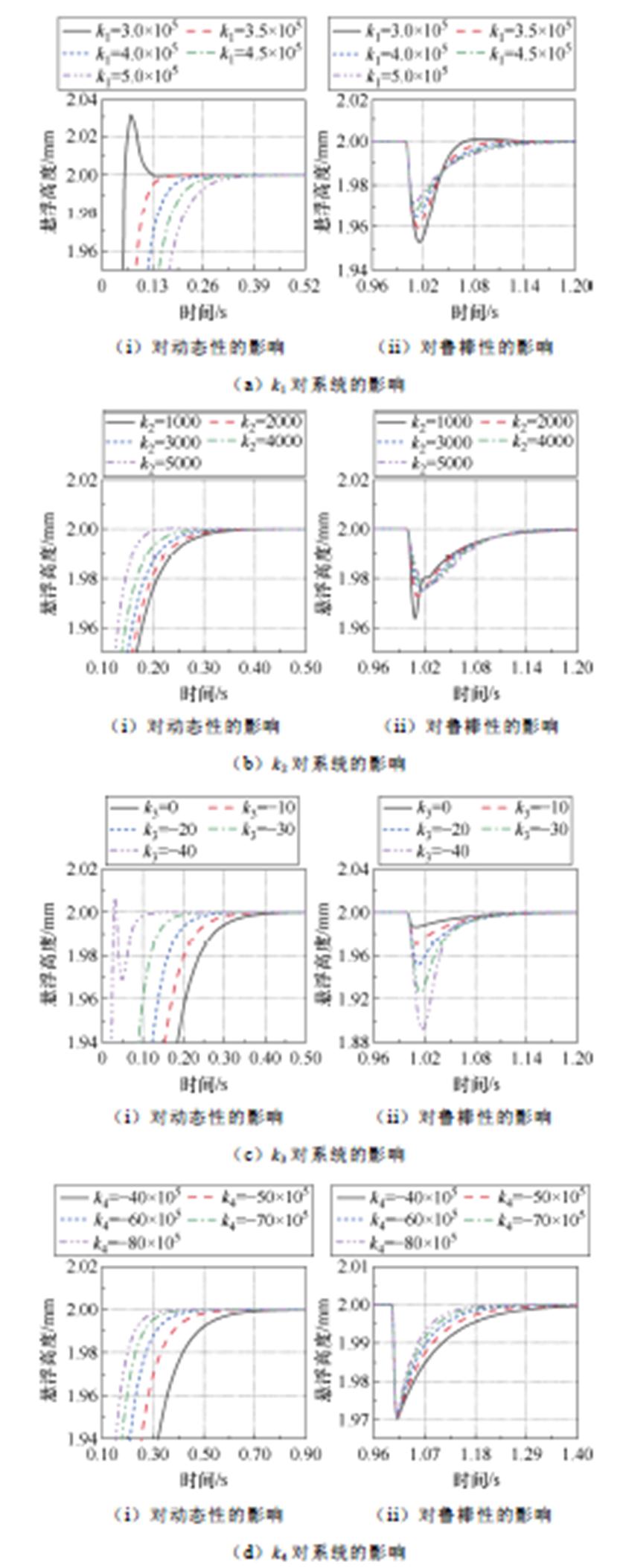
图5 k1～k4对系统的影响
Fig.5 Effect of k1～k4 on the system
（1）k1增大，会使得系统的快速性变差、鲁棒性增强。
（2）k2增大，会使得系统的快速性和鲁棒性都得到增强。
（3）k3减小，会使得系统的快速性增强、鲁棒性变差。
（4）k4减小，会使得系统的快速性和鲁棒性都得到增强。
因此，所设计的控制器需要使得k2较大、k4较小，根据系统表现出的快速性和鲁棒性，对k1和k3进行取舍。
2.3.2 p1～p4以及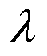
对k1～k4的影响
分别改变p1～p4以及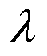，探究它们对k1～k4的影响，研究结果表明：
（1）改变p1，k1会小幅度地变化且整体呈正相关关系，k2、k3、k4基本不变。
（2）改变p2，k1、k2会小幅度变化且整体呈正相关关系，k3、k4基本不变。
（3）改变p3，k1会显著变化且整体呈正相关关系，k2、k4会小幅度变化且整体呈正相关关系，k3基本不变。
（4）改变p4，k1、k2、k3基本不变，k4会小幅度变化且整体呈负相关关系。
（5）改变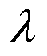，k1会小幅度变化，k2、k3基本不变，k4会显著变化呈正相关关系。
可以看出，加权矩阵的参数对k1～k4的影响非常复杂，但可以确定的是p4的选取必须要大，这样可以使得k4很小，从而增强系统的快速性和鲁棒性，其他参数的选择则需要综合控制器性能进行取舍。
本文设计的H∞鲁棒控制器加权矩阵以及求解出的控制器为
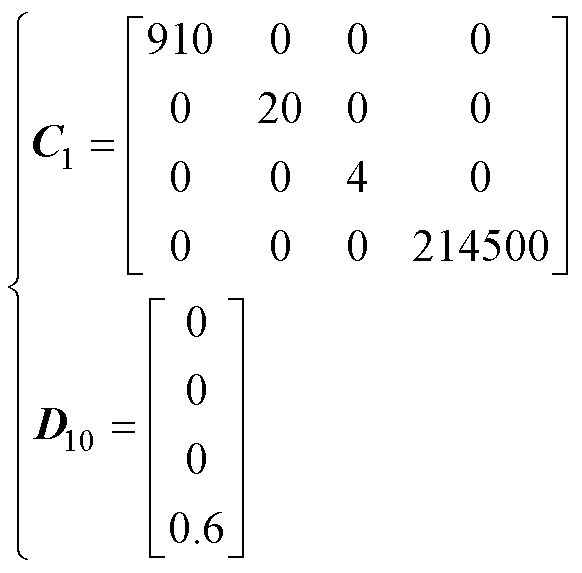（14）
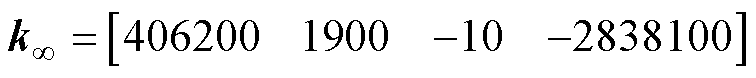（15）
本文设计的H2/H∞混合鲁棒控制器加权矩阵以及求解出的控制器为
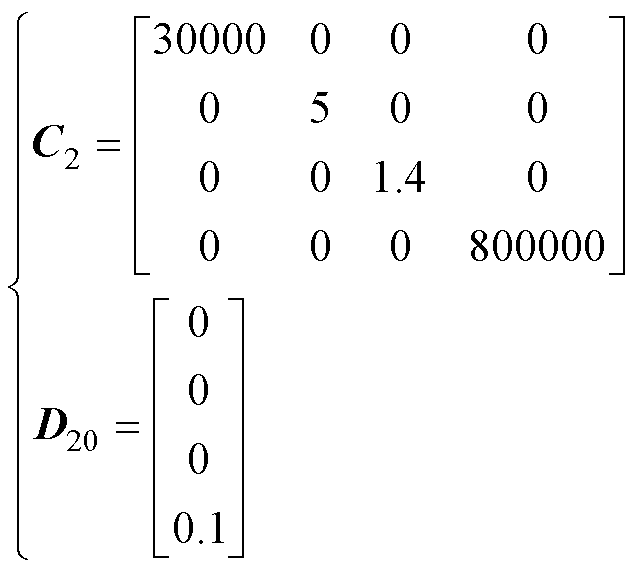（16）
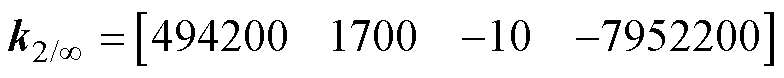（17）
对比H∞鲁棒控制器和H2/H∞混合鲁棒控制器的参数可以发现，主要的变化就在于k4的减小，较小的k4会使系统的快速性和鲁棒性都得到增强。这与2.3.1节分析的控制器参数对系统性能影响的结论相吻合。
由图4可以推导出磁悬浮系统的传递函数为
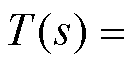
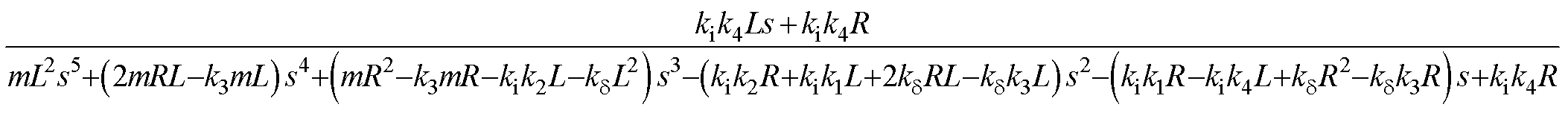（18）
式中，R为悬浮绕组电阻；L为悬浮绕组直轴电感。
由式（18），得到系统的零极点图、伯德图如图6、图7所示。
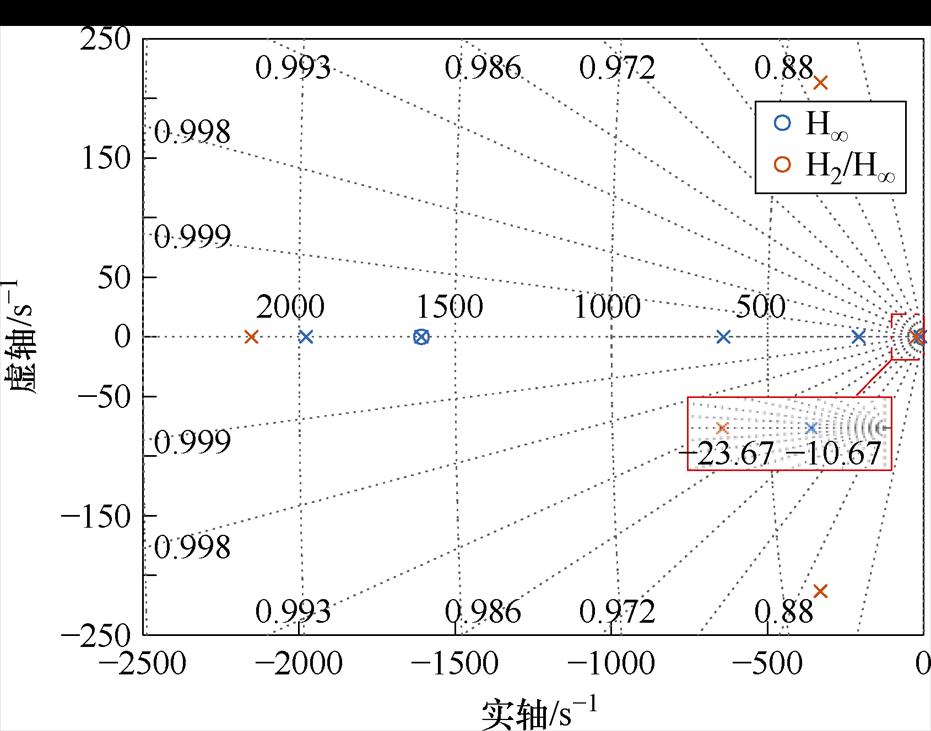
图6 系统的零极点图
Fig.6 Zero-pole diagram of the system
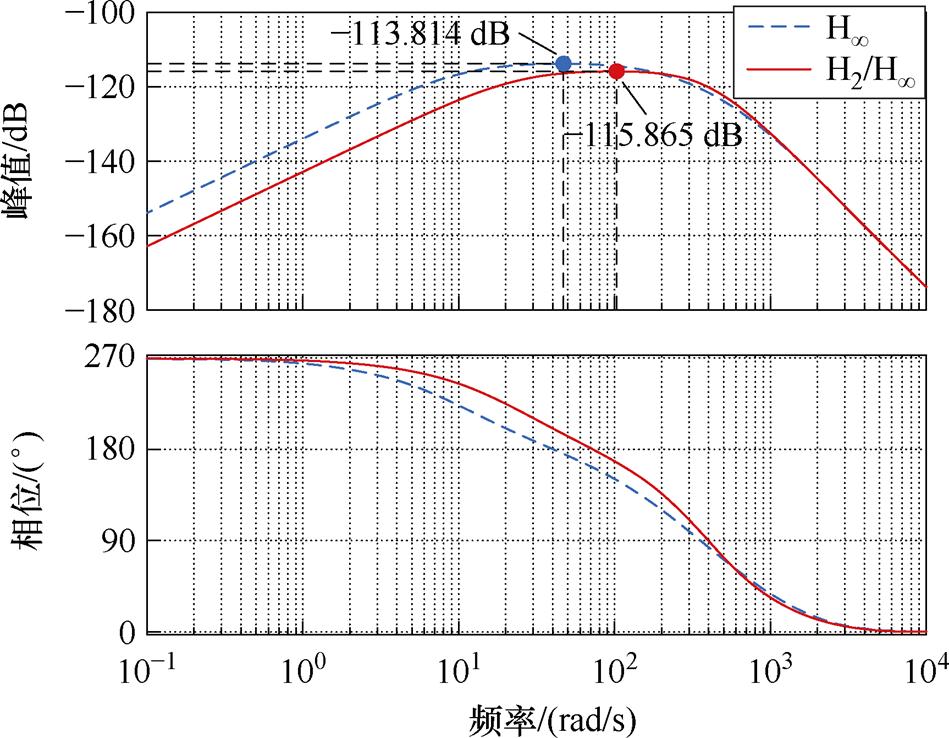
图7 系统的伯德图
Fig.7 Bode diagram of the system
图6表明，系统的极点均在虚轴的左半平面，系统是稳定的，同时在引入H2范数后，系统的主导极点进一步远离了虚轴，提升了系统的快速性。图7表明，所设计的H2/H∞混合鲁棒控制器能有效抑制系统的内外扰动。
MMT-MLPMLSM磁悬浮系统控制框图如图3所示。悬浮高度分别采用H∞鲁棒控制和H2/H∞混合鲁棒控制，两个控制器的参数如式（14）～式（17）所示；q轴电流采用PI控制，其中比例系数Kp= 27.117、积分系数Ki=43 620。
下层气隙初始高度为0，给定次级悬浮高度为2 mm，分别采用H∞鲁棒控制和H2/H∞混合鲁棒控制，得到的电机次级悬浮高度响应曲线如图8所示。图8表明，H∞鲁棒控制的系统响应速度较慢，在0.83 s达到给定悬浮高度；H2/H∞混合鲁棒控制的系统响应速度较快，在0.35 s达到给定悬浮高度。H∞鲁棒控制的调节时间是H2/H∞混合鲁棒控制的两倍以上。这表明H2/H∞混合鲁棒控制策略的起动性能优于H∞鲁棒控制策略。
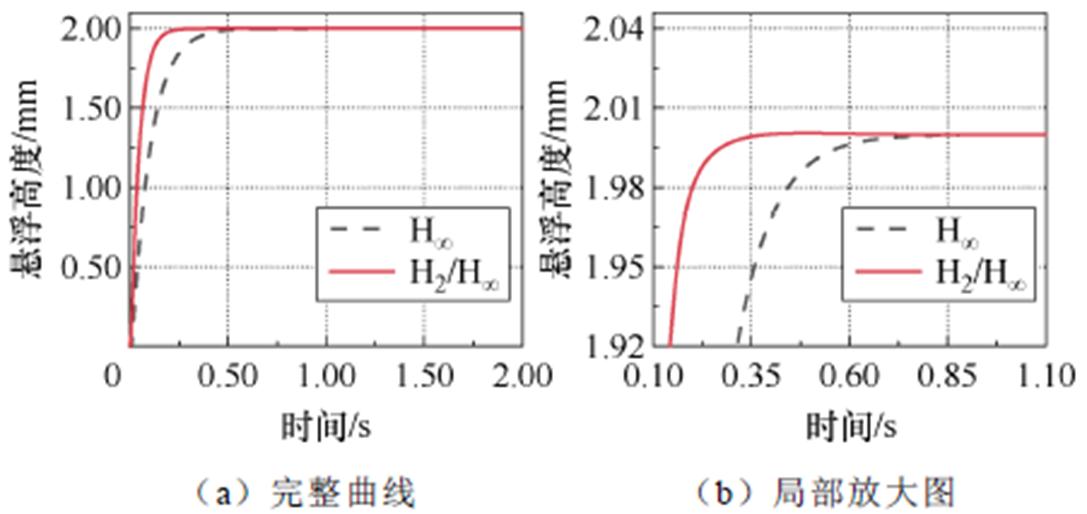
图8 起动性能对比曲线
Fig.8 Startup performance comparison curves
下层气隙初始高度为0，给定次级悬浮高度为2 mm，在1 s时加入20 N负载扰动，分别采用H∞鲁棒控制和H2/H∞混合鲁棒控制，得到的电机次级悬浮高度响应曲线如图9所示。图9表明，H∞鲁棒控制、H2/H∞混合鲁棒控制在系统加入扰动后的气隙高度分别下降了0.036 4 mm、0.029 mm，重新恢复到给定悬浮高度分别经历了0.6 s、0.2 s。仿真结果表明，H2/H∞混合鲁棒控制策略能够快速调节外部扰动，抗扰动性能明显优于H∞鲁棒控制策略。
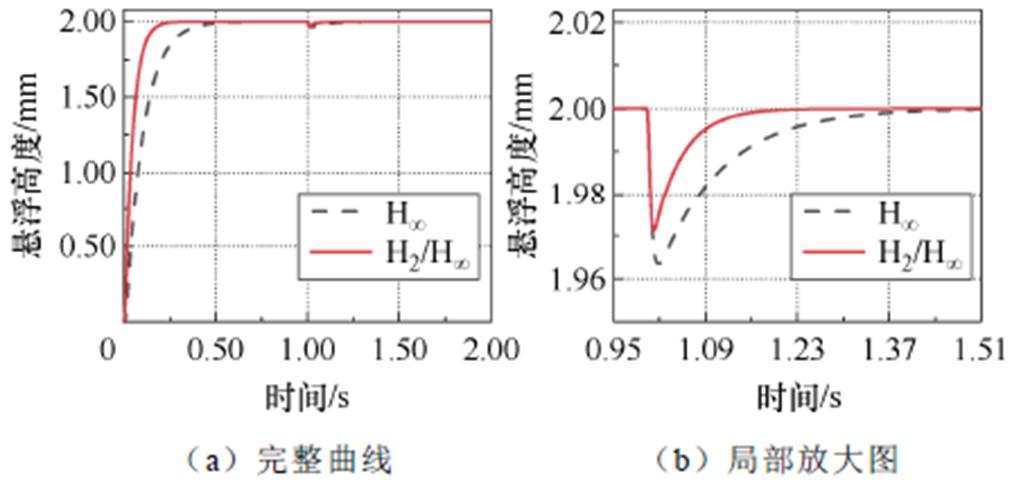
图9 抗干扰性能对比曲线
Fig.9 Anti-interference performance comparison curves
本文所研制的样机结构如图10所示，搭建的MMT-MLPMLSM磁悬浮实验平台如图11所示。实验平台主要由被测样机、电涡流传感器、激光传感器、电机驱动控制器和上位机组成。其中，悬浮子系统的位置环采用H2/H∞混合鲁棒控制器，q轴电流环采用PI控制器并把q轴电流iq调节为0。电涡流传感器对电机的悬浮高度和速度进行测量并反馈。激光传感器对电机进给方向的位移和速度进行反馈。电机驱动控制器以STM32F407ZET6作为主控芯片。
图10 MMT-MLPMLSM样机
Fig.10 The prototype of MMT-MLPMLSM
图11 悬浮系统实验平台
Fig.11 Experimental platform for levitation system
如果直接对传感器采集到的数据进行微分处理，速度波形会产生严重畸变，因此本文采用TD进行速度的计算，以达到良好的滤波效果。
推动电机次级做往返的直线运动，最高时速达0.3 m/s，分别采用经典微分器（Classical Differentiator, CD）、一阶低通滤波器（Low Pass Filter, LPF）和TD所求得的速度波形如图12所示。
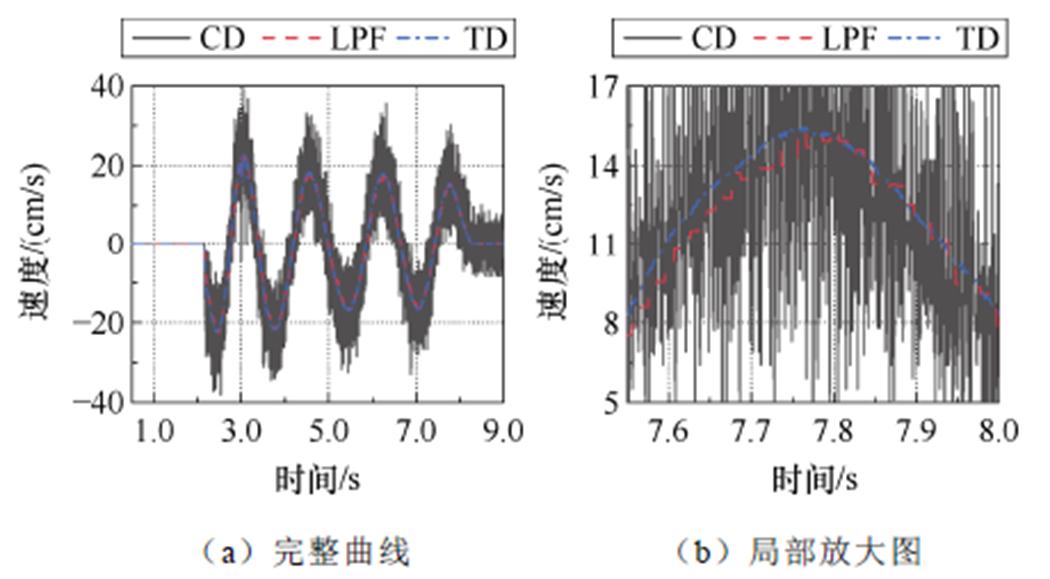
图12 三种方法下求解的速度波形
Fig.12 Speed waveforms solved by the three methods
实验结果表明，CD会使噪声被放大，导致速度波形产生许多毛刺；LPF能有效地对噪声进行滤波，使得速度波形变得相对平滑，但会造成一定的相位滞后；TD的滤波效果则更优于LPF，且基本没有相位滞后。
当电机次级紧贴下层初级起动时，由于下层磁场过强，悬浮绕组会产生较大的冲击电流，可能会烧毁电机，因此将电机次级垫高至下层气隙为0.9 mm位置起动，给定次级悬浮高度为2 mm，分别采用H∞鲁棒控制和H2/H∞混合鲁棒控制得到的电机次级悬浮高度响应曲线如图13所示，稳定悬浮后四个涡流传感器的读数如图14所示。
实验结果表明，H∞鲁棒控制的系统响应速度较慢，在0.32 s达到给定悬浮高度；H2/H∞混合鲁棒控制的系统响应速度较快，在0.21 s达到了给定悬浮高度。H2/H∞混合鲁棒控制策略能够有效地改善系统的动态性能。
四个传感器的编号如图11所示，1、4号传感器读数要略高于2、3号传感器，电机次级左侧要高于右侧20 mm，这是由于电机装配和加工误差所导致的，如电机次级下层永磁体或下层初级不平整导致初始位置时下层气隙不平，电机次级不对称导致重心偏移等，但误差在允许范围内。
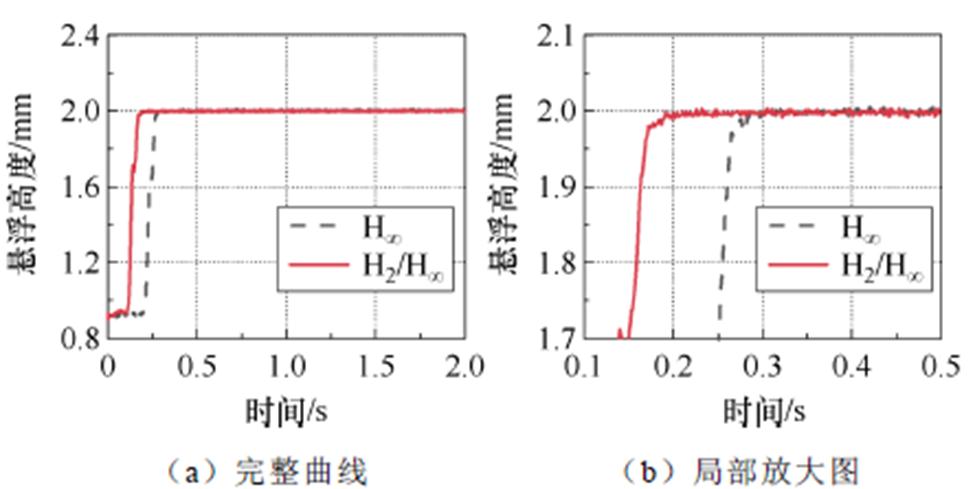
图13 实验的起动性能对比曲线
Fig.13 Startup performance comparison curves
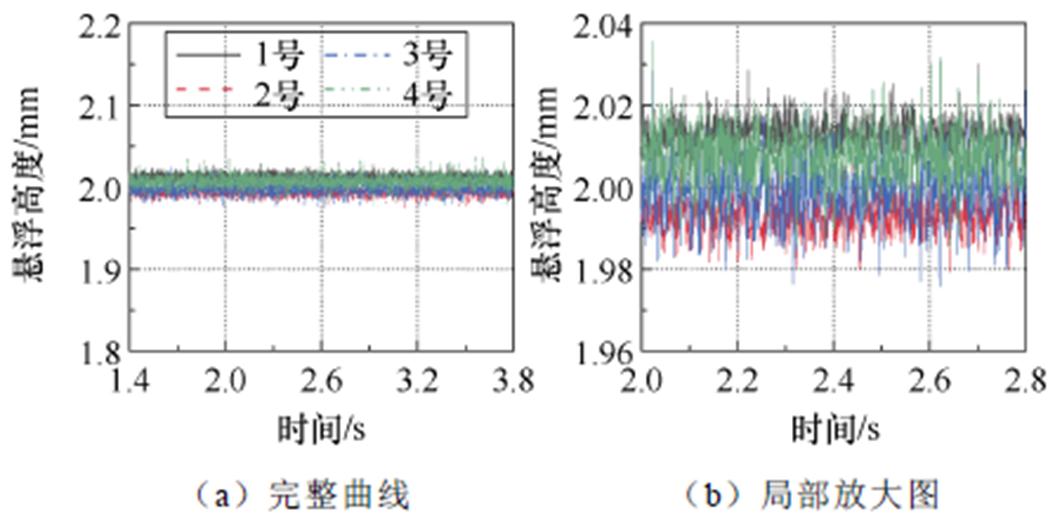
图14 四个传感器的读数
Fig.14 Four sensor readings
在与4.2节相同的起动条件下，当电机次级达到给定悬浮高度时，在次级上放置一个20 kg的砝码，分别采用H∞鲁棒控制和H2/H∞混合鲁棒控制得到的电机次级悬浮气隙高度响应曲线如图15所示。H∞鲁棒控制和H2/H∞混合鲁棒控制下系统的气隙高度分别下降了0.108 mm、0.09 mm，恢复到给定位置的时间分别为1.35 s、0.99 s。H2/H∞混合鲁棒控制策略能够快速调节外部扰动，抗负载扰动性能优于H∞鲁棒控制策略。
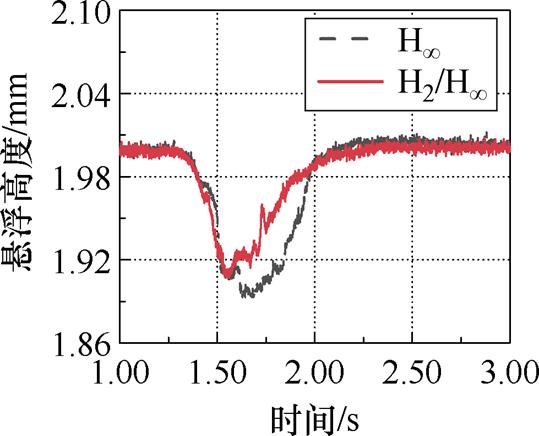
图15 实验的抗扰性能对比曲线
Fig.15 Anti-interference performance comparison curves
在与4.2节相同的起动条件下，3 s时电机次级已经稳定悬浮，此时分别使电机以0.01、0.05、0.1 m/s的速度进行进给运动，H∞鲁棒控制与H2/H∞混合鲁棒控制下次级悬浮高度响应曲线如图16～图18所示。
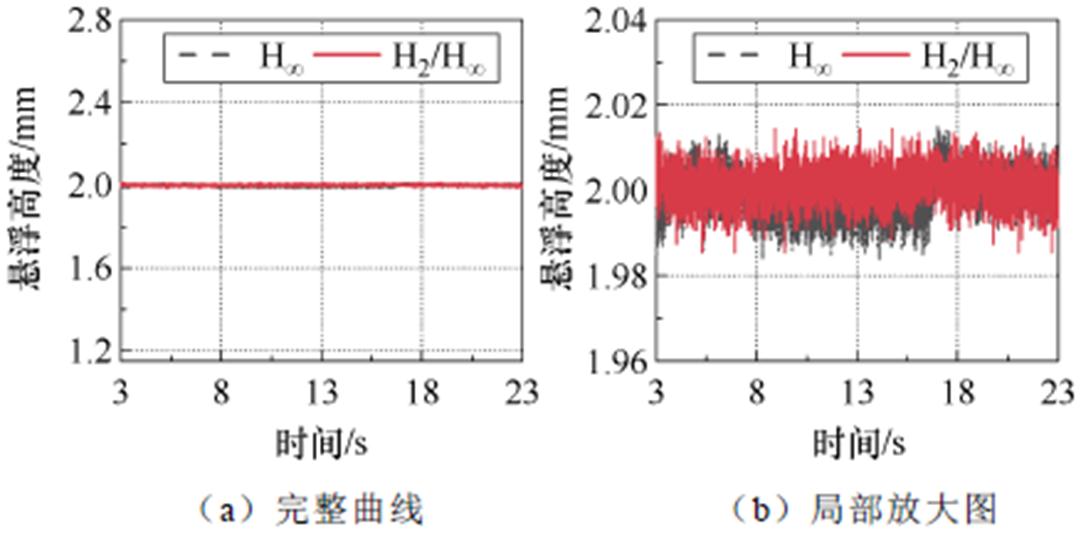
图16 0.01 m/s速度进给时悬浮高度响应曲线
Fig.16 Suspension height response curves at 0.01 m/s velocity feed
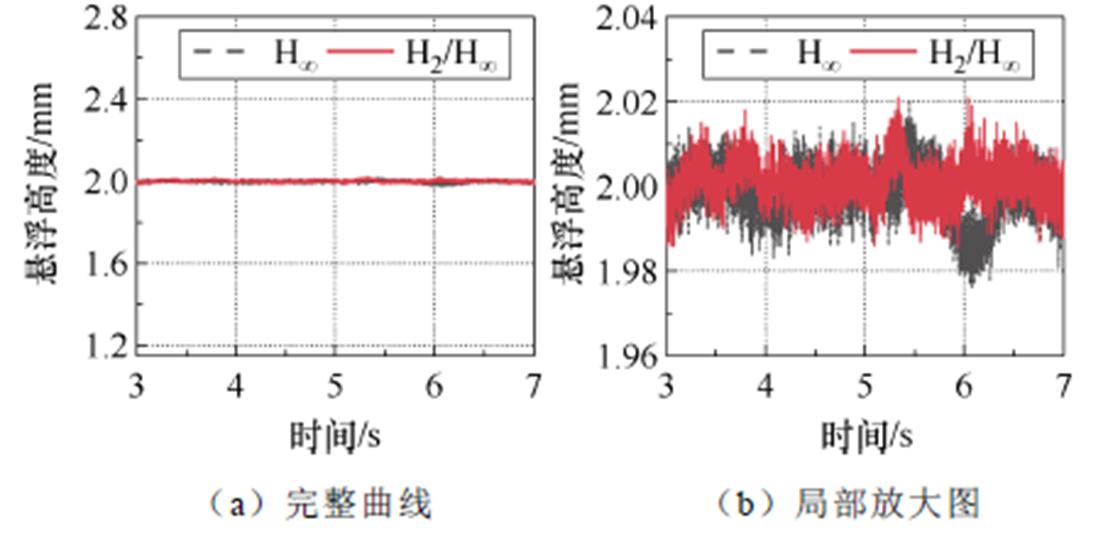
图17 0.05 m/s速度进给时悬浮高度响应曲线
Fig.17 Suspension height response curves at 0.05 m/s velocity feed
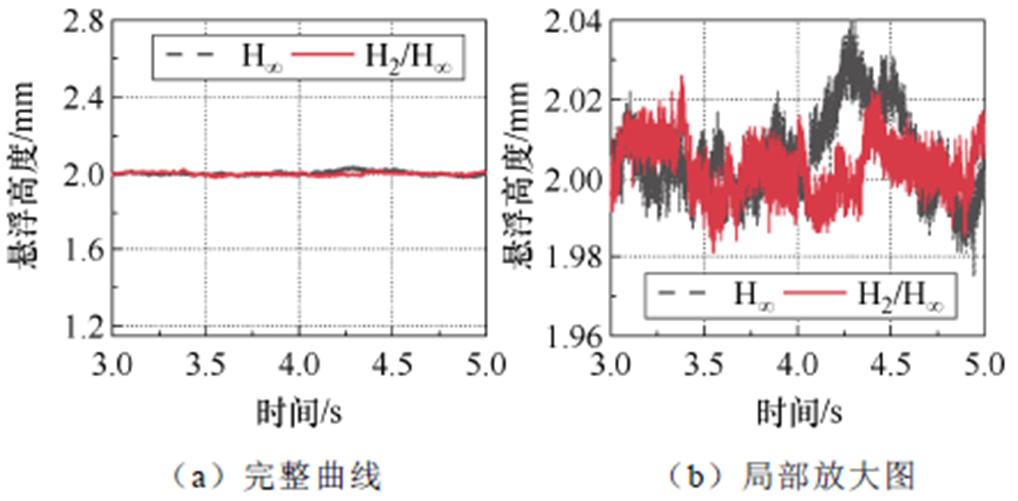
图18 0.1 m/s速度进给时悬浮高度响应曲线
Fig.18 Suspension height response curves at 0.1 m/s velocity feed
实验结果表明，在进给过程中电机次级会产生波动，随着速度的增大，波动幅度也会增大，具体分析如下：
（1）在0.01 m/s牵引速度时，H∞鲁棒控制下波动范围在±0.016 mm内；H2/H∞混合鲁棒控制下波动范围在±0.013 5 mm内，抗干扰性能相比于H∞鲁棒控制可以提升15.6%。
（2）在0.05 m/s牵引速度时，H∞鲁棒控制下波动范围在±0.024 mm内；H2/H∞混合鲁棒控制下波动范围在±0.02 mm内，抗干扰性能相比于H∞鲁棒控制可以提升16.7%。
（3）在0.10 m/s牵引速度时，H∞鲁棒控制下波动范围在±0.038 mm内；H2/H∞混合鲁棒控制下波动范围在±0.028 mm内，抗干扰性能相比于H∞鲁棒控制可以提升26.3%。
产生波动的原因是电机装配和加工误差，在x轴方向上，上下层气隙不均匀，电机次级不对称导致重心偏移等，但波动在允许范围内。
从实验结果可以看出，本文所提出的H2/H∞混合鲁棒控制抗干扰性要明显优于H∞鲁棒控制，在多种工况下都能进行有效控制。
本文针对一种双边、双绕组结构的MMT-MLP MLSM，建立了磁悬浮子系统的数学模型，提出并设计了一种H2/H∞混合鲁棒控制器，得出以下结论：
1）在磁悬浮系统数学模型的基础上，设计了H∞鲁棒控制器，对外部扰动产生了有效的抑制作用。
2）进一步引入H2范数，抑制了由磁悬浮力建模过程中的高次项所带来的内部扰动。还研究了权重矩阵参数对系统的影响，指导了参数的选择。
3）实验表明，所设计的H2/H∞混合鲁棒控制器相比于H∞鲁棒控制器能使系统的动态性能提升34.4%，抗扰性能提升16.7%，并能在多种牵引工况下实现对电机的有效控制。
参考文献
[1] Lan Yipeng, Zhang Wu, Zhang Fengge, et al. Research on design and control of direct magnetic suspension permanent magnet linear motor[C]//2011 International Conference on Electrical Machines and Systems, Beijing, China, 2011: 1-5.
[2] 秦伟, 马育华, 张洁龙, 等. 不均匀气隙工况下轴向磁通永磁电动式磁悬浮电机的磁场与力特性分析[J]. 电工技术学报, 2023, 38(4): 889-902.
Qin Wei, Ma Yuhua, Zhang Jielong, et al. Characteri- stic and magnetic field analysis of an axial flux permanent magnets maglev motor with non-uniform air gap[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 889-902.
[3] 石洪富, 邓自刚, 柯志昊, 等. 平板式永磁电动悬浮系统设计与实验研究[J]. 电工技术学报, 2024, 39(5): 1270-1283.
Shi Hongfu, Deng Zigang, Ke Zhihao, et al. Design and test of the flat-type permanent magnet elec- tromagnetic suspension system[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1270- 1283.
[4] Chang T. Research on the influence of additional air chamber on the dynamic characteristics of air springs[J]. Automotive and Driving Maintenance (Maintenance Edition), 2017(12): 146-147.
[5] Zhou Quan, Hu Yuanchao, Liu Qi, et al. Optimization design and simulation of an air suspension with auxiliary chamber and throttle valve[C]//2019 4th International Conference on Control and Robotics Engineering (ICCRE), Nanjing, China, 2019: 87-92.
[6] 杨帆, 袁野, 祝贵, 等. 12/14磁悬浮开关磁阻电机悬浮力全周期模型构建[J]. 电工技术学报, 2023, 38(2): 330-339.
Yang Fan, Yuan Ye, Zhu Gui, et al. Suspension force modeling for 12/14 bearingless switched reluctance motor considering flux multi teeth hinge[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(2): 330-339.
[7] Sokolov M, Saarakkala S E, Hosseinzadeh R, et al. A dynamic model for bearingless flux-switching permanent- magnet linear machines[J]. IEEE Transactions on Energy Conversion, 2020, 35(3): 1218-1227.
[8] Yoon J Y, Zhou Lei, Trumper D L. Linear stages for next generation precision motion systems[C]//2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 2019: 241-247.
[9] Zhang He, Lou Yuexuan, Zhou Lishan, et al. Modeling and optimization of a large-load magnetic levitation gravity compensator[J]. IEEE Transactions on Industrial Electronics, 2023, 70(5): 5055-5064.
[10] Kim H J, Yoon M H, Hong J P. Design and performance analysis of moving-coil type linear actuator[C]//2011 International Conference on Elec- trical Machines and Systems, Beijing, China, 2011: 1-4.
[11] 陆华才, 阮光正, 郭欣欣. 动圈式永磁平面电机无位置传感器控制策略[J]. 电机与控制学报, 2018, 22(11): 114-120.
Lu Huacai, Ruan Guangzheng, Guo Xinxin. Sensor- less control strategy on permanent-magnet planar motor with moving-coils[J]. Electric Machines and Control, 2018, 22(11): 114-120.
[12] Huang Weikang, Huang Wenxin, Dong Dingfeng, et al. Research and analysis of a novel voice coil motor with wireless power supply[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 2332-2341.
[13] Fu Xingdong, Huang Sudan, Cao Guangzhong, et al. Nonlinear modeling of a magnetic levitation system[C]// 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 2019: 1985-1989.
[14] 张丹, 姜建国. 高速磁悬浮永磁电机三电平无速度传感器控制[J]. 电工技术学报, 2022, 37(22): 5808- 5816.
Zhang Dan, Jiang Jianguo. Three-level sensorless control of high speed maglev permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5808-5816.
[15] 秦伟, 马育华, 张洁龙, 等. 不均匀气隙工况下轴向磁通永磁电动式磁悬浮电机的磁场与力特性分析[J]. 电工技术学报, 2023, 38(4): 889-902.
Qin Wei, Ma Yuhua, Zhang Jielong, et al. Characteristic and magnetic field analysis of an axial flux permanent magnets maglev motor with non- uniform air gap[J]. Transactions of China Elec- trotechnical Society, 2023, 38(4): 889-902.
[16] Kleijer M, Jansen J W, Lomonova E A. Optimization of quasi-halbach topologies to maximize the acceleration of moving-magnet planar motors[C]// 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 2022: 942-948.
[17] Lan Yipeng, Yang Wenkang, Zong Ming. Design of adaptive neural network backstepping controller for linear motor magnetic levitation system[C]//2019 IEEE Industry Applications Society Annual Meeting, Baltimore, MD, USA, 2019: 1-6.
[18] Zhang He, Kou Baoquan, Zhou Yiheng. Analysis and design of a novel magnetic levitation gravity compensator with low passive force variation in a large vertical displacement[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4797-4805.
[19] Mirić S, Küttel P, Tüysüz A, et al. Design and experimental analysis of a new magnetically levitated tubular linear actuator[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4816-4825.
[20] Zhou Lei, Trumper D L. Magnetically levitated linear stage with linear bearingless slice hysteresis motors[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(2): 1084-1094.
[21] Chi Song, Yan Jianhu, Guo Jian, et al. Double-sided single-set winding coordinated active levitation control of linear permanent magnet motor considering mover air-gap offset[J]. IEEE Transactions on Transportation Electrification, 2024, 10(3): 6801- 6811.
[22] Jeong J H, Ha Changwan, Lim J, et al. Analysis and control of the electromagnetic coupling effect of the levitation and guidance systems for a semi-high-speed MAGLEV using a magnetic equivalent circuit[J]. IEEE Transactions on Magnetics, 2016, 52(7): 8300104.
[23] Sun Yunpeng, Lan Yipeng. Optimal design of electromagnetic force of hidden: pole magnetic suspension linear motor[J]. IEEE Access, 2019, 7: 153675-153682.
[24] 蓝益鹏, 张明慧. 电励磁直线同步电动机磁悬浮系统H∞鲁棒控制的研究[J]. 制造技术与机床, 2022(1): 71-76.
Lan Yipeng, Zhang Minghui. Research on H∞ robust control of magnetic levitation system of electrically excitation linear synchronous motor[J]. Manufa- cturing Technology & Machine Tool, 2022(1): 71-76.
[25] Lan Yipeng, Li Jie, Zhang Fengge, et al. Fuzzy sliding mode control of magnetic levitation system of controllable excitation linear synchronous motor[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5585-5592.
[26] Feng Wei, Hao Jianhua, Wang Sen, et al. Adaptive terminal sliding mode control for magnetic levitation system with observer[C]//2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 2021: 788-792.
Hybrid H2/H∞ Robust Control Strategy for the Levitation Subsystem of Moving Magnet Type Magnetic Levitation Permanent Magnet Linear Synchronous Motor
Abstract With the continuous development of science and technology, CNC machine tools have become essential to IC manufacturing, playing a critical role in intelligent manufacturing. Magnetic suspension linear motor (MSLM) solves the friction problem of permanent magnet linear synchronous motor (PMLSM) and realizes the precision control of the feed system of CNC machine tools, which is one of the best choices for the ultra-precision linear positioning motion in the new generation of lithography machines and other high-end equipment. However, the electromagnetic characteristics of MLSM are complex, and the system is inherently coupled and unstable. Establishing a mathematical model of the magnetic levitation system to decouple the system is challenging. This paper studies a hybrid H2/H∞ robust control strategy, which utilizes the H2 paradigm to suppress the internal disturbances of the system.
Firstly, the structure and working principle of the motor are analyzed, and the mathematical model of the moving magnet type magnetic levitation permanent magnet linear synchronous motor (MMT-MLPMLSM) in the synchronous rotating coordinate system is deduced. Then, the closed-loop control system of the MMT- MLPMLSM is established. The developed mathematical model shows that the levitation system has strong nonlinear characteristics. As a positioning actuator, the magnetic levitation system needs to levitate stably at the equilibrium position. Accordingly, the Taylor expansion of the magnetic levitation force near the equilibrium point is helpful for the design of the controller. Finally, the state space equations of the motor are obtained based on the mathematical model.
Secondly, the H∞ robust controller and H2/H∞ hybrid robust controller are designed. The stability of the designed controller is verified using the Bird's plot and the zero-pole distribution graph. The effect of the weighting matrix on the dynamics and robustness of the system is investigated, guiding the parameter selection of the weighting matrix.
Finally, an experimental platform for the MMT-MLPMLSM suspension system based on STM32F407 is established. The simulation and experimental results verify the proposed hybrid H2/H∞ robust control strategy under steady state and dynamic conditions.
Compared with the H∞ robust controller, the H2/H∞ hybrid robust controller designed in this paper can improve the dynamic performance of the system by 34.4% regarding startup performance and the robustness of the system by 16.7% regarding disturbance immunity performance. Good control effects can be achieved under low-speed, medium-speed, and high-speed traction conditions, and the motor's secondary fluctuations can be suppressed efficiently.
Keywords：Moving magnet type magnetic levitation linear motor, mathematical model of magnetic levitation system, weighting matrix, H2/H∞ hybrid robust control
中图分类号：TM133
DOI: 10.19595/j.cnki.1000-6753.tces.241251
国家自然科学基金（52407052）、江苏省自然科学基金（SBK2022044339）和中国博士后科学基金（2023M731654）资助项目。
收稿日期 2024-07-14
改稿日期 2024-07-31
闫顺天 男，1999年生，硕士研究生，研究方向为动磁式磁悬浮永磁直线同步电机驱动控制。
E-mail: yanshuntian@nuaa.edu.cn
谭 强 男，1991年生，副研究员，硕士生导师，研究方向为精密永磁直线电机及相关技术、特种电机振动噪声抑制技术、磁悬浮系统及相关技术。
E-mail: tanqiang0213@nuaa.edu.cn （通信作者）
（编辑 崔文静）