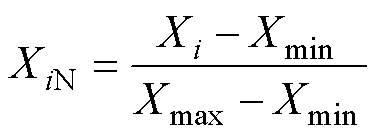（1）
摘要 针对分布式光伏点多面广、集中式光伏的异常检测技术难以在分布式光伏系统中应用等问题，该文提出一种采用模糊C均值聚类算法（FCM）和贝叶斯优化算法（BOA）优化时间卷积网络-门控循环单元神经网络（TCN-GRU）的分布式光伏发电异常检测方法。首先，对原始数据进行异常值处理和相关性分析筛选出最佳特征；其次，为了降低天气波动性对光伏出力预测结果的影响，提出一种基于权重的FCM-Frechet算法对数据进行两阶段相似日集群划分，将其划分为晴朗、多云和阴雨相似日；然后，为了提高不同相似日下光伏常态出力预测的准确性，提出一种基于BOA优化的TCN-GRU网络模型；最后，采用实际光伏电站进行案例分析，利用设定的规则进行异常判断。结果表明，该文所提方法相较于CNN-LSTM和Transformer-BiLSTM模型的准确率分别提高了11.24和3.92个百分点，验证了所提方法在分布式光伏异常检测上的有效性。
关键词：分布式光伏异常检测 时间卷积网络 门控循环单元 相似日聚类 贝叶斯优化
太阳能作为一种清洁、可再生、无污染的新能源，对其加以利用已成为世界各国应对全球变暖和环境污染的重要手段。近年来，随着我国“双碳”行动方案的实施，光伏发电成为利用太阳能最为有效的方式[1-3]。由于相关政策和技术的发展，截至2023年底，分布式光伏新增装机容量达到96.29 GW，同比增长88.4%，其中户用光伏占比45.16%，工商用光伏占比54.84%。分布式光伏设备多且位置分散，出现故障后人工巡检难以及时发现，严重影响光伏电站的正常运行。因此，研究分布式光伏发电异常检测方法对提高发电效率和降低维护成本等具有重要意义[4]。
目前分布式光伏发电系统异常检测方法主要有两种：一种是借助传感器、红外热成像及图像识别技术，直接在光伏组件层面上定位和识别异常[5]；另一种是数据挖掘方法，利用光伏历史数据和气象数据建立预测模型来检测异常[6]。后者根据有无标记的故障数据分为直接法和间接法[7]。直接法是使用预先标注的特征数据来训练异常检测模型[8]；间接法则是先通过光伏历史数据和环境数据构建模型预测光伏常态出力曲线，然后分析其与真实值之间的偏差检测异常[9]。然而，分布式光伏系统往往缺乏大量故障标注数据，且定位光伏组件的故障需要额外的辅助设备，直接法不适用于分布式光伏系统的异常检测，故本文采用间接法。
间接预测模型又分为物理模型、统计模型、传统机器学习模型[10]。物理模型是一种利用太阳辐射和温度的经验公式进行功率预测的模型。文献[11]通过构建一个单二极管模型，模拟光伏阵列的特性，并将一类支持向量机应用于残差模型进行故障检测。然而，基于先验知识的物理模型依赖特定的经验公式，受噪声和测量误差的影响较大，不具备普适性。统计模型主要包括模糊理论[12]、灰色理论[13]、马尔科夫链[14]、自回归[15]和回归模型[16]。这些模型主要依靠历史数据对不同变量进行相关性建模，虽然在特定数据集上的表现不错，但考虑到实际光伏出力与气象因素之间存在复杂的非线性关系，预测准确率和异常检测准确率会有所下降[17]。机器学习中的回归模型旨在预测样本中预期出现的常规模式，并通过比较实际值和预测值之间的差异确定样本是否存在异常[18]。聚类方法是指将远离聚类中心的样本识别为异常的方法[19]。然而这些方案受限于传统机器学习模型无法处理高维、多变量光伏运行数据和环境监测数据中的时间依赖性问题。深度学习模型因其在处理复杂和高维数据方面特别有效，被广泛应用于光伏发电异常检测中。递归神经网络及其变体是最常用的序列数据模型，其中，长短期记忆神经网络（Long Short-Term Memory, LSTM）[20]和门控循环单元（Gate Recurrent Unit, GRU）神经网络[21]是时间序列异常检测任务的首选[22]，已用于光伏系统[23]。文献[24]提出了基于预测的深度学习分布式光伏异常检测模型，然而，该模型只是利用周围光伏电站和阵列的运行数据，尚未考虑环境条件，很大程度地限制了其在实际应用中的准确性和通用性。文献[25]采用具有k近邻（k-Nearest Neigh- borhood, kNN）随机森林（Random Forest, RF）的监督机器学习对异常进行检测和分类，然而，此方法需要大量标注数据集，鉴于投资成本，用户侧很少配备专门的装置监测光伏系统的状态。综上所述，上述方法存在通用性差、检测准确率低、需要大量标注数据集等问题。
因此，本文提出了一种通过模糊C均值（Fuzzy C-Means, FCM）聚类算法和贝叶斯优化算法（Bayesian Optimization Algorithm, BOA）来优化时间卷积网络-门控循环单元神经网络（Temporal Convolutional Network-Gated Recurrent Unit, TCN- GRU）的分布式光伏发电异常检测方法。通过特征筛选、FCM-Frechet模型划分相似日和BOA-TCN- GRU模型进行光伏常态出力预测，结合双重动态阈值法判断分布式光伏发电系统的异常。该方法可以减少数据集的标注并提高光伏系统异常检测的准确率。本文的主要贡献如下：
1）提出一种基于权重的FCM-Frechet聚类模型对数据进行相似日集群划分，降低天气波动性对光伏预测结果的影响。
2）考虑环境条件，提出一种基于BOA的TCN- GRU网络模型，结合引入自适应因子的双重动态阈值法判断光伏系统的异常，提高了模型在光伏异常检测上的准确性和通用性。
3）实验结果表明本文所提模型准确率相较于CNN-LSTM和Transformer-BiLSTM有所提高。
由于实际采集的数据中会存在因传感器断电、自然环境因素及数据传输不稳定等导致的数据异常，这些异常数据的存在会对模型的训练造成严重影响。
采用统计分析方法对特征值进行异常检测，首先计算各种特征数据的标准化得分，根据3s 原则判断采样点的标准化得分是否大于3，若大于3则该点异常。为了保持数据的完整性，本文用异常点前后两点的均值代替异常值，用多项式插值填充缺失值。
在进行光伏系统性能分析时，由于涉及的变量通常具有不同的量纲和数量级，直接对原始数据进行分析可能会引起模型对某些变量的过度敏感，进而忽略其他变量，从而影响模型的预测精度。本文采用最大-最小归一化方法，即利用数据集中每个变量的最大值和最小值对数据集进行标准化处理，使标准化后的数值处于[0, 1]之间，计算式为
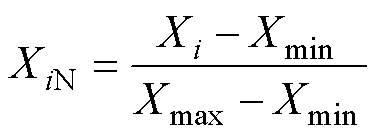（1）
式中，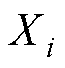
为数据集中第i个原始数据；
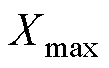和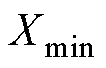
分别为数据集中变量的最大值和最小值；
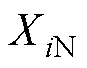为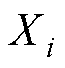归一化后的值。
本文用Pearson相关系数来衡量任意两个特征向量的相关密切程度，计算式为
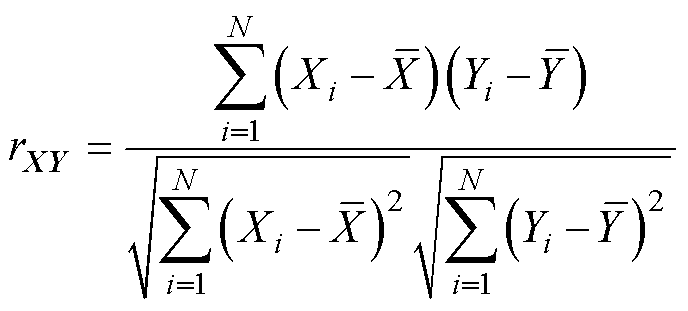（2）
式中，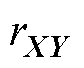
为特征向量X和Y的Pearson相关系数；
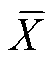和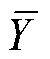
分别为向量X和Y中所有数据Xi和Yi的均值；
N为数据个数。rXY的取值范围为[-1, 1]，当rXY=1时，表明X和Y完全正相关；当rXY=0时，表明X和Y无线性相关关系；当rXY= -1时，表明X和Y完全负相关。图1所示为相关系数热点图，展示了多种特征数据之间的关联性。对光伏出力而言，电流、水平总辐射、气温、湿度、水平散射辐射和风速与其的相关性较强，风向和降雨量与其的相关性较弱，因此选择电流、水平总辐射、气温、湿度、水平散射辐射和风速作为输入来构建相似日聚类模型。
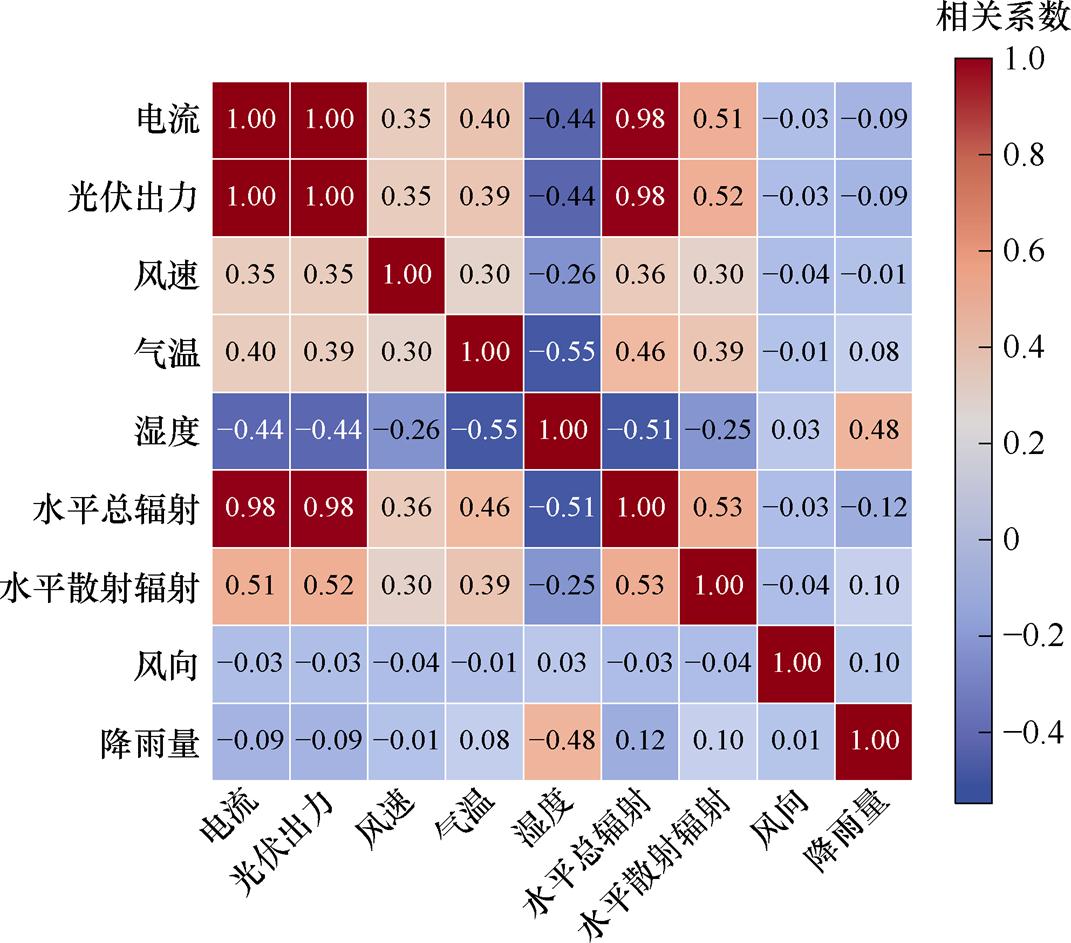
图1 相关系数热点图
Fig.1 Correlation coefficient hotspot map
为了降低天气波动性对光伏预测结果的影响，本节提出一种基于FCM-Frechet的相似日集群划分方法。首先，将1.3节筛选出的特征数据与光伏出力之间的皮尔逊相关系数作为各自的权重，采用模糊C均值（FCM）聚类算法对数据集进行数值相似性集群划分；然后，考虑数据集的形态相似性，采用离散Frechet距离对集群结果进行修正；最终得到相似日集群划分结果。相似日集群划分流程如图2所示。
FCM算法是一种用隶属度来表示每个数据之间的关系，从而确定每个数据点属于哪个聚类簇的聚类方法[26]。隶属度在[0, 1]之间，隶属度越高，数据之间的相似度越高。其目标函数和约束条件为
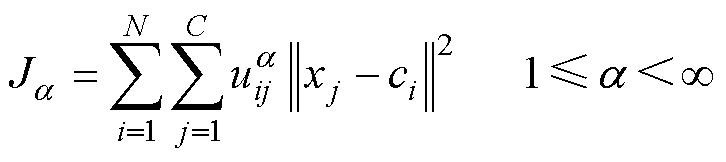（3）
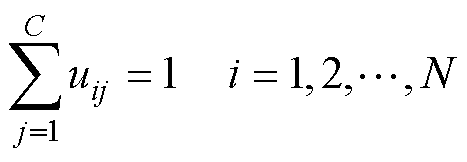（4）
式中，C为聚类中心数量；a为隶属度因子；uij为第j个样本数据xj隶属于第i个聚类中心ci的隶属度，满足每个对象都有属于每个类的隶属度，并且每个类中所有隶属度之和为1；||xj-ci||为xj到ci的欧氏距离。
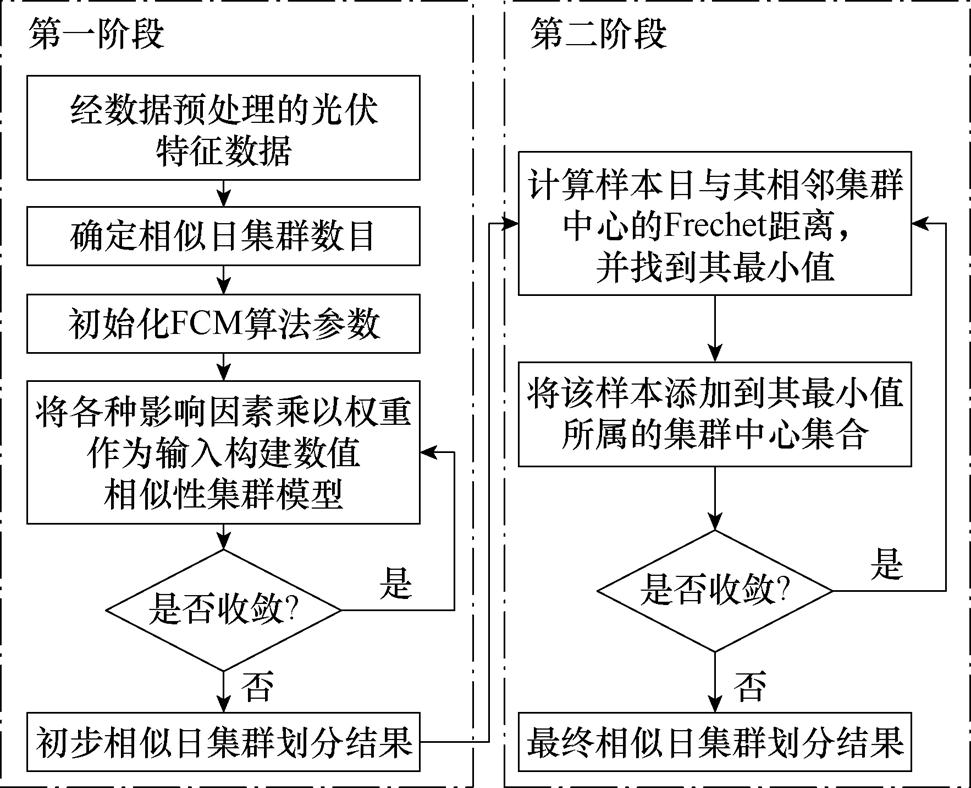
图2 相似日集群划分流程
Fig.2 Flow chart of cluster partition on similar days
由于FCM聚类方法只能从各样本数据之间的数值相似性进行判断，如气温、湿度、水平总辐射等，而忽略了曲线之间的形态相似性。离散Frechet距离是用来衡量两条离散曲线之间的相似度的一种度量方式，因此被用来修正FCM聚类结果，其求解方法为
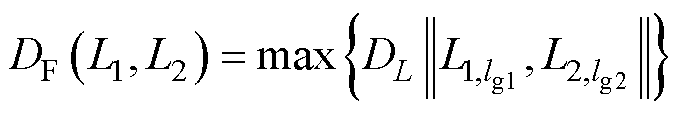（5）
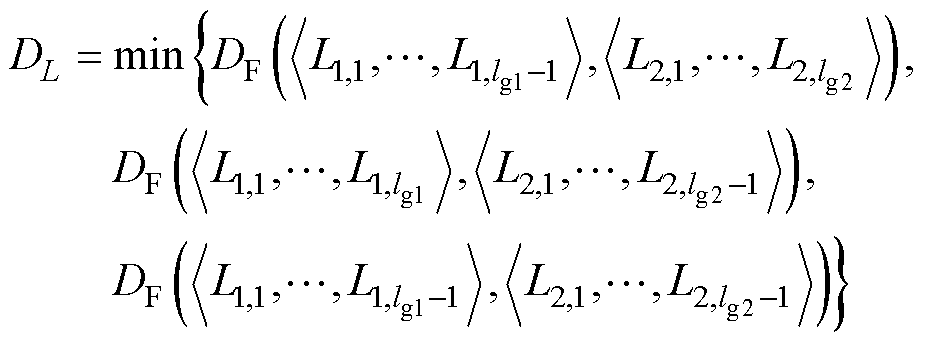（6）
式中，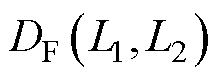
为曲线L1与L2的离散Frechet距离；
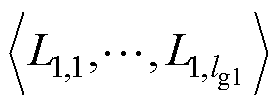为由L1的各点组成的有序子串；
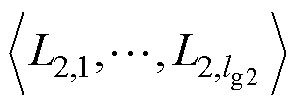为由L2的各点组成的有序子串；
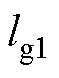和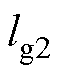
分别为曲线L1与L2上点的数量；
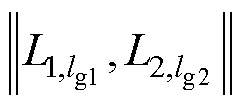为
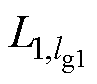与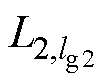
之间的欧氏距离。
时间卷积网络（TCN）的主要结构包括适合时序建模的膨胀因果卷积和解决深度神经网络在学习过程中遇到的性能退化问题的残差模块，能并行处理时间序列，有效地缓解梯度消失和梯度爆炸问 题[27]。在因果卷积的基础上增加膨胀系数d，扩大感受野范围，以指数方式增加对历史信息的考量，可以捕捉长序列光伏出力数据与其他特征数据之间的关系。4层膨胀因果卷积结构示意图如图3所示，其卷积核大小为3，膨胀系数依次为1、2、4，相应的感受野大小分别为3、5、9。
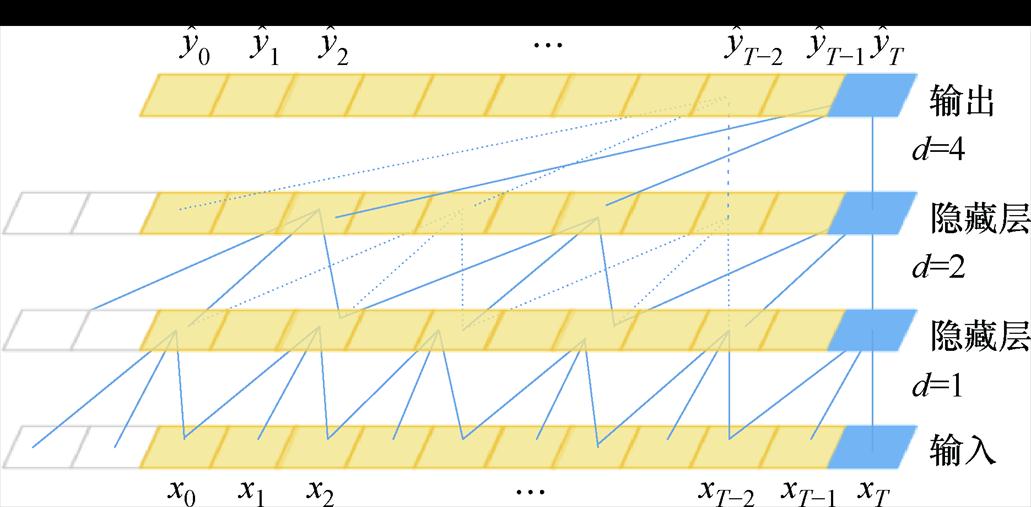
图3 膨胀因果卷积结构示意图
Fig.3 Dilated causal convolution structure schematic
由图3可知，卷积层在T时刻的输出只与T时刻和T时刻之前的输入序列有关，而与T时刻之后的输入序列无关。其卷积运算可表示为
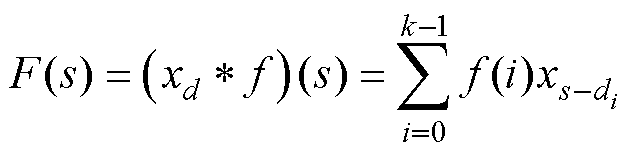（7）
式中，F(s)为卷积操作的结果，表示在位置s处的输出值；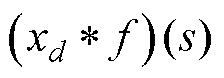
为输入序列xd和滤波器f的卷积在s处的值；s为卷积操作的输出位置索引；di为滤波器f的第i个权重在输入序列xd上的偏移位置；k为滤波器f的长度。
TCN网络可以通过堆叠多个卷积层来提取不同长度的特征，增强对时序数据中局部依赖关系的捕捉，同时，通过调整层数、卷积核大小等参数可以灵活处理不同长度的光伏出力数据。虽然增加网络深度能有效地挖掘各种数据之间的关联信息，但会导致梯度消失或梯度爆炸问题，所以，TCN网络通过引入残差连接以跨层的信息传递来训练深层网络，提高模型性能。残差模块的基本结构如图4所示。
本文采用互信息（Mutual Information, MI）[28]方法对预测模型的输入特征进行选择，通过计算输入特征与实际功率之间的互信息，选择互信息值较大的特征作为模型的输入，避免特征冗余。互信息的计算式为
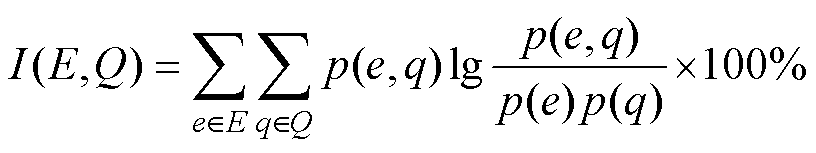（8）
式中，E为输入特征集合；Q为实际功率集合；p(e,q) 为输入特征e与实际功率q之间的联合概率分布；p(e)和p(q)分别为输入特征e和实际功率q的边缘概率分布。输入特征的互信息值如图5所示。
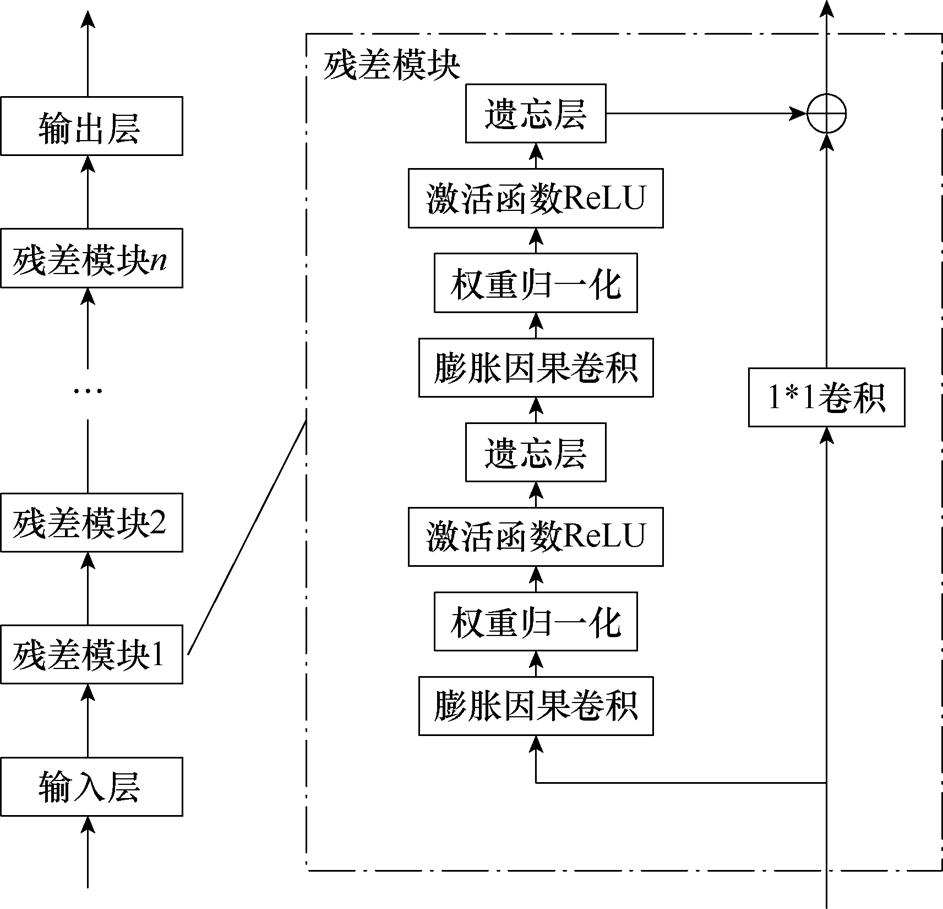
图4 残差模块基本结构
Fig.4 Residual block basic structure
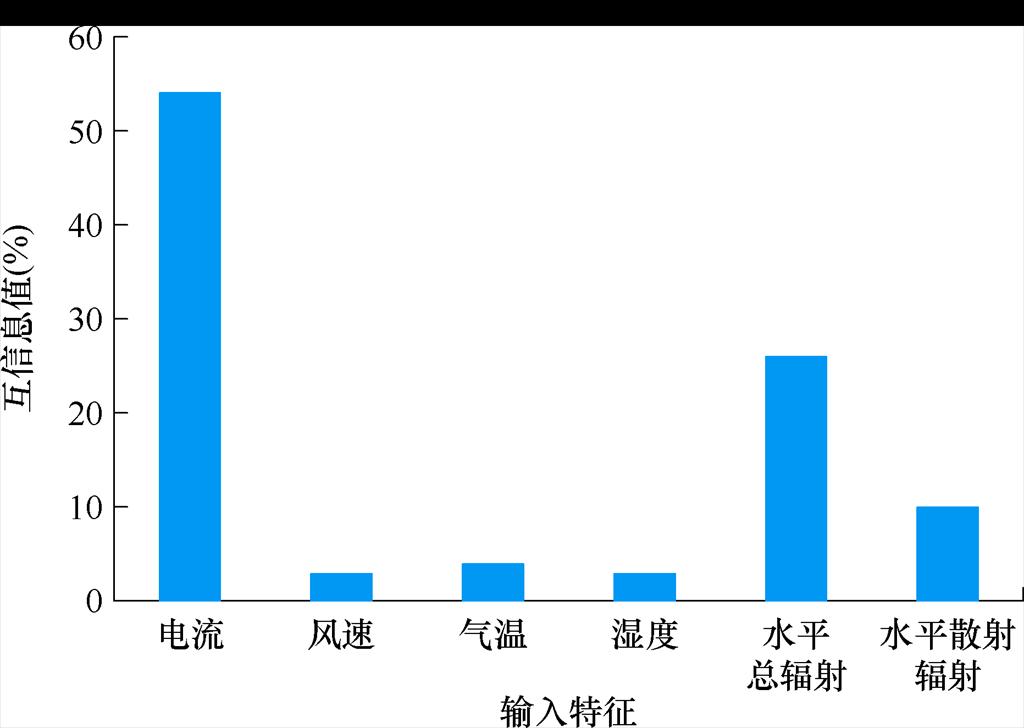
图5 输入特征的互信息值
Fig.5 Mutual information between input features
本文提出的预测模型输入为电流、水平总辐射和水平散射辐射三个特征，当输入时间序列包含多个变量时，TCN网络对数据局部特征的捕捉能力下降，会导致泛化能力降低等问题。
门控循环单元（GRU）网络能捕捉多变量输入数据中复杂的非线性特征，灵活处理可变长度的输入和输出序列[29]。因此，本文构建了基于TCN-GRU的光伏常态出力预测模型，通过TCN处理时间序列局部和全局的空间特征，GRU处理时间序列的时间特征，实现了特征的时空联合建模，提高了光伏常态出力的预测精度。TCN-GRU模型的基本结构如图6所示。
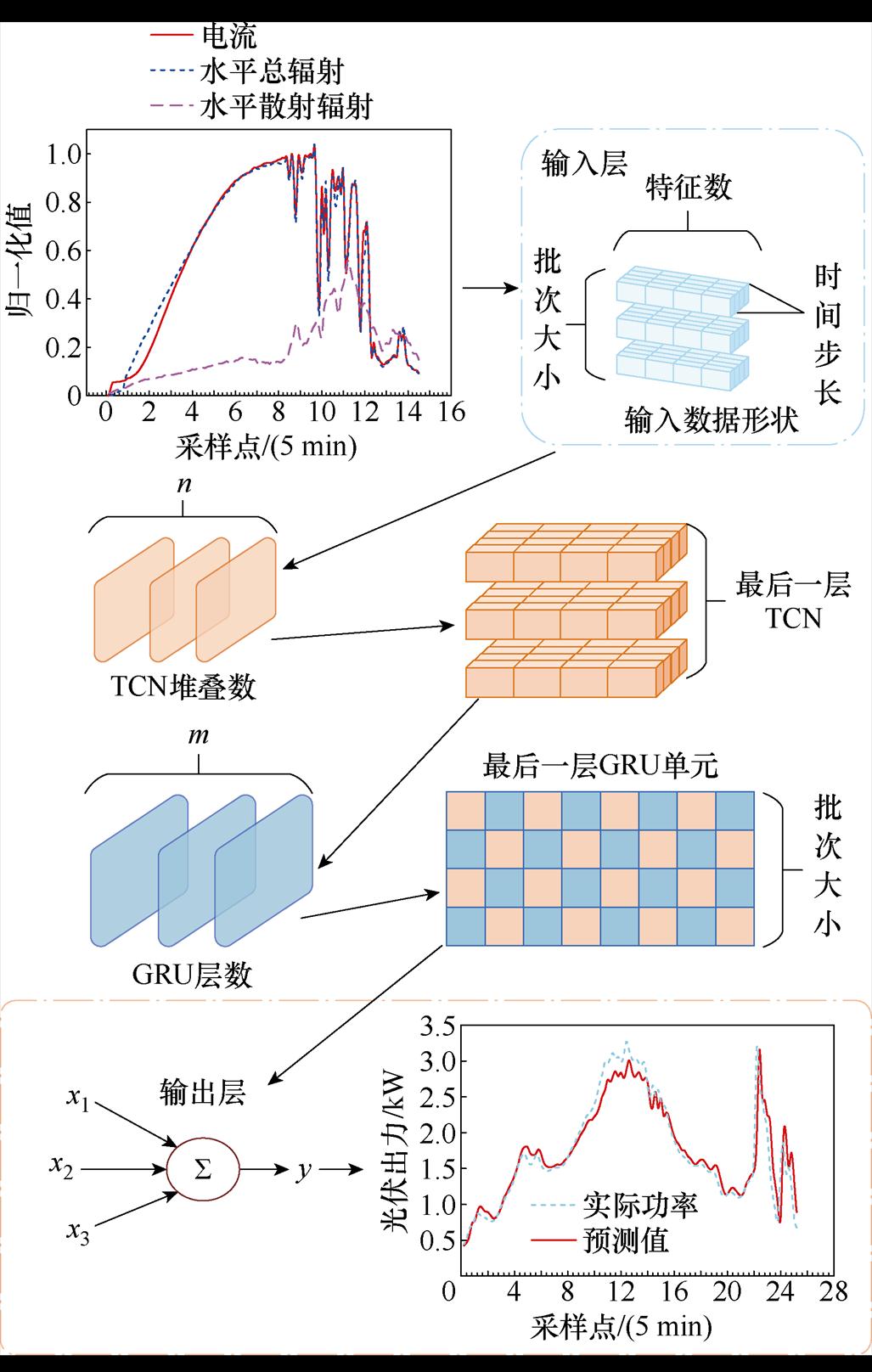
图6 TCN-GRU模型基本结构
Fig.6 TCN-GRU model basic structure
基于上述理论，通过组合FCM、Frechet、TCN和GRU构建光伏发电异常检测模型。其流程如图7所示，建模过程如下。
1）首先对光伏发电原始数据集进行数据预处理，去除数据中的异常值并填充缺失值，通过皮尔逊相关性分析，找出对光伏发电出力影响较大的特征变量。
2）将光伏发电出力与特征变量之间的Pearson相关系数作为权重，通过FCM对数据集进行数值相似性聚类。考虑光伏出力曲线的形态相似性，采用Frechet距离对FCM聚类结果进行修正，将数据集按天气类型分为晴朗日、多云日和阴雨日。
3）将三种聚类好的数据集按9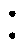
1的比例分别划分为训练集和测试集，经过互信息方法的特征筛选，分别输入各自的TCN-GRU模型进行训练，通过贝叶斯优化算法对TCN-GRU模型进行超参数优化，输出三种天气类型下光伏常态预测的最优结果。
4）将划分好的三种天气类型的测试集分别输入各自的模型，得到三种天气类型的常态光伏发电出力预测结果，再通过双重偏差法判断是否异常。具体方法为：对比预测值和真实值，先计算预测值的滚动标准差作为第一重阈值，再用预测值与真实值偏差的标准差作为第二重阈值，若某点预测值都超过阈值，则判断存在异常。为进一步优化阈值选择，引入自适应因子和历史数据的统计特性，根据当前光伏出力的波动性大小，动态调整阈值。
图7 基于FCM-BOA-TCN-GRU模型的光伏出力异常检测方法流程
Fig.7 Photovoltaic power output anomaly detection method based on FCM-BOA-TCN-GRU model flow chart
实验数据集选用位于澳大利亚沙漠地区的Alice Springs，数据由电气数据和环境数据组成，电气数据包括电流、光伏出力功率，环境数据包括环境温度、湿度、风速、风向、降雨量、水平太阳辐照度和散射辐射，数据间隔为5 min。选择2015年的数据用于构建光伏发电异常检测模型，该年数据因辅助设备的更换或线路检修等原因断电次数少，数据比较完整。因太阳辐照度是光伏发电的主要影响因素，所以仅考虑600—1800时段的数据。
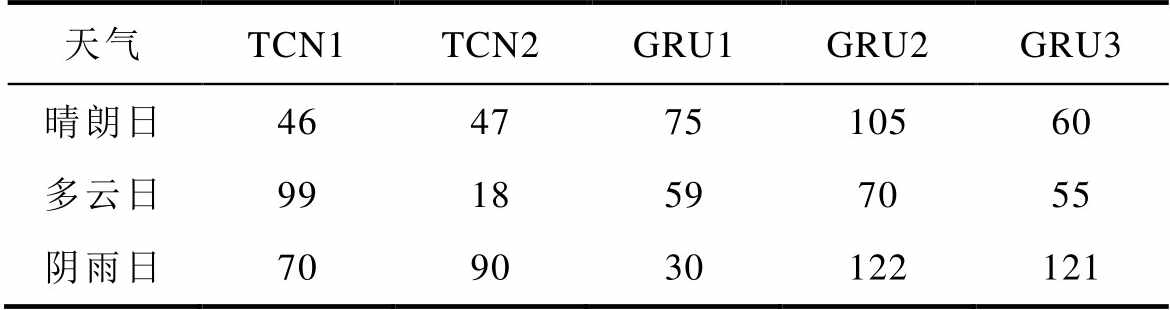
模型训练时采用AdamW优化器，AdamW优化器是Adam优化器的一种变体，通过改进权重衰减的方式，提高了算法的稳定性和泛化性能。损失函数L选取均方误差。TCN结构部分包含2个残差模块，卷积核大小为3，激活函数为ReLU，膨胀系数分别设置为1、2、4、8；全连接层的神经元数目与第3层GRU隐藏层神经元数目相同。贝叶斯优化后的TCN通道数、GRU隐藏层神经元数目等参数设置见表1。
表1 不同天气下的模型参数设置
Tab.1 Model parameter settings for different weather conditions
天气TCN1TCN2GRU1GRU2GRU3 晴朗日46477510560 多云日9918597055 阴雨日709030122121
本文选取方均根误差（Root Mean Squared Error, RMSE）、平均绝对误差（Mean Absolute Error, MAE）和决定系数R2来衡量光伏常态发电预测模型的性能。
异常检测部分用准确率、反正例率（False Positive Rate, FPR）、真正例率（True Positive Rate, TPR）作为评价指标。准确率表示正确预测异常值的比例；FPR表示预测异常实际为正常的样本数占正常样本数的比例；TPR表示预测为异常实际也为异常的样本数占异常样本数的比例。
综合考虑数据集和主要天气类型，应用FCM聚类与Frechet距离修正的算法将FCM的聚类数设置为3，隶属度因子设置为2，得到相似日集群结果如图8所示。由图8可知，晴朗相似日中光伏出力的周期性规律较强并且波动较小；阴雨相似日中光伏出力的数值较低且日间、日内波动较大；多云相似日的情况介于两者之间，受云层变化等因素的影响，光伏出力波动较大但数值比晴朗相似日低。
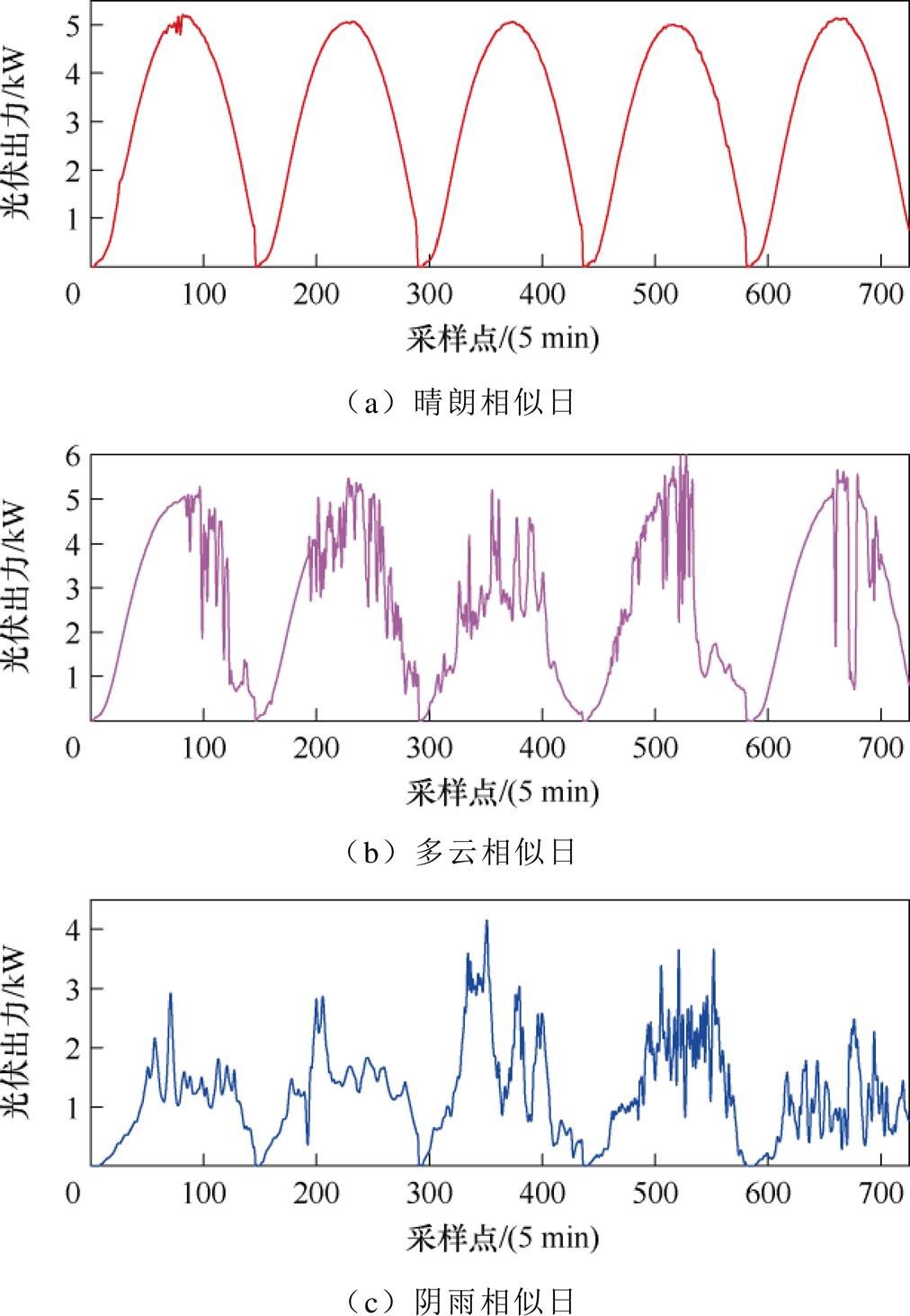
图8 相似日集群结果
Fig.8 Cluster results of similar days
本文提出一种基于FCM-BOA-TCN-GRU的光伏发电异常检测模型，并验证FCM和BOA算法在提高TCN-GRU模型对光伏常态发电功率预测精度方面的有效性。
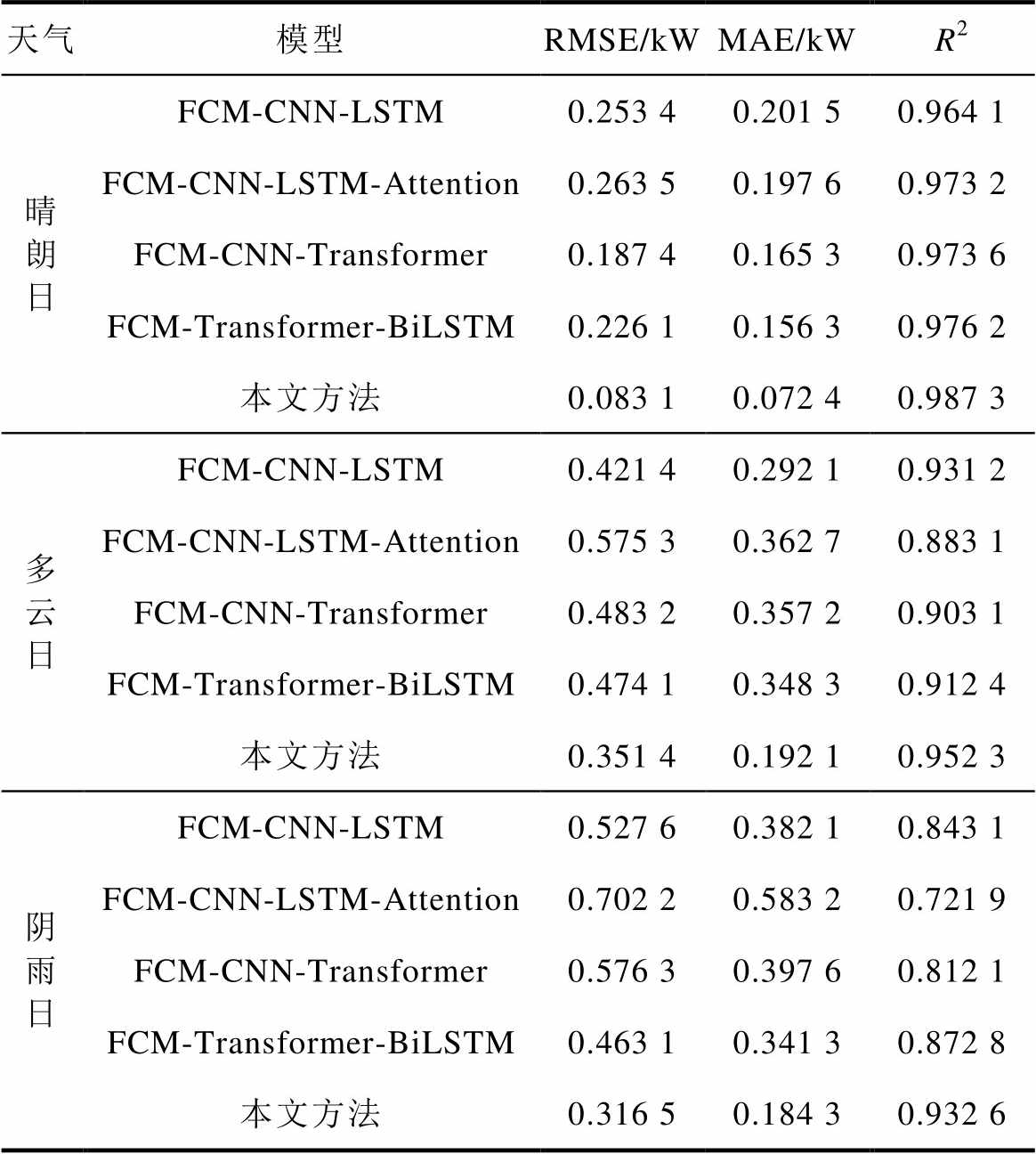
首先将本文所提模型与FCM-CNN-LSTM、FCM-CNN-LSTM-Attention、FCM-CNN-Transformer和FCM-Transformer-BiLSTM进行光伏常态发电功率预测比较，通过各种模型分别计算三种相似日下光伏常态功率预测的RMSE、MAE和R2，结果见表2，五种模型预测性能的雷达图如图9所示。
在不使用Frechet距离修正和BOA优化算法的前提下，除本文提出的方法外，其他算法的预测误差都偏大。引入Frechet距离修正和BOA算法后，在多云天气下，本文方法相较于FCM-CNN-LSTM- Attention的RMSE和MAE分别降低了0.223 9 kW和0.170 6 kW；在阴雨天气下，相较于FCM-CNN-LSTM-Attention的RMSE和MAE分别降低了0.385 7 kW和0.398 9 kW。由此说明了引入FCM聚类和BOA优化算法对光伏常态预测的有效性，为后文异常检测的准确性提供保障。而且由表2可知，本文所提方法在RMSE、MAE和R2指标方面均能到达较好的性能。
表2 各模型在不同天气类型下的实验结果对比
Tab.2 Experimental results comparison of various models under different weather types
天气模型RMSE/kWMAE/kWR2 晴朗日FCM-CNN-LSTM0.253 40.201 50.964 1 FCM-CNN-LSTM-Attention0.263 50.197 60.973 2 FCM-CNN-Transformer0.187 40.165 30.973 6 FCM-Transformer-BiLSTM0.226 10.156 30.976 2 本文方法0.083 10.072 40.987 3 多云日FCM-CNN-LSTM0.421 40.292 10.931 2 FCM-CNN-LSTM-Attention0.575 30.362 70.883 1 FCM-CNN-Transformer0.483 20.357 20.903 1 FCM-Transformer-BiLSTM0.474 10.348 30.912 4 本文方法0.351 40.192 10.952 3 阴雨日FCM-CNN-LSTM0.527 60.382 10.843 1 FCM-CNN-LSTM-Attention0.702 20.583 20.721 9 FCM-CNN-Transformer0.576 30.397 60.812 1 FCM-Transformer-BiLSTM0.463 10.341 30.872 8 本文方法0.316 50.184 30.932 6
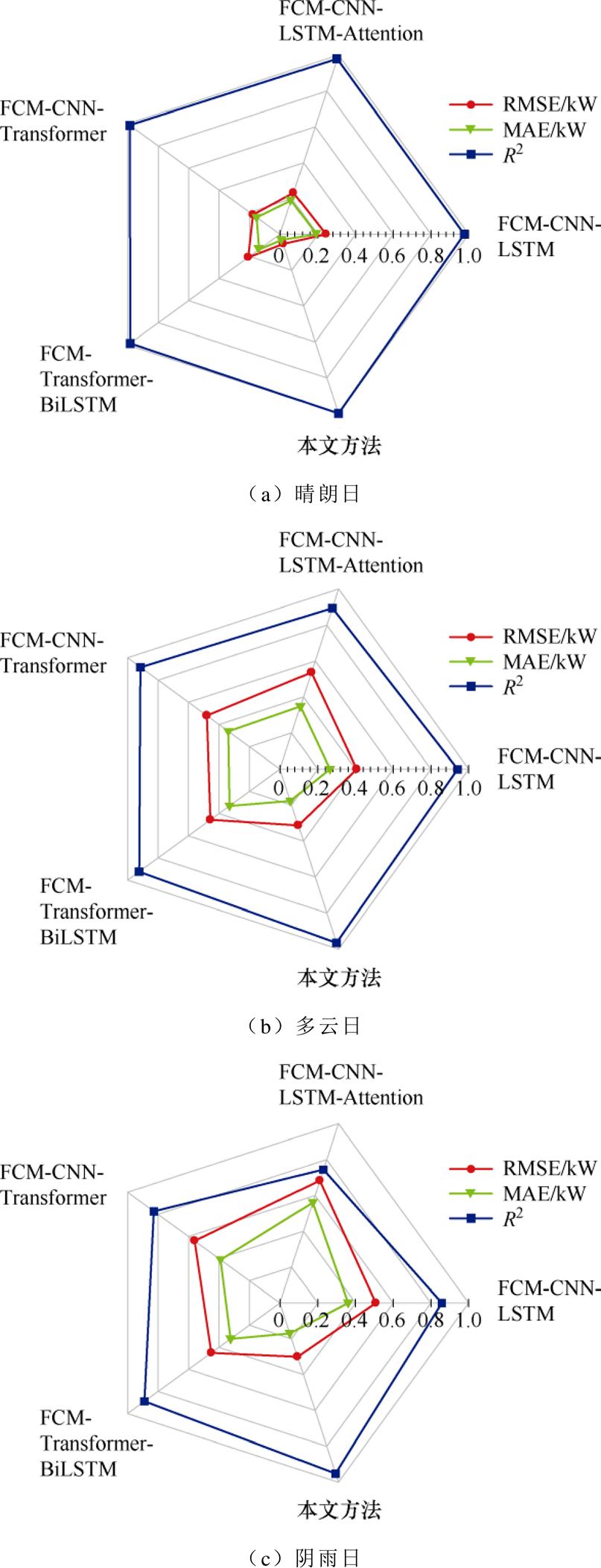
图9 各种模型在不同相似日下的预测性能雷达图
Fig.9 Radar map of predictive performance of various models under different similar days
为了更加直观地展示光伏发电预测的结果，所提方法在三种相似日下的预测结果对比如图10所示。由图10可知，当天气类型为晴朗日时，光伏的实际功率波动小，FCM-CNN-LSTM、FCM-CNN- LSTM-Attention和FCM-Transformer-BiLSTM不仅与实际值误差较大，其预测值的波动也较大，而所提方法与实际功率曲线拟合较好。多云天气时光伏的功率波动较大，FCM-Transformer-BiLSTM和所提模型表现较好，在浮云飘过导致光伏出力突然下降时，本文所提方法相较于其他模型能更早地做出反应，其他三种模型都未能准确预测光伏出力的变化。在光伏功率波动更大的阴雨天时，所提方法能准确地预测光伏功率的变化，其他模型表现均较差。综上所述，相较于其他对比模型，所提方法在光伏常态出力预测任务上展现出更好的天气普适性。
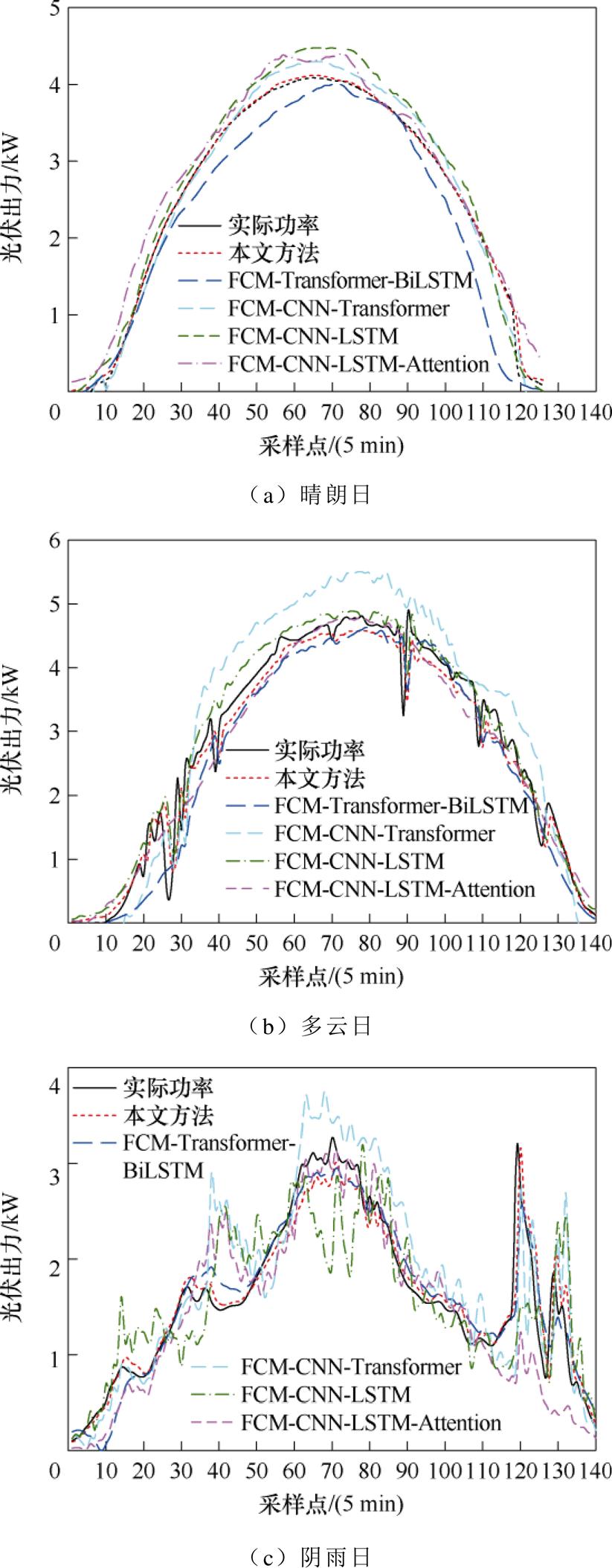
图10 不同相似日下的预测结果对比
Fig.10 Prediction results comparison under different similar days
为了验证所提方法的异常检测性能，在测试集的实验结果中截取部分包含正常和异常情况的典型片段，得到Alice Springs数据集的异常检测结果如图11所示，不同相似日下分布式光伏的异常检测结果见表3。
从表3和图11可知，晴朗日下所提方法相较于CNN-LSTM和Transformer-BiLSTM，FPR分别降低了40.38%和33.71%，准确率分别提高了11.24和3.92个百分点；在光伏出力波动较大的多云和阴雨天气下，本文所提方法的准确性均高于其他两种方法。因此所提方法不仅能准确地预测光伏常态出力曲线，还能通过预测值与实际值的偏差对比和异常判断规则识别出数据的异常，实现光伏发电的异常检测。光伏系统正常运行时，该方法能有效地避免对功率正常波动的误判，且线路发生损坏时也能及时识别异常。
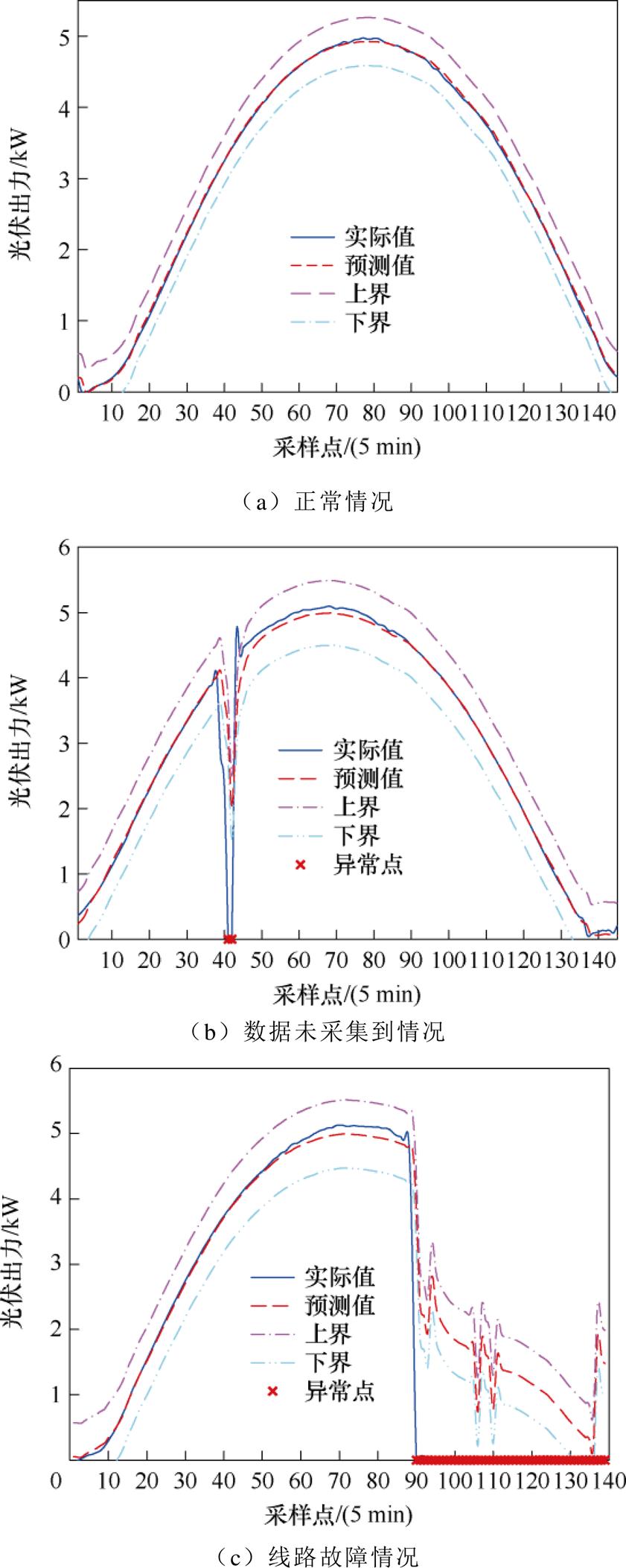
图11 Alice Springs数据集的异常检测结果
Fig.11 Anomaly detection results for the Alice Springs dataset
表3 分布式光伏异常检测结果
Tab.3 Distributed photovoltaic anomaly detection record
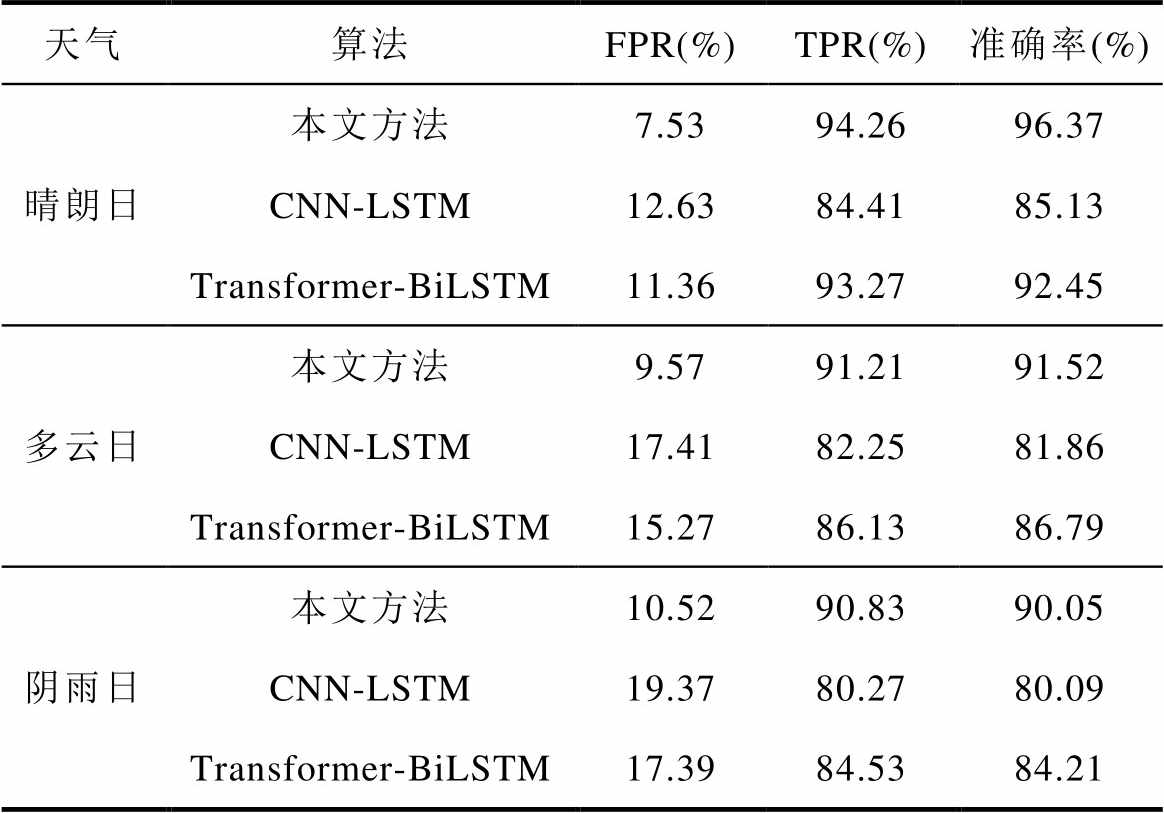
天气算法FPR(%)TPR(%)准确率(%) 晴朗日本文方法7.5394.2696.37 CNN-LSTM12.6384.4185.13 Transformer-BiLSTM11.3693.2792.45 多云日本文方法9.5791.2191.52 CNN-LSTM17.4182.2581.86 Transformer-BiLSTM15.2786.1386.79 阴雨日本文方法10.5290.8390.05 CNN-LSTM19.3780.2780.09 Transformer-BiLSTM17.3984.5384.21
为验证所提方法在其他数据集上的泛化能力，在另一数据集上进行了光伏常态出力预测和异常检测实验。实验数据采集自长沙市某楼宇屋顶光伏系统，采样间隔为5 min，参数设置与5.2节一致。首先在此基础上进行光伏常态出力预测实验，使用 本文所提方法与FCM-CNN-LSTM和FCM-CNN- Transformer方法的对比结果如表4和图12所示。
当天气类型为晴朗日时，光伏的实际功率波动小，三种模型都能达到较好的预测效果。多云天气时光伏的功率波动较大，FCM-CNN-LSTM和所提模型表现较好，在浮云飘过导致光伏出力突然下降时，本文所提方法相较于其他模型能更早地做出反应。在光伏功率波动更大的阴雨天时，所提方法能准确地预测光伏功率的变化，其他模型表现均较差。综上所述，相较于其他两种模型，所提方法在光伏常态出力预测任务上展现出更好的天气普适性。
表4 三种模型在不同天气类型下的实验结果对比
Tab.4 Comparison of experimental results of the three models under different weather types
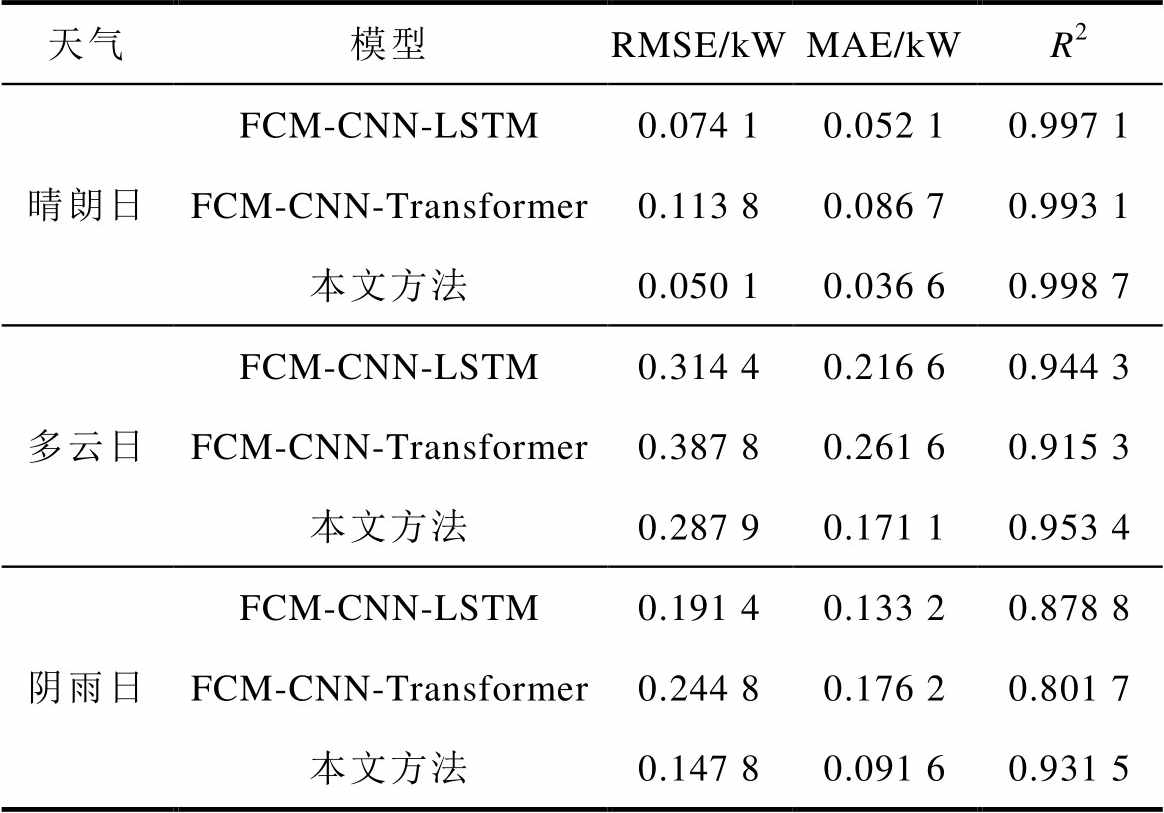
天气模型RMSE/kWMAE/kWR2 晴朗日FCM-CNN-LSTM0.074 10.052 10.997 1 FCM-CNN-Transformer0.113 80.086 70.993 1 本文方法0.050 10.036 60.998 7 多云日FCM-CNN-LSTM0.314 40.216 60.944 3 FCM-CNN-Transformer0.387 80.261 60.915 3 本文方法0.287 90.171 10.953 4 阴雨日FCM-CNN-LSTM0.191 40.133 20.878 8 FCM-CNN-Transformer0.244 80.176 20.801 7 本文方法0.147 80.091 60.931 5
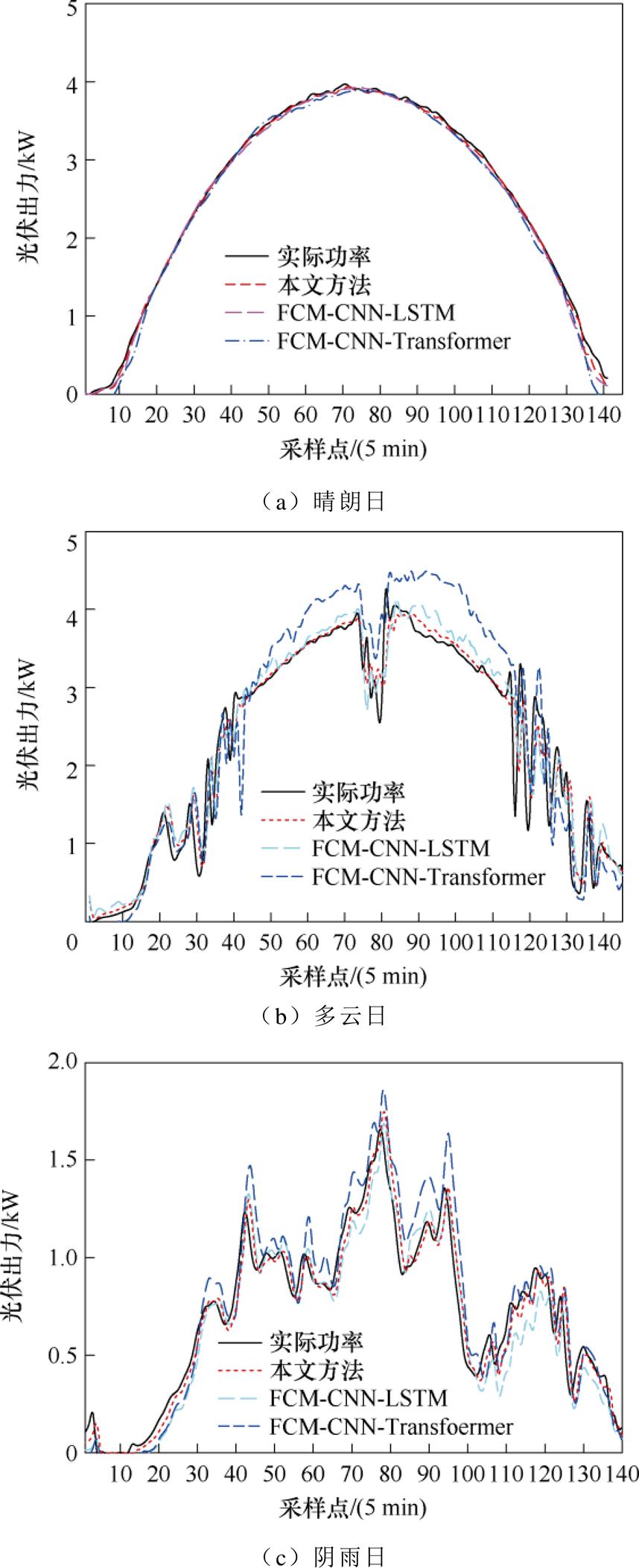
图12 不同相似日下三种模型的预测结果对比
Fig.12 Comparison of the prediction results of the three models under different similarity days
其次，为了验证所提方法的异常检测性能，在测试集的实验结果中截取部分包含正常和异常情况的典型片段，检测结果如图13所示。结果显示，CNN-LSTM和Transformer-BiLSTM两种方法的异常检测准确率分别为81.32%和85.43%，所提方法在其他数据集上仍能检测出光伏异常的情况，异常检测的准确率能达到90%。
本文提出了一种基于历史光伏出力数据和环境数据的分布式光伏发电异常检测方法，所提方法不仅能准确地预测光伏常态出力曲线，为异常检测的准确率提供保障，还能有效地识别光伏的异常情况。通过特征筛选、FCM-Frechet相似日集群划分、模型训练与双重动态阈值实现光伏的异常检测。实验结果表明，所提方法相较于CNN-LSTM和Transformer- BiLSTM，FPR分别降低了40.38%和33.71%，准确率分别提高了11.24和3.92个百分点。在光伏出力波动较大的多云和阴雨天气下，本文所提方法的准确性均高于其他两种方法。然而，本文模型在多云天气下光伏常态出力预测准确率较低，下一步将研究多云天气下云层移动和光伏出力关系的高精度时空建模方法，并提出该模型下用于识别光伏异常的检测方法。
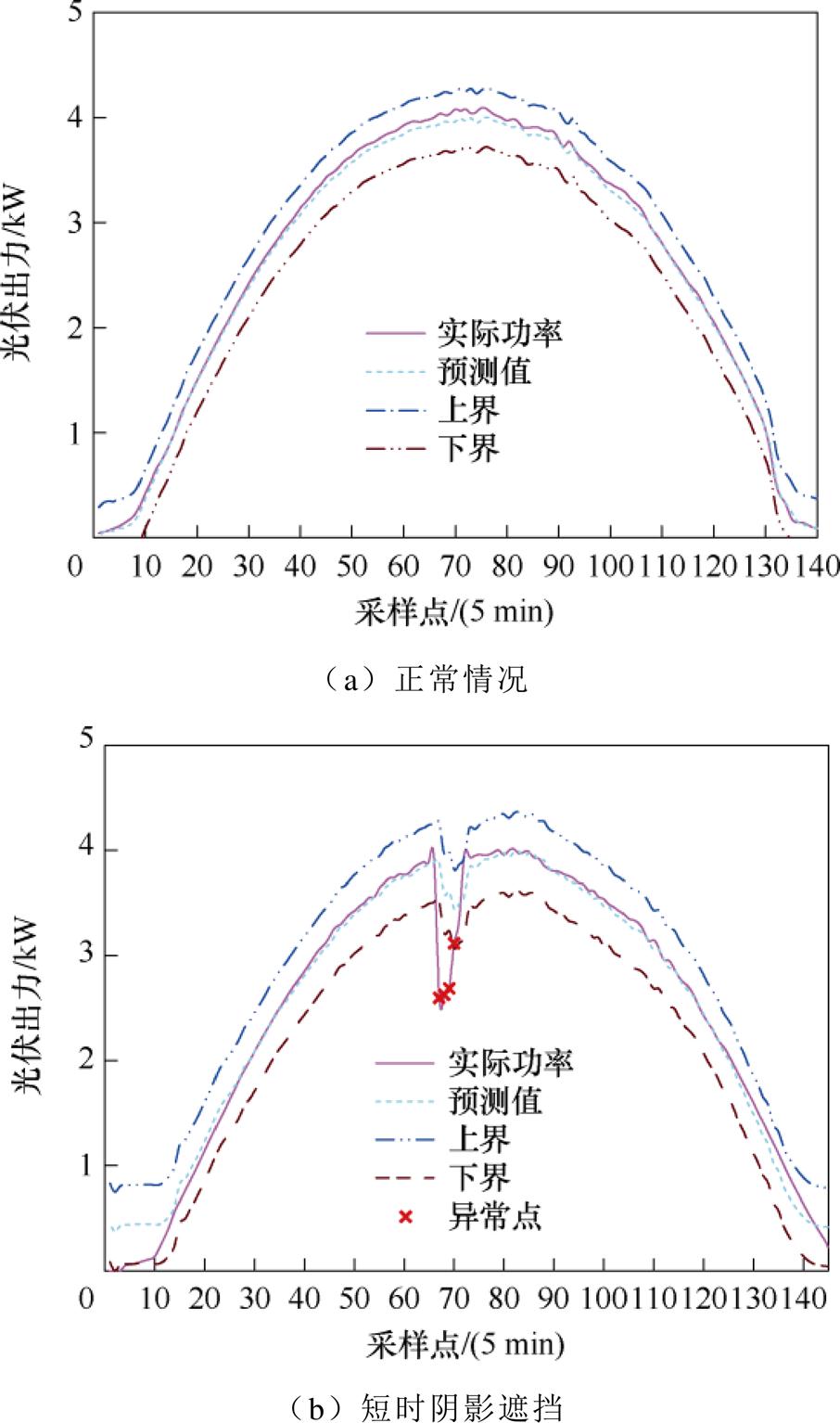
图13 异常检测结果
Fig.13 Anomaly detection results
参考文献
[1] 王小宇, 刘波, 孙凯, 等. 光伏阵列故障诊断技术综述[J]. 电工技术学报, 2024, 39(20): 6526-6543.
Wang Xiaoyu, Liu Bo, Sun Kai, et al. A review of photovoltaic array fault diagnosis technology[J]. Transactions of China Electrotechnical Society, 2024, 39(20): 6526-6543.
[2] 王玉庆, 徐飞, 刘志坚, 等. 基于动态关联表征与图网络建模的分布式光伏超短期功率预测[J]. 电力系统自动化, 2023, 47(20): 72-82.
Wang Yuqing, Xu Fei, Liu Zhijian, et al. Ultra- short-term power forecasting of distributed photo- voltaic based on dynamic correlation characterization and graph network modeling[J]. Automation of Electric Power Systems, 2023, 47(20): 72-82.
[3] 赵耀, 高少炜, 李东东, 等. 基于天气相似聚类与QRNN的短期光伏功率区间概率预测[J]. 电力系统自动化, 2023, 47(23): 152-161.
Zhao Yao, Gao Shaowei, Li Dongdong, et al. Short- term interval probability prediction of photovoltaic power based on weather similarity clustering and quantile regression neural network[J]. Automation of Electric Power Systems, 2023, 47(23): 152-161.
[4] 时珉, 许可, 王珏, 等. 基于灰色关联分析和GeoMAN模型的光伏发电功率短期预测[J]. 电工技术学报, 2021, 36(11): 2298-2305.
Shi Min, Xu Ke, Wang Jue, et al. Short-term photovoltaic power forecast based on grey relational analysis and GeoMAN model[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2298- 2305.
[5] Balachandran G B, Devisridhivyadharshini M, Ramachandran M E, et al. Comparative investigation of imaging techniques, pre-processing and visual fault diagnosis using artificial intelligence models for solar photovoltaic system—a comprehensive review[J]. Measurement, 2024, 232: 114683.
[6] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201- 1217.
Lai Changwei, Li Jinghua, Chen Bo, et al. Review of photovoltaic power output prediction technology[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1201-1217.
[7] Qu Jiaqi, Qian Zheng, Pei Yan, et al. An unsupervised hourly weather status pattern recognition and blending fitting model for PV system fault dete- ction[J]. Applied Energy, 2022, 319: 119271.
[8] Lu Xiaoyang, Lin Peijie, Cheng Shuying, et al. Fault diagnosis for photovoltaic array based on con- volutional neural network and electrical time series graph[J]. Energy Conversion and Management, 2019, 196: 950-965.
[9] Alippi C, Ntalampiras S, Roveri M. Model-free fault detection and isolation in large-scale cyber-physical systems[J]. IEEE Transactions on Emerging Topics in Computational Intelligence, 2017, 1(1): 61-71.
[10] Wang Kejun, Qi Xiaoxia, Liu Hongda. Photovoltaic power forecasting based LSTM-convolutional net- work[J]. Energy, 2019, 189: 116225.
[11] Harrou F, Dairi A, Taghezouit B, et al. An unsupervised monitoring procedure for detecting anomalies in photovoltaic systems using a one-class support vector machine[J]. Solar Energy, 2019, 179: 48-58.
[12] 乔楠, 蒋波涛, 郑雨, 等. 基于深度模糊神经网络的太阳总辐射预测研究[J]. 太阳能学报, 2024, 45(2): 59-64.
Qiao Nan, Jiang Botao, Zheng Yu, et al. Research on global solar radiation forecast based on deep fuzzy neural network[J]. Acta Energiae Solaris Sinica, 2024, 45(2): 59-64.
[13] Wang Chaofan, Shuai Jing, Ding Liping, et al. Comprehensive benefit evaluation of solar PV projects based on multi-criteria decision grey relation projection method: evidence from 5 counties in China[J]. Energy, 2022, 238: 121654.
[14] 丛伟伦, 张博, 夏亚东, 等. 基于马尔可夫链的光伏电站遮挡实时诊断算法[J]. 太阳能学报, 2020, 41(4): 67-72.
Cong Weilun, Zhang Bo, Xia Yadong, et al. Diagnosis algorithm for real-time shaded analysis of photo- voltaic power station based on Markov chain[J]. Acta Energiae Solaris Sinica, 2020, 41(4): 67-72.
[15] Ramírez A F, Valencia C F, Cabrales S, et al. Simulation of photo-voltaic power generation using copula autoregressive models for solar irradiance and air temperature time series[J]. Renewable Energy, 2021, 175: 44-67.
[16] Sahin G, Isik G, van Sark W G J H M. Predictive modeling of PV solar power plant efficiency con- sidering weather conditions: a comparative analysis of artificial neural networks and multiple linear regression[J]. Energy Reports, 2023, 10: 2837- 2849.
[17] Lindig S, Kaaya I, Weiss K A, et al. Review of statistical and analytical degradation models for photovoltaic modules and systems as well as related improvements[J]. IEEE Journal of Photovoltaics, 2018, 8(6): 1773-1786.
[18] Dey M, Rana S P, Simmons C V, et al. Solar farm voltage anomaly detection using high-resolution m PMU data-driven unsupervised machine learning[J]. Applied Energy, 2021, 303: 117656.
[19] Xiang Ling, Yang Xin, Hu Aijun, et al. Condition monitoring and anomaly detection of wind turbine based on cascaded and bidirectional deep learning networks[J]. Applied Energy, 2022, 305: 117925.
[20] 蔡雨思, 李泽文, 刘萍, 等. 基于间接健康特征优化与多模型融合的锂电池SOH-RUL联合预测[J]. 电工技术学报, 2024, 39(18): 5883-5898.
Cai Yusi, Li Zewen, Liu Ping, et al. Joint prediction of lithium battery state of health and remaining useful life based on indirect health features optimization and multi-model fusion[J]. Transactions of China Electro- technical Society, 2024, 39(18): 5883-5898.
[21] 杨童亮, 胡东, 唐超, 等. 基于SMA-VMD-GRU模型的变压器油中溶解气体含量预测[J]. 电工技术学报, 2023, 38(1): 117-130.
Yang Tongliang, Hu Dong, Tang Chao, et al. Prediction of dissolved gas content in transformer oil based on SMA-VMD-GRU model[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 117-130.
[22] Yu Wennian, Kim I Y, Mechefske C. Analysis of different RNN autoencoder variants for time series classification and machine prognostics[J]. Mechanical Systems and Signal Processing, 2021, 149: 107322.
[23] Ibrahim M, Alsheikh A, Awaysheh F, et al. Machine learning schemes for anomaly detection in solar power plants[J]. Energies, 2022, 15(3): 1082.
[24] Chang Zhonghao, Han Te. Prognostics and health management of photovoltaic systems based on deep learning: a state-of-the-art review and future perspectives[J]. Renewable and Sustainable Energy Reviews, 2024, 205: 114861.
[25] de Souza Silva J L, Mahmoudi E, Carvalho R R M, et al. Classification of anomalies in photovoltaic systems using supervised machine learning techniques and real data[J]. Energy Reports, 2024, 11: 4642- 4656.
[26] Liu Shujun, Xu Tong, Du Xiaoze, et al. A hybrid deep learning model based on parallel architecture TCN-LSTM with Savitzky-Golay filter for wind power prediction[J]. Energy Conversion and Management, 2024, 302: 118122.
[27] Limouni T, Yaagoubi R, Bouziane K, et al. Accurate one step and multistep forecasting of very short-term PV power using LSTM-TCN model[J]. Renewable Energy, 2023, 205: 1010-1024.
[28] Yang Shun, Du Yajun, Huang Jiaming, et al. Few-shot intent detection with mutual information and contrastive learning[J]. Applied Soft Computing, 2024, 167: 112338.
[29] Fantini D G, Silva R N, Siqueira M B B, et al. Wind speed short-term prediction using recurrent neural network GRU model and stationary wavelet transform GRU hybrid model[J]. Energy Conversion and Management, 2024, 308: 118333.
Distributed Photovoltaic Power Output Anomaly Detection Method Based on FCM-BOA-TCN-GRU
Abstract To address the challenges that the anomaly detection technology for centralized photovoltaic systems is difficult to apply in distributed photovoltaic systems due to the widespread and diverse nature of distributed photovoltaic points, this paper proposes a distributed photovoltaic power generation anomaly detection method based on the fuzzy C-means (FCM) clustering algorithm and Bayesian optimization algorithm (BOA) optimized TCN-GRU network. The method involves feature selection, the FCM-Frechet model for clustering similar days, and the BOA-TCN-GRU model for predicting normal photovoltaic power output, combined with a dual dynamic threshold method to determine anomalies in distributed photovoltaic power generation systems. This approach reduces the need for annotated datasets and improves the accuracy of photovoltaic system anomaly detection.
Firstly, the original data is treated for outliers and Pearson correlation analysis is conducted to select current, horizontal total radiation, temperature, humidity, horizontal scattered radiation, and wind speed as inputs to construct a similar day clustering model. Secondly, to mitigate the impact of weather volatility on photovoltaic power prediction results, a weighted FCM-Frechet algorithm is proposed for two-stage similar day clustering, categorizing weather into clear, cloudy, and rainy similar days. Then, using mutual information to screen redundant features, a BOA-optimized TCN-GRU network model is proposed. TCN processes local and global spatial features of time series, while GRU handles temporal features, achieving spatiotemporal joint modeling of features and improving the prediction accuracy of normal photovoltaic power output. Finally, the dual dynamic threshold method with an adaptive factor is used to determine photovoltaic system anomalies. The effectiveness of the proposed method is verified using the Alice Springs dataset from the Australian desert area and a building photovoltaic power generation dataset from Changsha City.
The results show that the proposed method achieves higher detection accuracy. This paper implements two simulations using Pytorch. The first simulation aims to predict normal photovoltaic power output and detect anomalies under different similar days using the proposed BOA-TCN-GRU model. The results indicate that under cloudy conditions, the proposed method reduces RMSE and MAE by 0.223 9 kW and 0.170 6 kW, respectively, compared to FCM-CNN-LSTM-Attention; under rainy conditions, RMSE and MAE are reduced by 0.385 7 kW and 0.398 9 kW, respectively. The proposed method demonstrates better weather generalizability in normal photovoltaic power prediction tasks. On clear days, the FPR is reduced by 40.38% and 33.71% compared to CNN-LSTM and Transformer-BiLSTM, respectively, with an accuracy increase of 11.24 and 3.92 percentage points. The second simulation aims to verify the generalization ability of the proposed anomaly detection model. The results show that the accuracy rates of CNN-LSTM and Transformer-BiLSTM are 81.32% and 85.43%, respectively, and the proposed method can still detect photovoltaic anomalies on other datasets, with an accuracy rate reaching 90%.
From the simulation analysis, the following conclusions can be drawn: (1) The weighted FCM-Frechet clustering model effectively reduces the impact of weather volatility on photovoltaic prediction results by clustering similar days. (2) Considering environmental conditions, the BOA-optimized TCN-GRU network model, combined with the dual dynamic threshold method with an adaptive factor, improves the accuracy and versatility of the model in photovoltaic anomaly detection. (3) Experimental results show that the proposed model improves accuracy by 11.24 and 3.92 percentage points compared to CNN-LSTM and Transformer-BiLSTM.
This paper identifies an issue with the inaccuracy of the model between moving clouds and photovoltaic output under cloudy weather conditions. The next step will involve researching high-precision spatiotemporal modeling methods for the relationship between cloud movement and photovoltaic output in cloudy weather and proposing detection methods for identifying photovoltaic anomalies under this model.
Keywords：Distributed photovoltaics anomaly detection, temporal convolutional network, gate recurrent unit, similar day clustering, Bayesian optimization
中图分类号：TM615; TP183
DOI: 10.19595/j.cnki.1000-6753.tces.241594
国家自然科学基金（62473065）、湖南省自然科学基金（2023JJ40053）、湖南省教育厅优秀青年基金（23B0321）和湖南省教育厅资助科研项目（23C0424）资助。
收稿日期 2024-09-09
改稿日期 2024-11-29
彭 昱 女，1993年生，博士，讲师，研究方向为电气设备故障诊断与健康管理、电网安全防御技术等。
E-mail: yupeng@csust.edu.cn
郭 昕 男，1994年生，博士，讲师，研究方向为智能控制算法。
E-mail: hnu_csgx@hnu.edu.cn（通信作者）
（编辑 李 冰）