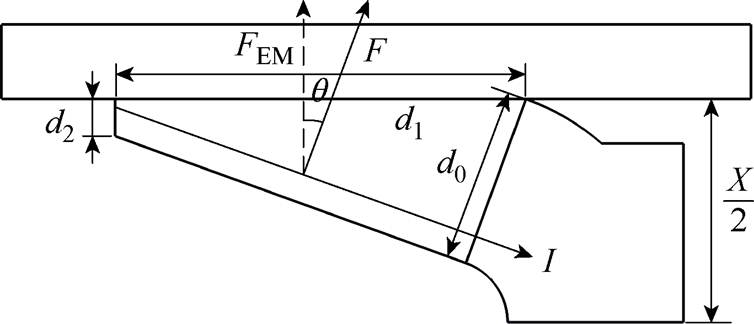
图1 电枢/轨道电磁接触压力示意图
Fig.1 Schematic of armature/rail electromagnetic contact pressure
摘要 一体C形电枢作为直线式电磁发射器中将电能转化为动能的重要部件,其性能的优劣直接影响发射器的整体性能,电枢尾翼倾角作为发射器典型结构参数会对其发射性能产生重要影响。该文从枢轨接触压力、电枢结构完整性和发射速度三方面考虑,以平面电枢为例,首先通过理论分析探究了枢轨接触压力与电枢结构完整性约束下尾翼倾角的取值范围,然后通过有限元仿真研究了电枢尾翼倾角对发射速度的影响。结果表明:在载流裕度系数为0.7~0.9的区间内,尾翼倾角的临界值随裕度系数的增大而减小,同时在考虑枢轨接触压力和电枢结构完整性的前提下,30 mm口径电枢尾翼倾角的取值范围为20°~30°;在驱动电流波形和额定发射速度均相同的条件下,电枢发射所需的轨道长度随尾翼倾角的增大而减小,尾翼倾角取30°时的轨道长度是取20°时的83%,增大倾角可以减小发射所需的电流幅值和轨道长度。
关键词:电磁轨道发射 C形电枢 尾翼结构参数 倾角
电磁轨道发射具有电流幅值高、发射时间短、发射速度快、安全可靠等优点[1-2],与传统发射方式相比,其电流密度高、相对运动速度大,处于一种极限工作条件。发射过程中,强脉冲电流通过轨道和电枢,轨道间的强磁场与电枢电流相互作用而产生洛伦兹力,推动载有弹丸的电枢不断加速。高温、大电流、强磁场这些因素将导致电枢工作在极其恶劣的环境中[3],作为将电能转化为动能的载体,电枢能否在这种恶劣的环境中保持结构完整性将直接关系轨道炮的工作状态[4]。
与其他类型的固体电枢相比,一体C形电枢结构简单,且具备相适应的结构特征[5-6]。一方面,尾翼能够提供接触压力,保证电枢/轨道间的良好电接触;另一方面,电枢尾翼倾角增大了枢轨间的摩擦力,阻碍电枢运动,进而影响电枢运动特性,且为防止电枢尾翼断裂,尾翼倾角也会受到电枢机械强度的约束。因此,探究电枢尾翼倾角的约束条件,在不同发射场景下选取合适的电枢尾翼结构参数,对于确保电枢结构完整、保证良好的电枢/轨道接触、获取较高的发射速度具有重要意义[7]。
目前已有较多学者针对C形电枢的结构参数进行了优化研究[8-11]。刘志明等确定了电枢和轨道的最佳几何形状及其相关参数的取值范围[12];陈立学等根据电枢材料的载流特征量计算了电枢喉部的最小厚度[7],并且分析了电枢接触压力及接触位置与电枢结构参数的直接关系[13];彭晓婷等根据最大电流密度对平面电枢头部厚度、侧面厚度、电枢长度和弧面半径四个参数进行了优化[14];李白等以电枢应力、温度及质量为目标对喉部厚度、臂长、尾翼长度和尾翼倾角四个参数进行了多目标优化[15];刘勇等在不显著改变电枢原有结构和接触力的前提下,增加枢轨界面面积,减小枢轨间距,并且使得接触压强分布更均匀[16]。
本文以平面电枢为例,从电枢的功能性出发,对C形电枢的尾翼倾角的取值范围进行研究:从电枢初始加速、结构完整性与发射速度三个方面考虑,首先基于枢轨接触压力的需求得到电枢尾翼倾角的上下限约束;然后在此基础上通过对电枢尾翼机械强度的分析得到电枢尾翼倾角临界值与载流裕度系数的关系;最后通过仿真研究电枢尾翼倾角对发射速度的影响,并对理论分析进行验证,为选取合适的电枢尾翼结构参数提供参考。
发射装置中与一体C形电枢尾翼结构相关的参数为:尾翼倾角q、尾翼转角厚度d0、尾翼长度d1、尾翼端部厚度d2,炮膛的口径和高度分别为X和Y。电枢与轨道电磁接触压力示意图如图1所示。

图1 电枢/轨道电磁接触压力示意图
Fig.1 Schematic of armature/rail electromagnetic contact pressure
流经电枢尾翼的电流I在电流产生的磁场B的作用下产生电磁力F,电磁力垂直于轨道的分力FEM即为电枢/轨道电磁接触压力。为简化分析,做出如下假设:①电枢后部炮膛中的磁场是均匀的;②电流从轨道进入尾翼的位置位于尾翼端部。
基于上述假设前提,可以得到电枢尾翼电磁接触压力FEM为
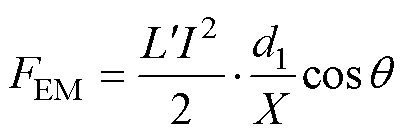 (1)
(1)
式中,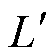 为轨道电感梯度。电枢结构参数间的关系为
为轨道电感梯度。电枢结构参数间的关系为
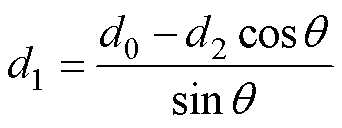 (2)
(2)
将式(2)代入式(1)可以得到电磁接触压力FEM与电枢尾翼结构参数的关系为
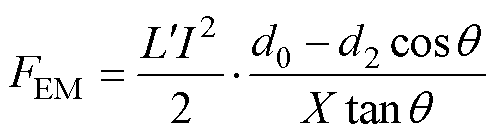 (3)
(3)
由式(3)可以看出,电磁接触压力FEM不但与尾翼转角厚度d0、尾翼长度d1、尾翼端部厚度d2和尾翼倾角q 有关,而且与电感梯度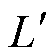 、电流幅值I和炮膛口径X有关。
、电流幅值I和炮膛口径X有关。
根据R. A. Marshall等提出的观点,电磁发射器电枢与轨道间的接触压力不应小于1 g/A[17],将其作为电磁接触压力的下限,则电磁接触压力FEM(N)与电流幅值I(A)在数值上满足不等式(4)。
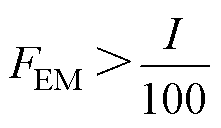 (4)
(4)
根据当电枢总推力大于摩擦力时,电枢才能加速的原理,将枢轨间的摩擦力作为电磁接触压力的上限,则电磁接触压力FEM满足不等式(5)。
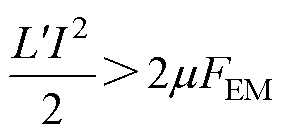 (5)
(5)
式中,m 为电枢/轨道动摩擦系数。
因此,可以得到枢轨电磁接触压力的取值范 围为
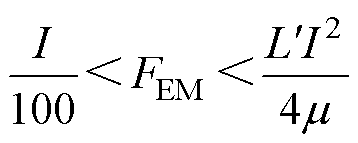 (6)
(6)
由式(6)可以看出,电枢/轨道电磁接触压力FEM的取值范围与发射器的电感梯度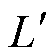 、驱动电流幅值I和电枢/轨道动摩擦系数m 有关。
、驱动电流幅值I和电枢/轨道动摩擦系数m 有关。
联立式(3)和式(6)可得
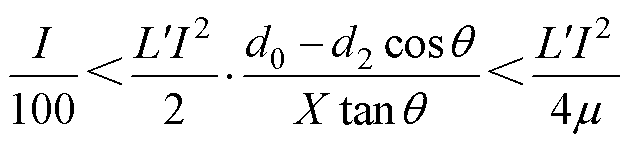 (7)
(7)
即
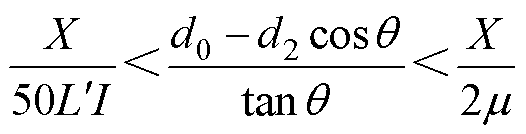 (8)
(8)
由于存在不等式
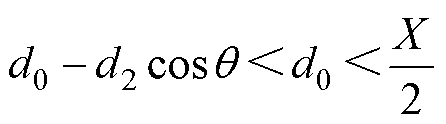 (9)
(9)
可以得到
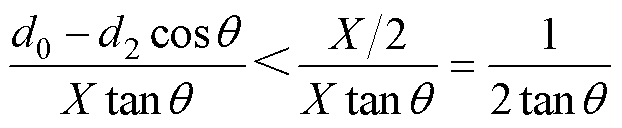 (10)
(10)
于是有
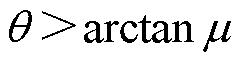 (11)
(11)
取m =0.1,则有q >6°。因此只要电枢尾翼倾角q >6°,则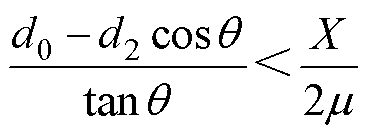 恒成立,此时枢轨间的电磁接触压力可以满足上限约束。
恒成立,此时枢轨间的电磁接触压力可以满足上限约束。
从式(8)可以看出,枢轨间电磁接触压力的下限约束由发射器的电感梯度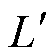 、炮膛口径X和驱动电流幅值I决定。
、炮膛口径X和驱动电流幅值I决定。
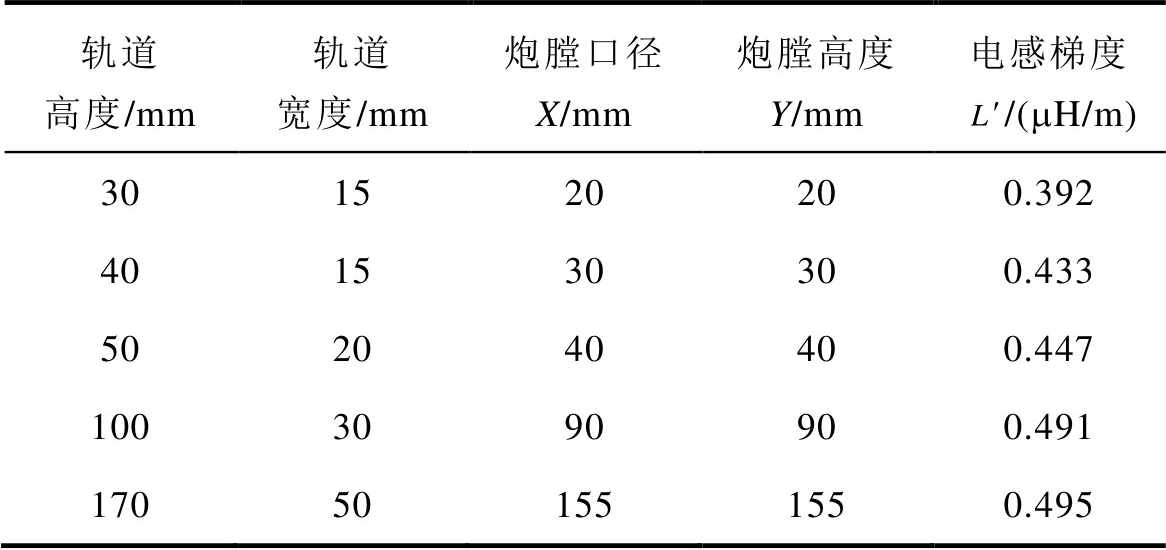
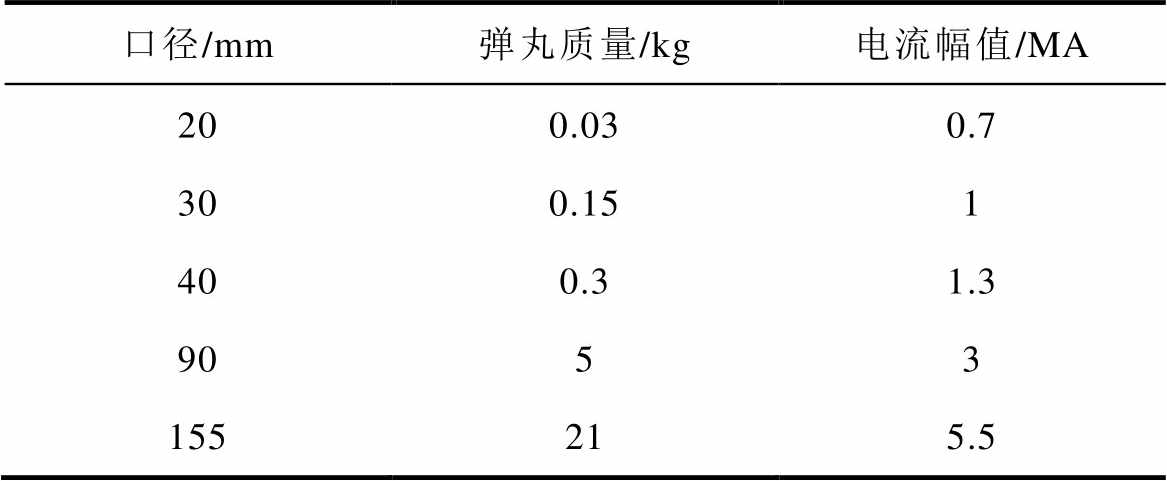
为简化分析,假设发射器的电感梯度为定值,由高频等效法计算得到的几种典型尺寸发射器的电感梯度见表1,不同口径发射器驱动电流幅值见表2。可见不同口径发射器的电感梯度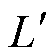 差别不大,驱动电流幅值I的差别较大。
差别不大,驱动电流幅值I的差别较大。
表1 发射器的结构尺寸和电感梯度的关系
Tab.1 Relationship between structural dimensions and inductance gradient of launcher
轨道高度/mm轨道宽度/mm炮膛口径X/mm炮膛高度Y/mm电感梯度/(mH/m) 301520200.392 401530300.433 502040400.447 1003090900.491 170501551550.495
表2 不同口径发射器的驱动电流幅值
Tab.2 Amplitude of drive current for launchers of different calibres
口径/mm弹丸质量/kg电流幅值/MA 200.030.7 300.151 400.31.3 9053 155215.5
为了保证电枢具有一定的柔性且肩部具有足够大的通流面积,尾翼倾角不宜过大,尾翼长度应大于电枢转角厚度的两倍,即d1>2d0,由此有q <30°,因此电枢尾翼结构参数中尾翼倾角q 的最大取值为30°。为验证该上限值的合理性,以30 mm和90 mm口径电枢为例,取不同的q 值,分别绘制上述两种尺寸电枢的电磁接触压力关于电流幅值的变化曲线,如图2所示。
从图2可以看出,随着电流幅值的增大,电磁接触压力呈二次方增大,即使在30°的尾翼倾角下,接触压力的值仍远大于1 g/A的接触压力需求。同时可以看出,在相同电流幅值下,电磁接触压力随q 的减小而增大,因此可以认为将30°作为尾翼倾角取值的上限是合理的。综上所述,从电磁接触压力的要求出发,电枢尾翼倾角的约束范围为
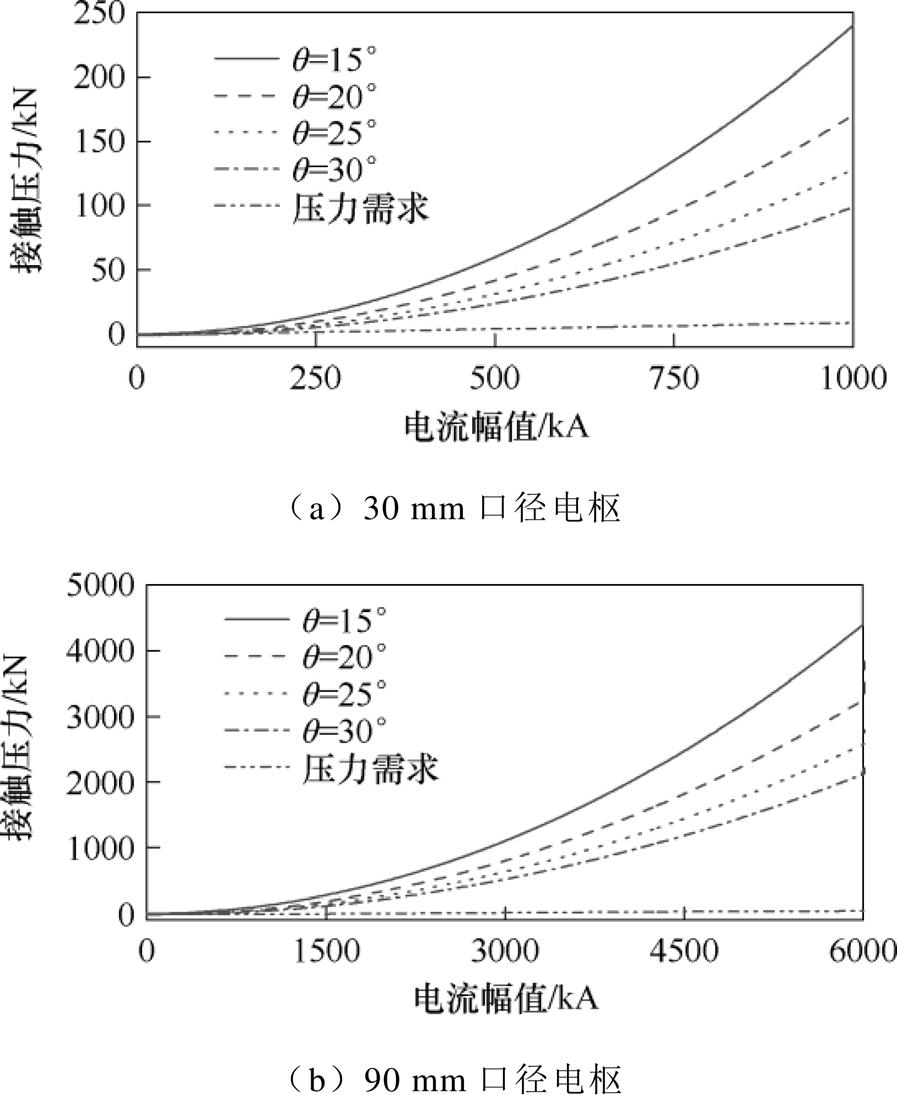
图2 不同q 下电磁接触压力与电流幅值的关系
Fig.2 Relationship between electromagnetic contact pressure and current amplitude for different q
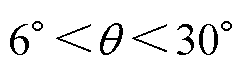 (12)
(12)
电磁发射过程中,电枢尾翼除电磁力外还要承受头部的拉力与轨道的摩擦力。发射过程中电枢温度较高,材料的机械强度较低,尾翼连接处易出现断裂。防止尾翼断裂、确保电枢结构完整是电磁发射器研究中不可回避的问题。选取头部的一个体积元为研究对象,该体积元的载流截面积为A1,长度为l1,电阻率为re,密度为rm,比热容为c,熔点为Tm,设通过该体积元的电流为I1,体积元的初始温度为T0,则该体积元的绝热温升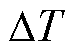 为
为
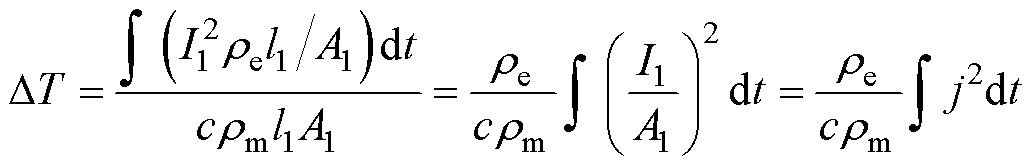 (13)
(13)
式中,j为电流密度。
当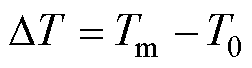 时,体积元开始熔化,此时对应的
时,体积元开始熔化,此时对应的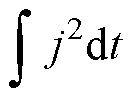 为熔化载流特征量G,表示为
为熔化载流特征量G,表示为
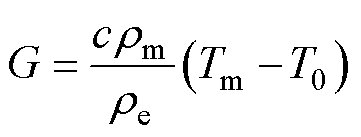 (14)
(14)
若电枢头部电流均匀分布,为保证头部不发生熔化,头部任意体积元的电流密度应满足
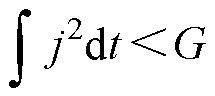 (15)
(15)
则电枢头部截面积A应满足
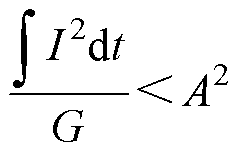 (16)
(16)
实际上电枢电流分布不均匀,受瞬态趋肤效应、速度趋肤效应及欧姆效应的影响,电枢电流集中在内侧表层,电流密度从内向外逐层递减。考虑截面电流分布不均匀,为避免通流截面发生熔化,需要对所需通流面积A的大小进行修正。为此引入载流裕度系数k(0<k<1),k值越小,电枢头部的通流截面积越大,由此可得
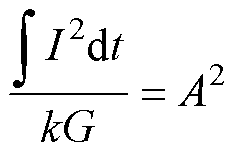 (17)
(17)
联立式(13)、式(14)和式(17)可得,电枢截面的平均温升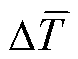 为
为
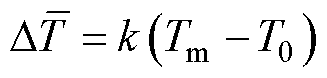 (18)
(18)
将电枢分为头部和尾翼两个部分,并对尾翼进行受力分析,示意图如图3所示。发射过程中,尾翼机械强度最薄弱的位置是尾翼转角处(图3中F0所在位置)。假设尾翼受到头部对尾翼的拉力F0,它与电磁力的分量Fsinq 共同克服摩擦力f,使电枢尾翼与电枢头部保持相同的加速度a向前运动。尾翼受到的加速力为
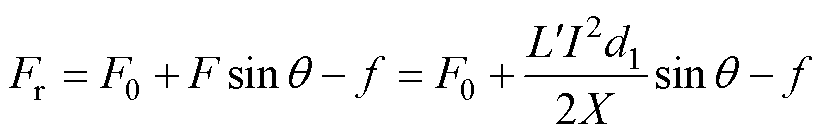 (19)
(19)
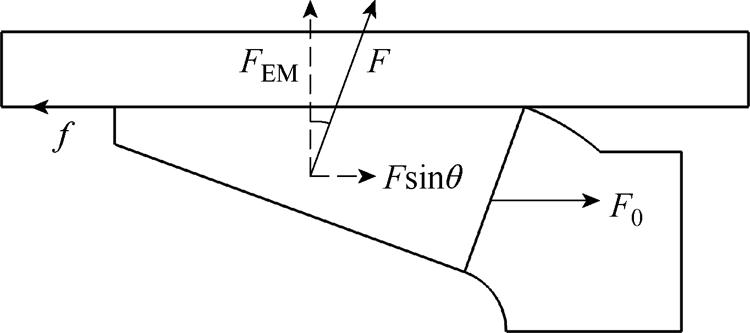
图3 电枢尾翼受力示意图
Fig.3 Schematic diagram of armature tail force
设电枢和弹丸的总质量为M,单侧尾翼的质量为m,电枢材料的密度为rm,由电枢尾翼与弹丸加速度相同可得
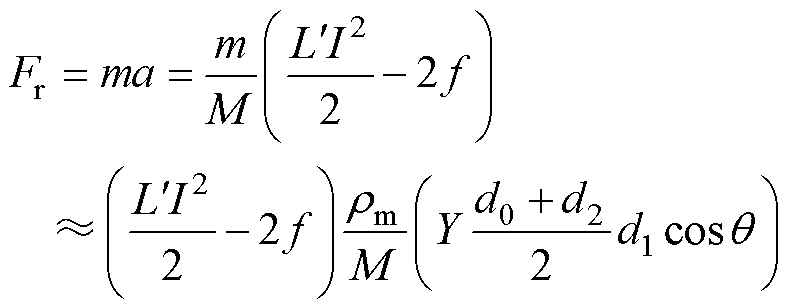 (20)
(20)
尾翼所受摩擦力为
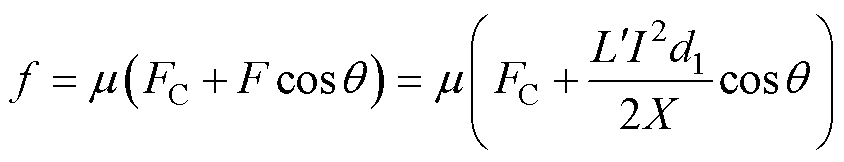 (21)
(21)
式中,FC为装配压力。联立式(19)~式(21)可得转角处拉力为
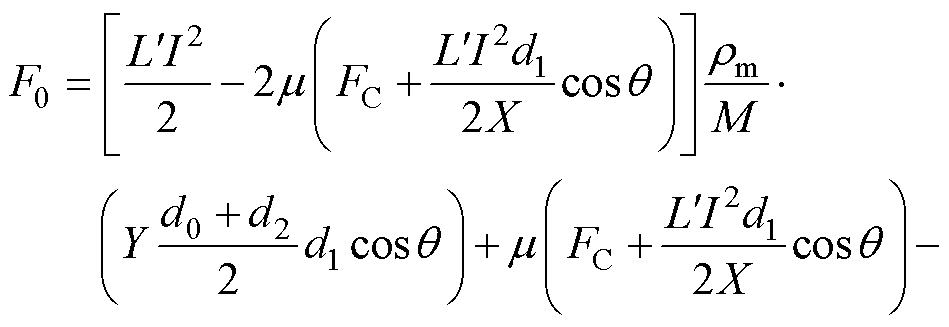
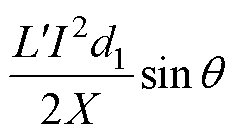 (22)
(22)
F0作用下电枢尾翼转角处的平均拉应力为
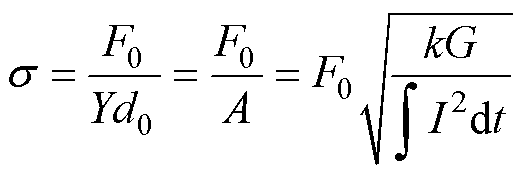 (23)
(23)
为保证电枢结构不被破坏,电枢尾翼受到的平均拉应力s 应小于电枢材料的固有抗拉强度s0以避免尾翼转角处损坏。而s0与温度T呈负相关,由式(18)可知,k值越大,电枢通流截面积的平均温升也越大,因此尾翼转角处的s0也与k呈负相关。k值较大时通流截面会发生熔化,此时尾翼转角处的s0较小。为避免尾翼转角发生损坏,s<s0(k)可等价于F0≤0,此时尾翼转角处温度很高,装配压力FC可以忽略,于是转角处的拉力可简化为
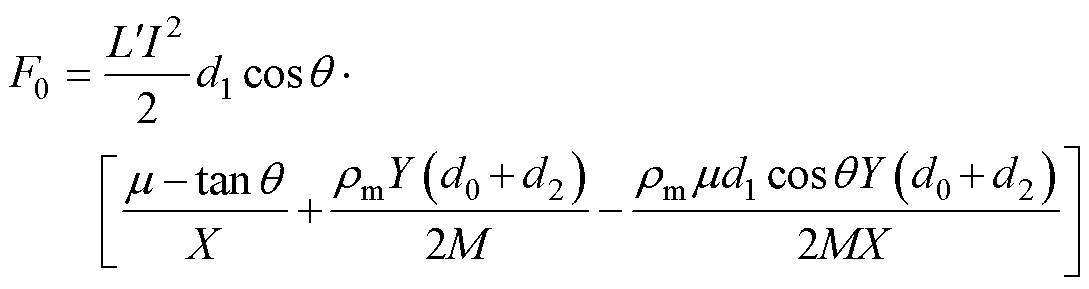 (24)
(24)
由式(24)可知,F0≤0等价于
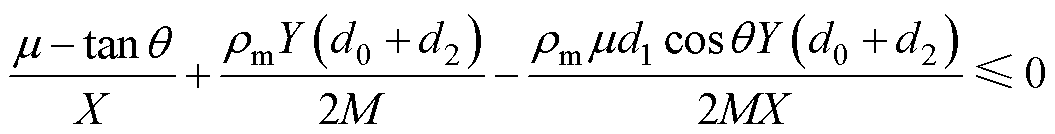 (25)
(25)
式(25)可进一步等价于
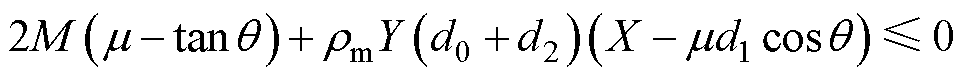 (26)
(26)
由于2d0<d1,式(26)可进一步等价于
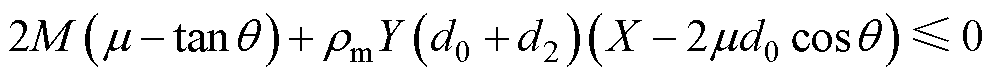 (27)
(27)
由电枢几何关系可知X>2d0cosq,于是有
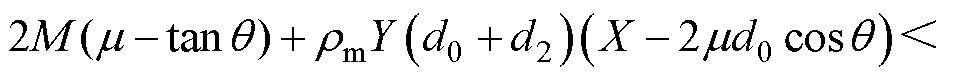
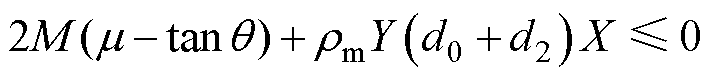 (28)
(28)
由于通流面积A=Yd0,于是有
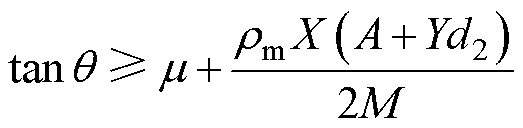 (29)
(29)
由发射速度v和电流积分的关系可得
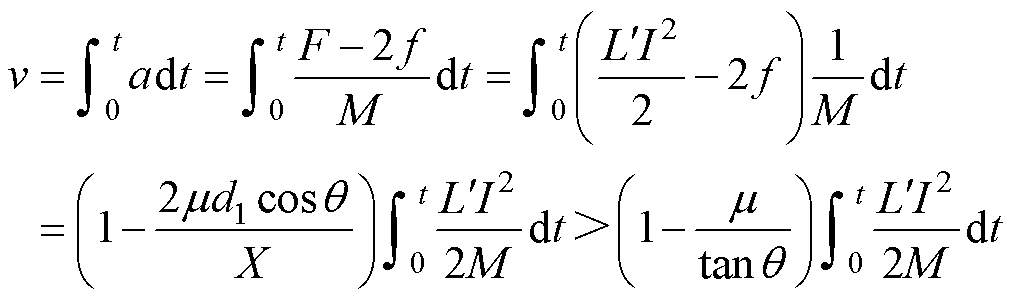 (30)
(30)
联立式(17)和式(30)可以得到
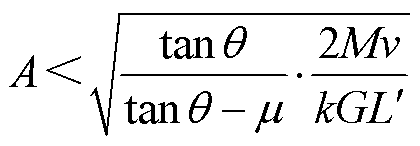 (31)
(31)
于是可以得到考虑电枢机械强度的尾翼倾角下限约束为
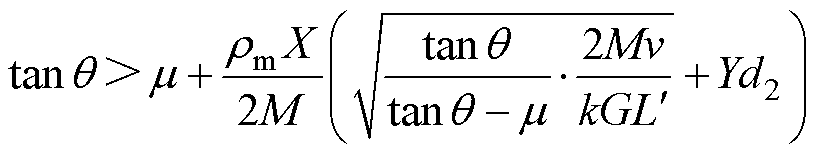 (32)
(32)
式(32)为尾翼倾角取值范围的隐式表达式,该式左侧为关于q 的增函数,右侧为关于q 的减函数,表明随着q 增大到某一值后,电枢机械强度约束可以被满足,该值即为考虑电枢机械强度约束的尾翼倾角极限取值。
与电枢受到的电磁推力相比,其摩擦力通常可以忽略不计,于是式(30)可以简化为
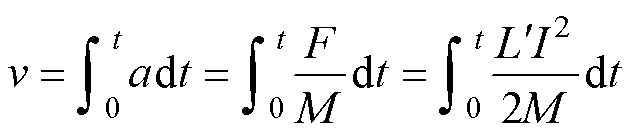 (33)
(33)
联立式(17)和式(33)可以得到
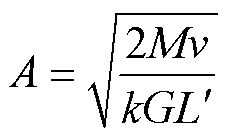 (34)
(34)
于是根据式(29)可以得到尾翼倾角取值范围的显式表达式为
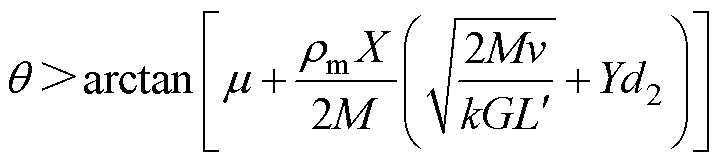 (35)
(35)
由式(32)和式(35)可知,在其他发射条件一致的前提下,载流裕度系数k会影响尾翼倾角的取值。下面以30 mm和90 mm口径电枢为例,依据式(32)和式(35)分别计算载流裕度系数k变化下,F0 =0时的电枢尾翼倾角q 的下临界值。取动摩擦系数m=0.1,电枢材料密度rm=2.7 g/cm3,发射速度v=2 500 m/s,熔化载流特征量G=20 000 (A/mm2)2∙s;30 mm口径电枢的发射质量M=150 g,炮膛高度Y= 30 mm,尾翼端部厚度d2=2.5 mm,电感梯度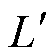 = 0.433 mH/m;90 mm口径电枢的发射质量M=5 kg,炮膛高度Y=90 mm,尾翼端部厚度d2=6 mm,电感梯度
= 0.433 mH/m;90 mm口径电枢的发射质量M=5 kg,炮膛高度Y=90 mm,尾翼端部厚度d2=6 mm,电感梯度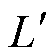 =0.491 mH/m。在载流裕度系数为0.7~0.9区间下电枢的尾翼倾角q 临界值曲线如图4所示。
=0.491 mH/m。在载流裕度系数为0.7~0.9区间下电枢的尾翼倾角q 临界值曲线如图4所示。
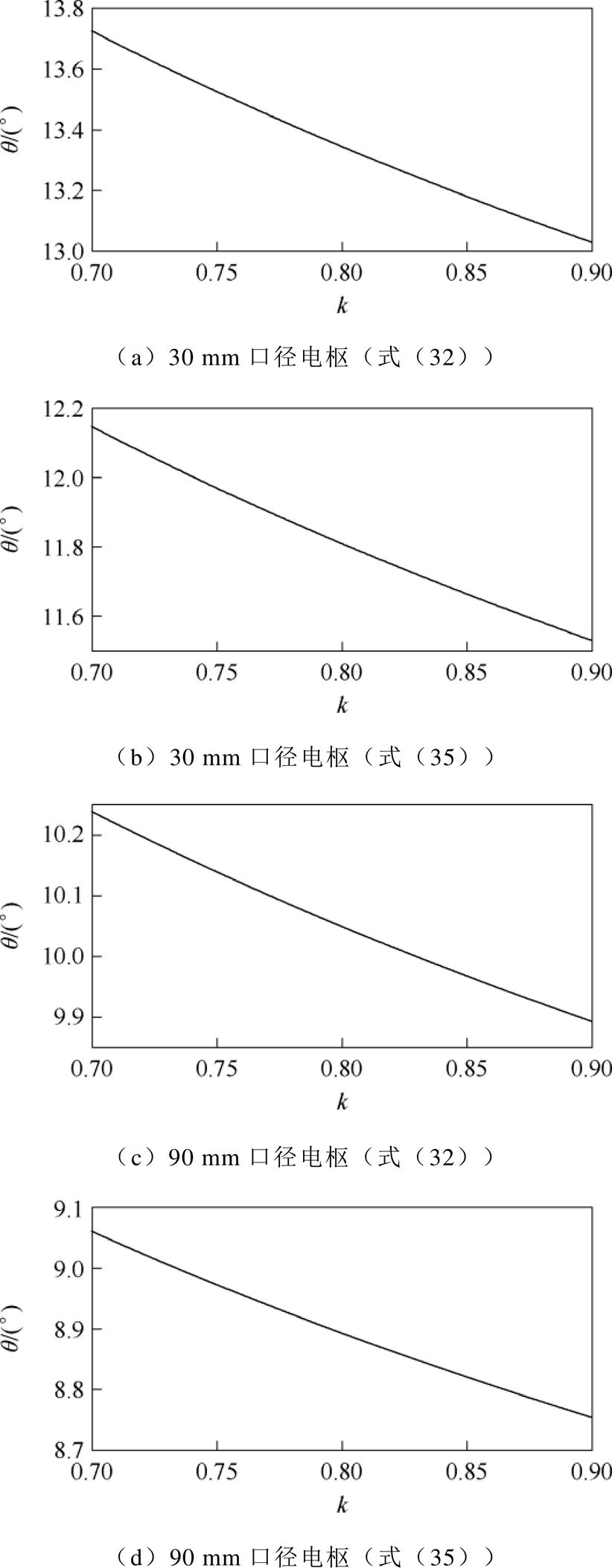
图4 电枢尾翼倾角的临界值与k的关系
Fig.4 Curve of critical values of armature tail inclination versus k
由图4可知,尾翼倾角q 的临界值随k的增大而减小,且由式(32)得到的尾翼倾角临界值大于式(35)的结果,二者存在约1°的差异。
综合本节和第1节的所有结果,若要同时满足枢轨间接触压力需求和电枢结构完整性约束,当k=0.7时,若考虑发射过程中枢轨摩擦力的影响,30 mm口径电枢的尾翼倾角q 的取值范围为14°≤q <30°,90 mm口径电枢的尾翼q 的取值范围为 11°≤q <30°;不考虑摩擦力时,30 mm口径电枢的尾翼倾角q 的取值范围为13°≤q <30°,90 mm口径电枢的尾翼倾角q 的取值范围为10°≤q <30°。
在实际发射过程中,发射器通入脉冲电流,由于瞬态趋肤效应和速度趋肤效应的影响,电流分布与假设不同。为进一步缩小电枢尾翼倾角的取值范围,使用2.2节中的几何参数,以30 mm口径电枢为例,在COMSOL中搭建有限元仿真模型进行模拟发射。根据文献[18]中对电枢的电热容量和质量的分析,0.7是k的合适取值。以k=0.7的电枢为例,根据式(31)取A的上限值可以得到d0和d1,进而确定电枢的形状。k=0.7时,发射器的1/4模型和模型的驱动电流波形如图5所示。驱动电流上升沿时间为0.5 ms,平顶期时间为1 ms,5.5 ms时电流下降为0,平顶期电流幅值为1 MA。
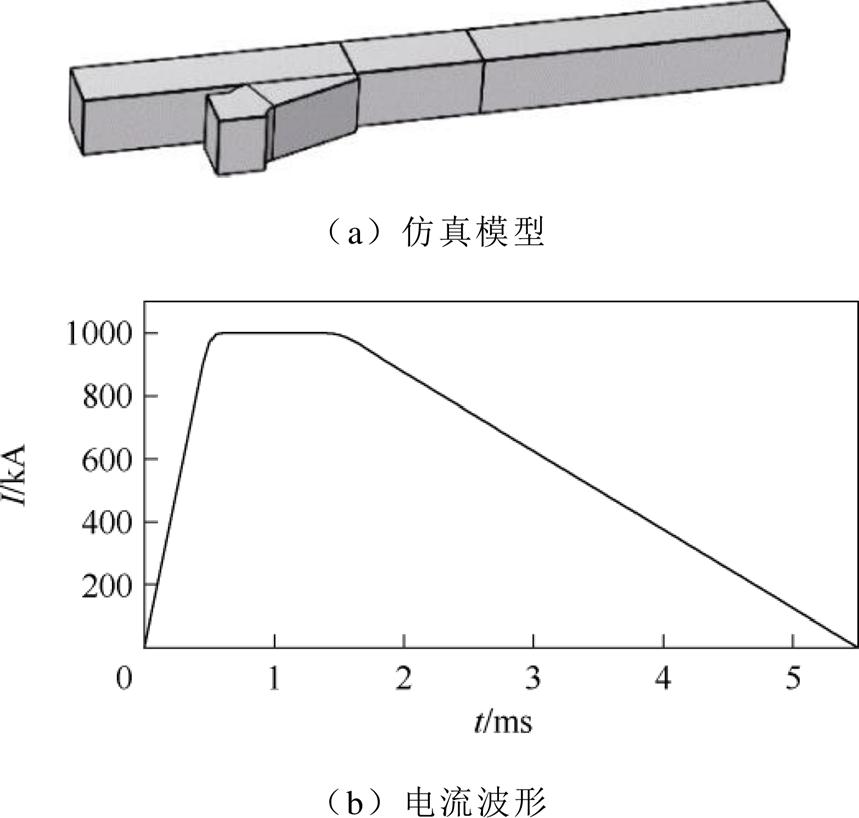
图5 仿真模型和发射器电流波形
Fig.5 Simulation model and current waveform of electromagnetic launcher
使用有限元仿真模型可以得到电枢在发射过程中受到的电磁力和摩擦力,进而根据式(30)计算得到不同尾翼倾角下电枢的速度。仿真计算得到的电枢速度位移曲线如图6所示。可以看出,相同时刻电枢的速度大小与q 呈正相关,q 越大,相同时刻下电枢的速度越大,电枢的出膛时刻越早。
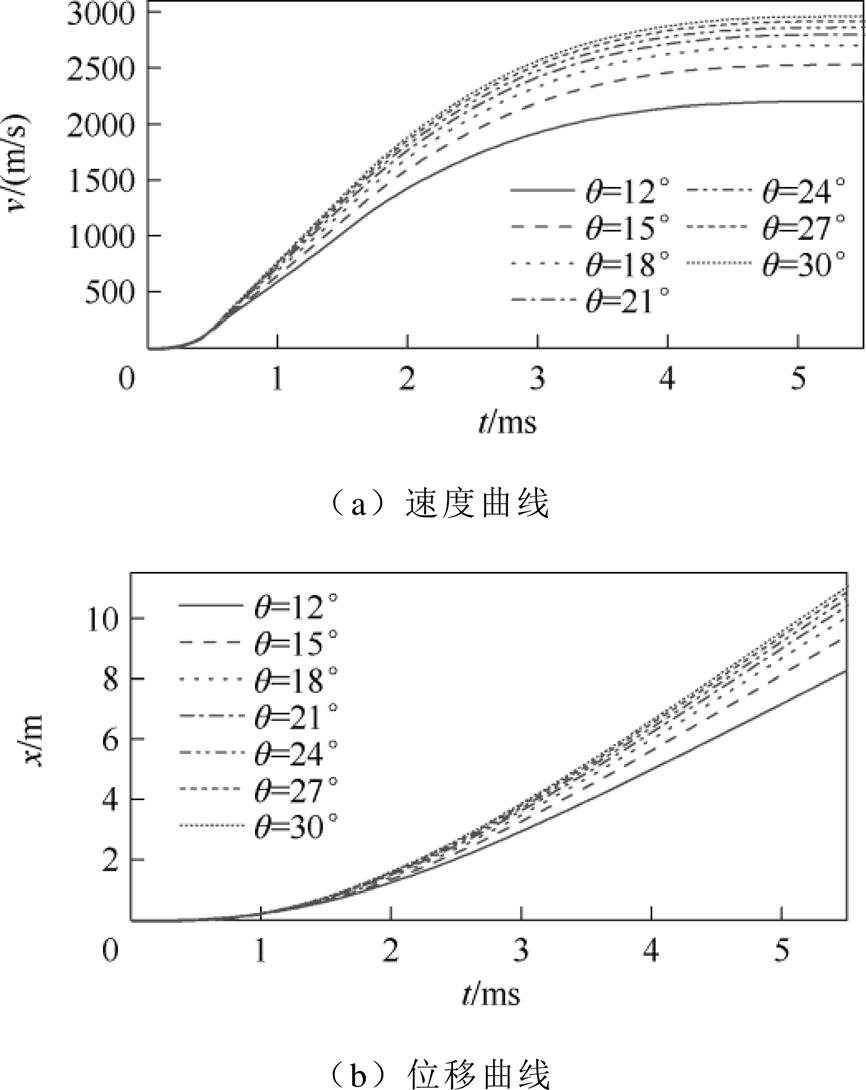
图6 不同q 下电枢的速度位移曲线
Fig.6 Velocity and displacement curves of the armature at different q
绘制发射所需轨道长度与q 的关系曲线如图7所示。可以看出,尾翼倾角q 越大,发射需要的轨道长度越短,30°时的轨道长度是15°时的63%,是20°时的83%,增大q 可以显著降低发射所需的轨道长度。
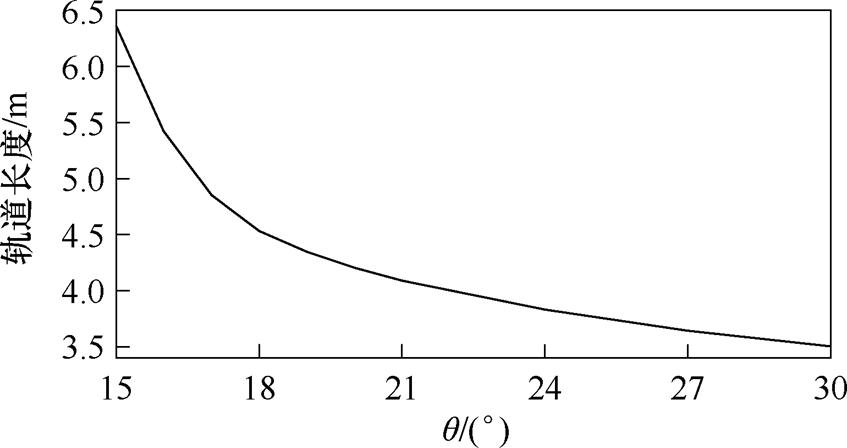
图7 发射所需轨道长度与q 的关系
Fig.7 Curve of the required rail length for launch versus q
根据第2节的分析结果,当头部对尾翼的拉力F0≤0时,电枢可以在发射过程中保证结构的完整性。根据此条件,由仿真计算的结果绘制尾翼对头部的推力与q 的关系如图8所示。可以看出,在尾翼不受头部拉力作用的情况下,发射过程中尾翼对头部的推力先增大后减小,然后再增大,最后减小到0。由受力曲线可以看出,当q >13°时,尾翼不再受到头部的拉力,此时电枢结构不会受到损坏。与图4b中k=0.7时的结果一致,此结果表明尾翼倾角约束范围的显式表达式(式(35))可以作为考虑电枢结构完整性约束下尾翼倾角取值范围的估算 方法。
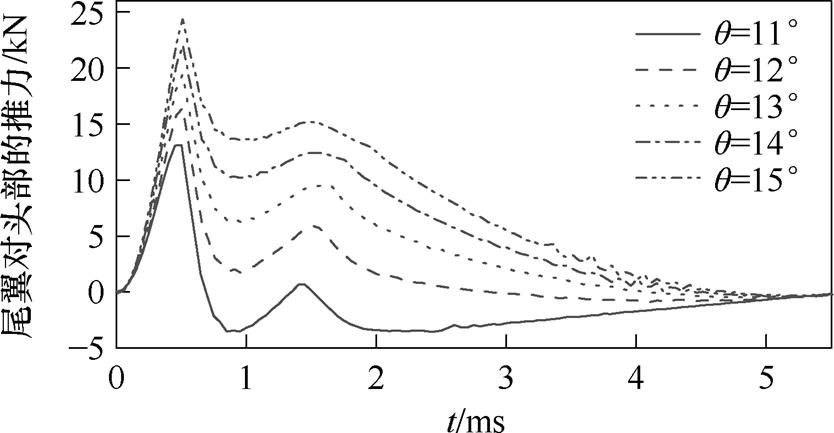
图8 尾翼对头部的推力与q 的关系
Fig.8 Tail thrust on the head versus q
为分析尾翼对头部的推力曲线变化的原因,以15°电枢尾翼为例,其在发射过程中受到的各种力如图9所示。由图9可以看出,尾翼对头部的推力如此变化的原因在于随着电流进入平顶期,电流在瞬态趋肤效应和速度趋肤效应的共同作用下由电枢表面向电枢内部扩散,尾翼受到的电磁推力先迅速下降然后趋于平稳,与持续下降的摩擦力和几乎不变的尾翼加速力共同作用,形成了第一个波谷;后续由于摩擦力仍迅速减小而尾翼受到的电磁推力几乎保持不变,造成了尾翼对头部的推力曲线的回升,摩擦力的迅速减小也解释了式(35)比式(32)的结果更接近仿真结果的原因;电流进入下降沿后尾翼受到的电磁力下降至0。
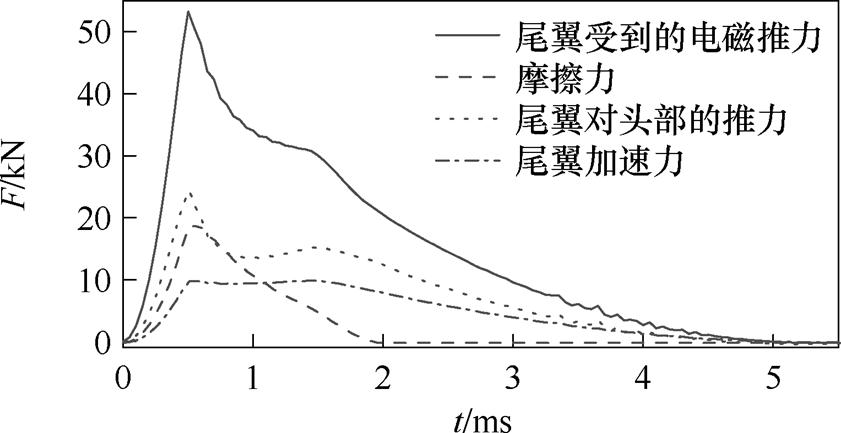
图9 尾翼在发射过程中受到的各种力
Fig.9 Various forces on the tail during the launch process
在尾翼对头部的推力的分析中可以发现,尾翼受到的摩擦力迅速减小,直到摩擦力降低为0,这意味着枢轨界面在发射过程中失接触。为分析尾翼倾角与1 g/A的接触压力需求下枢轨接触压力裕度的关系,绘制不同q 下的接触压力裕度曲线如图10所示。对比电枢的出膛时刻可以看出,当尾翼倾角小于20°时,枢轨接触压力裕度曲线的零点在电枢出膛时刻前,该结果表示当尾翼倾角小于20°时,无法在发射过程的后半段中保证枢轨间的良好电接触。
仿真分析结果表明,在同时考虑电枢结构完整性和保证发射过程后半段枢轨接触压力需求的条件下,当k=0.7时,电枢尾翼倾角最小值为20°,与理论分析的结果存在差异。其原因在于理论分析无法考虑电流波形导致的电磁场和电流分布的动态变化,而在电流下降沿由于瞬态趋肤效应和速度趋肤效应的影响,尾翼受到的横向电磁力反向,造成电枢与轨道失接触。但在实际发射过程中,下降沿阶段电枢已经拥有很高的速度,尾翼磨损严重,在电磁力的作用下电枢结构变形造成尾翼倾角增大,导致实际接触压力比仿真计算中更大;在电枢材料软化且存在液体铝自润滑的条件下,枢轨间的接触压力需求尚不明确,可能小于1 g/A,因此虽然式(35)得到的结果无法在电流下降沿满足假设的接触压力裕度,也可以作为电枢设计时的参考。在相同发射速度下,尾翼倾角越大,需要的轨道长度越小,30°时的轨道长度是20°时的83%,增大q 可以显著缩小发射所需轨道长度。
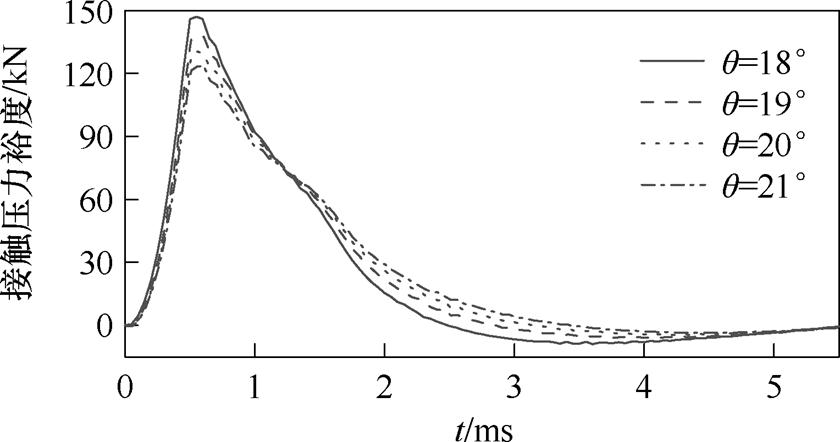
图10 发射过程中的接触压力裕度
Fig.10 Contact pressure margins during the launch
本文从实现电枢基本功能和保证发射过程中电枢结构完整性的角度出发,针对电枢尾翼倾角的取值范围进行了理论和仿真研究,取得了如下结果:
1)基于电枢机械强度约束得到了电枢尾翼倾角临界值的估算方法,获得了尾翼倾角随载流裕度系数k变化的显式和隐式表达式,并在仿真计算中验证了显式表达式的结果更加合理。显式表达式的结果显示,在k为0.7~0.9的区间内,临界值随着k的减小而增大。当k取值为0.7时,30 mm口径发射器中q 应不小于13°,90 mm口径发射器中q 应不小于10°。
2)电枢尾翼结构参数影响电枢/轨道的电磁接触压力,若要保证在发射过程的后半段中枢轨界面具有足够的接触压力,k=0.7时,30 mm口径电枢的尾翼倾角取值范围为20°<q <30°。当满足枢轨接触压力需求后,尾翼倾角的取值可以满足电枢机械强度的约束,此时电枢尾翼在发射过程中不会断裂。
3)在驱动电流波形和额定发射速度均相同的条件下,尾翼倾角越大的电枢出膛时刻越早,需要的轨道长度越小,30°时需要的轨道长度是20°时的83%,增大q 可以显著缩小发射所需轨道长度。但出膛时刻过早会导致发射器截流水平过高,造成电弧烧蚀,可以通过降低驱动电流幅值来缓解该问题。
参考文献
[1] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3943-3959.
Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3943-3959.
[2] 鲁军勇, 柳应全. 电磁发射用直线电机及其控制技术综述[J]. 电工技术学报, 2024, 39(19): 5899- 5913.
Lu Junyong, Liu Yingquan. Review on linear motor for electromagnetic launch and its control tech- nology[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5899-5913.
[3] 胡鑫凯, 鲁军勇, 李白, 等. 瞬态条件下电磁轨道发射装置绝缘体热损伤分析[J]. 电工技术学报, 2023, 38(21): 5673-5681.
Hu Xinkai, Lu Junyong, Li Bai, et al. Thermal damage analysis of insulator in electromagnetic rail launcher under transient conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5673-5681.
[4] McNa I R, Crawford M T, Satapathy S S, et al. IAT armature development[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 442-451.
[5] Haugh D C, Hainsworth G M G. Why “C” armatures work (and why they don’t!)[J]. IEEE Transactions on Magnetics, 2003, 39(1): 52-55.
[6] 肖铮, 陈立学, 夏胜国, 等. 电磁发射用一体化C形电枢的结构设计[J]. 高电压技术, 2010, 36(7): 1809-1814.
Xiao Zheng, Chen Lixue, Xia Shengguo, et al. Geometry design of monolithic C-shaped armature for EML system[J]. High Voltage Engineering, 2010, 36(7): 1809-1814.
[7] Chen Lixue, He Junjia, Xia Shengguo, et al. Some key parameters of monolithic C-type armature in rectangular caliber railgun[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1465-1469.
[8] Tian Wen, Zhao Weikang, Li Guochao, et al. Effects of launch mass on sliding electrical contact[J]. IEEE Transactions on Plasma Science, 2022, 50(7): 2263- 2269.
[9] Li Chengxian, Chen Lixue, Xu Jinghan, et al. Influence of caliber height on armature current melt erosion in rail gun[J]. IEEE Transactions on Plasma Science, 2020, 48(8): 2932-2938.
[10] Kim B K, Hsieh K T. Effect of rail/armature geometry on current density distribution and inductance gradient[J]. IEEE Transactions on Magnetics, 1999, 35(1): 413-416.
[11] Goyal G, Khatait J P, Mukherjee S. Design and analysis of hybrid armature for electromagnetic launch technology[J]. IEEE Transactions on Plasma Science, 2022, 50(10): 3468-3472.
[12] 刘志明, 孙江生, 王莹. 轨道炮固体电枢的设计[J]. 华北工学院测试技术学报, 2000, 14(3): 158-162.
Liu Zhiming, Sun Jiangsheng, Wang Ying. Design of a solid armature in a railgun[J]. Journal of Test and Measurement Technology, 2000, 14(3): 158-162.
[13] Chen Lixue, He Junjia, Xia Shengguo, et al. Study on tail structural parameters of monolithic C-type armature based on analysis of mechanical pre-contact pressure in non-equal-cross-section cantilever model[C]// 2012 16th International Symposium on Electro- magnetic Launch Technology, Beijing, China, 2012: 1-5.
[14] 彭晓婷, 马瑞, 李刚, 等. 基于响应面法的轨道炮C型电枢结构优化设计[J]. 弹道学报, 2014, 26(4): 102-106.
Peng Xiaoting, Ma Rui, Li Gang, et al. Structural optimization for C-shaped armature in rail gun based on response surface method[J]. Journal of Ballistics, 2014, 26(4): 102-106.
[15] 李白, 鲁军勇, 谭赛, 等. 多因素作用下的C形固体电枢优化设计方法[J]. 高电压技术, 2016, 42(9): 2870-2875.
Li Bai, Lu Junyong, Tan Sai, et al. Optimal method under the effect of multi-factor for C-shaped solid armature[J]. High Voltage Engineering, 2016, 42(9): 2870-2875.
[16] 刘勇, 国伟, 张涛, 等. 基于补偿法的电枢臂优化设计研究[J]. 高电压技术, 2019, 45(11): 3743-3750.
Liu Yong, Guo Wei, Zhang Tao, et al. Optimization design of armature’s arm based on compensation method[J]. High Voltage Engineering, 2019, 45(11): 3743-3750.
[17] (美) Marshall R A, 王莹. 电磁轨道炮的科学与技术[M]. 曹延杰, 译. 北京: 兵器工业出版社, 2006.
[18] Chen Lixue, He Junjia, Xia Shengguo, et al. Some key parameters for rectangular caliber railgun system[J]. IEEE Transactions on Plasma Science, 2013, 41(5): 1493-1497.
Abstract Electromagnetic rail launch has the advantages of short launching time, fast launching speed, safety and reliability. Compared with traditional launching method, it has high current density and high relative motion speed, which is in a kind of extreme working condition. As the carrier of converting electric energy into kinetic energy, the working condition of the armature will be directly related to the working condition of the launcher. Compared with other solid armatures, one-piece C-shaped armature has a simple structure and is equipped with a functionally appropriate structure. On one hand, the tail can provide contact pressure, which ensures the electrical contact between the armature/rail; on the other hand, the armature tail inclination increases the friction between the armature and the rail to impede the armature motion, which in turn affects the armature motion characteristics, and in order to prevent the armature tail from fracturing, the tail inclination is also subjected to the armature mechanical strength. Therefore, selecting appropriate structural parameters of the armature tail in different launch scenarios is important to ensure the structural integrity of the armature, ensure the armature/rail electrical contact, and obtain a high launch speed. This article taken the straight armature as an example to study the value range of the tail inclination angle of the C-type armature: First, the lower limit of the value of the tail inclination was obtained based on the principle of armature acceleration, and the upper limit of the range was obtained based on the armature rail contact pressure requirement and the relationship between inclination and contact pressure; Secondly, the force analysis is carried out at the corner of the tail, and under the condition of ensuring that the tail will not break in the launching process, the implicit and explicit expressions of the values of the tail inclination are obtained according to whether the friction force in the launching process is neglected, and their results are compared to determine the range of values of the tail inclination under different current-carrying margin coefficients; Thirdly, the effects of the values of the tail inclination on the launch speed and rail length were obtained by the finite element simulation model, and the tail force curves and contact pressure margin curves were obtained for different values of the inclination. The following results were obtained: The critical value of the tail inclination decreases with the increase of current carrying margin factor in the interval 0.7~0.9, and tail inclination is not less than 13° in 30 mm caliber launcher, and is not less than 10° in 90 mm caliber launcher; To fully ensure the contact pressure demand during launch, the value of inclination ranges from 20° to 30°, at this time, the armature tail will not break during the launching process; At the same drive current waveform and the rated launch speed, the armature with a larger tail inclination is discharged earlier, and the required rail length is smaller. The rail length at 30° is 83% of that at 20°, and increasing the tail inclination significantly reduces the required rail length for launching.
Keywords:Electromagnetic rail launch, C-shaped armature, tail structure parameters, inclination
中图分类号:TJ866; TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.241440
国家自然科学基金资助项目(92266301)。
收稿日期 2024-08-13
改稿日期 2024-10-21
陈立学 男,1984年生,博士,教授,研究方向为脉冲功率、电磁发射、滑动电接触、开关电器。
E-mail: chenlixue@hust.edu.cn(通信作者)
任 烨 女,1997年生,硕士研究生,研究方向为电磁发射。
E-mail: 936439516@qq.com
(编辑 李 冰)