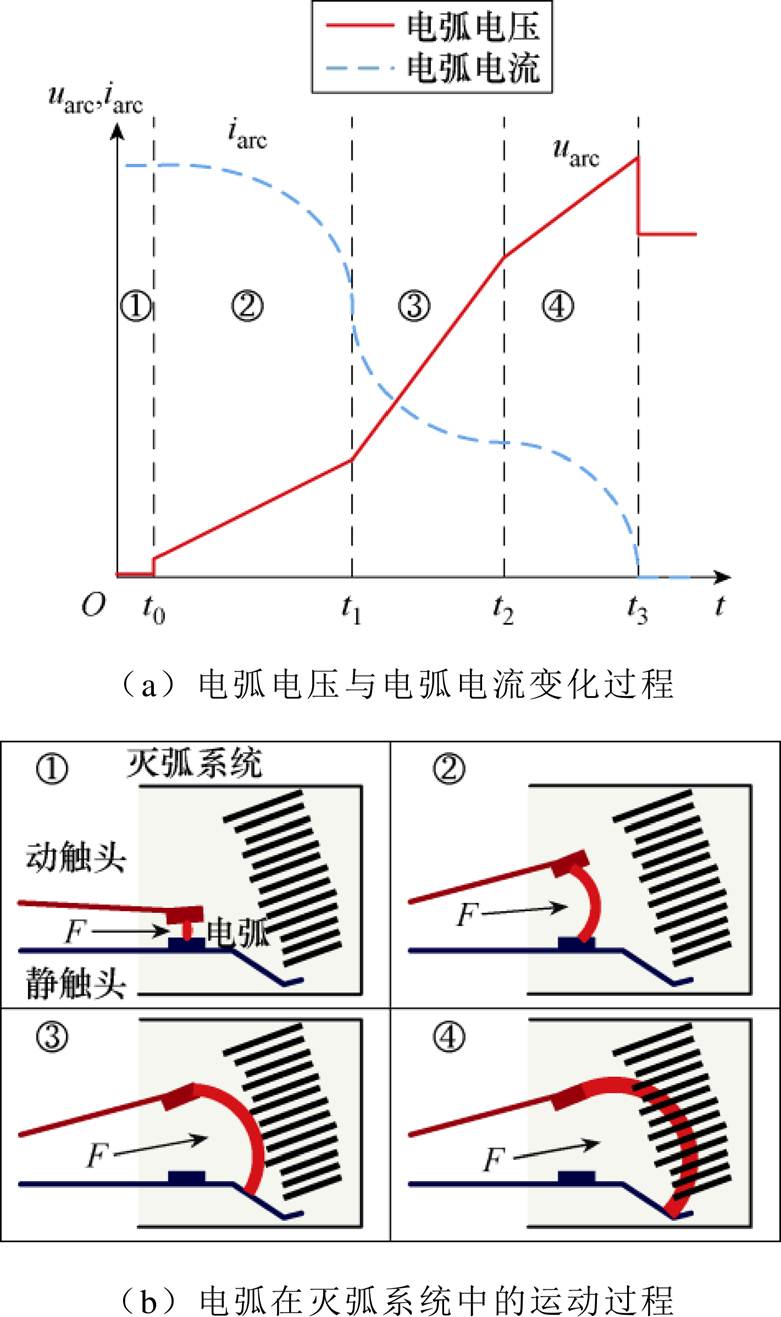
图1 直流电弧燃烧三个阶段示意图
Fig.1 The schematic diagram of three stages of direct current arc combustion
摘要 直流断路器是直流系统中的关键元件，其可靠性对电网的安全稳定运行至关重要。该文以直流断路器为研究对象，分析直流断路器的结构形式，研究直流电弧的物理特性和变化特征，提出直流电弧电压等效模拟方法；研究直流断路器电性能退化规律，采用燃弧能量来表征其电性能退化，提出基于电弧侵蚀的直流断路器剩余电寿命预测方法；建立基于性能退化的直流断路器剩余电寿命模型，开展电寿命实验研究，进行退化量的正态分布检验，基于实验数据进行剩余电寿命预测；建立基于Monte-Carlo法的电性能退化仿真模型，进行直流断路器电流开断过程仿真分析，基于仿真数据进行剩余电寿命预测。结果表明，基于电弧电压等效模拟方法的仿真结果与实验结果基本吻合，为直流断路器的可靠性仿真分析提供了依据。
关键词：直流断路器 电弧电压 触头电磨损 电性能退化 剩余电寿命
随着直流技术的广泛应用，直流系统的安全性和稳定性问题日益受到关注[1]。直流断路器作为直流系统中的核心保护设备，承担着防止短路、过载等故障对线路和设备造成损害的重要任务[2]，其可靠性至关重要。通过直流断路器性能退化分析，建立剩余寿命预测（Remaining Electrical Lifetime, REL）模型，是当前直流断路器可靠性研究的重要内容之一。
触头系统是直流断路器的核心，在服役过程中受到电弧侵蚀，是导致触头系统失效的重要因素[3-4]，通过电弧特性及触头磨损规律的研究，可以达到直流断路器电性能退化分析的目的。周学等[5]研究阻性和感性负载条件下的分断电弧特性，分析不同时间常数及分断电压等级对灭弧特性的影响机理。尹建宁等[6]建立了多并联接触系统模型，研究多个弧根之间的相互作用以及多个弧根运动特征，探究电弧运动过程中在极板接触处存在多个弧根的问题。吴翊等[7-9]对不同材料触头在不同气体介质的电弧烧蚀机理进行研究，实验电流范围为50～400 A，测量了触头质量损失，得到触头磨损变化规律。
在可靠性研究方面，学者们将研究重心从基于寿命数据的可靠性研究逐渐转为基于性能退化的可靠性研究上来。W. O. Meeker和C. J. Lu[10]最早引入了基于退化轨迹的方法，为基于性能退化的可靠性研究奠定了基础。翟国富等[11]基于时间序列理论，构建了一个以超程时间和吸合时间为双变量的寿命预测模型，相较于单变量模型更为准确。赵书涛 等[12]针对不同拓扑结构断路器，提出了一种评估其运行状态的方法，该方法通过Markov模型计算直流断路器状态转移概率，基于此得到直流断路器的可用率，并将其作为评估标准。段宇等[13]以交流接触器为研究对象，分析影响接触器电性能退化的主要因素，将累积燃弧能量作为性能退化量，并采用分段累计的方法，使其服从正态分布以满足Wiener过程。赵成晨等[14]将触头质量损失与三种燃弧特征量建立联系，研究交流断路器电性能退化过程，建立剩余寿命预测模型，在恒应力和变应力条件下验证模型的正确性。何志鹏等[15]通过从微型断路器性能退化过程中提取新的退化量，即电压跌落时刻与起弧时刻的时间差，验证了退化量随断路器动作次数的增加而逐渐变大，为微型断路器的电寿命预测提供理论支撑。
目前，不少学者针对开关电器电弧特性及触头磨损机理进行了许多研究，但对直流断路器电性能退化和剩余电寿命方面的研究还比较少。本文从电弧特性出发，开展直流断路器电性能退化研究。分析触头系统电弧电压变化特征，提出电弧电压等效模拟方法，建立直流断路器电性能退化模型，通过触头系统性能退化实验和仿真分析，实现直流断路器剩余电寿命预测。
一般情况下，直流断路器的燃烧过程可分为三个阶段：电弧拉长阶段、电弧运动阶段、电弧熄灭阶段[6]，其过程如图1所示。图中①代表起弧前的电压电流变化，②、③、④分别对应上述三个阶段。
图1 直流电弧燃烧三个阶段示意图
Fig.1 The schematic diagram of three stages of direct current arc combustion
触头分离前，电弧电压基本为0，此时尚未产生电弧，当触头两端出现电压，超过触头材料的最小起弧电压时，在触头间隙产生电弧，如图1a中的t0时刻，此时电弧电压为近极压降；电弧产生后的第一阶段为电弧拉长阶段，如图1a中的t0～t1时刻，电弧在洛伦兹力F作用下，向灭弧栅片移动，且弧根基本没有运动，电弧弯曲拉长，同时触头开距近似线性增加，电弧电压呈线性增长，电弧电压上升速率与电弧长度成正比；第二阶段为电弧运动阶段，如图1a中的t1～t2时刻，动触头完全打开，电弧在洛伦兹力作用下沿跑弧道快速移动，开始进入灭弧室，并被栅片切割，耗散功率也显著增加，电弧电压快速上升，电弧电流快速下降；第三阶段为电弧熄灭阶段，如图1a中的t2～t3时刻，当电弧完全进入灭弧室后，电弧与栅片完全接触，电弧电压增加速率变慢，由于电流下降使电弧电压继续上升，当电流接近0时，电弧电压达到最大，电弧完全熄灭。
根据图1b定义单次分断的燃弧时间tarc为
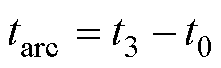（1）
由上述分析得，电弧电压在不同阶段存在不同的表现形式，具有一个起始点及两个分段点。起始点对应电弧产生的图1a中的t0时刻，电弧电压由近极材料决定；分段点1对应图1a中的t1时刻，电弧拉长并即将接触灭弧栅片，此时达到最大开距，电弧长度与触头灭弧系统的结构有关，其对应的电弧电压可认为恒定。分段点2对应图1a中的t2时刻，此时电弧完全进入灭弧室，对于栅片的利用率达到最大，切割的短弧数相同，故可认为该时刻的电弧电压不变。不同燃弧阶段的分段点受直流断路器结构、类型、灭弧系统、触头材料等因素的影响，但燃弧变化趋势相似，可通过分析不同动作次数下的电弧电压变化数据确定不同燃弧阶段的起始点及分段点电压值。
以某型号2极直流断路器展开可靠性研究，每极一个断口。其中一极触头称为触头1，另一极触头称为触头2。触头1、触头2的电弧电压及电弧电流典型波形如图2所示。由图2可知，0.2 ms时，触头开始分离，电弧产生。在0.2～4.1 ms和0.2～4.9 ms时间段内，触头1和触头2的电弧电压均保持在相对较低的水平，并随着触头间距的逐渐增大而匀速上升；电弧电流从分闸时刻的电流初始值开始下降，与图1a的t0～t1时刻对应，此时为电弧燃烧的第一阶段。随着触头的进一步分离，电弧被逐渐拉长。在4.1 ms时刻，触头1和触头2的开距达到最大，触头1进入第二阶段，在随后的4.1～4.9 ms，触头2出现平台，此时电弧长度基本不变。在4.9 ms后，触头2进入第二阶段，此时电弧逐渐接触灭弧栅片并逐渐进入灭弧室，与图1a的t1～t2时刻对应。触头1和触头2的电弧电压分别在随后的4.1～7.3 ms和4.9～7.9 ms时间段内上升速度更快。之后电弧电压继续上升，与图1a的t2～t3时刻对应，即第三阶段。最终，在8.3 ms时刻，电弧电流降至0，标志着电弧的完全熄灭。实际燃弧波形中电弧电压的变化过程存在三个阶段，与1.1节的理论分析一致。
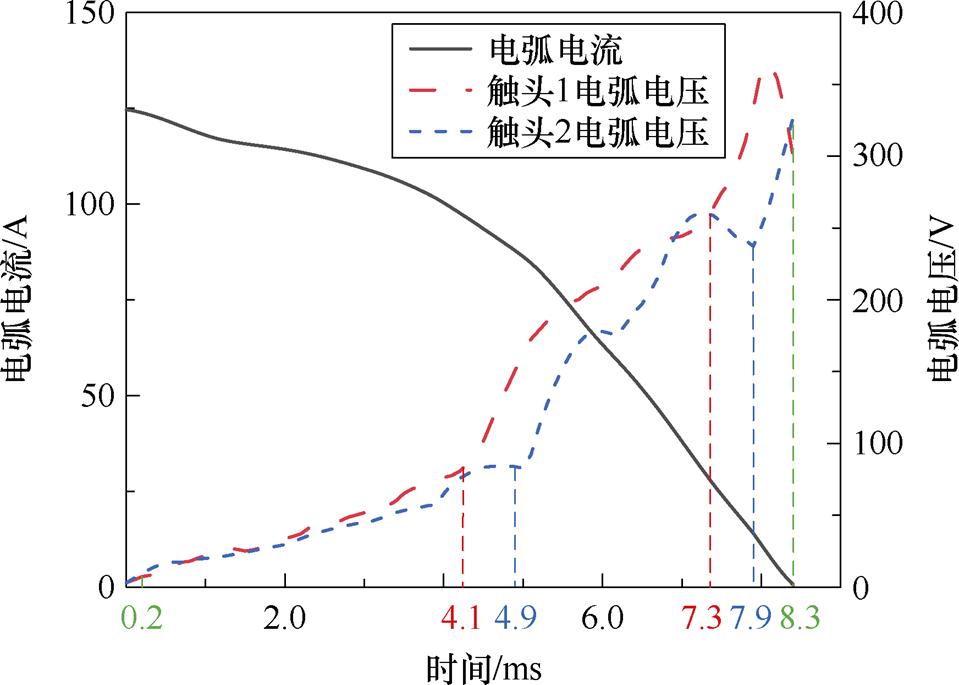
图2 触头1、触头2电弧电压及电弧电流典型波形
Fig.2 Typical waveforms of arc voltage and arc current of contact 1 and contact 2
准确描述电弧电压变化比较困难，可以根据电弧电压变化过程将其分为弧压变化率恒定不变和分段变化，如图3所示，其基本原则是：电弧电压与时间的关系曲线所围成的面积保持恒定，即电弧电压平均值不变。在此基础上将其分为弧压变化率恒定及弧压变化率分段恒定两种情况。
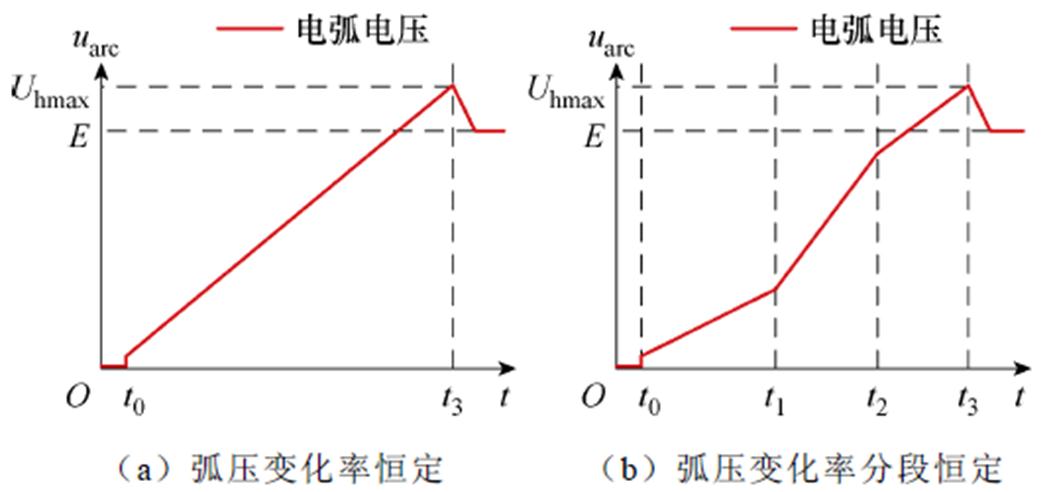
图3 电弧电压等效模拟方法
Fig.3 Equivalent simulation method of arc voltage
（1）弧压变化率恒定。电弧电压与电弧长度相关，在开断过程中，电弧不断被拉长，电弧电压也随之增加，如果灭弧室简单，电弧长度逐渐增加，电弧电压与长度有关，可以认为弧压变化率为定值，从起弧到熄弧整个过程将电弧电压线性化，电弧电压与横轴形成的面积与实际相等。
（2）弧压变化率分段恒定。如果灭弧室结构形式复杂，有灭弧栅片，在不同阶段电弧不仅长度增加，而且在灭弧室内不同区域（如电弧进入灭弧栅片前、后），电弧电压的变化有明显差异，因此依据电弧拉长、电弧位置、电弧电流变化情况，可以将直流电弧分为多个阶段，不同阶段弧压变化率不同，相同阶段电弧电压线性变化，不同阶段电弧电压与时间的关系曲线所围成的面积保持恒定，与实际值相等。
另外，即使灭弧室结构形式复杂，为简化计算，也可以假设弧压变化率恒定，但此时应保持简化后的电弧电流与实际变化波形相近。考虑到每次开断电弧电压变化的随机性，更好地模拟出电弧电流的实际变化，可以采用随机分布来描述弧压变化率与燃弧时间的随机性。
（1）弧压变化率恒定。对于2极直流断路器来说，接直流电源后，一对触头接电源的正极，另一对触头接电源负极，由于极性效应，造成两对触头的弧压变化及燃弧时间不同，在弧压变化率恒定下，其电弧电压Uhv为
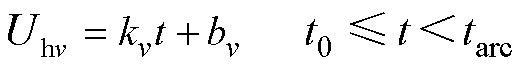（2）
式中，kv为触头v的弧压变化率，v=1, 2；bv为触头v电弧电压的初始值，即该类型直流断路器的起弧电压。
对简单直流电路列KVL方程，可以得到电流与电弧电压的关系为
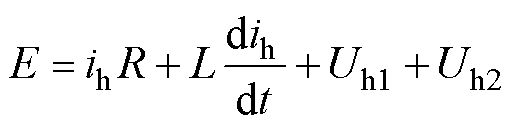
（3）
式中，E为电源电压；ih为电弧电流；R为电路中电阻；L为电路中的电感。
将Uh1和Uh2代入式（3），得到电弧电流ih为
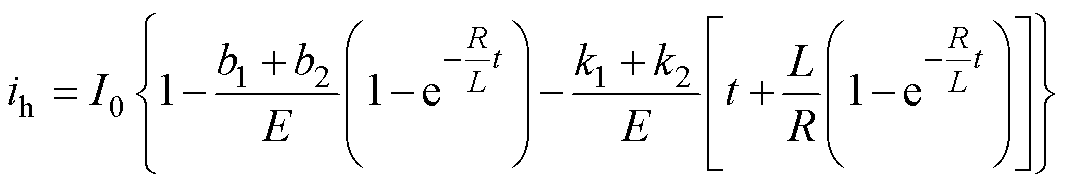（4）
式中，I0为断路器分闸时刻的电流初始值。
（2）弧压变化率分段恒定。根据弧压变化率分段恒定的假设可写出电弧电压Uhv的函数表达式为
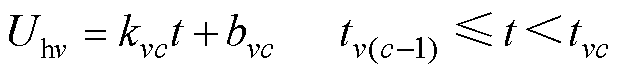（5）
式中，kvc为触头v第c阶段的弧压变化率；bvc为触头v第c阶段电弧电压的截距，可通过其求解对应分段点的电弧电压；tvc为触头v第c阶段的燃弧时间。
考虑到实际开断过程中两个灭弧室内电弧的运动速度存在差异，为使模拟电流变化与实际电流变化更接近，将电弧电流的变化过程分为图4所示的六个阶段，并认为各阶段终止点与下一阶段起始点重合。
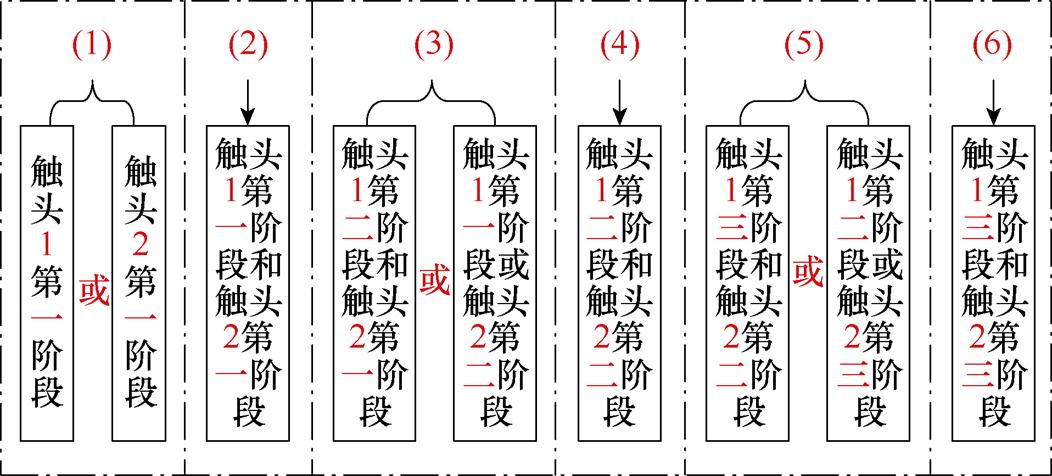
图4 直流电弧电压对电弧电流的影响阶段
Fig.4 The influence stage of DC arc voltage on arc current
将不同阶段Uhv代入式（4），可求解阶段d的电弧电流ihd为
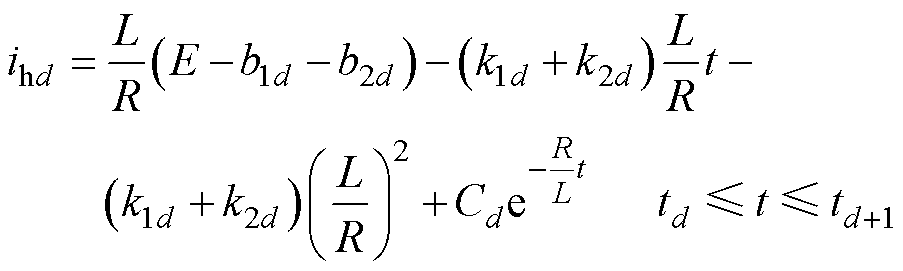（6）
式中，td为电弧电流d阶段的初始时刻。电弧电流不能发生突变，故可通过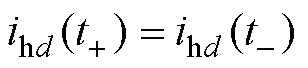
求解常数项Cd的数值解。kvd和bvd可通过阶段d的电弧电流判定，在不同阶段代入不同弧压变化率参数值，实现电弧电压等效模拟。
直流断路器的触头质量损失可通过电弧电压、电弧电流、燃弧时间等参数表征[8, 14]。单次分断的触头电磨损为
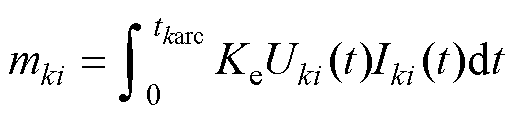（7）
式中，下标k表示不同的触头；下标i表示不同分闸操作；mki为触头质量损失；Uki(t)为电弧电压；Iki(t)为电弧电流；tkarc为燃弧时间；Ke为电弧侵蚀因子，反映触头质量损失与燃弧能量的关系。
单次分断过程中燃弧能量和电弧电压、电弧电流、燃弧时间的函数关系为
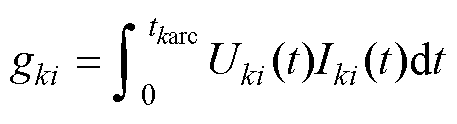（8）
式中，gki为触头k执行第i次分闸操作时的触头燃弧能量。单次分断的触头质量损失与燃弧能量的关系为
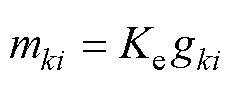（9）
多次操作后的触头累积质量损失为
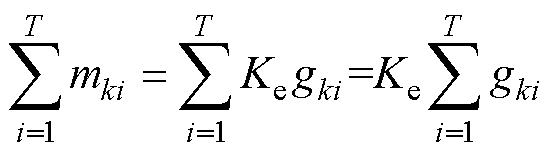
（10）
式中，T为直流断路器执行分闸操作次数。
2.1.1 直流断路器电性能退化过程
利用式（7）计算直流断路器每次开断的触头质量损失，并对触头质量损失进行分段累积。根据中心极限定理，分段累积的触头质量损失服从正态分布。每段的累积质量损失为
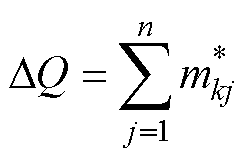
（11）
式中，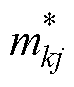
为第j段的累积质量损失。
令m=nm*，s2=ns*2，其中m、s分别为漂移参数、扩散参数，m*、s*分别为每段质量损失对应的漂移参数、扩散参数。使得直流断路器的电性能退化过程可以被描述为一个Wiener过程，则电性能退化规律可表示为
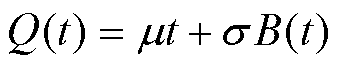（12）
式中，Q(t)为触头累积质量损失，Q(t)～N(mt, s2t)，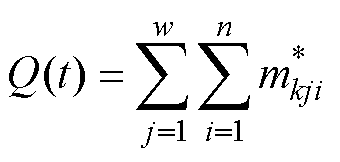
；将直流断路器电寿命平均分为w段，
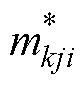为触头k每j段每i次分断操作的质量损失；B(t)为标准布朗运动。
2.1.2 直流断路器剩余电寿命预测方法
直流断路器的电寿命T可定义[15]为
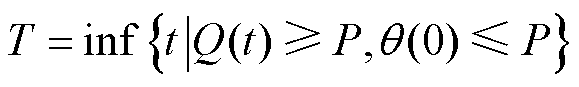（13）
式中，P为失效阈值。
平均电寿命E(T)为
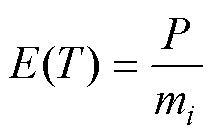（14）
式中，mi为触头质量损失。
Wiener过程首次达到某个特定点的时间分布服从逆高斯分布[6]，可计算出T的概率密度函数和可靠度函数，有
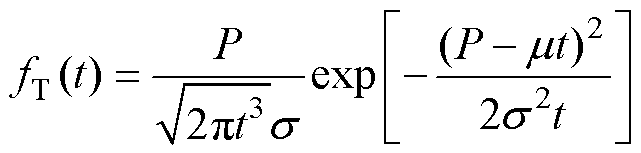（15）
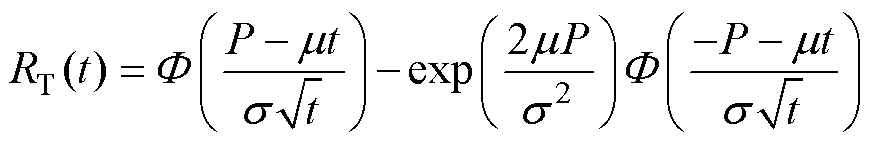（16）
直流断路器服役过程中需要考虑某一时刻T0时的剩余电寿命，根据此时触头累积质量损失P0，其REL可通过式（17）得到。
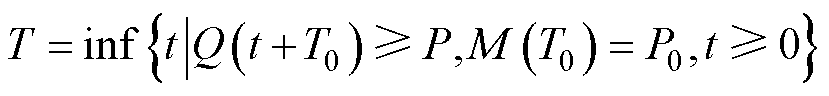（17）
直流断路器的电性能退化过程符合一元线性Wiener过程，在任意时刻T0的剩余电寿命REL，只与当前性能状态和失效阈值有关，与历史退化轨迹无关，将式（15）和式（16）中的失效阈值替换为当前状态的失效阈值P-P0即可。可计算出T0时刻REL的概率密度函数和可靠度函数分别为
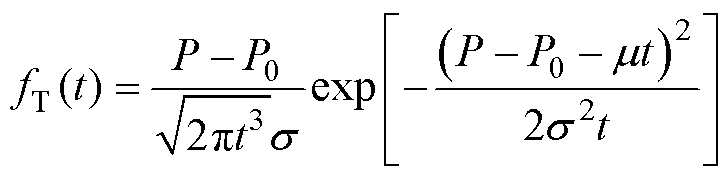（18）
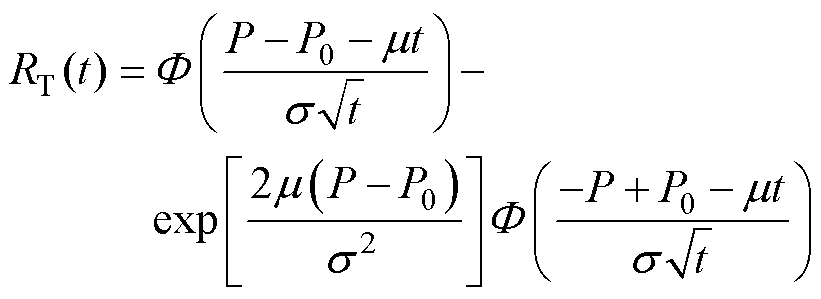（19）
REL的期望值为
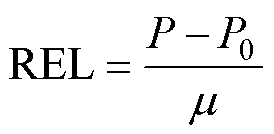（20）
利用直流断路器的性能退化数据，构建包含失效阈值P、漂移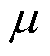参数
和扩散参数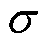
的似然函数，求解模型参数的最优估计值，有
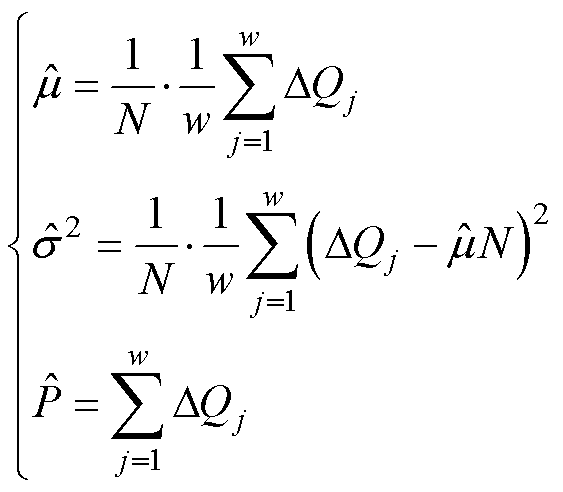（21）
式中，N为每段的断路器分合闸次数；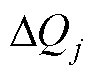
为第j段的累积退化量。同一批次产品具有相同的设计、规格、生产条件和工艺，同时在厂家的质量把控下，可认定同一批次直流断路器失效阈值P相同。收集同一批次产品的实验数据，利用统计分析和数据处理方法得到该批次直流断路器的失效阈值，在此基础上进行直流断路器剩余电寿命预测。预测过程如图5所示。
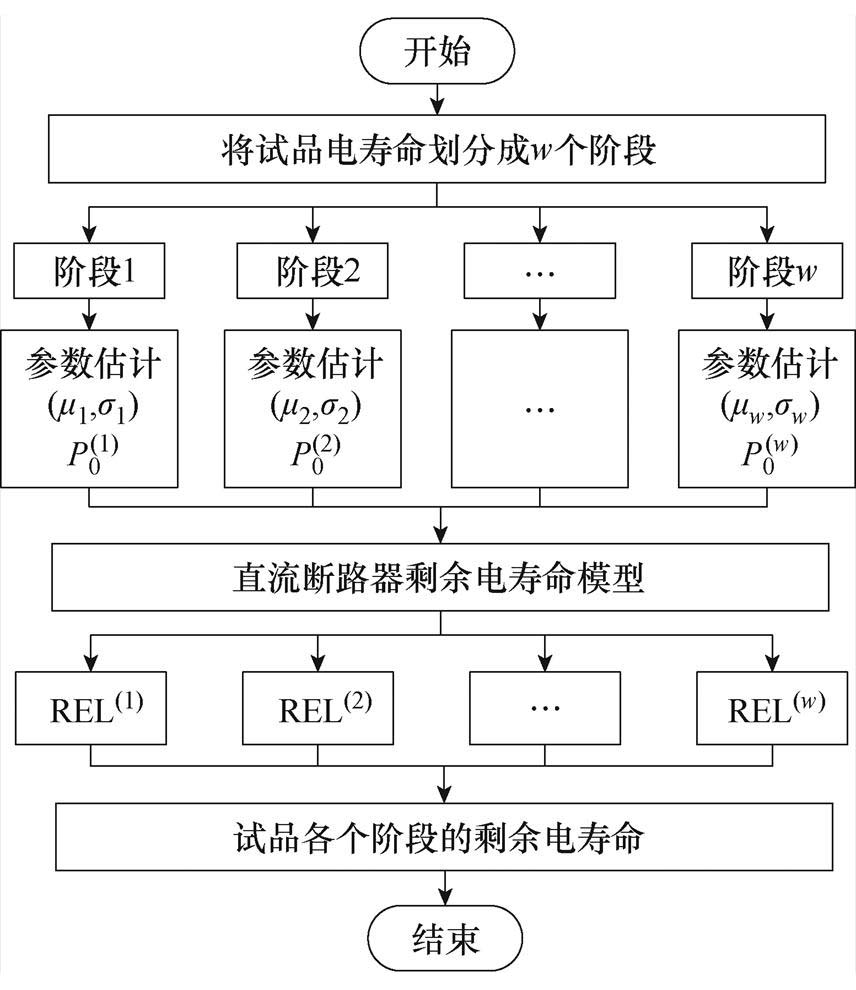
图5 直流断路器剩余电寿命预测方法
Fig.5 Residual life prediction method of DC circuit breaker
2.2.1 直流断路器电性能退化实验设计
对三台直流断路器（试品1～试品3）进行电性能退化实验，实验参数见表1，实验装置如图6所示。
表1 直流断路器电性能退化实验参数
Tab.1 Experimental parameters of electrical performance degradation of DC circuit breaker
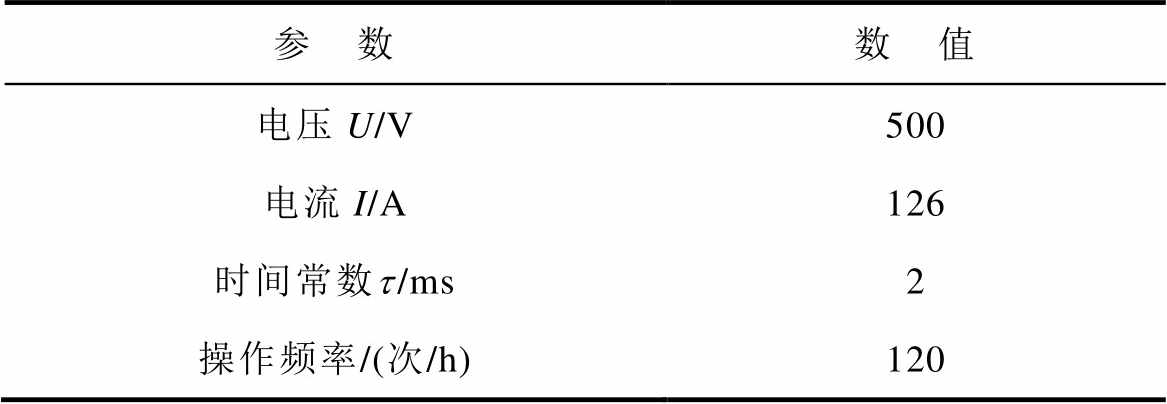
参 数数 值 电压U/V500 电流I/A126 时间常数t/ms2 操作频率/(次/h)120
图6 直流断路器电性能退化实验装置
Fig.6 DC circuit breaker electrical performance degradation experimental device
2.2.2 电性能退化实验结果及分析
图7为126 A电流应力水平下直流断路器的累计触头质量损失随动作次数的变化规律。对性能退化数据进行分析，随着动作次数增加，触头1和触头2累积质量损失均与动作次数呈线性关系。
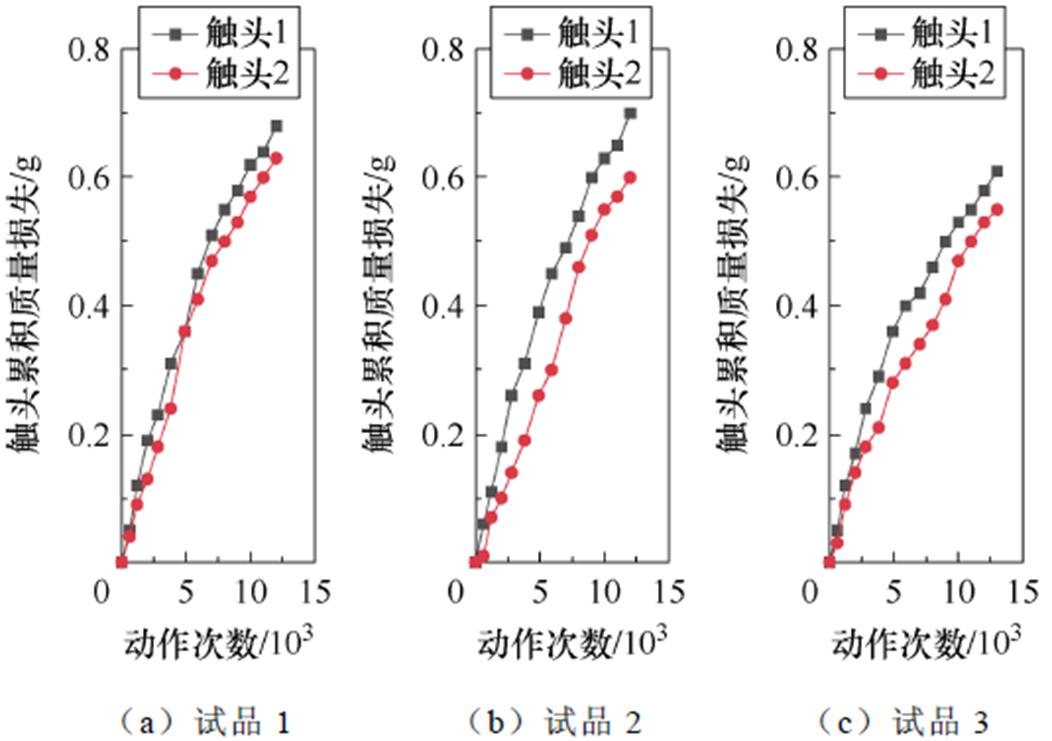
图7 126 A电流应力水平下触头累积质量损失
Fig.7 Cumulative mass loss at 126 A current stress level
3台试品的电寿命分别为13 025、12 525、13 026次，磨损最大相累积触头质量损失分别为0.71、0.70和0.61 g，失效模式分别为静触头损失量达到失效阈值、燃弧持续过长造成触头烧毁、弹簧断裂。对126 A电流应力水平下直流断路器的燃弧能量进行累计，如图8所示。
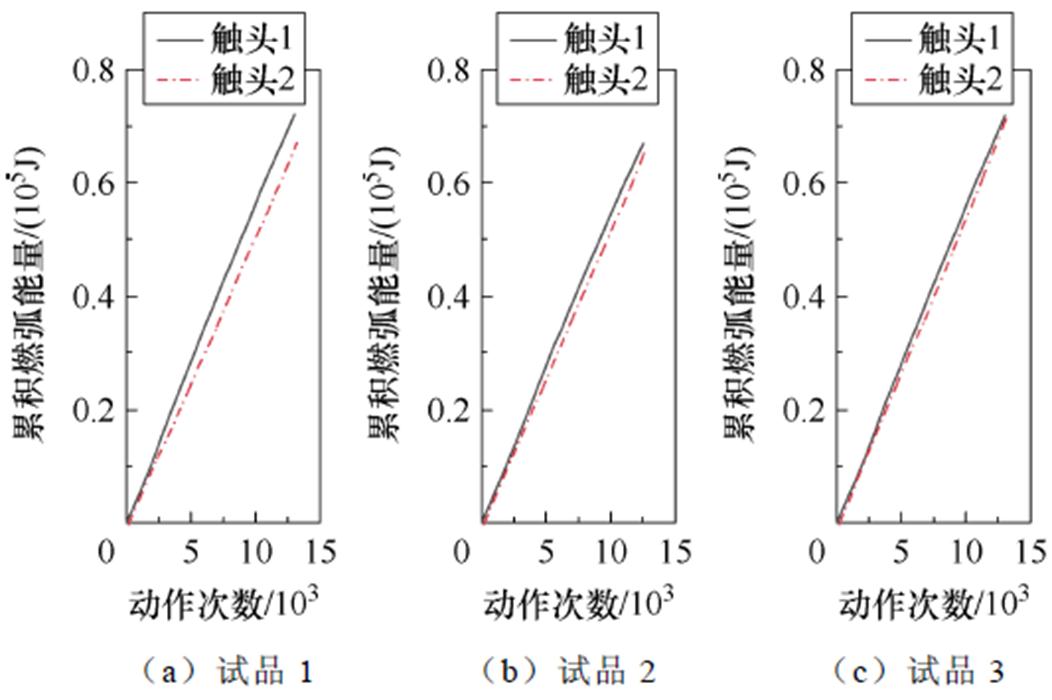
图8 126 A电流应力水平下累积燃弧能量
Fig.8 Accumulated arc energy at 126 A current stress level
随着动作次数的增加，触头1和触头2的累积质量损失与累积燃弧能量均表现为线性上升趋势，与动作次数具有较好的线性关系，整体退化速率基本不变。触头1的静触头为阳极，触头2的静触头为阴极，触头1的累积质量损失始终大于触头2，这是由于阳极表面温度高于阴极表面温度，导致阳极静触头产生较阴极静触头更为严重的电弧侵蚀现象[16]，其表现形式即为阳极触头1质量损失累积量大于阴极触头2。
采用线性拟合的方法，分析触头累积质量损失和累积燃弧能量的相关性，求得试品1～试品3累积质量损失与累积燃弧能量的相关系数，见表2。
表2 累积质量损失与累积燃弧能量的相关系数
Tab.2 The correlation coefficient between cumulative mass loss and cumulative arc energy
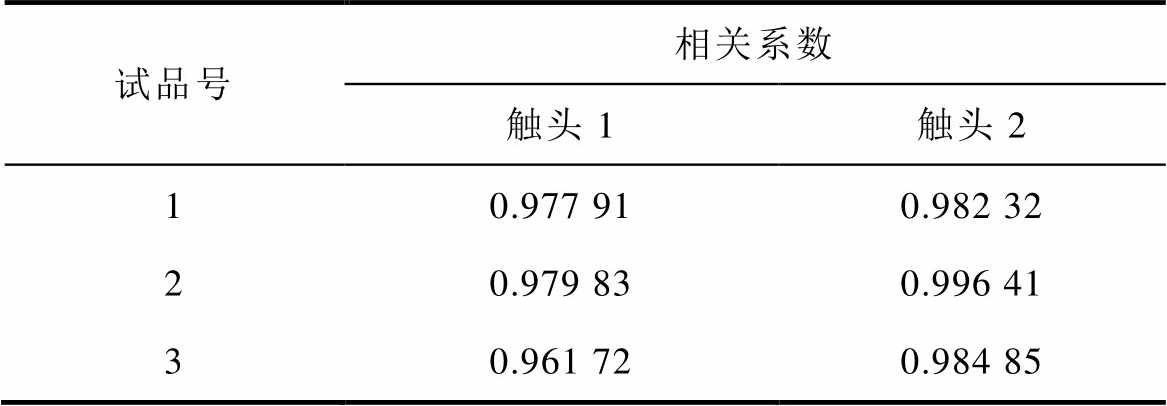
试品号相关系数 触头1触头2 10.977 910.982 32 20.979 830.996 41 30.961 720.984 85
试品1～试品3的触头1和2相关系数均在0.95以上，二者存在线性关系。图9为试品1中触头1和触头2累积质量损失与累积燃弧能量的线性拟合结果。
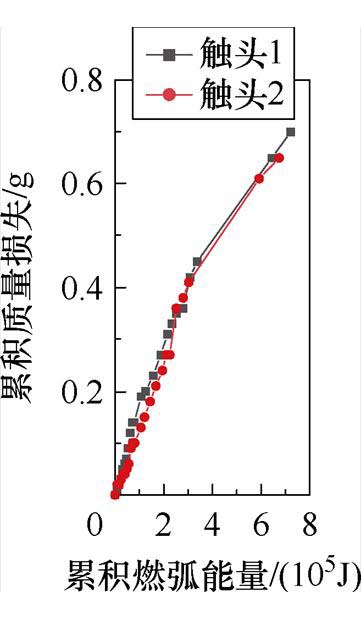
图9 试品1累积质量损失与累积燃弧能量线性拟合
Fig.9 Linear fitting of cumulative mass loss and cumulative arc energy of sample 1
2.2.3 基于实验结果的剩余电寿命预测
在实际服役过程中，电寿命由磨损最大的触头对决定。本文所选断路器阳极触头磨损值始终大于阴极触头，因此在剩余寿命预测工作中，以阳极触头的累积燃弧能量作为电性能退化过程的退化量。
1）退化量的正态分布检验
将试品1～试品3的燃弧能量进行分段累积，检验其是否满足Wiener过程条件，即是否服从正态分布。试品1～试品3的累积燃弧能量变化趋势一致，以试品1为例，对触头1的燃弧能量每50次进行一次累积，绘制了标准正态QQ（quantile-quantile）图，如图10所示。由图10可知，燃弧能量数据均在直线附近分布，代表累积燃弧能量服从正态分布，因此，可以选取累积燃弧能量作为退化量，利用Wiener过程描述电性能退化过程，进行剩余电寿命预测。
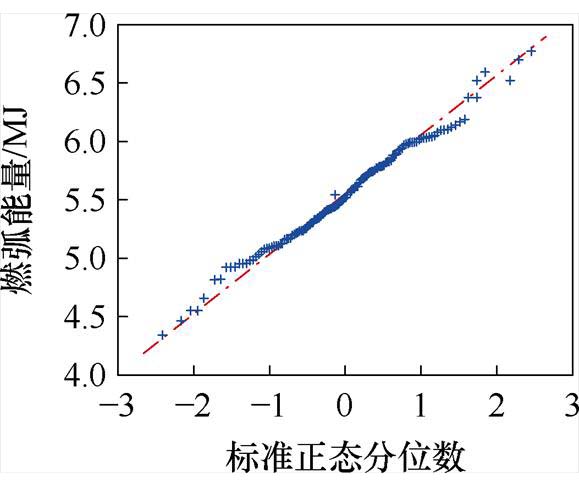
图10 试品1 QQ图
Fig.10 Quantile-quantile plot of sample 1
2）直流断路器剩余电寿命预测
由式（21）计算试品1～试品3的漂移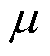参数和扩散参数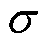估计值，并计算出三个试品的参数平均值，见表3。以试品1为例，将电性能退化过程的参数估计值代入式（16）、式（15）可计算出试品1的可靠度和概率密度函数表达式，分别为
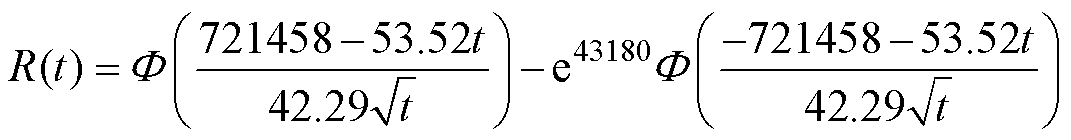（22）
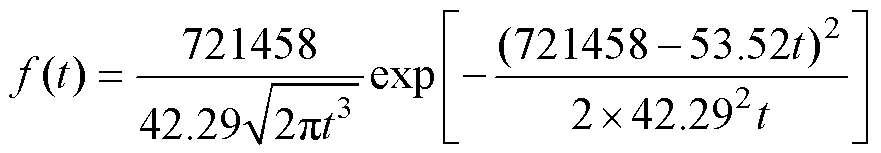（23）
表3 正态分布参数估计值
Tab.3 Parameter estimation of normal distribution （单位: J）
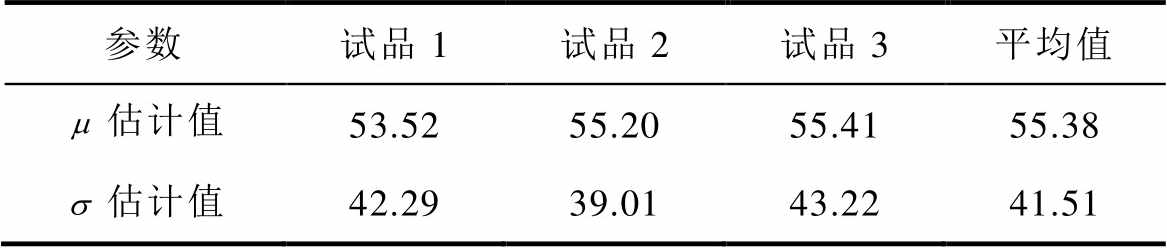
参数试品1试品2试品3平均值 估计值53.5255.2055.4155.38 估计值42.2939.0143.2241.51
根据函数式，可分别绘制试品1的可靠度函数曲线和概率密度函数曲线，如图11所示。由图11a可知，可靠度在经过12 884次左右分断操作后迅速下降。由图11b可知，概率密度函数的期望值为13 000次，与实际电寿命13 025次十分接近。利用试品2和试品3数据同时验证了每个试品的概率密度函数期望值与各自的实际电寿命均十分接近，可将概率密度函数期望值认定为电寿命的预测结果。
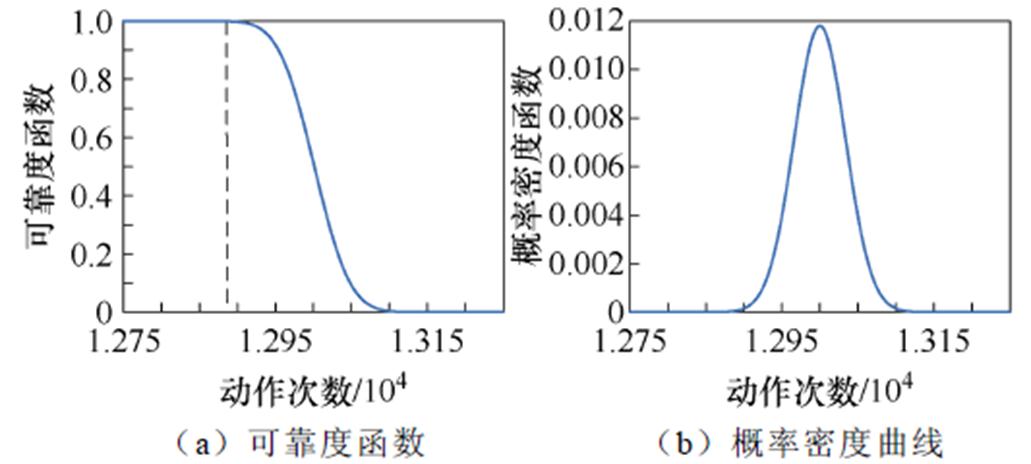
图11 试品1可靠度函数曲线和概率密度函数曲线
Fig.11 Reliability function curve and probability density function curve of sample 1
采取同批次产品：试品2、试品3的参数估计值及三个试品参数估计值的均值代入式（22）和式（23）替换试品1的参数估计值，分别预测试品1的电寿命，预测结果分别为13 457、12 999和13 166次。与试品1实际电寿命之间的相对误差分别为3.32%、0.20%和1.08%，预测误差均在5%之内。因此，在缺少本身性能退化数据的前提下，可利用同批次其他产品的性能退化参数进行剩余电寿命预测，且预测误差满足工程实际需求。
利用先验信息确定126 A电流应力水平下的失效阈值P，将电寿命分为六个不同的阶段，计算当前阶段的性能退化量并利用式（21）估计当前阶段的漂移参数和扩散参数，继而通过式（20）计算该阶段的剩余电寿命预测值。根据同批次产品的实验数据进行同类产品的剩余寿命预测。以试品1为例，列出基于自身数据的各阶段剩余电寿命预测结果，计算与实际值的相对误差，见表4。图12为根据不同试品的实验数据进行剩余电寿命预测的相对误差，均未超过10%。
表4 剩余电寿命预测值和实际值对比
Tab.4 The comparison between the predicted value and the actual value of the remaining electrical life
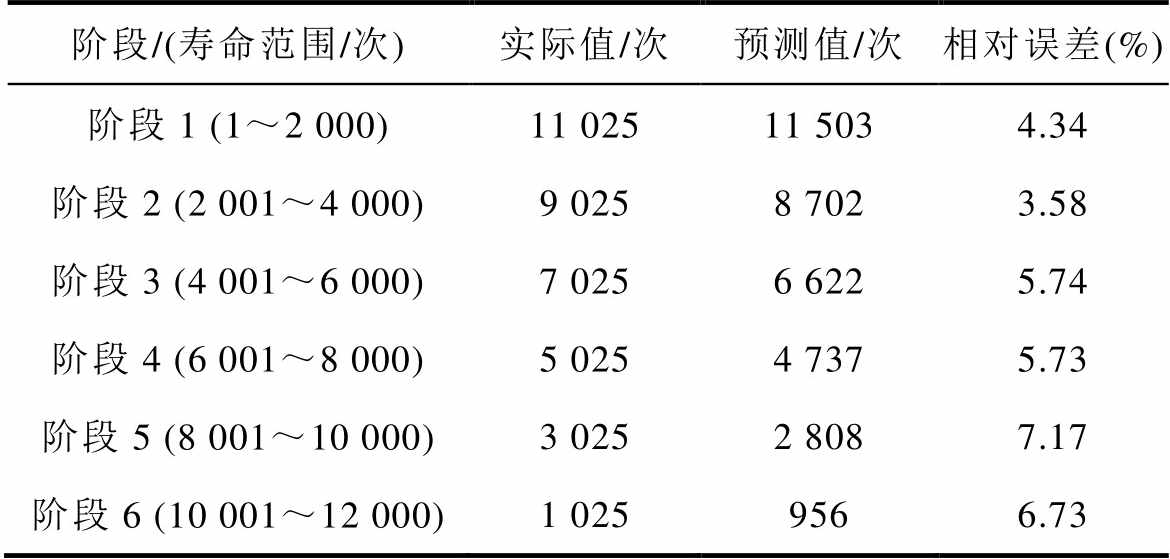
阶段/(寿命范围/次)实际值/次预测值/次相对误差(%) 阶段1 (1～2 000)11 02511 5034.34 阶段2 (2 001～4 000)9 0258 7023.58 阶段3 (4 001～6 000)7 0256 6225.74 阶段4 (6 001～8 000)5 0254 7375.73 阶段5 (8 001～10 000)3 0252 8087.17 阶段6 (10 001～12 000)1 0259566.73
3.1.1 电弧电压特征参数估计
电性能退化过程中每次分断操作的弧压变化率及燃弧时间存在随机性，根据最大熵原理可以假设
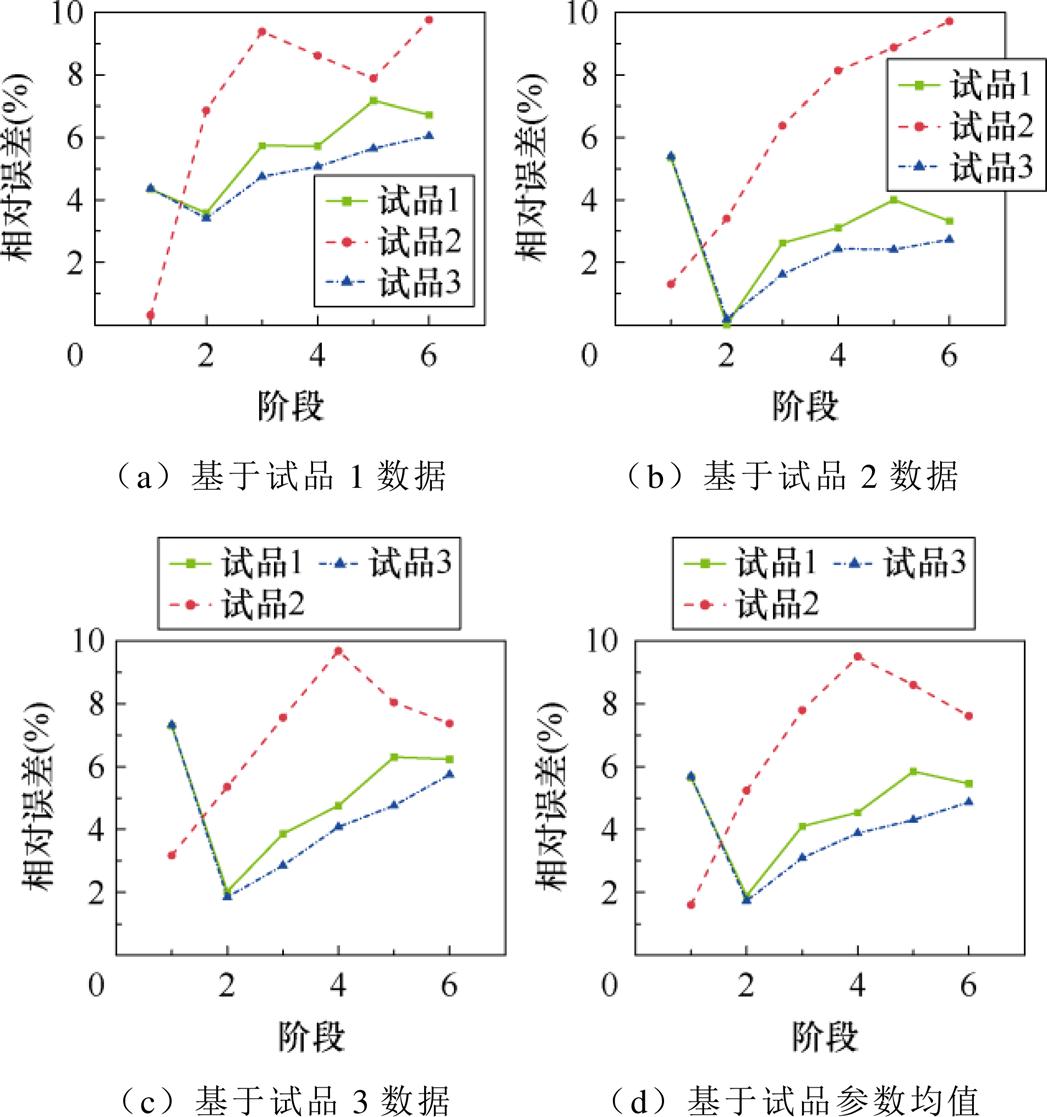
图12 剩余电寿命预测值与实际剩余电寿命的相对误差
Fig.12 The relative error between the predicted residual electrical life and the actual residual electrical life
不同操作时其参量服从正态分布。利用2.2节中的实验数据，进行弧压变化率及燃弧时间的估计。
1）弧压变化率恒定下分布检验及参数估计
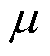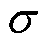根据实验数据提取每次直流断路器开断的弧压变化率及燃弧时间，进行正态分布检验，结果如图13所示。由图13可知，弧压变化率及燃弧时间均服从正态分布，其均值和标准差见表5。
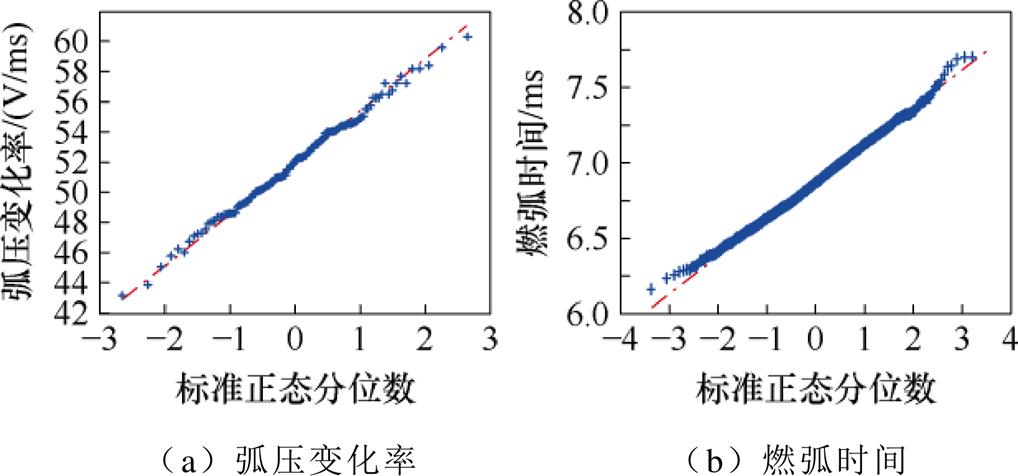
图13 各参量标准正态分布QQ图
Fig.13 The standard normal distribution QQ diagram of each parameter
表5 弧压变化率恒定下正态分布参数估计值
Tab.5 Normal distribution parameter estimation under constant voltage change rate
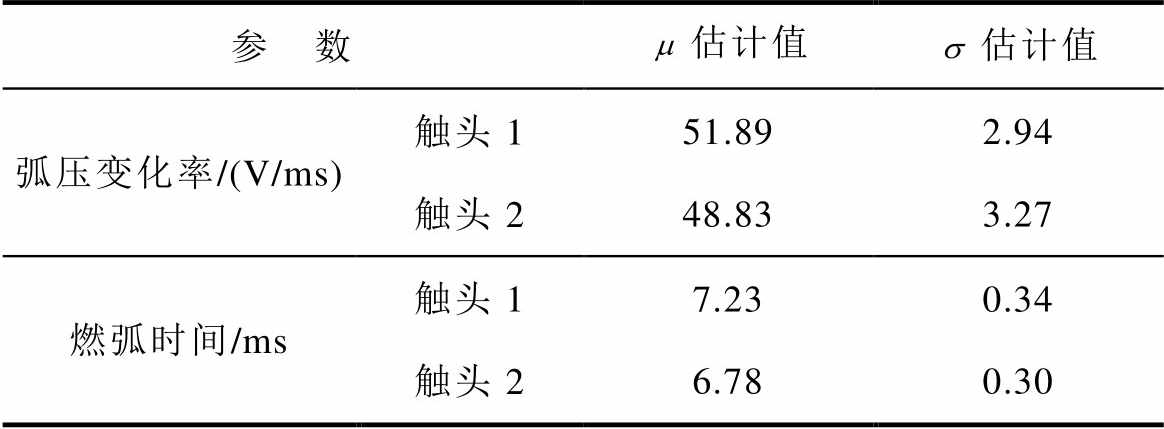
参 数估计值估计值 弧压变化率/(V/ms)触头151.892.94 触头248.833.27 燃弧时间/ms触头17.230.34 触头26.780.30
2）弧压变化率分段恒定下分布检验及参数估计
电弧电压变化的第一、二和三阶段弧压变化率的正态分布检验结果如图14所示。由图14可知，基于弧压变化率分段恒定的电弧电压等效模拟方法中的各阶段弧压变化率同样服从正态分布。两种电弧电压等效模拟方法的燃弧时间一致，其参数估计方法相同。触头1和触头2的各阶段弧压变化率均值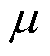和标准差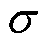估计值见表6。
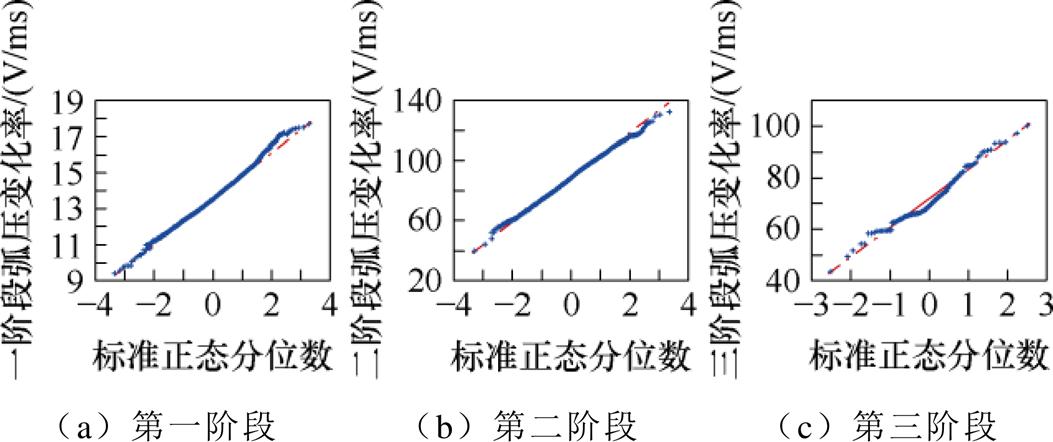
图14 弧压变化率标准正态分布QQ图
Fig.14 Standard normal distribution QQ plot of arc voltage change rate
表6 弧压变化率分段恒定下正态分布参数估计值
Tab.6 Normal distribution parameter estimation under piecewise constant arc voltage change rate （单位: V/ms）
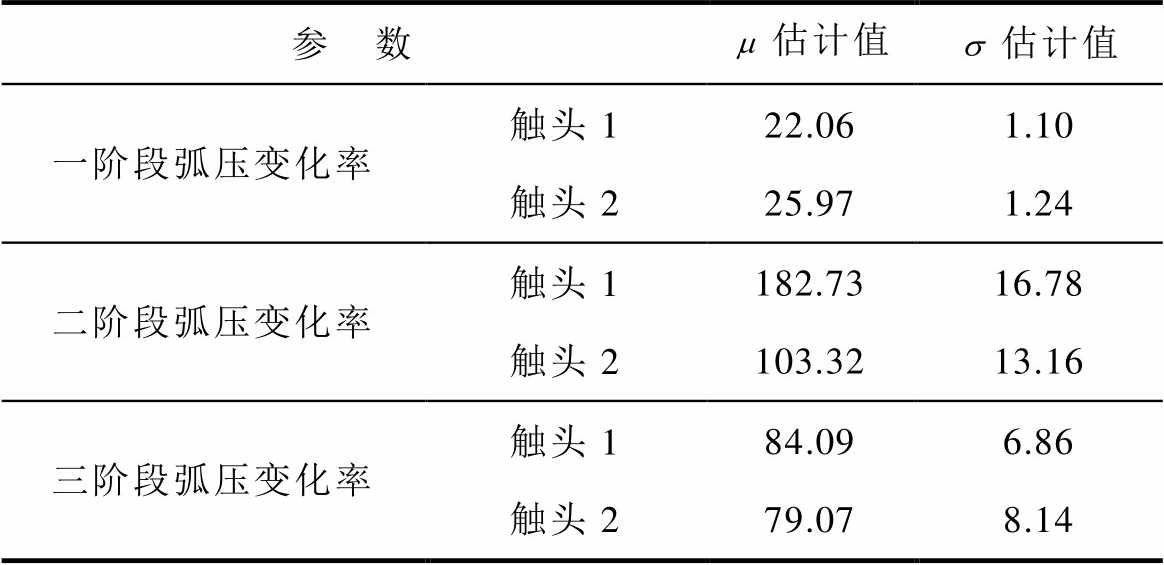
参 数估计值估计值 一阶段弧压变化率触头122.061.10 触头225.971.24 二阶段弧压变化率触头1182.7316.78 触头2103.3213.16 三阶段弧压变化率触头184.096.86 触头279.078.14
3.1.2 电性能退化仿真
电性能退化仿真流程如图15所示。
本文采用Monte-Carlo法，生成符合正态分布的弧压变化率及燃弧时间的数据集合，对电性能退化进行模拟仿真，以获得直流断路器在任意电流应力水平下的电寿命及性能退化数据，仿真过程如下：
（1）设定断路器样品个数及失效阈值。
（2）产生服从正态分布的燃弧时间tarc和弧压变化率kvc，取值范围为（m-3s, m+3s）。
（3）通过式（8）分别计算直流断路器基于两种电弧电压等效模拟方法的单次分断过程中的燃弧能量gki；利用式（7）计算单次分断过程中的触头质量损失mki（k=1, 2）。
（4）计算两对触头的累积质量损失Qk，比较两对触头中的最大值Qk与失效阈值P的大小。重复步骤（1）～步骤（3），当任一对触头的累积质量损失Qk达到或超过失效阈值P时，认为该试品失效，并记录此时的动作次数，即该台断路器的电寿命。
（5）进行步骤（2）～步骤（4）的操作流程，并记录每台试品的电性能退化过程数据及其电 寿命。
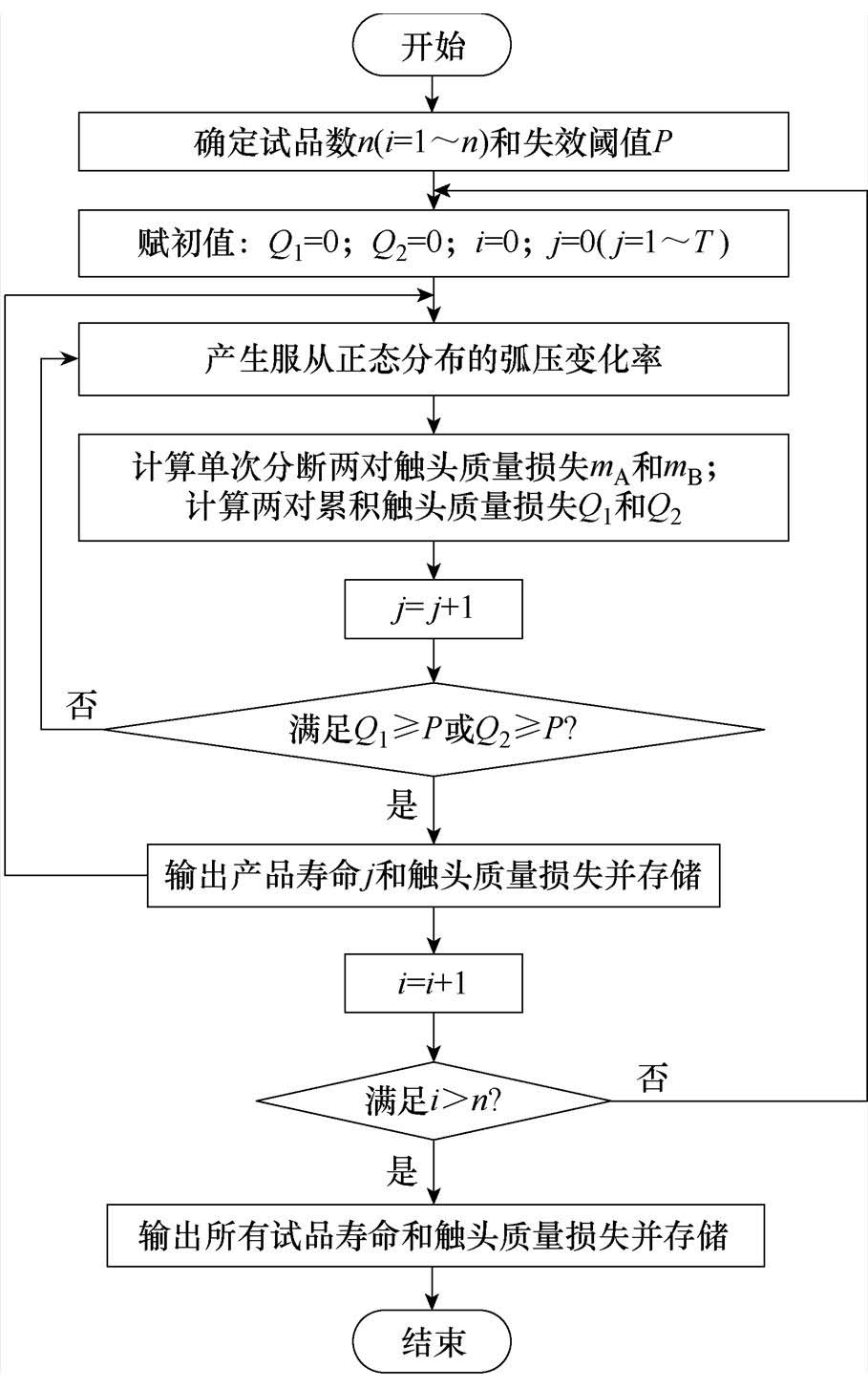
图15 电性能退化仿真流程
Fig.15 Electrical performance degradation simulation flow chart
3.1.3 基于仿真数据的剩余电寿命预测
1）基于弧压变化率恒定的剩余电寿命预测
产生1 000个样本，从仿真样本中随机选择100台进行电寿命和性能退化数据分析，如图16所示。
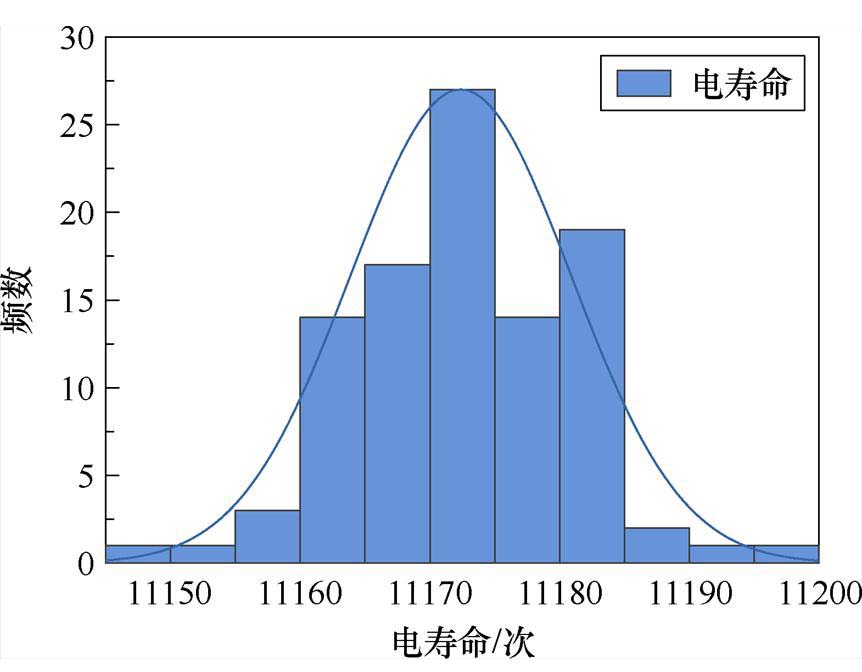
图16 基于弧压变化率恒定的电寿命仿真结果
Fig.16 Electrical life simulation results based on constant arc voltage change rate
由图16可知，在弧压变化率恒定条件下由仿真得到的样本的平均电寿命为11 170次，与该电流应力下的实际电寿命13 025次存在一定差距，误差为14.24%。这是因为基于该等效模拟方法得到的电压电流波形与实验波形存在差距，使得后续计算断路器每次分断造成的电磨损量与实际的电磨损量存在差距，由于质量损失经过多次累积达到失效阈值时判定断路器失效，差距进一步扩大，因此仿真电寿命与实际存在一定差距，但仍可在一定程度上实现对直流断路器电寿命的估计。
从100台样本中选取电寿命最大、中等和最小的电性能退化数据。将三台样本依次编号为样本1、样本2和样本3，电寿命分别为11 198次、11 172次、11 148次。样本1～样本3触头累积质量损失随动作次数的变化曲线如图17所示，触头1和触头2的质量损失均与动作次数呈线性关系，且触头1仿真磨损量始终高于触头2仿真磨损量。
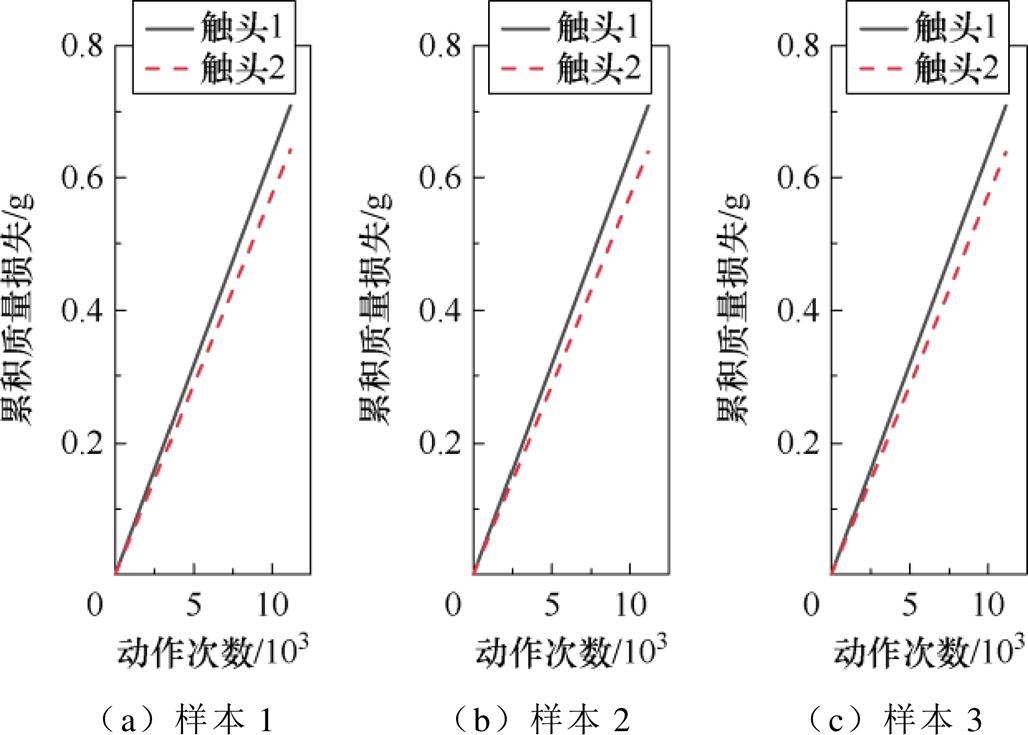
图17 基于弧压变化率恒定的触头累积质量损失
Fig.17 Cumulative mass loss of contact based on constant
2）基于弧压变化率分段恒定的剩余电寿命预测
从1 000台仿真数据中随机选取100个样本数据，电寿命仿真结果如图18所示。
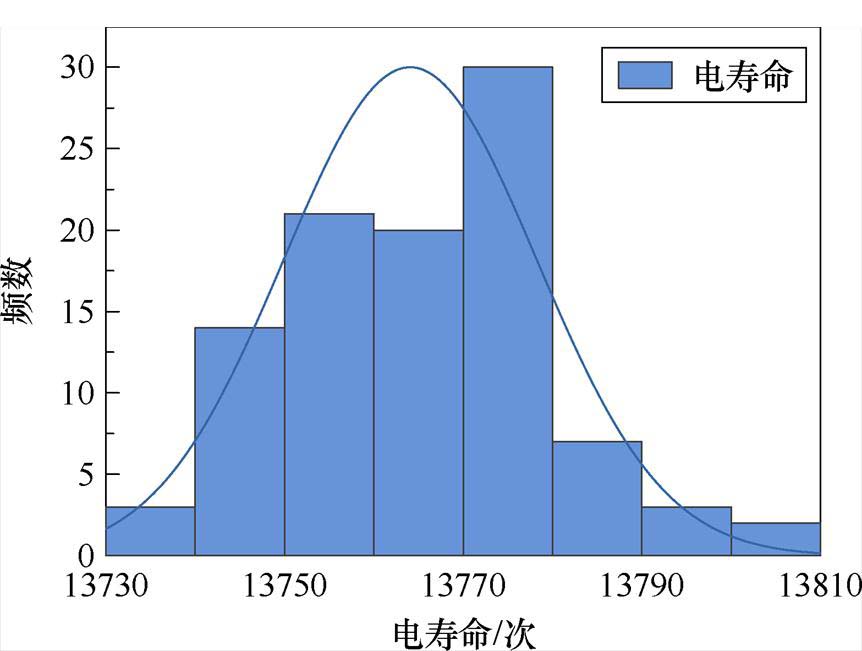
图18 电寿命仿真结果
Fig.18 The electrical life simulation results
由图18可知，样本的平均仿真电寿命为13 775次，误差为5.76%，小于恒压变化率恒定条件下误差，其原因是恒压变化率分段恒定条件下，电弧电压电流变化与实际更接近。
选取电寿命最大、中等和最小的电性能退化数据，依次编号为样本4、样本5和样本6。电寿命分别为13 805次、13 774次和13 738次。样本4～样本6触头累积质量损失变化曲线如图19所示。
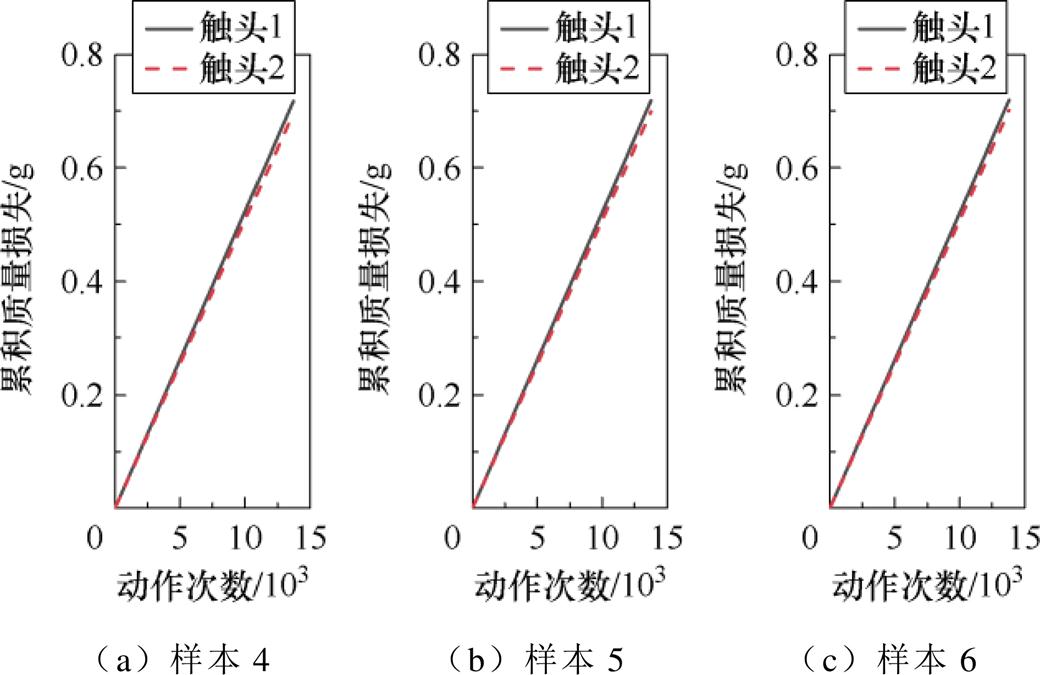
图19 触头累积质量损失
Fig.19 Cumulative mass loss
利用本文提出的电弧电压等效模拟方法可以对直流断路器电性能退化进行仿真，其结果可以反映直流断路器的性能退化过程。
3.2.1 燃弧波形的比较分析
选取任意一次动作次数的实验燃弧波形和仿真数据中燃弧时间与该次分断过程燃弧时间接近的燃弧波形数据进行对比，图20为126 A电流应力水平下的对比结果。
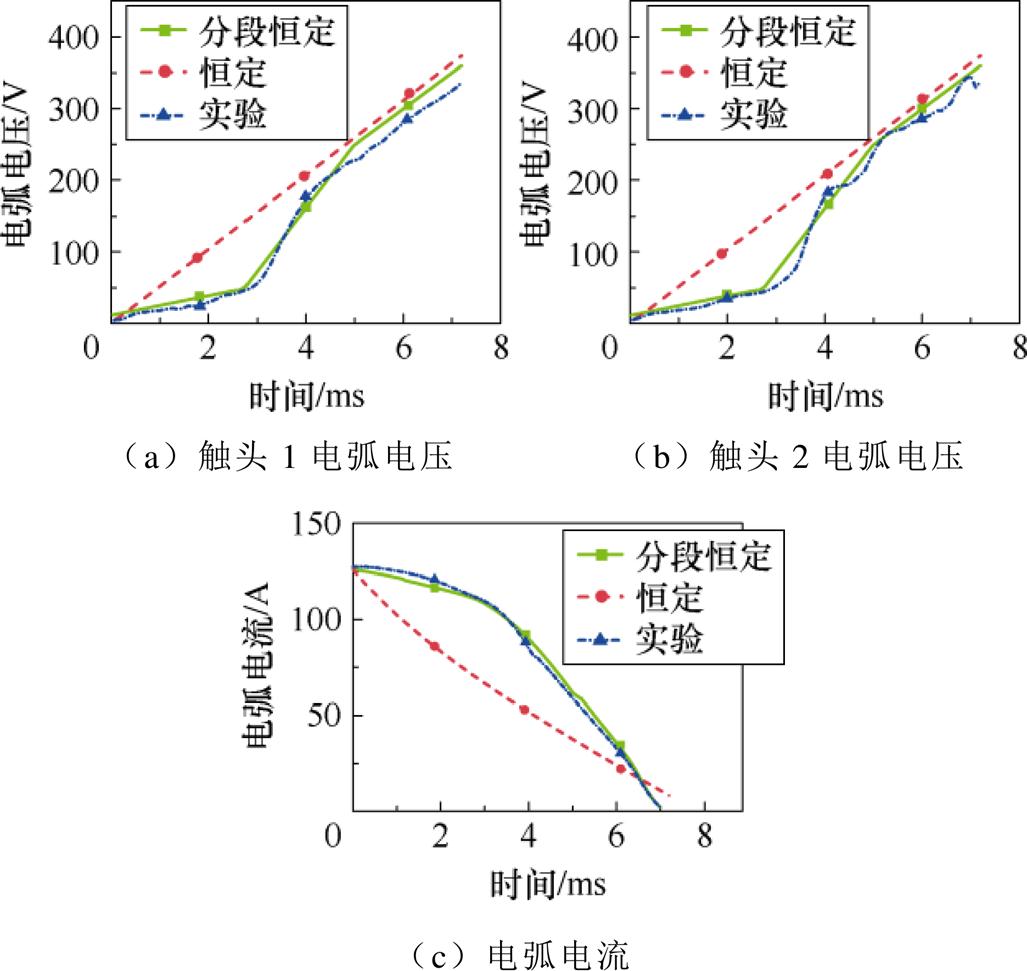
图20 仿真燃弧波形与实际燃弧波形对比
Fig.20 Comparison between the simulated arcing waveforms and the actual arcing waveforms
由图20可知，二者均可在一定程度上反映燃弧波形变化。由于假设的原则是电弧电压与横轴形成面积不变，即电弧电压平均值不变。弧压变化率分段恒定较弧压变化率恒定而言，其电弧电流变化过程更符合实际电流变化过程，弧压变化率分段的电弧电压等效模拟方法准确性较高，更接近实际燃弧波形。
3.2.2 燃弧能量的比较分析
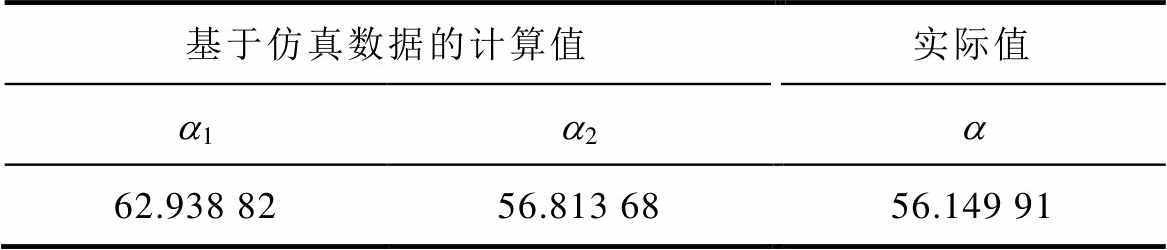
计算仿真样本2和样本5的累积燃弧能量，并与试品1实验结果进行比较，如图21所示，分段模型、恒定模型与实验结果退化量退化趋势一致，退化速率存在差别，燃弧能量退化速率a、a1、a2见表7，分段模型的燃弧能量退化速率与实际一致，而恒定模型需要乘以修正系数来确保等效原则。综上分析，通过仿真单次分断燃弧波形和累积燃弧能量两方面与实验数据进行对比，验证了基于弧压变化率分段的电弧电压等效模拟方法优于整体恒定的电弧电压等效模拟方法，基于弧压变化率分段的电性能退化仿真得到的电寿命数据与实际值更为接近，寿命预测准确性更高，而弧压变化率恒定的电弧电压等效模拟方法还需要乘以修正系数。
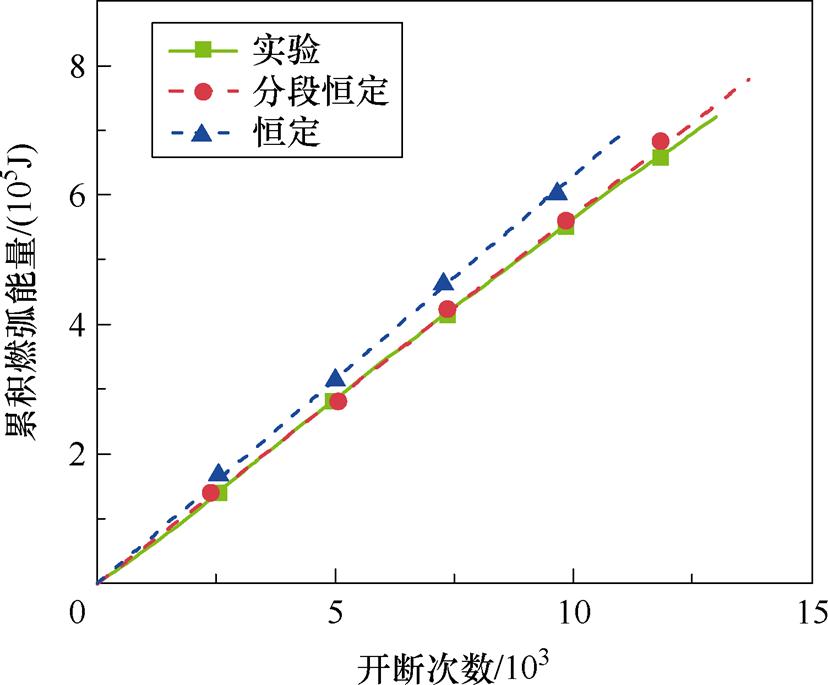
图21 仿真燃弧能量与实验对比
Fig.21 Experimental arcing energy and simulation comparison
表7 燃弧能量退化速率
Tab.7 Degradation rate of arcing energy （单位: J/次）
基于仿真数据的计算值实际值 a1a2a 62.938 8256.813 6856.149 91
本文针对直流断路器电性能退化开展研究，根据实验获得性能退化数据进行剩余电寿命预测，并提出了直流断路器电性能退化的仿真方法。结论如下：
1）研究直流电弧的物理特性和变化特征，提出了弧压变化率恒定和弧压变化率分段恒定两种电弧电压等效模拟方法，为电弧电压电流变化过程的仿真奠定了基础。
2）进行直流断路器电性能退化分析，建立了基于Wiener过程的直流断路器剩余电寿命预测模型，并根据电性能退化实验数据进行剩余电寿命预测，误差小于10%，可以满足工程实际需求。
3）建立了基于Monte-Carlo法的电性能退化仿真模型，并根据电弧电压等效模拟方法产生性能退化数据，实现了直流断路器的剩余电寿命预测的仿真分析。
参考文献
[1] 李静, 郭沛鑫, 彭世东, 等. 基于改进结构的自激式直流空气断路器小电流开断能力提升方法[J]. 电工技术学报, 2024, 39(22): 7278-7290.
Li Jing, Guo Peixin, Peng Shidong, et al. Enhance small current breaking performance of self-excited DC air circuit breaker based on an improved stru- cture[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7278-7290.
[2] 邢云琪, 王子涵, 杨广正, 等. 低压直流断路器双金属片性能退化特性及机理分析[J]. 电工技术学报, 2024, 39(22): 7266-7277.
Xing Yunqi, Wang Zihan, Yang Guangzheng, et al. Degradation characteristics and mechanism analysis of bimetal sheet of low voltage DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7266-7277.
[3] 何志鹏, 赵虎, 李伟林. 考虑弧根转移和开断电流的微型断路器电寿命评估方法[J/OL]. 电工技术学报, 2025: 1-12. (2025-04-27). https://link.cnki.net/ doi/10.19595/j.cnki.1000-6753.tces.241683.
He Zhipeng, Zhao Hu, Li Weilin. Electrical life evaluation of miniature circuit breakers considering arc root transfer and breaking current[J/OL]. Transa- ctions of China Electrotechnical Society, 2025: 1-12. (2025-04-27). https://link.cnki.net/doi/10.19595/j.cnki. 1000-6753.tces.241683.
[4] Shea J J. High current AC break arc contact erosion[C]//2008 Proceedings of the 54th IEEE Holm Conference on Electrical Contacts, Orlando, FL, USA, 2008: XXII-XLVI.
[5] 周学, 周雨馨, 孙会超, 等. 直流大功率接触器自磁场灭弧室电弧特性研究[J]. 电工技术学报, 2021, 36(增刊1): 292-302.
Zhou Xue, Zhou Yuxin, Sun Huichao, et al. Study on arc characteristics of self-magnetic arc extinguishing chamber of DC high-power contactor[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 292-302.
[6] Yin Jianning, Wang Qian, Li Xingwen. Simulation analysis of arc evolution process in multiple parallel contact systems[J]. IEEE Transactions on Plasma Science, 2018, 46(8): 2788-2793.
[7] Wu Yi, Cui Yufei, Rong Mingzhe, et al. Visualization and mechanisms of splashing erosion of electrodes in a DC air arc[J]. Journal of Physics D: Applied Physics, 2017, 50(47): 47LT01.
[8] Cui Yufei, Niu Chunping, Wu Yi, et al. Experimental study on the transformation of the W70Cu30 anode erosion mode in DC gaseous arcs-better insights into mechanisms of electrode erosion behavior using in situ diagnosis[J]. Journal of Physics D: Applied Physics, 2019, 52(47): 474001.
[9] Cui Yufei, Wu Yi, Niu Chunping, et al. Evolution of anodic erosion components and heat transfer effici- ency for W and W80Ag20 in atmospheric-pressure arcs[J]. Journal of Physics D: Applied Physics, 2020, 53(47): 475203.
[10] Lu C J, Meeker W O. Using degradation measures to estimate a time-to-failure distribution[J]. Techno- metrics, 1993, 35(2): 161-174.
[11] 翟国富, 王淑娟, 许峰, 等. 基于超程时间和吸合时间建模的继电器双变量寿命预测方法的研究[J]. 中国电机工程学报, 2002, 22(7): 76-80.
Zhai Guofu, Wang Shujuan, Xu Feng, et al. Research on double-variable life forecasting based on model- building of super-path time and pick-up time for relays[J]. Proceedings of the CSEE, 2002, 22(7): 76-80.
[12] 赵书涛, 王波, 华回春, 等. 基于马尔科夫模型的直流断路器可靠性评估方法[J]. 电工技术学报, 2019, 34(增刊1): 126-132.
Zhao Shutao, Wang Bo, Hua Huichun, et al. Reliability evaluation method of DC circuit breaker based on Markov model[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 126-132.
[13] 李奎, 段宇, 黄少坡, 等. 基于Wiener过程的交流接触器剩余电寿命预测[J]. 中国电机工程学报, 2018, 38(13): 3978-3986, 4039.
Li Kui, Duan Yu, Huang Shaopo, et al. Residual electrical life prediction of AC contactor based on the Wiener process[J]. Proceedings of the CSEE, 2018, 38(13): 3978-3986, 4039.
[14] 赵成晨, 李奎, 胡博凯, 等. 变应力条件下低压断路器剩余电寿命预测[J]. 中国电机工程学报, 2022, 42(21): 8004-8016.
Zhao Chengchen, Li Kui, Hu Bokai, et al. Residual electrical life prediction of low-voltage circuit breakers under varied stress[J]. Proceedings of the CSEE, 2022, 42(21): 8004-8016.
[15] 何志鹏, 赵虎. 微型断路器电寿命评估[J]. 电工技术学报, 2022, 37(4): 1031-1040.
He Zhipeng, Zhao Hu. Electrical lifespan evaluation of miniature circuit breakers[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 1031- 1040.
[16] Yin Jianning, Wang Qian, Li Xingwen. Simulation analysis of arc evolution process in multiple parallel contact systems[J]. IEEE Transactions on Plasma Science, 2018, 46(8): 2788-2793.
Abstract As key power equipment for protecting the DC system, the DC circuit breaker’s reliability and safety are crucial for the stable operation of the power grid. This paper proposes arc voltage equivalent simulation and contact electrical wear calculation. The degradation law for the electrical performance of the DC circuit breaker is investigated, and simulations are conducted to verify the consistency between the simulated and experimental results. The prediction of the residual electrical life for the DC circuit breaker is achieved.
The basic data, including arc voltage and arc current, are necessary to calculate the electrical wear of contact. Thus, the typical waveform of arc voltage and arc current are investigated, and two equivalent simulation methods for arc voltage are proposed. During the current-breaking process of the DC circuit breaker, the arc continuously elongates, and consequently, the arc voltage increases. A simplification method is proposed to deal with the arc voltage with the changing rate based on the principle that the average arc voltage remains constant. Two equivalence methods for arc voltage are proposed. One assumes that the arc voltage changing rate remains constant during the breaking process, and the other assumes that the arc voltage is piecewise linear.
In the case of a simple arc extinguishing chamber, the arc length increases gradually throughout the breaking process. The arc voltage is related to the arc length. Thus, the changing rate of the arc voltage can be considered as a fixed value. In the case of a complex arc extinguishing chamber structure, the changing rate of the arc voltage is markedly different before and after the arc enters the extinguishing grid. The arc voltage is considered piecewise linear, and the changing rate of the arc voltage remains the same within the same stage.
The mass loss of the contact is closely related to the arcing characteristics, which can be characterized by arc voltage, arc current, arcing time, and other parameters. According to the central limit theorem, the cumulative sum of contact mass loss over segments obeys a normal distribution, and the Wiener process can be used to describe the changing process of contact mass loss. Therefore, the residual electrical life prediction model for DC circuit breakers based on arc erosion is established. Since products from the same batch share the same design and production process, the failure threshold for DC circuit breakers within the same batch is considered identical. The electrical life of a DC circuit breaker ends when the contact mass loss reaches the failure threshold.
The electrical life experiment for the DC circuit breaker with a current of 126 A has been conducted. A normal distribution test for the arcing energy is performed. The arc energy is chosen as the performance degradation indicator, and the Wiener process is utilized to model the degradation process. An electrical life prediction method for the DC circuit breaker is proposed. According to the experimental data, the parameters in the Wiener process are estimated to predict the residual electrical life at various degradation stages. The prediction error is less than 10%.
Due to the influence of random factors, the arc voltage changing rate and arcing time of the DC circuit breaker are subject to randomness. According to the maximum entropy principle, assume that these parameters follow a normal distribution across different operations. The Monte Carlo method generates datasets of arc voltage change rate and arcing time that adhere to the normal distribution, enabling the simulation of electrical performance degradation. As a result, the electrical life and performance degradation data of the DC circuit breaker at any given current stress level can be obtained. The results indicate that the simulation with the arc voltage equivalent simulation method is fundamentally consistent with experimental results, and the residual electrical life of the DC circuit breaker can be predicted based on the Wiener process.
Keywords：DC circuit breaker, arc voltage, electrical wear of contact, electrical performance degradation, residual electrical life
中图分类号：TM561
DOI: 10.19595/j.cnki.1000-6753.tces.240986
国家自然科学基金资助项目（51937004）。
收稿日期2024-06-11
改稿日期 2024-08-01
李 奎 男，1965年生，教授，博士生导师，研究方向为电器可靠性与试验技术、电器智能化理论与技术。
E-mail: likui@hebut.edu.cn（通信作者）
张杰凯 男，1997年生，硕士研究生，研究方向为开关电器可靠性。
E-mail: zhangjiekai.hebut@foxmail.com
（编辑 崔文静）