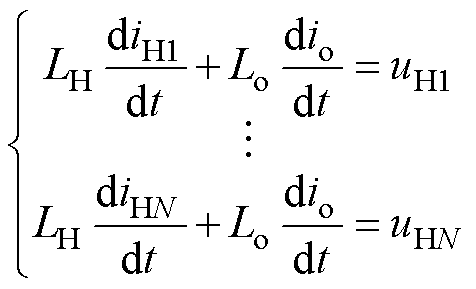 (1)
(1)
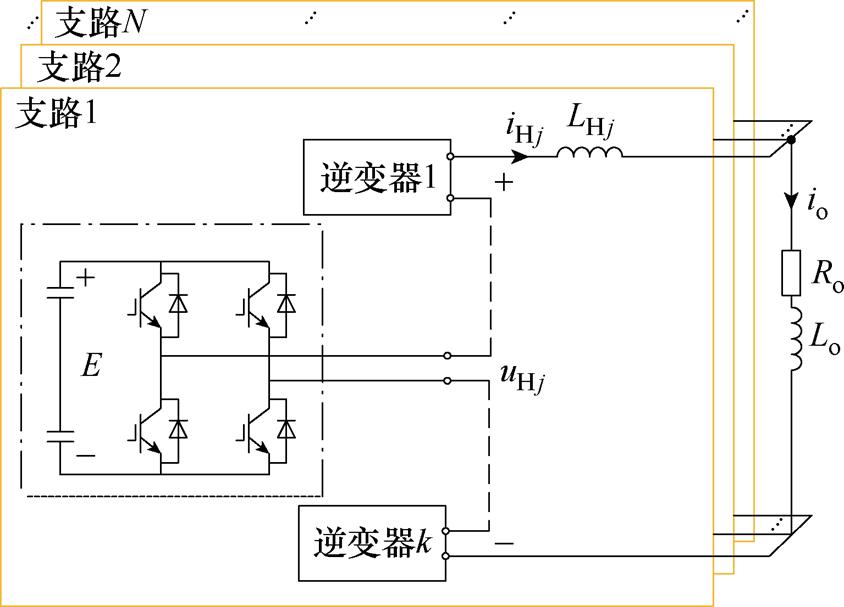
图1 EAST快控电源结构
Fig.1 EAST fast control power supply structure
摘要 全超导托卡马克核聚变发电装置(EAST)快控电源是实现可控核聚变中等离子体垂直位移控制的重要装置。EAST快控电源采用多个H桥逆变支路并联工作模式,电源的总输出电流对参考电流的快速跟踪控制直接影响等离子体的平衡控制,而各个并联支路的输出电流一致性对支路稳定工作十分重要。为加快EAST快控电源输出电流动态响应速度和保证各个支路电流平衡,该文提出一种改进灰色预测新型快速变幂次趋近率滑模控制方法,实现EAST快控电源输出电流的良好控制。为加快输出电流响应速度,在总输出电流反馈环节加入改进灰色预测,根据输出电流的凹凸性和积分思想对灰色预测背景值进行重构,将预测值加入到原始序列替换旧信息以实现滚动预测,可以有效提高输出电流的预测精度。设计以总电流跟踪参考电流和支路电流均衡为控制目的滑模面,提出一种新型快速变幂次趋近率以加快滑模系统的收敛速度。仿真和实验验证了提出的控制方法对比其他传统控制方法具有更好的支路电流一致性和更快的输出电流响应速度。
关键词:全超导托卡马克核聚变发电装置(EAST)快控电源 输出电流 灰色预测 滑模控制
全超导托卡马克核聚变发电装置(Experimental Advanced Superconducting Tokamak, EAST)是控制等离子体实现可控核聚变的重要装置,其中快速控制电源跟踪参考电流信号快速输出目标电流是实现等离子体垂直位移平衡控制的重要环节[1]。在实际工程应用中,EAST快控电源采用多个H桥逆变电路并联运行结构,根据参考电流快速输出目标电流是首要控制目的,各个支路输出电流均衡是维持EAST快控电源稳定工作的保障。现阶段工程上采用比例-积分(Proportional Integral, PI)控制实现EAST快控电源电流控制,但在输出电流快速性和支路电流均衡控制等方面还有较大优化空间。输出电流的预测控制能够实现轨迹预测以提高电流动态响应速度,非线性鲁棒控制在工作环境复杂的EAST快控电源中能够较好地保障控制的稳定性。
灰色预测只需少量的已知目标信息,即可实现目标量的预测,在经济社会趋势预测和电机运行故障诊断预测中发挥了良好的性能[2-3]。在EAST快控电源的应用中,灰色预测实现了输出电流轨迹的预测,文献[4-5]在EAST快控电源输出电流反馈环节中利用灰色预测提前预测输出电流轨迹,加快了输出电流响应速度。等离子体垂直位移信号为时变信号,参考电流信号存在突变过程,因此灰色预测需保证良好的预测精度才能实现精准的输出电流轨迹预测。EAST快控电源在数字控制过程中存在控制延时,在灰色预测累加序列构造的过程中得到的还原值曲线可能与实际电流曲线的凹凸性不一致,而传统灰色预测利用中值定理构造背景值的过程存在较大误差,以上问题均导致输出电流预测存在偏差。文献[6]采用一种新的削弱积累操作提高算法的预测能力,通过优化累加序列值来提高预测精度。文献[7]通过优化背景值和调整补偿系数,分别构建区间预测的单变量和多变量权重自适应灰色预测模型,实现了产值的精准预测。以上关于灰色预测中累加序列的处理均是通过复杂的变换算子来进行预处理,保证新信息优先性或者剔除杂乱信息,但不能从本质上改善原始序列的凹凸性,因此需要进一步设计改变累加序列曲线凹凸性的变换算子使得累加序列曲线的凹凸性与实际输出电流曲线的凹凸性一致。灰色预测的背景值构造过程是累加序列对时间的积分,但传统灰色预测利用中值定理来近似积分过程,导致背景值的构造存在一定误差。文献[8]利用粒子群算法进行权重因子的寻优调节来构造背景值。文献[9]应用矩形法对灰色预测背景权值进行优化,结合基于遗传算法求得约束条件下的最佳背景参数,以上关于背景值重构的过程较为复杂,需要经过大量的寻优计算来得到重构背景值,不利于应用于EAST快控电源的工程实际电流快速控制中。
滑模控制(Sliding Mode Control, SMC)是一种动态响应快速的非线性鲁棒控制方法,在DC-DC电路并联运行控制[10]、多电平级联H桥变换器控 制[11]、电机的电流轨迹跟踪控制[12-13]、模块化电源环流抑制控制[14]等多个类似于EAST快控电源的控制场合得到应用。同时滑模控制已在EAST快控电源电流跟踪控制和支路的环流抑制控制中得到应 用[15-16]。滑模控制过程中的收敛速度和抖振抑制问题是研究的热点问题,在EAST快控电源应用中,加速滑模面的收敛速度和抑制抖振,能够使得输出电流快速准确输出,同时保证各个支路的输出电流性能均衡,有效抑制支路间的环流。而对趋近率进行改进,能够有效加快滑模面的收敛速度和抑制抖振。文献[17]根据滑模面误差大小提出一种时变快速指数型双幂次快速趋近率。文献[18]提出一种改进型双幂次趋近率实现永磁同步电机的速度跟踪控制。文献[19]根据滑模运动情况提出一种时变改进幂次趋近率,以上基于幂次趋近率的改进均取得了良好的控制效果,但是在EAST快控电源的应用中可以进一步简化趋近率的结构。文献[20]提出了一种参数自适应的改进快速指数趋近率。文献[21]在指数趋近率中引入等速趋近率项实现快速平滑的电机调速控制。文献[22]基于改进饱和函数和滑模面误差余项对指数趋近率进行改进。文献[23]提出一种引入小脑模型关节控制的模糊滑模控制以提高滑模趋近阶段对系统的补偿能力和稳定性控制,以上对指数趋近率的改进能够加快滑模控制收敛速度和抑制抖振,但是控制参数整定以及趋近率结合的过程可以进一步简化以便实现快速准确的电流跟踪数字控制。基于指数趋近率和幂次趋近率进行趋近率的改进,能够结合滑模面误差大小,实现参数自适应时变控制,为EAST快控电源的电流跟踪滑模控制提供良好的借鉴。但处理器需要快速处理采样电流信号和参考电流信号以实现电流跟踪输出,因此趋近率的设计不应过于复杂,同时应尽量避免历史数据的积分应用和较为复杂的参数自适应调整过程,应尽可能减小处理器的运算负担。
为进一步提升EAST快控电源输出电流速度,保证各个支路电流均衡,实现EAST快控电源总输出电流快速控制和支路电流环流抑制,提出一种改进灰色预测方法对总输出电流轨迹进行预测,利用改进新型快速趋近率实现总输出电流和各个支路电流的控制。为进一步提升灰色预测精度,在传统灰色预测中提出三点改进:基于输出电流响应曲线的凹凸性,对累加序列进行重构保证累加序列的凹凸性与实际输出电流凹凸性一致;在背景值构造中结合微积分思想实现背景值重构以减小灰色预测误差;将第一次灰色预测输出值应用于原始序列中替换最老旧历史信息值,以实现两步滚动灰色预测来保证输出电流突变边沿的预测精度和补偿数字控制延时。为了加快滑模控制器收敛速度和抑制抖振,提出了一种参数时变指数型双幂次快速趋近率,使得趋近率参数能够根据滑模面误差自动调整。仿真和实验验证了改进改进灰色预测新型快速趋近率滑模控制器在EAST快控电源的总输出电流快速控制和支路电流环流抑制控制中具有良好的性能。
EAST快控电源结构如图1所示,N个支路并联,单支路采用k路H桥级联,现阶段工程上有N=6,k=3,后期将根据可控核聚变发展趋势进一步改进N和k的数值。图1中,uHj(j=1, 2,…, N)为逆变支路输出端电压,io为输出总电流,Lo为负载电感,Ro为线路等效电阻总和,E为单H逆变桥直流侧电压,iHj为各单支路输出电流,LHj为各个支路上值为LH的均流电抗器。
EAST快控电源各支路采用独立控制器,各支路输出电流iHj经过均流电抗器LH汇总到负载端,根据图1可得支路电流方程为
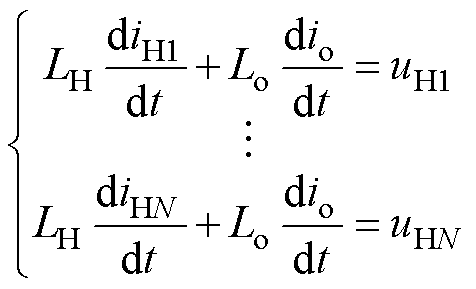 (1)
(1)

图1 EAST快控电源结构
Fig.1 EAST fast control power supply structure
结合国际热核实验堆磁体测试电源工程实际,在EAST快控电源中采用双闭环PI控制结构,其框图如图2所示。总输出电流io需要快速跟踪参考电流iref,跟踪误差经过参数为Kp1和Ki1的外环PI控制器后,得到内环各个支路电流的参考值,内环各个支路电流与参考的误差经过参数为Kp2和Ki2的内环PI控制器后实现级联H桥控制。
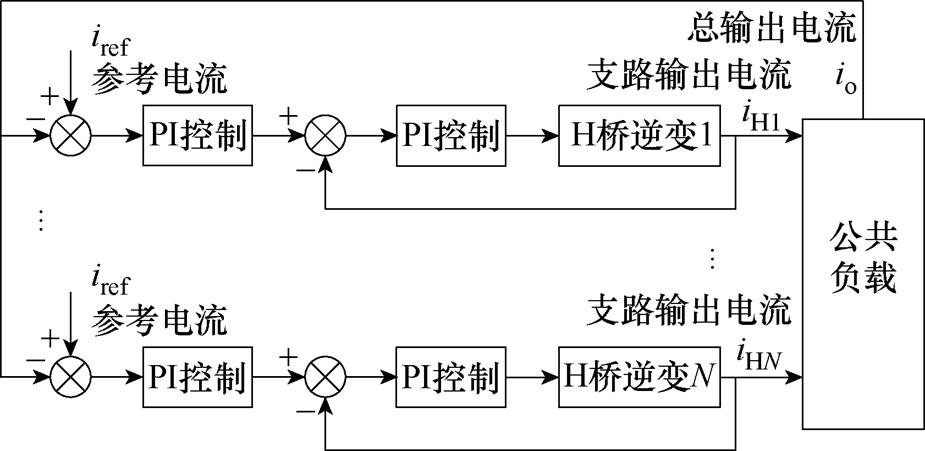
图2 双闭环PI控制框图
Fig.2 Control structure of dual closed-loop PI
在EAST快控电源工作过程中,总输出电流快速跟踪参考电流和实现各个支路输出电流均流是重要的控制目标,而双闭环PI控制在输出电流快速控制和各个支路输出电流均流控制中存在不足。为了加快输出电流建立速度,在输出电流建立之初根据部分已知采样电流值,利用灰色预测的指数变换增长趋势提前预测输出电流轨迹,同时利用滑模控制实现各个支路输出电流均流控制,设计的灰色预测滑模控制框图如图3所示。在输出电流反馈环节经过灰色预测提前预测总输出电流轨迹iop,使得输出电流快速建立。
灰色预测能够对输出电流轨迹进行预测,且在EAST快控电源中得到相关应用[4-5]。在EAST快控电源工作过程中,假设经采样得到的原始电流序列为
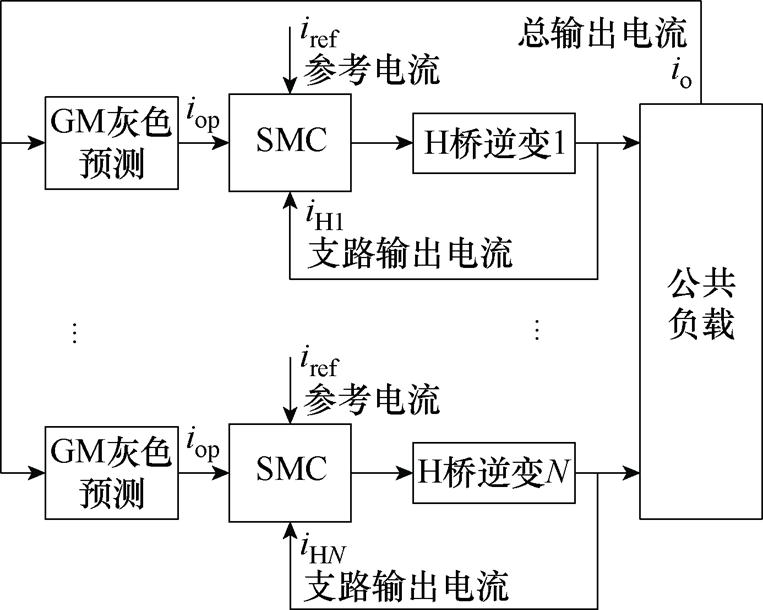
图3 灰色预测滑模控制框图
Fig.3 Control structure of grey prediction sliding mode
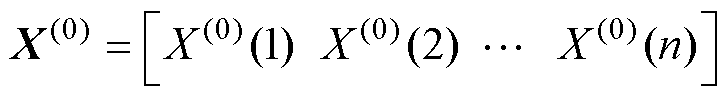 (2)
(2)
得到累加序列
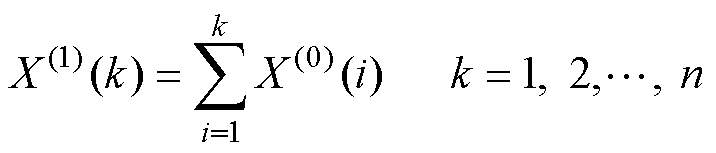 (3)
(3)
根据中值定理构造的序列累加背景值为
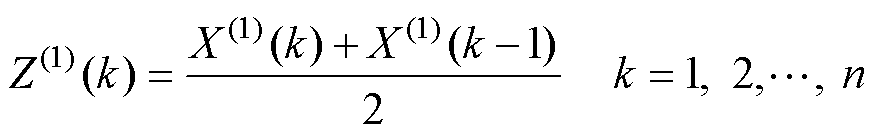 (4)
(4)
经过指数形式的时间响应得还原序列估计值为
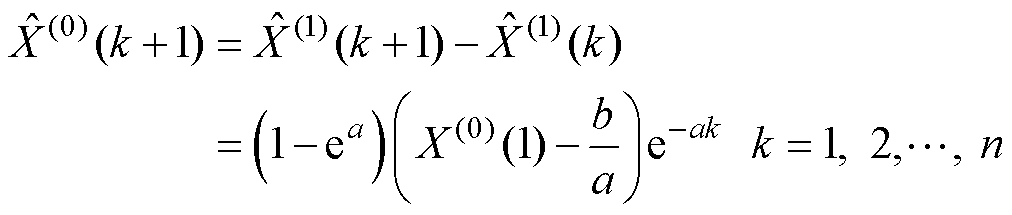 (5)
(5)
式中,a为发展系数;b为灰色量。a、b表示为
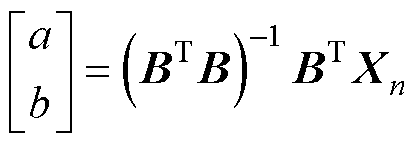 (6)
(6)
其中
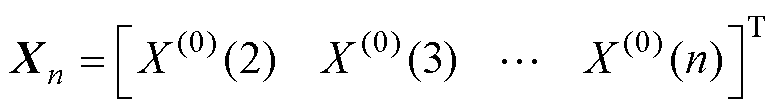 (7)
(7)
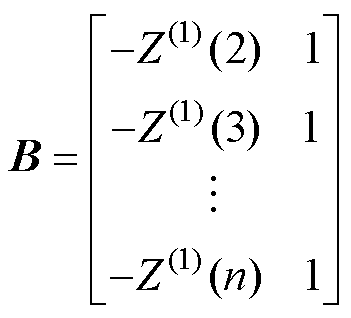 (8)
(8)
发展系数a的取值将会影响还原序列的特性,如图4所示,当a>0时,还原序列趋势将呈递增凸函数和递减凹函数的特性;当a<0时,还原序列趋势将呈递增凹函数和递减凸函数的特性。在输出电流实际建立过程中,上升时呈现递增凸函数且下降时呈现递减凹函数的形状,实际输出电流的特性曲线与a>0时的序列曲线类似。
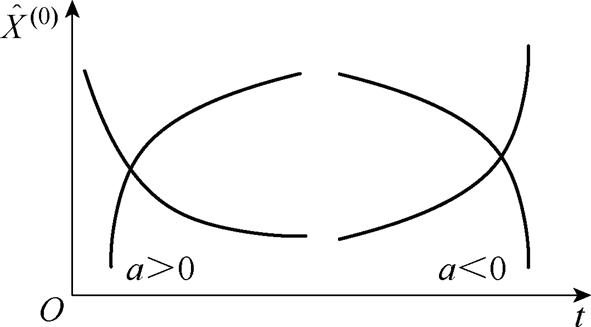
图4 a值与还原序列关系
Fig.4 Relationship between a and restoration sequence
将传统灰色预测应用于EAST快控电源过程中存在以下缺点:
(1)当a<0时,还原序列曲线与实际输出电流曲线趋势存在偏差,输出电流预测精度低。
(2)式(4)对背景值的构造存在较大误差,导致还原序列的预测存在误差。
(3)在数字控制过程中,存在固有的延时,在保证预测精度的同时,应该实现延时补偿保证输出电流快速建立。
为保证输出电流的预测精度,应使还原序列曲线与输出电流实际响应曲线趋势一致。因此,当a<0时,进行原始序列的变换,变换示意图如图5所示,原始序列变换前后的中值不发生改变,仅改变原始序列的凹凸性,使得a<0时还原序列曲线与输出电流实际响应曲线趋势一致。变换过程中将会重构序列累加背景值,使得重构后的原始序列预测曲线与输出电流实际响应曲线趋势一致。基于式(3),得到原始序列间误差为
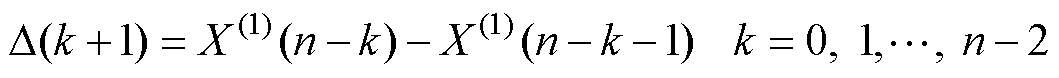 (9)
(9)
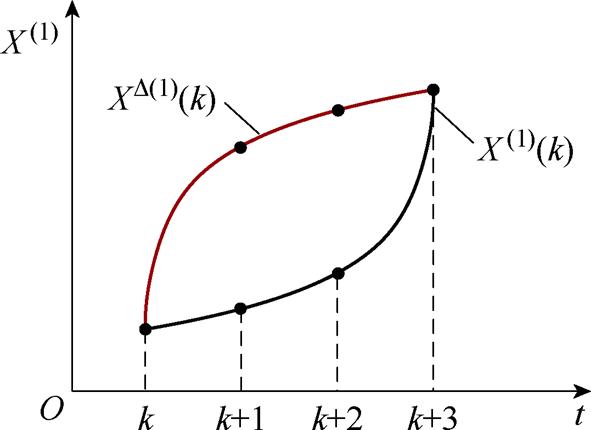
图5 累加序列变换示意图
Fig.5 Transformation of original accumulation sequence
重构的累加序列为
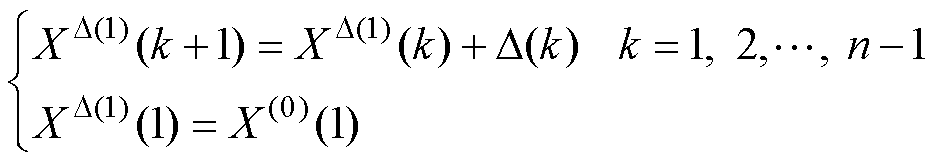 (10)
(10)
背景值重构过程实际为累加序列的积分过程,如图6曲线与时间轴的积分面积所示,而传统灰色预测利用式(4)中的平均值代替积分过程,如图6直角梯形面积所示,背景值构造中存在较大误差,使得输出电流的预测精度难以保证。为了减小近似误差和进一步逼近累加序列的积分过程,将累加序列曲线分割成l个矩形来代替直角梯形,以l个矩形的面积近似代替曲线积分值,如图6中l个矩形构成的总面积所示,背景值重构公式为
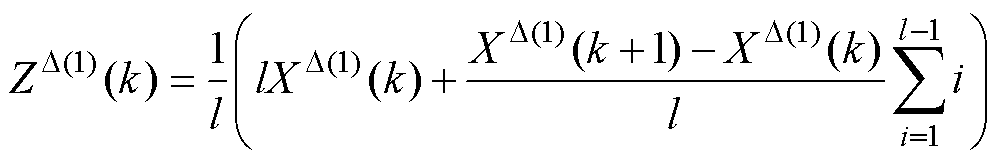
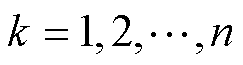 (11)
(11)
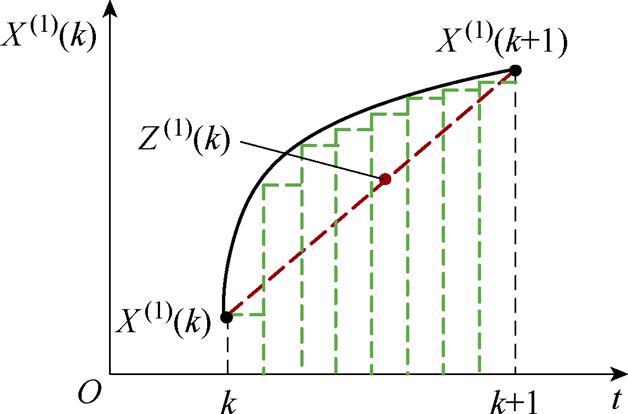
图6 背景值重构示意图
Fig.6 Background value reconstruction diagram
文献[5]分析了数字控制延时对EAST快控电源灰色预测的影响,同时基于新信息优先原则实现了输出电流的预测。根据传统灰色预测分析可知,需要采集k-3~k前4个周期输出电流信号构建原始序列,在第k个周期内实现k+1时刻输出电流i(k+1)的预测,并计算控制量u(k),且装载上周期计算得到的控制量u(k-1),故在第k+1个周期内采样到的电流值实际上是系统在控制量u(k-1)控制下得到的电流输出值,与系统期望得到的值存在偏差。当参考信号在某一时刻发生突变时,原始序列中存在突变前的输出电流值,使得输出电流的预测精度降低。为补偿数字延时,并改善参考电流突变过程中的输出电流预测精度,应及时舍弃老旧的原始序列值,实现滚动灰色预测,故在第k个周期内,将k+1时刻的预测值增加到原始序列,同时舍弃k-3时刻的原始序列值。根据k-2~k+1时刻的电流值预测k+2时刻输出电流,补偿了数字控制延时,及时舍弃老旧原始序列信息保证了预测过程中的预测精度。补偿数字延时过程如图7所示。
为提高灰色预测精度,实现EAST快控电源输出电流快速预测,对灰色预测的原始累加序列和背景值构造过程进行改进,并且利用滚动灰色预测补偿控制延时,改进灰色预测工作过程如图8所示。
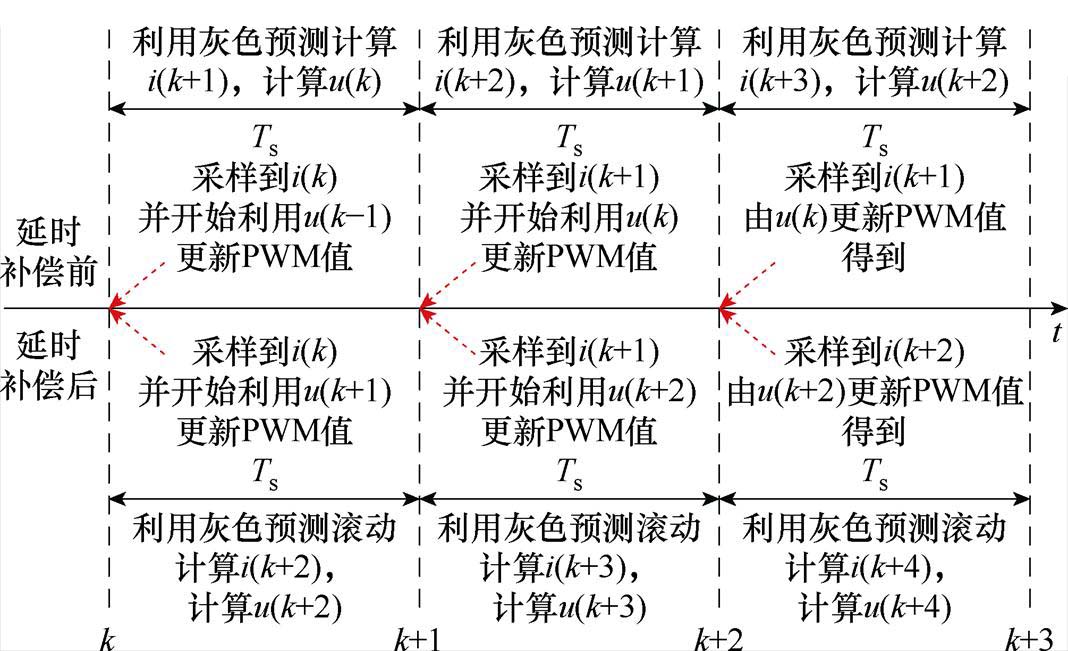
图7 补偿数字延时过程
Fig.7 Compensating for digital delay process
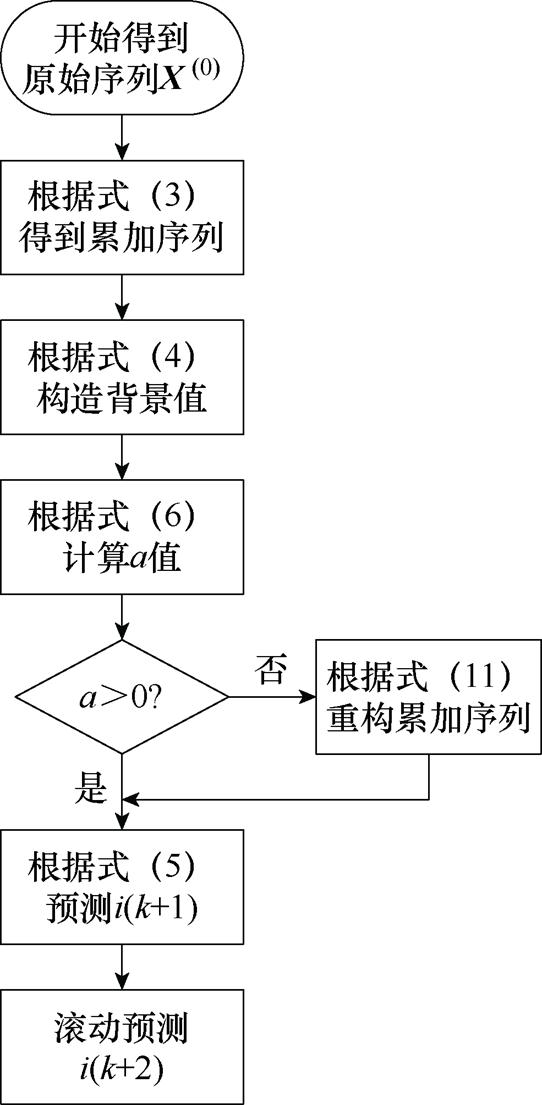
图8 改进灰色预测工作过程
Fig.8 Working process of improved grey prediction
以总输出电流快速跟踪参考电流和各个支路输出电流均衡为控制目的,建立滑模控制函数为
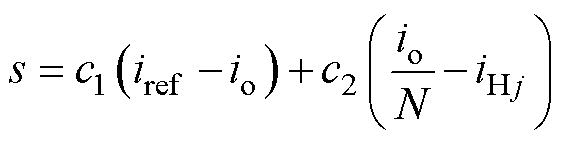 (12)
(12)
式中,c1和c2为滑模系数。
指数趋近率具有趋近速度快的优点,但在有限时间内不能达到滑模面,只能在滑模面附近来回滑动。幂次趋近率能在有限时间内达到滑模面,但趋近过程中会产生较大抖振且趋近速度可以进一步加快。基于指数趋近率和幂次趋近率,提出一种新型快速变幂次趋近率,新型趋近率为
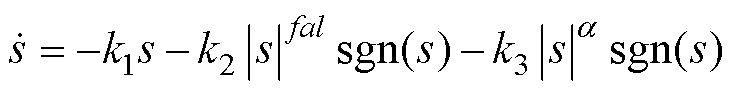 (13)
(13)
式中,k1、k2和k3为趋近系数;sgn(s)为符号函数;0<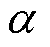 <1;fal为变幂次函数,fal表达式为
<1;fal为变幂次函数,fal表达式为
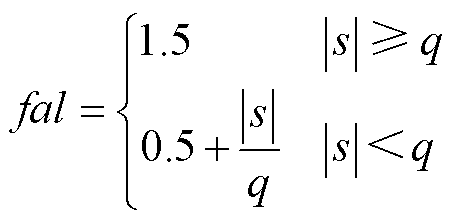 (14)
(14)
式中,q为滑模临界面。
结合式(13)和式(14)分析可知,整个趋近率呈现快速幂次趋近率的特性,当系统离滑模面较远时,fal函数取值较大保证系统快速趋近滑模面,当系统离滑模面较近而趋近临界面时,fal函数取值较小保证系统快速达到滑模面且减小抖振。
为进一步说明所提新型趋近率的优越性能,从可达性、稳态抖振抑制和趋近速度三方面分析新型趋近率的性能。
1)可达性
根据式(13)可知,存在
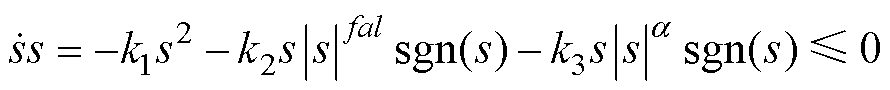 (15)
(15)
由系统连续性和滑模趋近率定理可知,当式(15)成立时,新型滑模趋近率满足存在及可达 条件。
2)稳态抖振抑制
传统指数趋近率表示为
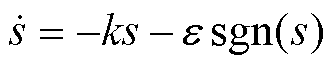 (16)
(16)
式中,k和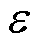 为趋近系数。
为趋近系数。
传统快速幂次趋近率表示为
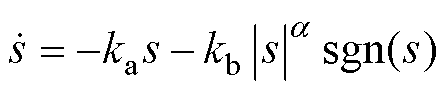 (17)
(17)
式中,ka和kb为趋近系数。
当系统趋近于滑模面时,式(13)和式(17)的极限形式均为0,式(16)的极限形式表示为
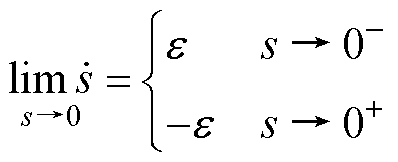 (18)
(18)
当系统趋于稳态阶段时,传统指数趋近率不能稳定在平衡点,而在平衡点附近做幅值为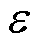 的来回抖振运动。设计的新型趋近率结合了快速幂次趋近率的优点,能在稳态时达到平衡点,有效消除系统抖振。
的来回抖振运动。设计的新型趋近率结合了快速幂次趋近率的优点,能在稳态时达到平衡点,有效消除系统抖振。
3)趋近速度
对于设计的新型趋近率,从任意初始位置s0趋近于平衡点s=0的过程,主要分为从s0到临界面q阶段和从临界面q到平衡点s=0阶段。
从s0到临界面q阶段中,fal变幂次函数取值较大,此阶段新型趋近率中快速趋近项可以简化为
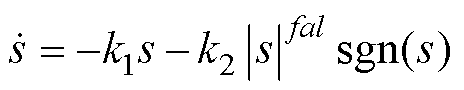 (19)
(19)
因此从s0到临界面q阶段历时应小于极限时间t1,根据式(19)可求得t1为
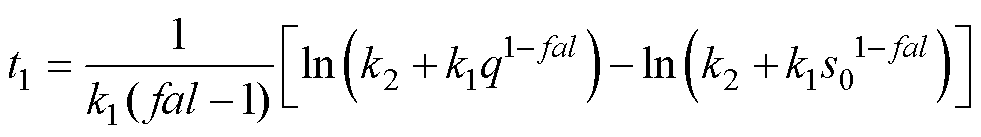 (20)
(20)
从临界面q到平衡点s=0阶段中,fal变幂次函数取值较小而影响较小,因此此阶段新型趋近率中快速趋近项可以简化为
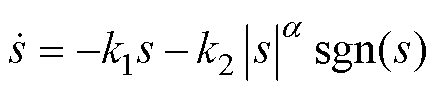 (21)
(21)
因此从临界面q到平衡点s=0阶段历时应小于极限时间t2,根据式(19)可求得t2为
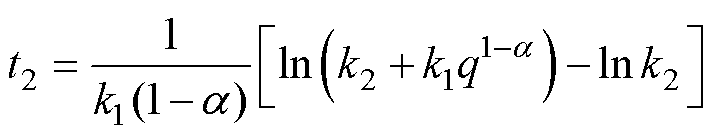 (22)
(22)
联立式(20)和式(22)可得,对于设计的新型趋近率,从任意初始位置s0趋近于平衡点s=0的过程中,历时时间应小于t1+t2。
根据式(17)可得,快速幂次趋近率从任意初始位置s0趋近于平衡点s=0的过程中,历时时间为
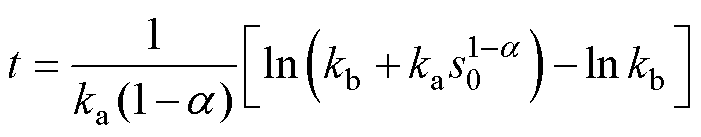 (23)
(23)
分析式(20)、式(22)和式(23)可知,当0.5<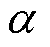 <1时,能够满足t1+t2<t,保证设计的新型趋近率比线性幂次趋近率具有更快的趋近速度。
<1时,能够满足t1+t2<t,保证设计的新型趋近率比线性幂次趋近率具有更快的趋近速度。
在Matlab中搭建由3个H桥级联组成支路的3支路并联仿真模型,对传统双闭环PI控制,传统灰色预测快速幂次趋近率滑模控制,所提的改进灰色预测新型快速变幂次趋近率滑模控制的控制性能进行对比。综合考虑输出电流快速性和支路电流一致性达到均衡,设计表1中合适的PI参数,其他仿真参数见表1。
表1 仿真参数
Tab.1 Simulation parameters

参 数数 值 E/V100 Lo/mH1 LH/mH0.2 Kp13 Ki11.5 Kp290 Ki28 l10 iref/A±30 (100 Hz) c110 c26 k17.5 k210.5 k3150 k1 000 ε600 α0.8 q2
对比所提趋近率与快速幂次趋近率的收敛速度,快速幂次趋近趋近率滑模控制下的输出电流iSM和所提新型快速变幂次趋近率滑模控制下的输出电流iISM对比如图9所示。iSM和iISM均能跟踪参考电流iref,且稳态跟踪波动小,均能有效抑制抖振,但iISM具有更快的跟踪收敛速度。
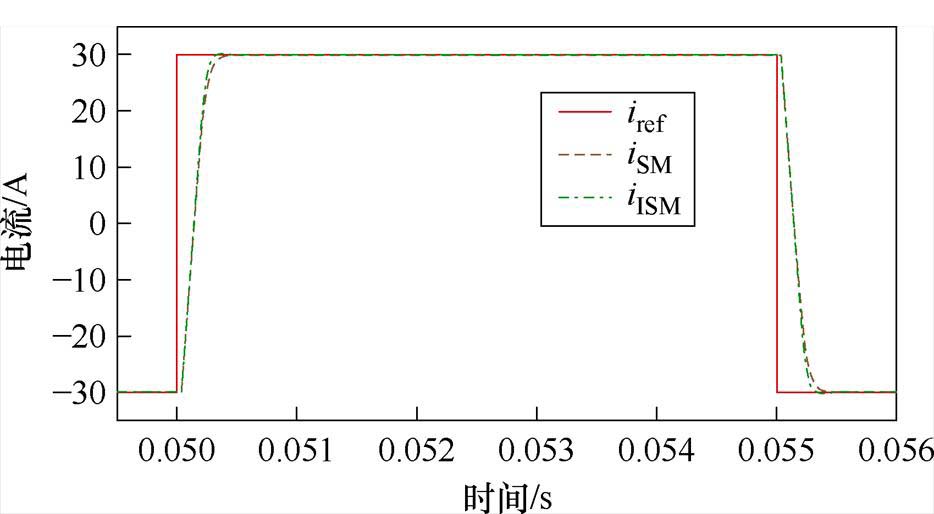
图9 两种滑模趋近率下输出电流对比
Fig.9 Comparison of output current with two reaching law
利用两种灰色预测对输出电流io进行独立预测,传统灰色预测电流iGM和改进灰色预测电流iIGM对比如图10所示。二者均能对给定的输出电流io进行预测,但是iGM在上升过程中出现较大的预测误差,且在整个预测过程中iIGM具有更快的响应速度和更好的预测精度。
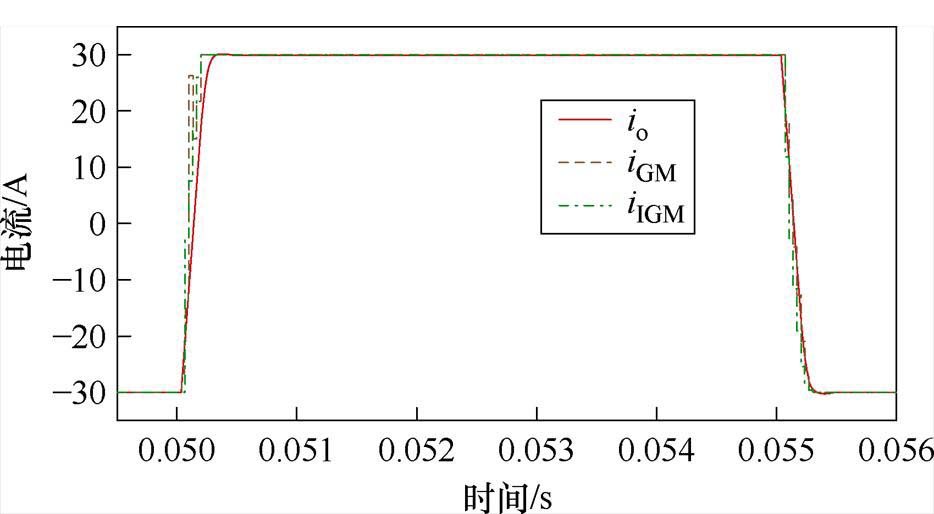
图10 两种灰色预测电流对比
Fig.10 Comparison of two grey prediction current
对比几种控制方法对参考电流的跟踪性能,双闭环PI控制下的输出电流iPI,传统灰色预测快速幂次趋近率滑模控制下的输出电流iGSM,所提改进灰色预测新型快速变幂次趋近率滑模控制下的输出电流iIGSM,对比如图11所示。三种控制方法均能跟踪参考电流输出±30 A (100 Hz) 的总电流,iPI中存在超调且跟踪速度最慢,iGSM和iIGSM均具有更好的跟踪性能,但iIGSM的跟踪速度最快。
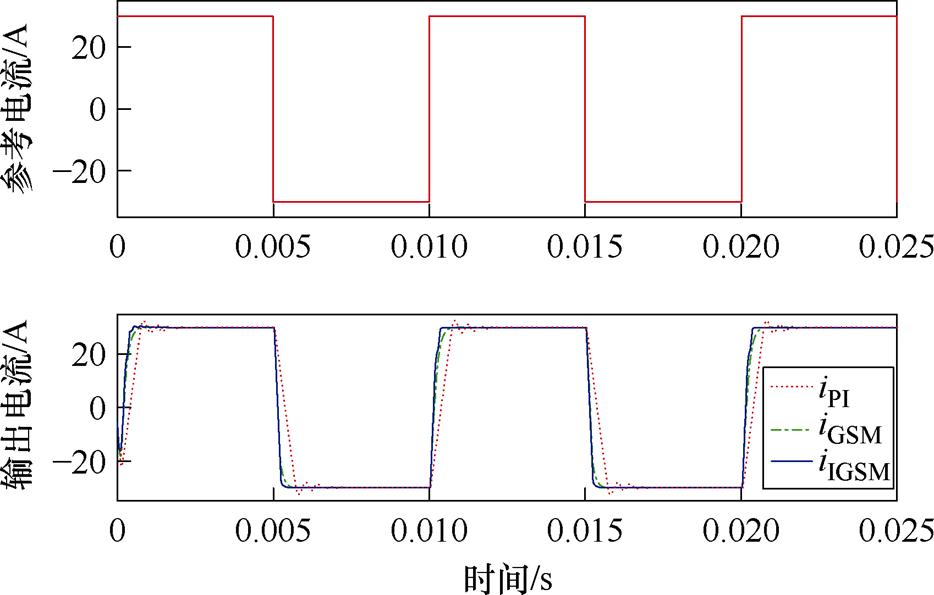
图11 输出电流跟踪性能对比
Fig.11 Comparison of output current tracking performance
对比支路电流的性能,iHPI1、iHPI2、iHPI3为双闭环PI控制下的支路电流,iHGSM1、iHGSM2、iHGSM3为传统灰色预测快速幂次趋近率滑模控制下的支路电流,iHIGSM1、iHIGSM2、iHIGSM3为所提改进灰色预测新型快速变幂次趋近率滑模控制下的支路电流,对比如图12所示。三种控制方法中支路电流趋势均一致,但是双闭环PI控制下支路电流在上升和下降动态过程中存在较大不一致性,滑模控制下的支路电流一致性更好。
以各支路实际输出电流与支路平均电流误差来评估支路电流一致性,ePI1、ePI2、ePI3为PI控制下支路电流误差,eGSM1、eGSM2、eGSM3为传统灰色预测快速幂次趋近率滑模控制下支路电流误差,eIGSM1、eIGSM2、eIGSM3为所提控制方法下支路电流误差,对比如图13所示。ePI1、ePI2、ePI3由于PI控制不能兼顾输出电流动态响应速度和支路电流均衡性,故调节各支路电流时带来了较大的支路电流误差,且误差集中在电流边沿处。两种滑模控制下支路电流误差较小,在电流边沿处存在误差但很快收敛至平均电流值,体现了滑模控制在动态响应控制和支路电流均衡控制方面性能良好。
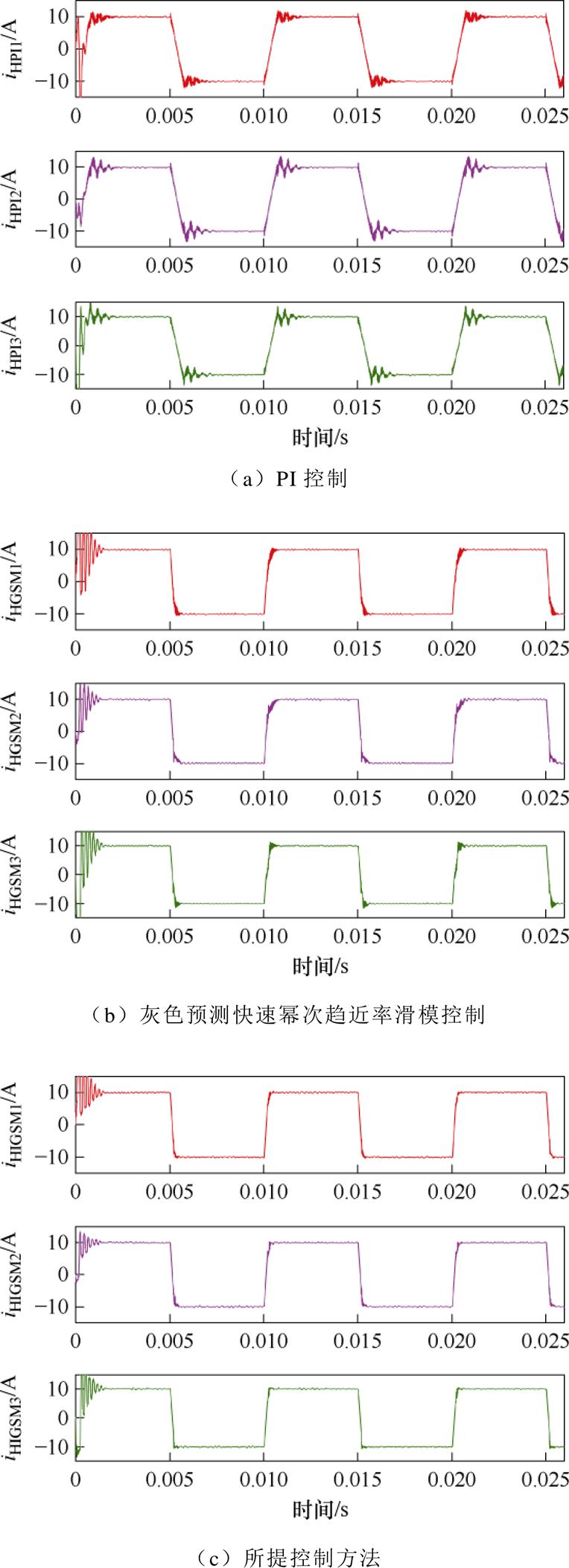
图12 支路电流性能对比
Fig.12 Comparison of branch current performance
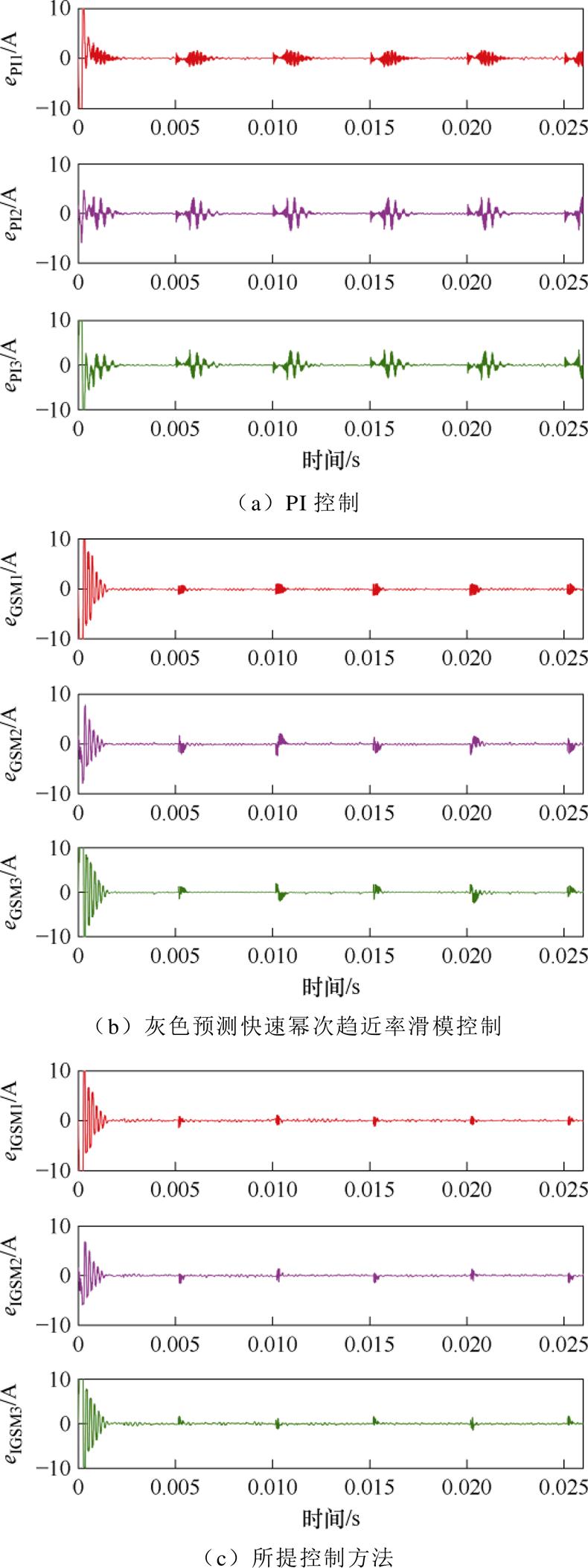
图13 支路电流误差对比
Fig.13 Comparison of branch current error
搭建实验样机对几种控制方法的控制性能进行验证,实验样机由3个支路并联组成,每支路由3个H桥逆变器级联而成。控制器选择TMS32028335数字处理器,IGBT开关管型号为SKM75GB12T4,实验样机如图14所示。考虑到实验过程中输出电流动态响应速度和支路电流一致性的均衡,选择合适的PI控制参数进行实验对比,实验参数见表2。

图14 实验样机
Fig.14 Experimental prototype
表2 实验参数
Tab.2 Experimental parameters

参 数数 值 E/V80 Lo/mH2 LH/mH0.4 Kp10.65 Ki10.05 Kp20.8 Ki20.02 l10 iref/A±10 (100 Hz) c13 c21 k12 k23 k310 k800 ε200 α0.8 q20
双闭环PI控制下输出电流iPI如图15所示,iPI能够跟踪参考电流iref,但是存在一定的波动。iPI跟踪iref的动态过程中,上升调节过程经历570 ms,下降调节过程经历560 ms。
快速幂次趋近率滑模控制下输出电流iSM如图16所示,iSM能够跟踪参考电流iref,跟踪性能良好。iSM跟踪iref的动态过程中,上升调节过程经历490 ms,下降调节过程经历510 ms。对比双闭环PI控制,滑模控制能够有效提升输出电流响应速度。
传统灰色预测快速幂次趋近率滑模控制下输出电流iGSM如图17所示,iGSM跟踪参考电流iref性能良好。iGSM跟踪iref的动态过程中,上升调节过程经历470 ms,下降调节过程经历470 ms。相对单一的滑模控制,灰色预测能够进一步提升输出电流响应速度,但是传统灰色预测在参考电流上升阶段对输出电流的预测存在一定预测误差。
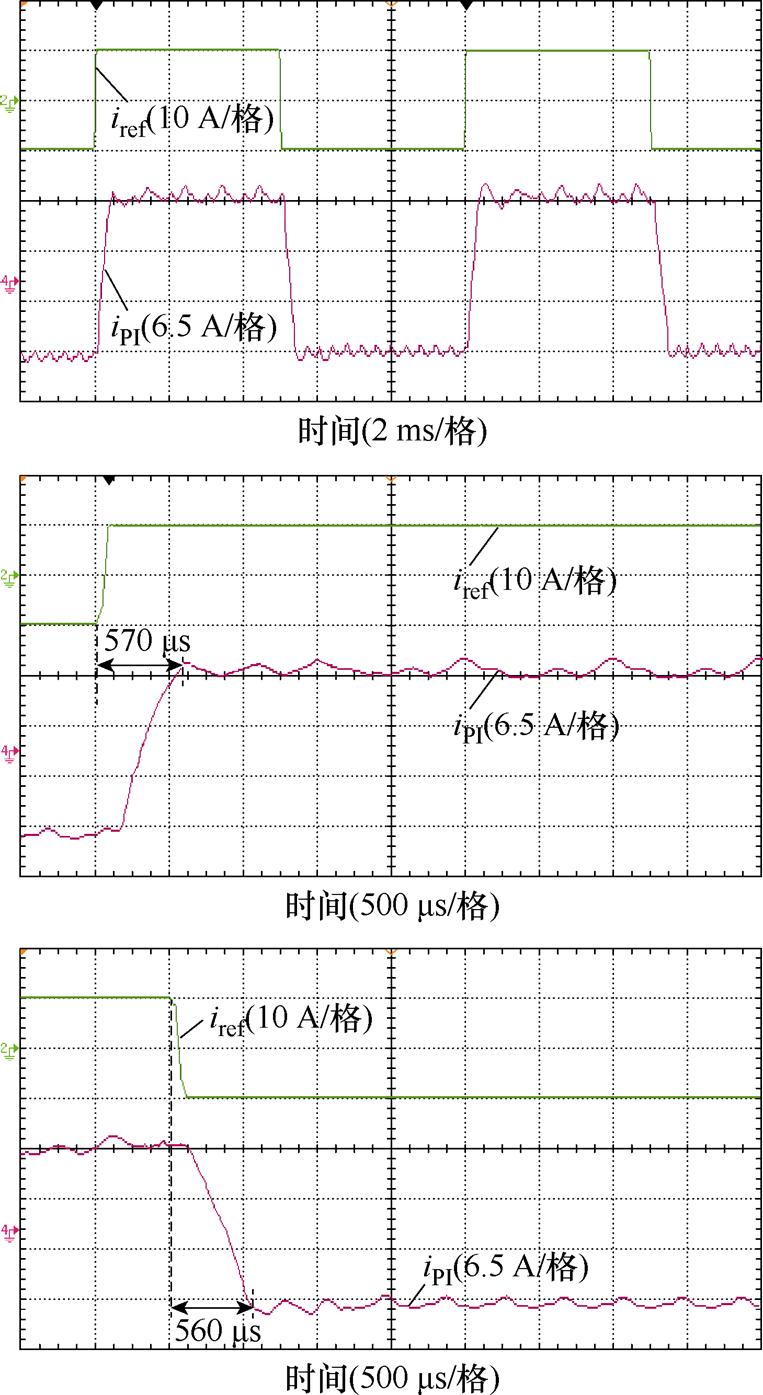
图15 PI控制下输出电流
Fig.15 Output current of PI control
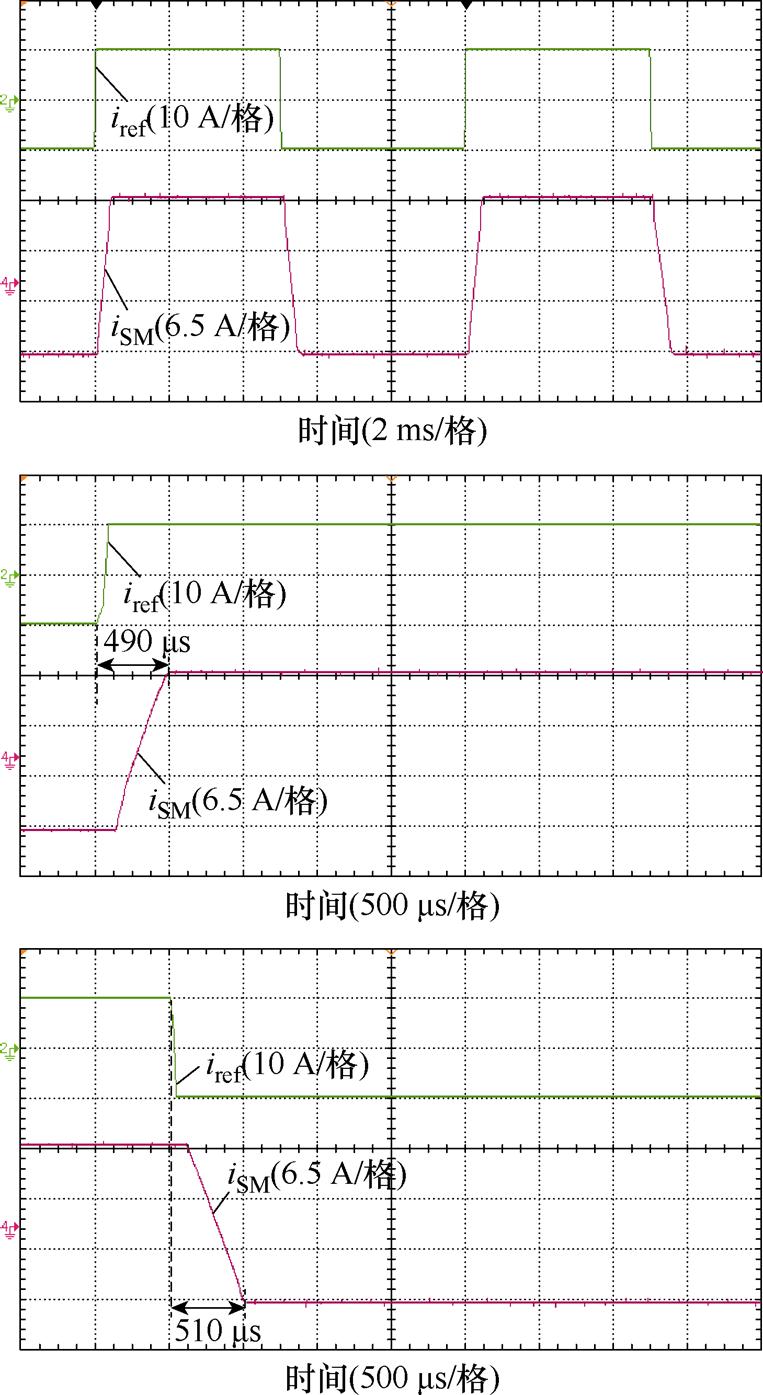
图16 快速幂次趋近率滑模控制下输出电流
Fig.16 Output current of fast power reaching law sliding mode control
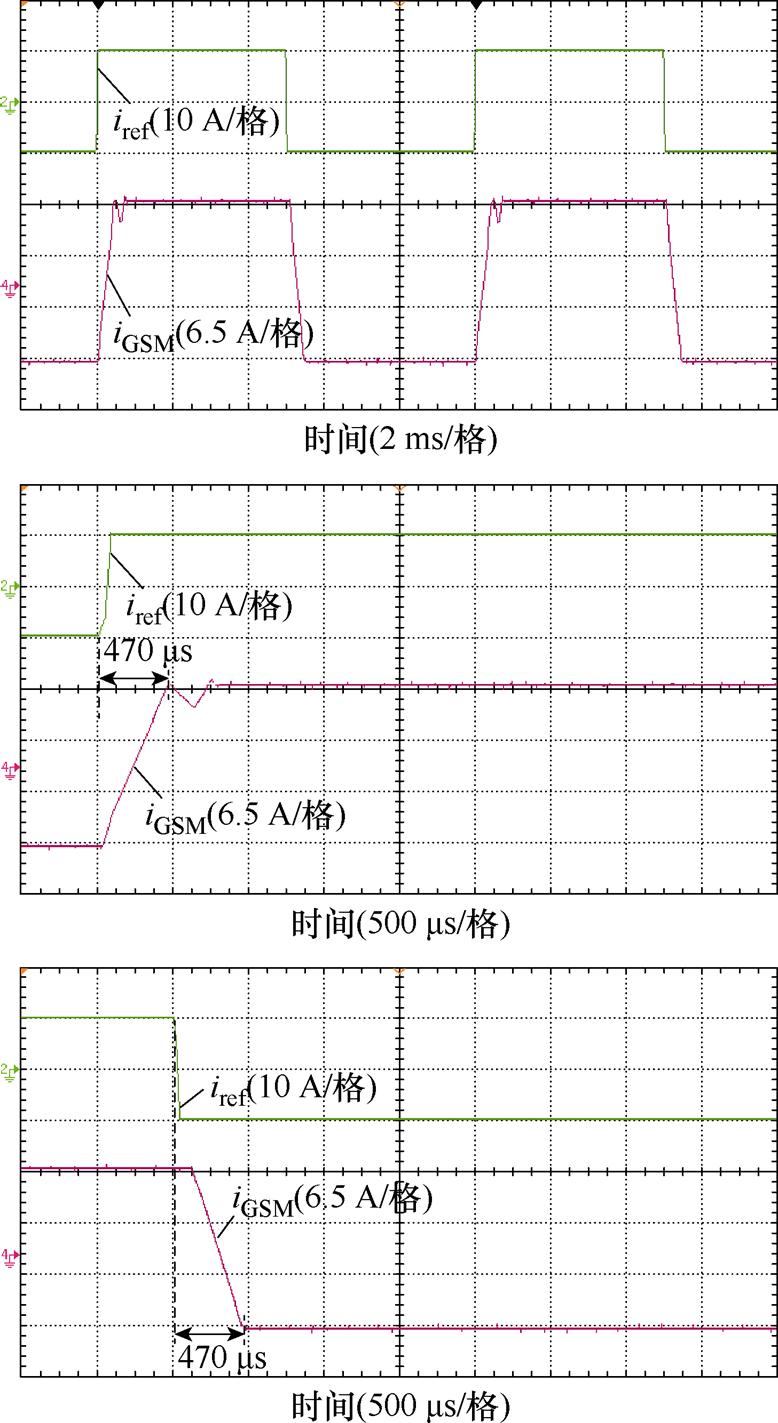
图17 灰色预测快速幂次趋近率滑模控制下输出电流
Fig.17 Output current of grey prediction fast power reaching law sliding mode control
所提改进灰色预测新型快速变幂次趋近率滑模控制下输出电流iIGSM如图18所示,iIGSM跟踪参考电流iref性能良好。iIGSM跟踪iref的动态过程中,上升调节过程经历410 ms,下降调节过程经历400 ms。对比双闭环PI控制和传统灰色预测快速幂次趋近率滑模控制,所提控制方法使得输出电流动态响应速度得到进一步提升,且改进的灰色预测对比传统的灰色预测具有更好的预测精度。
iHPI1、iHPI2、iHPI3为双闭环PI控制下支路电流,iHSM1、iHSM2、iHSM3为传统快速幂次趋近率滑模控制下支路电流,iHGSM1、iHGSM2、iHGSM3为传统灰色预测快速幂次趋近率滑模控制下支路电流,iHIGSM1、iHIGSM2、iHIGSM3为所提改进灰色预测新型快速变幂次趋近率滑模控制下支路电流,性能对比如图19~图22所示。iHPI1、iHPI2、iHPI3存在一定的波动,双闭环PI控制使得支路电流间一致性较差。iHSM1、iHSM2、iHSM3,iHGSM1、iHGSM2、iHGSM3,iHIGSM1、iHIGSM2、iHIGSM3几种支路电流一致性良好,支路电流平稳无波动,滑模控制能够有效抑制支路间电流差异。
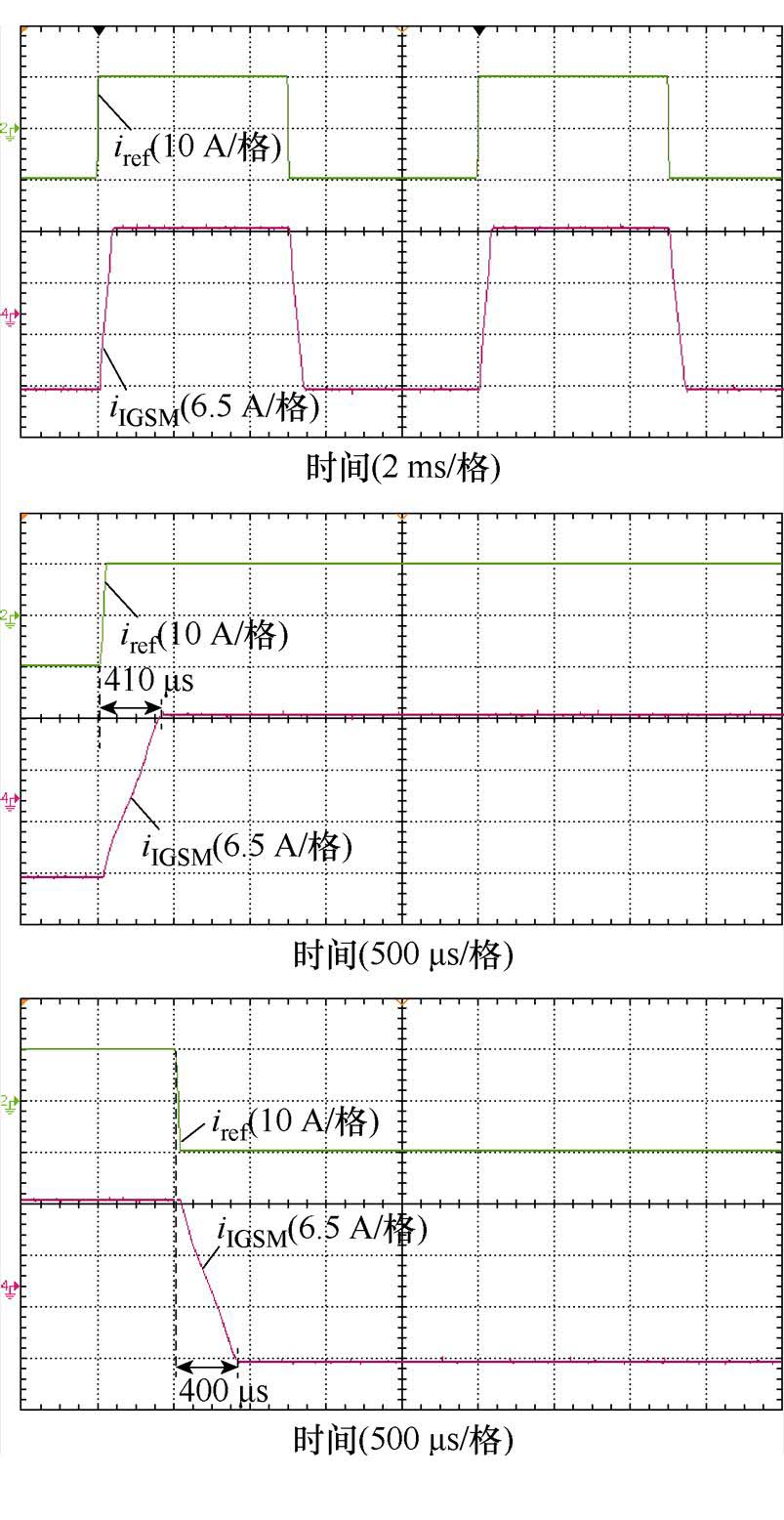
图18 所提控制方法下输出电流
Fig.18 Output current of proposed control method
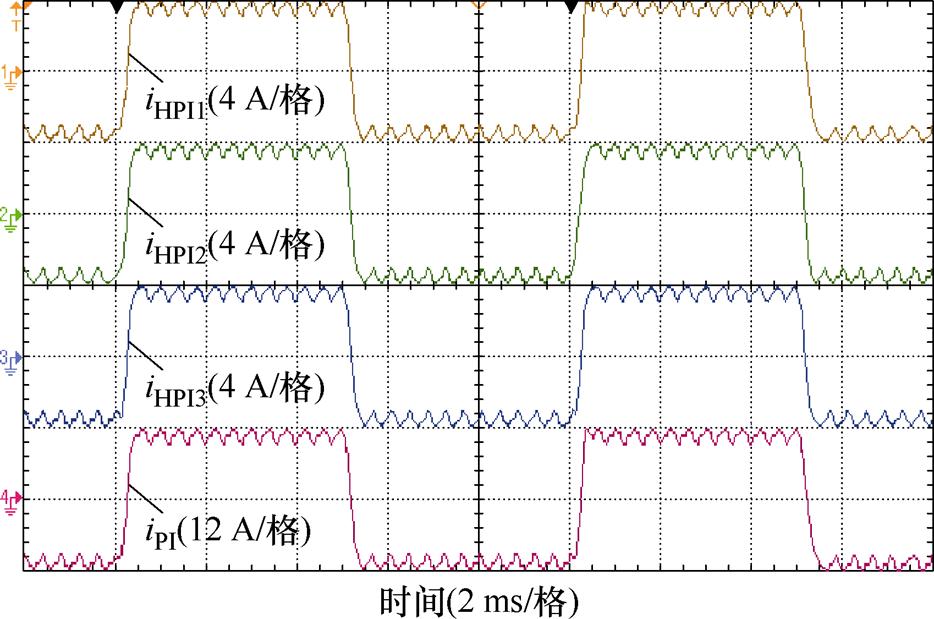
图19 PI控制下支路电流
Fig.19 Branch current of PI control
对几种控制方法性能进行对比,参考电流的跟踪动态响应时间和支路电流一致性对比见表3。根据表3可知,滑模控制对比双闭环PI控制具有更快的动态响应速度和更好的支路电流一致性,灰色预测能够有效预测输出电流以加快输出电流响应速度。对比传统灰色预测,改进灰色预测预测精度更高,所提改进灰色预测新型快速变幂次趋近率滑模控制下输出电流具有更快的动态响应速度。
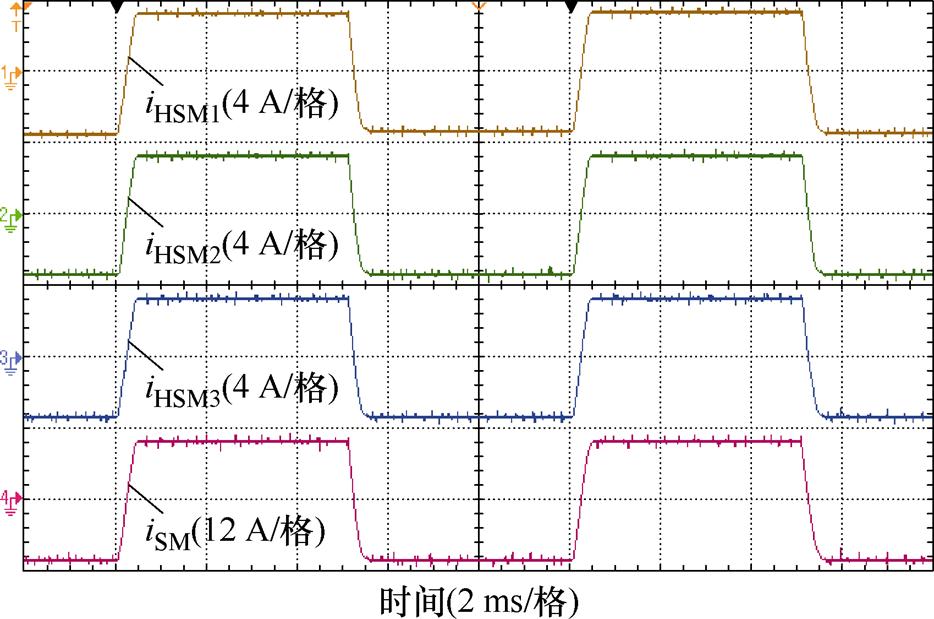
图20 快速幂次趋近率滑模控制下支路电流
Fig.20 Branch current of fast power reaching law sliding mode control
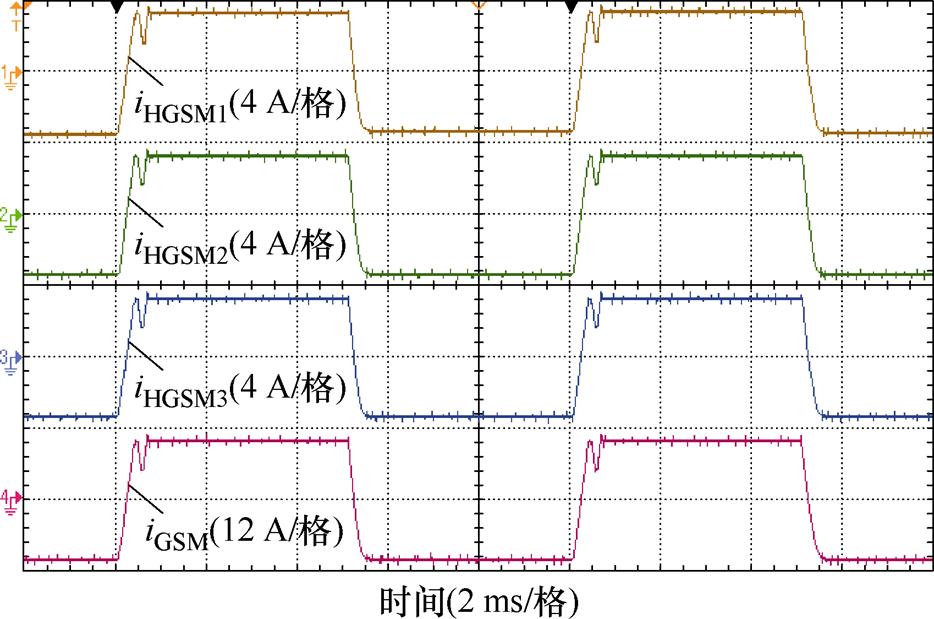
图21 灰色预测快速幂次趋近率滑模控制下支路电流
Fig.21 Branch current of grey prediction fast power reaching law sliding mode control
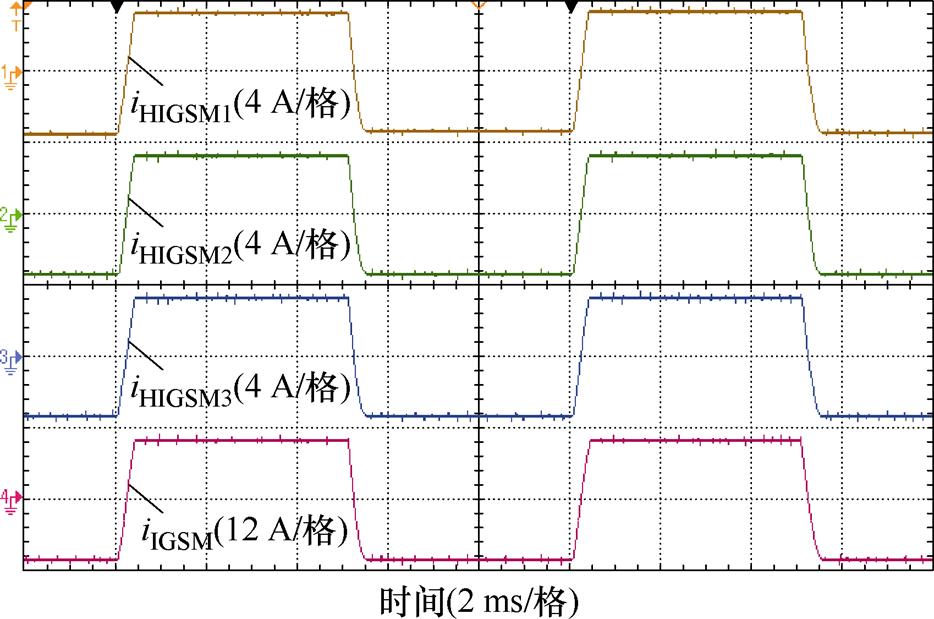
图22 所提控制方法下支路电流
Fig.22 Branch current of proposed control method
表3 几种方法控制性能对比
Tab.3 Performance comparison of different methods
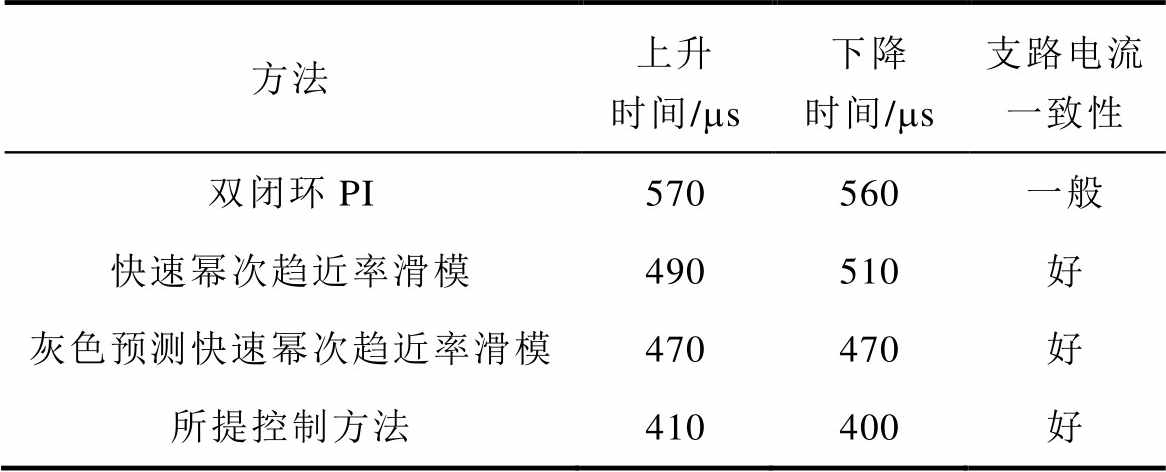
方法上升时间/ms下降时间/ms支路电流一致性 双闭环PI570560一般 快速幂次趋近率滑模490510好 灰色预测快速幂次趋近率滑模470470好 所提控制方法410400好
为实现EAST快控电源总输出电流快速控制和支路电流均衡控制,提出一种改进灰色预测方法对总输出电流轨迹进行预测,利用改进新型快速变幂次趋近率实现总输出电流和各个支路电流的一致性均衡控制。在输出电流反馈环节加入改进灰色预测,以实现输出电流的提前预测,对灰色预测背景值进行重构,将预测值加入到原始序列实现滚动预测,有效提高了灰色预测的精度。为加快总输出电流动态响应速度和解决各个支路输出电流不均衡问题,设计以总电流跟踪参考电流和支路电流均衡为控制目的的滑模面,提出一种新型快速变幂次趋近率以加快系统的收敛速度。仿真和实验结果表明所提控制方法对比几种传统方法具有以下优点:能有效提升输出电流动态响应速度;对输出电流的预测精度更加准确;支路电流一致性更好。
参考文献
[1] 黄海宏, 颜碧琛, 王海欣. 并联级联H桥电源电流跟踪优化与环流抑制的模型预测控制[J]. 电工技术学报, 2023, 38(16): 4376-4390.
Huang Haihong, Yan Bichen, Wang Haixin. Model predictive control of current tracking optimization and circulating current suppression for multi-parallel cascaded H-bridge power supplies[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4376- 4390.
[2] Wang Huiping, Zhang Zhun. A novel grey model with fractional reverse accumulation for forecasting natural gas consumption[J]. Computers & Industrial Engineering, 2023, 179: 109189.
[3] Li Peng, Xu Xiaosu, Yang Shirui, et al. Open circuit fault diagnosis strategy of PMSM drive system based on grey prediction theory for industrial robot[J]. Energy Reports, 2023, 9: 313-320.
[4] 黄海宏, 陈昭, 王海欣. 基于改进灰色预测单神经元PI的全超导托卡马克核聚变发电装置快控电源电流控制[J]. 电工技术学报, 2024, 39(6): 1886- 1897.
Huang Haihong, Chen Zhao, Wang Haixin. Current control of experimental advanced superconducting tokamak fast control power supply based on improved grey prediction single neuron PI[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1886- 1897.
[5] Chen Zhao, Huang Haihong, Wang Haixin. Current control of EAST fast control power supply based on improved grey prediction variable gain PI[J]. Journal of Fusion Energy, 2023, 42(2): 34.
[6] Liu Chong, Wu Wenze, Xie Wanli. A new grey intelligent prediction algorithm with multiobjective correction strategy[J]. Applied Mathematical Modelling, 2023, 118: 692-708.
[7] Ye Jing, Li Yan, Ma Zhenzhen, et al. Novel weight- adaptive fusion grey prediction model based on interval sequences and its applications[J]. Applied Mathematical Modelling, 2023, 115: 803-818.
[8] 王方, 王治中, 刘启明. DGGM(1, 1)双参优化模型及其应用研究[J]. 运筹与管理, 2023, 32(6): 82-88.
Wang Fang, Wang Zhizhong, Liu Qiming. Research on two-parameter optimization of DGGM(1, 1) model and its application[J]. Operations Research and Management Science, 2023, 32(6): 82-88.
[9] 孙波, 李娜, 张振威, 等. 基于改进灰色GM(1, 1)模型的轨道电路故障预测[J]. 电子测量技术, 2023, 46(12): 26-33.
Sun Bo, Li Na, Zhang Zhenwei, et al. Track circuit fault prediction based on modified grey GM(1, 1) model[J]. Electronic Measurement Technology, 2023, 46(12): 26-33.
[10] 陆珩, 胡长斌, 罗珊娜, 等. 基于模型预测与残差生成器的Buck变换器并联系统性能提升控制策略[J]. 中国电机工程学报, 2023, 43(24): 9696-9711.
Lu Heng, Hu Changbin, Luo Shanna, et al. Per- formance improvement control strategies for buck converter parallel systems based on model predictive control and residual generators[J]. Proceedings of the CSEE, 2023, 43(24): 9696-9711.
[11] Comparatore L, Ayala M, Kali Y, et al. Discrete-time sliding mode current control for a seven-level cascade H-bridge converter[J]. Energies, 2023, 16(5): 2481.
[12] 魏尧, 柯栋梁, 黄东晓, 等. 基于超局部化时间序列的永磁同步电机无模型预测电流滑模控制策略[J]. 电工技术学报, 2024, 39(4): 1022-1032.
Wei Yao, Ke Dongliang, Huang Dongxiao, et al. Model-free predictive sliding mode control using ultra-localized time-series for permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1022-1032.
[13] 汪凤翔, 杨奥, 于新红, 等. 基于自适应超螺旋滑模观测器的三相Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2024, 39(6): 1859-1870.
Wang Fengxiang, Yang Ao, Yu Xinhong, et al. Model-free predictive current control for three-phase Vienna rectifier based on adaptive super-twisting sliding mode observer[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1859-1870.
[14] Li Shaoling, Li Peike, Zheng Zheng, et al. Fractional order sliding mode control for circulating current suppressing of MMC[J]. Electrical Engineering, 2023, 105(6): 3791-3800.
[15] 黄海宏, 陈昭, 王海欣. 全超导托卡马克核聚变发电装置快控电源的干扰抑制离散积分滑模电流控制[J]. 电工技术学报, 2024, 39(10): 3141-3151.
Huang Haihong, Chen Zhao, Wang Haixin. Dis- turbance suppression discrete integral sliding mode current control of experimental advanced supercon- ducting tokamak fast control power supply[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3141-3151.
[16] Huang Haihong, Chen Zhao, Wang Haixin. Current tracking and circulating current suppression super- twisting sliding mode control for parallel operation of EAST fast control power supply[J]. Fusion Science and Technology, 2023: 1-19.
[17] Xiang Chuan, Cheng Qi, Zhu Yizheng, et al. Sliding mode control of ship DC microgrid based on an improved reaching law[J]. Energies, 2023, 16(3): 1051.
[18] 郭昕, 黄守道, 彭昱, 等. 基于改进型双幂次趋近律与全局快速终端滑模观测器的IPMSM调速系统滑模控制[J]. 电工技术学报, 2023, 38(1): 190-203.
Guo Xin, Huang Shoudao, Peng Yu, et al. Sliding mode control of IPMSM speed regulation system based on an improved double power reaching law and global fast terminal sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 190-203.
[19] Zuo Zhaoyang, Vafamand N, Mobayen S, et al. Finite-time tracking control with fast reaching condition for disturbed more electric aircraft direct current microgrid with constant power loads[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6695-6704.
[20] Zhang Dongdong, Zhang Hanquan, Li Xiang, et al. A PMSM control system for electric vehicle using improved exponential reaching law and proportional resonance theory[J]. IEEE Transactions on Vehicular Technology, 2023, 72(7): 8566-8578.
[21] 任萍, 朱景伟, 赵燕, 等. 基于双滑模控制器的开关磁阻电机调速策略[J]. 中国电机工程学报, 2024, 44(11): 4501-4513.
Ren Ping, Zhu Jingwei, Zhao Yan, et al. Speed control strategy for switched reluctance motor based on dual sliding mode controller[J]. Proceedings of the CSEE, 2024, 44(11): 4501-4513.
[22] Quan N V, Long M T. An improved control method for cascaded multilevel inverters based on sliding mode control technique[J]. Electrical Engineering, 2023, 105(5): 3293-3306.
[23] 聂永辉, 曲铭锐, 周恒宇, 等. 基于小脑模型-模糊滑模控制的电力系统低频振荡控制策略研究[J]. 电网技术, 2024, 48(2): 789-800.
Nie Yonghui, Qu Mingrui, Zhou Hengyu, et al. Control strategy of low-frequency oscillation supper- ssion in power system based on CMAC-FSMC[J]. Power System Technology, 2024, 48(2): 789-800.
Abstract Experimental advanced superconducting Tokamak (EAST) fast control power supply is vital for plasma vertical displacement control in controllable nuclear fusion. Multiple H-bridge inverter branches in parallel operation mode are adopted in the EAST fast control power supply. Plasma balance control is affected by output current tracking reference current, and branch current consistency is crucial for branches’ stable operation. At present, proportional-integral (PI) control is used in engineering to achieve EAST fast control of power supply current control. However, it has shortcomings regarding output current speed and branch current balance control.
This paper proposes an improved grey method based on fast variable power reaching law sliding mode control. Grey prediction is added to the total output current feedback loop to accelerate the response speed of the output current. The original sequence of grey prediction is transformed to ensure that the concavity and convexity of the original sequence are consistent with the actual output current. The integration idea is used to reconstruct the background value of grey prediction to reduce the prediction error from background value construction. T compensates for digital control delay, and the predicted current value is added to the original sequence to replace the oldest information and achieve multi-step rolling prediction. Grey prediction improvements enhance the EAST fast control of power supply output current prediction. The sliding mode surface with total current tracking reference current and branch current balancing as control objective is designed. In sliding mode control, according to the exponential reaching law and power reaching law, a new fast variable power reaching law is proposed to accelerate the convergence speed of the sliding mode control system. The output current dynamic response speed and branch current consistency are enhanced.
Simulation and experimental results show that output current response speed is effectively accelerated by grey prediction, and branch current balance control is ensured by sliding mode control. Compared with the traditional current grey prediction, the improved grey prediction enhances output current prediction accuracy and accelerates dynamic speed. Compared with the traditional reaching law sliding mode current control speed, convergence speed is accelerated by the proposed new fast variable power reaching law sliding mode current control. The proposed grey prediction has a faster output current dynamic response speed and better branch current consistency, effectively improving EAST fast control and ensuring stable balance control of plasma vertical displacement.
Keywords:Experimental advanced superconducting Tokamak (EAST) fast control power supply, output current, grey prediction, sliding mode control
中图分类号:TM93
DOI: 10.19595/j.cnki.1000-6753.tces.241221
国家自然科学基金区域创新发展联合基金资助项目(U22A20225)。
收稿日期 2024-07-10
改稿日期 2024-09-02
黄海宏 男,1973年生,教授,博士生导师,研究方向为新型大功率变流技术与电力电子技术等。
E-mail: hhaihong741@ 126.com
陈 昭 男,1996年生,博士研究生,研究方向为新型电能变换技术等。
E-mail: chenzhao_0202@163.com(通信作者)
(编辑 陈 诚)