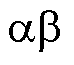 静止坐标系下的离散数学模型可以表示为
静止坐标系下的离散数学模型可以表示为摘要 为解决传统模型预测控制参数依赖性的问题,首先,该文提出一种适用于LC型滤波逆变器的三矢量无模型预测控制方法,构造了电流-电压梯度查表法,分析不同矢量对应的电感电流梯度与电容电压梯度之间的关系,从而实现了梯度全更新并基于梯度进行电流-电压的无模型预测值计算;其次,通过分析电流-电压采样值与参考值之间的相位幅值关系,构造基于采样信号相位差值的计算方法,实现LC型滤波逆变器的无参数参考值计算;再次,进一步建立电压-电流双目标价值函数,实现下一控制周期最优矢量的选取;最后,通过搭建实验平台,对所提方法与传统控制方法在不同运行工况下的输出电压纹波、总谐波畸变率以及预测误差等指标进行对比,以验证所提方法的有效性。所提控制方法实现了LC型滤波逆变器无模型预测控制,消除了传统无模型预测中参考值计算对系统参数的依赖,在参数失配条件下可有效降低输出电压预测误差,增强所提控制方法的参数鲁棒性,进一步改善参数失配条件下逆变器输出电压性能。
关键词:电压源逆变器 LC型滤波器 三矢量 无模型预测控制 无参数参考值
近年来,随着分布式能源(Distributed Energy Resources, DERs)的迅速发展与广泛应用,LC型滤波电压源逆变器(Voltage Source Inverter, VSI)成为了DERs的关键设备[1],相比L滤波型逆变器,其在高功率水平下具有更优良的谐波抑制能力、更好的紧凑性与更低的成本优势[2-4]。
为了保证LC型滤波电压源逆变器的输出电压性能,模型预测控制(Model Predictive Current Control, MPC)因其实现简单、响应快速和多目标控制[5-7]的优势而得到了广泛的研究与应用。MPC算法利用逆变器的离散模型基于系统采样值对系统未来时刻的状态进行推导,使用价值函数对VSI不同电压矢量所对应的系统状态进行评估,从而选择最优矢量进行开关动作[8-10]。然而该算法的控制性能十分依赖于预测模型中系统参数的准确性[11-12],当系统参数与实际参数发生失配时,价值函数对最优矢量的判断会受到影响,增加预测误差,导致输出次优矢量,从而影响逆变器稳定性。
为了消除传统MPC方法对系统参数的依赖,许多学者对无模型预测控制(Model-Free Predictive Control, MFPC)展开了研究,该方法往往基于系统采样数据而非系统参数来构造系统运行状态模型,常见的MFPC方法有超局部(Ultra-local model)[13-14]法,自回归输入(Auto Regressive with eXogenous input, ARX)法[15]以及查找表(Look-Up Table, LUT)[16-21]法。然而,基于超局部与ARX的MFPC往往需要大量存储空间来记录多个控制周期的电流、电压数据,这在一定程度上会影响MFPC的动态性能,同时在不同运行工况下这些算法需要设定不同的增益系数,否则MFPC的准确性与响应速度会受到影响。
基于LUT的MFPC利用存储在LUT中与8个基本电压矢量相对应的电流梯度来计算VSI的电流预测值[16],整个预测过程并不依赖系统参数,该方法只对LUT中被选择的电压矢量所对应的电流梯度进行更新,其余矢量对应的电流梯度则保持停滞,如此将会影响预测值计算的准确性。针对梯度更新问题,文献[17]基于历史3个控制周期的电流梯度来更新当前周期的电流梯度。文献[18-19]建立了两个相邻周期内不同电压矢量所对应的梯度关系,从而实现了所有梯度的更新。文献[20-21]采用三矢量控制方法,基于同一控制周期内3个应用矢量构建了梯度更新方程组,从而实现所有梯度的实时更新。以上文献主要针对L型滤波VSI展开研究,文献[21-22]将基于LUT的MFPC方法扩展到LC型滤波VSI上,对LC型滤波器的电感电流梯度与电容电压梯度之间的关系展开研究,构造了双梯度结构LUT,并实现了电流-电压梯度的更新。值得注意的是,上述文献主要通过电流(电压)梯度实现预测值的无模型计算,消除了预测过程对系统参数的依赖,而未考虑参考值计算过程中的参数敏感性问题,如文献[21-22]中桥臂侧电感电流参考值的计算需要使用LC型滤波器系统参数,其MFPC算法依然受到参数失配的影响。
本文针对LC型滤波逆变器提出了一种基于无模型预测与无参数参考的三矢量预测控制方法。首先,该方法建立了当前控制周期内应用的3个矢量所对应的电容电压梯度与桥臂侧电感电流梯度之间的关系,并推导了三矢量电压-电流梯度全更新公式,从而实现LC型滤波逆变器三矢量无模型预测值计算;其次,本文分析了电压-电流采样值与参考值之间的相位幅值关系,提出了一种基于相位差值的参考值无参数计算方法,消除传统参考值计算过程对参数的依赖,提高所提MFPC的参数鲁棒性;再次,通过建立电压-电流双目标价值函数来实现逆变器的多目标控制,提高了输出电能质量;最后,通过实验验证了所提方法的有效性。
如图1所示为LC型滤波VSI拓扑结构以及传统模型预测控制框图。根据零阶保持法,该拓扑在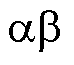 静止坐标系下的离散数学模型可以表示为
静止坐标系下的离散数学模型可以表示为
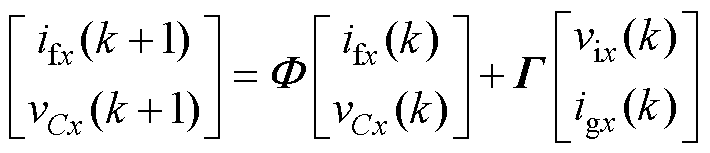 (1)
(1)
式中,x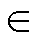 {
{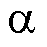 ,
, 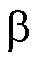 };ifx为逆变器桥臂侧电感电流;vCx为逆变器电容电压;vix为逆变器侧输出电压;igx为逆变器输出电流,参数矩阵
};ifx为逆变器桥臂侧电感电流;vCx为逆变器电容电压;vix为逆变器侧输出电压;igx为逆变器输出电流,参数矩阵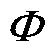 、
、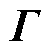 可表示为
可表示为
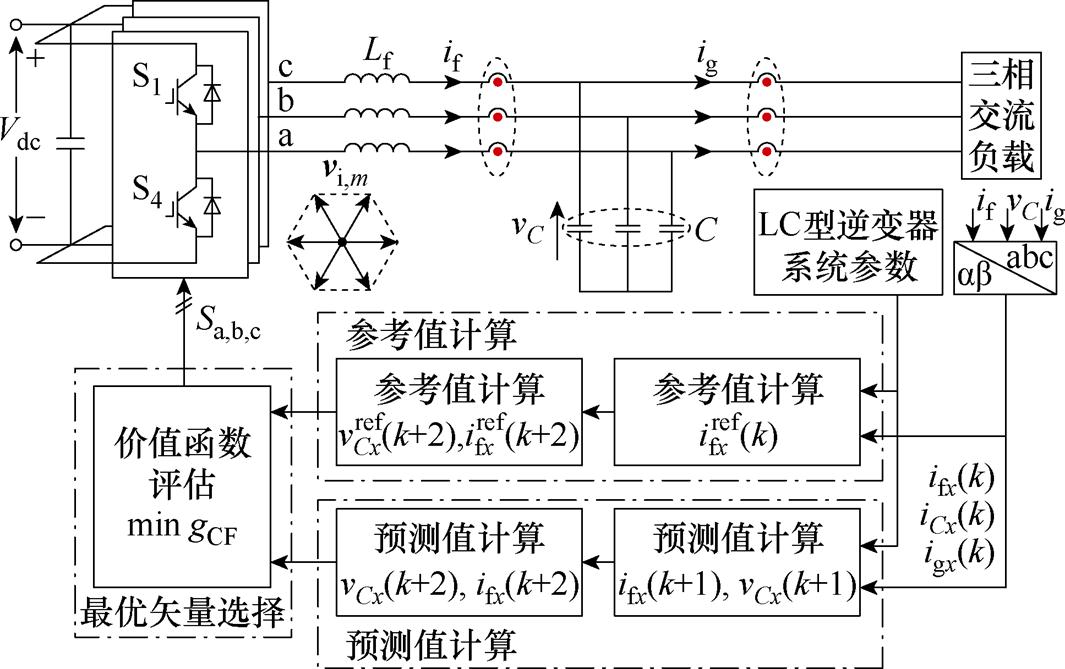
图1 传统LC型滤波逆变器模型预测控制框图
Fig.1 Topology of LC-filtered voltage source inverter
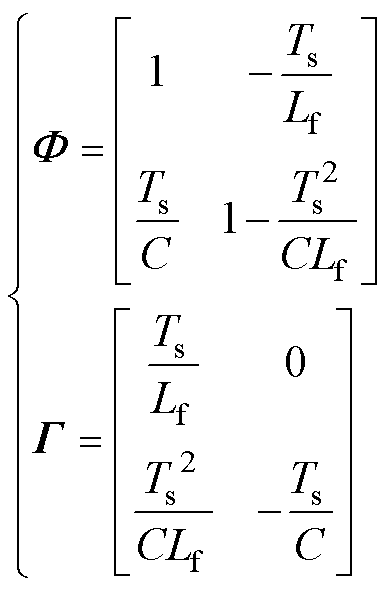 (2)
(2)
式中,Ts为系统控制周期;Lf为逆变器桥臂侧滤波电感;C为滤波电容。
为了补偿一个周期的控制延迟,系统在k+2时刻的电容电压预测值vCx(k+2)与桥臂侧电流预测值ifx(k+2)可以表示为
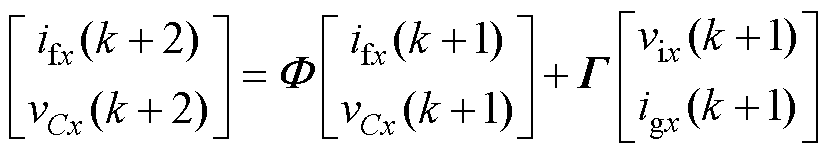 (3)
(3)
式中,vix(k+1)为逆变器k+1时刻输出电压,由于系统控制周期时间间隔极短,igx(k+1)可视作与igx(k)相等。
为了实现LC型滤波VSI的输出电压控制,并取得良好的谐振抑制效果,需要同时控制LC型滤波VSI的电容电压与桥臂侧电流[10]。电容电压参考矢量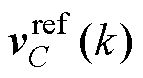 可以表示为
可以表示为
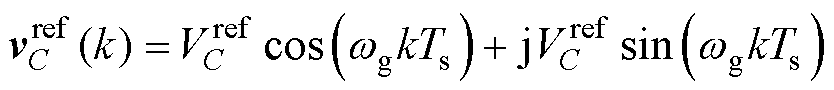 (4)
(4)
式中,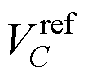 为参考电压幅值;
为参考电压幅值;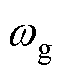 为电网基波角频率。
为电网基波角频率。
将式(4)代入式(1),可得到桥臂侧电感电流的参考矢量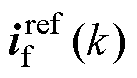 ,可表示为
,可表示为
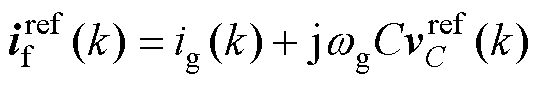 (5)
(5)
基于拉格朗日外推法[12],系统在k+2时刻的参考值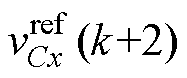 与
与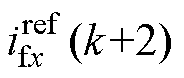 可分别表示为
可分别表示为
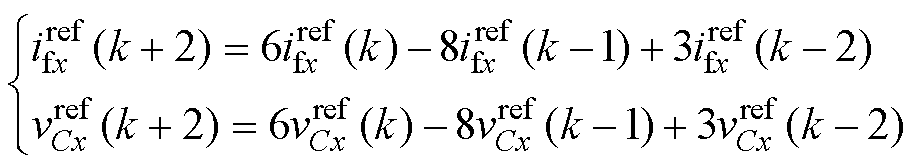 (6)
(6)
根据式(1)~式(5)可知,LC型滤波VSI的预测值计算以及参考值计算会受到模型参数的影响。
在Matlab/Simulink仿真平台搭建LC型滤波VSI的仿真模型。传统LC型滤波VSI在参数失配下的仿真预测误差如图2所示,当桥臂侧电感Lf以及电容C均无失配时(见图2中Case 1),输出电压预测误差保持在一个较低的水平;而当参考值与预测值计算中系统参数大于实际参数(Case 2与Case 3)或是小于实际参数时(Case 4与Case 5),逆变器输出电压预测误差明显增大。
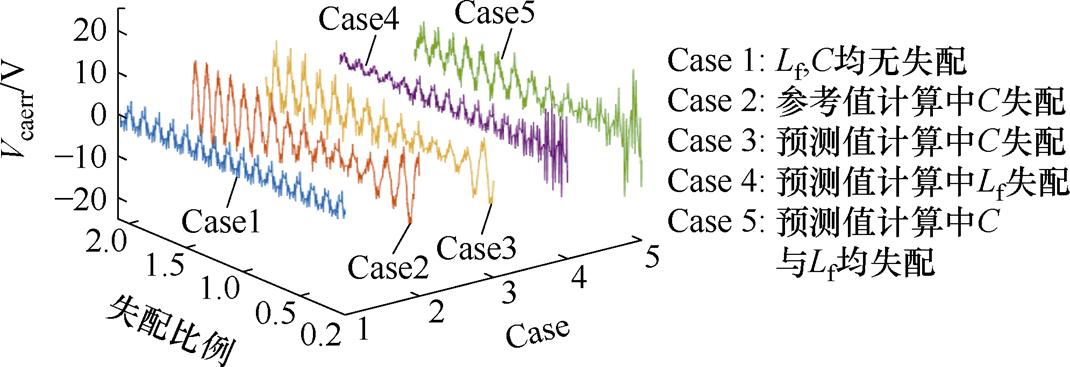
图2 传统LC型滤波VSI在参数失配下的仿真预测误差
Fig.2 Simulation results of prediction errors of vC in conventional MPC under parameters mismatches
为了消除传统控制方法的参数依赖性,本文提出了一种基于无模型预测与无参数参考的LC型滤波VSI无模型控制算法。所提的MFPC主要包含三个部分:三矢量无模型预测值计算方法、无参数参考值计算方法以及价值函数评估部分。
所提控制方法在每个控制周期中将应用3个基本电压矢量,其合成效果可用伏秒平衡原理表示为
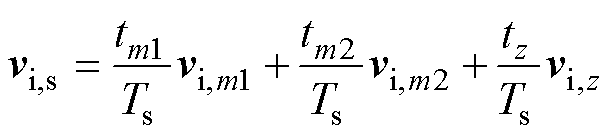 (7)
(7)
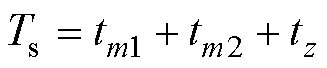 (8)
(8)
式中,vi,s为三矢量等效合成矢量;tm1与tm2分别为矢量vi,m1与vi,m2(m1与m2∈{1,…, 6}且m1≠m2)的作用时间;tz为零矢量vi,z(z∈{0,7})作用时间,则
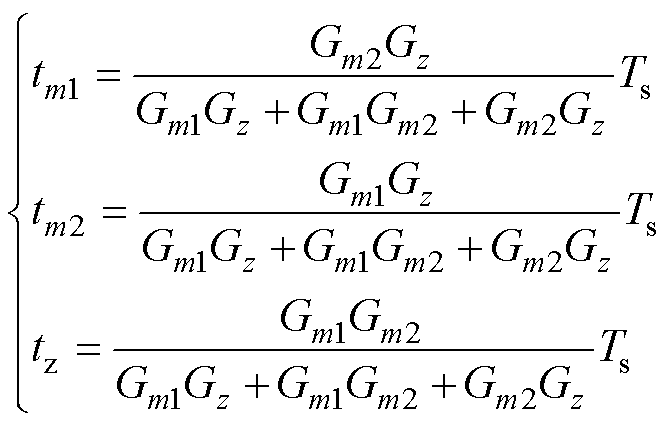 (9)
(9)
式中,Gm1、Gm2与Gz分别为三矢量vi,m1、vi,m2及vi,z的价值函数,其可表示为
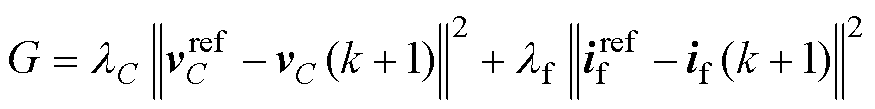 (10)
(10)
式中,lC、lf分别为电容电压与电感电流的权重系数。
该方法使每个控制周期同时采用电压矢量vi,m1、vi,m2及vi,z,其对应的七段式电流-电压梯度如图3所示。则第k-1个控制周期内桥臂侧电感电流梯度Difx(k)以及电容电压梯度DvCx(k)可表示为
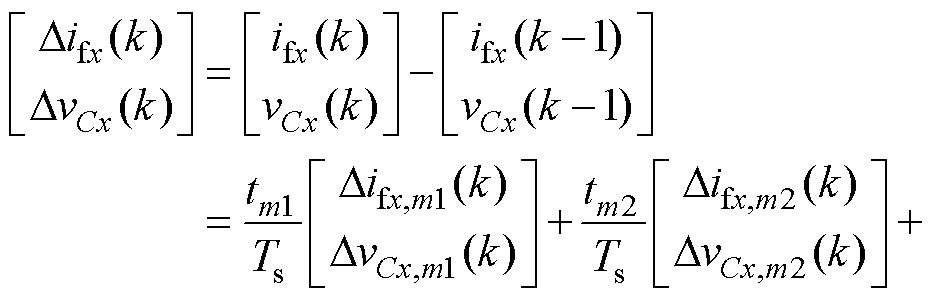
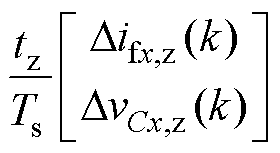 (11)
(11)
式中,Difx,m1(k)与DvCx,m1(k)由基本电压矢量vi,m1(k-1)产生;Difx,m2(k)与DvCx,m2(k)由基本电压矢量vi,m2(k-1)产生;Difx,z(k)与DvCx,z(k)由零矢量vi,z(k-1)产生。
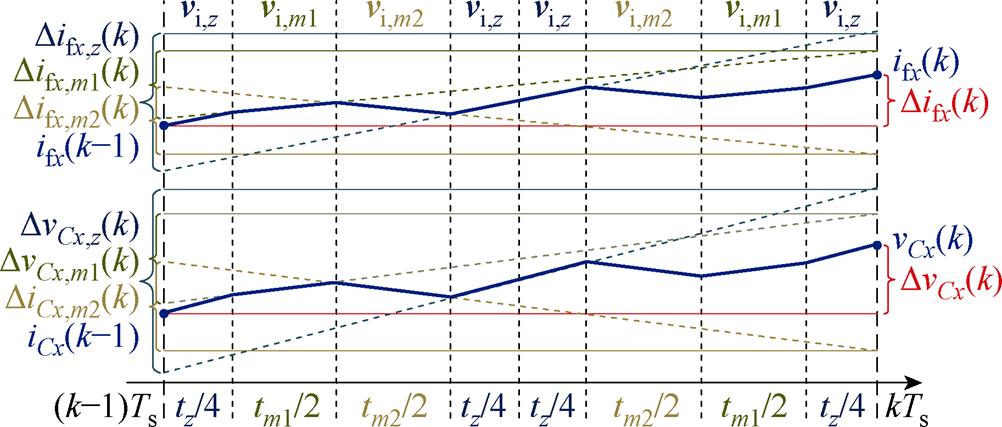
图3 三矢量作用下电流-电压梯度
Fig.3 Voltage-current gradients under triple vectors
基于式(1)、式(11),可将三矢量在第k-1个控制周期与第k-2个控制周期内所对应的梯度关系表示为
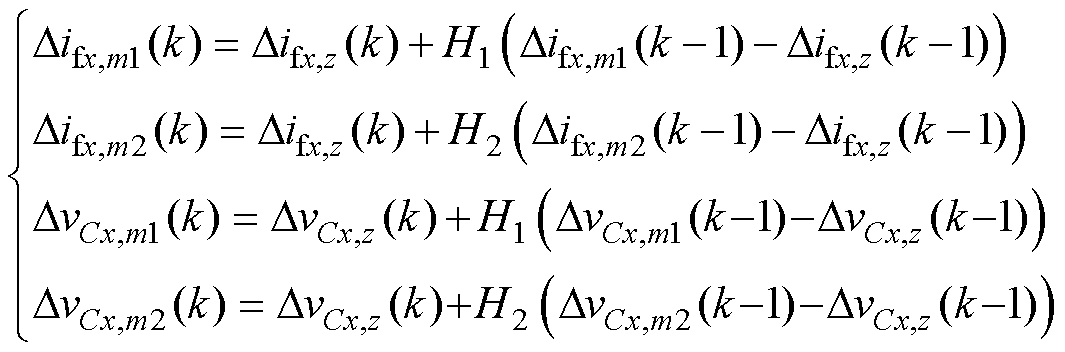 (12)
(12)
其中
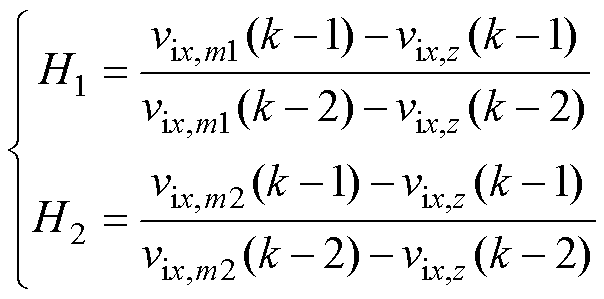 (13)
(13)
结合式(8)~式(13),可以解得三矢量所对应的电流-电压梯度,表示为
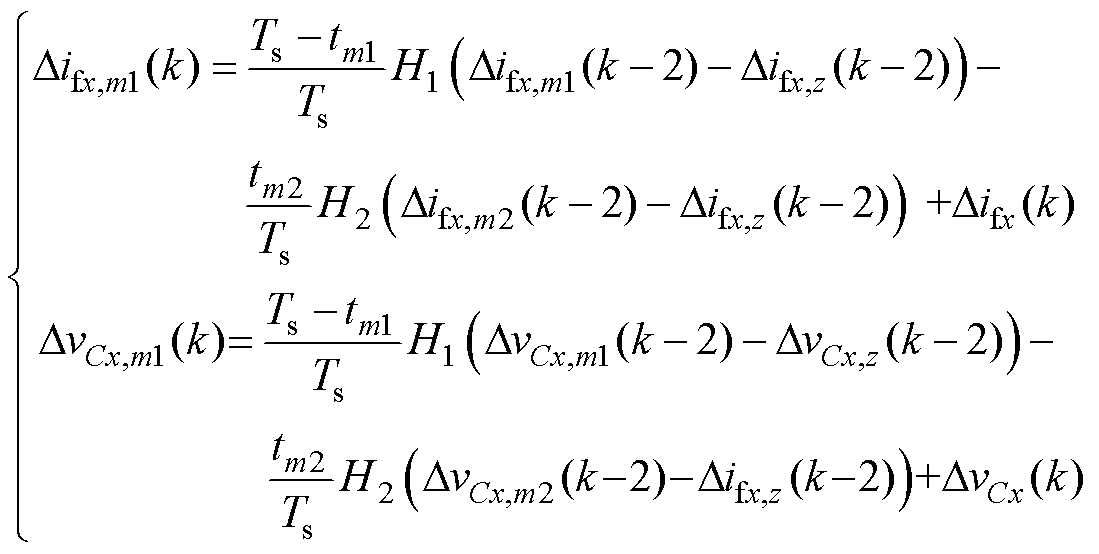 (14)
(14)
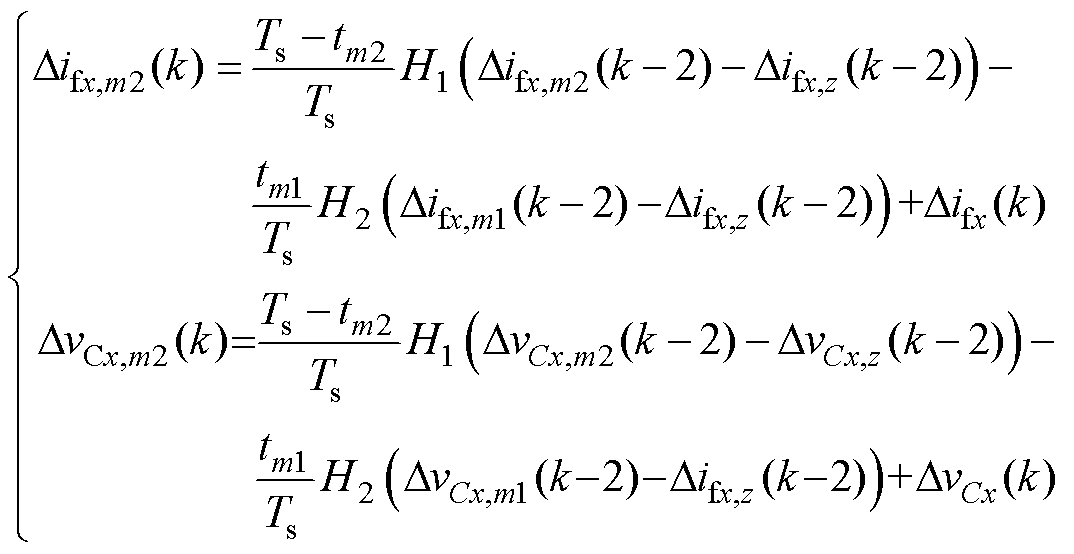 (15)
(15)
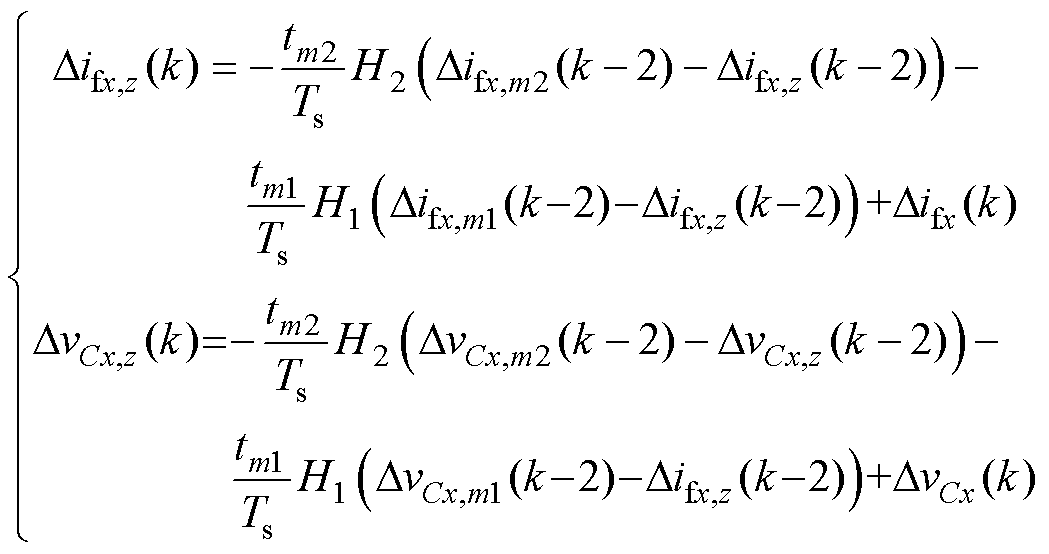 (16)
(16)
基于式(12),第k-1个控制周期内被选用的电压矢量vi,m(k-1)(m∈{m1, m2, 0,7})所对应的电流-电压梯度以及未被选用的电压矢量vi,n(k-1)(n≠m1, n≠m2且n∈{1, 2,…, 6})所对应的电流-电压梯度之间的关系可表示为
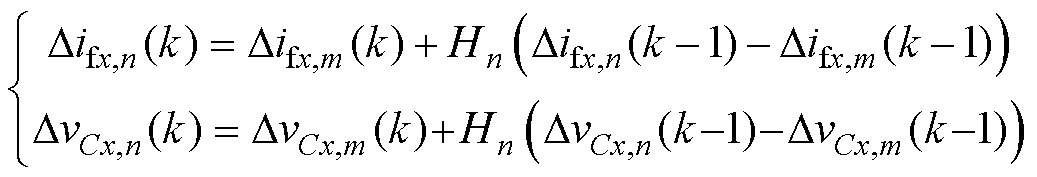 (17)
(17)
其中
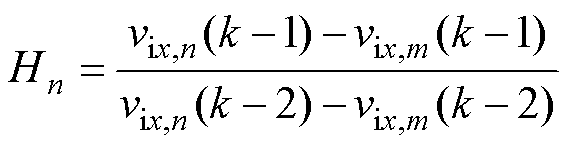 (18)
(18)
当Hn分母为0时,此时梯度更新公式为
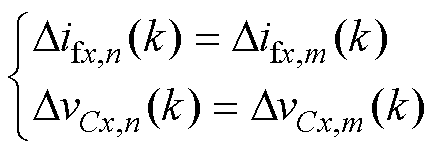 (19)
(19)
当Hn分母不为0时,此时Hn将会等于1,则梯度更新公式可被简化为
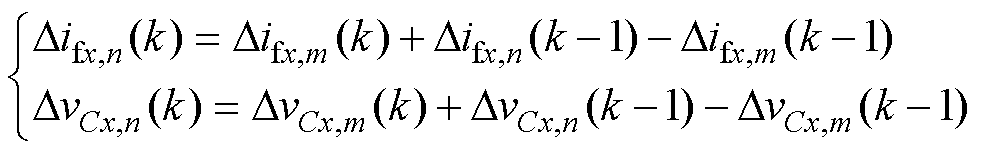 (20)
(20)
基于式(19)和式(20),第k个控制周期内LUT中所有电压矢量对应的电流-电压梯度皆可得到更新,更新停滞现象得以消除,如图4所示。
如图4所示,基于LUT中更新后的Difx(k)与DvCx(k),则第k+1时刻的预测值可被表示为
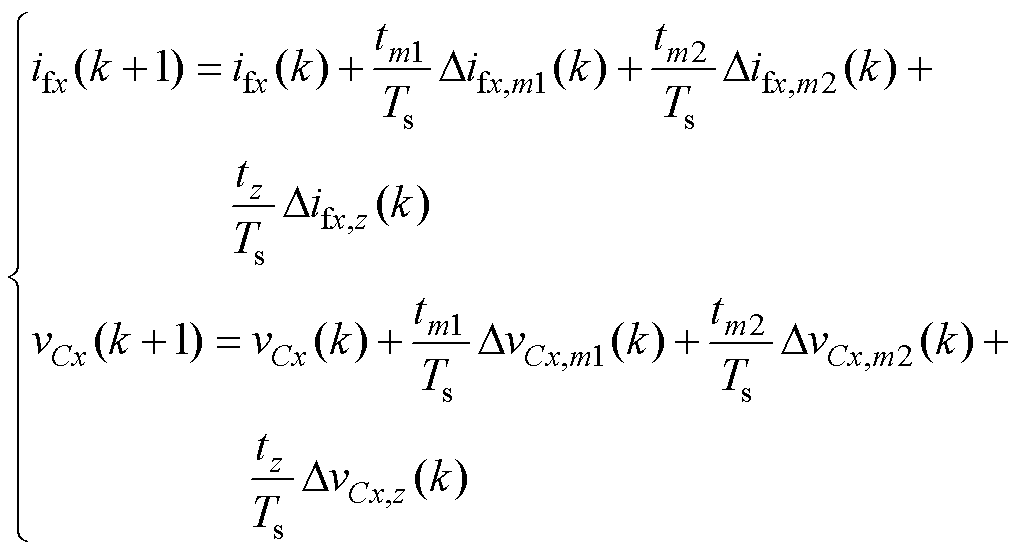 (21)
(21)
将基本电压矢量轮流代入进行第二步预测,则第k+2时刻的预测值可表示为
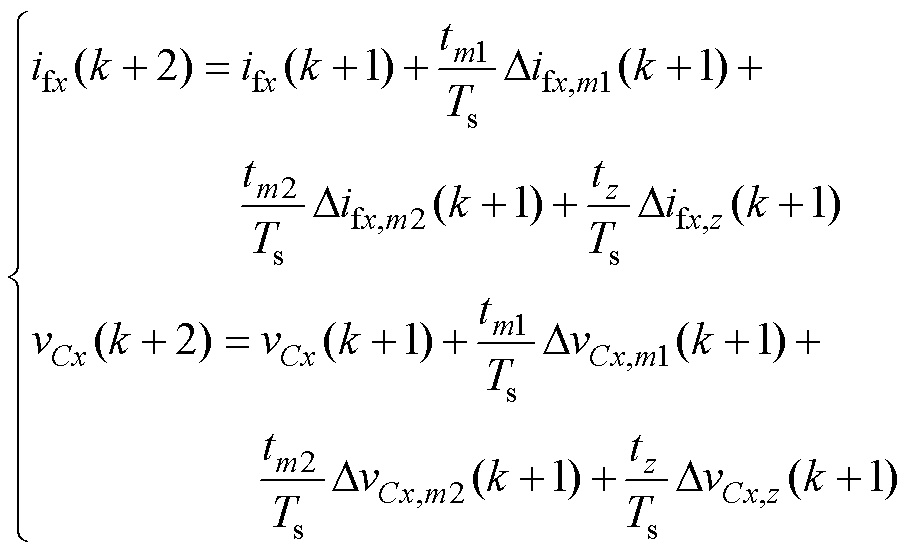 (22)
(22)
式(21)、式(22)取代了传统MPC方法中基于参数的预测值计算过程,消除了对系统参数的依赖,实现了预测值的无模型计算。
为了消除MPC方法中参考值计算对参数的依赖,实现参考值的无模型计算,本文提出了一种无参数参考值计算方法,可表示为
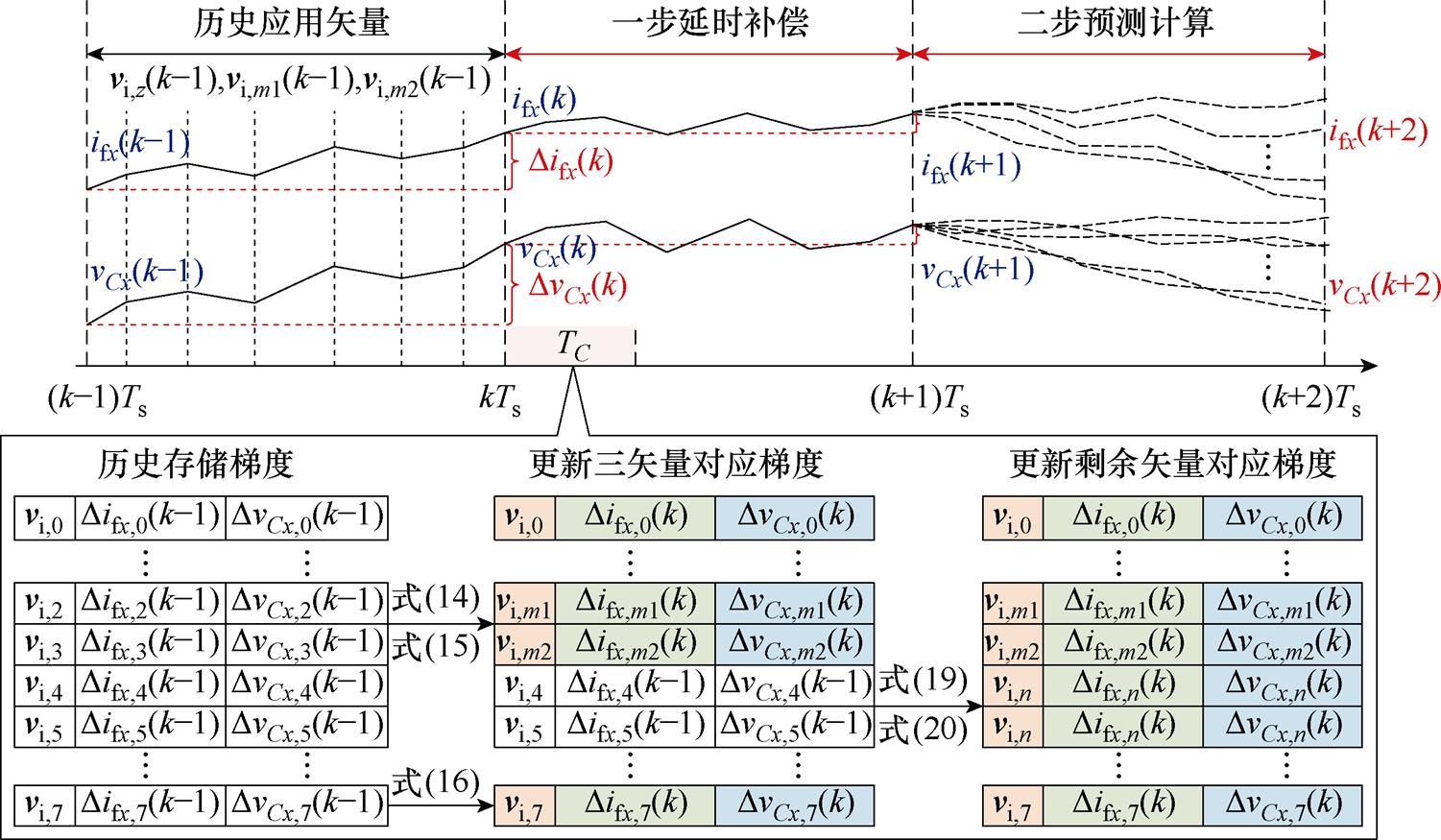
图4 所提基于电流-电压梯度的无模型预测方法
Fig.4 Proposed MFPC based on current-voltage gradients
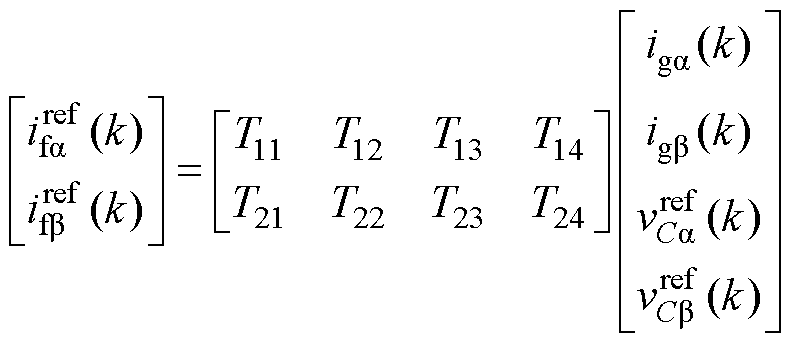 (23)
(23)
构建电感电流参考值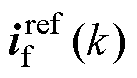 ,输出电流采样值ig(k),电容电压参考值
,输出电流采样值ig(k),电容电压参考值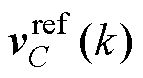 采样值vC(k)之间的关系可表示为
采样值vC(k)之间的关系可表示为
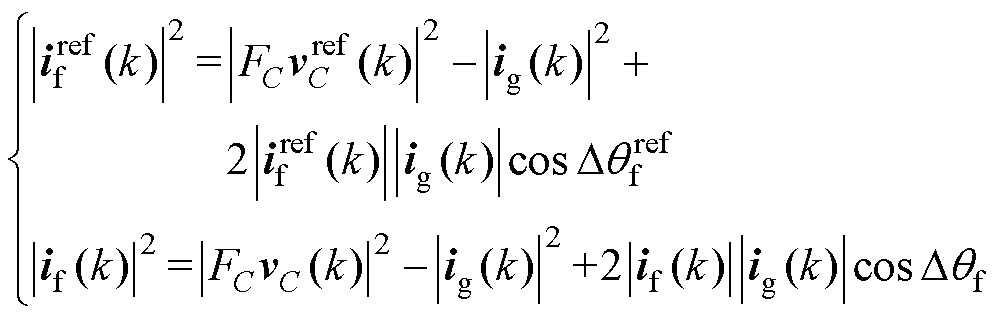 (24)
(24)
式中,FC为系统参数增益;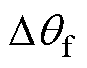 为if(k)与ig(k)之间的相位差;
为if(k)与ig(k)之间的相位差;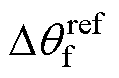 为
为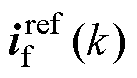 与ig(k)之间的相位差,其关系如图5所示。
与ig(k)之间的相位差,其关系如图5所示。
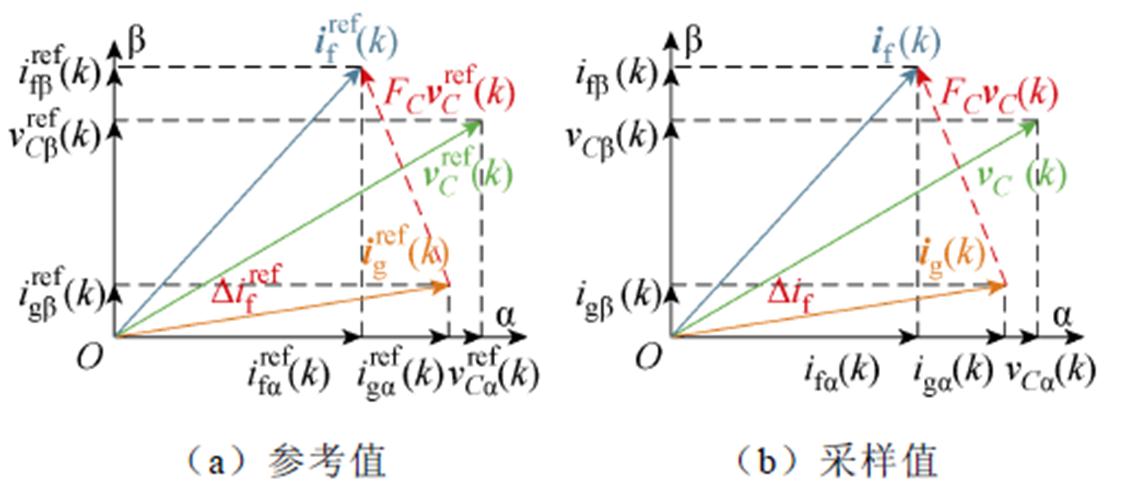
图5 幅值-相位关系
Fig.5 The amplitude and phase relationship
式(24)中的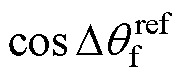 与
与 可分别表示为
可分别表示为
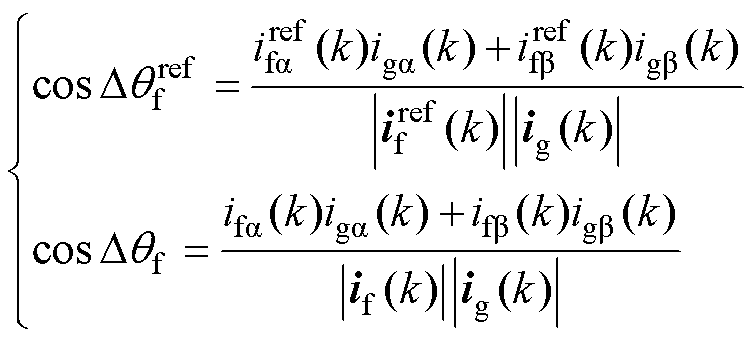 (25)
(25)
联立式(24)、式(25),消除系统参数增益FC,则式(23)中的系数矩阵T中的矩阵元素T11~T24可表示为
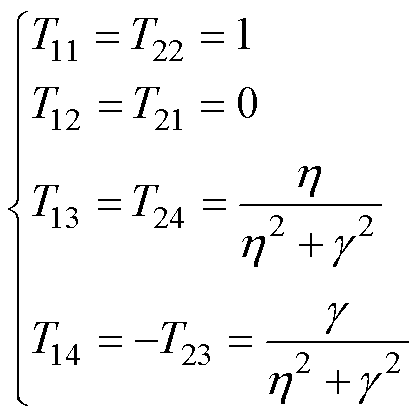 (26)
(26)
其中
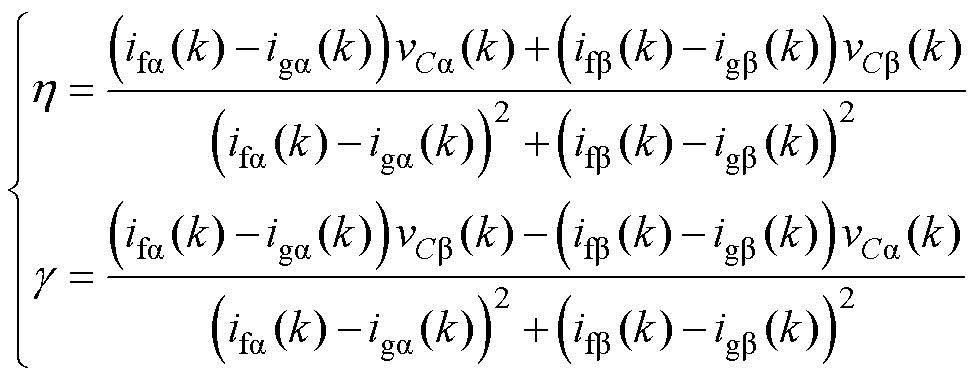 (27)
(27)
所提出的无参数参考值计算方法的计算框图如图6所示。基于式(25),通过电容电压采样值与桥臂侧电感电流采样值之间的相位差以及电容电压参考值与桥臂侧电感电流参考值之间的相位差代入式(24)的幅值-相位关系式中,消去系统参数增益,基于式(23)、式(26)与式(27)计算出桥臂侧电感电流参考值,从而消除了传统模型预测控制算法计算参考值过程中对参数的依赖性。
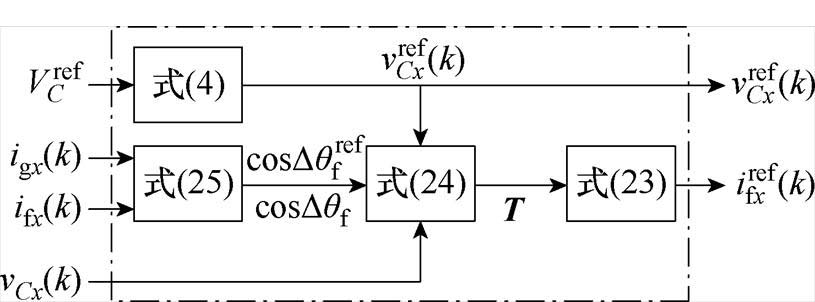
图6 所提出的无参数参考值计算方法
Fig.6 Proposed PL-reference calculation method
为了取得良好的谐振抑制效果与输出电压控制性能,同时确保桥臂侧电感电流预测值ifx(k+2)与电容电压预测值vCx(k+2)可以有效追踪桥臂侧电感电流参考值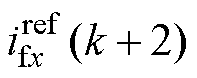 与电容电压参考值
与电容电压参考值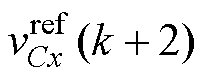 ,本文设计了多目标价值函数gCF,如下
,本文设计了多目标价值函数gCF,如下
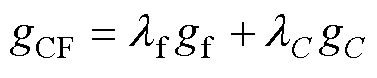 (28)
(28)
其中
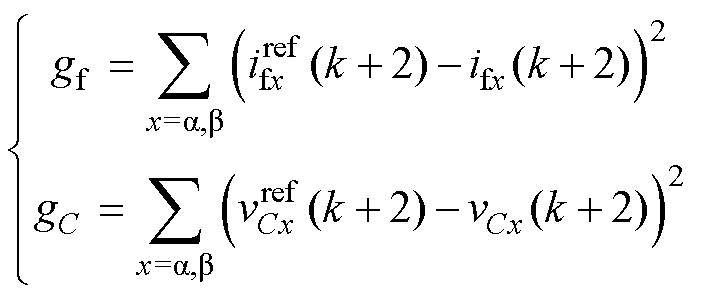 (29)
(29)
式中,gf与gC分别为桥臂侧电感电流以及电容电压的价值函数;lf、lC分别为gf与gC的权重因子。
如图7所示为所提TV-MFPC的控制框图,该方法主要由电流-电压梯度计算、无参数参考值计算、矢量作用时间与无模型预测值计算以及价值函数评估等部分组成。
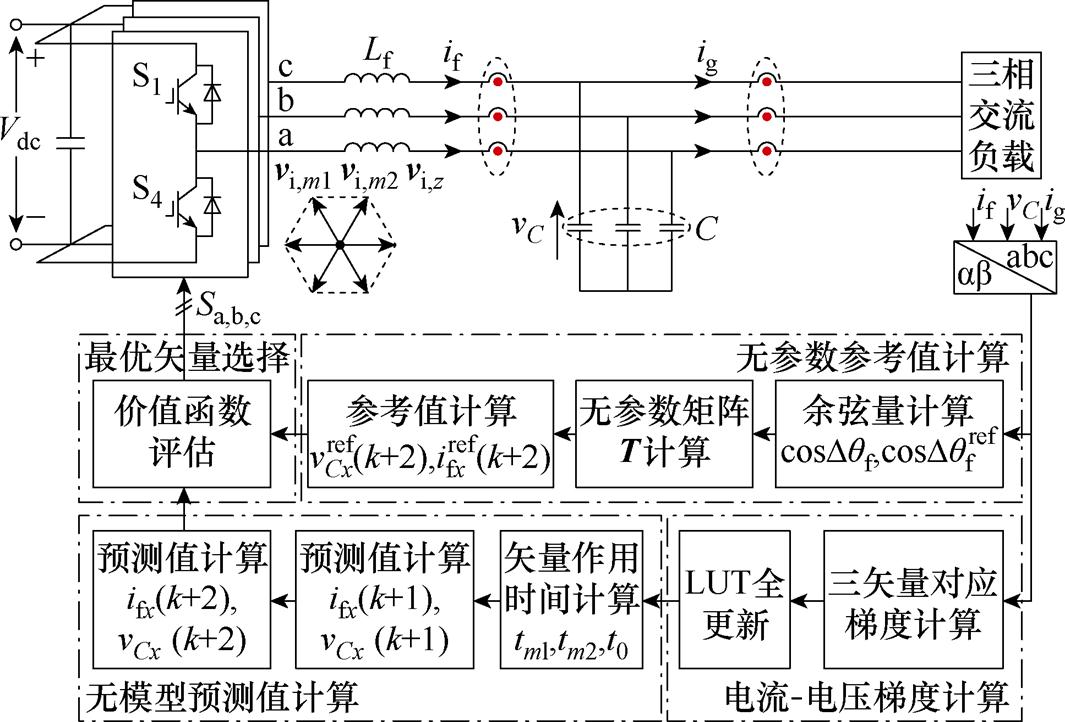
图7 所提LC型滤波VSI的MFPC控制框图
Fig.7 Control block diagram of proposed MFPC for LC-filtered VSI
本节通过如图8所示的两电平电压源逆变器实验平台验证了所提方法的有效性,示波器型号为LeCroy-HDO4034。控制算法在TMS320F28335中实现,系统和控制参数见表1。此外,式(11)为传统更新方法;文献[10]所提的方法为TV-MPC,文献[21]所提方法为TV-MFPC,本文所提方法为PLR-TV-MFPC。

图8 所提LC型滤波VSI的MFPC控制框图
Fig.8 Control block diagram of proposed MFPC for LC-filtered VSI
表1 VSI系统和控制参数
Tab.1 The parameters of VIS system and control
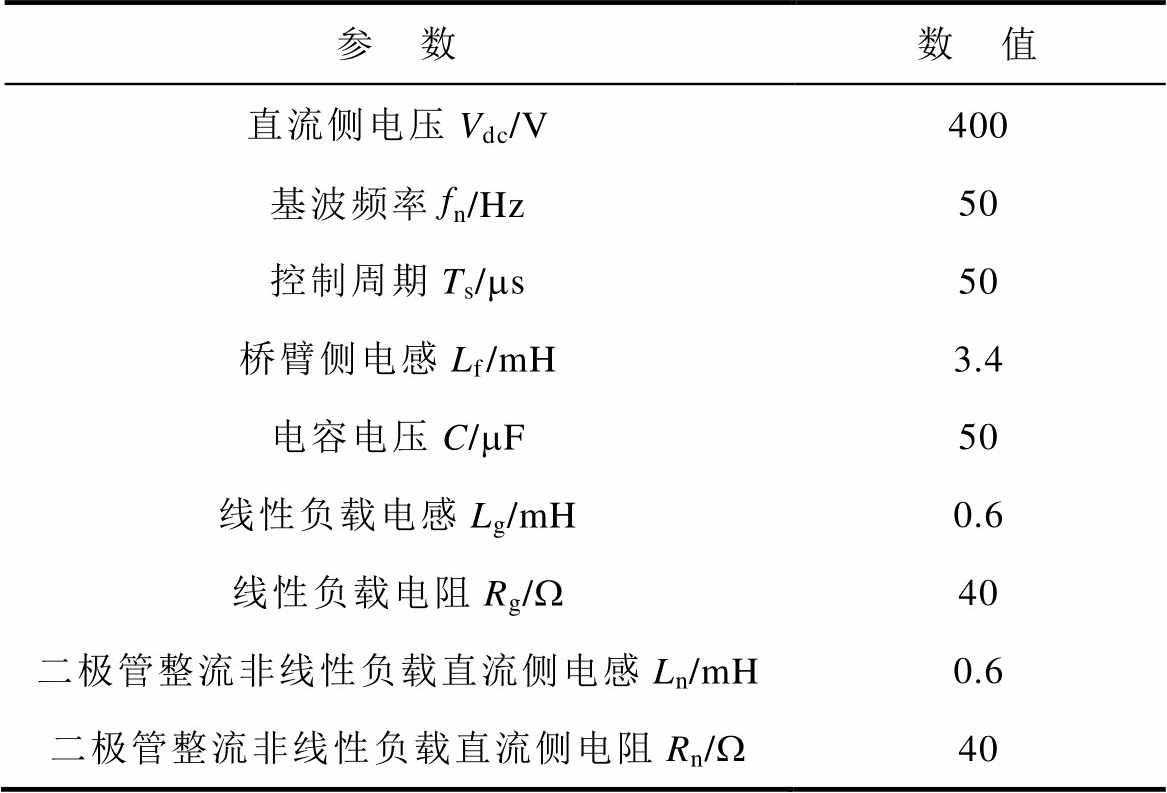
参 数数 值 直流侧电压Vdc/V400 基波频率fn/Hz50 控制周期Ts/ms50 桥臂侧电感Lf/mH3.4 电容电压C/mF50 线性负载电感Lg/mH0.6 线性负载电阻Rg/W40 二极管整流非线性负载直流侧电感Ln/mH0.6 二极管整流非线性负载直流侧电阻Rn/W40
图9对不同梯度更新方法的输出a相电压参考值、输出三相电压采样值、输出a相电压总谐波畸变率(Total Harmonic Distortion, THD)以及预测误差(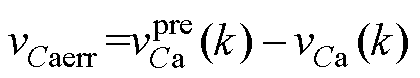 )进行了比较。其中,电压源输出电压参考值Vref设定为120 V。
)进行了比较。其中,电压源输出电压参考值Vref设定为120 V。
图9a为传统更新方法,该方法只对被选用的矢量对应的梯度进行更新,剩余梯度则出现更新停滞,其输出a相电压预测误差方均根有效值(Root Mean Squared Error, RMSE)为6.12 V,输出a相电压电压的THD=3.82%。图9b为本文所提三矢量电流-电压梯度全更新方法,本方法完全消除了LUT中梯度的更新停滞,降低了输出电压预测误差,此时输出a相输出电压预测误差RMSE=1.56 V,输出a相电压电压的THD=1.59%,明显低于传统更新方法下输出电压的THD,这体现了所提三矢量梯度全更新方法的正确性与有效性。
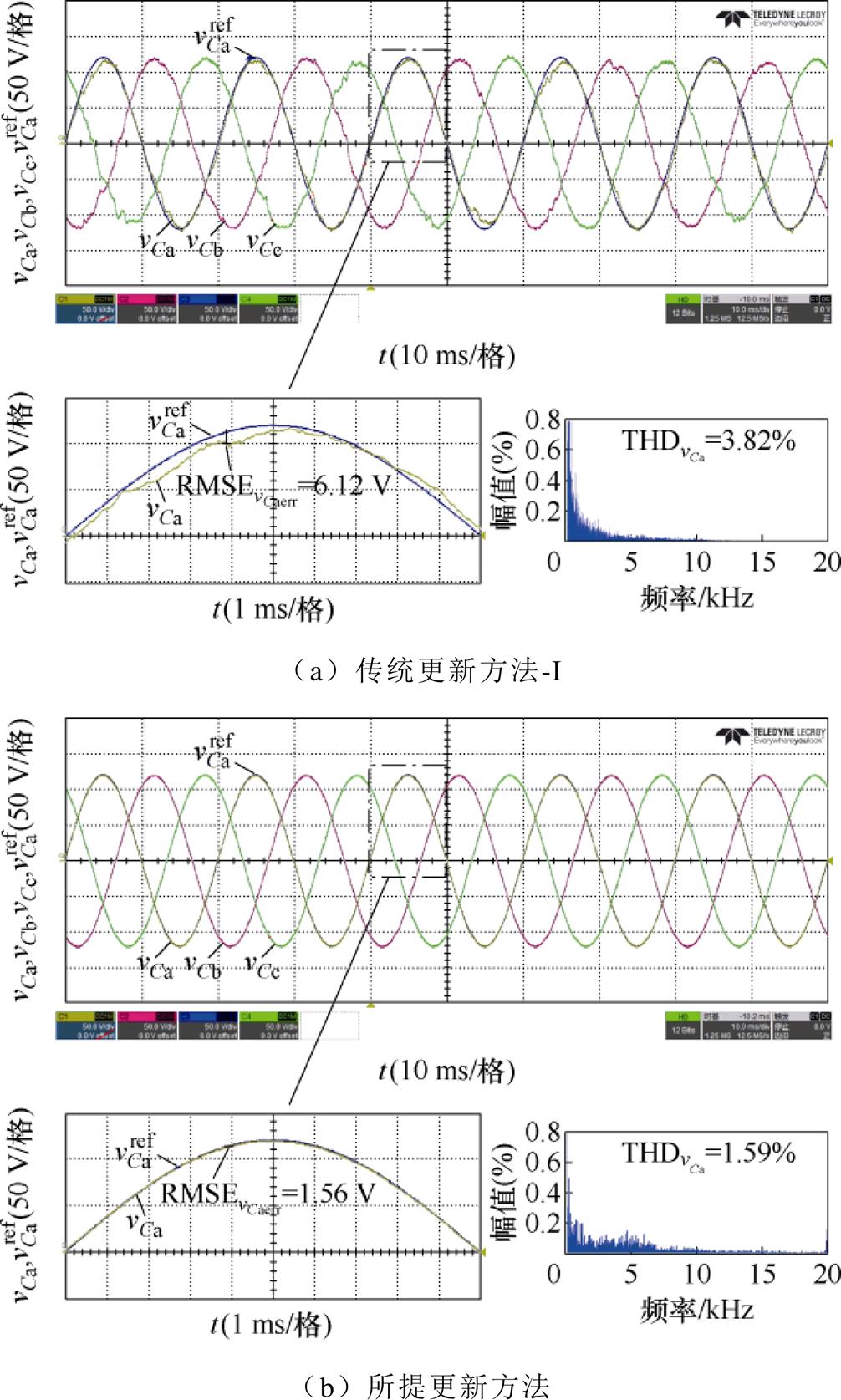
图9 不同梯度更新方法输出电压性能对比
Fig.9 Grid voltage performance comparison under different gradients updating methods
图10对文献[10]中所提TV-MPC方法与本文所提方法的输出三相电压纹波与三相电压预测误差进行比较,其中,输出电压参考值Vref设定为120 V。
如图10a所示,文献[10]中的传统TV-MPC方法在线性负载Ln=0.6 mH, Rn=40 W 下,其输出a相电压预测误差RMSE=0.89 V,输出a相电压的THD= 1.04%;在线性负载Ln=0.6 mH, Rn=20 W 下,其输出a相电压预测误差RMSE=0.98 V,输出a相电压的THD=1.08%;在二极管整流非线性负载Ln= 1.8 mH, Rn=40 W 下,其输出a相电压预测误差RMSE=1.05 V,输出a相电压电压的THD=1.26%;在二极管整流非线性负载Ln=1.8 mH, Rn=20 W 下,其输出a相电压预测误差RMSE=1.62 V,输出a相电压电压的THD=1.98%。
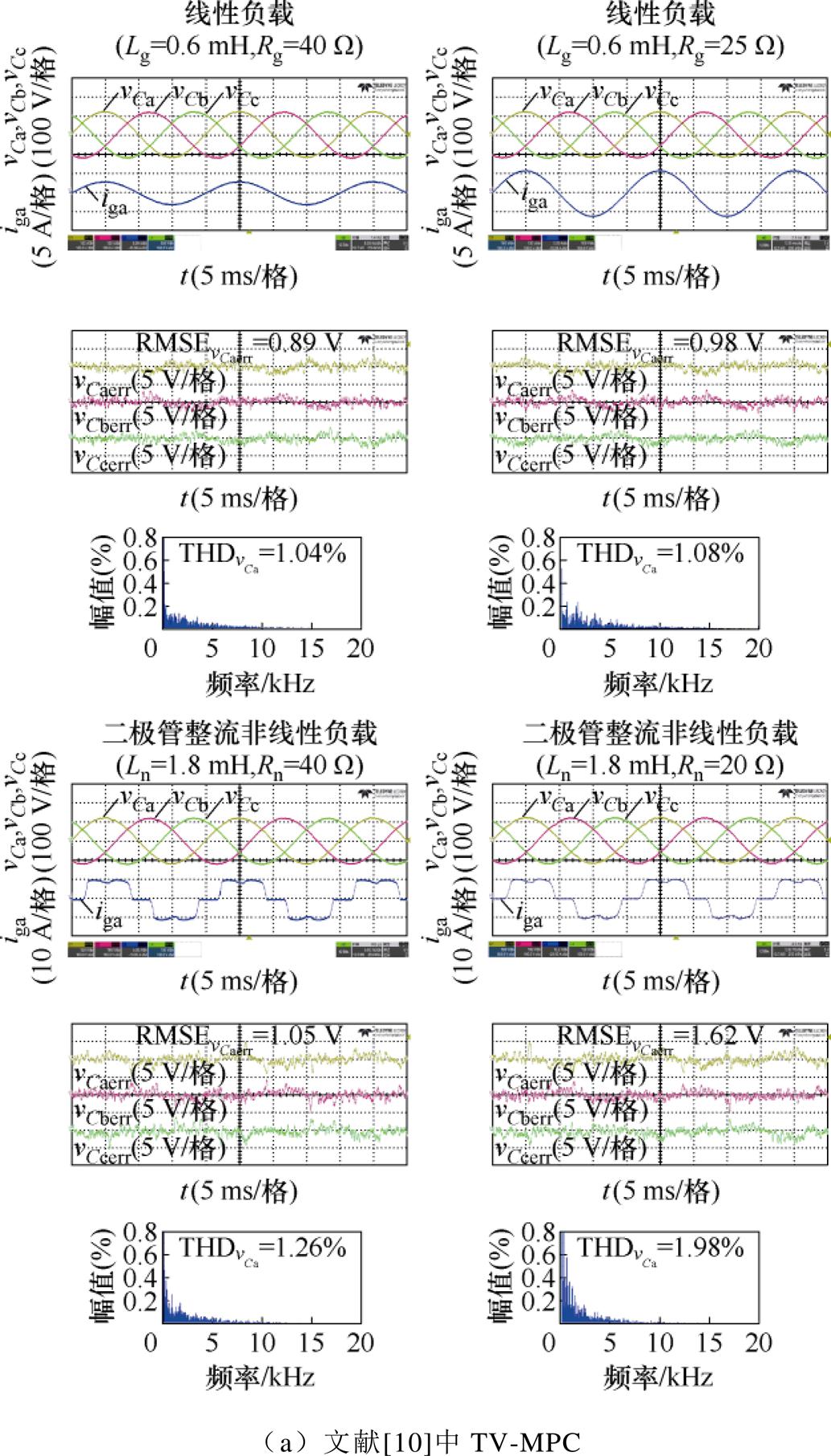
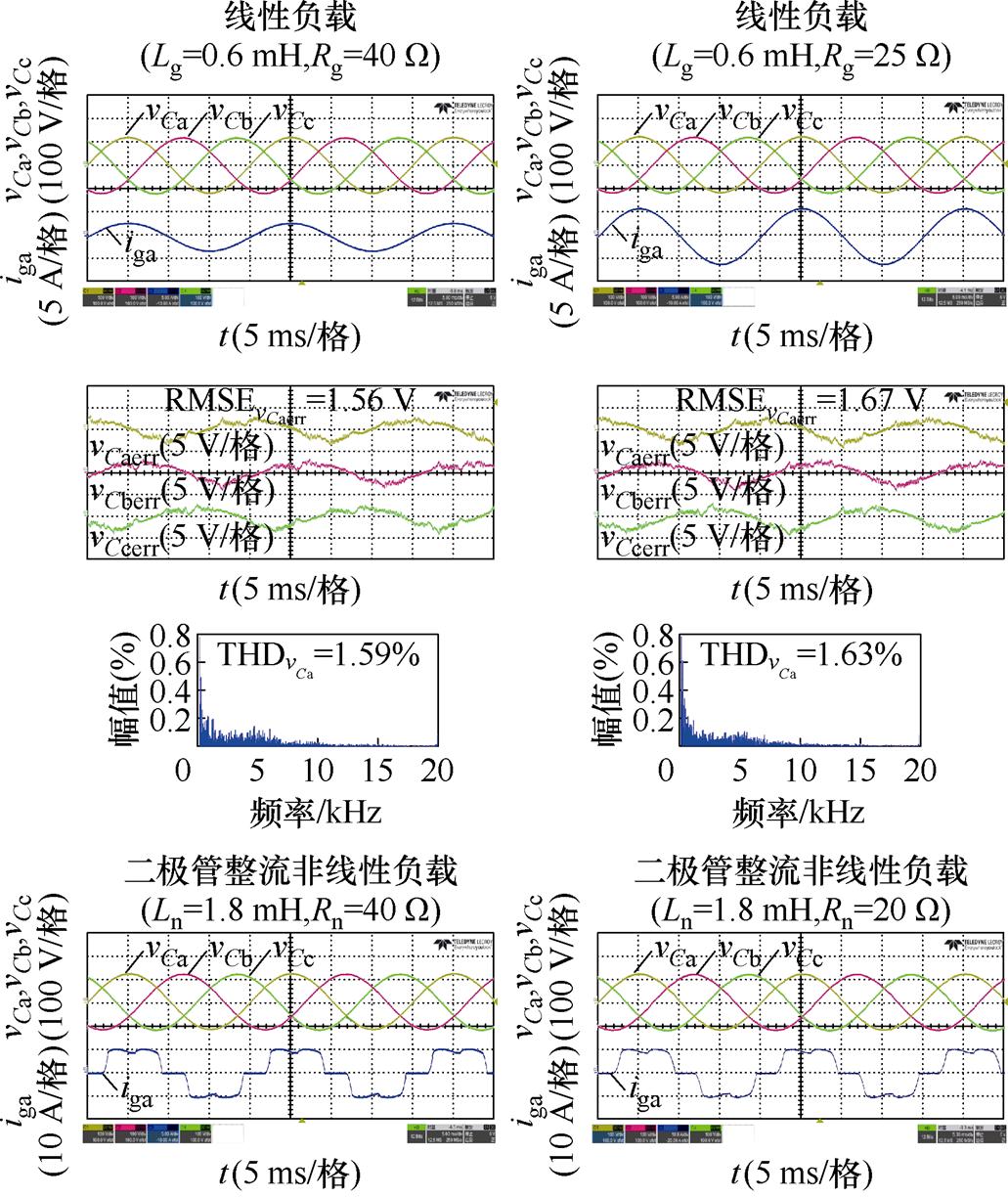
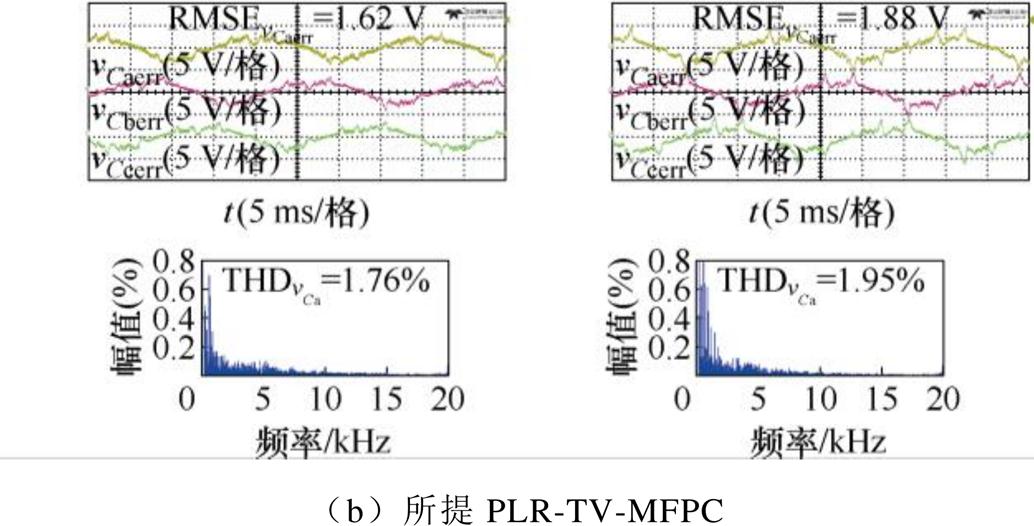
图10 不同控制方法输出电压性能对比
Fig.10 Output voltage performance under different methods
如图10b所示,本文所提的PLR-TV-MFPC方法在线性负载Ln=0.6 mH, Rn=40 W 下,其输出a相电压预测误差RMSE=1.56 V,输出a相电压的THD= 1.59%;在线性负载Ln=0.6 mH, Rn=20 W 下,其输出a相电压预测误差RMSE=1.67 V,输出a相电压的THD=1.63%;在二极管整流非线性负载Ln= 1.8 mH, Rn=40 W 下,其输出a相电压预测误差RMSE=1.62 V,其输出a相电压的THD=1.76%;二极管整流非线性负载Ln=1.8 mH, Rn=20 W 下,其输出a相电压预测误差RMSE=1.88 V,其输出a相电压的THD=1.95%。
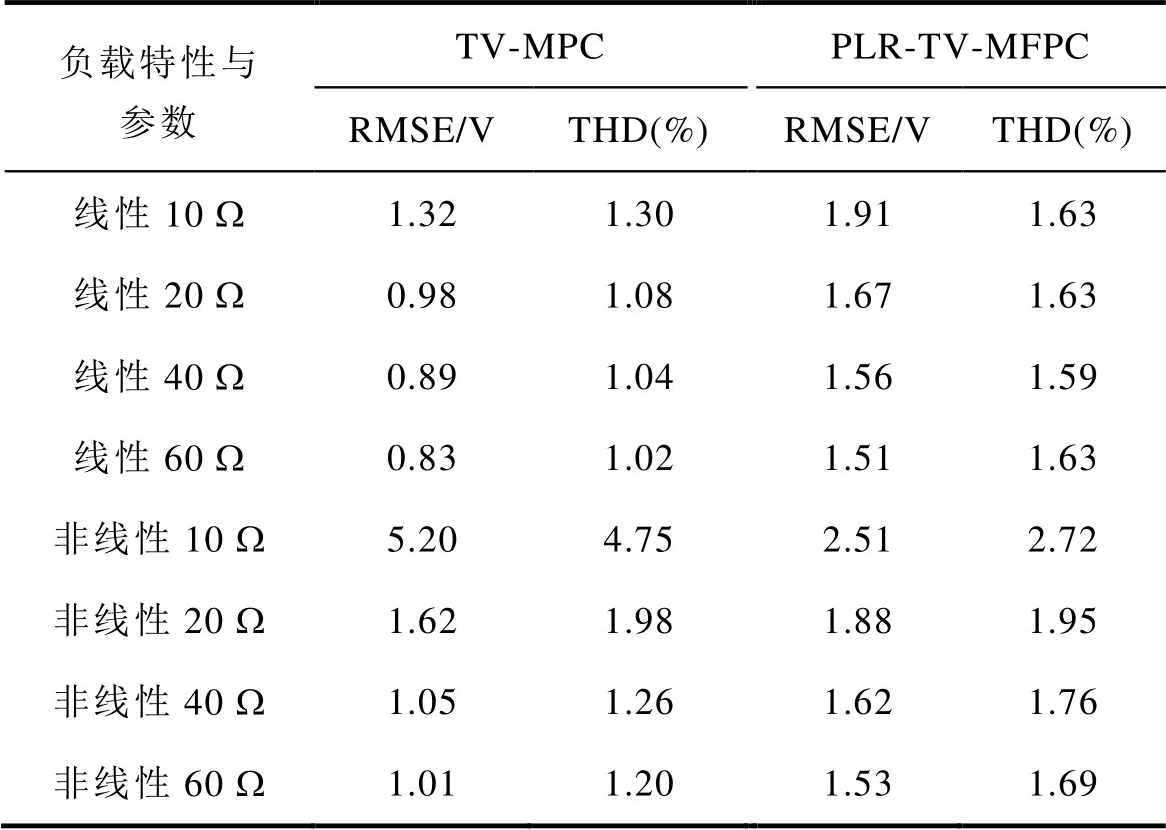
同时,在表2中展示了不同线性负载与非线性负载下的传统TV-MPC方法与本文所提PLR-TV- MFPC方法的输出电压预测误差RMSE以及a相输出电压THD,当非线性负载中的电阻为10 W 时,所提方法的输出电压预测误差RMSE=2.51 V,输出电压THD=2.72%,均低于传统MPC方法(5.20 V与4.75%);当非线性负载中的电阻为20 W 时,所提方法输出电压THD=1.95%,低于传统MPC方法(1.98%)。可见所提无模型方法具有与传统TV-MPC方法相近的输出电压性能,这体现了所提方法的正确性与有效性。
表2 不同负载下输出电压预测误差RMSE与输出电压THD比较
Tab.2 Prediction error RMSE and THD of output voltage under different loads
负载特性与参数TV-MPCPLR-TV-MFPC RMSE/VTHD(%)RMSE/VTHD(%) 线性10 W1.321.301.911.63 线性20 W0.981.081.671.63 线性40 W0.891.041.561.59 线性60 W0.831.021.511.63 非线性10 W5.204.752.512.72 非线性20 W1.621.981.881.95 非线性40 W1.051.261.621.76 非线性60 W1.011.201.531.69
图11与表3对不同方法在LC滤波器桥臂侧电感控制参数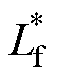 与电容控制参数
与电容控制参数 发生失配时的输出电压与输出电压预测误差进行了比较。其中,输出电压参考值Vref设定为120 V,逆变器带线性负载Ln=0.6 mH, Rn=40 W,参数失配比例从0.2变化为2.0。如图11a所示,当桥臂侧电感控制参数
发生失配时的输出电压与输出电压预测误差进行了比较。其中,输出电压参考值Vref设定为120 V,逆变器带线性负载Ln=0.6 mH, Rn=40 W,参数失配比例从0.2变化为2.0。如图11a所示,当桥臂侧电感控制参数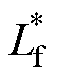 与电容控制参数
与电容控制参数 为实际值的2倍时,文献[10]中的TV-MPC方法输出电压预测误差最大值为16.4 V。如图11b所示,当桥臂侧电感控制参数
为实际值的2倍时,文献[10]中的TV-MPC方法输出电压预测误差最大值为16.4 V。如图11b所示,当桥臂侧电感控制参数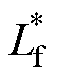 与电容控制参数
与电容控制参数 为实际值的50%时,文献[21]中TV-MFPC输出电压预测误差最大值为9.8 V。如图11c所示,所提的PLR-TV-MFPC输出电压性能几乎不受参数失配影响,其输出电压预测误差最大值降低为1.72 V,低于SV-MPC和TV-MFPC方法。
为实际值的50%时,文献[21]中TV-MFPC输出电压预测误差最大值为9.8 V。如图11c所示,所提的PLR-TV-MFPC输出电压性能几乎不受参数失配影响,其输出电压预测误差最大值降低为1.72 V,低于SV-MPC和TV-MFPC方法。
三种不同控制方法在不同参数失配情况下的输出电压预测误差最大值见表3,传统MPC方法的输出电压预测误差最大值在1.4~16.4 V左右浮动;文献[21]中的TV-MFPC方法的输出电压预测误差最大值在2.2~9.8 V左右浮动;本文提出的PLR-TV- MFPC方法的输出电压预测误差最大值为1.72 V,不受参数失配影响,具有良好的参数鲁棒性。
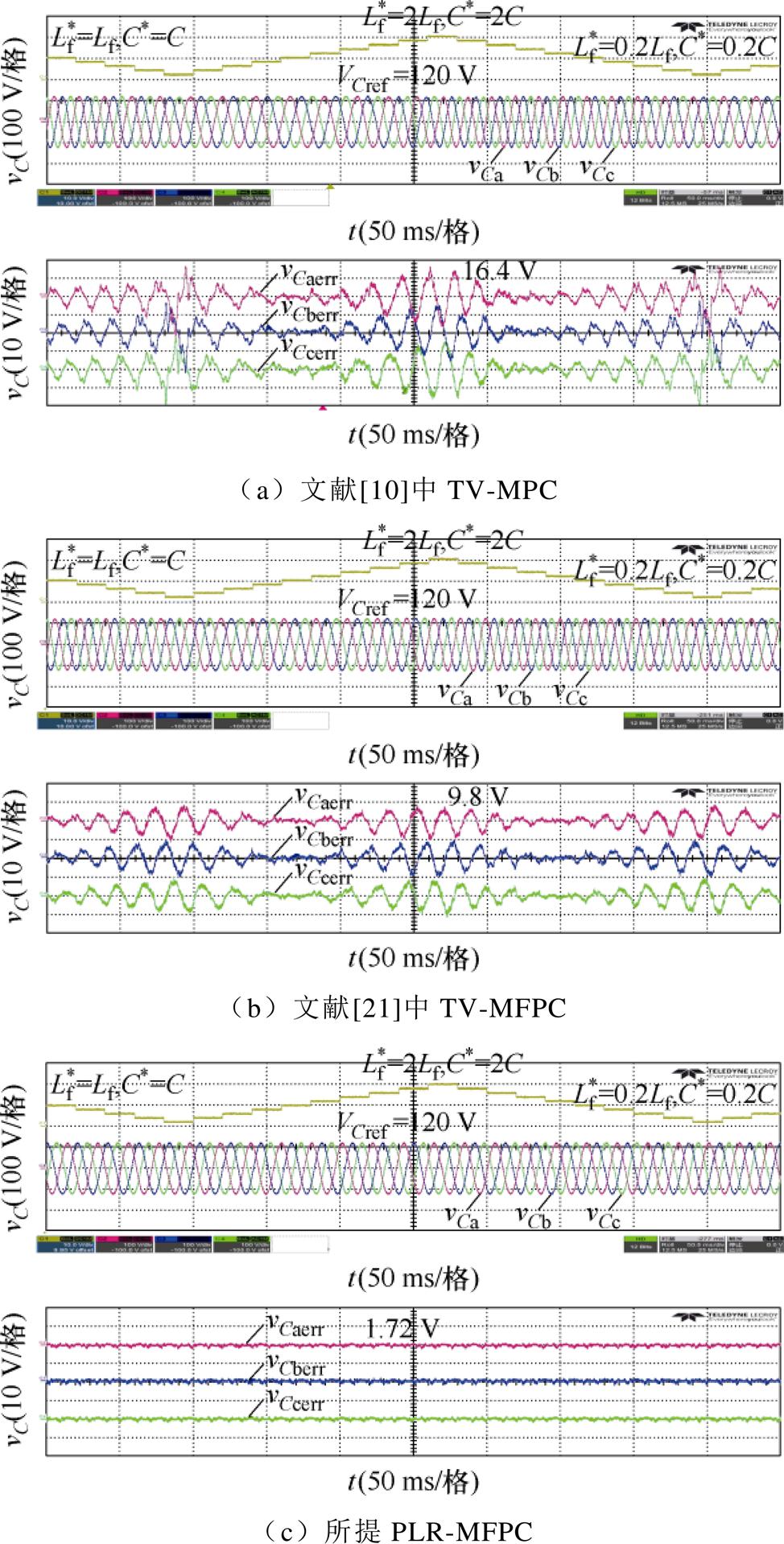
图11 参数失配时输出电压性能比较
Fig.11 Output voltage performance comparison under mismatched parameter
表3 参数失配时预测误差最大值比较
Tab.3 Comparision of prediction error maximum under mismatched parameters (单位: V)
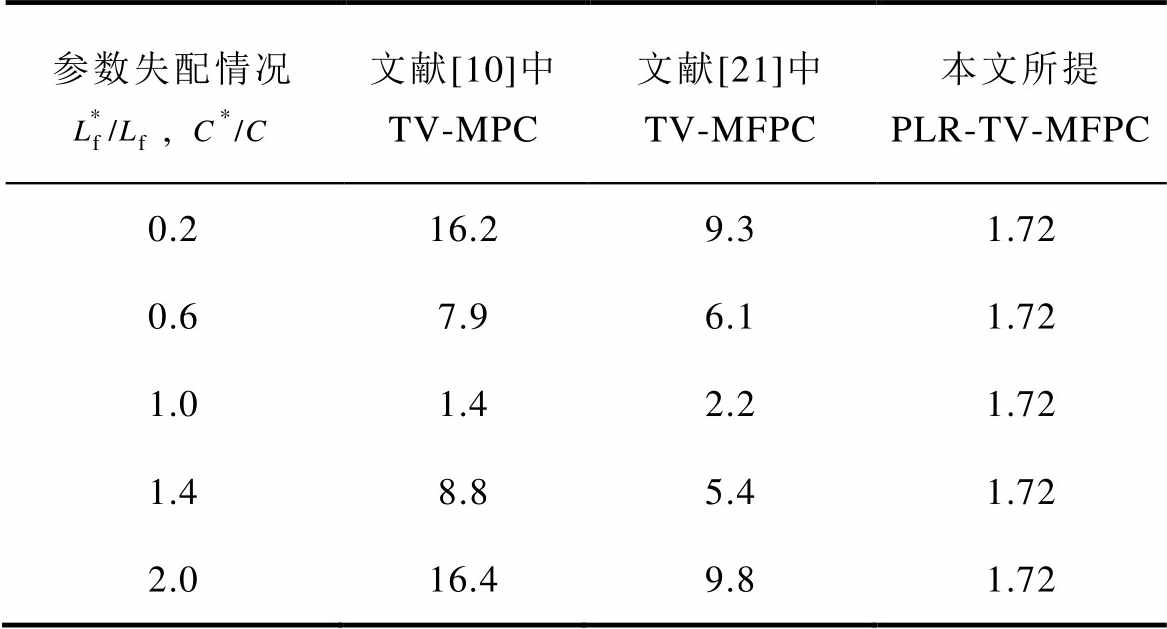
参数失配情况, 文献[10]中TV-MPC文献[21]中TV-MFPC本文所提PLR-TV-MFPC 0.216.29.31.72 0.67.96.11.72 1.01.42.21.72 1.48.85.41.72 2.016.49.81.72
本文提出了一种基于无模型预测值与无参数参考值的LC型滤波逆变器三矢量预测控制方法,并在三相LC型滤波逆变器实验平台上进行了测试。结果表明所提预测方法有以下优点:
1)该方法通过构造电流-电压梯度查找表,分析三矢量对应的电感电流梯度与电容电压梯度之间的关系,进行查找表中电流-电压梯度更新,通过梯度实现LC型滤波VSI的无模型预测值计算。
2)该方法通过分析电流-电压采样值与参考值之间的相位幅值关系,构造基于相位差值的计算方法,实现LC型滤波VSI的无参数参考值计算,消除了传统无模型预测中参考值计算对参数依赖性。
后续研究可以探讨所提方法在LC型并网逆变器以及LCL型并网逆变器中的应用。
参考文献
[1] Rodriguez J, Pontt J, Silva C A, et al. Predictive current control of a voltage source inverter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 495-503.
[2] Wang Xiongfei, Blaabjerg F, Wu Weimin. Modeling and analysis of harmonic stability in an AC power- electronics-based power system[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6421-6432.
[3] Safamehr H, Najafabadi T A, Salmasi F R. Adaptive control of grid-connected inverters with nonlinear LC filters[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1562-1570.
[4] Nauman M, Hasan A. Efficient implicit model- predictive control of a three-phase inverter with an output LC filter[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6075-6078.
[5] Falkowski P, Sikorski A. Finite control set model predictive control for grid-connected AC-DC con- verters with LCL filter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 2844-2852.
[6] 陈荣, 翟凯淼, 舒胡平. 永磁同步电机双矢量固定开关频率模型预测控制研究[J]. 电工技术学报, 2023, 38(14): 3812-3823.
Chen Rong, Zhai Kaimiao, Shu Huping. Predictive control of dual vector fixed switching frequency model for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3812-3823.
[7] 汪逸哲, 黄晟, 廖武, 等. 基于新型虚拟矢量调制方法的IPMSM模型预测电流控制方法[J]. 电工技术学报, 2024, 39(8): 2422-2433.
Wang Yizhe, Huang Sheng, Liao Wu, et al. IPMSM model predictive current control method based on a novel virtual vector modulation method[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(8): 2422-2433.
[8] Cortes P, Ortiz G, Yuz J I, et al. Model predictive control of an inverter with output LC filter for UPS applications[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1875-1883.
[9] Yaramasu V, Rivera M, Narimani M, et al. Model predictive approach for a simple and effective load voltage control of four-leg inverter with an output LC filter[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5259-5270.
[10] Zheng Changming, Dragičević T, Zhang Zhenbin, et al. Model predictive control of LC-filtered voltage source inverters with optimal switching sequence[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3422-3436.
[11] Young H A, Perez M A, Rodriguez J. Analysis of finite-control-set model predictive current control with model parameter mismatch in a three-phase inverter[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(5): 3100-3107.
[12] Martín Sanchez P, Machado O, Peña E J, et al. FPGA-based implementation of a predictive current controller for power converters[J]. IEEE Transactions on Industrial Informatics, 2013, 9(3): 1312-1321.
[13] Long Bo, Zhang Jiahao, Shen Dawei, et al. Ultralocal model-free predictive control of T-type grid- connected converters based on extended sliding-mode disturbance observer[J]. IEEE Transactions on Power Electronics, 2023, 38(12): 15494-15508.
[14] Zhao Tao, Zhang Mingzhou, Wang Chunlin, et al. Model-free predictive current control of three-level grid-connected inverters with LCL filters based on Kalman filter[J]. IEEE Access, 2023, 11: 21631- 21640.
[15] Heydari R, Young H, Flores-Bahamonde F, et al. Model-free predictive control of grid-forming inverters with LCL filters[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9200-9211.
[16] Lin Chengkai, Liu Tianhua, Yu J T, et al. Model-free predictive current control for interior permanent- magnet synchronous motor drives based on current difference detection technique[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 667-681.
[17] Yu Feng, Zhou Chenhui, Liu Xing, et al. Model-free predictive current control for three-level inverter-fed IPMSM with an improved current difference updating technique[J]. IEEE Transactions on Energy Con- version, 2021, 36(4): 3334-3343.
[18] Hu Cungang, Yin Zheng, Rui Tao, et al. A novel double-voltage-vector model-free predictive current control method for two-level voltage source inver- ters[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 5872-5884.
[19] 芮涛, 尹政, 汪凤翔, 等. 基于双矢量的并网逆变器无模型预测电流控制策略[J]. 电工技术学报, 2023, 38(14): 3759-3768.
Rui Tao, Yin Zheng, Wang Fengxiang, et al. Model-free predictive current control strategy of grid-connected inverter based on double-vector[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3759-3768.
[20] 胡存刚, 尹政, 芮涛, 等. 计及采样扰动抑制的电压源逆变器三矢量无模型预测电流控制方法[J]. 中国电机工程学报, 2024, 44(6): 2408-2417.
Hu Cungang, Yin Zheng, Rui Tao, et al. Three-vector model-free predictive current control method for voltage source inverter considering sampling dis- turbance suppression[J]. Proceedings of the CSEE, 2024, 44(6): 2408-2417.
[21] Hu Cungang, Xu Wanlun, Yin Zheng, et al. A novel modulated model-free predictive control for LC- filtered grid-forming inverters with double-difference updating[J]. IEEE Transactions on Industrial Elec- tronics, 2024, 71(9): 10806-10817.
[22] 尹政, 胡存刚, 芮涛, 等. LC滤波型电压源逆变器无模型预测电压控制策略[J]. 电工技术学报, 2023, 38(14): 3723-3732.
Yin Zheng, Hu Cungang, Rui Tao, et al. Model-free predictive voltage control strategy for LC-filtered voltage source inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3723-3732.
Abstract With the rapid development of distributed energy resources (DERs), LC-filtered voltage source inverters (VSI) have become an essential interface to connect the DERs with the grid due to their harmonic suppression capability and cost advantages at high power levels. In order to regulate the output performance of LC-filtered VSI with small voltage ripples and low total harmonic distortion (THD), model predictive control (MPC) has been widely investigated for its simple implementation, fast response, and multi-objective control. However, the direct use of discrete system models makes MPC prone to mismatches in system parameters, which increases prediction error and endangers system stability. The model-free predictive control (MFPC) methods utilize the sampled signals instead of system parameters to construct the predictive model of VSI. The sixteen current gradients generated by the eight basic voltage vectors (VVs) are calculated and stored in the look-up tables (LUTs) in each control period. Future state predictions can be obtained based on the current gradients, eliminating the impact of parameter mismatch on the prediction calculation. This paper proposes a model-free prediction and parameter-less reference-based triple-vector predictive control (PLR-TV-MFPC) for LC-filtered VSI, considering the parameter dependency of the reference calculation.
The triple vectors can improve the output performance of VSI and reduce the THDs of output voltage. The durations of applied vectors are calculated based on the ratios of their cost functions. Then, the inverter-side current gradients and capacitance voltage gradients of applied VVs can be obtained by analyzing the gradients corresponding to different VVs in different control periods. The gradients of the remaining VVs are summarized into two cases, where the components on the a-axis and b-axis are equal. The gradients updating equations are constructed, and the stagnation effect can be eliminated. Furthermore, the phase-amplitude relationship is analyzed with 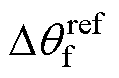 and
and 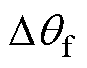 as the phase difference between the reference and sample signals of inverter-side current and capacitance voltage. The reference of inverter-side current can be obtained, and the system parameters are eliminated.
as the phase difference between the reference and sample signals of inverter-side current and capacitance voltage. The reference of inverter-side current can be obtained, and the system parameters are eliminated.
Finally, the proposed method is evaluated on the LC-filtered VSI experimental platform. The output voltage’s THD is 3.82 % and 1.59% using the conventional and the proposed methods. Under different load conditions, TV-MPC’s THD and prediction error are 0.89 V and 1.04%, and the proposed PLR-TV-MFPC’s are 1.56 V and 1.59%. The proposed PLR-TV-MFPC has a low and stable prediction error of 1.72 V when the system parameters of LC-filtered VSI mismatch from the actual values; the conventional TV-MPC and TV-MFPC vary from 1.4 V to 16.4 V and 2.2 V to 9.8 V, respectively.
Conclusions can be drawn as follows. (1) Using triple vectors and the update of all gradients in each control period can reduce the output voltage prediction error and THD of LC-filtered VSI. The output performance of the proposed method is similar to that of the conventional TV-MPC under accurate parameters. (2) The proposed PLR-TV-MFPC is robust against parameter mismatch. When the system parameters are inaccurate, the proposed method’s output voltage prediction errors and THD keep a low and stable value, verifying the effectiveness of the proposed model-free prediction and parameter-less reference methods. The proposed method can be extended to the LCL-filtered VSI in future studies or further tested under grid-tied conditions.
Keywords:Voltage source inverters, LC-filter, triple-vector, model-free predictive control, parameter-less reference
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.241065
国家自然科学基金资助项目(52377164, 52207184)。
收稿日期 2024-06-20
改稿日期 2024-08-07
吕立傲 男,1999年生,硕士研究生,研究方向为基于数据驱动的并网逆变器无模型预测控制。
E-mail: Z22301225@stu.ahu.edu.cn
胡存刚 男,1978年生,教授,博士生导师,研究方向为变流器的调制与控制技术。
E-mail: hcg@ahu.edu.cn
(编辑 陈 诚)