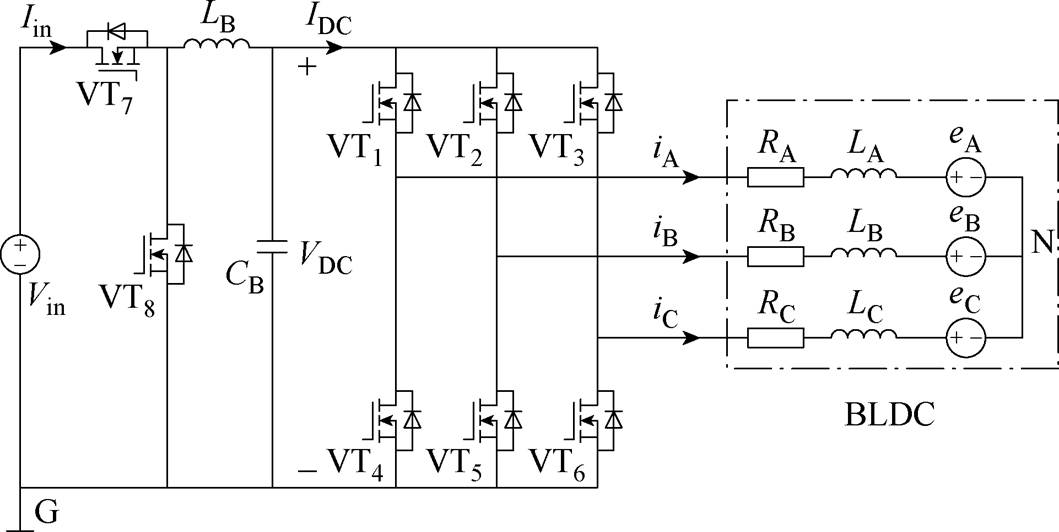
图1 BLDCM驱动系统主电路
Fig.1 BLDCM drive system main circuit
摘要 针对高速无刷直流电机控制中三相绕组参数不对称导致的换相误差以及换相点附近电感压降难以估测而导致的换相延迟问题,该文提出了一种基于改进线反电动势检测的非理想换相的校正策略。通过分析非理想电机参数不对称对线电压的影响,提出水平方向上电角度偏移可作为竖直方向上的电压偏移的参考量,并结合线反电动势交点间隔解算出每相的电角度偏移,通过PI算法恢复真实的线反电动势。同时,考虑了电感压降和电流噪声对线反电动势的影响,通过线性回归方程预测换向点附近的线反电动势,以实现准确换相。该方案可以有效地解决非理想电机的初始参数不对称问题,能一定程度地抵抗电机运行中参数扰动的影响。实验结果表明,该方法能在不同转速下将位置误差降低至±0.2个电角度,同时降低了电流峰峰值约10%。
关键词:线反电动势(LEMF) 参数不对称 无传感器控制 线性回归方程 无刷直流电机
无刷直流电机(Brushless Direct Current Motor, BLDCM)以其控制简单、运行可靠和高效率等优势而快速发展,广泛应用于高速空压机、晶圆切割、飞轮储能等系统[1-3]。BLDCM通常使用位置传感器检测转子位置,但传感器的应用不仅增加了系统成本和复杂性,而且对极端环境敏感[4],在超高速电机领域难以适用。无位置传感器因其低成本和高可靠性等优点得到了广泛研究。
但BLDCM无感控制系统在高速或大电流重载运行时,若无刷直流电机的参数存在非理想误差或受到极端环境下的参数扰动,可能导致电机电压偏离,进而引发严重的换相误差甚至失步问题。在实际应用中,许多因素可能导致电机参数不对称,如三相绕组布线问题、机械制造粗糙、转子偏心或绕组故障等[5-6]。特别是对于低电阻、低电感的高速无刷直流电机,其参数非常敏感。
针对无刷直流电机高速运行时的非理想换相问题,一般采用换相误差补偿策略。文献[7]分析了运行存在的换相误差问题和线电压差积分值的数学关系,解决了无刷直流电机运行中的换相误差问题,但该方法易带来较大的谐波,对滤波器的设计有较高的要求。文献[8]分析了低通滤波器(Low Pass Filter, LPF)延时、器件延时、软件延时等对换相的影响,得出了由各种延时导致的换相延时角度的精确表达式。
上述补偿方案鲁棒性较差,且难以有效解决非理想电机参数不对称的问题。文献[9]提出了一种基于电感法的定位方案,通过对脉冲电流响应差-转子位置曲线进行分析,对采样电流取差分值,消除了电机凸极性对电感变化的影响,但方案对电机本体参数要求较高。文献[10]深入分析了非对称电机参数,即相电阻和电感对无传感器换相的影响,并提出了相应的解决办法,但提出方法仅适用于相反电动势的换相策略。文献[11]研究了抗干扰性强的端电压尖峰脉冲信号的变化特性,并利用端电压尖峰脉冲设计了换相误差闭环控制方法,但该方法动态响应效果不佳,收敛速度较慢,且没有考虑电机运行过程中参数变化带来的影响。文献[12]在分析参数不对称时,利用相反电动势过零点间隔差,通过PI调节自适应门限值。但该方法有两个主要缺点:一是单纯通过调节门限值可能无法完全消除误差,会产生相同的超前角或滞后角;二是方法的收敛速度较慢,且收敛时电角度偏差噪声较大。
本文提出了一种改进方案,不仅解析了电机参数不对称问题与线反电动势交点(Electromotive Force Crossing Point, EMFCP)间隔之间的联系,还原了线反电动势(Line back Electromotive Force, LEMF),还通过预测局部的线反电动势,避免了电感压降和电流噪声对换相的影响。此外,考虑了高速下的低通滤波器延时和采样延时补偿。该方案可以有效解决非理想电机的初始参数不对称问题,能一定程度地抵抗电机运行中参数扰动的影响,使电机在高速下稳定运行。
基于脉幅调制(Pulse Amplitude Modulation, PAM)的BLDCM驱动系统、电机和采样电路的框架如图1所示。图1中,Vin、Iin分别为降压(Buck)变换器输入电压和电流,G为接地端,VT1~VT8均为功率器件,CB为直流侧电容;VDC、IDC分别为Buck变换器输出电压和电流;N为电机中性点。前端降压斩波电路进行的PAM,三相逆变桥只参与换相,不进行调制,可以减小高速无刷电机的转矩脉动[13]。

图1 BLDCM驱动系统主电路
Fig.1 BLDCM drive system main circuit
若忽略无刷直流电机齿槽效应和电枢反应,三相绕组电压方程可以表示为
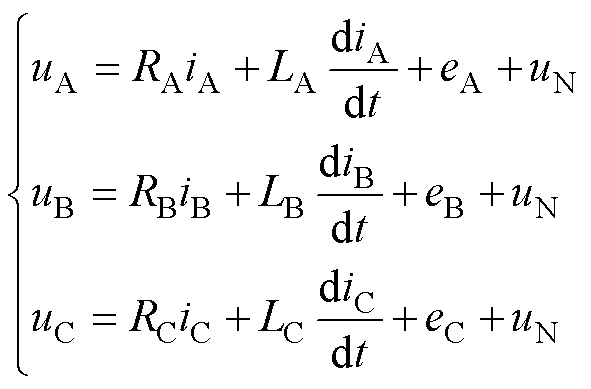 (1)
(1)
式中,uA、uB、uC为定子绕组端电压;iA、iB、iC为定子绕组相电流;RA、RB、RC为定子绕组电阻;eA、eB、eC为定子绕组的反电动势;LA、LB、LC为定子绕组等效电感;uN为电机中性点电压。
在电机系统中,线反电动势无法直接测量,可通过采集线电压和相电流进行解算。根据式(1)得线反电动势方程为
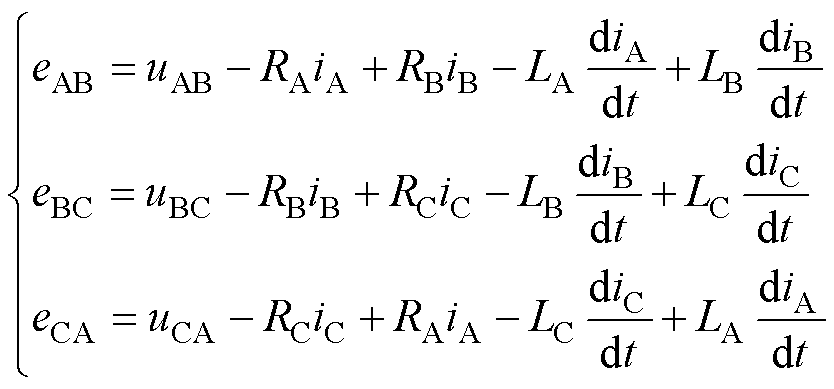 (2)
(2)
式中,uAB、uBC、uCA为三相线电压;eAB、eBC、eCA为三相线反电动势。
根据电机学原理,相反电动势可表示[14]为
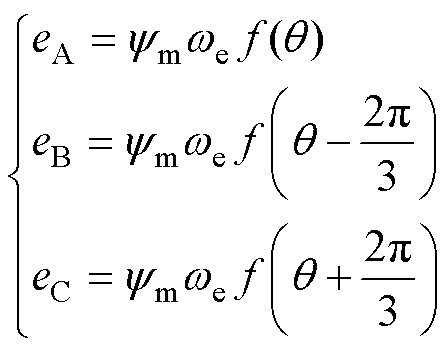 (3)
(3)
式中,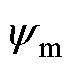 为每相绕组匝链永磁磁链的最大值;
为每相绕组匝链永磁磁链的最大值;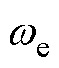 为电机的电速度;
为电机的电速度;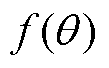 为BLDCM相反电动势梯型波。
为BLDCM相反电动势梯型波。
电机六步换相时,每一步均有两相处于导通状态,电流从上桥臂开通相流入到下桥臂开通相,另一相上下桥臂均关断处于悬空状态,A、B相悬空的等效电路如图2所示。
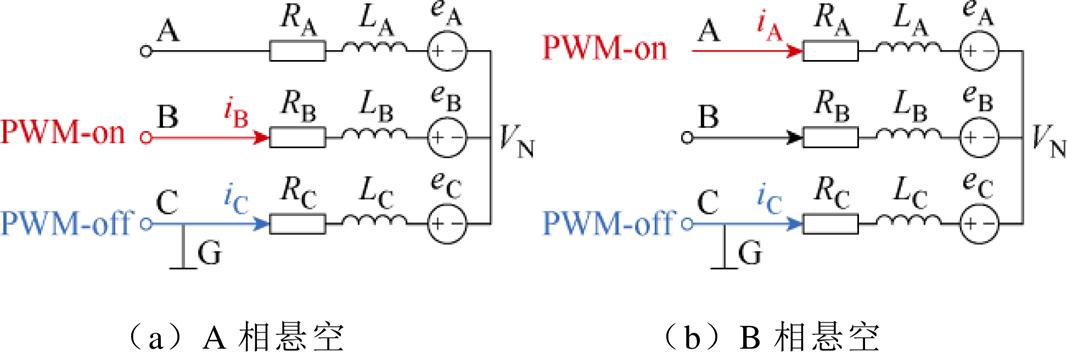
图2 A、B相悬空的等效电路
Fig.2 Equivalent circuit of phase A and B suspended
图2中,PWM-on表示MOS管导通并且与直流母线正端相接;PWM-off表示MOS管导通并且与直流母线负端相接;VN为电机中性点的电压。在图2a中,iA=0,根据式(2)得
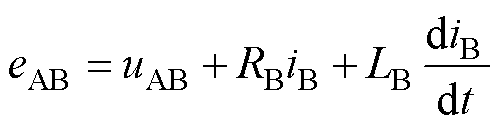 (4)
(4)
在图2b中,iB=0,同理可得
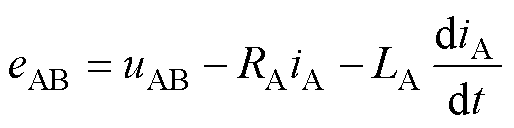 (5)
(5)
虽然线反电动势eAB在图2a、图2b都处于梯型波的腰线,但实际决定换相的是式(4)处于的状态。
根据图2,若电机参数不对称,以电机处于扇区Ⅰ时为例,有RB≠RC,LB≠LC,中性点电压VN会产生偏移,即式(4)可写为
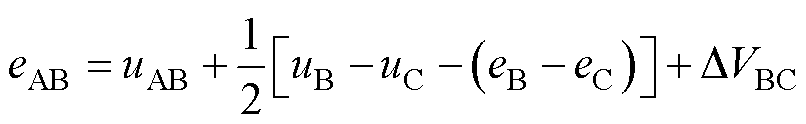 (6)
(6)
据式(3),可将式(6)化简得
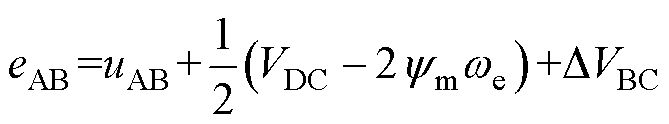 (7)
(7)
式中,DVBC为B相为高电平、C相为低电平、A相悬空时候由参数不对称引起的电压偏移。
A相悬空时候电压偏移表达式为
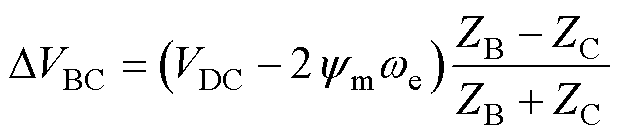 (8)
(8)
式中,ZX为该相的总阻抗,下标“X”表示A、B或C相。
根据式(8)易知,DVBC+DVCB=0。同理得另外两相电压偏差为
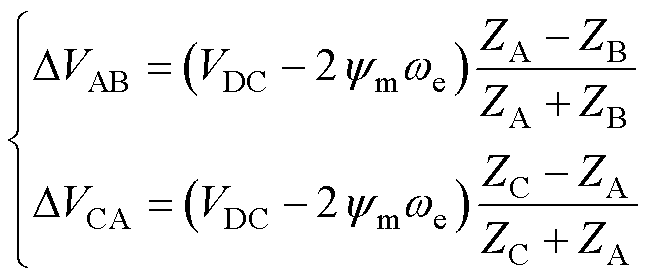 (9)
(9)
根据式(8)、式(9),三相电压偏差之和为
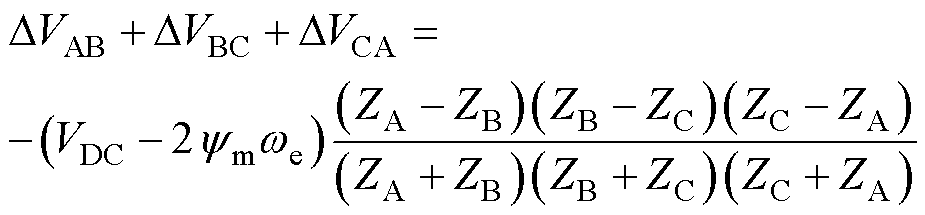 (10)
(10)
由于三相阻抗值比较接近,其差值的三次方趋近等于零,因此有
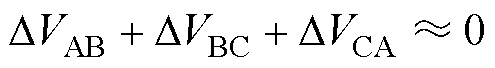 (11)
(11)
根据式(11)可以判断参数不对称存在顺时针不对称和逆时针不对称两种,顺时针不对称包括两个超前阶段和一个滞后阶段(即式中任意两个电压偏差项大于零,另外一项小于零),逆时针不对称包括两个滞后阶段和一个超前阶段(与顺时针不对称同理)。
基于图2a的分析,处于相同扇区时,线反电动势eCA同样处于梯型波的腰线,根据式(7),iA=0时,其线反电动势的变化为
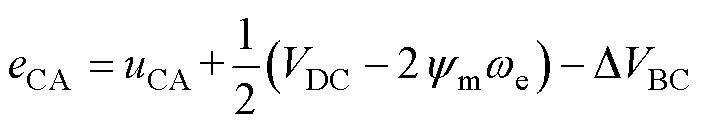 (12)
(12)
综上分析可知,电机参数不对称会使处于梯型波腰线的线电压发生竖直方向上的电压偏移,导致解算出的线反电动势发生相同的偏移,进而产生不同程度的换相误差,参数不对称下的换相分析如 图3所示。
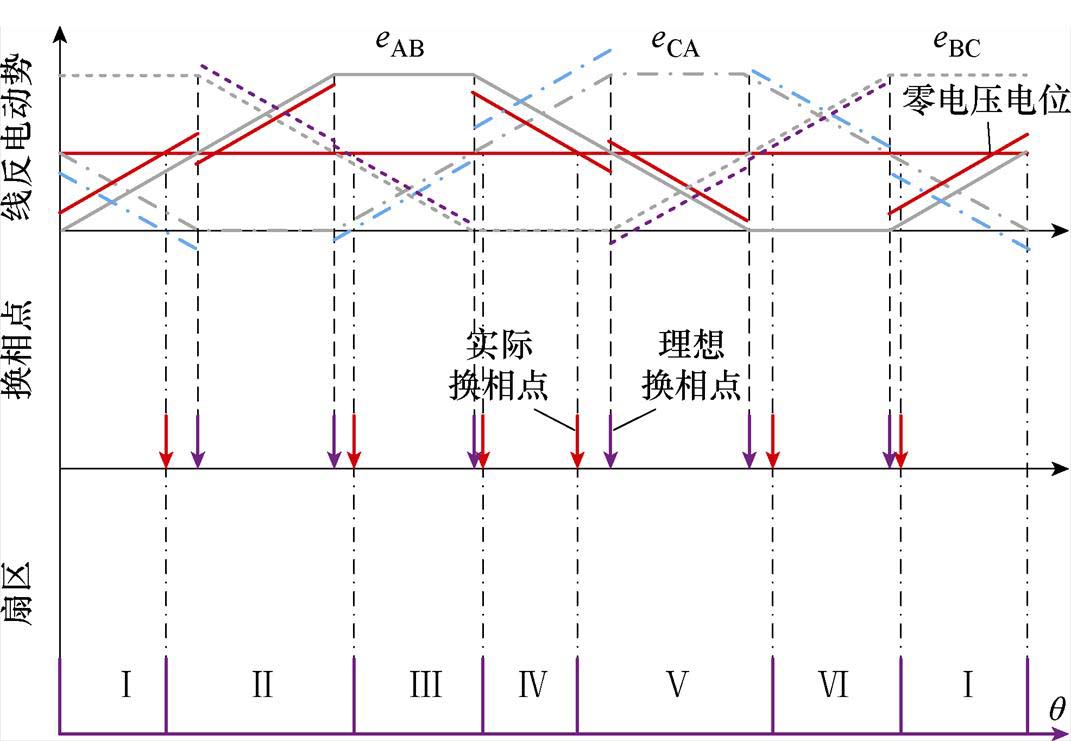
图3 参数不对称下的换相分析
Fig.3 Commutation analysis under asymmetric winding parameters
图3中,第一栏为理想线反电动势与实际线反电动势,红色为实际线反电动势eAB,蓝色为实际线反电动势eCA,紫色为实际线反电动势eBC,可以看到线反电动势换相存在不同程度的提前或者滞后;第二栏为理想换相点(紫色)与实际换相点(红色)对比,电机换相点为线反电动势过零点,可见电机参数不对称情况下换相的间隔是不均匀的,存在不同程度的换相误差;第三栏为非理想扇区,呈一定的规律分布,每三个连续扇区值之和相等。
为了探究线反电动势偏移对换相的影响,需要对换相时刻具体分析,非理想换相局部缩放如图4所示。
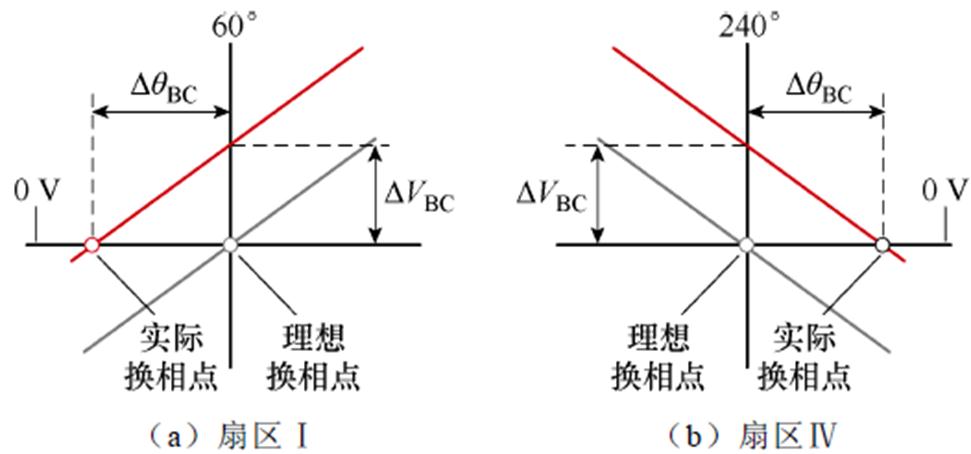
图4 非理想换相局部缩放
Fig.4 Non-ideal commutation local scaling
图4a、图4b分别为图3扇区Ⅰ和扇区Ⅳ中eAB的缩放图,蓝色虚线为理想线反电动势,蓝色实线为参数不对称引起的实际线反电动势。在扇区Ⅰ中,线反电动势向上移动了DVBC,使EAB提前过零,此时水平方向上的偏移电角度为DqBC;在扇区Ⅳ中,运动轨迹相反。从另一个角度来看,可以将线反电动势的竖直偏移看作水平偏移,即受电机参数不对称的影响会导致水平方向上的电角度偏差。理想情况下,换相点附近的线反电动势可近似看为一条斜率不变的直线,根据式(3)可得电压偏移误差与电角度偏移误差的线性关系为
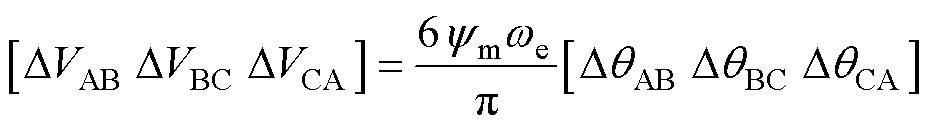 (13)
(13)
式中,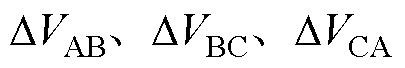 为电角度偏移误差。
为电角度偏移误差。
再结合式(11),三个电角度偏移误差之和为
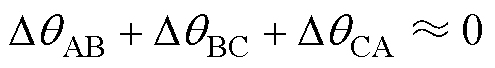 (14)
(14)
如图3所示,电角度偏差暴露在换相间隔之中,但是换相具有不确定性,无法直接利用换相间隔做指标,于是考虑利用线反电动势交点间隔解算电角度偏差。以扇区Ⅰ为例,根据式(2)得线反电动势交点为
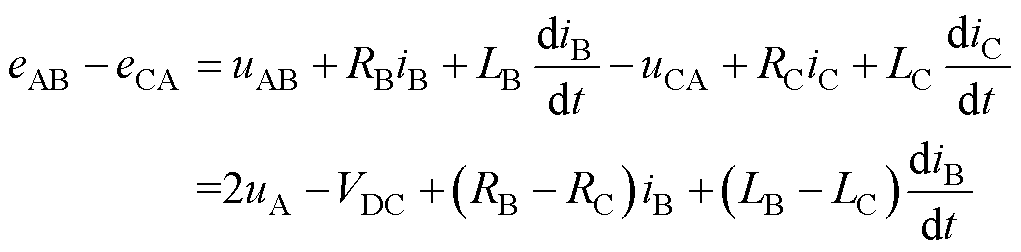 (15)
(15)
根据式(15),若参数对称时,假设端电压uA在t时刻等于1/2VDC,有eAB-eCA=0,此时为线反电动势交点;若参数不对称,在t+Dt时刻,式(15)等于0,根据式(8),此时uA(t+Dt)为
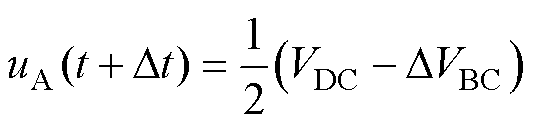 (16)
(16)
其他五个扇区同理可得。因此,可以确定水平方向上的电角度偏差会暴露在线反电动势交点间隔之中。绕组参数不对称情况下的EMFCP间隔偏差分析如图5所示,以电机参数逆时针不对称为例,六步换相周期有两个超前换相,四个滞后换相。
在图5中,第一栏为理想线反电动势与实际的线反电动势对比;第三栏为理想线反电动势交点(蓝色)与实际线反电动势交点(红色),阴影部分为理想与实际EMFCP偏差;第四栏为实际EMFCP间隔,其包含电角度偏差信号,每个交点用CPU定时器记录,Tn-6~Tn为记录的实际线反电动势交点;第五栏为理想扇区位置。以扇区Ⅰ为例,根据式(7)、式(12),A相处于悬空状态时,即eAB发生竖直方向上的偏移,而eCA向下偏移相同的电压。因此,线反电动势eAB、eCA同样可视作偏移了相同的电角度,且相对于换相点,二者偏移方向相同,则此时实际换相点相对于理想换相点向左偏移了2DqBC。由此可推,每个扇区都是相同的规律,EMFCP超前或滞后两倍的电角度偏差。
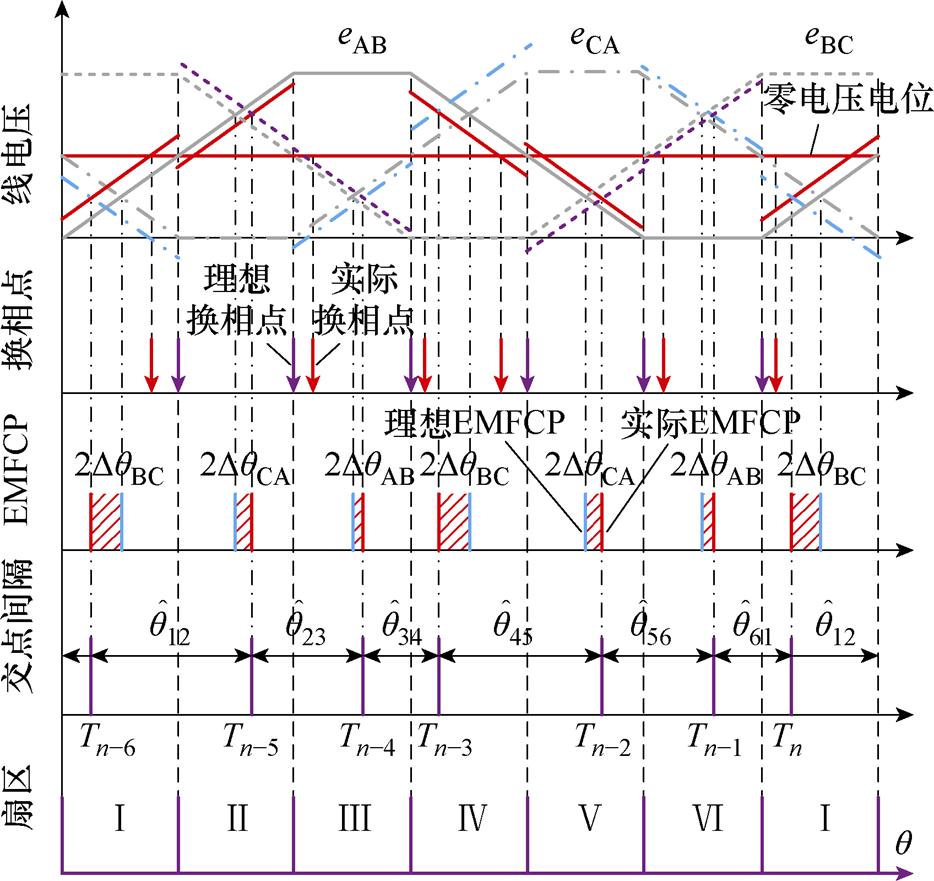
图5 绕组参数不对称情况下的EMFCP间隔偏差分析
Fig.5 Analysis of EMFCP interval deviation in the case of winding parameter asymmetry
根据图5,即使是参数非理想状态下,完整的六个EMFCP间隔之和也为360°,利用CPU定时器获取一个电周期时间为
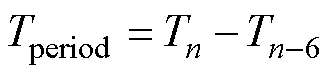 (17)
(17)
为了顺利地解算电角度偏差,先梳理了理想EMFCP与实际EMFCP之间的关系,如图6所示。
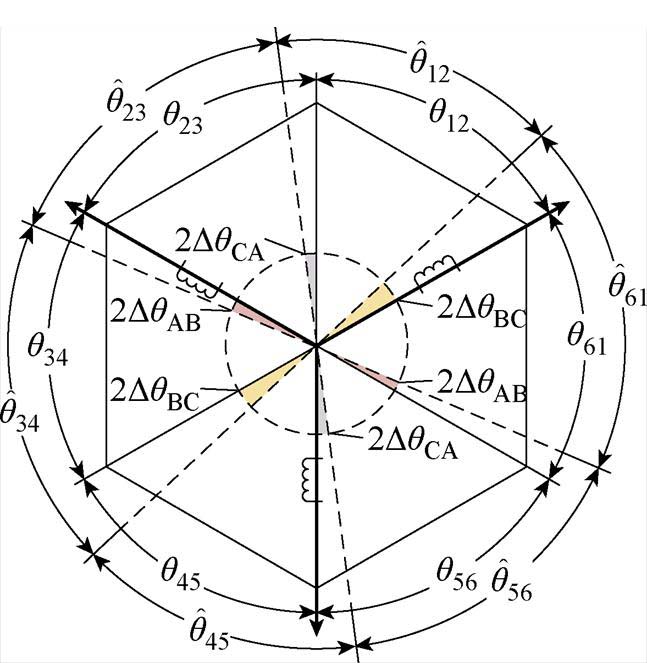
图6 理想与实际的EMFCP间隔偏差
Fig.6 Deviation between ideal and actual EMFCP intervals
在图6中,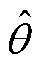 为EMFCP间隔估计值,图中彩色标记部分为电角度偏差。此时假设六个电角度偏差都包含正负号,且逆时针偏置,可以将电角度偏差建模为
为EMFCP间隔估计值,图中彩色标记部分为电角度偏差。此时假设六个电角度偏差都包含正负号,且逆时针偏置,可以将电角度偏差建模为
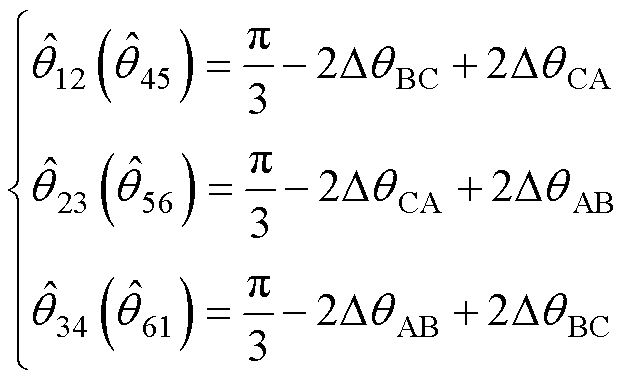 (18)
(18)
式中,括号中的值与变量值相等,如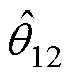 =
=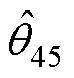 。
。
利用式(14)和式(18),可求解出任意的参数不确定误差为
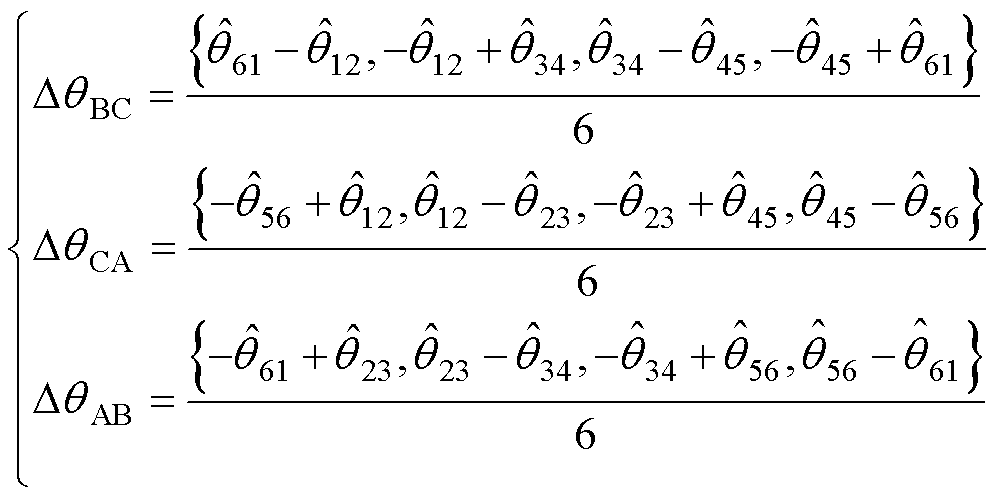 (19)
(19)
得到电角度偏差后,利用PI输出的电压值还原线反电动势,使得电角度偏差收敛至零。每个电角度偏差在一个电角度周期内,可以解算出六次,有效提高了PI的收敛速度。实际工程应用中,电角度偏差可以利用定时器测量的时间间隔来计算,有
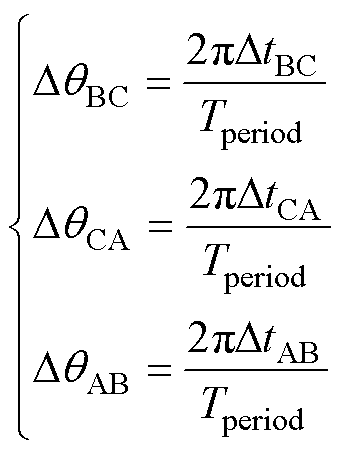 (20)
(20)
式中,DtBC、DtCA、DtAB为对应电角度偏差时间。
得到电角度偏差后,利用PI调节使线反电动势还原,从而消除换相误差。原方程详见表1,表中,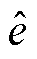 为线反电动势估计值。
为线反电动势估计值。
表1 基于三相绕组参数不对称的线反电动势还原
Tab.1 Line back EMF reduction based on three-phase winding parameter asymmetry
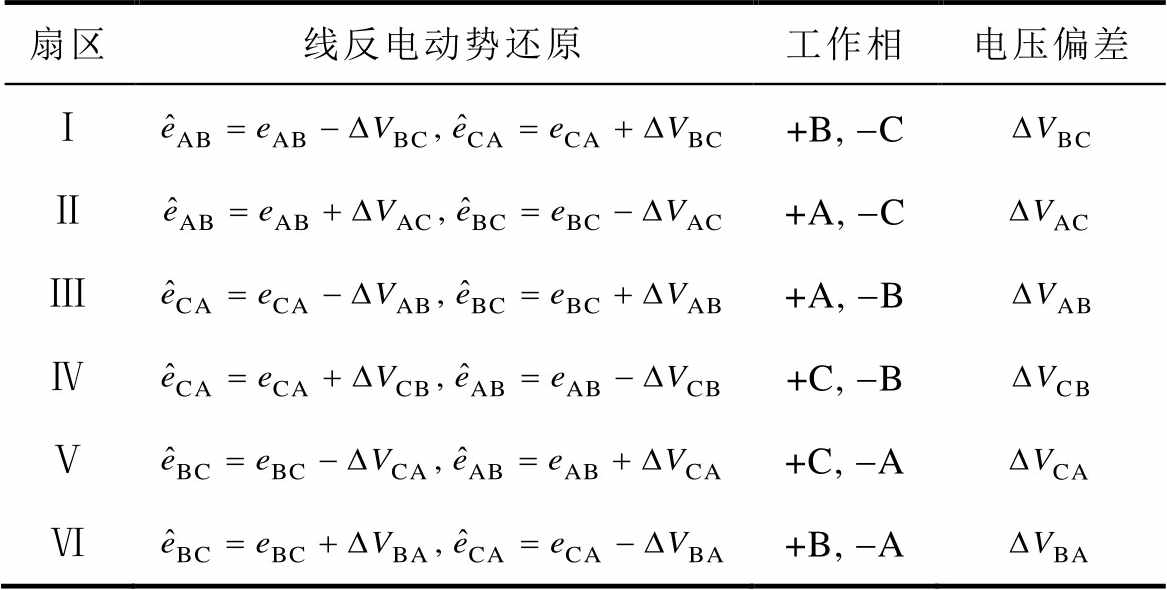
扇区线反电动势还原工作相电压偏差 Ⅰ+B, -C Ⅱ+A, -C Ⅲ+A, -B Ⅳ+C, -B Ⅴ+C, -A Ⅵ+B, -A
综上所述,考虑绕组参数不对称的非理想换相校正策略的主要原理是根据EMFCP的间隔解算出电角度偏差,然后利用PI输出的电压反馈到线反电动势上,从而消除电角度偏差,线反电动势非理想换相校正方案如图7所示。该方法在线反电动势还原过程中并不需要预先确定准确的电阻值,且具有一定的参数抗扰动性,总可以将线反电动势还原成合适的值。
理想状态下,线反电动势可以看成一个标准的梯型,但实际上电机中的电感可将反电动势平滑成更正弦的形状。由于电感电流的存在,解算出来的线反电动势在电流趋于稳态后是一段不断逼近理想线反电动势的曲线。考虑到电流传感器精度问题影响换相稳定性,且空载时电流信噪比低,影响线反电动势结算,会产生严重的换相误差问题。
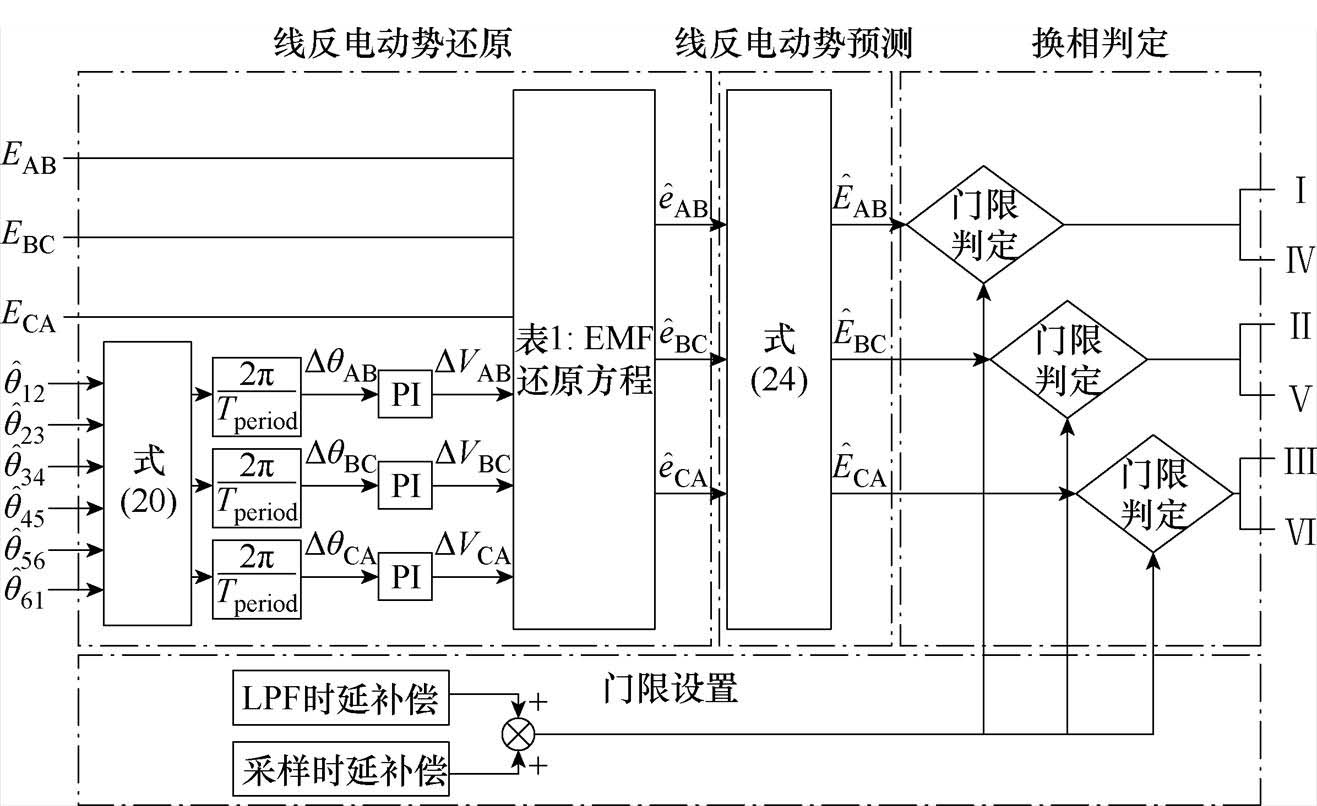
图7 线反电动势非理想换相校正方案
Fig.7 Non-ideal commutation correction scheme for line back EMF
针对这一问题,本文提出了一种数据拟合的方法[15],即将进入到下一个换相点之前的每个60°间隔划分为隔离区域、拟合区域以及预测区域三个部分,如图8所示。
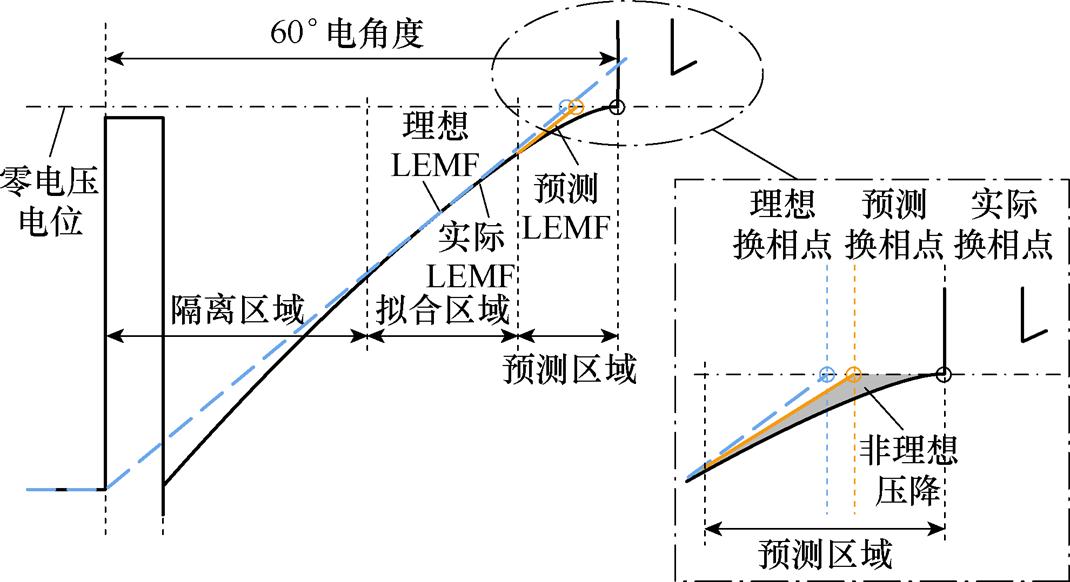
图8 基于线性回归方程的线反电动势预测
Fig.8 Line back EMF prediction based on linear regression equation
如图8所示,隔离区域为电流变化率较大的部分,该区域解算出来的线反电动势误差大,范围大致为30°。在拟合区域,每个中断记录一次线反电动势的值,借助大量的观测数据来给出数据最为相符的线性回归函数关系,范围大致为25°。预测区域采用拟合的线反电动势进行换相判定,规避线反电动势解算误差导致的换相误差或失败问题,范围大致为5°。
建立简单的一元线性拟合函数[16]为
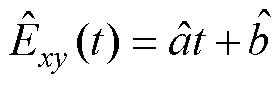 (21)
(21)
式中,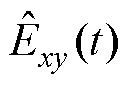 为线反电动势预测值;
为线反电动势预测值;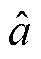 为直线斜率;
为直线斜率;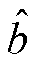 为截距;t为采样时间。
为截距;t为采样时间。
为作区分,线反电动势还原之后的估计值为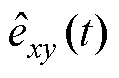 ,设t为采样点时间,其对应为t时刻的采样值(t的范围为20个电角度,t=1, 2,…, n,n=Tperiod/18)。
,设t为采样点时间,其对应为t时刻的采样值(t的范围为20个电角度,t=1, 2,…, n,n=Tperiod/18)。
由于预测值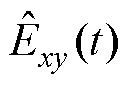 与还原之后的估计值
与还原之后的估计值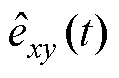 直接存在误差,建立误差函数
直接存在误差,建立误差函数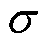 为
为
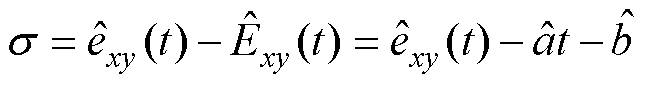 (22)
(22)
根据最小二乘法原则,需要使误差的二次方和最小,即总离差Q为
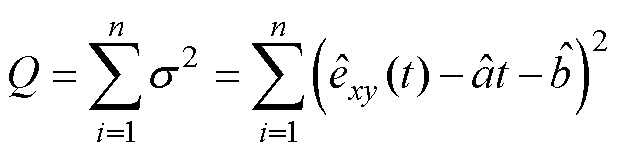 (23)
(23)
根据微分求极值的原理,对总离差函数中的斜率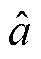 和截距
和截距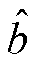 分别求偏导并等于0,得到方程组为
分别求偏导并等于0,得到方程组为
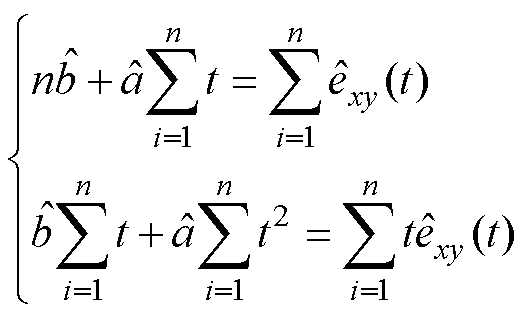 (24)
(24)
解方程组,求得拟合直线斜率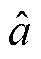 和截距
和截距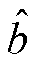 为
为
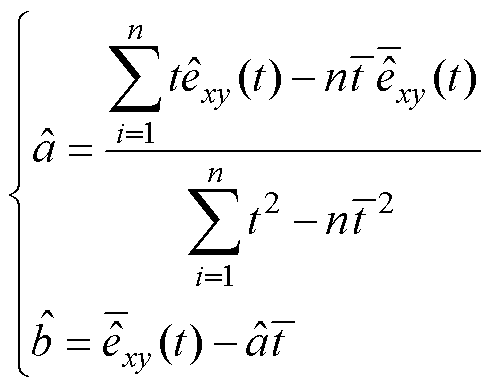 (25)
(25)
式中,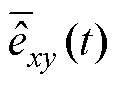 为拟合区域线反电动势的平均值;
为拟合区域线反电动势的平均值;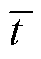 为拟合区域内不同区间段时间的平均值。
为拟合区域内不同区间段时间的平均值。
确定好线性方程的斜率和截距后,就可以预测下一步的线反电动势。
对于高速电机控制系统,在补偿了基于线反电动势参数不对称换相产生的影响之后,还需考虑低通滤波器引起的线反电动势过零点延迟问题,延迟角度qLPF[17]为
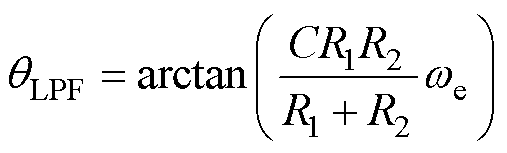 (26)
(26)
式中,R1、R2为滤波器两个采样电阻;C为滤波电路中的电容。
在高速无刷直流电机驱动系统中,若采样频率显著低于电机换相频率,换相信号的采样会导致较大的相位延迟,这一现象不容忽视。延迟角度qs[18]为
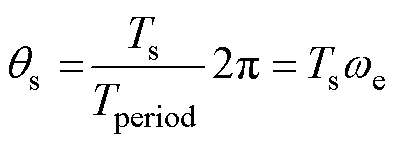 (27)
(27)
式中,Ts为数字处理器的采样周期。
因此,本文在无刷直流电机高速下考虑的低通滤波器延时问题和采样延时问题的综合补偿为
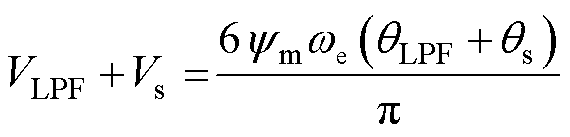 (28)
(28)
式中,VLPF为低通滤波器延时电压补偿;Vs为采样延时补偿。
由于二者延时问题会导致线反电动势统一的滞后,可以通过调整换相门限来消除延迟带来的影响,综合门限调整见表2。
表2 无刷直流电机高速下的时延门限调整
Tab.2 Delay threshold adjustment for high speed brushless DC motor

扇区换相时刻工作相 Ⅰ+B, -C Ⅱ+A, -C Ⅲ+A, -B Ⅳ+C, -B Ⅴ+C, -A Ⅵ+B, -A
根据上述分析,本文提出一种改进线反电动势检测的非理想电机换相补偿策略,该策略下的高速无刷直流电机控制框图如图9所示。构建的整体控制框架分为无感换相模块和控制模块两部分。图9中,D为电压PI控制器输出的占空比信号。控制模块为母线电流环加速度外环的双闭环控制结构。在无感换相模块中,首先进行电压和电流信号的采集,解算出线反电动势与EMFCP间隔差值;然后解算出电角度偏差后,利用PI还原线反电动势,校正电压偏差;最后针对高速下LPF时延和采样时延问题,通过设置换相门限的方式来补偿,再利用线反电动势线性预测来确保准确换相。
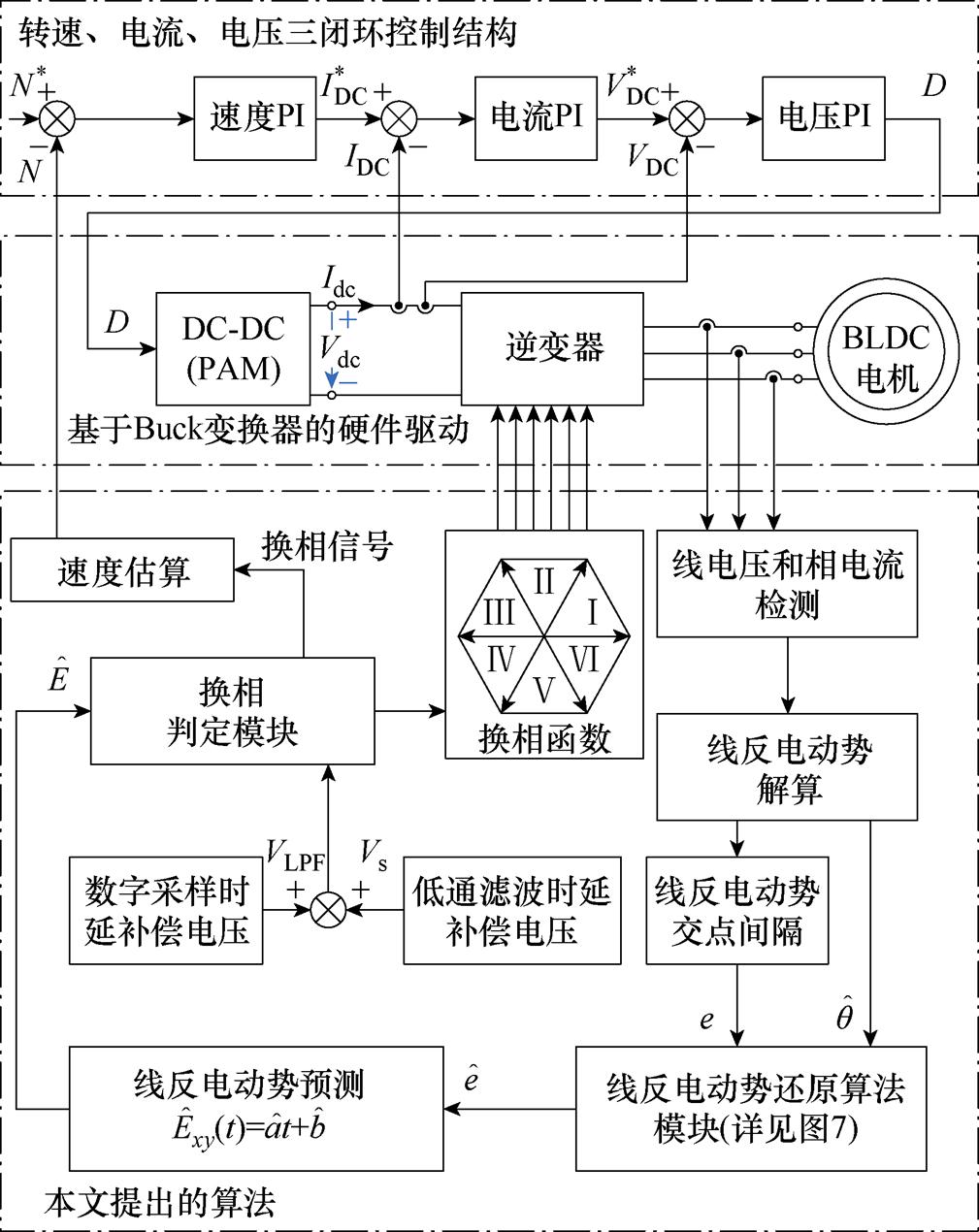
图9 高速无刷直流电机控制框图
Fig.9 High speed brushless DC motor control block diagram
本文首先在Matlab平台上进行了快速实验,验证了提出算法的有效性。然后,为了更好地适应实际工业应用场景,采用了由TI公司提供的TMS320F28379D芯片作为主控DSP并验证了所提出的补偿算法,实验平台如图10所示。

图10 基于DSP的实验平台
Fig.10 Experimental platform based on DSP
电机为高速空压机,通过涡轮扇叶提供巨大的负载转矩,其电阻和电感三相绕组值是不对称的。部分实验在高速对拖平台进行,用电机编码盘反馈的电速度,结合式(3),得到理想的线反电动势做参考,高速对拖电机与空压机电机参数详见表3。在线反电动势还原过程中,应用本文提出的非理想换相校正策略消除参数不对称造成的换相误差。
表3 电机参数
Tab.3 Motor parameters
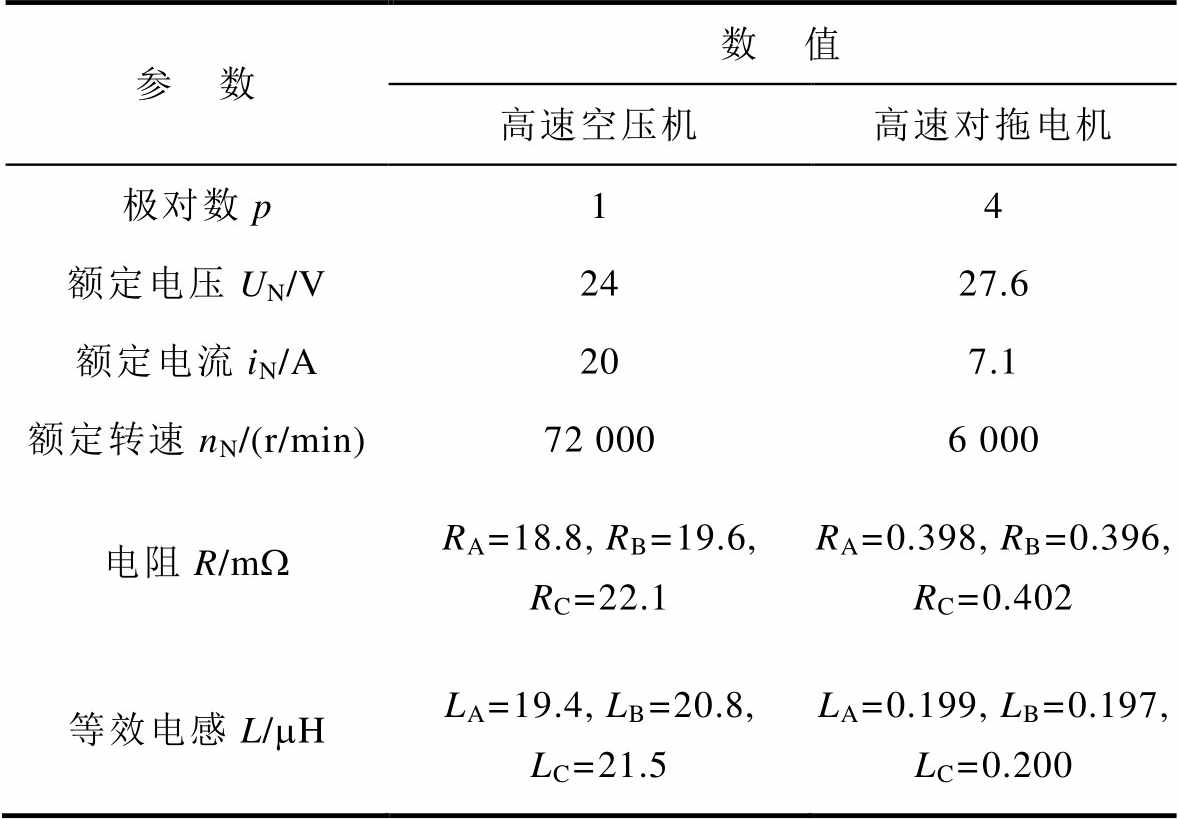
参 数数 值 高速空压机高速对拖电机 极对数p14 额定电压UN/V2427.6 额定电流iN/A207.1 额定转速nN/(r/min)72 0006 000 电阻R/mWRA=18.8, RB=19.6, RC=22.1RA=0.398, RB=0.396, RC=0.402 等效电感L/mHLA=19.4, LB=20.8, LC=21.5LA=0.199, LB=0.197, LC=0.200
图11为空压机电机36 000 r/min下的有无补偿算法的非理想过零点比较,曲线从上到下依次为EMFCP间隔、六步换相扇区、相电流iA和iB。在图11a中,由于参数不对称引起的电压偏移导致EMFCP间隔不一致,间隔最长为65.4°,最小为57.3°。而电压偏移也直接体现在相电流上,A、B相最大相电流峰峰值约为17.9 A。在图11b中,经过本文算法补偿后,EMFCP间隔差得到消除,间隔误差约为0.1°。同时,A、B相最大相电流峰峰值减小到16.2 A,换相电流偏差几乎为0。
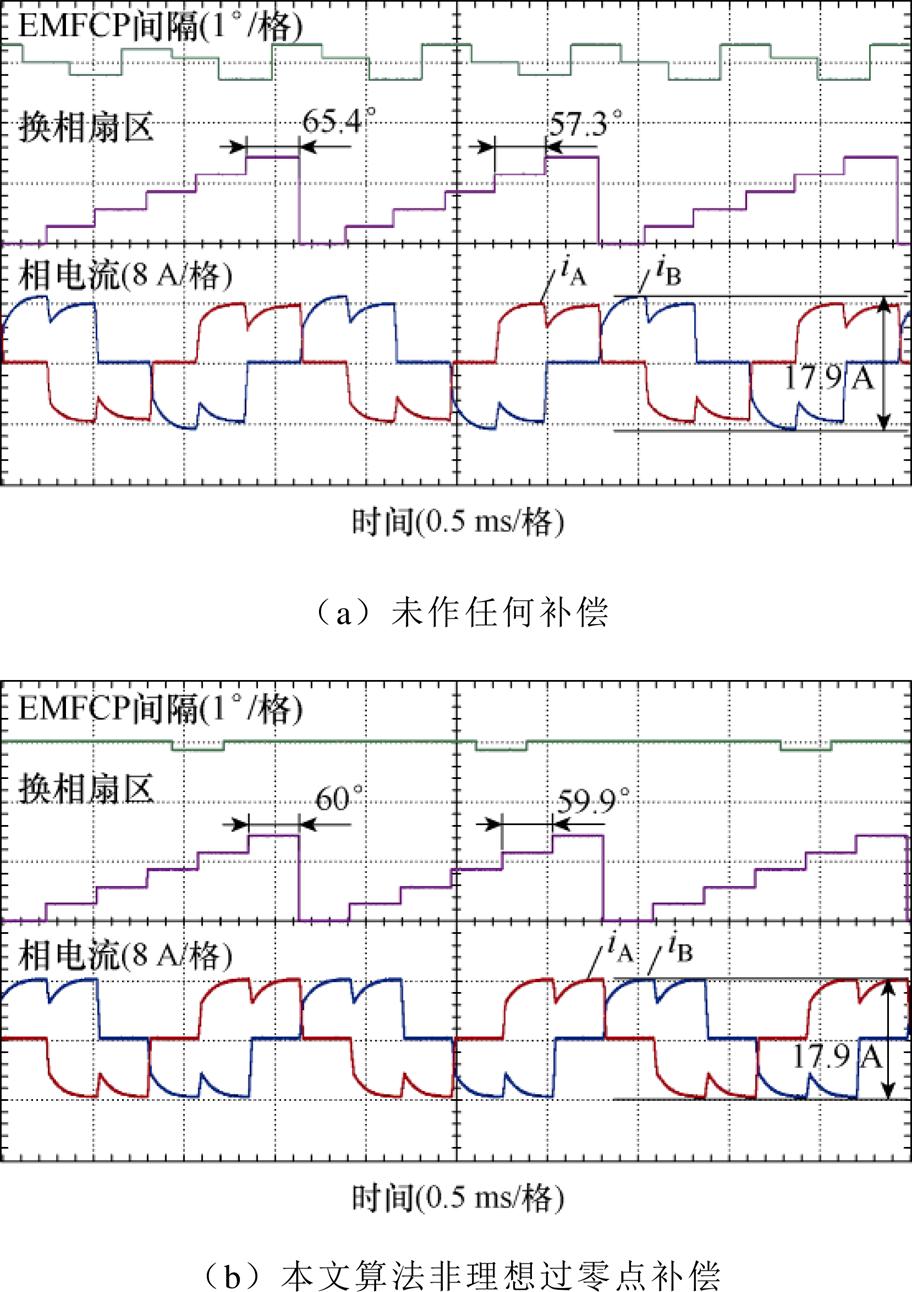
图11 在36 000 r/min下的非理想换相有无补偿比较
Fig.11 Comparison of non-ideal commutation with and without compensation at 36 000 r/min
图12为空压机电机72 000 r/min下的有无补偿算法的非理想过零点比较,在更高转速下的空压机负载转矩会急剧上升,引起更大电压偏移。在图12a中,EMFCP间隔最长为70.6°,最小为53.5°。而较大的电压偏移也使得相电流偏差变大,A、B相最大相电流峰峰值约为46.8 A。在图12b中,经过本文算法补偿后,EMFCP间隔差得到消除,间隔误差约为0.18°。同时,A、B相电流最大电流峰峰值减小到42 A,换相电流偏差几乎为0。
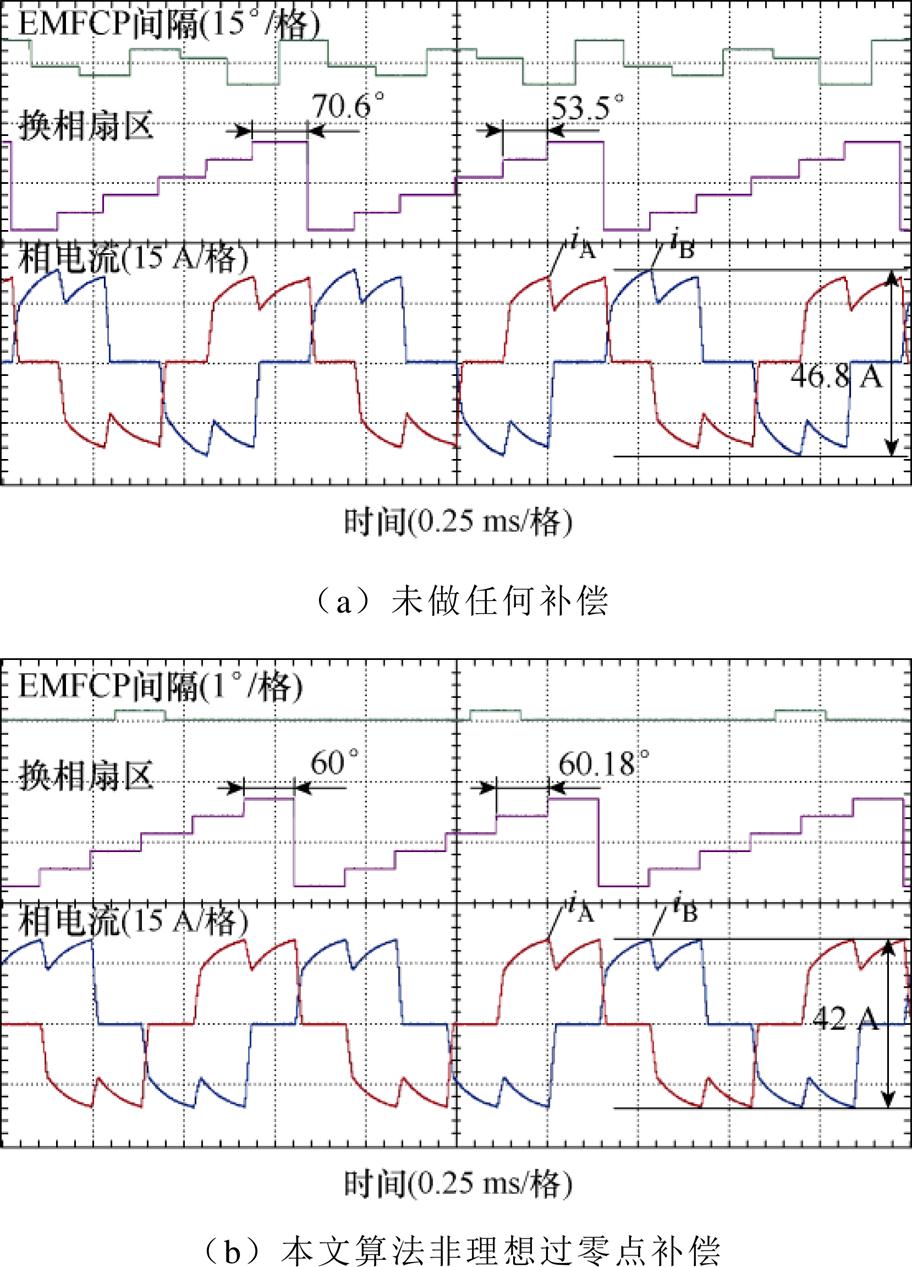
图12 在72 000 r/min下的非理想换相有无补偿比较
Fig.12 Comparison of non-ideal commutation with and without compensation at 72 000 r/min
从图11、图12中可以看出,传统方法换相不稳定,相电流的纹波较大,且无法有效消除相电流偏差。而文献[13]把电流换向时刻前后非换相相电流积分的差值作为PI的反馈量,动态响应较慢,本文算法可以在一个电周期计算出6次电角度偏差,收敛速度更快,且收敛后的换向误差仅有±0.2个电角度。文献[13]没有进行32 000 r/min以上的高速带载实验,当施加重载时,换相转矩脉动对积分计算有较大影响,此时该算法的补偿效果还有待商榷,而本文直接把线反电动势交点间隔差作为反馈量,不受此影响。使用本文的方案对非理想换相做补偿后,可以大幅度降低相电流峰峰值且减少相电流偏差,详见表4。
表4 电流峰峰值
Tab.4 Current ripple
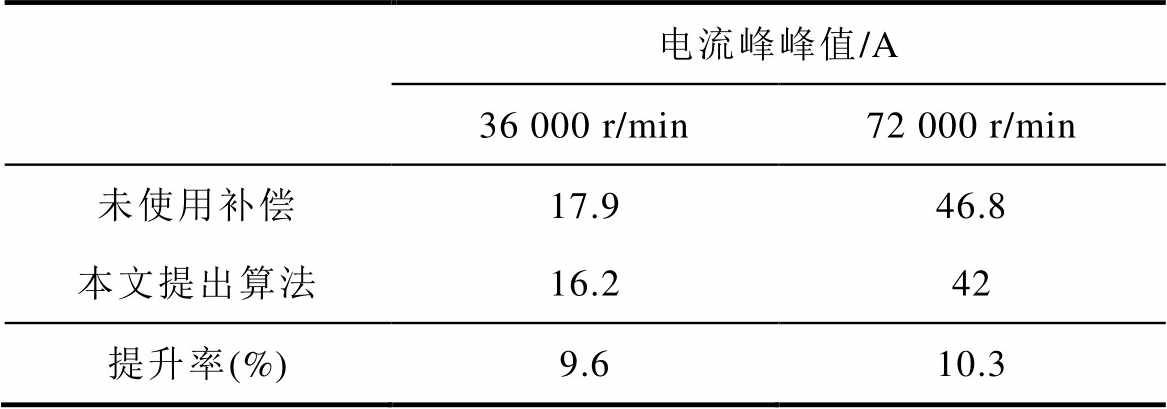
电流峰峰值/A 36 000 r/min72 000 r/min 未使用补偿17.946.8 本文提出算法16.242 提升率(%)9.610.3
图13为稳态过程中的电磁转矩有无补偿比较,曲线从上至下依次为电磁转矩、母线电流和a相相电流。电机受绕组参数不对称的非理想因素影响,会产生换相误差,超前或滞后换相会直接体现在相电流上。根据同步电机电磁转矩的表达式Te= 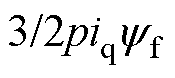 ,其中iq为q轴电流,
,其中iq为q轴电流,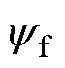 为永磁体磁链。本文利用采集的相电流与编码器反馈的角度通过坐标变换解耦出q轴电流,可以得到等效的电磁转矩。在图13a中,未作任何补偿时,电磁转矩与电流波动剧烈;而在图13b中,本文提出的算法可有效平滑由于参数不对称引起的转矩波动,降低了电流峰峰值。
为永磁体磁链。本文利用采集的相电流与编码器反馈的角度通过坐标变换解耦出q轴电流,可以得到等效的电磁转矩。在图13a中,未作任何补偿时,电磁转矩与电流波动剧烈;而在图13b中,本文提出的算法可有效平滑由于参数不对称引起的转矩波动,降低了电流峰峰值。
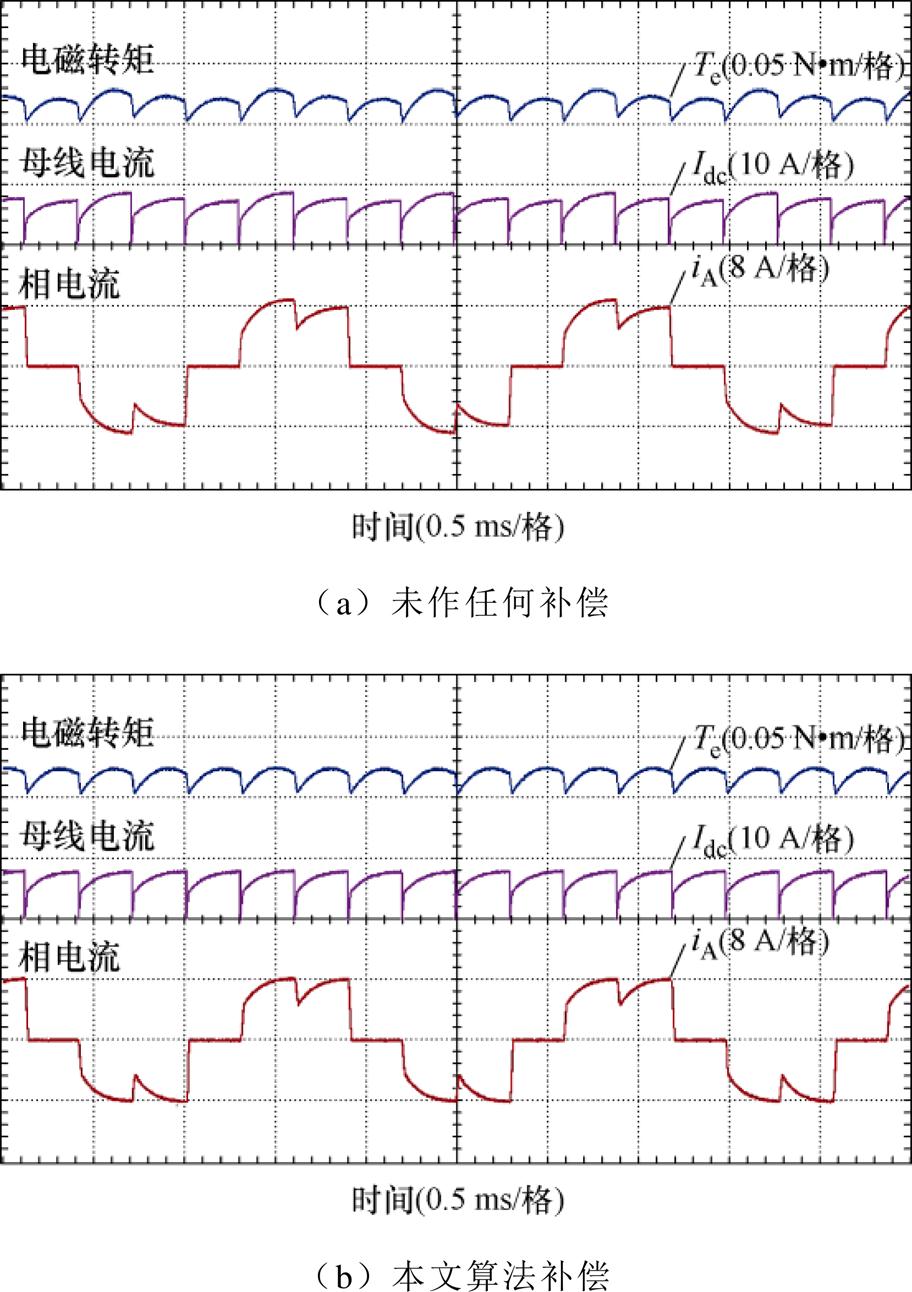
图13 稳态过程的电磁转矩有无补偿比较
Fig.13 Comparison of electromagnetic torque of steady-state process with and without compensation
图14为空压机电机加速与减速过程中有无补偿算法的非理想过零点比较,曲线从上到下依次为电机EMFCP换相间隔、电速度、相电流从36 000 r/min到72 000 r/min升速以及降速过程中的波形。在图14a中,非理想换相未作任何补偿,36 000 r/min时EMFCP换相间隔差为60°±3°;升到72 000 r/min时,EMFCP换相间隔差最大为60°± 5°,此时速度抖振较大,降速过程同升速过程一致。在图14b中,非理想换相得到本文算法补偿,36 000 r/min时EMFCP换相间隔差为60°±0.1°;升到额定转速时,EMFCP换相间隔差为60°±0.2°,此时速度抖振消除,降速过程同升速过程一致。可见,本文提出算法在电机变速响应时,仍可有效消除参数不对称引起的非理想换相误差。
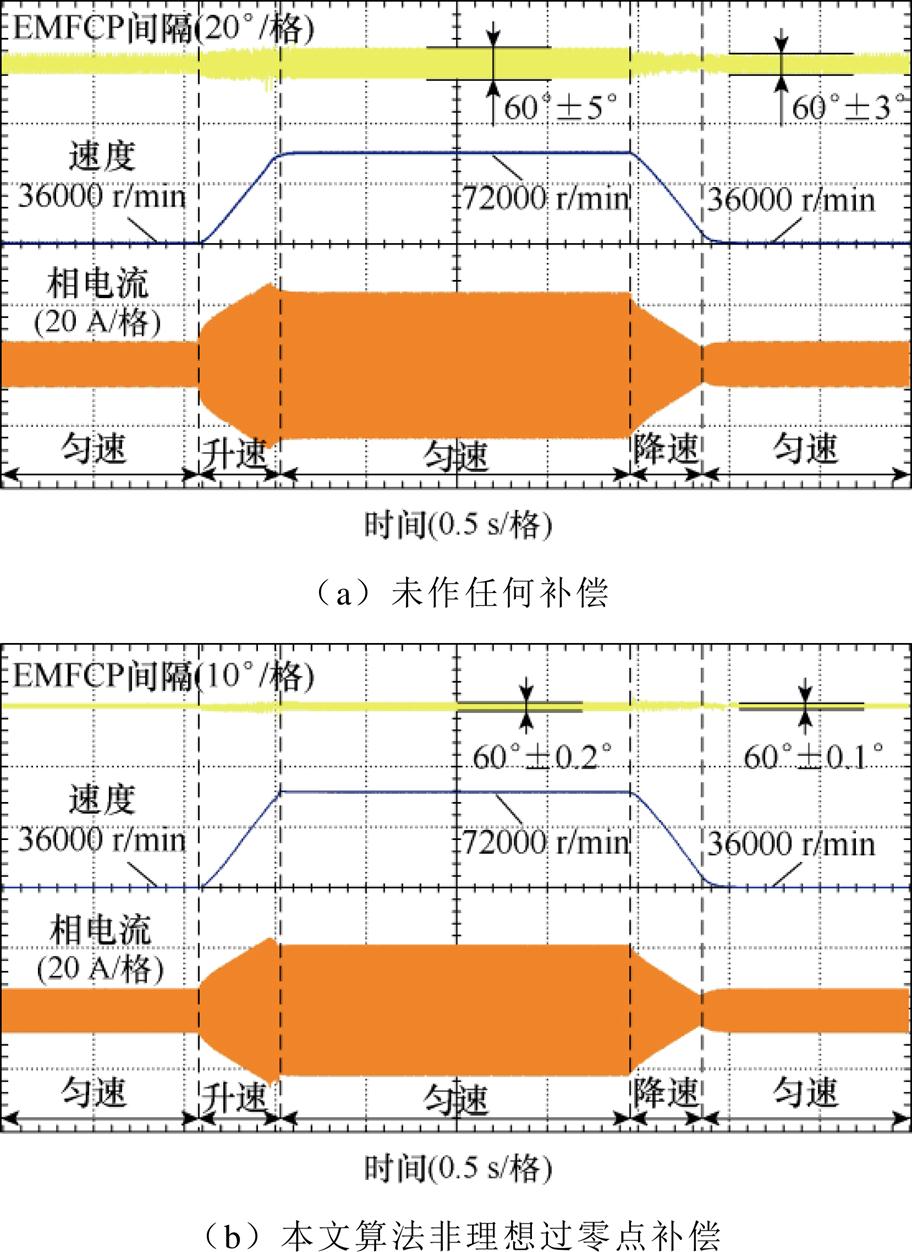
图14 变速过程中的非理想换相有无补偿比较
Fig.14 Comparison of non-ideal commutation with or without compensation in the variable speed process
图15为空压机恒定负载条件下PI作用的电角度偏差和电压偏差收敛的效果,曲线从上至下依次为电角度偏差和电压偏差。电角度偏差为参数不对称引起的超前或滞后的电角度,通过式(19)计算得到。电压偏差为参数不对称引起的电压竖直方向上的偏移,根据电角度偏差,可利用PI调节得到电压偏差。算法未生效时,参数不对称引起的电角度偏差最大为2.02个电角度,此时电压偏差未得到补偿;PI作用后,最大补偿电压为1.28 V并在1.5 s内趋于稳态,电角度偏差约为±0.18个电角度。需要注意的是,换相间隔是两倍的电角度偏差,所以算法未生效时换相间隔极不均匀,在高速情况下容易发生失步的情况。
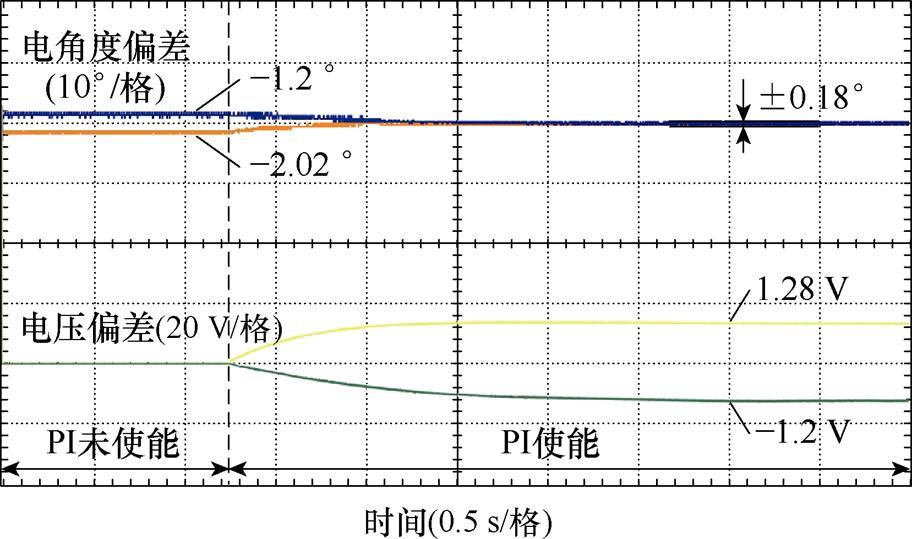
图15 非理想偏差收敛过程
Fig.15 Non-ideal bias convergence process
图16为高速对拖平台在2 000 r/min时的线反电动势还原过程比较,曲线蓝色为参数不对称情况下的线反电动势,橙色为理想线反电动势,绿色为线反电动势预测曲线。其中,缩略图为换相部分的放大曲线,左侧缩略图为线反电动势从负半轴到正半轴过零换向,右侧缩略图为线反电动势从正半轴到负半轴过零换向。可以看到,受电感电压影响的不对称线反电动势并不是规则的图形,并且在接近换相部分的线反电动势噪声较大,容易引起换相误差。在图16a中,未做算法补偿,不对称反电动势相对于理想反电动势在不同的扇区发生了一定的偏移。在缩放图中可以看到,上下两个半周期换相都是滞后相同的时间,电角度偏差约为0.45°。在图16b中,使用本文算法补偿之后,不对称线反电动势逐渐贴合理想线反电动势,电角度偏差缩小到约为0.09°。在图16c中,使用线性回归预测后,提高了换相精度,预测的线反电动势换相点几乎与理想线反电动势贴合,达到稳定、准确换相的目的。
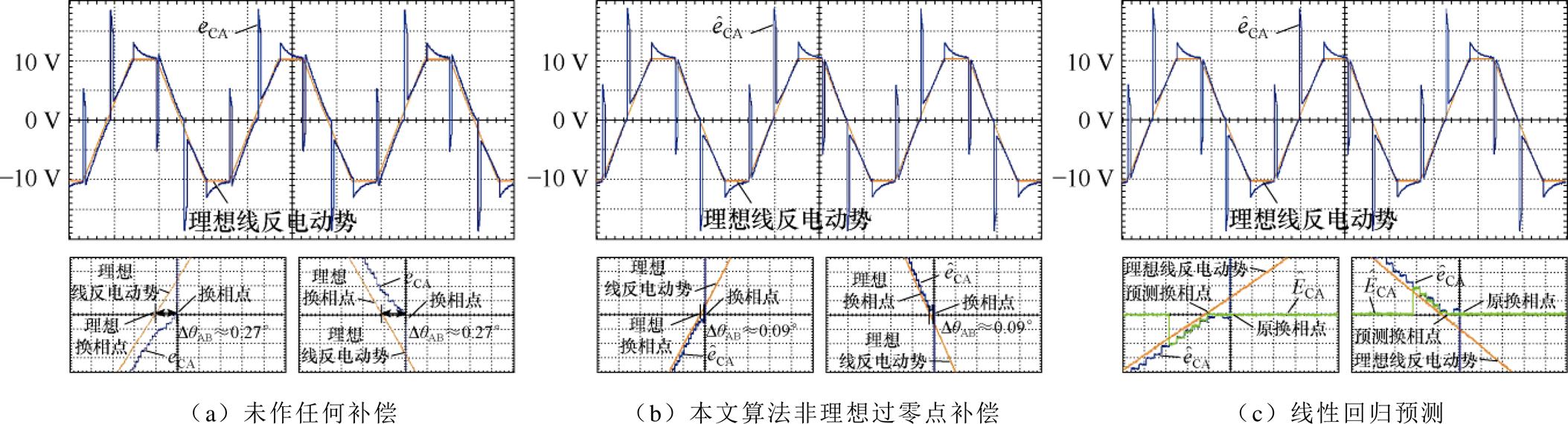
图16 线反电动势还原过程的有无补偿算法比较
Fig.16 Comparison of algorithms with and without compensation for line back EMF reduction process
本文研究了电机参数不对称导致的换相误差和换相点附近电感压降难以估测导致的换相延迟问题,在传统线反电动势检测的基础上提出一种改进方案,不仅解析了非理想电机参数不对称与EMFCP间隔之间的联系,还原线反电动势,还通过预测局部的线反电动势,避免了电感压降和电流噪声对换相的影响。提出的电机高速下的解决方案如下:
1)针对电机参数不对称导致的非理想换相问题,通过本文所提方案还原线反电动势,可以消除电机非理想因素的影响。
2)针对接近换相区域线反电动势的畸变问题,用线性回归方法预测线反电动势,确保准确换相。
3)针对电机高速下的低通滤波延时问题以及采样延时问题,通过设置合理的换相阈值,来消除换相延迟。
参考文献
[1] Zhang Hongjie, Yu Wenfei, Hua Wei. Design and key technology of oil-free centrifugal air compressor for hydrogen fuel cell[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 11-19.
[2] 黄文晖, 闵华松. 基于端电压尖峰的无刷直流电机无位置传感器换相控制策略[J]. 电机与控制学报, 2024, 28(5): 173-182.
Huang Wenhui, Min Huasong. Sensorless control strategy for brushless direct current motor based on terminal voltage spikes[J]. Journal of Electric Machines and Control, 2024, 28(5): 173-182.
[3] 于克训, 陈曦, 谢贤飞, 等. 无刷双馈电机研究综述与展望[J]. 电工技术学报, 2024, 39(2): 397-422.
Yu Kexun, Chen Xi, Xie Xianfei, et al. Overview and prospect of the brushless doubly-fed machine research[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 397-422.
[4] 王菁, 颜建虎, 季国东, 等. 一种基于双位置观测器的永磁同步电机低速无位置传感器控制方法[J]. 电工技术学报, 2023, 38(2): 375-386.
Wang Jing, Yan Jianhu, Ji Guodong, et al. A sensorless control method for permanent magnet synchronous machine based on dual position observers at low speed[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 375-386.
[5] Zhu Z Q, Azar Z, Ombach G. Influence of additional air gaps between stator segments on cogging torque of permanent-magnet machines having modular stators[J]. IEEE Transactions on Magnetics, 2012, 48(6): 2049- 2055.
[6] Xu P L, Zhu Z Q. Carrier signal injection-based sensorless control for permanent-magnet synchronous machine drives considering machine parameter asymmetry[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 2813-2824.
[7] 孙庆国, 卫功民, 刘旭. 自适应换相与转矩补偿的开关磁阻电机转矩脉动抑制[J]. 电机与控制学报, 2022, 26(6): 91-100, 111.
Sun Qingguo, Wei Gongmin, Liu Xu. Torque ripple suppression of switched reluctance motor with adaptive commutation and torque compensation[J]. Journal of Electric Machines and Control, 2012, 26(6): 91-100, 111.
[8] 郭金超, 孙津济, 陈少华. 基于端电压对称的高速磁悬浮无刷直流电机换相延时误差补偿方法[J]. 微电机, 2017, 50(4): 36-42.
Guo Jinchao, Sun Jinji, Chen Shaohua. A novel control method to correct commutation error of BLDC motor without position sensor based on symmetric phase voltage difference[J]. Micromotors, 2017, 50(4): 36-42.
[9] 李珍国, 韩启萌, 贾益丞, 等. 基于回馈升压逆变器的无刷直流电机宽速度范围转矩脉动抑制[J]. 电工技术学报, 2024, 39(6): 1725-1736.
Li Zhenguo, Han Qimeng, Jia Yicheng, et al. Torque ripple suppression of brushless DC motor with wide speed range based on feedback boost inverter[J]. Transactions of the China Electrotechnical Society, 2024, 39(6): 1725-1736.
[10] 余岳, 李诚, 刘建华, 等. 基于脉幅调制的超高速无刷直流电机过零点检测补偿策略[J]. 电工技术学报, 2024,39(15):4806-4819.
Yu Yue, Li Cheng, Liu Jianhua, et al. Proposed compensation strategy for ultra-high speed brushless DC motor based on pulse amplitude modulation zero crossing detection[J]. Transactions of China Elec- trotechnical Society, 2024, 39(15): 4806-4819.
[11] 黄文晖, 闵华松. 基于端电压尖峰的无刷直流电机无位置传感器换相控制策略[J]. 电机与控制学报, 2024, 28(5): 173-182.
Huang Wenhui, Min Huasong. Sensorless control strategy for brushless direct current motor based on terminal voltage spikes[J]. Electric Machines and Control, 2024, 28(5): 173-182.
[12] Yang Lei, Zhu Z Q, Shuang Bo, et al. Adaptive threshold correction strategy for sensorless high- speed brushless DC drives considering zero-crossing- point deviation[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5246-5257.
[13] 申永鹏, 刘迪, 梁伟华, 等. 三相桥式逆变电路电流检测方法综述[J]. 电工技术学报, 2023, 38(2): 465-484.
Shen Yongpeng, Liu Di, Liang Weihua, et al. Review of current detection methods for three-phase bridge inverter circuits[J]. Transactions of China Electro- technical Society, 2023, 38(2): 465-484.
[14] 李昊岩, 许海平, 陈曦. 定子无铁心永磁无刷直流电机驱动拓扑设计方案及对比[J]. 电工技术学报, 2023, 38(24): 6619-6631.
Li Haoyan, Xu Haiping, Chen Xi. Stator permanent magnet brushless DC motor drive without core topology design and comparison[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6619- 6631.
[15] Wang Ning, Li Jiayang. Efficient multi-channel thermal monitoring and temperature prediction based on improved linear regression[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 71: 9500809.
[16] Zhang Hengmin, Qian Feng, Zhang B, et al. Incorpo- rating linear regression problems into an adaptive framework with feasible optimizations[J]. IEEE Transactions on Multimedia, 2023, 25: 4041-4051.
[17] Wei Jiadan, Cai Zhengyou, Zhang Le, et al. The quadrature signals synchronous demodulation method for rotor position estimation of three-stage syn- chronous machine[J]. IEEE Transactions on Power Electronics, 2024, 39(6): 7351-7361.
[18] 李迎杰, 刘旭东. 基于高阶滑模观测器和改进PLL的永磁同步电机无传感器控制[J]. 电气工程学报, 2023, 18(4): 96-105.
Li Yingjie, Liu Xudong. Sensorless control of permanent magnet synchronous motor based on high- order sliding mode observer and improved PLL[J]. Journal of Electrical Engineering, 2023, 18(4): 96- 105.
Non-Ideal Commutation Correction Strategy for Brushless Direct Current Motor Based on Line Back Electromotive Force Detection
Abstract When the brushless DC motor non-inductive control system operates at high speed or with a high current and heavy load, if there is a non-ideal parameter error or if it is disturbed by an extreme environment, voltage deviation may occur, leading to serious commutation error or even out-of-step. Problems such as three-phase winding wiring, rotor eccentricity, or winding faults can cause parameter asymmetry in motors, especially for high-speed brushless DC motors with low resistance and low inductance, which are very sensitive to parameters during operation.
This study proposes a correction strategy for non-ideal commutation based on improved line-back electromotive force detection. First, by analyzing the impact of non-ideal motor parameter asymmetry on line voltage, the electrical angle offset in the horizontal direction can be used as a reference for the voltage offset in the vertical direction. Secondly, the electrical angle deviation is exposed in the commutation interval, but the commutation is uncertain, and the commutation interval cannot be directly used as an indicator. Therefore, the line back electromotive force intersection interval is used to solve the electrical angle offset of each phase, and each electrical angle deviation can be solved six times within one electrical angle cycle. Finally, the voltage value output by PI restores the line-back electromotive force so that the electrical angle deviation converges to zero. At the same time, the scheme considers the impact of inductance voltage drop and current noise on the line back electromotive force. The motor line back electromotive force is not a standard ladder. Thus, a data-fitting method is proposed. The area with a small local current change rate is selected for linear fitting. The linear regression equation predicts the line-back electromotive force near the commutation point to achieve accurate commutation.
Experimental results show that this method can reduce the position error to ±0.2 electrical angles at different rotational speeds, effectively smooth the torque fluctuations caused by parameter asymmetry, and reduce the peak-to-peak current by about 10%. This method avoids the commutation delay caused by the inherent inductance voltage of the traditional line-back electromotive force and the commutation error caused by parameter asymmetry. Its stator winding impedance changes have less impact on the identification accuracy of the rotor position. Moreover, this solution significantly improves the motor commutation accuracy and increases the upper limit of operating speed, broadening the application scenarios of speed sensorless ultra-high-speed brushless DC motors.
Keywords:Line back electromotive force (LEMF), parameter asymmetry, sensorless control, linear regression equation, brushless DC motor
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.241167
湖南省自然科学基金资助项目(2022JJ50082)。
收稿日期 2024-07-04
改稿日期 2024-07-29
余 岳 男,1978年生,博士,副教授,研究方向为电力电子及电力传动。
E-mail: yuyue@hut.edu.cn
李 诚 男,1997年生,硕士研究生,研究方向为电机系统及其控制。
E-mail: faith36521@outlook.com(通信作者)
(编辑 崔文静)