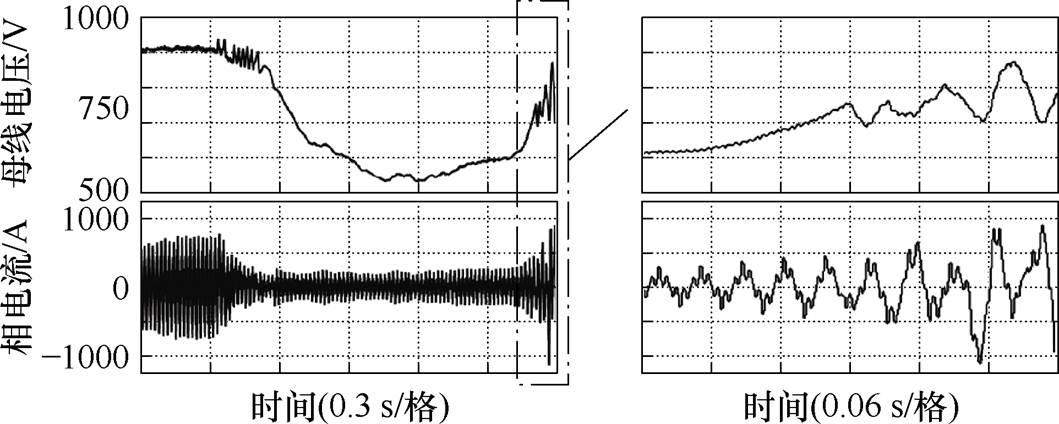
图1 传统矢量控制在110 t大型矿用自卸卡车测试中出现的不稳定现象
Fig.1 Instability occurred in tests of a 110 t large mining dump truck with conventional FOC
摘要 大型电动轮矿山自卸车在进行快速操作时,母线电压会产生剧烈波动,传统的矢量控制技术由于其转子磁链的调节速度较慢,可能导致控制系统失稳。该文针对上述问题,提出了一种低载波比工况下的高动态性能无差拍控制技术。首先,推导了感应电机的特征根离散化模型。然后,在离散域下设计了无差拍控制系统,通过状态变量的线性变换实现了系统的完全解耦,同时推导了状态变量间的额外约束条件,实现了同时考虑转子磁链幅值和定子电流矢量的三自由度无差拍控制。所提出的变步长无差拍控制系统具有动态响应速度快、电流谐波含量低的优点。最后,在仿真平台和大功率实验平台中对所提出的理论进行了验证。
关键词:无差拍控制 感应电机 低载波比 离散模型
感应电机凭借结构简单、成本低、鲁棒性强的特点,在大功率牵引系统中有着广泛应用。随着工业水平的不断进步,行业对大功率牵引传动系统性能的要求也在不断提高。
感应牵引电机的控制策略主要有矢量控制(Field Oriented Control, FOC)和直接转矩控制(Direct Torque Control, DTC)等。在大型电动轮矿车的控制系统中,电压等级高、输出电流大,受限于开关器件的开关损耗,其逆变器的开关频率通常只能达到几百赫兹,这就导致系统在中高速运行区间会进入低载波比工况。在低载波比工况下,FOC控制器控制延时增大、dq电流耦合加剧,导致控制带宽下降;DTC比FOC具有更简单的控制结构和更快的响应速度,但DTC缺少调制模块且开关频率不固定,控制器只考虑了控制误差的方向而不考虑其大小,控制精度严重依赖高控制频率,在低开关频率下存在谐波大和转矩波动大的缺点[1-2]。
上述两种控制策略广泛应用于轨道交通领域。对于大型电动轮矿山自卸车而言,受限于大型电池技术的发展,其直流母线多采用柴油发电机供电的模式。尽管配备了母线电容,但柴油发电机组的运行工况仍然会因为母线负载端的变化而变化,在面对复杂路段时,车辆油门踏板快速操作就会引起母线电压的快速跌落,导致电机驱动系统需要在短时间内进入深度弱磁工况。传统矢量控制在110 t大型矿用自卸卡车测试中出现的不稳定现象如图1所示,在母线电压剧烈变化时,传统控制器由于转子磁链的动态调节能力较差,控制系统失稳,无法满足可靠性要求。此外,转矩的快速调节能力能增强矿山自卸车在复杂路况的适应能力。因此,同时实现转矩和转子磁链的快速调节是控制系统稳定运行的迫切需求。

图1 传统矢量控制在110 t大型矿用自卸卡车测试中出现的不稳定现象
Fig.1 Instability occurred in tests of a 110 t large mining dump truck with conventional FOC
预测控制具有动态性能高、稳定性能好、控制目标多等优点,是一种非常有潜力的控制策略。常见的预测控制主要包括基于滞环的预测控制[3]、轨迹控制[4]、无差拍控制(Deadbeat Control, DBC)[5-6]和基于逆变器控制集的模型预测控制[7-10]。不同的预测控制具有相应的典型特征,如基于滞环或轨迹的控制目标、无差拍动态响应、代价函数等。
预测控制在低载波比工况下的应用面临较大的挑战。传统基于滞环的预测控制原理简单,但滞环的大小依赖开关频率的高低,低载波比工况下控制精度降低、转矩纹波增大,无法满足高性能应用需求[11-12]。经典的有限控制集模型预测控制不具备调制单元,在低开关频率下电流谐波会迅速增大。对此,国内外学者对低载波比下的预测控制进行了研究。大功率电机的轨迹控制最早由德国J. Holtz教授和B. Beyer博士在1993年提出[13]。该控制策略基于同步最优脉冲宽度调制(Synchronous Optimal Pules Width Modualtion, SOPWM)的脉冲模式进行设计,因此也被称为模型预测脉冲模式控制(Model Predictive Pulse Pattern Control, MP3C)。有学者分析了SOPWM和传统控制算法结合时转矩动态响应提升难的问题,指出MP3C能同时结合DTC的高动态响应和SOPWM的低谐波性能,是大功率系统控制策略的重要发展方向[14-15]。文献[16]采用无模型预测控制策略,有效降低了电机模型参数变化对预测控制的影响。在数字实现方面,有学者提出使用现场可编程逻辑门阵列进行电流过采样并添加扰动观测器可以减少参数变化对控制器性能的影 响[17]。在参考坐标系方面,有学者提出在各类旋转坐标系进行控制器设计,系统具有更好的谐波性能和参数鲁棒性[18],但推导转矩和定子磁链变化量与dq轴电压分量之间的关系较为困难[19]。
综上所述,虽然已有学者针对预测控制开展了相关工作,但同时控制转子磁链和定子dq轴电流的无差拍控制技术还有待进一步研究。在大型电动轮矿山自卸车的应用场景下,为了实现转矩和磁链的同时快速调节,需要设计一种三自由度的无差拍控制策略,以满足系统的运行需要。
本文提出了一种基于高精度离散模型的无差拍预测控制技术,该技术基于特征根离散模型设计,保证了低载波比工况下的高离散化精度。同时针对变流器极限边界区域设计了指令值计算方法和指令约束方程,同时实现了定子dq轴电流和转子磁链三个自由度的无差拍控制。对调制和控制器进行整体设计,在实现转子磁链和转矩无差拍动态响应的同时具有低电流谐波稳态性能。
本文首先推导了感应电机的高精度特征根离散化模型;其次,在高精度离散模型的基础上,设计了同时考虑转矩和转子磁链的无差拍控制器,对状态方程进行了状态解耦、坐标变换,并推导了dq轴电流和转子磁链间的额外约束性条件;然后,通过仿真和大功率实验对所提出的理论进行了验证;最后,对本文主要工作进行了总结。
为了使控制系统在低载波比工况下具有良好的调节性能,本文后续的设计推导将基于感应电机特征根离散化模型开展[20]。假设感应电机定子绕组三相对称、磁路无饱和、忽略涡流损耗和磁滞损耗,选择定子电流和转子磁链作为状态变量,则连续域的感应电机数学模型为
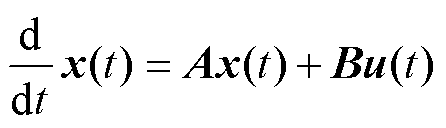 (1)
(1)
其中
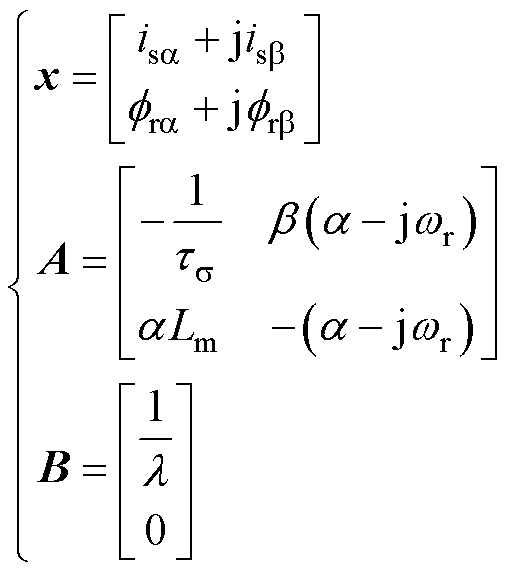 (2)
(2)
其中
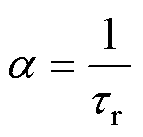
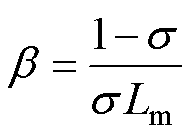
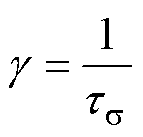
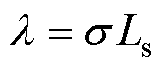
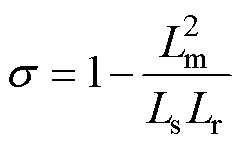
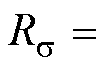
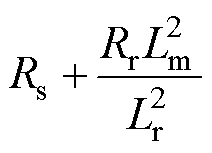
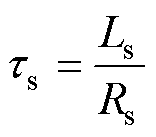
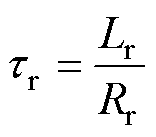
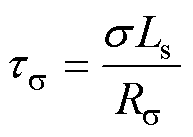
式中,x为状态向量;u(t)为电压输出变量;A为状态矩阵;wr为转子的电角速度;B为输入矩阵;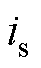 、
、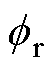 分别为定子电流、转子磁链;
分别为定子电流、转子磁链;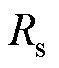 、
、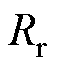 分别为定子电阻、转子电阻;
分别为定子电阻、转子电阻;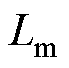 、
、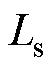 、
、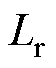 分别为励磁电感、定子电感、转子电感;
分别为励磁电感、定子电感、转子电感;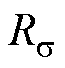 为定子等效电阻;
为定子等效电阻;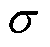 为漏磁系数;
为漏磁系数;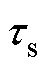 、
、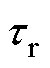 分别为定、转子时间常数;
分别为定、转子时间常数;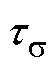 为等效定子瞬态时间常数;
为等效定子瞬态时间常数;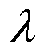 为定子瞬态电感。
为定子瞬态电感。
为方便起见,本文将电流、磁链等变量表示为复数向量。虚数算子用j表示。
根据式(3)中的微分方程,电机状态变量在连续时域的精确解为
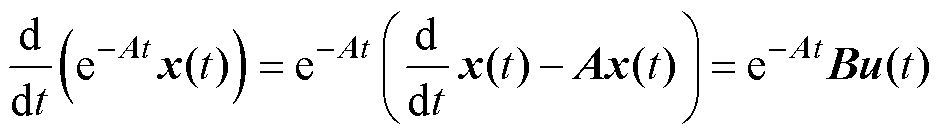 (3)
(3)
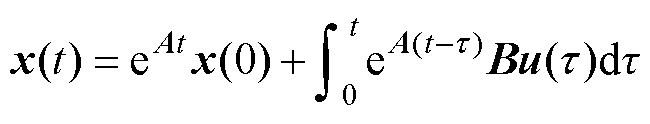 (4)
(4)
假设系统的采样步长为k、k+1两个相邻采样时刻之间的时间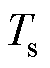 ,则状态变量在离散时域的精确解为
,则状态变量在离散时域的精确解为
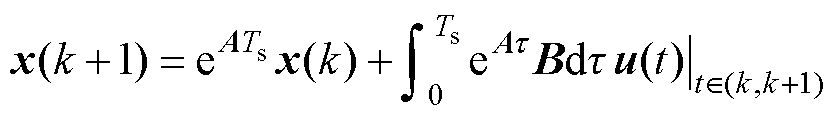 (5)
(5)
将离散模型中的状态矩阵和输入矩阵分别记为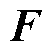 和
和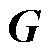 ,则有
,则有
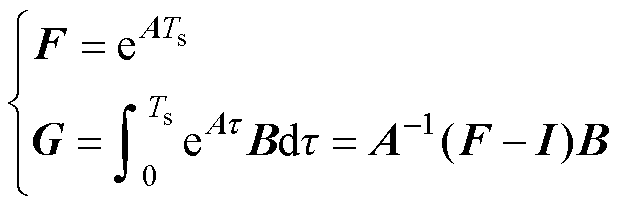 (6)
(6)
式中,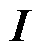 为单位矩阵。可以看出,精确求解状态矩阵系数
为单位矩阵。可以看出,精确求解状态矩阵系数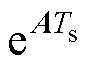 是获得高精度离散模型的关键。然而,根据其麦克劳林(Maclaurin)级数可知,
是获得高精度离散模型的关键。然而,根据其麦克劳林(Maclaurin)级数可知,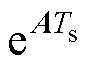 很难直接用式(7)所示的定义进行计算。传统的一阶欧拉离散化和二阶双线性离散化相当于式(7)的一阶或二阶近似,忽略了其高阶次,因此在低载波比下将出现过大的离散误差。事实证明,降阶的离散模型并不精确,尤其是在低载波比工况下。所以,需要推导一个精确的离散模型,满足无差拍控制器的设计需求。
很难直接用式(7)所示的定义进行计算。传统的一阶欧拉离散化和二阶双线性离散化相当于式(7)的一阶或二阶近似,忽略了其高阶次,因此在低载波比下将出现过大的离散误差。事实证明,降阶的离散模型并不精确,尤其是在低载波比工况下。所以,需要推导一个精确的离散模型,满足无差拍控制器的设计需求。
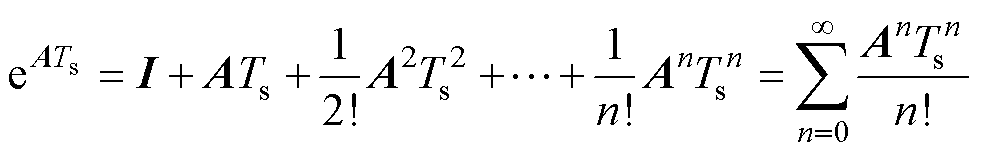 (7)
(7)
首先采用基于特征值的方法求解状态矩阵系数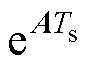 。根据矩阵的特征方程式(8),计算出特征值
。根据矩阵的特征方程式(8),计算出特征值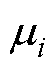 (i=1, 2),相应的特征值矩阵如式(9)所示,是一个对角矩阵。
(i=1, 2),相应的特征值矩阵如式(9)所示,是一个对角矩阵。
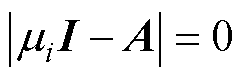 (8)
(8)
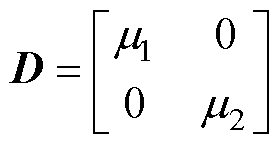 (9)
(9)
则状态矩阵A可以通过传递矩阵P变换至特征值对角矩阵D,如式(10)所示。因此,由矩阵的线性变换理论可以计算出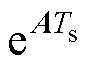 ,如式(11)所示。
,如式(11)所示。
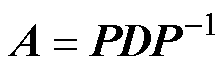 (10)
(10)
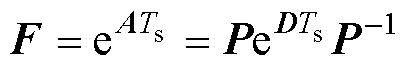 (11)
(11)
其中
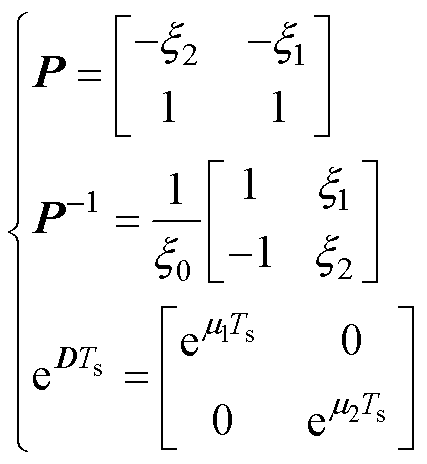 (12)
(12)
式(12)中的中间变量定义为
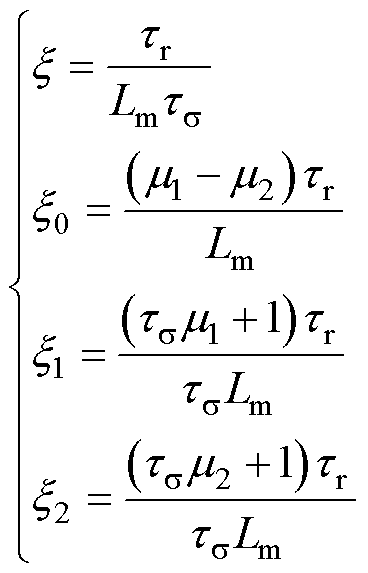 (13)
(13)
结合上述推导,基于特征根离散化的感应电机精确离散模型为
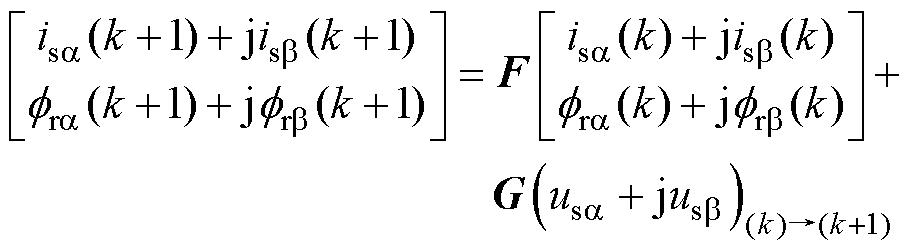 (14)
(14)
其中,状态矩阵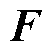 、输入矩阵
、输入矩阵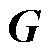 和中间变量
和中间变量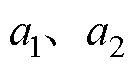 的精确表达式为
的精确表达式为
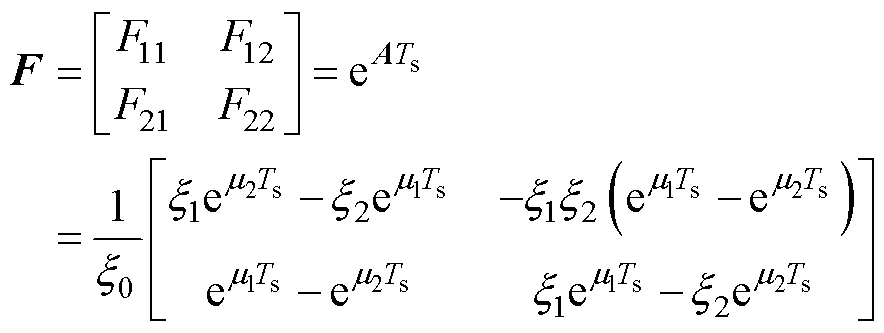 (15)
(15)
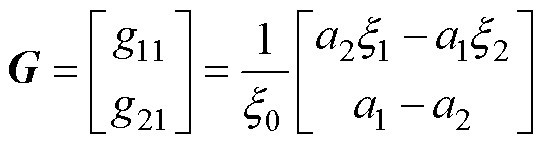 (16)
(16)
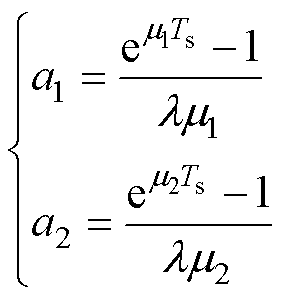 (17)
(17)
非对称采样系统中无差拍控制器的时序图如图2所示。与对称采样模式相比,非对称采样模式的采样频率和控制频率在相同开关频率下可提高一倍,能有效降低系统在低开关频率下的离散化误差,并将无差拍控制系统的动态响应时间缩短50%。因此,本文采用了非对称采样模式。
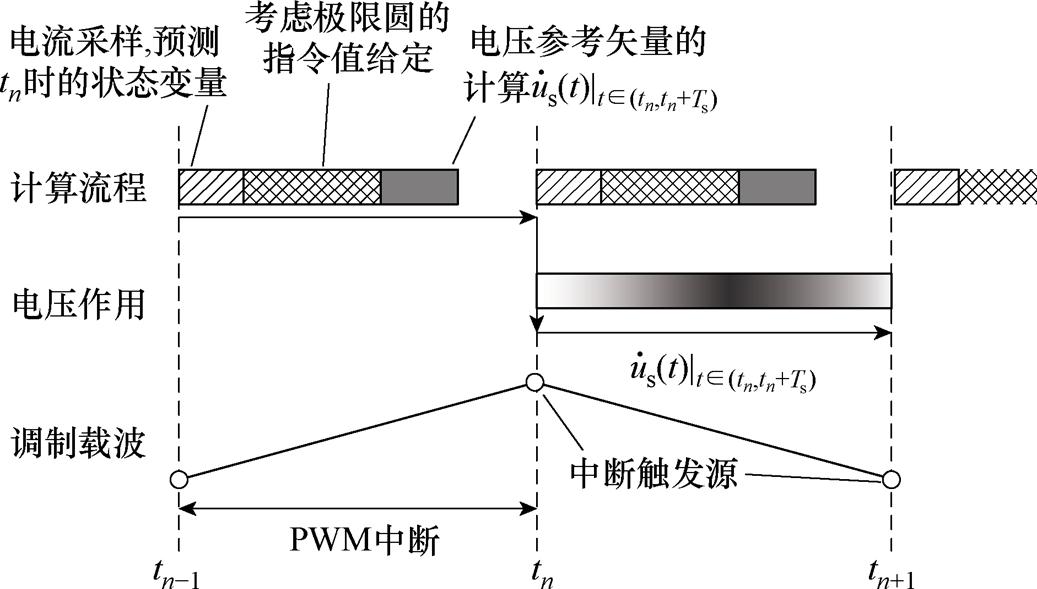
图2 非对称采样系统中无差拍控制器的时序图
Fig.2 Timing sequence chart of deadbeat control with asymmetrical sampling
无差拍控制是根据感应电机的离散数学模型设计的。考虑到实际单片机的时序逻辑是分步进行的,在单个采样周期内,k+1时刻的控制流可概括为以下三个步骤:
(1)在k-1时刻对母线电压和电机相电流采样。
(2)利用已知的电压指令值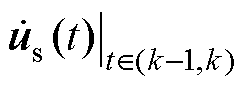 预测k时刻的状态变量。
预测k时刻的状态变量。
(3)计算状态变量由k时的初始值变化至k+1时的指令值需要作用的电压矢量指令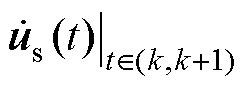 。
。
可以看出,给定的指令值是针对k+1时刻的,而系统的实际状态变量也将在k+1时刻跟上指令值,因此该控制器具有无差拍的极限动态跟踪特性。
无差拍控制器设计的基本思想是将式(14)中k+1时刻的状态变量设为指令值,求解状态方程,并根据k时刻的状态初始值获得电压指令值。然而,依照式(14)设计无差拍控制器仍然存在以下问题:
(1)由于输入矩阵G不是方阵,不存在逆矩阵,故状态方程不可反转,因此很难直接求取电压指令。
(2)式(14)处于静止ab坐标系中,所有状态变量都是交流量,进一步加大了指令值的计算难度。
为了解决上述问题,本小节将分别介绍状态解耦和坐标变换的推导过程,最终得到电压指令的计算表达式。
根据第1节的推导,感应电机的特征根离散化模型的系统矩阵F和输入矩阵G如式(6)所示。将式(6)代入精确离散模型式(14),左乘非奇异矩阵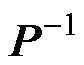 ,整理后得到解耦后的状态方程,如式(18)所示。
,整理后得到解耦后的状态方程,如式(18)所示。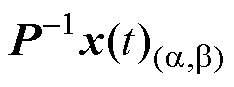 是原状态变量线性变换后得到的,由定子电流is和转子磁链
是原状态变量线性变换后得到的,由定子电流is和转子磁链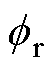 组成,将其作为线性变换后的新状态变量
组成,将其作为线性变换后的新状态变量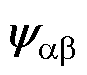 ,其表达式如式(19)所示。
,其表达式如式(19)所示。
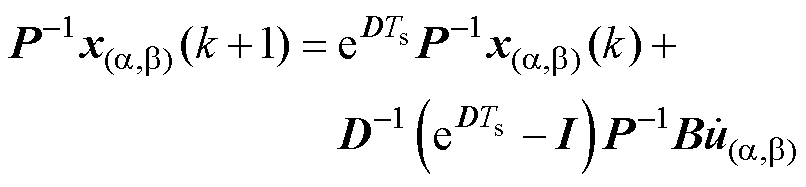 (18)
(18)
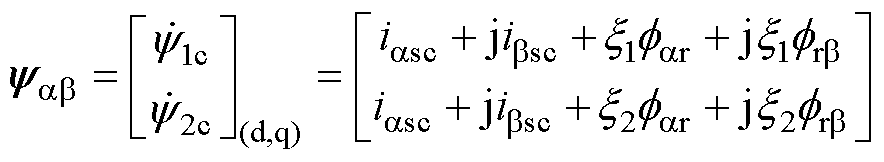 (19)
(19)
式中,we为同步角频率;上标“.”代表该物理量是一个复矢量。
以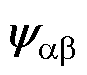 为状态变量建立状态方程如式(20)所示,可知状态矩阵
为状态变量建立状态方程如式(20)所示,可知状态矩阵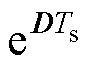 是一个对角矩阵,这表明离散方程是完全状态解耦的。
是一个对角矩阵,这表明离散方程是完全状态解耦的。
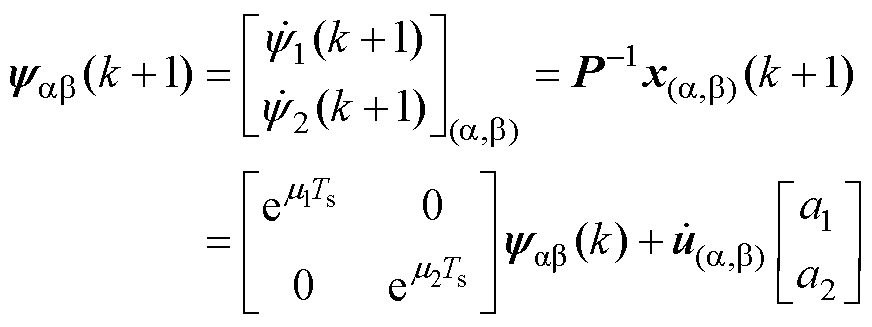 (20)
(20)
为了基于转子磁场定向来设计控制器,需要将离散模型从静止ab坐标系转换为转子磁场dq坐标系。根据完全解耦的状态方程,坐标变换可以用复数域中的旋转因子来表示,有
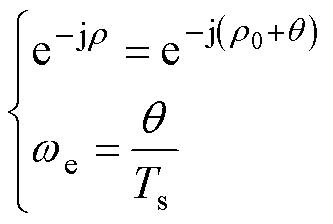 (21)
(21)
式中, 为
为 时转子磁链与静态参考a轴之间的位置角;
时转子磁链与静态参考a轴之间的位置角;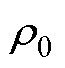 为
为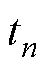 时转子磁链的角度,如图3所示;
时转子磁链的角度,如图3所示;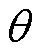 为电压矢量在一段时间Ts内旋转的电角度。
为电压矢量在一段时间Ts内旋转的电角度。
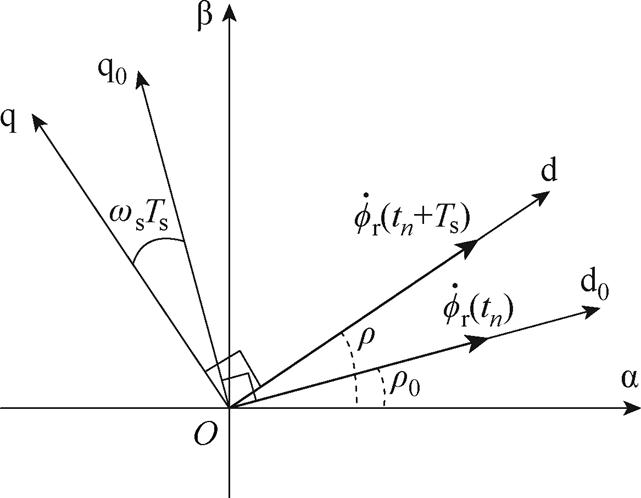
图3 特征根离散化模型从静止坐标系变换到转子磁场定向的离散旋转坐标系的示意图
Fig.3 Coordinate transformation of eigen-based discrete model from stationary frame to discrete coordinate with rotor flux oriented
对于上述变换过程,有以下两点值得注意:
(1)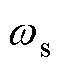 是一个采样周期内转子磁链旋转的平均角速度,在稳定状态下才等于电角频率
是一个采样周期内转子磁链旋转的平均角速度,在稳定状态下才等于电角频率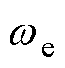 。
。
(2)图3中的坐标系为离散坐标系。对于感应电机而言,转子磁场的变化受该采样周期内电压的影响,在低载波比工况下影响更为严重。
将旋转因子式(21)代入状态方程式(20)即可得到转子磁场定向的状态方程,如式(22)所示。
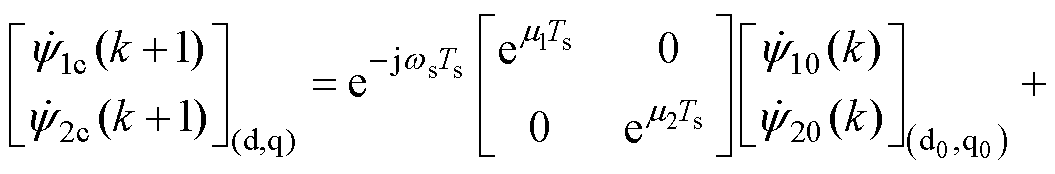
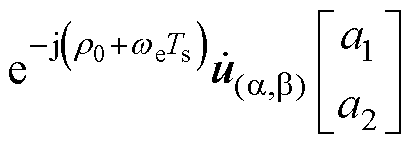 (22)
(22)
将式(22)按行展开并消去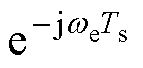 项,可以求解出电压指令的表达式为
项,可以求解出电压指令的表达式为
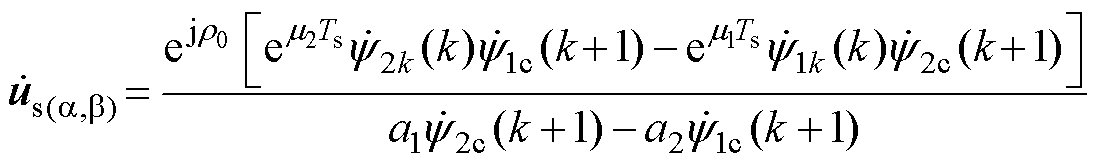 (23)
(23)
综上所述,无差拍控制器的控制结构如图4所示。在k-1时刻中断触发后,通过给定转矩、转子磁链幅值指令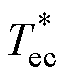 、
、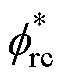 ,计算
,计算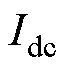 、
、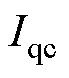 、
、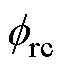 ,获得k+1时刻dq坐标系下的状态变量指令值
,获得k+1时刻dq坐标系下的状态变量指令值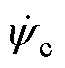 。此外,采样相电流、母线电压和转子速度,预测k时刻的定子电流和转子磁链,计算k时刻dkqk坐标系下的状态变量初始值
。此外,采样相电流、母线电压和转子速度,预测k时刻的定子电流和转子磁链,计算k时刻dkqk坐标系下的状态变量初始值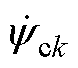 。最后,通过状态变量的指令值和初始值
。最后,通过状态变量的指令值和初始值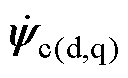 、
、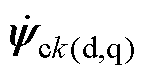 ,结合预测的k时刻的转子磁链角度
,结合预测的k时刻的转子磁链角度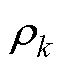 ,计算k~k+1时刻作用的电压
,计算k~k+1时刻作用的电压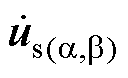 。
。
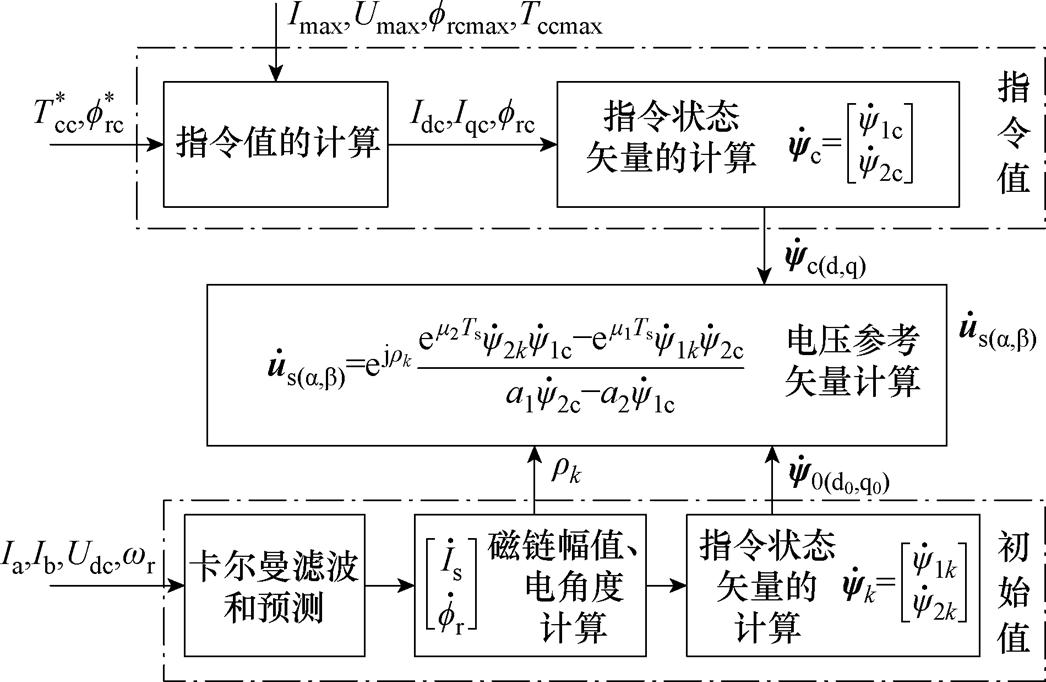
图4 无差拍控制系统的原理框图
Fig.4 The schematic of deadbeat control system
在低载波比工况下,采样频率仅为电频率的数倍,电机定子电流和转子磁链在一个采样周期内的变化较大。当k-1时刻的PWM中断触发时,必须提前对k时刻的状态变量进行预测,以补偿一个采样周期的数字延时。卡尔曼滤波器能有效结合多重信号来源,实现最佳状态估计,在工程上具有大量的应用。下面对其实现方法进行简要介绍。
已知k-1时刻的起始状态变量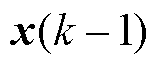 和k-1~k时刻即将作用的电压矢量,基于特征根离散电机模型式(14),通过式(24)即可获得k时刻的状态变量预测值。求解过程如图5所示。
和k-1~k时刻即将作用的电压矢量,基于特征根离散电机模型式(14),通过式(24)即可获得k时刻的状态变量预测值。求解过程如图5所示。
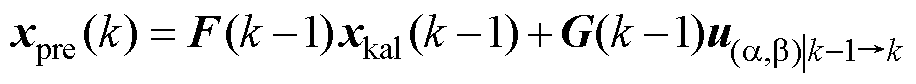 (24)
(24)
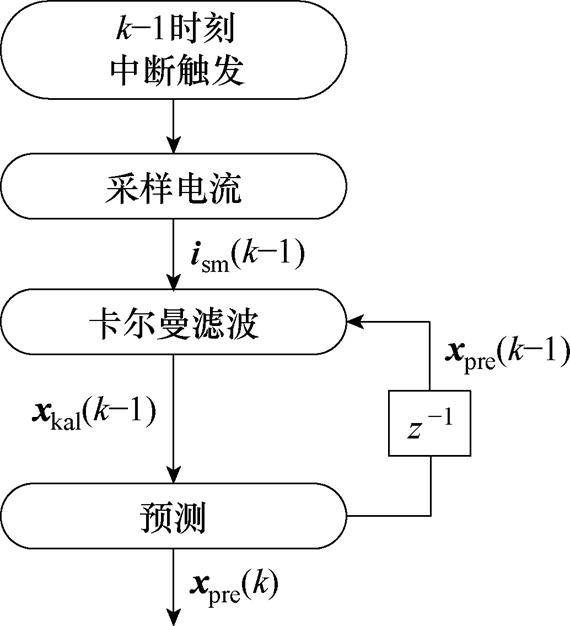
图5 卡尔曼滤波预测状态变量的实现流程
Fig.5 The process of state variables prediction by Kalman filter
k-1时刻的起始状态变量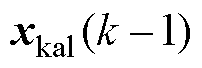 由卡尔曼滤波器获得,其表达式为
由卡尔曼滤波器获得,其表达式为
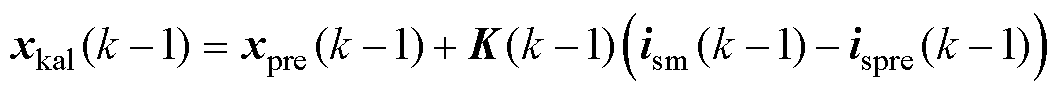 (25)
(25)
式中,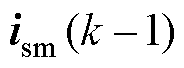 和
和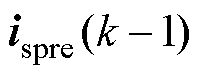 分别为定子电流的采样值和预测值;
分别为定子电流的采样值和预测值;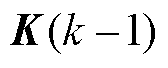 为卡尔曼滤波系数矩阵,其反映了对预测和测量变量的置信大小,当
为卡尔曼滤波系数矩阵,其反映了对预测和测量变量的置信大小,当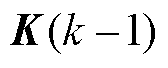 越小时,滤波结果更相信预测值,反之则观测值占比更大,其计算公式为
越小时,滤波结果更相信预测值,反之则观测值占比更大,其计算公式为
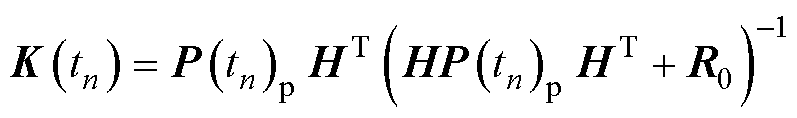 (26)
(26)
其中
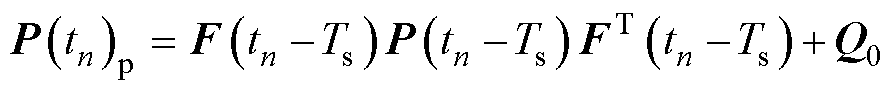 (27)
(27)
式中,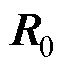 为测量扰动协方差矩阵,反映了采样噪声的统计特性;
为测量扰动协方差矩阵,反映了采样噪声的统计特性; 为输出矩阵,H=
为输出矩阵,H=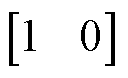 ;
;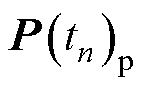 为预测误差的协方差矩阵;
为预测误差的协方差矩阵;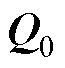 为状态预测扰动协方差矩阵,表示的是模型的不确定性。对于
为状态预测扰动协方差矩阵,表示的是模型的不确定性。对于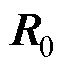 与
与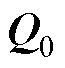 两个协方差矩阵,可以根据理论标定加上经验调试两步来确定其具体大小。
两个协方差矩阵,可以根据理论标定加上经验调试两步来确定其具体大小。
求出k-1时刻的最优估计状态变量值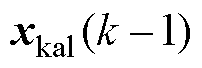 后,通过式(24)即可求得k时刻的状态变量预测值
后,通过式(24)即可求得k时刻的状态变量预测值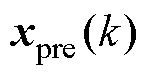 。该预测状态变量可用于2.1节中求解控制器的电压参考矢量。
。该预测状态变量可用于2.1节中求解控制器的电压参考矢量。
式(23)表示使状态变量变换至下一周期所需要的电压参考矢量,然而,该表达式的各个变量之间并不完全独立。输入电压矢量只有两个控制自由度,而控制命令值包含定子电流的dq轴分量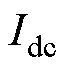 、
、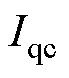 和转子磁链幅值
和转子磁链幅值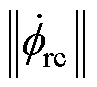 。仅具有两个控制自由度的电压矢量无法独立控制具有三个自由度的状态变量,必须找到控制变量间的额外约束条件,以实现对定子电流和转子磁链同时进行无差拍控制。
。仅具有两个控制自由度的电压矢量无法独立控制具有三个自由度的状态变量,必须找到控制变量间的额外约束条件,以实现对定子电流和转子磁链同时进行无差拍控制。
将状态方程式(22)的两行展开,去掉输入电压指令值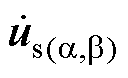 ,可以得到约束方程为
,可以得到约束方程为
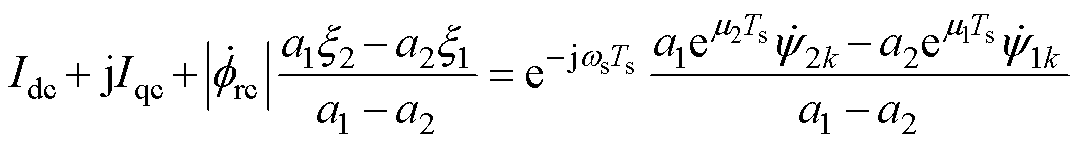 (28)
(28)
式(28)给出了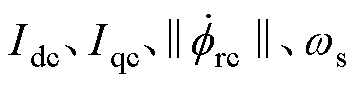 之间的约束关系,这是一个复数域方程,包含实部和虚部。将等号右侧的分式部分定义为一个幅值为
之间的约束关系,这是一个复数域方程,包含实部和虚部。将等号右侧的分式部分定义为一个幅值为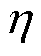 、相位为
、相位为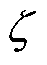 的旋转变量,如式(29)所示。再定义中间变量
的旋转变量,如式(29)所示。再定义中间变量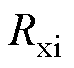 和
和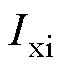 如式(30)所示。
如式(30)所示。
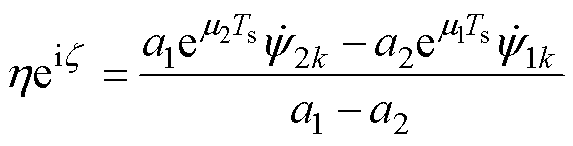 (29)
(29)
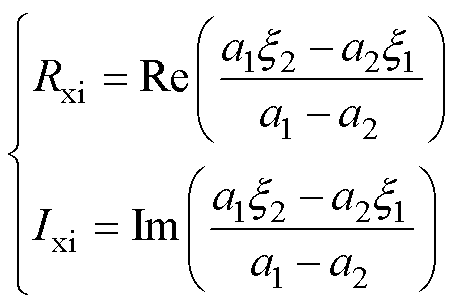 (30)
(30)
则式(28)中的限制条件可以根据实部方程或虚部方程简化为
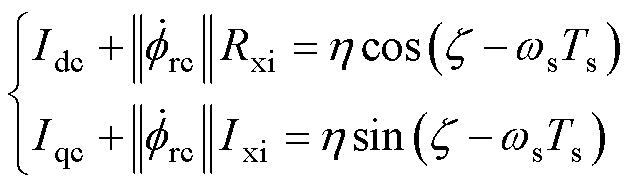 (31)
(31)
消去式(31)中的三角函数,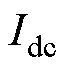 、
、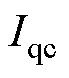 、
、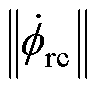 的指令约束条件为
的指令约束条件为
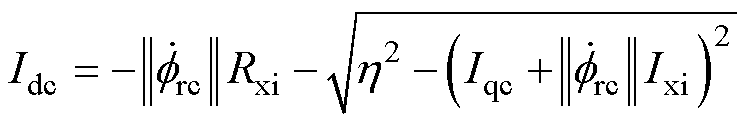 (32)
(32)
综上所述,为同时实现定子电流和转子磁链的无差拍响应,dq轴电流和转子磁链幅值的指令值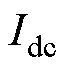 、
、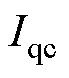 、
、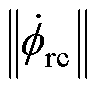 需满足式(32)的约束。
需满足式(32)的约束。
综合上述分析,同时考虑dq轴电流和转子磁链的无差拍控制系统框图如图6所示。调制策略采用连续载波比同步空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)[21]。控制系统的采样步长由调制模块统一调整,以实现输出电压矢量相位与参考电压矢量的同步。在PWM中断触发后,对电流进行同步采样以提取电流基波分量,再通过卡尔曼滤波器进行状态变量的预测。
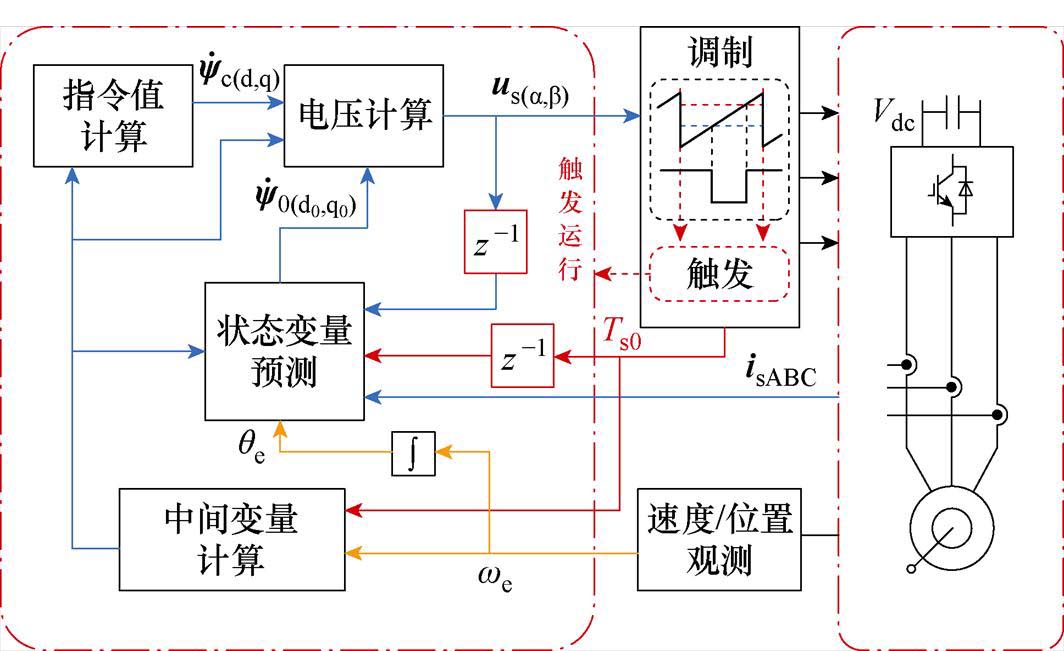
图6 无差拍控制系统框图
Fig.6 Block diagram of the deadbeat control
值得注意的是,由于预测单元和电压指令值计算单元分别在两个相邻的采样周期内执行,在分频数切换过程中两个相邻采样步长之间的差值较大,因此状态预测单元的时间需要滞后一个步长,如图6中的延迟模块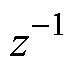 所示。
所示。
通过仿真分析和大功率平台实验,对本文提出的变步长无差拍控制系统进行了性能验证。逆变器的最高开关频率为400 Hz。测试电机的参数见表1。
表1 200 kW感应电机的相关参数
Tab.1 Machine parameters of 200 kW induction machine
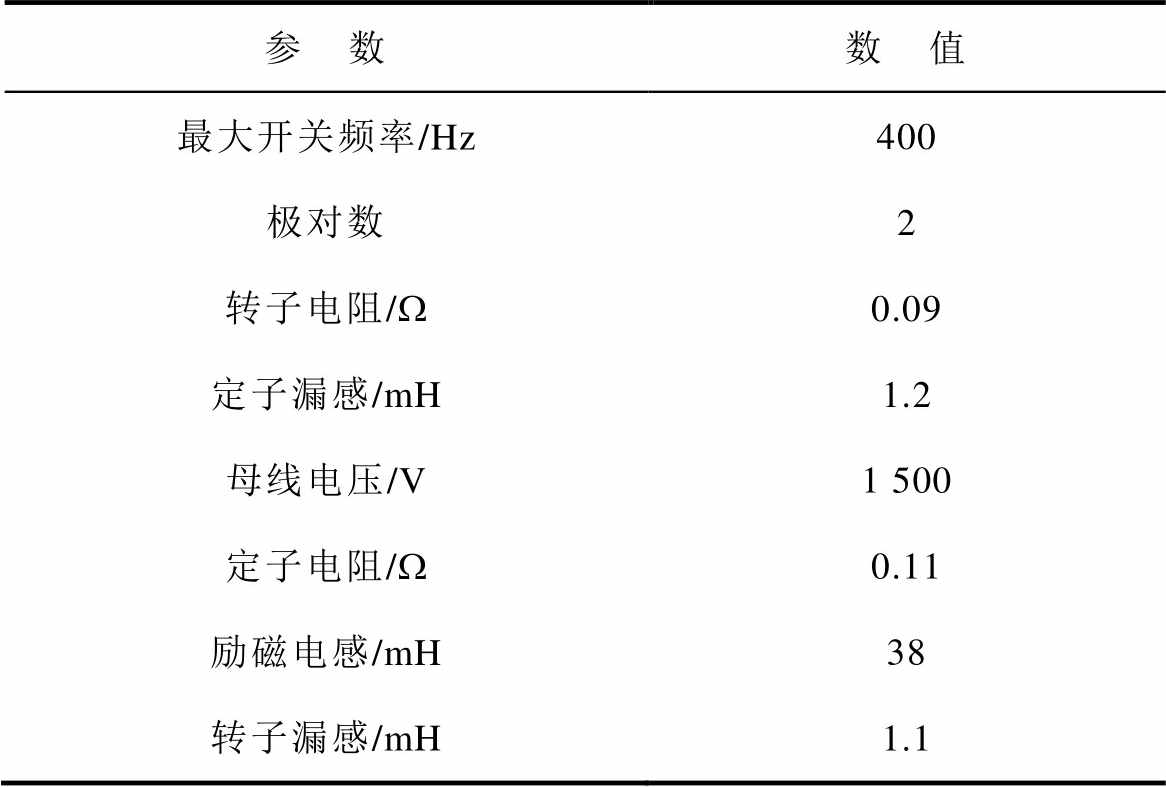
参 数数 值 最大开关频率/Hz400 极对数2 转子电阻/W0.09 定子漏感/mH1.2 母线电压/V1 500 定子电阻/W0.11 励磁电感/mH38 转子漏感/mH1.1
在Matlab/Simulink平台上对本文提出的系统进行仿真分析,与目前较为成熟的复矢量控制器进行对比,以凸显本文提出方案的优势。
图7的仿真结果显示了变步长无差拍控制系统转矩动态响应对比情况。图中,上标“*”表示指令值,无上标“*”表示真实值。仿真实验中,保持电机的转子机械角频率为80 rad/s,磁链指令为0.8 Wb,初始转矩指令为100 N·m,在0.5 s时对系统施加一个100~200 N·m的阶跃转矩指令。从结果中可以看出,本文提出的无差拍控制系统的转矩动态时间仅为1.1 ms,而传统复矢量控制器的转矩动态响应时间为23 ms,说明本文提出的无差拍控制系统具有较好的动态响应能力。
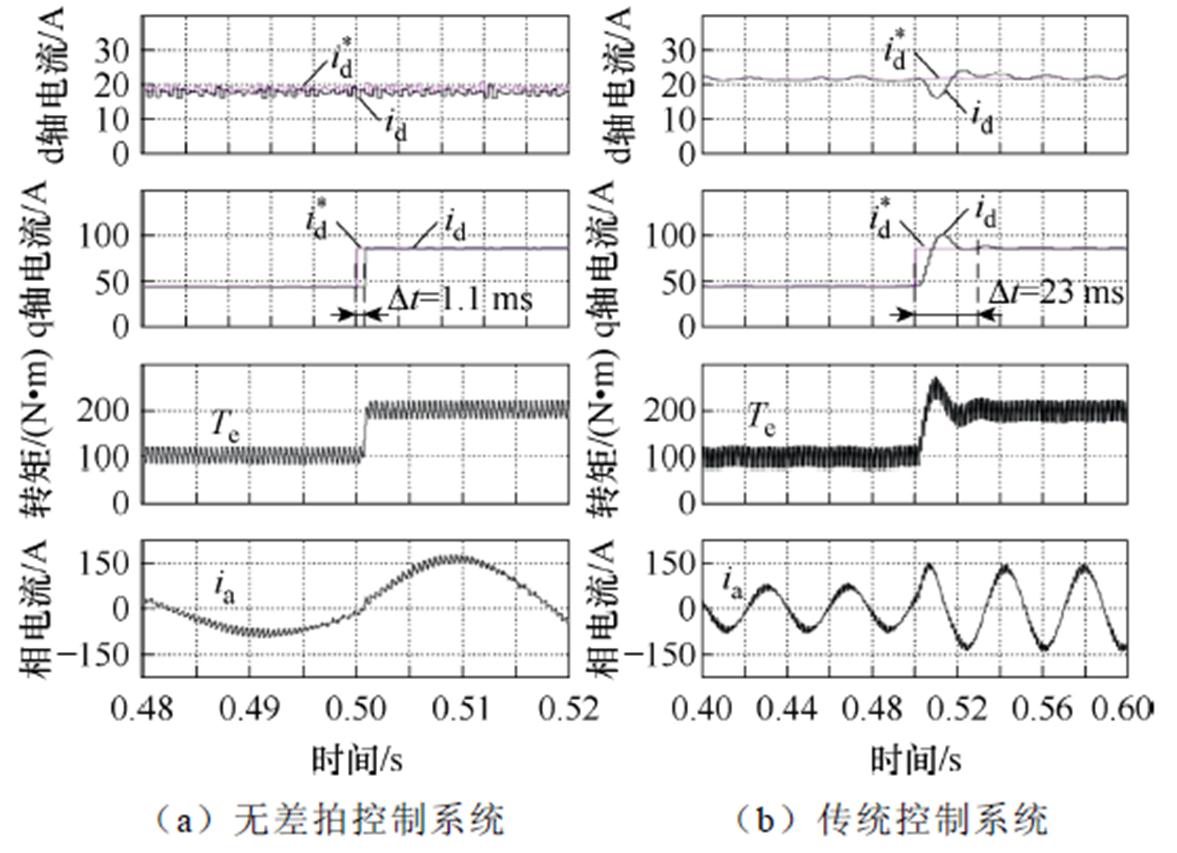
图7 无差拍控制系统与传统控制系统的转矩动态仿真对比结果
Fig.7 Torque dynamic performance of variable time step DBC and traditional control system in simulation
图8的仿真结果显示了变步长无差拍控制系统的转子磁链动态响应对比特性。仿真实验中,保持转子机械角频率为80 rad/s,转矩指令为100 N·m,初始转子磁链指令为0.7 Wb,在0.5 s时对系统施加一个0.7~1.2 Wb的阶跃转子磁链指令。从结果中可以看出,本文提出的无差拍控制系统的磁链调节速度非常快,仅有13 ms,而传统的复矢量控制器则需要380 ms,磁链动态性能的提升非常明显。在磁链动态过程中,无差拍控制系统的指令值计算模块认为,在允许的电流限制下,转子磁链从0.7~1.2 Wb的变化不可能在一个采样周期内实现,指令值计算模块会根据电压和电流限制重新计算指令值,在起动过程中,d轴电流被设置为最大电流值500 A,q轴电流设置为0,使系统处于极限励磁的状态。因此,实际的转子磁链指令值是以阶跃变化的形式出现的。在每个周期的动态过程中,dq电流和转子磁链的响应是无差拍的。
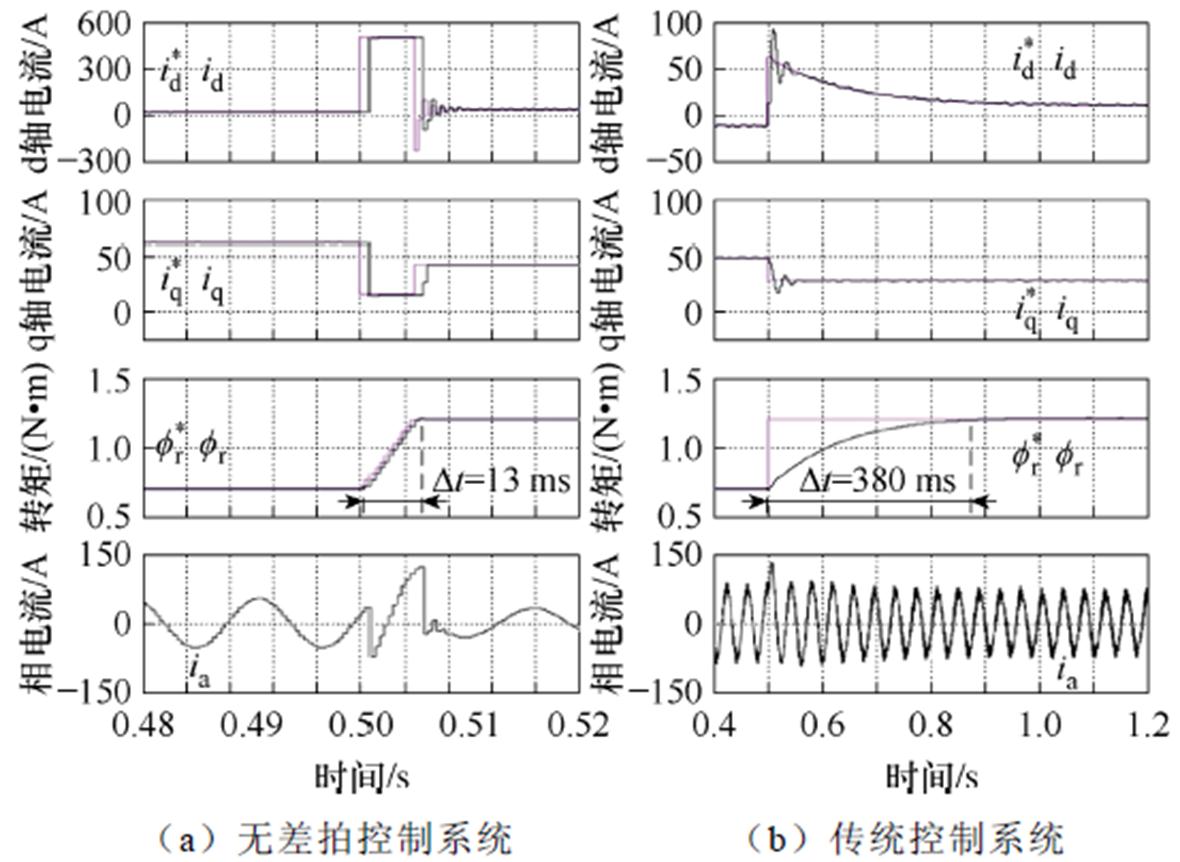
图8 无差拍控制系统与传统控制系统的磁链动态仿真对比结果
Fig.8 Rotor flux dynamic performance of variable time step DBC and traditional control system in simulation
本节将对所提出策略在同步SVPWM下的无差拍响应性能进行实验验证。大功率实验平台如图9所示。被测感应电机的相关参数见表1,其轴端外接转矩、转速测量仪,再通过变速箱和陪试直流电机连接,变速箱外接两套飞轮组以增加系统的转动惯量。陪试电机运行于发电模式,电枢绕组直接连接能耗电阻。电机控制程序运行于dSPACE MicroLabBox开发单元内。

图9 大功率实验平台
Fig.9 High-power experimental platform
图10给出了在转速500 r/min下调制采用脉冲模式 时,转矩从150 N·m突增至600 N·m的动态响应波形。调制系数MI表示定子电压矢量幅值与参考电压的比值,可以用于评估系统是否进入过调制状态,有
时,转矩从150 N·m突增至600 N·m的动态响应波形。调制系数MI表示定子电压矢量幅值与参考电压的比值,可以用于评估系统是否进入过调制状态,有
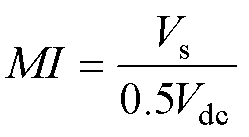 (33)
(33)
式中,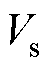 为基波电压矢量的幅值;
为基波电压矢量的幅值;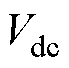 为母线电压幅值。
为母线电压幅值。
由于同步调制策略的应用,相电流波形呈现高度的周期一致性,同时d轴电流基本稳定,转子磁链实际值为1.2 Wb,和指令值基本重合。q轴电流响应时间为4 ms,且没有出现明显的超调。然而值得注意的是,4 ms的响应时间包含2个采样步长。 表明实际开关频率为电频率的15倍,即250 Hz。非对称采样方式的采样频率为开关频率的两倍,因此采样步长为2 ms。在两个采样周期中,无差拍控制器在第一个采样周期内通过状态预测补偿一拍的计算延时,并针对第二个采样周期结束时刻计算状态指令值,实际的定子电流和转子磁链在第二个采样周期结束时即可跟随上指令值,验证了系统的无差拍动态响应性能。控制器实际的动态调节时间仅为一个采样周期,即2 ms。
表明实际开关频率为电频率的15倍,即250 Hz。非对称采样方式的采样频率为开关频率的两倍,因此采样步长为2 ms。在两个采样周期中,无差拍控制器在第一个采样周期内通过状态预测补偿一拍的计算延时,并针对第二个采样周期结束时刻计算状态指令值,实际的定子电流和转子磁链在第二个采样周期结束时即可跟随上指令值,验证了系统的无差拍动态响应性能。控制器实际的动态调节时间仅为一个采样周期,即2 ms。
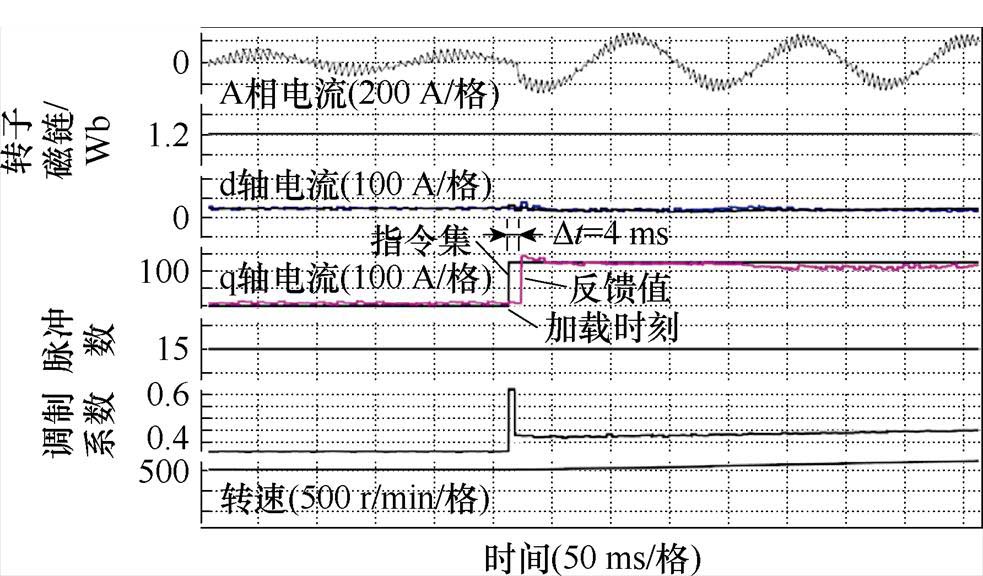
图10 无差拍控制系统在同步调制脉冲模式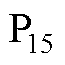 下的转矩指令阶跃上升实验结果
下的转矩指令阶跃上升实验结果
Fig.10 Torque dynamic performance of variable time step DBC with pulse pattern 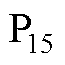 of synchronized SVPWM
of synchronized SVPWM
图11给出了在转速2 400 r/min下调制采用脉冲模式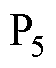 时,转矩从600 N·m突减至150 N·m的动态响应波形。当转矩突降时,对应的q轴电流响应时间间隔为3 ms,实际动态调节时间为1.5 ms,同样验证了系统的无差拍动态响应性能。
时,转矩从600 N·m突减至150 N·m的动态响应波形。当转矩突降时,对应的q轴电流响应时间间隔为3 ms,实际动态调节时间为1.5 ms,同样验证了系统的无差拍动态响应性能。
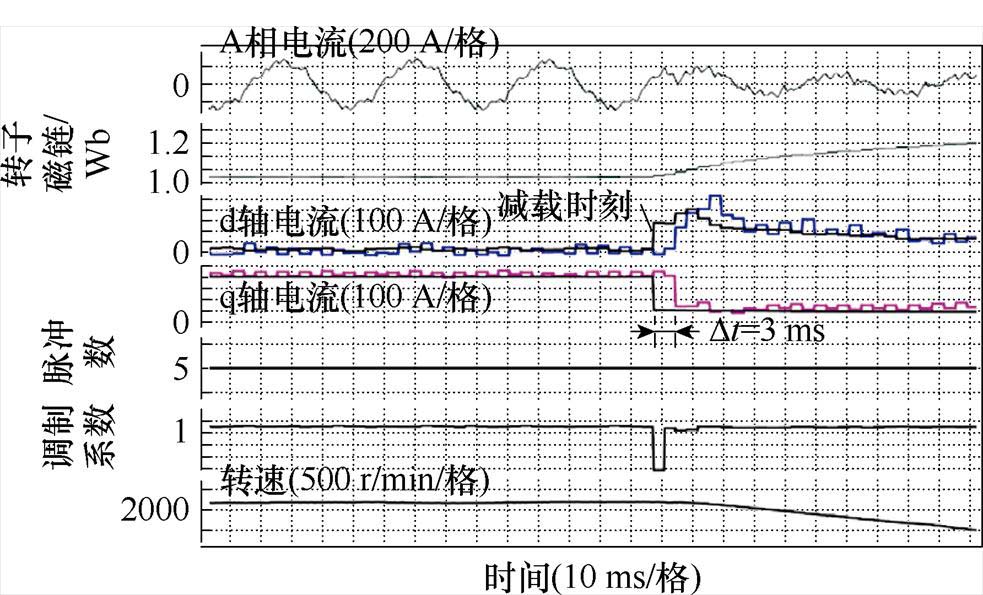
图11 无差拍控制系统在同步调制脉冲模式 下的转矩指令阶跃上升实验结果
下的转矩指令阶跃上升实验结果
Fig.11 Torque dynamic performance of variable time step DBC with pulse pattern  of synchronized SVPWM
of synchronized SVPWM
图12给出了在转速500 r/min下调制采用脉冲模式 时,转子磁场指令值阶跃下降和上升的实验结果。计算发现在一个采样周期内实现1.0 Wb转子磁链的无差拍跟踪所需要的电流将远超逆变器允许的最大电流值。因此,指令值计算单元将考虑电流极限圆重新计算转子磁链的指令值,在逆变器输出能力范围内快速调节磁链,导致实际的转子磁链指令值呈阶梯状下降,转子磁链在每次指令值变化时仍能实现无差拍动态性能。转子磁链从1.2 Wb至1.0 Wb的过程共花费16 ms。而传统矢量控制器即使忽略d轴电流的调节时间,实际磁链幅值仍需近4倍转子时间常数,即约1.74 s才能到达指令值。
时,转子磁场指令值阶跃下降和上升的实验结果。计算发现在一个采样周期内实现1.0 Wb转子磁链的无差拍跟踪所需要的电流将远超逆变器允许的最大电流值。因此,指令值计算单元将考虑电流极限圆重新计算转子磁链的指令值,在逆变器输出能力范围内快速调节磁链,导致实际的转子磁链指令值呈阶梯状下降,转子磁链在每次指令值变化时仍能实现无差拍动态性能。转子磁链从1.2 Wb至1.0 Wb的过程共花费16 ms。而传统矢量控制器即使忽略d轴电流的调节时间,实际磁链幅值仍需近4倍转子时间常数,即约1.74 s才能到达指令值。
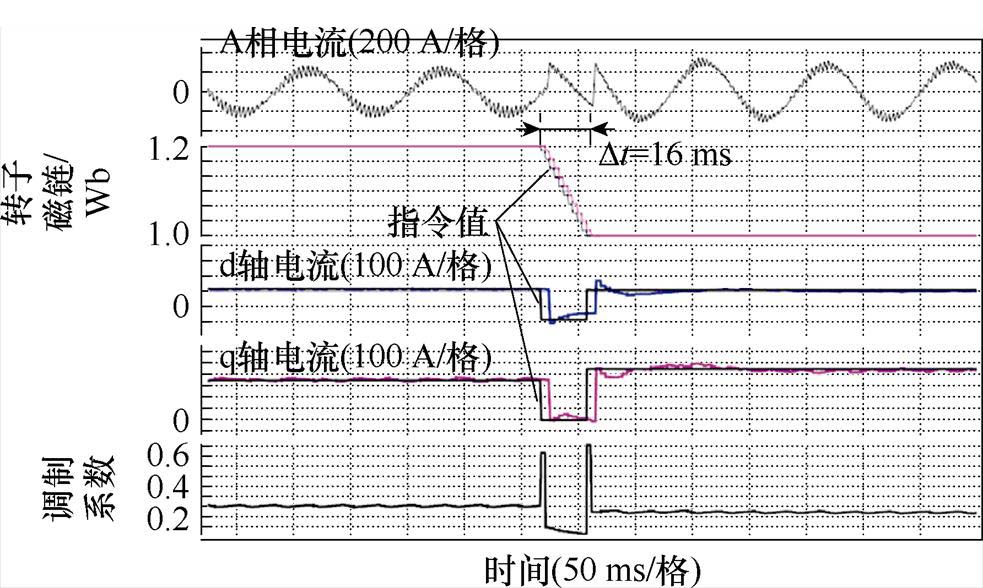
图12 无差拍控制系统在同步调制脉冲模式 下的转子磁链指令阶跃实验结果
下的转子磁链指令阶跃实验结果
Fig.12 Rotor flux dynamic performance of variable time step DBC with pulse pattern  of synchronized SVPWM
of synchronized SVPWM
图13给出了在转速2 400 r/min下调制采用脉冲模式 时,转子磁场指令值阶跃上升和下降的实验结果。转子磁链调节时间同样仅为16 ms,dq轴电流和转子磁链都能实现无差拍跟随,系统动态性能良好。
时,转子磁场指令值阶跃上升和下降的实验结果。转子磁链调节时间同样仅为16 ms,dq轴电流和转子磁链都能实现无差拍跟随,系统动态性能良好。
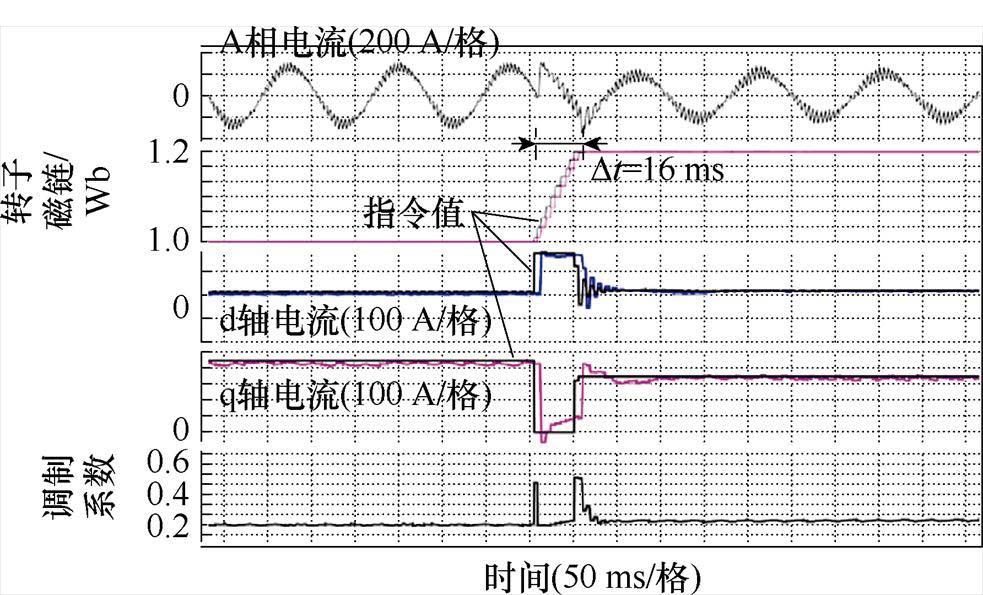
图13 无差拍控制系统在同步调制脉冲模式 下的转子磁链指令阶跃实验结果
下的转子磁链指令阶跃实验结果
Fig.13 Rotor flux dynamic performance of variable time step DBC with pulse pattern  of synchronized SVPWM
of synchronized SVPWM
在实际的系统中,驱动系统由柴油发电机组供电,在对车辆进行快速操作时,母线电压会随油门踏板的操作急剧变化,所以控制系统的抗母线扰动能力非常重要。通过网压突变实验来模拟这一工况,实验结果如图14所示。这是600 V直流母线供电机组突然分闸后的动态实验结果。机组分闸时,由于系统中存在支撑电容,母线电压按6.7 kV/s的速率变化。随着母线电压的持续降低,调制系数不断增加最后到达1.15。随后电机进入弱磁工况,dq电流波动且调制锁相环出现短暂振荡。最终,电流在波动30 ms后逐渐稳定,而同步调制也在100 ms内再次实现同步,系统整体表现出极高的抗扰动能力。
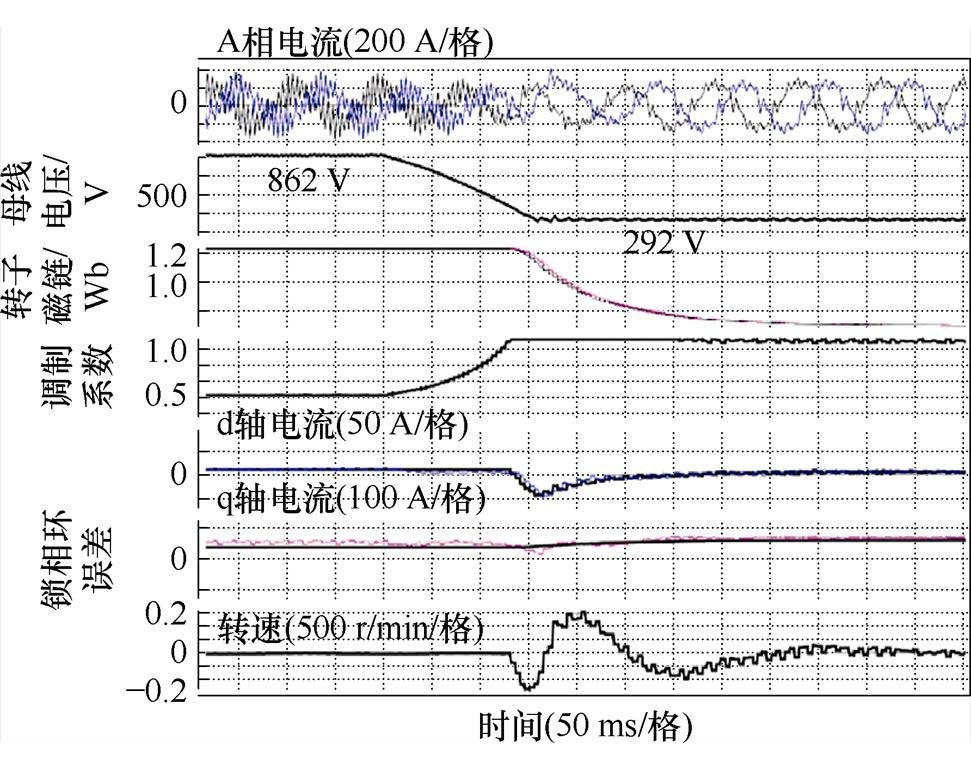
图14 断开600 V直流机组后系统进入弱磁工况的动态响应实验结果
Fig.14 The dynamic performance when the 600 V DC power disconnects and the control system runs into flux weakening operation
本文提出了适用于大功率感应牵引电机的变步长无差拍控制技术。首先,推导了高精度的感应电机特征根离散化模型,为控制器设计提供理论基础。然后,介绍了无差拍控制的时序逻辑,推导出控制器的三个主要组成部分,即参考电压矢量计算、初始状态变量预测和指令的约束条件,实现了转矩和转子磁链的无差拍控制,该系统不仅具有优异的动态性能,而且在稳态下保证了较低的电流谐波。最后,进行了仿真分析和大功率实验,验证了该系统的可行性。
参考文献
[1] 张希扬. 基于无差拍控制的异步电机模型预测转矩控制研究[D]. 杭州: 浙江大学, 2019.
Zhang Xiyang. Research on model predictive torque control of asynchronous motor based on deadbeat control[D]. Hangzhou: Zhejiang University, 2019.
[2] 韩硕, 张勇军, 肖雄, 等. 面向异步电机模型预测直接转矩控制的自适应谐波消除方法[J]. 电工技术学报, 2025, 40(4): 1078-1089.
Han Shuo, Zhang Yongjun, Xiao Xiong, et al. Adaptive harmonic elimination for model predictive direct torque control of asynchronous motor[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1078-1089.
[3] Khambadkone A, Holtz J. Low switching frequency and high dynamic pulsewidth modulation based on field-orientation for high-power inverter drive[J]. IEEE Transactions on Power Electronics, 1992, 7(4): 627-632.
[4] Steimel A. Direct self-control and synchronous pulse techniques for high-power traction inverters in com- parison[J]. IEEE Transactions on Industrial Elec- tronics, 2004, 51(4): 810-820.
[5] 刘国海, 孙汶超, 周华伟, 等. 五相永磁同步电机改进型无差拍直接转矩和磁链控制[J]. 电工技术学报, 2023, 38(24): 6658-6667.
Liu Guohai, Sun Wenchao, Zhou Huawei, et al. An improved deadbeat direct torque and flux control strategy of five-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6658-6667.
[6] 许爱德, 刘鑫, 李新宇, 等. 基于参数辨识的永磁辅助同步磁阻电机电流无差拍控制[J]. 电工技术学报, 2024, 39(18): 5626-5638.
Xu Aide, Liu Xin, Li Xinyu, et al. Current deadbeat control of permanent magnet-assisted synchronous reluctance motor based on parameter identification[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5626-5638.
[7] 兰志勇, 罗杰, 李延昊, 等. 基于快速选择表的永磁同步电机模型预测转矩控制[J]. 电工技术学报, 2023, 38(21): 5749-5757.
Lan Zhiyong, Luo Jie, Li Yanhao, et al. Model prediction torque control for permanent magnet synchronous motor based on the fast selection table[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5749-5757.
[8] 刘忠永, 范涛, 何国林, 等. 高性能永磁同步电机显式模型预测控制算法研究[J]. 电工技术学报, 2023, 38(22): 6039-6058.
Liu Zhongyong, Fan Tao, He Guolin, et al. Research on high-performance explicit model predictive control algorithm for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6039-6058.
[9] Liu Xicai, Wang Jin, Gao Xiaonan, et al. Continuous control set predictive speed control of SPMSM drives with short prediction horizon[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10166-10177.
[10] 肖海峰, 许宇豪, 李文真, 等. 五相永磁同步电机串级模型预测电流控制[J]. 电气技术, 2023, 24(8): 1-11, 21.
Xiao Haifeng, Xu Yuhao, Li Wenzhen, et al. Model predictive current control based on series cost function for five-phase permanent magnet syn- chronous machines[J]. Electrical Engineering, 2023, 24(8): 1-11, 21.
[11] Dey A, Rajeevan P P, Ramchand R, et al. A space-vector-based hysteresis current controller for a general n-level inverter-fed drive with nearly constant switching frequency control[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5): 1989-1998.
[12] Lascu C, Jafarzadeh S, Fadali M S, et al. Direct torque control with feedback linearization for induction motor drives[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2072-2080.
[13] Holtz J, Beyer B. Optimal synchronous pulsewidth modulation with a trajectory-tracking scheme for high-dynamic performance[J]. IEEE Transactions on Industry Applications, 1993, 29(6): 1098-1105.
[14] 刘勇, 梅文庆, 甘韦韦. 异步牵引电机定子磁链轨迹跟踪控制技术研究[J]. 机车电传动, 2016(2): 9-14.
Liu Yong, Mei Wenqing, Gan Weiwei. Research on stator flux trajectory tracking control for induction traction motor[J]. Electric Drive for Locomotives, 2016(2): 9-14.
[15] 冯江华. 轨道交通永磁电机牵引系统关键技术及发展趋势[J]. 机车电传动, 2018(6): 9-17.
Feng Jianghua. Key technology and development trend of permanent magnet motor traction system for rail transit[J]. Electric Drive for Locomotives, 2018(6): 9-17.
[16] 韩国强, 韩颖, 贾政, 等. 基于超局部模型的开关磁阻电机无模型预测电流控制方法[J/OL]. 电工技术学报, 1-13 [2025-03-03]. https://doi.org/10.19595/ j.cnki.1000-6753.tces.241471.
Han Guoqiang, Han Ying, Jia Zheng, et al. Model- free predictive current control method for switched reluctance motor with ultralocal model[J/OL]. Transactions of China Electrotechnical Society, 1-13 [2025-03-03]. https://doi.org/10.19595/j.cnki.1000-6753. tces.241471.
[17] Rovere L, Formentini A, Zanchetta P. FPGA imple- mentation of a novel oversampling deadbeat con- troller for PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2018, 66(5): 3731-3741.
[18] 储炜, 林黄达, 易新强. 基于三重旋转坐标变换的双三相永磁同步电机模型预测电流控制策略[J]. 电工技术学报, 2024, 39(增刊1): 51-63.
Chu Wei, Lin Huangda, Yi Xinqiang. Model predi- ctive current control strategy for dual three-phase permanent magnet synchronous motors based on triple rotating coordinate transformationp[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(S1): 51-63.
[19] Zuo Yuefei, Mei Jie, Jiang Chaoqiang, et al. Digital implementation of deadbeat-direct torque and flux control for permanent magnet synchronous machines in the M-T reference frame[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4610-4621.
[20] 张钦培, 李健, 卢阳, 等. 低载波比牵引系统的感应电机特征根离散化模型研究[J]. 电工技术学报, 2024, 39(2): 434-444.
Zhang Qinpei, Li Jian, Lu Yang, et al. Research on discretization model of induction motor for low switching-to-fundamental frequency ratio traction system[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 434-444.
[21] He Kun, Li Jian, Xiao Lifan, et al. Randomized pulse pattern strategy of synchronized SVPWM for low- frequency-ratio applications[J]. IEEE Transactions on Power Electronics, 36(6): 6404-6414.
Research on Deadbeat Control Technology with High Dynamic Performance for High-Power Induction Motors
Abstract In high-power motor drives, especially in high-power electric mining dump trucks, the switching frequency of the inverter is always strictly limited to avoid high switching losses, which will make the control system operate in a low pulse ratio condition. Therefore, the performance of traditional control strategies such as field-oriented control (FOC) and direct-torque control (DTC) will deteriorate. When a high-power electric mining truck is operated quickly, the DC bus voltage always has a dramatic variation, which may make the control system unstable since the response of rotor flux in traditional FOC is slow. This paper proposes a deadbeat control (DBC) strategy with high dynamic performance under a low pulse ratio to solve this problem. The proposed control strategy simultaneously achieves fast stator current & rotor flux dynamic responses and low current harmonics.
Firstly, the eigenvalue-based discrete model is derived. The mathematical model of the induction motor is modeled in the continuous domain using a state space description. The full-rank state matrix is diagonalized through the transformation matrix. The elements on the diagonal of the diagonal matrix are the corresponding stator's characteristic roots and the induction motor's rotor voltage equations. The exact solution of the system matrix can be obtained through the transformation matrix and the diagonal matrix. Thus, the eigenvalue-based discrete model of the induction motor is derived.
The deadbeat control system is designed in the discrete domain. The linear transformation is applied to the state variables, and a new state variable vector is defined. Then, the new state variable vector is transferred to the synchronized coordinate system. Since the violent oscillation of DC bus voltage in high-power electric mining dump trucks, the high dynamic performance of rotor flux and dq-axis current should be achieved simultaneously to keep the system stable. Therefore, the extra constraint of state variables is derived to control the rotor flux and stator current vector with three degrees of freedom.
Finally, the whole DBC system is introduced, and the simulation and high-power tests are performed. Simulation and experimental results show that the dq-axis current and rotor flux responses are deadbeat during the dynamic process. The torque response time reaches milliseconds, exhibiting an excellent dynamic torque performance. When the flux reference changes, the proposed system evaluates whether the flux tracking can be completed within one sampling period. If it cannot be completed, the system will control the flux by steps within several periods. However, the whole control process can also be maintained at tens of milliseconds, showing an excellent dynamic performance of rotor flux.
Keywords:Deadbeat control, induction machine, low pulse ratio, discretization model
中图分类号:TM301.2
DOI: 10.19595/j.cnki.1000-6753.tces.241258
国家重点研发计划(2023YFB4301500)和国家自然科学基金(52377051, 52207054)资助项目。
收稿日期2024-07-15
改稿日期 2024-11-15
周 正 男,1998年生,硕士研究生,研究方向为大功率感应电机控制技术。
E-mail: hust_zhouzheng@foxmail.com
卢 阳 男,1993年生,助理研究员,研究方向为电机设计与控制。
E-mail: luyang@hust.edu.cn(通信作者)
(编辑 崔文静)