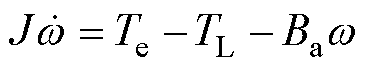 (1)
(1)
摘要 针对永磁同步电机(PMSM)伺服系统速度跟踪精度低的问题,提出一种基于复合观测器的分数阶快速终端滑模控制(FTSMC)方法。首先,建立含有不确定性的隐极式PMSM数学模型,采用分数阶FTSMC方法可以使系统状态轨迹在有限的时间内快速趋近到滑模面上,同时在滑模面中加入带有记忆属性的分数阶微积分算子,进而有效削弱抖振现象。其次,针对控制器参数选取困难,难以达到跟踪精度和抗扰性能动态最优的问题,采用模糊自适应方法对系统参数进行实时在线更新,提高速度跟踪精度。然后,为进一步提升系统对于负载扰动的抗扰性能,设计复合观测器结构对系统匹配扰动和非匹配扰动进行观测,有效提高系统的抗扰性能。最后,实验结果证明该方法能显著提高系统跟踪精度和抗扰性能。
关键词:永磁同步电机 分数阶微积分 快速终端滑模控制 模糊控制 复合观测器
随着我国现代工业的持续快速发展,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)已被广泛应用于纺织工业、工业机器人、医疗设备、家用电器、国防军事等领域[1-2]。PMSM具有结构简单、质量轻、功率密度高、驱动能力强等优点[3]。在实际应用中,PMSM多处于复杂工况下,对外部负载扰动、环境变化及内部参数变化等因素非常敏感,同时PMSM又具有多变量、非线性和强耦合性的特点,使其对伺服控制技术提出了较高的要求[4]。因此,PMSM精密伺服系统的研究愈发成为学术界的热点问题。
近些年来,为提高PMSM伺服系统的控制性能,国内外学者提出了许多新的控制策略,自抗扰控制[5-6]、动态面控制[7]、迭代学习控制[8]、模型预测控制[9]等方法被广泛应用于PMSM伺服系统中。滑模控制(Sliding Mode Control, SMC)是一种动态非线性控制方法,在控制过程中可根据系统的实时状态进行调整,具有对系统参数变化不敏感、鲁棒性强等优点,被广泛应用于伺服控制领域[10]。然而,传统SMC存在明显的抖振现象,在一定程度上降低了伺服跟踪精度,但是其系统响应速度较慢。快速终端滑模控制(Fast Terminal Sliding Mode Control, FTSMC)通过在滑模面中增加变速终端吸引子,使系统状态在远离平衡点时加快趋近速度,且跟踪误差可在有限时间内趋于零。因此,FTSMC被广泛应用于PMSM调速系统中。文献[11]设计积分型终端SMC方法,并通过径向基神经网络估计系统不确定性并补偿至控制律中,在提高系统跟踪精度的同时,有效地提高了系统的鲁棒性,但神经网络结构较为复杂且参数难以整定。文献[12]在积分型终端SMC的基础上设计了扩张状态观测器,将观测的系统扰动作为切换控制律的切换增益,避免了因较大切换增益造成的抖振现象,但是存在相位滞后现象,会对系统响应的快速性造成一定影响。文献[13]设计全局终端SMC,使系统初始时刻误差为零,同时采用龙贝格观测器观测系统误差,提高了系统的鲁棒性,但抖振现象并未明显改善。分数阶微积分具有记忆和遗传信息的特性,能量传递较为缓慢,将分数阶微积分与SMC结合可有效削弱抖振,提高稳态跟踪精度。观测器结构对被控对象进行数学建模,并经理论推导观测出未知的系统变量,将观测出的状态变量补偿至系统中,可有效提高系统跟踪精度和鲁棒性。文献[14]通过设计负载转矩观测器有效补偿了负载对系统的影响,提高了系统鲁棒性,但针对参数变化、非线性摩擦等非匹配扰动难以实现补偿。文献[15]通过设计扩张状态观测器(Extended State Observer, ESO)对系统集总扰动进行补偿,但ESO参数整定困难,对扰动的估计精度不高。
为提高PMSM速度伺服系统的跟踪性能和抗扰性能,本文设计了基于复合观测器的分数阶FTSMC方法。首先,在滑模面中引入分数阶微积分算子,可有效削弱系统抖振;其次,针对分数阶FTSMC的滑模面参数采用模糊自适应调节,根据系统状态在线调整控制器参数,可有效提高系统的响应速度和跟踪精度;然后,为提升系统的抗扰性能,设计复合观测器,对系统匹配扰动和不匹配扰动分别估计并补偿至控制律中,进而提升系统的综合控制性能;最后,通过实验证明了该方法的有效性,结果表明系统的跟踪性能更优、抗扰性能更强。
假设隐极式PMSM无磁路饱和现象,且磁滞和涡流损耗忽略不计。在dq坐标系下的运动方程和电磁转矩方程分别为
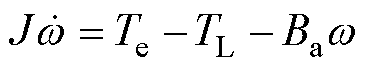 (1)
(1)
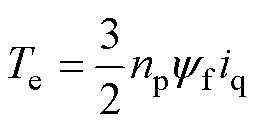 (2)
(2)
式中,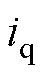 为q轴电流;
为q轴电流;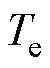 、
、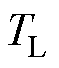 分别为电磁、负载转矩;
分别为电磁、负载转矩;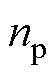 为极对数;
为极对数;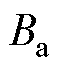 为阻尼系数;
为阻尼系数;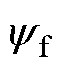 为绕组磁链;
为绕组磁链;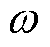 为机械角速度;J为转动惯量。
为机械角速度;J为转动惯量。
然而,PMSM易受到外部环境变化、内部参数变化等不确定性的影响,设系统集总不确定性为F,则PMSM的运动方程可表示为
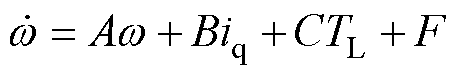 (3)
(3)
其中
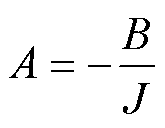
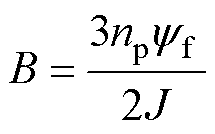
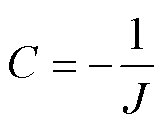
当考虑F对系统的影响时,PMSM的运动方程可改写为
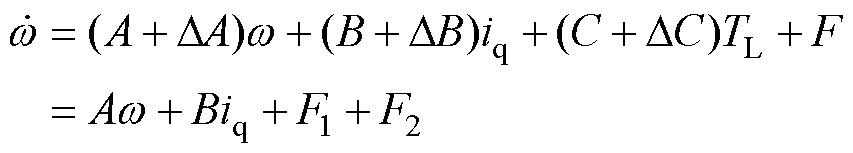 (4)
(4)
式中,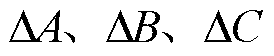 为系统参数不确定性和未建模量;F1为系统匹配不确定性,主要为系统负载扰动;
为系统参数不确定性和未建模量;F1为系统匹配不确定性,主要为系统负载扰动;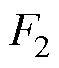 为系统非匹配不确定性,主要包括系统参数变化和系统未建模动态误差等,存在上界L。集总不确定性F存在上界H,且为缓慢变化的量,满足
为系统非匹配不确定性,主要包括系统参数变化和系统未建模动态误差等,存在上界L。集总不确定性F存在上界H,且为缓慢变化的量,满足
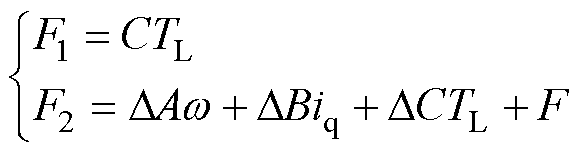 (5)
(5)
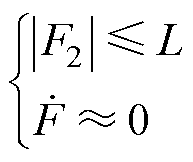 (6)
(6)
PMSM伺服系统结构框图如图1所示。速度参考信号与实际转速的差为速度误差e,e作为速度控制器的输入,经控制器计算,输出电流iq;电流环使用PI控制,输出d、q轴电压,经过Park逆变换、SVPWM和逆变器,向PMSM输出三相交流电压,通过电流传感器检测三相电流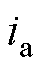 、
、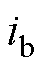 、
、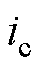 ,经过Clarke变换和Park变换构成电流反馈回路,在PMSM上通过速度传感器得到实际转速,与给定转速构成转速反馈回路,组成PMSM伺服系统。
,经过Clarke变换和Park变换构成电流反馈回路,在PMSM上通过速度传感器得到实际转速,与给定转速构成转速反馈回路,组成PMSM伺服系统。
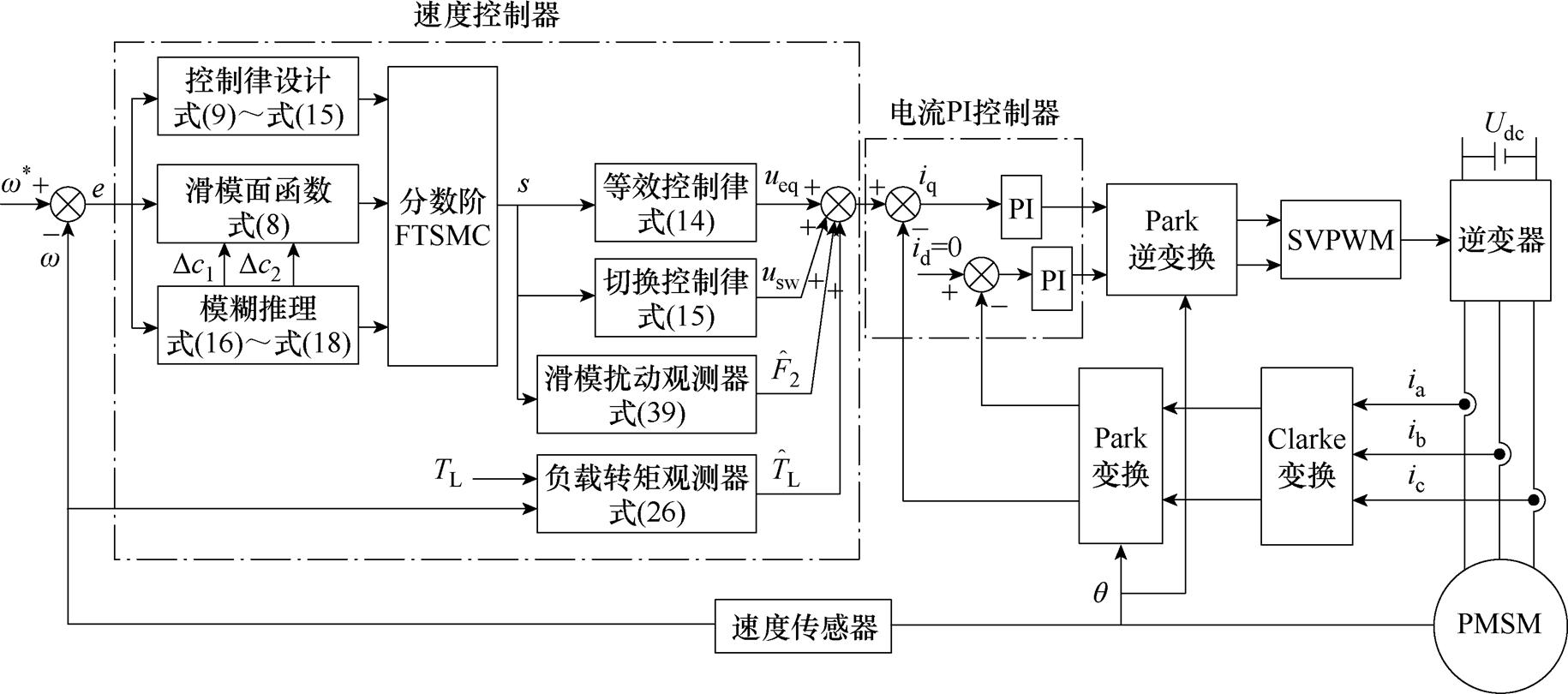
图1 PMSM伺服系统结构框图
Fig.1 Block diagram of PMSM servo system
定义状态变量x1、x2为
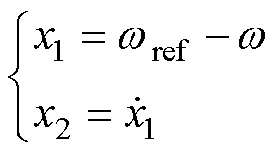 (7)
(7)
式中,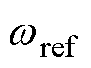 为PMSM给定角速度;
为PMSM给定角速度;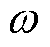 为实际角速度。定义分数阶FTSMC滑模面为
为实际角速度。定义分数阶FTSMC滑模面为
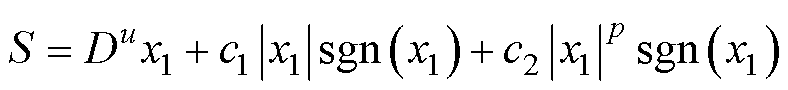 (8)
(8)
式中,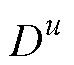 为分数阶微积分算子,采用分数阶FTSMC可使系统状态轨迹在有限时间内快速趋近滑模面,同时在滑模面中加入带有记忆属性的分数阶微积分算子,可通过改变系统状态穿越滑模面的速率和方向,使控制更加连续,进而有效削弱抖振;u为分数阶阶次,且
为分数阶微积分算子,采用分数阶FTSMC可使系统状态轨迹在有限时间内快速趋近滑模面,同时在滑模面中加入带有记忆属性的分数阶微积分算子,可通过改变系统状态穿越滑模面的速率和方向,使控制更加连续,进而有效削弱抖振;u为分数阶阶次,且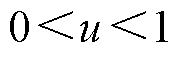 ;c1、c2为滑模面参数;p为滑模面参数;
;c1、c2为滑模面参数;p为滑模面参数;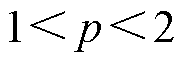 ;sgn( · )为符号函数。当系统状态远离平衡点时,
;sgn( · )为符号函数。当系统状态远离平衡点时,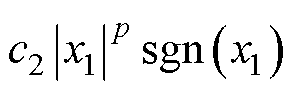 项起主要作用,适当增大可加快系统响应速度,但可能导致系统超调;当系统状态靠近平衡点时,
项起主要作用,适当增大可加快系统响应速度,但可能导致系统超调;当系统状态靠近平衡点时,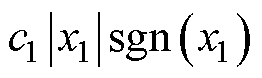 项起主要作用。
项起主要作用。
对式(8)在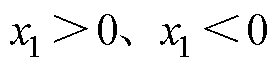 情况下求一阶导数,得
情况下求一阶导数,得
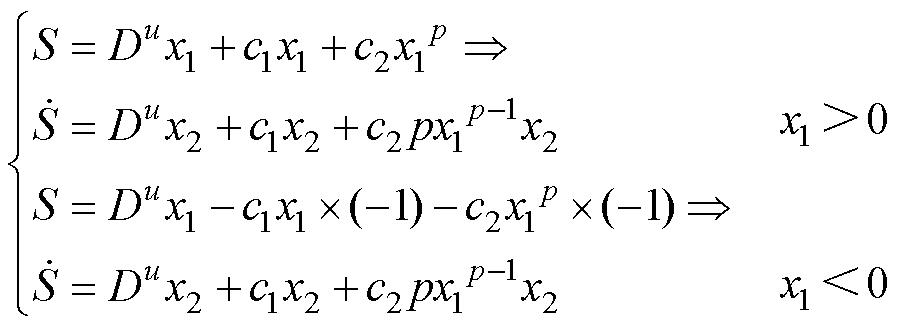 (9)
(9)
当忽略集总不确定性对系统的影响时,根据式(4)和式(7)可得
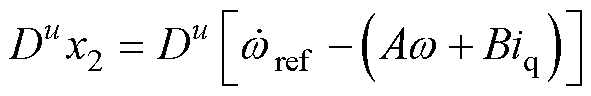 (10)
(10)
设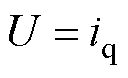 为系统总控制律,满足
为系统总控制律,满足
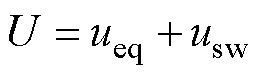 (11)
(11)
式中,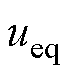 为系统的等效控制律,可使系统在理想状态下收敛至滑模面上;
为系统的等效控制律,可使系统在理想状态下收敛至滑模面上;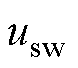 为系统的切换控制律,可保证系统的强抗扰性,在不确定性影响下仍能使系统跟踪误差收敛至零。
为系统的切换控制律,可保证系统的强抗扰性,在不确定性影响下仍能使系统跟踪误差收敛至零。
把式(11)代入式(10)可得
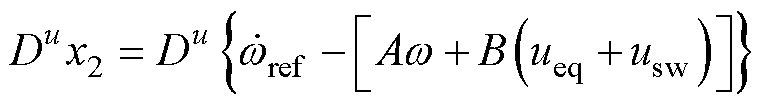 (12)
(12)
把式(12)代入式(9)得
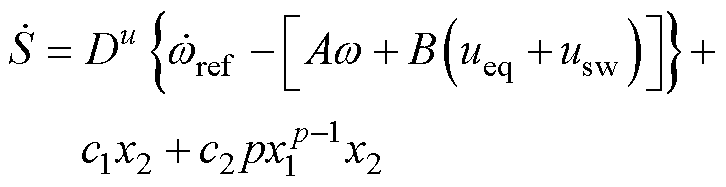 (13)
(13)
令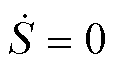 ,可得等效控制律为
,可得等效控制律为
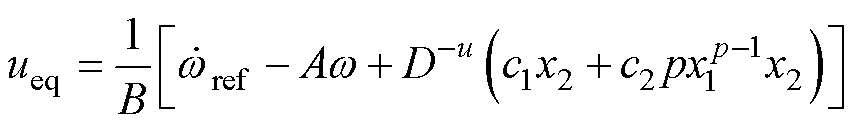 (14)
(14)
考虑到集总不确定性对系统的影响,设计切换控制律以保证系统的鲁棒性。
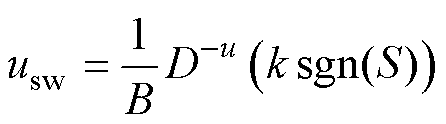 (15)
(15)
式中,k为切换控制律的切换增益,满足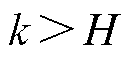 ,H为集总不确定性上限,是一数值未知的正常数。
,H为集总不确定性上限,是一数值未知的正常数。
为使控制器参数的选取更加合理,针对分数阶FTSMC的滑模面参数c1、c2采用模糊推理进行自适应调整,根据系统状态对参数进行在线更新,得到适合的参数值,进而提高系统的控制性能。针对式(8)中c1、c2的模糊推理结构框图如图2所示。
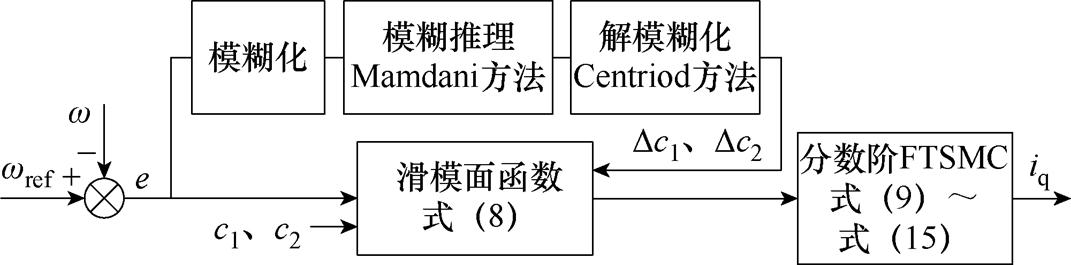
图2 参数c1、c2的模糊推理结构框图
Fig.2 Block diagram of fuzzy reasoning with parameters c1 and c2
模糊推理过程分为模糊化、模糊推理和解模糊化三部分。采用由X到Y的模糊关系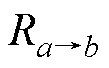 表示模糊语句if a then b,定义a为输入,b为输出,有
表示模糊语句if a then b,定义a为输入,b为输出,有
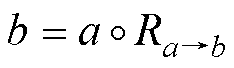 (16)
(16)
式中, 表示模糊合成运算。
表示模糊合成运算。
模糊关系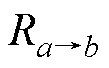 的Mamdani推理为
的Mamdani推理为
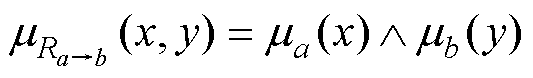 (17)
(17)
则由式(16)、式(17)得输出B的隶属度函数为
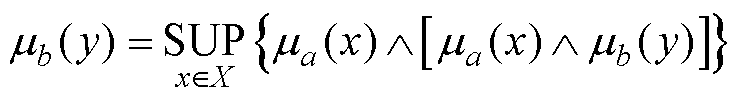 (18)
(18)
式中,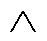 表示模糊交运算。
表示模糊交运算。
解模糊化采用重心法,对于式(8)中的滑模面参数c1、c2,选取误差e作为输入语言变量,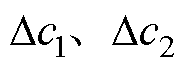 作为输出语言变量。输入变量的模糊子集为{负大、负小、零、正小、正大},记为{NB、NS、ZE、PS、PB};
作为输出语言变量。输入变量的模糊子集为{负大、负小、零、正小、正大},记为{NB、NS、ZE、PS、PB};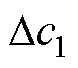 的模糊子集为{负大、负小、正小},记为{NB、NS、PS};
的模糊子集为{负大、负小、正小},记为{NB、NS、PS};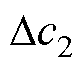 的模糊子集为{负小、正小、正大},记为{NS、PS、PB}。e的基本论域为[-0.03, 0.03],
的模糊子集为{负小、正小、正大},记为{NS、PS、PB}。e的基本论域为[-0.03, 0.03],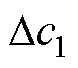 的基本论域为[-350, 150],
的基本论域为[-350, 150],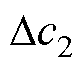 的基本论域为[-10, 20]。e的归一化隶属度曲线和
的基本论域为[-10, 20]。e的归一化隶属度曲线和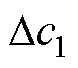 、
、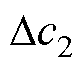 变化曲线分别如图3和图4所示。
变化曲线分别如图3和图4所示。
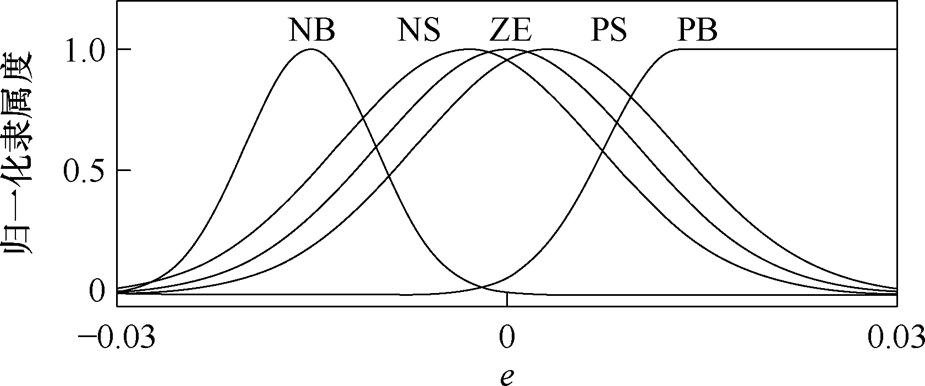
图3 误差e的归一化隶属度曲线
Fig.3 Normalized membership curves of the error e
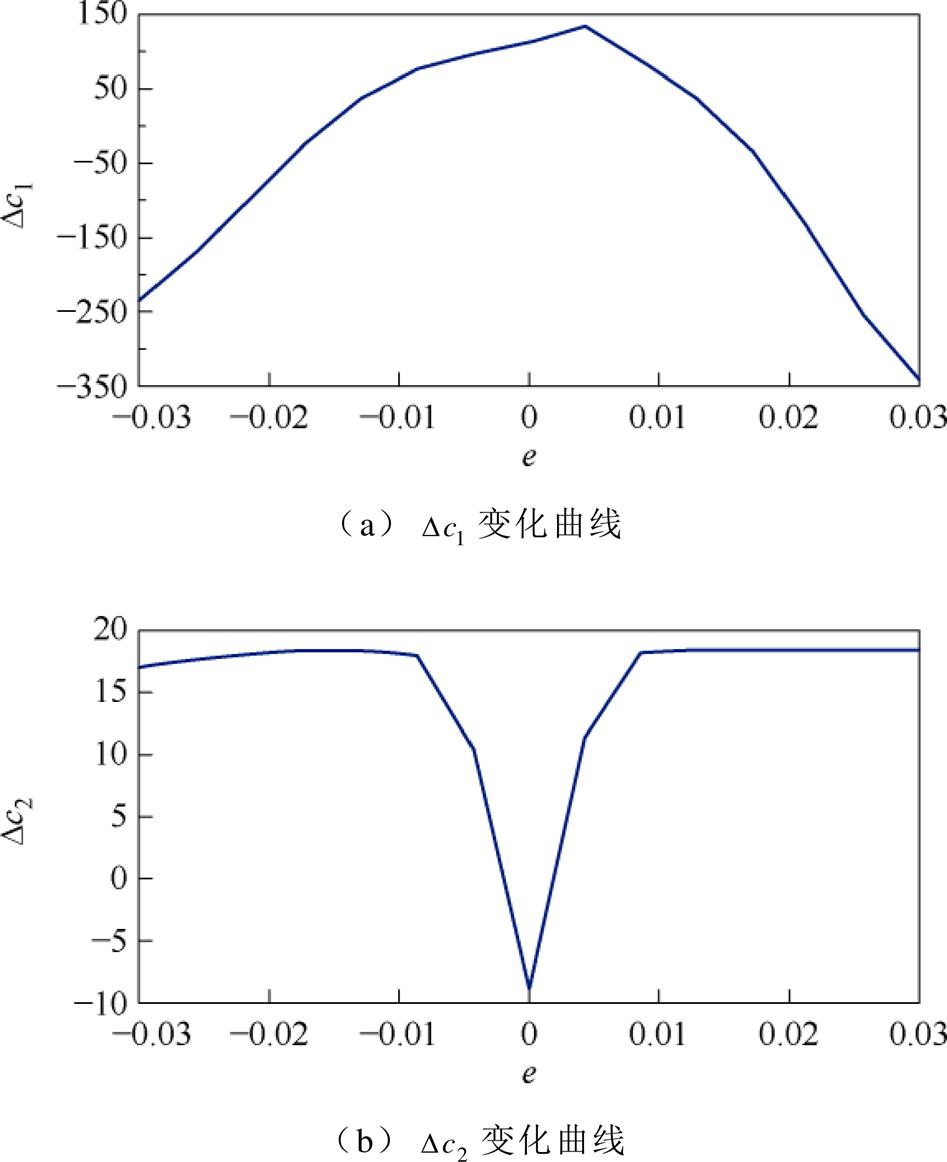
图4 控制器参数变化曲线
Fig.4 Curves of controller parameter variation
当e的绝对值偏大时,即控制器的状态变量与滑模面的距离较远。此时,式(8)中含c2的多项式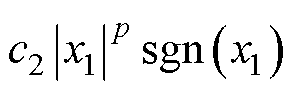 起主要作用,故应选取更小的c1和更大的c2。当输入量的绝对值偏小时,即控制器的状态变量近似趋近到了滑模面上,此时含c1的多项式
起主要作用,故应选取更小的c1和更大的c2。当输入量的绝对值偏小时,即控制器的状态变量近似趋近到了滑模面上,此时含c1的多项式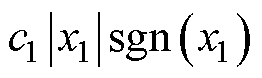 起主要作用,故应选取更大的c1和更小的c2。e与
起主要作用,故应选取更大的c1和更小的c2。e与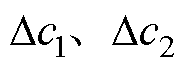 的模糊规则见表1。
的模糊规则见表1。
表1 模糊控制规则
Tab.1 Fuzzy control rule list

输入/输出Dc1Dc2 NBNBPB NSNSPS ZEPSNS PSNSPS PBNBPB
定义Lyapunov函数为
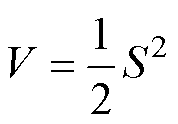 (19)
(19)
对式(19)求导,结合式(12)~式(15)可得
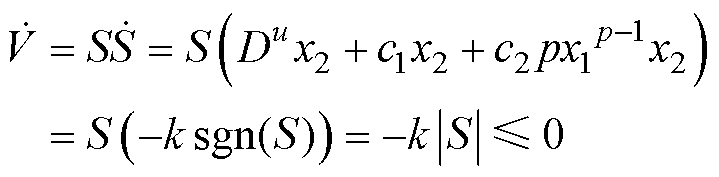 (20)
(20)
根据Lyapunov稳定性判据,可知分数阶FTSMC满足渐近稳定条件,系统状态轨迹可在有限时间内收敛至滑模面。针对系统实际收敛时间,存在如下定理:
定理1:在函数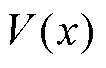 连续且满足正定的前提下,若满足
连续且满足正定的前提下,若满足
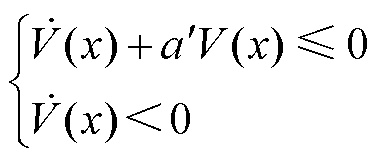 (21)
(21)
则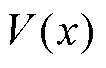 可在有限时间内稳定且收敛时间为
可在有限时间内稳定且收敛时间为
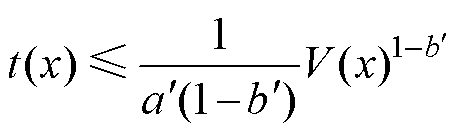 (22)
(22)
式中,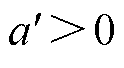 ;
;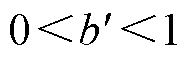 ;x为正实数。
;x为正实数。
根据式(21)、式(22),选取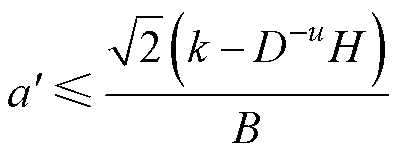 ,
,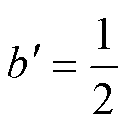 ,则分数阶FTSMC方法满足定理1中所要求的
,则分数阶FTSMC方法满足定理1中所要求的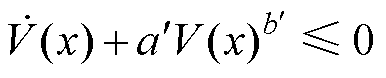 ,故系统的动态变量x可在有限时间内收敛至滑模面,且收敛时间满足
,故系统的动态变量x可在有限时间内收敛至滑模面,且收敛时间满足
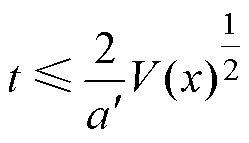 (23)
(23)
2.3.1 负载转矩观测器
为准确观测系统匹配扰动,提高系统的抗扰性能,本节设计负载转矩观测器对负载转矩进行观测,并补偿至系统控制律中。
根据式(3)和式(7),忽略系统非匹配扰动,建立基于转速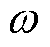 和负载转矩
和负载转矩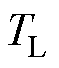 的系统状态方程为
的系统状态方程为
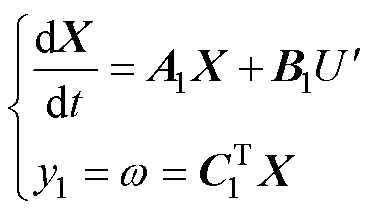 (24)
(24)
根据式(24)可得观测方程为
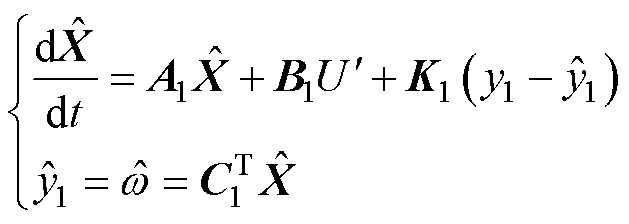 (25)
(25)
其中
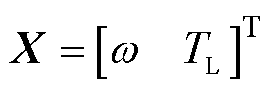
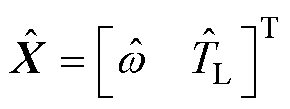
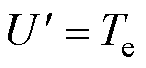
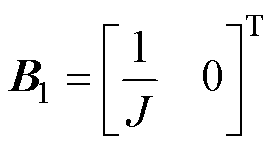
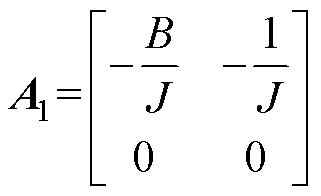
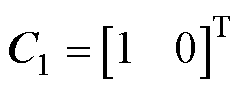
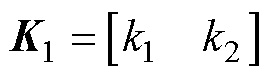
式中,k1、k2为观测参数。
将式(24)和式(25)相减,得到系统状态误差方程为
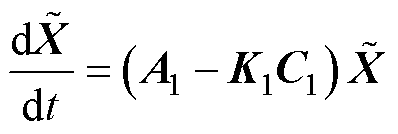 (26)
(26)
式中,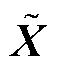 为观测误差矩阵,满足
为观测误差矩阵,满足
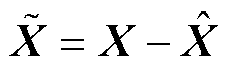 (27)
(27)
式(26)的特征方程可表示为
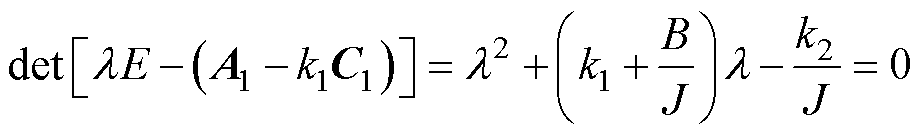 (28)
(28)
设式(26)状态方程的极点为m1、m2,联立式(28)得
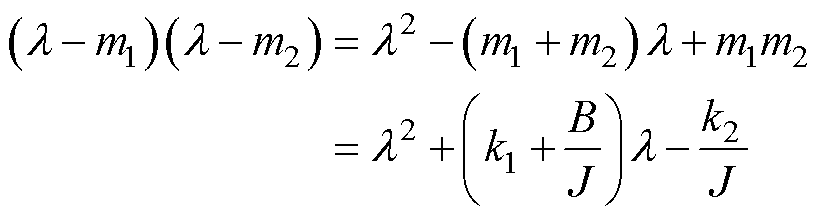 (29)
(29)
当系统极点位于复频域左半平面时,满足系统稳定条件,即满足: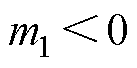 ,
,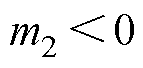 。
。
整理式(29)可得
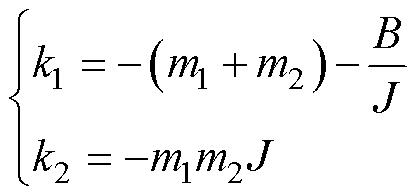 (30)
(30)
故通过选取符合系统稳定的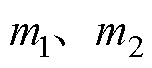 值,即可根据式(30)得到观测参数矩阵K1,完成对负载转矩的观测。
值,即可根据式(30)得到观测参数矩阵K1,完成对负载转矩的观测。
2.3.2 滑模扰动观测器
为进一步提升系统的抗扰性能并提高系统跟踪精度,本节设计基于低通滤波的滑模扰动观测器,针对系统非匹配扰动进行有效观测,削弱了观测器输出的抖振现象,有效提升了系统的综合控制品质。
考虑系统非匹配扰动F2对系统的影响,改写式(9)可得
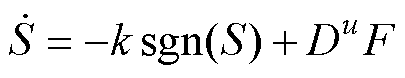 (31)
(31)
对式(31)进行u阶积分,可得

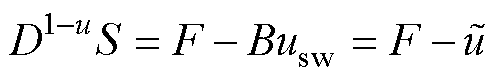 (32)
(32)
其中
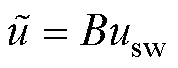
设计扰动观测器滑模面为
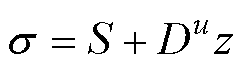 (33)
(33)
式中,z为待设计中间变量,满足
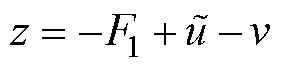 (34)
(34)
式中,v为待设计控制律。
对式(33)求导可得
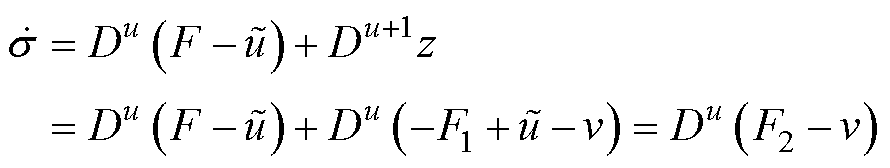 (35)
(35)
设计扰动观测器控制律为
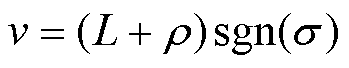
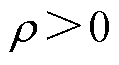 (36)
(36)
Lyapunov函数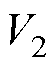 定义为
定义为
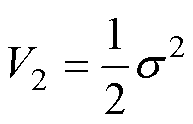 (37)
(37)
对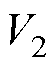 求导,可得
求导,可得
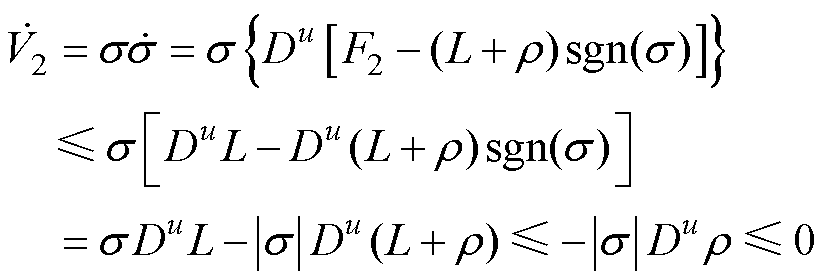 (38)
(38)
故系统满足渐近稳定条件,根据式(35)可知,控制律v能近似估计系统未知扰动F2。定义F2的估计值为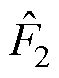 ,则满足
,则满足
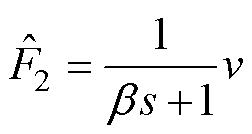 (39)
(39)
式中,s为Laplace变量;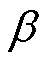 为滤波带宽。当
为滤波带宽。当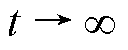 时,式(39)满足
时,式(39)满足
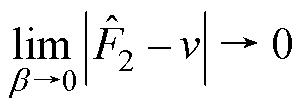 (40)
(40)
由式(39)、式(40)可知,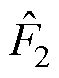 可被认为由v经低通滤波环节得到,当
可被认为由v经低通滤波环节得到,当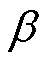 无限趋近于零时,观测误差也相应减小。滑模扰动观测器原理框图如图5所示。
无限趋近于零时,观测误差也相应减小。滑模扰动观测器原理框图如图5所示。
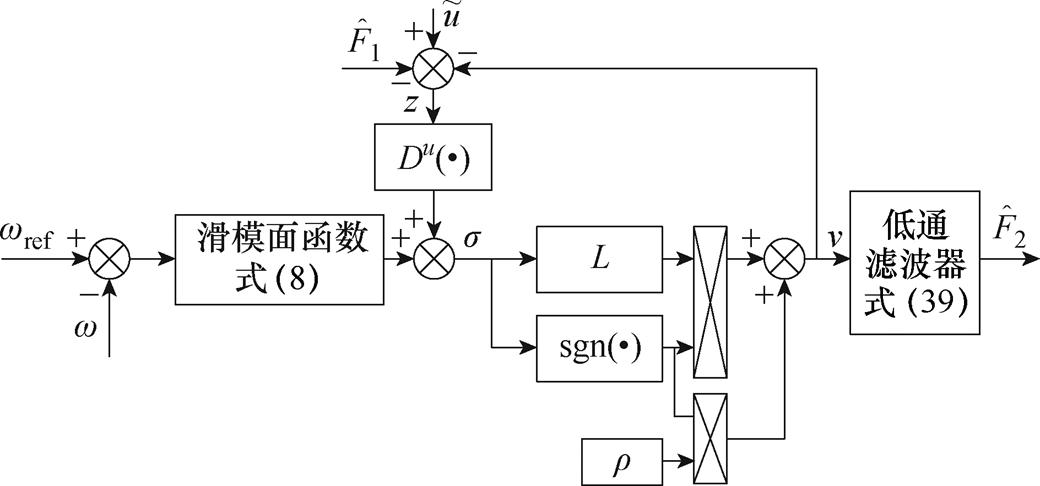
图5 滑模扰动观测器原理框图
Fig.5 Block diagram of the sliding mode disturbance observer principle
为验证基于复合观测器的PMSM分数阶FTSMC方法的有效性,利用Links-RT半实物仿真平台进行实验验证。实验平台主要包括:开发主机、Links-Box实时仿真机、转矩测量仪、PMSM、伺服驱动器等,如图6所示。实验使用的PMSM参数见表2。

图6 实验平台
Fig.6 The experimental platform
表2 实验电机参数
Tab.2 Experimental motor parameters
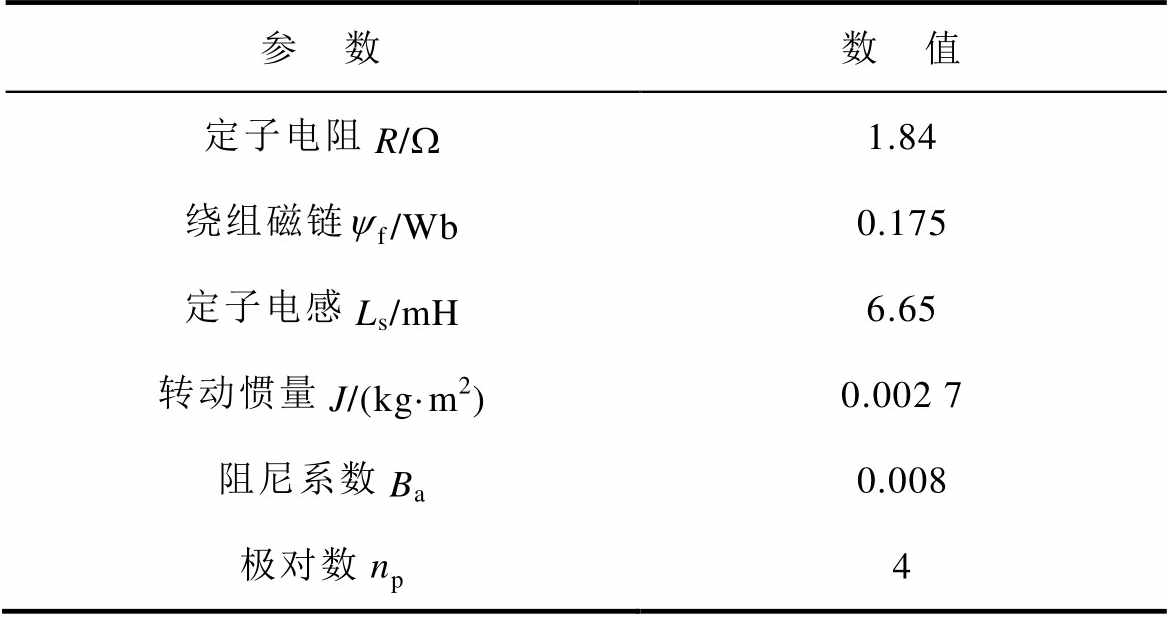
参 数数 值 定子电阻R/W1.84 绕组磁链yf/Wb0.175 定子电感Ls/mH6.65 转动惯量J/(kg·m2)0.002 7 阻尼系数Ba0.008 极对数np4
实验通过四种控制方法完成PMSM的调速过程,并将其实际控制效果进行对比。控制方法及相应参数选取如下:传统SMC方法(C1方法);文献[16]中采用的积分SMC方法(C2方法)。积分SMC的滑模面和切换控制律分别设计为
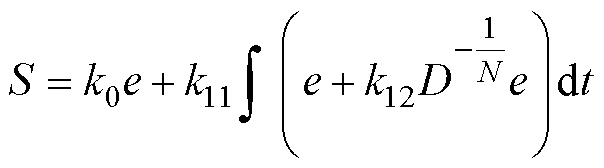 (41)
(41)
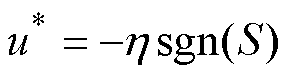 (42)
(42)
积分SMC的参数选取为: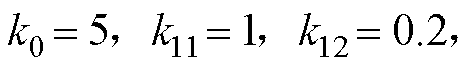
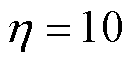 ,
,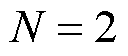 ;本文设计的分数阶FTSMC方法(C3方法),参数选取为:
;本文设计的分数阶FTSMC方法(C3方法),参数选取为: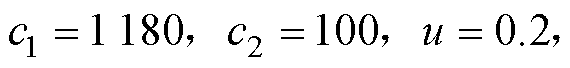
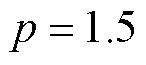 ,
,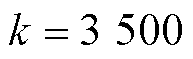 ;复合观测器-分数阶FTSMC 方法(C4方法),控制器参数选取为:
;复合观测器-分数阶FTSMC 方法(C4方法),控制器参数选取为: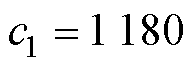 ,
,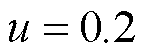 ,
,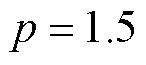 ,
,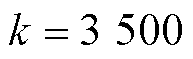 ,
,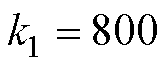 ,
,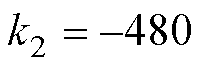 ,
,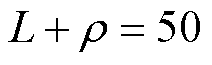 ,
,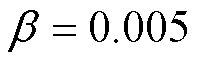 。
。
1)实验一:空载情况下转速跳变跟踪实验
速度给定信号为:0 s时给定1 000 r/min,0.4 s时转速下降至500 r/min,0.8 s时上升至1 300 r/min,实验时间为1.2 s。基于四种方法的转速跟踪、转速误差和电磁转矩曲线如图7~图9所示。根据图7可知,四种方法均对参考转速曲线有良好的跟踪效果。跟踪初态时,通过局部放大曲线可知,C1~C3方法均存在100~200 r/min的转速超调,而C4方法的超调接近于零,且由于终端吸引子的引入,响应时间(稳态转速误差±5 r/min)快于C1~C3方法。在转速拐点处,C4方法在快速性和瞬态响应速度上均优于C1~C3方法。由图8可直观地反映出系统稳态误差,C4在进入跟踪稳态后,由于扰动观测器的设计和参数模糊调整的引入,跟踪精度明显高于其他方法且曲线更为平滑。由图9可知,四种方法的转矩输出均较为平稳,无较大的转矩脉动。
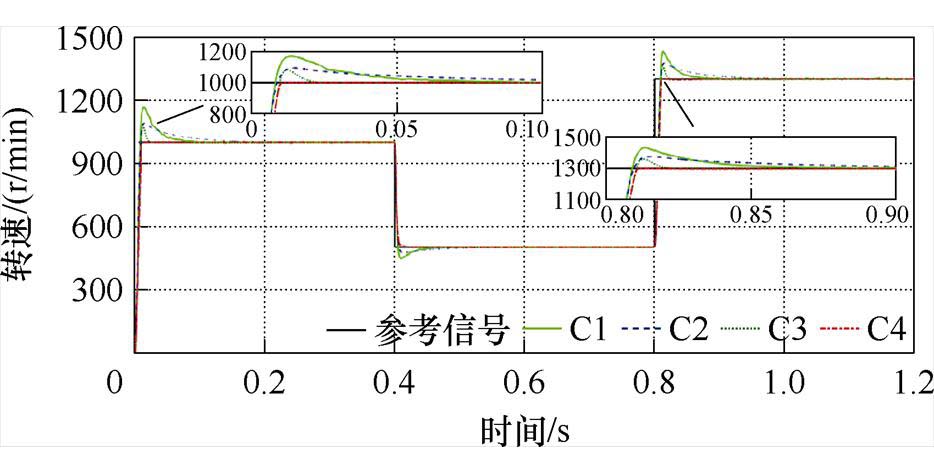
图7 空载条件下转速跟踪曲线
Fig.7 Curves of speed tracking under no-load given
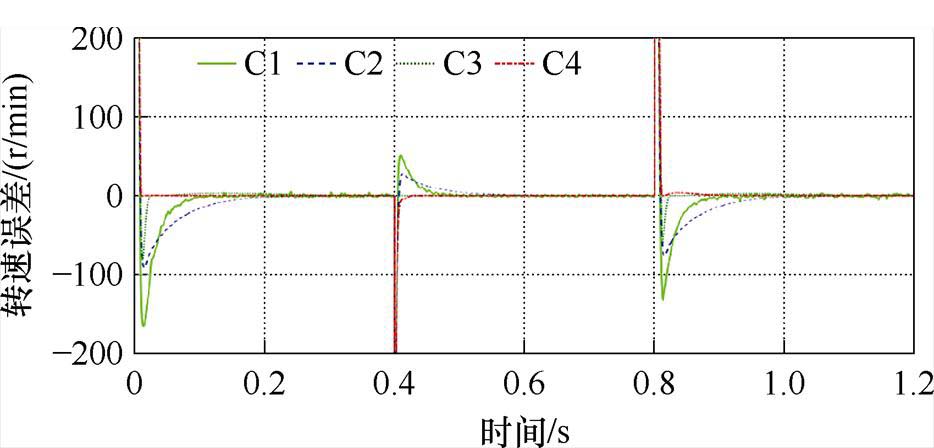
图8 空载方波给定下转速误差曲线
Fig.8 Curves of speed error given by no-load square wave
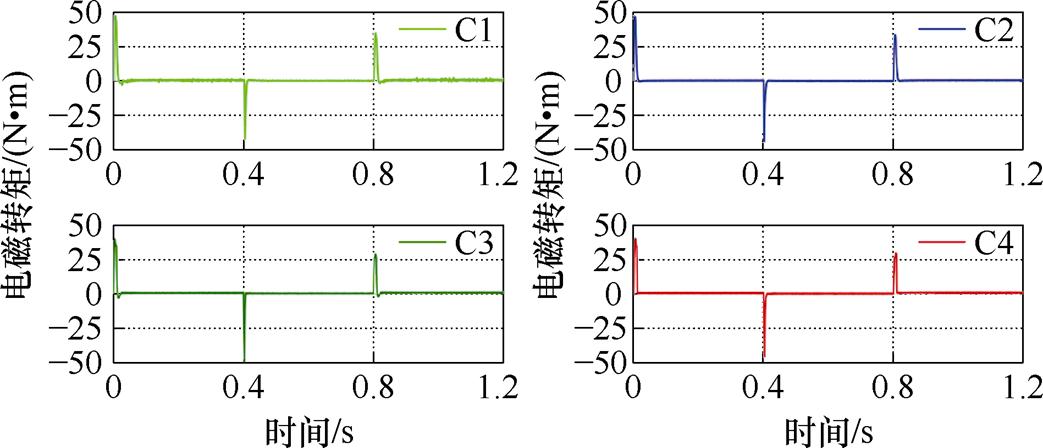
图9 空载方波给定下电磁转矩曲线
Fig.9 Curves of electromagnetic torque given by no-load square wave
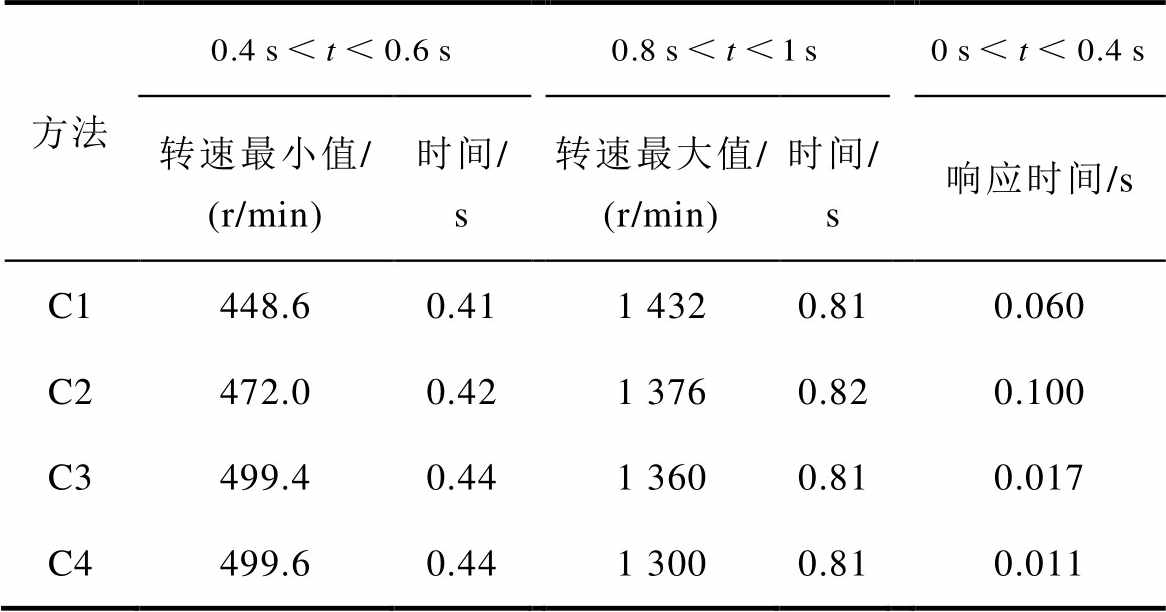
为进一步分析C1~C4方法的速度跟踪性能,针对不同时间段内的速度跟踪极值及响应时间进行整理与分析见表3,C4方法的响应速度较C1~C3分别提高了81.7%、89%、35.3%;在参考信号拐点处(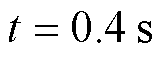 )的瞬态转速超调较C1~C3分别减小了99.2%、98.6%、33.3%;拐点处(
)的瞬态转速超调较C1~C3分别减小了99.2%、98.6%、33.3%;拐点处(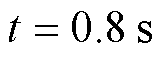 )的瞬态转速下降也显著降低。综上所述,C4方法在空载情况下的响应速度和跟踪精度较C1~C3方法有明显提升。
)的瞬态转速下降也显著降低。综上所述,C4方法在空载情况下的响应速度和跟踪精度较C1~C3方法有明显提升。
表3 空载转速跳变实验转速跟踪分析
Tab.3 Speed tracking analysis of no-load speed jump experiment
方法 转速最小值/(r/min)时间/s转速最大值/(r/min)时间/s响应时间/s C1448.60.411 4320.810.060 C2472.00.421 3760.820.100 C3499.40.441 3600.810.017 C4499.60.441 3000.810.011
2)实验二:突加负载情况下转速跟踪实验
转速给定信号为1 000 r/min,在0.5 s时施加10 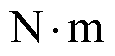 的负载转矩。基于四种方法的转速跟踪、转速误差、电磁转矩曲线分别如图10~图12所示。负载转矩观测曲线如图13所示。由图10可知,C4方法在瞬态跟踪精度和响应时间方面均优于C1~C3方法,在0.5 s突加负载时,C4的转速降落较C1~C3更小且恢复跟踪稳态时间更短,这是由于负载转矩观测器对负载转矩进行了有效观测并前馈补偿至系统中,从而提高了系统的抗扰性能。由图11可以看出,C4方法的稳态误差更小,这是由于扰动观测器对系统扰动进行有效补偿,提高了系统的跟踪精度,且分数阶算子的引入可有效削弱抖振,使跟踪曲线更为平滑。与实验一类似,由图12可知,C1~C4在跟踪稳态时的转矩输出均较为稳定,但C4在跟踪初态的瞬时转矩脉动明显小于C1~C3,具有更优的电磁转矩输出性能。由图13可知,负载转矩观测器能有效观测系统负载且响应时间较快。
的负载转矩。基于四种方法的转速跟踪、转速误差、电磁转矩曲线分别如图10~图12所示。负载转矩观测曲线如图13所示。由图10可知,C4方法在瞬态跟踪精度和响应时间方面均优于C1~C3方法,在0.5 s突加负载时,C4的转速降落较C1~C3更小且恢复跟踪稳态时间更短,这是由于负载转矩观测器对负载转矩进行了有效观测并前馈补偿至系统中,从而提高了系统的抗扰性能。由图11可以看出,C4方法的稳态误差更小,这是由于扰动观测器对系统扰动进行有效补偿,提高了系统的跟踪精度,且分数阶算子的引入可有效削弱抖振,使跟踪曲线更为平滑。与实验一类似,由图12可知,C1~C4在跟踪稳态时的转矩输出均较为稳定,但C4在跟踪初态的瞬时转矩脉动明显小于C1~C3,具有更优的电磁转矩输出性能。由图13可知,负载转矩观测器能有效观测系统负载且响应时间较快。
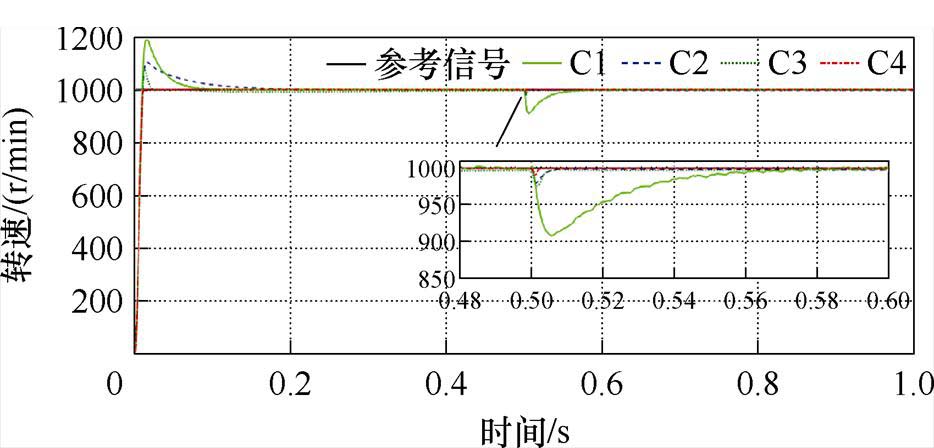
图10 突加负载情况下转速跟踪曲线
Fig.10 Curves of speed tracking under sudden load
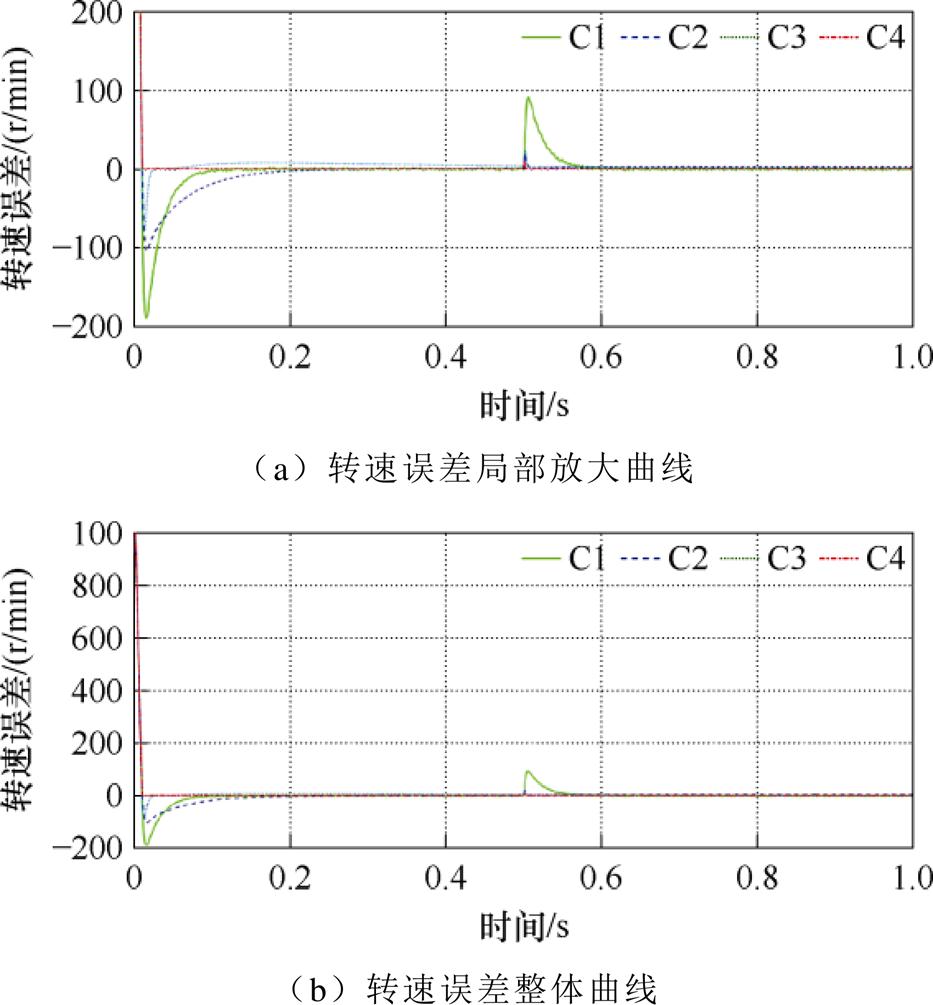
图11 突加负载情况下转速误差曲线
Fig.11 Curves of speed tracking error under sudden load
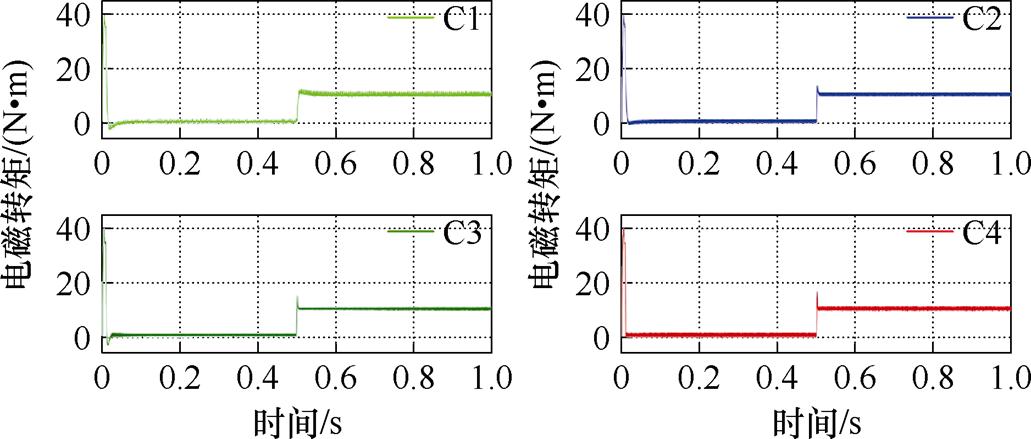
图12 突加负载情况下电磁转矩曲线
Fig.12 Curves of electromagnetic torque under sudden load
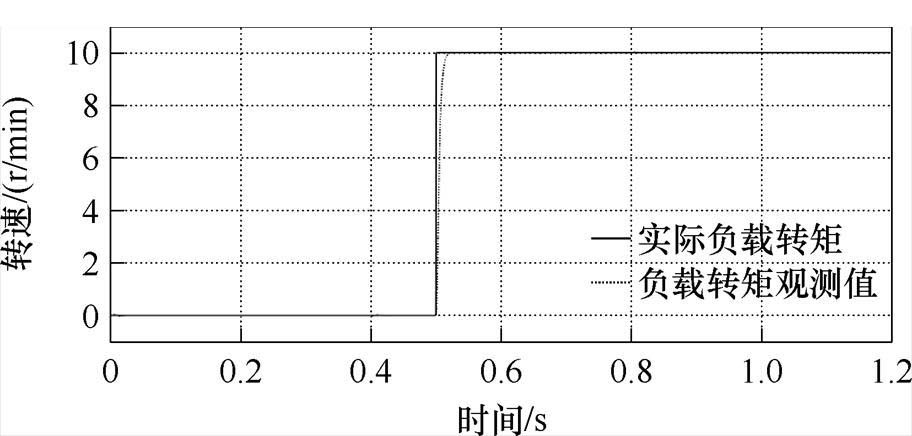
图13 突加负载转矩观测曲线
Fig.13 Observation curves of sudden load torque
此外,针对突加负载处的转速降落和恢复稳态时间进行分析,见表4,突加负载时,C4方法的转速下降较C1~C3分别降低了90.1%、55%和62.5%,转速恢复时间也更短,故负载转矩观测器使系统抗扰性能得到明显提高。
表4 突加负载实验转速跟踪分析
Tab.4 Speed tracking analysis of sudden load experiment
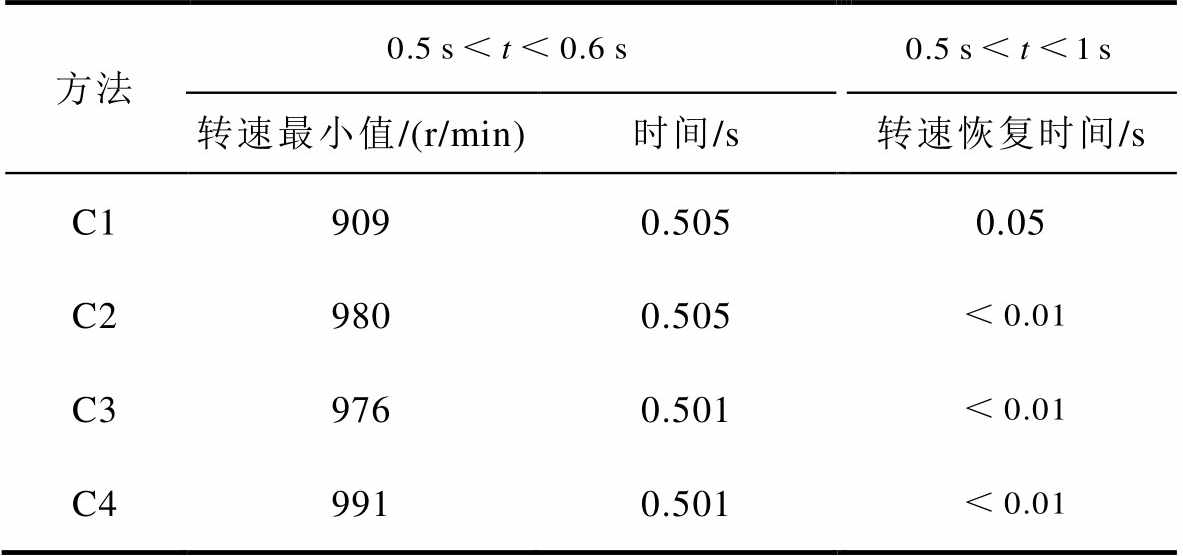
方法 转速最小值/(r/min)时间/s转速恢复时间/s C19090.5050.05 C29800.505 C39760.501 C49910.501
3)实验三:带载情况下转速跳变跟踪实验
转速参考信号同实验一,系统带动5 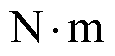 大小的负载起动,在0.6 s处再次施加大小为5
大小的负载起动,在0.6 s处再次施加大小为5 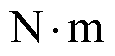 的负载转矩。基于四种方法的转速跟踪、转速误差、电磁转矩曲线分别如图14~图16所示。负载转矩观测曲线如图17所示。由图14可知,相较实验一的空载实验,系统带载起动使C4方法在跟踪初态存在一定的转速超调,但超调量较C1~C3方法更小,响应时间也更快,在0.6 s突加负载时,转速降落也更低,展现出其良好的抗扰性。从图15可知,C4的稳态跟踪误差更小且抖振较小,跟踪曲线平滑。由图16可知,C4在跟踪初态及参考曲线出现变化处的瞬态转矩脉动小于C1~C3,具有优秀的稳态电磁转矩输出特性。此外,由图17可知,负载转矩观测器对于系统负载有着良好的观测作用且跟踪时间较快。
的负载转矩。基于四种方法的转速跟踪、转速误差、电磁转矩曲线分别如图14~图16所示。负载转矩观测曲线如图17所示。由图14可知,相较实验一的空载实验,系统带载起动使C4方法在跟踪初态存在一定的转速超调,但超调量较C1~C3方法更小,响应时间也更快,在0.6 s突加负载时,转速降落也更低,展现出其良好的抗扰性。从图15可知,C4的稳态跟踪误差更小且抖振较小,跟踪曲线平滑。由图16可知,C4在跟踪初态及参考曲线出现变化处的瞬态转矩脉动小于C1~C3,具有优秀的稳态电磁转矩输出特性。此外,由图17可知,负载转矩观测器对于系统负载有着良好的观测作用且跟踪时间较快。
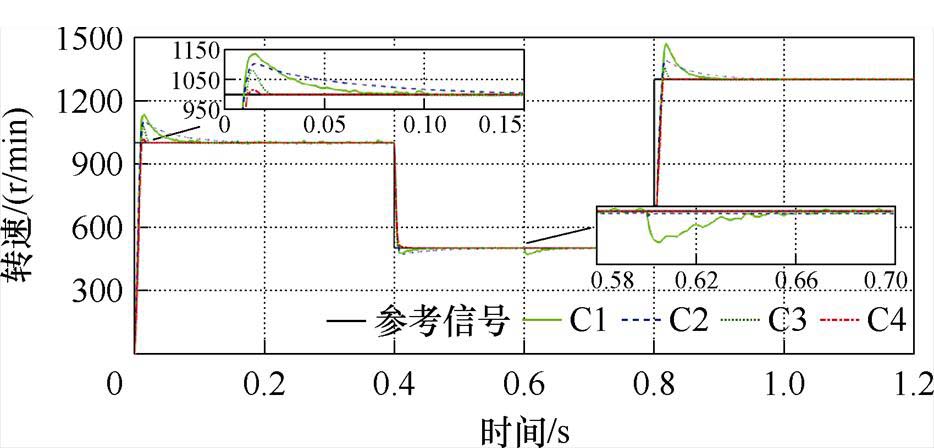
图14 带载起动情况下转速跟踪曲线
Fig.14 Curves of speed tracking in the case of starting with load
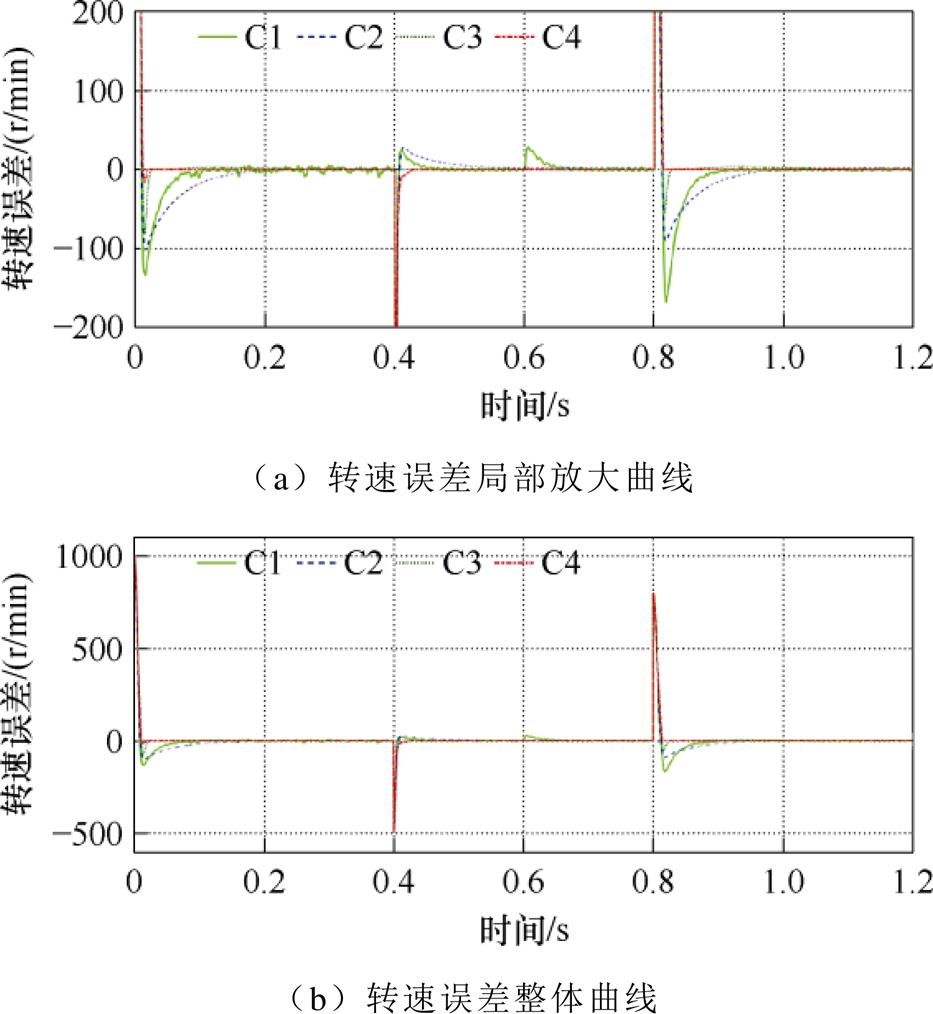
图15 带载起动情况下转速误差曲线
Fig.15 Curves of speed tracking error in the case of starting with load
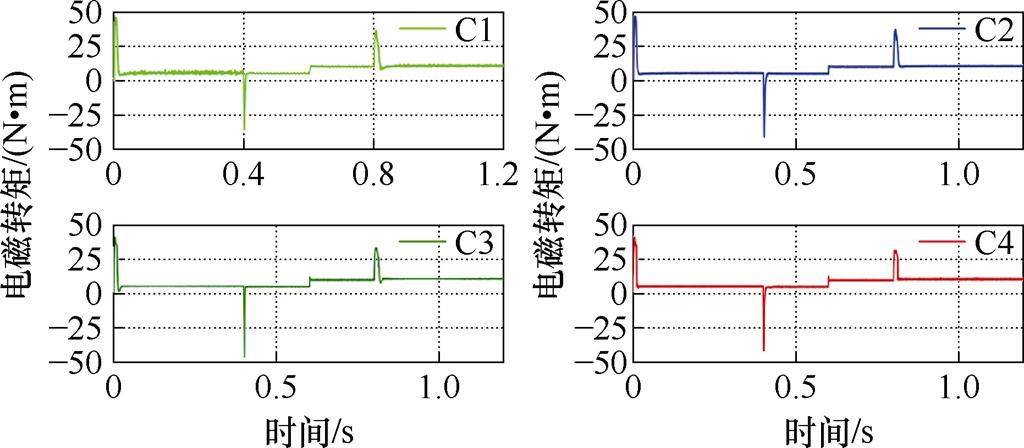
图16 带载起动情况下电磁转矩曲线
Fig.16 Curves of electromagnetic torque in the case of starting with load
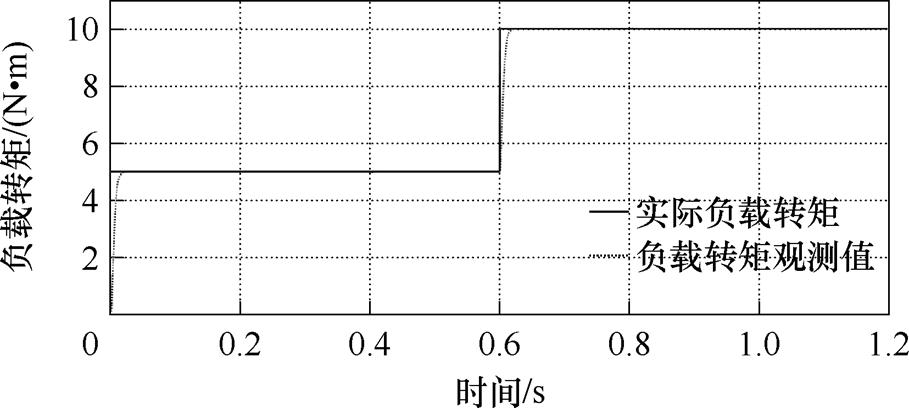
图17 带载起动负载转矩观测曲线
Fig.17 Curves of start load torque observation with load
与实验一、二相似,表5为带载起动实验中的转速分析。通过分析可知:在跟踪初态时,C4的转速跟踪超调较C1~C3分别降低了88.1%、84.2%和80.2%;在突加负载时的转速降落较C1~C3分别降低了92.4%、55.1%和54.2%。故在带载条件下,C4方法的跟踪精度、响应速度和抗扰性能均优于其他方法。
表5 带载起动实验转速跟踪分析
Tab.5 Rotational speed tracking analysis of starting experiment with load
方法 转速最大值/(r/min)时间/s转速最小值/(r/min)时间/s响应时间/s C11 1340.0154710.6050.100 C21 1010.015495.10.6000.120 C31 0810.014495.20.6000.025 C41 0160.014497.80.6000.020
4)实验四:变负载情况下转速跟踪实验
为体现在更多不同情况下的转矩变化,在同实验一的参考信号给定下进行电机的加减载实验。实验电机空载起动,在0.3 s处施加10 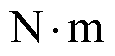 的负载转矩,在0.6 s处负载转矩减小为6
的负载转矩,在0.6 s处负载转矩减小为6 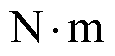 ,在0.9 s处减小为5
,在0.9 s处减小为5 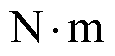 ,实验时间为1.2 s。本组实验仅将C3、C4方法的跟踪效果进行对比分析。基于C3、C4方法的转速跟踪、转速误差、电磁转矩曲线分别如图18~图20所示,负载转矩观测曲线如图21 所示。
,实验时间为1.2 s。本组实验仅将C3、C4方法的跟踪效果进行对比分析。基于C3、C4方法的转速跟踪、转速误差、电磁转矩曲线分别如图18~图20所示,负载转矩观测曲线如图21 所示。
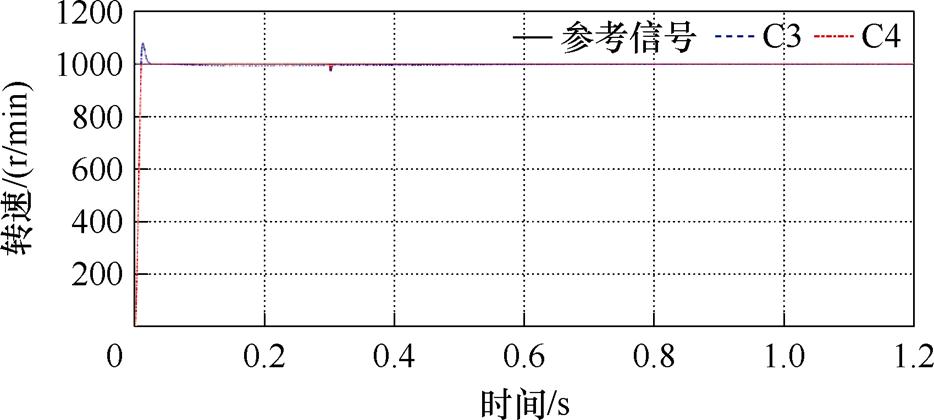
图18 加减载情况下的转速跟踪曲线
Fig.18 Speed tracking curves under loading and unloading conditions
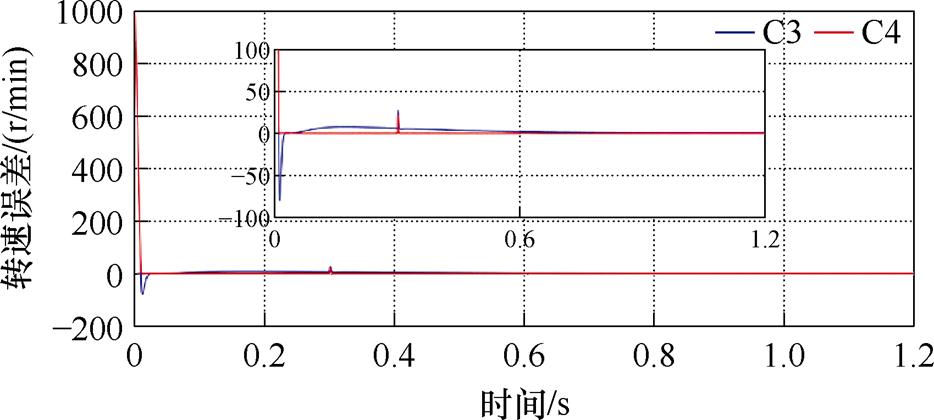
图19 加减载情况下的转速误差曲线
Fig.19 Speed error curves under loading and unloading condition
由图18、图19可知,空载起动时,C3方法存在100 r/min的转速超调,而C4方法的瞬态跟踪精度更高;在0.3 s突加负载时,C3方法存在约28 r/min左右的转速降落,而C4方法约为22 r/min,在复合观测器的前馈补偿作用下转速降落减小了约21.4%;而在0.6 s和0.9 s的减载点处,C3、C4方法的跟踪精度均保持在较高的水准,无明显转速降落,但C4的稳态跟踪精度更高。由图20可知,C4方法在加减载点处的电磁转矩能更快地恢复至稳态,较C3方法有效地削弱了电磁转矩波动。由图21可知,负载转矩观测器对系统负载有着良好的观测作用。
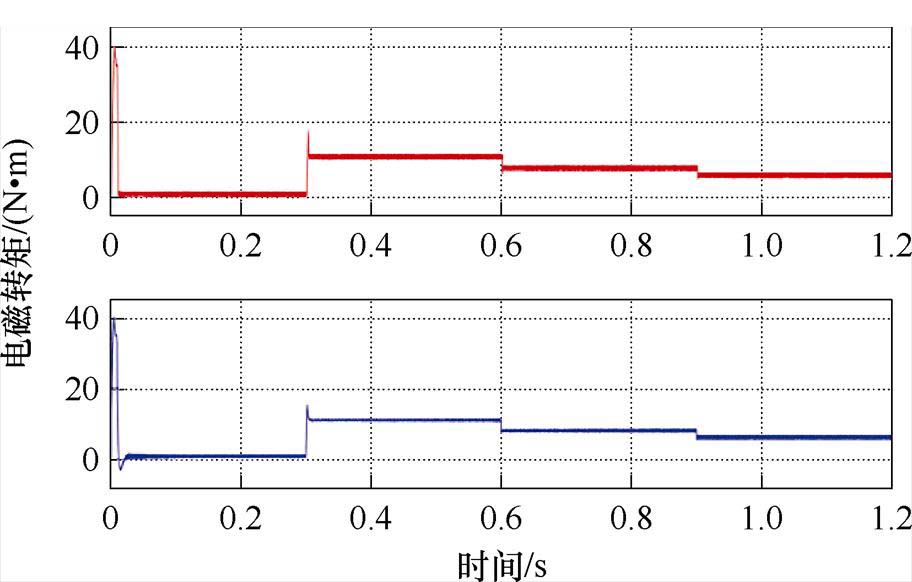
图20 加减载情况下的电磁转矩曲线
Fig.20 Electromagnetic torque curves under loading and unloading condition
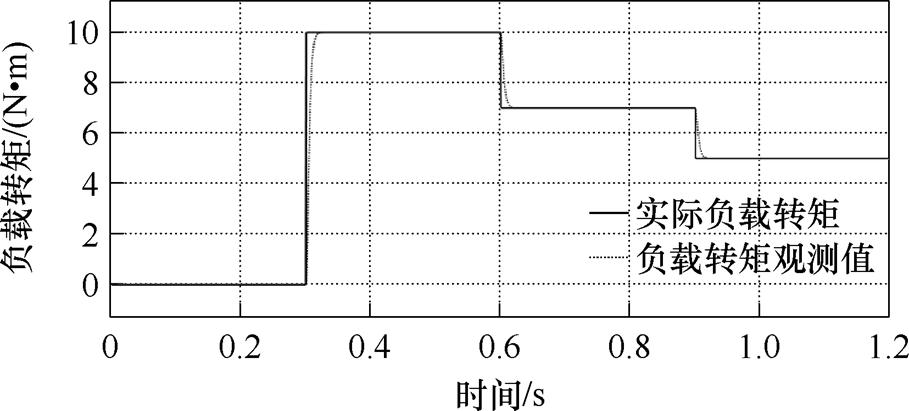
图21 加减载情况下的负载转矩观测曲线
Fig.21 Observation curves of load torque under loading and unloading condition
针对PMSM伺服系统的高精度跟踪要求,本文提出了一种复合观测器的PMSM分数阶FTSMC方法。针对传统控制方法跟踪精度较差且收敛速度较慢的问题,设计了基于分数阶FTSMC的速度控制器,由于在滑模面中加入了快速终端吸引子,且控制器参数根据系统状态进行模糊自适应调整,有效地提高了响应速度并提高了跟踪精度。同时,针对传统控制方法对系统扰动敏感且抗扰性能较差的问题,设计了复合观测器结构,即通过滑模扰动观测器和负载转矩观测器分别对系统非匹配扰动和匹配扰动进行观测,并补偿至系统控制律中,有效地提高了系统稳态跟踪精度和抗扰性能。实验结果表明,本文所提出的方法有效可行,在空载、加载和加减载情况下,均明显改善了系统的跟踪精度和抗扰 性能。
参考文献
[1] 陈荣, 翟凯淼, 舒胡平. 永磁同步电机双矢量固定开关频率模型预测控制研究[J]. 电工技术学报, 2023, 38(14): 3812-3823.
Chen Rong, Zhai Kaimiao, Shu Huping. Predictive control of dual vector fixed switching frequency model for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3812-3823.
[2] 刘忠永, 范涛, 何国林, 等. 高性能永磁同步电机显式模型预测控制算法研究[J]. 电工技术学报, 2023, 38(22): 6039-6058.
Liu Zhongyong, Fan Tao, He Guolin, et al. Research on high-performance explicit model predictive control algorithm for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6039-6058.
[3] 杨明, 刘铠源, 陈扬洋, 等. 基于PI-Lead控制的永磁同步电机双环位置伺服系统[J]. 电工技术学报, 2023, 38(8): 2060-2072.
Yang Ming, Liu Kaiyuan, Chen Yangyang, et al. Permanent magnet synchronous motor dual-loop position servo system based on PI-Lead control[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2060-2072.
[4] Guo Xin, Huang Shoudao, Lu Kaiyuan, et al. A fast sliding mode speed controller for PMSM based on new compound reaching law with improved sliding mode observer[J]. IEEE Transactions on Transpo- rtation Electrification, 2023, 9(2): 2955-2968.
[5] Xu Wei, Junejo A K, Liu Yi, et al. An efficient antidisturbance sliding-mode speed control method for PMSM drive systems[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6879-6891.
[6] 李思毅, 苏健勇, 杨贵杰. 基于自抗扰控制的永磁同步电机弱磁控制策略[J]. 电工技术学报, 2022, 37(23): 6135-6144.
Li Siyi, Su Jianyong, Yang Guijie. Flux weakening control strategy of permanent magnet synchronous motor based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6135-6144.
[7] Yu Jinpeng, Shi Peng, Dong Wenjie, et al. Neural network-based adaptive dynamic surface control for permanent magnet synchronous motors[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(3): 640-645.
[8] Mandra S, Galkowski K, Aschemann H. Robust guaranteed cost ILC with dynamic feedforward and disturbance compensation for accurate PMSM position control[J]. Control Engineering Practice, 2017, 65: 36-47.
[9] 杨帆, 赵希梅, 金鸿雁, 等. 基于广义比例积分观测器的永磁同步电机鲁棒谐振预测电流控制[J]. 电工技术学报, 2024, 39(10): 2995-3006.
Yang Fan, Zhao Ximei, Jin Hongyan, et al. Robust resonant predictive current control based on genera- lized proportional integral observer for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2995-3006.
[10] 东野亚兰, 杨淑英, 王奇帅, 等. 基于增强型扩张状态观测器的永磁同步电机低抖振高抗扰二阶终端滑模电流控制[J]. 电工技术学报, 2024, 39(8): 2434-2448.
Dongye Yalan, Yang Shuying, Wang Qishuai, et al. Enhanced extended state observer based second order terminal sliding mode current control for permanent magnet synchronous machine with low chattering and improved disturbance rejection[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2434- 2448.
[11] Mani P, Rajan R, Shanmugam L, et al. Adaptive fractional fuzzy integral sliding mode control for PMSM model[J]. IEEE Transactions on Fuzzy Systems, 2019, 27(8): 1674-1686.
[12] Ma Yuxiang, Li Dong, Li Yunhua, et al. A novel discrete compound integral terminal sliding mode control with disturbance compensation for PMSM speed system[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(1): 549-560.
[13] Zhu Changlin, Tu Qunzhang, Jiang Chengming, et al. Global fast terminal sliding mode control strategy for permanent magnet synchronous motor based on load torque Luenberger observer[J]. IEICE Electronics Express, 2021, 18(19): 20210348.
[14] 刘兴勇. 基于负载转矩观测器的船舶推进PMSM滑模控制研究[D]. 大连: 大连海事大学, 2015.
Liu Xingyong. Load torque observer based sliding mode control of ship propulsion PMSM[D]. Dalian: Dalian Maritime University, 2015.
[15] 任金霞, 何明晏, 姚广辉. 基于改进ESO和分数阶滑模的PMSM转速控制[J]. 组合机床与自动化加工技术, 2023(12): 137-141.
Ren Jinxia, He Mingyan, Yao Guanghui. PMSM speed control based on improved ESO and fractional sliding mode[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2023(12): 137-141.
[16] Calgan H. Novel tilt integral sliding mode controller and observer design for sensorless speed control of a permanent magnet synchronous motor[J]. COMPEL- the International Journal for Computation and Mathe- matics in Electrical and Electronic Engineering, 2022, 41(1): 455-470.
Abstract Due to their high efficiency, high power density, and compact structure, permanent magnet synchronous motors (PMSM) have been widely used in many fields, such as industrial robots, medical equipment, and household appliances. However, the PMSM system essentially has multivariable, nonlinear, and time-varying coupling characteristics, easily affected by external load disturbances and internal parameter fluctuations in practical applications. Traditional control methods are challenging in meeting the requirements of speed tracking accuracy in high-performance application scenarios. This paper proposes a fractional-order fast terminal sliding mode control (FTSMC) method based on a composite observer.
Firstly, the mathematical model of a non-salient pole PMSM with uncertainty is established. Then, the fractional-order calculus operator with memory property is introduced into the fast terminal sliding mode surface, and the fractional-order FTSMC method is designed. Thus, the system state trajectory can quickly approach the predefined sliding mode surface in a limited time. Fractional-order FTSMC has stronger flexibility and faster convergence speed than the traditional integer-order sliding mode control, which can effectively deal with the characteristics of nonlinear and time-varying systems. In addition, the fractional calculus operator with memory property is added to the sliding mode surface, which further weakens the chattering phenomenon common in traditional sliding mode control and improves the stability and control accuracy of the system.
Secondly, aiming at the difficulty of controller parameter selection, achieving the optimal anti-disturbance performance is difficult while ensuring tracking accuracy. We adopt the fuzzy adaptive method to update the system parameters in real-time. The control parameters are dynamically adjusted according to the system's current state through the fuzzy logic reasoning mechanism, and the system can maintain the best performance under different working conditions. This method not only simplifies the design process of the controller but also significantly improves the system's speed-tracking accuracy and anti-interference ability.
A composite observer structure is designed enhances the system's robustness to load disturbance. The sliding mode disturbance observer and the load torque observer record the system's mismatched and matched disturbances, improving the steady-state tracking accuracy and anti-disturbance performance. The experimental results show that the proposed method is practical and feasible, and the system's tracking accuracy and anti-interference performance are significantly improved.
Finally, experimental tests were conducted under no-load, loading, and unloading conditions. The experimental results show that this method exhibits excellent speed regulation ability and stability, significantly improving the tracking accuracy and anti-interference performance of the PMSM servo system.
Keywords:Permanent magnet synchronous motor, fractional calculus, fast terminal sliding mode control, fuzzy control, composite observer
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240952
辽宁省博士科研启动基金计划项目(2022-BS-177)和辽宁省科技厅揭榜挂帅项目(2023JI1, 11100004)资助。
收稿日期2024-06-04
改稿日期 2024-11-15
滕 然 男,1980年生,博士研究生,研究方向为伺服电机控制、滑模控制和预测控制等。
E-mail: TengRanTR@163.com
赵希梅 女,1979年生,教授,博士生导师,研究方向为现代伺服电机控制、机器人控制、智能控制。
E-mail: zhaoxm_sut@163.com(通信作者)
(编辑 崔文静)