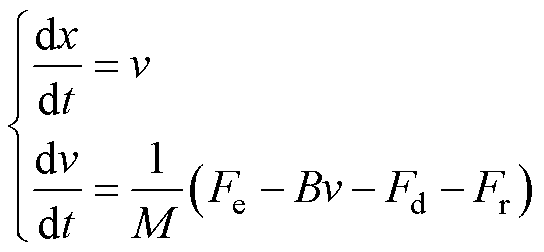 (1)
(1)
摘要 永磁直线同步电机(PMLSM)位置伺服系统运行时受到推力波动的影响容易导致位置跟踪精度不高。针对此问题,该文提出一种基于迭代学习预补偿策略的PMLSM推力波动抑制方法以提升系统控制性能。首先,对PMLSM的推力波动进行建模与分析,在PMLSM位置-电流双闭环控制结构中,利用加速度前馈控制器和扰动观测器构造二自由度位置控制器,初步抑制加减速阶段误差和推力波动。然后,利用预期迭代学习控制器进一步减小位置跟踪误差,并在此基础上拟合PMLSM的定位力扰动等效电流观测误差加以预补偿,从而改善迭代学习控制对运动模态的依赖,实现多工况下的推力波动抑制目的,提高位置跟踪精度。最后,通过实验验证该控制方案的有效性。
关键词:永磁直线同步电机 扰动观测器 迭代学习控制 推力波动抑制 预补偿
永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)具有推力密度高、动态响应快和不需要中间传动装置的特点[1-3],非常适合要求高速度和高精度的直线运动应用场合,如精密数控机床位置伺服系统等。通常情况下,精密数控机床平台的加工和测量过程为S形曲线轨迹,包含加速、匀速和减速阶段。然而,文献[4]指出精密运动系统在加减速阶段的位置跟踪误差与参考轨迹的特定阶导数成比例,因此PMLSM位置伺服系统在加减速阶段会产生较大的位置误差。此外,PMLSM存在由齿槽效应和端部效应引起的推力波动,也会直接影响伺服系统的跟踪性能和机床加工精度[5-8]。因此,如何抑制推力波动同时减小加减速阶段对位置跟踪精度的影响对于基于PMLSM的高精度位置伺服控制系统十分重要。
单自由度控制架构无法同时满足最优跟踪和抗扰要求,因此为了改善PMLSM位置伺服系统的控制性能,大多采用二自由度(2-Degree-of-Freedom, 2-DOF)控制架构。二自由度控制架构包括前馈控制器和反馈控制器。前馈控制可以在不影响系统稳定性的前提下提高系统的抗扰性能,从而辅助反馈控制系统[6]。在此基础上,国内外学者们提出了许多利用观测器抑制PMLSM推力波动的方法,将系统的扰动等效为集总扰动进行估计和补偿,如扰动观测器(Disturbance Observer, DO)和扩张状态观测器(Extended State Observer, ESO)。文献[9]提出了一种比例谐振内模扩张状态观测器来减小PMLSM推力波动引起的速度波动。文献[10]提出了一种基于多谐振扰动观测器的PMLSM推力波动抑制策略。文献[11]针对PMLSM的推力波动,设计了一种傅里叶变换补偿器和ESO的级联结构。文献[12]引入了自适应超螺旋扰动观测器并将观测结果进行前馈补偿从而降低速度跟踪误差。文献[13]在无铁心PMLSM伺服系统中采用了PID控制器、线性ESO和摩擦前馈控制器的控制方法,有效地降低了由推力波动和非线性摩擦力引起的位置跟踪误差。
然而,由于观测器的设计通常基于扰动缓慢变化的假设,并且为了抑制噪声需要限制带宽,因此难以进一步提高PMLSM位置跟踪精度。
迭代学习控制(Iterative Learning Control, ILC)可以在系统重复运动的基础上从先前操作中获得的经验中学习,沿着迭代方向逐次减小整个操作长度的跟踪误差[14]。ILC可以消除误差信号中的重复成分,对于系统的惯性滞后以及系统中的重复性扰动有很好的抑制作用。事实上,将ILC算法引入观测器是一种实用而有效的策略。文献[14]提出了一种基于ESO的数据驱动迭代学习控制方法,考虑了初始状态的非重复不确定性,不需要系统模型信息也能保证跟踪误差的收敛性。文献[15]针对不匹配扰动提出比例型ILC与ESO相结合的复合控制方法。文献[16]设计了一种基于ESO的循环迭代学习控制方法,以提高变化的连续系统的空间周期性抗扰性能。文献[17]通过采用高阶ESO来解决非重复不确定性和不确定系统模型的不良影响,从而提高ILC的跟踪精度。文献[18]提出了一种基于迭代学习原理的学习扰动观测器并成功应用于压电驱动系统。文献[19]提出了一种基于比例谐振内模扩展状态观测器的迭代学习推力波动抑制方法。文献[20]设计了一种基于ESO的变增益自适应ILC算法,有效提高了磁悬浮直线电机的跟踪性能和抗扰性能。上述文献提出的方法只适用于系统重复运动的特定工况,一旦系统运动状态发生改变,就需要重新进行迭代,限制了相应算法的适用范围。
受上述文献启发,针对PMLSM的S形曲线位置伺服系统高精度响应的运行要求,本文提出了一种基于迭代学习预补偿(Iterative Learning Pre- Compensation, ILPC)策略的PMLSM推力波动抑制方法。首先,设计了一种二自由度控制器,该控制器由加速度前馈控制器(Acceleration Feed-Forward Controller, AFFC)、反馈控制器以及扰动观测器构成,旨在初步抑制加减速阶段的误差以及推力波动。在此基础上,引入了预期迭代学习控制器(Anti- cipatory Iterative Learning Controller, AILC),利用迭代学习过程进一步抑制推力波动,从而提升系统的跟踪精度。
针对AILC在速度变化和负载状态变化后需要重新设置和学习的局限性,本文在迭代学习过程结束后,通过函数拟合建立了DO的定位力扰动等效电流观测误差与位置的函数模型,并将其应用于前馈预补偿中。与传统的二自由度控制器相比,本文提出的方法不仅能够进一步抑制推力波动造成的位置误差波动,还能减少ILC对运动模态的依赖,在不同的速度和负载状态下,该方法也能达到良好的推力波动抑制效果。最后,通过PMLSM实验平台验证了所提出的基于ILPC策略的推力波动抑制方法的有效性。
PMLSM的机械运动方程为
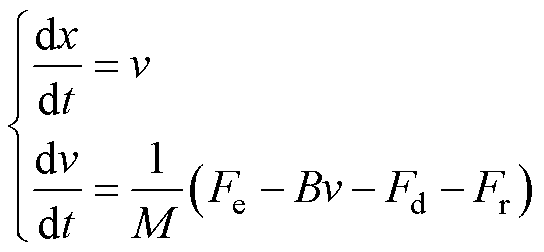 (1)
(1)
式中,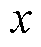 为动子位移;
为动子位移;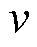 为动子速度;
为动子速度;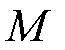 为动子质量;
为动子质量;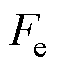 为电磁推力;
为电磁推力;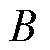 为黏滞摩擦系数;
为黏滞摩擦系数;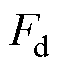 为定位力;
为定位力;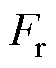 为包括线缆力在内的其余扰动的合力。
为包括线缆力在内的其余扰动的合力。
在dq同步坐标系下,PMLSM的电磁推力可以表示为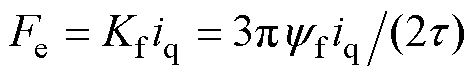 ,其中
,其中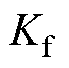 为推力系数,
为推力系数,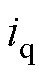 为q轴电流,
为q轴电流,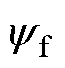 为永磁体磁链,
为永磁体磁链,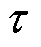 为电机极距。
为电机极距。
PMLSM的推力波动主要受端部效应和齿槽效应影响[21]。由于其初级铁心是断开的,特殊的端部效应使得电机气隙磁通密度产生畸变;铁心开槽导致的齿槽效应也会使气隙磁通密度发生变化,进而导致电机产生周期性的静磁阻力,二者的合力称为定位力,利用傅里叶级数展开的表达式[9]为
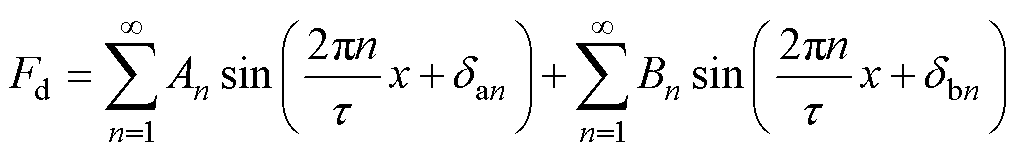 (2)
(2)
式中,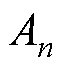 为端部力的傅里叶系数;
为端部力的傅里叶系数;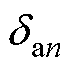 为端部力每一阶的相位;
为端部力每一阶的相位;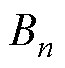 为齿槽力的傅里叶系数;
为齿槽力的傅里叶系数;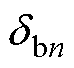 为齿槽力每一阶的相位。
为齿槽力每一阶的相位。
从式(2)可以看出,PMLSM的定位力只与电机位置有关,以极距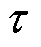 为基波周期,由不同频率不同幅值的正弦信号叠加而成。在位置伺服控制系统中,PMLSM的推力波动会产生相对应的位置误差波动,严重影响系统的控制精度和性能。
为基波周期,由不同频率不同幅值的正弦信号叠加而成。在位置伺服控制系统中,PMLSM的推力波动会产生相对应的位置误差波动,严重影响系统的控制精度和性能。
本文针对PMLSM位置伺服系统,采用位置-电流双闭环控制结构和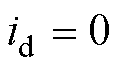 的矢量控制方式。在位置环中,反馈控制器采用PI控制器串联相位超前校正环节的PI-Lead控制器;而在电流环中,则采用传统的PI控制器。
的矢量控制方式。在位置环中,反馈控制器采用PI控制器串联相位超前校正环节的PI-Lead控制器;而在电流环中,则采用传统的PI控制器。
基于对PMLSM推力波动特性的深入分析,同时为了满足位置伺服控制系统的性能需求,本文设计了一种基于ILPC策略的PMLSM二自由度双闭环矢量控制结构,结构如图1所示,其控制流程如图2所示。
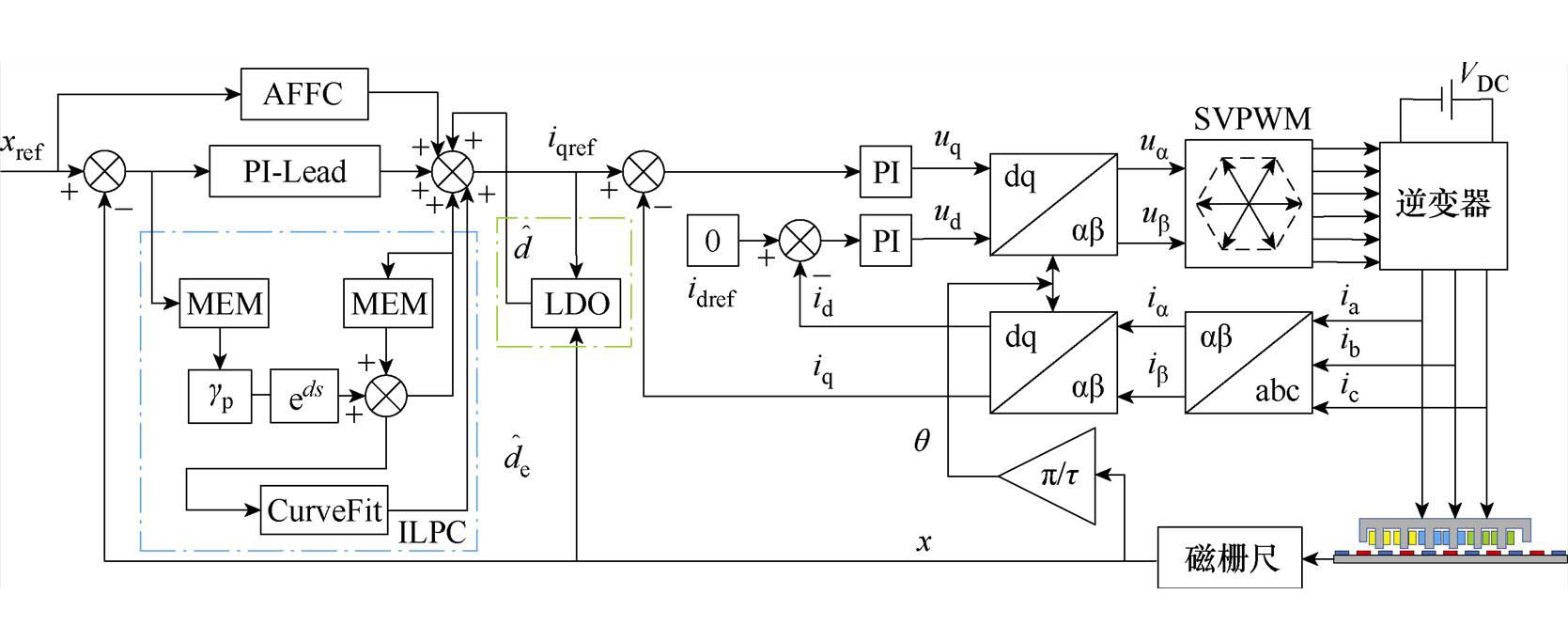
图1 基于ILPC策略的PMLSM二自由度双闭环矢量控制结构
Fig.1 Structural diagram of PMLSM 2-DOF double-closed-loop vector control based on ILPC strategy
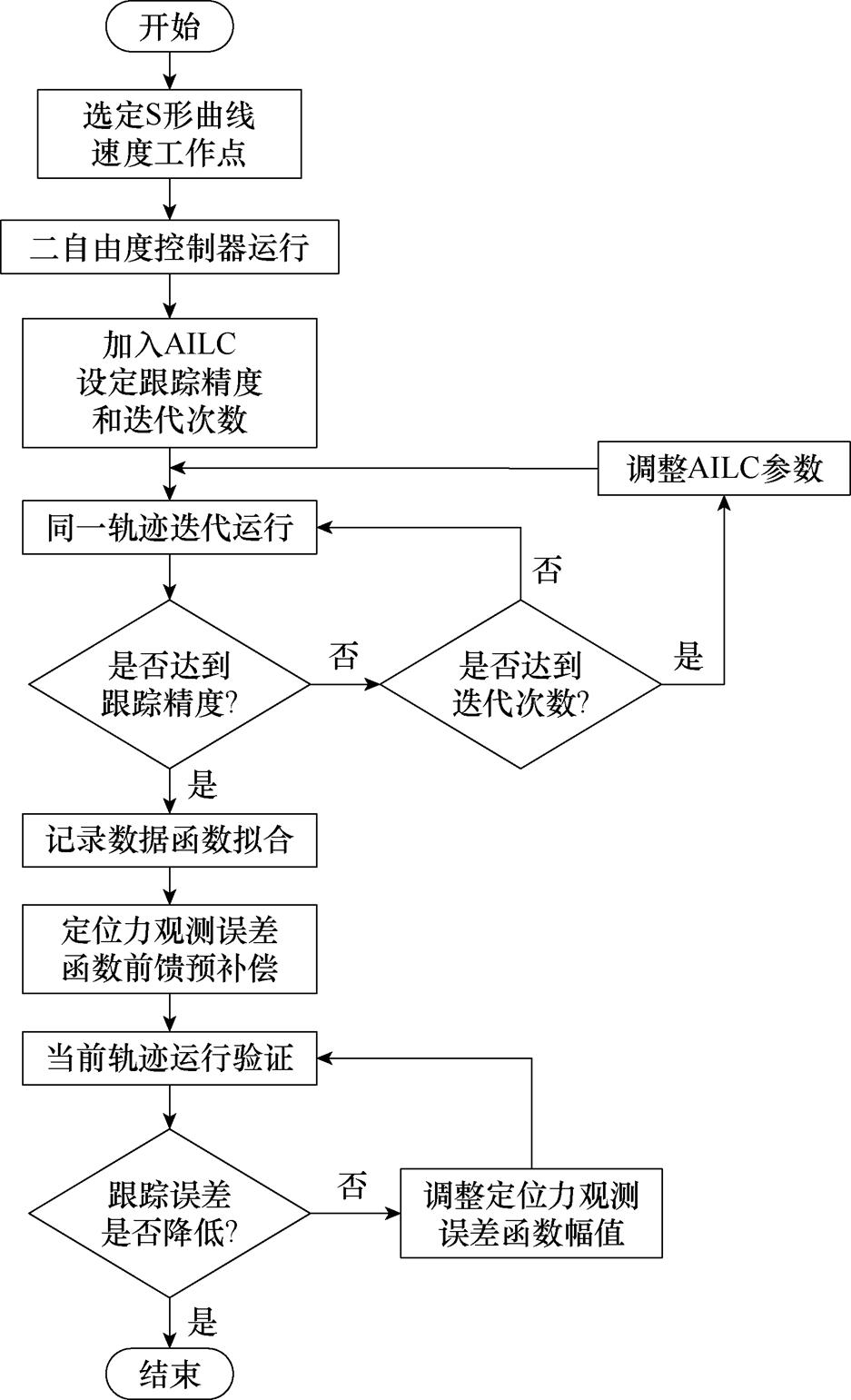
图2 ILPC策略控制流程
Fig.2 Control flow chart of ILPC strategy
本文提出的ILPC策略主要分为以下三个阶段:
(1)在迭代学习过程启动前,本文采用了由位置给定信号AFFC、DO以及PI-Lead反馈控制器组成的二自由度控制器,以初步抑制加减速阶段的误差和推力波动。
(2)在迭代学习阶段,引入了AILC以补偿DO的相位滞后和幅值失真,并将补偿信号前馈至q轴电流给定信号,进一步减少由周期性推力波动引起的位置误差。
(3)迭代学习过程完成后,AILC的前馈量使得整体位置跟踪误差降至可控范围内,推力波动中的重复分量也降低至一定水平。此时,系统控制信号中已包含大部分扰动信号。
鉴于PMLSM的定位力是由不同频率、不同幅值的正弦分量叠加而成,本文利用正弦函数和对AILC补偿信号进行拟合,建立了较为准确的基于位置的定位力扰动等效电流观测误差数学模型。通过将此正弦函数模型进行前馈预补偿,进一步抑制PMLSM的推力波动,从而提升系统的控制性能。
二自由度位置控制器由AFFC、PI-Lead反馈控制器以及DO构成,旨在保证系统稳定的情况下抑制推力波动,提高位置跟踪精度,其传递函数框图如图3所示。图中,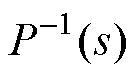 为PMLSM机械系统的名义逆模型,
为PMLSM机械系统的名义逆模型,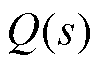 为低通滤波器,
为低通滤波器,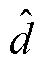 为DO输出的扰动补偿量。
为DO输出的扰动补偿量。
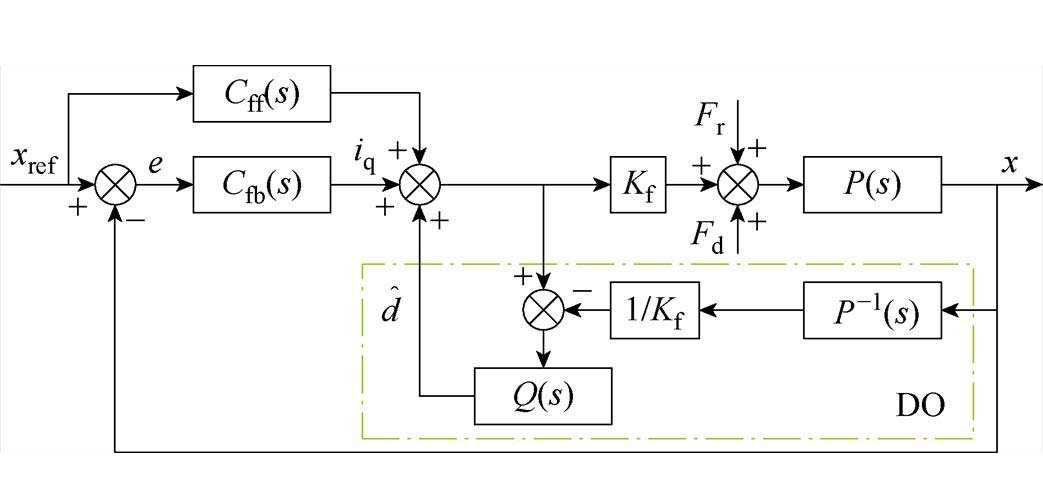
图3 二自由度控制器传递函数框图
Fig.3 Block diagram of the transfer function of a 2-DOF controller
PI-Lead反馈控制器传递函数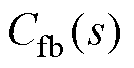 、AFFC传递函数
、AFFC传递函数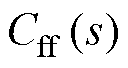 、被控对象传递函数
、被控对象传递函数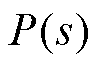 分别为
分别为
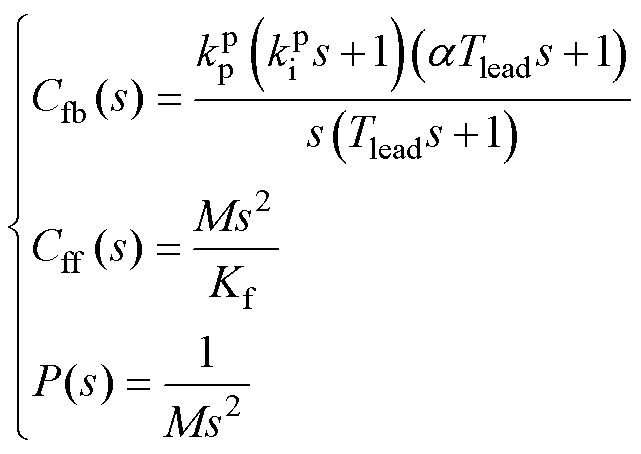 (3)
(3)
式中,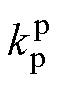 和
和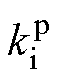 为位置环PI控制器参数;
为位置环PI控制器参数;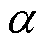 和
和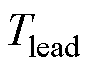 为位置环相位超前校正环节参数。
为位置环相位超前校正环节参数。
在PMLSM位置-电流双闭环控制器结构中,当位置环仅配置PI控制器时,双闭环系统开环传递函数表现为Ⅲ型系统,其中包含三个积分环节,这些积分环节引入了显著的相位滞后,导致系统的相位裕度为负值。根据频域分析判据可知,系统处于不稳定状态,因此必须引入相位补偿环节以稳定系统。
为了避免微分环节对系统噪声的放大效应,同时补偿相位滞后,位置环反馈控制器采用PI控制器串联相位超前校正环节的PI-Lead控制器,以实现系统的稳定性,同时维持原有的噪声抑制性能[22]。
此时,系统的开环传递函数表达式为
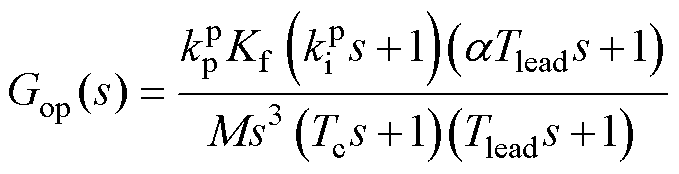 (4)
(4)
式中,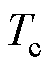 为电流环的等效惯性时间常数。
为电流环的等效惯性时间常数。
PI-Lead-PI双闭环系统的开环伯德图如图4所示。图中,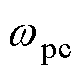 和
和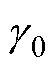 分别为相位校正前系统的开环截止频率和相位裕度,
分别为相位校正前系统的开环截止频率和相位裕度,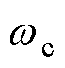 和
和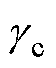 分别为相位校正后系统的开环截止频率和相位裕度,此时系统的相位裕度变为正值,伯德图清晰地展示了相位补偿的效果。
分别为相位校正后系统的开环截止频率和相位裕度,此时系统的相位裕度变为正值,伯德图清晰地展示了相位补偿的效果。
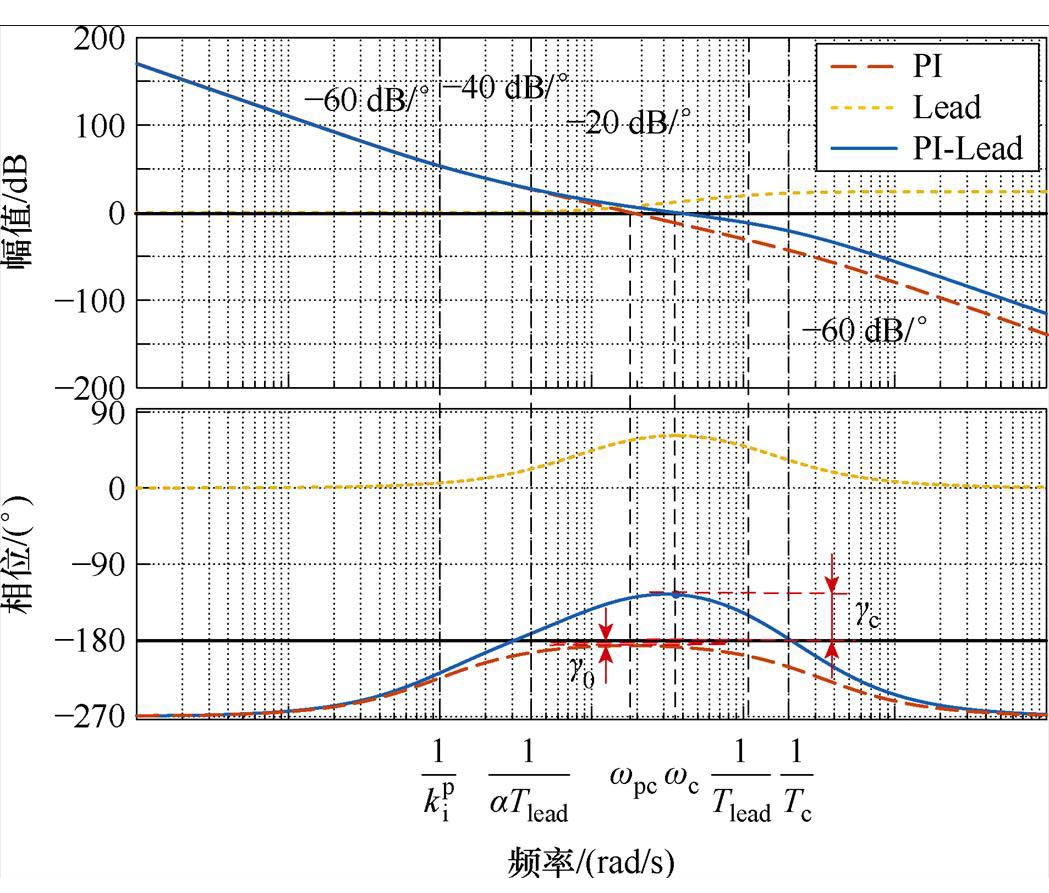
图4 PMLSM位置-电流双闭环系统开环伯德图
Fig.4 Open loop Bode diagram of PMLSM position-current double closed-loop system
基于模型的加速度前馈可以提高系统动态响应,减小S形轨迹的加减速阶段误差,而且并未改变原伺服系统内部回路结构,不会影响PI-Lead控制器的稳定性。
扰动观测器作为常用的抗扰策略,可以实时观测负载端扰动,并把扰动信号等效为q轴电流补偿量作为前馈补偿信号加在实际系统中,从而达到抑制扰动的目的。扰动观测器在PMLSM双闭环二自由度控制器中的应用原理如图3所示。
此时位置输出的表达式为
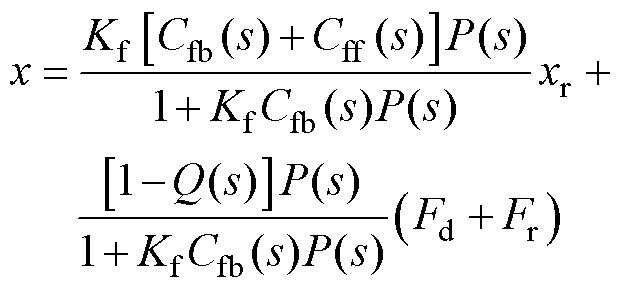 (5)
(5)
式中,xr为位置给定信号。
扰动灵敏度传递函数为
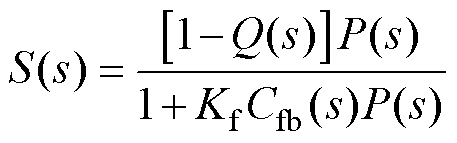 (6)
(6)
通过分析式(5)和式(6)可以观察到,DO作为内环的一部分,并未改变系统闭环传递函数的极点位置,因此不会对系统的稳定性造成影响。然而,DO的存在确实改变了系统的原始扰动灵敏度传递函数。为了有效抑制系统中的低频扰动,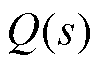 需被设计为低通滤波器。
需被设计为低通滤波器。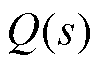 的阶数应与
的阶数应与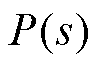 相同或更高,以确保名义逆模型的物理可实现性。在设计
相同或更高,以确保名义逆模型的物理可实现性。在设计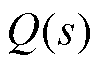 的带宽时,必须权衡系统的抗扰动性能与噪声抑制能力。带宽应选择在大于扰动信号带宽但小于噪声带宽的范围内,以避免噪声的放大。
的带宽时,必须权衡系统的抗扰动性能与噪声抑制能力。带宽应选择在大于扰动信号带宽但小于噪声带宽的范围内,以避免噪声的放大。
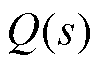 的合理设计对于提升系统性能至关重要。综合考虑滤波效果和系统复杂度,
的合理设计对于提升系统性能至关重要。综合考虑滤波效果和系统复杂度,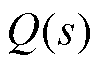 可以选择为通带范围内幅频特性最为平坦的巴特沃斯低通滤波器。由于被控对象是具有二阶积分性质的PMLSM机械系统,因此
可以选择为通带范围内幅频特性最为平坦的巴特沃斯低通滤波器。由于被控对象是具有二阶积分性质的PMLSM机械系统,因此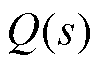 的阶数需要为二阶及以上,带宽需要大于实验电机额定速度下推力波动的基频频率,即
的阶数需要为二阶及以上,带宽需要大于实验电机额定速度下推力波动的基频频率,即
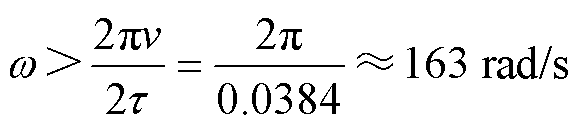 (7)
(7)
巴特沃斯低通滤波器的阶数分别选择二阶和三阶,带宽分别选择200 rad/s和500 rad/s,对比分析不同阶数和不同带宽下,1-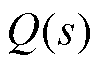 的伯德图如图5所示。
的伯德图如图5所示。
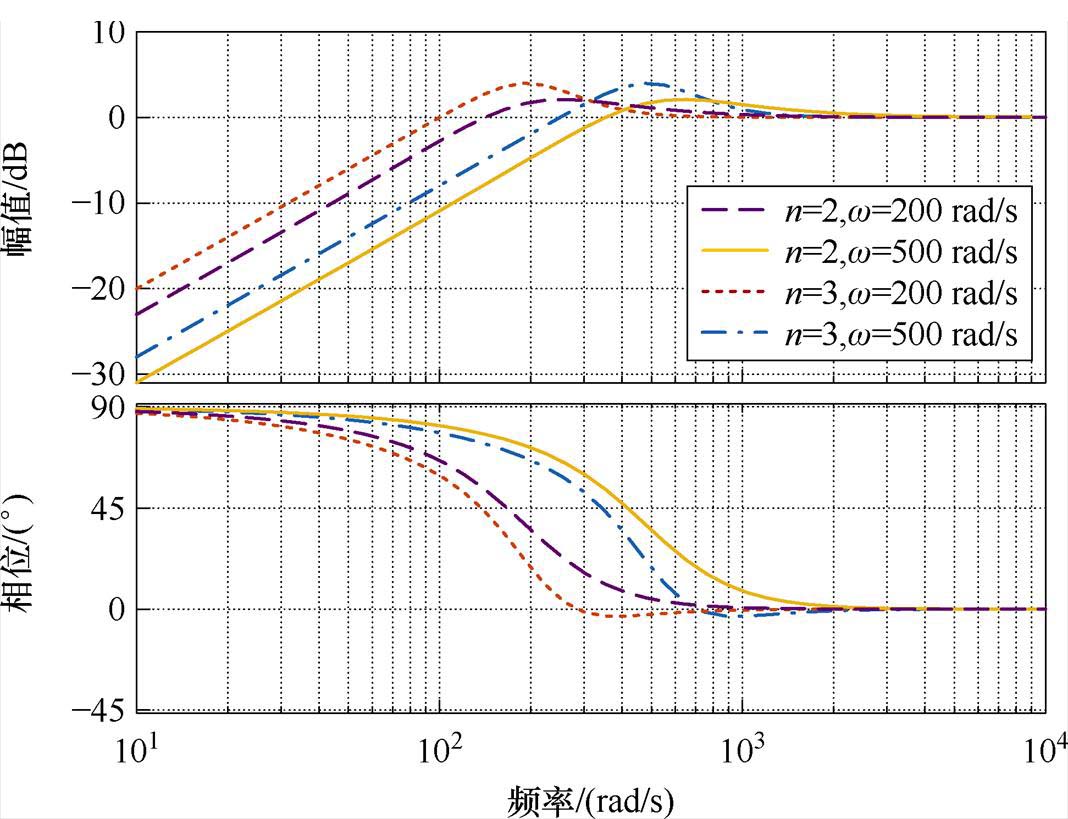
图5 不同阶数和不同带宽下1-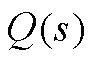 的伯德图
的伯德图
Fig.5 Bode plots of 1-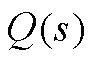 at different orders and bandwidths
at different orders and bandwidths
由图5可以看出,在相同的带宽下,DO的阶数越高,频率特性中0 dB以上的尖峰越大;在相同的阶数下,DO的带宽越高,系统对中高频噪声的抑制能力越差。综合以上分析,需要根据实际系统合理地选择DO的阶数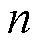 以及带宽
以及带宽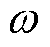 。
。
DO中低通滤波器的带宽有限,且相位滞后不可避免,以推力波动为主的外部扰动难以被准确观测并完全补偿。而迭代学习控制作为一种根据以往实验经验提供前馈控制输入的方法,可以抑制系统中的重复性扰动,显著提高系统跟踪精度。因为迭代学习控制依赖于系统在重复轨迹上的多次运行,而同一运行轨迹和运行状态下,推力波动在同一位置的幅值不变,因而具有周期性的特点,只要迭代学习控制参数满足收敛条件,推力波动在理论上可以被完全抑制。引入迭代学习控制可以补偿扰动观测器观测出的扰动的相位滞后和幅值失真,以进一步抑制推力波动,减小位置跟踪误差。
为了避免位置差分信号带来额外的噪声误差,同时提供超前相位补偿,ILC选用开环A型算法,学习增益用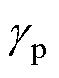 表示,超前时间系数用
表示,超前时间系数用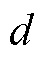 表示。
表示。
第j-1次位置误差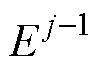 经AILC算法延迟并放大后与第j-1次迭代补偿前馈量
经AILC算法延迟并放大后与第j-1次迭代补偿前馈量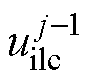 叠加,生成第j次迭代修正输入
叠加,生成第j次迭代修正输入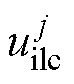 ,然后将
,然后将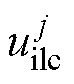 存入存储器中,作为下一迭代周期的补偿前馈量。AILC的输出传递函数可以表示[17]为
存入存储器中,作为下一迭代周期的补偿前馈量。AILC的输出传递函数可以表示[17]为
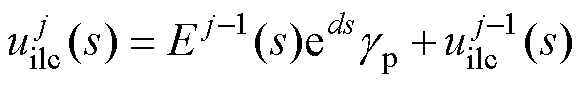 (8)
(8)
在结合AILC的二自由度控制器中,第j次迭代时的位置误差的表达式为
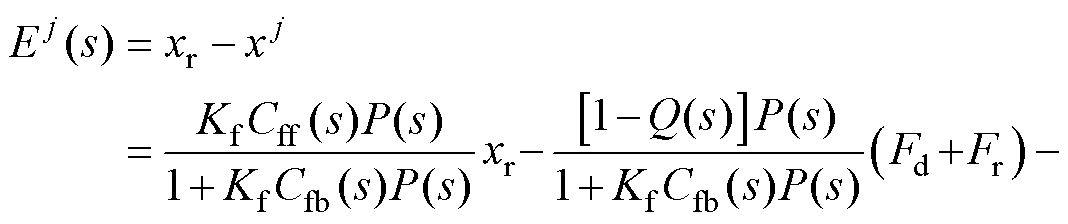
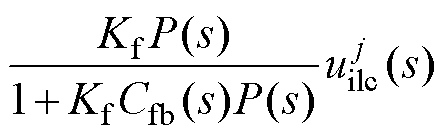 (9)
(9)
结合式(8)与式(9),可得递归形式的增量误差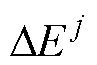 ,其中
,其中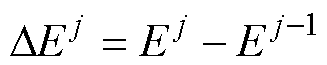 。
。
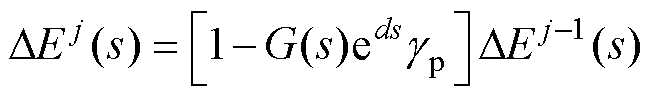 (10)
(10)
其中
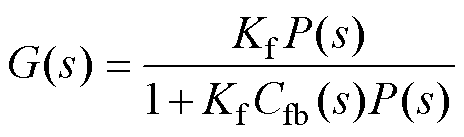
由式(10)可以推导出AILC的收敛条件为
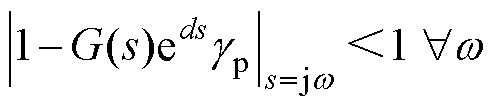 (11)
(11)
被控对象传递函数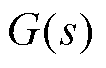 的频率响应可以表示为
的频率响应可以表示为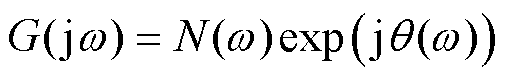 ,其中
,其中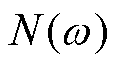 和
和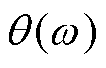 分别为其幅值特性和相位特性,此时收敛条件式(11)变为
分别为其幅值特性和相位特性,此时收敛条件式(11)变为
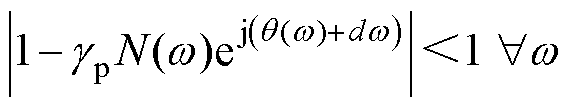 (12)
(12)
收敛条件可以分解为幅值和相位条件,即对于所有的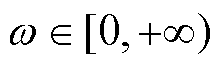 ,都有
,都有
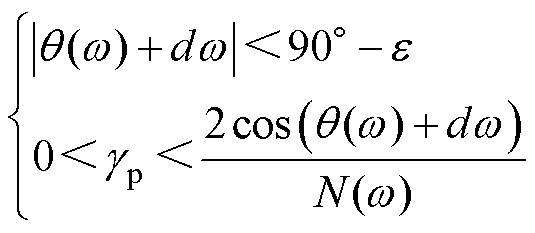 (13)
(13)
式中,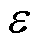 为相位裕度系数,是大于零的正实数。
为相位裕度系数,是大于零的正实数。
收敛条件中的相位条件至关重要,因为若满足相位条件,总能找到一个足够小的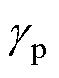 满足幅值条件。然而,对于大多数系统来说,并不能保证所有频率均满足该必要条件。收敛条件成立的频率范围称为学习频带,学习频带越宽,实际输出到期望输出的跟踪就越精确[23]。
满足幅值条件。然而,对于大多数系统来说,并不能保证所有频率均满足该必要条件。收敛条件成立的频率范围称为学习频带,学习频带越宽,实际输出到期望输出的跟踪就越精确[23]。
接下来探究基于AILC的PMLSM二自由度控制器中超前时间系数d对系统收敛性和学习频带的影响,相位裕度系数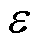 选取为10°,不同d值对系统的影响如图6所示。
选取为10°,不同d值对系统的影响如图6所示。
由图6可知,当d选取为0时,系统的学习频带最窄,仅为650 rad/s左右;当d选取为4时,系统的学习频带最宽,可以达到约6 000 rad/s。d值太小或者太大都会影响系统的学习频带,进而影响系统的跟踪性能。
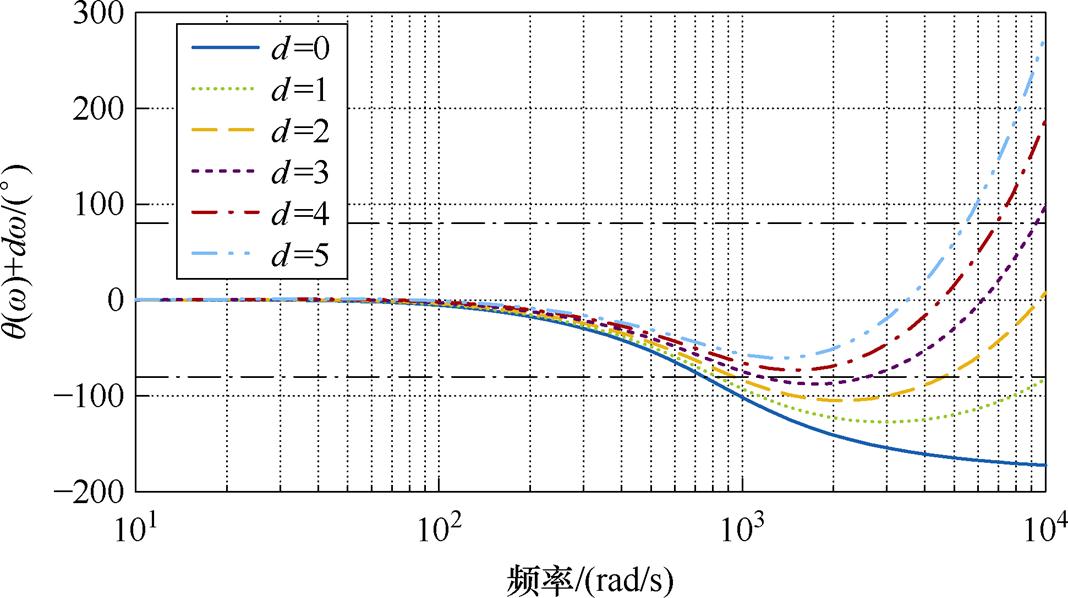
图6 不同d值的收敛条件曲线
Fig.6 Convergence condition curves for different values of d
为了验证所提推力波动抑制方法的可行性和有效性,在如图7所示的PMLSM实验平台上进行了不同控制器在不同工况下的对比实验,实验PMLSM的具体参数见表1。控制器主控芯片采用STM32F407,实验所用的PMLSM装配有Nidec公司生产的磁栅尺PLSH-050,其分辨率为0.5 mm,三相逆变器的开关频率和控制系统的采样频率均为10 kHz,实验数据和波形通过SEGGER公司出品的J-link与J-scope进行传输。

图7 PMLSM实验平台
Fig.7 PMLSM experimental platform
表1 PMLSM参数
Tab.1 Parameters of PMLSM
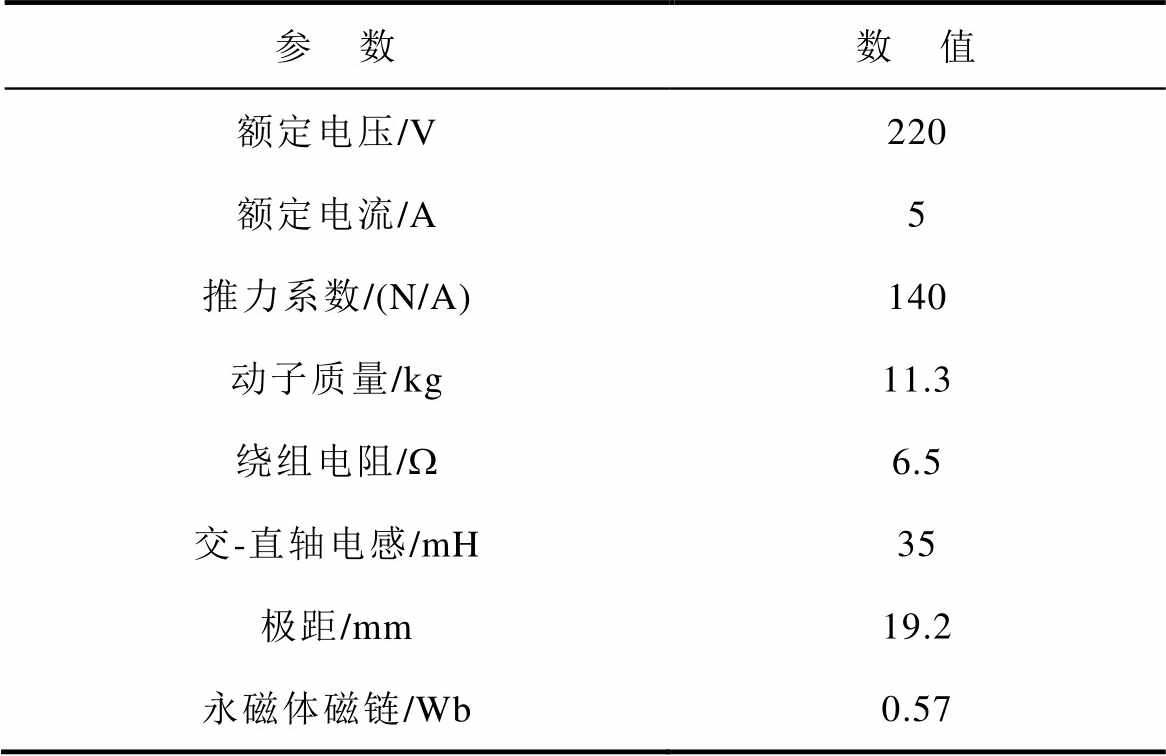
参 数数 值 额定电压/V220 额定电流/A5 推力系数/(N/A)140 动子质量/kg11.3 绕组电阻/W6.5 交-直轴电感/mH35 极距/mm19.2 永磁体磁链/Wb0.57
位置环PI-Lead反馈控制器参数设置为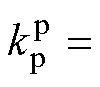 41 840,
41 840,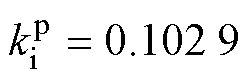 ,
,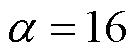 ,
,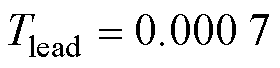 ;DO中的低通滤波器阶数设置为二阶,截止频率设置为
;DO中的低通滤波器阶数设置为二阶,截止频率设置为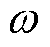 =200 rad/s;AILC的学习增益
=200 rad/s;AILC的学习增益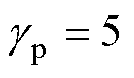 ,超前时间系数
,超前时间系数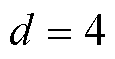 。AILC跟踪精度要求设置为误差绝对值不超过15 mm,迭代次数设置为20次。
。AILC跟踪精度要求设置为误差绝对值不超过15 mm,迭代次数设置为20次。
PMLSM位置伺服系统的应用场景之一是能够快速定位至给定位置,因此本节首先进行了定位响应速度对比实验。为了减小控制器积分饱和对位置跟踪性能产生的影响,位置给定信号规划二阶多项式S形轨迹,实际位移0.04 m,加速度a=50 m/s2,最高速度为v=1 m/s,引入AILC前后的实验结果如图8所示。
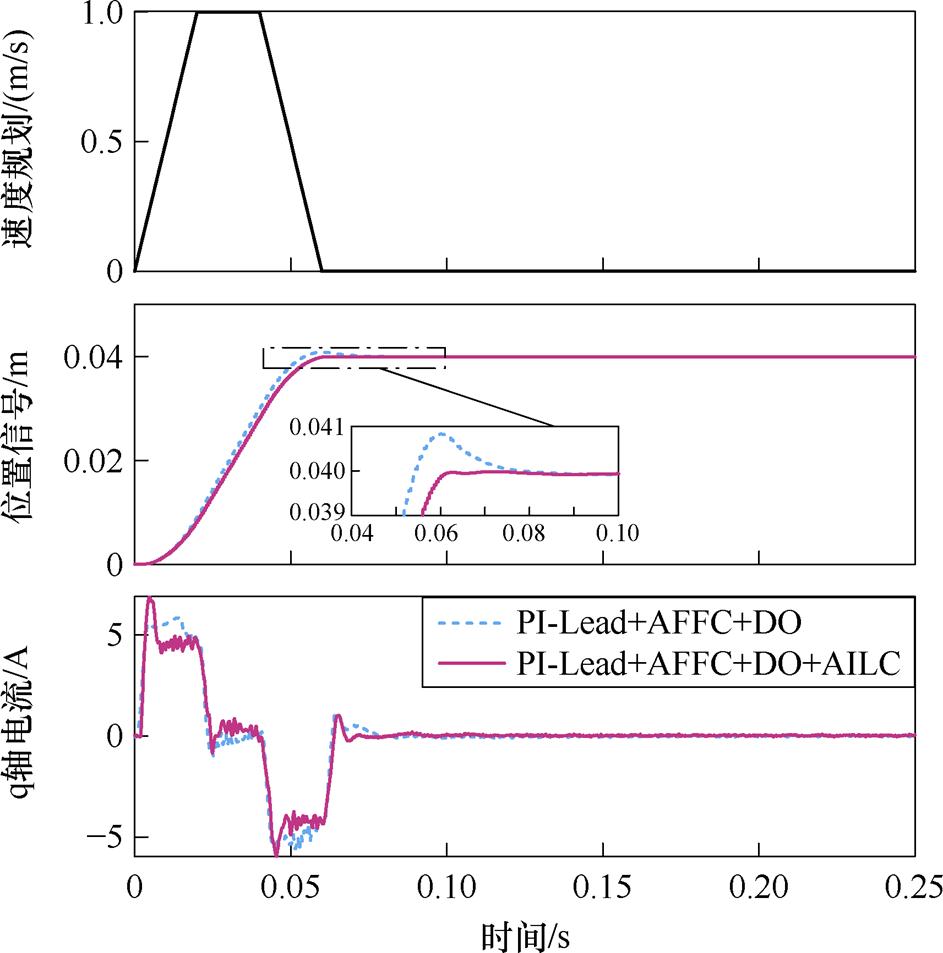
图8 响应速度实验结果
Fig.8 Experimental results of response speed
实验结果表明,引入AILC之后,通过20次重复迭代运行不仅消除了传统二自由度控制器响应的超调量,而且进一步缩短了定位所需时间,证明了结合AILC的PMLSM二自由度控制器在定位响应速度方面的优越性。
将电机动子定位之后,在实验平台上进行了不同工况下的PMLSM推力波动抑制对比实验,通过测量位置跟踪误差来对推力波动抑制效果进行评估。
PMLSM运动过程设置为二阶多项式S形轨迹,位移x=0.3 m,速度v=0.5 m/s,加速度a=5 m/s2。空载条件下三种控制器对应的实验结果如图9所示,位置跟踪误差的最大值、最小值和方均根值(Root Mean Square, RMS)见表2。
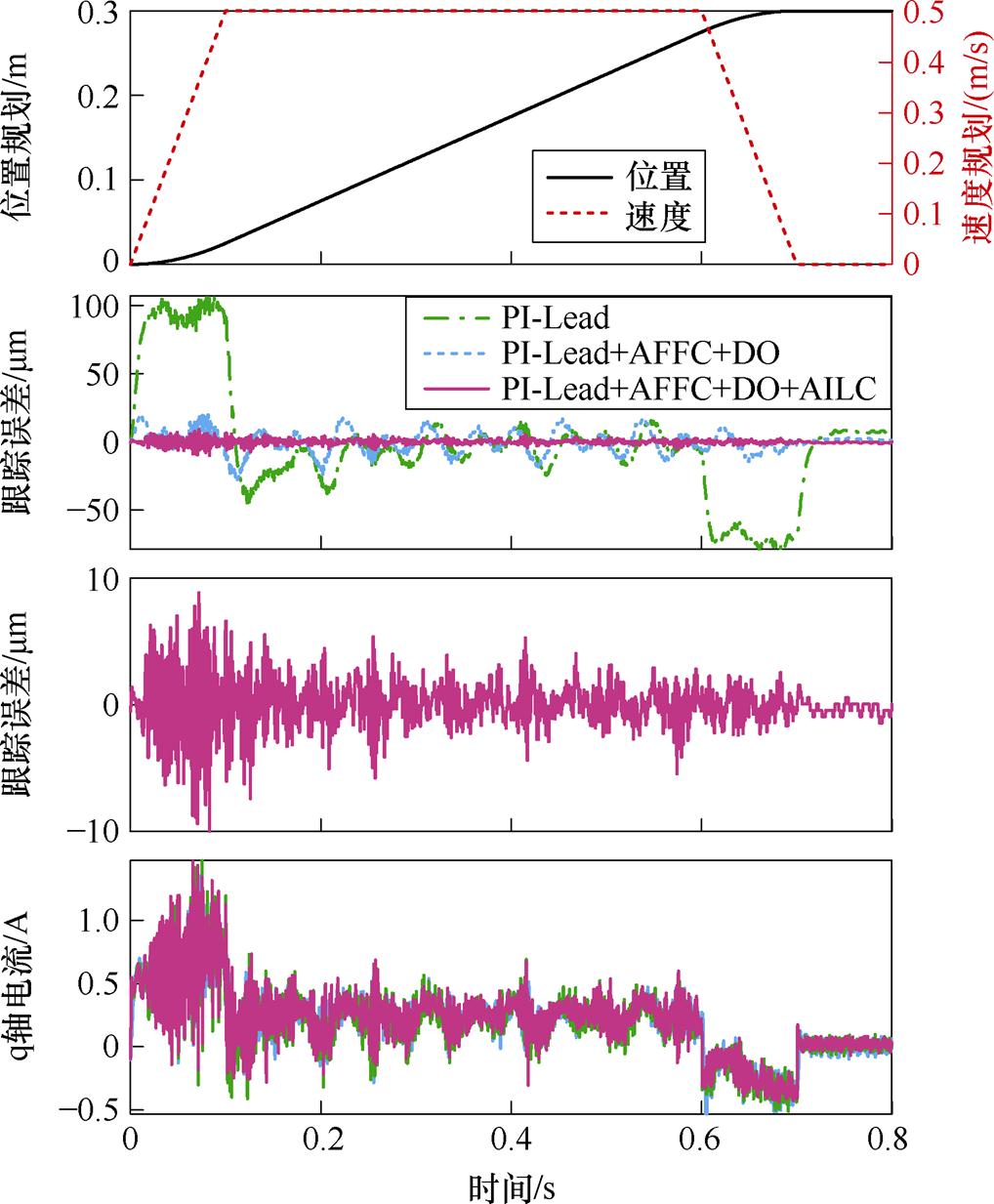
图9 v=0.5 m/s时三种控制器的实验结果
Fig.9 Experimental results of three controllers at the velocity of 0.5 m/s
表2 不同控制器的位置跟踪误差
Tab.2 Position tracking error for different controllers (单位: mm)
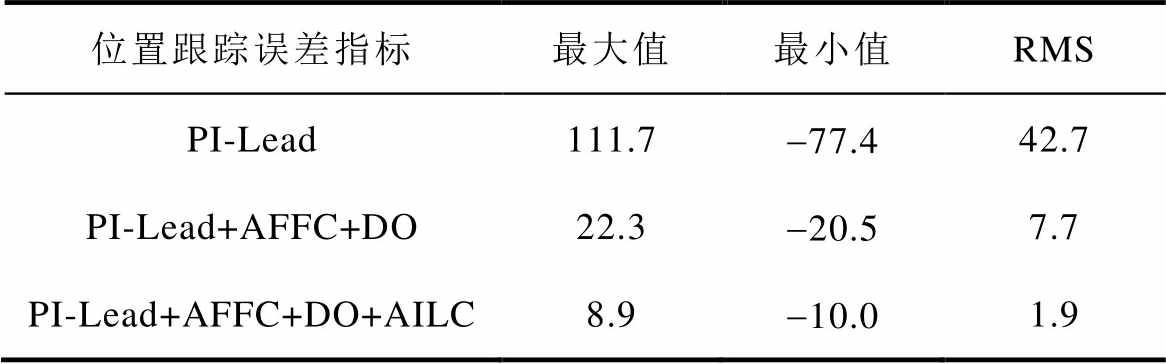
位置跟踪误差指标最大值最小值RMS PI-Lead111.7-77.442.7 PI-Lead+AFFC+DO22.3-20.57.7 PI-Lead+AFFC+DO+AILC8.9-10.01.9
由图9和表2可以看出,单自由度控制器(PI-Lead)在电机加减速阶段位置跟踪误差较大,匀速阶段由推力波动导致的误差波动非常明显,无法兼顾跟踪和抗扰要求;传统二自由度控制器(PI-Lead+AFFC+DO)极大地削弱了加减速阶段位置误差峰值,但是匀速段对于推力波动的抑制效果有限;而加入AILC的二自由度控制器在减小重复性扰动的同时抑制了非重复性干扰和随机误差,经过20次迭代之后误差方均根值降至1.9 mm,且运动全程位置跟踪误差未超过±10 mm,实现了跟踪精度要求和整体控制性能的提升。
电机机械参数失配会影响AFFC和DO的参数整定结果,进而影响位置跟踪精度。因此,在空载条件下和第3.2节设置的二阶多项式S形轨迹中,针对电机机械参数失配进行了AILC结合二自由度控制器的参数鲁棒性实验,通过改变动子质量标定值为实际值的80%和120%来模拟电机机械参数失配情况,两种控制器的跟踪误差和q轴电流如图10所示。
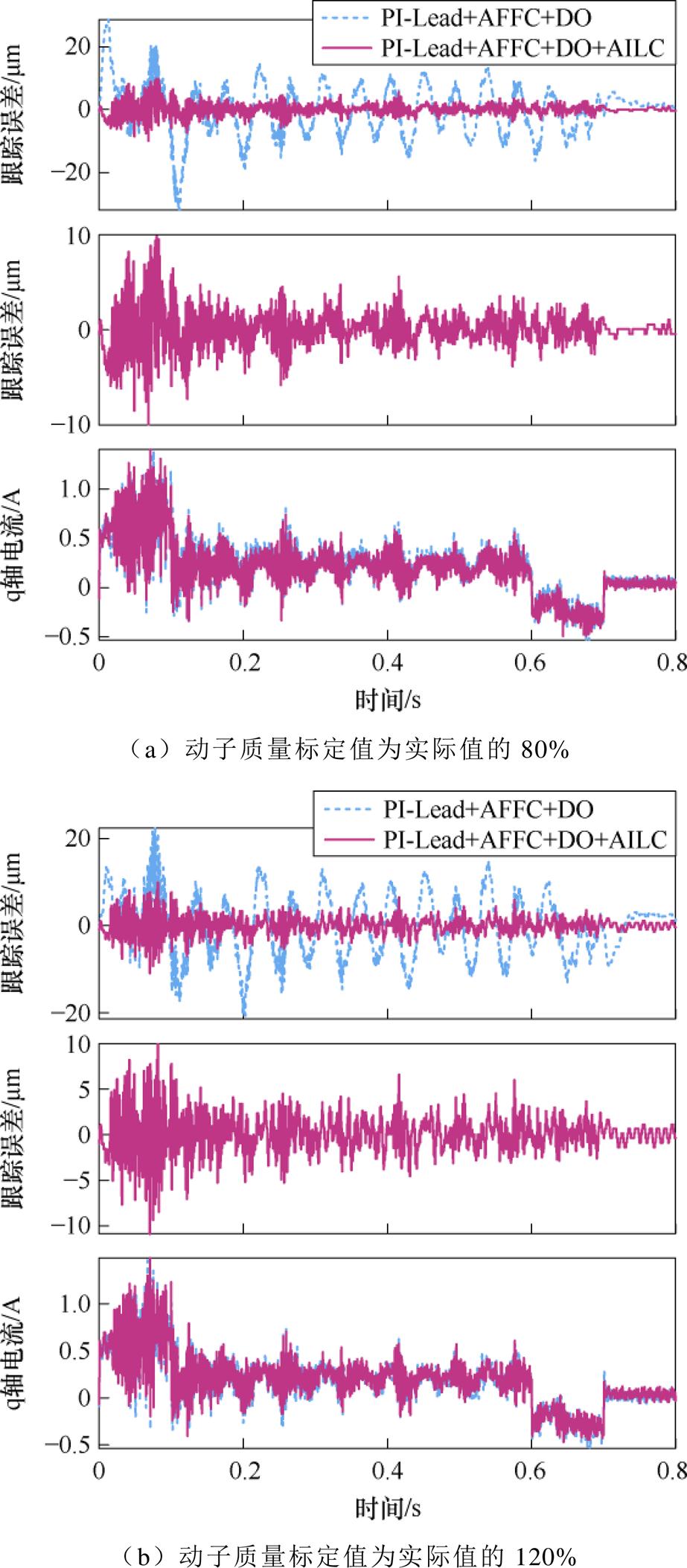
图10 v=0.5 m/s时机械参数失配情况下的实验结果 Fig.10 Experimental results of v=0.5 m/s when mechanical parameters are mismatched
实验结果表明,结合AILC的二自由度控制器在电机参数失配的情况下,经过20次迭代之后全程位置跟踪误差依然可以保持在±12 mm之内,能够抑制推力波动带来的位置跟踪误差波动,具有较强的参数鲁棒性。
将DO输出分离直流量之后,对AILC补偿前后的定位力扰动等效电流信号进行分析如图11所示。
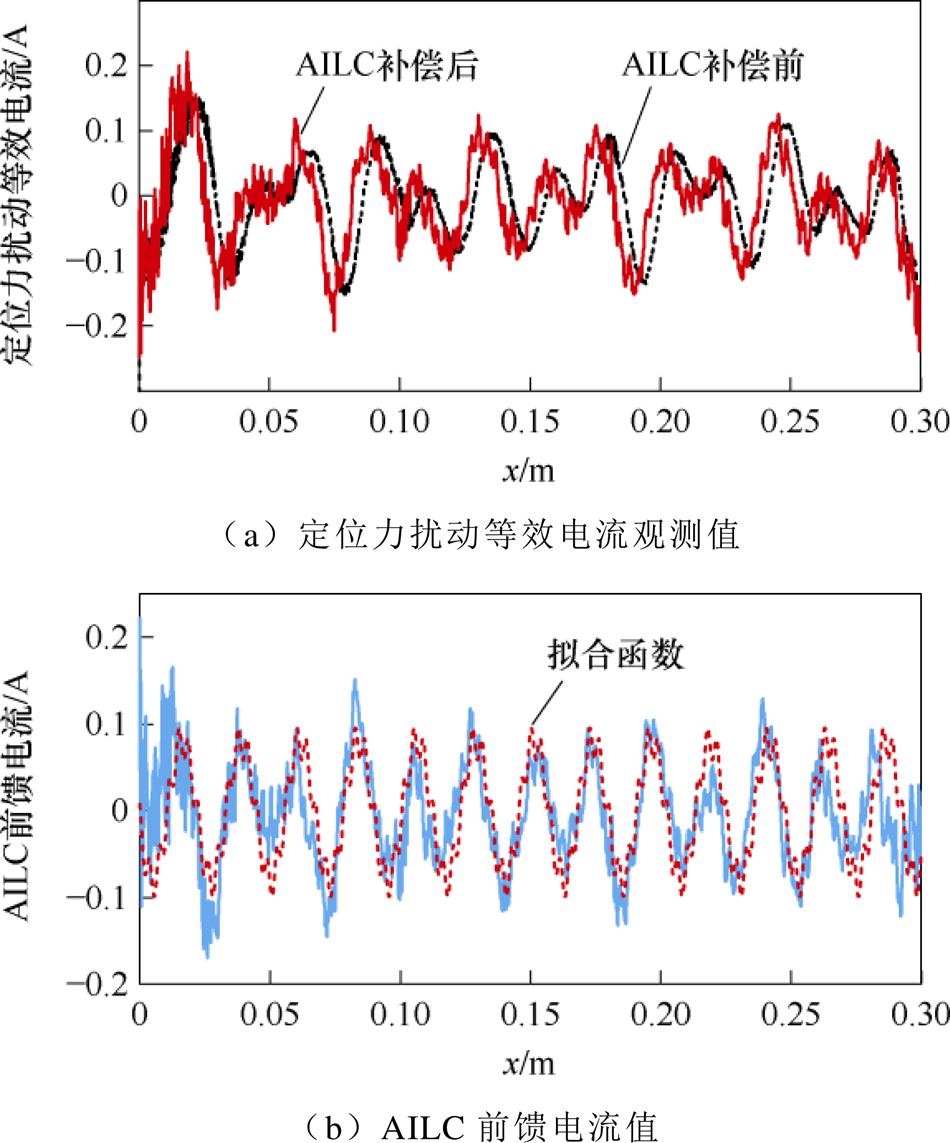
图11 AILC补偿信号分析
Fig.11 Analysis of AILC compensation signal
由图11a可以看出,虽然AILC的补偿会引入高频噪声,但是可以有效改善DO的相位滞后和幅值失真,准确定位力扰动等效电流显示的频率特征。由图11b可以看出,AILC前馈电流信号中主要包含基频信号和六倍频信号,对其利用正弦函数拟合,可以得到相对准确的基于定子位置的定位力扰动等效电流观测误差信号的频率和相位,函数拟合结果为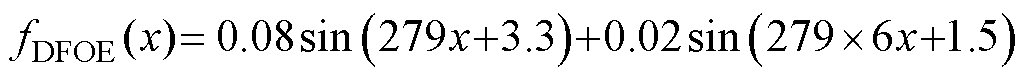 ,在二自由度控制器结构中将k倍
,在二自由度控制器结构中将k倍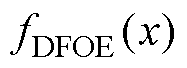 前馈补偿至匀速运动期间的q轴电流给定信号,其中
前馈补偿至匀速运动期间的q轴电流给定信号,其中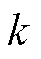 为与速度成正比的修正系数,设置
为与速度成正比的修正系数,设置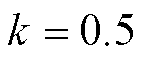 ,保持第3.2节设置的二阶多项式S形轨迹与速度不变继续运行进行验证。空载条件下,加入ILPC和未加入ILPC的跟踪误差、q轴电流对比结果如图12所示。
,保持第3.2节设置的二阶多项式S形轨迹与速度不变继续运行进行验证。空载条件下,加入ILPC和未加入ILPC的跟踪误差、q轴电流对比结果如图12所示。
由图12可知,引入ILPC前馈补偿电流后,空载条件下的位置跟踪误差RMS由7.7 mm下降至5.06 mm,降幅达到34.3%。实验结果证实,基于ILPC策略的PMLSM推力波动抑制方法能够有效地抑制定位力波动,提升二阶S形曲线的位置跟踪精度。
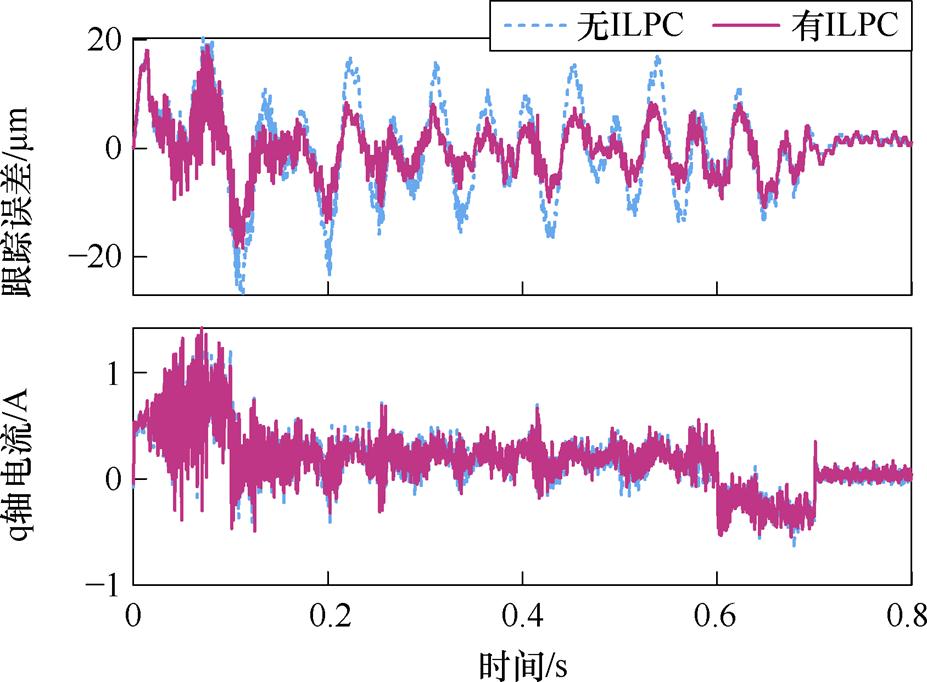
图12 v=0.5 m/s时的实验结果
Fig.12 Experimental results at the velocity of 0.5 m/s
ILPC策略可以改善迭代学习控制依赖特定的运动模态的缺点,为了验证这一结论,本文在保持二阶多项式S形轨迹规划位移0.3 m不变的条件下,对0.2 m/s(加速度a=2 m/s2)和1.0 m/s(加速度a=10 m/s2)高低两组速度工作点进行了空载条件下的推力波动抑制对比实验。空载工况下加入ILPC前后电机的位置跟踪误差、q轴电流、ILPC前馈补偿电流波形如图13所示。
由图13可知,引入ILPC后,空载条件下,电机运行速度为0.2 m/s时的位置跟踪误差RMS由5.94 mm下降至4.12 mm,降幅达到30.64%;电机运行速度为1.0 m/s时位置跟踪误差RMS由8.99 mm下降至7.43 mm,降幅达到17.35%。
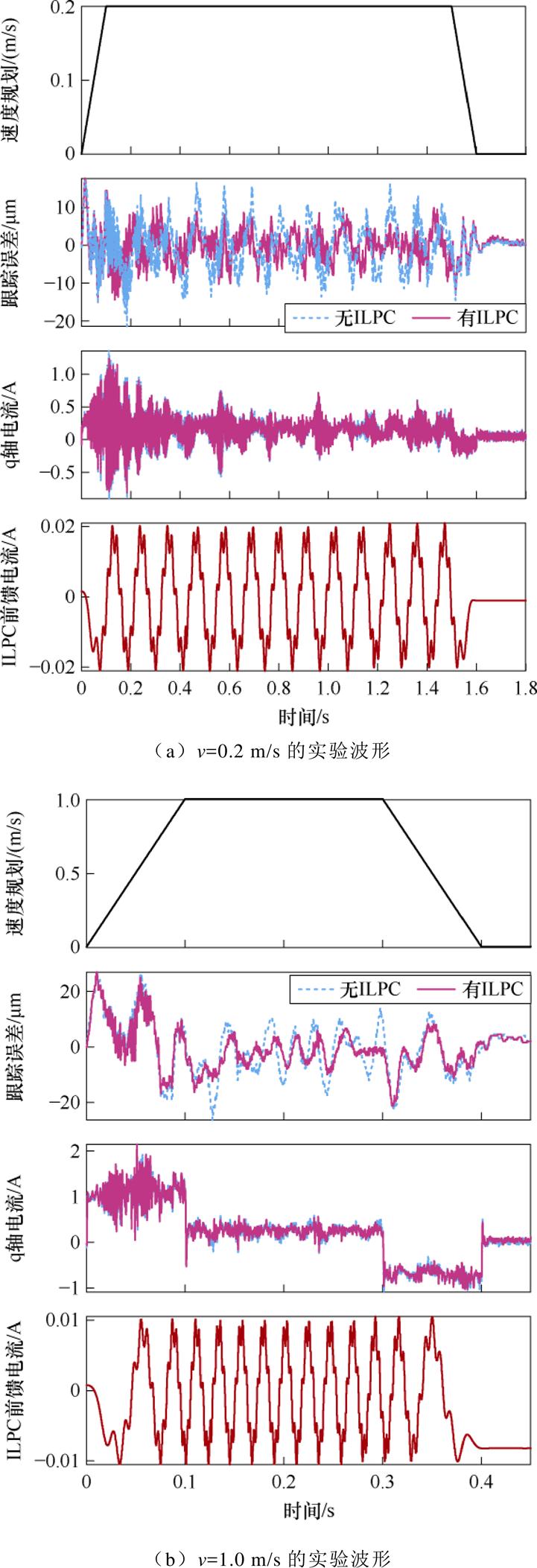
图13 不同速度下的实验结果
Fig.13 Experimental results under different velocity
实验结果表明,ILPC策略不依赖特定的运动模态,在其他速度工作点也能够有效地抑制定位力波动,提升二阶S形曲线的位置跟踪精度。
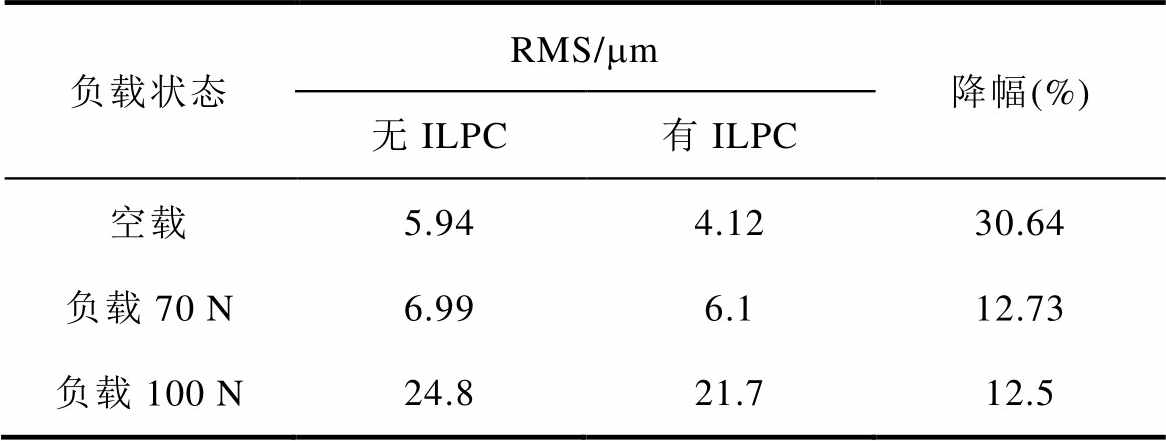
为了进一步验证ILPC策略的有效性,在0.2 m/s的速度工作点下进行了加载实验。实验平台的PMLSM额定推力为700 N,为了在保证实验安全的前提下模拟额定负载和过载的工况,本文采取缩小额定负载的方式,将电流环输出限幅至额定电流的1/10来降低电机额定推力,空载和不同轻载工况(负载70 N和负载100 N)下的实验波形如图14所示。
由图14可知,引入ILPC后,在0.2 m/s的运行速度下,电机空载时的位置跟踪误差RMS由5.94 mm下降至4.12 mm,降幅达到30.64%;电机负载70 N时的位置跟踪误差RMS由6.99 mm下降至6.1 mm,降幅达到12.73%;电机负载100 N时的位置跟踪误差RMS由24.8 mm下降至21.7 mm,降幅为12.5%。
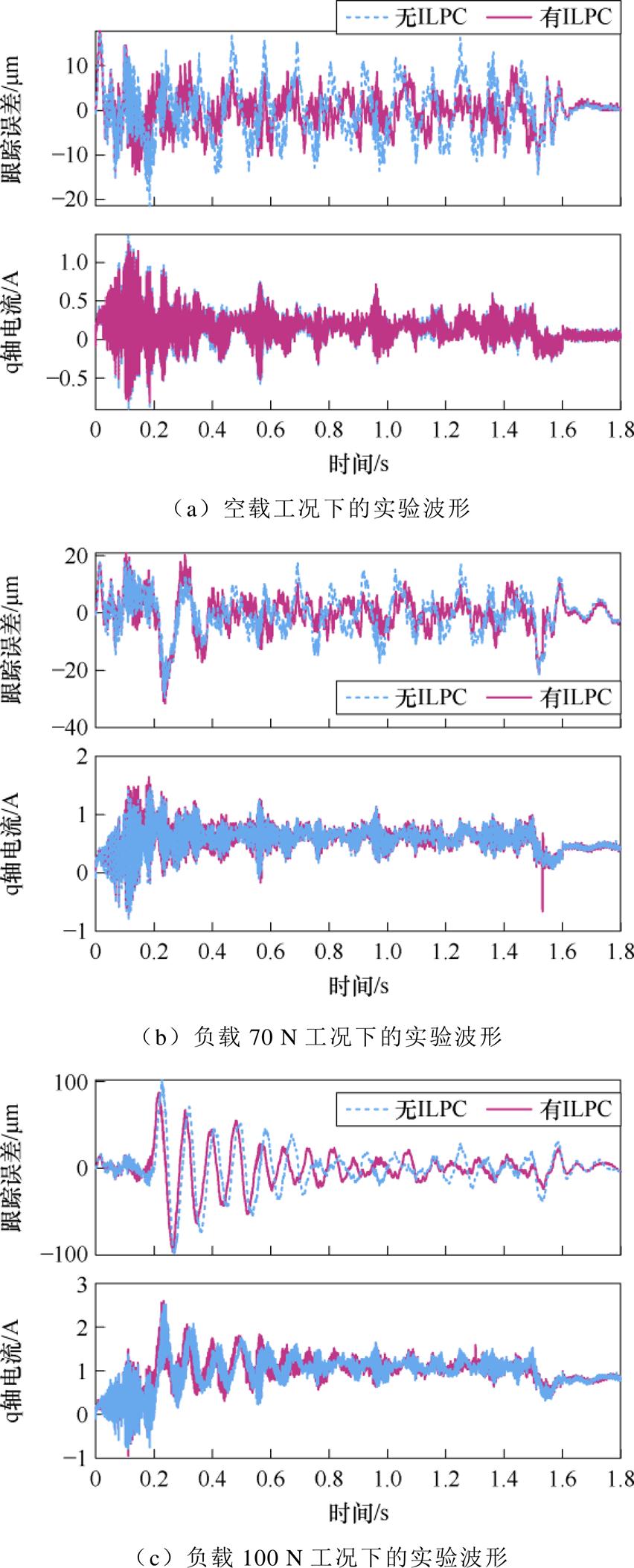
图14 不同轻载工况下时的实验结果
Fig.14 Experimental results under different light load conditions
将3.4节中引入ILPC推力波动抑制策略前后的不同工况下的实验结果进行汇总对比,不同速度下位置跟踪误差的RMS见表3,不同负载下位置跟踪误差的RMS见表4。
表3 不同速度下位置跟踪误差的RMS
Tab.3 RMS of position tracking error under different velocity
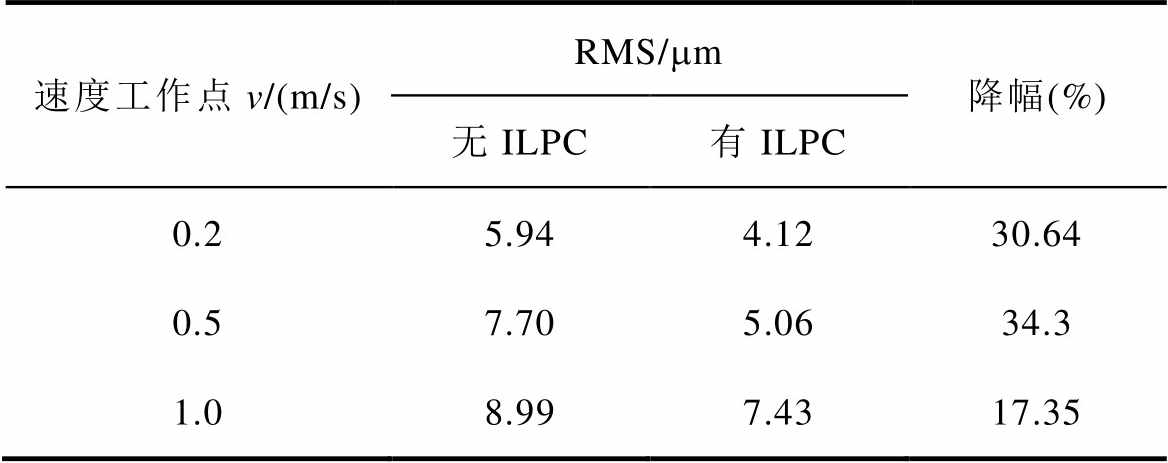
速度工作点v/(m/s)RMS/mm降幅(%) 无ILPC有ILPC 0.25.944.1230.64 0.57.705.0634.3 1.08.997.4317.35
表4 不同负载下位置跟踪误差的RMS
Tab.4 RMS of position tracking error under different load
负载状态RMS/mm降幅(%) 无ILPC有ILPC 空载5.944.1230.64 负载70 N6.996.112.73 负载100 N24.821.712.5
由表3和表4的实验结果可知,引入ILPC前馈补偿电流后,各个工况下的位置跟踪误差波动均有明显下降,RMS降幅最大可达34.3%,表明ILPC策略在不同速度、不同负载条件下对PMLSM的推力波动均有良好的抑制效果。
为了满足永磁直线同步电机位置伺服系统高速高精度响应的运行要求,本文提出了一种基于迭代学习预补偿策略的PMLSM推力波动抑制方法,得出以下结论:
1)在PMLSM位置-电流双闭环矢量控制结构的基础上,设计了结合AILC的二自由度控制器,在电机空载条件和参数失配条件下,实现了全程位置跟踪误差绝对值小于12 mm,满足了跟踪精度 要求。
2)进一步引入ILPC策略,通过信号分析与函数拟合,以电流前馈预补偿的方式推广至不同速度工作点和不同负载状态,改善了AILC依赖特定运动模态的缺点,验证了ILPC策略的泛化能力。
3)实验结果表明,本文提出的ILPC策略在不同速度、不同负载条件下对PMLSM的推力波动均有良好的抑制效果。具体而言,空载状态下,三个速度工作点的位置跟踪误差RMS值下降幅度均超过15%;不同轻载状态下,位置跟踪误差RMS下降幅度也都超过了10%,可以证明本文所提出的ILPC策略的正确性和有效性。
参考文献
[1] 张毅伟, 黄旭珍, 徐济安. 基于混合自适应扩展卡尔曼滤波的永磁同步直线电机等效机械参数辨识策略[J]. 中国电机工程学报, 2024, 44(3): 1162- 1173.
Zhang Yiwei, Huang Xuzhen, Xu Ji’an. Equivalent mechanical parameter identification of permanent magnet synchronous linear motor based on hybrid adaptive extended Kalman filter[J]. Proceedings of the CSEE, 2024, 44(3): 1162-1173.
[2] 宋琳, 聂子玲, 孙军, 等. 基于参数辨识的永磁同步直线电机循环神经网络多维观测器[J]. 电工技术学报, 2024, 39(22): 7059-7072.
Song Lin, Nie Ziling, Sun Jun, et al. Multidi- mensional observer of permanent magnet synchronous linear motor recurrent neural network based on parameter identification[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7059-7072.
[3] 鲍明堃, 周扬忠. 基于复合神经网络重构对象的永磁同步直线电机变参数型位移速度并行控制[J]. 电工技术学报, 2024, 39(8): 2470-2484.
Bao Mingkun, Zhou Yangzhong. Parallel dis- placement velocity control of permanent magnet synchronous linear motor with variable parameters based on composite neural network reconstruction object[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2470-2484.
[4] Dai Luyao, Li Xin, Zhu Yu, et al. The generation mechanism of tracking error during acceleration or deceleration phase in ultraprecision motion systems[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7109-7119.
[5] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[6] Wang Mingyi, Kang Kai, Zhang Chengming, et al. Precise position control in air-bearing PMLSM system using an improved anticipatory fractional- order iterative learning control[J]. IEEE Transactions on Industrial Electronics, 2024, 71(6): 6073-6083.
[7] 王立俊, 赵吉文, 于子翔, 等. 基于非线性时间延迟扰动估计的永磁同步直线电机无模型鲁棒位置跟踪控制[J]. 电工技术学报, 2024, 39(18): 5692- 5704.
Wang Lijun, Zhao Jiwen, Yu Zixiang, et al. Model- free robust position tracking control of permanent magnet synchronous linear motor based on nonlinear time delay disturbance estimation[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5692- 5704.
[8] 赵鑫宇, 王丽梅. 永磁直线同步电机自适应分数阶终端滑模控制[J]. 电工技术学报, 2023, 38(20): 5434-5443.
Zhao Xinyu, Wang Limei. Adaptive fractional-order terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5434-5443.
[9] 张国强, 赵新茹, 张恒, 等. 基于比例谐振内模扩张状态观测器的PMLSM推力波动抑制策略[J]. 电工技术学报, 2024, 39(8): 2449-2458.
Zhang Guoqiang, Zhao Xinru, Zhang Heng, et al. Proportional resonant internal model extended state observer based thrust ripple suppression strategy of PMLSM drives[J]. Transactions of China Electro- technical Society, 2024, 39(8): 2449-2458.
[10] Wang Anpeng, Li Liyi, Huang Xuzhen. A thrust ripple suppression strategy of PMLSM based on resonant disturbance observer with optimal gain and phase compensation[C]//2023 26th International Con- ference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 2023: 2600-2605.
[11] Zhang Heng, Zhang Guoqiang, Liu Wenlong, et al. Thrust ripple suppression of PMLSM drives based on Fourier transform compensator cascaded improved ESO[C]//IECON 2022-48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 2022: 1-6.
[12] 艾雄雄, 张博, 邓斌, 等. 基于扰动估计补偿的PMLSM固定时间积分滑模控制[J]. 电机与控制应用, 2023, 50(9): 28-34.
Ai Xiongxiong, Zhang Bo, Deng Bin, et al. Fixed time integral sliding mode control for PMLSM based on disturbance estimation compensation[J]. Electric Machines & Control Application, 2023, 50(9): 28-34.
[13] Liu Xiufeng, Cao Haiyin, Wei Wei, et al. A practical precision control method base on linear extended state observer and friction feedforward of permanent magnet linear synchronous motor[J]. IEEE Access, 2020, 8: 68226-68238.
[14] Hui Yu, Chi Ronghu, Huang Biao, et al. Extended state observer-based data-driven iterative learning control for permanent magnet linear motor with initial shifts and disturbances[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(3): 1881-1891.
[15] Sun Jiankun, Li Shihua, Yang Jun. Iterative learning control with extended state observer for iteration- varying disturbance rejection[C]//Proceeding of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 2014: 1148-1153.
[16] Wu Aijing, Huo Xin, Liu Qingquan, et al. ESO-based cyclic iterative learning control for continuous system with varying trials[C]//IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 2023: 1-6.
[17] Zhang Jingyao, Meng Deyuan. Improving tracking accuracy for repetitive learning systems by high-order extended state observers[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(12): 10398-10407.
[18] Jing Yajie, Hou Beibei, Liu Pengbo, et al. Learning disturbance observer-based repetitive control with application to fast tool servo system[C]//2024 IEEE 18th International Conference on Advanced Motion Control (AMC), Kyoto, Japan, 2024: 1-6.
[19] Zhang Guoqiang, Zhao Xinru, Wang Qiwei, et al. PR internal mode extended state observer-based iterative learning control for thrust ripple suppression of PMLSM drives[J]. IEEE Transactions on Power Electronics, 2024, 39(8): 10095-10105.
[20] 姜云风, 蓝益鹏, 孙伟栋. 基于ESO的磁悬浮直线同步电机变增益自适应迭代学习控制[J]. 电机与控制应用, 2023, 50(4): 1-7, 15.
Jiang Yunfeng, Lan Yipeng, Sun Weidong. Variable gain adaptive iterative learning control of magnetic levitation linear synchronous motor based on ESO[J]. Electric Machines & Control Application, 2023, 50(4): 1-7, 15.
[21] 谭强. 精密永磁直线同步电机电磁力波动分析与抑制研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
Tan Qiang. Analysis and suppression of electro- magnetic force fluctuation of precision permanent magnet linear synchronous motor[D]. Harbin: Harbin Institute of Technology, 2021.
[22] Chen Yangyang, Yang Ming, Liu Kaiyuan, et al. Reversed structure based PI-lead controller anti- windup design and self-commissioning strategy for servo drive systems[J]. IEEE Transactions on Indu- strial Electronics, 2022, 69(7): 6586-6599.
[23] Wang Danwei. On D-type and P-type ILC designs and anticipatory approach[J]. International Journal of Control, 2000, 73(10): 890-901.
Iterative Learning Pre-Compensation Strategy Based Active Disturbance Rejection Position Control Method of Permanent Magnet Linear Synchronous Motor Drives
Abstract The permanent magnet linear synchronous motor (PMLSM) has gained significant adoption in linear servo drive applications such as precision CNC machine tools due to its advantages of the direct drive mechanism, simplified structure, and high transmission efficiency. However, the inherent thrust ripple induced by the cogging effect and end effects in PMLSM systems adversely affects the tracking performance of servo mechanisms and machining accuracy, making thrust ripple suppression crucial. This paper presents a novel thrust ripple suppression method employing an iterative learning pre-compensation (ILPC) strategy to improve system control performance, thereby achieving high-dynamic and high-precision operation for PMLSM-driven systems.
Initially, a comprehensive modeling and analysis of the PMLSM and its thrust fluctuations are conducted. A two-degree-of-freedom controller is designed, comprising an acceleration feedforward controller (AFFC), a feedback controller, and a disturbance observer. This configuration preliminarily mitigates errors and thrust fluctuations during the acceleration and deceleration phases. The stability of the PI-Lead controller is validated through open-loop Bode plots. A comparative analysis assesses the impact of disturbance observers with varying orders and bandwidths on the system's disturbance rejection capabilities.
Subsequently, an anticipatory iterative learning controller (AILC) is introduced. The convergence of the AILC is rigorously demonstrated, and parameter tuning principles are investigated. The iterative learning process is leveraged to suppress thrust fluctuations further and enhance the system's tracking accuracy. Additionally, the equivalent current observation error of the PMLSM's detent force disturbance is fitted and pre-compensated, thereby reducing the dependency of iterative learning control on motion modes.
Finally, an experimental platform for PMLSM based on STM32F407 is established. The experimental results demonstrate that the proposed ILPC strategy effectively suppresses thrust fluctuations in PMLSM across different operating conditions. Specifically, under no-load conditions, the root mean square (RMS) value of position tracking error is reduced by more than 15% at three different speed setpoints. Under light-load conditions, the RMS value of position tracking error consistently reduces, exceeding 10%.
Keywords:Permanent magnet linear synchronous motor, disturbance observer, iterative learning control, thrust ripple suppression, pre-compensation
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.241022
国家自然科学基金资助项目(52277053)。
收稿日期2024-06-17
改稿日期 2024-10-16
梁万佳 男,1997年生,硕士研究生,研究方向为永磁直线同步电机驱动控制。
E-mail: liangwanjia@nuaa.edu.cn
黄旭珍 女,1985年生,教授,博士生导师,研究方向为直线电机系统。
E-mail: huangxuzhen@nuaa.edu.cn(通信作者)
(编辑 崔文静)