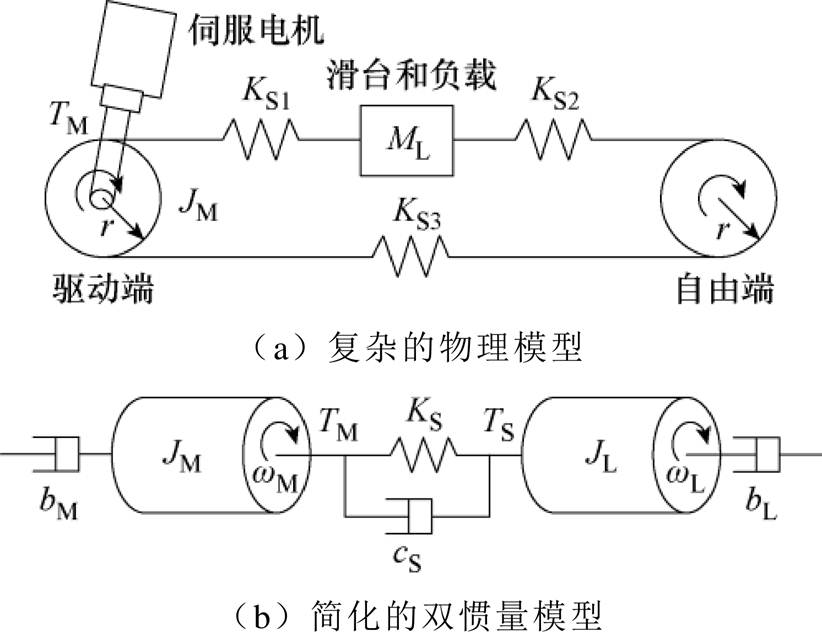
图1 同步带轮系统机械示意图
Fig.1 Mechanical diagram of the tooth belt drive system
摘要 针对弹性伺服系统带宽受反谐振频率限制问题，提出了两种基于状态反馈的位置控制器设计方法。含积分的状态反馈控制采用零极点对消法降低了闭环系统的阶数，频域上最优速度前馈设计提高了动态性能。无积分的状态反馈控制取消了速度环积分部分，用观测扰动补偿输出转矩，消除稳态误差。采用最大峰值灵敏度理论分析可得，取消速度环积分的设计有更大的增益边界，且所得极限增益为实际应用中带宽选择提供了合理的指导。在同步带轮伺服系统上验证了所提方法的有效性，实验表明，所提状态反馈位置控制具有良好的动态响应和较宽的增益选择 范围。
关键词：伺服控制 双惯量系统 状态反馈控制 增益边界
机械臂、数控机床类运动控制系统通过联轴器、减速器、同步带等传动机构连接负载，其传动机构并非完全刚性[1]。航空航天领域执行机构也越发要求传动机构采用复合材料，其材质轻，能满足较低自重比率[2-3]。这种机构运动时会严重扭曲以施加巨大驱动力，导致机械负载表现出弹性、柔性。随着伺服系统动态性能不断地提升，忽略弹性环节所带来的影响愈发显著。低阻尼扭转振动对伺服驱动系统伤害极大，会降低产品质量和系统可靠性，在某些情况下还会不稳定[1, 4]。而机械振动与控制器高增益有关，传统控制很难平衡稳定性和动态响应。
国内外许多文献针对机械共振抑制和带宽扩展进行研究，抑制方法大致可分为被动抑制和主动抑制两种。通过设计低通滤波器或陷波器，将其与经典速度控制器相结合，保证更高增益下的稳定性[5-6]。该方法原理简单、易实现，是目前工业伺服的常用工具。但传统陷波器法都对谐振频率特别敏感，频率偏移会使陷波器效果大打折扣，为了得到准确的谐振频率，机械参数辨识[7-8]和自适应频率识别[9-11]都是必要的。而位置控制末端抖动问题则需要对指令进行合理整形，以抵消系统的振动模态，使位置轨迹平滑[12-13]。整形参数与位置控制器参数密切相关，需仔细调试且无法对外部扰动有效阻尼。
主动抑制的核心思想是修正速度闭环传递函数，常用方法是比例-积分-微分（Proportional- Integral-Derivative, PID）控制器。根据不同惯量比设计极点，可保证闭环系统具有充足阻尼[14-15]。经典慢谐振比控制器通过等效调整电机侧惯量来增大系统阻尼，最优滤波器带宽选择能保证性能[16]。当需要扩展带宽时，基于PI+额外反馈的速度控制器能在极点配置上带来灵活性。反馈信号（轴矩、负载速度等）可分为三组进行对比测试，不同反馈所达动态效果不同，该方法切实突破了反谐振频率对带宽的限制[17]。由此，也衍生出了很多反馈控制方法。文献[18]采用转速负反馈法提取谐振信息，设计最优反馈系数和滤波时间常数提高阻尼。文献[19]通过反馈负载位置以增加控制器自由度，并详细分析了系统性能与参数的关系。通常情况，基于额外反馈的控制方法都需要加装传感器，这增加了系统成本，因此，观测器搭配状态反馈方法被广泛采纳。基于锁相环型扩张观测器与常规扩张观测器相比具有更高的带宽和更大的相位裕度，有助于提高谐振抑制算法的稳定性[20]。卡尔曼滤波器也被用于双惯量状态观测，实现降噪和观测器优化的效果[21-22]。固定增益滤波器用于克服卡尔曼观测器计算负担过重的问题，权衡了噪声和观测动态[23]。文献[24]指出全状态反馈控制搭配龙贝格观测器用以实现闭环极点的任意配置，其稳定性受转矩环滞后效应的影响，参数选择需详细分析。基于线性二次型在线优化状态反馈控制器参数，能实现预设的控制效果。但计算量偏大，且增益选择的稳定性和鲁棒性没有被讨论[25]。改进的五并联滑模观测器能在观测状态变量的同时实时辨识电机惯量、负载惯量、传动刚度等机械参数，极大地提高了控制器的鲁棒性，其性能远优于传统最小二乘辨识方法[26-27]。
一些高级控制算法，包括鲁棒控制器[28]、模型参考自适应[29]和模型预测控制[30]，在抑制谐振和抗扰方面取得了不错的效果。但高级算法过于复杂，不便在工业应用中推广。状态反馈控制（State Feedback Controller, SFC）设计方法理论上成熟，设计方便且动态性能提升明显，非常适合工业应用。但上述文献多讨论对速度环的状态反馈设计，重点集中在分母多项式的设计，对位置控制器和分子多项式的设计鲜有提及[31]。另一方面，SFC理论上可任意配置极点，但受制于自身谐振特性影响，带宽不能无限大。实际应用中如何选择控制器增益目前还没有文献详细讨论过。
为此，本文研究了针对双惯量系统的状态反馈位置控制器（State Feedback Position Controller, SFPC）设计方法。首先，提出了在状态反馈速度控制基础上设计位置环的方法，分析并阐明了该结构在带宽扩展上的限制。然后，在此基础上，提出基于状态空间的位置控制设计方法。该控制器与自抗扰速度控制结构类似[32]，取消积分环节而用观测扰动补偿转矩，控制结构得到简化。理论上该结构能进一步提高控制器增益，改善动态响应。采用最大峰值灵敏度理论评估增益边界，经过推导给出了能保证控制器鲁棒性的最大增益。最后，通过实验验证了本文方法的正确性和有效性。
本研究主要在同步带轮系统上实现，机械结构由同步带、带轮、联轴器、滑台和伺服电机构成，如图1所示。图1a给出了较为完整的同步带轮物理模型。由于滑台和作动端带轮对驱动系统起主导作用，忽略自由端后复杂物理模型可简化为典型的双惯量模型，如图1b所示。
图1 同步带轮系统机械示意图
Fig.1 Mechanical diagram of the tooth belt drive system
同步带轮双惯量模型表达式为
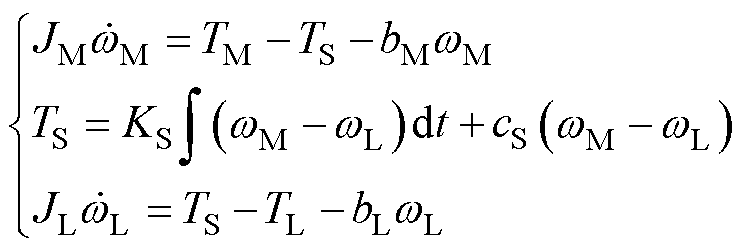（1）
式中，wM和wL分别为电机侧和负载侧角速度；TM为电磁转矩；TS为等效传动轴力矩；TL为滑台所受外力折算到电机侧的扰动；JM为电机侧惯量；JL为负载侧惯量；KS和cS分别为同步带刚度和带阻尼；bM和bL分别为电机侧和负载侧黏滞摩擦系数。通常来说，cS、bM和bL在控制器设计时可以被忽略。电机侧和负载侧角度qM、qL可表示为
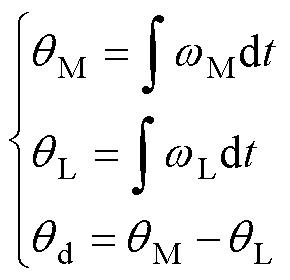（2）
惯量比R、反谐振频率wares和谐振频率wres为
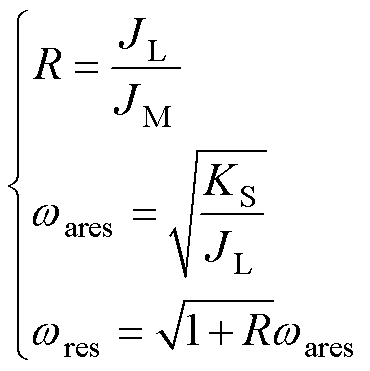（3）
电磁转矩TM、电机速度wM和负载速度wL对应的开环传递函数为
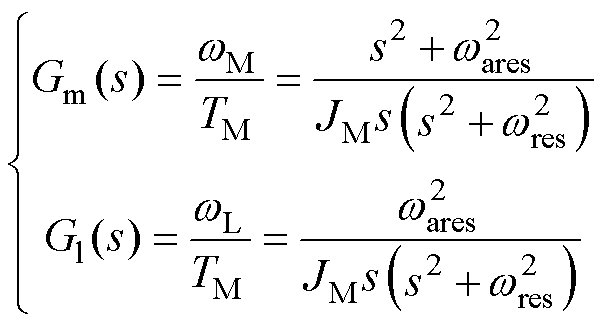（4）
图2a给出了双惯量系统框图，其频响特性如图2b所示。蓝色实线中凹陷和凸起部分为反谐振频率和谐振频率。谐振频率恶化了闭环系统稳定性，而反谐振频率限制了闭环系统的带宽[5, 14]。红色虚线为电磁转矩与负载速度的频响特性，其只包含谐振特性。
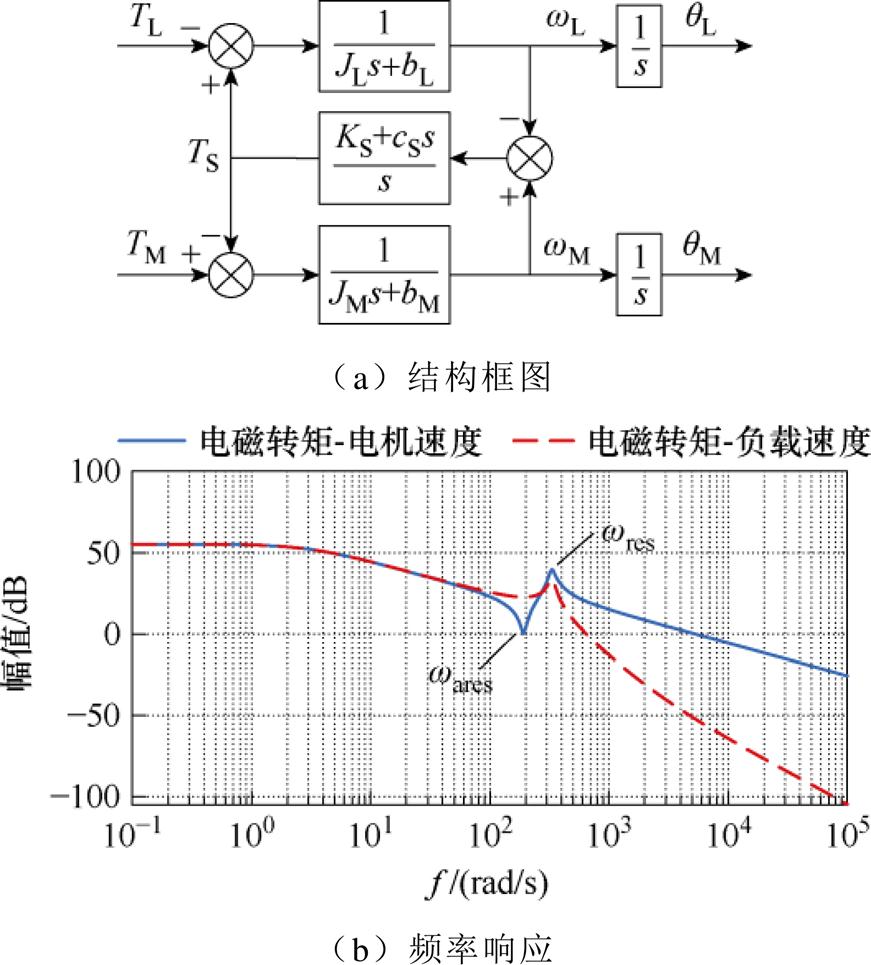
图2 双惯量系统特性
Fig.2 Characteristic of the two-mass system
传统P-PI位置控制结构如图3所示，图中，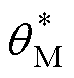
为位置指令，kpp和kpf分别为位置比例系数和速度前馈系数，kp为速度比例系数，ki为速度积分系数。由于阻尼振荡直接发生在速度环中，可基于速度环分析反谐振频率对带宽的影响。
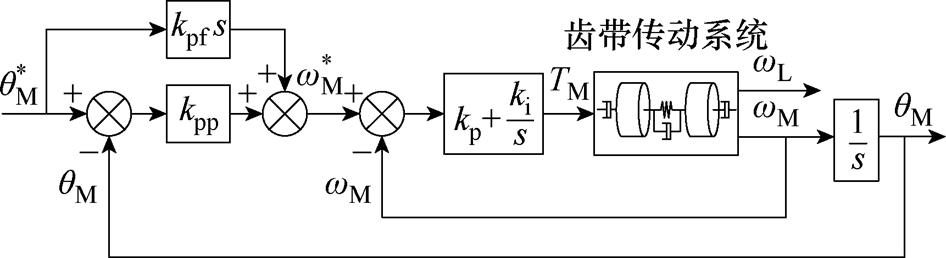
图3 传统P-PI位置控制结构
Fig.3 Structure of the traditional P-PI position controller
速度闭环传递函数表示为
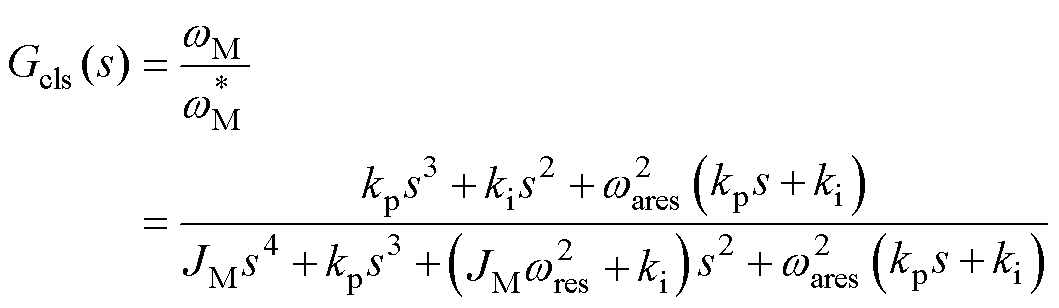（5）
设计式（5）的闭环极点为
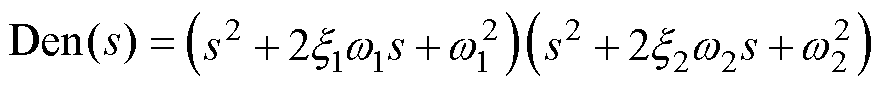（6）
式中，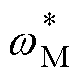
为位置环输出的参考速度；
、
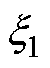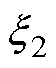和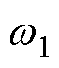
、
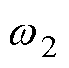分别为设计的阻尼和自然频率。结合式（5）、式（6）可推导出闭环系统受如下四个条件的限制。
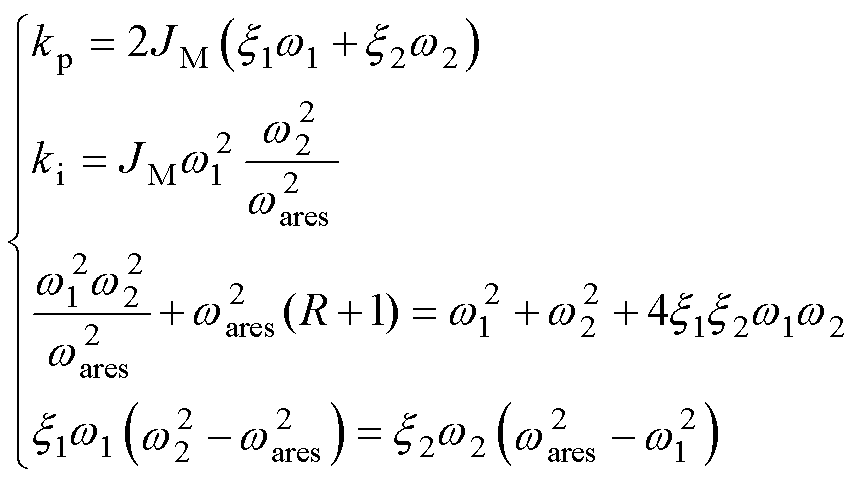（7）
由第四个条件可知，自然频率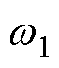、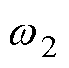满足
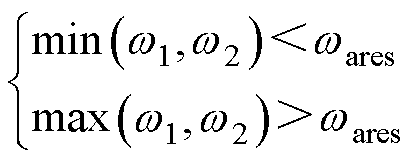（8）
因此，不管哪种极点配置方式，都无法兼顾动态和阻尼特性，这是传统PI控制的缺陷。额外反馈状态变量是实现高性能控制的方法，在合理设计特征多项式的同时，改善前馈增益对系统响应提升的影响非常可观。
状态反馈控制相关文献多集中在速度控制器设计，针对弹性伺服的位置控制器设计很少被提及。为了提高弹性伺服系统的位置控制动态特性，直观的思路是在状态反馈速度控制器外串联位置控制器。根据文献[22, 24-25]，双惯量系统速度控制框图如图4所示。图中，kn为速度环增益向量。基于积分-比例（Integral-Proportional, IP）的SFC闭环系统不包含零点，虽然阻尼效果好，但动态效果差。基于PI的SFC由kn1引入一个零点，动态效果提升显著。这里扰动前馈GFF(s)包含高阶微分，应用困难，而且在积分结构下闭环系统不存在稳态误差，前馈不是必要的。
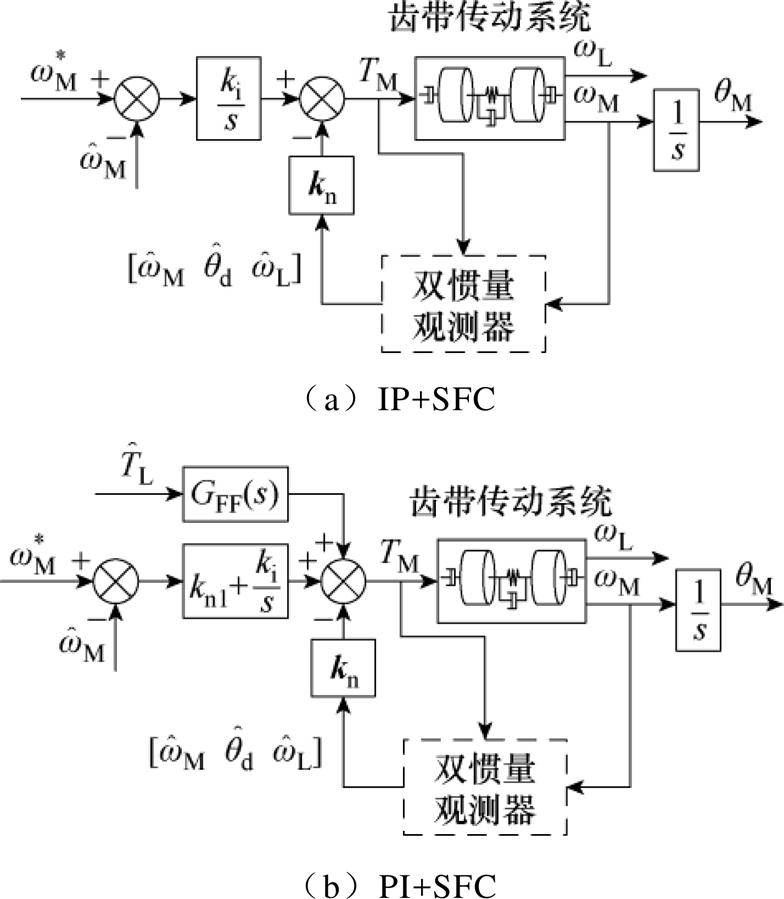
图4 双惯量系统状态反馈速度控制
Fig.4 State feedback speed controller of two-mass system
根据文献[22]，电机速度闭环传递函数为
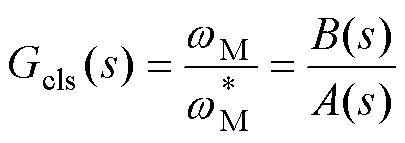（9）
其中
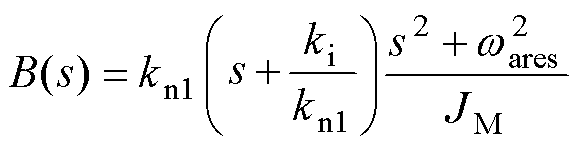
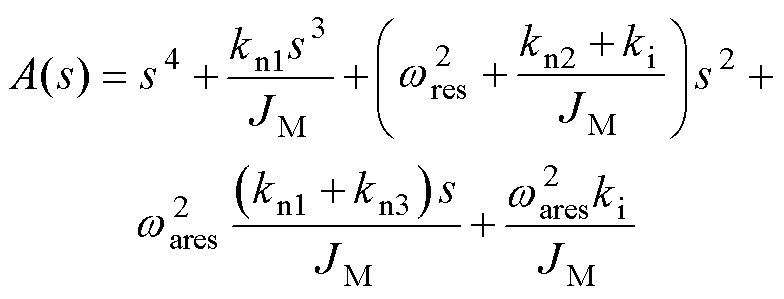
式中，kn1、kn2、kn3为增益向量kn的分量。
将位置增益kpp代入可得位置闭环传递函数为
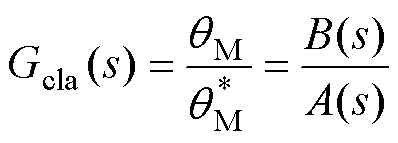（10）
其中
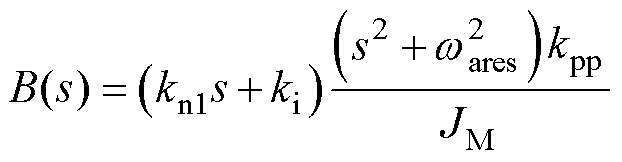
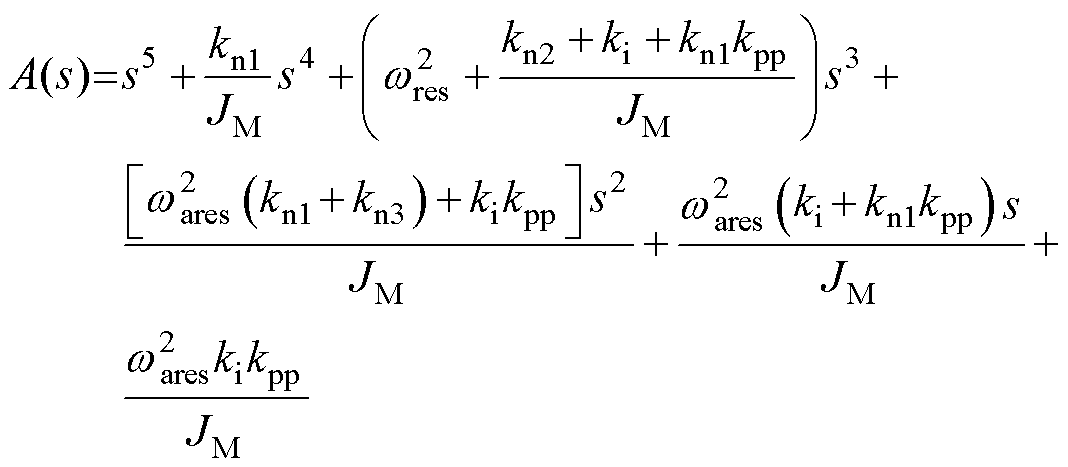
将特征方程设计为
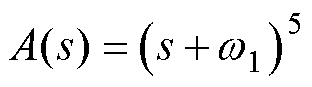（11）
对比式（10）和式（11），位置比例为
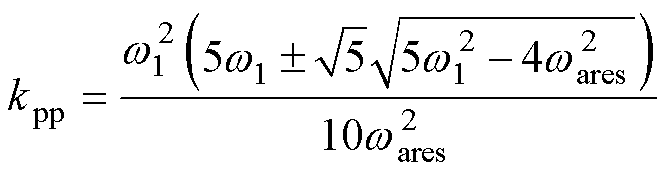（12）
可以看出，w 1＞0.894 4w ares时kpp才可实现，这显然不利于实际应用。增益向量kn可以自由配置速度环的分母多项式，但其唯一解和分子自由度受限于kn1。通过调整A(s)可能得到更宽的边界，但设计难度更大，实际应用困难。只能先根据文献[24]设计速度环，再调节位置环增益和前馈参数。
为了保证位置控制器的动态效果，速度比例项需要保留，但不能以图4b中的PI形式。本文提出的位置环设计方法如图5所示。与图4b不同的是引入kp前馈速度参考，分子和分母多项式都可以任意配置。
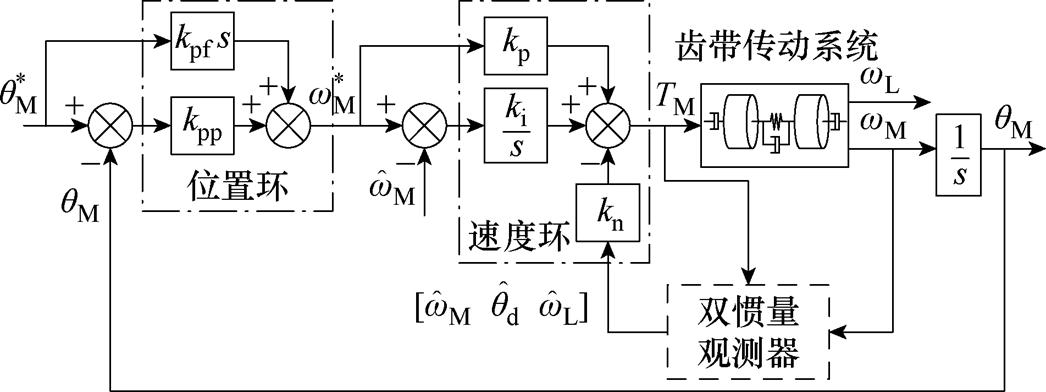
图5 含积分SFPC框图
Fig.5 Diagram of the SFPC with integral part
图5所示包含速度前馈的位置闭环传递函数可表示为
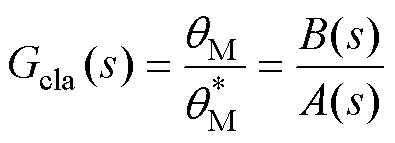（13）
其中
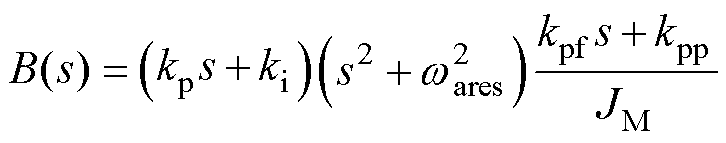
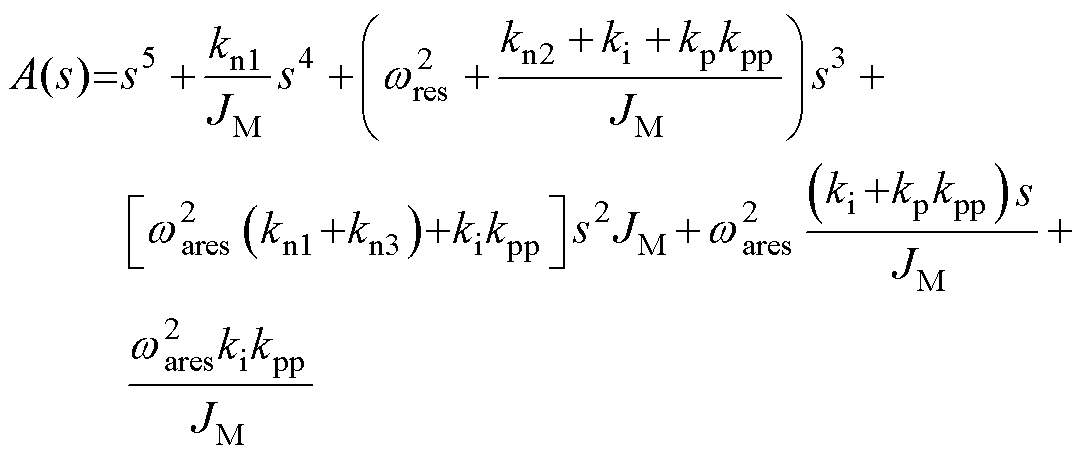
将特征方程设计为
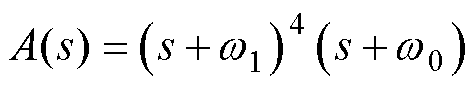（14）
式中，w 0为用于对消的极点。对比式（13）和式（14），并用kp对消w 0可得控制参数为
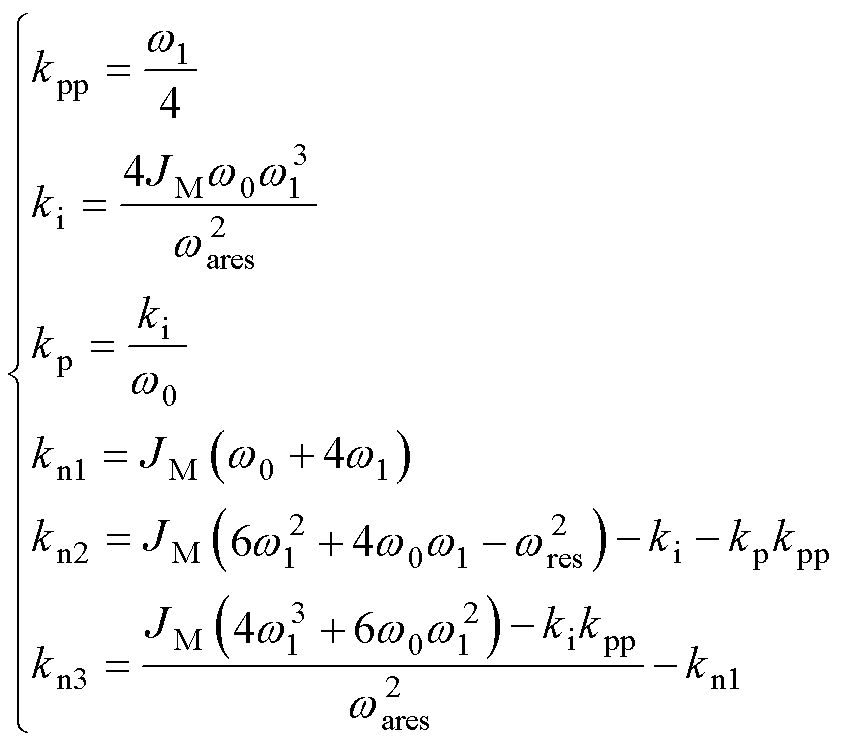（15）
根据式（1），wL与wM的传递函数为
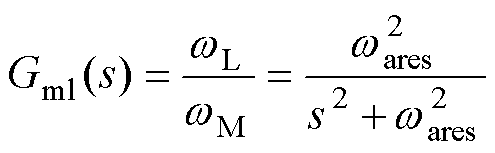（16）
则负载位置闭环传递函数可简化为
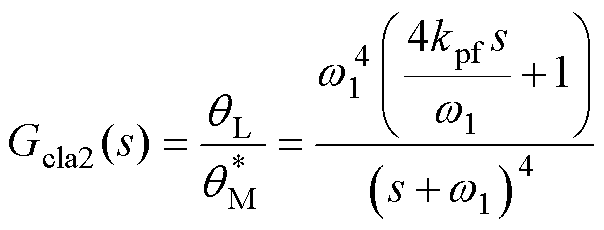（17）
为了进一步提升系统动态响应，也可以设计kpf=0.25对消w 1。但这种设计无法保证式（17）的幅频增益刚好小于0 dB，动态响应不是最优的。为此，计算式（17）的幅频增益可得
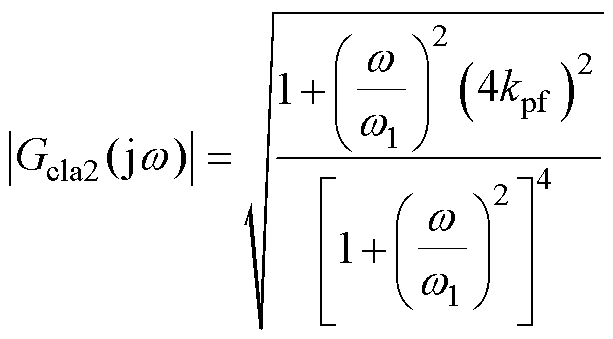（18）
式（18）的幅频增益主要受kpf和w 1的影响，且幅频增益是kpf的单调函数。kpf越大，w 1处的增益越大，响应越快。为了避免响应超调，使|Gcla2(jw)|=1，可得
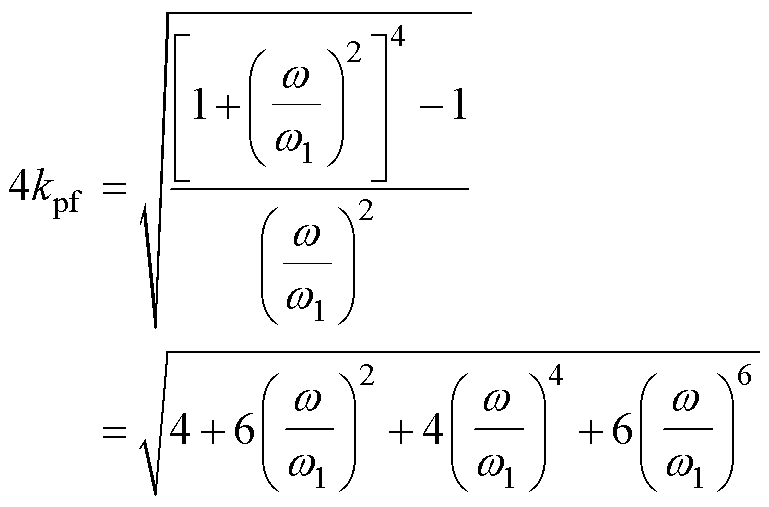（19）
由于式（19）随
增大而减小，=0 rad/s对应最大幅频增益（0 dB），则所提最优kpf取值为
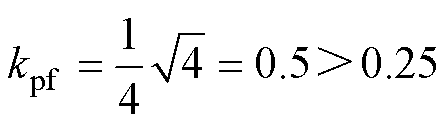（20）
式（20）表明，所设计的前馈增益kpf远大于零极点对消值0.25。图6所示为不同kpf下，式（18）的频率响应特性。可以看出，在式（20）的基础上稍微增大kpf会导致幅频增益大于0 dB，产生超调；减小kpf会使幅频增益更早地衰减，在期望频率处动态响应变差。因此，所设计的kpf是兼顾超调和动态响应的最优值。
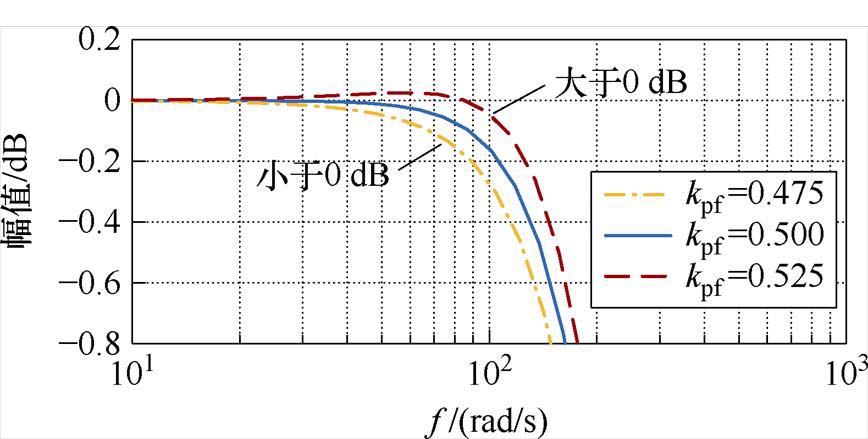
图6 不同kpf对式（18）的影响
Fig.6 Impact of different kpf on Eq. (18)
分析式（17）可知，w 0不影响闭环响应，为了设计方便，取w 0=w 1。对w 1而言，需从闭环稳定性和鲁棒性方面进行设计。速度控制器u可表示为
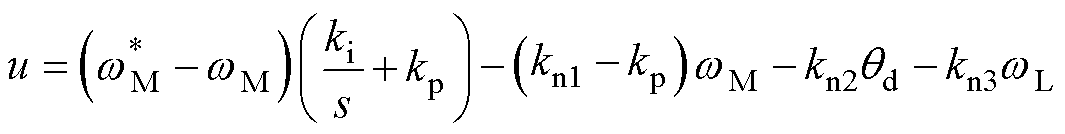（21）
由式（1）可知，状态变量qd与wM的传递函数为
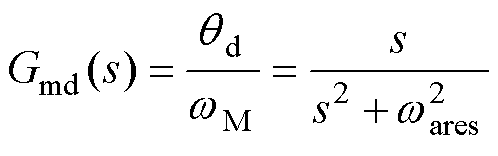（22）
则实际速度与参考速度的关系满足
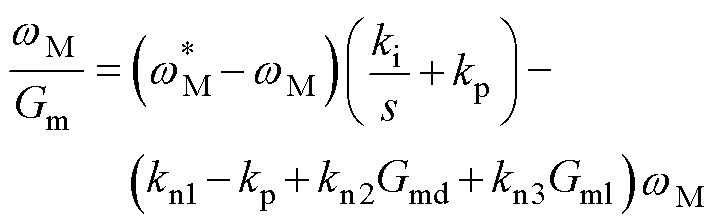（23）
化简可得速度开环传递函数为
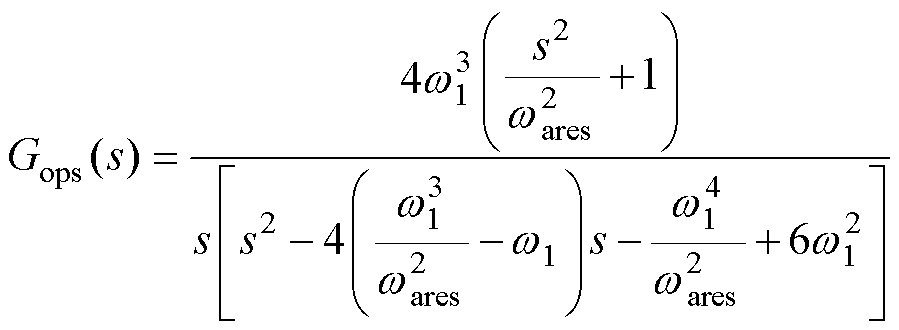（24）
根据式（24）可知，当w 1＞w ares时极点处于右半平面，闭环系统条件稳定，因此需保留足够的稳定裕度。这里通过最大峰值灵敏度函数S=[1+Gops(s)]-1来评估控制器鲁棒性。利用式（24）计算的灵敏度函数S只跟w ares相关，与惯量比无关，其频率响应如图7所示。可以看出，随着w1增大，幅频增益变大。在w 1=1.5w ares时最大峰值增益会大于6 dB，意味着追踪特性和鲁棒特性很差，些许扰动或不确定性都会恶化控制性能。因此，增益w 1的选择应小于1.4w ares，这适用于任意惯量比情况。
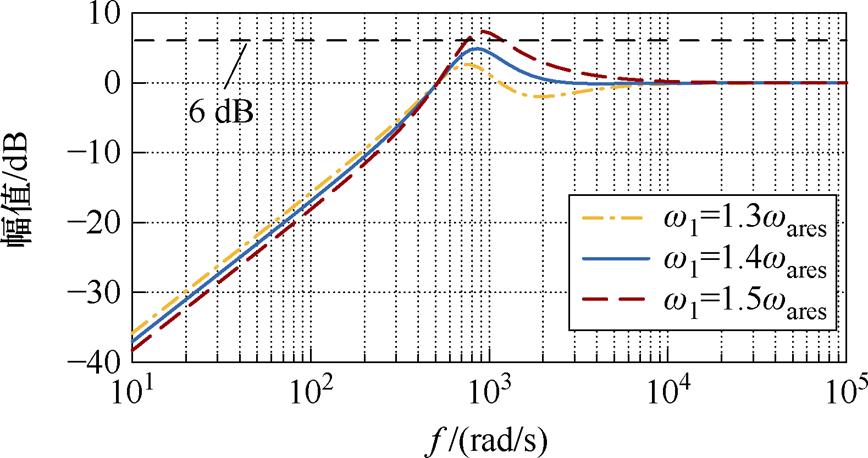
图7 不同w1时灵敏度函数S的特性
Fig.7 Feature of the sensitivity function S under different w1
积分环节虽然能消除稳态误差，但速度受扰动的影响也会被包含到积分作用中，降低了系统稳定裕度。本文提出在双惯量系统中设计无积分SFPC，以进一步扩展极限增益。通过补偿外部扰动以消除稳态误差。双惯量系统状态空间表达式为
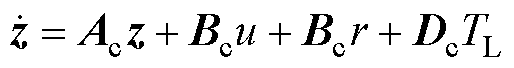（25）
其中
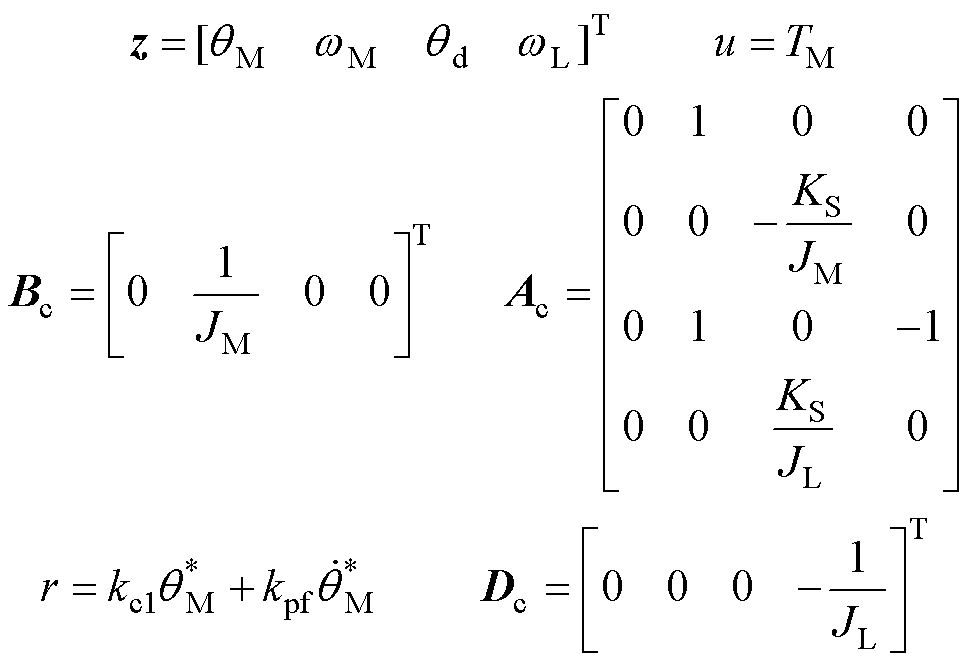
取控制率u=-kcz-kLTL，式（25）改写为
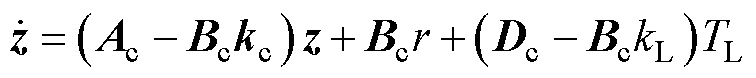（26）
其中
kc=[kc1kc2kc3kc4]
式中，I为单位矩阵；kL为扰动补偿系数。则电机位置闭环传递函数和扰动函数分别为
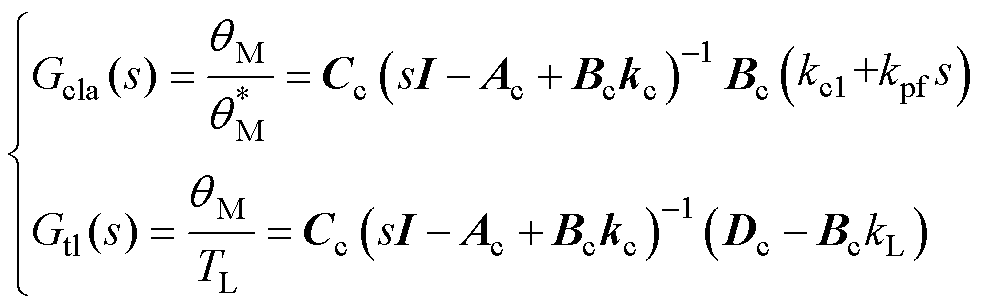（27）
其中
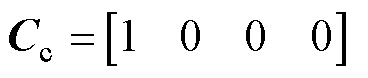
求解可得位置闭环传递函数为
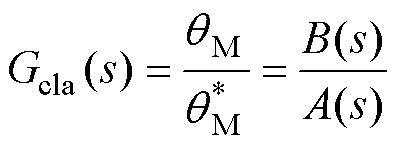（28）
其中
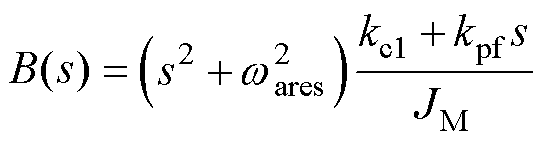
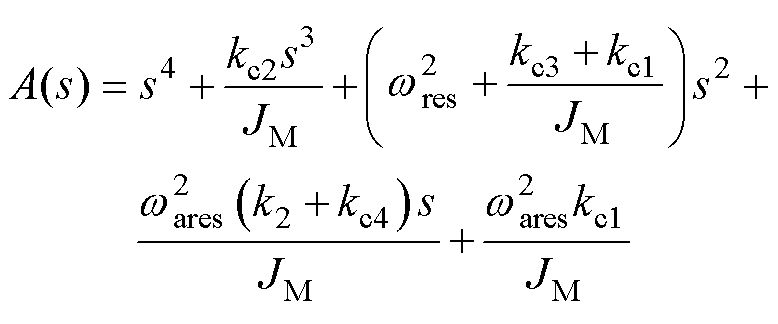
与式（11）对比可知，无积分SFPC已实现了闭环系统的降阶，不需要零极点对消。kL不影响式（28）的性能，只影响扰动函数，有
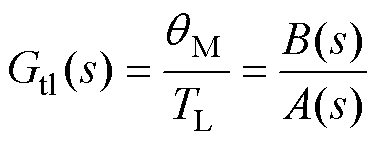（29）
其中
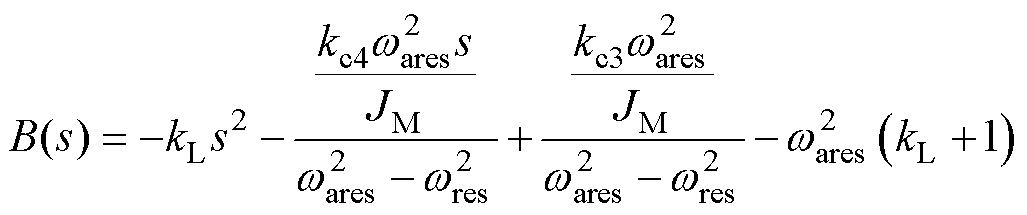
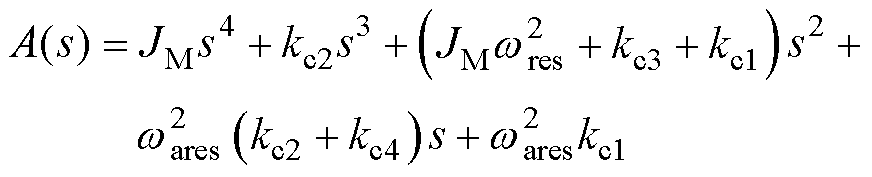
为了抑制常值扰动，设计kL消除B(s)的零阶项可得
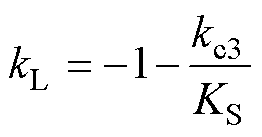（30）
因此，扰动函数呈高通滤波特性，稳态误差被消除。将特征方程设计为
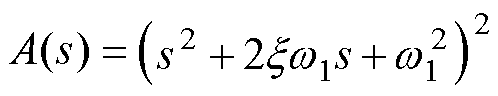（31）
式中，x 为设计阻尼。
对比式（28）和式（31），控制器参数为
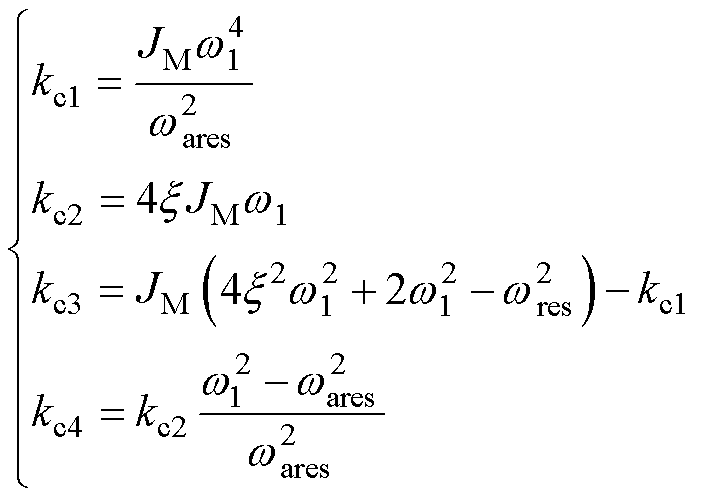（32）
将阻尼x 设计为1，负载位置闭环传递函数可简化为
（33）
类比式（18）和式（19），提出的最优前馈参 数为
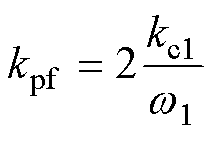（34）
前馈参数与式（20）显著不同。无积分可实现与含积分SFPC一致的位置闭环特性，其控制框图如图8所示，取消积分环节，用扰动估计TL补偿转矩以消除稳态误差。该结构更加简单，无需积分退饱和设计，观测器[25]需要扩张以估计扰动TL。
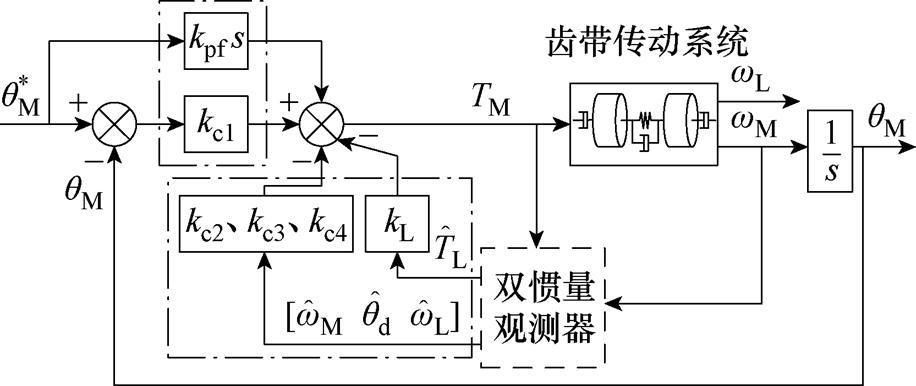
图8 提出的无积分SFPC框图
Fig.8 Diagram of the proposed SFPC without integral part
w 1的选择也需从闭环稳定性和鲁棒性方面进行设计。根据图8，假设等效参考速度为
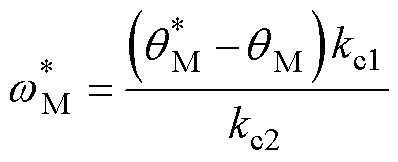（35）
考虑跟踪特性时控制器u可表示为
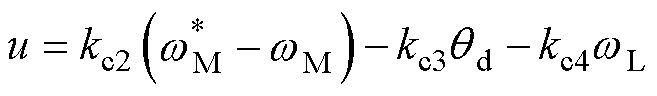（36）
则实际速度与等效参考速度的关系满足
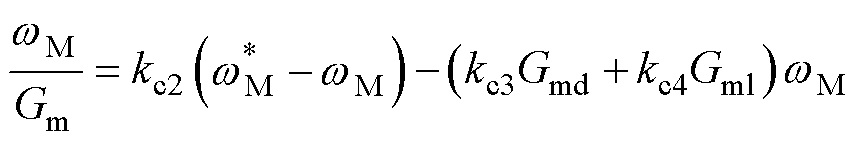（37）
化简可得开环传递函数为
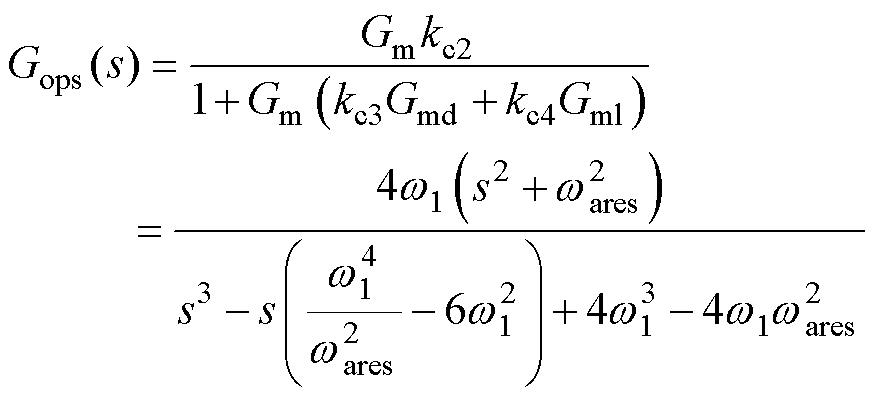（38）
将所提无积分SFPC转换为标准反馈控制系统，如图9所示。图中，GK为等效控制器。
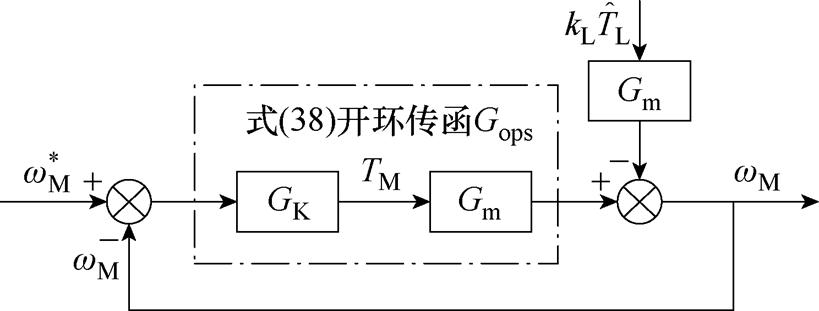
图9 标准反馈控制系统框图
Fig.9 Diagram of the standard feedback control system
推导可得扰动函数为
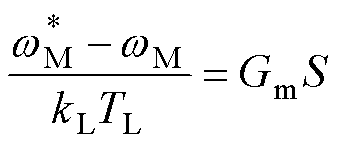（39）
由于控制对象是稳定系统，因此，扰动补偿稳定分析可等效于对灵敏度函数S的分析。对比式（24）可知，式（38）在w 1＞w ares时同样为条件稳定，但稳定裕度却大不相同。利用式（38）计算的灵敏度函数S的频率响应如图10所示。可以看出，随着w 1增大，幅频增益变大。在w 1=2.0w ares时最大峰值增益会大于6 dB，相比于图7提升了28%。w 1= 1.8w ares时最大峰值增益接近6 dB，因此增益w 1的选择可达到1.8w ares。从增益边界考虑，无积分SFPC有更大的选择空间。
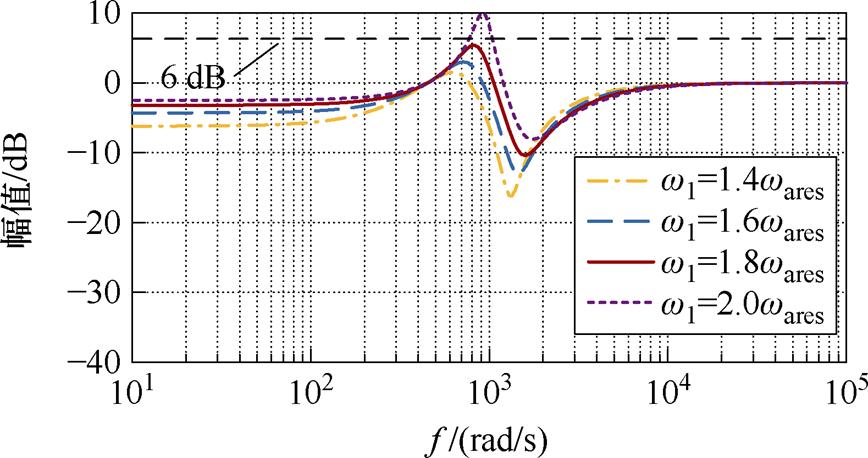
图10 无积分SFPC灵敏度函数S的特性
Fig.10 Feature of the sensitivity function S by using SFPC without an integral part
为了验证提出方法的有效性，在实验室搭建了同步带轮伺服控制系统。实验装置如图11所示，同步带轮将电机旋转运动转换为滑台的直线运动，通过滑台增加质量块改变惯量比，同步带的张力用来调节刚度。所提方法在法睿科公司Ker075高性能伺服驱动器上实现，伺服电机搭配23 bit绝对值编码器以匹配高性能控制算法。转矩环为矢量控制，算法迭代周期为10 kHz，机械和电气系统参数见表1。摩擦效应由位置指令微分前馈的方式进行补偿，补偿摩擦值为0.037 N∙m。
图11 同步带轮伺服驱动系统
Fig.11 Tooth belt servo drive system
传统P-PI控制在工业界广泛应用，参考单惯量系统设计能获得良好的动态效果。但为了抑制过量的末端抖动，速度积分不能太大，其参数设计为
表1 等效模型参数
Tab.1 Equivalent model parameters
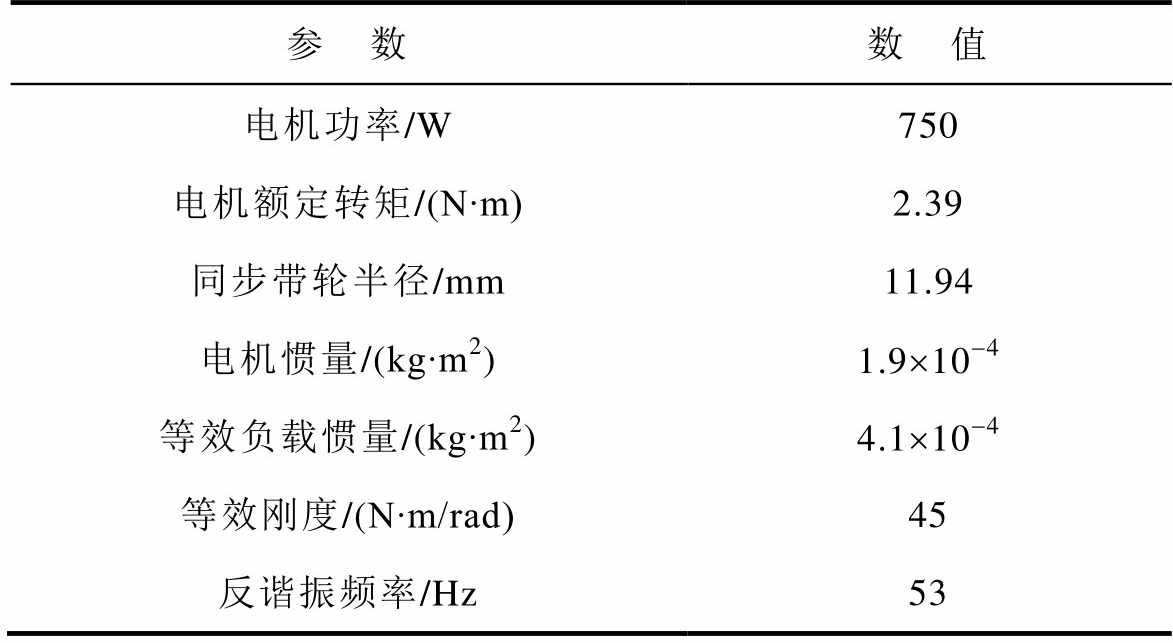
参 数数 值 电机功率/W750 电机额定转矩/(N∙m)2.39 同步带轮半径/mm11.94 电机惯量/(kg∙m2)1.9´10-4 等效负载惯量/(kg∙m2)4.1´10-4 等效刚度/(N∙m/rad)45 反谐振频率/Hz53
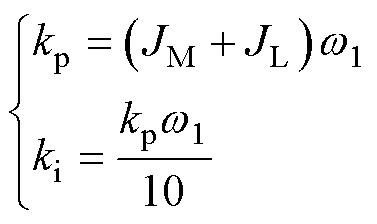（40）
传统结构与所提含积分SFPC结构类似，都包含位置和速度环。为方便对比，有
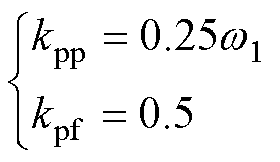（41）
实验验证所用负载惯量为4.1×10-4 kg·m2，约2倍惯量比，基于状态反馈的速度环响应实验结果如图12所示。可以看出，PI速度控制器超调22 r/min，调节时间为0.045 s，调节时间较长。为了降低调节时间，将积分增益ki增大4倍。积分增加确实将调节时间降低到0.030 s，但超调增大到了28 r/min。相比较而言，SFC调节时间为0.025 s，速度响应无超调。因此，PI控制无法兼顾速度响应的动态和超调特性，而状态反馈速度控制可以保证控制性能。
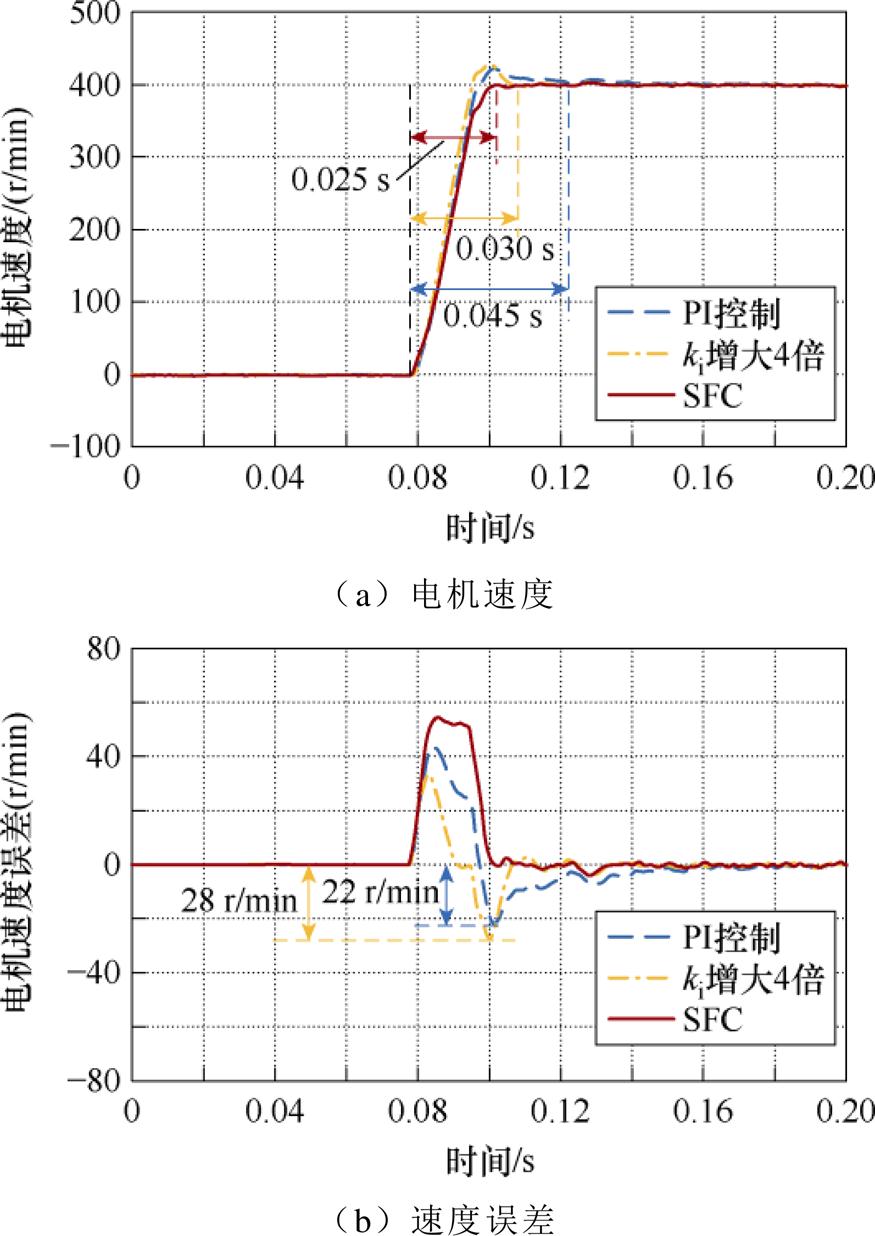
图12 w1=1.0w ares时，速度响应对比
Fig.12 Speed response comparison with w 1=1.0w ares
为验证所提含积分SFPC效果，图13给出了位置环响应波形并与传统P-PI控制进行对比。相同位置增益w 1=1.0w ares下，所提方法能更快到达指定位置且超调和抖动很轻微。实验中的速度误差受数模转换器输出的限制，只能显示出20 r/min以内的波形。根据式（40）和式（41）所设计的P-PI控制，位置响应抖动相较所提方法更大，且拖尾时间较长为0.10 s。为了缩短拖尾时间，将其积分增益ki增大4倍，可以看出，P-PI控制的拖尾时间缩短为0.07 s，但远达不到所提方法的效果。反而在调节过程（黑色虚线圆圈）中速度产生了明显的抖动，因此，所提方法在动态和振动抑制方面都优于传统 控制。
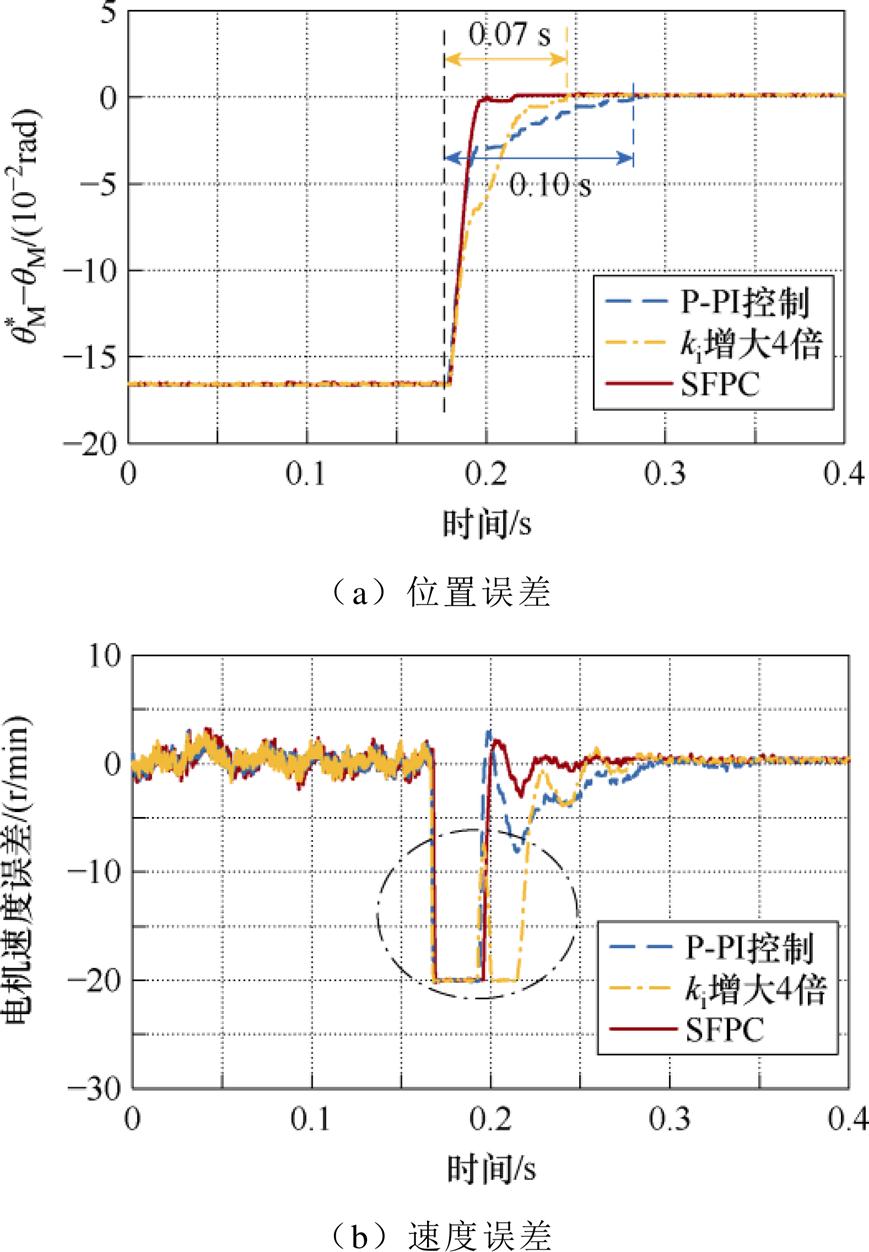
图13 w 1=1.0w ares时，位置环响应对比
Fig.13 Position response comparison with w 1=1.0w ares
PI+状态反馈速度环[22, 24]外串联位置环，参数按式（41）设计。调节速度环带宽以匹配外环，其不同增益下的位置响应如图14a所示。位置环直接串联PI+状态反馈速度环会造成一定的超调，其最大反转速度为10 r/min，由速度环PI结构引入的不可调零点影响了闭环系统的动态特性。当增益降低至w 1=0.7w ares时，位置响应拖尾明显且与降低增益前差异较大，需要进一步试凑各环节参数。如图14b所示，相同位置增益下，所提方法最大反转速度只有2.5 r/min，且增益改变前后位置环响应的形状基本一致，只是响应速度有所差异。因此，在不同增益下，所提含积分SFPC的响应特性能保持一致，且比直接串联速度环有更小的超调和抖动。
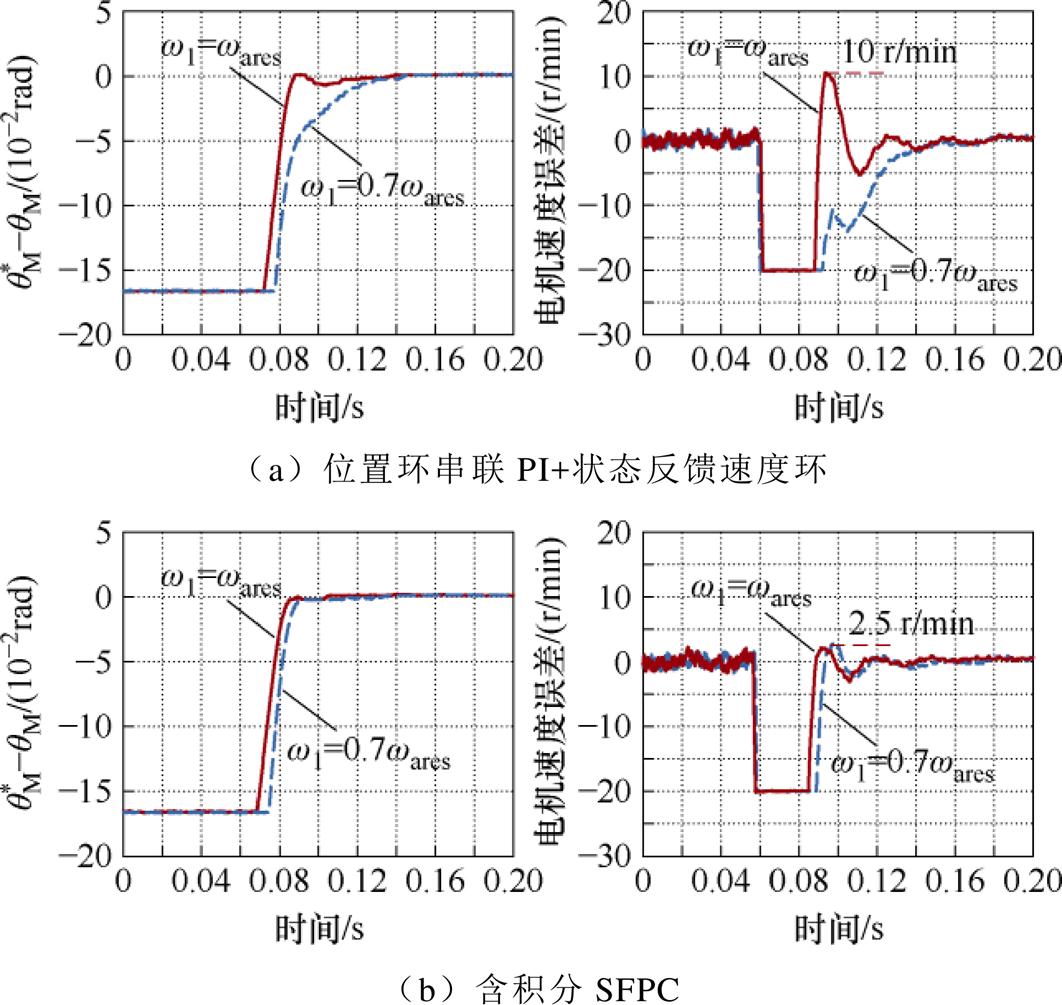
图14 不同w 1下，位置环响应对比
Fig.14 Position response comparison under different w 1
本文所提无积分与含积分SFPC的位置动态响应对比实验如图15所示。可以看出，无积分SFPC在相同增益下能实现与含积分方法一致的位置动态响应，拖尾阶段无超调且到位过程基本重合。从速度波形可以看出，无积分设计法的速度抖动略小。因此，本文所提两种结构能达到的控制性能在理论和实验效果上确实是一致的，但无积分状态反馈设计法控制结构更加简单。
虽然两种结构的动态响应一致，但按图7和图10分析，其鲁棒性大不相同。图16给出了临界增益下所提含积分的状态反馈控制速度和转矩的波形。可以看出，将增益w 1提升至1.3w ares时，速度响应依然平滑，转矩抖动较小。但如图16b所示，由于太接近6 dB的鲁棒边界，增益提升至1.4w ares时速度和转矩都出现了明显的抖动。尤其是在零速时，受摩擦扰动的影响，转矩和速度都出现了自持振荡。实际工业应用中，建议含积分SFPC的增益选择应小于1.4w ares。
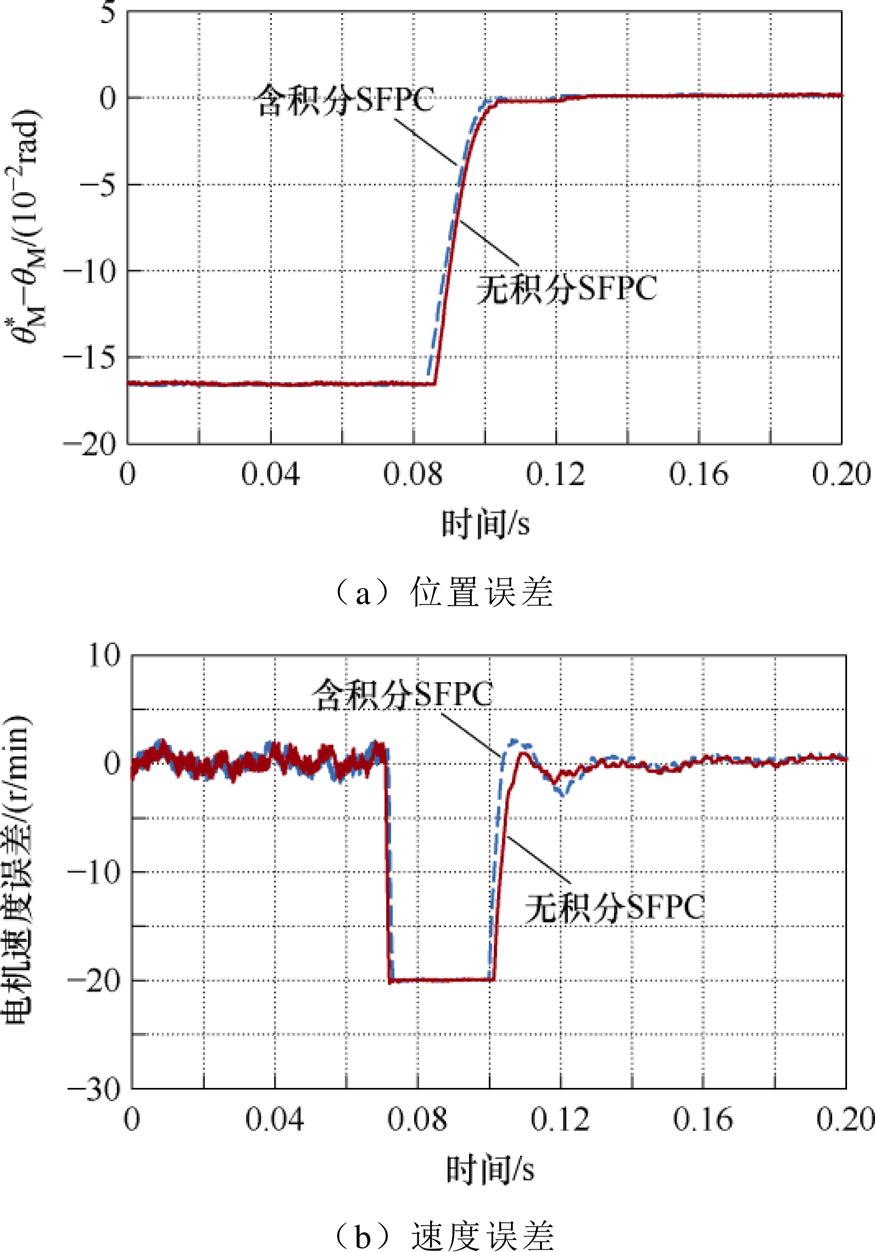
图15 w 1=1.0w ares时，两种SFPC结构的位置响应对比
Fig.15 Position response comparison between two kinds of SFPC structures with w 1=1.0w ares
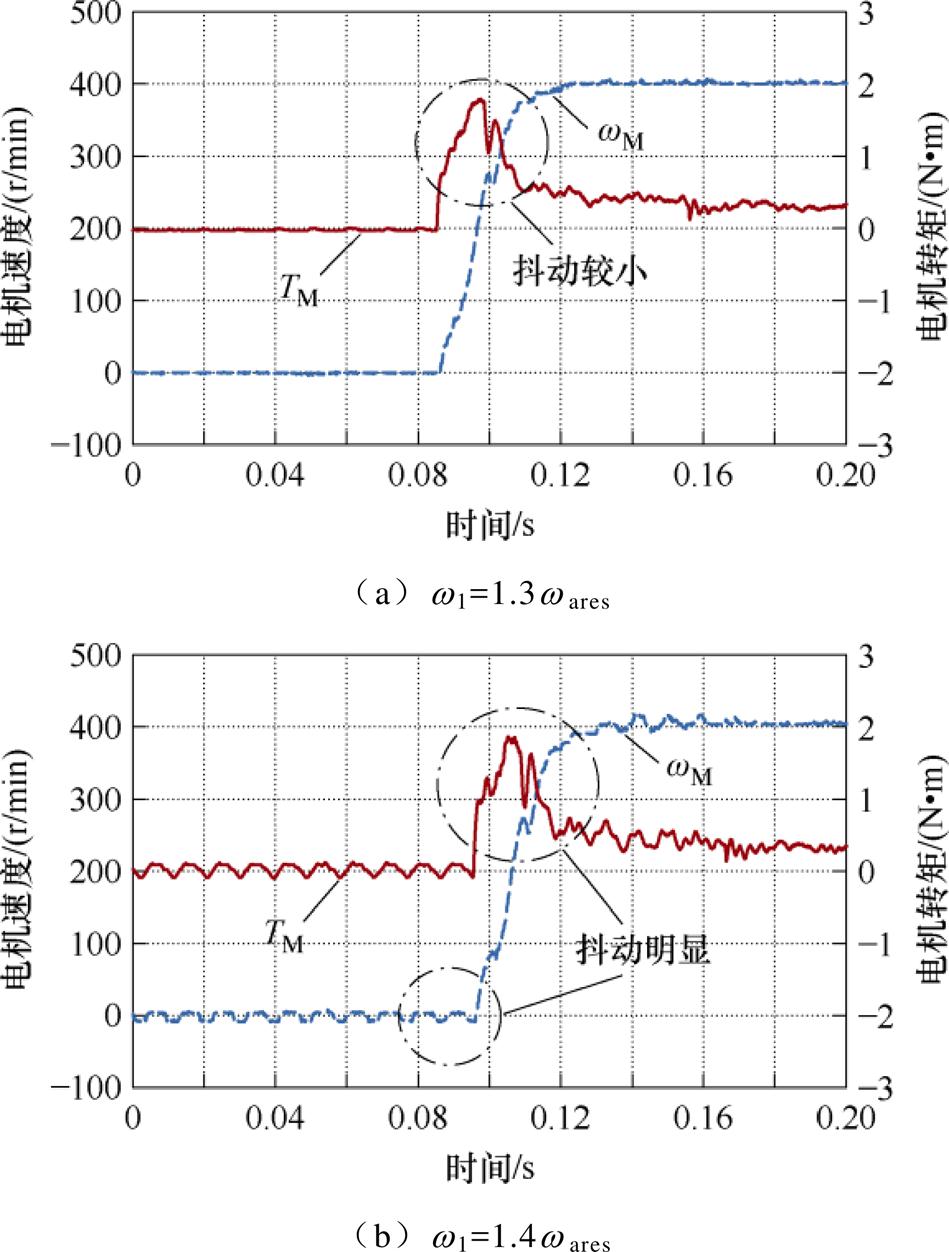
图16 含积分SFPC下增益边界附近的响应
Fig.16 Response around the gain boundary under the SFPC with integral part
无积分设计法在增益边界附近的响应如图17所示。当增益w 1提升至1.6w ares时，无积分设计法的速度和转矩响应依然平滑，而图16b中，增益达到1.4w ares时就已经出现了明显的自持振荡现象，积分环节是限制增益极限的主要因素。当增益进一步提升至1.8w ares时，速度和转矩都出现了明显的抖动，这意味着控制器鲁棒性显著降低。但系统依然稳定，并没有出现类似图16b的自持振荡，因此无积分SFPC扩展了28%的增益边界。
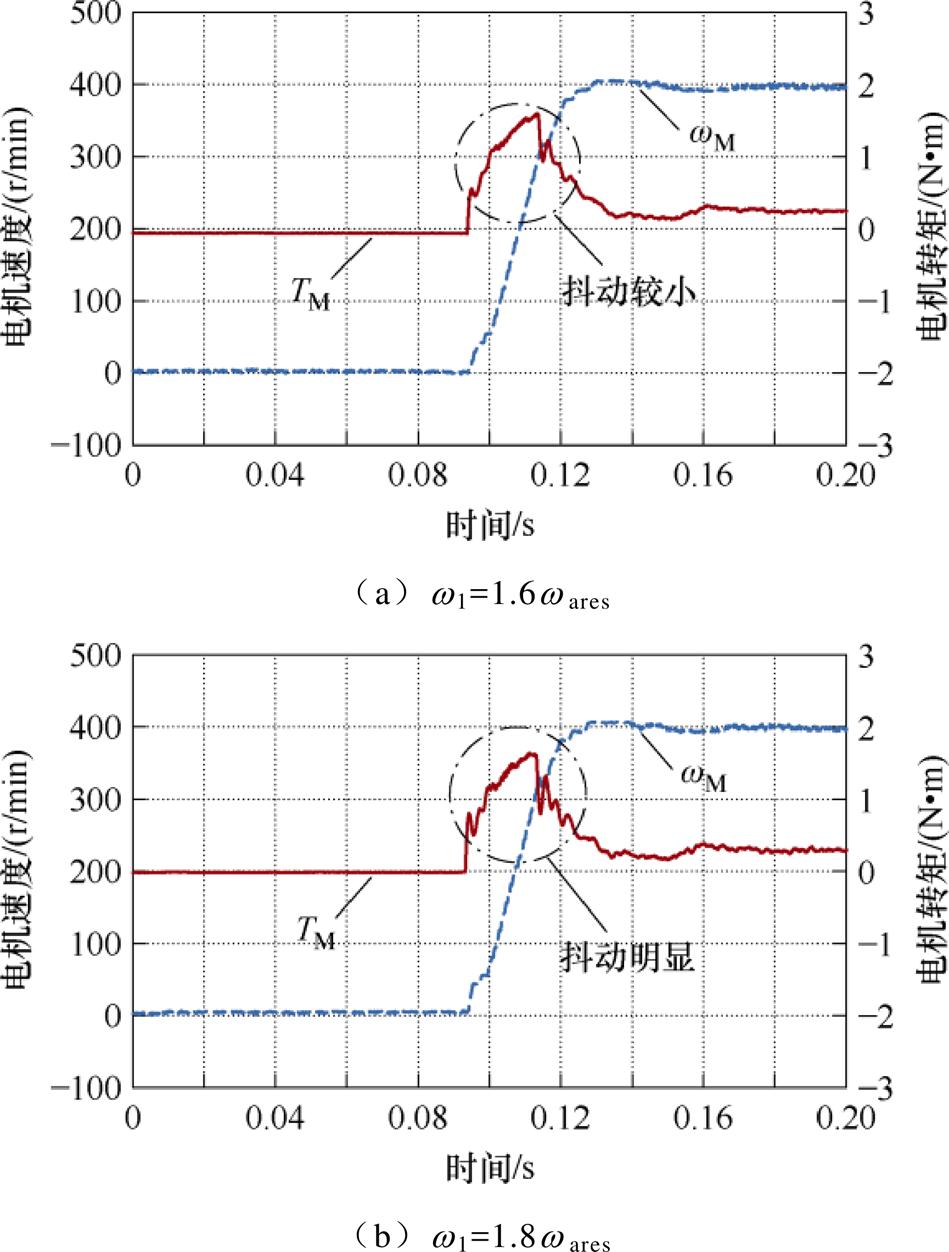
图17 无积分SFPC下增益边界附近的响应
Fig.17 Response around the gain boundary under the state feedback controller without integral part
图18验证了所提控制器对1 mm（折算到滑台）、1 Hz正弦位置指令的跟踪情况。含积分SFPC增益选择为1.4w ares，而无积分SFPC的增益为1.8w ares。可以看出，P-PI控制的跟踪误差最大为2.4 mm，含积分SFPC能显著减小跟踪误差至1.5 mm，无积分设计由于进一步提升了控制器增益，具有更小的跟踪误差。图18b表明，SFPC都有较为平滑的速度响应。但P-PI控制由于动态响应较慢，基于位置指令微分的摩擦补偿容易过度，使速度响应在过零时出现过冲现象。
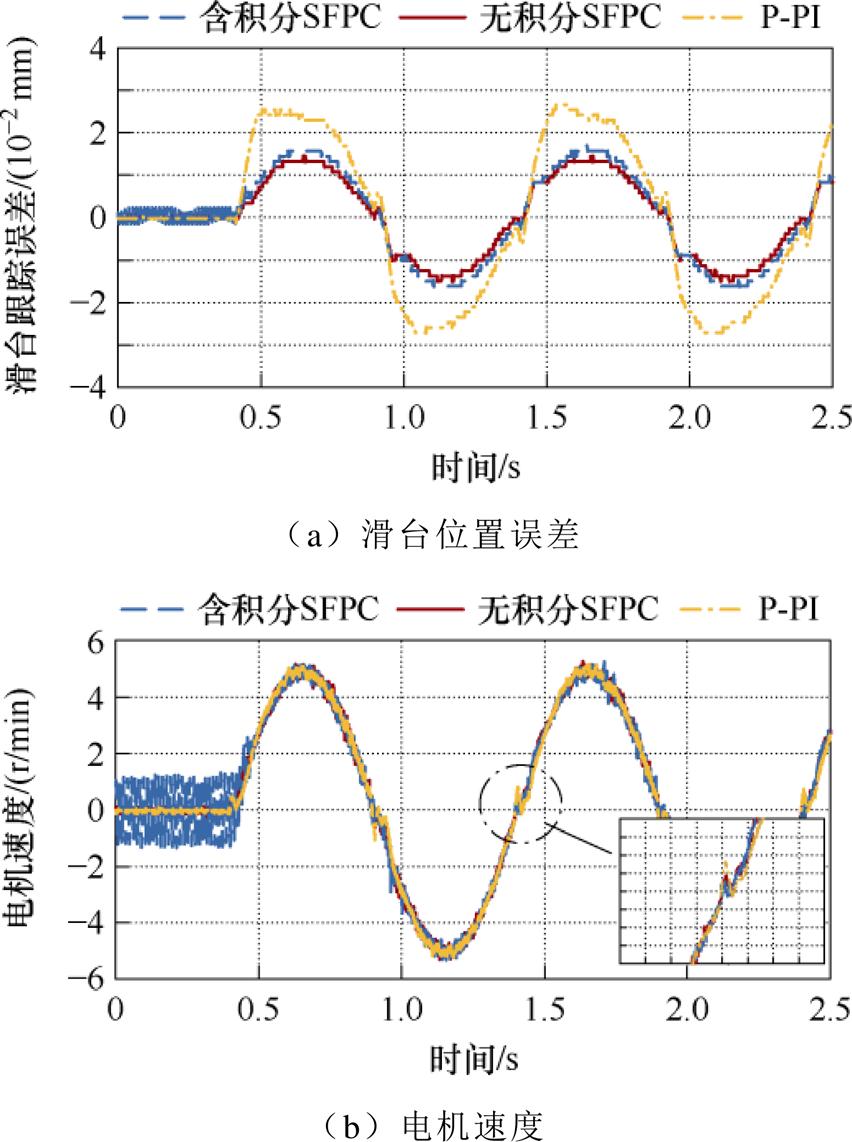
图18 正弦位置指令跟踪
Fig.18 Sinusoidal position reference tracking
本文研究了弹性伺服系统位置控制带宽扩展问题，分析了传统P-PI控制带宽受限的原因并提出了两种SFPC设计方法。通过理论分析和实验验证，得到如下结论：
1）在现有的PI+状态反馈速度控制外串联位置环，无法实现位置闭环系统的灵活设计。通过拆分速度环PI结构，增加了闭环系统分子多项式设计的自由度。
2）所提速度前馈设计能理论上保证临界无超调下最好的动态特性。与PI+状态反馈相比，响应的低通特性在不同增益选择下有很好的一致性，参数无需调整和试凑。
3）所提无积分SFPC取消了积分环节，控制结构得到简化，但理论上能实现与串联结构一致的动态特性。经过理论分析和实验验证，两种方法可选增益范围不同，无积分SFPC能提升28%的极限增益范围，更利于工业应用。
参考文献
[1] 王璨, 杨明, 栾添瑞, 等. 双惯量弹性伺服系统外部机械参数辨识综述[J]. 中国电机工程学报, 2016, 36(3): 804-817.
Wang Can, Yang Ming, Luan Tianrui, et al. A review of external mechanical parameter identification of two-mass elastic servo systems[J]. Proceedings of the CSEE, 2016, 36(3): 804-817.
[2] 朴敏楠, 陈志刚, 孙明玮, 等. 高超声速飞行器气动伺服弹性的自适应抑制[J]. 航空学报, 2020, 41(11): 623698.
Piao Minnan, Chen Zhigang, Sun Mingwei, et al. Adaptive aeroservoelasticity suppression of hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(11): 623698.
[3] 杨旭, 李超, 赵雅楠. 基于弹性连接模型的电动伺服机构频率特性研究[J]. 工程技术研究, 2023, 8(2): 8-10.
Yang Xu, Li Chao, Zhao Yanan. Research on frequency characteristics of electric servo mechanism based on elastic connection model[J]. Engineering and Technological Research, 2023, 8(2): 8-10.
[4] 倪启南, 杨明, 李云嵩, 等. 全闭环伺服驱动系统位置控制通信延时补偿技术[J]. 电工技术学报, 2022, 37(10): 2513-2522.
Ni Qinan, Yang Ming, Li Yunsong, et al. Com- munication delay compensation technology of full- closed loop position control for servo drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2513-2522.
[5] Chen Yangyang, Yang Ming, Long Jiang, et al. Analysis of oscillation frequency deviation in elastic coupling digital drive system and robust Notch filter strategy[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(1): 90-101.
[6] 杨明, 胡浩, 徐殿国. 永磁交流伺服系统机械谐振成因及其抑制[J]. 电机与控制学报, 2012, 16(1): 79-84.
Yang Ming, Hu Hao, Xu Dianguo. Cause and suppression of mechanical resonance in PMSM servo system[J]. Electric Machines and Control, 2012, 16(1): 79-84.
[7] 郑立楷, 吴玉香, 王孝洪, 等. 伺服系统弹性负载的闭环辨识方法[J]. 控制理论与应用, 2023, 40(3): 468-476.
Zheng Likai, Wu Yuxiang, Wang Xiaohong, et al. Closed-loop identification method for servo elastic load[J]. Control Theory & Applications, 2023, 40(3): 468-476.
[8] Niu Zenong, Huang Wenxin, Zhu Shanfeng. Online identification of mechanical systems using the simplified output error model[J]. IEEE Transactions on Industrial Electronics, 2023, 70(7): 6653-6662.
[9] 葛健, 宫逸凡, 徐伟, 等. 基于在线参数辨识及自适应谐波提取滤波器的改进型直线振荡电机无位置传感器控制[J]. 电工技术学报, 2024, 39(22): 7099-7110.
Ge Jian, Gong Yifan, Xu Wei, et al. Improved sensorless control of linear oscillatory machine based on online parameter identification and adaptive harmonic extraction filter[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7099-7110.
[10] 张放, 李佳欣, 史静舒. 基于基波同步相量的次/超同步振荡参数辨识探究: 频谱特性和关键问题[J]. 电工技术学报, 2024, 39(19): 6018-6038, 6053.
Zhang Fang, Li Jiaxin, Shi Jingshu. Research on subsynchronous/supersynchronous oscillation parameter identification based on fundamental synchrophasor: spectrum characteristics and essential issues[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6018-6038, 6053.
[11] 余洋, 余宗哲, 王孟云, 等. 机械弹性储能用永磁同步电机多源谐波提取及统一抑制[J]. 电工技术学报, 2024, 39(4): 1033-1045, 1073.
Yu Yang, Yu Zongzhe, Wang Mengyun, et al. Multi- source harmonic extraction and unified suppression of permanent magnet synchronous motor for mechanical elastic energy storage[J]. Transactions of China Elec- trotechnical Society, 2024, 39(4): 1033-1045, 1073.
[12] 杨明, 龙江, 唐思宇, 等. 永磁交流伺服系统定位末端抖动抑制[J]. 电机与控制学报, 2015, 19(6): 102-108.
Yang Ming, Long Jiang, Tang Siyu, et al. Suppression of positioning vibration for PMSM servo system[J]. Electric Machines and Control, 2015, 19(6): 102-108.
[13] Khoshdarregi M R, Tappe S, Altintas Y. Integrated five-axis trajectory shaping and contour error compensation for high-speed CNC machine tools[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(6): 1859-1871.
[14] Zhang G, Furusho J. Speed control of two-inertia system by PI/PID control[J]. IEEE Transactions on Industrial Electronics, 2000, 47(3): 603-609.
[15] 丁有爽, 肖曦. 基于极点配置的永磁同步电机驱动柔性负载PI调节器参数确定方法[J]. 中国电机工程学报, 2017, 37(4): 1225-1239.
Ding Youshuang, Xiao Xi. Parameter tuning methods based on pole placement for PI controllers of flexible loads driven by PMSM[J]. Proceedings of the CSEE, 2017, 37(4): 1225-1239.
[16] Hori Y, Sawada H, Chun Y. Slow resonance ratio control for vibration suppression and disturbance rejection in torsional system[J]. IEEE Transactions on Industrial Electronics, 1999, 46(1): 162-168.
[17] Szabat K, Orlowska-Kowalska T. Vibration suppression in a two-mass drive system using PI speed controller and additional feedbacks-comparative study[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 1193-1206.
[18] 杨影, 张杰鸣, 徐国卿, 等. 转速负反馈在伺服系统机械谐振抑制中的应用研究[J]. 电工技术学报, 2018, 33(23): 5459-5469.
Yang Ying, Zhang Jieming, Xu Guoqing, et al. Application research on speed negative feedback in mechanical resonance suppression in servo system[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5459-5469.
[19] 丁有爽, 肖曦. 基于负载位置反馈的永磁同步电机驱动柔性负载谐振抑制方法[J]. 电工技术学报, 2017, 32(11): 96-110.
Ding Youshuang, Xiao Xi. Resonance suppression method based on load position feedback for flexible load driven by PMSM[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 96-110.
[20] 吴春, 王超, 郑露华. 基于相环型扩张状态观测器的双惯量弹性伺服系统机械谐振抑制方法[J]. 电工技术学报, 2024, 39 (18): 5680-5691.
Wu Chun, Wang Chao, Zheng Luhua. A mechanical resonance suppression strategy for two-inertia elastic servo systems based on a phase locked loop-type extended state observ[J]. Transactions of China Elec- trotechnical Society, 2024, 39 (18): 5680-5691.
[21] Szabat K, Orlowska-Kowalska T. Application of the Kalman filters to the high-performance drive system with elastic coupling[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4226-4235.
[22] 丁有爽, 肖曦. 基于状态反馈和转矩补偿的永磁同步电机驱动柔性负载控制方法[J]. 中国电机工程学报, 2017, 37(13): 3892-3900.
Ding Youshuang, Xiao Xi. A resonance suppression method based on Kalman state estimation and load torque compensation for flexible load driven by permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(13): 3892-3900.
[23] Wang Can, Liu Jinliang, Xin Lekai, et al. Design of full-order state observer for two-mass joint servo system based on the fixed gain filter[J]. IEEE Transa- ctions on Power Electronics, 2022, 37(9): 10466- 10475.
[24] Saarakkala S E, Hinkkanen M. State-space speed control of two-mass mechanical systems: analytical tuning and experimental evaluation[J]. IEEE Transa- ctions on Industry Applications, 2014, 50(5): 3428- 3437.
[25] 赵寿华, 毛永乐, 许翠翠, 等. 基于自适应观测器和线性二次型调节器的高性能伺服系统谐振抑制[J]. 电工技术学报, 2016, 31(6): 108-117.
Zhao Shouhua, Mao Yongle, Xu Cuicui, et al. Torsional vibration suppression based on adaptive observer and linear quadratic regulator in high performance servo drives[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 108-117.
[26] 葛健, 宫逸凡, 徐伟, 等. 基于在线参数辨识及自适应谐波提取滤波器的改进型直线振荡电机无位置传感器控制[J]. 电工技术学报, 2024, 39(22): 7099-7110.
Ge Jian, Gong Yifan, Xu Wei, et al. Improved sensorless control of linear oscillatory machine based on online parameter identification and adaptive harmonic extraction filter[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7099-7110.
[27] Chang He, Lu Shaowu, Zheng Shiqi, et al. Integrated parameter identification based on a topological structure for servo resonance suppression[J]. IEEE Transactions on Industrial Electronics, 2024, 71(5): 4541-4550.
[28] 王立俊, 赵吉文, 于子翔, 等. 基于非线性时间延迟扰动估计的永磁同步直线电机无模型鲁棒位置跟踪控制[J]. 电工技术学报, 2024, 39(18): 5692- 5704.
Wang Lijun, Zhao Jiwen, Yu Zixiang, et al. Model- free robust position tracking control of permanent magnet synchronous linear motor based on nonlinear time delay disturbance estimation[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5692- 5704.
[29] Orlowska-Kowalska T, Szabat K. Control of the drive system with stiff and elastic couplings using adaptive neuro-fuzzy approach[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 228-240.
[30] Wang Can, Yang Ming, Zheng Weilong, et al. Vibration suppression with shaft torque limitation using explicit MPC-PI switching control in elastic drive systems[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11): 6855-6867.
[31] Niu Zenong, Huang Wenxin, Zhu Shanfeng, et al. Position controller design based on the extended state observer for servomechanism with elasticity[C]//2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 2023: 448-452.
[32] Zhu Shanfeng, Huang Wenxin, Zhao Yajun, et al. Robust speed control of electrical drives with reduced ripple using adaptive switching high-order extended state observer[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(2): 2009-2020.
High-Performance Position Controller Design and Gain Boundary Analysis for Elastic Servo Systems
Abstract High-performance servo drives are critical for the quality of industrial production. In traditional servo control schemes, motor position feedback modifies the speed closed-loop transfer function, characterized by two parameters: proportional and integral. For elastic mechanical loads, it is impossible to balance damping and dynamic response within the system. State feedback control (SFC) effectively improves speed dynamic response and suppresses residual vibration. This paper proposes two types of position controller design methods based on state feedback to address the bandwidth restrictions imposed by anti-resonance frequencies in elastic servo systems.
Firstly, the numerator polynomial in the speed proportional-integral (PI) structure has freedom restrictions. The proposed state feedback position control (SFPC) with an integral part combines PI with integral-proportional (IP) for a more flexible zero design. Zero-pole cancellation reduces the order of the closed-loop system, and optimal speed feedforward in the frequency domain improves dynamic performance. Secondly, the state feedback controller without an integral part removes the integral component from the speed loop, where estimated disturbances are compensated on the output torque. The disturbance function is modified with a parameter kL to provide a high-pass filter characteristic. Zero-pole cancellation is unnecessary for this simplified structure. Furthermore, the gain boundaries of these two SFPCs are analyzed using maximum peak sensitivity, demonstrating that the speed loop without an integral part has a larger gain boundary than the series structure. The maximum gain offers a reasonable guideline for bandwidth selection in practical applications. Finally, the effectiveness of the proposed methods is verified on a tooth belt servo system. The proposed SFPCs have good dynamic response and a wide gain selection boundary.
The following conclusions can be drawn. (1) The proposed SFPC with an integral part reaches the target position faster than the traditional method, with less overshoot and a 44% reduction in settling time. (2) Compared to state feedback speed control cascading a position loop, the response characteristics of the proposed SFPC remain consistent across different gains. (3) The position response of the SFPC with an integral part is in good agreement with the method that includes an integral, which achieves the same positional dynamic response at the same gain. (4) The optional gain boundaries of the two methods differ. The gain of the SFPC with and without an integral can approach 1.4wares with oscillations and 1.8wares without oscillations. The non-integral SFPC increases the gain boundary by 28%.
The proposed SFPC can balance dynamic response and residual vibration, broadening the maximum gain boundary to 1.8wares, which is beneficial for improving servo driver performance under elastic mechanical loads.
Keywords：Servo control, two-mass system, state feedback control, gain boundary
中图分类号：TM383.4
DOI: 10.19595/j.cnki.1000-6753.tces.241047
中央高校基本科研业务费资助项目（NT2023007）。
收稿日期2024-06-18
改稿日期 2024-10-11
牛泽农 男，1993年生，博士研究生，研究方向为永磁同步电机低载波比控制、高性能伺服控制系统设计。
E-mail: niuzenong@nuaa.edu.cn
黄文新 男，1966年生，教授，博士生导师，研究方向为电机系统及其控制、新型风力发电技术、电能变换、航空电源等。
E-mail: huangwx@nuaa.edu.cn（通信作者）
（编辑 崔文静）