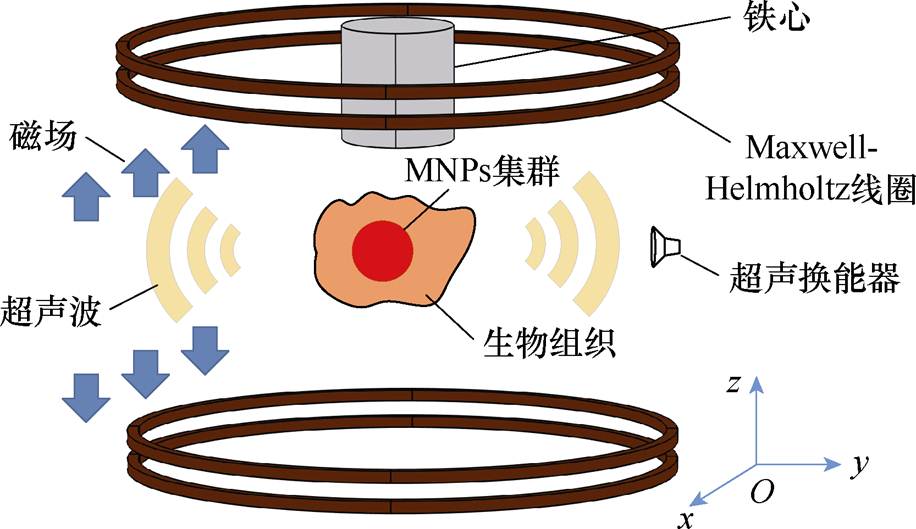
图1 MACT-MI成像原理
Fig.1 Principle of MACT-MI imaging
摘要 在相同电流激励条件下，为了提高感应式磁声磁粒子浓度成像（MACT-MI）装置产生的梯度磁场，该文提出一种由Maxwell-Helmholtz线圈和锥形铁心组成的磁场发生装置，相较于传统MACT-MI激励单元，在研究区域（ROI）新增一个由锥形铁心感生出的时变梯度磁场分量。首先研究了锥形铁心对MACT-MI电磁学与声学特性的影响，通过建立多目标优化模型，对铁心结构进行设计，并采用和谐搜索算法，得到最优铁心尺寸；最后采用有限元分析软件COMSOL对加铁心前后的激励效果进行了求解与比较。数值研究表明，与空心线圈相比，锥形铁心线圈在ROI的梯度磁场磁感应强度最大值提高了约6.9倍，轴线磁场梯度扩大了3倍，磁性纳米粒子（MNPs）在中心位置所受磁力增大了10.4倍。该研究为降低MACT-MI装置所需电流激励提供研究基础，使MACT-MI成像装置向生物医学的实际应用进一步迈进。
关键词：感应式磁声磁粒子浓度成像 锥形铁心线圈 磁力 声压
感应式磁声磁粒子浓度成像（Magnetoacoustic Concentration Tomography of Magnetic Nanoparticles with Magnetic Induction, MACT-MI）是一种电磁和超声相互耦合的多物理场成像方法。该方法可无创、低成本地实现目标组织内部磁性纳米粒子的定量估计，有望进一步提高成像分辨率[1]。然而在前期的研究中发现，当前MACT-MI需要借助高幅值的激励源装置来产生磁声信号，若要超声探头感应到声信号，至少需要在半径为0.4 m的Maxwell线圈通以大约200 A的脉冲电流[2]，这无疑对硬件配置提出了极高的要求，不利于实验工作的开展。在之前的工作中，文献[3]通过加入永磁体来提高磁场发生装置产生的静磁场，使磁声粒子（Magnetic Nanoparticles, MNPs）的磁化强度增大，进而增强磁声信号。然而，MNPs达到饱和磁化状态以后，所受磁力几乎不受静磁场影响，因此本文通过设计一种铁心线圈，同时提高研究区域（Region of Interest, ROI）内磁感应强度和梯度，从而使MNPs产生的磁声信号增大，适用性更广，且成本更低。
近年来，多位学者都验证了铁心线圈的优势，在线圈中嵌入铁磁材料是一种降低线圈能量需求的无源手段。2001年N. Al-Mutawaly等在新型slinky线圈中加入了铁心结构，铁心线圈产生的磁通密度几乎是空心线圈的2倍[4]。2007年R. Salvador等通过将一个高磁导率的C形铁心与设计的线圈相结合，发现铁心线圈可以减缓磁场衰减，增加磁场强度，并改善聚焦性，从而减少磁刺激器的负担[5]。2015年，Lai Lingfeng的主要关注点是铁心和高温超导线圈之间的相互作用，发现精心设计的铁心有利于降低交流损耗[6]。2017年P. Rastogi等在四蝶形线圈结构中添加了高导磁材料，使磁场聚焦程度提高了13.4%[7]。2021年，夏思萍等提出的“8”字形、双锥形铁心线圈结构提升了线圈刺激强度和聚焦性[8]。2022年，孙钰婷等分析五种铁心材料对线圈聚焦性能的影响，与空心线圈相比，硅钢材料最高可增强46.2%的磁场强度[9]。
相较于探索线圈的组合方式[10-11]，插入铁心更为简便易用；而与加入永磁体相比[12-13]，铁心材料成本更低。因此，本文通过在线圈中心插入铁心，新增一个由铁心感生出的时变梯度磁场分量，从而提升磁场发生装置产生的梯度磁场；并通过对优化目标进行归一化，得到最佳铁心尺寸。本文仿真研究了圆柱形与锥形铁心线圈相较于空心线圈在ROI内的梯度磁场特性，包括梯度磁场磁感应强度最大值、轴线磁场梯度及MNPs受力，结果显示，在这些方面锥形铁心线圈的提升尤为显著，而圆柱形铁心线圈也有一定提升，为MACT-MI成像装置的发展及其后续实验提供研究基础。
MACT-MI成像原理如图1所示。图中，铁心置于Maxwell-Helmholtz线圈的中心，除线圈本身产生的时变梯度磁场外，ROI新增一个由铁心感生出的时变梯度磁场分量，MNPs被磁化并受到更强的磁场力作用，激发粒子振动而产生声波，通过超声换能器检测其产生的声压信号，进而根据声压信号与MNPs浓度之间的关系，采用时间反演及有限差分法重构数量浓度分布图。
图1 MACT-MI成像原理
Fig.1 Principle of MACT-MI imaging
MNPs的受力情况可参考磁偶极子模型[14]，所受磁力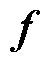
可描述为
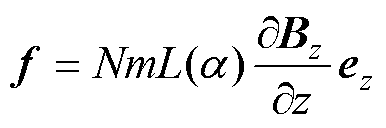（1）
式中，N为MNPs的浓度；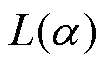
为Langevin函数；
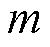为MNPs的磁矩；
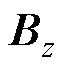为MNPs周围的磁通密度在z方向上的分量；
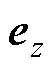为z方向的单位向量。
由于成像目标体在磁场源近场时，时变矢量可以由空间项、时间项的乘积来表示[15]，线圈产生z方向的时变磁场可以表示为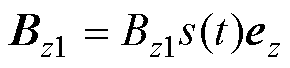
，其中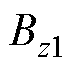
为线圈磁场的空间分布函数，
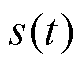描述其时间特性；铁心感生出的z方向的时变磁场为
，
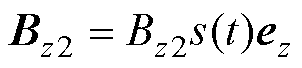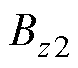为感生磁场的空间分布函数，由于感生磁场的时变过程也受到线圈电流的控制，同样可用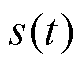近似描述其时间特性。
MNPs周围的磁场由Maxwell-Helmholtz线圈和铁心叠加产生，故铁心线圈磁体系统中的磁力可以表示为
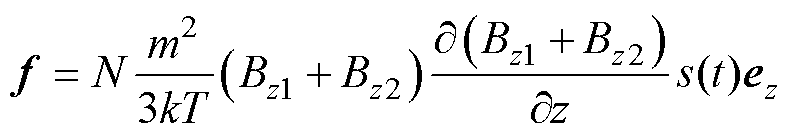（2）
式中，k为玻耳兹曼常数，k=1.38×10-23 J/K；T为温度（K）。
MNPs的磁化强度与外部磁场强度之间的关系为非线性的Langevin函数[16-17]，当外部磁场强度超过饱和磁场强度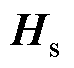
时，MNPs达到了饱和磁化状态，所受磁力为
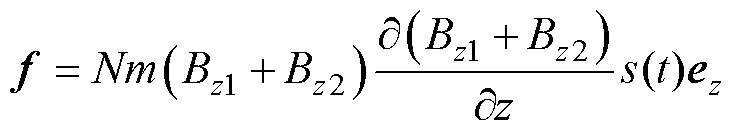（3）
因此，MNPs所受磁力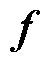与MNPs浓度N、ROI的磁场强度
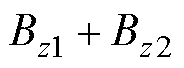和ROI的磁场梯度
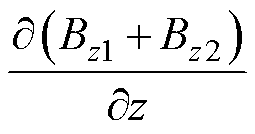有关：当ROI的磁场强度低于饱和磁场强度，即
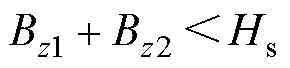时，采用式（2）对MNPs所受磁力进行计算，铁心的感生磁场分量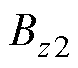可以提高ROI的磁场强度和梯度进而增强磁力；当ROI的磁场强度高于饱和磁场强度，即
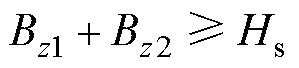时，采用式（3）对MNPs所受磁力进行计算，铁心的感生磁场分量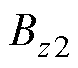同样可以通过提高ROI的磁场梯度来增强磁力。
以磁力散度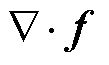
为声源项可得到线性声压波动方程，再根据无界空间格林函数法，求解无界声场的解析解为
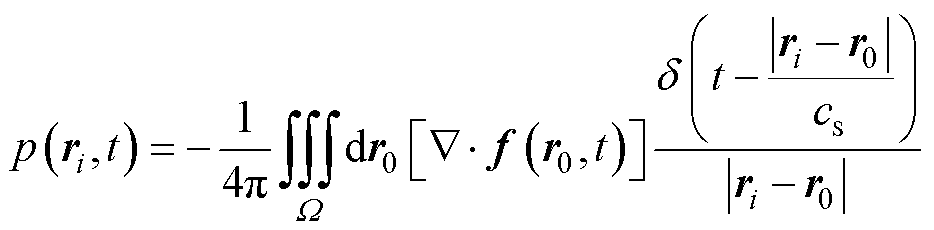（4）
式中，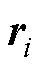
为声场中的任意一点；
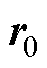为源点位置；
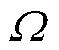为空间积分区域；
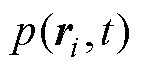为声场的时空分布；
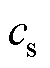为生物组织中的超声传播速度；
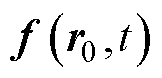为源点处MNPs受到的磁力。
通过对铁心的合理设计，可以提高ROI的磁场强度和磁场梯度，同时为确保ROI的磁场梯度方向一致，本文采用单边锥形结构的铁心[18]，MACT-MI磁场发生装置示意图如图2所示。图2中，h2为铁心总高度，h1为锥形部分铁心高度，R0为圆柱形部分铁心半径，Dw为Maxwell线圈半径。
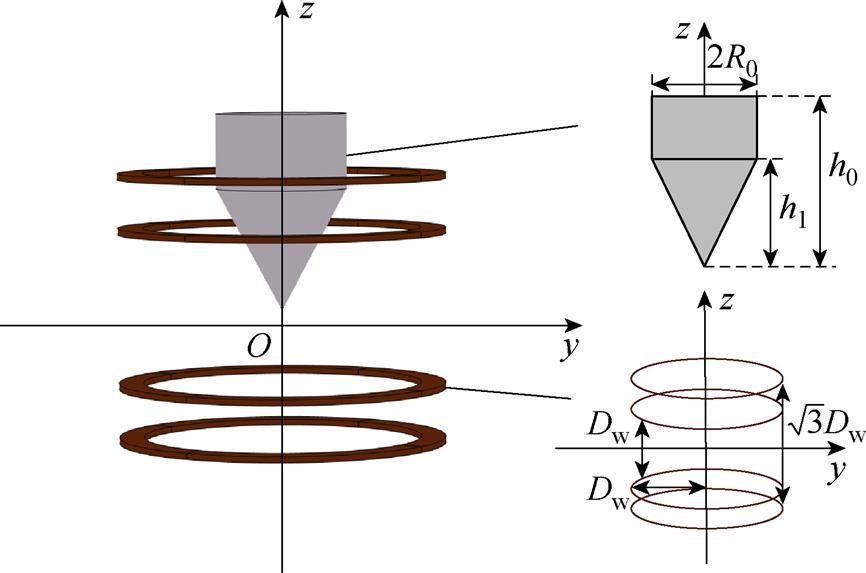
图2 MACT-MI磁场发生装置示意图
Fig.2 Schematic diagram of the MACT-MI magnetic field generator
为了简化计算模型，利用叠加原理计算线圈的磁场分布，并将锥形铁心变换为直径为2Dm（Dm为等效圆柱铁心的半径）的等效圆柱棒，锥形铁心线圈侧视图示意图模型如图3所示，其直径为Maxwell线圈中点位置对应的锥形铁心直径[19]。
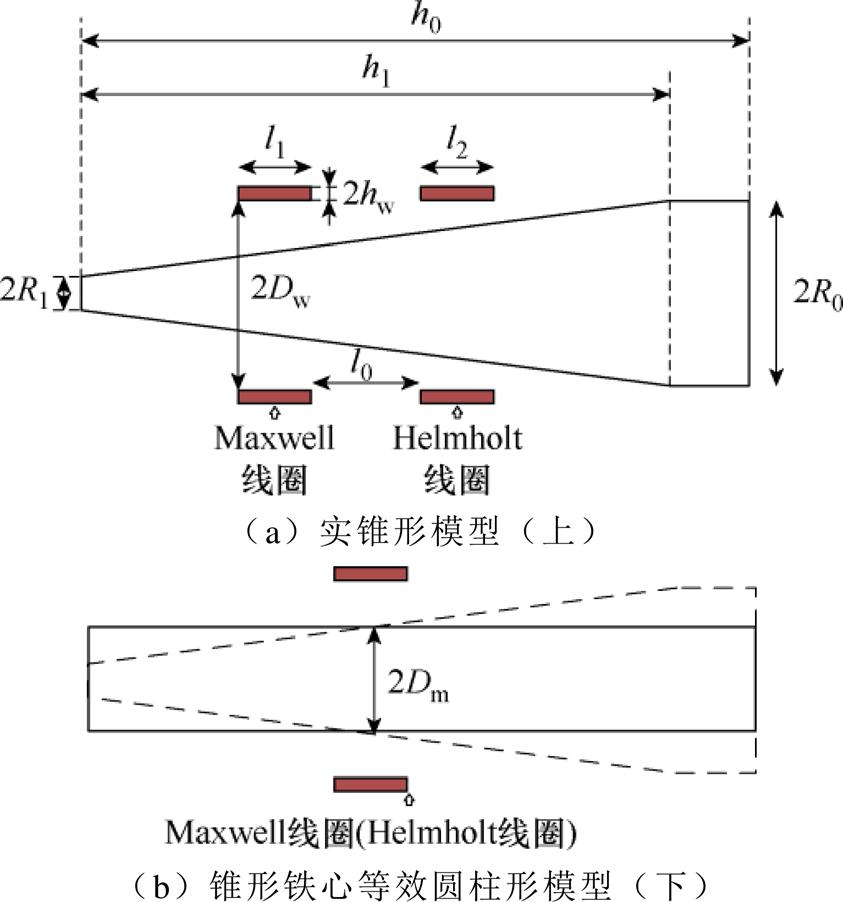
图3 锥形铁心线圈侧视图示意图模型
Fig.3 Conical core coil side view schematic model
计算Maxwell线圈作用下的磁场分布，仅考虑磁矢量势的方位分量，由柱面坐标系下的Maxwell方程可得磁矢势微分方程[20-22]为
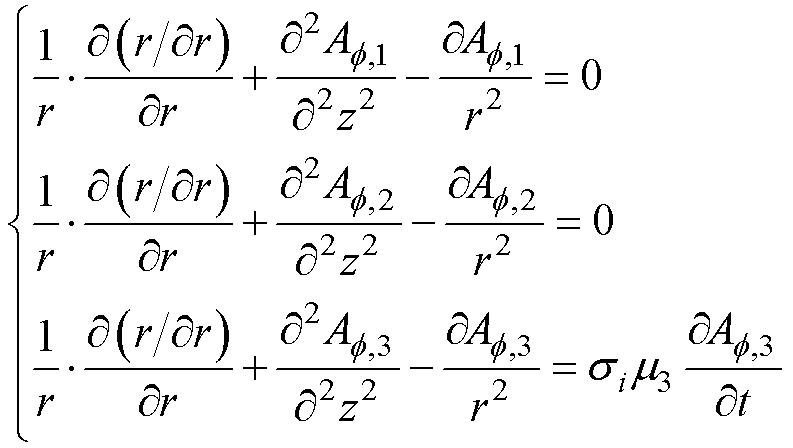（5）
式中，Af,1为线圈以外的空气区域1的磁矢势；Af,2为铁心和线圈之间气隙区域2的磁矢势；Af,3为铁心区域3的磁矢势；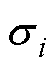
、
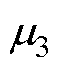分别为室温下铁心的电导率和磁导率。
采用分离变量法[19-20]求解得到
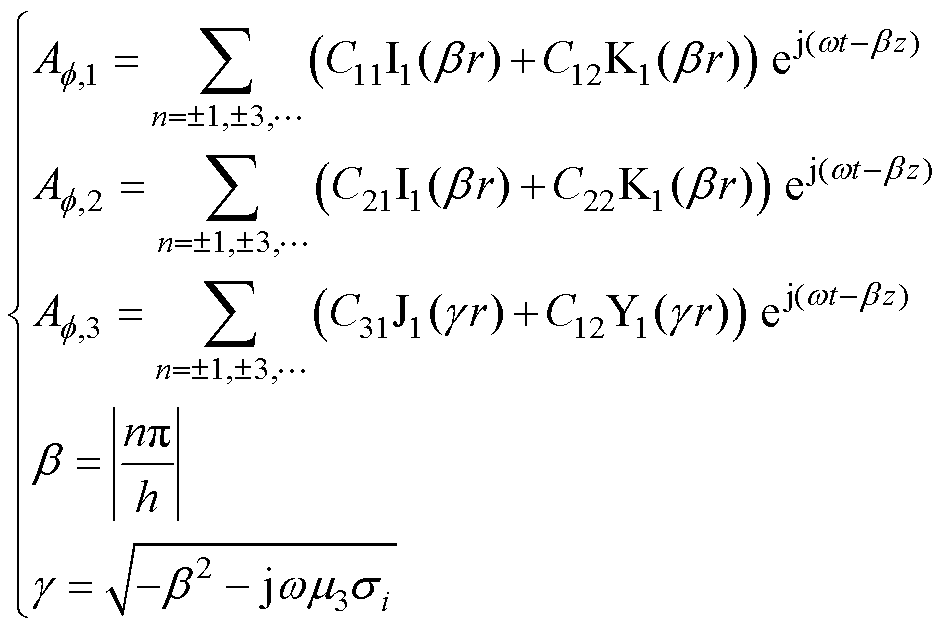（6）
式中，
、
、
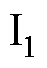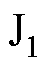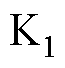和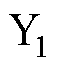
是1阶贝塞尔函数；
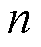为空间调和阶；
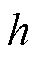为铁心的轴向长度；
、
、
、
、
、
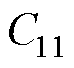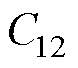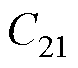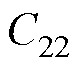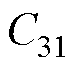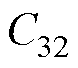是常数，由以下边界得到
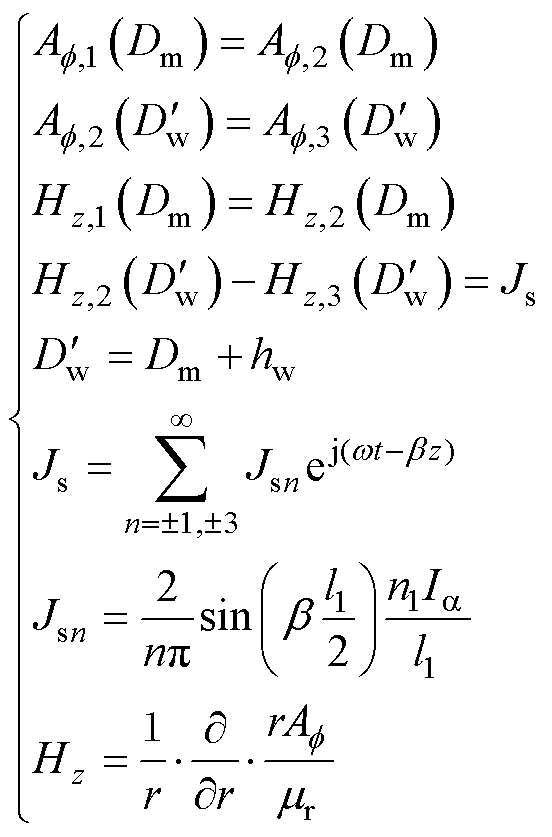（7）
式中，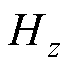
为磁场强度；hw为线圈厚度；Af 为在区域2和区域3之间的边界上的磁矢势；
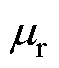为铁心表面的磁导率；
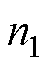为Maxwell线圈的匝数；
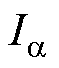为Maxwell的线圈电流；r为柱面坐标系中r方向，表示极轴到极面的距离。
同理可求Helmholt线圈作用下三个区域的磁矢势为Aq,1、Aq,2、Aq,3。
Maxwell-Helmholtz线圈会在z方向上产生梯度磁场，而在ROI的梯度磁场可近似[23]为
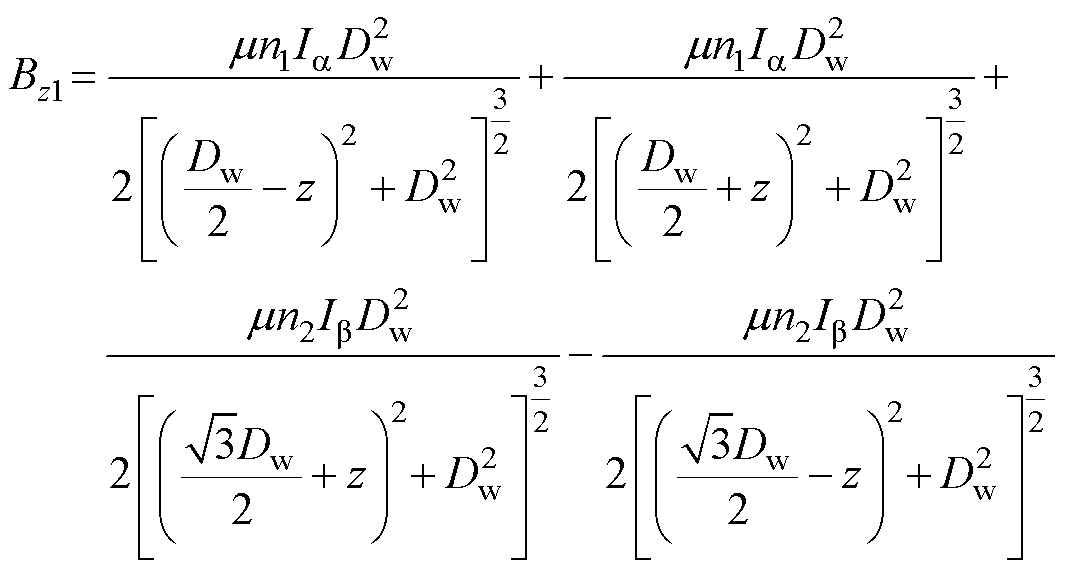（8）
式中，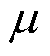
为ROI的磁导率；
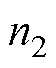为Helmholtz线圈的匝数；
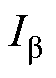为Helmholtz的线圈电流。
铁心线圈在ROI产生的磁场感应强度可以表示为
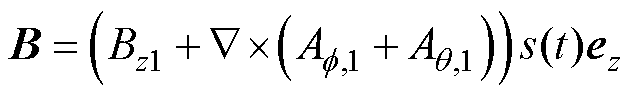（9）
首先利用COMSOL分析软件对铁心线圈的梯度磁场磁感应强度最大值、最小磁场增幅倍数和模拟磁力的表面平均值进行建模和计算，然后将上述结果导入Matlab进行优化，从而获得铁心的最佳尺寸。
由铁心尺寸决定的梯度磁场磁感应强度最大值、整体增幅倍数和模拟磁力这三个优化目标可能会相互冲突，一个目标的改进可能导致其他目标性能的下降，最优决策需要在两个或多个可能存在冲突的目标之间进行权衡。多目标优化方法常用于解决同一模型中存在多个非线性目标，需要进行优化以同时处理多个冲突目标的问题[24]。因此，本文通过在优化目标之间权衡，对铁心线圈进行优化设计。本文中的优化目标定义如下。
1）梯度磁场磁感应强度最大值[25]
式（9）可以描述铁心线圈在ROI产生的梯度磁场，其中磁感应强度最大值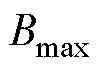
反映铁心的聚磁能力，应尽量增加梯度磁场磁感应强度最大值。
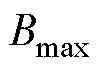2）最小磁场增幅倍数
本文中，最小磁场增幅倍数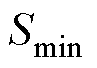
用于衡量线圈在ROI的磁场整体增幅强度，其定义为
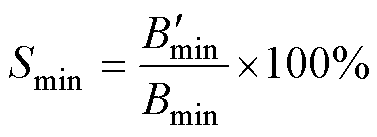（10）
式中，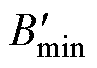
为铁心线圈在ROI内感生出的最小磁通密度；
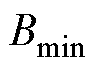为空心线圈在ROI内感生出的最小磁通密度。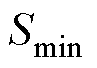值越大，磁场在ROI的整体聚焦越均匀。
3）模拟磁力的表面平均值
用式（2）可以表示铁心线圈作用下MNPs受到的磁力，模拟磁力的表面平均值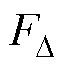
用于衡量ROI内MNPs产生声压信号的整体强弱程度，其定义为
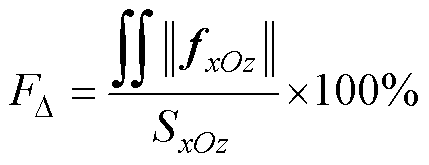（11）
式中，fxOz、SxOz分别为ROI内xOz截面的模拟磁力和截面积。
上述目标是由锥形铁心的尺寸决定的。因此本文的决策变量定义为铁心总高度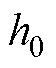
、锥形部分铁心高度
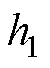、圆柱形部分铁心半径
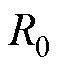和锥形尖端半径
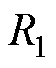（mm），如图3a所示。本文的多目标函数定义为
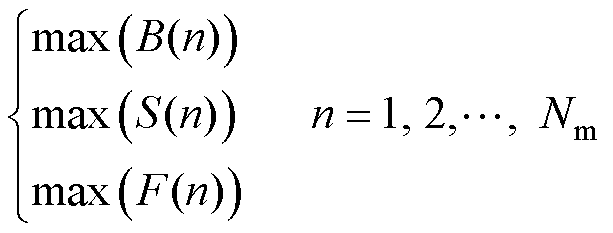（12）
式中，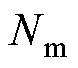
为决策变量的总数。B(n)为梯度磁场磁感应强度最大值，由第n个决策变量决定；S(n)为第n个决策变量的最小磁场增幅倍数；F(n)为第n个决策变量的模拟磁力的表面平均值。
函数可以转化为单个目标函数，每个目标的取值范围变化很大，因此应首先对其进行归一化以简化计算。采用min-max归一化[26]线性变换将原始数据转换到区间 (0, 1) 内。即
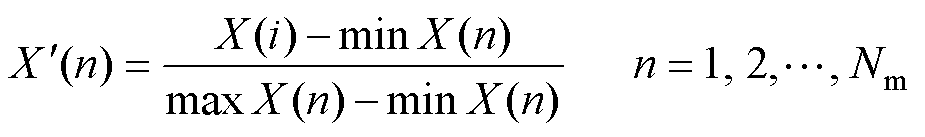（13）
式中，X(n)为决策变量的目标集合；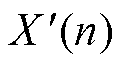
为归一化目标函数。
由式（13）得到归一化目标函数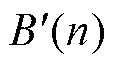
、
、
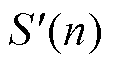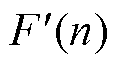。因此，将式（12）变换为
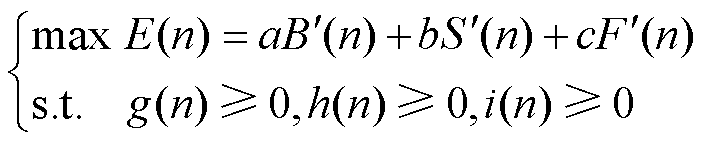
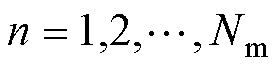（14）
不等式约束条件是铁心线圈的梯度磁场磁感应强度最大值、最小磁场增幅倍数和模拟磁力的表面平均值的限制。采用和谐搜索算法求解式（14），可以得到铁心尺寸的最优解。
决策变量是一个系统设置，其值由决策者指定，这些约束对决策方案施加了限制。在这种情况下，约束条件如下。
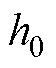的约束：圆柱形铁心总高度步长1 mm，进行了150组模拟，如图4所示，磁通密度和磁力表面平均值与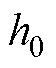呈正相关，考虑到铁心与线圈的适用性和制作成本，选择对
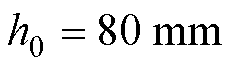的圆柱形铁心进行优化设计。
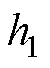的约束：锥形部分铁心高度不超过铁心总高度，即
。
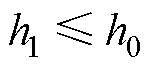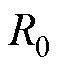的约束：铁心的尺寸要限制在线圈直径以内，即
。
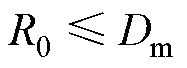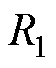的约束：考虑到ROI的大小，锥形尖端半径应不大于25 mm，即
。
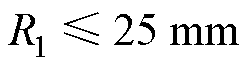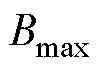的约束：锥形铁心线圈的梯度磁场磁感应强度最大值应至少为空心线圈的6倍。
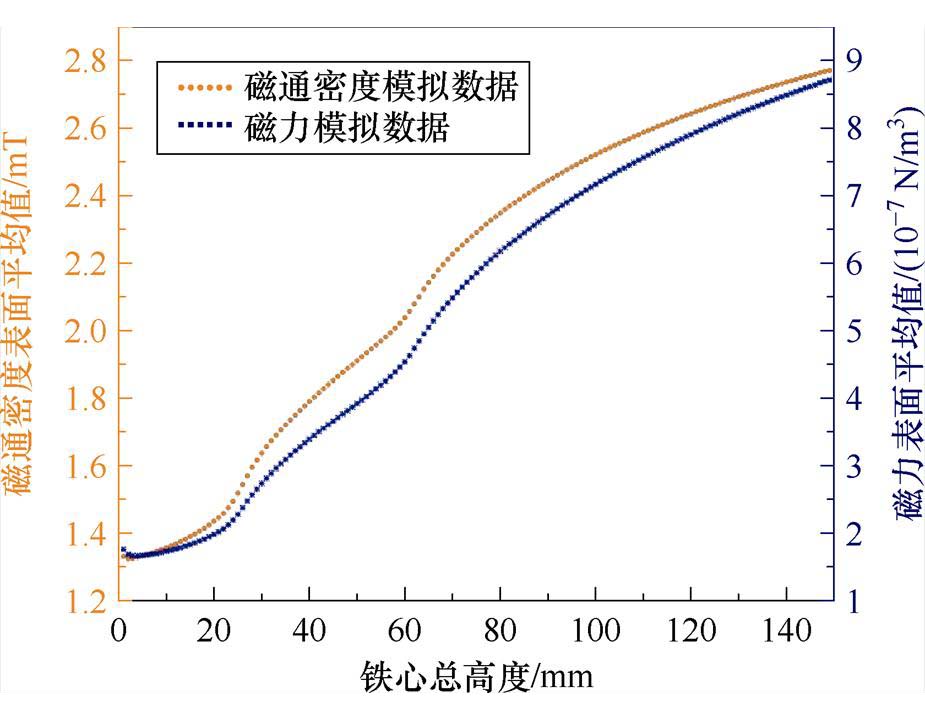
图4 铁心总高度对磁场、磁力的影响
Fig.4 Influence of total core height on magnetic field and magnetic force
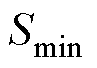的约束：为使ROI内磁场增幅尽可能均匀，最小磁场增幅倍数至少为空心线圈的1.6倍。
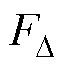的约束：锥形铁心线圈的磁力表面平均值应至少为空心线圈的6倍。
铁心锥形部分高度步长5 mm、圆柱形部分铁心半径步长5 mm、锥形尖端半径步长1 mm。进行了5 824组模拟，但只有28组决策变量合格，如图5所示。当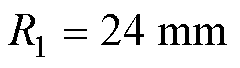
时，有16组数据（黄色散点）满足约束条件；当
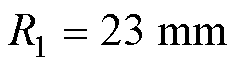时，有9组数据（绿色散点）满足约束条件；当
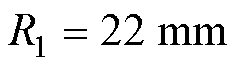时，只有三组数据（蓝色散点）符合约束条件。
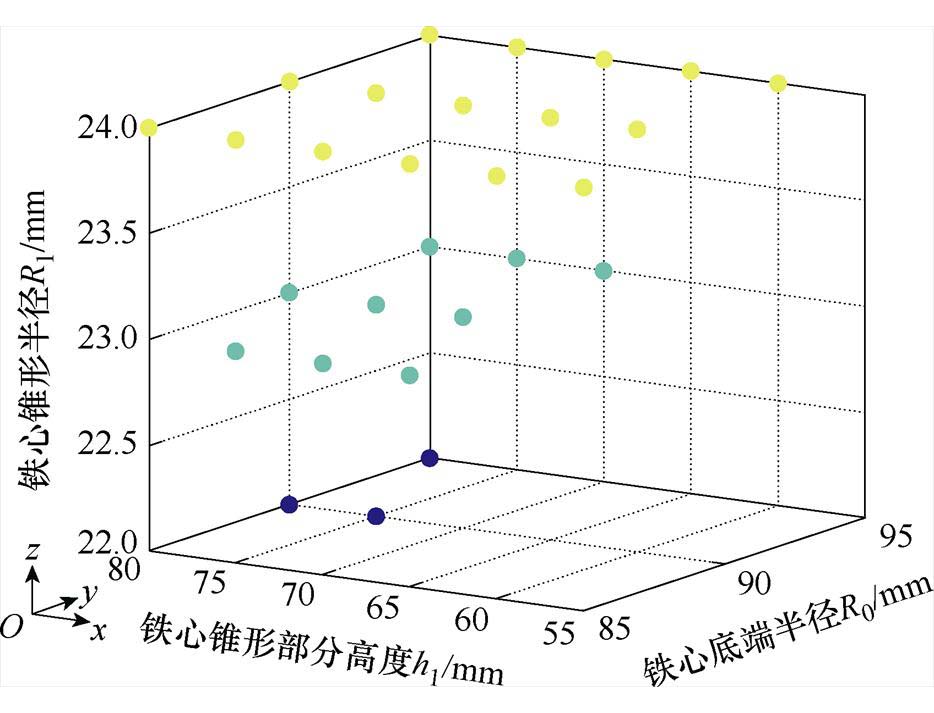
图5 决策变量满足约束的维度
Fig.5 The dimensions in which the decision variable satisfies the constraint
和谐搜索算法（Harmony Search Algorithm, HSA）是一种基于音乐的元启发式优化算法[27]。和谐搜索算法通过参数和声记忆概率（Harmony Memory Considering Rate, HMCR），音调微调概率（Pitch Adjusting Rate, PAR）和音调微调带宽（Band Width, BW）来控制算法的搜索能力，将音乐创作过程类比为种群进化过程。铁心几何结构优化设计流程如图6所示。本文的优化模型步骤如下：
（1）确定决策变量和约束条件。
（2）确定目标函数的表达式。
（3）初始化和声搜索算法参数，包括HMCR、PAR、BW等。
（4）随机生成初始和声库，并计算提取其中最优的和声条目。
（5）循环进行迭代和声库更新。
（6）根据目标函数判断是否满足成像需要，搜索最优设计。
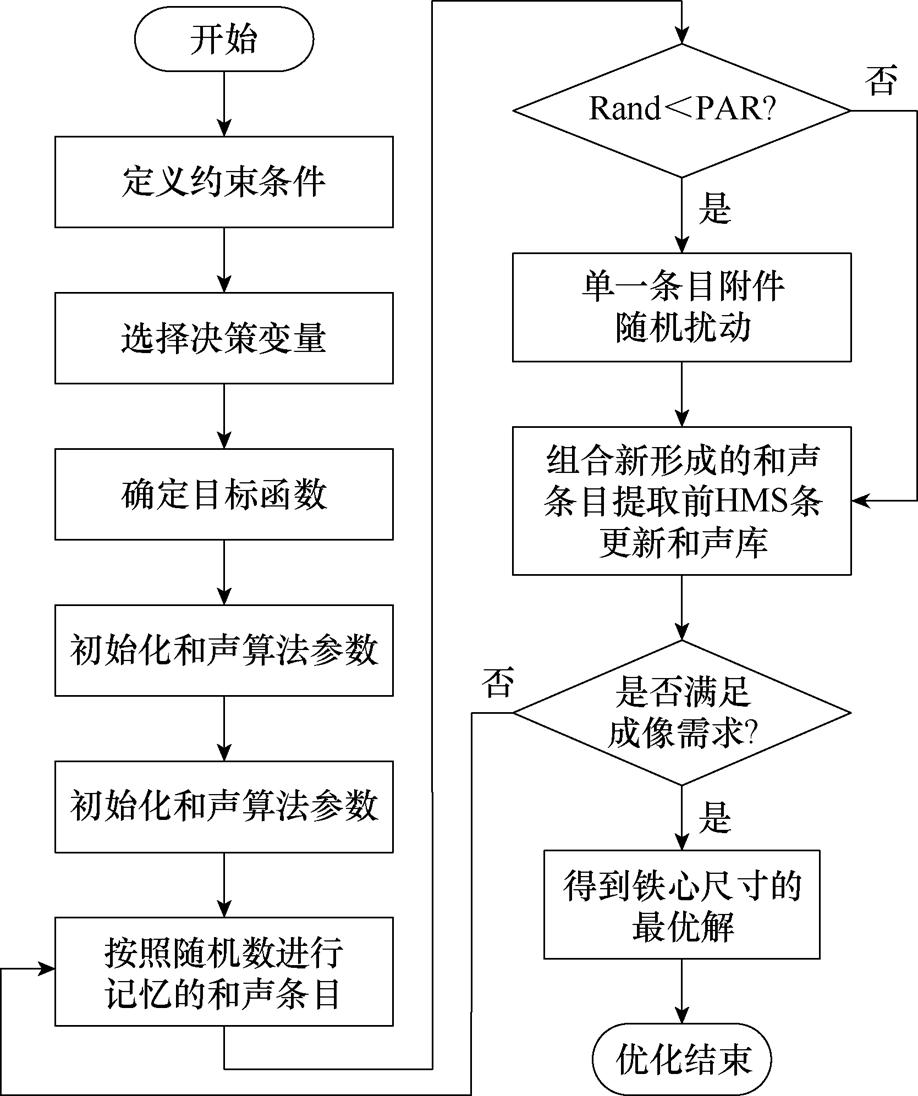
图6 铁心几何结构优化设计流程
Fig.6 Core geometry optimization design flow
铁心几何参数的优化选择及计算结果见表1。铁心优化前为圆柱形，根据其几何参数可计算目标变量的数值，即Opt.1。在实际应用中，首先要确定哪些性能需要改进，然后根据医疗应用的需求和制造商的生产能力来确定目标的优先顺序。因此，本文根据目标变量优先级的不同，得到了三组优化的铁心尺寸及目标变量，即Opt.2、Opt.3和Opt.4。
表1 铁心几何参数的优化选择及计算结果
Tab.1 Optimal selection and calculation results of geometric parameters of iron core
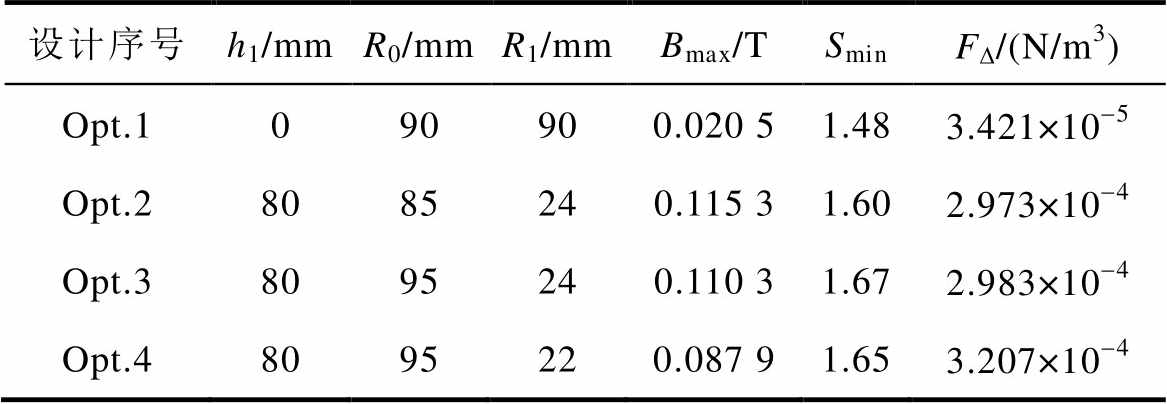
设计序号h1/mmR0/mmR1/mmBmax/TSminFD/(N/m3) Opt.1090900.020 51.483.421×10-5 Opt.28085240.115 31.602.973×10-4 Opt.38095240.110 31.672.983×10-4 Opt.48095220.087 91.653.207×10-4
锥形铁心线圈模型如图7所示，在Maxwell线圈的上线圈和Helmholtz线圈的上、下线圈中同时通入逆时针方向的电流，而在Maxwell线圈的下线圈中通入与前者大小相同的顺时针方向的电流。
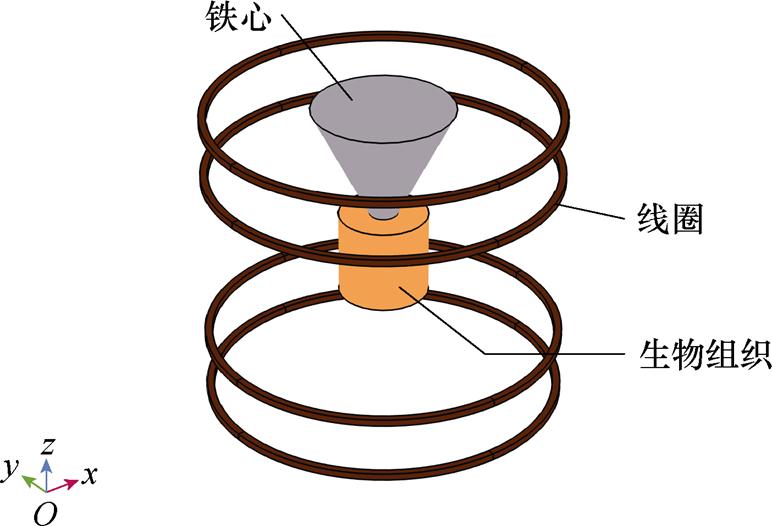
图7 锥形铁心线圈模型
Fig.7 Conical core coil model
线圈半径为100 mm，电流为一种正弦衰减截断波信号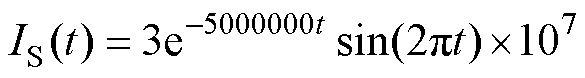
，时间特性线圈电流波形如图8所示，持续时间为2 ms，峰值出现在0.2 ms时刻。
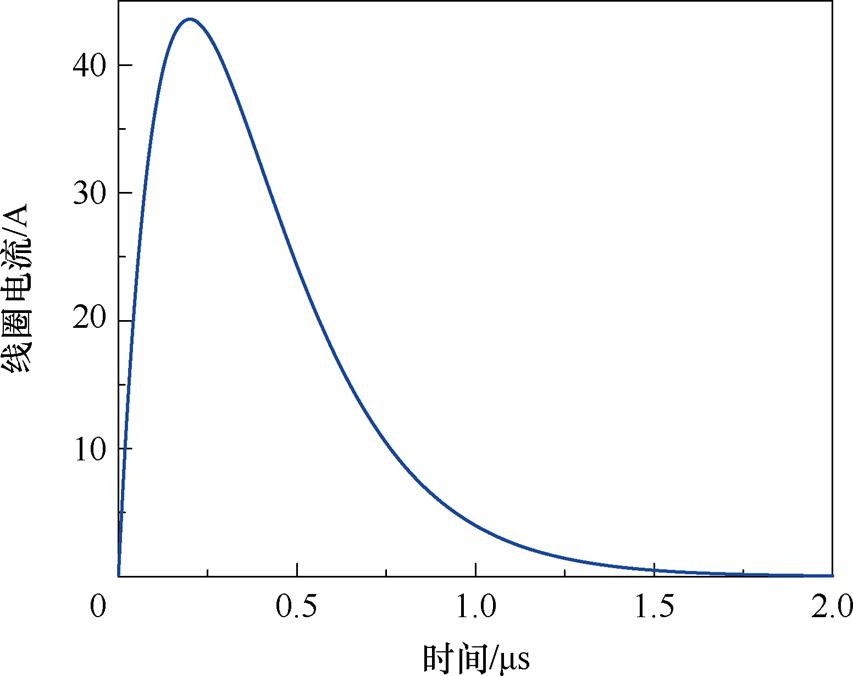
图8 线圈电流波形
Fig.8 Coil current waveform
铁心位于线圈的中心，铁心材质为Soft Iron，相对介电常数为1，其B-H曲线如图9所示，根据http:// cn.comsol.com/model/effective-nonlinear-magnetic- curves-calculator-30941上的有效非线性磁曲线计算器发现，当磁通密度B在0～0.5 T（本模型中的主要磁通密度范围）范围内时，该材料的有效相对磁导率在1 200左右。
成像目标体的仿真模型如图10所示，圆柱体和球体分别用来模拟生物组织和磁性纳米粒子集群，圆柱体底面半径为25 mm、高为50 mm，嵌入其中的球体半径为5 mm，球心坐标为(0, 0, 0)，磁性纳米粒子集群的参数取自水溶性超顺磁性纳米颗粒EMG 308（Ferrotec（USA） Corporation），其规格见表2。
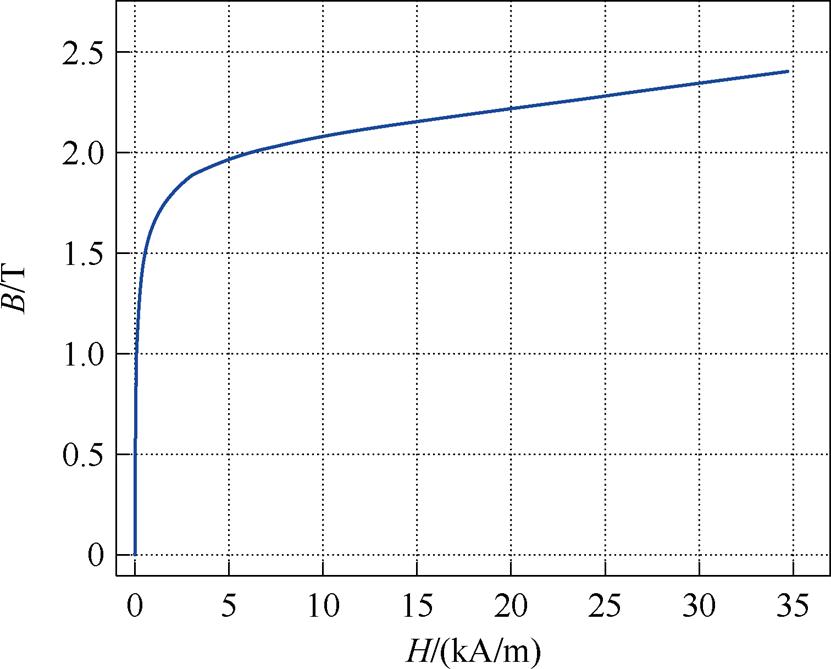
图9 铁心材料B-H曲线
Fig.9 Core material B-H curve
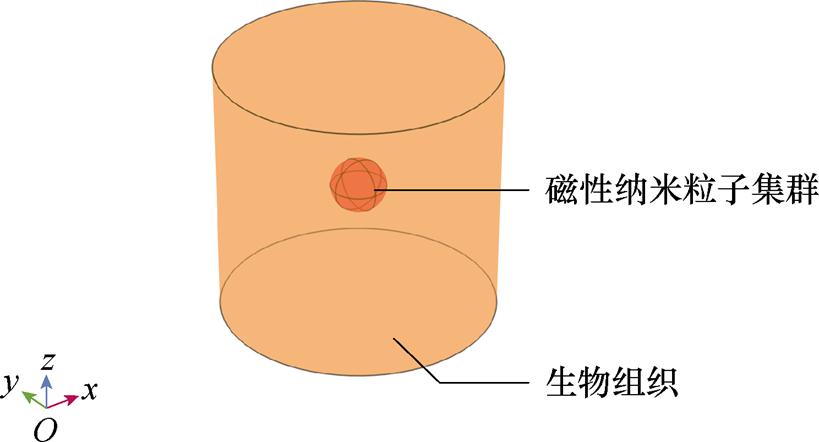
图10 生物组织模型
Fig.10 Biological tissue model
表2 EMG 308规格
Tab.2 EMG 308 specifications
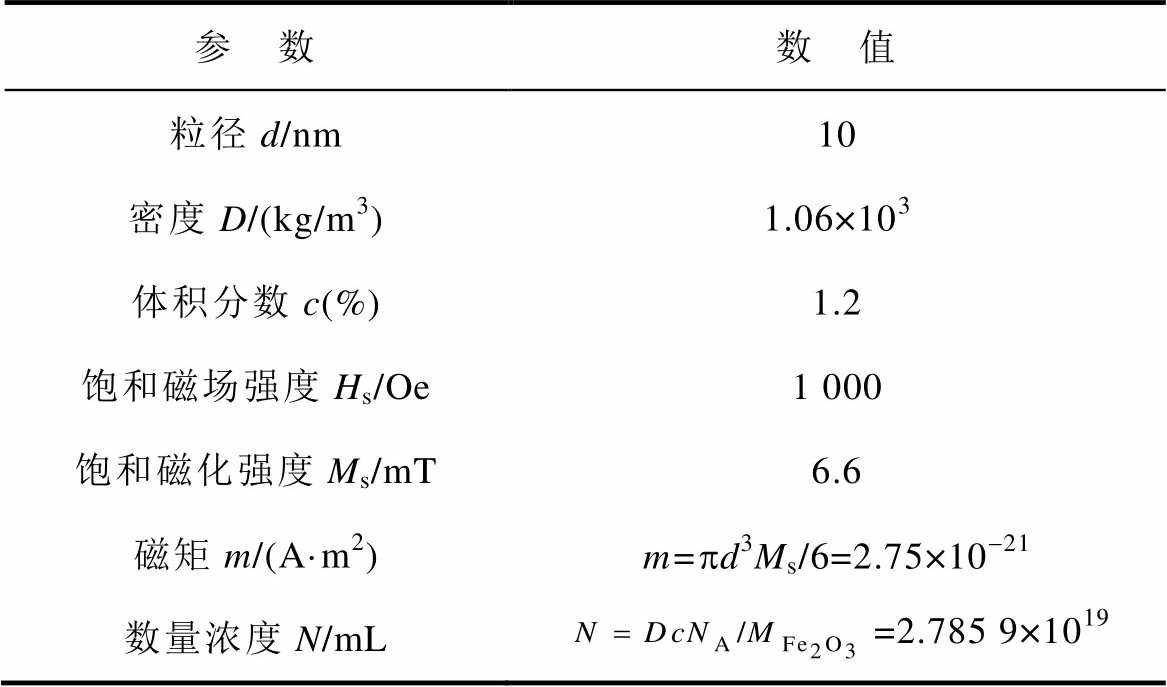
参 数数 值 粒径d/nm10 密度D/(kg/m3)1.06×103 体积分数c(%)1.2 饱和磁场强度Hs/Oe1 000 饱和磁化强度Ms/mT6.6 磁矩m/(A·m2)m=pd3Ms/6=2.75×10-21 数量浓度N/mL=2.785 9×1019
注：1Oe=79.577 5 A/m。
利用COMSOL得到Opt.1和Opt.2铁心线圈模型的磁通密度、磁力和声压的二维分布图及一维曲线图，并与空心线圈模型进行对比。0.2 ms时，三种线圈模型在ROI产生的磁场分布如图11所示，图11a中空心线圈在ROI内产生0.009～0.014 T的磁通密度，而图11b Opt.1圆柱形铁心线圈产生的磁通密度为0.012～0.02 T，图11c Opt.2锥形铁心线圈产生的磁通密度0.02～0.11 T，两种铁心模型对ROI内的磁场均有增强作用，其中锥形铁心的增强效果更明显。
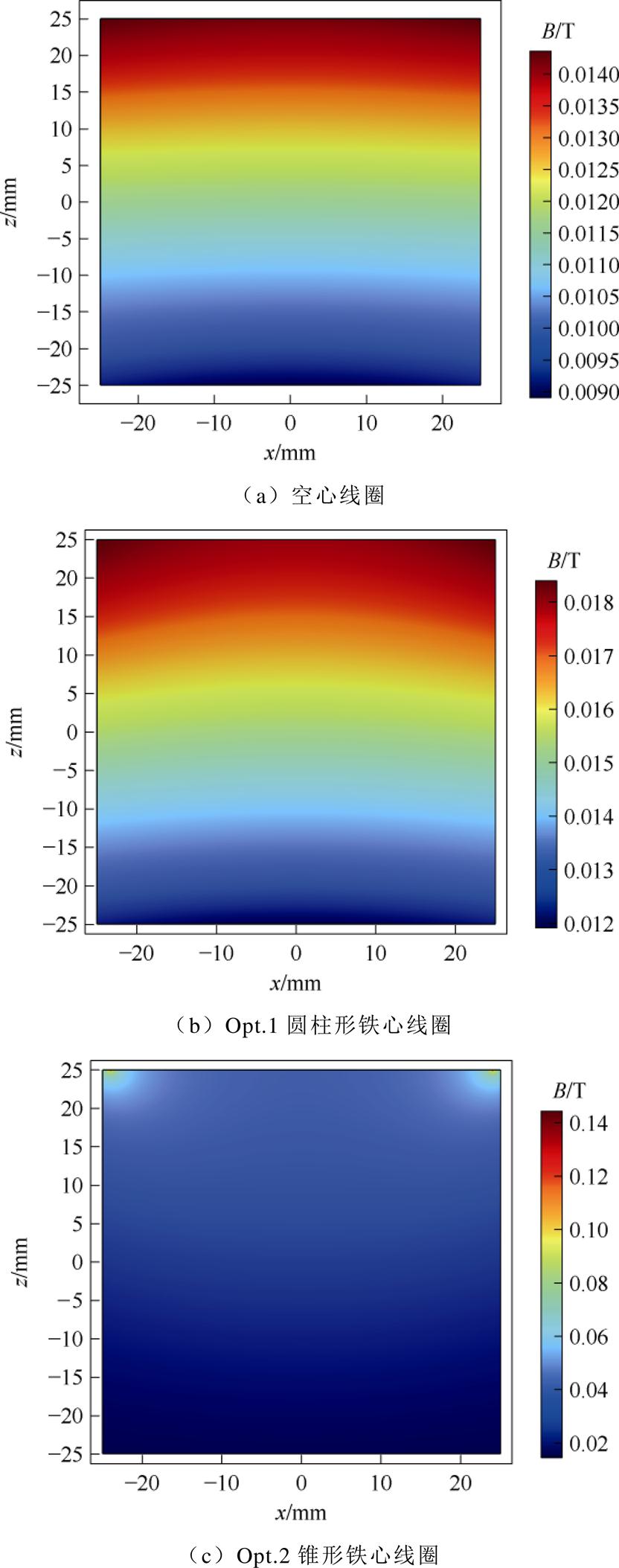
图11 磁场发生装置在ROI的xOz截面上产生的磁通密度
Fig.11 The magnetic flux density generated by a magnetic field generating device at the xOz cross-section of ROI
分析三种模型在中心区域产生的磁场强度，均低于EMG 308样品的饱和磁场强度，故用式（2）计算MNPs所受磁力。在xOz截面上产生的磁力分布如图12所示，仅有中心位置被MNPs标记的生物组织受到磁力作用，图12a中MNPs所受磁力约为1.804×10-5 N/m3，而图12b Opt.1中磁力约为2.809× 10-5 N/m3，图12c Opt.2中磁力能达到2.055× 10-4 N/m3，图12c中磁力分布略微不均匀，这是由于锥形铁心感生出磁场在上侧区域梯度较大。
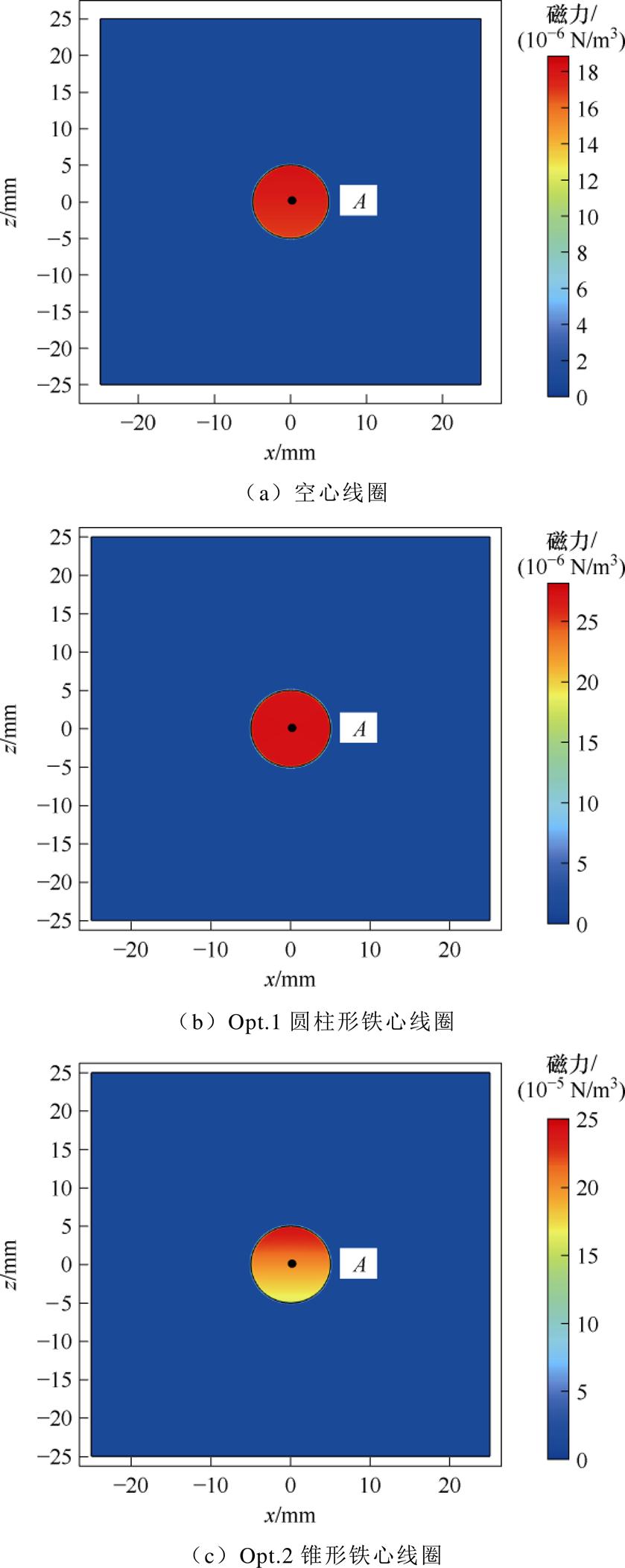
图12 0.2 ms磁力分布
Fig.12 t =0.2 ms, magnetic force distribution
取观测点A(0, 0, 0)，研究三种模型中MNPs所受磁力随时间的变化规律，其结果如图13所示，三种磁力曲线与线圈电流变化规律基本相同，且锥形铁心线圈作用下的磁力约为空心线圈的10.4倍。
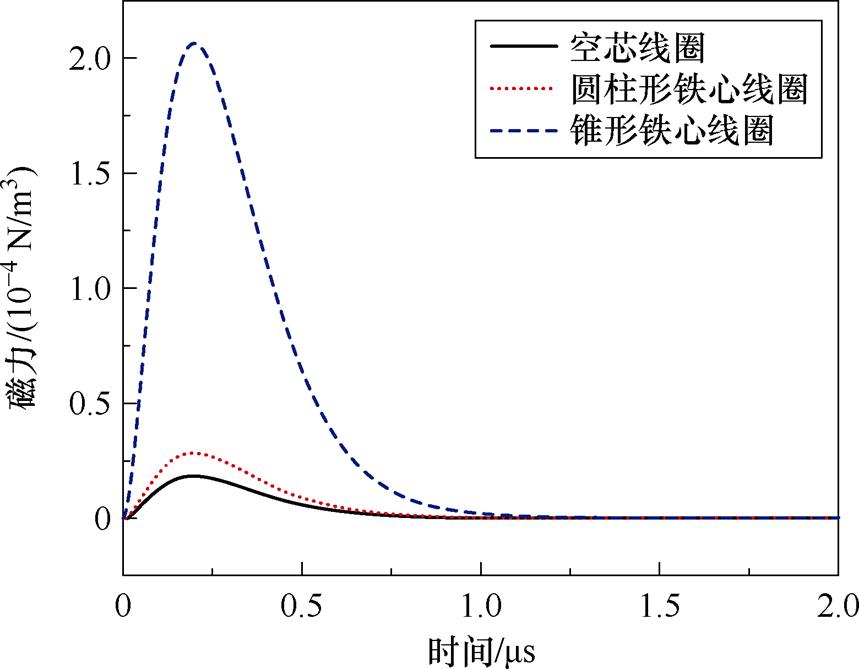
图13 磁力对比
Fig.13 Magnetic force comparison
根据MNPs所受磁力的仿真结果，进行电磁和超声相互耦合的多物理场有限元分析和对比，三种模型的声压分布如图14所示。图14a中磁性纳米粒子集群的上下边缘声压明显，z方向上声压分布较为均匀，且由于偶极声源特性，声压上下呈对称分布，方向相反；而图14b和图14c的声压分布与图14a大致相同，只是声压信号明显增大，其中图14c的声压分布略不对称，上侧声压较大，这是由于上
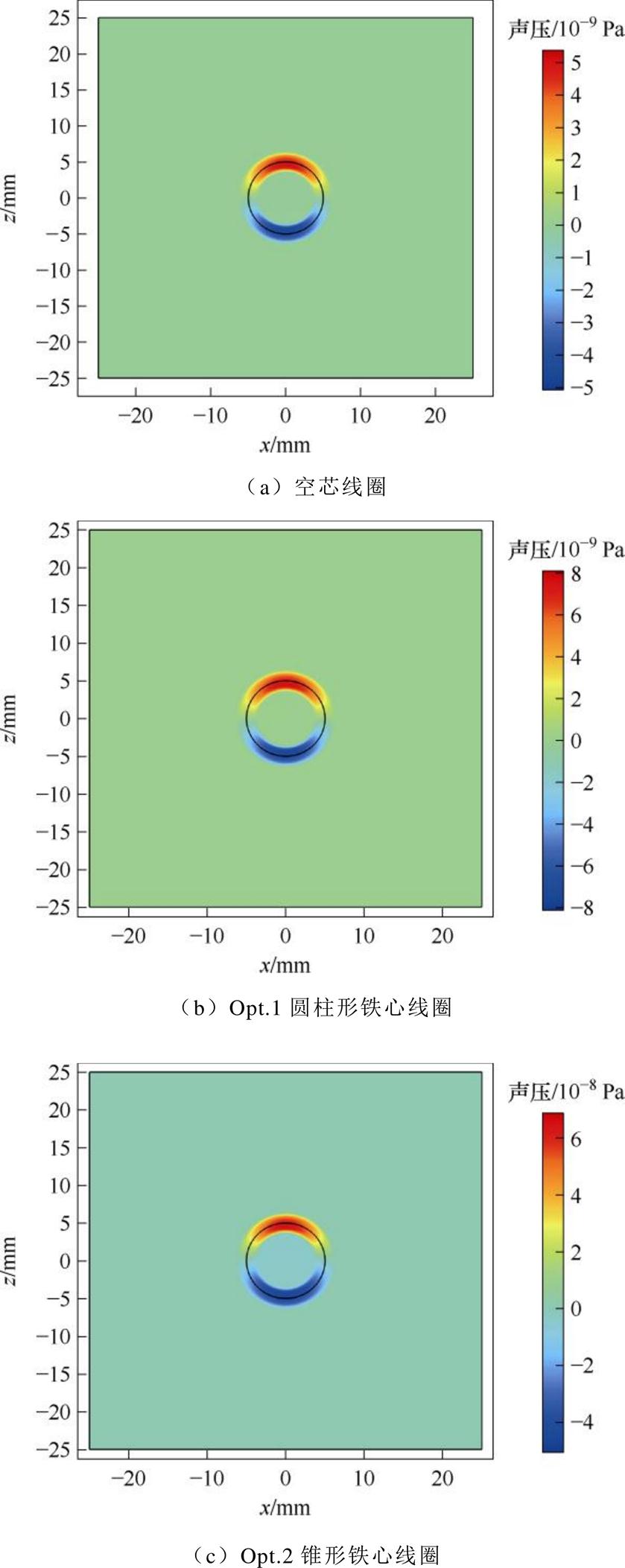
图14 t =1 ms声压分布
Fig.14 t =1 ms, sound pressure distribution
取观测点A(30 mm, 0 mm, 30 mm) 放置超声换能器，绘制40 ms内超声换能器接收到的声压曲线，如图15所示，根据超声换能器接收声压峰值时间差可计算磁性纳米粒子集群直径，在同一平面接收环扫一圈后的数据即可重建二维浓度边界。在三种模型中，超声换能器接收声压峰值时间差基本相同，声压与时间的变化规律也基本一致，只是铁心模型中的声压信号明显增大，圆柱铁心模型和锥形铁心模型中声压信号分别增大了0.55倍和10.4倍。
图15 超声换能器接收到的声压对比
Fig.15 Comparison of sound pressure received by ultrasonic transducer
本文经过优化设计的锥形铁心线圈可以有效提高磁场强度和梯度，进而增大MNPs所受磁力及其产生的声压信号，降低激励源要求，以上文铁心线圈为例，其规格参数见表3，可以看出：在43.57 A脉冲电流的激励条件下，空心线圈在ROI的梯度磁场磁感应强度最大值为0.014 T，轴线磁场梯度为0.1 T/m，中心位置MNPs所受磁力为1.804×10-5 N/m3。
表3 磁场发生装置模型规格
Tab.3 Model specifications for magnetic field generating devices
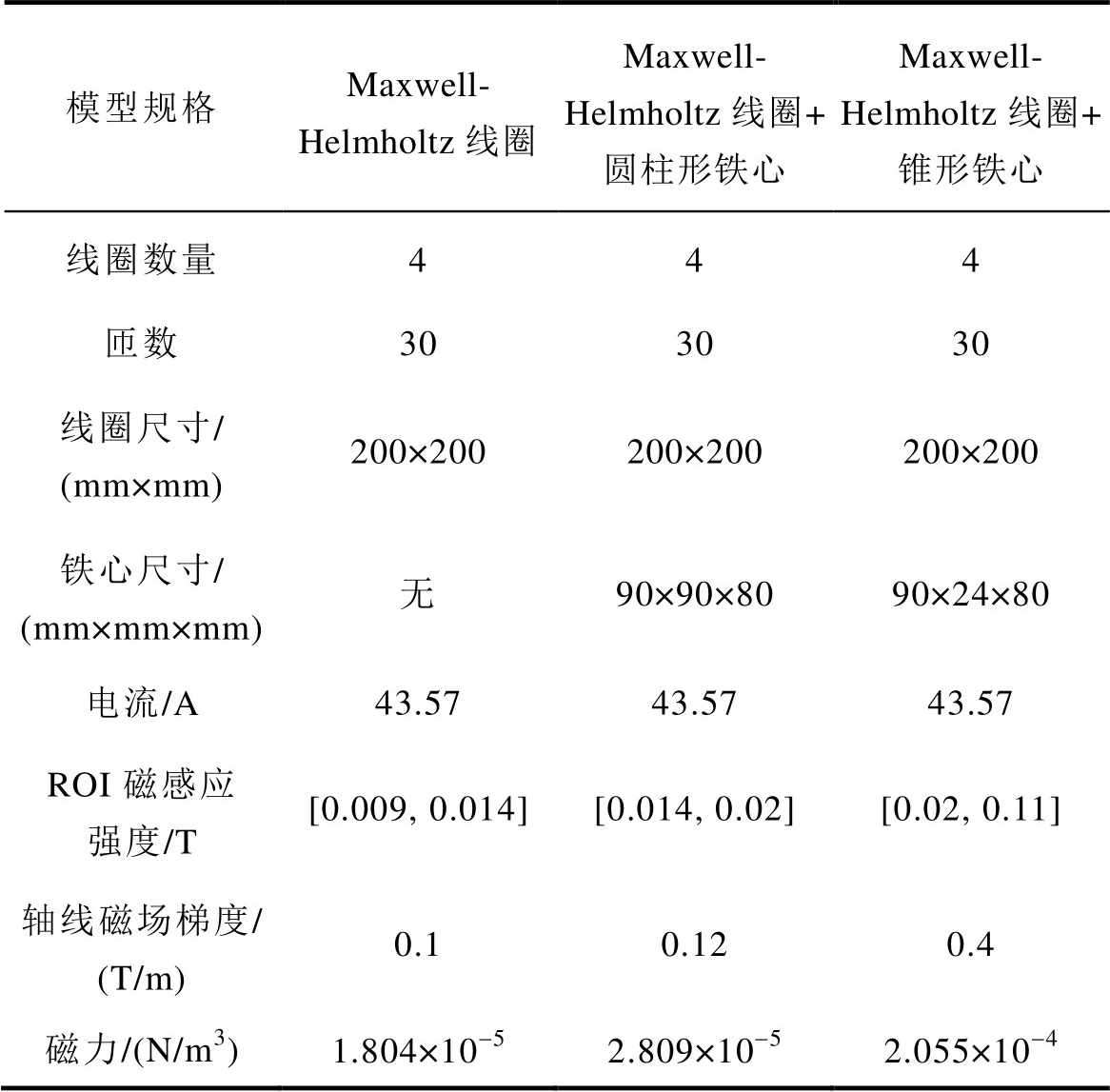
模型规格Maxwell-Helmholtz线圈Maxwell-Helmholtz线圈+圆柱形铁心Maxwell-Helmholtz线圈+锥形铁心 线圈数量444 匝数303030 线圈尺寸/(mm×mm)200×200200×200200×200 铁心尺寸/(mm×mm×mm)无90×90×8090×24×80 电流/A43.5743.5743.57 ROI磁感应强度/T[0.009, 0.014][0.014, 0.02][0.02, 0.11] 轴线磁场梯度/(T/m)0.10.120.4 磁力/(N/m3)1.804×10-52.809×10-52.055×10-4
本文为在相同电流激励条件下，提高了MACT- MI装置产生的梯度磁场，提出了一种锥形铁心线圈的优化设计方法。包括研究Maxwell-Helmholtz线圈与单边锥形铁心组合的磁场分布特征，推导MNPs受到的磁力公式，优化设计锥形铁心的结构参数，研究圆柱形铁心和锥形铁心模型对磁力及声压的影响。主要结论如下：
1）在Maxwell-Helmholtz线圈中加入单边锥形铁心，新增一个时变梯度磁场分量，可以有效地提高ROI内的磁场强度和梯度，进而增大MNPs所受磁力及其产生的声压，使MACT-MI成像装置向生物医学的实际应用进一步迈进。
2）以铁心的尺寸为决策变量，利用铁心线圈的梯度磁场磁感应强度最大值、最小磁场增幅倍数和模拟磁力的表面平均值构建多目标函数，采用和谐搜索算法，确定目标函数权重，从而得到锥形铁心尺寸的最优解。
3）在相同激励电流条件下，与空心线圈相比，圆柱形铁心线圈和锥形铁心线圈在ROI的梯度磁场磁感应强度最大值分别提高了约43%和6.9倍，轴线磁场梯度分别扩大了0.2和3倍，中心位置MNPs所受磁力分别增大了0.6和10.4倍。
本文设计的单边锥形铁心能增大MACT-MI装置产生的梯度磁场，通过与空心线圈进行数值对比表明，MNPs受到磁力和其产生的声压均有明显提升，使得MACT-MI成像装置的设计进一步迈进，但磁场汇聚的同时也必然会导致磁场分布的均匀性有所降低，在靠近铁心侧的区域磁场强度和梯度更大，使得在进行逆问题浓度成像时，计算复杂度增加。总之，本文进一步研究了MACT-MI成像装置的设计，为该方法的生物医学实际应用奠定了基础。
参考文献
[1] 闫孝姮, 李政兴, 孙迪, 等. 基于矩阵式线圈的感应式磁声磁粒子浓度成像研究[J]. 电工技术学报, 2022, 37(17): 4269-4283.
Yan Xiaoheng, Li Zhengxing, Sun Di, et al. Mag- netoacoustic concentration tomography of magnetic nanoparticles with magnetic induction based on matrix coil[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4269-4283.
[2] Shi Xiaoyu, Liu Guoqiang, Yan Xiaoheng, et al. Simulation research on magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction[J]. Computers in Biology and Medicine, 2020, 119: 103653.
[3] 闫孝姮, 李政兴, 潘也, 等. 相同极性永磁体对感应式磁声磁粒子浓度成像过程影响的仿真[J]. 电工技术学报, 2022, 37(8): 1926-1937.
Yan Xiaoheng, Li Zhengxing, Pan Ye, et al. Simu- lation of the influence of permanent magnets of the same polarity on the magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction process[J]. Transactions of China Electro- technical Society, 2022, 37(8): 1926-1937.
[4] Al-Mutawaly N, de Bruin H, Findlay D. Magnetic nerve stimulation: field focality and depth of penetration[C]//2001 Conference Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul, Turkey, 2001: 877-880.
[5] Salvador R, Miranda P C, Roth Y, et al. High- permeability core coils for transcranial magnetic stimulation of deep brain regions[C]//2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 2007: 6652-6655.
[6] Lai Lingfeng, Gu Chen, Qu Timing, et al. Simulation of AC loss in small HTS coils with iron core[J]. IEEE Transactions on Applied Superconductivity, 2015, 25(3): 4700905.
[7] Rastogi P, Tang Yalun, Zhang Bowen, et al. Quadruple butterfly coil with passive magnetic shielding for focused transcranial magnetic stimu- lation[J]. IEEE Transactions on Magnetics, 2017, 53(11): 5400305.
[8] 夏思萍, 徐雅洁, 顾卫国, 等. 经颅磁刺激铁芯线圈的优化设计研究[J]. 航天医学与医学工程, 2021, 34(4): 304-313.
Xia Siping, Xu Yajie, Gu Weiguo, et al. Research on optimal design of transcranial magnetic stimulation coil with iron core[J]. Space Medicine & Medical Engineering, 2021, 34(4): 304-313.
[9] 孙钰婷, 逯迈. 不同铁芯材料对经颅磁刺激电磁场分布的对比研究[J]. 生物医学工程研究, 2022, 41(4): 382-390.
Sun Yuting, Lu Mai. Comparative study on transcra- nical magnetic stimulation electromagnetic field distribution of different iron core materials[J]. Journal of Biomedical Engineering Research, 2022, 41(4): 382-390.
[10] 闫孝姮, 淡新贤, 陈伟华, 等. 基于改进目标场法梯度线圈的感应式磁声磁粒子浓度成像研究[J]. 电工技术学报, 2024, 39(14): 4305-4316.
Yan Xiaoheng, Dan Xinxian, Chen Weihua, et al. Magneto-acoustic magnetic particle concentration imaging based on improved target field method gradient coil[J]. Transactions of China Electro- technical Society, 2024, 39(14): 4305-4316.
[11] 万裁, 何为, 沈晟, 等. 超低场磁共振膝关节正交接收线圈设计[J]. 电工技术学报, 2024, 39(7): 1923-1931.
Wan Cai, He Wei, Shen Sheng, et al. Design of a quadrature receive coil for ultra-low-field knee mag- netic resonance imaging[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 1923-1931.
[12] 杨丹, 刘素羽, 张昊, 等. 基于永磁体和线圈复合结构的MPI零磁场研究[J]. 电工技术学报, 2025, 40(2): 335-345.
Yang Dan, Liu Suyu, Zhang Hao, et al. Research on MPI zero magnetic field based on permanent magnet and coil composite structure[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 335- 345.
[13] 董明, 李航辉, 马宏伟, 等. 高纯度横波蝶形线圈电磁超声换能器优化设计[J]. 电工技术学报, 2024, 39(11): 3270-3279.
Dong Ming, Li Hanghui, Ma Hongwei, et al. Optimi- zation design of high-purity shear wave electro- magnetic acoustic transducer with butterfly coil[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3270-3279.
[14] Zhao Zhiyuan, Torres-Díaz I, Rinaldi C. Brownian dynamics simulations of magnetic nanoparticles captured in strong magnetic field gradients[J]. The Journal of Physical Chemistry C, 2017, 121(1): 801- 810.
[15] 梁昆淼. 数学物理方法[M]. 4版. 北京: 高等教育出版社, 2010.
[16] Tobias K, M Buzug T. Magnetic Particle Imaging[M]. New York: Springer Science, 2012.
[17] Yan Xiaoheng, Li Jun, Xu Hong, et al. Numerical study on imaging of magnetic nanoparticles with ultrasound based on saturation magnetization[J]. Journal of Physics D: Applied Physics, 2022, 55(42): 425401.
[18] Cao Ruijie, Huang Yang, Guo Gepu, et al. Perfor- mance improvement of magnetoacoustic harmonic imaging for magnetic nanoparticles based on the electromagnetic excitation with a conical core[J]. Applied Acoustics, 2021, 180: 108105.
[19] Mirzaei M, Ripka P, Grim V. A novel position sensor with a conical iron core[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(11): 9178-9189.
[20] Binns K J, Lawrenson P J, Trowbridge C W. The Analytical and Numerical Solution of Electric and Magnetic Fields[M]. 1 ed, Wiley, 1992.
[21] Mirzaei M, Ripka P, Chirtsov A, et al. Eddy current linear speed sensor[J]. IEEE Transactions on Mag- netics, 55(1): 1-4.
[22] 郑涛, 何瑞, 潘志远, 等. MMC-HVDC换流变压器复杂性涌流产生机理及其影响分析[J]. 电力系统自动化, 2022, 46(23): 102-108.
Zheng Tao, He Rui, Pan Zhiyuan, et al. Analysis on generation mechanism and influence of complex inrush current in MMC-HVDC converter transfor- mer[J]. Automation of Electric Power Systems, 2022, 46(23): 102-108.
[23] Yan Xiaoheng, Pan Ye, Chen Weihua, et al. Simu- lation research on the forward problem of mag- netoacoustic concentration tomography for magnetic nanoparticles with magnetic induction in a saturation magnetization state[J]. Journal of Physics D: Applied Physics, 2021, 54(7): 075002.
[24] Ali M, Siarry P, Pant M. An efficient differential evolution based algorithm for solving multi-objective optimization problems[J]. European Journal of Opera- tional Research, 2012, 217(2): 404-416.
[25] 杨松松. 铁芯绕组结构的磁场分布与漏磁分析研究[D]. 昆明: 昆明理工大学, 2015.
Yang Songsong. Study on magnetic field distribution and magnetic leakage analysis of iron core winding structure[D]. Kunming: Kunming University of Science and Technology, 2015.
[26] Li Weijun, Liu Zhenyu. A method of SVM with normalization in intrusion detection[J]. Procedia Environmental Sciences, 2011, 11: 256-262.
[27] Kim J H, Geem Z W, Jung D, et al. Advances in Harmony Search, Soft Computing and Applications[M]. Cham: Springer International Publishing, 2020.
Abstract Based on the magneto acoustic coupling effect, inductive magnetic acoustic tomography (MACT-MI) is a novel technique for imaging magnetic nano particle concentration (MNPs). However, previous research indicates that the current MACT-MI necessitates the employment of a high-amplitude excitation source device to generate magneto acoustic signals. To enable the ultrasonic probe to detect these acoustic signals, passing a pulse current of approximately 200 amperes through a Maxwell coil with a radius of 0.4 meters imposes stringent requirements on hardware configuration and hinders the advancement of experimental work. This paper introduces a device composed of a Maxwell-Helmholtz coil and a conical iron core for generating magnetic fields. Compared to traditional MACT-MI excitation units, this device incorporates an additional time-varying gradient magnetic field component induced by the conical iron core within the region of interest (ROI). The iron core's design optimization enhances the magnetic field's intensity and gradient allowing MNPs to convert magnetic energy into acoustic energy more efficiently, amplifying the magneto acoustic signals and reducing the excitation source's required amplitude.
Firstly, the formula for the magnetic force acting on MNPs is derived, and the magnetic field distribution induced by the iron core in MACT-MI is analyzed. Secondly, three optimization objectives are identified: maximizing the magnetic induction intensity of the gradient magnetic field, the overall amplification intensity, and the simulated magnetic force. A multi-objective function is constructed, and the range of values for the decision variables is set. Then, the COMSOL simulation software is utilized to model and calculate all decision variables related to the iron core coil. Finally, constraint conditions are established after comprehensively considering the applicability and production cost of the iron core and coil. Two sets of optimized iron core dimensions are obtained by applying the harmony search algorithm to filter the decision variables.
COMSOL software is used to generate two-dimensional distribution maps and one-dimensional graphs of magnetic flux density, magnetic force, and sound pressure for the cylindrical and conical iron core coil models. Under identical excitation current conditions, the maximum magnetic induction intensity of the gradient magnetic field within the ROI for the cylindrical and conical iron core coils has increased by approximately 0.4 times and 6.9 times compared to the air-core coil. Furthermore, the axial magnetic field gradient has expanded by 0.2 times and 3 times, and the magnetic force experienced by the MNPs at the central position has intensified by 0.6 times and 10.4 times.
The single-sided conical iron core coil designed in this paper can significantly enhance the gradient magnetic field generated by the MACT-MI device, leading to a notable increase in the magnetic force experienced by MNPs and the acoustic pressure. However, although magnetic field focusing can amplify the magnetic field intensity and gradient in regions proximal to the iron core, it inevitably decreases the uniformity of the magnetic field distribution. In conclusion, this paper conducts an in-depth study on the design of MACT-MI imaging devices, marking a significant step towards the practical application of MACT-MI imaging technology in biomedicine.
Keywords：Magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction (MACT-MI), conical iron core coil, magnetic force, sound pressure
中图分类号：TM12
DOI: 10.19595/j.cnki.1000-6753.tces.241140
国家自然科学基金青年项目（52207008）和中国-波兰测控技术“一带一路”联合实验室开放课题项目（MCT202305）资助。
收稿日期 2024-06-30
改稿日期 2024-08-05
闫孝姮 女，1984年生，博士，副教授，博士生导师，研究方向为电磁探测与成像。
E-mail: xiaohengyan@163.com（通信作者）
王 兵 男，1996年生，硕士研究生，研究方向为电磁探测与成像。
E-mail: wangbing661045@163.com
（编辑 郭丽军）