集成AI的电工装备电磁场有限元仿真软件MBSE建模与应用
金 亮1,2 贾雨方1 刘 璐1 郭劭男1 马天赐1
(1. 智能配用电装备与系统全国重点实验室(河北工业大学) 天津 300401 2. 河北省电磁场与可靠性重点实验室(河北工业大学) 天津 300401)
摘要 电磁场有限元仿真软件在电磁设计和分析中至关重要。然而商业软件价格高昂且功能冗余,同时随着人工智能(AI)的发展,深度学习与传统数值模拟的结合提升了仿真精度和效率。为此,亟须开发自主可控、轻量化、面向企业定制的智能仿真软件。该文首先提出了双向耦合的设计方法,使仿真软件能适应复杂需求。然后,基于模型系统工程(MBSE)方法,建立四个层级的电磁场有限元仿真软件的架构设计流程,并完成软件的建模,实现了系统结构和行为的定义和可视化。最后,基于Python开发了集成AI的软件原型IFEM,并通过两个实际案例验证了其功能和准确性。研究成果提高了软件开发的质量、效率和知识传承能力,为数值模拟工业软件在AI for Science背景下的AI集成提供了有效思路。
关键词:模型系统工程(MBSE) 有限元 人工智能(AI) 电磁场计算
0 引言
电磁场有限元仿真软件作为电磁分析和设计的关键工具,承担着电磁场模拟、数据处理和用户交互等多层次、多维度的任务。在当今日益复杂的电磁场有限元仿真软件开发领域,采用先进的建模方法,对提高软件质量、开发效率和知识传承至关重要。同时,在人工智能迅猛发展的背景下,通过深度学习与数值模拟的联合,仿真分析电磁场,也成为一个重要的发展方向。
随着时代发展、计算机性能的提高,基于不同算法的电磁场仿真软件被开发出来,其中应用较为广泛的有Ansys、COMSOL和Abaqus等软件,这些软件在技术、产品、市场等多方面均以较大优势领先[1]。相对于国外,国内对于电磁场仿真软件的研究开展较晚,但在科技竞争加剧和软件自主开发的大环境下,我国多个企业、科研团队突破重重阻力,自主研发了一批较为实用的电磁场仿真软件,如云道智造Simdroid[2]、英特仿真INTESIM- Emag[3]和安世亚太PERA SIM LEmag等。目前,国内电磁场仿真软件功能全面,但短时间内难以赶超国外商业软件,如何寻求创新路径以缩小与国际先进水平的差距,成为相关研究人员需要突破的方向。
大型商业软件功能齐全、精度较高,但在提供通用性和易用性的同时,也带来了面对特定工程的使用门槛高、成本昂贵和功能冗余等问题。商业软件通常价格昂贵、且安装包庞大[1],企业在解决具体问题时往往仅需要软件提供一小部分功能,从使用门槛和成本角度来看,并不划算。此外,商业软件被视为“黑盒子”,使用时如果遇到问题很难精准判断缘由。由此,许多企业和科研人员为了实现特定工程的快速计算,基于国外商业软件进行二次开发。例如,2020年,韩志仁等基于Ansys二次开发型材拉弯有限元仿真模块[4]。但二次开发的工具内核终究存在依赖性。为了提供给企业端到端服务,助力电工装备性能分析与优化,亟须开发自主可控、轻量化、面向企业定制化的电磁场仿真软件。
在AI for Science背景下,研究集成AI的电磁场仿真软件构建方法,是发展企业定制化电磁场仿真软件的契机。自2006年G. E. Hinton等提出深度学习以来[5],AI经历了从AlphaGo到Chat GPT[6],再到2024年的视频生成模型Sora等一系列标志性的发展[7],这些进展开启了“AI for Science”时代。很多研究人员开始探索将AI算法用于电磁场仿真,并在提高计算精度、优化效率方面取得了初步成 效[8-12]。在人工智能迅猛发展的背景下,深度学习算法与传统数值模拟算法联合仿真屡见不鲜,如使用改进Linknet模型预测电机磁场云图[13]、通过深度学习预测线圈与电动机的磁场分布[14]、电机驱动效率图[15]、风电功率预测[16]、电磁场快速计算[17-18]等。但是,传统数值模拟与人工智能算法运行在不同平台,代码语言存在差异,多种算法混合使用时交互困难,这不利于两者深度结合。
电磁场有限元仿真软件的持续开发和更新过程,反映了复杂软件系统的典型特征-持续的适应性演化[19]。传统的电磁场有限元仿真软件,利用自然语言并基于文档载体的软件记录,存在信息一致性难以保证、描述内容存在二义性、结构更改困难等不足。因此,需要引入基于模型的系统工程(Model- Based Systems Engineering, MBSE),完成电磁场有限元仿真软件的架构设计。国际系统工程学会提出了MBSE方法论,使用可视化模型来定义系统的结构和行为,提供了一种更清晰、更准确的需求和设计表达方式[20]。MBSE提出后得到很多系统工程领域专家的认可,也被引入软件开发领域中[21-22]。
应用MBSE方法对软件设计进行建模,可清晰、准确地表达软件结构和组件关系。薛芳芳等提出基于MBSE的民机飞行管理软件开发方法,降低了软件研制成本,缩短了开发周期[23]。吕冠甫等将MBSE运用到无人机地面站应用系统软件的设计中,完成了架构设计[24]。俞超等提出基于MBSE和云计算的工业设计开发软件系统架构[25]。李清等指出,工业软件研发模式正朝着模型化和智能化方向发展,MBSE的理念和方法推动了工业软件变革[26]。宋羽等采用MBSE方法构建SysML模型用于导弹系统的设计和仿真,极大地减少了对飞行试验的依赖,降低了研发成本[27]。美国国家航天局将MBSE和可靠性与维护活动相结合,提出基于SysML的航天器控制系统故障管理模型与建模方法[28]。综上所述,MBSE方法在航空、无人机、工业设计、导弹系统等领域取得了显著成效,尤其是其在降低研发成本和缩短开发周期方面的贡献。但在电工领域的应用和研究仍不多见。主要原因可能包括电工领域对传统设计方法的依赖、MBSE方法在电工领域的推广不足以及缺乏具体的应用案例和成功经验,随着MBSE方法在其他领域的成功经验逐渐传播,电工领域也有望逐步引入和应用MBSE方法,提升系统开发效率。
根据系统工程的理论,这种复杂软件系统的演化需结合自动化决策和人工决策机制,形成一个双向耦合的决策机制,这种双重耦合决策机制来优化系统的响应性和功能性。因此,本文将MBSE建模思想引入电磁场有限元仿真软件的设计中,通过构建需求、功能和架构之间的关系,提出一种双向耦合决策机制。在这种机制下,以电磁场有限元仿真需求为导向,进行电磁场仿真软件的建模方法示例。有效克服了传统的基于文档的系统工程方法所存在的短板,保证需求和架构紧密结合,提高了需求和设计的一致性。
1 双向耦合的软件论证设计方法
一个复杂软件的开发过程是非线性的,需要综合权衡、不断迭代、逐步寻优。因此提出双向耦合的软件论证设计方法,为实现高效的知识传承和有效迭代奠定基础。“双向耦合”是指两方面:软件设计方和使用方的双向耦合;数值模拟和AI的双向耦合。
1.1 3软件设计方和使用方的双方耦合
在复杂软件系统的设计过程中,设计方和使用方之间的信息鸿沟常常导致设计和实施的不协调。为了克服这个问题,可以采用双向耦合的方法,使两个部门能够平衡发挥作用,确保软件的设计和使用相互协调。
目标设计采用自上而下的模式,根据战略目标将理论和概念转化为具体的任务和能力,通过场景化设计逐层分解任务,形成任务层次的能力树,并设计能力之间的相互支撑和协作关系。在不同外部影响条件下进行多次设计,以发现相对稳定的高层次能力和系统运用形态。软件设计则采用自下而上的模式,基于现有软件和技术趋势,通过构建典型应用场景,将预期目标逆向分解为复杂程度不同的任务的能力树,指导具体软件的设计和实现。
关键是要建立机制,确保目标设计和软件设计之间的信息有效交互。通过对目标设计中的场景进行提炼,形成每个场景的能力树和系统运用形态,目标设计和软件设计都将得到能力树,并将叶子节点能力归结为基础业务能力集合和基础系统能力集合。通过耦合分析,将目标设计的能力要求、技术预期的能力要求和现状能力要求进行对比,确定需要发展的能力及其重点方向,进而做出其他关联的设计决策。
通过双向耦合分析,设计方和使用方在各自领域内对基础能力进行分析和提炼,并在必要时进行耦合分析,最终确定需要发展的能力及对应的装备系统,有效解决设计方和使用方之间的信息鸿沟。这种方法确保了复杂软件系统的设计能够相互支持、协调一致,提升了系统整体的有效性和可靠性。
1.2 数值模拟和人工智能的双方耦合
人工智能的训练往往需要大量数据,这些数据来自实验测量或者数值模拟。实验数据受到实验条件影响,一些极端工况的实验数据获取难度大[29]。数值模拟可以模拟仿真实验难以实现的设备运行状态,用于生成人工智能模型的训练集[30]。此外,用传统数值模拟获取数据的计算量大、成本高,用人工智能代替数值模拟方法求解成本低且效率更高。
计算电磁学学科的发展和工业软件的发展息息相关。目前,面向数字孪生和智能制造等现代需求,为实现计算精度和计算速度的平衡需要不断融合新兴前沿技术。随着现代电工装备智能化及性能要求的提高,其面临着多时空尺度多物理场计算的困难,运用MBSE方法,将软件需求、设计和具体实现方案表示为采用统一建模语言和符号搭建的图形化模型,使得软件功能、组件及组件间交互关系得以清晰精准的表达,指导人工智能与数值模拟融合的软件开发。
基本思路:有限元(数值模拟)与神经网络(人工智能)结合的方法有很多,一种方法针对复杂非线性结构的动力学系统建模问题,可以将线性部分用有限元进行建模,非线性部分用神经网络描述(如输入非线性构件状态变量,输出其恢复力),再通过边界条件和连接条件将有限元模型部分和神经网络部分结合,得到混合模型。另一种方法是先通过有限元建立多种不同的模型,再将模态特性(即最终需要达到的设计要求)作为输出变量,将对应的模型结构参数作为输入变量,训练神经网络,利用神经网络的泛化特性得到设计参数的修正值。结合蒙特卡罗方法进行多组有限元分析,将数据输入神经网络中进行训练,可以用来分析结构的可靠度。
实施步骤如下:
(1)数值模拟引导。采用有限元方法对电磁问题进行精确的数值解。这一阶段,重点是建立一个全面和准确的物理模型,为AI提供训练数据和验证基准。
(2)AI增强,利用在第一阶段生成的数据训练机器学习模型。这些模型旨在学习电磁场的行为模式,以预测新的场景反应。训练完成后,AI模型可以在新的设计中快速提供解决方案,或者在参数研究中迅速扫描可能的配置。
(3)耦合迭代优化,将AI预测的结果与数值模拟进行比较,分析两者的偏差,并利用偏差信息反馈优化AI模型。AI可以指导数值模拟关注可能的关键区域,从而更高效地利用计算资源。
(4)集成应用,在仿真软件中集成双向耦合的框架,用户可以根据需要选择精确模式(数值模拟)或快速模式(AI驱动)。这样的集成不仅提升了软件的灵活性和用户体验,还大大增强了仿真任务的适应能力。
2 基于MBSE的软件架构设计流程
本节通过对MBSE三要素:建模方法、建模语言和建模工具进行对比分析[31],以上述软件需求分析和设计方案为指导,选取Arcadia建模方法、开源建模工具Capella、基于SysML改进并嵌入至Capella中隐式定义的建模语言Arcadia/Capella,完成电磁场有限元仿真软件架构设计。
常见的MBSE方法论和工具对比[32],见表1。其中,相比于其他建模工具来说,Arcadia建模方法所配套的Capella建模工具不仅能够完成建模任务,而且具有开源的特点,故本文选取Arcadia建模方法和Capella建模工具建立模型。
表1 常见MBSE方法论和工具比较
Tab.1 Comparison of common MBSE methodologies and tools
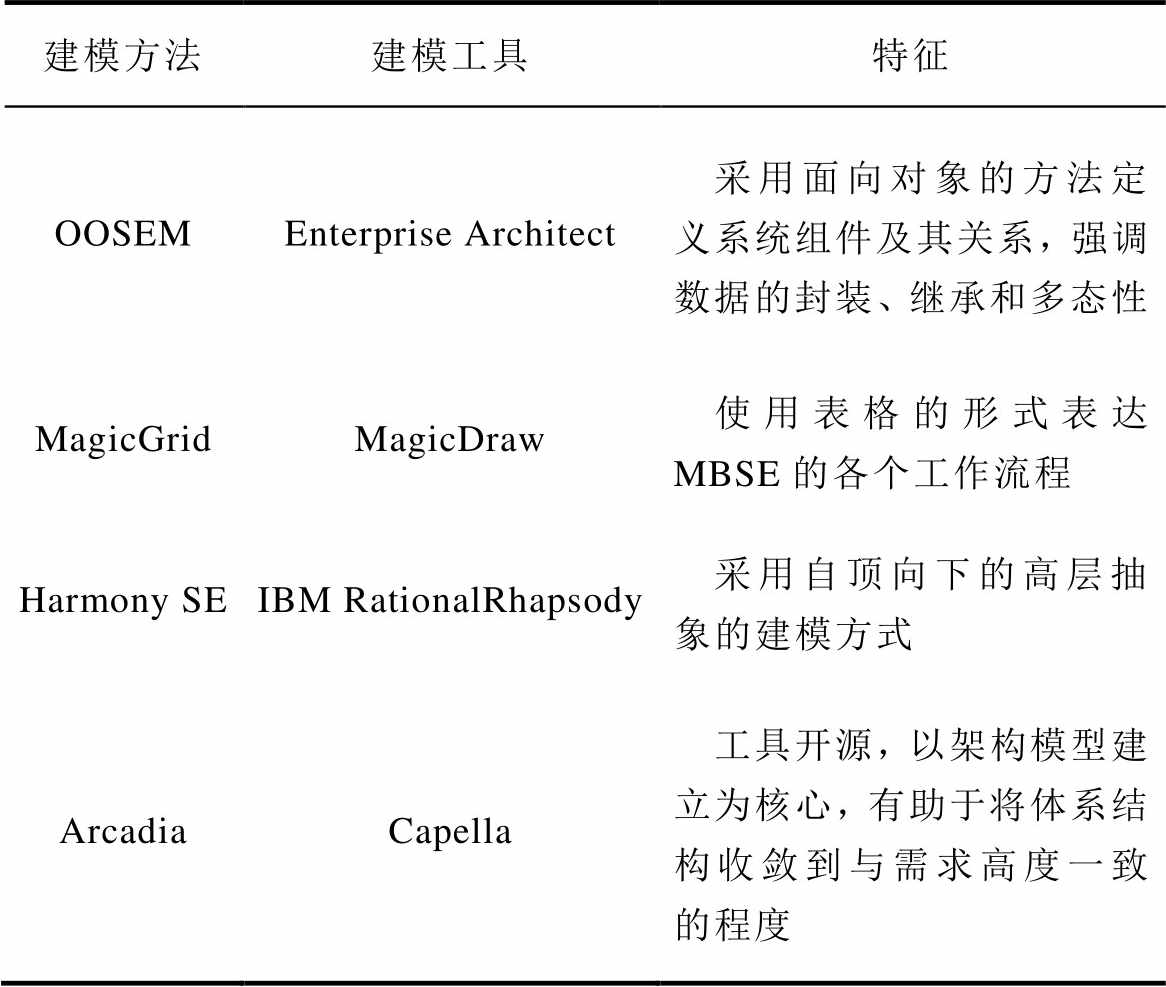
建模方法建模工具特征 OOSEMEnterprise Architect采用面向对象的方法定义系统组件及其关系,强调数据的封装、继承和多态性 MagicGridMagicDraw使用表格的形式表达MBSE的各个工作流程 Harmony SEIBM RationalRhapsody采用自顶向下的高层抽象的建模方式 ArcadiaCapella工具开源,以架构模型建立为核心,有助于将体系结构收敛到与需求高度一致的程度
Arcadia建模方法通过在运行分析、系统分析、逻辑架构、物理架构四个层级建立相关模型[33],支持从抽象的需求捕获到具体实现,将其用于电磁场有限元仿真软件开发,四个层级与软件开发阶段对应关系,见表2。
表2 Arcadia建模方法层级与自编软件开发阶段对应关系
Tab.2 Arcadia modeling methodology hierarchy corresponds to self-programming software development stages

Arcadia层级软件开发层级 运行分析需求分析 系统分析 逻辑架构总体架构设计模块化设计 软件架构具体实现
基于MBSE的软件架构设计以电磁场有限元仿真软件需求为驱动,通过四个层级需求分析和架构定义,层层递进,最终完成软件架构模型的构建。层级一:进行功能性需求的全面分析;层级二:细化需求,识别具体功能模块;层级三:定义各个模块的关系和接口,确保系统的整体协同和高效运行;层级四:完成细化的架构定义,结合具体技术实现细节,构建出高效、可靠的软件架构模型。这种层层递进的方法确保了从需求分析到技术实现的顺利过渡,逐步细化和实现软件的设计目标,最终构建出一个高效、可靠的软件架构模型。
2.1 设计流程概述
在电磁场有限元仿真软件的设计阶段,设计者需整合系统工程标准、用户、运行环境以及软硬件功能等多方面的需求,对电磁场有限元仿真软件进行总体规划及框架设计。在分析与设计过程中,设计者应充分理解并分配涉及所有利益相关方的需求,之后进一步细化仿真软件中各组成部分的子系统及功能、各个结构之间的关联以及数据传输的流向。这样的设计流程不仅确保软件的功能完整性,也优化了其性能和用户体验。
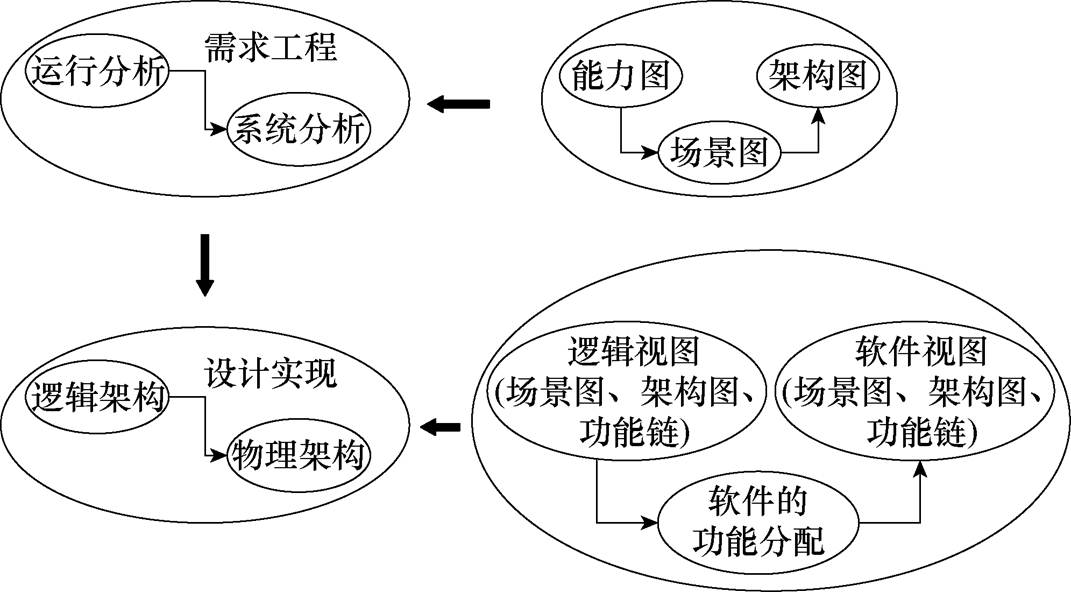
Arcadia方法将软件设计过程分为四个层级,广泛适用于各种复杂工业软件的设计,Arcadia方法的四个层级在电磁场有限元仿真软件中的针对性定义和建模方法,如图1所示。
2.2 需求捕获和分析
在电磁场仿真软件的开发初期,首先进行的是需求捕获和分析,确定软件应满足的核心需求。这些需求包括高精度的场模拟、多种边界条件的处理能力、高效的计算性能等。所有这些需求被转化为Arcadia中的模型,以确保在后续设计过程中能够被完整的跟踪和实施。
2.3 功能定义和行为建模
根据捕获的需求,通过Arcadia方法定义电磁场仿真软件的关键功能,并通过场景分析进一步细化这些功能的行为。例如,对于网格生成功能,定义其接受几何输入、应用网格细化算法和输出网格数据的具体行为。这些功能和行为通过使用功能图和场景图进行建模。
2.4 逻辑到软件的映射
最后一步是将逻辑架构转化为软件架构。这涉及将行为模型中定义的功能映射到实际的软件模块和代码库上。此过程需要确保软件的高性能和可扩展性,同时考虑未来可能的技术发展和新需求的融入。
3 基于MBSE的电磁场仿真软件建模
3.1 层级一:运行分析建模
运行分析层次确定系统用户的需要和目标,清晰地理解问题域,而不是提供解决方案。建模流程可分为三个阶段。
定义运行实体(Operational Entity, OE):将“用户”和“仿真软件”定义为运行实体,它们在后续各类模型图中投入使用,使得各个模型元素具有强关联性。
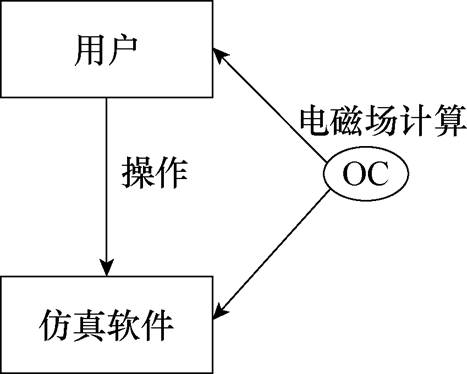
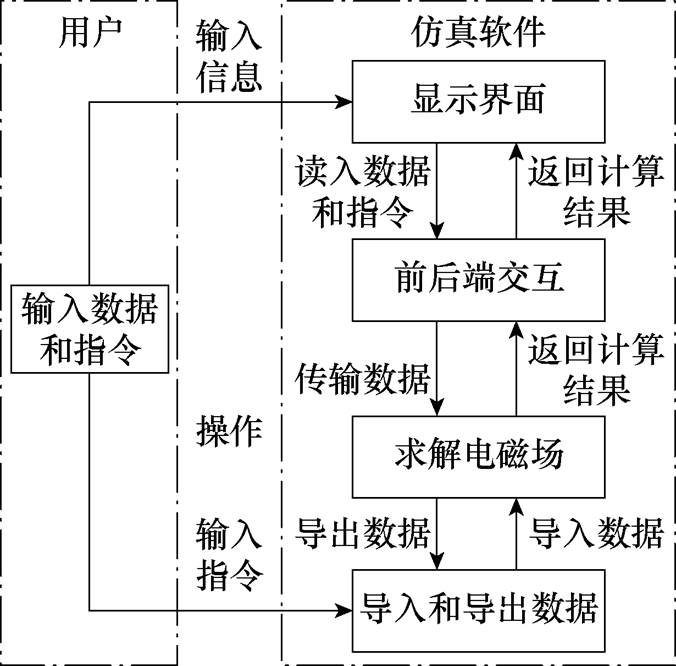
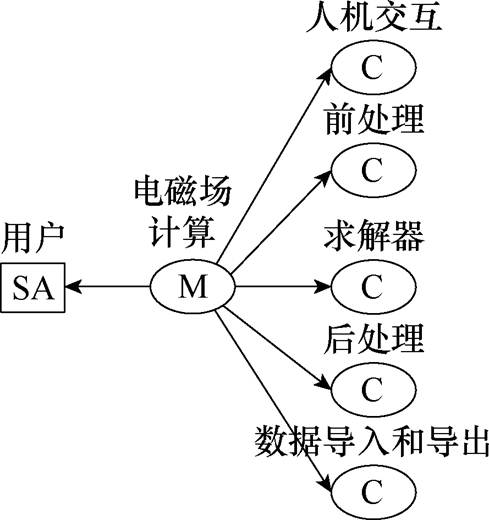
捕获运行能力(Operational Capabilities, OC):运行能力用于描述一个或多个运行实体提供的能力,并建立起与运行实体的交互关系。“电磁场计算”是软件应具备的运行能力,需要运行实体“用户”以及“仿真软件”共同作用,它们之间通过交互“操作”建立联系。描述运行能力相应的活动,并分配各运行实体:完成一个运行能力需要多个活动。“电磁场计算”运行能力由五个活动交互构成,根据图2中定义的关系,将“输入数据和指令”分配给用户,“显示界面”“前后端交互”“求解电磁场”“导入和导出数据”分配给仿真软件,得到运行架构,如图3所示。方框代表运行活动,箭头连线代表运行活动之间发生的交互。
3.2 层级二:系统分析建模
系统分析层次的目的是定义系统提供的功能,系统架构设计通过依次定义系统能力与任务、识别并分解系统功能及其交互,最终将这些功能分配到具体的系统元素上,形成完整的系统架构,确保系统功能需求的全面实现。建模流程可分为三个阶段。
定义系统能力(System Capability, SC)和系统任务(System Mission, SM):系统能力指系统应提供的能力,对应软件功能性需求;系统任务代表系统能力共同作用实现的目标。执行方(System Actor, SA)为与系统交互的外部元素。图4显示了软件所需要完成的系统任务“电磁场计算”,这个系统任务被五个系统能力实现。
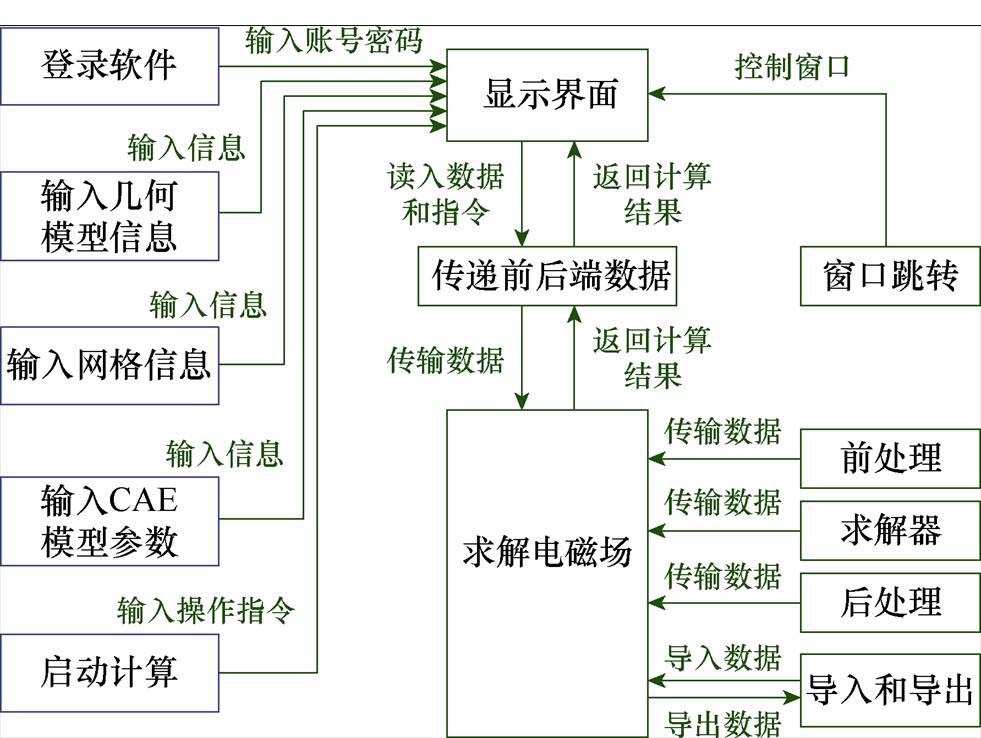
识别系统功能(System Function, SF)及其交互:将运行活动映射至系统功能,不仅保留了运行活动中涉及的对象,还继承了交互过程中涉及的各种数据流。为了更详细地体现软件功能性需求,将从运行分析层转化而来的系统功能进行分解。以用户的“输入数据和指令”为例,可分解为“登录软件”“输入几何模型信息”等五个具体功能,系统功能及交互可以用系统功能数据流描述,如图5所示。
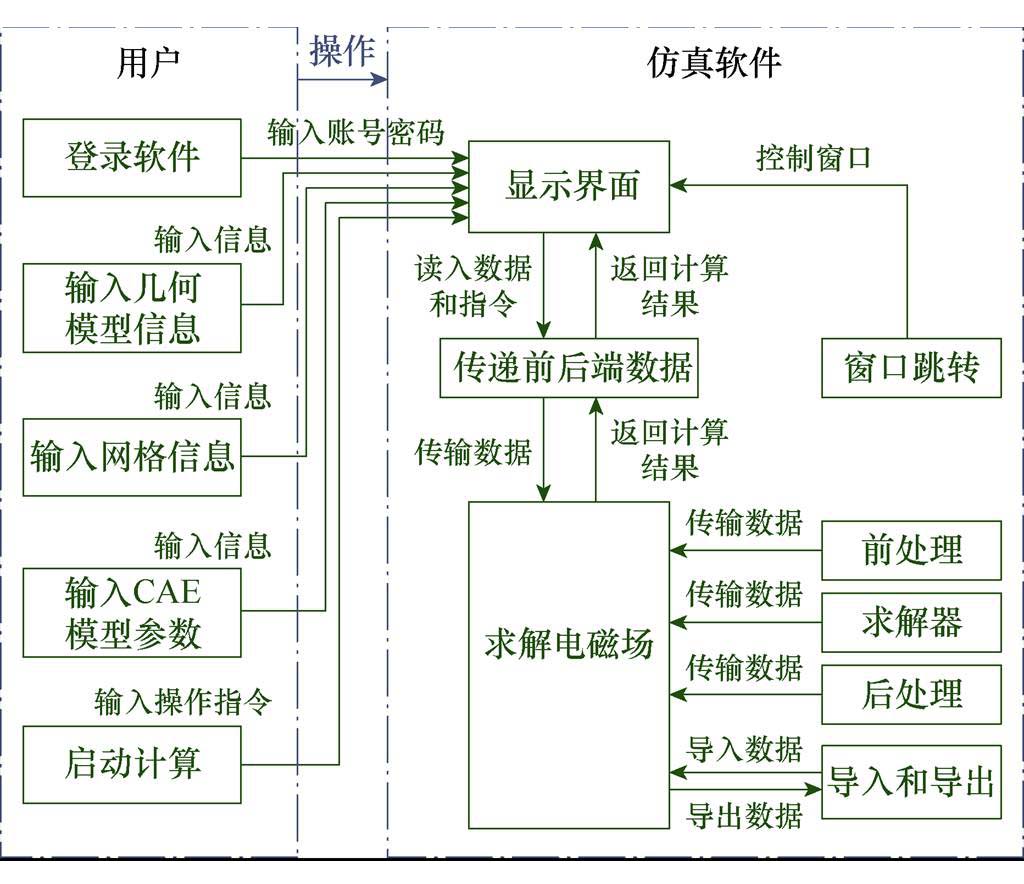
分配系统功能至系统元素:识别完所有系统功能后,将其分配至系统元素,获得提供系统层级全部信息的系统架构,如图6所示。
3.3 层级三:逻辑架构建模
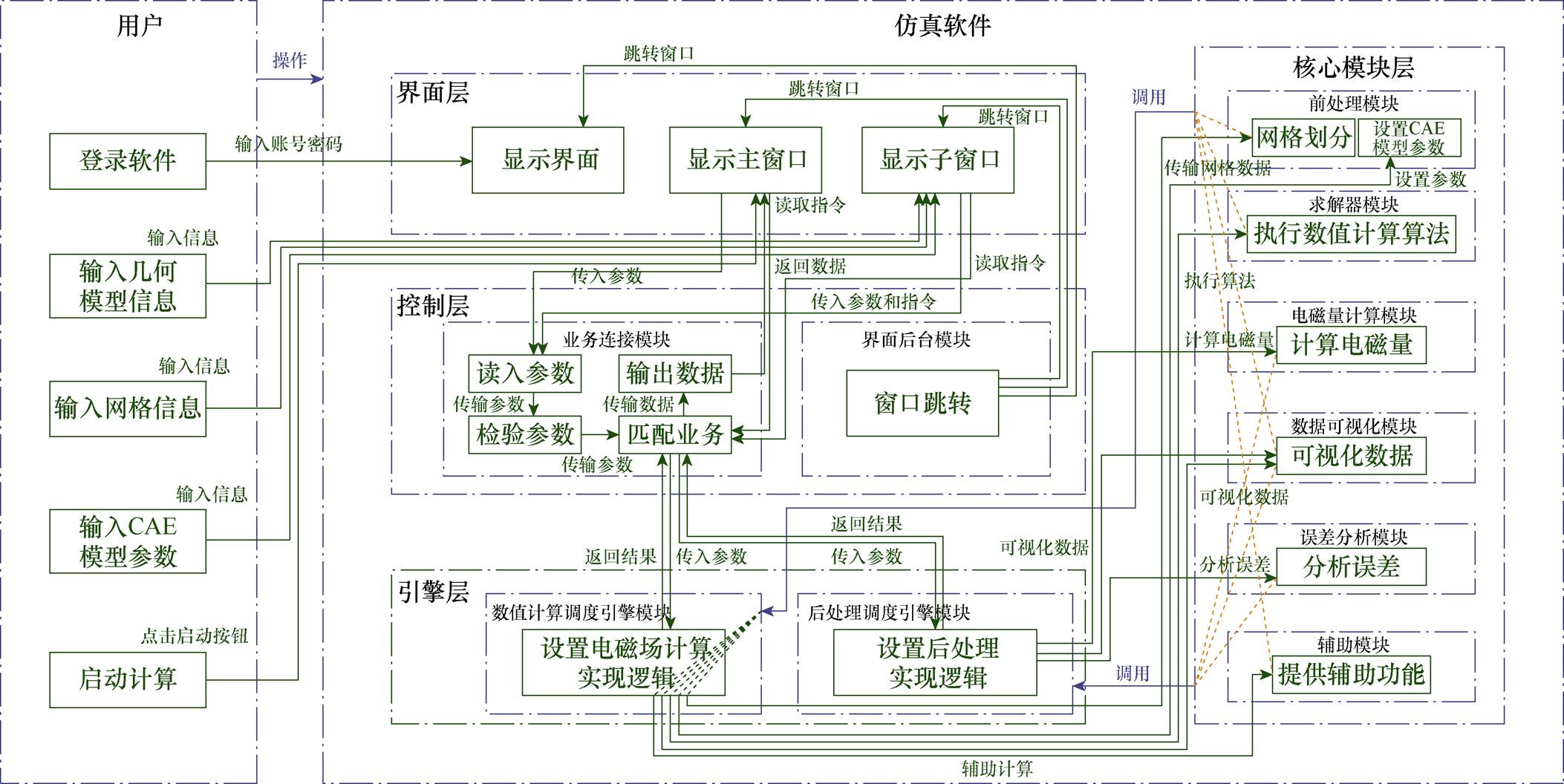
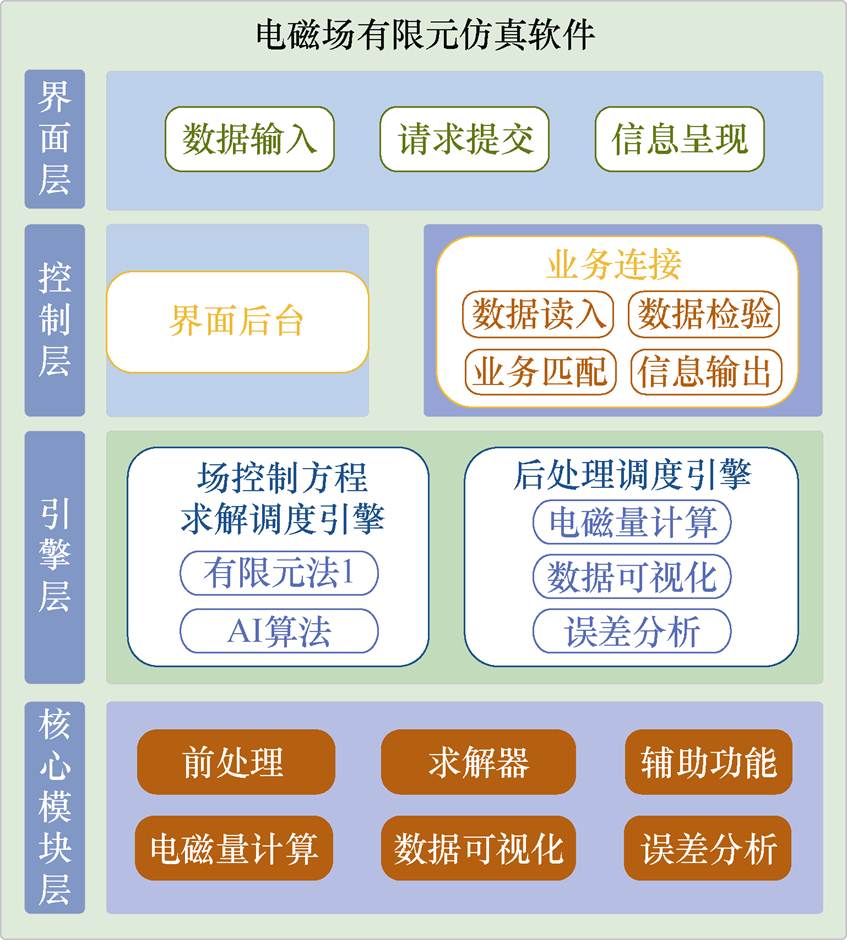
逻辑架构层级是建模过程从问题域转向解决方案的开始,旨在说明系统如何通过内部逻辑组件的关联达到期望的实现过程,而不过多地关注实现的技术细节。将系统模型转化、继承到逻辑架构层,系统执行方转换为逻辑执行方(Logical Actor, LA)。建模流程为:分析逻辑功能、定义逻辑组件和分配逻辑功能至逻辑组件。首先,基于系统功能定义逻辑功能(Logical Function, LF),并进一步细分以明确内部组件的具体功能。如,“后处理”逻辑功能可细分为“电磁量计算”“数据可视化”“误差分析”三个子功能。其次,用逻辑组件(Logical Component, LC)承接逻辑功能。将系统架构中的用户和仿真软件均转换为逻辑组件,并根据分解出的具体逻辑功能,在该层添加“界面层”“控制层”“引擎层”“核心模块层”等逻辑组件。最后,将逻辑功能分配给逻辑组件,通过逻辑组件以及逻辑功能之间的交互,建立完整的逻辑架构,如图7所示。
3.4 层级四:软件架构建模
软件架构层级的目标与逻辑架构层级类似,不同之处在于它定义了系统的最终架构。在该层级,将软件分解至最小设计颗粒度,将逻辑架构层中抽象的建模元素转换为具体技术,对应软件开发,即为将模块设计转换为具体的类实现,并将模块分配至软件功能层。详细建模过程可以分为三个阶段。
定义软件功能:基于对逻辑架构层级逻辑功能的转化和分解,定义软件功能。
定义软件组件:组件分为节点组件(软件功能模块)和行为组件(软件功能层)。其中,行为组件负责完成具体功能,节点组件负责调度相关行为组件。定义软件组件可构建实现逻辑架构的具体方案。
分配软件功能至组件:先把行为组件分配给节点组件,再将功能分配至行为组件,形成软件架构,如图8所示。
建模过程充分体现了使用Arcadia建模方法和Capella建模工具的优势。首先,MBSE方法通过采用统一的建模语言和符号、提供图形化模型,直观地呈现复杂的软件结构,这比自然语言更精确,确保合作开发者和后续继承者以相同的方式理解模型中的概念和关系,从而消除理解上的差异。其次,通过从需求分析逐步展开到详细的设计和实现,每一层建立在前一层的基础上,如上一层的功能在下一层得以继承和扩展,并且Capella提供一致性检查功能。这种逐层迭代和细化的分层方法使得不同的设计阶段保持连贯性和一致性,同时对系统进行扩展和改进。
在进行模型验证时,正确的功能架构模型需明确系统所需的能力、各功能的输入与输出、系统或外部环境的活动及其预设的答案或结果。这些要素在相应的场景中都应有明确的定义和说明,以确保功能场景中的信息和功能链中的预期功能消息一致。
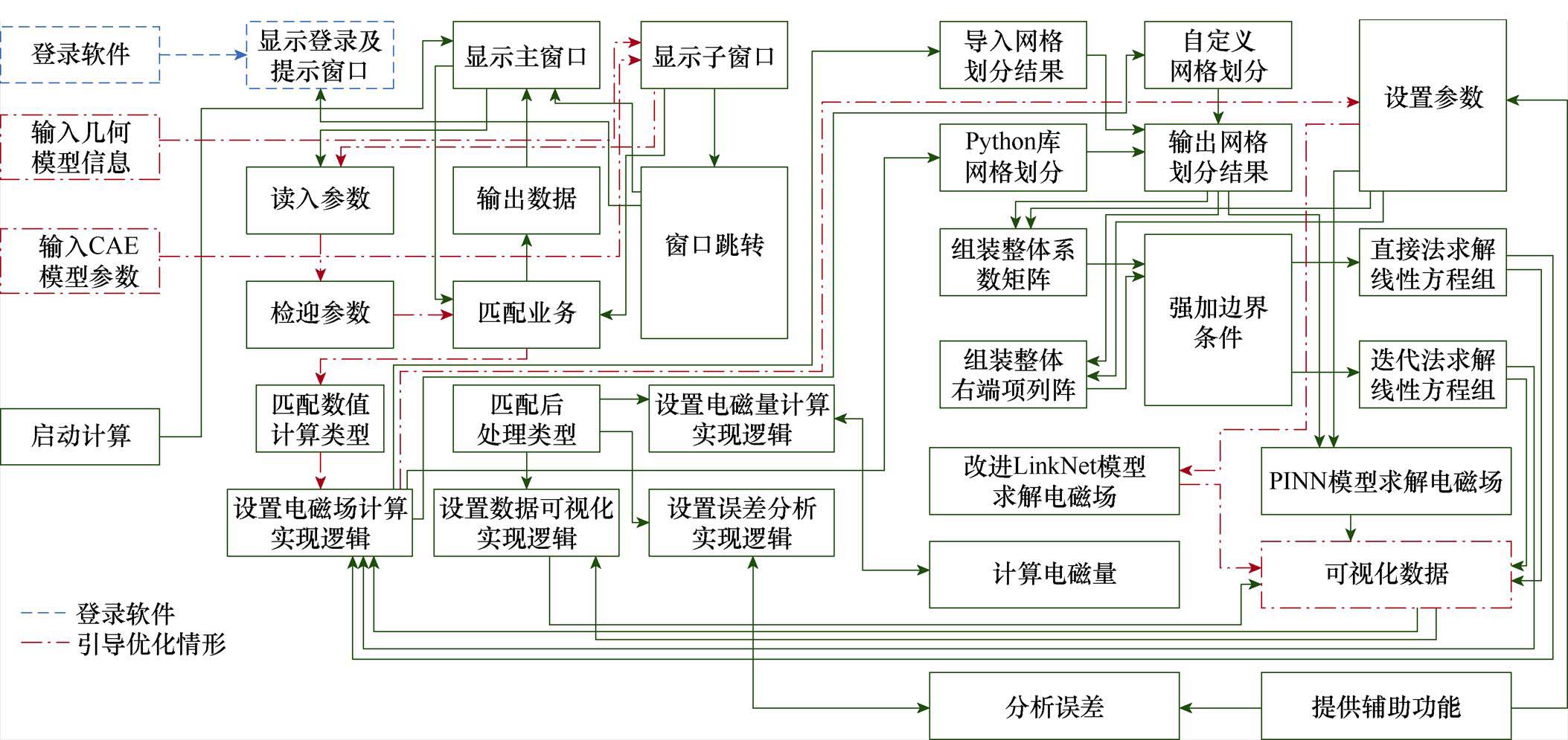
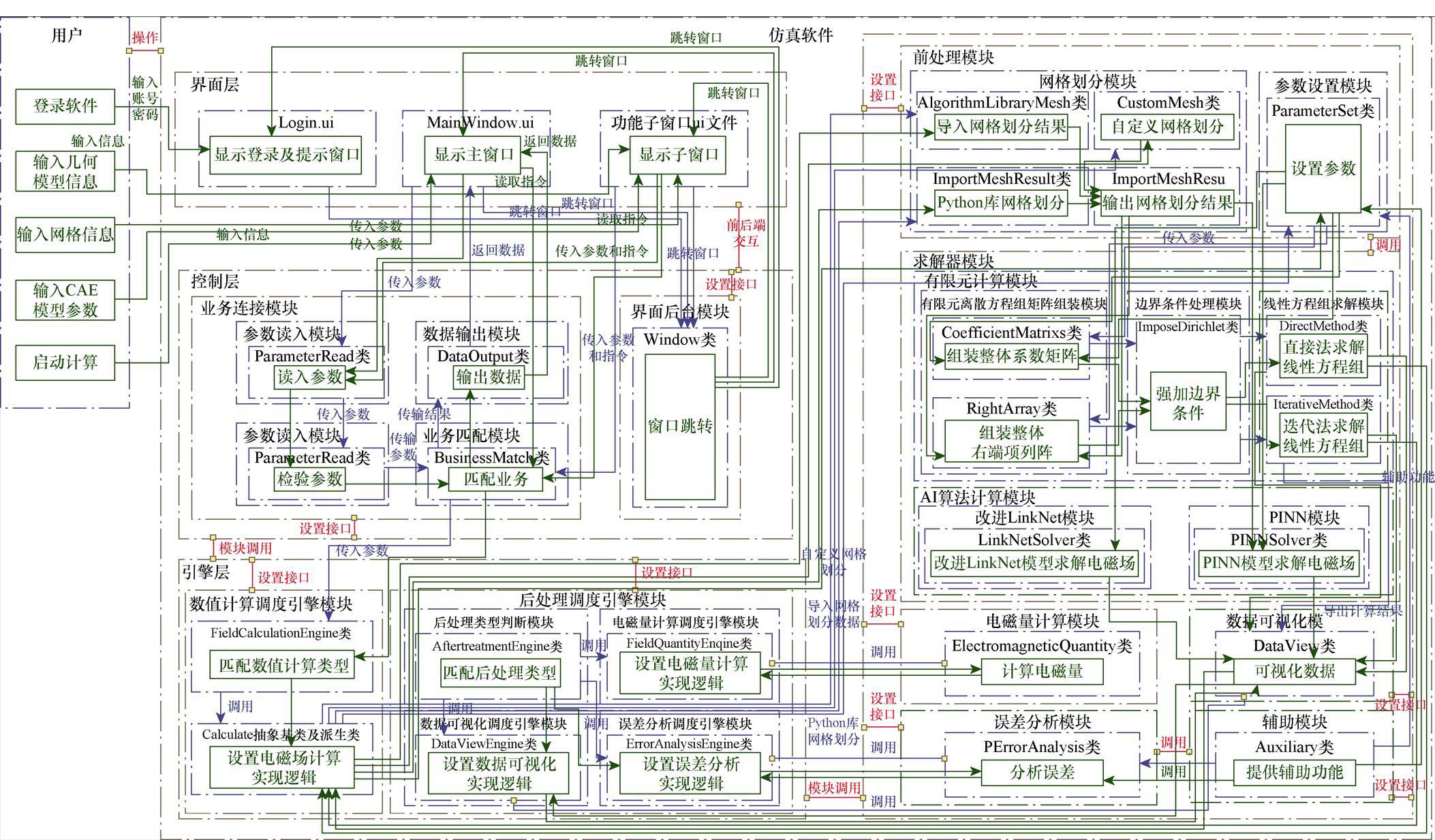
最后,采用Visio软件绘制的软件组件之间的复杂交互关系,其总体架构如图9所示。其可以展示组件间的关系,但在绘制时较为费力,且难以改动模块之间关系或者新增模块。相比之下,MBSE建模工具提供高亮模型元素和交互路径的功能,使得绘制和查看复杂模型变得高效便捷。当发生变化时,支持联动修改,即自动修改该层级其他位置该元素的变化。运用MBSE方法以模型描述软件需求、设计和实现,有助于促进软件合作开发、传承与扩展。
4 集成AI的电磁场有限元软件原型IFEM
AI for Science背景下轻量化、定制化电磁场有限元仿真软件无需同商业通用仿真软件一样功能完备,只需具备电磁场仿真流程中基础功能,针对特定工程问题再扩展。但从底层语言、架构、原型开发速度和成本等方面要为日益成熟的AI算法融合进电磁场仿真软件提供准备。电磁场有限元法仿真软件的开发工具选为Python及其基础算法库,可让软件开发者更关注算法逻辑,而不是基础代码编写。具体优势如下:①为数值模拟和AI算法提供统一的编程环境及运行平台;②贴近自然语言,代码简洁,易学易理解;③AI的迅速发展使Python算法库得以充分的迭代、测试、验证和优化,可通过Pip包管理工具,以简单的命令自动化安装、更新和管理50万以上的庞大第三方算法库及其依赖库,比C语言更方便、科学、规范;④虽然在密集型计算时Python代码执行速度不如C、C++等编译型语言,但其性能可通过多种方式提升[34],使得速度与C语言相似。
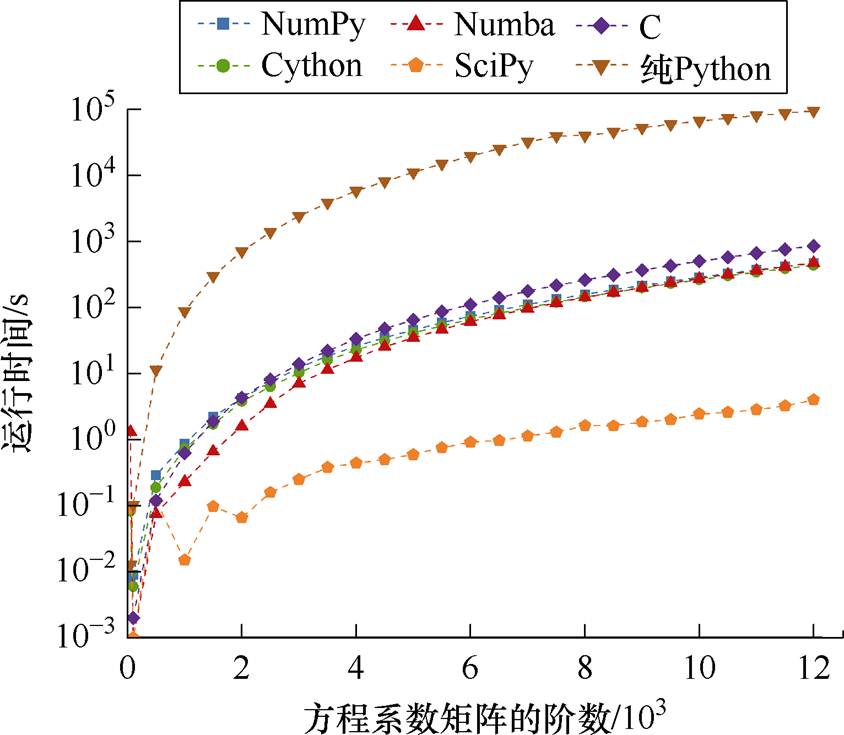
本文运用六种工具实现LU分解法求解线性方程组,分别为未经优化的C语言(作为性能基准)、纯Python(使用内置函数和循环)、Numba(将Python代码转换为机器码)、Cython(将Python代码编译成C代码)、底层使用C语言编写且经过优化的NumPy、SciPy库,对比如图10所示。纯Python计算速度远慢于C,Cython、Numba、NumPy与C相近,而SciPy快于C。经过性能提升后,其执行速度接近甚至超过C语言,这使得Python在处理大规模数据或计算密集型任务时仍具有竞争力,Python(SciPy)与C语言求解器的精度对比,见表3。
表3 Python(SciPy)与C语言求解器的精度对比
Tab.3 Precision comparison between Python (SciPy) and C language solvers
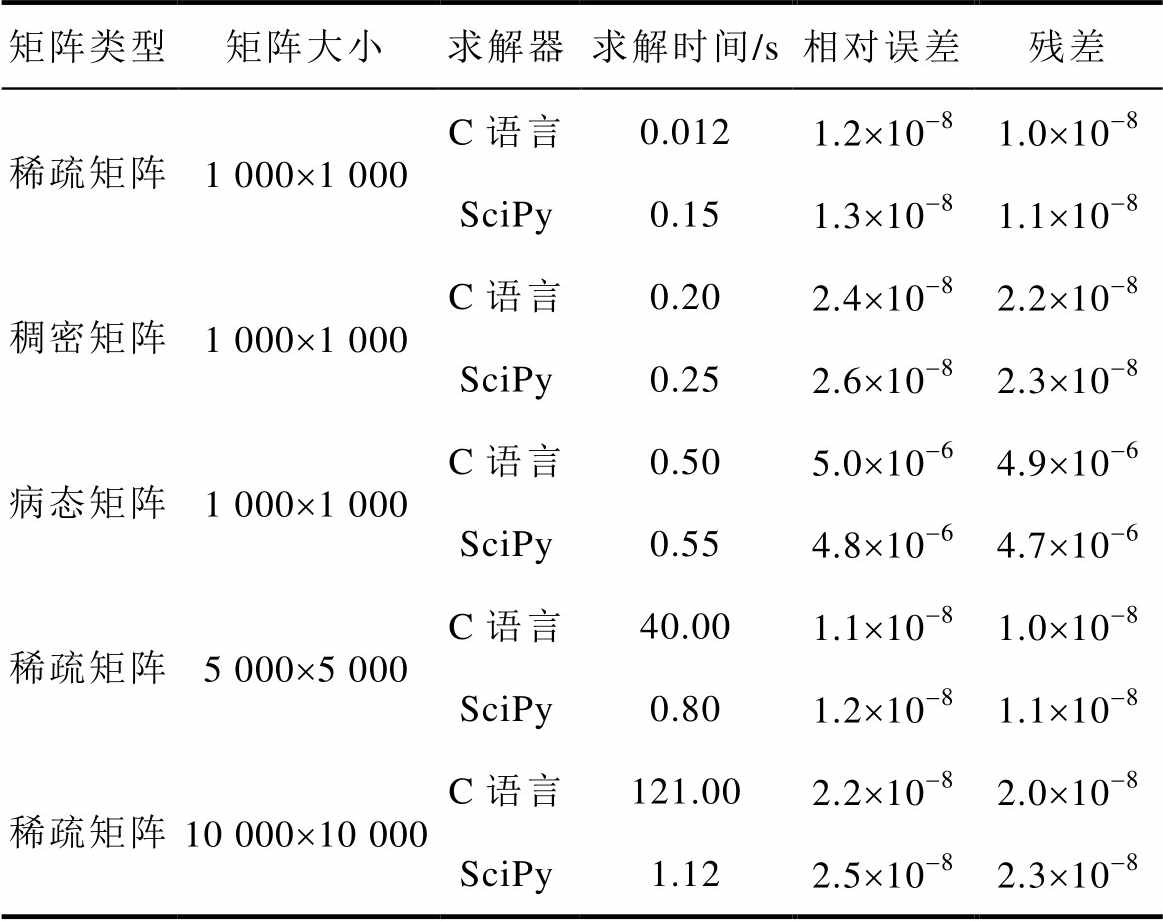
矩阵类型矩阵大小求解器求解时间/s相对误差残差 稀疏矩阵1 000´1 000C语言0.0121.2´10-81.0´10-8 SciPy0.151.3´10-81.1´10-8 稠密矩阵1 000´1 000C语言0.202.4´10-82.2´10-8 SciPy0.252.6´10-82.3´10-8 病态矩阵1 000´1 000C语言0.505.0´10-64.9´10-6 SciPy0.554.8´10-64.7´10-6 稀疏矩阵5 000´5 000C语言40.001.1´10-81.0´10-8 SciPy0.801.2´10-81.1´10-8 稀疏矩阵10 000´10 000C语言121.002.2´10-82.0´10-8 SciPy1.122.5´10-82.3´10-8
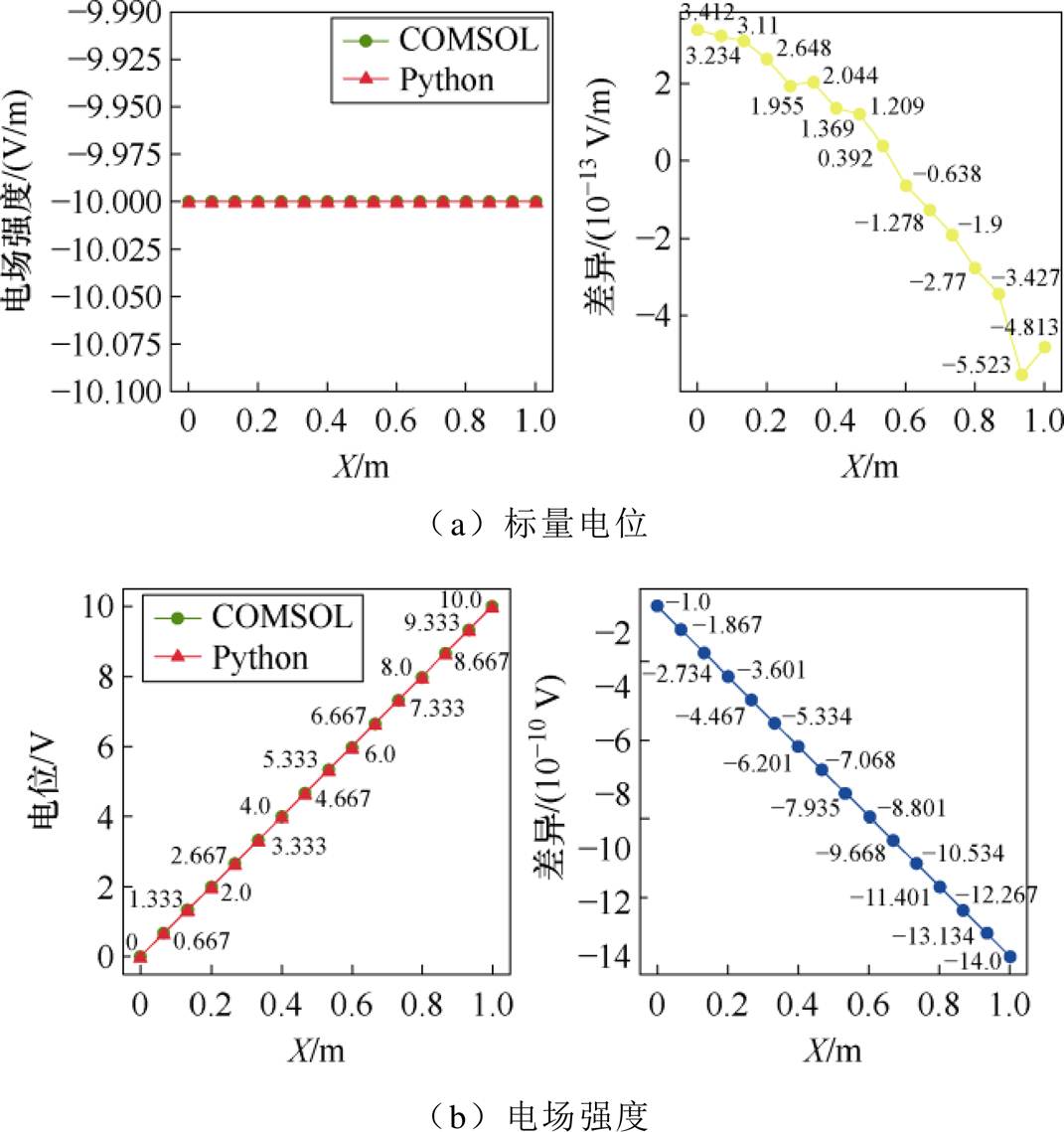
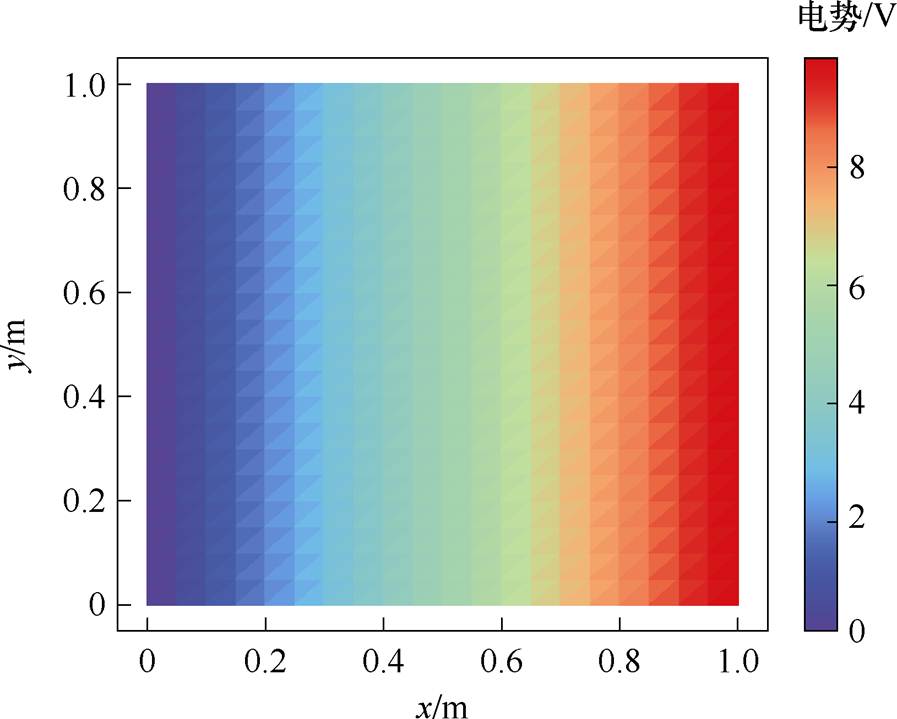
以求解长直导线电场分布为例,证明Python及其算法库的优势。假设长直导线长度为1 m,左端接地,右端电压为10 V,求解域内只包含线性、各向同性媒介,且无电荷存在。项目组基于Python和Numpy库实现了程序开发,涵盖了从算法库导入、前处理、求解到后处理的全部过程,程序仅由68行组成[35],突显了Python在实现数值仿真时的便利性。自编代码计算出的标量电位、电场强度及误差分布,如图11所示,结果与COMSOL计算结果对比整体误差,见表4。
表4 COMSOL和自编代码误差对比
Tab.4 Comparison of COMSOL and self-coding errors
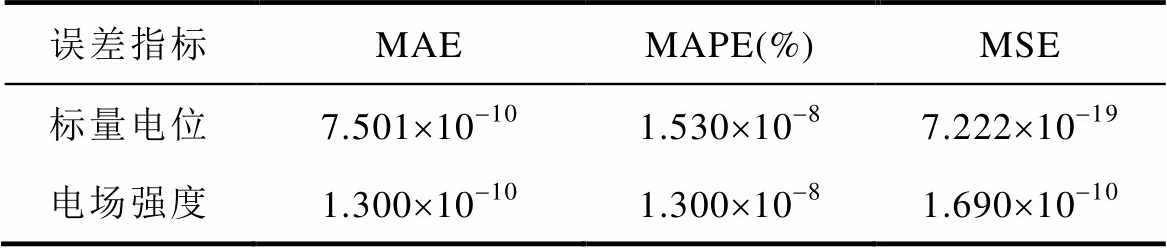
误差指标MAEMAPE(%)MSE 标量电位7.501´10-101.530´10-87.222´10-19 电场强度1.300´10-101.300´10-81.690´10-10
在电磁场有限元仿真软件开发中,引入数值模拟与AI的双向耦合设计方法,旨在实现两者的优势互补。数值模拟以其精确的物理和数学基础为仿真提供了坚实的科学支撑,而AI技术则利用其强大的数据处理能力和学习能力,增强仿真的效率和适应性。通过这种双向耦合,可以在保持仿真精度的同时,显著提高仿真速度,尤其在面对复杂电磁场问题时更显其优势。
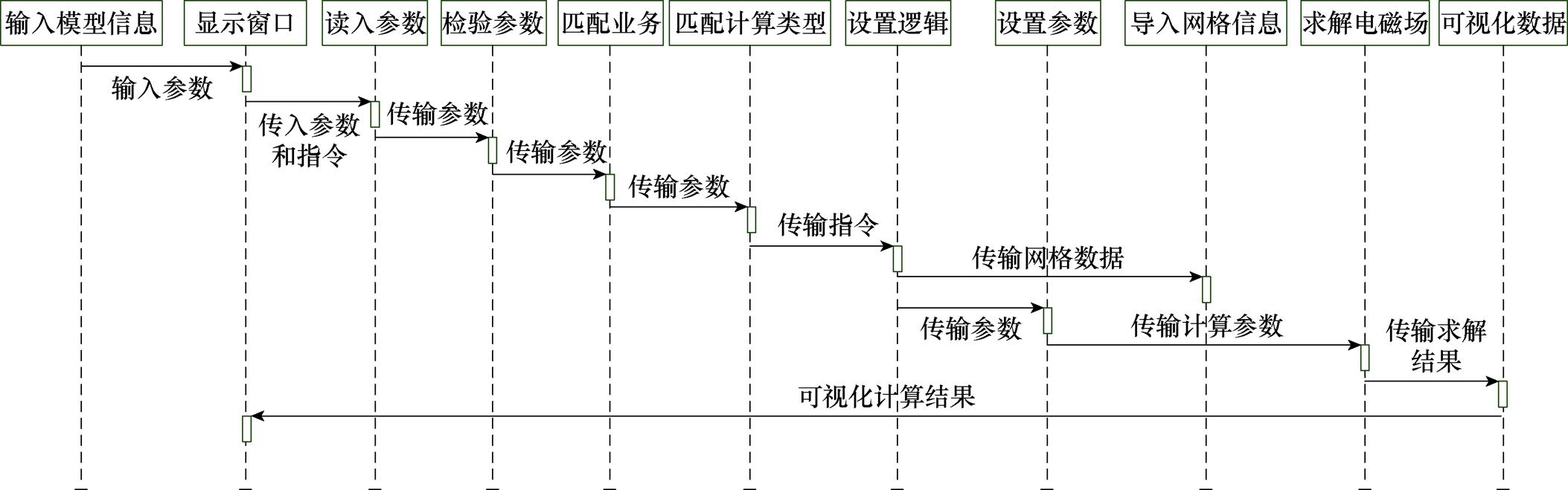
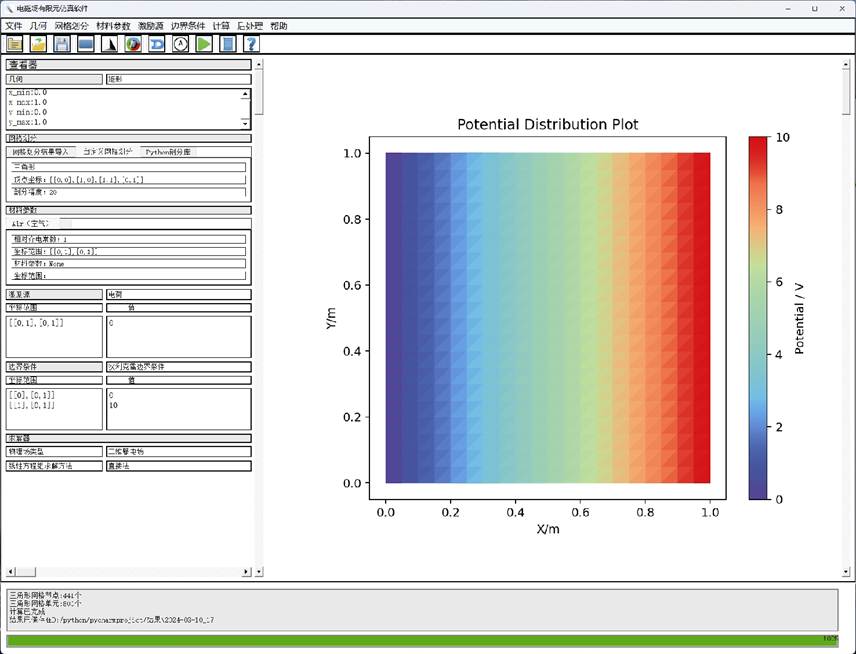
以集成AI的电磁场有限元仿真软件构建方法为指导,课题组完成了软件原型逆有限元法(Inverse Finite Element Method, IFEM)开发。用户输入电磁仿真任务各项数据后,主窗口的参数查看区随之自动更新,便于用户在参数设置每一步及完成后浏览和检查输入正确性。“开始计算”启动后端程序,进行场求解,并将位函数分布图显示在主窗口结果显示区。计算结果存储到默认的结果存储文件夹中,底部状态栏输出网格划分情况和提示信息,如图12所示。
IFEM采用面向对象编程方法和模块化思想,调用PyQt5、MeshPy、NumPy、SciPy和Matplotlib等Python基础算法库编写功能模块代码,并以包、.py文件的结构组织代码,形成层、模块、子模块。通过导入机制实现层、模块连接,完成界面开发及跳转、前后端数据交互、前后处理、节点有限元离散方程组矩阵组装、边界条件处理和线性方程组求解,以及物理信息神经网络(Physics-Informed Neural Networks, PINN)、改进LinkNet深度学习模型的集成。
为实现AI与数值模拟的集成开发,采用Python编程语言和PyCharm集成开发环境,统一进行有限元模块和AI模块的开发和调试,减少不同开发工具之间的兼容性问题;利用SciPy和NumPy等科学计算库,为AI模型提供高效的数据结构和运算支持,同时保证精确的数值模拟,确保大规模数据处理的效率;通过Python的Pandas库,在统一平台上实现数据传输,确保有限元仿真数据能直接用于AI模型的训练和预测。
下面就计算二维电极间电场分布和TEAM Workshop 第35基准问题,展开案例验证。
4.1 电极间电场计算
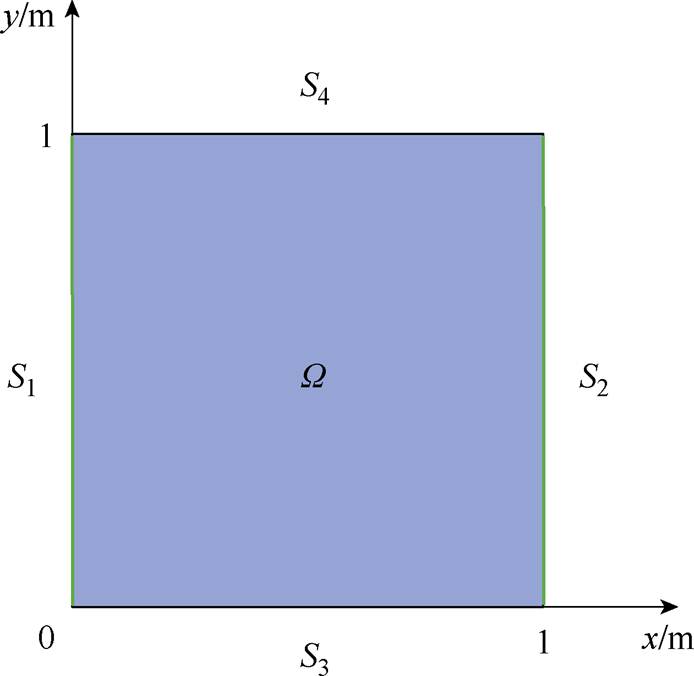
本节分别调用有限元法和PINN深度学习模型的两种求解器,计算二维电极间电场分布。如图13所示的正方形(1 m×1 m)求解域,左右边界为薄板导体,且左端给定电位0 V,右端给定电位10 V,两个导体之间为均匀线性电介质,相对介电常数为5。假设区域内不存在自由电荷。
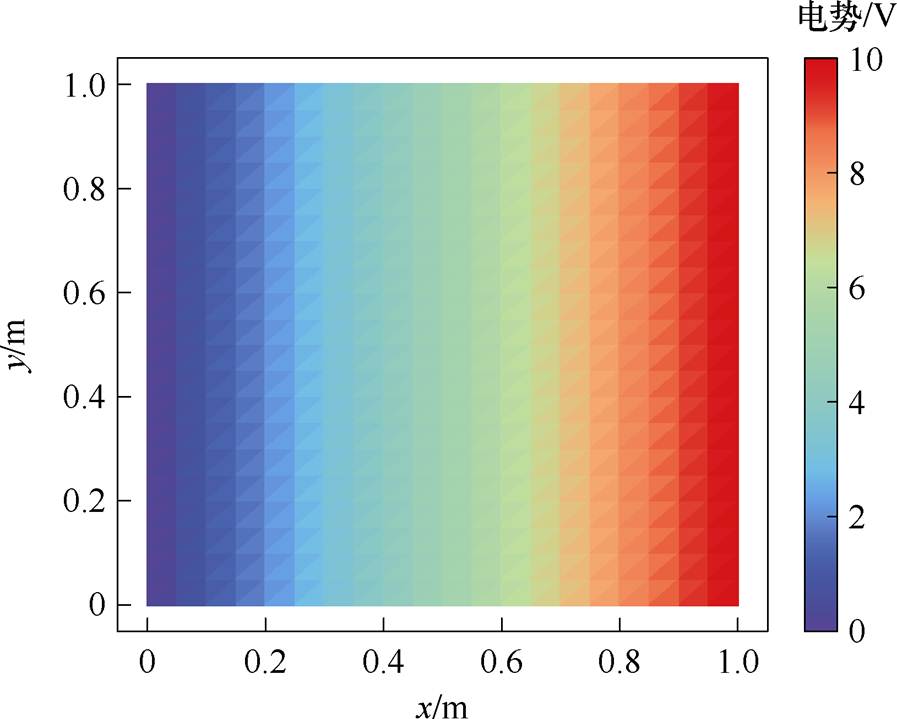
该算例求解域形状简单,采用自定义的规则化网格剖分方式,x、y方向的剖分数均为20,共有441个节点,800个单元。采用有限元法求解时,计算结果如图14所示。
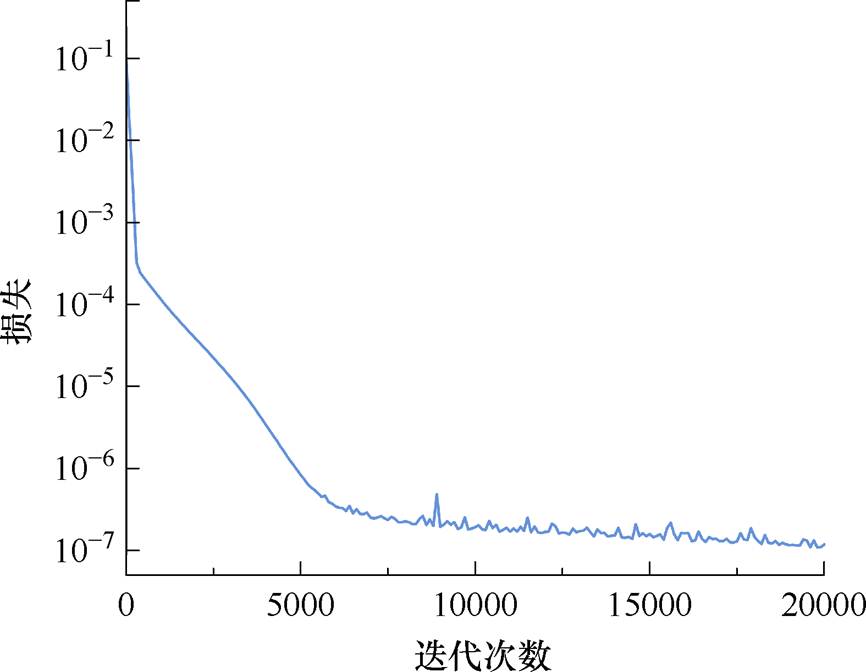
将求解器更改为深度学习模型PINN,该神经网络包含3个隐藏层,每层神经元数为150,激活函数为Tanh,对应的训练损失函数曲线,如图15所示。以求解域网格划分后的节点坐标作为PINN模型的输入,即可获得节点的电位离散值,分布图如图16所示。
为了验证IFEM后处理功能,将电位等值线可视化,计算电场强度并得到其离散值文件和幅值分布图。为了验证基于有限元法开发的求解器的正确性,以COMSOL结果为基准,对IFEM计算的节点电位、电场强度幅值进行整体误差分析,见表5。
表5 二维静电场算例的COMSOL与IFEM误差
Tab.5 COMSOL and IFEM error for the two-dimensional electrostatic field case

名称MAEMAPE(%)MSE 电位1.132´10-112.735´10-111.763´10-24 电场强度4.185´10-124.185´10-112.730´10-23
通过软件运行过程、IFEM计算结果与COMSOL的误差值,以及标量电位和电场强度数据对比情况,证明了IFEM前处理、求解、后处理等仿真功能的可用性以及二维静电场计算准确性。该算例适用于相同电磁问题的仅尺寸变化的场景,在不同结构(如复杂度增加或边界条件不同)或高度非线性的情况下,需进一步使用迁移学习方法,解决模型的适用性问题。
4.2 螺线管界面磁场优化
国际计算电磁学会提出的TEAM Workshop第35基准问题[36]是一个多目标、多变量优化问题,研究对象是轴对称空心螺线管,由上下对称的20匝串联线圈组成,每匝线圈宽度w=1 mm,高度h= 1.5 mm,第i匝螺线管线圈半径Ri变化范围为5~50 mm,输入激励电流为3 A。
在螺线管内部选取一个5×5 mm的二维控制区域,设计变量为螺线管半径Ri,第一个优化目标是使得控制区域内的磁通密度实际值与磁通密度规定值之间的差值最小化,即磁场分布尽可能均匀;第二个优化目标是使螺线管的功率损耗最小,设定线圈通过恒定电流供电,由式(1)推导可知,功率损耗与线圈半径成正比,故以线圈半径反映功率损耗,降低了目标函数复杂程度。
两个优化目标函数表达式为
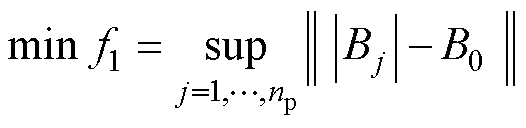 (2)
(2)
式中,P为功率损耗;I为电流值;r 为电阻率;l为导线长度;S为导线横截面积;nt为螺线管匝数;f1为第一个目标函数值;f2为第二个目标函数值;B0为目标磁通密度值,B0=2 mT;Bj为控制区域磁通密度实际值;np为采样点个数,取为66。
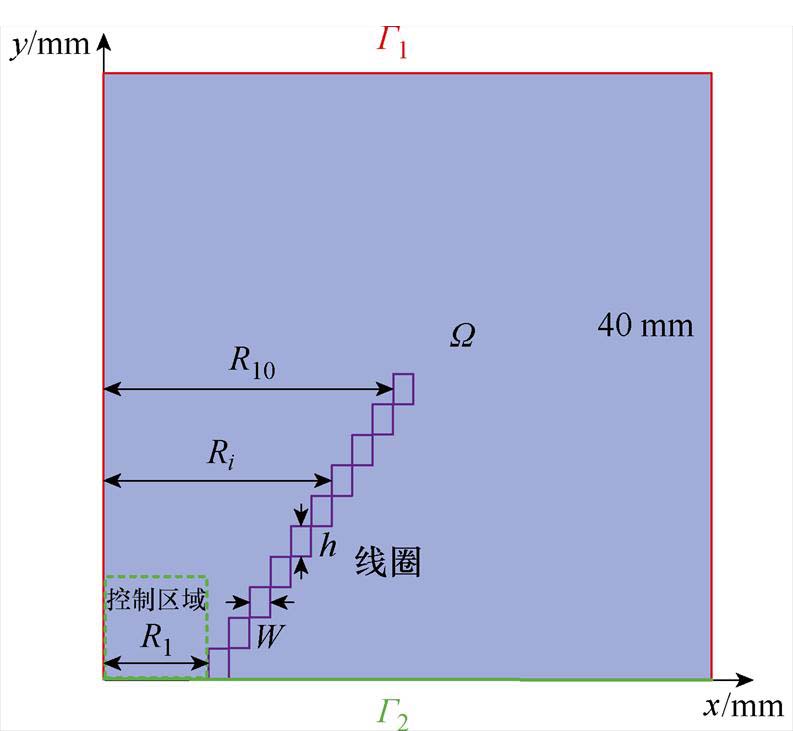
指定10个半径为5, 6, 7, 8, 9, 10, 11, 12, 13, 14 mm,计算螺线管周围磁场,并与COMSOL进行对比,验证IFEM计算正确性。由于几何模型、材料参数边界对称分布,故选取过中心截面的1/4,指定求解域为长度40 mm的正方形,左、右、上边界为第一类边界条件,下边界为自然边界条件。为了方便对比,同时避免插值带来的误差,直接导入COMSOL物理场控制网格较细化剖分的划分结果,即1 168个网格节点、2 224个网格单元,计算模型如图17所示。
对该二维平面场(x-y平面),电流密度J和矢量磁位A平行,且平行于z轴,即Ax=Ay=0,Jx=Jy=0。取矢量磁位z向分量Az为场变量函数,边值问题描述为
式中,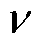 为磁阻率。
为磁阻率。
采用加权余量法作离散化处理,得到有限元离散化方程
式中,系数矩阵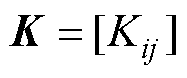 ,右端项列阵
,右端项列阵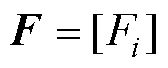 ,由各单元体的相应项叠加而成,其中,
,由各单元体的相应项叠加而成,其中,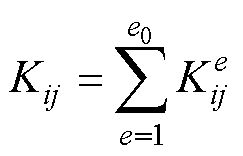 ,
,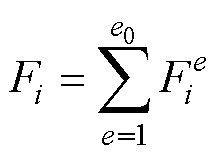 ,i、j代表单元e中所有节点的局部编号。
,i、j代表单元e中所有节点的局部编号。
根据加权余量法得到有限元离散公式为
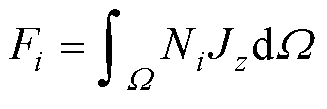 (7)
(7)
式中,Ni和Nj为基函数,i, j=K, M, N,代表三角形单元e的三个节点的编号。
运用三角形单元进行网格划分,得到单元对系数矩阵和右端项的贡献为
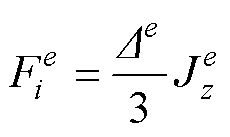 (9)
(9)
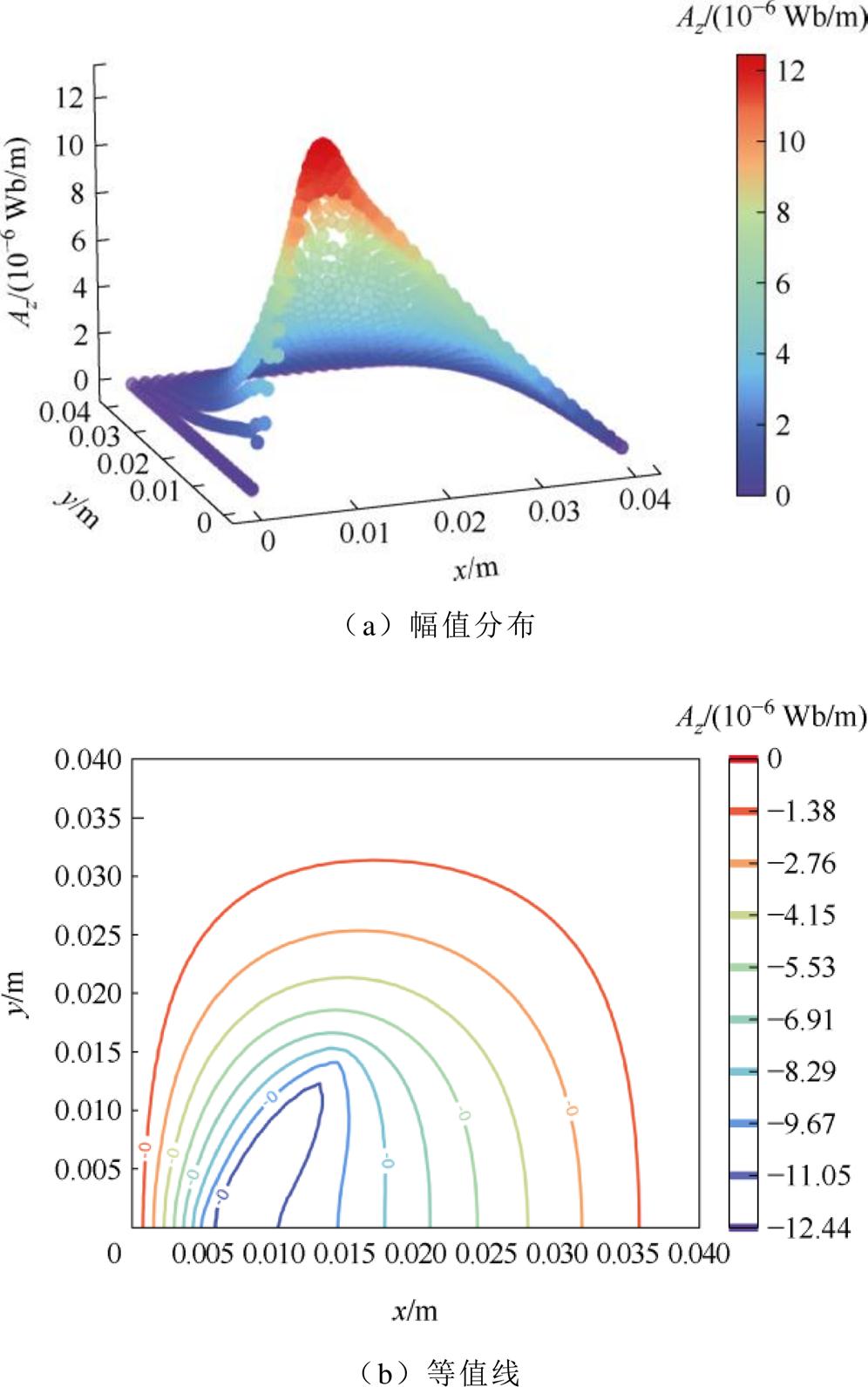
经计算,得到矢量磁位分量Az的离散值,绘制其幅值分布图和等值线,如图18所示。
经过误差分析,得出自编电磁场有限元仿真软件矢量磁位计算结果与COMSOL的误差值MAE为3.211×10-9、MAPE为0.054%、MSE为6.310×10-17。
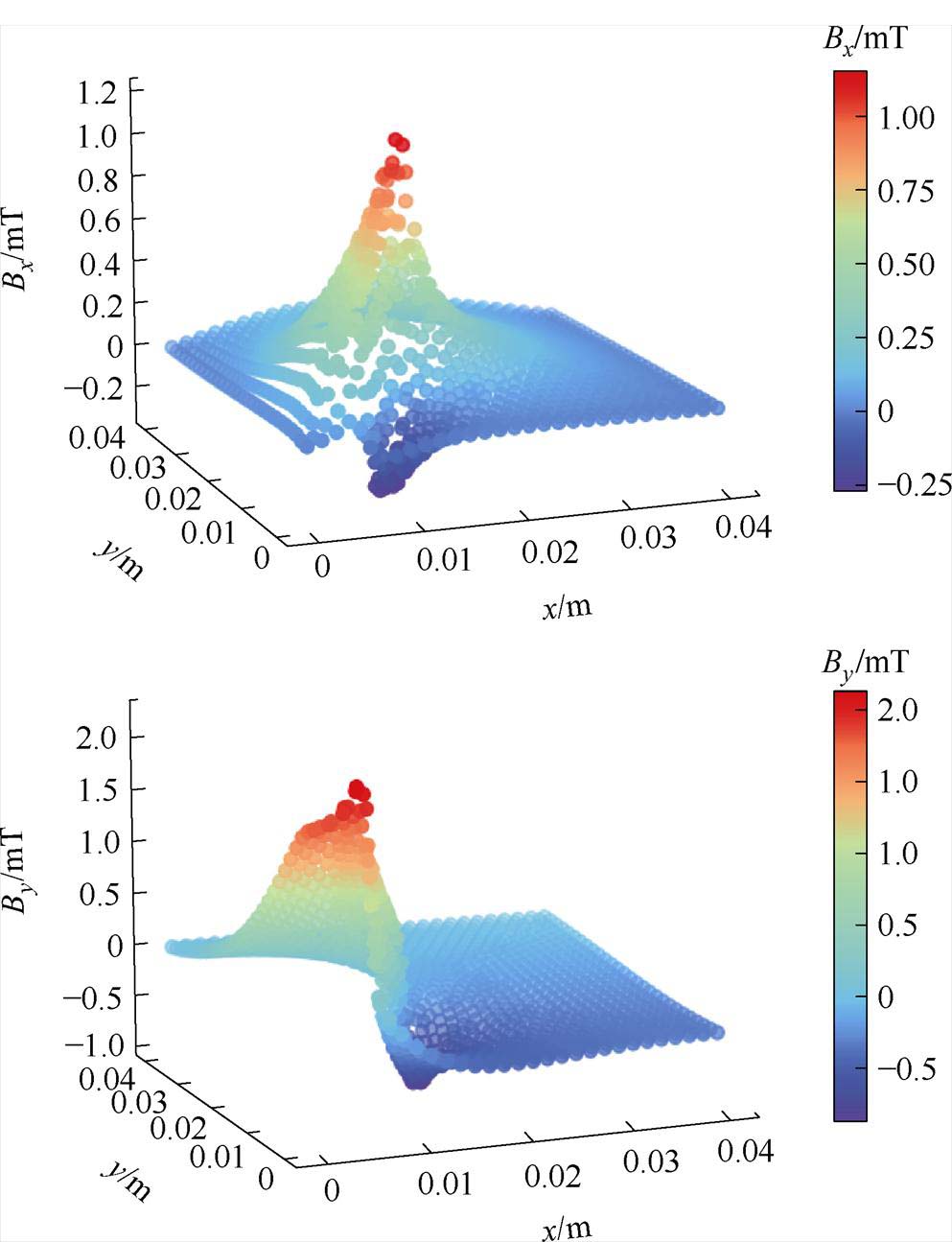
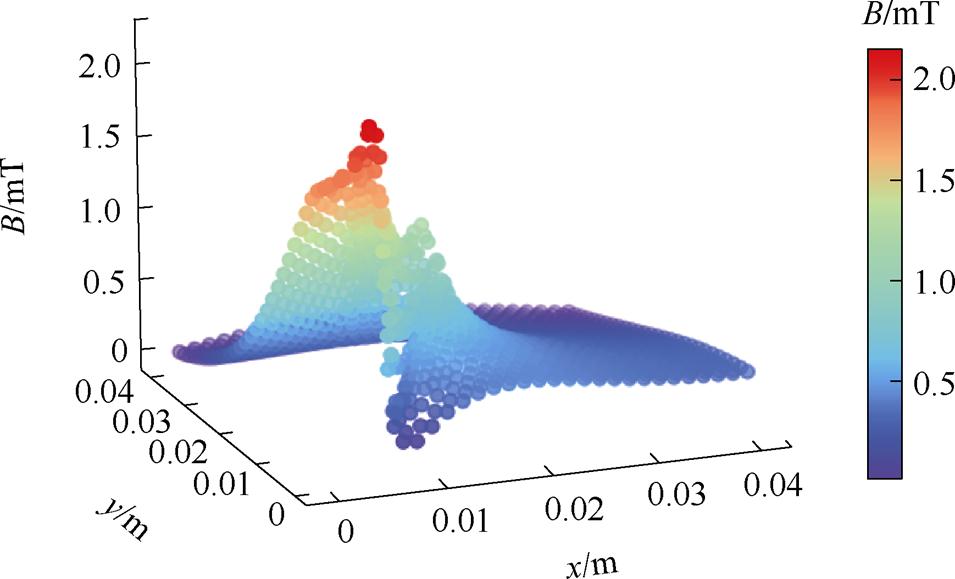
可由矢量磁位节点离散值计算单元及节点磁通密度各方向分量值以及合成量幅值,其分布如图19所示。
对比IFEM与COMSOL的磁通密度计算误差值,见表6。通过IFEM计算结果与COMSOL的误差值,以及矢量磁位和磁通密度分布对比情况,可见IFEM可以实现二维恒定磁场数值仿真功能。其中,矢量磁位IFEM计算误差较小,磁通密度的误差相比于矢量磁位,有扩大现象。考虑其原因是,IFEM求解器得出的矢量磁位A仅具有分片线性逼近精度,需计算其旋度得到磁通密度,在网格单元内对A求一阶导数后将得到分片插值,造成对B逼近精度存在不足。为了提升B逼近精度,可更改求解器模块对应代码,对A采用高阶有限元基函数进行展开。
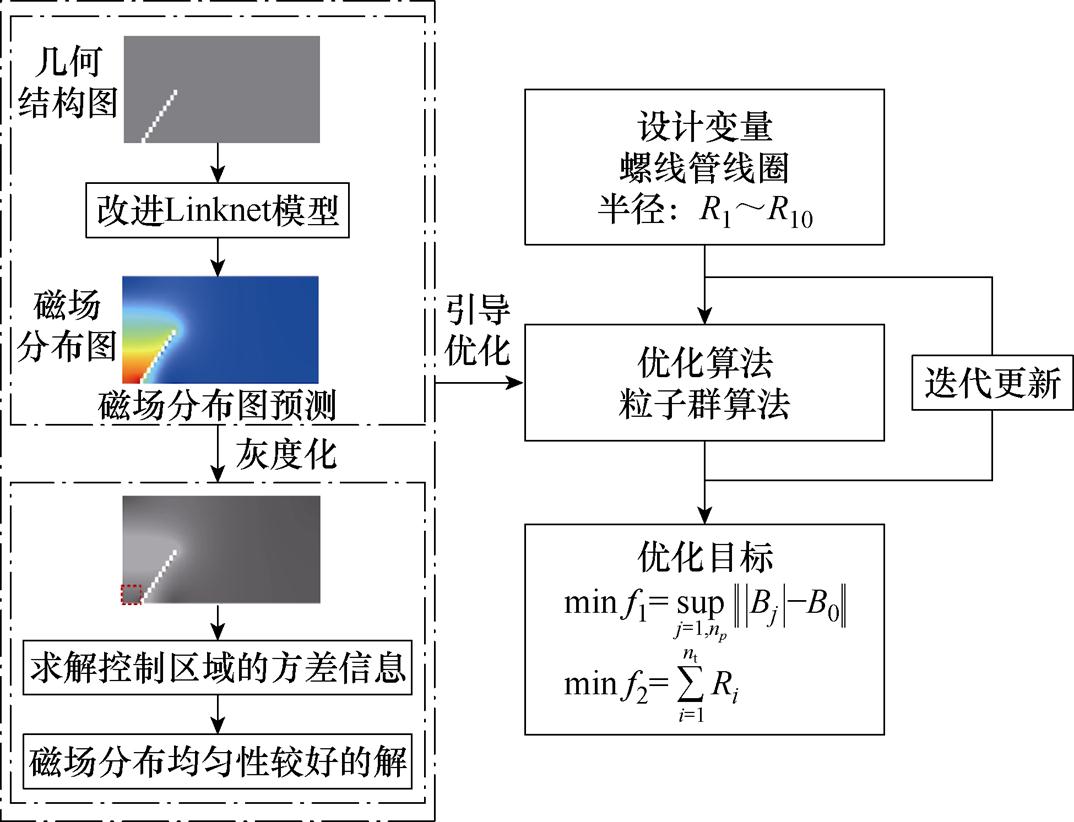
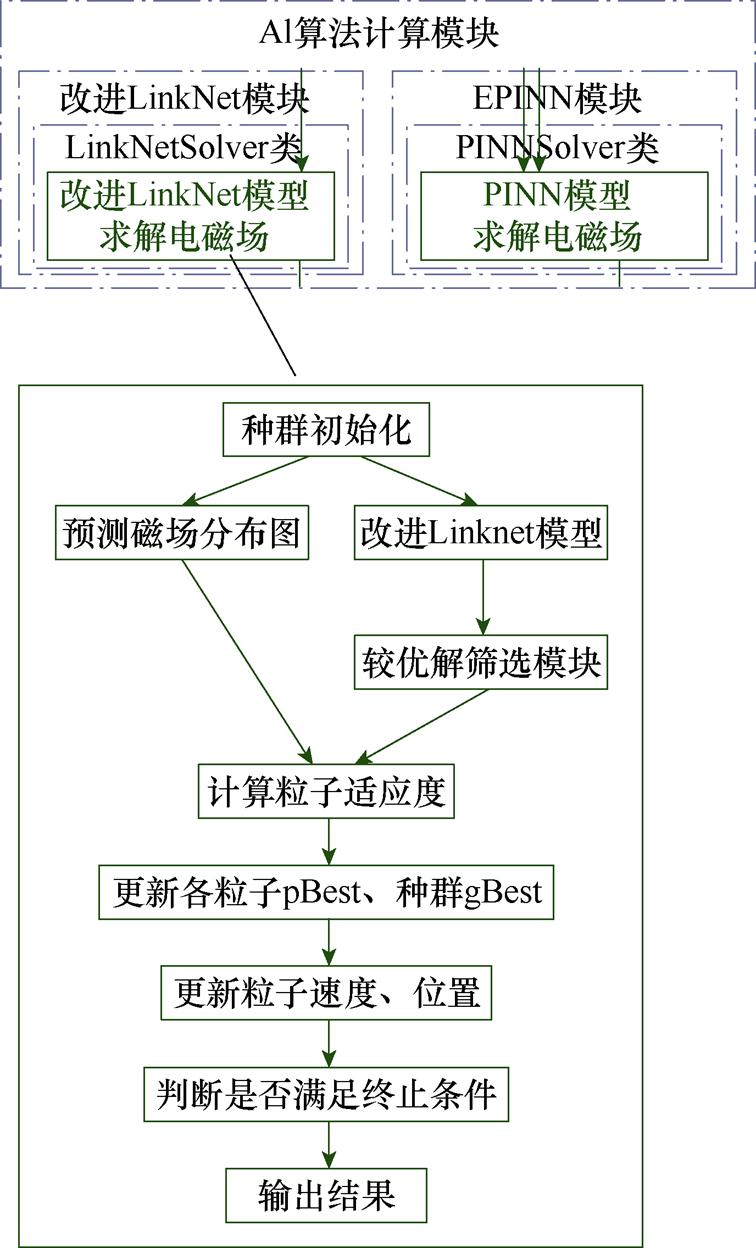
按照上述过程,由IFEM计算多组半径组合下的磁通密度值,作为改进LinkNet模型的训练数据集。应用引导优化算法,将训练完成的改进LinkNet模型作为代理模型,模型的输入为螺线管的几何结构图,基于粒子群优化算法,优化螺线管磁场分 布[13]。优化路线如图20所示。
Linknet与U-net具有相似的结构,可看作U-net的改进版本,不同之处在于LinkNet采用轻量级的编码器,减少了网络参数的数量,提高了训练速度,适用于内存受限的情况;其次,LinkNet具有更好的通用性,并且更适合于较小的数据集;并且LinkNet的编码器使用残差连接,可以有效地避免过拟合问题。改进LinkNet模型的具体改进思路如下:引入注意力机制,增强重要目标区域的特征提取能力,避免无关信息的干扰;借助Dropout来提高模型的泛化能力,避免网络层数过深而引起的过拟合问题;选择合适的损失函数,将LinkNet模型用于求解逐像素的回归预测问题。
表6 COMSOL与IFEM磁通密度误差
Tab.6 COMSOL and IFEM magnetic flux density error
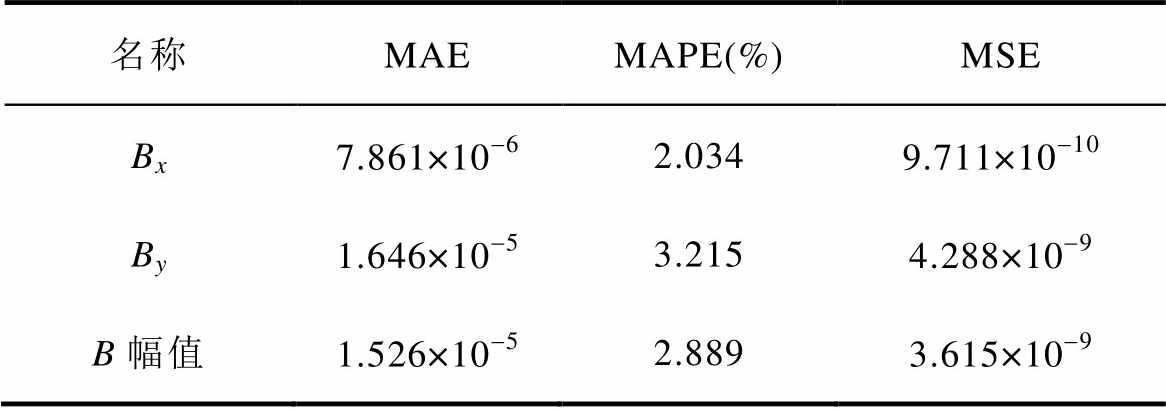
名称MAEMAPE(%)MSE Bx7.861×10-62.0349.711×10-10 By1.646×10-53.2154.288×10-9 B幅值1.526×10-52.8893.615×10-9
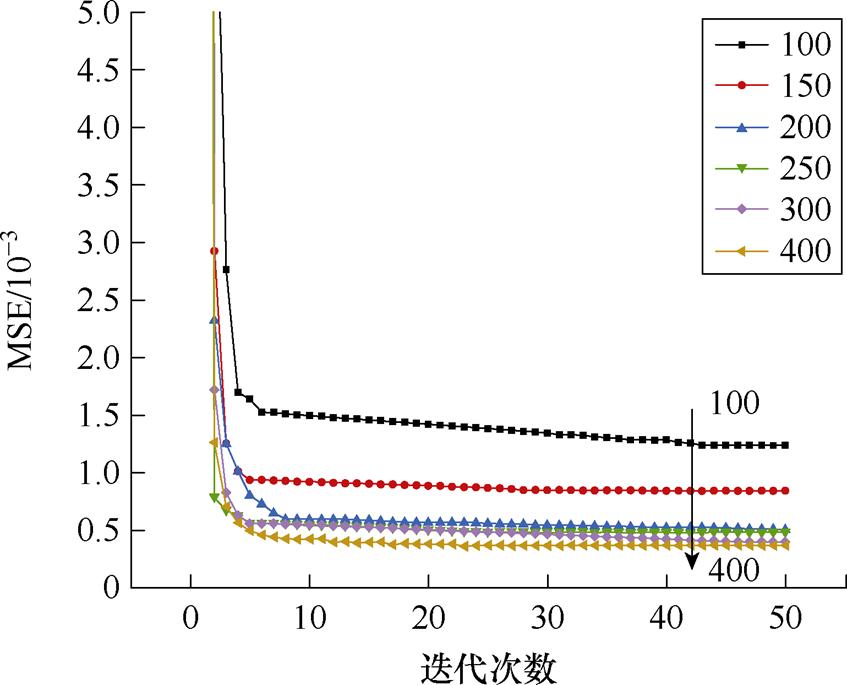
通过降低训练样本数量来验证改进Linknet的性能极限。针对不同的训练样本数量,100、150、200、250、300和400组进行模型训练,并记录训练过程中损失值随迭代次数的变化情况,如图21所示。经过50次训练后误差已基本稳定,完成模型训练,当训练样本数量为100组和150组时,预测效果较差,无法满足精度要求;当训练样本数为200~300组之间时,误差显著减小;训练样本数为400组时,训练消耗的时间会更长但准确度没有显著提高。因此,在保证训练速度和预测精度的前提下,可以将训练样本数减少到200~300组。当螺线管几何结构发生变化时,采用迁移学习的方法,即在已训练好的模型基础上,使用少量新样本对模型进行调整,来提高模型的适用性。
考虑到螺线管磁场云图是由图像表达的,不同颜色代表不同的磁感应强度值,而颜色正好是由像素值来表示的,当磁场分布发生变化时,磁场云图的颜色随之发生相应的改变,磁感应强度值的分布情况与磁场云图像素值的分布情况形成一一对应关系,因此可由像素值分布情况来反映磁感应强度值的分布情况,通过在控制区域内计算和对比磁场云图像素值的方差,可得到磁场分布尽可能均匀的较优解。
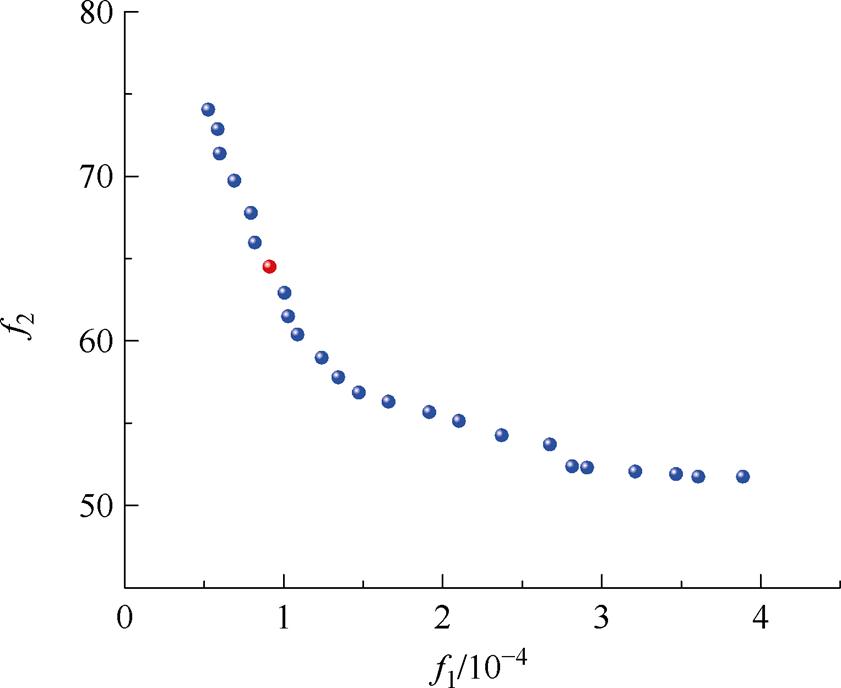
优化算法迭代次数为80,得到的帕累托前沿,如图22所示。
改进的LinkNet模型适用于几何结构较为固定、尺寸变化范围有限的螺线管磁场优化问题。如果几何结构发生显著改变,代理模型的精度可能下降。同时,模型的预测磁场,用粒子群算法实现优化,因此在优化求解时,受限于粒子群的限制,对于连续、平滑的优化问题较为适合。但对于复杂、不连续的优化空间,需进一步改进粒子群算法。
在IFEM开发过程中,采用了Arcadia建模方法、开源建模工具Capella以及Arcadia/Capella建模语言,并以双向耦合论证设计方法为指导,将引导优化模块融入电磁场有限元仿真软件架构中。MBSE支持多层级建模,在系统架构中集成LinkNet模块后,可直接在总架构中展开LinkNet模块,对其进行详细建模,这更有利于复杂软件的开发。引导优化模块展开如图23所示。MBSE在引导优化建模案例中的优势,可以通过功能链图和场景图来具体说明。
功能链图展示了系统中各个功能模块的依赖关系和数据流,帮助明确各模块之间的交互和信息传递路径,如图24所示。
通过功能链图,可以清晰地看到AI算法计算模块、调度引擎模块和数据可视化模块之间的数据流动。在模型搭建过程中,如因误操作删除功能链中的任意功能元素,Capella将会提示报错,大大降低软件研发过程中的错误率。
场景图展示了系统在不同使用场景下的行为,帮助理解系统在特定情况下的功能实现过程。在引导优化建模案例中,引导优化场景图如图25所示。
通过场景图,可以具体描述系统在处理TEAM Workshop第35基准问题时的行为,包括输入参数(如螺线管半径、输入电流等)和输出结果(如磁通密度分布、功率损耗等)。通过场景图,可以清晰地看到系统各部分的功能和交互方式,便于模块化开发,实现高效的开发流程。
MBSE在引导优化建模案例中的优势体现在系统化的需求管理、结构化的设计方案和模块化实现上。不仅提升了仿真软件的开发效率和质量,还增强了软件的灵活性和可维护性。通过MBSE方法,IFEM实现了从需求到设计再到实现的全流程反复迭代,确保了各功能模块的协调工作和信息一致性,使团队能够更高效地协作,并在复杂的工程项目中有效地管理和利用知识。
本节通过两个案例来验证双向耦合软件论证设计方法的可行性,通过统一软件平台(IFEM)集成AI与有限元算法,为AI技术在电磁场模拟中的应用提供了一个灵活、高效的平台。该软件平台结合了AI与有限元算法的优势,探索了电磁场仿真中的新型计算方法和优化策略。LinkNet模型训练成功后生成250组样本的时间为7.5 s,而有限元法生成250组样本时间为5 min43 s;文献[11]针对更为复杂变压器磁场预测模型,前期进行数据采样制作100组样本集及训练和计算的总时间需6.78 h,而有限元方法计算100个样本需近20 h,AI算法相比有限元法计算效率提高了66.1%。
5 结论
本文提出了一种基于MBSE的双向耦合架构设计方法,以电磁场有限元仿真软件需求为导向,完成了模型的搭建和软件示例,主要结论如下:
1)提出了双向耦合的软件论证设计方法。软件设计方-使用方、数值模拟-人工智能的两个双向耦合,使得电磁场有限元仿真软件,能够有效地适应复杂和动态变化的功能和设计需求。
2)建立了软件需求、设计和实现方案的设计流程,以及可视化模型,提升协作效率和知识可复用性。选取Arcadia建模方法、开源建模工具Capella、建模语言Arcadia/Capella,以双向耦合论证设计方法为指导,完成电磁场有限元仿真软件架构设计,采用基于MBSE的方法构建了界面层、控制层、引擎层和核心模块层的四层总体架构,提高了需求和设计的一致性,确保了软件复杂性和变化需求的可控性,提高了不同开发人员之间的协同工作效率。进一步划分为界面、前后处理、求解器等28个功能模块。分层架构和模块化设计增强了软件的可扩 展性。
3)建立集成AI的有限元软件原型IFEM,并完成计算案例验证。基于Python和统一的基础算法库、数据格式,建立集成AI的有限元计算软件原型IFEM,对二维静电场和电磁优化基准问题的求解,验证了IFEM软件计算结果的准确性。
通过基于MBSE的建模,提高了软件设计的透明度和团队间的沟通效率,允许在开发初期有效管理和解决潜在问题,提高了电磁场有限元仿真软件开发过程的系统性和效率。这为我国数值模拟工业软件,在AI for Science背景下的AI集成和专业领域的软件开发,提供了有效方法和新思路。未来的研究将进一步提升软件的扩展性和适用性,探索更多复杂工程问题中的应用场景,为电磁场仿真与优化提供更加高效和智能化的解决方案。
参考文献
[1] 程书灿, 赵彦普, 张军飞, 等. 电力设备多物理场仿真技术及软件发展现状[J]. 电力系统自动化, 2022, 46(10): 121-137.
Cheng Shucan, Zhao Yanpu, Zhang Junfei, et al. State of the art of multiphysics simulation technology and software development for power equipment[J]. Auto- mation of Electric Power Systems, 2022, 46(10): 121-137.
[2] 云道智造. 伏图(Simdroid)通用多物理场仿真PaaS平台[EB/OL]. https://www.ibe.cn/products/simdroid.
[3] 英特仿真. 多物理场仿真及优化平台INTESIM- MultiSim[EB/OL]. http://www.intesim.cn/Jmksh.
[4] 韩志仁, 罗雪磊. 基于ANSYS Workbench的型材拉弯有限元仿真模块开发[J]. 航空制造技术, 2020, 63(13): 64-68.
Han Zhiren, Luo Xuelei. Development of finite element simulate module of ANSYS Workbench on profile stretch-bending[J]. Aeronautical Manufacturing Technology, 2020, 63(13): 64-68.
[5] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.
[6] Miao Qinghai, Zheng Wenbo, Lü Yisheng, et al. DAO to HANOI via DeSci: AI paradigm shifts from AlphaGo to ChatGPT[J]. IEEE/CAA Journal of Automatica Sinica, 2023, 10(4): 877-897.
[7] Yu Hui, Liang Wei, Fan Lili, et al. Sora for social vision with parallel intelligence: social interaction in intelligent vehicles[J]. IEEE Transactions on Intelligent Vehicles, 2024, 9(3): 4240-4243.
[8] Zhang Weiwei, Li Xintao, Ye Zhengyin, et al. Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers[J]. Journal of Fluid Mechanics, 2015, 783: 72-102.
[9] Gao Chuanqiang, Zhang Weiwei, Li Xintao, et al. Mechanism of frequency lock-in in transonic buffeting flow[J]. Journal of Fluid Mechanics, 2017, 818: 528-561.
[10] 金亮, 王飞, 杨庆新, 等. 永磁同步电机性能分析的典型深度学习模型与训练方法[J]. 电工技术学报, 2018, 33(增刊1): 41-48.
Jin Liang, Wang Fei, Yang Qingxin, et al. Typical deep learning model and training method for per- formance analysis of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 41-48.
[11] 金亮, 尹振豪, 刘璐, 等. 基于残差U-Net和自注意力Transformer编码器的磁场预测方法[J]. 电工技术学报, 2024, 39(10): 2937-2952.
Jin Liang, Yin Zhenhao, Liu Lu, et al. Magnetic field prediction method based on residual U-Net and self-attention Transformer encoder[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2937- 2952.
[12] 魏蓉, 陈锦培, 仲林林. 基于深度算子网络的电磁轨道发射速度趋肤效应的快速计算方法[J]. 电工技术学报, 2025, 40(5): 1344-1354.
Wei Rong, Chen Jinpei, Zhong Linlin. A fast computational method for velocity skin effect of electromagnetic rail launch based on deep operator networks[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1344-1354.
[13] Jin Liang, Liu Yuankai, Yang Qingxin, et al. Prediction method of motor magnetic field based on improved Linknet model[J]. COMPEL-the Inter- national Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2023, 42(1): 90-100.
[14] Khan A, Ghorbanian V, Lowther D. Deep learning for magnetic field estimation[J]. IEEE Transactions on Magnetics, 2019, 55(6): 7202304.
[15] Khan A, Mohammadi M H, Ghorbanian V, et al. Efficiency map prediction of motor drives using deep learning[J]. IEEE Transactions on Magnetics, 2020, 56(3): 7511504.
[16] 李青, 张新燕, 马天娇, 等. 基于SSA-CNN-BiGRU- Attention的超短期风电功率预测模型[J]. 电机与控制应用, 2023, 50(5): 61-71.
Li Qing, Zhang Xinyan, Ma Tianjiao, et al. Ultra- short term forecasting model of wind power based on SSA-CNN-BiGRU-attention[J]. Electric Machines & Control Application, 2023, 50(5): 61-71.
[17] 张宇娇, 孙宏达, 赵志涛, 等. 基于物理信息神经网络的电磁场计算方法[J]. 电工技术学报, 2024, 39(17): 5251-5261.
Zhang Yujiao, Sun Hongda, Zhao Zhitao, et al. Electromagnetic field calculation method based on physical informed neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5251- 5261.
[18] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(9): 2730-2742.
Zhang Yujiao, Zhao Zhitao, Xu Bin, et al. Fast calculation method of electromagnetic field based on U-net convolutional neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2730- 2742.
[19] 王怀民, 吴文峻, 毛新军, 等. 复杂软件系统的成长性构造与适应性演化[J]. 中国科学: 信息科学, 2014, 44(6): 743-761.
Wang Huaimin, Wu Wenjun, Mao Xinjun, et al. Growing construction and adaptive evolution of complex software system[J]. Scientia Sinica: Infor- mationis, 2014, 44(6): 743-761.
[20] Henderson K, Salado A. Value and benefits of model- based systems engineering (MBSE): evidence from the literature[J]. Systems Engineering, 2021, 24(1): 51-66.
[21] 董梦如, 王国新, 鲁金直, 等. 基于WordCloud技术的MBSE发展态势研究[J]. 系统工程与电子技术, 2024, 46(2): 534-548.
Dong Mengru, Wang Guoxin, Lu Jinzhi, et al. Research on the development trend of MBSE based on WordCloud technology[J]. Systems Engineering and Electronics, 2024, 46(2): 534-548.
[22] 王文跃, 侯俊杰, 毛寅轩, 等. 面向复杂产品研制的MBSE体系架构及其发展趋势研究[J]. 控制与决策, 2022, 37(12): 3073-3082.
Wang Wenyue, Hou Junjie, Mao Yinxuan, et al. MBSE architecture for complex product development and trends[J]. Control and Decision, 2022, 37(12): 3073-3082.
[23] 薛芳芳, 王亮亮, 缪炜涛, 等. 基于MBSE的民机飞行管理软件设计[J]. 航空计算技术, 2019, 49(5): 111-116.
Xue Fangfang, Wang Liangliang, Miao Weitao, et al. Design of airborne flight management software based on MBSE[J]. Aeronautical Computing Technique, 2019, 49(5): 111-116.
[24] 吕冠甫. 基于MBSE的无人机地面站应用系统软件设计与实现[D]. 太原: 中北大学, 2020.
Lü Guanfu. Software design and implementation of UAV ground station application system based on MBSE[D]. Taiyuan: North University of China, 2020.
[25] Yu Chao, Li Qing, Liu Kui, et al. Industrial design and development software system architecture based on model-based systems engineering and cloud computing[J]. Annual Reviews in Control, 2021, 51: 401-423.
[26] 侯淑萍, 杨庆新, 陈海燕, 等. 新型高性能电工材料应用特性建模的模块化设计[J]. 电工技术学报, 2008, 23(10): 1-5.
Hou Shuping, Yang Qingxin, Chen Haiyan, et al. Modularity design of modeling for new high per- formance materials applied to electrical engineering[J].Transactions of China Electrotechnical Society, 2008, 23(10): 1-5.
[27] 王雨农, 毕文豪, 张安, 等. 基于DoDAF的民机MBSE研制方法[J]. 系统工程与电子技术, 2021, 43(12): 3579-3585.
Wang Yunong, Bi Wenhao, Zhang An, et al. DoDAF- based civil aircraft MBSE development method[J]. Systems Engineering and Electronics, 2021, 43(12): 3579-3585.
[28] Izygon M, Wagner H, Okon S, et al. Facilitating R&M in spaceflight systems with MBSE[C]//2016 Annual Reliability and Maintainability Symposium (RAMS), Tucson, AZ, USA, 2016: 1-6.
[29] 向超群, 尹雪瑶, 伍珣, 等. 基于物理信息神经网络的牵引变流器直流支撑电容参数辨识方法[J]. 电工技术学报, 2024, 39(15): 4654-4667.
Xiang Chaoqun, Yin Xueyao, Wu Xun, et al. Parameter identification of DC-link capacitor in traction converter based on physical information neural network[J]. Transactions of China Electro- technical Society, 2024, 39(15): 4654-4667.
[30] Ma Yaoyao, Xu Xiaoyu, Yan Shuai, et al. Extraction of interconnect parasitic capacitance matrix based on deep neural network[J]. Electronics, 2023, 12(6): 1440.
[31] Bashatah J, Sherry L. Usability analysis of an MBSE model of standard operating procedures[J]. INCOSE International Symposium, 2022, 32: 38-47.
[32] De Saqui-Sannes P, Vingerhoeds R A, Garion C, et al. A taxonomy of MBSE approaches by languages, tools and methods[J]. IEEE Access, 2022, 10: 120936- 120950.
[33] Biggs G, Juknevicius T, Armonas A, et al. Integrating safety and reliability analysis into MBSE: overview of the new proposed OMG standard[J]. INCOSE International Symposium, 2018, 28(1): 1322-1336.
[34] De Pra Y, Fontana F. Programming real-time sound in Python[J]. Applied Sciences, 2020, 10(12): 4214.
[35] 金亮, 刘璐, 贾雨方. Python语言下长直导线电场计算代码[EB/OL]. https://gitee.com/fang-xiaojia1123/ ifem.
[36] Di Barba P, Mognaschi M E, Lowther D A, et al. A benchmark TEAM problem for multi-objective Pareto optimization of electromagnetic devices[J]. IEEE Transactions on Magnetics, 2018, 54(3): 9400604.
Modeling and Application of Electromagnetic Field Finite Element Simulation Software MBSE for Electrical Equipment Integrated with AI
Jin Liang1,2 Jia Yufang1 Liu Lu1 Guo Shaonan1 Ma Tianci1
(1. State Key Laboratory of Intelligence Power Distribution and System Equipment Hebei University of Technology Tianjin 300401 China 2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province Hebei University of Technology Tianjin 300401 China)
Abstract Electromagnetic field finite element simulation software is crucial for electromagnetic design and analysis, particularly in the performance evaluation of complex electrical equipment, which often relies on costly foreign software with high barriers to entry. As the demand for electromagnetic field simulations continues to increase, existing commercial software fails to meet the specific customization needs of various engineering projects. It creates an urgent need to develop autonomous, lightweight, and intelligent simulation tools. This paper introduces the development of a prototype intelligent finite element simulation software, IFEM, which integrates artificial intelligence (AI) technology using a model-based systems engineering (MBSE) approach to create a visual software model.
Firstly, this paper proposes a bidirectional coupling software design method consisting of two key aspects: the bidirectional coupling between software developers and users as well as between numerical simulation and AI. The bidirectional coupling between developers and users aims to enable efficient information exchange, ensuring flexibility and adaptability in the software design process. Meanwhile, the bidirectional coupling between numerical simulation and AI retains the accuracy of numerical simulation while leveraging the efficiency of AI.
A four-layer architectural design process for the electromagnetic finite element simulation software is constructed, including operational analysis, system analysis, logical architecture, and software architecture. A graphical model represents the complex software structure, significantly enhancing transparency and improving collaboration among developers. During the development of the IFEM prototype, the bidirectional coupling of numerical simulation and AI is implemented using Python programming language and the PyCharm development environment, unifying the development and debugging of finite element and AI modules. It has the advantages of reduced programming workload, rich and user-friendly algorithm libraries, easy prototyping, and seamless AI integration.
Finally, a solver based on the node finite element method and Physics-Informed Neural Networks (PINN) is used to calculate the potential distribution between two-dimensional electrodes. Post-processing generates the electric field strength discrete values, field distribution maps, and contour lines. A comparison with COMSOL results shows that the mean absolute percentage errors (MAPE) for the potential and electric field strength are2.735×10-11 and 4.185×10-11, respectively. Additionally, an improved LinkNet model, integrated with the node finite element method, is used to optimize the magnetic field distribution of a solenoid. Compared to COMSOL, the MAPE for the 2D constant magnetic field vector potential and magnetic flux density magnitudes are0.054% and 2.889%, respectively. By replacing the finite element model with the improved LinkNet model, the Pareto front for solenoid optimization under two objectives is obtained. After training, the improved LinkNet model generates 250 samples in 7.5 seconds, whereas the finite element method takes 5 minutes and 43 seconds to generate the same number of samples.
Through case validation, IFEM demonstrates excellent computational accuracy and efficiency in solving problems such as 2D electrostatic fields and solenoid magnetic field optimization. The software also shows strong integration and scalability with AI algorithms. By adopting MBSE-based modeling, the transparency of the software design process and communication efficiency within the team are greatly improved, allowing for effective management and resolution of potential issues early in development. This approach has significantly enhanced the development efficiency of the electromagnetic field finite element simulation software. This paper provides effective methodologies for AI integration within specialized software development. Future research will focus on the software’s scalability and applicability enhancement, exploring complex engineering scenarios’ electromagnetic field simulation and optimization.
Keywords:Model-based systems engineering (MBSE), finite element, AI, electromagnetic field calculation
中图分类号:TM153
DOI: 10.19595/j.cnki.1000-6753.tces.241163
中央引导地方科技发展专项自由探索项目(226Z4503G)、国家自然科学基金面上项目(51977148)和国家自然科学基金重大研究计划项目(92066206)资助。
收稿日期 2024-07-02
改稿日期 2024-08-16
作者简介
金 亮 男,1982年生,教授,博士生导师,研究方向为电磁场数值模拟与智能计算。
E-mail: jinliang_email@163.com(通信作者)
贾雨方 男,1997年生,硕士研究生,研究方向为工程电磁场数值模拟软件开发。
E-mail: 710022490@qq.com
(编辑 郭丽军)





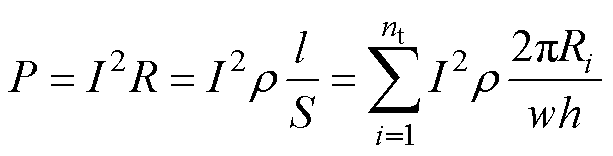 (1)
(1)
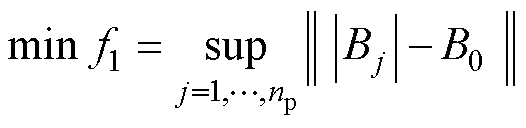 (2)
(2)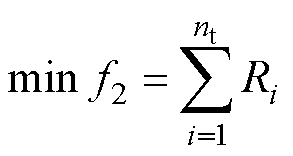 (3)
(3)
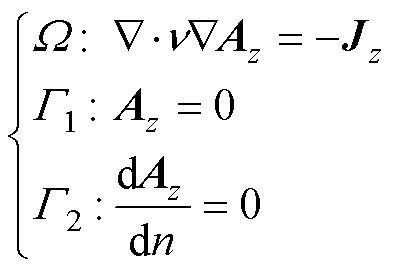 (4)
(4)
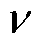 为磁阻率。
为磁阻率。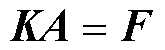 (5)
(5)
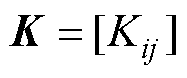 ,右端项列阵
,右端项列阵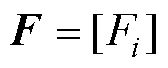 ,由各单元体的相应项叠加而成,其中,
,由各单元体的相应项叠加而成,其中,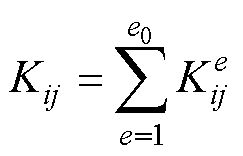 ,
,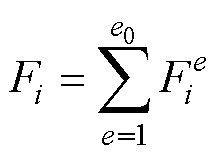 ,i、j代表单元e中所有节点的局部编号。
,i、j代表单元e中所有节点的局部编号。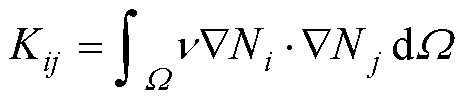 (6)
(6)
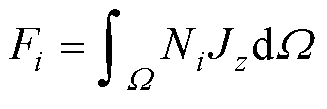 (7)
(7)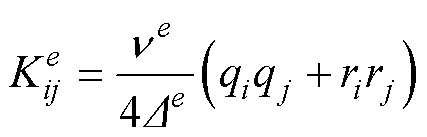 (8)
(8)
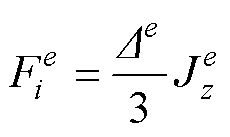 (9)
(9)