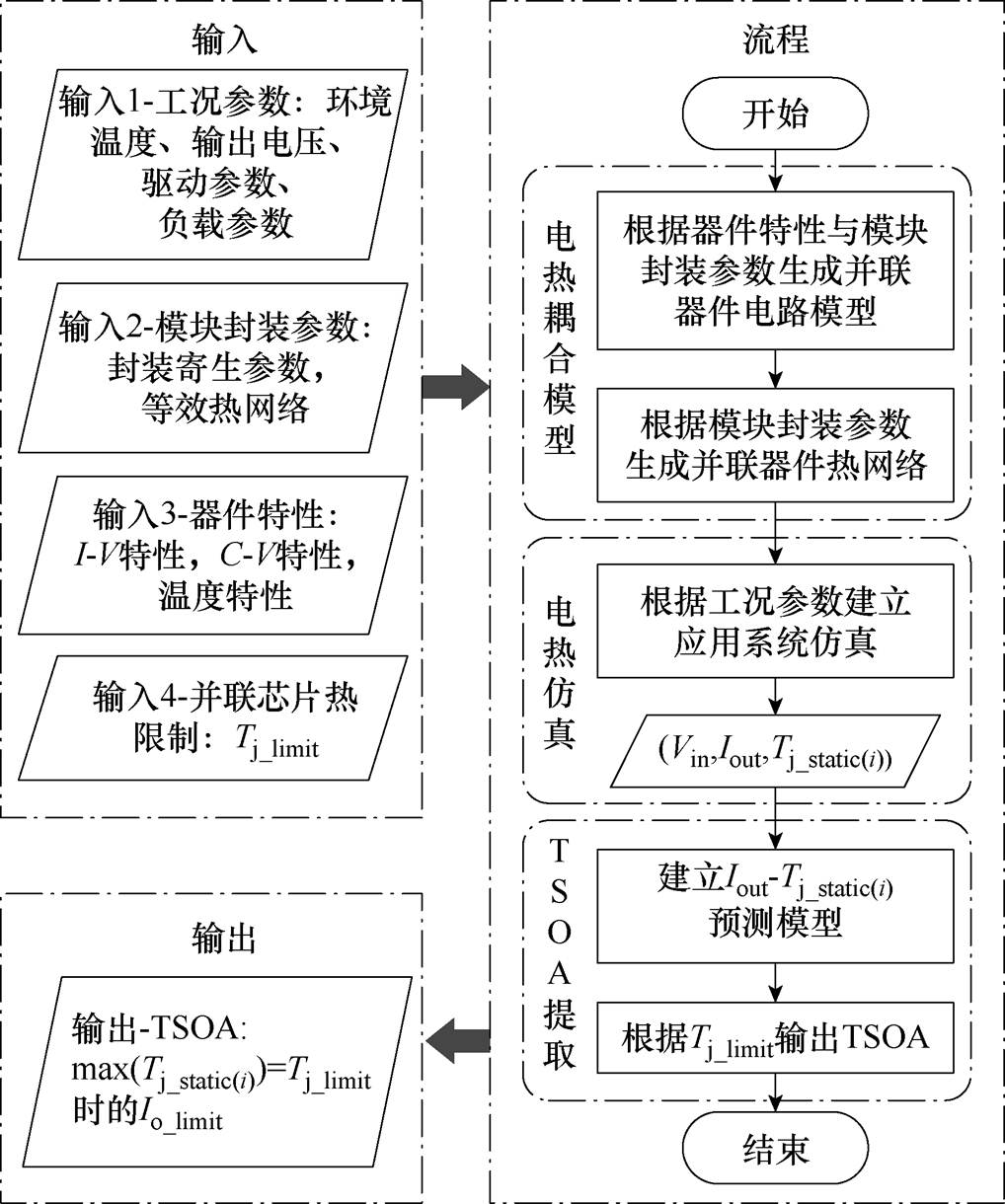
图1 多芯片并联功率模块TSOA提取流程
Fig.1 Flowchart for extracting the TSOA of multi-chip parallel power modules
摘要 SiC MOSFET功率模块通常由并联芯片组成,以实现应用系统所需的电流能力。然而,由于器件制备的工艺波动引起芯片参数分散性,叠加封装寄生参数与等效热阻非对称性,导致每个芯片的电热行为存在显著差异,使得相同最高结温限制下的工作区存在差异。因此,该文首先提出一种描述变换器应用中多芯片并联SiC MOSFET功率模块在给定最高结温限制下热安全工作区(TSOA)的评估方法,通过芯片级-模块级-系统级联合电热仿真并结合输出电流预测模型,能在减少仿真次数的基础上确定TSOA,并通过仿真与实验验证了所提TSOA评估方法的有效性。然后,运用蒙特卡罗(MC)模拟研究了芯片参数分散性在不同热限制、不同开关频率和分散范围下对多芯片并联SiC MOSFET TSOA的影响,发现TSOA的延拓或收缩在高开关频率下的主要影响因素为阈值电压与转移特性中达到额定电流时栅源电压的极差,而低开关频率下变为并联芯片导通电阻与跨导的均值。最后,提出TSOA延拓方法,通过变芯片参数分散范围的蒙特卡罗模拟并利用TSOA灵敏度进行多目标优化分组,提高单个多芯片并联功率模块的TSOA。
关键词:SiC功率模块 SiC MOSFET 芯片参数分散性 热安全工作区 蒙特卡罗模拟
受益于宽禁带半导体功率器件的发展,电力电子应用系统的功率密度与性能得以进一步提升[1-3]。碳化硅(SiC)金属-氧化物半导体场效应晶体管(MOSFET)由于具有宽带隙的优势,能够同时实现低功耗、高开关速度、高阻断电压和高工作温 度[4-6],使其电力电子系统的应用中极具潜力。而SiC MOSFET受到有源区面积及制造良率存在折中的制约[7],单颗芯片电流规格较小,应用中需要采用多芯片并联以满足高额定电流需求。而由于芯片制备对工艺水平的波动,芯片特性存在较大的分散性[8-10],同时影响并联均流与损耗均衡,使得器件的并联应用面临挑战。
在芯片参数分散性对并联均流影响的研究中发现,影响静态均流的主要参数为导通电阻。考虑导通电阻具有正向温度特性,结温较高的器件并联时流过的电流较小,有利于达到热平衡[8]。而影响多芯片并联动态均流的因素更多,机制更为复杂。阈值电压的负温度系数使得SiC MOSFET器件并联瞬态电流分配不均衡更为严重,芯片结温越高,阈值电压越低,导致该芯片的开通与关断电流越大[8, 11]。电流-电压(I-V)特性的分散性比电容-电压(C-V)特性的分散性对电流均衡的影响更大,尤其是平带电压、沟道长度调制系数及电流增益因子的分散性[12]。
在芯片参数分散性对结温均衡的影响研究方面,文献[10]运用蒙特卡罗(Monte Calro, MC)模拟发现阈值电压越小的芯片关断电流越大,关断损耗越大结温越高;文献[13]发现导通电阻较大的芯片开关能量更小,相同栅源电压下漏极电流更大的曲线对应的芯片开关能量更大,提出可以通过芯片参数对开关能量相互补偿,提升结温的均衡性;文献[14]研究了两个SiC MOSFET并联的热分布,发现导通损耗是电热自平衡的关键;文献[15]发现栅极外阻越小开通损耗越均衡,并在不考虑热耦合的情况下估计了样本集中两个芯片在升压斩波(Boost)电路中结温差的最大值。
上述对SiC MOSFET芯片参数分散性对并联电流均衡影响的研究往往是在封装寄生参数一致的前提下[8, 11-12],未考虑实际并联功率模块中会引起并联电热不均的封装寄生参数差异;另一方面,芯片参数分散性对结温分布影响的研究较少,同时器件电特性与温度的耦合关系考虑不充分,基本未考虑并联芯片间的热耦合[10, 13-15],导致预测的结温及相互结温差被低估[16],使得变换器设计的温度裕量减小,增加了热失效的风险。
因此,需要在同时考虑芯片参数波动性、封装寄生参数不对称性、等效热阻不均衡性以及芯片间热耦合的基础上,建立起电力电子系统与功率模块中并联芯片结温限制的关系,明确应用系统中并联芯片间最高结温达到热限制时的热安全工作区(Thermal Safe Operation Area, TSOA)。目前,还较少有文献关注SiC MOSFET芯片参数分散性对多芯片并联功率模块中结温热限制下输出电流能力的影响。而实际中芯片制造过程的波动是不可避免的,对于一定参数分散性下多芯片并联SiC MOSFET功率模块的TSOA评估便十分关键。
鉴于上述原因,首先,本文提出一种考虑封装寄生参数与等效热阻不均衡以及芯片间热耦合的多芯片并联功率模块TSOA评估方法,联系实际的电力电子系统应用,获得不同热限制下的输出能力。其次,对所提TSOA评估方法进行了验证。最后,运用蒙特卡罗模拟研究在不同热限制、不同分散范围、不同开关频率下芯片分散性对TSOA的影响,量化不同芯片参数对TSOA影响的重要性,提出延拓TSOA的芯片分选方法。
本文考虑并联芯片间最高结温的热限制,提出一种描述SiC MOSFET功率模块在变换器应用中TSOA的评估方法。该方法可以在考虑实际功率模块中的封装寄生参数不对称、等效热阻不均衡以及并联器件间热耦合的基础上,计算在单芯片最高结温达到热限制下的变换器输出能力,形成并联SiC MOSFET在应用中的TSOA,可作为多芯片并联功率模块选型的指导。
评估并联SiC MOSFET在应用中的TSOA同时考虑了工况参数、模块封装参数、器件特性及并联芯片热限制,其中工况参数包括了变换器工作的环境信息、负载参数、驱动参数以及输出规格,模块封装参数包括了封装的寄生电感、寄生电阻与等效热网络等,器件特性包括器件的I-V特性、C-V特性与温度特性,并联芯片热限制为并联芯片间的最高结温限制Tj_limit,具体的提取流程如图1所示。图中,Vin为变换器输入电压,Iout为变换器输出电流,Tj_static(i)为芯片i的稳态结温,Io_limit为并联芯片在达到热限制时的变换器输出电流。

图1 多芯片并联功率模块TSOA提取流程
Fig.1 Flowchart for extracting the TSOA of multi-chip parallel power modules
由于同时考虑实际功率模块中的封装寄生参数不对称、等效热阻不均衡以及并联器件间热耦合时难以进行解析计算,采用电热仿真是计算功率模块的电热应力的适用方法。因此,多芯片并联功率模块TSOA提取的核心步骤为电热耦合仿真。整个提取流程可以分为建立多芯片功率模块电热耦合模型、应用系统电热仿真及TSOA提取三大步骤。多芯片功率模块电热耦合模型用于开展应用系统电热仿真,获得变换器在不同运行工况下的结温分布与电流分布,然后根据仿真结果建立Iout-Tj_static(i)预测模型,最后获得并联芯片在达到热限制时的Io_limit,输出并联SiC MOSFET在系统应用中的TSOA。
1.2.1 SiC MOSFET芯片电模型
要模拟功率模块中并联芯片的结温分布,需要能准确再现芯片电气特性与损耗的电路模型。本文使用的芯片电路模型拓扑如图2所示。电特性模型由沟道电流源Ich、漂移区电阻Rd、栅漏电容Cgd、栅源电容Cgs、漏源电容Cds以及栅极内阻Rg,int组成。模型通过芯片结温Tj端子与耗散功率Pheat端子连接热网络(Thermal Network, TN),实现电热耦合。本文建立的考虑芯片间热耦合的等效热网络将在后文详细描述。
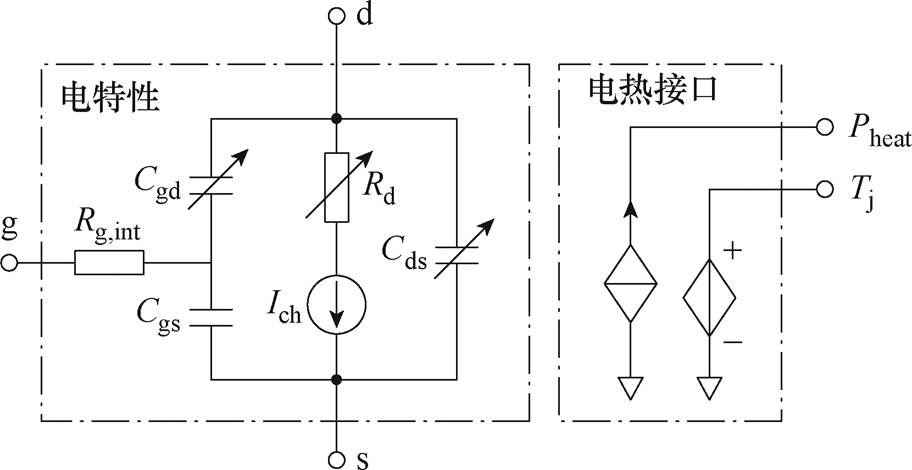
图2 SiC MOSFET芯片电路模型拓扑
Fig.2 Topology of the electrical model for the SiC MOSFET chip
沟道电流模型为简化的EKV模型[17],如式(1)所示,具有弱反型、中反型与强反型电流连续的特点,能够提升模型收敛性,同时包含由反型层下方势垒电容引起的夹断电压与栅极电压的关系变化。
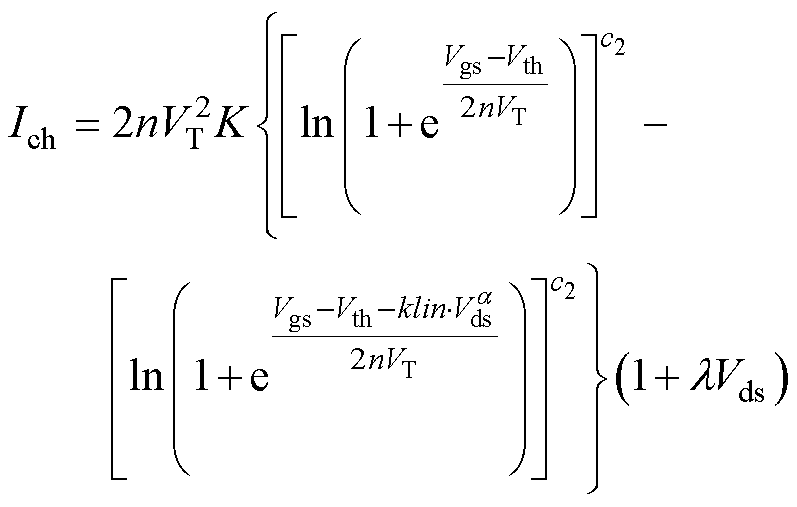 (1)
(1)
式中,Vds为漏源电压;Vgs为栅源电压;VT为热电压;n表示夹断电压与栅极电压呈非线性关系;K为电流系数;Vth为阈值电压;klin与a为线性区参数;c2为电流指数;l为沟道长度调制系数。
SiC MOSFET的温度特性由漂移区电阻Rd、K与Vth的温度依赖性实现,即
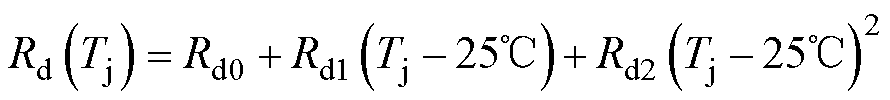 (2)
(2)
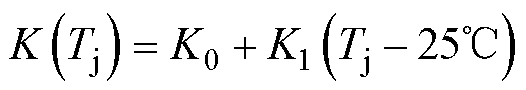 (3)
(3)
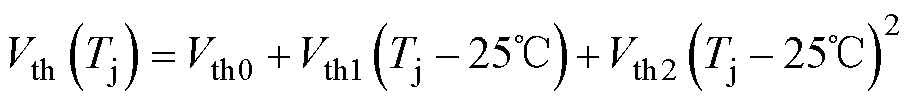 (4)
(4)
式中,Rd0为Tj=25℃时Rd的值;K0为Tj=25℃时K的值;Vth0为Tj=25℃时Vth的值;Rd1、Rd2、K1、Vth1、Vth2为各自的温度特性系数。
电容模型中,由于Cgs对偏置电压的依赖性很弱,所以采用固定值[18];Cds主要为漏极与源极的结电容构成,因此采用广泛使用的单边突变结耗尽电容模型[19];Cgd使用能反映低Vds下Cgd极速变化的行为模型[20]。Cds与Cgd的模型分别表示为
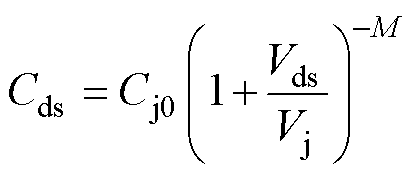 (5)
(5)
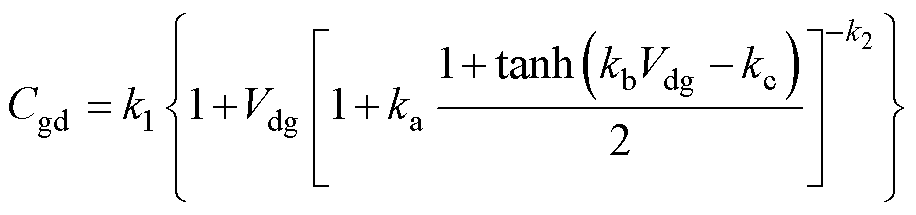 (6)
(6)
式中,Cj0为Vds=0时的Cds值;Vj为漏极与源极PN结内建电动势;M为增强模型灵活性的拟合指数;k1、k2、ka、kb、kc均为Cgd行为模型拟合参数。
1.2.2 考虑芯片间热耦合的热网络模型
提取TSOA的关键还在于热模型能准确地反映功率模块的热特性。在多芯片并联的功率模块中,为提高功率密度与减小封装寄生参数,往往会采用紧凑的芯片布局,从而使得并联器件间热量的横向传导效应更为显著,芯片间的散热路径相互交叠,存在明显的热耦合效应。因此,本文利用Foster网络,建立包含互热效应的二维等效热网络模型,当k个芯片并联时,模型拓扑如图3所示,图中,Tj(i)为第i个芯片的结温,i=1,…, k,Pheat(i)为第i个芯片的发热功率,Ta为环境温度。自热传热路径采用n阶Foster网络表示,互热传热路径采用m阶Foster网络表示,芯片i的热网络由Pheat(i)激励的自热网络串联除自身以外的其他芯片各自激励的互热网络构成,即各芯片结温表示为
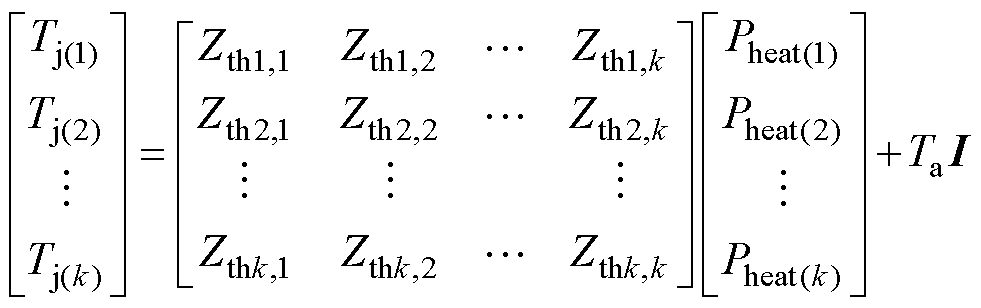 (7)
(7)
式中,Zthi,i为第i个芯片的自阻抗;Zthi,j为第j个芯片对第i个芯片的互阻抗,j=1,…, k,j≠i;I为单位矩阵。所有阻抗的具体参数,可对每个芯片分别进行阶跃响应的有限元仿真,得到结温的瞬态响应曲线,然后通过曲线拟合得到Foster网络参数[21]。
与芯片电模型进行双向耦合时,将各芯片的Pheat端子的电压值转化为对应等效电流源的激励电流Pheat(i),获得各芯片的自热温升与对其他芯片的互热温升,然后通过热网络中的Tj(i)端子将对应芯片的结温反馈至电模型的Tj端子,进而驱动电模型中与温度相关的参数随Tj变化实时更新,实现电-热双向动态耦合。
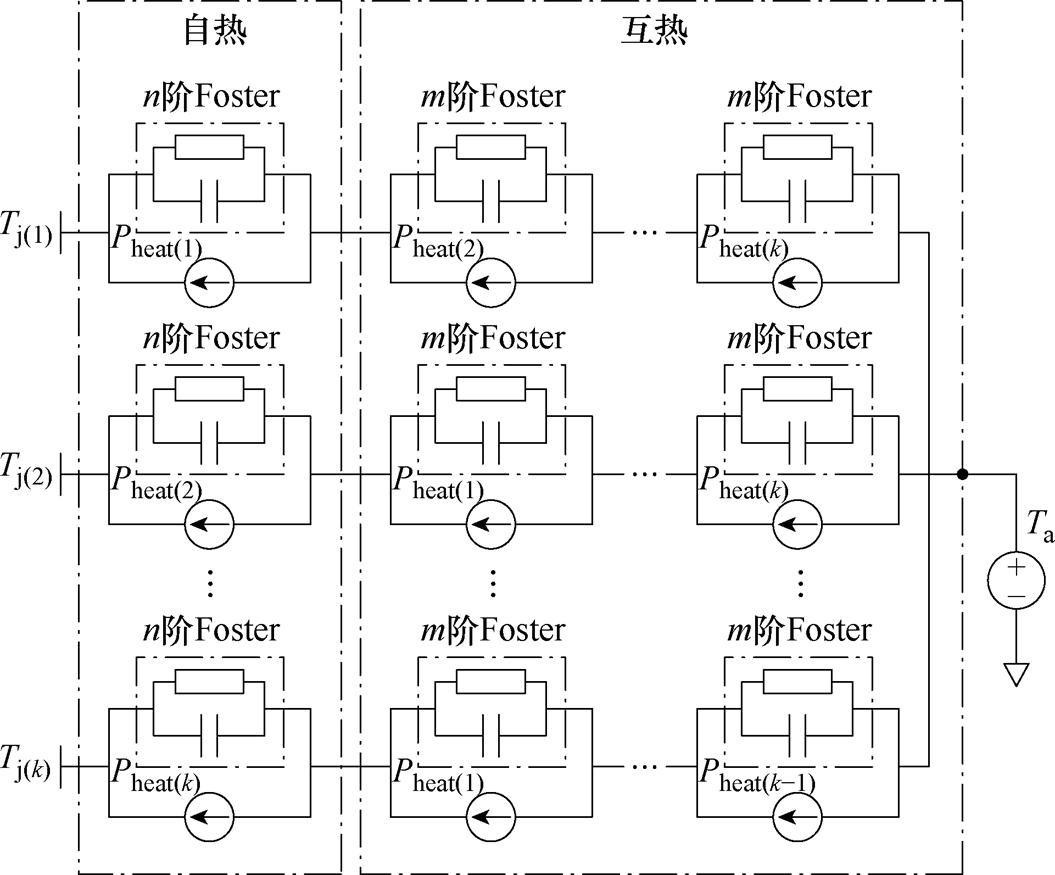
图3 功率模块二维热网络模型拓扑
Fig.3 Topology of the 2D thermal network model for the power module
要获得并联芯片中最高结温达到热限制时的变换器输出能力,通常可以通过步进输出电流的方 法[22]。但此种方式依赖通过解析计算得到稳态结温分布。由于实际功率模块中存在复杂的电热耦合,难以直接计算求解,适合采用电路仿真的方式获取。而热平衡所需时间一般在s级及以上,步进输出电流方式的仿真所需时间较长。因此,本文提出一种结温分布预测方法,建立了变换器输出电流到各芯片结温的映射关系。然后通过反函数计算达到最高结温上限Tj_limit时的输出电流Io_limit,得到TSOA。本文提出的结温预测模型以及热限制下的输出电流预测模型分别为
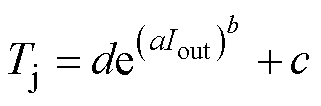 (8)
(8)
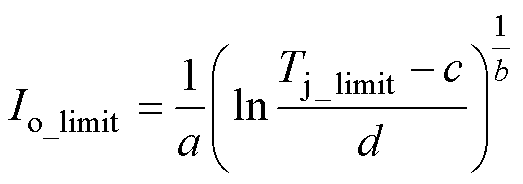 (9)
(9)
式中,a、b、c、d均为拟合参数。由于该模型具有4个参数,相应地至少需要4个数据点用于参数提取,因此,除去Iout=0时Tj=Ta的已知条件,相较于步进式仿真计算达到热限制时的输出电流,本文提出的方法所需系统电路仿真数量可减少至仅3个。
本节将对本文提出的SiC MOSFET并联芯片热安全工作区评估方法进行仿真与实验验证。本文选用62 mm封装1 200 V/300 A SiC MOSFET半桥功率模块作为研究对象。该模块的上下半桥均由6个1 200 V、25 mW SiC MOSFET并联组成,并带有反并联肖特基势垒二极管(SBD)。
静态特性模拟精度是芯片电模型能否准确预测器件动态行为及损耗的基础。为此,需首先验证其静态特性准确性。然而,实际功率模块中单个芯片的电流难以直接测量,因此本文选用两个1 200 V/ 32 A的SiC MOSFET分立器件(编号1号、2号)并联开展实验。利用功率器件静态特性测试仪测量其静态输出特性与电容特性。为避免自热效应干扰,输出特性测量采用窄脉冲、长时间间隔的脉冲电压激励。输出特性仿真与实验结果对比曲线如图4所示,电容特性仿真与实验结果对比曲线如图5所示,静态输出特性与电容特性的仿真结果与实验数据高度吻合,验证了单芯片电模型的静态特性模拟有效性。
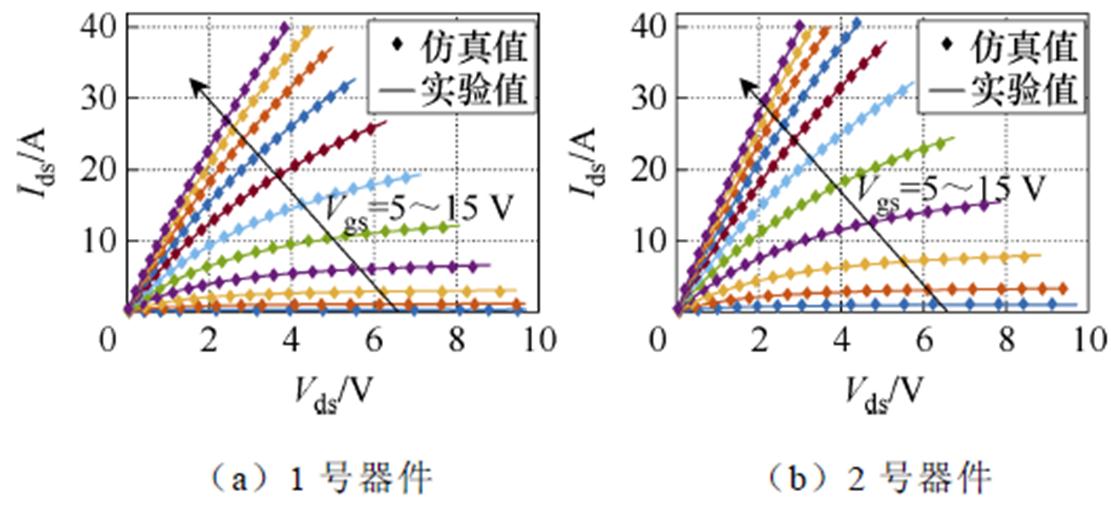
图4 输出特性仿真与实验结果对比曲线
Fig.4 Comparisons of output characteristic between simulation results and expiremental values
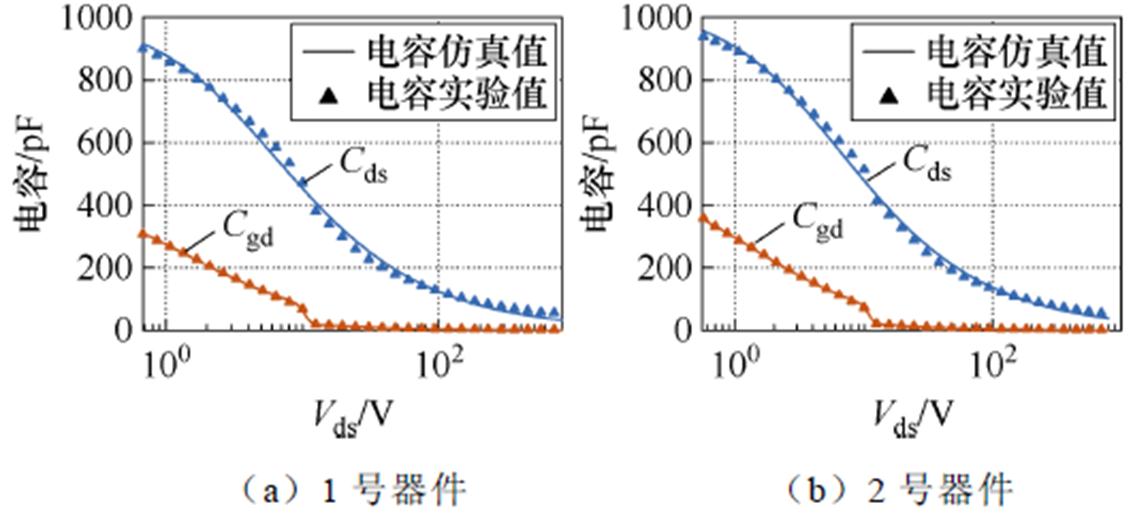
图5 电容特性仿真与实验结果对比曲线
Fig.5 Comparisons of capacitance characteristic between simulation results and expirement values
为验证模型在并联情况下对动态特性预测的有效性,本文使用如图6所示的双脉冲测试(Double Pulse Test, DPT)电路实验获得并联SiC MOSFET动态特性,并与模型仿真结果进行对比。图6中,Q1、Q2为被测器件,Vdc为母线电压,Cbus为母线电容,Lbus为功率回路等效寄生电感,Lload为负载电感,VD为续流二极管,Ldd,1与Ldd,2为器件漏极寄生电感,Lps1与Lps2为器件功率源极寄生电感,Lks1与Lks2为器件开尔文源极寄生电感,Lgg1与Lgg2为驱动支路寄生电感,Rg,ext1与Rg,ext2为驱动外电阻,Vdrive为驱动电压源。考虑到实验目的是验证芯片电路模型,两个并联器件的功率回路与驱动回路均采用对称布局,避免引入除器件模型外会影响动态特性的因素。续流二极管选用1 200 V SiC SBD,漏极电流测量选用HIOKI 3276,漏源极电压测量选用光隔离探头Micsig OIP200。
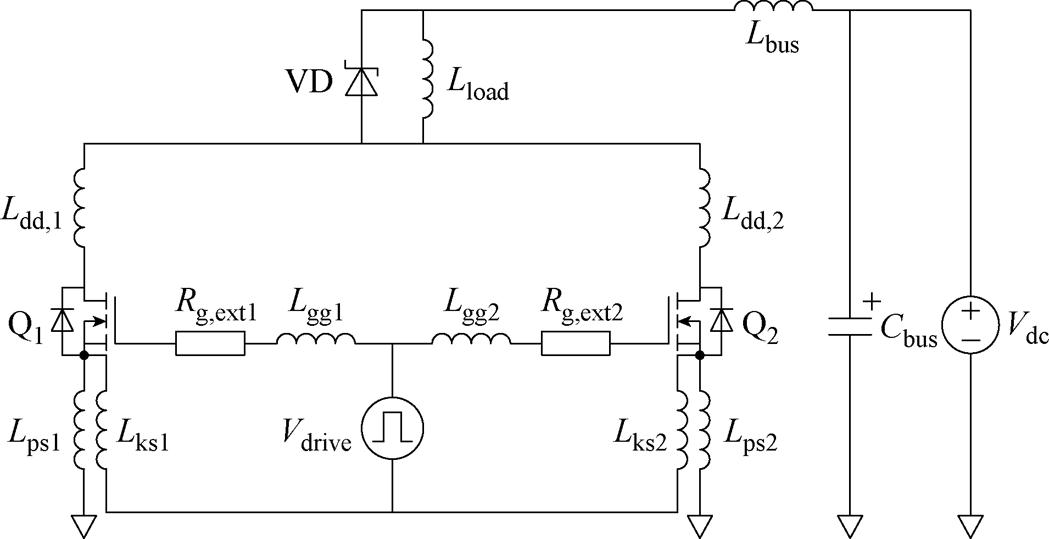
图6 并联SiC MOSFET DPT电路示意图
Fig.6 Schematic diagram of the DPT circuit for parallel SiC MOSFETs
母线电压为400 V,测试总电流为40 A的并联SiC MOSFET双脉冲测试的开通过程与关断过程的模型仿真与实验对比如图7所示,由图7可见,模型仿真较好地吻合了开关过程中并联器件的Vds和漏源电流Ids,并且很好地模拟芯片参数不同的两个器件并联电流的分配情况。在开通时电压Vds较大时,主要考虑的是高电压比电压探头引起的低压测试误差。开通与关断过程的损耗对比见表1,对比结果显示出,所提模型能有效地模拟并联器件的开关损耗情况。
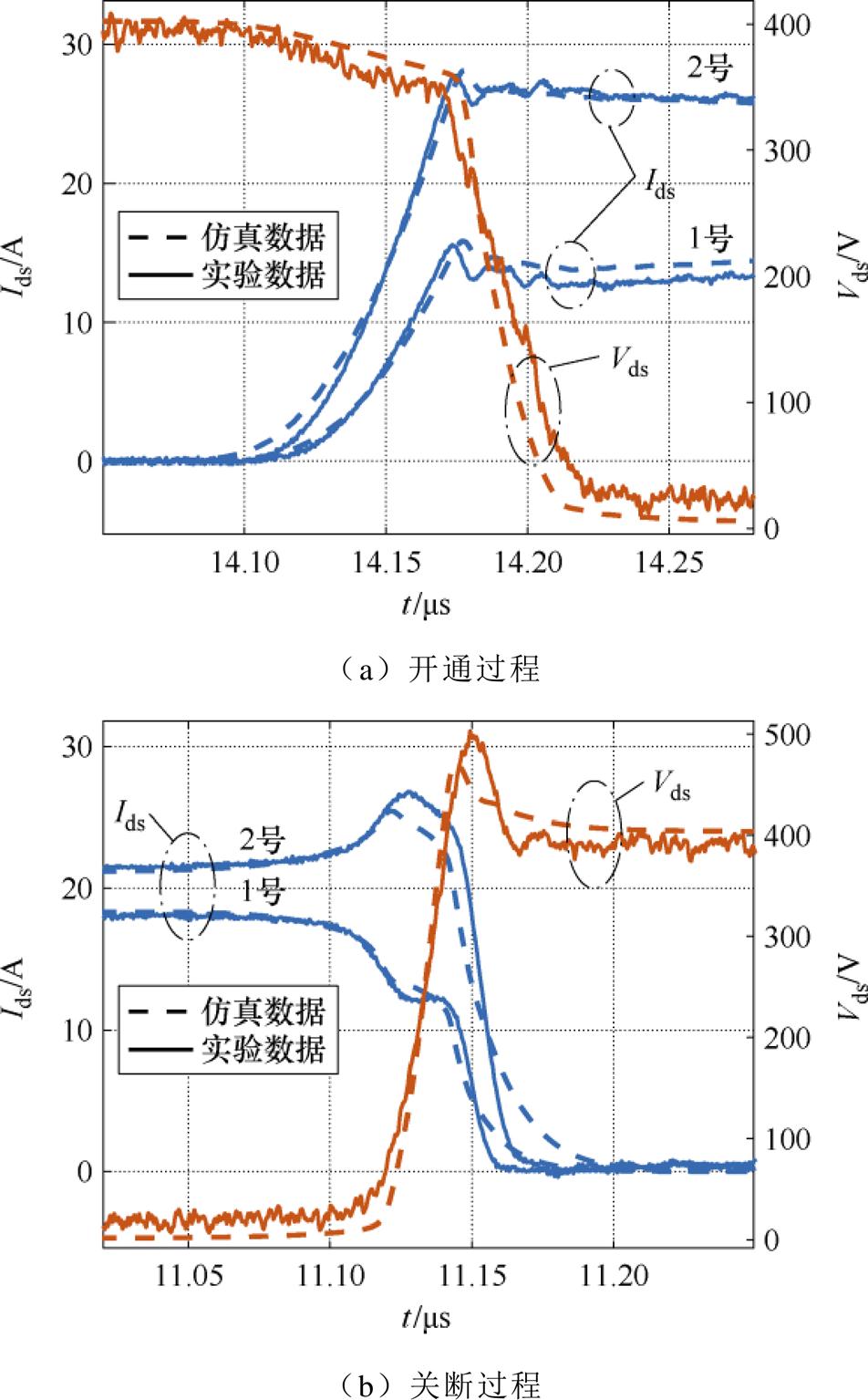
图7 开关过程仿真与实验波形对比
Fig.7 Comparison of turn-on and turn-off waveforms between simulation and experimental
表1 并联SiC MOSFET开关损耗对比
Tab.1 Comparison of switching losses of parallel SiC MOSFETs between simulation and expiremental values
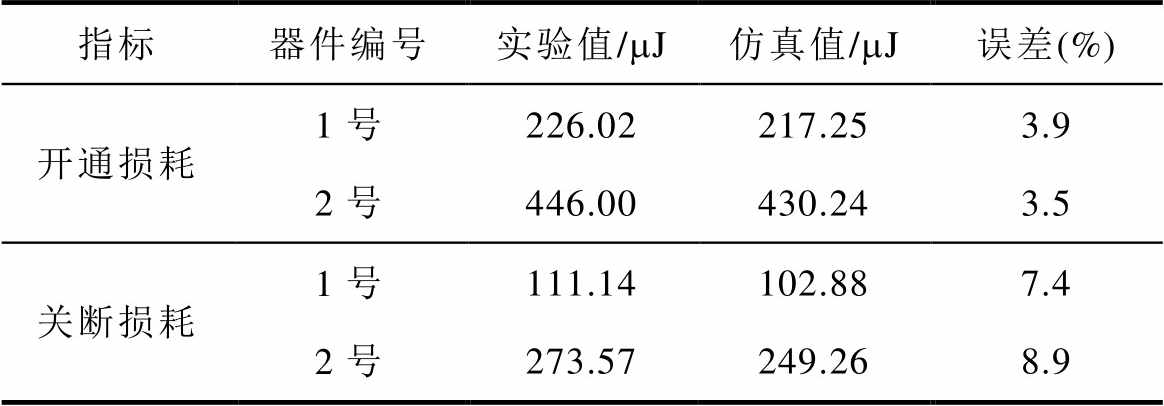
指标器件编号实验值/mJ仿真值/mJ误差(%) 开通损耗1号226.02217.253.9 2号446.00430.243.5 关断损耗1号111.14102.887.4 2号273.57249.268.9
本文考虑芯片间热耦合的二维热网络可以从瞬态热阻抗曲线中提取。对所选用的SiC MOSFET功率模块建立有限元(Finite Element, FE)模型进行瞬态热仿真,获得瞬态热阻抗曲线,所选模块的内部结构如图8所示。
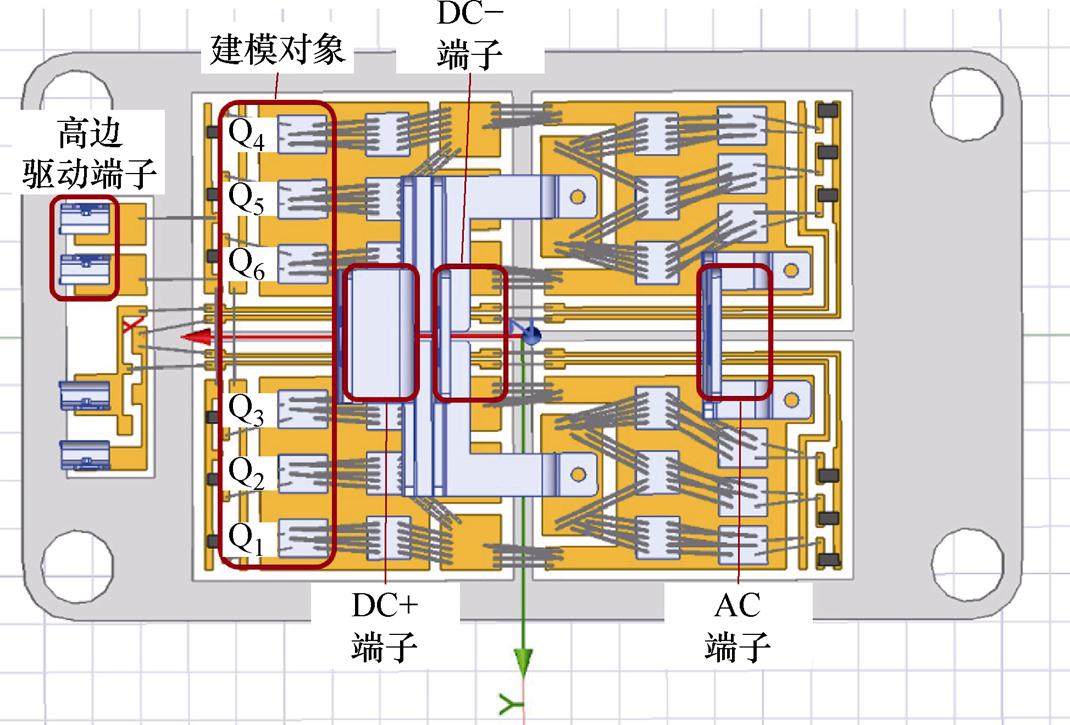
图8 所选多芯片并联SiC MOSFET功率模块结构
Fig.8 Layout of the selected multi-chip SiC MOSFET power module
以模块上半桥为例,底面传热系数为2 000 W/(m2·K)时,将Q1~Q6芯片分别作为热源,每个芯片的发热功率为50 W,环境温度为0℃,进行6个瞬态热响应仿真。采用10 ms+0.1t的动态线性变化步长,从10 ms到100 s进行模拟。利用仿真结果,提取自热网络为5阶、互热网络为1阶的热网络参数。验证仿真设置环境温度为20℃,Q1~Q6功率为17.5 W时R-C热网络与FE的瞬态热响应曲线的对比如图9所示,对比结果基本重合。改变Q1~Q6功率为62.5 W与107.5 W,对比结果中所有芯片的结温误差均小于3.5%,表明所提热网络模型的有效性。
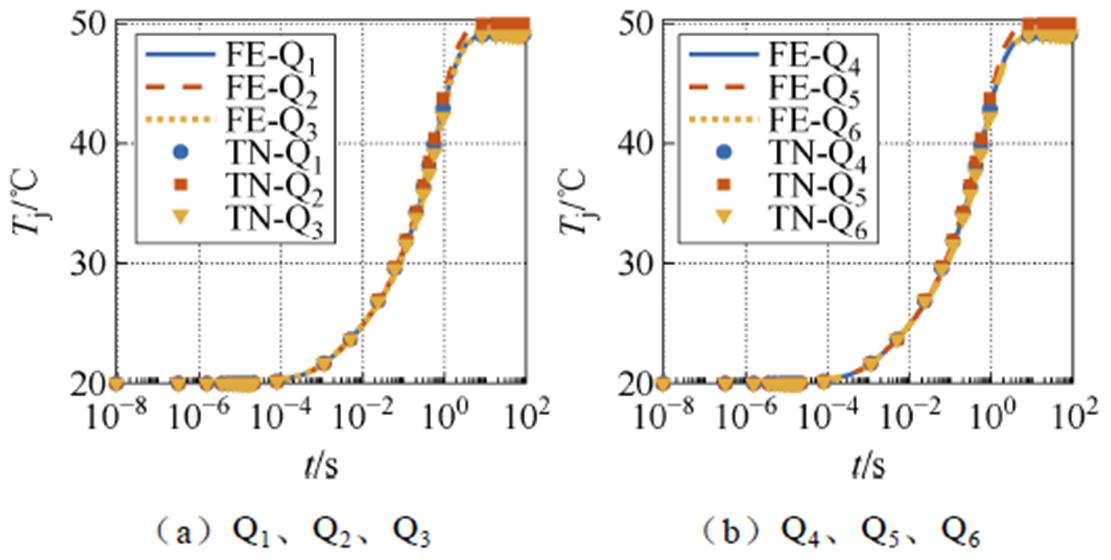
图9 热网络与FE瞬态热响应对比
Fig.9 Transient thermal response comparison between TN and FE
为了验证本文提出的热限制下的输出电流预测模型,采用电热耦合模型建模方法,以制造商提供的参数为基准值,对所选功率模块的上半桥进行建模。该模块的桥臂由6个SiC MOSFET并联组成,对应的考虑封装寄生参数的电路模型拓扑如图10所示,包括漏极D、栅极G、功率源极PS与开尔文源极KS四个端子,每个芯片的电热接口都与考虑芯片间热耦合的热网络对应端子连接。
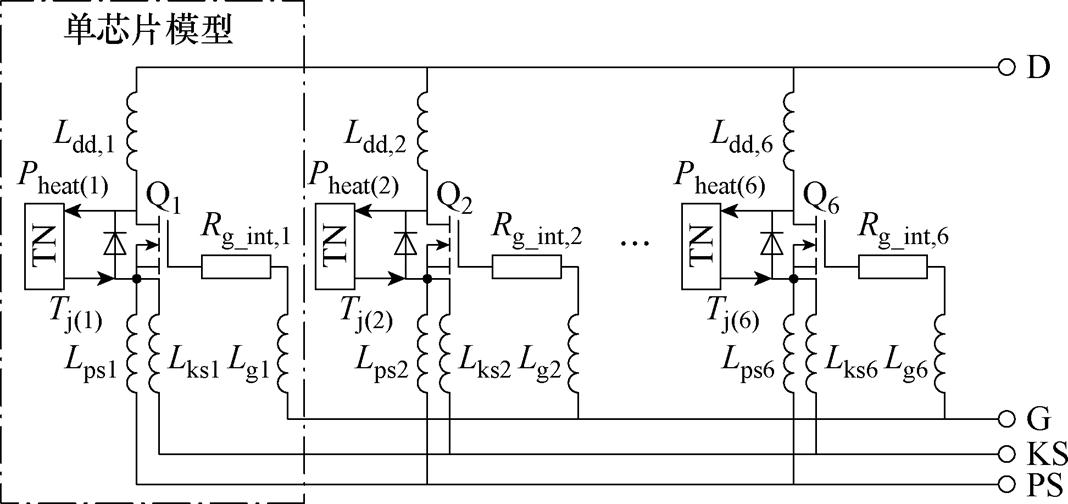
图10 六芯片并联功率模块上桥臂电路模型拓扑
Fig.10 Topology of the electrical model for the upper side six-chip parallelel SiC MOSFET power module
本文以降压(Buck)变换器为例,对热限制下的输出电流预测模型进行验证。Buck变换器电路示意图如图11所示,输入电压Vin=400 V,占空比D= 0.5。按照本文提出的TSOA评估方法,开展三组系统仿真。三组系统仿真的输出电流选用60 A、150 A、240 A,开关频率为50 kHz,驱动开通电压为20 V,驱动关断电压为-5 V,环境温度为40℃。续流SBD模型采用器件制造商提供的模型。按照本文所提TSOA评估方法,变换器输出电流到各芯片结温的映射关系如图12所示。图中原点表示仿真得到的稳态结温值。通过图中放大显示的输出电流为150 A下的匹配情况,说明了所提结温预测模型能有效地反映不同输出电流下的静态结温变化规律。
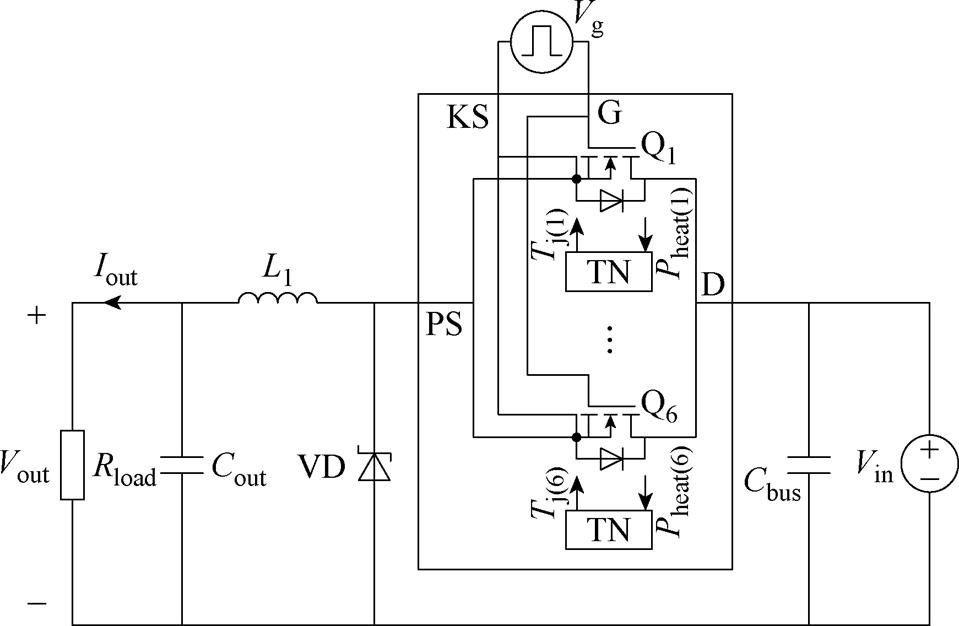
图11 Buck变换器电路示意图
Fig.11 Schematic diagram of the Buck converter
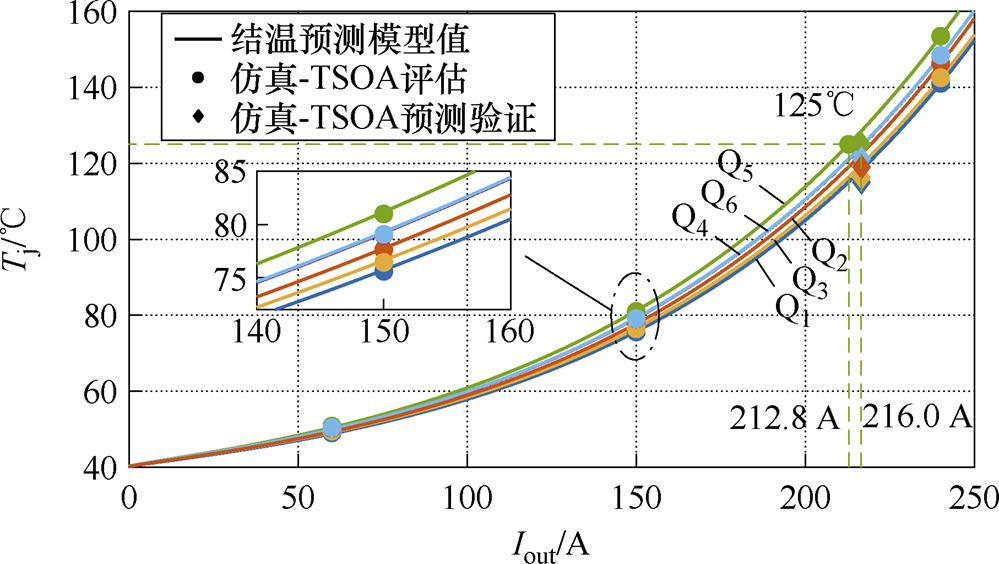
图12 热限制下输出电流预测值与仿真值对比
Fig.12 Comparison between predicted and simulated output current under the specific thermal constraint
为验证预测的准确性,以Tj_limit=125℃为例,输出电流预测模型计算得到功率模块达到设置的热限制125℃时的变换器输出电流为212.8 A。变换器输出电流从212 A到220 A采用1 A步进设置仿真,得到并联芯片间最高结温为125℃时的输出电流为216.0 A,误差为1.5%,表明了预测模型的有效性。
蒙特卡罗(MC)模拟是一种广泛应用于不确定性分析和灵敏度评估的方法。它通过随机生成输入参数的多个样本,模拟现实中可能的参数波动,利用统计方法评估参数波动对目标输出的影响,尤其适用于复杂非线性系统或存在多重随机变量的场景。因此,本文通过蒙特卡罗模拟方法研究芯片参数分散性对并联芯片TSOA的影响。
3.1.1 蒙特卡罗模拟的输入设置
在蒙特卡罗模拟中,输入参数的设置对模拟结果的准确性和可靠性具有重要影响。本文通过研究SiC MOSFET芯片参数分散性的相关文献[8-10, 23-27]发现,阈值电压Vth较导通电阻Rds(on)与跨导gfs的分散性更大。Vth的变异系数(CV)在8%~13.8%之间,Rds(on)的CV平均为4.2%,gfs或跨导系数的CV基本为3.8%。因此,本文根据现有研究中的SiC MOSFET芯片参数分散性范围及相对关系,通过对芯片电流模型中的b0、Vth0、klin、a、c2在基准值上进行随机波动,获得了600个芯片的电路模型,形成样本。其Vth、Rds(on)及gfs的均值(Mean)、标准差(Std)及CV见表2。
表2 600颗芯片样本样本I-V特性分散性统计结果
Tab.2 Statistics of I-V characteristic variations for sample of 600 chips
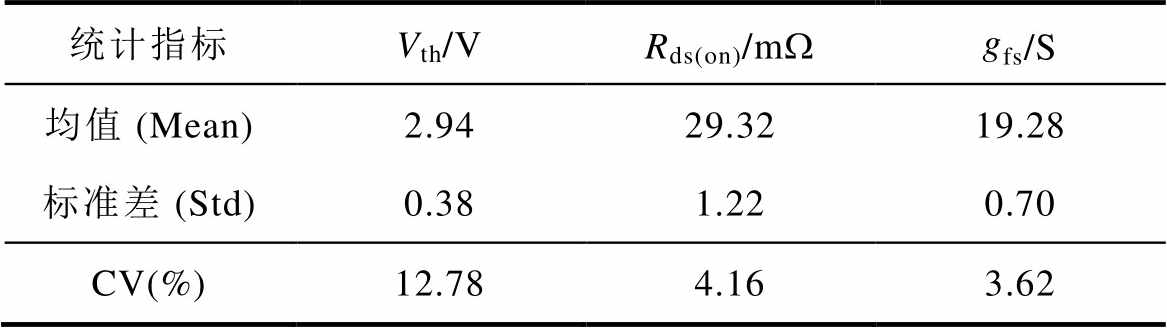
统计指标Vth/VRds(on)/mWgfs/S 均值 (Mean)2.9429.3219.28 标准差 (Std)0.381.220.70 CV(%)12.784.163.62
各项CV与文献[8-10, 23-27]中的分散性情况一致,并作为后续研究的芯片参数的总体统计模型。具体地,转移特性分散性如图13所示,在Ids= 50 A时的Vgs差异范围为2.59 V。阈值电压与跨导建立的样本累积分布函数(Cumulative Distribution Function, CDF)与拟合高斯分布的CDF之间的比较,如图14所示,表明生成样本芯片的阈值电压与跨导服从高斯分布,与文献[9-10]中实测的结果一致,进一步说明了本文输入参数设置的合理性。
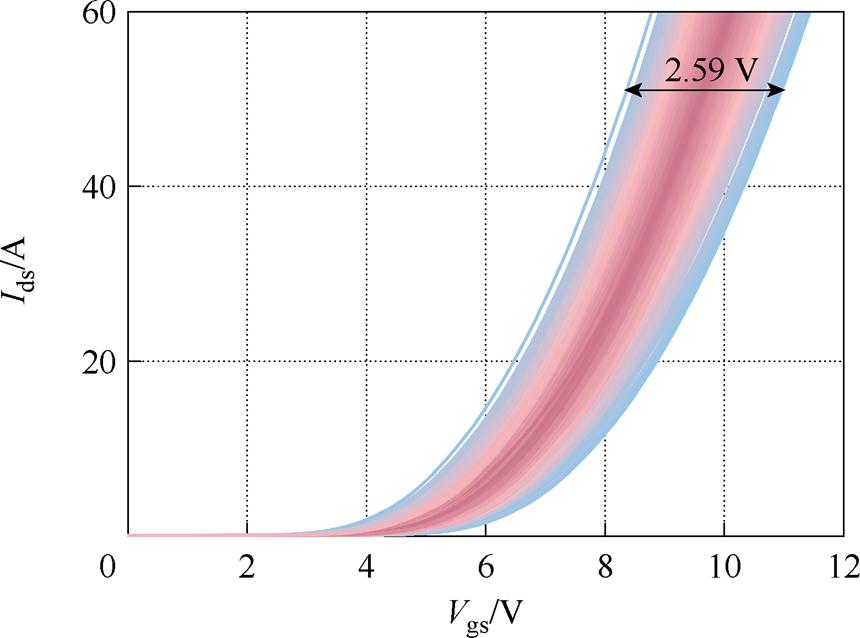
图13 600个器件的转移特性分散性
Fig.13 Spread of transfer characteristic of 600 devices
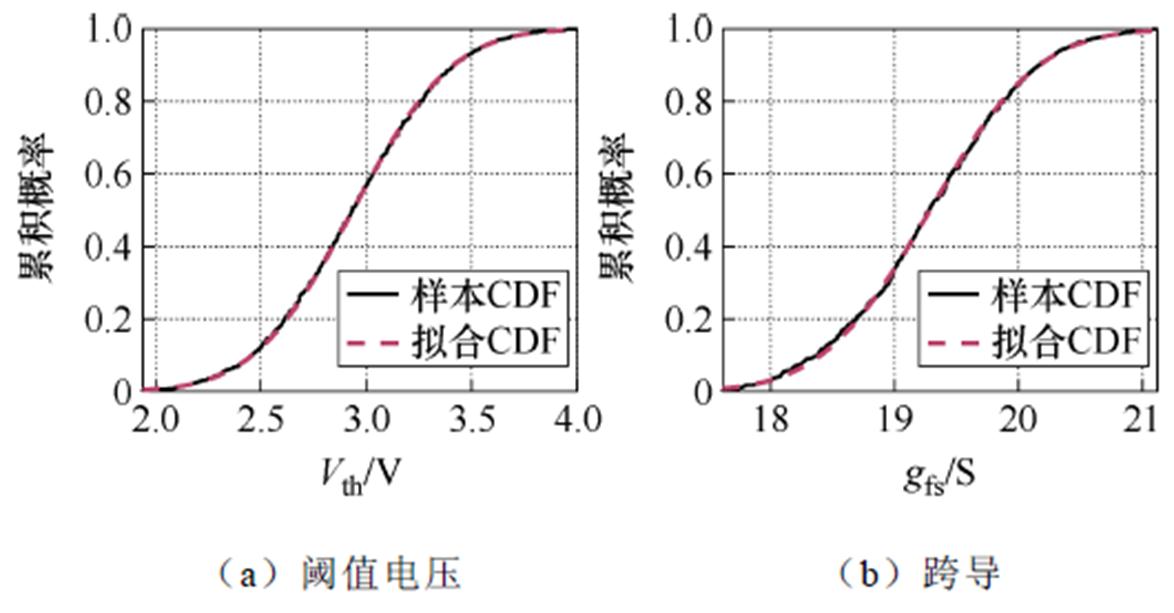
图14 样本CDF与拟合正态分布CDF对比
Fig.14 Comparison between empirical and analytical normal distribution CDF
3.1.2 蒙特卡罗模拟结果
为了评估芯片参数分散性对TSOA的影响,开展蒙特卡罗模拟。对样本芯片进行随机组合,得到100组六芯片并联模块,以图11所示的Buck变换器为例,按照本文所提的TSOA评估方法,在占空比D=0.5,开关频率为50 kHz,Vin为400 V、600 V、800 V下开展电热仿真,获得Tj_limit分别为75℃、100℃、125℃、150℃时的最大输出电流Io_limit。蒙特卡罗模拟得到的各并联模块在不同热限制下的TSOA如图15所示。
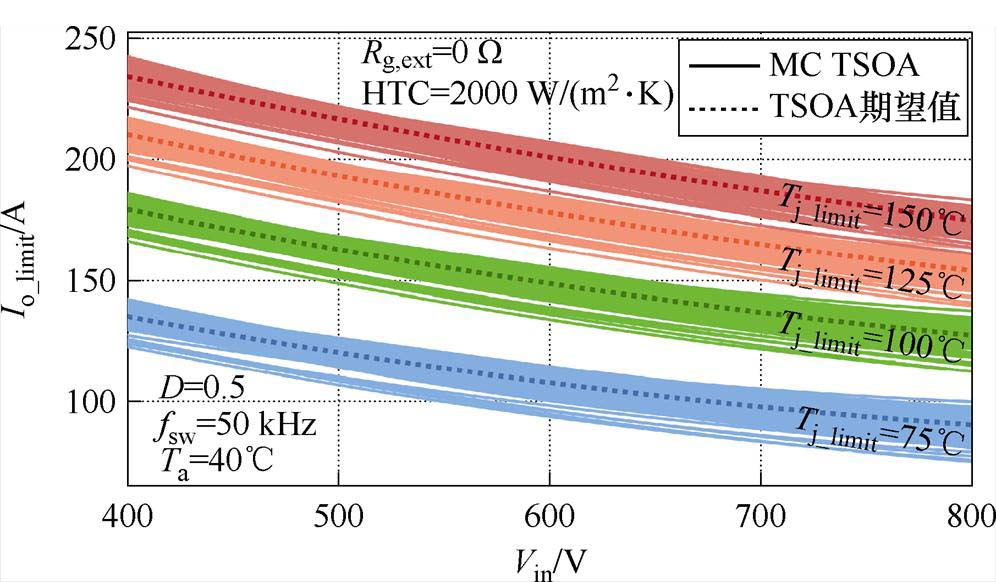
图15 不同热限制下的TSOA曲线
Fig.15 TSOA curves under different thermal constraints
为评估并联模块受芯片参数分散性引起的TSOA收缩程度,借鉴质量控制等领域常用的3s/m比值,衡量芯片参数分散性对TSOA的影响程度,即芯片参数分散性引起的热限制下输出能力下降的比例。假设一批次芯片的阈值电压、导通电阻及跨导等电气参数在整体电气参数的m-ns~m+ns的范围内,即芯片具有±ns参数分散性,定义该批量模块的最小输出电流为m(Io_limit)-3s(Io_limit),其期望输出电流能力m(Io_limit)与最小输出电流差值之比即为该批功率模块的总体TSOA收缩率b,即
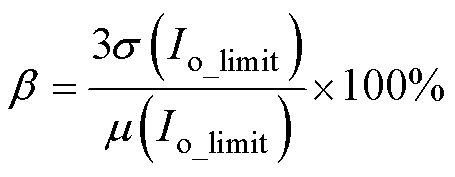 (10)
(10)
计算不同结温限制与输入电压下由3s芯片参数分散性引起的总体TSOA收缩率b如图16所示。
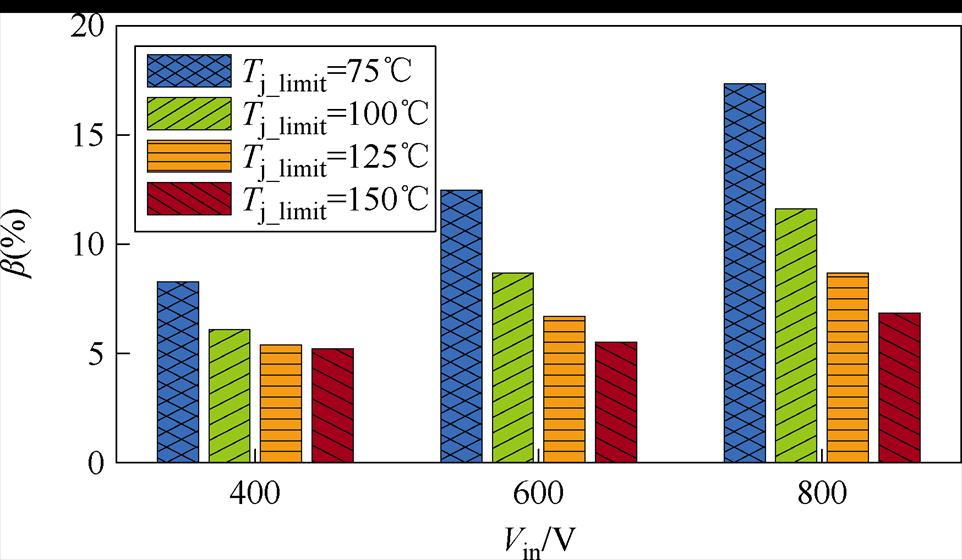
图16 不同热限制与输入电压下的总体TSOA收缩率
Fig.16 Overall TSOA reduction rate under different thermal constraints and input voltages
对最高结温要求越严格,芯片参数分散引起的TSOA收缩越严重。Tj_limit=75℃时,总体TSOA收缩率b最高近20%。而随着最高结温要求逐渐放宽,b减小,且b随输入电压的增加变化较小。Tj_limit= 150℃时,芯片参数分散性的影响趋向于稳定,约为7%。这一特性主要是由导通电阻较为明显的正温度系数特性以及开关损耗随结温增加的变化较小引起。稳态时,k个芯片并联中芯片i的电流可按照并联电阻电流分配的规律计算为
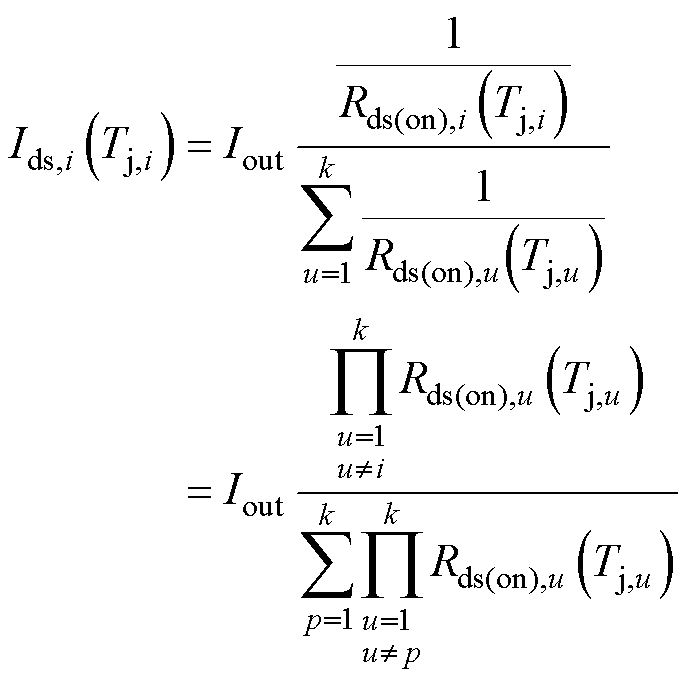 (11)
(11)
式中,Ids,i(Tj,i)为芯片i在结温为Tj,i时的稳态电流;Rds(on),i(Tj,i)为芯片i在结温为Tj,i时导通电阻值。当结温升高时,由式(11)可知,并联芯片间电流分配的比例因子分母相同,分子由其他芯片的导通电阻乘积决定。假设芯片i导通电阻变为原来的km,i倍,若结温升高较少,各芯片导通电阻变化比率km相近,使得芯片间Ids的不均衡性难以减小。而开关损耗温度依赖性较弱,主要取决于Ids,i,因此芯片间的电流差异仍将导致芯片间损耗分布不均。而当并联芯片间的最高结温限制升高时,芯片间km的差异得以扩大,使得Rds(on)的正温度系数性能发挥自调节作用,缩小芯片间的Ids差异,有利于损耗均衡,故TSOA的分散性更小。
为探究在一组并联芯片中,芯片间阈值电压、跨导、导通电阻各自的差异对其TSOA的影响的灵敏度,本文计算斯皮尔曼相关系数rs,通过取rs的绝对值并归一化,可以直接衡量不同芯片参数的重要性。基于rs的分析方法是一种低计算成本、适合于小样本与非线性模型的高效灵敏度评估工具,而被广泛应用[28]。灵敏度Si具体计算方法为
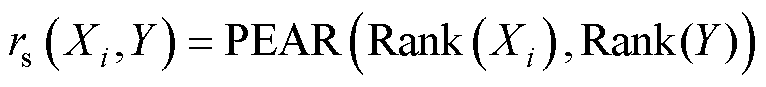 (12)
(12)
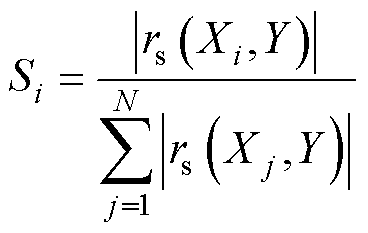 (13)
(13)
式中,N为自变量数量;Xi为第i个自变量;Y为因变量;Rank( · )为变量的秩;PEAR(X,Y)为X与Y的Pearson相关系数;Si为自变量Xi对因变量Y的灵敏度。
因变量Y以输出电流与输入电压围成的面积STSOA为指标,用于比较不同并联模块间的TSOA,其计算方法为
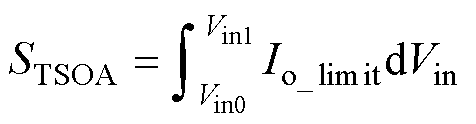 (14)
(14)
式中,Vin0为输入电压下限;Vin1为输入电压上限。
自变量X则包括并联芯片阈值电压、跨导、导通电阻的极差与均值,用RX表示X的极差大小,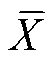 表示X的均值。除此之外,自变量还包括了单芯片转移特性中电流达到额定值的栅源电压Vgs@Id_rating,代表大信号电流增益的大小,本例中为Vgs@50 A。计算并联芯片参数对STSOA影响的Si值如图17所示。并联芯片的RVgs@50 A与RVth对TSOA影响最大。Tj_limit=75℃时,两者的影响比重约60%。而RRds(on)对TSOA的影响仅约10%,Rgfs的影响更小。均值因素中,Rds(on)与gfs的均值较Vgs@50 A与Vth的均值更为重要。这是因为Vgs@50 A与Vth主要影响并联芯片间由于电流分配引起的损耗差异,而Rds(on)与gfs主要代表芯片自身损耗大小。另一方面,随着Tj_limit的降低,TSOA对Vgs@50 A与Vth的极差灵敏度增加明显,而代表芯片自身损耗的Rds(on)与gfs的影响减小,表示在热限制较为严格时,要避免TSOA收缩,需要更为一致的芯片参数。
表示X的均值。除此之外,自变量还包括了单芯片转移特性中电流达到额定值的栅源电压Vgs@Id_rating,代表大信号电流增益的大小,本例中为Vgs@50 A。计算并联芯片参数对STSOA影响的Si值如图17所示。并联芯片的RVgs@50 A与RVth对TSOA影响最大。Tj_limit=75℃时,两者的影响比重约60%。而RRds(on)对TSOA的影响仅约10%,Rgfs的影响更小。均值因素中,Rds(on)与gfs的均值较Vgs@50 A与Vth的均值更为重要。这是因为Vgs@50 A与Vth主要影响并联芯片间由于电流分配引起的损耗差异,而Rds(on)与gfs主要代表芯片自身损耗大小。另一方面,随着Tj_limit的降低,TSOA对Vgs@50 A与Vth的极差灵敏度增加明显,而代表芯片自身损耗的Rds(on)与gfs的影响减小,表示在热限制较为严格时,要避免TSOA收缩,需要更为一致的芯片参数。
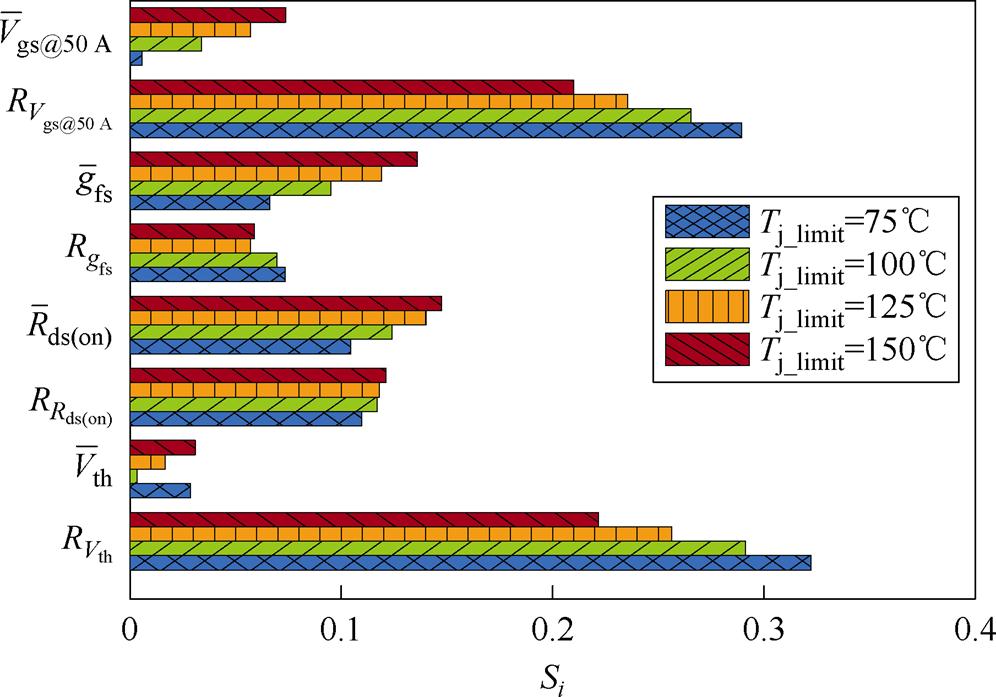
图17 并联芯片参数对STSOA影响的Si值
Fig.17 Si of parallelled chip parameters impacting on STSOA
本节研究了不同芯片参数分散性对TSOA的影响,并与并联芯片参数均一致的情况进行对比。
3.3.1 不同参数分散性范围下的TSOA
在3.1.1节中生成的总体概率分布下,以均值为中心,以m-ns~m+ns为采样窗口,得到±ns的样本集。以跨导为例,±s、±2s、±3s的采样范围如图18所示。
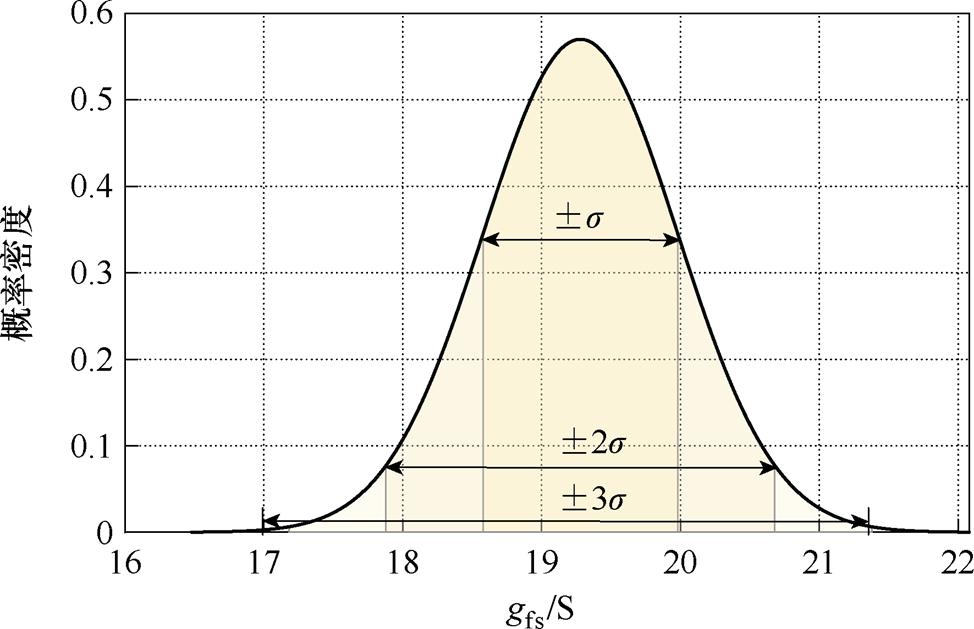
图18 不同分散范围的跨导采样范围示意图
Fig.18 Schematic diagram of transconductance sampling range under different variations
对生成的不同分散范围的芯片样本集按照前述过程分别开展蒙特卡罗模拟,设置系统工况为Vin= 800 V,fsw=50 kHz,D=0.5,Tj_limit=150℃。±s、±2s、±3s芯片参数分散性下蒙特卡罗模拟得到的最大输出电流分布如图19所示,总体TSOA收缩率b与期望的电流输出能力与芯片参数分散性的关系如图20所示。
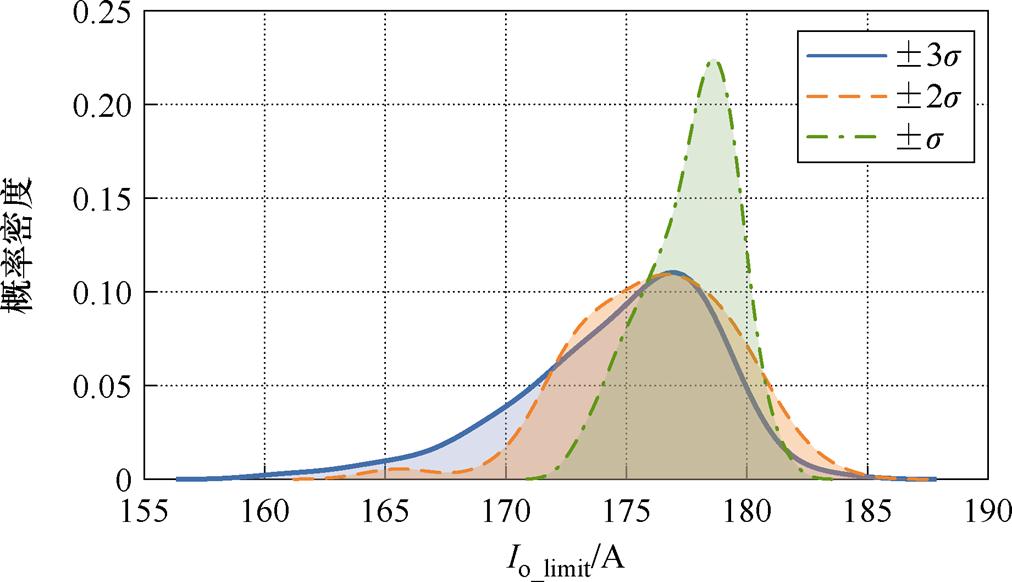
图19 不同芯片参数分散范围下输出电流能力分布
Fig.19 Distribution of output current capability under different chip parameter variations
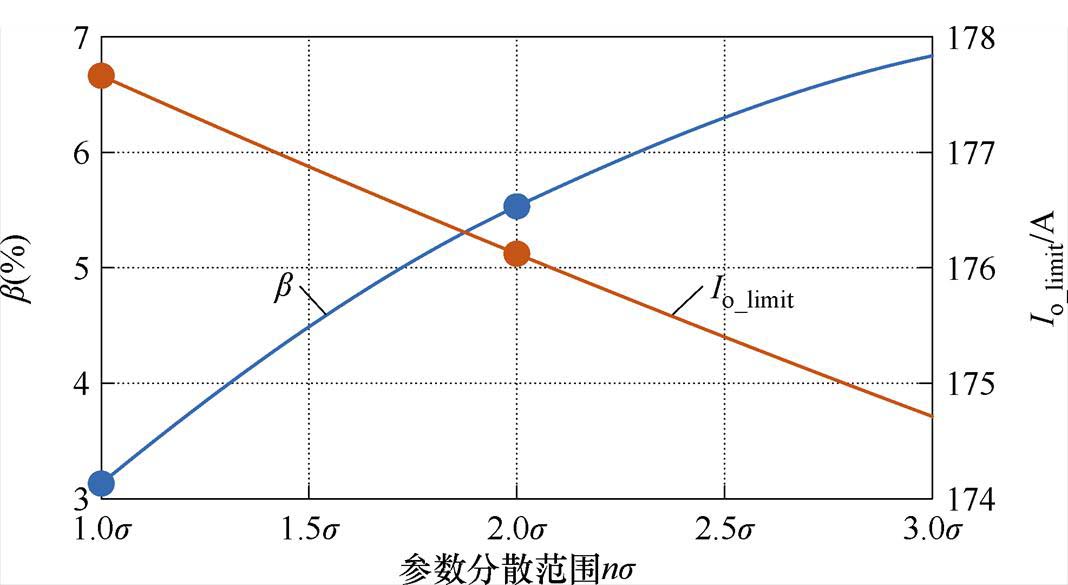
图20 不同参数分散范围下总体TSOA收缩率和期望输出电流的变化情况
Fig.20 Overall TSOA reduction rate and output current capability under different chip parameter variations
从图19与图20中可以看出,芯片参数分散性越大,TSOA的分散性越大,并联功率模块间的差异越大。当芯片参数分散范围从±s增加到±3s时,b从3.13%上升到6.84%,增加逾一倍。值得注意的是,随着芯片参数的分散性增加,期望的电流输出能力并未有明显的减小,再次表明了导通电阻对结温均衡的调节作用。
3.3.2 与并联芯片参数一致时的TSOA对比
传统多芯片并联功率模块封装中,存在并联芯片间的封装寄生参数非对称分布,导致芯片不均衡的损耗与暂态电流,引起芯片间的稳态结温差异,最终制约模块的TSOA。为研究芯片参数分散性对TSOA的独立影响,利用TSOA评估方法获得并联标称参数芯片的基线TSOA,并对±3s范围内波动芯片进行无分散性并联蒙特卡罗模拟,获得无并联芯片间分散性的TSOA。两者与3.1.2节中考虑并联芯片间分散性的TSOA对比情况如图21所示。
图21中,实线为基线TSOA,代表了给定封装时芯片在标称参数下的TSOA;浅灰色阴影表示考虑并联芯片间分散性后TSOA的分散范围,深灰色阴影表示无并联芯片间分散性的TSOA分散范围。可以看出,无并联芯片间分散性的TSOA期望与基线TSOA基本重合,表明当并联芯片间强制一致时,TSOA期望退化为期望的芯片参数并联后的TSOA,即基线TSOA。对比有无并联芯片间分散性的TSOA期望与分散范围可以发现,并联的芯片之间存在分散性后,虽然其期望TSOA较基线TSOA收缩较小,但TSOA分散范围显著扩大。因此,在实际批量生产中,为保障量产功率模块的性能一致性,还需控制芯片参数的差异。
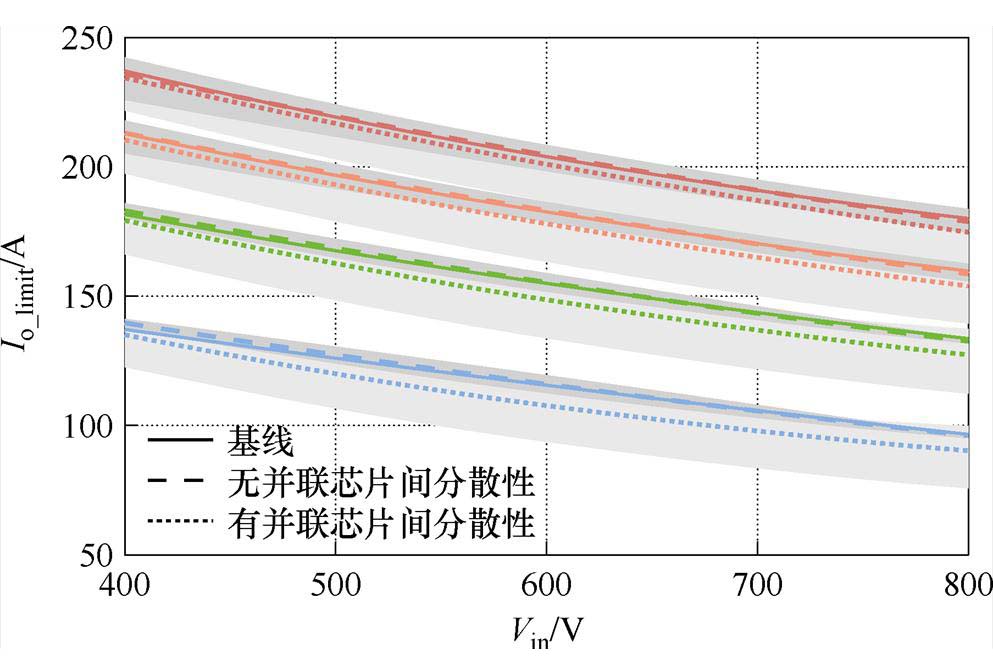
图21 与无芯片参数分散性的TSOA对比
Fig.21 Comparison with TSOA without chip parameter variations
SiC器件较传统硅基器件的优势之一体现在高频工况下,开关频率的提升,需直接调节开关损耗Psw与导通损耗Pcon的占比,而两类损耗对不同芯片参数分散性的敏感度存在显著差异。因此,为研究不同开关频率下芯片参数分散性对TSOA影响差异,改变开关频率至10 kHz,对3.1节所述随机组合的多芯片并联功率模块与基线模型构成的无分散性并联功率模块重新进行蒙特卡罗模拟,得到的TSOA如图22所示。与图15开关频率为50 kHz时TSOA的蒙特卡罗模拟结果进行对比,可以发现开关频率降低后,由于开关损耗与导通损耗的比例减小,导通电阻的正温度特性缓解开关过程中的电流不均,进而减少因电流分配不均引起的损耗差异,使得具有3s分散性的功率模块的TSOA期望值与基线TSOA几乎一致。芯片m开关损耗与导通损耗的比例hm以及芯片m与芯片n总损耗之比分别表示为
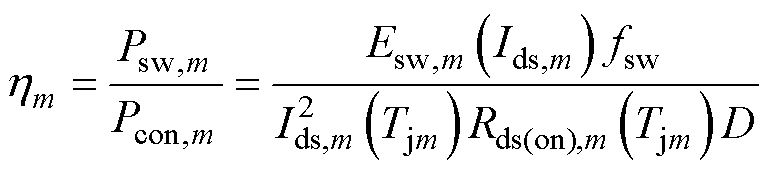 (15)
(15)
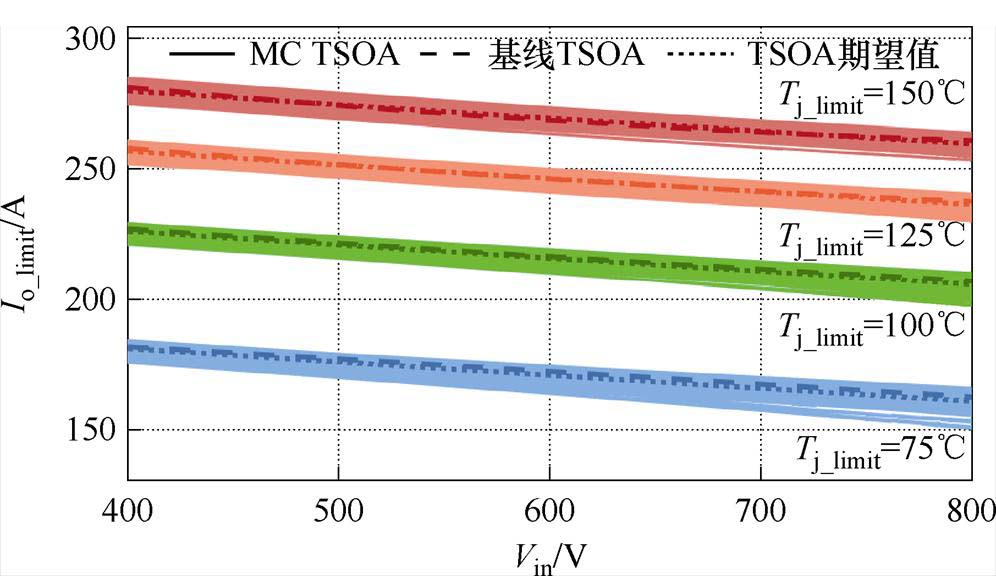
图22 开关频率为10 kHz的TSOA蒙特卡罗模拟结果
Fig.22 Monte Carlo simulation results of TSOA at a switching frequency of 10 kHz
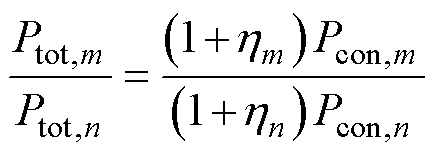 (16)
(16)
式中,Esw,m为芯片m的开关损耗;fsw为开关频率。当开关频率由50 kHz降至10 kHz时,Ptot,m/Ptot,n从主要由Esw,m/Esw,n的比例决定变为受Pcon,n/Rcon,m的比例影响,而器件在线性区的特性差异小,因而低开关频率时受芯片参数分散性的影响小。
统计开关频率分别为10 kHz与50 kHz时相较基线情况延拓了TSOA的组数,如图23所示。开关频率为10 kHz时,TSOA发生延拓的组数远超开关频率为50 kHz的TSOA,甚至Tj_limit=150℃时发生延拓的组数超过50%。表明在较小的开关损耗与导通损耗的比例下,芯片参数间的补偿作用可以减小芯片间的稳态结温差异,延拓TSOA。
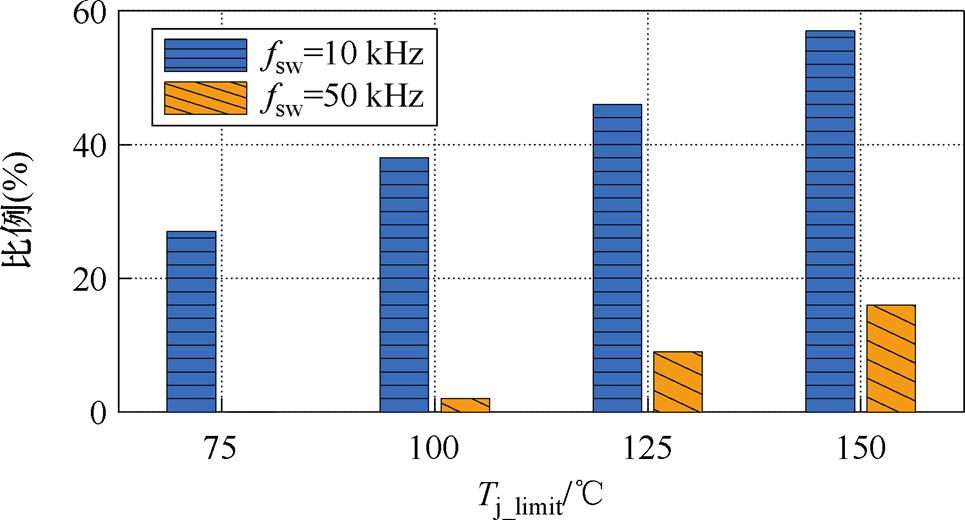
图23 不同开关频率下TSOA优于基线的组数占比
Fig.23 Proportion of groups in which TSOA outperforms baseline TSOA under different switching frequencies
进一步地,对比不同开关频率下Rds(on)、gfs、Vgs@50 A与Vth的均值与极值对TSOA影响的灵敏度如图24所示。开关频率降低后,Rds(on)、gfs、Vgs@50 A与Vth的均值的灵敏度增大,而表示并联芯片间gfs、Vgs@50 A与Vth分散性大小的极差对TSOA的灵敏度大幅减小。表明并联芯片间由于电流分配引起的损耗差异在低开关频率下对TSOA的影响不大,基本是由芯片本身的损耗大小来决定TSOA是延拓还是收缩。不同开关频率下芯片参数对TSOA影响的灵敏度不同,表明芯片分组可针对应用工况选择指标。
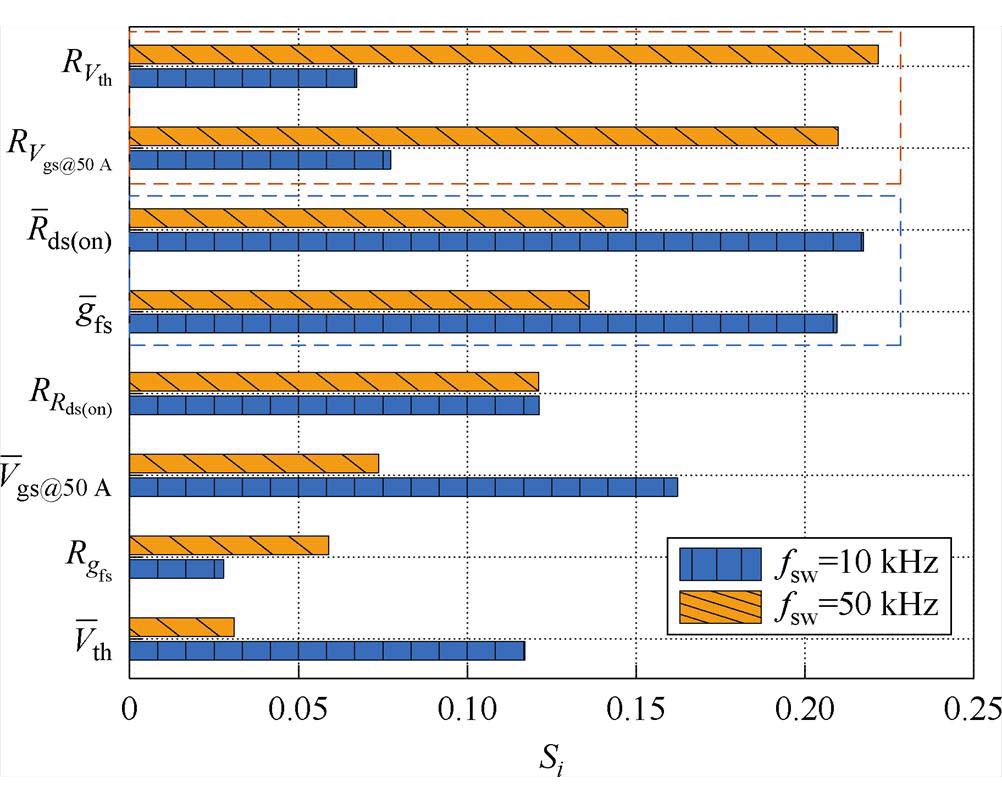
图24 不同开关频率下并联芯片参数对STSOA影响的Si值
Fig.24 Si of parallelled chip parameters impacting on STSOA under different frequencies
TSOA的延拓可以从两个方面入手:①筛选芯片,控制芯片参数分散型范围,降低同一批次的总体TSOA收缩率;②分选芯片,提高单个多芯片并联功率模块的TSOA,具体的延拓方法流程如图25所示。
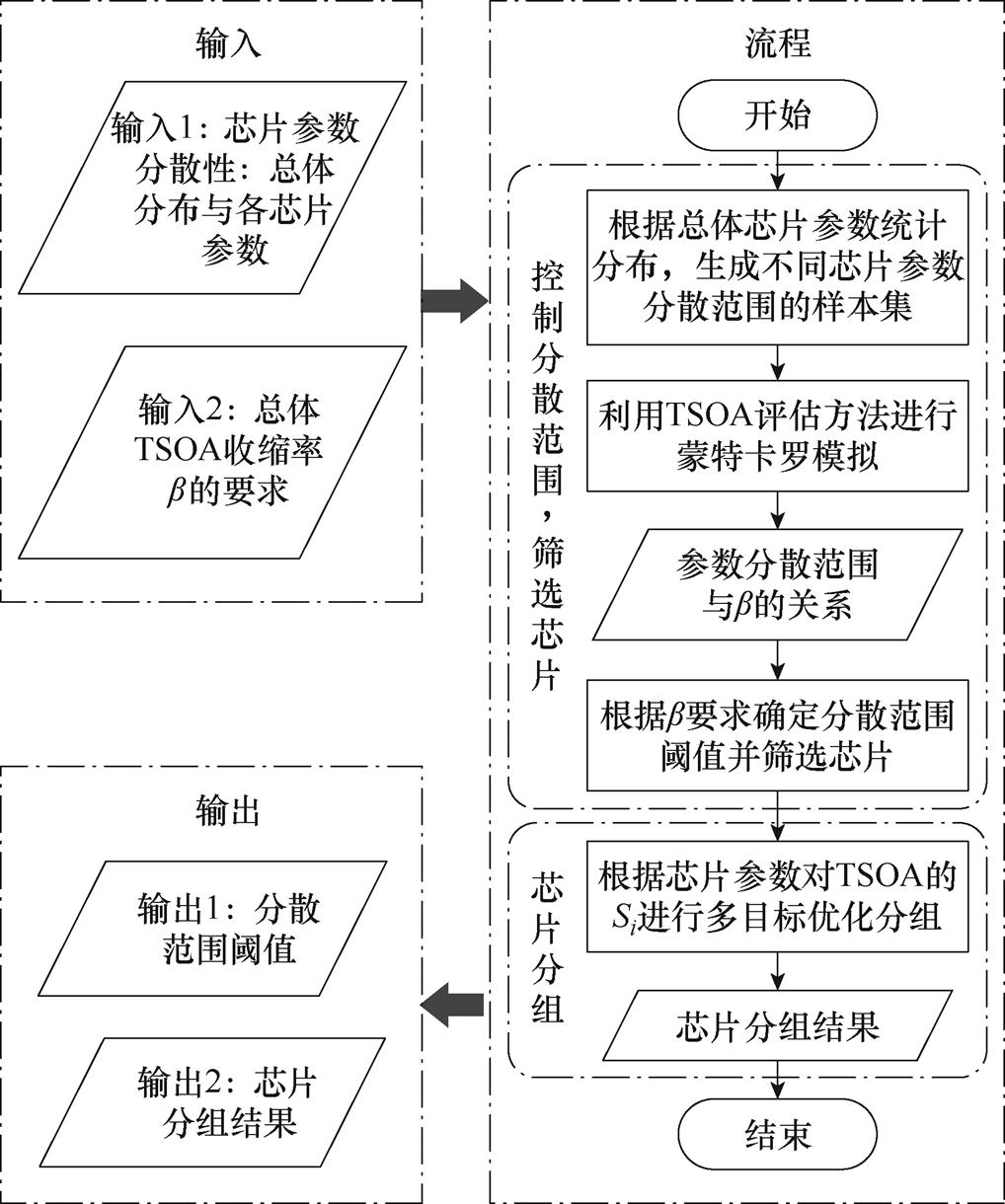
图25 延拓TSOA的方法流程
Fig.25 Flowchart of the methodology of enlarging TSOA
首先,在获取总体的芯片参数统计分布后,根据图18所示的不同芯片参数分散范围的采样窗口,生成对应的样本集,随后在目标应用工况下利用TSOA评估方法进行蒙特卡罗模拟,获得各分散范围下的TSOA分布,求得各芯片参数分散范围与总体TSOA收缩率之间的关系。随后根据总体TSOA收缩率的要求,确定分散性阈值,例如,对3.3.1节中±s、±2s、±3s分散范围的芯片样本集分别在开关频率为10 kHz和50 kHz的工况下进行蒙特卡罗模拟,计算得到的各芯片参数分散范围与总体TSOA收缩率之间的关系如图26所示。开关频率为10 kHz时,TSOA受分散性的影响较小,总体TSOA收缩率低,分散范围从±s扩大到±2s时,由1.26%增加到1.89%,而后保持稳定;开关频率为50 kHz时,TSOA受分散性的影响较大,总体TSOA收缩率增加明显,分散范围从±s扩大到±3s时,从3.13%增加到6.84%,扩大3.7%。因此,若希望总体TSOA收缩率控制在5%以内,对于低开关频率的应用,上述研究结果表明,无需额外控制,当前的芯片参数分散范围满足总体TSOA收缩率的要求。而对于高开关频率的应用,则需要将所用芯片的参数分散性阈值控制在约±1.7s以内。
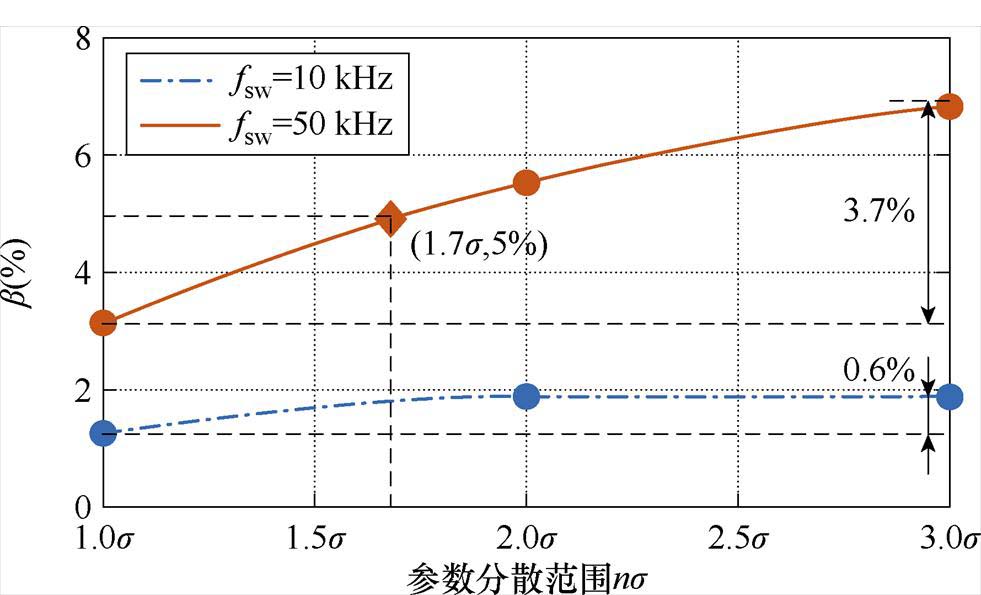
图26 不同开关频率下芯片参数分散性与总体TSOA收缩率的关系
Fig.26 Relationship between chip parameter variations and overall TSOA reduction rate under different switching frequencies
根据所得分散性阈值筛选芯片后,开展芯片分组。延拓TSOA的芯片分组的基本思想是满足高灵敏度因素的要求。从图17可知,Vth极差、Vgs@Id_rating极差、Rds(on)均值和gfs均值是影响TSOA的主要因素,四者影响占比为71.5%~78.2%。因而,可以以并联芯片组内Vth极差最小、Vgs@Id_rating极差最小、Rds(on)均值最小和gfs均值最大为目标,以灵敏度为参考权重,运用聚类算法、启发式算法等多目标优化算法进行芯片分组,以获得较宽的TSOA。
本文针对同时考虑封装寄生参数不均衡、等效热阻不均衡以及芯片间热耦合难以对并联电路解析求解的难点,提出了一种运用电热耦合仿真的多芯片并联功率模块TSOA评估方法,并通过蒙特卡罗模拟,研究了并联芯片参数存在分散性时,不同热限制、不同分散范围、不同开关频率对功率模块TSOA及其总体TSOA收缩率的影响。最后,提出了延拓功率模块TSOA的分选方法及分散性阈值确定方法。主要结论如下:
1)当Tj_limit越低时,总体TSOA收缩率b越高,且随Vin的升高而增大;当Tj_limit升高后,b减小,且升至150℃时,b随Vin的变化不明显。
2)不同分散范围对TSOA的影响需要结合器件的开关频率综合考虑。在较低开关频率下TSOA的期望值与基线TSOA几乎一致,随着芯片参数分散范围扩大,b增加0.6%且稳定在1.89%;在较高开关频率下,TSOA的期望值较基线TSOA发生明显收缩,分散范围扩大到±3s时,b增加到6.84%。
3)在较低开关频率下,TSOA的延拓或收缩主要受到并联芯片Rds(on)与gfs的均值大小的影响;在较高开关频率下,Vth与Vgs@Id_rating极差的灵敏度高。
4)提出TSOA延拓方法,首先通过变芯片参数分散范围的蒙特卡罗模拟,确定保障b在给定要求下的分散性阈值,筛选芯片。然后以组内并联芯片Vth极差最小、Vgs@Id_rating极差最小、Rds(on)均值最小和gfs均值最大为目标,进行多目标优化分组,以延拓多芯片并联功率模块的TSOA。
参考文献
[1] 钱照明, 张军明, 吕征宇, 等. 我国电力电子与电力传动面临的挑战与机遇[J]. 电工技术学报, 2004, 19(8): 10-22.
Qian Zhaoming, Zhang Junming, Lü Zhengyu, et al. Challenge and opportunity for power electronics and electrical drive in China[J]. Transactions of China Electrotechnical Society, 2004, 19(8): 10-22.
[2] 陈润田, 李楚杉, 姚文熙, 等. 基于等效励磁电感的SiC串联器件型中压双有源桥变换器的软开关技术[J]. 电工技术学报, 2024, 39(12): 3732-3745.
Chen Runtian, Li Chushan, Yao Wenxi, et al. Soft- switching technique for medium voltage dual active bridge converter with series-connected SiC devices based on equivalent magnetizing inductance[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3732-3745.
[3] 张少昆, 孙微, 范涛, 等. 基于分立器件并联的高功率密度碳化硅电机控制器研究[J]. 电工技术学报, 2023, 38(22): 5999-6014.
Zhang Shaokun, Sun Wei, Fan Tao, et al. Research on high power density silicon carbide motor controller based on parallel connection of discrete devices[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5999-6014.
[4] 王来利, 赵成, 张彤宇, 等. 碳化硅功率模块封装技术综述[J]. 电工技术学报, 2023, 38(18): 4947- 4962.
Wang Laili, Zhao Cheng, Zhang Tongyu, et al. Review of packaging technology for silicon carbide power modules[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4947-4962.
[5] 邹铭锐, 曾正, 孙鹏, 等. 基于变电阻驱动的SiC器件开关轨迹协同调控[J]. 电工技术学报, 2023, 38(16): 4286-4300.
Zou Mingrui, Zeng Zheng, Sun Peng, et al. Coor- dinated switching trajectory regulation of SiC device using variable resistance gate driver[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4286-4300.
[6] 丁四宝, 王盼宝, 王卫, 等. SiC/Si混合开关时间延迟及其信号调制方法[J]. 电工技术学报, 2025, 40(4): 1129-1144.
Ding Sibao, Wang Panbao, Wang Wei, et al. Analysis of SiC/Si HYS loss characteristics and its driving signal modulation circuit[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1129-1144.
[7] Li Helong, Zhao Shuang, Wang Xiongfei, et al. Parallel connection of silicon carbide MOSFETs: challenges, mechanism, and solutions[J]. IEEE Transactions on Power Electronics, 2023, 38(8): 9731-9749.
[8] Wang Gangyao, Mookken J, Rice J, et al. Dynamic and static behavior of packaged silicon carbide MOSFETs in paralleled applications[C]//2014 IEEE Applied Power Electronics Conference and Exposition- APEC 2014, Fort Worth, TX, USA, 2014: 1478-1483.
[9] Riccio M, Borghese A, Romano G, et al. Analysis of device and circuit parameters variability in SiC MOSFETs-based multichip power module[C]//2018 20th European Conference on Power Electronics and Applications (EPE'18 ECCE Europe), Riga, Latvia, 2018: 1-9.
[10] Borghese A, Riccio M, Fayyaz A, et al. Statistical analysis of the electrothermal imbalances of mismatched parallel SiC power MOSFETs[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(3): 1527-1538.
[11] Zhao Cheng, Wang Laili, Zhang Fan. Effect of asymmetric layout and unequal junction temperature on current sharing of paralleled SiC MOSFETs with kelvin-source connection[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7392-7404.
[12] Nakamura Y, Kuroda N, Yamaguchi A, et al. Influence of device parameter variability on current sharing of parallel-connected SiC MOSFETs[C]// 2020 IEEE 29th Asian Test Symposium (ATS), Penang, Malaysia, 2020: 1-6.
[13] 孙鹏, 赵志斌, 蔡雨萌, 等. 基于开关能量均衡的并联碳化硅MOSFET芯片筛选[J]. 中国电机工程学报, 2019, 39(19): 5613-5623.
Sun Peng, Zhao Zhibin, Cai Yumeng, et al. Chip screening for parallel silicon carbide MOSFET based on switching energy balancing[J]. Proceedings of the CSEE, 2019, 39(19): 5613-5623.
[14] Qin Haihong, Hu Haoxiang, Zhu Ziyue, et al. A fast forecasting model of electrothermal distribution for parallelled SiC MOSFETs[J]. Energy Reports, 2022, 8: 648-656.
[15] Piccioni A, Seltner N. Impact of parameter spread in parallel-operated SiC MOSFETs for hard-switching conversion[C]//PCIM Europe 2024; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nürnberg, Germany, 2024: 2675-2680.
[16] Li Xiang, Wang Yangang, Chang Guiqin, et al. Thermal imbalance among paralleling chips in power modules and the impact from traction inverter system view[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2231-2240.
[17] Pushpakaran B N, Bayne S B, Wang Gangyao, et al. Fast and accurate electro-thermal behavioral model of a commercial SiC 1200V, 80 mW power MOSFET[C]// 2015 IEEE Pulsed Power Conference (PPC), Austin, TX, USA, 2015: 1-5.
[18] Li Hong, Zhao Xingran, Sun Kai, et al. A non- segmented PSpice model of SiC MOSFET with temperature-dependent parameters[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(5): 4603-4612.
[19] Kimoto T, Cooper J A. Fundamentals of Silicon Carbide Technology: Growth, Characterization, Devices and Applications[M]. Singapore: John Wiley & Sons, 2014.
[20] Wolfspeed. All SPICE models[EB/OL]. cms.wolfspeed. com/download/21507, 2024-10-15.
[21] Li Jianfeng, Castellazzi A, Eleffendi M A, et al. A physical RC network model for electrothermal analysis of a multichip SiC power module[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2494-2508.
[22] Wang Jianpeng, Chen Wenjie, Zhang Jin, et al. A novel approach to model and analyze uneven temperature distribution among multichip high-power modules and corresponding method to respecify device SOA[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(4): 4626-4640.
[23] Ke Junji, Zhao Zhibin, Sun Peng, et al. Chips classification for suppressing transient current imbalance of parallel-connected silicon carbide MOSFETs[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(4): 3963-3972.
[24] Ke Junji, Zhao Zhibin, Sun Peng, et al. Influence of device parameters spread on current distribution of paralleled silicon carbide MOSFETs[J]. Journal of Power Electronics, 2019, 19(4): 1054-1067.
[25] Zhao Bin, Yu Qiuping, Sun Peng, et al. Device screening strategy for suppressing current imbalance in parallel-connected SiC MOSFETs[J]. IEEE Transa- ctions on Device and Materials Reliability, 2021, 21(4): 556-568.
[26] Zheng Fujun, Meng Hui, Zhou Ze, et al. Output curves based hierarchical clustering screening method with static/dynamic current balancing for paralleled SiC MOSFETs[J]. CPSS Transactions on Power Electronics and Applications, 2023, 8(3): 257-268.
[27] Yu Renze, Jahdi S, Mellor P. Impact of intrinsic parameter dispersion on short-circuit reliability of parallel-connected planar and trench SiC MOSFETs[J]. IEEE Transactions on Industrial Electronics, 2024, 71(12): 15599-15609.
[28] Saltelli A. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models[M]. Hoboken, NJ: Wiley, 2004.
Impact of Chip Parameter Variability on the Thermal Safe Operating Area of Multi-Chip Parallel SiC MOSFETs
Abstract SiC MOSFET power modules typically utilize parallel chip configurations to meet high-current demands in power electronic systems.However, inherent variations in the fabrication process cause chip parameter variability, which, along with the asymmetric package parasitic, uneven thermal resistance, and cross-chip thermal coupling within conventional module designs, creates significant electro-thermal (ET) imbalance among paralleled chips. It leads to divergent operational boundaries under specific temperature constraints at the junction. This paper proposes a thermal safe operation area (TSOA) assessment methodology for multi-chip paralleled power modules, investigating the impact of chip parameter variability on the TSOA through Monte Carlo simulations. A solution to expand TSOA is devised.
Firstly, ET co-simulation, spanning from chip-level to system-level, is combined with an output current prediction model, defined as the output capacity when the junction temperature of the hottest chip reaches thermal constraints. A simplified EKV model and a 2D thermal network model are used to analyze the ET behavior of a multi-chip parallel power module. ET simulations of its application circuit (e.g., buck converter) under different output currents predict the junction temperature of each chip. Then, a four-parameter model is developed to describe the relationship between junction temperature and output current. This ET- simulation-based approach addresses the analytical challenges posed by the asymmetric package parasitic, uneven thermal resistance, and inter-chip thermal coupling. Compared to traditional stepwise calculation for output current limits, this method determines TSOA more efficiently with just three ET simulations. The ET model is validated by the double pulse test experiment, exhibiting a discrepancy of less than 9% in switching loss prediction for two paralleled chips. The output current prediction model is further verified by stepwise ET simulation, achieving a 1.5% error in output current boundary estimation.
Secondly, Monte Carlo (MC) simulations are employed to analyze the impact of chip parameter variability on TSOA under various thermal constraints, ranges, and switching frequencies. The analysis quantifies frequency-dependent sensitivity to parameter variations and suggests a solution to expand TSOA. MC simulations are conducted to identify a variation threshold that keeps the overall TSOA reduction rate (b) within an acceptable range, followed by chip binning based on parameter sensitivities to extend TSOA.
The key findings are as follows. (1) The b increases with low junction temperature limits and high input voltages. However, this effect weakens as thermal constraints are relaxed, showing negligible voltage dependence. (2)The influence of parameter variability on TSOA is frequency dependent. At 10 kHz switching frequencies, TSOA remains nearly unchanged from the baseline, with b increasing by only 0.6% and stabilizing at 1.89% as variation expands. In contrast, at 50 kHz switching frequencies, TSOA contracts significantly, with b rising to 6.84% when the variation range reaches 3s. (3) Parameter sensitivity shifts with frequency. The mean value of on-state resistance (Rds(on)) and transconductance (gfs) dominate at low frequencies. In contrast, the ranges of threshold voltage (Vth) and gate-source voltage (Vgs@Id_rating) become critical at high switching frequencies, where the current reaches the rated value in the transfer characteristics. (4)To extend TSOA, a two-step approach is proposed. First, Monte Carlo simulations determine the parameter variation threshold to maintain the overall TSOA reduction rate within an acceptable range, thereby guiding the selection of chips. Next, multi-objective optimization forms parallel chip groups, thereby extending the TSOA of multi-chip parallel power modules.
Keywords:SiC power module, SiC MOSFET, chip parameter variability, thermal safe operation area, Monte Calro simulation
中图分类号:TN386
DOI: 10.19595/j.cnki.1000-6753.tces.250175
北京市科技新星计划资助项目。
收稿日期 2025-01-30
改稿日期 2025-03-07
蒋馨玉 女,1994年生,博士研究生,研究方向为碳化硅器件建模及并联可靠性。
E-mail: jiangxinyu@ncepu.edu.cn
孙 鹏 男,1994年生,讲师,博士后,研究方向为大功率电力电子器件封装、测试与状态检测。
E-mail: sunpeng@ncepu.edu.cn(通信作者)
(编辑 陈 诚)