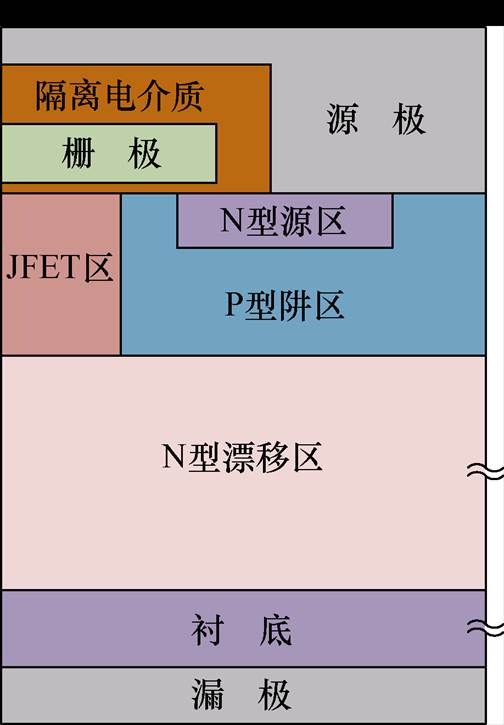
图1 国产6.5 kV SiC MOSFET元胞结构
Fig.1 Cell structure of the domestic 6.5 kV SiC MOSFET
摘要 碳化硅（SiC）MOSFET器件的短路耐受能力差是阻碍其广泛应用的关键难题，对于国产高压SiC MOSFET器件，其短路保护研发缺乏有力的技术、经验支撑。同时，缺乏快速、准确的仿真模型也是国产高压SiC MOSFET器件应用研发面临的核心问题之一。为此，该文提出一种适用于高压SiC MOSFET器件的、考虑器件实际物理特性的、可准确描述器件短路故障中电流、电压等外特性的行为模型。该行为模型针对高压SiC MOSFET的特点修正沟道电流模型中的电压，并基于元胞层面的电流路径对JFET区及漂移区电阻进行建模。该模型考虑了国产高压SiC MOSFET的实际器件设计、工艺等因素的影响，依据半导体、器件物理计算模型的关键参数，提升模型在短路故障仿真中的精度。并且，该文明确了模型所用参数的提取方法，其中关键参数获取自器件设计环节，建立起器件设计者与应用者之间的桥梁。最后，对国网智能电网研究院有限公司研制的6.5 kV/400 A SiC MOSFET器件开展短路测试实验，仿真结果与实验结果表现出较好的一致性，短路电流关键特征的相对误差小于2.5%，验证了该行为模型的准确性。
关键词：碳化硅MOSFET 高压功率器件 行为模型 短路故障 参数提取
以碳化硅（SiC）金属-氧化物-半导体场效应晶体管（MOSFET）为代表的宽禁带半导体器件具有开关速度快、工作温度高、漏电流小等优异特性[1-2]，其应用能够有效提升电力电子变换器的功率密度、工作效率和工作温度[3-7]，目前主要应用在电动汽车电机驱动、充电设备等中压、高功率密度的应用场景[8-12]。为拓展SiC器件在高压场景的应用，国网智能电网研究院有限公司成功研制国产6.5 kV SiC MOSFET模块，在智能电网、高电压等级电能转换、交直流配电网等领域具有广阔的应用前景[13]。
当前，阻碍SiC MOSFET应用的一个关键难题是其短路耐受能力远低于传统的硅（Si）功率器件[14]，一旦器件在电网应用中出现短路故障，将对整个设备产生严重损坏，甚至威胁输电、配电系统的运行稳定性，造成重大经济损失。但是，现有的SiC MOSFET短路保护通常面向1.7 kV以下电压等级的器件[15-16]。并且，传统的退饱和检测方法对SiC MOSFET无法实现绝对可靠的保护[17]。同时，由于缺乏针对高压器件的短路特性的测试数据，选用其他短路保护方式将面临保护阈值难以确定的问题。高压器件短路的故障保护电路设计缺乏有力的技术、经验支撑，这阻碍了高压SiC器件的短路保护研发。
在SiC MOSFET驱动、短路保护电路的设计中，基于器件行为模型的电路仿真是提升研发效率的有效方法[18]。但在国产高压SiC器件的驱动、保护电路等配套设备研发以及电力电子变换器设计等具体应用中，缺乏可用于电路参数设计的准确、快速的仿真模型是研究过程中遇到的核心难题之一。传统的SiC MOSFET行为模型注重拟合器件的转移特性、输出特性等静态参数以及结电容、反并联二极管等影响开关暂态的参数[19-20]，难以准确地描述器件在短路故障状态下的电压、电流等外特性。器件设计者在元胞设计中使用的半导体有限元仿真是模拟SiC MOSFET的短路故障外特性的常用方法[21-22]，但是有限元仿真速度极慢，且要求明确器件的元胞结构、掺杂等设计参数，以及考虑器件中复杂的物理效应，并不适合于辅助研究者进行电路设计。目前，器件设计者也难以根据现有的半导体级器件设计方便地向使用者提供可应用于电路仿真的模型。因此，为准确、快速地仿真6.5 kV SiC MOSFET的短路故障，支撑国产高压SiC器件短路保护电路设计，有必要以行为模型的形式对其进行描述。
截至目前，已经有许多研究者开始关注SiC MOSFET短路故障的行为建模[23-27]。文献[23-24]提出的短路模型采用公式拟合的方法考虑SiC MOSFET发生短路故障时漏极电流随结温的变化，模拟器件在短路故障中的电流外特性。拟合的方法无法清晰地描述器件短路故障中的实际物理过程，缺乏物理意义，通用性较差，将导致模型的仿真精度在不同工况的仿真中有所下降。文献[25]的短路行为建模关注SiC MOSFET短路故障中漏极电流上升初期的、受寄生参数影响的暂态电压、电流波形变化，无法准确地反映器件在短路故障中的电流变化。文献[26]提出了一种考虑物理的SiC MOSFET模型，通过对载流子迁移率、SiC/SiO2界面电荷的物理建模以计算沟道电流在不同结温下的变化，达到仿真器件短路行为的效果。该模型忽略了沟道电压的定义和通态电阻的建模，难以准确描述高压SiC器件的真实物理特性；虽然该模型具备一定的物理意义，但其中的部分核心参数（如阈值电压、掺杂浓度、界面态分布等）提取方法不明确，缺乏理论或数据支撑，需要经过大量调试。文献[27]提出一种能够同时涵盖SiC MOSFET短路及雪崩击穿故障的行为模型，其架构考虑了器件的故障演化底层物理过程，但其中的关键模型均通过公式拟合得到，不具备任何物理意义，同样削弱了模型的通用性。
目前的SiC MOSFET短路故障行为模型存在以下缺点：①针对1.7 kV及以下电压等级的SiC MOSFET开展建模、验证，其模型并不适用于高压器件；②大多基于公式拟合构建，缺乏物理基础，通用性较差，降低了模型在不同工况下的仿真准确性；③模型关键参数的提取方法不明确，需要依靠繁复的、缺乏物理根据的试错来调试模型关键参数，保证仿真精度。为克服上述问题，本文针对高压SiC MOSFET提出了一种基于器件底层物理机理的短路故障行为模型。该模型的主要优点如下：①相较于传统的1.7 kV及以下电压等级的SiC MOSFET模型，本文模型依据器件的真实元胞结构和元胞层面的电流路径引入JFET区、漂移区电阻模型，并对沟道电流公式的参数选取进行必要修正，使模型更加贴合高压器件的特征；②依据4H-SiC的材料性质以及SiC MOSFET中SiC/SiO2界面的实际条件和限制，计算本征载流子浓度、阈值电压和考虑多物理效应的沟道电子迁移率等关键参数，有助于准确仿真短路故障中电压、电流外特性；③本文明确了模型中关键参数的提取方法，其大多来自于材料特性和器件设计、工艺相关参数，均具有较强的物理依据和数据支撑，建立起器件设计者与应用研究者之间的桥梁，有助于国产器件的应用研发。本文对国网智能电网研究院有限公司生产的6.5 kV/400 A SiC MOSFET器件进行短路测试实验，并与仿真结果进行比对，验证了本文所提出短路故障行为模型的准确性。同时将本文模型与低压SiC MOSFET模型进行对比，验证了本文针对高压器件建立模型的必要性。
图1展示了国网智能电网研究院有限公司6.5 kV SiC MOSFET芯片的元胞结构示意图[21]，本文短路行为模型基于该器件的真实元胞结构提出，其电路如图2所示。该模型由以下五部分构成：①描述沟道电流的受控电流源ICH；②描述高温下器件漏电流的受控电流源IL；③对应元胞内寄生体二极管的反并联二极管VD；④概括器件栅、源、漏三级间寄生电容的CGS、CGD、CDS；⑤对应元胞内JFET区、漂移区电阻的漏极电阻RD。同时，为仿真故障过程中器件的暂态温度变化，模型引入热阻、热容网络模型计算器件结温。图2中，UDS为漏源电压，UCH为沟道电压，ID为漏极电流。
图1 国产6.5 kV SiC MOSFET元胞结构
Fig.1 Cell structure of the domestic 6.5 kV SiC MOSFET
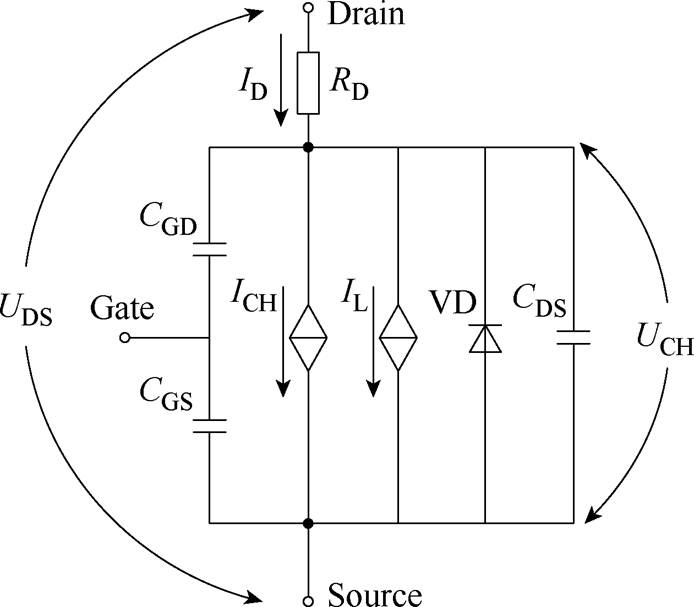
图2 本文短路行为模型电路
Fig.2 Circuit diagram of the proposed model
在1.7 kV及以下电压等级的SiC MOSFET中，由于N漂移区电阻及JFET区电阻对器件总导通电阻的占比较小，因此在器件建模中为使模型尽量简化，常将这部分电阻取为拟合所得的定值[28]，忽略其温度特性，甚至将该电阻直接忽略[29]。而在如图1所示6.5 kV的高压SiC MOSFET器件微观元胞结构中，外延层厚度大、掺杂浓度低，使得沟道电阻在总导通电阻中的占比相较1.7 kV及更低电压等级的器件有显著降低，漂移区电阻、JFET区电阻成为导通电阻的最主要组成部分。它们在高压器件总导通电阻中的占比可达50%甚至更高[30]，成为影响器件行为的关键因素。同时，漂移区电阻及JFET区电阻存在随温度变化的特性，在发生短路故障、结温陡增的工况下对器件特性的影响尤为明显。因此在高压器件的建模中，对器件漏极电阻RD的详细建模不可或缺。同时，RD还会影响沟道电流的计算，将在沟道电流、漏电流建模部分详细解释。
本节以下内容将逐一阐述短路行为模型中结温T、结电容CGS、CGD、CDS、体二极管VD、沟道电流ICH、漏电流IL、漏极电阻RD建模计算的详细方法。其中，T、CGS、CGD、CDS、VD的建模与传统1.7 kV及以下电压等级的SiC MOSFET器件模型基本一致；ICH、IL、RD建模则根据高压SiC MOSFET器件的微观结构特征特性进行了针对性优化建模。
当短路故障发生时，功率器件在高压、大电流应力下产生剧烈的功率耗散，导致短时间内的结温陡增，这是影响器件故障外特性的关键因素。为模拟故障中器件的结温变化，向模型其他部分的计算实时提供结温数据，本文模型选用5阶Foster热网络计算暂态结温T，如图3所示。
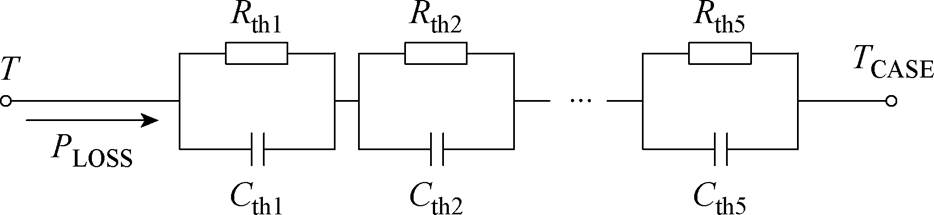
图3 5阶Foster热网络
Fig.3 5-orderFoster thermal network
热网络模型两端分别为器件的结温T与壳温TCASE，以实时的耗散功率PLOSS=UDSID作为输入。在单脉冲方波PLOSS激励下，该热网络的瞬态热阻抗Zth可用热网络阶数n、热阻Rthi、热容Cthi以及脉冲时间tp表示[26]为
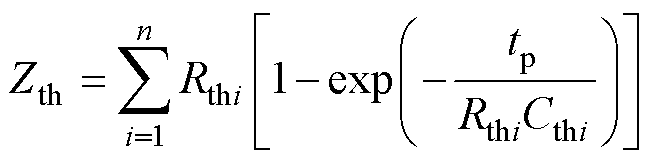（1）
使用式（1）拟合器件实测的单脉冲瞬态热阻抗ZthJC曲线，即可方便地提取Foster热网络模型中各热阻、热容值。
为模拟SiC MOSFET在开通、关断过程中的暂态特性，本文选用公式拟合的方法对高压SiC MOSFET的栅、源、漏三极间的寄生结电容CGS、CGD、CDS进行建模[28]。
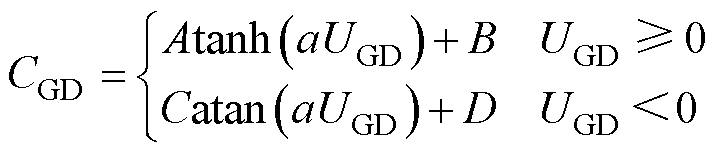（2）
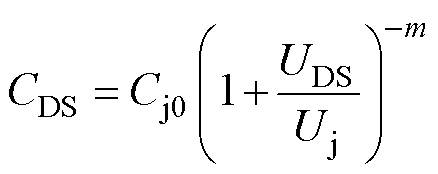（3）
式中，A、B、C、D、a、Cj0、Uj和m为曲线拟合所得参数。
在元胞层面，栅极和源极之间为厚度不变、性质稳定的隔离电介质层，因此在本文模型中忽略CGS的变化，将其简单建模为定值电容，其电容值可通过拟合输入电容曲线得到。
为反映实际器件的寄生体二极管特性，体二极管模型也是短路行为模型中不可或缺的一部分。但由于SiC MOSFET在短路故障中通常工作在正向导通状态，寄生体二极管对器件的短路特性影响较小，因此在本文模型中寄生体二极管使用简单的理想二极管进行建模。
后续的模型验证表明，CGS和VD的简化建模并未对本文短路行为模型描述6.5 kV SiC MOSFET短路故障外特性的准确程度产生比较大的影响。
本文短路故障行为模型中，SiC MOSFET的沟道电流ICH表示[31]为
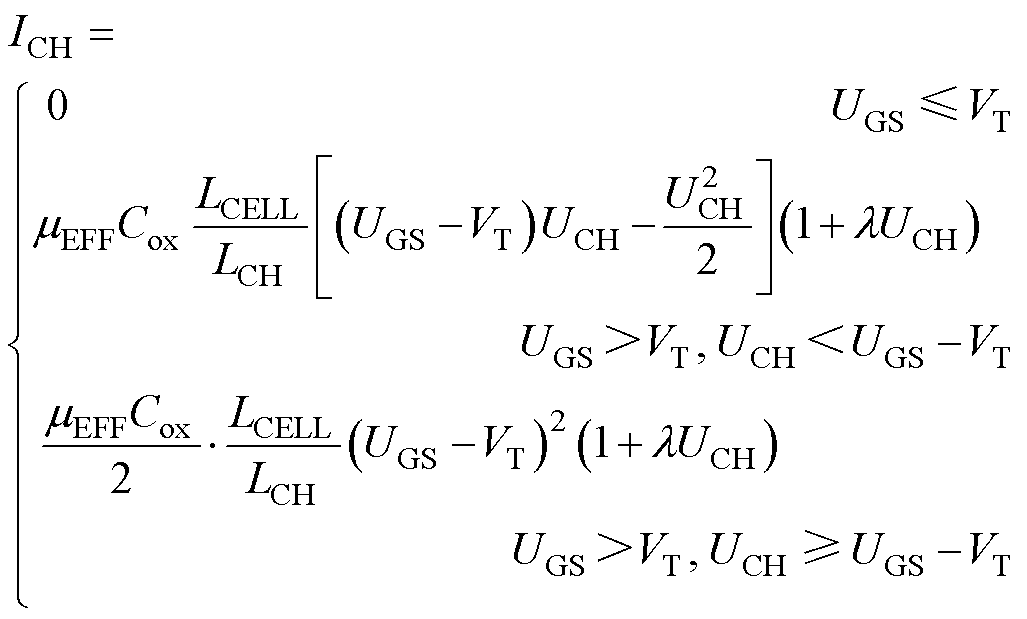（4）
式中，UGS为栅源电压；Cox为单位面积的栅氧化层电容，Cox=eSiC/tox；eSiC为4H-SiC材料的介电常数；tox为栅氧化层厚度；LCELL为条状元胞总长度，需要考虑不同电流等级器件的元胞并联；LCH为沟道长度；l 为器件的沟道长度调制系数；以上参数均为材料参数或拟合参数，UGS和UCH在建模时二者可直接根据电路模型的节点电压读取，其他参数提取方法见2.1节。mEFF为反型层的有效电子迁移率，VT为阈值电压，mEFF和VT均为决定MOSFET短路故障中沟道电流变化的关键参数，需根据物理模型做进一步计算，其计算方法将在2.2.2节中详细说明。
该公式是参考N沟道平面型MOSFET器件通过物理推导得到，同时考虑器件的沟道长度调制效应[31]。当短路故障发生时，器件的漏、源电压通常很高，故一般工作在饱和区，可用式（4）中第三式描述。
在1.7 kV及以下电压等级的MOSFET器件模型中，沟道电压UCH常用漏源电压UDS替代[26]。这是因为电压等级较低时SiC MOSFET沟道电阻在总导通电阻中占比很大，UCH仅略小于UDS，因此用UDS替代UCH产生的误差较小。然而在高压SiC器件中，更高的耐压意味着更低的外延层掺杂浓度和更厚的外延层厚度，即更大的外延层电阻[30]，也使得器件导通时UCH将远小于UDS。因此，本文短路模型考虑RD在UDS中的分压，将UDS修正为沟道电压UCH，令其更加符合高压器件的实际特征。
当结温较低时，SiC MOSFET的漏电流IL远小于流经器件的总电流ID，此时IL可以忽略。但在短路故障中，器件的结温可在极短时间内陡增至接近甚至超过1 000 K的极高值，此工况下的IL值不满足远小于ID的条件。因此，在器件短路故障特性的建模中，漏电流IL是一个不可忽略的部分。
在SiC MOSFET，漏电流通常由热产生（thermal generation）漏电流ITH、扩散（diffusion）漏电流IDIFF和雪崩（avalanche）漏电流IAV三部分组成[26, 32]，分别对应三种不同的漏电流产生机理。其中，ITH在IL中的占比远大于另外两类漏电流，所以本模型仅考虑ITH作为漏电流，则IL可表示[31]为
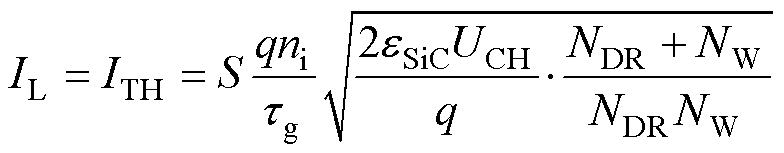（5）
式中，S为产生漏电流的PN结的等效面积；q为电子电荷量；tg为SiC的SRH复合（Shockley-Read-Hall Recombination）中的载流子寿命，属材料参数；ni为本征载流子浓度，是影响器件高温特性的关键物理参数之一，需根据物理模型做进一步计算，其建模计算方法将于2.2节详细阐述；NDR为漂移区掺杂浓度；NW为沟道净掺杂浓度。
尽管P型阱区和N型漂移区形成的从沟道到体二极管的整个PN结均产生漏电流，但文献[30]中的有限元仿真表明，在SiC MOSFET短路故障中沟道位置的漏电流密度远大于该PN结其他位置的漏电流密度[33]。据此，本文在计算漏电流时仅考虑流经沟道的漏电流，式（5）中以沟道电压UCH作为PN结两端的电压，以沟道净掺杂浓度NW=NA-NDR和漂移区掺杂浓度NDR表示PN结两侧的掺杂浓度，其中NA为沟道等效受主杂质掺杂浓度。上述掺杂浓度NDR、NW和PN结等效面积S均属器件设计与工艺参数，提取方法见2.1节。
在本文的短路行为模型中，以漏极电阻RD表示SiC MOSFET器件的导通电阻中除沟道电阻以外的部分，通常包括：衬底电阻RSUB、漂移区电阻RDR、JFET区电阻RJFET、源区电阻RS、接触电阻RC。由于衬底和源区均为高掺杂区，RSUB和RS很小，同时因为良好的欧姆接触工艺，RC同样较小。在6.5 kV SiC MOSFET中，上述三者均远小于RJFET和RDR，因此在本文模型中，忽略RSUB、RS和RC，以下对RJFET和RDR进行建模。
1.5.1 JFET区电阻RJFET
图4展示了高压SiC MOSFET正向导通时的元胞级电流路径示意图，图中JFET区的电流路径边界为P型阱区与JFET区之间PN结空间电荷区（Space Charge Region, SCR）的边界。为了降低JFET区电阻，在高压器件的实际工艺中通常会采用JFET区离子注入的方式提高JFET区掺杂浓度[21]。但高压SiC MOSFET的低外延层掺杂浓度使得P型阱区结深较大，形成了狭长的JFET区，导致JFET离子注入工艺增大掺杂浓度的效果无法作用于整个JFET区，仅其上部掺杂浓度有所增大。空间电荷区宽度因掺杂浓度的增大而变窄，令JFET区呈现“上宽下窄”的形貌。这是高压SiC MOSFET正向导通电流路径的特征，在1.7 kV及以下器件中几乎不存在该效应。
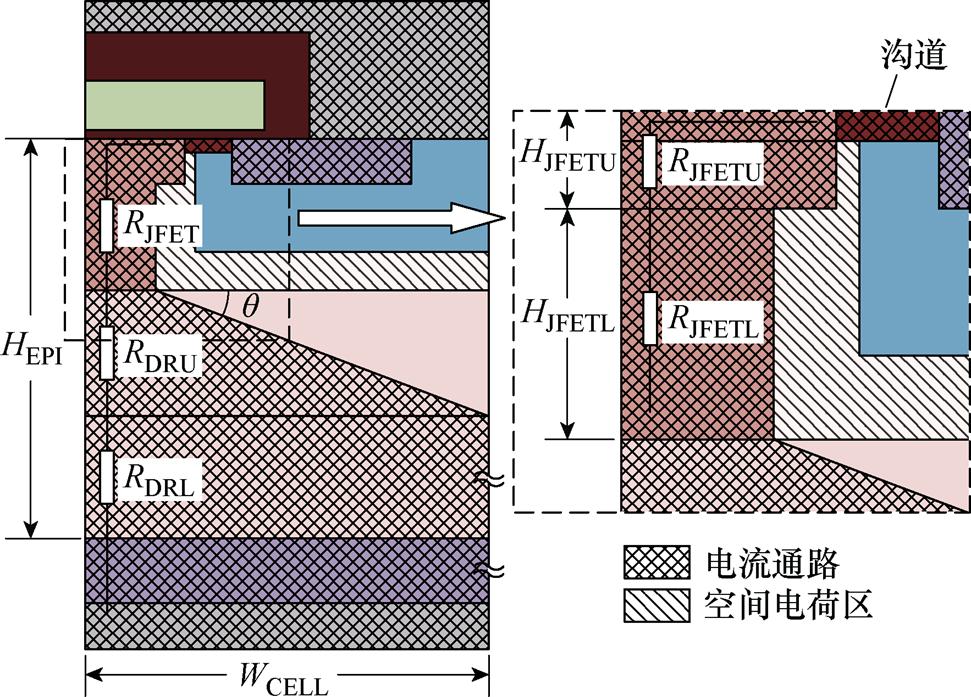
图4 高压SiC MOSFET正向导通时元胞内电流路径
Fig.4 The cell-level current path of high-voltage SiC MOSFET in forward conduction mode
据此，可将JFET区分为以下两部分进行电阻建模，分别定义为上方的JFET离子注入区电阻RJFETU以及下方的漂移层掺杂区电阻RJFETL。两电阻均可用以下公式进行计算。
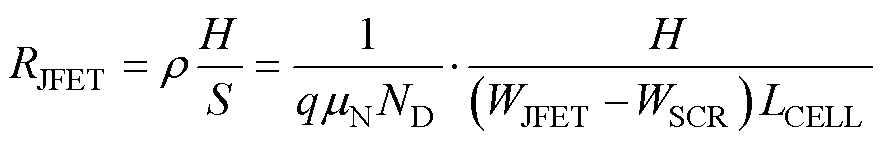（6）
式中，mN为JFET区的电子迁移率，是影响电阻温度特性的关键参数之一，需根据物理模型做进一步计算，详细计算方法见2.2.3节；WJFET为JFET区的设计宽度；LCELL为条状元胞总长度；WSCR为空间电荷区宽度，对于RJFETU和RJFETL分别记为WSCRU和WSCRL，计算公式[31]为
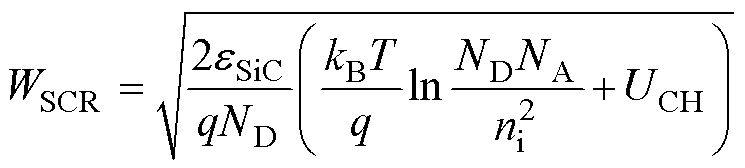（7）
H为对应部分JFET区的深度，对于RJFETU和RJFETL分别记为HJFETU和HJFETL，HJFETU可取JFET离子注入峰值掺杂的对应深度，HJFETL则可结合P型阱区的结深和该区域空间电荷区宽度进行计算
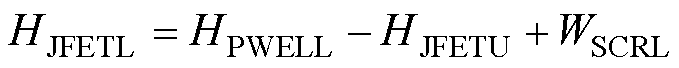（8）
ND为对应JFET区域内的掺杂浓度，对于RJFETU可取JFET离子注入掺杂浓度的均值NJFET，在RJFETL中等于漂移区掺杂浓度NDR；NA为P型阱区对应位置的掺杂浓度，对于RJFETU和RJFETL可分别取NAU和NAL，可根据P型阱区离子注入掺杂分布获取近似值。此处深度HJFETU、HJFETL和掺杂浓度NJFET、NAU、NAL均为器件设计与工艺参数，提取方法见2.1节。
1.5.2 漂移区电阻RDR
图4中，在N型漂移区的上部，电流受P型阱区与漂移区之间PN结的空间电荷区阻挡，导致电流从漂移区流入JFET区时形成可近似为梯形的电流扩散区，电流扩散面积随距离JFET区底部深度增加而线性增大，直至电流扩散至整个元胞区域。因此，亦可将漂移区电阻RDR分为两部分进行建模，分别为漂移区上部电流扩散区的电阻RDRU和漂移区下部电流均匀分布区域的电阻RDRL。
在电流扩散区，假设其边界与P型阱区底部空间电荷区边界的夹角q 不变，则RDRU可表示为
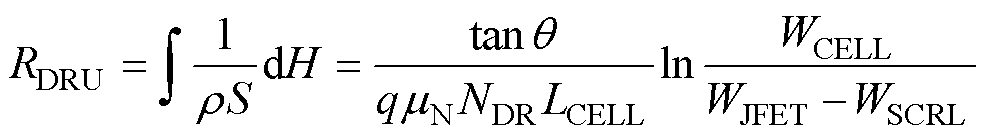（9）
式中，mN为漂移区的电子迁移率；WCELL为元胞宽度。RDRL则表示为
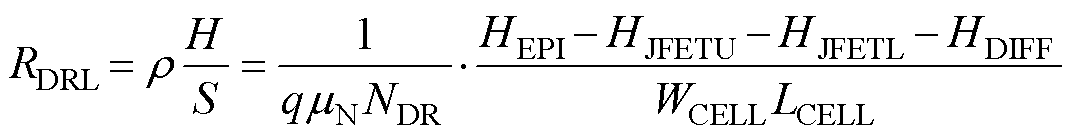（10）
式中，HEPI为SiC MOSFET的外延层厚度；HDIFF为电流扩散区深度。
综上所述，在本文6.5 kV SiC MOSFET短路行为模型中，漏极电阻RD可表示为
（11）
本节所述热网络模型、式（2）～式（11）所计算的结电容CGS、CGD、CDS、体二极管VD、沟道电流ICH、漏电流IL、漏极电阻RD共同构成本文的短路行为模型，能够在电路仿真中模拟高压、中压SiC MOSFET在短路故障中的电压、电流行为。其中，部分物理参数如本征载流子浓度ni、阈值电压VT、载流子迁移率等还需根据2.2节式（12）～式（26）进一步建模计算，以更加准确地模拟器件在故障中的特性。
本文短路故障行为模型基于SiC MOSFET在短路故障中的元胞级物理过程建立。但为提升电流等级，功率器件通常由多元胞并联构成芯片，多功率芯片并联又可以组合为功率模块。因此对于大电流等级的功率器件，本文模型在ICH、IL的模型中引入考虑元胞并联的条状元胞总长度LCELL，以及产生漏电流的PN结的总等效面积S使模型的电压、电流外特性与实际器件相符。利用不同建模对象的芯片有源区总面积除以元胞宽度，即可计算得到LCELL，LCELL乘以单一条状元胞中产生漏电流的PN结的等效宽度，即可得到S。由于芯片之间的特性差异，芯片并联后的通流能力可能小于各芯片通流能力之和，上述计算结果与实际器件的通流能力可能存在些许差异，根据器件实际通流能力在计算值的基础上进行微调即可。
模型中涉及的物理常数、材料参数由材料特性决定，对于不同的SiC MOSFET器件可以通用；其中的拟合参数和器件设计、工艺参数可从建模对象进行提取，将在第2.1节中详细阐述。
为提升仿真精度以及模型通用性，本文短路行为模型考虑了许多与国产6.5 kV SiC MOSFET的材料性质、器件设计、制造工艺相关的物理因素，这必将向模型中引入更多种类的参数。并且，这些参数涉及器件设计、制造、应用各环节，参数类型多且复杂。除上述直接获取的参数，本文行为模型还涉及部分难以直接测量，但对SiC MOSFET在短路故障中结温陡增条件下的行为影响巨大的关键物理参数，如本征载流子浓度ni、阈值电压VT、载流子迁移率mEFF、mN等，需要依据半导体物理原理对它们进行建模计算。
据此，本文模型中涉及的参数可分为以下五类：物理常数，材料参数，器件设计、工艺参数，拟合参数，关键物理参数。本节将介绍前四类参数的提取方法，并依据半导体物理原理介绍如何根据前四类参数对ni、VT、mEFF、mN等关键物理参数进行建模计算。
1）物理常数：模型使用了玻耳兹曼常数kB、普朗克常数h等常见的物理常数，其参数值获取十分容易。本文模型中的物理常数见表1。
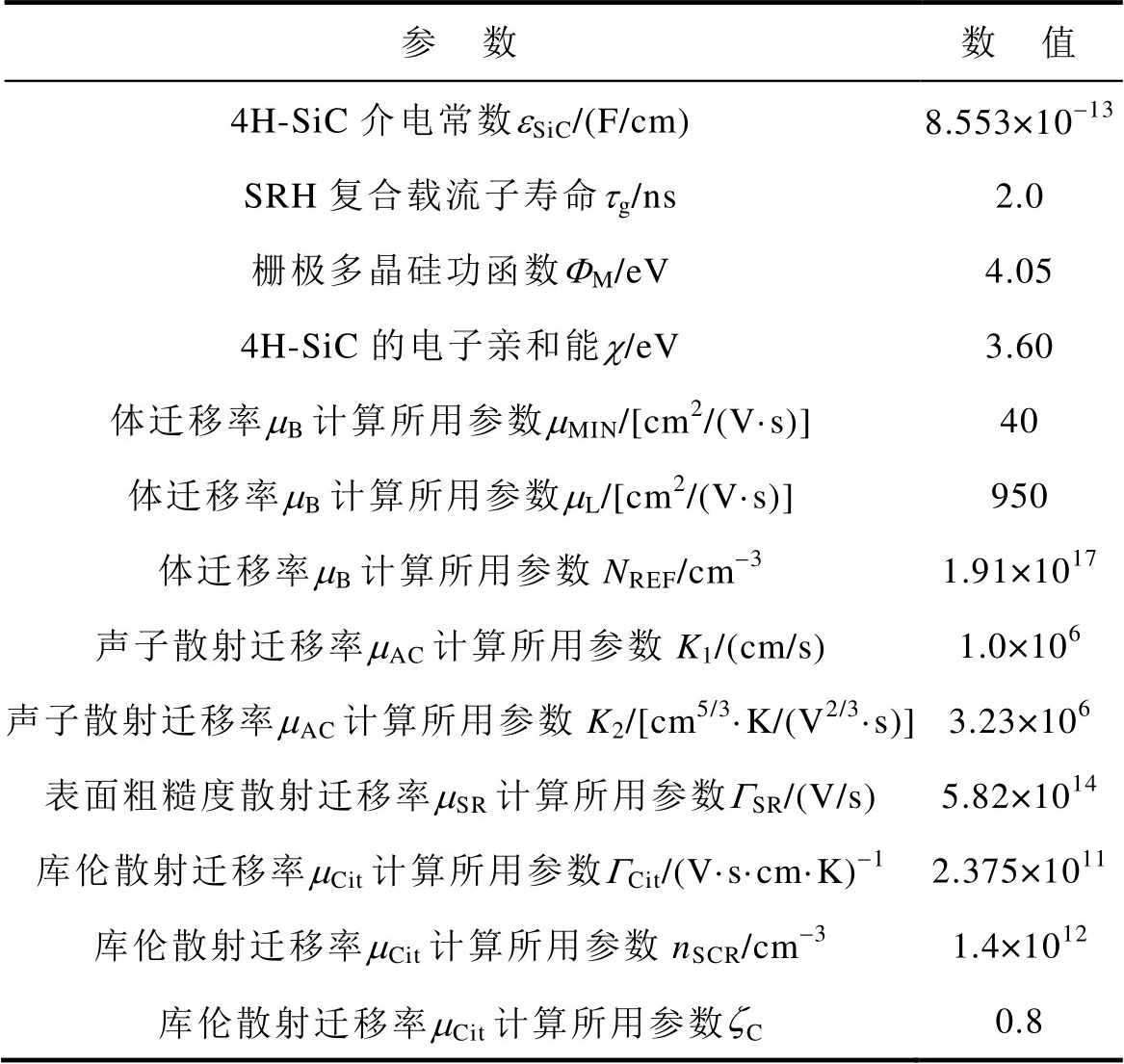
2）材料参数：用于描述4H-SiC材料的本征物理属性、载流子迁移率等性质的参数。其中，介电常数eSiC、电子亲和能c 等材料的本征物理属性可直接查阅相关材料参数手册得到[34]。在第1节中，载流子迁移率的物理模型引入了许多常数、系数以准确描述导致载流子迁移率退化的各项物理因素。这些参数均通过拟合4H-SiC材料或其反型层载流子迁移率测定实验的数据获取，可将其视为材料特性，在不同的SiC MOSFET器件中具有较好的通用性，因此选择常用值即可实现对不同器件中载流子迁移率的良好模拟。这些参数的常用值可从相关文献中直接获取。本文用到的材料特性参数见表2。
表1 本文模型中的物理常数
Tab.1 Physical constants in the proposed model
参 数数 值 电子电荷量q/C1.602×10-19 玻耳兹曼常数kB/(J/K)1.381×10-23 电子质量me/kg9.1×10-31 普朗克常数h/(kg·cm2/s)6.626×10-30
表2 本文模型中的材料参数
Tab.2 Material parameters in the proposed model
参 数数 值 4H-SiC介电常数eSiC/(F/cm)8.553×10-13 SRH复合载流子寿命tg/ns2.0 栅极多晶硅功函数FM/eV4.05 4H-SiC的电子亲和能c/eV3.60 体迁移率mB计算所用参数mMIN/[cm2/(V·s)]40 体迁移率mB计算所用参数mL/[cm2/(V·s)]950 体迁移率mB计算所用参数NREF/cm-31.91×1017 声子散射迁移率mAC计算所用参数K1/(cm/s)1.0×106 声子散射迁移率mAC计算所用参数K2/[cm5/3·K/(V2/3·s)]3.23×106 表面粗糙度散射迁移率mSR计算所用参数GSR/(V/s)5.82×1014 库伦散射迁移率mCit计算所用参数GCit/(V·s·cm·K)-12.375×1011 库伦散射迁移率mCit计算所用参数nSCR/cm-31.4×1012 库伦散射迁移率mCit计算所用参数zC0.8
3）器件设计、工艺参数：不同SiC MOSFET之间的主要差异在于元胞层面的各区域宽度、薄厚、掺杂浓度和芯片层面的元胞形貌、终端结构、有源区面积等设计不同，以及加工工艺中存在的工艺偏差。为准确描述SiC MOSFET的短路故障行为，需要对上述器件的设计、工艺参数进行提取。上文对模型的阐述中已经详细介绍了各参数的含义及其对应元胞内的区域或位点。在器件的设计研发阶段，元胞层级的半导体有限元仿真和针对部分设计参数、工艺参数的实验测定是必要环节。基于这些参数模型能够一定程度上反映器件的底层工作原理及器件设计，因此，该模型能够建立起器件设计者与应用研究者之间的桥梁。本文所使用的器件设计、工艺参数均来自器件设计者提供的元胞有限元仿真模型及实验测试结果中获取的实际值或近似值。然而，与器件的设计、工艺相关的许多参数均为器件设计方的核心技术细节，对于器件使用者、应用研究者而言获取难度较大，且由于对半导体、器件物理原理的不了解，器件使用者与应用者难以对这些参数进行合理调试，这是本文模型存在的局限性之一。
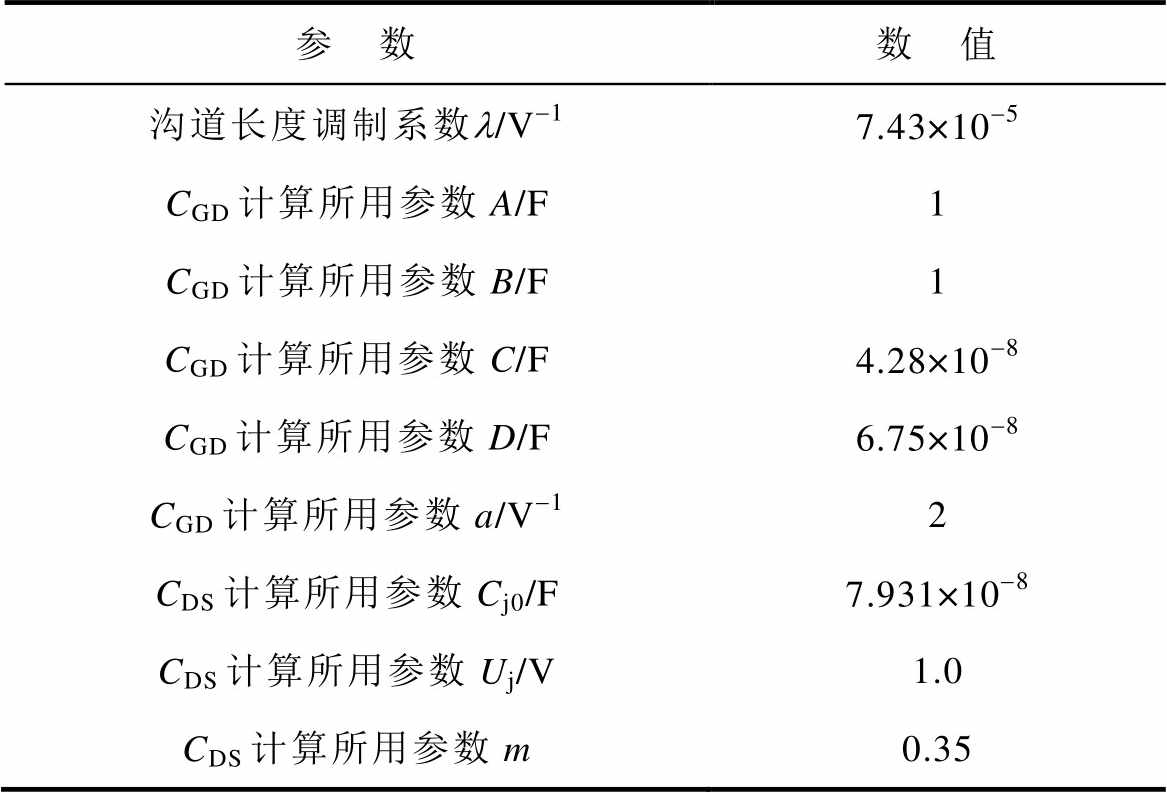
4）拟合参数：模型的一些部分尽管有其内涵的物理意义，但对其进行物理建模过于繁琐，会降低模型的运算速度和收敛性，选用足以准确描述其特性的公式对实验测定结果进行拟合或近似是更为简便、可行的方法。本文模型中所得拟合参数见表3。
表3 本文模型中的拟合参数
Tab.3 Fitting parameters in the proposed model
参 数数 值 沟道长度调制系数l/V-17.43×10-5 CGD计算所用参数A/F1 CGD计算所用参数B/F1 CGD计算所用参数C/F4.28×10-8 CGD计算所用参数D/F6.75×10-8 CGD计算所用参数a/V-12 CDS计算所用参数Cj0/F7.931×10-8 CDS计算所用参数Uj/V1.0 CDS计算所用参数m0.35
同时，本文模型采用1.1节中所述方法进行结温计算，用公式拟合国网智能电网研究院有限公司研制的6.5 kV/400 A SiC MOSFET器件的实测单脉冲瞬态热阻抗曲线，得到5阶热网络的热阻、热容值见表4。
表4 本文模型采用的热网络参数
Tab.4 Parameters of the thermal network used in the proposed model
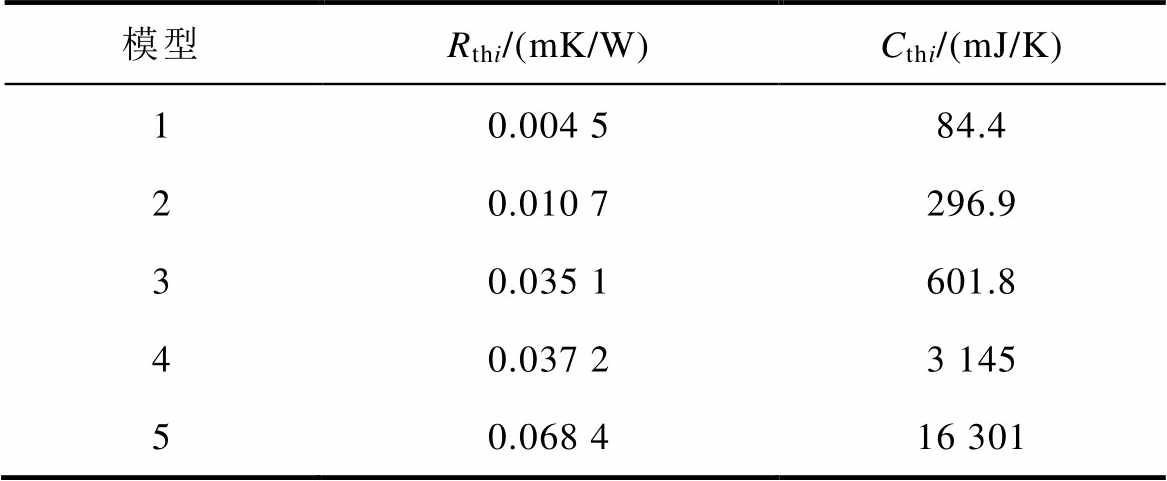
模型Rthi/(mK/W)Cthi/(mJ/K) 10.004 584.4 20.010 7296.9 30.035 1601.8 40.037 23 145 50.068 416 301
2.2.1 本征载流子浓度
本征载流子浓度是决定半导体材料高温特性的根源之一，是计算SiC MOSFET短路行为的核心参数。本文根据定义公式计算本征载流子浓度，可表示[31]为
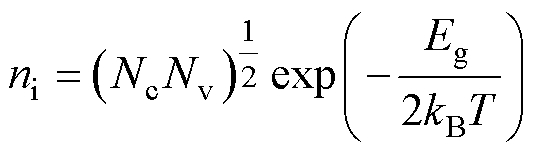（12）
式中，T为器件结温；Eg为禁带宽度[34]，即
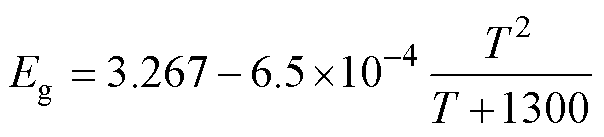（13）
式中，Nc、Nv分别为导带、价带的有效状态密度，计算公式[31]为
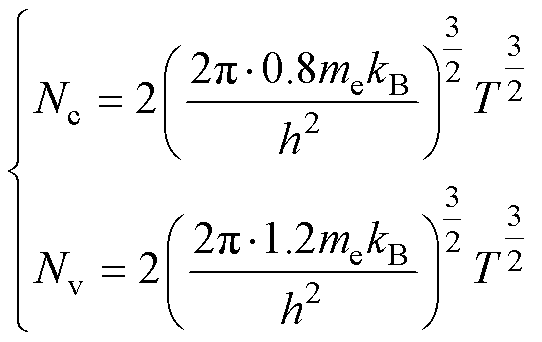（14）
式中，me为电子质量。
2.2.2 阈值电压
阈值电压是SiC MOSFET的温敏电气量，是影响器件高温特性的关键参数之一。在本文模型中，阈值电压VT的建模考虑了SiC MOSFET的实际沟道掺杂、SiC/SiO2界面固定电荷、界面陷阱电荷等物理因素，同时考虑对平带电压项中表面势的修正，将阈值电压的定义式表示[35]为
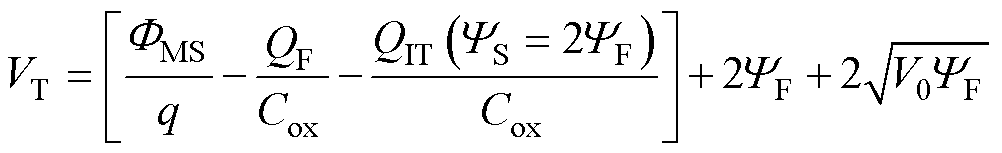（15）
式中，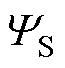
为沟道处SiC/SiO2界面处表面势；QF为栅氧化层固定电荷密度；QIT为界面陷阱电荷密度，是决定VT大小及其高温特性的关键参数，对mEFF同样存在显著影响，本文模型参考6.5 kV SiC MOSFET的实际界面特性对QIT进行建模，其推导、计算过程详见附录式（A17）～式（A25）；FMS为栅极选用的N型简并掺杂多晶硅与P型4H-SiC材料之间的功函数差，可用其定义计算公式[35]为
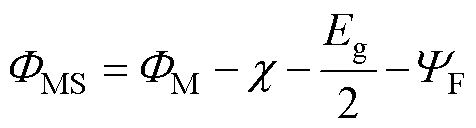（16）
式中，FM为栅极所使用的N型简并掺杂多晶硅的功函数；c 为4H-SiC材料的电子亲和能；YF为沟道处的费米势[31]，即
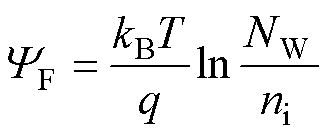（17）
V0为一个与材料性质、器件设计相关的常数[35]，表示为
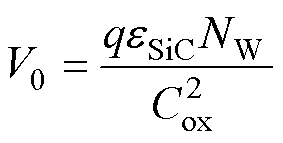（18）
2.2.3 载流子迁移率
载流子迁移率是决定半导体导电能力、性质的核心物理量，它也是影响SiC MOSFET高温性质，特别是导电沟道在高温下的导电能力的关键因素。在本文模型中，载流子迁移率是沟道电流ICH、漏极电阻RD的建模计算中的重要参数。但SiC MOSFET中的载流子迁移率受多种物理机制耦合影响[35]，简单的公式拟合难以对其进行准确计算。因此，为仿真6.5 kV SiC MOSFET的短路行为，对载流子迁移率的物理建模必不可少。
通常受多种物理机制耦合影响的总载流子迁移率可表示[31]为
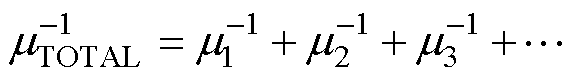（19）
式中，mTOTAL为考虑多种物理因素的总载流子迁移率；m1、m2、m3等为单物理因素影响下的载流子迁移率。在SiC MOSFET中，通常考虑四种载流子迁移率[26, 35-36]：体迁移率mB、声子（Acoustic phonon）散射迁移率mAC、表面粗糙度（Surface roughness）散射迁移率mSR、库伦（Columbic）散射迁移率mCit，分别对应不同的物理机制导致的载流子迁移率退化。
体迁移率mB表征材料内部自由载流子的迁移率，同时考虑电离杂质散射，即掺杂浓度增大导致载流子迁移率退化的物理效应，可表示[37]为
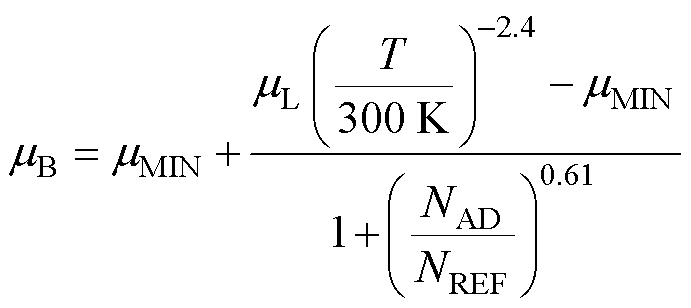（20）
式中，mMIN和NREF为考虑高掺杂下载流子迁移率退化引入的参数；mL为低掺杂下300 K时的载流子迁移率；NAD为对应区域施主、受主杂质掺杂浓度之和，在沟道处可取NAD=NA+NDR。
声子散射迁移率mAC表征SiC/SiO2界面声子散射，即电子受表面声子影响发生偏转导致的载流子迁移率退化，可表示[26, 35, 38]为
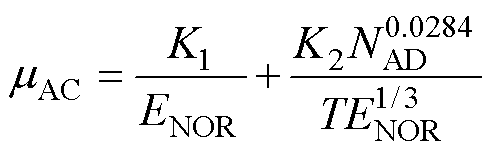（21）
式中，K1、K2为根据载流子迁移率测定实验结果进行理论拟合估算的参数，本文模型中选择其常用值；ENOR为沟道处垂直于SiC/SiO2界面的电场强度，可用电荷叠层模型（Charge sheet model）法计算，其详细推导过程见附录式（A1）～式（A16）。
表面粗糙度散射表征载流子受SiC/SiO2界面处的结构缺陷影响发生偏转导致的载流子迁移率退化，其一般形式[39-40]为
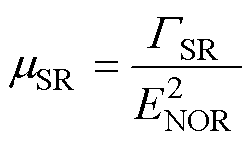（22）
式中，GSR为根据载流子迁移率测定实验结果获取的拟合参数，在本文模型计算中选用其常用值。
库伦散射迁移率表征SiC/SiO2界面库伦散射，即载流子受界面处固定电荷、界面陷阱电荷等带电中心的影响发生偏转导致的载流子迁移率退化，表达式[41-42]为
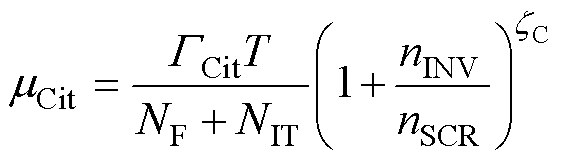（23）
式中，NF为SiC/SiO2界面固定电荷密度，由栅氧化层制造工艺决定；NIT为界面陷阱电荷密度，是限制SiC MOSFET器件沟道载流子迁移率的关键因素，其推导过程在附录中给出；GCit为与材料性质相关的常数，其计算公式在文献[41]中给出；nINV为反型层电子密度，同样可通过电荷叠层模型求解，其推导过程见附录式（A1）～式（A16）；nSCR和zC为根据载流子迁移率测定实验结果得到的拟合参数。
由于当前绝大多数SiC MOSFET为N沟道增强型，空穴几乎不参与器件的导电行为，此处仅考虑电子迁移率，空穴迁移率在模型中并未涉及。本文模型中，ICH和RD建模均用到载流子迁移率参数，但因其对应元胞内的位置不同，需考虑的物理因素也有所不同。ICH模型在元胞内对应沟道处的SiC/SiO2界面，受SiC MOSFET制造中刻蚀、热氧化等工艺当前工艺水平的限制，SiC/SiO2界面质量较差，表面粗糙度散射、声子散射以及库伦散射效应均非常显著，因此沟道反型层的载流子迁移率mINV可表示为
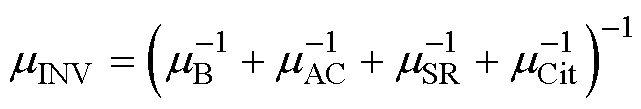（24）
由于mINV大于式（1）中使用的有效迁移率mEFF，且二者强相关[35-36, 38]，本文模型采用近似的方法将mEFF近似为mINV的倍数，即
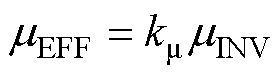（25）
式中，km 为沟道载流子迁移率近似系数，0＜km ＜1。RD模型在元胞内的对应位置是漂移层和JFET区，此处位于SiC材料内部，仅需考虑体迁移率，因此RD计算中采用的电子迁移率mN与mB相等，即
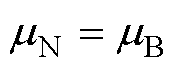（26）
同时应注意，4H-SiC的载流子迁移率存在各向异性。沟道电流近似垂直于4H-SiC晶格c轴，而流经漂移区和JFET区的电流近似平行于c轴，二者沿不同晶向流动。因此在ICH和RD建模中，载流子迁移率计算中的参数选取应考虑各向异性带来的参数值差异。
本文在Matlab/Simulink仿真平台建立6.5 kV SiC MOSFET短路行为模型并搭建短路测试电路进行短路故障仿真。为验证仿真结果的准确性，本文对国网智能电网研究院有限公司研制的6.5 kV/400 A SiC MOSFET器件开展短路特性测试实验，搭建如图5所示的高压SiC MOSFET短路测试实验平台，平台所使用的测量设备及其型号和参数见表5。
图5 高压SiC MOSFET短路测试实验平台
Fig.5 Short-circuit test experimental platform for high-voltage SiC MOSFET
表5 短路实验平台所用测量设备参数
Tab.5 Parameters of measuring equipments used in the short-circuit experimental platform
设备型号参数 示波器HDO6104A带宽1 GHz、采样速率10 GS/s 电流探头CP9121SA峰值电流12 kA、带宽30 MHz 电压探头HVD3605带宽100 MHz、量程6 000 V
短路测试实验平台的等效电路如图6所示。其中，Gate Driver为等效的栅极驱动电路；Rg为栅极电阻，本实验中对器件的开通、关断过程设置了不同的栅极电阻；Ri和Ci为减小开关振荡并联的输入电阻和输入电容。在功率回路，DUT为待测国产6.5 kV/ 400 A SiC MOSFET；Lloop1和Rloop1分别为吸收电容与器件之间的等效杂散电感与等效电阻；CS为吸收电容；Lloop2和Rloop2分别为母线电容与吸收电容之间的等效杂散电感与等效电阻；CDC为母线电容；VDC为等效直流电源。上述等效电路参数见表6。
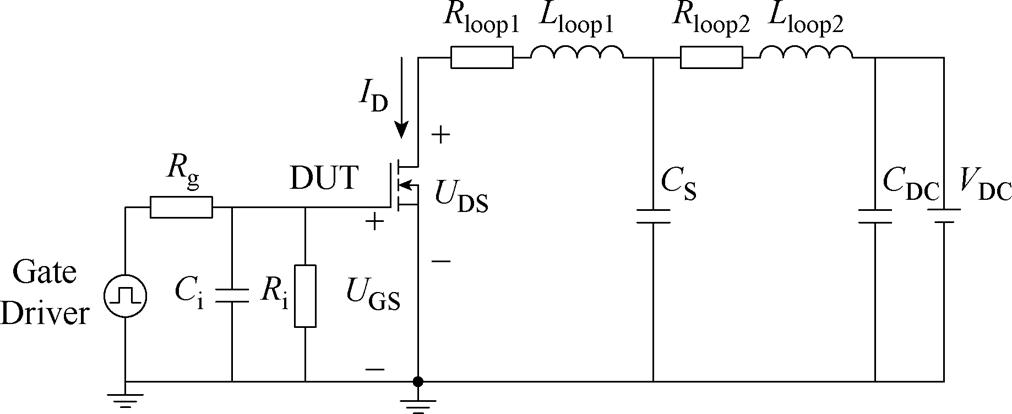
图6 高压SiC MOSFET短路测试实验平台等效电路
Fig.6 Equivalent circuit of the short-circuit test experimental platform for high-voltage SiC MOSFETs
表6 短路测试平台等效电路参数
Tab.6 Parameters in the equivalent circuit diagram of the short-circuit test experimental platform
参 数数 值 栅极电阻Rg/W(开通) 2.8 (关断) 5.5 输入电阻Ri/kW10 输入电容Ci/nF20 吸收电容CS/mF25.7 吸收电容与器件之间的等效杂散电感Lloop1/nH25 吸收电容与器件之间的等效电阻Rloop1/W0.02 母线电容与吸收电容之间的等效杂散电感Lloop2/nH55 母线电容与吸收电容之间的等效电阻Rloop2/W0.01 母线电容CDC/mF500
本文在VDC=3 300 V和VDC=2 470 V直流母线电压、2.5 ms短路时间的条件下对6.5 kV/400 A SiC MOSFET器件进行短路测试实验，得到漏极电流ID、栅源电压UGS、漏源电压UDS波形，并与短路行为模型的仿真结果对比，分别如图7和图8所示。图中，（红色）实线代表短路测试实验实测波形，（蓝色）虚线代表短路行为模型的仿真结果。同时，本文还对低压SiC MOSFET模型对6.5 kV SiC MOSFET短路行为的仿真效果进行评估，结果如图7、图8中（绿色）点画线所示。此处，低压SiC MOSFET行为模型忽略本文高压器件模型中关键的外延层、JFET区电阻建模，并将沟道电流ICH（式（4））计算中沟道电压UCH替换为低压SiC MOSFET模型中常见的漏源电压UDS。
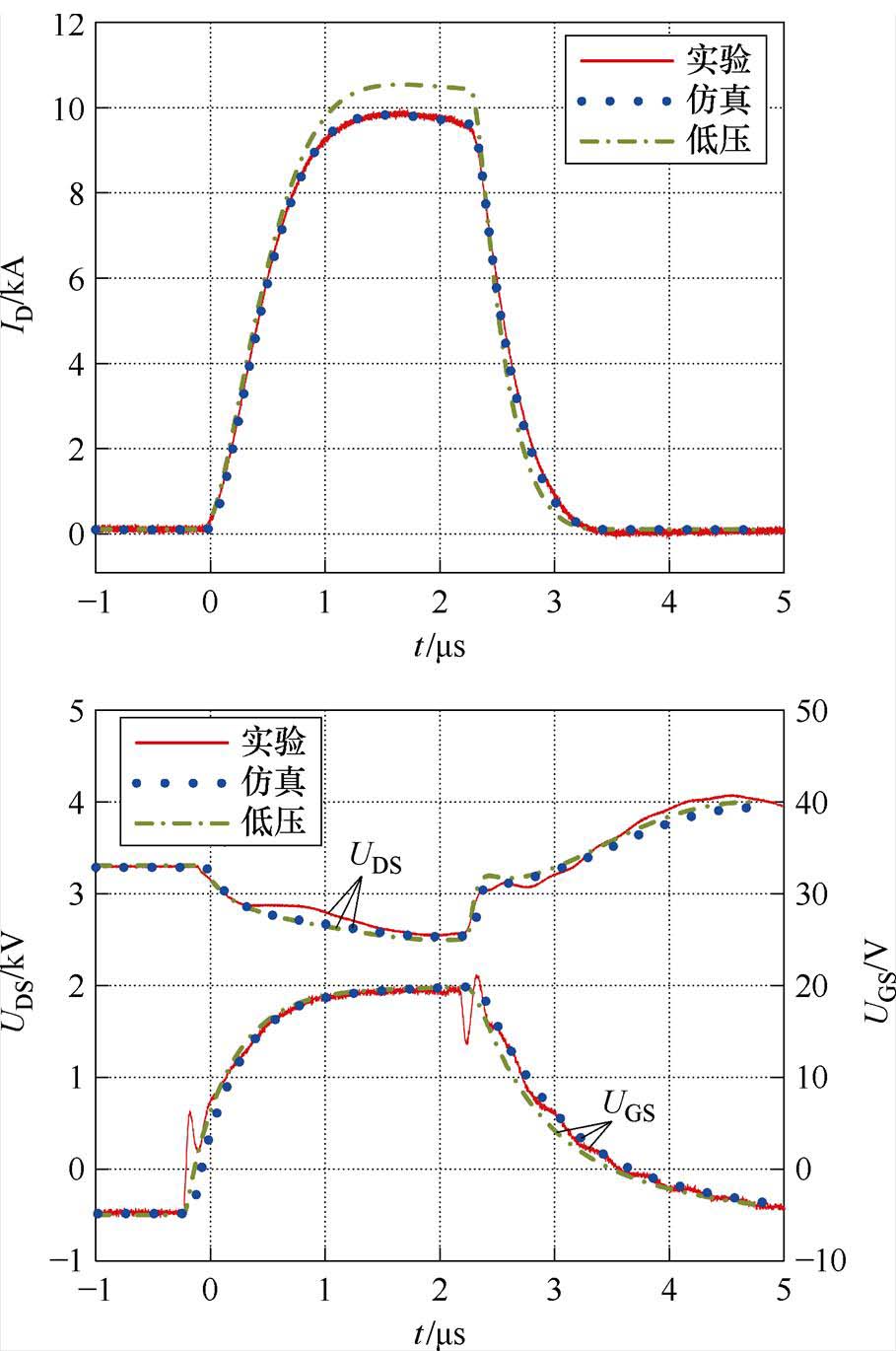
图7 VDC=3 300 V下短路测试实验与仿真波形
Fig.7 Short-circuit test experiment and simulation results under VDC=3 300 V
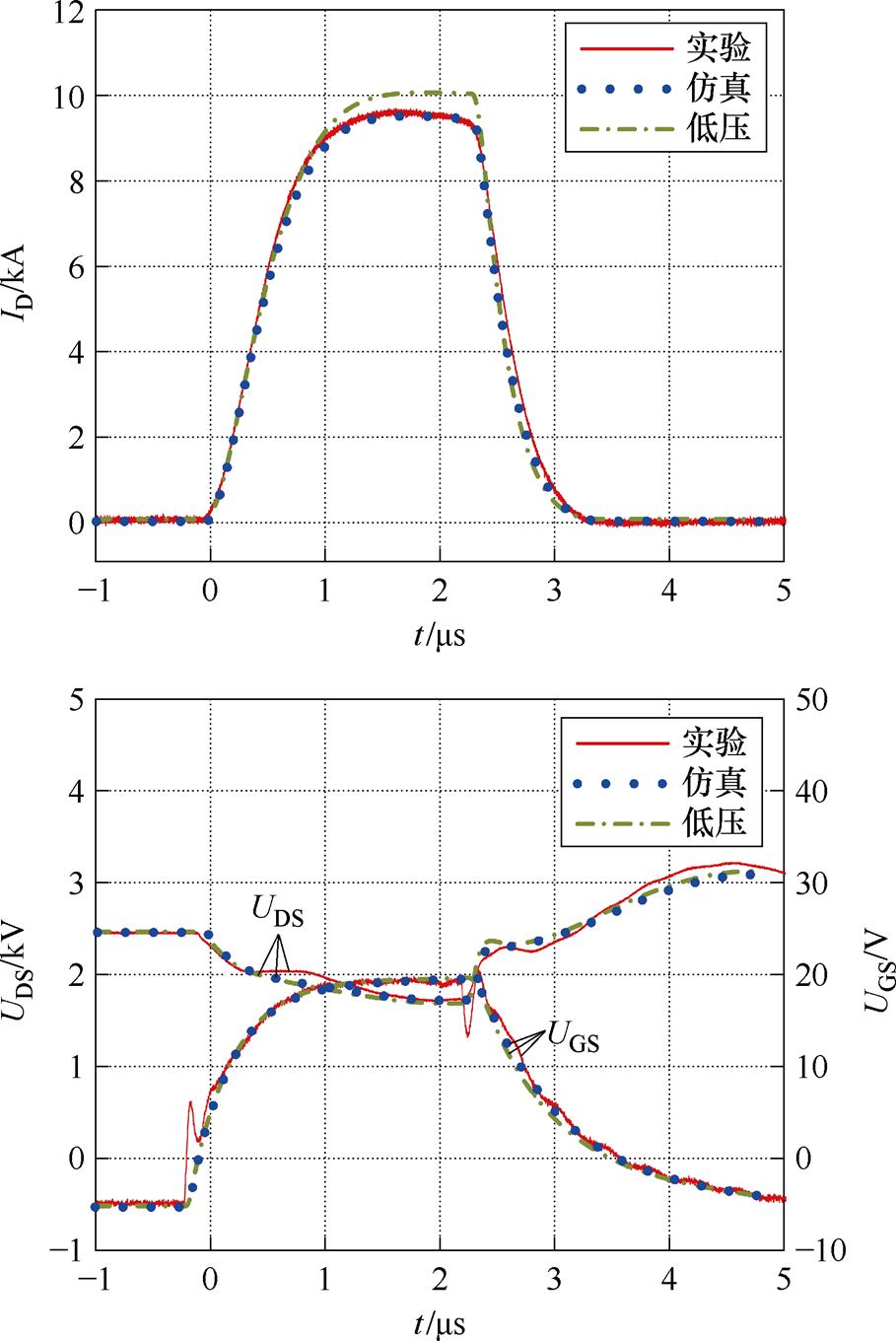
图8 VDC=2 470 V下短路测试实验与仿真波形
Fig.8 Short-circuit test experimental and simulation waveforms under VDC=2 470 V
UGS、UDS的仿真波形与实测结果比较相符，表明表7中提取的短路测试平台等效电路合理、参数准确。漏极电流ID是表征SiC MOSFET短路故障行为的重要电气量，表7对比了仿真和实验中器件ID的0～4 000 A上升率、电流峰值等关键特征，其误差均小于2.5%，表明短路行为模型的ID仿真结果均与实测结果十分符合，验证了本文模型能够准确描述国产6.5 kV SiC MOSFET器件在短路故障发生中的行为，同时验证了模型关键参数物理建模以及参数提取的准确性。在两种不同直流母线电压的工况下，短路行为模型的ID仿真结果均能与实测波形实现良好匹配，表明该模型在高压SiC MOSFET器件的短路特性仿真中具有较高的准确性和较好的通用性。
表7 仿真、实测短路电流ID关键特征对比
Tab.7 Comparison of the key features of simulated ID with the experimental results
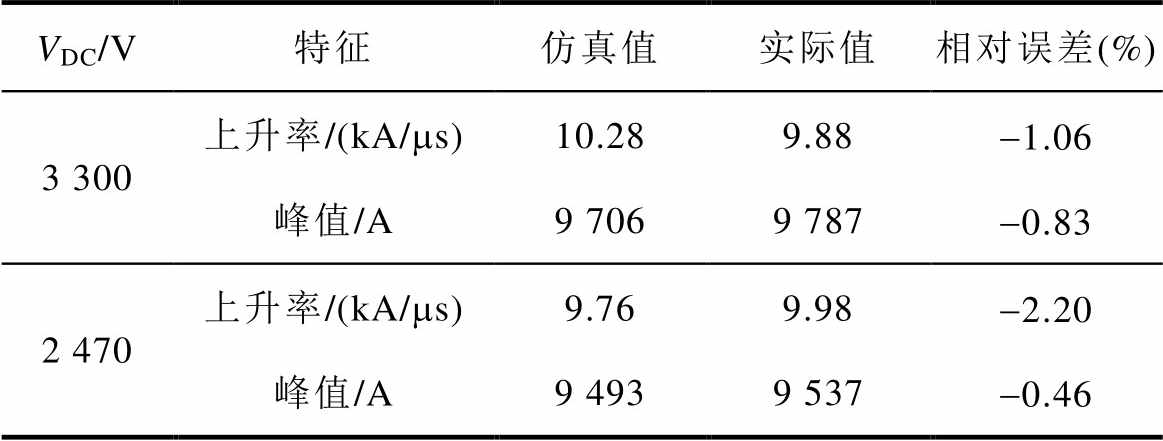
VDC/V特征仿真值实际值相对误差(%) 3 300上升率/(kA/ms)10.289.88-1.06 峰值/A9 7069 787-0.83 2 470上升率/(kA/ms)9.769.98-2.20 峰值/A9 4939 537-0.46
对比本文提出的高压SiC MOSFET短路故障行为模型与低压模型[23]在6.5 kV SiC MOSFET器件短路故障仿真中的电流波形。不难看出，本文提出的高压器件模型能够在不同工况下准确描述器件的短路电流上升率、峰值等关键特征，而低压SiC MOSFET模型的漏极电流ID仿真结果与实测波形存在显著差异。在VDC=3 300 V和VDC=2 470 V两种直流母线电压的工况下，其电流峰值分别为10 442 A和10 052 A，与实测电流的相对误差分别为7.58%和5.89%，其相对误差远大于本文提出的高压器件模型。产生误差的主要原因是：RD在短路故障中随温度升高而增大，且足以在器件的总导通电阻占据较大比例，若将其忽略，将使得器件模型的总导通电阻降低，导致短路电流仿真结果偏大。此外，电流上升率、下降率、到达电流峰值的时间也随之出现误差。该结果表明，本文模型针对高压器件的优化是必要的且准确的。
本文针对6.5 kV高压SiC MOSFET提出一种能够准确描述其短路故障中的电流、电压外特性的行为模型。相较于现有的1.7 kV以下电压等级的SiC MOSFET行为模型，本文模型根据高压器件中沟道电压占总漏源电压比例小的特征，修正沟道电流计算中的电压选取；同时，根据高压SiC MOSFET的元胞结构，以及器件导通时元胞层面的电流路径，对高压SiC MOSFET器件中占导通电阻比例较大的N型漂移区电阻和JFET区电阻进行建模。为考虑SiC MOSFET器件中决定短路故障行为的多种实际物理因素，本文基于半导体、器件物理对模型中涉及的本征载流子浓度、阈值电压及载流子迁移率等关键参数进行建模与计算。同时，本文明确了关键参数的含义及提取方法，模型中的大部分参数可直接提取自器件设计环节已知的材料特性、器件设计及工艺参数，少数参数可通过简单的拟合、近似得到，具有较强物理依据和数据支撑。但其中的部分参数属于器件设计方的核心技术细节，对于器件应用者难以准确获取及合理调试，这是本文模型尚存的局限性，但并不影响在明确上述参数后模型具有较高的准确性。
本文在不同直流母线电压工况下对短路行为模型进行仿真，并与国网智能电网研究院有限公司研制的6.5 kV/400 A SiC MOSFET器件的短路测试实验结果进行对比，验证了本文模型和参数提取方法的正确性。同时与低压SiC MOSFET模型进行对比，本文模型仿真结果的准确性相较其有显著提升，验证了本文模型针对高压器件进行建模的必要性和准确性。
附 录
反型层电荷密度QINV、沟道处垂直于SiC/SiO2界面的电场强度ENOR是沟道反型层载流子迁移率mINV计算中的关键参数；SiC/SiO2界面的界面陷阱电荷密度QIT则在阈值电压VT和mINV的计算中均起到决定性的作用。附录将详细阐述以上三个参数的建模与求解方法[26, 35, 38, 43-45]。
1）QINV和ENOR的建模
QINV和ENOR采用电荷叠层模型（Charge Sheet Model）法进行求解[38, 43]。在该方法中，QINV可表示为沟道位置SiC/SiO2界面处表面势YS的函数，有
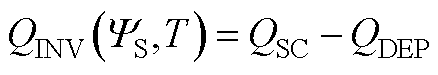（A1）
式中，QSC为空间电荷（Space charge）；QDEP为耗尽电荷（Depletion charge）。定义uS为
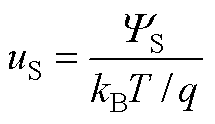（A2）
则QSC和QDEP均可表示为uS的函数。
QSC用公式计算式为
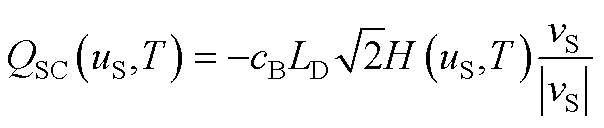（A3）
式（A3）中包含的参数cB、LD、H(uS,T)、vS可根据式（A4）～式（A11）求得。其中，考虑杂质不完全电离效应的沟道处自由载流子浓度cB可表示为
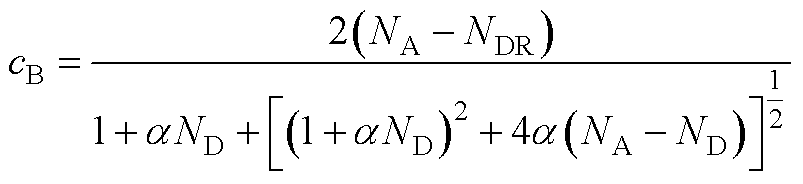（A4）
系数a 则定义为
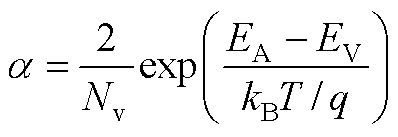（A5）
式中，EA、EV分别为受主杂质能级和价带能级；LD为德拜长度，即
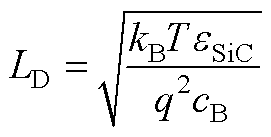（A6）
H(uS)可表示为
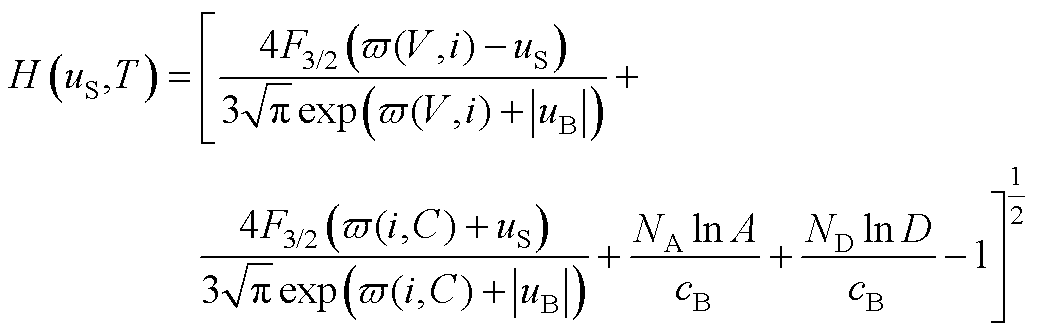（A7）
式中，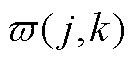
=(Ej-Ek)/(kBT)，Ej和Ek分别为载流子和禁带中央的能级，则A和D可定义为
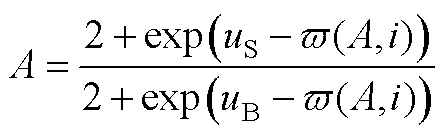（A8）
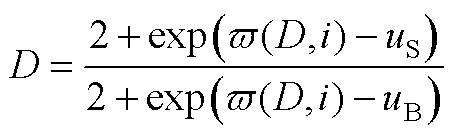（A9）
uB为沟道处远离SiC/SiO2界面的位置的费米能级，即
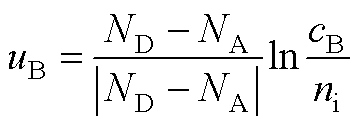（A10）
Fn[h]为费米-狄拉克积分，表示为
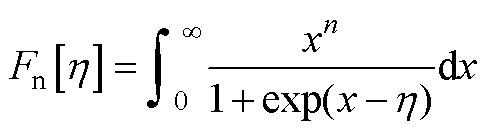（A11）
当SiC/SiO2界面费米能级低于导带或高于价带超过2kBT时，可采用其非退化表达式（Nondegenerate expression）简化求解[38, 43]。则vS可定义为
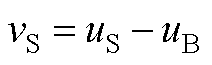（A12）
在电荷叠层模型法中，耗尽电荷定义为
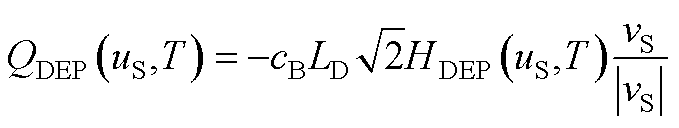（A13）
其中，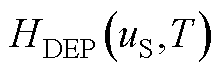
表示为
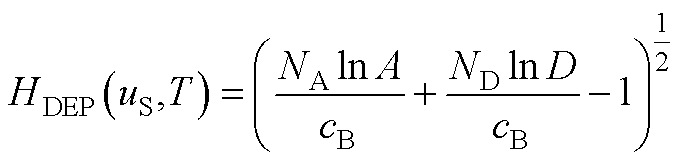（A14）
基于上述计算结果，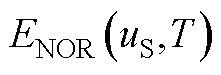
可表示为
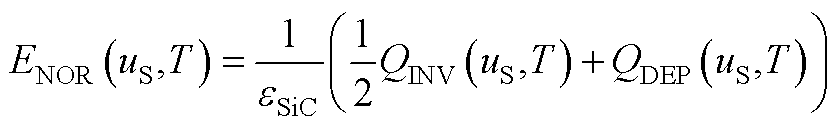（A15）
式（23）中的反型层电子密度nINV可表示为
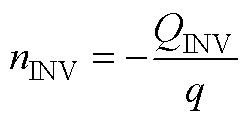（A16）
2）QIT的建模
本文选用如下公式计算界面陷阱电荷[26, 44-45]。
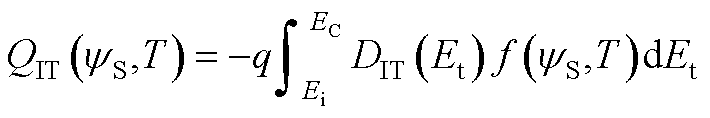（A17）
式中，EC、Ei分别为导带和禁带中央能级；DIT(Et)为SiC/SiO2界面的界面态密度分布，根据其实测结果[35]，可将其近似为
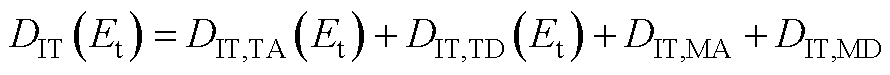（A18）
式中，DIT,TA(Et)和DIT,TD(Et)分别为靠近导带、价带边沿陡增的受主态、施主态密度，采用指数分布进行拟合；DIT,MA和DIT,MD分别为禁带中央两侧可视作均匀分布的受主态、施主态密度。由于N沟道SiC MOSFET在导通时费米能级位于禁带中央下方，施主态表现电中性，因此此处仅考虑受主态，则式（A18）可写作
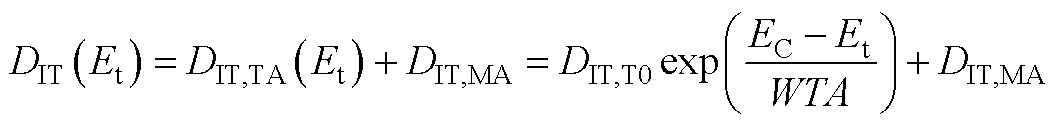（A19）
式中，DIT,T0为导带能级的界面态密度；WTA表征靠近导带边沿的界面态密度衰减；DIT,MA为靠近禁带中央的均匀分布的界面态密度。上述参数均与SiC MOSFET的栅氧化层制造工艺密切相关，可在器件设计者的设计、研发过程中测定、提取。
实际器件中，界面态是否被电荷占据受复杂的物理效应综合影响，难以理论概括，因此引入概率分布函数f(YS,T)模拟界面态的电荷占据情况，可表示为
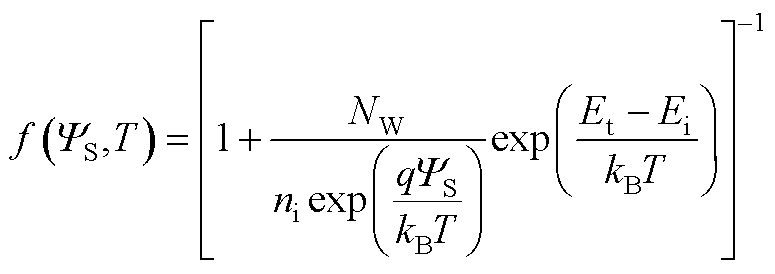（A20）
文献[45]给出了求解式所得的解析表达式为
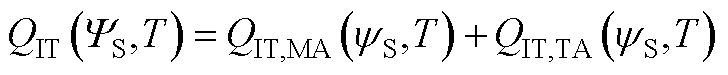（A21）
式中，QIT,MA(yS,T)和QIT,TA(yS,T)可分别写作
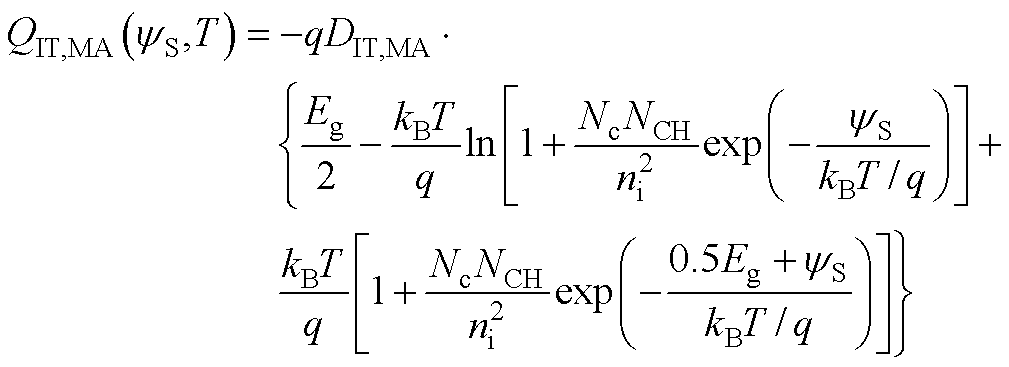（A22）
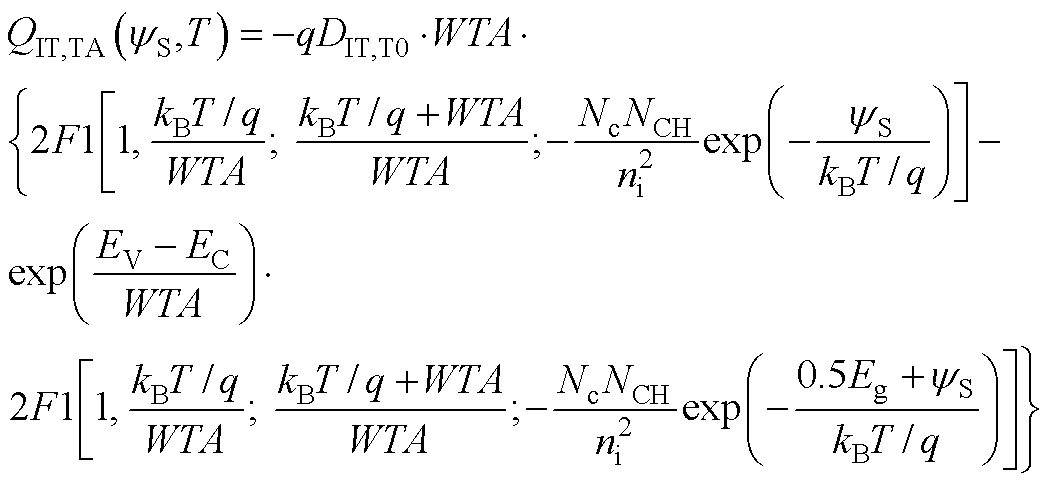（A23）
式中，2F1[a, b; c; z]为高斯超几何函数。
通过上述计算，可以获取确定表面势yS下的QINV、ENOR和QIT。
表面势yS与栅源电压UGS的对应关系可表示[26, 44]为
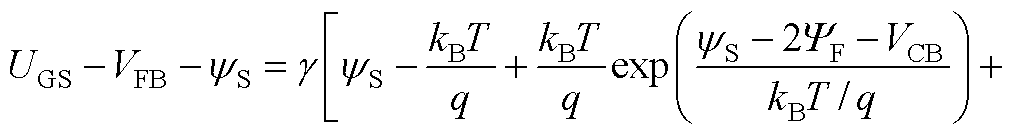
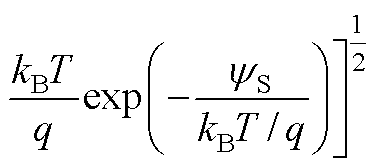（A24）
式中，平带电压VFB可用如下定义公式求解[35]。
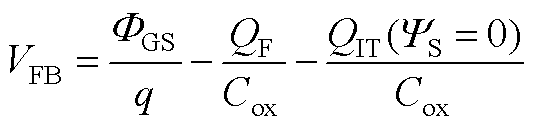（A25）
借此，QINV、ENOR和QIT均可表示为UGS的函数，可方便地在模型中进行求解。但由于式（A25）求解速度慢，若将其引入模型进行在线解算会严重降低模型的仿真速度。因而在本文模型中，QINV、ENOR和QIT均采用离线计算，计算三者随UGS、结温T变化的参数值并分别存入表格，在模型中即可通过查表的方式读取上述参数，提升仿真速度。
参考文献
[1] Kimoto T. Material science and device physics in SiC technology for high-voltage power devices[J]. Japanese Journal of Applied Physics, 2015, 54(4): 040103.
[2] 盛况, 任娜, 徐弘毅. 碳化硅功率器件技术综述与展望[J]. 中国电机工程学报, 2020, 40(6): 1741- 1753.
Sheng Kuang, Ren Na, Xu Hongyi. A recent review on silicon carbide power devices technologies[J]. Proceedings of the CSEE, 2020, 40(6): 1741-1753.
[3] 刘基业, 郑泽东, 李驰, 等. 电压自平衡碳化硅MOSFET间接串联功率模块[J]. 电工技术学报, 2023, 38(7): 1900-1909.
Liu Jiye, Zheng Zedong, Li Chi, et al. An indirect series-connected SiC MOSFET power module with voltage self-balance[J]. Transactions of China Elec- trotechnical Society, 2023, 38(7): 1900-1909.
[4] Zhang Lei, Yuan Xibo, Wu Xiaojie, et al. Perfor- mance evaluation of high-power SiC MOSFET modules in comparison to Si IGBT modules[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1181-1196.
[5] 朱小全, 刘康, 叶开文, 等. 基于SiC器件的隔离双向混合型LLC谐振变换器[J]. 电工技术学报, 2022, 37(16): 4143-4154.
Zhu Xiaoquan, Liu Kang, Ye Kaiwen, et al. Isolated bidirectional hybrid LLC converter based on SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4143-4154.
[6] 任鹏, 涂春鸣, 侯玉超, 等. 基于Si和SiC器件的混合型级联多电平变换器及其调控优化方法[J]. 电工技术学报, 2023, 38(18): 5017-5028.
Ren Peng, Tu Chunming, Hou Yuchao, et al. Research on a hybrid cascaded multilevel converter based on Si and SiC device and its control optimization method[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5017-5028.
[7] 黄天琪, 刘永前. 基于电-热-结构耦合分析的SiC MOSFET可靠性研究[J]. 电气技术, 2024, 25(8): 27-34.
Huang Tianqi, Liu Yongqian. Reliability study of SiC MOSFET based on electro-thermo-structural coupling analysis[J]. Electrical Engineering, 2024, 25(8): 27-34.
[8] Li Haoran, Zhang Zhiliang, Wang Shengdong, et al. A 300-kHz 6.6-kW SiC bidirectional LLC onboard charger[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(2): 1435-1445.
[9] 张栋, 范涛, 温旭辉, 等. 电动汽车用高功率密度碳化硅电机控制器研究[J]. 中国电机工程学报, 2019, 39(19): 5624-5634, 5890.
Zhang Dong, Fan Tao, Wen Xuhui, et al. Research on high power density SiC motor drive controller[J]. Proceedings of the CSEE, 2019, 39(19): 5624-5634, 5890.
[10] 付永升, 任海鹏, 李翰山, 等. SiC-MOSFET与Si-IGBT混合开关车载双向充电器中线桥臂设计及控制[J]. 中国电机工程学报, 2020, 40(19): 6330- 6345.
Fu Yongsheng, Ren Haipeng, Li Hanshan, et al. Neutral leg design and control of electric vehicle on-board bidirectional charger based on SiC- MOSFET and Si-IGBT hybrid devices[J]. Pro- ceedings of the CSEE, 2020, 40(19): 6330-6345.
[11] 胡嘉豪, 王英伦, 代豪豪, 等. SiC MOSFET器件栅氧可靠性研究综述[J]. 电源学报, 2024, 22(4): 1-11.
Hu Jiahao, Wang Yinglun, Dai Haohao, et al. Review on gate oxide reliability of SiC MOSFET devices[J]. Journal of Power Supply, 2024, 22(4): 1-11.
[12] 薄强, 王丽芳, 张玉旺, 等. 应用于无线充电系统的SiC MOSFET关断特性分析[J]. 电力系统自动化, 2021, 45(15): 150-157.
Bo Qiang, Wang Lifang, Zhang Yuwang, et al. Analysis of turn-off characteristics of SiC MOSFET applied to wireless charging system[J]. Automation of Electric Power Systems, 2021, 45(15): 150-157.
[13] 金晓行, 李士颜, 田丽欣, 等. 6.5kV高压全SiC功率MOSFET模块研制[J]. 中国电机工程学报, 2020, 40(6): 1753-1759.
Jin Xiaoxing, Li Shiyan, Tian Lixin, et al. Fabrication of 6.5kV high-voltage full SiC power MOSFET modules[J]. Proceedings of the CSEE, 2020, 40(6): 1753-1759.
[14] Ceccarelli L, Reigosa P D, Iannuzzo F, et al. A survey of SiC power MOSFETs short-circuit robustness and failure mode analysis[J]. Microelectronics Reliability, 2017, 76: 272-276.
[15] Sun Keyao, Wang Jun, Burgos R, et al. Design, analysis, and discussion of short circuit and overload gate-driver dual-protection scheme for 1.2-kV, 400-a SiC MOSFET modules[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 3054-3068.
[16] 王占扩, 童朝南, 黄伟超. SiC MOSFET短路特性及过流保护研究[J]. 中国电机工程学报, 2020, 40(18): 5751-5760.
Wang Zhankuo, Tong Chaonan, Huang Weichao. Research on short-circuit characteristics and over- current protection of SiC MOSFET[J]. Proceedings of the CSEE, 2020, 40(18): 5751-5760.
[17] 文阳, 杨媛, 宁红英, 等. SiC MOSFET短路保护技术综述[J]. 电工技术学报, 2022, 37(10): 2538-2548.
Wen Yang, Yang Yuan, Ning Hongying, et al. Review on short-circuit protection technology of SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2538-2548.
[18] Awwad A E, Dieckerhoff S. Short-circuit evaluation and overcurrent protection for SiC power MOSFETs[C]// 2015 17th European Conference on Power Electronics and Applications (EPE'15 ECCE-Europe), Geneva, Switzerland, 2015: 1-9.
[19] 李鑫, 罗毅飞, 史泽南, 等. 一种基于物理的SiC MOSFET改进电路模型[J]. 电工技术学报, 2022, 37(20): 5214-5226 .
Li Xin, Luo Yifei, Shi Zenan, et al. An improved physics-based circuit model for SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5214-5226.
[20] Stark R, Tsibizov A, Nain N, et al. Accuracy of three interterminal capacitance models for SiC power MOSFETs under fast switching[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9398-9410.
[21] Tian Lixin, Yang Fei, Niu Xiping, et al. Development and analysis of 6500V SiC power MOSFET[C]//2021 18th China International Forum on Solid State Lighting & 2021 7th International Forum on Wide Bandgap Semiconductors (SSLChina: IFWS), Shenzhen, China, 2021: 6-9.
[22] Romano G, Fayyaz A, Riccio M, et al. A com- prehensive study of short-circuit ruggedness of silicon carbide power MOSFETs[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(3): 978-987.
[23] Li Hong, Wang Yuting, Zhao Xingran, et al. A junction temperature-based PSpice short-circuit model of SiC MOSFET considering leakage current[C]//IECON 2019 - 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 2019: 5095-5100.
[24] Dumollard Y, Batista E, Dienot J M, et al. Equation-based modeling of the electrothermal behavior of a SiC MOSFET chip during a short circuit[C]//2020 IEEE Latin America Electron Devices Conference (LAEDC), San Jose, Costa Rica, 2020: 1-4.
[25] Xiang Pengfei, Hao Ruixiang, You Xiaojie, et al. Analytical modeling of SiC MOSFETs short-circuit behavior considering parasitic parameters[C]//2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020: 2835-2841.
[26] 周郁明, 蒋保国, 刘航志, 等. 包含SiC/SiO2界面电荷的SiC MOSFET的SPICE模型[J]. 中国电机工程学报, 2019, 39(19): 5604-5612, 5888.
Zhou Yuming, Jiang Baoguo, Liu Hangzhi, et al. SPICE model of SiC MOSFET including the trapped charge at SiC/SiO2 interface[J]. Proceedings of the CSEE, 2019, 39(19): 5604-5612, 5888.
[27] Riccio M, D’Alessandro V, Romano G, et al. A temperature-dependent SPICE model of SiC power MOSFETs for within and out-of-SOA simulations[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 8020-8029.
[28] Duan Zhuolin, Fan Tao, Wen Xuhui, et al. Improved SiC power MOSFET model considering nonlinear junction capacitances[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2509-2517.
[29] Hsu F J, Hung C C, Chu Kuoting, et al. A dynamic switching response improved SPICE model for SiC MOSFET with non-linear parasitic capacitance[C]// 2020 IEEE Workshop on Wide Bandgap Power Devices and Applications in Asia (WiPDA Asia), Suita, Japan, 2020: 1-4.
[30] (美)巴利加 B J. 先进的高压大功率器件: 原理、特性和应用[M]. 于坤山, 等译. 北京: 机械工业出版社, 2015.
[31] (美)尼曼 D A. 半导体物理与器件[M]. 赵毅强, 姚素英, 史再峰, 等译. 北京: 电子工业出版社, 2018.
[32] Wang Zhiqiang, Shi Xiaojie, Tolbert L M, et al. Temperature-dependent short-circuit capability of silicon carbide power MOSFETs[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(2): 1555- 1566.
[33] Zhao Xianlong, Li Tao, Liang Xiaobin, et al. Investigation on SiC MOSFET’s avalanche and short-circuit failure mechanism[C]//2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 2022: 3916-3921.
[34] (俄)莱温施泰因 M E, (俄)鲁缅采夫 S L. 先进半导体材料性能与数据手册[M]. (美)舒尔S M, 杨树人, 殷景志, 译. 北京: 化学工业出版社, 2003.
[35] (日)木本恒暢, (美)库珀J A. 碳化硅技术基本原理——生长、表征、器件和应用[M]. 夏经华, 潘艳, 杨霏, 等译. 北京: 机械工业出版社, 2018.
[36] Arnold E, Alok D. Effect of interface states on electron transport in 4H-SiC inversion layers[J]. IEEE Transactions on Electron Devices, 2001, 48(9): 1870- 1877.
[37] Masetti G, Severi M, Solmi S. Modeling of carrier mobility against carrier concentration in arsenic-, phosphorus-, and boron-doped silicon[J]. IEEE Transactions on Electron Devices, 1983, 30(7): 764-769.
[38] Pérez-Tomás A, Brosselard P, Godignon P, et al. Field-effect mobility temperature modeling of 4H-SiC metal-oxide-semiconductor transistors[J]. Journal of Applied Physics, 2006, 100(11): 114508.
[39] Zeng Y A, White M H, Das M K. Electron transport modeling in the inversion layers of 4H and 6H-SiC MOSFETs on implanted regions[J]. Solid-State Electronics, 2005, 49(6): 1017-1028.
[40] Tilak V, Matocha K, Dunne G. Electron-scattering mechanisms in heavily doped silicon carbide MOSFET inversion layers[J]. IEEE Transactions on Electron Devices, 2007, 54(11): 2823-2829.
[41] Dhar S, Haney S, Cheng L, et al. Inversion layer carrier concentration and mobility in 4H-SiC metal-oxide-semiconductor field-effect transistors[J]. Journal of Applied Physics, 2010, 108(5): 054509.
[42] Powell S K, Goldsman N, McGarrity J M, et al. Physics-based numerical modeling and characteri- zation of 6H-silicon-carbide metal-oxide-semiconductor field-effect transistors[J]. Journal of Applied Physics, 2002, 92(7): 4053-4061.
[43] Arnold E. Charge-sheet model for silicon carbide inversion layers[J]. IEEE Transactions on Electron Devices, 1999, 46(3): 497-503.
[44] Licciardo G D, Di Benedetto L, Bellone S. Modeling of the SiO2/SiC interface-trapped charge as a function of the surface potential in 4H-SiC vertical-DMOSFET[J]. IEEE Transactions on Electron Devices, 2016, 63(4): 1783-1787.
[45] Haasmann D, Dimitrijev S. Energy position of the active near-interface traps in metal-oxide- semi- conductor field-effect transistors on 4H-SiC[J]. Applied Physics Letters, 2013, 103(11): 113506.
Behavior Model of High-Voltage SiC MOSFET’s Short-Circuit Fault Based on Device Physics
Abstract The short-circuit ruggedness of silicon carbide (SiC) MOSFETs represents a significant challenge that impedes their widespread adoption in high-voltage applications. Developing effective short-circuit protection strategies in domestic high-voltage SiC MOSFETs is hampered by a lack of robust technical expertise and empirical experience. Furthermore, the absence of fast and accurate simulation models presents a fundamental obstacle to advancing research on the application of domestic high-voltage SiC MOSFETs. Traditional behavioral models focus on fitting these devices’ static and dynamic characteristics but fail to simulate fault conditions adequately. Recently, several models have been proposed for short-circuit scenarios. However, these models exhibit limitations, including low adaptability for high-voltage devices, insufficient universality, and inefficient parameter extraction. This paper introduces a behavioral model for high-voltage SiC MOSFETs, which incorporates practical physical characteristics. The proposed model can accurately simulate the device's behavior-such as voltage and current dynamics-throughout a short-circuit fault event.
The behavioral model comprises five primary components: a controlled current source (ICH) for calculating the current flowing through the channel, a controlled current source (ILEAK) for assessing the leakage current under high junction temperature conditions, a diode (D) representing the device's body diode, capacitors (CGS, CGD and CDS) for the junction capacitances, and a resistor (RD) denoting the total resistance of the drift layer and JFET region of the device. In high-voltage devices, the resistances associated with the drift layer and JFET region constitute a significantly large proportion of the total on-resistance compared to devices rated below 1.2 kV. The increased resistance markedly influences the device's behavior during short-circuit faults. Consequently, RD is carefully calculated based on the practical structure of high-voltage SiC MOSFETs and the current path during short-circuit events at the cell level. The model’s parameters are categorized into four types, each with detailed extraction methods. Furthermore, key physical parameters that are challenging to measure-such as intrinsic carrier concentration (ni), threshold voltage (VT), and carrier mobility (m)-are calculated based on semiconductor physics principles. The strong physical significance of the model's components and the parameters enhances the universality and portability of the proposed model.
A 6.5 kV/400 A SiC MOSFET produced by the State Grid Smart Grid Research Institute Co. Ltd is modeled. The model is developed, and short-circuit test simulations are conducted using Matlab/Simulink. A short-circuit test experimental platform is established for the selected device. Short-circuit tests are performed under a short-circuit duration (tSC) of 2.5 ms and DC-bus voltages (VDC) of 3 300 V and 2 470 V. The high consistency between the simulated and experimental waveforms indicates that the presented model effectively simulates the behavior of high-voltage SiC MOSFETs during short-circuit faults. The relative errors of the current rise rate and peak short-circuit current are less than 2.20% and 0.83%. Additionally, the relative errors of simulated peak currents with the low-voltage models are 7.58% and 5.89% under VDC=3 300 V and VDC=2 470 V, respectively, seven times those with the proposed model.
Keywords：Silicon carbide (SiC) MOSFET, high-voltage power devices, behavior model, short-circuit fault, parameter extraction
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.241066
国家电网有限公司科技资助项目（SGSNKY00KJJS2100291）。
收稿日期 2024-06-20
改稿日期 2024-07-12
巫以凡 男，1999年生，博士研究生，研究方向为电力电子与电力传动。
E-mail: wu-yf21@mails.tsinghua.edu.cn
郑泽东 男，1980年生，副教授，博士生导师，研究方向为电力电子与电气传动。
E-mail: zzd@mail.tsinghua.edu.cn（通信作者）
（编辑 郭丽军）