基于频域二次微分解谱法的油纸绝缘等效电路参数辨识
林智勇1,2 李荣华1,2 黄国泰3 邓东平4 张达敏1,2
(1. 厦门理工学院电气工程与自动化学院 厦门 361024 2. 厦门市高端电力装备及智能控制重点实验室 厦门 361024 3. 福建省电力物资有限公司 福州 350003 4. 国网漳平市供电公司 龙岩 364400)
摘要 变压器油纸绝缘介电响应等效电路是分析频域介电谱特征量与绝缘介质老化内在联系的重要分析途径。目前等效电路极化支路数绝大部分是人为假定,不能真正反映绝缘系统内部老化情况,且参数辨识需要复杂算法的迭代寻优,其效率和准确性不理想。该文对极化复电容实部表达式进行变换改造,构建极化复电容实部二次微分谱线,分析其子谱线的特性,提出利用极化复电容实部二次微分谱线峰值点数量和子谱线峰值点坐标分别辨识变压器油纸绝缘介电响应等效电路极化支路数和参数,并对多台不同老化状态的变压器进行验证。研究结果表明:极化复电容实部二次微分谱线判定等效电路极化支路数准确率为100%,等效电路参数辨识准确率达到98%以上,基于解谱法获取的复电容实部谱线与实测值拟合度达到97%以上,极化复电容实部二次微分谱线能够准确地辨识具有唯一性的等效电路参数,有效提高应用频域介电谱特征量辨识等效电路参数的可靠性和效率,为准确诊断变压器油纸绝缘老化状态奠定重要基础。
关键词:频域介电谱 油纸绝缘 等效电路 参数辨识 微分解谱法
0 引言
油浸式电力变压器作为电力系统的核心设备之一,在电力系统中发挥着电能传输与转换的重要作用[1-2],而油纸绝缘系统的老化状态与变压器运行的稳定性紧密相关[3-4]。研究发现,油纸绝缘在受到一些不可抗因素的作用后会产生老化劣化的现象,绝缘能力减弱,进而形成绝缘故障隐患,影响系统运行的安全可靠性[5-8]。因此,准确地判断变压器老化状态尤为重要。
目前扩展德拜模型等效电路参数能够有效反映油纸绝缘的老化状态[9-10],特别是极化支路数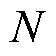 会随着老化程度的加深而不断增加[11],但是扩展德拜模型极化支路参数的准确辨识却是一大难题。文献[12]对支路数进行预设,采用粒子群算法对变压器进行参数辨识,可有效反映变压器绝缘老化状态,但是参数辨识具有随机性且不能准确地反映真实支路数。文献[13]通过遗传算法与Levenberg-Marquardt算法相结合的方法对变压器进行参数辨识,但其误差仅在一定范围内较小,辨识结果具有一定的局限性。文献[14]对回复电压谱线用峰值点确定极化支路数,采用末端随机取点的方式对极化支路进行参数辨识,对参数辨识具有参考意义,但是随机取点的方式不具有唯一性。文献[15]对复介电常数进行多次微分,研究分析1~4阶微分谱线峰值点特性,指出可通过4阶微分谱线峰值点判断极化支路数,但是计算公式较为复杂。文献[16]采用解谱法进行支路数判断和等效电路参数辨识,辨识结果与实测参数拟合度较高,有效地提高了极化支路参数辨识的准确度,但取点方式使辨识参数不唯一。文献[17]采用频域介电谱一次微分谱线进行参数辨识,通过一次微分谱线峰值点能够有效判定极化支路数,提高了参数辨识的可靠性,但有时存在峰值点不明显的缺点,需要进一步优化。
会随着老化程度的加深而不断增加[11],但是扩展德拜模型极化支路参数的准确辨识却是一大难题。文献[12]对支路数进行预设,采用粒子群算法对变压器进行参数辨识,可有效反映变压器绝缘老化状态,但是参数辨识具有随机性且不能准确地反映真实支路数。文献[13]通过遗传算法与Levenberg-Marquardt算法相结合的方法对变压器进行参数辨识,但其误差仅在一定范围内较小,辨识结果具有一定的局限性。文献[14]对回复电压谱线用峰值点确定极化支路数,采用末端随机取点的方式对极化支路进行参数辨识,对参数辨识具有参考意义,但是随机取点的方式不具有唯一性。文献[15]对复介电常数进行多次微分,研究分析1~4阶微分谱线峰值点特性,指出可通过4阶微分谱线峰值点判断极化支路数,但是计算公式较为复杂。文献[16]采用解谱法进行支路数判断和等效电路参数辨识,辨识结果与实测参数拟合度较高,有效地提高了极化支路参数辨识的准确度,但取点方式使辨识参数不唯一。文献[17]采用频域介电谱一次微分谱线进行参数辨识,通过一次微分谱线峰值点能够有效判定极化支路数,提高了参数辨识的可靠性,但有时存在峰值点不明显的缺点,需要进一步优化。
针对以上不足,本文提出一种基于频域介电谱二次微分解谱法的支路数判定和参数辨识方法,利用极化复电容实部二次微分谱线峰值点数量与坐标求解扩展德拜极化等效电路的极化支路数和极化支路参数。由于各个峰值点的显著性和唯一性,该方法能够避免现有参数辨识方法存在预设极化支路数和辨识结果不唯一等问题,从而提高了参数辨识的准确度。
1 扩展德拜模型等效电路参数与频域介电谱特征量关系
变压器油纸绝缘系统主要由绝缘油、绝缘纸、隔板及撑条等组成[18],在变压器的运行过程中绝缘油和绝缘纸存在各种复杂的弛豫过程[19-20]。为充分研究复杂的弛豫响应过程,通常采用扩展德拜等效电路模型[21]进行表征,如图1所示。
图1中,等效电路由几何等效电路和极化等效电路两部分组成,其中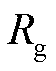 为绝缘电阻,
为绝缘电阻,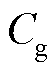 为工频下的几何电容,
为工频下的几何电容,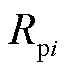 和
和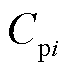 分别为第
分别为第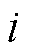 个极化支路的极化电阻和极化电容(
个极化支路的极化电阻和极化电容(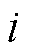 =1, 2,…,
=1, 2,…,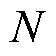 )。
)。
由图1可得,扩展德拜模型等效电路的导纳为
式(1)经过变换可得到复电容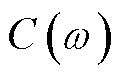 为
为
由式(2)可得复电容的实部和虚部分别为
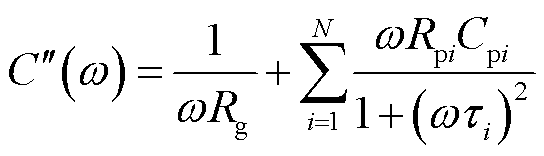 (4)
(4)
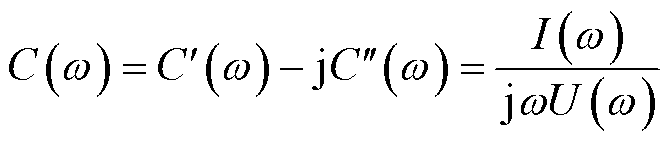 (5)
(5)
式中,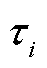 为第i个极化支路的时间常数,表征绝缘介质的极化弛豫速率,
为第i个极化支路的时间常数,表征绝缘介质的极化弛豫速率,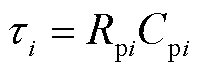 ;
;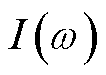 和
和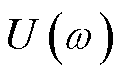 分别为施加的复电流和复电压。
分别为施加的复电流和复电压。
由式(5)可知,复电容是关于电压和电流的函数。不同频率的交变电场下绝缘介质内部会产生不同程度的电导响应和极化响应[22-23],对所测量的复电容幅值造成一定影响。因此在一定程度上复电容可以反映绝缘介质的电导与极化过程[24],进一步反映变压器内部绝缘介质的老化程度。
由式(3)可知,根据变压器实测频域介电谱复电容实部谱线末端稳定值可得到等效电路参数中的几何电容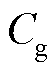 ,通过仪器可直接测量绝缘电阻数值。因此,可以通过直接测量获取几何等效电路的参数,变压器扩展德拜等效电路参数辨识的关键在于极化等效电路的参数辨识。由式(3)构建极化等效电路的极化复电容实部
,通过仪器可直接测量绝缘电阻数值。因此,可以通过直接测量获取几何等效电路的参数,变压器扩展德拜等效电路参数辨识的关键在于极化等效电路的参数辨识。由式(3)构建极化等效电路的极化复电容实部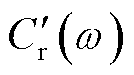 为
为
由式(6)可知,极化复电容实部由多个不同弛豫时间常数的子谱线叠加而成。研究发现,各个子谱线存在相互覆盖且影响范围较大的情况,因此不能通过直接解谱子谱线数量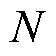 来判断极化支路数,需要对极化复电容实部
来判断极化支路数,需要对极化复电容实部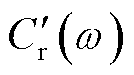 进行处理。
进行处理。
2 基于频域介电谱二次微分解谱法的极化等效电路参数辨识
2.1 频域微分介电谱的仿真分析
变压器油纸绝缘频域介电谱测量是在一定频域内对绝缘试品外加正弦电压,根据绝缘介质在交变电场下的极化特性,测量流过绝缘试品的电流峰值与相位,获得不同频率下的复电容值,从而进行绝缘介质的老化状态分析[25]。本文通过深入挖掘复电容实部曲线内部隐含的信息分析等效电路参数辨识的新方法。
对极化复电容实部进行微分处理,令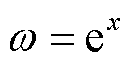 ,对
,对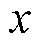 进行微分,得到极化复电容实部一次微分谱线
进行微分,得到极化复电容实部一次微分谱线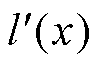 为
为
对式(7)两端同乘以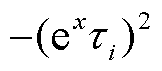 ,再进行微分得到极化复电容实部二次微分谱线
,再进行微分得到极化复电容实部二次微分谱线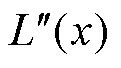 为
为
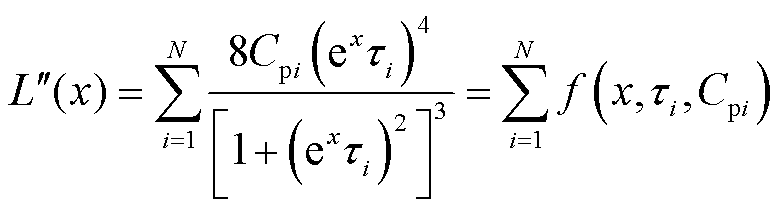 (8)
(8)
式中,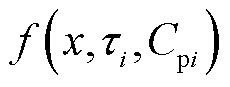 为极化复电容实部二次微分子谱线函数(以下称为子谱线函数,对应曲线称为子谱线)。
为极化复电容实部二次微分子谱线函数(以下称为子谱线函数,对应曲线称为子谱线)。
为研究子谱线函数的特性,现取三种不同时间常数的子谱线函数进行对比分析,其中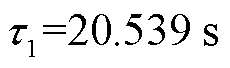 ,
,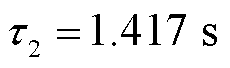 ,
,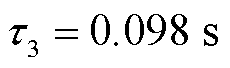 ,三种子谱线对比如图2所示。
,三种子谱线对比如图2所示。
由子谱线函数特性和图2对比结果可知,极化复电容实部二次微分谱线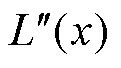 具有以下特性。
具有以下特性。
1)各个子谱线具有唯一峰值点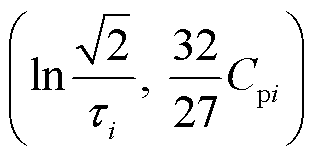 ,并向峰值两侧逐渐衰减为0,且子谱线随着
,并向峰值两侧逐渐衰减为0,且子谱线随着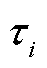 越小而整体向右偏移。
越小而整体向右偏移。
2)由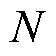 条具有不同时间常数的子谱线叠加而成,谱线峰值点数量即为扩展德拜等效模型的极化支路数。
条具有不同时间常数的子谱线叠加而成,谱线峰值点数量即为扩展德拜等效模型的极化支路数。
3)前一项子谱线对后一项子谱线影响较大,但后一项子谱线对前一项子谱线峰值点影响甚微。
4)从首个峰值点依次进行解谱,能够获取各个子谱线情况。
2.2 基于频域介电谱二次微分解谱法的参数辨识
通过对子谱线函数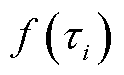 的分析可知,其峰值点的坐标为
的分析可知,其峰值点的坐标为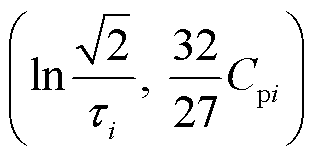 ,结合对应各个子谱线在实际坐标轴中峰值点坐标
,结合对应各个子谱线在实际坐标轴中峰值点坐标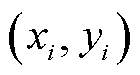 ,可求解不同极化支路的极化电容、时间常数和极化电阻,有
,可求解不同极化支路的极化电容、时间常数和极化电阻,有
具体参数辨识步骤如下:
1)将实测复电容实部谱线减去几何电容,获得极化复电容实部谱线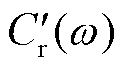 。
。
2)令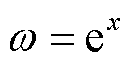 ,对极化复电容实部谱线
,对极化复电容实部谱线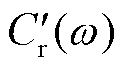 进行转换,再对其进行微分,获取极化复电容实部一次微分谱线
进行转换,再对其进行微分,获取极化复电容实部一次微分谱线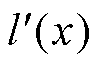 。
。
3)对极化复电容实部一次微分谱线乘以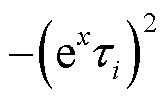 ,再进行微分得到极化复电容实部二次微分谱线
,再进行微分得到极化复电容实部二次微分谱线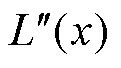 ,并将横坐标
,并将横坐标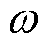 转换为
转换为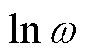 ,使得曲线峰值点更加清晰。
,使得曲线峰值点更加清晰。
4)选取极化复电容实部二次微分谱线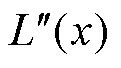 首个峰值点坐标
首个峰值点坐标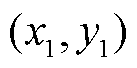 ,并结合式(10)求解第一条子谱线
,并结合式(10)求解第一条子谱线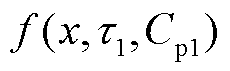 以及对应的极化支路1的极化电容
以及对应的极化支路1的极化电容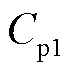 、时间常数
、时间常数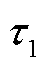 和极化电阻
和极化电阻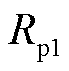 。
。
5)从当前微分谱线减去第一条子谱线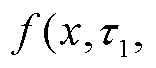
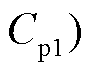 得到剩余谱线
得到剩余谱线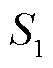 ;再从剩余谱线
;再从剩余谱线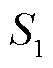 中选取首个峰值点坐标
中选取首个峰值点坐标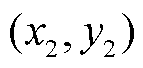 ,并结合式(10)求解第二条子谱线
,并结合式(10)求解第二条子谱线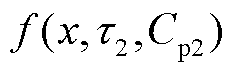 以及对应的极化支路2的极化电容
以及对应的极化支路2的极化电容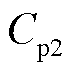 、时间常数
、时间常数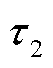 和极化电阻
和极化电阻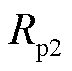 。
。
6)从当前微分谱线减去第二条子谱线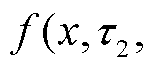
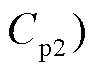 得到剩余谱线
得到剩余谱线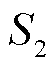 ,重复步骤4),以此类推直到最后一个峰值点
,重复步骤4),以此类推直到最后一个峰值点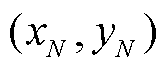 ,完成全部子谱线的解谱和极化支路参数辨识。
,完成全部子谱线的解谱和极化支路参数辨识。
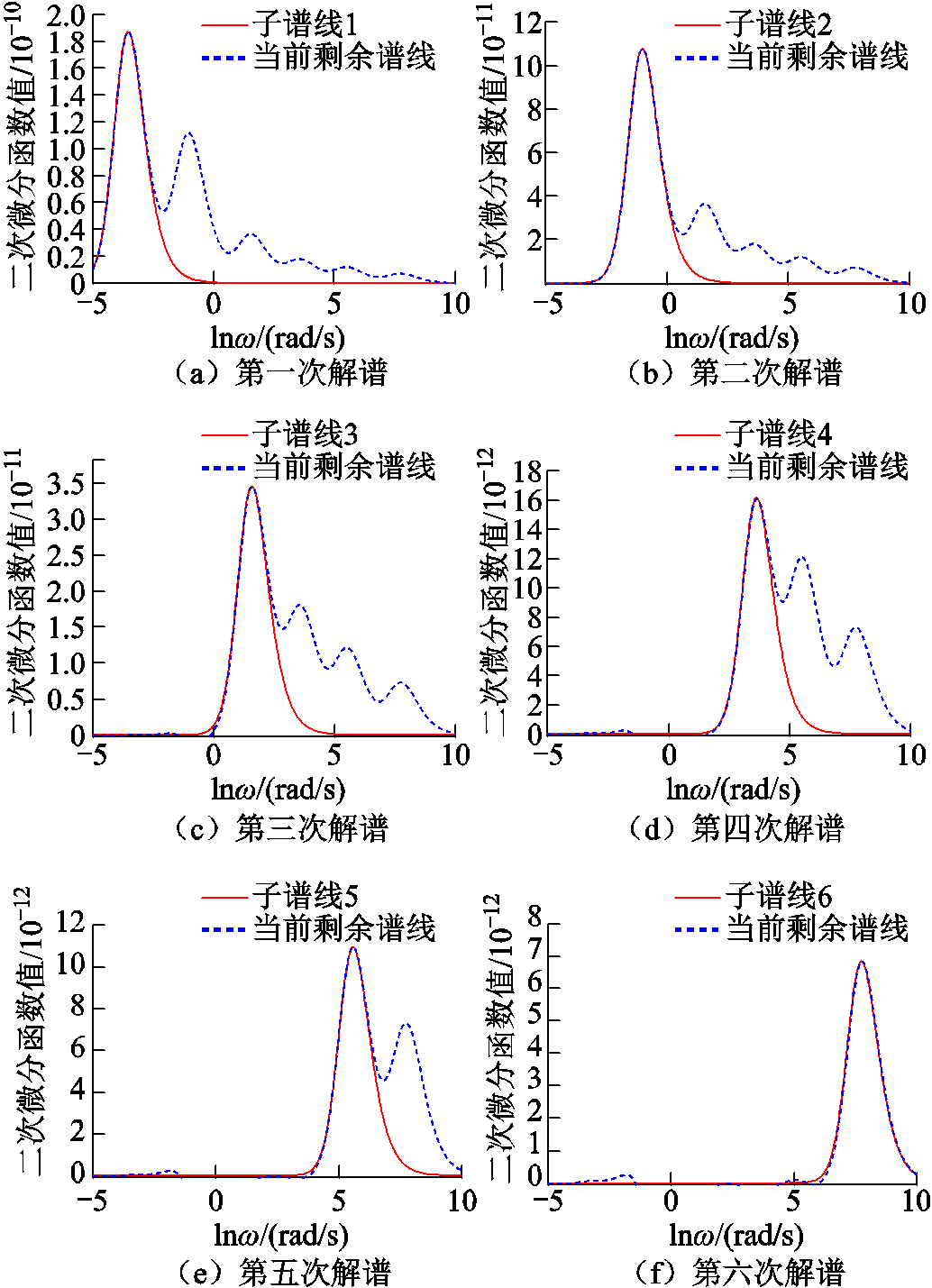
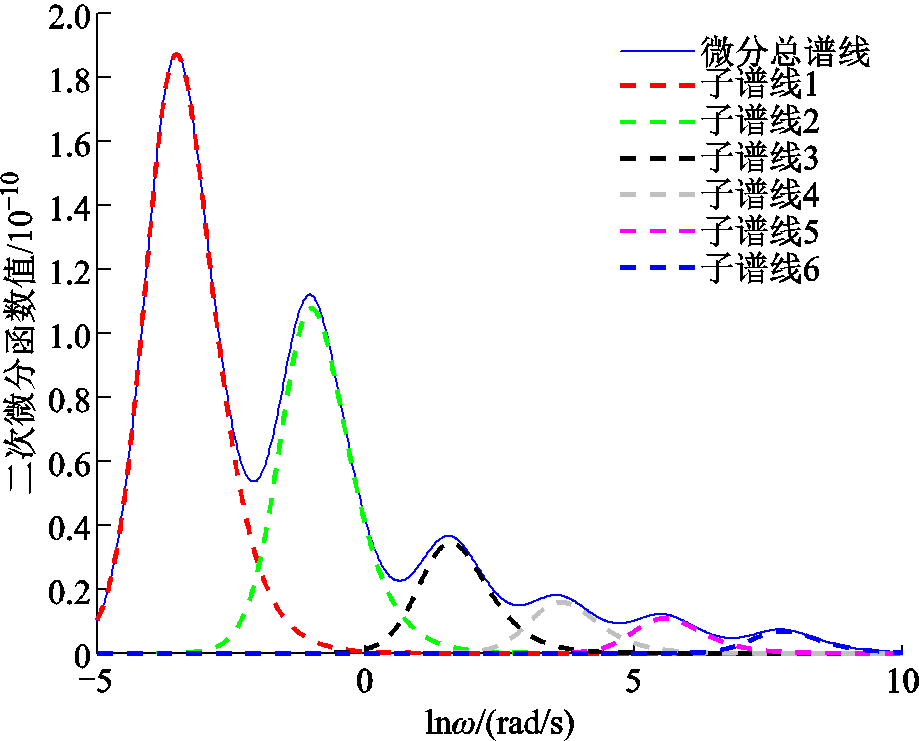
表1为某220 kV油浸式变压器T1扩展德拜等效电路参数。现对变压器T1的极化复电容实部采用本文所提方法进行微分解谱和等效电路参数辨识,解谱过程如图3所示,最终解谱结果如图4所示。
表1 变压器T1扩展德拜等效电路参数
Tab.1 Extended Debye equivalent circuit parameters of transformer T1

极化支路Rpi/GΩCpi/nFτi/s 1305.0710.15848.201 242.7530.0913.891 310.0162.91×10-20.291 42.7661.35×10-20.037 50.5829.23×10-35.37×10-3 60.1035.78×10-36.00×10-4
由图4可判定极化复电容实部二次微分谱线有6个峰值点,可判断该变压器油纸绝缘介电响应等效电路包含6条极化支路,与实际等效电路情况一致,验证了本文所提方法判定变压器油纸绝缘介电响应等效电路极化支路数的可靠性。图3中各个子谱线峰值点坐标情况见表2。结合式(10)辨识获得的各个极化支路参数见表3。
表2 各个峰值点坐标
Tab.2 Coordinates of each peak point

极化支路峰值点 1(-3.529, 1.872×10-10) 2(-1.006, 1.078×10-10) 3(1.577, 3.458×10-11) 4(3.634, 1.617×10-11) 5(5.586, 1.095×10-11) 6(7.763, 6.84×10-12)
表3 极化支路参数辨识结果
Tab.3 Identification results of polarized branch parameters
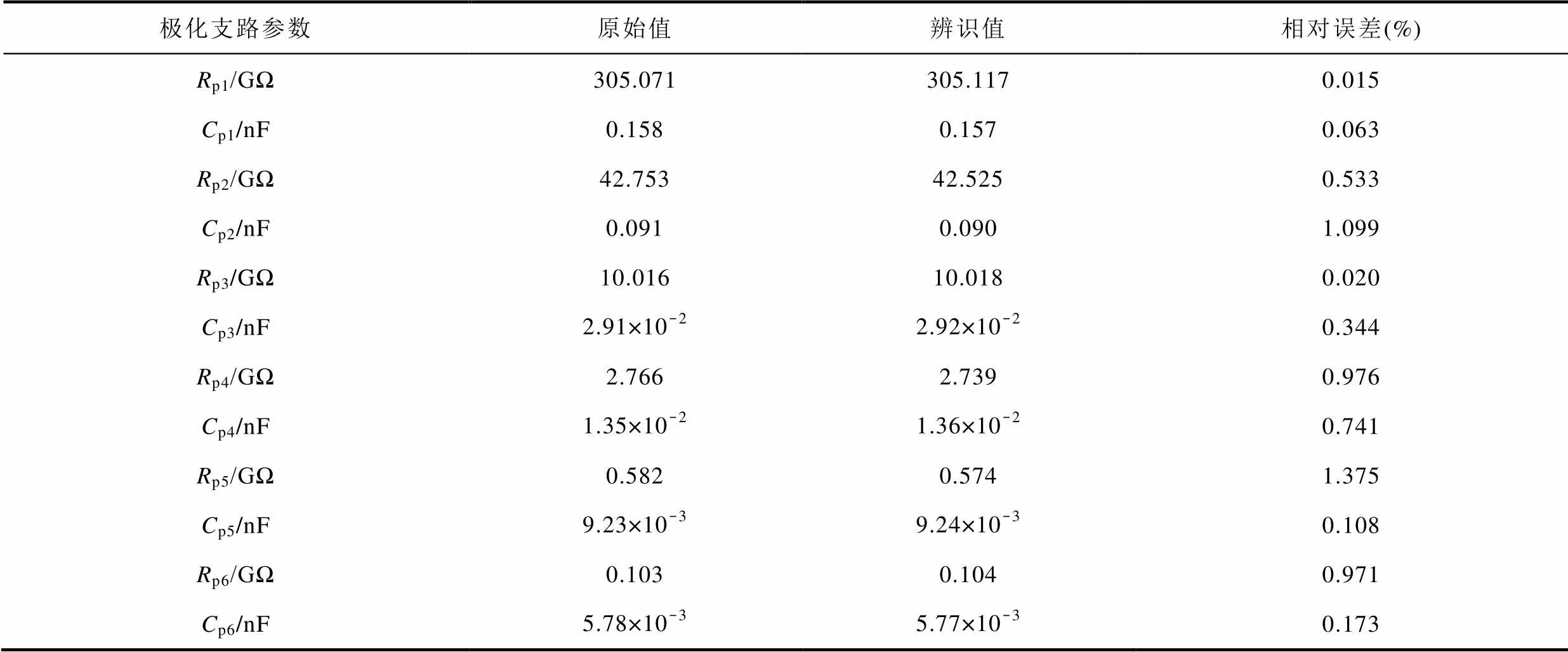
极化支路参数原始值辨识值相对误差(%) Rp1/GΩ305.071305.1170.015 Cp1/nF0.1580.1570.063 Rp2/GΩ42.75342.5250.533 Cp2/nF0.0910.0901.099 Rp3/GΩ10.01610.0180.020 Cp3/nF2.91×10-22.92×10-20.344 Rp4/GΩ2.7662.7390.976 Cp4/nF1.35×10-21.36×10-20.741 Rp5/GΩ0.5820.5741.375 Cp5/nF9.23×10-39.24×10-30.108 Rp6/GΩ0.1030.1040.971 Cp6/nF5.78×10-35.77×10-30.173
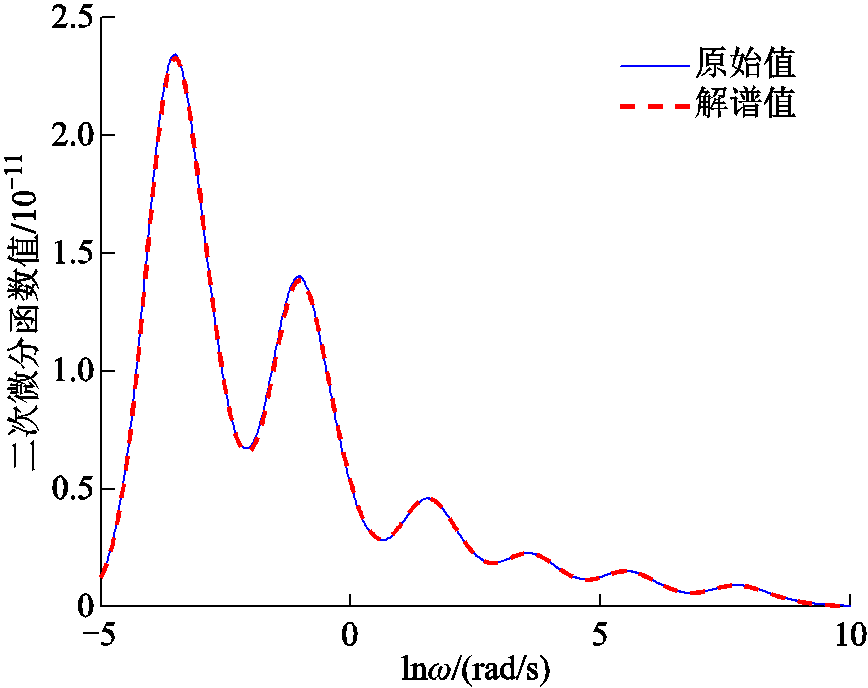
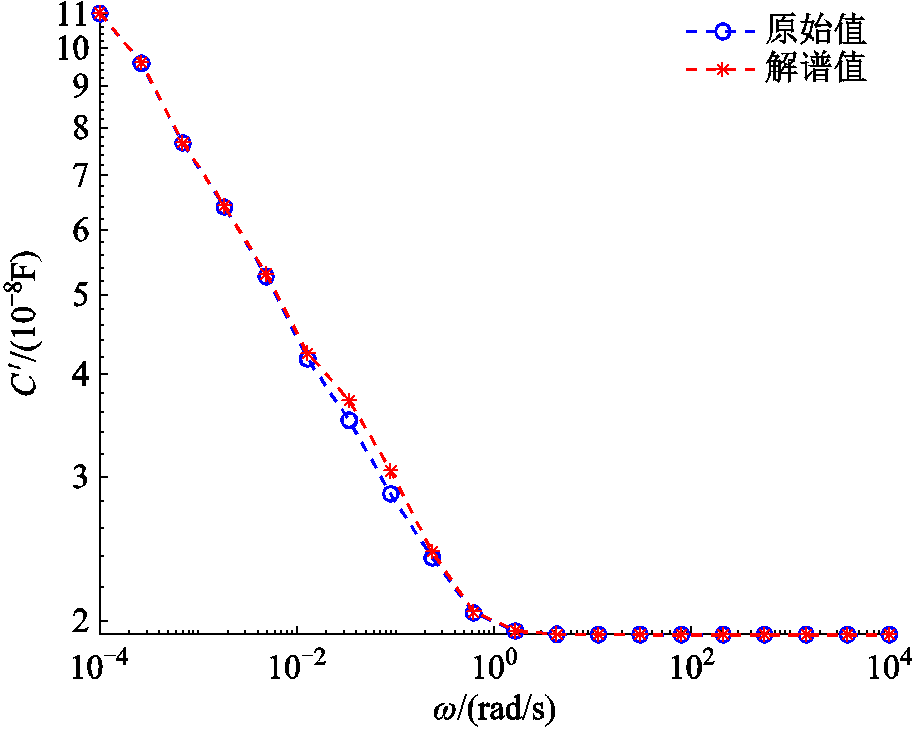
由表3可知,经极化复电容实部二次微分解谱法辨识得到的扩展德拜极化支路参数值与实测值的最高相对误差不超过2%。基于本文解谱法获得的极化复电容实部二次微分谱线和复电容实部谱线与各自实际谱线的对比分别如图5、图6所示。从图5、图6可直观看出基于本文解谱法获得两种谱线与各自实际谱线基本重合。
为进一步验证参数辨识的准确性,采用拟合度计算两条谱线的吻合情况,拟合度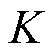 的表达式为
的表达式为
式中,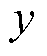 为实际值;
为实际值;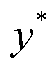 为计算值。
为计算值。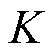 越接近1,代表实测所得谱线与辨识所得谱线的拟合度越高。
越接近1,代表实测所得谱线与辨识所得谱线的拟合度越高。
结合式(11)计算可得图5中两条谱线的拟合度为0.986,图6中两条谱线的拟合度为0.979,进一步验证了采用峰值点坐标辨识扩展德拜极化等效电路参数的准确性。
3 实例参数验证
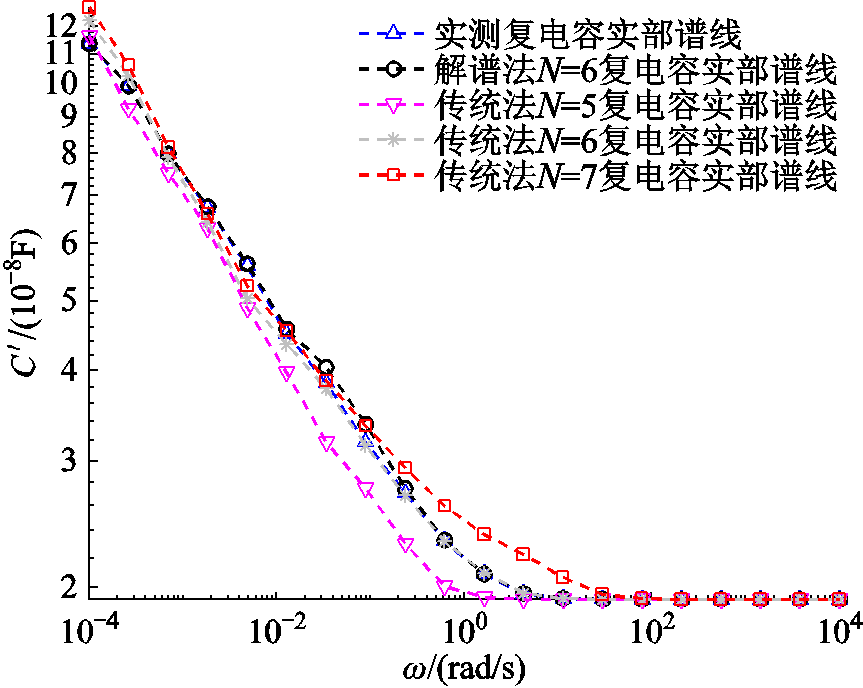
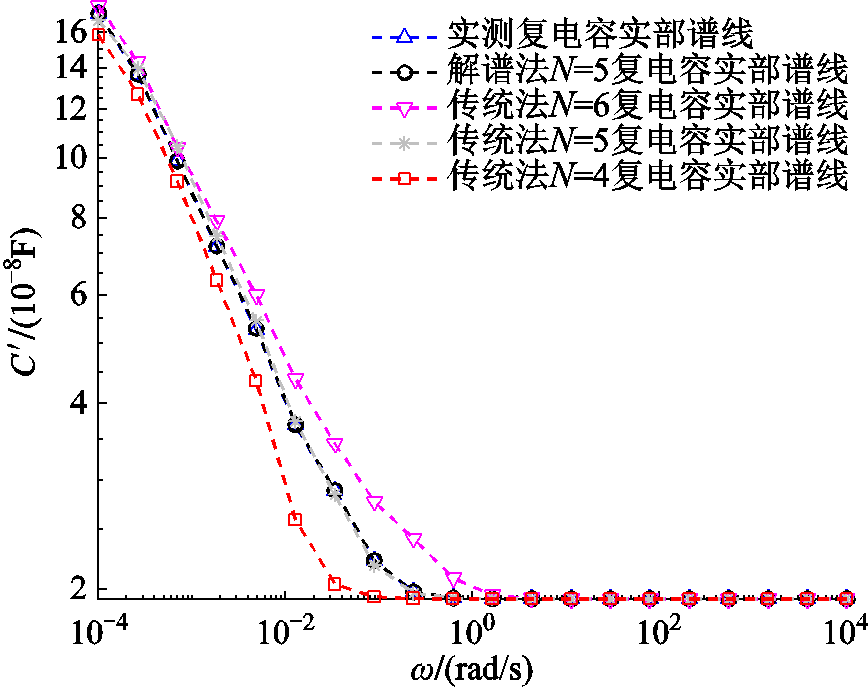
为验证本文提出的极化等效电路参数辨识方法的有效性,本文选取另外两台不同老化状态的变压器T2(型号为SFL-50000/110,运行10年,绝缘较好)、T3(型号为SFSE9-240000/220,刚投运,绝缘良好)进行分析。一方面,采用传统经验法(以下简称传统法)人为事先假定两台变压器油纸绝缘介电响应等效电路极化支路数,并结合智能算法进行等效电路参数辨识[14];另一方面,采用本文所提方法(以下简称解谱法)判定两台变压器各自的等效电路极化支路数并进行参数辨识。两种方法求解获得的等效电路参数见表4、表5,基于各自等效电路参数获取的复电容实部谱线与实测值对比分别如图7、图8所示,各个拟合度见表6。
从图7、图8可知,一方面,变压器T2含有6条极化支路的等效电路参数能够更准确地反映其频域介电谱,变压器T3含有5条极化支路的等效电路参数能够更准确地反映其频域介电谱,均与解谱法判定的极化支路数一样;另一方面,两台不同老化状态变压器基于解谱法求解获得的复电容实部谱线与实测值拟合情况均是最佳。
表4 两种方法求解获得的T2等效电路参数
Tab.4 Equivalent circuit parameters of T2 obtained by the two methods
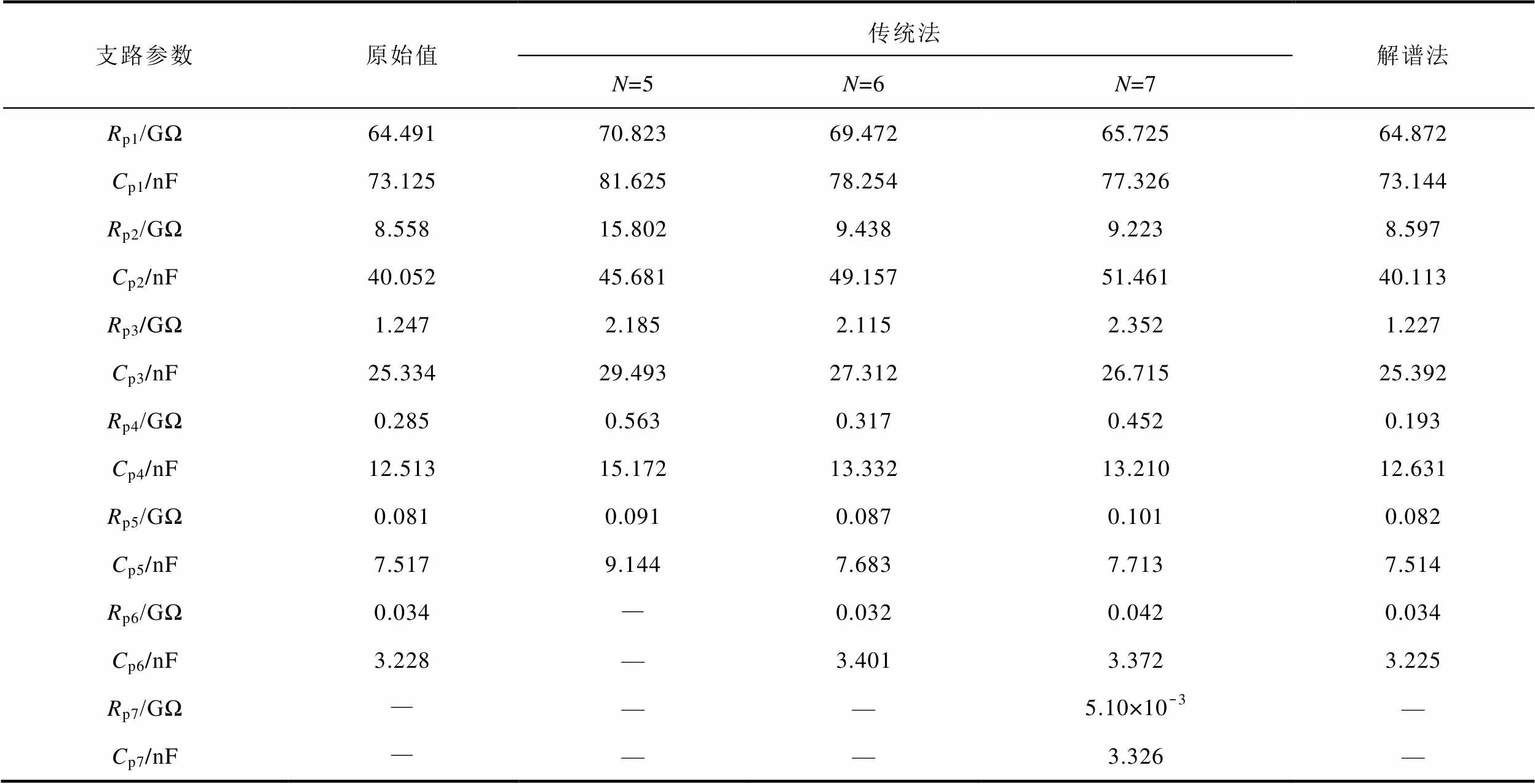
支路参数原始值传统法解谱法 N=5N=6N=7 Rp1/GΩ64.49170.82369.47265.72564.872 Cp1/nF73.12581.62578.25477.32673.144 Rp2/GΩ8.55815.8029.4389.2238.597 Cp2/nF40.05245.68149.15751.46140.113 Rp3/GΩ1.2472.1852.1152.3521.227 Cp3/nF25.33429.49327.31226.71525.392 Rp4/GΩ0.2850.5630.3170.4520.193 Cp4/nF12.51315.17213.33213.21012.631 Rp5/GΩ0.0810.0910.0870.1010.082 Cp5/nF7.5179.1447.6837.7137.514 Rp6/GΩ0.034—0.0320.0420.034 Cp6/nF3.228—3.4013.3723.225 Rp7/GΩ———5.10×10-3— Cp7/nF———3.326—
表5 两种方法求解获得的T3等效电路参数
Tab.5 Equivalent circuit parameters of T3 obtained by the two methods
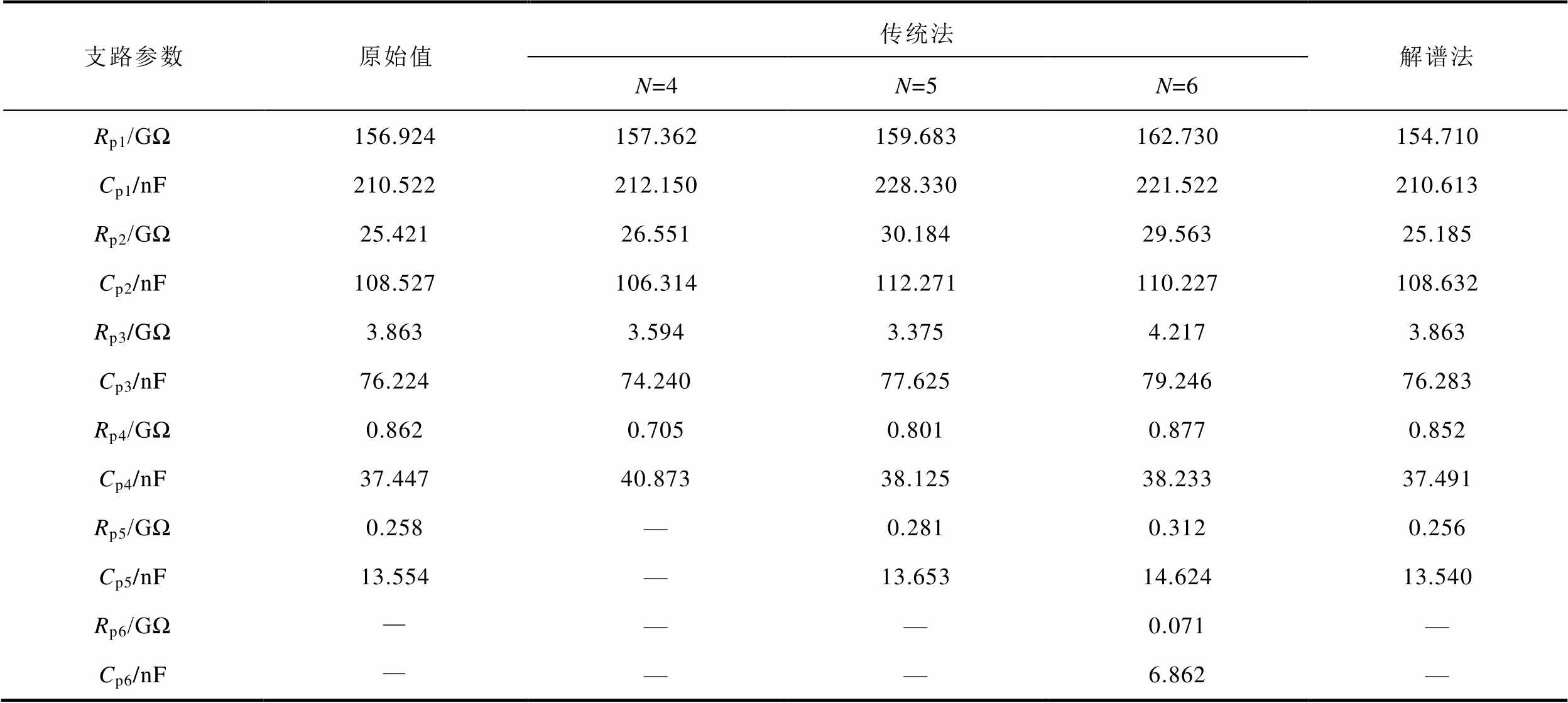
支路参数原始值传统法解谱法 N=4N=5N=6 Rp1/GΩ156.924157.362159.683162.730154.710 Cp1/nF210.522212.150228.330221.522210.613 Rp2/GΩ25.42126.55130.18429.56325.185 Cp2/nF108.527106.314112.271110.227108.632 Rp3/GΩ3.8633.5943.3754.2173.863 Cp3/nF76.22474.24077.62579.24676.283 Rp4/GΩ0.8620.7050.8010.8770.852 Cp4/nF37.44740.87338.12538.23337.491 Rp5/GΩ0.258—0.2810.3120.256 Cp5/nF13.554—13.65314.62413.540 Rp6/GΩ———0.071— Cp6/nF———6.862—
由表6的拟合度情况可知,变压器T2基于解谱法求解获得的复电容实部谱线与其实际值拟合度为0.979,比其他工况下的拟合度平均提升0.262。变压器T3基于解谱法求解获得的复电容实部谱线与其实际值拟合度为0.984,比其他工况下的拟合度平均提升0.266。
表6 两种方法求解获得的谱线拟合度
Tab.6 Fit condition of spectrum obtained by the two methods
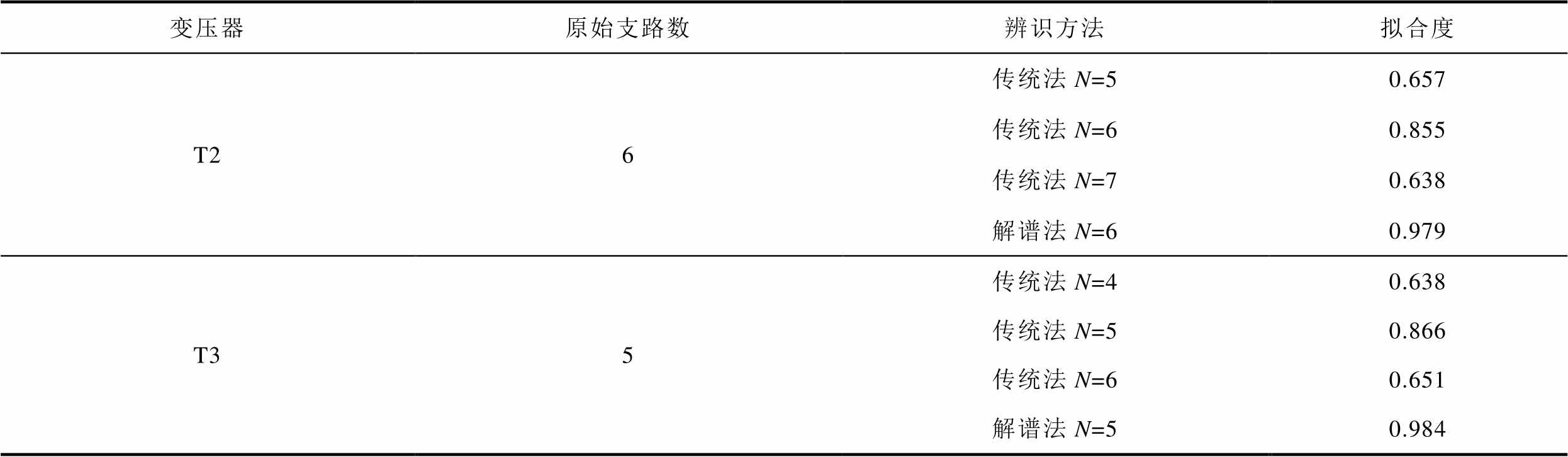
变压器原始支路数辨识方法拟合度 T26传统法N=50.657 传统法N=60.855 传统法N=70.638 解谱法N=60.979 T35传统法N=40.638 传统法N=50.866 传统法N=60.651 解谱法N=50.984
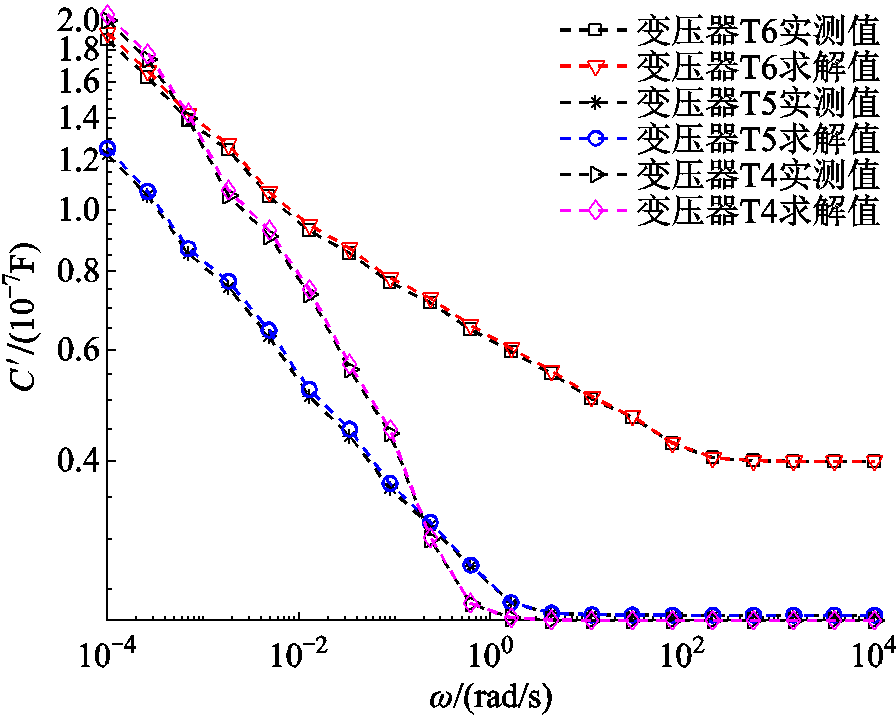
采用本文方法对另外三台不同老化程度的变压器进行等效电路参数辨识,对比各自复电容实部谱线求解值与实测值,并进行相应的拟合度计算,对比结果和计算结果分别如图9和表7所示。
表7 复电容实部谱线拟合情况
Tab.7 Fitting situation of real part spectrum of complex capacitance

变压器原始支路数老化状态判定支路数拟合度 T44绝缘良好40.991 T55轻微老化50.983 T67老化严重70.981
通过对以上六台不同老化状态的变压器分析可知,极化复电容实部二次微分谱线判定等效电路极化支路数准确率为100%,等效电路参数辨识准确率达到98%以上,基于解谱法获取的复电容实部谱线与实测值拟合度达到97%以上。
综上所述,通过对复电容实部谱线进行二次微分解谱,不但能够准确地判定变压器油纸绝缘介电响应等效电路的极化支路数,而且能够直接通过各个子谱线峰值点坐标辨识极化支路参数,所辨识的参数也能够准确地反映变压器复电容实部谱线,有利于后续应用变压器油纸绝缘介电响应等效电路参数和频域介电谱特征量综合分析变压器的绝缘老化情况。
4 结论
变压器油纸绝缘等效电路是分析变压器绝缘介质老化的重要途径,本文提出极化复电容实部二次微分谱线的构建方法,并利用子谱线数量和峰值点坐标直接判定极化支路数和辨识极化支路参数,解决了应用频域介电谱特征量难以判定等效电路极化支路数的难题,丰富了变压器油纸绝缘介电响应等效电路模型的构建方法。通过对多台不同老化程度的变压器研究,得出以下结论:
1)极化复电容实部二次微分谱线峰值点数量即为变压器油纸绝缘介电响应等效电路极化支路数,为后续准确辨识等效电路参数提供重要依据。
2)极化复电容实部二次微分谱线峰值点坐标能够直接准确地辨识等效电路参数,且峰值点坐标具有唯一性,有效地提高了等效电路参数辨识的准确度。
3)基于解谱法构建的等效电路模型能够准确地反映频域介电谱,为后续应用等效电路参数和频域介电谱特征量诊断变压器绝缘老化状态奠定了重要基础。
微分解谱法能够准确地判定变压器绝缘系统扩展德拜等效电路极化支路数,而随着变压器绝缘老化程度的加剧,其内部老化产物增多,介电响应更加复杂,对应的极化支路数也随之增多。因此,后续可以应用微分解谱法深入研究频域介电谱内部隐含的老化特征量,为变压器绝缘状态诊断提供新方法。
参考文献
[1] 赵洪山, 常杰英, 曲岳晗, 等. 基于二元非线性Wiener随机过程的变压器油纸绝缘剩余寿命预测方法[J]. 电工技术学报, 2023, 38(15): 4040-4049.
Zhao Hongshan, Chang Jieying, Qu Yuehan, et al. Residual life prediction method of transformer oil-paper insulation based on binary nonlinear Wiener random process[J]. Transactions of China Electro-technical Society, 2023, 38(15): 4040-4049.
[2] 郑玉平, 郝治国, 薛众鑫, 等. 大型电力变压器安全运行与主动保护技术探索[J]. 电力系统自动化, 2023, 47(20): 1-12.
Zheng Yuping, Hao Zhiguo, Xue Zhongxin, et al. Exploration of safe operation and active protection technology for large-capacity power transformers[J]. Automation of Electric Power Systems, 2023, 47(20): 1-12.
[3] 刘刚, 高成龙, 胡万君, 等. 基于改进的连续局部枚举采样和径向基函数响应面法的变压器静电环结构优化设计[J]. 电工技术学报, 2023, 38(23): 6266-6278.
Liu Gang, Gao Chenglong, Hu Wanjun, et al. Optimized design of transformer electrostatic ring based on radial basis function response surface method with enhanced successful local enumeration sampling[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6266-6278.
[4] 李唐兵, 童军心, 童涛, 等. 老化对特高压变压器油纸绝缘介电特性及特征量的影响[J]. 变压器, 2021, 58(7): 19-24.
Li Tangbing, Tong Junxin, Tong Tao, et al. Effect of aging on dielectric characteristic and characteristic parameter of oil-paper insulation in UHV transformer [J]. Transformer, 2021, 58(7): 19-24.
[5] 张明泽, 孟繁昊, 刘骥, 等. 变压器油纸绝缘频域介电响应非线性特性研究[J]. 中国电机工程学报, 2023, 43(2): 831-843.
Zhang Mingze, Meng Fanhao, Liu Ji, et al. Research on nonlinear characteristics for frequency domain dielectric response of transformer oil-paper insulation [J]. Proceedings of the CSEE, 2023, 43(2): 831-843.
[6] 梁一霖, 张明泽, 刘骥, 等. 复杂运行条件下非均匀老化油纸绝缘典型电场变化特性[J]. 高电压技术, 2024, 50(4): 1731-1741.
Liang Yilin, Zhang Mingze, Liu Ji, et al. Variation characteristics of typical electric field of non-uniform aging oil-paper insulation under complex operating conditions[J]. High Voltage Engineering, 2024, 50(4): 1731-1741.
[7] Münster T, Werle P, Hämel K, et al. Thermally accelerated aging of insulation paper for transformers with different insulating liquids[J]. Energies, 2021, 14(11): 3036.
[8] Wei Yanhui, Han Wang, Li Guochang, et al. Aging characteristics of transformer oil-impregnated insulation paper based on trap parameters[J]. Polymers, 2021, 13(9): 1364.
[9] 孔灿, 张大宁, 田杰, 等. 110 kV变压器油纸绝缘套管不均匀绝缘受潮劣化分析[J]. 智慧电力, 2020, 48(4): 119-124.
Kong Can, Zhang Daning, Tian Jie, et al. Non-uniform moisture degradation analysis of 110 kV transformer oil-paper insulation bushing[J]. Smart Power, 2020, 48(4): 119-124.
[10] 张寒, 万保权, 胡伟, 等. 热效应对胶浸纸套管绝缘性能的影响及温度反演方法[J]. 高电压技术, 2022, 48(10): 4124-4132.
Zhang Han, Wan Baoquan, Hu Wei, et al. Influence of thermal effect on insulation performance of resin impregnated paper bushing and temperature inversion method[J]. High Voltage Engineering, 2022, 48(10): 4124-4132.
[11] 史加奇, 赵春明, 许文燮, 等. 基于WOA-LM算法的变压器油纸绝缘等效模型参数辨识[J]. 水电能源科学, 2021, 39(8): 190-193.
Shi Jiaqi, Zhao Chunming, Xu Wenxie, et al. Parameter identification of transformer oil-paper insulation equivalent model based on WOA-LM algorithm[J]. Water Resources and Power, 2021, 39(8): 190-193.
[12] 刘雅琴, 张涛. 基于Debye模型分析变压器油纸绝缘频域介电谱特性研究[J]. 电工电气, 2017(1): 18-21.
Liu Yaqin, Zhang Tao. Analysis of frequency domain dielectric spectrum properties of transformer oil paper insulation based on Debye model[J]. Electrotechnics Electric, 2017(1): 18-21.
[13] 杜林, 杨峰, 蔚超, 等. 基于频域介电谱的油纸绝缘宽频等效模型参数辨识研究[J]. 电工技术学报, 2018, 33(5): 1158-1166.
Du Lin, Yang Feng, Wei Chao, et al. Parameter identification of the wide-band model of oil-impregnated paper insulation using frequency domain spectroscopy[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1158-1166.
[14] 蔡金锭, 刘永清, 蔡嘉. 油纸绝缘变压器极化等效电路分析及其老化评估[J]. 电工技术学报, 2016, 31(15): 204-212.
Cai Jinding, Liu Yongqing, Cai Jia. Analysis of equivalent circuit of oil-paper insulation transformer relaxation response and aging evaluation[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 204-212.
[15] Olmi R, Bittelli M. Dielectric data analysis: recovering hidden relaxations by fourth-order derivative spectroscopy[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(6): 3334-3340.
[16] 蔡金锭, 曾静岚. 基于二次时域微分解析法的油纸绝缘介质响应参数辨识[J]. 高电压技术, 2017, 43(6): 1937-1942.
Cai Jinding, Zeng Jinglan. Parameter identification for dielectric response of oil-paper insulation based on second time-differential analysis[J]. High Voltage Engineering, 2017, 43(6): 1937-1942.
[17] 邹阳, 林锦煌, 何津, 等. 基于频谱解构法的油纸绝缘扩展德拜模型参数辨识[J]. 电工技术学报, 2023, 38(3): 622-632.
Zou Yang, Lin Jinhuang, He Jin, et al. Parameter identification of oil paper insulation extended Debye model based on spectrum deconstruction method[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 622-632.
[18] 曲德宇, 丛培杰, 吴杰, 等. 基于分步拟合法的变压器油纸绝缘等效参数辨识研究[J]. 自动化与仪表, 2020, 35(11): 6-9, 14.
Qu Deyu, Cong Peijie, Wu Jie, et al. Research on equivalent parameter identification of oil paper insulation of transformer based on step fitting method[J]. Automation & Instrumentation, 2020, 35(11): 6-9, 14.
[19] Varakantham S R, Kliem H. Dielectric relaxational phenomena in interacting composite structures[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2021, 28(3): 845-852.
[20] 黄猛, 李怡然, 吴延宇, 等. 计及界面电荷和极性效应的油纸复合绝缘非线性电路等效模型[J]. 电工技术学报, 2024, 39(11): 3422-3432.
Huang Meng, Li Yiran, Wu Yanyu, et al. Equivalent nonlinear circuit model with interface charge and polarity effect for oil-paper composite insulation[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3422-3432.
[21] 马御棠, 束洪春, 钱国超, 等. 基于频域介电谱曲线分解的氧化锌避雷器老化状态评估[J]. 电工技术学报, 2024, 39(3): 901-913.
Ma Yutang, Shu Hongchun, Qian Guochao, et al. Method for evaluating the aging state of ZnO arrester based on curve decomposition of frequency domain dielectric spectrum[J]. Transactions of China Electro-technical Society, 2024, 39(3): 901-913.
[22] 廖浩泉, 吴智影, 饶红疆, 等. 非线性误差电流抑制算法的电力变压器绝缘电阻测量方案[J]. 高压电器, 2020, 56(7): 189-192.
Liao Haoquan, Wu Zhiying, Rao Hongjiang, et al. Measurement scheme of insulation resistance of power transformer based on nonlinear error current suppression algorithm[J]. High Voltage Apparatus, 2020, 56(7): 189-192.
[23] 徐晴川, 王圣康, 林福昌, 等. 基于时频域介电响应的绝缘油弛豫过程分析[J]. 电工技术学报, 2022, 37(9): 2355-2365.
Xu Qingchuan, Wang Shengkang, Lin Fuchang, et al. Analysis of relaxation process of insulating oil based on dielectric response in time and frequency domain[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2355-2365.
[24] 杨峰, 唐超, 周渠, 等. 基于等效电路的油纸绝缘系统受潮状态分析[J]. 电工技术学报, 2020, 35(21): 4586-4596.
Yang Feng, Tang Chao, Zhou Qu, et al. Analyzing the moisture state of oil-paper insulation system using an equivalent circuital model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4586-4596.
[25] 潘志城, 楚金伟, 张晋寅, 等. 提高试验电压对抑制高压交流油纸绝缘套管频域介电谱测试电磁干扰影响的研究[J]. 电瓷避雷器, 2021(2): 66-71.
Pan Zhicheng, Chu Jinwei, Zhang Jinyin, et al. Improving test voltage to suppress influence of electromagnetic interference in frequency domain dielectric spectrum test of high voltage AC oil-paper insulated bushing[J]. Insulators and Surge Arresters, 2021(2): 66-71.
Identification of Dielectric Response Equivalent Circuit of Transformer’s Oil-Paper Insulation Based on Quadratic Differential Decomposition Spectroscopy of Frequency Domain Spectroscopy
Lin Zhiyong1,2 Li Ronghua1,2 Huang Guotai3 Deng Dongping4 Zhang Damin1,2
(1. School of Electrical Engineering and Automation Xiamen University of Technology Xiamen 361024 China 2. Xiamen Key Laboratory of Frontier Electric Power Equipment and Intelligent Control Xiamen 361024 China 3. Fujian Electric Power Supplies Limited Fuzhou 350003 China4. State Grid Zhangping Electric Power Supply Company Longyan 364400 China)
Abstract This paper presents a novel approach in addressing the challenges where the number of polarization branches in equivalent circuits is often assumed, and parameter identification requires complex iterative optimization algorithms. By analyzing the relationship between the extended Debye model equivalent circuit and frequency domain spectroscopy characteristics, this paper researches the real part of the polarized complex capacitance. This study transforms and reconstructs it to create the quadratic differential spectral lines of the real part of the polarized complex capacitance. The characteristics of these sub-spectral lines are analyzed as follows: (1)Each sub-spectral line exhibits a unique peak point, gradually decaying to zero on both sides of the peak. The sub-spectral lines shift to the right as the time constant decreases. (2)The spectral line comprises several sub-spectral lines with different time constants. The number of peak points corresponds to the number of polarization branches in the extended Debye equivalent model. (3)Sub-Spectral Lines: The previous sub-spectral line significantly influences the subsequent one, while the latter has minimal impact on the peak of the former. (4)By performing spectral decomposition starting from the first peak point, the characteristics of each sub-spectral line can be obtained.
Based on the characteristics of these sub-spectral lines, this paper proposes a method to determine the number of polarization branches of the equivalent circuit by using the number of peak points of the quadratic differential spectral line of the real part of the polarization complex capacitance, and a method of using the coordinates of the peak points of the sub-spectral lines to determine the equivalent circuit parameters. Due to the significance and uniqueness of each peak point, this method can avoid the problems of presetting the number of polarization branches and the non-uniqueness of the identification results in the existing parameter identification methods, thus improving the accuracy of parameter identification. this paper proposes the parameter identification steps based on the frequency domain dielectric spectrum quadratic differential decomposition spectroscopy method. To verify the reliability of the proposed method, the real part of the polarized complex capacitance of a transformer is first identified by the proposed method for the quadratic differential decomposition spectroscopy and equivalent circuit parameters. Then, to verify the applicability of this method to transformers with different aging states, the polarization complex capacitance real part method is studied for multiple transformers with varying states of aging. To evaluate the effectiveness of this method for transformers in various aging states, the quadratic differential decomposition spectroscopy technique was applied to multiple transformers with differing conditions. The findings are as follows: This method achieves an impeccable 100% accuracy in identifying the number of polarization branches within the equivalent circuit. The technique surpasses 98% accuracy in identifying equivalent circuit parameters. The correlation between the spectrum obtained through spectral decomposition and the actual measured values exceeds 97%, the quadratic differential spectral line of the real part of the polarized complex capacitance can accurately and uniquely identify the equivalent circuit parameters. This approach effectively enhances the reliability and efficiency of identifying these parameters by utilizing the characteristics of the frequency domain spectroscopy. Additionally, it offers a novel method for accurately diagnosing the aging state of transformer oil-paper insulation.
Keywords:Frequency domain spectroscopy, oil-paper insulation, equivalent circuit, parameters identification, differential spectrum resolution
中图分类号:TH183;TM411
DOI: 10.19595/j.cnki.1000-6753.tces.241347
国家自然科学基金青年基金项目(51407151)、福建省自然科学基金资助项目(2020J01281)和福建省中青年教师教育科研项目(JZ230048)资助。
收稿日期 2024-07-28
改稿日期 2024-12-05
作者简介
林智勇 男,1989年生,博士,副教授,研究方向为电气设备绝缘监测与故障诊断。
E-mail:625720199@qq.com(通信作者)
李荣华 女,1999年生,硕士研究生,研究方向为电气设备绝缘监测与故障诊断。
E-mail:1534378433@qq.com
(编辑 赫 蕾)
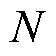 会随着老化程度的加深而不断增加[11],但是扩展德拜模型极化支路参数的准确辨识却是一大难题。文献[12]对支路数进行预设,采用粒子群算法对变压器进行参数辨识,可有效反映变压器绝缘老化状态,但是参数辨识具有随机性且不能准确地反映真实支路数。文献[13]通过遗传算法与Levenberg-Marquardt算法相结合的方法对变压器进行参数辨识,但其误差仅在一定范围内较小,辨识结果具有一定的局限性。文献[14]对回复电压谱线用峰值点确定极化支路数,采用末端随机取点的方式对极化支路进行参数辨识,对参数辨识具有参考意义,但是随机取点的方式不具有唯一性。文献[15]对复介电常数进行多次微分,研究分析1~4阶微分谱线峰值点特性,指出可通过4阶微分谱线峰值点判断极化支路数,但是计算公式较为复杂。文献[16]采用解谱法进行支路数判断和等效电路参数辨识,辨识结果与实测参数拟合度较高,有效地提高了极化支路参数辨识的准确度,但取点方式使辨识参数不唯一。文献[17]采用频域介电谱一次微分谱线进行参数辨识,通过一次微分谱线峰值点能够有效判定极化支路数,提高了参数辨识的可靠性,但有时存在峰值点不明显的缺点,需要进一步优化。
会随着老化程度的加深而不断增加[11],但是扩展德拜模型极化支路参数的准确辨识却是一大难题。文献[12]对支路数进行预设,采用粒子群算法对变压器进行参数辨识,可有效反映变压器绝缘老化状态,但是参数辨识具有随机性且不能准确地反映真实支路数。文献[13]通过遗传算法与Levenberg-Marquardt算法相结合的方法对变压器进行参数辨识,但其误差仅在一定范围内较小,辨识结果具有一定的局限性。文献[14]对回复电压谱线用峰值点确定极化支路数,采用末端随机取点的方式对极化支路进行参数辨识,对参数辨识具有参考意义,但是随机取点的方式不具有唯一性。文献[15]对复介电常数进行多次微分,研究分析1~4阶微分谱线峰值点特性,指出可通过4阶微分谱线峰值点判断极化支路数,但是计算公式较为复杂。文献[16]采用解谱法进行支路数判断和等效电路参数辨识,辨识结果与实测参数拟合度较高,有效地提高了极化支路参数辨识的准确度,但取点方式使辨识参数不唯一。文献[17]采用频域介电谱一次微分谱线进行参数辨识,通过一次微分谱线峰值点能够有效判定极化支路数,提高了参数辨识的可靠性,但有时存在峰值点不明显的缺点,需要进一步优化。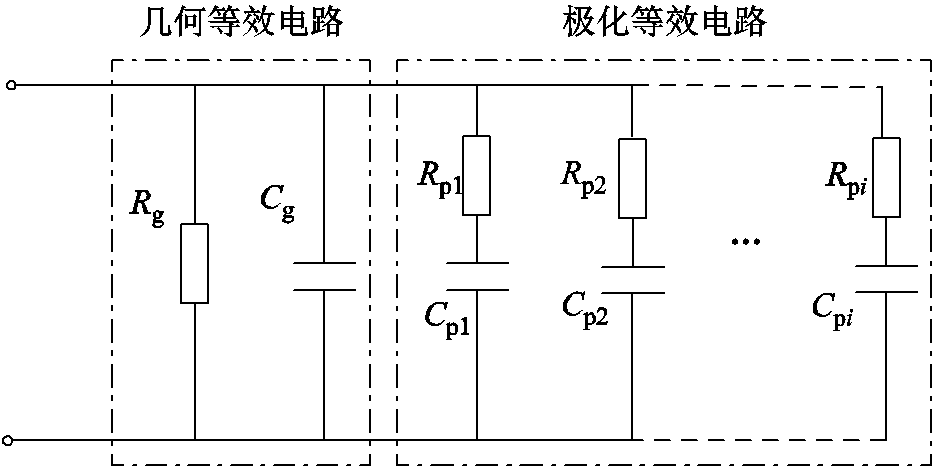
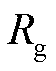 为绝缘电阻,
为绝缘电阻,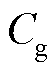 为工频下的几何电容,
为工频下的几何电容,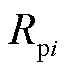 和
和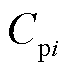 分别为第
分别为第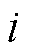 个极化支路的极化电阻和极化电容(
个极化支路的极化电阻和极化电容(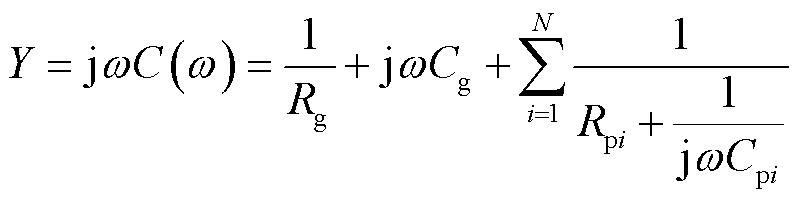 (1)
(1)
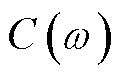 为
为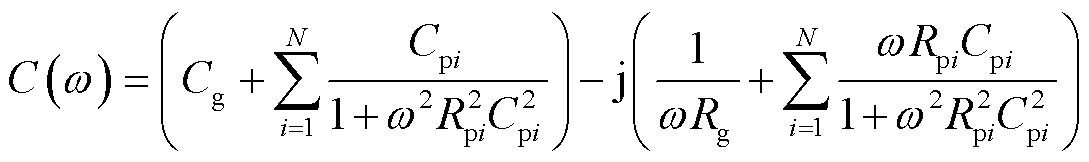 (2)
(2)
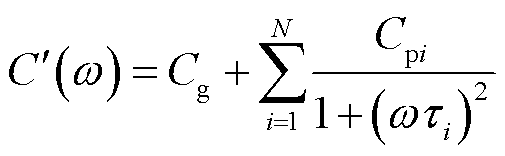 (3)
(3)
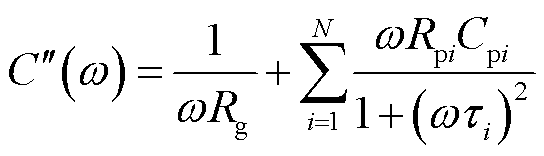 (4)
(4)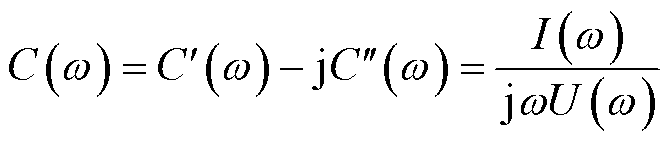 (5)
(5)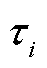 为第i个极化支路的时间常数,表征绝缘介质的极化弛豫速率,
为第i个极化支路的时间常数,表征绝缘介质的极化弛豫速率,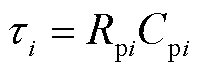 ;
;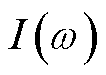 和
和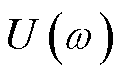 分别为施加的复电流和复电压。
分别为施加的复电流和复电压。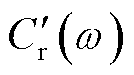 为
为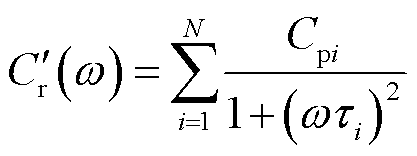 (6)
(6)
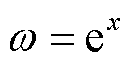 ,对
,对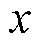 进行微分,得到极化复电容实部一次微分谱线
进行微分,得到极化复电容实部一次微分谱线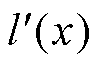 为
为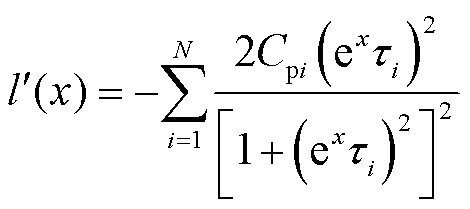 (7)
(7)
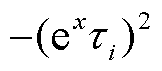 ,再进行微分得到极化复电容实部二次微分谱线
,再进行微分得到极化复电容实部二次微分谱线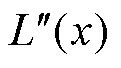 为
为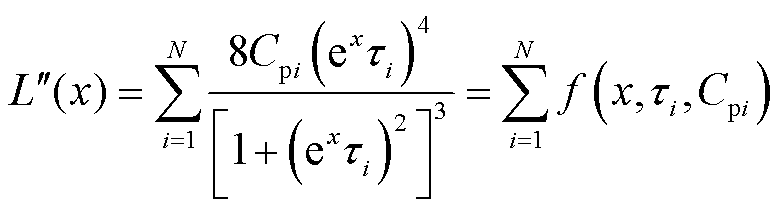 (8)
(8)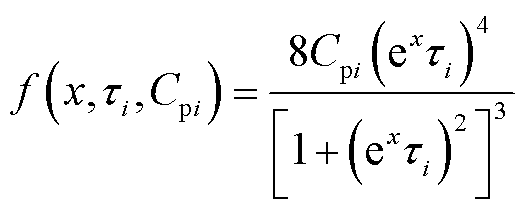 (9)
(9)
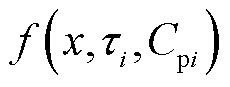 为极化复电容实部二次微分子谱线函数(以下称为子谱线函数,对应曲线称为子谱线)。
为极化复电容实部二次微分子谱线函数(以下称为子谱线函数,对应曲线称为子谱线)。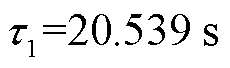 ,
,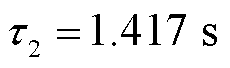 ,
,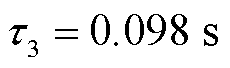 ,三种子谱线对比如图2所示。
,三种子谱线对比如图2所示。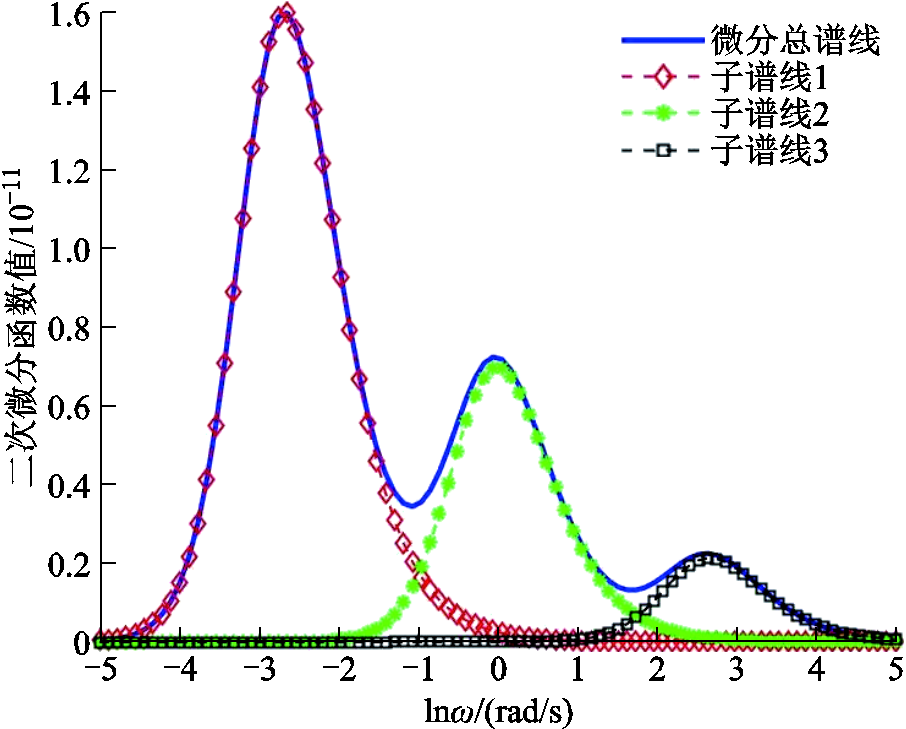
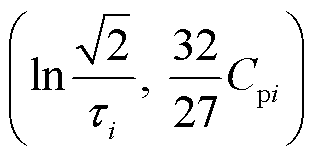 ,并向峰值两侧逐渐衰减为0,且子谱线随着
,并向峰值两侧逐渐衰减为0,且子谱线随着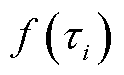 的分析可知,其峰值点的坐标为
的分析可知,其峰值点的坐标为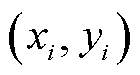 ,可求解不同极化支路的极化电容、时间常数和极化电阻,有
,可求解不同极化支路的极化电容、时间常数和极化电阻,有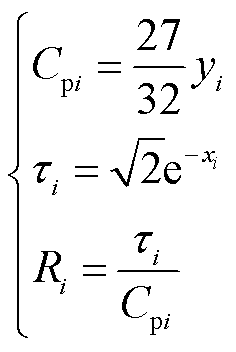 (10)
(10)
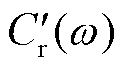 。
。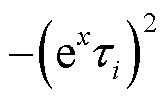 ,再进行微分得到极化复电容实部二次微分谱线
,再进行微分得到极化复电容实部二次微分谱线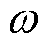 转换为
转换为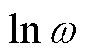 ,使得曲线峰值点更加清晰。
,使得曲线峰值点更加清晰。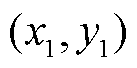 ,并结合式(10)求解第一条子谱线
,并结合式(10)求解第一条子谱线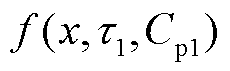 以及对应的极化支路1的极化电容
以及对应的极化支路1的极化电容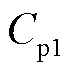 、时间常数
、时间常数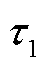 和极化电阻
和极化电阻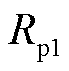 。
。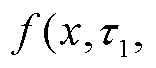
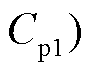 得到剩余谱线
得到剩余谱线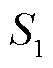 ;再从剩余谱线
;再从剩余谱线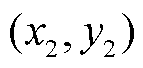 ,并结合式(10)求解第二条子谱线
,并结合式(10)求解第二条子谱线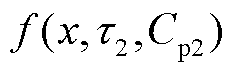 以及对应的极化支路2的极化电容
以及对应的极化支路2的极化电容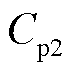 、时间常数
、时间常数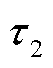 和极化电阻
和极化电阻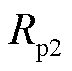 。
。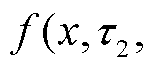
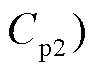 得到剩余谱线
得到剩余谱线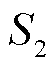 ,重复步骤4),以此类推直到最后一个峰值点
,重复步骤4),以此类推直到最后一个峰值点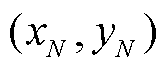 ,完成全部子谱线的解谱和极化支路参数辨识。
,完成全部子谱线的解谱和极化支路参数辨识。


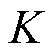 的表达式为
的表达式为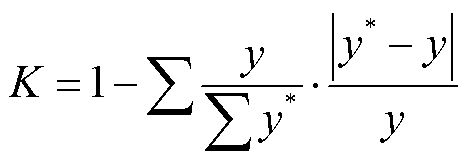 (11)
(11)
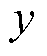 为实际值;
为实际值;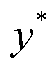 为计算值。
为计算值。