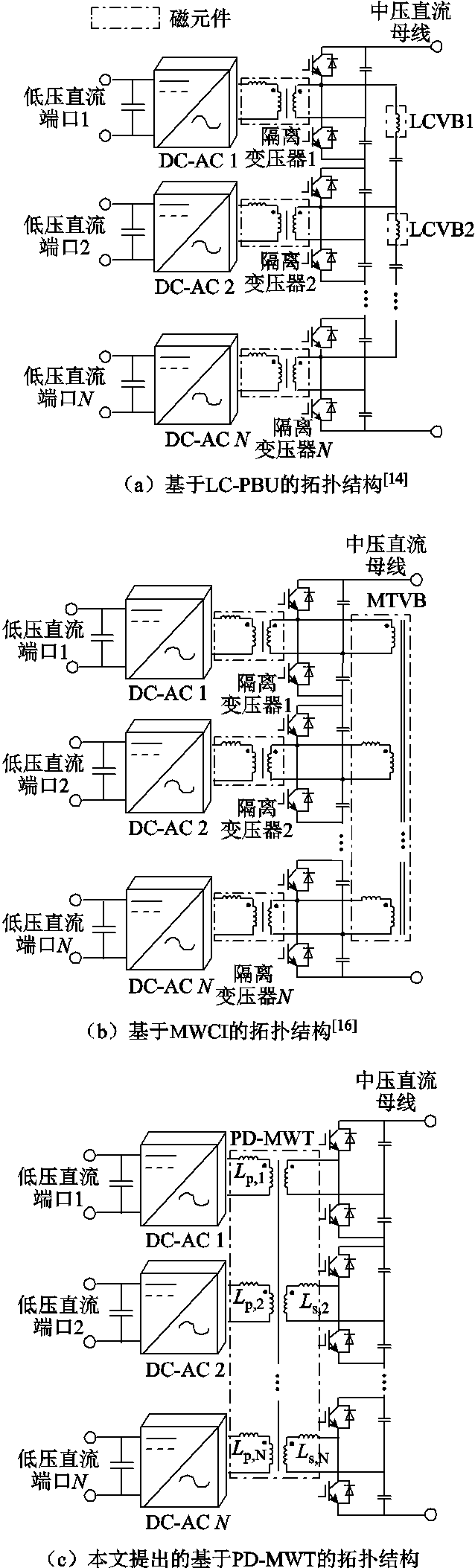
图1 多端口IIOS变换器拓扑结构比较
Fig.1 Multiport IIOS converter comparison
摘要 多端口输入独立输出串联(IIOS)型直流变换器具有独立最大功率点跟踪控制(MPPT)、高升压比和高效率等优点,适用于分布式光伏中压直流汇集场合。针对分布式光伏系统输入功率不匹配会造成子模块输出电压不均匀,会导致器件过电压和系统最大输出功率损失的问题,该文提出一种基于功率解耦多绕组变压器(PD-MWT)的多端口输入独立输出串联型双半桥变换拓扑结构,与现有其他多端口IIOS变换器相比,该拓扑结构将子模块变换器中的隔离变压器和用于电压均衡的多绕组变压器集成在一个PD-MWT中,可以显著地减小整个IIOS系统的体积和尺寸。此外,该变换器仅需在电路中配置较少的传感器就能实现MPPT控制和输出均压均衡,且网侧开关管比其他IIOS变换器具有更低的电流应力。最后通过Matlab/Simulink仿真和三模块900 W小型样机实验验证了该拓扑结构的工作原理和相关性能。
关键词:多端口DC-DC变换器 光伏直流汇集 中压直流 功率失配 电压均衡
为全力以赴促进实现“双碳”目标,目前我国电力绿色低碳转型不断加速,新能源发电占全部类型电源装机容量与发电量的比值不断增长[1]。随着电力电子技术和柔性直流输电技术发展,基于直流汇集的新能源外送系统将有望替代常规交流接入方式成为风电、光伏发电接入系统的可能解决方案[2]。其中光伏发电作为可再生能源开发利用的重要组成部分,是可供人类利用的储量最为丰富的清洁能源之一[3]。相比于传统以逆变器为核心的交流汇集方案,光伏发电采用中压直流(Medium Voltage DC, MVDC)汇集技术,无低次谐波污染和逆变器宽频振荡等问题,可有效改善系统的稳定性、电能质量与整体效率,因此得到了学术界的广泛关注与研究[4]。由于绝缘要求,大多数光伏阵列的耐压等级设计一般不超过1 kV,远低于中压直流母线的电压等级。因而常使用子模块变换器输出串联的模块化架构实现两个电压等级的匹配[5]。
基于输出串联结构,变换器系统可分为输入并联输出串联(Input-Parallel Output-Series, IPOS)和输入独立输出串联(Input-Independent Output-Series IIOS)两种类型[6]。由于IPOS变换器的输入端口数量有限,这使得它难以应对频繁发生的故障情况,特别是当低压直流侧发生短路故障时,整个系统将立即崩溃并退出运行[7]。对于隔离式多输入端口结构,当某个输入端口发生故障时,系统仍具有运行能力[8-9]。因此,分布式光伏中压直流汇集系统需要一种多端口输入独立输出串联的直流功率变换架构。
通常情况下,当分布式光伏阵列的光照强度和环境温度不一致时,光伏子模块变换器的输出功率将会不同。由于输出串联连接,输出端电流相同,IIOS系统中各子模块变换器将存在输出电压不均衡的问题,将会对系统正常运行产生不利影响[10]。为克服该问题,提出了许多具有功率平衡单元(Power Balance Unit, PBU)的输入独立输出串联型变换器。功率平衡单元作为传输不匹配功率的通道,可以被应用在输出侧的直流电容之间,使子模块变换器的输出电压达到平衡。文献[10]提出了一个三端口变换器(Three-Port Converter, TPC)系统来解决功率不匹配问题,功率只需传送一次即可到达目标模块,实现完全模块化。然而,该方法需要额外的低压直流母线,将会在一定程度上增加整个变换器系统的运维成本。文献[11]利用相邻移相全桥子模块(Submodules, SM)之间的双向Buck-Boost升降压网络作为电压平衡单元来传输不平衡功率。但这种方案使用了过多的功率开关器件,并且由于功率平衡单元中开关管的硬开关工作状态,整个变换器系统效率并没有得到显著提高。基于双向Buck-Boost均压结构,文献[12]提出了一种环形功率均衡拓扑方案及其效率优化控制策略,用以实现电压平衡。但是该方法没有减少变换器系统的有源开关器件,却增加了无源元件数量,且所采用的闭环控制策略较为复杂。
结合双向Buck-Boost升降压网络和串联LC支路,文献[13]提出了一种新的电压平衡单元,与文献[11]相比,节省了一半的开关器件数量,但以控制复杂为代价,且只能实现部分开关管的软开关。通过将LC支路嵌入相邻子模块变换器的输出桥臂中, 如图1a所示,IIOS模块化变换器可以通过模块间移相控制实现电压平衡[14]。由于开关器件复用,该方法具有高效率和低成本的优点。然而,为了实现相邻SM之间的闭环控制,需要N个(N代表SM数量)额外的传感器和闭环控制环路,这使得系统调制和控制策略复杂,增加了系统成本。此外,在文献[14]中,存在电网侧开关电流应力较高的问题。为了减少网侧开关电流应力,文献[15]提出了一种具有内移相的低电流峰值控制方法。然而,这种方法仅适用于双有源桥(Double Active Bridge, DAB)结构的SM变换器,需要更多的闭环传感器,这将进一步增加系统软硬件成本。文献[16]提出了在二次侧使用多绕组耦合电感的电压均衡拓扑结构(Multi-Winding Coupled-Inductor, MWCI),如图1b所示。该方法创建了一个可以将不匹配功率直接传输到目标SM的功率通道,提高了系统效率并减少了电网侧开关的电流应力,但是各子模块中均存在一个分离变压器,进而导致系统拓扑中使用了过多磁性元件。
基于文献[17-18]的磁集成技术和功率解耦多绕组变压器(Power Decoupling-Multi Winding Tranformer, PD-MWT),本文提出了一种适用于光伏中压直流汇集场合的多端口输入独立输出串联直流变换拓扑结构,如图1c所示。所提出的拓扑结构能够实现各输入端口的独立最大功率点跟踪(Maximum Power Point Tracking, MPPT)控制和高升压转换比。此外,该拓扑结构还具有以下工作特性:①用于实现电压均衡的变压器和子模块隔离变压器集成在一起,以隔离不同的电压等级并实现平均功率传输,进而可以在IIOS变换系统中实现更高的功率密度;②可以采用较少的传感器和闭环控制环路来实现输出电压均衡,降低了系统软硬件成本;③网侧开关管具有更低的电流应力,且与变换器系统功率不匹配程度无关。

图1 多端口IIOS变换器拓扑结构比较
Fig.1 Multiport IIOS converter comparison
本文详细描述了所提变换器拓扑的工作原理及其调制和控制策略,给出了变换器关键元件的参数设计选型准则,并与其他相关IIOS变换器进行了详细的性能比较。最后,通过Matlab/Simulink平台搭建模型进行了仿真分析,并建立了包含三个输入端口的低压等值硬件实验平台,对分析结果进行了测试验证。
本文所提出的基于多绕组变压器的IIOS变换器拓扑结构如图2所示,其拓扑结构包含N个一次电压源型半桥(Primary-Half Bridges, P-HBs)、N个二次电压源型半桥(Secondary Half-Bridges, S-HBs)和一个功率解耦多绕组变压器(PD-MWT)。P-HB半桥由Lin,k、C1,k和C2,k、Q1,k和Q2,k及其反并联二极管VD1,k和VD2,k组成。S-HB半桥由C3,k和C4,k、Q3,k和Q4,k及其反并联二极管VD3,k和VD4,k组成。N个一次侧半桥相互独立,与分布式光伏阵列相连,输入电流纹波相对较小;N个二次侧半桥串联,承受中压直流母线电压。在实际应用中P-HBs和S-HBs的数量并不一定相等,通过PD-MWT相连实现隔离和功率变换,PD-MWT的一次绕组匝数为np,二次绕组匝数为ns,匝比为nT=np:ns,因此变换器整体匝比为NnT。为了实现功率解耦,附加电感Lp,1~Lp,N被串联在PD-MWT所有一次绕组,同样附加电感Ls,2~Ls,N被串联在所有二次绕组(S-HB 1除外)。
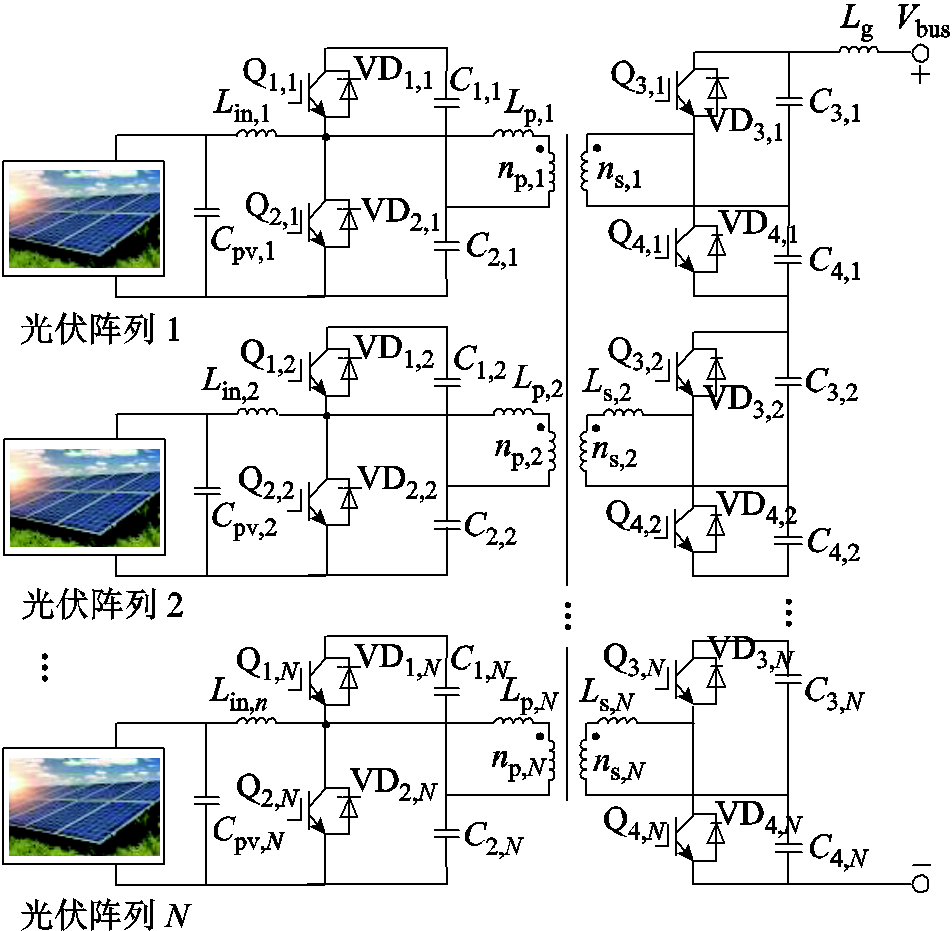
图2 本文提出的光伏中压直流汇集IIOS拓扑结构
Fig.2 Configuration of the proposed IIOS topology for PV MVDC integration
图3给出了所提变换器工作时的关键波形,由于所有P-HBs(S-HB 2~N)工作原理相似,故以下分析中仅选取P-HB k和S-HB j作为典型对所提变换器工作模态进行分析。图中,gQ3,1和gQ4,1(50%占空比包含死区)为开关管Q3,1和Q4,1的互补驱动信号,gQ3,j和gQ4,j为S-HB j中开关管Q3,j和Q4,j的互补驱动信号。同理,gQ1,k和gQ2,k为P-HB k中开关管Q1,k和Q2,k的互补驱动信号。gQ1,k与gQ3,1之间的相移比为dLp,k,gQ3,j与gQ3,1之间的相移比为dLs,j。
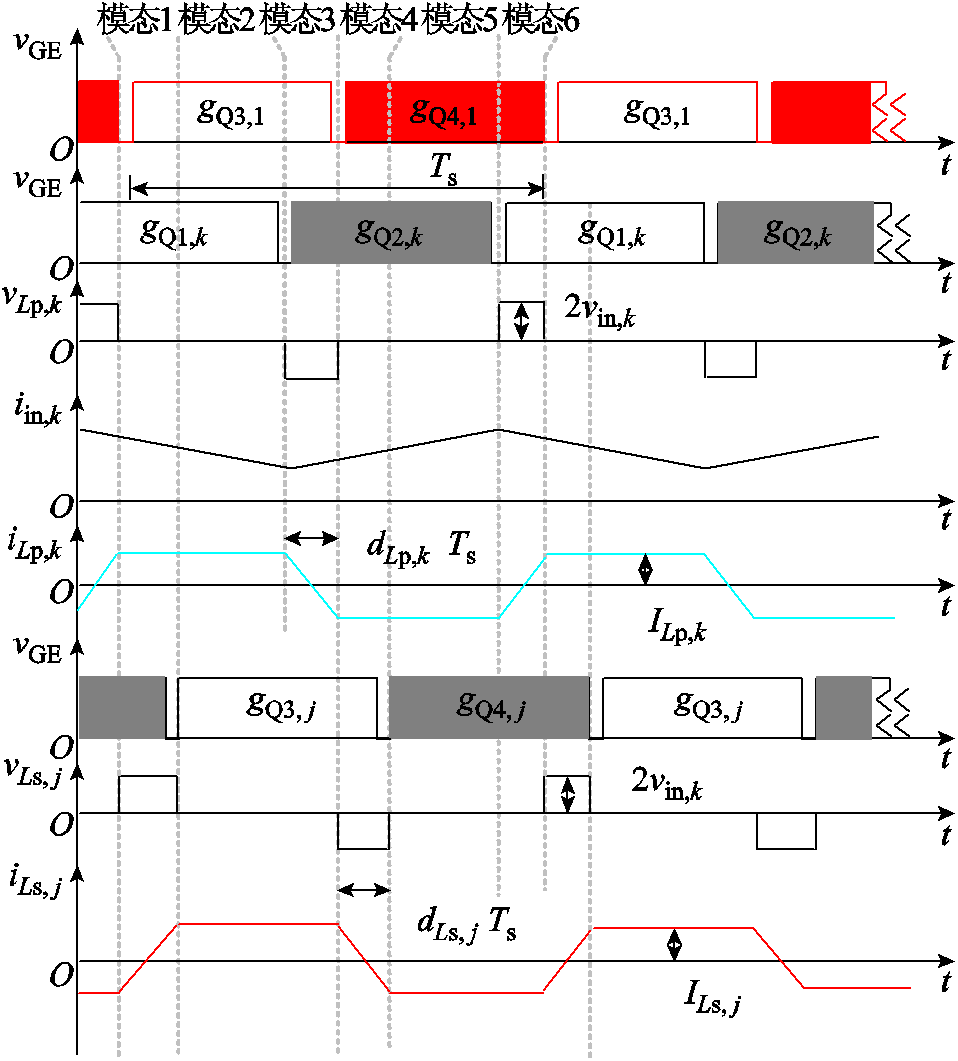
图3 所提拓扑结构在稳态时的关键工作波形
Fig.3 Key operation waveforms of topology in steady state
在一个开关周期内变换器可以分为六个工作模态,所提IIOS变换器在一个开关周期内的各模态等效电路如图4所示,由于S-HB 1汇入光伏能量并将平均功率传递给网侧其余S-HBs,故称其为变换器的松弛端口。为简化分析,假设变换器电容电压匹配并满足条件
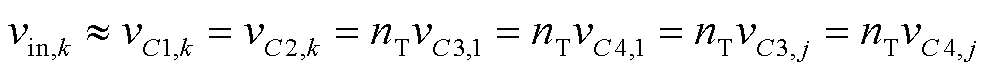 (1)
(1)
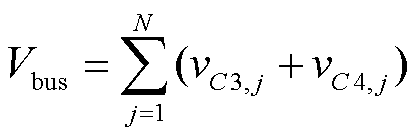 (2)
(2)
式中,vin,k为第k个光伏阵列的输入电压;vC1,k和vC2,k为P-HB k电容C1,k和C2,k电压;vC3, j和vC4, j为S-HB j电容C3, j和C4, j电压;Vbus为中压直流母线电压。
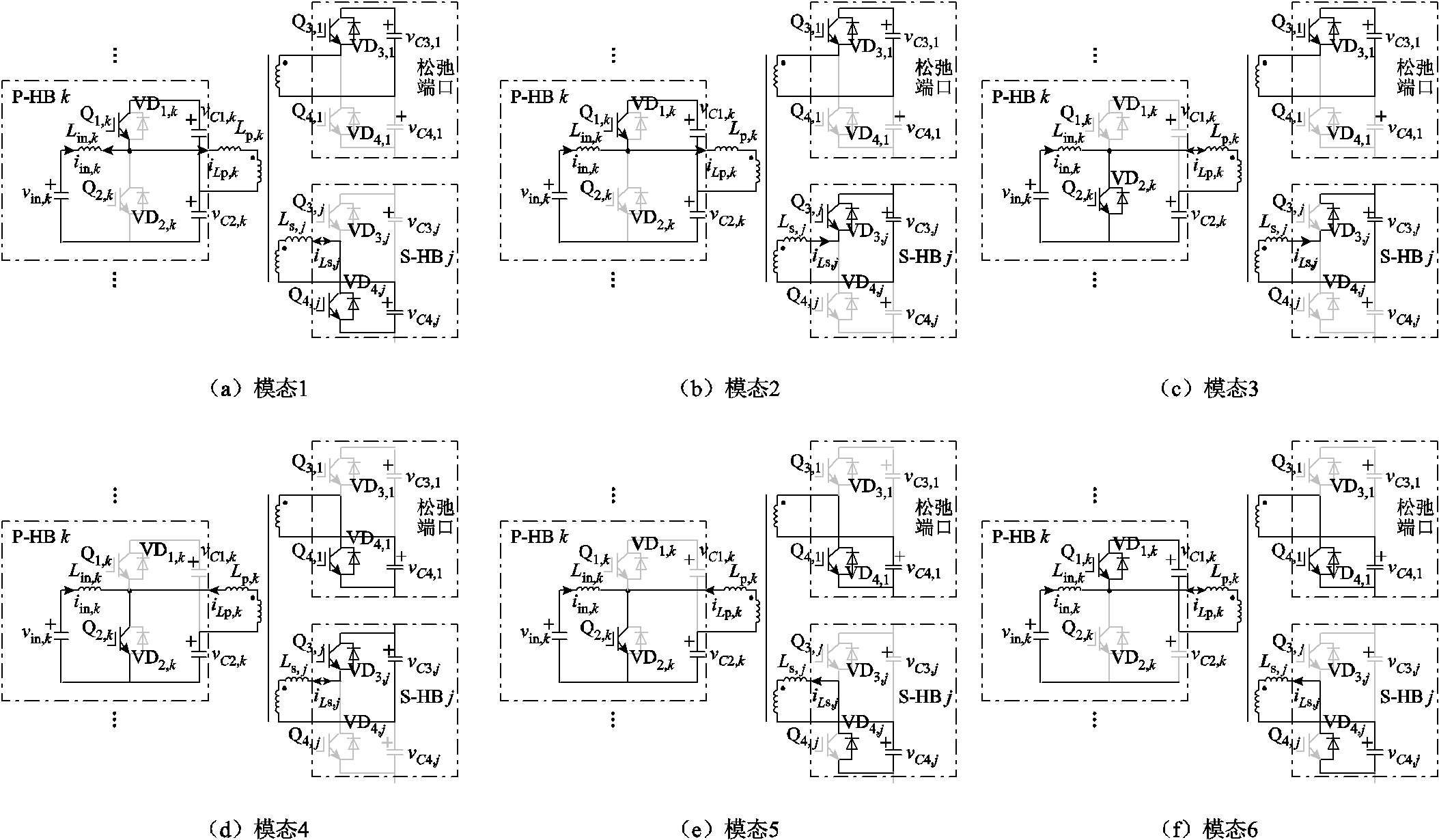
图4 所提IIOS变换器在一个开关周期内的各模态等效电路
Fig.4 Operating modes of the proposed IIOS converter during one switching period
模态1:如图4a所示,开关管Q4,j、Q1,k和Q3,1处于开通状态。由于电感Lp,k电压vLp,k为0,电感Lp,k电流iLp,k保持ILp,k不变。此外,电感Ls,j电压vLs,j为2 vin,k,电感Ls,j电流iLs,j将从负增加为正,Q4,j实现零电压开通(Zero Voltage Switching, ZVS)。
模态2:如图4b所示,Q4,j关闭,VD3,j导通续流,由于电感Ls,j电压vLs,j为0,电感Ls,j电流iLs,j保持ILs,j不变。
模态3:如图4c所示,Q1,k关闭,VD2,k导通续流,由于电感Lp,k电压vLp,k为-2vin,k,电感Lp,k电流iLp,k将从正降低为负,Q2,k实现ZVS。此外,电感Lin,k电压为vin,k,Lin,k的电流iin,k开始增大。
模态4:如图4d所示,开关管Q3,1开通,VD4,1导通续流。由于电感Lp,k电压vLp,k为0,电感Lp,k电流iLp,k保持ILp,k不变。此外,电感Ls,j电压vLs,j为-2vin,k,电感Ls,j电流iLs,j将从正降低为负,Q3,j实现ZVS。
模态5:如图4e所示,Q3,j关闭,VD4,j导通续流,由于电感Ls,j电压vLs,j为0,电感Ls,j电流iLs,j保持-ILs,j不变。
模态6:如图4f所示,Q2,k关闭,VD1,k导通续流,由于电感Lp,k电压vLp,k为2vin,k,电感Lp,k电流iLp,k将从负增大为正,Q1,k实现ZVS。此外,电感Lin,k电压为-vin,k,电感电流iin,k开始减小。
从上述模态分析可知,变换器各半桥间功率传输过程与传统单移相控制DAB变换器相似,故从P-HB k传输到松弛端口的功率Pin,k计算式为
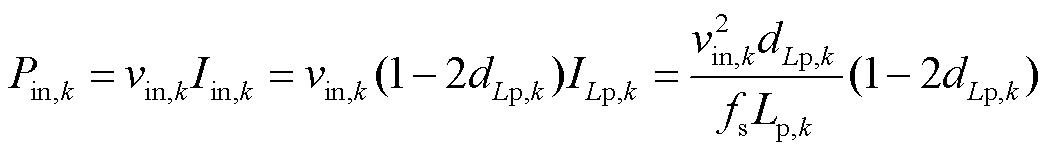 (3)
(3)
式中,Iin,k为P-HB k的平均输入电流;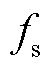 为开关管工作频率。
为开关管工作频率。
同样地,从松弛端口传输到S-HB j的功率PB,j计算式为
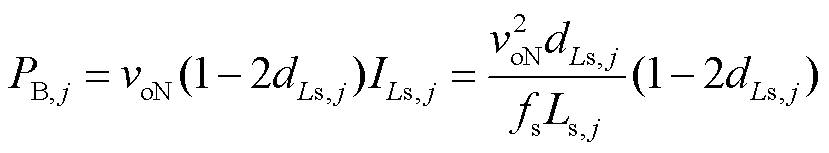 (4)
(4)
式中,voN为S-HBs的额定输出电压,voN=Vbus/N = vC3,j+vC4,j。
所提变换器控制策略与开关管驱动信号产生原理图如图5所示。图5中,Gc1和Gc2均为PI(比例积分)调节器模块,PSM为移相调制模块。其原理可以描述为:基于式(3)采集变换器输入端光伏阵列的电压电流信号并调节移相比dLp,k对光伏阵列进行独立的MPPT控制;基于式(4),通过控制移相比dLs由松弛端口S-HB1向S-HB 2~S-HB N传输平均功率,平均功率Pave的计算式为
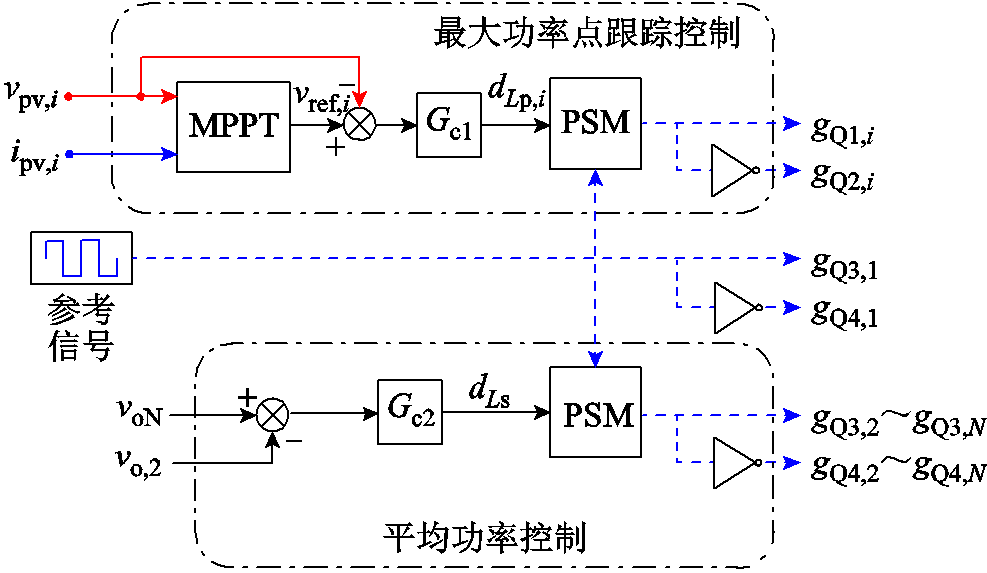
图5 提出的控制与调制策略框图
Fig.5 Block diagram of the proposed control and modulation strategy
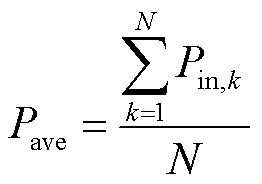 (5)
(5)
若电感Ls,2~Ls,N具有一致性,则只需采集单个vo,2~vo,N信号,S-HB 2~S-HB N开关管驱动信号共享dLs。由于只接收平均功率(PB,2=PB,3=PB,4 =…=PB,N),S-HBs电压将自然均衡。
为了对控制器Gc2进行参数设计,所提变换器平均功率控制的小信号模型可以通过线性化方法推导得到。根据电容C3的物理特性,其状态方程为
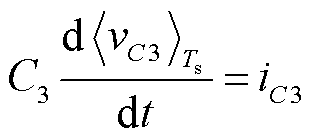 (6)
(6)
式中,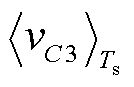 为一个开关周期内电容C3的平均电压。在稳态下引入小信号扰动并引入增益函数G1,则式(6)可改写为
为一个开关周期内电容C3的平均电压。在稳态下引入小信号扰动并引入增益函数G1,则式(6)可改写为
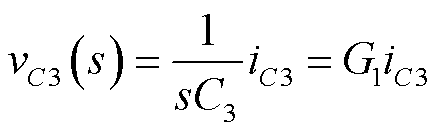 (7)
(7)
同理,式(4)可改写为
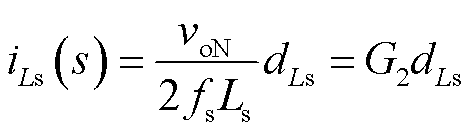 (8)
(8)
根据基尔霍夫电流定律(Kirchhoff’s Current Law, KCL)对电容C3列写KCL方程
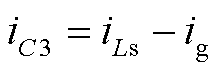 (9)
(9)
式中,ig为所提变换器整体输出电流。结合式(7)~式(9)可建立变换器平均功率控制下控制到输出的系统小信号模型,用图6所示的信号流图表示,据此可以得到控制系统开环传递函数为
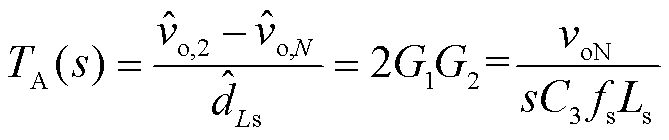 (10)
(10)
式中,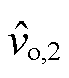 和
和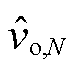 分别为
分别为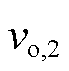 、
、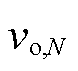 的小信号量;
的小信号量;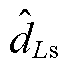 为
为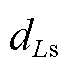 的小信号量。
的小信号量。
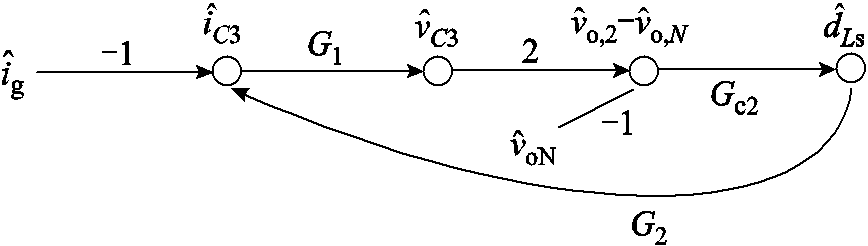
图6 平均功率控制信号流图
Fig.6 Average power control signal flow diagram
为了确保系统的稳定性,控制器Gc2需要对系统进行校正以获得足够的相位裕度,若将截止频率设计为fc,相位裕度设计为φ,选取PI控制器对系统进行补偿,则控制器参数计算式为
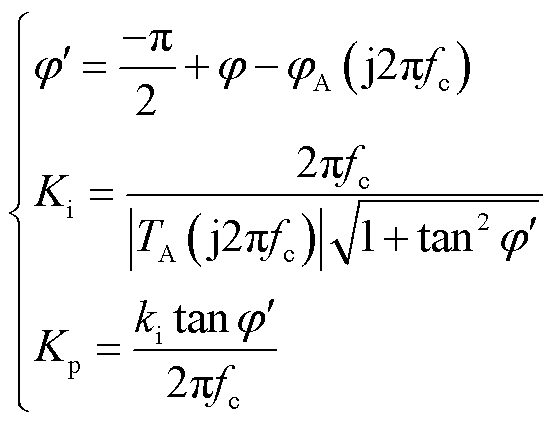 (11)
(11)
式中,φA为TA的相位。
现有的调整控制器的方法可以分为三种:试错法、传递函数法以及时域目标函数的优化。本文结合了第一种和第二种方法,根据式(11)求出闭环Kp和Ki,然后使用试错法调整这些参数。最终确定Kp=0.52,Ki=100,并绘制开环传递函数的伯德图用于分析变换器稳定性,如图7所示。根据伯德图可知在截止频率处的相位裕度大于45°,因此系统是稳定的。
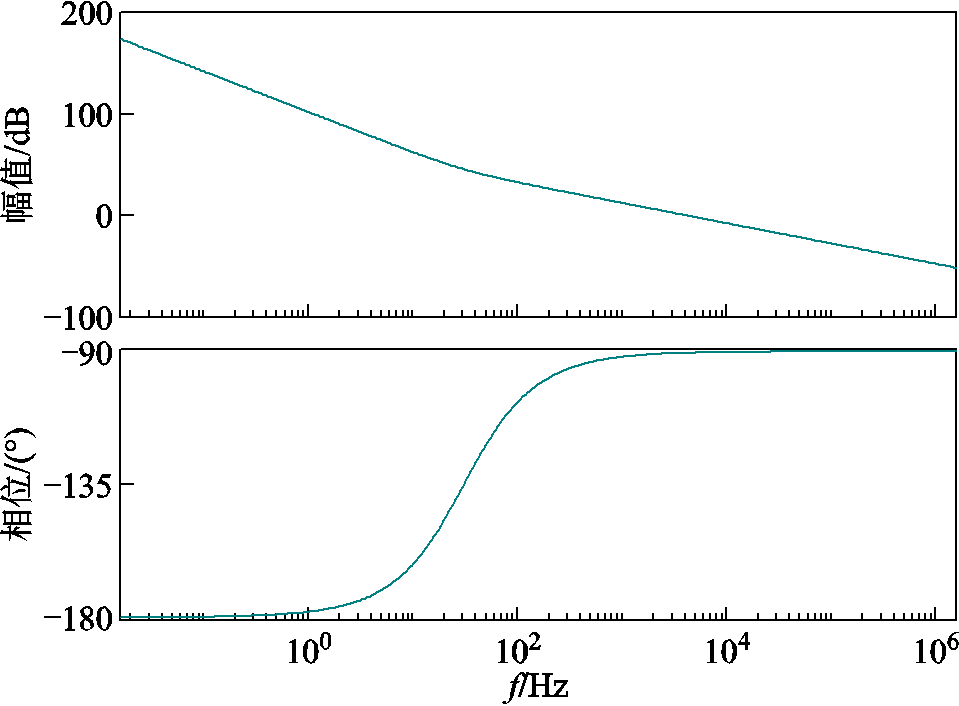
图7 变换器系统开环传递函数伯德图
Fig.7 Bode diagram of open-loop transfer function for the proposed converter system
如1.2节所述,多绕组变压器是所提拓扑进行功率变换的关键元件,所有一次、二次侧半桥单元均通过其相连接,构成了点对点的功率传输模式。基于多绕组变压器构建直流变换器存在以下两点挑战:①半桥单元间存在的移相比差与绕组间的磁耦合导致端口间将自然存在功率的交叉耦合;②功率耦合带来复杂的电流传输路径,使得开关器件电流应力分析与器件选型困难。下面对所提变换器的功率解耦特性与松弛端口电流特性进行分析。
1.4.1 功率解耦特性分析
文献[19]提出可以在负载端口中放置额外的电感以实现功率解耦,并在文中进行了实验验证。根据图1和1.2.1节描述,附加电感Lp,1~Lp,N被串联在多绕组变压器所有一次绕组,Ls,2~Ls,N被串联在所有二次绕组(S-HB 1除外),定义S-HB 1为“松弛端口”,作为功率传输的中间节点。耦合电感的等效电路可以用励磁电感Lm和每个端口的漏电感Lσ,k表示。在耦合电感的第i个端口和第j个端口之间的等效耦合电感LSB,ij可表示为
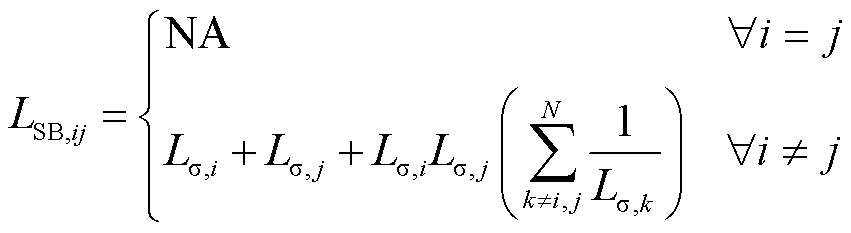 (12)
(12)
图8给出了功率解耦多绕组变压器简化功率传输模型,图中已将多绕组变压器一次侧电感全部折算到二次侧,即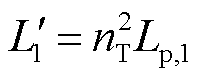 、
、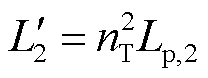 、
、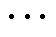 、
、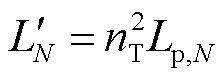 ,同时二次侧电感
,同时二次侧电感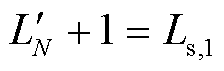 、
、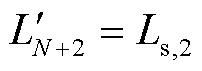 、
、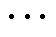 、
、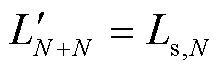 。由于松弛端口的电感量Ls,1(图中未标出)近似为零,远小于其他半桥单元,松弛端口半桥单元逆变得到的方波电压将直接调节多绕组变压器励磁电感电压与励磁电流。因此,式(12)可以改写为
。由于松弛端口的电感量Ls,1(图中未标出)近似为零,远小于其他半桥单元,松弛端口半桥单元逆变得到的方波电压将直接调节多绕组变压器励磁电感电压与励磁电流。因此,式(12)可以改写为
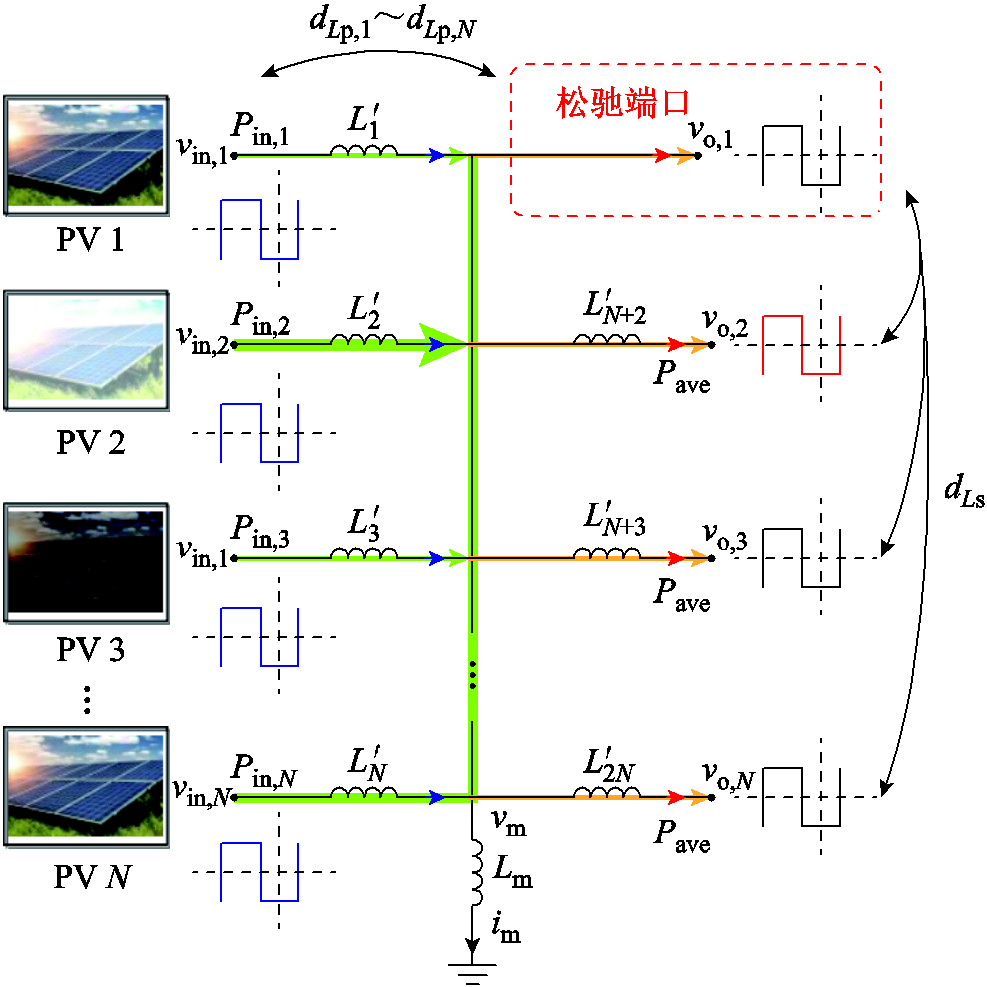
图8 功率解耦多绕组变压器简化功率传输模型示意图
Fig.8 Schematic diagram of simplified power transmission model for power decoupling multi winding transformers
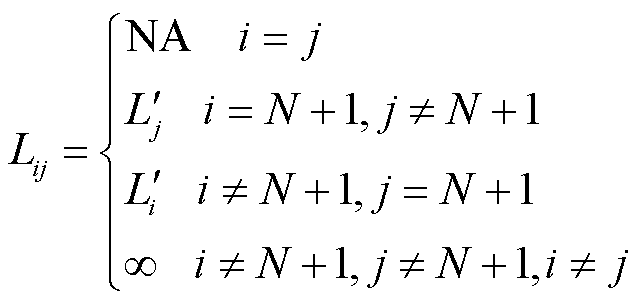 (13)
(13)
结合式(3)和式(4)可知,松弛端口与其他端口之间的功率传输具有一般性,符合DAB变换器工作准则,但由于其他端口间等效电感无穷大,即使存在移相比,可认为不存在其他端口间的功率传输,因此所提控制策略中将松弛端口作为功率传输中间节点的方法具有理论依据。
1.4.2 松弛端口电流特性分析
由1.2节工作原理分析可知,松弛端口吸收光伏输出功率并传递平均功率到余下S-HBs的输出电容,故流过开关管Q3,1和Q4,1的电流将较其他开关器件复杂,下面对其电流特性进行详细分析。根据KCL,开关管Q3,1的电流为P-HB 1~P-HB N和S-HB 2~S-HB N电流的叠加,可以表示为
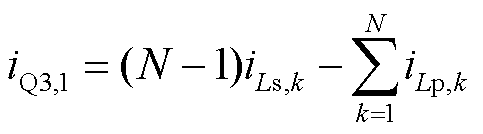 (14)
(14)
以N=2为例,所提变换器工作波形如图9所示。图中,电流iLp,1、iLp,2和iLs,1在电流反向阶段的斜率定义为kLp,1、kLp,2和kLs,1;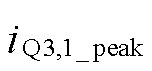 为
为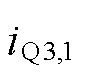 的峰值电流,
的峰值电流,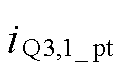 由其他端口功率传输电流决定,因此可以表示为其他端口功率传输电流的代数和。
由其他端口功率传输电流决定,因此可以表示为其他端口功率传输电流的代数和。
由于输入功率单向流动,gQ1,1和gQ1,2总是超前gQ3,1。同样地,由于松弛端口总是发出功率,gQ3,1总是超前gQ3,2。结合式(3)、式(4)和式(7)可以得到开关管Q3,1的峰值电流IQ3,1_peak与功率传输电流IQ3,1_pt分别为
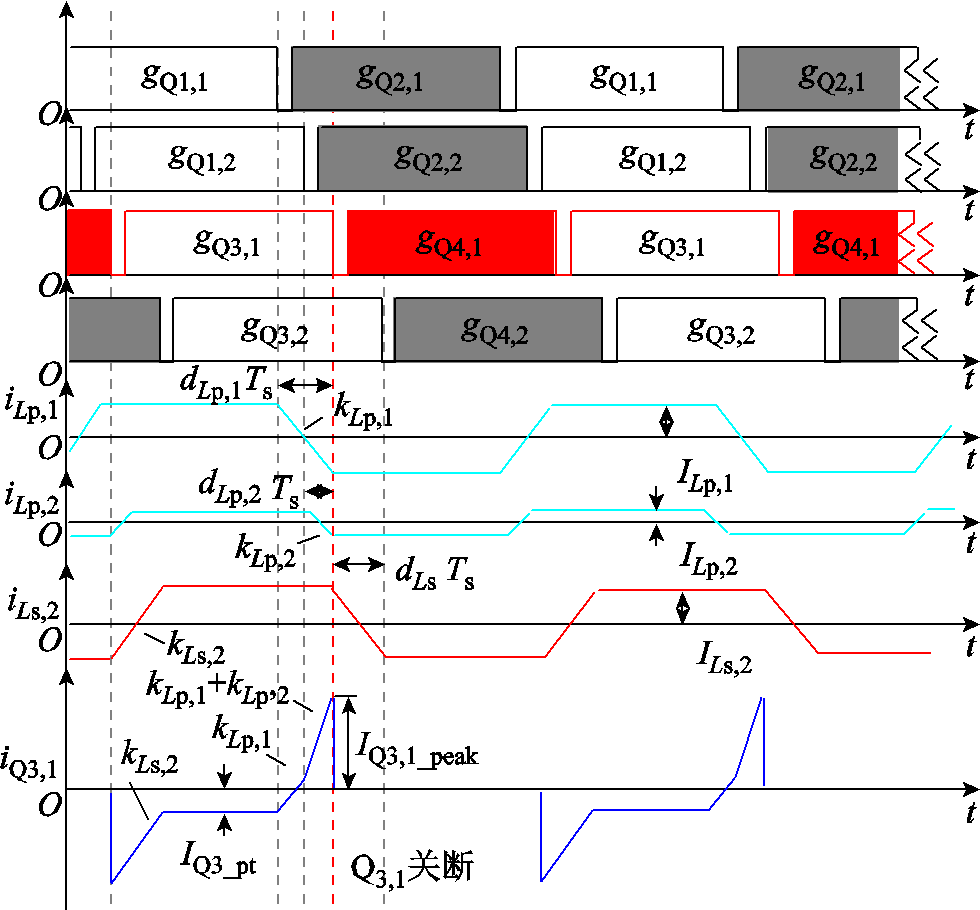
图9 N=2时所提变换器驱动信号与电流波形
Fig.9 The driving signal and current waveforms of the proposed converter when N=2
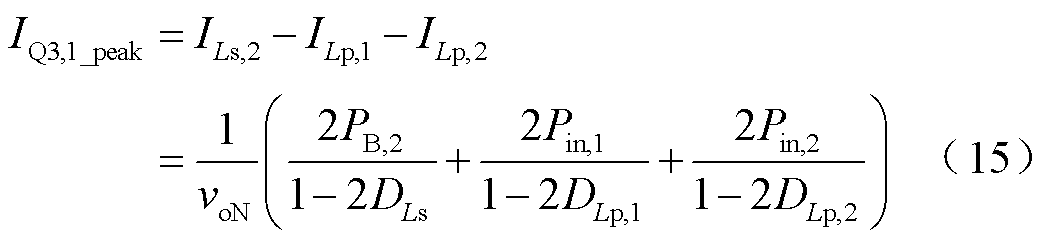
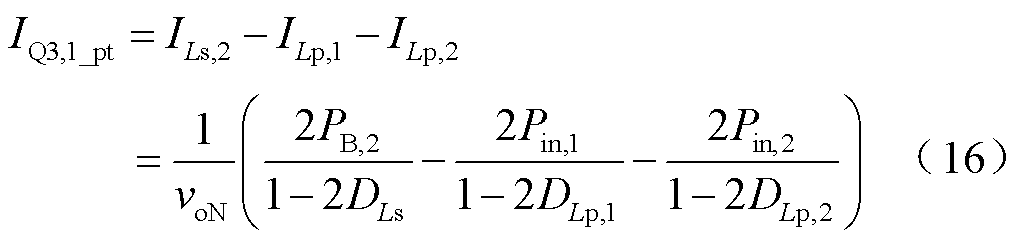
式中,DLs、DLp,1和DLp,2分别为dLs、dLp,1和dLp,2的稳态值。
同理可推导得到一般情形下开关管的电流特性为
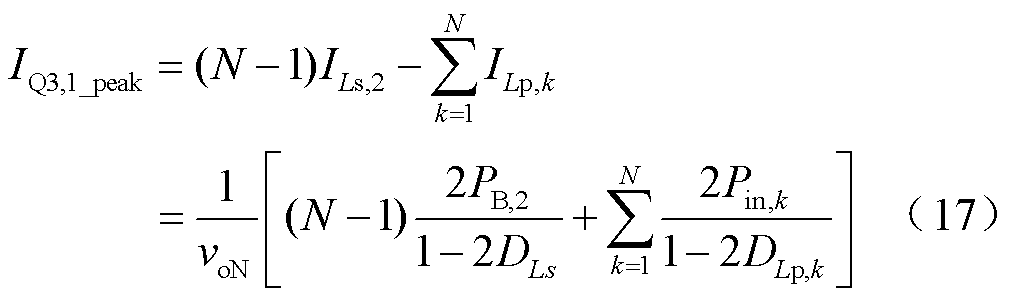
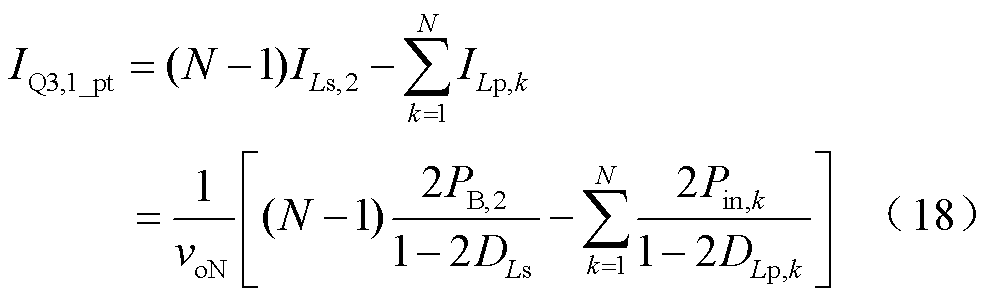
由于Q4,1的工作原理与Q3,1相同,此处忽略讨论。
2.1.1 输入电感Lin设计
输入电感Lin的充放电状态与传统升压变换器相同。因此,电感Lin可以根据输入电流纹波进行设计。基于前面的工作模态分析,输入电流纹波计算式为
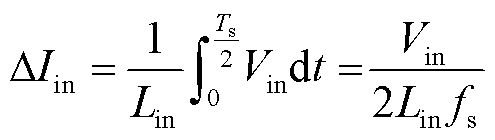 (19)
(19)
式中,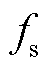 为开关管工作频率。
为开关管工作频率。
如果将最大输入电流纹波比定义为rii=ΔIin/Iin,则电感Lin应满足
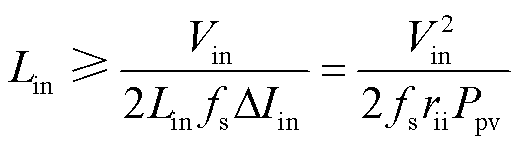 (20)
(20)
式中,Ppv和Iin分别为光伏额定输出功率和平均输入电流。
2.1.2 电容C1和C2设计
根据1.2节中的工作原理分析,在一次电压源型半桥P-HBs功率传输过程中,电容C1的电流可以近似计算为
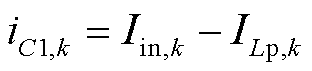 (21)
(21)
假设输入电流纹波相对较小且忽略电流换向过程,C1的电压纹波可以表示为
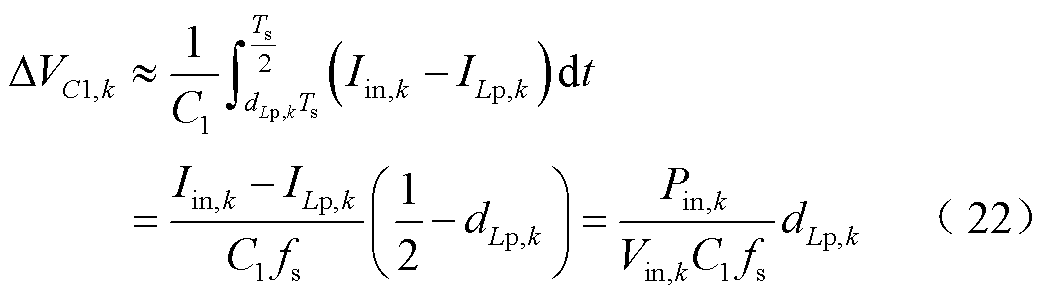
如果将电容电压纹波比设置为riv=ΔvC1/vC1,则电容C1的表达式应满足
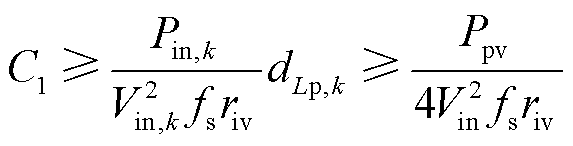 (23)
(23)
电容C2在半个周期内的电流为Iin,C2的电压纹波可以表示为
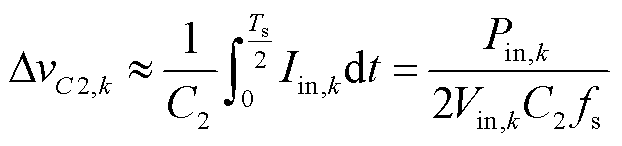 (24)
(24)
因此,电容C2的设计表达式应满足
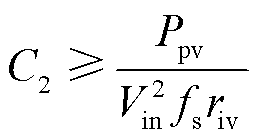 (25)
(25)
PD-MWT是本文所提IIOS变换器中的主要功率传输元件。其中,进行适当的绕组配置对MWT是很有利的,且传统双绕组变压器中已建立使用的绕组结构可用于配置到本文的MWT。对于具有独立输入端口的IIOS结构,有必要建立输出端口之间的阻抗,以减轻不期望的交叉耦合效应。在这方面,交错堆叠的绕组结构可能具有优势[20],E型铁心的交错堆叠绕组结构如图10所示。
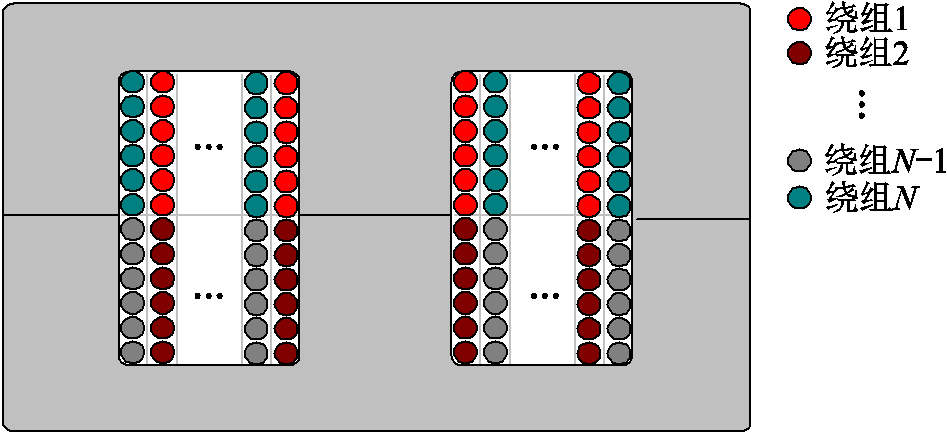
图10 E型铁心的交错堆叠绕组结构
Fig.10 Interleaved stacked winding structures for E-cores
为了实现PD-MWT的功率流解耦,额外的附加漏感Lp,1~Lp,N和Ls,2~Ls,N是必要的。根据式(3),当dLp=0.25时,光伏阵列达到最大输出功率Ppv,进而可以得到电感Lp的范围为
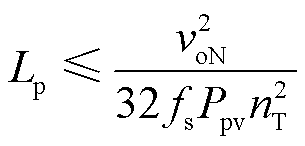 (26)
(26)
为实现低压直流输入和中压直流母线之间的电压等级匹配,所需的变压器匝比nT应满足
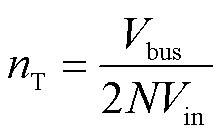 (27)
(27)
类似地,当dLs=0.25时,从松弛端口S-HB 1传递到其他二次电压源型半桥S-HB的功率达到最大值。因此,电感Ls的范围可以推导得到
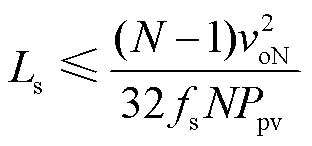 (28)
(28)
假设本文所提IIOS变换器系统的输出电流为Iout,当Q3,k关闭时,半个周期内C3的电流等于Iout。则电容C3的电压纹波为
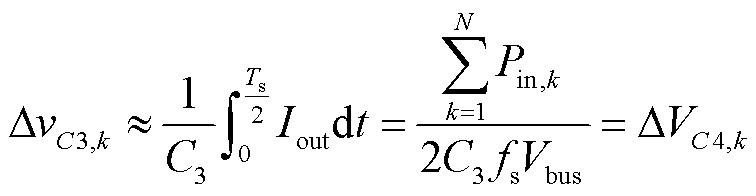 (29)
(29)
由于C3和C4对称工作,基于电压纹波限制,可以得出C3和C4的最小值为
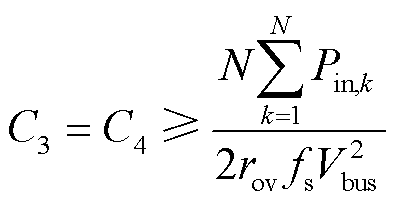 (30)
(30)
式中,rov为输出电压纹波比。
为了更直观地展示所提变换器的性能优势,针对拓扑结构、控制复杂度以及器件应力三个方面与同类型变换器(文献[14, 16]拓扑)进行了性能比较。
图1a和图1b分别给出了文献[14]和文献[16]的拓扑结构,它们由N个传统的DAB变换器和N个电压均衡电路(文献[14]采用LCVB,文献[16]采用MTVB)组成。
根据文献[14, 16]中变换器的拓扑结构与控制方式,表1列出了三种变换器所使用的有源和无源元件以及控制回路的数量。由于所提变换器一次侧采用升压半桥,其磁性元件数量(电感和变压器)与文献[16]相同。然而相比于传统DAB变换器,该结构能提供更低的输入电流纹波与更少的开关元件数量。若所提变换器一次侧配置为全桥结构,由于磁性元件数量最少,变换器在体积方面将更具有优势。此外,由表1可知文献[14]和文献[16]拓扑分别使用了3N-1个采样电路和2N-1个控制环路,比本文所提变换器更多,控制实现更为复杂。
表1 变换器性能比较
Tab.1 Performance comparison with other IIOS converters
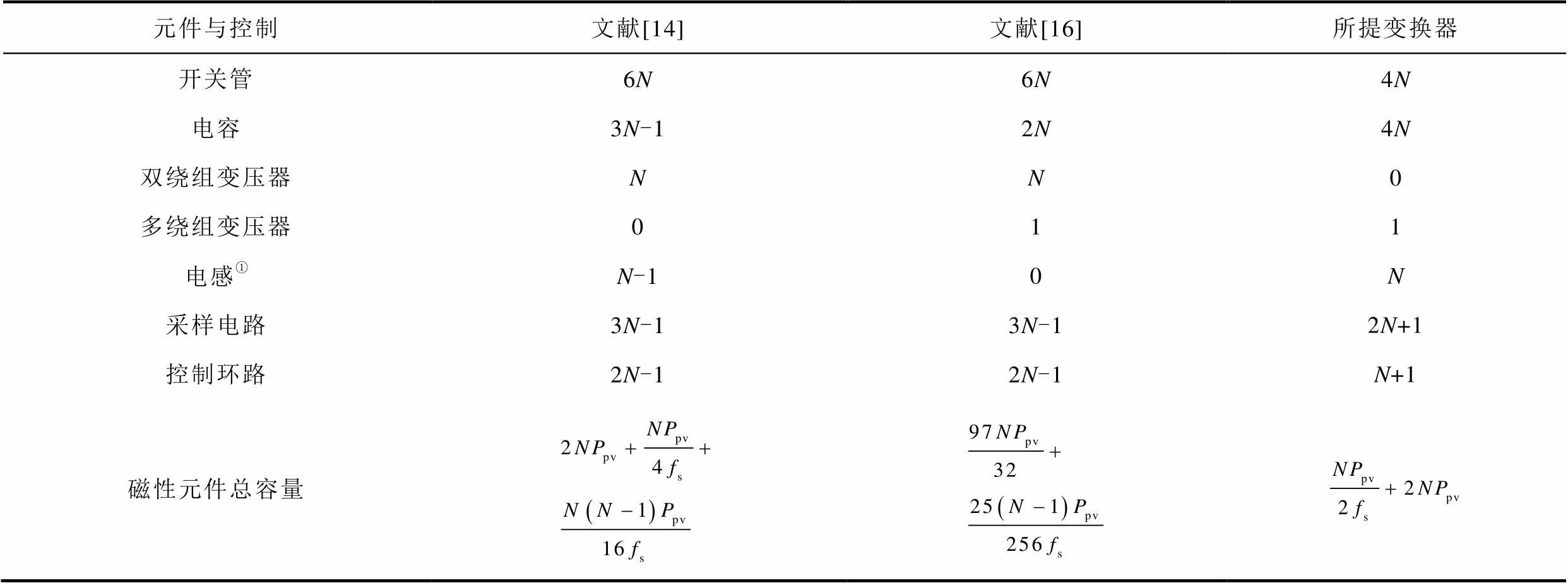
元件与控制文献[14]文献[16]所提变换器 开关管6N6N4N 电容3N-12N4N 双绕组变压器NN0 多绕组变压器011 电感①N-10N 采样电路3N-13N-12N+1 控制环路2N-12N-1N+1 磁性元件总容量
①通过将漏感Lp和Ls纳入两端口和多端口变压器设计中实现。
因为三种拓扑的升压比相同,因此同样的电压等级,所用子模块数量N相同,取N=6,开关频率fs=50 kHz,图11绘制出了三种拓扑磁性元件总容量与光伏阵列输入功率的关系曲线。从图11中可以看到,S14_max与Smax几乎完全重合,且其磁性元件总容量都低于文献[16]。
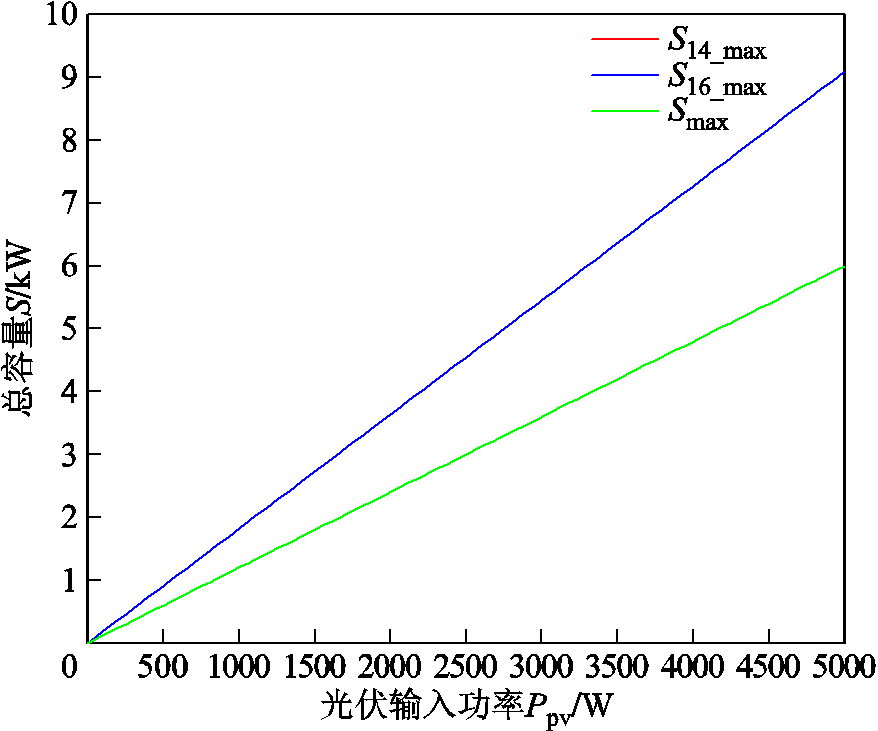
图11 三种拓扑磁性元件总容量与光伏阵列输入功率的关系曲线
Fig.11 The relationship curves between the total capacity of magnetic components and the input power of PV arrays for these three topologies
上述三种变换器同属于IIOS结构,在相同的工作条件下,由于开关器件应力中电流应力具有主要差异,故本节主要对其电流应力进行分析,最后给出了三种变换器开关器件容量的比较结果。
3.2.1 松弛端口电流应力
同样将被比较变换器二次侧第一半桥定义为松弛端口,文中1.4节已对所提变换器松弛端口的电流特性进行讨论。假设移相比足够小,式(15)和式(16)可改写为
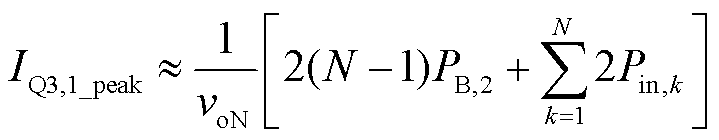 (31)
(31)
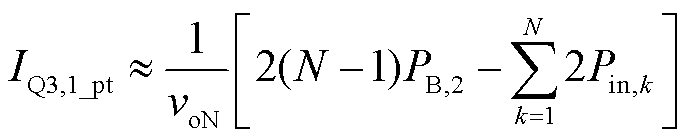 (32)
(32)
根据式(31)和式(32),可得IQ3,1_peak的最大值IQ3,1_peak,max与IQ3,1的方均根IQ3,1_rms分别为
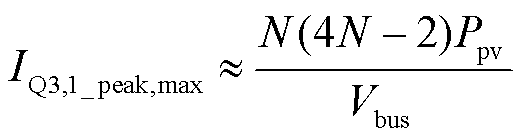 (33)
(33)
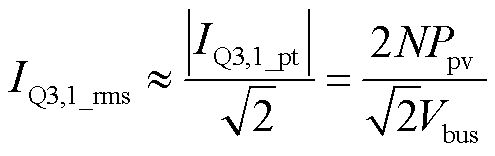 (34)
(34)
此处,Ppv表示Pin,k的最大值。
3.2.2 Q3,k和Q4,k的电流应力
Q3,k(Q4,k)为除第一半桥外的其余半桥开关管,以下均称为网侧开关管。图12展示了相同工作条件下三种拓扑的网侧开关管电流波形。由图12可知,文献[14, 16]拓扑的二次电流为子模块变换器电流与电压均衡器件电流之和,因此其电流应力大于传统DAB变换器,其电流峰值取决于子模块传递功率与不均衡功率大小。对于所提变换器,网侧开关管功率来自松弛端口,其电流波形与传统DAB变换器相同,其电流应力在三种拓扑中最小。
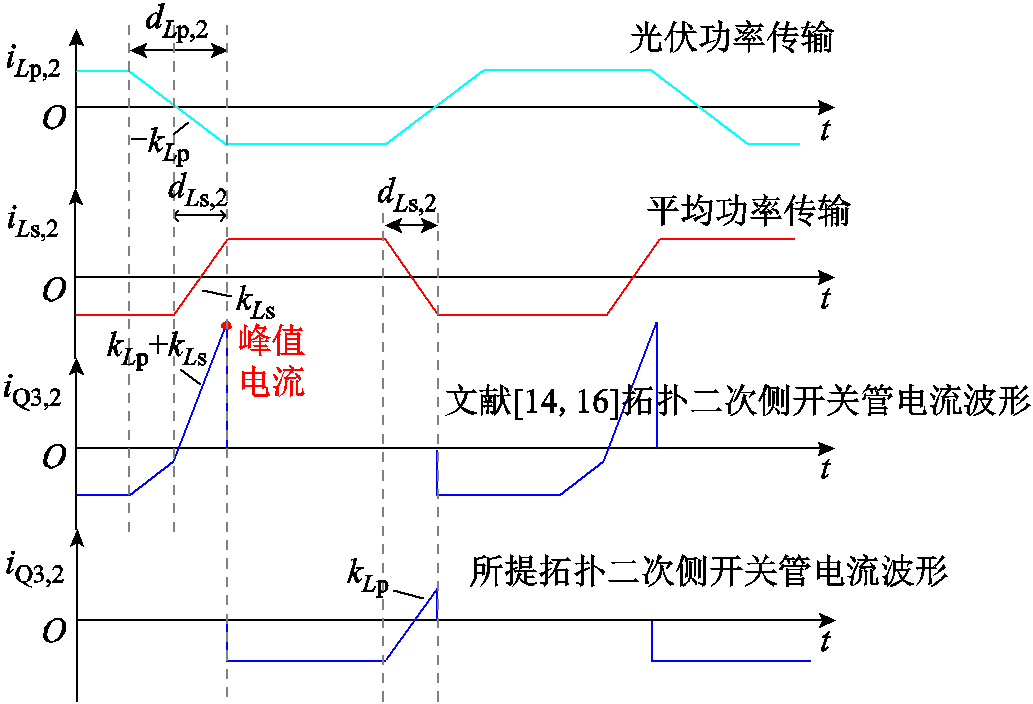
图12 三种IIOS拓扑结构中网侧开关管的电流波形
Fig.12 The current waveforms of switches on the grid side for three IIOS topologies
类似地,所提变换器网侧开关管电流IQ3,2~N的峰值IQ3,2~N_peak,max和方均根IQ3,2~N_rms计算式分别为
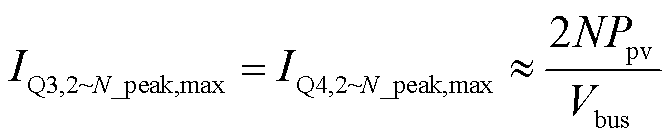 (35)
(35)
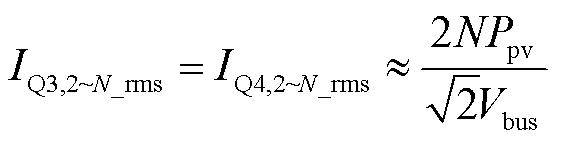 (36)
(36)
3.2.3 开关器件容量
根据式(33)和式(35),网侧开关器件容量Pcap计算式为
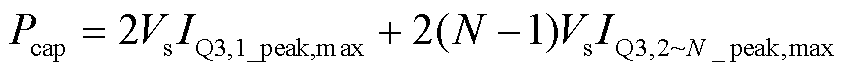 (37)
(37)
式中,Vs为网侧开关器件电压应力,Vs=voN。
根据式(33)、式(35)和式(37),并结合表2中给定参数,图13给出了三种IIOS拓扑开关电流应力Ipeak和容量Pcap与子模块数量N之间的关系曲线比较,并由图13a可知所提变换器松弛端口的电流峰值应力最大。然而,由图13b可以看出所提变换器其他网侧开关管电流应力均小于拓扑文献[14, 16]拓扑。在图13c的对比中,可以发现所提变换器的开关容量Pcap位于拓扑文献[14]和文献[16]之间。
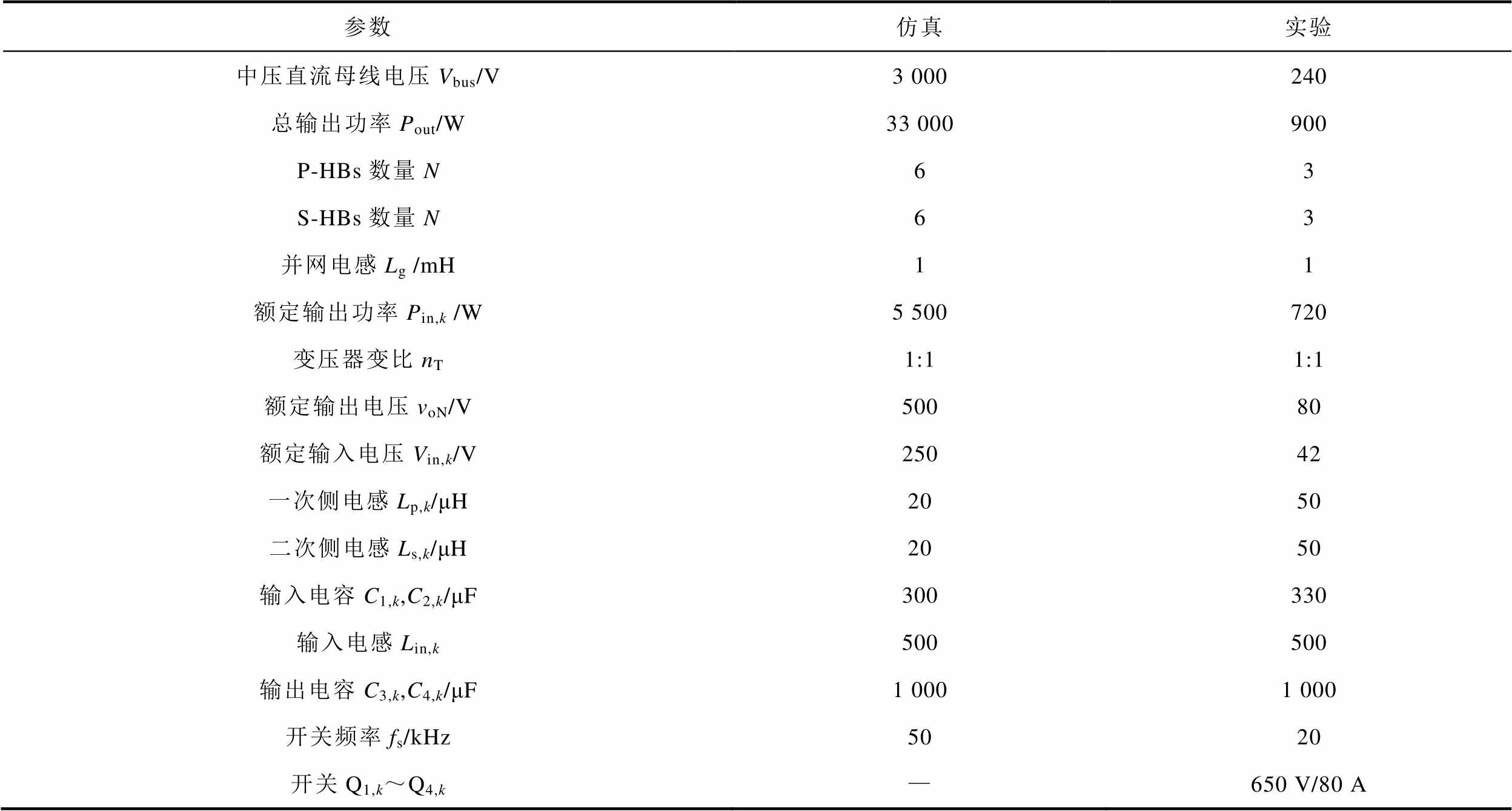
表2 IIOS变换器仿真及实验参数
Tab.2 Simulation and experimental parameters of the proposed IIOS converter
参数仿真实验 中压直流母线电压Vbus/V3 000240 总输出功率Pout/W33 000900 P-HBs数量N63 S-HBs数量N63 并网电感Lg /mH11 额定输出功率Pin,k /W5 500720 变压器变比nT1:11:1 额定输出电压voN/V50080 额定输入电压Vin,k/V25042 一次侧电感Lp,k/μH 2050 二次侧电感Ls,k/μH2050 输入电容C1,k,C2,k/μF300330 输入电感Lin,k500500 输出电容C3,k,C4,k/μF1 0001 000 开关频率fs/kHz5020 开关Q1,k~Q4,k—650 V/80 A
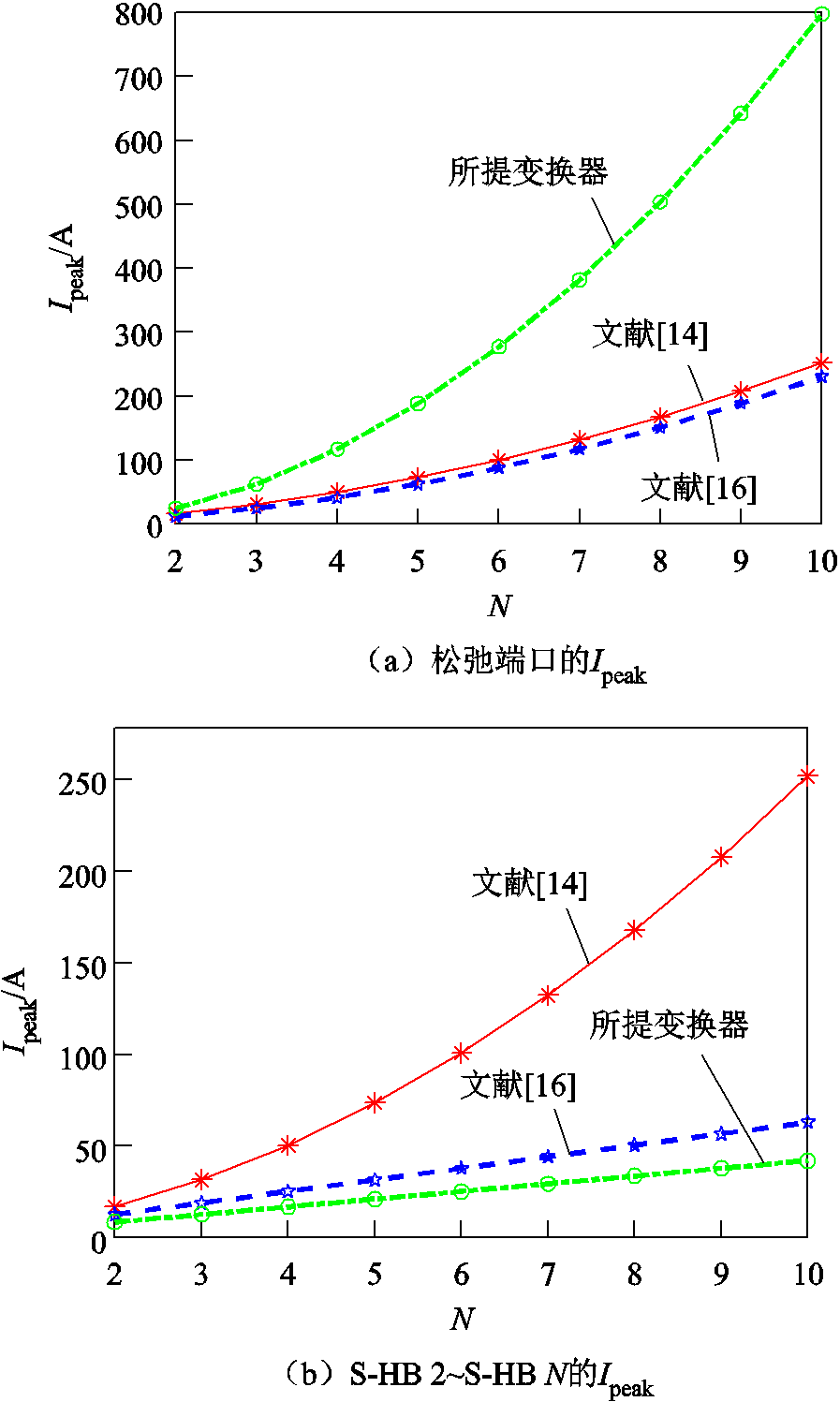
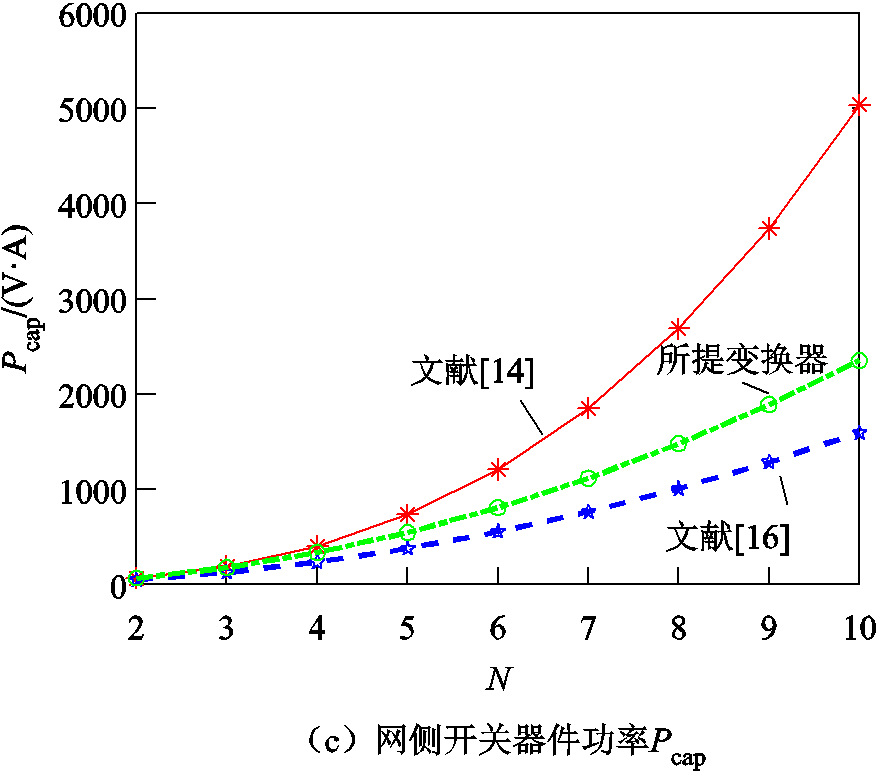
图13 三种IIOS拓扑网侧开关管电流峰值应力和器件容量比较
Fig.13 Comparison of peak current Ipeak and Pcap for these three IIOS converters
为了验证所提变换器工作原理的正确性,本文基于Matlab/Simulink平台搭建了仿真模型,并在小容量实验样机平台进行测试给出了实验波形。
本文搭建了总输出功率为33 kW、中压直流母线电压为3 kV的仿真模型来验证所提基于PD-MWT的IIOS变换器的可行性与正确性。仿真与实验中的关键参数见表2,为模拟实际工况,在仿真过程中每个分布式光伏阵列变化的给定光照强度已在表3中给出。
表3 光伏阵列给定光照强度
Tab.3 Photovoltaic array set light intensity
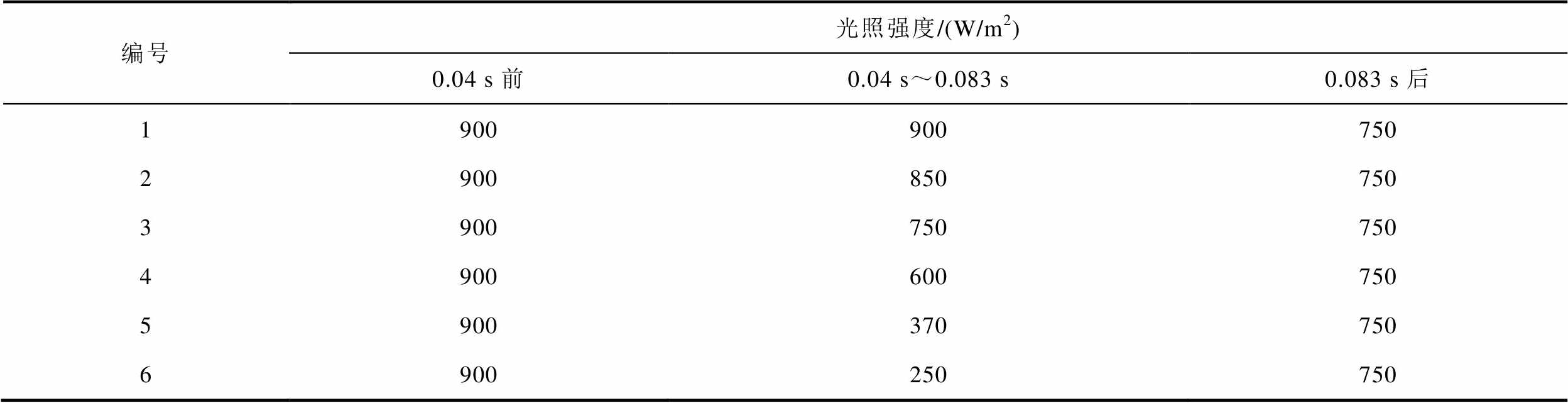
编号光照强度/(W/m2) 0.04 s前0.04 s~0.083 s0.083 s后 1900900750 2900850750 3900750750 4900600750 5900370750 6900250750
图14展示了仿真中每个P-HB的输入电流(iin,i i=1~6对应P-HB1~6)和每个S-HB输出电压(vo,i i=1~6对应S-HB1~6)变化波形。如图14a所示,初始6个光伏阵列的光照强度相同且输入电流保持一致,平均输入电流21 A。在t=0.04 s时光伏阵列光照强度突变导致输入电流出现差异,在t=0.083 s时光照强度再次相同。

图14 输入电流的波形和每个S-HB的输出电压
Fig.14 Waveforms of input PV currents and output voltages of each S-HB
如图14b所示,由于变换器整体输入功率在t=0.04 s时降低,松弛端口的功率无法支撑其余S-HB 2~6的电容电压,松弛端口的电压出现暂态下跌(Dv1=32 V, Dt1=5 ms)。通过闭环控制调节dLs,使松弛端口电压重新维持额定值。类似地,在t=0.083 s时,由于变换器整体输入功率增大,松弛端口电压上升产生一定的过电压(Dv2=10 V, Dt1= 4 ms),之后电压仍将保持稳定。以上仿真结果与理论分析保持一致。
图15a展示了P-HB 1在功率传输过程中的工作波形,通过控制gQ3,1和gQ1,1之间的移相比dLp,1实现最大功率传输。如图15b所示,变换器总输入功率的平均值通过控制移相比dLs,2实现,进而可以实现输出电压均衡。
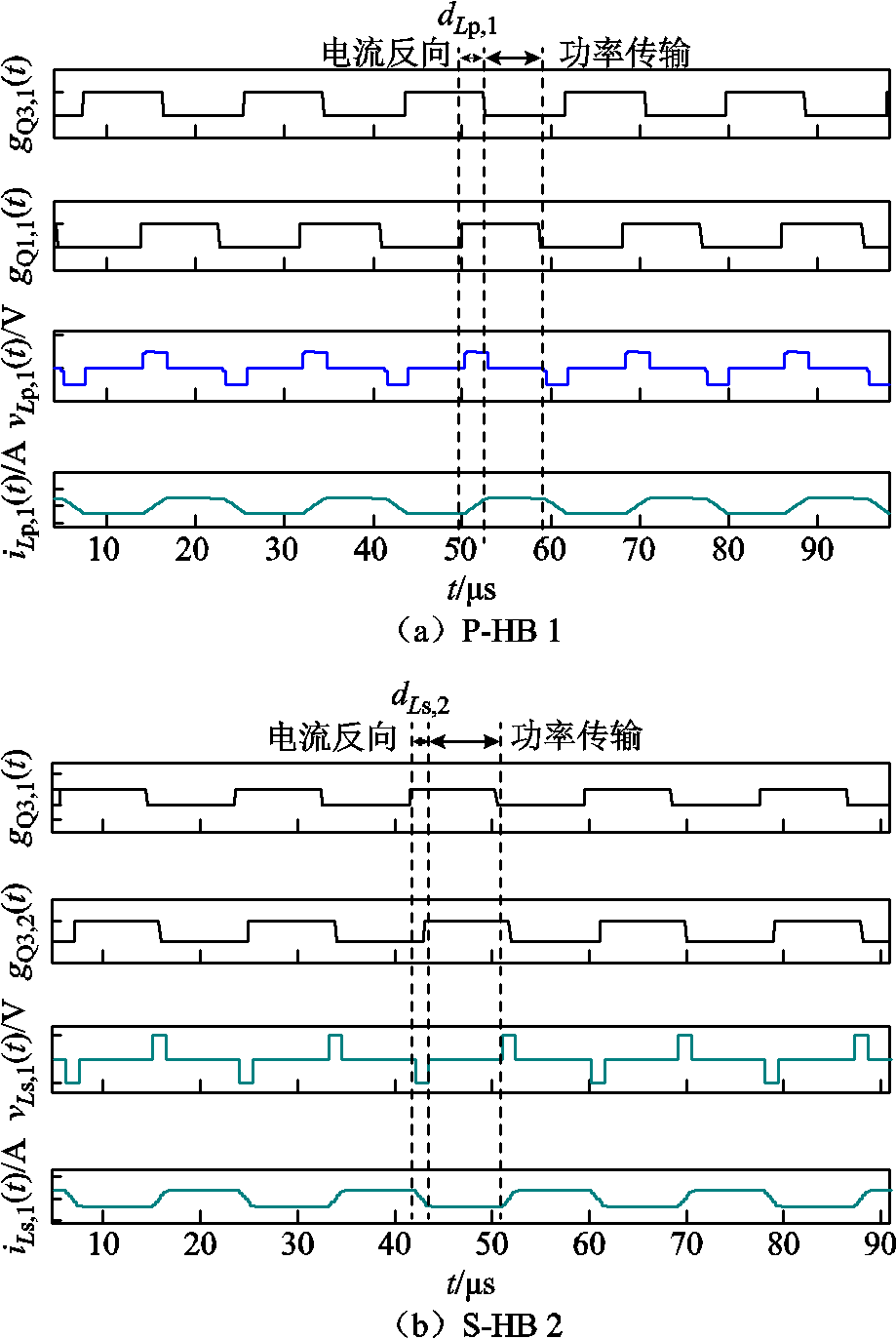
图15 P-HB 1和S-HB 2的工作波形
Fig.15 Operation waveforms of P-HB 1 and S-HB 2
图16给出了光照条件渐变前后各子模块的关键运行波形,包括光照强度、子模块输入电流和输出电压。如图16a所示,为了模拟实际工况,在0.02 s时设置了子模块光伏阵列发生光照变化,变化时间为0.02~0.08 s,其中子模块1~3光照强度分别缓慢增强至900、800、700 W/m2,子模块4~6光照强度分别缓慢减弱至500、400、300 W/m2。如图16b所示,初始6个光伏阵列的光照强度相同且输入电流保持一致,平均输入电流13 A。在t=0.02 s时光伏阵列光照强度渐变导致输入电流出现差异,在t=0.08 s时光照强度保持固定不变,输入电流维持稳定。如图16c所示,各子模块输出电容上的功率被平均分配,使得子模块输出电压均衡。由于光照强度渐变,在输出电压仿真波形中几乎看不出子模块在该状况下输出电压的波动,均压效果较之前的光照突变效果更好。因而,可以得出本文提出的基于多绕组变压器的模块化输入独立输出串联光伏直流汇集变换器在光照渐变时均压时间短且几乎不存在电压过冲。

图16 光照强度渐变时的仿真结果
Fig.16 Simulation results during gradual changes in lighting radiation intensity
图17给出了实验室搭建的小功率样机测试平台示意图。原理样机由一次侧三个P-FB单元和二次侧三个S-HB组成,每个输入端口与42 V直流电源相连,变换器整体的输出电压为240 V。实验样机数字控制器型号为DSPF28335,功率器件型号为TPW60R028DFD,电压电流采样器件型号为C87A2211HPC,实验详细参数见表2。使用恒流控制器对输入电流iin,1、iin,2和iin,3进行调节,以模拟不同环境条件下的光伏阵列行为,使用电子负载连接变换器输出端口并调至恒压挡模拟中压直流母线。

图17 实验硬件平台
Fig.17 Hardware platform of the proposed IIOS converter
图18展示了不同输入功率条件下一次侧第一全桥单元的电流电压波形,与传统的DAB变换器传输过程相类似,调节移相比dLp可改变一次侧输入端口功率传输大小。在实验中三个端口的初始输入功率均为150 W,此时S-HBs的电感电流iLs,1、iLs,2和iLs,3波形如图19所示,由图19可知,iLs,2和iLs,3与iLs,1为同相位,表明松弛端口吸收电源侧功率并传递平均功率给S-HB 2和S-HB 3。

图18 一次侧全桥电压和电流实验波形
Fig.18 Voltages and currents experimental waveforms of P-FB unit
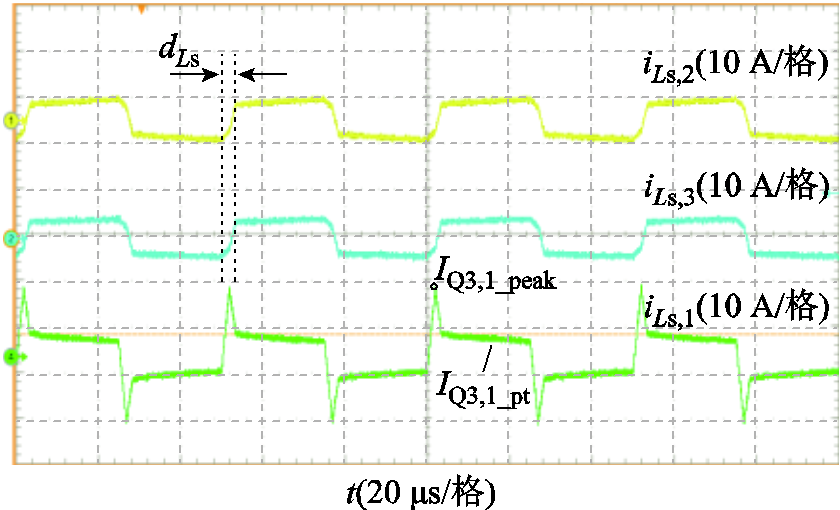
图19 S-HB电流的实验波形
Fig.19 Experimental waveforms of the S-HB currents
图20展示了松弛端口与其余半桥开关器件的开关过程。从图中可看出,开关管两侧的电压vQ1,1和vQ3,1在驱动信号gQ1,1和gQ3,1到来之前先降为0,其他开关管工作原理相同,故所有开关管均能实现零电压开通。

图20 零电压开关的实现波形
Fig.20 ZVS realization waveforms
此外,当考虑端口1输入功率变化时,测量得到所提出的转换器的动态响应如图21所示。从图21a可以看出,为了响应输入电流控制器的功率指令,P-FB 1端口的输入电流由3.6 A变为5.7 A。这三个子模块的实测输出电压波形如图21b所示。从图21b中可以看出,在输入功率变化前后,子模块输出电压得到了很好的平衡,并稳定在80 V左右。因此,充分证实了所提变换器和控制策略在输入功率不平衡条件下的有效均压能力。
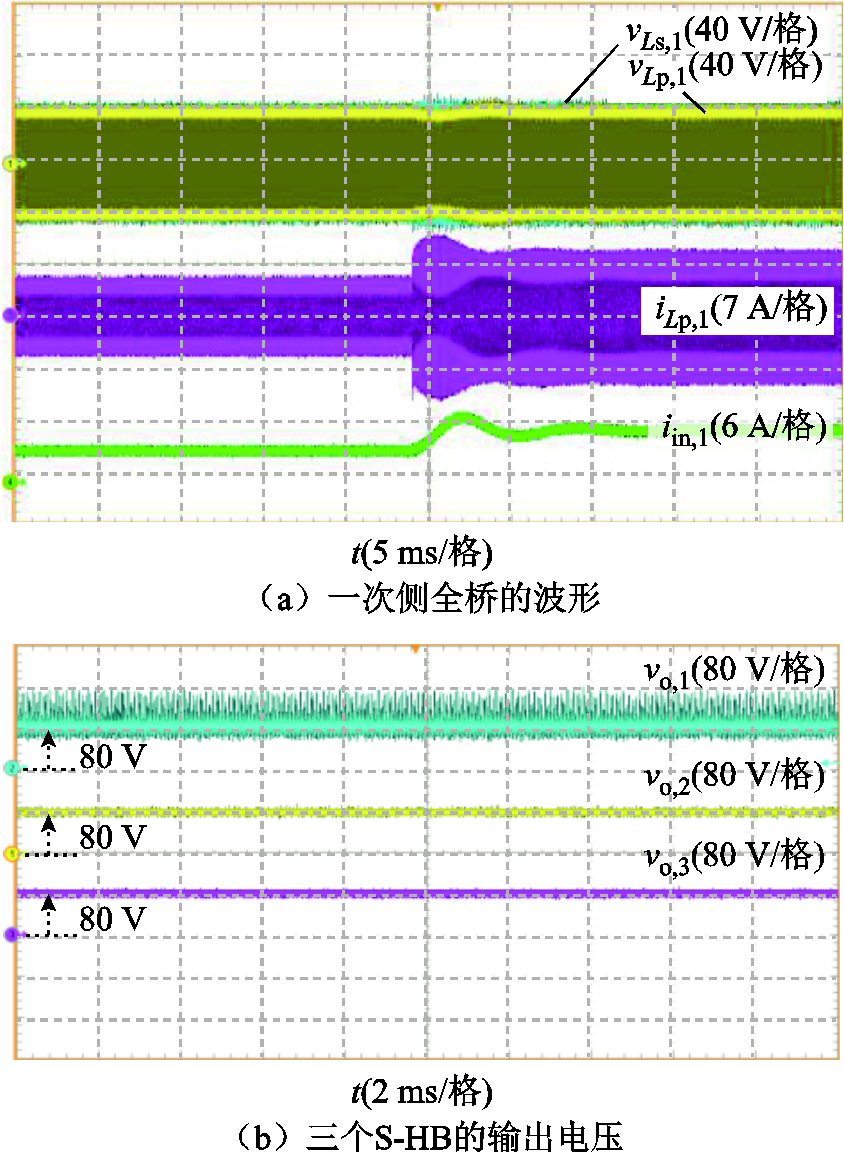
图21 当考虑输入功率变化时,所提出的转换器的动态响应
Fig.21 Dynamic response of the proposed converter when considering input power changes
输入独立输出串联变换器具有多端口、高升压转换比和独立MPPT控制的优点,但存在子模块输出电压不均衡的问题。为解决这一问题,本文提出了一种基于多绕组变压器的IIOS变换器拓扑结构及其调制策略,分析了该变换器的工作模态、多绕组变压器功率解耦特性与松弛端口的电流特性。基于所提出的拓扑结构和控制方法,可实现各输入端口的独立MPPT控制和子模块输出电压均衡。此外,所有功率开关管都可实现零电压开通,并与现有其他同类型IIOS变换器进行了性能比较,最后通过仿真分析和实验验证相结合证实了所提变换器工作原理的可行性和正确性。
参考文献
[1] 黄蔓云, 费有蝶, 卫志农, 等. 高比例新能源下的交直流配电网预测辅助区间状态估计[J]. 电力系统自动化, 2023, 47(16): 34-43.
Huang Manyun, Fei Youdie, Wei Zhinong, et al. Interval state estimation aided by forcasting for AC/DC distribution network with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2023, 47(16): 34-43.
[2] 付宇, 白浩, 李跃, 等. 面向高比例光伏消纳的低压交直流混合配电网时-空协调优化方法[J]. 南方电网技术, 2023, 17(1): 84-93.
Fu Yu, Bai Hao, Li Yue, et al. Spatial-temporal coordinated optimization method of low voltage hybrid AC/DC distribution network for accommodation of high-proportion PVs[J]. Southern Power System Technology, 2023, 17(1): 84-93.
[3] 谢芝东, 陈璐, 汪晓彤, 等. 光伏电站电压无功快速精准控制策略研究及应用[J]. 电气工程学报, 2023, 18(1): 235-243.
Xie Zhidong, Chen Lu, Wang Xiaotong, et al. Research and application of fast accurate voltage and reactive power control strategy for photovoltaic power station[J]. Journal of Electrical Engineering, 2023, 18(1): 235-243.
[4] 高圣伟, 祝庆同. 一种独立光储发电系统用宽输入范围非隔离三端口变换器[J]. 电工技术学报, 2023, 38(4): 970-982.
Gao Shengwei, Zhu Qingtong. A wide input range non-isolated three-port converter for stand-alone PV storage power generation system[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 970-982.
[5] 王斌, 张裕, 罗晨. 高比例光伏接入的配电网分布式运行优化技术[J]. 南方电网技术, 2024, 18(6): 121-130.
Wang Bin, Zhang Yu, Luo Chen. Distributed operation optimization technology of distribution network with high proportion of photovoltaic access[J]. Southern Power System Technology, 2024, 18(6): 121-130.
[6] 李嘉进, 马翔, 谢宇帆, 等. 输入串联输出并联型三电平双有源桥变换器功率与电压平衡控制策略[J]. 电工技术学报, 2024, 39(10): 3082-3092.
Li Jiajin, Ma Xiang, Xie Yufan, et al. Power and voltage balance control strategy of series input parallel output type three-level dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3082-3092.
[7] 潘尧, 孙孝峰, 蔡瑶, 等. 一种拓展模块化多电平变换器的光伏系统稳定运行范围的谐波补偿调制策略[J]. 电工技术学报, 2024, 39(4): 1132-1146.
Pan Yao, Sun Xiaofeng, Cai Yao, et al. A harmonic compensation modulation strategy for extending steady operation range of modular multilevel converter-based photovoltaic system[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1132-1146.
[8] 罗朋, 潘锦超, 洪濬哲, 等. 用于直流微电网的高升压变换器设计及效率优化[J]. 电工技术学报, 2023, 38(20): 5530-5546.
Luo Peng, Pan Jinchao, Hong Junzhe, et al. Design and efficiency optimization of a high step-up converter for DC microgird[J]. Transactions of China Electro-technical Society, 2023, 38(20): 5530-5546.
[9] 何晓坤, 胡仁杰, 陈武. 一种适用于新能源中压直流汇集的无环流零电流软开关三电平谐振式复合全桥变换器[J]. 电工技术学报, 2023, 38(19): 5274-5287.
He Xiaokun, Hu Renjie, Chen Wu. A novel circulating current free zero current switching three-level resonant composite full bridge converter for new energy medium voltage DC collection system[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5274-5287.
[10] Lu Yangjun, Wu Hongfei, Dong Xiaofeng, et al. A three-port converter based DC grid-connected PV system with autonomous output voltage sharing control[C]//2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 2017: 2057-2061.
[11] Li Xiuyi, Zhu Miao, Li Yunwei, et al. Cascaded MVDC integration interface for multiple DERs with enhanced wide-range operation capability: concepts and small-signal analysis[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1182-1188.
[12] 庄一展, 刘飞, 黄艳辉, 等. 模块化串联光伏直流变换器的环形功率均衡拓扑及效率优化策略[J]. 中国电机工程学报, 2022, 42(5): 1657-1669.
Zhuang Yizhan, Liu Fei, Huang Yanhui, et al. A circular power balancing topology with efficiency optimization strategy for modular cascaded photovoltaic DC/DC converter[J]. Proceedings of the CSEE, 2022, 42(5): 1657-1669.
[13] Huang Yanhui, Liu Fei, Zhuang Yizhan, et al. Bidirectional buck-boost and series LC-based power balancing units for photovoltaic DC collection system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 6726-6738.
[14] Zhuang Yizhan, Liu Fei, Huang Yanhui, et al. A multiport modular DC-DC converter with low-loss series LC power balancing unit for MVDC interface of distributed photovoltaics[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7736-7749.
[15] Zhuang Yizhan, Liu Fei, Huang Wenhui, et al. A peak current reducing method for input-independent and output-series modular converters with LC-branch-based power balancing unit[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 418-429.
[16] Diao Xiaoguang, Liu Fei, Zhuang Yizhan, et al. A novel voltage balance topology with high efficiency and low current stress for MVDC interface of distributed PV[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3867-3877.
[17] Zumel P, Garcia O, Cobos J A, et al. Magnetic integration for interleaved converters[C]//Eighteenth Annual IEEE Applied Power Electronics Conference and Exposition, 2003. APEC '03, Miami Beach, FL, USA, 2003: 1143-1149.
[18] Sullivan C R, Chen Minjie. Coupled inductors for fast-response high-density power delivery: discrete and integrated[C]//2021 IEEE Custom Integrated Circuits Conference (CICC), Austin, TX, USA, 2021: 1-8.
[19] Bandyopadhyay S, Purgat P, Qin Zian, et al. A multiactive bridge converter with inherently decoupled power flows[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2231-2245.
[20] Pereira T, Hoffmann F, Zhu Rongwu, et al. A comprehensive assessment of multiwinding transformer-based DC-DC converters[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10020-10036.
Modular Input Independent Output Series Photovoltaic DC Collection Converter Based on Multi-Winding Transformer
Abstract The multiport input-independent and output-series (IIOS) DC-DC converter is adaptive to medium-voltage DC (MVDC) photovoltaic (PV) integration for its independent maximum power point tracking (MPPT) control, high boost ratio, and high efficiency. However, the mismatched input power of distributed PV will cause output voltage inequality, which leads to device overvoltage and the loss of system maximum output power.
Based on the magnetic integration technology, a multiport IIOS dual half-bridge topology based on the power-decoupled multi-winding transformer (PD-MWT) is presented in this paper. The proposed topology is capable of realizing independent MPPT, high voltage conversion ratio, and isolation for distributed PV integration. Moreover, it has the following advanced features: (1) The isolation transformer and voltage balancing multi-winding transformer of the proposed topology are integrated into one PD-MWT to isolate different voltage levels and achieve average power delivery, which can significantly reduce the system volume size and achieve higher power density in the IIOS system. (2) Based on the proposed control method, the MPPT and output voltage-balance can be realized merely by configuring fewer sensors and close-control loops in the circuit, which can reduce the system costs. (3) All the power switches can achieve zero-voltage-switching, the switching current stresses on grid side can be reduced, and it is independent of the power mismatch degree.
The system structure of the proposed IIOS converter is consisted of N primary-side boost half-bridges (P-HBs), N secondary-side half-bridges (S-HBs) and one PD-MWT. The N primary-side half-bridges are independent of each other and are connected to their respective independent distributed PV panels with low input current ripple, while N secondary-side half-bridges are connected in series to withstand MVDC bus voltage. It should be noted that the number of P-HBs and S-HBs are not necessarily equal. One PD-MWT is installed to link the P-HBs and S-HBs, and to achieve isolation and voltage conversion. The operating principle of the proposed topology is described and the key operation waveforms are plotted, the system parameter design guidelines, such as inductance, capacitance and active switches selection, are also provided in the paper.
The down-scale hardware experimental setup with three input-port is built and tested. The input voltage of each submodule converter is 42 V, the desired output voltage of the proposed IIOS converter is 240 V. It can be seen from the experimental results that the power transferring from primary side to secondary side can be achieved by regulating phase-shift ratio dLp. The initial input power of these three ports is 150 W identically. The current iLs,2 and iLs,3 are in phase with iLs,1, which indicate that the slack-port absorbs power from source side and deliver average power to S-HB2 and S-HB3. Moreover, the dynamic response of the proposed converter when considering port 1 input power changes are measured and presented. In response to the power reference of input current controller, the input current of port 1 is changed from 3.6 A to 5.7 A. The output voltage waveforms of these three submodules are measured. And one can find that the submodule output voltages are well balanced and kept stable at 80 V before and after the input power changes. Therefore, the effectiveness and voltage equalization capability of the proposed converter and control strategy under input power unbalanced conditions are fully confirmed.
Keywords:Multiport DC-DC converter, PV integration, medium-voltage DC (MVDC), power mismatch, voltage balancing
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.241133
直流输电技术全国重点实验室开放基金资助项目(SKLHVDC-2023-KF-11)。
收稿日期2024-06-29
改稿日期 2024-08-12
周月宾 男,1987年生,博士,正高级工程师,研究方向为直流输电与电力电子技术。
E-mail:zhouyb@csg.cn
朱小全 男,1990年生,博士,讲师,硕士生导师,研究方向为直流输电与电力电子技术。
E-mail:ijruexq@nuaa.edu.cn(通信作者)
(编辑 郭丽军)