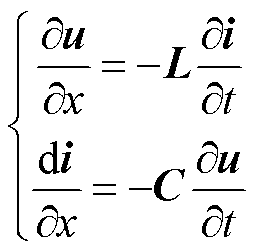 (1)
(1)
摘要 配电网线路短、行波过程极其短暂,在已知故障分支区段的前提下,实现单相接地故障的精确定位仍然具有一定的挑战性。为解决上述问题,该文综合传统单端法、双端法的优势,提出一种消去波速、且不依赖双端同步对时的单相接地故障测距方法。首先,基于模量波速差算法对就地化模量时差进行数学计算,用以表征故障位置;其次,在对两侧线模、零模首波头分别标定的前提下,提出故障位置的计算方法,无须对零模波速进行估计,有效地提升了故障定位的精度,并利用PSCAD/EMTDC与配电网动模实验系统进行验证;最后,基于数值分析理论,将误差限引入行波测距算法的评估,通过推导传统算法与所提算法的误差限,探讨了波头标定误差与零模波速估计误差对测距结果的影响,揭示了上述精度提升的理论本质。结果显示,在不考虑对时误差的仿真结果下,所提方法与双端法的精度大幅度地高于基于模量波速差的算法;考虑对时误差后,分析得到所提方法精度高于双端法。
关键词:配电网 单相接地故障 故障测距 零模行波 误差限
配电网处于电力系统的末端,线路故障概率高,其中单相接地故障占比80%以上。为减轻人工巡线负担、实现配电网的快速故障恢复,单相接地故障的精确定位是长期以来的研究热点。然而,由于配电网分支线路众多、结构复杂,利用单端测量信号、一次性地精确定位故障面临较大的困难[1],因此常利用多个阶段分步实现故障定位,可分为故障诊断[2-4]、区段定位、线路精确定位三个阶段。
随着配电自动化技术的不断进步,尤其是通信水平、信号处理技术的发展,以及馈线终端单元(Feeder Terminal Unit, FTU)的不断升级改造[5-6],在接地故障选线的基础上[7-8]进一步实现区段定位也成为了可能[9-11]。为进一步提高故障定位的精度,在现有故障区段定位的基础上研究测距技术将更为高效,但仍面对如下挑战:相对于输电线路,馈线的长度较短、行波过程极为短暂,微小的误差即可导致严重的测距结果偏差,甚至偏离线路的实际长度。因此,以双端行波测距法为主、单端法为辅的输电网故障定位模式难以直接套用在配电网中。例如,单端法在输电网中应用良好[12-13],其测距误差通常处于可接受范围(500 m)内,而在多分支的配电网中则难以识别故障点反射波[14]。双端法在精度方面具有一定的优势,但对采集装置的对时精度要求较高,误差需保持在μs级。
为此,诸多专家和学者都在测距算法方面做出努力,旨在有效地减小测距误差。文献[15]提出基于模量波速差的单端测距算法,基本不受分支线路的影响,仅需标定单端的故障零、线模首波头到达时刻。文献[16]提出基于模量波速差的双端测距算法,该算法保留了双端行波测距精度高的优点且无须同步对时。然而,零模分量传播时具有依频特性和衰减特性,其波速是随传播距离增加而衰减的变量,与行波的频率分量、线路的结构参数以及运行状态相关,要获得精确的零模波速相当困难。当前采用基于模量波速差的测距算法时,对零模波速的选取仍有一定主观性,影响了测距结果的准确性。
针对零模波速难以选取的问题,目前的改进方法有三类:第一类为波速估计法。文献[17-19]分别通过波头李氏指数、故障距离、零模行波首波头到达两端的时间差等相关特征量拟合零模波速曲线,考虑波速变化特性后,测距精度有较大提升。然而,配电网分支多且运行环境复杂,拟合零模波速曲线需要针对不同的线路与工况建立模型,工作量大且难以保证拟合的准确度。文献[20]利用故障距离、行波频率与零模波速的关系构造迭代公式提取零模波速,提高了准确性及抗干扰能力,但需大量数据才能拟合频率分量与故障距离之间的非线性关系。因此,波速估计法在配电网中难以实现。第二类为迭代法[21]。该类方法拟合零模波速关于故障距离或频率的函数,再结合基于模量波速差的单端测距公式,不断迭代缩小故障定位的范围,直到达到精度要求。该类方法在原理上消除了波速衰减的影响,但同样需要针对具体线路拟合,且迭代的计算量较大。第三类为数学消除法。针对输电线路,文献[22]利用初始行波及其后故障点反射波,建立多个方程来消除波速的影响,实现短路故障测距。文献[23-24]分别通过增加行波检测点、对线路注入高压脉冲构建多方程,在数学层面消除了波速变量,避免了波速估算这一难题,但具有多测点成本高、注入法操作复杂等问题。
为解决上述问题,并针对配电网多分支导致反射波难识别的特点,本文采用模量初始行波作为检测波,在现有的配电网故障区段定位基础上,提出一种不依赖同步对时的改进型双端测距方法:首先,基于模量波速差算法对就地化模量时差进行了数学计算,通过数学消除法,提出了故障位置的计算方法;其次,结合变分模态分解(Variational Mode Decomposition, VMD)和Teager能量算子(Teager Energy Operator, TEO)实现了计算过程所需的线模、零模波头能量标定与到达时刻提取;然后,基于数值分析中对算法误差分析的理论与方法,将误差限引入行波测距算法的评估,探讨了波头标定误差与零模波速估计误差对算法误差限的影响,揭示了本文所提方法精度更高的理论本质,并通过仿真,实现了理论基础与测试结果的循环验证;最后,讨论了不同噪声干扰对所提测距方法的影响,并通过动模实验验证了该方法具备良好的工程实用性。
在均匀换相的三相线路中,各点电压、电流均满足波动方程组,即
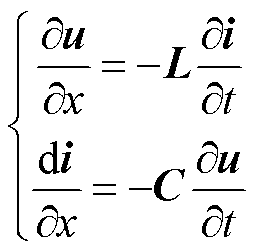 (1)
(1)
式中,u、i分别为相电压、相电流列向量,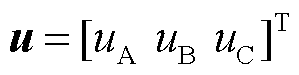 ,
,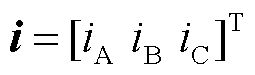 ;x为首端和测量点之间的距离;L、C分别为线路单位长度的串联电感矩阵和并联电容矩阵,由于多导体线路之间存在电磁耦合现象,故L、C矩阵为满秩矩阵。式(1)变换后得到二阶偏微分方程组,即平行多导体线路的波动方程,表示为
;x为首端和测量点之间的距离;L、C分别为线路单位长度的串联电感矩阵和并联电容矩阵,由于多导体线路之间存在电磁耦合现象,故L、C矩阵为满秩矩阵。式(1)变换后得到二阶偏微分方程组,即平行多导体线路的波动方程,表示为
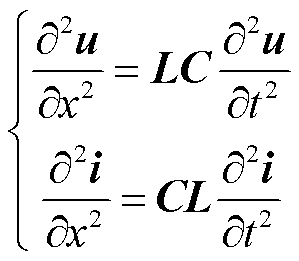 (2)
(2)
为了实现上述方程的解耦与解析求解,采用凯伦贝尔相模变换得到线模、零模信号,使得变换后对应方程的各个分量相互独立,其相模变换公式为
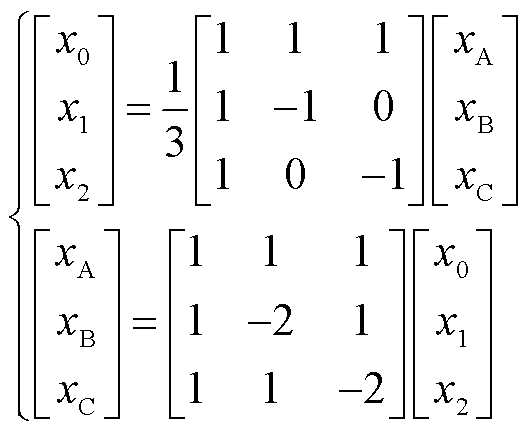 (3)
(3)
式中,x0、x1、x2为所得模量,本文取1模作为线模分量进行分析。
行波模量示意图如图1所示。不失一般性,假设配电线路AB段发生单相接地故障,故障点为F。
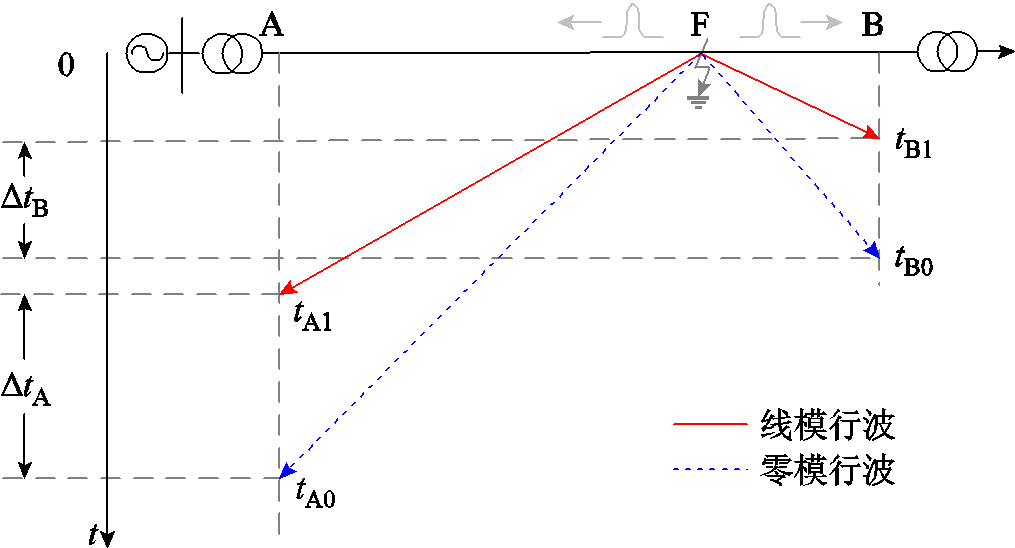
图1 行波模量示意图
Fig.1 Schematic of traveling wave modal components
图1中,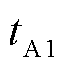 、
、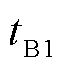 分别为故障初始行波线模分量的波头抵达线路A、B端检测点的时刻;
分别为故障初始行波线模分量的波头抵达线路A、B端检测点的时刻;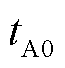 、
、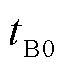 分别为故障初始行波零模的波头抵达线路A、B端检测点的时刻;
分别为故障初始行波零模的波头抵达线路A、B端检测点的时刻;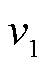 、
、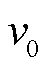 分别为线模、零模行波波速;线路AB段的长度为
分别为线模、零模行波波速;线路AB段的长度为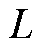 。假设
。假设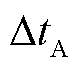 、
、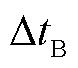 分别为行波线模和零模分量到达线路A、B端测量点处的时间差,
分别为行波线模和零模分量到达线路A、B端测量点处的时间差,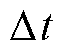 为A端与B端模量时差的差值,
为A端与B端模量时差的差值,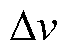 为线模与零模行波的波速差,则
为线模与零模行波的波速差,则
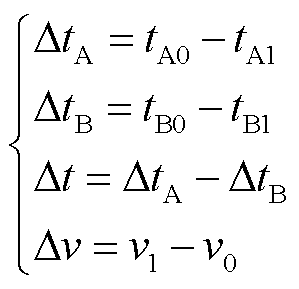 (4)
(4)
其中
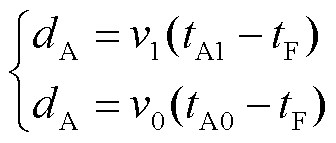 (5)
(5)
式中,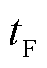 为故障发生时刻。消去
为故障发生时刻。消去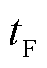 后可得A侧基于模量波速差的单端测距算法为
后可得A侧基于模量波速差的单端测距算法为
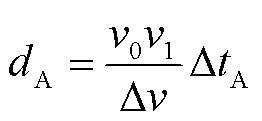 (6)
(6)
同理,可得B侧的单端测距公式为
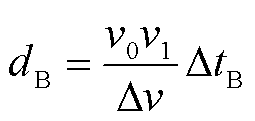 (7)
(7)
故障点到A、B两端距离之差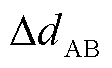 为
为
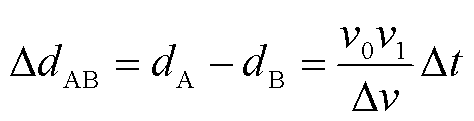 (8)
(8)
进而得到基于模量波速差的双端测距算法为
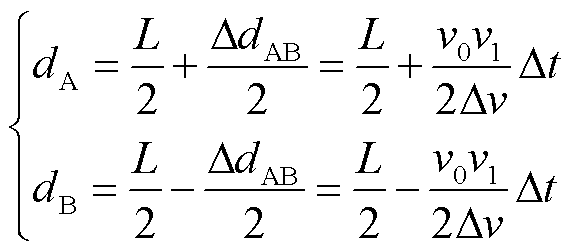 (9)
(9)
单独应用上述基于模量波速差的单端、双端测距方法,不仅要检测模量行波到达首端的时间,还要确定所对应的模量行波的准确波速。将式(6)、式(7)分别与式(9)的第一、第二个方程联立,可得基于模量传输时差的改进型双端测距公式为
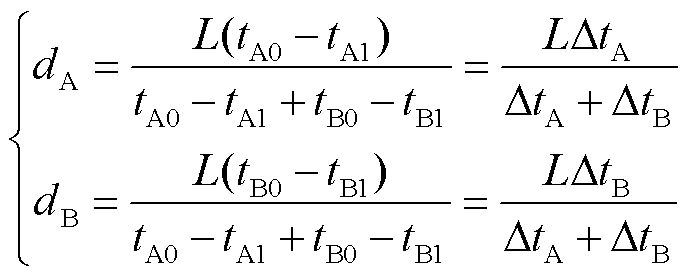 (10)
(10)
相比基于模量波速差的单端、双端算法,本算法消去具有衰减特性的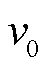 变量,无需估算零模行波波速,且无需双端的同步对时,易于实现。
变量,无需估算零模行波波速,且无需双端的同步对时,易于实现。
行波波头的准确标定对故障精确定位至关重要。小波变换[25](Wavelet Transform, WT)、经验模态分解[26](Empirical Mode Decomposition, EMD)与经验小波变换(Empirical Wavelet Transform, EWT)等是标定波头的经典算法。然而,WT的效果依赖所选择的小波基函数,这是其主要挑战;EMD具有数据驱动的自适应性,但引入了模态混叠和边缘效应的问题;EWT结合了EMD的自适应分解思想与WT的紧支撑框架,解决了模态混叠问题,但其通过自动分割信号频谱提取模态,因噪声频谱能量与信号成分混杂,在噪声环境下鲁棒性较差。相比之下,VMD[27]通过变分优化自适应分解信号,将其分为频带有限的本征模态函数(Intrinsic Mode Functions, IMFs),并最小化各模态的带宽,克服了模态混叠和边缘效应等问题,表现出更好的噪声鲁棒性与降噪效果。
VMD的基本原理为,在保证所有IMFs之和等于待分解电压行波信号的前提下,使各IMF估计带宽之和最小,约束变分模型表达式为
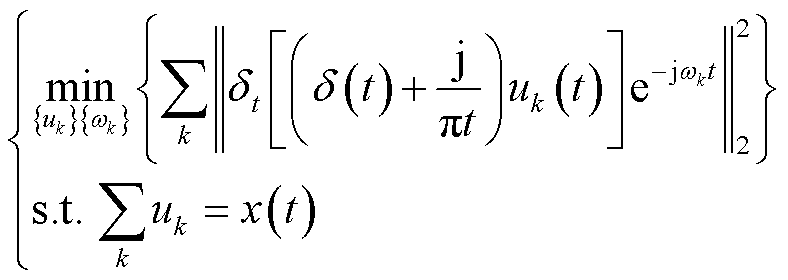 (11)
(11)
式中,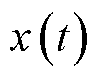 为模量信号;t为时间参数;
为模量信号;t为时间参数;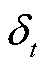 为随时间变换的偏导数;j为虚数单位;
为随时间变换的偏导数;j为虚数单位;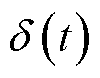 为脉冲函数;
为脉冲函数;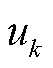 为分解得到的第k个IMF分量;
为分解得到的第k个IMF分量; 为各分量的中心频率。引入Lagrange乘法算子
为各分量的中心频率。引入Lagrange乘法算子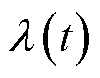 和二次惩罚因子α以求取表达式的最优解。增广Lagrange函数表达式为
和二次惩罚因子α以求取表达式的最优解。增广Lagrange函数表达式为
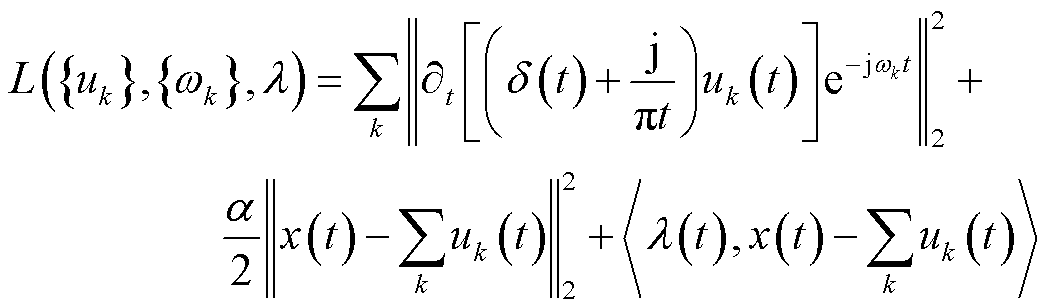 (12)
(12)
在第n步更新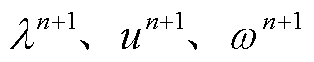 的公式为
的公式为
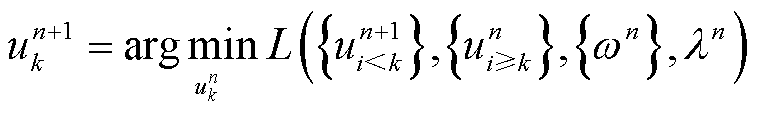 (13)
(13)
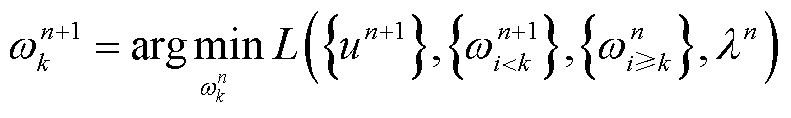 (14)
(14)
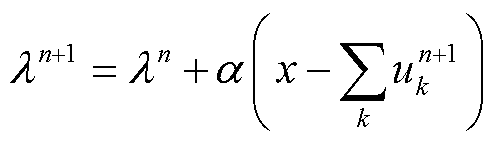 (15)
(15)
更新至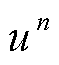 达到收敛精度
达到收敛精度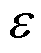 (
(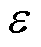 =
=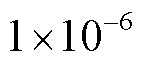 ),即
),即
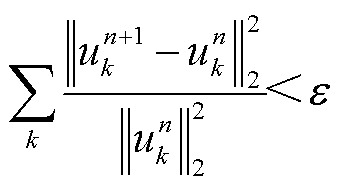 (16)
(16)
最终分解获得k个IMF分量。
针对传统提取调频调幅信号瞬时能量谱和频率谱方法,计算原理复杂、计算时间长的问题,本文采用TEO运算替代传统方法,快速而准确地提取并标定调频调幅信号瞬时能量谱和频率谱。TEO在信号振幅与频率两方面对瞬时信号进行能量评估,准确跟踪信号的变化,对信号进行实时处理,其计算公式为
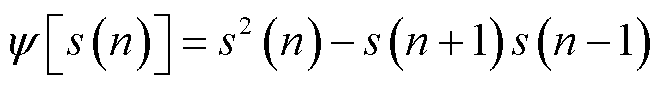 (17)
(17)
式中,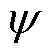 [s(n)]为能量算子;s(n)为待分析信号。由于VMD变换后的第一个IMF分量(IMF1)具有明显的波头突变特征,易于准确标定,本文对IMF1进行TEO运算,并将其能量谱第一个峰值对应的时间标定为行波到达时刻。
[s(n)]为能量算子;s(n)为待分析信号。由于VMD变换后的第一个IMF分量(IMF1)具有明显的波头突变特征,易于准确标定,本文对IMF1进行TEO运算,并将其能量谱第一个峰值对应的时间标定为行波到达时刻。
本测距法流程如图2所示,具体步骤如下。
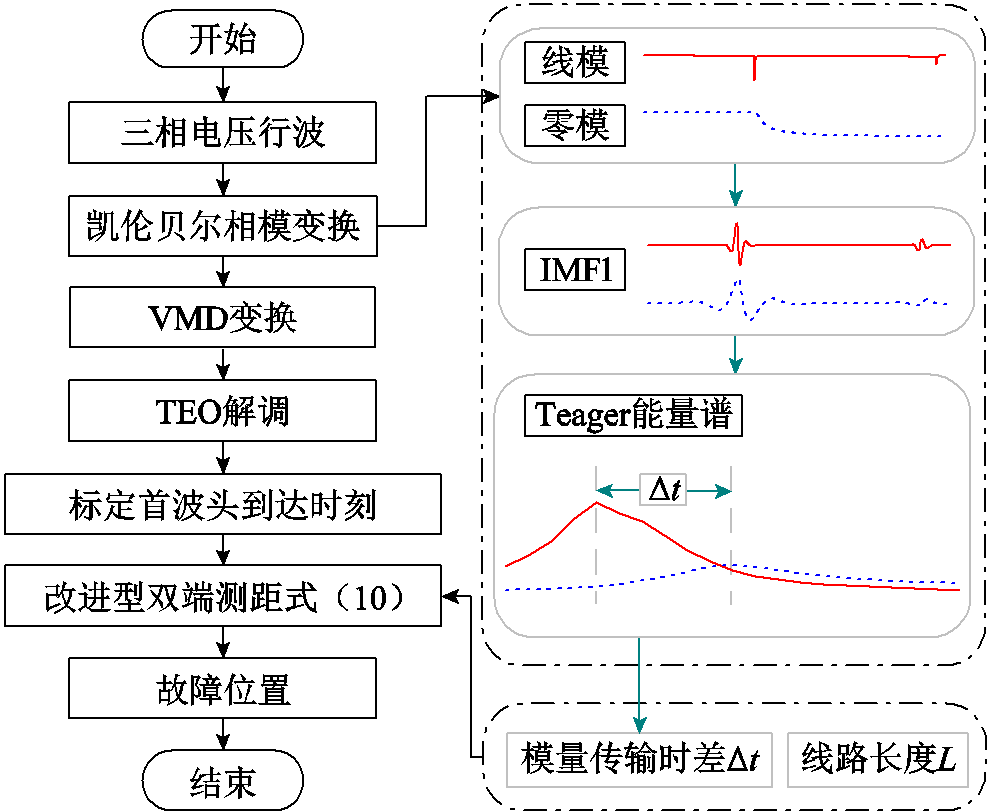
图2 所提测距方法流程
Fig.2 Flow chart of the proposed fault location method
1)信号采集:在线路两端采集三相电压行波,经凯伦贝尔相模变换计算其对应的零模、线模分量。
2)波头标定:对零模与线模行波作VMD变换,标定IMF1的Teager能量谱第一个峰值对应的时间为行波到达时刻。
3)计算故障距离:将线路两端模量传输时差与线路长度代入式(10),得到故障位置。
在PSCAD/EMTDC中搭建如图3所示的10 kV配电网模型。架空线路采用频变参数模型,从而反映线路的暂态与谐波特性。导线采用LGJ-120,线路阻抗为Z=0.263+j0.348 Ω/km,其参数设置方法如图4所示,50 Hz下三相配电线路的电感和电容模量参数见表1。变压器采用YNd11联结,电压比为110 kV/10.5 kV,末端负荷采用恒定功率。
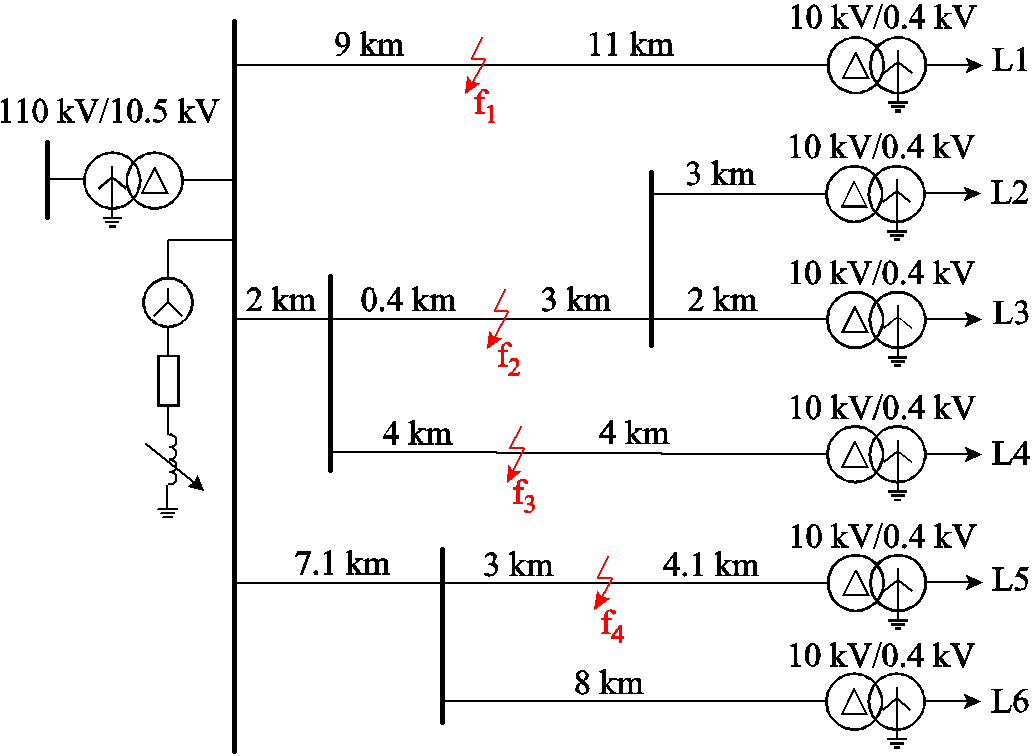
图3 配电网结构示意图
Fig.3 Structure chart of the distribution network

图4 线路参数设置方法
Fig.4 Line parameter setting method
表1 线路参数
Tab.1 Line parameters

相序电容/(10-6µF/km)电感/(μH/km) 正序10.6781.058 零序2.8715.018
在配电网首端母线处及各分支线路末端配置行波检测装置。单相接地故障发生后,首先进行故障区段的定位[9-11],然后确定与故障点相邻的行波检测装置,通过相邻检测装置提取故障电压行波。例如,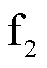 处故障时,采用线路3首末端的检测信号。
处故障时,采用线路3首末端的检测信号。
不同于输电线路,配电网线路短、行波过程极其短暂,只能通过提升采样率的方式获取首波头相关特征。其中,现有研究中所使用的采样率为10~20MHz[28],本文设置采样率为10MHz。在图3所示的仿真系统中,距离电源侧9km的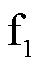 处发生单相接地故障,过渡电阻10
处发生单相接地故障,过渡电阻10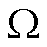 ,故障初相角10°。
,故障初相角10°。
故障发生后,由FTU得到故障点位于线路1,再将线路首末端检测所得的三相电压行波信号经凯伦贝尔相模变换解耦,分别得到故障后100ms的电源侧、负荷侧模量行波,波形如图5所示。分别对线模、零模行波进行VMD变换,本文选定二次惩罚因子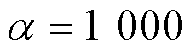 ,分解层数
,分解层数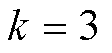 ,得到的电源侧IMFs如图6所示。对分解所得IMF1分量进行TEO运算,其瞬时能量谱上首个能量峰值对应的时间即为行波波头到达时刻,波头标定结果如图7所示。
,得到的电源侧IMFs如图6所示。对分解所得IMF1分量进行TEO运算,其瞬时能量谱上首个能量峰值对应的时间即为行波波头到达时刻,波头标定结果如图7所示。
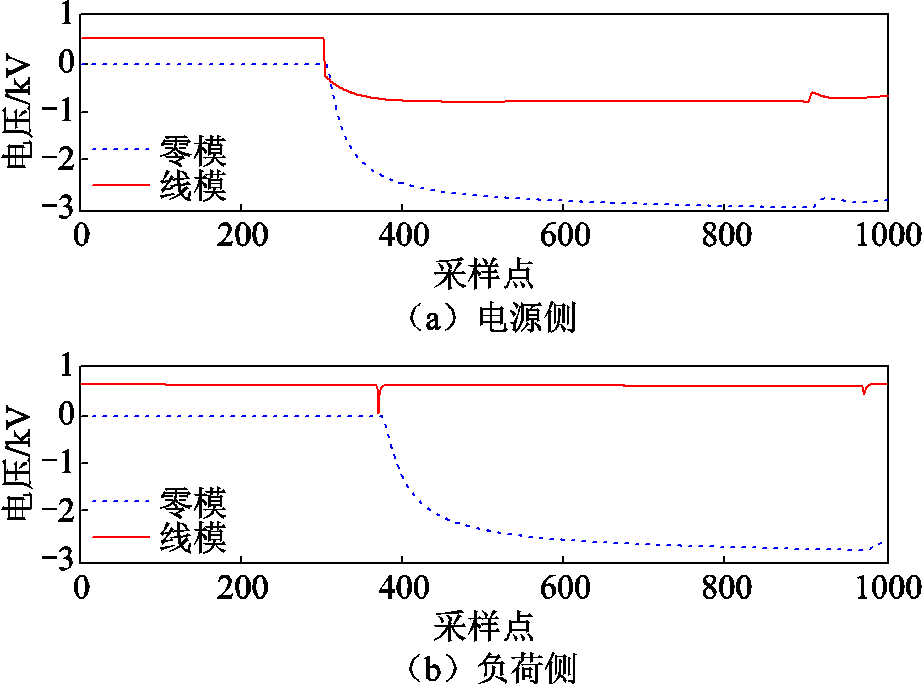
图5 线模、零模行波
Fig.5 Zero- and aerial-modal traveling waves
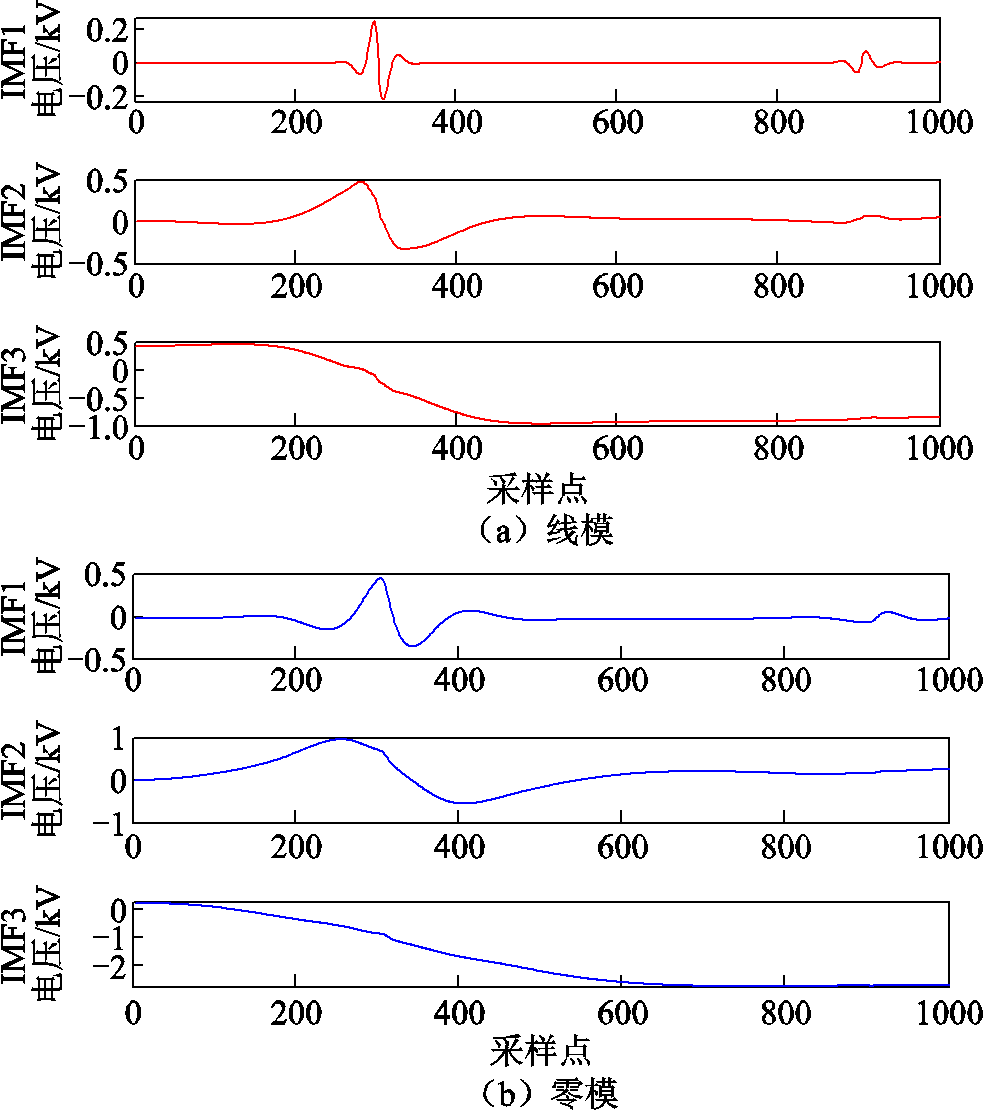
图6 电源侧线模、零模行波VMD变换结果
Fig.6 VMD results of zero- and aerial-modal traveling waves on the source side
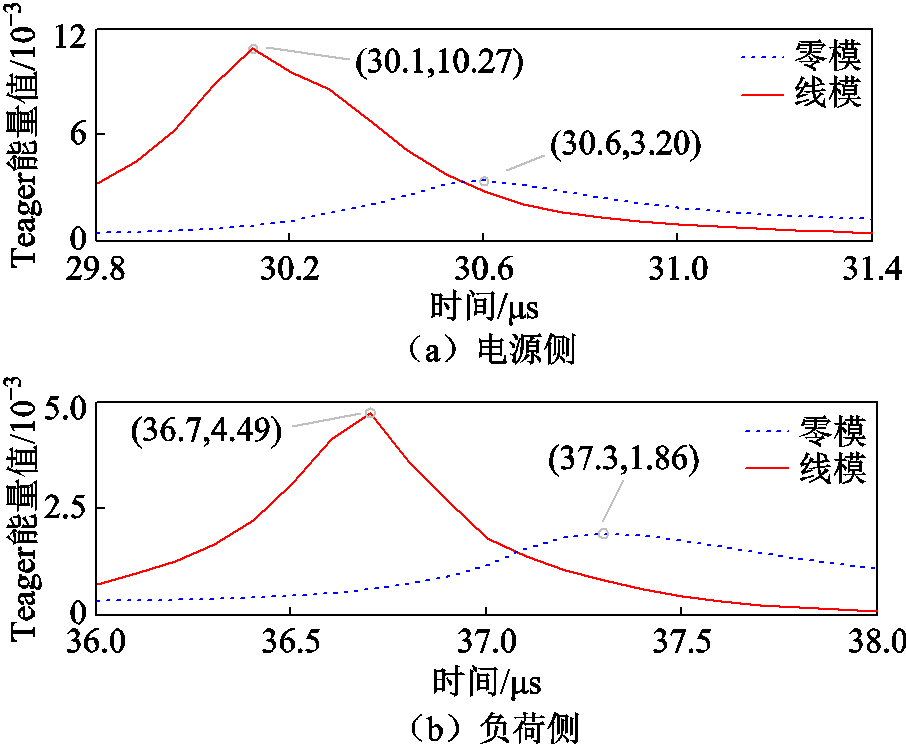
图7 波头标定结果
Fig.7 Results of wavefront calibration
可以算得,电源侧、负荷侧的线模、零模行波到达时差分别为0.5ms、0.6ms。根据式(10)可得故障位置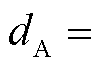 9 090.91 m。故障测距绝对误差
9 090.91 m。故障测距绝对误差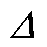 定义为
定义为
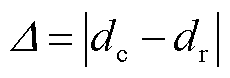 (18)
(18)
故障测距相对误差e定义为
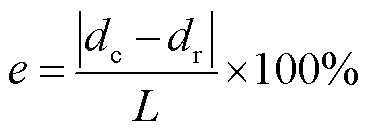 (19)
(19)
式中,dc为测量故障距离;dr为真实故障距离。
可知上述场景下的测距绝对误差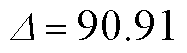 m,相对误差e=0.45%。
m,相对误差e=0.45%。
为验证本文所提算法的适用性,在图3所示模型中的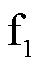 点,分别进行不同过渡电阻与故障初相角的仿真。固定故障初相角为5°,改变过渡电阻后的负荷侧模量行波能量谱如图8所示;固定过渡电阻为2 Ω,改变故障初相角后的负荷侧模量行波能量谱如图9所示。由图8、图9可知,随着过渡电阻与故障初相角的改变,检测到各模量行波的幅值变化,但对第一个波头的形状基本没有影响,相应Teager能量谱首个峰值的对应时刻也没有发生变化,即测距结果不受影响。
点,分别进行不同过渡电阻与故障初相角的仿真。固定故障初相角为5°,改变过渡电阻后的负荷侧模量行波能量谱如图8所示;固定过渡电阻为2 Ω,改变故障初相角后的负荷侧模量行波能量谱如图9所示。由图8、图9可知,随着过渡电阻与故障初相角的改变,检测到各模量行波的幅值变化,但对第一个波头的形状基本没有影响,相应Teager能量谱首个峰值的对应时刻也没有发生变化,即测距结果不受影响。
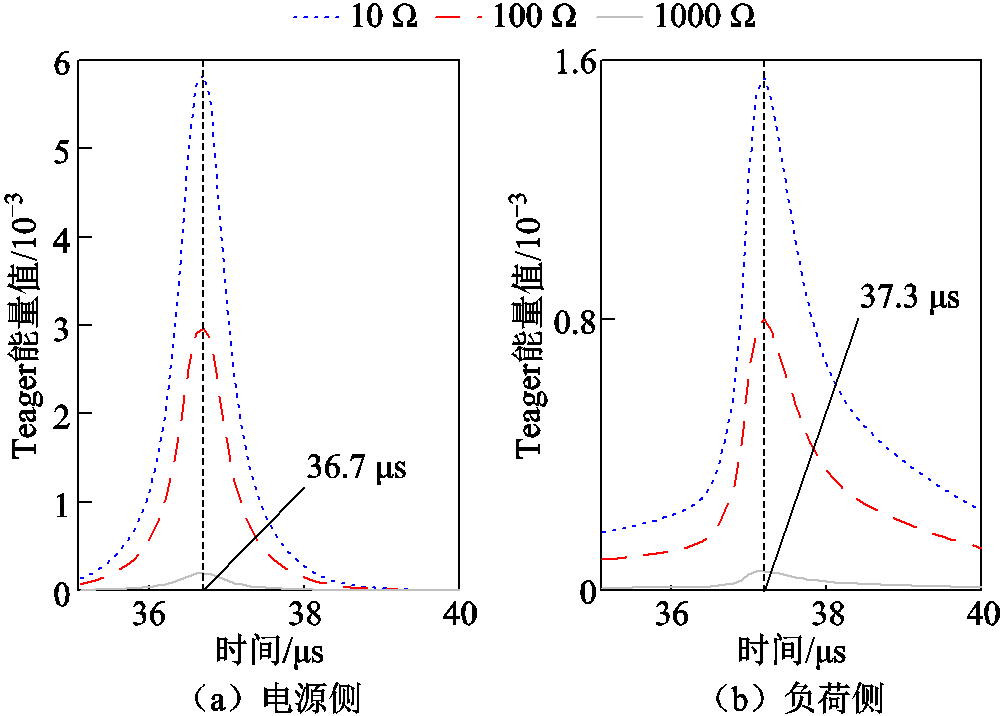
图8 不同过渡电阻下线模与零模标定结果
Fig.8 Calibration results of aerial- and zero-modal traveling waves under different fault resistances
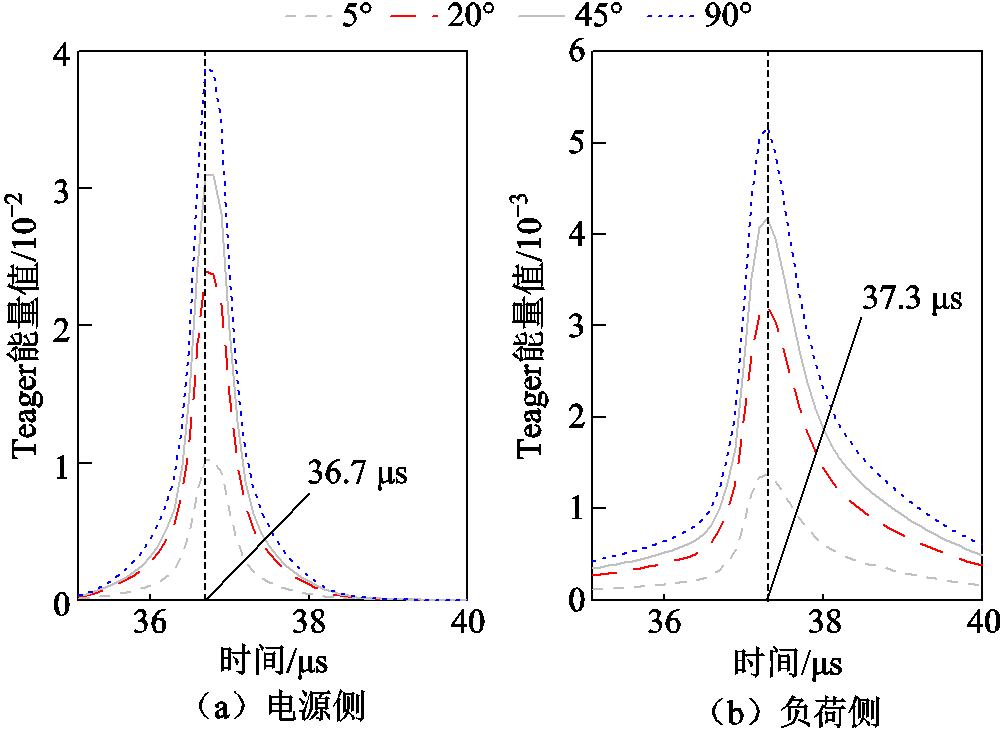
图9 不同故障初相角下线模与零模标定结果
Fig.9 Calibration results of aerial- and zero-modal traveling waves under different fault angles
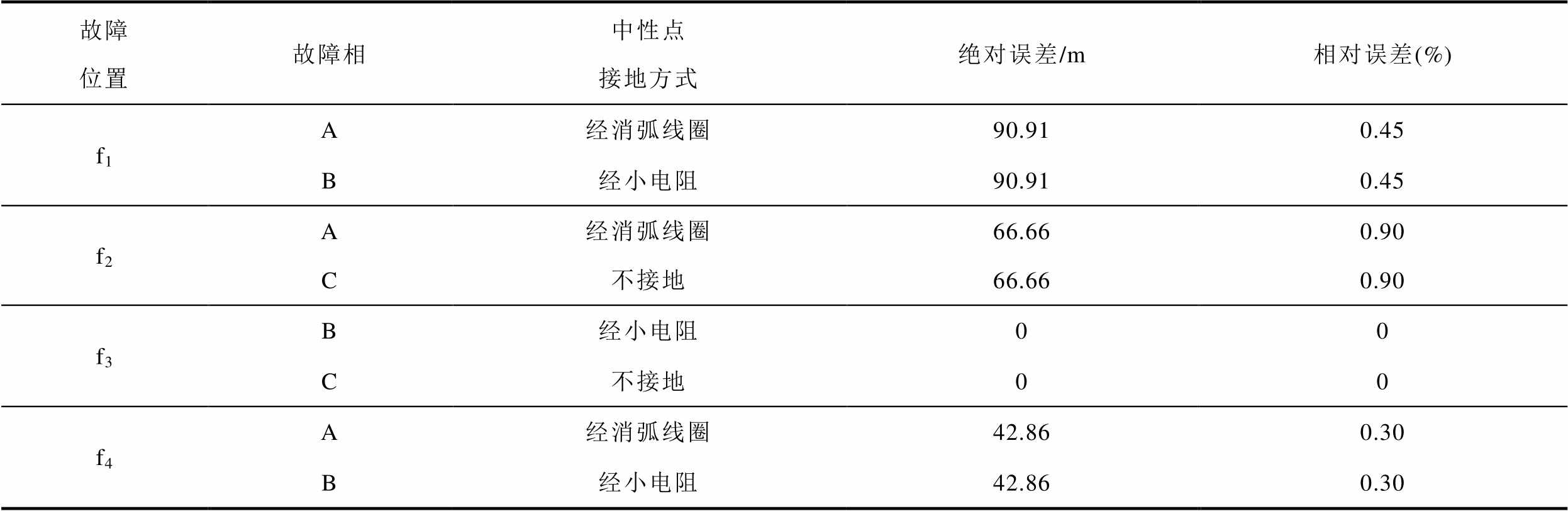
在保持过渡电阻为2 Ω、故障初相角为5°的条件下,分别改变故障位置、故障相和中性点接地方式,测距结果见表2。对于C相接地故障,采用相模变换后的2模作为线模分析,其余采用1模。由表2可得,不同故障相与中性点接地方式对测距结果没有影响。此外,在不同故障位置下,本文所提算法的定位精度较高,测距相对误差分别为0.45%、0.90%、0%、0.30%。
表2 不同故障场景测距结果
Tab.2 Fault location results for different fault scenarios
故障位置故障相中性点接地方式绝对误差/m相对误差(%) f1A经消弧线圈90.910.45 B经小电阻90.910.45 f2A经消弧线圈66.660.90 C不接地66.660.90 f3B经小电阻00 C不接地00 f4A经消弧线圈42.860.30 B经小电阻42.860.30
设x为准确值,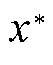 为x的一个近似值,称
为x的一个近似值,称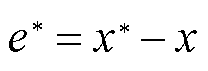 为近似值的误差。通常只能根据测量工具或计算情况估计误差的绝对值不超过某正数
为近似值的误差。通常只能根据测量工具或计算情况估计误差的绝对值不超过某正数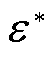 ,即误差绝对值的上界,称
,即误差绝对值的上界,称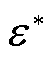 为近似值的误差限。由于误差无法确定正负与大小,故由绝对值不等式计算误差限,通过所得误差限对基于模量波速差的单端、双端算法与本文所提算法进行误差分析。
为近似值的误差限。由于误差无法确定正负与大小,故由绝对值不等式计算误差限,通过所得误差限对基于模量波速差的单端、双端算法与本文所提算法进行误差分析。
假设基于模量波速差单端、双端测距法在估计零模波速时引入误差eV0,线路A、B端零-线模波头标定时间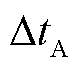 、
、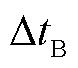 的误差分别为
的误差分别为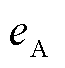 、
、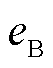 。基于模量波速差单端测距法的误差
。基于模量波速差单端测距法的误差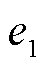 为
为
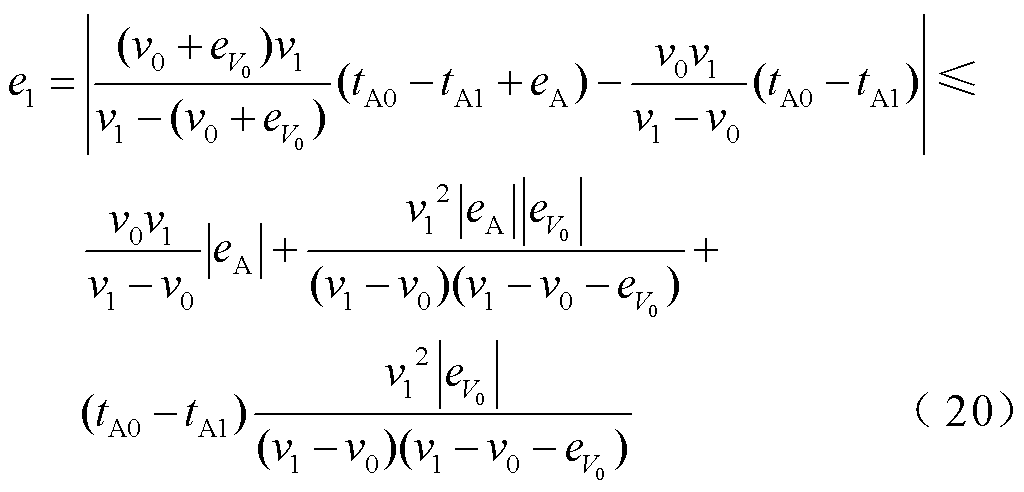
基于模量波速差双端测距法的误差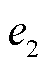 为
为
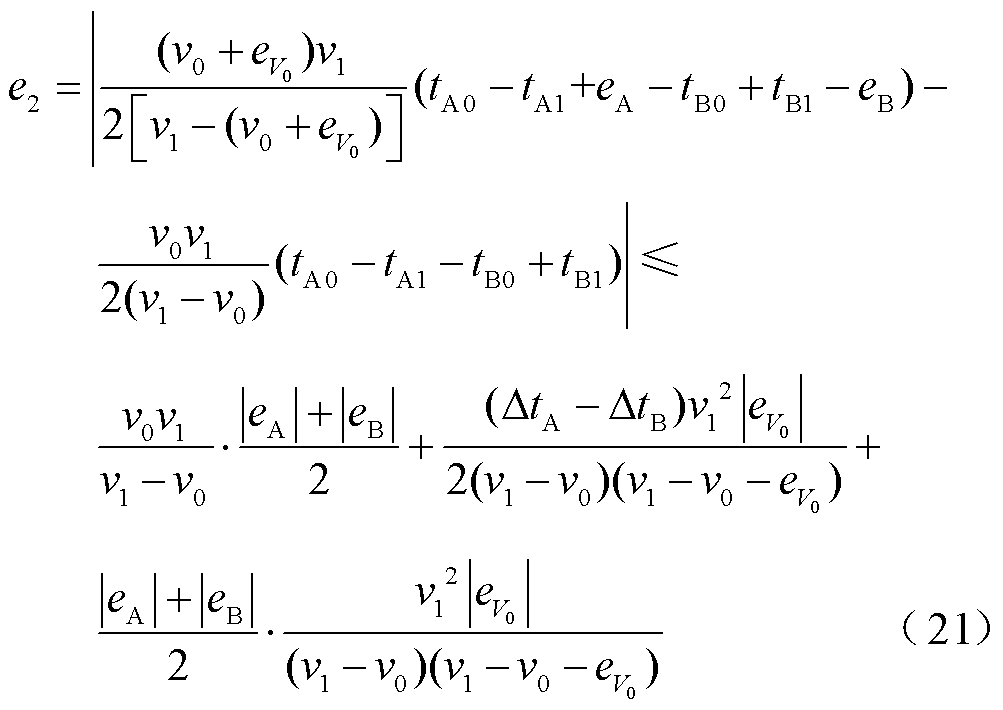
本文所提算法误差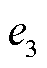 为
为
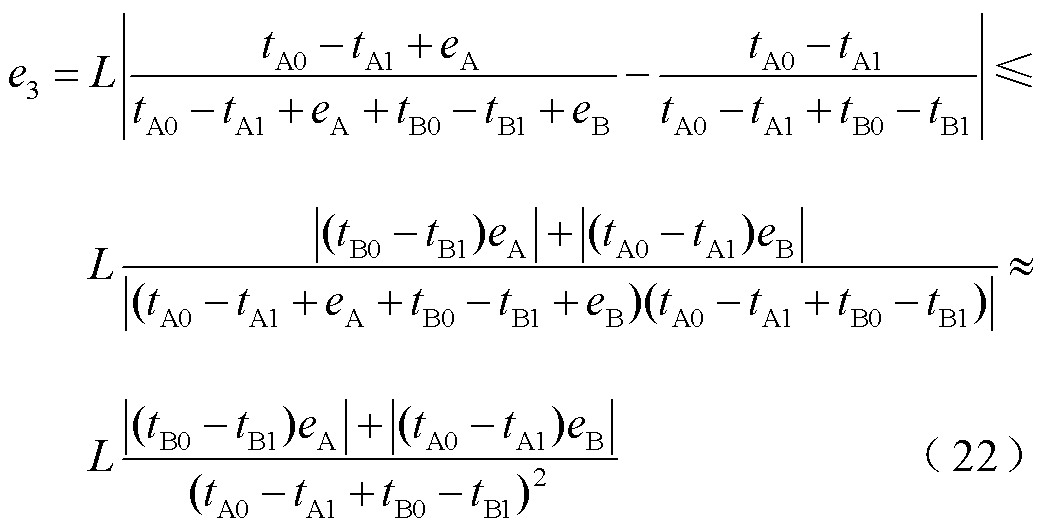
式中,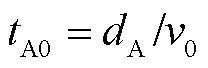 ;
;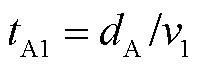 ;
;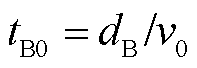 ;
;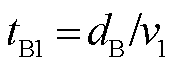 ;化简可得
;化简可得
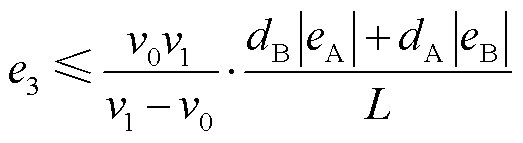 (23)
(23)
综上所述,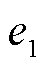 、
、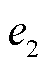 、
、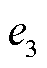 的误差限
的误差限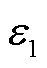 、
、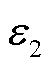 、
、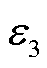 分别为
分别为
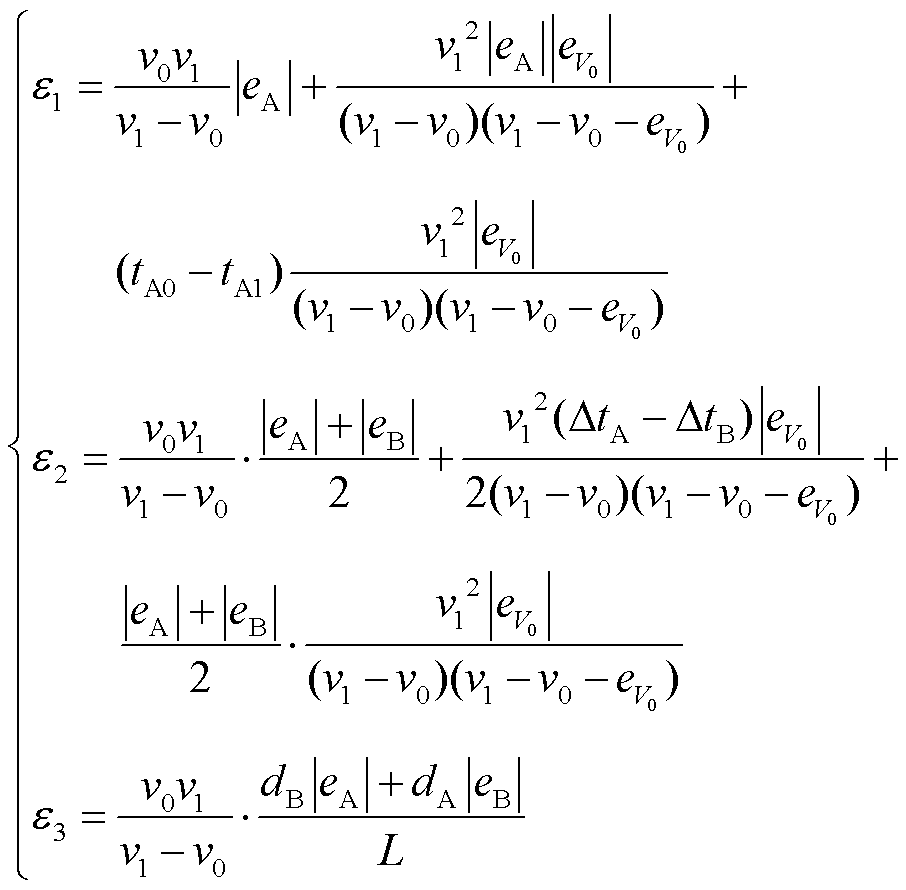 (24)
(24)
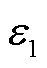 、
、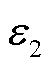 与
与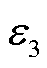 首项的公共因子为
首项的公共因子为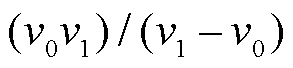 ,乘数分别为
,乘数分别为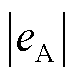 、
、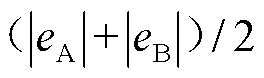 、
、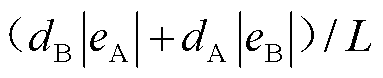 。由于故障发生地点的随机性,
。由于故障发生地点的随机性,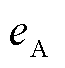 、
、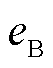 误差服从同一分布,故
误差服从同一分布,故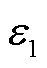 、
、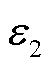 首项的数学期望相等。现对比
首项的数学期望相等。现对比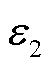 首项与
首项与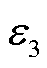 。考虑行波零模分量随着传输距离增加而衰减,相同的波头标定算法得到的结果误差随之增大,即假设
。考虑行波零模分量随着传输距离增加而衰减,相同的波头标定算法得到的结果误差随之增大,即假设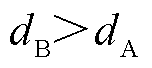 时,有
时,有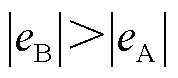 ,则
,则
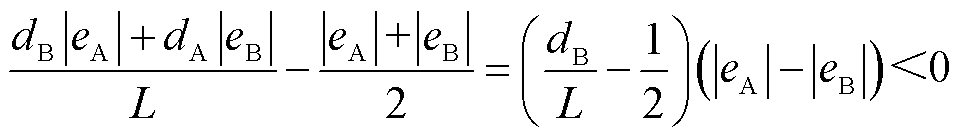 (25)
(25)
得到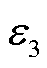 小于
小于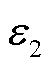 首项,即本算法的误差项与其系数成反比,具有自适应减小误差的效果。由此可见,仅考虑另外两种算法误差限首项,即不考虑波速估计的误差时,本文所提算法的误差限已最小。
首项,即本算法的误差项与其系数成反比,具有自适应减小误差的效果。由此可见,仅考虑另外两种算法误差限首项,即不考虑波速估计的误差时,本文所提算法的误差限已最小。
图10为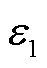 、
、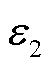 与
与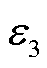 的余项关于零模波速估计误差的函数曲线。由于
的余项关于零模波速估计误差的函数曲线。由于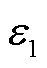 、
、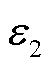 的余项皆为εV0的非线性函数,当零模波速的估计值与理论值有较大偏差时,余项被非线性放大,且都为非负数,对测距结果产生较大影响;而本文所提算法没有相应的余项,不受零模波速取值误差的影响。
的余项皆为εV0的非线性函数,当零模波速的估计值与理论值有较大偏差时,余项被非线性放大,且都为非负数,对测距结果产生较大影响;而本文所提算法没有相应的余项,不受零模波速取值误差的影响。
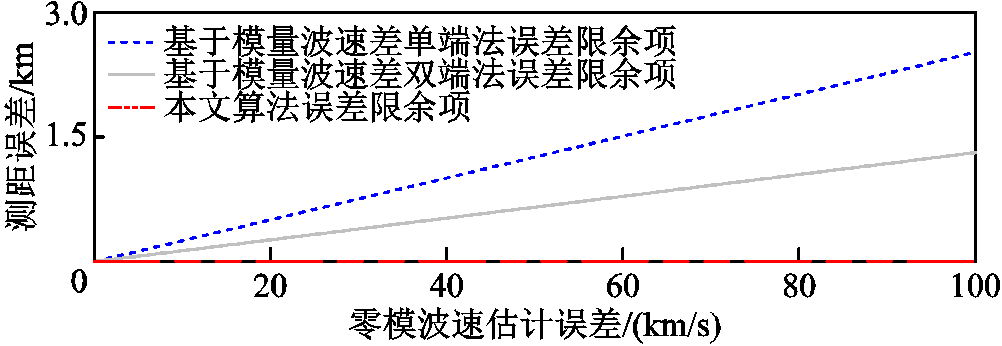
图10 误差限余项关于零模波速估计误差的函数曲线
Fig.10 The function curves of the error limit remainder versus the estimation error of the zero-modal wave velocity
由误差限分析得到,各算法误差从低到高排序为:本文所提算法、基于模量波速差双端法、基于模量波速差单端法。
基于PSCAD/EMTDC的仿真结果,对文中所提算法、传统双端行波测距方法和基于零模线模时差的单端、双端行波故障测距方法进行对比验证。其中,模量波速计算公式为
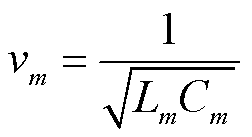 (26)
(26)
式中,m为模量,m=0, 1,分别表示零模、线模。将表1的线路参数代入式(26),计算得到50 Hz下线模波速v1=2.975×108 m/s、零模波速v0=2.635× 108 m/s。
3.2.1 测距精度对比
将仿真数据代入各类测距算法,得到的测距结果见表3。由表3可知,对于不同故障场景,本文所提方法在不考虑双端同步对时误差的场景下,其精度仅次于传统双端测距算法;此外,50 Hz条件下的线路参数计算所得零模波速与实际波速有一定差距,导致基于模量波速差的测距算法具有较大误差,而这在本文所提出的方法中已得到了改善。
表3 不同算法测距结果
Tab.3 Results of fault location by different algorithms

故障位置故障距离/m测距误差/m 本文算法基于模量波速差单端法基于模量波速差双端法双端法(不考虑对时误差) f19 00090.91>2 000884.863.31 f22 40066.66>2 0001 184.865.79 f36 0000>2 000884.863.31 f410 10042.86>2 000>2 0009.92
3.2.2 零模波速取值影响
以f1故障仿真数据为例,分析不同零模波速取值对各类测距算法的影响。以50 Hz下的零模波速为取值起点,代入基于模量波速差单端、双端测距公式,所得基于模量波速差算法与本文所提算法误差对比如图11所示,可见基于模量波速差算法的准确度高度依赖零模波速的选取。仅在极少零模波速取值区间内,即2.926×108~2.935×108 m/s,基于模量波速差的算法精度高于本文所提算法,而在配电网中准确的零模波速估计难以实现。由图11可知,各类测距算法受零模波速取值影响程度由高至低为:基于模量波速差单端法、基于模量波速差双端法、本文算法,与本文的误差限分析所得结论一致。
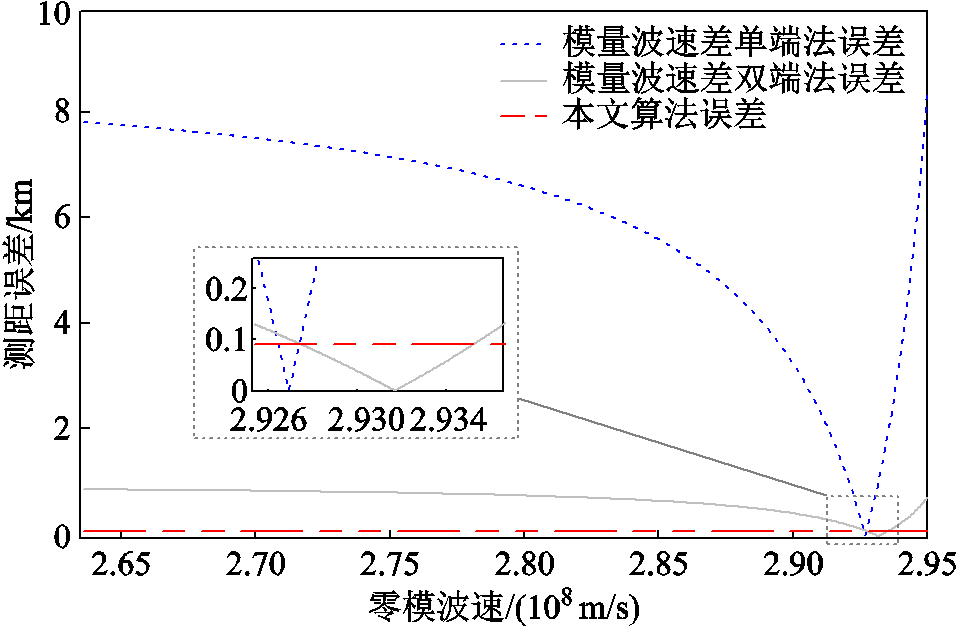
图11 不同零模波速下测距误差对比
Fig.11 Comparison of fault location errors under different zero-modal traveling wave velocities
3.2.3 对时误差影响
由表2可知,不考虑对时误差时,传统双端测距算法精度最高。而在电力行业标准DL/T 357—2019《输电线路行波故障测距装置技术条件》中,要求行波故障测距装置采用自带对时功能情况下,与标准时间系统的对时误差应小于1 ms。实际工程应用中,双端故障定位装置的时钟误差在±1 ms,定位误差约±300 m[29]。随着对时装置的改进,对时精度不断提高,但仍难以保证对时装置的运行状态在复杂的配电网环境中一直保持稳定。由图12可知,当对时误差超过0.59 ms时,双端测距算法误差便超过本文所提算法误差。因此,相较于依赖同步对时的传统双端测距法,本文所提免对时改进型双端测距法可在此场景下弥补其不足。
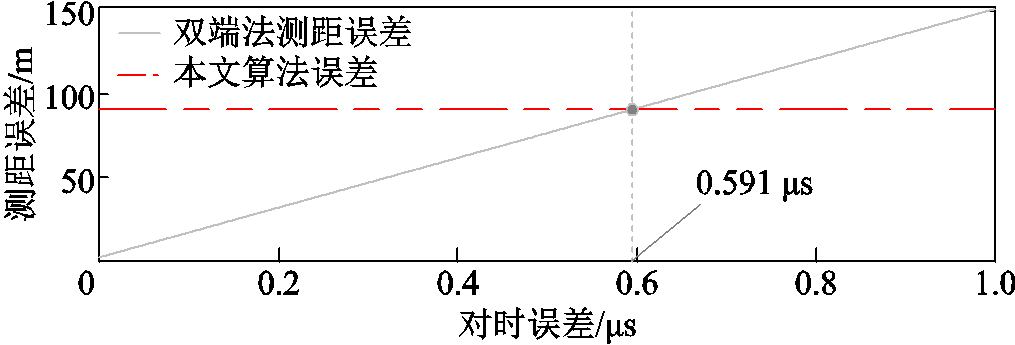
图12 不同对时精度下测距误差对比
Fig.12 Comparison of fault location errors under different time synchronizing precisions
在图3所示的仿真系统中,保持过渡电阻和故障初相角不变,在不同故障位置下,分别使用VMD-TEO、小波模极大值法、EMD-TEO和EWT-TEO进行波头标定,测距误差对比如图13所示。其中,WT方法选择bior1.3小波为母小波。由图13的对比可知,VMD-TEO的标定准确度最高,测距误差均保持在100 m以内,其次为EWT-TEO。
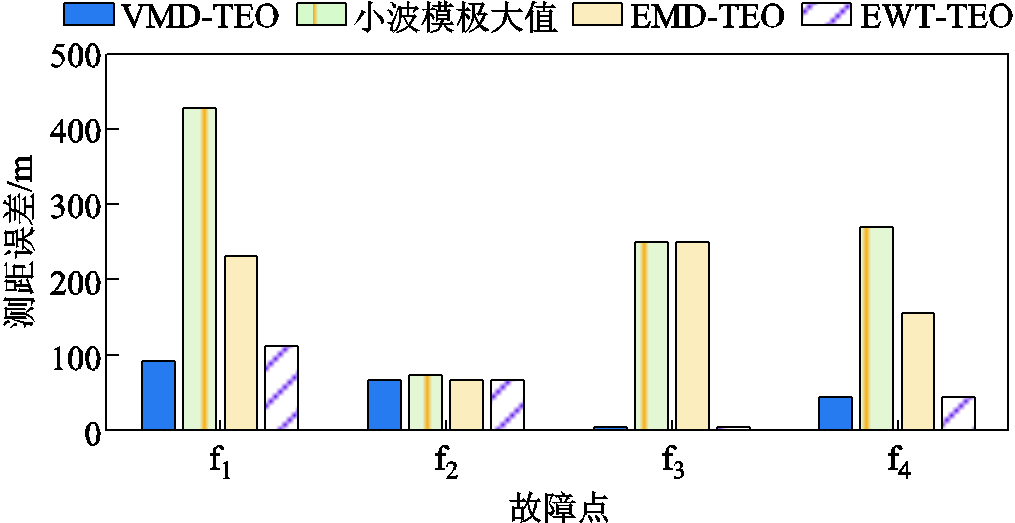
图13 不同波头标定方法下测距误差对比
Fig.13 Comparison of fault location errors under different wavefront calibration methods
在图3所示的仿真系统中,以故障点f1、过渡电阻10 Ω、初相角10°的A相接地故障场景为例,对电源侧线模行波依次加入45、43、40 dB的高斯白噪声,并根据VMD-TEO的变换结果标定波头,不同噪声下波头标定结果如图14所示。在45 dB噪声下,波头的突变特征明显,标定准确;在40 dB噪声下,虽然波头仍能正确标定,但其可辨识度已接近极限。由此得出,未经降噪处理时,VMD-TEO对噪声的抗干扰极限为40 dB。
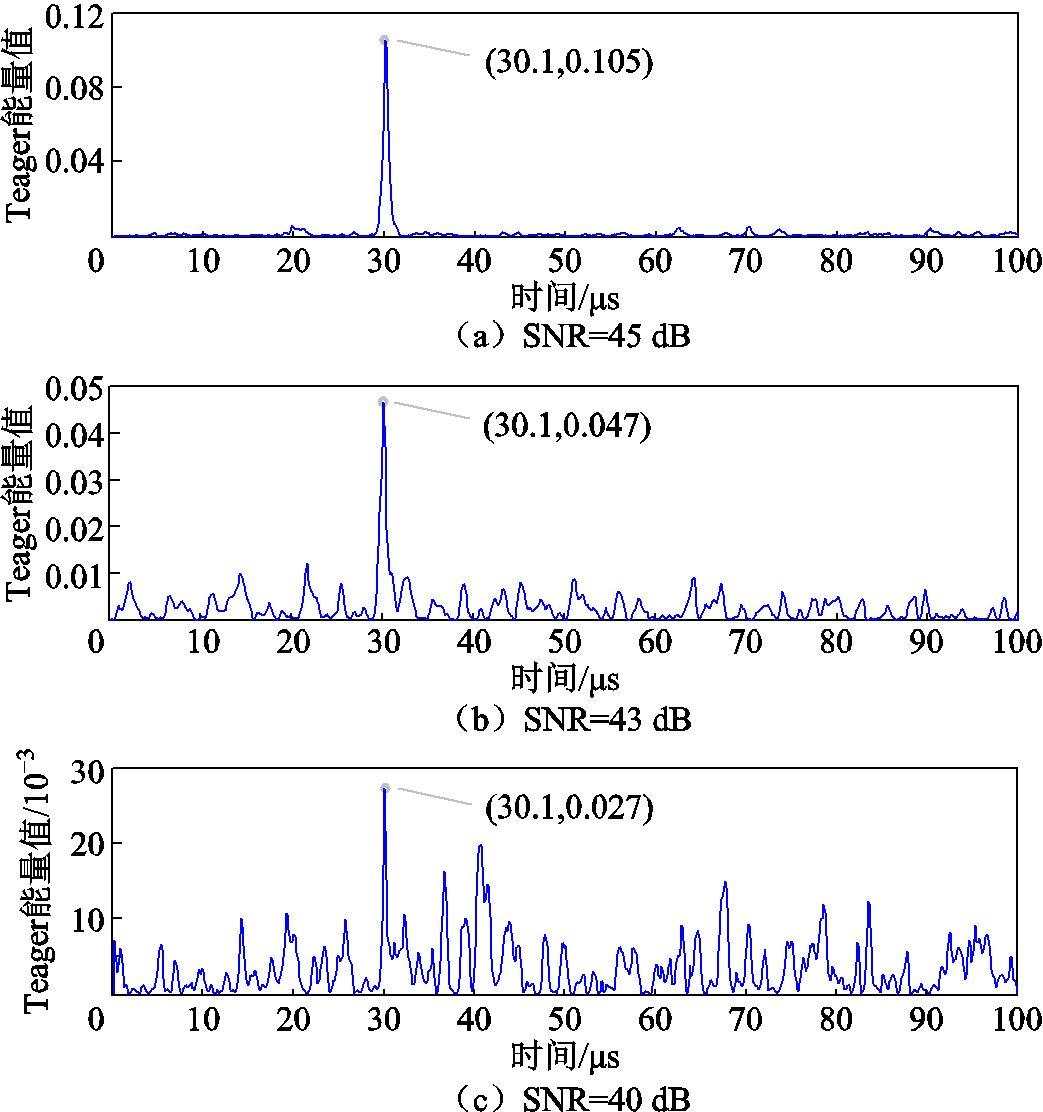
图14 不同噪声下波头标定结果
Fig.14 Calibration results under different noise conditions
为验证上述结论,对电压行波加入40 dB的噪声。改变故障位置、过渡电阻与故障初相角后,测距结果见表4。结果表明,40 dB噪声的引入并未影响波头的准确标定,在不同故障场景下依然能够保持故障定位的准确性。
表4 带噪声行波(SNR=40 dB)测距结果
Tab.4 Results of fault location under 40 dB noise

故障位置故障类型过渡电阻/Ω故障初相角/(°)中性点接地方式绝对误差/m f1AG1005经小电阻90.91 f2CG10025经消弧线圈66.66 f3BG50045不接地0 f4AG1 00090经消弧线圈42.86
然而,在实际工程中,可能面临更严重的噪声干扰(SNR<40 dB),导致波头难以识别。在此情况下,可采用降噪方法对行波信号进行预处理,如本文动模实验中采用的中值滤波[30]与多次滑动均值滤波[31],以确保在恶劣测试环境下波头的准确标定。
为验证本文所提测距方法的工程实用性,采用配电网动模实验系统进行验证,如图15a所示。该系统电压等级为380 V,包括1座变电站、1台容量为30 kV·A的主变压器及6条线路。在线路1中接入电缆电线,构建了用于行波故障测距的动模实验系统。实验台如图15b所示,实验中使用高压差分探头采集电缆双端信号,并通过示波器监测相电压变化。电压探头的电压比为100:1,接入的电缆电线长度为1.4 km。

图15 动模实验
Fig.15 Dynamic simulation test
在电缆电线距离电源端600 m处设置A相金属性接地故障,边沿触发故障录波,录波数据如图16所示,录波时间为100 ms,采样率为10 MHz。以波头到达前500 µs作起始时间点,截取随后1 ms时间窗口内的三相电压波形,相模变换后得到的线模、零模行波如图17所示,其中含有10 000个采样点。
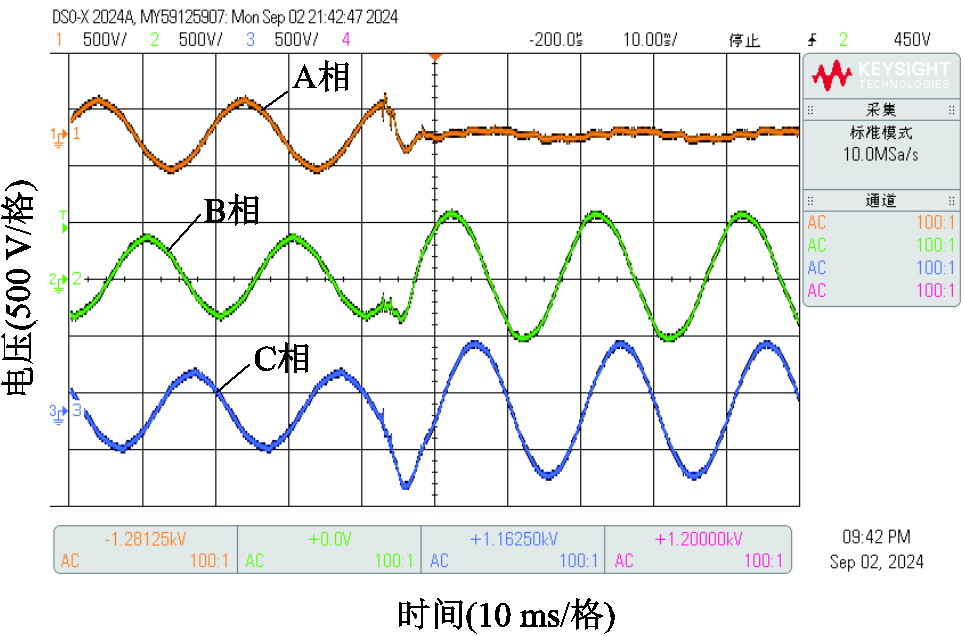
图16 接地故障三相电压录波数据
Fig.16 Recording data of grounding fault three-phase voltage
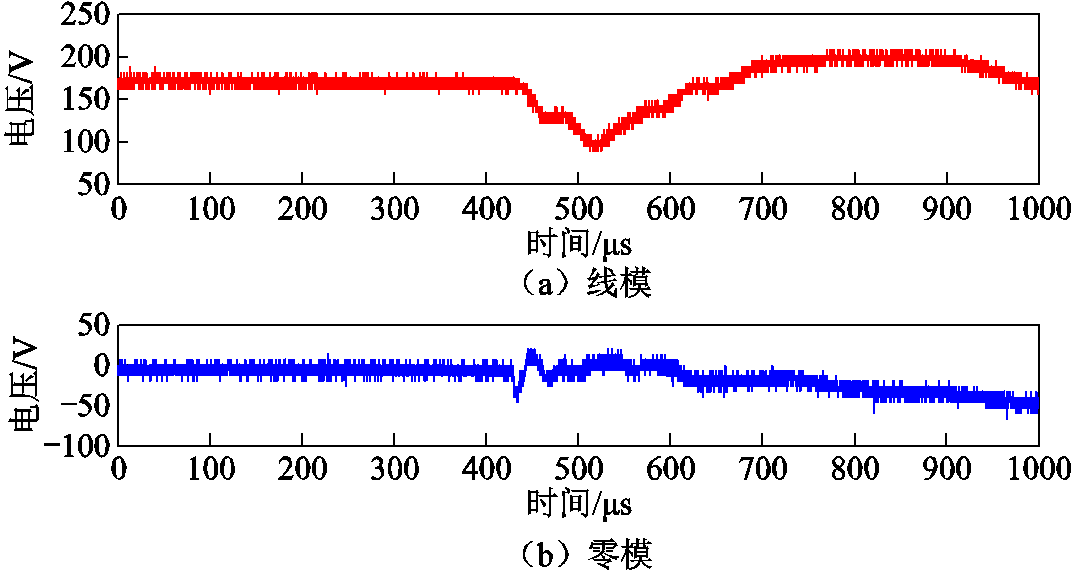
图17 线模、零模行波
Fig.17 Zero- and aerial-modal traveling waves
由图17可见,动模实验得到的电压波形中含有大量白噪声干扰,且在波头起始处存在明显的脉冲噪声,这给波头的精确标定带来了挑战。对此,采用多次滑动均值滤波(滑窗大小为10 µs,滤波次数为2)减少白噪声,并采用中值滤波(窗口长度为70 µs)消除脉冲噪声。滤波后的线模、零模行波如图18所示。对其进行VMD-TEO变换后,根据IMF1的Teager能量谱进行波头标定,结果如图19所示,电源侧线模、零模行波到达时差为29.6 µs。
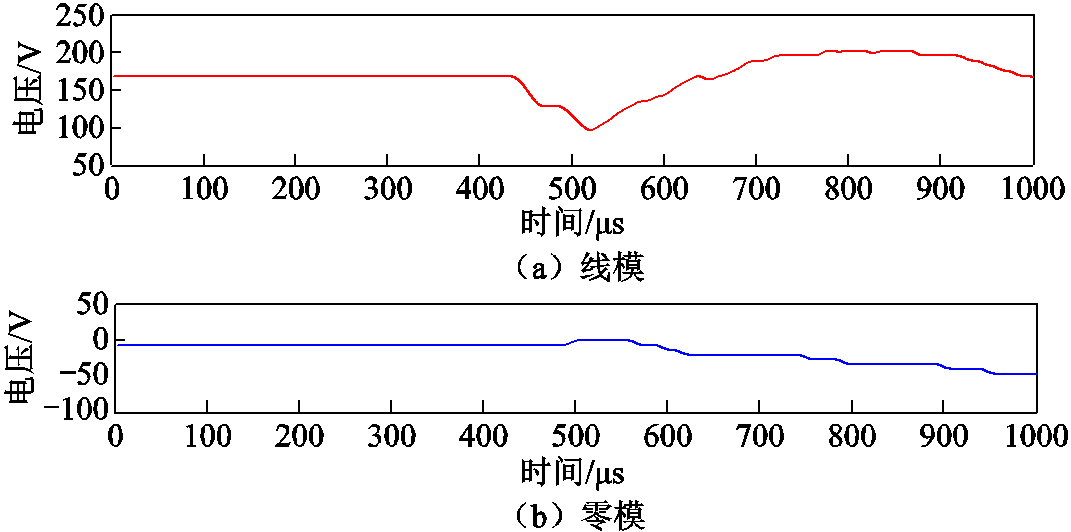
图18 模量行波滤波结果
Fig.18 Filtering results of modal traveling waves
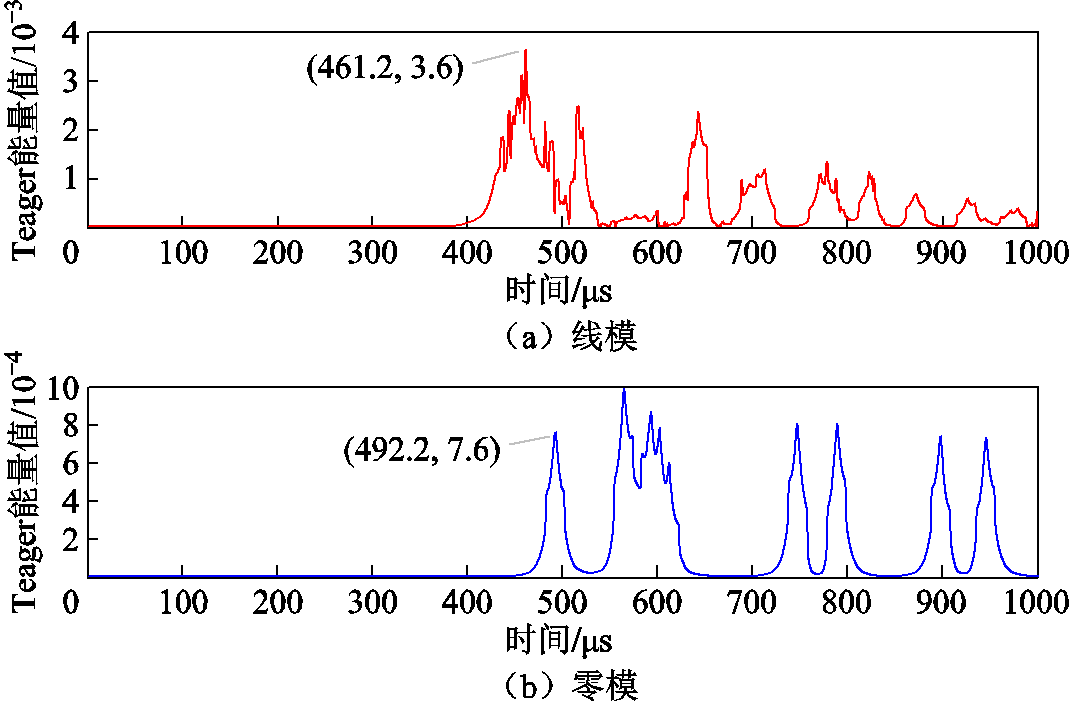
图19 电源侧线模、零模行波波头标定结果
Fig.19 Wavefront calibration of zero- and aerial-modal traveling waves on the source side
负荷侧采用与电源侧相同的处理方法,标定结果如图20所示,线模、零模行波到达时差为46.8 µs。根据本文所提测距公式计算,得到故障距离为581.15 m,测距结果的绝对误差D=18.85 m,相对误差e=1.26%。通过动模实验验证,本文提出的测距方法展现出较高的准确性,具备良好的工程实用性。
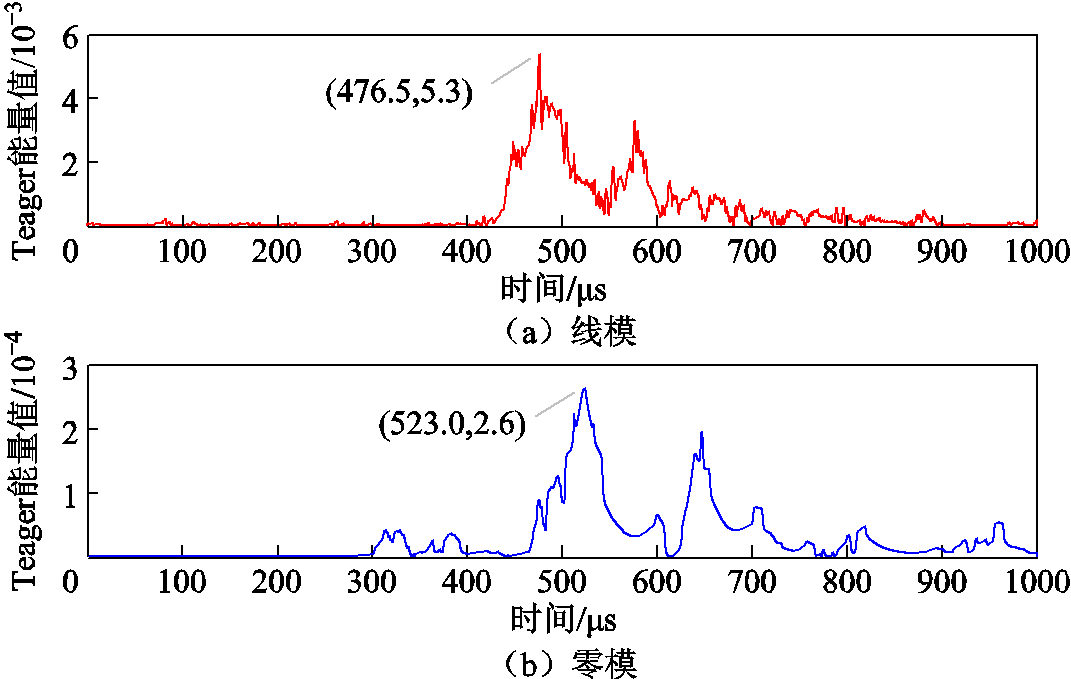
图20 负荷侧线模、零模行波波头标定结果
Fig.20 Wavefront calibration of zero- and aerial-modal traveling waves on the load side
针对传统双端测距算法依赖高精度对时,以及基于模量波速差算法测距精度受制于不稳定的零模波速的问题,本文提出不依赖同步对时的改进型双端行波测距方法。该方法以基于FTU的故障区段定位结果作为前置条件,其可实施性将随着配电网测量与通信条件的改善而不断增强。主要结论如下:
1)将基于模量波速差的单端、双端测距公式相结合,消除波速变量。所得测距算法仅需标定零模、线模首波头,无需对时与估计波速;基于PSCAD/ EMTDC的仿真结果显示,所提出的测距方法能够快速、可靠地定位配电网架空线路单相接地故障,不同故障场景下的测距误差都在100 m以内。
2)经测试,单独使用本文所提算法的抗噪声边界为40 dB。当测量环境的噪声水平较高(SNR<40 dB)、存在一定比例的脉冲干扰时,结合多次滑动均值滤波(抑制白噪声)和中值滤波(抑制脉冲干扰)的降噪方法,能够确保波头提取的准确性。动模实验结果表明,所提方法在强噪声环境中依然能准确地定位故障,测距相对误差为1.26%,具备良好的工程应用价值。
3)相比于基于模量波速差的方法,所提出的方法由于无需估计零模行波的波速度,因此可以获得更高的准确性。相比于传统双端法,所提出的方法在误差数量级上与之保持一致,在不考虑对时误差的情况下精度稍有劣势,但考虑对时误差后,所提出方法的精度仍然能够得到保证,优势更加明显。将与标准时间系统的对时误差1 ms作为上限(假设为1 ms),传统双端法误差超过了本文所提出的方法。
4)本文基于数值分析中对算法误差分析的理论与方法,推导了本文所提算法与基于模量波速差算法的误差限。针对波头标定误差,得到本文所提算法具有自适应减小误差的优势;针对零模波速估计误差,证明了基于模量波速差的算法测距结果受此影响较大,而本文所提方法不含该误差。通过仿真对比算例验证了上述理论的正确性。
参考文献
[1] Shu Hongchun, Duan Danni, Tian Xincui. Single-ended fault location for direct distribution overhead feeders based on characteristic distribution of traveling waves along the line[J]. Electric Power Systems Research, 2020, 185: 106345.
[2] 黄杨, 张广斌, 王潜, 等. 基于图像特征的输电线路故障行波存续性判别[J]. 电工技术学报, 2023, 38(5): 1339-1352.
Huang Yang, Zhang Guangbin, Wang Qian, et al. Identification of the existence and persistence of faulted traveling waves for transmission lines based on image features[J]. Transactions of China Electro-technical Society, 2023, 38(5): 1339-1352.
[3] 吴宇奇, 肖澍昱, 黎钊, 等. 基于二次振荡波过程的交流电网相继速动判据[J]. 电工技术学报, 2023, 38(24): 6695-6708.
Wu Yuqi, Xiao Shuyu, Li Zhao, et al. The fast sequential action principle for AC power grid based on the secondary travelling waves processes[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6695-6708.
[4] Zeng Xinjie, Tong Xiangrui, Tong Ning. A novel protection relay for neutral effectively grounded distribution networks independent on sequence components[J]. International Journal of Electrical Power & Energy Systems, 2024, 159: 110036.
[5] 董新洲, 陈彬书, 董启环, 等. 应用分布式电压传感技术的配电线路行波故障测距[J]. 电网技术, 2023, 47(12): 4837-4847.
Dong Xinzhou, Chen Binshu, Dong Qihuan, et al. Traveling waves fault location of distribution lines based on distributed voltage sensing technology[J]. Power System Technology, 2023, 47(12): 4837-4847.
[6] Lin Jiahao, Guo Moufa, Zheng Zeyin. Active location method for single-line-to-ground fault of flexible grounding distribution networks[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 3524712.
[7] 郭谋发, 刘世丹, 杨耿杰. 利用时频谱相似度识别的配电线路接地选线方法[J]. 中国电机工程学报, 2013, 33(19): 183-190, 4.
Guo Moufa, Liu Shidan, Yang Gengjie. A novel approach to detect fault lines in distribution network using similarity recognition based on time-frequency spectrum[J]. Proceedings of the CSEE, 2013, 33(19): 183-190, 4.
[8] 吴宇奇, 李正天, 林湘宁, 等. 基于变电站高频滤波边界特性的配电网线模行波选线方法[J]. 电工技术学报, 2024, 39(7): 2072-2088.
Wu Yuqi, Li Zhengtian, Lin Xiangning, et al. The faulty line selection method using line mode traveling wave based on high-frequency filtering characteristics of the substation line boundary in the distribution network[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2072-2088.
[9] 童宁, 张雪松, 赵波, 等. 基于相电流有效能量循迹法的配电网单相故障定位[J]. 电力系统自动化, 2018, 42(19): 140-147.
Tong Ning, Zhang Xuesong, Zhao Bo, et al. Fault location method for single-phase grounding fault in distribution network based on trajectory of phase current valid energy[J]. Automation of Electric Power Systems, 2018, 42(19): 140-147.
[10] 肖文妍, 郭谋发, 林佳壕, 等. 基于多频带多特征融合的配电网单相接地故障选段方法[J]. 电气技术, 2024, 25(7): 7-14.
Xiao Wenyan, Guo Moufa, Lin Jiahao, et al. Single-phase-to-ground fault section location method of distribution network based on multi-frequency band and multi-feature fusion[J]. Electrical Engineering, 2024, 25(7): 7-14.
[11] Gao Jianhong, Guo Moufa, Lin Shuyue, et al. Advancing high impedance fault localization via adaptive transient process calibration and multiscale correlation analysis in active distribution networks[J]. Measurement, 2024, 229: 114431.
[12] Deng Feng, Zhong Yihan, Zeng Zhe, et al. A single-ended fault location method for transmission line based on full waveform features extractions of traveling waves[J]. IEEE Transactions on Power Delivery, 2023, 38(4): 2585-2595.
[13] 邓丰, 徐帆, 曾哲, 等. 基于多源暂态信息融合的单端故障定位方法[J]. 电工技术学报, 2022, 37(13): 3201-3212.
Deng Feng, Xu Fan, Zeng Zhe, et al. Single-ended fault location method based on multi-source transient information fusion[J]. Transactions of China Electro-technical Society, 2022, 37(13): 3201-3212.
[14] 季涛, 孙同景, 徐丙垠, 等. 配电混合线路双端行波故障测距技术[J]. 中国电机工程学报, 2006, 26(12): 89-94.
Ji Tao, Sun Tongjing, Xu Bingyin, et al. Study on fault location of distribution mixed feeders based on double terminal method of traveling waves[J]. Proceedings of the CSEE, 2006, 26(12): 89-94.
[15] 李友军, 王俊生, 郑玉平, 等. 几种行波测距算法的比较[J]. 电力系统自动化, 2001, 25(14): 36-39.
Li Youjun, Wang Junsheng, Zheng Yuping, et al. Comparison of several algorithms of travelling wave based fault location[J]. Automation of Electric Power Systems, 2001, 25(14): 36-39.
[16] 胡冰颖, 李梅. 基于零模线模时差的配电网双端行波故障测距[J]. 电力工程技术, 2021, 40(2): 114-120.
Hu Bingying, Li Mei. Double ended traveling wave fault location in distribution network based on the time difference of zero-mode and line-mode[J]. Electric Power Engineering Technology, 2021, 40(2): 114-120.
[17] 张帆, 潘贞存, 张慧芬, 等. 树型配电网单相接地故障行波测距新算法[J]. 中国电机工程学报, 2007, 27(28): 46-52.
Zhang Fan, Pan Zhencun, Zhang Huifen, et al. New algorithm based on traveling wave for location of single phase to ground fault in tree type distribution network[J]. Proceedings of the CSEE, 2007, 27(28): 46-52.
[18] 张怿宁, 徐敏, 刘永浩, 等. 考虑波速变化特性的直流输电线路行波故障测距新算法[J]. 电网技术, 2011, 35(7): 227-232.
Zhang Yining, Xu Min, Liu Yonghao, et al. A novel travelling wave fault location algorithm for HVDC transmission lines considering variation characteristics of wave speed[J]. Power System Technology, 2011, 35(7): 227-232.
[19] 王炜, 王全金, 尹力, 等. 基于零模行波波速量化的高压输电线路双端故障定位方法[J]. 电力自动化设备, 2022, 42(12): 165-170.
Wang Wei, Wang Quanjin, Yin Li, et al. Two-terminal fault location method for high-voltage transmission line based on zero-mode traveling wave velocity quantization[J]. Electric Power Automation Equipment, 2022, 42(12): 165-170.
[20] 唐金锐, 尹项根, 张哲, 等. 零模检测波速度的迭代提取及其在配电网单相接地故障定位中的应用[J]. 电工技术学报, 2013, 28(4): 202-211.
Tang Jinrui, Yin Xianggen, Zhang Zhe, et al. Iterative extraction of detected zero-mode wave velocity and its application in single phase-to-ground fault location in distribution networks[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 202-211.
[21] 刘永浩, 蔡泽祥, 徐敏, 等. 基于波速优化与模量传输时间差的直流线路单端行波测距新算法[J]. 电力自动化设备, 2012, 32(10): 72-76.
Liu Yonghao, Cai Zexiang, Xu Min, et al. Single-end fault location algorithm based on traveling wave speed optimization and modal propagation time difference for DC transmission line[J]. Electric Power Automation Equipment, 2012, 32(10): 72-76.
[22] 张广斌, 束洪春, 于继来, 等. 不依赖双侧时钟同步的输电线双端行波测距[J]. 电工技术学报, 2015, 30(20): 199-209.
Zhang Guangbin, Shu Hongchun, Yu Jilai, et al. Double-ended travelling wave fault location indepen-dent of two side time synchronization[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 199-209.
[23] 高艳丰, 朱永利, 闫红艳, 等. 基于改进双端法的输电线路行波故障定位[J]. 电测与仪表, 2015, 52(1): 41-46, 52.
Gao Yanfeng, Zhu Yongli, Yan Hongyan, et al. Traveling waves fault location of transmission lines based on improved double-end method[J]. Electrical Measurement & Instrumentation, 2015, 52(1): 41-46, 52.
[24] 何晓, 雷勇, 周聪聪, 等. 消除零模波速影响的配电网单端行波故障测距算法[J]. 电力系统保护与控制, 2016, 44(23): 39-45.
He Xiao, Lei Yong, Zhou Congcong, et al. A single-terminal fault location algorithm in distribution network for eliminating the effect of the velocity of zero-mode traveling wave[J]. Power System Protection and Control, 2016, 44(23): 39-45.
[25] Tong Ning, Chen Le, Wang Weikang, et al. Local-measurement-based high-speed protection for half-wavelength UHV lines[J]. IEEE Transactions on Power Delivery, 2020, 35(5): 2481-2494.
[26] 赖纪东, 崔玉妹, 苏建徽, 等. 基于希尔伯特-黄变换的微电网主动小干扰稳定性评估方法[J]. 电力系统自动化, 2023, 47(13): 149-158.
Lai Jidong, Cui Yumei, Su Jianhui, et al. Active small-signal stability assessment method for microgrid based on Hilbert-Huang transform[J]. Automation of Electric Power Systems, 2023, 47(13): 149-158.
[27] 李英顺, 阚宏达, 郭占男, 等. 基于数据预处理和VMD-LSTM-GPR的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(10): 3244-3258.
Li Yingshun, Kan Hongda, Guo Zhannan, et al. Prediction of remaining useful life of lithium-ion battery based on data preprocessing and VMD-LSTM-GPR[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3244-3258.
[28] 徐伟宗. 采样频率对行波测距影响的仿真分析[J]. 电力系统及其自动化学报, 2014, 26(6): 76-80.
Xu Weizong. Simulation analysis of impacts of sampling frequency on traveling wave ranging[J]. Proceedings of the CSU-EPSA, 2014, 26(6): 76-80.
[29] 何智强, 牛捷, 刘兰兰, 等. 基于分布式电流行波监测的输电线路故障精确定位装置研制[J]. 科学技术与工程, 2023, 23(18): 7798-7808.
He Zhiqiang, Niu Jie, Liu Lanlan, et al. Development of transmission line fault precise location device based on distributed current traveling wave monitoring[J]. Science Technology and Engineering, 2023, 23(18): 7798-7808.
[30] 安春莲, 杨古月, 杨延菊. 基于中值滤波预处理的强冲击噪声背景测向方法[J]. 电子学报, 2021, 49(6): 1159-1166.
An Chunlian, Yang Guyue, Yang Yanju. DOA estimation under strong impulsive noise based on Median value filtering[J]. Acta Electronica Sinica, 2021, 49(6): 1159-1166.
[31] 田博文, 张志禹, 杨梦飞. 基于多次滑动均值滤波的混合储能功率分配与定容研究[J]. 电工技术学报, 2024, 39(5): 1548-1564.
Tian Bowen, Zhang Zhiyu, Yang Mengfei. Research on hybrid energy storage power allocation and capacity determination based on multiple moving average filtering[J]. Transactions of China Electro-technical Society, 2024, 39(5): 1548-1564.
A Double-Terminal Traveling Wave Grounding Fault Location Scheme in Distribution Networks Independent of Time Synchronization and Its Error Analysis
Abstract The distribution network is at the end of the power system, with a high probability of line faults, among which single-phase ground faults account for over 80%. To reduce the burden of manual line inspections and achieve rapid fault restoration in the distribution network, accurate localization of single-phase ground faults has been a long-standing research focus. However, the distribution network line is short, and the traveling wave process is extremely brief. Even with known fault branch segments, achieving precise localization of single-phase grounding faults remains challenging. Existing fault location algorithms often rely on zero-modal components, but the instability and difficulty in estimating the zero-modal wave velocity introduce significant errors in the location results. To address these issues, this paper proposes a single-phase grounding fault location method that combines the advantages of traditional single- and double-terminal methods, while eliminating the dependence on zero-modal wave velocity estimation and synchronization between terminals.
Firstly, mathematical calculations of the on-site modal time difference are performed based on the modal wave velocity difference, which is then used to characterize the fault location. Variational mode decomposition (VMD) and the Teager energy operator (TEO) are applied to separately calibrate the first wavefronts of the aerial and zero-modal components on both sides of the fault. The modal time differences from both sides are then substituted into the fault location formula to calculate the fault distance. This approach eliminates the need for estimating the zero-modal wave velocity and avoids the challenges of synchronization and detecting reflected waves, effectively improving the accuracy of fault location. Simulation results based on PSCAD/EMTDC show that the proposed fault location method can quickly and reliably locate single-phase grounding faults in overhead distribution network lines, with an error of less than 100 meters across various fault scenarios, including different fault resistances, fault angles, fault locations, fault phases, and grounding methods of the neutral point. Testing has shown that the noise resistance threshold of the proposed algorithm is 40 dB. When the noise level in the measurement environment is high (SNR<40 dB) and there is a certain proportion of impulse noise, the combination of multiple moving average filters (to suppress white noise) and median filters (to suppress impulse noise) ensures the accuracy of wavefront calibration. Results from dynamic simulation tests demonstrate that the proposed method can still accurately locate faults in high-noise environments, with a relative error of 1.26%.
Finally, based on numerical analysis theory, error bounds are derived for both the single- and double-terminal methods based on the modulus wave speed difference, as well as for the proposed algorithm. The impact of wavefront calibration errors and zero-modal wave velocity estimation errors on the error bounds is explored, revealing the theoretical basis for the improved accuracy. Validation cases using the PSCAD/EMTDC simulation platform confirm these findings. The results indicate that, without considering synchronization errors, the proposed method and the double-terminal method achieve significantly higher accuracy than the algorithm based on the modal wave velocity difference. After accounting for synchronization errors, the proposed method demonstrates higher accuracy than the double-terminal method.
Keywords:Distribution networks, single-phase grounding fault, fault location, zero-modal traveling wave, error bounds
中图分类号:TM773
DOI: 10.19595/j.cnki.1000-6753.tces.241340
国家自然科学基金资助项目(51677030)。
收稿日期2024-07-28
改稿日期2025-01-13
郑雨霖 女,2001年生,硕士研究生,研究方向为配电网单相接地故障行波测距。
E-mail:230127003@fzu.edu.cn
郭谋发 男,1973年生,博士,教授,博士生导师,研究方向为配电网单相接地故障信息处理、保护控制及柔性消弧等。
E-mail:gmf@fzu.edu.cn(通信作者)
(编辑 赫 蕾)