图1 配电网的单芯电缆
Fig.1 The single-core cables in distribution networks
摘要 单芯电缆因其质量轻、耐温等级高、输送功率大等优势在城市配电网中占比高。配电网三相单芯电缆多导体耦合的复杂结构，且存在邻近效应与趋肤效应，因而发生单相接地故障时的特征微弱多变，导致复杂配电网精准故障定位困难。为此，该文提出一种基于单芯电缆矩阵变换与故障特征模态分析的区段定位方法。首先，针对配电网单芯电缆导体与屏蔽层间的复杂耦合，提出了在一定频率条件下实现系统完全解耦的相模变换方法；其次，从本质上分析解耦后各模态信号的暂态故障特征变化情况与量测可行性，从而合理筛选故障特征模态；最后，构建拓扑结构测点分布矩阵、电流α模态极性矩阵和对角元占优的最终判据矩阵，利用矩阵间的信息交互实现逻辑判断，从而在减少测点数量、节省成本的同时实现高精度故障定位。仿真结果表明，该方法不仅能够实现复杂条件下单相接地故障的精准定位，且与现有方法相比，计算量小、存储容量小、耗时少、时效性高。
关键词：完全解耦 特征模态 矩阵变换 单相接地故障 配电电缆
近年来，电缆线路因其质量轻、耐温等级高、输送功率大、占地面积小等优势，在城市配电网中得到广泛应用[1]。因电缆深埋于地下，会受潮湿环境侵蚀、机械外力破坏、长期过载运行等因素影响，其内绝缘劣化产生缺陷，且随时间发展逐渐演变为主绝缘击穿，从而形成贯穿电缆故障相缆芯至大地的放电通道，发生缆芯-屏蔽单相接地故障。配电网拓扑结构复杂、电缆长度短且分支多，发生单相接地故障后，故障特征微弱、多变[2-3]。因此，单相接地故障在复杂配电网的精准定位十分困难。
目前，常见的定位方法有主动注入法[4-6]、故障信号法[7-14]。其中，故障信号法基于信息维度可以分为单一特征法与信息融合法[7-8]，而基于信号时间可分为稳态分量[9-10]与暂态分量法[11-17]，暂态分量法根据信号频谱又分为行波法[11-13]与非行波法[14-17]。
文献[4]利用电感电流与电容电流的幅值比，该方法克服了S注入导致电流分流而误判的缺陷，但对故障指示器配置和通信条件要求高；文献[5]依据虚拟注入电流比与故障位置的对应关系实现故障定位，精度高，但成本也较高；文献[6]提出了一种将节点负序电压方程与贝叶斯压缩感知理论相结合的故障定位方法，在拓扑结构复杂条件下，该方法的虚拟注入节点多、计算量大。因此，主动注入法的可靠性受拓扑结构和测量设备的影响，在实际应用中受到限制。而故障信息法属于被动探测，无需额外添加注入设备，更适合电缆型复杂配电网的定位研究。
文献[7]利用零序电流、暂态相电流信号构造故障方向测度，建立多指标决策优化模型，该优化求解思路提高了故障定位的鲁棒性，但需要通信，存储容量大；文献[8]基于暂态电流在故障区段的差异构造了5个特征量，用于多特征融合的单相接地故障区段检测，但适用于暂态零序电流的最优分解还有待研究；文献[9]提出利用零序电流突变量进行带电故障定位的方法；文献[10]凭借各区段零序电流稳态特征的变化情况进行故障区段定位。但实际中，稳态分量法容易受到配电网线路参数和过渡电阻的影响，从而故障特征微弱、易受噪声干扰，因此，基于稳态信号定位的可靠性和准确率难以保证。
文献[11]构建了故障位置搜索矩阵，将双端法与多端初始行波到达时刻相结合，克服了配电网行波波头标定不准确的难题，但存储容量大；文献[12]利用故障暂态信号的时间特性实现故障区段辨识，但在最佳量测装置配置下才能精准定位，可行性受到限制；文献[13]针对暂态电压信号，将固有频率与电磁时间反演相结合，实现了多分支配电网的故障定位，但受端口选取的影响较大，可靠性难以保证。电缆型配电网节点多、分支短的网架结构导致行波的折反射更加复杂，行波波头到达时刻的准确标定困难，对测量装置的硬件需求较高，其可靠性与经济性难以同时满足，因此非行波法相对具有优势。
文献[14]利用暂态电流变化量的比值及方向实现接地故障的判别；文献[15]分析了首容性分量的故障特征，依据暂态能量实现故障定位，但其耐过渡电阻的能力有待提升；文献[16]利用相电流工频变化量的比值实现故障区段定位，该方法耐过渡电阻能力强，但需要通信交换各终端信息；文献[17]利用电流特征模量的幅值和极性，结合空间位置构建测量矩阵以实现故障区段定位，该方法只适用于三芯电缆的解耦，不适用于架空线路与单芯电缆。
通过研究与分析，归纳现有电缆型配电网单相接地故障定位方法存在的一些技术难点：
1）三相单芯电缆结构复杂，各金属导体间存在电磁耦合，且电气参数不对称。现有架空线路与三芯电缆的解耦方法难以适应。配电网发生单相接地故障时，其故障特征微弱，在噪声、高阻等干扰下，筛选暂态故障特征分量困难，难以保证定位精度。
2）电缆型配电网节点多、分支短的网架结构导致行波的折反射更加复杂，行波波头到达时刻难以准确标定，对测量装置及通信设备的硬件需求高，其可靠性与经济性难以同时满足。
针对以上问题，本文提出了基于单芯电缆矩阵变换与模态分析的电缆型配电网区段定位方法，贡献如下：
1）考虑了单芯电缆的多导体耦合结构，提出了一种适合配电网三相单芯电缆两端接地方式下的矩阵变换方法，以实现系统的完全解耦。进而筛选故障特征模态，充分反映故障前后暂态特征变化，为故障区段的精准定位奠定条件。
2）结合配电网拓扑结构的空间位置合理分布测点，构建拓扑结构测点分布矩阵、电流α模态极性矩阵和最终判据矩阵，利用矩阵间的信息交互实现逻辑互补，进而在减少测点分布、节省成本的同时实现故障区段的精准定位。
3）本文利用电压σ模态能量与电流α模态极性的暂态特征构造判据，无需增加额外的量测投资，该方法具有可行性与适应性。该方法构造的最终判据矩阵属于对角元占优的稀疏矩阵，其计算量小、存储内存要求低、耗时少，具有一定工程价值。
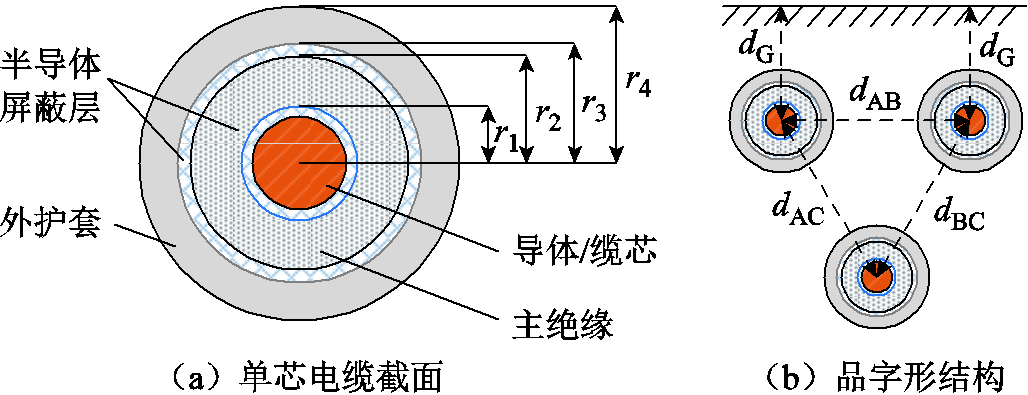
交流电缆常用三根单芯电缆安装，城市配电网中常用的单芯电缆的截面如图1a所示，包含导体、主绝缘、外护套和半导体屏蔽层，且三根电缆一般呈品字形排列敷设，如图1b所示，其串联阻抗矩阵为6×6阶矩阵。矩阵第一列和第一行表示A相导体，第二列和第二行表示A相屏蔽层，其他列和行以相同的顺序代表B相和C相。因此，主对角线元素分别是导体、屏蔽层的自阻抗，而矩阵的上、下三角是互阻抗，由此得到对称的阻抗矩阵。
图1 配电网的单芯电缆
Fig.1 The single-core cables in distribution networks
相模变换的本质就是寻求一个矩阵，将电缆的阻抗矩阵与导纳矩阵的乘积矩阵ZY与YZ同时对角化，实现三相系统的解耦。因此，首先探讨如图2a所示单芯电缆的复杂耦合结构的系统解耦条件。为了实现线路精准建模，将基尔霍夫定律应用到如图2b所示的线路微元段等效单相电路中，推导频域方程，进而得到波动方程，然后将其化简成式（1）与式（2）的形式，以完成相域到模态域的转换。
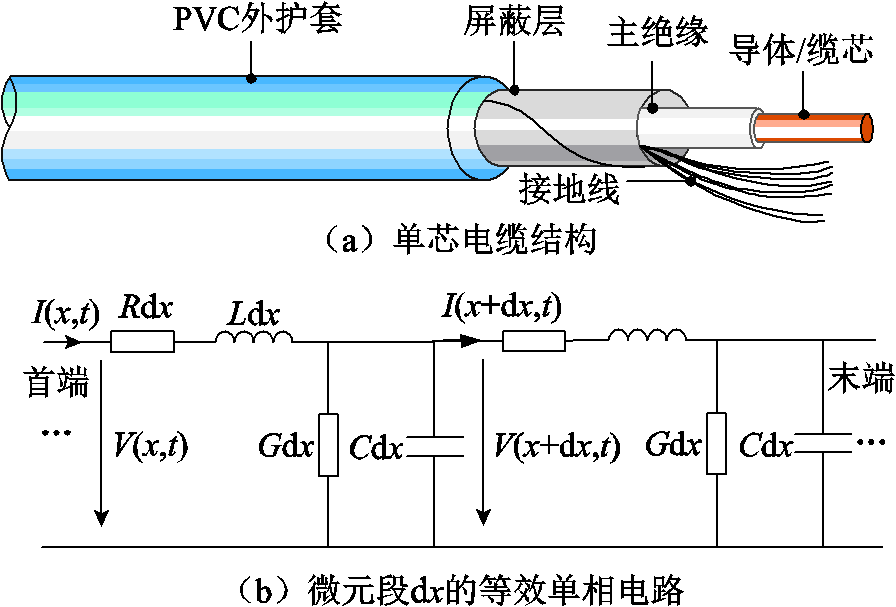
图2 长度为dx电缆的等效单相电路
Fig.2 Equivalent single-phase circuit withdx cable length
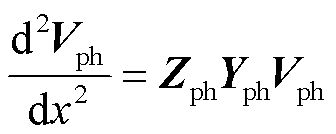（1）
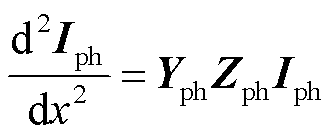（2）
式中，Vph、Iph分别为相域中电压、电流；Zph、Yph分别为相域中电缆的串联阻抗矩阵与并联导纳矩阵。
相域和模态域中，电压之间的关系为
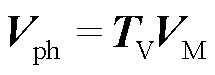（3）
联立式（1）～式（3）得到
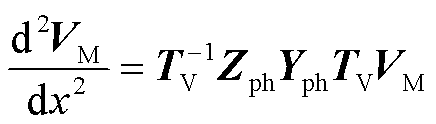（4）
式中，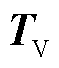
为电压变换矩阵；VM为模态域中的电压。利用变换矩阵使得乘积ZphYph对角线化，特征值即为方程（5）的对角元素。
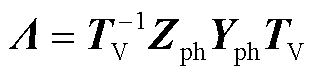（5）
因此，式（4）可简化为
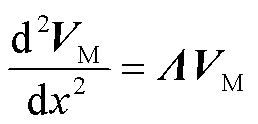（6）
电流的推导与电压相似。同理，可得出结论：电流变换矩阵TI与电压变换矩阵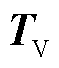间关系表示为
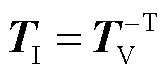（7）
串联阻抗矩阵Zph和并联导纳矩阵Yph均与频率相关。变换矩阵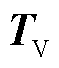、TI及特征值均为与频率相关的复数。当且仅当矩阵满足式（8）时，才能彻底解耦。
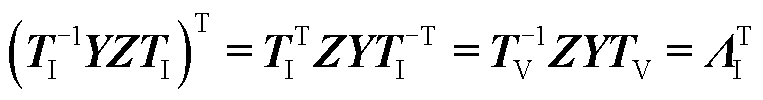（8）
因此，矩阵必须是Hermitian矩阵或酉矩阵。然而，分析可知，主对角线上必然存在实数项，且无法构成正交基，因此，乘积矩阵不满足解耦条件。此时，模态分解的有效性降低，变换矩阵会随着频率改变，无法完全耦合。但随着频率的增加，乘积矩阵的虚部逐渐趋近于零。此时，矩阵接近实数阵，进而可实现对角化。因此，考虑在较高频率完成系统解耦。通过仿真可得，频率超过200 Hz，误差小于10%；频率超过1 kHz时，误差小于1%。
通过上述推导与分析，以10 kV城市配电网常用电缆型号YJV-8.7/10kV-1×300为例，进行三相单芯电缆的解耦，YJV-8.7/10kV-1×300电缆参数见表1。具体步骤如下。
表1 YJV-8.7/10kV-1×300电缆参数
Tab.1 YJV-8.7/10kV-1×300 cable parameters
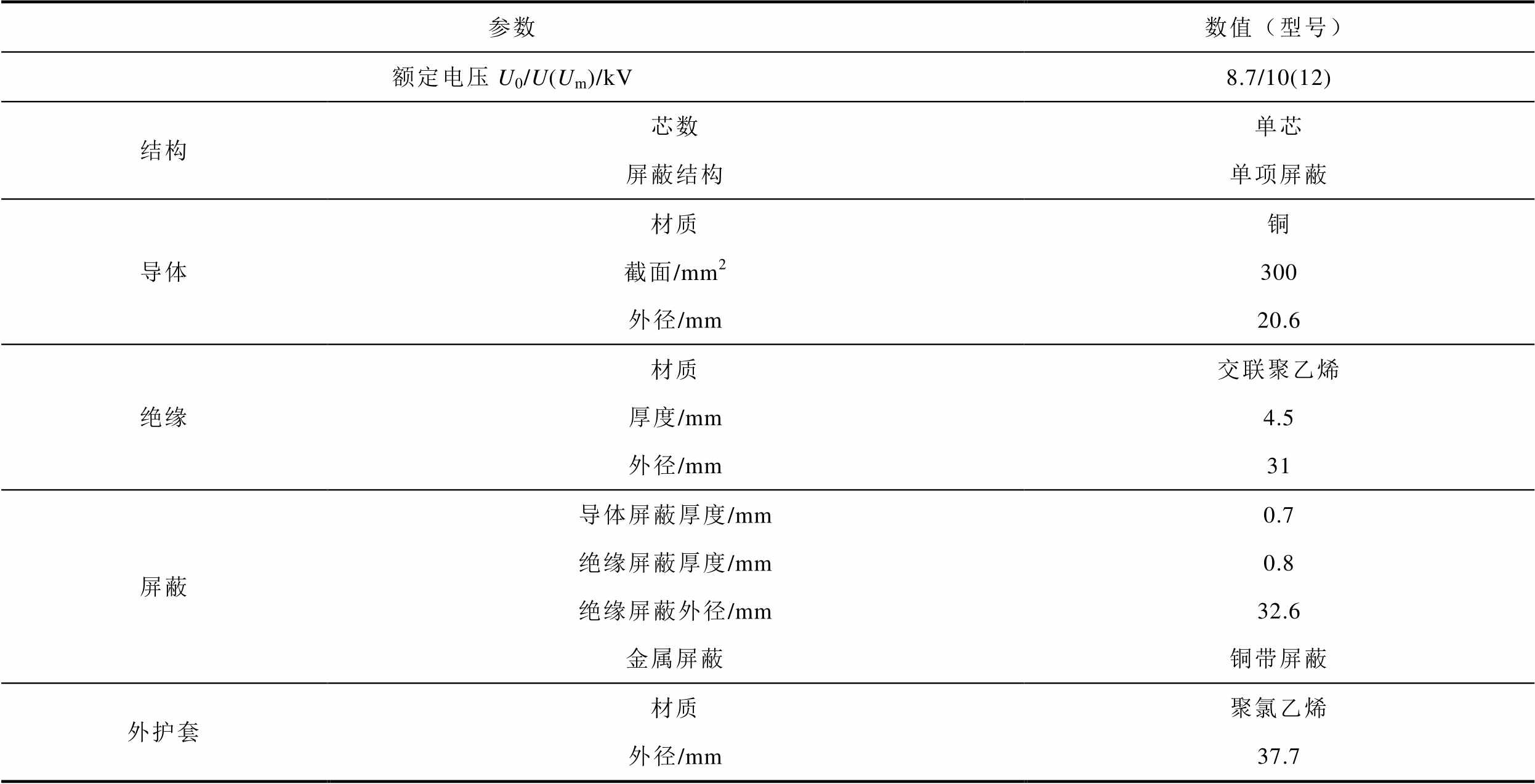
参数数值（型号） 额定电压U0/U(Um)/kV8.7/10(12) 结构芯数单芯 屏蔽结构单项屏蔽 导体材质铜 截面/mm2300 外径/mm20.6 绝缘材质交联聚乙烯 厚度/mm4.5 外径/mm31 屏蔽导体屏蔽厚度/mm0.7 绝缘屏蔽厚度/mm0.8 绝缘屏蔽外径/mm32.6 金属屏蔽铜带屏蔽 外护套材质聚氯乙烯 外径/mm37.7
1）代入表1所示的试验电缆技术参数，计算得到相应的阻抗矩阵式（9）和导纳矩阵式（10）。
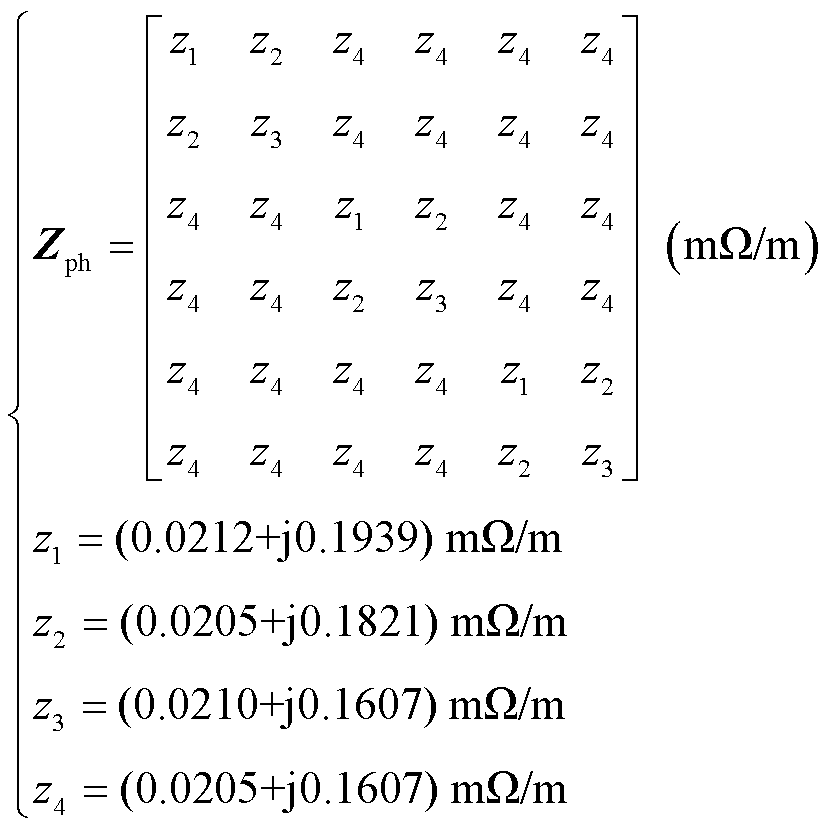（9）
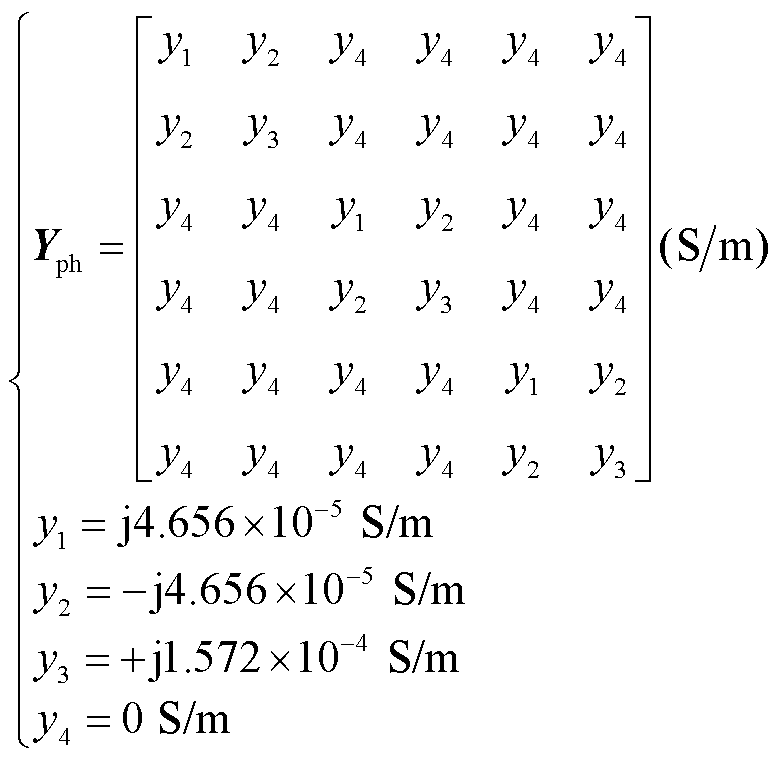（10）
通过分析得出串联阻抗矩阵Zph具有以下特征：①矩阵对称；②只含有4个不同元素值：缆芯自阻抗z1=(0.021 2+j.1939) mΩ/m，屏蔽自阻抗z3= (0.021 0+j0.1607) mΩ/m，缆芯-屏蔽互阻抗z2= (0.0205+j0.1821) mΩ/m，相间互阻抗z4=(0.020 5+ j0.160 7) mΩ/m；③自阻抗大于互阻抗；④同相互阻抗大于相间互阻抗（实部相同，虚部的差异）。导纳矩阵式（10）的计算相对容易。其中，考虑到半导体层的存在，绝缘体介电常数需要修正为
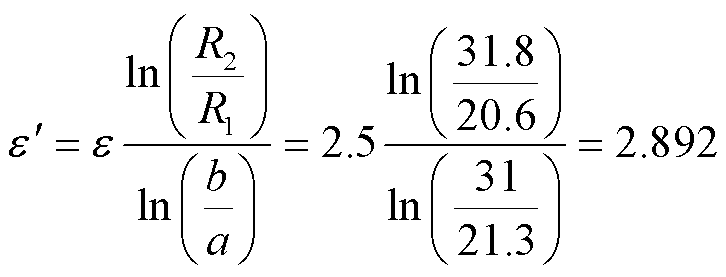（11）
2）调换矩阵列向量的顺序为：缆芯A-缆芯B-缆芯C-屏蔽层A-屏蔽层B-屏蔽层C，计算矩阵Zph和矩阵Yph的乘积矩阵ZphYph，如式（12）所示。
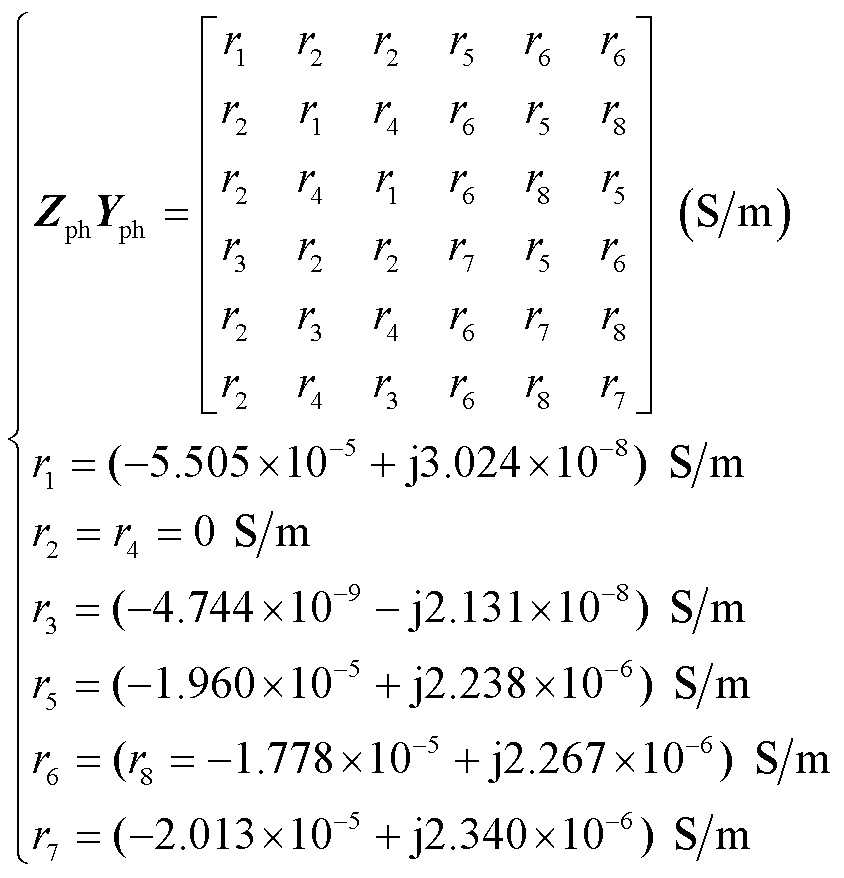（12）
3）计算矩阵的特征值与特征向量，存在某一固定矩阵S，使得S-1ZphYphS=SYphZphS-1=对角阵V。
4）通过计算，电压变换矩阵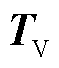和电流变换矩阵TI的具体数值解为
（13）
（14）
根据式（13）、式（14）可知，其解耦后对应的六个模态信号（以电压为例）可分别记作：ua(t)、ub(t)、ug(t)、uh(t)、uq(t)和us(t)。虽然理论上电流也有6个模态，但根据式（14）可知，除了电流α模态，其余模态均无法通过实测信号计算得到。
分析系统解耦后所得结果的物理意义，并描述矩阵式（13）所示的六种传播模态。三相单芯电缆的传输模态可分为：3个同轴模态、2个护套间模态与1个接地模态。各模态的电流路径详细如图3所示。同轴模态对应于电缆的导体-屏蔽层回路，其中，导体电流在同一电缆的屏蔽层中完全返回，如图3a所示。护套间模态对应于电缆的屏蔽层-屏蔽层回路，在屏蔽层中流动的电流从其他电缆的屏蔽层中返回，如图3b所示。护套和大地之间的接地模态，对应于屏蔽层-大地回路，是一个零序模态，相同的电流在三个屏蔽层中注入并从大地返回。通过这些模态的特性，可归纳总结出另一种分类方式：①零序模态：相同的电流注入三相中；②导体间模态：电流从一相注入，经另两相返回；③导体模态：电流注从一相注入，并从另一相返回。
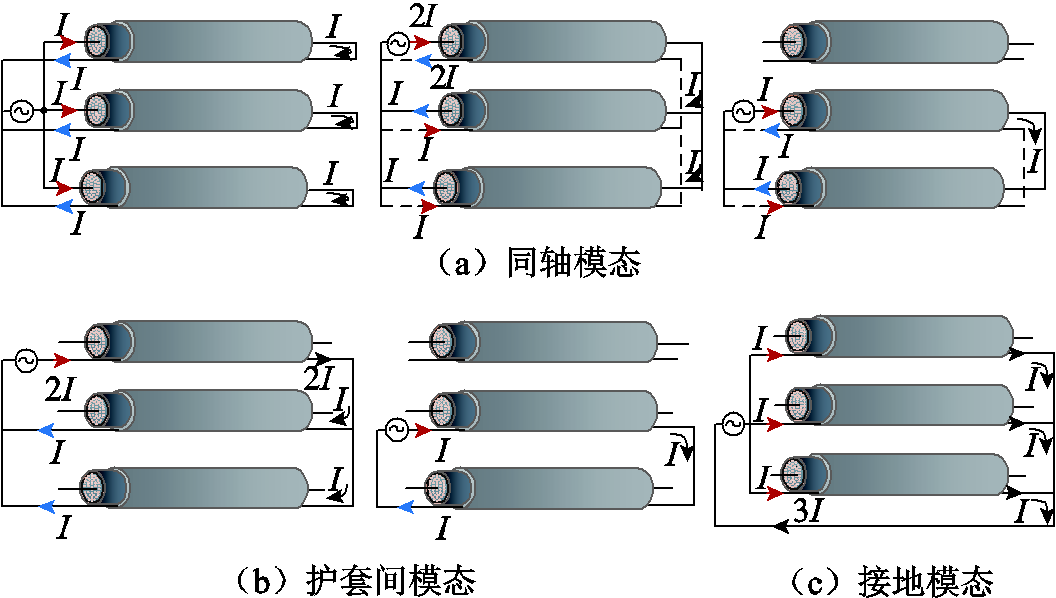
图3 解耦后各模态电流路径
Fig.3 Decoupled current paths for each mode
10 kV城市配电网中的电缆线路常采用两端接地的方式，因而电压h模量、电流a模量中包含接地线上部分微弱信号分量。当电缆发生故障，故障导体电压突变，电压不再对称。此时，相当于在故障点处叠加了一个反向电源，使得三相缆芯对地电压与三相导体电流发生变化，导致解耦后电压、电流模态发生突变。单相接地故障（过渡电阻Rg=300 Ω）发生前后，电缆的三相电压、三相电流，以及解耦后的各电压、电流模态的变化情况如图4所示。
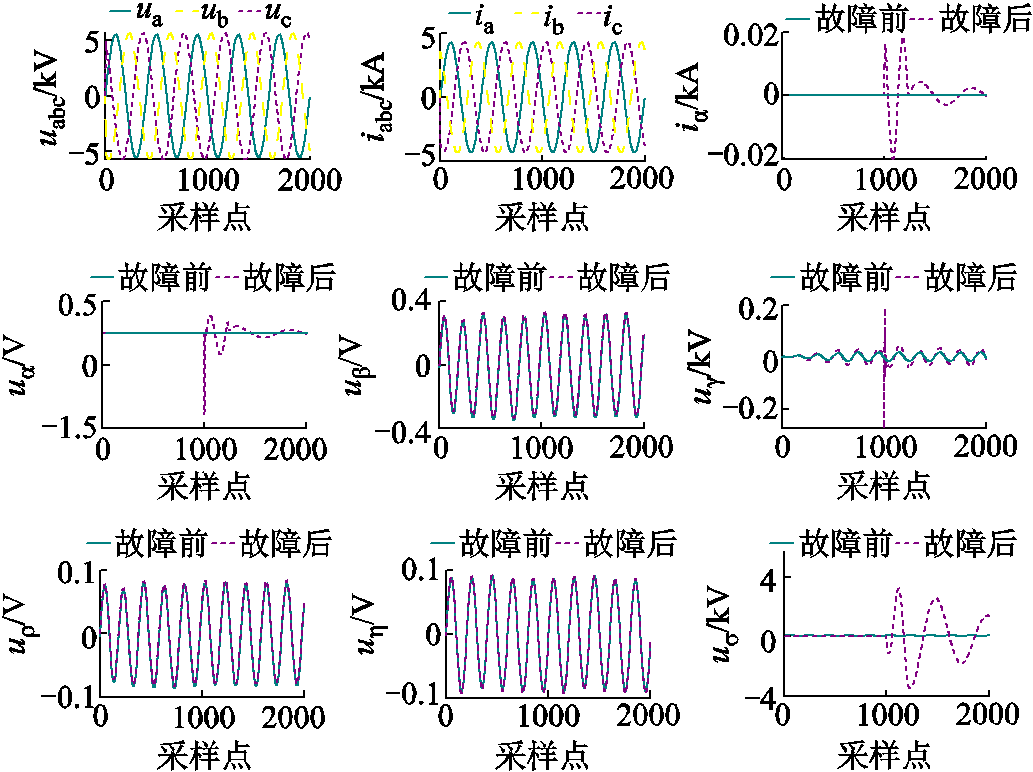
图4 各模态故障前后的变化情况
Fig.4 Changes before and after faults in each mode
由图4可以看出，发生单相接地故障后，电压与电流的变化不明显，而解耦后的电流α模态、电压α、g及σ模态在故障前几乎为零，故障后发生突变，尤其是属于接地模态的电压σ模态突变剧烈，易于辨识。相比之下，电压g模态的幅值较小、不易测量，电流α模态的极性变化趋势明显。因此，针对电缆型配电网的单相接地故障，本文利用电压σ模态的能量与电流α模态的极性构造定位判据。
由于与电缆末端的故障相连接，两端接地电缆的电流通过大地、故障相半导体屏蔽层和正常相屏蔽层返回，如图5所示。其中，Zcp_x、Zsp_x分别为p相导体与屏蔽层的阻抗，p=a,b,c相，Zg_x为屏蔽层公共接地阻抗，x为首端或末端。
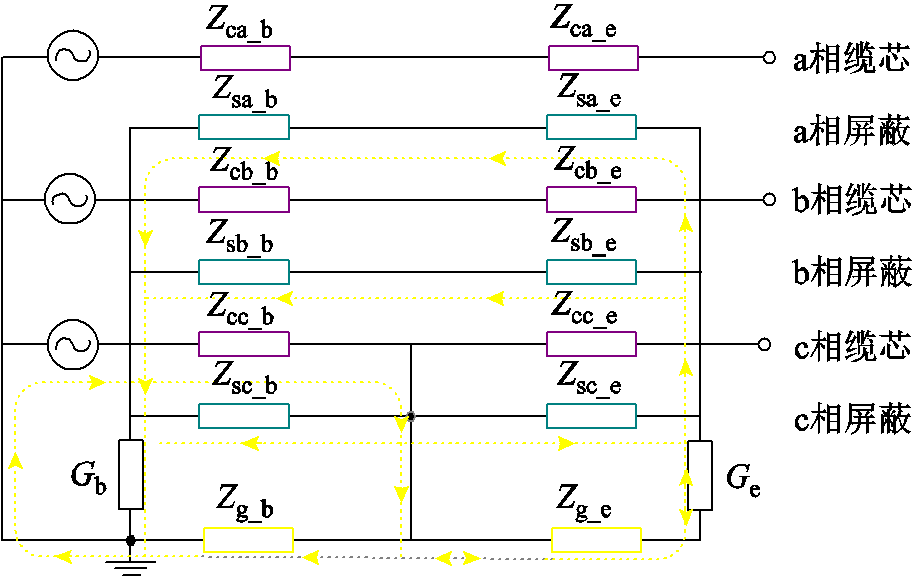
图5 单相接地故障的电流回路
Fig.5 Current circuit for single-phase ground fault
导体电压模态Mc和接地电压模态Mg分别为
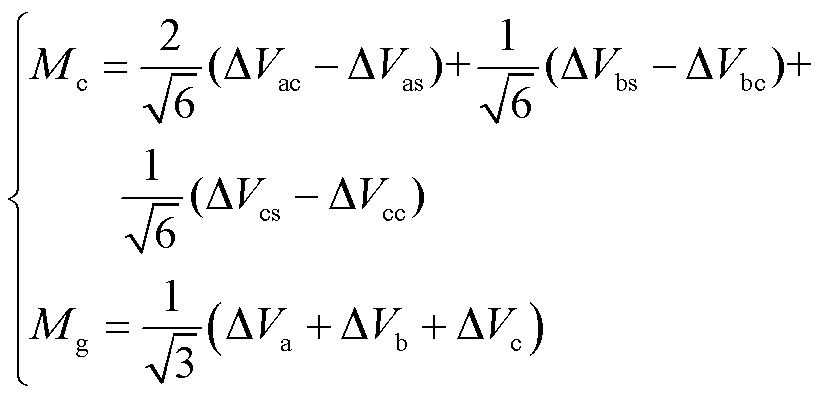（15）
式中，ΔVp为p相电压变化量；ΔVpc、ΔVps分别为p相导体与屏蔽层的电压变化量。
导体间模态对a相电压为零，且不影响暂态现象；导体模态表明，a相中暂态电压的幅值是其他两相的2倍，且与其他两相的极性相反。接地模态的幅值通常大于导体模态，ΔVa约为l(pu)，而ΔVb和ΔVc的大小取决于系统结构且均小于1(pu)。通过电压σ模态的能量首先确定故障区段的一个端点。电压σ模态的能量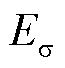
的计算式为
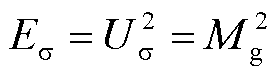（16）
由于交联聚乙烯电缆绝缘的介电常数较大，单位长度的缆芯与屏蔽之间的等效电容通常为nF级，且配电网中单根电缆长度一般不超过10 km。因此，三相缆芯与屏蔽间的电容Ccs_x很小，当与屏蔽层接地电阻并联时等效为开路。正常运行时，缆芯-护套电流Ics_x非常小，三相电压对称且相等，三相屏蔽电流之和近似为零。当电缆主绝缘损坏时，缆芯将直接与屏蔽相连，进而损坏电缆外部护套，且随着时间发展逐渐演变为主绝缘击穿，从而形成贯穿电缆故障相缆芯至大地的放电通道。本文分析的电缆故障类型为缆芯-屏蔽单相接地故障，以a相接地为例，等效电路如图6所示。由图6可知，故障点处，缆芯经过故障电阻Rf与屏蔽相连，Uf是等效电压源。上游故障电流回路如图6中的绿色点线箭头所示：部分故障电流通过上游电容返回故障点，剩余电流则通过电缆首端屏蔽层接地线流向大地，再由末端屏蔽层接地线返回故障点。同样地，下游故障电流以相似的方式返回故障点，如图6中的红色点画线箭头所示。
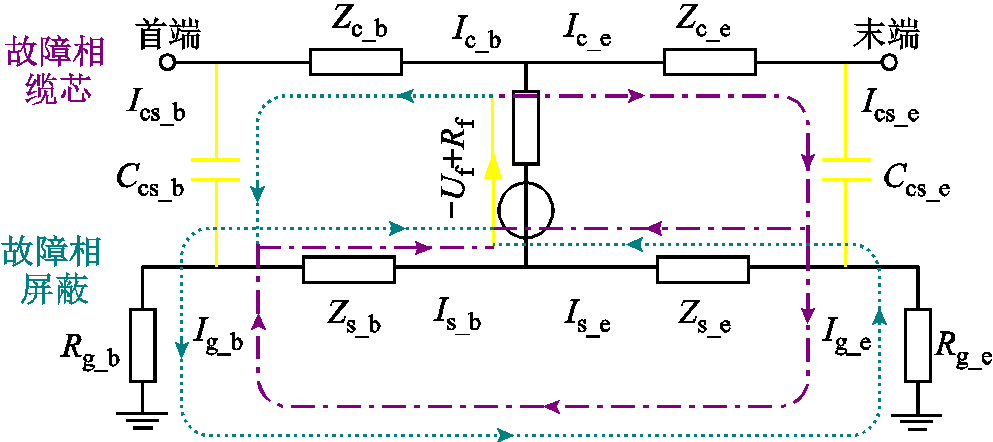
图6 缆芯-屏蔽单相接地故障的等效电路
Fig.6 Circuit of core-shield single-phase ground fault
若电缆j发生故障，故障电流方向如图7所示。其中，Cg_∑为健全电缆的缆芯-屏蔽等效电容，Rg_∑为屏蔽层接地线的等效电阻，Zg_∑为缆芯等效阻抗，Ig_∑为通过健全电缆的故障电流。单根电缆故障电流的分布规律在配电网中同样适用。因此，故障电流通过缆芯-护层间电容Ccs_b流到屏蔽层并返回故障点，其余通过健全电缆线路流入大地，并通过故障电缆的两个屏蔽接地线返回故障点。网络故障等效电路如图8所示。其中，Zi,c、Zi,s分别健全线路i的缆芯阻抗与屏蔽层阻抗，Ci,cs_b、Ci,cs_e分别为首末端缆芯与屏蔽间的等效电容，Ri,g_b和Ri,g_e分别为首末端屏蔽接地线的等效电阻，Zexi,cg_∑为除电缆i以外的健全电缆对地阻抗。
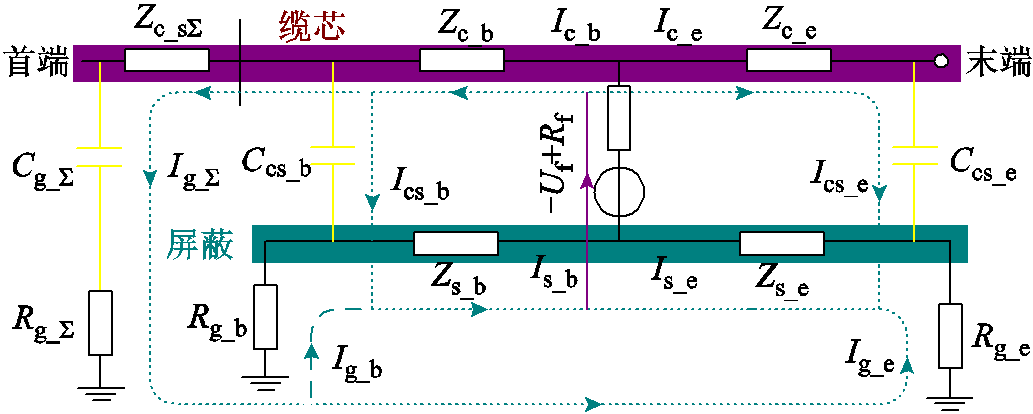
图7 故障电流方向
Fig.7 The direction of fault current
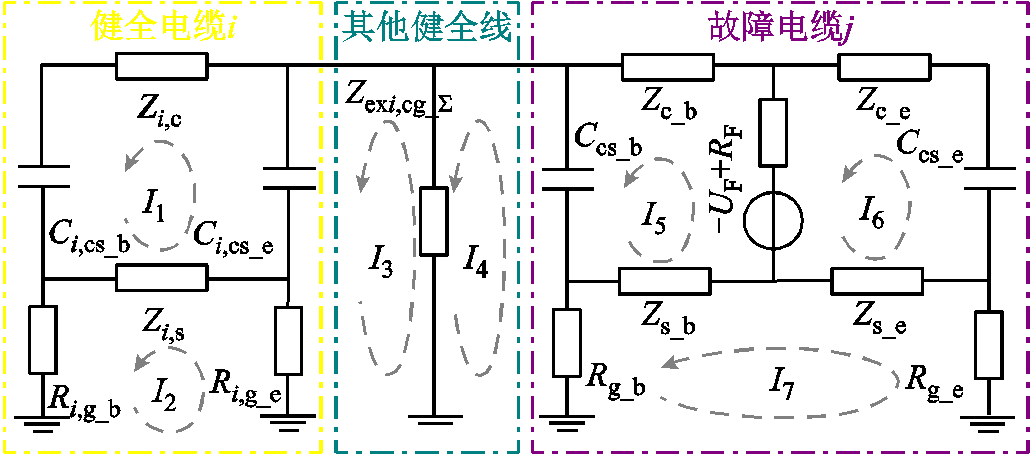
图8 配电网故障电流回路
Fig.8 Fault current circuit in distribution network
根据图8列写基尔霍夫电压定律方程得到
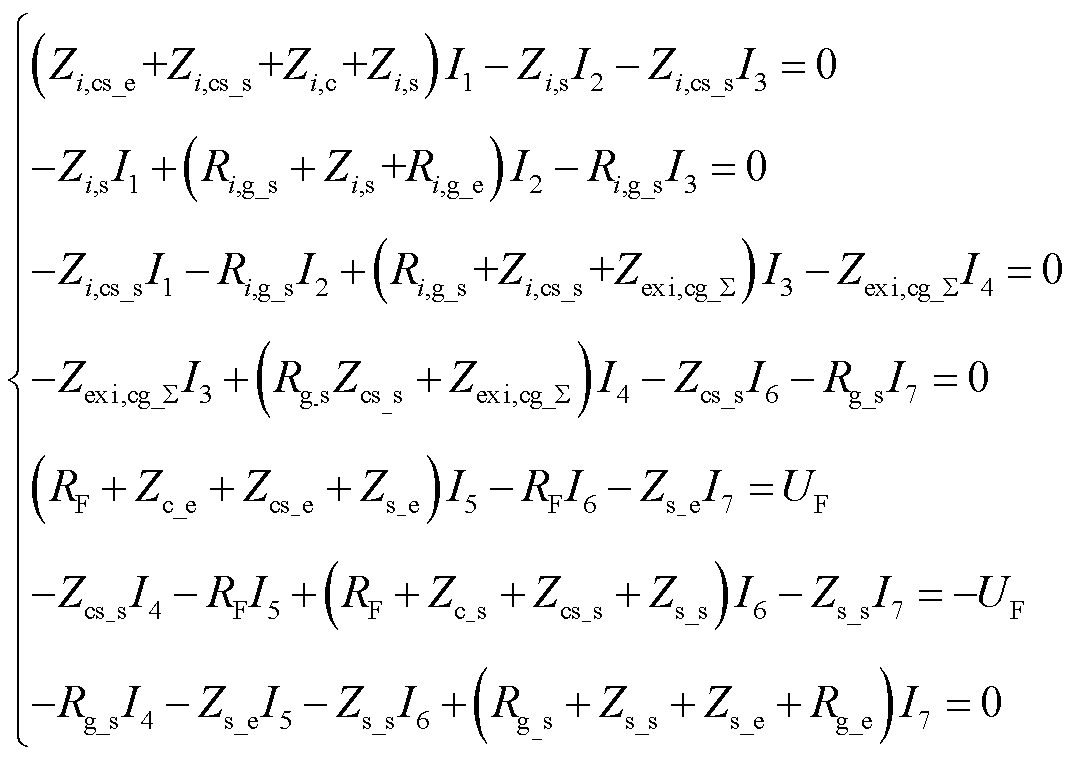（17）
求解式（17）所示的节点电压方程组，明确I1与I4的电流流向的关系为
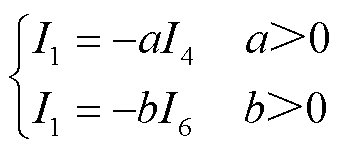（18）
式中，a、b均为大于零的实数。
健全馈线的缆芯对地电流在电缆j的屏蔽接地线处聚集，并通过屏蔽层流回故障点。故障点上游的电流流向与下游的电流流向以及其他健全电缆电流流向相反。当A相接地时，选取故障后电流α模态作为参考电流，根据本文所提解耦方法，参考电流Iα的表达式可以由式（14）得到，其为零序电流的倍数。因此，通过矩阵变换后的电流α模态极性依旧满足式（18）。
由2.2节分析可知，当发生单相接地故障时，故障电缆导体电压会发生突变，此时三相电压不再对称，可通过电压的不对称度来判断故障定位流程是否启动。通常将系统的电压负序分量与正序分量的比值称为电压不对称度。本文将电压不对称度定义为电压σ模态与电压α模态的比值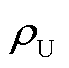
。供电系统的三相电压不对称度不应超过额定电压5%UN。考虑不对称负载的裕度，因此，当电压不对称度大于0.1UN时，故障区段定位流程启动，即
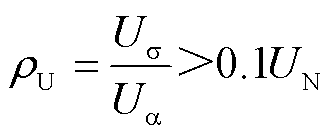（19）
针对不同接地方式，分析了启动判据的适应性，以小电阻接地为例，其仿真结果见表2。表2中，S为故障距离。
表2 小电阻接地方式的适应性分析
Tab.2 Adaptability analysis of low-resistance to ground
lnS/kmRg/Ω启动判据结果 lAB2.03002 685＞1 000正确启动 lBC2.48002 240＞1 000正确启动 lCD4.31 5001 754＞1 000正确启动 lML1.53 0001 256＞1 000正确启动
通过仿真结果看出，随着过渡电阻的增大，电压不对称程度会逐渐减小，当过渡电阻为3 000 Ω时，该方法仍然能够正确启动。因此，该启动判据在小电阻接地方式下具有较强适应性，而在消弧线圈接地方式下，该判据的适应性会有一定程度的降低。
一般情况下，对于k个节点、n条出线的拓扑结构，需要n-1个电流测点才可判断电流极性[18]。而本文考虑配电网空间位置，通过对测点进行合理部署，从而利用矩阵间的信息交互实现电缆上下区段的逻辑判断，在降低成本的同时实现故障区段精准定位的目的。测点的部署策略具体如下：①在主线（电气距离最长的线路定义为主线，其他均为分支线）每级线路的首端安装测点；②当末端电缆所在节点的分支数b≥2时，该节点添加b-1个测点。如图9所示，该拓扑具有14条电缆线路，仅需11个测点即可判断电流α模态的极性。如若在更加繁复的拓扑结构中，该方法的优势将愈发明显。
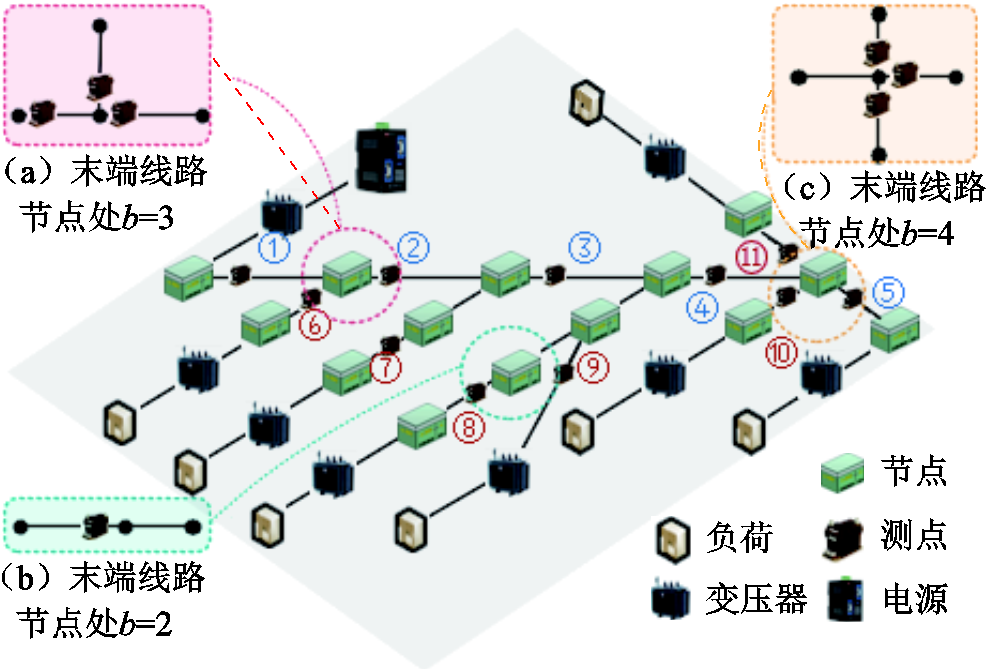
图9 测点部署策略
Fig.9 Deployment strategy for measurement points
归纳电缆型配电网实现故障区段定位的流程：首先，利用电缆首端暂态电流与暂态电压进行相模变换，完成矩阵解耦，得到能够辨识单相接地故障前后差异特征的电压σ模态与电流α模态；其次，通过计算电压σ模态的能量大小确定故障区段的一个端点；最后，利用电流α模态的极性特征——故障点上游的电流流向与下游的电流流向以及其他健全电缆电流流向相反，确定最终故障区段。其中，构造拓扑结构测点分布矩阵、电流α模态极性矩阵，以及最终判据矩阵的具体方法如下：
1）构造拓扑结构测点分布矩阵X：确定拓扑空间位置测点分布。
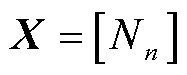（20）
式中，Nn为0-1变量，Nn=1表示有测点，Nn=0表示无测点。
2）构造电流α模态极性矩阵Y：确定电流α模态极性。
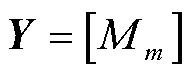（21）
式中，Mm为各节点电流α模态的极性，将线路指向故障点的方向定义为正方向，记为Mm=1，Mm=-1表示反方向，Mm =0表示无测点。
3）构造节点s与节点l之间的最终判据矩阵Zsl：将配电网空间位置的拓扑结构与电流α模态的极性相结合，综合反映各节点的电流流向。
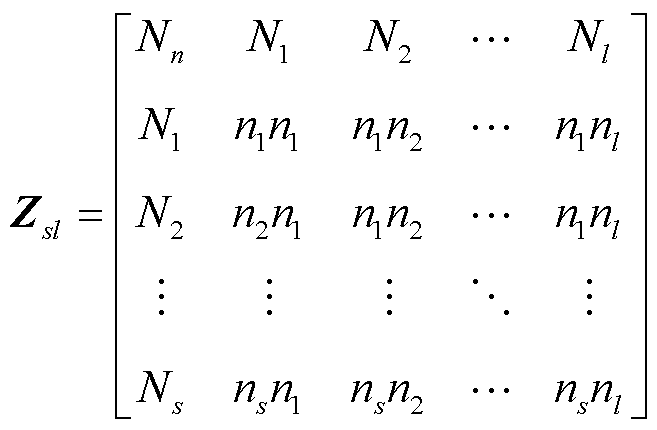（22）
当满足如式（23）所示规律时，说明单相接地故障发生在该区段内。
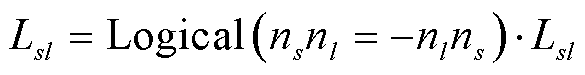（23）
式中，Lsl为节点s、l构成的区段；Logical(·)为逻辑判断函数，判断正确则输出1，否则为0。
通过比较区段的长度来精确定位故障区段SF，从而排除伪故障区段以缩小检修范围。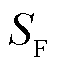
表示为
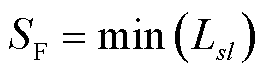（24）
具体的故障区段定位流程如图10所示。
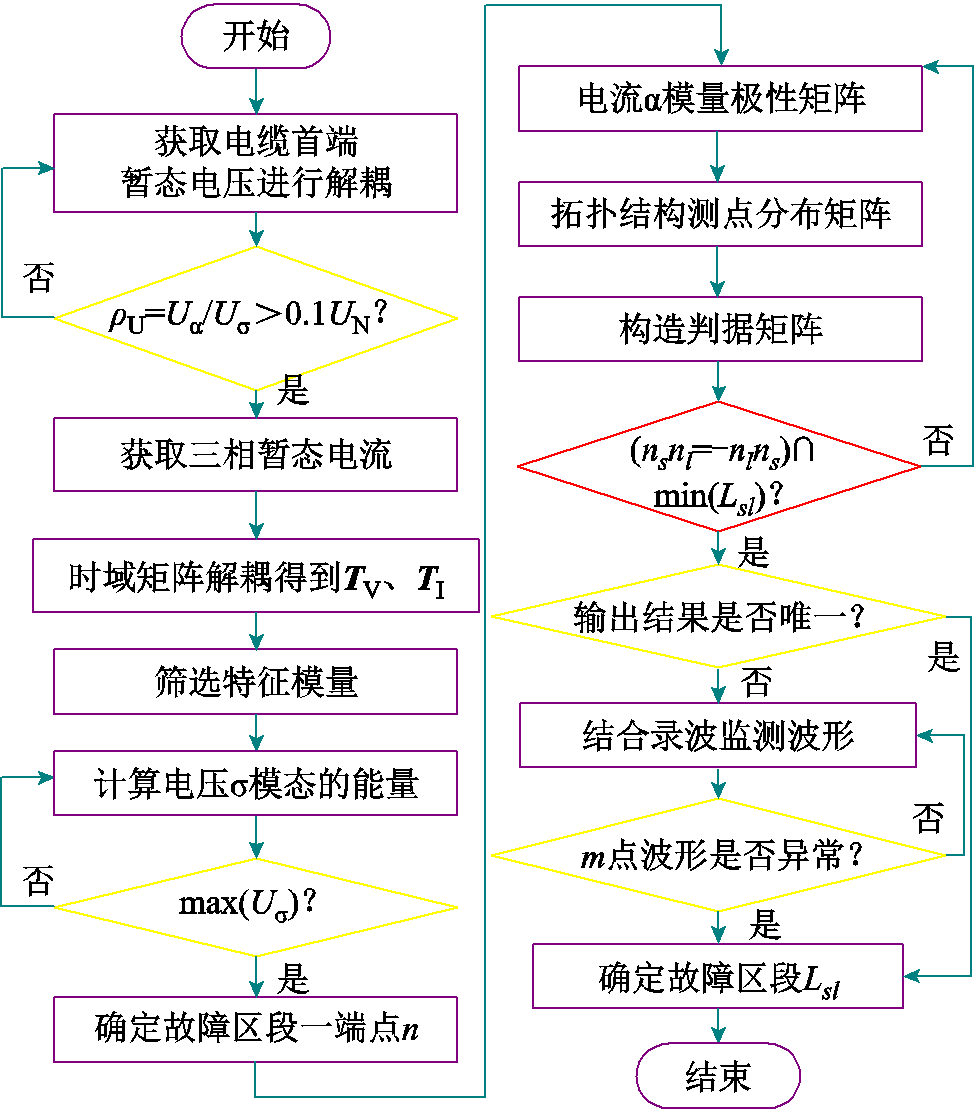
图10 故障区段定位流程
Fig.10 Fault section localization process
为了验证本文方法的有效性与可靠性，在PSCAD中搭建如图11所示的10 kV电缆型配电网模型。其中，有22条电缆线路，黑点表示电缆分支节点或者末端节点，详细编号如图11所示。仿真中，采用依频特性呈品字形排列的电缆模型，电缆型号为YJV-8.7/10kV-1×300。消弧线圈电感L根据过补偿度8%设置，接地电阻Rg为10 Ω。仿真频率为10 kHz。测点按照3.1小节的优化策略进行合理部署。以馈线lAB发生200 Ω接地故障为例，接地方式为小电阻接地，初相位为90°。对各测点的电压、电流进行矩阵分解，计算电压σ模态的能量结果，见表3。
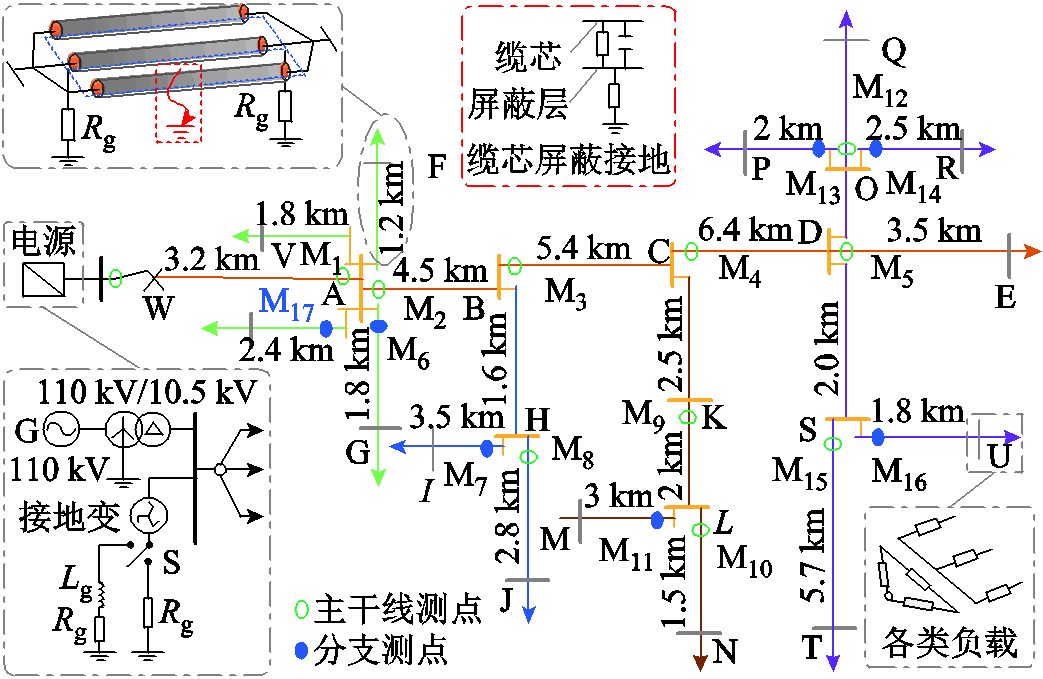
图11 电缆型配电网拓扑结构
Fig.11 Cable type distribution network topology structure
表3 各节点电压σ模态的能量
Tab.3 The energy of the voltage σ-mode at each node （单位：kV2）
测点能量测点能量测点能量测点能量 M11.82M50.13M90.56M130.06 M22.26M61.92M100.28M140.05 M31.75M71.29M110.24M150.12 M40.60M81.24M121.97M160.09
通过表3看出，不同测点对应节点的电压σ模量的能量不同，且距离故障位置较近的节点的能量相对较大。其中，测点M2对应节点A的能量最大。由此，确定故障区段的一个端点为点A。进而，构造拓扑结构测点分布矩阵X与电流α模态极性矩阵Y，确定最终判据矩阵Zsl实现定位，其定位结果如图12所示。通过进行不同故障位置、不同过渡电阻的单相接地故障仿真，验证该方法的有效性，其定位结果见表4。通过表4可以看出，当过渡电阻增大时，电压σ模态能量逐渐减小，而电流α模态的极性基本不受影响。由此可知，该方法能够实现故障区段定位。
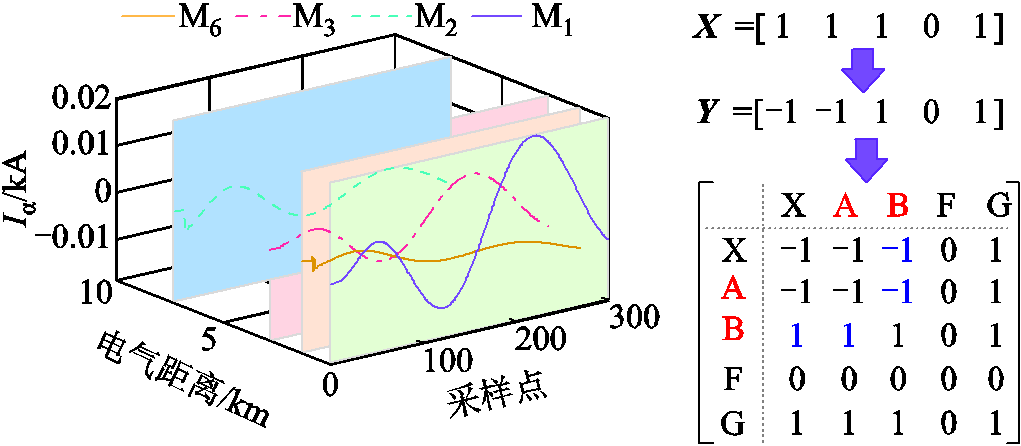
图12 三个矩阵与定位结果
Fig.12 Three matrices and location results
表4 不同工况下的定位结果
Tab.4 Location results under different conditions
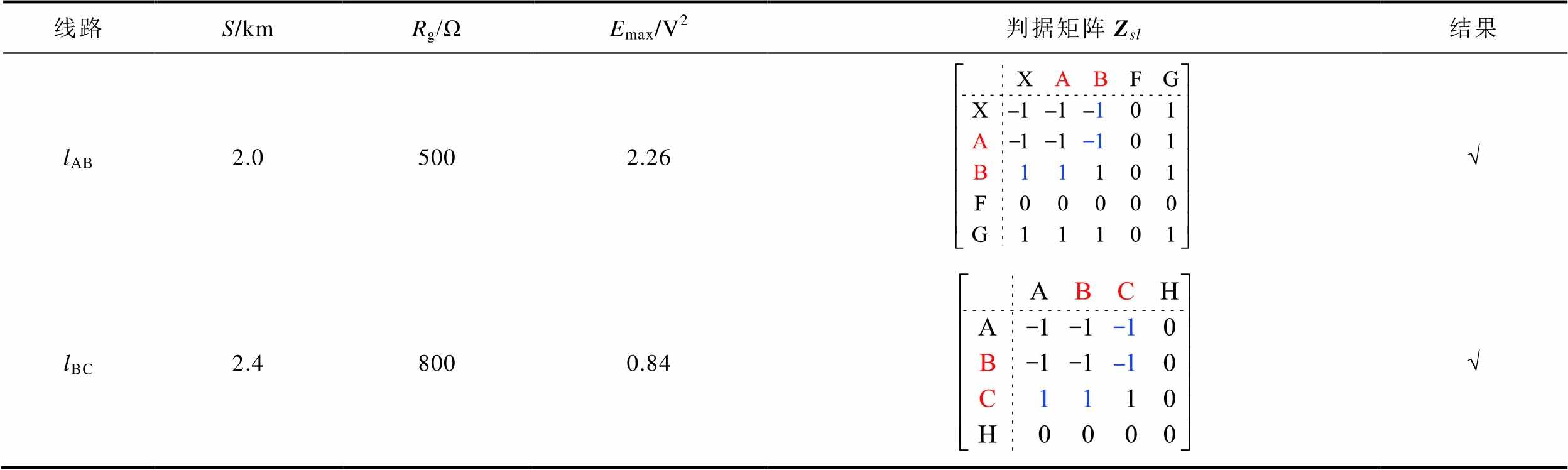
线路S/kmRg/ΩEmax/V2判据矩阵Zsl结果 lAB2.05002.26√ lBC2.48000.84√
（续）
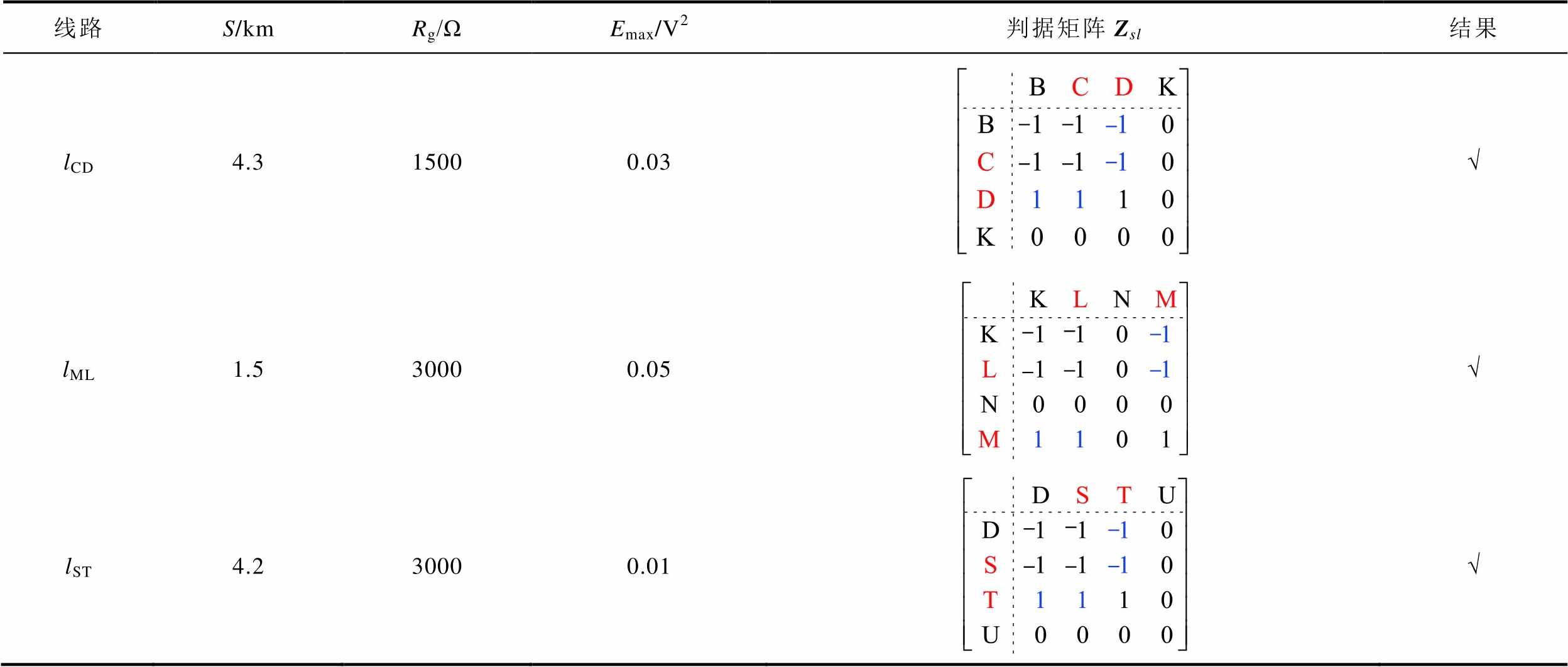
线路S/kmRg/ΩEmax/V2判据矩阵Zsl结果 lCD4.315000.03√ lML1.530000.05√ lST4.230000.01√
考虑测点采集的电气信号会受背景噪声的影响，因此，在三相电压、电流信号中添加不同信噪比的白噪声模拟环境噪声，具体设置如下：在距离lAB始端2.4 km处设置单相接地故障，进行四组不同故障电阻Rg与故障初相位的模拟试验，并添加不同信噪比SNR（10、20、30、50 dB）的高斯白噪声进行仿真验证，其结果见表5。其中，由于篇幅问题，下文简写判据矩阵Zsl为最小区段min(Lsl)的形式。由表5可以看出，当故障电阻Rg为1 Ω，信噪比SNR为50 dB时，处在环境噪声下的故障特征明显。而随着故障电阻增大与噪声增强，当Rg=1 kΩ，SNR=20 dB时的电压、电流波形如图13a所示，很难凭借其波形特征实现故障定位。但通过解耦后的电压σ模态依旧能够辨识单相接地故障，实现精准定位，如图13b所示，噪声对于电流α模态极性矩阵的构建基本没有影响，而对电压σ模态的影响较小。由此可见，该方法可以适用于噪声环境。
表5 不同噪声条件下的定位结果
Tab.5 Location results under different noise conditions
δ/(°)Rg/ΩSNR/dBEmax/kV2判据矩阵Zsl结果 01504 994√ 30100305.817√ 601 000200.063√ 902 000100.016√
考虑不同采样频率对故障定位的影响，分别设置3.2、6.4、10、20和40 kHz的采样率来获取三相电气信号。通过矩阵分解与判据计算确定故障区段，其结果见表6。
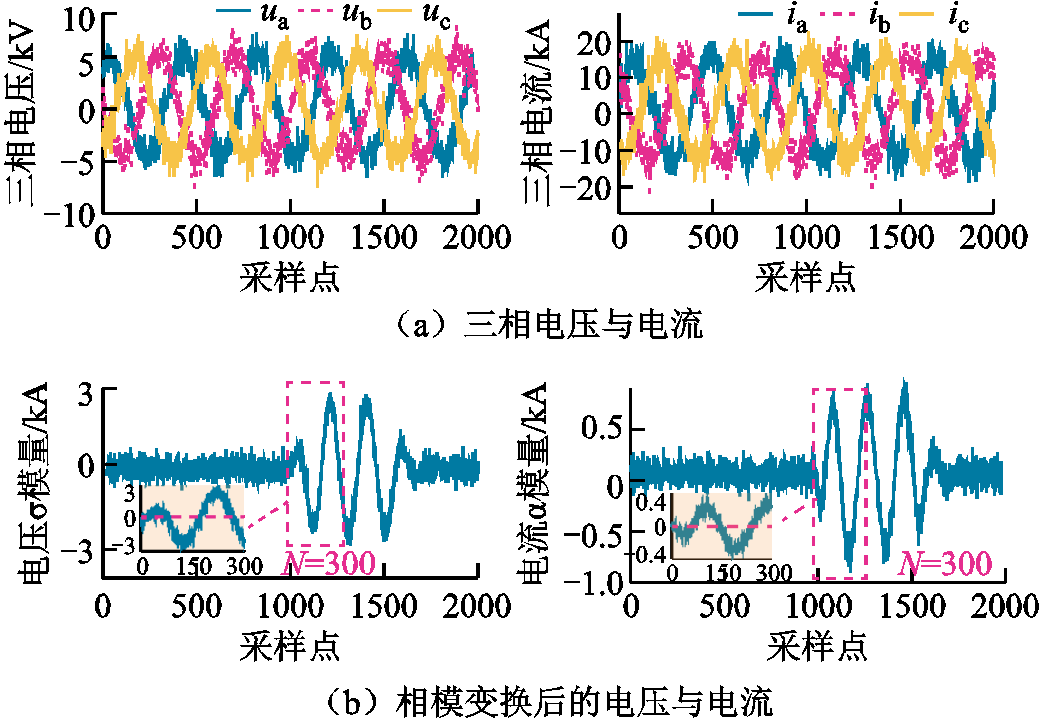
图13 1 kΩ，20 dB波形特征
Fig.13 Waveforms characteristics under 1 kΩ, 20 dB
表6 不同采样率下的定位结果
Tab.6 Location results at different sampling rates
线路S/kmRg/Ω采样率/kHz时间/ms结果 lAB2.01003.20.019√ lBC2.43006.40.035√ lCD4.3500100.047√ lML1.51 000200.086√ lST4.22 000400.167√
当采样率f=3.2 kHz时，电压σ模态和电流α模态的波形如图14所示。不同采样率下的情况如图15所示。该方法使用的是故障后的暂态信号，因此定位的精度会受到采样率的影响，但相模变换后的电压σ模态的能量分布与电流α模态的极性基本不受影响。结合表6与图15可以看出，不同采样率下的区段定位结果相同，随着采样率升高，定位的准确性进一步提升，且耗时随采样率的增大而增大，但均满足工程要求。该方法能在3.2 kHz的采样率下实现故障定位，在更高采样率下定位效果更佳。
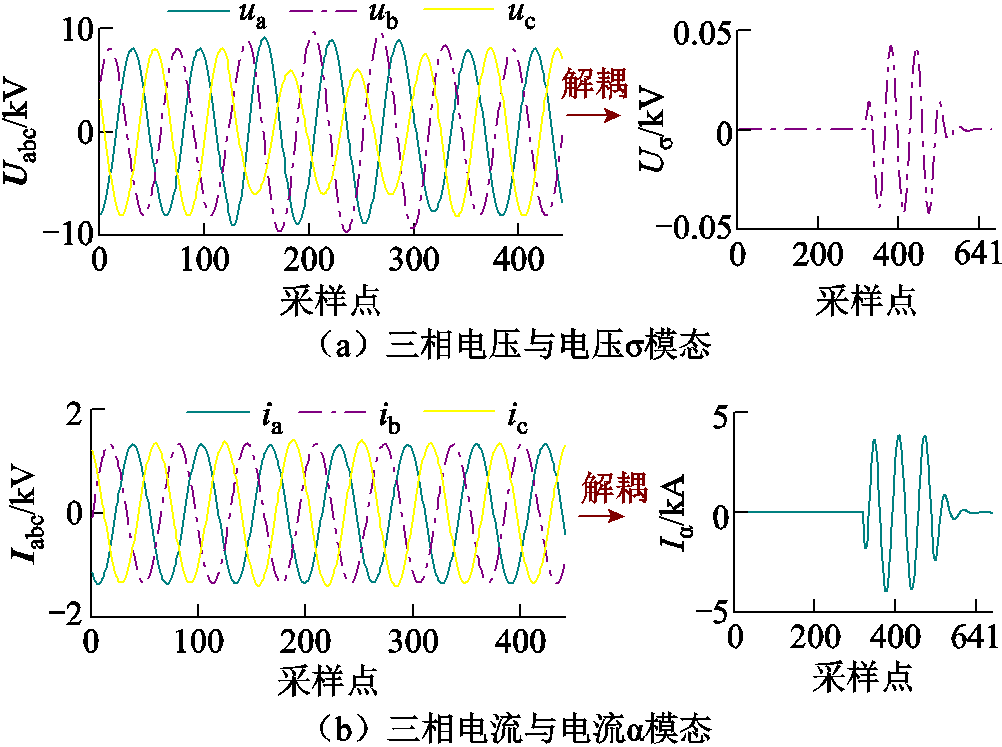
图14 f=3.2 kHz时的特征模态
Fig.14 Eigen-mode at f=3.2 kHz
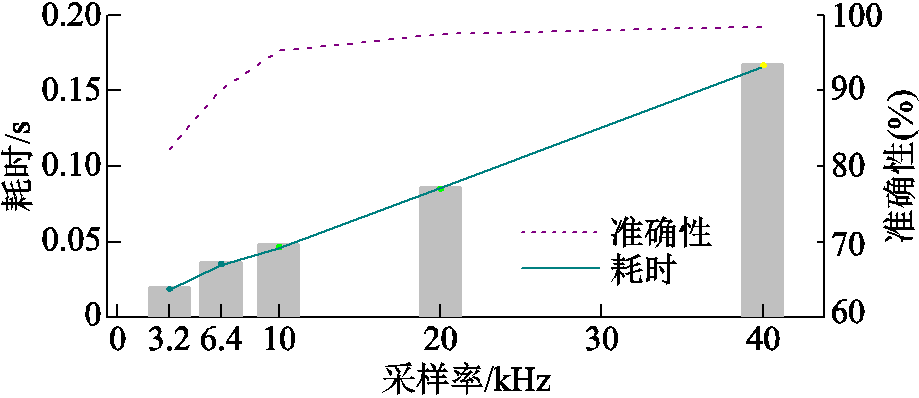
图15 不同采样率下的情况
Fig.15 The situation at different sampling rates
结合图11所示的配电网结构，考虑测点失效这一情况，以电缆lBC发生单相接地故障为例，进行讨论分析，若节点B处测点M2故障，有以下三种情况：
1）仅能获取电压信号：通过电压σ模态的能量确定B点（EB=0.835 1 kV2）为故障区段的端点；无法测取BC段极性，拓扑结构测点分布矩阵为X=[A B F G]=[1 0 1 1]，结合电流α模态极性矩阵Y=[-1 0 1 0]，得到判据矩阵Z1，如图16a所示。由此判定故障区段为lAC，增大了故障范围。此时，结合录波数据，监测节点B处测点M2的电流信号异常或畸变，通过这一信息回馈，根据定位流程可正确判定故障区段为lBC。
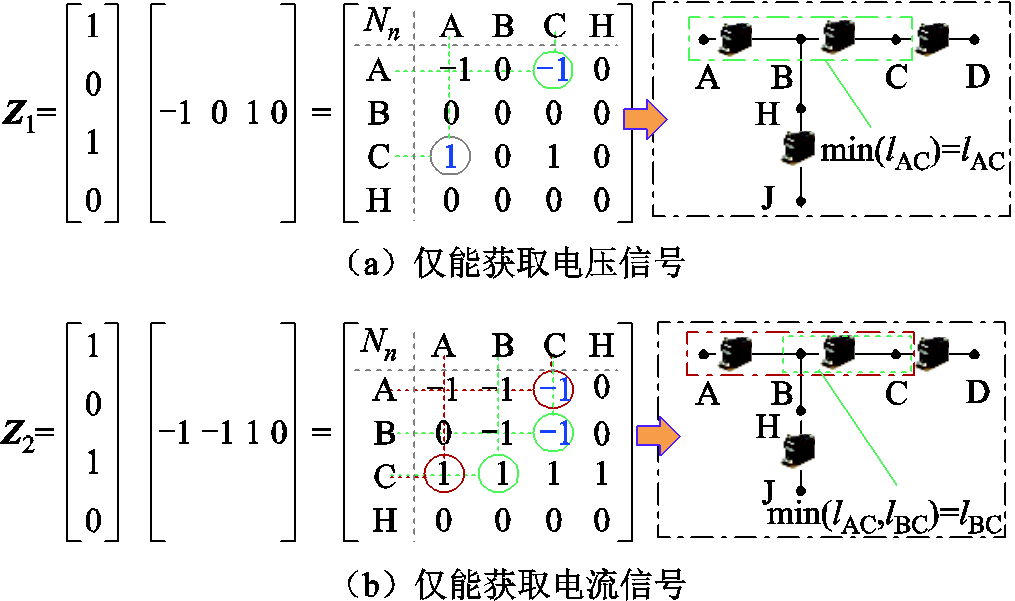
图16 测点失效下的判据矩阵
Fig.16 The criterion matrix for measuring point failure
2）仅能获取电流信号：计算电压σ模态的能量确定C点为能量最大值点（EC=0.771 1 kV2），X=[A B F G]=[1 0 1 0]，Y=[-1 -1 1 0]，由此得到判据矩阵Z2，如图16b所示。由AC=-CA，BC=-CB，且结合min(lAC, lBC)可正确判定lBC为故障区段。
3）电压、电流信号均失效：测点M2的电压信号缺失，首先确定C点为故障区段的一端点，无法测得BC段电流极性，Y=[B C D K]=[0 1 1 0]，通过判据矩阵Z3无法确定故障区段。此时，结合录波数据，通过节点B处测点M2信号异常这一信息回馈，可判定故障区段的另一端点为B点，故障区段为lBC。
综上所述，配电网拓扑部署的某一测点故障导致电压、电流无法测量时，通过所提方法可实现故障定位。当出现电压、电流信号均失效的极端情况时，在一定程度上增大了区段范围，但城市配电网的电缆线路长度短，增加一段电缆的搜索范围，工程实践中可以接受，且本文为了实现100%精准定位，结合录波数据监测运行情况，添加逻辑判断，进而，能够准确实现故障定位。
考虑配电网拓扑结构变化对该方法的影响，对如图11所示的拓扑结构进行改变。单相接地故障均发生在lAB，具体分为以下几种情况：①含测点M6的电缆线lAL退出运行；②带测点M17的电缆线lAX投入运行；③不带测点的电缆线lAV退出运行或④不带测点的电缆线lAV投入运行，定位结果见表7。拓扑结构变化会从两方面影响该方法的定位结果：一是参数解耦的变化，由于投入或退出一段电缆（长度不会很长），影响不大；二是测点配置，当投入或退出不含测点的电缆时，判据矩阵中该节点对应元素置零，不影响定位结果。由表7也可以看出，拓扑结构变化对该方法的定位结果影响不大。因此，该方法适用于拓扑结构变化的情况。
表7 不同线路拓扑下的定位结果
Tab.7 Location results under different line topologies
工况Rg/ΩS/kmEmax/kV2判据矩阵Zsl结果 ①2000.50.418√ ②5001.00.195√ ③1 0001.50.108√ ④3 0002.00.091√
在实际现场中，配电网线路参数不是恒定的。电缆敷设于地下，受环境、温度等影响，会随着时间发展导致绝缘下降，参数也会相应变化。根据文献[19]可知，绝缘老化导致绝缘电阻下降、电容增大，参数变化下的定位结果见表8，故障发生在lCD。其中，“-”表示阻抗减小；“+”表示电容增加。由表8可以看出，整体性缺陷造成的线路参数改变对于解耦的影响较小，故电缆参数变化后，定位结果基本不受影响。因此，该方法适用于参数变化的情况。
表8 不同线路参数下的故障区段定位
Tab.8 Location results under different line parameters
工况R(%)C(%)Emax/kV2判据矩阵Znm结果 ①-0.1+0.30.195 3√ ②-0.2+0.40.107 9√ ③-0.5+0.80.190 9√
实际上，配电网中存在多点三相不对称负荷，本节主要分析不对称负荷对所提方法的影响。图17a、图17b分别展示了10 kV配电网正常运行与负荷不对称的情况。当电缆lAG距首端1 km发生A相接地，故障初相位90°，接地电阻800 Ω，考虑接单相负载与两相负载的不对称情况进行仿真分析，结果如图18所示。图18a为该工况下的三相电流波形，图18b为通过该方法解耦后的电压σ模量与电流α模态的波形，图18c和图18d为相应的电流α模态的极性与电压σ模量能量的计算结果。观察图18可知，当电缆末端三相负荷不对称时，所提方法不受影响，且能够准确地实现故障区段定位。
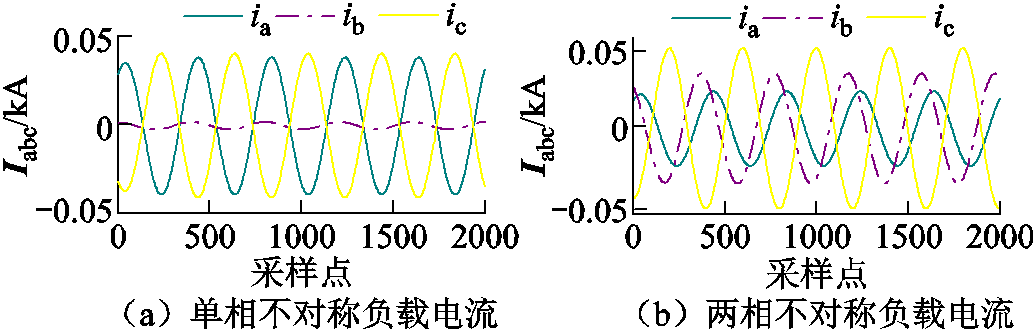
图17 系统三相电流
Fig.17 Three-phase current of system
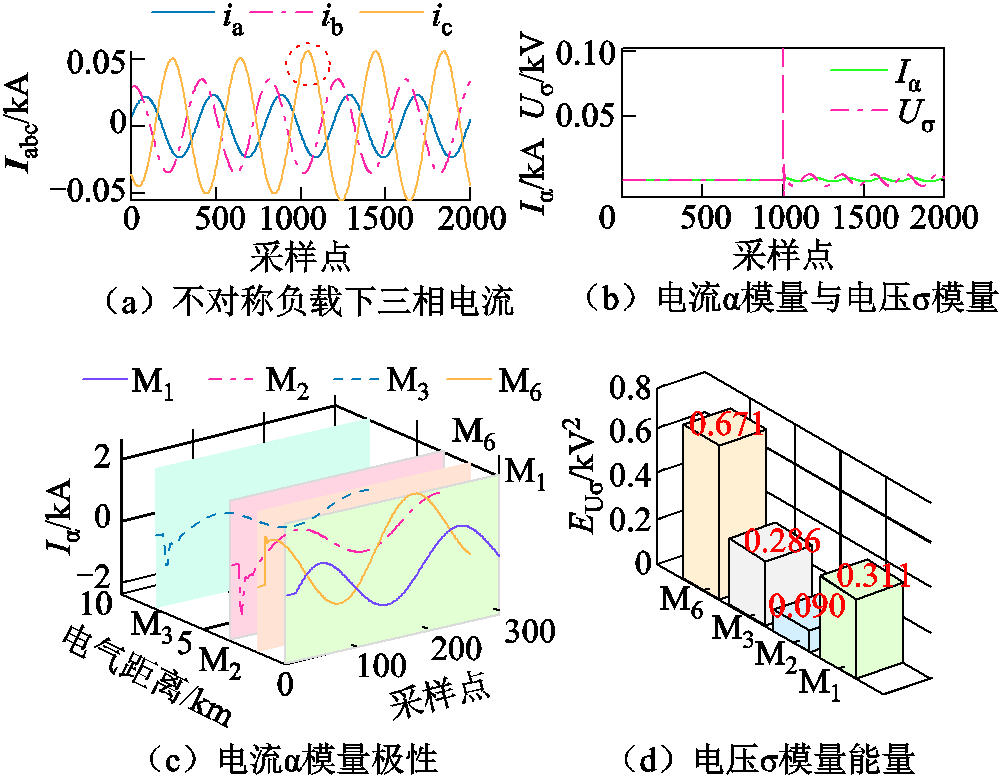
图18 不对称负荷下的定位结果
Fig.18 Location results under asymmetric loading
本节通过对不同接地方式以及不同接地方式系统并网运行下的单相接地故障进行仿真，以分析该方法的适应性，其故障仿真初始条件见表9。利用所提解耦方法，获取各测点暂态特征模量信号。不同接地方式下的模态信号如图19所示。
表9 不同故障工况的初始条件
Tab.9 Initial conditions for different fault conditions
工况接地方式不同的系统ln-S/kmRg/Ωδ/(°) ①小电阻接地系统l2-1.530090 ②消弧线圈接地系统l4-3.350060 ③小电阻接地系统与消弧线圈接地系统并网运行l6-0.880030
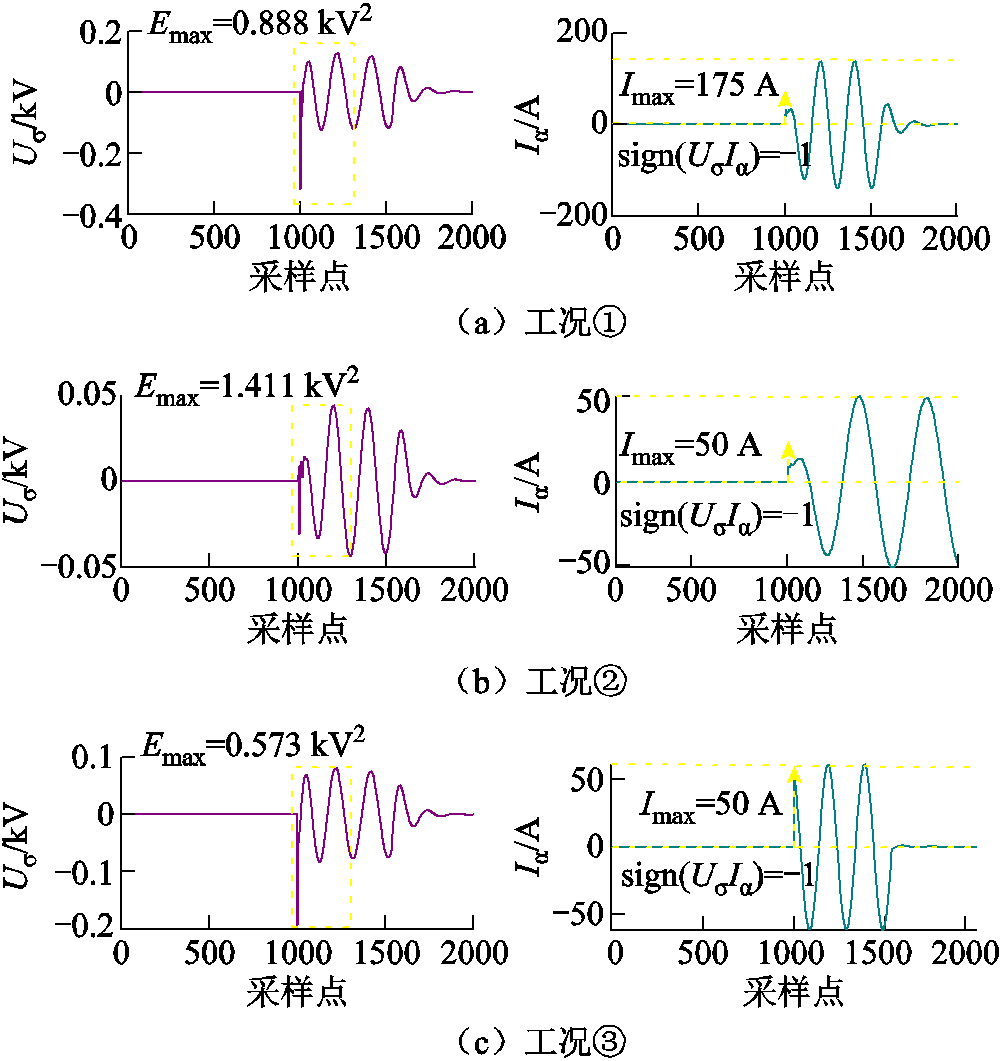
图19 不同接地方式下的模态信号
Fig.19 Mode signals under different grounding methods
由图19看出，电压σ模态的能量分布均满足上述规律。根据式（23）可知，电流α模态与三相电流大小有关，且本质上属于零序模态，因此主要分析不同接地方式下，电流α模态的极性是否普遍满足所提方法的规律：工况①，小电阻接地方式下，单相接地故障发生在距离母线电气距离较近的位置，且叠加中性点小电阻补偿的阻性电流，电流α模态约为175 A，因而能准确实现区段定位；工况②，经消弧线圈接地方式下，故障距离母线电气距离较远的CD区段，由于消弧线圈的补偿作用，此时故障区段电流较小，电流α模态约为50 A，但根据其极性仍可正确定位故障区段。如图19c所示，当小电阻接地系统与消弧线圈系统并网运行时发生接地故障，距离母线的电气距离较近，此时电流α模态的大小约为 50 A，且极性依旧满足上述规律。因此，小电阻接地、消弧线圈接地、以及不同接地系统并网运行下，均可通过最终矩阵判据正确判定故障区段。
将该方法与现有其他主流方法进行对比分析，从测量装置配置、适应性、时效性等方面进行分析，验证其优越性，对比结果见表10。
表10 不同方法的对比情况
Tab.10 Comparison of different methods
对比方法测点配置耦合结构Rg/ΩSNR/dB耗时/ms时效性(pu) 文献[10]全网未考虑100未考虑30000.31 文献[17]部分考虑3 000未考虑1009.80 文献[20]部分考虑3 000未考虑1208.08 文献[21]部分考虑3 000301206.83 本文部分考虑3 000109011.10
表10中，故障区段定位的时效性Te为
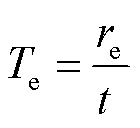（25）
式中，t为不同故障区段定位方法的耗时；re为故障区段定位的准确性。通过分析表10，得出以下结论：首先，该方法在测点配置上具有优势，根据文献[10]可知，测点需要全网配置，根据文献[17]可知，在具有n个节点的系统中需要n-1个测点，而本文通过构造判据矩阵、添加空间结构的逻辑判断，从而合理优化测点配置，具有一定经济性；其次，本文考虑了交联聚乙烯电缆的多导体耦合结构，在PSCAD软件建模时，修正了相对介电常数，使电缆系统的解耦更加精准，该方法的适用性也较强，与文献[20-21]所提方法相比，其耐过渡电阻能力达到3 kΩ，抗噪声干扰能力达到10 dB，能够普遍适应一些极端工况，在测点失效、高阻故障、不同接地方式系统并网等场景上均具有一定优势；最后，该方法构造的三个矩阵属于对角元占优的稀疏矩阵，根据表10可以看出，该方法计算量小，且对存储内存要求低，因而执行耗时少、时效性高，具有一定工程价值。
本文提出了基于单芯电缆矩阵变换与故障特征模态的电缆型配电网区段定位方法。与现有方法对比验证了本文方法的有效性与优越性，并得出以下结论：
1）考虑电缆多导体耦合结构，提出一种适合三相单芯电缆的矩阵变换方法，揭示了乘积矩阵随频率增加趋于实数阵的现象，实现了电缆系统的完全解耦。
2）电压σ模态与电流α模态在单相接地故障前后的变化明显，可作为故障特征模态，且满足以下规律：电压σ模态幅值变化剧烈；电流α模态在故障点上游的流向与下游以及其他健全电缆线路的流向完全相反。
3）结合配电网拓扑结构的空间位置合理配置测点，构建拓扑结构测点分布矩阵、电流α模态极性矩阵和最终判据矩阵，能够在减少测点分布、节省经济成本的同时实现故障区段的精准定位。
4）与现有方法相比，本文所提方法在测点配置、解耦程度、耐过渡电阻与抗噪声干扰能力上均具有优势。判据矩阵属于对角元占优的稀疏矩阵，其计算量小、存储内存要求低、耗时少、时效性高，具有一定的工程价值。
参考文献
[1] Yang Shiwu, Jiao Yang, Chen Qing, et al. A single-phase to ground fault identification method based on extremely low frequency current detection in distribution grids[J]. IEEE Transactions on Power Delivery, 2022, 37(6): 5214-5223.
[2] 徐星, 陈向荣, 杜振东, 等. 基于非解耦节点导纳矩阵的随桥电缆接地方式研究[J]. 电工技术学报, 2021, 36(17): 3664-3674.
Xu Xing, Chen Xiangrong, Du Zhendong, et al. Study on bridge-cable grounding system based on the non-decoupling nodal admittance matrix[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3664-3674.
[3] 邓丰, 徐帆, 曾哲, 等. 基于多源暂态信息融合的单端故障定位方法[J]. 电工技术学报, 2022, 37(13): 3201-3212.
Deng Feng, Xu Fan, Zeng Zhe, et al. Single-ended fault location method based on multi-source transient information fusion[J]. Transactions of China Electro-technical Society, 2022, 37(13): 3201-3212.
[4] 叶雨晴, 马啸, 林湘宁, 等. 基于SOP的主动式谐振接地配电网单相接地故障区段定位方法[J]. 中国电机工程学报, 2020, 40(5): 1453-1465.
Ye Yuqing, Ma Xiao, Lin Xiangning, et al. Active fault locating method based on SOP for single phase grounding faults in the resonant grounding distribution network[J]. Proceedings of the CSEE, 2020, 40(5): 1453-1465.
[5] 李浩, 张禄亮, 栾云飞, 等. 基于子系统划分和注入电流比的配电网故障定位方法[J]. 电力系统保护与控制, 2023, 51(8): 63-72.
Li Hao, Zhang Luliang, Luan Yunfei, et al. Fault location method for a distribution network based on subsystem division and injection current ratio[J]. Power System Protection and Control, 2023, 51(8): 63-72.
[6] 贾科, 李论, 杨哲, 等. 基于贝叶斯压缩感知理论的配网故障定位研究[J]. 中国电机工程学报, 2019, 39(12): 3475-3486.
Jia Ke, Li Lun, Yang Zhe, et al. Research on distribution network fault location based on Bayesian compressed sensing theory[J]. Proceedings of the CSEE, 2019, 39(12): 3475-3486.
[7] 贾清泉, 郑旭然, 刘楚, 等. 基于故障方向测度的配电网故障区段定位方法[J]. 中国电机工程学报, 2017, 37(20): 5933-5941.
Jia Qingquan, Zheng Xuran, Liu Chu, et al. A method of fault section location in distribution networks based on fault direction measures[J]. Proceedings of the CSEE, 2017, 37(20): 5933-5941.
[8] 杜政奇, 王敬华, 张新慧, 等. 基于多特征融合与优化支持向量机的小电流接地故障区段定位方法[J]. 电力系统及其自动化学报, 2023, 35(9): 103-111.
Du Zhengqi, Wang Jinghua, Zhang Xinhui, et al. Location method for small current grounding fault segment based on multi-feature fusion and optimized support vector machine[J]. Proceedings of the CSU-EPSA, 2023, 35(9): 103-111.
[9] 倪广魁, 鲍海, 张利, 等. 基于零序电流突变量的配电网单相故障带电定位判据[J]. 中国电机工程学报, 2010, 30(31): 118-122.
Ni Guangkui, Bao Hai, Zhang Li, et al. Criterion based on the fault component of zero sequence current for online fault location of single-phase fault in distribution network[J]. Proceedings of the CSEE, 2010, 30(31): 118-122.
[10] 刘斯琪, 喻锟, 曾祥君, 等. 基于零序电流幅值连调的小电流接地系统故障区段定位方法[J]. 电力系统保护与控制, 2021, 49(9): 48-56.
Liu Siqi, Yu Kun, Zeng Xiangjun, et al. Fault location method of a non-effective earthed system based on zero sequence current amplitude continuous regulation [J]. Power System Protection and Control, 2021, 49(9): 48-56.
[11] 邓丰, 李欣然, 曾祥君, 等. 基于多端故障行波时差的含分布式电源配电网故障定位新方法[J]. 中国电机工程学报, 2018, 38(15): 4399-4409, 4640.
Deng Feng, Li Xinran, Zeng Xiangjun, et al. A novel multi-terminal fault location method based on traveling wave time difference for radial distribution systems with distributed generators[J]. Proceedings of the CSEE, 2018, 38(15): 4399-4409, 4640.
[12] 胡明峰, 刘洋, 华斌. 量测装置优化配置下的分布式配电网故障定位方法[J]. 电网技术, 2021, 45(7): 2616-2622.
Hu Mingfeng, Liu Yang, Hua Bin. Distributed fault location for distribution networks under optimal configuration of measuring devices[J]. Power System Technology, 2021, 45(7): 2616-2622.
[13] 杨庆, 胡逸, 崔浩楠, 等. 固有频率与电磁时间反演结合的多分支配网故障定位方法[J]. 高电压技术, 2025, 51(3): 1103-1113.
Yang Qing, Hu Yi, Cui Haonan, et al.A fault location method for multi-terminal distribution network combined with natural frequency and electromagnetic time reversal[J].High Voltage Engineering, 2025, 51(3): 1103-1113.
[14] 朱秀香, 刘肖骢, 姚敏东, 等. 配电网接地故障下相电流暂态变化量的分析及应用[J]. 电力系统自动化, 2022, 46(24): 187-196.
Zhu Xiuxiang, Liu Xiaocong, Yao Mindong, et al. Analysis and application of transient change of phase current under grounding fault in distribution network [J]. Automation of Electric Power Systems, 2022, 46(24): 187-196.
[15] 王雪文, 石访, 张恒旭, 等. 基于暂态能量的小电流接地系统单相接地故障区段定位方法[J]. 电网技术, 2019, 43(3): 818-825.
Wang Xuewen, Shi Fang, Zhang Hengxu, et al. A single-phase earth fault location method based on transient energy for non-effectively grounded system [J]. Power System Technology, 2019, 43(3): 818-825.
[16] 廖芳群, 李海锋, 陈嘉权, 等. 小电阻接地系统高灵敏性接地故障区段定位方法[J]. 电力系统保护与控制, 2021, 49(21): 150-158.
Liao Fangqun, Li Haifeng, Chen Jiaquan, et al. High sensitive ground fault location in a low-resistance grounded system[J]. Power System Protection and Control, 2021, 49(21): 150-158.
[17] 梁睿, 彭楠, 张政一, 等. 暂态特征模量时频分析的电缆型配电网单相接地故障区段定位[J]. 中国电机工程学报, 2023, 43(23): 9098-9114.
Liang Rui, Peng Nan, Zhang Zhengyi, et al. Single-phase grounding fault section location of the distribution cable networks based on the time-frequency analysis of the transient featured moduli[J]. Proceedings of the CSEE, 2023, 43(23): 9098-9114.
[18] 林骏捷, 林佳壕, 郭谋发. 基于多暂态特征量聚类的配电网接地故障区段定位方法[J]. 电气技术, 2023, 24(5): 16-22.
Lin Junjie, Lin Jiahao, Guo Moufa. A method of grounding fault location in distribution network based on multi-transient characteristic cluster[J]. Electrical Engineering, 2023, 24(5): 16-22.
[19] 王晓卫, 王雪, 王毅钊, 等. 基于图像信息熵与多元变分模态分解的电缆局放信号去噪方法[J]. 电工技术学报, 2024, 39(13): 4100-4115, 4152.
Wang Xiaowei, Wang Xue, Wang Yizhao, et al. A denoising algorithm for cable partial discharge signals based on image information entropy and multivariate variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4100-4115, 4152.
[20] Zhang Peng, Jin Mohan, Liang Rui, et al. Faulty cable segment identification of low-resistance grounded active distributions via grounding wire current-based approach[J]. IEEE Transactions on Industrial Informatics, 2024, 20(5): 7708-7718.
[21] Zhang Peng, Kong Lingchang, Liang Rui, et al. Fault location method for three-core cable using amplitude ratio of shield-grounding wire currents[J]. IEEE Transactions on Industrial Informatics, 2023, 19(6): 7456-7467.
Abstract Cables in urban distribution networks have advantages such as lightweight, high-temperature resistance, and high transmission power. However, over time, they can be affected by erosion, mechanical forces, and long-term overload operation, leading to insulation degradation and defects. Locating single-phase grounding faults in distribution networks is difficult due to the complex structure and short cable length. Furthermore, the existing decoupling methods for overhead lines and three-core cables are challenging to adapt.
The complex structure of multi-conductor coupling in three-phase single core cables of distribution networks, which is easily affected by proximity and skin effects, and the weak and variable characteristics of single-phase grounding faults in practical applications, as well as the difficulty of precise fault location in complex distribution networks, have not been solved. Many scholars have conducted extensive research in recent years on the precise positioning problem of cable-type distribution networks. Further analysis has found that there are still two problems with existing fault positioning technologies: (1) The multi-conductor structure coupling of three-phase single-core cables in distribution networks is complex, and the electrical parameters are asymmetric, making it difficult to transplant existing decoupling methods. (2) The grid structure of a cable-type distribution network with multiple nodes and short branches makes the refraction and reflection of traveling waves more complex, requiring high hardware requirements for measurement devices and communication equipment, making it difficult to meet both reliability and economy simultaneously.
This paper proposes a section location method based on single-core cable matrix transformation and fault characteristic modal analysis to address the problems of existing methods. Specifically, (1) Based on the complex coupling between the conductor and shielding layer of a single-core cable in the distribution network, a phase mode transformation method is proposed to achieve complete system decoupling under frequency conditions. (2) Analyze the transient fault characteristic changes and measurement feasibility of decoupled modal signals to screen fault characteristic modes reasonably. (3) A topology measurement point distribution matrix, a current alpha mode polarity matrix, and a final criterion matrix dominated by diagonal elements are constructed. The information exchange between matrices is utilized to achieve logical judgment, thereby reducing the number of measurement points and saving costs while achieving high-precision fault location. The simulation results show that this method can accurately position single-phase grounding faults under complex conditions and has advantages such as low computational complexity, small storage capacity, low time consumption, and high timeliness compared to existing methods. The following conclusions have been drawn through research: (1) A matrix transformation method is proposed for three-phase single-core cables to achieve complete decoupling of the cable system. (2) The voltage σ mode and current α mode can be used as fault characteristic modes before and after single-phase grounding faults. (3) By configuring measuring points based on the spatial location of the distribution network, accurate fault section positioning can be achieved while saving costs. (4) This method offers advantages in measuring point configuration, decoupling degree, and resistance to noise interference compared to existing methods. The criterion matrix has low computational complexity and high timeliness, with certain engineering values.
Keywords：Complete decoupling, characteristic mode, matrix transformation, single-phase grounding fault, distribution cables
中图分类号：TM77
DOI: 10.19595/j.cnki.1000-6753.tces.241234
国家自然科学基金资助项目（52177114, 61403127）。
收稿日期 2024-07-16
改稿日期2025-01-06
王晓卫 男，1983年生，博士，副教授，博士生导师，研究方向为配电网故障选线与定位、高阻故障检测、5G在配网中的应用。
E-mail：proceedings@126.com（通信作者）
王 雪 女，2000年生，硕士研究生，研究方向为配电电缆绝缘监测与故障定位、信号处理。
E-mail：shield_wx@126.com
（编辑 赫 蕾）