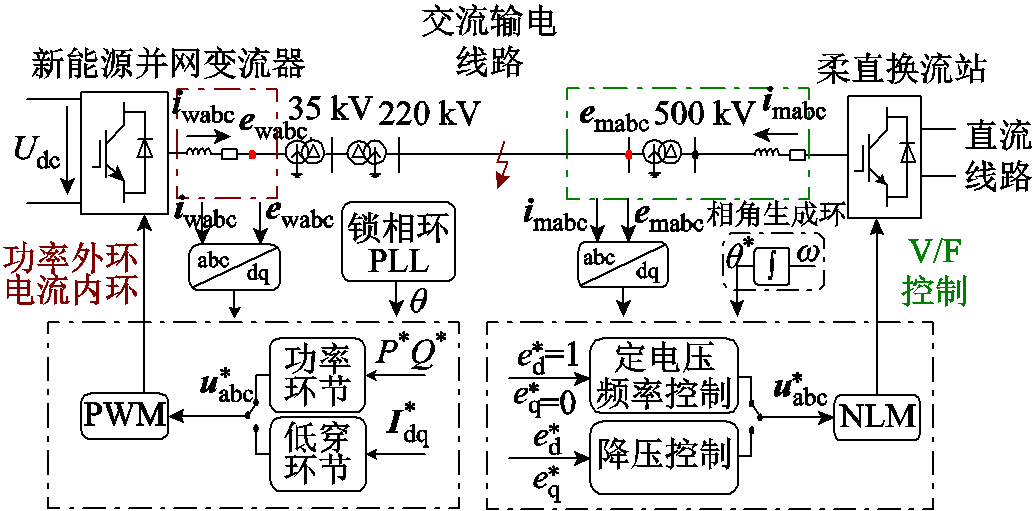
图1 新能源大基地柔直外送系统示意图
Fig.1 Schematic diagram of flexible and direct external transmission system for new energy base
摘要 新能源大基地经柔直外送，柔直换流站提供的短路电流受新能源及自身控制特性的影响，耦合特性复杂，导致现有方法难以确保暂态特性计算的精度。针对上述问题，该文采用分区计算的思路对柔直换流站与新能源大基地交互影响进行解耦，并提出了复数域数理法对计及柔直换流站控制响应特性的dq分量进行解耦，计算得到柔直换流站短路电流解析式。在硬件在环实验平台中搭建了新能源大基地柔直送出系统测试平台，不同故障场景下所提方法的计算误差均小于5%，验证了所提方法的有效性和准确性。
关键词：新能源 柔直换流站 短路电流 复数域解耦
为贯彻落实“双碳”目标，我国将加快推进新能源大基地建设，截至2030年，我国规划的新能源大基地总装机容量将达到4.55亿kW[1]。面对新能源大基地输电距离远、配套的常规能源少的问题，新能源大基地经柔性直流送出供电成为主要解决方式之一[2-4]。相较于新能源直接接入交流系统，由新能源接入柔直系统呈现的双端电力电子受控特征导致柔直侧短路电流故障机理发生根本性变化[5]，而现有的柔直侧故障电流解析侧重于稳态解析，对于暂态特性的解析由于缺乏考虑两侧电力电子源的控制响应过程，导致其暂态解析与实际波形差异较大，无法满足保护的实际需求。因此，亟须研究计及新能源耦合特性的柔直换流站短路电流解析方法。
对于柔直换流站的故障特性解析方法，现有方法可分为电磁暂态精细化仿真建模和时频方程计算方法两大类。
基于电磁暂态精细化仿真建模的解析方法主要通过在仿真软件中构建精细化仿真模型，利用精细化模型实现对不同场景下柔直换流站的故障特性进行仿真分析[6-11]。然而，该类方法本质上是利用复杂的电气特性和控制特性进行迭代计算，因此，其计算所需要的时间成本高，不适合大规模开展研究[12]。并且利用这类方法难以获得解析解，无法得到柔直换流站提供的短路电流的数学模型，缺乏理论分析，同时该方法也不可能对所有的故障场景进行仿真分析，难以为保护原理提供参考依据[13]。
相较于电磁暂态精细化仿真建模的方法，时频方程计算方法可以得到柔直换流站的解析解。然而，目前此类方法无法准确地刻画柔直换流站暂态阶段的短路电流特性。其中文献[14-16]提出了将柔直换流站等效为电压源的简化计算方式，这种方法能够实现对柔直换流站的稳态响应特性进行解析；文献[17-18]则利用变流器之间的功率关系对柔直换流站短路电流的稳态特性进行解析，然而由于该类方法未考虑两侧电力电子变流器的控制响应特性，导致此类型方法暂态解析精度较低；文献[19]利用拉氏变换，构建了考虑两侧变流器耦合特性的频域传递函数，然而由于传递函数阶数较高，导致该方法无法通过拉氏反变换得到柔直换流站侧短路电流的时域解析式。
针对新能源大基地柔直外送系统在交流送出线路发生故障时，送端柔直换流站提供的短路电流难以解析的问题，本文提出了计及新能源耦合特性的送端柔直换流站短路电流解析方法。采用分区计算的思路实现了柔直换流站与新能源大基地交互影响下的解耦计算，并基于复数域数理方法实现了对计及控制响应过程的柔直换流站dq轴分量解耦，得到柔直换流站短路电流时域解析式，解决了现有方法难以解析柔直换流站暂态特性的难题。在硬件在环实验平台验证了所提方法的计算精度。结果表明，在不同故障场景下所提算法的最大误差均小于5%，验证了所提方法的有效性。
新能源大基地柔直外送系统示意图如图1所示。本文的关注重点是220 kV交流输电线路发生故障时柔直换流站的故障电流特性。
图1 新能源大基地柔直外送系统示意图
Fig.1 Schematic diagram of flexible and direct external transmission system for new energy base
220 kV线路两侧分别连接新能源与柔直变流设备，下面分别从不同变流设备控制策略的角度分析两侧的故障特征。
新能源并网变流器采用功率外环、电流内环双环控制策略，当发生故障时，采用低电压穿越控制策略，此时外环切除，控制策略如图2所示。
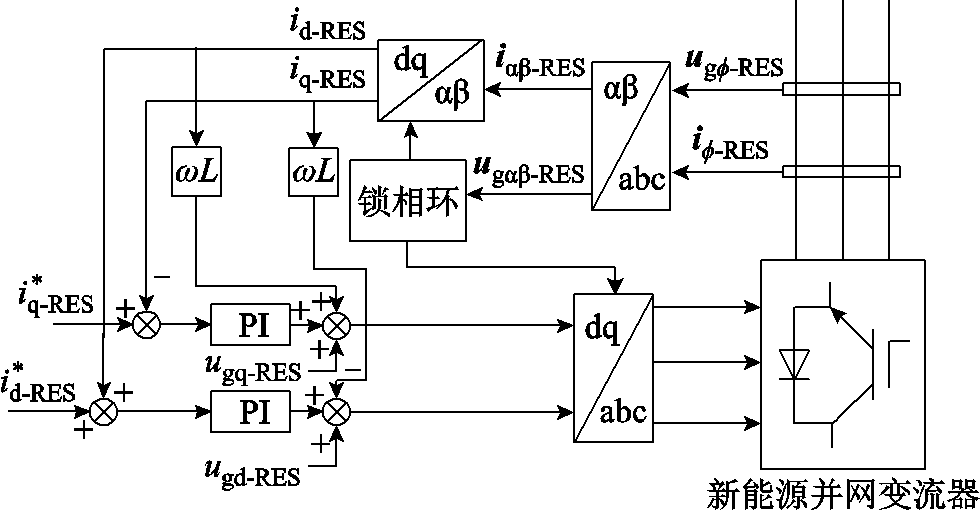
图2 新能源并网变流器控制策略示意图
Fig.2 Schematic diagram of control strategy for new energy grid connected inverters
由图2可知，功率外环在故障发生后立即关闭，因此可以忽略外环控制回路的影响[20-21]。此时新能源并网变流器仅依赖电流单环控制，dq坐标系的电流指令值根据低电压穿越控制策略直接给定。在低电压穿越控制期间dq坐标系的电流指令值[22]为
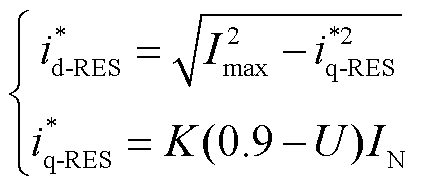（1）
式中，Imax为故障期间逆变器最大允许电流值；IN为额定电流；K为无功电流补偿系数；U为并网点电压标幺值。
根据风电并网变流器控制系统可以得到dq坐标系下的控制方程为
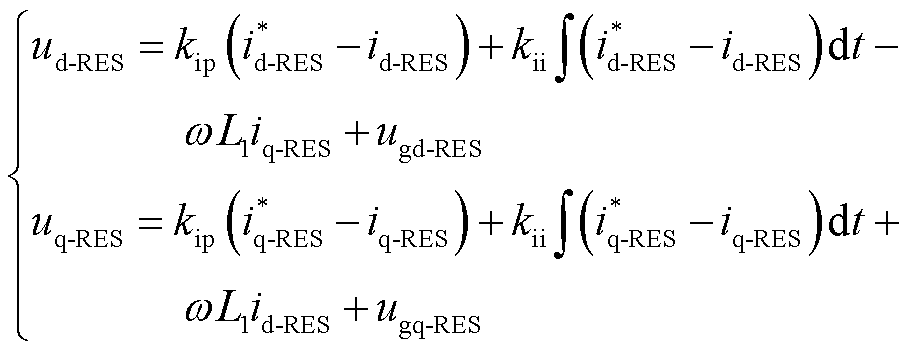（2）
式中，kip、kii分别为电流控制环的比例、积分调节系数；
、
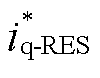分别为d、q轴电流指令值；id-RES、iq-RES分别为d、q轴电流实际值；ud-RES、uq-RES分别为新能源并网变流器d、q轴端口电压值；ugd-RES、ugq-RES分别为新能源并网变流器d、q轴并网点电压值；L1为并网变流器端口到并网点的等效电感。
由式（2）可知，风电并网变流器控制的设计由于考虑了线路方程，因此存在前馈解耦项，从而抵消了由于电感造成的dq轴电气量耦合。
为了确保风电场正常运行，送端变流器需要给风电场提供稳定的电压和频率，因此采用电压-频率控制方式[23]。当发生故障时，采用降低电压指令值的方式防止柔直换流站侧短路电流过电流，控制策略如图3所示。
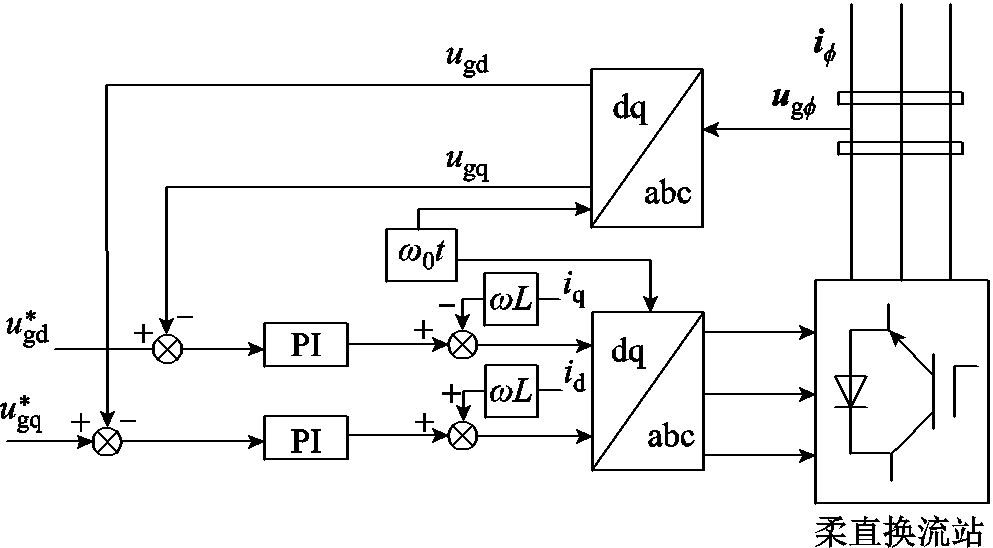
图3 柔直换流站控制策略示意图
Fig.3 Schematic diagram of control strategy for flexible and direct converter station
由于新能源并网变流器需要与同步交流电源相连才能正常运行，因此，柔直换流站在低电压穿越期间的控制策略仍然需要固定电压频率。
但为了防止过电流，低电压穿越期间柔直换流站的电压指令值会降低。现有的电压指令值降低方式分为梯度降压法[24-25]和虚拟阻抗降压法[26]两种。在低电压穿越控制阶段，对于两种电压指令值降低方式的dq坐标系的电压指令值如下。
梯度降压法的电压指令方式为
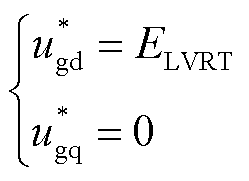（3）
虚拟阻抗降压法的电压指令计算方式为
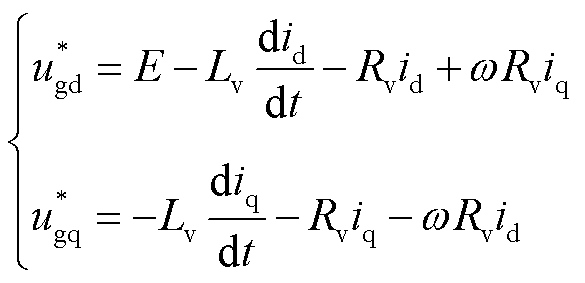（4）
式中，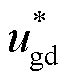
、
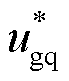分别为d、q轴电压指令值；ELVRT为低电压穿越控制阶段的电压指令值，ELVRT＜1(pu)；E为正常运行时电压指令值，E=1(pu)；Rv为虚拟电阻值；Lv为虚拟电感值；id、iq分别为柔直换流站提供的d、q轴电流值。
对于目前的两种电压指令值降低方式，其中梯度降压法的电压指令值可以理解为虚拟阻抗降压法中Rv与Lv取值为0的情况，并且改变电压指令值，因此，现有的电压指令值降低方式可以归一为
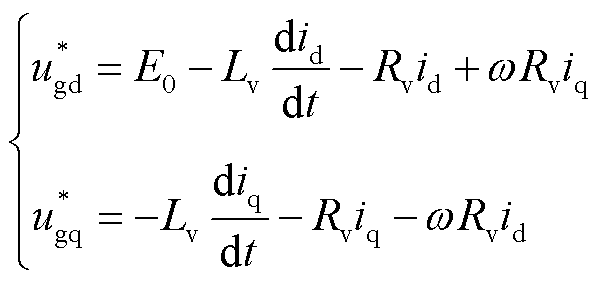（5）
式中，E0的取值在梯度降压法时小于1(pu)，在虚拟阻抗降压法时为1(pu)。
由于两种类型的指令值均是对于电压环的直接控制，因此根据柔直换流站控制响应环节可以得到dq坐标系下的控制方程为
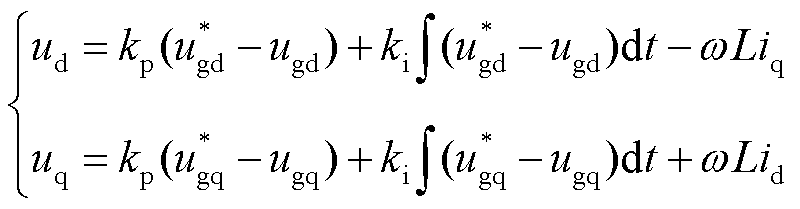（6）
式中，kp为电压-频率控制的比例调节系数；ki为电压-频率控制的积分调节系数；ugd、ugq分别为d、q轴电压实际值。
由式（6）可知，由于柔直换流站的控制方程是通过对电压指令值的控制来间接控制柔直换流站提供的电流，因此在计算柔直换流站提供的短路电流时需要考虑对侧新能源提供的电流的影响。
对于柔直换流站提供的短路电流计算需要考虑新能源提供的短路电流。由于新能源并网变流器的低电压穿越控制策略考虑线路方程设计，因此可直接联立新能源侧线路方程和控制方程，消除耦合项实现新能源侧短路电流的解析。所以柔直换流站的短路电流解析可进行分区求解，先对新能源侧短路电流进行解析，再将新能源侧短路电流代入柔直侧线路方程，对柔直换流站侧短路电流进行解析。
当发生故障时，新能源侧线路方程为
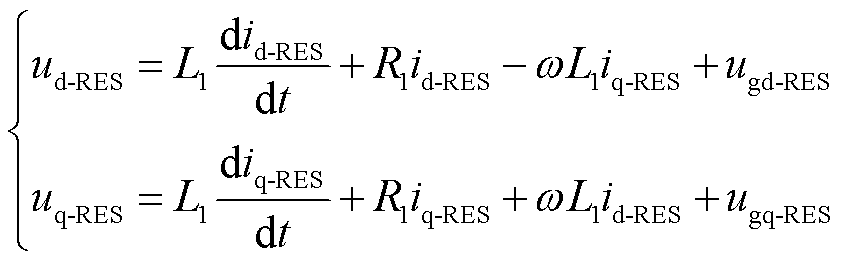（7）
式中，R1和L1分别为并网变流器端口到并网点间的等效电阻和电感。
将式（2）与式（7）联立，由于dq轴控制方程与线路方程的耦合项抵消，因此可以得到不含耦合项的二阶dq轴电流微分方程为
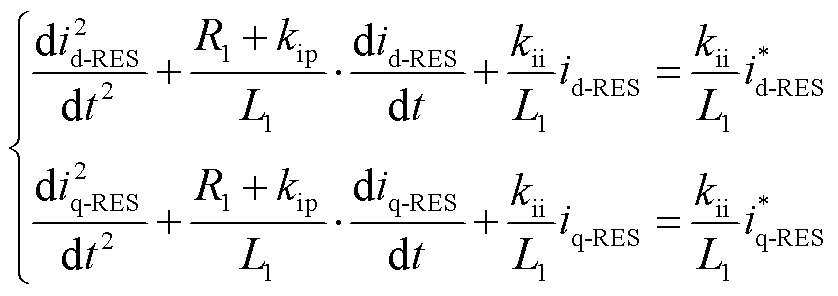（8）
解析可得新能源侧短路电流解析式为
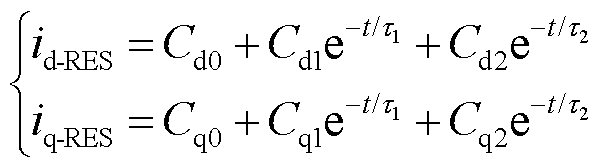（9）
式中，Cd0、Cd1、Cd2、Cq0、Cq1、Cq2为系数；τ1、τ2为衰减分量。
然而，对于柔直换流站的短路电流解析，由于其指令值为电压量，无法通过单条线路方程对解析式解耦来消除电压量，同时其电压量会受到对侧新能源故障特征的影响，因此需要通过多故障回路实现对柔直换流站采用不同控制策略时的故障特性进行分析。其故障回路包括三条回路：故障回路1为柔直换流站端口至故障点；故障回路2为公共连接点至故障点；故障回路3为新能源侧短路电流注入至故障点。
根据三条故障回路可以列写线路方程为
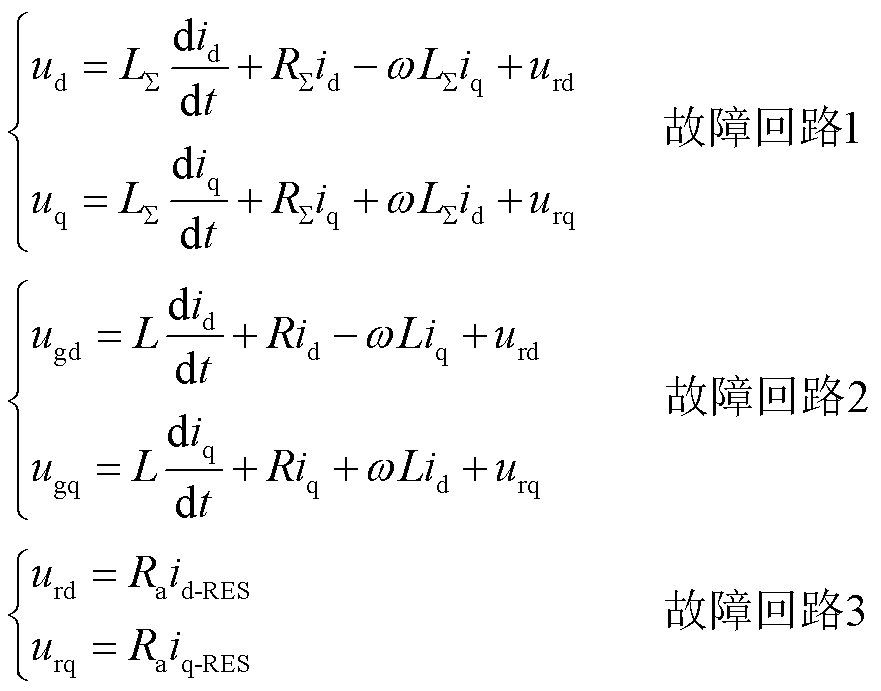（10）
式中，RΣ和LΣ分别为柔直换流站端口到故障点间的等效电阻和电感；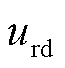
、
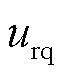分别为d、g轴的故障点电压；R和L分别为公共连接点到故障点间的等效电阻和电感；Ra为过渡电阻。
计及三条故障回路方程，对于降压控制环节，其控制方程如式（6）所示，联立式（10）的线路方程以及电压指令值方程式（5），可以得到包含耦合项的dq轴电流的二阶微分方程为
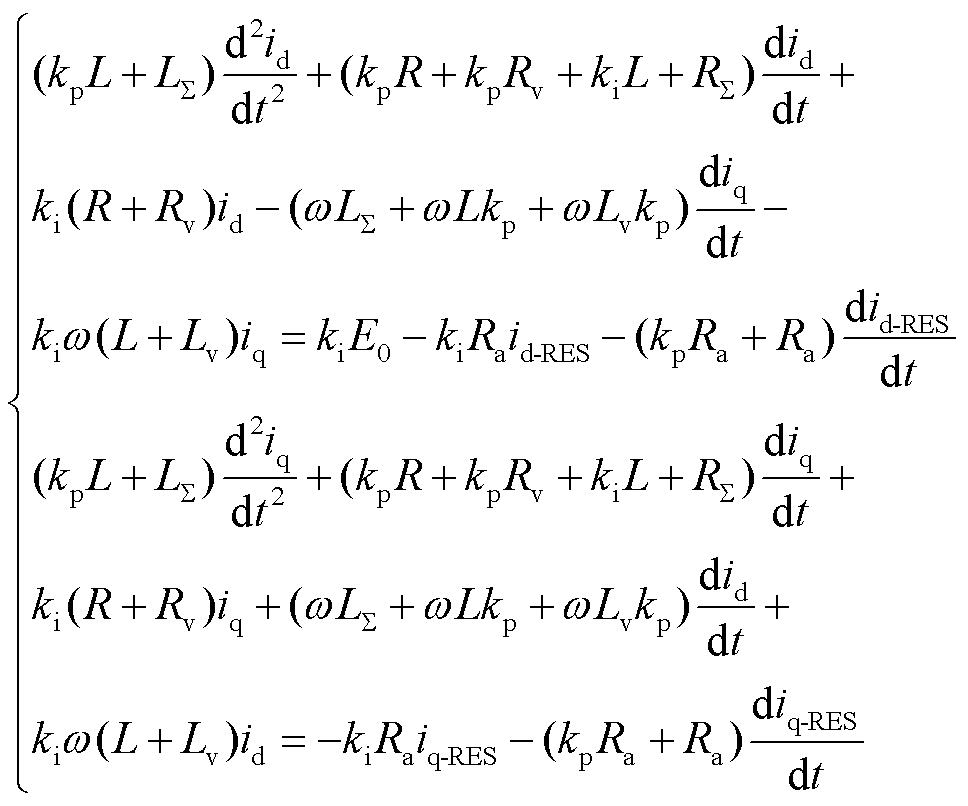（11）
此时的二阶微分方程组存在耦合项，如果采用时域解析的方法，通过列写特征方程，对特征值和特征相量进行求解。然而由于其系数包含多种类型的参数，无法得到特征值的解析解，进而导致无法得到时域解析式，仅能得到的数值解将导致无法对柔直换流站提供的短路电流的故障特征进行分析。如果采用拉氏域解析，将二阶时域微分方程组转换到拉氏域进行求解，能够对二阶微分方程组实现解耦，然而解耦后在拉氏域的阶数较高，且解析过程不存在有效极点，难以进行拉氏反变换，因此也无法应用该类型的方法。
针对柔直换流站侧短路电流微分方程组由于存在耦合分量导致其难以得到解析解的问题，本节提出了一种基于复数域的短路电流微分方程组解耦方法。
为了方便后续解耦计算，将式（11）的形式简化为
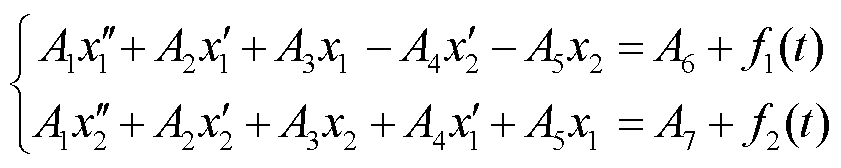（12）
式中，x1、x2分别为dq轴电流； A1、A2、A3、A4、A5、A6、A7对应式（11）中微分方程组的系数；f1(t)、f2(t)分别为式（11）中新能源提供的短路电流部分。
对比式（12）微分方程组中上、下两式的系数，可以发现两式的对应系数相等或者互为相反数。因此对于dq轴电流的耦合，可通过将两式按不同倍数相加得到
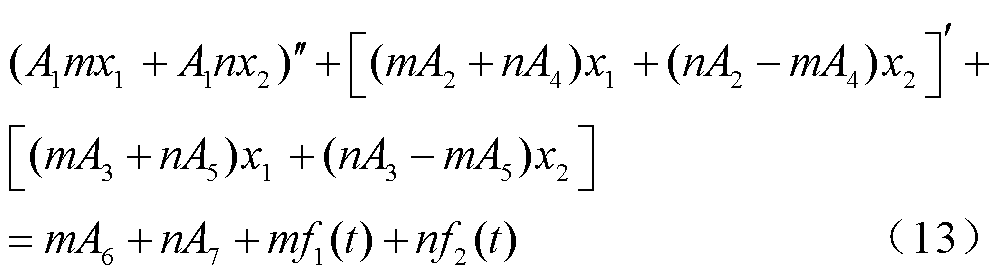
式中，m、n分别为式（12）中两式所乘的倍数。
为了确保对于dq轴电流的耦合能够实现解耦，需确保式（13）在各阶次的系数比相同，即
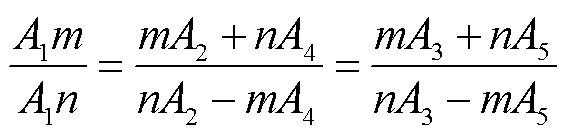（14）
为了满足式（14），设m=1，经计算可得n=±j，此时将结果代入，可构建两个变量y1、y2，其中y1=x1+jx2，y2=x1-jx2，从而得到二阶微分方程组为
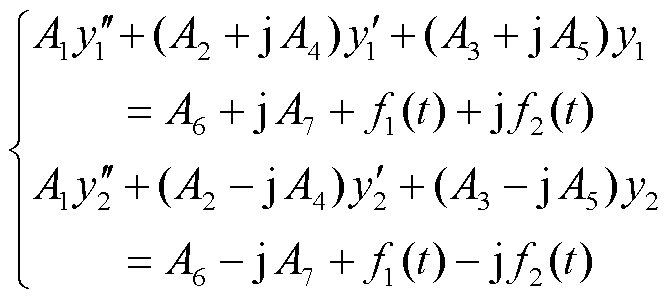（15）
由式（15）可知，此时上、下式均为二阶常系数微分方程，不存在耦合项，因此可以直接求解，得到y1、y2的解析式。结合y1、y2与x1、x2之间的线性关系，可以得到对应的dq轴电流的解析式计算方法，其中id=(y1+y2)/2，iq=(y1-y2)/(2j)，因此可得到柔直换流站解析式为
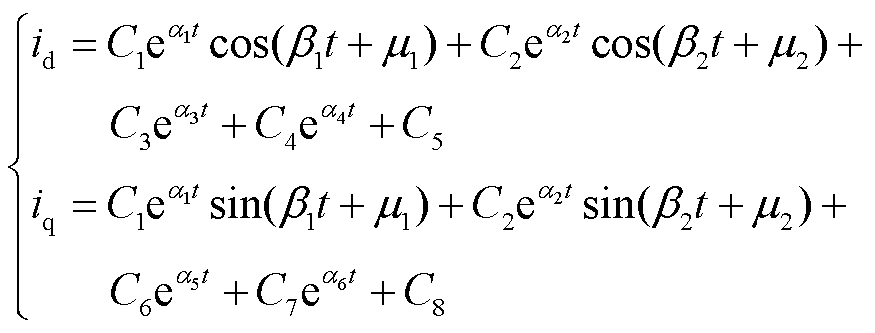（16）
式中，C1、C2、C3、C4、C5、C6、C7、C8为系数；α1、α2、α3、α4、α5、α6为衰减分量；β1、β2为角频率；μ1、μ2为相角。
通过对新能源并网变流器与柔直换流站进行分区求解，并采用复数域解耦方法，可实现对于柔直换流站提供的短路电流的解析，得到解析式如式（16）所示。由式（16）可知，故障发生后，柔直换流站提供的dq轴短路电流分为三部分：①两组衰减周期分量；②两组衰减直流分量；③直流分量。对于衰减周期分量部分，dq轴电流的衰减速度和振荡频率相同；而对于衰减直流分量部分，dq轴电流的衰减速度和幅值均不同，即暂态过程中dq轴电流的衰减时间和衰减速度并不相同。
为了检验计及新能源耦合特性的柔直换流站短路电流计算的有效性，以藏东南新能源大基地工程的相关参数为例，构造了新能源大基地柔直系统模型，拓扑结构如图1所示。其中新能源大基地与柔直换流站之间的距离为40 km，选取F1～F5五个故障点，其中F1为距离新能源大基地0 km处，F1～F5之间依次距离10 km，其他模型参数见附表1。基于此模型搭建了硬件在环实验平台，如图4所示。
图4 硬件在环实验平台
Fig.4 Hardware-in-the-loop experimental platform
为了验证所提短路电流计算方法的有效性，在F3处设置过渡电阻为5 Ω的故障，所得仿真结果与计算结果如图5所示。其中计算结果包括所提短路电流计算方法与现有短路电流计算方法[14]的计算结果。
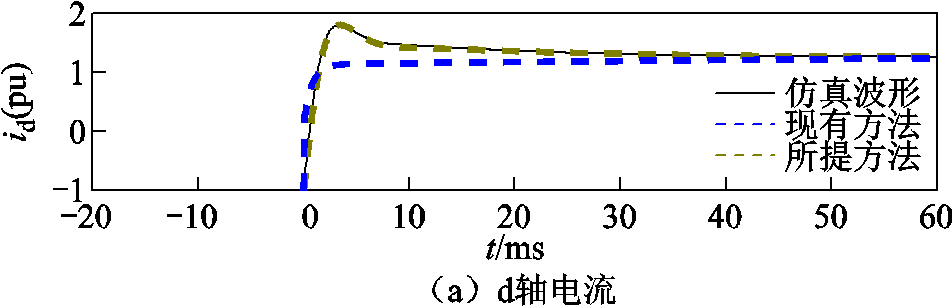
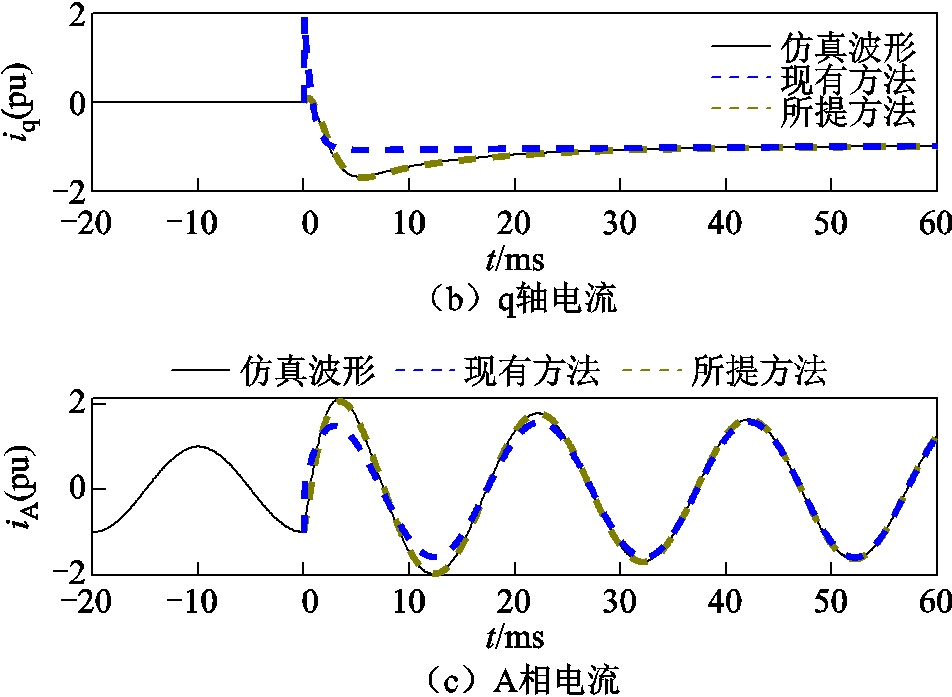
图5 柔直换流站故障电流仿真计算对比
Fig.5 Comparison of fault current simulation and calculation of flexible straight converter station
由图5可知，对于暂态阶段，利用所提短路电流计算方法得到的电流波形与仿真波形更加吻合，而现有的计算方法由于在暂态阶段忽略了柔直换流站控制的响应过程，认为电压实际值瞬时响应指令值，因此导致其在暂态阶段与柔直换流站提供的实际电流波形存在较大的差异。为了进一步量化对比两种方法在不同阶段的拟合特性，通过分析实验结果与计算值之间的瞬态电流误差，利用故障发生后60 ms内30个离散时刻的实验结果与计算结果，可计算各离散时刻瞬时电流误差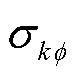
（k为离散时刻，k=2, 4, 6, …,60 ms），误差计算公式为
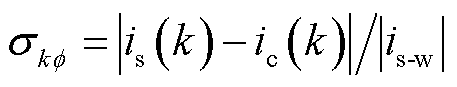。其中is为短路电流实验值，ic为短路电流计算值，is-w为短路电流稳态值，误差比较的结果如图6所示。
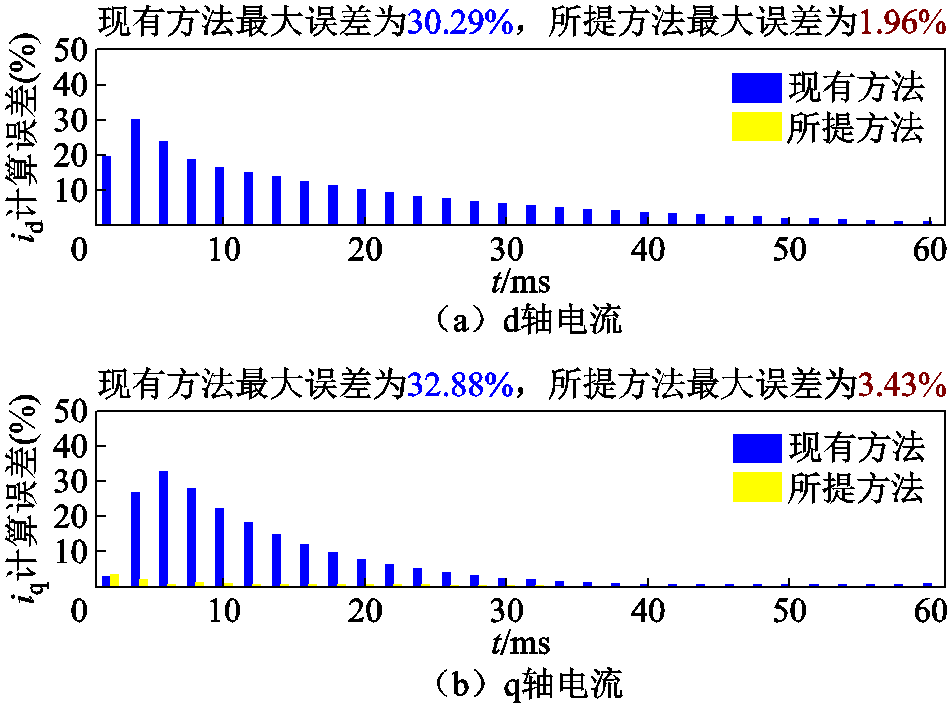
图6 柔直换流站短路电流不同计算方法误差对比
Fig.6 Comparison of error of different calculation methods of short-circuit current of flexible straight converter station
由图6可知，所提方法在故障暂态过程中的瞬时电流计算误差明显小于现有方法。现有方法的dq轴平均电流计算误差分别为30.29%和32.88%，基于所提方法的电流最大计算误差分别为1.96%和3.43%。与现有方法相比，所提出的方法在dq轴的解析精度分别提高了28.33个百分点和29.45个百分点，证明了所提方法的准确性。
为了进一步验证不同场景下所提算法的适用性，在后续的验证中给出了实验和计算电流值之间的误差比较结果，除了需要对比修改的参数，实验系统中的其他参数与3.1节相同，结果见表1。
表1 不同故障场景下短路电流计算误差
Tab.1 Calculation error of short-circuit current in different fault scenarios
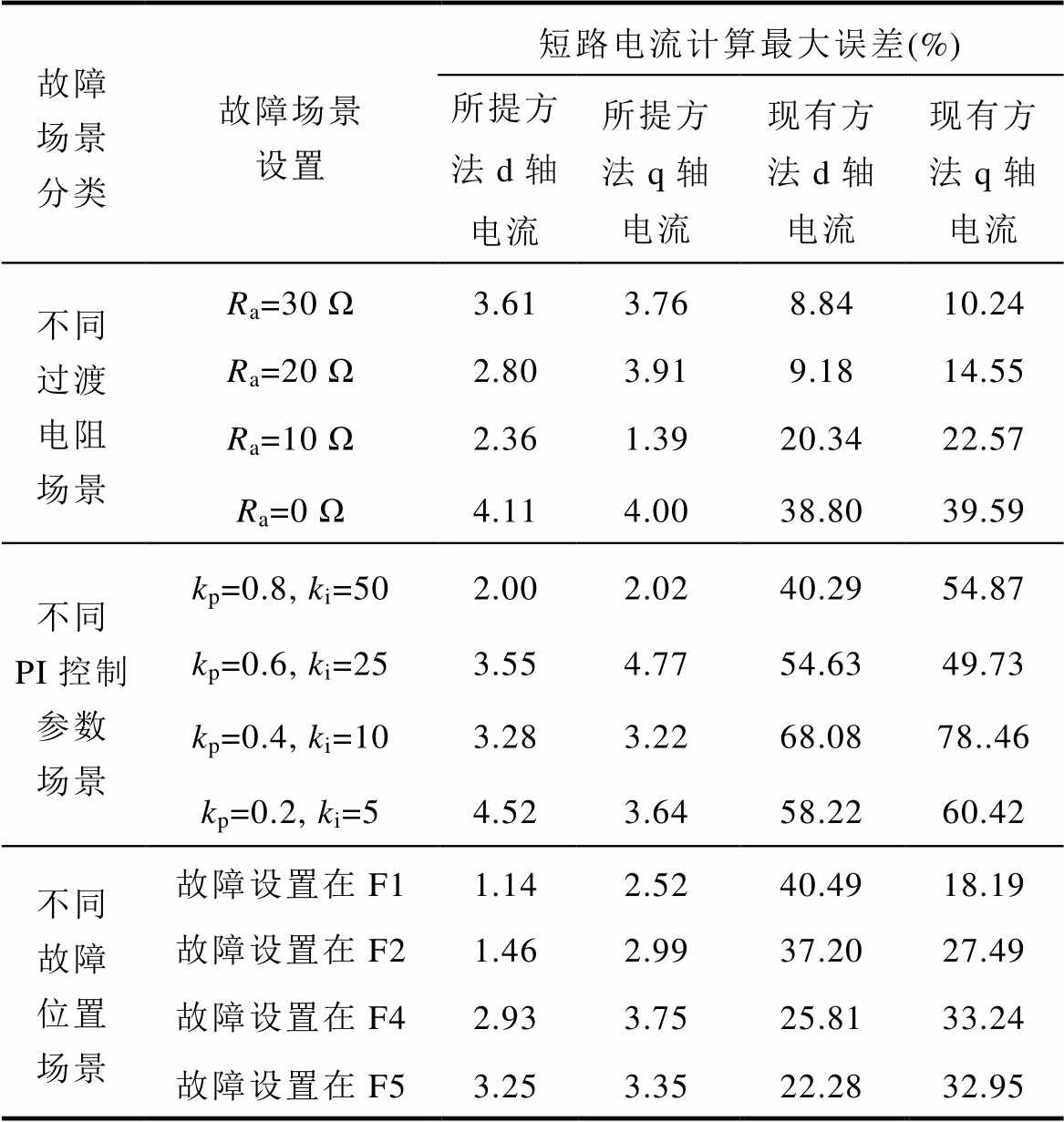
故障场景分类故障场景设置短路电流计算最大误差(%) 所提方法d轴电流所提方法q轴电流现有方法d轴电流现有方法q轴电流 不同过渡电阻场景Ra=30 Ω3.613.768.8410.24 Ra=20 Ω2.803.919.1814.55 Ra=10 Ω2.361.3920.3422.57 Ra=0 Ω4.114.0038.8039.59 不同PI控制参数场景kp=0.8, ki=502.002.0240.2954.87 kp=0.6, ki=253.554.7754.6349.73 kp=0.4, ki=103.283.2268.0878..46 kp=0.2, ki=54.523.6458.2260.42 不同故障位置场景故障设置在F11.142.5240.4918.19 故障设置在F21.462.9937.2027.49 故障设置在F42.933.7525.8133.24 故障设置在F53.253.3522.2832.95
由表1可知，在不同过渡电阻场景下，随着过渡电阻减小，柔直换流站暂态阶段短路电流衰减速度逐渐减小。由于现有方法难以准确地刻画暂态特性，随着暂态特征持续时间变长，计算误差逐渐增大，d轴最大误差达到38.80%，q轴最大误差达到39.59%；而所提方法在不同过渡电阻场景下的d轴最大误差达到4.11%，q轴最大误差达到4.00%，与现有方法相比，所提出的方法在dq轴的解析精度分别提高了34.69个百分点和35.59个百分点。
由于PI参数变化和线路阻抗变化也会影响暂态衰减速度，因此选取不同PI控制参数场景和不同故障位置场景对所提方法与现有方法的计算精度进行分析。分析结果表明，现有方法在两种场景下的d轴最大误差达到68.08%，q轴最大误差达到78.46%；而所提计算方法d轴最大误差达到4.52%，q轴最大误差达到4.77%，所提出的方法在dq轴的解析精度分别提高了63.56个百分点和73.69个百分点。
因此，通过测试不同场景下所提计算方法与现有计算方法的计算精度，结果表明现有计算方法在不同场景下的计算误差最大将达到78.46%，所提计算方法在不同场景下的计算误差均小于5%，能够精确地刻画柔直换流站侧的暂态特性。
本文研究了新能源及柔直换流站控制响应特性对柔直换流站短路电流的影响机理，推导并解析了计及新能源耦合特性的柔直换流站短路电流，并得到以下结论：
1）故障暂态期间两侧电力电子变流器的控制响应会导致dq轴电流发生耦合，现有的研究方法对该阶段进行了简化，但无法保证暂态阶段计算精度。
2）采用分区计算的思路解决了新能源控制响应对柔直换流站短路电流的耦合影响，并提出复数域数理法实现了柔直换流站控制响应引发的dq轴电流耦合的解耦。通过硬件在环实验验证了所提解析方法的有效性。实验结果表明所提方法在不同场景下的最大计算误差均小于5%。
附 录
附表1 仿真模型参数
App.Tab.1 The parameters of simulation model
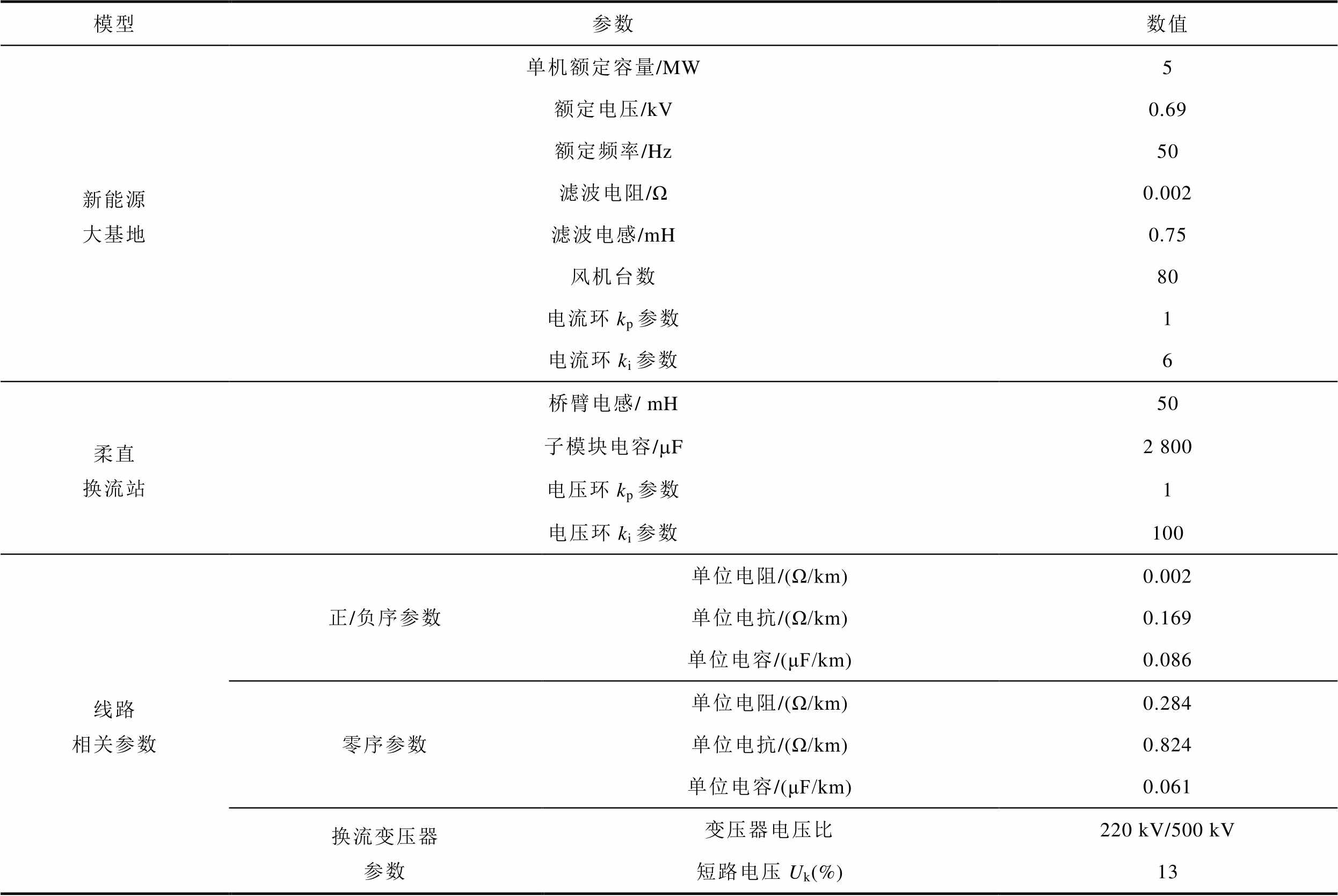
模型参数数值 新能源大基地单机额定容量/MW5 额定电压/kV0.69 额定频率/Hz50 滤波电阻/Ω0.002 滤波电感/mH0.75 风机台数80 电流环kp参数电流环ki参数16 柔直换流站桥臂电感/ mH50 子模块电容/mF2 800 电压环kp参数1 电压环ki参数100 线路相关参数正/负序参数单位电阻/(Ω/km)0.002 单位电抗/(Ω/km)0.169 单位电容/(μF/km)0.086 零序参数单位电阻/(Ω/km)0.284 单位电抗/(Ω/km)0.824 单位电容/(μF/km)0.061 换流变压器参数变压器电压比220 kV/500 kV 短路电压Uk(%)13
参考文献
[1] 蔡希鹏, 黄伟煌, 李桂源, 等. 大规模光伏集群经柔性直流构网送出的运行控制技术研究[J]. 中国电机工程学报, 2023, 43(22): 8734-8745.
Cai Xipeng, Huang Weihuang, Li Guiyuan, et al. Research on operation control strategy of large-scale photovoltaic cluster transmission via grid-forming VSC-HVDC[J]. Proceedings of the CSEE, 2023, 43(22): 8734-8745.
[2] 饶宏, 黄伟煌, 郭知非, 等. 柔性直流输电技术在大电网中的应用与实践[J]. 高电压技术, 2022, 48(9): 3347-3355.
Rao Hong, Huang Weihuang, Guo Zhifei, et al. Practical experience of VSC-HVDC transmission in large grid[J]. High Voltage Engineering, 2022, 48(9): 3347-3355.
[3] 郑涛, 李紫肖, 陈云飞, 等. 基于等效故障区段的柔性直流输电线路单端量保护方案[J]. 电工技术学报, 2025, 40(3): 771-785.
Zheng Tao, Li Zixiao, Chen Yunfei, et al. Single terminal protection scheme for flexible DC transmission lines based on equivalent fault section [J]. Transactions of China Electrotechnical Society, 2025, 40(3): 771-785.
[4] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[5] 郑涛, 马家璇, 吕文轩, 等. 基于暂态负序电流积聚量比值的海上风电交流汇集线路保护[J]. 电力系统自动化, 2023, 47(12): 137-144.
Zheng Tao, Ma Jiaxuan, Lü Wenxuan, et al. Protection for AC collection line of offshore wind power based on ratio of transient negative-sequence current accumulation[J]. Automation of Electric Power Systems, 2023, 47(12): 137-144.
[6] 林思齐, 熊永新, 姚伟, 等. 基于MATLAB/ Simulink的新一代电力系统动态仿真工具箱[J]. 电网技术, 2020, 44(11): 4077-4088.
Lin Siqi, Xiong Yongxin, Yao Wei, et al. MATLAB/Simulink-based dynamic simulation toolbox for new generation power system[J]. Power System Technology, 2020, 44(11): 4077-4088.
[7] 黄颂开, 徐晋, 汪可友, 等. 基于谐波状态空间模型的MMC解析仿真方法[J]. 中国电机工程学报, 2024, 44(15): 6110-6123.
Huang Songkai, Xu Jin, Wang Keyou, et al. MMC analytical simulation method based on harmonic state space model[J]. Proceedings of the CSEE, 2024, 44(15): 6110-6123.
[8] 许建中, 王乐, 武董一, 等. 采用子模块相关性坐标变换解耦的混合模块化多电平换流器可靠性建模[J]. 电工技术学报, 2019, 34(18): 3821-3830.
Xu Jianzhong, Wang Le, Wu Dongyi, et al. Reliability modeling of hybrid modular multilevel converter using coordinate transformation based on decoupled sub-module correlations[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3821-3830.
[9] 刘若平, 屠卿瑞, 李银红, 等. 适用于交流保护整定的MMC-HVDC接入母线故障等效模型[J]. 电力系统自动化, 2019, 43(18): 145-153.
Liu Ruoping, Tu Qingrui, Li Yinhong, et al. Equivalent model of MMC-HVDC for AC protection setting with access bus fault[J]. Automation of Electric Power Systems, 2019, 43(18): 145-153.
[10] 许建中, 徐义良, 赵禹辰, 等. 多类型子模块MMC电磁暂态通用建模和实现方法[J]. 电网技术, 2019, 43(6): 2039-2048.
Xu Jianzhong, Xu Yiliang, Zhao Yuchen, et al. Generalized electromagnetic transient equivalent modeling and implementation of MMC with arbitrary multi-type submodule structures[J]. Power System Technology, 2019, 43(6): 2039-2048.
[11] 王洁聪, 刘崇茹, 徐东旭, 等. 基于RTDS的模块化多电平换流器闭锁状态仿真建模方法[J]. 电工技术学报, 2018, 33(16): 3686-3696.
Wang Jiecong, Liu Chongru, Xu Dongxu, et al. Simulation method of modular multilevel converter blocking state based on RTDS[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3686-3696.
[12] Chiniforoosh S, Jatskevich J, Yazdani A, et al. Definitions and applications of dynamic average models for analysis of power systems[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2655-2669.
[13] 贾科, 刘浅, 杨彬, 等. 计及锁相环动态特性的逆变电源故障暂态电流解析[J]. 电网技术, 2021, 45(11): 4242-4250.
Jia Ke, Liu Qian, Yang Bin, et al. Transient fault current analysis of the inverter-interfaced renewable energy sources considering the dynamic characteristicsof the phase-locked loop[J]. Power System Technology, 2021, 45(11): 4242-4250.
[14] 郑黎明, 贾科, 毕天姝, 等. 海上风电接入柔直系统交流侧故障特征及对保护的影响分析[J]. 电力系统保护与控制, 2021, 49(20): 20-32.
Zheng Liming, Jia Ke, Bi Tianshu, et al. AC-side fault analysis of a VSC-HVDC transmission system connected to offshore wind farms and the impact on protection[J]. Power System Protection and Control, 2021, 49(20): 20-32.
[15] 余越, 王聪博, 沙兆义, 等. 基于矩阵突变特征的风电经柔直送出交流线路保护[J]. 中国电机工程学报, 2023, 43(14): 5441-5450.
Yu Yue, Wang Congbo, Sha Zhaoyi, et al. AC transmission line protection for wind farms integrated with VSC-HVDC system based on matrix mutation characteristics[J]. Proceedings of the CSEE, 2023, 43(14): 5441-5450.
[16] Zheng Liming, Jia Ke, Yang Bin, et al. Singular value decomposition based pilot protection for transmission lines with converters on both ends[J]. IEEE Transactions on Power Delivery, 2022, 37(4): 2728-2737.
[17] 曹润彬, 聂少雄, 芮智, 等. 对称单极柔性直流输电系统不对称交流故障解析模型[J]. 南方电网技术, 2021, 15(8): 48-54, 70.
Cao Runbin, Nie Shaoxiong, Rui Zhi, et al. Analytical modeling of asymmetric AC faults in symmetric single-pole MMC-HVDC power transmission system [J]. Southern Power System Technology, 2021, 15(8): 48-54, 70.
[18] 秦继朔, 贾科, 杨彬, 等. 风电多端柔性直流并网系统交流送出线故障短路电流解析[J]. 电力系统自动化, 2021, 45(14): 47-55.
Qin Jishuo, Jia Ke, Yang Bin, et al. Short-circuit fault current analysis of AC transmission line of MMC-MTDC system for wind power intergration[J]. Automation of Electric Power Systems, 2021, 45(14): 47-55.
[19] 温志文, 刘昊霖, 贾科, 等. 风电接入海上换流站的交流汇集出线高速保护[J]. 中国电机工程学报, 2024, 44(12): 4775-4788.
Wen Zhiwen, Liu Haolin, Jia Ke, et al. High speed protection of AC convergence outgoing lines for wind power integration into offshore converter stations [J]. Proceedings of the CSEE, 2024, 44(12): 4775-4788.
[20] 孔祥平, 张哲, 尹项根, 等. 含逆变型分布式电源的电网故障电流特性与故障分析方法研究[J]. 中国电机工程学报, 2013, 33(34): 65-74, 13.
Kong Xiangping, Zhang Zhe, Yin Xianggen, et al. Study on fault current characteristics and fault analysis method of power grid with inverter interfaced distributed generation[J]. Proceedings of the CSEE, 2013, 33(34): 65-74, 13.
[21] 孔祥平, 袁宇波, 黄浩声, 等. 光伏电源故障电流的暂态特征及其影响因素[J]. 电网技术, 2015, 39(9): 2444-2449.
Kong Xiangping, Yuan Yubo, Huang Haosheng, et al. Fault current transient features and its related impact factors of PV generator[J]. Power System Technology, 2015, 39(9): 2444-2449.
[22] 国家市场监督管理总局, 国家标准化管理委员会. 风电场接入电力系统技术规定第1部分：陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[23] 郑涛, 章若竹, 吕文轩, 等. 故障主动控制下计及分布电容影响的海上风电交流汇集线路时域距离保护[J]. 电工技术学报, 2025, 40(1): 122-138.
Zheng Tao, Zhang Ruozhu, Lü Wenxuan, et al. Time domain distance protection for offshore wind power AC collection lines considering the influence of distributed capacitance under active fault control[J]. Transactions of China Electrotechnical Society, 2025, 40(1): 122-138.
[24] 贾科, 董学正, 毕天姝, 等. 接入换流站的新能源交流汇集系统低电压穿越方法[J]. 电网技术, 2024, 48(6): 2385-2393.
Jia Ke, Dong Xuezheng, Bi Tianshu, et al. Low-voltage ride-through method of AC collection system for renewable energy connected to converter station[J]. Power System Technology, 2024, 48(6): 2385-2393.
[25] Hou Junjie, Gao Qiangqiang, Song Guobing, et al. Research on fault control strategy for two terminal weak feed systems considering step-down V/f control[C]//2023 IEEE International Conference on Advanced Power System Automation and Protection (APAP), Xuchang, China, 2023: 150-155.
[26] Huo Junda, Wang Yi, Meng Jianhui, et al. Current limiting control strategy of grid-forming MMC based on adaptive virtual impedance[C]//2023 5th International Conference on Power and Energy Technology (ICPET), Tianjin, China, 2023: 508-513.
Analysis of Short-Circuit Current in Flexible DC Converter Stations Considering the Coupling Characteristics of New Energy Sources
Abstract The new energy base is transmitted through flexible direct transmission, and the short-circuit current provided by the flexible direct converter station is affected by the new energy and its own control characteristics, resulting in complex coupling characteristics, making it difficult for existing methods to ensure the accuracy of transient characteristic calculations.
The existing methods for analyzing the fault characteristics of flexible DC converter stations can be divided into two categories: electromagnetic transient fine simulation modeling and time-frequency equation calculation methods.
In the analytical method based on electromagnetic transient fine simulation modeling, it mainly constructs a fine simulation model in simulation software, and uses the fine model to simulate and analyze the fault characteristics of flexible DC converter stations in different scenarios. However, this type of method essentially uses complex electrical and control characteristics for iterative calculation. Therefore, the time cost required for its calculation is high, and it is not suitable for large-scale research. Moreover, it is difficult to obtain analytical solutions using this type of method, and the mathematical model of the short-circuit current provided by flexible DC converter stations cannot be obtained, lacking theoretical analysis. At the same time, this method cannot simulate and analyze all fault scenarios, making it difficult to provide reference for protection principles.
Compared with the method of electromagnetic transient fine simulation modeling, the time-frequency equation calculation method can obtain analytical solutions for flexible DC converter stations. However, existing methods of this kind cannot accurately characterize the short-circuit current characteristics of flexible DC converter stations during the transient phase.
In response to the problem of difficulty in analyzing the short-circuit current provided by the flexible DC converter station at the transmission end when the AC transmission line fails in the flexible DC transmission system of the new energy base, this paper proposes a short-circuit current analysis method for the flexible DC converter station at the transmission end that takes into account the coupling characteristics of new energy. The decoupling calculation of the interaction between the flexible DC converter station and the new energy base is achieved by adopting the idea of partition calculation. Based on complex domain mathematical methods, the dq axis component of the flexible DC converter station is decoupled for the calculation and control response process, and the time-domain analytical formula for the short-circuit current of the flexible DC converter station is obtained, which solves the problem that existing methods are difficult to analyze the transient characteristics of the flexible DC converter station. The calculation of the proposed method is verified on the hardware in the loop experimental platform. The accuracy shows that the maximum error of the proposed algorithm is less than 5% in different fault scenarios, Verified the effectiveness of the proposed method.
Keywords：Renewable energy, flexible direct converter station, short circuit current, decoupling of complex fields
中图分类号：TM615
DOI: 10.19595/j.cnki.1000-6753.tces.241122
国家电网公司科技项目资助（SGZJDK00FZJS2250083）。
收稿日期 2024-06-29
改稿日期 2024-09-04
刘昊霖 男，1999年生，博士研究生，研究方向为新能源大基地并网系统保护与控制。
E-mail：871100549@qq.com
贾 科 男，1986年生，教授，博士生导师，研究方向为新能源电力系统保护与控制、新型配电网故障定位与系统恢复控制等。
E-mail：ke.jia@ncepu.edu.cn（通信作者）
（编辑 赫 蕾）