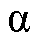 、
、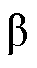 轴分量分别经过SOGI,利用其输出正交和滤波特性,实现对输入电压信号的正交分相和谐波抑制;然后经PNSC计算得到电压正、负序分量;最后由SRF-PLL将正序电压
轴分量分别经过SOGI,利用其输出正交和滤波特性,实现对输入电压信号的正交分相和谐波抑制;然后经PNSC计算得到电压正、负序分量;最后由SRF-PLL将正序电压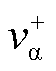 及
及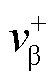 经Park变换至同步旋转坐标系,再通过闭环控制使
经Park变换至同步旋转坐标系,再通过闭环控制使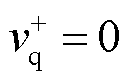 完成锁相,实现dq参考坐标系下相位和电网频率的检测[20]。
完成锁相,实现dq参考坐标系下相位和电网频率的检测[20]。摘要 当新能源并网系统发生故障时会出现电压跌落并伴随相位跳变,负荷不均衡分配及不对称故障等因素会进一步产生三相电压幅值、相位不平衡的问题,并导致双二阶广义积分器锁相环(DSOGI-PLL)产生锁相偏差,从而对新能源输出特性造成影响。该文首先通过分析电网电压不平衡影响电压正序相位跳变机理,同时考虑DSOGI-PLL动态过程影响,基于小信号模型推导得到锁相偏差动态解析式,并根据波形拟合法得到适用于大相位跳变下的锁相偏差解析式;然后以光伏并网逆变器为例,分析PLL动态响应过程对逆变器输出特性的影响,推导了逆变器出口故障电流解析表达式,进而提出了基于锁相偏差动态解析式的相位补偿方案,实现了PLL在动态追踪过程中对公共耦合点(PCC)电压相位的快速同步追踪;最后基于Matlab/Simulink仿真验证了所提相位补偿方案的有效性。
关键词:新能源并网系统 锁相环 锁相偏差 故障特性 相位补偿
在能源短缺的严峻形势下,为保障能源供给、加快能源转型,世界各国正加大对光伏、风电等可再生能源的开发和利用[1]。随着“双碳”战略目标的提出,我国新能源发电技术水平与装机容量不断提高[2]。截至2023年底,全国的新能源装机容量已达到15亿kW,进入跃升发展的全新阶段[3]。
大量电力电子设备的接入会影响电压的稳定性,新能源并网系统需要相应的控制策略与手段来调控电压[4]。通常采用锁相环(Phase-Locked Loop, PLL)实现对电网电压频率、相位等信号的跟踪,确保新能源侧与网侧的同步性[5]。同步参考坐标系锁相环(Synchronous Reference Frame PLL, SRF-PLL)因其结构简单而被广泛应用,但由于有限的抗干扰能力,SRF-PLL在系统电网电压不平衡或存在谐波情况下的性能显著下降。为此,文献[6]对传统的SRF-PLL进行改进,提出基于双二阶广义积分器的锁相环(Double Second-Order Generalized Integrator PLL, DSOGI-PLL)。DSOGI-PLL可以实现正负序分离,并在一定程度上抑制谐波分量[7],在电网电压不平衡及系统中谐波含量较低的情况下,能够准确、即时地跟踪公共耦合点(Point ofCommon Coupling, PCC)的正序电压相位信号,实现逆变器出口侧与网侧相位的同步。但在高渗透率分布式新能源的影响下,电网表现出低短路比的弱电网特性[8]。此时,电网发生故障后,由于PCC电压发生相位跳变,锁相环的动态响应过程会对新能源输出特性造成影响,进而引发电网稳定性问题[9]。
近年来,已有较多研究围绕锁相环动态响应过程对并网逆变器输出特性的影响进行理论分析,并提出相应的改进策略。文献[10-12]计及锁相环的动态响应特性,分析了PLL的锁相偏差对光伏并网系统故障电流解析计算的影响。其中,文献[10]通过分析逆变器输出故障电流中二次谐波产生机理,推导得到二次谐波解析表达式,并指出光伏并网系统中产生的二次谐波对变压器保护可靠性的负面影响。文献[11]考虑锁相环动态响应特性,建立了相应的故障电流解析计算模型,明确了故障电流的谐波特性。文献[12]为提高变压器差动保护可靠性提出了基于记忆电压和限幅系数的锁相环改进方案。但是,以上文献全部基于对称故障下锁相环的动态响应特性进行分析,未对电网电压不平衡的情况展开研究。而考虑负荷不均衡分配及不对称故障等因素,电网电压幅值、相位不平衡的情况不容忽视[13]。
考虑电网电压不平衡的情况,文献[14-18]对新能源并网系统故障特性进行分析,并建立解析计算模型或提出改进方案。文献[14-15]针对逆变器控制策略进行分析,但未考虑锁相环动态响应特性的影响。文献[16]提出一种计及PLL输出动态特性的逆变电源故障暂态电流解析方法,能够精准刻画逆变器故障暂态电流的欠阻尼特征及振荡衰减特性。但是,其理论推导基于在稳态点处对非线性环节线性化处理的线性模型(即小信号模型),并运用线性理论分析电网稳定性问题[17],而这种分析方法仅适用于电网发生小扰动的情况,在大扰动下所求并网逆变器输出表达式的解析精度难以保证。文献[18]通过对三相电压不平衡与锁相误差内在关系的理论推导,提出一种锁相误差的补偿方法以实现精准锁相。但其理论推导及其补偿仅针对电压相位进行分析,忽略了电网电压幅值不平衡对锁相偏差及逆变器输出特性的影响[19]。
综上所述,本文首先通过分析电网电压不平衡影响电压正序相位跳变机理[18],并考虑DSOGI-PLL动态过程影响,基于小信号模型推导得到锁相偏差动态解析式,且基于波形拟合法得到适用于大相位跳变下的锁相偏差解析式;然后以光伏并网逆变器为例,分析PLL动态响应过程对逆变器输出特性的影响,推导了逆变器出口故障电流解析表达式,进而提出了基于锁相偏差动态解析式的相位补偿方案,实现了PLL在动态追踪过程中对PCC电压相位的快速同步追踪;最后通过仿真验证了所提改进方案的有效性。
基于DSOGI-PLL能够在电网电压不平衡条件下准确地获取电网电压正、负序分量的相位、幅值及频率信息,其基本组成单元包括三部分:基于二阶广义积分器的正交信号发生器(Second-Order Generalized Integrator, SOGI)、正/负序分量计算模块(Positive/Negative-Sequence Calculator, PNSC),以及SRF-PLL,其结构框图如图1所示。
DSOGI-PLL的锁相原理如下:首先将输入DSOGI-PLL的三相电压通过Clark变换转换至两相静止坐标系,再将所得电网电压的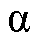 、
、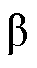 轴分量分别经过SOGI,利用其输出正交和滤波特性,实现对输入电压信号的正交分相和谐波抑制;然后经PNSC计算得到电压正、负序分量;最后由SRF-PLL将正序电压
轴分量分别经过SOGI,利用其输出正交和滤波特性,实现对输入电压信号的正交分相和谐波抑制;然后经PNSC计算得到电压正、负序分量;最后由SRF-PLL将正序电压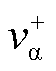 及
及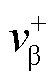 经Park变换至同步旋转坐标系,再通过闭环控制使
经Park变换至同步旋转坐标系,再通过闭环控制使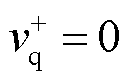 完成锁相,实现dq参考坐标系下相位和电网频率的检测[20]。
完成锁相,实现dq参考坐标系下相位和电网频率的检测[20]。
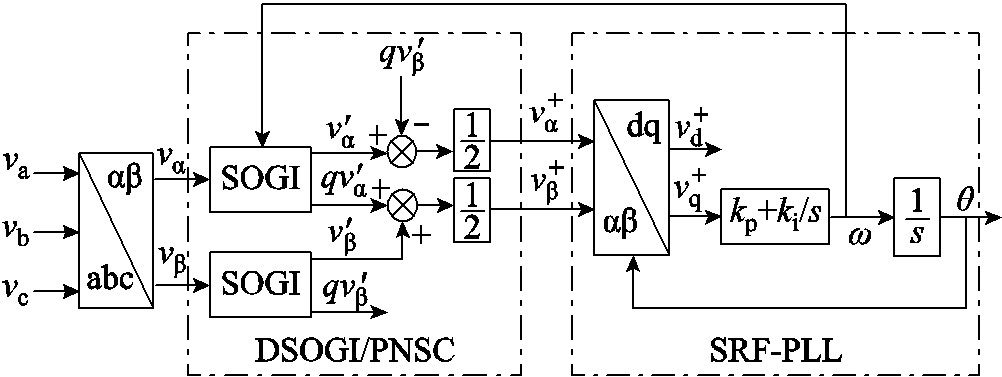
图1 DSOGI-PLL结构框图
Fig.1 Schematic diagram of DSOGI-PLL
传统的SRF-PLL小信号模型如图2所示[21]。图中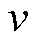 为输入并网电压幅值,
为输入并网电压幅值,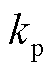 、
、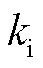 分别为PI环节的比例和积分系数,
分别为PI环节的比例和积分系数,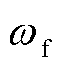 为基波角频率,
为基波角频率,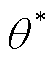 和
和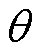 分别为SRF-PLL小信号模型的输入和输出电压相位,
分别为SRF-PLL小信号模型的输入和输出电压相位,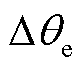 为PLL的锁相偏差。
为PLL的锁相偏差。
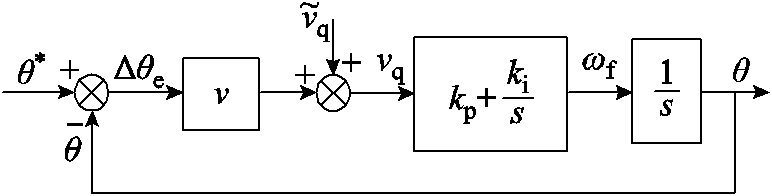
图2 SRF-PLL小信号模型
Fig.2 Small signal model of SRF-PLL
DSOGI/PNSC的结构在dq坐标系下可等效为低通滤波器(Low-Pass Filter, LPF)与陷波器级联[22]。考虑PLL带宽较小,可以忽略陷波器带来的影响[23-24],因此结合SRF-PLL的小信号模型,得到DSOGI-PLL的等效小信号模型如图3所示。图中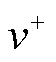 为输入正序并网电压幅值,
为输入正序并网电压幅值,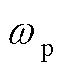 为前置低通滤波器的截止频率。
为前置低通滤波器的截止频率。
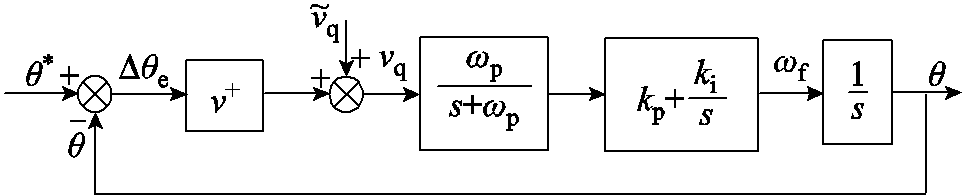
图3 DSOGI-PLL小信号模型
Fig.3 Small signal model of DSOGI-PLL
由图3可得系统的闭环传递函数为
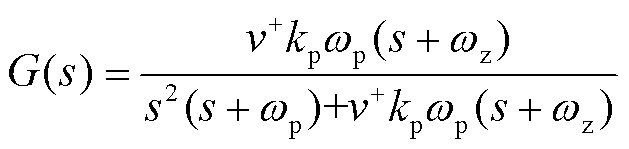 (1)
(1)
式中,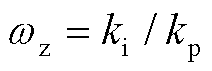 。
。
当新能源并网系统发生故障,外部网络拓扑结构发生相应改变,会导致PCC电压跌落并伴随相位跳变,且负荷不均衡分配及不对称故障等因素会造成三相电压幅值、相位不平衡的现象。三相不平衡下PCC正序电压相位的跳变信息难以确定,进而导致DSOGI-PLL无法进行同步精准锁相,因此亟须对三相不平衡下正序电压相位跳变的机理进行分析。
现有研究基于三相电压不平衡分量推导得到正序电压相位跳变角表达式[18],但其推导以故障前后A相电压相位不变为前提,仅考虑了BC两相电压的相位跳变,且忽略了电压幅值不平衡对正序电压相位跳变的影响。本文在上述方法的基础上进一步改进,综合分析三相电压幅值、相位不平衡下的正序电压相位跳变机理,推导得到了更具有普遍意义的PCC正序电压相位跳变角的精确表达式,具体阐述如下。
假设A相电压初相位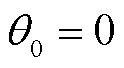 ,则故障后的三相不平衡电压可表示为
,则故障后的三相不平衡电压可表示为
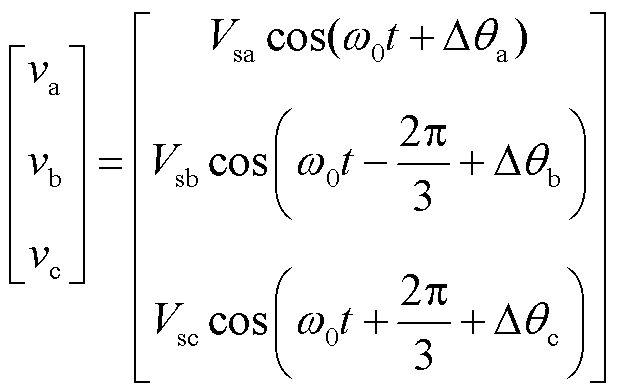 (2)
(2)
式中,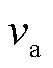 、
、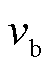 、
、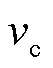 分别为A相、B相及C相电压;
分别为A相、B相及C相电压;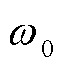 为电压基频角频率;
为电压基频角频率;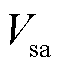 、
、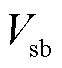 、
、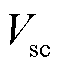 及
及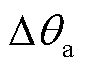 、
、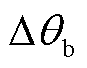 、
、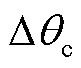 分别为故障后各相的电压幅值及相位跳变角。
分别为故障后各相的电压幅值及相位跳变角。
将式(2)所示不平衡三相电压作为DSOGI-PLL的输入信号,经Clark变换得到两相静止坐标系下的不平衡电压分量为
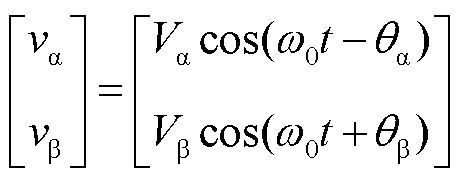 (3)
(3)
式中,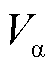 、
、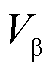 及
及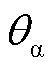 、
、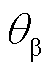 为关于
为关于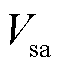 、
、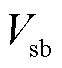 、
、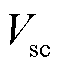 及
及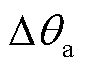 、
、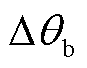 、
、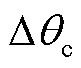 的函数,其表达式见附录中式(A1)。
的函数,其表达式见附录中式(A1)。
将电网电压的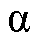 、
、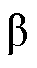 轴分量经SOGI正交分相,再经PNSC计算可得电压正序分量。该电压正序分量经过Park变换可得
轴分量经SOGI正交分相,再经PNSC计算可得电压正序分量。该电压正序分量经过Park变换可得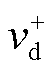 及
及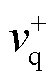 分别为
分别为
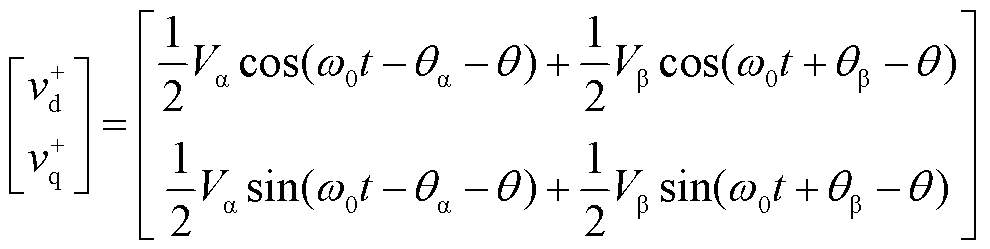 (4)
(4)
式中,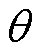 为d轴与a轴的夹角。故障前后PCC电压相位变化示意图如图4所示,将故障后PCC正序电压的相位跳变角记为
为d轴与a轴的夹角。故障前后PCC电压相位变化示意图如图4所示,将故障后PCC正序电压的相位跳变角记为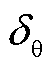 ,则有
,则有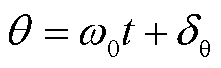 。
。
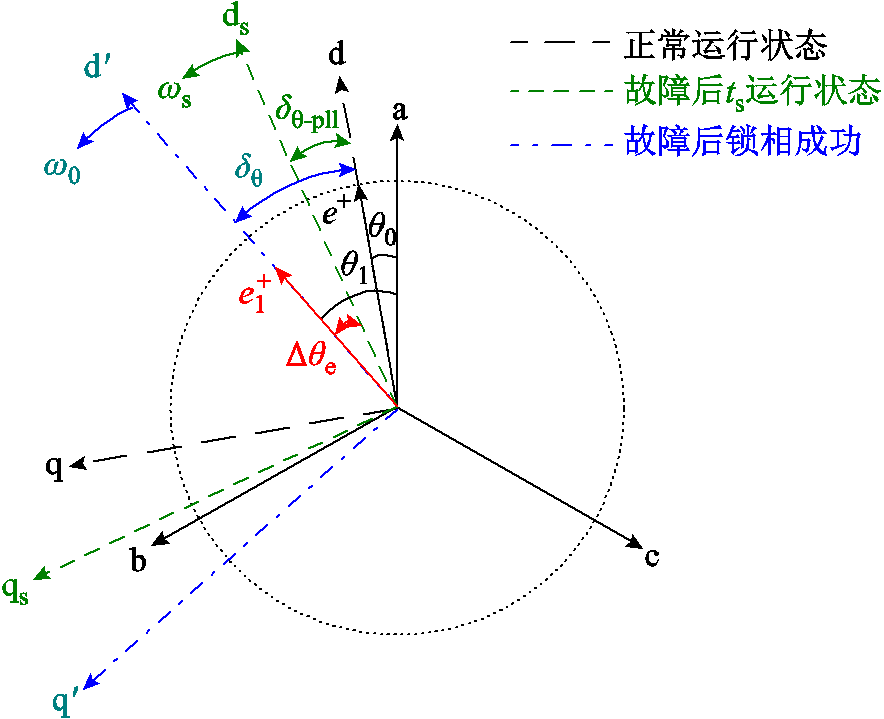
图4 故障前后PCC电压相位变化示意图
Fig.4 Schematic diagram of the change in phase angle of PCC voltage before and after the fault
根据锁相的稳态关系,令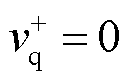 得到三相不平衡下的
得到三相不平衡下的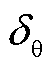 为
为
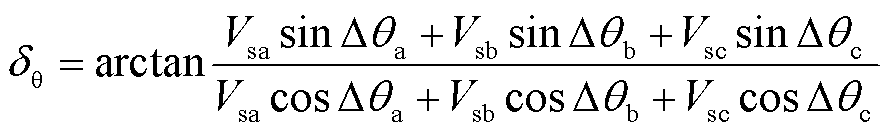 (5)
(5)
由式(5)可知,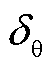 受三相不平衡电压幅值及相位跳变角共同影响,二者缺一不可。
受三相不平衡电压幅值及相位跳变角共同影响,二者缺一不可。
当新能源并网系统发生故障时,PCC电压跌落并伴随相位跳变,PLL对PCC电压相位的跟踪存在一个短时动态过程,产生锁相偏差。锁相偏差通过影响Park变换与反变换过程影响逆变器输出特性,导致逆变器输出电流中含有较大谐波分量[23]。
以系统发生不对称故障为例进行分析,故障前后PCC正序电压相位变化示意图如图4所示。故障时刻,PCC正序电压相位发生阶跃变化,即由图4中的d轴跃变为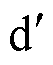 轴[11]。图4中
轴[11]。图4中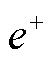 与
与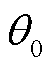 分别为并网系统正常运行时PCC的正序电压及其相位;
分别为并网系统正常运行时PCC的正序电压及其相位;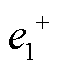 与
与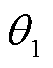 分别为并网系统发生不对称故障后PCC的正序电压及其相位;
分别为并网系统发生不对称故障后PCC的正序电压及其相位;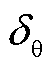 为故障前后的d轴相位差,即
为故障前后的d轴相位差,即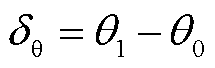 ;将PCC电压相位跳变后,在PLL动态追踪过程中已追踪到的相位定义为PLL动态相位追踪角,记作δθ-pll;将PLL动态追踪过程中尚未追踪到的相位定义为PLL的锁相偏差,记作
;将PCC电压相位跳变后,在PLL动态追踪过程中已追踪到的相位定义为PLL动态相位追踪角,记作δθ-pll;将PLL动态追踪过程中尚未追踪到的相位定义为PLL的锁相偏差,记作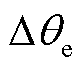 。由图4可知,
。由图4可知,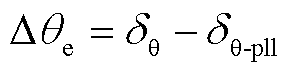 。
。
故障前后DSOGI-PLL小信号模型输入相位的变化量即为正序电压相位跳变角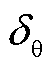 ,则正序电压相位阶跃信号为
,则正序电压相位阶跃信号为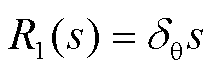 。根据式(1)所示基于小信号模型的PLL闭环传递函数,将其与
。根据式(1)所示基于小信号模型的PLL闭环传递函数,将其与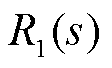 相乘得到锁相系统的频域响应为
相乘得到锁相系统的频域响应为
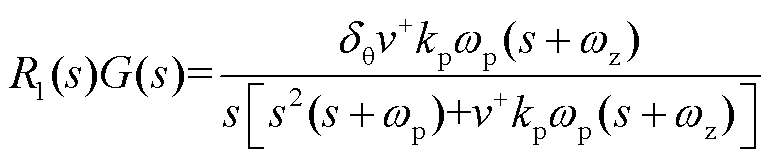 (6)
(6)
故障前后DSOGI-PLL小信号模型输出相位的变化量即为PLL动态相位追踪角δθ-pll。因此,将锁相系统频域响应式(6)反变换至时域可得 δθ-pll为
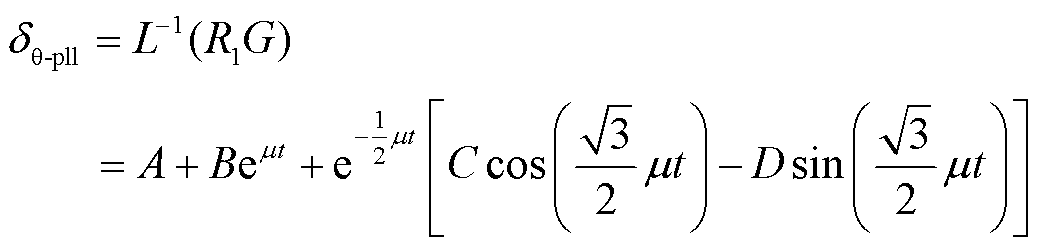 (7)
(7)
式中,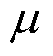 及A、B、C、D的具体表达式见式(A2)。
及A、B、C、D的具体表达式见式(A2)。
根据图4及式(7)可得锁相偏差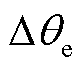 为
为
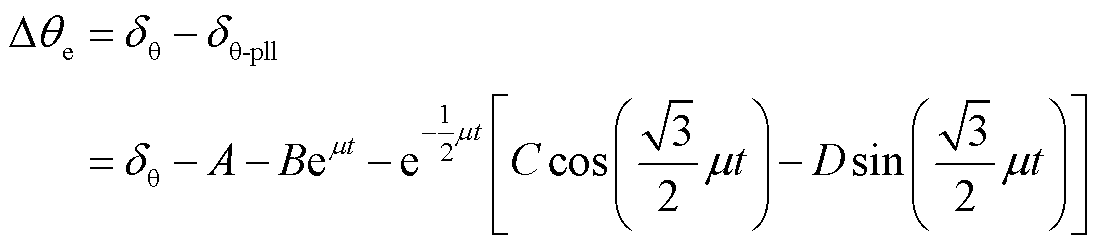 (8)
(8)
由式(8)可得,锁相偏差受PCC正序电压幅值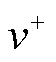 、PI环节参数
、PI环节参数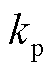 、
、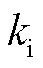 和
和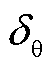 等多种因素共同影响。锁相偏差
等多种因素共同影响。锁相偏差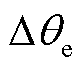 随时间变化,在故障发生时刻
随时间变化,在故障发生时刻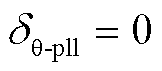 且
且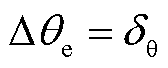 ,即故障发生瞬间,锁相偏差与正序电压相位跳变角相等。而随着时间的推移,锁相偏差逐渐减小,直至PLL追踪到正序电压相位跳变角为止,此时
,即故障发生瞬间,锁相偏差与正序电压相位跳变角相等。而随着时间的推移,锁相偏差逐渐减小,直至PLL追踪到正序电压相位跳变角为止,此时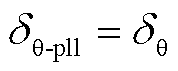 且
且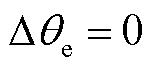 。当系统发生三相对称故障时,系统中无负序、零序分量,PCC正序电压相位跳变角
。当系统发生三相对称故障时,系统中无负序、零序分量,PCC正序电压相位跳变角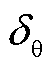 在数值上与A相电压相位跳变角
在数值上与A相电压相位跳变角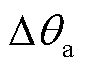 相等,此时锁相偏差动态解析式(8)仍适用,仅需将其中的PCC正序电压幅值
相等,此时锁相偏差动态解析式(8)仍适用,仅需将其中的PCC正序电压幅值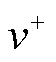 调整为A相电压
调整为A相电压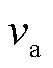 ,且将PCC正序电压相位跳变角
,且将PCC正序电压相位跳变角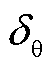 调整为A相电压相位跳变角
调整为A相电压相位跳变角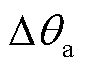 。
。
然而,前文所得锁相偏差动态解析式是基于小信号模型推导得出,而小信号模型成立的前提是稳态相位误差较小[25],即
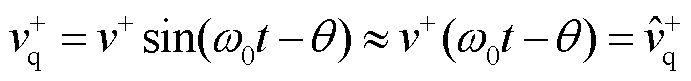 (9)
(9)
因此式(8)仅适用于网侧电压在故障前后相位跳变角较小的情况。利用百分比误差公式计算锁相偏差动态解析式适用范围,如式(10)所示。
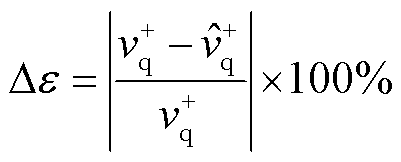 (10)
(10)
当平均绝对百分比误差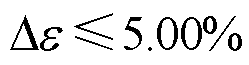 时,认为泰勒公式简化后小信号模型的锁相结果在误差允许范围内[26]。此时,将式(8)、式(9)代入式(10),可得
时,认为泰勒公式简化后小信号模型的锁相结果在误差允许范围内[26]。此时,将式(8)、式(9)代入式(10),可得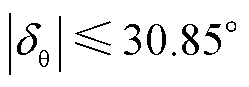 。当网侧电压相位在故障前后变化较大(
。当网侧电压相位在故障前后变化较大(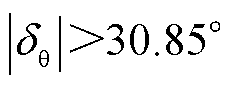 )时,由于难以对非线性环节进行线性化处理,小信号模型不再适用。
)时,由于难以对非线性环节进行线性化处理,小信号模型不再适用。
由2.2节分析可知,当PCC电压相位在故障前后变化较大(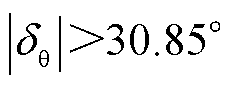 )时,小信号模型不再适用。对此,本文采用波形拟合的方法进行分析。工程实际中一般利用最小二乘法进行波形拟合,即通过最小化误差的平方和寻找已知数集的最佳函数匹配[27]。因此本文在故障前后相位跳变角较大的情况下,基于最小二乘法,通过离线采样大量数据构造函数,对PLL动态相位追踪角波形进行拟合。
)时,小信号模型不再适用。对此,本文采用波形拟合的方法进行分析。工程实际中一般利用最小二乘法进行波形拟合,即通过最小化误差的平方和寻找已知数集的最佳函数匹配[27]。因此本文在故障前后相位跳变角较大的情况下,基于最小二乘法,通过离线采样大量数据构造函数,对PLL动态相位追踪角波形进行拟合。
以t=0.5 s时发生三相对称故障,故障后PCC电压相位较故障前滞后75°的情况为例,对PLL动态相位追踪角δθ-pll的波形进行处理与分析,波形对比如图5所示。如图5a所示,将系统稳态运行时的PCC相位波形与故障后PLL输出相位波形相减,得到PLL动态相位追踪角相反数的波形,如图5b中红色实线所示。由于相位锯齿波的波形特征及锁相偏差的存在会导致PLL动态相位追踪角波形出现离群点,进而影响拟合函数解析式的求取,故首先对PLL动态相位追踪角实际波形进行数据预处理,利用线性插值法去掉相位差波形的离群点,如图5b中蓝色虚线所示,再进行波形拟合。
当拟合函数波形与预处理波形的方均根误差(Root-Mean-Square Error, RMSE)达到0.05以下,认为拟合优度较高[28-29]。以故障时刻为零时刻时的拟合函数波形与预处理波形对比图如图5c所示,相应的拟合波形函数表达式如式(11)所示,其表达式为指数函数和三角函数的线性组合。
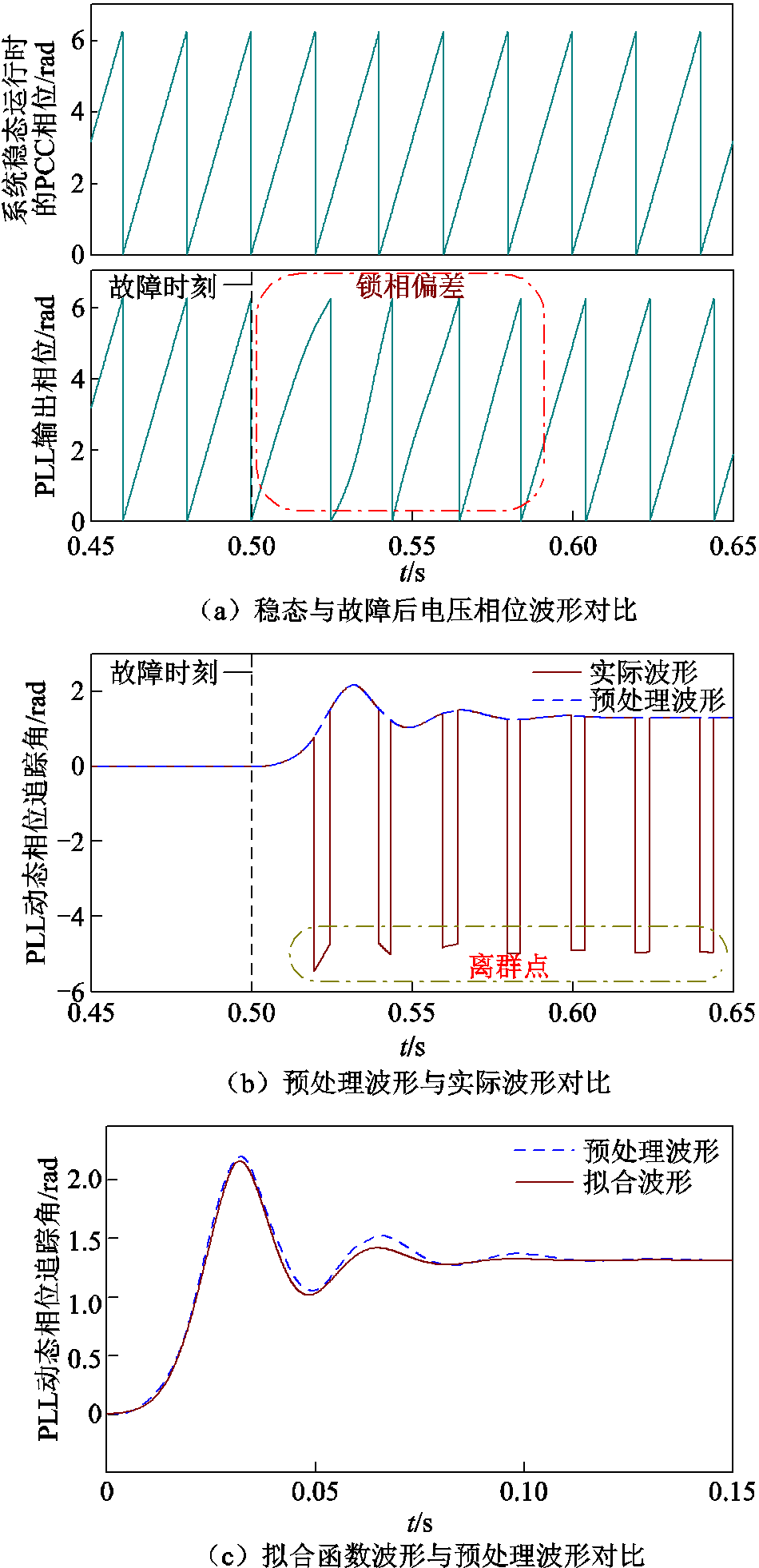
图5 波形对比
Fig.5 Waveforms comparison
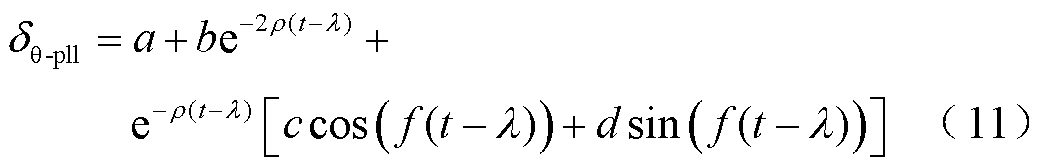
式中,系数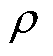 、
、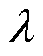 、
、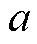 、
、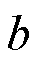 、c、
、c、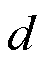 、f的具体数值见式(A3)。
、f的具体数值见式(A3)。
此时,锁相偏差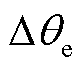 的拟合波形函数表达式为
的拟合波形函数表达式为
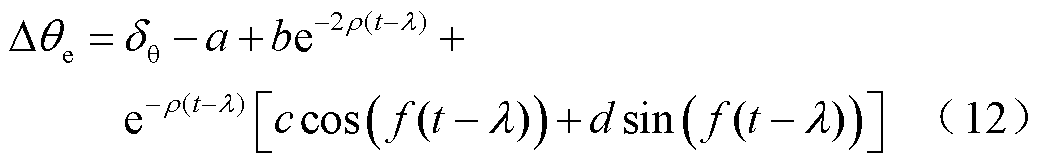
光伏并网系统的结构控制图如图6所示。光伏电源经逆变器并网,控制系统中的PLL跟踪PCC电压相位。光伏并网逆变器在正常运行时采用双闭环的电网电压定向矢量控制技术[30]。图6中KVP、KVI和KiP、KiI分别为外环电压和内环电流PI调节器的比例、积分系数;Ts为滞后时间常数;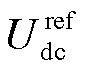 为直流母线电压参考值。
为直流母线电压参考值。
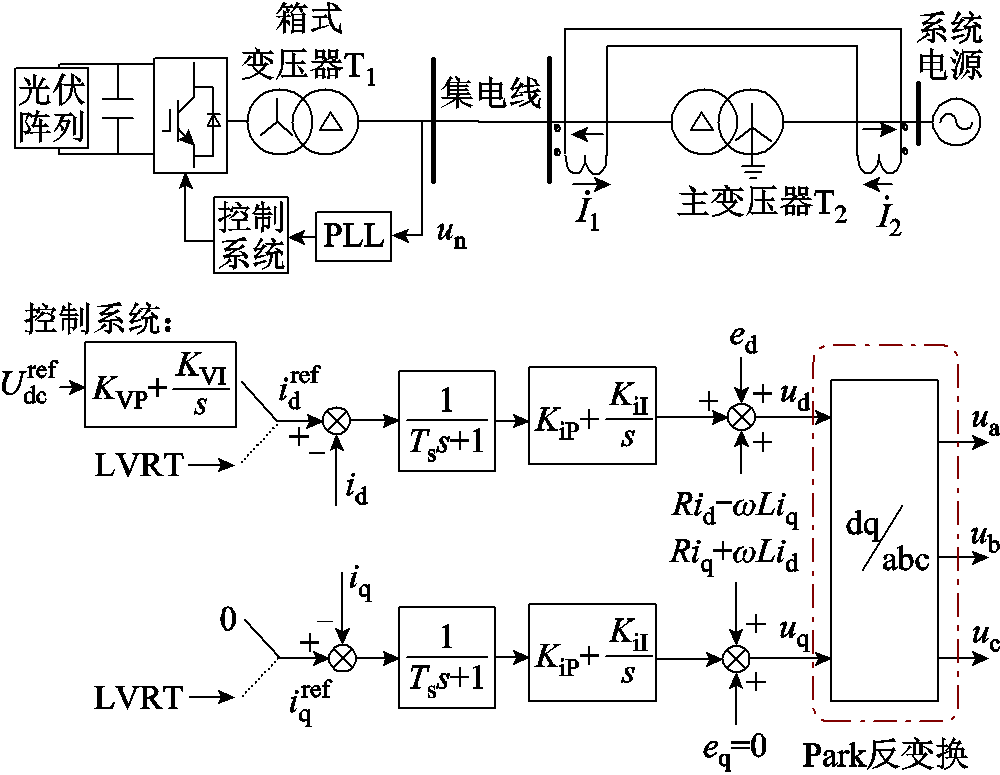
图6 光伏并网系统结构控制图
Fig.6 Grid-connected structure diagram of PV
Park反变换矩阵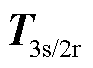 为
为
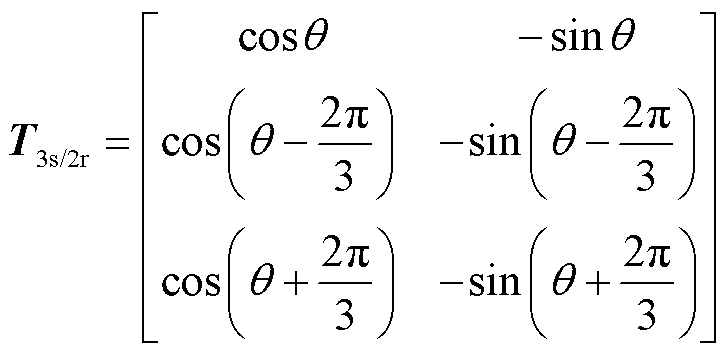 (13)
(13)
系统正常运行时,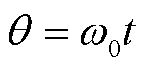 ;当系统故障后,电压发生相位跳变,此时
;当系统故障后,电压发生相位跳变,此时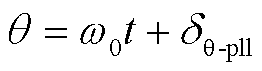 。
。
考虑PLL动态响应过程的影响,将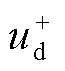 、
、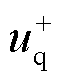 经Park反变换后得到三相静止坐标系下的逆变器输出电压,并利用泰勒展开公式进行化简得
经Park反变换后得到三相静止坐标系下的逆变器输出电压,并利用泰勒展开公式进行化简得
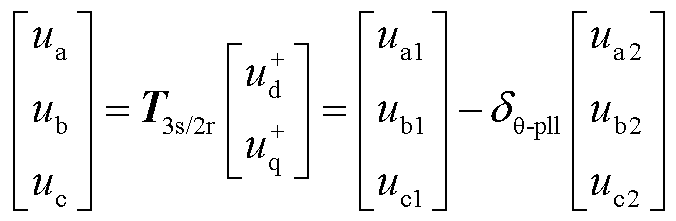 (14)
(14)
式中,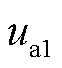 、
、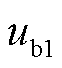 、
、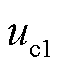 及
及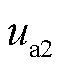 、
、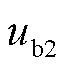 、
、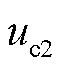 的具体表达式见式(A4)。由式(14)可知,PLL动态响应过程通过影响Park反变换过程改变光伏输出特性。
的具体表达式见式(A4)。由式(14)可知,PLL动态响应过程通过影响Park反变换过程改变光伏输出特性。
以A相为例对式(14)展开得
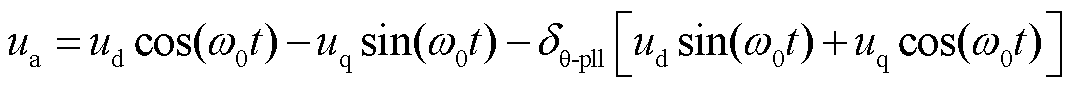 (15)
(15)
当网侧电压相位在故障前后变化较小时,将基于小信号模型推导得出的式(7)代入式(15),可得考虑PLL动态响应过程影响下逆变器输出电压表达式为
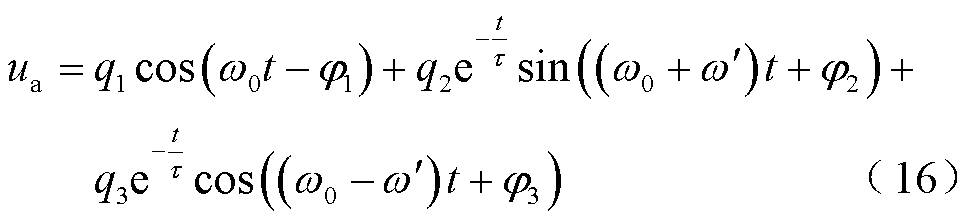
式中,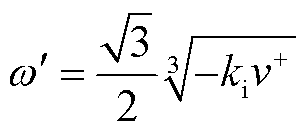 ,可得非整数次角频率
,可得非整数次角频率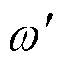 受PI环节参数
受PI环节参数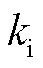 、正序电压幅值跌落程度
、正序电压幅值跌落程度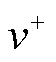 共同影响。此外,
共同影响。此外,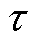 、
、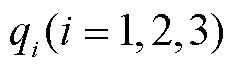 、
、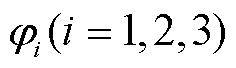 的具体表达式见式(A5)。
的具体表达式见式(A5)。
逆变器端口电压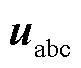 与输出电流
与输出电流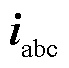 之间的关系表达式为
之间的关系表达式为
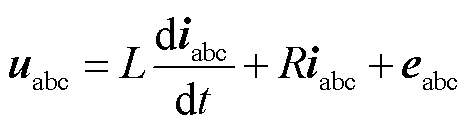 (17)
(17)
式中,L为逆变器端口到PCC点之间的等效电感;R为逆变器端口到PCC点之间的等效电阻;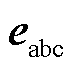 为PCC点电压。
为PCC点电压。
以A相为例对此线性微分方程进行求解,并代入相关变量,即可得到故障电流的解析表达式为
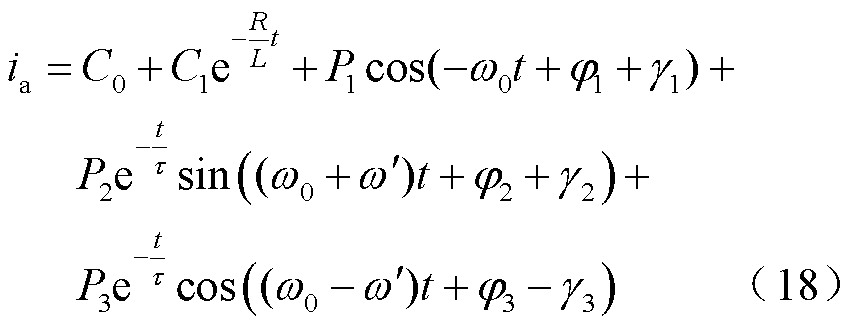
式中,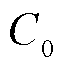 、
、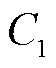 为微分方程通解中的待定系数,
为微分方程通解中的待定系数,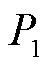 、
、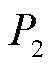 、
、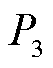 、
、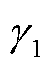 、
、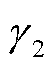 、
、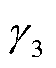 具体表达式见式(A6)。
具体表达式见式(A6)。
由2.3节分析可知,在故障后正序电压相位跳变角较大时,基于波形拟合所得PLL动态相位追踪角解析式为指数函数和三角函数的线性组合,与基于小信号模型所得解析式形式近似。同理可得,此时解析式中的非工频次分量会导致逆变器出口电压中存在非整数次频率分量,感应至输出电流即导致输出电流中谐波含量较高。
理想情况下故障电流只含基频分量,而当计及PLL动态响应过程的影响时,无论网侧电压相位在故障前后变化大小,逆变器输出电压除基频分量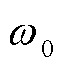 外,都含有
外,都含有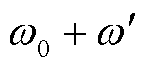 和
和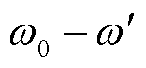 等非整数次频率分量。故障下PLL的动态响应过程作用于光伏逆变器控制系统会使输出电压中含有非整数次谐波,进而在输出电流中同样感应出非整数次谐波。在外部电网为弱电网的情况下,光伏输出电流在主变压器差动电流中占比较高,此时光伏输出电流波形畸变对差动保护的影响不可忽略。
等非整数次频率分量。故障下PLL的动态响应过程作用于光伏逆变器控制系统会使输出电压中含有非整数次谐波,进而在输出电流中同样感应出非整数次谐波。在外部电网为弱电网的情况下,光伏输出电流在主变压器差动电流中占比较高,此时光伏输出电流波形畸变对差动保护的影响不可忽略。
若要降低新能源并网系统逆变器输出电流中的谐波分量,维护电网的安全稳定运行,理想方案是利用故障后PCC的正序电压相位跳变角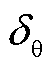 对锁相环进行补偿,即在故障发生的瞬间,将
对锁相环进行补偿,即在故障发生的瞬间,将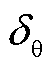 补偿至锁相环出口侧。此时,对PLL进行相位补偿的具体步骤为:首先,测得三相不平衡电压幅值和相位
补偿至锁相环出口侧。此时,对PLL进行相位补偿的具体步骤为:首先,测得三相不平衡电压幅值和相位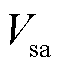 、
、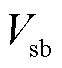 、
、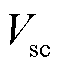 及
及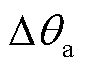 、
、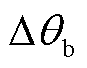 、
、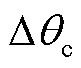 ;其次,将实测值代入正序电压相位跳变角表达式求解
;其次,将实测值代入正序电压相位跳变角表达式求解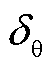 ;最后,将
;最后,将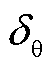 补偿至锁相环出口,消除PLL锁相偏差。
补偿至锁相环出口,消除PLL锁相偏差。
但是,三相不平衡电压幅值和相位的实测值一般利用快速傅里叶变换(Fast Fourier Transform, FFT)得到,而FFT由于整周期采样的特性,在故障后的第一个周期内为数据窗提取幅值和相位会存在一定的误差。因此要得到三相不平衡电压幅值和相位的精准实测值,至少需要一个周期的时间,即利用式(5)进行相位补偿这一方案无法在故障瞬间完成。以工频量为例,通过FFT实测三相不平衡电压幅值和相位的过程至少需要0.02 s。
由2.1节分析可知,锁相偏差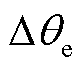 随时间动态变化,故障发生瞬间其数值与正序电压相位跳变角
随时间动态变化,故障发生瞬间其数值与正序电压相位跳变角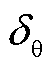 相等,随着时间的推移逐渐减小。在故障后0.02 s时,若对锁相环的相位补偿延用原思路,仍将
相等,随着时间的推移逐渐减小。在故障后0.02 s时,若对锁相环的相位补偿延用原思路,仍将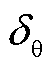 补偿至PLL出口,则会导致逆变器出口和PCC间的相位仍不相等。因此,如果相位补偿需要在0.02 s的延时下进行,就不应以
补偿至PLL出口,则会导致逆变器出口和PCC间的相位仍不相等。因此,如果相位补偿需要在0.02 s的延时下进行,就不应以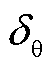 作为补偿量,应以此刻的锁相偏差实际值进行补偿,即相位补偿量
作为补偿量,应以此刻的锁相偏差实际值进行补偿,即相位补偿量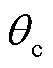 为
为
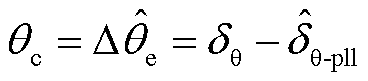 (19)
(19)
式中,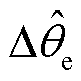 为故障后0.02 s的锁相偏差;
为故障后0.02 s的锁相偏差;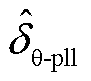 为故障后0.02 s的PLL动态相位追踪角。
为故障后0.02 s的PLL动态相位追踪角。
相位补偿环节中,锁相偏差具体数值的确定是关键。当网侧电压相位在故障前后变化较小(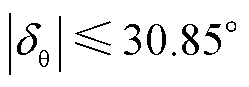 )时,锁相偏差动态解析式(即式(8))成立。该解析式中除并网电压幅值
)时,锁相偏差动态解析式(即式(8))成立。该解析式中除并网电压幅值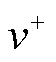 及正序电压相位跳变角
及正序电压相位跳变角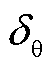 外,均为光伏并网系统正常运行时的已知量,而当
外,均为光伏并网系统正常运行时的已知量,而当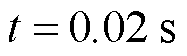 时,
时,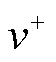 和
和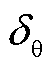 也将基于FFT及式(5)求得。因此当
也将基于FFT及式(5)求得。因此当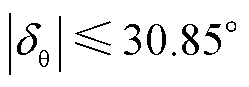 时,锁相偏差
时,锁相偏差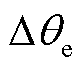 可以通过锁相偏差动态解析式得出。而由2.3节分析可知,当网侧电压相位在故障前后变化较大时,锁相偏差动态解析式无法直接求解,需要通过波形拟合的方式获得,因此无法通过解析式求得锁相偏差
可以通过锁相偏差动态解析式得出。而由2.3节分析可知,当网侧电压相位在故障前后变化较大时,锁相偏差动态解析式无法直接求解,需要通过波形拟合的方式获得,因此无法通过解析式求得锁相偏差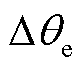 ,故本文采用波形拟合离线整定后进行在线匹配的方式来分析。
,故本文采用波形拟合离线整定后进行在线匹配的方式来分析。
离线整定是对系统中可能出现的几乎所有运行方式进行提前假设组合,根据不同的运行方式组合离线计算得出目标值[31]。由式(18)可知,要获得相对精确的锁相偏差,就需获取PLL动态相位追踪角δθ-pll的精准值。PLL动态相位追踪角的稳态值即为正序电压相位跳变角,因此可通过确定正序电压相位跳变角的变化范围对PLL动态相位追踪角的稳态值进行整定。经多组仿真验证,综合考虑故障位置、故障类型及并网点短路容量等对相位变化大小的影响,在本文研究场景下故障后PLL动态相位追踪角δθ-pll最大不会超过80°。此外,考虑测量误差和计算误差的影响,以及需要留有一定的裕度等因素,适当扩大离线整定的相位范围,因此将相位补偿方案中离线整定的相位范围限制在30°~90°。在误差允许的范围内,每隔10°进行一次波形拟合,得到30°~90°内所有δθ-pll的波形拟合函数。据此通过所求正序电压相位跳变角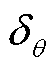 的具体数值进行在线匹配确定δθ-pll,并即时计算得到锁相偏差数值,对PLL进行相位补偿。
的具体数值进行在线匹配确定δθ-pll,并即时计算得到锁相偏差数值,对PLL进行相位补偿。
综上所述,只需对所有故障情况下的PLL动态相位追踪角δθ-pll进行离线整定,即可实时进行在线匹配,求得锁相偏差并进行相位补偿,进而满足实时控制要求。PLL动态相位追踪角的离线整定、在线匹配所需拟合函数集如图7所示。
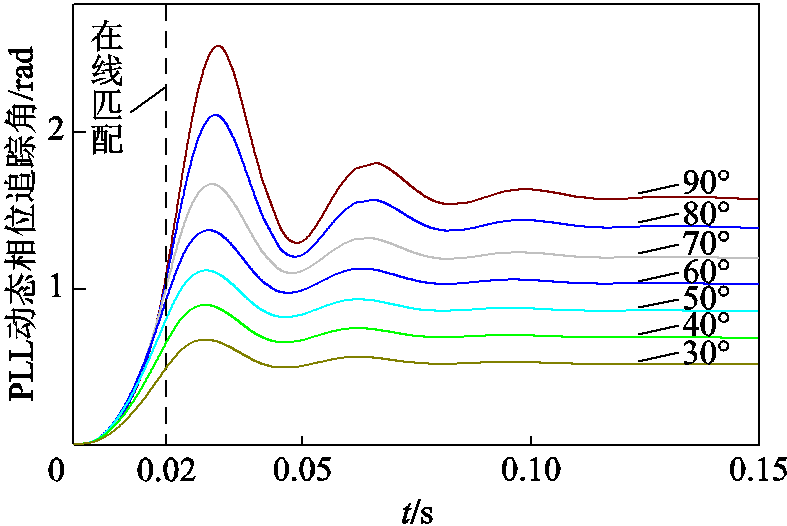
图7 离线整定、在线匹配所需拟合函数集
Fig.7 Offline tuning and online matching of the required set of fitting functions
根据3.2及3.3节分析,可以通过对DSOGI-PLL进行相位补偿来减小其锁相过程中的动态偏差。增设相位补偿环节的DSOGI-PLL控制图如图8所示,在PLL出口处加入相位补偿环节,补偿故障后PLL的锁相偏差,实现PLL在动态追踪过程中对PCC电压相位的快速同步追踪。新加入的相位补偿环节不影响原有的DSOGI-PLL特性,改进后的PLL不存在稳定性问题,可有效解决因三相电压不平衡造成的锁相失败及因锁相偏差导致的光伏输出电流波形畸变。
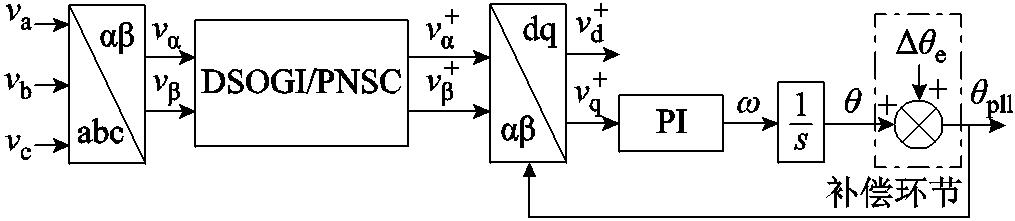
图8 增设相位补偿环节的DSOGI-PLL控制图
Fig.8 Control diagram of DSOGI-PLL with added phase angle compensation component
基于锁相偏差动态解析式的相位补偿方案如图9所示。首先,当检测到电网某相电压幅值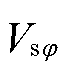 (φ=a, b,c)跌落到门槛值
(φ=a, b,c)跌落到门槛值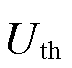 以下时,判定系统出现电压跌落或三相电压不平衡的情况。根据国家标准GB/T 12325—2008《电能质量供电电压偏差》,35 kV及以上供电电压正、负偏差绝对值之和不超过标称电压的10%,因此
以下时,判定系统出现电压跌落或三相电压不平衡的情况。根据国家标准GB/T 12325—2008《电能质量供电电压偏差》,35 kV及以上供电电压正、负偏差绝对值之和不超过标称电压的10%,因此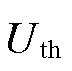 取0.9。其次,以检测到的电压跌落或电压三相不平衡开始时间点为故障时刻
取0.9。其次,以检测到的电压跌落或电压三相不平衡开始时间点为故障时刻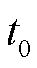 ,经一个周期的采样后由FFT得到三相不平衡电压幅值和相位跳变角
,经一个周期的采样后由FFT得到三相不平衡电压幅值和相位跳变角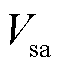 、
、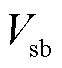 、
、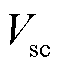 及
及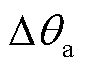 、
、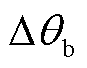 、
、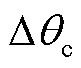 ,并将实测值代入正序电压相位跳变角表达式求解
,并将实测值代入正序电压相位跳变角表达式求解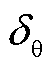 。然后,由所得
。然后,由所得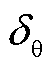 数值大小判断选取锁相偏差动态解析式或是利用拟合函数进行离线整定在线匹配,即时得到此时的锁相偏差
数值大小判断选取锁相偏差动态解析式或是利用拟合函数进行离线整定在线匹配,即时得到此时的锁相偏差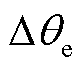 。最后,在PLL出口处利用所得
。最后,在PLL出口处利用所得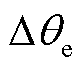 进行相位补偿。
进行相位补偿。
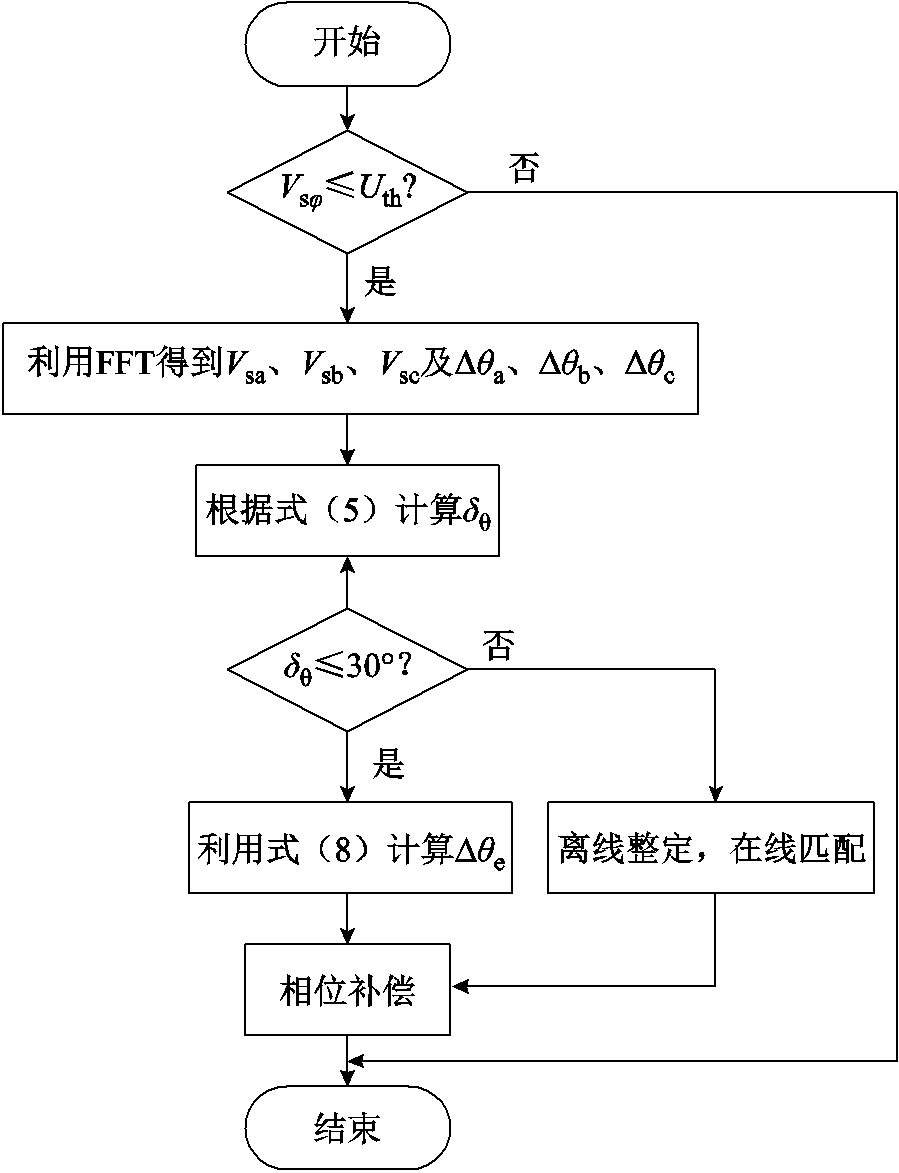
图9 基于锁相偏差动态解析式的相位补偿方案
Fig.9 Phase angle compensation scheme based on dynamic analytical formula of phase-locked deviation
本文所提相位补偿方案具有普适性。不论离线整定的相位范围以及PLL动态相位追踪角波形如何变化,只要能考虑到系统所有故障情况对PLL动态相位追踪角进行整定,得到相位补偿方案中完整的整定配置数据,都可以实现“离线整定、在线匹配”,进而实现本文所提出的相位补偿方案。
本文以光伏并网系统为例进行仿真分析,基于Matlab/Simulink仿真平台搭建如图10所示的光伏并网仿真模型,仿真不同故障类型下PLL的性能,验证相位补偿改进措施的有效性。锁相环采用DSOGI-PLL,仿真数据均取标幺值,基准容量SB=50 MV·A,基准电压取平均额定电压。仿真系统参数见表1。
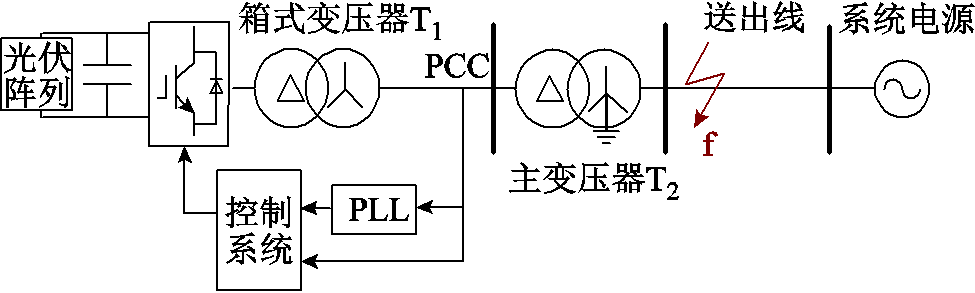
图10 光伏并网系统拓扑
Fig.10 Topology diagram of photovoltaic grid connected system
表1 仿真系统参数
Tab.1 Simulation system parameters

参数数值 光伏场站容量/MW50 集电线线正序阻抗/Ω0.6+j2 集电线零序阻抗/Ω1.5+j5.1 变压器T2联接方式YNd11 变压器T2电压比110/38.5 变压器T2额定容量/(MV·A)50
如图10所示,设置主变压器高压侧在t=0.5 s发生三相短路故障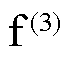 ,故障后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图11a和图11b所示。可以看出,三相短路故障期间PLL采集的输入电压发生约80%的电压跌落,PLL输出相位发生延迟,跟踪性能下降。PLL输出电流波形发生明显畸变,二次谐波含量高。图11a和图11b所示仿真结果与前文对锁相偏差动态解析与光伏输出特性分析相符。
,故障后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图11a和图11b所示。可以看出,三相短路故障期间PLL采集的输入电压发生约80%的电压跌落,PLL输出相位发生延迟,跟踪性能下降。PLL输出电流波形发生明显畸变,二次谐波含量高。图11a和图11b所示仿真结果与前文对锁相偏差动态解析与光伏输出特性分析相符。
在上述故障条件下,基于3.4节提出的相位补偿方案对PLL进行相位补偿。故障后经0.02 s的采样得到A相电压相位跳变角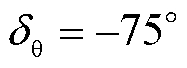 ,此时
,此时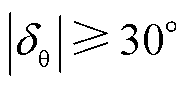 ,采用波形拟合进行函数在线匹配,得到
,采用波形拟合进行函数在线匹配,得到
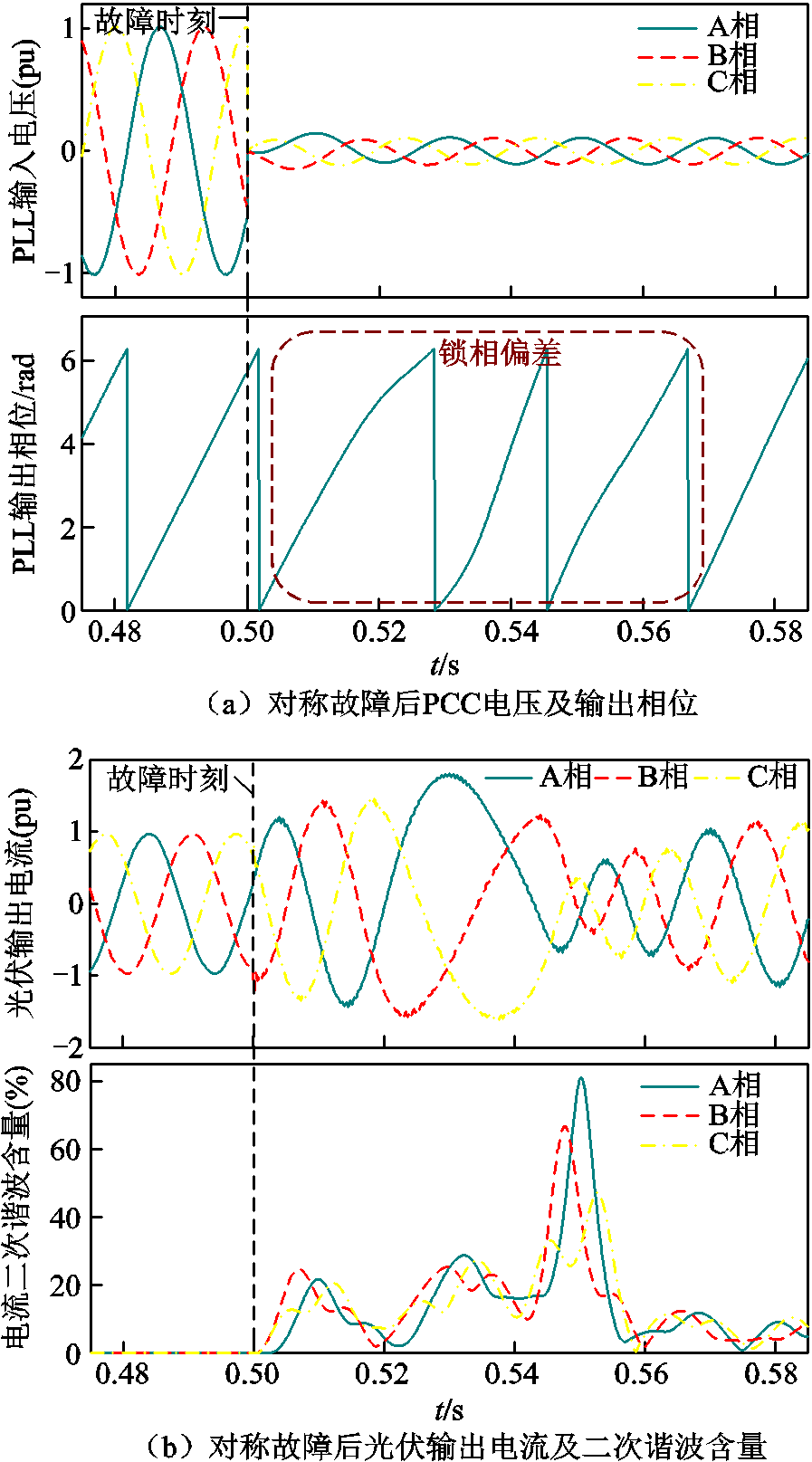
图11 对称故障后PCC电压及相位、光伏输出电流及谐波
Fig.11 PCC voltage and phase angle, photovoltaic output current and harmonic diagram after symmetry fault
PLL动态相位追踪角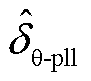 的相反数为39.06°,因此
的相反数为39.06°,因此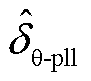 的实际值为-39.06°,可得
的实际值为-39.06°,可得
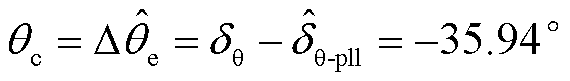 (20)
(20)
当t=0.52 s时将 补偿至PLL出口处,得到相位补偿后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图12a和图12b所示。可以看出,相位补偿后PLL输出相位不再有跟踪延迟,输出电流的频率维持在50 Hz左右,波形不再有明显畸变,且电流中的二次谐波含量降低。图12a和图12b所示仿真结果验证了相位补偿方案的有效性。
补偿至PLL出口处,得到相位补偿后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图12a和图12b所示。可以看出,相位补偿后PLL输出相位不再有跟踪延迟,输出电流的频率维持在50 Hz左右,波形不再有明显畸变,且电流中的二次谐波含量降低。图12a和图12b所示仿真结果验证了相位补偿方案的有效性。
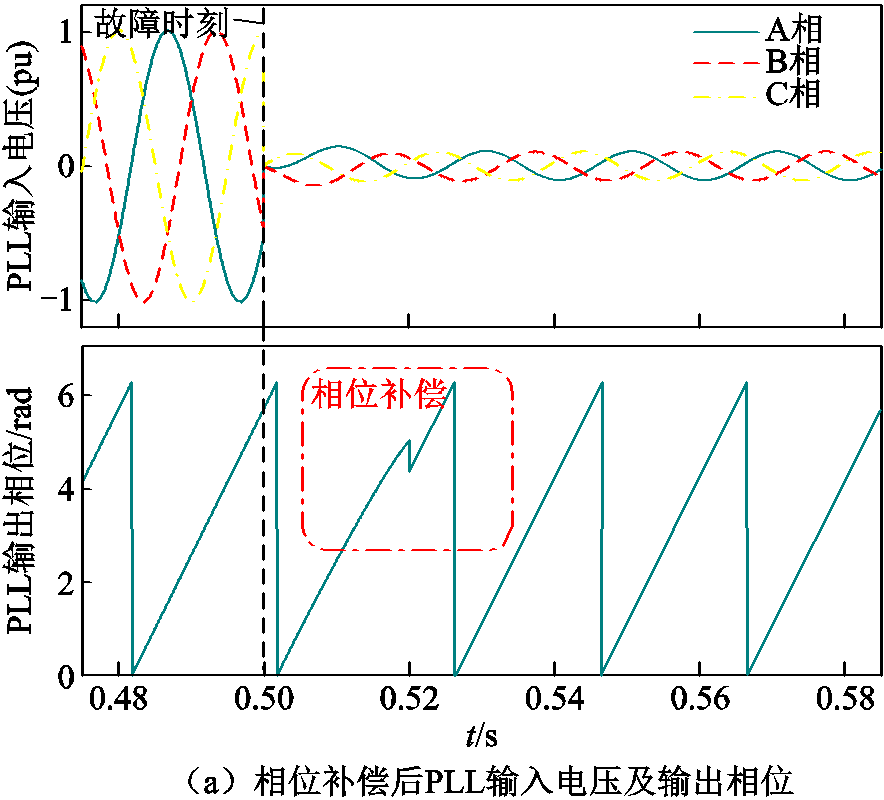
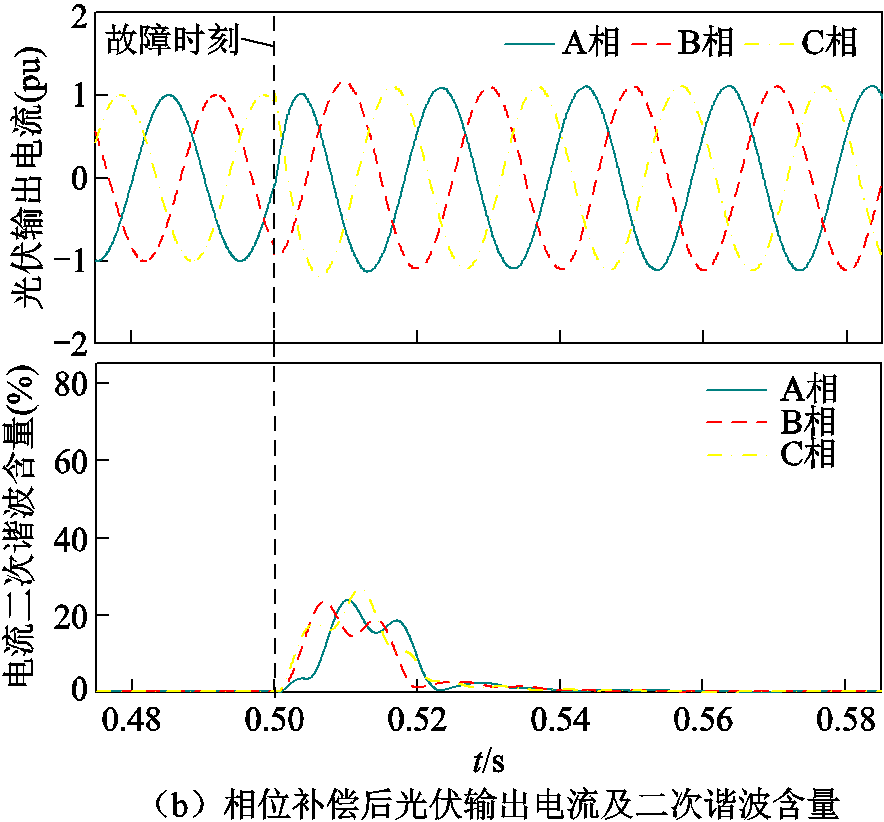
图12 对图11所示故障相位补偿后PCC电压及相位、光伏输出电流及谐波
Fig.12 PCC voltage and phase angle, photovoltaic output current and harmonic diagram after fault phase angle compensation shown in Fig.11
如图10所示,以主变压器高压侧在t=0.5 s发生BC两相接地故障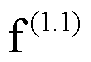 为例进行不对称故障下PLL性能及相位补偿的验证。故障后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图13a和图13b所示。可以看出,BC两相接地短路故障期间PLL输入电压发生不同程度的电压跌落,电压幅值与相位三相不平衡。PLL输出相位发生延迟,PLL输出电流波形由于负序抑制仅发生不明显畸变,电流中二次谐波含量在故障后升高。图13a和图13b所示仿真结果与前文对锁相偏差动态解析与光伏输出特性分析相符。
为例进行不对称故障下PLL性能及相位补偿的验证。故障后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图13a和图13b所示。可以看出,BC两相接地短路故障期间PLL输入电压发生不同程度的电压跌落,电压幅值与相位三相不平衡。PLL输出相位发生延迟,PLL输出电流波形由于负序抑制仅发生不明显畸变,电流中二次谐波含量在故障后升高。图13a和图13b所示仿真结果与前文对锁相偏差动态解析与光伏输出特性分析相符。
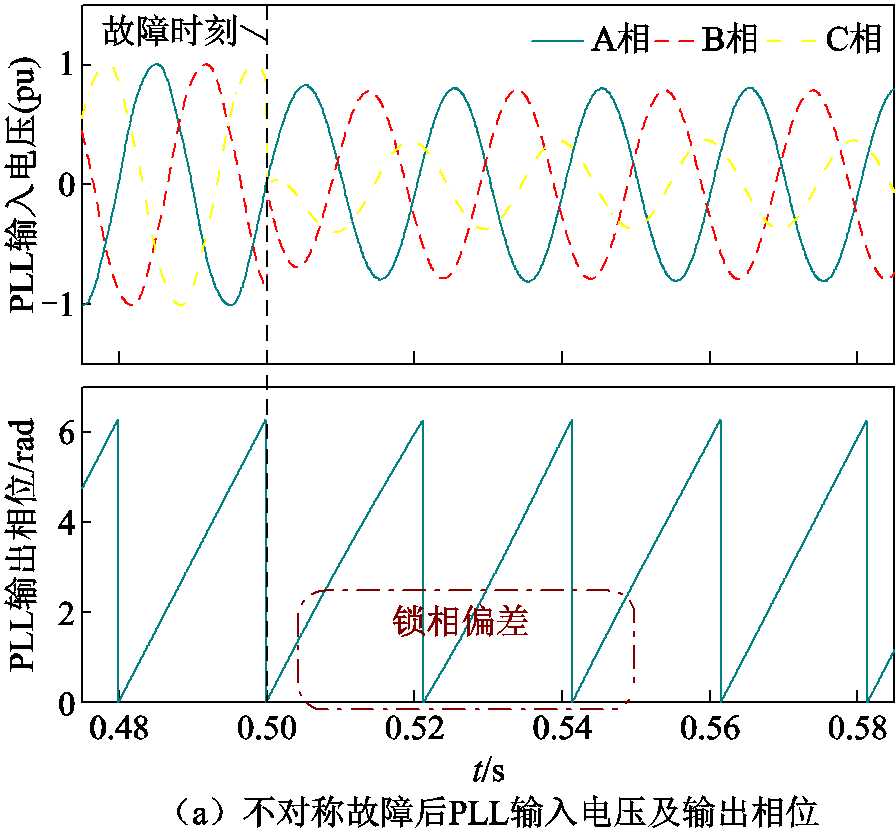
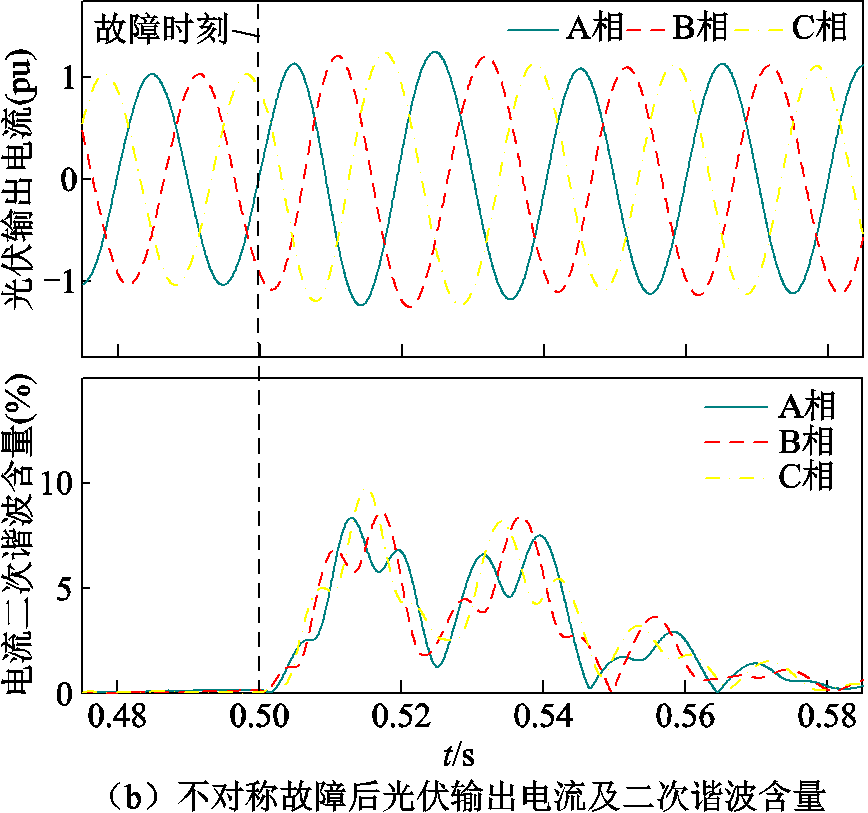
图13 不对称故障后PCC电压及相位、光伏输出电流及谐波
Fig.13 PCC voltage and phase angle, photovoltaic output current and harmonic diagram after asymmetrical fault
在上述故障条件下,基于3.4节提出的相位补偿方案对PLL进行相位补偿。故障后经0.02 s的采样由式(5)计算得到正序电压相位跳变角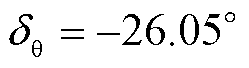 ,此时
,此时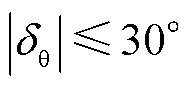 ,采用锁相偏差动态解析式求解锁相偏差,可得t=0.52 s时的锁相偏差为
,采用锁相偏差动态解析式求解锁相偏差,可得t=0.52 s时的锁相偏差为
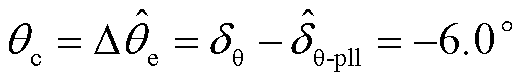 (21)
(21)
当t=0.52 s时将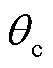 补偿至PLL出口处,得到相位补偿后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图14a和图14b所示。可以看出,相位补偿后PLL输出相位不再有跟踪延迟,输出电流的频率维持在50 Hz左右,波形不再有明显畸变,且电流中的二次谐波含量降低。图14a和图14b所示仿真结果验证了相位补偿方案的有效性。
补偿至PLL出口处,得到相位补偿后PLL输入电压及其相位、光伏输出电流及其二次谐波含量如图14a和图14b所示。可以看出,相位补偿后PLL输出相位不再有跟踪延迟,输出电流的频率维持在50 Hz左右,波形不再有明显畸变,且电流中的二次谐波含量降低。图14a和图14b所示仿真结果验证了相位补偿方案的有效性。
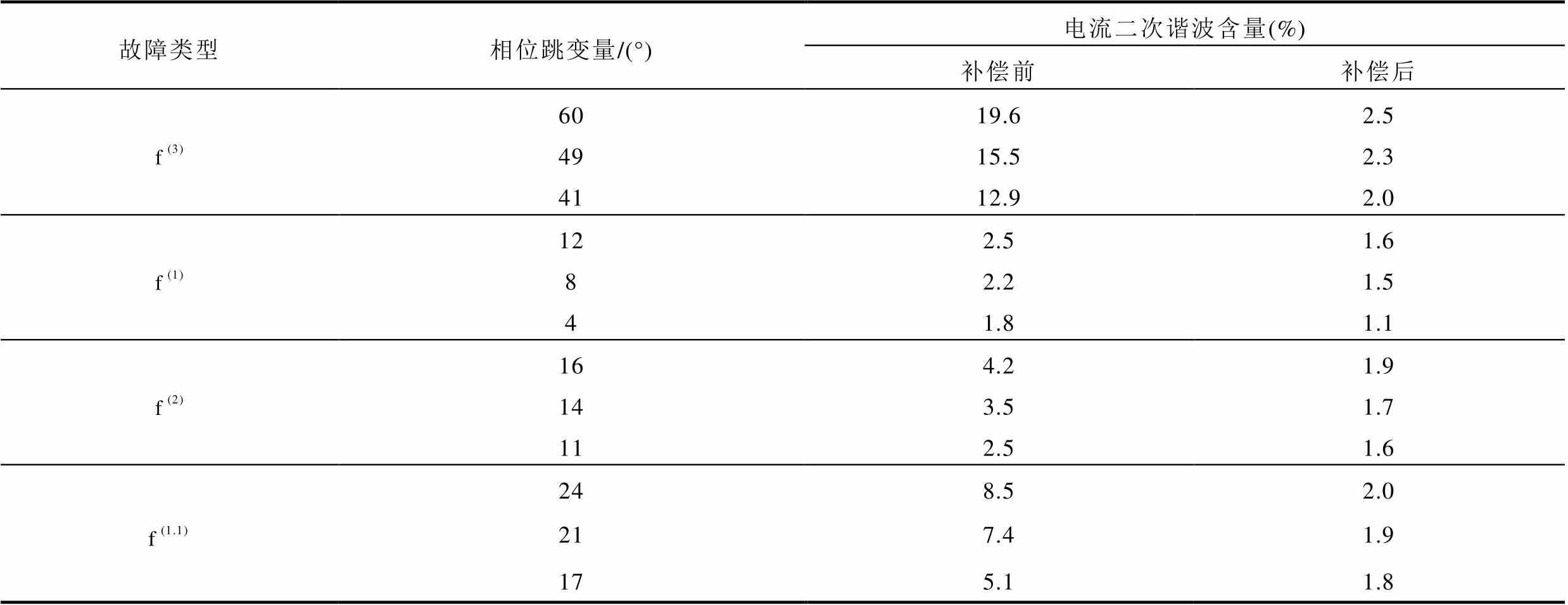
此外,本文设置了多组不同故障位置、故障类型、过渡电阻及并网点短路容量大小的故障进行比对,以故障两周波后逆变器输出电流的二次谐波含量(取三相中的含量最大值)为依据,验证不同故障情况下本文所提相位补偿方案的有效性和鲁棒性。设置系统运行至0.5 s时,在图10的f处分别发生三相短路故障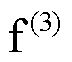 、单相接地短路故障
、单相接地短路故障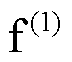 、两相短路故障
、两相短路故障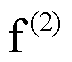 以及两相接地短路故障
以及两相接地短路故障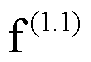 ,仿真结果见表2。由表2可知,在上述故障工况下,经相位补偿后光伏逆变器输出电流中的二次谐波含量均有不同程度的降低,降低程度受故障类型及正序电压相位跳变角大小等因素的影响。因此,本文所提基于锁相偏差动态解析式的相位补偿方案能有效减小锁相偏差,使逆变器输出电流中的谐波含量降低,有助于系统的安全稳定运行。
,仿真结果见表2。由表2可知,在上述故障工况下,经相位补偿后光伏逆变器输出电流中的二次谐波含量均有不同程度的降低,降低程度受故障类型及正序电压相位跳变角大小等因素的影响。因此,本文所提基于锁相偏差动态解析式的相位补偿方案能有效减小锁相偏差,使逆变器输出电流中的谐波含量降低,有助于系统的安全稳定运行。
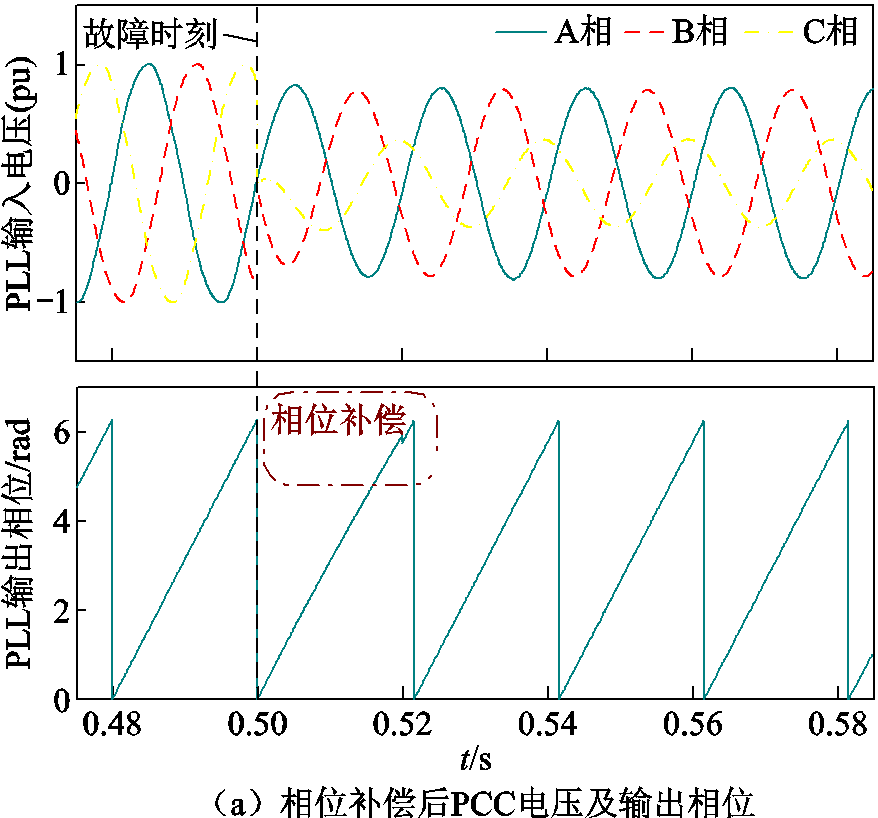
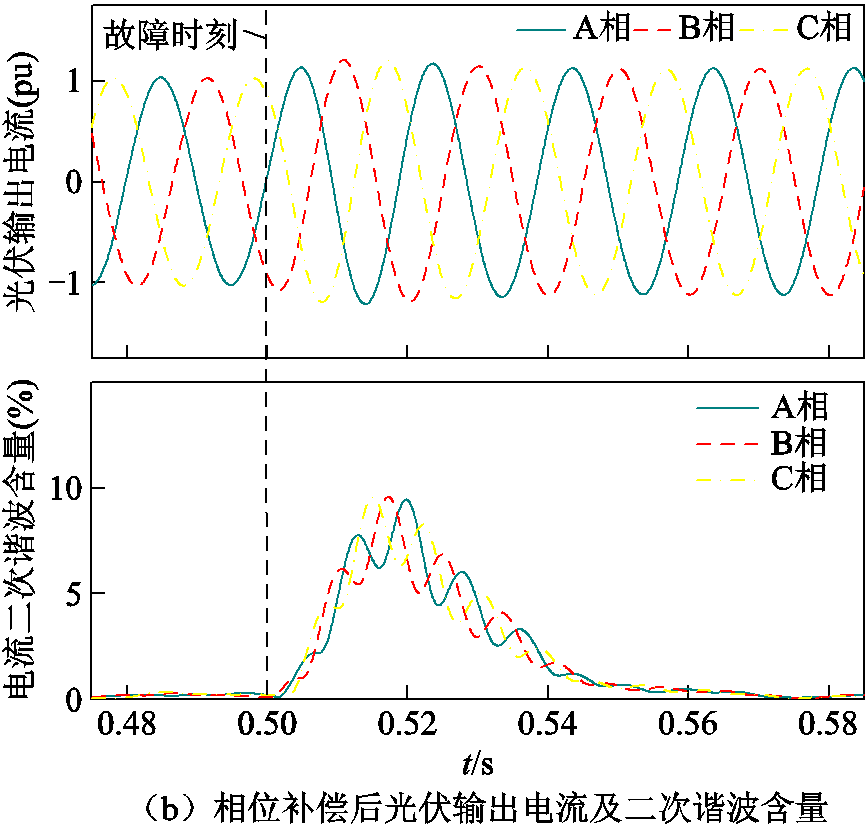
图14 对图13所示故障相位补偿后PCC电压及相位、光伏输出电流及谐波
Fig.14 PCC voltage and phase angle, photovoltaic output current and harmonic diagram after fault phase angle compensation shown in Fig.13
表2 多组不同过渡电阻下不同类型故障的验证
Tab.2 Verification of different types of faults under multiple sets of different transition resistances
故障类型相位跳变量/(°)电流二次谐波含量(%) 补偿前补偿后 6019.62.5 4915.52.3 4112.92.0 122.51.6 82.21.5 41.81.1 164.21.9 143.51.7 112.51.6 248.52.0 217.41.9 175.11.8
在此以文献[18]为例,与本文提出的相位补偿改进方案进行对比,以验证本文所提方案的有效性。
文献[18]通过对三相电压不平衡与锁相误差内在关系的理论推导,提出一种锁相误差的补偿方法以实现精准锁相。但文献[18]未计及电压幅值不平衡对锁相误差的影响,其推导得出的锁相误差公式为
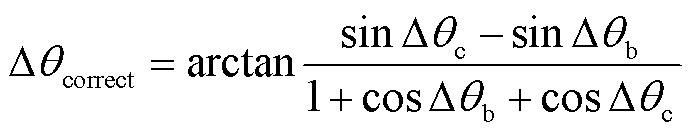 (22)
(22)
式中,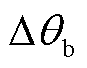 、
、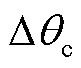 分别为以A相电压为基准的B相和C相的不平衡相位;
分别为以A相电压为基准的B相和C相的不平衡相位;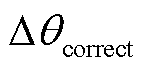 为锁相误差。
为锁相误差。
其不平衡相位检测方法为
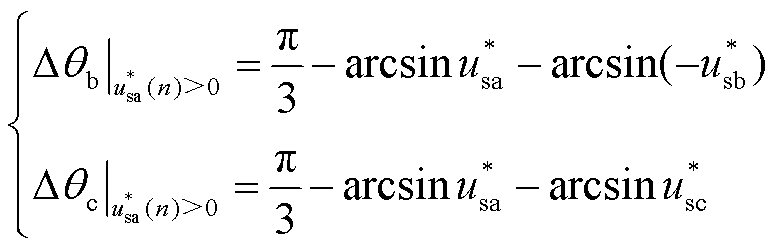 (23)
(23)
式中,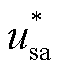 、
、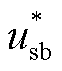 、
、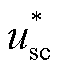 为三相不平衡电压瞬时值。
为三相不平衡电压瞬时值。
如图10所示,以主变压器高压侧在t=0.5 s发生AB两相短路接地故障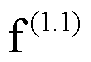 为例,进行本文所提方案效果与文献[18]关于PLL性能及相位补偿的对比。故障后PLL输出电压及相位、光伏输出电流及其二次谐波含量如图15a、图15b所示。
为例,进行本文所提方案效果与文献[18]关于PLL性能及相位补偿的对比。故障后PLL输出电压及相位、光伏输出电流及其二次谐波含量如图15a、图15b所示。
首先以文献[18]的相位补偿方案进行锁相误差求解及相位补偿。由图15a中0.505 s时的采样值及式(23)可以得出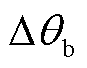 、
、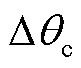 ,代入式(22)可得所要补偿的锁相误差为
,代入式(22)可得所要补偿的锁相误差为
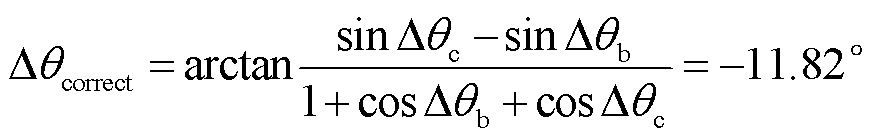 (24)
(24)
在0.505 s将所求锁相误差补偿至PLL出口处,得到相位补偿后PLL输出相位、光伏输出电流及其二次谐波含量如图16所示。可见,补偿后波形畸变有一定减弱,且电流中的二次谐波含量有一定降低。
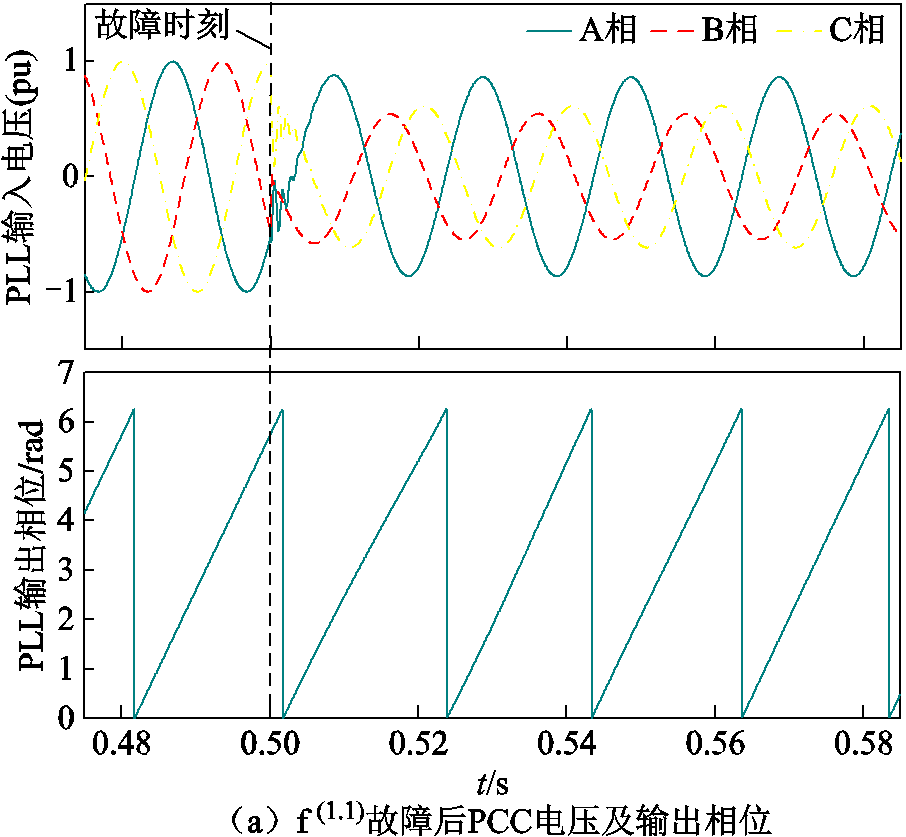
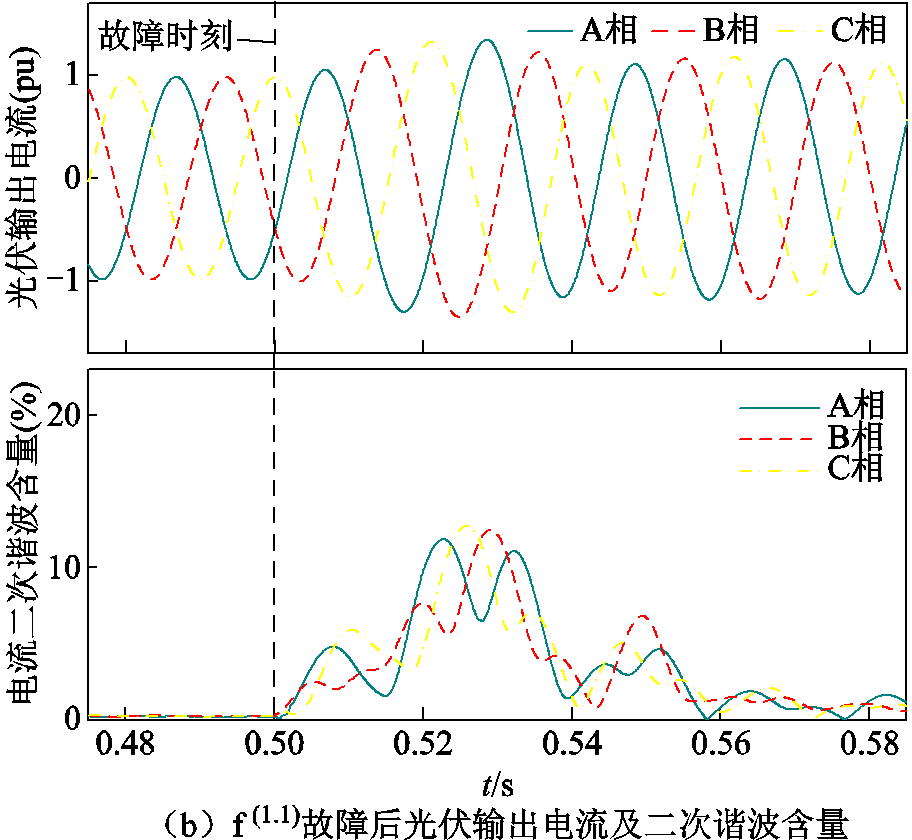
图15 f(1.1)故障后PLL输入电压及相位、光伏输出电流及谐波
Fig.15 PCC voltage and phase angle, photovoltaic output current and harmonic diagram after fault f(1.1)
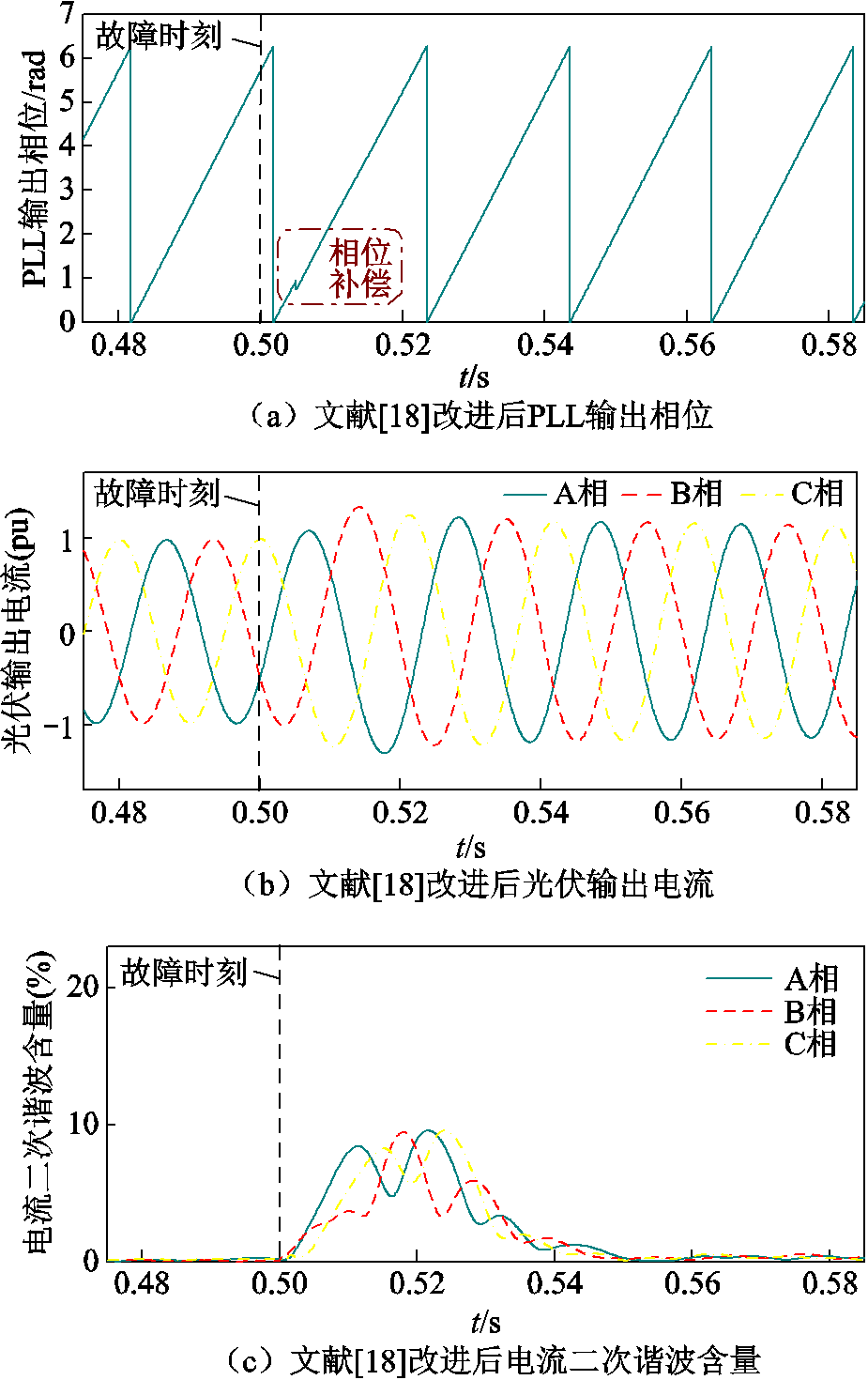
图16 对故障f(1.1)文献[18]相位补偿改进效果
Fig.16 Improvement effect diagram of phase compensation for fault f(1.1) in Ref.[18]
其次以本文的相位补偿方案进行锁相偏差求解及相位补偿。由式(5)可以得到正序电压相位跳变角数值为
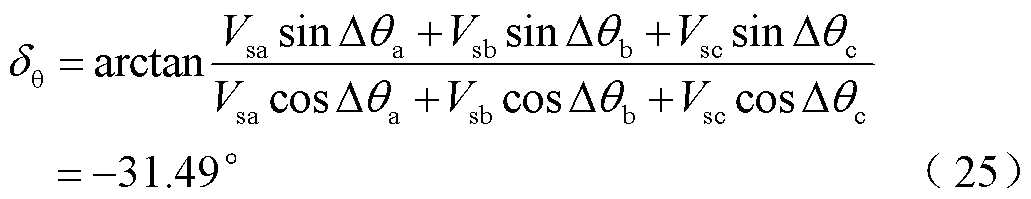
此时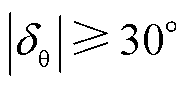 ,采用波形拟合进行函数在线匹配,得到PLL动态相位追踪角
,采用波形拟合进行函数在线匹配,得到PLL动态相位追踪角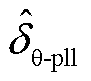 为-23.82°,可得相位补偿量即0.02 s时的锁相偏差为
为-23.82°,可得相位补偿量即0.02 s时的锁相偏差为
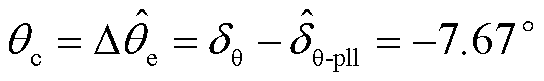 (26)
(26)
在t=0.52 s将所求锁相偏差值补偿至PLL出口处,得到相位补偿后PLL输出相位、光伏输出电流及其二次谐波含量如图17所示。对比图16b、图16c及图17b、图17c可见,大相位跳变场景下,相比于文献[18]的补偿方案,本文补偿后波形不再有明显畸变,且电流中的二次谐波含量显著降低。此外,针对小相位跳变场景的仿真见附录。
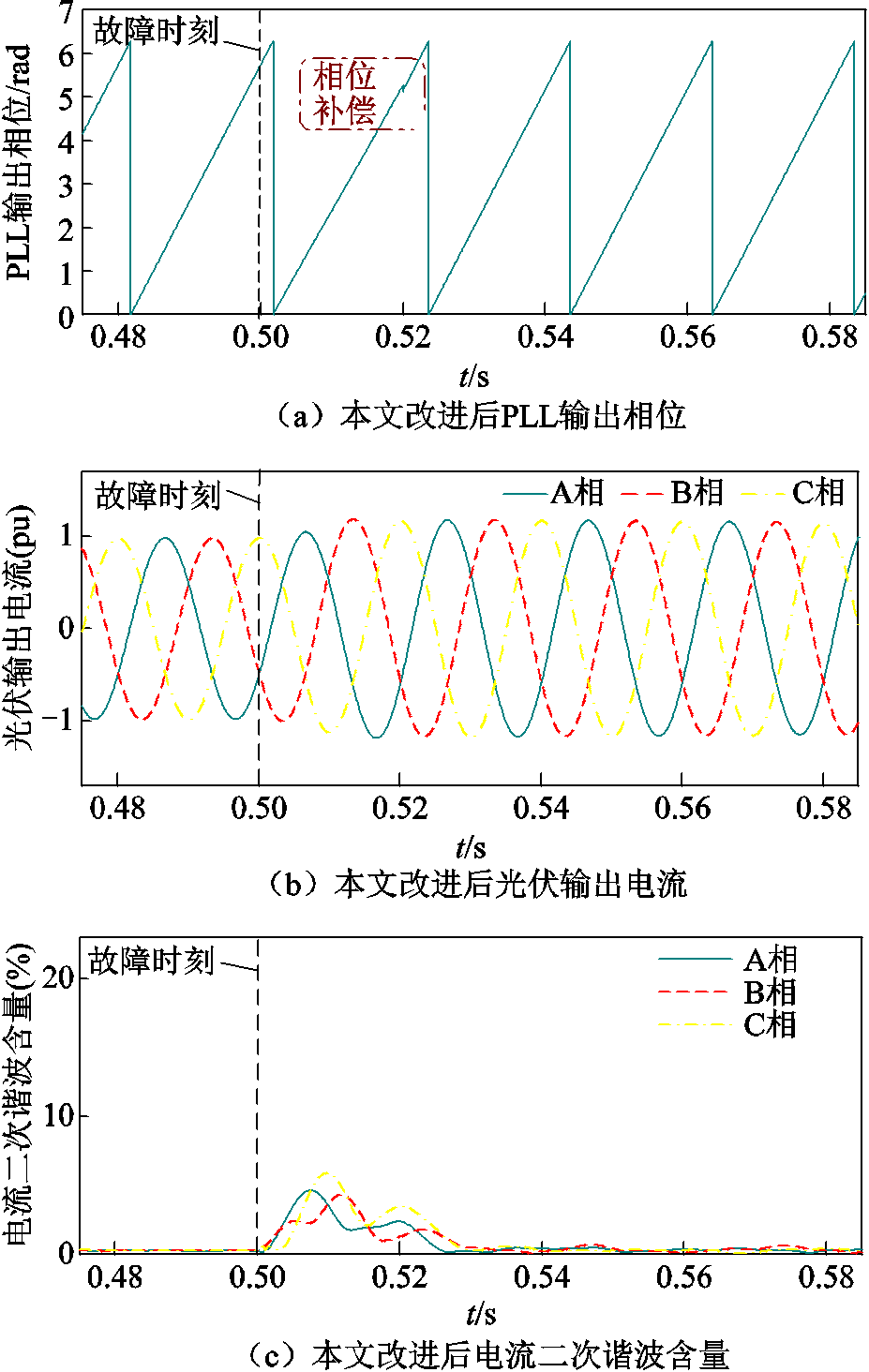
图17 对故障f(1.1)本文相位补偿改进效果
Fig.17 Improvement effect diagram of phase compensation for fault f(1.1) in this article
综上所述,本文所提方案及文献[18]所提方案均可改进PLL性能,降低电流二次谐波含量。但是相比于文献[18],本文所提方案综合分析三相电压幅值、相位不平衡下的正序电压相位跳变机理,且考虑了PLL动态响应过程及相位补偿量实测所需的固有时间给补偿带来的影响,无论在大相位跳变还是小相位跳变的情况下,均可对锁相偏差进行有效的补偿,并降低PLL动态响应过程对光伏输出特性的影响,因此相位补偿效果更好,改进后PLL性能更佳,更具有可行性。
新能源并网系统发生故障时会出现电压跌落并伴随相位跳变,DSOGI-PLL产生锁相偏差,从而导致新能源输出电流中含有大量谐波分量。为解决上述问题,本文提出了一种计及DSOGI-PLL动态过程影响的锁相偏差检测及相位补偿方案,主要结论如下:
1)分析了电网电压不平衡下的正序电压相位跳变机理,并考虑DSOGI-PLL动态过程影响,基于小信号模型推导得到锁相偏差动态解析式,且基于波形拟合得到适用于大扰动下的锁相偏差解析式。
2)在分析PLL动态响应过程对光伏输出特性影响的基础上,提出了减小PLL锁相偏差影响的相位补偿方案,实现了PLL在动态追踪过程中对PCC电压相位的快速同步追踪。
3)提出的相位补偿方案能够减小PLL锁相偏差的影响,并显著降低新能源输出电流中的谐波分量,但本方案仍有0.02 s的延时,后续将针对该问题展开进一步研究。
附 录
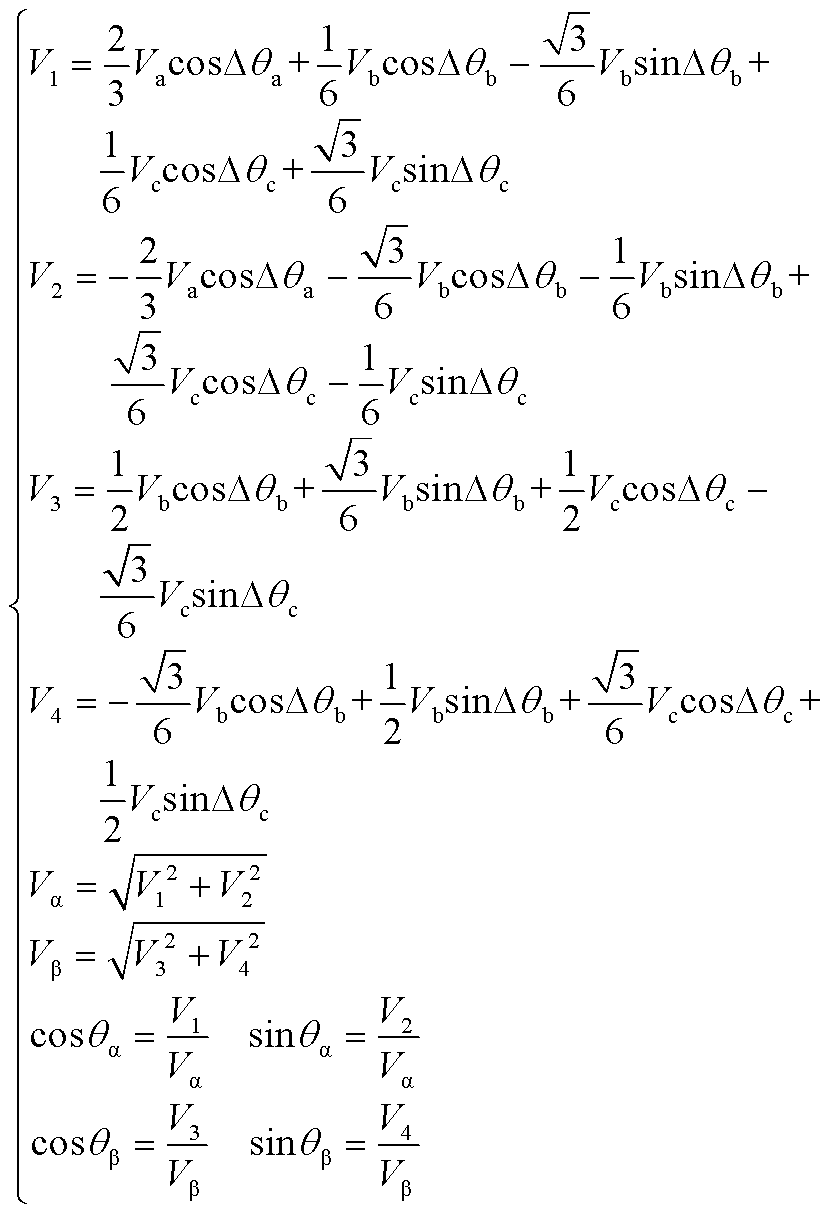 (A1)
(A1)
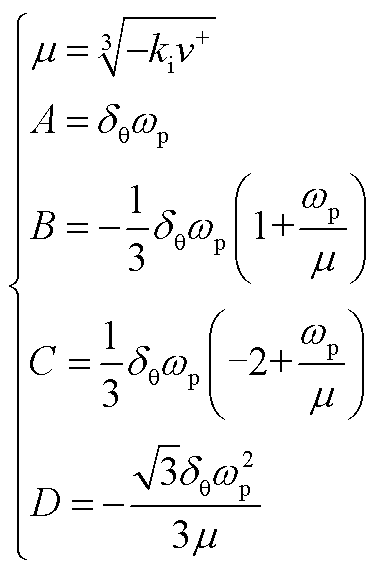 (A2)
(A2)
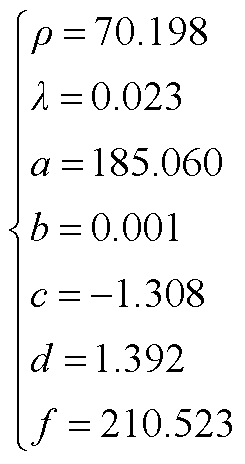 (A3)
(A3)
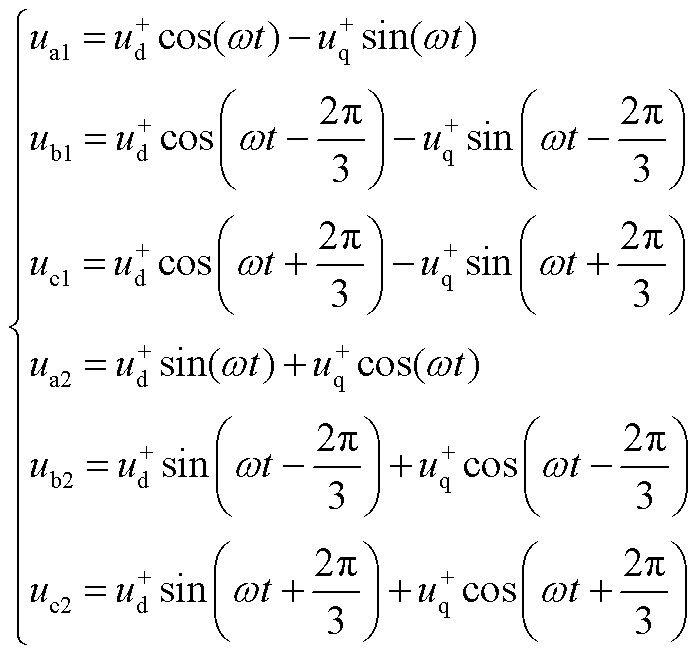 (A4)
(A4)
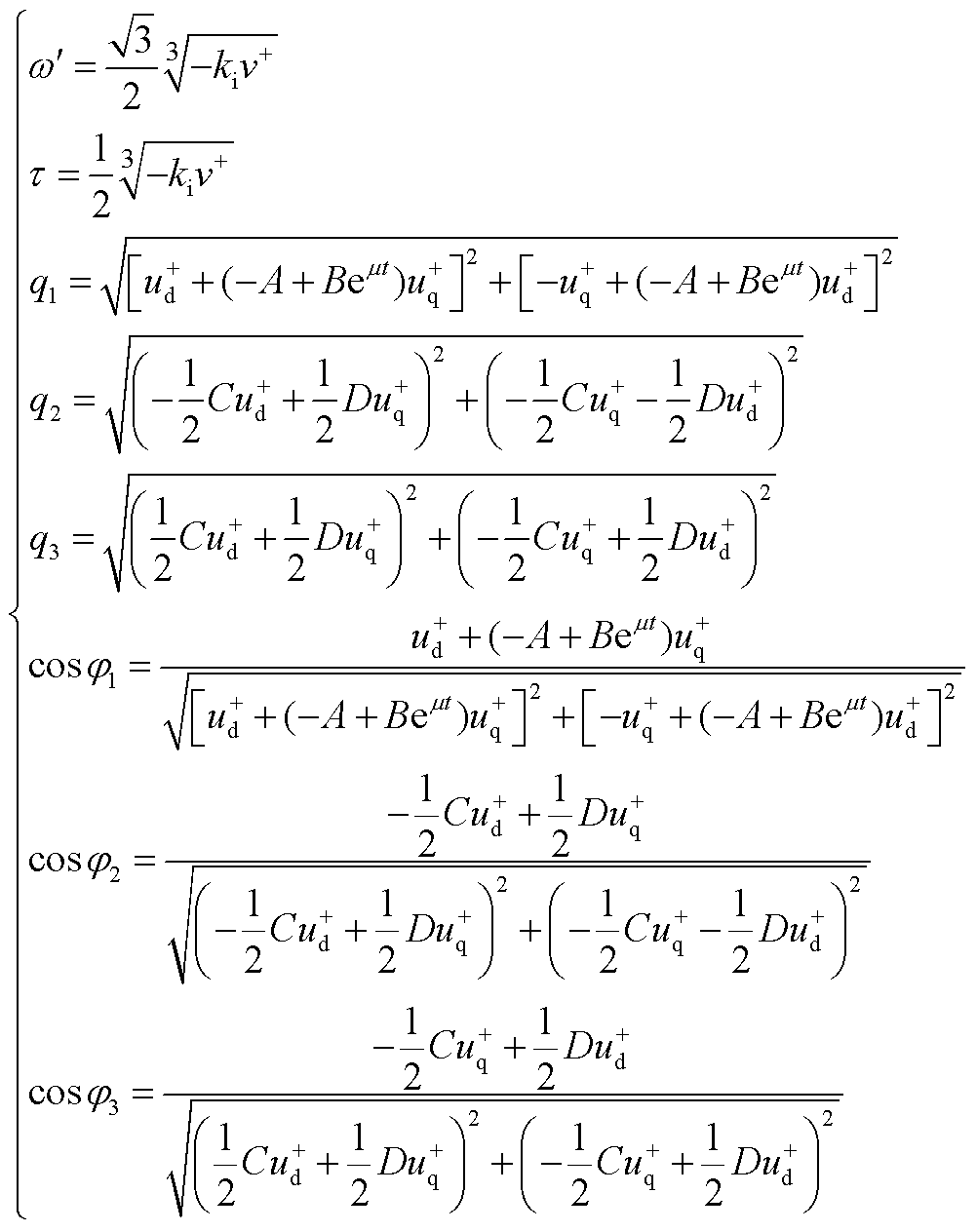 (A5)
(A5)
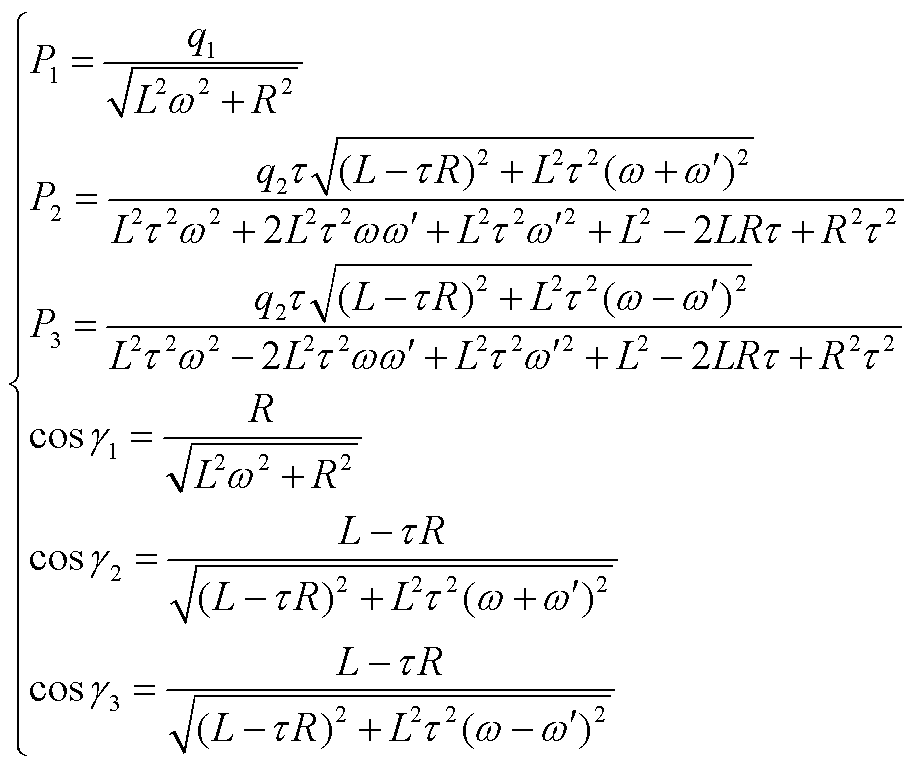 (A6)
(A6)
如图10所示,以主变压器高压侧在t =0.5 s发生AB两相短路故障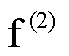 为例进行本文所提方案效果与文献[18]关于PLL性能及相位补偿的对比。f(2)故障后PCC电压及相位、光伏输出电流及谐波如附图1所示。
为例进行本文所提方案效果与文献[18]关于PLL性能及相位补偿的对比。f(2)故障后PCC电压及相位、光伏输出电流及谐波如附图1所示。
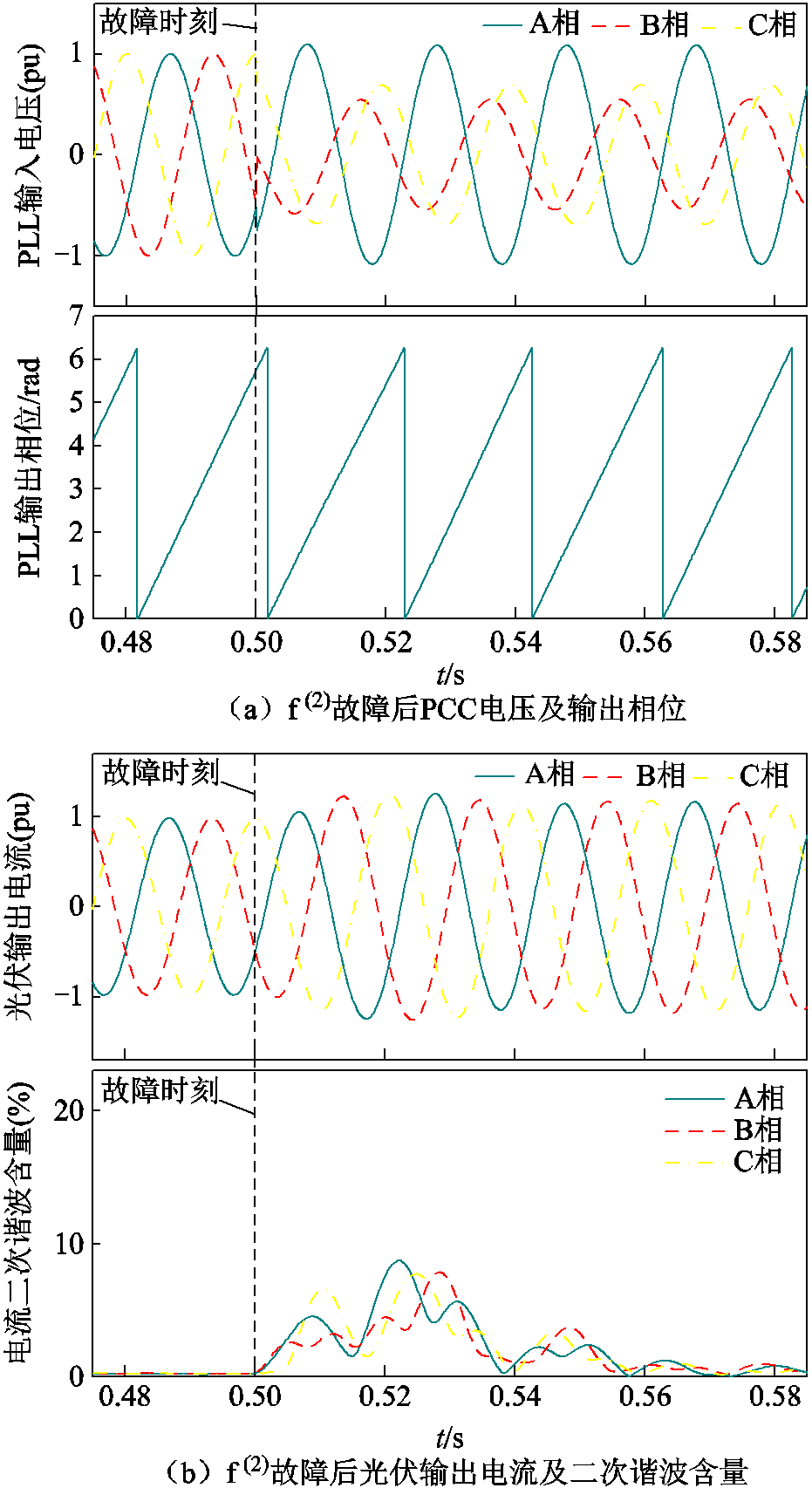
附图1 f(2)故障后PCC电压及相位、光伏输出电流及谐波
App.Fig.1 PCC voltage and phase angle, photovoltaic output current and harmonic diagram after fault f(2)
首先以文献[18]的相位补偿方案进行锁相误差求解及相位补偿。由附图1a中0.505 s时的采样值及式(23)可以得出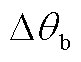 、
、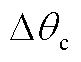 并代入式(22)可得所要补偿的锁相误差为°
并代入式(22)可得所要补偿的锁相误差为°
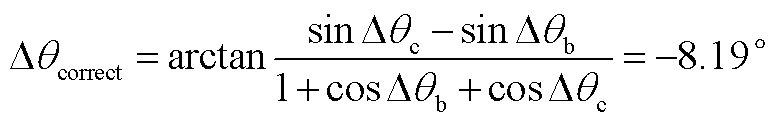 (A7)
(A7)
在0.505 s将所求锁相误差补偿至PLL出口处,得到相位补偿后PLL输出相位、光伏输出电流及其二次谐波含量如附图2所示。可见,补偿后波形畸变减弱,且电流中的二次谐波含量降低。
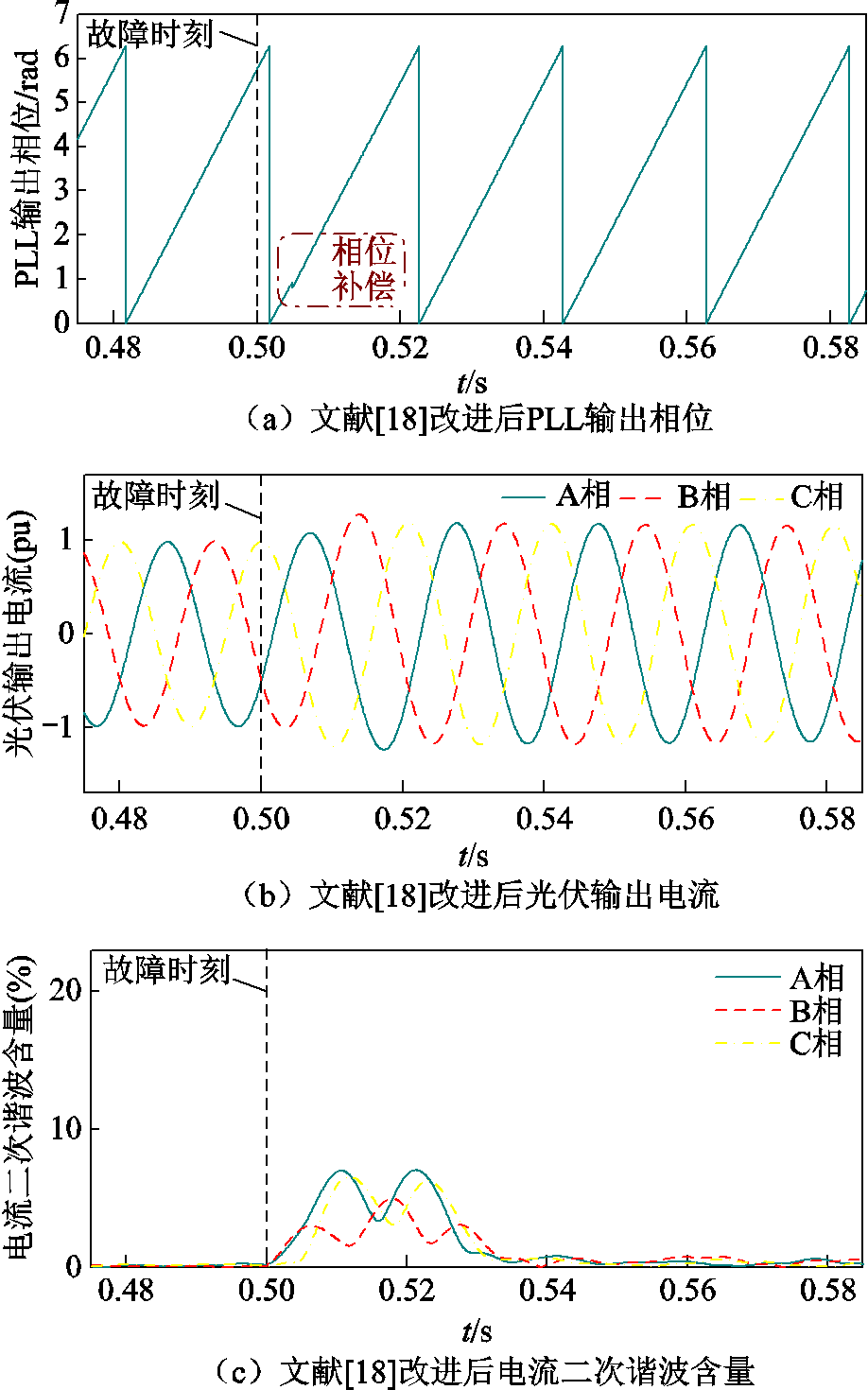
附图2 对故障f(2)文献[18]相位补偿改进效果
App.Fig.2 Improvement effect diagram of phase compensation for fault f(2) in Ref.[18]
其次以本文的相位补偿方案进行锁相偏差求解及相位补偿。由式(5)可以得到正序电压相位跳变角数值为
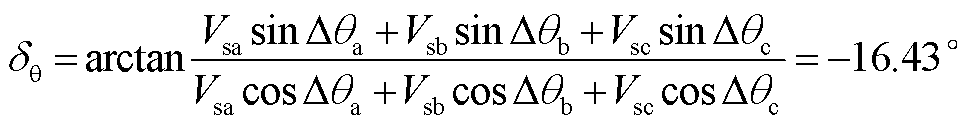 (A8)
(A8)
此时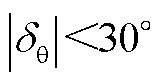 ,采用锁相偏差动态解析式求解锁相偏差角,可得相位补偿量即0.02 s时的锁相偏差为
,采用锁相偏差动态解析式求解锁相偏差角,可得相位补偿量即0.02 s时的锁相偏差为
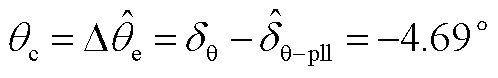 (A9)
(A9)
在t=0.52 s将所求锁相偏差值补偿至PLL出口处,得到相位补偿后PLL输出相位、光伏输出电流及其二次谐波含量如附图3所示。
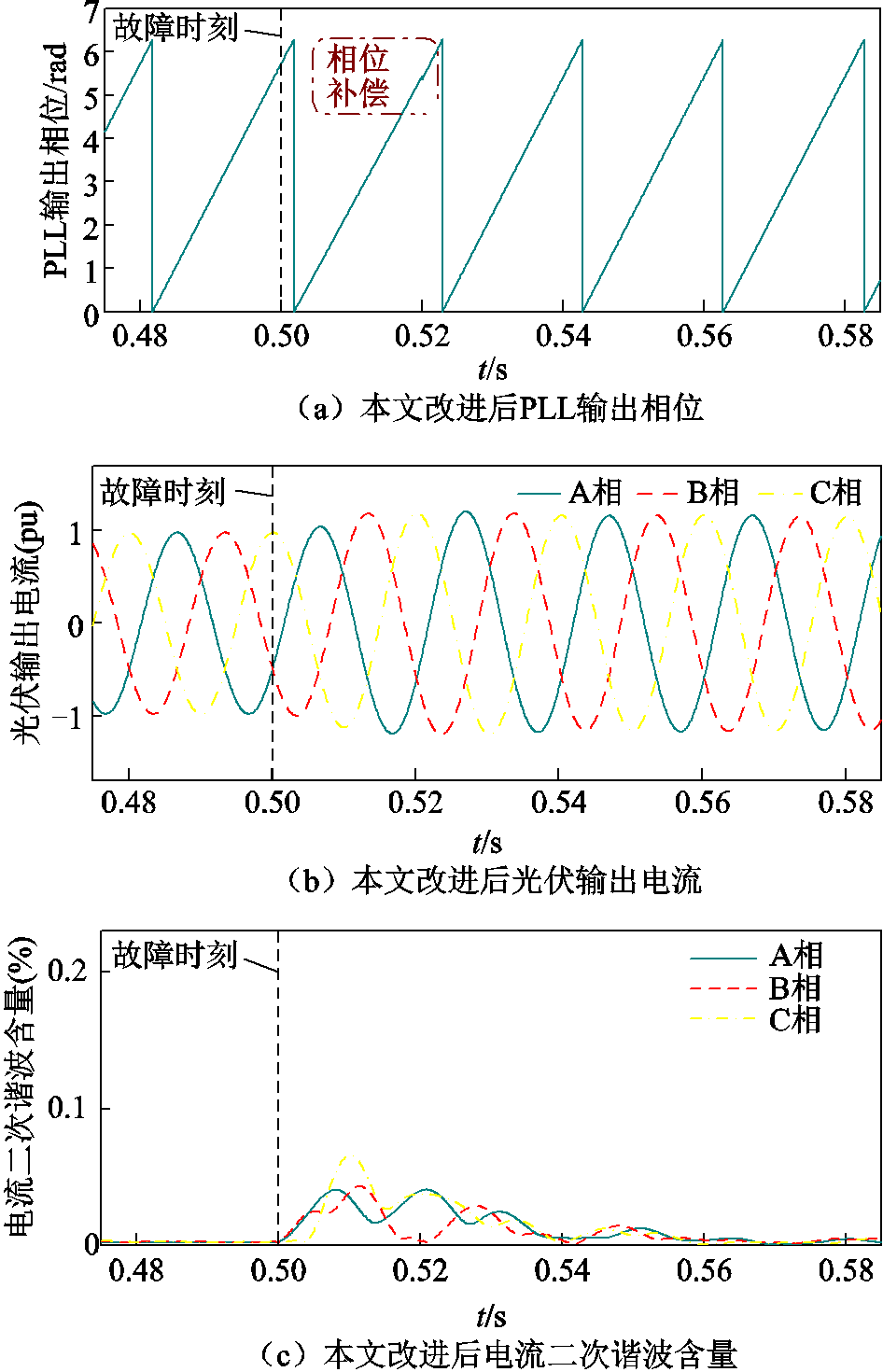
附图3 对故障f(2)本文相位补偿改进效果
App.Fig.3 Improvement effect diagram of phase compensation for fault f(2) in this article
对比附图2b、附图2c及附图3b、附图3c可见,在小相位跳变场景下,本文提出的补偿方案与文献[18]采用的补偿方案效果相似,波形不再有明显畸变,且电流中的二次谐波含量降低。
参考文献
[1] 赵旭东, 王艺博, 王博闻, 等. 考虑差异化工业高载能负荷灵活性挖掘的市场实施及调度模型研究综述[J]. 电工技术学报, 2025, 40(7): 2043-2062, 2161.
Zhao Xudong, Wang Yibo, Wang Bowen, etc. Review of market implementation and scheduling models considering the flexibility extraction of differentiated industrial energy-intensive loads[J] Transactions of China Electrotechnical Society, 2025, 40(7): 2043-2062, 2161.
[2] 罗远翔, 王云龙, 冯扬, 等. 高比例新能源并网含抽蓄的联合系统变时段日前调度[J]. 电力系统及其自动化学报, 2024, 36(8): 115-121, 132.
Luo Yuanxiang, Wang Yunlong, Feng Yang, et al. Variable-time day-ahead dispatching of high-proportion new energy grid-connected joint system with pumped storage[J]. Proceedings of the CSU-EPSA, 2024, 36(8): 115-121, 132.
[3] 马秀达, 文继锋, 严伟, 等. 张北柔性直流工程电压单环控制策略应用分析[J]. 电力系统自动化, 2025, 49(2): 198-207.
Ma Xiuda, Wen Jifeng, Yan Wei, et al. Application analysis of single-loop voltage control strategy in Zhangbei flexible DC project of China[J]. Automation of Electric Power Systems, 2025, 49(2): 198-207.
[4] 余墨多, 黄文焘, 邰能灵, 等. 逆变型分布式电源并网运行暂态稳定机理与评估方法[J]. 电工技术学报, 2022, 37(10): 2596-2610.
Yu Moduo, Huang Wentao, Tai Nengling, et al. Transient stability mechanism and judgment for inverter interfaced distributed generators connected with public grids[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2596-2610.
[5] 郑宇婷, 肖凡, 谢伟杰, 等. 基于并网变流器电流稳定运行域的锁相环参数设计方法[J]. 电工技术学报, 2025, 40(10): 3181-3194.
Zheng Yuting, Xiao Fan, Xie Weijie, et al. A phase-locked loop parameter design method based on current stable operation domain of grid-connected converter [J]. Transactions of China Electrotechnical Society, 2025, 40(10): 3181-3194.
[6] Rodríguez P, Teodorescu R, Candela I, et al. New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions[C]//2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea (South), 2006: 1-7.
[7] 涂娟, 汤宁平. 基于改进型DSOGI-PLL的电网电压同步信号检测[J]. 中国电机工程学报, 2016, 36(9): 2350-2356.
Tu Juan, Tang Ningping. Synchronizing signal detection for grid voltage based on modified DSOGI-PLL[J]. Proceedings of the CSEE, 2016, 36(9): 2350-2356.
[8] 杨明, 杨倬, 李玉龙, 等. 高渗透率下基于并网逆变器阻抗重塑的锁相环设计方法[J]. 电工技术学报, 2024, 39(2): 554-566.
Yang Ming, Yang Zhuo, Li Yulong, et al. A phase-locked loop design method based on impedance remodeling of grid-connected inverter under high permeability[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 554-566.
[9] 葛豪宇, 杨明, 方聪, 等. 弱电网下计及并网逆变器耦合效应的新型锁相环设计方法及其稳定性分析[J]. 电网技术, 2024, 48(12): 5108-5117.
Ge Haoyu, Yang Ming, Fang Cong, et al. A new phase-locked loop design method and stability analysis considering the coupling effect of grid-connected inverter under weak grid[J]. Power System Techno-logy, 2024, 48(12): 5108-5117.
[10] 郑涛, 黄予园, 宗伟, 等. 光伏并网系统故障二次谐波产生机理及其对变压器保护的影响[J]. 电力系统保护与控制, 2020, 48(12): 13-22.
Zheng Tao, Huang Yuyuan, Zong Wei, et al. Second harmonic generation mechanism of a photovoltaic grid-connected system fault and its influence on transformer protection[J]. Power System Protection and Control, 2020, 48(12): 13-22.
[11] 郑涛, 邹芃蓥, 王子鸣. 计及锁相环动态响应特性的光伏并网系统故障电流解析计算[J]. 电网技术, 2022, 46(12): 4656-4667.
Zheng Tao, Zou Pengying, Wang Ziming. Fault current analysis of photovoltaic grid-connected system considering dynamic response characteristics of PLL[J]. Power System Technology, 2022, 46(12): 4656-4667.
[12] Zheng T, Zhang R, Chen Y, et al. Improved scheme based on memory voltage for transformer differential protection considering the effects of PLL[J]. IET Generation Transmission Distribution, 2024, 18: 214-225.
[13] 陈晓龙, 朱雨葭, 张浩, 等. 光伏电站主变压器比率差动保护对单相接地短路故障的适应性分析[J]. 电力自动化设备, 2023, 43(10): 217-224.
Chen Xiaolong, Zhu Yujia, Zhang Hao, et al. Adaptability analysis of photovoltaic power station main transformer ratio differential protection to single-phase grounding short circuit fault[J]. Electric Power Automation Equipment, 2023, 43(10): 217-224.
[14] 刘素梅, 毕天姝, 王晓阳, 等. 具有不对称故障穿越能力逆变型新能源电源故障电流特性[J]. 电力系统自动化, 2016, 40(3): 66-73.
Liu Sumei, Bi Tianshu, Wang Xiaoyang, et al. Fault current characteristics of inverter interfaced renewable energy generators with asymmetrical fault ride-through capability[J]. Automation of Electric Power Systems, 2016, 40(3): 66-73.
[15] 毕天姝, 刘素梅, 薛安成, 等. 逆变型新能源电源故障暂态特性分析[J]. 中国电机工程学报, 2013, 33(13): 165-171.
Bi Tianshu, Liu Sumei, Xue Ancheng, et al. Fault characteristics of inverter-interfaced renewable energy sources[J]. Proceedings of the CSEE, 2013, 33(13): 165-171.
[16] 贾科, 刘浅, 杨彬, 等. 计及锁相环动态特性的逆变电源故障暂态电流解析[J]. 电网技术, 2021, 45(11): 4242-4251.
Jia Ke, Liu Qian, Yang Bin, et al. Transient fault current analysis of the inverter-interfaced renewable energy sources considering the dynamic characteristics of the phase-locked loop[J]. Power System Technology, 2021, 45(11): 4242-4251.
[17] 程成, 谢少军, 张晴晴, 等. 计及锁相环动态的单相并网逆变器建模及稳定性研究综述[J]. 中国电机工程学报, 2024, 44(1): 255-269.
Cheng Cheng, Xie Shaojun, Zhang Qingqing, et al. Overview of modeling and stability analysis for single-phase grid-connected inverters considering phase-locked loop dynamics[J]. Proceedings of the CSEE, 2024, 44(1): 255-269.
[18] 祁永胜, 李凯, 高畅毓, 等. 三相电压不平衡下DDSRF-PLL与DSOGI-PLL的锁相误差检测与补偿方法[J]. 电工技术学报, 2024, 39(2): 567-579.
Qi Yongsheng, Li Kai, Gao Changyu, et al. Phase estimation error detection and compensation method of DDSRF-PLL and DSOGI-PLL under three-phase voltage unbalance[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 567-579.
[19] 岑扬, 黄萌, 査晓明. 电网电压不平衡跌落下同步参考坐标系锁相环瞬态响应分析[J]. 电工技术学报, 2016, 31(增刊2): 28-38.
Cen Yang, Huang Meng, Cha Xiaoming. The Transient Response Analysis of SRF-PLL under the Unbalance Grid Voltage Sag [J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 28-38.
[20] Lee C R, Chun T W, Lee H H. A second-order generalized differentiator method for eliminating DC component in the three-phase PLL for grid-connected inverters[C]//2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-5.
[21] 李红, 梁军杨, 王振民, 等. 跟网型变换器的小扰动同步稳定机理分析与致稳控制[J]. 电工技术学报, 2024, 39(12): 3802-3815.
Li Hong, Liang Junyang, Wang Zhenmin, et al. Small signal synchronization stability analysis and improved control strategy for grid following converter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3802-3815.
[22] 闫培雷, 葛兴来, 王惠民, 等. 弱电网下新能源并网逆变器锁相环参数优化设计方法[J]. 电网技术, 2022, 46(6): 2210-2221.
Yan Peilei, Ge Xinglai, Wang Huimin, et al. PLL parameter optimization design for renewable energy grid-connected inverters in weak grid[J]. Power System Technology, 2022, 46(6): 2210-2221.
[23] Golestan S, Monfared M, Freijedo F D. Design-oriented study of advanced synchronous reference frame phase-locked loops[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 765-778.
[24] Lei Jiaxing, Quan Xiangjun, Feng Shuang, et al. Accurate modeling of PLL with frequency-adaptive prefilter: on the positive feedback effect[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3747-3752.
[25] 王铭灏. 计及电压扰动的光伏输出特性及其对保护的影响研究[D]. 北京: 华北电力大学, 2021.
Wang Minghao. Research on characteristics of photovoltaic output and its impact on the protection considering voltage disturbance[D]. Beijing: North China Electric Power University, 2021.
[26] 孙雷强, 王冲, 王丽艳, 等. Buck-Boost变换电路DCM动态建模分析[J]. 电机与控制应用, 2019, 46(11): 88-93.
Sun Leiqiang, Wang Chong, Wang Liyan, et al. Modeling and simulation analysis of buck-boost converter circuit in DCM[J]. Electric Machines & Control Application, 2019, 46(11): 88-93.
[27] 李济山, 刘清平, 乔进军, 等. 应用最小二乘法对电网电压拟合波形函数[J]. 价值工程, 2018, 37(22): 182-186.
Li Jishan, Liu Qingping, Qiao Jinjun, et al. Application of least square method to power grid voltage fitting waveform function[J]. Value Engineering, 2018, 37(22): 182-186.
[28] 陆秋贤, 马刚, 涂孟夫. 基于IEWT-FE-BO-LSTM模型的超短期风功率预测[J]. 水电能源科学, 2023, 41(1): 217-220.
Lu Qiuxian, Ma Gang, Tu Mengfu. Ultra-short-term wind power prediction based on IEWT-FE-BO-LSTM model[J]. Water Resources and Power, 2023, 41(1): 217-220.
[29] 周颖, 乔婧, 陈宋宋, 等. 基于麻雀搜寻优化算法的代理购电用户用电量多维度协同校核[J]. 电网技术, 2025, 49(2): 604-612.
Zhou Ying, Qiao Jing, Chen Songsong, et al. Multi-dimensional collaborative checking of power consumption of purchasing agent users based on ISSA optimization algorithm[J]. Power System Technology, 2025, 49(2): 604-612.
[30] Li Jishan, Liu Qingping, Qiao Jinjun, et al. Application of least squares method for fitting waveform functions to grid voltage[J]. Value Engineering, 2018, 37(22): 182-186.
[31] 冯翔. 复杂环网后备保护在线整定方法研究[D]. 成都: 电子科技大学, 2022.
Feng Xiang. Research on online setting method of backup protection in complex ring network[D]. Chengdu: University of Electronic Science and Technology of China, 2022.
Phase-Locked Deviation Detection and Phase Angle Compensation Scheme Considering the Influence of Dynamic Process of DSOGI-PLL
Abstract Voltage drop and the abrupt change of phase will occur when a fault occurs in the power system integrated with renewable energy sources (RESs). Factors, such as imbalanced load and asymmetric faults, will further cause the imbalanced amplitude and phase of three-phase voltage, leading to the phase-locked deviation of the double second-order generalized integrator phase-locked loop (DSOGI-PLL), which are commonly used in the real project. This deviation affects the output characteristics of the RESs, and some recent studies have analyzed the impact of the dynamic response of the PLL on the output characteristics of the grid-connected inverter. However, most of the above studies focus on the symmetrical faults and few studies quantitatively analyze the impact of the imbalanced amplitude of the grid voltage and the large abrupt change of phase of the voltage at the point of common coupling (PCC) on the phase-locked deviation under asymmetrical faults. The compensation method for the phase-locked deviation is also lacked. Therefore, a phase compensation method based on the dynamic analytical formula of phase-locked deviation is proposed in this paper, which realizes the fast and synchronous tracking of the DSOGI-PLL on the PCC voltage phase.
Firstly, the abrupt change mechanism of positive sequence voltage phase under imbalanced three-phase voltage amplitude and phase is comprehensively analyzed. Considering the influence of the dynamic response of the DSOGI-PLL, the analytical phase-locked deviation equation applicable to small disturbances is obtained using the small-signal model. Besides, the analytical equation applicable to large disturbances is obtained based on the waveform fitting. Secondly, a phase compensation scheme is proposed by analyzing the impact of the DSOGI-PLL dynamic response on the output characteristics of photovoltaic (PV), reducing the influence of PLL phase-locked deviation. The phase-locked deviation of the DSOGI-PLL under faults is compensated in real time by adding a compensation link in the DSOGI-PLL control, realizing the fast and synchronous tracking of the PCC voltage phase during the dynamic tracking process. Finally, a large number of simulations are carried out in the PV grid-connected system and simulation results show that the phase compensation scheme proposed in this paper can effectively reduce the phase-locked deviation, whether the abrupt change of PCC voltage phase after faults is small or large in the PV grid-connected system, benefiting the safe and stable operation of the system.
The following conclusions can be drawn from theoretical analysis and simulation verification: (1) The abrupt change of positive-sequence voltage phase is affected by the imbalanced amplitude and phase of three-phase voltage. (2) A phase compensation scheme is proposed based on the analysis of phase-locked deviation during the dynamic response of DSOGI-PLL to reduce the negative impact. The phase-locked deviation of the DSOGI-PLL after a fault is compensated in real time by adding a phase compensation link in the DSOGI-PLL control. (3) The phase compensation scheme proposed in this paper realizes the fast and synchronous tracking of PCC voltage phase by the DSOGI-PLL in the dynamic tracking process, effectively reducing the phase-locked deviation of DSOGI-PLL after grid-connected system faults and facilitating the safe and stable operation of the system.
Keywords:New energy grid connected system, phase-locked loop, phase-locked deviation, fault characteristics, phase angle compensation
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.241136
国家自然科学基金联合基金资助项目(U2166205)。
收稿日期2024-06-30
改稿日期2024-11-26
郑 涛 男,1975年生,教授,博士生导师,研究方向为电力系统继电保护及其自动化等。
E-mail:zhengtao_sf@126.com
刘昱彤 女,2000年生,硕士研究生,研究方向为电力系统继电保护。
E-mail:1037612885@qq.com(通信作者)
(编辑 赫 蕾)