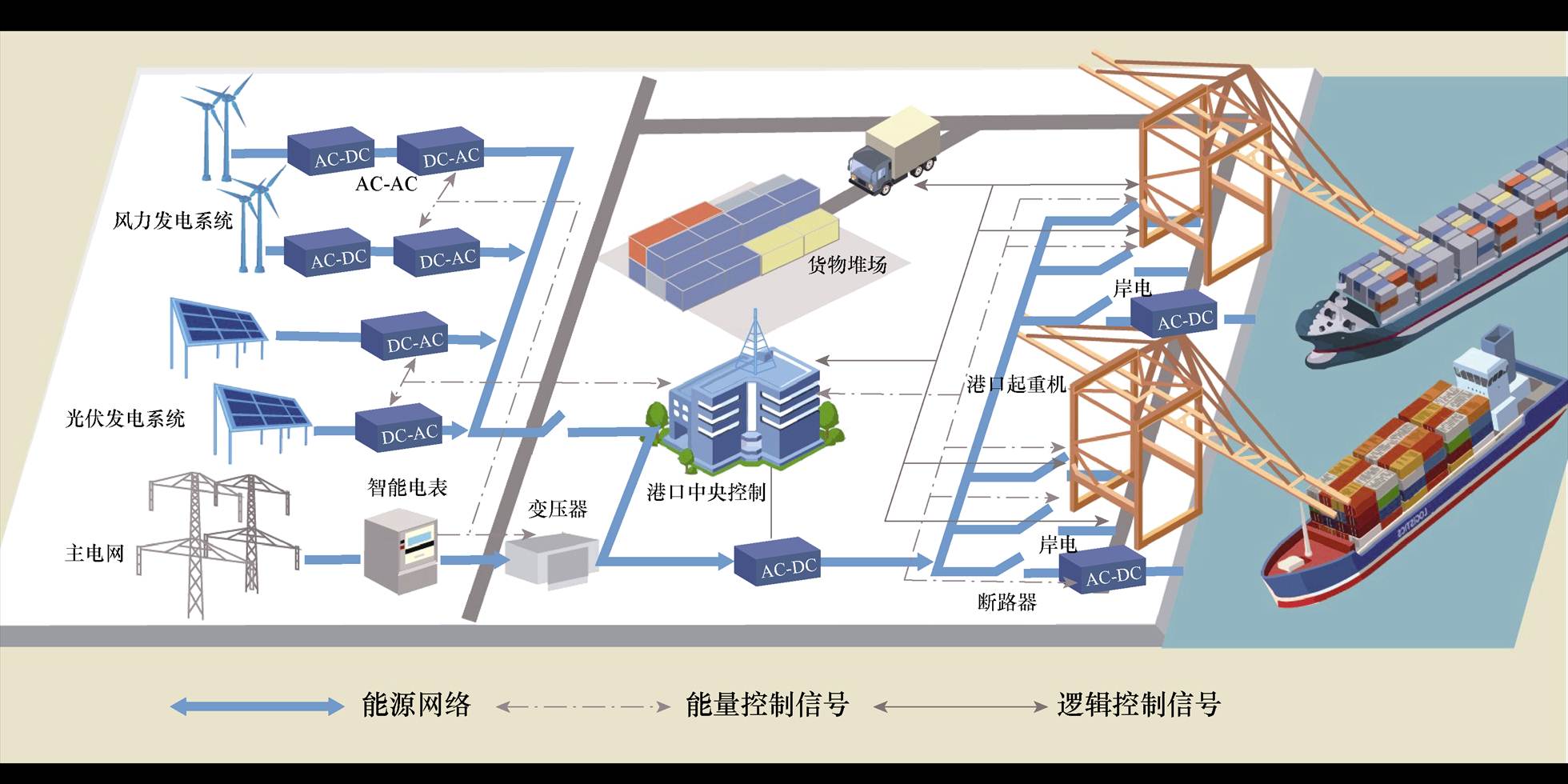
图1 港口微能源系统框架
Fig.1 Framework of port microgrid system
摘要 为有效地满足绿色港口集群优化调度中港口电网与公共电网、港口与港口、港口与船舶等多个利益主体需求,该文建立了一种基于双层博弈理论的绿色港口集群优化调度模型。博弈上层,港口集群区域电网作为领导者管理当地港口集群的能源,并决定能源的价格,以实现经济效益最大化;博弈下层,各港口微能源系统作为追随者决定供能和用能策略,在满足港区负荷的同时,为规模化接入港口岸电的船舶提供能量和服务。然后,将双层博弈模型转换为双层优化问题进行高效求解。算例分析表明,所提出的新型绿色港口集群能源优化方法突破了陆上园区综合系统的场景限制,克服了传统调度方法无法满足多利益主体需求的不足,同时可显著地提高港口集群区域电网的经济效益,增强新能源消纳水平,提升环境友好性。
关键词:绿色港口集群 双层博弈理论 领导者-追随者框架 经济性优化调度
作为海洋强国发展的战略支柱,港口在维护海洋生态和发展海洋经济方面具有至关重要的作用。近年来,随着“双碳”目标的提出,新型电力系统规划加快推进[1],绿色港口集群建设成为其中重要一环,水上交通网络与电气网络深度融合将成为必然趋势[2]。然而,随着港口自身的负荷和各类大容量船舶负荷的增长以及港口集群规模的扩张,港口电网单一的供能方式已无法满足日益增长的用电需求,高比例新能源与规模化船舶负荷的接入给港口能源系统的优化运行与协调控制带来了严峻的挑 战[3-4]。因此,在绿色港口集群场景下,考虑新能源、船舶等各类负荷特性,研究港口集群能源的经济调度和低碳调度具有重大意义。
目前,针对港口综合能源系统的能源配置和调度问题,研究者们从经济性、节能减排等角度开展了相关研究。文献[5]在港口综合能源系统场景下,以系统运行成本最低为目标,提出了一种基于综合需求响应的优化策略,建立了港口综合能源系统运行优化模型。文献[6]建立了一种能源-物流系统耦合的海港综合能源系统,综合多种能源利用形式,对海港综合能源系统协同优化,以日前海港数据实现电力网与天然气网耦合运行,并降低了系统成本。文献[7]通过建立风机模型、储能模型和港口供电系统模型,提出适用于港口新能源供给系统的两级优化架构,从功率平衡、容量限制等角度出发,有效地降低了港口供电系统的投入成本。文献[8]重点研究了港口岸电技术在提升能源利用效率和提升港口整体经济效益中的作用。文献[9]提出了一种基于多层代理系统的双层结构的实时分布式需求响应系统,有效地解决了传统控制系统在实现众多端口柔性负载实时控制中的弊端,确保了船舶排放的实时限制,降低了当地风电场的运营成本,并利用基于模糊逻辑的系统估算了岸电所需的利用率。文献[10]同样在多层代理系统的概念上,提出利用智慧能源网络和全面电气化的设备来限制港口的温室气体排放,并提高电力系统的运行效率,满足岸电船舶负载、陆上各类其他电动设备,尤其是柔性负载的电力供应需求。然而,以上研究侧重于研究单个港口内的能量耦合及优化配置和调度问题,缺乏对多个港口间能源互补以及上层区域电网影响的考虑,忽略了港口集群场景下不同港口利益主体的需求。
然而,计及多利益主体的港口集群优化鲜有研究,目前的研究大多基于陆地电网中的园区综合能源系统。其中,不同的园区综合能源系统代表不同的利益主体,不同利益主体做出符合自身利益的决策,这类决策问题可以转换为博弈论的均衡问题进行解决[11-12]。例如,文献[13]将快速充电站与电动汽车用户之间的成本效益交互建模为斯塔克尔伯格博弈,对电动汽车充电和预留进行管理;文献[14]提出一种非合作博弈论来优化智能电网与插电式电动汽车之间的能量交换,其中电网是领导者,电动汽车是追随者;文献[15]引入社区能源互联网框架,提出了社区运营商和产消者群的主从博弈模型,提升了两者的综合效益,优化了系统的负荷特性。此外,还有相关研究将博弈方法应用于园区系统能源优化配置[16]、电碳耦合交易[17]、平抑负荷波动[18]和电力系统扩容[19]等。然而,普通的陆上园区综合能源系统中不涉及港口中规模化船舶的动态行为,也不具备靠港船舶接受港口装卸服务和充电服务的特殊性,且目前的研究大多局限于单一的电力系统,鲜有集群场景下的考虑,因此传统的博弈方法无法用于解决绿色港口集群场景下的多利益主体问题。
综上所述,针对绿色港口集群场景下的能源经济优化调度问题,本文在考虑船舶与港口协同运行的基础上,提出了一种基于双层博弈的适用于绿色港口集群的能源经济优化调度方法,突破了传统博弈方法应用于陆上园区综合能源系统的场景限制,充分利用港口之间的能源调度实现不同港口利益主体的效用最优。首先,在港口微能源系统中引入新能源设备与港口岸电系统,构建绿色港口微能源系统;其次,搭建包含多个港口的区域港口集群电网架构,并在此基础上,将绿色港口集群区域电网能源的经济优化调度问题建成双层博弈模型,构建评价不同港口利益主体需求满足程度的效用函数,实现多个利益主体的共赢;进一步地,在博弈均衡的计算中,考虑不同港口主体的个体化差异,采用双层优化结构求取能量调度过程中的利益平衡解;最后,通过仿真验证基于双层博弈理论的绿色港口集群能源经济优化调度的优越性。
在绿色港口微能源系统中,电能来源于可再生能源发电和从上级电网购电,这些电能被输送至港口微能源系统内部,以满足日常的用电负荷。这部分负荷包括港口常规负荷和由港口岸电系统连接的船舶负荷。此外,发电系统所产生的部分过剩的能量可以回馈给上级电网,起到一定的调峰作用。港口微能源系统框架如图1所示。
1.1.1 港口岸电系统
随着“海洋双碳”目标的提出,“绿色港口”建设加速推进。港口岸电系统作为港口与船舶低碳、协同运行的关键装备,以及港口集群中能量路由和友好互动的必备设备,已在各海洋与内河航运港口积极布局。以港口岸电系统为核心设备的港口微能源系统具有区别于其他园区综合能源系统的特征,具体如下:

图1 港口微能源系统框架
Fig.1 Framework of port microgrid system
1)虽然港口能源网络中发电和负荷种类较多,但是网络比较集中,常把港口能源系统看作微电网系统,即满足功率平衡,可认为系统是稳定的。
2)港口岸电系统能向船舶提供岸上电力,这形成了特殊的能量流动形式。这部分电力具备两个作用:一方面可以使船舶靠港时关闭自身的发电机,利用岸上电力满足船舶停靠时的负荷,有利于减轻环境污染;另一方面可以面向电力船舶提供充电服务,满足船舶电力需求。
3)部分岸电系统可以接收电力船舶的余电,附加削峰填谷的功能,可作为港口微电网运行的友好支撑,提升了系统灵活性。
4)港口岸电系统需要结合船舶的移动性需求,以满足船舶在不同时间和泊位的能源需求,即需兼顾港口的物流特性。
本文根据是否配备了港口岸电系统,将港口分为两种主要类型。
1)传统港口:传统港口由于没有配备港口岸电系统,无法向船舶提供岸上电力,因此只能通过向船舶提供装卸货物的服务而获益。
2)新型港口:新型港口配备了港口岸电系统,可以向船舶提供岸上电力,其收入还包括向船舶提供充电服务的部分。需要说明的是,本文考虑的是绿色港口集群的层面,因此暂未考虑船舶主体的利益和需求,仅将其看作港口中的一类负荷,由充放电功率和装卸功率构成。
1.1.2 可再生能源发电及负荷
在绿色港口集群的近水区域,风光资源天然充沛,且风力发电在一定程度上可与光伏发电形成资源互补的格局,因此以风力发电和光伏发电为代表的可再生能源发电系统可作为港口微能源系统的重要发电设备。根据文献[20],本文采用的新能源发电模型为
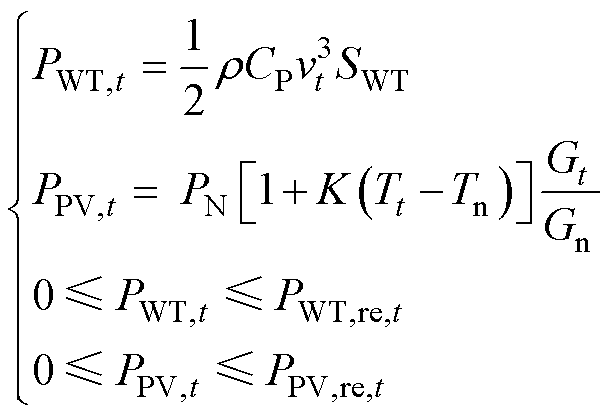 (1)
(1)
式中,对于风力发电系统,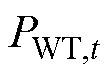 为
为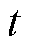 时刻风机出力功率;
时刻风机出力功率;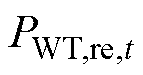 为t时刻风机的预测功率;r 为当前大气环境下的空气密度;CP为风能转化相关系数;vt为t时刻风速;SWT为风力发电设备的扫风截面积。对于光伏发电系统,
为t时刻风机的预测功率;r 为当前大气环境下的空气密度;CP为风能转化相关系数;vt为t时刻风速;SWT为风力发电设备的扫风截面积。对于光伏发电系统,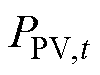 为t时刻光伏出力功率;
为t时刻光伏出力功率;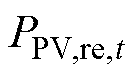 为t时刻光伏的预测功率;Tn为标况下的温度;Gn为标况下的光照度;PN为光伏板在运行时的额定功率;K为光伏板的温度转化相关系数;Tt、Gt分别为光伏板t时刻的工作实况温度和辐射照度。
为t时刻光伏的预测功率;Tn为标况下的温度;Gn为标况下的光照度;PN为光伏板在运行时的额定功率;K为光伏板的温度转化相关系数;Tt、Gt分别为光伏板t时刻的工作实况温度和辐射照度。
针对港口负荷,除常规负荷外,还包括港船互联部分的负荷。其中,港口通过岸电系统向船舶提供岸上电力的功率会受到船舶自身特性的约束,其储能电池的充放电约束为
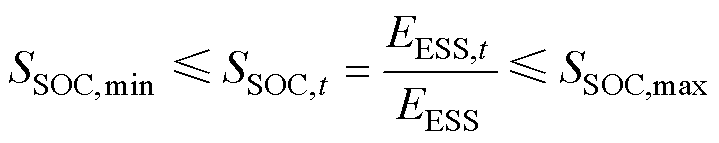 (2)
(2)
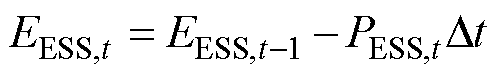 (3)
(3)
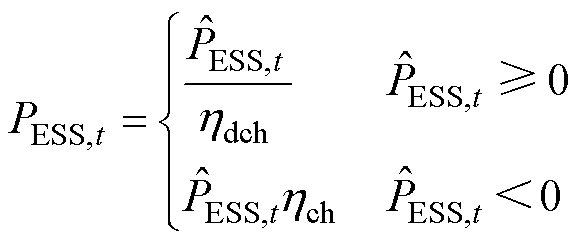 (4)
(4)
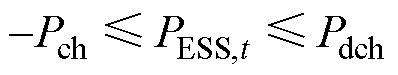 (5)
(5)
式中,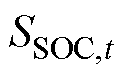 为t时刻的储能荷电状态(State of Charge, SOC);
为t时刻的储能荷电状态(State of Charge, SOC);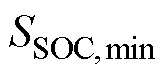 与
与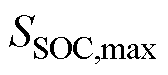 分别为储能荷电状态的下限和上限;
分别为储能荷电状态的下限和上限;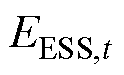 为t时刻储能系统的能量;
为t时刻储能系统的能量;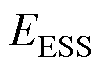 为储能系统的额定能量;
为储能系统的额定能量;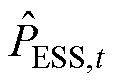 为t时刻储能的出力;
为t时刻储能的出力;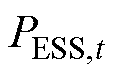 为t时刻储能的充放电功率;
为t时刻储能的充放电功率;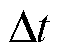 为计步时长;
为计步时长;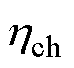 和
和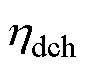 分别为储能系统的充电和放电效率;
分别为储能系统的充电和放电效率;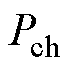 和
和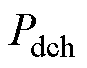 分别为储能最大充电功率和最大放电功率。
分别为储能最大充电功率和最大放电功率。
港口使用港口岸桥起重机进行装卸的功率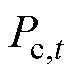 如式(6)所示[21],这是船舶靠港服务的主要形式。
如式(6)所示[21],这是船舶靠港服务的主要形式。
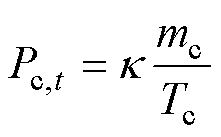 (6)
(6)
式中,k 为装卸货物的速率;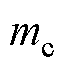 为船上货物的质量;
为船上货物的质量;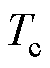 为船舶在港口的服务时间。
为船舶在港口的服务时间。
本文构建的绿色港口集群在能源层面由多个港口微能源系统组成,每个港口微能源系统由风力发电和光伏发电等新能源发电系统构成,并与上级电网连接。
绿色港口集群区域电网架构如图2所示。将绿色港口集群区域电网架构考虑为辐射状网架,每个港口都是一个能源和交通枢纽,代表不同的利益主体,并接入区域电网。在能量耦合的前提下,利用不同港口源荷不平衡的特征,通过能量路由器等设备,将能量在各个港口间进行调度,以实现不同港口间能源的削峰填谷,也降低对区域电网的依赖性。
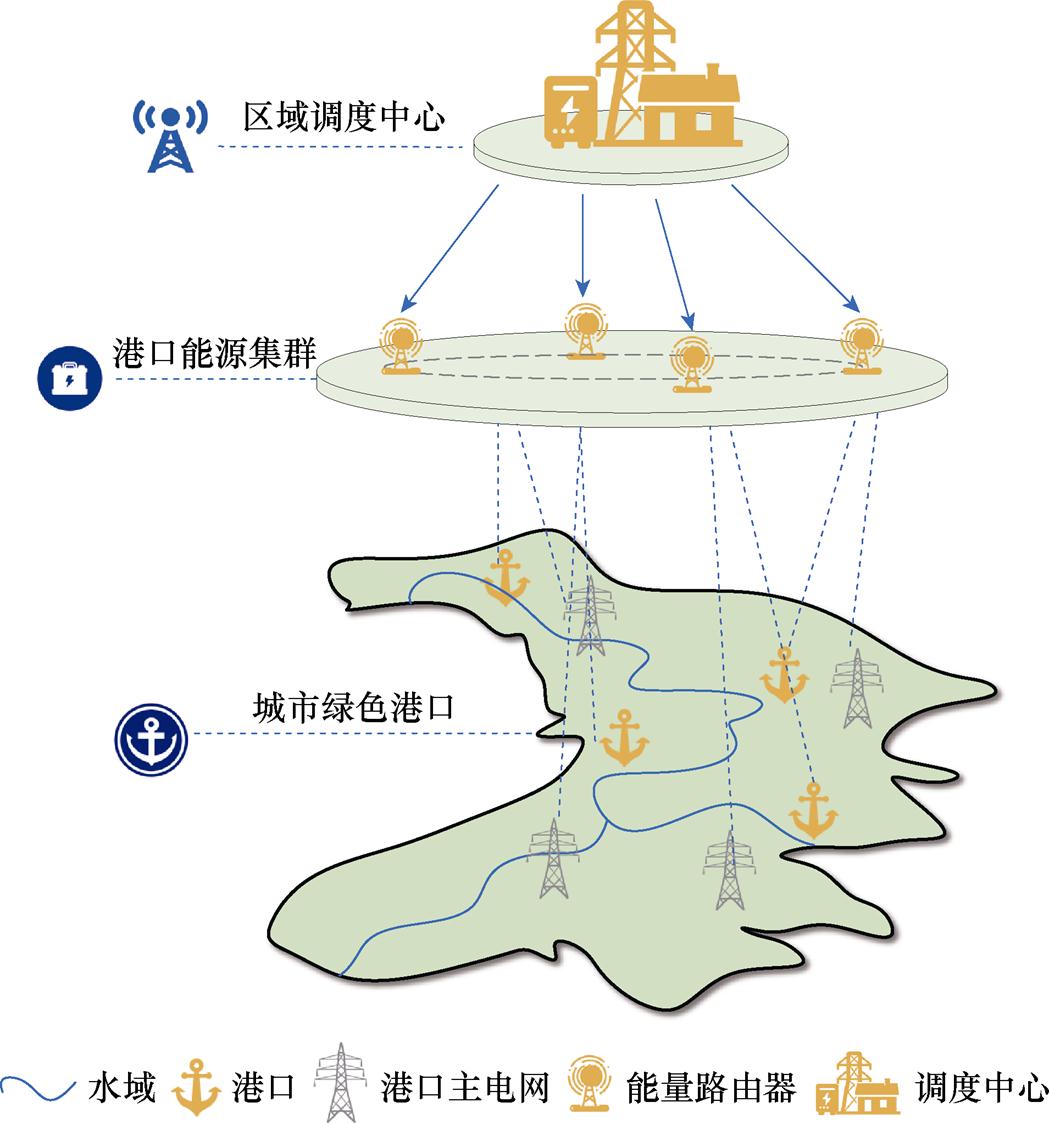
图2 绿色港口集群区域电网架构
Fig.2 Regional grid architecture in green port cluster
为保证能源能够在港口集群之间进行调度,本文建立了基于绿色港口集群区域电网的能源交易市场模型,用于优化港口集群的定价策略与能源调度策略,其管理流程可用图3表示。
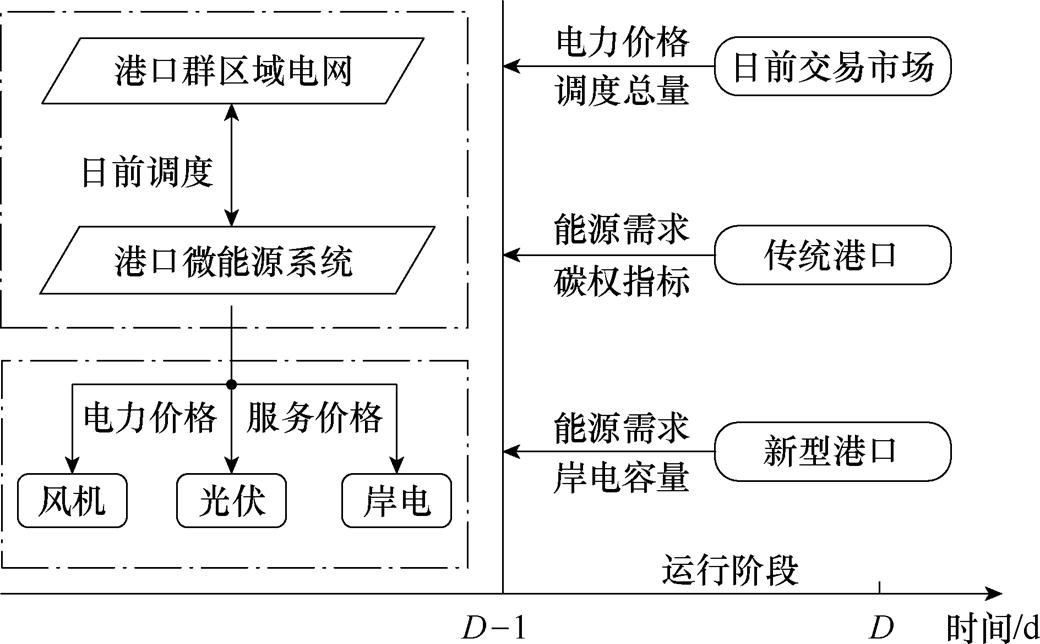
图3 日前能源市场管理流程
Fig.3 Schematic flow chart of day-ahead management
其中,港口集群区域电网与港口微能源系统之间的能源调度是日前调度,港口集群区域电网提前一天响应能源供需总量的变化,作为能源代理商参与电力市场的电能申报与交易,并制定与下级港口间的日前能源交易价格,以获得区域电网的最大经济效益。参与能源交易市场的下层港口根据自身日内的能源需求和经济效益需求,选择不同的能源供应策略和能源交易策略,完成日内的能源调度。同时,为提升整体中长期的效益,区域电网会根据下层港口的交易策略动态调整未来的电价设定,这是区域电网进行市场化电价定制的手段,目前已经具备充分的政策可行性[22]。
港口集群区域电网的协同优化问题涉及区域电网与港口、港口与港口等多个利益主体的竞争,为了深入研究多个独立参与者(跟随者)对主导参与者(领导者)做出的决策响应,本文拟基于双层博弈理论,设计绿色港口集群多层级协同优化策略,其中将港口微能源系统当作跟随者,区域电网当作领导者,所提出的博弈决策表示为
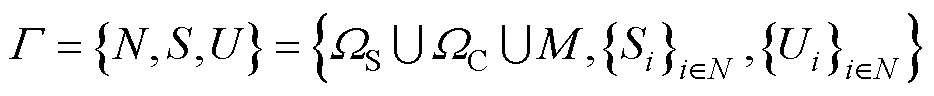 (7)
(7)
式中,N、S、U分别为参与者集合、纯策略集合和效用函数集合;下标i为港口对应的编号;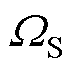 为配备港口岸电系统的新型港口集合;
为配备港口岸电系统的新型港口集合;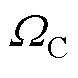 为传统港口集合;M为绿色港口集群区域电网。上述物理量的细分如下:
为传统港口集合;M为绿色港口集群区域电网。上述物理量的细分如下:
1)绿色港口都归属于港口集群集合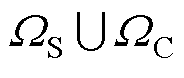 ,在博弈中担任跟随者的角色。
,在博弈中担任跟随者的角色。
2)效用函数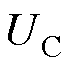 代表传统港口的效用,包含其通过购买上级电网的电力和利用新能源发电来满足日常负荷,并向船舶提供泊位服务获得的经济效益。其策略空间
代表传统港口的效用,包含其通过购买上级电网的电力和利用新能源发电来满足日常负荷,并向船舶提供泊位服务获得的经济效益。其策略空间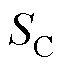 代表港口向上级电网购电、新能源发电等功率调度策略。
代表港口向上级电网购电、新能源发电等功率调度策略。
3)效用函数 代表新型港口的效用,与传统港口的不同之处在于其可以提供岸电服务,面向船舶的种类更多,综合效益更佳。其策略空间
代表新型港口的效用,与传统港口的不同之处在于其可以提供岸电服务,面向船舶的种类更多,综合效益更佳。其策略空间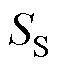 还包括面向港口岸电和全电力船舶的功率调度策略。
还包括面向港口岸电和全电力船舶的功率调度策略。
4)效用函数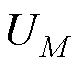 代表整个绿色港口集群区域电网的效用,其通过向各类港口售电获得经济效益,并对各港口进行能量的调节。其策略空间
代表整个绿色港口集群区域电网的效用,其通过向各类港口售电获得经济效益,并对各港口进行能量的调节。其策略空间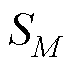 对应电价设定和能量调度的策略。
对应电价设定和能量调度的策略。
港口区域电网决定电力的价格,以增加自身收入。各港口提前向区域电网发送能源信息以进行能量交换,每个参与港口的信息对其他港口都是不可见的,有效地保护了各利益主体的隐私信息,但同时也和其他港口产生了竞争关系,即本文的双层博弈是非合作博弈[23]。
2.1.1 效用函数的性质
每个传统港口的能源调度计划会根据不同的利益需求有所不同,本文定义了一类效用函数,用于衡量不同利益主体在能源调度中的满意度水平。设定xi代表港口i的决策,x-i代表其他港口的决策,这类决策包含港口微能源系统的功率调度情况;并设定ai和bi均为港口i对能源价格的敏感参数,代表港口每调度一单位能量所能达到的满意度,但两者与价格的相关性相反。ai体现的是港口i在能源交易过程中的支付能力上限,与其可调度的能源总量相关,ai越大表示港口愿意支付给上级电网的价格越高,在不同港口利益主体中对于日内能源调度的满意程度也会越大,其效用值更高。ai值的设定一般与电价相匹配,如果ai的值低于当前电价,说明该港口认为当前电价设置高于其期望,经济效益的满意度会变差。bi体现的是港口i在能源交易过程中对经济效益的期望和态度,bi越大表示港口对价格越敏感。对于同样价格的能源,bi越大的港口购买量就会越少,整体的效用值越低,这与经营该港口的管理者对经济效益的态度相关。单位电力的价格也会影响港口的效用。因此,效用函数必须满足以下性质。
1)效用函数是一个非递减的函数,因为每个港口都愿意调度更多的能源,在满足自身能源需求的约束下,获得更多的经济效益。
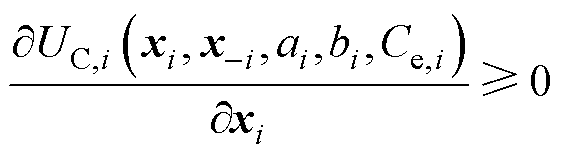 (8)
(8)
式中,UC,i( · )为传统港口i的效用函数;Ce,i为港口i的电价。
2)港口的边际效益是一个非递增的函数,当港口进行更多的能源交易后,满意度会提升。
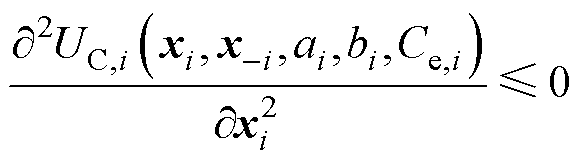 (9)
(9)
3)根据对价格敏感参数的定义,在能源交易水平相同的情况下,ai越大效用越高,bi越大效用越低。
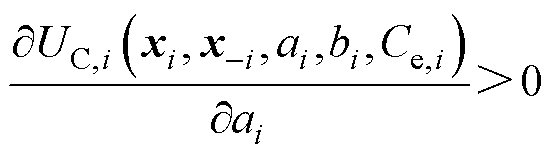 (10)
(10)
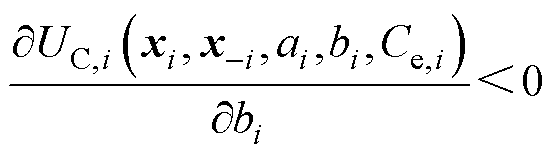 (11)
(11)
4)港口集群区域电网制定的价格影响港口的效用,电价越高,效用越低。
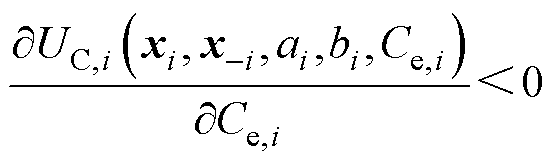 (12)
(12)
2.1.2 下层优化的效用函数
基于上述分析,本文提出了面向双层博弈模型中下层传统港口和新型港口的效用函数,其能够反映各港口对于能源供应和经济效益的利益需求满意程度。
传统港口的效用函数定义为
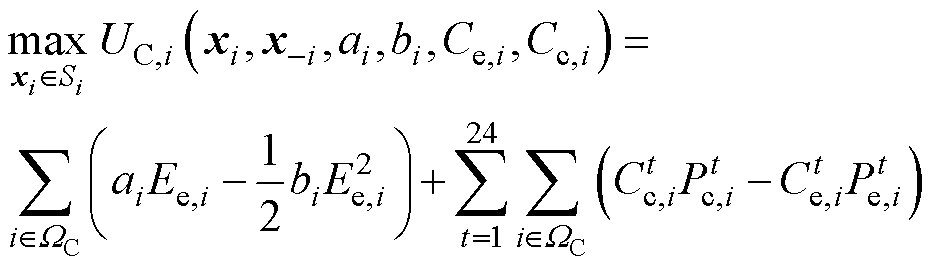 (13)
(13)
式中,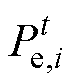 为t时刻港口i能源调度的功率;
为t时刻港口i能源调度的功率;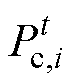 为t时刻港口i起重机装卸货物的功率,即船舶进行港口服务的功率;
为t时刻港口i起重机装卸货物的功率,即船舶进行港口服务的功率;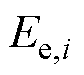 为港口i参与能源调度的总量;
为港口i参与能源调度的总量;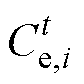 为t时刻港口i的电价;
为t时刻港口i的电价;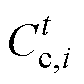 为t时刻港口i船舶参与港口服务的价格。同理,将新型港口的效用函数定义为
为t时刻港口i船舶参与港口服务的价格。同理,将新型港口的效用函数定义为
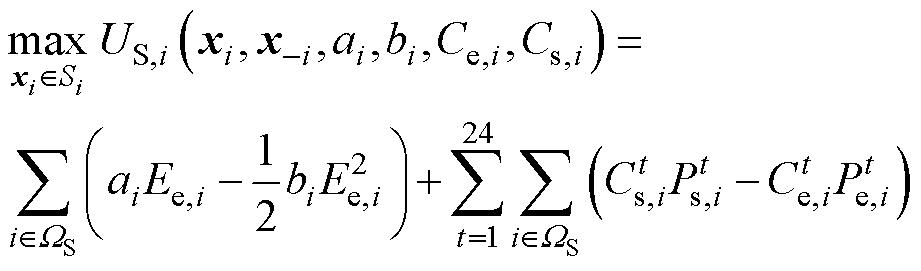 (14)
(14)
式中,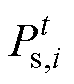 为t时刻港口i岸电向停靠的全电力船舶充电的功率;
为t时刻港口i岸电向停靠的全电力船舶充电的功率;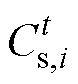 为t时刻港口i这部分岸电的效益,这是新型港口区别于传统港口之处,它可以为停靠的全电力船舶提供电力服务而获得能源上的收益。
为t时刻港口i这部分岸电的效益,这是新型港口区别于传统港口之处,它可以为停靠的全电力船舶提供电力服务而获得能源上的收益。
由式(13)和式(14)可知,港口的效用与能源调度的总量、价格敏感程度以及能源和服务的单价有关。其中,第一项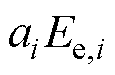 用于衡量港口对能源调度情况的满意水平,港口的支付能力越高、能源调度总量越多,其对于日内的运营情况满意度将越高;第二项
用于衡量港口对能源调度情况的满意水平,港口的支付能力越高、能源调度总量越多,其对于日内的运营情况满意度将越高;第二项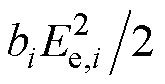 用于衡量港口对经济效益需求的满意度水平,港口对经济效益需求预期越高,在同样的经济效益下,其满意度水平将越低;第三项
用于衡量港口对经济效益需求的满意度水平,港口对经济效益需求预期越高,在同样的经济效益下,其满意度水平将越低;第三项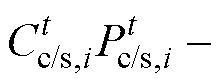
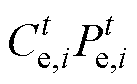 用于衡量港口的运营获利情况。
用于衡量港口的运营获利情况。
2.1.3 下层优化的约束条件
港口的功率调度受到最大功率和港口微能源系统实际能源水平的限制,因此下层优化模型需满足以下约束条件:
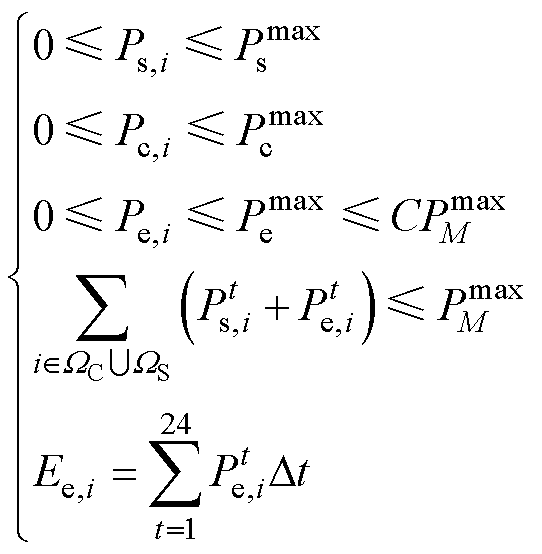 (15)
(15)
式中,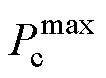 为港口起重机的最大功率;
为港口起重机的最大功率;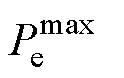 、
、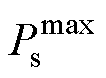 分别为主电网、港口岸电的最大传输功率,前者一方面与每个港口微能源系统的新能源发电水平和负荷水平相关,另一方面会受到区域电网分配的碳权指标的限制,区域电网将根据各个下级港口的碳权指标分配电力,而后者与港口岸电设备能够承载的功率上限相关;C为碳权系数,其设置借鉴了文献[19]中碳流率的考虑,在新型电力系统建设推进下,为达成减碳目标,需要对特定对象做出一定的碳约束;
分别为主电网、港口岸电的最大传输功率,前者一方面与每个港口微能源系统的新能源发电水平和负荷水平相关,另一方面会受到区域电网分配的碳权指标的限制,区域电网将根据各个下级港口的碳权指标分配电力,而后者与港口岸电设备能够承载的功率上限相关;C为碳权系数,其设置借鉴了文献[19]中碳流率的考虑,在新型电力系统建设推进下,为达成减碳目标,需要对特定对象做出一定的碳约束;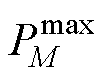 为整个港口集群区域电网的功率传输上限。
为整个港口集群区域电网的功率传输上限。
2.1.4 上层优化的效用函数
作为双层博弈的上层领导者,绿色港口集群区域电网通过设定合理的电价,在区域的能源交易中获得经济效益,其效用函数定义为
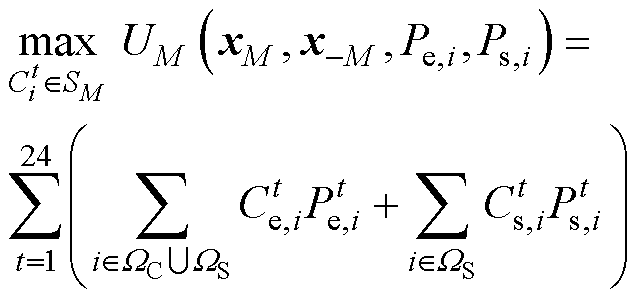 (16)
(16)
式中,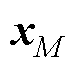 为港口集群的决策;
为港口集群的决策;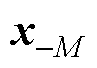 为除集群外其他参与者的决策;
为除集群外其他参与者的决策;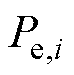 为港口i与主电网之间的调度功率;
为港口i与主电网之间的调度功率;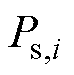 为港口i与岸电系统间的调度功率。
为港口i与岸电系统间的调度功率。
2.1.5 上层优化的约束条件
在考虑如图2所示的辐射状网架的基础上,港口集群区域电网与下层港口的功率调度需要考虑节点功率平衡约束,即
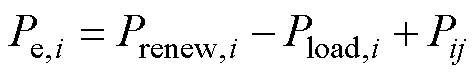 (17)
(17)
式中, 为港口i的风机、光伏出力;
为港口i的风机、光伏出力;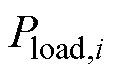 为港口i的负荷需求,主要包括港口起重机和港口岸电系统的负荷需求;
为港口i的负荷需求,主要包括港口起重机和港口岸电系统的负荷需求;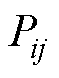 为港口i、j之间的调度功率。
为港口i、j之间的调度功率。
博弈均衡就是求解问题的策略,其存在性由如下定理说明[24]。
定理1:给定双层博弈问题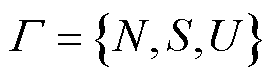 ,当且仅当满足下列不等式集时,策略
,当且仅当满足下列不等式集时,策略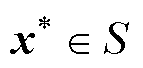 构成该问题的均衡解。
构成该问题的均衡解。
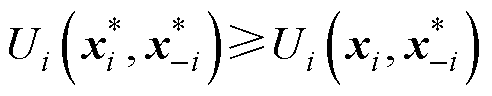
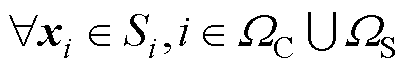 (18)
(18)
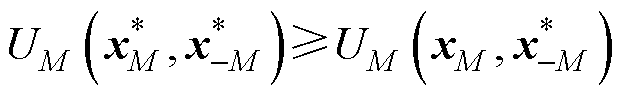
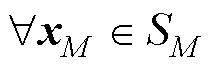 (19)
(19)
为了计算该博弈的均衡,可将双层博弈转换为双层优化问题,即
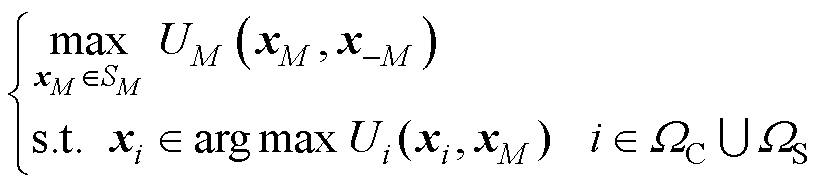 (20)
(20)
在求解该双层优化问题时,首先下层港口根据港口集群区域电网的定价形成能源调度的最优策略,并将其作为上层港口集群区域电网效用最大化函数的约束条件,最终解得绿色港口集群的效用最大值。
需要说明的是,该双层优化问题的解就是转换前双层博弈的均衡解。根据本文对港口微能源系统的效用函数的定义,当所有bi>0时,两类效用函数都是求最大值的凸二次规划问题,根据文献[25],这类问题具有全局最优解。
此外,每个港口的策略选择,即效用函数的博弈均衡解,对于上层区域电网设定的电价是唯一的。因此,双层优化问题可以表示为
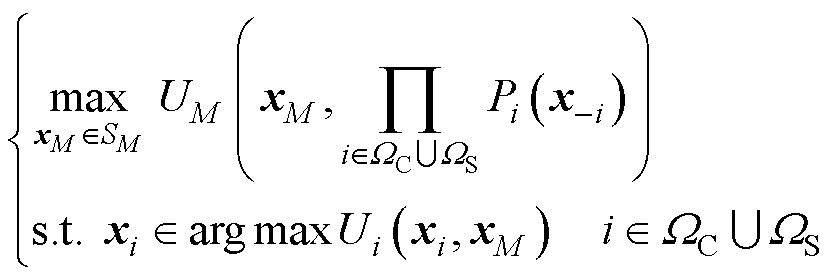 (21)
(21)
式中,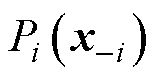 为港口集群的博弈对手(即下层各港口)的策略。
为港口集群的博弈对手(即下层各港口)的策略。
从港口集群区域电网的角度,式(21)可以被看作一个由下层港口的策略集合给定隐式约束的数学优化问题。该问题的最优解使得区域电网的效用最大化,同时捕捉到每个港口对应的最优能源调度策略,并且满足式(18)和式(19)中对博弈均衡解的定义。可见,将双层博弈均衡问题转换为双层优化问题可以求得全局最优解。
2.3.1 求解框架
本文提出的绿色港口集群能源经济优化调度的双层博弈模型求解框架如图4所示,其主要包含两个层面。
1)港口集群区域电网作为博弈领导者,提前一天响应能源供需总量的变化,作为能源代理商参与电力市场的电能申报与交易,并制定与下级港口间的日前能源交易价格。
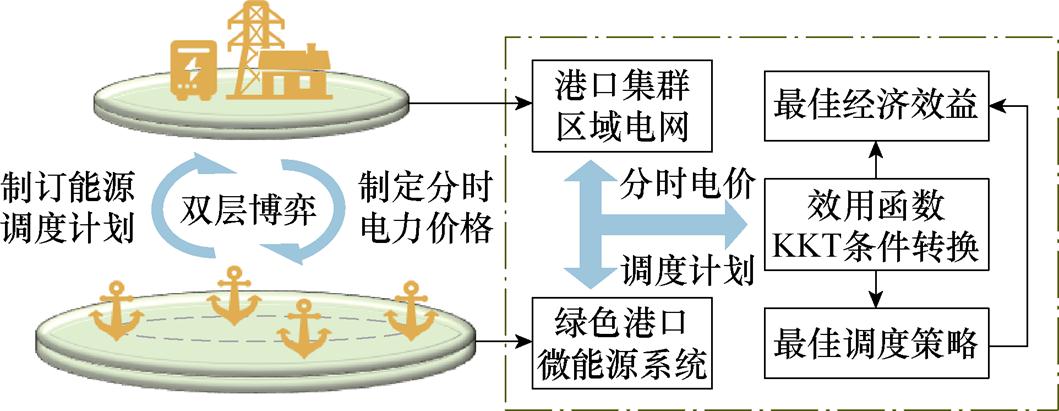
图4 求解框架
Fig.4 Solution framework
2)各港口微能源系统作为博弈跟随者,根据区域电网的所报电价,在不了解其他港口的能源需求的情况下,在满足自身负荷需求与系统约束的基础上,以自身利益最优为目标,与上级电网之间进行能源的调度。
为求解该“领导者-跟随着”模式双层数学优化问题,结合该问题模型的凸性,可以用等价Karush- Kuhn-Tucker(KKT)条件转换求解,将在2.3.2节详述。
2.3.2 求解方法与流程
利用等价KKT条件,将下层问题转换为一组约束条件,然后将这些KKT形式的约束条件整合到上层问题中,从而将原始的双层优化问题转换为一个包含额外约束的单层优化问题,具体过程如下:
首先,引入拉格朗日乘子,将下层效用函数用KKT条件的形式进行重构。KKT条件主要包括两个方面:一方面为下层问题的目标函数关于决策变量的梯度为零,另一方面必须满足不等式约束的互补松弛性,即
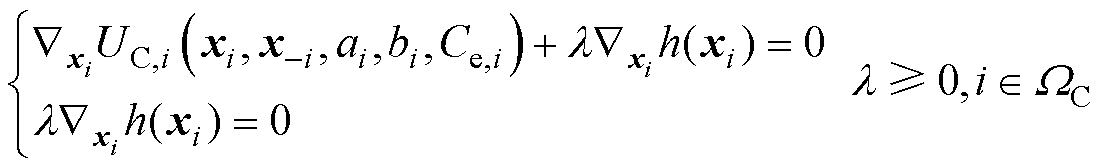 (22)
(22)
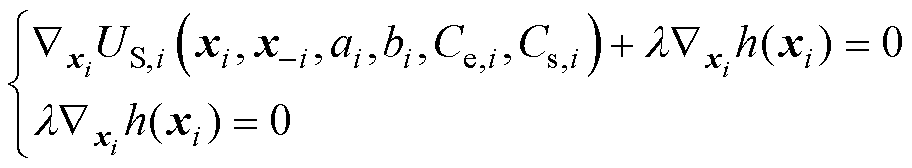
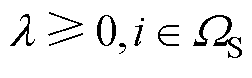 (23)
(23)
式中,l 为拉格朗日乘子;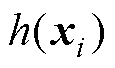 为绿色港口微能源系统和区域电网的约束条件。
为绿色港口微能源系统和区域电网的约束条件。
其次,将这些KKT约束条件整合到上层问题中,上层效用函数可以写为
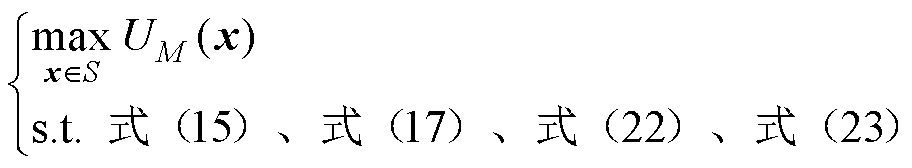 (24)
(24)
可见,将原始的双层优化问题转换为一个包含额外约束的单层优化问题,最终可解得该双层优化问题的最优解,即为双层博弈的均衡解。算法流程如图5所示,详细转换过程可参考附录。
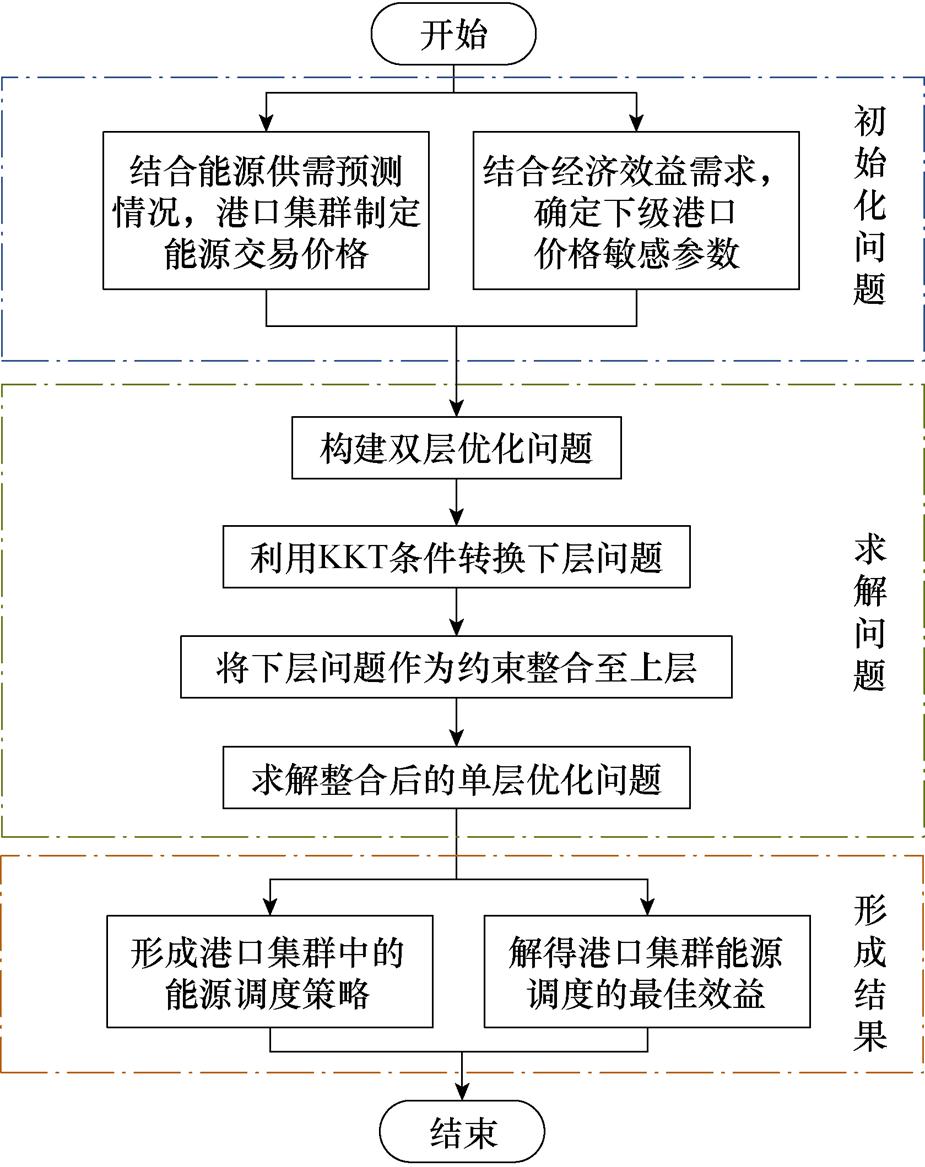
图5 算法流程
Fig.5 Algorithm flow chart
本文选取中国江苏省苏州的四个沿江、内河港口为研究对象,其中包括吴江港口(港口1)、振南港口(港口2)两个传统港口,兴华港口(港口3)、新泰港口(港口4)两个配备港口岸电系统的新型港口,进而分析两类港口和该港口集群区域电网的效益和策略。该绿色港口集群的新能源发电功率和负荷功率如图6所示。此外,根据下级港口微能源系统的能源需求情况,为最大化港口集群的整体利益,作为能源代理商的港口集群区域电网结合电价设定的一般情况所设置的交易电价见表1。
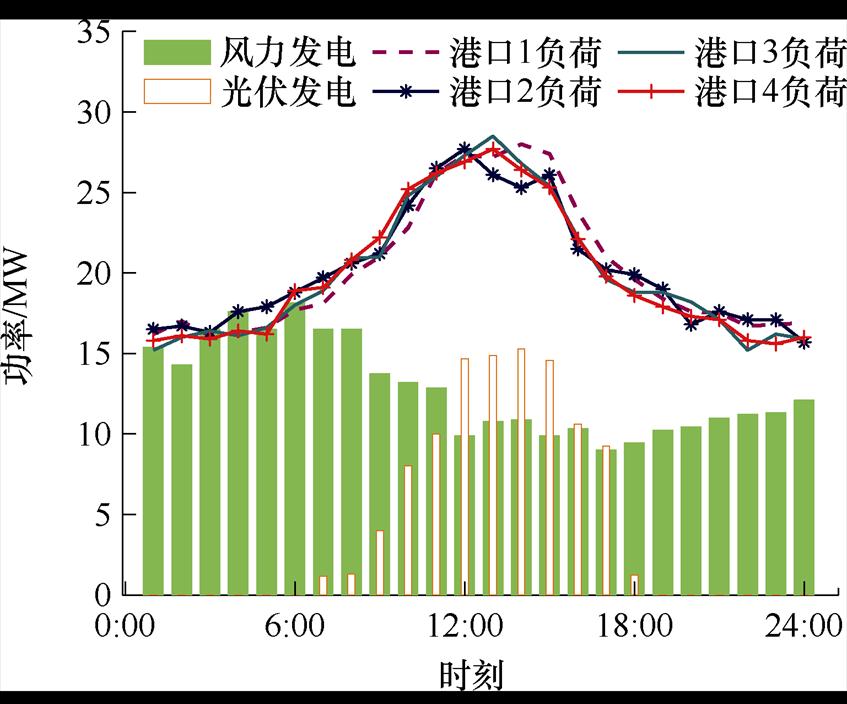
图6 绿色港口集群新能源发电功率和负荷功率
Fig.6 Renewable energy generation capacity and load power of green port clusters
表1 港口集群电价
Tab.1 Electric price in port cluster
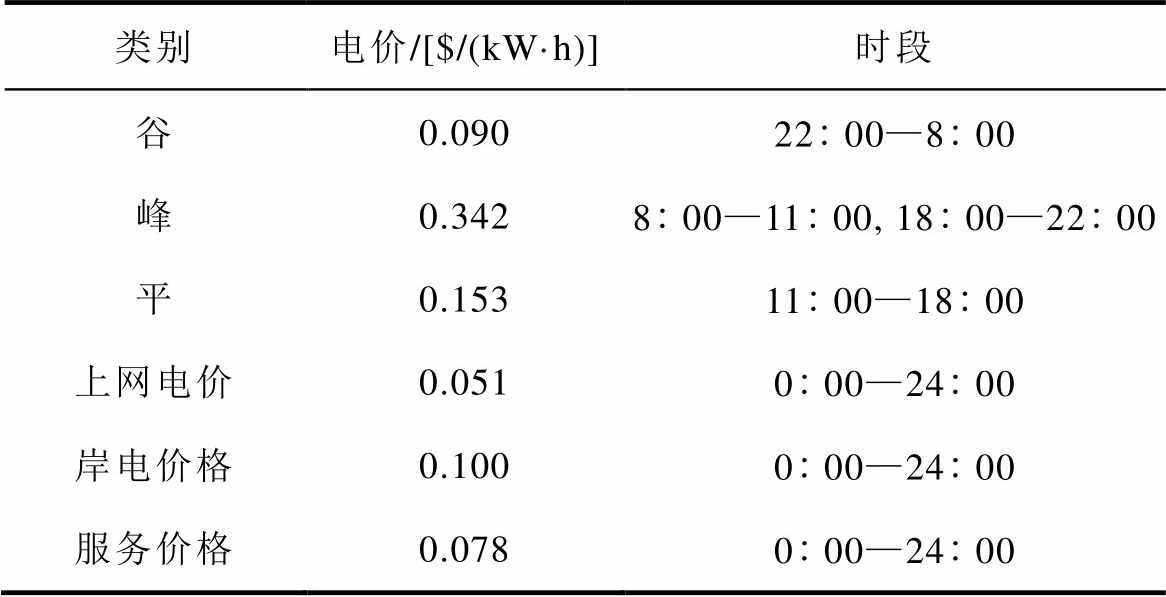
类别电价/[$/(kW·h)]时段 谷0.0902200—800 峰0.342800—1100, 1800—2200 平0.1531100—1800 上网电价0.051000—2400 岸电价格0.100000—2400 服务价格0.078000—2400
为验证本文所提方法的有效性,采取以下对照场景进行对比仿真。其中,场景1与场景3的对比是为了突出本文所提的双层博弈方法在港口集群能源联合调度中的有效性,场景2与场景3的对比是为了说明因博弈产生的利益冲突并不会降低港口集群整体的综合效益。
场景1:各港口微能源系统单独运行,不受区域电网支配,仅满足各自能源需求。这种场景下港口之间不存在功率的调度和交换,每个港口微能源系统的功率就地平衡,多余的新能源将被舍弃。
场景2:区域电网整体调度整个港口集群的能源,使得港口集群内港口的经济效益最大化。这种模式下港口微能源系统的个性化利益需求将不被考虑,仅从港口集群整体的经济效益出发。
场景3:采用双层博弈的思想,考虑上层区域电网和下层绿色港口的不同利益主体的效用,发挥不同利益主体主动调度功率的功能,使港口集群各利益主体综合效益最大化。
考虑电价的影响,参考文献[13-14]的思路,设置各港口的价格敏感参数见表2。ai的范围设定为[0.8Ce,i, Ce,i],用于表示港口愿意支付的价格;bi的范围设定为[0.08, 0.10],用于表示港口对于经济效益的预期需求。bi的范围下限若过低会导致该项对效用函数的影响偏低,bi的范围上限若过高则可以认为该港口不愿意参与集群的博弈,故综合上述考虑设置bi的范围。此外,碳权系数分配见表3。碳权系数越高表示区域电网接受其碳排放量的上限越高,因此,给予其越少的碳约束,允许其调度的功率上限越高。
不同场景下的绿色港口集群能源调度的效用见表4。
表2 各港口的价格敏感参数
Tab.2 The price sensitive parameters of each port
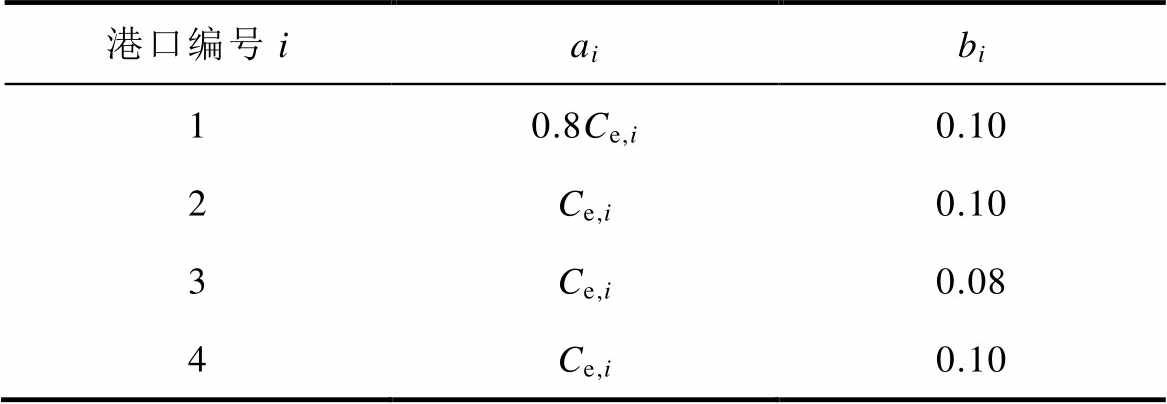
港口编号iaibi 10.8Ce,i0.10 2Ce,i0.10 3Ce,i0.08 4Ce,i0.10
表3 绿色港口碳权系数
Tab.3 Carbon right factors of green port

港口碳权系数 传统港口10.85 传统港口20.9 新型港口30.95 新型港口41
表4 不同场景下绿色港口集群的效用
Tab.4 The utility of green port cluster under different cases (单位: 104 $)
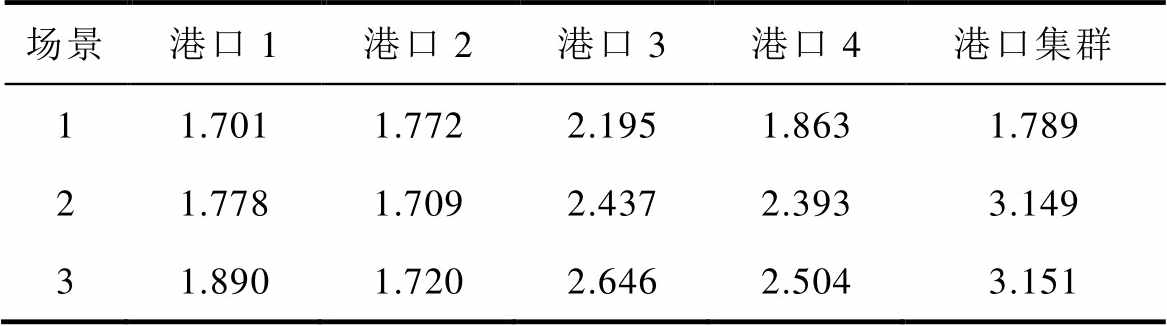
场景港口1港口2港口3港口4港口集群 11.7011.7722.1951.8631.789 21.7781.7092.4372.3933.149 31.8901.7202.6462.5043.151
相较于场景1,场景3下绿色港口的总运行效用提升了16.32%,原因在于,场景3是基于双层博弈的港口集群能源调度模型,通过绿色港口与区域电网的能源交易,大大减少了各绿色港口独立运行时能源不平衡的情况,港口可以通过向区域电网回馈多余的能源而获益,同时也大幅降低了弃风和弃光的水平。此外,相较于场景1,场景3下传统港口的运行效用提升了3.94%,新型港口的运行效用提升了26.91%。新型港口的效用提升情况较高有两方面的原因:一方面,新型港口可以向船舶主体提供充电服务从而获得来自岸电系统的收益;另一方面,由于新型港口减碳效应更佳,受到区域电网的碳约束较低,能源调度的功率上限较高,更易在能源调度中获得更大的效益。其中,新型港口3的运行效用在场景3下是最大的,相比其他三个港口的效用值分别高出40.00%、53.84%和5.67%,这一方面是由于其新型港口的属性,另一方面是由于新型港口3对价格的敏感程度较低,因此其对能源调度运行的满意度更高。
相较于场景1,场景3下绿色港口集群区域电网的效用提升了76.13%,这是因为区域电网在场景3中作为双层博弈的领导者,将下级四个港口的能源连接起来,通过回收下级港口的余电,有大量的能源可以供给下级港口,并以此获利。而在场景1中,区域电网与下级港口是割裂的,区域电网只能向每个单独的港口售电,能源的利用率有所下降,经济效益也相应降低。
对比场景2与场景3,场景3的绿色港口的总运行效用提升了5.33%。其中,相较于场景2,场景3下传统港口的运行效用提升了3.53%,新型港口的运行效用提升了6.63%。这是由于在场景2的模式下,港口微能源系统的个性化利益需求不被考虑,仅从港口集群整体的经济效益出发,因此下层港口的效益满足程度将变差,不符合多利益主体的需求。而从上层区域电网的角度而言,双层博弈场景下的博弈均衡解与场景2的最优解基本保持一致,即港口集群的综合效益并不会因为不同利益主体间的博弈关系而下降,场景3所描述的博弈场景也能保障每个利益主体的效益。因此综合来看,场景1削弱了港口集群区域电网的利益,场景2削弱了港口主体的利益,而场景3下基于双层博弈的绿色港口集群能源调度模型是最优的方案,实现了多利益主体的共赢。
在双层博弈的场景3下,该绿色港口集群的功率调度情况如图7所示,上级港口区域电网从下级港口获得的效益如图8所示。
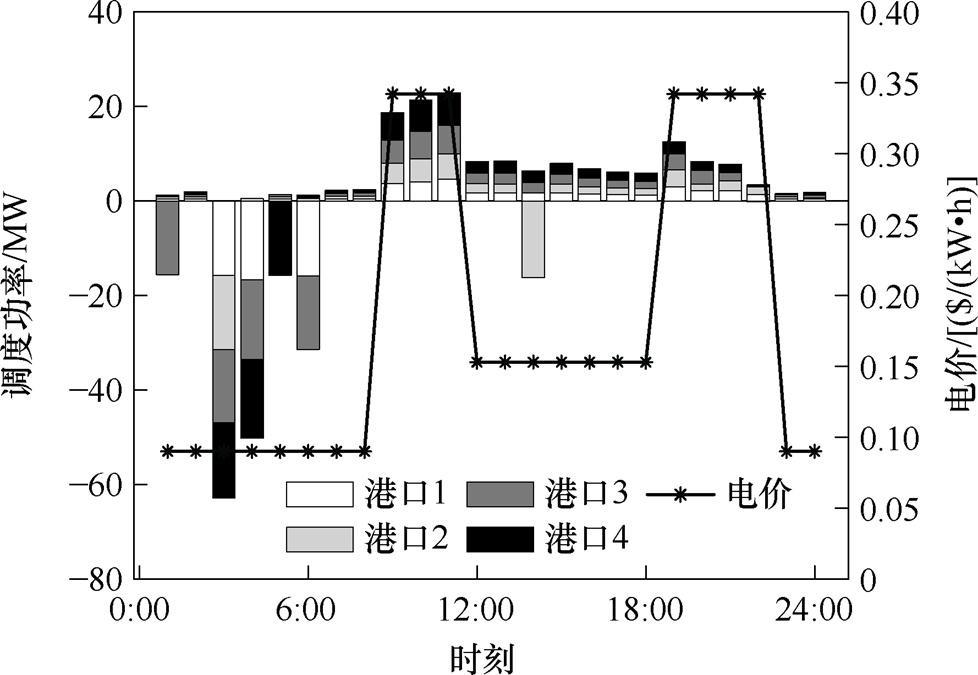
图7 绿色港口集群双层博弈场景功率调度(阶梯碳权)
Fig.7 Power dispatching in green port cluster under two-stage game theory
从图7和图8中可以分时段分析双层博弈场景下的不同利益主体的功率调度情况和获利方式。在夜间至早晨,即22 00—7
00—7 00的时间段内,港口内负荷较少,而此时风能资源较丰富,因此港口在满足自身负荷需求的前提下,将部分余电存储在储能系统中或者直接进行余电上网,可获得一定的经济效益。在负荷高峰的9
00的时间段内,港口内负荷较少,而此时风能资源较丰富,因此港口在满足自身负荷需求的前提下,将部分余电存储在储能系统中或者直接进行余电上网,可获得一定的经济效益。在负荷高峰的9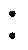 00—11
00—11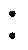 00与19
00与19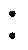 00—21
00—21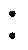 00,风能出力下降,光伏出力较弱,新能源发电不能满足负荷需求,由于此时港口集群区域电网设定的电价相对较高,港口需要调用储能系统中的电能来降低发电成本,但其向上级电网购买的电力也相对较多。这一现象说明双层博弈模型既满足了港口自身的发电要求,也给上级电网带来了效益,实现了博弈均衡。而在11
00,风能出力下降,光伏出力较弱,新能源发电不能满足负荷需求,由于此时港口集群区域电网设定的电价相对较高,港口需要调用储能系统中的电能来降低发电成本,但其向上级电网购买的电力也相对较多。这一现象说明双层博弈模型既满足了港口自身的发电要求,也给上级电网带来了效益,实现了博弈均衡。而在11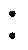 00—19
00—19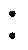 00的时间段内,由于光伏出力增加,港口为提升自己的经济效益,其向上级电网购买的电力也相对减少。这也说明港口愿意更多地使用新能源设备进行发电而降低成本,并同时实现碳排放量的降低。而在各港口独立运行的场景下,各港口在某些时段出现了能源的盈余或匮乏,没有利用好不同港口之间的多能互补的特性,能源利用率不及双层博弈场景下的功率调度情形。
00的时间段内,由于光伏出力增加,港口为提升自己的经济效益,其向上级电网购买的电力也相对减少。这也说明港口愿意更多地使用新能源设备进行发电而降低成本,并同时实现碳排放量的降低。而在各港口独立运行的场景下,各港口在某些时段出现了能源的盈余或匮乏,没有利用好不同港口之间的多能互补的特性,能源利用率不及双层博弈场景下的功率调度情形。
图8 区域电网从下级港口获得的效益
Fig.8 The utility of regional grid from subordinate ports
需要指出的是,不同港口和上级区域电网的调度在总体上趋势一致,但是由于受到自身负荷需求和碳权系数的限制,不同港口的调度功率有所区别。在大部分时间段内,新型港口4的调度功率相对较大,参与的能源交易更多,这是因为区域电网向其分配的碳权系数较高,其受到的碳约束小,可供其调度的功率也相应较大,而其他港口受到的碳约束相对较大。将新型港口4和传统港口1进行对比可知,传统港口1受碳权限制较高,为降低发电成本提高自身效益,传统港口1会尽可能地减少在集群内的功率调度与电力消费,更大比例地使用负荷低谷时段储存的新能源电力,长期来看,这也将迫使其在未来增加新能源发电的比例、配备港口岸电系统,以更好地满足港口内部的负荷需求;而新型港口4在不受碳权限制的前提下,会尽可能多地利用港口集群区域电网进行功率调度,包括在电价较低时购电、新能源余电上网等,这不仅提高了自身的效益,也起到了较好的削峰填谷效果。因此,碳权系数的设置有利于减少集群整体的碳排放量,并迫使碳排放量较高的利益主体加快减碳改造,进一步提升集群的综合效益。此外,在部分时间点,由于不同港口的负荷功率不同,功率调度情况具有特殊性,这说明在双层博弈的框架下,不同利益主体会根据自身需求选取相应的调度策略,并不会因为博弈造成综合效益的损失。可见,本文所提出的基于双层博弈的港口集群能源调度模型对调节能源供应、提升经济效益以及协调碳排放量都有一定的作用。
此外,本文对比了统一设置四个港口碳权系数的方案,此时该绿色港口集群的功率调度情况如图9所示。从两类碳权系数设置情形下的功率调度情况来看,若实行统一的碳权系数,传统港口在与新型港口进行竞争时将不再面临成本上的劣势。进一步观察分时的功率调度情况,夜间时段由于新能源发电能力较弱,四个港口的功率调度策略呈现较高的相似性;然而在日间时段,传统港口向上级电网的购电量相较于阶梯式碳权系数设置情形下有了显著提升。出现这一现象的原因在于,传统港口在减碳方面不再承受额外的成本压力,因此在日间新能源发电无法满足负荷需求时,它们更倾向于直接向上级电网购电,而这种策略的综合效用并不逊色于新型港口。然而,这种趋势将直接导致港口集群内的碳排放量增加,使得配置新能源发电的成本优势不再明显,从长期来看,这将对港口集群的减碳进程构成不利影响。
图9 绿色港口集群双层博弈场景功率调度(统一碳权)
Fig.9 Power dispatching in green port cluster under two-stage game theory (unified carbon rights)
为进一步说明所提出求解算法的效率,本文还采用了粒子群优化算法求解场景3下的双层博弈问题。粒子群优化算法作为智能搜索算法,一般适用于下层问题非凸非线性的情况。本文选取不同参数进行计算,结果见表5。
表5 不同参数下粒子群算法求解结果
Tab.5 Solution of particle swarm optimization algorithm under different parameters
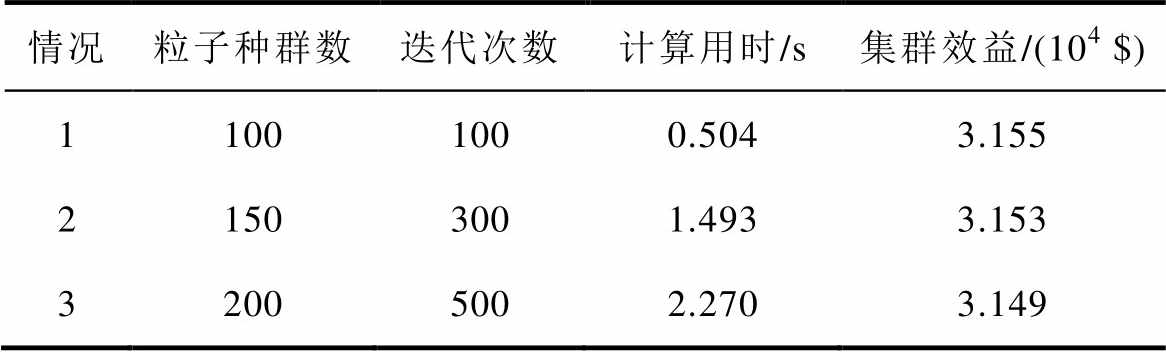
情况粒子种群数迭代次数计算用时/s集群效益/(104 $) 11001000.5043.155 21503001.4933.153 32005002.2703.149
在采用本文方法求解时,求解时间为0.029 s,显著小于采用粒子群优化算法的情况;且粒子群优化算法迭代过程具有随机特征,最终结果依赖粒子种群数和迭代次数,算法的不稳定性较大。可见本文的求解算法具有更加快速且准确的优势。即使规模较大,如在符合客观实际的条件下扩大集群规模、纳入更多数量的港口,求解方法依然有效,求解的时间尺度仍然较小。相反,如采用启发式搜索算法等智能算法求解博弈均衡问题,在规模较大时为更好地收敛,迭代次数将显著增多,求解效率将变差。
在“双碳”目标的背景下,本文以绿色港口集群为研究对象,基于双层博弈理论,提出了考虑港口集群与公共电网、港口与港口等不同利益主体需求的绿色港口集群能源经济优化调度模型。为验证所提方法的有效性,选取苏州四个沿江、内河码头和港口进行分析,得到主要结论如下:
1)本文所提出的基于双层博弈绿色港口集群能源经济优化调度模型综合考虑了港口集群和区域电网的利益需求,利用不同港口“源荷”的差异性,以区域电网为领导者,实现了能源的经济性优化调度。与不考虑双层博弈的场景进行对比,运行效用提升了16.32%,新能源的消纳水平得到进一步 增强。
2)不同绿色港口的效用与其自身的能源水平和经济需求密切相关。本文不仅考虑了经济成本,还考虑了多个港区的自然资源禀赋和对价格的敏感程度,从而满足了不同港口的利益需求,进一步达到了绿色港口集群整体效益最优。
3)同等场景下,配备港口岸电系统的新型港口的综合效益比传统港口的综合效益更高,这能有效地激励港口配备岸电设备,增加对新能源发电设备的投入,进一步降低港口的碳排放量。
未来,将在绿色港口集群的场景下,重点探索如何更准确地评估新能源与负荷的不确定性对绿色港口集群能源调度的影响,形成计及新能源预测不确定性与经济性调度两阶段联合优化模型,使本文提出的双层博弈模型在绿色港口集群下具备更加丰富的实用价值。
附录 双层优化问题转换过程
针对所构建的双层模型,下层函数的原始问题可以概括为如下目标函数与约束条件。
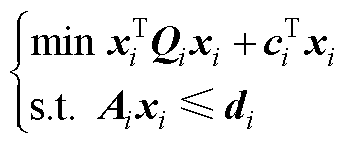 (A1)
(A1)
式中,xi为第i个港口的策略解;Qi和ci为其对应目标函数系数矩阵;同理,Ai和di分别为其对应约束条件的系数矩阵和边界矩阵。
将其转换成拉格朗日问题模型L,并写出KKT条件,有
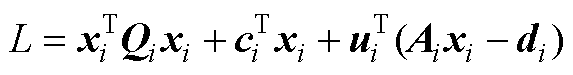 (A2)
(A2)
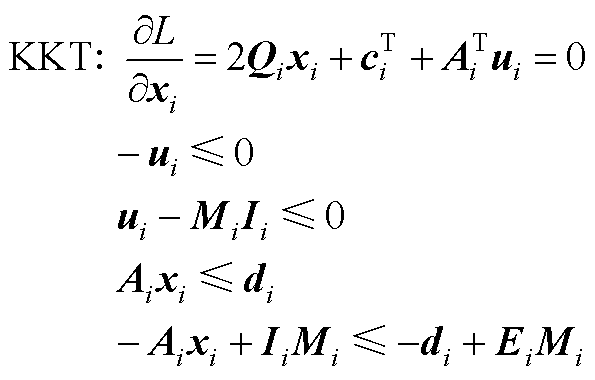 (A3)
(A3)
式中,ui为拉格朗日乘子矩阵;Mi、Ei、Ii为拉格朗日过程的约束矩阵,用于保证有界性。
如此,原始问题就转换为如下目标函数和约束条件形式。
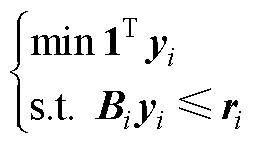 (A4)
(A4)
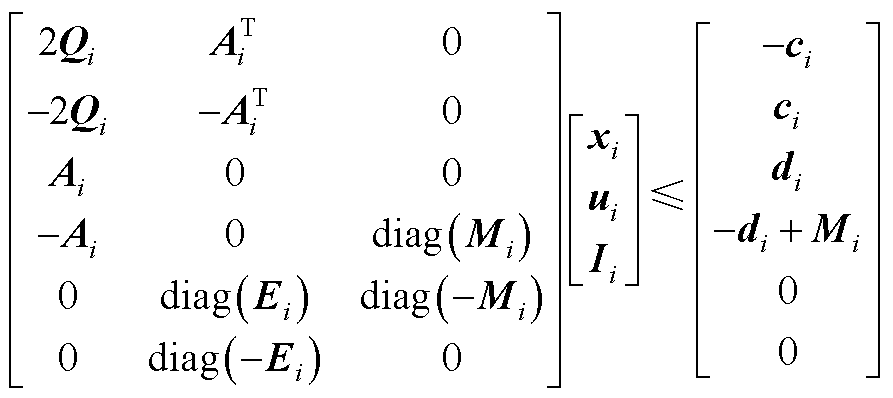 (A5)
(A5)
式中,yi为转换后的求解目标;Bi和ri分别为转换后的约束条件的系数矩阵和边界矩阵。
而针对上层问题,则可以转换为
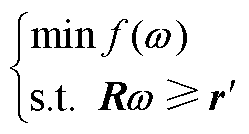 (A6)
(A6)
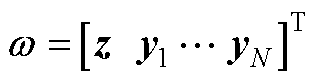 (A7)
(A7)
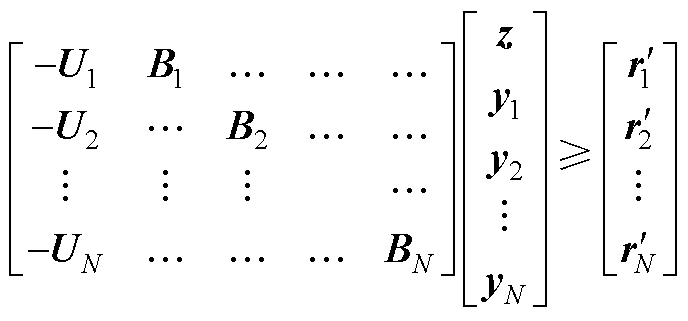 (A8)
(A8)
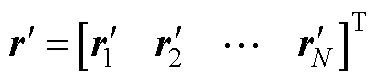 (A9)
(A9)
式中,w 为转换后的策略矩阵,包含上层策略z与下层策略y;U为上层约束的系数矩阵;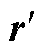 为整合了上层约束条件边界的约束条件边界矩阵。
为整合了上层约束条件边界的约束条件边界矩阵。
可见,下层问题中的KKT约束条件整合到了上层问题中,从而将原始的双层优化问题转换为一个包含额外约束的单层优化问题进行求解。
参考文献
[1] 胡博, 谢开贵, 邵常政, 等. 双碳目标下新型电力系统风险评述: 特征、指标及评估方法[J]. 电力系统自动化, 2023, 47(5): 1-15.
Hu Bo, Xie Kaigui, Shao Changzheng, et al. Commentary on risk of new power system under goals of carbon emission peak and carbon neutrality: characteristics, indices and assessment methods[J]. Automation of Electric Power Systems, 2023, 47(5): 1-15.
[2] 方斯顿, 赵常宏, 丁肇豪, 等. 面向碳中和的港口综合能源系统(一): 典型系统结构与关键问题[J]. 中国电机工程学报, 2023, 43(1): 114-134.
Fang Sidun, Zhao Changhong, Ding Zhaohao, et al. Port integrated energy systems toward carbon neutrality (part I): typical topology and key prob- lems[J]. Proceedings of the CSEE, 2023, 43(1): 114-134.
[3] 吴任博, 黄奕俊. 高比例可再生能源接入下含自愈性能的分布式配电网重构策略研究[J]. 发电技术, 2024, 45(5): 975-982.
Wu Renbo, Huang Yijun. Research on reconfiguration strategy of distributed distribution network with self-healing performance under high-proportion renew- able energy access[J]. Power Generation Techno- logy, 2024, 45(5): 975-982.
[4] 林森, 文书礼, 朱淼, 等. 海港综合能源系统低碳经济发展研究综述[J]. 中国电机工程学报, 2024, 44(4): 1364-1386.
Lin Sen, Wen Shuli, Zhu Miao, et al. Review on low-carbon and economic development of seaport integrated energy system[J]. Proceedings of the CSEE, 2024, 44(4): 1364-1386.
[5] 普月, 纪历, 刘皓明. 考虑综合需求响应的港口能源系统优化运行[J]. 电力需求侧管理, 2021, 23(1): 11-17.
Pu Yue, Ji Li, Liu Haoming. Optimal operation of port energy system considering integrated demand response[J]. Power Demand Side Management, 2021, 23(1): 11-17.
[6] 黄逸文, 黄文焘, 卫卫, 等. 大型海港综合能源系统物流-能量协同优化调度方法[J]. 中国电机工程学报, 2022, 42(17): 6184-6196.
Huang Yiwen, Huang Wentao, Wei Wei, et al. Logistics-energy collaborative optimization scheduling method for large seaport integrated energy system[J]. Proceedings of the CSEE, 2022, 42(17): 6184-6196.
[7] Yin Jingyuan, Yang Jie, Li Guanqi, et al. Research on integration model of shore-to-ship power supply system with high proportion renewable energy[J]. IOP Conference Series: Earth and Environmental Science, 2019, 371(4): 042056.
[8] Parise G, Parise L, Martirano L, et al. Wise port and business energy management: port facilities, electrical power distribution[J]. IEEE Transactions on Industry Applications, 2016, 52(1): 18-24.
[9] Gennitsaris S G, Kanellos F D. Emission-aware and cost-effective distributed demand response system for extensively electrified large ports[J]. IEEE Transa- ctions on Power Systems, 2019, 34(6): 4341-4351.
[10] Kanellos F D, Volanis E M, Hatziargyriou N D. Power management method for large ports with multi-agent systems[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1259-1268.
[11] 王灿, 张羽, 田福银, 等. 基于双向主从博弈的储能电站与综合能源系统经济运行策略[J]. 电工技术学报, 2023, 38(13): 3436-3446, 3472.
Wang Can, Zhang Yu, Tian Fuyin, et al. Economic operation of energy storage power stations and integrated energy systems based on bidirectional master-slave game[J]. Transactions of China Elec- trotechnical Society, 2023, 38(13): 3436-3446, 3472.
[12] 王波, 王蔚, 马恒瑞, 等. 基于Wasserstein两阶段分布鲁棒的多主体多能微网合作博弈优化调度[J/OL]. 电工技术学报, 2024: 1-18[2024-11-12]. http://kns.cnki.net/kcms/detail/11.2188.tm.20241025. 1338.002.html.
Wang Bo, Wang Wei, Ma Hengrui, et al. Multi-agent multi-energy microgrid cooperative game scheduling based on wasserstein two stage robust optimi- zation[J/OL]. Transactions of China Electrotechnical Society, 2024: 1-18[2024-11-12]. http://kns.cnki.net/ kcms/detail/11.2188.tm.20241025.1338.002.html.
[13] Zhao Tianyang, Li Yuanzheng, Pan Xuewei, et al. Real-time optimal energy and reserve management of electric vehicle fast charging station: hierarchical game approach[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5357-5370.
[14] Tushar W, Saad W, Poor H V, et al. Economics of electric vehicle charging: a game theoretic approach[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 1767- 1778.
[15] 马丽, 刘念, 张建华, 等. 基于主从博弈策略的社区能源互联网分布式能量管理[J]. 电网技术, 2016, 40(12): 3655-3662.
Ma Li, Liu Nian, Zhang Jianhua, et al. Distributed energy management of community energy Internet based on leader-followers game[J]. Power System Technology, 2016, 40(12): 3655-3662.
[16] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in indu- strial park integrated energy system based on Stackelberg game[J]. Transactions of China Electro- technical Society, 2021, 36(3): 507-516.
[17] 董雷, 李扬, 陈盛, 等. 考虑多重不确定性与电碳耦合交易的多微网合作博弈优化调度[J]. 电工技术学报, 2024, 39(9): 2635-2651.
Dong Lei, Li Yang, Chen Sheng, et al. Multi- microgrid cooperative game optimization scheduling considering multiple uncertainties and coupled electricity-carbon transactions[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2635- 2651.
[18] 杨雪莹, 祁琪, 李启明, 等. 奖励机制与用户意愿结合的高峰期负荷博弈调度策略[J]. 电工技术学报, 2024, 39(16): 5060-5074.
Yang Xueying, Qi Qi, Li Qiming, et al. Peak load game scheduling strategy combining reward mechanism and user willingness[J]. Transactions of China Elec- trotechnical Society, 2024, 39(16): 5060-5074.
[19] 曹逸滔, 王丹, 贾宏杰, 等. 考虑多能碳流约束的区域综合能源系统双层博弈扩展规划[J]. 电力系统自动化, 2023, 47(7): 12-22.
Cao Yitao, Wang Dan, Jia Hongjie, et al. Bilevel Nash-Stackelberg game expansion planning of regional integrated energy system considering multi- energy carbon flow constraints[J]. Automation of Electric Power Systems, 2023, 47(7): 12-22.
[20] 赵冬梅, 宋晨铭, 冯向阳, 等. 100%新能源场景下考虑频率稳定约束的源网荷储一体化系统储能优化配置[J]. 电工技术学报, 2025, 40(7): 2146-2161.
Zhao Dongmei, Song Chenming, Feng Xiangyang, et al. The optimal configuration of energy storage in the source-grid-load storage integrated system con- sidering frequency stability constraints in 100% new energy scenarios[J]. Transactions of China Electro- technical Society, 2025, 40(7): 2146-2161.
[21] Iris Ç, Pacino D, Ropke S. Improved formulations and an adaptive large neighborhood search heuristic for the integrated berth allocation and quay crane assignment problem[J]. Transportation Research Part E: Logistics and Transportation Review, 2017, 105: 123-147.
[22] 国家发展改革委. 国家发展改革委关于进一步深化燃煤发电上网电价市场化改革的通知[EB/OL]. (2021-10-11)[2024-08-14]. https://www.gov.cn/zhengce/ zhengceku/2021-10/12/content_5642159.htm.
[23] Myerson R B. Game Theory[M]. Cambridge: Harvard University Press, 1997.
[24] Frihauf P, Krstic M, Basar T. Nash equilibrium seeking in noncooperative games[J]. IEEE Transa- ctions on Automatic Control, 2012, 57(5): 1192-1207.
[25] Boyd S P, Vandenberghe L. Convex optimization[M]. Cambridge, UK: Cambridge, 2004.
Two-Level Game Theory-Based Economic Scheduling of Multi-Energy in Green Port Clusters
Abstract The optimization scheduling of energy systems within green port clusters poses a multifaceted challenge, encompassing intricate relationships among port grids, public grids, inter-port dynamics, and ship connections. A comprehensive and sophisticated approach is necessary for addressing these diverse and conflicting interests. This study proposes a tailored two-level game theory-based optimization scheduling model, which is designed for green port clusters. The aim of this is to enhance the economic efficiency of the regional grid, improve the utilization of renewable energy resources, and foster environmental sustainability within the broader framework of port cluster development.
The methodology employed in this study is grounded in the establishment of a hierarchical game model. At the first level, the regional grid of the port cluster acts as a pivotal leadership role, which is tasked with managing energy distribution within the local port cluster and determining energy prices in a way that maximizes economic benefits while ensuring the stability and reliability of the energy supply. The regional grid considers the complex dynamics of energy demand and supply within the port cluster, as well as the potential ripple effects of its decisions on the interconnected public grid. This comprehensive understanding allows the regional grid to formulate strategies that strike a balance between economic efficiency and energy security. At the second level, individual port microgrid systems act as followers, devising energy supply strategies that cater to ships accessing port onshore power while ensuring adequate power supply within the port area. These microgrid systems operate within the broader framework set by the regional grid, adjusting their strategies in response to changes in energy prices and supply conditions. This two-level interaction creates a dynamic and responsive energy system that can adapt to the evolving needs of the port cluster.
The two-level game model is then transformed into a two-level optimization problem, which was reformulated into a single-level optimization problem for efficient solution. The simulation results demonstrated that the proposed novel energy optimization approach for green port clusters transcends the limitations of onshore integrated systems, overcoming the shortcomings of conventional scheduling methods in addressing the diverse requirements of multiple stakeholders, while enhancing the economic efficiency of the regional grid within the port cluster, augmenting the utilization of renewable energy resources, and fostering environmental sustainability.
The following conclusions can be drawn from the simulation analysis: (1) The proposed two-level game model for green port clusters optimizes energy scheduling by balancing the interests of port clusters and regional power grids, leveraging port-specific energy differences. This results in a 16.32% increase in operational efficiency and enhanced renewable energy integration. (2) Considering economic costs, natural resource endowments, and price sensitivity, the model satisfies diverse port interests, optimizing the overall benefits of green port clusters. (3) Ports with shore power systems outperform traditional ports, with a 57.22% increase in benefits under the two-level game scenario. This incentivizes investment in renewable energy and shore power equipment, meanwhile reducing carbon emissions.
Keywords:Green port cluster, two-level game theory, leader-follower framework, optimal economy scheduling
中图分类号:TM734
DOI: 10.19595/j.cnki.1000-6753.tces.241447
国家电网有限公司总部科技项目资助(5400-202218430A-2-0-ZN)。
收稿日期 2024-08-14
改稿日期 2024-10-31
董晊兴 男,2000年生,硕士研究生,研究方向为港口与船舶多能源协同运行技术。
E-mail: dzx0013@sjtu.edu.cn
文书礼 男,1987年生,副教授/博士生导师,研究方向为海洋交通电气化、储能优化配置、深度学习与智能算法等。
E-mail: wenshuli@sjtu.edu.cn(通信作者)
(编辑 李 冰)