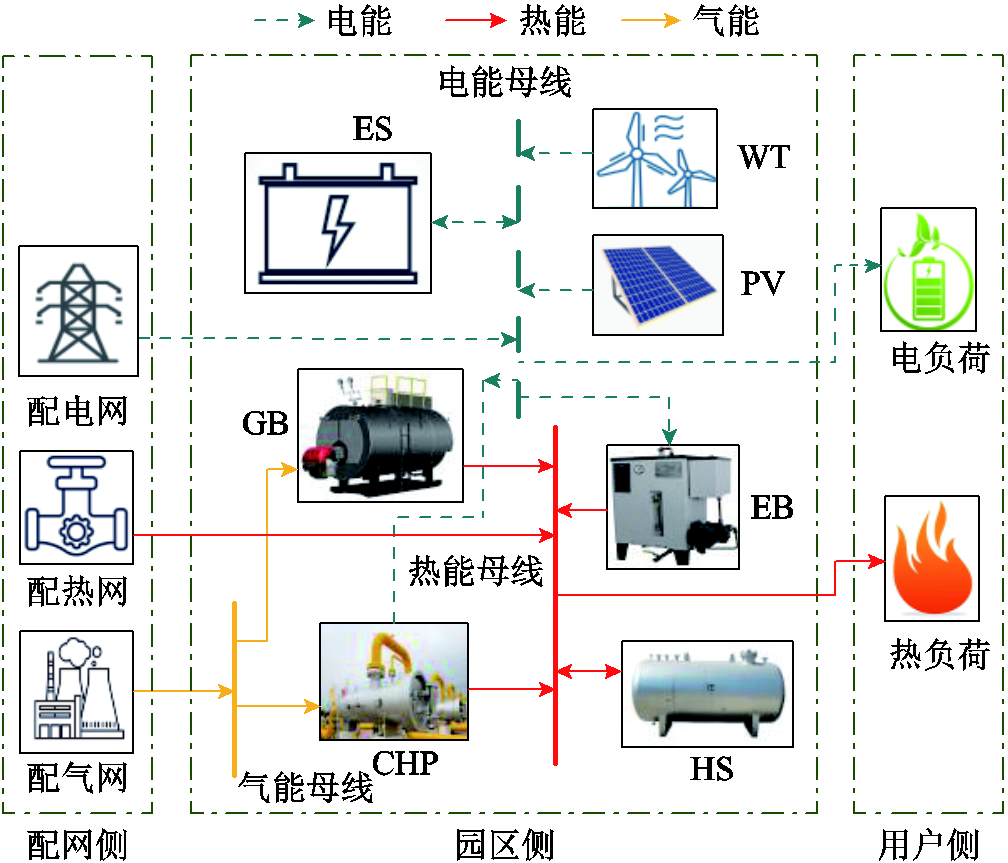
图1 单园区综合能源微网能量流动示意图
Fig.1 Energy flow diagram of the park's integrated energy microgrid
摘要 制定合理的多园区综合能源微网的碳交易策略能够有效引导园区低碳运行,推进“双碳”目标的实现。为此,该文提出一种考虑两阶段碳交易的多园区综合能源微网混合博弈优化运行方法。首先,提出在第一阶段碳交易中由微网运营商向各园区综合能源微网购售碳配额,在第二阶段碳交易中由微网运营商参与外部碳交易市场的两阶段碳交易策略;其次,构建以微网运营商为领导者,多园区综合能源微网为跟随者的主从博弈模型,并考虑微网间电能交易,构建多园区综合能源微网间的合作博弈模型;然后,构建由微网运营商与多园区综合能源微网的主从博弈和多园区综合能源微网间合作博弈组成的混合博弈模型;最后,采用二分法和交替方向乘子法分布式求解该混合博弈模型,并通过仿真验证了所提方法的优越性。
关键词:多园区综合能源微网 低碳优化运行 混合博弈 纳什议价 分布式优化
随着经济的快速发展,气候变暖和能源危机是当前人类所面临的问题,为实现可持续发展,节能减排和绿色发展成为全球共识[1]。当前,以能源高效清洁利用为目标,结合微型发电机组和多元储能形成的多园区综合能源微网具有显著的低碳效益。同时,通过多微网间资源共享能够有效地提高新能源消纳,降低对上级能源网的依赖性,进一步促进可持续发展[2-3]。然而,多园区综合能源微网在碳交易中存在多主体交互问题,如何兼顾多方利益,构建与能源系统对应的多层级的碳交易机制,是多园区综合能源微网低碳运行的关键制约因素[4-5]。
近年来,随着多园区综合能源微网的不断发展,制定合理的碳交易策略,促进微网低碳转型成为国内外学者研究的热点。碳交易机制作为一种促进园区碳减排的重要手段,其通过碳排放权的分配与交易能够提高园区节能减排的积极性[6-7]。文献[8]构建了考虑碳捕集技术和碳交易机制的园区综合能源系统模型。随着能源共享理念的引入,同一区域内多个园区综合能源系统通过能源共享能够实现更高的低碳效益[9]。文献[10]以能源中心为基础,建立了计及碳交易成本的多区域综合能源系统分散调度模型。文献[11]提出一种考虑碳排权购买约束的多区域综合能源系统联合优化运行碳交易成本联合优化运行方法。文献[12]考虑互联系统碳排放量约束,提出了一种分布式低碳经济调度优化方法。针对碳交易市场中碳价是非时变的,无法与能量市场进行良好耦合等问题,文献[13-14]建立了考虑分时碳价的多供能商的电-碳耦合交易市场,并验证了其在低碳效益方面的有效性。文献[15]提出一种基于主从博弈的最优能源-碳配额定价模型,通过园区运营商发布动态分时电价、碳价,引导用户同时参与园区能量与碳配额交易。然而,上述文献中园区综合能源微网只能被动地接受上级碳交易市场的决策,无法与上级碳交易市场形成有效的互动。
博弈理论能够有效地分析多主体利益交互关系,寻找各主体利益最大化的策略,因此在园区综合能源微网优化运行中得到了广泛的运用[16-17]。文献[18]针对含电能交互的多微网综合能源系统,提出了一种基于综合需求响应和主从博弈优化调度策略,并通过算例验证了所提出的策略能够兼顾多微网系统和用户的利益。文献[19]针对灵活性资源调节积极性不高的问题,提出了一种考虑灵活性补偿的高比例风电与多元灵活性资源主从博弈优化的调度方法。然而,主从博弈中利益分配多侧重于保证领导者的利益,无法实现多主体合理的利益分配。合作博弈能够兼顾整体和个体的利益,因此也得到了广泛的应用[20]。文献[21]提出了一种基于纳什议价模型的合作博弈运行策略,并将该模型转换为两个子问题进行分布式求解。文献[22]建立了考虑多重不确定性和电碳耦合交易的多微网合作博弈模型,验证了所提模型能够有效提高各微网效益。文献[23]提出了一种基于合作博弈的共享储能与分布式光伏容量协同规划方法。当前,针对微网运营商参与的博弈优化策略也得到了广泛的研究。文献[24]针对多能耦合的共享储能进一步增加多微网之间协调运行难度的问题,提出了一种以微网运营商为领导者的考虑多能耦合共享储能参与的混合博弈模型。但在上述文献中微网运营商与微网多为能量交易,并未考虑微网运营商在碳交易市场中的作用。
目前已有文献研究多微网P2P电-碳耦合交易。文献[25]提出了一种考虑电-碳交易的多微网合作运行优化策略,仿真结果表明,考虑微网间电-碳交易后各微网的购电成本与碳交易成本都得到了降低。文献[26]提出了一种电碳耦合市场下的能量和碳配额P2P交易模型,仿真结果表明考虑微网间能量和碳配额P2P交易后各微网成本得到了降低。但仅在微网间P2P电能交易的基础上考虑微网间P2P碳交易只对各微网的经济性存在一定的促进作用,无法使各微网的碳排放量得到降低。
综上所述,本文以同一微网运营商领导下的多园区综合能源微网为研究对象,提出了一种考虑两阶段碳交易的多园区综合能源微网混合博弈优化运行方法。主要创新和贡献如下:
1)提出了两阶段碳交易策略:由微网运营商向多园区综合能源微网购售碳配额为第一阶段,微网运营商参与外部碳交易市场为第二阶段,旨在由微网运营商通过各微网反馈的信息制定时变碳价引导各微网低碳运行,使得多园区综合能源微网在碳交易机制下与上级市场形成有效的互动。
2)建立了由微网运营商和多园区综合能源微网的主从博弈以及多园区综合能源微网间的合作博弈组成的混合博弈模型。其中,微网运营商为领导者,以最大化自身利益为目标,制定碳价并下发至各园区综合能源微网;多园区综合能源微网为跟随者,以最小化综合成本为目标,通过合作的方式响应微网运营商的策略。
3)本文采用二分法和交替方向乘子法分布式求解该混合博弈模型。在混合博弈求解过程中,各主体仅需交换各自的决策信息,从而有效地保证了各主体隐私。
园区综合能源微网中涵盖了能源的生产、传输、储存和利用等环节,其中,单园区综合能源微网能量流动示意图如图1所示,主要由光伏(Photovoltaic, PV)、风电(Wind Turbine, WT)、热电联产机组(Combined Heat and Power, CHP)、电热锅炉(Electric Boiler, EB)、燃气锅炉(Gas Boiler, GB)、储电(Electric Storage, ES)、储热(Heat Storage, HS)等设备,以及电、热负荷组成。

图1 单园区综合能源微网能量流动示意图
Fig.1 Energy flow diagram of the park's integrated energy microgrid
本文对多园区综合能源微网展开研究,多园区综合能源微网架构如图2所示。
多园区综合能源微网不仅能够通过微网运营商与外部配网和碳交易市场进行交易,也能够通过各园区间的联络线进行园区间的电能交易。在本文中,微网运营商对于电能、热能和气能均以原价进行购售,不通过差价获利。
园区综合能源微网不仅能够和邻近微网进行能量交易,也能够与上级市场进行交互[9]。碳交易市场作为一个上级市场,能够通过碳交易机制达到各园区碳减排的目的。碳市场针对碳排放量设定上限并设立交易市场,通常分为一级碳市场和二级碳市场。一级碳市场通常为政府无偿分配或者拍卖交易,实现碳配额的初始分配;二级碳市场为短时间尺度的碳配额现货交易市场,碳价具有分时波动性[13]。但传统的碳交易机制使得微网侧只能被动地接受碳市场的决策,无法与碳市场形成良好的互动。为此,在二级碳市场的碳配额交易背景下,本文提出了一种考虑分时碳价的两阶段碳交易策略。在两阶段碳交易中,微网运营商通过低买高卖的方式向各微网购售碳配额来获利。其中,微网运营商的碳配额售价需低于外部碳交易市场,否则微网直接参与外部碳交易市场;微网运营商的碳配额购价需高于外部碳交易市场,否则微网直接将碳配额出售给外部碳交易市场,由此,在该策略中微网运营商和各微网都可获利。同时,微网运营商拥有碳价的决定权,所以在交互过程中占据领导地位,但多园区综合能源微网之间在能量交互过程中彼此属于合作关系,因此,单一的模型无法满足多个主体的利益诉求。为此,本文在两阶段碳交易策略的基础上,提出了一种多园区综合能源微网混合博弈框架,如图3所示。由图3可知,考虑两阶段碳交易的多园区混合博弈框架主要包括:
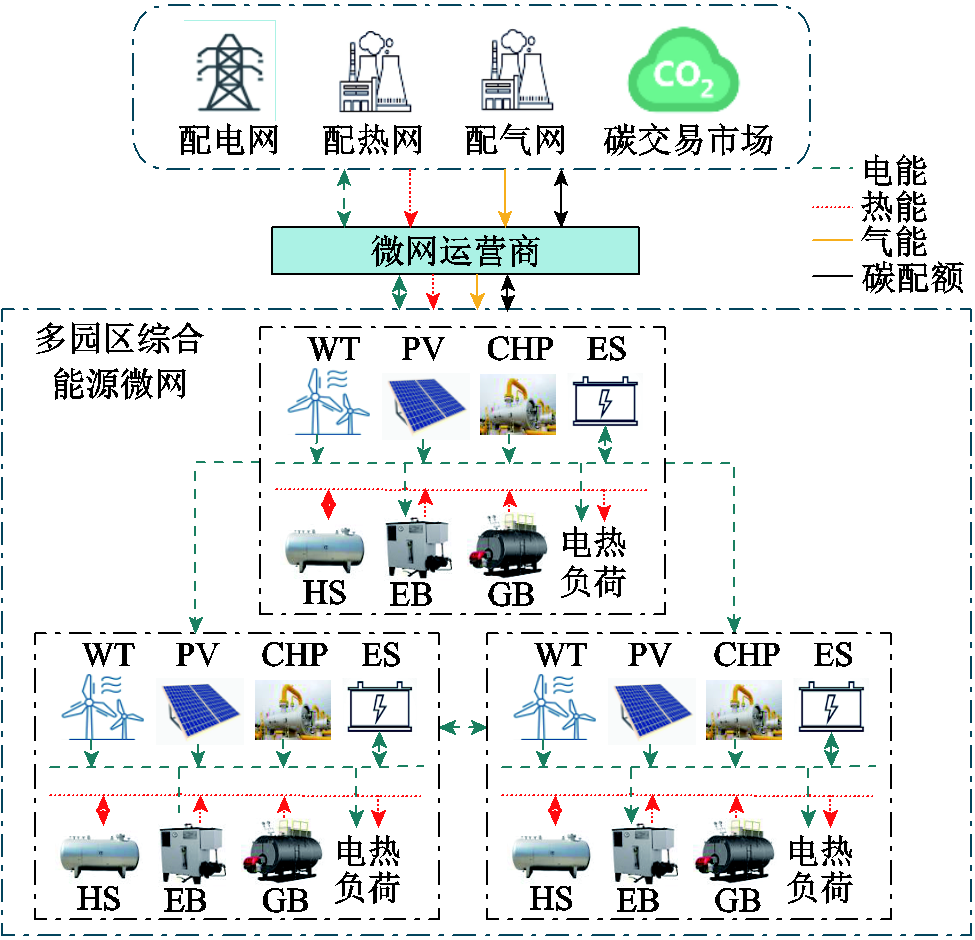
图2 多园区综合能源微网架构
Fig.2 Architecture of district multi-energy microgrid
1)两阶段碳交易策略
(1)第一阶段碳交易中,由微网运营商制定分时碳价并向各微网进行购售碳配额,以此来引导微网侧进行低碳运行;微网侧以合作的方式进行电能交互以此来响应微网运营商的决策。
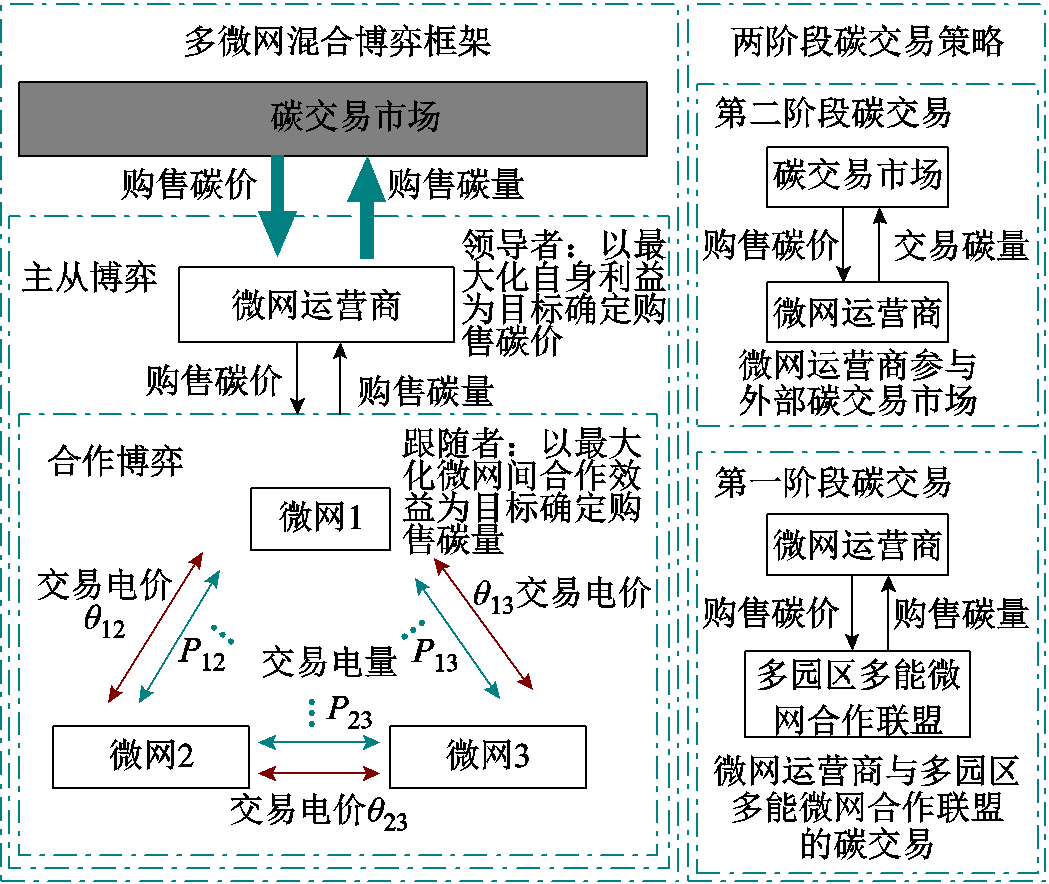
图3 考虑两阶段碳交易的多微网混合博弈框架
Fig.3 Multi-microgrid hybrid game frame considering two-stage carbon trading
(2)第二阶段碳交易中,微网运营商代表各微网参与外部碳交易市场,以此来出售多余碳配额或购买缺少的碳配额。
2)多微网混合博弈框架
考虑上述两阶段碳交易策略,本文提出了由微网运营商和多园区综合能源微网的主从博弈,以及多园区综合能源微网间的合作博弈组成的混合博弈模型。其中,微网运营商为领导者,以最大化自身利益为目标确定微网的购售碳价,并将其下发给各微网;多园区综合能源微网合作联盟为跟随者,以最大化微网间合作效益为目标确定各微网的购售碳量,并将购售碳信息传递给微网运营商。
为满足各方利益诉求,本文基于第1节提出的多园区综合能源微网混合博弈框架建立了混合博弈模型。
作为两阶段碳交易的参与者,微网运营商的目标为使自身利益最大化,即
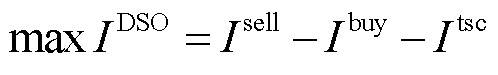 (1)
(1)
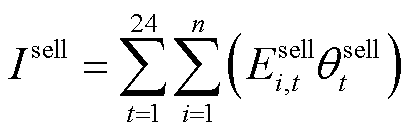 (2)
(2)
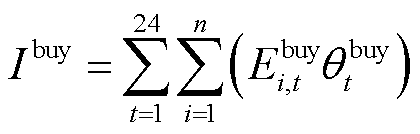 (3)
(3)
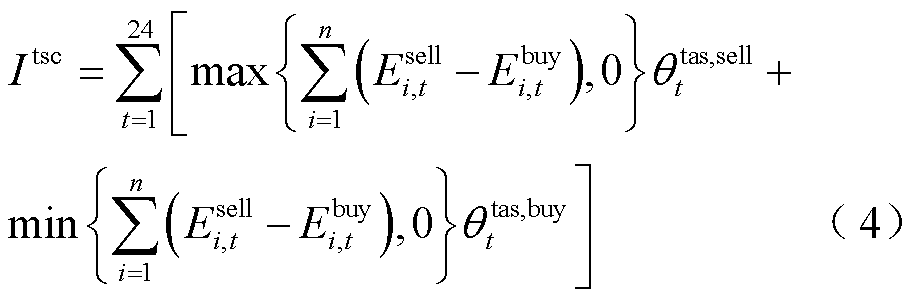
式中,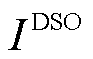 为微网运营商总收益;
为微网运营商总收益;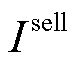 和
和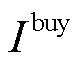 分别为微网运营商向各微网出售碳配额的收益和购买碳配额的成本;
分别为微网运营商向各微网出售碳配额的收益和购买碳配额的成本;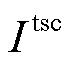 为微网运营商参与外部碳交易市场的成本;
为微网运营商参与外部碳交易市场的成本;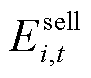 和
和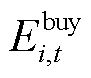 分别为微网运营商在t时段向第i个微网出售和购买的碳配额;
分别为微网运营商在t时段向第i个微网出售和购买的碳配额;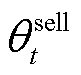 和
和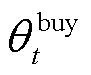 分别为微网运营商在t时段向微网出售和购买碳配额的价格;
分别为微网运营商在t时段向微网出售和购买碳配额的价格;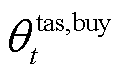 和
和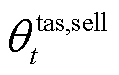 分别为外部碳交易市场在在t时段购、售碳配额的价格;n为微网数量。
分别为外部碳交易市场在在t时段购、售碳配额的价格;n为微网数量。
在混合博弈模型中,微网运营商作为领导者,拥有定价权。为避免微网运营商为追求自身利益将购买碳配额的价格制定过低,将出售碳配额的价格制定过高,需要对其增加相应的价格约束,即
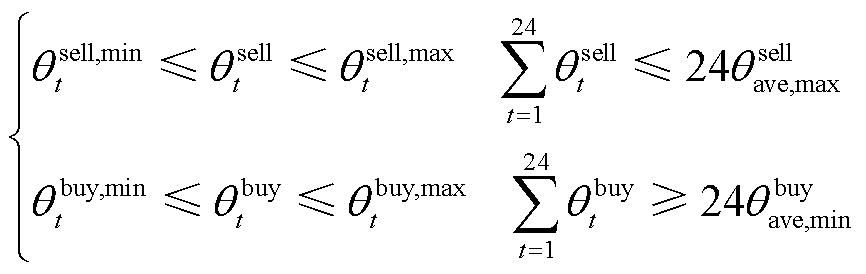 (5)
(5)
式中,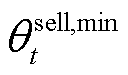 和
和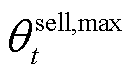 分别为微网运营商在t时段制定的碳配额售价下限和上限;
分别为微网运营商在t时段制定的碳配额售价下限和上限;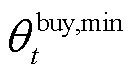 和
和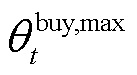 分别为微网运营商在t时段制定的碳配额购价下限和上限;
分别为微网运营商在t时段制定的碳配额购价下限和上限;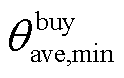 和
和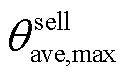 分别为微网运营商向微网购买碳配额价格的平均值下限和向微网出售碳配额价格的平均值上限,该值为预先设定的值。
分别为微网运营商向微网购买碳配额价格的平均值下限和向微网出售碳配额价格的平均值上限,该值为预先设定的值。
多园区综合能源微网混合博弈模型中的主从博弈均衡解存在且唯一,具体证明详见附录。
2.2.1 园区综合能源微网模型
园区综合能源微网作为独立的博弈参与者,不仅能够与邻近微网进行电能交易,也能够与上级市场进行交互,其目标为使自身综合成本最小。
1)目标函数
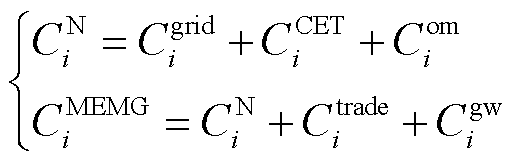 (6)
(6)
式中,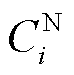 和
和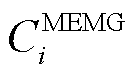 分别为微网i不考虑电能交易时的总成本和考虑电能交易时的总成本;
分别为微网i不考虑电能交易时的总成本和考虑电能交易时的总成本;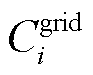 、
、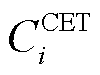 、
、 、
、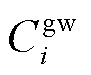 和
和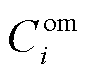 分别为第i个微网的购能成本、碳交易成本、微网间电能交易成本、微网间电能交易过网费用和设备运维成本。
分别为第i个微网的购能成本、碳交易成本、微网间电能交易成本、微网间电能交易过网费用和设备运维成本。
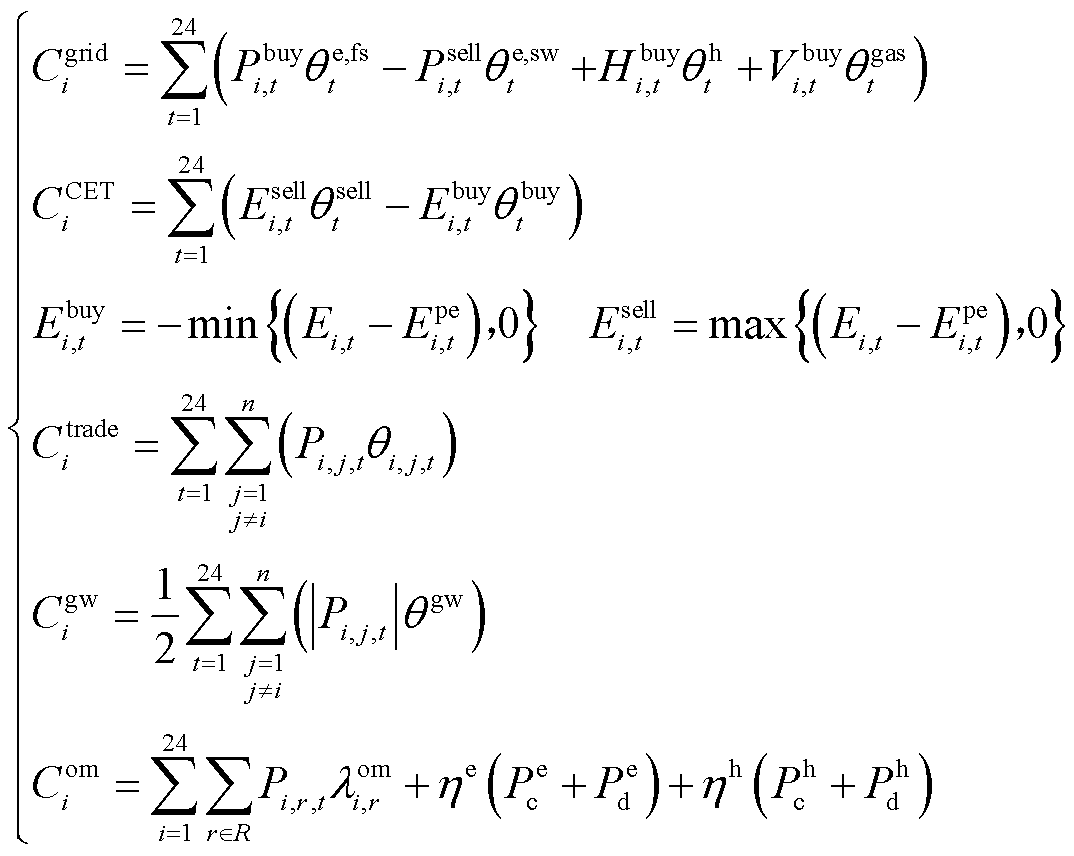 (7)
(7)
式中,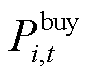 、
、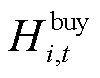 和
和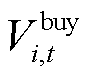 分别为在t时段微网i的外网购电量、购热量和购气量;
分别为在t时段微网i的外网购电量、购热量和购气量;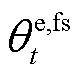 、
、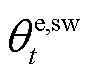 、
、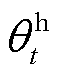 和
和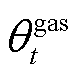 分别为在t时段电网分时电价、电网上网电价、热网售热价和气网售气价;
分别为在t时段电网分时电价、电网上网电价、热网售热价和气网售气价;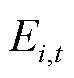 和
和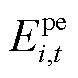 分别为在t时段碳排放量和碳配额量,碳配额量为单位发电、热量碳配额系数与单位发电、热量的乘积,其中碳排放量计算公式见文献[9],碳配额量计算公式见附录;
分别为在t时段碳排放量和碳配额量,碳配额量为单位发电、热量碳配额系数与单位发电、热量的乘积,其中碳排放量计算公式见文献[9],碳配额量计算公式见附录;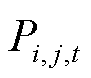 和
和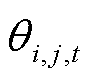 分别为t时段微网i与微网j的电能交互量和电能交互价格;
分别为t时段微网i与微网j的电能交互量和电能交互价格;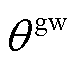 为微网间电能交互的过网费系数;
为微网间电能交互的过网费系数;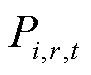 和
和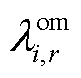 分别为微网i中第r个设备的运行功率以及运行损耗系数;R为园区内除储能设备外的全部设备集合;
分别为微网i中第r个设备的运行功率以及运行损耗系数;R为园区内除储能设备外的全部设备集合;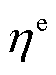 和
和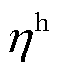 分别为电储能和热储能的充、放能损耗系数;
分别为电储能和热储能的充、放能损耗系数;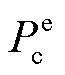 、
、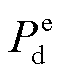 和
和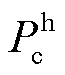 、
、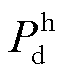 分别为电储能和热储能的充、放能功率,其中各类设备模型见文献[10]。
分别为电储能和热储能的充、放能功率,其中各类设备模型见文献[10]。
需要指出的是,本文所采用的碳交易成本计算模型为统一型碳交易成本计算模型,即碳交易成本为碳排放量和碳配额量的差值乘以碳价,具体描述见附录。
2)约束条件
园区综合能源微网在运行中需要考虑能量平衡约束,包括系统内电、热的供需平衡约束,即
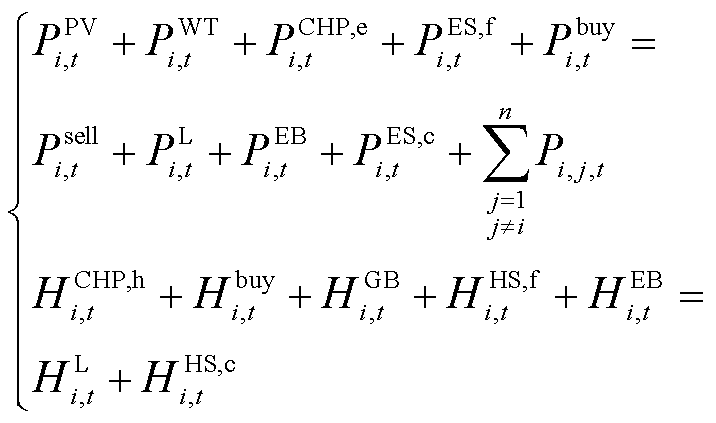 (8)
(8)
式中,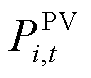 、
、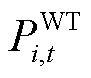 、
、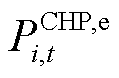 、
、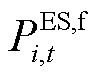 和
和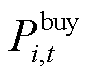 分别为第i个微网在t时段光伏、风电、CHP机组、储能放电和电网购电的功率;
分别为第i个微网在t时段光伏、风电、CHP机组、储能放电和电网购电的功率;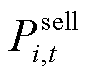 、
、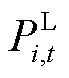 、
、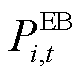 、
、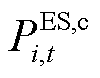 分别为第i个微网在t时段向电网售电、电负荷、电热锅炉耗电、储能充电功率;
分别为第i个微网在t时段向电网售电、电负荷、电热锅炉耗电、储能充电功率;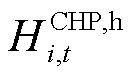 、
、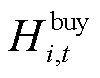 、
、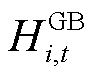 、
、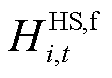 和
和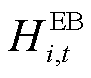 分别为第i个微网在t时段CHP机组产热、向热网购热、GB产热、储能放热和EB产热的热量;
分别为第i个微网在t时段CHP机组产热、向热网购热、GB产热、储能放热和EB产热的热量;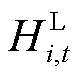 和
和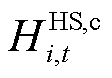 分别为第i个微网在t时段的热负荷和储能充热的热量,需要指出的是,本文未考虑负荷侧的需求响应(若考虑负荷侧需求响应,仅需应用本文所提方法即可)。
分别为第i个微网在t时段的热负荷和储能充热的热量,需要指出的是,本文未考虑负荷侧的需求响应(若考虑负荷侧需求响应,仅需应用本文所提方法即可)。
能量传输约束包括与上级能源网交互功率约束和微网间交互功率约束,即
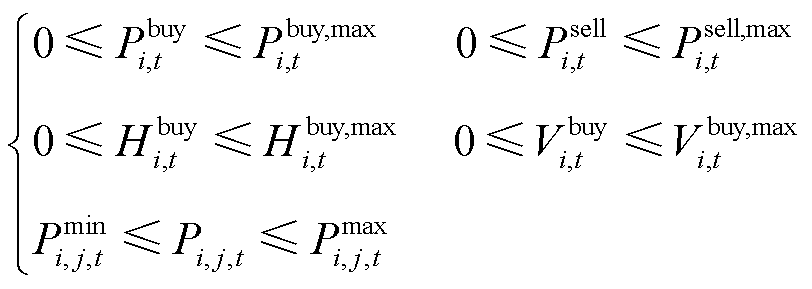 (9)
(9)
式中,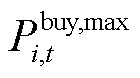 和
和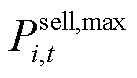 分别为第i个微网在t时段外网购电量和出售给电网的电量上限;
分别为第i个微网在t时段外网购电量和出售给电网的电量上限;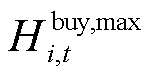 和
和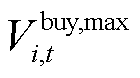 分别为外网购热量和外网购气量的上限;
分别为外网购热量和外网购气量的上限;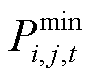 和
和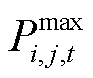 分别为微网i和j之间电能交互功率的下限和上限。
分别为微网i和j之间电能交互功率的下限和上限。
园区综合能源微网中设备约束包括设备出力上下限约束,即
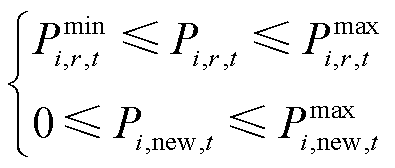 (10)
(10)
式中,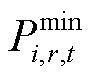 和
和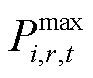 分别为第i个微网在t时段第r个设备的出力下限和出力上限;
分别为第i个微网在t时段第r个设备的出力下限和出力上限;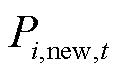 和
和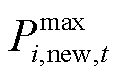 分别为第i个微网在t时段新能源出力值和新能源出力上限。
分别为第i个微网在t时段新能源出力值和新能源出力上限。
2.2.2 多园区综合能源微网合作博弈模型
各园区综合能源微网在与其他微网交互中拥有独立选择权[21]。某一微网能够与其他微网进行合作的前提是合作后能够进一步降低自身成本,否则该微网拒绝合作。纳什谈判属于合作博弈,能够在实现合作联盟效益最大化的基础上实现利益的合理分配。为此,本文建立了基于纳什谈判理论的多园区综合能源微网合作博弈模型,有
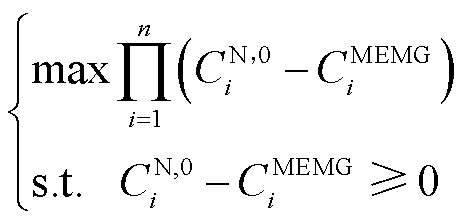 (11)
(11)
式中,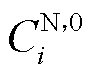 为第i个微网的谈判破裂点;
为第i个微网的谈判破裂点;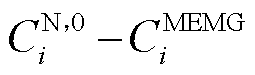 表示第i个微网通过合作所得到的收益。
表示第i个微网通过合作所得到的收益。
本文所建立的多园区综合能源微网混合博弈模型包括微网运营商和多园区综合能源微网的主从博弈模型,以及多园区综合能源微网间的合作博弈模型。由于微网间合作博弈模型为非凸非线性模型,因此,本文基于纳什议价理论将该合作博弈模型转换为两个子问题,进而采用二分法[27]和交替方向乘子法[28]求解该混合博弈模型。
针对启发式算法在计算过程迭代的收敛性不一定总是得到保证,并且可能出现振荡等问题,本文采用二分法分布式优化算法求解该主从博弈模型。二分法的主要思路是为目标提供一个区间,该区间始终包含所求结果,并在每次迭代中通过更新下界或上界逐渐缩小该区间,最终求得结果。具体的求解流程如图4所示。
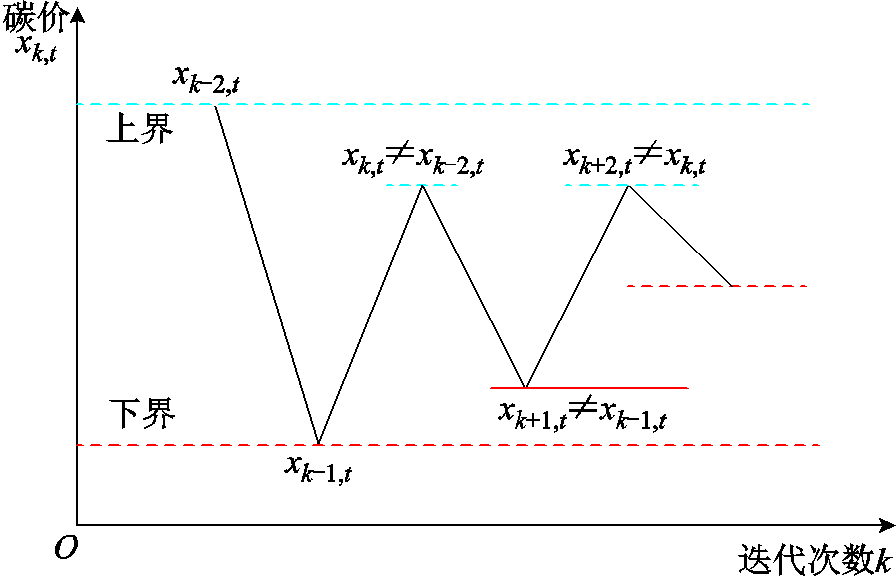
图4 二分法求解流程
Fig.4 Dichotomy solution flow chart
图4中,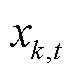 为在t时段第k次迭代中的碳价。在求解过程中,二分法会判断第k次迭代结果和第k-2次迭代结果,如果结果相同,则用二分法缩小该价格区间;如果结果不同则添加不等式约束。
为在t时段第k次迭代中的碳价。在求解过程中,二分法会判断第k次迭代结果和第k-2次迭代结果,如果结果相同,则用二分法缩小该价格区间;如果结果不同则添加不等式约束。
假设此时的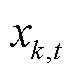 为上界,当
为上界,当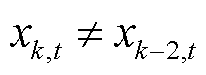 时,添加约束式(12)。
时,添加约束式(12)。
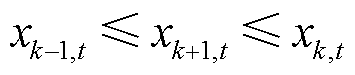 (12)
(12)
当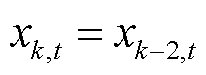 时,添加约束式(13)。
时,添加约束式(13)。
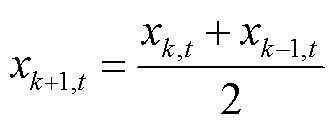 (13)
(13)
通过上述方式能够不断地更新价格区间的上界和下界,每次迭代中都会依据收敛判据判断是否收敛,如果满足收敛条件则跳出循环,输出均衡解,收敛判据为
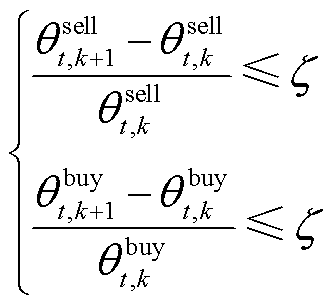 (14)
(14)
式中,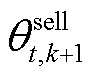 和
和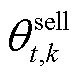 分别为第k+1次和k次迭代中微网运营商售碳价格;
分别为第k+1次和k次迭代中微网运营商售碳价格;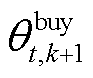 和
和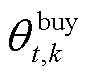 分别为第k次迭代中微网运营商购碳价格;
分别为第k次迭代中微网运营商购碳价格;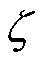 为二分法的收敛判据。
为二分法的收敛判据。
由于本文中微网运营商所制定的碳配额售价不能高于外部市场的碳配额售价,所制定的碳配额购价不能低于外部市场的碳配额购价,而为了保证微网运营商能够从中获利,则需要保证微网运营商各个时刻所制定的碳配额售价要高于所制定的碳配额购价,所以本文确定的二分法的初始区间为[0.15, 0.4],即外部碳交易市场碳配额售价作为区间上限和外部碳交易市场碳配额购价作为区间下限。
3.2.1 合作博弈模型转换
式(11)中多园区综合能源微网合作博弈模型为非凸非线性模型,无法直接求解。为此,本文参考文献[21]中的方法将模型转换为两个子问题,模型具体的转换过程见附录,转换后的模型如下。
1)子问题1:合作联盟成本最小化
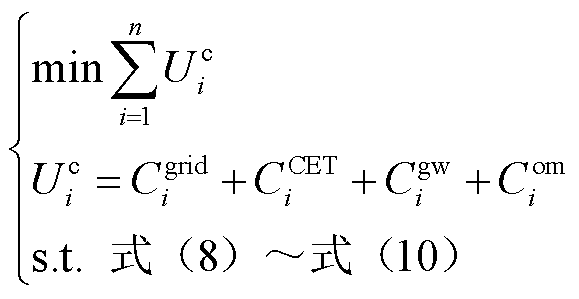 (15)
(15)
式中,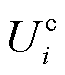 为子问题1的优化目标。
为子问题1的优化目标。
2)子问题2:电能交易支付议价子问题
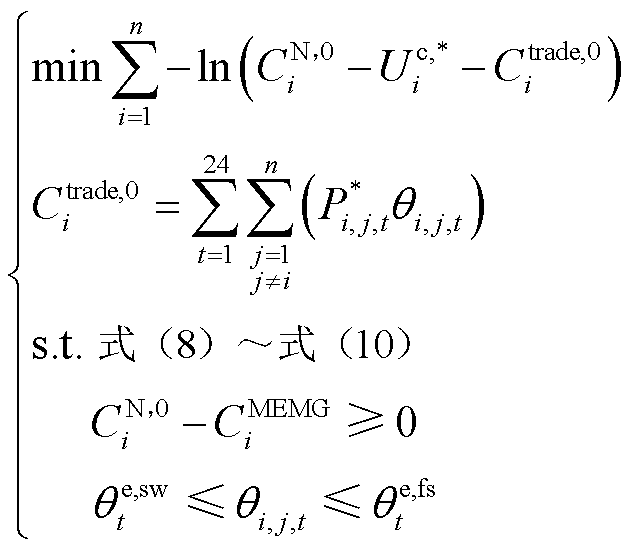 (16)
(16)
式中,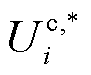 为子问题1求得的最优解;
为子问题1求得的最优解; 为子问题1求得电能交易量后的电能交易成本;
为子问题1求得电能交易量后的电能交易成本;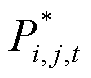 为子问题1求得的电能交易量。
为子问题1求得的电能交易量。
上述两个子问题能够通过分布式算法进行求解。
3.2.2 合作博弈模型求解
经过上述模型的转换,本文将微网间合作博弈模型转换为两个子问题,进而运用交替方向乘子法进行分布式求解。
1)合作联盟成本最小化子问题求解
在求解合作联盟成本最小化子问题中,优化目标为最小化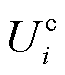 ,电能交互量为耦合变量,需要满足
,电能交互量为耦合变量,需要满足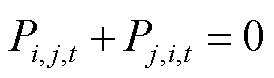 的约束条件,为此,构造增广拉格朗日函数为
的约束条件,为此,构造增广拉格朗日函数为
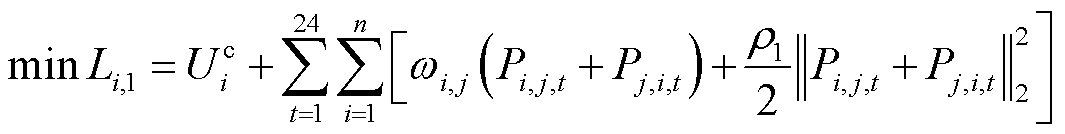 (17)
(17)
式中,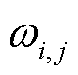 和
和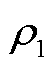 分别为子问题1的拉格朗日乘子和惩罚因子。
分别为子问题1的拉格朗日乘子和惩罚因子。
首先设置迭代初始数据,各微网在收到迭代初始数据后,在各微网内进行内部优化,并输出各自的交易电量,具体的迭代计算步骤为
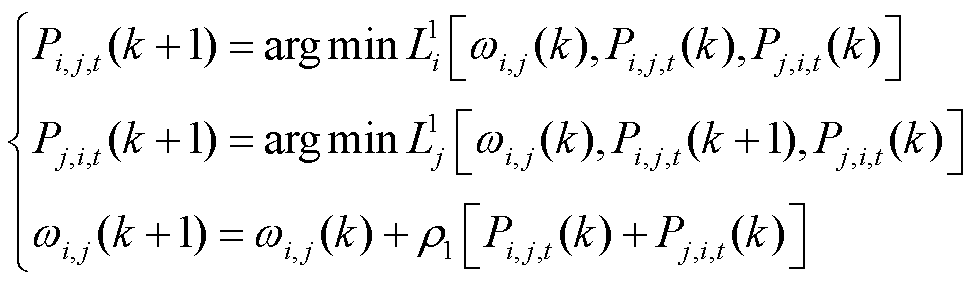 (18)
(18)
式中,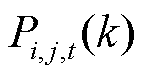 和
和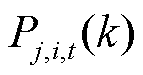 分别为第k次迭代中在t时段微网i、j的电能交互量和微网j、i的电能交互量;
分别为第k次迭代中在t时段微网i、j的电能交互量和微网j、i的电能交互量;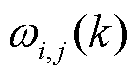 为第k次迭代中子问题1的拉格朗日乘子。
为第k次迭代中子问题1的拉格朗日乘子。
在每次迭代中各微网都会更新自身的交易电量,并依据收敛判据判断是否收敛,如果满足收敛条件则跳出循环,收敛判据为
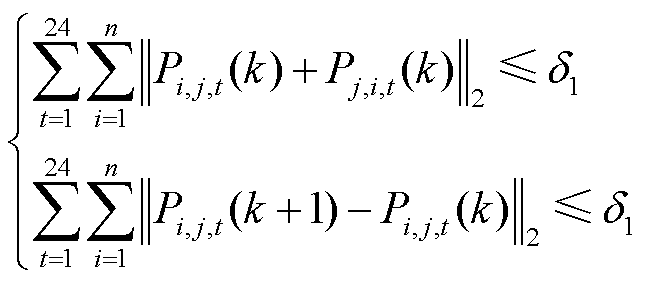 (19)
(19)
式中,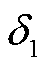 为子问题1的迭代收敛判据。
为子问题1的迭代收敛判据。
在每次迭代中都会依据收敛判据判断是否收敛,如果满足收敛条件则跳出循环;如果不收敛则继续迭代,直到满足收敛条件。
2)电能交易支付议价子问题求解
在求解电能交易支付议价子问题中,电能交互价格为耦合变量,需要满足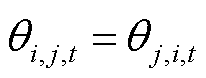 的约束条件,为此,构造增广拉格朗日函数为
的约束条件,为此,构造增广拉格朗日函数为
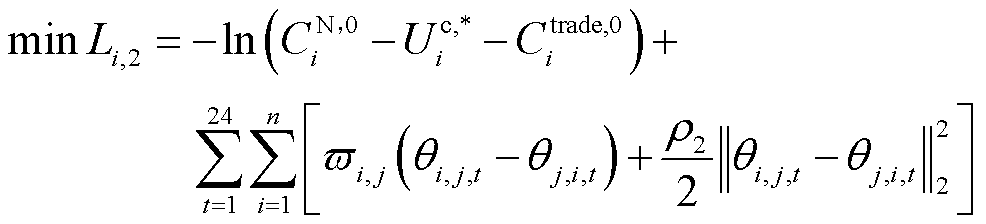 (20)
(20)
式中, 和
和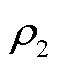 分别为子问题2的拉格朗日乘子和惩罚因子。
分别为子问题2的拉格朗日乘子和惩罚因子。
子问题2的具体迭代计算步骤为
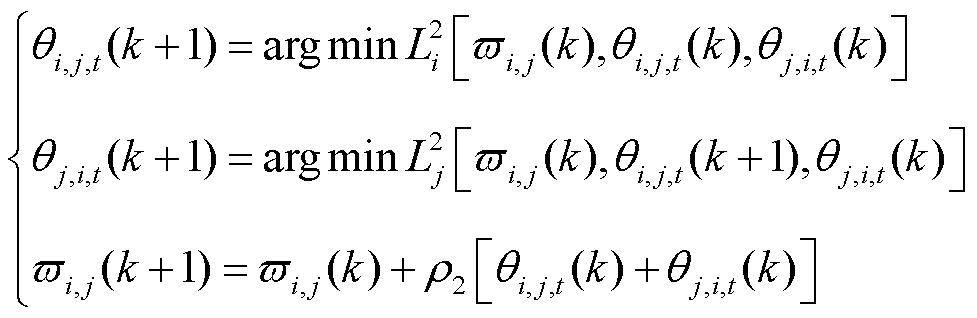 (21)
(21)
式中,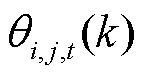 和
和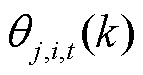 分别为第k次迭代中在t时刻微网i、j的电能交易价格和微网j、i的电能交易价格;
分别为第k次迭代中在t时刻微网i、j的电能交易价格和微网j、i的电能交易价格;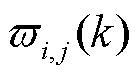 为第k次迭代中子问题2的拉格朗日乘子。
为第k次迭代中子问题2的拉格朗日乘子。
子问题2的收敛判据为
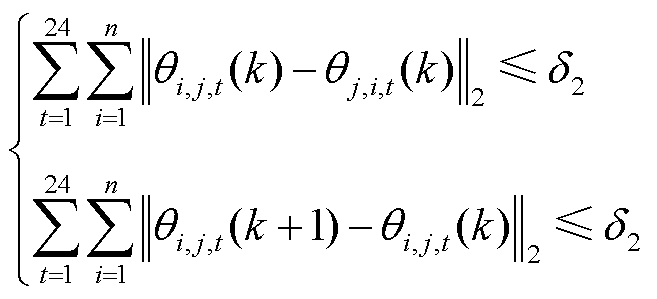 (22)
(22)
式中,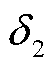 为子问题2的迭代收敛判据。
为子问题2的迭代收敛判据。
本文建立了由微网运营商和多园区综合能源微网的主从博弈、多园区综合能源微网间的合作博弈组成的混合博弈模型。为在保护各主体隐私的基础上对模型进行高效的求解,本文采用二分法和交替方向乘子法求解上述混合博弈模型,具体的求解流程如图5所示。图5中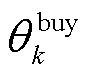 、
、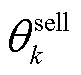 、
、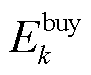 和
和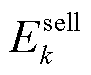 分别为第k次迭代中24 h的碳配额购售价格和碳配额购售量。由图4可知,本文求解方法能够在各主体交换极少信息的情况下求解该混合博弈模型。
分别为第k次迭代中24 h的碳配额购售价格和碳配额购售量。由图4可知,本文求解方法能够在各主体交换极少信息的情况下求解该混合博弈模型。
本文算例选自某智慧小镇,其中单园区综合能源微网能量流动与图1一致,多园区综合能源微网的系统结构和交互方式与图2一致,负荷及风光出力均采用日前预测数据,各微网内设备参数、风光预测数据、负荷预测数据、电网及外部碳交易市场的电价和碳价等相关参数见附件,调度周期为24 h。在Matlab2021b环境下,采用YALMIP调用CPLEX求解器对模型进行了求解。
为验证本文所提方法的有效性,设置了以下不同的方案进行对比分析,仿真结果见表1。
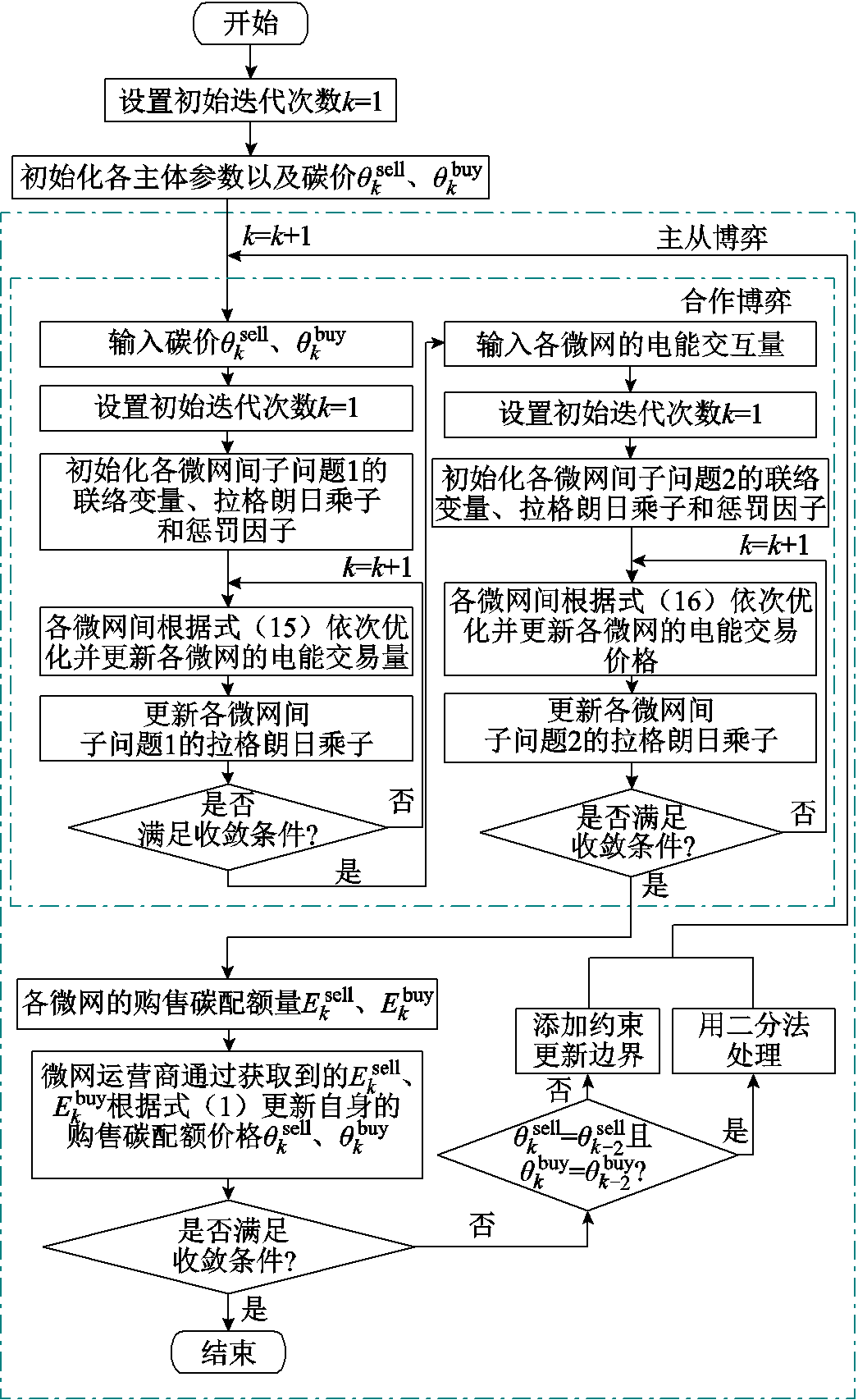
图5 模型求解流程
Fig.5 Model solving flow chart
表1 不同方案下的优化结果对比
Tab.1 Comparison of optimization results under different schemes
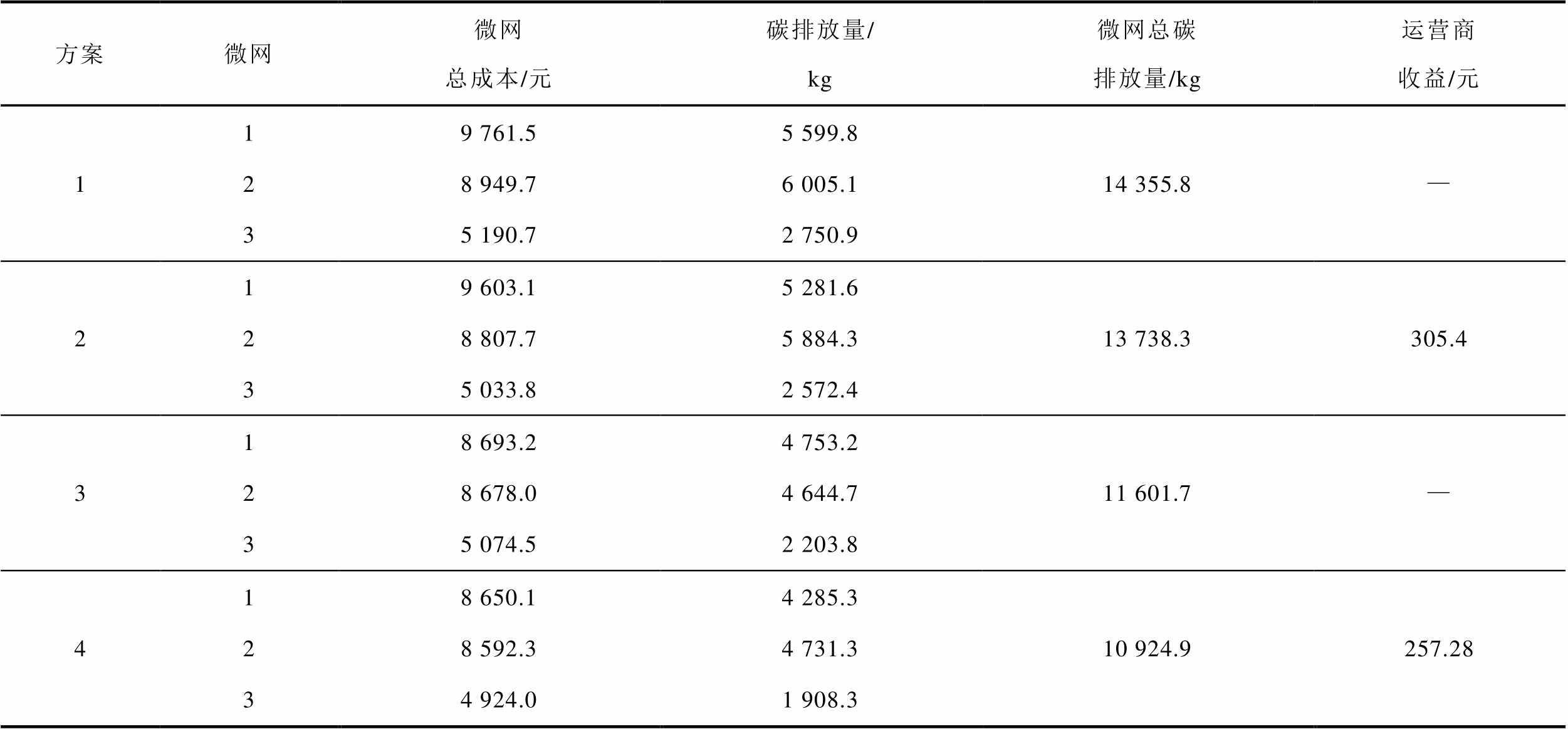
方案微网微网总成本/元碳排放量/kg微网总碳排放量/kg运营商收益/元 119 761.55 599.814 355.8— 28 949.76 005.1 35 190.72 750.9 219 603.15 281.613 738.3305.4 28 807.75 884.3 35 033.82 572.4 318 693.24 753.211 601.7— 28 678.04 644.7 35 074.52 203.8 418 650.14 285.310 924.9257.28 28 592.34 731.3 34 924.01 908.3
方案1:各微网单独运行,不考虑微网运营商和各微网的主从博弈,采用常规的碳交易机制,即各微网直接参与外部碳交易市场且碳价非时变。
方案2:各微网单独运行,考虑微网运营商和各微网的主从博弈,采用本文提出的两阶段碳交易策略。
方案3:考虑微网间的合作博弈,不考虑微网运营商和各微网的主从博弈,采用常规的碳交易机制。
方案4:考虑微网间的合作博弈,以及微网运营商和各微网的主从博弈,采用本文提出的两阶段碳交易策略。
对比方案1和方案2可以看出,在考虑本文所提出的两阶段碳交易策略后,微网1、2和3的总成本分别下降了158.4、142、156.9元,碳排放量分别下降了318.2、120.8、178.5 kg,三个微网的总碳排放量减少了617.5 kg。这是由于在考虑两阶段碳交易策略后,微网运营商制定的碳配额售价低于外部碳交易市场,且微网运营商制定的碳配额购价高于外部碳交易市场,低买高卖下不仅满足了微网运营商的利益,同时也使得微网与碳交易市场形成了良好的互动,激励微网尽可能地降低自身碳排放量,以此出售多余的碳配额,从而获得更大的利润。对比方案1和方案3可以看出,在考虑微网间合作博弈后,各微网的总成本和碳排放量都得到了下降,这是由于微网之间通过电能交易实现能量互补互济,提高了整个多园区综合能源微网的综合效益。
从表1可以看到,相较于方案1,方案4在考虑多园区综合能源微网混合博弈后,微网1、2和3的总成本分别下降了1 111.4、357.4、266.7元,碳排放量分别下降了1 314.5、1 274.1、842.6 kg,三个微网的总碳排放量减少了3 431.2 kg,这是由于在考虑混合博弈后各主体的利益都得到了保证,使得整个系统的效益得到了提高;而方案4中的微网运营商的收益相较于方案2有所降低,这是由于各微网合作运行后降低了对上级市场的依赖,从而导致微网运营商的利益下降。同时,通过表1可以看出,在考虑混合博弈后的方案要优于考虑单一博弈模型的方案。
本文构建了微网运营商和多园区综合能源微网间的主从博弈模型,旨在通过微网运营商制定碳价引导多园区综合能源微网低碳运行,方案4中的主从博弈的结果如图6和图7所示。
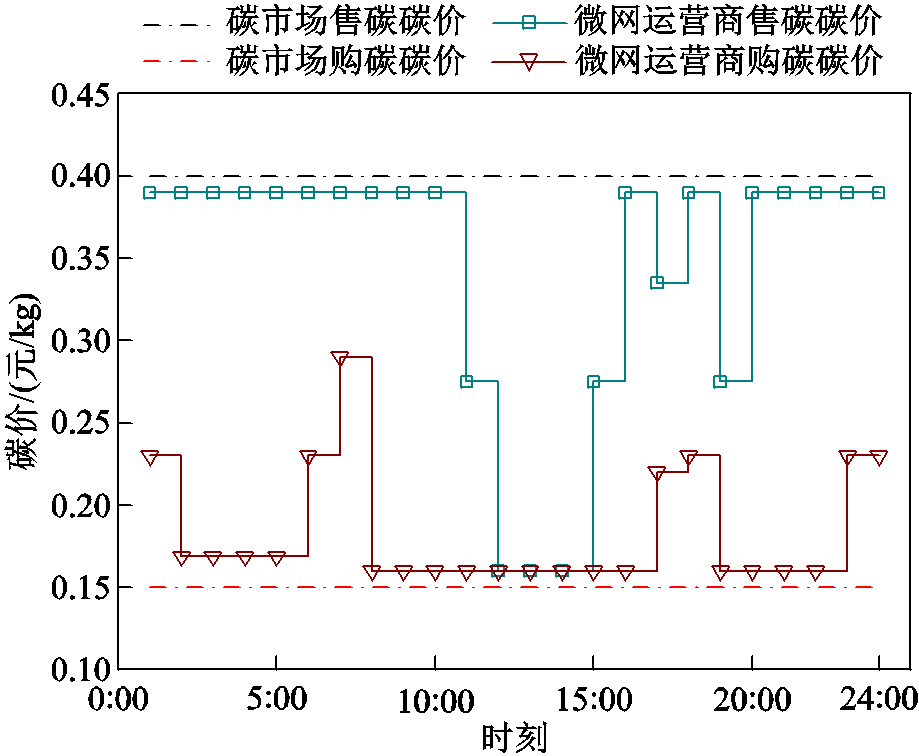
图6 微网运营商购售碳价
Fig.6 Microgrid operators buy and sell carbon prices
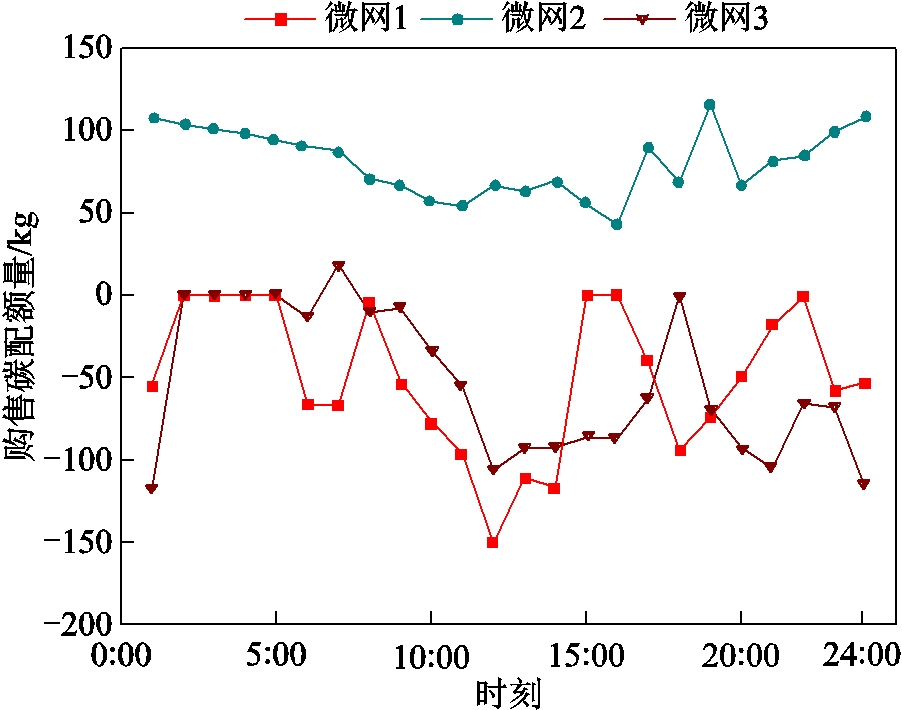
图7 各微网购售碳配额量
Fig.7 The amount of carbon allowances purchased and sold by each microgrid
从表1和图7可以看出,微网2为碳排放较高的微网,其碳配额购买量较高,而微网1和微网3为碳排放较低的微网,其碳配额出售量较高。分析图7可知,微网2碳配额购买量在10:00—16:00时段较低,在其他时段较高;而微网运营商所制定的碳配额售价在11:00—15:00时段较低,在其他时段较高。这就使得微网2能够尽可能地调整自身机组和储能系统的调度策略,以此来提高自身在11:00—15:00时段的碳配额购买量,降低其他时段的碳配额购买量,最终使微网2的碳排放量得到了下降。微网1和微网3碳排放较低的微网,出售碳配额的主要时段为10:00—15:00和19:00—21:00;而微网运营商所制定的碳配额购价在6:00—7:00、17:00—18:00和23:00—1:00时段较高,其他的时段较低。这就使得微网1和微网3尽可能地调整自身机组和储能系统的调度策略,通过降低碳配额售价较高时段的碳排放量获得更大的收益。
方案4中合作博弈求解的电能交易价格和电能交易量如图8和图9所示。
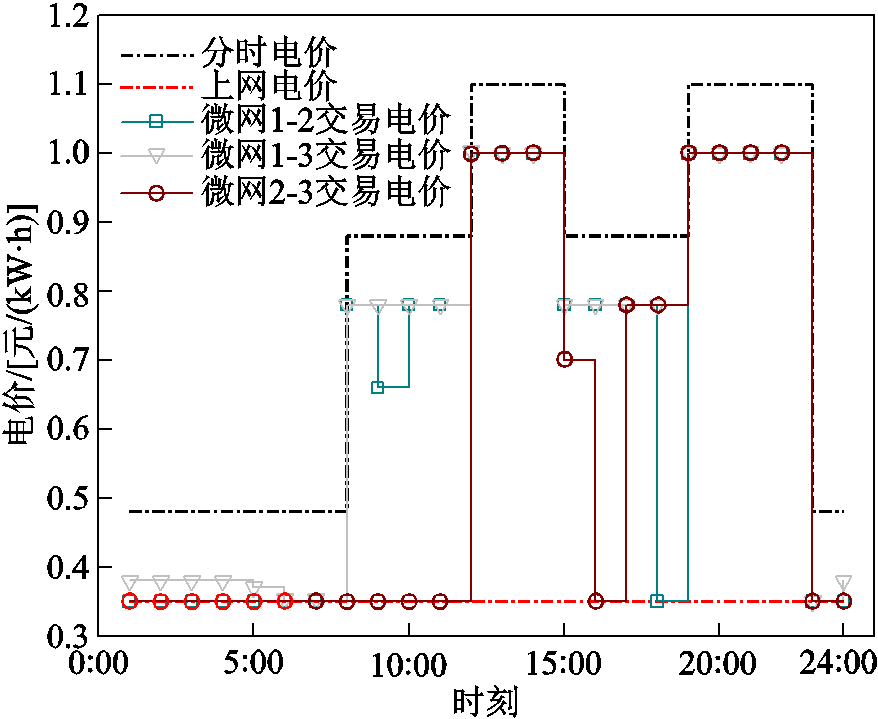
图8 微网间电能交易价格
Fig.8 Price of electricity transaction between microgrids
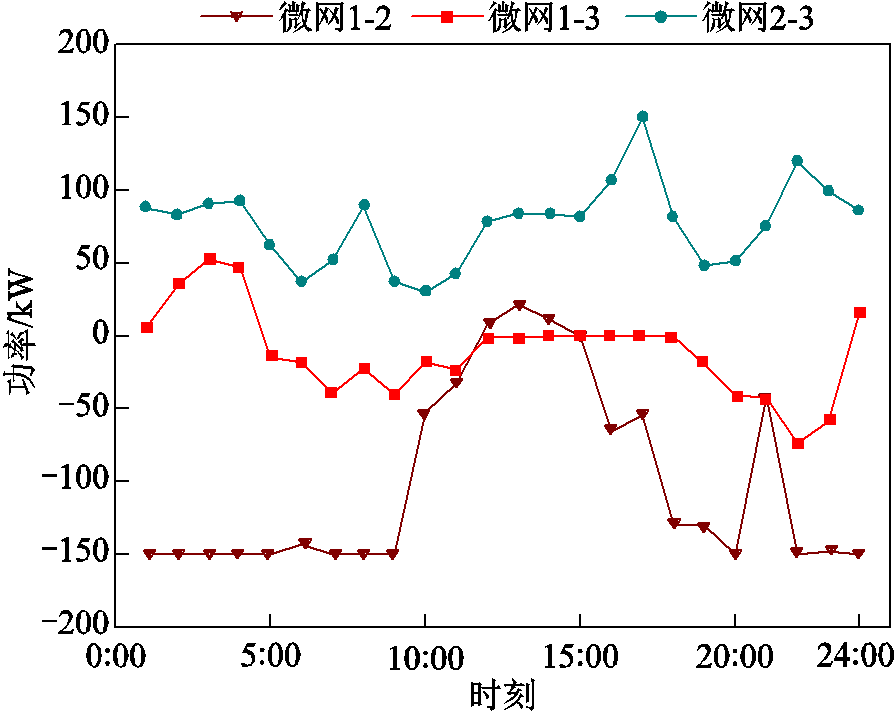
图9 微网间电能交易量
Fig.9 Power transaction volume between microgrids
由图8和图9可以看出,微网2向微网1和微网3的电能出售量较高,这是由于微网2自身的电负荷量较小,在合作博弈整体利益最大化的优化过程中需要提高自身的电能出售量,以此保证整体效益的最大化。微网1和微网3之间的电能交互较低,主要集中在0:00—3:00和19:00—23:00时段。合作博弈利益分配见表2。
表2 合作博弈利益分配结果
Tab.2 Profit distribution results of cooperative game (单位:元)

微网独立运行总成本合作后成本合作支付收益最终成本 19 761.57 394.6-1 255.58 650.1 28 949.71 06752 082.78 592.3 35 190.74 112.5-811.494 924.0
对比表1和表2可以看到,在合作前和合作后微网2的总成本只降低了271.7元,这是由于合作博弈的目标是联盟整体效益最大化,为了提高整体的效益,微网2需要不断提高自身的出售电量以提高整个系统效益。
微网1合作后电能、热能运行结果如图10和图11所示。可以看出,微网1获取电能的方式主要为风电、光伏、CHP产电和其他区供电,获取热能的方式主要为CHP产热、外网购热和储能放热。其中,微网1中电热供给主要靠CHP机组和风光出力,在电价较高的时刻,CHP机组出力较高,配合电热储能,能够有效满足电热负荷的需求;在电价较低的时刻,CHP机组出力较低,微网内电能供给需要由风光以及其他园区供电的补充,热能供给需要通过热网购热进行补充,以维持系统内电热平衡。
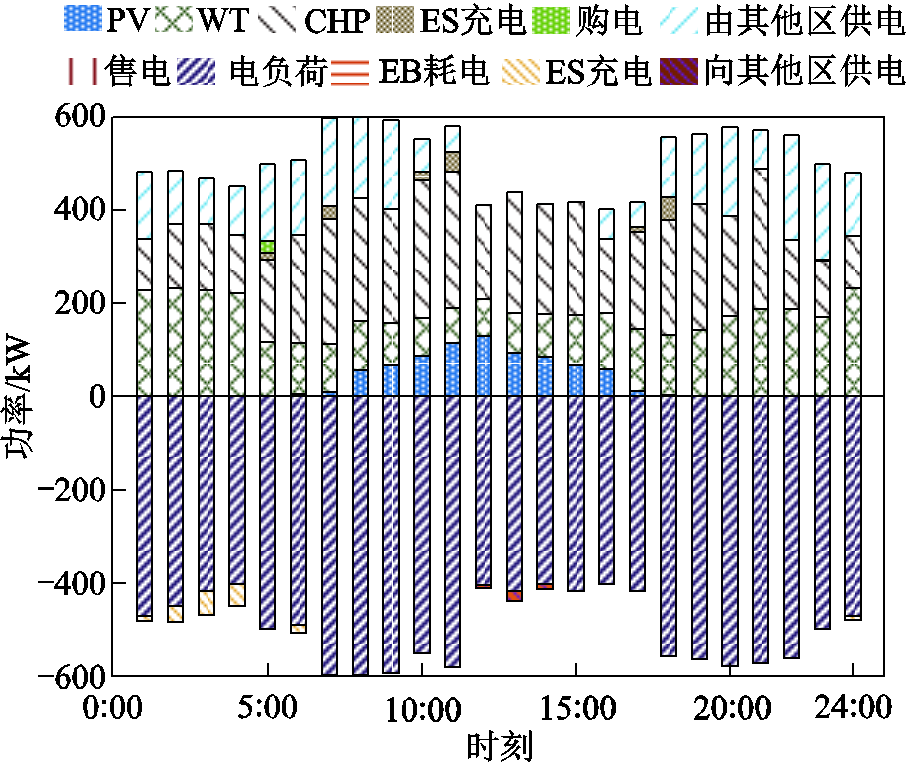
图10 微网1电功率平衡图
Fig.10 Microgrid 1 electrical power balance diagram
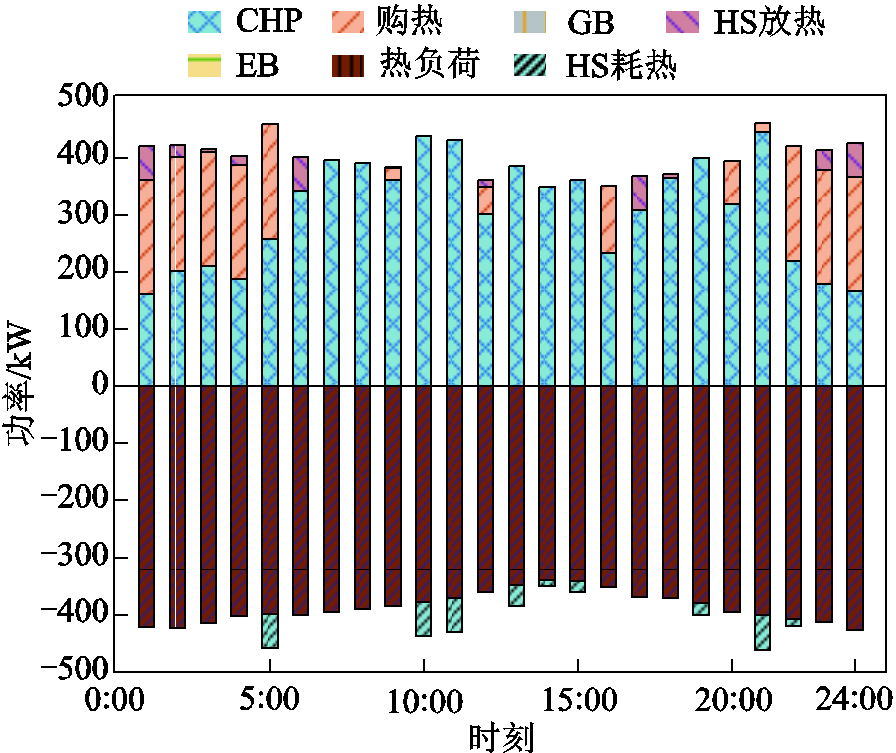
图11 微网1热功率平衡图
Fig.11 Microgrid 1 thermal power balance diagram
对比方案1和方案2可知,考虑两阶段碳交易策略后,各微网的总成本和碳排放量都有所下降。考虑两阶段碳交易策略前后的24 h碳配额购售量如图12所示。
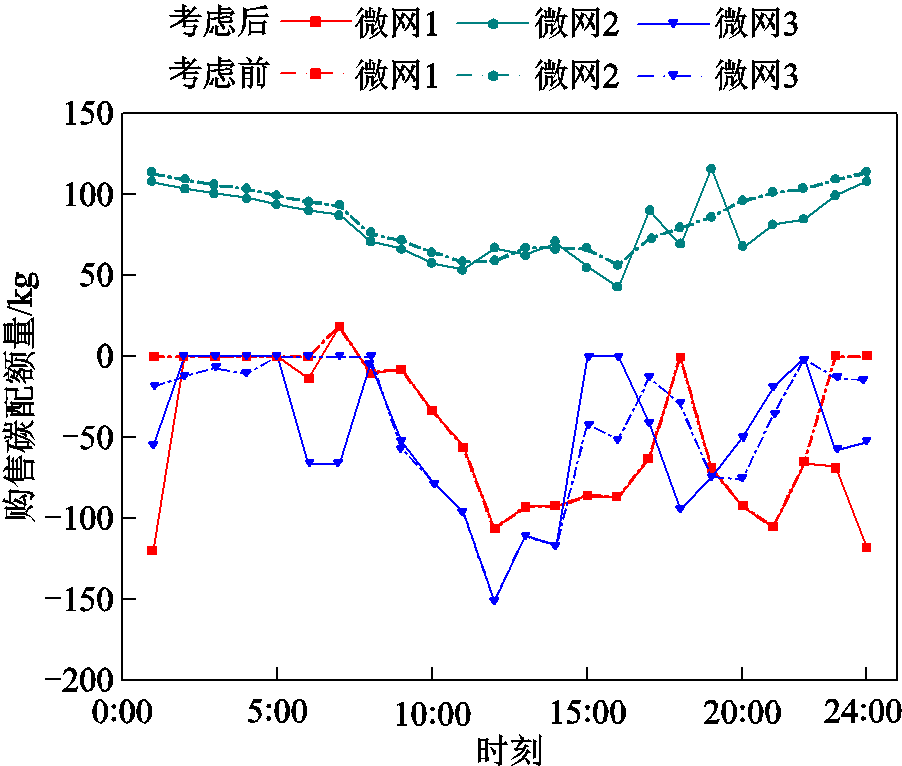
图12 考虑两阶段碳交易策略前后各微网碳配额购售量
Fig.12 The amount of carbon allowances purchased and sold in each microgrid before and after the two-stage carbon trading tactics is considered
由图12可知,微网2在考虑两阶段碳交易策略后整体碳配额购买量有所下降,但在17:00和19:00这两个时刻购买量有所提高,这是由于运营商在这两个时刻碳配额售价较低,使得微网2能够调整自身碳排放以此来获得更大的利益。微网1在考虑两阶段碳交易策略后整体碳配额出售量有所下降。微网3在两阶段碳交易策略后自身的碳配额出售量在15:00—17:00和20:00—21:00时段有所降低,在17:00—18:00有所提高。这是由于微网运营商在17:00—18:00碳配额购价较高,而在15:00—17:00和20:00—21:00碳配额购价较低。其中,考虑两阶段碳交易策略前后各微网碳排放量变化如图13所示。
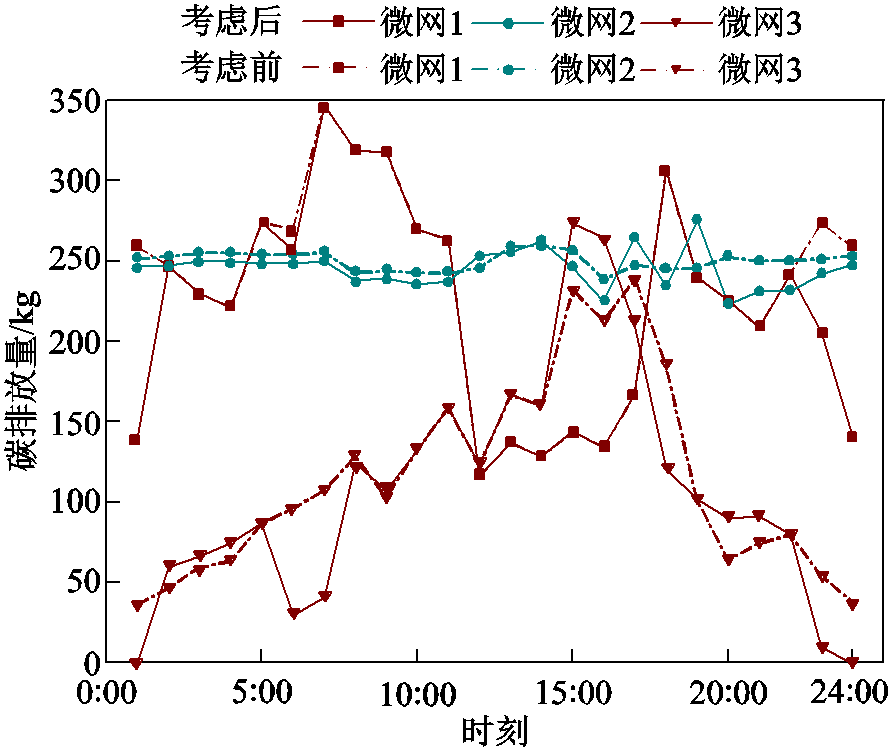
图13 考虑两阶段碳交易策略前后各微网碳排放量
Fig.13 The carbon emissions of each microgrid before and after the two-stage carbon trading tactics is considered
从图13中可以看出,在考虑两阶段碳交易策略后微网1和微网3的碳排放量在多数时段得到了下降,这是由于微网运营商在这些时段的碳配额购价较高,激励微网在这些时段降低碳排放以获得更大收益。在考虑两阶段碳交易策略后微网2在17:00和19:00这两个时刻碳排放升高了,而其他时段均有所降低,这是由于在17:00和19:00这两个时刻运营商的碳配额售价较低,导致微网2在这两个时刻的碳排放量有所提高。
相较于传统启发式算法,二分法具有更好的收敛性和更快的收敛速度,不同算法的优化结果对比见表3。
表3 不同算法对比
Tab.3 Comparison of different algorithms

算法迭代次数迭代时间/s微网运营商收益/元 二分法28526257.28 粒子群算法791 753253.34
由表3可知,二分法具有更少的迭代次数和更短的优化时间,实现了对模型的高效求解,不同算法的迭代次数与微网运营商收益对比如图14所示。
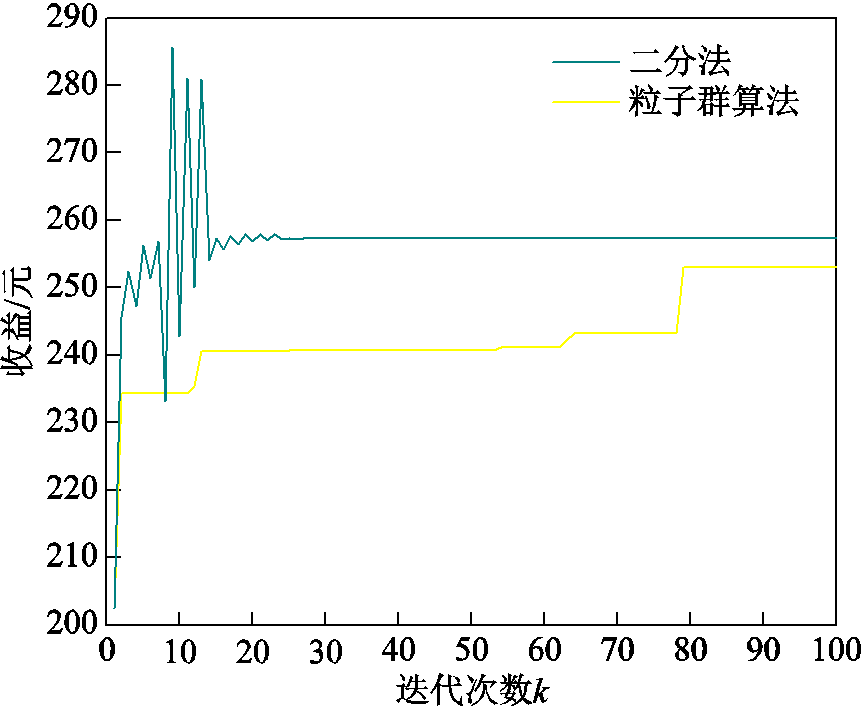
图14 不同算法迭代效果对比
Fig.14 Different algorithms iteration effect comparison
本文以同一微网运营商领导下的多园区综合能源微网为研究对象,提出了一种考虑两阶段碳交易的多园区综合能源微网混合博弈优化运行策略,主要结论如下:
1)与单独运行相比,微网间通过电能交易能够有效地降低各微网的碳排放量和总成本。
2)所提的两阶段碳交易策略不仅使微网侧总碳排放量下降了617.5 kg,实现了微网侧低碳运行,同时也降低了各微网的总成本。
3)所构建的混合博弈模型使得微网运营商的利润增加了257.28元,各微网的成本分别下降了 1 111.4、357.4、266.7元,该结果表明所提模型能够在保证微网运营商和各微网协调运行的基础上,实现各主体的利益最大化。
4)采用二分法和交替方向乘子法能够在保护各主体隐私的基础上,对模型进行高效的求解,其中二分法共迭代了28次,使得模型求解时间大为降低。
附 录
1. 碳交易模型
统一型碳交易成本计算模型为
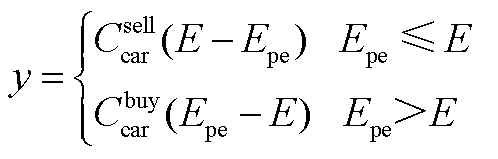 (A1)
(A1)
式中,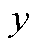 为碳交易成本;
为碳交易成本;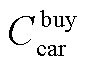 和
和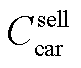 分别为上级市场购、售碳价;
分别为上级市场购、售碳价;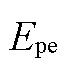 和E分别为碳配额量和碳排放量。
和E分别为碳配额量和碳排放量。
2. 合作博弈模型转换
根据算术-几何均值不等式,式(11)中的目标函数取得最大值需要满足
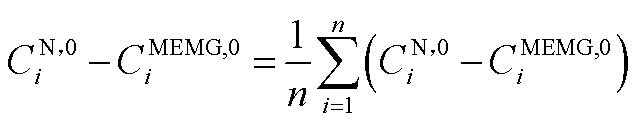 (A2)
(A2)
式中,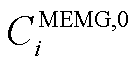 为微网i参与议价的最优成本,各微网间电能交易中电能交互量为相反数,电能交易价格相等,即
为微网i参与议价的最优成本,各微网间电能交易中电能交互量为相反数,电能交易价格相等,即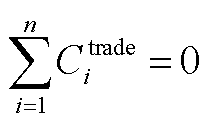 。令
。令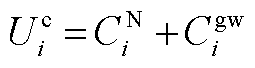 代入式(A2),则目标函数可转换为
代入式(A2),则目标函数可转换为
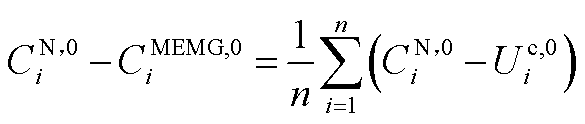 (A3)
(A3)
式中,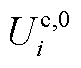 为
为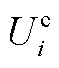 的最优解。将式(A3)代入式(11)可得
的最优解。将式(A3)代入式(11)可得
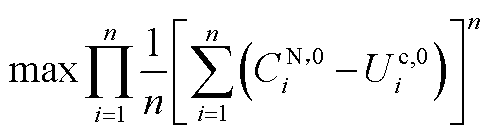 (A4)
(A4)
进一步将问题转换为
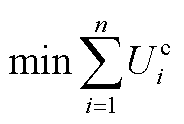 (A5)
(A5)
式(A5)为合作博弈模型转换后子问题1所求的目标函数。该子问题为标准的凸问题,能够通过分布式算法求得微网间电能交互功率。
将子问题1所求得的结果代入式(11)可得
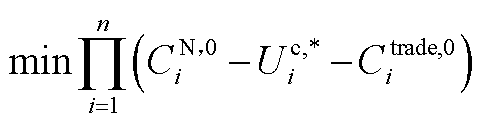 (A6)
(A6)
式中,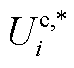 和
和 为子问题1所求的解。
为子问题1所求的解。
对式(A6)取对数后乘积问题转换为求和问题,即
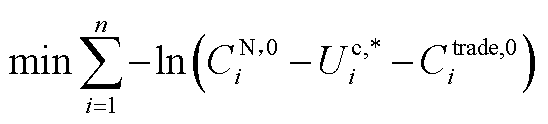 (A7)
(A7)
式(A7)为合作博弈模型转换后子问题2所求的目标函数。该子问题也为标准的凸问题,同样可采用分布式算法求得微网间电能交易价格。
3. 主从博弈均衡证明
本文建立的主从博弈模型为微网运营商将碳价下发给各园区综合能源微网,各园区综合能源微网基于微网运营商下发的碳价进行内部优化,再将自身的碳配额购售量传递给微网运营商。由正文中建立的模型可知,微网运营商、多园区综合能源微网的目标函数均为其博弈策略集的连续函数且对于各个博弈策略集拟凸,则可知该主从博弈的均衡解存在。
为证明主从博弈的均衡解的唯一性,需要满足以下条件:
1)对于微网运营商做出的决策,多园区综合能源微网存在唯一的最优策略。
2)对于多园区综合能源微网做出的决策,微网运营商存在唯一的最优策略。
对于式(15)分别求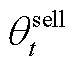 和
和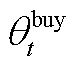 的二阶偏导,有
的二阶偏导,有
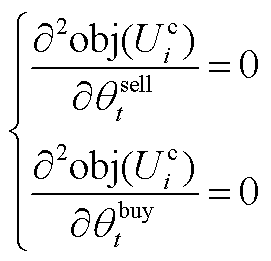 (A8)
(A8)
对式(1)分别求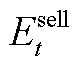 和
和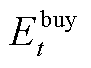 的二阶偏导,有
的二阶偏导,有
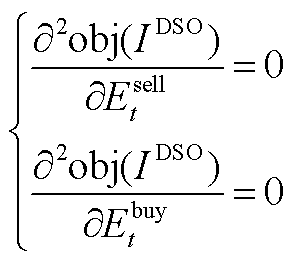 (A9)
(A9)
以上二阶偏导数均为0,则可证明该主从博弈的均衡解具有唯一性。
综上所述,主从博弈均衡解存在且唯一。
4. 储能设备模型
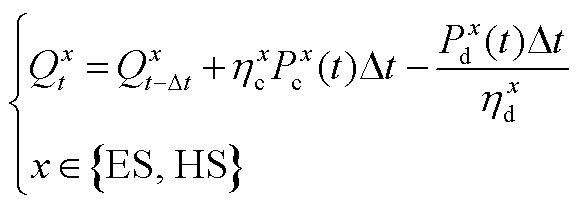 (A10)
(A10)
式中,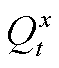 为第x类储能在第t时刻的储能量;
为第x类储能在第t时刻的储能量;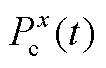 和
和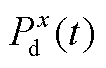 分别为第x类储能在t时刻的充、放能功率;
分别为第x类储能在t时刻的充、放能功率;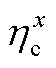 和
和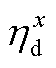 分别为第x类储能的充、放能效率;ES和HS分别为电储能和热储能。本文充、放能效率取值相同,具体取值见附表1。
分别为第x类储能的充、放能效率;ES和HS分别为电储能和热储能。本文充、放能效率取值相同,具体取值见附表1。
5. 初始碳配额计算公式
我国电力行业一般采用无偿的方式分配初始碳排放额,本文采用基准线法计算微网的碳配额,即
附表1 各设备运行参数
App.Tab.1 Operational parameters of the equipment
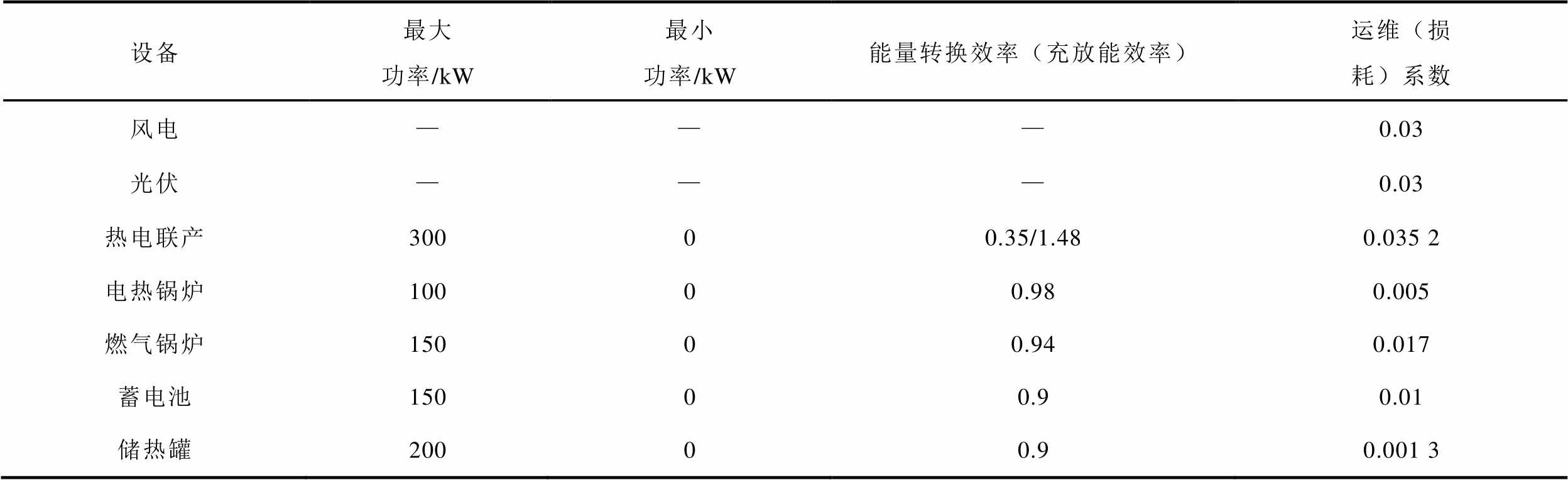
设备最大功率/kW最小功率/kW能量转换效率(充放能效率)运维(损耗)系数 风电———0.03 光伏———0.03 热电联产30000.35/1.480.035 2 电热锅炉10000.980.005 燃气锅炉15000.940.017 蓄电池15000.90.01 储热罐20000.90.001 3
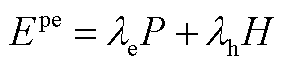 (A11)
(A11)
式中,P和H分别为微网通过消耗天然气的发电量和供热量;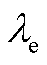 和
和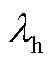 分别为单位发电量碳配额系数和单位供热量碳配额系数,分别取0.728 t/(MW·h)[10]和0.102 t/GJ[10]。
分别为单位发电量碳配额系数和单位供热量碳配额系数,分别取0.728 t/(MW·h)[10]和0.102 t/GJ[10]。
6. 仿真参数
附图1 各微网风电预测曲线
App.Fig.1 Wind power prediction curves for each microgrid
附图2 各微网光伏预测曲线
App.Fig.2 Prediction curves of photovoltaic power generation in each microgrid
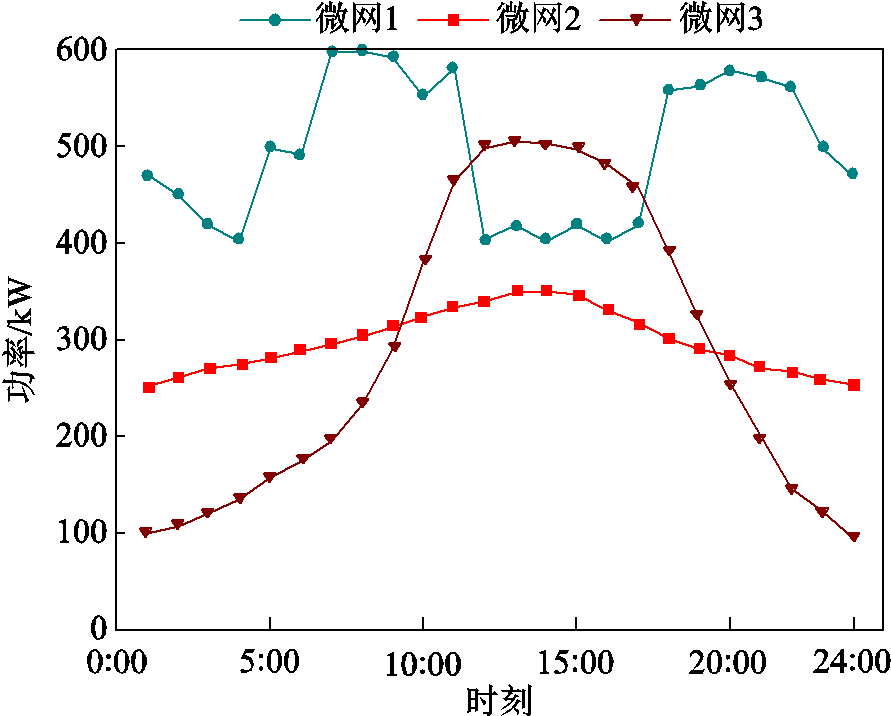
附图3 各微网电负荷预测曲线
App.Fig.3 Electric load forecasting curves of each microgrid
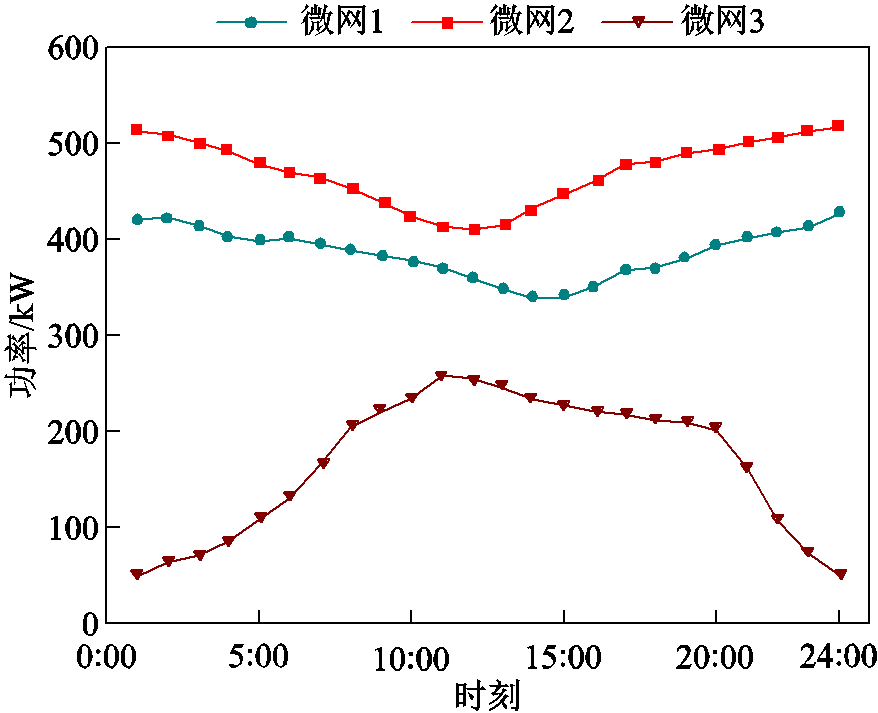
附图4 各微网热负荷预测曲线
App.Fig.4 Heat load prediction curves of each microgrid
7. 混合博弈收敛图
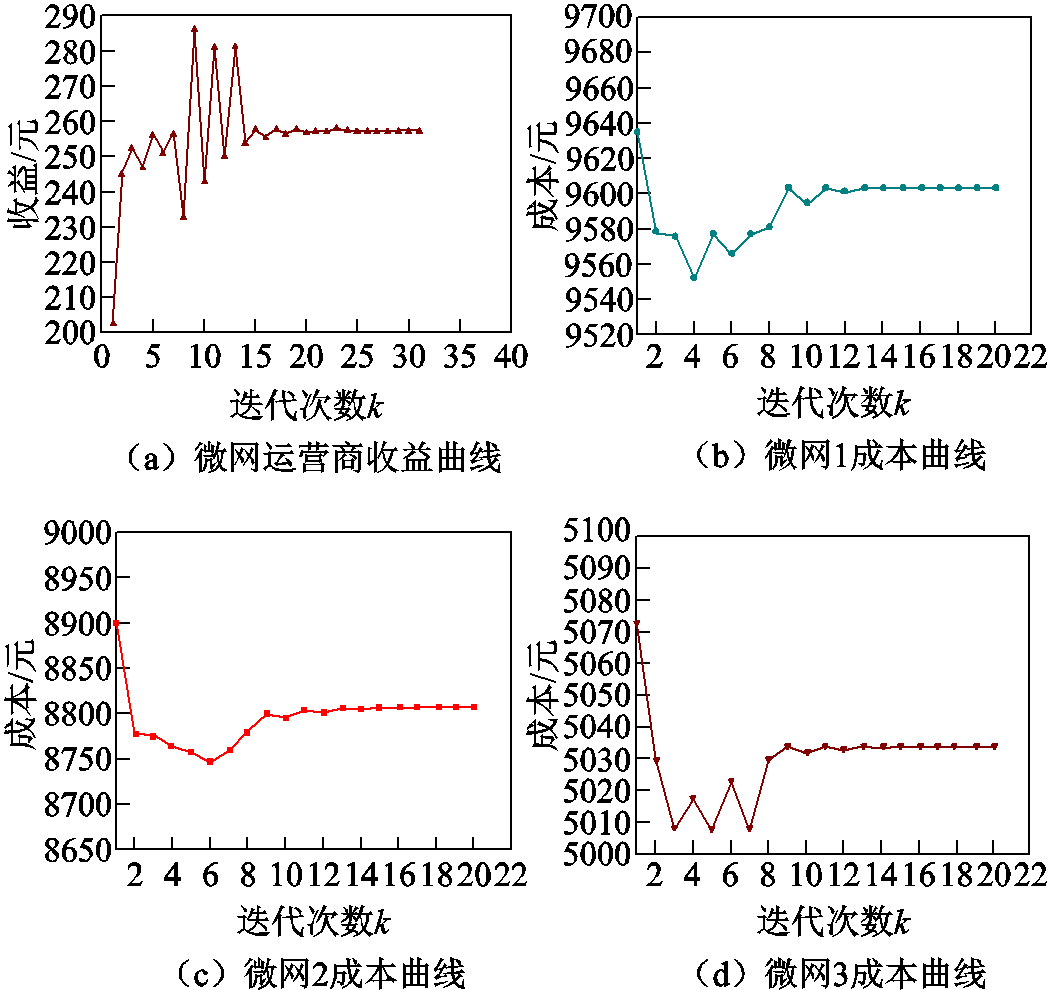
附图5 主从博弈收敛图
App.Fig.5 Master-slave game convergence diagram
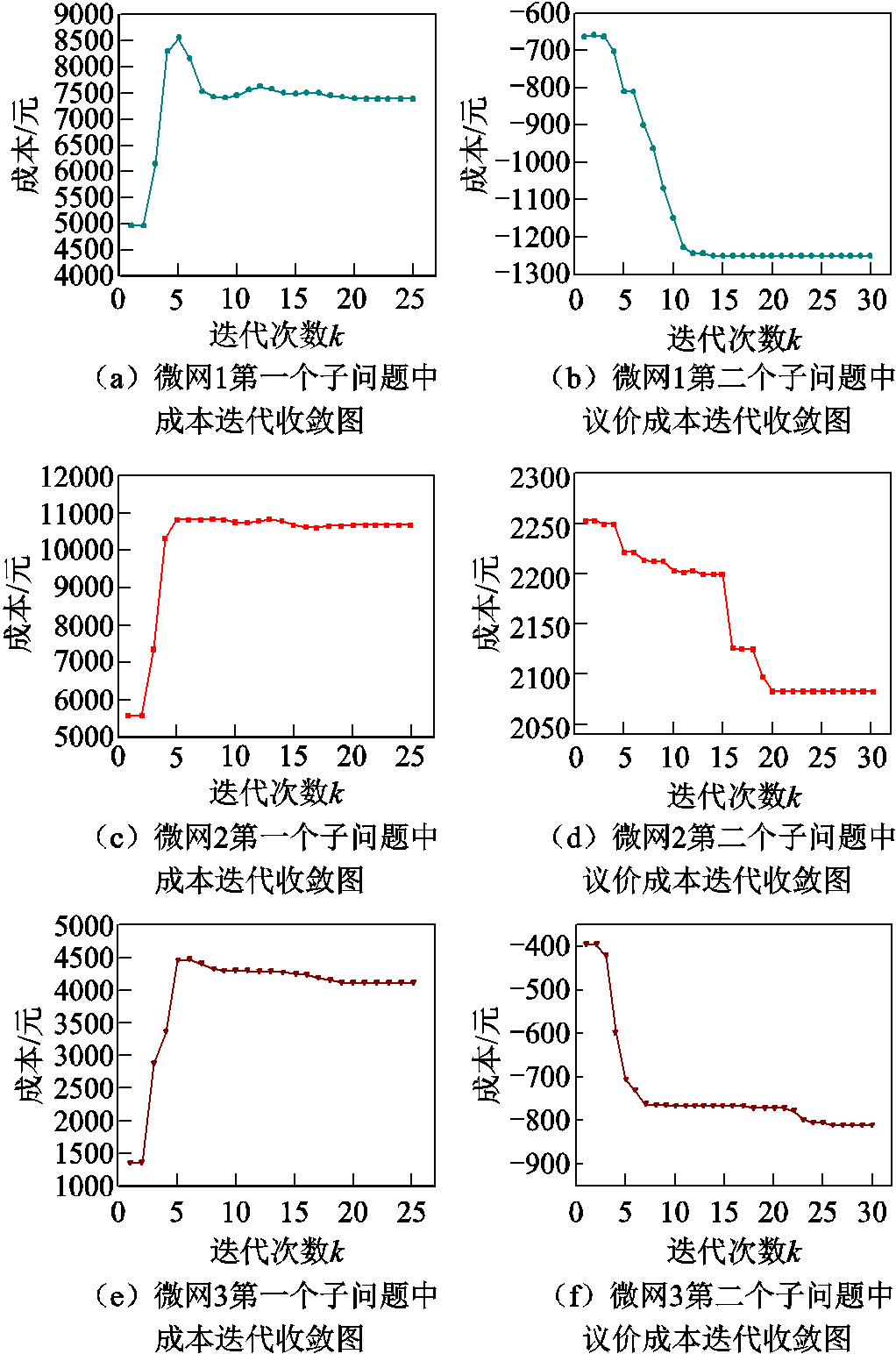
附图6 合作博弈收敛图
App.Fig.6 Convergence diagram of cooperative game
8. 微网相关参数
附表2 外部市场电价与碳价
App.Tab.2 External market electricity price and carbon price
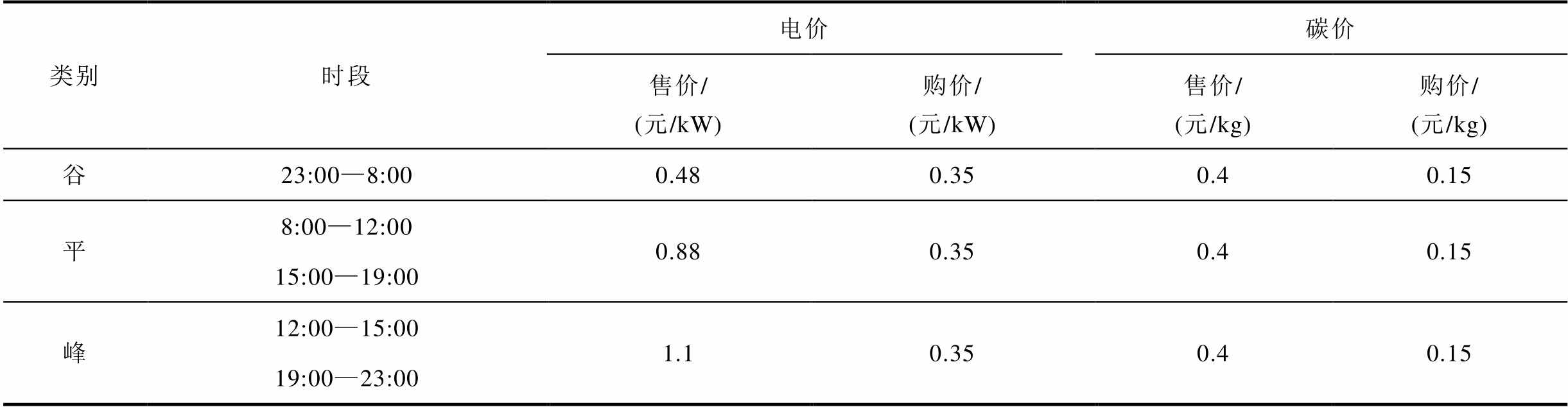
类别时段电价碳价 售价/(元/kW)购价/(元/kW)售价/(元/kg)购价/(元/kg) 谷23:00—8:000.480.350.40.15 平8:00—12:000.880.350.40.15 15:00—19:00 峰12:00—15:001.10.350.40.15 19:00—23:00
参考文献
[1] Li Peng, Wang Zixuan, Liu Haitao, et al. Bi-level optimal configuration strategy of community integrated energy system with coordinated planning and operation[J]. Energy, 2021, 236: 121539.
[2] 董雷, 杨子民, 乔骥, 等. 基于分层约束强化学习的综合能源多微网系统优化调度[J]. 电工技术学报, 2024, 39(5): 1436-1453.
Dong Lei, Yang Zimin, Qiao Ji, et al. Optimal scheduling of integrated energy multi-microgrid system based on hierarchical constraint reinforcement learning[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1436-1453.
[3] 闫佳佳, 滕云, 邱实, 等. 计及供能可靠性动态约束与碳减排的充能型微电网互联系统优化模型[J]. 电工技术学报, 2022, 37(23): 5956-5975.
Yan Jiajia, Teng Yun, Qiu Shi, et al. Optimization model of charging microgrid interconnection system considering dynamic constraints of energy supply reliability and carbon emission reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5956-5975.
[4] Li Peng, Wang Zixuan, Wang Jiahao, et al. A multi-time-space scale optimal operation strategy for a distributed integrated energy system[J]. Applied Energy, 2021, 289: 116698.
[5] Wang Zixuan, Li Peng, Zhou Yue, et al. Coordinated configuration strategy of multi-energy systems based on capacity-energy-information sharing[J]. Energy, 2023, 277: 127699.
[6] Sun Hongxia, Yang Jie. Optimal decisions for competitive manufacturers under carbon tax and cap-and-trade policies[J]. Computers & Industrial Eng-ineering, 2021, 156: 107244.
[7] Li Xiaojuan, Xie Wanjun, Xu Le, et al. Holistic life-cycle accounting of carbon emissions of prefabricated buildings using LCA and BIM[J]. Energy and Buildings, 2022, 266: 112136.
[8] 李嘉祺, 陈艳波, 陈来军, 等. 工业园区综合能源系统低碳经济优化运行模型[J]. 高电压技术, 2022, 48(8): 3190-3200.
Li Jiaqi, Chen Yanbo, Chen Laijun, et al. Low-carbon economy optimization model of integrated energy system in industrial parks[J]. High Voltage Eng-ineering, 2022, 48(8): 3190-3200.
[9] 岳子宜, 刘华志, 李永刚. 基于多阶段双重博弈的多园区随机场景低碳分布式调度优化[J]. 中国电机工程学报, 2024, 44(22): 8860-8874.
Yue Ziyi, Liu Zhihua, Li Yonggang. Low-carbon distributed scheduling optimization for multi-park stochastic situations based on a multi-stage dual game[J]. Proceedings of the CSEE, 2024, 44(22): 8860-8874.
[10] 瞿凯平, 黄琳妮, 余涛, 等. 碳交易机制下多区域综合能源系统的分散调度[J]. 中国电机工程学报, 2018, 38(3): 697-707.
Qu Kaiping, Huang Linni, Yu Tao, et al. Decentralized dispatch of multi-area integrated energy systems with carbon trading[J]. Proceedings of the CSEE, 2018, 38(3): 697-707.
[11] 刘英培, 黄寅峰. 考虑碳排权供求关系的多区域综合能源系统联合优化运行[J]. 电工技术学报, 2023, 38(13): 3459-3472.
Liu Yingpei, Huang Yinfeng. Joint optimal operation of multi-regional integrated energy system considering the supply and demand of carbon emission rights[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3459-3472.
[12] 李军徽, 邵岩, 朱星旭, 等. 计及碳排放量约束的多区域互联电力系统分布式低碳经济调度[J]. 电工技术学报, 2023, 38(17): 4715-4728.
Li Junhui, Shao Yan, Zhu Xingxu, et al. Carbon emissions constraint distributed low-carbon economic dispatch of power system[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4715-4728.
[13] 孙晓聪, 丁一, 包铭磊, 等. 考虑发电商多时间耦合决策的碳-电市场均衡分析[J]. 电力系统自动化, 2023, 47(21): 1-11.
Sun Xiaocong, Ding Yi, Bao Minglei, et al. Carbon-electricity market equilibrium analysis considering multi-time coupling decision of power producers[J]. Automation of Electric Power Systems, 2023, 47(21): 1-11.
[14] 葛少云, 程雪颖, 刘洪, 等. 园区多微网P2P电-碳耦合交易市场设计[J]. 高电压技术, 2023, 49(4): 1341-1349.
Ge Shaoyun, Cheng Xueying, Liu Hong, et al. Market design of P2P electricity carbon coupling transaction among multi-microgrids in a zone[J]. High Voltage Engineering, 2023, 49(4): 1341-1349.
[15] 刘靓颖, 蒋凯, 刘念, 等. 基于主从博弈的园区多主体能量-碳配额共享机制[J]. 中国电机工程学报, 2024, 44(6): 2119-2131.
Liu Liangying, Jiang Kai, Liu Nian, et al. Multi-agent energy-carbon sharing mechanism for parks based on Stackelberg game[J]. Proceedings of the CSEE, 2024, 44(6): 2119-2131.
[16] Tushar W, Saha T K, Yuen C, et al. A motivational game-theoretic approach for peer-to-peer energy trading in the smart grid[J]. Applied Energy, 2019, 243: 10-20.
[17] 宋晓通, 陈佳琪, 师芊芊. 多主体博弈背景下的综合能源微网优化调度[J]. 高电压技术, 2023, 49(8): 3163-3178.
Song Xiaotong, Chen Jiaqi, Shi Qianqian. Optimal scheduling of integrated energy microgrid under the background of multi-agent game[J]. High Voltage Engineering, 2023, 49(8): 3163-3178.
[18] 李鹏, 吴迪凡, 李雨薇, 等. 基于综合需求响应和主从博弈的多微网综合能源系统优化调度策略[J]. 中国电机工程学报, 2021, 41(4): 1307-1321, 1538.
Li Peng, Wu Difan, Li Yuwei, et al. Optimal dispatch of multi-microgrids integrated energy system based on integrated demand response and Stackelberg game[J]. Proceedings of the CSEE, 2021, 41(4): 1307-1321, 1538.
[19] 潘郑楠, 邓长虹, 徐慧慧, 等. 考虑灵活性补偿的高比例风电与多元灵活性资源博弈优化调度[J]. 电工技术学报, 2023, 38(增刊1): 56-69.
Pan Zhengnan, Deng Changhong, Xu Huihui, et al. Game optimization scheduling of high proportion wind power and multiple flexible resources considering flexibility compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 56-69.
[20] 马腾飞, 裴玮, 肖浩, 等. 基于纳什谈判理论的风-光-氢多主体能源系统合作运行方法[J]. 中国电机工程学报, 2021, 41(1): 25-39, 395.
Ma Tengfei, Pei Wei, Xiao Hao, et al. Cooperative operation method for wind-solar-hydrogen multi-agent energy system based on Nash bargaining theory[J]. Proceedings of the CSEE, 2021, 41(1): 25-39, 395.
[21] 崔明勇, 宣名阳, 卢志刚, 等. 基于合作博弈的多综合能源服务商运行优化策略[J]. 中国电机工程学报, 2022, 42(10): 3548-3564.
Cui Mingyong, Xuan Mingyang, Lu Zhigang, et al. Operation optimization strategy of multi integrated energy service companies based on cooperative game theory[J]. Proceedings of the CSEE, 2022, 42(10): 3548-3564.
[22] 董雷, 李扬, 陈盛, 等. 考虑多重不确定性与电碳耦合交易的多微网合作博弈优化调度[J]. 电工技术学报, 2024, 39(9): 2635-2651.
Dong Lei, Li Yang, Chen Sheng, et al. Multi-microgrid cooperative game optimization scheduling considering multiple uncertainties and coupled electricity-carbon transactions[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2635-2651.
[23] 王再闯, 陈来军, 李笑竹, 等. 基于合作博弈的产销者社区分布式光伏与共享储能容量优化[J]. 电工技术学报, 2022, 37(23): 5922-5932.
Wang Zaichuang, Chen Laijun, Li Xiaozhu, et al. Capacity optimization of distributed PV and shared energy storage of prosumer community based on cooperative game[J]. Transactions of China Electro-technical Society, 2022, 37(23): 5922-5932.
[24] 林墨涵, 刘佳, 唐早, 等. 考虑多能耦合共享储能的微网多智能体混合博弈协调优化[J]. 电力系统自动化, 2024, 48(4): 132-141.
Lin Mohan, Liu Jia, Tang Zao, et al. Coordinated optimization of mixed microgrid multi-agent game considering multi-energy coupled shared energy storage[J]. Automation of Electric Power Systems, 2024, 48(4): 132-141.
[25] 张忠会, 熊骁跃, 万昶, 等. 计及电-碳交易与综合贡献率的多微网合作运行优化策略[J]. 电网技术, 2024, 48(8): 3258-3268.
Zhang Zhonghui, Xiong Xiaoyue, Wan Chang, et al. Multi-microgrids cooperative operation optimization strategy considering electricity-carbon trading and comprehensive contribution rate[J]. Power System Technology, 2024, 48(8): 3258-3268.
[26] Yan Mingyu, Shahidehpour M, Alabdulwahab A, et al. Blockchain for transacting energy and carbon allowance in networked microgrids[J]. IEEE Transactions on Smart Grid, 2021, 12(6): 4702-4714.
[27] Cheng Yaohua, Zhang Ning, Zhang Baosen, et al. Low-carbon operation of multiple energy systems based on energy-carbon integrated prices[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1307-1318.
[28] 孔令国, 史立昊, 石振宇, 等. 基于交替方向乘子法的园区电-氢-热系统低碳优化调度[J]. 电工技术学报, 2023, 38(11): 2932-2944.
Kong Lingguo, Shi Lihao, Shi Zhenyu, et al. Low-carbon optimal dispatch of electric-hydrogen-heat system in park based on alternating direction method of multipliers[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2932-2944.
Multi-Park Integrated Energy Microgrids Hybrid Game Optimization Strategy Considering Two-Stage Carbon Trading
Abstract The park's integrated energy microgrid covers the production, transmission, storage and utilization of energy, and combines electricity, thermal units and energy storage to improve energy utilization and reduce carbon emissions in the system. However, with the increasing number of entities in the microgrid, the existing carbon trading mechanism cannot meet the interests of each entity. In this context, how to take into account the interests of multiple parties and build a multi-level carbon trading strategy corresponding to the energy system is a key constraint for low-carbon operation of multi-park integrated energy microgrids. Therefore, this paper proposes a hybrid game optimization operation method for multi-park integrated energy microgrids that considers two-stage carbon trading. The aim is to formulate a reasonable carbon trading strategy of multi-park integrated energy microgrids to effectively guide the low-carbon operation of the park and promote the realization of the "double carbon" goal.
First, a two-stage carbon trading mechanism is proposed in which microgrid operators buy and sell carbon quotas to integrated energy microgrids in various parks in the first stage of carbon trading. In the second stage of carbon trading, microgrid operator s participate in external carbon trading markets. The purpose is that the operators of the microgrid will set time-varying carbon prices through the carbon quota purchase and sale information fed back by each microgrid, so as to guide the low-carbon operation of each microgrid, and enable the multi-park integrated energy microgrids to form an effective interaction with the upper market under the carbon trading mechanism. Secondly, a master-slave game model with the microgrid operators as the leader and the multi-park integrated energy microgrids as the follower are constructed, and a cooperative game model between the multi-park integrated energy microgrids is constructed considering the electricity transaction between the microgrid. On this basis, the cooperative alliance built by the multi-park integrated energy microgrids cooperation game model is taken as the follower of the master-slave game, and the microgrid operator is taken as the leader of the master-slave game, and the multi-park integrated energy microgrids hybrid game model is constructed. Among them, microgrid operators are the leaders, with the goal of maximizing their own interests, setting carbon prices and distributing them to the integrated energy microgrid of each park. The multi-park integrated energy microgrids are the follower, with the goal of minimizing the comprehensive cost, and responds to the strategy of microgrid operators through cooperation. Finally, the cooperative game model of multi-park integrated energy microgrids is transformed into two sub-problems by Nash bargaining theory, and then the mixed game model is solved by dichotomy and alternating direction multiplier method. The superiority of the proposed method is verified by simulation.
The results show that: (1) The two-stage carbon trading strategy proposed in this paper can improve the economy and low-carbon performance of each microgrid, and ensure the low-carbon operation of each microgrid in the system; (2) The multi-microgrid hybrid game optimization model constructed in this paper improves the economy of both microgrid operators and each microgrid in the system and guarantees the economy of each entity; (3) Using dichotomy and alternating direction multiplier method can solve the mixed game model efficiently on the basis of protecting the privacy of each entity.
Keywords:Multi-park integrated energy microgrids, low carbon optimized operation, hybrid game, Nash bargaining, distributed optimization
中图分类号:TM732
DOI: 10.19595/j.cnki.1000-6753.tces.241302
国家自然科学基金资助项目(52177084)。
收稿日期 2024-07-22
改稿日期 2024-11-05
李 鹏 男,1965年生,博士,教授,研究方向为新能源电力系统、综合能源系统与微网、储能技术应用、人工智能在智慧能源中的应用。
E-mail:ncepulp@ncepu.edu.cn
刘 浩 男,1999年生,硕士研究生,研究方向为综合能源系统优化运行。
E-mail:lh17303223906@163.com(通信作者)
(编辑 赫 蕾)