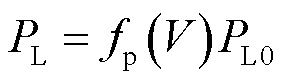 (1)
(1)
摘要 虚拟电厂(VPP)是挖掘需求侧灵活性的重要手段。现有研究多将需求侧资源划分为可控和不可控两类,在优化模型中将后者视为与决策无关的参数。然而,由于负荷客观存在静态电压特性,VPP调控引发的节点电压变化必然影响不可控资源的实际功率,导致VPP难以实现精准调控。为此,该文提出考虑负荷静态电压特性的VPP精准调控方法。首先,建立了考虑负荷静态电压特性的VPP运行模型,在优化模型中精细化地考虑不可控资源功率受决策变量被动变化的影响关系;其次,针对负荷静态电压特性引入所产生的模型求解难题,建立了适应VPP控制策略的负荷静态电压特性方程,实现高效的模型在线求解;最后,基于实际系统的算例分析发现,该文方法可以在VPP运行问题中准确考虑不可控资源受其他资源调控带来的影响,进而以更小的调节代价达到合格的功率目标跟踪精度。该研究解决了当前VPP因调节粗略而仅在削峰填谷等单一场景应用的不足,为VPP发挥负荷跟踪、自动功率控制、运行备用等多类型调节作用奠定基础。
关键词:静态电压特性 虚拟电厂 精准调控 需求侧资源
在“双碳”战略目标指导下,我国提出了建设以新能源为主体的新型电力系统的目标,亟须扎实推进新型电力系统建设[1]。随着高比例的新能源发电接入电网,新能源的波动性导致的灵活调节能力匮乏成为新型电力系统的核心矛盾,电力系统的安全高效运行面临新的挑战[2]。如何挖掘电力需求侧泛在的灵活性潜力成为关键问题[3]。
近年来,虚拟电厂(Virtual Power Plant, VPP)的概念和技术得到快速发展,完成了从无到有的突破[4]。VPP旨在连接聚合需求侧海量的分布式资源(Distributed Energy Resources, DERs),将其作为一个整体参与电网调节,为新型电力系统提供必不可缺的调节能力[5-6]。从不同时间尺度来看,VPP可提供的服务包括:①开展日前到h级的能量调节,达到削峰填谷、促进新能源消纳等作用;②开展min~s级的快速功率调节,起到快速备用等效果以及提供电压频率支撑等辅助服务,应对电力系统的各种异常运行状态;③发挥需求侧事故备用等作用,实现s级以内的快速负荷调节,增强系统稳定性[7]。目前,上海、冀北、广东等诸多省市和地区都建设了VPP示范项目,可调节资源可达百万kW级[8]。
但是,如何实现VPP精准调控仍是有待突破的关键技术[9]。对电力系统而言,VPP只有在具备精准调控的能力下,才能发挥负荷跟踪、自动功率控制(Automatic Power Control, APC)、运行备用等作用,向电力系统提供类似电化学储能等高品质的调节服务,起到弥补传统机组调节能力的作用;对VPP自身而言,具备精准调控能力才能以更低的代价获得更高的运行收益,实现可持续运营。
VPP调节能力的最终来源是泛在分布的DERs。现有的研究通常将VPP内的资源划分为可控资源和不可控资源两大类,在优化调度可控资源的同时,将不可控资源作为优化问题的参数进行考虑。例如,文献[10]考虑经济性目标,对风电、储能系统(Energy Storage System, ESS)等需求侧资源进行调控,文献[11]以电动汽车为调控对象,文献[12]则将光伏、储能和电动汽车充电桩都纳入考虑范围之中,以实现优化运行和响应调控指令的目的。然而,现有的研究主要存在两方面局限:①将不可控资源视为刚性的恒定功率负荷,忽视了负荷特性的调节空间;②缺乏对VPP内部网络拓扑结构的系统建模。
在电力系统中,负荷特性对系统的稳态和动态性能都有重要的影响,对电力系统的正确分析需要准确的负荷模型[13]。根据时间尺度和应用场景,负荷模型可分为静态模型和动态模型。静态模型描述负荷功率与电压、频率等电气量的稳态关系;动态模型则还需考虑电气量的变化率,多用于暂态的研究场景中[14-15],由于动态模型对数据采样密度要求极高[16],因此仅在特定场景下加装高性能采样设备时适用。考虑到VPP的调控场景主要关注min级的时间尺度,本文重点研究负荷的静态特性,特别是静态电压特性。
在实际配电系统中,当电压偏离额定点时,负荷特性会发生改变[17],可能表现出恒功率、恒电流、恒阻抗或其组合特性,从而影响系统的潮流分布[18],这就是所谓的负荷静态电压特性。换言之,不可控资源的功率大小在VPP内部优化调度问题中并非参数,而应该是与决策变量相关的函数。忽略负荷的静态电压特性,可能导致VPP对外输出功率偏离预设值,于系统层面产生调节偏差,在VPP内部资源层面产生不必要的调节损失。为此,有必要在VPP内部优化调度中充分考虑不可控资源的负荷静态电压特性。
目前,负荷电压特性仅在电力系统分析与规划[19-20]、电压稳定性分析[21-22]等领域得到关注和考虑,但VPP等资源优化控制领域研究中鲜有考虑[23]。而在VPP中考虑负荷静态电压特性面临诸多挑战:①需要建立完整的VPP内部拓扑模型,包括网络结构、潮流约束和各类资源的运行特性;②需要准确描述调控策略-电压变化-负荷响应-潮流改变-输出调整的全过程模型,体现不可控资源与决策变量间的复杂关联;③需要设计高效的求解算法,在保证模型准确性的同时满足实际应用对计算速度的要求。
针对上述问题,本文提出了一种考虑负荷静态电压特性的VPP精准调控方法。主要工作点包括:①建立了包含可控资源、不可控资源和园区网络的完整VPP运行模型,实现了对内部拓扑结构的精细化描述;②提出了适用于VPP控制策略的负荷静态电压特性方程,揭示了不可控资源与决策变量的关联机理;③设计了高效的模型求解方法,实现了优化结果的快速收敛。算例分析表明,本文方法可以准确把握不可控资源受其他DERs调控带来的影响,显著提高了VPP功率调节的精准性,同时降低了调节成本。
VPP中的可控资源与不可控资源是由电力网络耦合起来的,可控资源接收到调控指令改变自身功率会引起网络潮流和节点电压的变化。不可控资源由于其静态电压特性的存在,当电压发生变化时,自身的功率也会相应发生变化,可记作
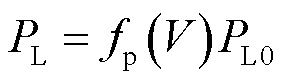 (1)
(1)
式中,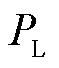 为负荷实际功率;
为负荷实际功率;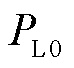 为额定电压下该负荷的标准功率;
为额定电压下该负荷的标准功率;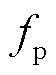 用来描述功率变化与电压的关系,其具体的数学形式将在本文2.2节中详细讨论。由于负荷功率与电压关系的存在,VPP的精准调控需要下沉到DERs末端,精确计及VPP内部网络拓扑约束与负荷静态电压特性。
用来描述功率变化与电压的关系,其具体的数学形式将在本文2.2节中详细讨论。由于负荷功率与电压关系的存在,VPP的精准调控需要下沉到DERs末端,精确计及VPP内部网络拓扑约束与负荷静态电压特性。
为此,本文将精细化考虑电网拓扑的VPP称作园区VPP。园区泛指各类型工业园、校园、科技园等,园区是现代人类社会工作与生活最重要的物理载体,也是需求侧最典型的综合能源节点,包含了能源的生产、消费、存储各个环节。在“双碳”目标推动下,大量的园区建设了光伏、储能等DERs,在能源的生产和消费端都占据着重要的位置。将广泛存在的园区建设为VPP,既为园区运营带来新的机遇,也可充分挖掘需求侧资源灵活性潜力[24-26]。园区中的资源调控流程如图1所示。
园区中的资源聚合成为园区级别的VPP,由园区向上级电网上报自己的调节能力,由与上级电网连接的公共耦合点(Point of Common Coupling, PCC)反映自己的调节能力。当上级电网出现调节需求时,根据园区VPP上报的调节能力给出PCC的跟踪目标,给出的跟踪目标应当在VPP的跟踪能力范围内[27-28]。园区应当综合考虑园区内部各DERs的运行参数以及内部负荷的静态电压特性制定并下发DERs的运行策略,最后由上级电网对PCC功率进行考核,衡量调控效果。
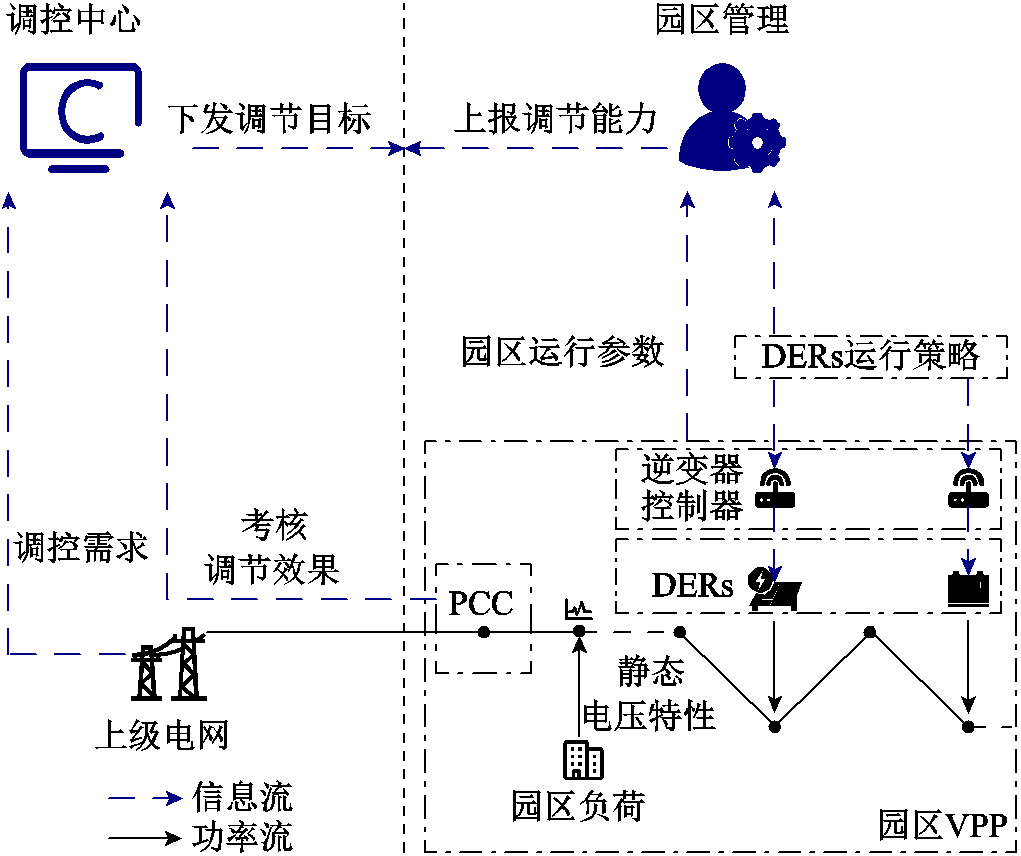
图1 园区资源参与调控流程
Fig.1 Process of participation of park DERs in regulation
园区VPP中常见的可控资源包括光伏、储能等。本文主要以光伏和储能的调控方法为研究对象,提出园区VPP中可控资源参与调控的模型;涉及其他典型资源的情况仅需补充或替换相应资源模型即可。
2.1.1 光伏
园区中的光伏通过逆变器连接到网络中,光伏的发电能力既受辐照、温度等环境参数影响,又受逆变器容量的制约。考虑到光伏逆变器的调节能力,可以认为光伏资源的有功功率可在0(完全弃光)与最大功率点之间任意调节;无功功率则在有功功率确定后,受逆变器容量制约,使复功率不超出逆变器容量的范围,即
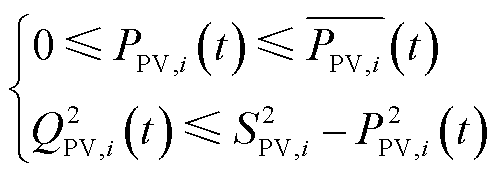 (2)
(2)
式中,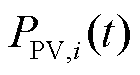 为节点
为节点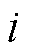 中光伏在
中光伏在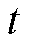 时刻的有功功率;
时刻的有功功率;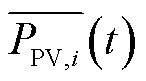 为该光伏设备在
为该光伏设备在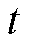 时刻受辐照等物理条件影响的最大有功功率;
时刻受辐照等物理条件影响的最大有功功率;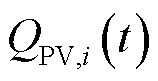 为t时刻下该光伏的无功功率;
为t时刻下该光伏的无功功率;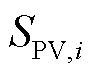 为该光伏逆变器的容量。由于光伏无功所受的约束具有一定的复杂性,为简化问题,同时不失其无功的调节灵活性,考虑在实际运行中,对光伏工作允许的最小功率因数
为该光伏逆变器的容量。由于光伏无功所受的约束具有一定的复杂性,为简化问题,同时不失其无功的调节灵活性,考虑在实际运行中,对光伏工作允许的最小功率因数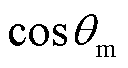 进行限制,使得光伏不至于吸收或输出过多的无功功率。光伏可行域简化示意图如图2所示。
进行限制,使得光伏不至于吸收或输出过多的无功功率。光伏可行域简化示意图如图2所示。
从而将其改写[29]为
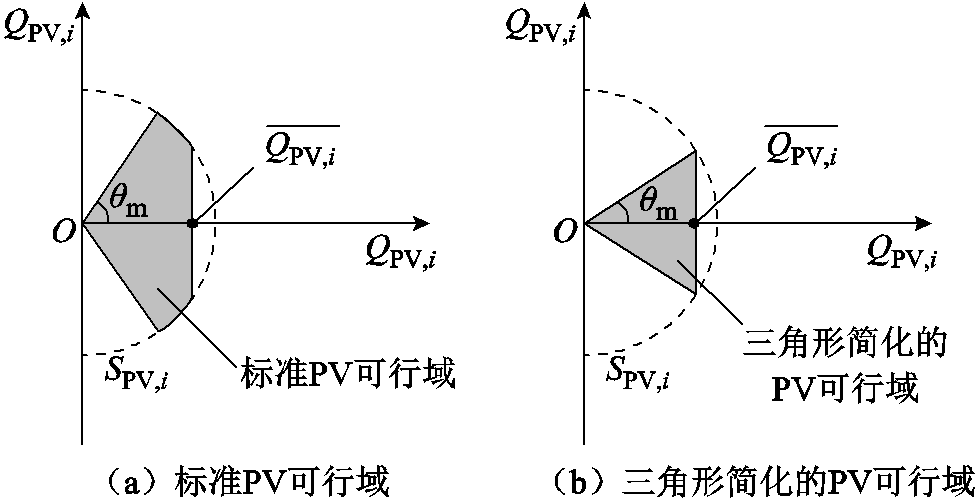
图2 光伏可行域简化示意图
Fig.2 Simplified PV feasible domains
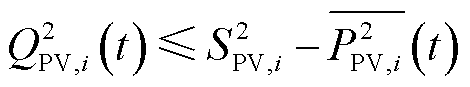 (3)
(3)
式(3)将光伏的可行域简化为三角形约束,从而降低了优化的复杂程度。
光伏资源的调节偏离了其原本的最大功率点跟踪策略,需要付出调节的代价,因此采用效用损失函数的方式对光伏的调节代价进行衡量。光伏的效用损失函数一方面需要表示弃光造成的效益损失,另一方面也要表征无功调节对逆变器容量占用造成的效益损失,有
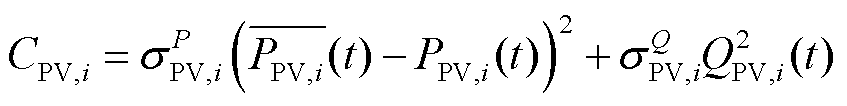 (4)
(4)
式中,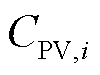 为调节该光伏的效用损失函数;
为调节该光伏的效用损失函数;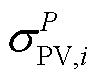 和
和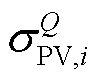 分别为调节该光伏有功和无功的效用系数。
分别为调节该光伏有功和无功的效用系数。
2.1.2 储能
储能资源除其功率的调节限制之外,由于其能量的储存释放特性,还存在时间维度的耦合关系,通常需要考虑其工作状态在全时段范围内的约束,即其荷电状态(State of Charge, SOC)的范围约束。
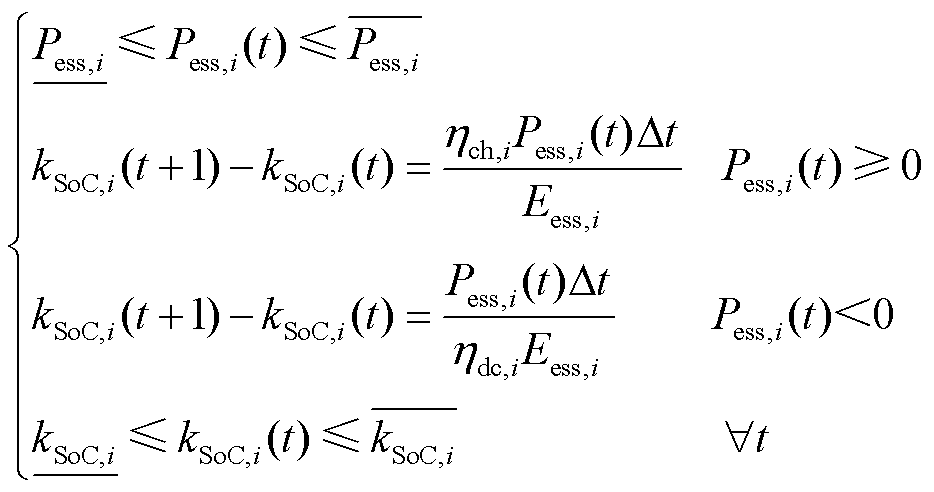 (5)
(5)
式中,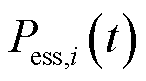 为
为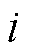 节点下储能的充放电功率,规定储能充电功率为正,放电功率为负,受最大充电功率
节点下储能的充放电功率,规定储能充电功率为正,放电功率为负,受最大充电功率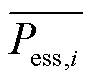 与最大放电功率
与最大放电功率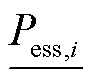 限制;
限制;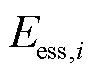 为该储能的容量;
为该储能的容量;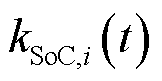 为储能在
为储能在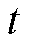 时刻的荷电状态;
时刻的荷电状态;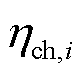 和
和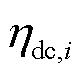 分别为充电效率和放电效率;
分别为充电效率和放电效率;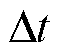 为相邻时刻的时间差;
为相邻时刻的时间差;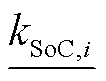 与
与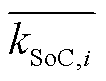 分别为该储能运行全时段的荷电状态下限和上限要求。
分别为该储能运行全时段的荷电状态下限和上限要求。
在本文关注的问题中,由于调控的时段通常不会太长,在给定的时段内,储能全充电或者全放电下都不会触及SOC的上下限限制,因此,可以将储能的模型简化为
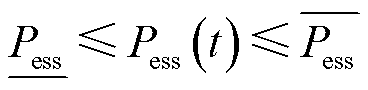 (6)
(6)
储能的无功通常不作调节,因此,储能的效用损失函数可表示为
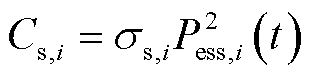 (7)
(7)
式中,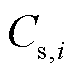 为调节储能的效用损失函数;
为调节储能的效用损失函数;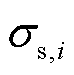 为调节储能的效用系数。在该效用损失函数下,储能充电和放电造成的效用损失等价,在调节过程中,为追求最小的调节代价,不会出现储能在同一时刻既充电又放电的优化结果,故而可以免于添加充放电的逻辑约束,使得模型保持为较简单的形式,具体说明如下。
为调节储能的效用系数。在该效用损失函数下,储能充电和放电造成的效用损失等价,在调节过程中,为追求最小的调节代价,不会出现储能在同一时刻既充电又放电的优化结果,故而可以免于添加充放电的逻辑约束,使得模型保持为较简单的形式,具体说明如下。
假设对于某特定时刻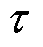 ,除各ESS外各项参数已经确定,各ESS需协同满足某一确定功率目标
,除各ESS外各项参数已经确定,各ESS需协同满足某一确定功率目标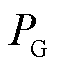 。假设
。假设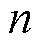 台ESS各自的功率为
台ESS各自的功率为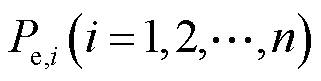 ,各自的效用系数为
,各自的效用系数为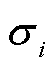 ,有
,有
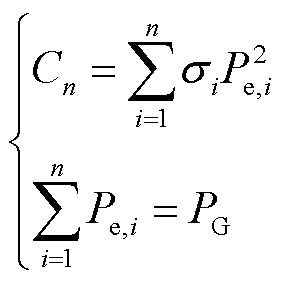 (8)
(8)
要最小化其效用损失函数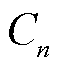 ,采用拉格朗日乘数法进行求解,可以得出
,采用拉格朗日乘数法进行求解,可以得出
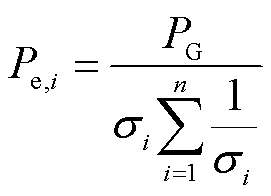 (9)
(9)
即各ESS的充放电行为取决于功率目标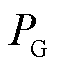 的正负。式(9)说明,在平方型的效用损失函数下,不同ESS分别处于充电和放电将会在不影响其他条件的情况下导致效用损失函数的增大,因此该效用损失函数可以控制ESS不出现同一时刻既充电又放电的优化结果。该结论在考虑SOC约束且不考虑充放电效率时仍然成立,但当考虑ESS充放电效率时,由于充放电行为会导致SOC变化情况的差异,仍需要将充放电功率进行区分。
的正负。式(9)说明,在平方型的效用损失函数下,不同ESS分别处于充电和放电将会在不影响其他条件的情况下导致效用损失函数的增大,因此该效用损失函数可以控制ESS不出现同一时刻既充电又放电的优化结果。该结论在考虑SOC约束且不考虑充放电效率时仍然成立,但当考虑ESS充放电效率时,由于充放电行为会导致SOC变化情况的差异,仍需要将充放电功率进行区分。
现有的研究中,多将不可控的资源负荷视为刚性的恒功率负荷,未考虑负荷功耗与电压之间的依赖关系。在本文的研究中,引入负荷的静态电压模型以考虑不可控资源在VPP调控后,由于自身功耗变化对于网络潮流变化的影响。
刻画负荷静态电压特性的模型有多种,最常用的包括幂指数模型和ZIP模型[30]。幂指数模型可表示为
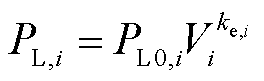 (10)
(10)
式中,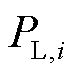 为节点
为节点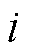 上的负荷的功耗;
上的负荷的功耗;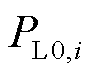 为节点
为节点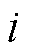 上的负荷在额定电压下的标准功耗;
上的负荷在额定电压下的标准功耗;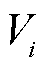 为节点
为节点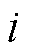 的电压幅值的标幺值;
的电压幅值的标幺值;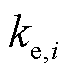 为节点
为节点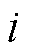 上的负荷的电压灵敏度,表征负荷因电压的变化引起的功耗变化,对于刚性负荷,
上的负荷的电压灵敏度,表征负荷因电压的变化引起的功耗变化,对于刚性负荷,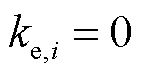 。
。
ZIP模型根据负荷中不同组分对电压敏感性的不同,将其分为恒阻抗分量(Z)、恒电流分量(I)与恒功率分量(P),从而可以将负荷的功率电压关联关系表示为
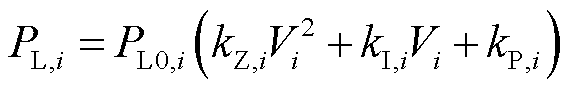 (11)
(11)
式中,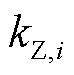 、
、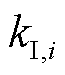 、
、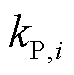 分别为节点
分别为节点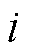 上负荷的恒阻抗分量系数、恒电流分量系数与恒功率分量系数。由于负荷在额定电压
上负荷的恒阻抗分量系数、恒电流分量系数与恒功率分量系数。由于负荷在额定电压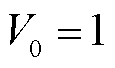 下有标准功耗,因此有
下有标准功耗,因此有
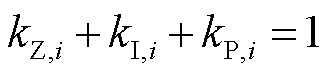 (12)
(12)
从式(12)也可以看出,负荷ZIP模型对应系数的物理含义即负荷组成中,具有恒阻抗、恒电流和类恒功率三种类型负荷的占比。当忽略负荷组成中的恒阻抗和恒电流成分时,ZIP模型将退化为不可控的刚性负荷模型。
负荷的幂指数模型和ZIP模型之间可以互相转换。ZIP模型可以视为电压灵敏度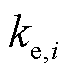 在分别取2、1、0的情况下进行的加权求和,而幂指数模型中的
在分别取2、1、0的情况下进行的加权求和,而幂指数模型中的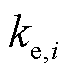 可以通过展开的方式与ZIP模型中的参数相对应,即
可以通过展开的方式与ZIP模型中的参数相对应,即
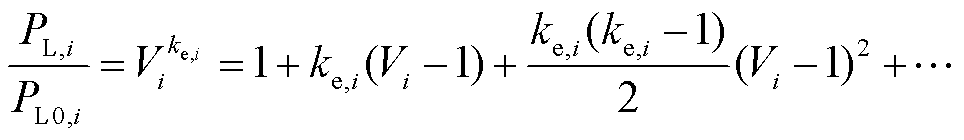 (13)
(13)
舍去高阶项后,整理可得
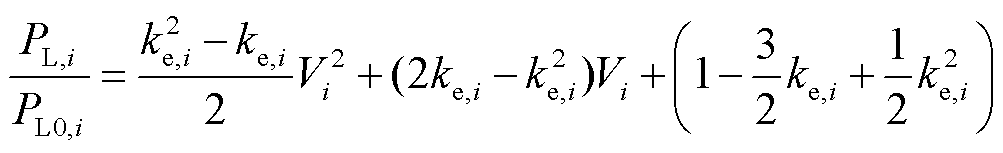 (14)
(14)
对比可得,幂指数模型等效的ZIP模型中各参数与原电压灵敏度的关系为
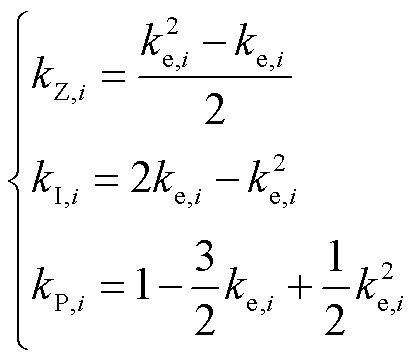 (15)
(15)
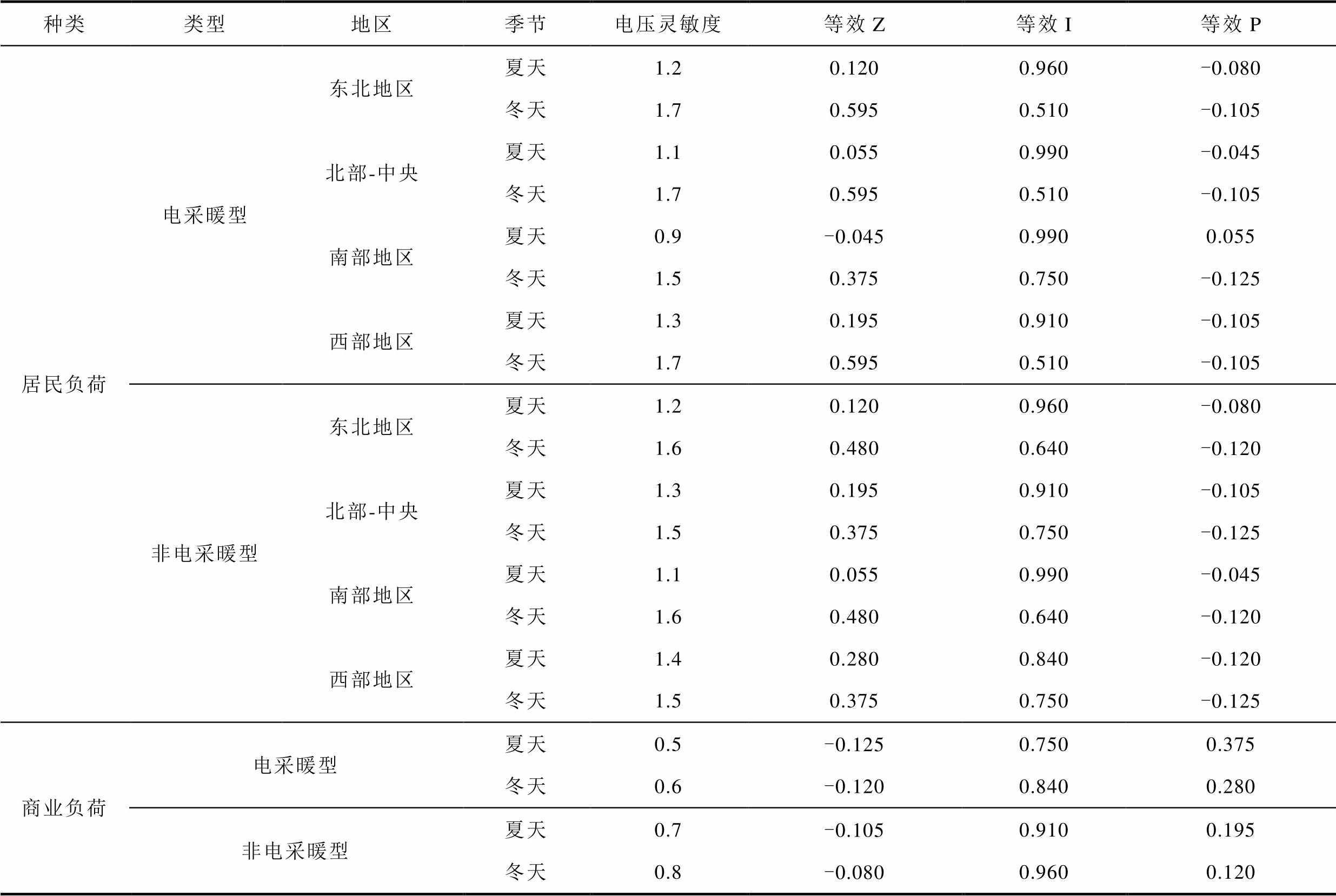
尽管幂指数模型和ZIP模型可以进行等效转换,但ZIP模型较幂指数模型更加灵活,有限地增加参数不会带来过大的测量与辨识负担,同时可以提高模型的刻画精准程度,因此本文选用ZIP模型描述负荷的静态电压特性。文献[14]总结了北美地区居民、商业、工业等不同性质的负荷类型的典型电压灵敏度值,根据式(15),可得到各类负荷的典型ZIP参数值,见附表1。可以发现,居民负荷有更明显的电压特性,具有相当多的恒阻抗成分和恒电流成分;而商业负荷以恒电流成分为主导;某些类型的工业负荷恒功率成分具有比较明显的特征。
为考虑调控过程中节点电压的变化以及对不可控资源的影响,需要考虑网络拓扑约束。本文考虑10 kV电压等级的园区配电网络,主要基于以下原因:①在该电压等级下,各类DERs资源和负荷已经完成了一定程度的聚合;②该电压等级下的电压-功率耦合特性较为明显,便于研究负荷静态电压特性的影响。在10 kV电压等级下,园区的网络结构在正常运行时与配电网具有类似的放射状结构[31],因此,在考虑其网络拓扑约束时,可以类似地参照配电网络的分析方法,建立最优潮流问题。最常用的模型是DistFlow模型[32],在忽略网损时有
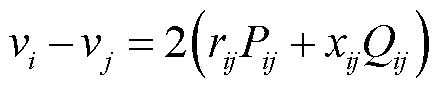 (16)
(16)
式中,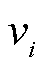 为节点i的电压幅值的二次方,即
为节点i的电压幅值的二次方,即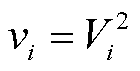 ;
;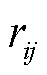 和
和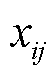 分别为线路
分别为线路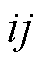 的电阻和电抗;
的电阻和电抗;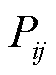 和
和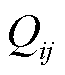 分别为线路
分别为线路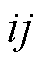 上流经的有功功率和无功功率。
上流经的有功功率和无功功率。
除支路上的潮流外,由于网络是放射状的,因此各节点功率与支路潮流关系为
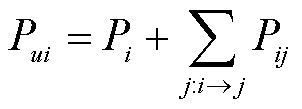 (17)
(17)
式中,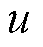 为节点
为节点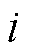 的上游节点;
的上游节点;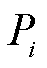 为节点
为节点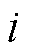 的注入功率。节点注入功率即该节点的净功耗需求,为
的注入功率。节点注入功率即该节点的净功耗需求,为
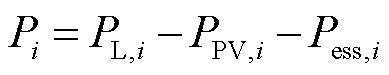 (18)
(18)
式(18)面向存在光伏和储能资源的节点定义。对于网络中一般性的节点,仅需要补充定义,当节点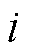 不存在光伏或储能资源时,视作该类资源对应功率恒为0,即可对于任一节点成立。
不存在光伏或储能资源时,视作该类资源对应功率恒为0,即可对于任一节点成立。
因此,考虑到全网络中各节点的净功耗之和来自PCC从上级电网注入的功率,可以得到描述电力电量平衡的关系为
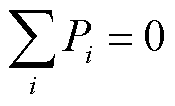 (19)
(19)
特别地,对于网络与上级电网相连的PCC,其功率存在的关系为
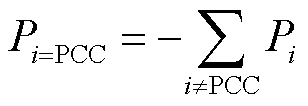 (20)
(20)
考虑到对于上级电网而言,通常关心的是下级网络对外表现的总负荷特性,为符合习惯,将PCC从上级电网接收的总功率记作边界节点功率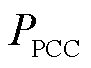 ,即
,即
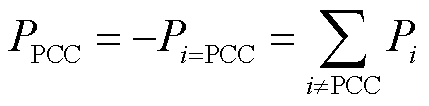 (21)
(21)
另外,为了保障园区内的人员用电安全与电器设备正常运行,节点电压应当运行在允许的范围内,即
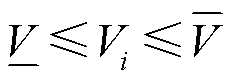 (22)
(22)
式中,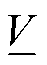 和
和 分别为电压安全容许范围的下限与上限,在标幺值下,该界限通常为0.95(pu)与1.05(pu),即允许电压在
分别为电压安全容许范围的下限与上限,在标幺值下,该界限通常为0.95(pu)与1.05(pu),即允许电压在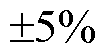 的范围内浮动。
的范围内浮动。
VPP的调控有多种形式,常见的包括削峰、填谷,以及跟随外界给出的跟踪目标,完成负荷跟踪调节服务。本文以负荷跟踪为例作为VPP调控的应用场景。在南方能源监管局印发的《南方区域电力并网运行管理实施细则》与《南方电力辅助服务管理实施细则》中,对于负荷的调节精度给出了规定,即负荷响应出力与其控制要求之间的差值[33]。在不同场景下,对于不同类型的资源调节精度有不同的要求。对于负荷目标跟踪场景,对调节精度的要求为
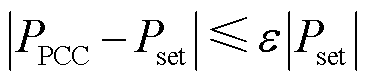 (23)
(23)
式中,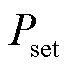 为上级电网给园区下发的负荷跟踪目标曲线;
为上级电网给园区下发的负荷跟踪目标曲线;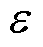 为负荷跟踪精度要求。式(23)可改写为
为负荷跟踪精度要求。式(23)可改写为
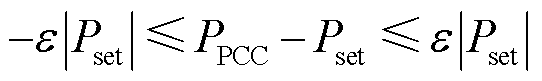 (24)
(24)
基于2.1节~2.4节所述,可将园区层级的VPP调控问题建立为如下的优化问题。
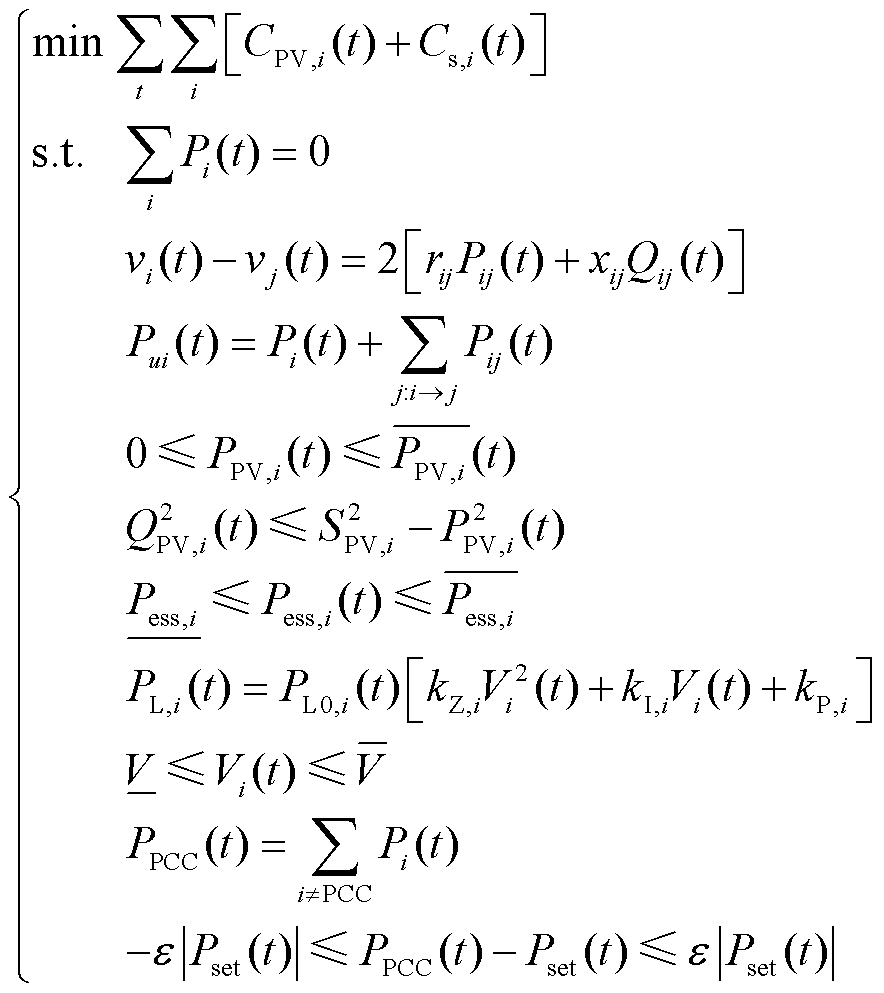 (25)
(25)
式(25)中,目标函数是对所有DERs调节的效用损失最小。在考虑VPP中负荷可控资源与不可控资源通过网络耦合对于网络潮流的影响后,建立了如式(25)所示的模型,调控的对象是园区网络中分散的光伏、储能等DERs在各时刻的有功功率、无功功率。
然而,由于上述模型精细化地考虑了负荷静态电压特性,给整个优化模型引入了非凸的约束,对问题的求解带来复杂性和难度,难以直接应用。
为了使第2节中的VPP调控模型能够高效地进行求解,本节提出一种线性化的手段,以处理负荷静态电压特性带来的非凸性,从而将其转换为可快速求解的问题。
ZIP模型可以衡量负荷的功耗和电压之间的依赖关系,然而,其表达式是一个多项式,在优化问题中会带来复杂性和求解的难度,因此需要对其形式进行一些处理,从而可以适应于控制方法的框架中[34]。
考虑到节点电压安全要求的限制,网络中各节点电压变化幅度相对于其额定电压很小,因此,当节点电压在额定电压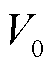 附近波动时,在标幺制下,有
附近波动时,在标幺制下,有
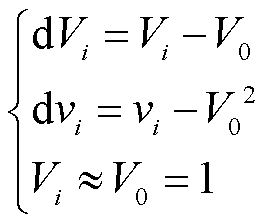 (26)
(26)
式中,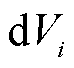 为节点电压幅值标幺制下的变化量;
为节点电压幅值标幺制下的变化量;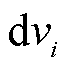 为节点电压幅值的二次方在标幺制下的变化量。
为节点电压幅值的二次方在标幺制下的变化量。
考虑引入参量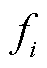 以衡量不可控的负荷资源功率变化幅度与电压的关系,即
以衡量不可控的负荷资源功率变化幅度与电压的关系,即
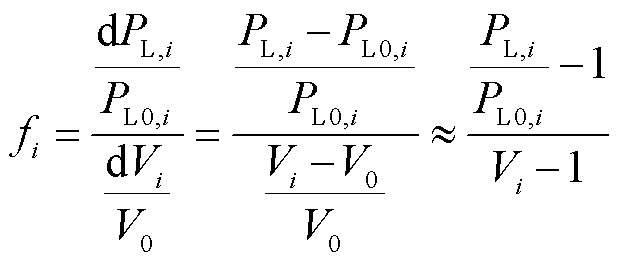 (27)
(27)
式中,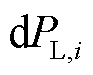 为因节点电压变化引起的负荷功率变化,即负荷的功率与负荷基准功率之差。
为因节点电压变化引起的负荷功率变化,即负荷的功率与负荷基准功率之差。
由式(26),有
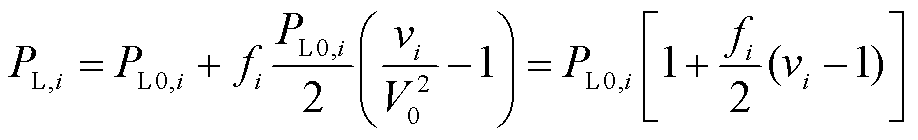 (28)
(28)
将式(11)代入式(27)并求导,有
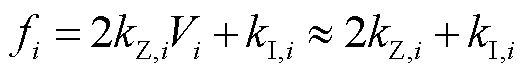 (29)
(29)
故式(28)可改写为
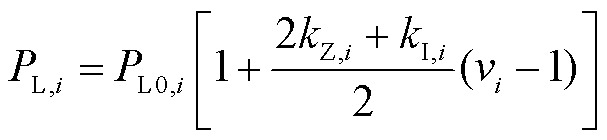 (30)
(30)
式(26)~式(30)证明,在节点电压安全范围内,可以通过参量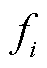 将ZIP模型由多项式近似为关于节点电压幅值二次方
将ZIP模型由多项式近似为关于节点电压幅值二次方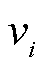 的线性关系。由于式(16)描述的潮流方程是关于
的线性关系。由于式(16)描述的潮流方程是关于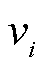 的关系,因此该线性化处理将原约束转换为线性约束,从而大幅简化问题的复杂程度。该近似的本质可以认为是负荷的ZIP模型在节点电压
的关系,因此该线性化处理将原约束转换为线性约束,从而大幅简化问题的复杂程度。该近似的本质可以认为是负荷的ZIP模型在节点电压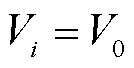 处的泰勒展开舍弃高阶项后的近似,在不过多损失精度的同时获得线性性质,利于求解。
处的泰勒展开舍弃高阶项后的近似,在不过多损失精度的同时获得线性性质,利于求解。
实际上,参量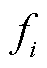 与实施降压节能(Conservation Voltage Reduction, CVR)技术时的CVR系数定义一致。CVR系数的物理意义是衡量电压波动造成的负荷功率变化的幅度,使用功率变化的百分比与电压变化的百分比的比值。在西北能源效率联盟(Northwest Energy Efficiency Alliance, NEEA)的相关研究中发现,夏季CVR系数为0.67,冬季CVR系数为0.20[35]。加拿大魁北克水电公司在2005年的CVR试点项目中发现总体的CVR系数为0.4[36]。在关于纽约市节能效益的相关研究中,算例结果表明其网络的CVR系数在0.5~1[37]。与本文不同的是,降压节能技术多通过改接变压器抽头、无功补偿等手段以降低全网络节点的电压,从而降低网络负荷功耗达到节能的目的,但其本质同样是利用负荷的静态电压特性。CVR系数的大小也可以作为网络整体负荷静态电压特性的衡量指标。
与实施降压节能(Conservation Voltage Reduction, CVR)技术时的CVR系数定义一致。CVR系数的物理意义是衡量电压波动造成的负荷功率变化的幅度,使用功率变化的百分比与电压变化的百分比的比值。在西北能源效率联盟(Northwest Energy Efficiency Alliance, NEEA)的相关研究中发现,夏季CVR系数为0.67,冬季CVR系数为0.20[35]。加拿大魁北克水电公司在2005年的CVR试点项目中发现总体的CVR系数为0.4[36]。在关于纽约市节能效益的相关研究中,算例结果表明其网络的CVR系数在0.5~1[37]。与本文不同的是,降压节能技术多通过改接变压器抽头、无功补偿等手段以降低全网络节点的电压,从而降低网络负荷功耗达到节能的目的,但其本质同样是利用负荷的静态电压特性。CVR系数的大小也可以作为网络整体负荷静态电压特性的衡量指标。
另外,将表示幂指数模型的式(10)代入式(27),得到
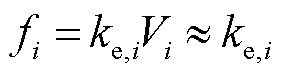 (31)
(31)
因此,电压灵敏度与CVR系数在数值上吻合,在衡量负荷静态电压特性大小时具有等效性。式(28)与式(30)的线性化处理手段同样可适用于幂指数的负荷模型。下文将该线性化模型简称为负荷的CVR模型,参量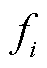 称为负荷的等效CVR系数。
称为负荷的等效CVR系数。
3.2.1 不同ZIP模型的等效CVR系数
不同ZIP模型的静态电压特性如图3所示。可以看到,当等效的CVR系数相等时,曲线在电压安全的范围内差异非常小,因此CVR系数相近的负荷具有接近的负荷静态电压特性。
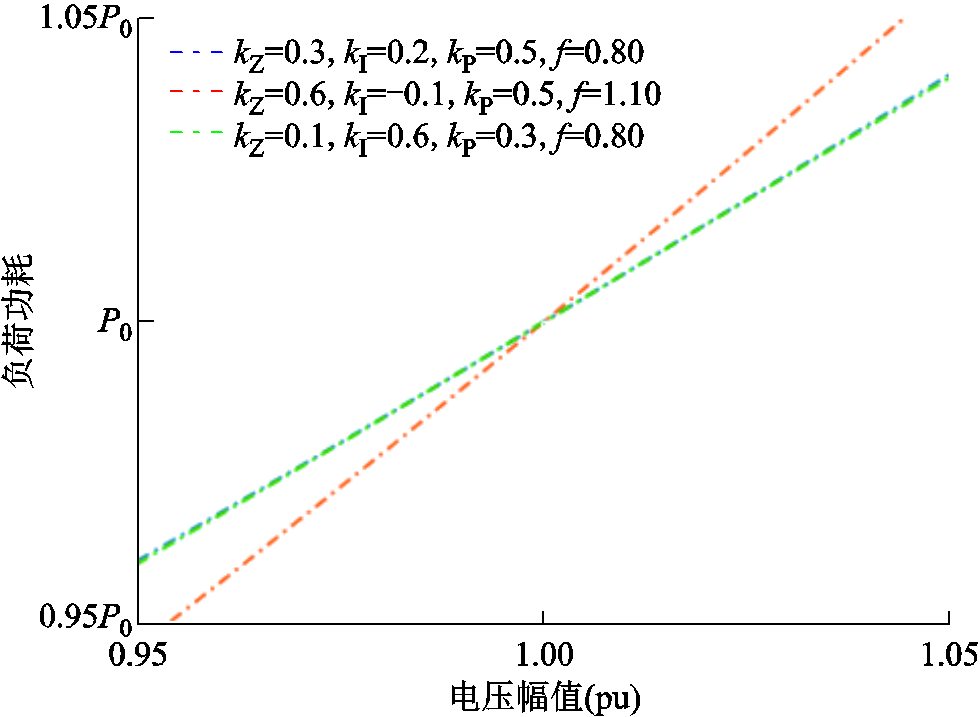
图3 不同ZIP模型的静态电压特性
Fig.3 Static voltage load characteristics of different ZIP models
3.2.2 ZIP模型和CVR模型
基于附表1中的典型负荷ZIP参数值,选取了部分数据作为居民负荷、商业负荷和工业负荷的代表参数,见表1。根据表1中的参数,对于式(11)描述的ZIP模型和式(30)描述的CVR模型,可以得到相应的静态电压特性曲线,如图4所示。
表1 典型ZIP参数
Tab.1 Typical ZIP parameters

类型恒阻抗分量恒电流分量恒功率分量 居民负荷0.5950.510-0.105 商业负荷-0.1200.8400.280 工业负荷-0.0450.1900.855
从图4中可以得知,对于不同类型的负荷,在电压安全容许的调节范围内,其ZIP模型和CVR模型描述的负荷静态电压特性非常接近,具备等效性。
通过CVR模型的代换,式(25)中由于负荷静态电压特性产生的非凸约束已经转换为凸约束,原问题转换为凸优化问题,可基于成熟的优化算法和工具加以求解,进而得到各DERs的运行策略,即各时刻不同DERs的有功和无功出力要求。
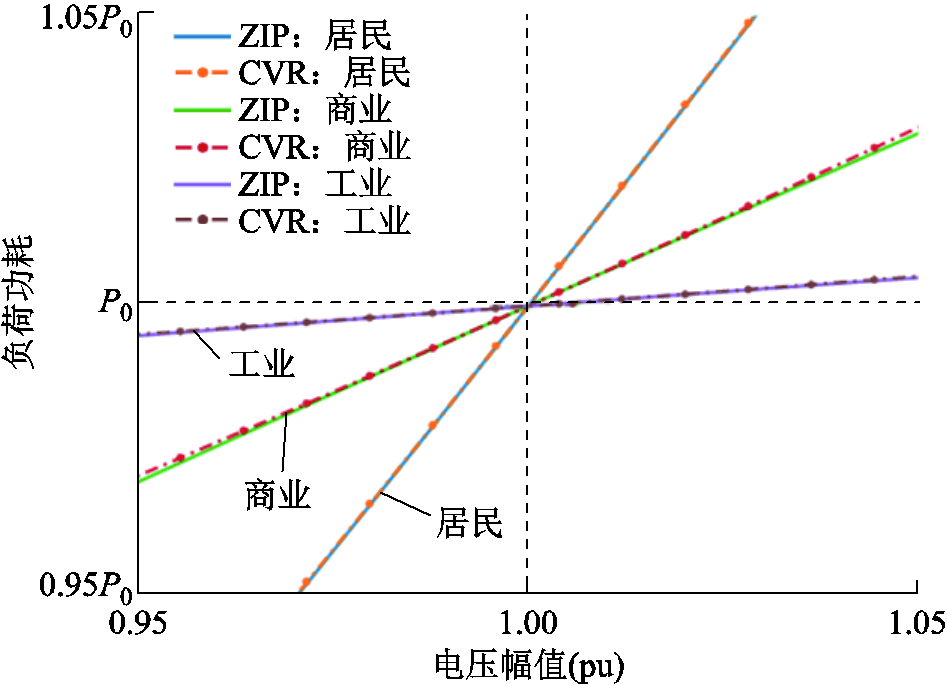
图4 采用ZIP模型和等效CVR系数模型描述的静态电压特性
Fig.4 Static voltage characteristics under ZIP model and equivalent CVR factor models
在调控时段,调控中心基于调控需求和园区管理上报的调节能力下发调控目标,园区管理通过本地表计得到园区内负荷在调控时段的静态电压特性参数,并计算得到参量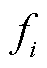 ,结合园区内资源的信息作为调控方法的输入,优化得到资源的运行策略。在实际应用中,可通过递归最小二乘法[38]、加权最小二乘法[39]、深度学习[40]等方法从用电信息中获取负荷特性的参数。调控中心在边界节点的计量将会与调控目标进行比较,考核调控效果。考虑负荷静态电压特性的调控方法流程如图5所示。
,结合园区内资源的信息作为调控方法的输入,优化得到资源的运行策略。在实际应用中,可通过递归最小二乘法[38]、加权最小二乘法[39]、深度学习[40]等方法从用电信息中获取负荷特性的参数。调控中心在边界节点的计量将会与调控目标进行比较,考核调控效果。考虑负荷静态电压特性的调控方法流程如图5所示。
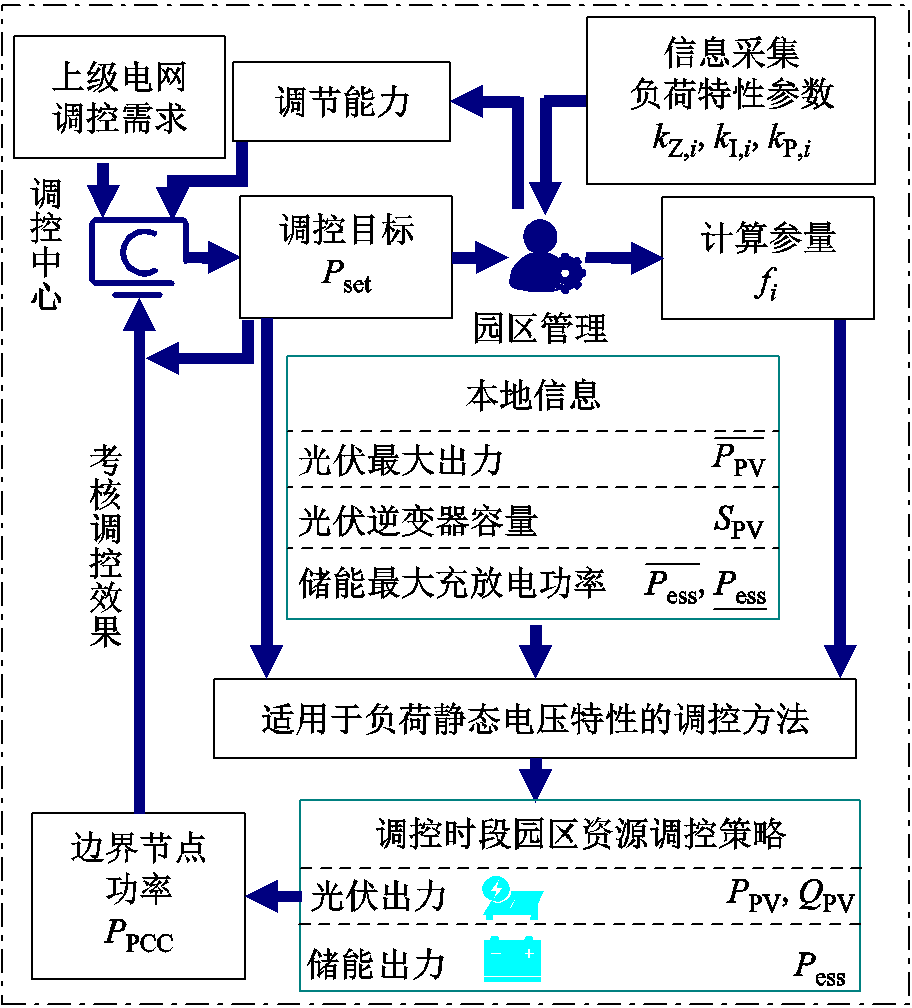
图5 考虑负荷静态电压特性的调控方法流程
Fig.5 Flow chart of the regulation method considering static voltage load characteristics
根据文献[31]中的典型工业园区网络拓扑,结合海南省某园区实际DERs类型与相关参数搭建算例,基于pvlib[41]和pandapower[42]进行算例测试。pvlib工具可结合环境信息与实际光伏组件、逆变器参数生成光伏全天的最大发电功率;pandapower工具可更精准地计算网络潮流,在本文算例中用于模拟测量,以反映负荷静态电压特性对于潮流的影响。算例园区网络系统拓扑如图6所示。
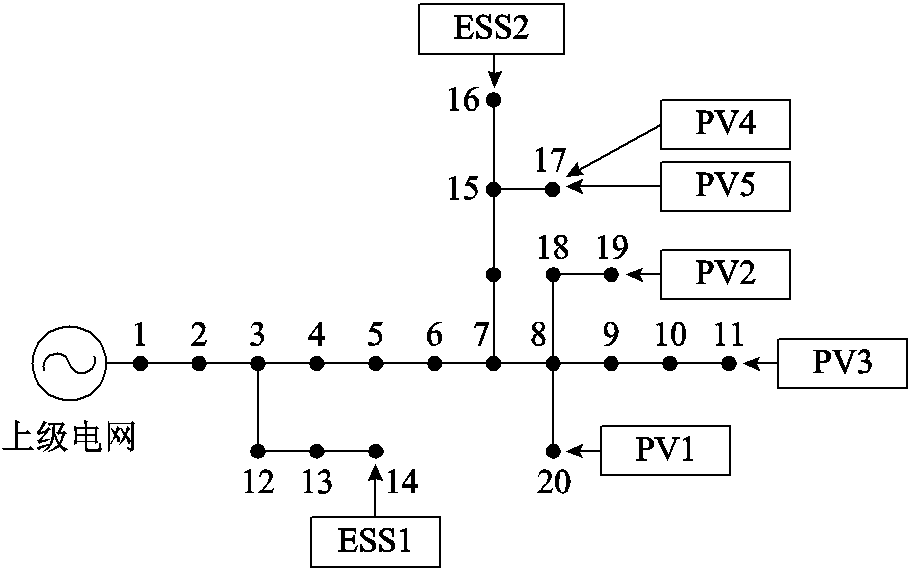
图6 算例园区网络系统拓扑
Fig.6 Topology of park network system in case
为分析负荷静态电压特性对于园区VPP制定DERs控制策略的影响,分别建立考虑负荷静态电压特性的负荷跟踪优化问题与传统的负荷跟踪优化问题,调控时段选取为某一典型日的14:00—15:00,设置以下调控策略进行对比。
1)S1:刚性负荷调控
将网络中的负荷视为刚性模型进行优化,即
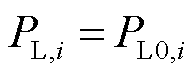 (32)
(32)
从优化结果得到DERs的控制策略,包括光伏、储能在调控时段内的有功功率、无功功率。
2)S2:引入量测反馈修正的刚性负荷调控
在S1基础上,根据模拟测量结果与跟踪目标之间的偏差进行修正;根据储能最大出力按比例对修正量进行分配,相应调整储能的控制策略,即
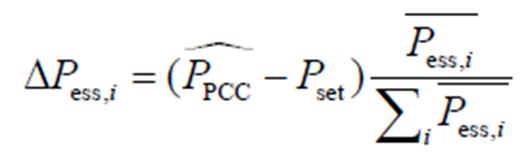 (33)
(33)
式中,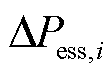 为
为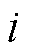 节点的储能功率相对于原本工作状态的功率修正量;
节点的储能功率相对于原本工作状态的功率修正量;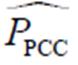 为采取S1控制策略后,
为采取S1控制策略后,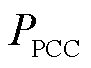 的模拟测量值。
的模拟测量值。
3)S3:考虑负荷静态电压特性的调控(本文所提方法)
考虑负荷的静态电压特性进行优化,即式(30)。从优化结果得到DERs的控制策略,包括光伏、储能在调控时段内的有功功率、无功功率。
通过上述调控策略得到DERs控制策略后,基于负荷的ZIP模型,通过pandapower工具进行模拟测量,得到调控策略对于边界节点的实际功率控制效果。优化模型通过Gurobi求解,测试硬件环境为Intel i5-11400H 2.70 GHz CPU,16 GB内存。算例参数见表2,网络拓扑参数与静态电压特性参数见附表2与附表3,DERs的参数见附表4。光伏的最大功率曲线如附图1所示,各节点负荷标准电压下的标准功耗曲线如附图2所示。
表2 算例参数
Tab.2 Case paramaters

参数数值 3 2 2 0.03
表2中前三个参数没有加下标节点i,表示在本文算例中对于所有同类资源统一地设置效用损失系数,针对不同的应用场景,可单独对DER个体设置效用损失系数。
不作调节时的边界节点功率与调控时段采取调控策略后的结果如图7所示。图7采用S3的调控策略作为示例,图中阴影表示由于DERs调节导致的边界节点功率调节量。
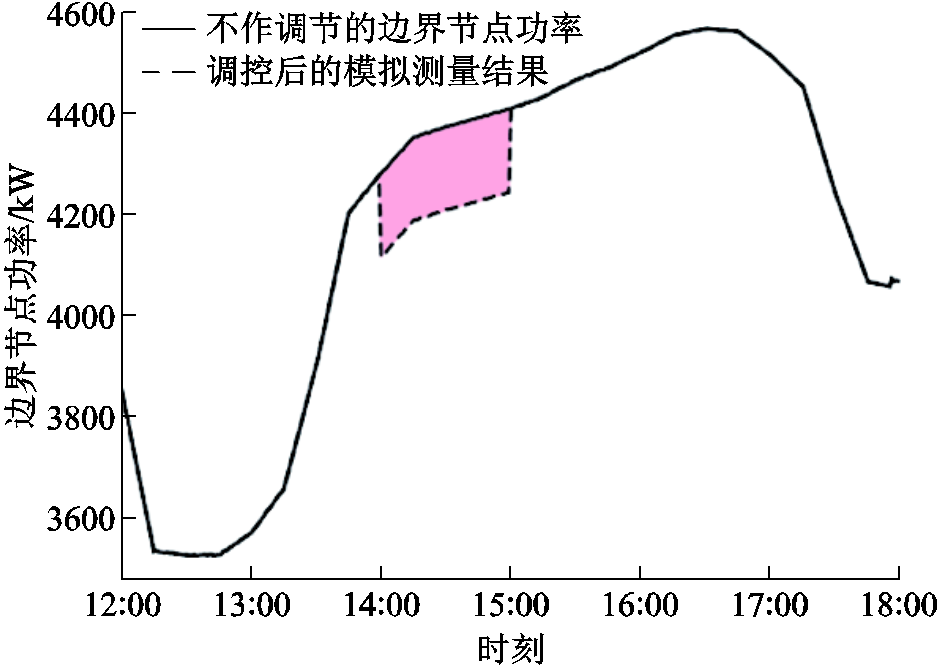
图7 PCC功率与调控结果
Fig.7 PCC power and load following results
考虑调控策略的跟踪效果和调节效益,采用如下指标对上述的三种调控策略进行评价。
1)平均跟踪相对误差
采用平均相对误差(Mean Relative Error, MRE)评价根据三种调控策略模拟测量得到的边界节点功率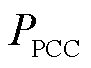 与跟踪目标
与跟踪目标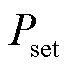 之间的偏差,即
之间的偏差,即
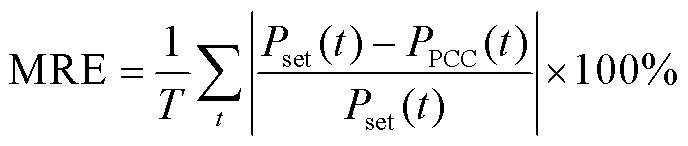 (34)
(34)
式中,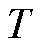 为调控时长。该指标用来衡量调控策略的跟踪效果。
为调控时长。该指标用来衡量调控策略的跟踪效果。
2)调节效用损失
由于对DERs的调控被认为是对设备造成了损耗,采用二次型的调节效用损失来衡量。在跟踪精度允许的范围内,调控策略被期望造成尽可能小的效用损失。因此,使用调节效用损失指标评价调控策略的调节效益,有
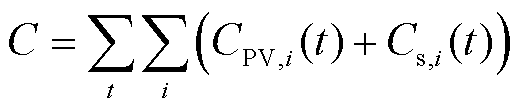 (35)
(35)
在同一跟踪目标下,分别采用S1~S3的调控策略,PCC功率跟踪效果如图8所示。
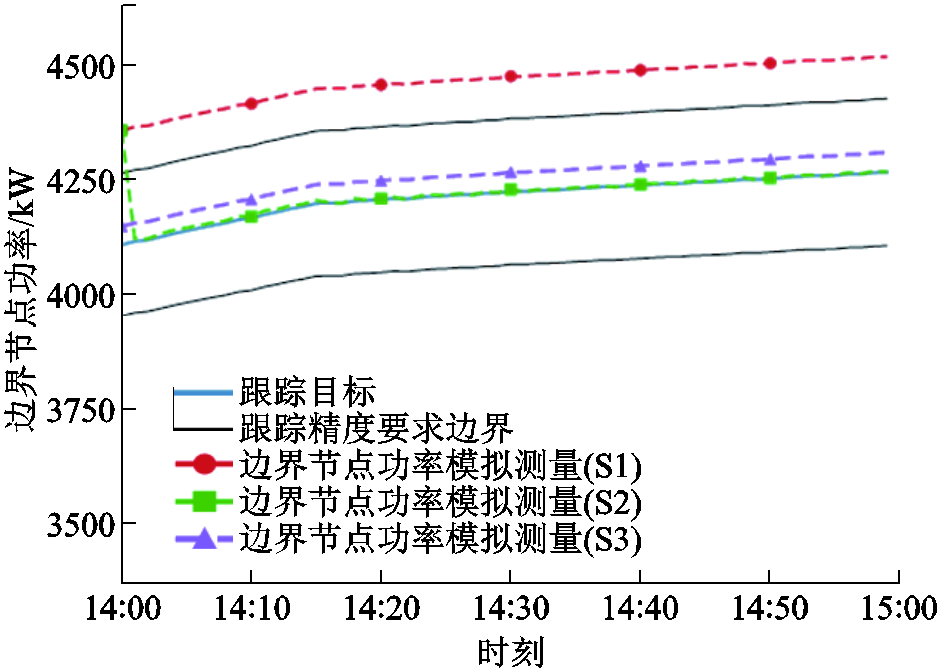
图8 PCC功率跟踪效果
Fig.8 PCC power following effects
从图8中可以看到,S1由于忽略了负荷的静态电压特性,在该条件下未达到功率跟踪精度要求;S2在S1基础上进行了基于量测的修正,在初时刻后可以达到跟踪功率精度要求;S3可以满足功率跟踪的精度要求。各调控策略的评价指标见表3。
表3 不同调控策略的评价指标
Tab.3 Evaluation indicators for different strategies

调控策略MRE(%)调节效用损失 S14.82— S20.132.49 S30.781.62
由于调控策略S1的结果未达到功率跟踪精度要求,因此评价其调节效用损失无意义,在表3中对S2和S3的调节效用损失进行了评价。在该条件下,S1不可行,而忽略初始时刻的S2和S3都达到了功率跟踪的精度要求,且S3的调节效用损失更低。
上面的这种现象是由于S1和S3中的优化模型对于负荷的ZIP模型的描述差异造成的。PCC功率优化结果与模拟测量如图9所示。在S1中采用了刚性负荷的模型进行优化,优化结果中,边界节点的功率在跟踪精度要求的范围内,但S1确定的DERs控制策略在ZIP负荷下进行模拟测量时,得到的模拟测量结果超出了跟踪目标的范围,发生了功率偏移的现象;而S3采用等效CVR系数模型进行优化,其优化结果在跟踪范围边界上,模拟测量的结果仍落在跟踪精度要求范围内。因此S1的结果未能达到功率跟踪精度要求,而S3的结果可以满足要求。
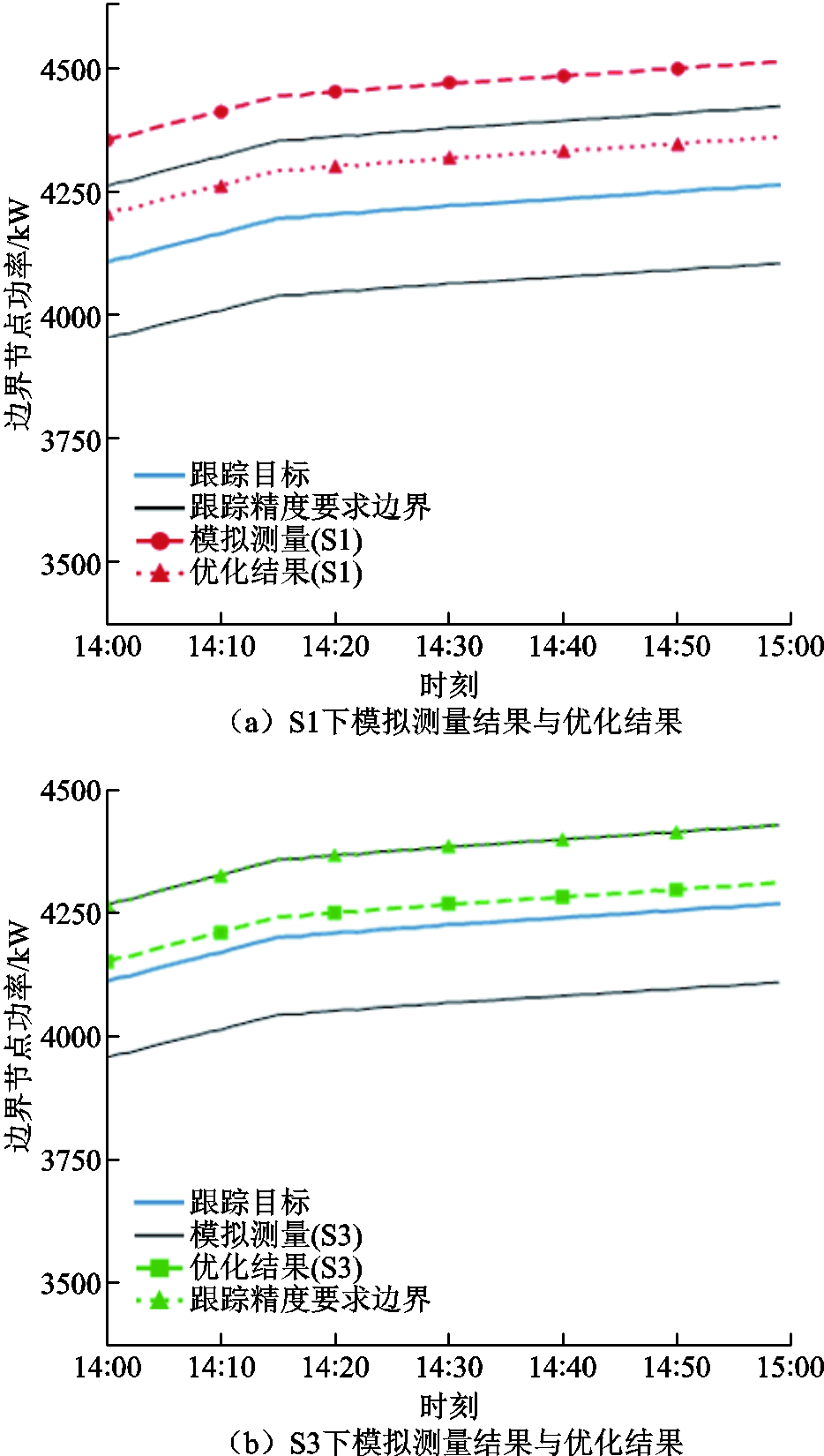
图9 PCC功率优化结果与模拟测量
Fig.9 Optimization results and simulated measurements of PCC power
除此之外,调控策略的跟踪效果受到负荷静态电压特性的大小、跟踪目标的位置设置、调控跟踪精度要求等因素的影响,因此下文针对这些因素对调控策略的效果进行分析。
在同一跟踪目标下,分析ZIP系数综合作用下对于负荷跟踪效果的影响,在等效CVR系数更高和更低的情况下,分别采用S1~S3的策略进行调控。参考文献[14]中不同类型负荷的典型静态电压特性设置ZIP参数,详见附表5,跟踪效果对比如图10所示。
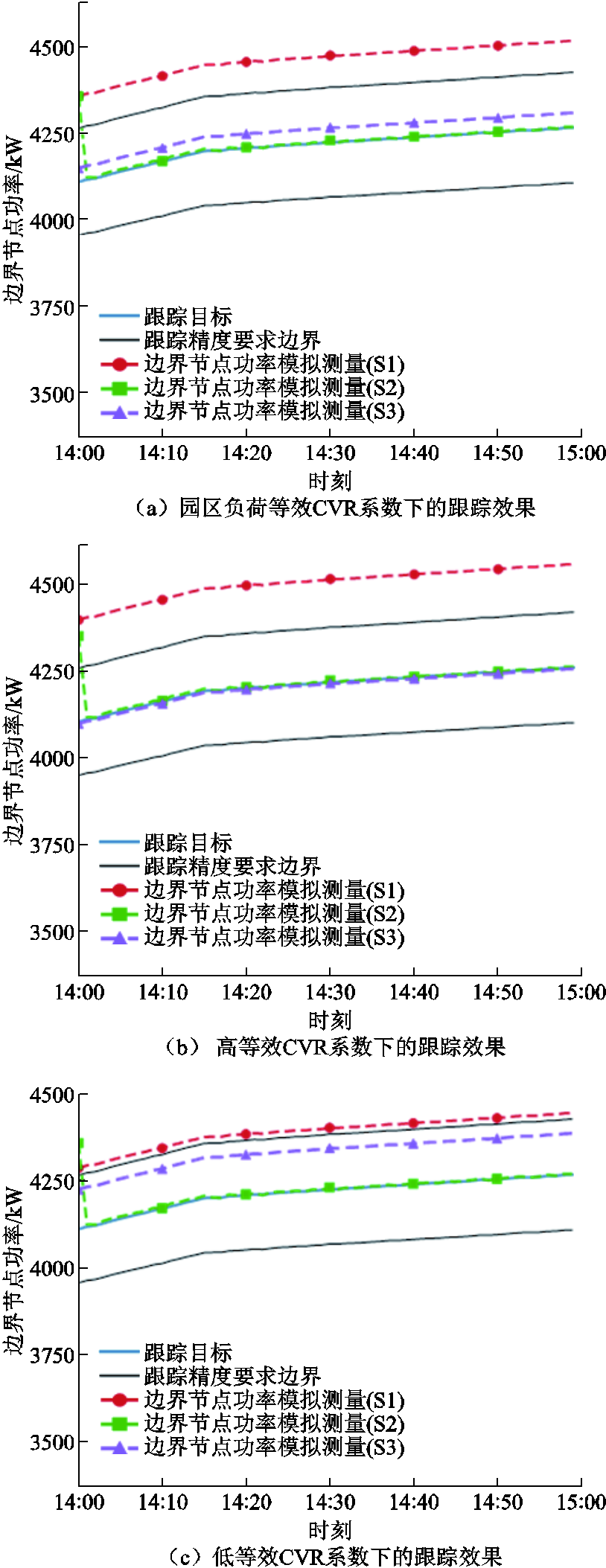
图10 不同等效CVR系数下跟踪效果
Fig.10 PCC power following effects under different equivalent CVR factors
从图10中可以得到类似的结论,调控策略S1的结果在不同的静态电压特性下均未达到功率跟踪的精度要求,忽略初始时刻的S2和S3都达到了功率跟踪的精度要求。在等效CVR系数更高的情况下,S3的跟踪效果显著优于S1,与量测反馈修正后的S2更接近;而在等效CVR系数更低的情况下,S3的跟踪效果更接近S1,因为此时静态电压特性较为不明显,负荷表现出的特性更接近刚性负荷。不同等效CVR系数下各策略的评价指标见表4。
表4 不同等效CVR系数下各调控策略的评价指标
Tab.4 Evaluation indicators for different strategies under different equivalent CVR factors
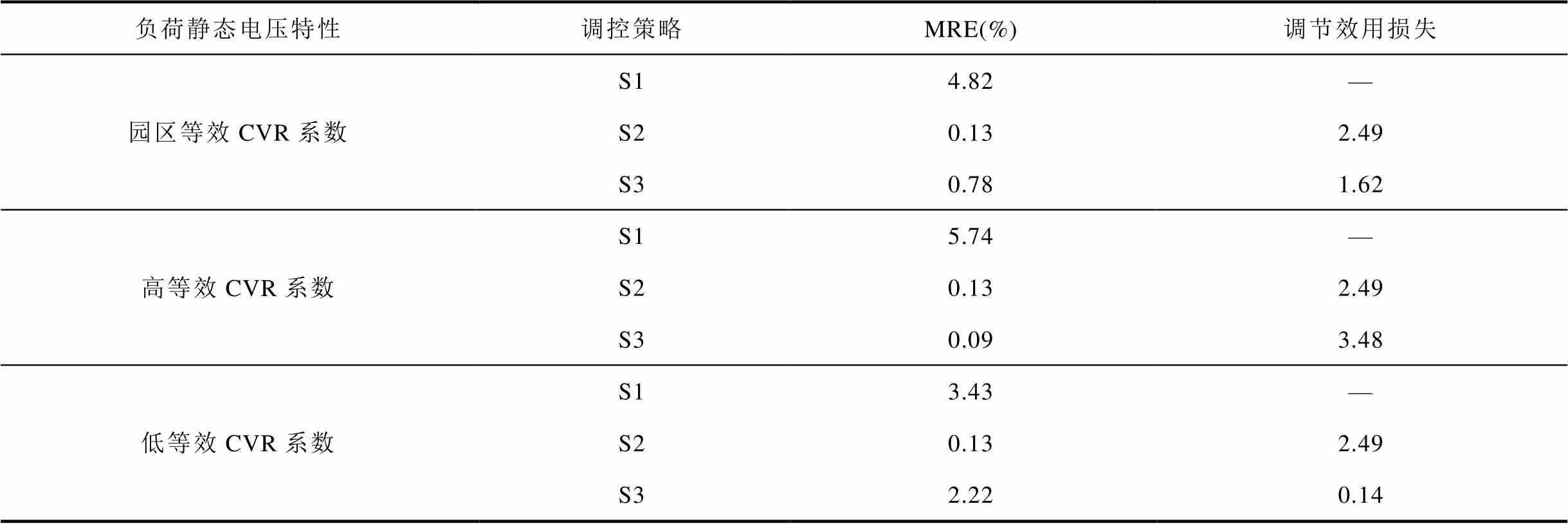
负荷静态电压特性调控策略MRE(%)调节效用损失 园区等效CVR系数S14.82— S20.132.49 S30.781.62 高等效CVR系数S15.74— S20.132.49 S30.093.48 低等效CVR系数S13.43— S20.132.49 S32.220.14
跟踪目标的位置设置同样可能会对跟踪效果产生影响。为分析跟踪目标位置对各调控策略调控效果的影响,通过参数调节深度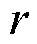 来决定跟踪目标的位置,有
来决定跟踪目标的位置,有
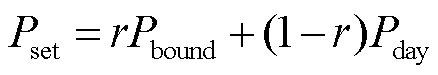 (36)
(36)
式中,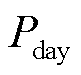 为不作调节时的PCC功率;
为不作调节时的PCC功率;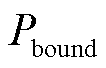 为评估的调节目标边界,通过网络净功耗最小时的边界节点功率估计得到。不同跟踪目标下各策略的评价指标见表5。
为评估的调节目标边界,通过网络净功耗最小时的边界节点功率估计得到。不同跟踪目标下各策略的评价指标见表5。
表5 不同跟踪目标下各调控策略的评价指标
Tab.5 Evaluation indicators for different strategies under different following loads
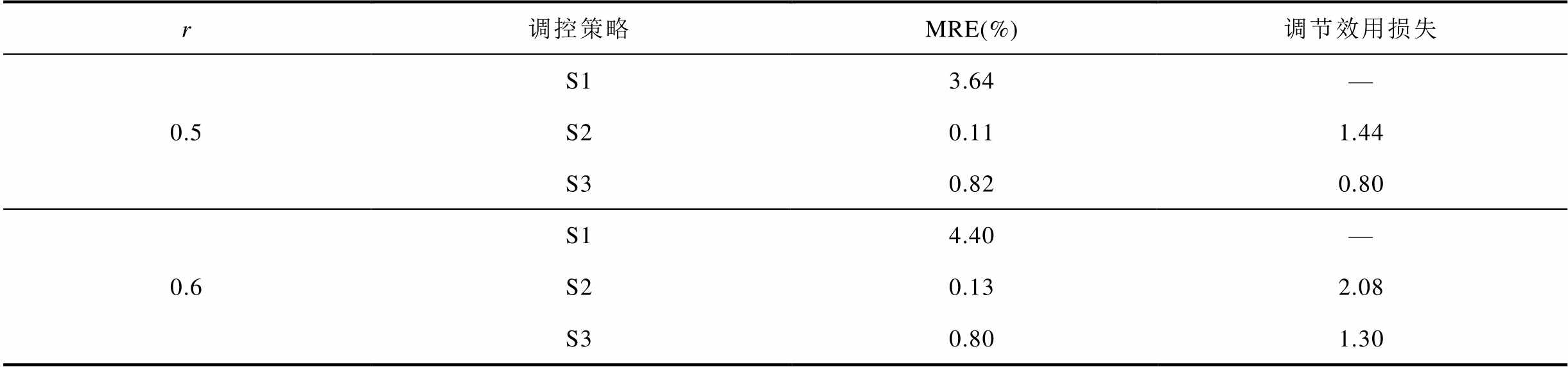
r调控策略MRE(%)调节效用损失 0.5S13.64— S20.111.44 S30.820.80 0.6S14.40— S20.132.08 S30.801.30
(续)
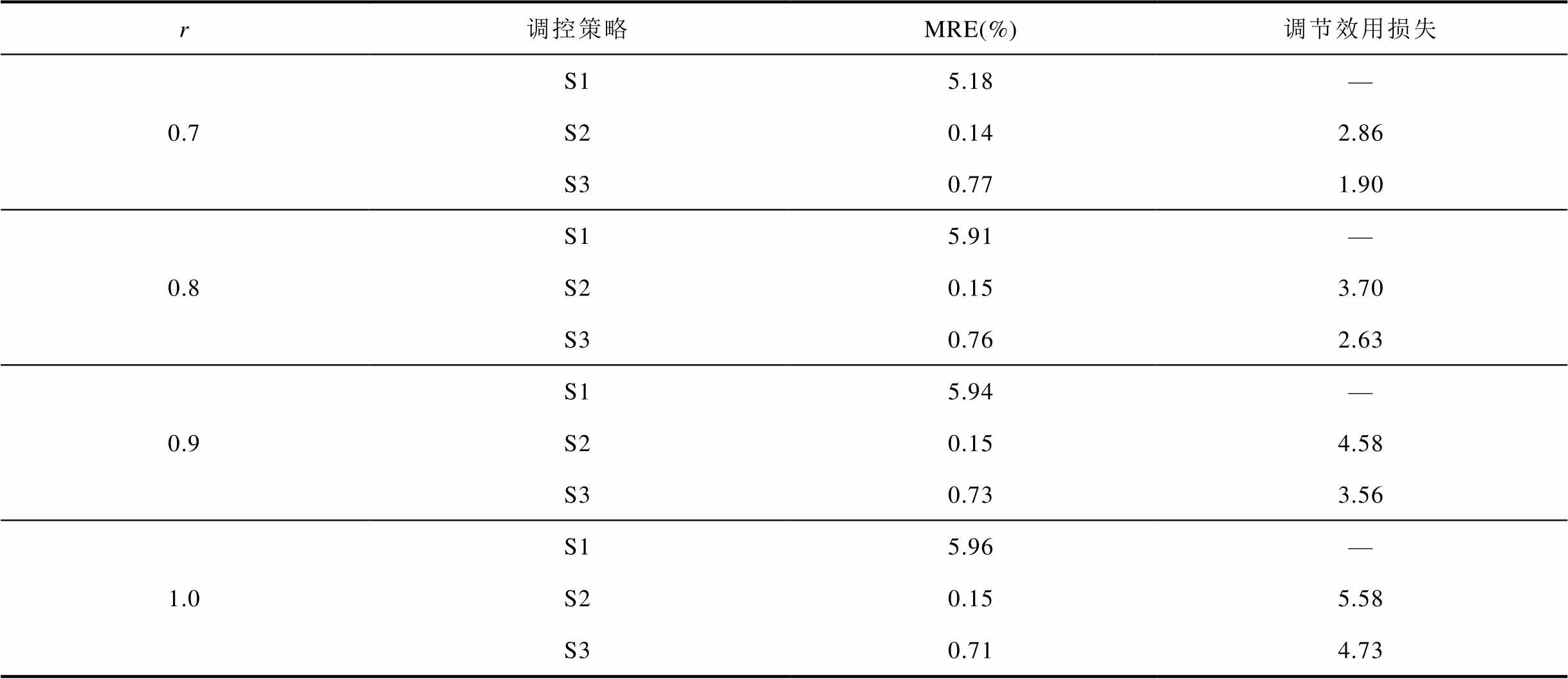
r调控策略MRE(%)调节效用损失 0.7S15.18— S20.142.86 S30.771.90 0.8S15.91— S20.153.70 S30.762.63 0.9S15.94— S20.154.58 S30.733.56 1.0S15.96— S20.155.58 S30.714.73
表5中,调节深度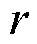 取值从0.5~1.0时,S1的跟踪精度都不满足跟踪精度要求,而S2和S3都达到了跟踪精度要求,且S3的调节效用损失始终比S2低。调节深度r更小时,由于跟踪目标与不作调节时的位置偏差过小,本身已经落在跟踪精度要求范围内,无法比较各调控策略的跟踪效果,因此不列入表5中。
取值从0.5~1.0时,S1的跟踪精度都不满足跟踪精度要求,而S2和S3都达到了跟踪精度要求,且S3的调节效用损失始终比S2低。调节深度r更小时,由于跟踪目标与不作调节时的位置偏差过小,本身已经落在跟踪精度要求范围内,无法比较各调控策略的跟踪效果,因此不列入表5中。
在调控时段内,对各调控策略下各时刻负荷跟踪的相对误差采用箱线图进行统计,不同跟踪策略下跟踪相对误差分布如图11所示。由于S2在调控起始时刻不在误差容许范围内,故不计入图11。
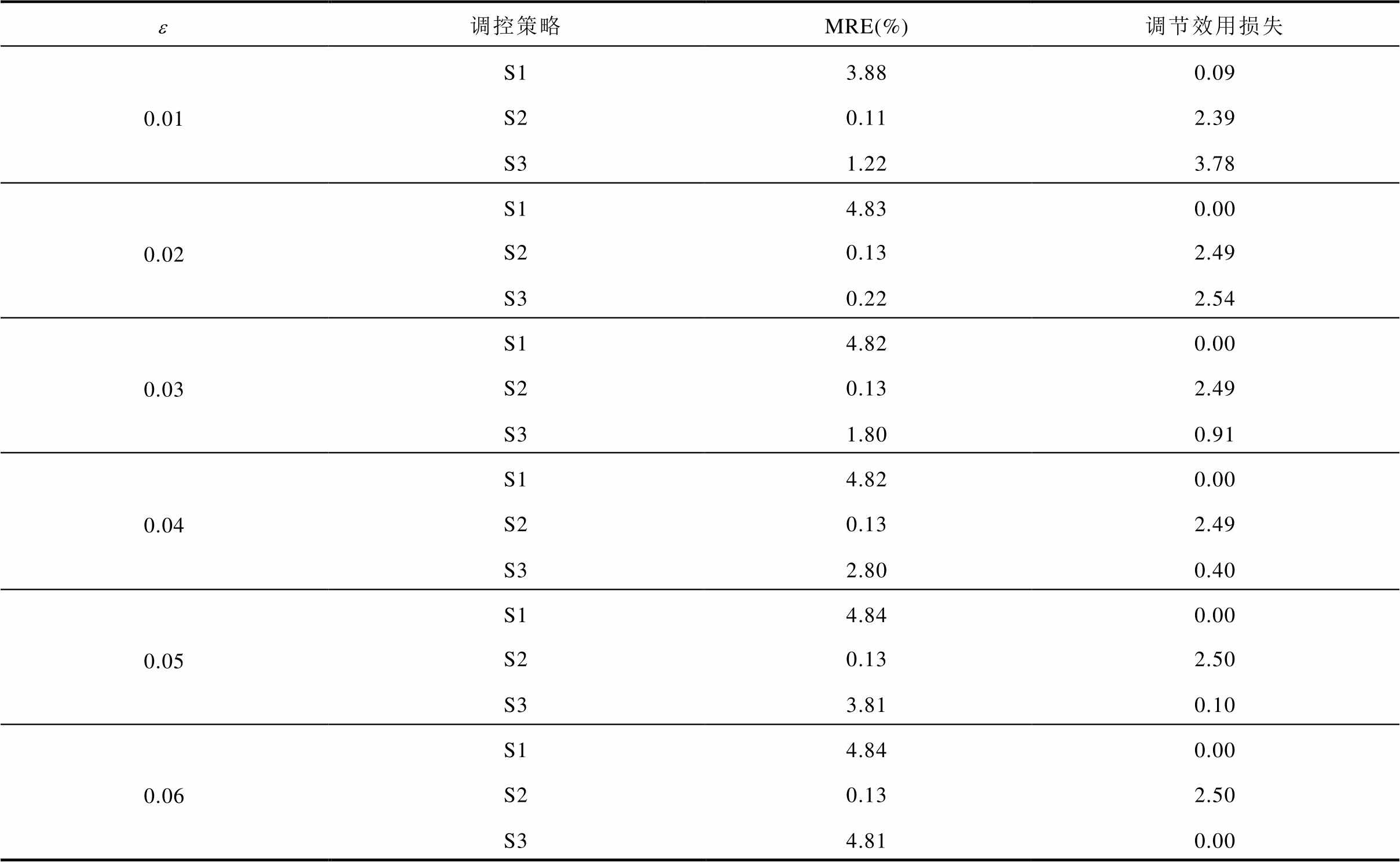
跟踪精度要求不同时,S1~S3也会有不同的跟踪效果。不同跟踪精度要求下各策略的评价指标见表6。
表6显示,当跟踪精度要求过高时,S1难以满足跟踪精度需求,S3表现比S2稍差;而跟踪精度要求稍放宽后,S3可以满足跟踪精度要求,且调节效用损失显著优于S2;进一步放宽跟踪精度要求后,S1采用刚性负荷模型对ZIP负荷模型的刻画误差已经小于跟踪精度的要求,因此S1与S3没有太大差别。S2与跟踪精度需求无关,实时根据量测偏差反馈进行调节,有相对更好的调节精度,但会产生较大的调节效用损失。
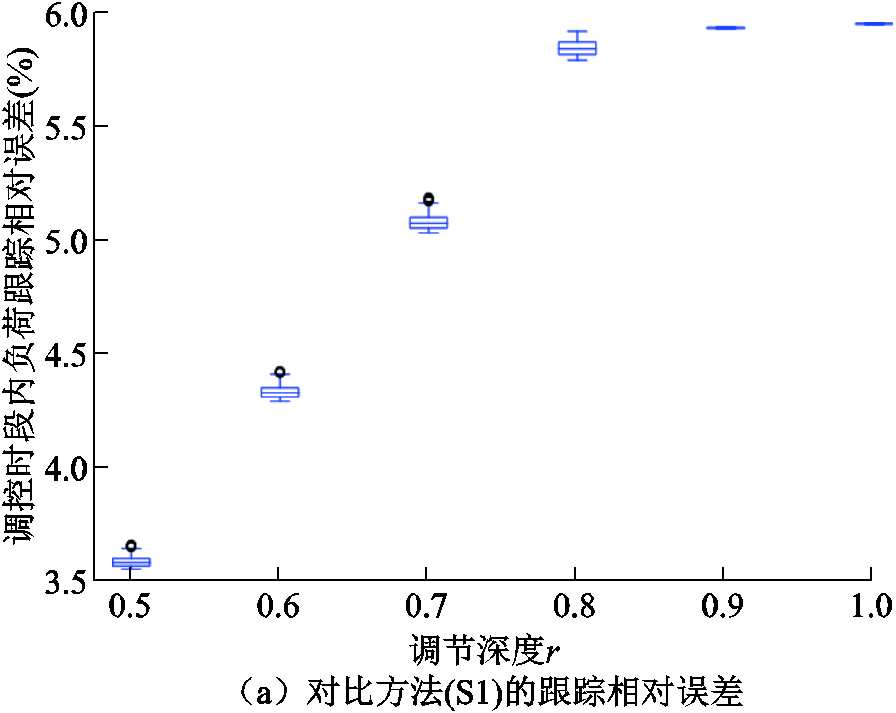
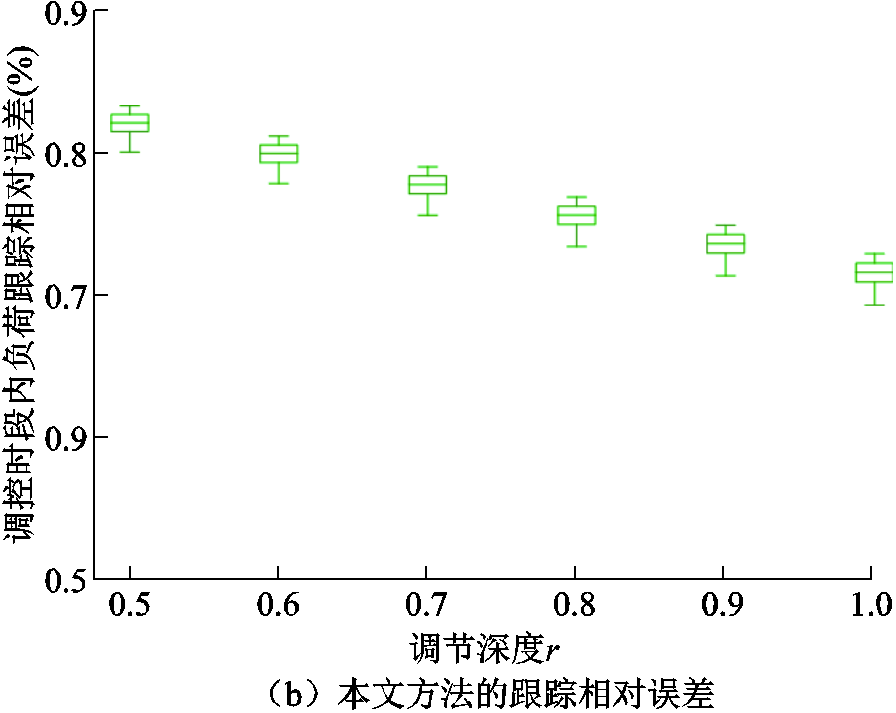
图11 不同跟踪策略下跟踪相对误差分布
Fig.11 Distribution of following relative errors under different following strategies
表6 不同精度要求下各策略的评价指标
Tab.6 Evaluation indicators for different strategies under different accuracy requirements
调控策略MRE(%)调节效用损失 0.01S13.880.09 S20.112.39 S31.223.78 0.02S14.830.00 S20.132.49 S30.222.54 0.03S14.820.00 S20.132.49 S31.800.91 0.04S14.820.00 S20.132.49 S32.800.40 0.05S14.840.00 S20.132.50 S33.810.10 0.06S14.840.00 S20.132.50 S34.810.00
本文针对VPP中大量负荷受静态电压特性影响而导致整体调节精度不足的问题,提出内嵌负荷静态电压特性的VPP精准调控方法。建立了计及园区的低压电网拓扑的VPP运行架构,并从可控资源、不可控资源与网络潮流等角度建立考虑负荷静态电压特性的VPP调控模型,提出了模型线性化方法和基于量测反馈的模型校准机制,保障模型的快速在线求解。算例结果表明:
1)相较于传统方法中将负荷视为刚性负荷建立的调控策略,本文方法可将平均跟踪相对误差从4.82%降低至0.78%,且调节效用损失比基于量测反馈的储能下垂控制修正策略降低35%。
2)网络中的负荷静态电压特性越显著,本文方法的优势越明显。在高等效CVR系数下,所提方法的平均跟踪相对误差仅为0.09%,而传统方法达到5.74%。
3)在低等效CVR系数下,本文方法仍可保持2.22%的跟踪误差。在不同调节深度和跟踪精度要求下,本文方法均能保持稳定的跟踪效果,表现出良好的适应性。
本文研究的方法中,调控时段较短,因此可以忽视储能SOC带来的限制,然而,在更长的调控时段,乃至常态化的调控中,储能SOC带来的时空耦合约束影响将不可忽略。模型更加复杂的DERs也会给调控方法增加复杂程度,例如,在实际应用中,要考虑光伏系统实际存在的弃光成本,则需要通过蒙特卡洛等方法考虑光伏预测的不确定性等问题,从这个角度出发,本文光伏模型中的二次型效用损失函数模型对实际情况的考量还可以进一步提升。此外,网络中的负荷也分散存在各个节点中,实现海量泛在的各类资源进行不间断的数据采集与协同调控,对资源量测体系和控制系统提出了新的挑战。本文着重探讨了具有静态电压特性的负荷对VPP调控精度的影响机理,特别是其被动电压响应特性。然而,工商业负荷中还蕴含着大量的主动调节潜力,如空调等柔性负荷不仅具有静态电压特性,还可通过主动控制参与需求响应。这种被动响应与主动调节的耦合机制,以及如何将其纳入VPP的整体调控策略,将成为未来的重要研究方向。因此,研究计及更长时段、更多DERs类型、更精确的DERs模型、更精细尺度以及柔性负荷与静态电压特性协同优化的VPP精准调控方法将成为后续的研究重点。
附 录
附表1 负荷的典型ZIP参数值
App.Tab.1 Typical ZIP parameters for the load
种类类型地区季节电压灵敏度等效Z等效I等效P 居民负荷电采暖型东北地区夏天1.20.1200.960-0.080 冬天1.70.5950.510-0.105 北部-中央夏天1.10.0550.990-0.045 冬天1.70.5950.510-0.105 南部地区夏天0.9-0.0450.9900.055 冬天1.50.3750.750-0.125 西部地区夏天1.30.1950.910-0.105 冬天1.70.5950.510-0.105 非电采暖型东北地区夏天1.20.1200.960-0.080 冬天1.60.4800.640-0.120 北部-中央夏天1.30.1950.910-0.105 冬天1.50.3750.750-0.125 南部地区夏天1.10.0550.990-0.045 冬天1.60.4800.640-0.120 西部地区夏天1.40.2800.840-0.120 冬天1.50.3750.750-0.125 商业负荷电采暖型夏天0.5-0.1250.7500.375 冬天0.6-0.1200.8400.280 非电采暖型夏天0.7-0.1050.9100.195 冬天0.8-0.0800.9600.120
(续)

种类类型地区季节电压灵敏度等效Z等效I等效P 工业负荷典型工业负荷0.1-0.0450.1900.855 原铝产业1.80.720.360-0.080 钢铁厂0.6-0.120.8400.280 电厂辅助设备0.1-0.0450.1900.855 农用泵1.40.280.840-0.120
附表2 算例园区网络拓扑参数
App.Tab.2 Park network topology parameters in case
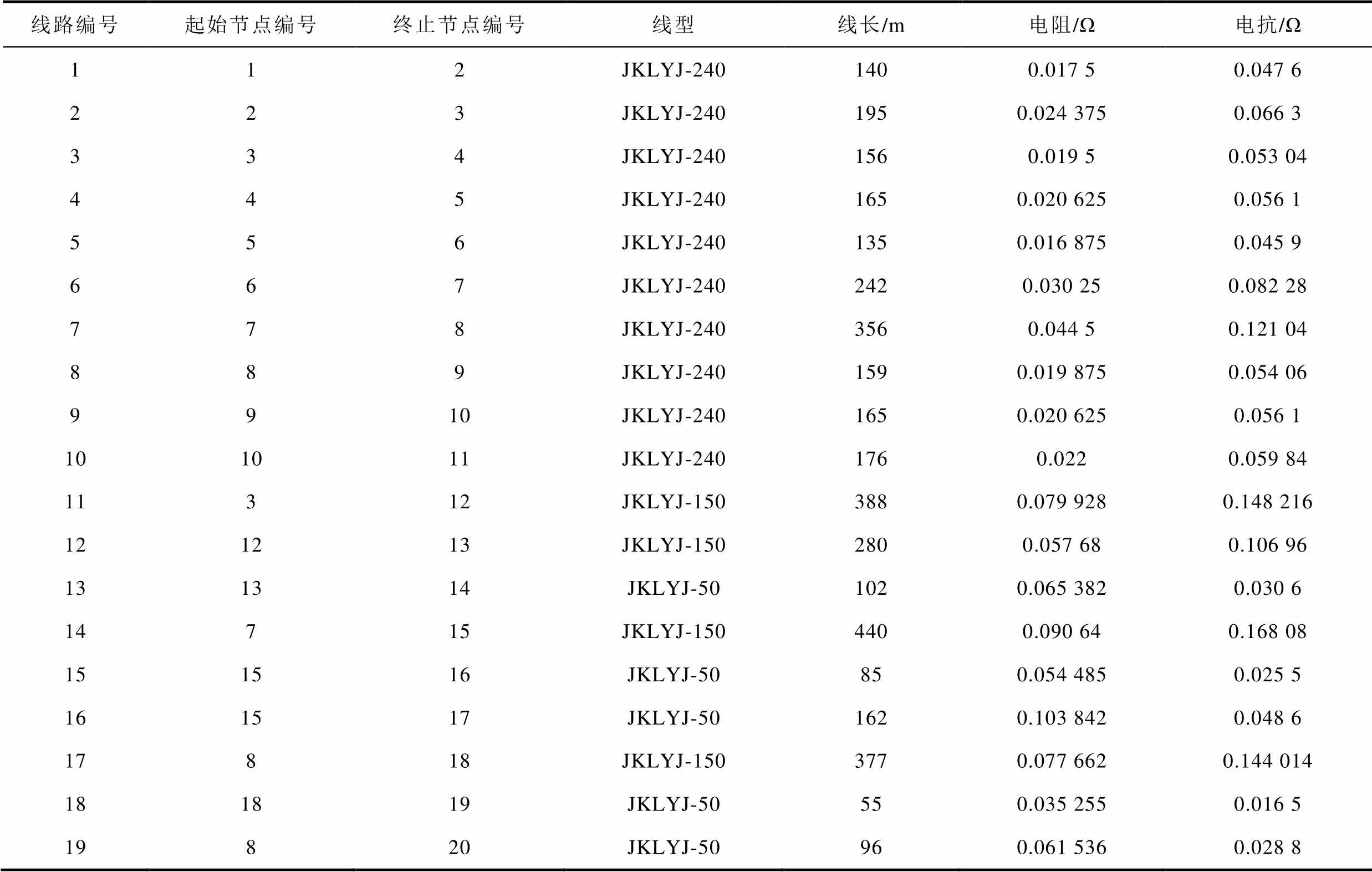
线路编号起始节点编号终止节点编号线型线长/m电阻/Ω电抗/Ω 112JKLYJ-2401400.017 50.047 6 223JKLYJ-2401950.024 3750.066 3 334JKLYJ-2401560.019 50.053 04 445JKLYJ-2401650.020 6250.056 1 556JKLYJ-2401350.016 8750.045 9 667JKLYJ-2402420.030 250.082 28 778JKLYJ-2403560.044 50.121 04 889JKLYJ-2401590.019 8750.054 06 9910JKLYJ-2401650.020 6250.056 1 101011JKLYJ-2401760.0220.059 84 11312JKLYJ-1503880.079 9280.148 216 121213JKLYJ-1502800.057 680.106 96 131314JKLYJ-501020.065 3820.030 6 14715JKLYJ-1504400.090 640.168 08 151516JKLYJ-50850.054 4850.025 5 161517JKLYJ-501620.103 8420.048 6 17818JKLYJ-1503770.077 6620.144 014 181819JKLYJ-50550.035 2550.016 5 19820JKLYJ-50960.061 5360.028 8
附表3 园区负荷静态电压特性参数
App.Tab.3 Static voltage load characteristic parameters of park load
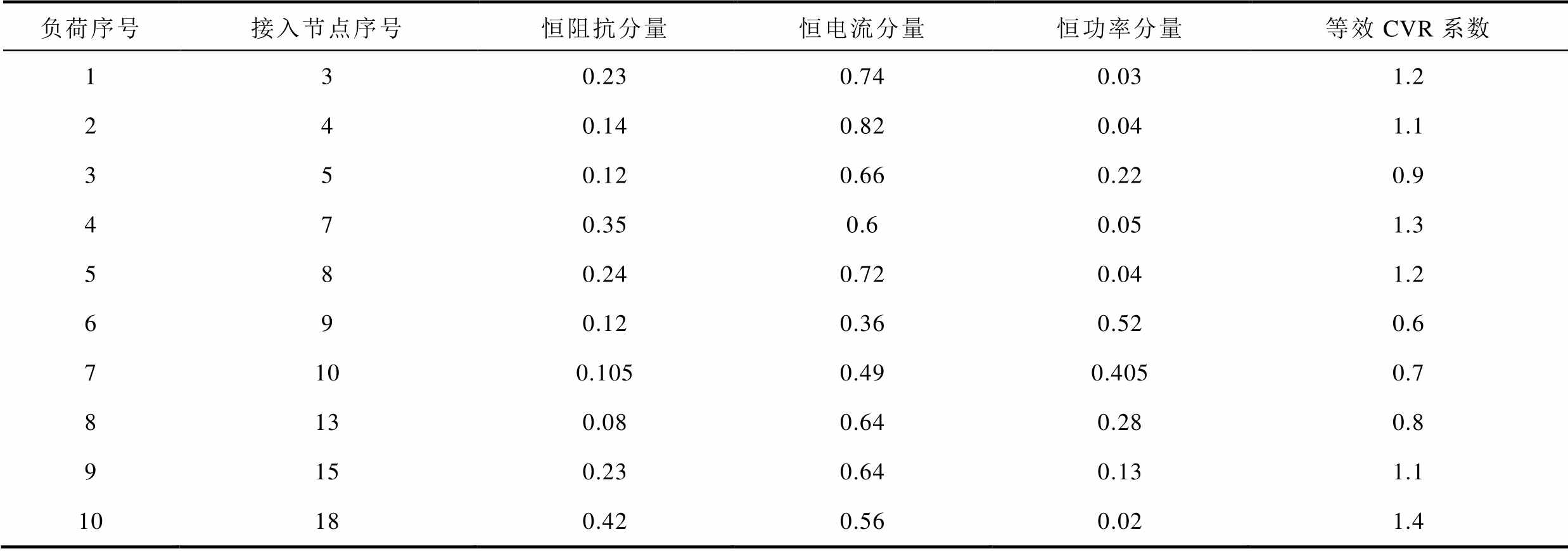
负荷序号接入节点序号恒阻抗分量恒电流分量恒功率分量等效CVR系数 130.230.740.031.2 240.140.820.041.1 350.120.660.220.9 470.350.60.051.3 580.240.720.041.2 690.120.360.520.6 7100.1050.490.4050.7 8130.080.640.280.8 9150.230.640.131.1 10180.420.560.021.4
附表4 园区分布式资源参数
App.Tab.4 Distributed resources parameters in park

资源类型资源名称接入节点序号有功调节下限/kW有功调节上限/kW逆变器容量/kW 光伏PV120022.1430 PV219026.2430 PV311026.2430 PV417026.2430 PV517019.6830 储能ESS114-200200 ESS216-100100
附表5 对照组园区负荷静态电压特性参数
App.Tab.5 Static voltage load characteristic parameters of park load in control group
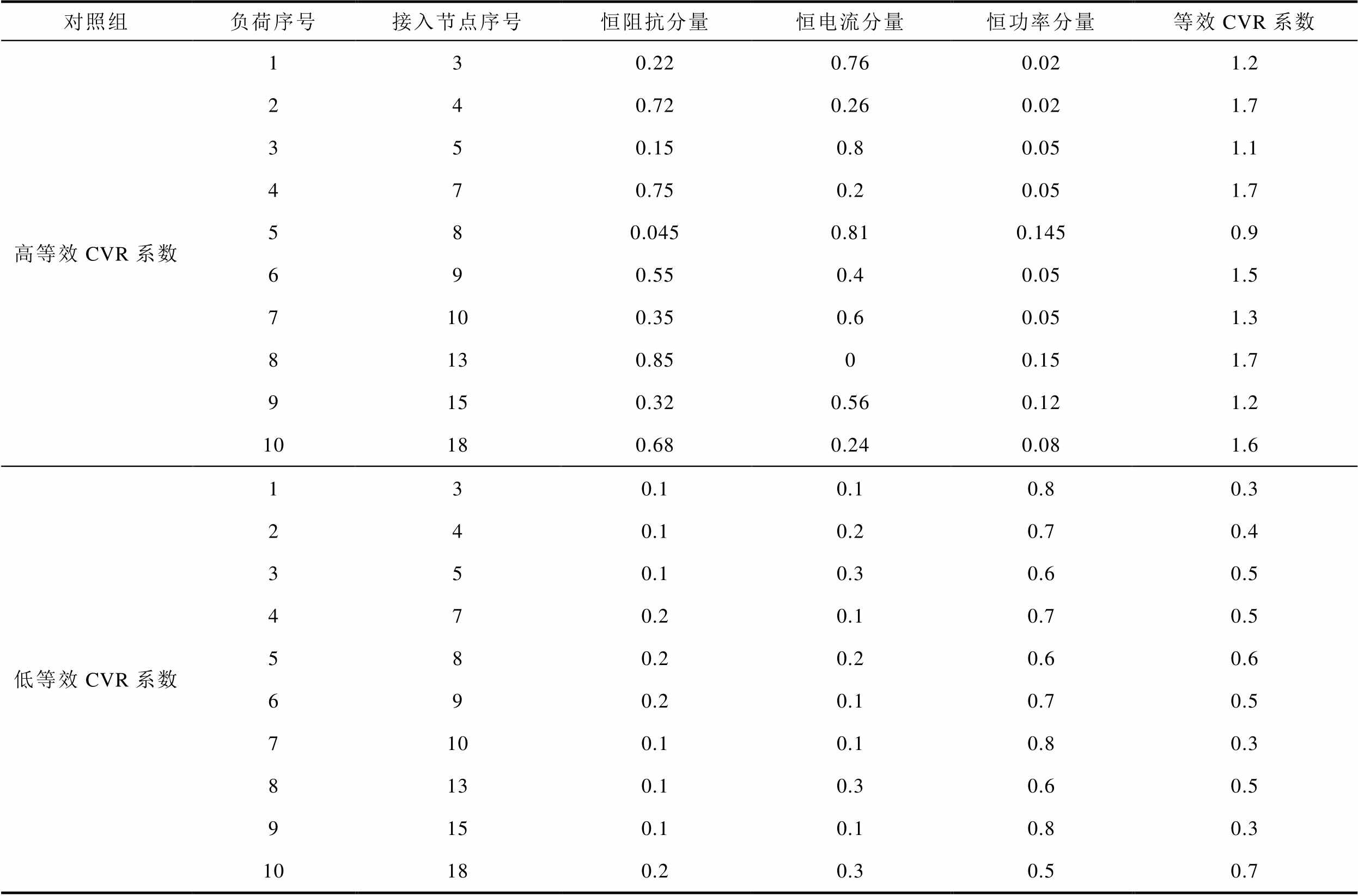
对照组负荷序号接入节点序号恒阻抗分量恒电流分量恒功率分量等效CVR系数 高等效CVR系数130.220.760.021.2 240.720.260.021.7 350.150.80.051.1 470.750.20.051.7 580.0450.810.1450.9 690.550.40.051.5 7100.350.60.051.3 8130.8500.151.7 9150.320.560.121.2 10180.680.240.081.6 低等效CVR系数130.10.10.80.3 240.10.20.70.4 350.10.30.60.5 470.20.10.70.5 580.20.20.60.6 690.20.10.70.5 7100.10.10.80.3 8130.10.30.60.5 9150.10.10.80.3 10180.20.30.50.7
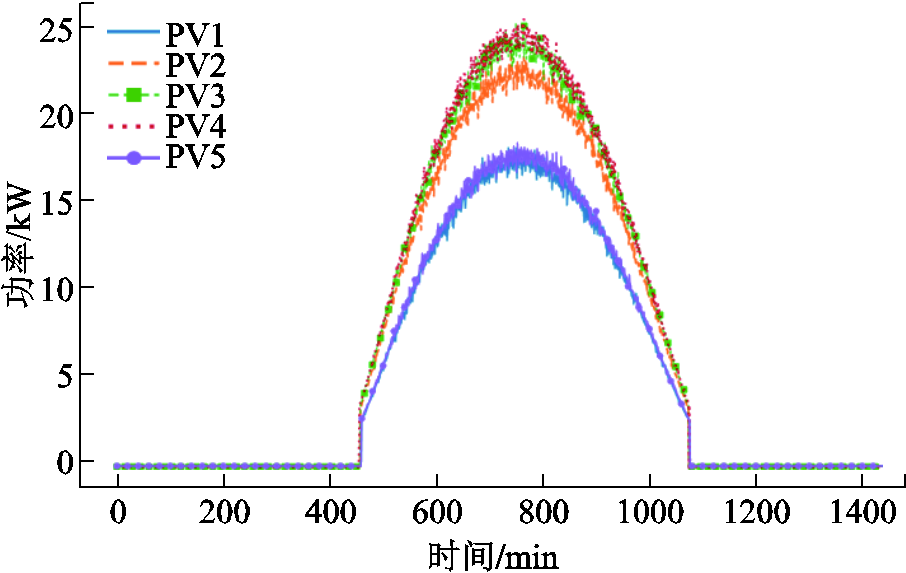
附图1 光伏最大功率曲线
App.Fig.1 Maximum power curves of PVs
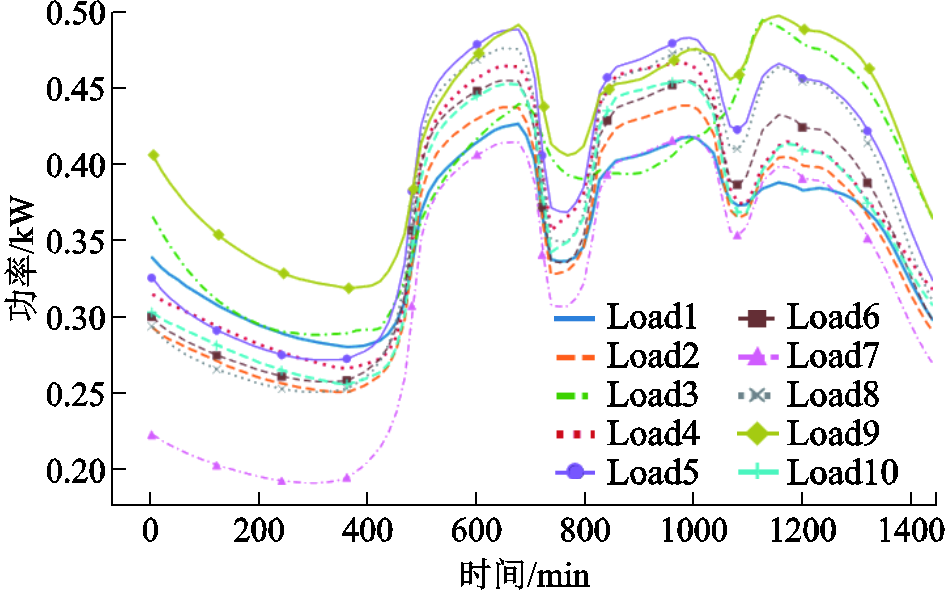
附图2 负荷标准电压下的标准功耗
App.Fig.2 Standard power consumption under standard voltage
参考文献
[1] 辛保安, 张智刚. 奋进新时代新征程展现新气象新作为[N]. 国家电网报, 2022-01-01.
[2] 范帅, 危怡涵, 何光宇, 等. 面向新型电力系统的需求响应机制探讨[J]. 电力系统自动化, 2022, 46(7): 1-12.
Fan Shuai, Wei Yihan, He Guangyu, et al. Discussion on demand response mechanism for new power systems[J]. Automation of Electric Power Systems, 2022, 46(7): 1-12.
[3] 范帅, 郏琨琪, 王芬, 等. 基于负荷准线的大规模需求响应[J]. 电力系统自动化, 2020, 44(15): 19-27.
Fan Shuai, Jia Kunqi, Wang Fen, et al. Large-scale demand response based on customer directrix load[J]. Automation of Electric Power Systems, 2020, 44(15): 19-27.
[4] 孟琰, 肖居承, 洪居华, 等. 计及需求响应不确定性的节点负荷准线: 概念与模型[J]. 电力系统自动化, 2023, 47(13): 28-39.
Meng Yan, Xiao Jucheng, Hong Juhua, et al. Nodal customer directrix load considering demand response uncertainty: concept and model[J]. Automation of Electric Power Systems, 2023, 47(13): 28-39.
[5] 李翔宇, 赵冬梅. 分散架构下多虚拟电厂分布式协同优化调度[J]. 电工技术学报, 2023, 38(7): 1852-1863.
Li Xiangyu, Zhao Dongmei. Distributed coordinated optimal scheduling of multiple virtual power plants based on decentralized control structure[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1852-1863.
[6] 李宗晟, 张璐, 张志刚, 等. 考虑柔性资源多维价值标签的交直流配电网灵活调度[J]. 电工技术学报, 2024, 39(9): 2621-2634.
Li Zongsheng, Zhang Lu, Zhang Zhigang, et al. A flexible scheduling method of AC/DC hybrid distribution network considering the multi-dimensional value tags of flexible resources[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2621-2634.
[7] Xiao Jucheng, He Guangyu, Fan Shuai, et al. Decentralized transfer of contingency reserve: framework and methodology[J]. Applied Energy, 2020, 278: 115703.
[8] 王健, 郑峻峰, 黄际元, 等. 虚拟电厂关键技术综述与发展展望[J]. 供用电, 2023, 40(12): 43-54, 86.
Wang Jian, Zheng Junfeng, Huang Jiyuan, et al. Key technology and development prospects of virtual power plants[J]. Distribution & Utilization, 2023, 40(12): 43-54, 86.
[9] 吴潇雨, 曹雨辰, 时庆. 一味追捧虚拟电厂概念不可取[N]. 中国能源报, 2023-02-06.
[10] 李翔宇, 赵冬梅. 基于模糊-概率策略实时反馈的虚拟电厂多时间尺度优化调度[J]. 电工技术学报, 2021, 36(7): 1446-1455.
Li Xiangyu, Zhao Dongmei. Research on multi-time scale optimal scheduling of virtual power plant based on real-time feedback of fuzzy-probability strategy[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1446-1455.
[11] 王明月, 刘东, 魏力鹏, 等. 电动汽车参与虚拟电厂优化调控的状态推演策略研究[J]. 供用电, 2024, 41(1): 14-25, 41.
Wang Mingyue, Liu Dong, Wei Lipeng, et al. Research on state inference strategies for electric vehicles participating in the optimal regulation of virtual power plants[J]. Distribution & Utilization, 2024, 41(1): 14-25, 41.
[12] 戴睿鹏, 窦晓波, 喻洁, 等. 含光储充的配网虚拟电厂二次调频随机模型预测控制策略[J]. 电网技术,2024, 48(8): 3228-3237.
Dai Ruipeng, Dou Xiaobo, Yu Jie, et al. Secondary frequency control strategy for photovoltaic-storage-charging distribution-level virtual power plant based on stochastic model predictive control[J]. Power System Technology,2024, 48(8): 3228-3237.
[13] Yamashita K, Djokic S, Matevosyan J, et al. Modelling and aggregation of loads in flexible power networks–scope and status of the work of CIGRE WG C4.605[J]. IFAC Proceedings Volumes, 2012, 45(21): 405-410.
[14] Khodayar M, Wang Jianhui. Probabilistic time-varying parameter identification for load modeling: a deep generative approach[J]. IEEE Transactions on Industrial Informatics, 2021, 17(3): 1625-1636.
[15] AlMuhaini M, Yahaya A, AlAhmed A. Distributed generation and load modeling in microgrids[J]. Sustainability, 2023, 15(6): 4831.
[16] Lee S H, Son S E, Lee S M, et al. Kalman-filter based static load modeling of real power system using K-EMS data[J]. Journal of Electrical Engineering and Technology, 2012, 7(3): 304-311.
[17] Schneider K P, Fuller J C, Tuffner F K, et al. Evaluation of conservation voltage reduction (CVR) on a national level[R].Richland, WA: Pacific Northwest National Laboratory, 2010.
[18] 朱星阳, 张建华, 刘文霞, 等. 考虑负荷电压静特性的含分布式电源的配电网潮流计算[J]. 电网技术, 2012, 36(2): 217-223.
Zhu Xingyang, Zhang Jianhua, Liu Wenxia, et al. Power flow calculation of distribution system with distributed generation considering static load characteristics[J]. Power System Technology, 2012, 36(2): 217-223.
[19] Arif A, Wang Zhaoyu, Wang Jianhui, et al. Load modeling: a review[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 5986-5999.
[20] Yang Jing, Wu Min, He Yong, et al. Identification and application of nonlinear dynamic load models[J]. Journal of Control Theory and Applications, 2013, 11(2): 173-179.
[21] Shair J, Li Haozhi, Hu Jiabing, et al. Power system stability issues, classifications and research prospects in the context of high-penetration of renewables and power electronics[J]. Renewable and Sustainable Energy Reviews, 2021, 145(7): 1-16.
[22] Wu Hao, Li Jing, Yang Haibo. Research methods for transient stability analysis of power systems under large disturbances[J]. Energies, 2024, 17(17): 4330.
[23] 毛文博, 曹冬志, 姚良忠, 等. 考虑感应电机负荷特性的主动配电网电压模型预测控制[J].电力自动化设备, 2024, 44(8): 92-99.
Mao Wenbo, Cao Dongzhi, Yao Liangzhong, et al. Voltage model predictive control of active distribution network considering load characteristics of induction motor[J]. Electric Power Automation Equipment, 2024, 44(8): 92-99.
[24] 田壁源, 常喜强, 戚红燕, 等. 基于混合博弈的园区虚拟电厂广义储能共享与协同优化调度[J]. 电力需求侧管理, 2023, 25(4): 8-14.
Tian Biyuan, Chang Xiqiang, Qi Hongyan, et al. Generalized energy storage sharing and collaborative optimal scheduling of park-level virtual power plants based on mixed game[J]. Power Demand Side Management, 2023, 25(4): 8-14.
[25] 李山山, 李华强, 金智博, 等. 基于共享经济理念的园区分布式能源共享服务机制[J]. 中国电机工程学报, 2022, 42(1): 56-71.
Li Shanshan, Li Huaqiang, Jin Zhibo, et al. Distributed energy sharing service mechanism for park based on the concept of sharing economy[J]. Proceedings of the CSEE, 2022, 42(1): 56-71.
[26] 刘雨佳, 樊艳芳, 白雪岩, 等. 基于优化计算型区块链系统的虚拟电厂模型与调度策略[J]. 电工技术学报, 2023, 38(15): 4178-4191.
Liu Yujia, Fan Yanfang, Bai Xueyan, et al. Virtual power plant model and scheduling strategy based on optimized computing block-chain system[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4178-4191.
[27] 杨宜龙, 范帅, 蔡思烨, 等. 内嵌调节目标的分布式能源调节能力分层分类聚合方法[J]. 电力系统自动化, 2025, 49(9): 84-95.
Yang Yilong, Fan Shuai, Cai Siye, et al. A hierarchical and classified aggregation method for distributed energy resources regulation capability with embedded regulation targets[J]. Automation of Electric Power Systems, 2025, 49(9): 84-95.
[28] 周欢, 王芬, 李志勇, 等. 虚拟电厂自趋优负荷跟踪控制策略[J]. 中国电机工程学报, 2021, 41(24): 8334-8349.
Zhou Huan, Wang Fen, Li Zhiyong, et al. Load tracking control strategy for virtual power plant via self-approaching optimization[J]. Proceedings of the CSEE, 2021, 41(24): 8334-8349.
[29] Fan Shuai, Liu Jiang, Wu Qing, et al. Optimal coordination of virtual power plant with photovoltaics and electric vehicles: a temporally coupled distributed online algorithm[J]. Applied Energy, 2020, 277: 115583.
[30] Bokhari A, Alkan A, Dogan R, et al. Experimental determination of the ZIP coefficients for modern residential, commercial, and industrial loads[J]. IEEE Transactions on Power Delivery, 2014, 29(3): 1372-1381.
[31] 孙充勃, 李敬如, 罗凤章, 等. 考虑分布式电源接入的配电系统典型算例设计[J]. 电力建设, 2020, 41(10): 47-62.
Sun Chongbo, Li Jingru, Luo Fengzhang, et al. Typical case design of distribution system considering DG integration[J]. Electric Power Construction, 2020, 41(10): 47-62.
[32] Baran M E, Wu F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.
[33] 国家能源局南方能源监管局.关于印发《南方区域电力并网运行管理实施细则》《南方区域电力辅助服务管理实施细则》的通知[EB/OL]. (2022-06-13) [2024-06-30].https://nfj.nea.gov.cn/xxgk/fdzdgknr/ scjg/202402/t20240208_240258.html.
[34] Jha R R, Dubey A, Liu C C, et al. Bi-level volt-VAR optimization to coordinate smart inverters with voltage control devices[J]. IEEE Transactions on Power Systems, 2019, 34(3): 1801-1813.
[35] Short T A, Mee R W. Voltage reduction field trials on distributions circuits[C]//PES T&D 2012, Orlando, FL, USA, 2012: 1-6.
[36] Lefebvre S, Gaba G, Ba Ao, et al. Measuring the efficiency of voltage reduction at Hydro-Québec distribution[C]//2008 IEEE Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 2008: 1-7.
[37] Diaz-Aguiló M, Sandraz J, Macwan R, et al. Field-validated load model for the analysis of CVR in distribution secondary networks: energy conservation [J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2428-2436.
[38] Wang Zhaoyu, Wang Jianhui. Time-varying stochastic assessment of conservation voltage reduction based on load modeling[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2321-2328.
[39] Wang Chong, Wang Zhaoyu, Wang Jianhui, et al. Robust time-varying parameter identification for composite load modeling[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 967-979.
[40] Cui Mingjian, Khodayar M, Chen Chen, et al. Deep learning-based time-varying parameter identification for system-wide load modeling[J]. IEEE Transactions on Smart Grid, 2019, 10(6): 6102-6114.
[41] Anderson K S, Hansen C W, Holmgren W F, et al. Pvlib Python: 2023 project update[J]. Journal of Open Source Software, 2023, 8(92): 5994.
[42] Thurner L, Scheidler A, Schäfer F, et al. Pandapower: an open-source Python tool for convenient modeling, analysis, and optimization of electric power systems [J]. IEEE Transactions on Power Systems, 2018, 33(6): 6510-6521.
Accurate Regulation Method for Virtual Power Plants Considering Static Voltage Load Characteristics
Abstract Virtual power plant (VPP) serves as an effective mechanism for exploiting flexibility from demand-side resources in modern power systems. Current research typically categorizes demand-side resources into controllable and uncontrollable types, treating the latter as parameters independent of decision variables in optimization models. However, loads inherently possess static voltage characteristics, meaning voltage variations induced by VPP regulation inevitably affect the actual power consumption of uncontrollable resources. This phenomenon causes difficulties in achieving accurate VPP regulation and limits its application scope to simple scenarios such as peak shaving.
This study proposes an accurate regulation method for VPPs that accounts for the static voltage load characteristics. The objective is to overcome the limitations of conventional approaches where uncontrollable resources are inaccurately modeled, leading to suboptimal regulation performance. The research addresses a critical gap in VPP operation strategies by recognizing that uncontrollable loads should not be considered as fixed parameters but as functions related to decision variables through network voltage profiles.
The methodology involves three main components. First, a comprehensive VPP operation model is developed that incorporates the topology of the low-voltage distribution network within the park area. This model explicitly represents how uncontrollable loads passively respond to voltage changes caused by control actions on other resources. Second, to address the computational challenges introduced by load static voltage characteristics, a model linearization method and a measurement feedback-based model calibration mechanism are proposed. These approaches enable efficient online solution of the optimization problem while maintaining modeling accuracy. Third, an integrated control framework is established that minimizes adjustment utility losses while meeting regulation targets. This framework optimizes the dispatch of various controllable resources including distributed generators, energy storage systems, and flexible loads, while accounting for their impact on uncontrollable loads through voltage variations.
Results from case studies demonstrate that the proposed method significantly improves regulation accuracy compared to conventional approaches. Specifically, compared to traditional methods that treat loads as rigid in control strategies, the proposed method reduces the average tracking relative error from 4.82% to 0.78%. Additionally, the adjustment utility loss is reduced by 35% compared to the energy storage droop control correction strategy based on measurement feedback. The advantages of the proposed method become more pronounced as the load static voltage characteristics in the network become more significant. Under high equivalent conservation voltage reduction (CVR) coefficients, the proposed method maintains an average tracking relative error of only 0.09%, while traditional methods reach 5.74%. Even under low equivalent CVR coefficients, the proposed method still maintains a tracking error of 2.22%. The method demonstrates good adaptability by maintaining stable tracking performance under various regulation depths and tracking accuracy requirements.
The proposed methodology resolves limitations of current VPP implementations that typically offer only single-scenario applications such as peak shaving. By enabling more precise control, this approach establishes a foundation for VPPs to provide multiple types of regulation services including load following, automatic generation control, and operating reserves. The method enhances the overall efficiency and reliability of VPP operations in distribution networks with high penetration of demand-side resources.
This research primarily focuses on the impact mechanism of loads with static voltage characteristics on VPP regulation accuracy, particularly their passive voltage response characteristics. The current study has several limitations that warrant future research. The control period is relatively short, thus neglecting the constraints from energy storage state of charge (SOC). In longer control periods or normalized control scenarios, the temporal and spatial coupling constraints from energy storage SOC cannot be ignored. More complex distributed energy resources (DERs) models would introduce new complexities to the control method. For instance, considering the actual curtailment costs of photovoltaic (PV) systems would require addressing uncertainties in PV forecasting through methods such as Monte Carlo simulation. Additionally, implementing continuous data collection and coordinated control of various dispersed resources throughout the network poses new challenges to resource measurement systems and control systems. Future research should focus on VPP precise control methods that consider longer time periods, more DER types, more accurate DER models, finer granularity, and collaborative optimization of flexible loads with static voltage characteristics.
Keywords:Static voltage load characteristics, virtual power plant, accurate regulation, demand-side resources
中图分类号:TM732
DOI: 10.19595/j.cnki.1000-6753.tces.241169
国家自然科学基金(52207123)和国家重点研发计划(2021YFB1507104)资助项目。
收稿日期2024-07-04
改稿日期2025-03-14
田济源 男,2000年生,硕士研究生,研究方向为智能用电与虚拟电厂。
E-mail:aveckbeko@sjtu.edu.cn
范 帅 男,1993年生,博士,研究方向为需求响应与虚拟电厂等。
E-mail:fanshuai@sjtu.edu.cn(通信作者)
(编辑 赫 蕾)