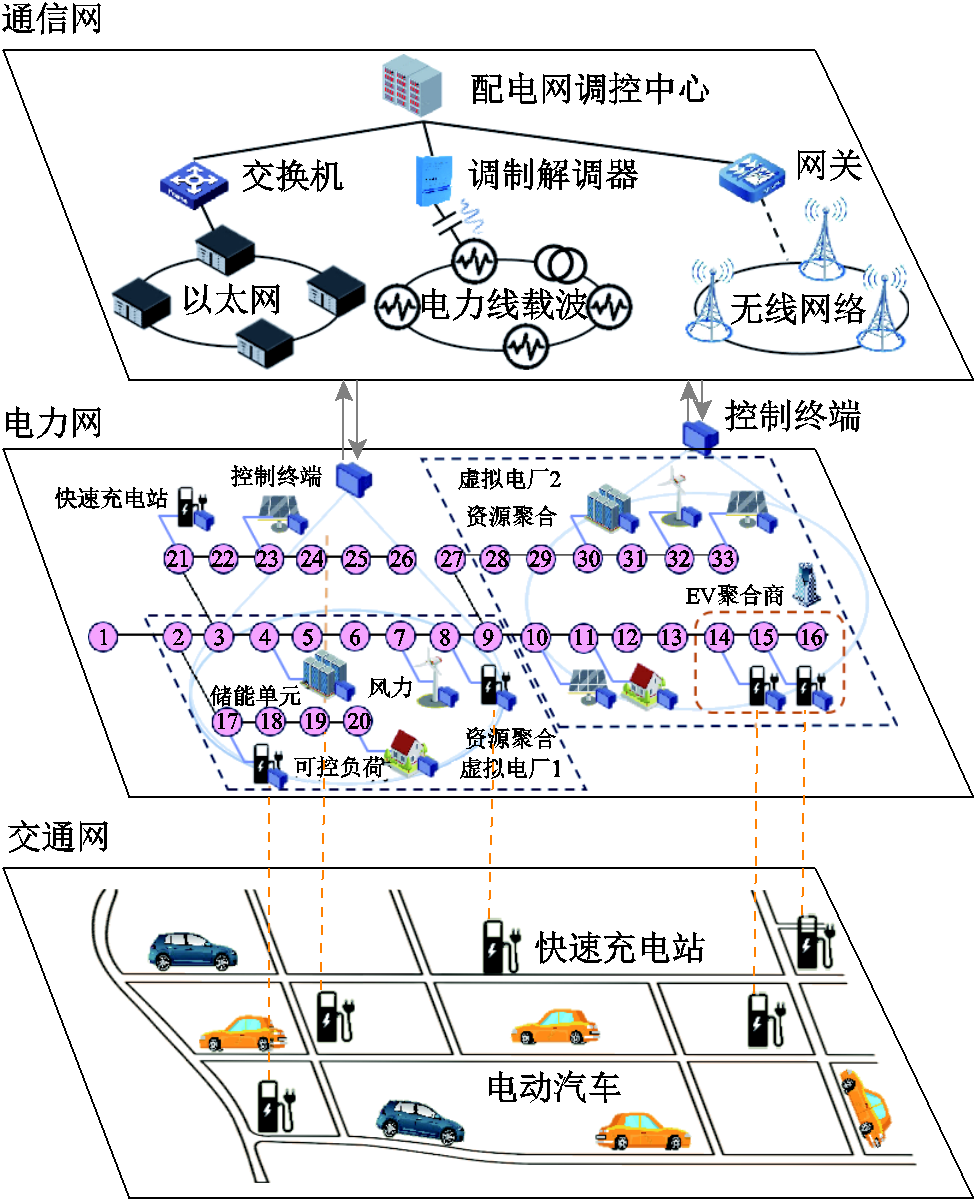
图1 电力-通信-交通耦合网络架构
Fig.1 Architecture of power-communication-transportation coupling network
摘要 电力-通信-交通耦合网络中,虚拟电厂(VPP)通过先进的控制、通信、信息采集技术对分布式资源进行规模化聚合调控并积极响应电网需求,能够提高电网运行的稳定性。然而,现有VPP优化调度方法忽略了电力-通信-交通耦合网络中不确定性因素对VPP需求响应优化调度的影响,导致调度成本高、鲁棒性差。针对上述问题,首先,该文构建电力-通信-交通耦合网络模型,并以最小化网损、节点电压偏差、VPP经济成本的加权和为目标建立优化问题;其次,分析来自电力-通信-交通三个网络的不确定性因素,并构建计及电力-通信-交通耦合网络不确定性的VPP鲁棒优化调度问题;然后,提出一种基于联邦对抗深度Q网络(DQN)的VPP鲁棒优化调度求解算法,通过双智能体之间的不断迭代,实现鲁棒最优策略的对抗求解;最后,对所提算法进行仿真验证,仿真结果表明,所提算法能够有效降低不确定性因素对VPP优化调度的影响,提高电网运行的可靠性与稳定性。
关键词:电力-通信-交通 虚拟电厂 不确定性 鲁棒优化调度 联邦对抗深度Q网络(DQN)
随着可再生能源发电、电气化交通等交叉技术的不断创新发展,电力-通信-交通三个系统间的联系日益紧密[1-2]。交通系统作为重要的电能负荷来源,在通信网的支撑下与电力系统在用户、电能、信息等层面产生了频繁的交互,给电网的安全稳定运行带来巨大挑战[3-4]。虚拟电厂(Virtual Power Plant, VPP)利用先进的控制、通信、信息采集技术对分布式资源进行规模化聚合和智能调控,并积极响应电网需求,提高电网运行的稳定性[5-6]。然而,在三网耦合网络中,可再生能源出力、调控指令通信时延以及电动汽车(Electric Vehicle, EV)充放电行为等均具有高度的不确定性,这将会直接影响VPP需求响应调度决策。因此,研究计及电力-通信-交通耦合网络不确定性的VPP需求响应鲁棒优化调度方法,对于提升系统的可靠性、安全性与经济性具有重要意义。
电力-通信-交通三网耦合关系复杂,传统VPP需求响应优化调度方法常依赖预先设定的规则或机制,在面对动态多变的环境时往往存在局限性。深度强化学习(Deep Reinforcement Learning, DRL)结合深度学习的复杂信息处理能力和强化学习的决策能力,能够高效处理复杂多维的环境信息,做出快速响应,现已广泛应用于VPP需求响应优化调度。文献[7]考虑交通网侧EV的充放电行为,针对包含EV的VPP,提出一种基于深度确定性策略梯度的VPP优化调度方法,在提高EV收益的同时改善VPP整体运行性能。文献[8]设计一种VPP云边协同架构,在云边协同通信网络支撑下,提出一种基于改进深度Q网络(Deep Q-network, DQN)的VPP需求响应优化调度方法,以降低VPP运营成本。联邦深度强化学习(Federated Deep Reinforcement Learning, FDRL)支持多VPP通过分布式训练、集中式聚合实现调度策略经验知识共享,从而有效提高学习效率和优化调度性能[9]。文献[10]面向VPP中EV部署与可再生能源整合场景,以VPP内部功率平衡为优化目标,提出基于FDRL的VPP功率控制策略。文献[11]提出一种基于联邦柔性行动者-评论家算法的VPP优化调度策略,通过动态调整各VPP对外出力,实现配电网电压最优控制。然而,上述研究忽略了三网耦合网络中可再生能源出力、调控指令通信时延以及EV充放电行为等不确定性因素对VPP需求响应优化调度的影响,导致调度成本高、鲁棒性差。
针对VPP需求响应优化调度过程中的不确定性问题,当前求解方法主要包括鲁棒优化、模糊规划、随机规划等。文献[12]提出一种计及用户需求响应不确定性的分布鲁棒优化方法,在促进多方利益最大化的基础上提升VPP的经济性、电网友好性和用户舒适性。文献[13]针对分布式光伏和负荷需求的双重不确定性,基于模糊规划方法建立最小化损耗的目标函数,并通过改进粒子群优化算法进行求解。文献[14]针对高光伏渗透率配电网中传统规划方法难以应对光伏与负荷不确定性的问题,构建了一种考虑不确定因素的综合能源系统两阶段规划模型,并采用灰狼优化算法求解,以提升系统在高渗透率场景下的适应性与经济性。现有研究考虑的不确定性因素主要有基站动态功耗和业务场景的差异化时延需求等。文献[15]考虑到基站的用电功耗对通信负载量的变化较为敏感,其中动态功耗受接入车辆用户数量的影响较大,因此将通信网络的不确定性因素纳入耦合网络。文献[16]针对电网可调节资源分级调控的通信系统服务质量问题,将各业务场景的时延、可靠性等通信指标纳入耦合网络模型。
尽管上述研究在VPP需求响应优化调度领域已经取得一些进展,但仍面临以下挑战。首先,现有方法忽略了电力-通信-交通耦合网络不确定性因素的影响,导致VPP需求响应优化调度策略鲁棒性较差。其次,现有方法在马尔可夫决策过程(Markov Decision Process, MDP)建模过程中,无法根据VPP资源实际响应值与调控值之间的偏差动态调整动作空间,难以适配三网耦合复杂场景下VPP需求响应鲁棒优化。最后,传统基于单智能体决策的深度强化学习求解方法忽略了鲁棒优化过程中确定性变量与不确定性变量之间的对抗性,存在收敛速度慢、鲁棒性弱等问题,难以实现VPP需求响应鲁棒优化调度。
针对上述问题,本文提出计及电力-通信-交通耦合网络不确定性的VPP鲁棒优化调度方法。首先,构建电力-通信-交通耦合网络模型,并以最小化网损、节点电压偏差、VPP经济成本的加权和为目标建立优化问题;其次,分析来自电力-通信-交通三个网络的不确定性因素,并构建计及电力-通信-交通耦合网络不确定性的VPP鲁棒优化调度问题;然后,提出一种基于联邦对抗DQN的VPP鲁棒优化调度求解算法,通过双智能体之间的不断迭代,实现鲁棒最优策略的对抗求解;最后,通过仿真分析验证本文所提算法的有效性。
电力-通信-交通耦合网络架构如图1所示。在三网耦合网络中,电网侧由VPP实现可再生能源、储能、可控负荷以及EV等资源的聚合,并调控这些资源参与电网需求响应。交通网侧由快速充电站实现与电网的耦合,一方面为EV提供充电服务,另一方面经由EV聚合商聚合参与VPP调控。通信网侧VPP通过以太网、电力线载波、无线网络等异构通信方式与配电网调控中心以及下辖资源进行参数信息交互与调控指令下发。

图1 电力-通信-交通耦合网络架构
Fig.1 Architecture of power-communication-transportation coupling network
该三网耦合网络中形成了电能流-信息流-交通流之间的交互,如图2所示,相互之间存在复杂且动态的影响,伴随着大量不确定性因素。
电能流的不确定性主要源于分布式电源出力的波动,由此引起电力供需不平衡、负荷过载等问题,增加快速充电站的故障风险和电能供应不稳定性。信息流的不确定性主要体现在通信时延、通信设备可靠性和通信质量等方面,网络堵塞、设备故障、数据丢失等问题均会阻碍需求响应调控指令的传输和执行,进而影响VPP调控效果。交通流的不确定性与EV出行及充放电特性直接相关,包括入网时间、离网时间、入网荷电状态(State of Charge,SOC)等,以上不确定性因素使得VPP需求响应优化调度变得更加复杂和困难。
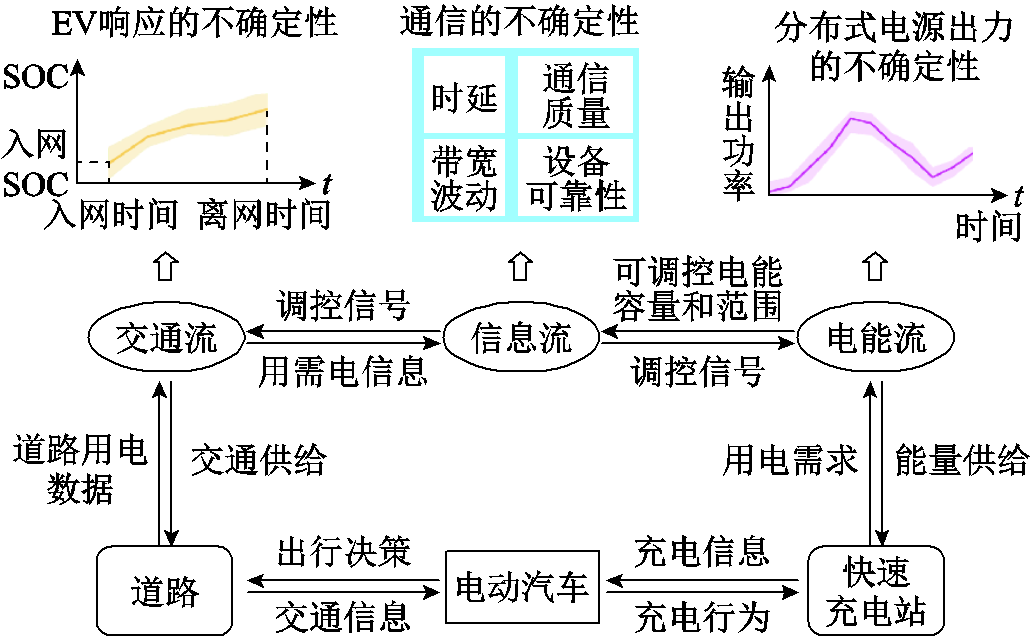
图2 电力-通信-交通耦合网络不确定性因素
Fig.2 Uncertainty factors of power-communication-transportation coupling network
本文以最小化配电网网损、节点电压稳定性及VPP经济成本的加权和为优化目标构建优化问题,表示为
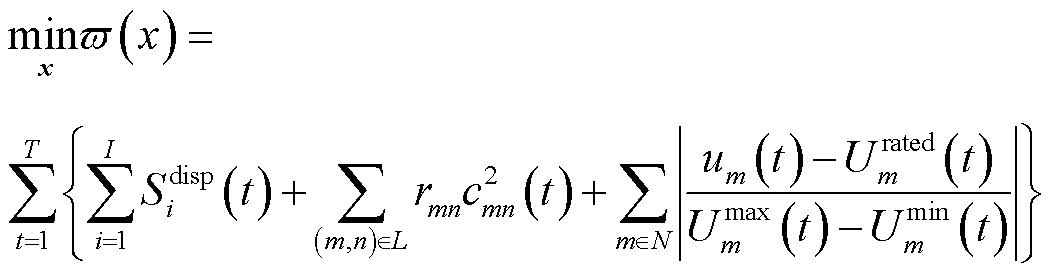 (1)
(1)
式中,x为优化变量集合,包括可控负荷、储能单元与EV聚合商的调控功率;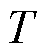 为优化时隙总数;L和N分别为配电网所有线路组成的集合与所有节点组成的集合;
为优化时隙总数;L和N分别为配电网所有线路组成的集合与所有节点组成的集合;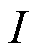 为VPP数量;
为VPP数量;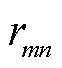 和
和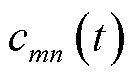 分别为支路
分别为支路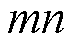 的电阻与电流;
的电阻与电流;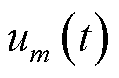 、
、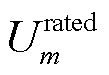 、
、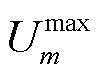 和
和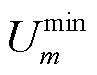 分别为节点
分别为节点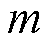 处第
处第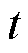 时隙的电压、额定电压、最大和最小容许电压;
时隙的电压、额定电压、最大和最小容许电压;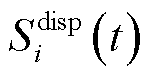 为第
为第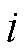 个VPP的经济成本,表示为
个VPP的经济成本,表示为
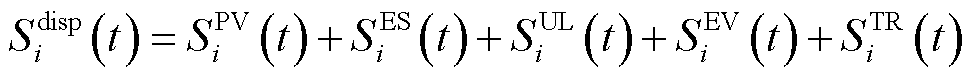 (2)
(2)
式中,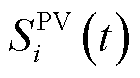 为光伏运维成本;
为光伏运维成本;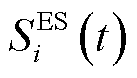 为储能单元调控成本;
为储能单元调控成本;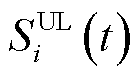 为可控负荷调控成本;
为可控负荷调控成本;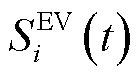 为EV聚合调控成本;
为EV聚合调控成本;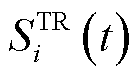 为购售电成本。分别表示如下。
为购售电成本。分别表示如下。
1)储能单元调控成本
储能单元调控成本表示为
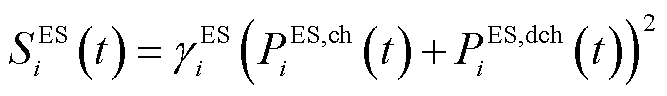 (3)
(3)
式中,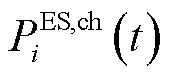 、
、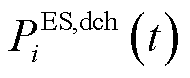 分别为储能单元的充、放电功率;
分别为储能单元的充、放电功率;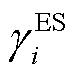 为储能单元调控成本系数。
为储能单元调控成本系数。
2)可控负荷调控成本
本文考虑的可控负荷主要指电网中工业负荷等传统负荷,此类负荷参与需求响应调控时通常按照计划执行,计划性较强,不确定性较弱,其调控成本表示为
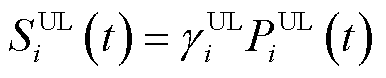 (4)
(4)
式中,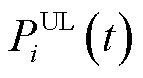 为可控负荷调控功率;
为可控负荷调控功率;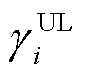 为可控负荷调控成本系数。
为可控负荷调控成本系数。
3)EV聚合调控成本
EV聚合调控成本表示为
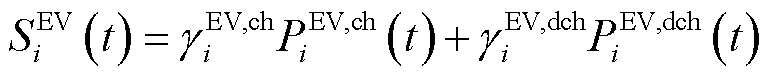 (5)
(5)
式中,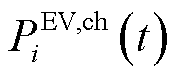 、
、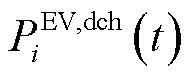 分别为EV的聚合充、放电功率;
分别为EV的聚合充、放电功率;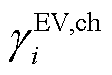 、
、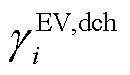 分别为充、放电价。
分别为充、放电价。
4)光伏运行维护成本
光伏运行维护成本表示为
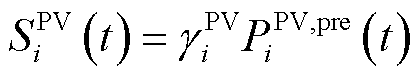 (6)
(6)
式中,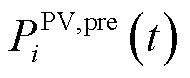 为光伏预测出力功率;
为光伏预测出力功率;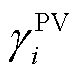 为光伏运维成本系数。
为光伏运维成本系数。
5)购售电成本
当VPP内部发电功率不足或过多时,VPP可以向上级电网购售电,购售电成本表示为
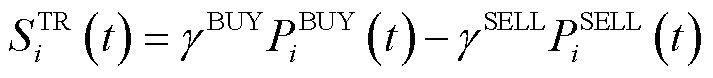 (7)
(7)
式中,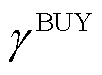 和
和 分别为购、售电价;
分别为购、售电价;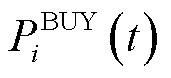 、
、 分别为购、售电功率。
分别为购、售电功率。
1.2.1 潮流约束
采用支路潮流约束,表示为
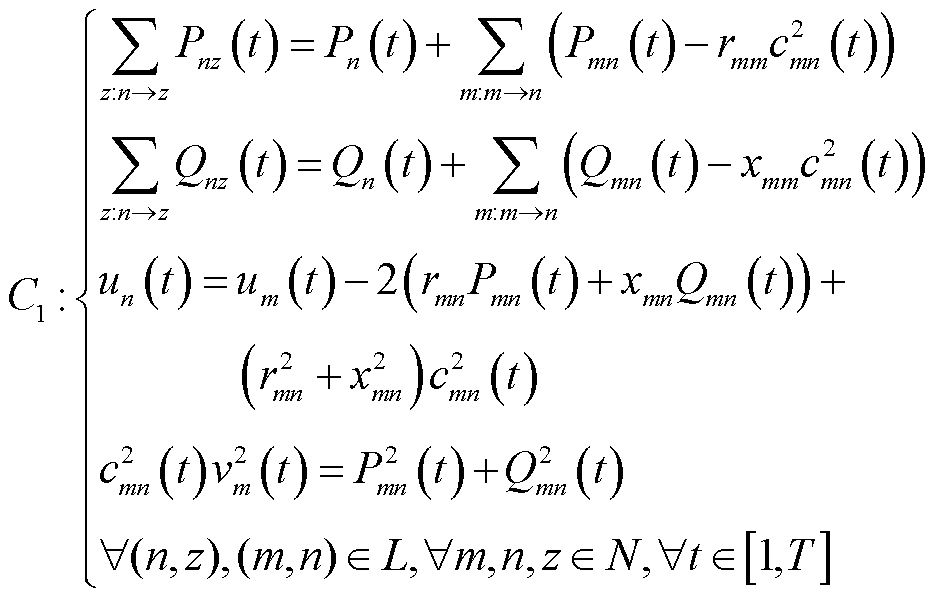 (8)
(8)
式中,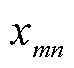 为支路
为支路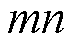 的电抗;
的电抗;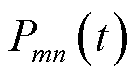 、
、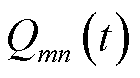 分别为节点
分别为节点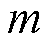 流向节点
流向节点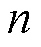 的有功功率、无功功率;
的有功功率、无功功率;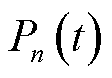 、
、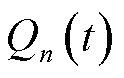 分别为节点
分别为节点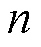 注入的有功功率、无功功率。
注入的有功功率、无功功率。
1.2.2 节点电压与支路电流安全约束
节点电压与支路电流安全约束表示为
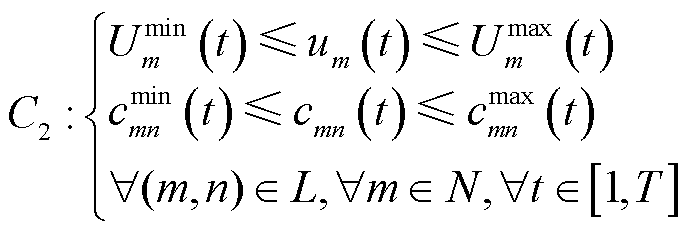 (9)
(9)
1.2.3 功率平衡约束
VPP内部需要满足功率平衡约束,表示为
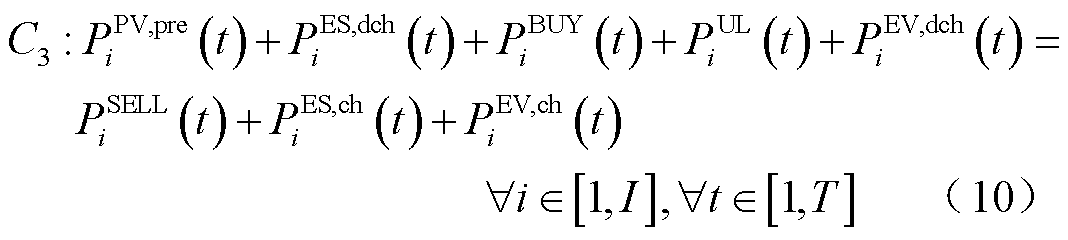
1.2.4 光伏运行约束
分布式光伏运行约束表示为
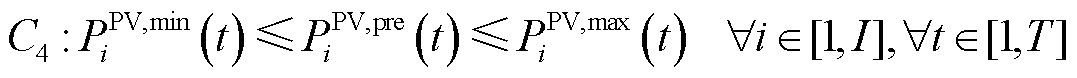 (11)
(11)
式中,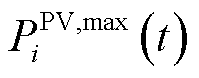 、
、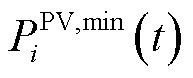 分别为光伏出力最大、最小值[17]。
分别为光伏出力最大、最小值[17]。
1.2.5 可控负荷出力约束
可控负荷的出力约束表示为
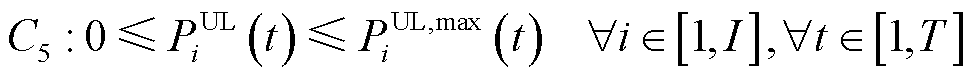 (12)
(12)
式中,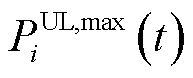 为可控负荷功率最大可削减量。
为可控负荷功率最大可削减量。
1.2.6 分布式储能出力约束
分布式储能出力约束主要包含充放电状态约束、储能容量约束和充放电功率约束,表示为
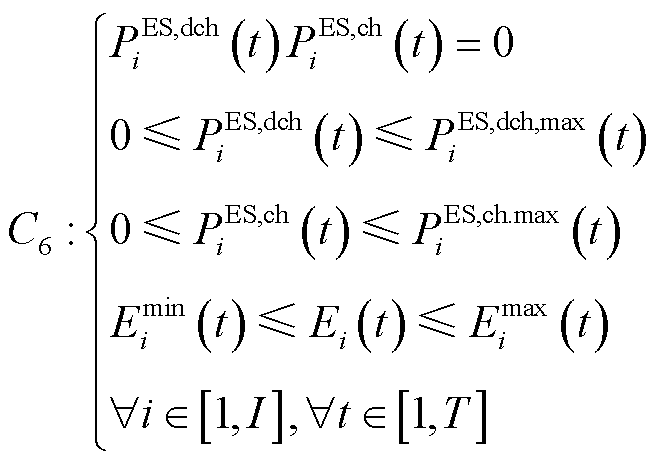 (13)
(13)
式中,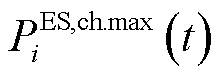 、
、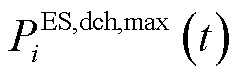 分别为分布式储能最大充放电功率;
分别为分布式储能最大充放电功率;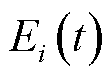 为储能容量;
为储能容量;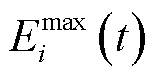 、
、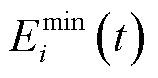 分别为储能容量上、下限。
分别为储能容量上、下限。
1.2.7 EV聚合调控约束
EV聚合调控约束主要包括充放电状态约束、充放电功率约束和SOC约束,表示为
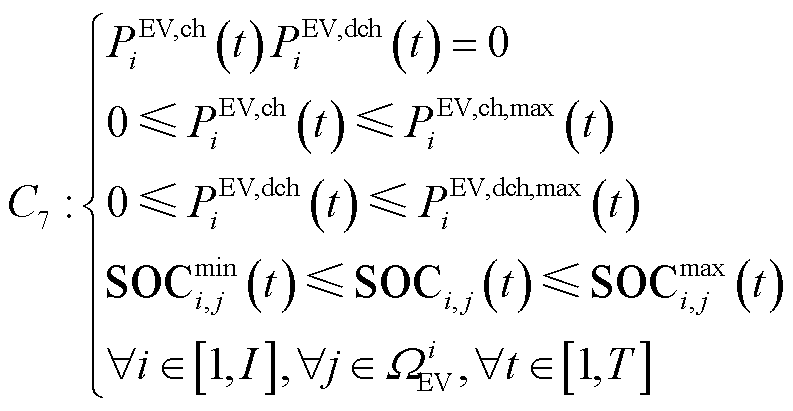 (14)
(14)
式中,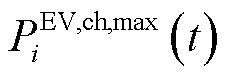 、
、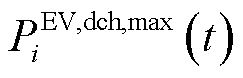 分别为VPP中EV聚合商所能聚合的最大充、放电功率;
分别为VPP中EV聚合商所能聚合的最大充、放电功率;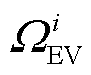 为第
为第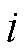 个VPP所聚合的EV集合;
个VPP所聚合的EV集合;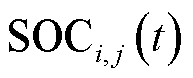 为第
为第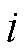 个VPP所聚合第
个VPP所聚合第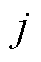 辆EV的荷电状态;
辆EV的荷电状态;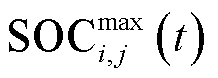 、
、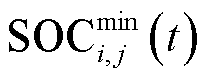 分别为荷电状态上、下限。
分别为荷电状态上、下限。
1.2.8 购售电约束
VPP向电网的购售电约束表示为
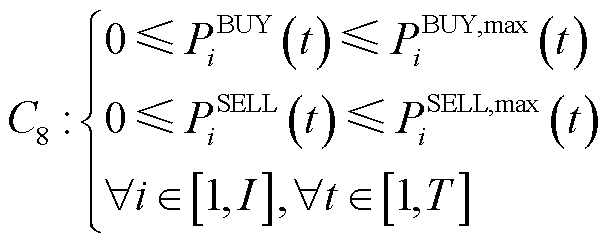 (15)
(15)
式中,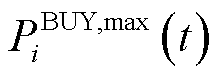 、
、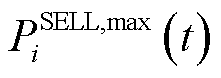 分别为最大购、售电功率。
分别为最大购、售电功率。
2.1.1 通信不确定性
VPP调控各类资源参与需求响应依赖各资源控制终端的可靠运行以及通信网络对调控指令和响应信号的有效传输,因此,通信网侧的不确定性因素主要有控制终端运行可靠性、通信带宽波动有效性、调控指令通信时延和通信质量。
控制终端运行可靠性 定义为
定义为
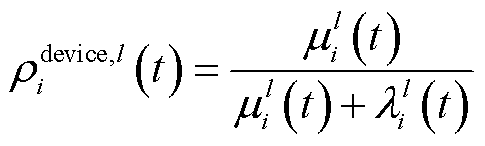 (16)
(16)
式中,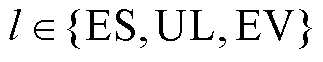 表示资源类型;
表示资源类型;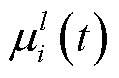 、
、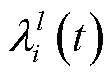 分别为资源
分别为资源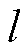 控制终端的修复率与失效率。
控制终端的修复率与失效率。
通信带宽波动的有效性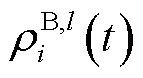 定义为
定义为
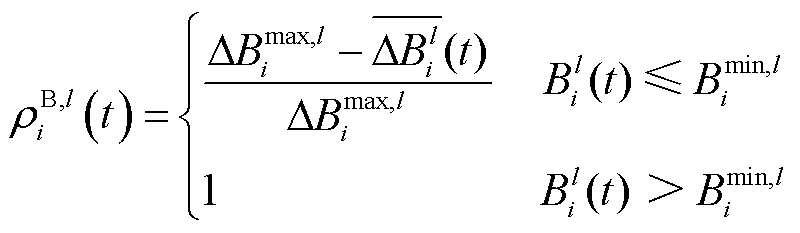 (17)
(17)
式中,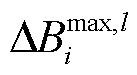 为资源
为资源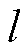 参与调控时能接受的最大通信带宽波动;
参与调控时能接受的最大通信带宽波动;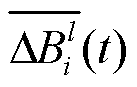 为资源
为资源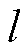 通信设备当前的平均带宽波动;
通信设备当前的平均带宽波动;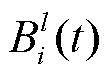 为资源
为资源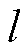 通信设备当前带宽;
通信设备当前带宽;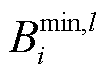 为资源l通信设备有效带宽阈值,超过该阈值时通信带宽冗余充足,波动不会影响通信有效性。
为资源l通信设备有效带宽阈值,超过该阈值时通信带宽冗余充足,波动不会影响通信有效性。
调控指令通信时延有效性 定义为
定义为
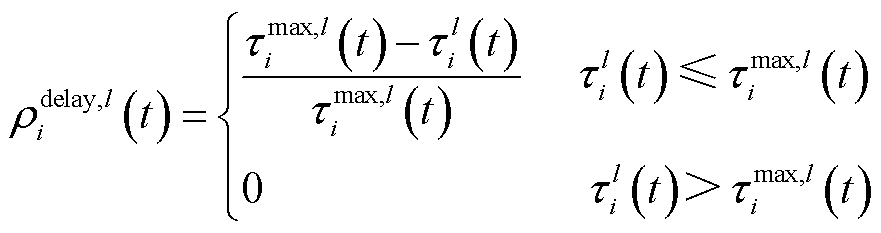 (18)
(18)
式中,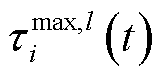 为资源
为资源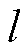 参与调控时能接受的最大调控指令通信时延;
参与调控时能接受的最大调控指令通信时延;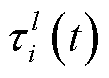 为资源
为资源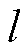 通信设备当前的平均通信时延。
通信设备当前的平均通信时延。
通信质量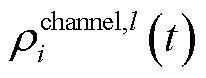 采用丢包率进行衡量,表示为
采用丢包率进行衡量,表示为
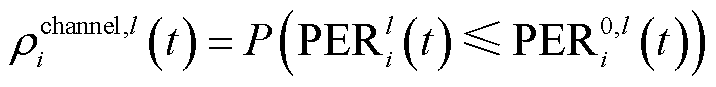 (19)
(19)
式中,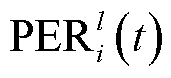 为丢包率;
为丢包率;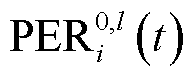 为丢包率阈值;
为丢包率阈值;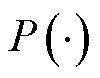 表示事件发生概率。
表示事件发生概率。
因此,通信可靠性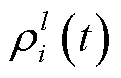 表示为
表示为
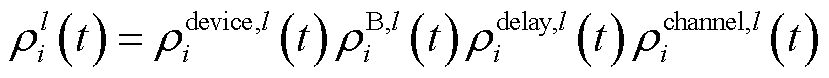 (20)
(20)
VPP中各类资源计及通信不确定性的出力功率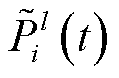 表示为
表示为
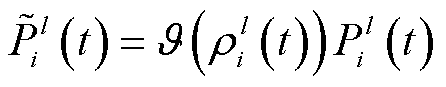 (21)
(21)
式中,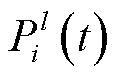 为
为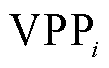 中资源
中资源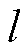 的调控功率;
的调控功率;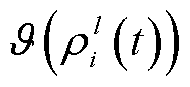 为通信不确定性变量,表示为
为通信不确定性变量,表示为
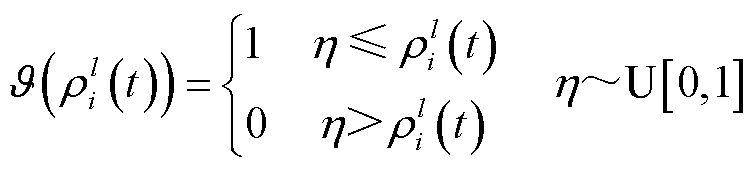 (22)
(22)
2.1.2 电力不确定性
电力不确定性主要来源于可再生能源出力的不确定性,本节以分布式光伏出力不确定性为例进行电力不确定性建模。将光伏实际出力功率建模为功率预测值与功率偏差值两部分,表示为
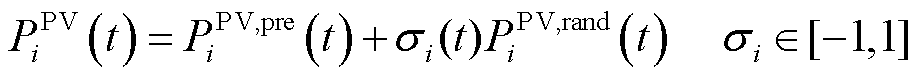 (23)
(23)
式中,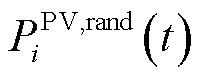 为光伏出力功率偏差值;
为光伏出力功率偏差值;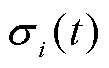 为光伏不确定性因子。
为光伏不确定性因子。
根据光伏设备的物理约束可以确定其出力功率的最大值与最小值,因此,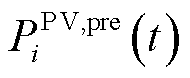 和
和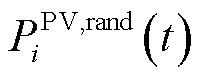 可以进一步表示为
可以进一步表示为
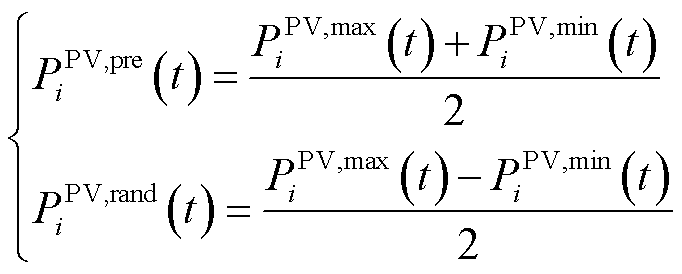 (24)
(24)
将式(21)代入式(20)可得计及不确定性的光伏出力模型,表示为
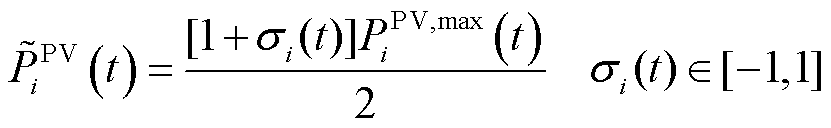 (25)
(25)
2.1.3 交通不确定性
交通网的不确定性主要来源于EV需求响应的不确定性。配电网调控中心发布分时电价,通过电价激励来引导EV参与需求响应,然而,EV私人属性较强,其入网时间、离网时间、入网SOC等都具有较强的不确定性,导致EV对激励电价的响应程度在一定范围内波动。本节采用韦伯-费希纳定律[18]量化EV在不同激励电价下需求响应的不确定性,EV充、放电响应率表示为
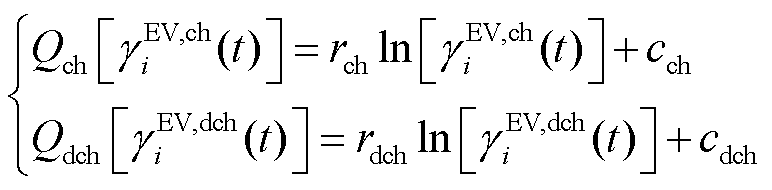 (26)
(26)
式中,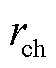 、
、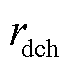 分别为充、放电响应系数;
分别为充、放电响应系数;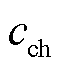 、
、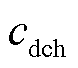 分别为充、放电响应常数。
分别为充、放电响应常数。
根据EV的需求响应率,第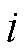 个VPP中EV聚合商的可调控功率表示为
个VPP中EV聚合商的可调控功率表示为
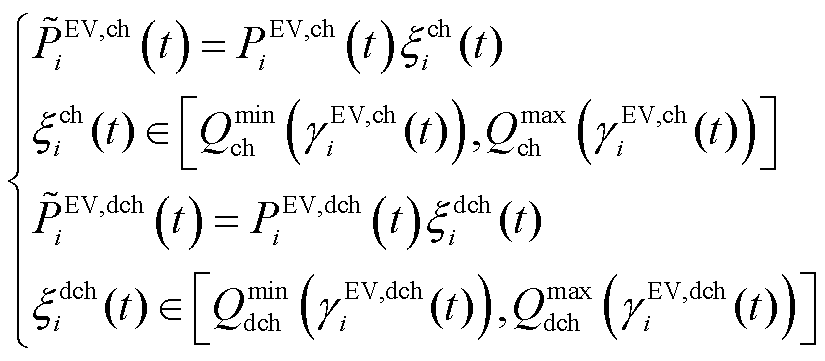 (27)
(27)
式中,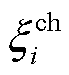 、
、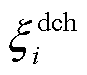 分别为EV充、放电不确定性因子。
分别为EV充、放电不确定性因子。
将上述计及不确定性的资源出力功率替换式(1)中的相应变量,即可得到计及电力-通信-交通耦合网络不确定性的VPP鲁棒优化调度问题,表示为
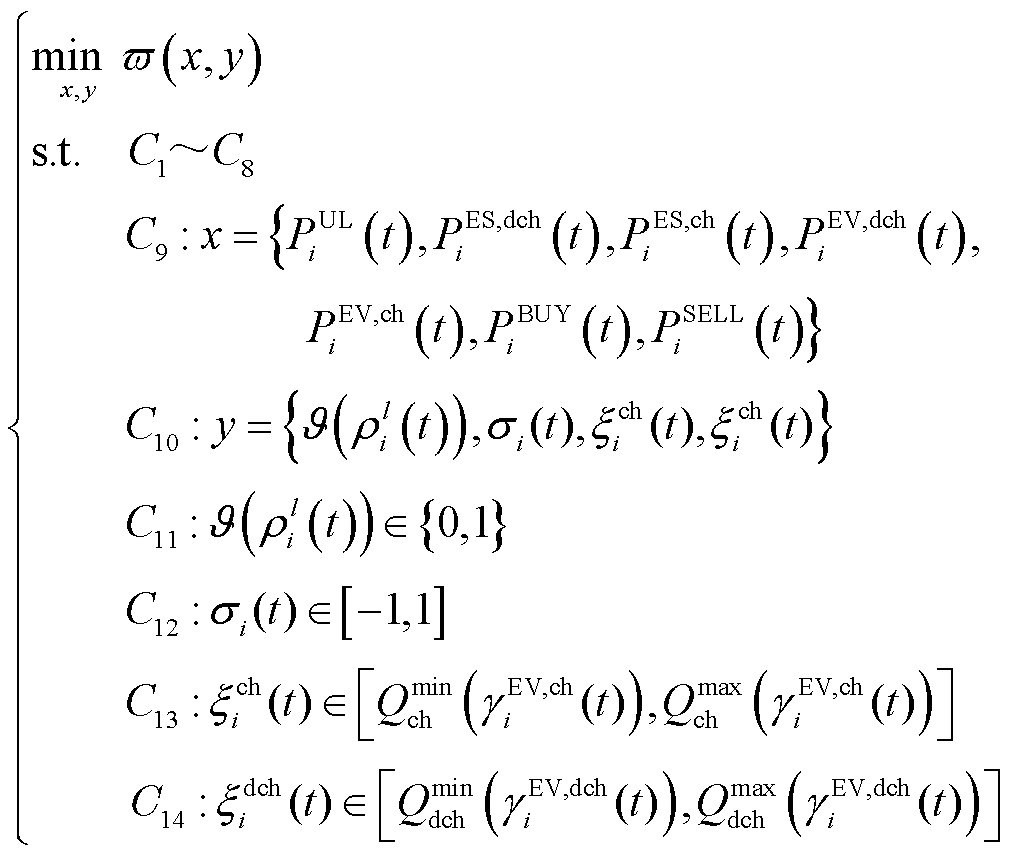 (28)
(28)
式中,x为确定性变量集合;y为不确定性变量集合;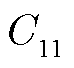 ~
~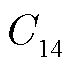 分别为不确定性变量取值约束。
分别为不确定性变量取值约束。
对优化问题(25)进行鲁棒对等变换之后,采用割平面法进行解耦[19],原优化问题转换为两个迭代求解的单层优化问题,具体表示为
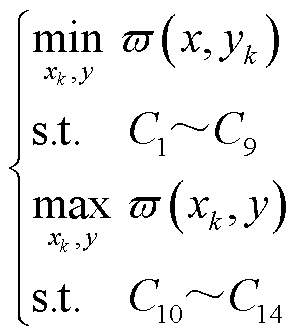 (29)
(29)
式中,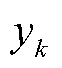 由max优化问题在第
由max优化问题在第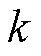 次迭代中求得;
次迭代中求得;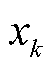 由min优化问题在第
由min优化问题在第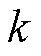 次迭代中求得。二者交替迭代求解,直到max优化问题与min优化问题目标函数相等,即可得到鲁棒最优解。
次迭代中求得。二者交替迭代求解,直到max优化问题与min优化问题目标函数相等,即可得到鲁棒最优解。
由于式(26)需要交替迭代求解,同时考虑了电力-通信-交通多方面的不确定因素,传统求解方法适配性差,收敛速度慢,且没有考虑调控指令通信时延与丢包对VPP调度策略执行情况的影响。针对上述问题,本节提出基于调控指令通信时延与丢包感知的鲁棒对抗MDP模型,分别在每个VPP侧构建智能体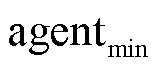 和
和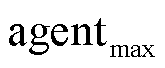 进行对抗迭代求解,考虑调控指令通信时延与丢包对VPP中各资源需求响应功率出力的影响,设计对应状态与动作,同时基于Shapley值法进行奖励函数设计,保证利益分配合理性,促进全局收益最大化,具体介绍如下。
进行对抗迭代求解,考虑调控指令通信时延与丢包对VPP中各资源需求响应功率出力的影响,设计对应状态与动作,同时基于Shapley值法进行奖励函数设计,保证利益分配合理性,促进全局收益最大化,具体介绍如下。
3.1.1 智能体状态
智能体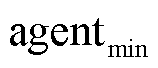 和
和 的状态分别为
的状态分别为
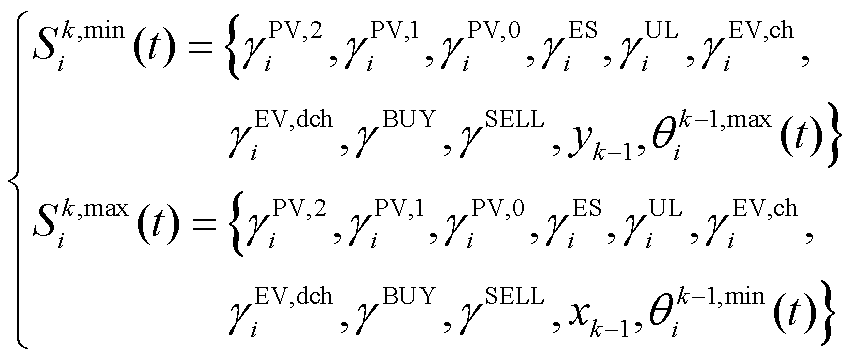 (30)
(30)
式中,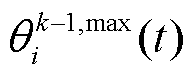 、
、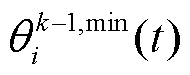 分别为
分别为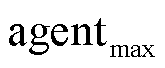 和
和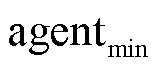 第
第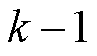 次迭代对抗的奖励。
次迭代对抗的奖励。
3.1.2 智能体动作
智能体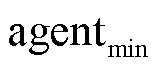 和
和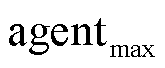 的动作分别为
的动作分别为
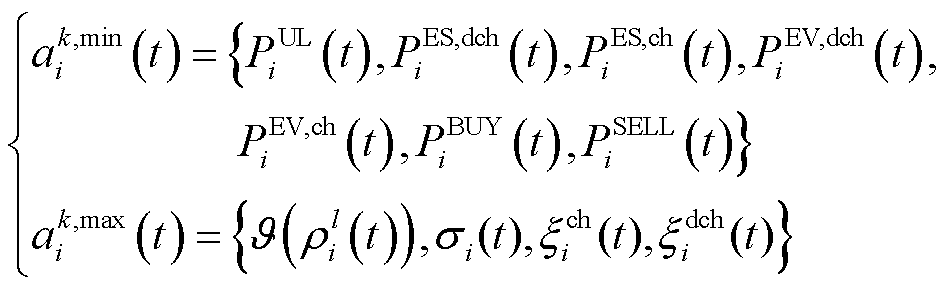 (31)
(31)
调控指令通信时延过高乃至产生丢包,将会导致VPP内部资源无法及时响应,使得资源实际响应量与调控量偏差较大,VPP经济成本增大,鲁棒性较差。因此,基于VPP调控指令通信时延和丢包率对智能体动作空间进行自适应调整,当某种资源调控指令通信时延或丢包率过高时,则相应降低其出力功率上限,减小其出力在所有资源中的比重,从而降低其无法及时响应引起的调控偏差。以可控负荷为例,智能体动作空间调整方法如下。
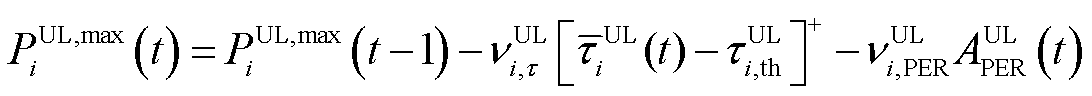 (32)
(32)
式中,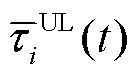 为可控负荷截至当前时隙的平均调控指令通信时延;
为可控负荷截至当前时隙的平均调控指令通信时延;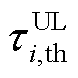 为调控指令通信时延阈值;
为调控指令通信时延阈值; 为截至当前时隙的总丢包次数;
为截至当前时隙的总丢包次数;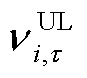 、
、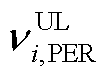 分别为可控负荷出力上限对时延和丢包的调整系数。
分别为可控负荷出力上限对时延和丢包的调整系数。
采用类似方法可实现对VPP其他资源出力上限的调整,同时,为简化问题求解,基于自适应调整之后的出力上限,对智能体动作进行均匀离散化。
3.1.3 智能体状态
智能体奖励包含本地奖励与全局奖励,本地奖励为VPP经济成本,全局奖励包含网损、节点电压稳定性,采用Shapley值方法对全局奖励进行分配,第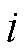 个VPP的全局奖励表示为
个VPP的全局奖励表示为
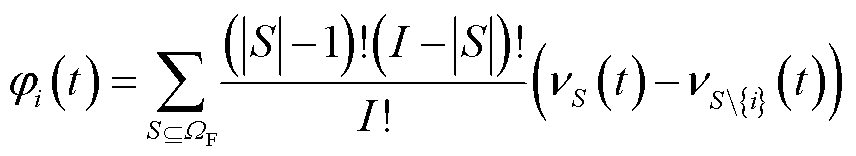 (33)
(33)
式中,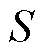 为VPP联盟;
为VPP联盟;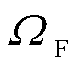 为所有可能的VPP联盟集合;
为所有可能的VPP联盟集合; 为集合
为集合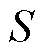 中元素数量;
中元素数量;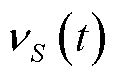 为联盟
为联盟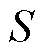 参与需求响应的网损与节点电压偏差加权和,具体见式(1);
参与需求响应的网损与节点电压偏差加权和,具体见式(1);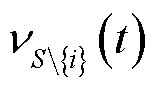 为联盟
为联盟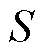 除去第
除去第 个VPP时,参与需求响应的网损与节点电压偏差加权和。
个VPP时,参与需求响应的网损与节点电压偏差加权和。
考虑本地奖励与全局奖励,智能体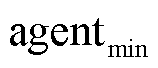 和
和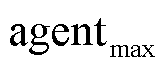 的奖励函数分别表示为
的奖励函数分别表示为
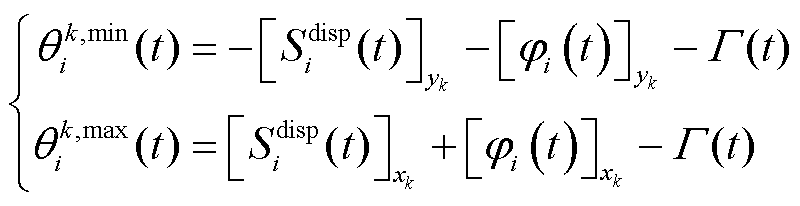 (34)
(34)
式中,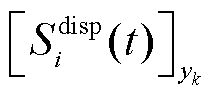 为不确定性变量取值为
为不确定性变量取值为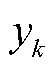 情况下VPP的经济成本;
情况下VPP的经济成本;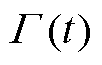 为配电网安全约束惩罚项,具体表示为
为配电网安全约束惩罚项,具体表示为
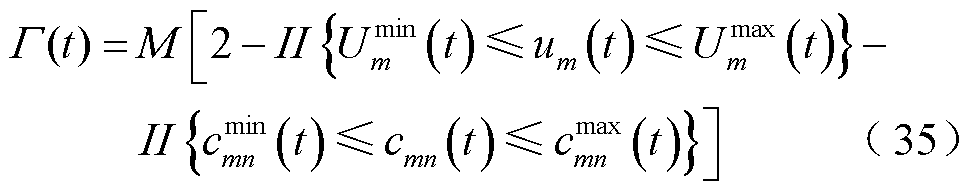
式中,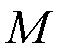 为很大的正数;
为很大的正数;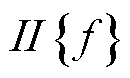 为事件函数,若
为事件函数,若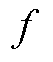 为真,则
为真,则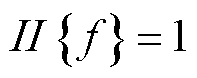 ,反之,
,反之,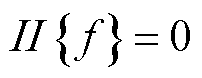 。
。
为求解VPP鲁棒优化调度问题,本文提出联邦对抗DQN算法,其原理如图3所示。每个VPP包含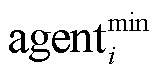 和
和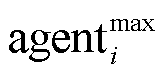 两个智能体,分别用于求解解耦之后的最小化和最大化优化问题,从而实现VPP鲁棒优化调度问题的对抗求解。两智能体结构对称,以
两个智能体,分别用于求解解耦之后的最小化和最大化优化问题,从而实现VPP鲁棒优化调度问题的对抗求解。两智能体结构对称,以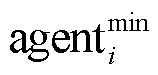 为例,包括评估网络
为例,包括评估网络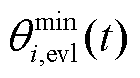 、目标网络
、目标网络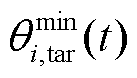 以及经验回放池
以及经验回放池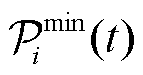 等结构。其中,
等结构。其中,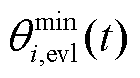 负责量化和拟合高维状态空间下的状态-动作价值,即表征动作累积奖励值的Q值
负责量化和拟合高维状态空间下的状态-动作价值,即表征动作累积奖励值的Q值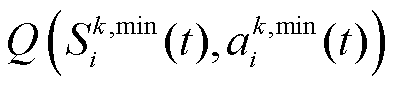 ,并以此为依据优化VPP的鲁棒调控策略。
,并以此为依据优化VPP的鲁棒调控策略。
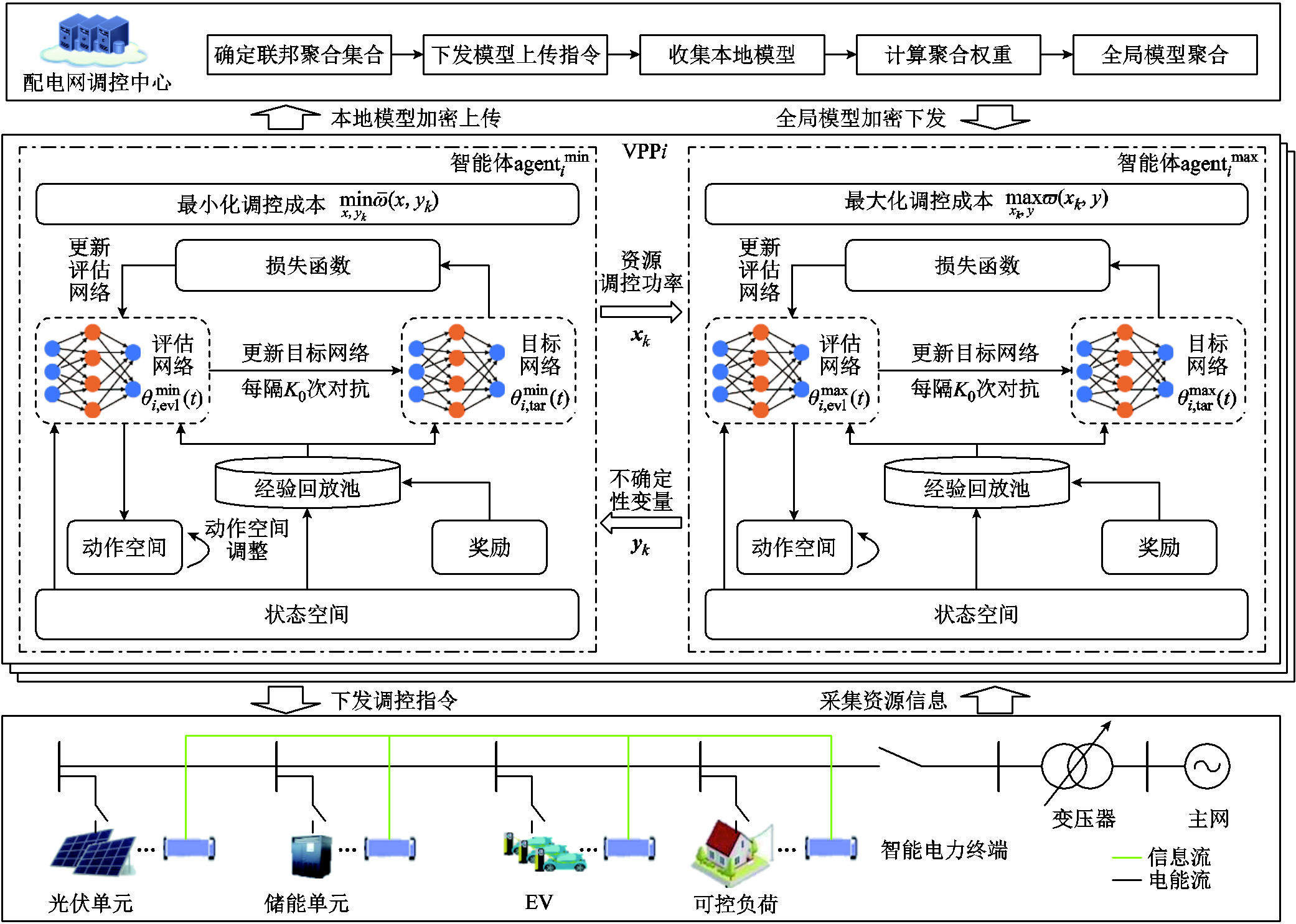
图3 基于联邦对抗DQN的VPP需求响应鲁棒优化调度算法
Fig.3 Principle of federated adversarial DQN-based robust optimization scheduling algorithm for VPP demand response
两个智能体与环境进行持续交互,学习最优需求响应调度策略,并结合另一智能体的输出结果训练模型,互相迭代对抗,提高算法的收敛速度,得到鲁棒最优解。VPP基于智能体对抗求解的鲁棒调控策略调控其所覆盖资源参与需求响应,并且每隔一定时间将其本地智能体网络模型参数上传至配电网调控中心;调控中心在收集到所有VPP的本地智能体模型参数之后,进行全局模型的联邦聚合,并及时将全局模型参数下发至各个VPP。各VPP通过调控中心所下发的全局模型在保证自身数据隐私安全的情况下实现经验共享,有效提高VPP本地智能体学习效果。所提算法流程如图4所示,主要包括对抗初始化、需求响应策略对抗优化与执行、本地模型训练和全局联邦聚合四个步骤,具体步骤介绍如下。
1)对抗初始化
各VPP初始化本地模型参数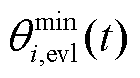 、
、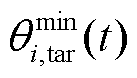 和
和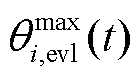 、
、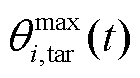 ,并与环境进行预交互以初始化经验回放池
,并与环境进行预交互以初始化经验回放池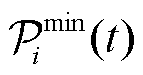 。
。
2)需求响应策略对抗优化与执行
(1)设置不确定性变量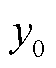 为其下界,设置对抗终止条件
为其下界,设置对抗终止条件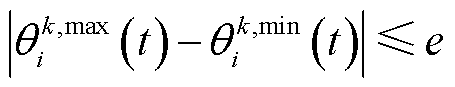 ,其中,
,其中,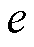 为迭代精度,初始化对抗轮次
为迭代精度,初始化对抗轮次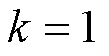 。
。
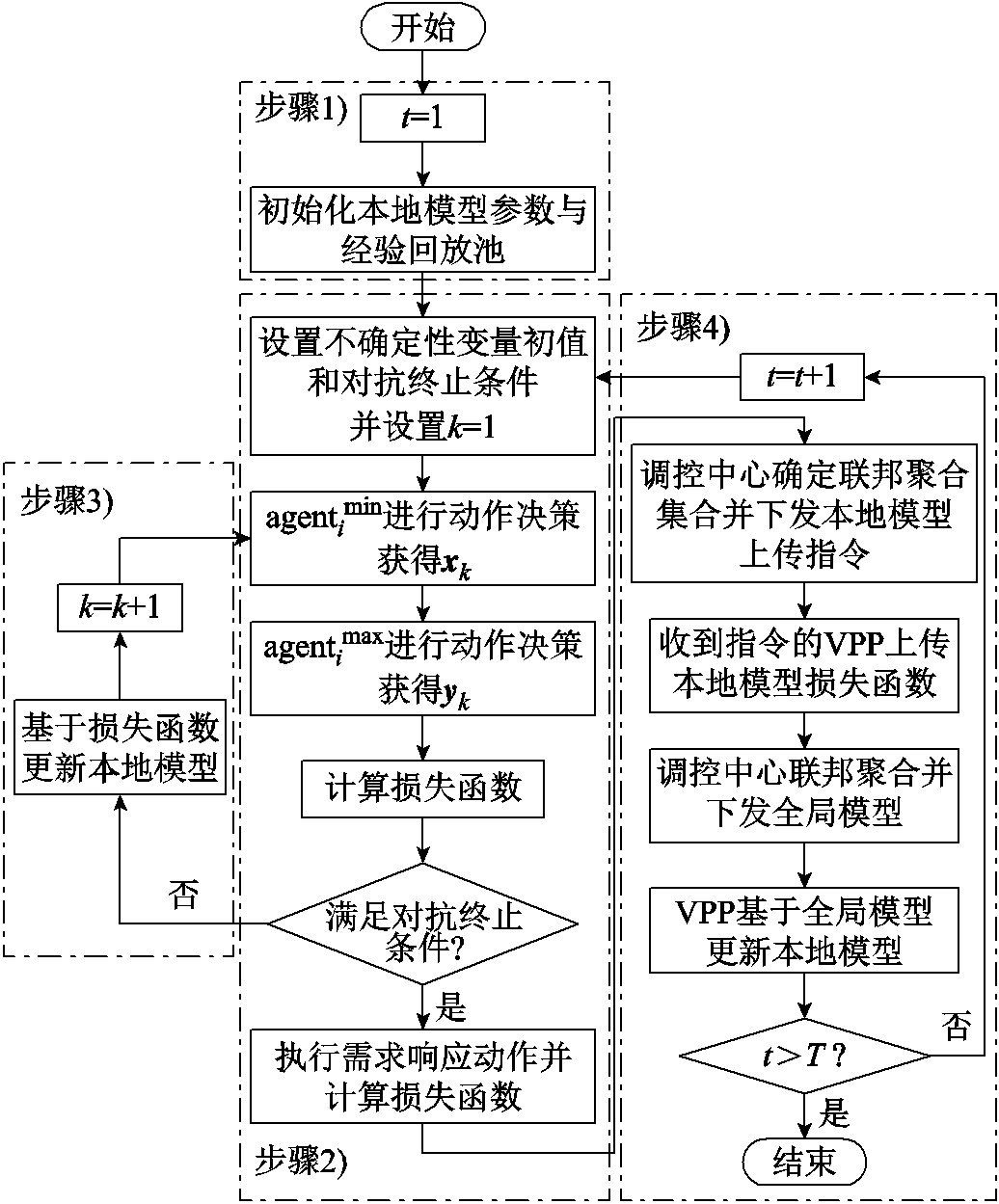
图4 所提算法流程
Fig.4 Proposed algorithm flow chart
(2)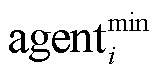 根据不确定性变量
根据不确定性变量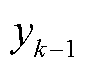 确定状态
确定状态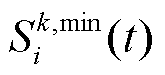 ,并将状态输入评估网络
,并将状态输入评估网络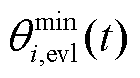 ,得到状态-动作Q值,并基于Q值选择动作,表示为
,得到状态-动作Q值,并基于Q值选择动作,表示为
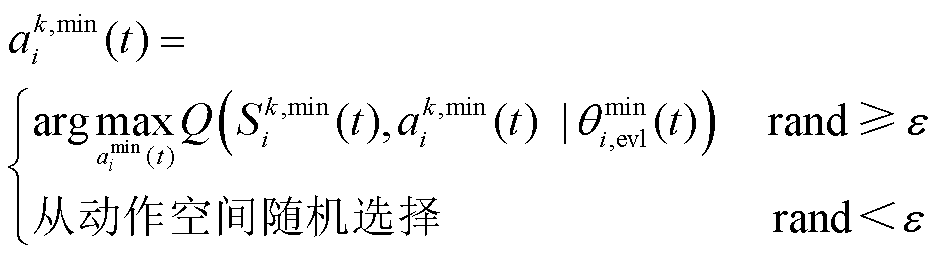 (36)
(36)
(3)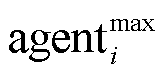 根据
根据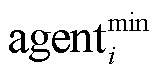 所选动作
所选动作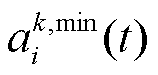 确定状态向量
确定状态向量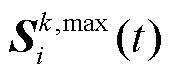 ,并将状态输入评估网络
,并将状态输入评估网络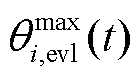 ,得到状态-动作Q值,然后采用类似方法选择动作
,得到状态-动作Q值,然后采用类似方法选择动作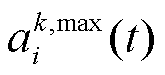 。
。
(4)VPP基于两个智能体的动作,根据式(34)计算奖励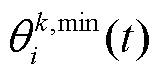 和
和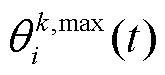 ,并将新的经验信息存入经验回放池。然后,从
,并将新的经验信息存入经验回放池。然后,从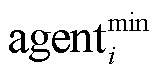 经验回放池中随机抽取一组经验数据集
经验回放池中随机抽取一组经验数据集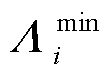 ,计算其损失函数为
,计算其损失函数为
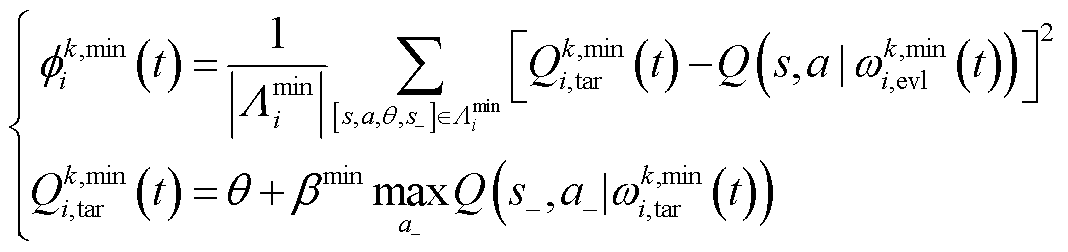 (37)
(37)
式中,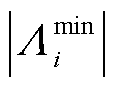 为所抽取样本数量;
为所抽取样本数量;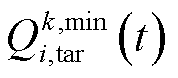 为目标Q值;
为目标Q值;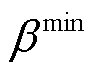 为折扣因子。采用类似方法计算
为折扣因子。采用类似方法计算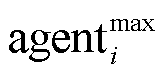 损失函数
损失函数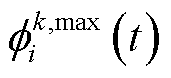 。
。
(5)判断是否满足对抗终止条件,若不满足,则继续执行步骤3);若满足,则VPP执行动作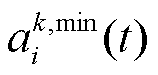 和
和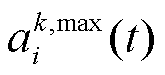 ,调控其内部资源参与需求响应,并执行步骤4)。
,调控其内部资源参与需求响应,并执行步骤4)。
3)本地模型训练
根据损失函数更新两个智能体的本地模型,更新方法为
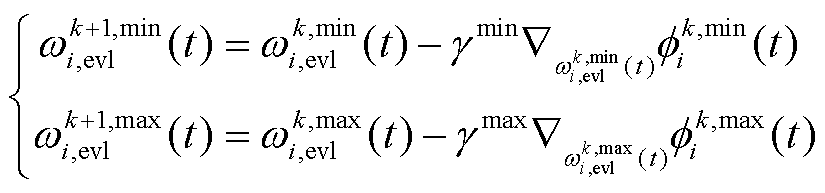 (38)
(38)
式中,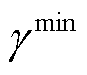 和
和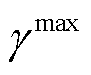 分别为两个智能体的学习速率。
分别为两个智能体的学习速率。
每隔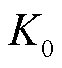 次对抗,两个智能体将评估网络参数复制于目标网络,以此来提高学习效果的稳定性。
次对抗,两个智能体将评估网络参数复制于目标网络,以此来提高学习效果的稳定性。
设置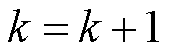 ,重复执行步骤2)到步骤3)。
,重复执行步骤2)到步骤3)。
4)全局联邦聚合
(1)配电网调控中心根据各个VPP全局贡献确定联邦聚合集合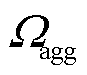 ,设定贡献阈值
,设定贡献阈值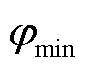 ,全局贡献不低于上述阈值的VPP将会被放入集合中,参与全局模型联邦聚合;反之,全局贡献低于上述阈值的VPP则不参与聚合。
,全局贡献不低于上述阈值的VPP将会被放入集合中,参与全局模型联邦聚合;反之,全局贡献低于上述阈值的VPP则不参与聚合。
(2)调控中心向集合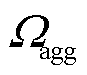 中的VPP下发本地模型上传指令,接收到指令的VPP将其损失函数
中的VPP下发本地模型上传指令,接收到指令的VPP将其损失函数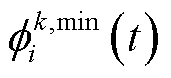 上传至调控中心。调控中心接收到所有VPP的损失函数之后,基于各VPP的全局贡献,进行全局模型联邦聚合,具体表示为
上传至调控中心。调控中心接收到所有VPP的损失函数之后,基于各VPP的全局贡献,进行全局模型联邦聚合,具体表示为
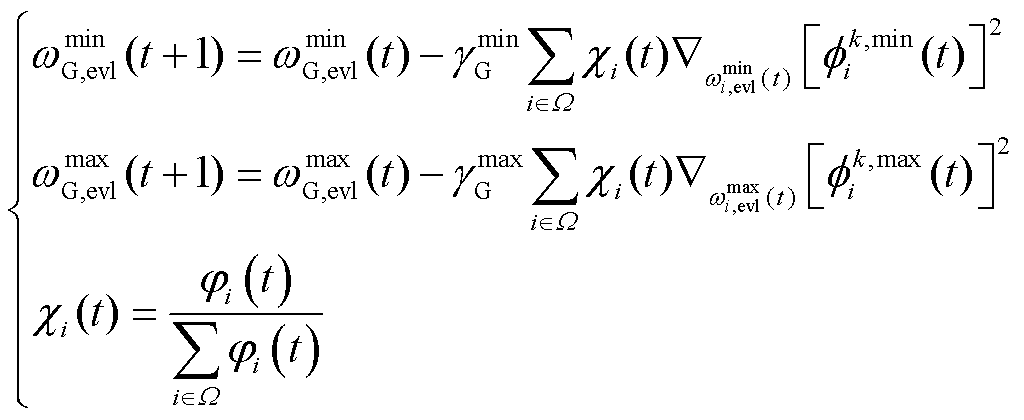 (39)
(39)
(3)配电网调控中心完成全局模型联邦聚合之后,将全局模型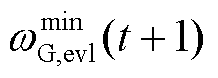 和
和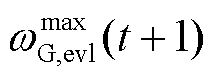 下发至各VPP。各VPP收到全局模型之后,将全局模型参数赋值于本地模型实现本地模型的更新。
下发至各VPP。各VPP收到全局模型之后,将全局模型参数赋值于本地模型实现本地模型的更新。
设置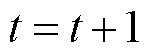 ,重复执行步骤2)~步骤4),直到
,重复执行步骤2)~步骤4),直到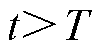 。
。
为了验证所提算法及模型的有效性,本文构建电力-通信-交通耦合网络的仿真场景,场景基于改进IEEE 33节点模型,如图5所示,其中电力网络包含四个VPP,各VPP内的资源具体分布见表1[20-21],其中EV聚合商容量与实时在网EV数量有关,本文考虑500辆EV随机分布在各VPP中,EV电池容量、充放电功率及初始荷电状态等参数参考文献[22-23]设置,当EV离网时需要满足其目标荷电状态要求。仿真所使用的计算机配置为Intel(R) Core(TM) i7-10875H CPU@2.30 GHz,16 GB内存。
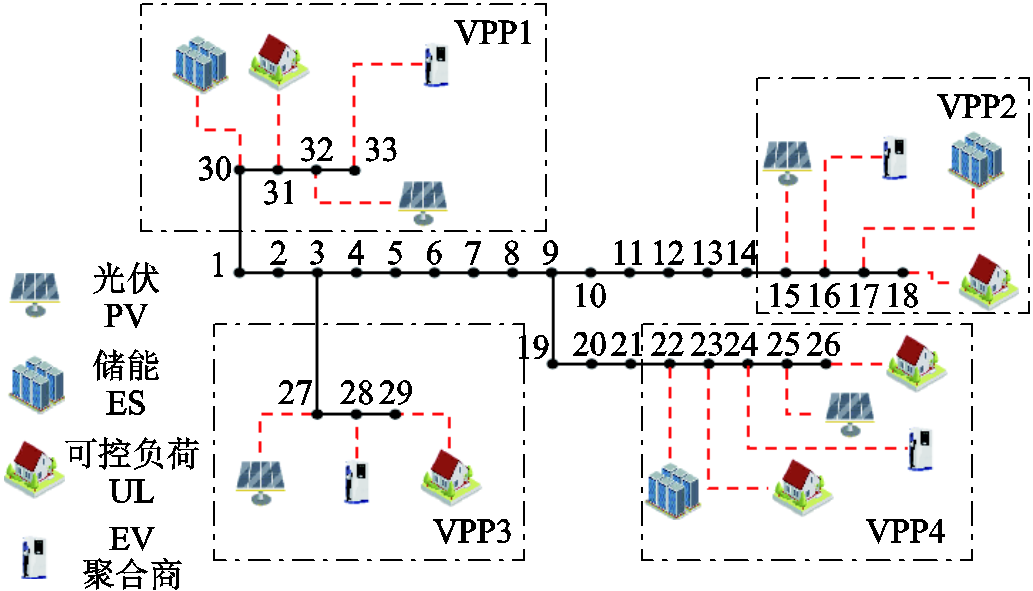
图5 仿真场景
Fig.5 Simulation scenario
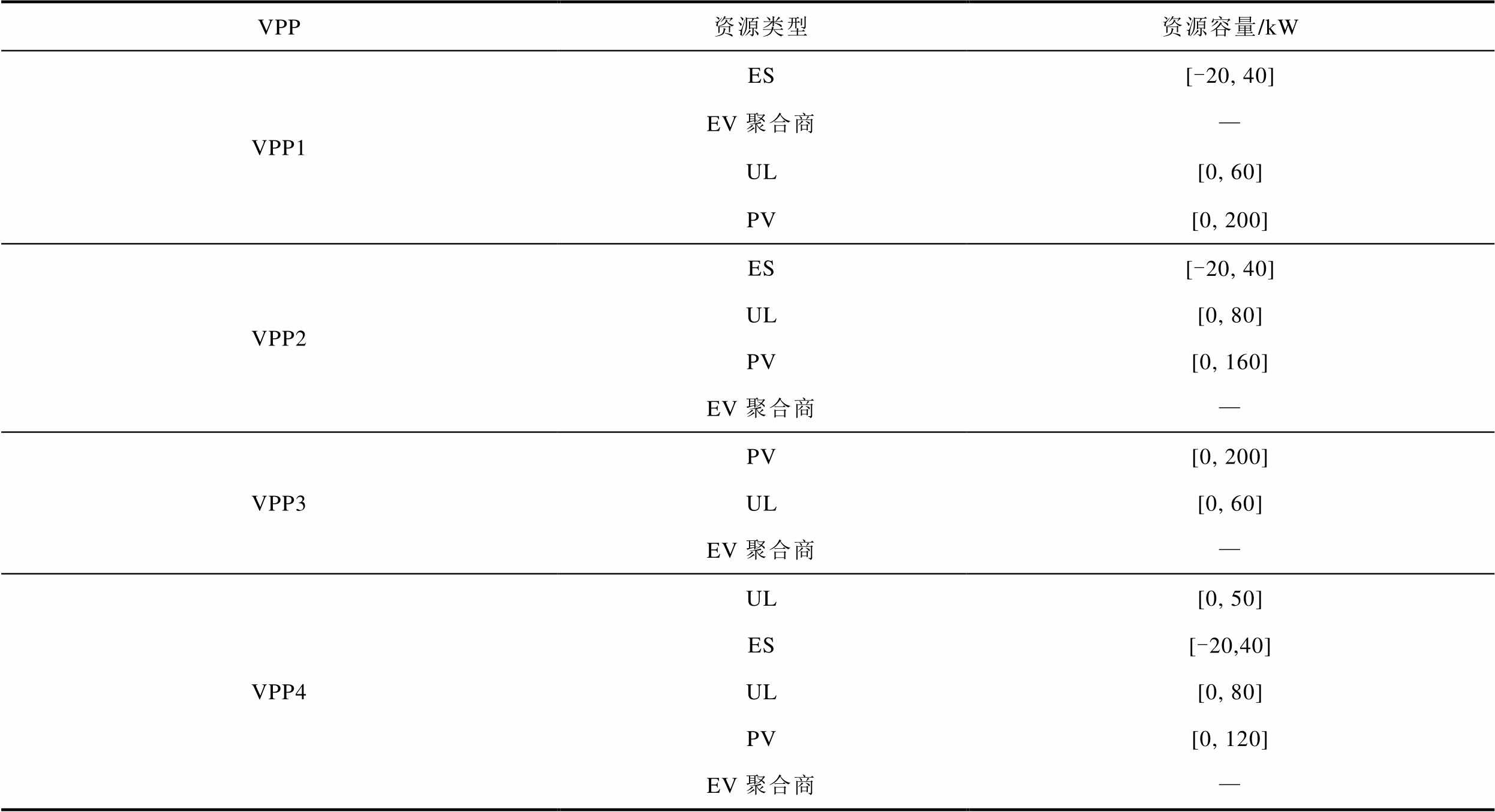
表1 仿真场景资源设置
Tab.1 Simulation scenario resource settings
VPP资源类型资源容量/kW VPP1ES[-20, 40] EV聚合商— UL[0, 60] PV[0, 200] VPP2ES[-20, 40] UL[0, 80] PV[0, 160] EV聚合商— VPP3PV[0, 200] UL[0, 60] EV聚合商— VPP4UL[0, 50] ES[-20,40] UL[0, 80] PV[0, 120] EV聚合商—
调控指令通信时延存在不确定性,在时间区间55 ms内服从高斯分布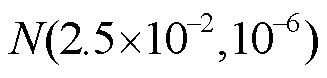 [24]。接口设备的平均恢复时间和平均失效时间分别为12 h和168 000 h,通信链路的平均恢复时间和平均失效时间分别为4 h和11 750 000 h[25]。修复率
[24]。接口设备的平均恢复时间和平均失效时间分别为12 h和168 000 h,通信链路的平均恢复时间和平均失效时间分别为4 h和11 750 000 h[25]。修复率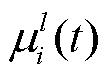 可以根据平均恢复时间求得,失效率
可以根据平均恢复时间求得,失效率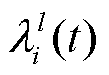 可以通过平均失效时间求得,其余通信网参数参考文献[26-27]设置。文献[28]设置分时电价,EV参与需求响应存在不确定性,在设置的充放电价下,EV充、放电响应率范围分别为
可以通过平均失效时间求得,其余通信网参数参考文献[26-27]设置。文献[28]设置分时电价,EV参与需求响应存在不确定性,在设置的充放电价下,EV充、放电响应率范围分别为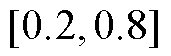 与
与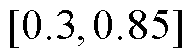 。其余仿真参数见表2。
。其余仿真参数见表2。
表2 仿真参数
Tab.2 Simulation parameters

参数数值 T24 I4 /(元/kW)0.2 400 0.4 ,0.35,0.2 0.1 ,0.001
为了验证所提算法的有效性,本文将所提算法与两种现有算法进行对比,对比算法1采用传统DQN算法,基于单智能体进行分布式求解。对比算法2首先将双层优化问题的内层max问题做对偶变换,将原优化问题转换合并为单层优化问题,然后采用粒子群算法进行求解[29]。
图7展示了不同算法对于VPP1内部各资源参与需求响应优化的对比结果。由图7a可知,经过所提算法优化后,VPP1内部的负荷峰谷差从173.9 kW降低至113.7 kW,下降了34.62%。由图7b、图7c可知,两种对比算法优化后的负荷峰谷差分别为135.9 kW和155.9 kW,相较所提算法分别高19.53%和37.12%。此外,对比三种算法的储能容量变化曲线可知,所提算法在电价谷段、强光照时段充分调控储能资源存储电能,进而在电价峰段调控储能资源出力,有效降低全局成本。而两种对比算法的储能容量曲线变化幅度较小,无法在不确定性因素下充分利用储能资源。其原因在于,所提算法考虑可控负荷、购售电、储能、EV等多种方式充分消纳具有不确定性的光伏出力功率,保障了节点电压稳定性及较低网损,提高了不确定性情况下的全局收益。各VPP的经济成本对比见表3,所提算法总成本相较于对比算法1和对比算法2分别下降了15.13%和24.33%,这是由于所提算法通过Shapley值法对全局奖励进行分配,对各智能体学习方向进行有效引导,提高了智能体学习效果,有效降低了总经济成本。
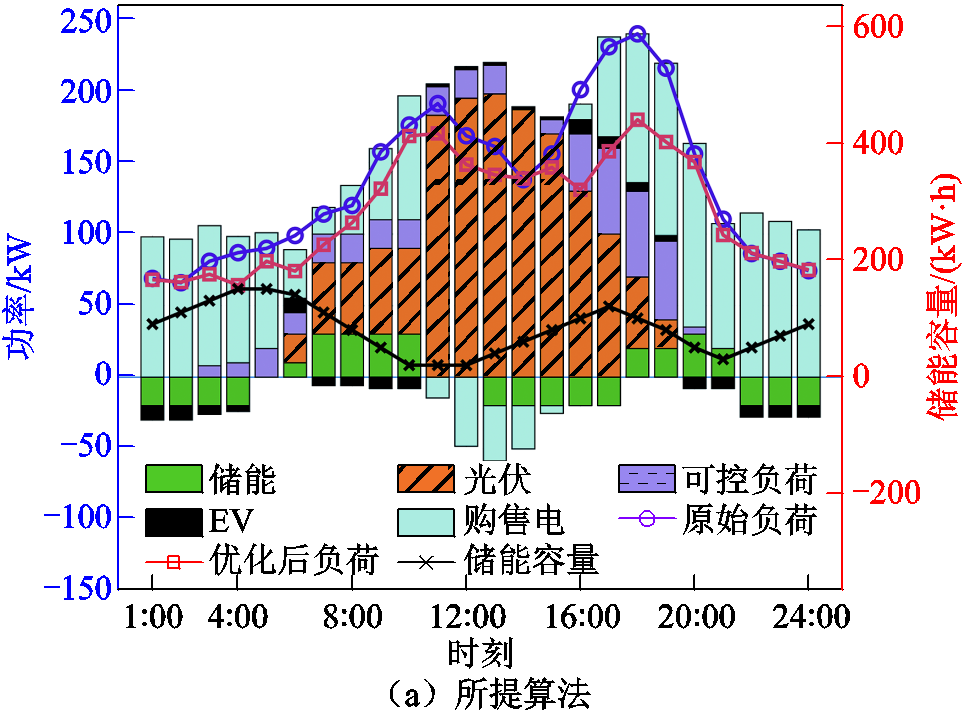

图6 不同算法下VPP1需求响应结果及ES容量变化曲线
Fig.6 Demand response results and energy storage capacity curves of VPP1 under different algorithms
表3 经济成本对比
Tab.3 Economic cost comparison (单位:元)

算法VPP1VPP 2VPP 3VPP 4总成本 所提算法1 940.51 628.51 844.21 552.36 965.5 对比算法12 135.51 968.12 214.31 889.28 207.1 对比算法22 525.52 237.22 328.52 113.39 204.5
图7展示了50次仿真中配电网网损及节点电压波动的优化结果。所提算法的平均网损相较于对比算法分别下降了14.83%和19.76%,且50次实验的波动区间明显小于对比算法。此外,相比于对比算法,所提算法节点电压波动分别降低了11.79%和18.54%。这是由于所提算法采用了联邦学习的方式训练智能体,在保障各智能体数据安全的同时,促进智能体间的经验交流,共享全局经验,从而避免各智能体陷入本地局部最优解,促进各智能体相互协调搜索全局最优解,有效地提高全局效益。同时,所提算法充分考虑了通信不确定性的影响,基于通信指标设计了智能体动作空间调整机制,可以降低通信差的资源的出力占比,有效地提高了系统鲁棒性,减小各种场景下的网损波动。
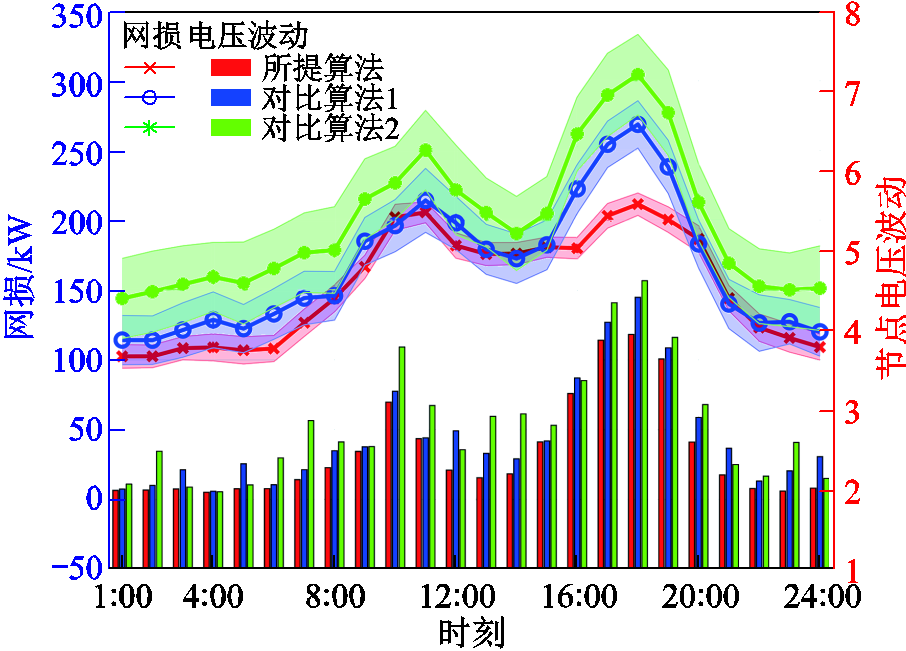
图7 配电网网损优化结果
Fig.7 Distribution grid loss optimization results
表4展示了不同资源数量下各算法收敛时间,由表可知,所提算法在资源数量较少时,收敛时间没有明显优势,随着资源数量上升,所提算法收敛时间的增幅远小于传统DQN算法,在调控20个资源的情况下,所提算法收敛速度相比传统DQN提升了12.1%。这是由于所提算法构建了对抗DQN分别求解双层优化问题,互相迭代对抗,提高算法的收敛速度,同时考虑了多VPP间的联邦学习,通过VPP间的模型共享,进一步提升了算法收敛速度。
表4 不同资源数量下各算法收敛时间
Tab.4 Convergence time of each algorithm under different number of resources (单位:s)

资源数量1214161820 所提DQN384449621843978 传统DQN3725186979321 096
为验证所提算法的鲁棒性和经济性,选择12:00—13:00时段,通过蒙特卡洛模拟方法,对节点处光伏不确定性因子、通信不确定性变量和EV充放电响应率进行随机采样,构建了80个随机场景,其中恶劣程度排名前3的场景分别为80、68与23。将所有场景代入鲁棒优化模型进行求解,为了验证所提算法的鲁棒性,将场景的不确定性变量设定为已知量,求解出实时最优解与所提算法求得的鲁棒最优解进行对比。
图8、图9分别展示了不同场景的节点电压分布及配电网网损、调控成本。由图8b可知,鲁棒最优解导致的电压分布未出现电压越界场景,电压约束得到满足。通过图8a、图8b对比可知,鲁棒最优解的电压优化效果稍差于实时最优解,这是由于所提算法在不确定性情况下为了保证最劣情况下的最优收益,采用了保守性策略,相对牺牲了一般情况下的全局收益。由图9可知,一般情况下鲁棒最优解的网损和调控成本表现均差于实时最优解,场景恶劣程度越高二者越接近,在最劣场景80下二者的表现一致。最劣场景80实时最优解的网损和成本最大,但鲁棒最优解的网损和成本最小,这说明场景80确实造成了最劣场景,同时鲁棒最优解在最极端的情况下具有最优性。

图8 不同场景的节点电压分布
Fig.8 Voltage distribution of nodes in different scenarios
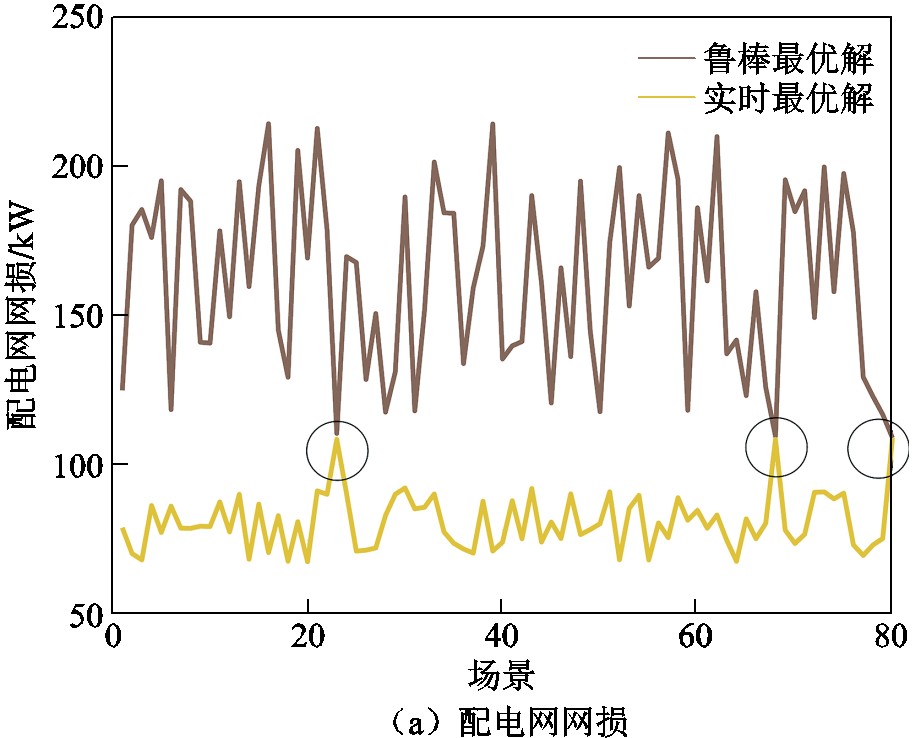
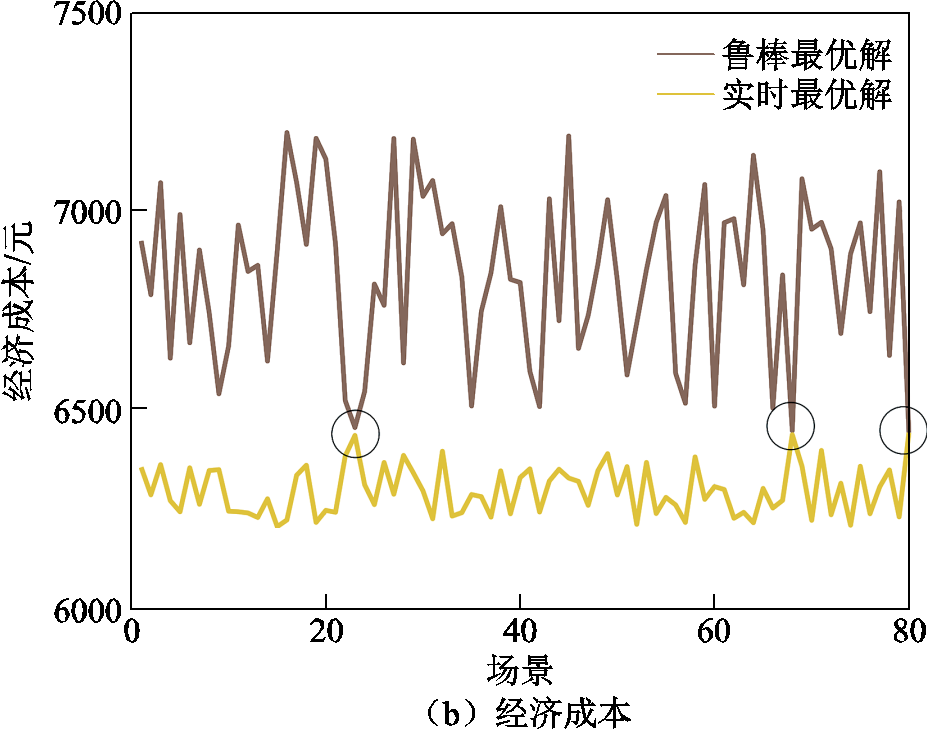
图9 网损和经济成本的鲁棒最优解与实时最优解对比
Fig.9 Comparison of robust and real-time optimal solutions for grid loss and economic cost
为提高电力-通信-交通耦合网络不确定性场景下VPP优化调度鲁棒性,本文提出计及电力-通信-交通耦合网络不确定性的VPP鲁棒优化调度方法。首先,构建电力-通信-交通耦合网络模型,并以最小化网损、节点电压偏差、VPP经济成本的加权和为目标建立优化问题。其次,分析来自电力-通信-交通三个网络的不确定性因素,并构建计及电力-通信-交通耦合网络不确定性的VPP鲁棒优化调度问题。最后,提出一种基于联邦对抗DQN的VPP鲁棒优化调度求解算法,通过双智能体之间的不断迭代,实现鲁棒最优策略的对抗求解。仿真结果表明,在考虑电力-通信-交通耦合网络不确定性因素的场景中,所提算法在保障鲁棒性的同时实现了极端场景下的性能最优,相较于对比算法,所提方法的VPP经济成本分别降低了15.13%和24.33%,网损分别降低了14.83%和19.76%,节点电压波动降低了11.79%和18.54%。在未来研究中,作者将考虑实时动态交通流变化对VPP需求响应优化调度的影响。此外,为了进一步提升整体调控收益,作者将进一步结合市场规律,开展计及三网耦合不确定性的日前-日内双阶段鲁棒优化研究。
参考文献
[1] 姜飞, 刘利波, 裴翔羽, 等. 综合能源系统智慧运维技术综述及展望[J]. 电气工程学报, 2025, 20(1): 170-187.
Jiang Fei, Liu Libo, Pei Xiangyu, et al. Review and prospect of intelligent operation and maintenance of integrated energy systems[J]. Journal of Electrical Engineering, 2025, 20(1): 170-187.
[2] 杨蒙, 陈玥, 徐潇源, 等. 电力-交通融合研究综述:模型、算法与关键问题[J]. 电力系统自动化, 2025, 49(9): 1-16.
Yang Meng, Chen Yue, Xu Xiaoyuan. Review on research of power-transportation fusion: models, algorithms and key problems[J]. Automation of Electric Power Systems, 2025, 49(9): 1-16.
[3] 陈亚鹏, 杨阳, 姚锦清, 等.计及双网耦合特性的电力业务风险自适应均衡方法[J].中国电机工程学报, 2025, 45(4): 1359-1369.
ChenYapeng, YangYang, Yao Jinqing, et al. An Adaptive risk equalization method for power services considering dual-network coupling characteristics[J]. Proceedings of the CSEE, 2025, 45(4): 1359-1369.
[4] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477.
Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electro-technical Society, 2022, 37(21): 5462-5477.
[5] 李翔宇, 赵冬梅. 分散架构下多虚拟电厂分布式协同优化调度[J]. 电工技术学报, 2023, 38(7): 1852-1863.
Li Xiangyu, Zhao Dongmei. Distributed coordinated optimal scheduling of multiple virtual power plants based on decentralized control structure[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1852-1863.
[6] 韩丽, 王冲, 于晓娇, 等. 考虑风电爬坡灵活调节的碳捕集电厂低碳经济调度[J]. 电工技术学报, 2024, 39(7): 2033-2045.
Han Li, Wang Chong, Yu Xiaojiao, et al. Low-carbon and economic dispatch considering the carbon capture power plants with flexible adjustment of wind power ramp[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2033-2045.
[7] 李明扬, 窦梦园. 基于强化学习的含电动汽车虚拟电厂优化调度[J]. 综合智慧能源, 2024, 46(6): 27-34.
Li Mingyang, Dou Mengyuan. Optimal scheduling of virtual power plants integrating electric vehicles based on reinforcement learning[J]. Integrated Intelligent Energy, 2024, 46(6): 27-34.
[8] 张超, 赵冬梅, 季宇, 等. 基于改进深度Q网络的虚拟电厂实时优化调度[J]. 中国电力, 2024, 57(1): 91-100.
Zhang Chao, Zhao Dongmei, Ji Yu, et al. Real time optimal dispatch of virtual power plant based on improved deep Q network[J]. Electric Power, 2024, 57(1): 91-100.
[9] Huang Huakun, Xue Sihui, Zhao Lingjun, et al. Privacy-preserving smart energy management by consumer-electronic chips and federated learning[J]. IEEE Transactions on Consumer Electronics, 2024, 70(1): 2200-2209.
[10] Feng Bin, Liu Zhuping, Huang Gang, et al. Robust federated deep reinforcement learning for optimal control in multiple virtual power plants with electric vehicles[J]. Applied Energy, 2023, 349: 121615.
[11] Liu Haotian, Wu Wenchuan. Federated reinforcement learning for decentralized voltage control in distribution networks[J]. IEEE Transactions on Smart Grid, 2022, 13(5): 3840-3843.
[12] 刘鑫, 李扬, 史云鹏, 等. 计及用户参与不确定性的虚拟电厂分布鲁棒优化模型[J]. 电力自动化设备, 2022, 42(7): 84-93.
Liu Xin, Li Yang, Shi Yunpeng, et al. Distributionally robust optimization model of virtual power plant considering user participation uncertainty[J]. Electric Power Automation Equipment, 2022, 42(7): 84-93.
[13] Wu Huayi, Dong Ping, Liu Mingbo. Distribution network reconfiguration for loss reduction and voltage stability with random fuzzy uncertainties of renewable energy generation and load[J]. IEEE Transactions on Industrial Informatics, 2020, 16(9): 5655-5666.
[14] 顾佳琪, 郭左, 孙翔宇, 等. 高光伏渗透下考虑源荷不确定性的含分布式储能的综合能源系统规划[J]. 电气工程学报, 2024, 19(3): 362-376.
GuJiaqi, GuoZuo, SunXiangyu, et al. Integrated energy system planning with distributed energy storageconsidering source load uncertainty under high PV penetration[J]. Journal of Electrical Engineering, 2024, 19(3):362-376.
[15] 张巍, 祝童童, 苏瑾. 考虑电动汽车和5G基站的电力-信息-交通耦合网络需求响应策略[J]. 电力系统自动化, 2024, 48(7): 116-126.
Zhang Wei, Zhu Tongtong, Su Jin. Demand response strategy for power-cyber-transportation coupling network considering electric vehicles and 5G base stations[J]. Automation of Electric Power Systems, 2024, 48(7): 116-126.
[16] 肖钰皓, 李科, 苏军, 等. 大规模可调节资源多级聚合参与互动响应数据需求及潜力分析方法[J]. 四川电力技术, 2024, 47(1): 28-34, 71.
Xiao Yuhao, Li Ke, Su Jun, et al. Interactive response data demand and potential analysis method for multilevel aggregation of large-scale adjustable resources[J]. Sichuan Electric Power Technology, 2024, 47(1): 28-34, 71.
[17] Yan Xingyu, Gao Ciwei, Song Meng, et al. An IGDT-based day-ahead co-optimization of energy and reserve in a VPP considering multiple uncertainties[J]. IEEE Transactions on Industry Applications, 2022, 58(3): 4037-4049.
[18] 袁桂丽, 苏伟芳. 计及电动汽车不确定性的虚拟电厂参与AGC调频服务研究[J]. 电网技术, 2020, 44(7): 2538-2548.
Yuan Guili, Su Weifang. Virtual power plants providing AGC FM service considering uncertainty of electric vehicles[J]. Power System Technology, 2020, 44(7): 2538-2548.
[19] 康田园, 刘科研, 贾东梨, 等. 计及分布式电源出力不确定性的虚拟电厂鲁棒优化调度[J]. 电力信息与通信技术, 2024, 22(2): 16-24.
Kang Tianyuan, Liu Keyan, Jia Dongli, et al. Robust optimal scheduling of virtual power plant considering output uncertainty of distributed generation[J]. Electric Power Information and Communication Technology, 2024, 22(2): 16-24.
[20] 许翔泰, 张仰飞, 陈光宇, 等. 计及光伏发电的电动汽车充电优化调度研究[J]. 智慧电力, 2019, 47(10): 44-50.
Xu Xiangtai, Zhang Yangfei, Chen Guangyu, et al. Optimal scheduling of charging for electric vehicle considering photovoltaic power generation[J]. Smart Power, 2019, 47(10): 44-50.
[21] 刘友波, 王晴, 曾琦, 等. 能源互联网背景下5G网络能耗管控关键技术及展望[J]. 电力系统自动化, 2021, 45(12): 174-183.
Liu Youbo, Wang Qing, Zeng Qi, et al. Key technologies and prospects of energy consumption management for 5G network in background of energy Internet[J]. Automation of Electric Power Systems, 2021, 45(12): 174-183.
[22] 侯慧, 唐俊一, 王逸凡, 等. 价格与激励联合需求响应下电动汽车长时间尺度充放电调度[J]. 电力系统自动化, 2022, 46(15): 46-55.
Hou Hui, Tang Junyi, Wang Yifan, et al. Long-time-scale charging and discharging scheduling of electric vehicles under joint price and incentive demand response[J]. Automation of Electric Power Systems, 2022, 46(15): 46-55.
[23] 潘超, 汤中卫, 廖海君, 等. 基于非对称一致性学习的多类型电动汽车协同参与需求响应方法[J]. 电工技术学报, 2025, 40(7): 2178-2190.
Pan Chao, TangZhongwei, Liao Haijun, et al. Asymmetric consensus learning-based multi-type electric vehicle collaborative participation demand response method[J]. Transactions of China Ele-ctrotechnical Society, 2025, 40(7): 2178-2190.
[24] 孟广雨, 于洁潇, 杨挺. 基于随机网络演算的分布式能源调控系统时延上界计算[J]. 电工技术学报, 2020, 35(11): 2360-2371.
Meng Guangyu, Yu Jiexiao, Yang Ting. Upper bound calculation of delay of distributed energy resource coordinated-control system based on stochastic network calculus[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2360-2371.
[25] 任惠, 陆海涛, 卢锦玲, 等. 考虑信息物理系统耦合和用户响应差异的负荷聚合商需求响应特性分析[J]. 电网技术, 2020, 44(10): 3927-3936.
Ren Hui, Lu Haitao, Lu Jinling, et al. Analysis of LA demand response characteristics considering cyber physical system coupling and user’s response difference [J]. Power System Technology, 2020, 44(10): 3927-3936.
[26] 陈亚鹏, 杨阳, 舒乙凌, 等. 基于业务性能偏差感知的电力通信网路由优化策略[J]. 电工技术学报, 2024, 39(11): 3411-3421.
Chen Yapeng, Yang Yang, Shu Yiling, et al. Service performance deviation awareness-based power communication network routing optimization strategy [J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3411-3421.
[27] 陈亚鹏, 周振宇, 韩东升, 等. 电力+5G前传网中融合时延敏感网络技术的流量调度方法[J]. 电子学报, 2023, 51(5): 1141-1147.
Chen Yapeng, Zhou Zhenyu, Han Dongsheng, et al. TSN-integrated flow scheduling method in Power+5G fronthaul network[J]. Acta Electronica Sinica, 2023, 51(5): 1141-1147.
[28] 徐智威, 胡泽春, 宋永华, 等. 基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报, 2014, 34(22): 3638-3646.
Xu Zhiwei, Hu Zechun, Song Yonghua, et al. Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs[J]. Proceedings of the CSEE, 2014, 34(22): 3638-3646.
[29] 齐彩娟, 陈宝生, 韦冬妮, 等. 考虑主从博弈定价模式的共享储能分布鲁棒优化配置方法研究[J]. 中国电力, 2024, 57(7): 40-53.
Qi Caijuan, Chen Baosheng, Wei Dongni, et al. Distributionally robust optimal configuration for shared energy storage based on stackelberg game[J]. Electric Power, 2024, 57(7): 40-53.
Robust Optimization Scheduling of Virtual Power Plant Considering the Uncertainty of Power-Communication-Transportation Coupling Network
Abstract As innovations in intersecting technologies, such as renewable energy generation and electrified transportation, continue to progress, the connections among the power, communication, and transportation systems are becoming increasingly closer. In the coupling network of the power-communication-transportation system, virtual power plant (VPP) utilizes advanced control, communication, and information collection technologies to aggregate and intelligently control distributed resources, actively responding to grid demands, thereby enhancing grid operational stability. However, existing VPP optimization scheduling methods overlook the impact of uncertainties in the power-communication-transportation coupling network on the optimization scheduling of VPP demand response, leading to high costs and poor robustness of scheduling. Therefore, researching a robust optimization scheduling method for VPP demand response that considers the uncertainties in the power-communication-transportation coupling network is of great significance for enhancing system reliability, security, and economic efficiency. To address this issue, this paper proposes a robust optimization scheduling method of VPP considering the uncertainty of the power-communication-transportation coupling network.
Firstly, a model of the coupling power-communication-transportation system is constructed. In the power-communication-transportation coupling model, the power grid side achieves the aggregation of resources such as renewable energy, energy storage, controllable loads, and EVs through the VPP, coordinating these resources to participate in demand response. On the transportation network side, fast-charging stations facilitate coupling with the power grid by providing charging services for EVs and allowing aggregated EV resources to participate in VPP control through EV aggregators. On the communication network side, the VPP interacts with the distribution network control center and its associated resources, exchanging parameter information and issuing control commands via heterogeneous communication methods such as Ethernet, power line carrier, and wireless networks.The optimization problem is formulated with the objective of minimizing the weighted sum of grid loss, node voltage deviation, and VPP economic cost.
Subsequently, uncertainties from the three networks are analyzed. The main uncertainty factors on the communication network side include the operational reliability of control terminals, the effectiveness of communication bandwidth fluctuations, communication delay in control commands, and communication quality. Uncertainty factors on the power grid originate from the variability in renewable energy output. This paper models power grid side uncertainty using the example of distributed photovoltaic output uncertainty. The transportation network side uncertainty mainly stems from the unpredictability of EV demand response, as the response level of privately owned EVs to incentive pricing fluctuates within a certain range. Based on the uncertainty model, a robust optimization scheduling problem considering uncertainties in the power-communication-transportation network is developed for VPP. A federated adversarial deep Q-network (DQN) based algorithm for robust optimization scheduling of VPP is proposed, where robust optimal strategies are achieved through iterative adversarial solution between two agents.
Finally, to verify the effectiveness of the proposed algorithm and model, this paper constructs a simulation scenario of a power-communication-transportation coupling network based on an improved IEEE-33 node model. The simulation results show that, compared to two traditional algorithms, the proposed algorithm reduces the VPP economic cost by 15.13% and 24.33%, network losses by 14.83% and 19.76%, and node voltage fluctuations by 11.79% and 18.54%, respectively. Under adverse conditions, the proposed algorithm can still ensure the safety of node voltage, achieving optimal performance in extreme scenarios while maintaining robustness. The algorithm effectively enables efficient and robust control of the VPP while accounting for uncertainty factors in the power-communication-transportation coupling network. In future research, the author will consider the impact of real-time dynamic traffic flow changes on the optimization scheduling of VPP demand response. Additionally, to further enhance overall control benefits, the author will conduct a two-stage robust optimization study that takes into account the uncertainties in the three-network coupling, integrating market dynamics into the analysis.
Keywords:Power-communication-transportation, virtual power plant, uncertainty, robust optimization scheduling, federated adversarial deep Q-network (DQN)
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.241189
国家电网有限公司总部科技项目(52094021N010 (5400-202199534A-0-5-ZN))和中国南方电网有限责任公司科技项目(1500002023030103JL00320)资助。
收稿日期2024-04-12
改稿日期2024-10-14
潘 超 男,1998年生,博士研究生,研究方向为智能电网分布式资源调控及物联网技术。
E-mail:chao_pan@ncepu.edu.cn
周振宇 男,1983年生,教授,博士生导师,研究方向为新型电力系统与虚拟电厂、无线通信网络与新技术、能源互联网信息通信技术等。
E-mail:zhenyu_zhou@ncepu.edu.cn(通信作者)
(编辑 郭丽军)