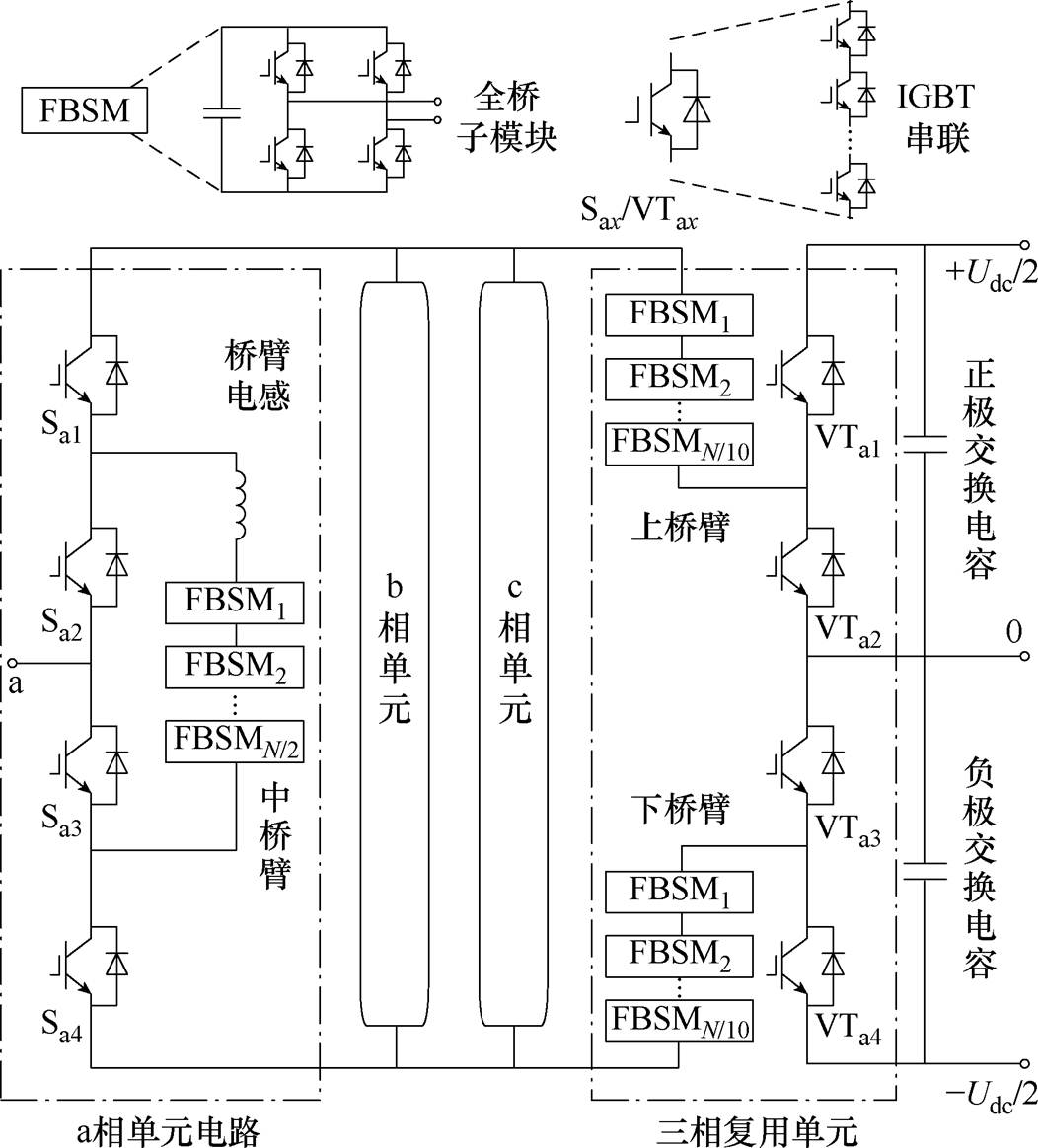
图1 混合复用型多电平换流器
Fig.1 Hybrid multiplexing MMC
摘要 为提高模块化多电平换流器(MMC)的轻型化程度,并实现混合型MMC的宽调制范围运行,该文基于桥臂时分复用和三相复用的思想引入交直流侧开关组及复用桥臂,提出了混合复用型多电平换流器(HM-MMC)及其能量均衡控制策略。在交流侧,HM-MMC通过开关组的交替导通实现桥臂的全周期时分复用,提高子模块利用率;在直流侧,HM-MMC通过三相复用桥臂和开关组的配合,构建桥臂的间接能量交换回路,并通过能量均衡控制稳定子模块电容电压,实现换流器的宽范围运行。与传统MMC相比,该混合复用型MMC拓扑的子模块数量可以降低72%左右。与混合型MMC相比,该拓扑可实现桥臂能量均衡,解决了运行范围受限问题,将固定调制比拓展为[0, 4/p]。最后,基于Matlab/Simulink的仿真结果和HM-MMC实验平台的实验结果验证了所提拓扑及控制策略的可行性。
关键词:高压直流 模块化多电平换流器 桥臂复用 能量均衡策略
模块化多电平换流器(Modular Multilevel Con- verter, MMC)凭借其模块化、拓展性强、输出波形质量高等优势,已成为柔性直流输电系统的首选方案,广泛应用于长距离高压直流(High Voltage Direct Current, HVDC)输电工程[1-2]。受电力电子器件耐压能力的限制,MMC通常采用增加级联子模块数量的方法应对高压应用场景。然而,这也导致其子模块数量过多,造成换流站占地面积大、质量重、成本高等缺点[3]。根据现有工程可知,MMC中电容的质量和体积在子模块中占比达到了80%[4]。因此,研究如何减少子模块和电容的使用对于降低建设成本、提高MMC的功率密度和实现MMC的轻型化具有重要意义。
目前,降低容值和减少电容数量是实现MMC轻型化的两种主要研究方向。在降低容值方面,已经有环流抑制、环流控制和三次谐波注入等多种方法可以通过控制手段来减小电容电压纹波,从而降低换流器对容值的要求。但MMC子模块基数较大,导致该类方法的轻型化程度有限[5]。与降低容值相比,通过改进拓扑直接减少电容数量能够更有效地实现MMC的轻型化。文献[6-13]提出了多种混合型多电平换流器来实现轻型化。该类拓扑主要包含电力电子器件串联形成的开关和子模块级联构成的桥臂。
文献[6-7]提出了一种桥臂复用模块化多电平换流器(Arm Multiplexing MMC, AM-MMC)。该换流器将每相分成三个桥臂,并对中间桥臂进行时分复用,从而减少了25%的电容器数量,提高了子模块利用率。文献[8-10]提出了一种桥臂交替多电平换流器(Alternate Arm Multilevel Converter, AAMC)。该拓扑通过在上、下桥臂分别配置开关实现桥臂的交替导通,从而使得所需的子模块数量下降。文献[11]在AM-MMC的基础上结合AAMC的桥臂交替的思想,提出了半波交替型模块化多电平换流器(Half Wave Alternating MMC, HA-MMC)。该拓扑通过导通开关和切换开关的相互配合进行桥臂子模块的复用,实现了子模块数量的进一步下降。此外,还有针对故障穿越[12]或开关损耗[13]的混合型MMC拓扑。
但此类混合型拓扑普遍存在运行点固定,无法实现宽范围调压的问题。如AAMC和HA-MMC都需要运行在固定的调制比才能实现桥臂的能量均衡。这要求交直流侧电压必须严格满足电压关系,导致换流器稳定性脆弱,轻微的电压波动都有可能在换流器中积累能量导致失稳,使用场景受限。为解决该问题,文献[14-25]提出并发展了以谐波注入、重叠角、移相角为主的多种能量均衡方式。文献[14]提出了三次谐波电流注入方法,可以大幅拓展调制范围,但需新增电流源设备,存在调制比偏离固定点时注入电流过大的问题。文献[15]则采用三次谐波电压注入,在实现能量均衡的基础上完成了电容控制优化,进一步发展了AAMC的均衡策略。文献[16-19]研究的短重叠法,存在重叠周期较短(一般为15°~18°),导致其不能在低调制比下运行的问题。此外,长重叠法[20-22]以及移相角法[23]也存在宽范围调压下拓扑子模块数量增加较多等问题。
为解决以上问题,本文在混合型拓扑的基础上,提出基于桥臂复用与三相复用的混合复用型多电平换流器(Hybrid Multiplexing MMC, HM-MMC)。针对轻型化问题,该拓扑每相单元基于桥臂复用的思想,通过交流侧开关的配合,将MMC的上下桥臂改为单一的复用桥臂,进一步降低了子模块数量,从而大幅降低了电容的使用,实现轻型化。针对固定运行点问题,拓扑通过三相复用的直流侧单元在每个周期内构建能量交换回路,大幅扩展了可控能量交换时间,使其调制比不再受限。由此,通过对桥臂的混合复用,HM-MMC可以在轻型化的基础上实现宽范围运行。
本文首先提出HM-MMC的拓扑结构,分析其桥臂模块混合复用的运行原理,并给出相应的分时调制策略;其次,针对HM-MMC的运行模式构建了桥臂能量均衡的数学模型,并在此基础上提出了均衡电流控制的方法,以实现该换流器的宽范围运行;最后,通过Matlab/Simulink搭建的仿真模型和HM-MMC的实验平台分析并验证了所提拓扑及控制策略的可行性。
为实现拓扑的轻型化,需要对MMC桥臂中的子模块数量进行优化。由于MMC在正常运行时总有上/下桥臂处于闲置状态,导致子模块的利用率较低。因此,本文所提拓扑引入桥臂时分复用的思想,从而降低子模块数量。此外,本文拓扑通过引入直流侧单元的三相复用,实现换流器的宽范围运行,形成混合复用。
所提HM-MMC的拓扑结构如图1所示,三相桥臂并联于三相复用单元两端,并由该单元连接到直流电容上。图1中b、c相与a相电路结构完全相同,每相单元由交流侧开关组(Sjx,j=a, b, c)、桥臂电感和中桥臂组成,三相复用单元含有上、下桥臂和直流侧开关组(VTjx, j=a, b, c),且与交换电容并联在直流电压Udc两端。上、中、下桥臂均由具备双极性电压输出能力的全桥子模块(Full Bridge Submodule, FBSM)级联组成,即图1所示的FBSM模块,用以控制交流侧电压的输出波形。开关由绝缘栅双极型晶体管(Insulated-Gate Bipolar Transistor, IGBT)串联构成,用以控制通断。其中,相单元的桥臂复用降低了子模块数量,而直流单元的三相复用则在此基础上实现了灵活调制。

图1 混合复用型多电平换流器
Fig.1 Hybrid multiplexing MMC
在混合复用的基础上,通过开关组的配合,中桥臂能够全周期输出交流电压,使得HM-MMC相单元仅需MMC每相子模块数量的1/4(0.5N),N为MMC单桥臂中子模块的数量。对于三相复用的上/下桥臂,当其子模块数量为0.1N,两桥臂子模块数量共0.2N时,换流器可实现宽范围运行。由此,该拓扑可将总子模块数由6N(MMC三相总子模块数)降至1.7N,降低约72%。
HM-MMC一方面通过相单元的桥臂复用实现轻型化;另一方面又由直流侧单元的三相复用构建交换回路,实现能量均衡。本节首先分析混合复用运行原理,并在此基础上提出适用于该换流器的分时调制策略。
HM-MMC的混合复用运行在工频周期内可分为整体的相单元复用运行和间隔插入的三相复用运行:①相单元复用运行,其运行模式分为正、负压引导模式,如图2所示;②三相复用运行,其运行模式分为正、负极交换模式,如图3所示。两种复用交替运行构成混合复用。
2.1.1 相单元复用运行
为简化分析,首先说明相单元桥臂复用的运行模式。如图2a所示,HM-MMC通过交流侧开关组的配合,实现中桥臂的交替复用。相单元每半个周期进行模式切换,分别运行在正、负压引导模式下。这种模式切换通过轮流导通中桥臂,全周期复用其桥臂电压,从而降低子模块数量并维持交流侧电压的高质量输出。
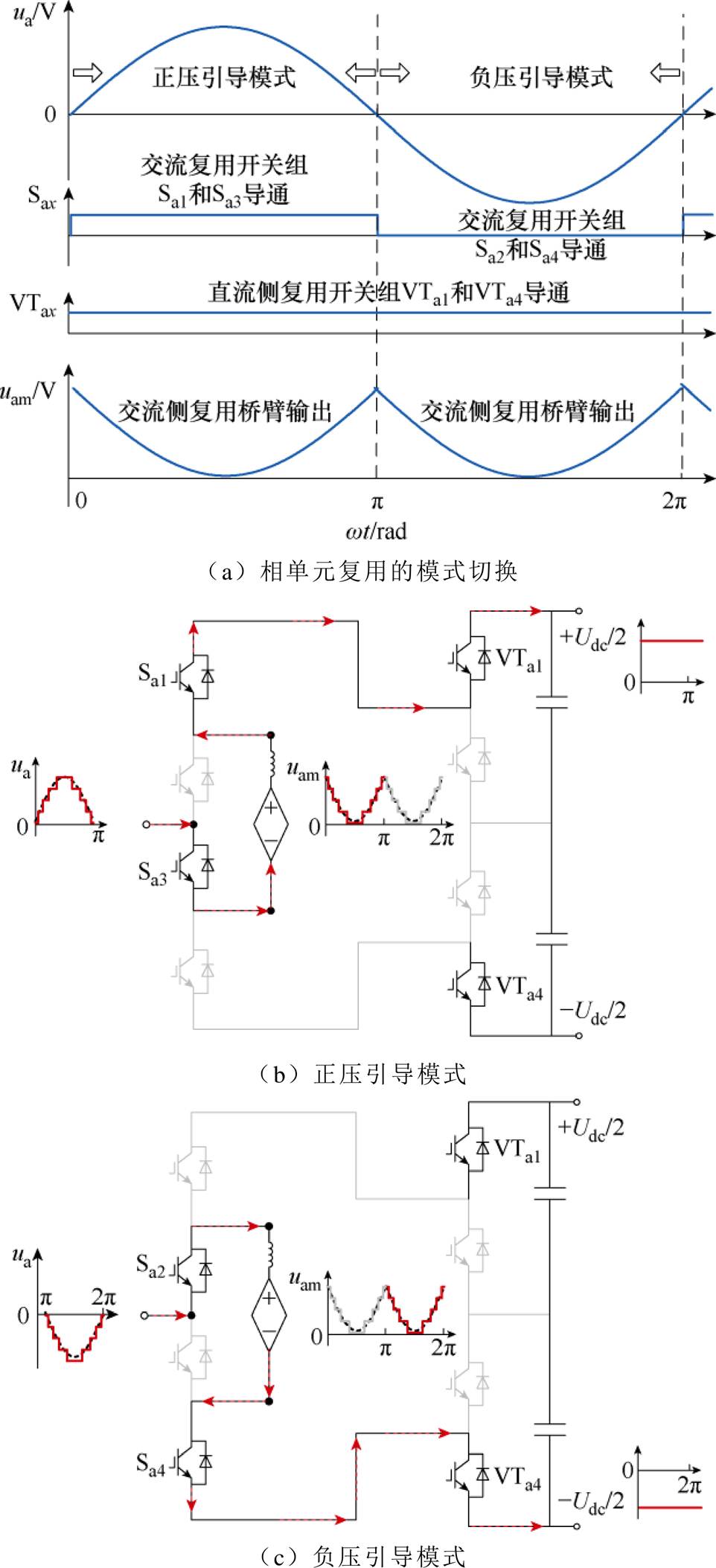
图2 HM-MMC正、负压引导模式
Fig.2 Positive and negative voltage guided operations of HM-MMC
定义Fa为a相单元的运行模式开关函数,即
 (1)
(1)
通过控制子模块的投切,中桥臂可等效为电压源。图2中a相单元等效电路,中桥臂电压uam和电流iam可分别表示为
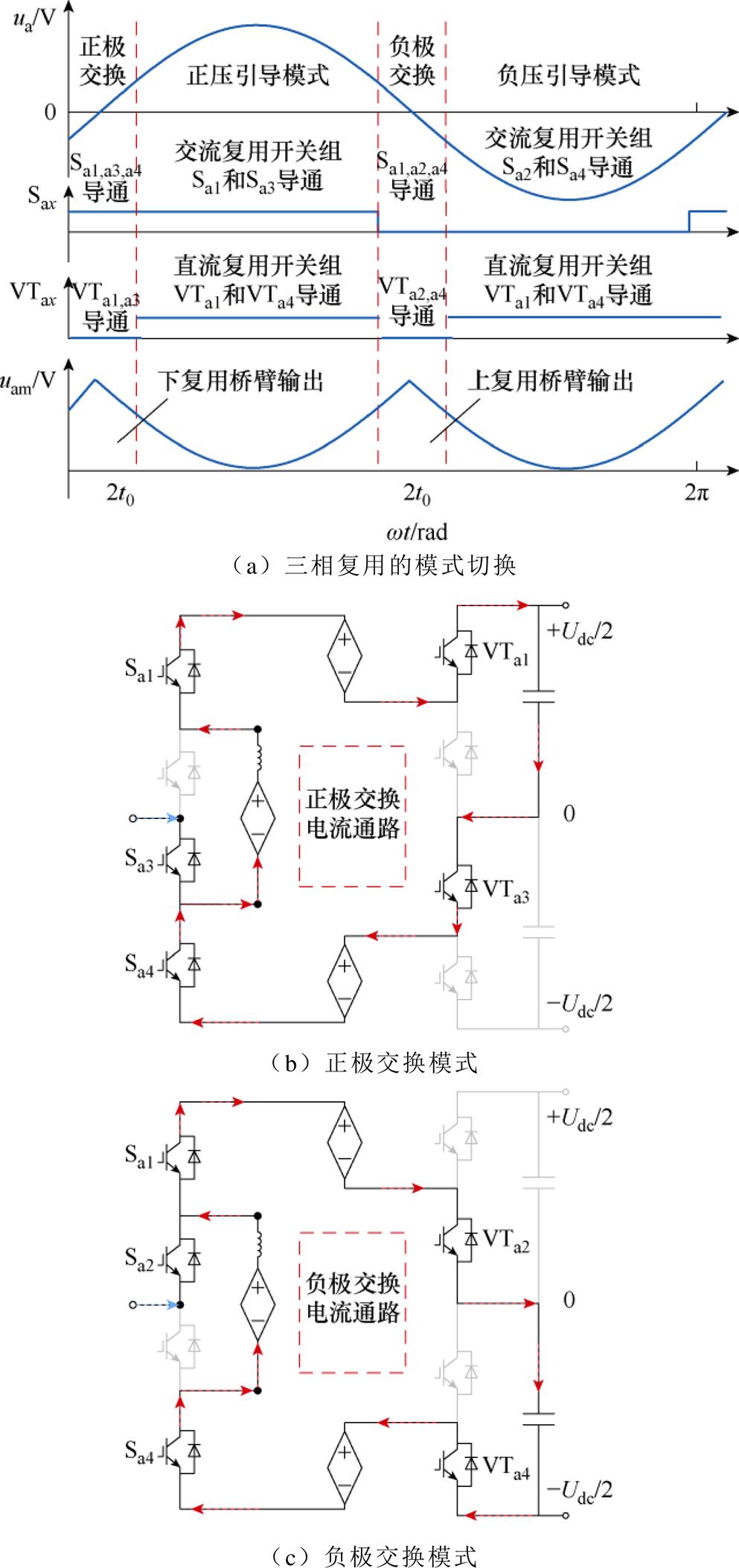
图3 HM-MMC正、负极交换模式
Fig.3 Positive and negative polarity switching operations of HM-MMC
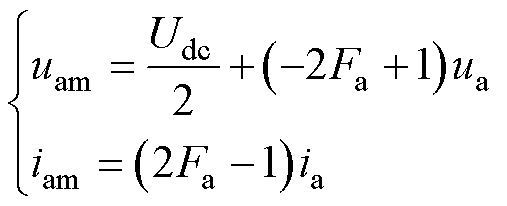 (2)
(2)
式中,ia为a相输出电流;ua为a相输出电压。
以图2b正压引导运行模式为例,此时Fa=1,根据式(2),交流侧输出电压ua为
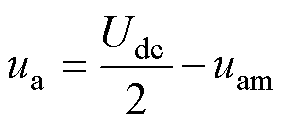 (3)
(3)
即HM-MMC通过开关的配合,以电压差的形式实现了桥臂波形的翻转,输出了交流侧的正弦交流电压。根据式(2),中桥臂输出电压所需的最大值为Udc/2,对应的每相所需子模块为N/2。同理,负压引导模式通过与负压-Udc/2的压差实现桥臂波形的下降。即交流侧开关组互补导通,将桥臂半波电压整形为正弦电压输出,且通断频率为工频。
2.1.2 三相复用运行
混合复用运行是指在相单元复用的基础上,增加了三相复用。其变化在于在图2a的基础上新增了三相复用的运行区间,即图3a中的正、负极交换区间。下面仅对三相复用区间的运行模式进行分析。
在该区间内,三相复用主要配合直流侧开关组,并由此实现两个目标:①维持交流侧电压输出; ②构建能量交换回路,实现桥臂能量均衡。
为维持交流侧电压输出,以正极交换为例,在正弦参考波上升沿过零点的两端,HM-MMC交换持续时间为2t0。正极交换模式的导通回路如图3b所示。与正、负压引导模式不同,在不投入上、下桥臂时,a相中桥臂两端电位为+Udc/2和0,交流侧输出被钳位在零电位,中桥臂被旁路。为了交流侧能够持续输出正弦电压,需要下桥臂的配合。此时
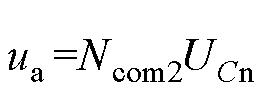 (4)
(4)
式中,Ncom2为下桥臂投入的子模块数量;UCn为子模块额定电压。
因此在正极交换期间,下桥臂根据a相正弦参考波调制。为了充分利用下桥臂全桥子模块的负压输出能力,HM-MMC在参考波过零点的正负两侧都进行交换调制。相比只能正压输出的半桥子模块,全桥子模块的交换时间可增大为半桥子模块交换时间的两倍。
与正极交换相似,在正弦参考波下降沿过零点两侧期间,电路切换到负极交换模式,交换持续时间也为2t0。负极交换模式的导通回路如图3c所示,此时直流侧开关组投切与正极交换相反。同理,由上桥臂配合输出交流电压。
为实现能量均衡,在以上两种交换运行中,通过开关组的协调配合,a相桥臂直接连接到交换电容,形成可交换能量的电流回路。通过该回路,拓扑可以将桥臂盈余/缺少的能量对电容进行充/放电,从而实现子模块电容电压的稳定。如图3b所示,HM-MMC可以通过控制通路中三个桥臂总子模块的投切数量,由桥臂与正极电容的压差实现回路电流的控制。根据基尔霍夫电压定律可得
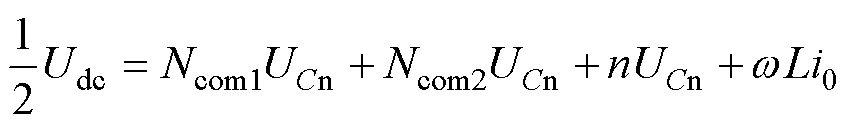 (5)
(5)
式中,Ncom1为上桥臂投入的子模块数量;n为中桥臂投入的子模块数量;L为桥臂电感值;i0为交换电流。
由式(5)可知,桥臂在周期内积累能量需要向电容放电时,控制三桥臂电压之和大于Udc/2,则电感电压与中桥臂电压反向,此时的电流即由中桥臂流向交换电容,从而实现桥臂的盈余能量释放。
综上所述,通过相单元复用和三相复用的交替运行组成混合复用,区间划分如图3a所示,HM- MMC可以实现灵活的宽范围运行。
2.1节以a相为例对混合复用运行进行了研究,b、c相的运行原理与a相完全相同。三相分别在自身调制波过零点两侧t0进行交换,并轮流复用直流侧单元,故周期内每相进行2次交换,三相共进行6次交换。
受交换影响,HM-MMC在调制期间不仅要考虑参考电压调制波的大小,还要考虑三相复用的直流单元影响,因此需要在最近电平逼近的基础上进行分时调制。HM-MMC三相调制区间划分如图4所示。
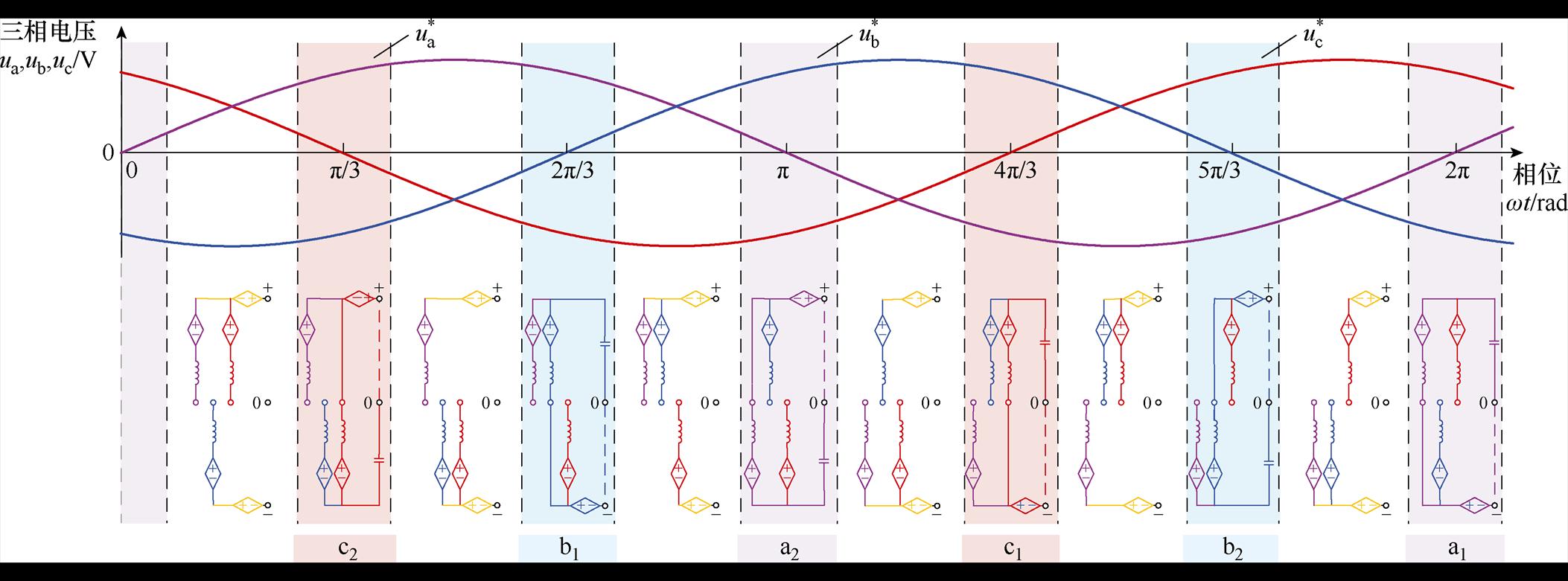
图4 HM-MMC三相调制区间划分
Fig.4 Three-phase modulation interval division of HM-MMC
图4中,ua、ub、uc分别为三相交流侧输出电压。为简化起见,以桥臂的上、下区分正、负压引导模式,以电容的上、下和回路的颜色区分正、负极交换模式。下面以a相分时调制为例,对Ⅰ、Ⅱ、Ⅲ三类区间进行说明。
Ⅰ类区间:当a、b、c三相均处于正负压引导运行模式,不存在交换区间,即图中未标号区域,此时a相不受其他相交换影响。该电路可采用最近电平逼近法进行调制。a相中桥臂的参考电压如图紫色曲线所示。此时,中桥臂依据参考波计算出的阶梯波进行调制,进而形成逼近参考波的等效阶梯波。
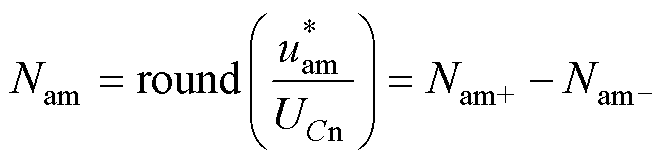 (6)
(6)
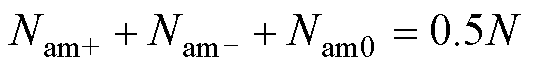 (7)
(7)
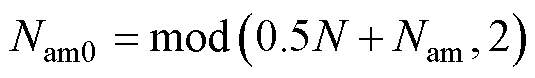 (8)
(8)
式中,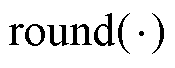 和
和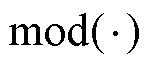 分别为取整函数和求余函数;
分别为取整函数和求余函数;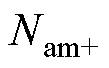 、
、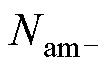 、
、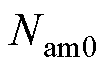 分别为正投入、负投入和旁路的子模块数;
分别为正投入、负投入和旁路的子模块数;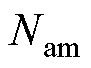 为中桥臂的输出电平数。
为中桥臂的输出电平数。
Ⅱ类区间:a相进行正负极交换运行时,即a1、a2区域,中桥臂的子模块投入受能量均衡电流控制,这将在后文3.2节进行阐述。
Ⅲ类区间:当其他相进行交换时,即b1、b2、c1、c2区域,a相调制受到影响。交换区间构建直流回路时,a、b、c三相的中桥臂两端电压均减半,这会影响到非交换相的调制电压。以图4中c相正极交换(c1区间)对a相的影响为例,对c1区间的电路的运行状态省略开关并且仅突出路径,得到c相正极交换对a、b相的影响如图5所示。此时直流侧开关动作,c相桥臂与正极电容构建电流回路。相单元两端电位分别为+Udc/2和0。同时,由下桥臂输出c相交流侧的阶梯波。
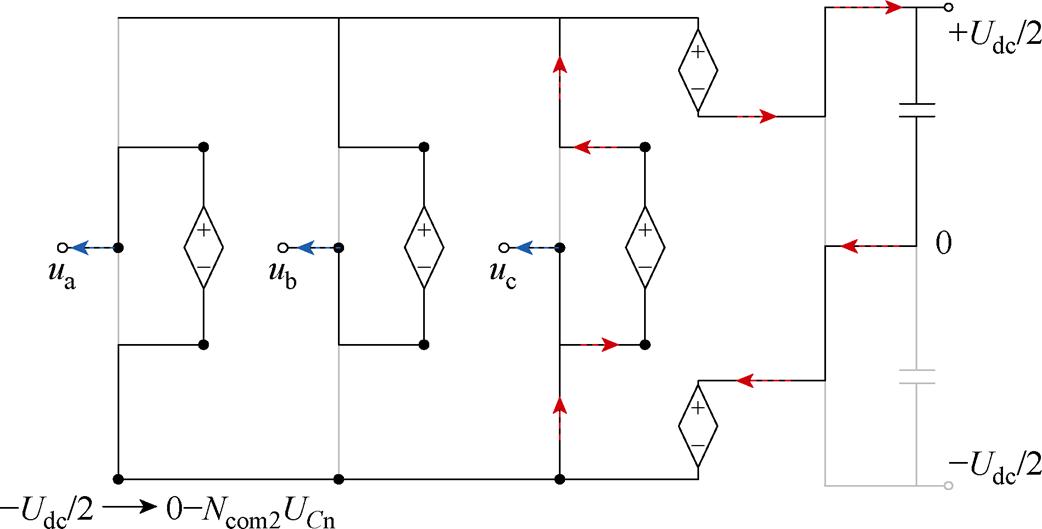
图5 c相正极交换对a、b相的影响
Fig.5 Effects of positive polarity switching of phase c on phase a and phase b
由基尔霍夫电压定律可知,此时a相负压引导下的桥臂调制电压公式为
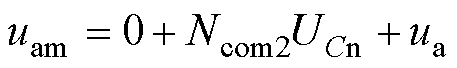 (9)
(9)
对比式(2)可知,受c相正极交换的影响,此时a相桥臂的直流侧电位由负压引导区间的-Udc/2变为0-Ncom2UCn。
同理,在b相和c相交换区间,都受到复用直流侧影响的相单元。此时需要适时地改变中桥臂调制电压来输出交流电压波形。
在前文的基础上,结合四种运行模式及分时调制策略,可以给出在正弦调制波下的各桥臂电压、电流的理论波形。图6和图7所示为采用了m=1,cosj=1,上、下桥臂Ncom1/2=1的简化工况,即桥臂无负投入、电压、电流无相位差的波形。图6中,在增加交换区间后,上、下桥臂分别负责输出负极和正极交换时的正弦电压,同时中桥臂受到分时调制的影响,需要输出一部分负压。图7中,桥臂电流在交换区间受控于交换电流,而上、下桥臂电流在非交换区间为六脉动电流,在交换区间则流过反向的交换电流。其中,Im、I0、Idc分别为交流侧电流、交换电流、直流侧电流的幅值。
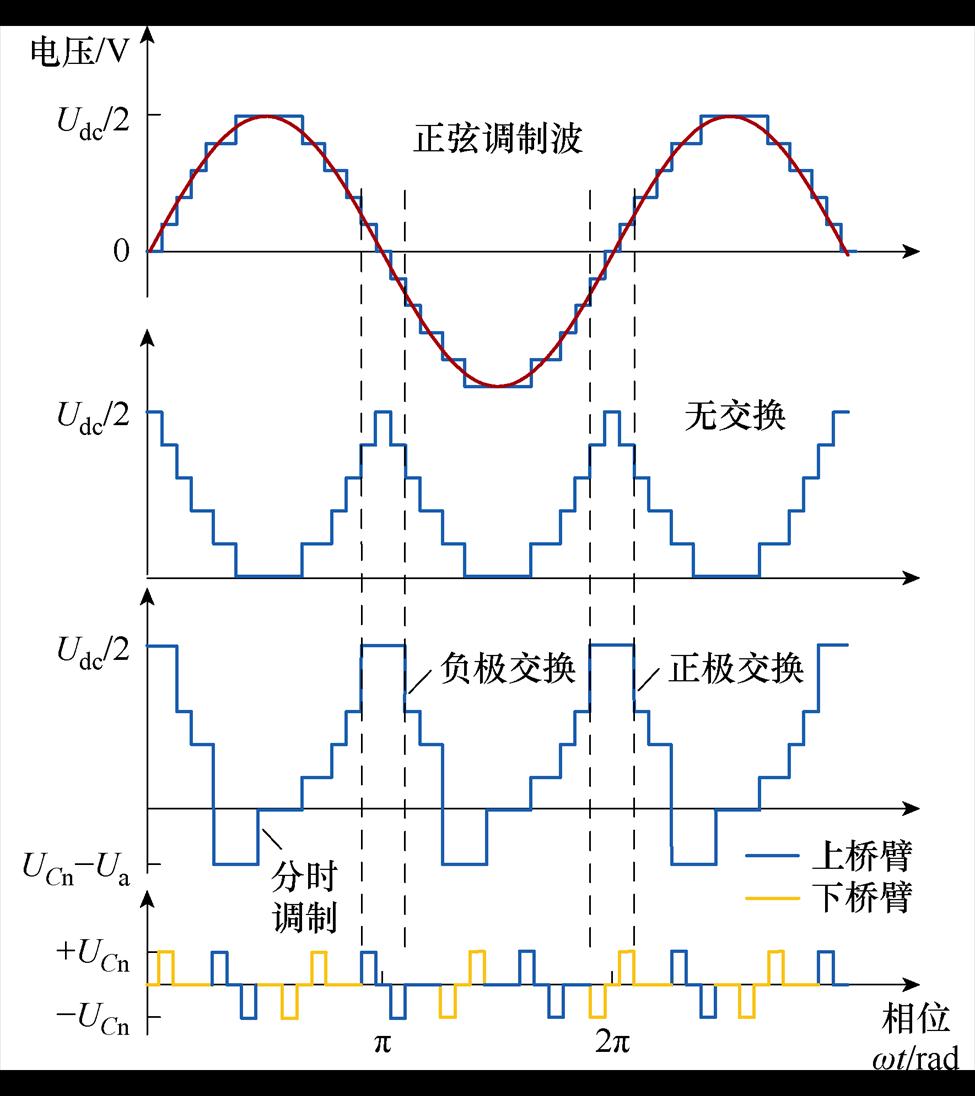
图6 各桥臂电压理论波形
Fig.6 Theoretical voltage waveforms of each bridge arm
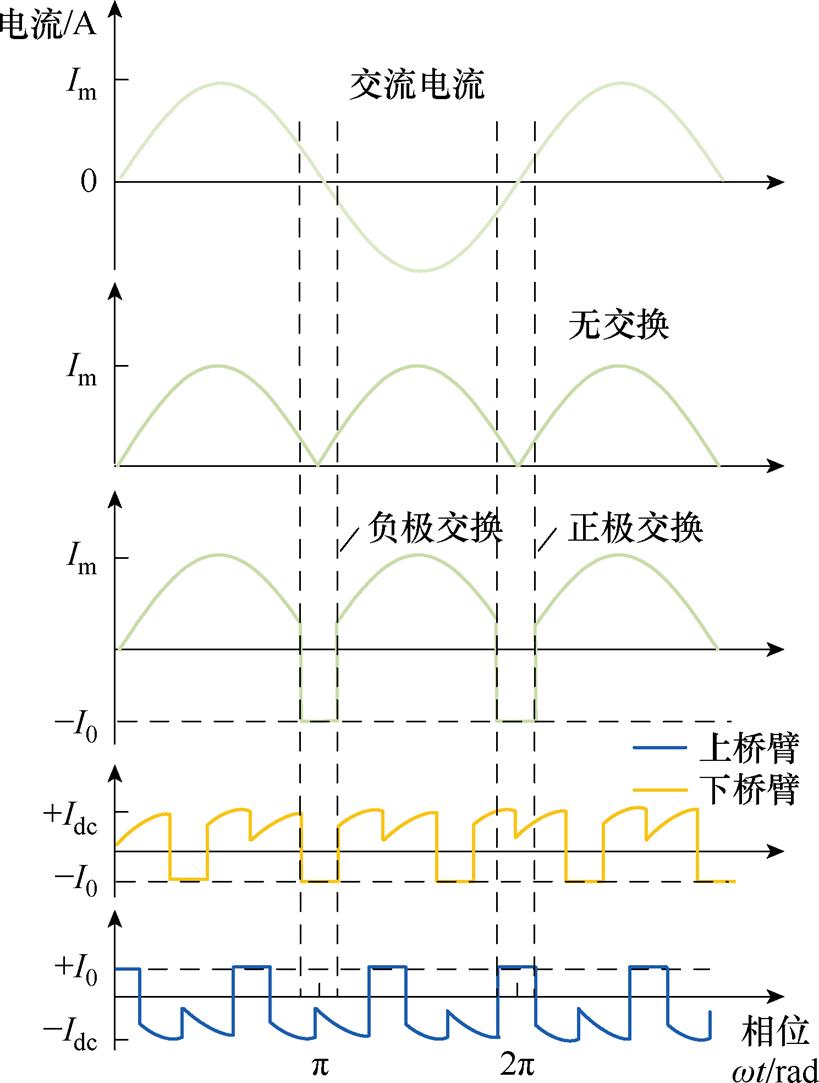
图7 各桥臂电流理论波形
Fig.7 Theoretical current waveforms of each bridge arm
本文拓扑通过三相复用单元以及正负极交换配合运行实现了桥臂能量均衡,达到了灵活调制的效果。其中,三相复用的上、下桥臂子模块只需要简单的均压排序算法即可实现能量均衡。而占HM- MMC绝大多数子模块的中桥臂则需要进行交换区间的均衡电流控制。为此,主要针对中桥臂进行能量均衡的机理分析和电流控制的阐述。
在一个周期内,HM-MMC分别运行在正负压引导模式和正负极交换模式。当处于前者的运行区间时,相单元与直流侧不存在直接相连的回路,无法进行能量交换。这就导致在非最佳调制比的工况时,相单元会在该区间内积累/减少能量。然而,当处于正负极交换模式时,HM-MMC构建了如图8所示以电容为缓冲的能量交换回路,通过对回路电流的控制可以对引导模式中产生的能量偏移进行平衡。
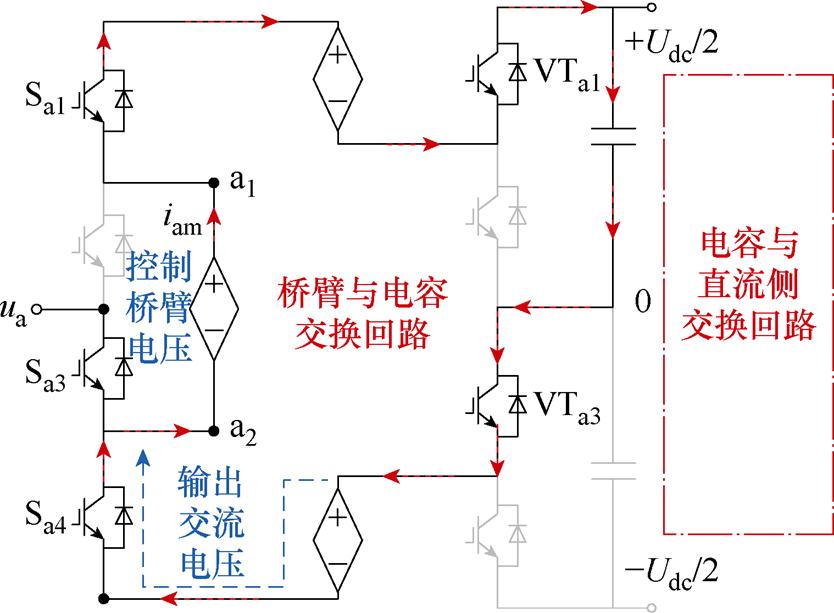
图8 HM-MMC能量交换机理
Fig.8 Energy exchange mechanism of HM-MMC
因此在轻型化基础上,HM-MMC能够实现桥臂的能量均衡。在这种情况下,两种类型的复用桥臂具有明确的分工。以图8中正极交换运行为例,中桥臂负责控制桥臂电压,并通过该电压来控制交换电流以实现能量均衡。上/下桥臂负责在交换期间输出交流电压,则对应的下/上桥臂通过改变自身电压,辅助中桥臂控制回路电流。
为简化起见,先考虑不增加三相复用时的受限调制情况,即只有相单元复用运行时的能量平衡条件。假设交流侧输出电压和电流不含任何谐波,定义a相电压和电流的表达式为
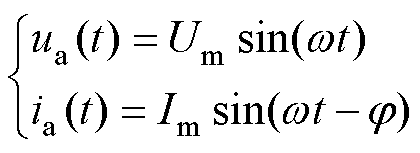 (10)
(10)
式中,Um、Im分别为相电压和电流的幅值;w为角频率;j为功率因数角。则可将中桥臂电压uam和电流iam分别表示为
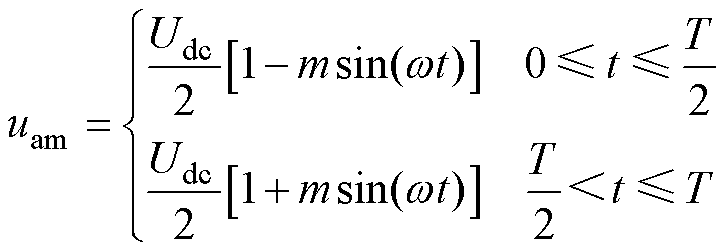 (11)
(11)
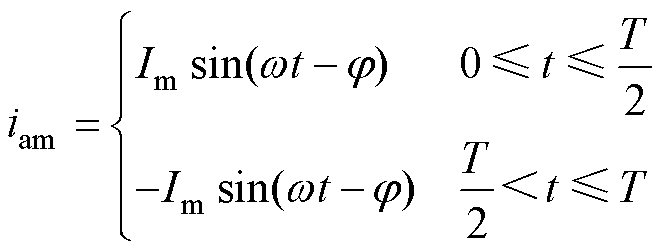 (12)
(12)
式中,m为电压调制比,m=2Um/Udc;T为工频周期。
根据式(11)、式(12),则拓扑在不采用缓冲能量交换时,要使得桥臂在一个周期T内的能量积累DEam为零,即能够持续工作运行,有
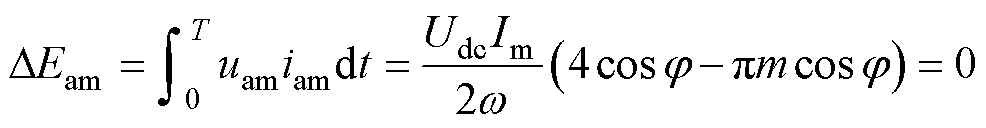 (13)
(13)
则调制比m必须满足
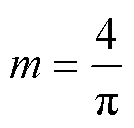 (14)
(14)
与AAMC相似,该拓扑的调压范围被限制在过调制状态。在此基础上考虑三相复用的加入,分析混合复用运行模式下的桥臂能量均衡。
如前文所述,HM-MMC在[-t0, t0]和[T/2-t0, T/2+t0]时间内进行能量交换,中桥臂电压uam和电流iam可分别表示为
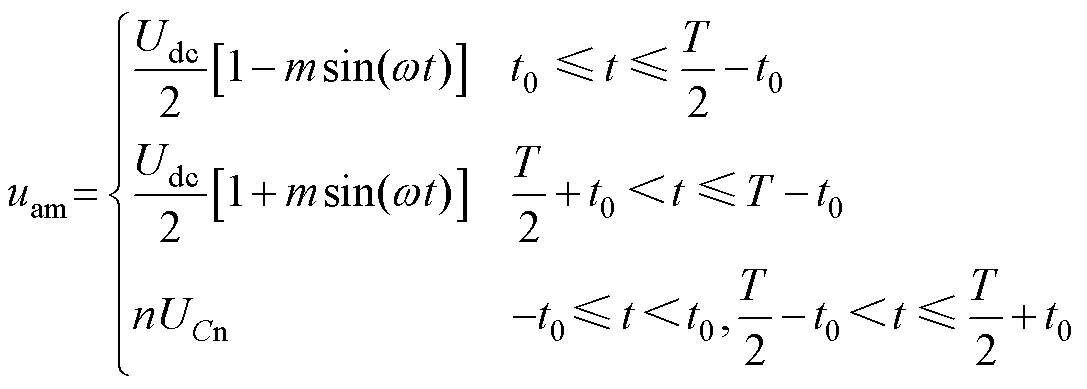 (15)
(15)
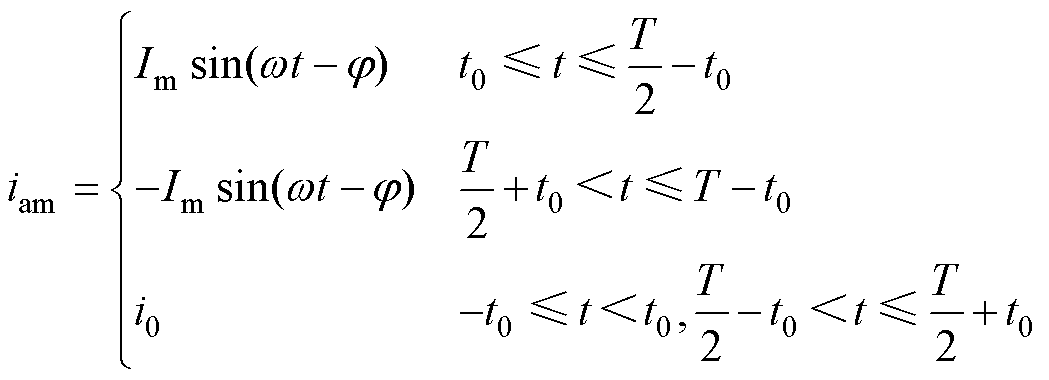 (16)
(16)
式中,2t0为交换时间;i0可正可负。
对于中桥臂,根据式(15)、式(16)可知桥臂在一个周期中非交换区间内积累的能量DE1为
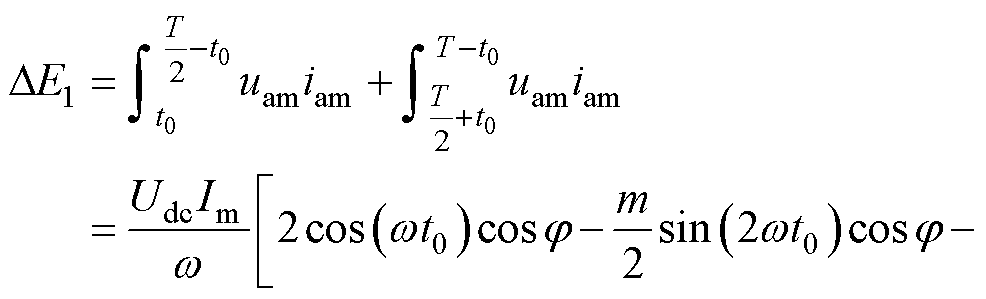
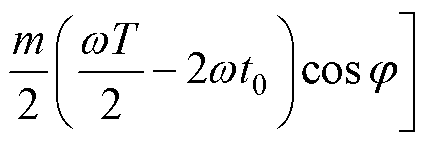 (17)
(17)
根据式(15)、式(16),交换区间内中桥臂向电容充/放电的能量DE2为
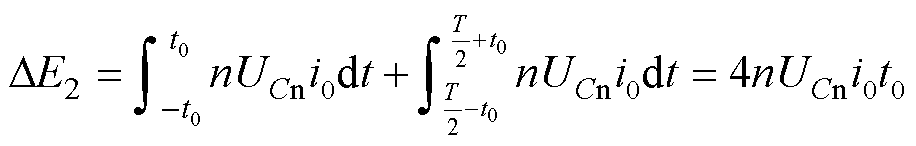 (18)
(18)
缓冲能量交换的目标是在调制比m变化的工况下,确保桥臂周期能量平衡,从而维持子模块电容电压稳定,实现HM-MMC的宽范围运行,因此需要满足
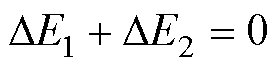 (19)
(19)
根据式(17),DE1是随m变化的值,m与固定调制比4/p的差值越大,DE1的值就越大。根据式(18),DE2受到了交换时投入子模块数量、交换电流和交换时间的影响。其中交换电流由回路中投入子模块数量决定,所以DE2可看作主要受交换电流和交换时间两个自由度影响。本文通过固定交换时间,改变交换电流大小来实现桥臂能量均衡。
此外,对于直流侧的交换电容组,其电压受到桥臂充放电的影响。如图8所示,由于电容与直流侧始终直接形成回路,能够在整个周期内将多余或缺失的能量交换到直流侧。因此,即使电容电压在一个周期内有波动,但总体上能维持在额定值。
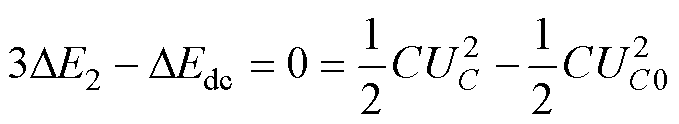 (20)
(20)
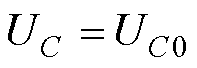 (21)
(21)
式中,C为交换电容的电容值大小;UC0、UC分别为交换电容初始电压值和一个周期内的最终电压值;DEdc为一个周期内交换电容向直流侧充放电的能量。
从式(20)可知,该电容的容值要求较低。因为UC0为高电压等级,即电容的基础总能量较大,这就导致一个周期内较小的DE2对电容总能量的影响较小。同时,电容也在持续地向直流侧交换能量。其中,能量交换策略对该电容的要求为控制直流电压的波动率,因此其容值受到直流电压等级、电压波动率以及直流侧电流幅值的影响。
在前文所述能量均衡分析的基础上,为尽可能地减少上、下桥臂的子模块数量,本文采用固定交换时间,控制交换电流的能量均衡方法。
当t0为定值,根据式(17)~式(19)可以得出目标交换电流i0为
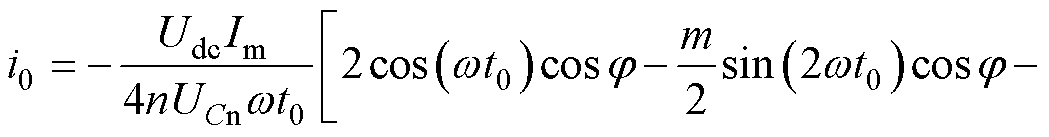
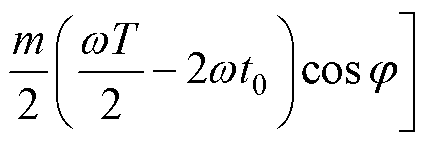 (22)
(22)
在控制过程中,根据式(22),首先需要确定交换时间,然后才能确定交换电流的目标值。其中,在调制比不变的条件下,交换电流的大小取决于交换时间,交换时间越短,交换电流就越大。而关于交换时间,根据前文对正负极交换运行模式的分析,HM-MMC在交换区间内由上、下桥臂输出交流侧电压,因此交换时间的长短由上、下桥臂投入的子模块数量确定,其交换时间通过角度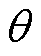 表示为
表示为
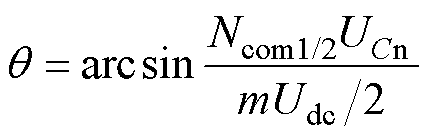 (23)
(23)
式中,Ncom1/2为上/下桥臂的子模块数量。调制比m分式的分子为三相复用桥臂可提供的最大电压,分母为交流侧电压的峰值。
三相复用子模块数量与交换时间、调制比关系如图9所示。从图9可以看出,由三相复用桥臂输出交换区间内正弦交流电压的优越性。调制比越远离4/p,桥臂所积累的能量就越多。然而,对于相同子模块数量的三相复用桥臂来说,能够提供的交换时间也会相应延长。这就使得调制比偏离自然平衡点时的能量交换压力大幅降低,使三相复用桥臂能够在维持少量子模块的同时将调制范围拓展到极低的工况。由于该特性,可以验证Ncom1/2=0.1N时足以实现m∈[0, 4/p]的调制范围。
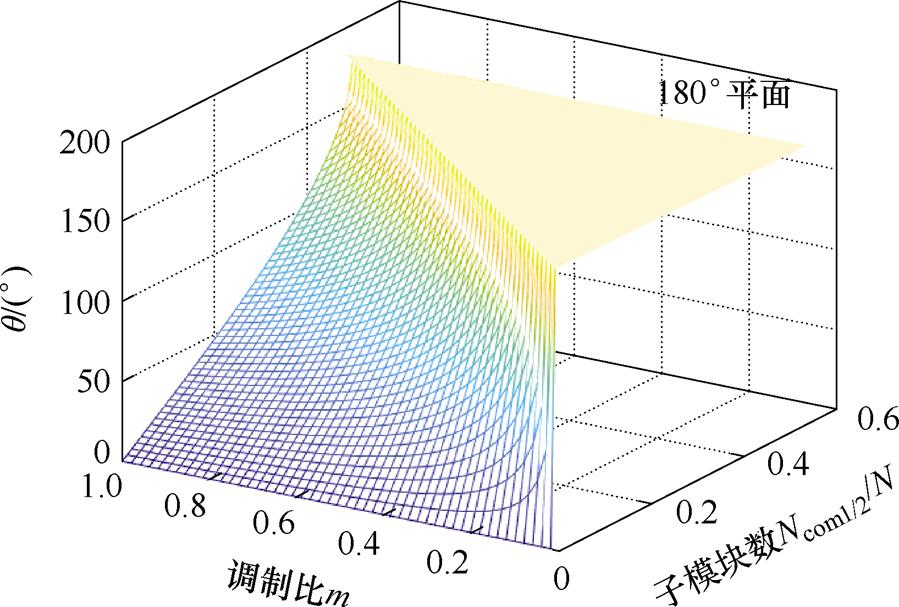
图9 三相复用子模块数量与交换时间、调制比关系
Fig.9 Relationship between the number of common submodules, exchange time and modulation ratio
在确定交换时间后,可根据式(22)计算出交换电流的大小,并通过增加或减少回路中投入的子模块数量来控制目标电流,控制式同式(5),由中桥臂和非调制的三相复用桥臂共同完成。HM-MMC采用如图10所示的桥臂电流iam滞环控制器。当交换电流i0过大或过小时,对回路中投入的总子模块数Nall进行减小或增大。同时,电流控制器在工况改变的情况下需要重新计算交换电流的大小并与电流阈值i_lim比较。若电流过大,则增加三相复用桥臂子模块,从而增加交换时间,降低交换电流。综上所述,得到含能量均衡电流控制的综合调制策略流程如图10所示。
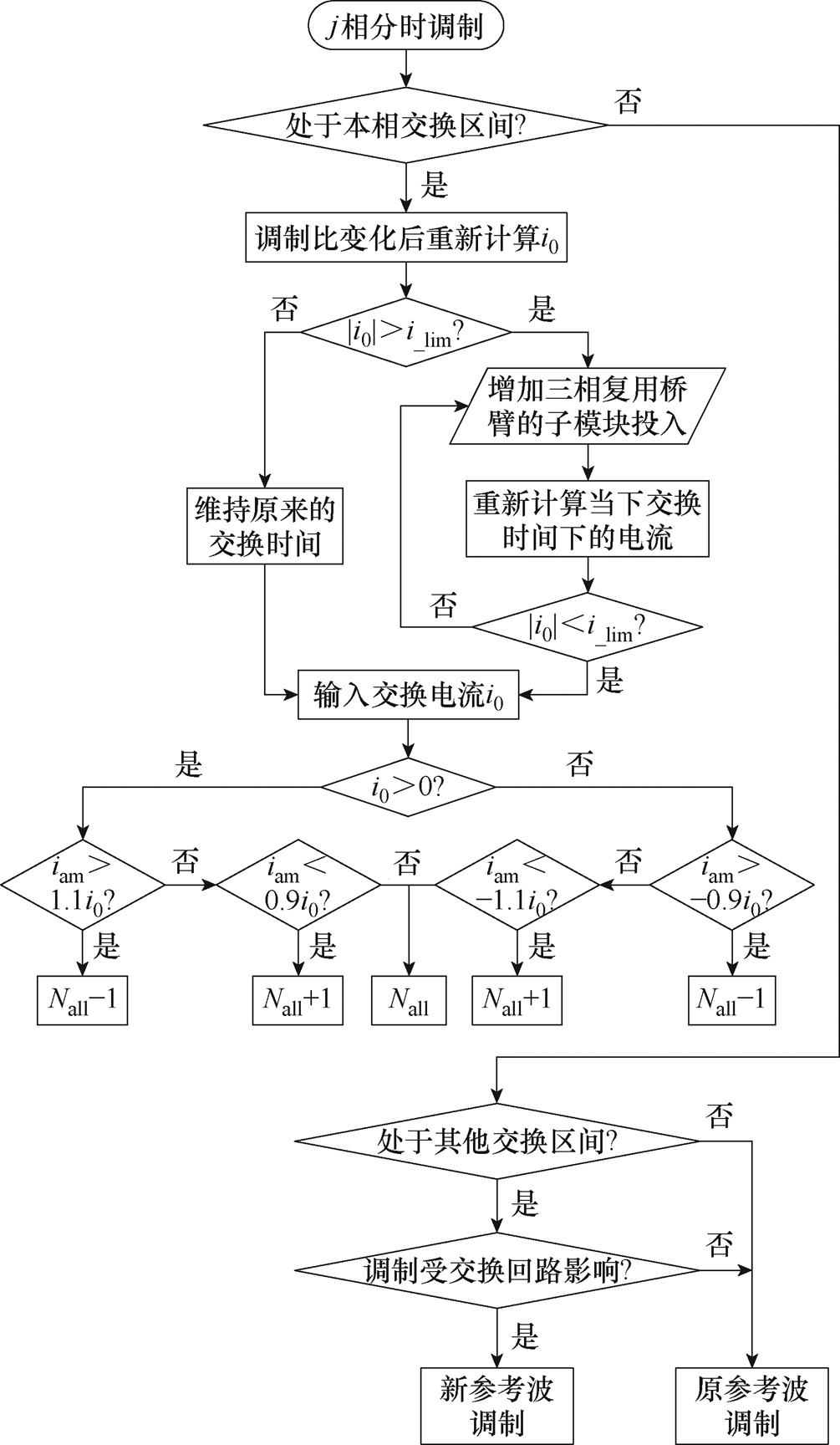
图10 HM-MMC含能量均衡电流控制的综合调制策略流程
Fig.10 Flow chart of integrated modulation strategy with energy balance current control of HM-MMC
为验证所提拓扑及控制策略的波形质量、宽范围运行性能等,本文基于Matlab/Simulink平台搭建了固定调制比下的AAMC、HM-MMC以及宽运行范围下的HM-MMC仿真模型。通过与AAMC的比较,验证HM-MMC良好的波形质量。更进一步地,通过搭建宽运行范围下m=0.9时的HM-MMC仿真模型,对比其能量均衡前后的变化并研究其电压电流等内特性。其基本仿真参数见表1。
表1 仿真参数
Tab.1 Simulation parameters
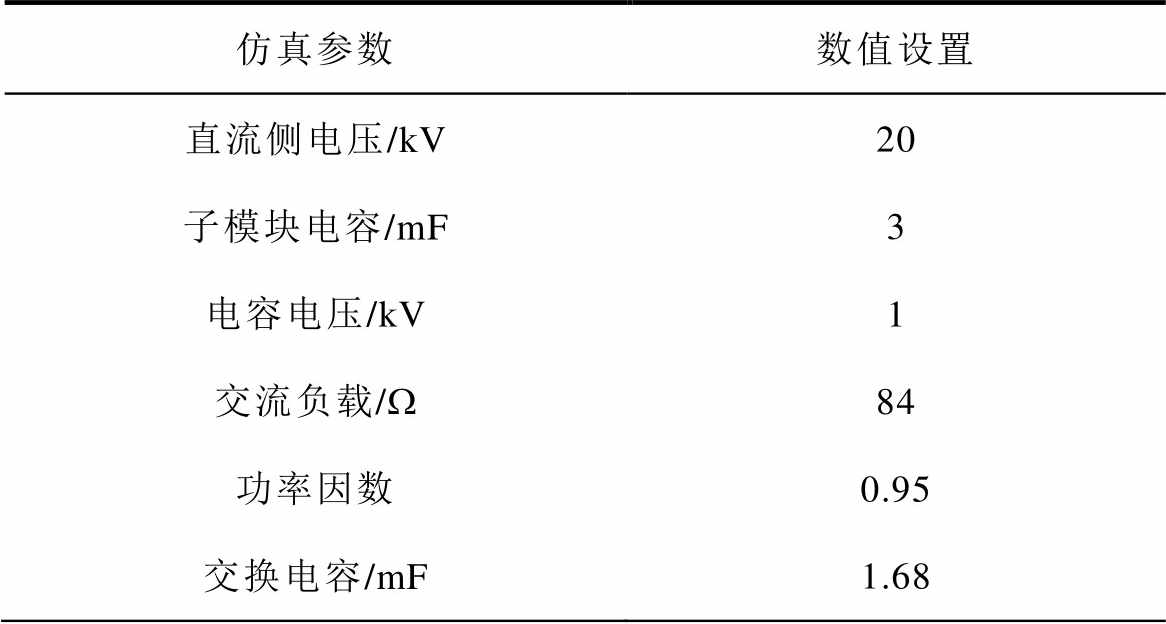
仿真参数数值设置 直流侧电压/kV20 子模块电容/mF3 电容电压/kV1 交流负载/W84 功率因数0.95 交换电容/mF1.68

换流器单相子模块 AAMCN=20 HM-MMC0.5N=10 宽范围HM-MMC0.567N≈11
AAMC与HM-MMC的特性对比如图11所示,可以看到在相同的调制策略下,HM-MMC与AAMC输出电平数相同,交流电压的总谐波畸变率(Total Harmonic Distortion, THD)分别为3.24%和3.42%,较为接近。此外,两者交直流侧电流的特性也十分相似,交流侧电流THD较低,分别为0.42%与0.54%,直流侧电流为六脉动特性,均需要进行滤波。其中,HM-MMC的直流侧电流受到正负压模式切换的影响,会出现轻微波动。此外,HM-MMC的子模块电容电压波动率约为4.2%,小于AAMC的5.3%,这说明该拓扑对子模块电容值的要求可以进一步降低。如图11所示,本拓扑即使减少了一半的子模块,也能够实现与AAMC相近的效果,达到近乎一致的外部输出特性。

图11 AAMC与HM-MMC的特性对比
Fig.11 Comparison of the characteristics between AAMC and HM-MMC
在增加三相复用桥臂的子模块数为0.1N后,HM-MMC的调制比拓展到[0, 4/p]。此时设定调制比m=0.9,不再处于过调制状态。宽范围HM-MMC的电压特性如图12所示。在该工况下,电压的畸变率轻微上升,这可能是受到了能量交换时状态切换的影响。此外,电容电压的波动进一步下降,这充分说明了能量交换的可行性。综上所述,能量交换策略不仅保持了桥臂的能量均衡,还降低了电容电压纹波。
除此之外,图12中也以a相桥臂为例,分别给出了HM-MMC三个桥臂的电压波形。可以看到图中1 s和1.01 s左右,a相分别进行负极交换和正极交换。负极交换时由上桥臂输出a相交流侧电压,即先后输出-1 kV、0和+1 kV的阶梯电压。正极交换时,同理由下桥臂输出阶梯电压。
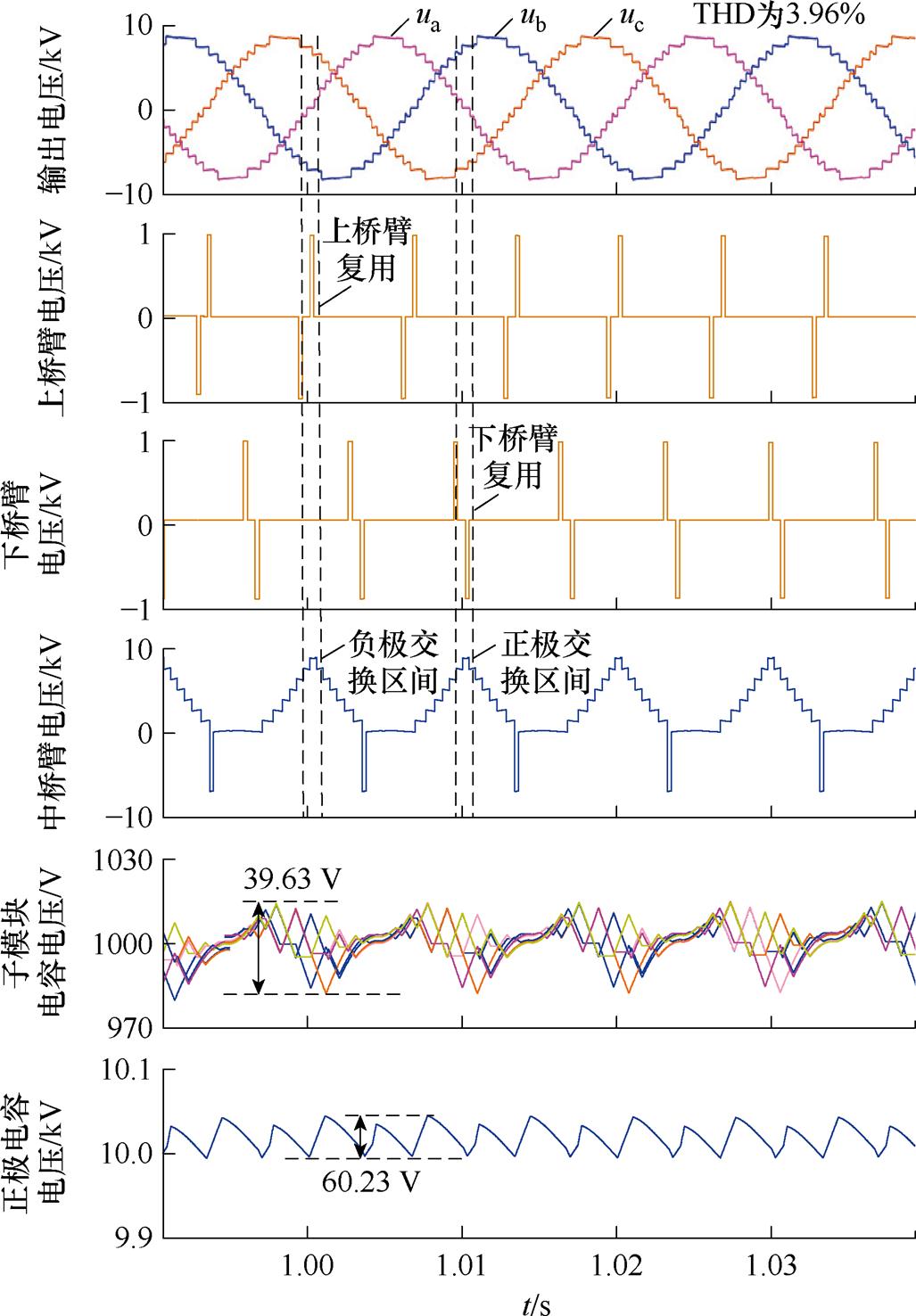
图12 宽范围HM-MMC的电压特性
Fig.12 Voltage characteristics of the wide-range HM-MMC
此外,中桥臂存在全桥的负投入,这部分电压主要是受到非交换相运行调制的影响,即a相在b、c相进行交换时受复用直流侧单元电平选择的影响。与AAMC中负压利用率较低不同,这就使得HM-MMC中全桥子模块的负投入也得以充分利用。最后,图12中给出了正极交换电容的电压波动。正如前文推导所示,该电容在容值较低的情况下,波动范围也很小,波动幅度维持在0.6%左右。这使得交换电容值与同电压等级下AAMC的滤波电容相当即可,电容成本大幅下降。
图13所示为HM-MMC的内部电流特性。其中,a相交流侧电流在正负压运行和正负极交换的模式切换过程中,交流电流的输出波形良好。两个模式间的开关切换也可以较好地续流,这就使得交流电流的THD较小。由直流侧单元的输入电流可以观察到每个周期内三相桥臂的6次放电交换电流。其交换电流幅值均在可控范围内,并且对直流侧电流(即直流侧单元流出电流)的影响较小。
为验证HM-MMC动态响应能力,对有功功率指令阶跃工况进行仿真。宽范围HM-MMC的动态响应波形如图14所示。在1.2 s之前,换流器在额定工况下稳定运行,输出有功功率标幺值为1(pu)。1.2 s时刻发出有功功率标幺值阶跃为0.6(pu)的指令,控制器进行有限幅的功率变化,即图中的梯形斜坡。此时三相交流电流无明显畸变和波动,波形品质良好。直流侧的正负极交换电容及子模块电容电压在有功功率变化时波动相对较小。
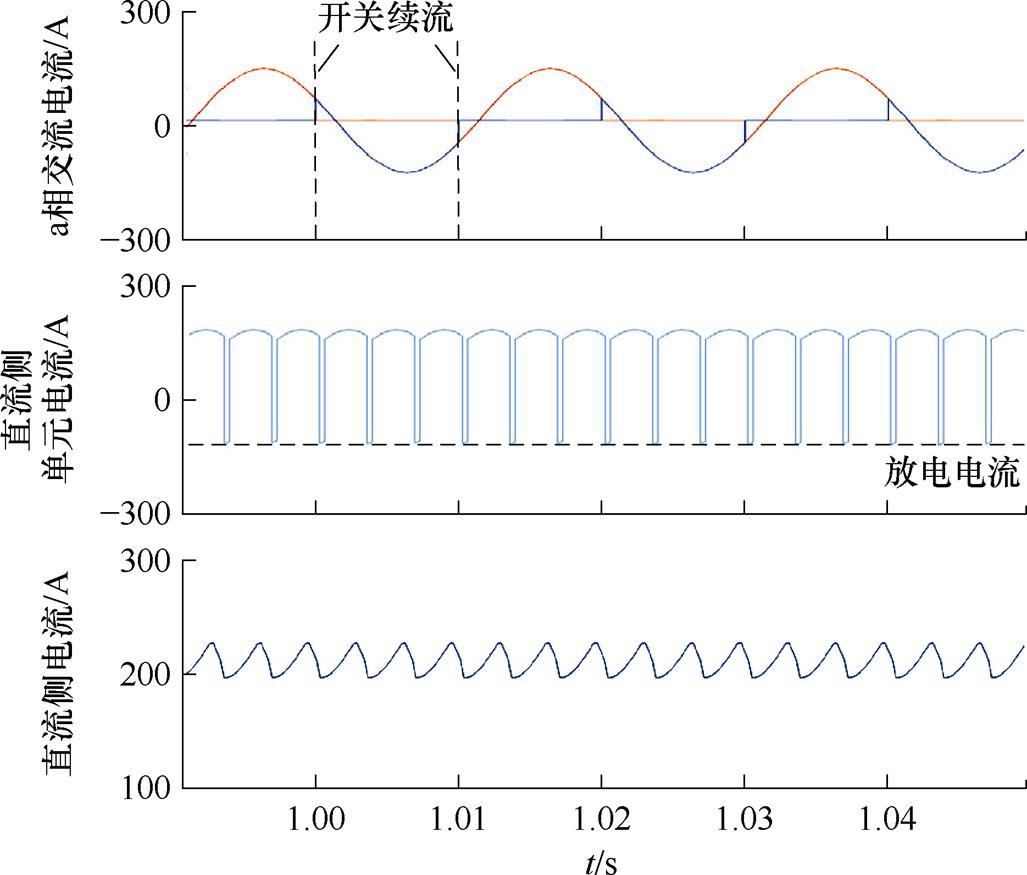
图13 宽范围HM-MMC的电流特性
Fig.13 Current characteristics of the wide-range HM-MMC

图14 宽范围HM-MMC的动态响应波形
Fig.14 Dynamic response waveforms of HM-MMC
为进一步验证所提拓扑的可行性,团队搭建了HM-MMC的实验平台。HM-MMC实验平台如图15所示。分别运行在调制比为0.9和1两种工况下并进行对比。该低电压等级、子模块较少的实验系统参数修改见表2。

图15 HM-MMC实验平台
Fig.15 The experimental platform of HM-MMC
表2 实验参数
Tab.2 Experimental parameters
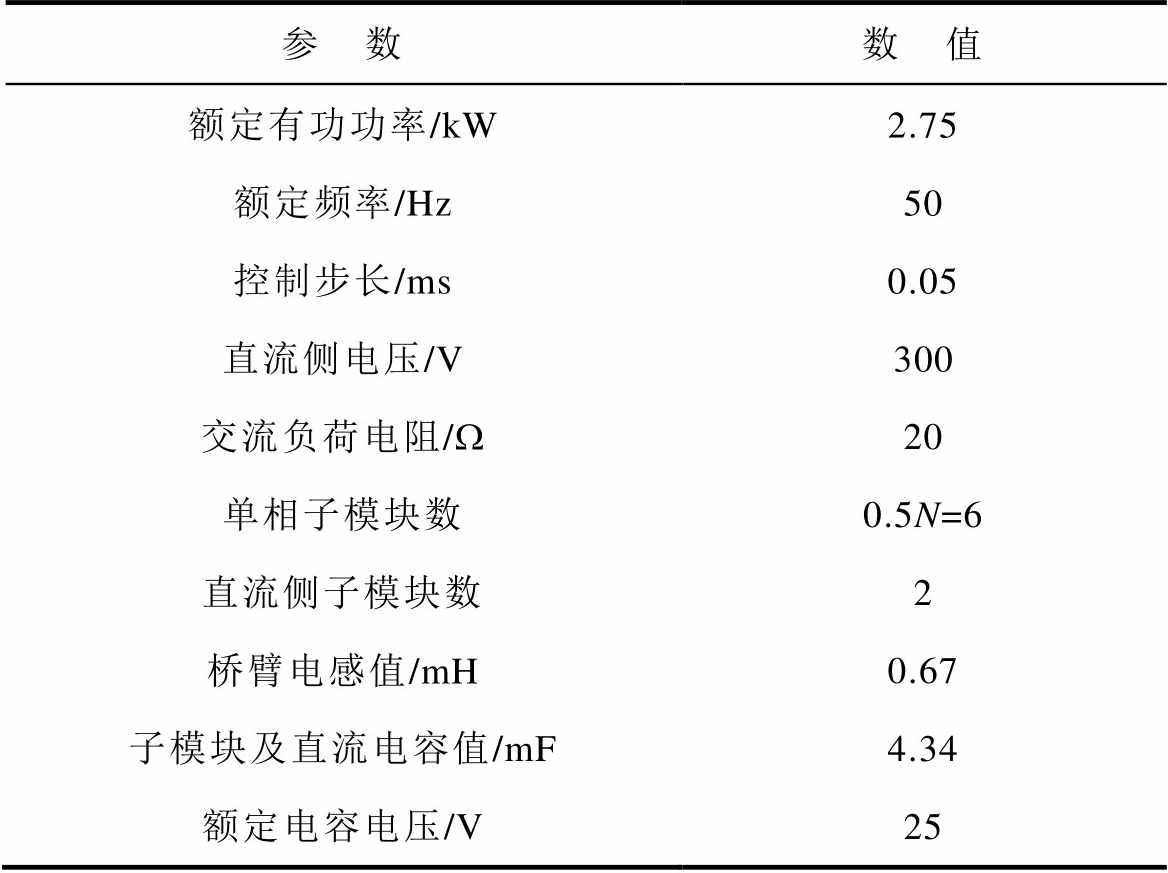
参 数数 值 额定有功功率/kW2.75 额定频率/Hz50 控制步长/ms0.05 直流侧电压/V300 交流负荷电阻/W20 单相子模块数0.5N=6 直流侧子模块数2 桥臂电感值/mH0.67 子模块及直流电容值/mF4.34 额定电容电压/V25
HM-MMC的输出电压、电流如图16所示。在桥臂全桥子模块数N=6,以17电平输出交流电压的条件下,HM-MMC输出交流侧电压的实验波形谐波畸变率较小,不同调制比下分别为5.69%和6.41%。在子模块较少的条件下输出的波形质量良好,具有拓扑可行性。在调制比减小之后,可以观察到交流侧电压的下降以及电流的增大。
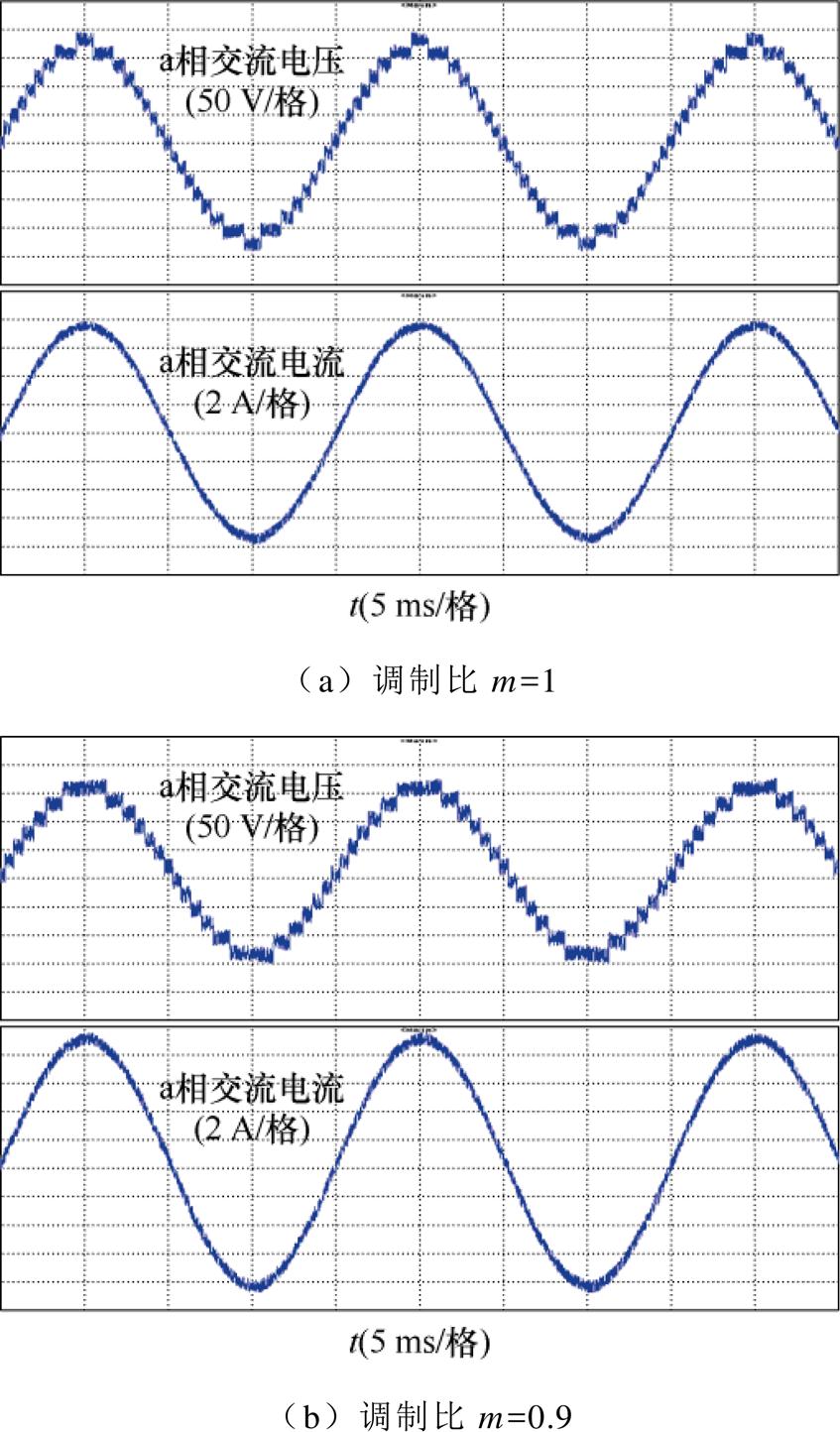
图16 HM-MMC的输出电压、电流
Fig.16 Output voltages and currents of HM-MMC
图17以a相为例给出了子模块电容电压、直流侧交换电容电压和直流侧电流。其中,在调制比发生变化后,子模块电容电压也能够始终保持稳定,且周期内充放电波动较小,波动率分别为4.3%与5.2%,随调制比减小略有增加。与仿真相同,保持了子模块电容电压波动率较低的特点。这充分证明了能量均衡策略的有效性。

图17 HM-MMC的子模块电容电压、直流侧交换电容电压、直流侧电流
Fig.17 The capacitor voltages of submodules, DC-side capacitor voltages, DC-side currents of HM-MMC
此外,交换电容电压在三相交换区间充电,形成六脉动的充放电波形,在调制比下降时,因充电功率增加,电压波动增大。直流侧电流在功率恒定的条件下保持稳定,持续输出六脉动的电流,实现交直流功率传输,并且受调制比影响较小。
为解决混合型MMC轻型化和宽运行范围难以兼顾的问题,本文引入桥臂时分复用和三相复用的思想,提出了混合复用型多电平换流器及其能量均衡控制策略,得出如下结论:
1)HM-MMC通过开关组实现中桥臂的时分复用,在保证输出电压质量的基础上最大程度地减少了相单元桥臂中子模块的数量,平均每相子模块数量可减少72%,实现了拓扑轻型化设计。其中,开关组的通断频率为工频或者三倍工频,均不存在高频开关的情况,对串联IGBT的动态均压和开关一致性的要求有所降低。
2)针对因周期能量不均衡导致的调制比受限问题,HM-MMC通过三相复用直流侧单元构建桥臂的能量交换回路。通过该回路,子模块可以进行受控的充放电维持电容电压稳定,调制范围拓宽至[0, 4/p],使得HM-MMC的总子模块数仅为1.7N。
3)为实现两种复用方式的协调配合,本文提出了能量均衡电流控制、混合复用运行模式及分时调制策略,形成HM-MMC的综合控制策略。该策略在MMC轻型化的基础上实现了可控的能量均衡,并通过分时调制策略实现了构建交换回路时相单元交流电压的输出。
本文所提拓扑在器件成本和占地成本上具有一定的经济性,并且在复用桥臂的子模块数量和子模块结构方面仍有一定的优化空间,具备进一步研究的意义和价值。此外,针对HM-MMC的直流故障穿越以及交流不对称运行等工况,未来还需做进一步的分析、优化及实验验证,以提升所提拓扑的理论完整性与工程可实现性。
参考文献
[1] 刘欣, 袁易, 王利桐, 等. 柔性直流输电系统三端口混合参数建模及其稳定性分析[J]. 电工技术学报, 2024, 39(16): 4968-4984.
Liu Xin, Yuan Yi, Wang Litong, et al. Three-port hybrid parameter modeling and stability analysis of MMC-HVDC system[J]. Transactions of China Elec- trotechnical Society, 2024, 39(16): 4968-4984.
[2] 武鸿, 王跃, 刘熠, 等. 基于广义电容电压不平衡度的MMC子模块开路故障诊断策略[J]. 电工技术学报, 2023, 38(14): 3909-3922.
Wu Hong, Wang Yue, Liu Yi, et al. Open circuit fault diagnosis strategy of MMC sub-module based on generalized capacitor voltage unbalance[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3909-3922.
[3] 侯玉超, 郭祺, 涂春鸣, 等. 面向输出性能优化的高低频混合型模块化多电平变换器及其调控策略[J]. 电工技术学报, 2024, 39(14): 4467-4479.
Tu Chunming, Wang Xin, Wang Ying, et al. A high and low frequency hybrid modular multilevel converter for output performance optimization and its control strategy[J]. Transactions of China Electro- technical Society, 2024, 39(14): 4467-4479.
[4] Rao N P, Shukla A. Analysis of capacitor voltage unbalance in hybrid MMC and its novel operation with reduced submodule capacitance[J]. IEEE Journal of Emerging and Selected Topics in Power Elec- tronics, 2022, 10(6): 7271-7284.
[5] 许建中, 李钰, 陆锋, 等. 降低MMC子模块电容电压纹波幅值的方法综述[J]. 中国电机工程学报, 2019, 39(2): 571-584, 654.
Xu Jianzhong, Li Yu, Lu Feng, et al. A review of suppression methods for sub-module capacitor voltage ripple amplitudes in modular multilevel converters[J]. Proceedings of the CSEE, 2019, 39(2): 571-584, 654.
[6] 王琛, 陶建业, 王毅, 等. 桥臂复用型模块化多电平换流器的拓扑及控制研究[J]. 中国电机工程学报, 2022, 42(9): 3373-3385.
Wang Chen, Tao Jianye, Wang Yi, et al. Research on topology and control of arm multiplexing modular multilevel converter[J]. Proceedings of the CSEE, 2022, 42(9): 3373-3385.
[7] 李宇薇, 王毅, 高玉华, 等. 桥臂复用模块化多电平变流器单极接地故障无闭锁穿越及能量均衡[J]. 电工技术学报, 2025, 40(1): 190-202.
Li Yuwei, Wang Yi, Gao Yuhua, et al. Pole-to-ground fault riding-through and energy balance of arm- multiplexing modular multilevel converter[J]. Transa- ctions of China Electrotechnical Society, 2025, 40(1): 190-202.
[8] Merlin M M C, Green T C, Mitcheson P D, et al. The alternate arm converter: a new hybrid multilevel converter with DC-fault blocking capability[J]. IEEE Transactions on Power Delivery, 2014, 29(1): 310- 317.
[9] Farr E, Feldman R, Watson A, et al. A sub-module capacitor voltage balancing scheme for the alternate arm converter (AAC)[C]//2013 15th European Con- ference on Power Electronics and Applications (EPE), Lille, France, 2013: 1-10.
[10] Wickramasinghe H R, Sun Pingyang, Konstantinou G. A hybrid VSC-HVDC system based on modular multilevel converter and alternate arm converter[C]// IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, Singapore, 2020: 4141-4146.
[11] 高玉华, 王琛, 王毅, 等. 基于半波交替的轻型化MMC拓扑及控制策略[J]. 电力系统自动化, 2023, 47(17): 149-159.
Gao Yuhua, Wang Chen, Wang Yi, et al. Topology and control strategy of light-weight modular multi- level converter with half-wave alternating[J]. Auto- mation of Electric Power Systems, 2023, 47(17): 149-159.
[12] 范世源, 杨贺雅, 杨欢, 等. 具有故障穿越能力的T型桥臂交替多电平换流器及其调制策略[J]. 电力系统自动化, 2021, 45(8): 41-50.
Fan Shiyuan, Yang Heya, Yang Huan, et al. T-type alternate arm multilevel converter with fault ride- through capability and its modulation strategy[J]. Automation of Electric Power Systems, 2021, 45(8): 41-50.
[13] 任鹏, 涂春鸣, 侯玉超, 等. 基于Si和SiC器件的混合型级联多电平变换器及其调控优化方法[J]. 电工技术学报, 2023, 38(18): 5017-5028.
Ren Peng, Tu Chunming, Hou Yuchao, et al. Research on a hybrid cascaded multilevel converter based on Si and SiC device and its control optimization method[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5017-5028.
[14] 薛英林, 徐政, 王峰. 基于三次谐波电流注入的AAMC电容电压均衡策略[J]. 电工技术学报, 2013, 28(9): 104-111.
Xue Yinglin, Xu Zheng, Wang Feng. Capacitor voltage balancing strategy base on third harmonic current injection for the alternate-arm multilevel converter[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 104-111.
[15] 王顺亮, 廖鑫, 张芮, 等. 基于三次谐波注入的桥臂交替换流器子模块电容优化方法[J]. 电力系统自动化, 2024, 48(12): 165-176.
Wang Shunliang, Liao Xin, Zhang Rui, et al. Submodule capacitance optimization method for alternate arm converter based on third harmonic injection[J]. Automation of Electric Power Systems, 2024, 48(12): 165-176.
[16] Reddy G A, Karaka N R, Shukla A. Constant overlap-time based SMS capacitor voltage balancing scheme for alternate arm converter[C]//2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 2021: 2595-2600.
[17] Yang Heya, Qu Qiannan, Chen Cong, et al. Sub- module capacitor voltage control for alternate arm converter with current commutation modulation[J]. IEEE Transactions on Power Delivery, 2024, 39(1): 635-646.
[18] Farr E M, Feldman R, Clare J C, et al. The alternate arm converter (AAC): “short-overlap” mode operation: analysis and design parameter selection[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5641-5659.
[19] Wickramasinghe H R, Konstantinou G, Pou J. Gradient-based energy balancing and current control for alternate arm converters[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1459-1468.
[20] Farr E M, Feldman R, Clare J C, et al. The alternate arm converter “extended-overlap” mode: AC faults[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5371-5388.
[21] Merlin M M C, Soto-Sanchez D, Judge P D, et al. The extended overlap alternate arm converter: a voltage- source converter with DC fault ride-through capa- bility and a compact design[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3898-3910.
[22] Liu Shenquan, Saeedifard M, Wang Xifan. Zero- current switching control of the alternate arm HVDC converter station with an extended overlap period[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 2355-2365.
[23] Zhang Rui, Wang Shunliang, Ma Junpeng, et al. Capacitor voltage balancing for alternate arm converter based on conduction angle and zero- sequence voltage[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 3268-3280.
[24] Chivite-Zabalza J, Trainer D R, Nicholls J C, et al. Balancing algorithm for a self-powered high-voltage switch using series-connected IGBTs for HVDC applications[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(9): 8481-8490.
[25] Wickramasinghe H R, Konstantinou G, Ceballos S, et al. Alternate arm converter energy balancing under parameter variation[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 2996-3000.
A Hybrid Multiplexing MMC Topology with Wide Operating Range and Energy Balance Control Strategy
Abstract The modular multilevel converter (MMC) faces challenges due to the excessive number of submodules, which causes disadvantages such as a large area, heavyweight, and high cost of the converter station. A hybrid multiplexing modular multilevel converter (HM-MMC) is proposed to address this issue. On the AC side, HM-MMC achieves full-cycle multiplexing of the bridge arms through the alternating conduction of switch groups. Thus, the number of submodules in HM-MMC is reduced. An energy exchange circuit is established between the bridge arm and the DC side on the DC side, which balances energy in the bridge arms and facilitates wide-range voltage regulation.
Firstly, by applying the coordination of switch groups, two MMCs’ bridge arms at each phase are changed into a single multiplexed bridge arm in HM-MMC, reducing submodules and capacitors for lightweight construction. The topology features positive and negative guided operation modes that alternate every half cycle, allowing the multiplexing of bridge arms. These arms are designed to output a sinusoidal half-wave under two guided operation modes. With the help of switch groups, the HM-MMC achieves half-wave inversion, thereby generating a full sinusoidal wave on the AC side. Furthermore, a controlled energy exchange circuit is constructed using the DC side unit in each cycle, with the bridge arm directly connected to the DC side capacitor. This circuit allows surplus or missing energy from the bridge arms to charge or discharge the capacitor on the DC side, ensuring the voltage stability of submodules. Due to the structure and control strategy of HM-MMC, a slight increase in the number of submodules extends the energy exchange time, thereby removing limitations on the modulation ratio.
Through simulation and experimental results, the following conclusions can be drawn:
(1) Through the cooperation of the switch groups, the full-cycle multiplexing of the bridge arm submodules is realized. The number of submodules is reduced by about 72% compared to conventional MMC. Besides, the operating frequency of the multiplexing switch groups is the power frequency or triple power frequency. There are no high-frequency switching actions during the operation of HM-MMC, which reduces the requirements for dynamic voltage balancing and switching consistency of the series insulated gate bipolar transistors (IGBTs).
(2) HM-MMC establishes an energy exchange circuit for the bridge arms by multiplexing DC side units. Accordingly, the submodules in arms can carry out controlled charge or discharge to maintain capacitor voltage stability, and the modulation range of HM-MMC is extended to [0, 4/p]. In addition, due to the coordination of the DC unit and the switch groups, when more submodules are required at a low modulation ratio, the exchange time of the bridge arm is extended. The average number of submodules per phase of HM-MMC is 0.567N.
(3) The proposed energy balance, current control, hybrid multiplexing operation modes, and time-sharing modulation strategy form a comprehensive control strategy of HM-MMC. This strategy achieves a controllable energy balance based on lightweight MMC and avoids the influence on the output AC voltage of the phase unit.
Keywords:High voltage direct current, modular multilevel converter, bridge arm multiplexing, energy balance strategy
中图分类号:TM721.1
DOI: 10.19595/j.cnki.1000-6753.tces.241474
国家自然科学基金项目(52077079)和国网浙江省电力有限公司科技项目(5211DS24000D)资助。
收稿日期 2024-08-19
改稿日期 2024-10-22
王 锐 男,2001年生,硕士研究生,研究方向为柔性直流输电。
E-mail: mxc_irony@qq.com
王 毅 男,1977年生,教授,博士生导师,研究方向为新能源与储能构网控制、柔性直流输配电网拓扑与控制。
E-mail: yi.wang@ncepu.edu.cn(通信作者)
(编辑 郭丽军)