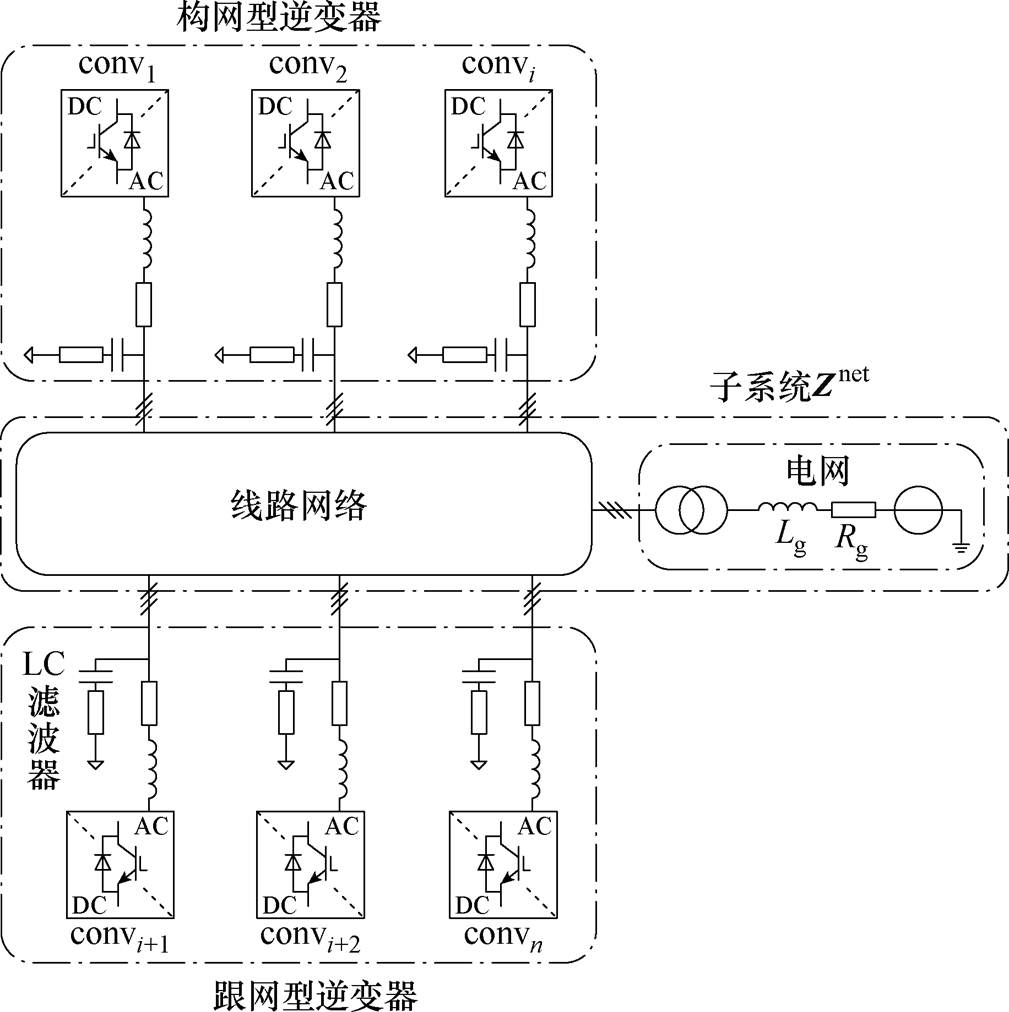
图1 多变流器并网系统
Fig.1 Multi-converter grid-tied system
摘要 高比例新能源经大量电力电子变换器并网容易诱发系统不稳定,近年来针对多变流器并网系统的小干扰稳定性分析已成为研究热点。为简化分析过程,该文将构网型与跟网型逆变器统一表示为诺顿等效电路,在此基础上推导了含构网型与跟网型逆变器的多机系统小干扰稳定性判据,该判据适用于任意网络结构,且考虑了变流器序阻抗的频率耦合效应,具有很好的普适性。依据所提出的稳定性判据,给出系统稳定性分析步骤,该方法简单易行且有助于分析各变流器对系统小干扰稳定性的影响;同时,通过详细分析虚拟同步发电机(VSG)输出序阻抗矩阵行列式在50 Hz频点处的频率特性,提出其Nyquist曲线在50 Hz处的补线原则,实现了VSG输出序导纳矩阵行列式右半平面极点数量的准确获取;最后,结合算例对多变流器系统进行了小干扰稳定性分析,并将临界稳定下系统的时域仿真结果、硬件在环实验结果和理论分析结果进行对比,定量验证了所提出的稳定性分析方法的准确性。
关键词:多变流器系统 构网型逆变器 跟网型逆变器 小干扰稳定性 硬件在环仿真
随着新能源渗透率的不断提高,电力系统的形态由同步发电机为主的传统电力系统逐步转化为电力电子主导的新型电力系统[1]。电力电子逆变器具有高度可控性和灵活性等优点,但也给系统稳定性带来了巨大挑战[2]。研究表明,跟网型逆变器,又称电流型控制逆变器(Current Control Inverter, CCI),在弱电网下容易与系统感性阻抗交互作用而诱发系统小干扰不稳定;而对于构网型逆变器,如虚拟同步发电机(Virtual Synchronous Generator, VSG),因其具备与同步发电机相似的频率电压支撑能力,有助于增强电网强度[3],但其在强电网场景下也存在小干扰失稳问题。鉴于跟网型与构网型逆变器在控制策略上可实现优势互补,含构网型和跟网型的多变流器系统近年来受到了广泛关注,其交互稳定性问题已成为研究的热点。
目前,针对逆变器并网系统的稳定性分析方法主要包括状态空间法和阻抗分析法。状态空间法通过构建电源与负载的整体状态空间模型,利用特征值轨迹对系统进行稳定性分析[4-8]。由于状态空间法需要建立包含功率电路和控制系统的统一状态空间模型,对于多变流器系统,其模型阶数很高,导致稳定性分析非常复杂[9]。此外,由于状态空间模型是对系统的整体描述,因而难以分析出各逆变器间的交互特性。
相比于状态空间法,阻抗分析法具有物理意义明确、便于模块化建模以及测量方便和容易实现等诸多优点,其主要应用于单个并网逆变器系统的稳定性分析。2011年,美国伦斯勒理工学院的孙建教授首次将阻抗法应用于单逆变器并网的小信号稳定性分析[10],受到了大量学者的青睐并逐渐成为电力系统小干扰稳定性分析的主流方法。该方法通常是将待分析系统划分为逆变器和电网两个独立的子系统,分别建立两者的输入和输出阻抗/导纳模型,采用回比矩阵[11-13]或回差矩阵[14]结合奈奎斯特稳定性判据[15-16]或广义奈奎斯特判据(Generalized Nyquist Stability Criterion, GNC)[17-20]对系统进行稳定性分析。需要说明的是,在稳定性分析中,通常根据运行外特性来选定逆变器的电路形式,构网型与跟网型逆变器一般分别表示为戴维南模型(“Z”型子系统)和诺顿模型(“Y”型子系统),其目的是保证回比矩阵或回差矩阵不存在右半平面(Right Half Plane, RHP)极点,仅依据奈奎斯特曲线或伯德图即可实现系统稳定性分析。
随着单机并网稳定性分析方法的日趋成熟,多变流器系统的小信号稳定性分析已成为关注的热点问题[21-23],并且相应地提出了一系列稳定性分析方 法[24-29]。文献[24]提出了一种用于分析多变流器系统的多环路嵌套稳定性分析方法,但该方法是建立在逆变器阻抗/导纳不含RHP极点的前提之上。文献[25]针对同时含有跟网型和构网型逆变器的多机系统,提出了一种适用于分析具有网状结构的多变流器系统稳定性的方法,但采用此种方式仅能判断系统整体的稳定性而无法分析单个变流器对稳定性的影响。文献[26]与文献[25]思路相近,可以避免引入附加RHP极点,但其是以各跟网型逆变器、各构网型逆变器以及集电线路分别具有相同的阻抗/导纳为前提,且仍仅适用于分析整个系统的稳定性。而且文献[24-26]所提方法均未考虑正、负序阻抗之间的频率耦合效应,可能会导致稳定性误判。文献[27]提出了一种基于沉降角的多变流器并网系统稳定性分析方法,但由于多节点网络中变流器的沉降角不易计算,故其仅适用于具有单母线结构的系统。为改进文献[27]的不足,文献[28]基于节点导纳矩阵的相位信息,提出了一种可分析多母线结构系统稳定性的改进方法,但该方法并未考虑VSG输出导纳矩阵行列式可能含有RHP极点的情况。文献[29]将无源网络建立为与之相适应的多口混合参数矩阵,提出了一种基于开环传递函数矩阵特征值的稳定性分析方法,该方法可避免引入附加RHP极点,但对于复杂网络,其所建立的数学模型阶数较高,且Nyquist曲线也难于观察。
综上所述,针对同时含构网型和跟网型逆变器的多变流器系统所提出的小干扰稳定性分析方法,仍有如下关键问题需要进一步改进:
(1)RHP极点数量计算。对于同时含有跟网型和构网型逆变器的多变流器系统,因不同类型变流器阻抗/导纳的RHP极点存在差异性,盲目忽略阻抗/导纳RHP的极点数量将可能导致稳定性误判。
(2)变流器模型的选择。多变流器系统中,对于单个变流器而言,由于外部网络为含有变流器的有源网络,其可能因变流器与无源网络间的相互作用而引入新的RHP极点[24, 27]。当外部网络结构较为复杂时,其端口阻抗/导纳解析式将难以推导。将跟网型和构网型变流器统一表示为“Y”型子系统则可避免此问题,但必须对构网型变流器导纳矩阵RHP极点加以讨论。
(3)特定变流器对整体稳定性影响的评估。部分文献提出的系统小信号稳定性分析方法可避免RHP极点计算的问题,但其仅可分析系统的整体稳定性,难以评估单个变流器对系统稳定性的影响。
(4)分析方法难度高。现有的大部分针对多机系统的小信号稳定性分析方法建立的是整个系统的数学模型,其阶数较高,开环传递函数矩阵特征值的数值求解必然会引入误差。同时,分析结构复杂的系统时,通过观察获取数条奈奎斯特曲线绕(-1, j0) 的圈数也并非易事。
(5)奇异点的处理。由于控制器中积分器的存在,导纳矩阵在50 Hz处存在奇异点,忽视该问题同样可能造成稳定性误判问题,然而现有文献均未对此问题进行过深入的讨论。
此外,大量的研究已经证实,稳定性分析中必须计及变流器正负序阻抗/导纳之间的耦合效应[30],即系统为一个多输入多输出系统,其数学模型将更为复杂。
针对上述问题,本文在构建系统的多输入多输出整体模型的基础上,通过数学推导,提出了一种适用于分析含有跟网型和构网型逆变器的多变流器系统小干扰稳定性的通用方法。该方法无须将系统进行划分,可避免复杂的解析公式推导,分析过程简单易行。同时,本文所提出的方法还有助于分析各个变流器对系统稳定性的影响。此外,本文针对构网型变流器导纳矩阵在50 Hz处存在奇异点的问题,讨论了该频点处的逆变器阻抗特性,实现了回比矩阵中的RHP极点数目的准确获取。最后,结合算例,对临界稳定条件下的系统完成了时域仿真以及硬件在环(Hardware-in-the-Loop, HIL)实验,仿真与实验结果同理论分析结果进行对比,证明了本文所提方法的准确性。
图1给出了多变流器并网系统的示意图,其含有n台逆变器,其中,一部分为构网型逆变器,另一部分为跟网型逆变器,线路网络可为单母线或多母线结构。

图1 多变流器并网系统
Fig.1 Multi-converter grid-tied system
采用VSG控制策略的逆变器的主电路拓扑及控制框图如附图1所示[31-32]。采用谐波线性化的方法对VSG序阻抗模型进行推导,可得VSG输出序阻抗[33],即
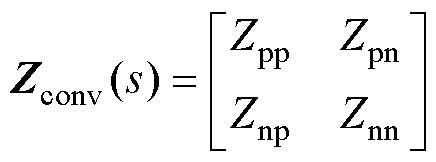 (1)
(1)
式中,Zpp和Znn分别为正、负序阻抗;Zpn与Znp为正负序耦合阻抗,具体表达式如附录式(A1)~式(A4)所示。
跟网型CCI的主电路拓扑与VSG相同,其控制框图如附图2所示[34]。同样采用谐波线性化的方法可以建立考虑频率耦合效应的CCI的序阻抗模型,其具体表达式如附录式(A5)~式(A8)所示。
考虑到各变流器连接至公共耦合点(Point of Common Coupling, PCC)的线路阻抗不尽相同,故进行稳定性分析时需统一坐标系。选定PCC构建全局坐标系,第n台变流器自身的局部旋转坐标系与全局旋转坐标系相差一个角度en,则经坐标系转换后,可得变流器输出序导纳模型为[35]
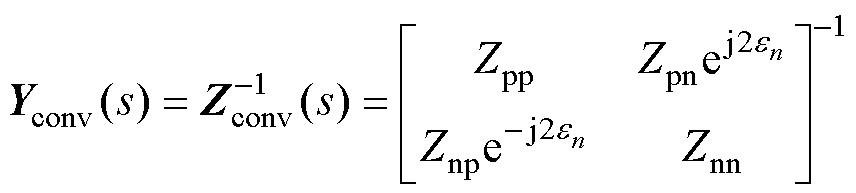 (2)
(2)
跟网型逆变器和构网型逆变器因控制策略不同而分别对外呈现电流源和电压源特性。现有文献在分析单个变流器并网稳定性问题时,为避免引入开环传递函数RHP极点,对于跟网型逆变器通常采用阻抗比形式的判据,对于构网型逆变器,则可采用阻抗和的形式[36]。而对于同时含有跟网型与构网型逆变器的“Z+Y+Z型”系统,相应的稳定性分析方法尚有待改进。此外,分析各逆变器对系统稳定性的影响也具有较高的实用价值。因此,本文通过构建系统整体模型,提出了一种适用于同时含有跟网型和构网型逆变器的多变流器系统的稳定性分析方法。
将图1中所有变流器convi均表示为诺顿等效电路,如图2所示,其中Ui和Ii分别为第i个变流器端口的正负序电压和电流列向量,ISi为表征变流器稳态工作点的电流源列向量,Yi为第i个变流器的序导纳矩阵。Znet表示2n阶开路阻抗矩阵,其可以用于描述任意结构的网络连接关系。
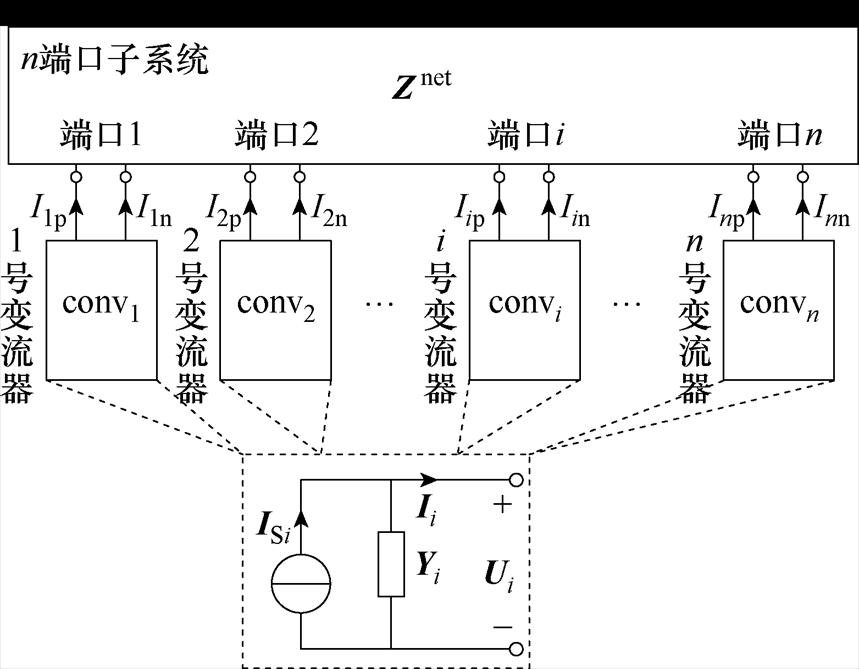
图2 多变流器系统等效电路
Fig.2 Equivalent circuit of multi-converter system
将所有变流器增广为一个2×n端口网络,则该网络所对应的诺顿形式的数学模型为
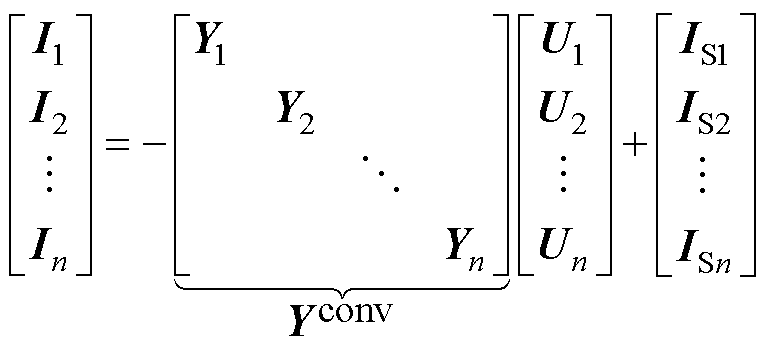 (3)
(3)
需要说明的是,因计及频率耦合效应,矩阵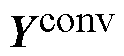 中所有元素Yi均为2阶方阵。将由线路所构成的无源网络亦视为一2×n端口网络,相应的开路阻抗参数方程为
中所有元素Yi均为2阶方阵。将由线路所构成的无源网络亦视为一2×n端口网络,相应的开路阻抗参数方程为
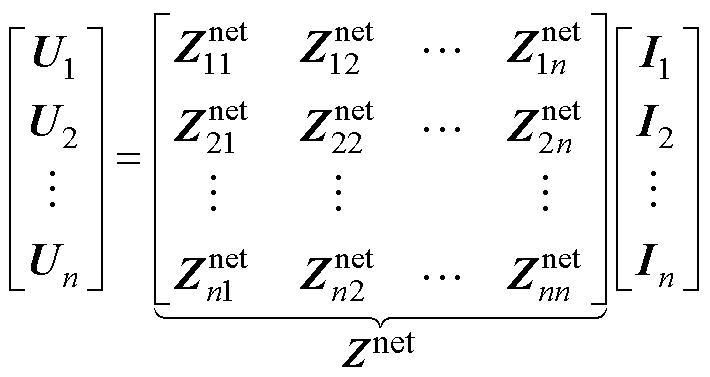 (4)
(4)
结合式(3)和式(4),可得整个系统的数学模型为
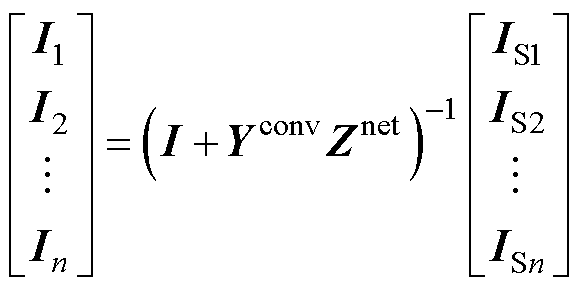 (5)
(5)
式中,I为单位矩阵。
由式(5)可知,该多变流器系统的回差矩阵为
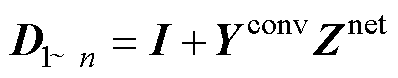 (6)
(6)
根据GNC,系统整体的闭环RHP极点数为
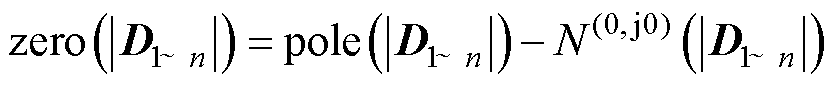 (7)
(7)
式中,pole(|D1~n|)表示|D1~n|的RHP极点数;N(0, j0)(|D1~n|)表示|D1~n|的Nyquist曲线逆时针包围或穿越 (0, j0) 的次数。
理论上,根据式(7)即可判断系统的小干扰稳定性,但由于D1~n的阶数较高,推导出其行列式的解析表达式并非易事,这将导致pole(|D1~n|)的获取十分困难,故式(7)本身的实际应用价值不高,需要在其基础上给出一种更加简单实用的判稳方法。
根据式(6),可将pole(|D1~n|)表示为
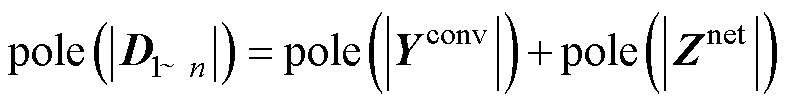 (8)
(8)
考虑到无源网络的开路阻抗矩阵Znet的RHP极点数为0,且Yconv为分块对角矩阵,则式(8)可改写为
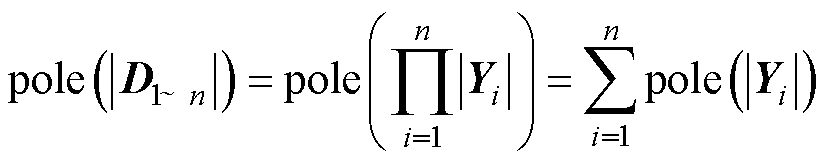 (9)
(9)
将式(9)代入式(7)中,可将其进一步化 简为
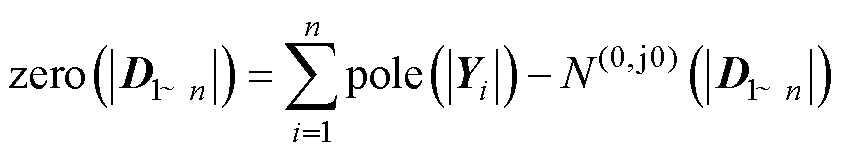 (10)
(10)
相较于式(7)中的pole(|D1~n|),式(10)中的pole(|Yi|)仅需各变流器的序导纳矩阵Yi即可获取,故式(10)更具实用价值。根据GNC,若zero(|D1~n|)=0,则系统稳定;若zero(|D1~n|)>0,则说明系统闭环传递函数矩阵存在RHP极点,系统失稳。
虽然式(10)可实现系统整体的稳定性分析,但当变流器数量较多时,D1~n的阶数较高,为2n阶,对应有2n个特征值,因此回差矩阵行列式|D1~n|或回比矩阵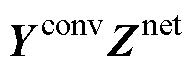 的特征值的Nyquist曲线均较为复杂,其绕 (0, j0) 点或 (-1, j0) 点的圈数难于观察。此外,式(10)仅可表征系统整体的稳定性,无法评价各个变流器对系统稳定性的影响。为解决上述问题,下文将给出一种更为简单实用的多变流器系统稳定性分析方法。
的特征值的Nyquist曲线均较为复杂,其绕 (0, j0) 点或 (-1, j0) 点的圈数难于观察。此外,式(10)仅可表征系统整体的稳定性,无法评价各个变流器对系统稳定性的影响。为解决上述问题,下文将给出一种更为简单实用的多变流器系统稳定性分析方法。
基于矩阵变换,可将式(6)所示的回差矩阵的行列式表示为
 (11)
(11)
其中
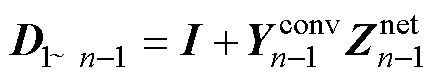 (12)
(12)
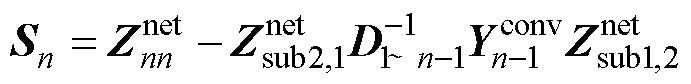 (13)
(13)
式(12)和式(13)中各导纳和阻抗矩阵分别为
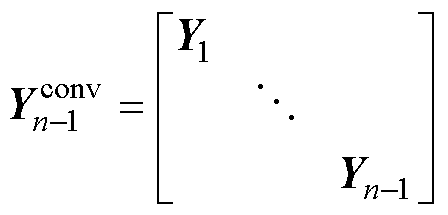 (14)
(14)
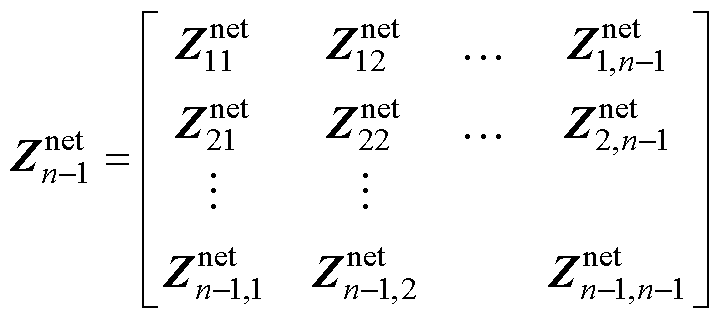 (15)
(15)
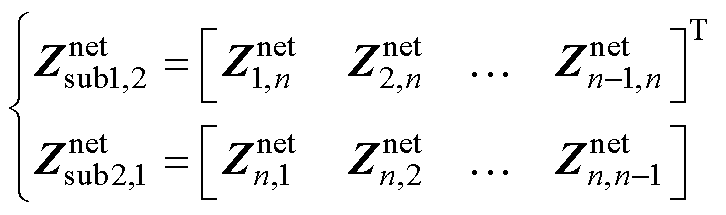 (16)
(16)
将(12)和式(6)进行对比可知,D1~n-1的含义为:除n号变流器外,其余1~n-1号变流器接入电网所组成的子系统的回差矩阵。同时经进一步分析表明,Sn也具有明确的物理含义,下文将予以解释。
令U1~n-1=[U1U2 … Un-1]T、I1~n-1=[I1I2 … In-1]T分别为1~n-1端口的电压和电流列向量,并将式(3)和式(4)分别改写为分块形式,即
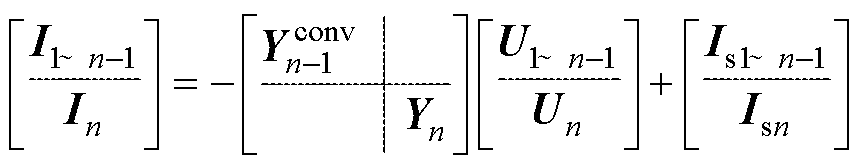 (17)
(17)
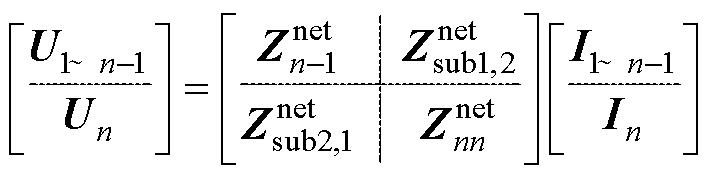 (18)
(18)
考虑到式(17)中稳态电流源不会影响阻抗矩阵,将其省略,综合式(17)和式(18),消去中间变量U1~n-1和I1~n-1,经推导可得
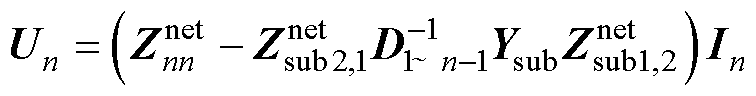 (19)
(19)
将式(13)和式(19)中的系数矩阵进行对比,可见二者完全相同,由此可知Sn的物理含义为:当1~n-1号变流器接入系统时,从n号端口看入的输入阻抗。
通过上述针对D1~n-1和Sn物理含义的解释,说明式(11)的含义为:对第n号变流器并网所得的回差矩阵行列式|1+YnSn|和n-1台变流器与电网所构成的子系统的回差矩阵行列式|D1~n-1|进行RHP零点分析,可判定第n号变流器接入后系统能否保持稳定。
进一步观察式(11)发现,其具有递推形式,则式(11)可以进一步表示为
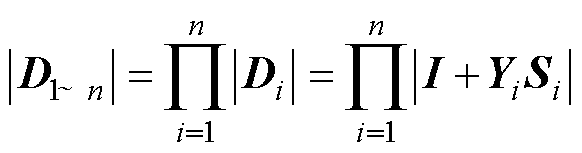 (20)
(20)
将式(20)代入式(10),可得
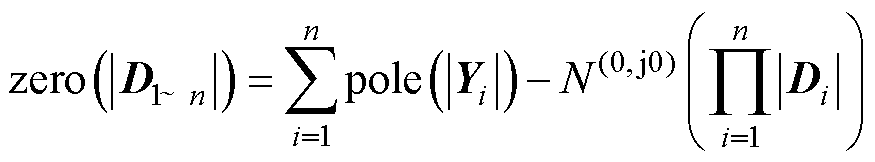 (21)
(21)
基于GNC,式(21)等号右侧第二项可表示为
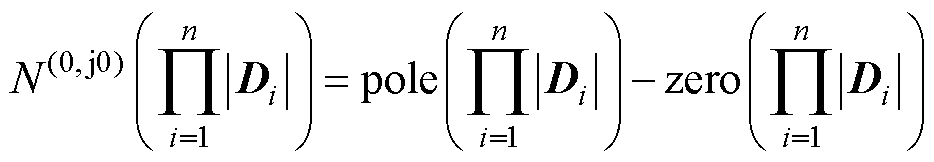
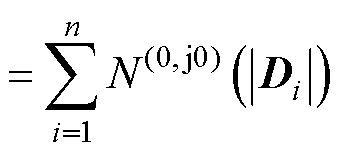 (22)
(22)
将式(22)代入式(21),可得n台变流器系统的稳定性判据为
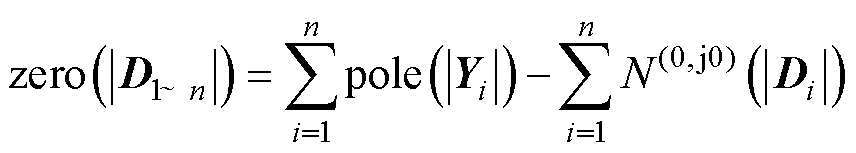 (23)
(23)
式(23)即本文所提出的多变流器系统稳定性判据,其含义为:当各子系统回差矩阵行列式的Nyquist曲线沿逆时针方向环绕 (0, j0) 点的总圈数等于全部变流器导纳矩阵行列式的RHP极点数之和时,则整个系统稳定。
为便于分析各变流器的接入对系统稳定性的影响,对于n-1台变流器系统,根据式(23),显然有
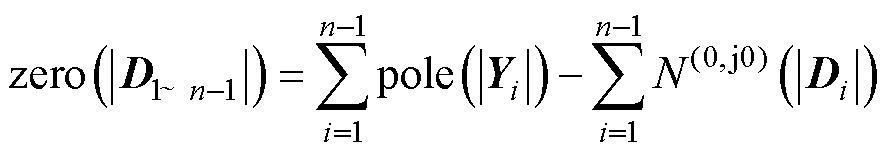 (24)
(24)
再将式(24)代入式(23),可得
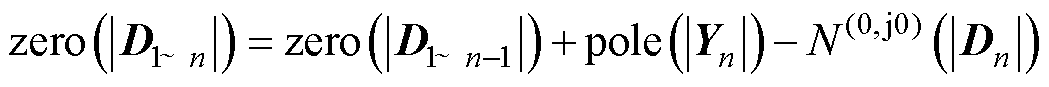 (25)
(25)
考虑到回比矩阵相比回差矩阵更便于评估系统的稳定裕度,结合式(20),可将式(25)改写为
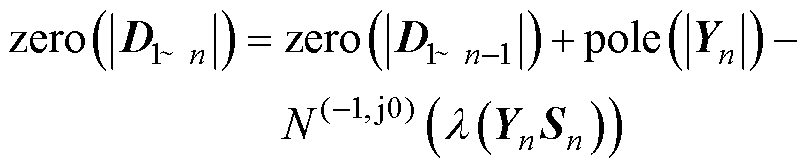 (26)
(26)
式中,l(YnSn)为矩阵YnSn的特征值。根据前文给出的关于Yn及Sn的物理含义解释,可知YnSn的含义为:在1~n-1号变流器接入电网的基础上,接入n号变流器所形成的回比矩阵。对比式(23),YnSn仅为二阶矩阵,其两个特征值均可解析计算,且其Nyquist曲线包围 (-1, j0) 的情况更加易于观察,可有效降低稳定性分析的难度。
观察式(26)等号右侧第二项和第三项可知,其表征了某变流器接入后现有系统与原系统回差矩阵行列式零点数量之差,即当pole(|Yn|)和N(-1, j0)(l|YnSn|) 二者相等时,其将不会影响原系统的稳定性;当二者不相等时,它们的差值可用于评估当前所接入的变流器对于整个系统稳定性的影响。
需要说明的是,在运用式(26)所示的稳定性判据时,需要预知各变流器的导纳矩阵行列式的RHP极点数量。众所周知,对于跟网型变流器CCI,由于其自身连接理想电压源时可保持稳定,因此,其导纳矩阵行列式不会含有RHP极点;但对于构网型变流器,其导纳矩阵行列式可能含有RHP极点,因此,下一节将对构网型逆变器导纳矩阵行列式的RHP极点数量进行详细讨论。
构网型变流器的控制策略主要包含下垂控制和VSG控制等,其对外均呈现电压源特性。分析变流器网络交互稳定性的前提是各逆变器自身稳定,即当其连接理想电流源时是稳定的,因此,构网型变流器序阻抗矩阵行列式不会含有RHP极点。然而,由于无法保证其是最小相位系统,其导纳矩阵行列式可能存在RHP极点,故需予以详细讨论。需要说明的是,鉴于构网型变流器阻抗/导纳矩阵均具有上述特点,本文仅针对VSG控制下变流器进行讨论,但所给出的分析方法同样适用于其他控制策略下的构网型变流器。
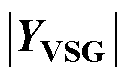 右半平面极点数量计算原理
右半平面极点数量计算原理根据序导纳矩阵和序阻抗矩阵二者之间的关系,即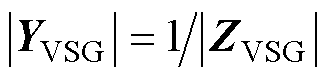 ,则有
,则有
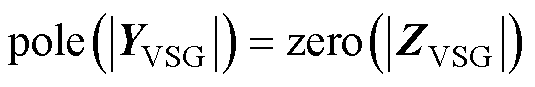 (27)
(27)
因VSG的序阻抗不一定是最小相位系统,则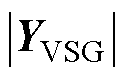 的RHP极点数可能不为0。这说明构网型逆变器阻抗矩阵行列式的RHP零点对系统的稳定性的影响不可忽视。鉴于针对单机VSG并网稳定性分析时往往是利用其阻抗矩阵,目的是避开其导纳矩阵行列式存在RHP极点的问题,故现有文献未对如何确定
的RHP极点数可能不为0。这说明构网型逆变器阻抗矩阵行列式的RHP零点对系统的稳定性的影响不可忽视。鉴于针对单机VSG并网稳定性分析时往往是利用其阻抗矩阵,目的是避开其导纳矩阵行列式存在RHP极点的问题,故现有文献未对如何确定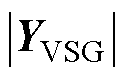 的RHP极点数量加以详细讨论。
的RHP极点数量加以详细讨论。
根据GNC, 的零点数可以表示为
的零点数可以表示为
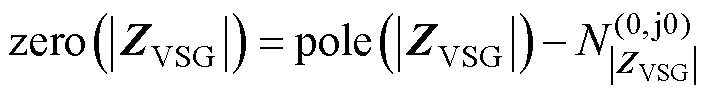 (28)
(28)
式中,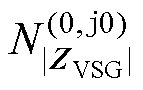 表示
表示 的Nyquist曲线逆时针包围(0, j0) 点的圈数,由于已知
的Nyquist曲线逆时针包围(0, j0) 点的圈数,由于已知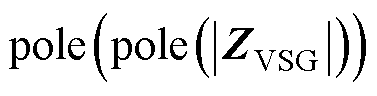 等于0,根据式(27),则
等于0,根据式(27),则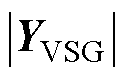 的RHP极点数为
的RHP极点数为
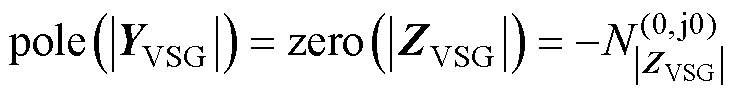 (29)
(29)
表面上,利用式(29)获得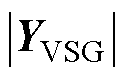 的RHP极点数并非难事,但在绘制
的RHP极点数并非难事,但在绘制 的Nyquist曲线时仍需特别关注以下问题:
的Nyquist曲线时仍需特别关注以下问题:
(1)由VSG的输出序阻抗公式可知,PI控制器中的积分环节将使得序阻抗公式中存在ki/(s-jw0)项(ki为PI控制器积分系数),同时VSG的有功功率控制环节还将包含1/[J(s-jw0)2+Dp(s-jw0)]项(J为VSG的虚拟惯性系数,Dp为VSG的P-f下垂系数),二者均将导致VSG输出序阻抗在复频率s= jw0=j2p×50处存在奇异点,无法直接计算。
(2)VSG输出序阻抗行列式分子的阶数往往大于分母的阶数,这将使得 在∞ Hz处趋于无穷大,因此在绘制∞ Hz处
在∞ Hz处趋于无穷大,因此在绘制∞ Hz处 的Nyquist曲线时必须进行人为补线。
的Nyquist曲线时必须进行人为补线。
综上所述,需要有针对性地对VSG在50 Hz和∞ Hz频点处输出序阻抗的频率特性进行讨论,方可实现系统稳定性的准确判定。
当系统中注入fp=50 Hz的正序电流扰动时,考虑到频率耦合效应,经过控制系统的作用将会产生f1=50 Hz的正序电压分量,以及f2=-50 Hz的负序电压分量,注入扰动分量亦为50 Hz的正序电压分量。说明当系统注入fp=50 Hz的正序电流扰动时,并网逆变器的输出中仅含频率为50 Hz的正序电压响应。因此,有别于其他频率,50 Hz的电流/电压仅含相同的序分量,说明该频率下的系统是镜像频率解耦的[37],即50 Hz下的正负序阻抗之间不存在耦合关系,此时输出序阻抗矩阵的非对角元素将均为0,即Zpn=Znp=0。
此外,正频率f下的正序输出阻抗与负频率-f下的负序输出阻抗存在共轭关系[38],即
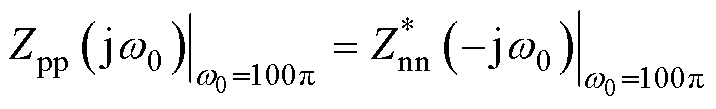 (30)
(30)
式中,Zpp(s)和Znn(s)分别为正序和负序输出阻抗;上标“*”表示共轭运算。此种关系亦可以通过全频域范围内的输出序阻抗模型给予验证,如图3所示。
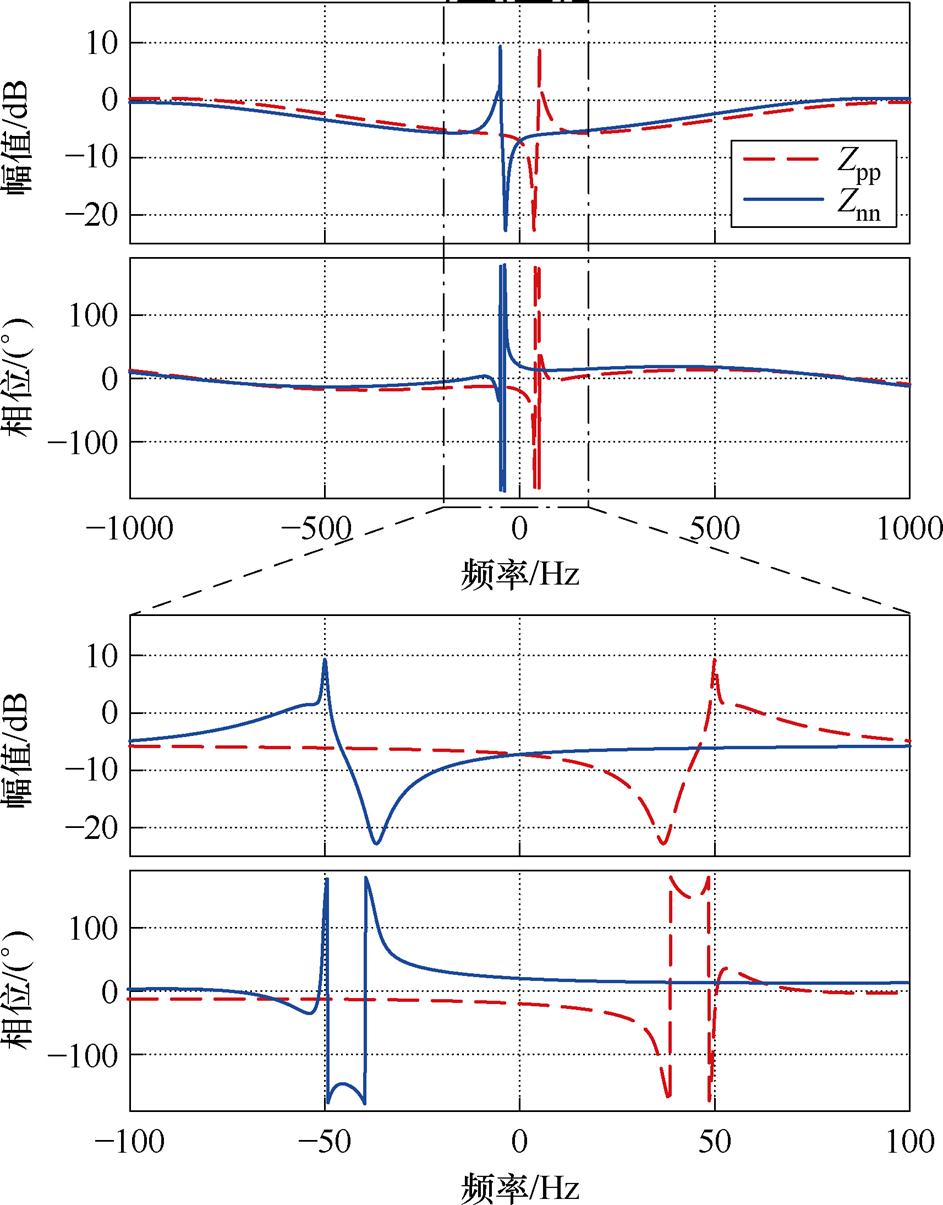
图3 VSG正负序输出阻抗频率特性曲线
Fig.3 Positive and negative sequence output impedance frequency characteristics of VSG
结合式(30),可得50 Hz下的 为
为
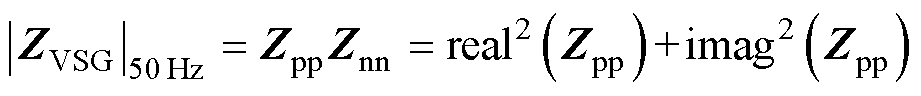 (31)
(31)
式中,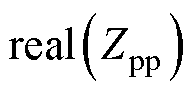 和
和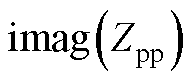 分别为50 Hz频点处Zpp的实部和虚部。显然,
分别为50 Hz频点处Zpp的实部和虚部。显然, 始终是一个大于0的实数,因此,
始终是一个大于0的实数,因此, 的Nyquist曲线在50 Hz频点处应位于正实轴上,对
的Nyquist曲线在50 Hz频点处应位于正实轴上,对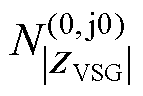 的数值不会产生影响。图4给出了某
的数值不会产生影响。图4给出了某 的Nyquist曲线,基于上述结论,对于50- Hz到50+ Hz的Nyquist曲线段,应从fp=50- Hz处的Nyquist曲线端点经原点右侧补充一条穿越正实轴的曲线,并与fp=50+ Hz对应的端点相接,如图4b中虚线所示。
的Nyquist曲线,基于上述结论,对于50- Hz到50+ Hz的Nyquist曲线段,应从fp=50- Hz处的Nyquist曲线端点经原点右侧补充一条穿越正实轴的曲线,并与fp=50+ Hz对应的端点相接,如图4b中虚线所示。
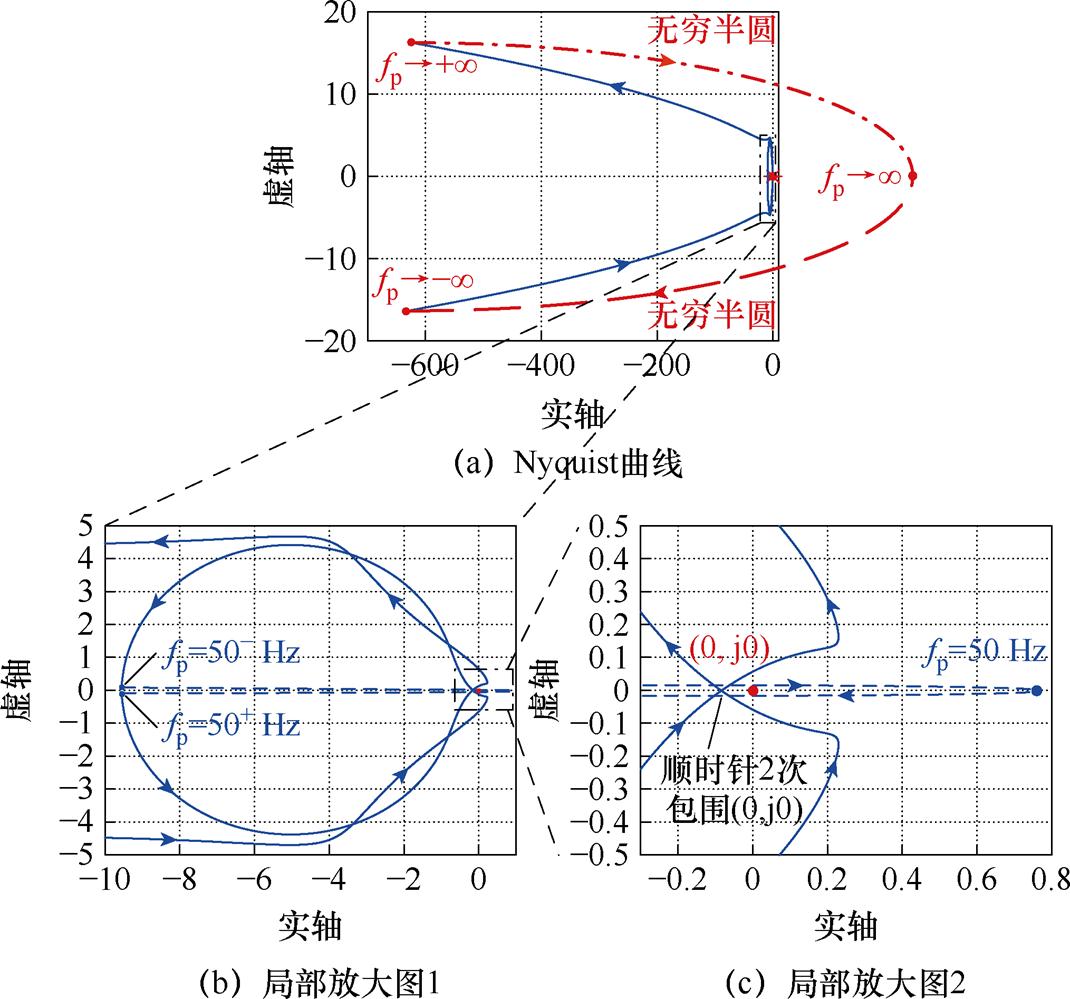
图4 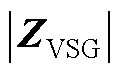 的Nyquist曲线
的Nyquist曲线
Fig.4 Nyquist curve of 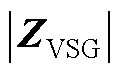
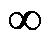 Hz频点处的VSG序阻抗频率特性分析
Hz频点处的VSG序阻抗频率特性分析如前所述,频率为∞ Hz处的Nyquist曲线亦需特殊讨论,下面以正频率fp为例,说明其由+∞变化至∞再变化至-∞对应的Nyquist曲线的补线方法[25]。
图5展示了 的Bode图,当频率趋近于∞ Hz时,
的Bode图,当频率趋近于∞ Hz时, 的幅值趋近于无穷大,且幅频特性斜率为40 dB/dec,由此可判断
的幅值趋近于无穷大,且幅频特性斜率为40 dB/dec,由此可判断 的复频域表达式分子比分母高2阶,故当频率由+∞至∞的变化过程中,相频曲线将减小180°,如图5中蓝色虚线所示。
的复频域表达式分子比分母高2阶,故当频率由+∞至∞的变化过程中,相频曲线将减小180°,如图5中蓝色虚线所示。
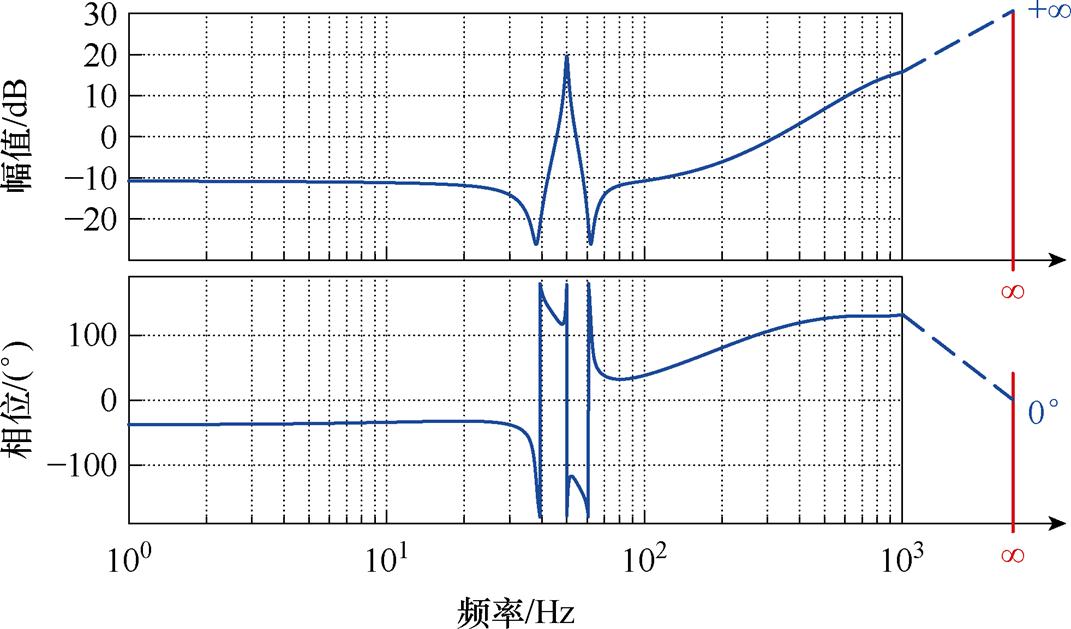
图5 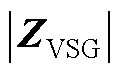 的Bode图
的Bode图
Fig.5 Bode diagram for 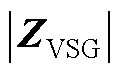
图4为图5所示Bode图对应的Nyquist曲线。当频率为∞ Hz时,其于+∞处穿越实轴;当频率为+∞ Hz和-∞ Hz时其在实轴上的投影均位于-∞处。因此,当fp为∞时,其相位为0°,当fp为±∞时,其相位则约为180°。图4a中的红色点画线和虚线共同呈现了频率由+∞变化至∞再变化至-∞对应的补线图,其补线过程为:在fp从+∞变化至∞的过程中, 的Nyquist轨迹段将从第二象限经第一象限顺时针旋转180°至正实轴,如图4a红色点画线所示。图4a中红色虚线则展示了在fp从∞变化至-∞的过程中,
的Nyquist轨迹段将从第二象限经第一象限顺时针旋转180°至正实轴,如图4a红色点画线所示。图4a中红色虚线则展示了在fp从∞变化至-∞的过程中, 的Nyquist轨迹段经第四象限顺时针旋转约180°至第三象限。
的Nyquist轨迹段经第四象限顺时针旋转约180°至第三象限。
根据3.2节的分析,频率由50- Hz变化至50 Hz再变化至50+ Hz对应的补线如图4b和图4c所示。当fp为50+ Hz和50- Hz时,曲线在虚轴上的投影分别位于正、负半轴上,且趋近于0,如图4b所示。而曲线在50 Hz频点时,由于高频率下 为正实数,因此
为正实数,因此 的Nyquist轨迹将位于正实轴,如图4c所示。
的Nyquist轨迹将位于正实轴,如图4c所示。
通过对比图4中经50 Hz和∞ Hz补线前后的Nyquist曲线可知,若忽视f=50 Hz和∞ Hz时 的特性,而将其Nyquist曲线假定为一条全频段平滑连续的曲线,则
的特性,而将其Nyquist曲线假定为一条全频段平滑连续的曲线,则 的Nyquist曲线仅会顺时针包围原点1次。而经补线后,实际上
的Nyquist曲线仅会顺时针包围原点1次。而经补线后,实际上 的Nyquist曲线将包围原点2次。这说明若忽视50 Hz和∞ Hz处的阻抗矩阵特性,将因
的Nyquist曲线将包围原点2次。这说明若忽视50 Hz和∞ Hz处的阻抗矩阵特性,将因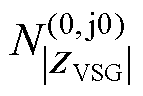 的错误计算而导致稳定性误判。
的错误计算而导致稳定性误判。
综合第2节和本小节所得结论,可将本文提出的多变流器系统小干扰稳定性分析步骤总结如下:
(1)获得系统中线路网络的开路阻抗矩阵以及各逆变器的输出序导纳/阻抗矩阵。
(2)对于跟网型逆变器,因其连接理想电压源稳定,故认定跟网型逆变器的序导纳矩阵的行列式不含RHP极点;对于VSG,绘制 的Nyquist曲线,利用本小节的方法补全其在50 Hz和∞ Hz频点处的曲线,获得
的Nyquist曲线,利用本小节的方法补全其在50 Hz和∞ Hz频点处的曲线,获得 的零点数,即
的零点数,即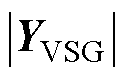 的极点数。
的极点数。
(3)将各逆变器逐个接入系统,统计逆变器导纳矩阵行列式的RHP极点数及回比矩阵特征值Nyquist曲线逆时针绕 (-1, j0) 的圈数,依据式(26)计算各变流器接入后系统的RHP闭环极点数量,判定系统的稳定性。
不失一般性,本文以两个场景来验证本文所提判稳方法的有效性,各变流器的详细参数列于附表1中,两算例系统所有工况短路比SCR<6。
基于第3节关于VSG序导纳行列式RHP极点的获取方法,可得本文中变流器有
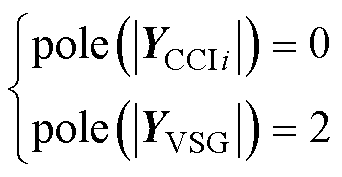 (32)
(32)
两算例中VSG的给定输出功率均为10 kW,且CCI的参数一致。两算例中CCI给定输出功率均由额定值提升10%,用于模拟临界稳定工况,以定量验证本文方法的准确性。两算例中的SCR、PI控制器与LC滤波器参数亦有所不同,并通过Simulink离线仿真和硬件在环实验两种方式分别进行仿真,为验证所提分析方法的正确性提供有力支撑。
算例1多变流器网络连接关系如图6所示,变压器10 kV侧电网线路阻抗Zg归算到380 V侧,各线路阻抗参数见附表2,两CCI额定输出由140 kW调整至160 kW,以分析相同拓扑、不同参数下系统的小信号稳定性。
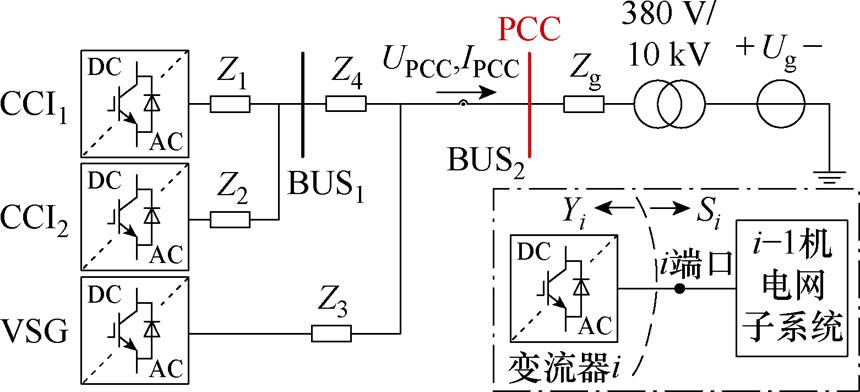
图6 算例1多变流器网络
Fig.6 Case 1 multi-converters network
当两台CCI的给定输出功率为140 kW、VSG的额定功率为10 kW时,CCI1、CCI2和VSG依次接入系统所对应的回比矩阵Y1S1、Y2S2和Y3S3特征值的Nyquist曲线如图7所示。
由图7a可知,CCI1接入电网后,Y1S1特征值的Nyquist曲线未包围 (-1, j0) 点,依据式(26)可得
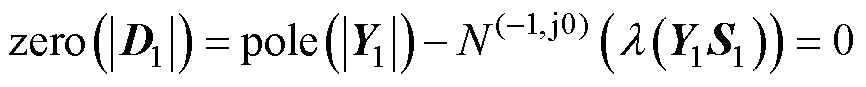 (33)
(33)
在CCI1接入系统的基础上接入CCI2,所得Y2S2特征值的Nyquist曲线如图7b所示,曲线仍未包围 (-1, j0) 点。将式(32)和式(33)代入式(26),可得
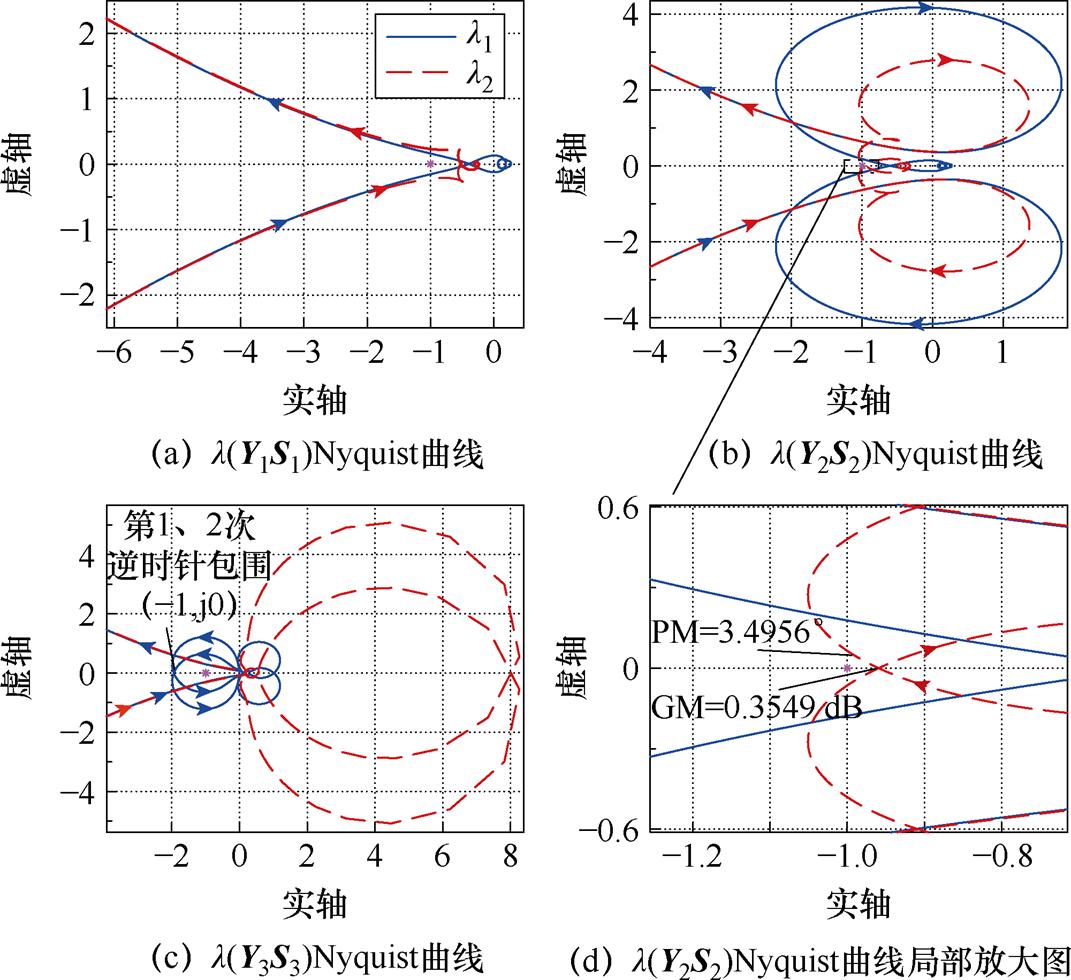
图7 稳定算例1:l(YiSi) Nyquist曲线
Fig.7 Stable case: Nyquist curves of l(YiSi)
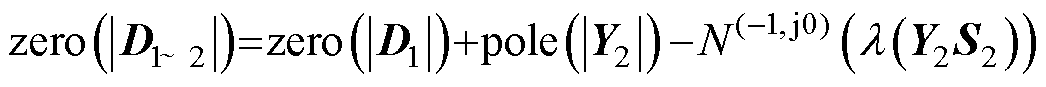
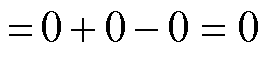 (34)
(34)
继续接入VSG,此时Y3S3特征值的Nyquist曲线将逆时针包围 (-1, j0) 点2次,如图7c所示。由于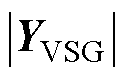 自身具有两个RHP极点,故可得系统闭环传递函数的RHP极点数量为
自身具有两个RHP极点,故可得系统闭环传递函数的RHP极点数量为
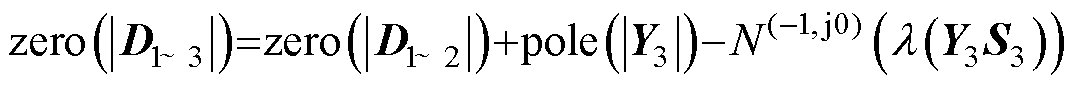
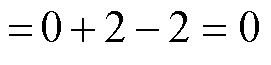 (35)
(35)
将上述分析结果总结为表1,可以看出,经过三步分析后可得出结论:由CCI1、CCI2和VSG并网组成系统计算所得zero(|D1~3|)=0,这表示闭环传递函数RHP极点数为0,故各变流器接入系统时均可保持稳定。
表1 稳定算例:稳定性分析过程
Tab.1 Stable case: results of stability analysis procedures

工况稳定性 a (i=1)000稳定 b (i=2)000稳定 c (i=3)220稳定
此外,相比于CCI1单独接入系统,CCI2的接入将使系统的相位裕度和幅值裕度分别减小为3.495 6°和0.354 9 dB,如图7d所示。可以预想,若CCI的输出功率进一步增加,SCR随之减小,系统强度被削弱,相应的Nyquist曲线与负实轴交点将继续向左移动,会包围 (-1, j0) 点,这说明相较弱电网而言,大功率的跟网型变流器接入会导致稳定裕度下降,甚至造成系统失稳。
将算例1中两台CCI的额定功率调整为160 kW,VSG的额定输出功率仍为10 kW,各变流器接入系统所对应的回比矩阵Y1S1、Y2S2、Y3S3的特征值的Nyquist曲线绘于图8中。当仅有CCI1接入系统时,Y1S1特征值的Nyquist曲线未包围 (-1, j0) 点,从而可得
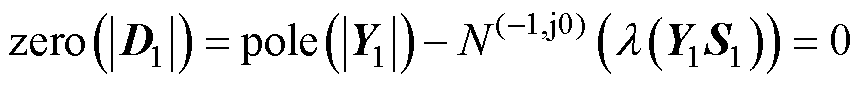 (36)
(36)
再接入CCI2,Y2S2特征值的Nyquist曲线顺时针包围 (-1, j0) 点2次,此时有
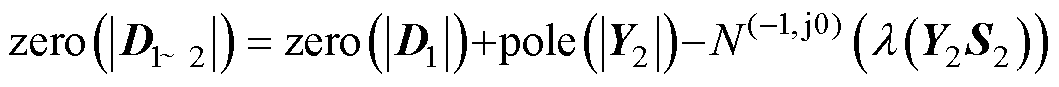
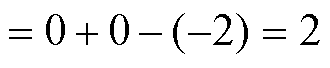 (37)
(37)
继续接入VSG,Y3S3特征值的Nyquist曲线将沿逆时针方向穿过 (-1, j0) 两次,结合式(32)和式(37),可得此时系统闭环传递函数的RHP极点数量为
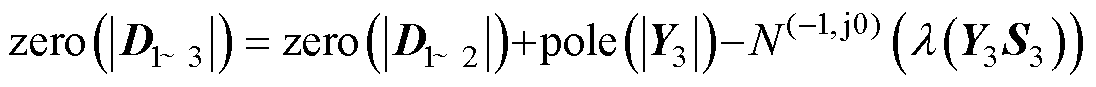
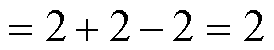 (38)
(38)
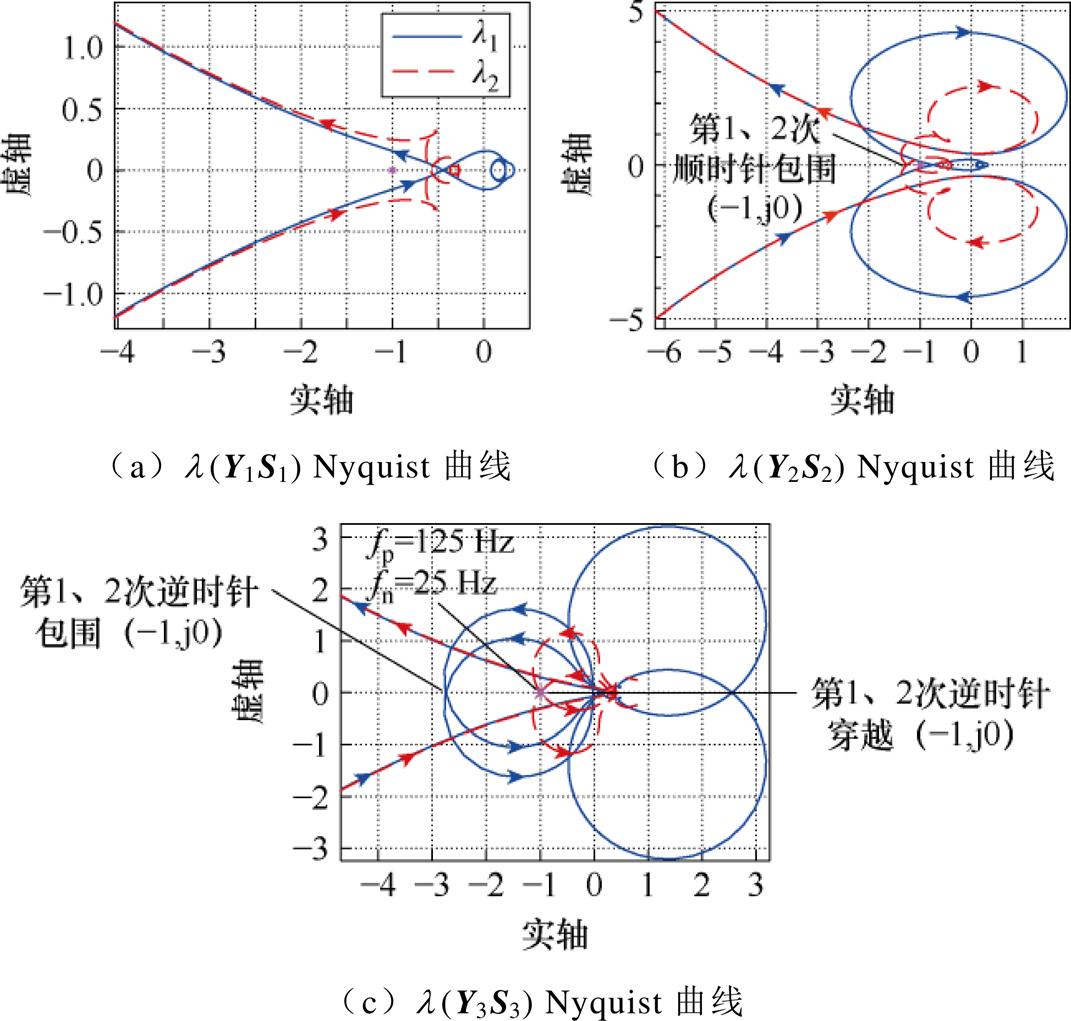
图8 临界稳定算例:l(YiSi) Nyquist曲线
Fig.8 Critical stable case: Nyquist curves of l(YiSi)
上述分析结果的总结见表2,可以看出,本算例中两台160 kW的CCI接入系统会导致zero(|D1~2|)>0,造成失稳,而VSG的接入有助于提升系统稳定性。
此外,由于此时Y3S3特征值的Nyquist曲线两次穿过 (-1, j0) 点,此时zero(|D1~3|)=0,可以判定系统处于临界稳定状态,且此两次穿越所对应的频率为125 Hz和25 Hz,分别为正序和负序的临界振荡频率。
表2 临界稳定算例:稳定性分析过程
Tab.2 Critical stable case: results of stability analysis procedures

工况稳定性 a (i=1)000稳定 b (i=2)0-22不稳定 c (i=3)22 (穿越(-1, j0))2临界稳定
算例2多变流器网络结构如图9所示,变压器10 kV侧电网线路阻抗Zg归算到380 V侧,各线路阻抗参数见附表3。本算例中整个系统包含3台CCI和2台VSG,其中各CCI和VSG的额定输出功率分别为70 kW和10 kW。利用本文所提方法,按照图9中下标顺序依次接入电网,通过将CCI输出功率增加10%以分析系统的小扰动稳定性。
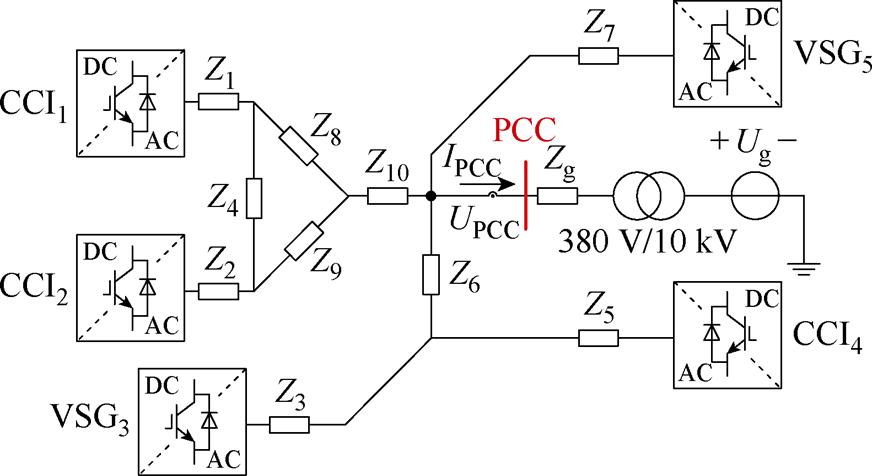
图9 算例2多变流器网络
Fig.9 Case 2 multi-converters network
各变流器按顺序接入系统所对应五种工况的回比矩阵依次为Y1S1、Y2S2、Y3S3、Y4S4和Y5S5,其特征值的Nyquist曲线如图10所示,利用本文方法所得的各步骤系统RHP闭环极点数列于表3之中,相应计算过程为
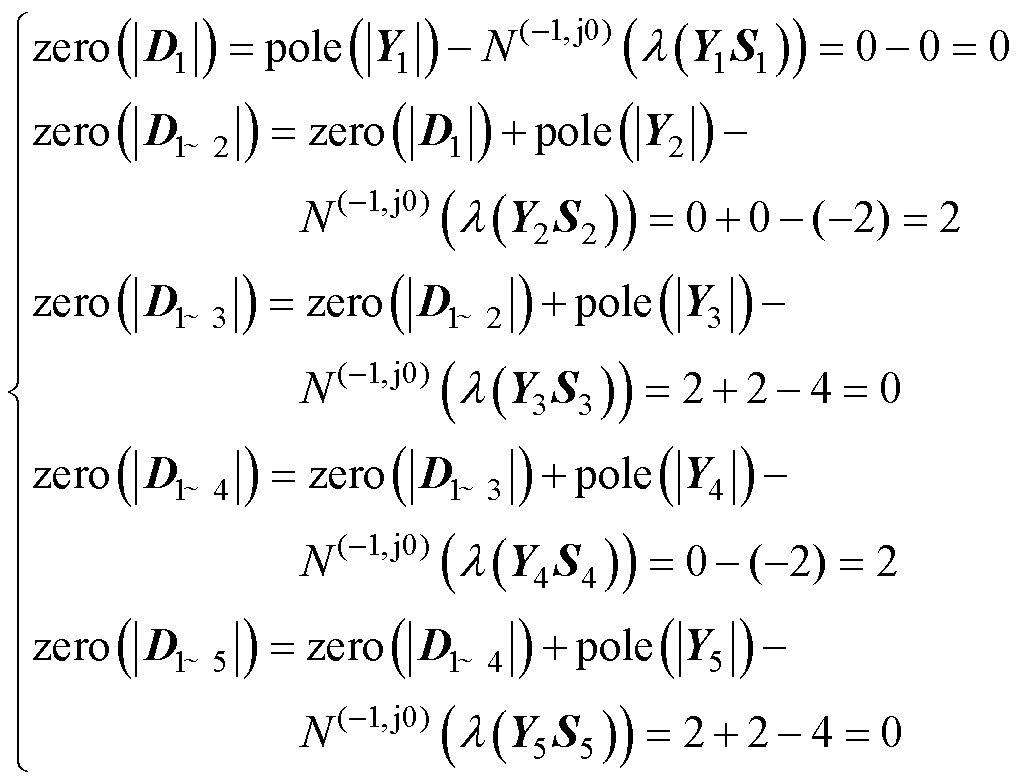 (39)
(39)

图10 5台变流器算例:l(YiSi) Nyquist曲线
Fig.10 Five-converter case: Nyquist curves of l(YiSi)
表3 稳定性分析过程
Tab.3 Results of stability analysis procedures
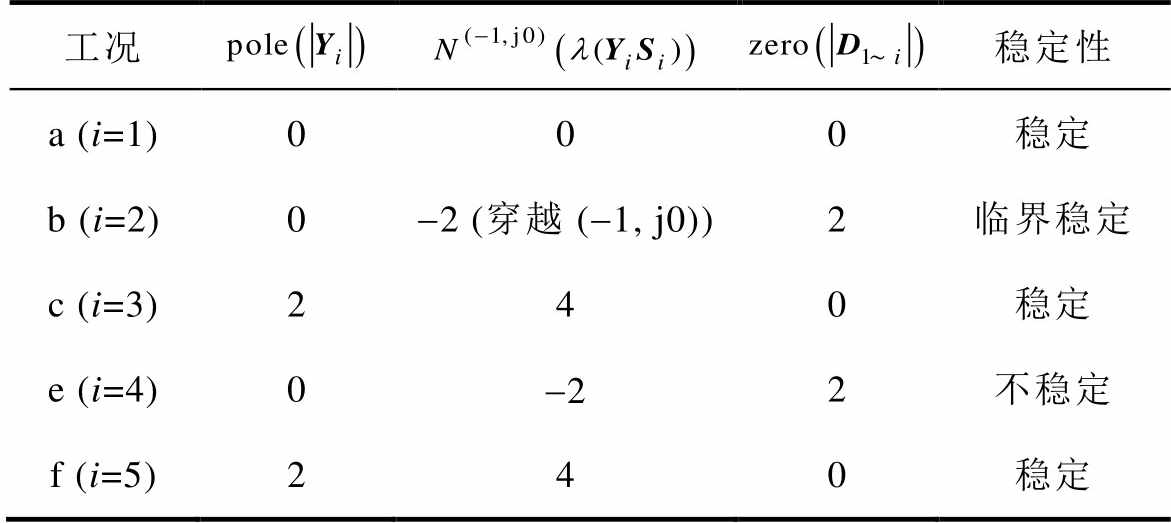
工况稳定性 a (i=1)000稳定 b (i=2)0-2 (穿越 (-1, j0))2临界稳定 c (i=3)240稳定 e (i=4)0-22不稳定 f (i=5)240稳定
具体为:CCI1接入下,由于l(Y1S1) 的Nyquist曲线未包围 (-1, j0) 点,系统将稳定运行,如图10a所示;图10b则呈现了当CCI2接入后的Nyquist曲线,此时l(Y2S2)顺时针穿越 (-1, j0) 点2次,系统处于临界稳定状态,且两次穿越对应的频率为正序115 Hz和负序15 Hz;继而接入VSG3,图10c中l(Y3S3) 逆时针包围 (-1, j0) 点4次,考虑到VSG3序导纳Y3存在2个RHP极点,根据式(39)计算结果可知,此时系统不存在RHP闭环极点,系统处于稳定状态;继续接入CCI4,l(Y4S4) 顺时针包围 (-1, j0) 点2次,如图10d所示,根据式(39)计算结果,此时系统存在2个RHP闭环极点,系统失稳;最后,接入一台输出功率为10 kW的VSG5,可以看出图10e中l(Y5S5) 逆时针包围 (-1, j0) 点4次,考虑到VSG5序导纳矩阵自身含有2个RHP极点,经式(39)计算,此时系统无RHP闭环极点,系统稳定。
总体上,系统回比矩阵YS的特征值Nyquist曲线共计顺时针穿越 (-1, j0) 点4次,逆时针包围 (-1, j0) 点8次,结合两台VSG序导纳矩阵各自含有2个RHP极点,五机系统将不含有RHP闭环极点,整个系统可稳定运行。
经上述分析可总结出如下规律:随着CCI型变流器的依次接入,馈入系统的总功率增加,由于外部的网络结构和线路阻抗没有变化,系统SCR降低,电网的强度变弱,系统稳定裕度减少而趋于失稳。相较而言,构网型逆变器VSG的接入对电网电压和频率起到支撑作用,尤其是在弱电网的场景下,有助于提高系统的小信号稳定性。
为验证上述稳定性分析,本节在Matlab/Simulink中搭建仿真模型,通过时域仿真验证算例1中所提方法分析结果的正确性。
为进一步提高本文所提多机稳定性分析方法的可信度,本节采用搭载NI-LinuxRT系统的NI PIXe- 1082实时仿真机作为下位机,运用现场可编程门阵列(FPGA)实现信号传输与硬件资源配置,上位机以EasyGoDeskSim软件为基础,完成了算例2的模型搭建,最终利用硬件在环(HIL)仿真平台实现了多母线多变流器系统的在线仿真模拟。
系统拓扑如图6所示,各变流器和线路参数与4.1节一致,VSG给定功率始终保持在10 kW。t=1 s时,将两台跟网型逆变器给定功率由140 kW调整为160 kW,以模拟相同拓扑、不同参数下的系统发生小干扰后系统的动态过程。
图11给出了不同工况下的PCC电流波形。其中图11a为单台CCI接入系统的电流波形,可以看出,两工况在发生小扰动后,电流均保持标准正弦波形,系统稳定,与表1和表2中工况a均一致。两台跟网型CCI接入系统的电流波形如图11b所示,当二者的给定功率为140 kW时,小信号扰动下系统保持稳定,与表1工况b的分析结果相符;t=1.0 s,当二者给定功率调整为160 kW后,受小信号扰动影响,PCC电流波形发生畸变,系统失稳,与表2中工况b的分析结果吻合。
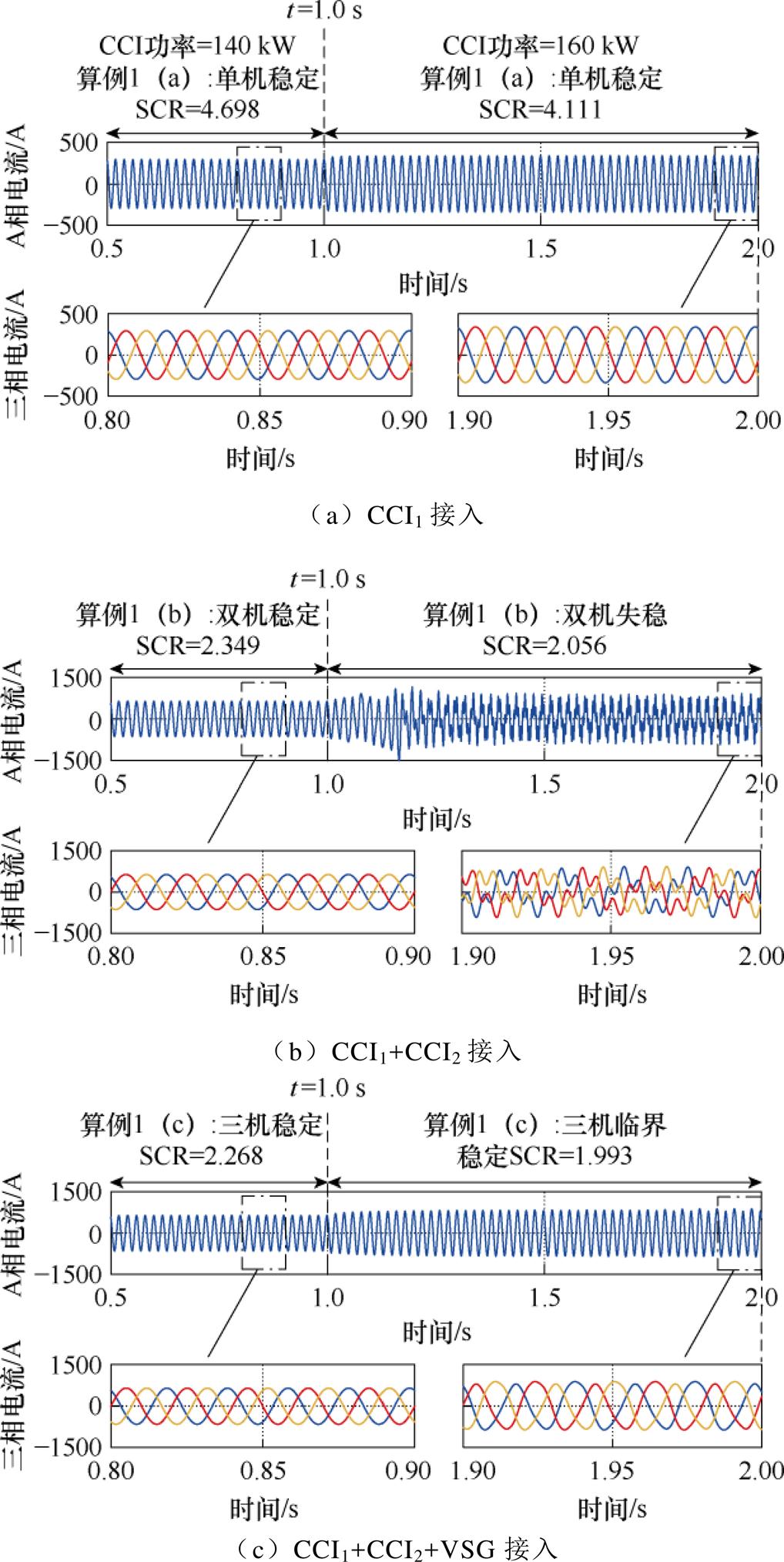
图11 算例1:PCC电流波形
Fig.11 Case 1: current waveforms at PCC
由两台跟网型CCI和一台构网型VSG组成的多变流器系统的仿真结果如图11c所示。可以看出,t=1.0 s前,系统在小扰动下保持稳定状态,与表1工况c所给出的分析结论一致。当在t=1.0 s将两台CCI给定功率由140 kW调整为160 kW,并加入小扰动后,PPC电流波形发生畸变,但与图11b相比,其畸变程度明显变小,系统稳定性有所改善,原因是VSG的接入起到了增强电网强度的作用。
进一步对1.5~2.5 s时段内的PCC电流波形进行傅里叶分析,得到的电流频率成分如图12所示。可以看出,其含有的主要谐波频率为125 Hz(正序)和25 Hz(负序),与4.1节中图8c的理论分析结果相一致,从定量角度验证了本文所提出的稳定性分析方法的准确性。若进一步提升VSG的给定功率,系统将恢复稳定,鉴于篇幅有限,本文未予给出。
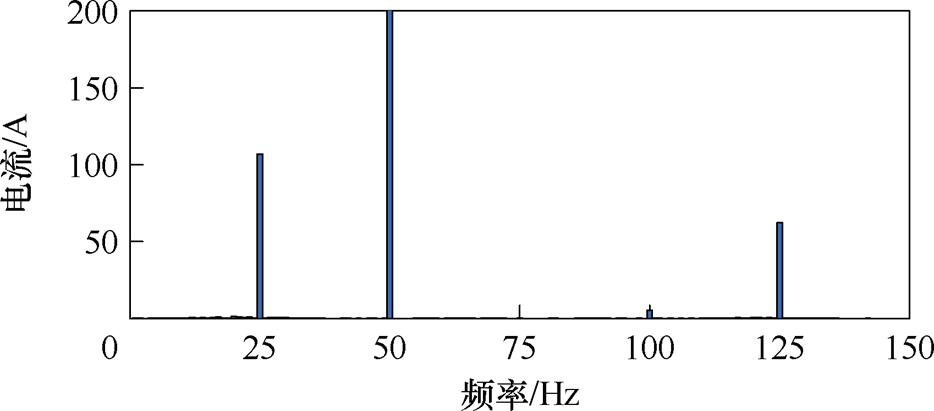
图12 算例1:PCC电流频率成分
Fig.12 Case 1: FFT analysis of current at PCC
系统拓扑如图9所示,各变流器和线路参数与4.2节一致。图13为HIL仿真平台,HIL仿真相比于全数字仿真可以更加真实地模拟多变流器系统的闭环运行状态信息。HIL实验中,电气回路的仿真步长为1 ms,控制回路的仿真步长为100 ms。
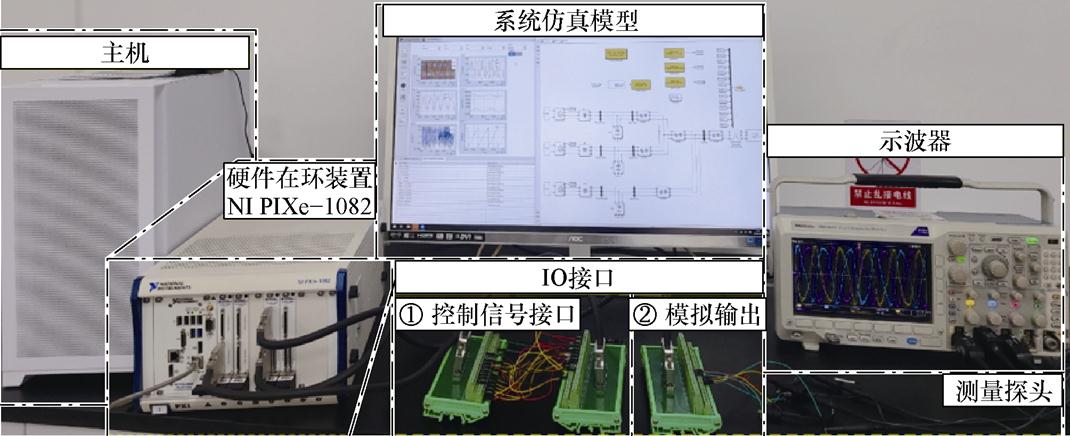
图13 HIL仿真平台
Fig.13 HIL simulation platform
仿真平台由HIL装置NI PIXe-1082、IO接口、测量探头、示波器以及上位机等组成。上位机显示器利用EasyGoDeskSim软件的UI界面一方面实现系统运行状态监视,另一方面实时调节所有系统参数,以模拟不同工况;硬件在环装置能够快速且精准地求解系统状态量,利用FPGA与IO接口实现电气与控制系统的交互,以及在示波器输出电压、电流曲线,观察其变化以判断该系统运行是否稳定。
基于HIL仿真平台开展仿真实验,与表3中五种工况对应的PCC电流波形如图14所示。系统发生扰动前,所有工况电流波形均为标准正弦波,系统均处于稳定状态,为节省篇幅不再给出。从图14可以看出,输出功率为70 kW的CCI1和CCI2先后接入电网,电网短路比由5.472下降至2.736,电网强度逐步变弱,电流波形发生畸变,如图14b所示,即系统由稳定运行进入临界稳定状态。对其进行傅里叶分析,PCC频率成分柱状图如图15所示,其含有正序115 Hz和负序15 Hz谐波分量,与图10b中Nyquist曲线两次穿越 (-1, j0) 点时的频率相一致。继而接入VSG3后,PCC的电流波形如图14c所示,其恢复为标准正弦波形,系统回到稳定状态。在此基础上,继续接入CCI4,此时系统SCR进一步下降到1.741,电流波形紊乱,如图14d所示,系统失稳。此时再次接入一台构网型逆变器VSG5,电流波形如图14e所示,系统又可恢复稳定运行。

图14 算例2:PCC电流波形
Fig.14 Case 2: current waveforms at PCC
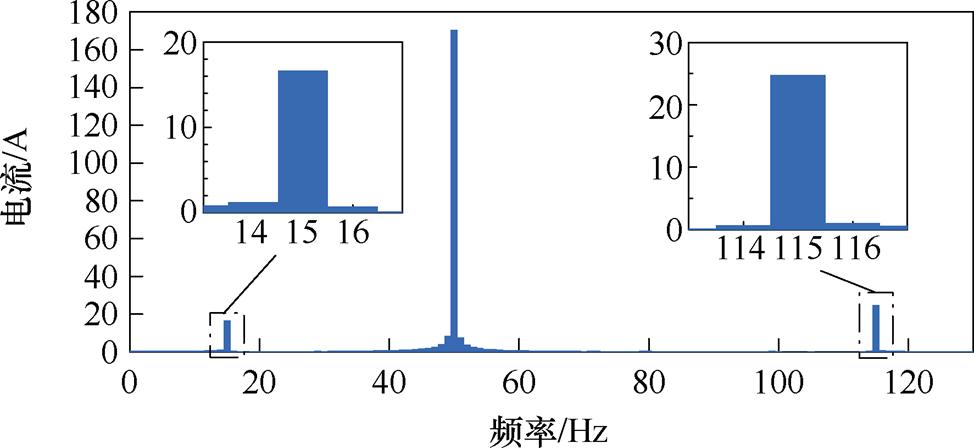
图15 算例2:PCC电流频率成分
Fig.15 Case 2: FFT analysis of current at PCC
综上所述,由于构网型逆变器对电网具有电压和频率支持作用,有助于提升系统小信号稳定性。同时,上述五种工况下的HIL实验结果均与4.2节表3分析结果一致。说明了本文所提稳定性分析方法的正确性。
本文针对由跟网型逆变器与构网型逆变器组成的多变流器系统的小干扰稳定性分析方法和构网型逆变器输出序导纳RHP极点数量的获取方法进行了全面系统的研究,所得结论如下:
1)本文通过将跟网型和构网型逆变器统一表示为“Y”型子系统,推导了一种适用于分析多变流器系统小干扰稳定的通用判据,其具有如下优点:①该方法适用于任意网络结构的多变流器系统小干扰稳定性分析;②该方法具有递推形式,适用于任意数量变流器并网的系统,具有很好的通用性;③在准确评估系统整体稳定性的同时还有助于分析各变流器对系统稳定性的影响;④所提方法避免了对高维矩阵行列式RHP极点及高维矩阵特征值Nyquist曲线的分析,且特征值具有解析计算公式而无需数值求解,简单易行,准确可靠。
2)为实现系统小干扰稳定性的准确评估,本文对构网型逆变器输出序阻抗矩阵行列式在50 Hz与∞ Hz处的频率特性进行了详细讨论,基于所得结论,给出了其Nyquist曲线在奇异点处的补线原则,实现了VSG输出序导纳矩阵行列式极点数量的准确获取。
3)结合典型算例,本文对同时含有构网型与跟网型变流器的多变流器系统进行了小干扰稳定性分析,获得了各逆变器接入后闭环系统的RHP极点数量,并分析了各变流器接入对系统稳定性的影响。针对所分析的典型算例开展了Simulink时域仿真与硬件在环实验,并对临界稳定场景下PCC电流所含的频率成分进行了傅里叶分析。通过分析发现:理论分析所得系统稳定性与仿真实验结果一致,定性验证了所提方法有效性;进一步,通过对比理论分析所得Nyquist图两次穿越 (-1, j0) 点的频率与仿真实验中PCC的扰动电流频率,二者基本相等,定量说明了本文方法用于评估系统的小干扰稳定性的准确性。
附录 主要公式及仿真参数
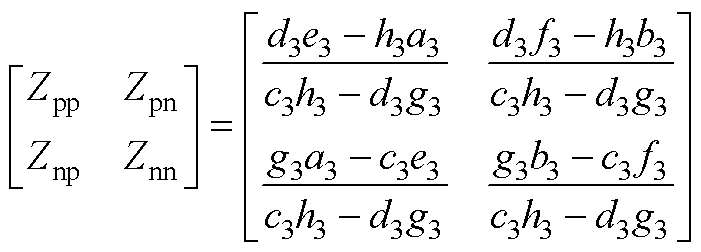 (A1)
(A1)
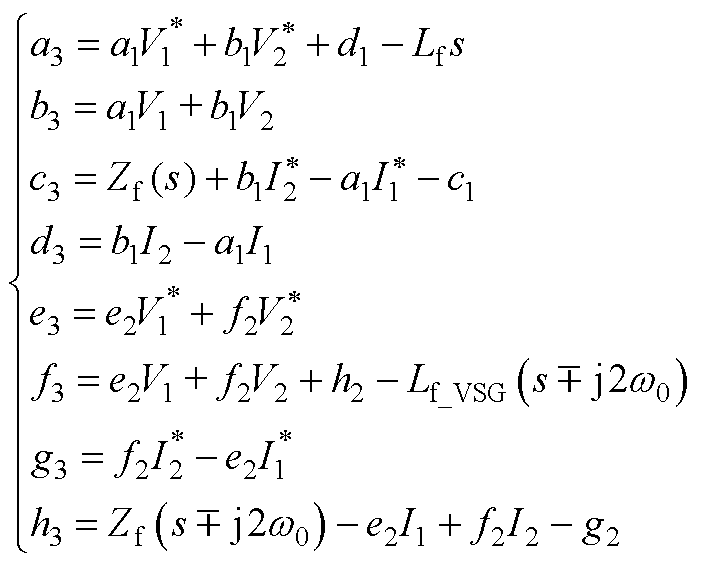 (A2)
(A2)
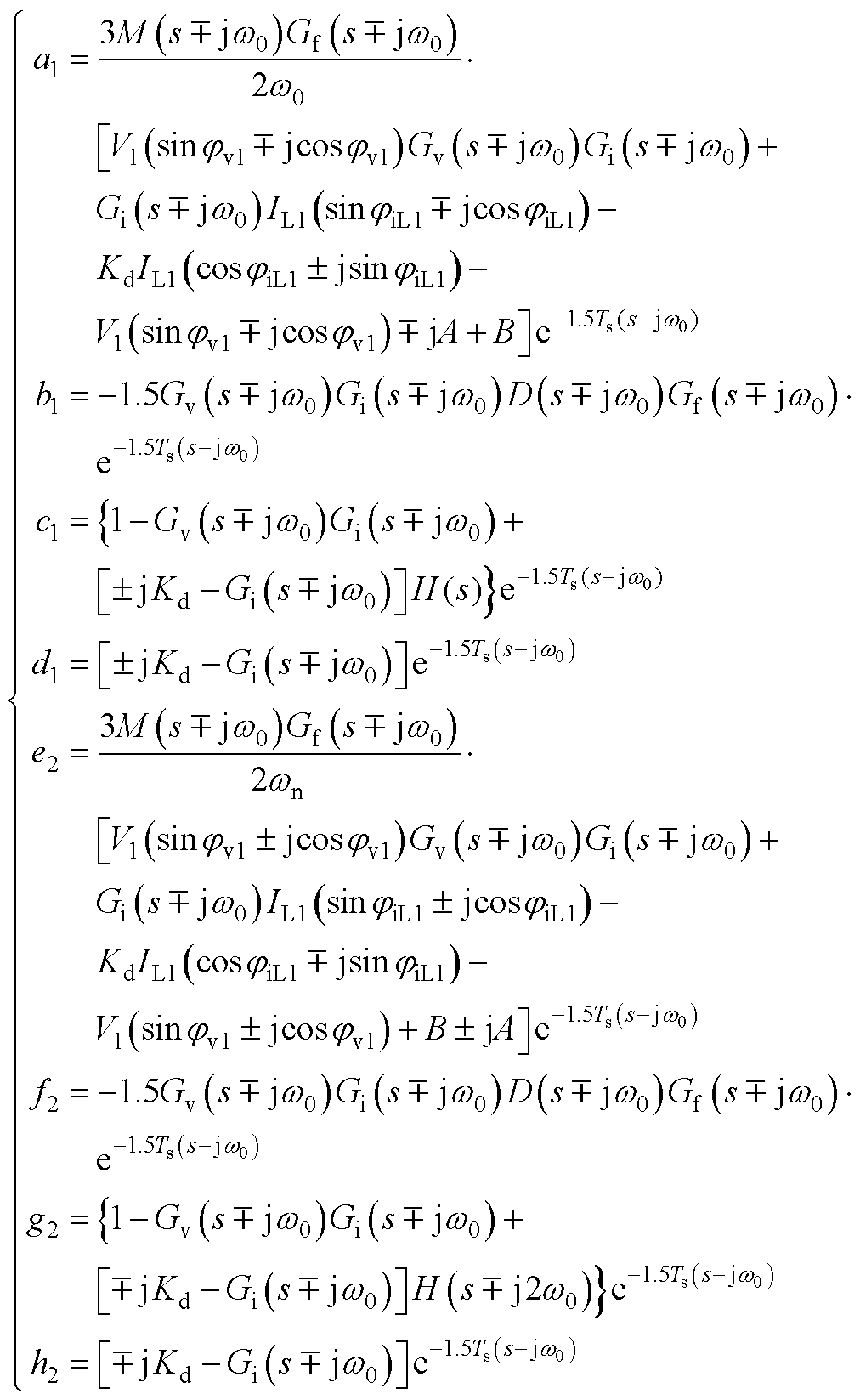 (A3)
(A3)
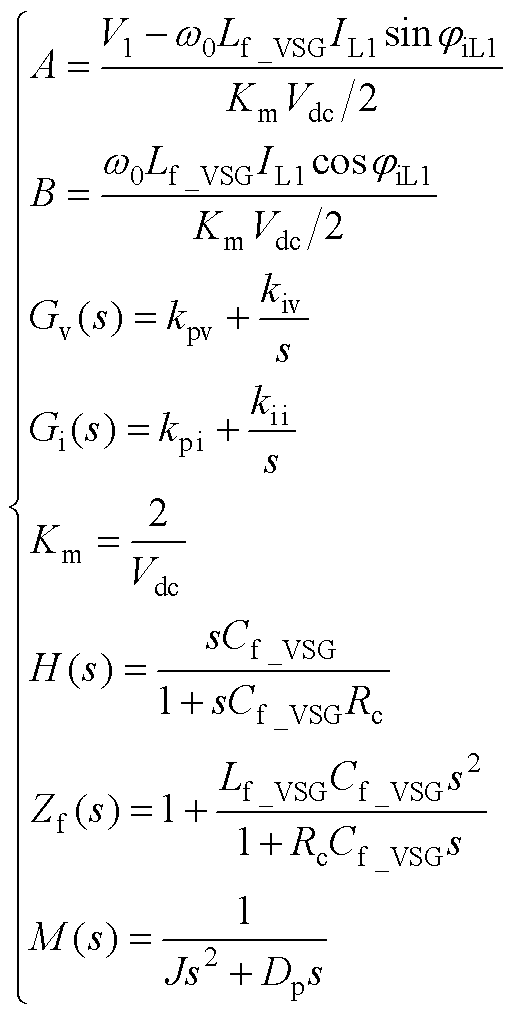 (A4)
(A4)
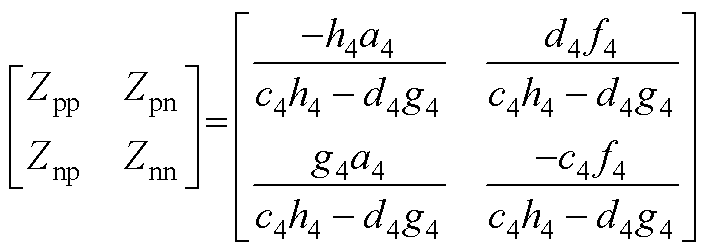 (A5)
(A5)
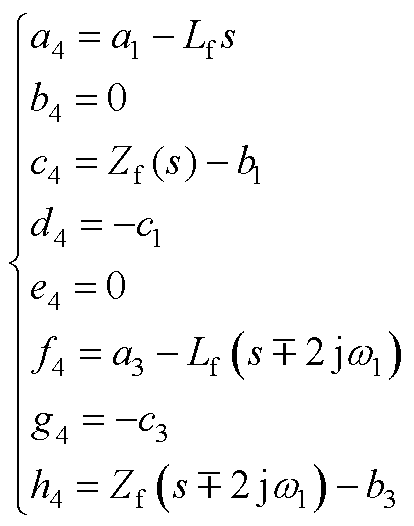 (A6)
(A6)
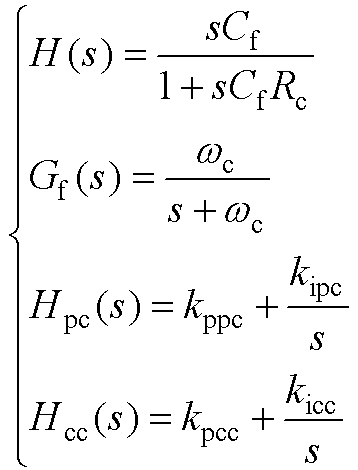 (A7)
(A7)
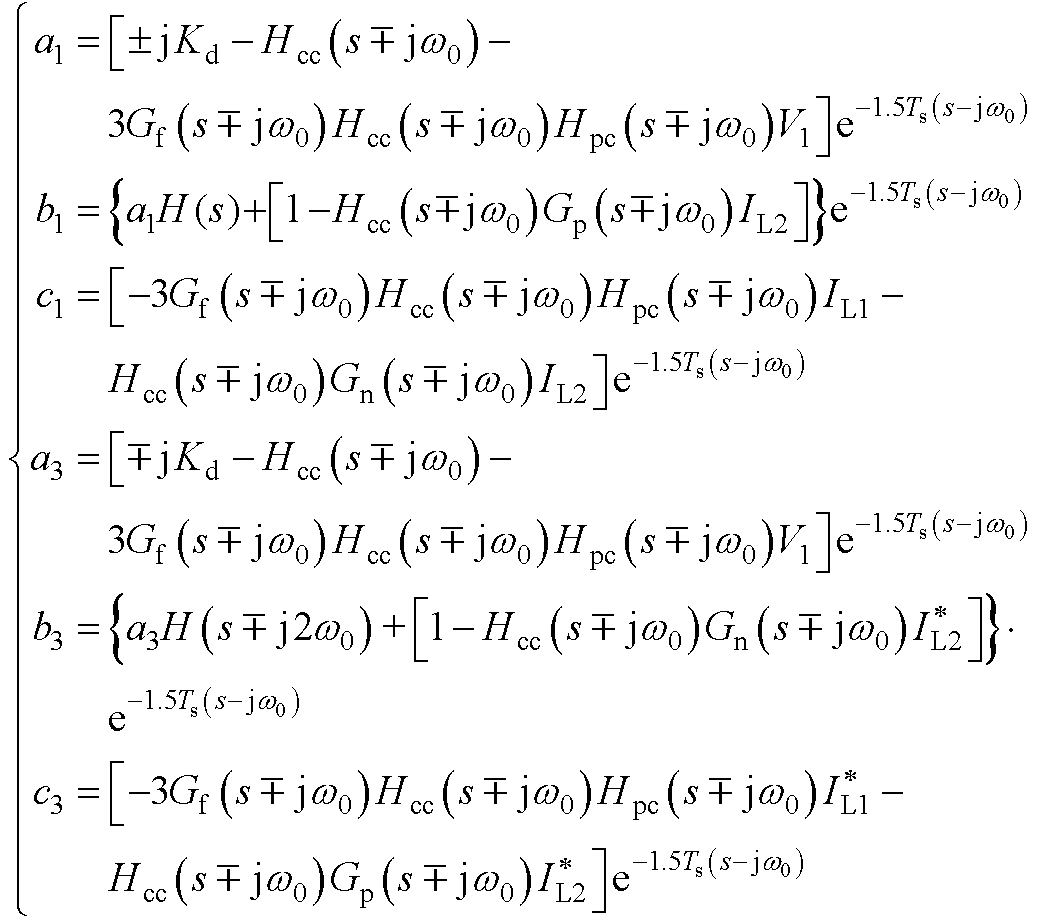 (A8)
(A8)
附表1 VSG与CCI的电路和控制参数
App.Tab.1 Parameters of VSG and CCI
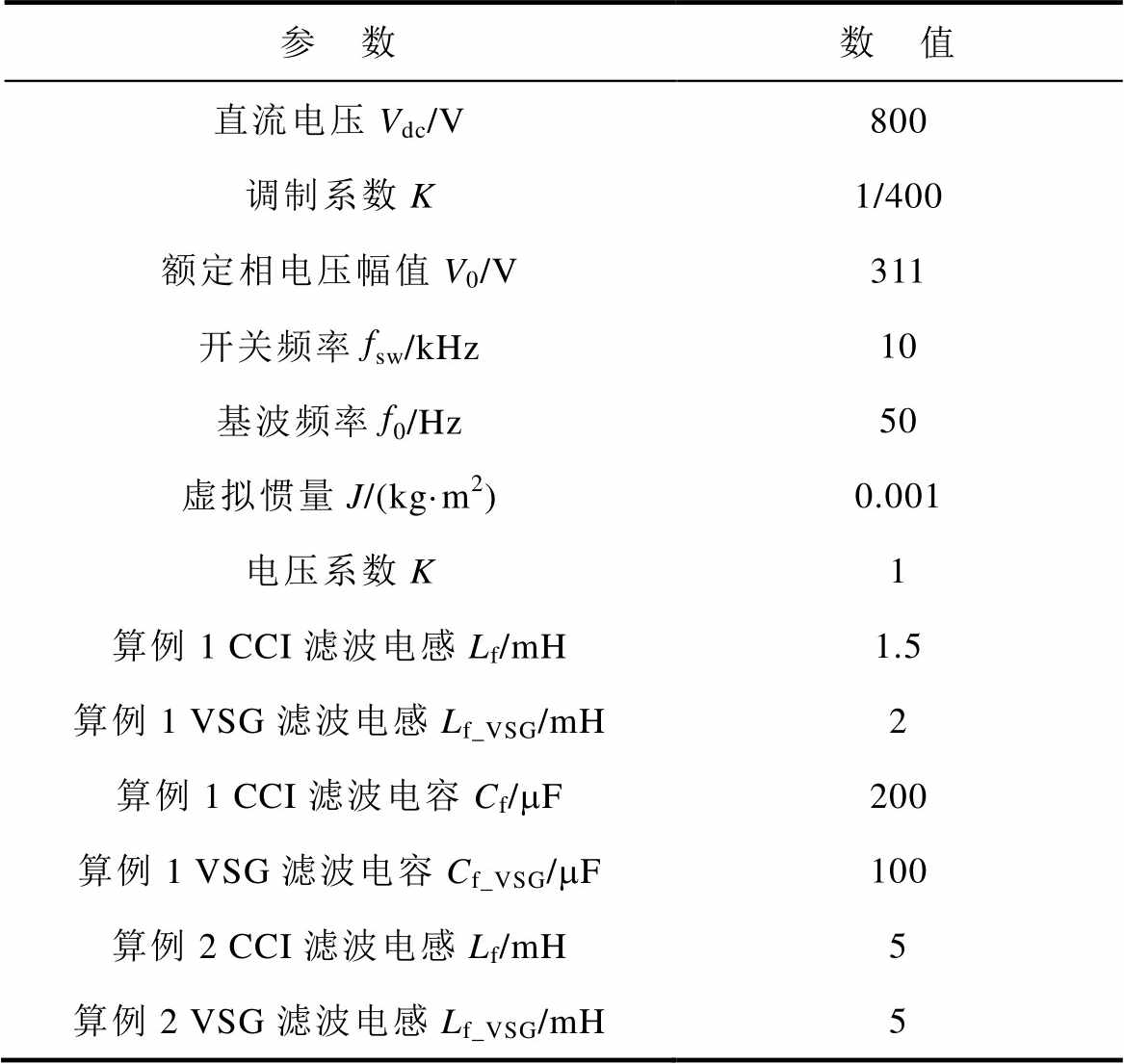
参 数数 值 直流电压Vdc/V800 调制系数K1/400 额定相电压幅值V0/V311 开关频率fsw/kHz10 基波频率f0/Hz50 虚拟惯量J/(kg·m2)0.001 电压系数K1 算例1 CCI滤波电感Lf/mH1.5 算例1 VSG滤波电感Lf_VSG/mH2 算例1 CCI滤波电容Cf/mF200 算例1 VSG滤波电容Cf_VSG/mF100 算例2 CCI滤波电感Lf/mH5 算例2 VSG滤波电感Lf_VSG/mH5
(续)

参 数数 值 算例2 VSG滤波电容Cf_VSG/mF500 算例2 CCI滤波电感Lf/mF500 P-f下垂系数Dp15 Q-V下垂系数Dq321 VSG电压外环比例系数kpv2 VSG电压外环积分系数kiv50 算例1 VSG电流内环比例系数kpi1 VSG电流内环积分系数kii50 CCI锁相环比例系数kpPLL0.531 8 CCI锁相环积分系数kiPLL31.008 算例1 CCI功率外环比例系数kppc0.002 4 算例1 CCI功率外环积分系数kipc0.1 算例1 CCI电流内环比例系数kpcc1 算例1 CCI电流内环积分系数kicc1 000 算例2 CCI功率外环比例系数kppc0.001 6 算例2 CCI功率外环积分系数kipc0.05 算例2 CCI电流内环比例系数kpcc20 算例2 CCI电流内环积分系数kicc1 000 算例2 VSG电流内环比例系数kpi4
附表2 算例1系统线路参数
App.Tab.2 Parameters of lines in system of case 1

参 数数 值 R1/W, L1/mH0.01, 0.2 R2/W, L2/mH0.01, 0.2 R3/W, L3/mH0.01, 0.2 R4/W, L4/mH0.02, 0.4 Rg/W, Lg/mH0.02, 0.4
附表3 算例2系统线路参数
App.Tab.3 Parameters of lines in system of case 2
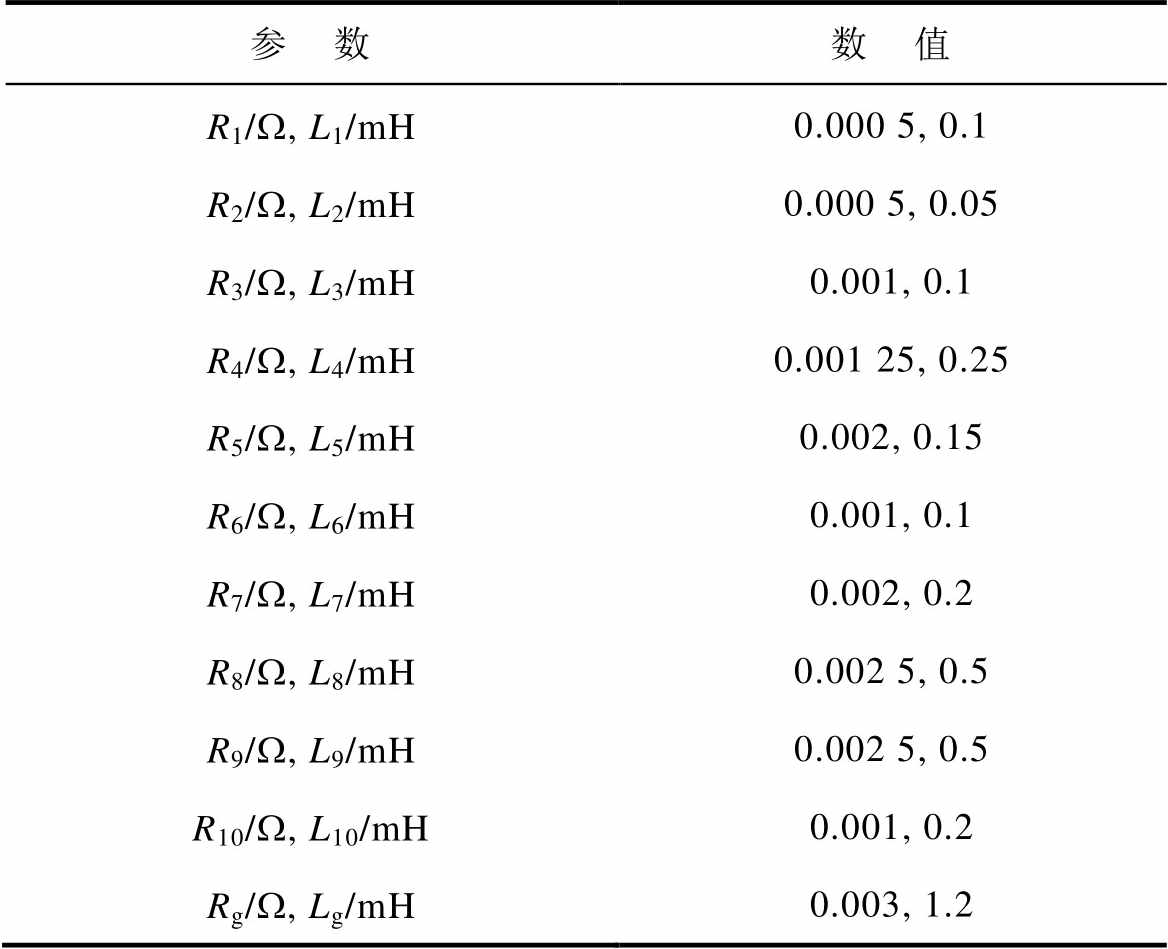
参 数数 值 R1/W, L1/mH0.000 5, 0.1 R2/W, L2/mH0.000 5, 0.05 R3/W, L3/mH0.001, 0.1 R4/W, L4/mH0.001 25, 0.25 R5/W, L5/mH0.002, 0.15 R6/W, L6/mH0.001, 0.1 R7/W, L7/mH0.002, 0.2 R8/W, L8/mH0.002 5, 0.5 R9/W, L9/mH0.002 5, 0.5 R10/W, L10/mH0.001, 0.2 Rg/W, Lg/mH0.003, 1.2
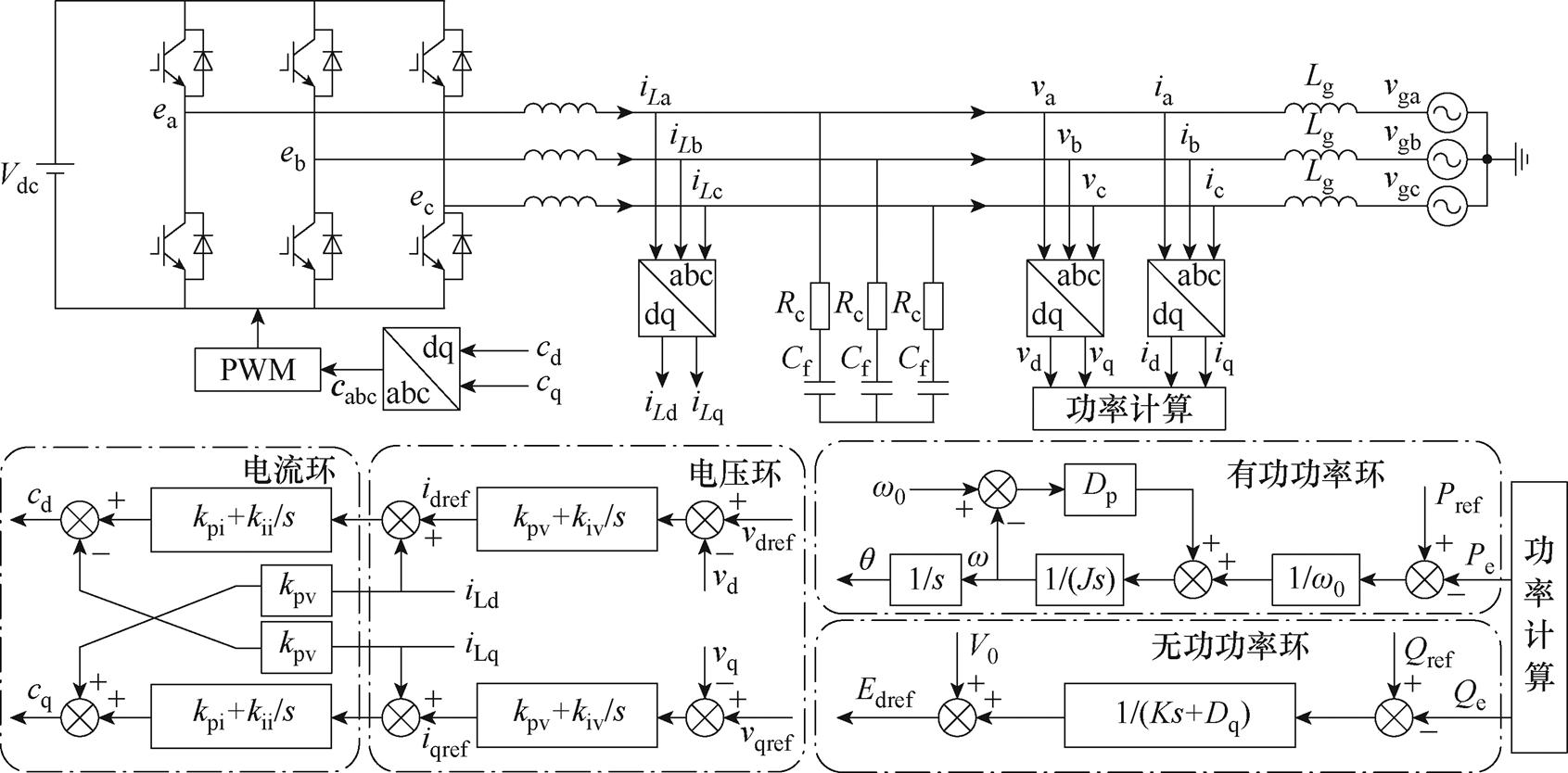
附图1 VSG主电路拓扑与控制框图
App.Fig.1 VSG main circuit topology and control block diagram
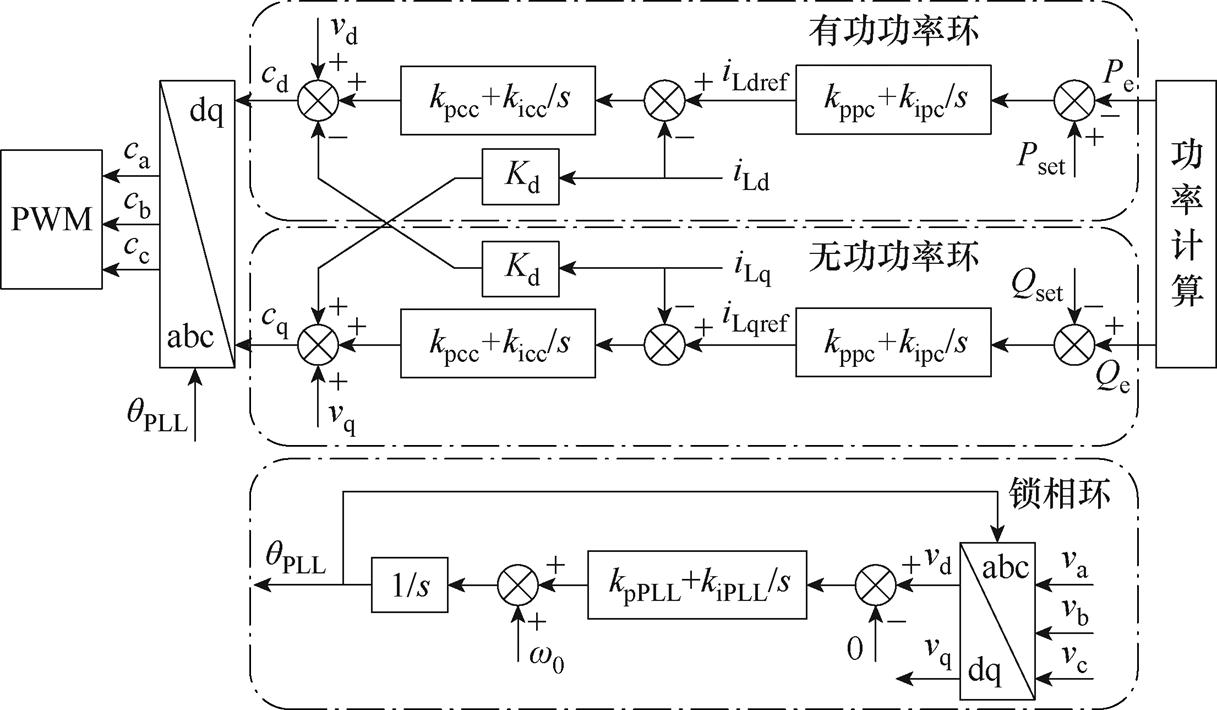
附图2 CCI控制框图
App.Fig.2 CCI control block diagram
参考文献
[1] 雷雨, 李光辉, 王伟胜, 等. 跟网型和构网型新能源并网控制阻抗对比与振荡机理分析[J]. 中国电机工程学报, 2025, 45(1): 150-163.
Lei Yu, Li Guanghui, Wang Weisheng, et al. Com- parison of impedance characteristics and oscillation mechanism for grid following and grid forming renewable energy[J]. Proceedings of the CSEE, 2025, 45(1): 150-163.
[2] 黄萌, 凌扬坚, 耿华, 等. 功率同步控制的构网型变流器多机交互分析与稳定控制研究综述[J]. 高电压技术, 2023, 49(11): 4571-4583.
Huang Meng, Ling Yangjian, Geng Hua, et al. An overview on multi-VSCs interaction analysis and stability controls of grid-forming converters with power synchronization control[J]. High Voltage Engineering, 2023, 49(11): 4571-4583.
[3] Harnefors L, Hinkkanen M, Riaz U, et al. Robust analytic design of power-synchronization control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 5810-5819.
[4] Zhou Yuhan, Xin Huanhai, Wu Di, et al. Small-signal stability assessment of heterogeneous grid-following converter power systems based on grid strength analysis[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2566-2579.
[5] Yang Dongsheng, Wang Xiongfei. Unified modular state-space modeling of grid-connected voltage- source converters[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9700-9715.
[6] Zhu Yue, Gu Yunjie, Li Yitong, et al. Impedance- based root-cause analysis: comparative study of impedance models and calculation of eigenvalue sensitivity[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1642-1654.
[7] Liao Shuhan, Huang Meng, Zha Xiaoming, et al. Emulation of multi-inverter integrated weak grid via interaction-preserved aggregation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4153-4164.
[8] Gao Xian, Zhou Dao, Anvari-Moghaddam A, et al. Stability analysis of grid-following and grid-forming converters based on state-space model[C]//2022 Inter- national Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 2022: 422-428.
[9] 陈新, 王赟程, 龚春英, 等. 采用阻抗分析方法的并网逆变器稳定性研究综述[J]. 中国电机工程学报, 2018, 38(7): 2082-2094, 2223.
Chen Xin, Wang Yuncheng, Gong Chunying, et al. Overview of stability research for grid-connected inverters based on impedance analysis method[J]. Proceedings of the CSEE, 2018, 38(7): 2082-2094, 2223.
[10] Sun Jian. Impedance-based stability criterion for grid- connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[11] Wu Heng, Wang Xiongfei, Kocewiak Ł H. Impedance- based stability analysis of voltage-controlled MMCs feeding linear AC systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 4060-4074.
[12] Guo Jian, Chen Yandong, Wu Wenhua, et al. Wideband dq-frame impedance modeling of load-side virtual synchronous machine and its stability analysis in comparison with conventional PWM rectifier in weak grid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 2440-2451.
[13] 涂春鸣, 邹凯星, 高家元, 等. 基于不对称正负反馈效应的PQ功率控制并网逆变器稳定性分析[J]. 电工技术学报, 2023, 38(2): 496-509.
Tu Chunming, Zou Kaixing, Gao Jiayuan, et al. Stability analysis of grid-connected inverter under PQ power control based on asymmetric positive- negative-feedback effects[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 496-509.
[14] 唐圣德, 胡海涛, 肖冬华, 等. 基于阻抗测量信息的电气化铁路“多车共网”系统稳定性分析[J]. 电工技术学报, 2024, 39(19): 6039-6053.
Tang Shengde, Hu Haitao, Xiao Donghua, et al. Stability analysis of electrified railway multiple train- network system based on impedance measurement information[J]. Transactions of China Electrotech- nical Society, 2024, 39(19): 6039-6053.
[15] Bode H W. Network Analysis and Feedback Amplifier Design[M]. New York: D. Van Nostrand Co. Inc, 1945.
[16] 郝艺, 周瑀涵, 刘晨曦, 等. 含跟网型储能的新能源多馈入系统小扰动电压支撑强度分析[J]. 电工技术学报, 2024, 39(11): 3569-3580.
Hao Yi, Zhou Yuhan, Liu Chenxi, et al. Small- disturbance voltage support strength analysis for renewable multi-infeed system with grid-following energy storage[J]. Transactions of China Electro- technical Society, 2023, 38(21): 5758-5770.
[17] Zhang Haitao, Wang Xiuli, Mehrabankhomartash M, et al. Harmonic stability assessment of multiterminal DC (MTDC) systems based on the hybrid AC/DC admittance model and determinant-based GNC[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1653-1665.
[18] Zhang Haitao, Mehrabankhomartash M, Saeedifard M, et al. Stability analysis of a grid-tied interlinking converter system with the hybrid AC/DC admittance model and determinant-based GNC[J]. IEEE Transa- ctions on Power Delivery, 2022, 37(2): 798-812.
[19] Wen Bo, Boroyevich D, Burgos R, et al. Inverse Nyquist stability criterion for grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1548-1556.
[20] 李信栋, 苟兴宇. 多输入多输出线性定常系统稳定裕度的分析与改进[J]. 控制理论与应用, 2014, 31(1): 105-111.
Li Xindong, Gou Xingyu. Analysis and improvement of stability margin for multi-input multi-output linear time-invariant systems[J]. Control Theory & Appli- cations, 2014, 31(1): 105-111.
[21] Liu Fangcheng, Liu Jinjun, Zhang Haodong, et al. Stability issues of Z+Z type cascade system in hybrid energy storage system (HESS)[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5846-5859.
[22] Xue Danhong, Liu Jinjun, Liu Zeng. Impedance-based stability analysis of two- terminal cascaded voltage source converter system[C]//2019 4th IEEE Work- shop on the Electronic Grid (eGRID), Xiamen, China, 2019: 1-5.
[23] 于彦雪, 马慧敏, 陈晓光, 等. 弱电网下基于准静态模型的混合控制微电网逆变器同步稳定性研究[J]. 电工技术学报, 2022, 37(1): 152-164.
Yu Yanxue, Ma Huimin, Chen Xiaoguang, et al. Synchronous stability research of inverters in hybrid microgrid based on the quasi-static models under weak grid[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 152-164.
[24] Wang Xiongfei, Blaabjerg F, Loh P C. An impedance- based stability analysis method for paralleled voltage source converters[C]//2014 International Power Elec- tronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 2014: 1529-1535.
[25] Cao Wenchao, Ma Yiwei, Wang F. Sequence- impedance-based harmonic stability analysis and controller parameter design of three-phase inverter- based multibus AC power systems[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(10): 7674- 7693.
[26] Guo Zixuan, Zhang Xing, Li Ming, et al. Stability analysis and capacity distribution of multi-paralleled current-controlled inverters and voltage-controlled VSGs grid-connected system[C]//2021 IEEE 12th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Chicago, IL, USA, 2021: 1-8.
[27] Jiang Shan, Zhu Ye, Konstantinou G. Settling angle- based stability criterion for power-electronics- dominated power systems[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 2972-2984.
[28] Jiang Shan, Zhu Ye, Konstantinou G. Stability analysis of multi-bus power electronics defined power systems using phase information of nodal admittance matrix[J]. IEEE Transactions on Power Systems, 2024, 39(4): 6063-6075.
[29] Yang Dongsheng, Sun Yin. SISO impedance-based stability analysis for system-level small-signal stability assessment of large-scale power electronics- dominated power systems[J]. IEEE Transactions on Sustainable Energy, 2022, 13(1): 537-550.
[30] Zhang Chen, Cai Xu, Rygg A, et al. Sequence domain SISO equivalent models of a grid-tied voltage source converter system for small-signal stability analysis[J]. IEEE Transactions on Energy Conversion, 2018, 33(2): 741-749.
[31] 杜燕, 赵韩广, 杨向真, 等. 考虑频率耦合效应的虚拟同步发电机序阻抗建模[J]. 电源学报, 2020, 18(6): 42-49.
Du Yan, Zhao Hanguang, Yang Xiangzhen, et al. Sequence impedance modeling of virtual synchronous generator considering frequency coupling effect[J]. Journal of Power Supply, 2020, 18(6): 42-49.
[32] 徐少博, 徐永海, 陶顺, 等. 计及边带分量频率耦合的电压源型换流器输入导纳建模[J]. 电工技术学报, 2023, 38(11): 2883-2893.
Xu Shaobo, Xu Yonghai, Tao Shun, et al. Voltage source converter input admittance model considering frequency coupling of sideband components[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2883-2893.
[33] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impe- dance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[34] 李红, 梁军杨, 王振民, 等. 跟网型变换器的小扰动同步稳定机理分析与致稳控制[J]. 电工技术学报, 2024, 39(12): 3802-3815.
Li Hong, Liang Junyang, Wang Zhenmin, et al. Smallsignal synchronization stability analysis and improved control strategy for grid following con- verter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3802-3815.
[35] Gu Yunjie, Li Yitong, Zhu Yue, et al. Impedance- based whole-system modeling for a composite grid via embedding of frame dynamics[J]. IEEE Transa- ctions on Power Systems, 2021, 36(1): 336-345.
[36] Cao Wenchao, Ma Yiwei, Wang F. Harmonic stability analysis and controller parameter design of three- phase inverter-based multi-bus AC systems based on sequence impedances[C]//2016 IEEE Energy Con- version Congress and Exposition (ECCE), Milwaukee, WI, USA, 2016: 1-8.
[37] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[38] Shah S, Parsa L. Impedance modeling of three-phase voltage source converters in DQ, sequence, and phasor domains[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1139-1150.
Abstract In recent years, small-signal stability analysis of multi-converter grid-tied systems has gained significant research attention. Existing methods in the literature often overlook three critical aspects: (1) calculating the number of right-half-plane (RHP) poles in the closed-loop transfer function, (2) addressing the singularities of the converter admittance matrix at 50 Hz, and (3) evaluating the impact of individual converters on system stability. To address these gaps, this study investigates small-signal stability analysis methods for multi-converter systems comprising grid-forming (GFM) and grid-following (GFL) inverters, with a focus on determining the number of RHP poles in the sequence admittance of GFM inverters.
First, a Norton-form mathematical model of the multi-converter system is established based on sequence admittance modeling. On the basis, the small signal stability analysis method of the multi-converter system is derived, and the step-by-step stability assessment procedures are presented. Secondly, due to the possibility of RHP poles in the sequence admittance matrix of the GFM converters, the frequency characteristic of the output sequence impedance matrix of the grid-forming converter, virtual synchronous generator (VSG), at 50 Hz is analyzed. A principled approach is proposed to construct the Nyquist curve at 50 Hz, enabling accurate calculation of the RHP poles in the VSG admittance matrix. Third, two case studies of multi-converter systems are analyzed to demonstrate how individual converters influence system stability. Finally, time-domain simulations and hardware-in-the-loop experiments validate the proposed method by comparing critical stability conditions with theoretical predictions.
Key findings include: (1) The proposed Norton-form model accommodates arbitrary network topologies and any number of GFM/GFL converters, enabling holistic stability analysis while quantifying the impact of individual converters. Stability margins are computed using Nyquist curves, with mirror-frequency effects accounted for to prevent misjudgment. (2) Analysis of VSG admittance RHP poles reveals that ignoring impedance matrix behavior at 50 Hz and ∞Hz leads to erroneous pole counts and stability assessments.
Three conclusions are drawn: (1) The recursive formulation of the proposed method supports systems with arbitrary converter counts, while the use of open-circuit impedance matrices generalizes the approach to any grid structure. (2) The method circumvents high-dimensional eigenvalue analysis of closed-loop transfer functions, relying instead on analytical eigenvalue formulas without numerical approximations. (3) By resolving the 50 Hz singularity in GFM admittance matrices, the correct count of RHP poles in the return ratio matrix is ensured, eliminating stability misclassification.
Keywords:Multi-converter system, grid-forming inverters, grid-following inverters, small-signal stability analysis, hardware-in-the-loop experiment
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241348
国家自然科学基金资助项目(52207102)。
收稿日期 2024-07-28
改稿日期 2024-11-09
刘 欣 男,1980年生,博士,副教授,硕士生导师,研究方向为新能源发电系统建模与控制、电力电子系统可靠性。
E-mail: liuxinhust@163.com(通信作者)
邓 昊 男,2000年生,硕士研究生,研究方向为新能源发电系统建模、控制与稳定性分析。
E-mail: 13872751222@163.com
(编辑 郭丽军)