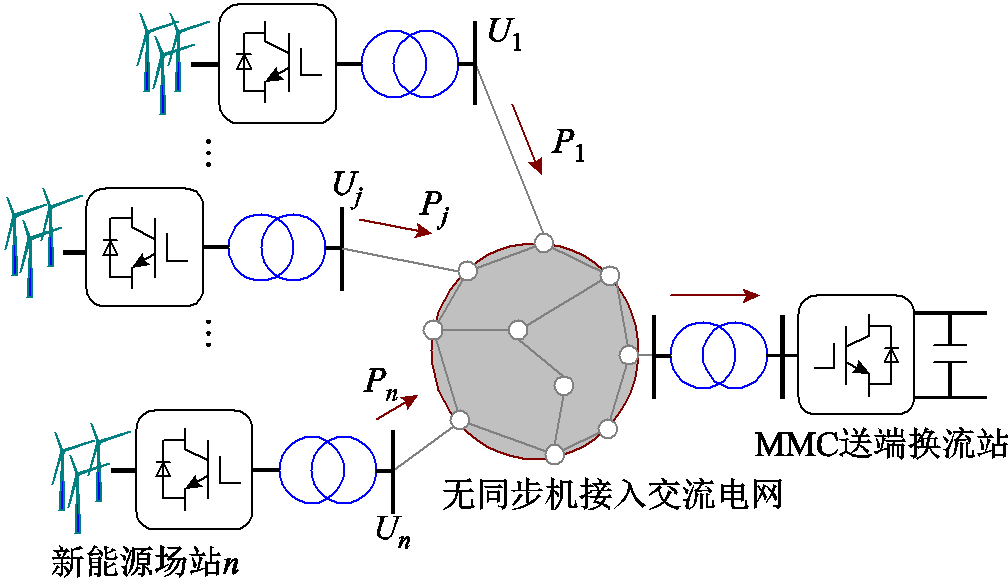
图1 新能源经MMC-HVDC送出的结构
Fig.1 Renewables with MMC-HVDC transmission system
摘要 基于广义短路比指标的电压支撑强度(简称“系统强度”)可用于评估额定工况下新能源经两电平直流送出系统的稳定性。然而目前新能源基地大多采用模块化多电平变流器柔性直流系统(MMC-HVDC)送出,相比于两电平直流,MMC-HVDC内部控制特性复杂,其对系统的电压支撑作用难以表征。此外,新能源实际运行工况多变,基于额定工况定义的短路比指标难以应用。为此,该文从灵敏度视角提出了基于广义运行短路比的新能源经MMC-HVDC送出系统(简称送出系统)强度评估方法。首先,建立了系统频域闭环传递函数矩阵模型,利用灵敏度方程刻画了送出系统的系统电压对电流小扰动的响应特性;其次,基于阻抗矩阵的最大奇异值等效刻画了MMC-HVDC的宽频段电压支撑能力,并提出MMC-HVDC等效方法;进而,将广义运行短路比推广到送出系统强度评估;最后,仿真算例验证了所提方法的有效性。
关键词:新能源 模块化多电平变流器柔性直流系统(MMC-HVDC) 系统强度 广义运行短路比
随着我国“双碳”战略目标的深入推进,电力系统呈现高比例可再生能源、高比例电力电子化的发展趋势[1]。大规模海上风电场、“沙戈荒”风光基地经过柔性直流输电系统与交流电网互联系统成为新型电力系统典型场景之一。由于模块化多电平换流器(Modular Multilevel Converter, MMC)具有谐波含量低、开关损耗较少的优势,是柔性直流输电主流方案。随着新能源场站规模的扩大,新能源场站到送端模块化多电平变流器柔性直流系统(Modular Multilevel Converter High Voltage Direct Current System, MMC-HVDC)的电气距离逐渐增加。与此同时,新能源装机容量不断提升,导致系统电压支撑强度下降,进而带来宽频振荡问题[2]。
为解决上述振荡失稳问题,目前已有的研究主要聚焦新能源单机与MMC-HVDC交互的振荡机理分析,研究方法可分为时域仿真分析法、基于状态空间模型的特征值分析法[3-5]及基于频域的阻抗法。例如,文献[6]将多个新能源场站等效为单机,针对新能源单机与送端柔直互联的两机系统给出了稳定性判据;文献[7]利用序阻抗法分析了送出系统的全频段振荡机理以及主导交互环节。然而上述研究主要针对单个新能源场站并网系统,在多个新能源馈入系统稳定性分析中存在不足。例如,特征值法在多馈入场景下状态空间维数过高,计算量庞大;当新能源场站大规模接入时,利用电磁暂态仿真进行时域分析较为繁琐,难以对复杂多变的运行工况进行实时快速评估;阻抗法难以解析多机场景下的稳定性判据,难以衡量稳定裕度。而基于短路比指标的系统强度稳定裕度分析方法具有计算简便、物理意义明确的优势[8]。单馈入系统的传统短路比定义为同步机提供的短路容量与接入设备的额定容量之比,通过比较短路比与临界短路比的相对大小即可判断系统的电压稳定性。
为描述多个电力电子设备接入交流电网的系统电压稳定性,目前已有多种多馈入短路比指标[8-12]。然而这些指标的研究场景中均存在常规同步机主导的外部交流电网为电力电子设备并网点提供短路容量,也就是说上述短路比指标分析的前提是电网存在同步机提供短路电流/短路容量,而送出系统中仅由送端MMC-HVDC提供电压支撑,不存在常规同步机,MMC-HVDC内部控制的非线性因素导致短路电流存在限幅,短路容量难以表征送端MMC-HVDC维持并网点电压幅值恒定的能力,因而以往的多馈入短路比指标难以适用于无同步机的送出系统[13]。为此,文献[14]基于短路比的灵敏度本质,提出了无同步机支撑的两电平直流送出系统强度量化方法。
然而,文献[14]仅考虑了两电平变流器类型的直流换流站,而实际送出系统中大多采用MMC类型的换流站。相比于两电平直流,MMC-HVDC动态特性复杂,目前尚不明确小扰动同步稳定性分析中MMC-HVDC的电压支撑能力应当如何量化。此外,文献[14]仅分析了额定工况条件下的系统强度,忽略了各个新能源场站的输出有功功率、端电压的差异性。但在系统实际运行过程中,新能源场站的运行工况复杂多变,发出有功功率和端电压往往偏离额定值,并且非额定工况条件对系统的稳定性有较大影响[12],进一步加大了送出系统强度量化的难度。
为此,本文从灵敏度视角提供了一种MMC-HVDC宽频段电压支撑能力量化的思路,由此提出了考虑实际工况的送出系统强度量化方法,即利用短路比指标对系统稳定性进行快速评估。首先,建立了送出系统的闭环频域传递函数矩阵模型,利用灵敏度方程刻画了系统电压对电流小扰动的响应特性;其次,基于阻抗矩阵的最大奇异值等效刻画了MMC-HVDC的宽频段电压支撑能力,并提出了MMC-HVDC等值方法,进而将广义运行短路比应用到送出系统强度评估;最后,仿真案例验证了所提方法的有效性。
典型的新能源经MMC-HVDC送出的结构如图1所示,包括n个新能源场站,每个新能源场站内部由单位功率因数运行的外特性相似的变流器型发电设备(Converter-Interfaced Generator, CIG)构成。各个场站发出的功率经过场站出口处的升压变压器汇入交流电网,最后汇集到送端MMC-HVDC送出。
针对图1无同步机提供电压支撑的三相对称稳态运行的送出系统,本文聚焦送出系统次同步振荡问题。该振荡模态的主导因素是新能源变流器的锁相环及MMC-HVDC的定交流电压外环之间的交互作用[3,7]。而在本文关注的频段内,送端交流系统、直流系统与受端交流系统的振荡模态相互解耦[15],故为方便讨论,假设控制直流电压的受端换流站能够维持直流电压恒定,对应送端MMC-HVDC的直流侧的电压恒定[6]。

图1 新能源经MMC-HVDC送出的结构
Fig.1 Renewables with MMC-HVDC transmission system
此外,本文提到的系统强度特指系统电压支撑强度,不涉及频率支撑强度的讨论,重点研究的是稳态平衡点附近的小扰动同步稳定性问题。因此在分析过程中忽略了小扰动后系统频率变化,大干扰后的频率变化不在本文讨论范围内。
基于上述假设条件,本文要解决的问题可以归纳为:
1)送出系统中仅由送端MMC-HVDC提供电压支撑,系统在稳定运行点受到小扰动后送端MMC-HVDC宽频段电压支撑能力应当如何量化?
2)考虑新能源场站实际运行工况,小扰动同步稳定性视角下如何量化评估新能源经MMC-HVDC送出系统的系统强度?
图1所示的系统动态可以分成两大类,分别是电力电子设备(Power Electronics Equipment, PEE)侧动态(包括新能源场站及送端MMC-HVDC)和网络侧动态。对于图1所示的送出系统的稳定性分析,系统动态特性可以由稳定工作点处的线性化方程描述。在全局同步旋转坐标系下建立各个并网节点输入电流扰动ΔIxy=[ΔI1x ΔI1y ΔI(n+1)x ΔI(n+1)y]T到并网节点电压微增量ΔUxy=[ΔU1x ΔU1y
ΔI(n+1)x ΔI(n+1)y]T到并网节点电压微增量ΔUxy=[ΔU1x ΔU1y ΔU(n+1)x ΔU(n+1)y]T的闭环模型,如图2所示。
ΔU(n+1)x ΔU(n+1)y]T的闭环模型,如图2所示。
图2中YPEE(s)、Ynet(s)分别为电力电子设备与交流网络的导纳矩阵,反映了节点电压微增量与电流微增量之间的灵敏度关系。下面对交流网络、新能源场站及送端MMC-HVDC分别建立灵敏度方程模型。
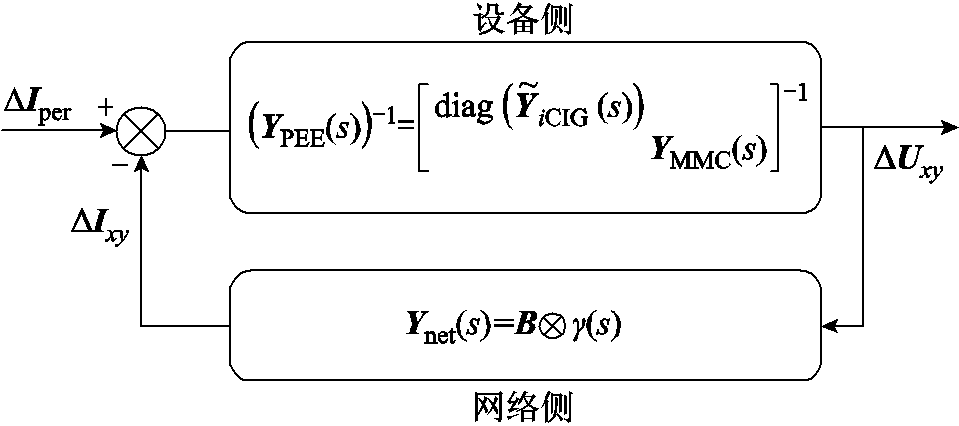
图2 送出系统闭环传递函数矩阵模型
Fig.2 System closed-loop transfer function matrix model
假设n个新能源场站的节点编号为1~n,送端MMC-HVDC位于第n+1节点。在电网感性占优的条件下[16],系统中注入网络的节点电流微增量列向量ΔIxy和各节点的母线电压微增量构成的列向量ΔUxy的灵敏度关系可以由网络侧导纳矩阵表示,具体为
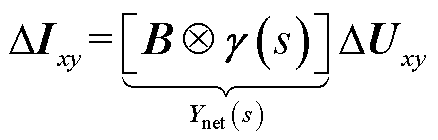 (1)
(1)
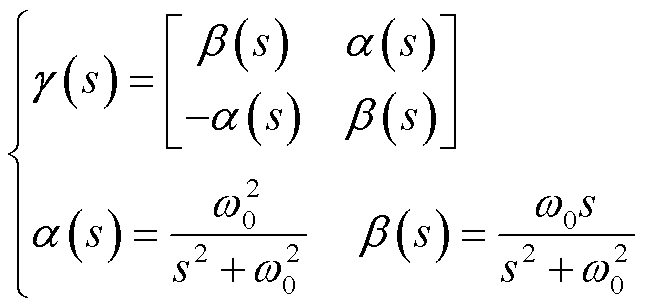 (2)
(2)
式中,ΔIix与ΔIiy分别为全局同步坐标系下流入网络节点i的电流x轴与y轴分量;ΔUix与ΔUiy分别为全局同步坐标系下节点i的电压x轴与y轴分量;i=1, 2, …, n+1;B为网络结构的节点导纳矩阵,其具体表达式可参考文献[16];Ä表示Kronecker积。需要注意的是,式(1)中的节点导纳矩阵是将无源节点消去后得到的,仅保留了各个新能源场站和MMC-HVDC的端口信息,因此可以推广到不同网络结构的拓扑中。
为便于分析,考虑场站内部各个新能源发电设备均由附图1所示的控制参数相同的跟网型变流器构成,且功率因数为1。各个新能源场站采用单机倍乘模型进行建模,即通过容量倍乘原则等效为单台变流器[17]。此外,由于新能源直流侧电容解耦作用,新能源机侧变流器动态予以忽略[3]。
跟网型变流器在全局同步旋转坐标下的动态端口特性解析表达式如式(3)所示[12],反映了注入节点i的电流微增量[ΔIix ΔIiy]T与节点电压微增量[ΔUix ΔUiy]T的灵敏度关系。
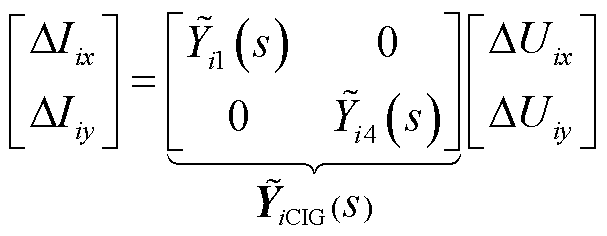 (3)
(3)
为体现运行工况信息,式(3)也可以改写为
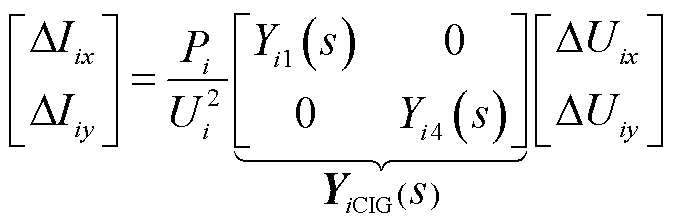 (4)
(4)
送出系统的异构特征表现为新能源场站的并网母线的电压与发出的有功功率偏离额定点。相比于式(3),式(4)中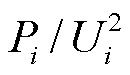 作为整体表征了第i个新能源场站的大部分运行工况信息,Yi1(s)与Yi4(s)的具体表达式参考文献[12],分子和分母均为端电压的一次函数,能够减小不同设备动态特性由于运行工况不同导致的差异性[12]。
作为整体表征了第i个新能源场站的大部分运行工况信息,Yi1(s)与Yi4(s)的具体表达式参考文献[12],分子和分母均为端电压的一次函数,能够减小不同设备动态特性由于运行工况不同导致的差异性[12]。
送端MMC-HVDC第k相(k = a, b, c)主电路的拓扑结构如图3所示。每个桥臂由N个半桥型功率模块构成,子模块(Sub-Module, SM)的投入与切除由调制信号控制。图3中Larm与Rarm分别为桥臂电感和桥臂电阻,Csm为子模块电容,udc为MMC-HVDC直流侧的电压,uk与ik分别为并网点的第k相交流电压和流入电流,ikp与ikn分别为第k相的上桥臂与下桥臂的桥臂电流,两者的共模量为第k相环流icirk。送端MMC-HVDC的典型控制结构如图4所示[3],环流控制能够有效抑制环流中的二次谐波分量。环流控制环节及双环主控的输出信号经过最近电平逼近调制(Nearest Level Modulation, NLM)生成上下桥臂的三相调制信号mp与mn。图4中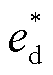 与
与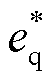 分别为MMC主控部分输出的基频参考电压d轴与q轴分量;
分别为MMC主控部分输出的基频参考电压d轴与q轴分量;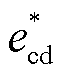 与
与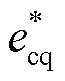 分别为MMC环流控制部分输出的二倍频参考电压d轴与q轴分量,具体控制方式见附录;uabc与iabc分别为送端MMC-HVDC并网点三相电压和电流,经Park变换后得到同步坐标系下的形式udq和idq;icirabc为三相桥臂环流,经Park变换后得到同步坐标系下的形式icirdq;udref和uqref分别为定交流电压的d轴与q轴参考值;icirdref与icirqref分别为环流抑制d轴与q轴参考值。
分别为MMC环流控制部分输出的二倍频参考电压d轴与q轴分量,具体控制方式见附录;uabc与iabc分别为送端MMC-HVDC并网点三相电压和电流,经Park变换后得到同步坐标系下的形式udq和idq;icirabc为三相桥臂环流,经Park变换后得到同步坐标系下的形式icirdq;udref和uqref分别为定交流电压的d轴与q轴参考值;icirdref与icirqref分别为环流抑制d轴与q轴参考值。
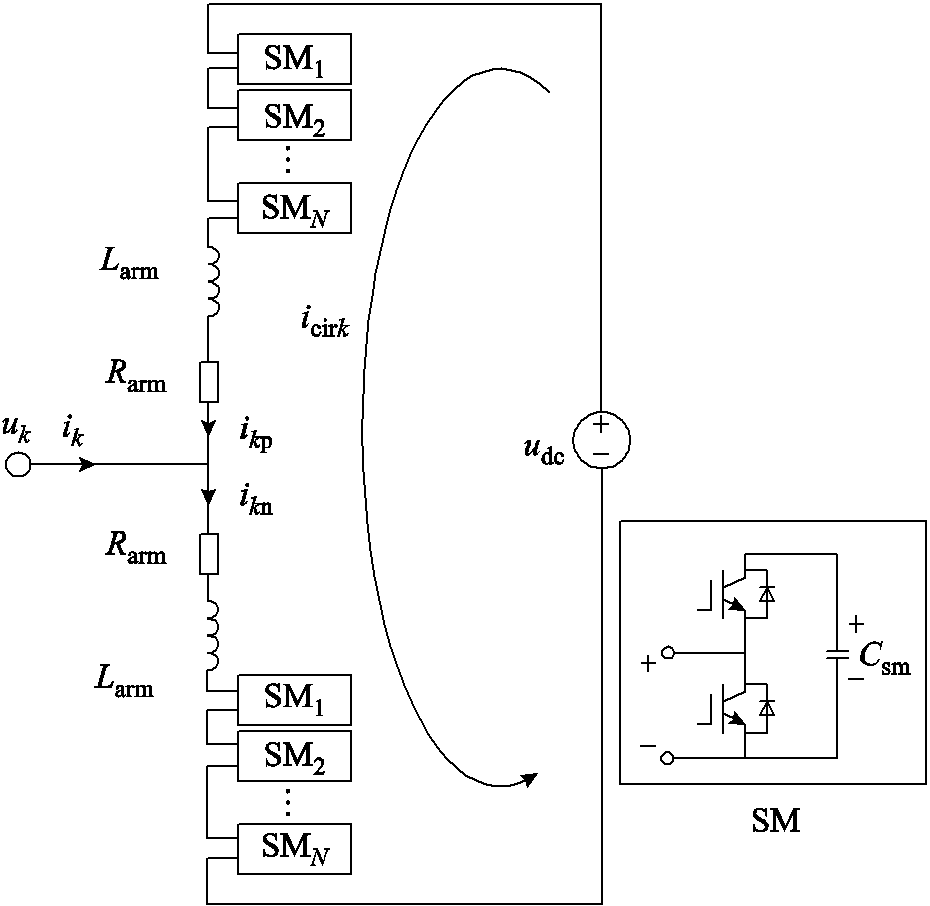
图3 半桥型MMC-HVDC单相电路与子模块结构
Fig.3 Half-bridge MMC-HVDC single-phase circuit and submodule diagram
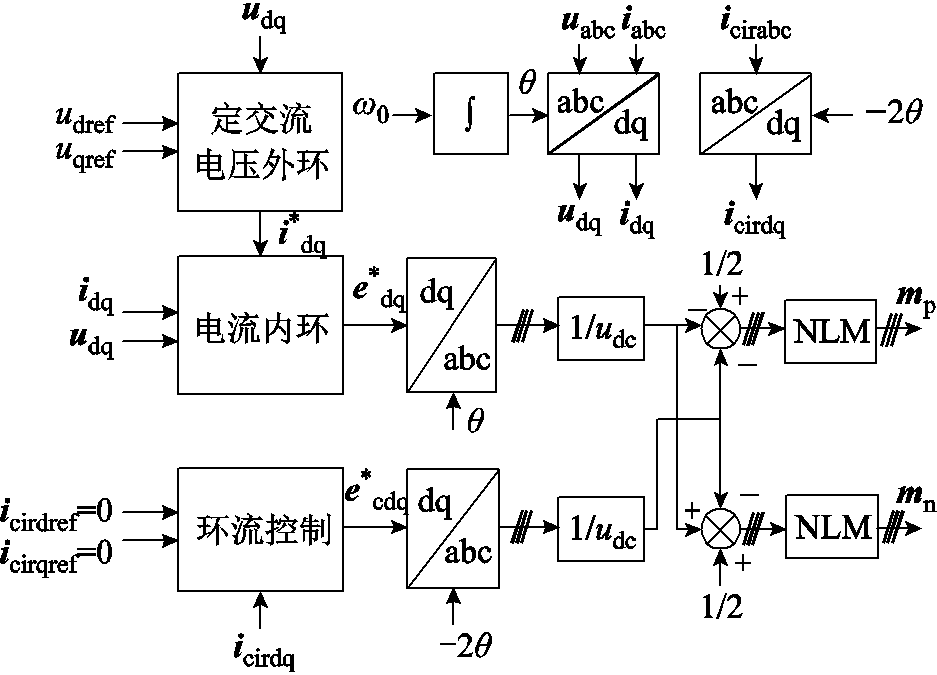
图4 送端MMC-HVDC定V/F控制框图
Fig.4 Sending-end MMC-HVDC constant V/F control diagram
定V/F闭环控制运行的MMC-HVDC阻抗建模已有较多研究[4,18],本文在此不作展开,具体可参考附录。送端MMC-HVDC阻抗矩阵ZMMC(s)如式(5)所示,在全局同步旋转坐标系下呈现了流出送端MMC-HVDC的节点电流微增量与并网点电压之间的灵敏度关系,下标xy表示全局同步旋转坐标系。
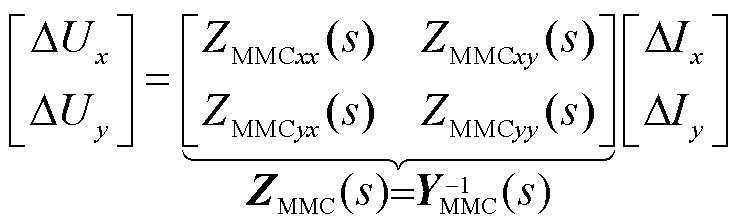 (5)
(5)
除了采用MMC-HVDC阻抗理论模型,在工程中也可利用端口扫频的方法获得阻抗特性[19]。阻抗测量法的优势是能够减小解析建模过程带来的误差,并且无需“白箱”模型,即使参数未知也可以通过测量获得其阻抗外特性。
综合上述建模,联立式(3)与式(5),系统设备侧灵敏度关系可以写为
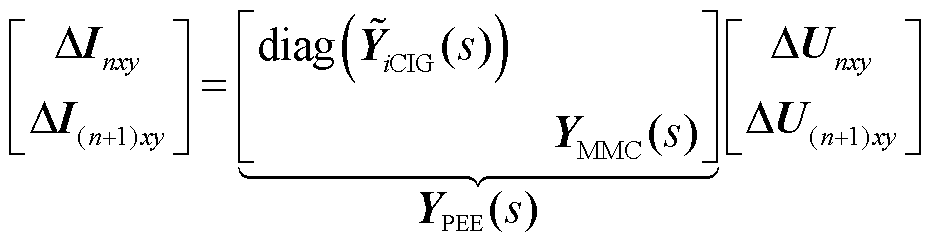 (6)
(6)
式中,ΔInxy为n个新能源场站的节点电流微增量构成的列向量,ΔInxy=[ΔI1x ΔI1y… ΔInx ΔIny]T;ΔUnxy为n个新能源场站节点电压微增量构成的列向量,ΔUnxy=[ΔU1x ΔU1y… ΔUnx ΔUny]T;ΔI(n+1)xy为MMC-HVDC所在节点电流微增量构成的列向量,ΔI(n+1)xy=[ΔI(n+1)x ΔI(n+1)y]T;ΔU(n+1)xy为MMC-HVDC所在节点电压微增量构成的列向量,ΔU(n+1)xy= [ΔU(n+1)x ΔU(n+1)y]T;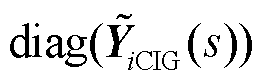 为n个新能源场站导纳矩阵构成的对角矩阵。
为n个新能源场站导纳矩阵构成的对角矩阵。
联立设备侧灵敏度方程(6)和网络侧灵敏度方程(1),即可得到送出系统Σp的特征方程为
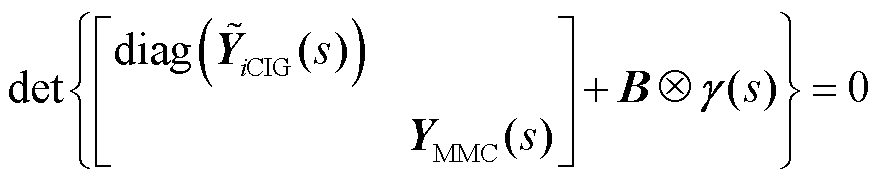 (7)
(7)
式中,det(∙)为求矩阵的行列式;s为拉普拉斯算子。
系统强度描述了受扰后系统响应性能,反映了跟网型设备/场站对MMC-HVDC支撑电网的耐受度与电网电源MMC-HVDC的电压支撑能力的匹配程度[20],因此系统强度评估需要对送端MMC-HVDC的电压支撑能力进行量化。
本节首先基于矩阵奇异值理论量化了送端MMC-HVDC的电压支撑能力,提出MMC-HVDC等值方法,进而将广义运行短路比推广到新能源经MMC-HVDC送出系统中,提出系统强度评估方法。
已有研究表明,MMC-HVDC的阻抗特性在锁相环频段由定交流电压外环主导,呈现电压源特性[7]。送端MMC-HVDC采用定V/F的控制结构,从而为送端交流系统提供电压支撑。这与常规同步机的电压支撑作用类似,从物理本质的角度出发,送端MMC-HVDC可以等值为含感性内阻抗的电压源[7, 21]。
对于理想电压源而言,即任意端口电流的条件下并网点电压始终恒定,电压微增量恒为0,而由于ZMMC(s)的存在,可以认为送端MMC-HVDC并网点和理想电压源之间存在电气距离。为方便分析,采用等值电感动态近似ZMMC(s)动态特性。
具体地,阻抗矩阵ZMMC(s)本质上反映了MMC-HVDC并网点的节点电压微增量对单位电流微增量的响应关系,矩阵的奇异值可以表征该响应的增益程度。矩阵ZMMC(s)的最大奇异值可理解为ZMMC(s)对单位向量的最大增益。相反地,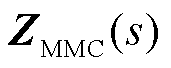 的最小奇异值表征了矩阵对单位向量的最小增益。矩阵ZMMC(s)的最大奇异值与谱范数相等,即
的最小奇异值表征了矩阵对单位向量的最小增益。矩阵ZMMC(s)的最大奇异值与谱范数相等,即
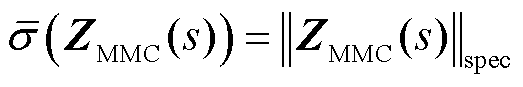 (8)
(8)
假设MMC-HVDC的等值电感为Leq,其阻抗矩阵ZLeq(s)的最小奇异值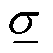 (·)为
(·)为
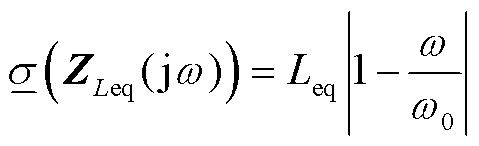 (9)
(9)
为了保证等值结果的保守性,电感Leq的阻抗矩阵ZLeq(s)对单位电流微增量的增益作用应当不小于MMC-HVDC阻抗矩阵在某一频段对单位电流微增量的增益作用。具体而言,对于本文关注的次同步频段,MMC-HVDC阻抗矩阵ZMMC(jω)在频段内的最大奇异值等于ZLeq(jω)在对应频率ωc处的最小奇异值,计算公式为
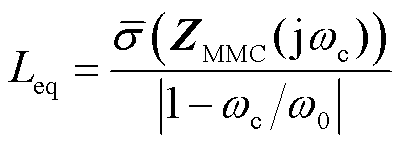 (10)
(10)
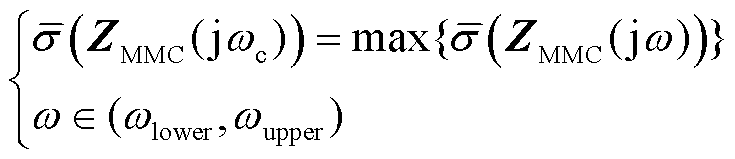 (11)
(11)
式中,ωlower和ωupper分别为频域的下界与上界,构成了关注频域Ω。对于本文关注的新能源变流器锁相环模态主导的次同步振荡问题,取ωlower=0,ωupper=50 Hz。另外,送端MMC-HVDC的阻抗特性与其运行功率基本无关[22],因此等值电感与MMC-HVDC运行功率基本无关。
式(10)利用等值电感Leq表征了MMC-HVDC动态过程中并网母线电压在任意方向上对电流扰动的最大响应增益程度。由于采用等值电感Leq阻抗矩阵的最小增益包络MMC-HVDC阻抗矩阵的最大增益,因此该方法具有保守性,能在一定程度上保证系统强度量化指标的鲁棒性。
值得一提的是,基于静止坐标系的正负序阻抗矩阵经正负工频ω0频移后,得到的同步旋转坐标系下的正负序阻抗矩阵与同步旋转坐标系下的全局xy阻抗矩阵ZMMC(s)是酉等价的[23],因此两种阻抗的最大奇异值相同,式(10)对于序阻抗也适用。
另外,分析送出系统静态电压稳定性时,其电压支撑能力量化可以视为关注频域Ω缩小至s=0点处的结果。而根据图5,阻抗矩阵的最大奇异值在s=0处为0,那么此时等值电感为0,送端MMC-HVDC在静态电压稳定分析中等效为幅值恒定的电压源。因此本文所提的MMC-HVDC电压支撑能力量化方法可以兼顾小扰动同步稳定性分析与静态电压稳定性分析。
以采用附表3所示典型参数的送端MMC-HVDC为例,利用附图2所示的额定工况下阻抗矩阵进行分析,对各个频率点ωk的复数矩阵ZMMC(jωk)进行奇异值分解,求得对应频率的最大奇异值,构成了关注频段的最大奇异值集合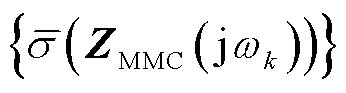 ,额定工况下的送端MMC-HVDC阻抗矩阵最大奇异值曲线如图5所示。根据式(9)、式(10)求得附表3参数条件下MMC-HVDC等值电感计算结果为0.0562(pu)。对于定V/F构网控制的MMC-HVDC,其阻抗矩阵的最大奇异值越小表明越接近理想电压源,提供的电压支撑能力越强。
,额定工况下的送端MMC-HVDC阻抗矩阵最大奇异值曲线如图5所示。根据式(9)、式(10)求得附表3参数条件下MMC-HVDC等值电感计算结果为0.0562(pu)。对于定V/F构网控制的MMC-HVDC,其阻抗矩阵的最大奇异值越小表明越接近理想电压源,提供的电压支撑能力越强。
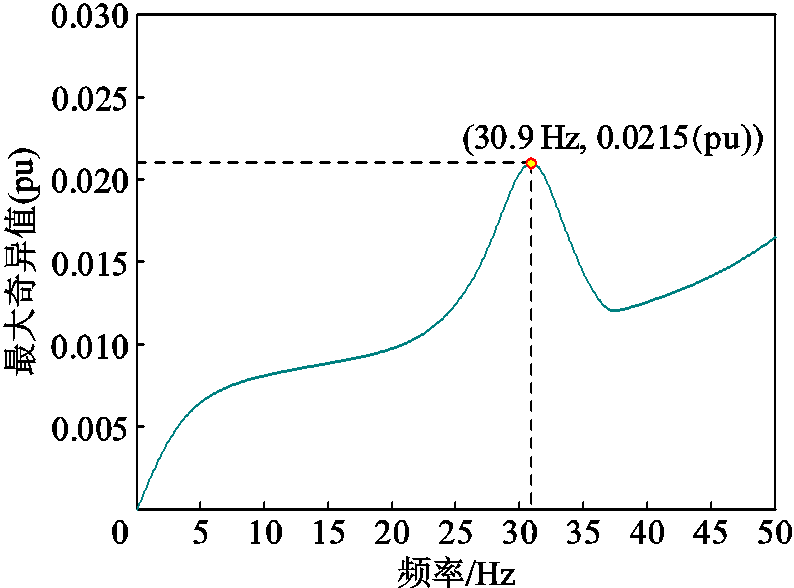
图5 送端MMC-HVDC阻抗矩阵的最大奇异值曲线
Fig.5 Curve of maximum singular value of MMC-HVDC impedance matrix
3.1节将送端MMC-HVDC等效为含有内电感的电压源,故在式(7)中可以将YMMC(s)折算到网侧导纳矩阵,相当于在MMC-HVDC所在的第n+1个节点增加一条对地支路,因此式(7)改写为
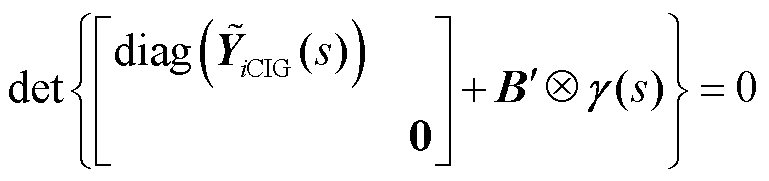 (12)
(12)
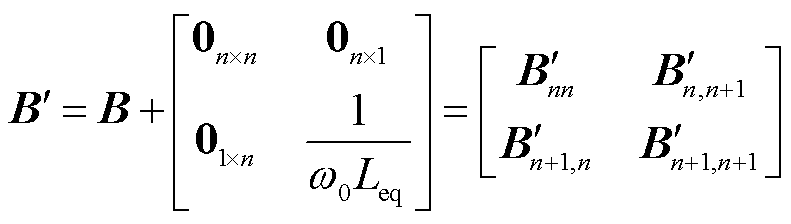 (13)
(13)
B'为修正后的n+1阶导纳矩阵,可以划分为如式(13)所示的四个子矩阵。进一步将第n+1个节点消去,仅保留新能源场站所在的第1~n个节点,式(12)可等价变形为
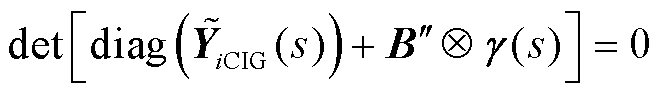 (14)
(14)
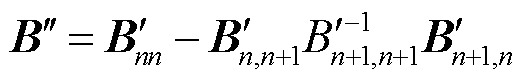 (15)
(15)
将式(4)代入式(14)可得
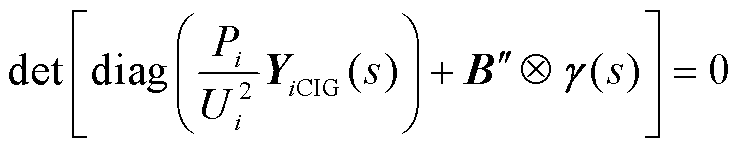 (16)
(16)
为了将各个新能源场站的运行工况与端口动态解耦,将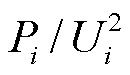 等价折算到网络侧得到
等价折算到网络侧得到
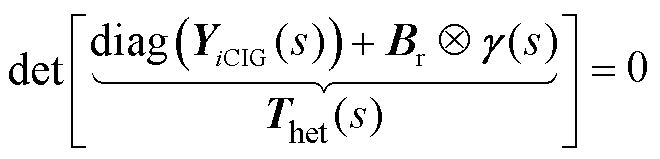 (17)
(17)
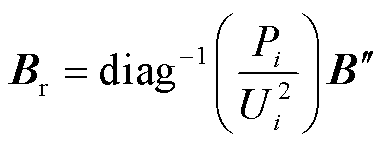 (18)
(18)
式中,Thet(s)为送端MMC-HVDC等值后的异构系统Σ的系统矩阵;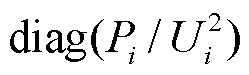 为n维对角矩阵,第i个对角元素为
为n维对角矩阵,第i个对角元素为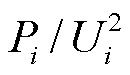 ;Br为消去无源节点的拓展导纳矩阵。由于Br具有正定性质[17],其特征值均大于0,则矩阵Br⊗I2具有n个二重特征值λk(k=1,…,n),其中I2为2阶单位矩阵,特征值λk对应的左右特征向量为yk与xk,其分别对应的左右特征子空间为
;Br为消去无源节点的拓展导纳矩阵。由于Br具有正定性质[17],其特征值均大于0,则矩阵Br⊗I2具有n个二重特征值λk(k=1,…,n),其中I2为2阶单位矩阵,特征值λk对应的左右特征向量为yk与xk,其分别对应的左右特征子空间为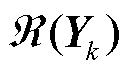 与
与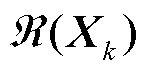 ,
,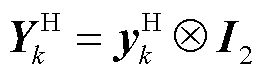 ,
,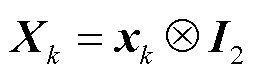 。
。
式(17)表征了异构系统Σ的特征方程,将设备动态与实际运行工况近似解耦后,系统Σ中设备异构特征仅来源于设备实际端口电压间差异。然而异构多馈入系统的模态难以解耦,一种可行的思路是构造新能源场站外特性相似的等效同构系统Σ0,从而基于特征子空间摄动理论,利用等效同构系统的特征子空间求解异构系统的特征子系统,其能够近似异构系统的稳定性,基于此可定义指标,以实现异构系统的强度量化[24]。
具体地,首先,可以根据Br⊗I2最小特征值λ1对应的特征子空间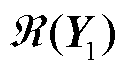 与
与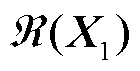 构造等效同构系统Σ0[24]:n个新能源变流器场站的外特性按照参与因子进行加权得到等效同构场站外特性ŶCIG(s),类似于式(17),其特征方程为
构造等效同构系统Σ0[24]:n个新能源变流器场站的外特性按照参与因子进行加权得到等效同构场站外特性ŶCIG(s),类似于式(17),其特征方程为
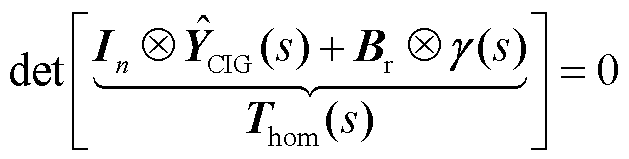 (19)
(19)
式中,Thom(s)为等效同构系统Σ0的系统矩阵;In为n阶单位矩阵。
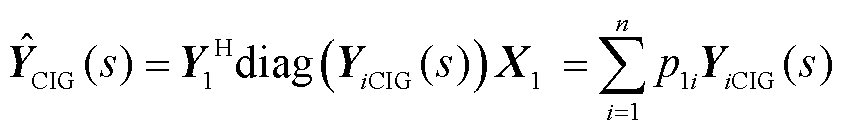 (20)
(20)
式中,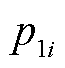 为第i个新能源场站的参与因子,满足和为1。
为第i个新能源场站的参与因子,满足和为1。
进一步地,由于等效同构系统与原异构系统稳定性近似且基于特征子空间摄动理论,Thet(s)可以视为Thom(s)的摄动,那么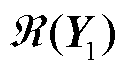 与
与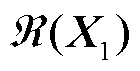 即为Thet(s)的特征子空间的近似,所以其作用于Thom(s)得到的最易失稳的等效单馈入系统Σs即为异构系统的特征子系统,其特征方程为
即为Thet(s)的特征子空间的近似,所以其作用于Thom(s)得到的最易失稳的等效单馈入系统Σs即为异构系统的特征子系统,其特征方程为
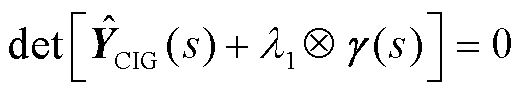 (21)
(21)
上述结论的证明类似于文献[12],限于文章篇幅,本文不再展开。综上所述,异构系统稳定等价于n个等效单馈入系统均稳定。对于跟网型变流器单馈入系统,短路比λk越小,系统的失稳风险越大[8],因此具有最小短路比的等效单馈入系统的失稳风险最大,可以用于判断异构系统的稳定性。
基于第3.2节分析过程,新能源经MMC-HVDC送出的广义运行短路比gOSCR可定义为系统拓展导纳矩阵Br的最小特征值,即
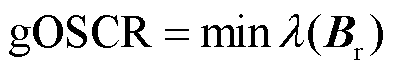 (22)
(22)
式中,λ(∙)表示求特征值。
由于系统稳定性随广义运行短路比的减小而下降,因此存在等效单馈入系统Σs临界稳定时的运行短路比,即临界运行短路比CgOSCR。CgOSCR反映了新能源场站对MMC-HVDC支撑的交流电网的耐受度[20]。根据第3.2节的分析,CgOSCR对应于等效同构系统Σ0解耦后最易失稳的等效单馈入系统的主导共轭特征根实部为0的运行短路比,满足
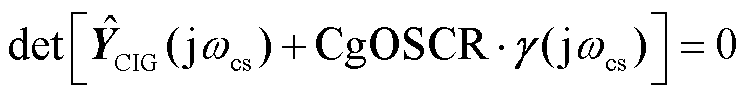 (23)
(23)
式中,ωcs为等效单馈入系统临界振荡的角频率。临界运行短路比可以由式(23)的解析方法获得,也可以由仿真或半实物测试的方法获得[20]。
基于上述分析可知,送出系统的广义运行短路比考虑了新能源实际运行工况及MMC-HVDC对网络动态的修正,能够反映等效电网强度;而等效单馈入系统的临界运行短路比主要与新能源设备的控制参数有关,能够反映新能源设备对电网强度的耐受能力。基于源-网协同的思路,给出系统强度稳定性判据:gOSCR≥CgOSCR时系统稳定;gOSCR<CgOSCR时系统失稳。
进一步利用广义运行短路比与临界运行短路比的归一化差值定义为送出系统强度的稳定裕度指标β,即
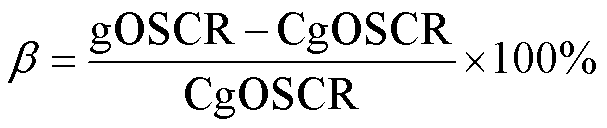 (24)
(24)
由于实际系统存在不确定因素,判断送出系统的稳定性时往往根据实际工程经验保留一定的临界稳定裕度β0(β0>0),即要求β≥β0。
综上所述,新能源场站经MMC-HVDC送出系统的系统强度评估流程如图6所示。
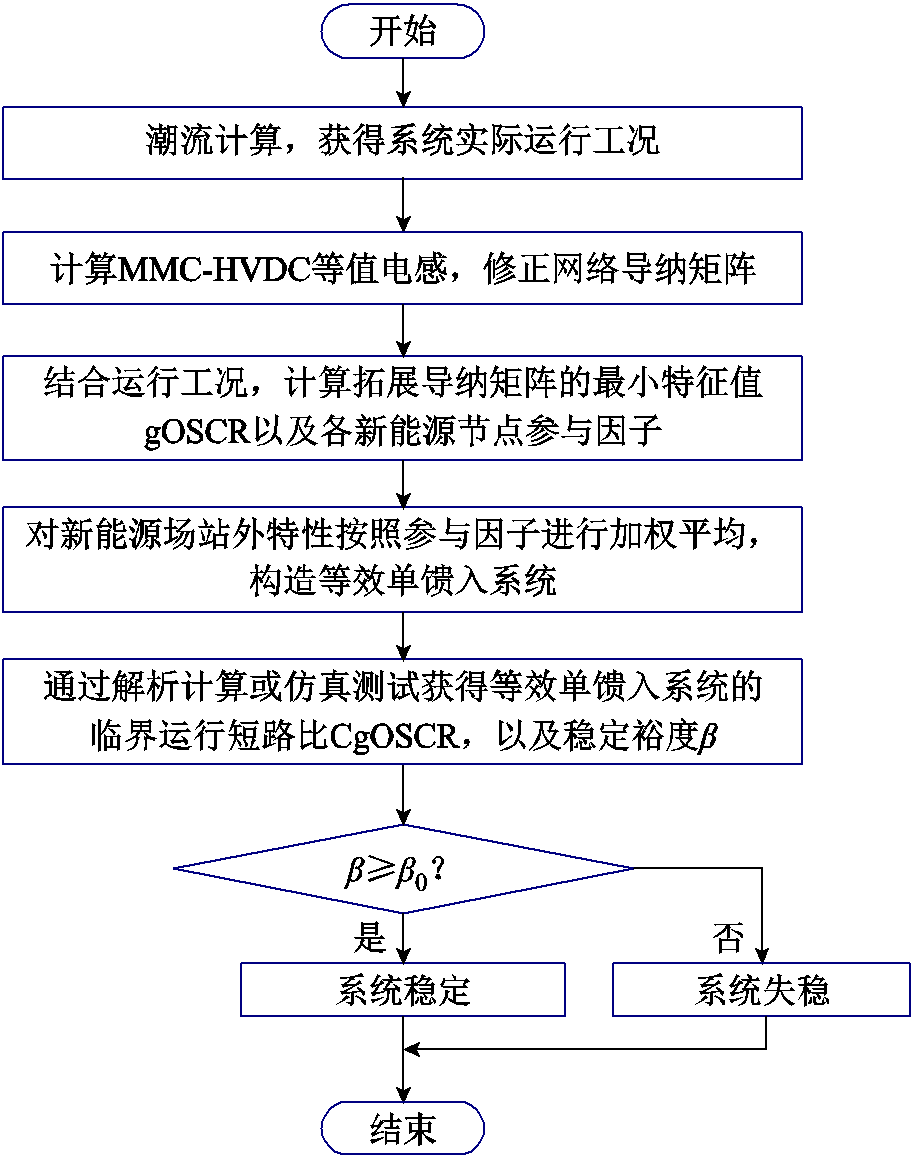
图6 送出系统强度量化评估流程
Fig.6 System strength evaluation flow chart
送出系统强度量化评估可以总结为以下步骤:
1)计算送出系统的潮流,获得实际运行工况。
2)求取送端MMC-HVDC的等值电感。通过端口扫频或者解析建模的方法获得MMC-HVDC在全局同步坐标系下的阻抗外特性,然后根据式(9)、式(10)计算关注频域内的等值电感。
3)计算拓展导纳矩阵Br。将送端MMC-HVDC等值电感折算到网络导纳矩阵中,消去无源节点,仅保留新能源接入节点,具体参考式(13)~式(18)。
4)计算送出系统广义运行短路比gOSCR。拓展导纳矩阵Br的最小特征值即为系统广义运行短路比,根据最小特征值的左右特征向量获得各个新能源场站的参与因子。
5)构造等效单馈入系统。根据各新能源设备的参与因子对场站外特性进行加权平均,得到等效同构系统,进而解耦得到等效单馈入系统。
6)计算等效单馈入系统的临界运行短路比CgOSCR。可以由解析计算或仿真获得。
7)计算送出系统稳定裕度。根据广义短路比与临界运行短路比的相对差值计算稳定裕度指标β。
静态电压稳定评估流程与上述小扰动同步稳定性评估过程类似,可视为小扰动同步稳定性问题在s = 0处的特例。
为验证本文所提方法的可行性,在Matlab/ Simulink中搭建图7所示的含4个新能源场站的MMC-HVDC送出系统电磁暂态仿真模型。其中4个新能源场站均为光伏发电场站,均采用单机倍乘模型,控制结构示意图附图1所示。各个新能源场站通过0.69 kV/110 kV升压变压器接入交流电网,再通过110 kV/120 kV变压器汇入MMC-HVDC,交流线路参数以及MMC-HVDC的详细参数见附表1~附表3。
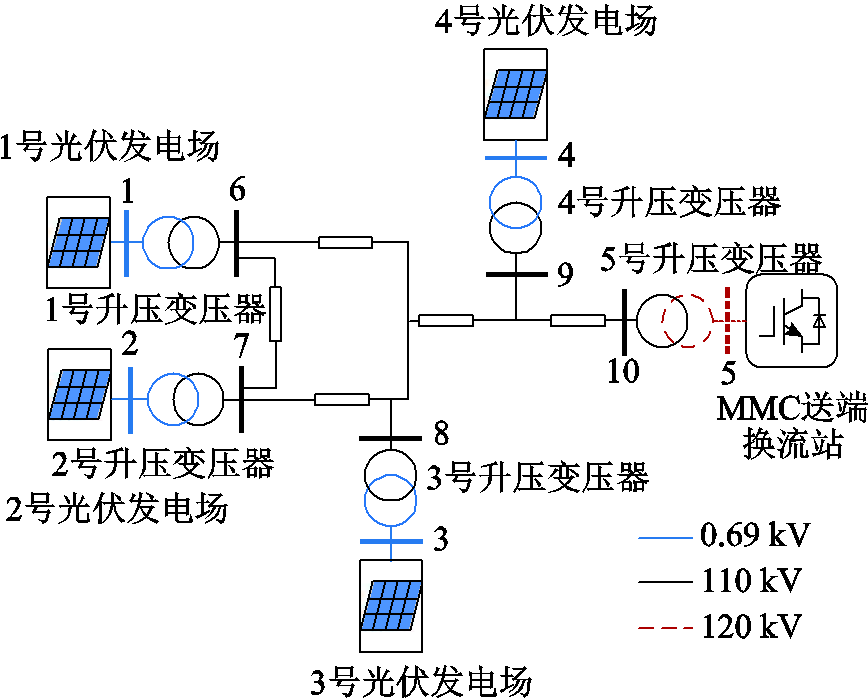
图7 新能源场站经MMC-HVDC送出系统仿真示意图
Fig.7 One-line diagram of renewables with MMC-HVDC
表1给出了4个新能源场站不同运行工况(Pi, Ui)的5组算例信息,网络参数、新能源场站以及MMC-HVDC控制参数保持不变。表1中i为节点编号;Pi为正数表示流入交流电网,负数为流出,以系统额定容量为基准值;Ui为经过各自电压等级标幺化后的节点电压幅值。按照图7所示的小扰动同步稳定性评估流程,首先利用阻抗扫频或理论建模方法获取送端MMC-HVDC的全局同步坐标系阻抗矩阵数据集{ZMMC(jω)},然后根据式(9)、式(10)求得MMC-HVDC相应的等值电感为0.0562(pu),从而通过式(13)和式(15)修正网络导纳矩阵。
表1 送出系统实际运行工况
Tab.1 Operational conditions of the system

算例Pi (i = 1, 2, 3, 4, 5)(pu)Ui (i = 1, 2, 3, 4, 5)(pu) 10.04, 0.04, 0.04, 0.08, −0.201.020, 1.019, 1.019, 1.013, 1 20.08, 0.06, 0.06, 0.12, −0.321.014, 1.014, 1.013, 1.008, 1 30.12, 0.08, 0.10, 0.16, −0.461.004, 1.004, 1.003, 0.999, 1 40.14, 0.14, 0.15, 0.40, −0.830.966, 0.966, 0.965, 0.964, 1 50.20, 0.20, 0.20, 0.40, −1.000.920, 0.920, 0.919, 0.925, 1
由式(17)~式(23)分别计算5组不同运行工况下送出系统的gOSCR与CgOSCR,为了便于分析,临界稳定裕度取0,系统强度计算结果及判稳结果见表2。
表2 5组算例的gOSCR、CgOSCR和稳定性评估结果
Tab.2 The gOSCR, CgOSCR and stability assessment results in five cases

算例gOSCRCgOSCRb(%)稳定性评估结果 111.322.94285.03稳定 26.892.74151.46稳定 34.632.7369.60稳定 42.582.68−3.73失稳 51.863.04−38.82失稳
根据式(21),可以计算出等效单馈入系统的主导特征根。表3以及图8给出了送出系统Σp的主导特征根与等效单馈入系统Σs的主导特征根的校验情况。从图8中可以看到,等效单馈入系统能够较好地拟合送出系统的主导特征根,验证了本文所提方法的可行性。
表3 等效单馈入系统和原始送出系统的主导特征根
Tab.3 The dominant eigenvalue of the equivalent single-infeed system and the original transmission system

算例等效单馈入系统原始送出系统 1−2.10±86.3i−2.09±86.7i 2−1.57±86.2i−1.57±86.5i 3−0.98±85.9i−1.01±86.1i 40.04±84.4i±84.3i 50.47±82.7i0.50±82.1i
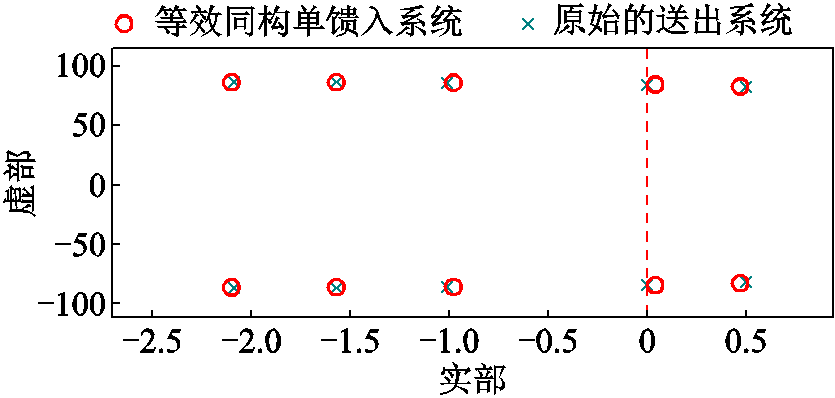
图8 特征根对比
Fig.8 Eigenvalue comparison chart
进一步地,图9给出了算例1~5的小扰动测试时域仿真结果。5组算例均在稳定运行条件下向送端MMC-HVDC的并网耦合点处端电压注入0.01(pu)的扰动并迅速清除。图9中展示了1号和2号新能源场站的端电压幅值的时域波形。算例1~3波形振荡收敛(系统稳定),算例5波形振荡发散(系统失稳),与表2的判稳结果相符;算例4的波形为等幅振荡,表明系统临界稳定,而此时b判断为失稳,说明所提评估方法在误差允许范围内具有保守性,相对误差较小,为3.73%,能够满足工程应用需求。
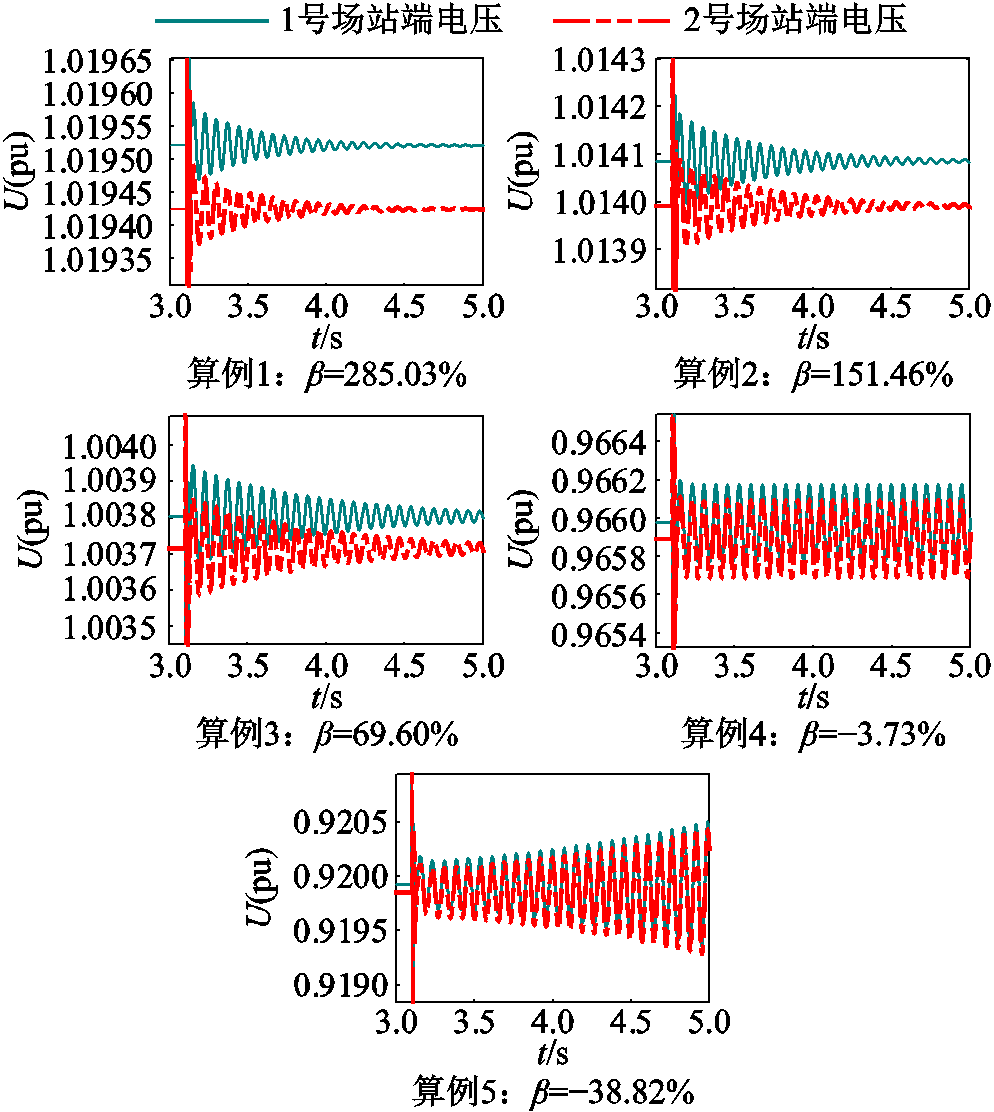
图9 5组算例的小扰动测试时域仿真波形
Fig.9 Time-domain simulation waveforms of 5 cases
另外,从图9可以看出随着裕度指标β的下降,系统受到小扰动后振荡的收敛速度下降,也就是说β越小,系统的主导特征根逐渐向复平面右半平面移动,更加靠近虚轴。
结合表1和表2的信息可知,当新能源场站出力增加时,新能源场站的端电压逐渐下降,送出系统的系统稳定裕度β逐渐下降,系统稳定裕度降低。因此本文提出的系统强度评估方法能够较为准确地评估运行工况对系统稳定性的影响。
作为对比,如果在分析过程中不考虑实际运行工况,仅利用新能源场站的额定容量信息计算广义短路比,由于网络参数没有发生变化,因此即使新能源场站运行工况改变,广义短路比和临界短路比仍保持相同。以算例1为例,广义短路比gSCR为2.19,而临界短路比CgSCR为2.56,gSCR<CgSCR,判断结果为系统失稳。然而此时新能源场站出力较小,系统是稳定的,基于广义短路比的稳定性评估结果与实际不符。因此在评估送出系统的系统强度时有必要考虑实际新能源实际运行工况。
为进一步验证所提方法的可行性,在固定运行工况、网络参数以及新能源设备参数的条件下,针对不同MMC-HVDC外环控制参数的送出系统进行系统强度评估。以表1的算例3运行工况为例,设置表4所示的定交流电压外环PI控制参数进行系统强度评估,其他参数均与算例3相同。不同MMC-HVDC外环参数下的仿真波形如图10所示。
表4 不同交流电压外环参数下的系统强度评估结果
Tab.4 System strength evaluation results under different AC voltage control parameters

算例外环PI控制参数Leq(pu)gOSCRCgOSCRb(%)判稳结果 6(0.2, 10)0.58702.192.73−19.78失稳 7(1, 25)0.11514.142.7351.65稳定 8(5, 40)0.02304.992.7382.78稳定
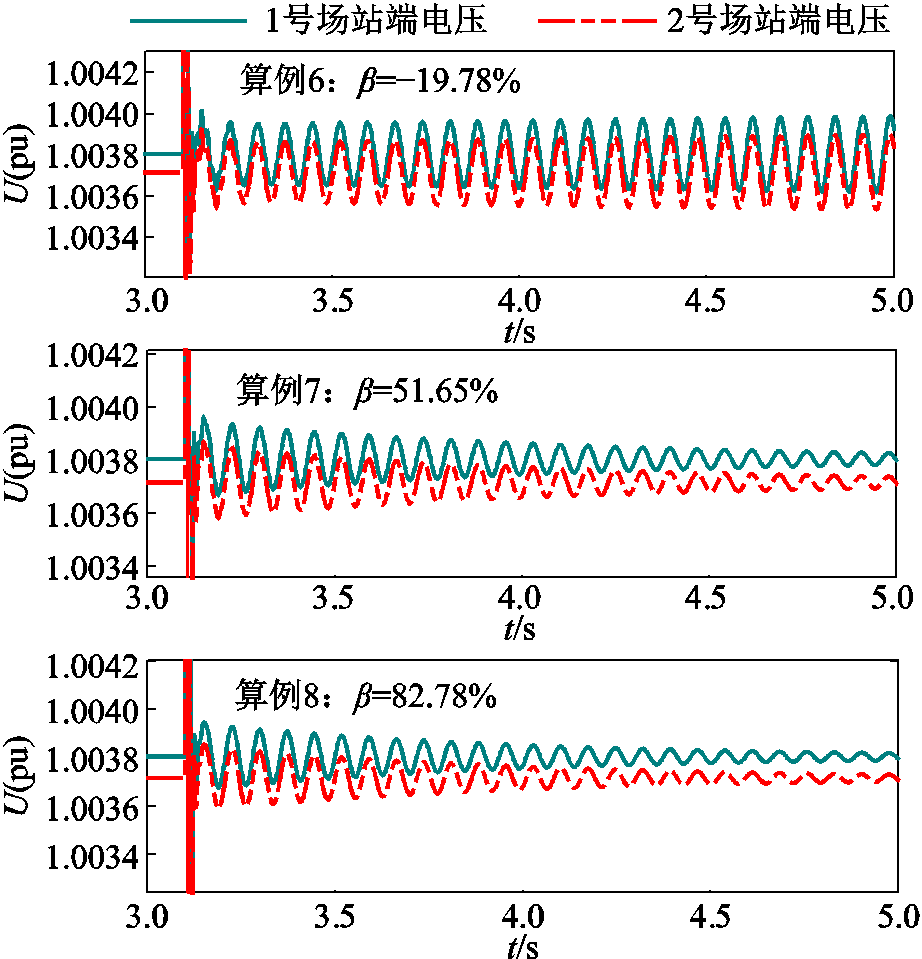
图10 不同MMC-HVDC外环参数下的仿真波形
Fig.10 Time-domain simulation waveforms under different outer loop control parameters of MMC-HVDC
从表4与图10的结果可以看到,不同交流电压外环参数对应的送端MMC-HVDC的闭环阻抗外特性不同,等值电感不同。外环PI控制系数越大,等值电感越小,送端MMC-HVDC越接近理想电压源,电压支撑能力越强,系统更稳定。因此本文提出的电压支撑能力量化方法能够反映送端MMC-HVDC的定交流电压控制效果。另外从算例结果可以发现,等值电感归算到网络侧后导致广义运行短路比变化,从而影响系统强度和系统稳定裕度,基于广义运行短路比指标的系统强度判据可以直观反映不同MMC-HVDC控制参数下的系统小扰动同步稳定性,对不同控制参数的MMC-HVDC具有适用性。
本文提出了考虑实际运行工况下的新能源经MMC-HVDC送出的系统强度量化评估原理方法。主要结论为:
1)针对送端MMC-HVDC电压支撑作用难以表征的问题,基于阻抗矩阵的最大奇异值提出了送端MMC-HVDC宽频段电压支撑能力的量化方法。
2)提出了考虑新能源场站的实际运行工况(有功出力与端电压)的新能源经MMC-HVDC送出系统强度量化评估方法,将广义运行短路比推广到无同步机支撑的送出系统中,能够快速量化评估系统的稳定裕度,不仅可应用于工况复杂多变的运行场景中,也可以用于规划阶段(可视为各新能源场站出力均为额定的情况)。
未来将研究送出系统的控制参数优化、调相机配置、构网型储能优化选址等强度提升方法,结合本文提出的系统强度评估方法,迭代提升系统强度。
附 录
1. 仿真参数
附表1 变压器以及电网参数
App.Tab.1 Parameters of transformers and grids

变压器参数数值(pu)线路电感参数数值(pu) L1-60.01L6-70.06 L2-70.01L6-80.08 L3-80.01L7-80.05 L4-90.01L8-90.2 L5-100.01L9-100.3
附表2 新能源场站参数
App.Tab.2 Parameters of the renewable base

参数(函数)数值(表达式) 系统额定容量SB/(MV·A)200 场站额定容量Si (i=1,2,3,4)/(MV·A)40, 40, 40, 80 额定交流电压UN/kV0.69 额定直流电压UdcN/kV1.5 直流侧电容Cdc(pu)0.038 滤波电感Lf(pu)0.05 滤波电容Cf(pu)0.05 直流电压外环传递函数Hdc(s)1.1+16/s 电流内环传递函数Hi(s)0.8+50/s 电压前馈滤波传递函数GFF(s)1/(1+0.001s) 锁相环传递函数Hpll(s)(6+7306/s)/s
附表3 送端MMC-HVDC参数
App.Tab.3 Parameters of sending-end MMC-HVDC

参数数值 系统额定容量SB/(MV·A)200 MMC额定容量SMMC/(MV·A)200 额定交流电压UN/kV120 额定直流电压UdcN/kV200 桥臂电感Larm/mH30 桥臂电阻Rarm/W1 子模块电容CSM/mF15 桥臂子模块个数N250 环流抑制环节传递函数Gcir(s)8+100/s 电流内环传递函数Gi(s)6.5+100/s 定交流电压外环传递函数Gv(s)2+50/s
2. MMC-HVDC阻抗矩阵建模
送端MMC-HVDC采用图4所示的定V/F控制,为送端交流网络提供电压与频率支撑,MMC-HVDC本地dq同步坐标系的旋转角速度直接给定为工频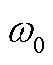 ,与全局同步坐标系旋转速度相同,因此不妨假设全局xy同步坐标系与MMC-HVDC的本地dq同步坐标系重合对齐。为获得送端MMC-HVDC的控制闭环运行下的阻抗矩阵,需要对主电路与控制两部分的动态方程进行建模。值得一提的是,本文的阻抗建模中考虑了谐波耦合特性,由于本文关注的振荡模态中三倍频及以上的谐波分量参与程度非常低[3-4],因此本文对三倍频及以上的谐波分量予以忽略。
,与全局同步坐标系旋转速度相同,因此不妨假设全局xy同步坐标系与MMC-HVDC的本地dq同步坐标系重合对齐。为获得送端MMC-HVDC的控制闭环运行下的阻抗矩阵,需要对主电路与控制两部分的动态方程进行建模。值得一提的是,本文的阻抗建模中考虑了谐波耦合特性,由于本文关注的振荡模态中三倍频及以上的谐波分量参与程度非常低[3-4],因此本文对三倍频及以上的谐波分量予以忽略。
MMC-HVDC的主电路动态方程的具体表达式参考文献[4,18]。控制部分的动态方程为
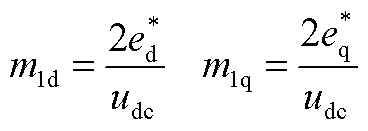 (A1)
(A1)
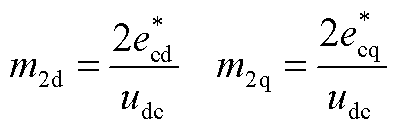 (A2)
(A2)
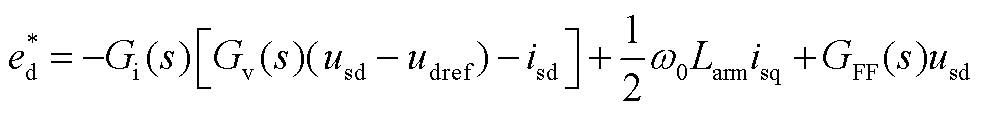 (A3)
(A3)
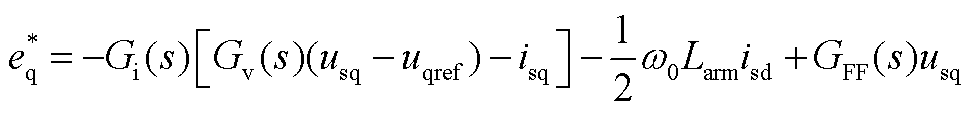 (A4)
(A4)
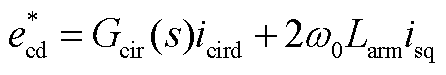 (A5)
(A5)
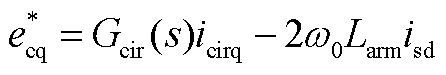 (A6)
(A6)
在稳态运行工作点对状态空间方程进行线性化可得
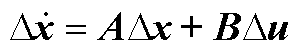 (A7)
(A7)
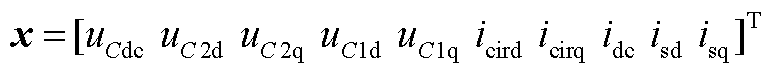 (A8)
(A8)
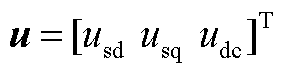 (A9)
(A9)
式中,“Δ”表示微增量;uCdc、uC2d、uC2q、uC1d、uC1q分别为下桥臂电容总电压的直流分量、二倍频d轴与q轴分量、基频d轴与q轴分量;isd、isq分别为流入MMC-HVDC的交流电流d轴与q轴分量;icird与icirq分别为桥臂环流电流的d轴与q轴分量;usd、usq分别为MMC-HVDC并网耦合点的交流电压d轴与q轴分量;udc、idc分别为送端MMC-HVDC直流侧的电压与电流,由前文假设可知Δudc = 0。
选取输出变量Δy为[−Δisd −Δisq]T,输入变量Δu为[Δusd Δusq]T,根据式(A10)求得送端MMC-HVDC的本地dq频域导纳矩阵YMMC(s),求逆得到阻抗矩阵ZMMC(s)。由于本地dq坐标系与全局xy坐标系对齐,因此本地dq阻抗与全局xy阻抗解析式相同。
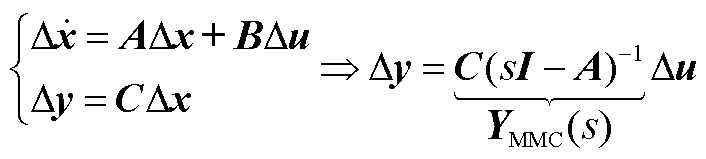 (A10)
(A10)
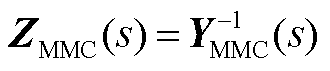 (A11)
(A11)
式中,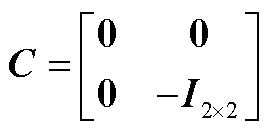 ;I为单位矩阵。
;I为单位矩阵。
以额定工况运行的送端MMC-HVDC为例,采用附表3所示的典型参数,在Matlab/Simulink中搭建MMC-HVDC仿真系统。送端MMC-HVDC在本文关注频段的阻抗扫频结果与理论模型的结果如附图2所示,可以看到两种方法的得到的外特性结果一致。
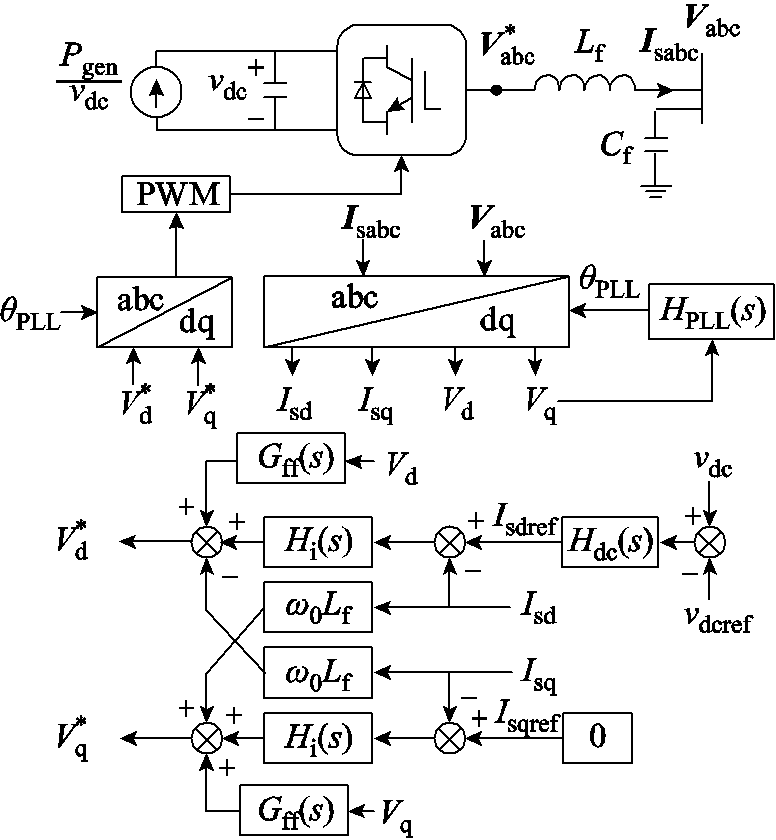
附图1 跟网型变流器控制框图
App.Fig.1 Control scheme of the grid-side inverter of GFL
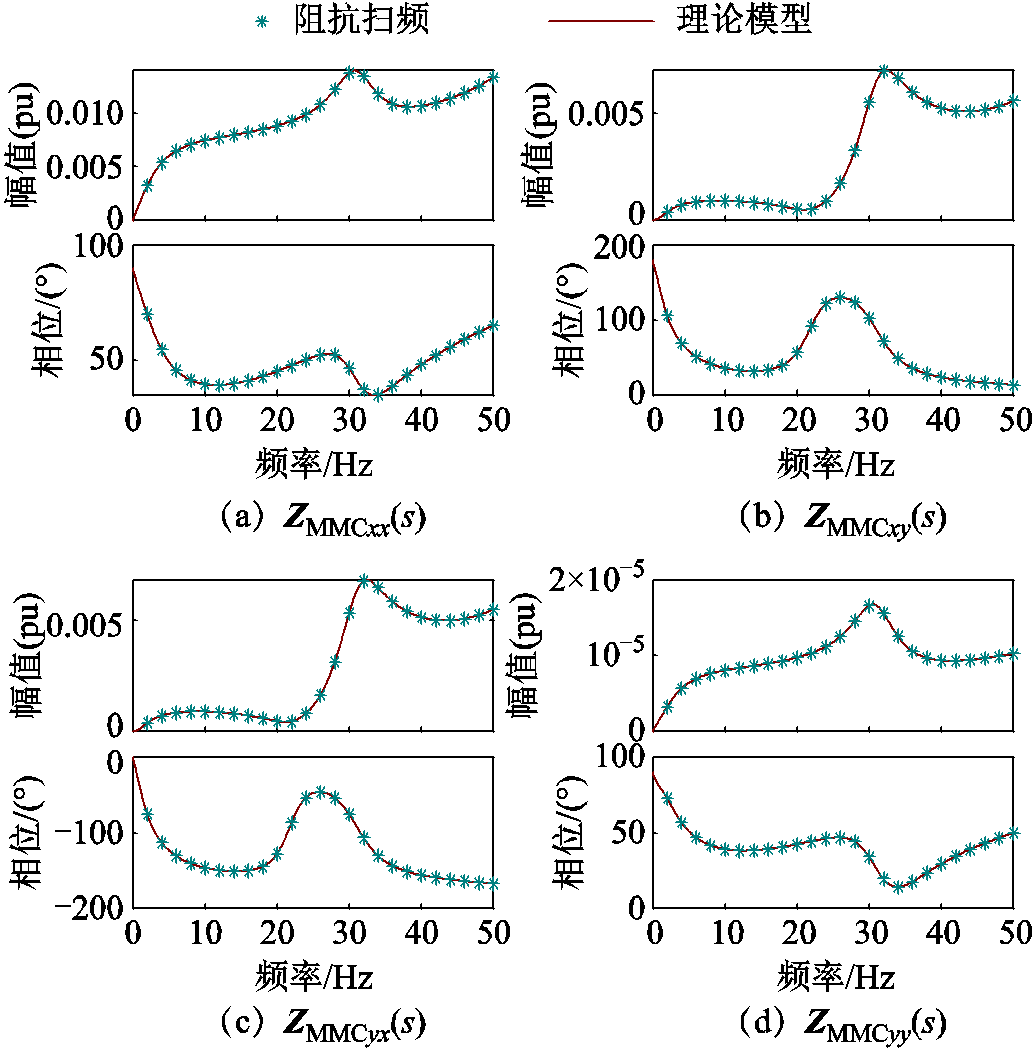
附图2 送端MMC-HVDC阻抗扫频与理论模型对比
App.Fig.2 Comparison of impedance scan results with theoretical model of sending-end MMC-HVDC
参考文献
[1] 杨鹏, 刘锋, 姜齐荣, 等. “双高”电力系统大扰动稳定性: 问题、挑战与展望[J]. 清华大学学报(自然科学版), 2021, 61(5): 403-414.
Yang Peng, Liu Feng, Jiang Qirong, et al. Large disturbance stability of “double high” power system: problems, challenges and prospects[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(5): 403-414.
[2] Wang Weisheng, Li Guanghui, Guo Jianbo. Large-scale renewable energy transmission by HVDC: challenges and proposals[J]. Engineering, 2022, 19: 252-267.
[3] Wang Yifan, Zhao Chengyong, Guo Chunyi, et al. Dynamics and small signal stability analysis of PMSG-based wind farm with an MMC-HVDC system[J]. CSEE Journal of Power and Energy Systems, 2020, 6(1): 226-235.
[4] 郭贤珊, 李云丰, 谢欣涛, 等. 直驱风电场经柔直并网诱发的次同步振荡特性[J]. 中国电机工程学报, 2020, 40(4): 1149-1160, 1407.
Guo Xianshan, Li Yunfeng, Xie Xintao, et al. Sub-synchronous oscillation characteristics caused by PMSG-based wind plant farm integrated via flexible HVDC system[J]. Proceedings of the CSEE, 2020, 40(4): 1149-1160, 1407.
[5] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes' participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[6] 王一凡, 赵成勇, 郭春义. 双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J]. 电工技术学报, 2019, 34(10): 2116-2129.
Wang Yifan, Zhao Chengyong, Guo Chunyi. Small signal stability and oscillation suppression method for islanded double fed induction generator-based wind farm integrated by modular multilevel converter based HVDC system[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2116-2129.
[7] 李光辉, 王伟胜, 郭剑波, 等. 风电场经MMC-HVDC送出系统宽频带振荡机理与分析方法[J]. 中国电机工程学报, 2019, 39(18): 5281-5297, 5575.
Li Guanghui, Wang Weisheng, Guo Jianbo, et al. Broadband oscillation mechanism and analysis for wind farm integration through MMC-HVDC system[J]. Proceedings of the CSEE, 2019, 39(18): 5281-5297, 5575.
[8] 辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027.
Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[9] 辛焕海, 甘德强, 鞠平. 多馈入电力系统广义短路比: 多样化新能源场景[J]. 中国电机工程学报, 2020, 40(17): 5516-5527.
Xin Huanhai, Gan Deqiang, Ju Ping. Generalized short circuit ratio of power systems with multiple power electronic devices: analysis for various renewable power generations[J]. Proceedings of the CSEE, 2020, 40(17): 5516-5527.
[10] CIGRE Working Group B4.41. Systems with multiple DC infeed[R]. Paris, France: CIGRE, 2008.
[11] 于琳, 孙华东, 赵兵, 等. 新能源并网系统短路比指标分析及临界短路比计算方法[J]. 中国电机工程学报, 2022, 42(3): 919-929.
Yu Lin, Sun Huadong, Zhao Bing, et al. Short circuit ratio index analysis and critical short circuit ratio calculation of renewable energy grid-connected system [J]. Proceedings of the CSEE, 2022, 42(3): 919-929.
[12] 刘晨曦, 辛焕海. 考虑实际工况的新能源多馈入系统广义运行短路比[J]. 电力系统自动化, 2025, 49(8): 12-20.
Liu Chenxi, Xin Huanhai. Generalized operational short circuit ratio of renewable energy multi-infeed systems considering actual operating conditions[J]. Automation of Electric Power Systems, 2025, 49(8): 12-20.
[13] 徐政. 新型电力系统背景下电网强度的合理定义及其计算方法[J]. 高电压技术, 2022, 48(10): 3805-3819.
Xu Zheng. Reasonable definition and calculation method of power grid strength under the background of new type power systems[J]. High Voltage Engineering, 2022, 48(10): 3805-3819.
[14] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessmentmethod for renewables VSC-HVDC delivery system[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[15] 张志强, 李秋彤, 余浩, 等. 海上直驱风电经柔直并网系统的次/超同步振荡特性分析[J]. 上海交通大学学报, 2022, 56(12): 1572-1583.
Zhang Zhiqiang, Li Qiutong, Yu Hao, et al. Analysis of sub/super-synchronous oscillation of direct-drive offshore wind power grid-connected system via VSC-HVDC[J]. Journal of Shanghai Jiao Tong University, 2022, 56(12): 1572-1583.
[16] Dong Wei, Xin Huanhai, Wu Di, et al. Small signal stability analysis of multi-infeed power electronic systems based on grid strength assessment[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1393-1403.
[17] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725.
Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[18] 李探, Aniruddha M.Gole, 赵成勇. 考虑内部动态特性的模块化多电平换流器小信号模型[J]. 中国电机工程学报, 2016, 36(11): 2890-2899.
Li Tan, Gole A M, Zhao Chengyong. Small-signal model of the modular multilevel converter considering the internal dynamics[J]. Proceedings of the CSEE, 2016, 36(11): 2890-2899.
[19] Wang Zhong, Lü Jing, Rao Yiming, et al. Data-driven impedance identification and stability online assessment of DFIG-based wind farm integration with MMC-HVDC[C]//2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 2023: 4500-4504.
[20] 周瑀涵, 辛焕海, 鞠平. 基于广义短路比的多馈入系统强度量化原理与方法: 回顾、探讨与展望[J]. 中国电机工程学报, 2023, 43(10): 3794-3811.
Zhou Yuhan, Xin Huanhai, Ju Ping. System strength quantification principle and method of multi-infeed systems based on generalized short-circuit ratio: reviews, discussions and outlooks[J]. Proceedings of the CSEE, 2023, 43(10): 3794-3811.
[21] 迟永宁, 江炳蔚, 胡家兵, 等. 构网型变流器: 物理本质与特征[J]. 高电压技术, 2024, 50(2): 590-604.
Chi Yongning, Jiang Bingwei, Hu Jiabing, et al. Grid-forming converters: physical mechanism and characteristics[J]. High Voltage Engineering, 2024, 50(2): 590-604.
[22] 吕敬, 蔡旭. 提高风场柔直并网系统稳定性的控制器参数优化设计[J]. 中国电机工程学报, 2018, 38(2): 431-443, 674.
Lü Jing, Cai Xu. Controller parameters optimization design for enhancing the stability of wind farm with VSC-HVDC system[J]. Proceedings of the CSEE, 2018, 38(2): 431-443, 674.
[23] Fang Qiao, Xing Facai, Jiang Zhe, et al. Equivalence analysis of different sequence impedance modeling methods[C]//2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 2023: 3800-3805.
[24] 辛焕海, 刘晨曦, 黄林彬, 等. 基于特征子系统的广义短路比导出原理及计算方法[J]. 中国电机工程学报, 2025, 45(7): 2447-2461.
Xin Huanhai, Liu Chenxi, Huang Linbin, et al. Derivation principle and calculation method for generalized short-circuit ratio based on eigen-subsystems[J]. Proceedings of the CSEE, 2025, 45(7): 2447-2461.
System Voltage Support Strength Evaluation for Renewables HVDC Transmission System Considering Operating Condition
Abstract Large-scale renewable energy transmission via high voltage direct current system (HVDC) has become a typical scenario in modern power system. The evaluation method of voltage support strength (referred to as system strength) based on the generalized short-circuit ratio index can describe the stability margin of renewable energy transmission system via two-level converter HVDC. However, modular multilevel converter high voltage direct current system (MMC-HVDC) is more commonly utilized in power transmission of renewable bases. Compared with the two-level converter HVDC, MMC-HVDC is more complicated in dynamical characteristic because of complex harmonic coupling. Consequently, it remains unclear how to quantify the voltage support capability of the ac grid containing MMC-HVDC, especially when analyzing small-disturbance voltage stability. Furthermore, the operating conditions of renewables are changing in the actual operating system. Operating conditions have a significant impact on the stability of the system, further increasing the difficulty of assessing the system strength. To solve the challenge mentioned above, this paper proposes the system strength assessment method considering operating conditions, focusing on small-disturbance voltage stability.
Firstly, the frequency-domain closed-loop transfer function matrix of the renewables MMC-HVDC transmission system (RMTS) is established by linearization of the state equations at the stable operating point. The sensitivity relationship between bus voltage response and small-disturbance current is described by impedance matrix. Based on the transfer function matrix, the closed-loop characteristic equation of RMTS is derived. Secondly, the small-disturbance voltage support capability of MMC-HVDC is analyzed equivalently based on the maximum singular value of its impedance matrix, and an equivalent model of MMC-HVDC is proposed accordingly. This equivalence results in modification to the ac grid admittance matrix. Then, the definition of generalized operational short-circuit ratio (gOSCR) is extended to RMTS considering operating conditions. The relative difference between gOSCR and critical gOSCR is defined as the stability margin of RMTS, as performing the evaluation of the system strength. Finally, the effectiveness of the proposed methods is verified by electromagnetic transient simulation of 4-infeed RMTS in varied operating conditions. The results show that the evaluation results correspond with time-domain simulation waveform.
The following conclusion can be drawn: (1) The critical gOSCR reflects the tolerance of renewable energy devices to the ac grid strength supported by MMC-HVDC, which is related to the characteristics of devices. The gOSCR characterizes the voltage support capability of ac grids with MMC-HVDC. By comparing the gOSCR and critical gOSCR, the small-disturbance voltage stability of RMTS can be assessed in a rapid way, avoiding massive work of electromagnetic transient modeling. The proposed method can be applied in both the operational scenario and the planning phase. (2) The variation of power output and bus voltage of renewable energy are reflected in gOSCR. When the output of the renewables increases, the bus voltage of the renewables gradually decreases, leading to reduction in the system stability margin of RMTS and thus a decrease in system stability margin. (3) The gOSCR is also determined by the voltage support dynamic characteristics of MMC-HVDC. When the voltage support dynamic of MMC-HVDC approaches ideal voltage source, the gOSCR increases, resulting in increment of RMTS stability margin.
Keywords:Renewables, modular multilevel converter high voltage direct current system (MMC-HVDC), system strength, generalized operational short-circuit ratio
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241215
国家重点研发计划资助项目(2023YFB2405900)。
收稿日期2024-07-10
改稿日期2024-09-26
王祥宇 男,1999年生,硕士研究生,研究方向为新能源并网稳定分析与控制。
E-mail:wangxiangyu@zju.edu.cn
辛焕海 男,1981年生,教授,博士生导师,研究方向为高比例新能源电力系统稳定性分析和控制。
E-mail:xinhh@zju.edu.cn(通信作者)
(编辑 赫 蕾)