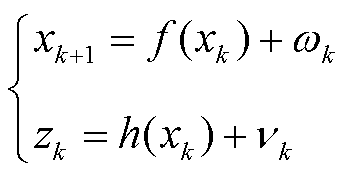 (1)
(1)
摘要 快速准确地获取整个系统的实时状态,对于随机性和波动性大大增强的新型电力系统变得更为重要。为减小未知测量噪声的影响,准确获取系统状态,该文提出了一种基于自适应抗差扩展卡尔曼滤波(IAREKF)算法的混合测量状态估计方法。首先,通过量测变换技术实现混合量测的融合,并基于系统的时空特性构造伪量测;其次,引入自适应遗忘因子,改进噪声估计算法,能够更快速准确地估计时变系统噪声,提高算法的动态跟踪能力;然后,分析量测装置特性来估计量测噪声,并基于标准新息构造抗差因子以抑制不良数据;最后,基于IEEE 39节点系统进行仿真验证,结果表明所提方法在模型参数未知、系统状态变化和不良数据的影响下,均有良好的估计性能及较强的抗差性。
关键词:状态估计 混合量测 卡尔曼滤波 抗差估计
状态估计是电网调度控制中心能量管理系统的核心功能之一,通过分析采集的量测数据,计算补全整个电力网络的运行状态,实现对电力系统的实时监测[1]。随着新能源的大量接入,大功率电力电子设备的广泛应用,现代电力系统的随机性和波动性大大增强,电网的运行方式和动态特性越来越复杂多变,因而对快速准确地获取系统状态提出了更高要求[2]。电力系统状态估计需要提高估计精度和频次,以支撑系统动态参数辨识、暂态稳定评估等应用[3-5]。
同步相量测量单元(Phase Measurement Unit, PMU)的发展和广域测量系统(Wide Area Measurement System, WAMS)的建设,提供了高同步、高精度、高刷新频率的测量数据,为快速准确地获取电力系统的实时状态提供了新途径[6-7]。然而,受限于经济成本和配置环境,目前PMU还不能在电网中广泛配置。为满足系统的可观测性,需要结合电网中原有的数据采集与监控系统(Supervisory Control and Data Acquisition, SCADA)、智能电能表等常规量测系统形成混合量测以提高测量的冗余度。因此研究混合量测下的电力系统状态估计更具有现实意义[8]。目前,WAMS与SCADA等量测系统在数据成分、采样时刻、刷新频率及数据精度等方面存在较大差异[9]。为提高量测信息的一致性和状态估计的准确性,需要融合多源量测数据[10-13]。
依靠高频PMU量测数据可以实现电力系统的实时状态感知,但在PMU量测不足时需加入伪量测[14]才能确保系统的快速全局估计。线性插值法[15]是常见的伪量测构造方法,文献[16]基于SCADA量测的预测值,采用分段插值法,在每个子区间构造三次样条插值多项式生成伪量测。但伪量测精度受制于预测值的准确性,且在系统状态波动较大时,基于插值法的伪量测无法体现系统动态变化。因此构造伪量测需要充分利用量测数据在空间和时间的相关性[17]。文献[18]采用数据驱动和概率统计方法,计算历史量测数据的概率分布并生成伪量测。
电力系统状态估计通过量测方程建立量测与待求状态间的关系,求解获得当前时间断面的运行状态,可分为静态状态估计和动态状态估计两种方法。目前静态状态估计的应用较为成熟,以最小二乘法等为主要求解方法,但该方法仅利用单时间断面的量测数据,忽略了系统状态在连续时刻下的动态变化及其关联性。随着智能电网的发展,电力系统呈现更为明显的动态特性。动态状态估计基于多断面量测数据生成状态预测值,并结合最新测量值估计系统运行状态,能更好地反映系统的动态变化[19]。目前,动态状态估计算法主要基于卡尔曼滤波(Kalman Filter, KF)[20]设计,针对如电力系统的非线性系统,延伸出扩展卡尔曼滤波(Extended Kalman Filter, EKF)[21]、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)[22]和容积卡尔曼滤波(Cubature Kalman Filter, CKF)[23]等算法。EKF通过对非线性函数进行泰勒展开,并省略高阶项,实现非线性函数线性化,但也因此引入了线性化误差,当系统非线性较强时,会产生较大的估计误差。文献[24]基于广义极大似然估计提出迭代扩展卡尔曼滤波方法(Generalized Maximum Likelihood Iterated Extended Kalman Filter, GMIEKF),利用迭代消除了线性化误差,且对新息和量测的离群值点具有鲁棒性。UKF和CKF通过点集采样方式获取非线性变换后的统计特性,避免了线性化误差[25],但在计算效率上不及EKF。同时,以上三种算法基于KF框架,对模型精确度要求较高,只有在掌握系统噪声统计特性时才能实现准确估计。针对具有模型不确定性和系统噪声统计特性未知的电力系统,文献[26]采用Sage-Husa噪声估计器,根据一段窗口内的新息统计特性,实时调整过程噪声协方差,以适应系统的动态变化。文献[27]在上述基础上引入渐消记忆指数加权法,通过遗忘因子提高最新采样数据的权重,逐渐遗忘陈旧数据,进而准确估计时变噪声。文献[28]提出了一种自适应H¥扩展卡尔曼滤波器(Adaptive H¥ Extended Kalman Filter, AHEKF),能够抑制噪声模型统计不确定性的不利影响。但上述文献中的遗忘因子都采用定值,不能合理调整对陈旧数据的遗忘程度,影响估计结果的稳定性和准确性。
高频次、高精度的状态估计不仅是新型电力系统运行调度的要求,也能够为后续各方面的应用提供有力支撑。据此,本文提出了一种混合量测下基于改进自适应抗差扩展卡尔曼滤波算法(Improved Adaptive Robust Extended Kalman Filter, IAREKF)的电力系统状态估计方法。针对多源数据融合问题,采用量测变换技术实现量测方程线性化,并基于节点状态间的时空相关性构造伪量测,实现混合量测的融合;针对系统模型不确定性和噪声统计特性未知,基于计算效率较高的EKF算法,设计了一种遗忘因子自适应方法来改进Sage-Husa噪声估计器,根据新息判定滤波效果并调整遗忘程度,可以提高过程噪声自适应估计的准确性,从而提高算法对系统状态的动态追踪能力。此外,通过分析量测装置统计特性来估计量测噪声,并根据标准新息构造等价权函数,修正量测噪声协方差,以提高算法的抗差性。
电力系统动态状态估计模型可由状态方程和量测方程构成,有
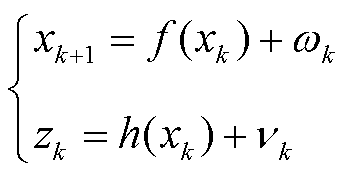 (1)
(1)
式中,x为系统状态值;z为系统量测值;k为采样时刻;f(x)为状态转移方程,反映电力系统运行状态的动态变化;h(x)为系统量测方程,反映状态量和量测量的关系;w和n分别为系统过程噪声和量测噪声,通常假设为相互独立、均值为零、协方差已知的高斯白噪声。
由于电力系统的动态变化十分复杂,难以用线性模型精准表示状态变化过程,因此,状态方程一般采用Holt指数平滑法表示[15]。Holt指数平滑法能够根据数据在时间序列中的特征,进行短期状态预测。具体过程表示为
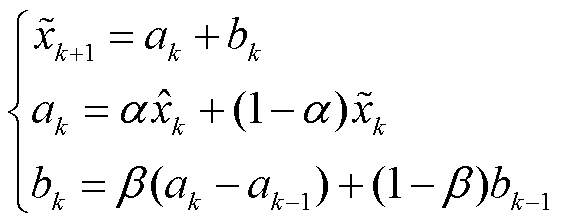 (2)
(2)
式中,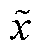 为状态预测值;
为状态预测值;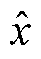 为状态估计值;
为状态估计值;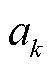 和
和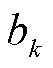 分别为Holt指数平滑的水平分量和垂直分量;α、β为平滑系数。
分别为Holt指数平滑的水平分量和垂直分量;α、β为平滑系数。
虽然PMU量测数据具有高精度、高刷新频率的特点,但受限于装置的配置成本和技术要求,目前仅依靠PMU量测难以保证系统的可观测性。为满足实际应用需求,需要将PMU量测和传统的SCADA量测数据融合,形成混合量测。
1.2.1 PMU量测
在电力网络支路简化成的p型等效支路i-j中,由欧姆定律和基尔霍夫定律可将电流相量用电压相量表示为
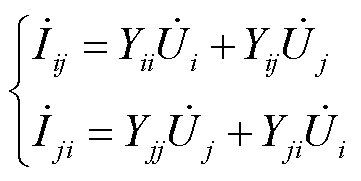 (3)
(3)
式中,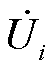 、
、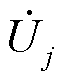 、
、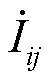 和
和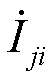 分别为支路i-j的节点电压相量和支路电流相量;
分别为支路i-j的节点电压相量和支路电流相量;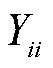 、
、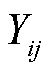 、
、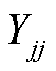 和
和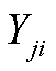 为支路导纳。
为支路导纳。
由于PMU能够直接测量节点电压相量和支路电流相量,以节点电压相量为状态量,可以得到基于PMU的线性量测方程为
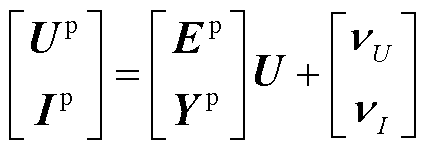 (4)
(4)
式中, 为节点电压状态量;
为节点电压状态量;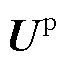 和
和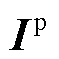 分别为由PMU节点电压相量和支路电流相量构造的向量;上标p表示PMU量测;
分别为由PMU节点电压相量和支路电流相量构造的向量;上标p表示PMU量测;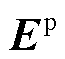 为单位矩阵;
为单位矩阵;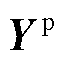 为节点-支路导纳矩阵;
为节点-支路导纳矩阵;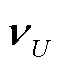 和
和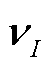 分别为电压和电流的量测误差。
分别为电压和电流的量测误差。
以节点电压为状态量,根据式(1)可将式(4)的PMU量测方程简化为
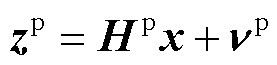 (5)
(5)
式中,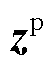 为基于PMU的量测向量,
为基于PMU的量测向量,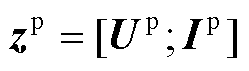 ;
;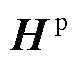 为量测方程中的系数矩阵,
为量测方程中的系数矩阵,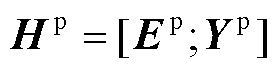 ;
;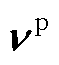 为量测噪声向量,
为量测噪声向量,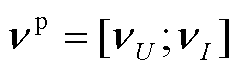 。
。
1.2.2 SCADA量测
融合SCADA量测数据后将引入功率量测,造成量测方程非线性。为提高计算效率,需要对SCADA数据进行量测变换[29],将支路功率量测和节点注入功率量测转换成等效支路电流相量量测和等效节点注入电流相量量测,转换公式为
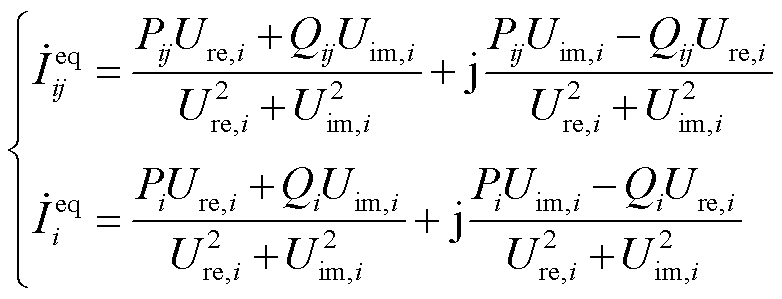 (6)
(6)
式中,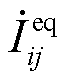 和
和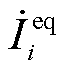 分别为等效支路电流相量和等效节点注入电流相量;
分别为等效支路电流相量和等效节点注入电流相量;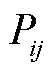 、
、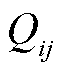 和
和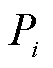 、
、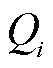 分别支路i-j的有功功率、无功功率和节点i的注入有功功率、注入无功功率;
分别支路i-j的有功功率、无功功率和节点i的注入有功功率、注入无功功率;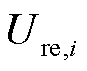 和
和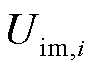 分别为节点电压的实部和虚部。
分别为节点电压的实部和虚部。
采用量测变换后得到基于SCADA的线性量测方程为
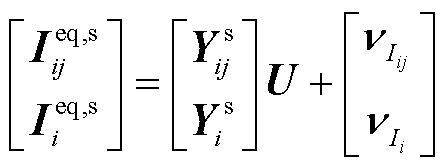 (7)
(7)
式中,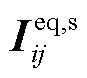 和
和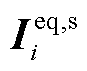 分别为由SCADA数据经过量测变换得到的等效支路电流相量和等效节点注入电流相量构造的向量;上标s表示SCADA量测;
分别为由SCADA数据经过量测变换得到的等效支路电流相量和等效节点注入电流相量构造的向量;上标s表示SCADA量测;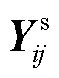 和
和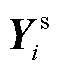 分别为节点-支路导纳矩阵和节点导纳矩阵;
分别为节点-支路导纳矩阵和节点导纳矩阵;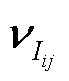 和
和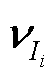 为等效电流的量测误差。以节点电压为状态量,根据式(1)可将式(7)的SCADA量测方程简化为
为等效电流的量测误差。以节点电压为状态量,根据式(1)可将式(7)的SCADA量测方程简化为
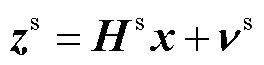 (8)
(8)
式中,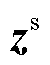 为基于SCADA的量测向量,
为基于SCADA的量测向量,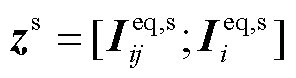 ;
;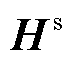 为系数矩阵,
为系数矩阵,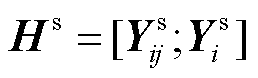 ;
;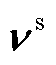 为量测噪声向量,
为量测噪声向量,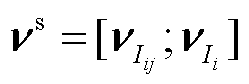 。
。
将PMU和SCADA的量测数据融合,最终得到基于混合量测的量测方程为
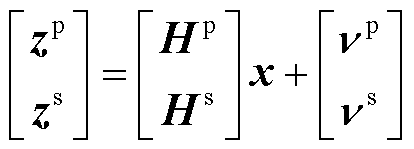 (9)
(9)
当PMU配置不满足系统可观测性时,仅基于PMU量测进行动态状态估计无法反映系统全局状态。虽然结合SCADA数据形成的混合量测能够满足系统可观,但由于SCADA更新频率较慢,为快速追踪电力系统的动态变化,仍需要在非SCADA更新时刻给PMU不可观测节点构造伪量测,以支撑系统的全局状态估计。
节点间潮流示意图如图1所示。根据数据在空间的相关性和时间的相关性,由PMU量测推导出PMU不可观节点的伪量测。
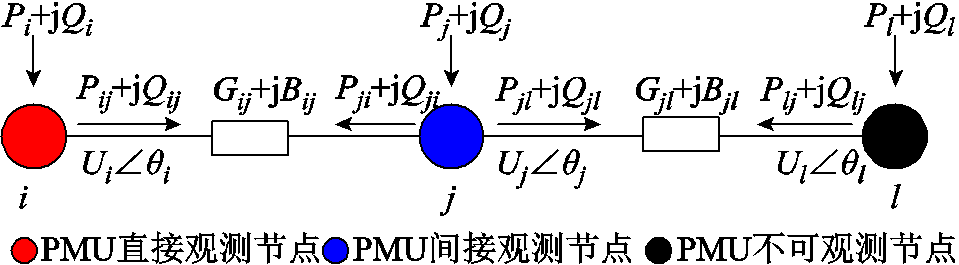
图1 节点间潮流示意图
Fig.1 Diagram of power flow between bus
1.3.1 间接量测
假设节点i配置了PMU,而节点j没有配置PMU,则节点j的电压和电流可以通过节点i的量测间接计算[30]得到,即
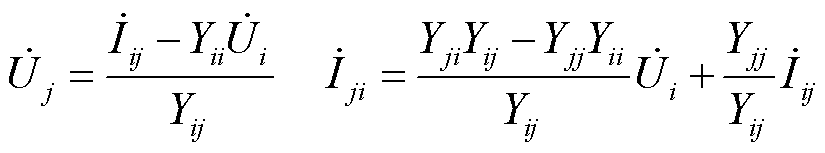 (10)
(10)
1.3.2 基于功率转移分布因子的功率伪量测构造
根据直流潮流计算公式可得支路功率和节点注入功率与节点电压间的关系为
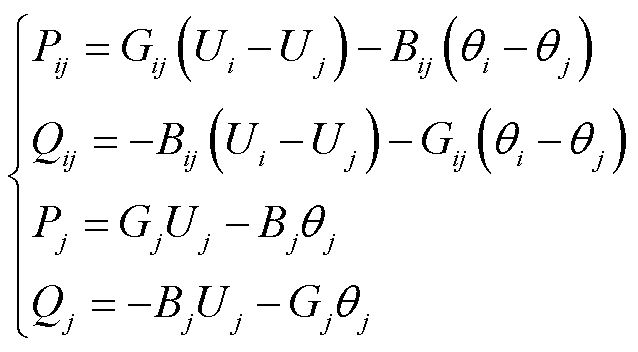 (11)
(11)
式中,U、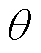 分别为电压的幅值和相位;P、Q分别为有功功率和无功功率;G、B分别为支路的电导和电纳。
分别为电压的幅值和相位;P、Q分别为有功功率和无功功率;G、B分别为支路的电导和电纳。
当节点注入功率变化时,根据式(11)可以推导出节点电压的变化为
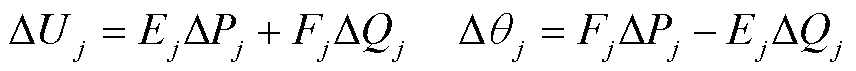 (12)
(12)
通过变量E和F建立功率和电压间的关系,得到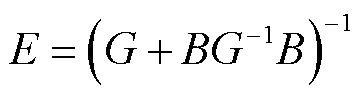 ,
,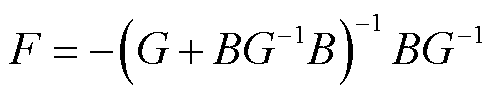 。
。
根据式(11)和式(12),由节点注入功率变化量可以计算获得支路功率变化量为
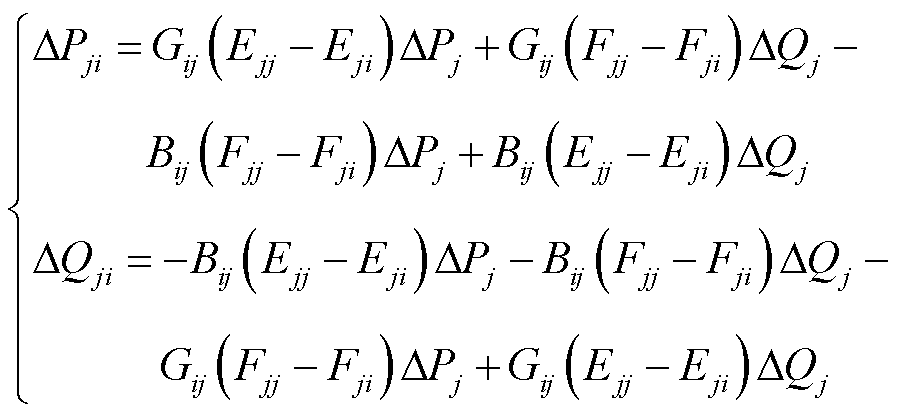 (13)
(13)
进而,由PMU间接量测支路功率变化量可以推导出PMU间接量测节点注入功率变化量为
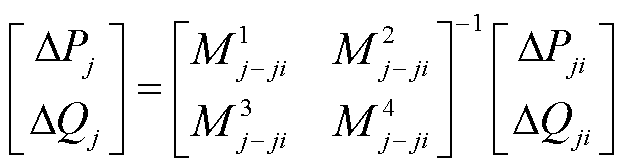 (14)
(14)
式中,M表示支路功率量测变化量和节点注入功率变化量的关系,有
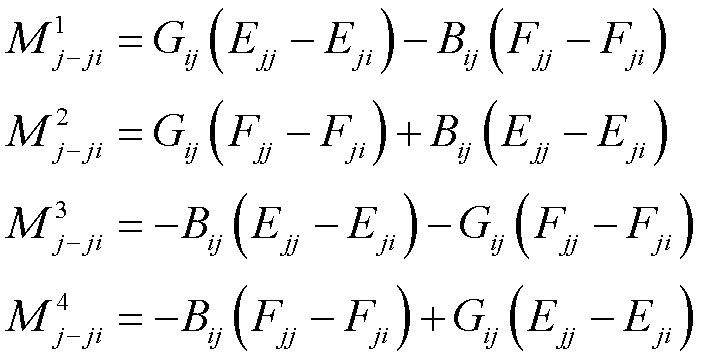
同理,通过计算PMU间接量测节点的注入功率变化量,可以推导出PMU不可观测支路的功率变化量为
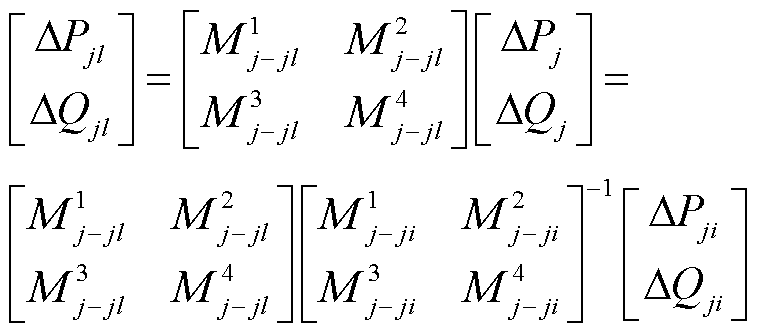 (15)
(15)
最终,以SCADA在k时刻测量的支路j-l功率量测为起点,根据PMU量测计算支路j-i在k~k+1时刻间的功率变化量,结合式(15)可得PMU不可观测支路j-l的功率变化量,从而生成支路j-l在k+1时刻的功率伪量测为
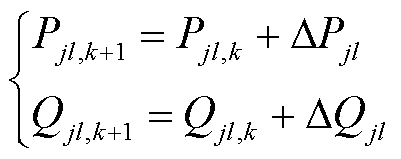 (16)
(16)
将得到的PMU不可观测支路功率伪量测根据式(6)转换成等效电流伪量测,融入PMU量测方程中,与不可观测节点建立状态联系,通过状态估计可以实现电力系统的完全可观性。
1.3.3 基于时间相关性的伪量测构造
电力系统中以发电机为代表的众多元件都是动态元件,这些元件根据输入和历史状态做出响应,使得电力系统当前状态与先前状态紧密相关,因此,系统状态存在着强烈的时间相关性。同样,同一节点的各个注入功率间也存在着明显的时间相关性。根据同一节点的各个注入功率在一段时间内的变化关系,设计出基于时间相关性的伪量测构造方法,表示为
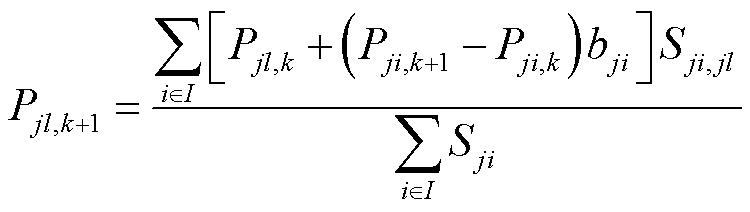 (17)
(17)
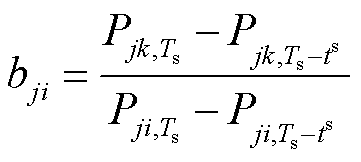 (18)
(18)
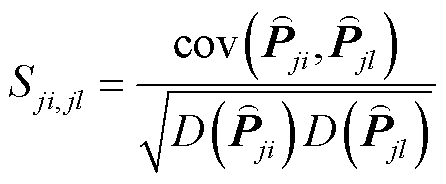 (19)
(19)
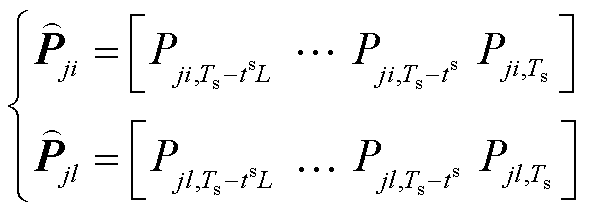 (20)
(20)
式中,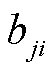 为趋势系数,为最近两次SCADA更新时刻支路j-i和支路j-l的功率比;
为趋势系数,为最近两次SCADA更新时刻支路j-i和支路j-l的功率比;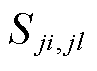 为相关性系数,为一段时间窗口L内支路j-i和支路j-l的相关系数;
为相关性系数,为一段时间窗口L内支路j-i和支路j-l的相关系数;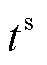 为SCADA量测周期;
为SCADA量测周期;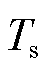 为最近一次SCADA更新时刻;I为与节点j相连的可观测节点数集合;cov(·)为协方差矩阵函数;D(·)为方差函数。
为最近一次SCADA更新时刻;I为与节点j相连的可观测节点数集合;cov(·)为协方差矩阵函数;D(·)为方差函数。
1.3.4 基于时空相关性的伪量测构造
为提高伪量测精度,分别将基于功率转移分布因子构造的伪量测和基于时间相关性构造的伪量测与状态估计值作差,并采用指数函数设置权重,加权求和形成基于时空相关性的伪量测为
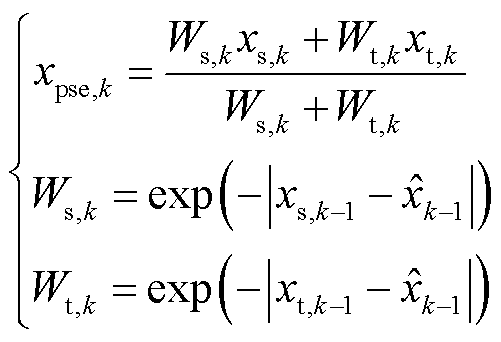 (21)
(21)
式中,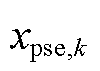 为基于时空相关性构造的伪量测;
为基于时空相关性构造的伪量测;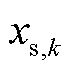 和
和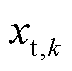 分别为在k时刻基于功率转移分布因子构造的伪量测和基于时间相关性构造的伪量测;
分别为在k时刻基于功率转移分布因子构造的伪量测和基于时间相关性构造的伪量测;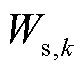 和
和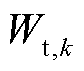 为对应的权重。
为对应的权重。
将两种伪量测结合,分别基于时间相关性和空间结构关系,并结合动态状态估计结果,能够抑制伪量测估计在状态估计次数增加时估计发散的问题,进一步提高伪量测的估计精度。
基于混合量测的状态估计架构如图2所示。图2中,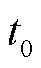 为第一次SCADA采样时刻,
为第一次SCADA采样时刻,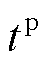 为PMU量测周期。当SCADA量测更新时采用混合量测进行状态估计;在非SCADA量测更新时,采用PMU量测结合伪量测进行状态估计。
为PMU量测周期。当SCADA量测更新时采用混合量测进行状态估计;在非SCADA量测更新时,采用PMU量测结合伪量测进行状态估计。
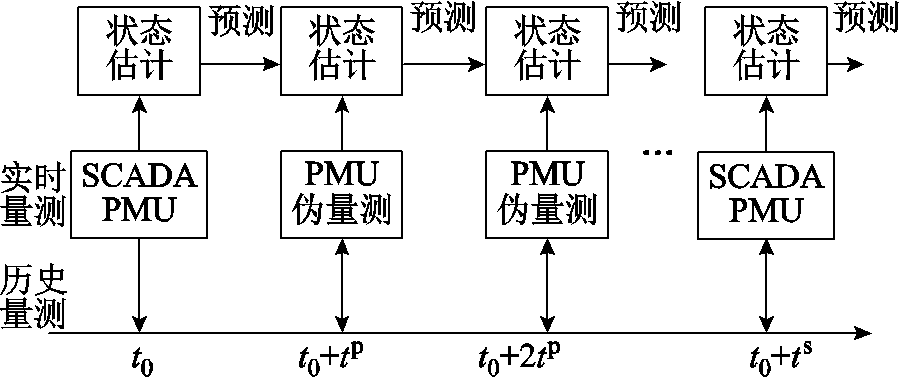
图2 基于混合量测的状态估计架构
Fig.2 State estimation framework based on hybrid measurements
对非线性的电力系统进行动态状态估计时,通常可采用扩展卡尔曼滤波算法。扩展卡尔曼滤波基于动态状态估计模型,根据噪声的统计特性,遵循线性无偏最小均方差准则,滤除量测信息中的随机干扰,得到状态变量的最佳估计值。卡尔曼滤波可分为状态预测和状态滤波两个过程[31],具体过程如下。
状态预测过程为
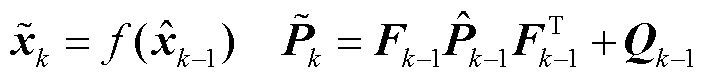 (22)
(22)
状态滤波过程为
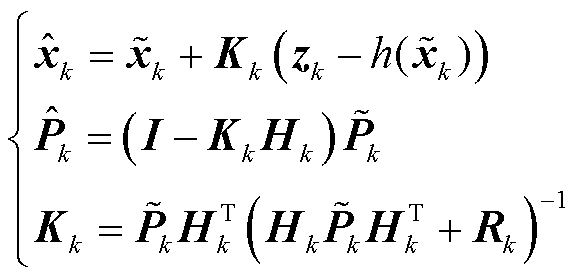 (23)
(23)
式中,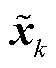 为状态预测值;
为状态预测值;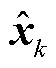 为状态估计值;
为状态估计值;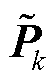 为预测误差协方差矩阵;
为预测误差协方差矩阵;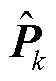 为估计误差协方差矩阵;
为估计误差协方差矩阵;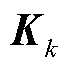 为卡尔曼增益;
为卡尔曼增益;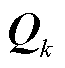 和
和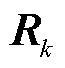 分别为过程噪声
分别为过程噪声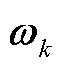 和量测噪声
和量测噪声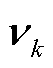 的协方差矩阵;
的协方差矩阵;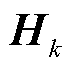 为量测方程的雅克比矩阵,
为量测方程的雅克比矩阵,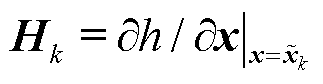 ,在混合量测下可根据式(9)求得;
,在混合量测下可根据式(9)求得;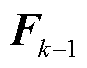 为状态转移方程的雅克比矩阵,
为状态转移方程的雅克比矩阵,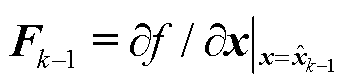 ,根据Holt指数平滑法可由式(2)求得。
,根据Holt指数平滑法可由式(2)求得。
由于实际电力系统的量测误差存在不确定性,采用固定的Q和R可能会导致状态估计效果变差,需要对Q和R根据实际情况进行自适应调整。量测噪声协方差矩阵R与量测设备的特性有关,可通过分析装置的误差特性,用量测误差方差表示。
PMU量测的幅值和相位通常被认为独立地遵循零均值高斯分布。假设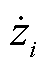 是PMU量测的一个元素,其幅值和相位的量测误差分别为
是PMU量测的一个元素,其幅值和相位的量测误差分别为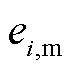 和
和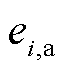 ,根据欧几里德距离,
,根据欧几里德距离,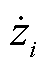 的量测误差
的量测误差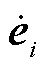 可表示为
可表示为
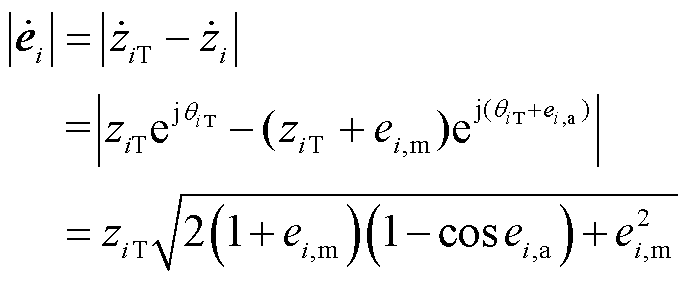 (24)
(24)
式中,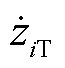 为
为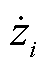 的真实值,
的真实值,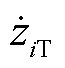 =
=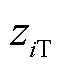 ∠
∠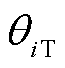 。
。
假设PMU量测的幅值误差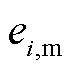 和相位误差
和相位误差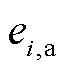 是均值为
是均值为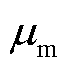 和
和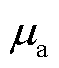 、标准差为
、标准差为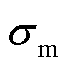 和
和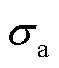 的随机变量,则相量误差
的随机变量,则相量误差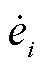 的均值可表示为
的均值可表示为
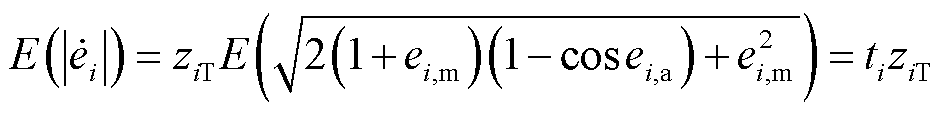 (25)
(25)
式中,E(·)为均值函数;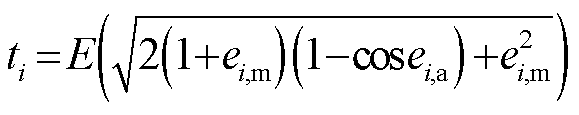 。对
。对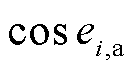 进行泰勒展开,忽略高阶项可得
进行泰勒展开,忽略高阶项可得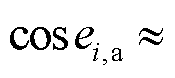
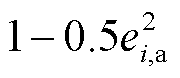 ,因此相量误差
,因此相量误差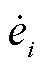 的方差表示为
的方差表示为
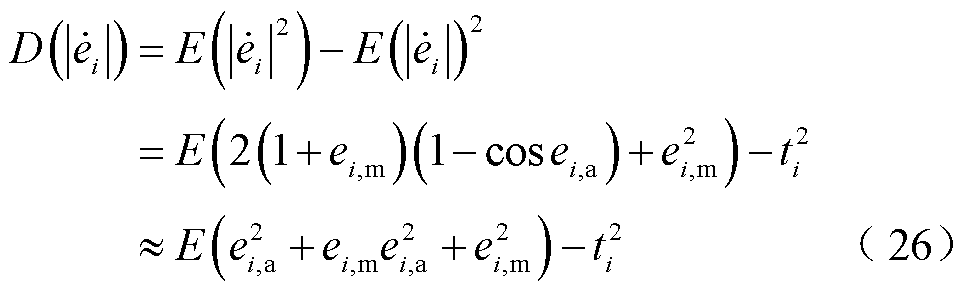
由于PMU量测的幅值和相位通常被认为独立地遵循零均值的高斯分布,则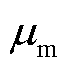 和
和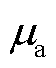 都等于0,且
都等于0,且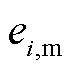 和
和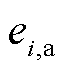 相互独立,相量误差
相互独立,相量误差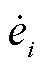 的方差可进一步简化为
的方差可进一步简化为
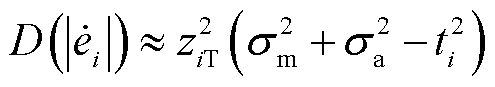 (27)
(27)
由于PMU幅值误差一般为幅值真实值的千分之几,在对PMU不良数据进行识别和处理后,可以用相量幅值测量值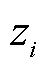 来代替未知相量幅值真值
来代替未知相量幅值真值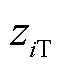 。在已知
。在已知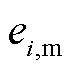 和
和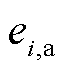 的统计性质的情况下,
的统计性质的情况下,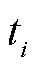 的值可以通过数理统计方法近似地估计出来。
的值可以通过数理统计方法近似地估计出来。
SCADA的功率量测经过量测变换后,量测方差也随之改变,根据误差传递理论[32],可得等效电流相量的量测方差为
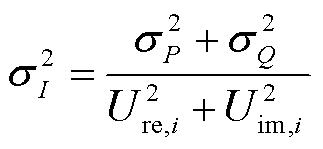 (28)
(28)
式中,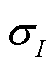 为等效电流量测误差标准差;
为等效电流量测误差标准差;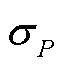 和
和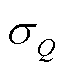 分别为SCADA有功和无功功率量测误差标准差。
分别为SCADA有功和无功功率量测误差标准差。
通过量测误差方差的对角矩阵设置量测噪声协方差矩阵R,可在每次状态估计前根据最新量测自适应地估计量测噪声为
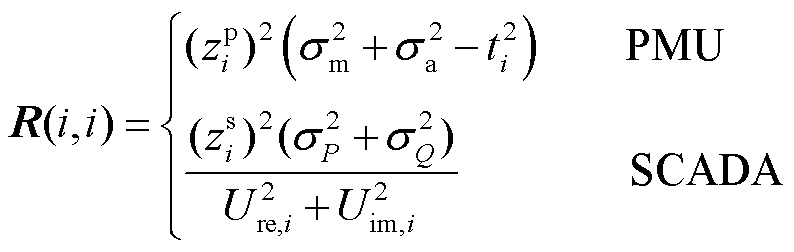 (29)
(29)
式中,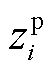 为PMU量测的某一元素;
为PMU量测的某一元素;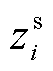 为SCADA量测的某一元素。
为SCADA量测的某一元素。
考虑到实际应用中会不可避免地出现不良数据,为避免不良数据对状态估计造成不良影响,采用标准新息对不良数据进行辨识与处理。新息为测量值与预测值之差,有
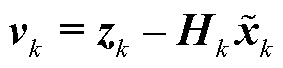 (30)
(30)
式中,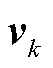 为新息值。
为新息值。
新息协方差理论值可表示为
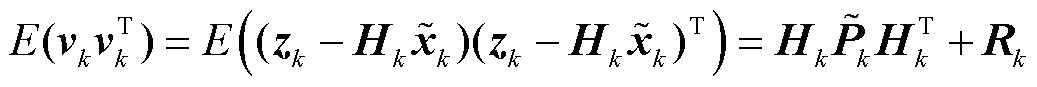 (31)
(31)
将新息标准化得到标准新息得到
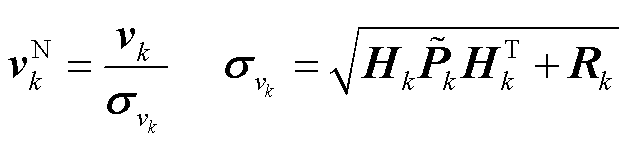 (32)
(32)
式中,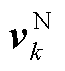 为标准新息。
为标准新息。
基于标准新息引入抗差因子对量测噪声进行修正。抗差因子采用IGGⅢ权函数[33]生成,即
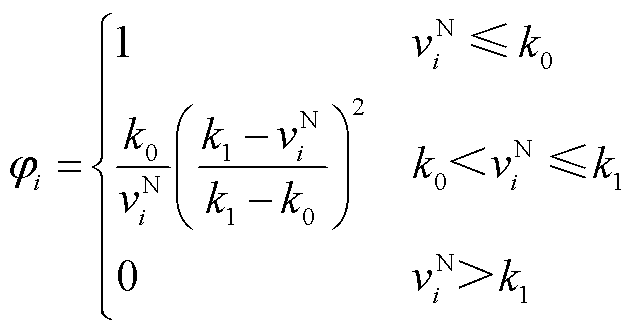 (33)
(33)
式中,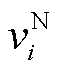 为
为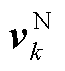 中的第i个元素;
中的第i个元素;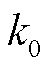 和
和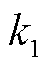 为衡量测量值好坏的参数。为确保量测冗余下抑制不良数据,本文取
为衡量测量值好坏的参数。为确保量测冗余下抑制不良数据,本文取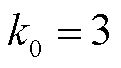 、
、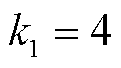 ,即当量测数据的标准新息大于3倍标准差时被判定为不良数据,并进行抗差处理,降低其在状态估计中的权重;当量测数据的标准新息大于4倍标准差时剔除该不良数据。
,即当量测数据的标准新息大于3倍标准差时被判定为不良数据,并进行抗差处理,降低其在状态估计中的权重;当量测数据的标准新息大于4倍标准差时剔除该不良数据。
相比于标准残差,标准新息考虑了预测状态,并避免了残差污染。最终得到修正后的量测噪声协方差矩阵为
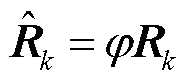 (34)
(34)
2.3.1 过程噪声自适应估计
Sage-Husa噪声估计[26]利用最新时刻的新息值对过程噪声协方差序列进行调整,通过引入渐消记忆指数加权方法[27],根据系统变化程度对新数据赋予权重,能够更好地反映系统过程噪声的实时变化。
根据式(1)的动态状态估计状态方程,过程噪声为状态真值与状态预测值之差。由于系统真实状态未知,故用状态的估计值近似估计过程噪声,有
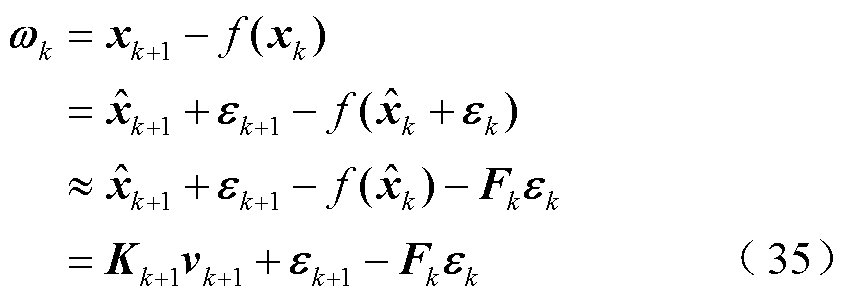
式中,e为估计误差。
当样本空间的采样数为N时,过程噪声协方差的无偏估计为
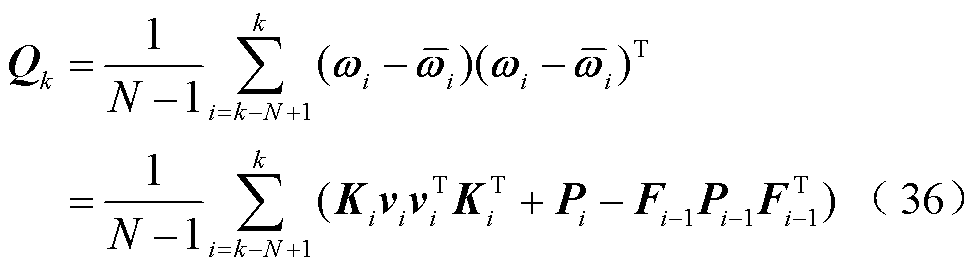
在这N次采样中,最新采样数据更能反映当前过程噪声的时变特性,故引入权重因子,为最新采样数据赋予较大权重,权重因子为
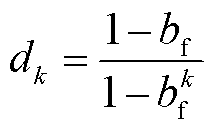 (37)
(37)
式中,d为权重因子;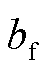 为遗忘因子,系统过程噪声变化越大,
为遗忘因子,系统过程噪声变化越大,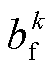 的取值越小。
的取值越小。
因此,可将过程噪声协方差修改为
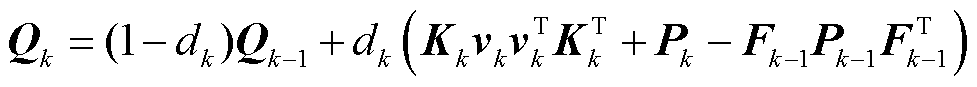 (38)
(38)
2.3.2 自适应遗忘因子
为了能更好地适应时变噪声系统的动态变化,设计一种遗忘因子自适应调整方法,以进一步提高算法在各种运行工况下对过程噪声的估计能力。
由新息方差与新息协方差矩阵迹比值设计中间变量h衡量当前状态估计的整体滤波效果[34],即
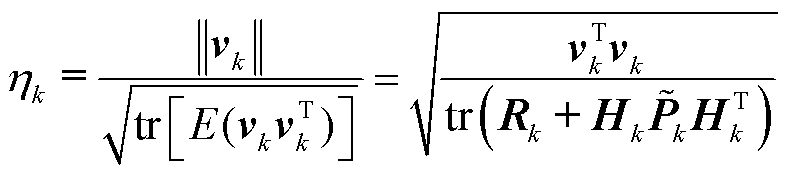 (39)
(39)
式中,tr为矩阵的迹。
根据滤波效果对遗忘因子进行自适应调整,有
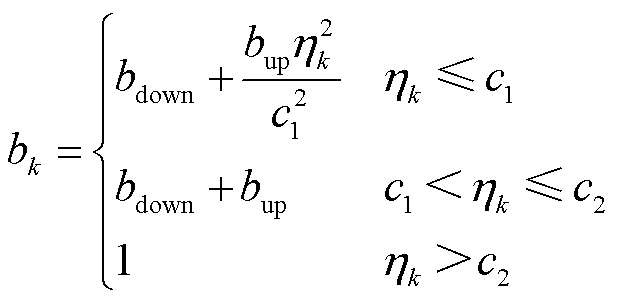 (40)
(40)
式中,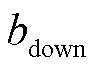 、
、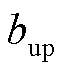 分别为遗忘因子下限和自适应变化上限,为了确保算法运行稳定性,遗忘因子下限
分别为遗忘因子下限和自适应变化上限,为了确保算法运行稳定性,遗忘因子下限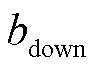 可取0.6,
可取0.6,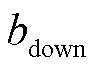 +
+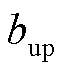 可取0.95~0.995;c1、c2为衡量滤波效果好坏的参数,本文取
可取0.95~0.995;c1、c2为衡量滤波效果好坏的参数,本文取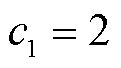 ,
,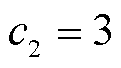 。当
。当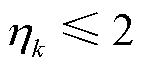 ,即新息标准差之和小于2倍理论标准差时,判定为滤波效果良好,降低遗忘因子b以提高遗忘程度,使过程噪声快速追踪准确值;当
,即新息标准差之和小于2倍理论标准差时,判定为滤波效果良好,降低遗忘因子b以提高遗忘程度,使过程噪声快速追踪准确值;当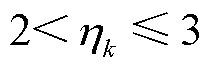 ,判定为滤波效果一般,保持遗忘因子b稳定,使过程噪声平稳估计;当
,判定为滤波效果一般,保持遗忘因子b稳定,使过程噪声平稳估计;当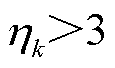 ,说明滤波过程受到干扰,遗忘因子b=1,过程噪声不更新。同时,若系统突变,基于平稳系统产生的预测值将产生较大误差,应提高过程噪声协方差,以降低预测值在卡尔曼滤波的权重。
,说明滤波过程受到干扰,遗忘因子b=1,过程噪声不更新。同时,若系统突变,基于平稳系统产生的预测值将产生较大误差,应提高过程噪声协方差,以降低预测值在卡尔曼滤波的权重。
综合上述分析,本文融合PMU量测和SCADA量测形成混合量测集,当存在PMU不可观测节点时,基于数据的时空相关性构造伪量测。通过分析量测误差方差估计量测噪声,采用标准新息估计过程噪声,并引入抗差因子和遗忘因子实时自适应调整噪声估计,形成IAREKF的基本框架。整体流程如图3所示。
1)参数初始化。
2)量测集形成:在采用SCADA时刻,结合最新时刻PMU量测,按式(4)~式(9)形成混合量测集;在非SCADA更新时刻,按式(5)形成PMU量测集;若此时PMU不满足系统可观,按式(10)~式(21)构造伪量测,并融入PMU量测集。
3)状态预测:按式(2)进行状态预测。
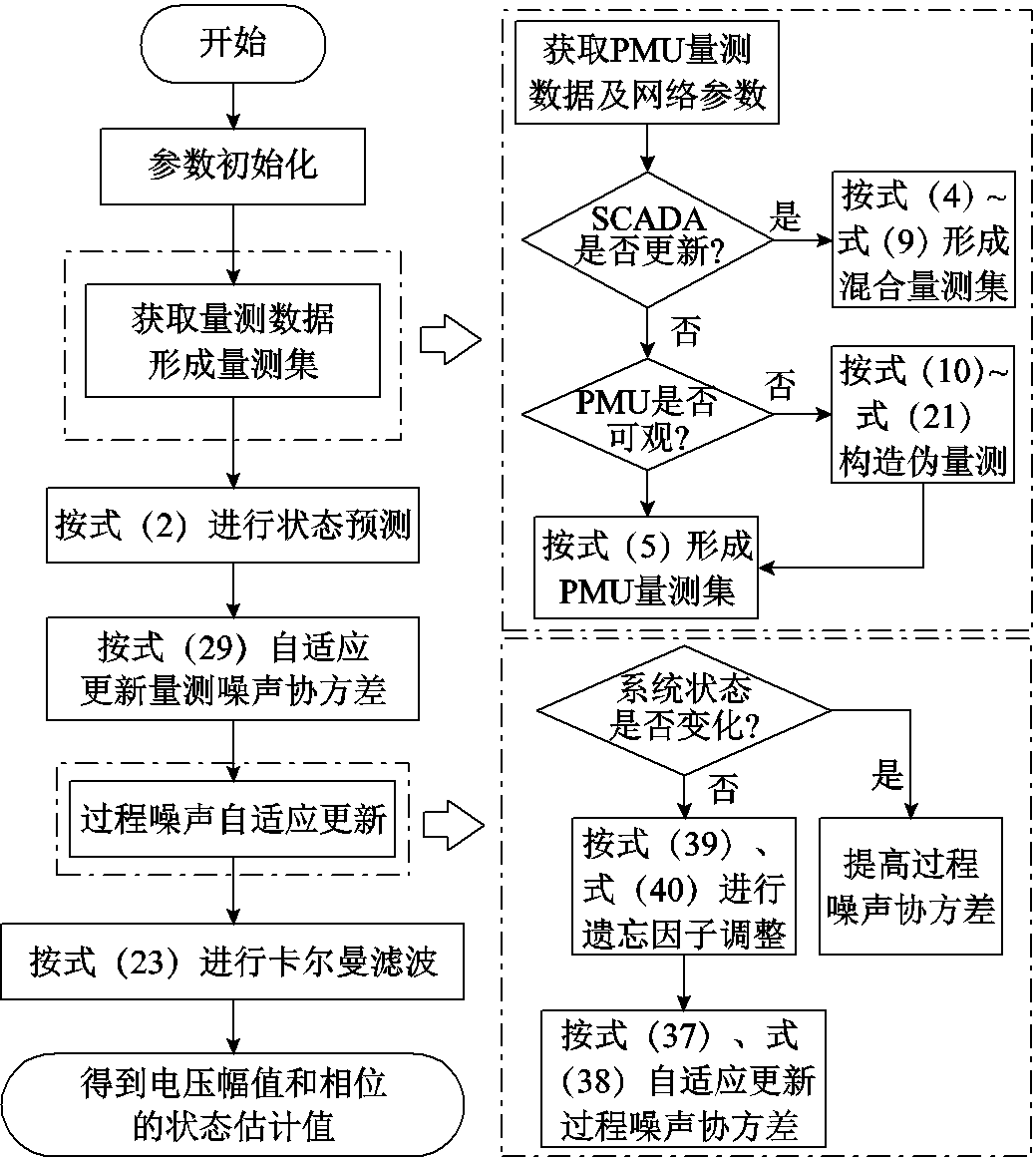
图3 基于IAREKF的动态状态估计整体流程
Fig.3 Overall flow chart of dynamic state estimation based on IAREKF
4)量测噪声协方差矩阵R设置:根据最新量测按式(29)进行量测噪声协方差自适应更新。
5)过程噪声协方差矩阵Q设置:根据新息分布进行暂稳态分析,若系统状态发生变化,则提高过程噪声协方差;否则按式(39)、式(40)计算遗忘因子,按式(37)、式(38)估计过程噪声。
6)状态滤波:按式(23)进行扩展卡尔曼滤波,得到IAREKF的估计结果。
为验证本文所提方法的可行性与准确性,在IEEE 39节点系统上进行仿真测试,仿真软件为Matlab 2018b,采用Matpower 7.1获取网络拓扑信息。为模拟电力系统的运行状态,设置负荷PQ在额定值±10%范围内波动,真实值通过对仿真案例进行潮流计算获得,测量值在真实值上添加零期望高斯分布的测量误差获得,本文仿真的测量误差标准差见表1。PMU按照0.01 s间隔进行采样,SCADA按照1 s间隔进行采样,每次动态状态估计的间隔为0.01 s。
表1 测量误差的标准差
Tab.1 Standard deviation of measurement errors

PMU电压测量PMU电流测量SCADA功率测量(%) 幅值(%)相位/(°)幅值(%)相位/(°) 0.30.40.40.71
为了衡量估计结果的准确性,引入平均绝对误差(Mean Absolute Error, MAE)、方均根误差(Root Mean Square Error, RMSE)和平均相量误差(Mean Vector Error, MVE)作为评价算法估计精度的指标,三种评价指标的定义分别为
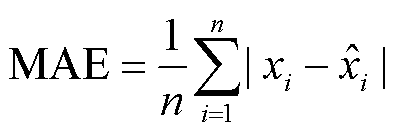 (41)
(41)
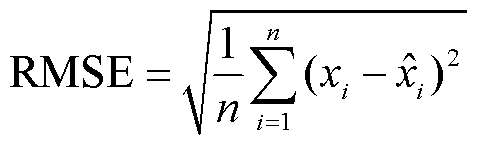 (42)
(42)
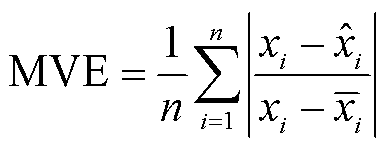 (43)
(43)
式中,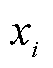 为状态量真实值第i个分量;
为状态量真实值第i个分量;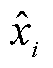 为状态量估计值第i个分量;
为状态量估计值第i个分量;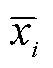 为状态量测量值第i个分量;n为状态量维数。
为状态量测量值第i个分量;n为状态量维数。
为体现所提出基于时空相关性伪量测构造方法的有效性,分别采用方法一(将上一时刻估计结果作为当前时刻的伪量测)、方法二(基于功率转移分布因子的伪量测构造方法)和本文所提方法对IEEE 39节点系统的不可观测节点构造伪量测。PMU配置在节点3、8、11、19、23、26,此时系统不完全可观。选取不可观测节点31的电压伪量测结果对比如图4所示。
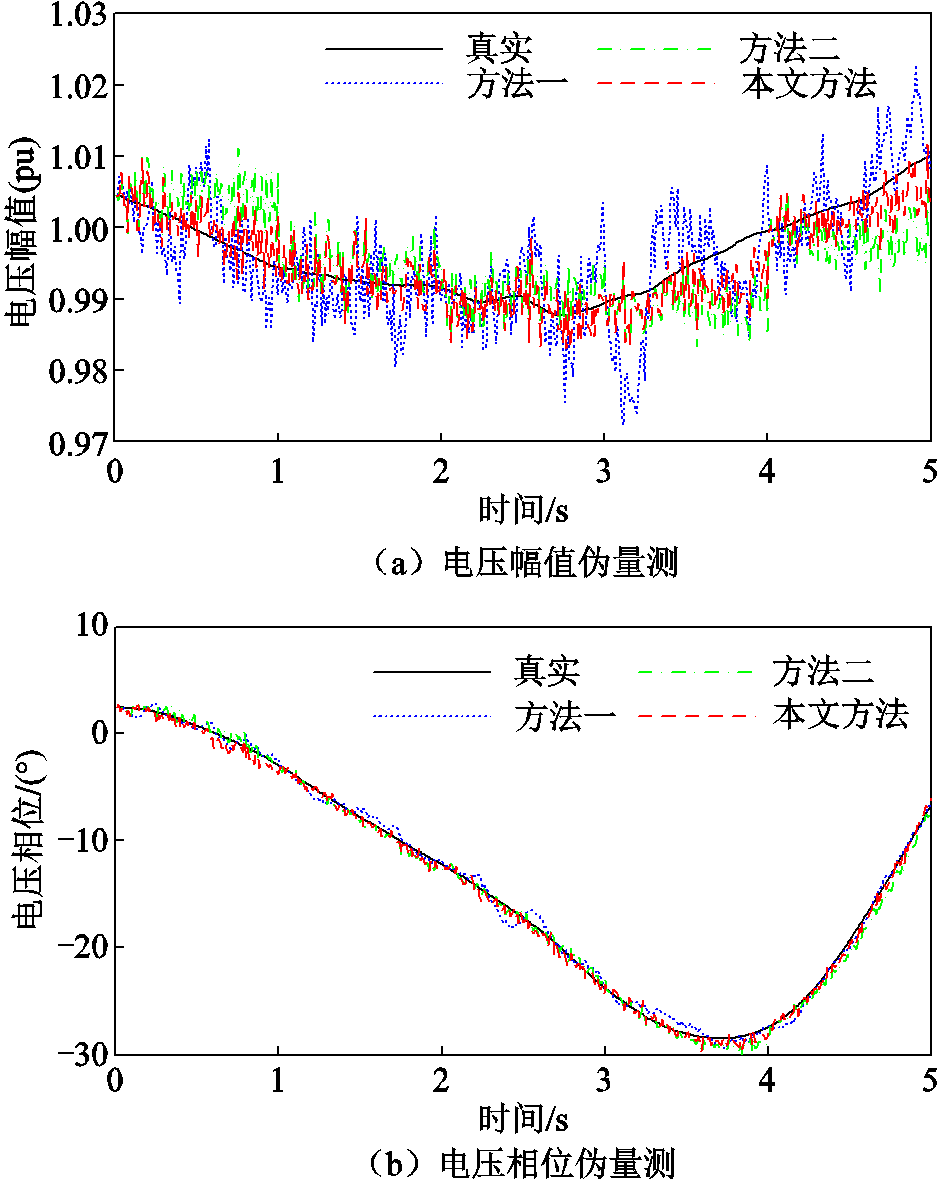
图4 不可观测节点31的电压伪量测结果对比
Fig.4 Comparison of voltage state estimation results for bus 31 with consideration of pseudo-measurements
从图4可以看出,方法一在真实值附近出现较大波动;方法二考虑相邻节点量测,起初有较好的估计效果,但随着估计次数增加会逐渐出现偏移;本文方法结合节点间时空相关性,在一定程度上抑制了不可观测节点估计结果的偏移,能较好地贴近真实值。
为分析所构造伪量测与PMU真实量测的差别,将三种方法构造的伪量测与PMU量测进行对比,具体计算结果见表2。
表2 三种伪量测构造方法的MAE指标对比
Tab.2 Comparison of MAE for three pseudo-measurement construction methods

方法MAE 电压幅值(10-4pu)电压相位/(°) PMU量测24.762 20.319 913 方法一49.946 20.543 861 方法二31.912 30.509 007 本文方法29.257 50.488 961
从表2可以看出,本文方法的MAE值最接近PMU量测,表示该方法能较好地反映PMU量测的效果。为量化分析引入伪量测对不可观测节点状态估计效果和对可观测节点状态估计的影响,分别引入三种伪量测进行状态估计。可观测节点和不可观测节点的电压估计MAE指标对比见表3。
表3 三种伪量测构造方法下的状态估计MAE指标对比
Tab.3 Comparison of MAE for state estimation for three pseudo-measurement methods
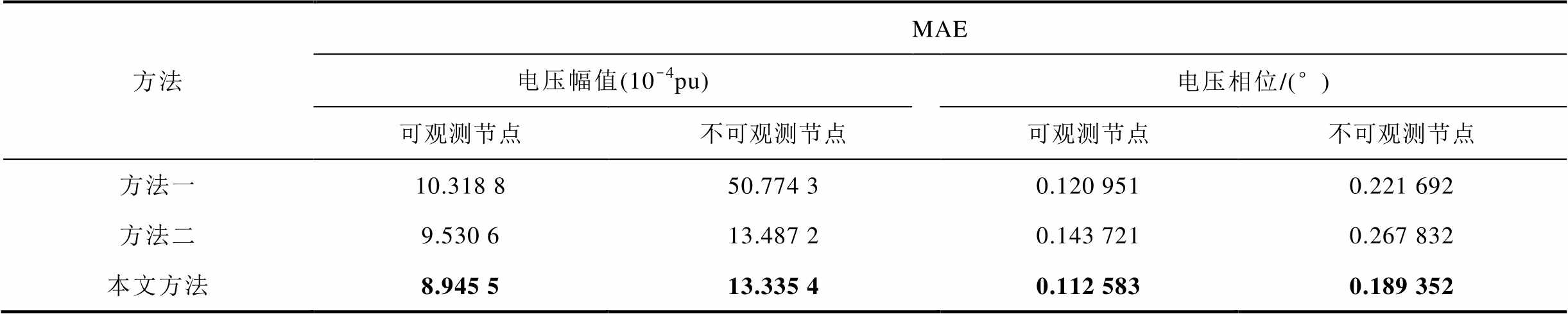
方法MAE 电压幅值(10-4pu)电压相位/(°) 可观测节点不可观测节点可观测节点不可观测节点 方法一10.318 850.774 30.120 9510.221 692 方法二9.530 613.487 20.143 7210.267 832 本文方法8.945 513.335 40.112 5830.189 352
从表3可以看出,采用本文所提出的伪量测构造方法进行状态估计对于可观测节点和不可观测节点都比方法一和方法二有更高的估计精度,说明所提方法不但对不可观测节点的状态估计有更高的准确性,对可观测节点状态估计的影响也是最小的。
基于IEEE 39节点系统仿真案例,算法中涉及的初始参数和经验参数经过多次不同运行方式不同案例下的蒙特卡洛仿真实验优化得到:过程噪声Q和测量噪声R的初始方差分别设为10−6、10−4时状态估计的效果最佳;Holt指数平滑法的平滑系数α、β分别选取为0.85、0.35时状态预测的效果最佳。
为了评估本文IAREKF状态估计算法在电力系统动态状态估计中的有效性和准确性,以广义极大似然迭代扩展卡尔曼滤波算法[24]、自适应H¥扩展卡尔曼滤波算法[28]和EKF算法作为对比验证,在IEEE 39节点系统上进行动态状态估计仿真,四种算法的状态估计结果图和MAE指标如图5和图6所示。
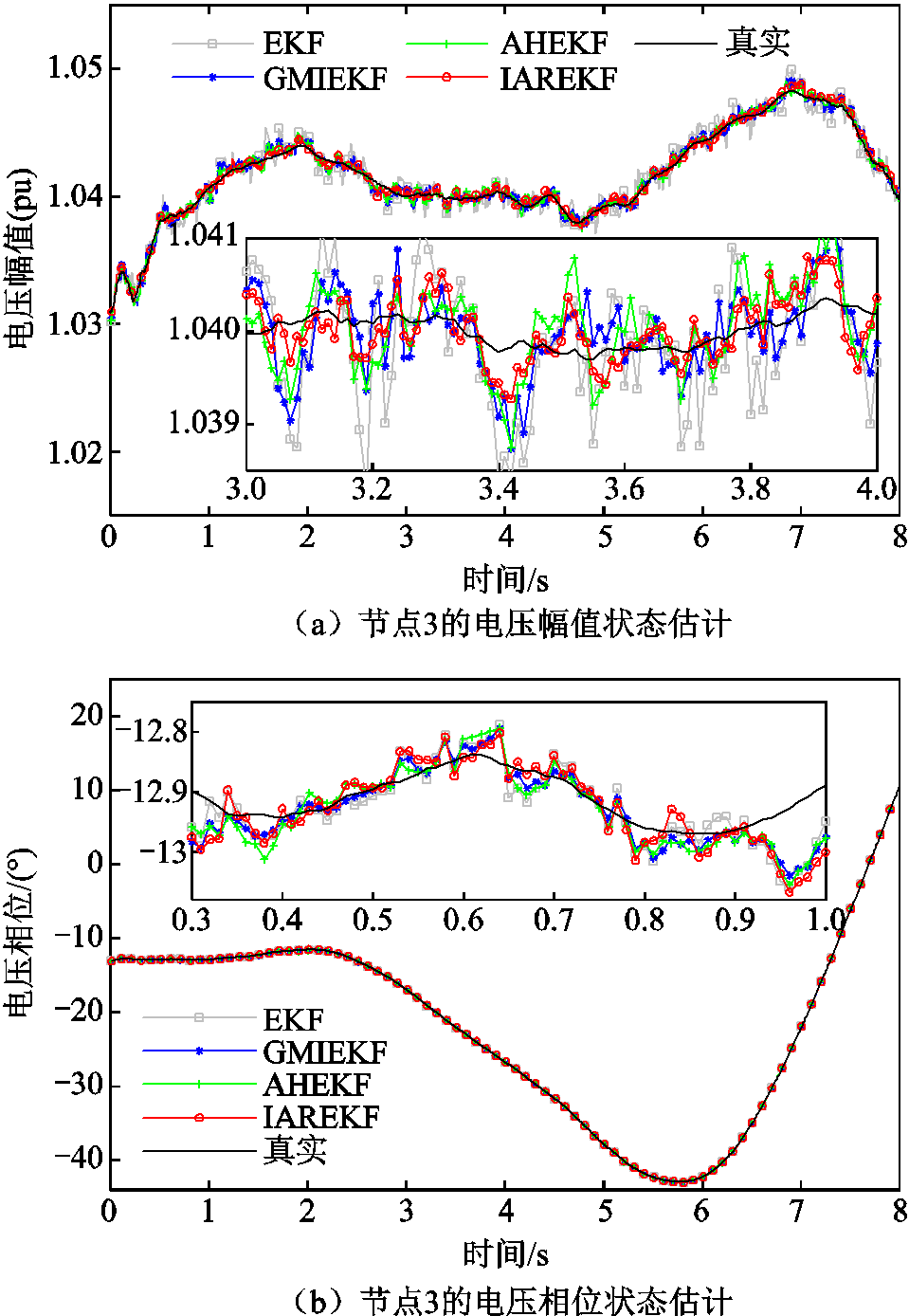
图5 节点3的状态估计结果对比
Fig.5 State estimation results comparison for bus 3
从图5和图6可以看出,在能够获得准确的模型参数时,四种状态估计算法都能很好地追踪系统动态变化,而AHEKF、GMIEKF和IAREKF相较于EKF估计效果更加平稳,具有更小的估计误差。
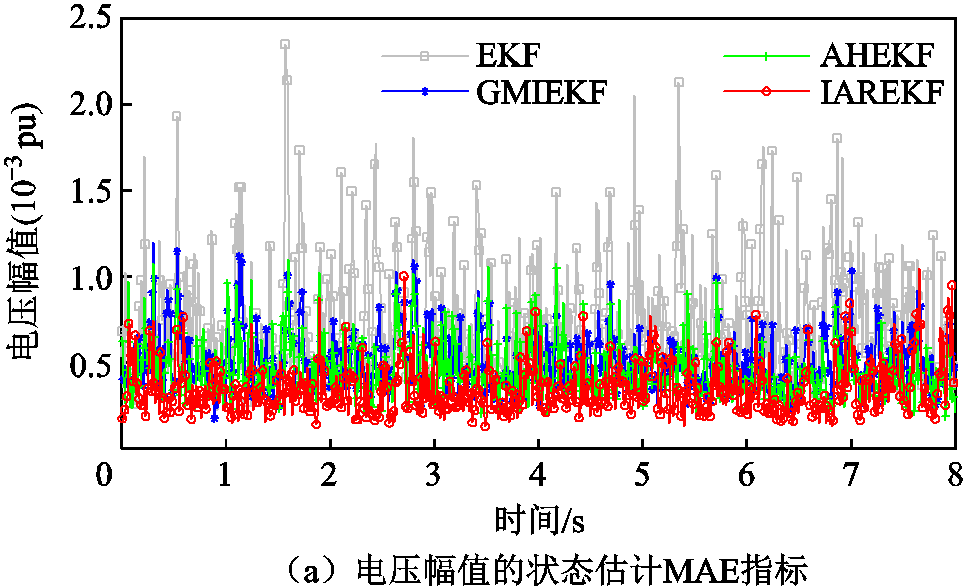
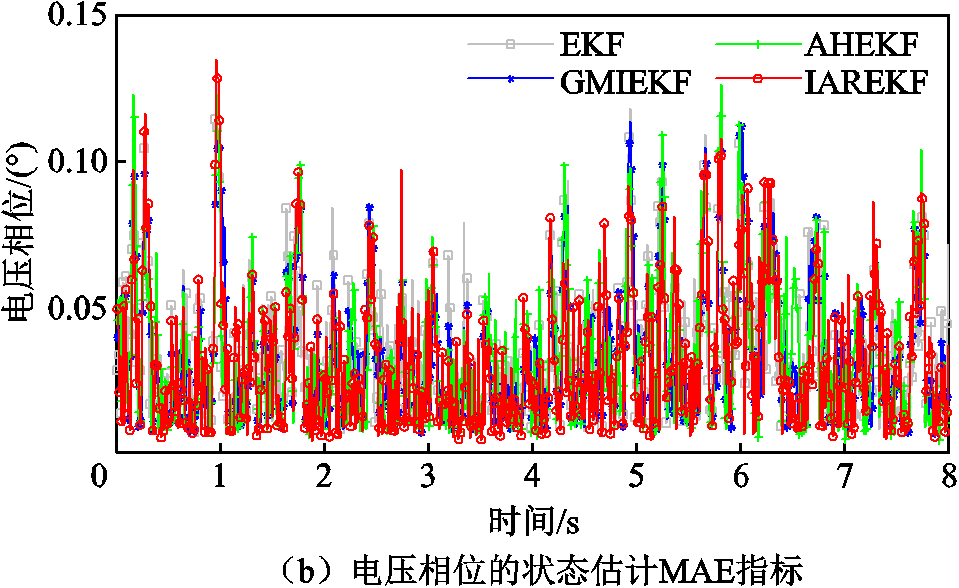
图6 四种状态估计算法的MAE指标对比
Fig.6 Comparison of MAE for four state estimation algorithms
为了量化分析四种动态状态估计算法的估计精度,对比四种状态估计算法评价指标,结果见表4。
表4 四种状态估计算法评价指标对比
Tab.4 Comparison of evaluation indices for four state estimation algorithms
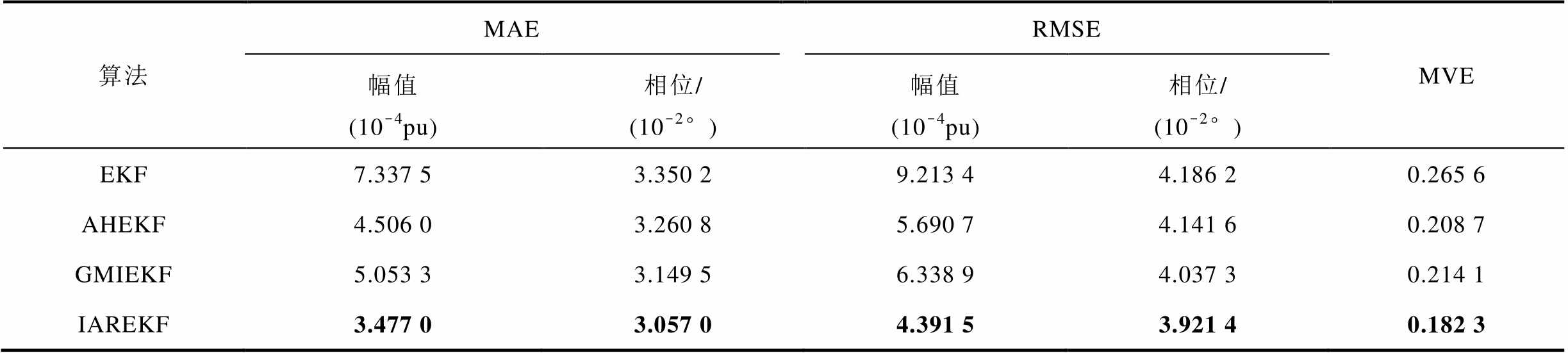
算法MAERMSEMVE 幅值(10-4pu)相位/(10-2°)幅值(10-4pu)相位/(10-2°) EKF7.337 53.350 29.213 44.186 20.265 6 AHEKF4.506 03.260 85.690 74.141 60.208 7 GMIEKF5.053 33.149 56.338 94.037 30.214 1 IAREKF3.477 03.057 04.391 53.921 40.182 3
从表4可以看出,虽然四种状态估计算法都展现出较高的估计精度,但IAREKF相较于AHEKF和GMIEKF在幅值和相位上都能有更小的估计误差,对EKF估计精度的提升更为显著。
为验证本文IAREKF算法对模型噪声的自适应估计能力,假定模型噪声参数未知,设置过程噪声Q和测量噪声R的初始方差分别为10-5、10-5,并采用四种算法进行状态估计。图7和表5分别给出了该场景下四种算法的状态估计评价指标。
从表5可以看出,在模型噪声参数未知下,本文IAREKF状态估计RMSE误差评价指标较AHEKF和GMIEKF算法,在幅值、相位上分别降低42.21%、21.47%和37.51%、14.97%,展现出最高的估计精度。结合表4和表5可以看出,在模型噪声参数未知下,本文IAREKF仍然具有和已知噪声参数时一样的估计能力,而其他三种算法的估计精度均有所下降,说明该算法能够快速准确地估计模型噪声,体现了所提自适应估计算法的有效性和优越性。
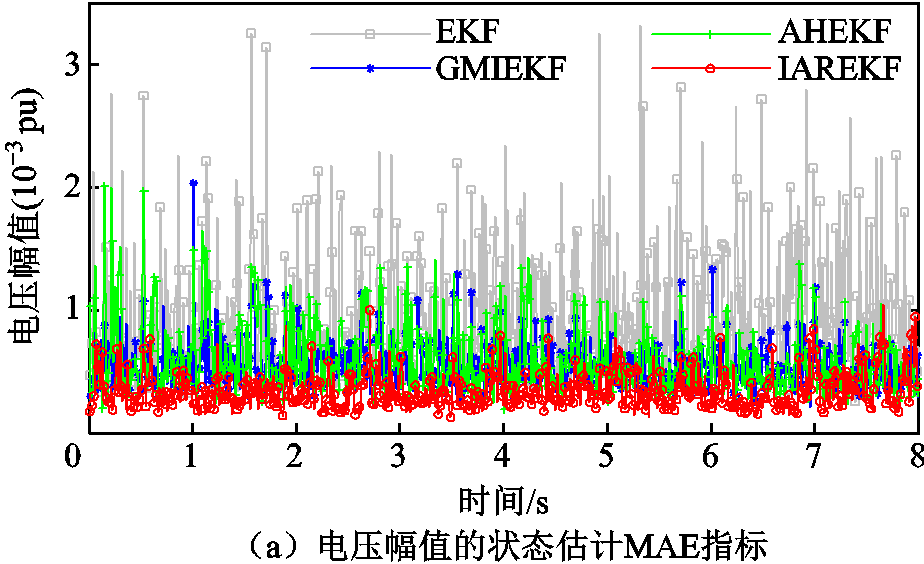
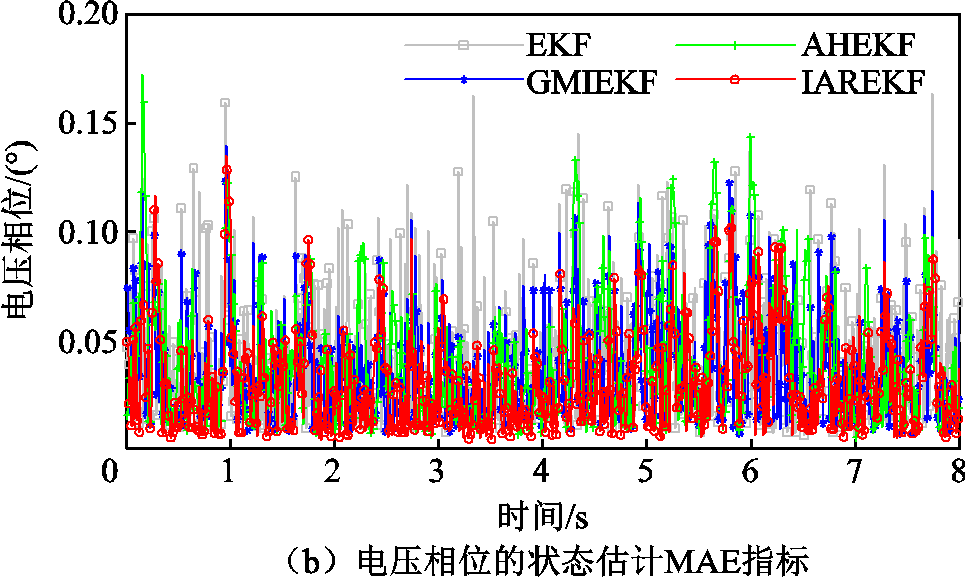
图7 噪声未知下四种状态估计算法的MAE指标对比
Fig.7 Comparison of MAE for four state estimation algorithms under unknown model parameters
表5 模型参数未知下四种状态估计算法评价指标对比
Tab.5 Comparison of evaluation indices for four state estimation algorithms under unknown model parameters
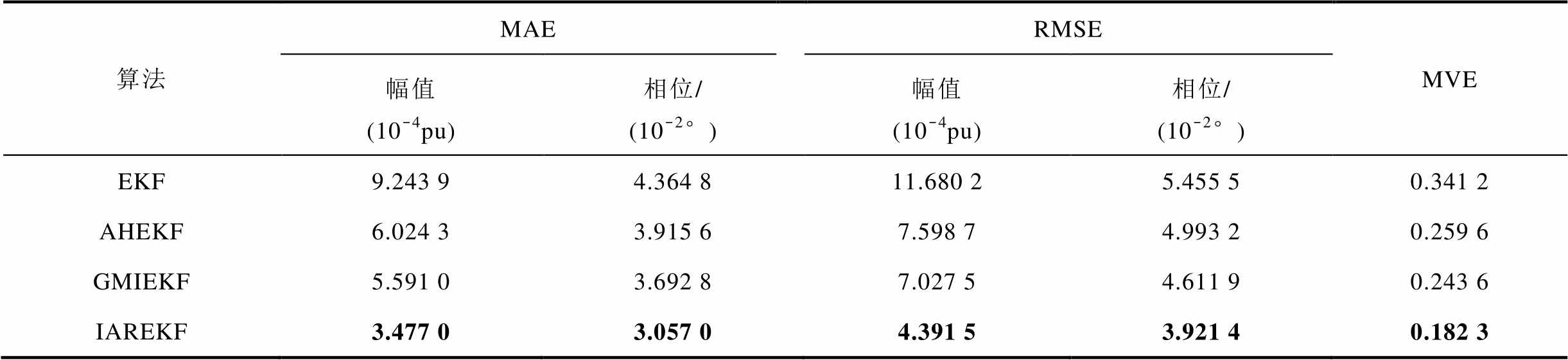
算法MAERMSEMVE 幅值(10-4pu)相位/(10-2°)幅值(10-4pu)相位/(10-2°) EKF9.243 94.364 811.680 25.455 50.341 2 AHEKF6.024 33.915 67.598 74.993 20.259 6 GMIEKF5.591 03.692 87.027 54.611 90.243 6 IAREKF3.477 03.057 04.391 53.921 40.182 3
在电力系统发生突变后,预测值的准确度和可靠性将大大降低,过程噪声协方差矩阵需要快速调整以适应实际运行工况。为验证本文IAREKF算法在暂态过程下的自适应估计能力,在IEEE 39节点系统的节点4上添加短路故障,并在0.1 s后切除故障,在此暂态期间进行状态估计,任选节点3的电压幅值和相位的状态估计结果对比如图8所示。
从图8可以看出,没有自适应调整能力的EKF算法在暂态期间的估计状态结果严重偏离真实值;AHEKF、GMIEKF和本文IAREKF都能适应系统状态变化,在暂态期间展现良好的动态追踪能力。
为进一步比较四种方法的估计性能,表6给出了暂态期间四种状态估计算法的评价指标。
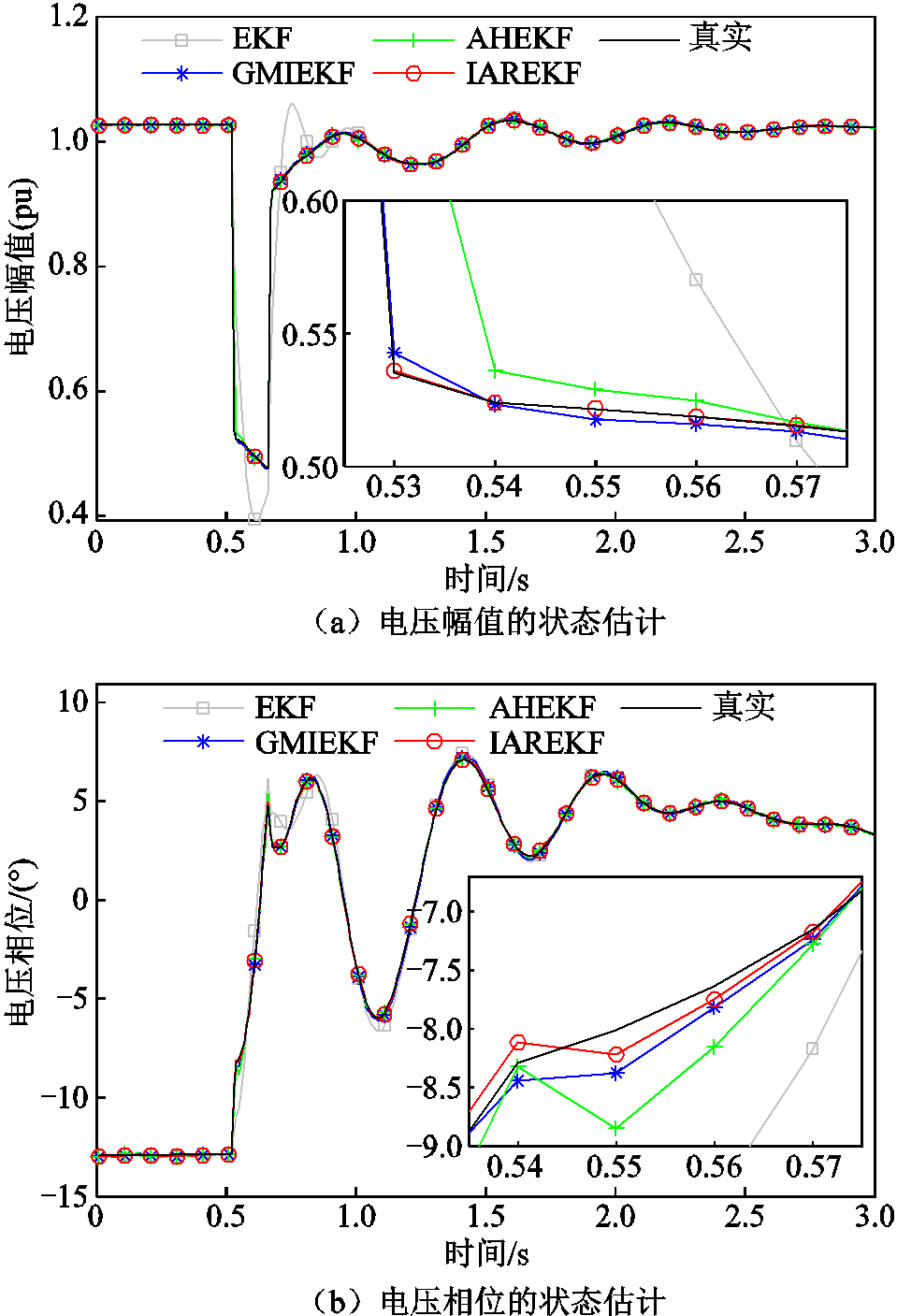
图8 暂态期间节点3的状态估计结果对比
Fig.8 Transient period state estimation results comparison for bus 3
表6 暂态期间四种状态估计算法评价指标对比
Tab.6 Transient period comparison of evaluation indices for four state estimation algorithms
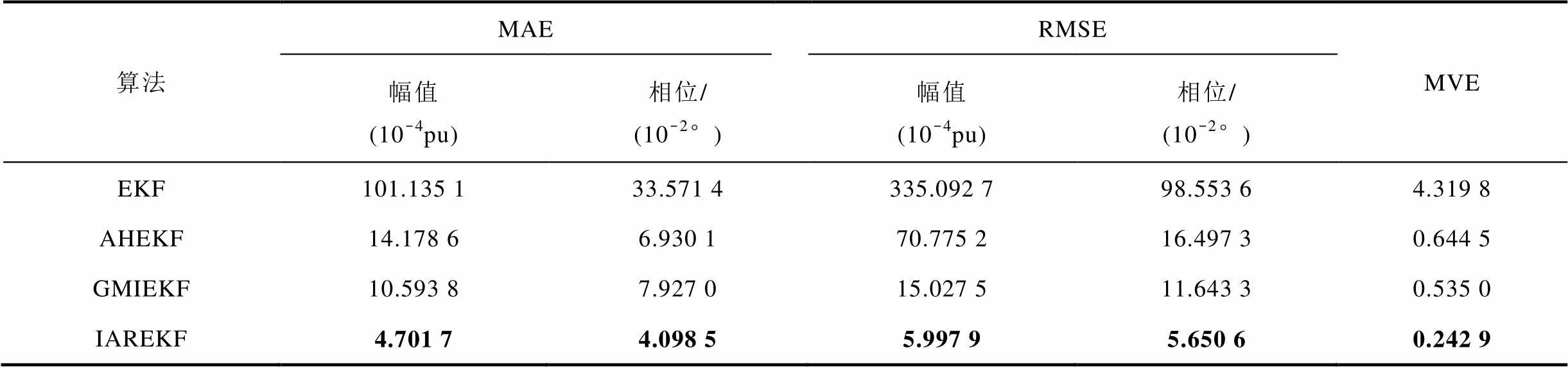
算法MAERMSEMVE 幅值(10-4pu)相位/(10-2°)幅值(10-4pu)相位/(10-2°) EKF101.135 133.571 4335.092 798.553 64.319 8 AHEKF14.178 66.930 170.775 216.497 30.644 5 GMIEKF10.593 87.927 015.027 511.643 30.535 0 IAREKF4.701 74.098 55.997 95.650 60.242 9
从表6可以看出,在暂态期间,EKF的MVE大于1,状态估计失效。AHEKF和GMIEKF虽然仍能有效地进行状态估计,但估计精度严重下降。本文IAREKF通过遗忘因子自适应调整,能迅速遗忘先前的统计信息,准确调整过程噪声协方差以适应新的运行工况,在暂态期间仍然保持较高的估计效果。
为验证本文IAREKF对不良数据的抗差性,给电压测量值随机添加不良数据(不良数据设置为幅值大于真实值的±3%,相位大于3°),任选节点3的电压幅值和相位的状态估计结果如图9所示,表7给出了不良数据下四种状态估计算法评价指标对比。
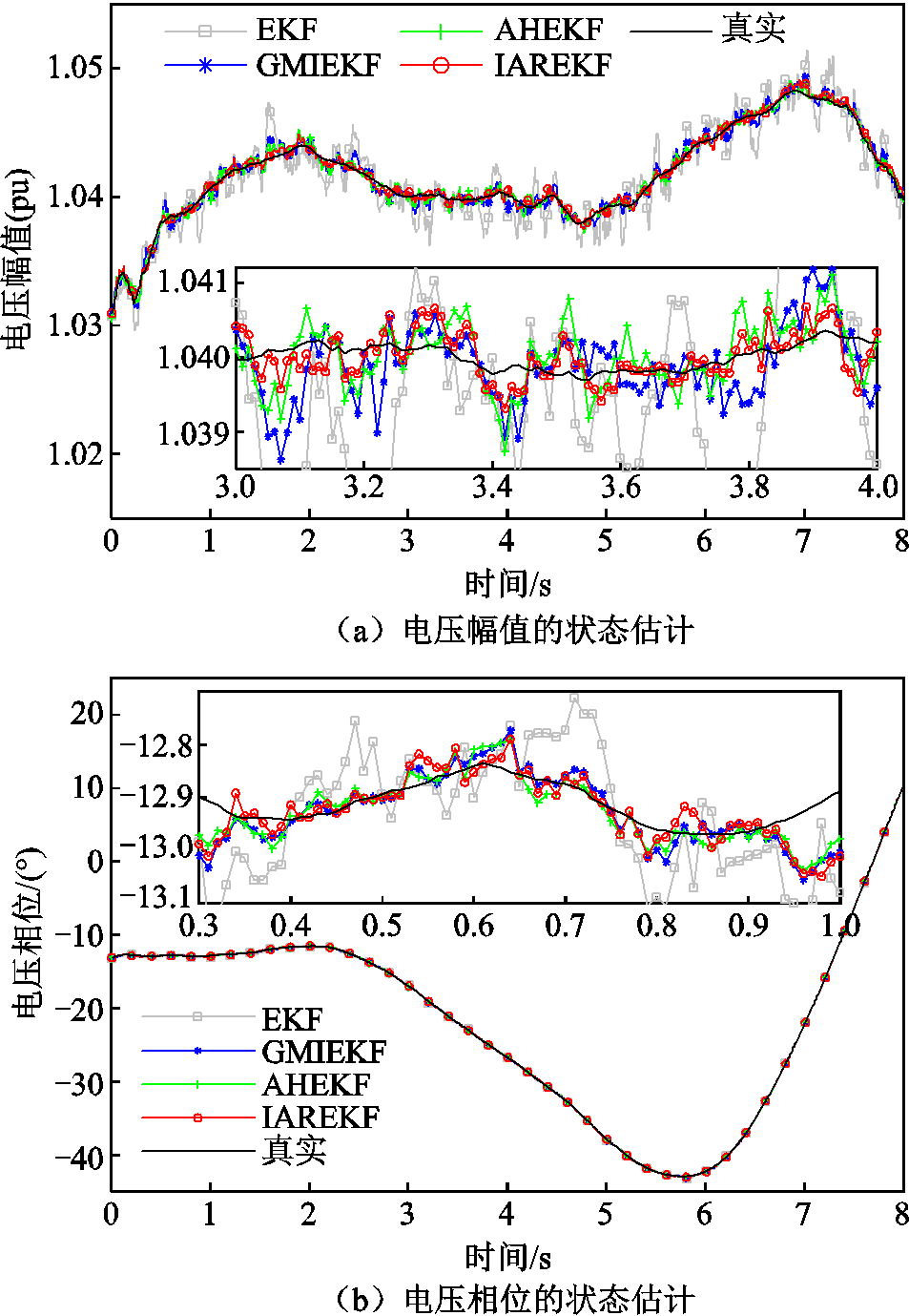
图9 不良数据下节点3的状态估计结果对比
Fig.9 Comparison of state estimation results for bus 3 under bad data conditions
表7 不良数据下四种状态估计算法评价指标对比
Tab.7 Comparison of evaluation indices for four state estimation algorithms under bad data conditions
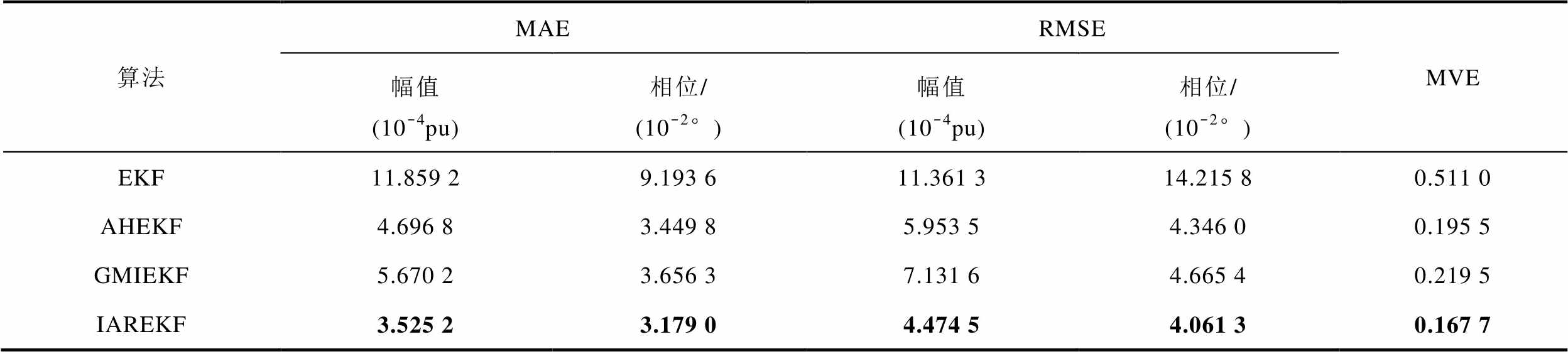
算法MAERMSEMVE 幅值(10-4pu)相位/(10-2°)幅值(10-4pu)相位/(10-2°) EKF11.859 29.193 611.361 314.215 80.511 0 AHEKF4.696 83.449 85.953 54.346 00.195 5 GMIEKF5.670 23.656 37.131 64.665 40.219 5 IAREKF3.525 23.179 04.474 54.061 30.167 7
结合图9和表7可以看出,在不良数据的影响下,EKF估计精度明显下降,由于其他三种算法具有抗差性,在不良数据的影响下仍有较高的估计精度,而本文IAREKF状态估计RMSE误差评价指标相比AHEKF和GMIEKF,在幅值、相位上分别降低24.84%、6.55%和37.26%、12.95%,具有最低的估计误差,展现出良好的抗差性。
针对混合测量下的电力系统状态估计问题,本文提出了一种基于自适应抗差扩展卡尔曼滤波的动态状态估计算法,能减小未知系统噪声和不良数据的影响,准确地获取系统状态,并基于IEEE 39节点系统进行各类场景下的动态状态估计仿真验证,得出结论如下:
1)针对不同量测系统的特性差异,采用量测变换技术实现混合量测的融合。基于系统的时空特性构造PMU不可观测节点的伪量测,提高状态估计的频率到与PMU采样同步,更快速地获取系统的动态变化。
2)通过分析量测装置的特性估计量测噪声,并基于标准新息构造抗差因子调整量测噪声协方差矩阵,在不良数据下具有良好的抗差性。
3)针对时变系统过程噪声难以获取的问题,采用基于自适应遗忘因子的过程噪声估计算法,相较于传统的Sage-Husa噪声估计方法,能更快速地遗忘先前失效的统计信息,更准确地估计过程噪声,在系统发生扰动或突变下有更高的估计精度。
参考文献
[1] 陈艳波, 于尔铿. 电力系统状态估计[M]. 北京: 科学出版社, 2021.
[2] 马燕峰, 李金媛, 王子建, 等. 基于量测数据的新能源电力系统区域等效惯量评估方法[J]. 电工技术学报, 2024, 39(17): 5406-5421.
Ma Yanfeng, Li Jinyuan, Wang Zijian, et al. Assessment method of regional equivalent inertia of new energy power system based on measured data[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5406-5421.
[3] Wang Ying, Song Wenchao, Lin Junjie, et al. Data improvement for ambient signal based load modeling via wide-area state estimation[J]. International Journal of Electrical Power & Energy Systems, 2022, 141: 108173.
[4] Zhu Lipeng, Wen Weijia, Qu Yinpeng, et al. Robust representation learning for power system short-term voltage stability assessment under diverse data loss conditions[J]. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(5): 6035-6047.
[5] Zhu Lipeng, Hill D J, Lu Chao. Hierarchical deep learning machine for power system online transient stability prediction[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2399-2411.
[6] 刘晟源, 林振智, 李金城, 等. 电力系统态势感知技术研究综述与展望[J]. 电力系统自动化, 2020, 44(3): 229-239.
Liu Shengyuan, Lin Zhenzhi, Li Jincheng, et al. Review and prospect of situation awareness technologies of power system[J]. Automation of Electric Power Systems, 2020, 44(3): 229-239.
[7] 严正, 孔祥瑞, 徐潇源, 等. 微型同步相量测量单元在智能配电网运行状态估计中的应用[J]. 上海交通大学学报, 2018, 52(10): 1195-1205.
Yan Zheng, Kong Xiangrui, Xu Xiaoyuan, et al. Applications of micro synchronous phasor measurement units in state estimation of smart distribution network[J]. Journal of Shanghai Jiao Tong University, 2018, 52(10): 1195-1205.
[8] Dobakhshari A S, Abdolmaleki M, Terzija V, et al. Robust hybrid linear state estimator utilizing SCADA and PMU measurements[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1264-1273.
[9] Sun Kang, Huang Manyun, Wei Zhinong, et al. A real-time recursion correction hybrid linear state estimator using stream processing[J]. IEEE Transactions on Industrial Informatics, 2023, 19(3): 2317-2329.
[10] 李诗伟, 骆晨, 何叶, 等. 多源量测环境下计及时延融合的配电网区间状态估计[J]. 电力系统自动化, 2024, 48(12): 120-129.
Li Shiwei, Luo Chen, He Ye, et al. Interval state estimation for distribution network considering time-delay fusion in multi-source measurement environment [J]. Automation of Electric Power Systems, 2024, 48(12): 120-129.
[11] Kabiri M, Amjady N. A new hybrid state estimation considering different accuracy levels of PMU and SCADA measurements[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(9): 3078-3089.
[12] Darmis O, Korres G. A survey on hybrid SCADA/ WAMS state estimation methodologies in electric power transmission systems[J]. Energies, 2023, 16(2): 618.
[13] 徐俊俊, 吴在军, 张腾飞, 等. 融入多源量测数据的配电网分布式区间状态估计[J]. 中国电机工程学报, 2022, 42(24): 8888-8900.
Xu Junjun, Wu Zaijun, Zhang Tengfei, et al. A distributed interval state estimation framework of distribution networks based on multi-source measurements[J]. Proceedings of the CSEE, 2022, 42(24): 8888-8900.
[14] Angioni A, Schlösser T, Ponci F, et al. Impact of pseudo-measurements from new power profiles on state estimation in low-voltage grids[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(1): 70-77.
[15] 巫春玲, 郑克军, 徐先峰, 等. 基于自适应插值强跟踪扩展卡尔曼滤波的电力系统动态状态估计研究[J]. 电网技术, 2023, 47(5): 2078-2091.
Wu Chunling, Zheng Kejun, Xu Xianfeng, et al. Dynamic state estimation of power system based on adaptive interpolation strong tracking extended Kalman filter[J]. Power System Technology, 2023, 47(5): 2078-2091.
[16] 宋雨露, 樊艳芳, 刘牧阳, 等. 基于SC-DNN和多源数据融合的新能源电力系统状态估计方法[J]. 电力系统保护与控制, 2023, 51(9): 177-187.
Song Yulu, Fan Yanfang, Liu Muyang, et al. State estimation method of a new energy power system based on SC-DNN and multi-source data fusion[J]. Power System Protection and Control, 2023, 51(9): 177-187.
[17] 赵洪山, 吴雨晨, 温开云, 等. 基于时空注意力机制的台区多用户短期负荷预测[J]. 电工技术学报, 2024, 39(7): 2104-2115.
Zhao Hongshan, Wu Yuchen, Wen Kaiyun, et al. Short-term load forecasting for multiple customers in A station area based on spatial-temporal attention mechanism[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2104-2115.
[18] Dehghanpour K, Wang Zhaoyu, Wang Jianhui, et al. A survey on state estimation techniques and challenges in smart distribution systems[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2312-2322.
[19] Zhao Junbo, Netto M, Huang Zhenyu, et al. Roles of dynamic state estimation in power system modeling, monitoring and operation[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2462-2472.
[20] 李江, 王义伟, 魏超, 等. 卡尔曼滤波理论在电力系统中的应用综述[J]. 电力系统保护与控制, 2014, 42(6): 135-144.
Li Jiang, Wang Yiwei, Wei Chao, et al. A survey on the application of Kalman filtering method in power system[J]. Power System Protection and Control, 2014, 42(6): 135-144.
[21] 巫春玲, 胡雯博, 孟锦豪, 等. 基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2021, 36(24): 5165-5175.
Wu Chunling, Hu Wenbo, Meng Jinhao, et al. State of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion extended Kalman filtering algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5165-5175.
[22] 马文涛, 寇晓, 郭耀松, 等. 基于扩展KRSL无迹卡尔曼滤波的约束动态状态估计[J]. 电力系统自动化, 2023, 47(6): 185-196.
Ma Wentao, Kou Xiao, Guo Yaosong, et al. Constrained dynamic state estimation based on extended kernel risk sensitive loss unscented Kalman filter[J]. Automation of Electric Power Systems, 2023, 47(6): 185-196.
[23] 朱茂林, 刘灏, 毕天姝. 考虑风电场量测相关性的双馈风力发电机鲁棒动态状态估计[J]. 电工技术学报, 2023, 38(3): 726-740.
Zhu Maolin, Liu Hao, Bi Tianshu. Robust dynamic state estimation of doubly-fed induction generator considering measurement correlation in wind farms[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 726-740.
[24] Zhao Junbo, Netto M, Mili L. A robust iterated extended Kalman filter for power system dynamic state estimation[J]. IEEE Transactions on Power Systems, 2017, 32(4): 3205-3216.
[25] 王永刚, 孙羽苗, 张楠楠, 等. 基于无迹卡尔曼滤波的非线性解耦方法在火电机组中的应用研究[J]. 电气技术, 2021, 22(8): 15-24.
Wang Yonggang, Sun Yumiao, Zhang Nannan, et al. Application of nonlinear decoupling method based on unscented Kalman filter in thermal power units[J]. Electrical Engineering, 2021, 22(8): 15-24.
[26] 王彤, 高明阳, 黄世楼, 等. 基于自适应容积卡尔曼滤波的双馈风力发电机动态状态估计[J]. 电网技术, 2021, 45(5): 1837-1845.
Wang Tong, Gao Mingyang, Huang Shilou, et al. Dynamic state estimation for doubly fed induction generator wind turbine based on adaptive cubature Kalman filter[J]. Power System Technology, 2021, 45(5): 1837-1845.
[27] 张静, 毕天姝, 刘灏. 考虑过程噪声时变后验统计的自适应同步发电机动态状态估计[J]. 中国电机工程学报, 2022, 42(19): 6973-6985.
Zhang Jing, Bi Tianshu, Liu Hao. Adaptive dynamic state estimation for synchronous machines considering time-varying posteriori statistics of process noise[J]. Proceedings of the CSEE, 2022, 42(19): 6973-6985.
[28] Wang Yi, Sun Yonghui, Dinavahi V. Robust forecasting-aided state estimation for power system against uncertainties[J]. IEEE Transactions on Power Systems, 2020, 35(1): 691-702.
[29] 陈艺煌, 邵振国, 林俊杰, 等. 融合多源量测数据的区间型抗差谐波状态估计[J]. 电工技术学报, 2024, 39(23): 7394-7405.
Chen Yihuang, Shao Zhenguo, Lin Junjie, et al. Interval harmonic robust state estimation method based on multi-source measurement data fusion[J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7394-7405.
[30] 方陈, 姚维强, 魏新迟, 等. 考虑节点时空相关性的有限配电网PMU装置优化部署[J]. 电网与清洁能源, 2023, 39(8): 105-115.
Fang Chen, Yao Weiqiang, Wei Xinchi, et al. Optimal placement of limited distribution PMU considering spatiotemporal correlation of nodes[J]. Power System and Clean Energy, 2023, 39(8): 105-115.
[31] 高崇, 邵在康, 康忠健, 等. 基于扩展卡尔曼滤波的水中放电阶段辨识方法[J]. 电工技术学报, 2024, 39(11): 3475-3485.
Gao Chong, Shao Zaikang, Kang Zhongjian, et al. Method for identifying stages of discharge in water based on extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3475-3485.
[32] 程浩忠, 袁青山, 汪一华, 等. 基于等效电流量测变换的电力系统状态估计方法[J]. 电力系统自动化, 2000, 24(14): 25-29.
Cheng Haozhong, Yuan Qingshan, Wang Yihua, et al. A state estimation method of power systems based on equivalentcurrent measurement transformation[J]. Automation of Electric Power Systems, 2000, 24(14): 25-29.
[33] 张恩政, 唐宁敏, 陈刚, 等. 基于改进IGG3权函数距离误差模型的工业机器人标定[J]. 中国机械工程, 2021, 32(13): 1539-1546.
Zhang Enzheng, Tang Ningmin, Chen Gang, et al. Industrial robot calibration based on improved IGG3 weight function of distance error model[J]. China Mechanical Engineering, 2021, 32(13): 1539-1546.
[34] 杨元喜, 景一帆, 曾安敏. 自适应参数估计与内外部精度的关系[J]. 测绘学报, 2014, 43(5): 441-445.
Yang Yuanxi, Jing Yifan, Zeng Anmin. Adaptive parameter estimation and inner and external precision[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 441-445.
Power System Adaptive Robust Dynamic State Estimation Based on Hybrid Measurements
Abstract State estimation is a key function of the energy management system in the power grid dispatching control center, which can be used to estimate the operating status of the entire power network and enable real-time monitoring of the power system. Currently, the availability of phasor measurement units (PMUs) alone is insufficient to meet the observability requirements for state estimation. To address this, integrating conventional measurement systems, like supervisory control and data acquisition (SCADA), into a hybrid measurement setup can effectively enhance measurement redundancy. Meanwhile, the Kalman filter algorithm used for dynamic state estimation in power systems demands high model accuracy, yet its tracking capability and estimation precision are compromised under the influence of unknown time-varying noise. To mitigate the impact of unknown measurement noise and accurately obtain system states, this paper proposes a hybrid measurement state estimation method based on the improved adaptive robust extended Kalman filter (IAREKF) algorithm.
Firstly, the power measurements of SCADA are converted into equivalent current phasor measurements by the measurement transformation strategy, which linearizes the measurement equations and enhances computational efficiency. Simultaneously, a spatio-temporal pseudo-measurement generation method is devised that incorporates power transfer distribution factors and temporal correlations, thereby supplementing missing state information and enabling the fusion of hybrid measurements. Secondly, the measurement noise covariance is estimated by analyzing the statistical characteristics of the measurement devices. An equivalent weight function is constructed based on the standardized innovation to modify the measurement noise covariance, thereby enhancing the robustness of the algorithm. Finally, an adaptive forgetting factor method is employed to refine the Sage-Husa noise estimator. Quantify the overall filtering performance of the current state estimation utilizing the ratio of the trace of the innovation variance matrix to the trace of the innovation covariance matrix as a metric. An adaptive forgetting factor is determined using this metric, adjusting the level of discounting applied to outdated data during the estimation of the process noise covariance matrix. This method enhances the precision of the adaptive estimation of process noise, thereby improving the algorithm′s dynamic tracking performance of the system state.
Simulation results show that in the IEEE 39-bus power system, under conditions of unknown model and noise parameters, the proposed method achieves a mean absolute error (MAE) of 3.477×10-4(pu) for voltage phase angle estimation, and MAE of 0.03057° for voltage phase angle estimation. Compared to the generalized maximum likelihood iterated extended Kalman filter (GMIEKF) and adaptive H¥ extended Kalman filter (AHEKF) algorithms, the MAE reductions are 37.51% and 42.21% for voltage magnitude estimation, and 14.97% and 21.46% for voltage phase angle estimation, respectively. Under the influence of bad data, the MAE reductions are 37.26% and 24.84% for voltage magnitude estimation, and 12.95% and 6.55% for voltage phase angle estimation, demonstrating excellent robustness. During system transients, the proposed method maintains high estimation accuracy, showcasing its superior dynamic tracking capability.
The following conclusions can be obtained through simulation analysis: (1) Facing the differences in characteristics among various measurement systems, the measurement transformation technology is adopted to achieve the fusion of hybrid measurements. Pseudo-measurements are constructed based on the spatio-temporal characteristics of the system to increase the frequency of state estimation to synchronize with PMU sampling, enabling a more rapid acquisition of the system's dynamic changes. (2) The measurement noise covariance is estimated by analyzing the characteristics of measurement devices. Furthermore, a robust factor is constructed based on the standardized innovation to adjust the measurement noise covariance matrix, ensuring robustness against bad data. (3) An adaptive forgetting factor-based process noise estimation algorithm is proposed. Compared to the traditional Sage-Husa noise estimation method, this algorithm can more quickly forget previously invalid statistical information, leading to a more accurate estimation of process noise. Consequently, it achieves higher estimation accuracy under system disturbances or abrupt changes.
Keywords:State estimation, hybrid measurements, Kalman filter, robust estimation
中图分类号:TM711
DOI: 10.19595/j.cnki.1000-6753.tces.241387
国家自然科学基金项目(52407087)和新型电力系统运行与控制全国重点实验室开放基金课题(SKLD23KZ06)资助。
收稿日期 2024-08-05
改稿日期 2024-09-18
林俊杰 男,1992年生,博士,副教授,研究方向为同步相量测量技术、电力系统状态估计。
E-mail:linjunjie@fzu.edu.cn
江昌旭 男,1990年生,博士,副教授,研究方向为人工智能技术在电力系统中的应用、电力−交通融合网。
E-mail:cxjiang@fzu.edu.cn(通信作者)
(编辑 赫 蕾)