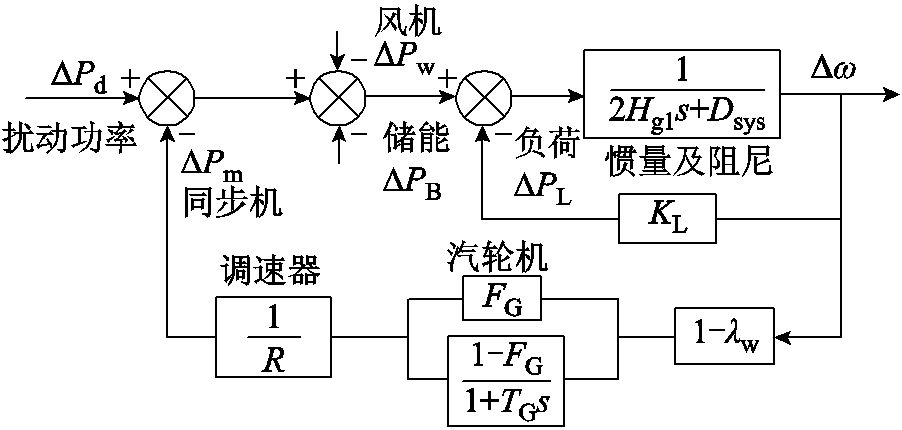
图1 风储联合系统虚拟转速响应模型
Fig.1 Virtual speed response model of wind-storage system
摘要 依据频率安全指标约束,利用风电机组和储能的功率协同支撑潜力以满足系统调频要求,是保障新能源高渗透区域电网安全运行的关键。该文首先建立风储并网发电系统的虚拟转速动态响应模型,针对风储系统的频率调整需求及特点,提出包含频率偏离、风储转换与频率恢复三阶段的风机、储能虚拟转速多段协同调节过程划分方法;其次,计算系统转速响应极值时间,并分析其关键影响因素,在频率安全指标约束下,提出风、储虚拟多段协同调速控制策略,以满足风储并网发电系统的惯量支撑和一次调频需求;最后,搭建风储并网仿真系统,验证虚拟多段调速有利于明晰风储协同支撑功能,满足保障系统频率安全需求。
关键词:调频要求 虚拟转速 极值时间 协同调速 频率安全
近年来,新能源发电处于高速发展期,通过电力电子换流器并网的新能源在矢量控制下虽然可实现最大功率点跟踪(Maximum Power Point Tracking, MPPT)运行,但缺少了惯性响应与励磁系统,导致其无法主动响应电网频率、电压变化,加之风光出力具有波动性,新能源高比例接入后系统稳定运行将面临严峻挑战[1-3]。其中,新能源高渗透电网的惯性及调频能力不足已不容忽视,如在美国加州“8·14”、南澳“9·28”停电等事故中,风机参与系统调频能力不足被认为是事故发生的重要原因之一[4-5]。在新能源高占比区域电网中,储能可快速补偿风功率扰动,已成为与新能源配套装设的重要设备[6-8]。尽管并网规范已要求配置储能,但如何利用储能的功率支撑潜力,与风电机组配合保障系统频率安全,目前仍需要进一步探讨,这也是新能源安全消纳的关键技术瓶颈。
为提升风能利用效率,风电机组通常采用最大功率跟踪控制,无法对系统频率起到调节作用,不具备惯量与一次调频支撑能力[9-10]。为提升风电高渗透率电网的频率稳定性能,风机频率控制技术不断完善,如文献[11]提出超速减载控制,风机功率跟踪曲线右移,使机组可以保留一部分有功备用,但当发生频率抬升事件时风机却无法参与调频。文献[12]采用变桨距角控制,在高风速时限制风能捕获,但由于响应速度较慢,其对频率突变无法做出及时处理。文献[13]提出了风机虚拟惯性控制减缓频率波动的速度。文献[14-15]在风机转子侧换流器电流指令中采用PID控制,使其快速响应系统的频率波动。上述控制策略在风机有功控制环附加控制,开发了风机转子动能模拟惯性响应的潜力,但虚拟惯量如何评估尚需探讨,这也导致了控制参数设计依据不足。
具备能量储备的储能装置拥有快速的调节与响应能力,可通过附加有功控制参与系统调频。与风电机组相似,储能也可以通过虚拟惯性减缓系统频率变化速度,甚至可利用能量储备,采用下垂控制减小系统一次调频的稳态偏差[16-17]。文献[18]根据频率动态变化过程,加入虚拟惯性、下垂控制比例系数分配器,提高控制过程中频率暂态响应的表现。文献[19-20]考虑储能实际运行时的荷电状态量(State of Charge, SOC),通过将储能SOC与调频指标相结合,提出基于动态任务系数的储能辅助一次调频策略,并兼顾了减小储能充放电次数和保障系统频率稳定的双重目标。理论上,储能可以准确地追踪功率指令,响应速度远快于传统调频机组,但当前储能成本较高,单独依靠储能参与调频成本受限严重[21]。
随着新能源调频需求日益提高,仅依靠风机或储能,调频能力有限且深度出力不利于风储安全运行,如何充分发挥风、储各自的调频优势,实现风储之间的协同配合,将是提高系统频率稳定性的关键。文献[22]根据储能荷电状态量依次启动储能控制、风机变桨控制参与系统频率调节,但其未能开发风储调频技术的互补优势。文献[23]提出基于虚拟同步机(Virtual Synchronous Generator, VSG)控制的风储配合策略,其调频功能本质是VSG的有功-频率下垂控制,以实现VSG有功输出随电网系统频率变化的自适应调节,但该策略中储能优先参与系统功率支撑,导致储能容量配置高,经济性相对较低。文献[24]研究了基于风机转子转矩控制的风储联合调频策略,但其侧重于风机频率响应能力,未能充分开发储能的调频优势。文献[25]采用凸优化模型,调用Gurobi完成所提风储调频辅助服务市场多时间尺度出清调度策略进行求解与验证。文献[26]提出基于频率分析与运行优化深度融合需求,可构造适用于凸优化问题的新能源系统频率安全约束,用于保证优化方案的全局最优性。但凸优化标准形应用求解可能会使得问题没有可行解,在应对维数、精度较高问题时求解复杂度显著增加,兼顾多目标稳定控制的优化算法仍需深入探讨。文献[27]关注风储联合调频时的功率分配方案,减小了风电场弃风情况,同时考虑了储能充放电问题,但风储控制器参数设计依赖在线评估,无法准确满足实际工程的系统调频需求。综上所述,当前风储协同控制仍存在控制器参数整定依赖实时在线数据,惯性、一次调频参数配合逻辑复杂等问题。此外,风储虚拟惯量控制启停条件易受干扰也是制约风储协同发展的重要因素。若风储协同控制能紧密围绕系统同步转速各阶段的变化特性,对风储间惯性、一次调频参数进行设计,同时避免风储惯量控制存在的缺陷,则可极大地提高风储并网支撑的可靠性,保障系统频率安全稳定运行。
风储协同频率支撑应将系统频率安全指标需求作为控制目标,为此本文提出了风储三阶段协同调速区间划分方法,明晰了各阶段风储调频任务分配原则,提出了根据系统调频需求划分扰动区间,并生成调频指令的风储协同频率支撑方法,可靠地保障新能源高比例电力系统的频率安全。为解决风储频率支撑控制存在的不足,本文首先采用系统频率响应模型[28-29],建立了风储联合系统虚拟转速动态响应模型,分析了风储并网发电系统的同步转速响应特性,将系统转速响应过程分为频率偏离、风储转换与频率恢复三个阶段;其次,计算系统转速响应极值时间,并分析了极值时间的影响因素;然后,分析了多段协同调速三个阶段的调频需求及目标任务,并提出风储虚拟惯量与一次调频双目标多段协同调速控制策略;最后,搭建风储高占比仿真系统,验证所提控制对系统频率稳定性的提升效果。
随着新型电力系统中新能源渗透率的不断提高,同步机组惯量支撑及一次调频能力越发不足,当系统所受扰动较大时,仅依靠同步机的调速能力,无法满足系统频率安全需求。因此,具有能量储备的风储附加调频控制,参与系统功率支撑,分担系统转速调节压力,将是保证风储并网发电系统稳定安全运行的必要措施。
对于复杂电力系统,需要根据电网的拓扑结构和电气特性对系统节点进行合并,将复杂的发电机组简化为单机等值模型,等值处理方式也是目前电力系统成熟的频率调整措施进行参数设计时普遍采用的方法[30-31]。为分析风储并网发电系统同步转速的动态特性,本文建立了图1所示包含同步机、风储模块的虚拟转速响应模型。功率信号中,ΔPd为系统扰动功率;ΔPm为同步机机械功率;ΔPw、ΔPB分别为风电机组和储能的功率;ΔPL为负荷调节信号。系统参数中,Δw为系统转速变化量;lw为系统的风电渗透率;TG为再热过程时间常数;FG为高压涡轮机功率占比系数;R为同步机调差系数;KL为负荷调节系数;Dsys为系统阻尼;Hg1为考虑风电占比时同步机的惯性时间常数,Hg1=Hg(1-lw),Hg为同步机组固有惯性时间常数。系统参数的具体取值及范围可参见表1[32]。
依据图1可得风储系统的转速响应表达式为

图1 风储联合系统虚拟转速响应模型
Fig.1 Virtual speed response model of wind-storage system
表1 风储系统转速响应模型参数
Tab.1 Parameters of the wind-storage system’s speed response model

参数取值范围数值 Dsys0~10.5 KL0~11 R0.04~0.10.05 TG/s6~146 FG0.15~0.40.3 Hg/s3~98
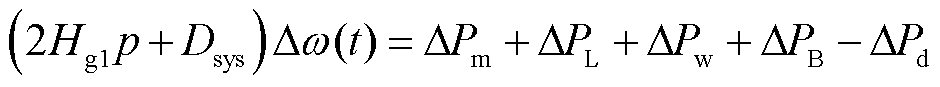 (1)
(1)
式中,p为微分算子;负荷输出信号ΔPL=KLΔω,同步机功率输出信号ΔPm与lw、R、FG、TG等系统参数相关,可表示为
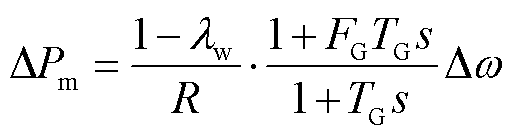 (2)
(2)
风、储采用微分控制后具备和同步机等效的惯性响应能力,可将其虚拟惯量与同步机惯量进行合并[33],则式(1)表示为
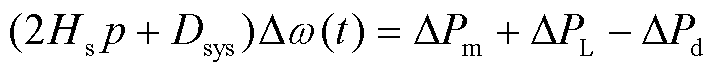 (3)
(3)
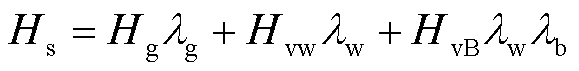 (4)
(4)
式中,Hvw、HvB分别为风机虚拟惯量、储能虚拟惯量;Hs为系统总惯量;lg为系统中同步机所占比例;lb为储能占风机容量的比例。
将同步机功率输出ΔPm、负荷调节信号ΔPL代入式(1)中,可得复数域下风储系统转速响应模型为
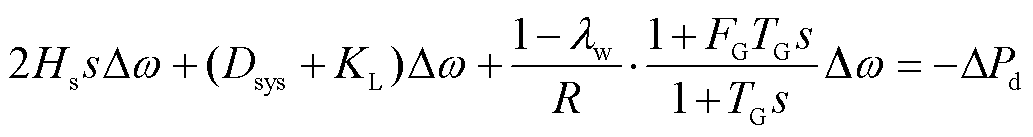 (5)
(5)
进一步由式(5)可得转速响应方程的二阶微分时域表达式为
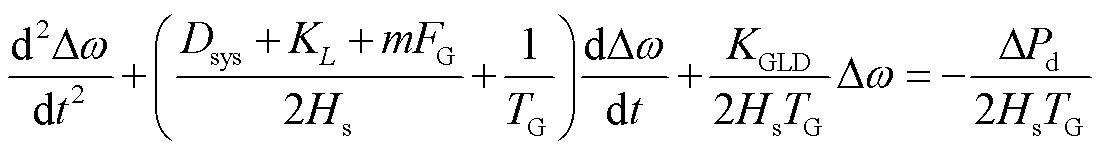 (6)
(6)
式中,m为计及风电渗透率下的同步机组一次调频系数;KGLD为风储系统的等效一次调频系数。
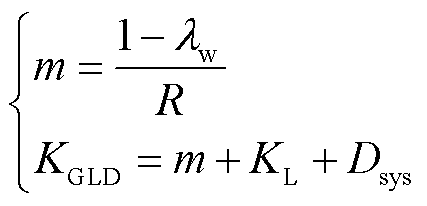 (7)
(7)
假设在t=0时刻系统出现负荷扰动,负荷扰动发生时刻的初始条件为
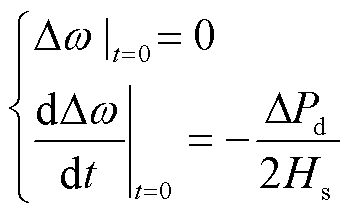 (8)
(8)
则可求得Δw与时间t的微分方程的解析解为
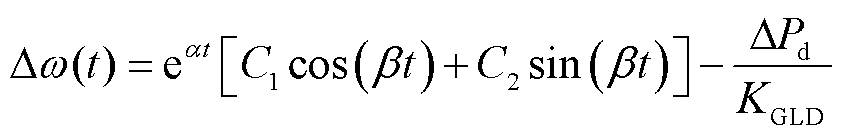 (9)
(9)
其中
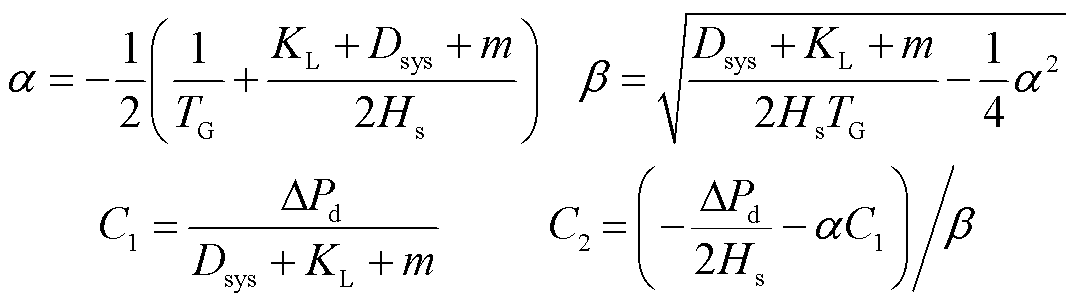 (10)
(10)
由式(9)可知,风储系统FG、TG、R等固有参数确定,风储系统转速响应方程也随之确定,进而可通过对转速方程的分析获得系统转速变化特性及其过程对应的各个指标。本文建立的转速响应模型在求解过程中,可以定量反映系统惯量及一次调频系数需求,且极值时间求解形式简单,便于划分系统频率响应阶段,也是根据每个阶段的频率安全指标明晰风储调频任务与协同控制逻辑,进而满足系统惯量与一次调频双重目标需求的基础。
在新能源高占比区域电网内,系统惯量与一次调频支撑均可分担系统调速负担,但二者控制规律不同。具体表现在惯量支撑可以快速响应系统角频率变化率,但惯量支撑是一个非常短时的冲击型功率支撑,其产生的累积能量有限,当系统角频率不再变化时其功率支撑为0;而一次调频响应的是系统角频率偏差量,系统角频率变化初期偏差量较小,一次调频功率出力也较小,但一次调频功率是一个持续的功率支撑,只要系统角频率偏差存在,一次调频功率就一直存在,从而使系统角频率维持在一个新的稳态水平继续运行。以负荷突增导致转速跌落为例,系统动态响应过程如图2所示。其中,t0时刻系统受到外部扰动,t1时刻系统一次调频开始动作,tex时刻系统同步转速跌落至最低,t2时刻一次调频阶段结束;ΔPH、ΔPF分别为系统的惯量支撑与一次调频支撑功率。
本文将风储系统动态响应过程分为三个阶段,其中,[t0, tex]为频率偏离阶段(dw/dt<0),在t0时刻,系统发生功率突增扰动,导致系统同步转速迅速下跌。此阶段中,风储可通过附加惯量控制响应转速变化向系统提供功率支撑,减小系统转速的跌落速率,分担系统调频负担。
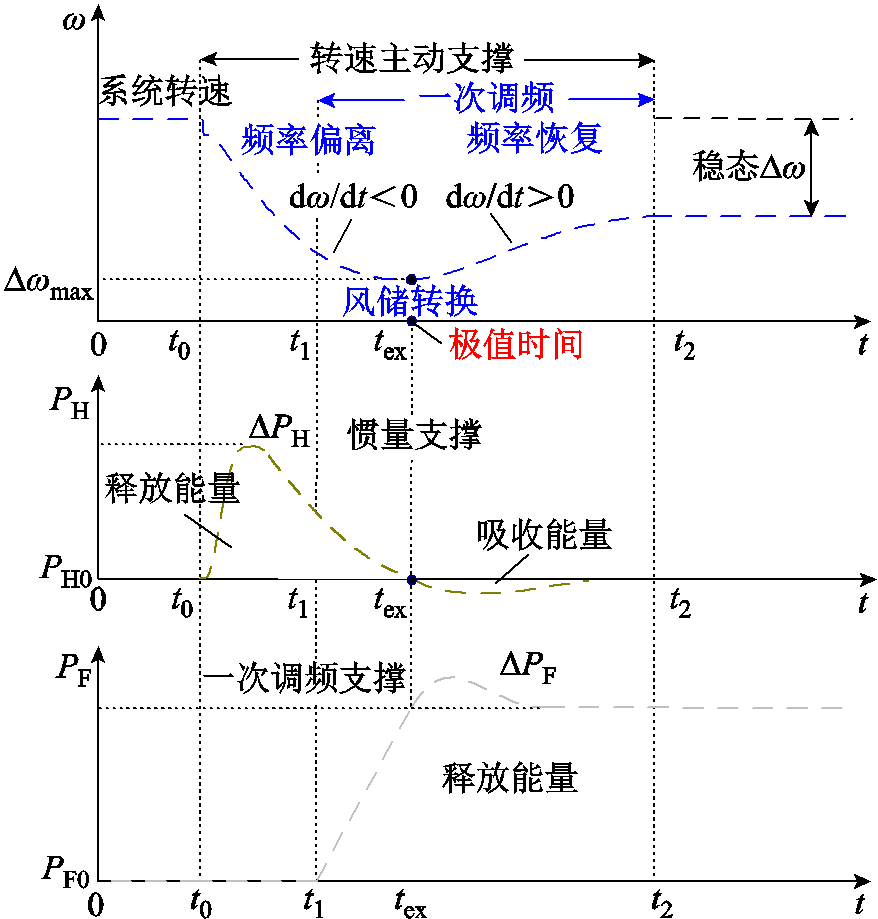
图2 风储系统动态响应特性
Fig.2 Dynamic response characteristics of wind-storage system
(tex, t2]为频率恢复阶段(dw/dt>0)。此阶段中,风机和储能附加惯量控制不仅无法向系统提供功率,反而会吸收功率,增加系统的调频压力,不利于系统频率恢复,甚至会造成频率的二次跌落。因此,在惯性支撑结束后,即转速跌落至极值tex时刻应及时闭锁风储的惯性响应,并将惯量控制转换为一次调频控制,由风储一次调频响应提供功率支撑,促进系统同步转速快速恢复,该阶段为风储转换阶段。
为了规范风电并网技术,我国的风电并网国家标准GB/T 19963.1—2021《风电场接入电力系统技术规定 第1部分:陆上风电》中要求风机惯性响应需满足:Δf·df/dt>0。然而,微分控制在系统频率响应过程中存在高频噪声,控制器误动作可能性较大。若能准确地预估扰动下风储系统内发电机转速跌落至极值的时间,在本文划分出的三个阶段中,通过风、储进行虚拟调速辅助发电机转速尽快恢复,则不仅能有效避免因频率微分信号监测误差较大而导致的控制器误操作,使风储惯量控制具备安全切除的保障,还有利于明晰转速响应过程中系统的调频需求,进而为系统转速及频率安全下的惯量及一次调频协同提供更加可靠的控制逻辑,显著提升风储并网发电系统频率支撑的可靠性。
系统转速响应极值时间是将风储虚拟多段调速区间划分为频率偏离、风储转换与频率恢复阶段的重要依据。
对式(9)进行求导,导数为0的时刻即为转速响应极值点时刻,计算可得系统转速响应极值时间tex为
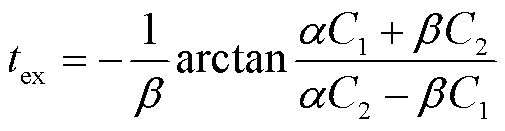 (11)
(11)
由式(11)可知,风储系统转速响应极值时间与系统惯量Hs及扰动功率ΔPd密切相关,接下来将对转速响应极值时间的影响因素做进一步分析。
风储不附加控制参与系统惯量支撑,即式(4)中Hs=Hglg时,设置在3 s时系统受到外部扰动,扰动ΔPd(pu)大小为0.1,依据表1中的典型参数,不同风电渗透率下风储系统的转速响应如图3所示。
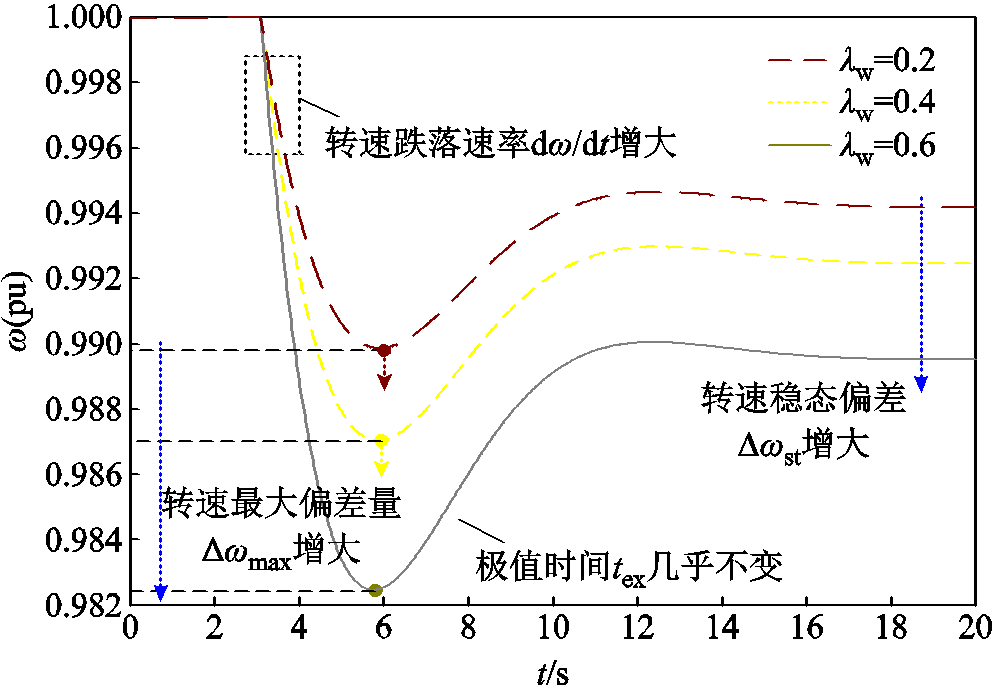
图3 风储无附加控制时系统转速响应
Fig.3 Dynamic speed response of wind-storage system without additional control
根据图3,风储无惯量支撑时,风电渗透率变化主要影响系统的转速跌落速率dw/dt、最大转速偏差量Δwmax和转速稳态偏差Δwst三个指标,对转速响应极值时间tex的影响不大。在相同的功率扰动ΔPd下,随着常规控制的风电接入比例的提升,系统惯量减小,转速跌落速率变大,最大转速偏差与转速稳态偏差变大,风电渗透率持续增大,系统的转速安全将无法得到保障。
风储参与系统功率支撑时,即风储系统惯量Hs=Hglg+Hvwlw+HvBlwlb时,设置风储虚拟惯量Hvw与HvB分别为8 s与10 s,储能容量占比lb为10%,扰动ΔPd为0.1(pu),风储系统在不同风电渗透率下的转速响应曲线如图4所示。
附加惯性控制后,风储可响应同步转速变化向系统提供惯量支撑。由图4可知,在相同的功率扰动下,随着风电渗透率提高,系统惯量增大,转速跌落速率减小,最大转速偏差量减小,极值时间tex增大。
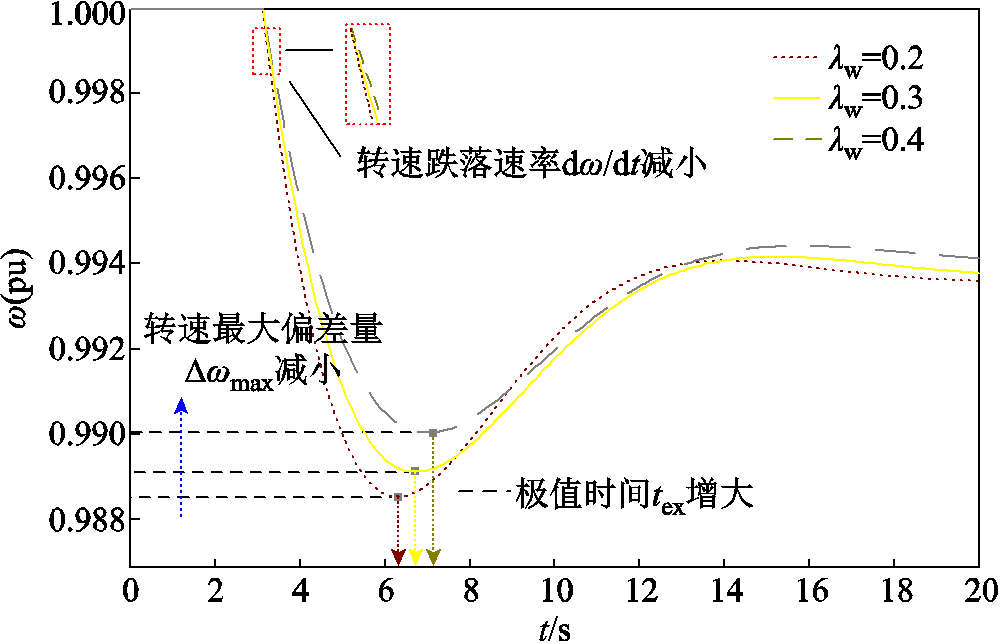
图4 风储虚拟惯性控制下系统转速响应
Fig.4 Dynamic response of wind-storage system speed under virtual inertial control
分析扰动对系统转速响应的影响,设置风电渗透率为0.3,储能容量占比lb=10%,此时风储系统惯量为Hs=0.7Hg+0.3Hvw+0.03HvB,3 s时向系统施加扰动。风储系统在不同扰动下的转速响应曲线如图5所示。
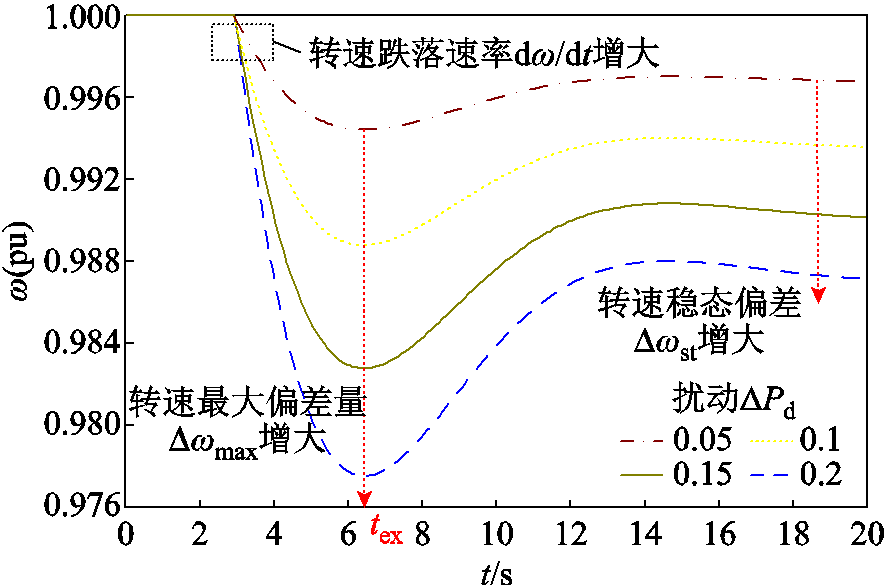
图5 不同扰动下系统转速响应
Fig.5 Dynamic speed response of wind-storage system under different perturbations ΔPd
由图5可知,随着扰动功率增大,系统的转速跌落极值时间tex几乎不变,系统转速跌落速率变大,最大转速偏差量与转速稳态偏差变大。当扰动ΔPd继续增大,系统同步转速安全指标将不满足要求,风储需进行虚拟调速将系统同步转速限制在安全范围以内。
基于上述分析,风储系统采用虚拟惯量控制前,风电渗透率及扰动的增大会增加系统同步转速跌落速率、转速最大偏差量和转速稳态偏差,但系统转速响应极值时间tex几乎不变。因此,可根据系统参数预估系统转速响应极值时间,降低风储协同调速控制的在线需求。
同步机组中含有调速器控制模块,主要用于响应机组转速变化,完成一次调频工作。类比同步机中传统的调速模块,本文提出风储系统中虚拟调速控制策略,用于响应系统角频率变化,完成系统的惯量支撑与一次调频支撑。标幺值系统下,系统同步转速即为系统频率,两者大小及变化规律相同,即Δf=Δw,系统转速跌落速率、转速最大偏差量和转速稳态偏差,分别对应着系统频率变化率df/dt、频率最大偏差量Δfmax与频率稳态偏差Δfst,转速响应极值时间也即频率响应极值时间。因此可通过分析系统频率变化指标对同步转速进行限制,进而分析风储虚拟协同调速控制原理及系统调频需求。
结合风储并网发电系统同步转速变化特性,本文将系统调速控制分为三个阶段,即虚拟三段式协同调速控制,以满足系统惯量与一次调频的双目标需求。第一阶段,频率偏离阶段,该阶段系统频率支撑主要依靠惯性响应完成,需要采取转速安全控制措施降低系统转速跌落速率,控制目标是动态过程中的最大转速变化率符合安全指标,以满足系统的惯量需求;第二阶段,风储转换阶段,该阶段系统频率支撑主要依靠一次调频响应完成,需要采取转速安全控制措施降低系统转速最大跌落幅值,控制目标是动态过程中系统转速偏差最大值符合安全指标,满足系统一次调频需求;第三阶段,频率恢复阶段,该阶段系统频率支撑主要靠一次调频响应完成,需采取转速安全控制措施避免系统角频率长期偏离正常范围,控制目标是故障后系统转速稳态偏差符合安全指标,满足系统一次调频需求。综上所述,本文将所提虚拟多段协同调速控制分为三个阶段,新能源调频各阶段的控制逻辑更加明确。但是,不能将三个阶段的调速控制策略割裂开,三个阶段的控制措施仍需要协调配合,后一阶段的频率安全控制策略需计及前一阶段控制策略实施后的影响。
为提高风能利用效率,保障风机经济性,当前风电场控制中通常没有足够的预留容量来参与系统的一次调频工作,在该情况下,虚拟惯性响应将是风机参与系统频率支撑调整的主要方式。相较于风机,储能灵活便捷,短时间内可调用自身存储的能量,附加微分与下垂控制为系统提供功率支撑。基于以上分析,本文风储虚拟多段协同调速支撑控制中,惯量支撑由同步机组、风机和储能共同完成,一次调频则由同步机组与储能承担。针对新能源高比例电力系统频率安全需求,能够可靠地满足系统安全指标是相对合理的控制参数设计方案,该控制方式下新能源参与调频保障系统频率安全即完成了预期任务,不会因为附加控制诱发其他稳定问题。
频率偏离阶段主要研究系统的惯量支撑情况,控制目标为保证系统频率及转速变化率满足安全约束,其主要步骤为:①分析系统频率及转速最大变化率安全约束;②根据系统同步转速最大变化率约束,明确系统惯量需求;③根据系统最小惯量需求,计算系统启动频率偏离阶段虚拟调速控制时的临界扰动功率ΔPd1。
频率快速响应过程中,系统惯量水平制约着系统频率变化速度。目前英国、爱尔兰、比利时等国家研究表明,风电高渗透系统受到功率扰动后的频率变化率应限制在0.125~1 Hz/s [34-35]。
系统初始频率下降速度与初始功率缺额有关,有功功率缺额越大,频率下降越快。扰动发生初期,系统频率变化率最大,其动态响应方程为
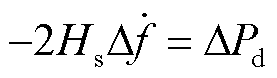 (12)
(12)
本文将0.5 Hz/s设置为系统最大频率变化率约束限值,即系统转速变化率限值为prad/s2,标幺值为0.01(pu)。若负荷扰动初期的转速变化率小于限值,即可认为系统转速在整个调整期间均满足转速变化率约束。基于转速变化率约束下的系统最小惯量需求为
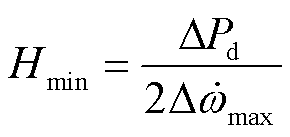 (13)
(13)
当系统转速变化率不满足安全指标时,需利用风、储附加惯量控制将系统转速变化率约束在安全范围以内。风储惯量需求表达式可表示为
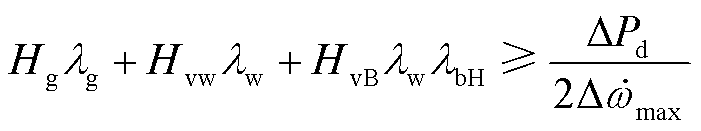 (14)
(14)
式中,lbH为用于惯量支撑的储能容量占风机容量的比例。
根据式(14),已知系统中风机容量占比,即可得到风、储需向系统提供的惯量支撑功率HWB为
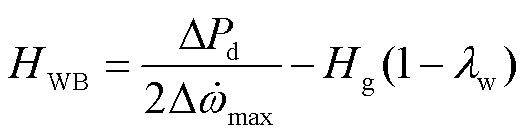 (15)
(15)
由式(15)可知,在系统转速变化率安全约束下,风储虚拟惯量的需求HWB主要取决于扰动功率ΔPd和风电渗透率lw。取Hg=6 s、(dΔw/dt)max =0.01(pu),代入式(15)得风储虚拟惯量需求HWB如图6所示。
从图6可知,在系统惯量需求确定的情况下,系统应对扰动的能力随着系统风电占比的提高逐渐降低。如当风电渗透率达到0.4时,系统可应对的功率扰动低于0.072(pu);风电渗透率达到0.6时,系统可应对的功率扰动低于0.048(pu),难以应对系统中诸多典型故障类型(扰动达到0.05(pu),此时需要风、储提供惯量支撑以满足系统角频率稳定要求。
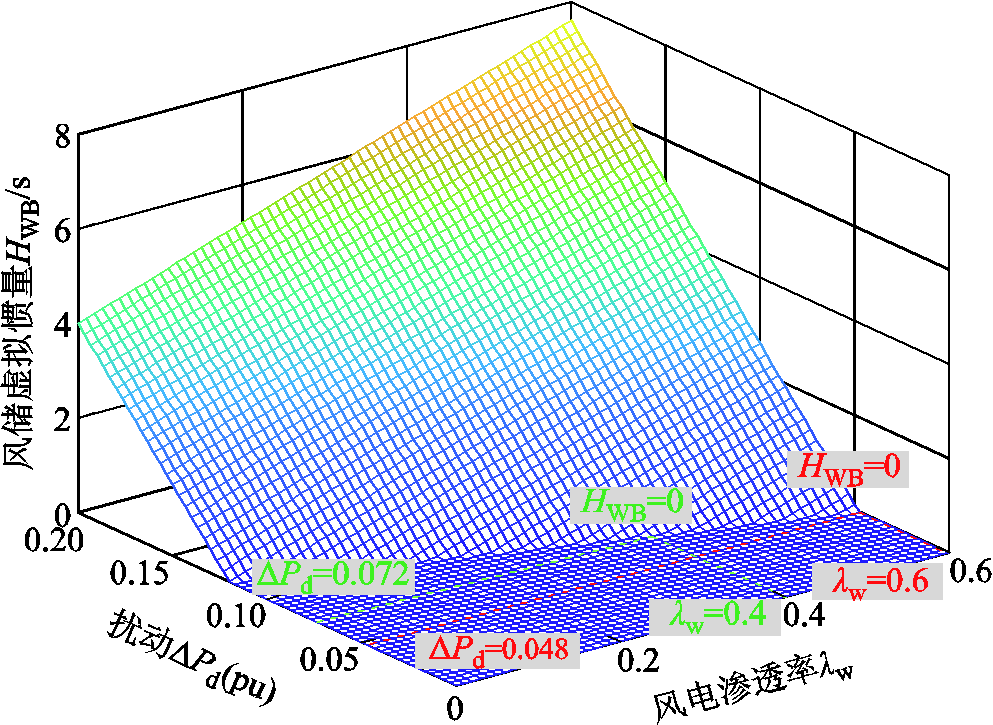
图6 风储系统虚拟惯量需求
Fig.6 Virtual inertia requirements of wind-storage system
系统转速变化率安全约束下,启动频率偏离阶段控制的临界扰动功率ΔPd1可表示为
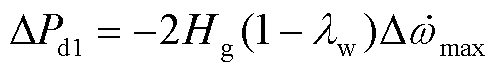 (16)
(16)
当系统实际扰动功率大于ΔPd1时,即应启动频率偏离阶段调速控制,保证系统转速及频率变化率满足安全约束。
风储转换阶段主要任务为闭锁风储惯量控制,防止风储从系统倒吸功率,同时研究储能一次调频支撑情况,控制目标为保证系统频率及转速最大偏差量满足安全约束,其主要步骤为:①分析系统频率及转速最大偏差量安全约束;②基于转速响应极值时间tex,根据系统转速最大偏差量约束,确定系统一次调频需求最小值Kmin1;③确定储能需向系统提供的一次调频系数最小需求值Kbmin1,计算启动风储转换阶段虚拟调速控制时的临界扰动功率ΔPd2。
为防止大负荷扰动下触发电力系统低频减载装置动作,我国对电力系统频率波动极值进行了限制,在发生大功率扰动事件时,电力系统频率最低值不得低于49 Hz[36]。
本文将频率偏差量最大值Δfmax设定为1 Hz,即系统同步转速偏差量限值为2p rad/s,标幺值为0.02(pu)。在系统满足最小惯量需求,即Hs=Hmin时,将Hmin表达式代入式(10)可得惯量需求约束下的参数α1、β1、C11与C22,进一步计算出系统的转速响应极值时间tex,即可确定系统的转速最大偏差量,可表示为
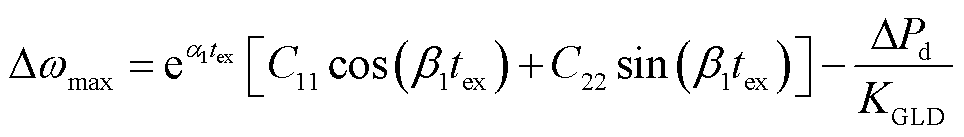 (17)
(17)
根据式(17),在系统最大转速偏差量Δwmax为0.02(pu)的约束下,根据故障扰动功率ΔPd即可计算出系统所需的一次调频系数最小值Kmin1,可表示为
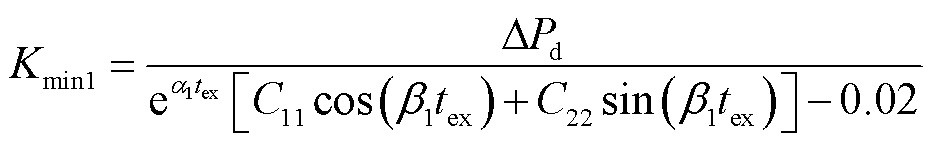 (18)
(18)
当系统一次调频能力不足时,储能可通过下垂控制快速参与系统转速调节,其对系统提供的功率支撑可表示为
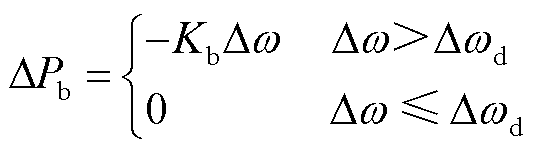 (19)
(19)
式中,Kb为储能的快速调频系数;Δwd为转速死区限值。
标准DL/T 2246.7—2021中规定储能的快速调频系数应为50~200,储能参与系统一次调频后,向系统提供的一次调频系数Kbmin1可表示为
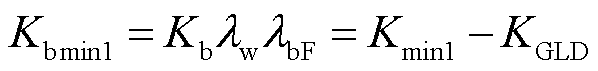 (20)
(20)
式中,lbF为用于一次调频支撑的储能容量占风机容量的比例。
系统转速最大偏差量安全约束下,启动风储转换阶段控制的临界扰动功率ΔPd2可表示为
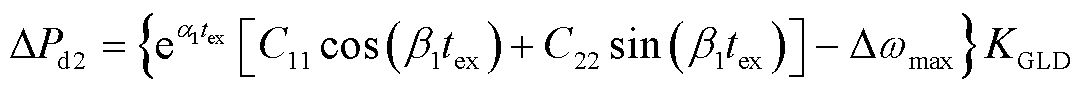 (21)
(21)
当系统扰动功率大于ΔPd2时,即应启动风储转换阶段调速控制,保证系统转速及频率最大偏差量满足安全约束。
频率恢复阶段主要研究系统一次调频支撑情况,控制目标为保证系统频率及转速稳态偏差满足安全约束,其主要步骤为:①分析系统频率及转速稳态偏差安全约束;②基于转速响应方程,综合系统转速稳态偏差与转速最大偏差量约束,确定系统一次调频需求最小值Kmin;③确定储能需提供的一次调频系数最小需求值Kbmin,计算系统启动频率恢复阶段虚拟调速控制时的临界扰动功率ΔPd3。
系统频率稳态偏差反映了扰动后系统工作运行的新状态,我国系统频率响应过程的稳态值一般在49.5~50.5 Hz之间[37-38],新能源发电系统一次调频时间一般在20~30 s,以0.033 Hz的系统频率偏差量作为系统调频死区[39]。
本文结合所提转速响应方程,以扰动发生30 s时刻系统稳态频率偏差Δfst≤0.5 Hz为约束条件,即系统同步转速稳态偏差限值为p rad/s,标幺值为0.01(pu),进一步对系统一次调频系数Kmin2进行限制。
将t1=30 s代入转速响应表达式(9),此时系统一次调频系数Kmin2应满足
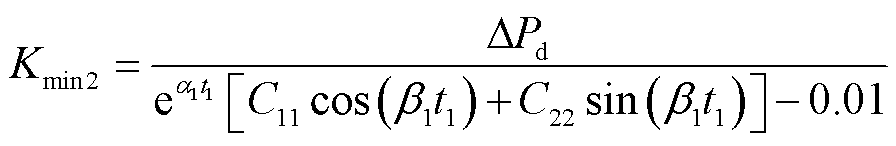 (22)
(22)
综合式(18)与式(22),为同时满足系统最大转速偏差量约束与转速稳态偏差约束,系统一次调频系数Kmin应取Kmin1与Kmin2中较大值,储能所需提供的一次调频系数Kbmin应依据Kmin而定,可表示为
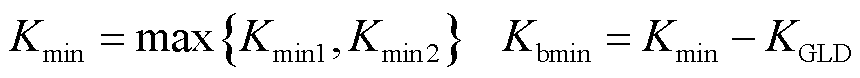 (23)
(23)
系统转速稳态偏差安全约束下,启动频率恢复阶段控制时的临界扰动功率ΔPd3可表示为
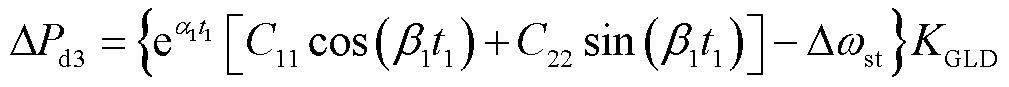 (24)
(24)
当系统扰动功率大于ΔPd3时,即应启动频率恢复阶段调速控制,保证系统转速及频率稳态偏差满足安全约束。
风储虚拟多段协同调速频率支撑技术中,依据系统转速安全的三个指标分别启动对应阶段控制。风机负责提供惯量支撑,储能作为备用容量负责提供惯量与一次调频支撑以满足系统频率及转速安全需求。风储虚拟协同调速控制下,其功率支撑可表示为
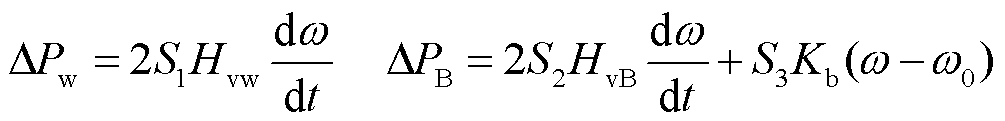 (25)
(25)
式中,S1、S2与S3分别为风机惯量支撑、储能惯量支撑与储能一次调频支撑的控制系数,依据调频指令取0或1;w0为同步转速基准值,标幺值取1(pu)。
风储功率支撑情况依据系统调频需求而定,但实际系统运行中并无相关测量仪器可直接获得风储在线惯量及一次调频需求,因此通过比较系统扰动功率ΔPd与三阶段安全控制临界扰动功率ΔPd1、ΔPd2、ΔPd3来确定虚拟调速控制中风、储模块的参与指令,满足系统的调频需求。
频率偏离阶段,为明确风、储惯量支撑情况,引入风机惯量支撑启动参考功率ΔPdH1与储能惯量支撑启动参考功率ΔPdH2。综合式(16),考虑系统转速变化率约束,风储启动惯量支撑的扰动参考功率ΔPdH1、ΔPdH2可表示为
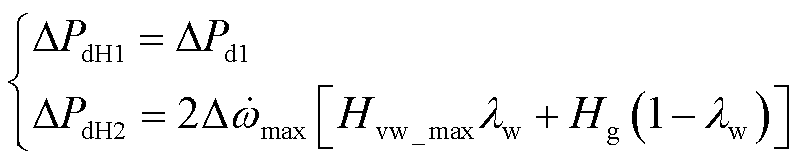 (26)
(26)
式中,Hvw_max为系统转速安全约束下风机的保守评估惯性时间常数。
量化过程中,当ΔPd≤ΔPdH1时,系统的惯量需求等于同步机的等值惯量Hg1,风储无需提供惯量支撑;当ΔPdH1<ΔPd≤ΔPdH2时,风机应提供惯量支撑,系统的惯量需求等于Hg1与风机可提供的惯量Hvw加权和;当ΔPd>ΔPdH2时,需风储协同向系统提供惯量支撑,此时系统的惯量需求等于Hg、Hvw与储能可提供的惯量HvB的加权和。
因此,当系统实际扰动功率大于ΔPd1时,即应启动频率偏离阶段调速控制,并根据ΔPd与ΔPdH1、ΔPdH2大小关系确定风储惯量支撑参与情况,保证系统转速变化率满足安全约束。
风储转换阶段,根据系统参数计算风储频率响应极值时间tex,并在tex时刻闭锁风储惯量响应,防止风储倒吸功率增加系统调频负担。当系统实际扰动功率大于ΔPd2时,即应启动风储转换阶段调速控制,保证系统最大转速偏差量满足安全约束。
此外,为明确储能一次调频支撑情况,引入储能一次调频支撑启动参考功率ΔPdF。量化过程中,当ΔPd≤ΔPdF时,储能无需向系统提供一次调频功率支撑,系统的一次调频需求等于风储无出力下系统等效调频系数KGLD;当ΔPd>ΔPdF时,需储能提供一次调频功率支撑,系统的一次调频需求为KGLD与储能提供的一次调频系数Kb之和。
频率恢复阶段,同理比较实际扰动ΔPd与ΔPd3的大小关系确定该阶段控制启动情况。同时考虑系统最大转速偏差量与转速稳态偏差约束,储能一次调频支撑启动参考功率ΔPdF可表示为
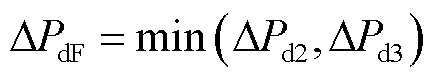 (27)
(27)
风储系统虚拟惯量及一次调频参与方案见表2。其中,ΔPmax为系统扰动量最大值。在实际运行中,由于系统扰动量无法准确预知,可参考历史数据,评估系统遭遇扰动的风险。进一步通过表2判断扰动所在区间生成风、储调频信号,即可确定风储协同调速控制下系统的惯量及一次调频分配方案。当系统遭遇较大扰动后,如直流闭锁等,结合可能出现的功率损失缺额,系统可采取紧急措施启动对应扰动区间的频率协同控制策略,确保系统频率安全。
表2 风储虚拟惯量及一次调频分配方案
Tab.2 Virtual inertia and primary frequency regulation allocation scheme of wind power and energy storage

ΔPd[0, ΔPdH1](ΔPdH1, ΔPdH2](ΔPdH2, ΔPmax](ΔPdF, ΔPmax] Hvw_set0HvwHvwHvw HvB_set00HvBHvB Kb_set000Kb
为满足风储并网系统频率安全需求,本文提出虚拟多段协同调速频率安全支撑策略,其包括风储惯量及一次调频需求评估、转速响应极值时间及调频指令生成、风机虚拟惯量控制、储能虚拟惯量控制与储能一次调频控制五个部分,控制框图如图7所示。
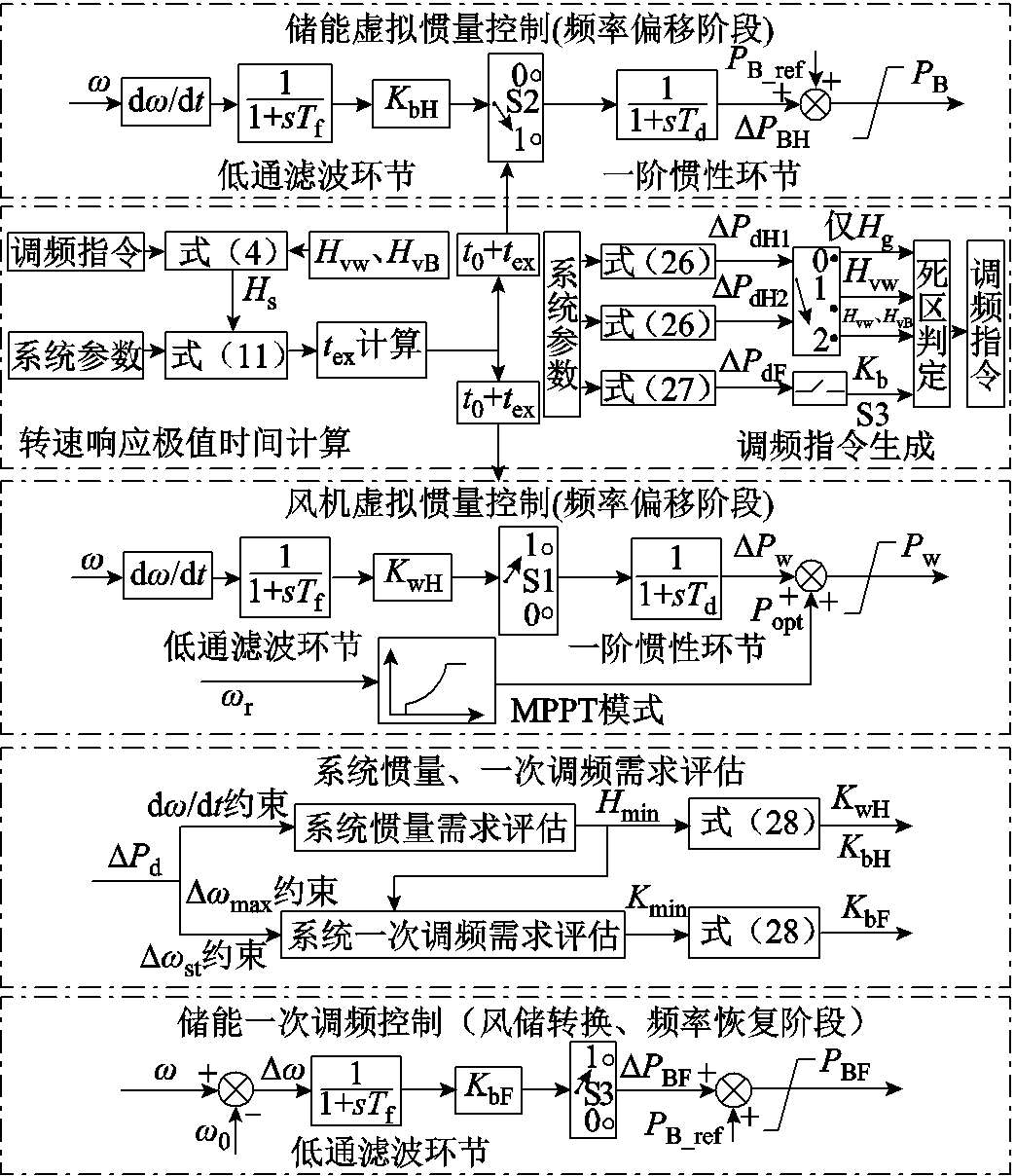
图7 虚拟多段协同调速频率支撑控制器
Fig.7 Virtual multi-stage coordinated speed regulation frequency support controller
所提控制中,风储需协同配合来满足系统最小惯量及一次调频需求。其中,频率偏离阶段,根据式(14),系统惯量水平不足时,风机优先提供虚拟惯量,储能其次;风储转换阶段,在转速响应极值时间tex退出风储惯量控制,防止风储倒吸功率增加系统调频负担;频率恢复阶段,根据式(23),当系统一次调频能力不足时,即启动储能一次调频控制,当频率恢复至频率稳态偏差范围内时,储能的一次调频控制退出。风储频率支撑效果应考虑系统测试延迟等因素影响。为此,本文在风储功率输出中设置了一阶惯性环节模拟系统延时响应,同时减弱高频噪声对风储功率输出的影响。
当风机采用惯量控制、储能采用惯量控制与一次调频控制时,控制器对应参数分别为KwH、KbH与KbF,对于一个确定的风储系统,确定系统扰动功率,则可确定控制器对应参数的取值,可表示为
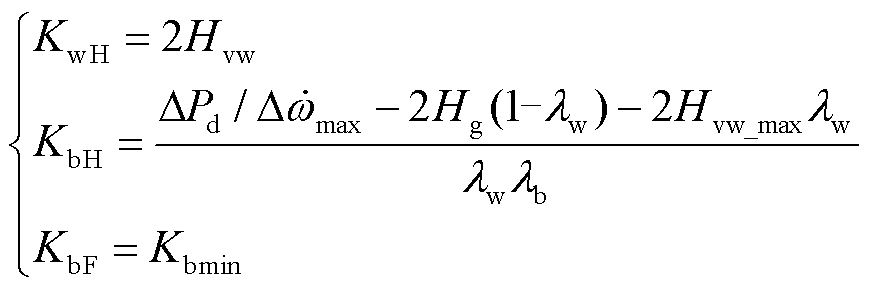 (28)
(28)
风储虚拟惯量控制环节增设判断模块S1与S2,依据调频指令,当t≤t0+tex时,判断模块配合输出1进行风储惯性响应,否则输出0实现惯性响应闭锁。储能一次调频控制增设判断模块S3,当系统频率稳态偏差不满足安全约束时输出1进行储能一次调频响应,否则输出0退出储能一次调频。通过比较系统扰动功率ΔPd与三阶段安全控制临界扰动功率ΔPd1、ΔPd2、ΔPd3确定虚拟调速控制中风、储模块的参与指令。当遭遇扰动时,判断模块S1、S2、S3视系统调频需求可同时启停,以满足系统频率安全需求。风储惯量支撑投入时,判断模块S1、S2启动,直至系统转速响应极值时间处闭锁;储能一次调频支撑控制投入时,判断模块S3启动,系统频率恢复至稳态偏差范围内闭锁。同时,为避免系统小幅频率波动造成控制器频繁启停,也可在判断模块中加入控制死区,根据实际系统要求灵活设计。
本文在DIgSILENT/PowerFactory电力系统仿真分析软件中建立了图8所示的风储3机9节点仿真模型,以验证所提虚拟多段协同调速策略控制效果。该模型中包含负荷LA,其容量为600 MW;电源包含一个由150台2 MW双馈风电机组(Doubly fed Induction Generator, DFIG)组成的风电场,火电机组G1、G2和G3的容量分别为200、500和200 MW,同时包含了一组容量为60 MW的集中式储能,该仿真系统中风电渗透率为0.25。
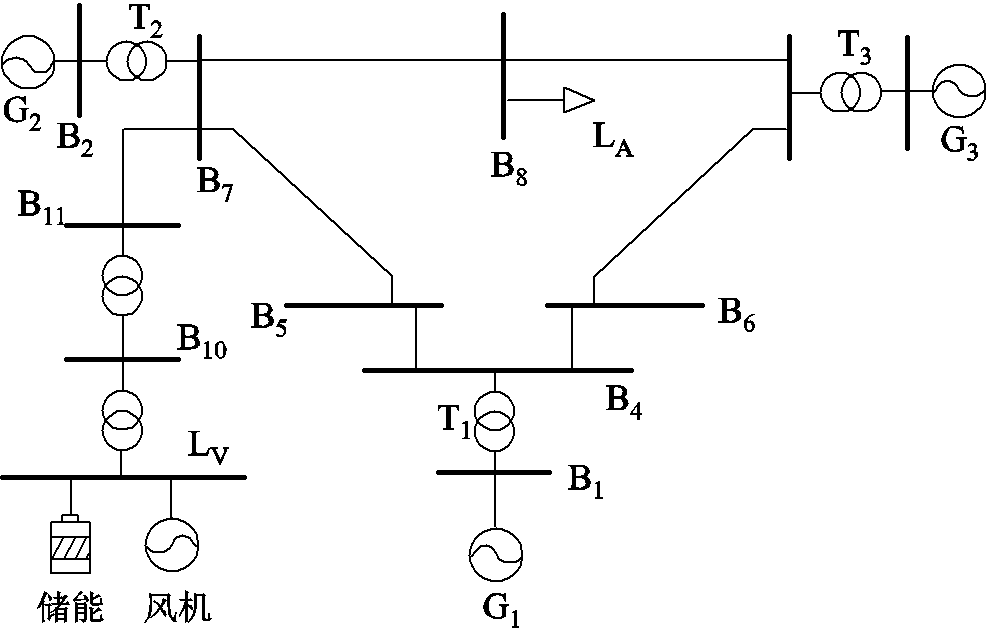
图8 仿真系统结构
Fig.8 Simulation system structure
为验证系统转速响应模型分析计算的准确性,设置系统负荷LA在3 s时刻突增0.1(pu),风储无附加控制下系统的同步转速及功率支撑的响应曲线如图9所示。
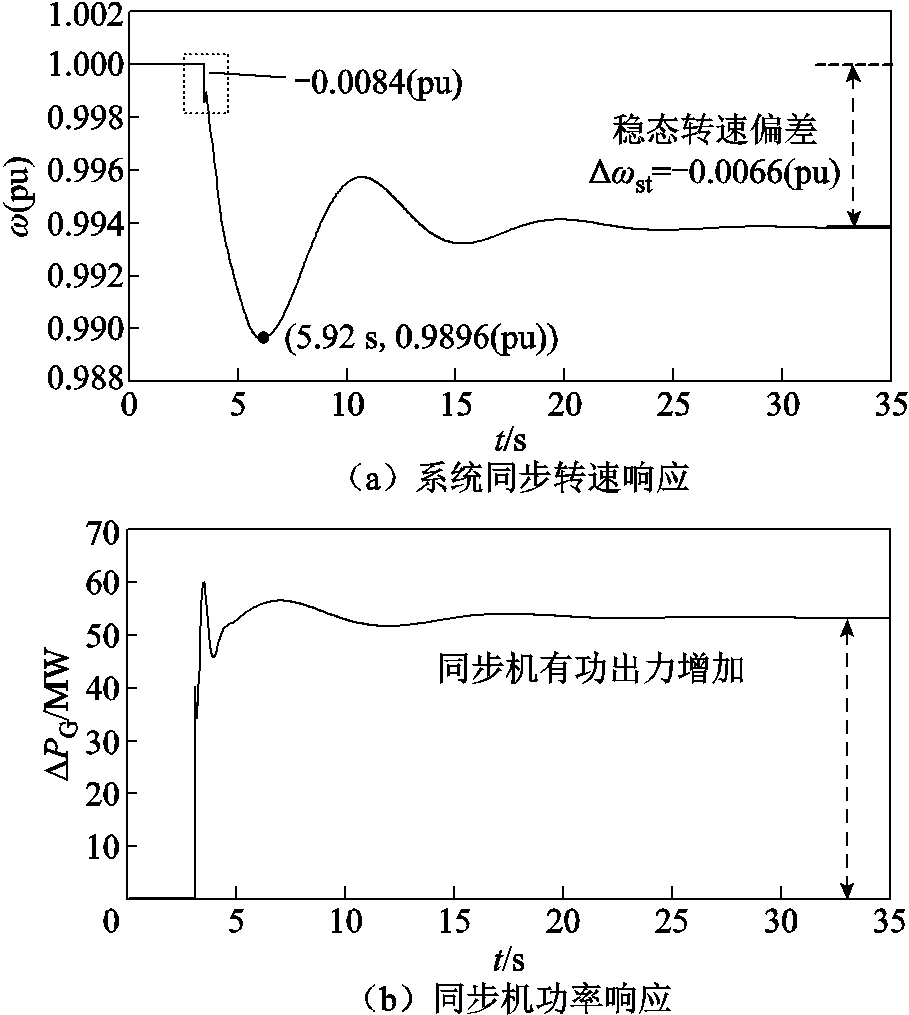
图9 无虚拟惯量控制时测试系统的动态响应
Fig.9 Dynamic response of the test system without virtual inertia control
由图9可知,负荷突增10%,系统同步转速下降,同步机G2有功增加响应系统角频率变化。根据图9a所示系统转速特性,对比转速响应极值时间tex、转速最大变化率(dw/dt)max、最大转速偏差量Δwmax以及转速稳态偏差Δwst的仿真数据和理论计算数据,可得具体分析结果见表3。
表3 转速响应模型指标分析
Tab.3 Speed response model indexes analysis

指标tex/s(dw/dt)max(pu)Δwmax(pu)Δwst(pu) 计算数据2.98-0.008 8-0.010 6-0.006 8 仿真数据2.92-0.008 4-0.010 4-0.006 6 误差2.01%4.55%1.89%2.94%
考虑到仿真中包含变压器和线路等诸多元件,实际系统比理论建模结果复杂,因此仿真与理论数据间会存在一定的误差。对比表3关键参数可知,tex、(dw/dt)max、Δwmax和Δwst指标误差均在5%内,所提转速响应极值时间及转速响应模型的准确性得以验证。
在实际工程应用中,风电机组运行会受到风速波动影响自身功率支撑,为测试风速波动对系统调频效果的影响,将DFIG设置为在随机风速条件下运行,在MPPT控制与所提协同控制策略下,风速v、系统频率f、同步机G2有功功率PG和DFIG有功功率Pw的动态响应如图10所示。
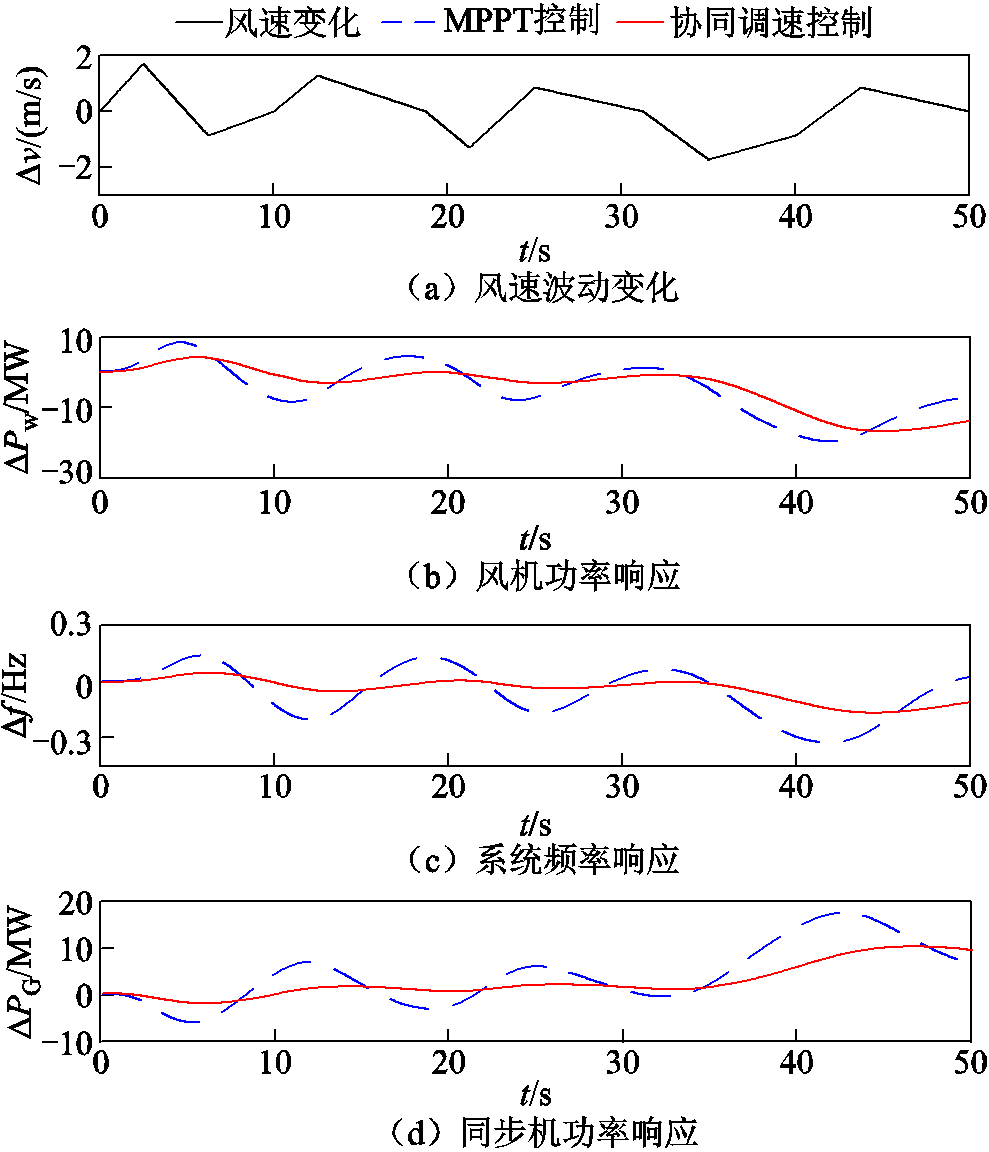
图10 随机风速下系统动态响应
Fig.10 System dynamic response under random wind speed
如图10所示,当风速变化导致风机功率输出大幅变化后,系统频率发生了较大波动。采用MPPT控制时,DFIG的输出功率由风速所决定,自身固有惯量仅能够起到平滑自身功率的作用,无法为系统提供频率支撑,系统频率波动范围达到-0.32~0.15 Hz。在本文所提控制策略下,风电机组可以响应频率变化为系统提供功率支撑,同步发电机的功率波动显著减小,系统频率波动得到了有效抑制,其变化范围减小至-0.17~0.05 Hz。测试结果表明,本文所提控制在变风速条件下也可保证风电机组有效参与系统频率调节。
为验证所提虚拟多段协同调速频率支撑控制策略的优越性,本文将其分别与MPPT控制和风储微分控制下的系统的调频性能进行对比。目前研究中,尾流效应在时间尺度相对较长的新能源电力系统规划研究方向中常作为风电机组出力的约束条件,对于短时间频率支撑控制的影响相对不大[40-41]。由于风机惯量支撑为短时功率调节(约为2~3 s),本文忽略了尾流效应对单台风电机组短时调频效果的影响。
以ΔPd>0为例,设置风机初始转速wr0为0.84(pu),保守评估下风机虚拟惯量Hvw为6.72 s。通过式(26)、式(27)可计算得到扰动参考功率 ΔPdH1为0.12(pu),ΔPdH2为0.153 6(pu),ΔPdF为 0.165 2(pu),据此设计四种工况,风储协同调速控制器相关参数见表4。
表4 工况1~4中的参数
Tab.4 Simulation parameters in Scenarios 1~4

工况ΔPd(pu)Hmin/sKsminHvw/sHvB/sKwHKbHKbF 10.151000000 20.136.513.0120400 30.16816.016.7212.813.4425.60 40.18918.0110.4515.5220.931.0460.4
工况1:设置扰动ΔPd=0.1(pu),根据式(13)可得系统最小惯量需求Hmin=5 s,此时同步机可提供的惯量为6 s,风、储无需启动虚拟多段协同调速控制。
工况2:设置扰动ΔPd=0.13(pu),此时系统最小惯量需求Hmin=6.5 s,由于ΔPdH1<ΔPd<ΔPdH2,频率偏离阶段控制启动,风机需具备惯量支撑能力。依据式(15),风机需提供惯性响应时间为2 s,储能无需参与系统频率支撑。
工况3:设置扰动ΔPd=0.16(pu),此时系统最小惯量需求Hmin=8 s,由于ΔPd>ΔPdH2,频率偏离阶段控制启动,储能也需附加惯量控制向系统提供功率支撑。依据仿真参数与式(15),风机需提供惯性响应时间为6.72 s,储能需提供的惯性时间常数为12.8 s。
工况4:设置扰动ΔPd=0.18(pu),根据式(23)可得系统一次调频需求Kmin=18.01 MW/Hz,由于Kmin>KGLD,系统一次调频能力不足,储能应具备一次调频能力,频率恢复阶段控制启动。
系统采用MPPT控制时,设置控制器参数KwH=0,KbH=0;采用风储微分控制时,设置参数KwH=6,KbH=10;采用所提多段协同调速控制时,KwH、KbH与KbF设置为基于式(28)的调整值。
工况1中,系统转速响应如图9所示,最大转速偏差量为-0.010 4(pu),系统频率最大跌落速率为-0.008 4(pu),稳态偏差为-0.006 6(pu),满足转速安全约束,系统无需启动虚拟多段协同调速控制,避免了风储频繁动作。
工况2下,系统动态响应曲线如图11所示,可知,ΔPd=0.13(pu)时,MPPT控制下系统最大转速偏差量Δwmax为-0.013 7(pu),稳态转速偏差Δwst为 -0.008 1(pu),满足转速安全约束,但扰动初期系统转速跌落速率dw/dt为-0.013 6(pu),超过转速变化率安全限制,需启动频率偏离阶段协同调速控制,将系统转速及频率变化率约束在安全范围内。
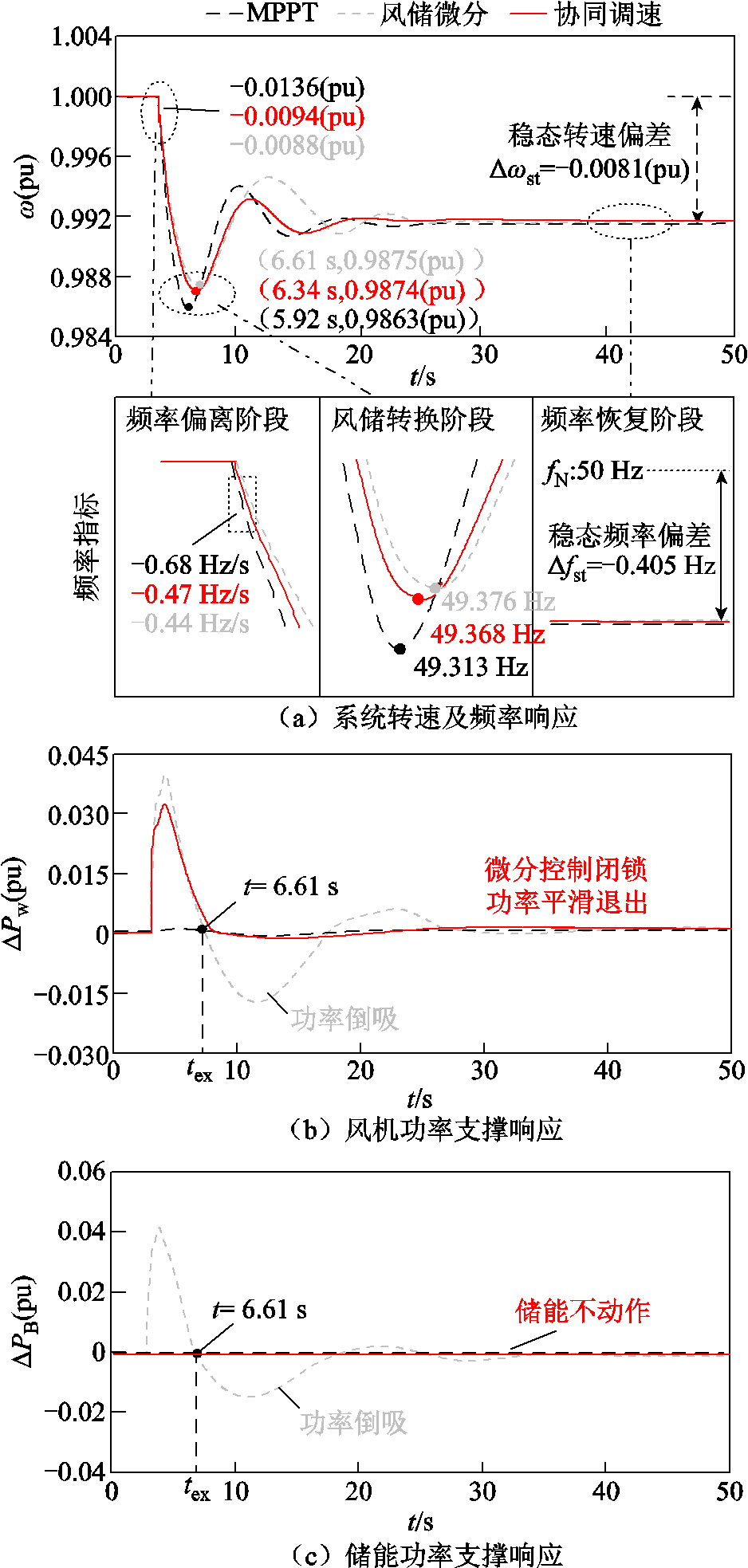
图11 工况2下系统动态响应曲线
Fig.11 System dynamic response curves in Scenario 2
风储微分控制下,风储惯量参数固定,扰动开始时刻,系统转速跌落速率为-0.008 8(pu),Δwmax为-0.012 5(pu),扰动较小的情况下虽然能满足转速安全约束,但风储微分控制不能及时启停,导致风机在转速恢复过程倒吸功率,不利于系统角频率恢复,应启动风储转换阶段协同调速控制闭锁风机惯性响应。
采用本文所提协同调速控制后,频率偏离阶段与风储转换阶段协同调速控制启动。由图11可知,所提控制下系统最大转速偏差量Δwmax和变化率dw/dt分别为-0.012 6(pu)和-0.009 4(pu),在转速安全限值以内;系统频率最大偏差量Δfmax与频率变化率df/dt分别为-0.632 Hz和-0.47 Hz/s,满足频率安全约束。虽然所提控制在转速及调频指标需求上与风储微分控制效果相差不大,但风储转换阶段控制启动,风机微分控制在tex闭锁,惯性响应功率平滑退出,系统角频率恢复过程中超调量明显减小。此外,在工况2中,风储微分控制下风机提供固定惯量支撑3 s,实际风机仅需提供2 s即可,风机出力盈余,本文所提控制下风机出力减小,减少了风机功率波动,更利于风机自身的稳定运行。由于在工况2中,扰动未达到储能启动惯量或一次调频控制的条件,因此储能无需出力,这可以减少储能充放电次数,有利于延长储能寿命。
工况3下系统动态响应曲线如图12所示。由图12可知,ΔPd=0.16(pu)时,MPPT控制下系统转速稳态偏差Δwst为-0.009 8(pu),扰动初期转速跌落速率为-0.016 2(pu),转速最大偏差量Δwmax为-0.016 3(pu),其中转速跌落速率已不满足系统转速安全指标。采用风储微分控制时,系统Δwmax减小为-0.015 1(pu),dw/dt降低为-0.013(pu),仍无法满足转速变化率安全约束,且风储在系统角频率恢复期倒吸功率,加重了系统调速负担。
采用本文所提控制,频率偏离阶段、风储转换阶段协同调速控制启动,系统Δwmax与dw/dt分别减小至-0.013 7(pu)与-0.008 4(pu),符合系统转速安全指标。由图12可知,在协同调速控制下,系统频率指标Δfmax与df/dt均优于MPPT与风储微分控制,分别为-0.684 Hz与-0.42 Hz/s,满足了系统频率安全需求,同时,依据系统调频指令,风储均启动惯量控制参与系统功率支撑,且在极值时间tex平滑退出,系统角频率恢复过程中超调量减小。由图12a可知,该工况下系统转速稳态偏差Δwst<0.01(pu),在安全约束内,系统无需启动频率恢复阶段调速控制,但由于所设置扰动ΔPd(0.16(pu))与ΔPdF(0.165 2(pu))接近,系统转速稳态偏差已临近约束限值。
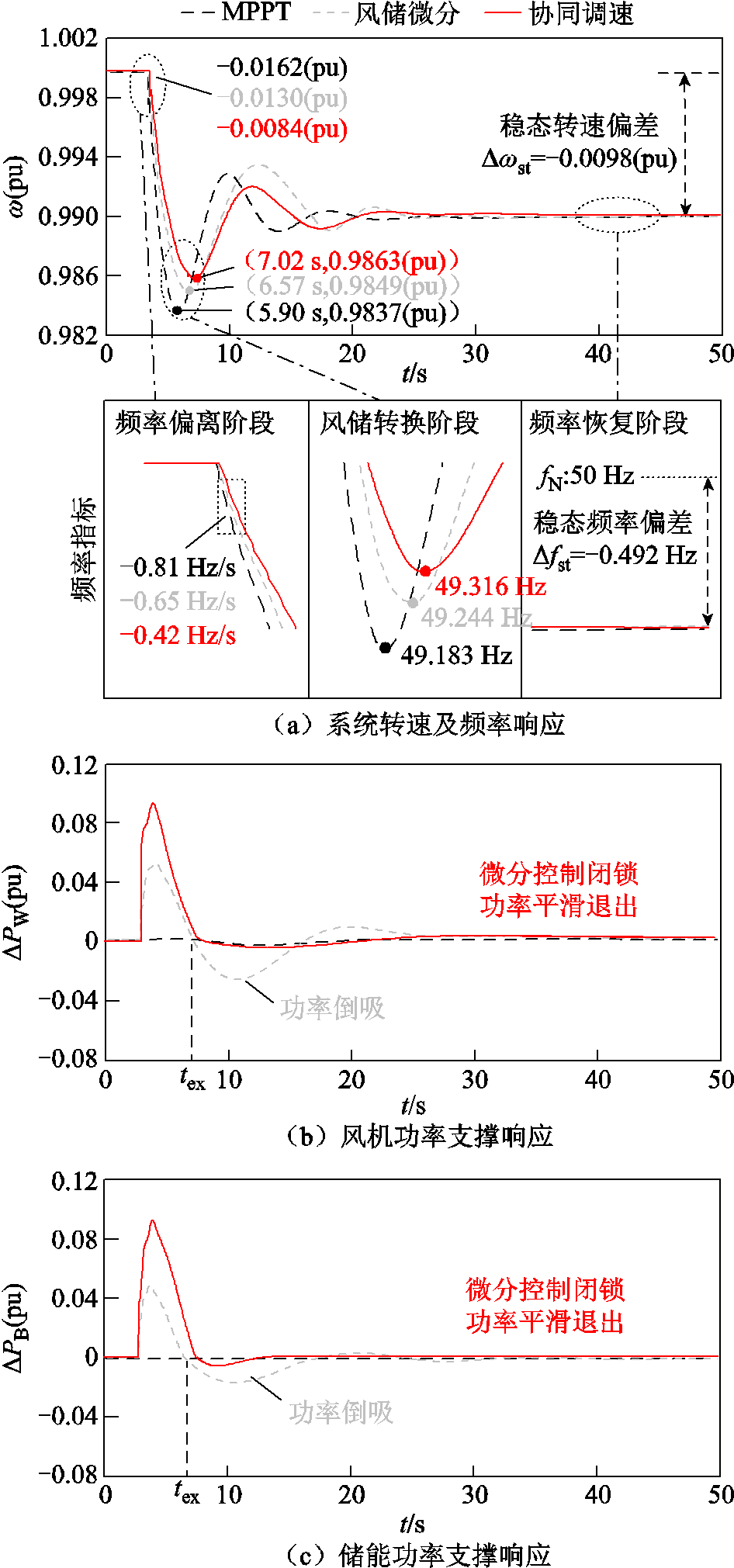
图12 工况3下系统动态响应曲线
Fig.12 System dynamic response curves in Scenario 3
工况4下系统动态响应曲线如图13所示,所设ΔPd>ΔPdF,系统频率恢复阶段调速控制动作,储能启动一次调频控制参与系统调频工作。由图13可知,ΔPd=0.18(pu)时,MPPT控制下系统转速跌落最大幅值Δwmax为-0.019 1(pu),接近转速最大偏差量约束边界,存在失稳风险;系统转速最大变化率dw/dt为 -0.019(pu),转速稳态偏差Δwst为-0.011 3(pu),已不满足转速安全约束。风储微分控制下,系统Δwmax减小为-0.017 7(pu),dw/dt减小为-0.013 8(pu),系统转速变化率仍不满足安全指标。
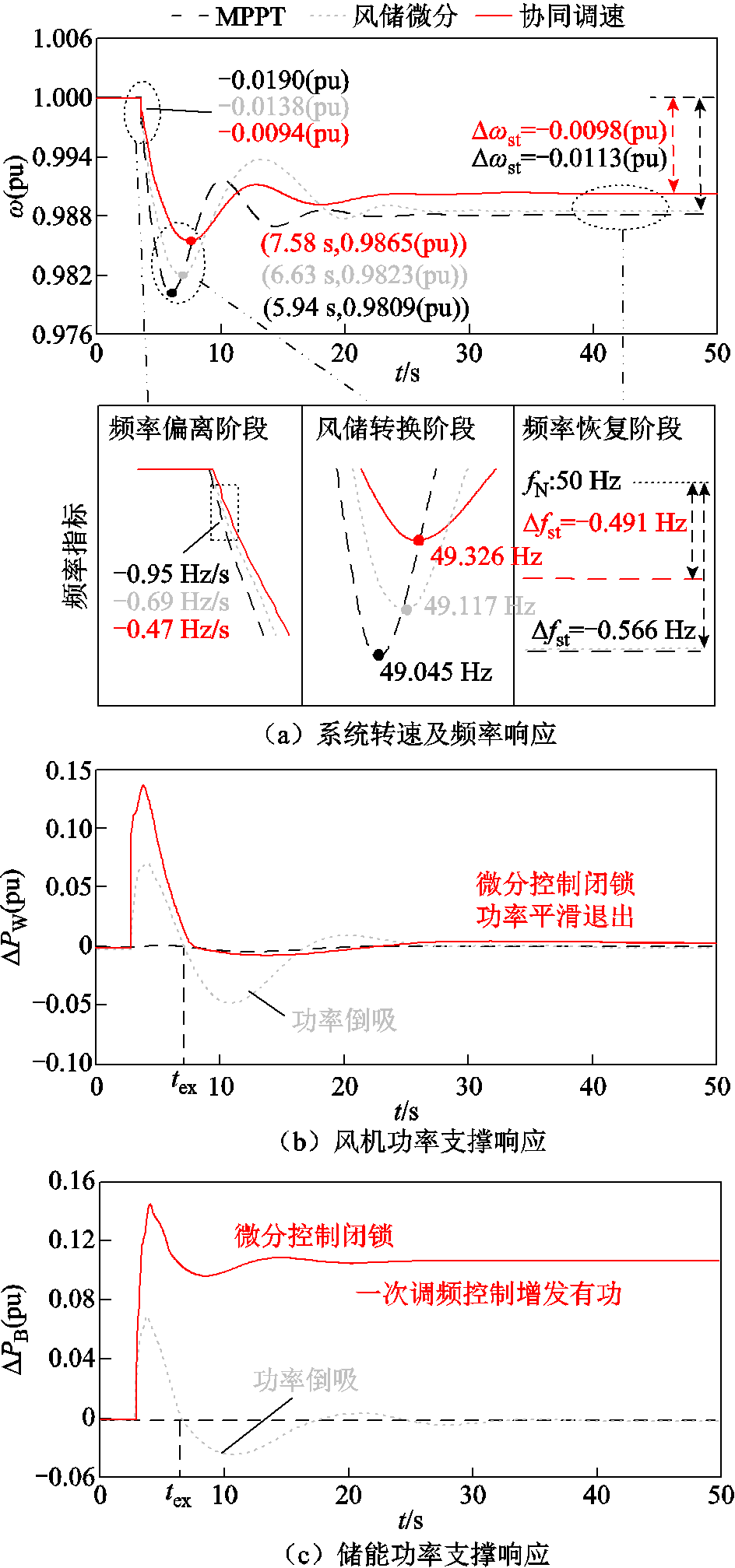
图13 工况4下系统动态响应曲线
Fig.13 System dynamic response curves in Scenario 4
采用本文所提控制,系统频率偏离、风储转换与频率恢复三个阶段协同调速控制启动,系统Δwmax、Δwst与dw/dt分别减小至-0.013 5(pu)、-0.009 8(pu)与-0.009 4(pu),满足了系统转速安全约束。由图13可知,所提控制下,系统频率最大偏差量Δfmax和频率变化率分别减小至-0.674 Hz和-0.47 Hz/s,优于MPPT与风储微分控制,满足系统频率安全指标,风储微分控制在tex时刻闭锁,惯性响应功率平滑退出。同时,储能启动一次调频控制迅速增发有功功率,弥补同步机一次调频能力的不足。系统稳态频率偏差在恢复过程中显著减小,由MPPT控制下的-0.566 Hz减至-0.491 Hz,满足了系统频率安全需求。
综上所述,纵向观察工况1~4中系统的转速及频率响应,MPPT控制下,系统转速响应极值时间tex几乎不变,约为5.9 s;风储微分控制下由于风储所提供的惯性时间常数不变,tex大小也几乎不变,约为6.6 s;本文所提协同调速控制下,极值时间tex随风储惯性出力增加而增大,这有利于系统的频率稳定,也与第2节风储系统转速响应影响因素规律相符,验证了所提转速响应模型的适用性。此外,在所提控制策略中,频率信号采集于新能源并网点。若区域频率波动造成本地电网频率变化,所提控制可以通过监测新能源并网点所在区域电网的频率安全关键指标,调用风储功率储备,缓解本区域同步机的调频负担,将区域电网频率限制在安全范围以内。
为提升风储并网系统的频率稳定性,本文针对风电机组、储能的频率支撑性能及系统转速响应过程,提出了包含频率偏离、风储转换与频率恢复三阶段的虚拟多段协同调速频率支撑控制策略,通过分析验证得到主要结论如下:
1)风储可模拟同步发电机组的响应特性参与系统调频,其控制应在兼顾系统转速变化率、转速最大偏差量及稳态偏差三个安全需求约束的基础上,合理地分配风储调频任务,主动完成系统频率支撑。
2)本文建立了风储联合系统转速响应模型,提出了风储协同三阶段调速区域划分方法。利用转速响应极值时间,风储可在频率偏离阶段根据系统转速变化率约束确定系统惯量需求;在风储转换与频率恢复两阶段则满足频率最大偏差量及稳态偏差约束需求,完成一次调频任务。
3)本文提出根据系统调频需求划分扰动区间,生成三阶段风储协同调频指令,完成虚拟多段调速参与系统频率支撑的控制策略。测试结果表明,所提控制策略有利于明晰分配风储调频任务,可有效地调用新能源功率储备,将系统频率约束在安全范围内,可靠满足频率支撑需求。
参考文献
[1] 季克勤, 卢昊威. 考虑多元灵活性资源的配电网协同优化调度[J]. 电气技术, 2024, 25(7): 23-31.
Ji Keqin, Lu Haowei. Coordinative optimization and dispatching of distribution network considering multi-flexible resources[J]. Electrical Engineering, 2024, 25(7): 23-31.
[2] 付媛, 王毅, 张祥宇, 等. 变速风电机组的惯性与一次调频特性分析及综合控制[J]. 中国电机工程学报, 2014, 34(27): 4706-4716.
Fu Yuan, Wang Yi, Zhang Xiangyu, et al. Analysis and integrated control of inertia and primary frequency regulation for variable speed wind turbines[J]. Proceedings of the CSEE, 2014, 34(27): 4706-4716.
[3] 李雪, 李佳奇, 张儒峰, 等. 计及风电出力相关性和条件价值风险的电力系统概率可用输电能力评估[J]. 电工技术学报, 2023, 38(15): 4162-4177.
Li Xue, Li Jiaqi, Zhang Rufeng, et al. Probabilistic available transfer capability assessment in power system considering conditional value-at-risk and correlated wind power[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4162-4177.
[4] 印永华, 郭剑波, 赵建军, 等. 美加“8.14”大停电事故初步分析以及应吸取的教训[J]. 电网技术, 2003, 27(10): 8-11, 16.
Yin Yonghua, Guo Jianbo, Zhao Jianjun, et al. Preliminary analysis of large scale blackout in interconnected North America power grid on August 14 and lessons to be drawn[J]. Power System Technology, 2003, 27(10): 8-11, 16.
[5] 孙华东, 许涛, 郭强, 等. 英国“8·9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192.
Sun Huadong, Xu Tao, Guo Qiang, et al. Analysis on blackout in great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[6] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804.
Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1791-1804.
[7] 董天翔, 翟保豫, 李星, 等. 风储联合系统参与频率响应的优化控制策略[J]. 电网技术, 2022, 46(10): 3980-3989.
Dong Tianxiang, Zhai Baoyu, Li Xing, et al. Optimal control strategy for combined wind-storage system to participate in frequency response[J]. Power System Technology, 2022, 46(10): 3980-3989.
[8] 林莉, 林雨露, 谭惠丹, 等. 计及SOC自恢复的混合储能平抑风电功率波动控制[J]. 电工技术学报, 2024, 39(3): 658-671.
Lin Li, Lin Yulu, Tan Huidan, et al. Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 658-671.
[9] Gautam D, Goel L, Ayyanar R, et al. Control strategy to mitigate the impact of reduced inertia due to doubly fed induction generators on large power systems[J]. IEEE Transactions on Power Systems, 2011, 26(1): 214-224.
[10] Gevorgian V, Zhang Yingchen, Ela E. Investigating the impacts of wind generation participation in interconnection frequency response[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 1004-1012.
[11] 李世春, 黄悦华, 王凌云, 等. 基于转速控制的双馈风电机组一次调频辅助控制系统建模[J]. 中国电机工程学报, 2017, 37(24): 7077-7086, 7422.
Li Shichun, Huang Yuehua, Wang Lingyun, et al. Modeling primary frequency regulation auxiliary control system of doubly fed induction generator based on rotor speed control[J]. Proceedings of the CSEE, 2017, 37(24): 7077-7086, 7422.
[12] Cardenas R, Pena R, Alepuz S, et al. Overview of control systems for the operation of DFIGs in wind energy applications[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7): 2776-2798.
[13] 周天沛, 孙伟. 高渗透率下变速风力机组虚拟惯性控制的研究[J]. 中国电机工程学报, 2017, 37(2): 486-496.
Zhou Tianpei, Sun Wei. Study on virtual inertia control for DFIG-based wind farms with high penetration[J]. Proceedings of the CSEE, 2017, 37(2): 486-496.
[14] 陈萌, 肖湘宁, 赖柏竹. 基于虚拟同步发电机控制的微电网分层频率控制[J]. 高电压技术, 2018, 44(4): 1278-1284.
Chen Meng, Xiao Xiangning, Lai Baizhu. Hierarchical frequency control strategy of microgrids with virtual synchronous generators[J]. High Voltage Engineering, 2018, 44(4): 1278-1284.
[15] Wong W C, Chung C Y. Coordinated damping control design for DFIG-based wind generation considering power output variation[J]. IEEE Transactions on Power Systems, 2012, 27(4): 1916-1925.
[16] 张祥宇, 李凌斐, 边子轩. 基于混合静止能量的虚拟转动惯量控制技术[J]. 电力自动化设备, 2019, 39(11): 50-56.
Zhang Xiangyu, Li Lingfei, Bian Zixuan. Virtual moment inertia control based on hybrid static energy storage[J]. Electric Power Automation Equipment, 2019, 39(11): 50-56.
[17] 孟建辉, 彭嘉琳, 王毅, 等. 考虑储能荷电状态及频率恢复特性的改进型灵活虚拟惯性控制[J]. 电力自动化设备, 2020, 40(6): 100-111.
Meng Jianhui, Peng Jialin, Wang Yi, et al. Improved flexible virtual inertial control considering SOC of energy storage and characteristics of frequency recovery[J]. Electric Power Automation Equipment, 2020, 40(6): 100-111.
[18] 李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J]. 电工技术学报, 2019, 34(18): 3897-3908.
Li Xinran, Cui Xiwen, Huang Jiyuan, et al. The self-adaption control strategy of energy storage batteries participating in the primary frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3897-3908.
[19] 李军徽, 高卓, 李翠萍, 等. 基于动态任务系数的储能辅助风电一次调频控制策略[J]. 电力系统自动化, 2021, 45(19): 52-59.
Li Junhui, Gao Zhuo, Li Cuiping, et al. Control strategy for dynamic task coefficient based primary frequency regulation of wind power assisted by energy storage[J]. Automation of Electric Power Systems, 2021, 45(19): 52-59.
[20] 吴启帆, 宋新立, 张静冉, 等. 电池储能参与电网一次调频的自适应综合控制策略研究[J]. 电网技术, 2020, 44(10): 3829-3836.
Wu Qifan, Song Xinli, Zhang Jingran, et al. Study on self-adaptation comprehensive strategy of battery energy storage in primary frequency regulation of power grid[J]. Power System Technology, 2020, 44(10): 3829-3836.
[21] 王灿, 张羽, 田福银, 等. 基于双向主从博弈的储能电站与综合能源系统经济运行策略[J]. 电工技术学报, 2023, 38(13): 3436-3446, 3472.
Wang Can, Zhang Yu, Tian Fuyin, et al. Economic operation of energy storage power stations and integrated energy systems based on bidirectional master-slave game[J]. Transactions of China Electro-technical Society, 2023, 38(13): 3436-3446, 3472.
[22] Dang J, Seuss J, Suneja L, et al. SOC feedback control for wind and ESS hybrid power system frequency regulation[C]//2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 2012: 1-7.
[23] 张冠锋, 杨俊友, 王海鑫, 等. 基于虚拟同步机技术的风储系统协调调频控制策略[J]. 电工技术学报, 2022, 37(增刊1): 83-92.
Zhang Guanfeng, Yang Junyou, Wang Haixin, et al. Coordinated frequency modulation control strategy of wind farm-storage system based on virtual synchronous generator technology[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 83-92.
[24] 赵晶晶, 李敏, 何欣芹, 等. 基于限转矩控制的风储联合调频控制策略[J]. 电工技术学报, 2019, 34(23): 4982-4990.
Zhao Jingjing, Li Min, He Xinqin, et al. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4982-4990.
[25] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039.
Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[26] 陈春宇, 黄宸恺, 王剑晓, 等. 考虑风电不确定性的调频辅助服务市场多时间尺度出清调度策略[J]. 电工技术学报, 2024, 39(21): 6804-6818.
Chen Chunyu, Huang Chenkai, Wang Jianxiao, et al. Multi-time-scale frequency regulation market clearing and dispatch strategy considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6804-6818.
[27] 张程铭, 柳璐, 程浩忠, 等. 考虑频率安全的电力系统规划与运行优化研究综述与展望[J]. 电网技术, 2022, 46(1): 250-265.
Zhang Chengming, Liu Lu, Cheng Haozhong, et al. Review and prospects of planning and operation optimization for electrical power systems considering frequency security[J]. Power System Technology, 2022, 46(1): 250-265.
[28] Anderson P M, Mirheydar M. A low-order system frequency response model[J]. IEEE Transactions on Power Systems, 1990, 5(3): 720-729.
[29] Larsson M. An adaptive predictive approach to emergency frequency control in electric power systems[C]//Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 2005: 4434-4439.
[30] 汪兴强, 丁明, 韩平平. 互联电力系统可靠性评估的改进等效模型[J]. 电工技术学报, 2011, 26(9): 201-207.
Wang Xingqiang, Ding Ming, Han Pingping. An improved equivalent model for reliability evaluation in interconnected power system[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 201-207.
[31] 刘翔宇, 李晓明, 朱介北, 等. 新型电力系统的频率响应模型综述及展望[J]. 南方电网技术, 2022, 16(10): 38-47.
Liu Xiangyu, Li Xiaoming, Zhu Jiebei, et al. Review and prospect on frequency response models of new power system[J]. Southern Power System Technology, 2022, 16(10): 38-47.
[32] Shi Qingxin, Li Fangxing, Cui Hantao. Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6355-6367.
[33] 孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5192.
Sun Huadong, Wang Baocai, Li Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5192.
[34] Polajžer B, Dolinar D, Ritonja J. Estimation of area’s frequency response characteristic during large frequency changes using local correlation[J]. IEEE Transactions on Power Systems, 2016, 31(4): 3160-3168.
[35] Meng Xin, Liu Jinjun, Liu Zeng. A generalized droop control for grid-supporting inverter based on comparison between traditional droop control and virtual synchronous generator control[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5416-5438.
[36] 叶婧, 林涛, 张磊, 等. 考虑动态频率约束的含高渗透率光伏电源的孤立电网机组组合[J]. 电工技术学报, 2017, 32(13): 194-202.
Ye Jing, Lin Tao, Zhang Lei, et al. Isolated grid unit commitment with dynamic frequency constraint considering photovoltaic power plants participating in frequency regulation[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 194-202.
[37] Ju Ping, Zheng Yi, Jin Yuqing, et al. Analytic assessment of the power system frequency security[J]. IET Generation, Transmission & Distribution, 2021, 15(15): 2215-2225.
[38] 国家能源局. 电力系统自动低频减负荷技术规定: DL/T 428—2010[S]. 北京: 中国电力出版社, 2011.
[39] 赵熙临, 林震宇, 付波. 基于风机运行边界分析的电网频率控制方法[J]. 电网技术, 2020, 44(9): 3450-3457.
Zhao Xilin, Lin Zhenyu, Fu Bo. Frequency control method in grid based on boundary analysis of wind turbine operation[J]. Power System Technology, 2020, 44(9): 3450-3457.
[40] Hu Zhengyang, Gao Bingtuan, Mao Yongheng. Nonlinear model predictive control-based active power dispatch strategy for wind power plant considering dynamic wake effect[J]. International Journal of Electrical Power & Energy Systems, 2023, 148: 108996.
[41] 韩帅, 张峰, 丁磊, 等. 基于混合Copula函数的风电场可用惯量评估方法[J]. 电力自动化设备, 2021, 41(3): 189-195, 210.
Han Shuai, Zhang Feng, Ding Lei, et al. Available inertia evaluation method of wind farm based on mixed Copula function[J]. Electric Power Automation Equipment, 2021, 41(3): 189-195, 210.
Abstract With the increasing proportion of new energy units in power system, the inertia and primary frequency regulation capability are insufficient. Although the grid-connected specificationsmandating wind power and energy storage standards, there is still a room for improvement on how to use the power from energy storage in conjunction with wind turbines to ensure the safety of the system frequency. According to the frequency safety index constraint, a virtual multi-stage coordinated speed regulation scheme of the wind power and energy storage was proposed in this paper.
Firstly, based on the frequency regulation demand and characteristics of the wind-storage system, a virtual multi-stage coordinated speed regulation process of wind power and energy storage was proposed, which includes three stages: frequency deviation, wind-storage transition and frequency recovery. Secondly, the speed extreme value time of the system was calculated, and its influencing factors were analyzed. Under the constraint of frequency safety indices, a novel virtual multi-stage coordinated speed regulation control strategy of wind power and energy storage was proposed and the design basis of controller parameters were given. Finally, a grid-connected wind-storage simulation system was built to verify that the virtual multi-stage speed regulation can effectively assist the rapid recovery of the system frequency and ensure the safety of the system frequency.
Simulation results show that compared to maximum power point tracking (MPPT) or differential control of the wind power and energy storage, the proposed virtual multi-stage speed regulation control scheme can effectively reduce the frequency drop rate of the system, and the inertia response power of the wind power and energy storage smoothly can exit at the extreme time, the overshoot decreases obviously during the recovery of system speed. When the disturbance power is small, the wind power and energy storage does not need to participate in the system power support. When the disturbance power is large, the frequency regulation of wind power and energy storage need to be invested successively to provide power support to ensure the frequency safety of the system.
The main conclusions by simulation analysis and verification are as follows: (1) The wind turbine and energy storage devices can adopt primary frequency regulation and virtual inertia control to participate in system frequency regulation. The control should take into the three safety requirements,namely,the rate of change of system speed (dw/dt), the maximum frequency deviation (Δwmax) and the steady-state frequency deviation (Δwst). (2) By using the proposed method of three-stage speed regulation region division and speed response extremum time calculation, the inertia demand of the system can be determined according to the (dw/dt)max at the frequency deviation stage, the primary frequency regulation demand can be determined according to the Δwmax and Δwst at the wind-storage conversion and frequency recovery stage. (3) According to the frequency regulation demand of the system, the disturbance interval was divided and a three-stage wind storage cooperative frequency regulation command was generated. The test results show that the proposed control strategy is conducive to clearly allocating the frequency regulation tasks of the wind power and energy storage, effectively invoke the new energy power reserve, limiting the system frequency within the safe range, and reliably meeting the frequency support requirements.
Keywords:Frequency regulation demand, virtual speed, extreme value time, coordinated speed regulation, frequency safety
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.241464
国家自然科学基金(52277100)、河北省自然科学基金(E2023502038)和中央高校基本科研业务费(2023MS101)资助项目。
收稿日期 2024-08-18
改稿日期2024-11-08
张祥宇 男,1984年生,副教授,博士生导师,研究方向为风力发电控制技术。
E-mail:zh.xy.sq@163.com(通信作者)
邵孜建 男,1999年生,硕士研究生,研究方向为新能源发电控制技术。
E-mail:1933431446@qq.com
(编辑 赫 蕾)