 )与腐蚀算子(
)与腐蚀算子( )分别为
)分别为摘要 针对交流接触器运行状态特征数据模态混叠和分辨率低难以有效降噪的问题,该文提出一种基于自适应多尺度形态学滤波(AMMF)的特征数据降噪方法。首先,利用曲线包络将特征数据分解为多尺度分量,并引入Triangle阈值与自适应结构元素来改进传统形态学滤波技术,使其适应不同尺度频谱分布差异,构建AMMF降噪模型。然后,根据分量自相关函数特性辨别含噪分量,使用AMMF提取含噪分量有效频段,并对该频段逆变换重构为特征数据。最后,对比六种常见降噪技术,以信噪比、互相关系数与平均自相关系数为指标,结合实例进行分析,结果表明所提方法可有效降低交流接触器特征数据含噪量。
关键词:交流接触器 形态学滤波 数据降噪 包络分解 自相关系数
交流接触器是一种用于频繁接通和断开电机或负载主电路的控制电器,其稳定性对被控系统的安全至关重要。随着触头动作次数增加,触头表面受电弧烧蚀而发生熔焊,导致线路失控[1-4]。因此,对交流接触器进行可靠性分析显得尤为关键,而这一分析依赖于高质量的运行状态特征数据。然而,电气干扰和测量误差等因素常导致数据被噪声淹没,故需要对特征数据进行有效降噪处理。
目前,经验模态分解(Empirical Mode Decom- position, EMD)、小波降噪(Wavelet Denoising, WD)、奇异值分解(Singular Value Decomposition, SVD)、中值滤波等方法广泛运用于各领域数据降噪研究。以SVD、中值滤波为代表的统计学降噪方式[5-6]可以快速降低数据复杂度,但会丢失物理意义。WD与EMD将原始数据分解为多尺度分量,进而结合峭度等指标剔除特定尺度分量以滤除噪声[7]。然而,WD对参数设置较为敏感,且易受稳态噪声影响而出现高频残留[8-10];EMD对稳态噪声有较好的鲁棒性,但辨别具有相似主频的虚假分量严重依赖专家经验[11-12]。部分研究者提出联合降噪方法,如EMD- WD,解决了高频残留和虚假分量辨别问题,但未充分考虑参数敏感和维数灾问题。文献[13-14]提出基于高斯分布三倍标准差范围的有效频段降噪技术,但受中心频率偏移影响而保留高频噪声。上述方法在多个领域得到广泛应用和深入研究,但针对交流接触器特征数据的降噪研究却相对匮乏。作为控制系统中的关键组件,接触器的特征数据质量对于设备性能评估和故障诊断至关重要。因此,确定一种适合交流接触器特征数据的降噪方法对提高控制系统可靠性具有重要意义。
相较于上述传统方法,神经网络和形态学滤波技术在处理非线性数据时表现更为出色。神经网络的自适应学习能力使其能够捕捉数据中的复杂非线性关系,但其对基底知识要求过高,否则信息提取与隐藏表示难以解释[15-16],而形态学滤波则专注于数据的主要形态,通过集合运算来平滑数据,能有效去除毛刺和异常值,且过程更为直观,结果更易于解释。文献[17-18]将形态学滤波直接运用于振动信号处理和风机叶片疲劳测试,取得了较好的降噪效果。文献[19-20]结合多尺寸结构元素对形态学滤波进行改进以提高在复杂数据上的降噪分辨率和降噪效果。上述研究将形态学滤波运用于其他领域并取得了预期效果,但结构元素尺寸和阈值方法设置仍旧依赖主观经验且单一。因此,为使该技术能有效处理接触器特征数据,确定合适的结构元素尺寸与二值化阈值方法至关重要。
综上所述,针对交流接触器运行特征数据模态混叠和分辨率低导致现有降噪技术难以有效降噪的问题,本文提出一种基于自适应多尺度形态学滤波(Adaptive Multi-scale Morphological Filter, AMMF)的降噪方法。首先,引入包络分解、自适应结构元素与Triangle阈值对传统形态学滤波技术进行改进,缓解模态混叠等现象对降噪效果的影响,提高降噪分辨率;其次,引入自相关函数界定含噪分量,降低输入维度;然后,利用改进形态学滤波技术提取含噪分量有效频段,并逆变换重构为降噪后特征数据;最后,对比六种常见降噪技术,以基于谱估计的信噪比等三种指标评判降噪效果。结果表明,本文方法可有效降低交流接触器特征数据含噪量,并保留有效信息。
形态学滤波是一种应用广泛的非线性数据降噪技术,能够保留数据主要形态特征而滤除噪声。对于时序数据x(n)(n=1, 2,…, N)与结构元素序列g(m)(m=1, 2,…, M),定义膨胀算子( )与腐蚀算子(
)与腐蚀算子( )分别为
)分别为
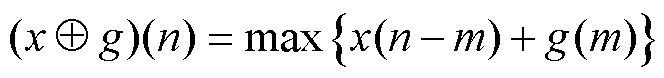 (1)
(1)
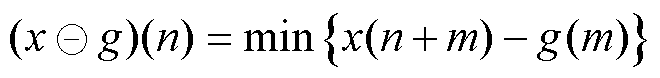 (2)
(2)
据膨胀算子与腐蚀算子的顺序组合,定义形态开算子(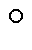 )和形态闭算子(
)和形态闭算子(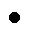 )分别为
)分别为
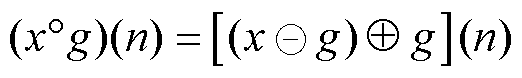 (3)
(3)
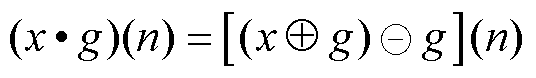 (4)
(4)
开算子消除数据毛刺。闭算子填充数据细小间隙,平滑数据。由开闭算子组合而成的级联形态学滤波技术定义为
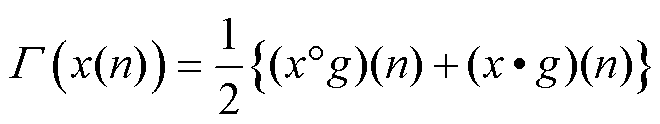 (5)
(5)
稀疏信号分辨率较高,这种降噪方式有较好的降噪效果[17-18]。但实际数据稀疏度和分辨率较低,间隙与毛刺无法被精准识别,存在过度平滑风险。
考虑交流接触器运行状态特征数据的复杂程度,本文对传统形态学滤波做三部分改进:引入多尺度分量概念、调整结构元素计算方式和引入Triangle阈值。
1.2.1 多尺度分量
根据数据包络,将该数据分解为有限个本征模态函数(Intrinsic Mode Function, IMF)和残差分量,过程如下:
(1)搜寻x(n)在时域内所有极值点,利用三次样条插值对极值点序列拟合,产生上包络线emax,1(n)和下包络线emin,1(n),计算上下包络线均值eavg,1(n)为
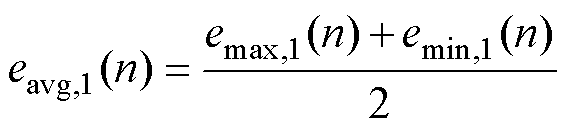 (6)
(6)
(2)以x(n)与eavg,1(n)的差值为第一个IMF分量c1(n),有
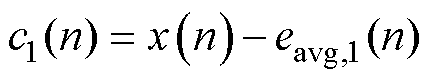 (7)
(7)
(3)将r2(n)作为待分解的原始数据,重复式(6)~式(8)直至分解出的分量为单调函数。
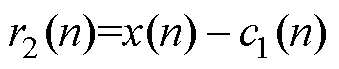 (8)
(8)
(4)最终,x(n)被分解为Z个IMF分量和1个残差分量,有
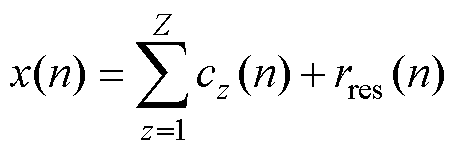 (9)
(9)
式中,rres(n)为残差分量且单调。
1.2.2 自适应结构元素
为了使结构元素能够精准识别复杂实际数据的细小间隙与毛刺,本文调整结构元素计算方式:
(1)由于c1(n)由稳态噪声主导,故将其剔除。定义cz(n)(z=2,…, Z)为待处理分量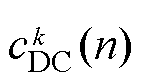 (k=1,…, Z-1),并对
(k=1,…, Z-1),并对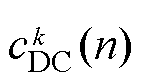 进行傅里叶变换,有
进行傅里叶变换,有
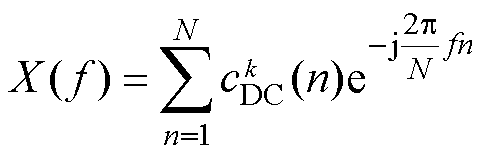 (10)
(10)
式中,N和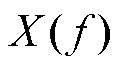 分别为
分别为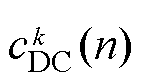 长度和频域表示;f为频率;j为虚数。
长度和频域表示;f为频率;j为虚数。
(2)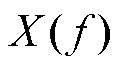 的频率与幅值分别记为f(i)={fi|i= 1, 2,…, F}和A(i)={Ai|i=1, 2,…, F},其中,F为频域长度。由于g(m)为长条形结构元素序列,故m为g(m)宽度。
的频率与幅值分别记为f(i)={fi|i= 1, 2,…, F}和A(i)={Ai|i=1, 2,…, F},其中,F为频域长度。由于g(m)为长条形结构元素序列,故m为g(m)宽度。
(3)X(f)所有极值点的频率与幅值,分别记为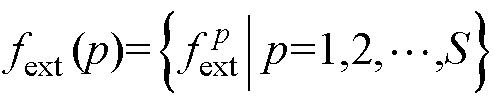 和
和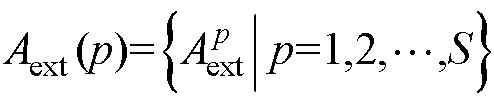 ,其中,S为局部极值点个数。
,其中,S为局部极值点个数。
(4)归一化Aext(p),得到归一化极点幅值 Anorm(p)为
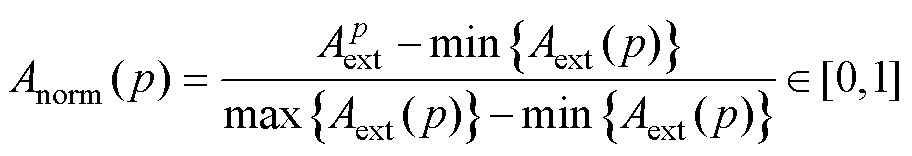 (11)
(11)
(5)定义非线性映射函数h以确定第i个频率对应的元素结构宽度mi为
 (12)
(12)
式中,s为相邻两个局部极值点间的频率个数;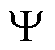 为向上取整函数。
为向上取整函数。
1.2.3 Triangle阈值
相较于时域,从频域分辨数据所含成分更简易,因此本文从分量频域进行降噪。考虑到频谱具有直方图特征,本文采用Triangle阈值法,该法是使用直方图确定阈值的几何方法,实现原理为:记频谱最低点为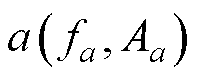 ,向频率尖峰侧搜索所有极大值点
,向频率尖峰侧搜索所有极大值点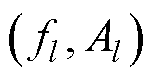 (l=b, b+1,…, a),其中,
(l=b, b+1,…, a),其中,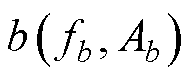 为频谱最高点。连接
为频谱最高点。连接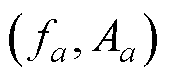 与
与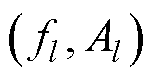 ,记每条直线到频谱的最远垂线为
,记每条直线到频谱的最远垂线为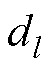 ,将
,将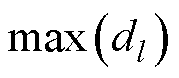 对应的幅值
对应的幅值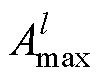 作为阈值T。
作为阈值T。
基于该阈值的二值化原理为:若频率幅值低于该阈值则置0,高于该阈值则置1;根据式(1)~式(12)对数据进行降噪,过程如图1所示。
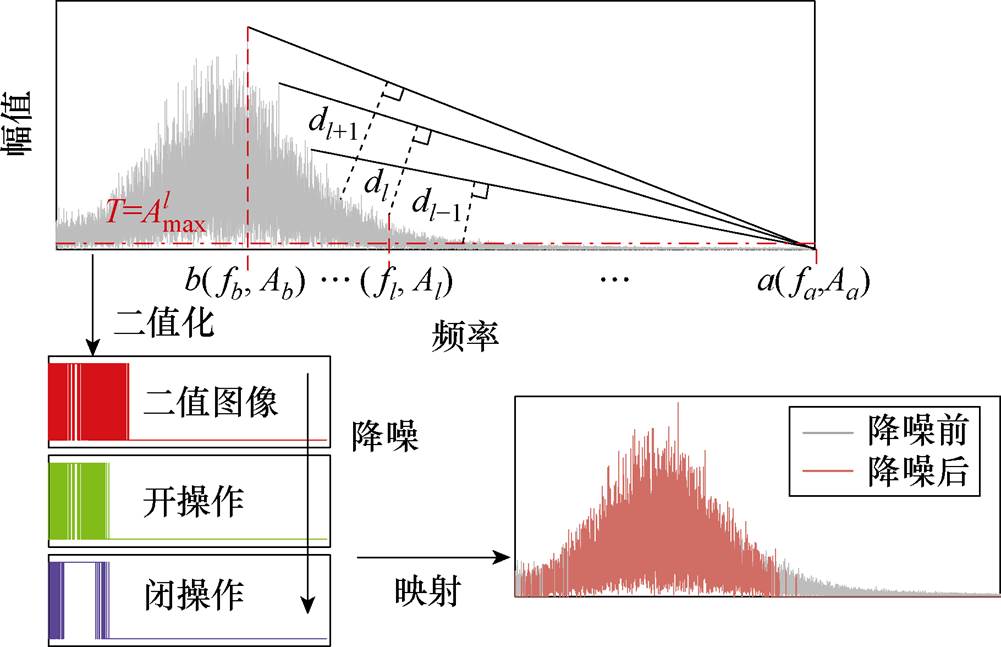
图1 引入Triangle阈值法的二值化过程
Fig.1 Binarization process employing the Triangle thresholding method
特征数据是一种在系统模型未知的情况下提取的时序数据,即x(n)是未知信号,无法利用特定指标来辨别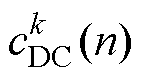 含噪程度。因此,本文引入自相关函数作为信噪分界点确定方法[21-23]。
含噪程度。因此,本文引入自相关函数作为信噪分界点确定方法[21-23]。
自相关函数(Autocorrelation Function, ACF)用来描述同一时序数据在不同时刻的依赖关系。由于噪声在时域中具有随机性,通常表现为短期自相关;而纯净分量含特定变化规律,表现为长期自相关,因此通过数据在延迟周期的相关性可确定分量含噪程度。若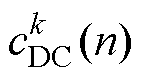 (n=t)为含噪分量,有
(n=t)为含噪分量,有
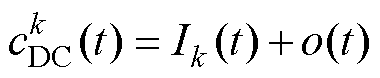 (13)
(13)
式中,Ik(t)为纯净分量;o(t)为噪声。
则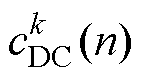 自相关函数为
自相关函数为
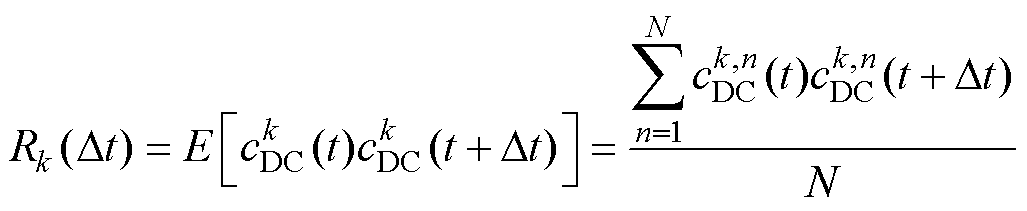
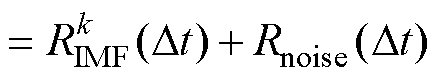 (14)
(14)
式中,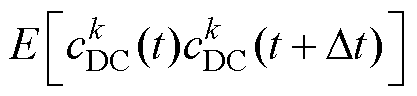 为时序数据
为时序数据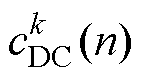 在t时刻与t+Dt时刻元素乘积的均值;
在t时刻与t+Dt时刻元素乘积的均值;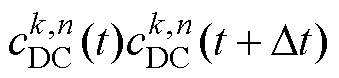 为第n个不同元素的乘积;
为第n个不同元素的乘积;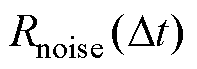 为噪声的自相关系数;
为噪声的自相关系数;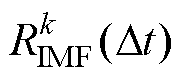 为纯净分量的自相关系数。
为纯净分量的自相关系数。
由于o(t)具有短期自相关性,故当Dt≠0时,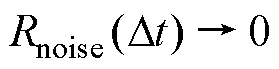 ,
,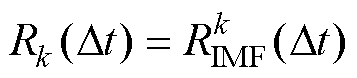 。根据关联度标准(见表1),当Dt≠0时,若
。根据关联度标准(见表1),当Dt≠0时,若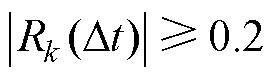 ,该分量具有长期自相关性,属于纯净分量;反之,属于含噪分量,需要降噪处理。基于AMMF的降噪技术路线如图2所示。
,该分量具有长期自相关性,属于纯净分量;反之,属于含噪分量,需要降噪处理。基于AMMF的降噪技术路线如图2所示。
表1 关联度标准
Tab.1 Correlation standards

相关性负正 无相关[0, -0.2[0, 0.2 弱相关[-0.2, -0.4[0.2, 0.4 中等相关[-0.4, -0.6[0.4, 0.6 强相关[-0.6, -0.8[0.6, 0.8 极强相关[-0.8, -1.0][0.8, 1.0]
安全稳定是控制系统的基本要求,故交流接触器开断动作必须可靠准确,为此开展交流接触器全寿命试验并从电压/电流信号提取其重要特征。根据GB 14048.4—2010搭建交流接触器全寿命试验平台,部分试验条件见表2。
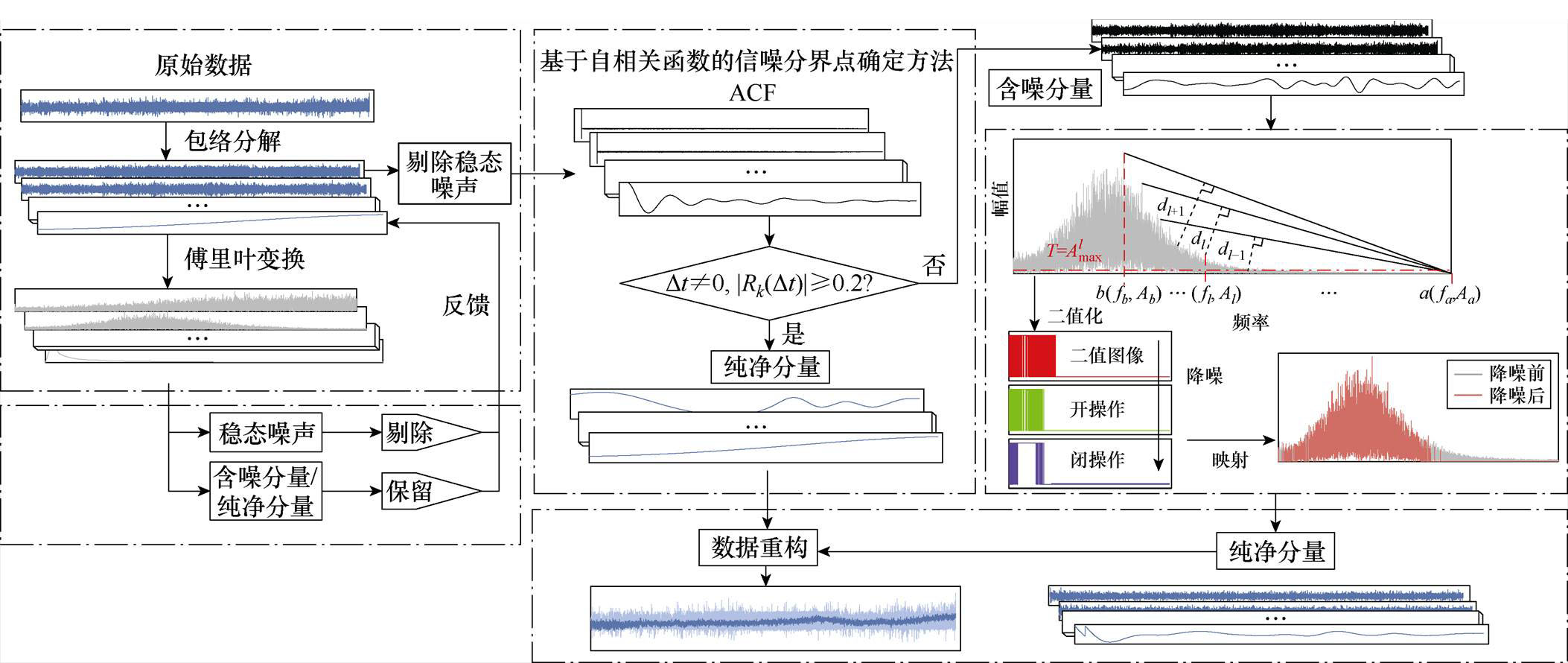
图2 基于AMMF的降噪技术路线
Fig.2 Roadmap of denoising technology based on AMMF
表2 试验条件
Tab.2 Experimental conditions
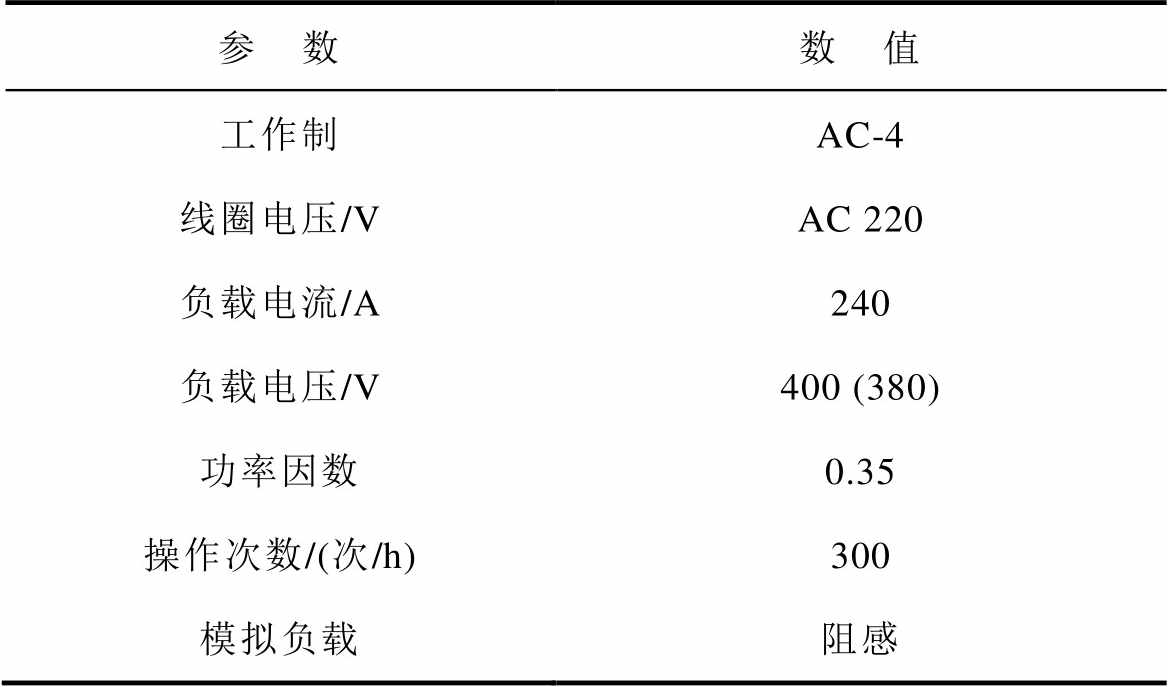
参 数数 值 工作制AC-4 线圈电压/VAC 220 负载电流/A240 负载电压/V400 (380) 功率因数0.35 操作次数/(次/h)300 模拟负载阻感
该试验平台采用USB6356型高速数据采集卡作为采集模块,数据采集卡主要参数见表3,试验平台实物如图3所示。为方便处理数据,数据采集卡采样率设置为1.0 MS/s。另外,本文采用LV25-400、LF310-S和LT58-S7传感器分别测量线圈/触头电压信号、触头电流信号和线圈电流信号,三种传感器主要参数见表4,测量范围和裕量均满足表2试验条件。
表3 数据采集卡主要参数
Tab.3 Main parameters of data acquisition card

参 数数 值 单通道最大值/(MS/s)1.25 模拟转换器分辨率/bit16 模拟输入通道带宽/MHz1 输入耦合DC 定时精度采样率的50×10-6 工作电压范围/V±11
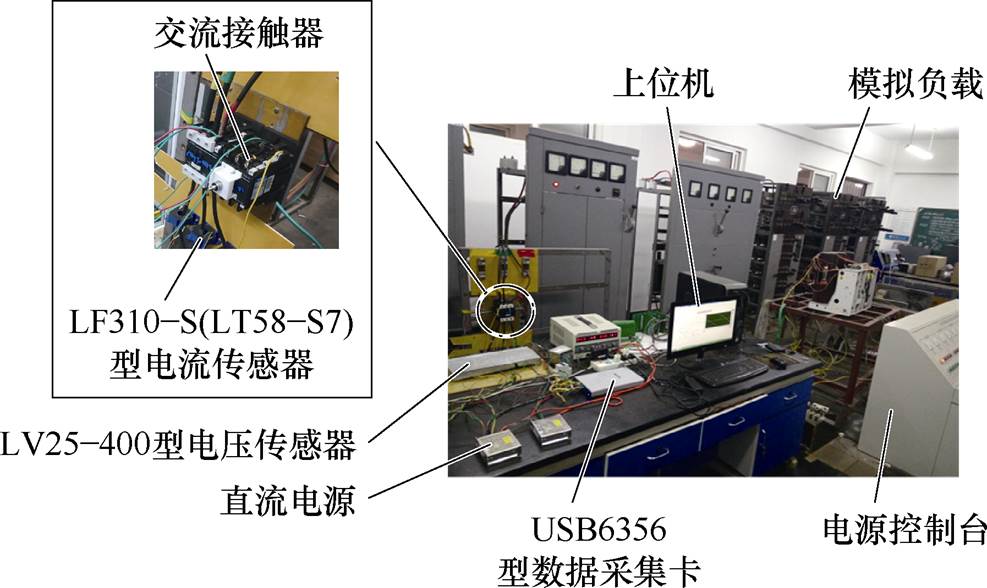
图3 试验平台实物
Fig.3 Physical setup of the experimental platform
表4 传感器主要参数
Tab.4 Main parameters of sensors
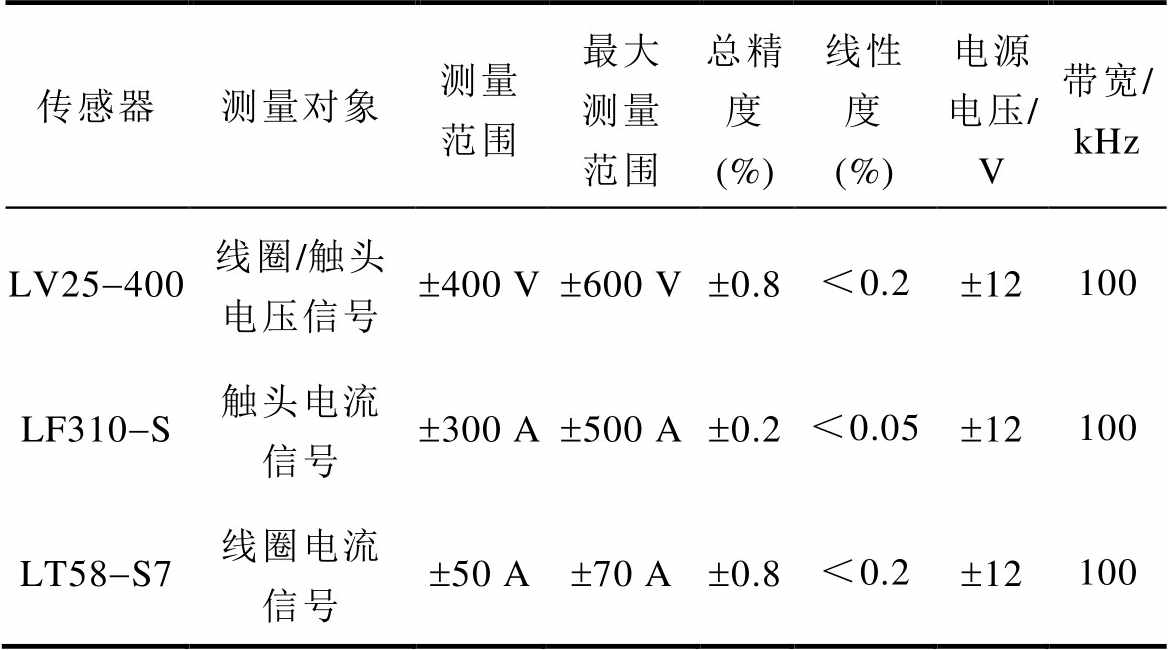
传感器测量对象测量范围最大测量范围总精度 (%)线性度 (%)电源电压/ V带宽/ kHz LV25-400线圈/触头电压信号±400 V±600 V±0.8<0.2±12100 LF310-S触头电流信号±300 A±500 A±0.2<0.05±12100 LT58-S7线圈电流信号±50 A±70 A±0.8<0.2±12100
图4所示为接触器通断过程中电压电流信号,其中,线圈电流信号放大100倍以确保坐标一致性。t1时刻,线圈得电,触头间电磁吸力增大。t2时刻,吸力大于弹簧反力,动静触头第一次吸合,但由于弹簧作用,触头持续弹跳。该过程可提取特征:吸合时间txh,物理意义为线圈得电到触头第一次吸合所需要的时间,有
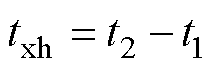 (15)
(15)
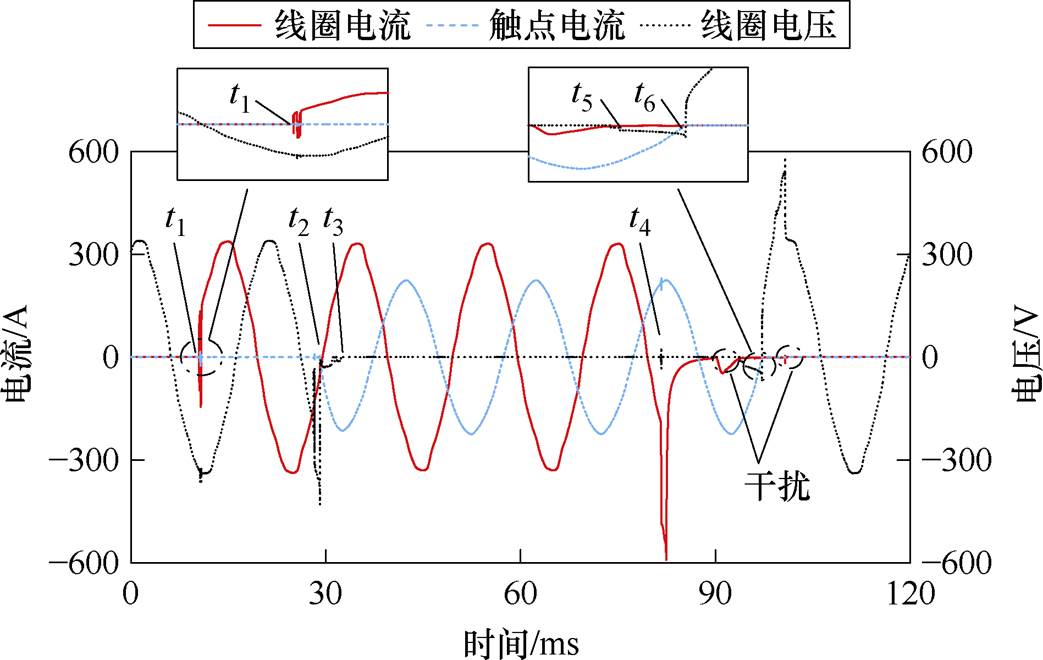
图4 电压电流信号
Fig.4 Voltage and current signals
t3时刻,弹跳消失,触头稳定吸合。该过程可提取特征:弹跳时间ttt,物理意义为触头第一次吸合到稳定吸合所需要的时间,有
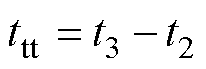 (16)
(16)
t4时刻,线圈失电,电磁吸力减小。t5时刻,吸力不足以维持吸合状态,触头分离。该过程可提取特征:释放时间tsf,物理意义为线圈掉电到触头刚分所需要的时间,有
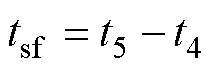 (17)
(17)
上述三种特征从响应动作方面表征触头运行状态[2, 21],是常用的可靠性分析指标。在触头分离时,电弧产生并不断烧蚀触头表面。t6时刻,电流过零,电弧熄灭。该过程触头表面接触电阻发生不可逆改变,从触头表面形态方面表征触头运行状态,其计算方式为
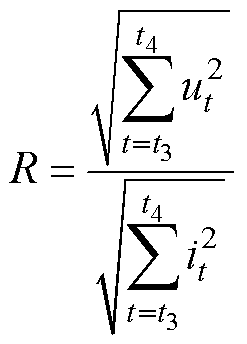 (18)
(18)
式中,ut和it分别为触头稳定吸合到线圈掉电时间段内电压和电流。
四种重要特征的时域趋势如图5所示。根据阈值判断时刻点时,外界干扰会造成程序误判,致使时刻点前移或滞后从而产生异常值或毛刺。线圈电流幅值大于1 A是t1的阈值标准,但当干扰幅值大于1 A时,该干扰会被误判为t1,如图4中t5附近存在两处与特征无关且幅值较大的干扰。同时,t2和t3等时刻的阈值相近,程序除误判干扰外还会将t2判断为t3,致使数据存在负值,如图5弹跳时间所示。另外,触头表面不同位置的劣化程度不同,吸合时电阻会因接触位置不同而有所差异,这也是毛刺现象的原因之一。图5所示为四种特征数据的原始趋势,不难发现,各特征数据存在毛刺和异常值突出现象,需要降噪处理以平滑数据。
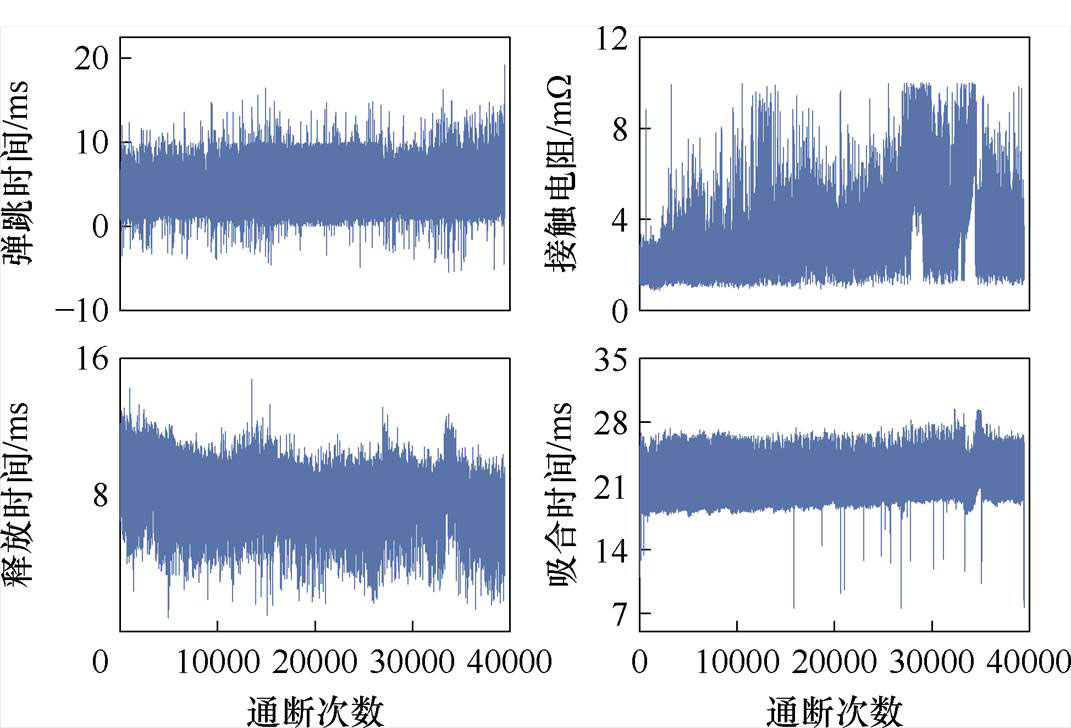
图5 四种重要特征的时域趋势
Fig.5 The time-domain trends of four important features
形态学滤波技术本质上是将数据二值化为01序列,并使用结构元素对该序列进行集合运算,运算结果为元素1则保留原值;反之,则使用邻近值 替代。
图6所示为传统形态学滤波技术处理弹跳时间数据的结果。可以发现,频域数据二值序列含有大量0元素,稀疏度比时域数据高。使用多种细小结构元素对二者进行处理,结果可知,时域数据稀疏性降低,序列中端0元素被全部置1,仅在序列两端保留元素0,即降噪前后数据没有明显变化;而频域数据二值序列稀疏度高,不同尺寸结构元素均取得明显结果。究其原因,频域数据优势频率与非优势频率幅值差异大,二值化后序列稀疏度高,结构元素可更好辨别01元素而提高降噪分辨率,故本文采用频域降噪方式处理特征数据。另外,考虑到图6b所示频谱较为平坦,无法辨别主要频率所处位置,为将元素1集中于主要频率处,本文根据曲线包络将原始数据分解为不同尺度分量,使各分量在特定尺度上具有明显尖峰分布,结果如图7所示。
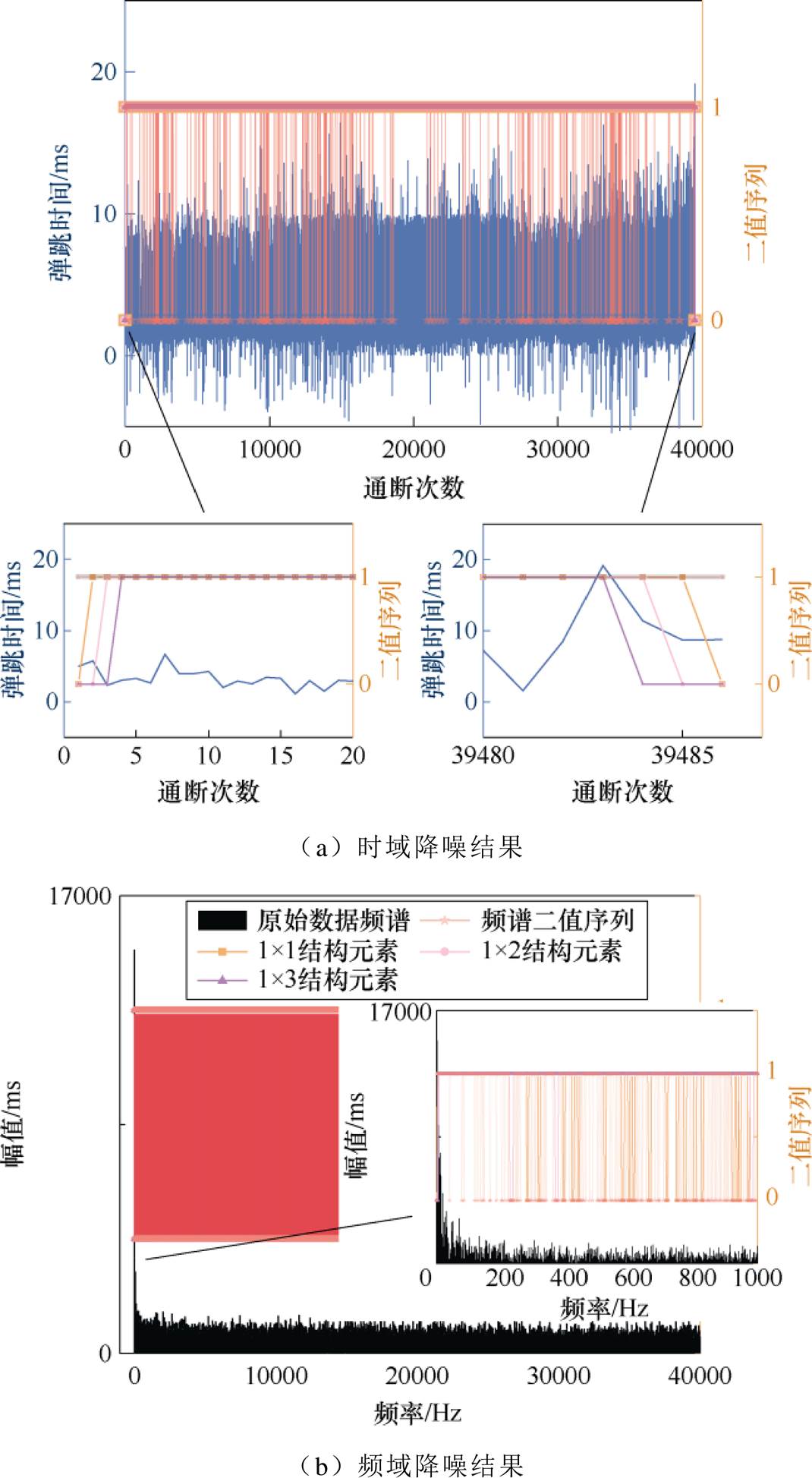
图6 传统形态学滤波技术的降噪结果
Fig.6 Denoising results of traditional morphological filtering technology
由图7b可知,相较于原始数据,分量的集中分布情况有所改善。IMF1主要分布于高频范围且幅值相对其他分量较小,一般认为是噪声主导的分量,故将IMF1直接剔除。IMF2~IMF15主要分布于低频范围,但部分分量含有高频成分,表明这些分量发生模态混叠,受高频成分干扰,需截取有效频段以重构高质量数据。
由1.1节分析可知,形态学滤波的两个核心组件是二值化阈值方法和结构元素,阈值用于将数据转换为二值序列,而结构元素则对这些二值序列进行形态学操作。然而,图6及其分析表明,均值阈值方法易受极值分布的影响,尤其在分量频谱中,优势频率幅值远大于尾部频率幅值,导致阈值偏高,尾部截断现象明显,如图8a所示。针对该问题,本文提出了Triangle阈值方法,其效果如图8b所示,降噪后频谱尾部较平缓,截断现象不明显,利于降噪后数据平滑性。
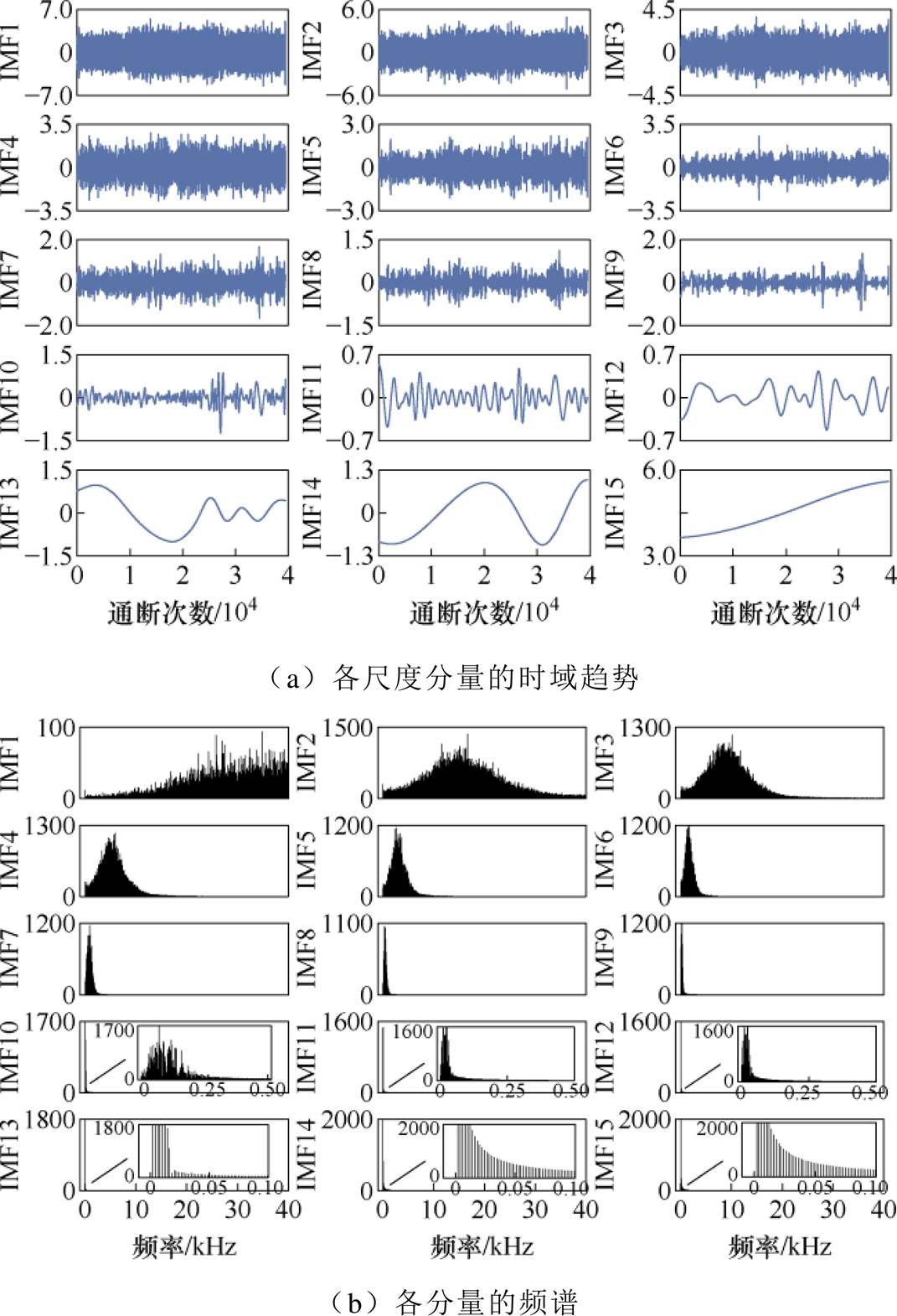
图7 不同尺度分量及其频谱
Fig.7 Different components and their respective spectra
结构元素尺寸设置同样关键,其直接影响降噪效果。单一尺寸结构元素在不同分量上的降噪效果有限,如图9所示,在IMF3中截取低频成分而滤去高频成分,但在相邻尺度IMF2中则过度平滑,仅保留部分优势频率而缺失细节。因此,本文以自适应结构元素替代单一结构元素,实现对不同尺度分量的批量处理,提高所提方法的适应性。
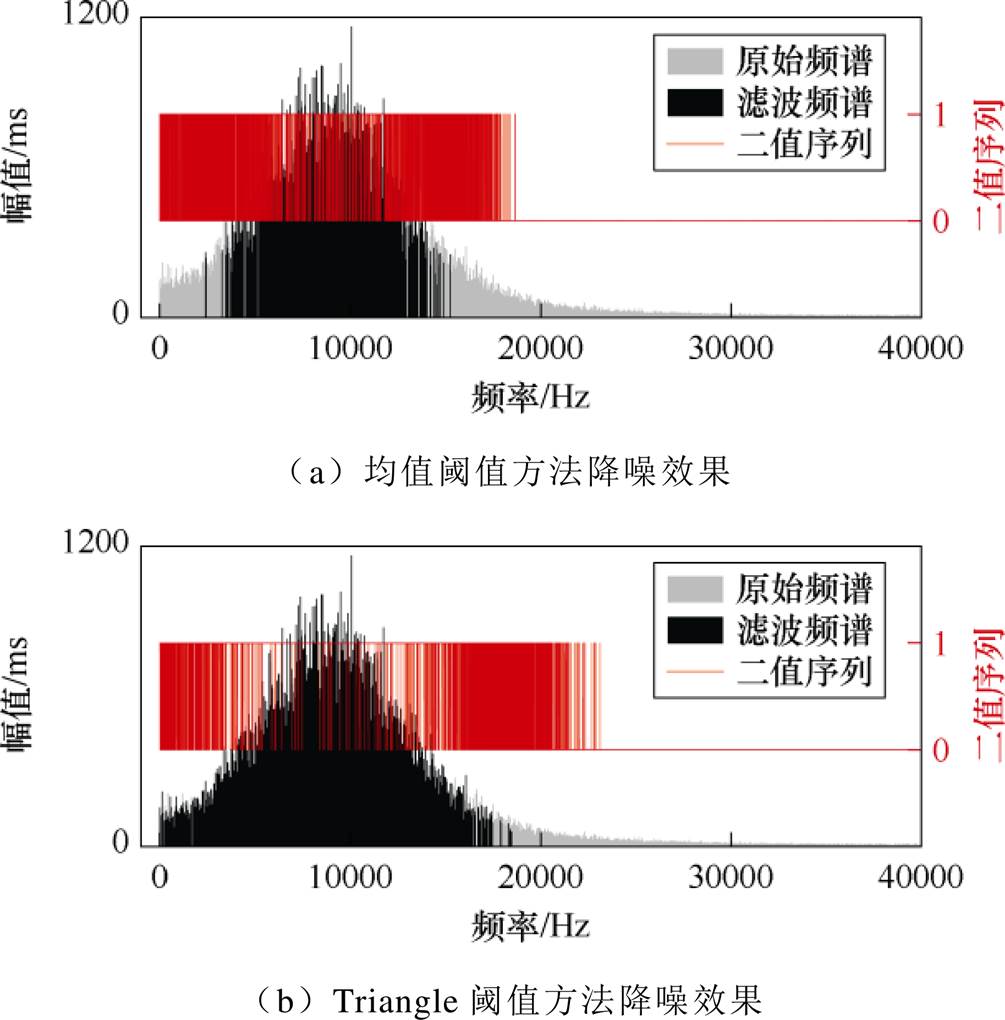
图8 不同阈值方法的降噪效果
Fig.8 Denoising effects of different thresholding methods
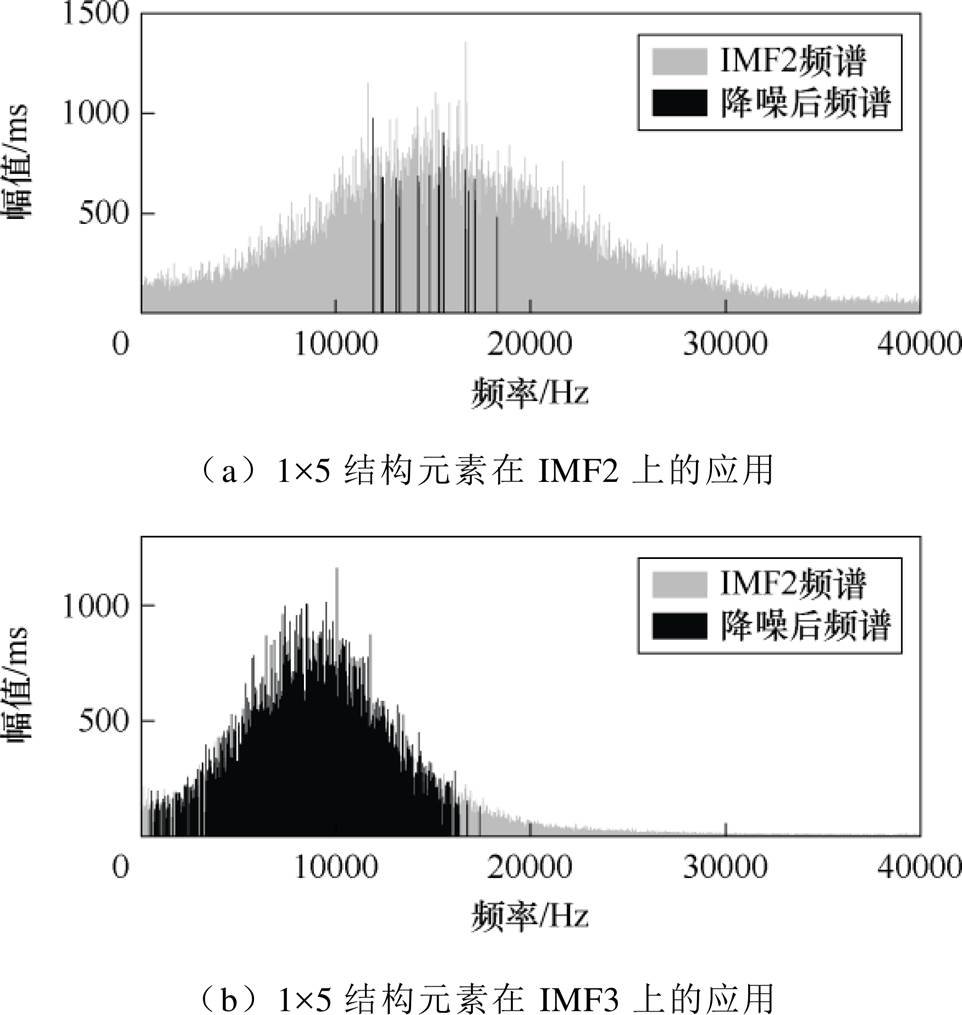
图9 单一结构元素在不同分量上的降噪效果
Fig.9 Denoising effects of a single structuring element on different components
部分文献认为随机噪声以模态混叠形式存在于分量中,可通过波形畸变程度判断噪声含量。如在图7a中,IMF9和IMF10在30 000次通断时幅值有较大变化,属于含噪分量。然而,这种方法在处理如IMF2~IMF5更高频分量时,难以通过肉眼直接判断畸变程度,效率低且主观性大。因此,根据1.3节信噪分界点确定方法,计算IMF2~IMF15中各个分量的自相关函数来确定分量含噪程度,结果如图10所示。根据表1相关性标准,IMF2~IMF12在零延迟时刻自相关系数大于0.2,非零延迟时刻系数小于0.2,表明这些分量受随机噪声干扰而呈现短期自相关性,需要降噪处理;IMF13~IMF15在长期延迟中自相关系数大于0.2且振荡缓慢,说明这些分量趋势未被噪声淹没,是纯净分量。因此,将IMF13~IMF15直接用于数据重构,而IMF2~IMF12作为含噪分量用于降噪处理。
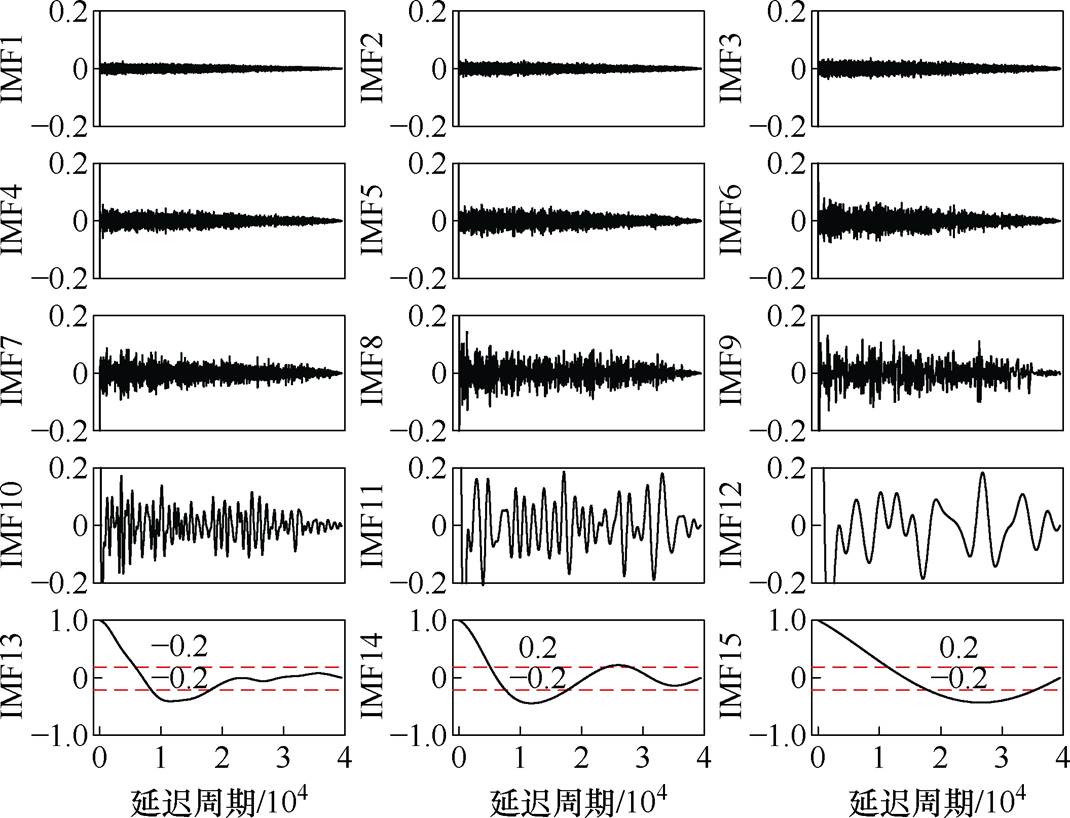
图10 IMF时域自相关函数图
Fig.10 Image of autocorrelation function of IMF component in time series
使用1.2节构建的AMMF提取分量有效频段,结果如图11所示。图11中,各分量频谱降噪前后有明显变化,IMF2剔除了主频两端能量较小的频率,IMF3~IMF12主要剔除频谱右端高频成分。将这些有效频段逆变换回时域并加和重构为降噪后特征数据,降噪结果如图12所示。
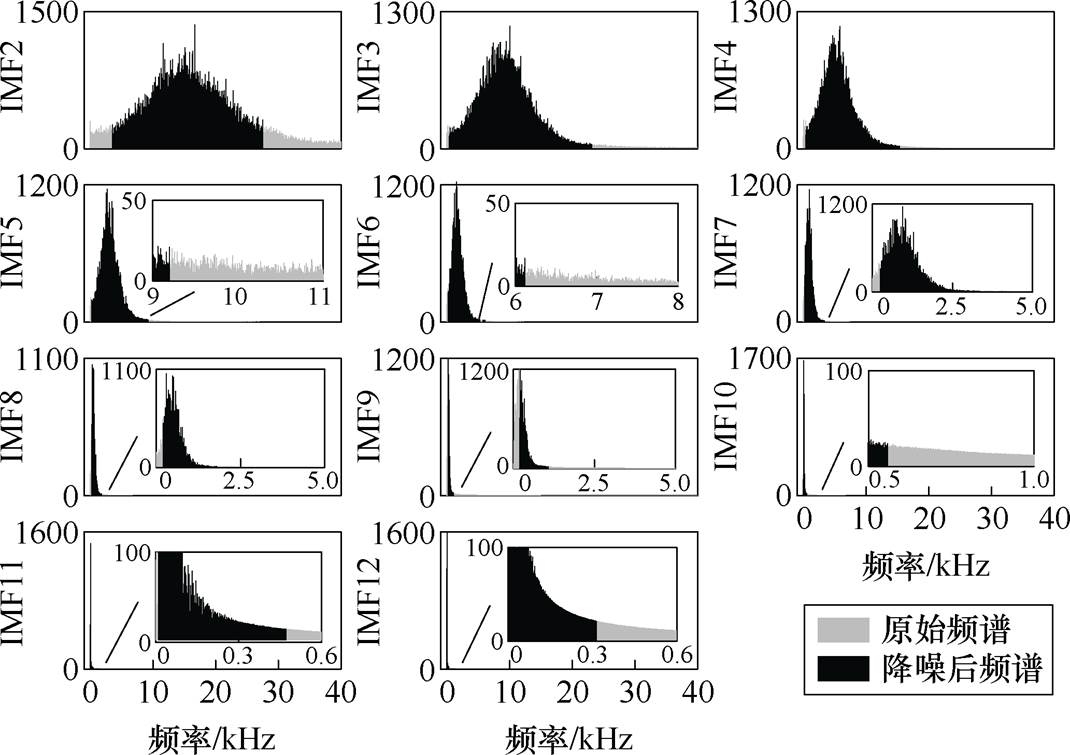
图11 降噪前后频谱对比
Fig.11 Comparison of spectra before and after denoising
图12所示为降噪前后特征数据趋势的对比。为衡量特征数据的平滑情况,本文以方差作为指标。具体来说,降噪前弹跳时间、接触电阻、释放时间和吸合时间的方差分别为7.165、2.786、2.566和5.719。经过AMMF降噪后,这些特征的方差分别降低至1.501、1.643、0.785和0.765。与降噪前相比,弹跳时间、接触电阻、释放时间和吸合时间的方差分别降低了79.05%、41.03%、69.40%和86.62%。结果表明,本文提出的AMMF降噪技术能够有效平滑交流接触器运行状态特征数据。
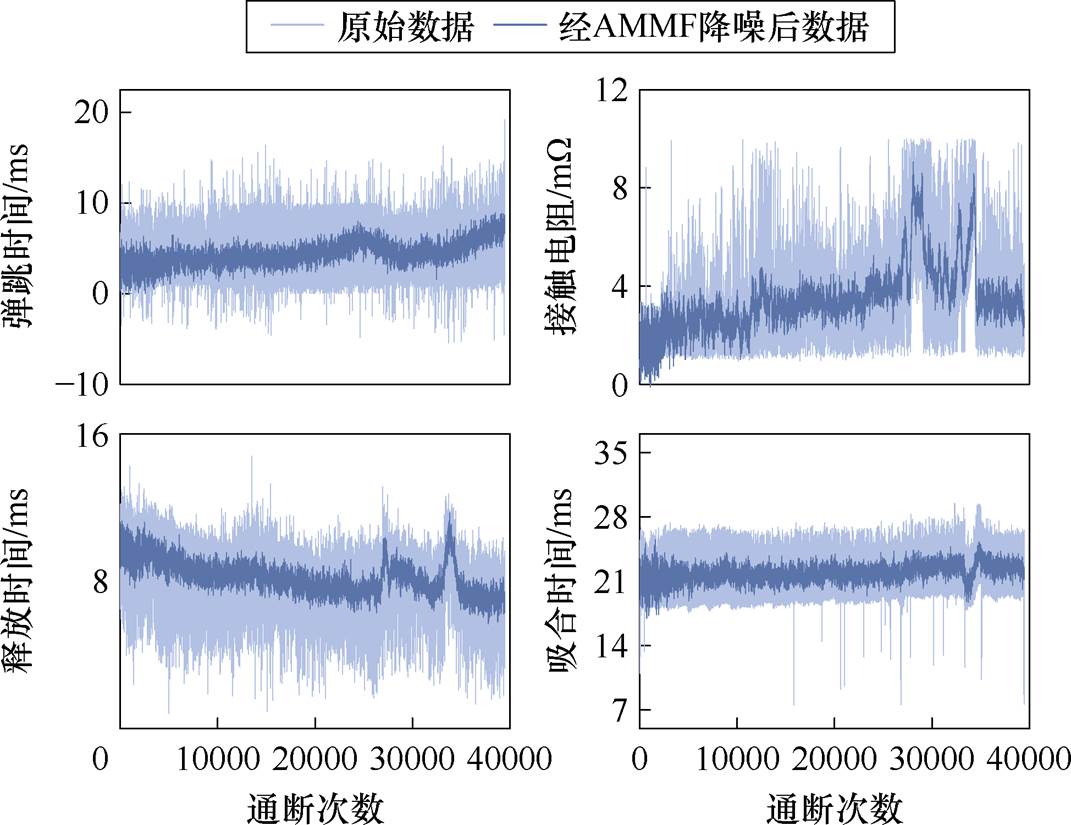
图12 特征数据降噪前后时域对比
Fig.12 Time-domain comparison of feature data before and after denoising
为说明本文提出的AMMF降噪技术不仅平滑能力好,而且在保留有效信息方面具有较大优势,本节以多种常用降噪技术作为对比方法:
(1)EMD:剔除IMF1后重构其余分量[11-12]。
(2)集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD):在数据中加入白噪声并多次进行EMD分解,然后对得到的IMF进行平均,以减少模态混叠并提高分解的稳定性和可靠性。
(3)WD:使用优化算法设置合适的小波系数、分解层数、阈值系数和阈值[8-9]。
(4)小波包分解(Wavelet Packet Decomposition, WPD):在WD基础上,WPD引入最优基概念,即在多层次频带划分后,根据数据特征自适应选择最佳基函数以提高高频分量的分辨率[10]。
(5)联合降噪技术(Joint Denoising technology, JD):使用EMD将原始数据分解为多尺度分量,剔除IMF1,后使用WD对剩余分量进行降噪[12]。
(6)有效频段(Effective Frequency band, EF)法:对频谱进行拟合,根据高斯分布三倍标准差原则截取频段并逆变换为时域数据[13-14]。
未知信号因缺失理想参考信号而无法通过信噪比、方均误差等指标评价降噪效果,但可以通过基于谱估计的信噪比及降噪前后数据对同一参数的不同表现形式来评价降噪效果。因此,本文使用基于谱估计的信噪比(Signal to Noise Ratio, SNR)、自相关函数和降噪后参量数据与接触器寿命的互相关函数Pcoff作为评价指标。
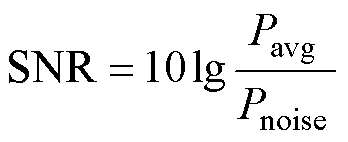 (19)
(19)
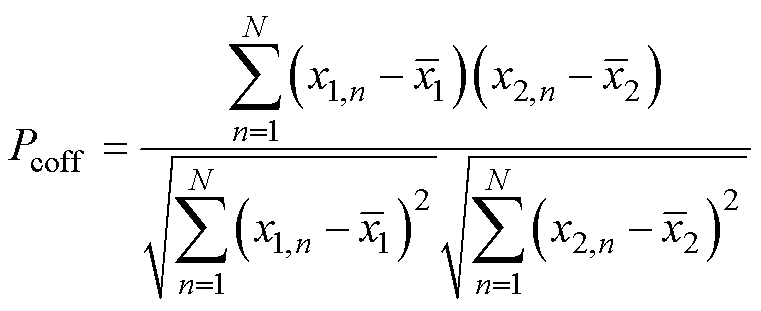 (20)
(20)
式中,Pavg和Pnoise分别为数据平均功率和噪声平均功率;Pcoff为x1与x2两特征之间的互相关值;x1,n与x2,n为两特征的时序数据;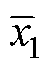 和
和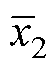 为数据均值。
为数据均值。
图13所示为多种降噪技术处理后的四种重要特征的自相关函数。WD和EEMD未表现出明显波动趋势,存在高频残留现象。相较而言,WPD和EMD趋势明显,原因在于,EEMD引入的白噪声与数据所含噪声混叠且迭代平均后未能滤除同等白噪声,而WD对高频信息的处理远不如WPD。结合EF和AMMF分析,二者均将高频成分置0处理,自相关趋势波动较缓且振幅大。由此可知,混叠的高频成分降低了数据前后时刻相关性。
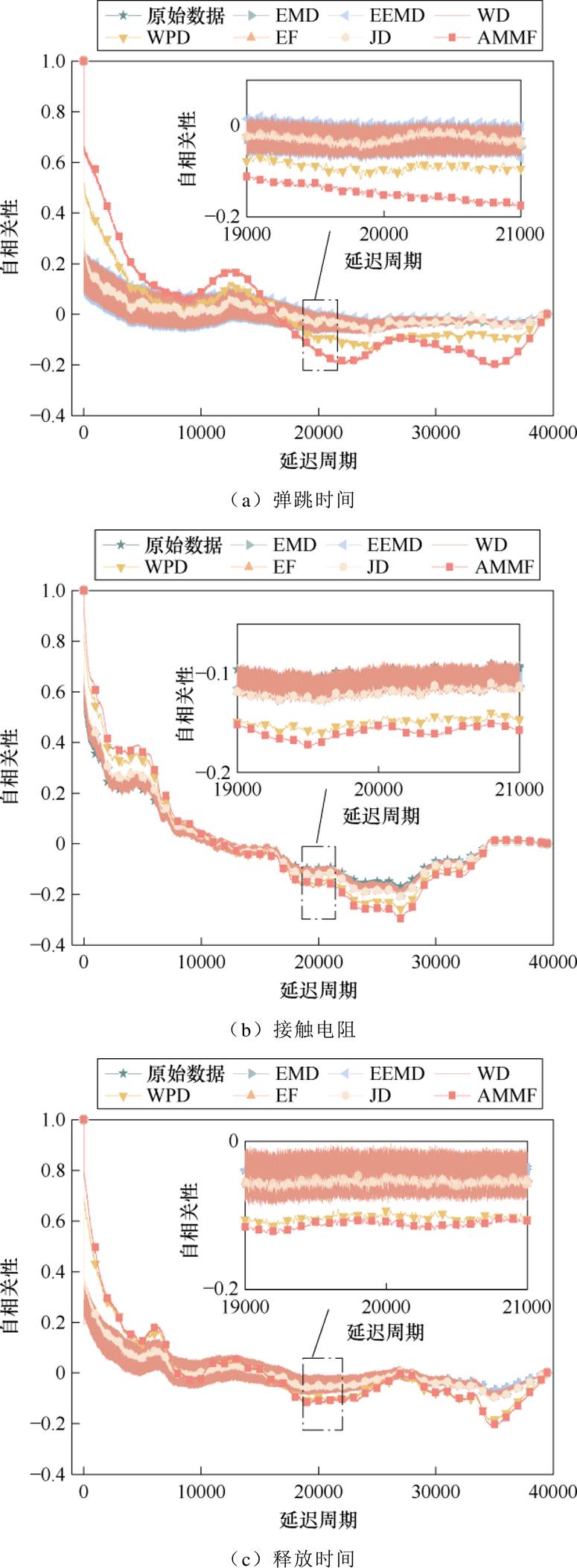
图13 特征数据自相关函数
Fig.13 Autocorrelation function diagrams of feature data
统计全延迟周期内平均自相关系数,结果如图14所示。相较于其他方法,EF、WPD和AMMF这类能够处理高频成分的方法平均自相关系数更高。其中,EF只考虑三倍标准差范围内频段,受频谱集中分布程度和中心频率偏移影响,适应性较差,仅在弹跳时间这一数据上表现较好;AMMF和WPD通过数据分解来提高降噪分辨率,各频率成分能够被精确识别,且自适应性能确保二者处理不同分布的分量数据,故二者表现优于EF。在处理高频信息时,WPD选择将高频分量继续向下分解,而AMMF将高频成分置0。这两种不同处理方式导致WPD和AMMF处理后数据有所差异,AMMF因高频成分更少而表现较优。结合图12~图14来看,本文所提AMMF能够加强特征数据前后时刻的联系性,凸显变化趋势。
接触器寿命具有不可逆性,将其作为参考信号可以判断特征数据表征触头退化规律的能力[5]。根据表1相关性标准,相关系数绝对值在0.4~0.6为中等相关,0.6~0.8为强相关。由图15a可知,WPD和AMMF与接触器寿命的相关性均达到0.4以上,即达到中等相关程度,而其他方法均在0.3左右,相关性较弱。其中,AMMF四种数据相关性分别为0.68、0.61、-0.58和0.48,而WPD分别为0.53、0.57、-0.56和0.41,说明AMMF处理后数据单调性得到加强,与接触器寿命的不可逆性有较强关联,可以有效表征触头长期退化规律。该结论也可通过图13和图14佐证,自相关函数本质上是描述同一时序数据在不同时刻的差值变化,当数据的单调增减趋势明显且增减幅值相近时,数据自相关性较强。由此可得,AMMF所得特征数据长期表征能力优于其他对比方法。
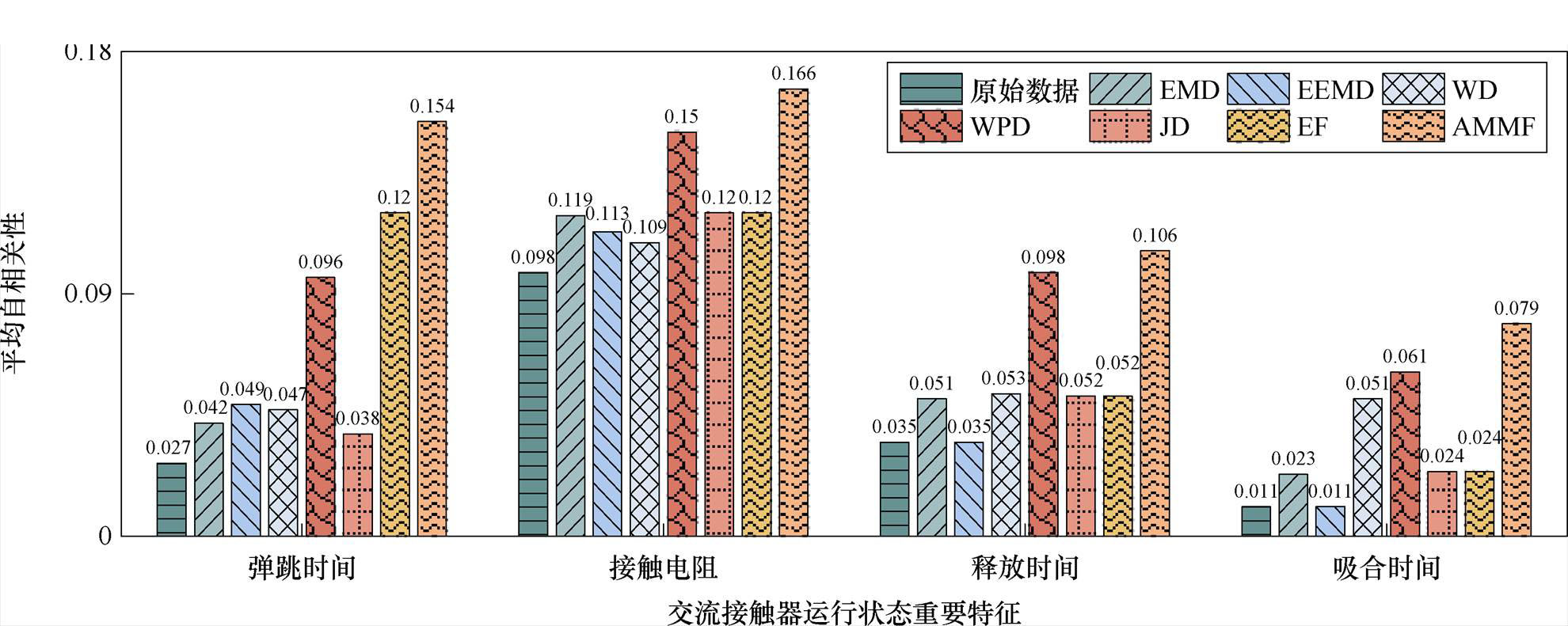
图14 特征数据全延迟周期平均自相关系数
Fig.14 Average autocorrelation coefficient over the full delay period of feature data
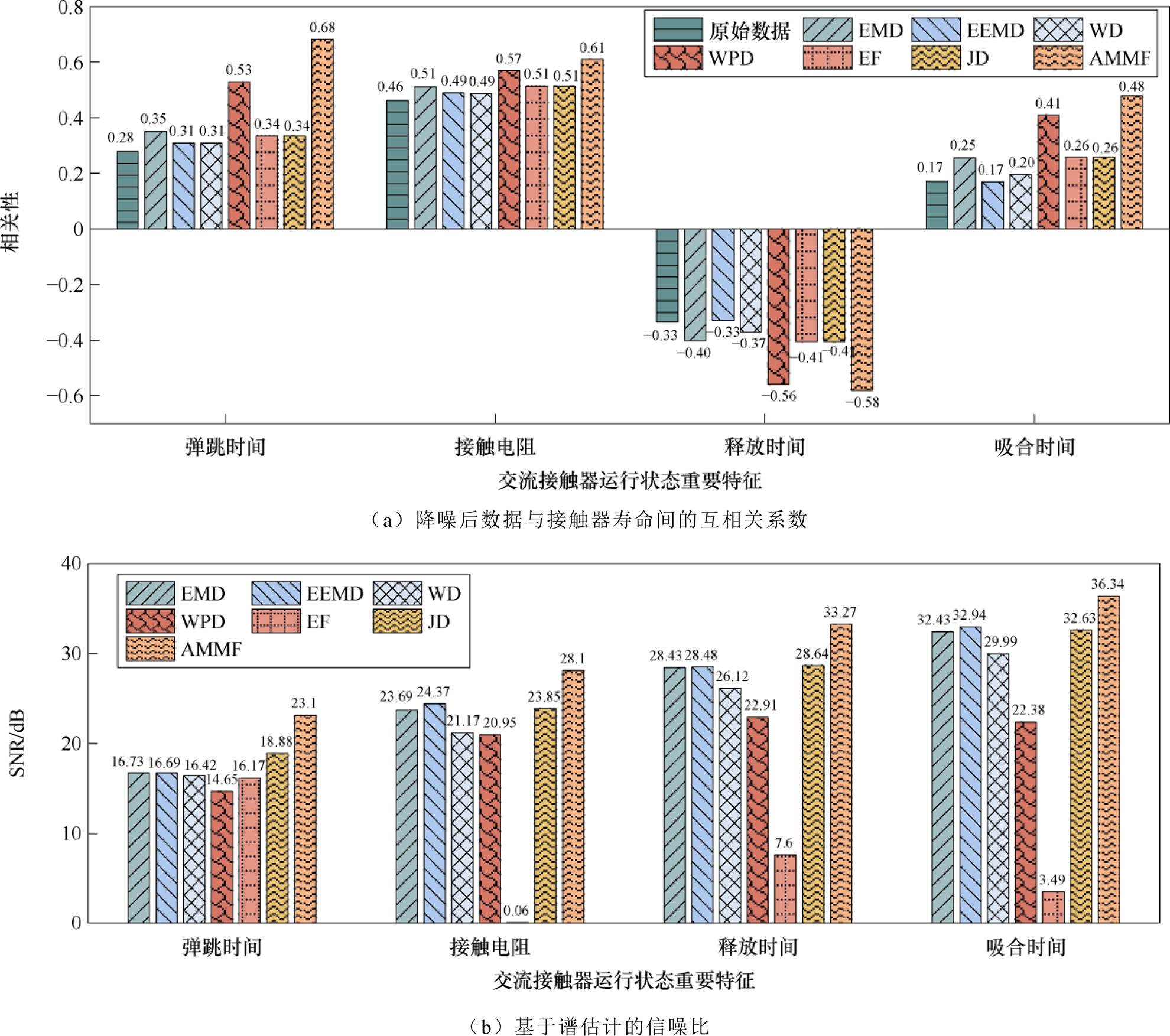
图15 不同降噪方法的效果对比
Fig.15 Comparison of the effects of different denoising methods
此外,为说明AMMF保留局部信息的能力也优于其他方法,本文还使用了基于谱估计的信噪比作为评价指标,结果如图15b所示。在该指标上,AMMF四种数据信噪比分别为23.1、28.1、33.27和36.34 dB,均高于其他对比方法。综上所述,本文所提AMMF降噪方法可以有效降低交流接触器特征数据噪声程度,并保留有效信息。
针对交流接触器运行特征数据含噪量大且传统降噪技术无法有效降噪的问题,本文提出一种基于AMMF的降噪方法,结合实例,有以下结论:
1)本文以包络分解策略、自适应结构元素和Triangle阈值法改进传统形态学滤波技术,使形态学滤波能够适应和处理交流接触器运行状态特征 数据。
2)本文引入基于自相关函数的信噪分界点确定方法,一定程度上解决未知噪声难以辨别的问题。
3)以六种常用降噪技术作为对比,以信噪比、互相关系数及自相关系数为指标,证明本文方法在降低噪声程度和保留信息方面具有较大优势。
参考文献
[1] 刘向军, 杨程, 周煜源. 基于多反馈参量的交流接触器自适应吸持控制策略[J]. 电工技术学报, 2023, 38(2): 554-562.
Liu Xiangjun, Yang Cheng, Zhou Yuyuan. Adaptive holding control strategy of AC contactor based on multiple feedback parameters[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 554-562.
[2] 蒋幸伟, 曹云东, 刘洋, 等. 基于多特征增强融合的交流接触器状态表征[J]. 高电压技术, 2024, 50(1): 282-291.
Jiang Xingwei, Cao Yundong, Liu Yang, et al. State characterization of AC contactor based on multi- feature enhanced fusion[J]. High Voltage Engineering, 2024, 50(1): 282-291.
[3] Liu Shuxin, Gao Shuyu, Peng Shidong, et al. Residual-electrical-endurance prediction of AC contactor based on CNN-GRU[J]. Machines, 2022, 10(11): 1067.
[4] Abirami S, Ruthvik S, Sathiq Ali M, et al. AC contactor electrical health estimator model[J]. IOP Conference Series: Materials Science and Engineering, 2021, 1145(1): 012070.
[5] 刘树鑫, 周柱, 刘洋, 等. 基于振动信号的交流接触器触头系统退化阶段划分[J]. 高电压技术, 2023, 49(12): 4971-4981.
Liu Shuxin, Zhou Zhu, Liu Yang, et al. Degradation phase division of AC contactor contact system based on vibration signal[J]. High Voltage Engineering, 2023, 49(12): 4971-4981.
[6] 于春雨, 张文韬, 张庆海, 等. 基于EMD-AR与改进宽度学习系统的滚动轴承故障诊断方法[J]. 中国电机工程学报, 2023, 43(22): 8944-8955.
Yu Chunyu, Zhang Wentao, Zhang Qinghai, et al. Fault diagnosis method of a rolling bearing on EMD-AR and improved broad learning system[J]. Proceedings of the CSEE, 2023, 43(22): 8944-8955.
[7] 唐志国, 李阳. 基于改进无参尺度空间经验小波变换的变压器高频电流局放噪声抑制研究[J]. 高压电器, 2024, 60(1): 144-153.
Tang Zhiguo, Li Yang. Research on partial discharge noise suppression of transformer based on improved parameterless scale space empirical wavelet trans- form[J]. High Voltage Apparatus, 2024, 60(1): 144- 153.
[8] 刘帼巾, 刘达明, 缪建华, 等. 基于变分模态分解和改进灰狼算法优化深度置信网络的自动转换开关故障识别[J]. 电工技术学报, 2024, 39(4): 1221- 1233.
Liu Guojin, Liu Daming, Miao Jianhua, et al. Fault identification of automatic transfer switching equipment based on VMD-WPE and IGWO optimized DBN[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1221-1233.
[9] 王晓卫, 王雪, 王毅钊, 等. 基于图像信息熵与多元变分模态分解的电缆局放信号去噪方法[J]. 电工技术学报, 2024, 39(13): 4100-4115, 4152.
Wang Xiaowei, Wang Xue, Wang Yizhao, et al. A denoising algorithm for cable partial discharge signals based on image information entropy and multivariate variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4100- 4115, 4152.
[10] 李忠. 基于小波包与回声状态网的风电功率预测[J]. 电气工程学报, 2021, 16(3): 123-129.
Li Zhong. Wind power forecasting based on wavelet packet and echo state network[J]. Journal of Electrical Engineering, 2021, 16(3): 123-129.
[11] Shamaee Z, Mivehchy M. Dominant noise-aided EMD (DEMD): extending empirical mode decomposition for noise reduction by incorporating dominant noise and deep classification[J]. Biomedical Signal Pro- cessing and Control, 2023, 80: 104218.
[12] Chen Wuge, Li Junning, Wang Qian, et al. Fault feature extraction and diagnosis of rolling bearings based on wavelet thresholding denoising with CEEMDAN energy entropy and PSO-LSSVM[J]. Measurement, 2021, 172: 108901.
[13] 陈太聪, 张奇. 基于频谱能量形态拟合的加速度积分方法研究[J]. 振动与冲击, 2019, 38(13): 7-12, 20.
Chen Taicong, Zhang Qi. Acceleration integration method based on frequency spectral energy morphological fitting[J]. Journal of Vibration and Shock, 2019, 38(13): 7-12, 20.
[14] 李展铨, 陈太聪. 基于Welch功率谱的加速度积分改进方法研究[J]. 振动与冲击, 2022, 41(18): 41- 46, 54.
Li Zhanquan, Chen Taicong. Improved acceleration integration method based on Welch power spectrum[J]. Journal of Vibration and Shock, 2022, 41(18): 41-46, 54.
[15] 陈媛, 段文献, 何怡刚, 等. 带降噪自编码器和门控递归混合神经网络的电池健康状态估算[J]. 电工技术学报, 2024, 39(24): 7933-7949.
Chen Yuan, Duan Wenxian, He Yigang, et al. State of health estimation of lithium ion battery based on denoising autoencoder-gated recurrent unit[J]. Transactions of China Electrotechnical Society, 2024, 39(24): 7933-7949.
[16] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(1): 289-302.
Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
[17] 闫晓丽. 基于数学形态学与混沌理论的滚动轴承故障诊断研究[D]. 北京: 华北电力大学, 2022.
Yan Xiaoli. Research on rolling bearing fault diagnosis based on mathematical morphology and chaos theory[D]. Beijing: North China Electric Power University, 2022.
[18] Li Dewang, Ma Qiang, Bai Xuezong, et al. A morphological filtering-based strain data processing method for biaxial fatigue testing of wind turbine blades[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2023, 237(17): 4005-4016.
[19] 方志法, 王维民, 曹颜玉, 等. 基于自适应变尺度形态学滤波的冲击提取方法[J]. 振动测试与诊断, 2023, 43(4): 698-704, 828.
Fang Zhifa, Wang Weimin, Cao Yanyu, et al. Impact feature extraction based on the adaptive variable scale morphological filter[J]. Journal of Vibration, Mea- surement & Diagnosis, 2023, 43(4): 698-704, 828.
[20] 王晓龙, 石海超, 熊江涛, 等. 基于自适应多尺度形态学梯度乘积运算的发电机振动信号特征增强检测[J]. 中国电机工程学报, 2025, 45(8): 3195- 3205.
Wang Xiaolong, Shi Haichao, Xiong Jiangtao, et al. Enhanced detection of generator vibration signals characteristic based on adaptive multi-scale morpho- logical gradient product operation[J] Proceedings of the CSEE, 2025, 45(8): 3195-3205.
[21] 李文华, 姜惠, 赵正元, 等. 基于波形匹配端点延拓法优化的经验模态分解算法在铁路继电器参数降噪上的应用[J]. 电工技术学报, 2022, 37(10): 2656-2664.
Li Wenhua, Jiang Hui, Zhao Zhengyuan, et al. Application of empirical mode decomposition algorithm based on waveform matching endpoint continuation method in noise reduction of railway relay parameters[J]. Transactions of China Electro- technical Society, 2022, 37(10): 2656-2664.
[22] Ni Zexing, He Dan, Wang Xiufeng, et al. Research on the detection of axle abnormal noise based on maximum autocorrelation kurtosis deconvolution[J]. Applied Acoustics, 2023, 203: 109228.
[23] 王中, 李振华, 成俊杰, 等. Rogowski线圈电流互感器故障的早期诊断研究[J]. 高压电器, 2023, 59(2): 162-168.
Wang Zhong, Li Zhenhua, Cheng Junjie, et al. Research on early diagnosis of fault of current transformer with Rogowski coil[J]. High Voltage Apparatus, 2023, 29(2): 162-168.
Abstract High-quality operating state feature data is crucial for the reliability analysis of AC contactors and serves as the foundation for research on residual life prediction and state identification of AC contactors. However, factors such as the singularity of the feature extraction program, electrical interference, and measurement errors often result in a significant amount of noise in the feature data. Moreover, traditional noise reduction technologies struggle to effectively reduce noise content due to issues of modal aliasing and low denoising resolution in feature data. Therefore, this paper proposes a denoising method for feature data based on the adaptive multi-scale morphological filter (AMMF).
Initially, this paper employs curve envelopes to decompose feature data into multi-scale components and introduces Triangle thresholds and adaptive structural elements to enhance traditional morphological filtering techniques. Accordingly, the method can adapt to differences in the distribution of various scale spectra, thereby constructing the AMMF denoising model. Subsequently, the autocorrelation function characteristics of the components are utilized to identify noisy components. The AMMF is then applied to extract the effective frequency bands of these noisy components, which are inversely transformed and reconstructed into feature data. Finally, this paper compares the proposed method with six denoising techniques, using signal-to-noise ratio, cross-correlation coefficient, and average autocorrelation coefficient as evaluation metrics. The results demonstrate that the proposed method effectively reduces the noise content in AC contactor feature data.
Regarding the autocorrelation coefficient metric, the temporal correlation of feature data processed by AMMF is significantly enhanced. Specifically, the full-period average autocorrelation coefficients of four critical feature data—bounce time, contact resistance, release time, and closing time—improve from 0.027, 0.098, 0.035, and 0.011 to 0.154, 0.166, 0.106, and 0.079, respectively. Concurrently, the signal-to-noise ratios of these four datasets after processing reach 23.1, 28.1, 33.27, and 36.34 dB, respectively, with correlation coefficients relative to contactor life amounting to 0.68, 0.61, -0.58, and 0.48, respectively. These numerical values of the three metrics indicate that the AMMF outperforms comparison methods in processing AC contactor operating state feature data.
The following conclusions are drawn from the case analysis. (1) The improved morphological filtering technique mitigates the issues of modal aliasing and low denoising resolution in feature data. (2) The method of determining the signal-to-noise boundary using the autocorrelation coefficient can effectively reduce the subjectivity of traditional methods in identifying noisy components. (3) Compared to traditional denoising techniques, the proposed method exhibits significant advantages in noise reduction and information retention.
keywords:AC contactor, morphological filter, data denoising, envelope decomposition, autocorrelation coefficient
DOI: 10.19595/j.cnki.1000-6753.tces.241143
中图分类号:TM572.2
国家自然科学基金(51977132)、辽宁省科技重大专项(2020JH1/10100012)和辽宁省科技厅“揭榜挂帅”科技攻关专项(2022JH1/10800015)资助项目。
收稿日期 2024-07-02
改稿日期 2024-11-15
刘树鑫 男,1982年生,教授,博士生导师,研究方向为电器状态监测与电器智能化。E-mail: liushuxin@sut.edu.cn
祁新智 男,1999年生,硕士研究生,研究方向为电器状态监测与电器智能化等。E-mail: Qixinzhi_1999@163.com(通信作者)
(编辑 崔文静)