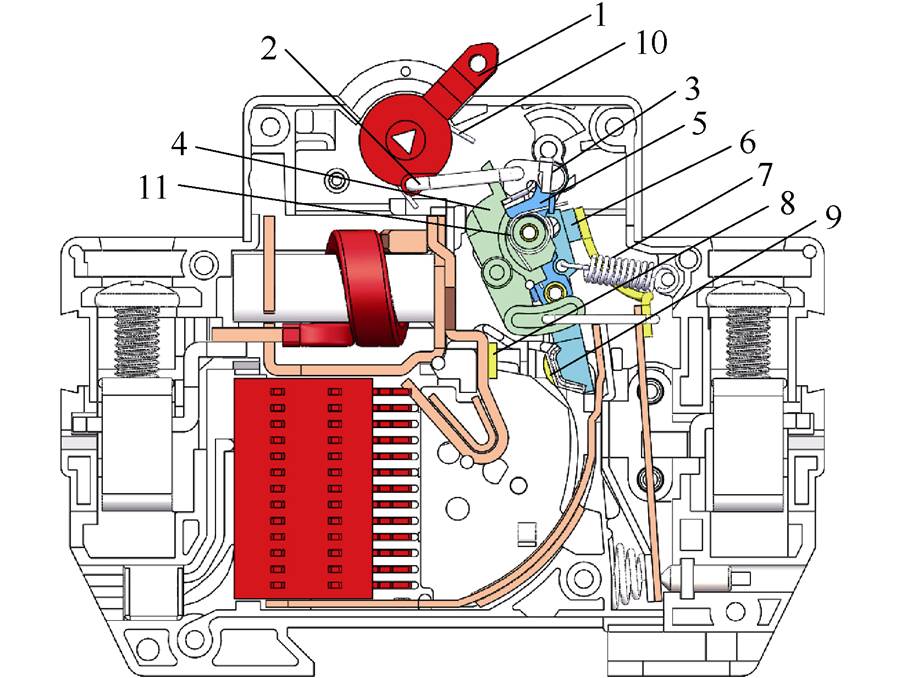
图1 微型断路器结构示意图
摘要 微型断路器是低压配电系统中的重要保护设备，随着微型断路器操作次数的增加，其性能退化，机械参数随之变化，最终导致微型断路器丧失操作性能，影响低压配电系统的安全可靠运行，因此如何有效识别微型断路器的服役状态是当前亟需解决的问题。该文建立微型断路器操作机构的动力学仿真模型，研究合闸过程中手柄操作力矩变化规律，提取表征手柄操作力矩变化特征的刚合角度和合闸最大转矩；分析触头超程退化特征和触头弹簧性能退化特征，确定微型断路器服役性能退化特征与手柄操作力矩特征参数的关系；根据触头磨损程度将微型断路器服役状态分为正常、退化、危险、故障四种等级，确定每种等级下刚合角度和合闸最大转矩的阈值区间。进行微型断路器性能退化模拟实验，验证所提服役状态辨识方法的有效性，实现微型断路器在不同退化特征下服役状态的准确识别。
关键词：微型断路器 操作机构 机械特性 动力学模型 服役状态辨识
微型断路器是低压配电系统中广泛使用的电力设备，能接通正常工作回路并通过过载保护与短路保护切除故障回路[1-2]。微型断路器在服役过程中承受电应力和机械应力，引起不同部件发生劣化，当劣化至一定程度时会造成微型断路器合分闸失败。因此，有效且准确地辨识微型断路器状态并诊断性能退化部件及退化程度非常重要。
国内外学者开展了很多关于断路器状态辨识与故障诊断的研究，监测的特征信号主要有触头行程、振动信号、声音信号、线圈电流等[3-8]。为掌握断路器内部件的工作状态并达到故障预警的目的，有学者通过监测触头角位移监测部件的运动状态，A. A. Razi-Kazemi等[9]通过监测行程曲线实现弹簧驱动操作机构的机械故障判别；胡博凯等[10]分析框架断路器动触头和操作机构不同位置铰接点的位移，研究特征量随不同部件退化的变化规律。监测触头位移的方法较为直接，可从位移中计算得到合分闸时间、合分闸速度等关键机械参数，该方法对安装位置要求较高。振动信号中蕴含诸如操作机构与传动部件碰撞、动静触头撞击等机械状态信息[11]。许多学者通过振动信号对断路器进行状态辨识，杨秋玉等[12]针对断路器振动信号研究边际谱能量与触头超程的规律，实现断路器触头超程状态识别。刘会兰等[13]建立支持向量机模型对不同运行状态下的断路器振动特征，进行操作机构状态的准确辨识。马莉等[14]利用变分模态分解（Variational Mode Decomposition, VMD）对高压断路器振动和声音信号进行分解，构造相应Hilbert边际谱，求取能量熵作为特征向量，利用支持向量机（Support Vector Machine, SVM）方法建立训练模型，实现高压断路器机械状态辨识。然而，振动信号的采集受传感器安装位置影响较大，且仅对零件松动和间歇性接触等故障的敏感性更高。李永丽[15]和孙曙光等[16]通过分析断路器机械故障对分合闸线圈电流的影响，实现断路器状态的在线监测与故障诊断。以上研究为断路器状态辨识工作提供了参考，但研究对象大多为高压断路器，在微型断路器的状态辨识研究方面鲜有应用。
断路器在服役过程中发生触头电磨损、触头弹簧疲劳断裂等问题，而这些问题导致断路器运行可靠性降低。断路器的服役状态和可靠性与运行电压、电流及其相关电性能特征量密切相关[17]。王振兴 等[18]采用支持向量回归法预测和评估了不同电弧电流烧蚀后的断路器接触电阻和触头质量损失，完成对断路器服役状态的精确评估，但是触头质量损失测量一般需要对断路器部件进行拆卸，在微型断路器上实施较为困难。赵成晨等[19-20]通过研究触头质量损失和燃弧特征量（电弧电量、焦耳积分和燃弧能量）的关系，建立不同电流范围内平均触头质量损失率数学模型，完成低压断路器的剩余电寿命预测。通过观测燃弧特征量的累积变化可准确判断断路器服役状态，需要逐次测量并计算单次开断的燃弧特征量，并进行累积才能得到需要的特征量，且需要在线监测断路器每次开断的电压和电流。
断路器触头电磨损和触头弹簧断裂等问题会引起机械特性发生改变，因此断路器的机械性能参数与其服役状态密切相关。手柄操作力矩是微型断路器的重要机械性能参数：①手柄操作力矩的测量能在不破坏微型断路器结构的情况下完成，且可以在服役过程中进行，定期获得服役状态信息；②与其他检测方法相比，检测手柄操作力矩相对简单，且检测成本低。
本文根据微型断路器的机械特性，分析机械特征量随触头磨损、触头弹簧断裂等不同因素变化的规律，进行服役状态辨识的研究，为评价微型断路器的可靠性奠定基础。
微型断路器主要由触头灭弧系统、保护系统和机械操作系统组成。机械操作系统主要由手柄、U形连杆、跳扣、锁扣、中心支架、触头杠杆组成，并含有两个扭簧和一个触头弹簧，微型断路器三维实体模型如图1所示。
微型断路器的操作性能主要由操作机构和触头系统决定，机构中任何机械部件产生磨损或断裂等均会导致机构的运动发生改变。操作机构示意图及等效的机构如图2所示。操作机构由手柄BC、U形连杆CD、跳扣DE、锁扣DF、触头杠杆FG、中心支架DEKF等部件组成。根据机构中不同部件在合分闸过程中的运动特性和配合关系，将一些形状不规则的部件等效为一定长度的连杆，通过等效后的操作机构模型进行机构在合分闸过程中的分析。
图1 微型断路器结构示意图
1—手柄 2—U形连杆 3—跳扣 4—锁扣 5—中心支架 6—触头杠杆 7—触头弹簧 8—静触头 9—动触头 10—扭簧Ⅰ 11—扭簧Ⅱ
Fig.1 Structure composition of miniature circuit breaker
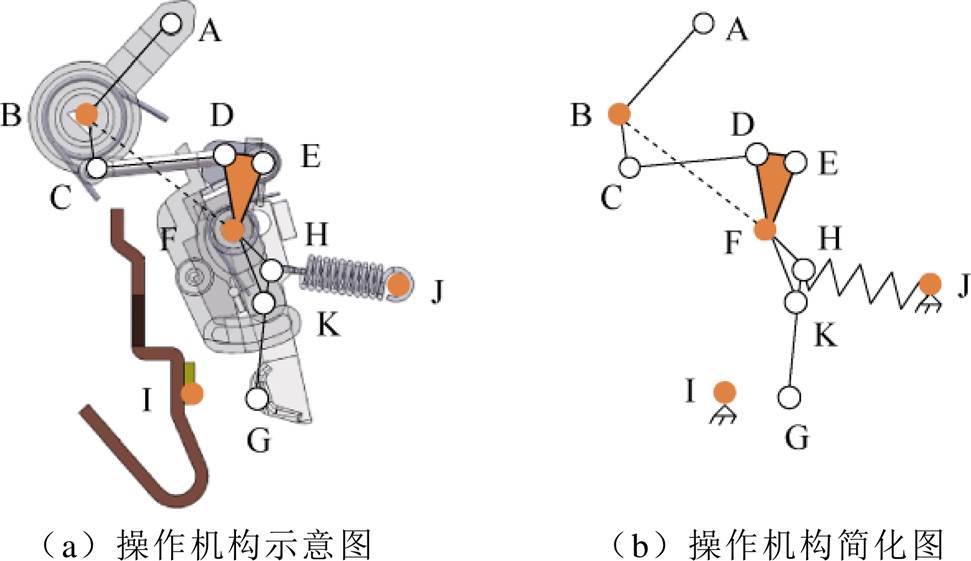
图2 微型断路器操作机构及简化示意图
Fig.2 Operating mechanism and its schematic diagram of miniature circuit breaker
以手柄B点为原点，与轴销F点连线的所在直线为x轴，垂直于x轴方向的直线为y轴，建立平面直角坐标系。设手柄BC为杆1，U形连杆CD为杆2，铰接点D到轴销F的距离DF为杆3，初始位置的机构受力分析如图3所示。
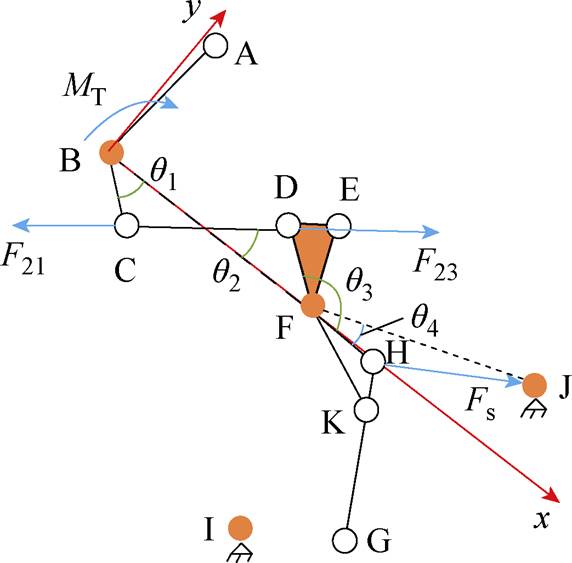
图3 微型断路器初始位置受力示意图
Fig.3 Schematic diagram of initial position force on miniature circuit breakers
根据动静触头的相对运动关系，将微型断路器合闸过程中的运动过程分为空行程阶段和超程阶段。空行程阶段为手柄转动到动静触头刚合前的过程，假设手柄以角速度w1匀速转动，扭簧Ⅰ和U形连杆对手柄提供阻力，因此在手柄B点关系为
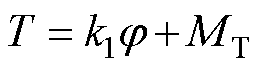（1）
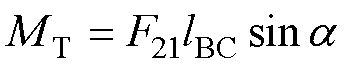（2）
式中，T为手柄操作力矩；k1为扭簧Ⅰ的刚度系数；j 为手柄从初始位置到当前位置的转动角度；MT为U形连杆对手柄的力矩；F21为U形连杆对手柄的推力；lBC为手柄B点与铰接点C的距离；a 为F21与连杆BC的夹角。
空行程阶段中，手柄驱动U形连杆和触头组件以四连杆形式运动，有
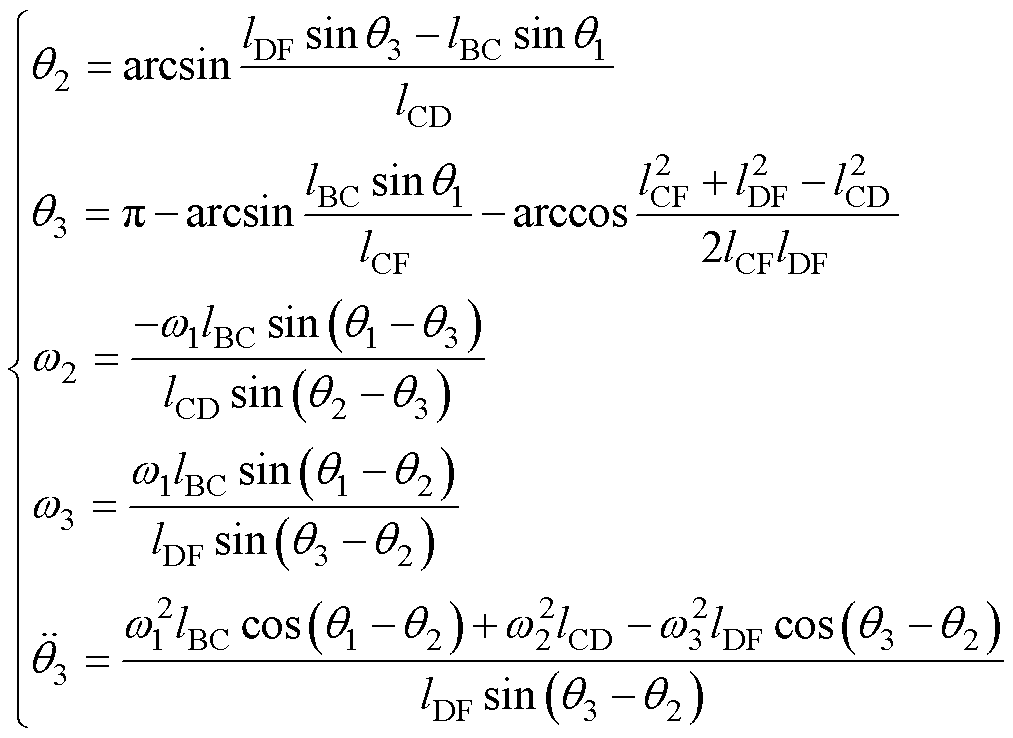（3）
式中，q1、q2、q3分别为杆BF与杆BC、杆CD、杆DF的夹角；w2、w3为杆2和杆3的转动角速度；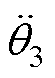
为杆3转动角加速度。
空行程阶段中，U形连杆推动锁扣使触头组件（跳扣、锁扣、中心支架、触头杠杆）围绕轴销F点做定轴转动，因此在F点的力矩关系为
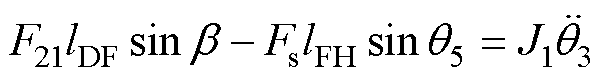（4）
式中，b 为推力F23与杠杆DF夹角；Fs为触头弹簧对触头杠杆的拉力；q5为弹簧拉力与杠杆FH夹角；J1为触头组件系统转动惯量。
微型断路器合闸过程操作机构运动示意图如图4所示。在触头刚合后进入超程阶段，如图4b所示，动触头G点不再移动，操作机构仍围绕F点以角速度w3转动，铰接点K带动触头杠杆HG围绕G点以角速度wH逆时针转动。动触头G点力矩关系为
（5）
式中，FK为铰接点K对触头杠杆HG的作用力；yH, xH、yJ, xJ分别为H点和J点的坐标值；J3为触头杠杆转动惯量。
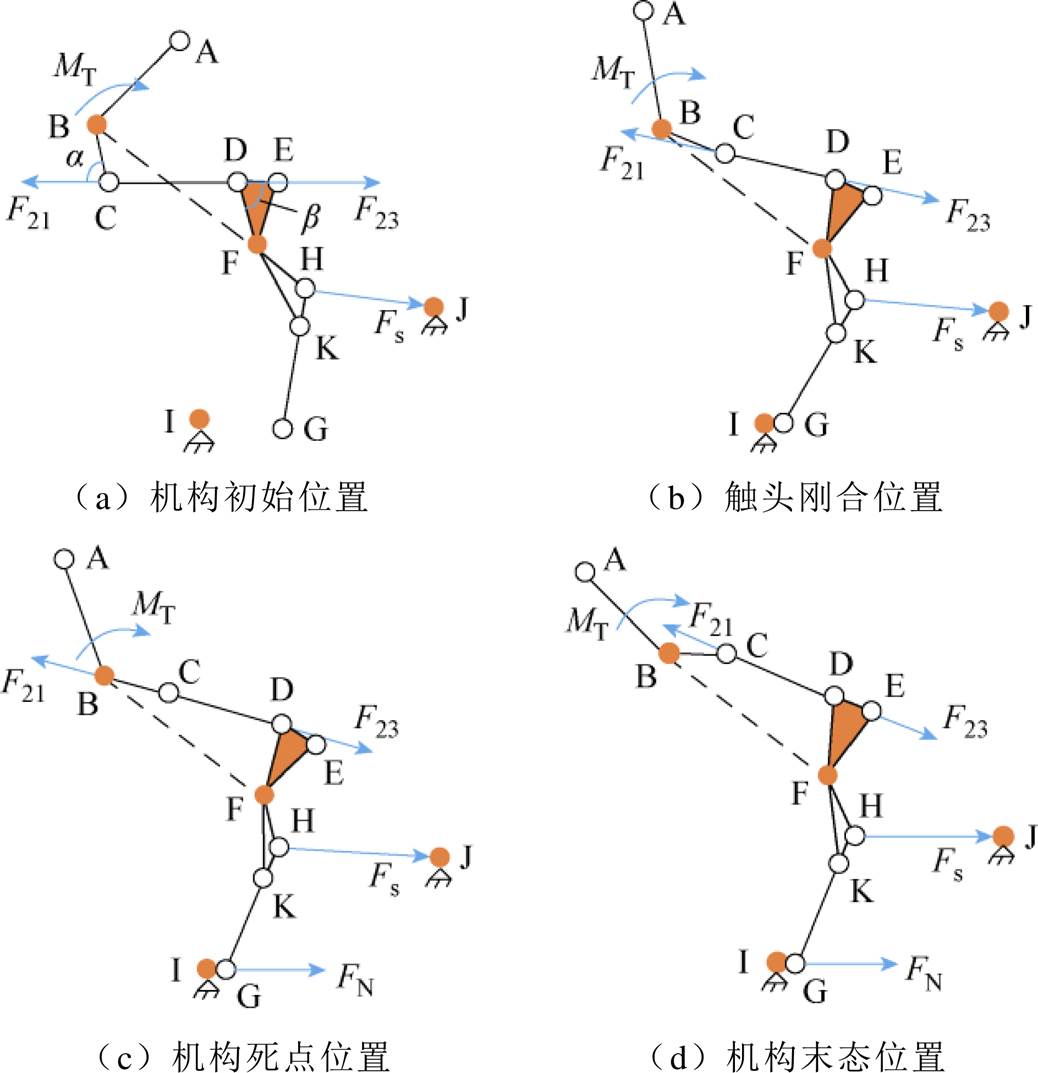
图4 微型断路器合闸过程操作机构运动示意图
Fig.4 Movement of operating mechanism during opening process
轴销F点力矩关系为
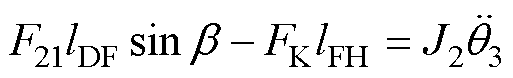（6）
式中，J2为触头组件系统转动惯量（不含触头杠杆）。
综上分析，可得合闸全过程中手柄操作力矩T与手柄转动角度j 的关系。
通过建立微型断路器操作机构虚拟样机模型，模拟合闸过程中各部件运动规律，计算机械特征量随手柄转动的变化，仿真流程如图5所示。
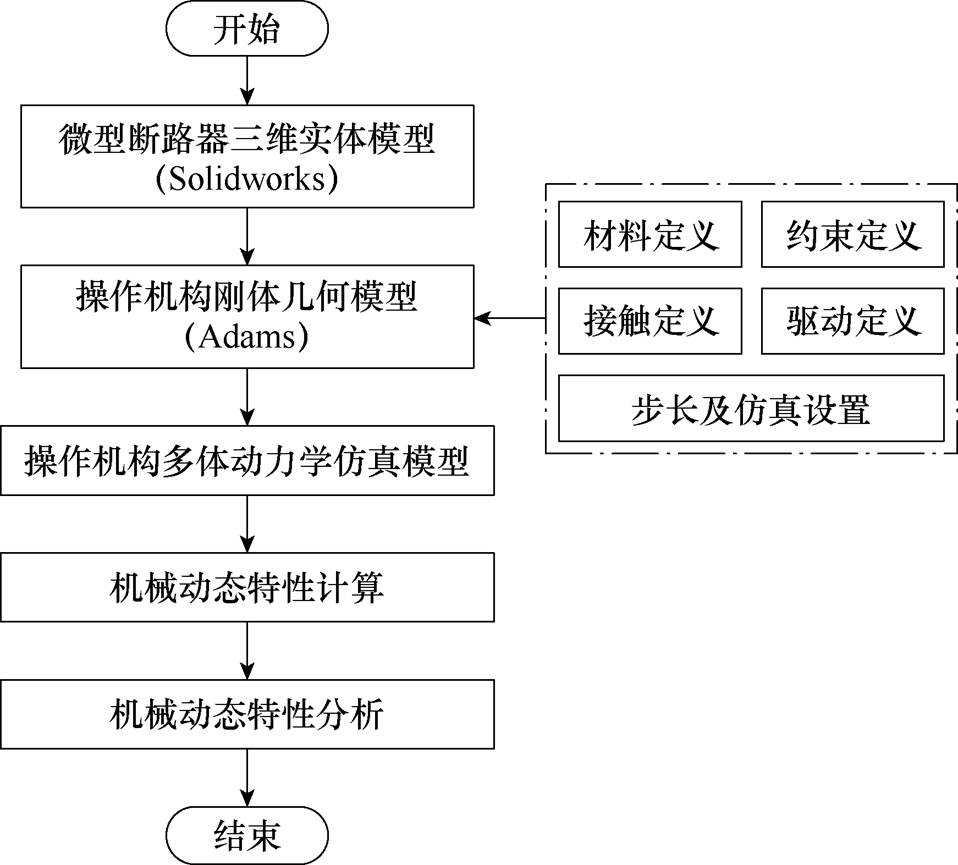
图5 微型断路器虚拟样机仿真流程
Fig.5 Miniature circuit breaker virtual prototype simulation process
首先建立微型断路器的三维实体模型，对动静触头、U形连杆、跳扣、锁扣、中心支架、触头杠杆等主要部件进行材料设置，定义手柄的转动角度和扭簧、触头弹簧的刚度系数，对不同部件间添加正确的固定副、运动副、手柄驱动方式、部件间接触力等约束条件后得到虚拟样机模型，手柄处逆时针方向箭头表示驱动，其他铰接点处的逆时针方向箭头表示转动副，锁形表示固定副，如图6所示。
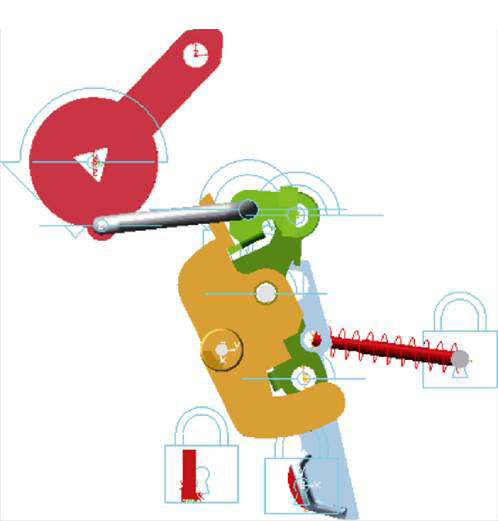
图6 微型断路器虚拟样机模型
Fig.6 Virtual mockup model of miniature circuit breaker dynamics
合闸过程机构动力学分析如图7所示。假设手柄处为恒转速转动，手柄操作力矩等于扭簧扭矩与U形连杆对手柄的转矩之和。在空行程阶段，手柄受到扭簧Ⅰ和U形连杆CD的阻力，触头弹簧HJ对触头杠杆HG提供拉力。手柄开始转动后扭簧Ⅰ不断被压缩，对手柄的阻力矩逐渐增大，同时随连接点H转动，触头弹簧HJ对中心支架阻力增大，导致U形连杆提供的阻力矩与扭簧Ⅰ扭矩之和呈上升趋势，如图7d所示，因此在该阶段内手柄操作力矩逐渐增大。
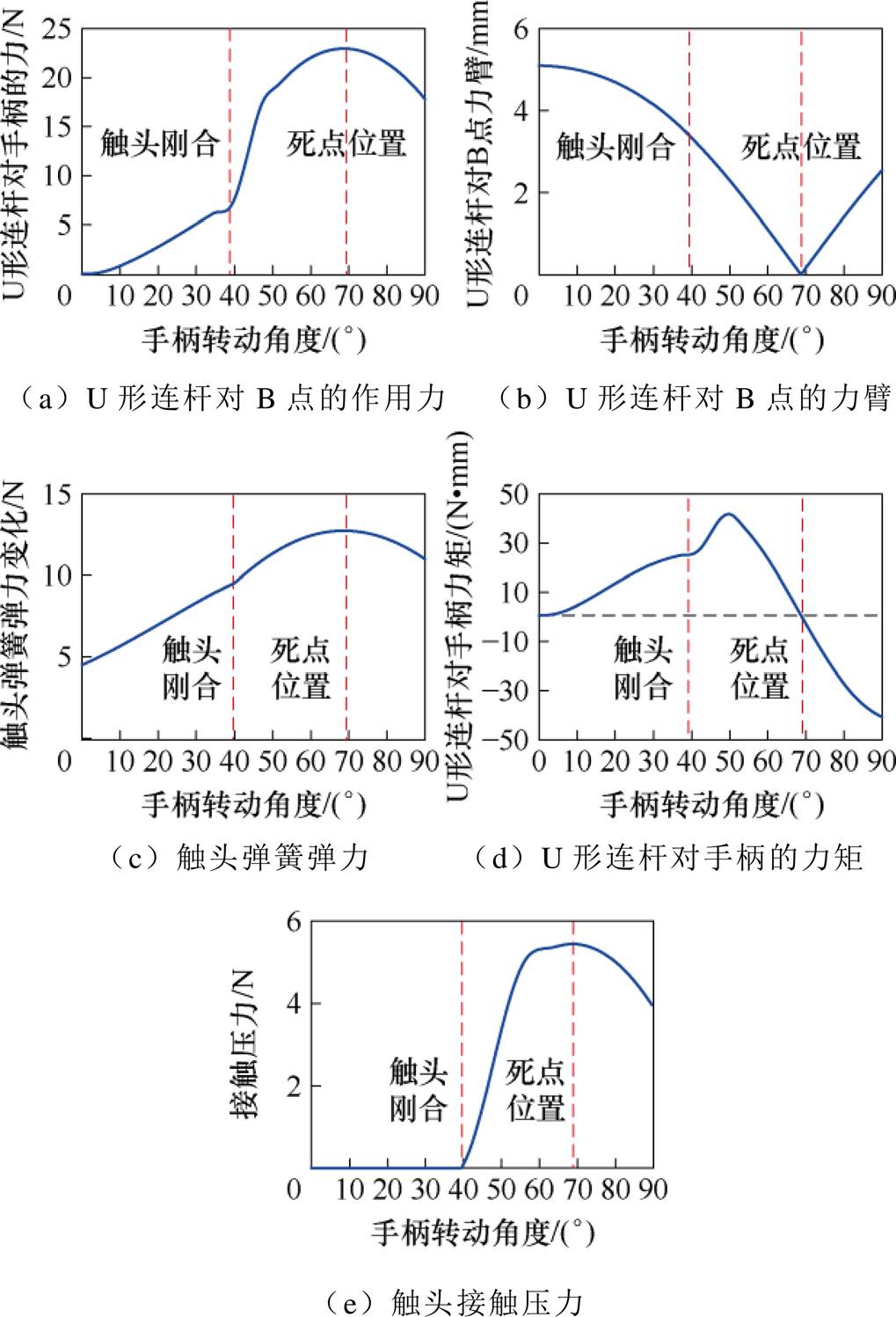
图7 合闸过程机构动力学分析
Fig.7 Dynamic analysis of the closing process mechanism
在动静触头接触后至转到死点位置（CD与BC共线）前，触头杠杆与中心支架整体发生相对移动，触头弹簧对触头杠杆的拉力增加。同时动静触头接触后产生接触压力，且接触压力随着操作机构转动而逐渐增大。触头弹簧的拉力和触头间接触压力对手柄均起阻力作用，且在该过程内阻力作用逐渐增大，造成手柄阻力矩增速变快，因此该过程中手柄操作力矩呈增大且增速变快趋势。
此外，机构继续运动，触头弹簧和扭簧Ⅰ继续形变，由图7a、图7b可知，到机构运动至死点位置前，U形连杆CD对手柄的阻力臂逐渐减小且减小的趋势逐渐变快，U形连杆CD对手柄的推力F21逐渐增大并在死点位置达到最大，因此手柄操作力矩T在死点位置前达到极值Tmax后逐渐减小。
在死点位置到末态位置阶段，U形连杆CD对手柄的推力F21由阻力转变为动力且逐渐减小，动力臂逐渐增大，经仿真计算得出U形连杆对手柄的动力矩逐渐增大，且该过程中U形连杆给手柄的动力矩大于扭簧Ⅰ的阻力矩，导致手柄的阻力矩逐渐减小，因此手柄操作力矩T继续减小，直至手柄到达合闸末态位置，微型断路器进入合闸保持状态。
通过仿真得到合闸过程中手柄操作力矩与手柄转动角度的关系，如图8所示。
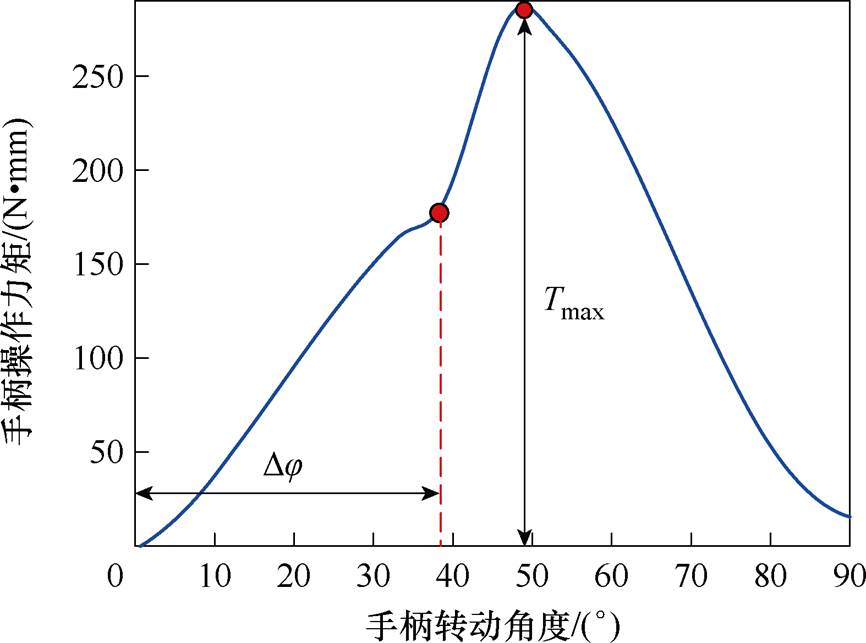
图8 合闸过程中手柄操作力矩仿真波形
Fig.8 Simulation waveform of the operating torque of the handle during the closing process
根据合闸过程中的手柄操作力矩的变化规律，提取能够表征断路器服役状态的特征量，见表1。
表1 合闸过程中手柄操作力矩特征量
Tab.1 Characteristics of mechanism during closing process
操作过程机械特征量物理意义 合闸过程Dj手柄开始转动至触头刚合的手柄转角 Tmax合闸过程中手柄的最大转矩
随着微型断路器操作次数的增加，触头系统以及内部不同机械部件均会发生不同程度的退化以及突发性的部件断裂，当某关键部件退化至临界值时或发生突发性断裂均会导致断路器失效。由电弧侵蚀和机械损伤引起的机械部件性能退化或缺陷主要包括触头磨损和触头弹簧断裂。这些缺陷发生后会引起操作机构的机械特性改变，因此可以根据操作机构的机械特性变化，分析触头退化或机械部件损伤后对于微型断路器机械特征量和服役性能的影响。
2.1.1 单极情况下机械特征量与触头磨损的关系
微型断路器触头系统在接通和分断过程中产生电弧，电弧产生的高温导致触头表面发生熔化与磨损，同时动静触头间的机械应力引起触头表面形变并加剧磨损。随着微型断路器动作次数的增加，机械应力、电弧侵蚀等因素对触头产生的累积损伤效应愈发严重，微型断路器的触头磨损量逐渐增加。触头磨损前后动、静触头接触时机械机构位置发生变化，如图9所示，H1、K1、G1表示触头完好情况下各部件所在位置，H2、K2、G2表示触头磨损情况下各部件所在位置。
由于动静触头的厚度变薄导致触头间的超程减少，因此触头杠杆HG需要比触头磨损前多转动一定角度才能使动静触头可靠接触，这使得动静触头磨损后接触时间发生延后，因此触头的刚合角度随触头磨损的增加而逐渐增大。此外，由图9可知，触头开距增大导致合闸末态位置的触头超程减小，进而造成动静触头接触后触头弹簧对触头杠杆铰接点H的拉力Fs减小，动静触头间接触压力减小，触头终压力和弹簧末态形变量随触头磨损的变化如图10所示。
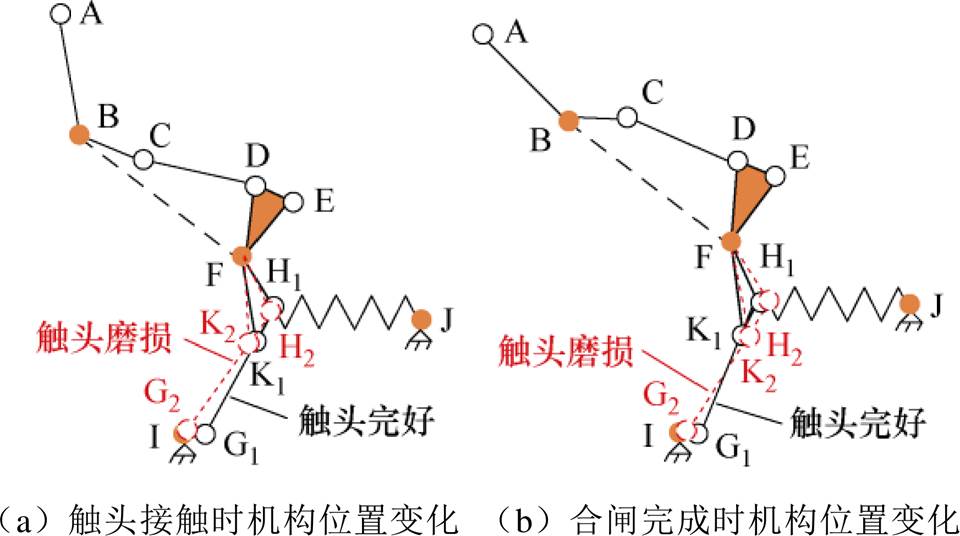
图9 触头磨损前后机构位置变化示意图
Fig.9 Mechanism position change before and after contact abrasion
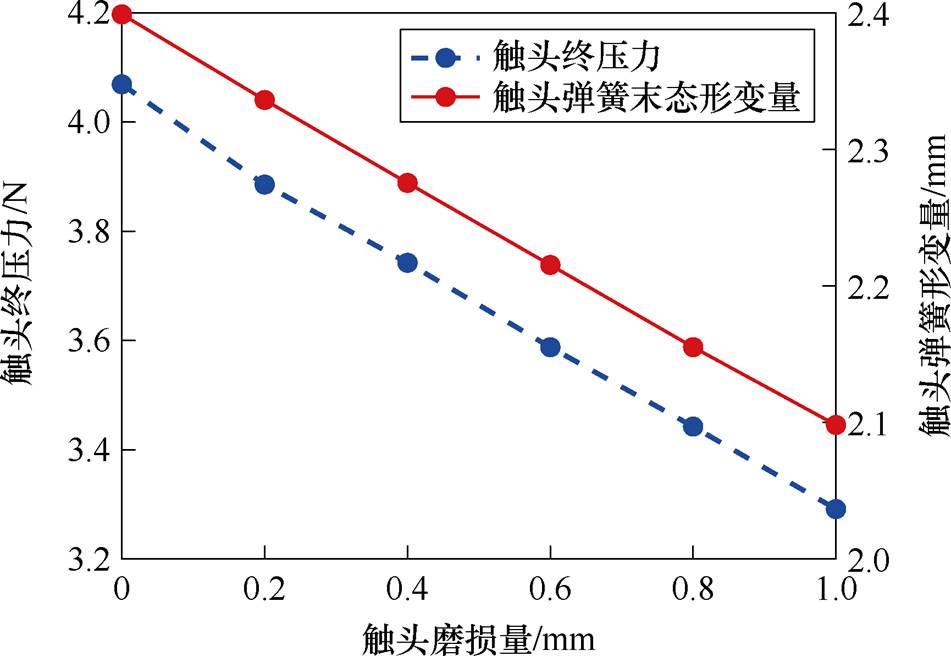
图10 触头终压力和弹簧末态形变量随触头磨损的变化
Fig.10 The variation of contact end pressure and spring end state deformation with contact wear
在触头间接触压力减小后，跳扣对U形连杆产生的推力F32减小，经U形连杆传递，对手柄产生的推力F21减小，进而导致动静触头接触后，手柄操作力矩T相应减小。因此，通过手柄操作力矩与手柄转动角度的关系可以仿真得到单极断路器在不同触头磨损量下的机械特征量，结果见表2。
表2 单极下触头磨损量与机械特征量的关系
Tab.2 Relationship between wear of single pole contact and mechanical characteristic quantity
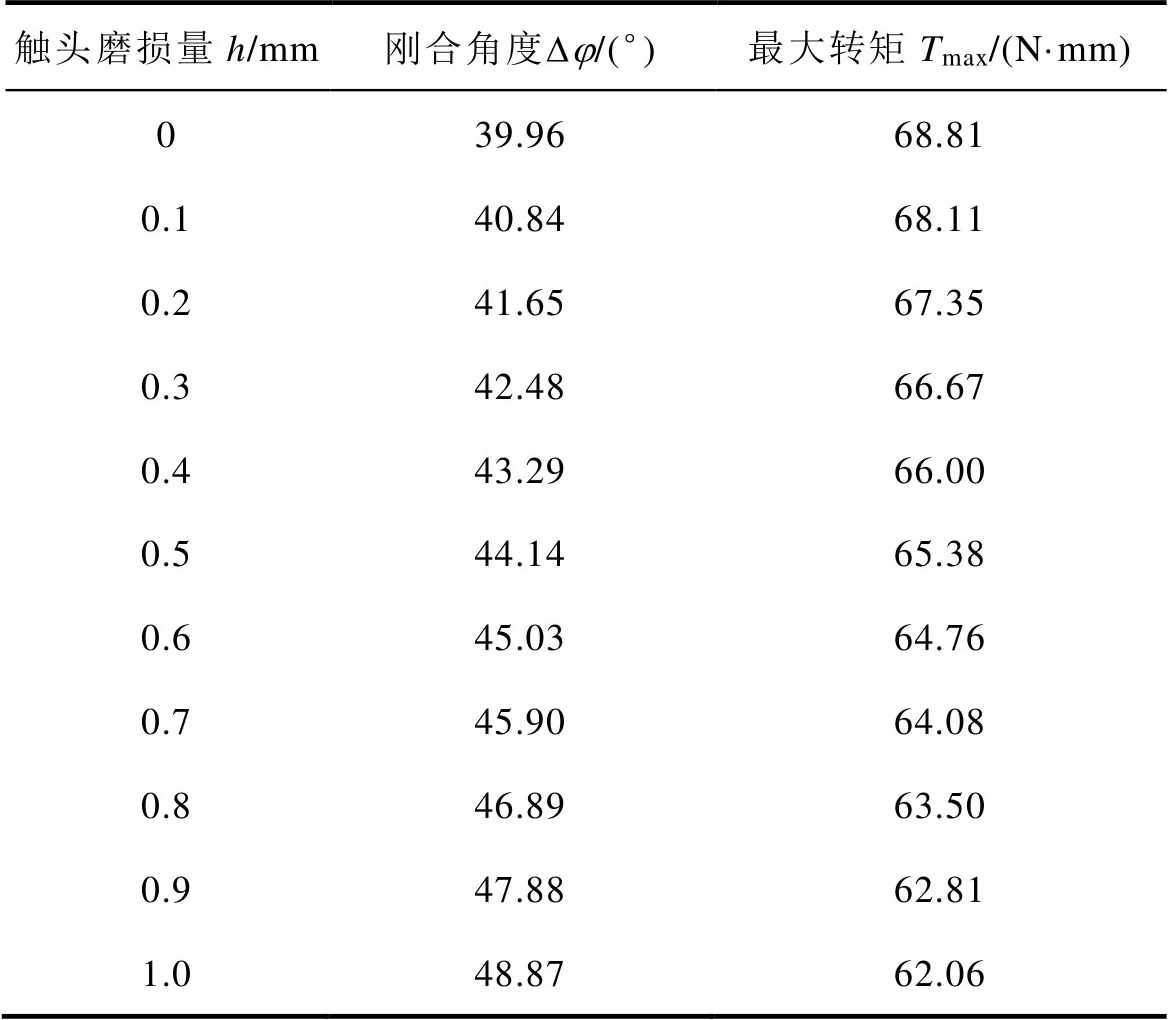
触头磨损量h/mm刚合角度Dj/(°)最大转矩Tmax/(N·mm) 039.9668.81 0.140.8468.11 0.241.6567.35 0.342.4866.67 0.443.2966.00 0.544.1465.38 0.645.0364.76 0.745.9064.08 0.846.8963.50 0.947.8862.81 1.048.8762.06
单极触头磨损量与特征量的变化如图11所示。由图11看出，单极断路器的刚合角度随触头磨损线性增加，最大转矩随触头磨损线性减少。
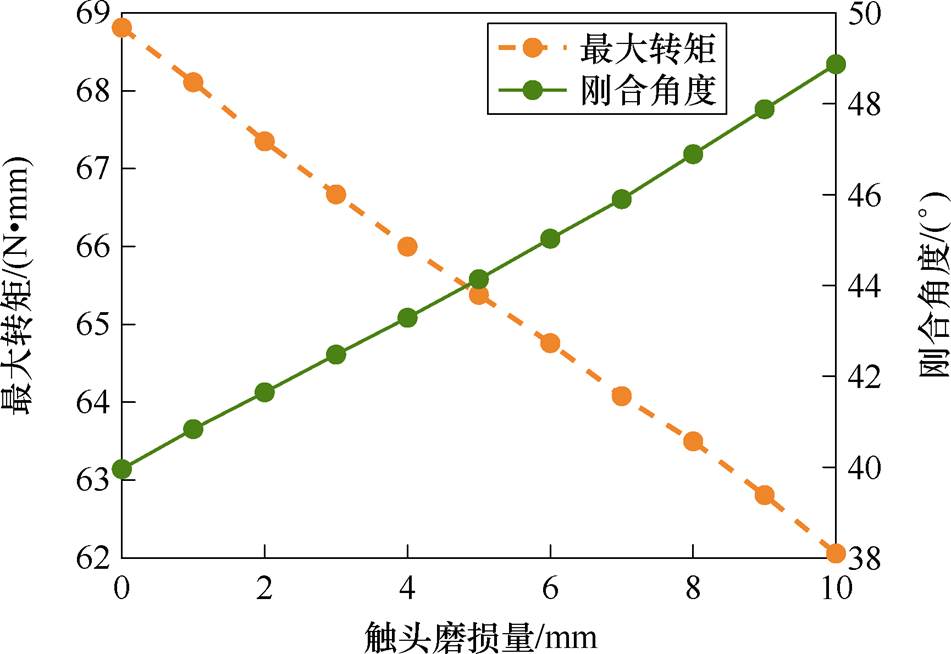
图11 单极触头磨损量与特征量的变化
Fig.11 Relationship between wear of single pole contact and characteristic quantity
2.1.2 多极情况下机械特征量与触头磨损的关系
微型断路器的总操作力矩T与单极操作力矩存在线性叠加关系：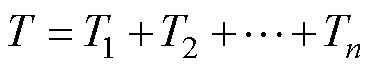
，其中n为断路器极数。假设n极断路器的初始参数完全一致，当n极触头均匀磨损时，满足
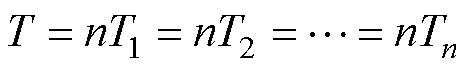（7）
因此，每极断路器的刚合角度Dj 均相等，即
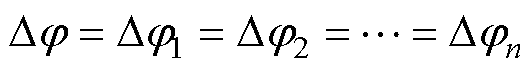（8）
断路器的总最大转矩Tmax也分别满足各极断路器最大转矩Tmaxi的和，即
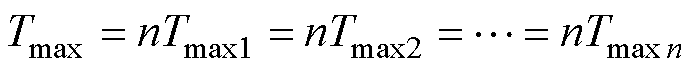（9）
在所有触头均匀磨损情况下，多极断路器的刚合角度Dj 变化与单极断路器相同，最大转矩Tmax为单极的n倍，根据表2易得出多极断路器触头均匀磨损时特征量的对应结果。
当触头磨损不均匀时，断路器总操作力矩T满足各单极断路器的操作力矩之和，但由于触头接触时刻不同，不均匀磨损情况下的特征量并不是通过单极断路器的特征量直接叠加而来。因此，通过动力学仿真模型计算不均匀磨损下特征量的变化。以四极微型断路器为例，对于设计和制造工艺成熟的同一批微型断路器，可认为其机械参数一致。
由于断路器分闸操作是随机且独立的，起弧相位产生具有随机性和独立性，当操作次数较多时，A、B、C三极触头的磨损量相差不大，N极触头在正常情况下磨损量非常少，因此考虑A、B、C极触头均匀磨损，N极触头不磨损的情况。
由于触头不均匀导致触头接触存在先后，因此取多极触头中刚合角度最大值，即
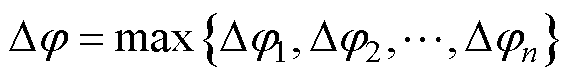（10）
将上述磨损情况进行仿真，得到机械特征量与触头磨损量的关系，结果见表3。
表3 机械特征量与触头磨损量的关系
Tab.3 Relationship between wear of mechanical characteristic quantity and contacts
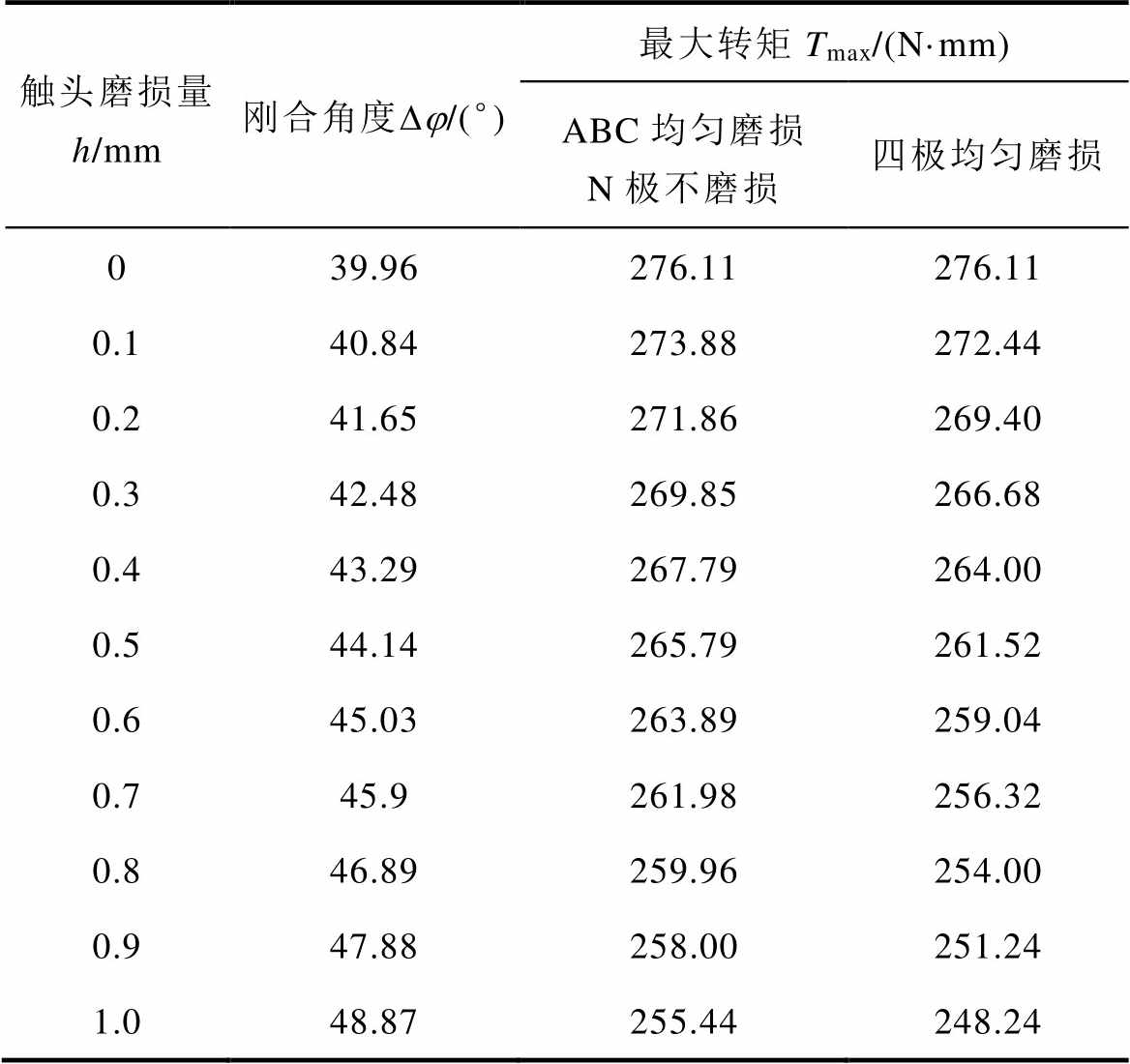
触头磨损量h/mm刚合角度Dj/(°)最大转矩Tmax/(N·mm) ABC均匀磨损 N极不磨损四极均匀磨损 039.96276.11276.11 0.140.84273.88272.44 0.241.65271.86269.40 0.342.48269.85266.68 0.443.29267.79264.00 0.544.14265.79261.52 0.645.03263.89259.04 0.745.9261.98256.32 0.846.89259.96254.00 0.947.88258.00251.24 1.048.87255.44248.24
四极断路器机械特征量与触头磨损量的变化关系如图12所示。由图12得出，当四极断路器N极触头不磨损而其他三极触头均匀磨损时，刚合角度随触头磨损呈线性增加，最大转矩随触头磨损呈线性减少。四极触头均匀磨损时，刚合角度变化与前者一致，最大转矩随触头磨损线性减少，但是下降速度比前者更快。
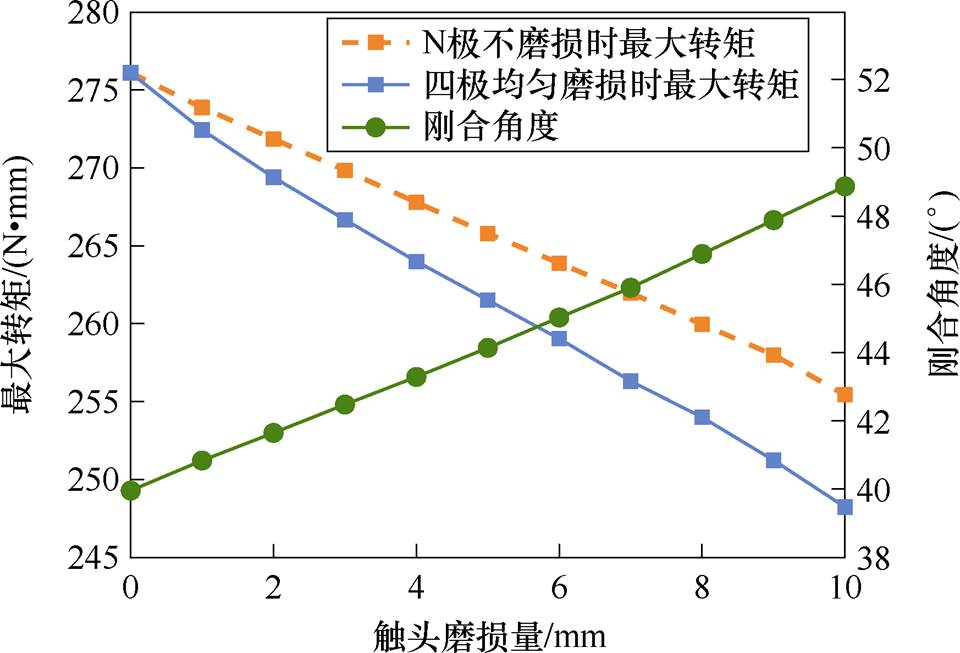
图12 四极断路器机械特征量与触头磨损量的变化关系
Fig.12 Relationship between wear of mechanical characteristic quantity and contacts
综上分析，触头磨损会使刚合角度呈线性上升趋势，使手柄最大转矩呈线性下降趋势，因此刚合角度、最大转矩均可表征微型断路器的性能退化，可通过观测其变化判断触头的磨损程度。
随着微型断路器服役时间的增长，触头弹簧长期处于拉伸状态，可能导致弹簧的塑性形变增加，同时断路器在分合闸过程中，触头间拉出的电弧会产生高温，以及触头弹簧距离软连接很近甚至在合分闸过程中会发生接触，这两种情况导致触头弹簧受到较高温度的影响，进而使弹簧应力松弛，塑性形变与应力松弛均会导致弹簧刚度系数减小。
当手柄转至死点位置后，U形连杆CD对手柄的作用由阻力转变为动力，当触头弹簧刚度系数减小时，弹簧对触头杠杆的拉力Fs减小，导致U形连杆CD对手柄的推力F21减小，力臂lBCsina 不变，可知手柄在转到死点前阻力矩减小，转过死点位置后动力矩减小。若只有触头弹簧刚度系数下降，则手柄操作力矩T在整个合闸过程中都减小，因此可得出最大转矩Tmax随触头弹簧刚度系数下降而减小。此外，刚度系数下降并不影响触头弹簧形变量，因此触头刚合角度不受弹簧刚度系数影响。对于多极断路器，每极触头弹簧疲劳程度相同，仍可根据式（8）和式（9）进行分析。根据手柄操作力矩T随弹簧刚度系数变化特征可以计算弹簧疲劳程度与机械特征量之间的变化关系，仿真计算结果见表4。
表4 弹簧疲劳程度与机械特征量的关系
Tab.4 Relationship between fatigue degree of unipolar spring and mechanical characteristic quantity
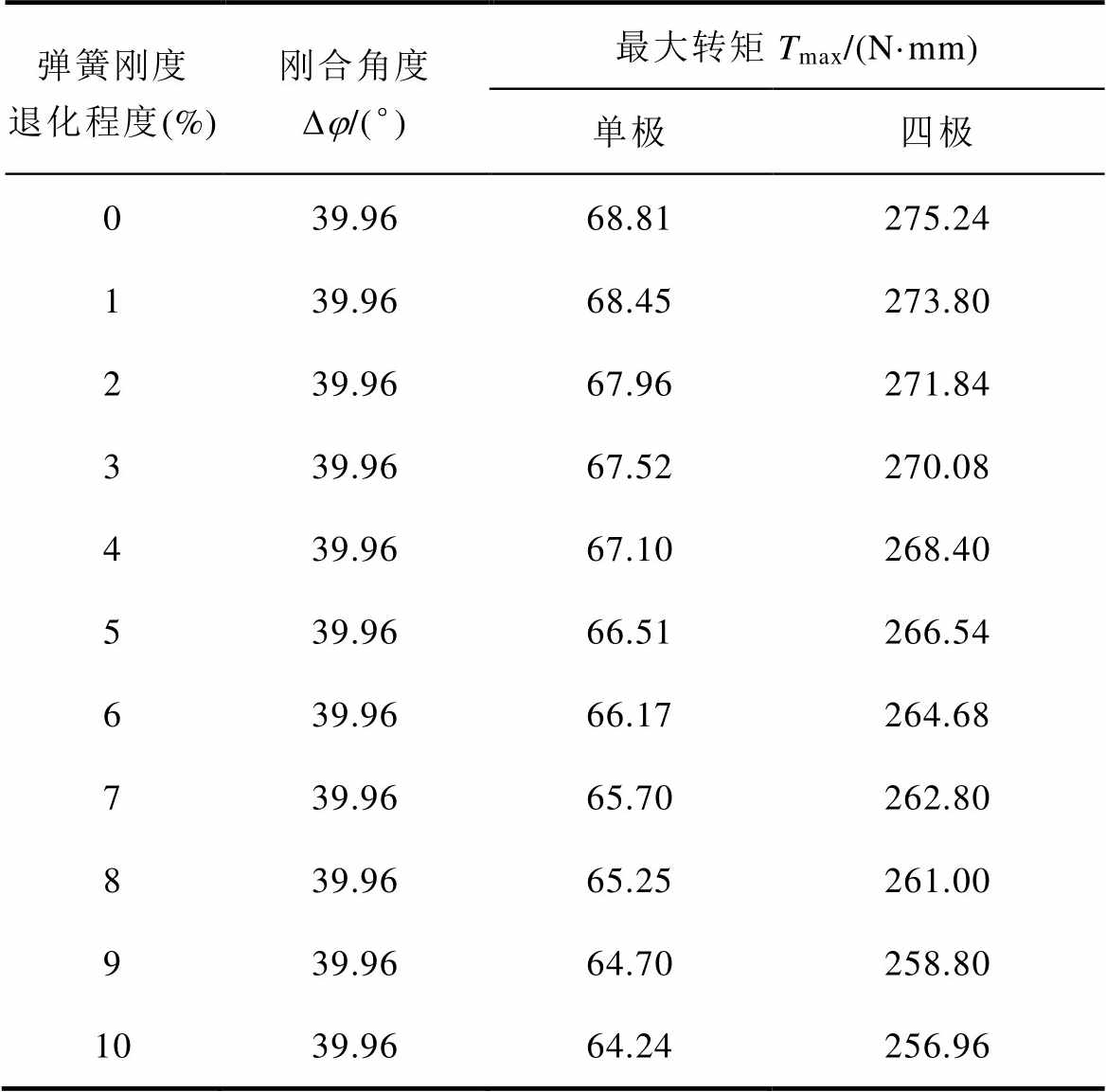
弹簧刚度退化程度(%)刚合角度Dj/(°)最大转矩Tmax/(N·mm) 单极四极 039.9668.81275.24 139.9668.45273.80 239.9667.96271.84 339.9667.52270.08 439.9667.10268.40 539.9666.51266.54 639.9666.17264.68 739.9665.70262.80 839.9665.25261.00 939.9664.70258.80 1039.9664.24256.96
机械特征量随触头弹簧退化的变化关系如图13所示。由图13可看出，触头弹簧退化会导致最大转矩Tmax减小，但并不影响刚合角度Dj 大小。
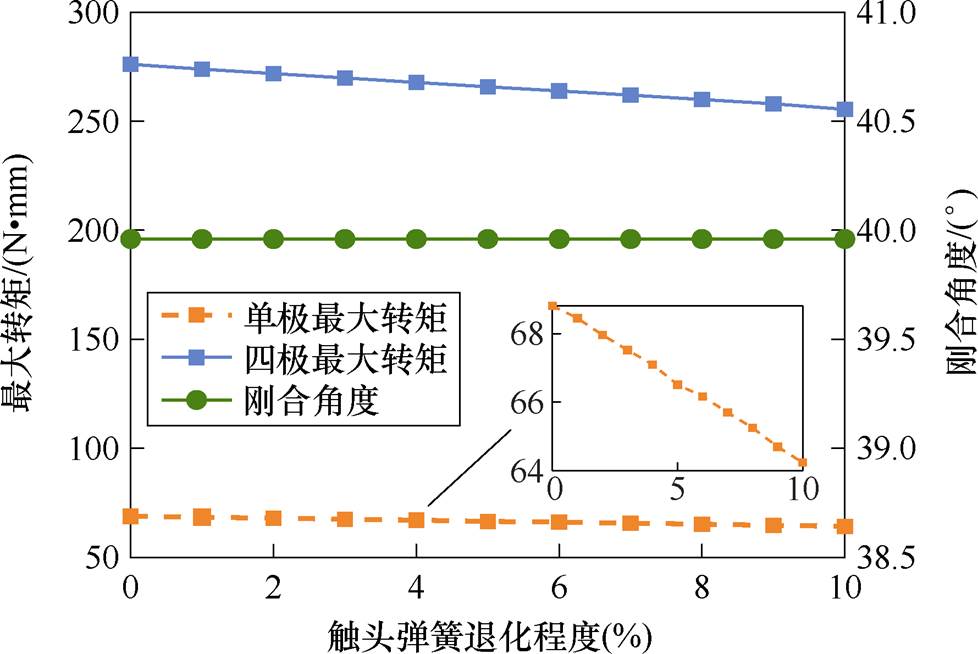
图13 机械特征量随触头弹簧退化的变化关系
Fig.13 Relationship between mechanical characteristic quantities and degradation of contact spring
在微型断路器操作过程中，触头弹簧钩环处发生应力集中现象，弹簧表面产生裂纹，随着操作次数的增加，触头弹簧表面裂纹逐渐扩展，当累积疲劳损伤超过弹簧承受范围时，触头弹簧断裂。
当触头弹簧发生断裂后，触头弹簧对触头杠杆的拉力Fs消失，为触头提供接触压力的动力大幅下降，使得触头间的接触压力发生骤降，对于中心支架对铰接点K的拉力FK而言，接触压力属于阻力，阻力骤降后，完成同样的合闸过程所需要的FK就相应骤降，因此跳扣对U形连杆的作用力F32骤降，力臂lBCsina 不变，导致U形连杆对手柄的力矩发生骤降。分别仿真分析单极和四极情况下机械特征量的变化情况，其结果见表5。
表5 触头弹簧断裂对机械特征量的影响
Tab.5 The influence of single pole contact spring fracture on mechanical characteristic quantities
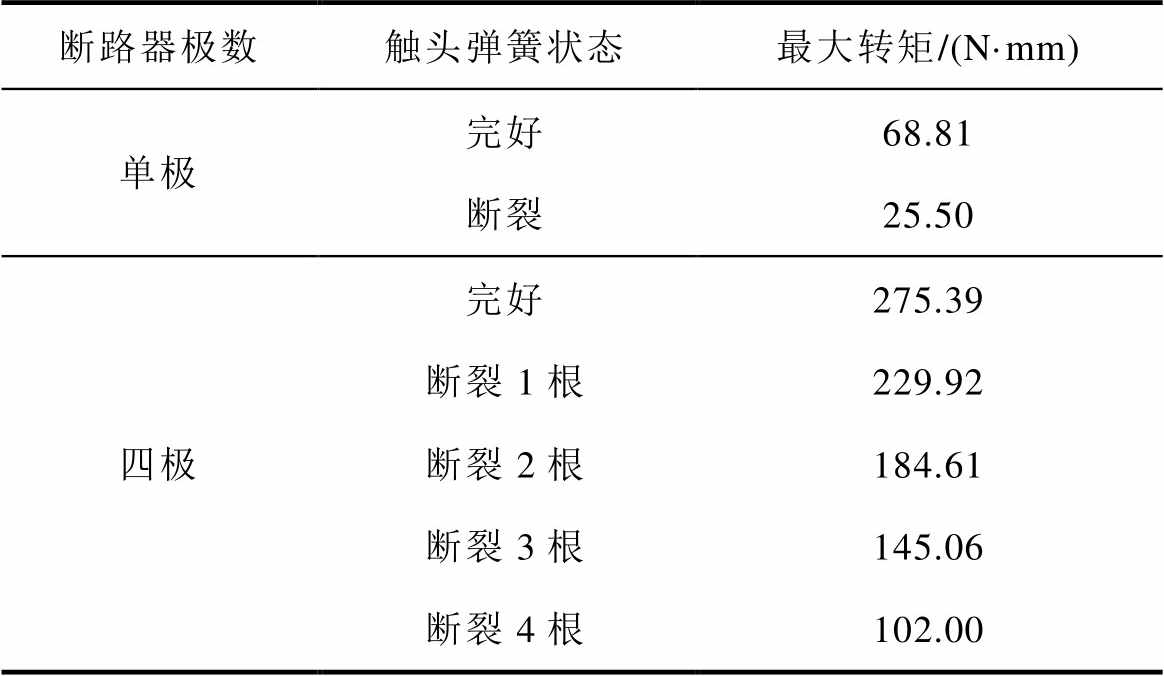
断路器极数触头弹簧状态最大转矩/(N·mm) 单极完好68.81 断裂25.50 四极完好275.39 断裂1根229.92 断裂2根184.61 断裂3根145.06 断裂4根102.00
由表5可看出，触头弹簧断裂使得最大转矩Tmax出现阶跃下降。因此，可通过观测最大转矩Tmax是否阶跃变化判断微型断路器是否发生触头弹簧断裂。
触头弹簧断裂后，触头杠杆缺少触头弹簧的弹力作用而导致动静触头间接触压力急剧减小，在软连接的牵拉作用下，动静触头能接触但接触压力很小，在电动力作用下触头很容易斥开。
在微型断路器服役过程中，触头受电弧侵蚀导致触头磨损，且随操作次数的增加，弹簧发生断裂失效。这两种失效形式是常见故障形式，因此在微型断路器服役状态等级划分时可考虑这些因素。
在触头退化方面，当触头磨损在25%范围以内时，断路器能正常完成线路的接通和断开；当触头磨损50%时，断路器服役性能已经发生一定程度的退化；当触头磨损至75%时，动静触头间能接触，但是触头超程退化和触头终压力减小较多，断路器转移至危险状态；当触头磨损90%以上，触头不能可靠接触，认为断路器处于故障状态。在触头弹簧方面，当触头弹簧断裂时，动静触头间接触压力很小，可能引起触头斥开、熔焊故障，因此认为触头弹簧断裂时，断路器转移至故障状态。
由于实际服役过程中微型断路器的外壳不可拆卸，无法对触头磨损量进行测量，根据2.1～2.3节分析可知，触头磨损量和刚合角度、最大转矩之间存在线性关系，因此可以通过刚合角度、最大转矩进行状态阈值划分，本文把四极微型断路器的服役状态分为四个等级，相应机械特征量范围见表6。
表6 微型断路器服役状态划分
Tab.6 Rule for dividing the service status of miniature circuit breaker
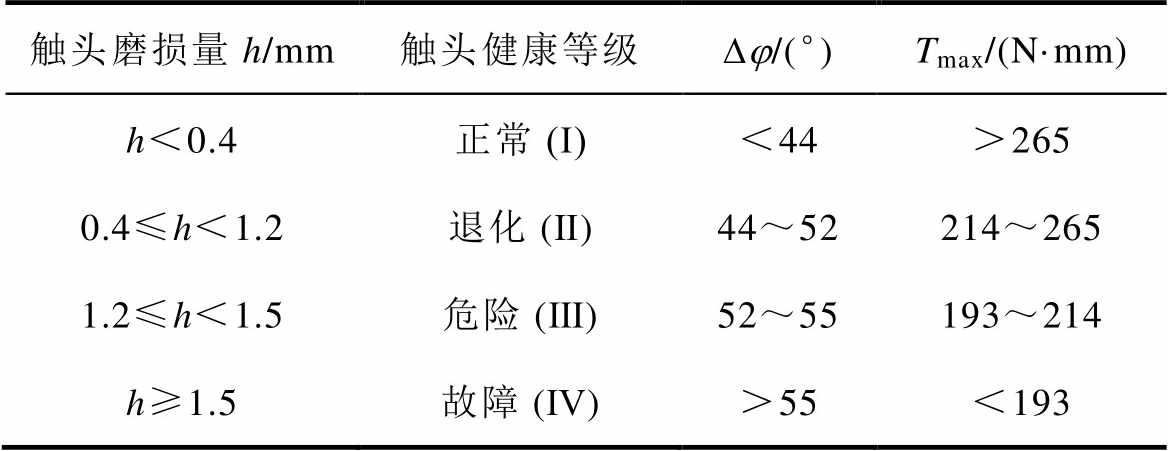
触头磨损量h/mm触头健康等级Dj/(°)Tmax/(N·mm) h＜0.4正常 (Ⅰ)＜44＞265 0.4≤h＜1.2退化 (Ⅱ)44～52214～265 1.2≤h＜1.5危险 (Ⅲ)52～55193～214 h≥1.5故障 (Ⅳ)＞55＜193
通过检测微型断路器的刚合角度、最大转矩，可以对触头磨损、触头弹簧断裂状态进行识别。微型断路器操作性能观测与状态辨识过程如图14所示。
服役状态辨识流程具体步骤如下：
（1）根据完好状态下微型断路器参数进行调整并设定特征量的状态阈值。
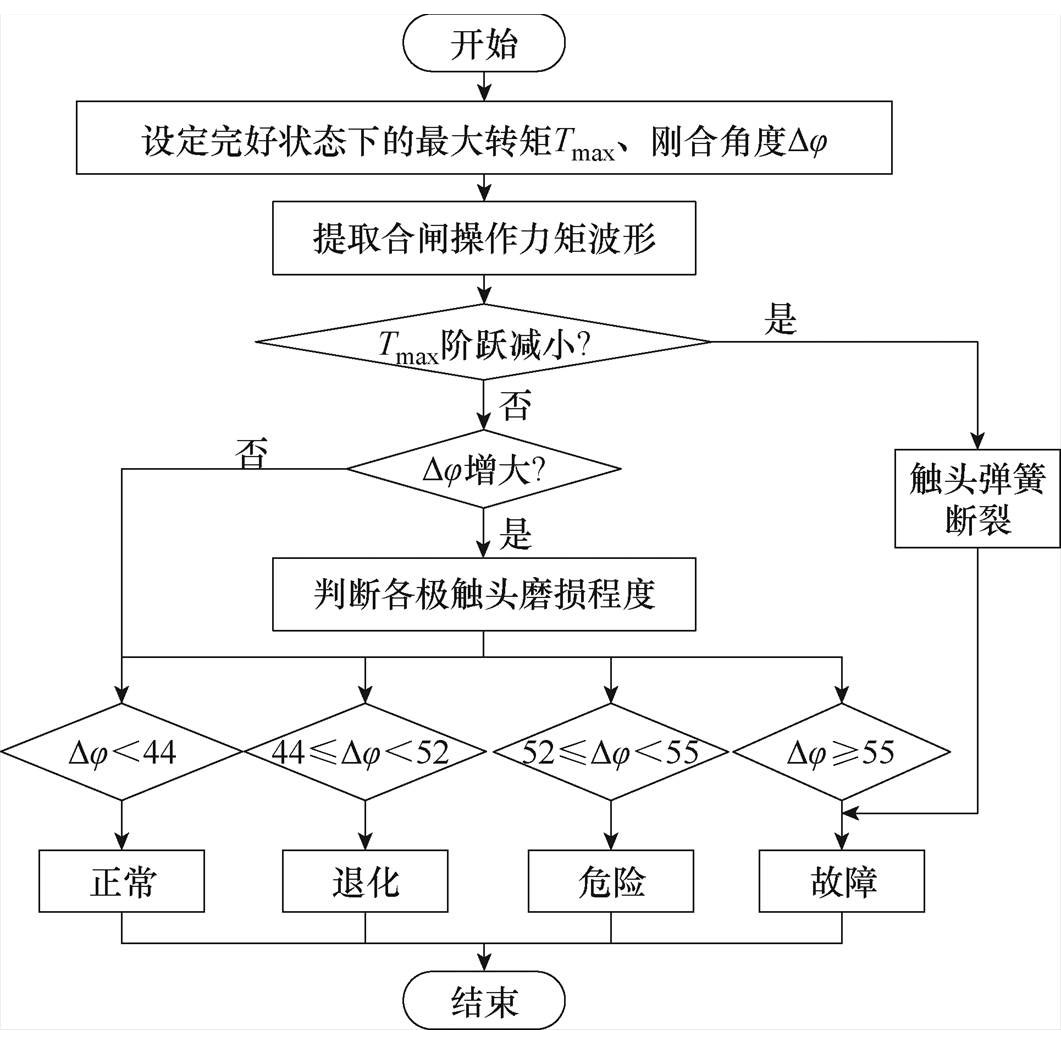
图14 微型断路器服役状态辨识流程
Fig.14 Process for identifying the service status of miniature circuit breakers
（2）采集机构合闸过程的手柄操作力矩波形，并提取刚合角度Dj 和最大转矩Tmax。
（3）根据Tmax判断微型断路器是否发生触头弹簧断裂，若发生断裂则判定为断路器失效，并报警；若无断裂则执行后续操作。
（4）根据Dj 判断微型断路器的触头系统是否发生磨损，若有磨损，得出触头磨损程度，并根据状态阈值判断触头当前服役状态，若磨损达到故障阈值，则判定微型断路器状态为故障，若未达故障阈值，根据Dj 所处区间给出触头当前服役状态，并执行结束操作。
本文搭建了微型断路器手柄转矩测量平台，进行微型断路器机械特性参数的测量、分析和验证，实验平台原理如图15a所示。
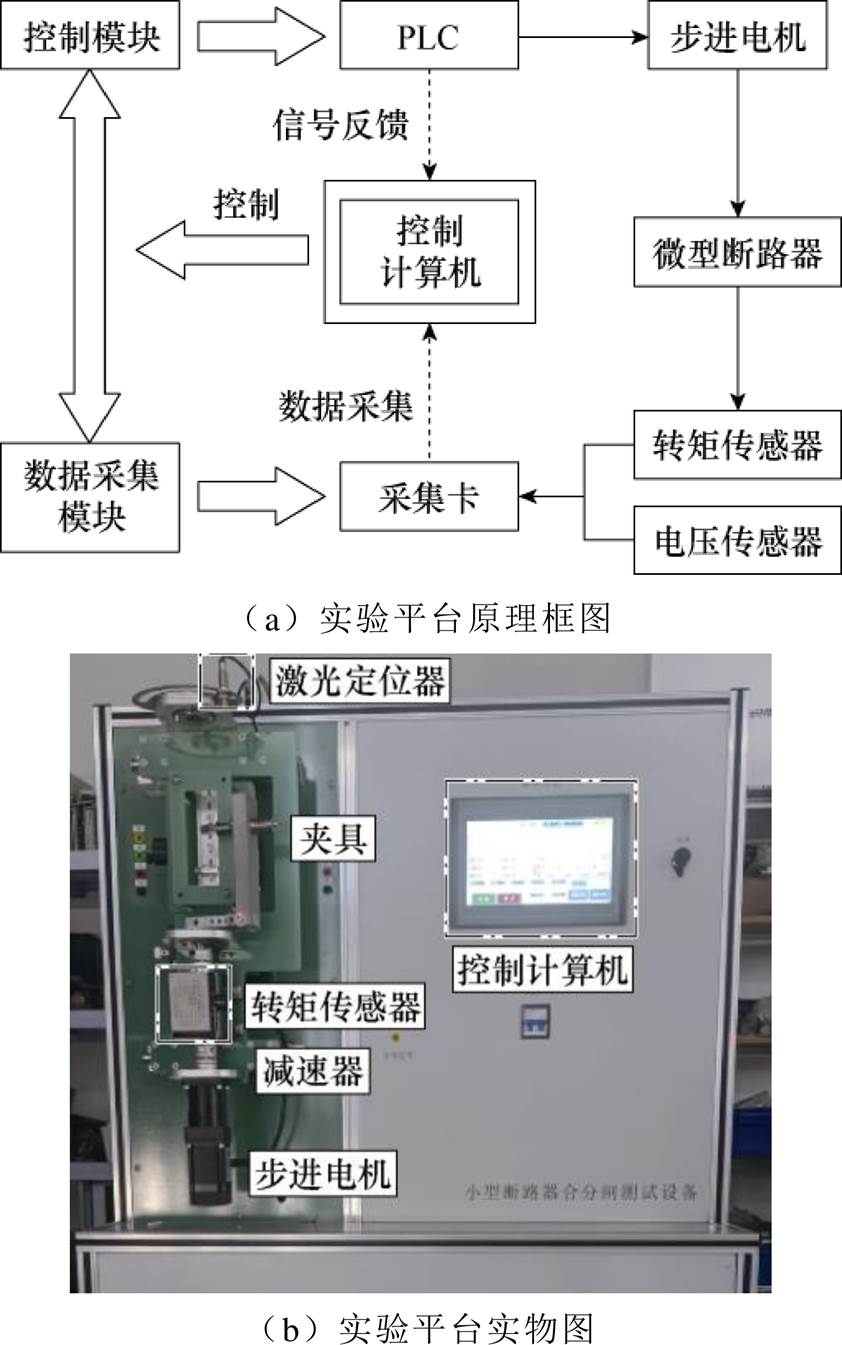
图15 微型断路器转矩测量平台
Fig.15 Miniature circuit breaker torque test platform
控制计算机通过总线控制PLC驱动步进电机匀速转动，用以控制断路器的合分闸操作，同时也控制采集卡对手柄转矩信号和触头信号进行数据采集并上传到控制计算机显示系统，完成采集信号的显示和存储。
测量平台的结构如图15b所示，手柄转矩测量平台包括激光定位器、手柄夹具、动态转矩传感器、电压传感器、9 V直流电源、减速器、步进电机等。通过检测微型断路器来判别触头的刚合状态。
采集微型断路器合闸过程中手柄操作力矩后，对波形信号进行滤波处理，结果如图16所示，仿真和采集的手柄转矩波形整体变化趋势一致。
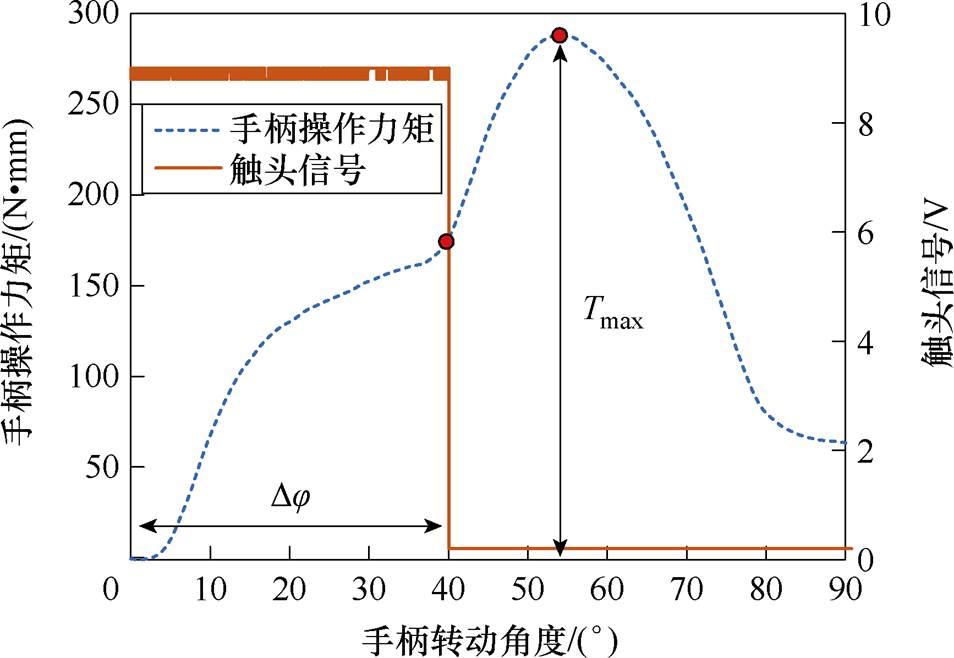
图16 合闸过程中手柄操作力矩波形
Fig.16 Operating torque waveform of handle during the closing process
机构初始位置卡涩示意图如图17所示。在图17中，跳扣DE和锁扣DF间存在间隙，连杆CD对E的作用力指向E点内侧，导致机构开始运动时U形连杆和跳扣产生卡涩现象。手柄刚开始转动的一段时间内，通过U形连杆水平推动跳扣及触头组件，连杆CD对锁扣的力指向E点内侧，该时间段内手柄阻力矩增加量较大，手柄转动一定角度后，跳扣锁扣啮合，连杆CD对E的作用力指向E点外侧，卡涩现象消失，U形连杆对手柄阻力矩的增速减小，因此手柄操作力矩增长先快后慢。在仿真分析中并未考虑卡涩现象，因此在动静触头接触前，手柄操作力矩变化仿真结果与实测有一定误差，但变化趋势相同。触头一旦接触，仿真结果和实测结果吻合度高。
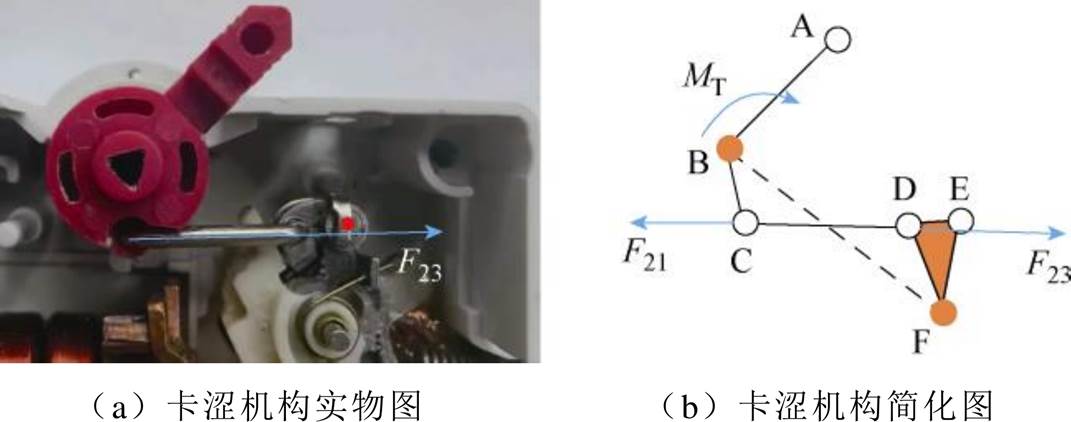
图17 机构初始位置卡涩示意图
Fig.17 Schematic diagram of mechanism initial position jamming
4.2.1 触头磨损情况下特征量实验验证
对四极微型断路器进行触头磨损模拟实验，将微型断路器A、B、C 三极触头均匀磨损1 mm，每磨损0.2 mm进行手柄操作力矩特征量的采集，共采集六组特征量，即完好状态、磨损0.2 mm、磨损0.4 mm、磨损0.6 mm、磨损0.8 mm、磨损1 mm。结果如图18所示。
由图18可知，触头磨损后会导致刚合角度Dj 增大，最大转矩Tmax减小，刚合角度增大的原因是断路器动触头与静触头接触的时间后延，最大转矩减小的原因是触头超程减小引起手柄合闸过程中的阻力矩减小。基于仿真得出的触头磨损后两个特征量变化趋势与实验中所得变化趋势相同，最大相对误差在13%以内。
4.2.2 触头弹簧断裂情况下特征量实验验证
通过拆除方法来模拟断路器触头弹簧断裂情况，模拟四极断路器中每极触头弹簧断裂，可分为五种情况，即：无弹簧断裂、A极弹簧断裂、B极弹簧断裂、C极弹簧断裂、N极弹簧断裂。结果如图19所示。
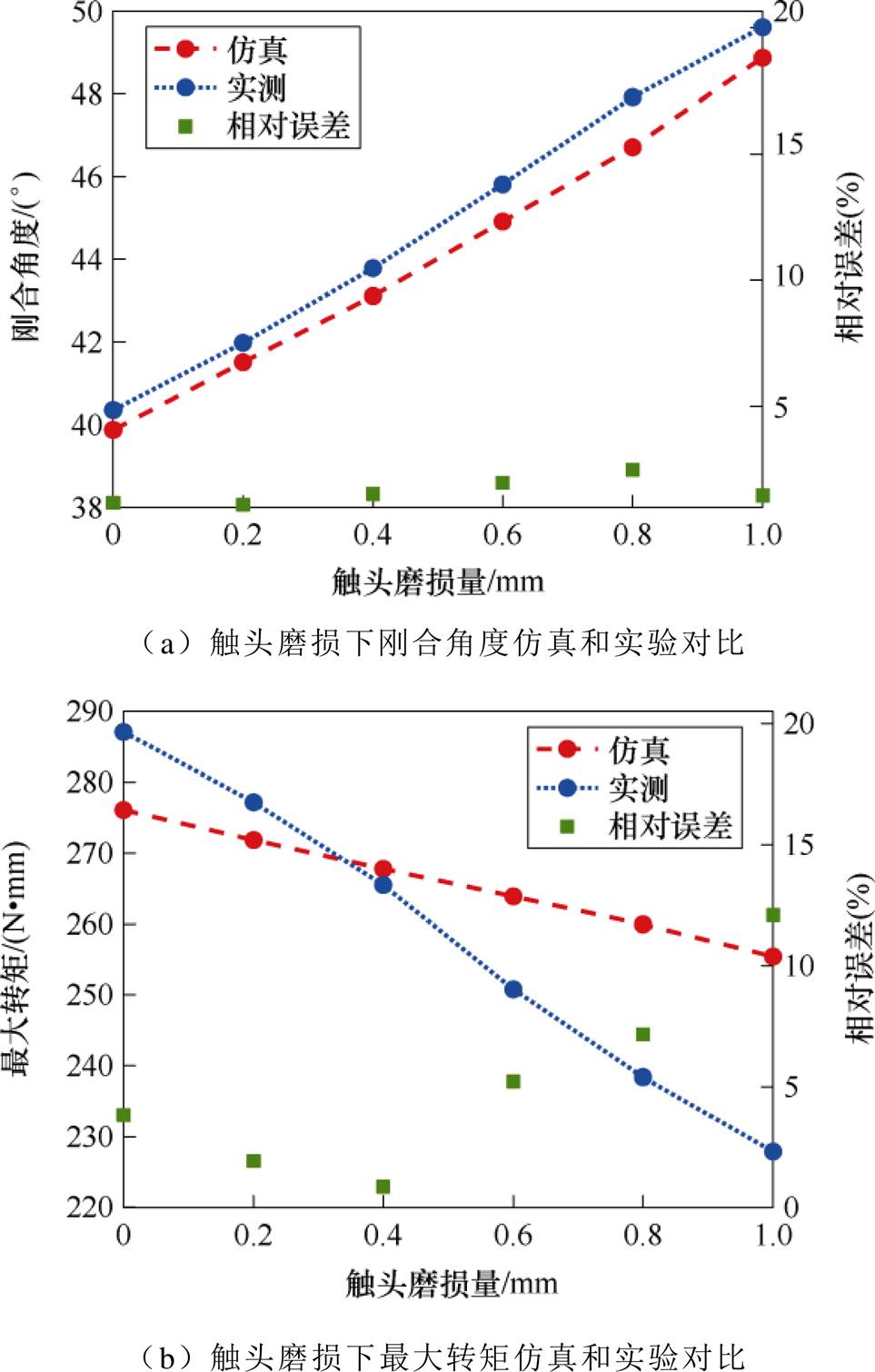
图18 触头磨损下机械特征量的仿真和实验对比
Fig.18 Simulation and experimental comparison of mechanical characteristic quantities under contact wear
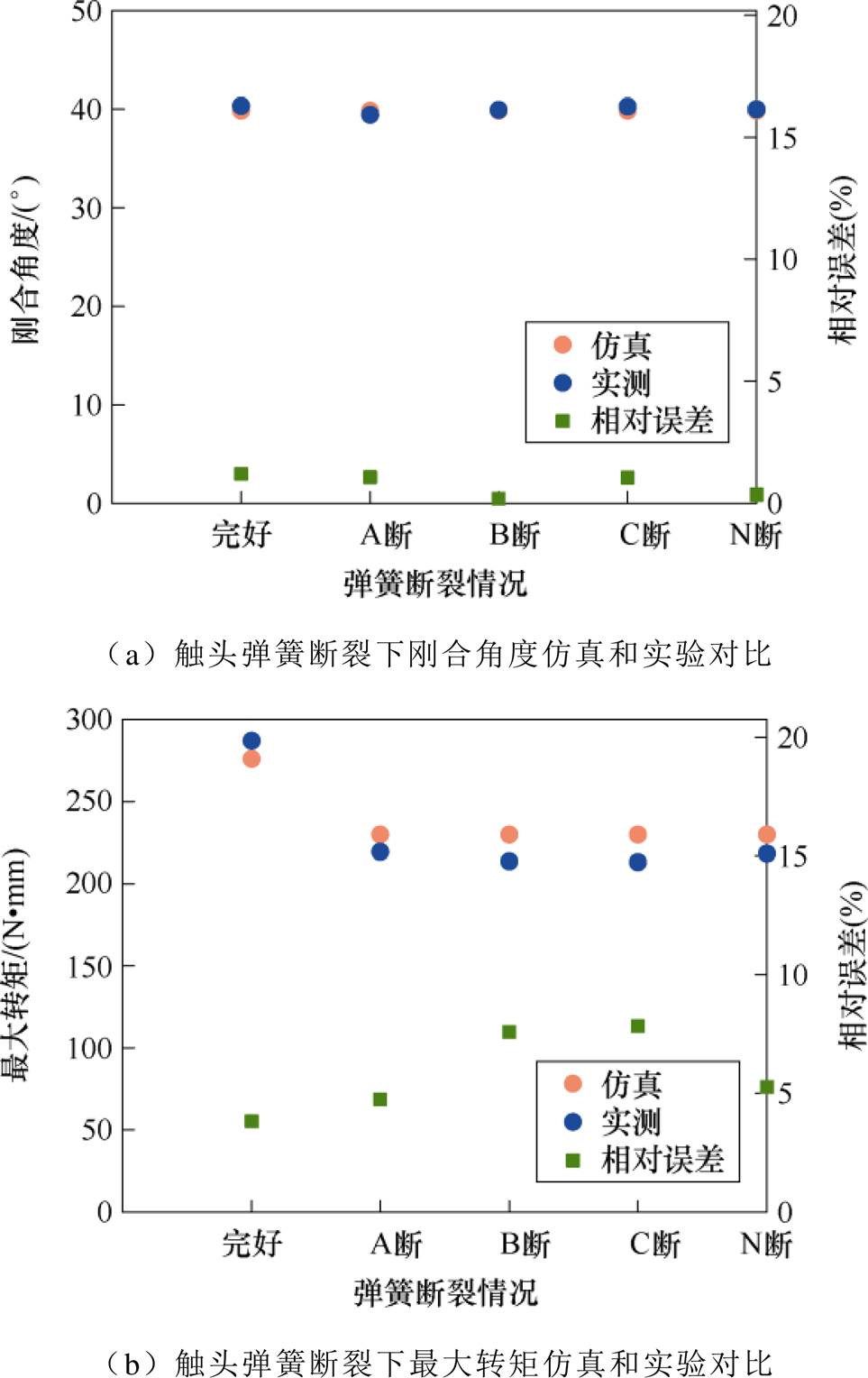
图19 触头弹簧断裂下机械特征量仿真和实验对比
Fig.19 Simulation and experimental comparison of mechanical characteristic quantities under contact spring fracture
由图19可知，当四极微型断路器有一极触头弹簧断裂后，刚合角度不变，最大转矩阶跃下降。理论上不同极弹簧断裂时最大转矩下降变化量应当相同，但由于实际产品中的不同极触头弹簧存在分散性，实测每一极弹簧断裂的最大转矩下降变化量存在差异，仿真与实验的相对误差在8%以内。
在实验中受各种偶然因素的影响，实验结果与理论仿真结果存在一定误差，有些情况相差较大，相对误差在10%～20%之间一般认为是可接受的[21-22]。仿真模型中各部件间的配合与装配进行简化处理，忽略不同部件间铰接时存在的间隙、运动副间摩擦等，此外，杆件尺寸公差也会造成仿真计算结果与实测数据不同。因此，可以认为上述两种情况下刚合角度和最大转矩的仿真结果与实验结果一致，验证了理论分析的正确性和所提方法的可行性。
本文对微型断路器操作机构动力学特性进行仿真分析，提出采用手柄操作力矩表征微型断路器的服役性能退化的方法，并开展了相关研究。主要结论如下：
1）根据操作机构动力学特性，建立微型断路器动力学仿真模型，分析合闸过程中手柄操作力矩随手柄转动角度的变化特征，通过手柄操作力矩变化曲线可以确定出触头刚合角度和合闸最大转矩。
2）提出了采用触头刚合角度和合闸最大转矩表征微型断路器性能退化的方法，通过手柄操作力矩的分析可以判定微型断路器性能退化程度。分析触头磨损、触头弹簧疲劳断裂等因素对微型断路器机械特征量的影响，可以发现，当触头磨损增加，刚合角度增加，最大转矩减小；当触头弹簧断裂，刚合角度不变，最大转矩阶跃下降。
3）提出基于机械特性的微型断路器服役状态辨识方法，将微型断路器服役状态划分为正常、退化、危险、故障四个等级，根据不同服役状态下刚合角度和最大转矩的状态阈值实现微型断路器服役性能退化状态的辨识。进行实验和仿真分析，验证了本文提出方法的有效性。
参考文献
[1] Li Xiaodong, Liu Xiangjun, Xu Zhihong. Simulation and research on short circuit breaking arc characteristics of micro circuit breaker[C]//The Proceedings of the 18th Annual Conference of China Electrotechnical Society, Singapore, 2024: 32-40.
[2] 何志鹏, 赵虎. 微型断路器电寿命评估[J]. 电工技术学报, 2022, 37(4): 1031-1040.
He Zhipeng, Zhao Hu. Electrical lifespan evaluation of miniature circuit breakers[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 1031- 1040.
[3] Tahvilzadeh M, Aliyari-Shoorehdeli M, Razi-Kazemi A A. Model-aided approach for intelligent fault detection system for SF6 high-voltage circuit breaker with spring operating mechanism[J]. IEEE Transa- ctions on Power Delivery, 2023, 38(5): 3356-3365.
[4] 范兴明, 许洪华, 李涛, 等. 基于SMA-VMD和能量熵的高压断路器故障诊断[J]. 高电压技术, 2024, 50(12): 5248-5258.
Fan Xingming, Xu Honghua, Li Tao, et al. Fault diagnosis of high-voltage circuit breakers based on SMA-VMD and energy entropy[J]. High Voltage Engineering, 2024, 50(12): 5248-5258.
[5] 李辰辉, 褚继峰, 龙潇, 等. 基于弧触头接触振动特征分析的高压SF6断路器电寿命在线监测方法[J]. 电工技术学报, 2024, 39(15): 4883-4895.
Li Chenhui, Chu Jifeng, Long Xiao, et al. Online monitoring method of electrical life of high voltage SF6 circuit breaker based on analysis of arcing contact vibration characteristics[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4883-4895.
[6] 孙玉伟, 罗林根, 陈敬德, 等. 含噪背景下基于盲源分离与NSVDD的断路器机械故障诊断方法[J]. 高电压技术, 2022, 48(3): 1104-1112.
Sun Yuwei, Luo Lingen, Chen Jingde, et al. Mechanical fault diagnosis method of circuit breaker based on blind source separation and NSVDD under noisy background[J]. High Voltage Engineering, 2022, 48(3): 1104-1112.
[7] 段梵, 李先允, 单光瑞, 等. 基于融合特征和残差神经网络的10 kV高压断路器机械故障声纹识别方法[J]. 高压电器, 2025, 61(3): 205-213.
Duan Fan, Li Xianyun, Shan Guangrui, et al. Voiceprint recognition method for mechanical faults of 10 kV circuit breaker based on fusion feature residual neural network[J]. High Voltage Apparatus, 2025, 61(3): 205-213.
[8] 钟声, 李晓洋, 梁胜乐, 等. 基于线圈电流信号及动态时间规整的高压断路器状态评估方法[J]. 高压电器, 2023, 59(4): 24-31.
Zhong Sheng, Li Xiaoyang, Liang Shengle, et al. Condition assessment method on high voltage circuit breaker based on coil current signal and dynamic time warping[J]. High Voltage Apparatus, 2023, 59(4): 24-31.
[9] Razi-Kazemi A A, Niayesh K, Nilchi R. A probabi- listic model-aided failure prediction approach for spring-type operating mechanism of high-voltage circuit breakers[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1280-1290.
[10] 胡博凯, 李奎, 牛峰, 等. 低压断路器机械特性状态监测方法研究[J]. 电工技术学报, 2022, 37(13): 3317-3330.
Hu Bokai, Li Kui, Niu Feng, et al. Research on condition monitoring method of mechanical characteristics of low-voltage circuit breaker[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3317-3330.
[11] 韩翔宇, 纽春萍, 何海龙, 等. 电磁式断路器状态监测与智能评估技术综述[J]. 电工技术学报, 2023, 38(8): 2191-2210.
Han Xiangyu, Niu Chunping, He Hailong, et al. Review of condition monitoring and intelligent assessment of electromagnetic circuit breaker[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2191-2210.
[12] 杨秋玉, 阮江军, 黄道春, 等. 基于振动信号的高压断路器触头超程状态识别[J]. 电机与控制学报, 2019, 23(6): 27-34.
Yang Qiuyu, Ruan Jiangjun, Huang Daochun, et al. Over-travel state identification for electrical contact of high-voltage circuit breaker using vibration signature[J]. Electric Machines and Control, 2019, 23(6): 27-34.
[13] 刘会兰, 常庚垚, 赵书涛, 等. 溯源弹簧形变过程的断路器振动信号递归量化分析辨识方法[J]. 电工技术学报, 2024, 39(8): 2567-2577.
Liu Huilan, Chang Gengyao, Zhao Shutao, et al. Circuit breaker state identification method based on tracing spring deformation process and recurrence quantitative analysis of vibration signals[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(8): 2567-2577.
[14] 马莉, 霍耀佳, 吴杨, 等. 基于VMD和KFCM- SVM的高压断路器声振联合故障诊断方法[J]. 高压电器, 2024, 60(8): 53-62.
Ma Li, Huo Yaojia, Wu Yang, et al. Acoustic and vibration joint fault diagnosis method of high voltage circuit breaker based on VMD and KFCM-SVM[J]. High Voltage Apparatus, 2024, 60(8): 53-62.
[15] 卢扬, 李永丽. 基于实时状态评估与剩余寿命计算的高压断路器预测性维护策略[J]. 高电压技术, 2022, 48(7): 2716-2726.
Lu Yang, Li Yongli. Predictive maintenance policy for high-voltage circuit breakers based on real-time state estimation and remanent useful life calcu- lation[J]. High Voltage Engineering, 2022, 48(7): 2716-2726.
[16] 孙曙光, 杨飞龙, 陈静, 等. 基于振动-电流广域特征与软共享机制的断路器多故障诊断[J]. 仪器仪表学报, 2024, 45(1): 46-59.
Sun Shuguang, Yang Feilong, Chen Jing, et al. Multi-fault diagnosis of circuit breaker based on vibration-current wide-domain features and soft sharing mechanism[J]. Chinese Journal of Scientific Instrument, 2024, 45(1): 46-59.
[17] 赵书涛, 黄伟杰, 刘会兰, 等. 高压断路器触头烧蚀及电寿命评估研究综述[J]. 高电压技术, 2024, 50(2): 489-502.
Zhao Shutao, Huang Weijie, Liu Huilan, et al. Review of research on contact ablation and electrical life assessment of high-voltage circuit breakers[J]. High Voltage Engineering, 2024, 50(2): 489-502.
[18] 王振兴, 刁目鑫, 肖光宇, 等. 基于QPSO-SVR算法的SF6断路器触头烧蚀状态评估[J]. 高电压技术, 2023, 49(9): 3919-3930.
Wang Zhenxing, Diao Muxin, Xiao Guangyu, et al. Evaluation of contact ablation state of SF6 circuit breaker based on QPSO-SVR algorithm[J]. High Voltage Technology, 2023, 49(9): 3919-3930.
[19] Li Kui, Zhao Chengchen, Niu Feng, et al. Electrical performance degradation model and residual electrical life prediction for AC contactor[J]. IEEE Transactions on Components, Packaging and Manufa- cturing Technology, 2020, 10(3): 400-417.
[20] 赵成晨, 李奎, 胡博凯, 等. 变应力条件下低压断路器剩余电寿命预测[J]. 中国电机工程学报, 2022, 42(21): 8004-8016.
Zhao Chengchen, Li Kui, Hu Bokai, et al. Residual electrical life prediction of low-voltage circuit breakers under varied stress[J]. Proceedings of the CSEE, 2022, 42(21): 8004-8016.
[21] 孔倩, 赵义豪, 姜根山, 等. 流场声学层析成像测量方法仿真和实验研究[J/OL]. 仪器仪表学报, 2024: 1-12. (2024-08-12). http://kns.cnki.net/KCMS/detail/ detail.aspx? filename=YQXB2024080900X&dbname= CJFD&dbcode=CJFQ.
Kong Qian, Zhao Yihao, Jiang Genshan, et al. Simulation and experimental study on acoustic tomography measurement method of flow field[J/OL]. China Industrial Economics, 2024: 1-12. (2024- 08-12). http://kns.cnki.net/KCMS/detail/detail.aspx? filename=YQXB2024080900X&dbname=CJFD& dbcode=CJFQ.
[22] 李东晖, 周学, 王傲, 等. 考虑制造参数的批量化真空交流接触器机械寿命预测[J]. 电工技术学报, 2023, 38(7): 1982-1990.
Li Donghui, Zhou Xue, Wang Ao, et al. Mechanical life prediction of batch electromagnetic switches considering manufacturing parameters[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(7): 1982-1990.
Abstract Miniature circuit breakers (MCBs) are important protection devices in low-voltage distribution systems. They can automatically de-energize the power supply immediately in the event of electrical failures, protecting the power distribution system from fire or other serious hazards. MCBs are subject to electrical and mechanical stresses during service. The operational performance of an MCB can gradually degrade with the increasing number of operations, which affects the safe operation of the power distribution system. Therefore, it is of great significance to accurately identify the service status of an MCB.
Firstly, the basic structure of the circuit breaker is analyzed, and the irregular parts in the operating mechanism are processed equivalently. The closing process can be divided into two stages: empty-stroke and over-stroke. The relationship between the handle operating torque and rotation angle is investigated. A dynamic simulation model of the operating mechanism is built using virtual prototype technology to simulate the actual closing motion process of the part. Moreover, the changes in the handle operating torque during closing are studied. The mechanical characteristics representing the state of service, the initial closing angle, and the maximum torque of the closing are extracted.
Secondly, the contact’s overtravel degradation characteristics and the contact spring’s performance degradation characteristics are analyzed, and the relationship between the service performance degradation characteristics of the MCB and the characteristic parameters of handle operating torque is determined. Contact wear, contact spring degradation, or fracture of an MCB can occur after arc erosion and mechanical fatigue damage, which reflects the mechanical characteristic quantity. The results show that the contact wear can linearly increase the initial closing angle and decrease the maximum torque. Additionally, the degradation of the contact spring only reduces the maximum torque without affecting the initial closing angle. It is also found that the contact spring fracture may cause a stepwise decrease in the maximum torque.
Finally, based on the degree of contact wear and the state of the contact spring, the service state of an MCB can be categorized into four levels: normal, degraded, dangerous, and faulty. Then, the threshold range of the initial closing angle and the maximum torque can be determined under different levels. A service state identification method based on mechanical characteristics can be proposed. An experimental platform was set up to simulate contact wear and spring fracture. When compared, the simulation results show the same trend of changes as the experimental results, with an acceptable range of maximum relative errors. This paper presents a novel approach to evaluating the reliability and state identification of the MCB.
keywords：Miniature circuit breaker, operating mechanism, mechanical properties, dynamic model, service status identification
DOI: 10.19595/j.cnki.1000-6753.tces.240987
中图分类号：TM561
国家自然科学基金重点资助项目（51937004）。
收稿日期 2024-06-11
改稿日期 2024-10-24
李 奎 男，1965年生，博士，博士生导师，研究方向为电器可靠性与智能化、故障诊断与电气设备的寿命预测等。E-mail: likui@hebut.edu.cn（通信作者）
王 鹏 男，1997年生，硕士，研究方向为电器可靠性。E-mail: 1223830942@qq.com
（编辑 崔文静）