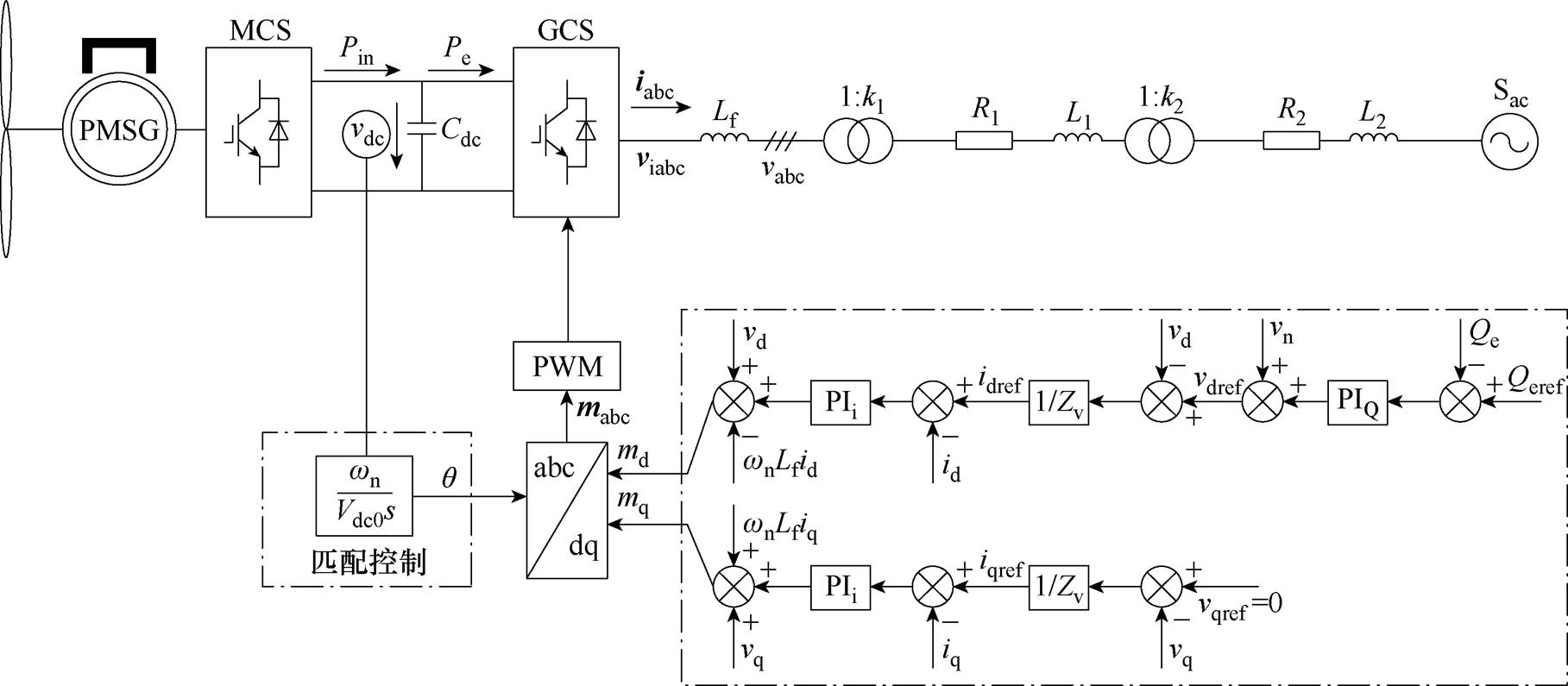
图1 匹配控制型直驱风机并网系统结构
Fig.1 Matching control type direct drive fan grid connected system structure
摘要 近年来,匹配控制型直驱风机并网系统的稳定性问题得到广泛关注,其阻抗特性对新型电力系统稳定性分析具有重要意义。首先,该文建立匹配控制型直驱风机的序阻抗模型,分析其接入不同强度电网时系统的稳定性。然后,基于所建阻抗解析模型,利用频域灵敏度分析影响匹配控制型直驱风机阻抗特性的主导参数,并确定提高系统稳定性的参数优化方案。最后,通过时域仿真验证所建阻抗模型及理论分析的正确性。结果表明,匹配控制型直驱风机具有良好的弱电网稳定性,但在强电网下存在次同步振荡的风险;网侧变流器的无功外环比例系数、电流内环比例系数和虚拟阻抗是影响匹配控制型直驱风机阻抗特性的主导参数。仿真算例中,适当减小无功外环比例系数、增大电流内环比例系数或虚拟阻抗可以提高匹配控制型直驱风机并网系统的稳定性。
关键词:匹配控制 构网型直驱风机 次同步振荡 阻抗分析
21世纪以来,风电、光伏等新能源机组在电力系统中所占比重不断提高,“双高”特性成为新型电力系统的重要技术特征[1]。传统跟网型新能源机组基于锁相环(Phase-Locked Loop, PLL)实现与电网间的同步。当大容量新能源场站经长输电线路并网时,电力系统会呈现弱电网特性[2],其引发的次同步振荡(Sub-Synchronous Oscillation, SSO)问题日益突出[3-4]。因此,具有弱电网适应能力的构网型新能源机组,在未来极有可能成为这一问题的解决方案。构网型控制技术通过模拟同步发电机的外特性,实现全功率变流器与电网间的自主同步。相较于传统跟网型变流器,构网型变流器不仅可以为系统提供更优的阻尼与惯性控制,而且具有主动支撑电网电压的能力。
目前,国内外学者提出的构网型控制策略主要包括:虚拟同步机(Virtual Synchronous Generator, VSG)控制、下垂控制和匹配控制[5]。其中,VSG控制和下垂控制以输出功率为控制目标,适用于输入功率稳定、可控的变流器。对于以直流电压为控制目标且输入功率具有间歇性和波动性的风电机组网侧变流器,更适合采用基于直流电压同步的匹配控制策略[6]。一方面,匹配控制仅需测量全功率变流器的直流母线电压即可实现与电网间的自主同步,具有较快的响应速度;另一方面,直流电容积分环节直接提供系统的等效惯性,无需再额外模拟惯性[7]。凭借上述优势,匹配控制型直驱风电机组已在北京、湖北、甘肃等地开展测试和验证[8-9],在未来具有广泛的应用前景。
虽然构网型变流器在弱电网下有较好的稳定性,但相关研究表明其在其他工况下仍然存在稳定性问题。文献[10]从稳态工作点、小信号稳定性和大信号稳定性三个方面对现有构网型变流器稳定性研究结果进行了总结,指出构网型变流器在弱电网下有较好的小信号稳定性,而在强电网条件下存在失稳风险,需要对其控制参数进行合理设计。
现阶段常用的构网型风电机组并网稳定性的分析方法主要有特征值分析法和阻抗分析法[11]。特征值分析法通过求解系统的状态矩阵,并分析其特征根轨迹来判断系统的稳定性[12]。文献[13]利用特征值分析法对匹配控制型直驱风电机组进行小信号建模,并借鉴阻尼转矩法分析了构网型直驱风电场的振荡机理。文献[14]利用复转矩系数法分析附加惯量传递控制对风电机组弱电网运行稳定裕度的影响,并提出增加机侧、网侧变流器阻尼的致稳控制策略。然而随着系统复杂程度的增加,该方法在建模时存在“维数灾”问题,系统特征值的求解将变得困难。
相较于特征值分析法,阻抗分析法具有物理意义清晰、建模灵活等优势,逐渐成为分析新能源电力系统宽频振荡问题的一种有效方法[15-17]。阻抗分析法将新能源场站和电网看成两个子系统,首先通过建立各子系统相应的阻抗模型来描述其各自的端口外特性,然后结合电路理论和控制理论分析系统的稳定性[17-18]。阻抗建模按其所处坐标系可以分为dq轴阻抗建模和序阻抗建模。文献[19]通过建立直驱风电机组的dq轴阻抗模型分析了影响系统稳定性的控制参数,提出了参数优化方案。文献[20]通过建立构网型直驱风机的dq轴阻抗模型研究了多台风电机组之间的交互问题,提出了多机稳定性分析方法。相较于dq阻抗建模方法,基于谐波线性化方法建立的序阻抗模型具有正负序解耦、物理意义清晰、便于进行实际的工程测量等优点[21]。文献[22-23]基于谐波线性化建立了VSG的序阻抗模型,并对其并网稳定性进行分析。然而尚未有文献建立匹配控制型直驱风机的序阻抗模型,利用频域灵敏度对影响匹配控制型直驱风机并网稳定性的控制参数进行分析更是鲜有研究。
本文针对匹配控制型直驱风机的序阻抗模型及SSO稳定性展开研究。首先,基于谐波线性化原理建立匹配控制型直驱风机的输出序阻抗模型,并通过阻抗扫频验证模型的准确性。其次,结合阻抗稳定性判据,分析不同电网强度时并网系统的稳定性。然后,利用频域灵敏度分析影响匹配控制型直驱风机阻抗特性的主导参数,并提出提高并网系统稳定性的参数优化方法。最后,基于PSCAD/EMTDC电磁暂态仿真平台验证理论分析的正确性。
本文所研究的匹配控制型直驱风机并网系统如图1所示。图1中,Pin为机侧变流器(Machine Side Converter, MSC)输出的有功功率,Pe为网侧变流器(Grid Side Converter, GSC)输入的有功功率;Qe为风机实际输出的无功功率;Cdc、vdc分别为直驱风机的直流侧电容和直流电容电压;Lf为滤波电感;R1、L1为35 kV线路电阻和电感;R2、L2为110 kV线路电阻和电感;viabc和iabc分别为GSC交流侧三相电压和电流;vabc为并网点处三相交流电压;mabc为GSC输出的电压调制信号;各物理量中,下标d、q表示变量dq坐标系下d轴、q轴的分量,下标ref表示各变量的指令值;q 为GSC调制电压的相位;vn为调制电压幅值的额定值;wn为电网额定角速度;Vdc0为稳态时直流母线电压。构网型直驱风机输出电能通过一级升压变和汇集线路接入35 kV场站,之后经二级升压变和输电线路送入110 kV电网。

图1 匹配控制型直驱风机并网系统结构
Fig.1 Matching control type direct drive fan grid connected system structure
构网型直驱风机的MSC采用基于转子磁链定向的双环控制结构,GSC通过“匹配控制”策略产生输出电压的相位,通过无功功率控制外环、电流控制内环生成dq轴调制信号的指令值。并且在GSC的双环控制中加入虚拟阻抗控制来调节输出阻抗,提高系统的稳定性。
本节采用谐波线性化方法建立匹配控制型直驱风机的序阻抗模型,主要过程为:首先,将交流电压、交流电流及调制信号转换至频域,建立稳态工作点;然后,在交流电压上叠加一个特定频率的小信号扰动,通过推导交流电流对交流电压扰动的小信号响应,建立匹配控制型直驱风机的小信号频域阻抗模型。
值得说明的是,对于通过构网型变流器并网的直驱风电机组而言,由于MSC与GSC之间的直流电容的缓冲隔离作用,直驱风机在次同步频率范围内的动态特性受同步发电机和MSC的影响较小,主要取决于GSC及其控制。因此,在采用谐波线性化方法推导直驱风机阻抗模型时,本文将MSC及其左侧部分(风力机、同步电机等)等效为大小可控的理想直流电流源Idc,通过调整该电流源的大小模拟原动机功率变化,以GSC为主来分析直驱风机整体的阻抗模型,以便在保证研究精度的前提下简化模型推导,提高建模和分析效率[24]。
在风机并网点处施加频率为fp的正序小信号电压扰动,考虑到频率耦合效应,GSC的输出电压中会出现同频率的正序分量和相差二倍频的负序分量fp-2 f1,直流电压含有频率为fp-f1的小信号分量。将各稳态分量按稳态频率序列[-2 f1 -f1 0 f1 2f1]T的顺序排列5个列向量,小信号分量按小信号频率序列[ fp-2 f1 fp-f1 fp fp+f1 fp+2f1]T的顺序排列成5行列向量,各变量表示为
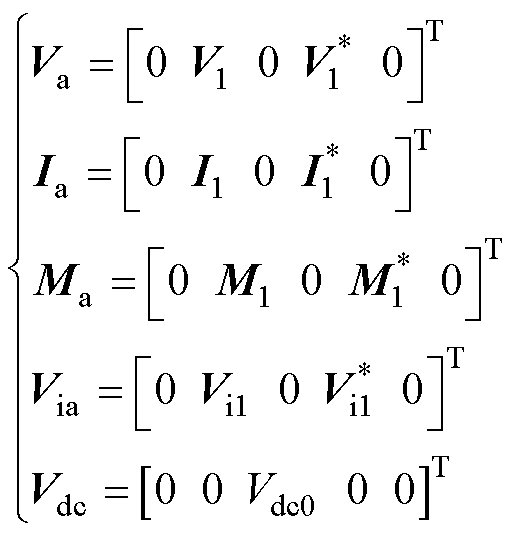 (1)
(1)
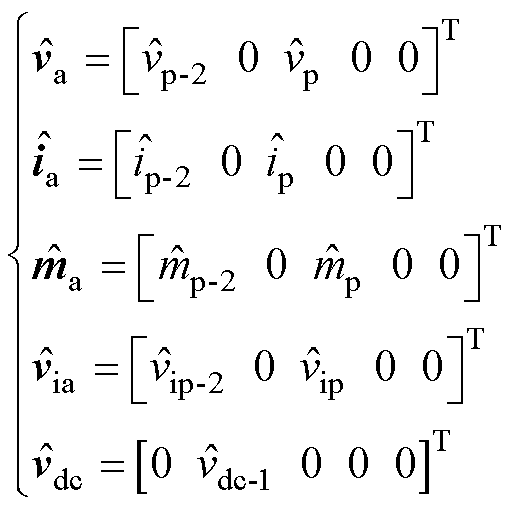 (2)
(2)
式中,Va为并网点电压稳态列向量;Ia为并网点电流稳态列向量;Ma为调制电压稳态列向量;Via为变流器出口电压稳态列向量;Vdc为直流母线电压稳态列向量;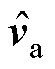 为并网点电压小信号分量;
为并网点电压小信号分量;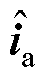 为并网点电流小信号分量;
为并网点电流小信号分量;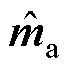 为调制电压小信号分量;
为调制电压小信号分量;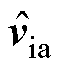 为变流器出口电压小信号分量;
为变流器出口电压小信号分量;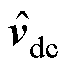 为直流母线电压小信号分量;列向量中各变量为对应各频率序列分量;上标“*”代表共轭。
为直流母线电压小信号分量;列向量中各变量为对应各频率序列分量;上标“*”代表共轭。
1)主电路模型
当假定变流器直流端口输入为理想电流源时,根据交、直流端口功率平衡关系,得到直流母线频域小信号模型为
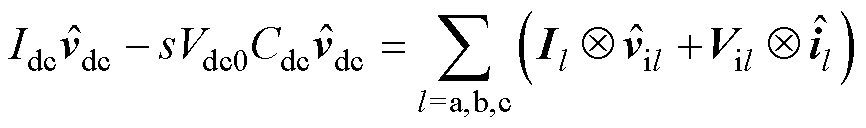 (3)
(3)
式中,s为拉普拉斯算子;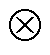 为卷积运算符号。
为卷积运算符号。
整理得到直流母线电压、调制电压和交流电流的小信号之间关系的矩阵表达式为
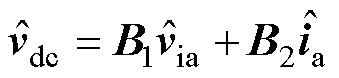 (4)
(4)
式中,B1、B2为五阶方阵,具体表达式见附录式(A1)和式(A2)。
由图1可知,主电路a相频域小信号模型为
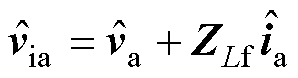 (5)
(5)
式中,ZLf为小信号频率序列下交流滤波电感阻抗,ZLf =j2pLf·diag( fp-2 f1, fp-f1, fp, fp+f1, fp+2 f1)。
2)参考角小信号模型
GSC通过匹配控制策略生成相位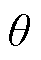 作为同步旋转参考角。由图1可知,直流电容积分环节根据直流电压波动生成参考角的扰动分量。输出相位小信号分量
作为同步旋转参考角。由图1可知,直流电容积分环节根据直流电压波动生成参考角的扰动分量。输出相位小信号分量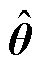 的表达式为
的表达式为
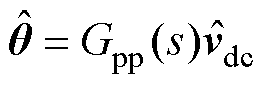 (6)
(6)
式中,Gpp(s)为匹配控制传递函数,Gpp(s)=wn/(sVdc0)。
3)dq轴电压、电流小信号模型
根据派克变换将abc坐标系的电流和电压小信号分量投影到dq轴,并且考虑到输出相位的小信号分量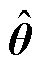 后,得到交流电流和电压dq轴小信号向量表达式为
后,得到交流电流和电压dq轴小信号向量表达式为
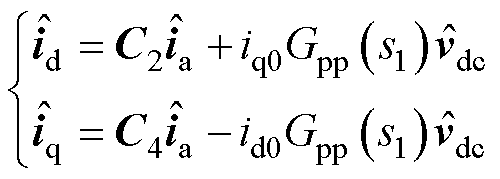 (7)
(7)
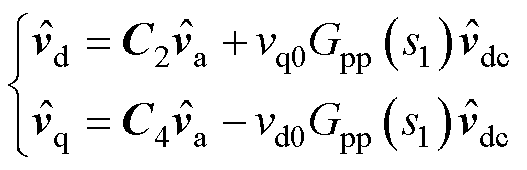 (8)
(8)
式中,s1=j2p(fp-f1);id0、iq0分别为d、q轴电流初始值;vd0、vq0分别为d、q轴电压初始值;C2、C4为五阶方阵,具体表达式见附录式(A3)和式(A4)。
4)交流调制电压的小信号模型
由PWM原理可得a相调制电压的小信号表达式为
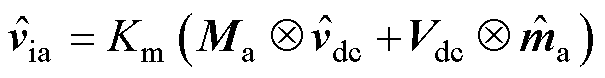 (9)
(9)
式中,Km为调制系数,Km=1/Vdc0。
根据派克逆变换公式,并且考虑到输出相位小信号分量,得到a相调制信号的表达式为
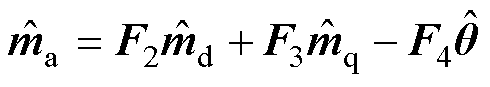 (10)
(10)
式中,F2、F3、F4为五阶方阵,具体表达式见附录式(A5)~式(A7)。联立式(6)、式(9)和式(10),得到a相调制电压的小信号表达式为
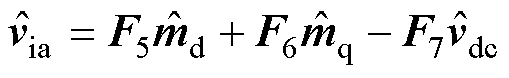 (11)
(11)
式中,F5、F6、F7为五阶方阵,具体表达式见附录式(A8)和式(A9)。
5)控制环节小信号模型
由图1所示控制结构得到dq轴调制信号的小信号分量的表达式为
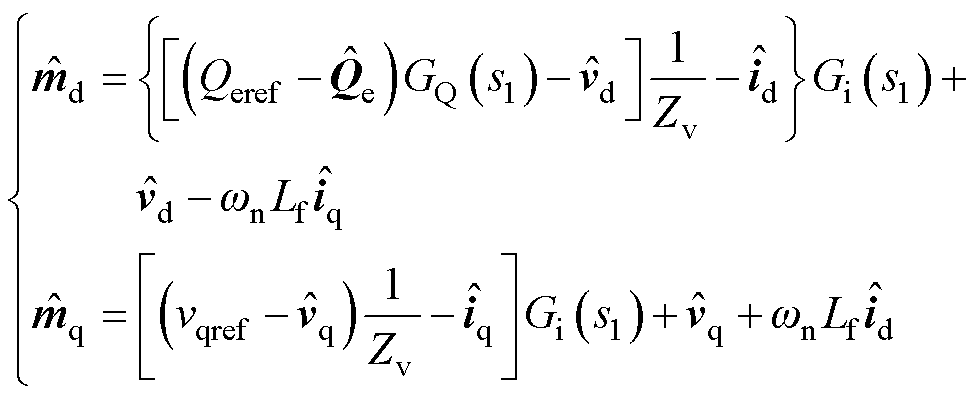 (12)
(12)
式中,下标“ref”表示参考值;Gi(s)=kip+kii/s,kip、kii分别为电流内环比例系数和积分系数;GQ(s)= kQp+kQi/s,kQp、kQi分别为无功外环比例系数和积分系数。
变流器输出无功功率的小信号分量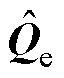 为
为
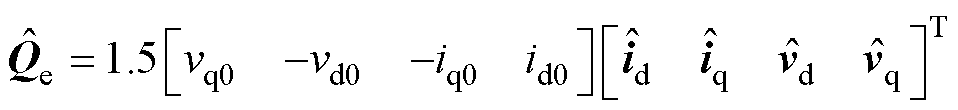 (13)
(13)
联立式(12)和式(13),得到dq轴调制信号小信号分量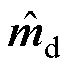 、
、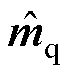 与dq轴电压、电流小信号分量的矩阵关系式为
与dq轴电压、电流小信号分量的矩阵关系式为
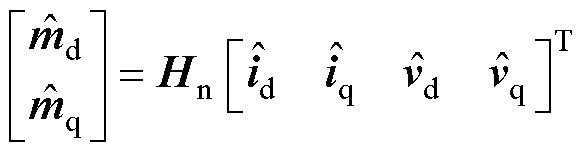 (14)
(14)
式中,Hn为2×4阶矩阵,其中各分量表达式见附录式(A10)。
6)交流端口导纳模型
将dq轴电压电流小信号的表达式代入式(14)后与式(11)联立,得到a相调制电压的小信号表达式为
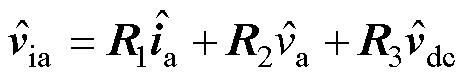 (15)
(15)
式中,矩阵R1、R2、R3的表达式具体见附录式(A11)。
将式(4)与式(15)联立,化简得到a相调制电压与变流器输出电压、电流之间的关系式为
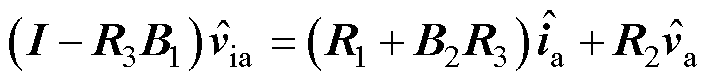 (16)
(16)
式中,I为五阶单位矩阵。
将式(5)主电路频域小信号模型与式(16)联立得到匹配控制型直驱风机的输出导纳模型为
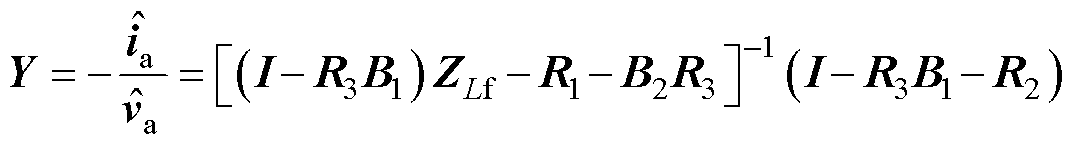 (17)
(17)
将GSC交流电压、电流小信号向量与交流端口导纳在扰动频率和耦合频率处的关系重新表述为
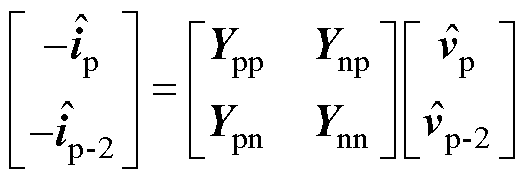 (18)
(18)
式中,二阶交流端口导纳矩阵表达式为
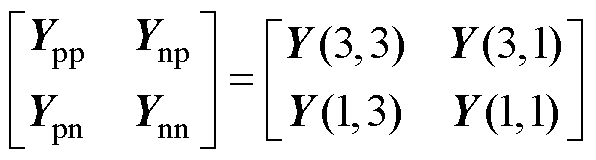 (19)
(19)
7)等效序阻抗模型
根据式(18)可知,匹配控制型直驱风机并网系统是一个多输入多输出(Multi-Input and Multi- Output, MIMO)系统,需要采用广义奈奎斯特稳定性判据分析系统的稳定性,分析较为复杂繁琐。文献[25]表明,可以将MIMO模型等效转化为单输入单输出(Single Input and Single Output, SISO)模型,进而采用等效奈奎斯特判据对其进行稳定性分析。
当考虑控制结构不对称引起的频率耦合时,匹配控制型直驱风机频率耦合效应关系如图2所示。由图2可知,在并网点处叠加频率为fp的正序小信号电压扰动后,由于控制环节的不对称,电流响应中会产生频率为fp的正序分量以及频率为fp-2f1的负序分量。这两种频率的并网电流扰动通过电网阻抗Zg产生对应频率的电压扰动Vp和Vp-2,扰动电压又通过控制环路和主电路各自产生两个对应频率的并网扰动电流,形成闭环。
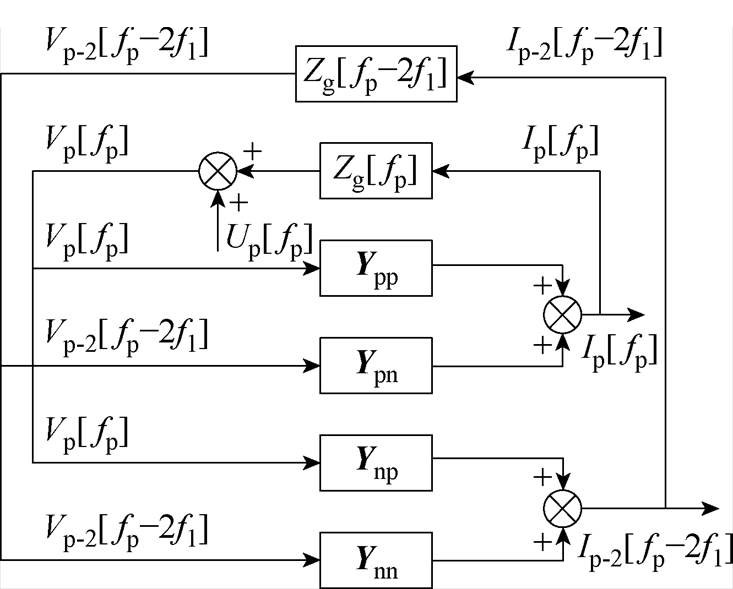
图2 频率耦合效应关系
Fig.2 Frequency coupling effect relationship
根据频率耦合关系,引入电网阻抗Zg将导纳矩阵中的耦合项消除,使MIMO模型等效转化为SISO模型[26]。匹配控制型直驱风机SISO等效正序阻抗Zp的表达式为
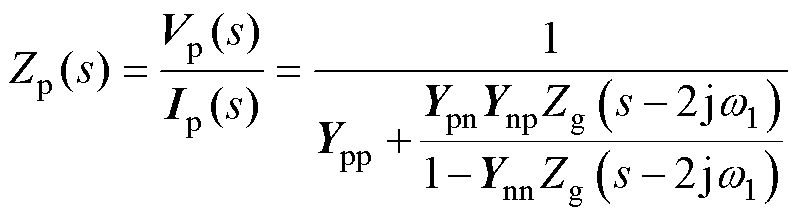 (20)
(20)
根据正、负序阻抗之间的转化关系,可以得到SISO模型中的负序阻抗为
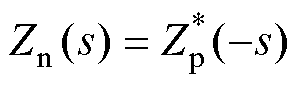 (21)
(21)
将式(19)中各导纳分量和电网阻抗的表达式代入式(20),即可得到匹配控制型直驱风机并网系统的SISO等效序阻抗模型的表达式。
为验证所建序阻抗模型的正确性,基于PSCAD/ EMTDC电磁暂态仿真平台搭建匹配控制型直驱风机并网系统仿真模型,主要元件参数和控制参数见表1。在风机并网点处采用谐波注入的方法进行阻抗扫频,仿真中注入的电压谐波幅值为基频分量的10%。
表1 系统参数及控制参数
Tab.1 System parameters and controller parameters
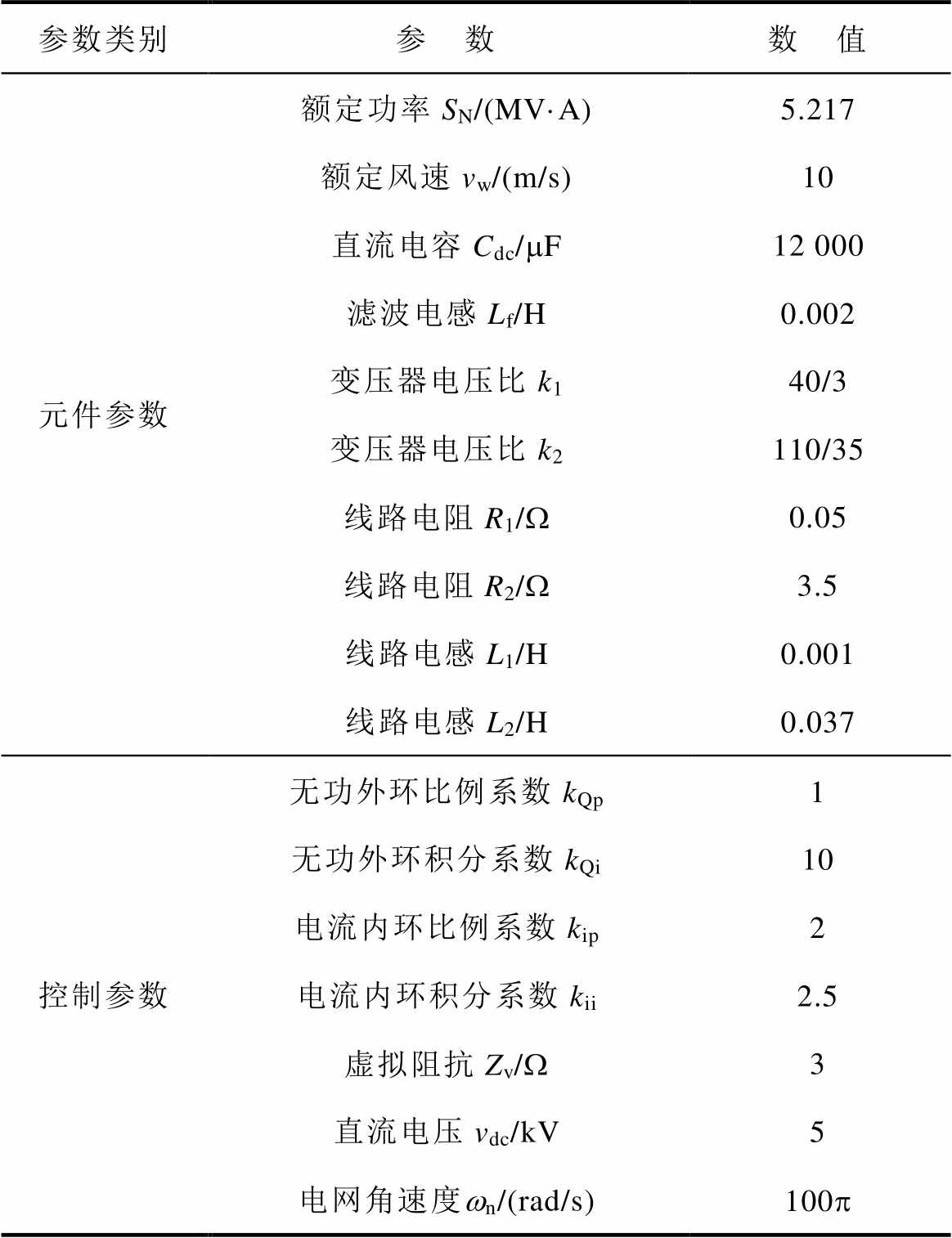
参数类别参 数数 值 元件参数额定功率SN/(MV·A)5.217 额定风速vw/(m/s)10 直流电容Cdc/mF12 000 滤波电感Lf/H0.002 变压器电压比k140/3 变压器电压比k2110/35 线路电阻R1/W0.05 线路电阻R2/W3.5 线路电感L1/H0.001 线路电感L2/H0.037 控制参数无功外环比例系数kQp1 无功外环积分系数kQi10 电流内环比例系数kip2 电流内环积分系数kii2.5 虚拟阻抗Zv/W3 直流电压vdc/kV5 电网角速度wn/(rad/s)100p
匹配控制型直驱风机SISO等效序阻抗解析曲线与扫频结果如图3所示。对比图3结果可知,理论解析曲线与仿真扫频结果吻合得较好,验证了本节所建立匹配控制型直驱风机序阻抗模型的正确性。
实际工程的直驱风机并网系统中,电网一般呈现“正电阻+感性”的阻感特性,因此直驱风机阻抗特性中“负电阻+容性”区域易与感性电网发生谐振。由图3可知,在表1所示控制参数下匹配控制型直驱风机的正序阻抗模型在低频段呈感性,在次同步频段存在负阻尼区间,在54.5~65.7 Hz频段范围内呈容性,相位在-90°以内;负序阻抗模型在低频段呈容性,之后变为感性,容性频段的相位在-90°以内。因而构网型直驱风机与感性电网的阻抗相位差均在180°以内,即说明基于匹配控制策略的构网型直驱风机不易与感性电网构成负阻尼振荡回路,具有较好的并网稳定性。
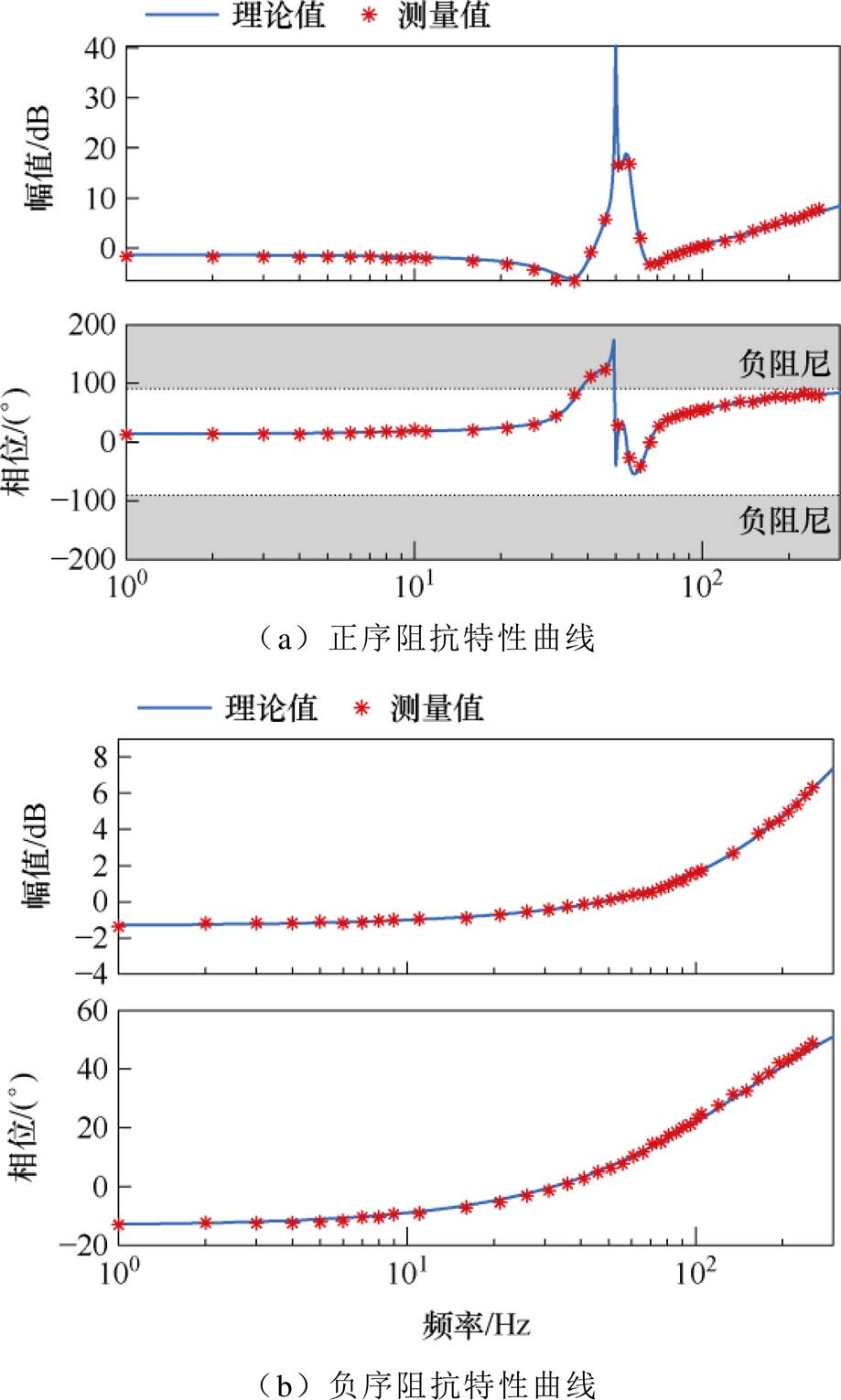
图3 SISO等效序阻抗的理论曲线和仿真结果
Fig.3 Theoretical curves and simulation results of SISO equivalent sequence impedance
新能源机组接入交流电网的振荡现象可以等效为RLC电路发生串联谐振。构网型直驱风机的阻抗模型存在容性负电阻频段时,可以等效为电阻、电感和电容的串联。感性电网的阻抗可等效为电阻与电感的串联形式,其模型结构如图4所示。
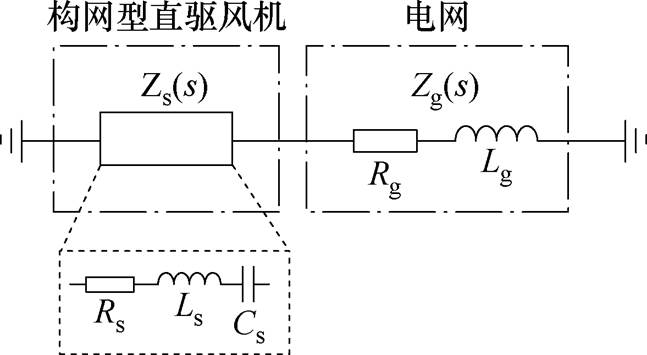
图4 等效RLC模型
Fig.4 Equivalent RLC circuit model
基于等效RLC模型,系统总阻抗可表示为Zall= Zs+Zg。一般认为实际中直驱风机和电网均可独立稳定工作,则当系统总阻抗的虚部(Xall=Im(Zall(s)))等于0时,系统发生振荡,振荡特性由总阻抗的实部(Rall=Re(Zall(s)))决定。基于等效RLC电路阻抗模型的稳定判据[27-29](下文简称为“阻抗稳定性判据”)具体表述如下:
(1)随着测量频率的增加,系统等效电抗Xall从负到正穿越零点时,若对应频率下系统等效电阻Rall为正,则系统稳定;反之,系统不稳定。
(2)随着测量频率的增加,系统等效电抗Xall从正到负穿越零点时,若对应频率下系统等效电阻Rall为负,则系统稳定;反之,系统不稳定。
本节针对匹配控制型直驱风机并入不同强度电网的稳定性进行分析。通过系统的短路比(Short Circuit Ratio, SCR)来描述电网强度[13]。设置电网1、电网2和电网3的SCR分别为1.61、2.82和11.14,风机的控制参数见附表1。匹配控制型直驱风机与电网1、电网2和电网3并网系统的等效序阻抗模型的实部-频率、虚部-频率曲线如图5所示。其中,电网1为极弱电网,电网2为弱电网,电网3为强电网。
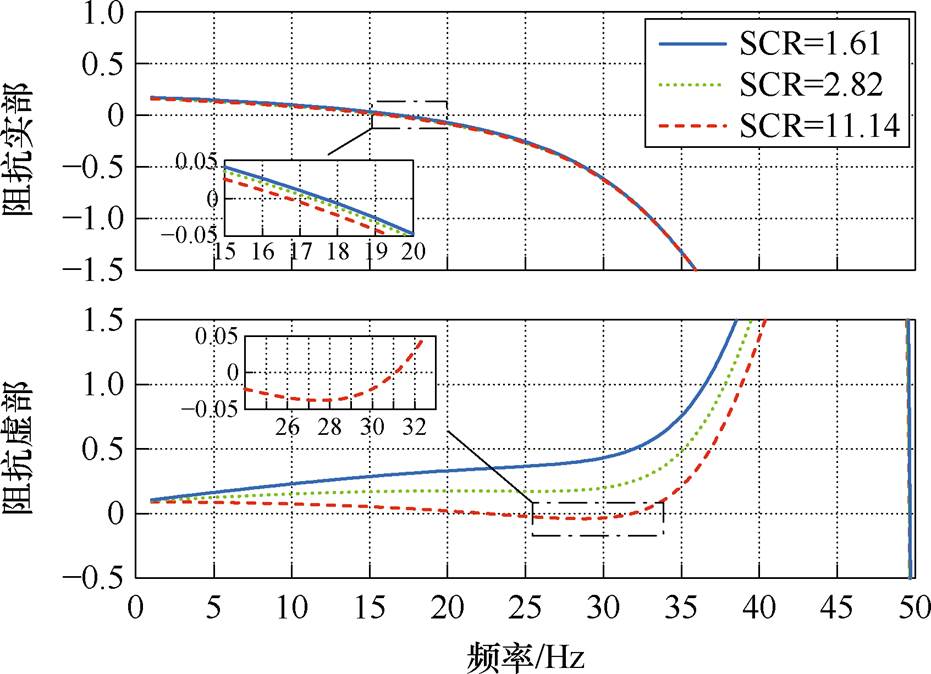
图5 不同SCR下系统的阻抗曲线
Fig.5 Impedance curves of systems under different SCR conditions
由图5可以看出,当风机并入SCR为1.61和2.82的弱电网时,系统阻抗虚部在0~50 Hz的频率区间内不存在过零点,即系统不会出现次同步振荡现象,表明匹配控制型直驱风机在弱电网下具有较好的稳定性。当风机并入SCR为11.14的强电网时,系统阻抗虚部在31 Hz由负到正过零,且对应阻抗实部小于零。根据3.1节给出的阻抗稳定性判据可以判断,系统在SCR=11.14时会出现频率为31 Hz的振荡现象,说明匹配控制型直驱风机在强电网下存在振荡的风险。相同参数条件下利用奈奎斯特判据对系统进行稳定性分析的结果如附图1所示,其结果与图5分析一致。
根据并网稳定性分析结果可知,匹配控制型直驱风机具有良好的弱电网适应性,但接入强电网运行时可能存在振荡风险。这是由于匹配控制型直驱风机对外可以等效为一个受控电压源,其并网特性类似于两个电压源并联,因此当电网阻抗较小,即电网较强时,匹配控制型直驱风机并网系统的联络阻抗较小,不利于电压源并联,因此在强电网下存在振荡风险[10]。
设置匹配控制型直驱风机并网系统在2 s时系统SCR从1.61变为11.14,得到直流电容电压的波形如图6所示。采用PSCAD/EMTDC电磁暂态仿真平台元件库中的快速傅里叶变换(Fast Fourier Transform, FFT)分析模块对3.0~3.5 s内直流电容电压和并网点电压进行FFT分析,得到频谱图如图7和图8所示。
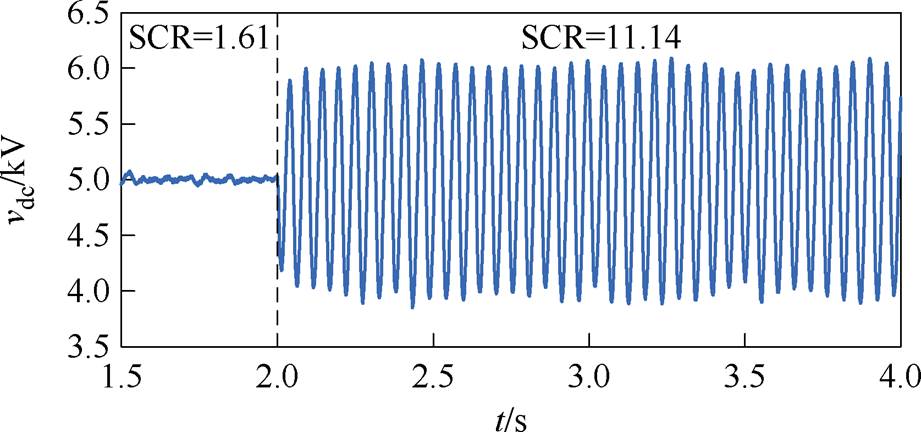
图6 直流电容电压波形
Fig.6 DC capacitor voltage waveform
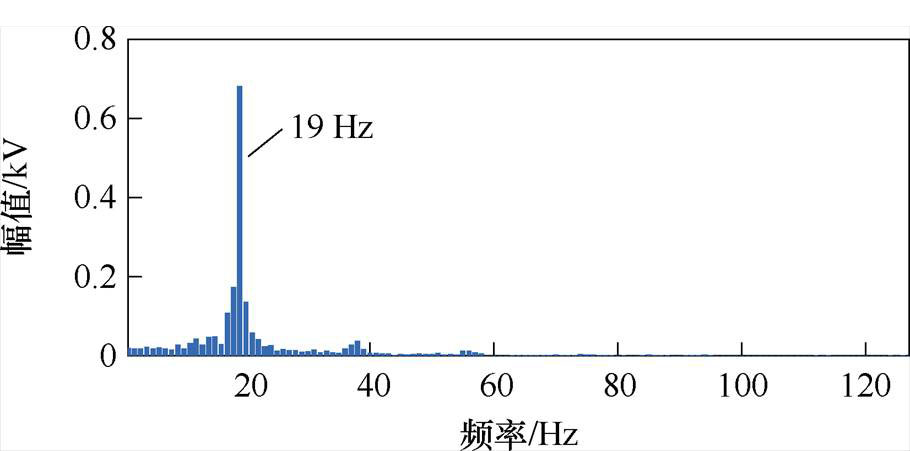
图7 直流电容电压FFT分析结果
Fig.7 FFT analysis results of DC capacitor voltage
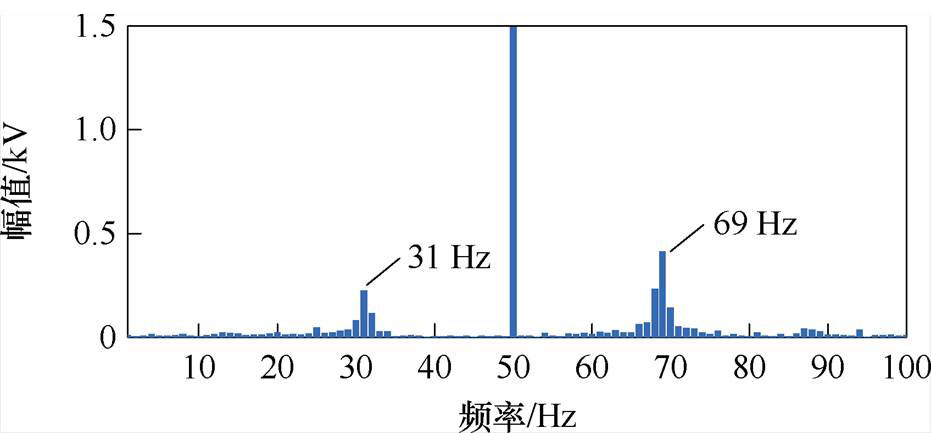
图8 a相电压FFT分析结果
Fig.8 FFT analysis results of phase a voltage
由图6可知,当匹配控制型直驱风机并入弱交流电网时,直流电容电压稳定,表明系统能够稳定运行;当匹配控制型直驱风机并入强交流电网时,直流电容电压出现振荡现象。由图7和图8可知,直流电容电压中出现频率为19 Hz的谐波分量,系统并网点电压中出现频率为31 Hz的谐波分量,同时存在频率为69 Hz的耦合分量。说明在该并网条件下系统运行不稳定。该时域仿真结果与3.2节中稳定性理论分析结果一致。
为提高匹配控制型直驱风机的并网稳定性,本节分析各控制参数变化对系统阻抗特性的影响。首先,根据各控制参数的频域灵敏度,确定影响系统阻抗特性的主导参数。然后,分析各个主导参数对系统阻抗特性的影响,给出提高系统稳定性的参数优化方法。最后,通过时域仿真验证理论分析的正确性。
将第2节中建立的构网型直驱风机的正序阻抗表达式视为复数域上的传递函数H(s),采用实部灵敏度、虚部灵敏度表示该传递函数的频域特性[30]。频域灵敏度的具体表达式如下。
1)频域灵敏度
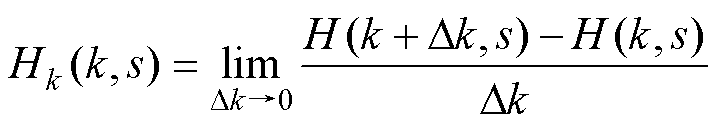 (22)
(22)
2)实部灵敏度
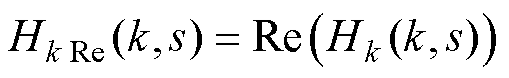 (23)
(23)
3)虚部灵敏度
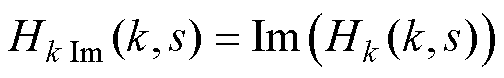 (24)
(24)
由灵敏度表达式的定义可知,借鉴频域灵敏度概念的阻抗灵敏度就是阻抗表达式关于某参数的偏导值,反映各控制参数对系统阻抗的影响程度。阻抗灵敏度的绝对值反映了参数变化对系统阻抗影响的程度,绝对值越大表示参数变化对系统阻抗特性的影响程度越大;阻抗灵敏度的正负反映了系统阻抗的实部/虚部随参数变化的方向,灵敏度为正时,阻抗实部/虚部的幅值随参数的增大而增大,灵敏度为负时则相反。
为对比分析匹配控制型直驱风机中各控制参数对其阻抗特性的影响程度,本小节将计算各控制参数的阻抗灵敏度,所分析的控制参数包括GSC无功外环比例系数kQp与积分系数kQi、GSC电流内环比例系数kip与积分系数kii、虚拟阻抗Zv。根据灵敏度分析结果确定在次同步频段内影响系统阻抗特性的主导参数。
根据4.1节中频域灵敏度的定义和计算方式,得到系统总阻抗对各参数的阻抗灵敏度表达式,基于附表1所示参数得到与之相对应的阻抗实部、虚部灵敏度曲线如图9所示。
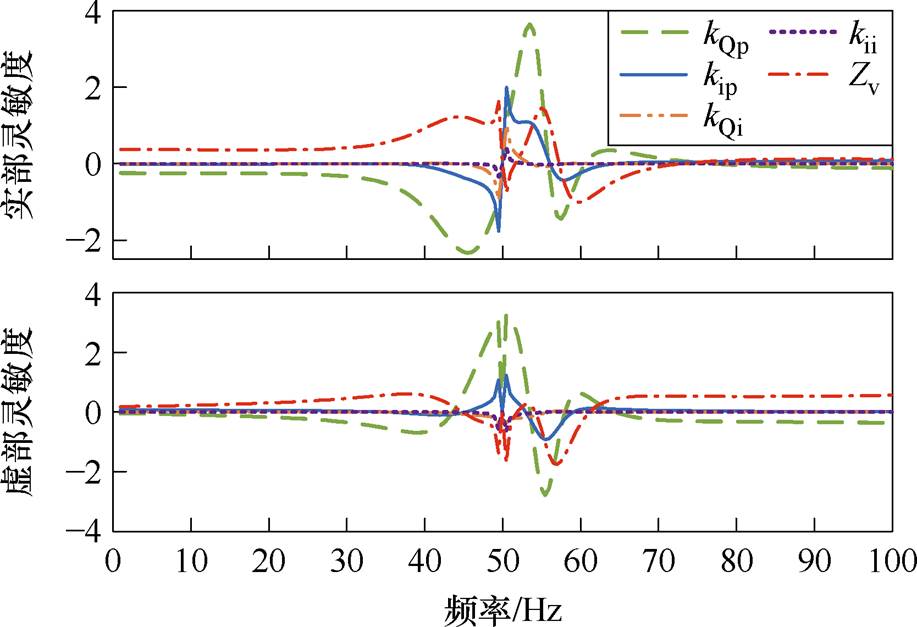
图9 阻抗灵敏度曲线
Fig.9 Impedance sensitivity curves
据图9分析,无功外环比例系数、电流内环比例系数和虚拟阻抗的阻抗灵敏度幅值较大,相较而言,无功外环积分系数和电流内环积分系数的阻抗灵敏度幅值较小。根据各参数的阻抗灵敏度幅值大小可知,无功外环比例系数、电流内环比例系数和虚拟阻抗为影响匹配控制型直驱风机阻抗特性的主导参数。因此,在考虑调整控制参数抑制系统SSO时,应首先考虑调节电流内环和无功外环的比例系数以及虚拟阻抗的大小。
由3.2节分析可知,匹配控制型直驱风机在次同步频段内存在振荡风险,因此对次同步频段内各参数的阻抗灵敏度进行具体分析,将图9分为两个图进行说明。其中图10所示为次同步频段内主导参数的阻抗灵敏度曲线,而对阻抗特性影响较小的积分系数的阻抗灵敏度曲线如附图2所示,在此不作具体分析。
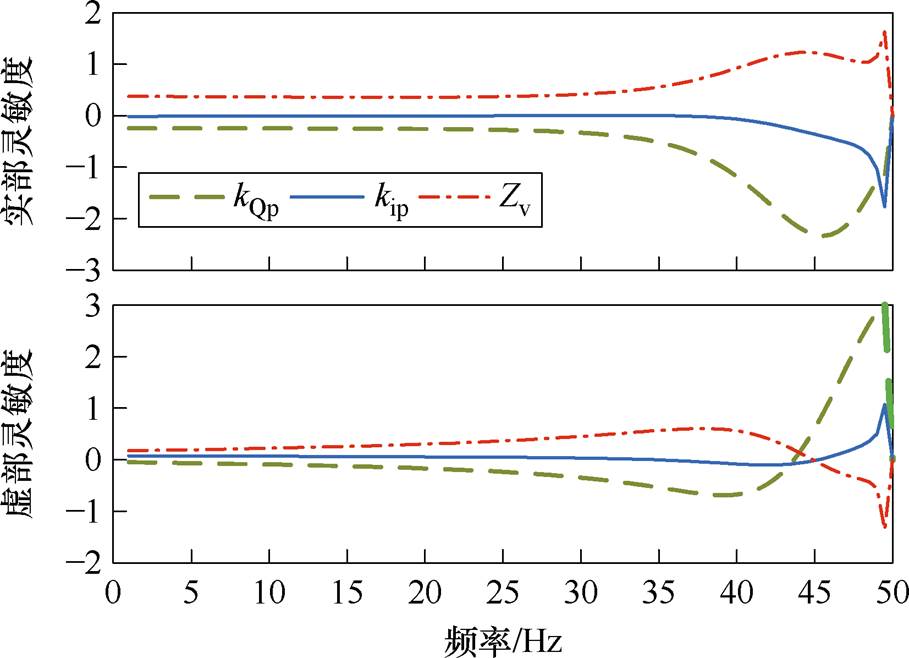
图10 阻抗灵敏度曲线(局部)
Fig.10 Impedance sensitivity curves (partial)
由图10可知,在次同步频段内,kQp的实部灵敏度小于0,虚部灵敏度在频率小于45 Hz时也小于0,之后就大于0。说明随着频率的增加,阻抗实部一直随kQp的增加而减小,阻抗虚部先随kQp的增加而减小,之后随kQp的增加而增加。对kip和Zv的灵敏度分析与之类似,结论如下:随着频率的增加,阻抗实部一直随kip的增加而减小,阻抗虚部在35~45 Hz频率区间内随kip的增加而减小,其余频段内随kip的增加而增加;保持其他控制参数不变时,阻抗实部一直随Zv的增加而增加,阻抗虚部先随Zv的增加而增加,之后随Zv的增加而减小。
4.3.1 无功外环比例系数kQp对阻抗特性的影响
图11所示为保持其余控制参数不变,改变kQp,得到的系统等效序阻抗模型的实部-频率、虚部-频率曲线。由图11可知,kQp=4, 2, 1时,系统阻抗虚部存在过零点,且由负到正的过零点处频率所对应的阻抗实部小于0,依据阻抗稳定性判据可知,系统处于不稳定状态。kQp=0.5时,系统阻抗虚部不存在过零点,系统在该工况下处于稳定状态。
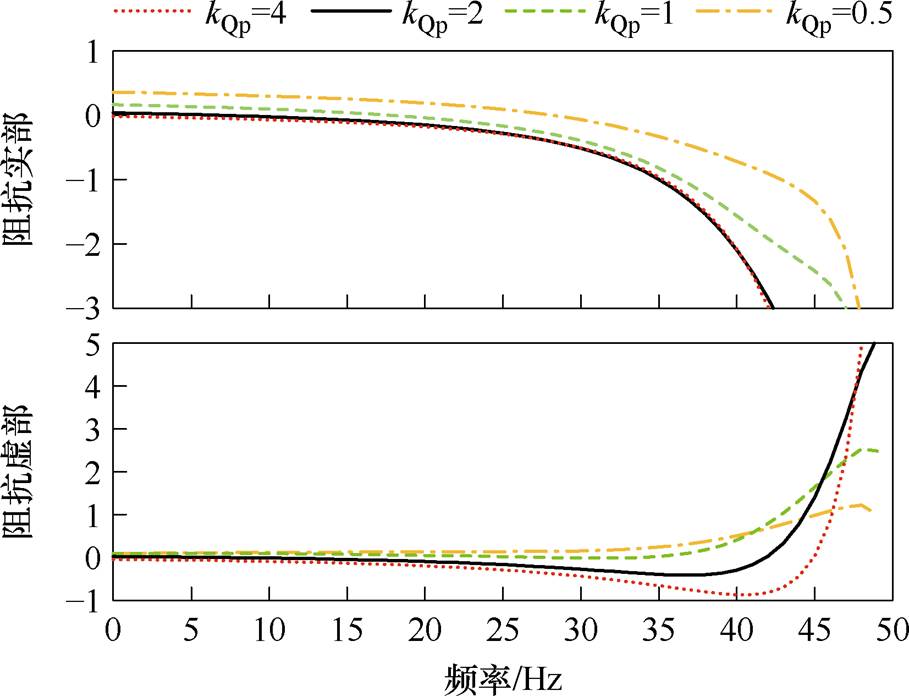
图11 无功外环比例系数的影响
Fig.11 The influence of reactive power external loop proportion coefficient
根据4.2节中对各参数阻抗灵敏度的分析,系统总阻抗实部随着kQp的减小而增大;阻抗虚部先随着kQp的减小而增大,后随着kQp的减小而减小。因此,随着kQp的减小,阻抗虚部过零点的频率降低,阻抗实部由正到负过零点的频率增加。通过减小kQp使得阻抗虚部不存在过零点或过零点处对应阻抗实部大于0时,系统运行稳定。综上所述,减小无功外环比例系数有利于提高系统的稳定性。
4.3.2 内环比例系数kip对系统阻抗特性的影响
图12所示为保持其余控制参数不变,改变kip,得到的系统等效序阻抗模型的实部-频率、虚部-频率曲线。由图12可知,kip=0.5, 1, 2时,系统阻抗虚部存在过零点,且由负到正的过零点处所对应阻抗实部小于0,依据阻抗稳定性判据可知,系统处于不稳定状态。kip=4时,系统阻抗虚部不存在过零点,系统在该工况下处于稳定状态。
根据灵敏度分析可知,系统总阻抗实部随着kip的减小而增加;虚部曲线在33 Hz以内随着kip的减小而减小,在33~45 Hz频率区间内随着kip的减小而增加。即随着kip的增加,阻抗实部由正到负过零点频率减小,但总体变化不大;阻抗虚部曲线逐渐抬升,由负到正过零点频率增加直至没有过零点。通过增大kip使阻抗虚部不存在过零点时,系统由不稳定状态变为稳定状态。综上所述,合理增大电流内环比例系数可以提高系统稳定性。
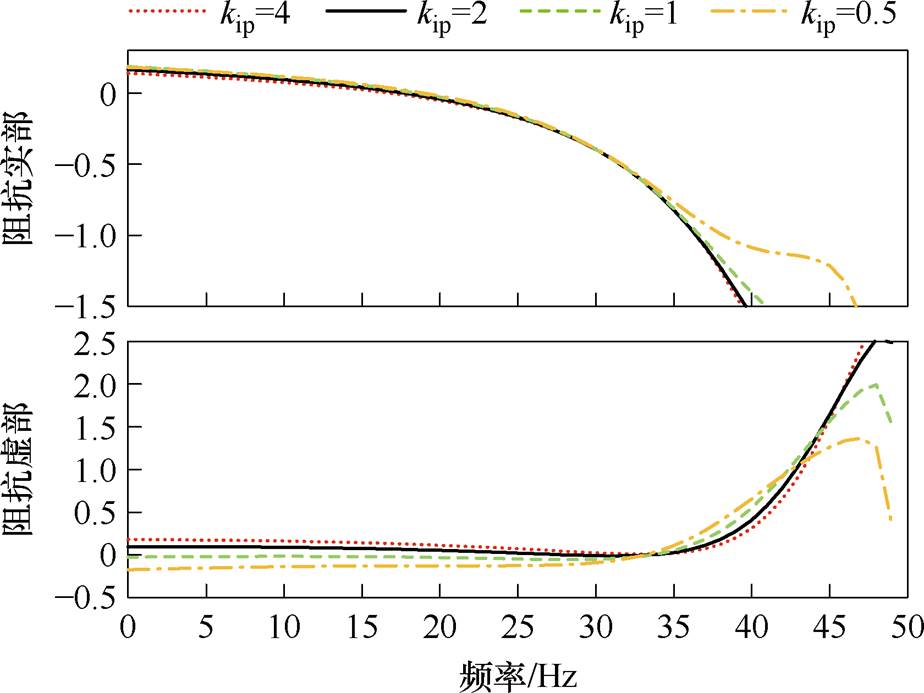
图12 电流内环比例系数的影响
Fig.12 The influence of the proportion coefficient of the current inner loop
4.3.3 虚拟阻抗Zv大小对阻抗特性的影响
为了增强系统在强电网条件下的稳定性,在直驱风机GSC的控制环节引入Zv。图13所示为保持其余控制参数不变,改变Zv得到的系统等效序阻抗模型的实部-频率、虚部-频率曲线。由图13可知,Zv=0.5 W 、Zv=1 W 时,系统阻抗虚部存在过零点,且由负到正的过零点处所对应阻抗实部小于0,依据阻抗稳定性判据可知,系统处于SSO不稳定状态。Zv=2 W 、Zv=4 W 时,系统阻抗虚部不存在过零点,系统处于SSO稳定状态。
根据灵敏度分析结果可知,系统总阻抗实部随着Zv的减小而减小;阻抗虚部先随着Zv的减小而减小,后随着Zv的减小而增加。因此,随着Zv的增加,阻抗实部由正到负过零点频率增加;阻抗虚部由负到正的过零点的频率减小,直至虚部不存在过零点。因此,通过增大Zv使得阻抗虚部无过零点或过零点处对应阻抗实部大于0时,系统能够稳定运行。综上所述,增大Zv能够提高系统的稳定性。
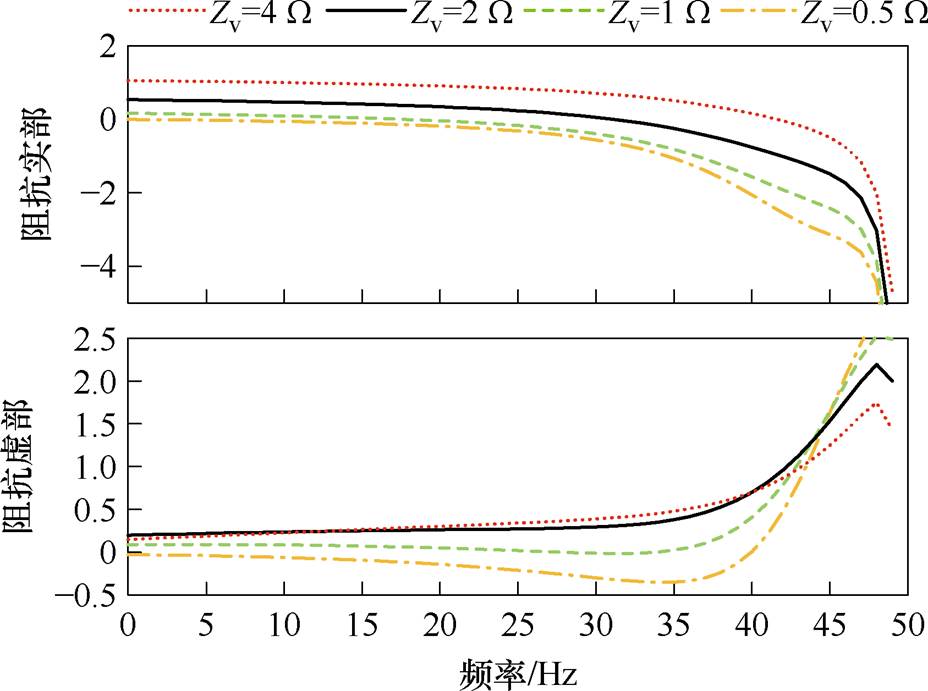
图13 虚拟阻抗的影响
Fig.13 The impact of virtual impedance
由第4.3节对各参数阻抗灵敏度的分析可知,在一定范围内,减小kQp、增大kip或增大Zv可以提高构网型直驱风机并网系统的稳定性。
为验证上述参数优化方案的正确性,按附表1设置仿真模型参数,2 s时系统SCR由1.61变为11.14,在保持其他参数不变的情况下,在3 s时增大虚拟阻抗Zv,得到直流电容电压波形如图14所示;在3 s时增大电流内环比例系数kip,得到直流电容电压波形如图15所示;在3 s时减小无功外环比例系数kQp,得到直流电容电压波形如图16所示。
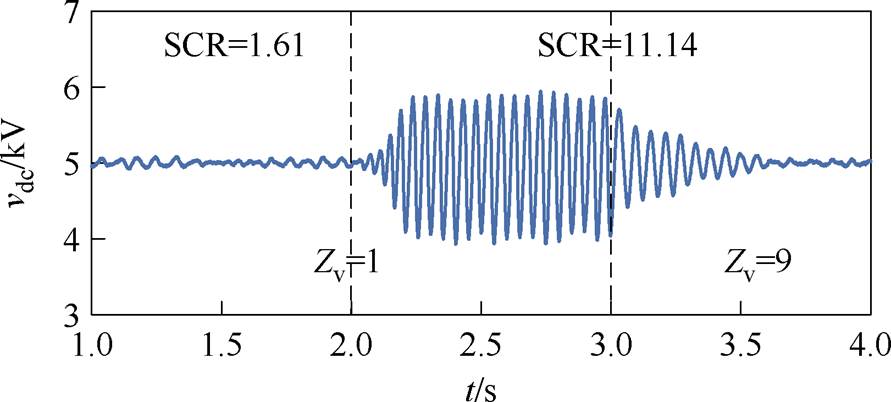
图14 改变Zv时直流电压波形
Fig.14 DC voltage waveform when changing Zv
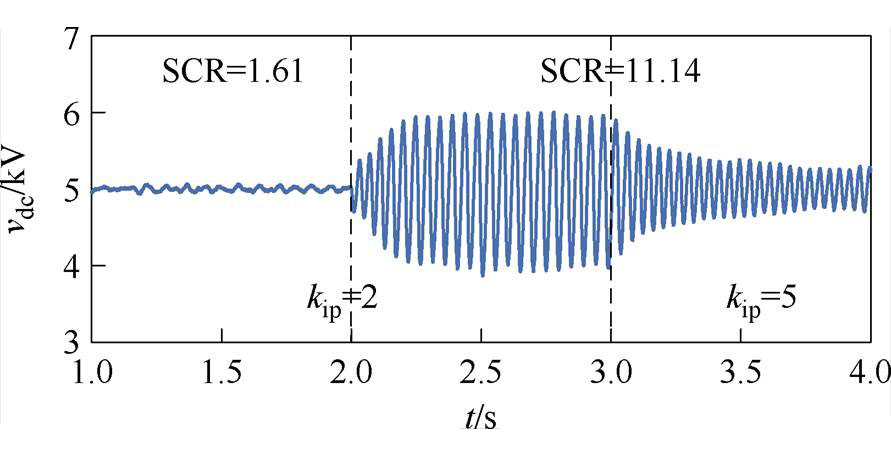
图15 改变kip时直流电压波形
Fig.15 DC voltage waveform when changing kip
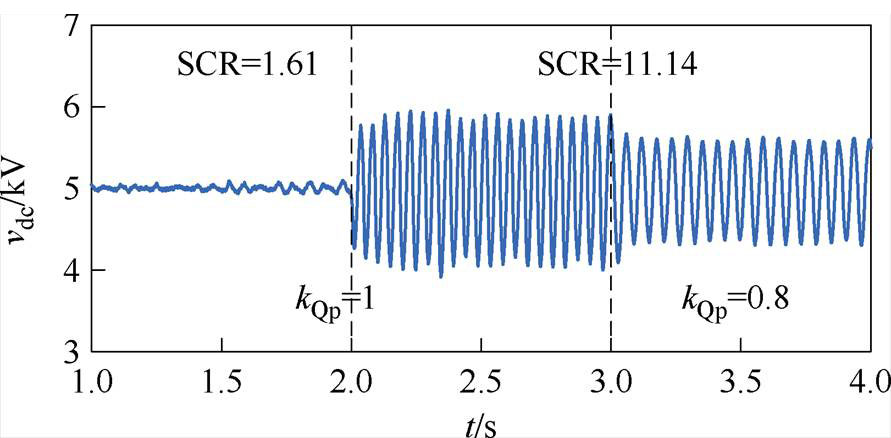
图16 改变kQp时直流电压波形
Fig.16 DC voltage waveform when changing kQp
图14~图16时域仿真结果表明,虚拟阻抗由1增大到9时,系统由振荡逐渐收敛,系统稳定性提高;电流内环比例系数kip由2增大到5时,系统由振荡转变为振荡收敛,振荡幅值减小,系统稳定性提高;无功外环比例系数kQp由1减小为0.8时,振荡幅值减小,系统稳定性提高。以上时域仿真结果验证了4.3节中控制参数分析结果的正确性和有效性。
本文建立了匹配控制型直驱风机的序阻抗模型,通过阻抗分析法研究了系统SSO特性,并且利用阻抗灵敏度分析了影响匹配控制型直驱风机阻抗特性的主导参数,给出了提高系统稳定性的参数优化方法。主要结论如下:
1)与常规跟网型风电机组不同,基于匹配控制的构网型直驱风机的输出阻抗在次同步频段呈现阻感特性,不易与感性的弱电网发生电气谐振。因此,匹配控制策略可以改善直驱风机阻抗特性,增强直驱风机并网系统的弱电网稳定性。
2)匹配控制型直驱风机在弱电网下具有良好的稳定性,但在强电网下存在稳定性问题,通过优化控制参数能够提高匹配控制型直驱风机并网系统的SSO稳定性。
3)根据各参数的阻抗灵敏度可知,无功外环比例系数、电流内环比例系数和虚拟阻抗为影响系统阻抗特性的主导参数。在本文仿真算例中,减小GSC的无功外环比例系数、增大电流内环比例系数或虚拟阻抗可以提高构网型直驱风机并网系统的SSO稳定性。
本文针对匹配控制型直驱风机阻抗建模及次同步振荡稳定性展开研究,所建立的匹配控制型直驱风机的序阻抗模型可表示控制结构相同、控制参数一致的匹配控制型直驱风电场的阻抗模型,用于风电场并网稳定分析。对于进一步指导匹配控制型直驱风机参数设计、匹配控制型直驱风电场并网等实际工程问题具有一定的参考价值。
附 录
1. 第2.1节公式推导补充
B1、B2为五阶方阵,除下述元素外,其余元素均为0。
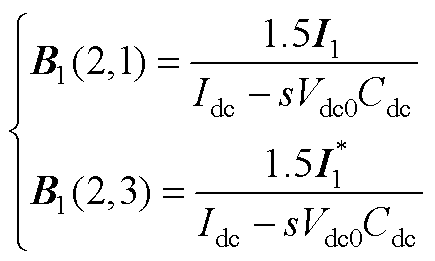 (A1)
(A1)
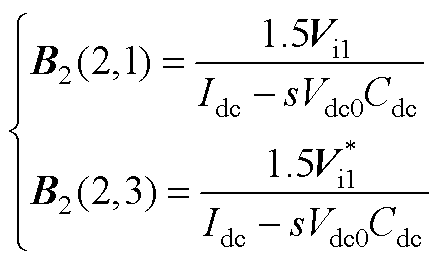 (A2)
(A2)
C2、C4为五阶方阵,除下述元素外,其余元素均为0。
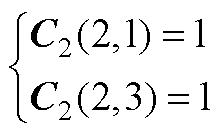 (A3)
(A3)
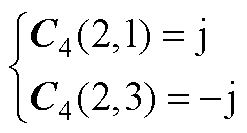 (A4)
(A4)
F2、F3、F4为五阶方阵,除下述元素外,其余元素均为0。
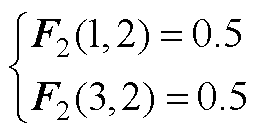 (A5)
(A5)
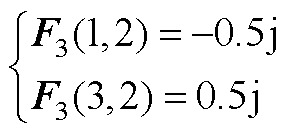 (A6)
(A6)
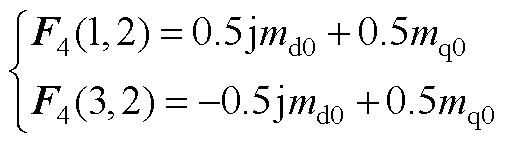 (A7)
(A7)
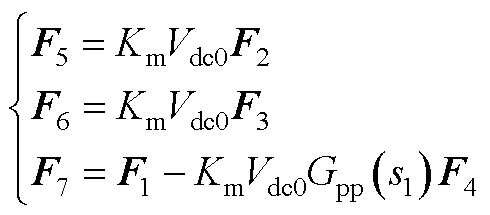 (A8)
(A8)
F1为五阶方阵,除下述元素外,其余元素均为0。
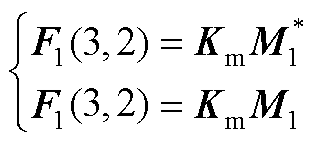 (A9)
(A9)
Hn的具体表达式为
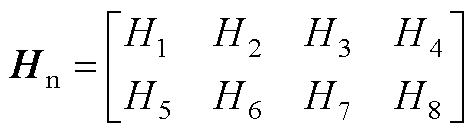 (A10)
(A10)
其中
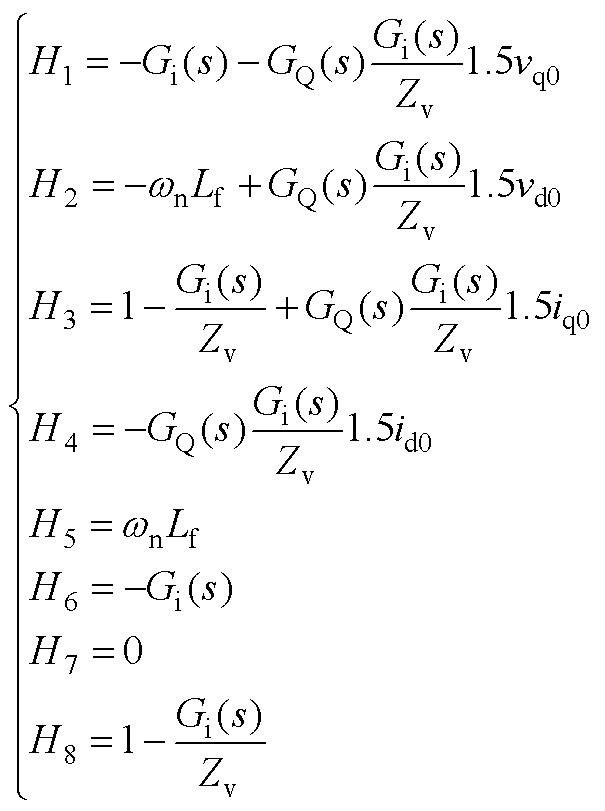
R1、R2、R3的表达式具体为
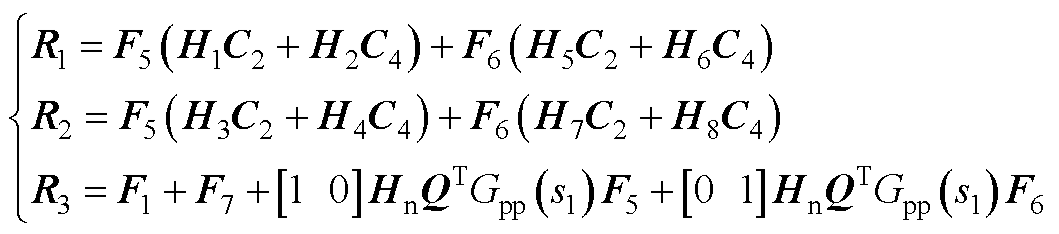 (A11)
(A11)
其中
QT=[iq0 -id0 vq0 -vd0]T
2. 系统参数说明
附表1 控制器参数1
App.Tab.1 Controller argument 1

控制器参 数数 值 匹配控制型直驱风机GSC无功外环比例系数kQp1 无功外环积分系数kQi10 电流内环比例系数kip2 电流内环积分系数kii2.5 虚拟阻抗Zv/W1 直流电压vdc/kV5
3. 构网型直驱风机并网系统SSO稳定性
根据奈奎斯特稳定性判据,直驱风机-电网互联系统中风机与电网的幅频特性曲线交点频率处对应的相角裕度大于零时,系统稳定;反之,系统不稳定。
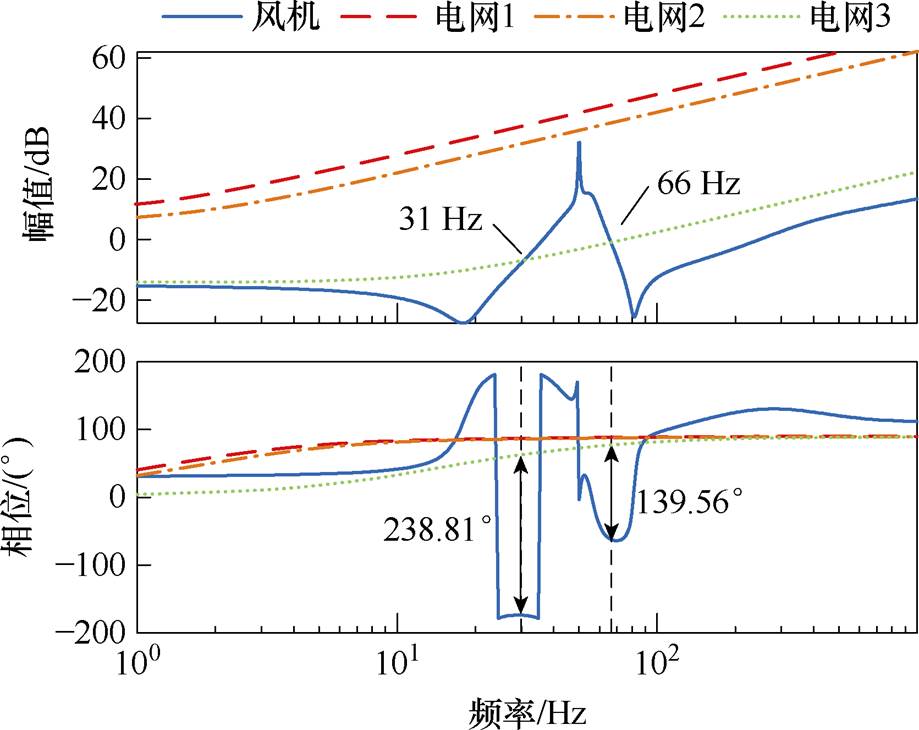
附图1 直驱风机并网系统阻抗特性曲线
App.Fig.1 Impedance characteristic curves of direct drive fan grid connected system
由附图1可知,风机与电网1(SCR=1.61)和电网2(SCR=2.82)的阻抗幅频特性曲线不存在交点,表明匹配控制型直驱风机在弱电网下具有较好的稳定性。风机与电网2(SCR=11.14)的阻抗幅频特性曲线在31 Hz和66 Hz处存在交点,其中31 Hz处相位差为238.81°,即相位裕度为-58.81°<0°,系统不稳定。表明匹配控制型直驱风机在强电网下存在振荡的风险。
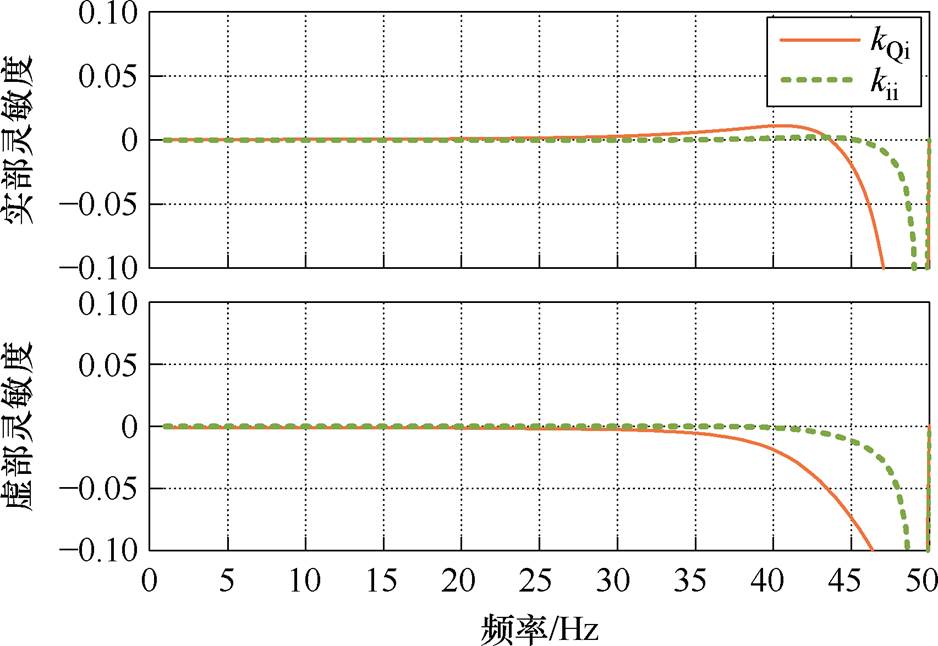
附图2 阻抗灵敏度曲线(局部)
App.Fig.2 Impedance sensitivity curve (partial)
参考文献
[1] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205.
Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205.
[2] 桑顺, 高宁, 蔡旭, 等. 功率-电压控制型并网逆变器及其弱电网适应性研究[J]. 中国电机工程学报, 2017, 37(8): 2339-2351.
Sang Shun, Gao Ning, Cai Xu, et al. A power-voltage controlled grid-connected inverter and its adaptability research under weak grid conditions[J]. Proceedings of the CSEE, 2017, 37(8): 2339-2351.
[3] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.
Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[4] 董文凯, 杜文娟, 王海风. 弱连接条件下锁相环动态主导的并网直驱风电场小干扰稳定性研究[J]. 电工技术学报, 2021, 36(3): 609-622.
Dong Wenkai, Du Wenjuan, Wang Haifeng. Small- signal stability of a grid-connected PMSG wind farm dominated by dynamics of PLLs under weak grid connection[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 609-622.
[5] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3595.
Xu Jieyi, Liu Wei, Liu Shu, et al. Current state and development trends of power system converter grid-forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3595.
[6] 桑顺, 徐婷, 齐琛, 等. 惯性同步构网型变换器定量感知电网频率的机理及抗干扰控制策略[J]. 电网技术, 2023, 47(4): 1395-1408.
Sang Shun, Xu Ting, Qi Chen, et al. Mechanism of quantitatively sensing grid frequency and anti- disturbance control strategy for the grid-forming converter[J]. Power System Technology, 2023, 47(4): 1395-1408.
[7] Arghir C, Dörfler F. The electronic realization of synchronous machines: model matching, angle tracking, and energy shaping techniques[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4398-4410.
[8] 秦世耀, 齐琛, 李少林, 等. 电压源型构网风电机组研究现状及展望[J]. 中国电机工程学报, 2023, 43(4): 1314-1334.
Qin Shiyao, Qi Chen, Li Shaolin, et al. Review of the voltage-source grid forming wind turbine[J]. Pro- ceedings of the CSEE, 2023, 43(4): 1314-1334.
[9] 人民网-湖北频道. 国网湖北电力首次实现国内无储能支撑新能源电压源机组运行[EB/OL]. (2022- 03-14)[2024-06-16].http://hb.people.com.cn/n2/2022/0314/c194063-35173448.html.
[10] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339- 2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[11] 邢华栋, 张叔禹, 尹柏清, 等. 风电并网系统次同步振荡稳定性分析与控制方法研究综述[J]. 电测与仪表, 2020, 57(24): 13-21.
Xing Huadong, Zhang Shuyu, Yin Baiqing, et al. Review of sub-synchronous oscillation stability analysis and control method for grid-connected wind power system[J]. Electrical Measurement & Instru- mentation, 2020, 57(24): 13-21.
[12] 年珩, 杨洪雨. 不平衡运行工况下并网逆变器的阻抗建模及稳定性分析[J]. 电力系统自动化, 2016, 40(10): 76-83.
Nian Heng, Yang Hongyu. Impedance modeling and stability analysis of grid-connected inverters under unbalanced operation conditions[J]. Automation of Electric Power Systems, 2016, 40(10): 76-83.
[13] 高本锋, 邓鹏程, 孙大卫, 等. 基于匹配控制的构网型直驱风电场次同步振荡机理与特性研究[J]. 电工技术学报, 2024, 39(9): 2755-2770.
Gao Benfeng, Deng Pengcheng, Sun Dawei, et al. Mechanism and characteristics of subsynchronous oscillation of grid-forming direct-drive wind farm based on matching control[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2755-2770.
[14] 桑顺, 张琛, 蔡旭, 等. 全功率变换风电机组的电压源控制(一): 控制架构与弱电网运行稳定性分 析[J]. 中国电机工程学报, 2021, 41(16): 5604- 5616.
Sang Shun, Zhang Chen, Cai Xu, et al. Voltage source control of wind turbines with full-scale converters (part Ⅰ): control architecture and stability analysis under weak grid conditions[J]. Proceedings of the CSEE, 2021, 41(16): 5604-5616.
[15] 陈新, 王赟程, 龚春英, 等. 采用阻抗分析方法的并网逆变器稳定性研究综述[J]. 中国电机工程学报, 2018, 38(7): 2082-2094, 2223.
Chen Xin, Wang Yuncheng, Gong Chunying, et al. Overview of stability research for grid-connected inverters based on impedance analysis method[J]. Proceedings of the CSEE, 2018, 38(7): 2082-2094, 2223.
[16] 伍文华, 周乐明, 陈燕东, 等. 序阻抗视角下虚拟同步发电机与传统并网逆变器的稳定性对比分 析[J]. 中国电机工程学报, 2019, 39(5): 1411- 1421.
Wu Wenhua, Zhou Leming, Chen Yandong, et al. Stability comparison and analysis between the virtual synchronous generator and the traditional grid- connected inverter in the view of sequence impe- dance[J]. Proceedings of the CSEE, 2019, 39(5): 1411-1421.
[17] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[18] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source con- verters[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
[19] 王利超, 于永军, 张明远, 等. 直驱风电机组阻抗建模及次同步振荡影响因素分析[J]. 电力工程技术, 2020, 39(1): 170-177.
Wang Lichao, Yu Yongjun, Zhang Mingyuan, et al. Impedance model and analysis of subsynchronous oscillation influence factors for grid-connected full-converter wind turbines[J]. Electric Power Engineering Technology, 2020, 39(1): 170-177.
[20] 桑顺, 张琛, 蔡旭, 等. 计及内、外部交互模态的电压源型风电场-电网稳定性量化分析[J]. 高电压技术, 2022, 48(7): 2840-2853.
Sang Shun, Zhang Chen, Cai Xu, et al. Quantitative analysis of the voltage-source-type wind farm-weak grid’s stability considering the internal and external interaction modes[J]. High Voltage Engineering, 2022, 48(7): 2840-2853.
[21] 胡宇飞, 田震, 查晓明, 等. 构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J]. 电力系统自动化, 2022, 46(24): 121-131.
Hu Yufei, Tian Zhen, Zha Xiaoming, et al. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid- following converters[J]. Automation of Electric Power Systems, 2022, 46(24): 121-131.
[22] 伍文华, 陈燕东, 周乐明, 等. 虚拟同步发电机接入弱电网的序阻抗建模与稳定性分析[J]. 中国电机工程学报, 2019, 39(6): 1560-1571, 1853.
Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability analysis for virtual synchronous generator connected to the weak grid[J]. Proceedings of the CSEE, 2019, 39(6): 1560-1571, 1853.
[23] 杨伊茜, 陈杰, 万雨朦, 等. 电网电压前馈控制VSG的阻抗建模与并网稳定性分析[J]. 电力工程技术, 2021, 40(6): 52-61.
Yang Yiqian, Chen Jie, Wan Yumeng, et al. The impedance modelling and stability analysis of VSG with grid voltage feedforward control[J]. Electric Power Engineering Technology, 2021, 40(6): 52- 61.
[24] 谢小荣, 刘华坤. 风电并网系统次/超同步振荡的分析与控制[M]. 北京: 科学出版社, 2022.
Xie xiaorong, Liu Huakun. Analysis and control of sub/ultra synchronous oscillations in wind power grid connected systems[M]. Beijing: Science Press, 2022.
[25] Zhang Chen, Cai Xu, Rygg A, et al. Sequence domain SISO equivalent models of a grid-tied voltage source converter system for small-signal stability analysis[J]. IEEE Transactions on Energy Conversion, 2018, 33(2): 741-749.
[26] 杜燕, 赵韩广, 杨向真, 等. 考虑频率耦合效应的虚拟同步发电机序阻抗建模[J]. 电源学报, 2020, 18(6): 42-49.
Du Yan, Zhao Hanguang, Yang Xiangzhen, et al. Sequence impedance modeling of virtual synchronous generator considering frequency coupling effect[J]. Journal of Power Supply, 2020, 18(6): 42-49.
[27] 曾锋, 李崇涛, 舒进, 等. 基于阻抗法的稳定性判据论证及其适用性分析[J]. 电力系统自动化, 2021, 45(8): 146-154.
Zeng Feng, Li Chongtao, Shu Jin, et al. Demon- stration of stability criterion based on impedance method and analysis on its applicability[J]. Auto- mation of Electric Power Systems, 2021, 45(8): 146-154.
[28] 张海华, 李中烜, 沈鑫, 等. 基于序阻抗模型的直驱风机并网系统RLC稳定判据研究[J]. 湖北电力, 2019, 43(6): 78-85.
Zhang Haihua, Li Zhongxuan, Shen Xin, et al. Research on RLC stability criterion of sequence- impedance-model-based direct driven wind-turbine generator grid-connected system[J]. Hubei Electric Power, 2019, 43(6): 78-85.
[29] 孙焜, 姚伟, 文劲宇. 双馈风电场经柔直并网系统次同步振荡机理及特性分析[J]. 中国电机工程学报, 2018, 38(22): 6520-6533.
Sun Kun, Yao Wei, Wen Jinyu. Mechanism and characteristics analysis of subsynchronous oscillation caused by DFIG-based wind farm integrated into grid through VSC-HVDC system[J]. Proceedings of the CSEE, 2018, 38(22): 6520-6533.
[30] 张明远, 肖仕武, 田恬, 等. 基于阻抗灵敏度的直驱风电场并网次同步振荡影响因素及参数调整分析[J]. 电网技术, 2018, 42(9): 2768-2777.
Zhang Mingyuan, Xiao Shiwu, Tian Tian, et al. Analysis of SSO influencing factors and parameter adjustment for grid-connected full-converter wind farm based on impedance sensitivity[J]. Power System Technology, 2018, 42(9): 2768-2777.
Abstract When the new energy units, mainly wind power and photovoltaic, are connected to the AC grid on a large scale through power electronic converters, the power system is prone to form a weak AC grid environment, which brings severe challenges to the stable operation of traditional grid-following new energy units. In recent years, scholars at home and abroad have proposed various grid-forming control strategies based on virtual synchronous generator control, sagging control, and matching control, enabling inverters to have suitable voltage and frequency support capabilities. Matching control only measures the DC voltage to realize the autonomous synchronization function and has a fast response speed, receiving widespread attention. However, research on grid-forming new energy units based on matching control focuses on supporting capacity and inertia response characteristics of AC grid, and the impedance characteristics and related influencing factors still need to be studied.
This paper first establishes the positive and negative sequence impedance model of matching-control-type direct drive wind turbines (DDWT) using the harmonic linearization method. The impedance analytical model is verified by combining the impedance sweep method. The stability of the matching-control-type DDWT system when connected to AC grids of different intensities is analyzed based on the equivalent RLC stability criterion. Furthermore, the dominant parameters affecting the impedance characteristics of matching-control-type DDWT are analyzed using impedance sensitivity, and a parameter optimization scheme is determined to improve system stability. Finally, the theoretical analysis is verified through PSCAD/EMTDC electromagnetic transient simulation.
It can be concluded that the positive sequence impedance model of matching-control-type DDWT is inductive in the low-frequency range and has a negative damping range in the sub-synchronous frequency range, but the phase is within -90°. The negative sequence impedance model exhibits capacitive behavior in the low-frequency range, then becomes inductive, and the phase of the capacitive frequency range is within -90°. Therefore, matching-control-type DDWT makes it challenging to form negative damping oscillation circuits with inductive AC grids. The stability analysis results based on the RLC stability criterion indicate that matching-control-type DDWT has suitable stability in weak AC grids but has a risk of oscillation in strong AC grids. Furthermore, the impedance sensitivity of each control parameter is calculated, and the dominant parameter that affects the impedance characteristics is determined based on the magnitude of the impedance sensitivity amplitude. According to the impedance’s real-imaginary frequency characteristic curve, a parameter adjustment method is obtained to improve the grid stability of matching-control-type DDWT in strong power grids.
The proportional coefficient of the reactive outer loop, the proportional coefficient of the current inner loop, and the virtual impedance of the grid side converter mainly affect the impedance characteristics. Properly reducing the reactive outer loop’s proportional coefficient and increasing the current inner loop’s proportional coefficient or virtual impedance can improve the stability of the matching-control-type DDWT grid-connected system.
keywords:Matching control, grid-forming direct-drive wind turbine, sub-synchronous oscillation, impedance analysis
DOI: 10.19595/j.cnki.1000-6753.tces.241097
中图分类号:TM712
国家电网公司总部科技资助项目《接入弱电网的新能源场站主动支撑控制技术研究》(4000-202414073A-1-1-ZN)。
收稿日期 2024-06-25
改稿日期 2024-07-16
高本锋 男,1981年生,博士,副教授,研究方向为高压直流输电和电力系统次同步振荡。E-mail: gaobenfeng@126.com
王秋文 女,2000年生,硕士研究生,研究方向为新能源电力系统的分析与控制。E-mail: 1261744942@qq.com(通信作者)
(编辑 郭丽军)